Soliton Generation in Negative Thermal Expansion Materials

Strain solitons have been observed statically in several 2D materials and dynamically in substrate materials using ultrafast laser pulses. The latter case relies on lattice relaxation in response to ultrafast heating in a light-absorbing transducer material, a process which is sensitive to the thermal expansion coefficient. Here we consider an unusual case where the sign of the thermal expansion coefficient is negative, a scenario which is experimentally feasible in light of rapid and recent advances in the discovery of negative thermal expansion materials. We present numerical solutions to a nonlinear differential equation which has been repeatedly demonstrated to quantitatively model experimental data and discuss the salient results using realistic parameters for material linear and nonlinear elasticity. The solitons that emerge from the initial value problem with negative and positive thermal expansion are qualitatively different in several ways. The new case of negative thermal expansion gives rise to a nearly-periodic soliton train with chirped profile and free of an isolated shock front. We suggest this unanticipated result may be realized experimentally and assess the potential for certain applications of this generic effect.

1 Introduction

The propagation of strain waves through materials originating from an initial disturbance is of high interest to a variety of theoretical, experimental, and technological efforts. A practical method of realizing this context involves use of a laser light pulse incident on an opaque material surface. The resultant energy absorption, heating, and subsequent thermal expansion can generate a dynamic strain profile capable of propagating over macroscopic distances. Early ultrafast laser experiments at low laser fluence (energy density) generated and subsequently detected acoustic strain pulses and related this observed sound propagation to the linear elastic properties of the propagation medium (Thomsen et al., 1984; Eesley et al., 1987; Wright, 1992). As experimentation with ultrafast lasers advanced, experiments were developed which are sensitive to the nonlinear elastic properties as well (Hao and Maris, 2001; Muskens, 2004). In particular, strongly pumped materials are observed to generate solitary solutions called solitons which move at supersonic speeds and do not disperse in contrast to the weakly-pumped experimental regime. To our knowledge, all such experiments have been performed on materials with positive thermal expansion (PTE).

For many years, mention of negative thermal expansion (NTE), a materials tendency to shrink when heated, evoked discussion of liquid water ice expansion responsible for icebergs and the 4 K temperature window above the ice water phase boundary where phase fluctuations occur. However, since the late 1990s, many materials have been identified and discovered which have strong NTE (Sleight, 1998; Goodwin et al., 2008; Miller et al., 2009; Azuma et al., 2011; Lind, 2012; Takenaka, 2012; Dove and Fang, 2016; Qu et al., 2017; Attfield, 2018; Takenaka et al., 2019) over a large range of temperatures and material compositions. NTE materials hold promising application potential in stabilizing fiber Bragg gratings for high-speed telecommunication (Fleming et al., 1997; Kowach and Ramirez, 2002), substrates for devices which benefit from controllable stresses, and rigid composite materials with engineered thermal characteristics through combinations of PTE and NTE components (Balch and Dunand, 2004; De Buysser et al., 2004; Lommens et al., 2005; Sullivan and Lukehart, 2005; Lind et al., 2011). Here we explore the potential use of NTE materials as strain pulse transducers.

2 Strain Pulse Production and Detection in Solids

Figure 1 shows a typical scheme capable of demonstrating the development of strain solitons. An ultrafast laser pulse (∼10–200 fs) delivers energy Q over an area A of a light-absorbing transducer film (reflectivity R, volumetric specific heat C) deposited on a substrate. The deposited energy per unit area (1-R)Q/A is absorbed by the transducer film, first heating electrons which thermalize with the lattice degrees of freedom within a few picoseconds. Immediately following electron-lattice thermalization, heat distributed within the optical absorption depth ζ drives a depth-dependent temperature profile ΔT(z), where z is the direction of propagation into the sample (Matsuda et al., 2015). The resultant ultrafast heating introduces a sudden thermal stress within the illuminated volume σ_T = −3Bα_LΔT where B is the bulk modulus and α_L is the linear coefficient of thermal expansion (CTE) (Hao and Maris, 2001; Matsuda et al., 2015). This thermal stress induces a thermal strain ${\eta }_0=\frac{3B{\alpha }_L(1-R)Q}{AC\zeta \rho c_0^2}$, which depends on the equilibrium mass density ρ and the sound speed c₀ in the direction normal to the surface, but is also proportional to the linear CTE α_L in a direction perpendicular to the plane of the film. Here, we consider only transducer films of cubic crystal symmetry. As observed in many experiments (Hao and Maris, 2001; Wright et al., 2001; Muskens et al., 2004; Péronne and Perrin, 2006; Schmidt et al., 2008; Wang et al., 2010; Péronne et al., 2017), this initial strain profile enters the underlying substrate and evolves as a propagating strain wave which can be detected after propagation over macroscopic mm-lengths scales typical of sample dimensions.

FIGURE 1

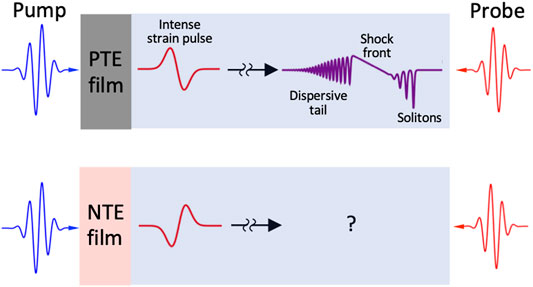
FIGURE 1. (A) Schematic of PTE film on substrate with laser pulse incident, then propagating strain pulse through PTE bulk sample, forming a shock front trailing a set of well-separated solitons. (B) Schematic of NTE film on substrate with laser pulse incident, then propagating strain pulse through PTE bulk sample.

For small amplitude of the initial strain η₀, evolution of the propagating strain pulse η(z, t) moves at the speed of sound with subtle shape changes which can be described by the dispersion ${\omega }_{LA}(\vec{k})$ of the longitudinal acoustic wave appropriate in the regime of linear (Hooke’s law) elasticity. For larger amplitude of the initial strain pulse, where nonlinear elastic properties of the substrate material govern strain evolution, solitons can be observed after propagation through the substrate. These phenomena are sensitive to the nonlinear elasticity, sound wave dispersion, and density and can be described quantitatively in this context using a one-dimensional Korteweg-deVries equation (Korteweg and de Vries, 1895; Gardner et al., 1974; Whitham, 1999; Debnath, 2007):

$\frac{\partial \eta }{\partial t}+\frac{C_3}{2c_0\rho }\eta \frac{\partial \eta }{\partial y}+\gamma \frac{{\partial }^3\eta }{\partial y^3}=0(1)$

Here, C₃ is the appropriate nonlinear elastic parameter, γ quantifies the curvature of the acoustic dispersion ${\omega }_{LA}(\vec{k})=c_{0}k-\gamma k^3+\dots$, and y is a co-moving spatial coordinate which moves at the sound speed c₀: y = z − c₀t. A key feature of the solutions of Eq. 1 is the emergence of solitons, which are local regions of high density which move at supersonic speeds and propagate without distortion. Below we present numerical solutions (Landau and Pez, 2018) of Equation 1 using various initial strain profiles corresponding to a transducer with conventional positive (PTE) or negative (NTE) thermal expansion and substrate parameters corresponding to sapphire with strain wave propagation along the 100 direction, a specific case where much experimental work has been done (Hao and Maris, 2001; Wright et al., 2001; Muskens et al., 2004; Péronne et al., 2017). For the case of conventional CTE in the transducer film, the initial pulse front is compressive but the detailed shape depends upon a number of factors. Naively, the exponentially extinguished profile of the incident laser light pulse sets up an exponential temperature profile and therefore an exponential strain profile. However, known effects of electronic diffusion affect the electron-lattice thermalization (Tas and Maris, 1994; Wright, 1994) on a similar time scale to the light absorption in typical laser systems. A recent direct measurement using ultrafast Sagnac interferometry and a propagation analysis accounting for acoustic dispersion has been observed to have a Gaussian-derivative profile (Péronne et al., 2017):

$\eta (y,t=0)=-{\eta }_0\frac{y}{\sigma }{e}^{-\frac{y^2}{2{\sigma }^2}}.(2)$

We use this initial strain profile in the simulations presented here. In real experiments, the transducer film is typically aluminum, gold, palladium alloys, or other opaque materials with conventional thermal expansion α_L > 0 (Wang et al., 2010). The primary consequence of a transducer with positive thermal expansion is a compressive front and η₀ > 0, corresponding to negative strain followed by a dilatational trailing edge. After discussing these PTE results, we will compare the evolution for the NTE case with η₀ < 0. Numerical solutions to Equation 1 with the initial strain profile in Eq. 2 were performed using a finite difference scheme following (Landau and Pez, 2018). Here, the first-time step is solved using a forward difference scheme while the remaining time steps use a central difference scheme, following other analyses of experimental data (Muskens, 2004; Mogunov et al., 2020).

The material dependent dispersion and nonlinear parameters used in the numerical calculation were those for a z-cut (1,000) sapphire (Al₂O₃) substrate. In all calculations we used the known parameters (Hao and Maris, 2001) C₃ = −18.3 × 10¹¹ g/(mm s²), c₀ = 11.23 × 10⁶ mm/s, ρ = 3.98 × 10^–3 g/mm³, and γ = 3.50 × 10^–8 mm³/s.

Figure 2A shows that with η₀ = + 3.0 × 10^–4 the initial profile shown for 0 ns evolves dynamically according to Equation 1 into a linear-sloped shock front near y = 0. In addition, several well-separated compressive solitons emerge on the supersonic side of the shock front y > 0. The leading solitons are strongest and the strength decreases linearly with soliton number as the shock front is approached around y = 100 nm. Under these conditions, numerical solution of Eq. 1 comports with experiments and describes well the evolution of an initial strain pulse into a shock front and a set of supersonic solitons followed by a dispersive tail - an oscillatory strain profile traveling at subsonic speeds. These phenomena are labeled in Figure 1 and have been demonstrated in a host of materials (e.g. MgO (Hao and Maris, 2001), Sapphire (Hao and Maris, 2001; Muskens, 2004), GaAs (Péronne et al., 2017)).

FIGURE 2

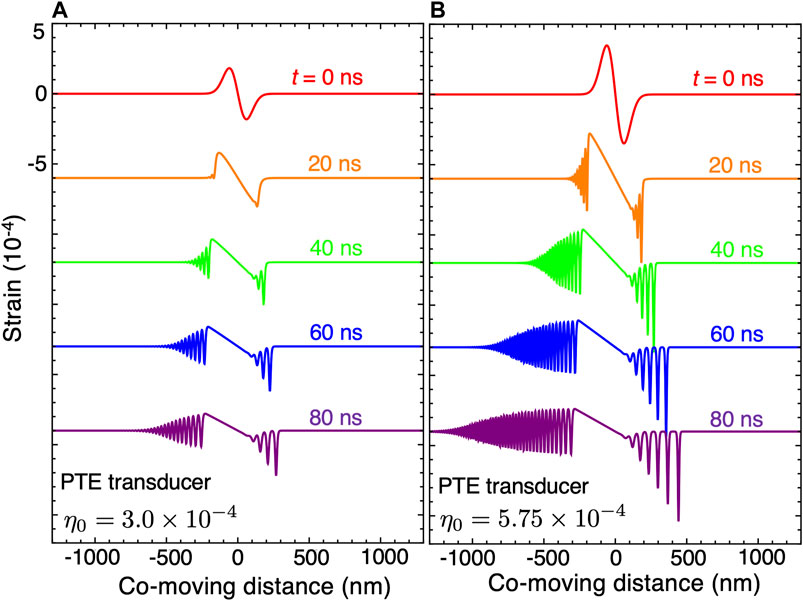
FIGURE 2. Evolution of strain pulses generated in materials with conventional thermal expansion for initial strain amplitudes (A)η₀ = +3.0×10^–4 and (B)η₀ = +5.75 ×10^–4.

Figure 2B shows that increasing the initial strain amplitude to η₀ = 5.75 × 10^–4 increases the number of solitons produced, steepens the shock front, and extends the dispersive tail. The increase in the number of solitons is expected from theoretical grounds where the number of solitons can be related to the number of bound states of a Schrodinger equation whose potential shape is set by the initial strain profile (Gardner et al., 1974; Debnath, 2007). Since increasing the initial strain profile effectively deepens the potential, more bound states and therefore solitons are expected. The initial strain profiles considered here are shown as the t = 0 ns traces in Figures 2A,B, 3A,B.

FIGURE 3

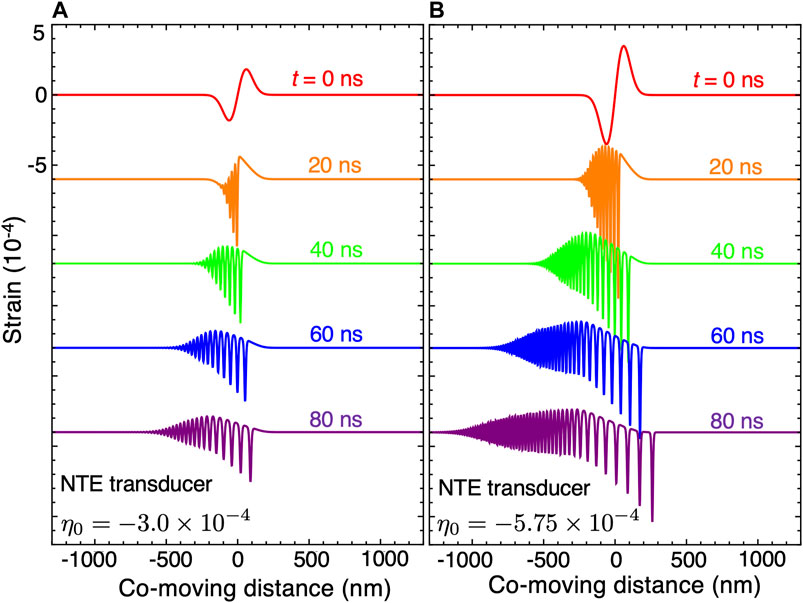
FIGURE 3. Evolution of strain pulses generated in materials with negative thermal expansion for initial strain amplitudes (A)η₀ = −3.0×10^–4 and (B)η₀ = −5.75 ×10^–4.

3 Results: Strain Waves Produced in Materials With Negative Thermal Expansion

Recent discoveries in synthesis of materials with low and negative thermal expansion in a wide variety of material contexts has motivated us to explore how the production of solitons would be impacted by the case α_L < 0. There is much interest in systems which exhibit this remarkable material behavior, particularly because strong NTE has been observed in the vicinity of low-temperature phase transitions. For example, insulating perovskite ScF₃ appears to have an incipient structural instability (Handunkanda et al., 2015; Wendt et al., 2019; Bird et al., 2020) while semiconducting Sm_1−xY_xS (Takenaka et al., 2019; Mazzone et al., 2020) shows an unusual magnetic transition at low temperature. Experiments of the type proposed here are nondestructive and sensitive to other lattice-related materials properties and may benefit NTE research in certain contexts.

Specific candidates of opaque NTE films include metallic perovskite ReO₃ (Chatterji et al., 2009a; Chatterji et al., 2009b; Rodriguez et al., 2009), semiconducting Sm_0.8Y_0.2S (Takenaka et al., 2019; Mazzone et al., 2020), and insulating Si (Shah and Straumanis, 1972) or CdTe (Greenough and Palmer, 1973; Jovanovic et al., 2014) at low temperature at pump photon energies exceeding their band gap (1 and 1.51 eV at 300 K respectively (Bludau et al., 1974; Jovanovic et al., 2014)). Given recent advances in high-harmonic generation of laser sources, any NTE material could be considered if the photon energy exceeds the candidate material band gap. For the sake of exploring the physics of soliton evolution from NTE transducers, we assume the substrate would again be sapphire oriented along the 100 direction and we repeat the calculations of Figure 2 with η₀ < 0 describing the initial strain pulse. Physically this means the initial pulse has a dilatational/low density front and compressive/high density tail.

Figure 3 shows results of KdV evolution of a strain pulses produced from a NTE transducer with the same magnitudes as in Figure 2. Both PTE and NTE cases produce a similar extended dispersive tail for y < -300 nm and clearly produce solitons. An exact correspondence is expected between the number of solitons in the NTE and PTE cases because the number of Schrodinger bound states of the initial strain profiles, which are related by a simple mirror reflection around y = 0, are exactly the same. However, strong differences in both the form of the shock front and distribution of solitons are apparent. For example, the soliton train in the PTE case emerges from the leading edge of the shock front discontinuity while for the NTE case solitons emerge from the back of the shock front. As for the case of a PTE transducer, several isolated supersonic solitons are produced within a few 10 s of ns. However, unlike the PTE case, they appear to merge continuously with the oscillatory tail and appear without a clearly isolated shock front.

4 Section: Fitting Solitons for PTE and NTE Cases

The KdV equation permits analytic expressions describing isolated solitons and in this section we apply these to our numerical solutions to determine and compare the distribution of solitons produced by NTE and PTE transducer films.

The KdV Eq. 1 has as solutions

$\eta (y,t)={\eta }_s{\text{sech}}^2\left(\frac{\sqrt{{\eta }_s}(y-y_s)}{w}\right)(3)$

where η_s is a measure of the strength of the soliton, y_s is the co-moving coordinate position where the soliton peaks, and w = $\sqrt{24\rho c_0\gamma /C_3}$ is a material-dependent length which quantifies the soliton width. Specifically, the half-width-half maximum of the free soliton in Eq. 3 is $\delta =warccosh\sqrt{2}/\sqrt{{\eta }_s}\simeq 0.881w/\sqrt{{\eta }_s}$. We model the shock front as a linear background with slope s which terminates at a critical value of the co-moving coordinate y_c. We sum each soliton contribution and the shock front in a nonlinear fit at late times and in the y range where solitons appear. Each soliton is parametrized by its strain η_s and the global material-dependent w = 0.143 nm was fixed in both fits. The shock slope and intercept y_c was allowed to adjust between the NTE and PTE cases.

Figure 4 shows the result of the fitting procedure and particularly Figure 4C compares the strain parameter η_s versus soliton number as labelled in Figures 4A,B. Interestingly, the leading soliton (labelled 1) has similar strength in the PTE and NTE cases, but for the PTE case, the strength linearly decreases to zero as a function of soliton number, a phenomenon pointed out long ago (Zabusky and Kruskal, 1965). In contrast, the NTE transducer case shows that η_s is more uniform and so the soliton speed U = c₀ + C₃η_s/6ρc₀ is also more uniform within the experimentally-accessible range considered here. This reveals a potential advantage of NTE transducers in retaining a periodic strain texture capable of propagating over long distances in functional acousto-optic devices.

FIGURE 4

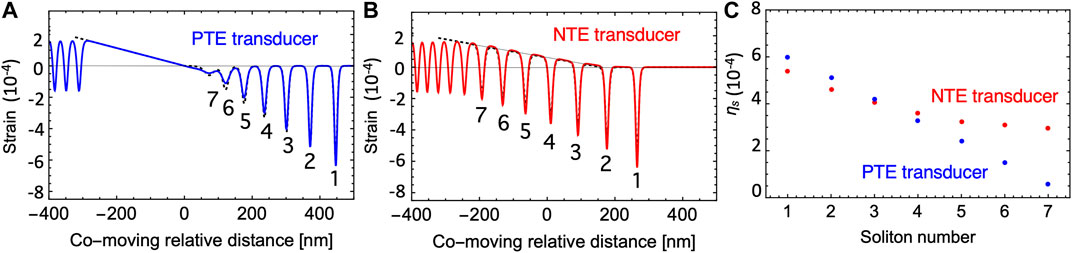
FIGURE 4. Fits of the simulated strain profile at t = 80 ns and |η₀| = 5.75×10^–4 to isolated solitons on a linear background for the case of (A) a PTE transducer and (B) a NTE transducer. The material-specific parameter w was held fixed according to the parameters of the simulation at 0.14324 nm appropriate to sapphire 100 longitudinal propagation. (C) shows the distribution of strain over the solitons for each case.

5 Discussion

Our simulations reveal qualitative differences in soliton trains generated from NTE and PTE transducer films. The phenomena are expected to be found for any NTE film on any substrate or within a single crystal of NTE material. Here we address possibilities for applications.

The ability to create well-defined propagating strain textures on nanometer length scales and nanosecond time scales portends functionality in novel electronic and acoustic device construction. Recent work analyzing the transient spectral response of excitons in GaAs to incident solitons (Scherbakov et al., 2007) has shown definitively an electronic-soliton coupling is present in this common device material. Recent investigations in 2D materials (Alden et al., 2013; Edelberg et al., 2020) have shown that static strain solitons form under certain conditions related to twisted van der Waals stacking patterns. These static solitons could be used to confine electronic states and one can consider dynamic soliton trains and the interaction between static and dynamic solitons may be sufficient to manipulate the charge states in novel device schemes.

Another clear feature of NTE-generated pulse trains is that they are more periodic than their PTE-generated counterparts. Figure 5 compares the spatial Fourier transforms of the pulse trains at different times and reveals that at early times, the NTE-generated pulse train is comprised of spatial frequencies much higher than in the PTE case, with significant spectral weight at Fourier wavevectors as large as k ≃ 0.4 nm⁻¹, corresponding to fine periodic textures with space of order 2π/k ≃15 nm. This length scale corresponds to industry-leading features in integrated circuits and may present an inroad to novel devices. Furthermore, one may consider use of the fine periodic strain texture in potential applications related to transient diffraction gratings appropriate to photons in the vacuum ultraviolet and soft X-ray regimes. Currently, static diffraction gratings are constructed from conventional photolithography or novel contact-mode lithography methods (Gleason et al., 2017). If an appropriately conditioned periodic train of strain solitons can be produced simultaneously with arrival of an X-ray pulse, one may be able to produce a transient grating with configurable characteristics from an atomically smooth surface.

FIGURE 5

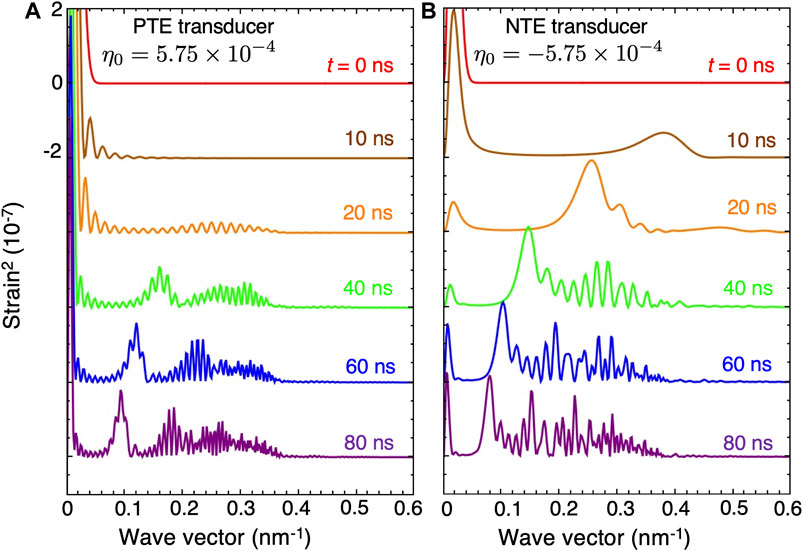
FIGURE 5. Fourier transform of strain pulses generated in materials with (A) positive thermal expansion for initial strain amplitude 5.75 ×10^–4 and (B) negative thermal expansion for initial strain amplitude -5.75 ×10^–4.

Importantly, the evolution of strain is related to the linear and nonlinear elasticity of the propagation medium. Here we have presented results for an opaque transducer film and compare the results of propagation through sapphire. However, similar considerations could model the case of an opaque single crystal specimen with unusual NTE. In the pursuit of mechanistic descriptions of NTE capable of leading materials discovery efforts, anomalous behavior of such elastic parameters is of interest. In cases such as ScF₃ and Hg₂I₂, the low-temperature behavior has been difficult to study due to proximity of a ferroelastic instability and a competing structural phase. Some methods of studying elasticity such as resonant ultrasound spectroscopy may be too invasive to be effective and the relatively weak perturbations of ultrasonic pulses are promising at addressing this experimental challenge.

6 Summary and Conclusion

In summary, we have provided the first assessment of the use of NTE materials as acousto-optic transducers for strain wave generation. In the case of strong, nonlinear acoustic response, unconventional strain textures are anticipated when the strain is generated from a NTE transducer film in comparison to the conventional PTE type where many experiments have been performed. In particular, while both the NTE and PTE cases ultimately produce the same number of solitons as anticipated, the NTE case delivers a soliton train with more uniform distribution of strain over the solitons present and significantly higher spatial frequencies at early times. Furthermore, while nonlinear strain profiles generated from conventional PTE transducer films have always been observed with clear separation of the shock front and solitons, in the NTE case the shock front and soliton train interacts strongly over the entire experimentally accessible time scale for the case we have considered. We have suggested several technologically relevant applications for the effects observed. However, while we have considered a prevalent case of a thin transducer film on a z-cut sapphire substrate, solitons have been observed in many other applicable materials, suggesting more diverse phenomena beyond the scope of this work. Future efforts are needed to experimentally observe NTE solitons as well as understand their interactions and variability across materials classes.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Work at UConn is supported by the National Science Foundation Grant No. NSF-DMR-1905862 with additional support from the U.S. Department of Energy, Basic Energy Sciences, Grant No. DE-SC0016481.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alden, J. S., Tsen, A. W., Huang, P. Y., Hovden, R., Brown, L., Park, J., et al. (2013). Strain Solitons and Topological Defects in Bilayer Graphene. Proc. Natl. Acad. Sci. 110, 11256–11260. doi:10.1073/pnas.1309394110

PubMed Abstract | CrossRef Full Text | Google Scholar

Attfield, J. P. (2018). Mechanisms and Materials for NTE. Front. Chem. 6, 371. doi:10.3389/fchem.2018.00371

PubMed Abstract | CrossRef Full Text | Google Scholar

Azuma, M., Chen, W.-t., Seki, H., Czapski, M., Olga, S., Oka, K., et al. (2011). Colossal Negative thermal Expansion in Binio3 Induced by Intermetallic Charge Transfer. Nat. Commun. 2, 347. doi:10.1038/ncomms1361

PubMed Abstract | CrossRef Full Text | Google Scholar

Balch, D. K., and Dunand, D. C. (2004). Copper-zirconium Tungstate Composites Exhibiting Low and Negative thermal Expansion Influenced by Reinforcement Phase Transformations. Metall. Mat Trans. A. 35, 1159–1165. doi:10.1007/s11661-004-0042-7

CrossRef Full Text | Google Scholar

Bird, T. A., Woodland-Scott, J., Hu, L., Wharmby, M. T., Chen, J., Goodwin, A. L., et al. (2020). Anharmonicity and Scissoring Modes in the Negative thermal Expansion Materials ScF₃ and CaZrF₆. Phys. Rev. B. 101, 064306. doi:10.1103/PhysRevB.101.064306

CrossRef Full Text | Google Scholar

Bludau, W., Onton, A., and Heinke, W. (1974). Temperature Dependence of the Band gap of Silicon. J. Appl. Phys. 45, 1846–1848. doi:10.1063/1.1663501

CrossRef Full Text | Google Scholar

Chatterji, T., Freeman, P. G., Jimenez-Ruiz, M., Mittal, R., and Chaplot, S. L. (2009). Pressure- and Temperature-inducedM3phonon Softening in ReO₃. Phys. Rev. B. 79, 184302. doi:10.1103/PhysRevB.79.184302

CrossRef Full Text | Google Scholar

Chatterji, T., Hansen, T. C., Brunelli, M., and Henry, P. F. (2009). Negative thermal Expansion of Reo₃ in the Extended Temperature Range. Appl. Phys. Lett. 94, 241902. doi:10.1063/1.3155191

CrossRef Full Text | Google Scholar

De Buysser, K., Lommens, P., De Meyer, C., Bruneel, E., Hoste, S., and Van Driessche, I. (2004). ZrO₂-ZrW₂O₈ Composites with Tailor-Made thermal Expansion. Ceram. Silik. 48, 139–144.

Google Scholar

Debnath, L. (2007). A Brief Historical Introduction to Solitons and the Inverse Scattering Transform-A Vision of Scott Russell. Int. J. Math. Edu. Sci. Tech. 38, 1003–1028. doi:10.1080/00207390600597849

CrossRef Full Text | Google Scholar

Dove, M. T., and Fang, H. (2016). Negative thermal Expansion and Associated Anomalous Physical Properties: Review of the Lattice Dynamics Theoretical Foundation. Rep. Prog. Phys. 79, 066503. doi:10.1088/0034-4885/79/6/066503

PubMed Abstract | CrossRef Full Text | Google Scholar

Edelberg, D., Kumar, H., Shenoy, V., Ochoa, H., and Pasupathy, A. N. (2020). Tunable strain soliton networks confine electrons in van der waals materials. Nat. Phys. 16, 1097–1102. doi:10.1038/s41567-020-0953-2

CrossRef Full Text | Google Scholar

Eesley, G. L., Clemens, B. M., and Paddock, C. A. (1987). Generation and Detection of Picosecond Acoustic Pulses in Thin Metal Films. Appl. Phys. Lett. 50, 717–719. doi:10.1063/1.98077

CrossRef Full Text | Google Scholar

Fleming, D., Johnson, D., and Lemaire, P. (1997). A Temperature Compensated Optical Fiber Refractive Index Grating. Patent US5694503A.

Google Scholar

Gardner, C. S., Greene, J. M., Kruskal, M. D., and Miura, R. M. (1974). Korteweg-devries Equation and Generalizations. Vi. Methods for Exact Solution. Comm. Pure Appl. Math. 27, 97–133. doi:10.1002/cpa.3160270108

CrossRef Full Text | Google Scholar

Gleason, S., Manton, J., Sheung, J., Byrum, T., Jensen, C., Jiang, L., et al. (2017). “Intrinsic Resolving Power of XUV Diffraction Gratings Measured with Fizeau Interferometry,” in Advances in Metrology for X-Ray and EUV Optics VII. Editors L. Assoufid, H. Ohashi, and A. K. Asundi (San Diego: International Society for Optics and Photonics (SPIE)), 10385, 22–34.

CrossRef Full Text | Google Scholar

Goodwin, A. L., Calleja, M., Conterio, M. J., Dove, M. T., Evans, J. S. O., Keen, D. A., et al. (2008). Colossal Positive and Negative thermal Expansion in the Framework Material Ag₃[co(cn)₆]. Science 319, 794–797. doi:10.1126/science.1151442

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenough, R. D., and Palmer, S. B. (1973). The Elastic Constants and thermal Expansion of Single-crystal CdTe. J. Phys. D: Appl. Phys. 6, 587–592. doi:10.1088/0022-3727/6/5/315

CrossRef Full Text | Google Scholar

Handunkanda, S. U., Curry, E. B., Voronov, V., Said, A. H., Guzman-Verri, G. G., Brierley, R. T., et al. (2015). Large Isotropic Negative thermal Expansion above a Structural Quantum Phase Transition. Phys. Rev. B. 92, 134101. doi:10.1103/physrevb.92.134101

CrossRef Full Text | Google Scholar

Hao, H.-Y., and Maris, H. J. (2001). Experiments with Acoustic Solitons in Crystalline Solids. Phys. Rev. B. 64, 064302. doi:10.1103/PhysRevB.64.064302

CrossRef Full Text | Google Scholar

Jovanovic, S. M., Devenyi, G. A., Jarvis, V. M., Meinander, K., Haapamaki, C. M., Kuyanov, P., et al. (2014). Optical Characterization of Epitaxial Single crystal Cdte Thin Films on Al₂o₃ (0001) Substrates. Thin Solid Films 570, 155–158. doi:10.1016/j.tsf.2014.09.027

CrossRef Full Text | Google Scholar

Korteweg, D. J., and de Vries, G. (1895). Xli. On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 39, 422–443. doi:10.1080/14786449508620739

CrossRef Full Text | Google Scholar

Kowach, G. R., and Ramirez, A. P. (2002). Handbook of Materials Selection. New York: John Wiley & Sons. doi:10.1002/9780470172551

CrossRef Full Text

Landau, R. H., and Pez, M. J. (2018). Computational Problems for Physics: With Guided Solutions Using Python. 1st edn. USA: CRC Press.

Lind, C., Coleman, M. R., Kozy, L. C., and Sharma, G. R. (2011). Zirconium Tungstate/polymer Nanocomposites: Challenges and Opportunities. Phys. Stat. Sol. (B) 248, 123–129. doi:10.1002/pssb.201083967

CrossRef Full Text | Google Scholar

Lind, C. (2012). Two Decades of Negative thermal Expansion Research: Where Do We Stand? Materials 5, 1125–1154. doi:10.3390/ma5061125

PubMed Abstract | CrossRef Full Text | Google Scholar

Lommens, P., De Meyer, C., Bruneel, E., De Buysser, K., Van Driessche, I., and Hoste, S. (2005). Synthesis and thermal Expansion of ZrO₂/ZrW₂O₈ Composites. J. Eur. Ceram. Soc. 25, 3605–3610. doi:10.1016/j.jeurceramsoc.2004.09.015

CrossRef Full Text | Google Scholar

Matsuda, O., Larciprete, M. C., Li Voti, R., and Wright, O. B. (2015). Fundamentals of Picosecond Laser Ultrasonics. Ultrasonics 56, 3–20. doi:10.1016/j.ultras.2014.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Mazzone, D. G., Dzero, M., Abeykoon, A. M., Yamaoka, H., Ishii, H., Hiraoka, N., et al. (2020). Kondo-induced Giant Isotropic Negative thermal Expansion. Phys. Rev. Lett. 124, 125701. doi:10.1103/PhysRevLett.124.125701

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, W., Smith, C. W., Mackenzie, D. S., and Evans, K. E. (2009). Negative thermal Expansion: a Review. J. Mater. Sci. 44, 5441–5451. doi:10.1007/s10853-009-3692-4

CrossRef Full Text | Google Scholar

Mogunov, I. A., Lysenko, S., Fedianin, A. E., Fernández, F. E., Rúa, A., Kent, A. J., et al. (2020). Large Non-thermal Contribution to Picosecond Strain Pulse Generation Using the Photo-Induced Phase Transition in Vo2. Nat. Commun. 11, 1690. doi:10.1038/s41467-020-15372-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Muskens, O. L. (2004). High-Amplitude, Ultrashort Strain Solitons in Solids. Ph.D. thesis. Utrecht, Netherlands: Universiteit Utrecht.

Google Scholar

Muskens, O. L., Akimov, A. V., and Dijkhuis, J. I. (2004). Coherent Interactions of Terahertz Strain Solitons and Electronic Two-Level Systems in Photoexcited Ruby. Phys. Rev. Lett. 92, 035503. doi:10.1103/PhysRevLett.92.035503

PubMed Abstract | CrossRef Full Text | Google Scholar

Péronne, E., Chuecos, N., Thevenard, L., Perrin, B., and Thevenard, L. (2017). Acoustic Solitons: A Robust Tool to Investigate the Generation and Detection of Ultrafast Acoustic Waves. Phys. Rev. B. 95, 64306. doi:10.1103/Phys.10.1103/physrevb.95.064306

CrossRef Full Text | Google Scholar

Péronne, E., and Perrin, B. (2006). Generation and Detection of Acoustic Solitons in Crystalline Slabs by Laser Ultrasonics. Ultrasonics 44, e1203–e1207. doi:10.1016/j.ultras.2006.05.072

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, J., Kadic, M., Naber, A., and Wegener, M. (2017). Micro-Structured Two-Component 3D Metamaterials with Negative Thermal-Expansion Coefficient from Positive Constituents. Sci. Rep. 7, 40643. doi:10.1038/srep40643

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez, E. E., Llobet, A., Proffen, T., Melot, B. C., Seshadri, R., Littlewood, P. B., et al. (2009). The Role of Static Disorder in Negative thermal Expansion in Reo₃. J. Appl. Phys. 105, 114901. doi:10.1063/1.3120783

CrossRef Full Text | Google Scholar

Scherbakov, A. V., van Capel, P. J. S., Akimov, A. V., Dijkhuis, J. I., Yakovlev, D. R., Berstermann, T., et al. (2007). Chirping of an Optical Transition by an Ultrafast Acoustic Soliton Train in a Semiconductor Quantum Well. Phys. Rev. Lett. 99, 057402. doi:10.1103/PhysRevLett.99.057402

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, A. J., Chen, X., and Chen, G. (2008). Pulse Accumulation, Radial Heat Conduction, and Anisotropic thermal Conductivity in Pump-Probe Transient Thermoreflectance. Rev. Scientific Instr. 79, 114902. doi:10.1063/1.3006335

CrossRef Full Text | Google Scholar

Shah, J. S., and Straumanis, M. E. (1972). Thermal Expansion Behavior of Silicon at Low Temperatures. Solid State. Commun. 10, 159–162. doi:10.1016/0038-1098(72)90371-7

CrossRef Full Text | Google Scholar

Sleight, A. W. (1998). Negative thermal Expansion Materials. Curr. Opin. Solid State. Mater. Sci. 3, 128–131. doi:10.1016/S1359-0286(98)80076-4

CrossRef Full Text | Google Scholar

Sullivan, L. M., and Lukehart, C. M. (2005). Zirconium Tungstate (ZrW₂O₈)/Polyimide Nanocomposites Exhibiting Reduced Coefficient of Thermal Expansion. Chem. Mater. 17, 2136–2141. doi:10.1021/cm0482737

CrossRef Full Text | Google Scholar

Takenaka, K., Asai, D., Kaizu, R., Mizuno, Y., Yokoyama, Y., Okamoto, Y., et al. (2019). Giant Isotropic Negative thermal Expansion in Y-Doped Samarium Monosulfides by Intra-atomic Charge Transfer. Sci. Rep. 9, 122. doi:10.1038/s41598-018-36568-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Takenaka, K. (2012). Negative thermal Expansion Materials: Technological Key for Control of thermal Expansion. Sci. Tech. Adv. Mater. 13, 013001. doi:10.1088/1468-6996/13/1/013001

CrossRef Full Text | Google Scholar

Tas, G., and Maris, H. J. (1994). Electron Diffusion in Metals Studied by Picosecond Ultrasonics. Phys. Rev. B. 49, 15046–15054. doi:10.1103/PhysRevB.49.15046

CrossRef Full Text | Google Scholar

Thomsen, C., Strait, J., Vardeny, Z., Maris, H. J., Tauc, J., and Hauser, J. J. (1984). Coherent Phonon Generation and Detection by Picosecond Light Pulses. Phys. Rev. Lett. 53, 989–992. doi:10.1103/PhysRevLett.53.989

CrossRef Full Text | Google Scholar

Wang, Y., Park, J. Y., Koh, Y. K., and Cahill, D. G. (2010). Thermoreflectance of Metal Transducers for Time-Domain Thermoreflectance. J. Appl. Phys. 108, 43507. doi:10.1063/1.3457151

CrossRef Full Text | Google Scholar

Wendt, D., Bozin, E., Neuefeind, J., Page, K., Ku, W., Wang, L., et al. (2019). Entropic Elasticity and Negative thermal Expansion in a Simple Cubic crystal. Sci. Adv. 5, eaay2748. doi:10.1126/sciadv.aay2748

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitham, G.(1999). Shock Dynamics. Linear and Nonlinear Waves. John Wiley Sons, Ltd. doi:10.1002/9781118032954.ch8

CrossRef Full Text | Google Scholar

Wright, O. B., Perrin, B., Matsuda, O., and Gusev, V. E. (2001). Ultrafast Carrier Diffusion in Gallium Arsenide Probed with Picosecond Acoustic Pulses. Phys. Rev. B. 64, 081202. doi:10.1103/PhysRevB.64.081202

CrossRef Full Text | Google Scholar

Wright, O. B. (1992). Thickness and Sound Velocity Measurement in Thin Transparent Films with Laser Picosecond Acoustics. J. Appl. Phys. 71, 1617–1629. doi:10.1063/1.351218

CrossRef Full Text | Google Scholar

Wright, O. B. (1994). Ultrafast Nonequilibrium Stress Generation in Gold and Silver. Phys. Rev. B. 49, 9985–9988. doi:10.1103/PhysRevB.49.9985

CrossRef Full Text | Google Scholar

Zabusky, N. J., and Kruskal, M. D. (1965). Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. 15, 240–243. doi:10.1103/PhysRevLett.15.240

CrossRef Full Text | Google Scholar