
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Mater., 17 September 2021
Sec. Ceramics and Glass
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.741560
This article is part of the Research TopicRecent Advances in Low-Positive, Zero, and Negative Thermal Expansion Materials: Fundamentals and ApplicationsView all 5 articles
This review presents the history of materials in the A2M3O12 and related ceramic families, including their unusual thermal expansion and the present understanding of its mechanism, and related factors such as hydroscopicity and the monoclinic to orthorhombic phase transition. Other properties, including thermomechanical, thermal and ionic conduction and optical properties, are presented in terms of current knowledge, challenges and opportunities for applications. One of the largest challenges is the production of monoliths, and various methods for consolidation and sintering are summarized. These ceramics have considerable promise when combined with other materials, and recent advances in such composites are presented. These matters are placed in the context of the potential applications of negative and near-zero thermal expansion ceramics, which still present challenges for future materials researchers.
The A2M3O12 ceramic family,1 in which A stands for a trivalent cation, in the range of cation radii from Al3+ to Dy3+ and M generally stands for W6+ or Mo6+, offers extraordinary flexibility in terms of chemistry, while preserving the same basic crystal structure. Many of the members of this family display negative thermal expansion along one or more lattice vectors, leading to unusual (near-zero, negative or low-positive) values of the coefficient of thermal expansion. The origins of this unusual behavior and its relationship to materials chemistry, structure, and physical properties, is the main topic of this review. More general aspects of negative thermal expansion materials have been addressed thoroughly in our previous review (Romao et al., 2013).
In addition to the vast range of options for A3+ ions, it is also possible to substitute A3+ with a mixture of tetravalent, trivalent and/or divalent cations with concomitant partial substitution of M6+ with pentavalent cations to preserve charge neutrality, while maintaining the same general structure (Figure 1). Therefore, it is possible to categorize materials from such cation replacements into three major sub-families according to the degree of M6+ substitution by pentavalent cations, as ABM3O12, ABM2XO12 and A2MX2O12. These subfamilies are described briefly here, with the main focus of this review on A2M3O12.
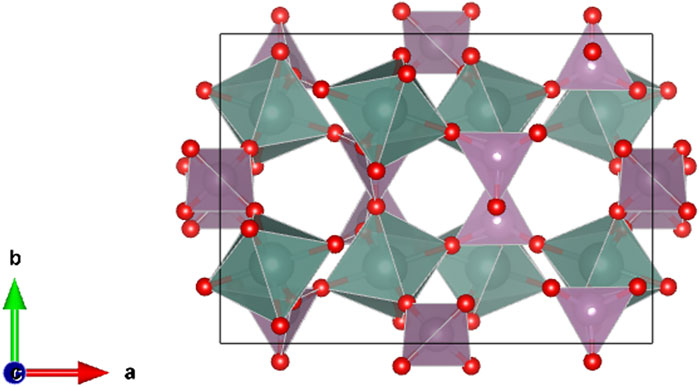
FIGURE 1. Sc2W3O12-type orthorhombic structure (Pbcn space group), shown for Y2Mo3O12 at room temperature, oriented along the c-axis direction, indicating void spaces due to vacant dodecahedral, 8-fold sites (which are fully occupied in the garnet structure).
The ABM3O12 sub-family requires A and B as tetravalent and divalent cations, respectively. Their presence in 1:1 atomic ratio does not require substitution of W6+/Mo6+ with pentavalent cations. Since the 2004 report of HfMgW3O12 (Suzuki and Omote, 2004), many other compounds from this sub-family have been reported (Baiz et al., 2008; Marinkovic et al., 2008a; Omote et al., 2011; Song et al., 2013; Zhang et al., 2015; Romao et al., 2015b; Li et al., 2017). Most of these compounds are tungstates or molybdates of Hf4+/Zr4+ and Mg2+. Therefore, these three elements are archetypical for A4+ and B2+ in ABM3O12. The ABM3O12 structure maintains the same framework connectivity of octahedra and tetrahedra through the vertices as in A2M3O12 (see Figure 1 and Section 2 for structure details), although in the orthorhombic Pna21 space group. However, A4+ and B2+ occupy crystallographically unique atomic sites, thereby splitting the single A3+ site in A2M3O12. In some instances, A4+ can be shared by two tetravalent cations Hf4+/Zr4+ (Shen et al., 2018), while in some other materials B2+ can be a mixture of two divalent cations such as Mg2+ and Zn2+ (Li et al., 2018; Madrid et al., 2020; Marinkovic et al., 2021). The special importance of the substitution at B2+ is due to HfMg1-xZnxMo3O12 and ZrMg1-xZnxMo3O12, which have near-zero thermal expansion. Intermediate compounds between A2M3O12 and ABM3O12 such as In0.5(ZrMg)0.75Mo3O12 (Prisco et al., 2016a), In(HfMg)0.5Mo3O12 (Miller et al., 2012b) and Cr(ZrMg)0.5Mo3O12 (Song et al., 2014) also exist.
The ABM2XO12 sub-family requires the A and B cations to be tetravalent and trivalent, respectively. Therefore, 1/3 of W6+ or Mo6+ must be replaced with P5+ or V5+, as in the case of HfScW2PO12 and related materials (Zhang et al., 2015; Cheng et al., 2016; Ge et al., 2016c; Cheng et al., 2017). Even more complex substitution patterns are possible in ABM2XO12 (Liang et al., 2017; Yuan et al., 2020) permitting further adjustments of their physical properties. The structures from this sub-family preserve the same framework connectivity through vertices as in A2M3O12, and also take on the same orthorhombic space group (Pbcn).
The A2MX2O12 sub-family was reported (Piffard et al., 1987) prior to the first report of negative thermal expansion in A2M3O12 (Evans et al., 1997). They presented studies of Zr2SP2O12 and since then it is known that this sub-family shares exactly the same crystal structure and space group as the A2M3O12 family. In the A2MX2O12 family, A is necessarily a tetravalent cation, which offers only limited chemical flexibility since A4+ could be only Hf4+ or Zr4+, with Zr4+ generally reported (Evans et al., 1995; Cetinkol et al., 2009; Cetinkol and Wilkinson, 2009; Shang et al., 2013). To preserve charge neutrality, the compounds from the A2MX2O12 sub-family have 2/3 of the W6+, Mo6+ or S6+ ions replaced by P5+.
Negative and near-zero thermal expansion are common for all these sub-families, and therefore their properties and insights complement studies of the A2M3O12 family.
Although this review centers on properties of materials in the A2M3O12 family, some comments concerning synthesis are pertinent. Most of the materials in the A2M3O12 and related sub-families can be synthesized through the classical solid-state reaction method (Romao et al., 2013). This method is simple, straightforward and avoids sophisticated chemistry, so its use is understandable when the goal is to prepare novel materials and to evaluate their fundamental physical properties. However, due to the inherent drawbacks of the synthesized powders, solid-state reactions are usually not useful to produce powders to form the monolithic bodies required for many applications (see Section 8), even with consolidation and sintering (see Section 6). The inherent drawbacks of the powders prepared by solid-state reaction methods are phase inhomogeneity (i.e., formation of secondary phases), and large and strongly agglomerated particles. These characteristics do not permit the required formation of highly dense solids with fine microstructure. From an industrial viewpoint, this method also is expensive since it uses high temperatures and long processing times.
Therefore, soft-chemistry routes are better to provide nanometric to sub-micronic powders with high specific area and low agglomeration. There are currently significant efforts aimed at the development of protocols capable of providing powders with desired properties, including co-precipitation (Yordanova et al., 2012; Pontón et al., 2017; Pourmortazavi et al., 2017; Marzano et al., 2019), sol-gel methods (Zhang et al., 2008; Ari et al., 2011; Prisco et al., 2013), non-hydrolytic sol-gel methods (Gates et al., 2006; Baiz et al., 2008; Truitt et al., 2015; Young et al., 2016) and hydrothermal routes (Li et al., 2019; Isobe et al., 2020). Low-temperature combustion was also reported for preparation of fine Al0.5Sc1.5W3O12 powders (Dasgupta et al., 2012).
The present review presents the history of studies of materials in the A2M3O12 and related ceramic families, the findings of unusual thermal expansion and the present understanding of the mechanism, and related factors such as hydroscopicity, and the monoclinic to orthorhombic phase transition. Other properties, including thermomechanical, thermal and electric conduction and optical properties, are presented in terms of current knowledge, challenges and opportunities for applications. One of the largest challenges is the production of monoliths, and various methods for consolidation and sintering are summarized. These ceramics have considerable promise when combined with other materials, and recent advances in such composites are presented. All of these matters are placed in the context of the applications of the A2M3O12 and related ceramic families, which still present challenges for future materials researchers.
Before negative thermal expansion (NTE, also known as thermomiotic behavior) and near-zero thermal expansion (NZTE) were discovered in the orthorhombic crystal phases (space group 60: Pbcn, alternatively Pnca) of A2M3O12 and related compounds in the late 1990s (Evans et al., 1997), many of these materials were already known and studied for other purposes.
An 1895 paper (Hitchcock, 1895) on co-precipitation synthesis of several tungstates and molybdates from the A2M3O12 family likely is the first report in the scientific literature of A2M3O12 phases. There is scant other new information until the 1963 report (Borchardt, 1963a) of Y2W3O12 (denoted as Y2O3 × 3WO3 in the paper), synthesized through a solid-state reaction route, which acknowledged that the unit cell, space group and crystal structure of this new compound were not known at the time. The author reported that the X-ray diffraction (XRD) pattern of Y2W3O12 at room temperature was characterized by a few broad and weak diffraction lines, providing the first, although indirect, observation of hygroscopicity in the A2M3O12 family.
Soon after, Borchardt published another study (Borchardt, 1963b) on the rare-earth (Sc to Lu) tungstates in the A2M3O12 family. That report concentrated on optical properties with special interest in their luminescence (see also Section 5.3). Although the crystal structure was not determined, the author preliminarily indicated three different types of X-ray powder diffraction (XRPD) patterns, depending on the size of the rare-earth cations. The author suggested the existence of three structures at room temperature: one for the tungstates in the ranges from La to Dy, another from Ho to Y, and a third for the tungstates of Lu and Sc which are the two smallest rare-earth cations. Interestingly, Borchardt (1963a) discerned that Dy2W3O12, when quenched from a temperature higher than 1273 K, adopts the structure of the tungstates from the Ho-Y group, which led the author to propose that Dy2W3O12 transforms to a Ho2W3O12-type structure above 1273 K. This finding was confirmed in 2016 (Cao et al., 2016).
Shortly after Borchardt’s pioneering research, it was suggested (Nassau et al., 1964) that four different crystal structures exist for the rare-earth tungstates from La to Lu, depending on cation size, and also on temperature. For the first time, the orthorhombic crystal system was ascribed to some of the A2M3O12 tungstates, such as Yb2W3O12 and Sc2W3O12. A year later the same authors published a landmark paper (Nassau et al., 1965) which described synthesis of 66 different tungstates and molybdates from A2M3O12 family, encompassing the phases with rare-earth and non-rare-earth trivalent cations, as well as some solid solutions. The authors distinguished several tungstate crystal structures. The tungstates from La to Dy appeared to be isostructural, adopting the monoclinic space group C2/c with four chemical formulae per unit cell at room temperature. The crystal structure for Eu2W3O12 had been solved a few years prior (Templeton and Zalkin, 1963), showing that W6+ occupied two independent tetrahedra sites, while Eu3+ was coordinated by eight oxygens. Nassau et al. concluded that all tungstates from La to Dy adopted this same structure, with unit cell dimensions decreasing in accord with the lanthanide contraction rule, with the exception of Tb2W3O12. In addition, they recognized explicitly, for the first time, the existence of hydrated phases at room temperature for tungstates and molybdates of heavy rare earths, for Y and Dy to Lu. When heated to 393 K, these materials lost water and converted into orthorhombic phases, as demonstrated by high-temperature X-ray diffraction. In the same report (Nassau et al., 1965), they also correctly proposed the space group of the orthorhombic phases as Pnca. The same authors also suggested that the molybdates from La to Nd and from Sm to Gd crystallized in two different structures, but did not give further details. They also referred to a tetragonal structure adopted, supposedly, by the molybdates with trivalent cations from Pr to Ho, and observed that tungstates and molybdates of non-rare-earth trivalent cations were not hygroscopic.
Soon after those reports, the crystal structure of orthorhombic Sc2W3O12 was reported (Abrahams and Bernstein, 1966). This was a significant step forward and Sc2W3O12 became the archetypal structure, shared by other 23 tungstates and molybdates from the A2M3O12 family, mainly those containing heavy rare-earth and non-rare-earth cations, e.g., Al2W3O12 (Craig and Stephenson, 1968). In contrast with the Eu2W3O12 structure, where the trivalent cations adopt 8-fold coordination, in the Sc2W3O12 structure the trivalent cations adopt octahedral coordination. The Sc2W3O12-type structure also has W6+ in two independent crystallographic positions, and oxygens in six independent crystallographic sites, with four formula units per unit cell.
The division between the two types of structure (Eu2W3O12 and Sc2W3O12) for the series of rare-earth elements from La to Lu obeyed the first Pauling rule (coordination number dictated by radius ratio) quite well (Abrahams and Bernstein, 1966). A cation-to-anion radius ratio >0.732 led to 8-fold cation coordination, while lower ratios favored octahedral (6-fold) coordination. Also, for the first time, it was recognized that octahedra and tetrahedra in the orthorhombic Sc2W3O12-type structure shared mutual vertices (more specifically, each octahedron is connected to six tetrahedra through vertices, while each tetrahedron is connected to four octahedra at the same manner) (Abrahams and Bernstein, 1966), a feature that would be identified, 3 decades later, as the essential structural motif underlying the vibrational mechanism of NTE or NZTE.
In those early days the potential for applications of A2M3O12-type materials was already recognized, in the high intrinsic optical transparency of A2M3O12 phases over a wide wavelength range from 0.35 to 5 μm, including visible and infra-red ranges (Nassau et al., 1965), and the use of Gd2Mo3O12 as a laser host material when doped with Nd (Borchardt and Bierstedt, 1966).
The unit cell parameters of some rare earth molybdates, from Sm to Dy, were reported in 1971 (Brixner et al., 1971). A few years later a milestone paper was published (Sleight and Brixner, 1973), showing that phases with the orthorhombic structure (Sc2W3O12-type) could undergo a displacive phase transformation at lower temperatures to the monoclinic space group P21/a (space group 14). Even more importantly, the authors correlated the temperatures of the phase transformations with the electronegativity of the trivalent cations, showing that higher electronegativity of the trivalent cations results in phase transitions at higher temperatures. Although there are a few exceptions from this electronegativity correlation, such as the case of ScAlMo3O12 (Truitt et al., 2015), the plot constructed by Sleight and Brixner for five different A2M3O12 molybdates has been generally affirmed in many further investigations (Romao et al., 2013) and is still of fundamental importance to understanding the main mechanism controlling this important phase transition in the A2M3O12 family.
A thorough review on rare-earth molybdates was published in 1979 (Brixner et al., 1979). The authors explicitly delineated the phase transition temperatures and structural types for all molybdates from La to Lu, while also showing that the unit cells of molybdates adopting the Pba2 space group (defined as the β’ modification) obey the lanthanide contraction in the range from Pr to Ho. In the same timeframe, the crystal structure for the monoclinic, lower-temperature modification of heavy rare-earth and non-rare-earth tungstates and molybdates was solved for Fe2Mo3O12 (Chen, 1979).
Luminescence studies of Al2W3O12, Sc2W3O12 and Lu2W3O12, undoped and doped with Eu3+ or Cr3+, were published in 1980 but the last two tungstate phases were found to be so hygroscopic that their luminescence was not efficient (Blasse and Ouwerkerk, 1980).
In the late 1980s, Zr2SO4(PO4)2 was synthesized and shown to be isostructural with Sc2W3O12 (Piffard et al., 1987). This report was the first time a phase with two chemically different tetrahedra and with a tetravalent cation in an octahedral position had been identified as having the orthorhombic Sc2W3O12 structure. More recently, similar materials have been denoted as the A2MX2O12 sub-family of A2M3O12 (Madrid et al., 2020). It has been suggested that S6+ and P5+ are randomly distributed over two independent tetrahedral sites at room temperature (Piffard et al., 1987).
In 1995, Evans et al. published the crystal structure of Zr2WO4(PO4)2, another compound isostructural to Zr2SO4(PO4)2 and Sc2W3O12 (Evans et al., 1995). The authors discussed the relationship between this structure and the garnet structure. Although this issue had been previously discussed in Russian literature (Plyasova et al., 1967), Evans et al. importantly pointed out that the Sc2W3O12-type structure can be understand as a deficient garnet structure, with completely vacant 8-coordinated sites (Figure 1). This structural feature allows the Sc2W3O12-type structure to accommodate atomic and molecule species within the empty 8-fold sites, which form continuous channels along the c-crystallographic direction (for the Pbcn space group; for Pcna, the channels are directed along the a-axis). The properties, such as hygroscopicity (Marinkovic et al., 2005) and high ionic conductivity (Imanaka et al., 1998) of some A2M3O12 phases with large channels owing to large A site cations, are likely a direct consequence of the deficient garnet structure. Evans et al. (1995) concluded their paper by anticipating unusual negative thermal expansion in Zr2WO4(PO4)2 and of some other (unspecified) Sc2W3O12-type materials. Surprisingly, 30 years after the original report of the synthesis of Y2W3O12 (Borchardt, 1963a), aside from a brief report in the Russian literature (Balashov et al., 1975), no study on thermal expansion of A2M3O12 family had been reported and the issue remained obscure. The 1995 paper by Evans et al. ended the pre-NTE period and brought new research insights concerning this vast group of ceramics.
Figure 2 summarizes the timeline of the main discoveries and milestone papers in the pre-NTE period of the A2M3O12 family.
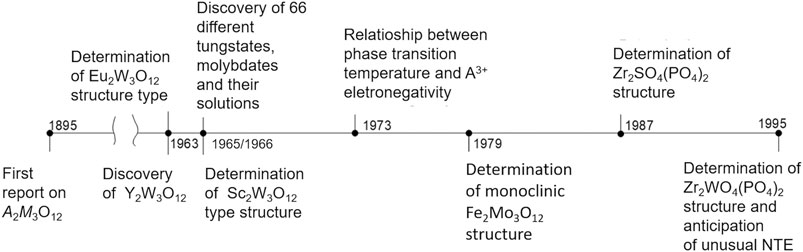
FIGURE 2. Timeline of the main discoveries and milestone papers in the pre-NTE era of the A2M3O12 family of ceramics.
The first report of NTE and NZTE in the A2M3O12 family was in 1997 (Evans et al., 1997): linear coefficients of thermal expansion (CTE) for 21 tungstates and molybdates, mainly measured by dilatometry, although some CTEs were measured by XRPD. Most of the reported tungstates and molybdates were based on Al3+ and Sc3+, partially substituted by different rare-earth or non-rare-earth cations. In addition, a few members of the related A2MX2O12 family (A = Zr4+ or Hf4+; X = P5+; M = W6+ or Mo6+) also were reported. An NTE mechanism for the A2M3O12 family was proposed in the seminal 1997 paper and discussed further from a more general viewpoint in related subsequent publications (Sleight, 1998; Evans et al., 1998a; Evans et al., 1998b; Evans, 1999) and in more detail for Sc2W3O12 (Evans et al., 1998b) and Sc2Mo3O12 (Evans and Mary, 2000).
In the late 1990s, the mechanism proposed for NTE and NZTE in the A2M3O12 leaned heavily on understanding of the unusual thermal expansion and phase transitions in a structurally related family, the framework silicates such as quartz and cristobalite (Giddy et al., 1993; Swainson and Dove, 1995; Hammonds et al., 1996). The known mechanism for the framework silicates, where SiO4 tetrahedra share vertices in an open crystal structure, explained the phase transition between high- and low-temperature structures, and also addressed NTE and NZTE observed in β-quartz and β-cristobalite (the high-temperature forms). The mechanism was based on low-energy phonon modes capable of tilting rigid SiO4 units in a correlated manner, causing NTE or NZTE over relatively limited temperature ranges, well above room temperature. In β-quartz and β-cristobalite, this unusual negative contribution to the overall thermal expansion overwhelmed the well-understood positive contribution due to bond-length (Si-O in this case) extension with increased temperature, originating from the inherent asymmetry of the interatomic potential well (Figure 3). There is no doubt that the small thermal dilatation of the strong Si−O bonds, ∼0.02 Å, along a wide temperature range of ∼1273 K (Tucker et al., 2000), together with the framework vertex-shared structure, were the fundamental factors for emergence of the unusual dimensional response to temperature changes in β-quartz and β-cristobalite. In addition, an earlier contribution (Blackman, 1957) concerning softening of low-energy vibrational modes with volume reduction in structures composed from polyhedra with low coordination numbers (i.e., with low-density, open crystal structures) was also indirectly used early on to rationalize the mechanism causing NTE/NZTE in the A2M3O12 family.
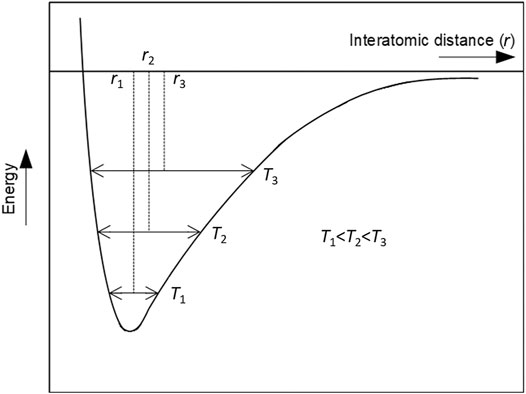
FIGURE 3. Schematic representation of an asymmetric interatomic potential well. The positions r1, r2 and r3 show the evolution of mean interatomic distances with increasing temperature, with the mean interatomic distance increasing with increasing temperature as in normal (positive) thermal expansion.
The mechanism causing NTE/NZTE in the A2M3O12 family is now understood as asymmetrical framework librations, caused by low-energy phonons, leading to coupled tilting of quasi-rigid polyhedra. Since the 1966 report (Abrahams and Bernstein, 1966) it is known the materials in the A2M3O12 family have framework structures when orthorhombic (Figure 1) with polyhedra connected through vertices. Therefore, the oxygens, which are shared by two polyhedra (an octahedron and a tetrahedron), are coordinated by only two cations (one A3+ and one M6+). This structural feature permits the vertex-shared oxygens to be capable of vibrating in a transverse manner on heating. When free of interstitial ions/molecules, such a lattice arrangement presents no steric hindrance to the librational movements guided by 2-fold oxygens.
With the local structural motif of A2M3O12 composed from one octahedron and one tetrahedron connected through a vertex, an asymmetric transverse vibration of the 2-fold oxygen is capable of contracting the A−M non-bonding distance and decreasing the A−O−M angle (Figure 4A). The six crystallographically different A−O−M angles in orthorhombic A2M3O12 are never equal to 180°, and their angles, which some decrease with temperature, are between 140° and 175° (Evans et al., 1998b; Evans and Mary, 2000; Marinkovic et al., 2009).
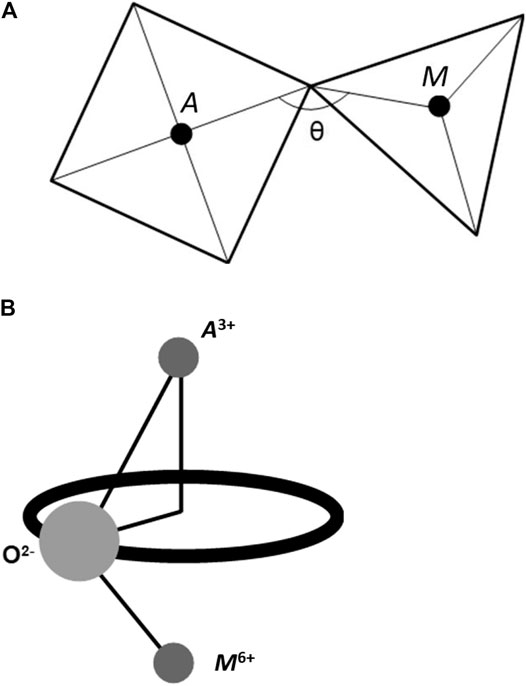
FIGURE 4. (A) Contraction of the A−M non-bonding distance and decrease of the A−O−M angle (θ) in the octahedron-tetrahedron local structural motif in an A2M3O12 structure, arises with increasing temperature due to the asymmetric transverse vibration of the 2-fold oxygen at the shared vertex, and leads to negative thermal expansion. (B) Transverse thermal vibrations of 2-fold oxygens in the A2M3O12 family, describing a torus geometrical figure, causing reduction of the apparent bond distances (A3+−O2- and, especially, M6+−O2-).
The peculiar lattice dynamics in the A2M3O12 family, with the existence of many low-energy vibrational modes, has been demonstrated by several different experiments.
Especially for ceramics and minerals, the constituent additivity model, based on constituent oxides, can accurately predict heat capacities of complex ceramics, such as, for example, sodalite (Qiu and White, 2001). However, the constituent additivity model underestimates the heat capacity at low temperatures for the NTE/NZTE A2M3O12 phases. For example, in HfMgMo3O12 the constituent additivity model does not accurately described the low-temperature experimental heat capacity below 150 K, since its constituent (positive CTE) oxides, HfO2, MgO and MoO3, do not present low-energy vibration modes (Miller et al., 2012a).
Another experimental proof of the contribution of low-energy modes to NTE/NZTE is the finding of negative mode Grüneisen parameters (γn) for low-energy vibration modes (Liang et al., 2008; Torres Dias et al., 2013). The softening of low-energy vibration modes with reduction of volume in keeping with the relationship:
where ωn is the frequency of mode n and V is the volume of the unit cell, contributes to negative thermal expansion in A2M3O12 materials.
The quasi-rigidity of polyhedra in A2M3O12 with changing temperature was first suggested for Sc2W3O12 (Evans et al., 1998b), demonstrating that small distortions of polyhedra occur. The distortions can be evaluated, for example, through temperature evolution of individual ScO6ca. 90° angles, showing, on average, not higher than 0.53° change over a temperature interval of more than several hundred Kelvin. Another study (Marinkovic et al., 2009) showed a mean variation of YO6∼ 90° angles over 723 K as high as 1.23°, corroborating the quasi-rigidity of polyhedra in A2M3O12. The earlier investigation (Evans et al., 1998b) also concluded that the apparent Sc−O and W−O bond lengths decreased with increasing temperature. This feature was later reported for many other A2M3O12 materials (Forster and Sleight, 1999; Marinkovic et al., 2009; Marinkovic et al., 2010) and likely can be understood as an artefact partially caused by the Rietveld analysis of Bragg lines in XRPD of the A2M3O12 structure where the vibrations of 2-fold oxygens are complex and cannot be described by simple thermal spheres or ellipsoids. This apparent bond-length reduction has no physical relationship to true bond lengths, and is not the origin of NTE. It is a consequence of transverse thermal vibrations of 2-fold oxygen ions, which possibly describe a torus (Figure 4B), not an ellipsoid, between the two neighboring cations. This artefact is enhanced due to strong A−O and, especially, W−O/Mo−O bonds with very low individual thermal expansion coefficients (Hazen and Prewitt, 1977). Another factor is that the tetrahedra, such as WO4, are even more rigid than the octahedra (Evans et al., 1998a). This finding has been corroborated by showing that YO6 are intrinsically more distorted than MoO4 (Marinkovic et al., 2009).
The AO6 and MO4 polyhedra are slightly distorted from their ideal shapes and volumes, even at very low temperatures, close to 0 K (Marinkovic et al., 2009), possibly in order to satisfy connectivity of polyhedra in a framework made by vertex sharing (Forster and Sleight, 1999). In addition, it has been suggested that the NTE mechanism in the A2M3O12 structure is intrinsically associated with continuously increasing slight distortions of the quasi-rigid polyhedra with increasing temperature (Forster and Sleight, 1999). This rationalization was proven for octahedra by XRPD (Marinkovic et al., 2009): octahedral distortion, calculated as volume distortion parameter, increased with increasing temperature. This structural feature is a peculiarity of the A2M3O12 structure and is not observed for ZrW2O8, another classic NTE material (Marinkovic et al., 2009). In the next section, it will be shown that larger AO6 octahedra distort more with temperature than smaller octahedra, a feature which intrinsically controls CTE in the A2M3O12 family.
The A2M3O12 crystal framework presents a pseudo two-dimensional structure since b-c layers are connected along the a-crystallographic direction (in the Pbcn space group) by only a few oxygen linkages per unit area, which is distinct from the situation in the other two crystallographic directions. This is reflected in the elastic tensors, which show reduced stiffness along a compared to b and c (Romao et al., 2016); this elastic anisotropy is reduced as the CTE becomes more negative, indicating a correlation between three-dimensional network-like behavior and NTE. Such a crystal framework causes, in general, NTE along the b and c directions, while the a-axis shows positive thermal expansion. However, the overall volume (aV) and average linear CTEs (αℓ =
At this point it should be highlighted that XRPD and dilatometry do not necessary give the same values for CTE for A2M3O12 materials. This situation is distinct from cubic materials, such as AM2O8, and is a result of the anisotropic A2M3O12 structure. The differences in CTEs are attributed to microstructural factors, principally microcracks (Evans et al., 1997), which can grow on sintering due to thermal stresses caused by mismatched CTEs along different crystallographic directions in orthorhombic A2M3O12 (For further discussion, see Section 5.1). On subsequent heating in a dilatometer, sintering tends to close the microstructural flaws. This factor leads to lower dilatomeric CTEs than from XRPD, which additionally can vary from sample to sample due to inhomogeneous microstructures. Therefore, CTEs of A2M3O12 materials are classified as either: 1) intrinsic CTE, originating from intrinsic competition of two crystal lattice factors such as bond-length thermal dilatation and asymmetric librations due to low-energy phonons, as determined by XRPD, or 2) extrinsic CTE determined by dilatometry, which additionally includes microstructural factors.
The existence of an orthorhombic-to-monoclinic phase transition is deleterious to these materials since the monoclinic phase shows normal, high, positive thermal expansion (Gates et al., 2006; Marinkovic et al., 2010), while the orthorhombic phase exhibits NTE or NZTE. In this section the focus is on the mechanism of the phase transition. (The factors controlling the widely ranging transition temperatures within the A2M3O12 family, varying from ∼180 to ∼780 K, are discussed in Section 4.3.) The orthorhombic modifications in A2M3O12 are considered to be the higher-temperature form, capable of transforming to monoclinic at lower temperatures, although in some rare cases this transition appears to be completely absent at ambient pressure (Romao et al., 2013).
The transition from the monoclinic to the orthorhombic form is a displacive, endothermic, low enthalpy change (typically ΔH ∼ 1 kJ mol−1), reversible phase transition (Varga et al., 2007). Thermodynamically, this phase transition is driven by the increase of thermal (vibrational) entropy on transition to the lower-density orthorhombic form. No primary bonds are broken during this phase transition. Thus, from the thermodynamic viewpoint, the monoclinic phase is enthalpically stabilized on cooling. But what is happening from the lattice dynamic and structural viewpoints? The low-energy phonons, responsible for NTE/NZTE in the higher-temperature orthorhombic phase, freeze out on cooling through the transition, due to the formation of secondary van der Waals interactions between 2-fold oxygens from the neighboring polyhedra motifs (Figure 5), therefore frustrating transverse vibrations and increasing the density of the newly formed monoclinic phase. This event leads to an abrupt decrease in volume on transition to the low-temperature phase (Figure 6), loss of most of the symmetry elements of the orthorhombic phase, and consequent reduction of the crystal symmetry to the monoclinic P21/a space group. Without the NTE contribution of lower-energy phonons, the only contribution to thermal expansion is bond-length thermal expansion, resulting in positive thermal expansion (PTE) of the monoclinic form.
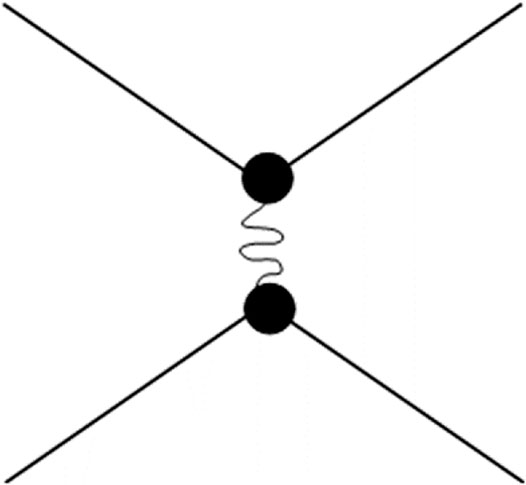
FIGURE 5. The orthorhombic-to-monoclinic phase transition on cooling coincides with formation of secondary van der Waals bonds (as represented here by a spring) between 2-fold oxygens from the neighboring octahedra-tetrahedra motifs. Asymmetric framework librations freeze out at the phase transition to the monoclinic form.
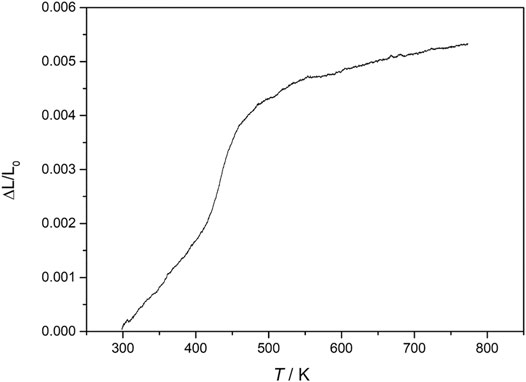
FIGURE 6. Dilatometric heating curve of AlInW3O12 phase, showing change in length (ΔL) relative to the original length (L0) and the monoclinic-to-orthorhombic phase transition at ca. 473 K. The low-temperature monoclinic form has higher density (lower molar volume), and therefore, there is volume expansion on transition to the lower-density (higher molar volume) orthorhombic form (Cerón Cortés et al., 2021).
Most of the studies on A2M3O12 phases and their solid solutions are driven by the vast chemical flexibility of this family while preserving the Sc2W3O12-type structure, and the consequent possibility to change, control and even finely tune the CTE through chemical substitutions, especially of the cations at the crystallographically unique octahedral site (Wu et al., 2006; Wu et al., 2007a; Wu et al., 2007b; Xiao et al., 2008b; Wu et al., 2009a; Miller et al., 2012b; Prisco et al., 2016a; Muller et al., 2019; Machado et al., 2021).
However, are the influences of the cation substitutions to be relegated to empirical approaches, through trial-and-error, or are there rational rules governing their influence on CTE in A2M3O12 materials and related sub-families?
In an early short report, it was shown (Forster et al., 1998) that complete substitution of Sc3+ [r(VI) = 0.745 Å, where r is the ionic radius and “VI” stands for octahedral coordination] by Lu3+ [r(VI) = 0.861 Å] made the value of the linear CTE more negative, changing it from −2.2 × 10–6 K−1 for Sc2W3O12 to −6.8 × 10–6 K−1 for Lu2W3O12. Those authors anticipated that Ho2W3O12 would have the most negative linear CTE among tungstates, since Ho3+ [r(VI) = 0.901 Å] is the largest cation capable of forming the orthorhombic Sc2W3O12-type structure at room temperature. Their prediction concerning the highest negative linear CTE for Ho2W3O12 was experimentally confirmed as −8.25 × 10–6 K−1 (Liu Q. et al., 2015). The same tendency was observed (Sumithra et al., 2005) for a series of tungstates including the trivalent cations of Lu, Yb, Er and Y, where negative linear CTEs increased from Lu2W3O12 to Y2W3O12, following the increase of cationic radius from Lu to Y in the A crystallographic site. The same trend was identified for molybdates, for example in the Yb2-xCrxMo3O12 system where the partial substitution of larger Yb3+ by smaller Cr3+ changed the linear CTE to less negative values, in the compositional range 0 ≤ x ≤ 0.4 (Wu et al., 2009b).
Therefore, early reports directly correlated values of linear CTE with the radius of A3+, i.e., larger cation radius causes more negative linear CTE. This relationship was rationalized in terms of capacity for distortion of AO6, which would increase with increased cationic radius (Forster et al., 1998). In their view, distortions of AO6 would be required to permit asymmetrical framework librations and, therefore, NTE or NZTE. Larger cations form larger polyhedra and favor polyhedral deformability through reduction of oxygen-to-oxygen repulsions, since oxygen-to-oxygen distances are increased inside larger polyhedra.
However, with more information it became evident that the A3+ radius was not the only factor that influences the CTE (Ari et al., 2008; Peng et al., 2008; Yu et al., 2008; Xiao et al., 2008a). It was shown that some phases and solid solutions did not follow the A3+ radius model (Ari et al., 2008): Cr3+ [r(VI) = 0.62 Å] has a smaller radius than Fe3+ [r(VI) = 0.65 Å], but the linear CTE of Cr2Mo3O12 was smaller (0.67 × 10–6 K−1) than for Fe2Mo3O12 (1.72 × 10–6 K−1). The linear CTE of Cr2Mo3O12, almost identical to the value measured by Ari et al., was also reported by other authors (Wu et al., 2009b). Furthermore, some phases within the Al2-xFexMo3O12 solid solution (x = 1 and 1.4) presented linear CTEs higher than for pure Al2Mo3O12 and Fe2Mo3O12 (Ari et al., 2008), a feature which would not be expected based on the A3+ radius model. Similarly, reports for Y2-xNdxW3O12 (Peng et al., 2008), Y2-xSmxW3O12 (Yu et al., 2008) and Sc2-xAlxW3O12 (Liu H. et al., 2021) showed that partial substitution with rare earths with higher ionic radius, such as Nd and Sm for Y and Al for Sc did not cause a continuous change of CTE between the limits of CTEs of the end-member phases; instead the linear CTE seemed to change in a random fashion.
A more general rule has been proposed concerning control of CTE in A2M3O12 and related families (Marinkovic et al., 2009; Marinkovic et al., 2010; Romao et al., 2015b). The principal parameter that correlates with linear CTE is the inherent volume distortion parameter for AO6. The volume distortion parameter of polyhedra was previously reported in the literature as a general quantitative measure of polyhedral deformability (Makovicky and Balic-Zunic, 1998). In the present context, the inherent volume distortion parameter was defined as deformation at the lowest temperature from which diffraction data are available (Marinkovic et al., 2009). The accurate calculation of the inherent volume distortion parameter is based on correctly refined atomic site coordination, obtained via the Rietveld method or from single-crystal diffraction. Increasing inherent volume distortion of AO6 correlates well with decreasing linear CTE (Figure 7), i.e., more distorted octahedra contribute more to the mechanism causing NTE/NZTE (Marinkovic et al., 2009).
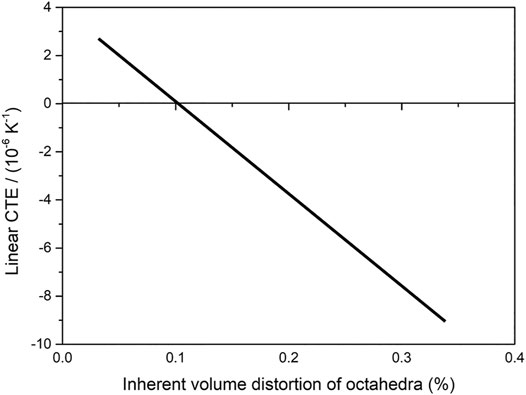
FIGURE 7. Schematic representation of the dependence between linear CTE and inherent volume distortion of octahedra. The increase of inherent volume distortion of AO6 corresponds to decrease in linear CTE (styled from data in Marinkovic et al., 2009).
Although inherent volume distortion can be correlated with cation radius, this correlation is non-linear and increases more rapidly for larger cations, as can be seen from Figure 8 (Romao et al., 2015b). Higher octahedral distortion in rare earths with larger radii, such as Er, Y and Ho (and probably of Dy, when stabilized in Sc2W3O12) might be a sign of decreasing stability of the octahedral coordination as the cationic size increases, since rare-earth cations with radii as large or larger than Dy adopt 8-fold coordination. Also, there is another interesting feature of octahedral distortion that makes its correlation with cationic radii more complex. In some cases, such as ZrO6 and MgO6 in ZrMgMo3O12, two octahedra with nearly the same cationic radii present rather different inherent volume distortions (Romao et al., 2015b).
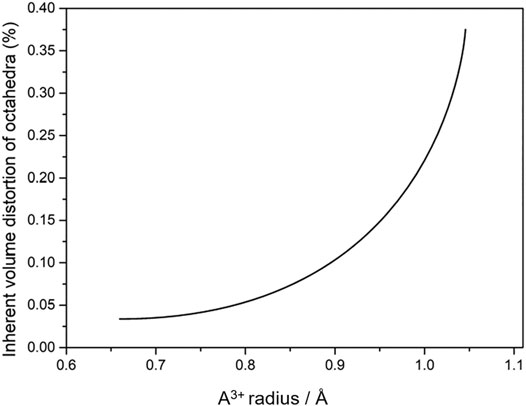
FIGURE 8. Schematic view of the dependence between inherent volume distortion of octahedra and radius of A3+ in the A2M3O12 family (styled from data in Romao et al., 2015b).
In this matter, it is critical to evaluate the temperature evolution of octahedral volume distortion of each type of octahedron with temperature to determine if it is rigid or quasi-rigid. Quasi-rigid polyhedra are fundamental for sustaining the NTE mechanism in the A2M3O12 family as the topology of the Sc2W3O12 structure is too constrained to permit rigid unit modes (Hammonds et al., 1998), and therefore transverse vibrations of the type shown in Figure 4 necessarily distort the coordination polyhedra. For example, volume distortion of YO6 increases linearly with temperature over a temperature span of approximately 1673 K (Forster and Sleight, 1999; Marinkovic et al., 2009) showing that these octahedra are quasi-rigid and contribute to NTE mechanism.
The extent of polyhedral distortion can be rationalized at a more fundamental physical level as a function of A−O bond attractive energies or forces. The attractive energy, Ea, in a predominantly ionic bond, is described as
where Z1 is the valence of the cation, Z2 is the valence of the anion, e is the elementary charge, ε0 is electrical permittivity in vacuum and R is the sum of the cation and anion radii (i.e., equilibrium bond length). The attractive ionic force (Fa) is the first derivative of the attractive energy with respect to interionic distance. More rigid polyhedra are those with highly attractive ionic energy (strong force), which hampers bond and angle deformation within the polyhedra as temperature increases, and thus inhibits the NTE mechanism within A2M3O12. Figure 9 shows schematically the relationship between linear CTE and ionic force (given in nN) between A3+ and O2- (Romao et al., 2015b). This view explains why Al2W3O12 and Al2Mo3O12 have the most positive linear CTE since their ionic forces between A3+ and O2- are the highest.
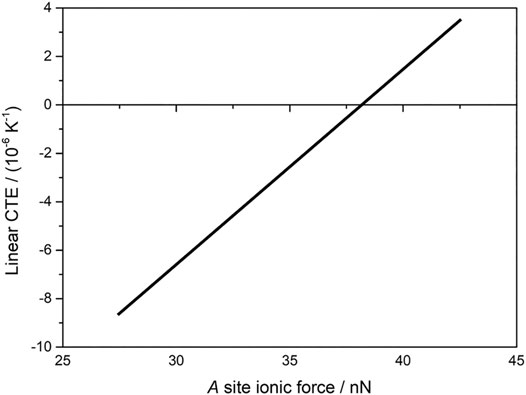
FIGURE 9. Schematic view of the relationship between linear CTE and ionic force between A3+ and O2- in the A2M3O12 family (styled from data in Romao et al., 2015b).
Another interesting feature is that the tetrahedra are less intrinsically distorted than the octahedra in these structures, and their distortion increases with temperature less than for octahedra (Marinkovic et al., 2009). On this basis, the tetrahedral contribution to the NTE mechanism seems to be minor, which can be understood in terms of highly attractive ionic forces between M6+ and O2- which hamper deformation of the tetrahedra. That tetrahedra are more rigid than octahedra in A2M3O12 was also concluded through ab initio lattice dynamics calculations (Rimmer and Dove, 2015). Those authors pointed out that O-Y-O bond angles, and therefore YO6, significantly deform on NTE, while WO4 remain rigid. In addition, Weck et al., studying Zr2WO4(PO4)2 using density functional perturbation theory, showed that ZrO6 octahedra distort significantly, while WO4 and PO4 tetrahedra remain almost ideal (Weck et al., 2018). The authors pointed out that the bond angle variances for ZrO6 were as high as 20.4°, while for WO4 and PO4 they were as low as 0.5° and 0.4°, respectively.
Based on the data currently available in the literature for the A2M3O12 family, the intrinsic linear CTEs vary widely, from −11.6 × 10–6 K−1 for Ho2Mo3O12 from 200 to 700°C (Xiao et al., 2008a) to about 3 × 10–6 K−1 for Al1.4Fe0.6Mo3O12 from 593 to 1023 K (Ari et al., 2008). For a thorough table of linear CTEs for the A2M3O12 family, the reader is directed to another recent review (Liu H. et al., 2021).
Hygroscopic behavior in A2M3O12 materials can lead to material degradation, and can suppress NTE/NZTE. Furthermore, it has been reported that Y2Mo3O12 partially amorphizes in air at temperatures below 403 K due to its hygroscopic behavior (Marinkovic et al., 2005). Hygroscopicity also was confirmed in all other tungstates and molybdates of the heavy rare earths from Lu to Ho (Wu et al., 2007b; Xiao et al., 2008a; Wu et al., 2009b; Wu et al., 2012; Wu et al., 2016). On the other hand, tungstates and molybdates of non-rare-earth A3+ cations, which have smaller cationic radii, are not hygroscopic (Muller et al., 2019). The channels are the key structural feature permitting entrance and accommodation of water molecules in the interior of the open orthorhombic Sc2W3O12-type structure. These empty one-dimensional spaces are aligned along the c-axis directions (Figure 1). Their diameters are controlled by the size of A3+, and therefore smaller cations form narrow channels, which can inhibit uptake of water.
Another possible explanation why tungstates and molybdates of smaller trivalent cations are not hygroscopic has been presented based on a first-principles study (Wu et al., 2016): the chemical interactions between water molecules and the crystal framework in the tungstate and molybdates of smaller A3+ are weaker and lead to lower absorption energies. Therefore, these phases are resistant to humidity. Water molecules likely interact with the framework through hydrogen bonding and it has been proposed that the oxygen atoms from water molecules intact with A3+ or M6+, while hydrogen atoms from water molecules interact with the framework 2-fold oxygens (Wu et al., 2016). These interactions between water molecules and the framework can cause amorphization in molybdates and tungstates (Marinkovic et al., 2005; Yu et al., 2008; Li et al., 2012) or even change the crystal symmetry in some tungstates (Kol’tsova, 2001; Sleight, 2003; Cao et al., 2016; Pontón et al., 2017; Machado et al., 2021). Symmetry lowering by transformation to the monoclinic phase, or the presence of water molecules in channels, will inhibit, or attenuate, the asymmetrical framework librations of the quasi-rigid polyhedra, due to freezing of polyhedra rocking motions or due to steric effects, respectively. A similar feature has been reported for some zeolites, such as ZSM-5 (Marinkovic et al., 2004; Marinkovic et al., 2008b). Although zeolites neither amorphize in the hygroscopic form nor change symmetry, their NTE is inhibited unless totally dehydrated, proving that water molecules, or any other atom/molecule which occupies void spaces in the deficient garnet structure, will inhibit NTE (Marinkovic et al., 2004; Marinkovic et al., 2008b).
It is important to distinguish between hygroscopicity in molybdates and tungstates. Molybdates become amorphous when hygroscopic and lose water at temperatures higher than 403 K (Sumithra and Umarji, 2004; Sumithra and Umarji, 2006). Tungstates, on the other hand, lose water more easily, at temperatures not higher than 373 K and do not necessary become amorphous (Yu et al., 2008; Muller et al., 2019; Machado et al., 2021). It has been proposed that differences in hygroscopicity between tungstates and molybdates are due to lower absorption energies of water molecules into the crystal framework in tungstates (Wu et al., 2016).
There are two main ways to reduce or inhibit hygroscopicity in tungstates and molybdates. One is to partially substitute larger A3+ for smaller cations, such as in the cases of Er2-xFexMo3O12 and Yb2-xGaxW3O12 (Cheng et al., 2007; Machado et al., 2021). Suppression of hygroscopic behavior also has been achieved by coating the hygroscopic A2M3O12 material with a hydrophobic material, such as C3N4 (Liu et al., 2017).
The orthorhombic to monoclinic phase transformation is another property of great importance for practical applications of A2M3O12 materials. It appears, however, that the temperatures of this phase transition vary widely within the A2M3O12 family, for example 785 K for Fe2Mo2O12 and 178 K for Sc2Mo3O12 (Evans and Mary, 2000; Ari et al., 2008). For a thorough table of phase transition temperatures, see another recent review (Liu H. et al., 2021).
Interestingly, the phase transition has not been detected for a few A2M3O12 materials; for example, for Y2Mo3O12 and Y2W3O12 it has not been detected at temperatures as low as 2 and 10 K, respectively (Forster and Sleight, 1999; Marinkovic et al., 2009), suggesting that the monoclinic form is not stable under ambient pressure. Note that at higher pressures and ambient temperature, Y2Mo3O12 transforms to a lower-symmetry structure, likely the monoclinic phase (Torres Dias et al., 2013).
The main question, however, is which feature or features govern the temperature of the orthorhombic-to-monoclinic phase transition. This information could be important to control the transition temperature and especially to suppress the monoclinic phase stability range to below room temperature, allowing broader use of the special CTE properties of the orthorhombic phase. Based on five different molybdates, an electronegativity rule which linearly correlates the electronegativity of the trivalent cations with the temperature of phase transition has been proposed (Sleight and Brixner, 1973). Higher electronegativities of the trivalent cations lead to higher phase transition temperatures.
The physics behind the proposed rule is relatively simple. More electronegative trivalent cations, such as Fe [1.83; electronegativities here on the Allred scale (Allred, 1961)] and Cr (1.66), would diminish the effective oxygen anion charge far from the nominal value of −2, much more than, for example, Y (1.22) or Sc (1.36). Since oxygen anions, with reduced effective valences, would then be able to interact with each other through induced dipole secondary interactions (Figure 5), low-energy phonons would be frozen and the higher-density monoclinic form would be stable up to higher temperatures. It is worth noting that similar oxygen−oxygen interactions are responsible for the existence of molecular oxides, such as OsO4 and RuO4 (Evans et al., 1997; Pley and Wickleder, 2005).
Most of the A2M3O12 materials and their solid solutions, such as Al2-xFexMo3O12, Al2-xCrxMo3O12 and Cr2-xFexMo3O12 (Ari et al., 2008), to mention just a few, closely obey the electronegativity rule (Figure 10). However, there are some exceptions, such as AlScMo3O12 (Truitt et al., 2015) and some materials in the Al2-xInxW3O12 (x = 0.2; 0.4 and 0.7) family (Cerón Cortés et al., 2021). Since Al2Mo3O12 and Sc2Mo3O12 have phase transitions at 473 and 178 K, respectively, it would be expected that the phase transition in AlScMo3O12 might occur at around 340 K, but it does not occur at all, at least not above 100 K (Truitt et al., 2015). It is still not clear why this phase does not follow the electronegativity rule, although it has been suggested that the great difference between cationic radii for Al [r(VI) = 0.54 Å] and Sc [r(VI) = 0.75 Å] might contribute in some manner to this deviation (Truitt et al., 2015).
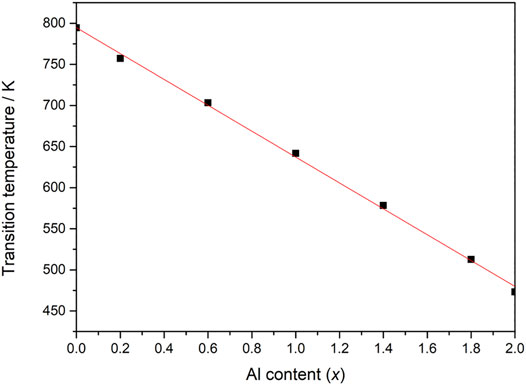
FIGURE 10. Temperature of monoclinic-to-orthorhombic phase transition in Fe2-xAlxMo3O12 as a function of Al content (x) (styled from data in Ari et al., 2008).
The reports on the existence of the orthorhombic structure of Fe1.5Y0.5Mo3O12 down to 103 K (Li et al., 2011) and AlInW3O12 at room temperature (Mary and Sleight, 1999) are still under debate (Truitt et al., 2015).
Thermoelasticity (i.e., how a material’s elastic properties and stress/strain state change with temperature) is inherently connected to thermal expansion and therefore to NTE and NZTE. A theoretical background is presented here, in order to expose a deeper understanding of this important property, starting with the CTE−elastic connection from Grüneisen’s definition of the thermal expansion for a cubic or isotropic solid as:
where Ce is the volumetric heat capacity at constant strain, K is the bulk modulus, and γ is the Grüneisen parameter (Grüneisen, 1912). (Note that the Grüneisen parameter presented in Equation 1, γn, is for a given vibrational mode n, whereas γ of Equation 3 is for the overall lattice. The connection between the mode Grüneisen parameters γn and the bulk Grüneisen parameter γ is made through the quasiharmonic approximation.) Dimensional analysis reveals that Ceγ has SI units of J m−3 K−1 = Pa K−1, and therefore the numerator of Equation 3 represents a thermal pressure, arising from vibrational anharmonicity, which acts against the bulk modulus to cause thermal expansion. Therefore, in general, stiffer materials will have smaller magnitudes of the thermal expansion coefficient.
The general connection between stiffness and elasticity was investigated early on by Barker, who found that for a broad range of metals, alloys, polymers, and polymer-matrix composites, there is a general relationship between linear thermal expansion, αℓ, and Young’s modulus (Y) at room temperature following Yαℓ2≈ 15 Pa K−2 (Barker, 1963). Within Barker’s sample of conventional materials, those with low CTEs (αℓ < 10–6 K−1) have γ ≈ 1, those with intermediate CTEs (10–6 K−1 < αℓ < 10–5 K−1) have γ ≈ 2, and those with the largest CTEs (αℓ > 10–5 K−1) somewhat surprisingly have the smallest Grüneisen parameters (γ < 1), because they are polymers with many vibrational degrees of freedom that involve stiff C–C bonds (Barker, 1963). Therefore, for conventional materials, differences in thermal expansivity can largely be explained by differences in stiffness rather than differences in vibrational anharmonicity.
Of course, network solids such as amorphous SiO2 and many thermomiotic materials do not follow this simple relationship, but stiffness and the magnitude of NTE can still be expected to be inversely related. A direct reduction of the bulk modulus by entropic elasticity (i.e., an increase in entropy upon compressive strain) has been found in floppy networks, including ScF3 (Tkachenko and Zaliznyak, 2021), indicating an underlying mechanism that reduces the bulk modulus in flexible frameworks. This relationship is not absolute (e.g., α-ZrW2O8 is stiffer than the thermomiotic A2M3O12 oxides and has a more negative CTE (Drymiotis et al., 2004; Varga et al., 2006; Romao et al., 2016; Young et al., 2018)), because the Grüneisen parameters of thermomiotic materials vary considerably, and because of the effects of anisotropy, which require further discussion.
The relationship expressed in Equation 3 applies only to materials with isotropic thermal expansion. In anisotropic materials, there are distinct Grüneisen parameters for each independent element of the CTE tensor, each of which is related to the elastic properties of that axis. In the limit of zero external pressure, directional thermal expansion can be related to directional Grüneisen parameters (γii) and directional Young’s moduli (Yii) through:
by defining the corresponding directional mode Grüneisen parameters of mode n (γii,n) in relation to uniaxial stress (σ) perturbations along direction i (Romao, 2017):
Therefore, the coefficient of thermal expansion in an arbitrary direction is inversely proportional to the elastic stiffness in that direction. The definition of the directional Grüneisen parameters given in Equation 5 is simpler than the form given in Barron and Munn (1967) which is based on uniaxial strain perturbations; the definition given by Equation 5 (Romao, 2017) has the significant advantage that the thermal expansion along each axis is related to a single Grüneisen parameter, allowing identification of the modes which lead to anomalous thermal expansion even in anisotropic materials (Dolabdjian et al., 2018; Romao, 2019). Many thermomiotic materials have flexible structures, i.e., they have a mixture of stiff and compliant directions.
Application of Equation 4 along with the constraints of crystallographic symmetry on the thermal expansion and elastic tensors allows understanding of how anisotropic elasticity and thermal expansion are connected, as maxima and minima in the CTE tensor lie in directions corresponding to stiffness minima, as shown in Figure 11 (Romao, 2017). Maxima in the stiffness tensor lie near minima in the magnitude of the CTE, which necessarily correspond to nodal planes due to the symmetry of the CTE tensor (for orthotropic systems). The relationship between structural flexibility and anisotropic thermal expansion even allows mechanisms of bending to be deduced from structural changes upon heating (Rather and Saha, 2021).
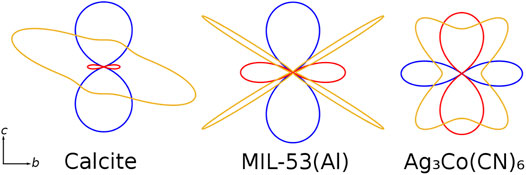
FIGURE 11. Indicatrices of directional thermal expansion (positive: blue; negative: red) and Young’s modulus (orange) for three materials with axial NTE (Rao et al., 1968; Ramachandran and Srinivasan, 1972; Goodwin et al., 2008; Ortiz et al., 2012; Fang et al., 2014b; Nanthamathee et al., 2015). Maxima in stiffness correspond to minima in the magnitude of the CTE, following Equation 4; symmetry constraints on the CTE tensor cause these minima to correspond to nodal planes and a mixture of directional PTE and NTE results. Adapted from Romao (2017).
Other connections between NTE and elasticity exist outside of the Grüneisen theory, including the tendency of thermomiotic materials to undergo pressure-induced softening (Fang et al., 2013a; Fang and Dove, 2013b; Fang et al., 2014b; Hester et al., 2016; Wei et al., 2020). For simple solids, the pressure derivative of the bulk modulus can be expressed as follows:
and therefore modes with negative Grüneisen parameters decrease the pressure derivative of the bulk modulus (Hofmeister, 1991). Pressure-induced softening can be seen to arise from simple models of chains of atoms which exhibit the tension effect (Fang et al., 2014a), suggesting that the softening is a consequence of thermomiotic materials’ tendency to undergo buckling of floppy linkages upon the application of both pressure and temperature. The pressure-induced softening reaches values of up to (∂K/∂p)T = −220 in ScF3 (Wei et al., 2020), much larger in magnitude than the value of (∂K/∂p)T ≈ 4 seen in many conventional materials (Hofmeister, 1991). Thermal expansion is also directly connected to the temperature derivatives of the elastic constants, as these depend on the anharmonicity of the interatomic force constants (Rao, 1974). Changes in the elastic constants with temperature can therefore directly affect the CTE (Karunarathne et al., 2021). Other mechanical properties beyond the elastic regime, such as hardness and even creep, can show pronounced temperature-induced softening in NTE materials (Heinen et al., 2018).
These relationships between thermal expansion and elasticity are therefore required to understand the origins of thermal expansion, and are also important for many potential applications of thermomiotic materials, especially those where NTE is used to compensate for PTE. In such applications, the mechanical interactions between the PTE and NTE components, which reduce the overall thermal strain, lead to thermal stresses in both components (Holzer and Dunand, 1999; Jakubinek et al., 2010; Miller et al., 2010; Zhou et al., 2017). The magnitudes of these thermal stresses, and, in fact, the thermal strains (and therefore the amount of NTE component required to achieve a desired degree of thermal expansion reduction) all depend on the elastic and thermomechanical properties of the components. The thermal stresses are a necessary consequence of the CTE mismatch, and are proportional both to the difference in CTE and to material stiffness (Kreher, 1990).
In a randomly mixed composite material, the interactions between the components can result in different behavior ranging from the rule of mixtures (ROM), where the bulk CTE is an average of the components (White, 2019), and that described by the Turner model, where the bulk CTE is an average of the components weighted by their bulk moduli (Schapery, 1968). These two behaviors refer to two different types of stress distribution in the composite: in the ROM case the stresses are fully isochoric and in the Turner model case the stresses are fully volumetric. Therefore, in the usual intermediate case, the ability of a thermomiotic material to compensate for PTE will depend on its stiffness. This effect is seen experimentally in cases where large amounts of relatively compliant NTE filler are required (Sharma et al., 2012; Shi et al., 2016) and offers an argument in favour of using, for example, non-vibrational thermomiotic materials in composites for applications which only require a relatively narrow temperature range of use (Takenaka and Ichigo, 2014), due to their higher bulk moduli (Nakamura et al., 2009), or other non-conventional thermomiotic materials such as carbon nanotubes (Shirasu et al., 2017). The properties of microstructured (e.g., lamellar) composites do not necessarily fall between the ROM and Turner limits (Lim, 2011), and therefore their design offers another route to control thermal expansion. It has even been demonstrated that the combination of two materials with different CTEs and void space in a structured fashion can generate metamaterials with arbitrary CTEs, although stiffness consequently falls off at the CTE extremes (Sigmund and Torquato, 1997; Wang et al., 2016; Qu et al., 2017). Another possibility is the creation of composite materials whose dimensions and elastic properties are constant over some temperature range (Keuter et al., 2020).
The ability of thermomiotic materials to counteract PTE is also affected by the fact that vibrational NTE is related to proximity to dynamic instability, and therefore pressure-induced phase transitions are common (Occhialini et al., 2018). These phase transitions can cause significant reductions in volume and the magnitude of the CTE, and therefore, in combination with the pressure-induced softening described above, present a significant challenge to the use of materials which exhibit vibrational NTE in composites (Holzer and Dunand, 1999; Zhou et al., 2017), especially those using stiff PTE components. Interestingly, a stiff matrix might be able to stabilize an intermediate state during a pressure-induced phase transition, wherein the filler undergoes constrained collapse and therefore has negative stiffness (Romao and White, 2016). This intermediate state would therefore be unable to effectively counteract PTE, but its negative stiffness could be useful in the design of novel metamaterials (Kochmann and Bertoldi, 2017).
Thermal stress also influences the properties of single-phase materials when they are polycrystalline and anisotropic. This stress arises from CTE mismatch between grains, which can be severe enough to reach GPa levels of stress (Romao et al., 2016), leading to microcracking, decreased material strength and decreased thermal shock resistance (Prisco et al., 2013; Prisco et al., 2019). These issues can be ameliorated by achieving a high degree of consolidation and small crystallite size (see Section 6). The CTE mismatch within polycrystals can cause their bulk CTEs to differ from those of the corresponding powder, not only because of microcracking and microcrack healing effects which are observable in dilatometry (Prisco et al., 2013) but also because elastic anisotropy leads to the CTEs of the stiffer axes having a larger impact on the bulk CTE (Kreher, 1996). This effect can lead to relatively large discrepancies in CTE for materials with volumetric CTEs close to zero (up to several 10–6 K−1 in the A2M3O12 family) (Romao et al., 2016). An extreme example of this phenomenon is found in CaRuO4−y polycrystals, where CTE anisotropy, elastic anisotropy, and the presence of voids combine to increase the bulk NTE nearly sevenfold over that of the corresponding powder (Takenaka et al., 2017; Takezawa et al., 2018).
The elastic properties of A2M3O12 materials are known to vary significantly with composition and therefore with their CTEs, with the magnitude of NTE being negatively correlated with stiffness (Varga et al., 2005; Romao et al., 2016). As shown in Figure 12, NTE is also correlated with elastic anisotropy; local stiffness maxima coincide with the [011] and [100] directions (in Pbcn or P21nb settings) (Romao et al., 2016). A2M3O12 materials are also prone to pressure-induced phase transitions and/or amorphization (Secco et al., 2001; Karmakar et al., 2004; Varga et al., 2005), although these instabilities often require pressures on the order of 1 GPa and therefore lie well beyond the expected compressive strengths of these materials. The use of A2M3O12 materials as thermomiotic components in applications therefore depends on finding methods to compensate for their relatively low stiffnesses and the generation of thermal stress due to thermal expansion mismatch. These goals can be accomplished by, for example, the use of compliant matrices and processing techniques which enhance material strength, as described in Section 7.4.
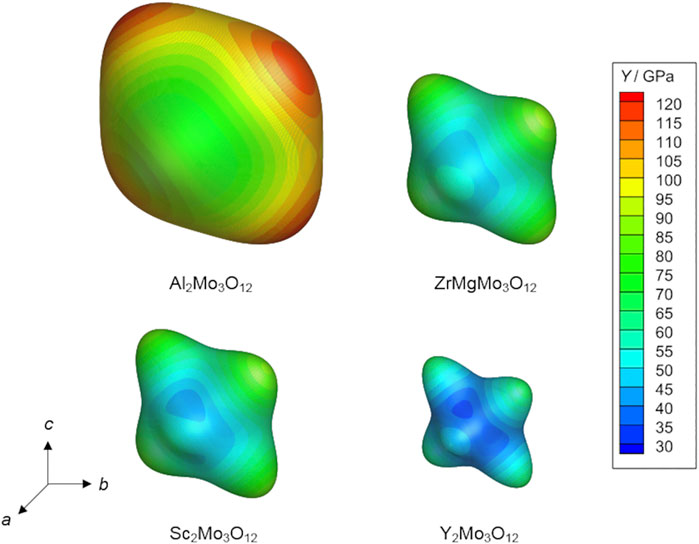
FIGURE 12. Directional Young’s moduli of orthorhombic Al2Mo3O12, ZrMgMo3O12, Sc2Mo3O12, and Y2Mo3O12 (Romao et al., 2014; Romao et al., 2016) in the Pbcn or P21nb setting, shown as contour plots generated using the nanoHUB Anisotropy Calculator – 3D Visualization Toolkit (Zuluaga et al., 2014). Adapted from Romao et al. (2016).
A major aim for NZTE materials is to allow the material to withstand large changes in temperature without fracture. This property can be quantified as the thermal shock resistance coefficient, Rs:
where κ is the thermal conductivity, σ is the material strength and Y is the Young’s modulus (White, 2019), and higher values of Rs indicate greater resilience on thermal shock. Clearly, the closer the absolute value of the CTE is to zero, the greater the thermal shock resistance. However, the thermal conductivity also plays a role, with high values preferable, as they reduce temperature gradients within the material and hence lead to high thermal shock resistance.
The thermal conductivity of an insulating solid can be approximated by the Debye model:
where CV is the heat capacity per unit volume, νs is the mean phonon speed (speed of sound) and λ is the phonon mean free path (White, 2019). High thermal conductivity is favoured by stiff materials (high speed of sound) and high purity (long phonon mean free path).
The flexible structures of the “traditional” AB2O8 NTE materials are associated with low-frequency optic modes which can interfere with the heat-carrying acoustic modes, lowering the phonon mean free path and leading to low thermal conductivity, 0.51 W m−1 K−1 at room temperature for Zr2W2O8 (Kennedy and White, 2005) and 0.64 W m−1 K−1 for HfMo2O8 (Kennedy et al., 2007). Furthermore, both Zr2W2O8 and HfMo2O8 exhibit glass-like thermal conductivity, low and decreasing as the temperature drops. Normally the phonon mean free path has a very strong and opposite dependence on temperature, such as 1 nm at T = 300 K and 104 nm at T = 2 K for a rigid inorganic solid (White, 2019), which leads to a peak in the temperature profile of the thermal conductivity for a typical crystalline solid. For Zr2W2O8 and HfMo2O8 the mean free path is very short and less temperature dependent. The main temperature-dependent factor in the thermal conductivity is the heat capacity which falls as T → 0 K, leading to glass-like thermal conductivity (Kennedy and White, 2005; Kennedy et al., 2007).
In the A2M3O12 and related families, thermal conductivities have been reported for HfMgMo3O12 (Miller et al., 2012a), Y2Mo3O12 (Romao et al., 2014) and Al2W3O12 (Prisco et al., 2016b) and again are low with room-temperature values of 1.04, 0.80 and 0.63 W m−1 K−1, respectively. By comparison, oxides developed specifically to have low thermal conductivities and thus to act as thermal barrier coatings, have higher values of κ at room temperature, ranging from ∼1 to ∼3 W m−1 K−1 (Pan et al., 2012). Furthermore, the thermal conductivity for Y2Mo3O12 drops as the temperature goes down, again due to the short phonon mean free path: ∼1 nm at T = 300 K and ∼30 nm at T = 6 K (Romao et al., 2014). HfMgMo3O12 behaves similarly (Miller et al., 2012a). However, despite the low thermal conductivity, the thermal shock resistance of Al2W3O12 has been shown to be as high as for sapphire (Prisco et al., 2016b), the state-of-the-art material for thermal-shock resistant infrared windows, largely due to the relatively low magnitude of the CTE (even though not as low as some A2M3O12 compounds) and the low Young’s modulus due to the flexible lattice, which both mitigate against the low thermal conductivity.
Typically, ceramics in the A2M3O12 and related families are electrical insulators. A theoretical investigation of Y2Mo3O12 showed an indirect band gap of 3.6 eV at T = 0 K (Romao et al., 2014).
However, high ionic conductivity has been observed in some compounds in this family, including 2.5 × 10–2 Ω−1 m−1 for MgHfW3O12 at 600°C (Omote et al., 2011) and 4.1 × 10–4 Ω−1 m−1 for ZrMgMo3O12 at 520°C (Romao et al., 2015b). The ionic conductivity mechanism is likely due to motion of the Mg2+ ions, which are arranged alternately with the Hf/Zr ions along the (010) direction, as they move with low activation energies of ca. 80 kJ mol−1 through cavities provided by the AO6 and MO4 polyhedra (Omote et al., 2011; Romao et al., 2015b). With the potential for low thermal expansion combined with high electrical conductivity, such materials could have applications in the field of solid electrolytes and electrode materials for batteries (Andersen et al., 2018).
The A2M3O12 and related ceramics exhibit interesting optical properties, stemming both from the intrinsic ceramics, and also via doping. The flexibility of choice of A and M again is an asset. The low magnitude CTE is a special attribute for several optical properties, allowing both dimensional stability with changing temperature and also temperature-independent interatomic distances and correspondingly stable optical properties over a wide temperature range. The ability to prepare some of the structures from the melt is an advantage over ceramics that have competing high-temperature phases.
An important optical property was reported in early studies of A2M3O12 ceramics, namely very high optical transparency, over wavelengths from 350 to 4500 nm, of single crystals pulled from the melt, for Sc2W3O12 and Gd2Mo3O12, with the latter showing close to 100% transparency (Nassau et al., 1965). The low CTE combined with high transparency in the visible-to-infrared range makes these oxides promising for optical applications, including as hosts for rare earth ions due to lack of interference from intrinsic effects. (See also Section 8.)
Another early work (Borchardt, 1963b) on the rare-earth (from Sc to Lu) tungstates in the A2M3O12 family reported optical properties with special interest in their luminescence. While most of the tungstates were white powders, most also exhibited luminescence through a broad band within the white light spectra, peaking between 475 and 500 nm. The luminescence mechanism was attributed to W6+, while in some cases, such as Eu2W3O12 and Tb2W3O12, narrower emissions were found and attributed to rare-earth emission following energy transfer from W6+. For example, in the case of Eu2W3O12 and Tb2W3O12, the W6+ ion acted as sensitizer (Borchardt, 1963b).
Further early luminescence studies were carried out for Al2W3O12, Sc2W3O12 and Lu2W3O12, both undoped and doped with Eu3+ or Cr3+ (Blasse and Ouwerkerk, 1980). The undoped compounds did not luminesce at room temperature, but blue-green emission under UV excitation was observed at lower temperatures, increasing with decrease in temperature to 4 K. Eu3+-doped samples showed a medium-intensity red emission at room temperature, and doping with Cr3+ resulted in a deep red/infrared emission. As noted elsewhere, Sc2W3O12 and Lu2W3O12 are highly hygroscopic, but the Eu3+ emission can be used to quantify the moisture content (Blasse and Ouwerkerk, 1980).
Also in the 1980s, the use of Al2W3O12 as the host for Cr3+ for solid-state high-gain laser applications was shown (Petermann and Mitzscherlich, 1987). Laser action was observed at 800 nm.
In more recent work, HfScW2PO12 has been shown to have intense blue photoluminescence from room temperature to 10 K (Cheng et al., 2017). The authors conclude that this ceramic could have potential applications as a near-UV LED-convertible blue-emitting phosphor for white LEDs. The low magnitude CTE (1.3 × 10–6 K−1) over the temperature range 140–1469 K leads to good thermal stability in the photoluminescence (Cheng et al., 2017), which would be an asset for optical applications. (See also Section 8).
Investigations of ZrxAl2-xMo3-xVxO12 have shown broad band luminescence from 370 to 650 nm, i.e., across almost the entire visible spectrum, becoming most intense at x = 0.5 (Wang et al., 2021). The luminescence was ascribed to the Zr4+ (replacing Al3+) and V5+ (replacing Mo6+) ions, which introduce donor and acceptor levels in the band gap. The structure has four formula units, allowing for multiple distinct pairs of donor (centre of octahedron) and acceptor (centre of tetrahedron) sites, with different donor-acceptor spacings and therefore different fluorescence bands, giving a total luminescence band that covers most of the visible range. For x = 0.5, the monoclinic to orthorhombic transition was at ca. 420 K, and the CTE was 2.53 × 10–6 K−1 over the temperature range 420–773 K. The low CTE and the essentially white luminescence show considerable potential for LEDs and other optoelectronic devices (Wang et al., 2021). See also Section 8.
The A2M3O12 and related ceramic families have aroused the interest of researchers mainly due to their chemical flexibility, and the possibility of obtaining negative thermal expansion and near-zero thermal expansion. Consolidation and sintering processes play a critical role in determination of the final properties of monolithic (bulk) ceramic materials. To obtain a ceramic with high thermal shock resistance, for instance, it is necessary to have a high-density microstructure, with mean grain sizes smaller than the critical size for crack formation (Prisco et al., 2016b). Optical transparency also requires ceramics with small grain and pore sizes and low porosity. These features can be only reached through careful consolidation and sintering stages. The current best approaches to consolidation and sintering of A2M3O12 and related ceramic families and current understanding of related properties are reviewed in this section.
In a study from 2012, Al0.5Sc1.5W3O12 powder was synthesized by the low-combustion-temperature method (Dasgupta et al., 2012). The as-prepared powder was suspended in n-butanol to form a slurry with 70 mass% solid in the load, aiming to fabricate slip-cast compacts. To stabilize the slurry, a phosphate ester dispersant was used, and 9 mass% polyethylene glycol (PEG) was added as a binder to enhance the strength of the compacts. To obtain an agglomerate-free powder, the suspension (slurry) was planetary milled for 3 h at 300 rpm using 5 mm diameter stabilized zirconia as the grinding medium. According to the authors, reduction of the powder agglomeration did not significantly influence its specific surface area. However, the milling process allowed the powder to pack more efficiently, which led to green bodies with higher densities. The slurry was cast into plaster molds and, after drying, conventional sintering was carried out in air at 1373 K for 3 h, followed by hot isostatic pressing (HIP) for 2 h at 1373 K and 100 MPa in an 80% Ar/20% O2 atmosphere. The conventionally sintered compacts revealed a density of 97% of the theoretical density (TD), while after HIPing the compacts reached very high bulk density of 99.5% TD, with grain sizes between 2 and 3 µm. The investigators also determined linear CTE from high temperature XRPD (−0.32 × 10–6 K−1 from 303 to 873 K) and by dilatometry measurements (−0.15 × 10–6 K−1 from 298 to 973 K). The difference between the two CTEs, intrinsic and extrinsic, respectively, was attributed to the presence of microcracks (see also Section 3.1). The authors also evaluated infrared optical properties of the bulk ceramic after HIPing, on a 1.03 mm thick disk. The sample showed an in-line transmittance of 64–73% within the 3–5 µm mid-IR wavelength range. The theoretical maximum reflection-limited transmission for the studied phase was about 86–88% near 2500 cm−1 (4.0 μm). The peak transmittance of 73% at 2300 cm−1 (4.3 μm) represents an optical loss of about 14%. This optical loss was attributed to optical scatter at grain boundaries and pores. Therefore, the authors achieved an excellent combination of near-zero CTE and high IR transmittance, two important properties for some high thermal shock resistance applications (Dasgupta et al., 2012).
In another study (Prisco et al., 2013), Al2Mo3O12 powder in its orthorhombic form, stable at T > 473 K, was used to investigate the influence of mean grain size on the linear coefficient of thermal expansion, as evaluated by dilatometry. The grain size investigation was motivated by knowledge that microcrack formation occurs when the grain sizes of ceramic body exceed a certain critical size, giving rise to a discrepancy between the intrinsic and extrinsic CTE. Nanometric and micrometric powders of Al2Mo3O12 were used to produce monolithic ceramics. Both powders were pressed at 1 GPa for 1 min to form green bodies. Sintering was performed at 1063 K over 24 h, and this procedure resulted in cylindrical bulk samples with low densities, 54.8% TD and 82.3% TD for the nanometric and micrometric powder, respectively. The sample prepared from the nanometric powder showed (Prisco et al., 2013) a bulk linear CTE (0.9 × 10–6 K−1 from 473 to 973 K) closer to the intrinsic CTE (2.4 × 10–6 K−1 between 523 K and 973) than for the sample prepared from the micrometric powder (−2.2 × 10–6 K−1 in the range from 473 to 923 K). The two samples presented completely different microstructures. The one from nanometric powders was very porous and had crystals of ca. 100 nm diameter, whereas the one from micrometric powders had crystals larger than 5 µm and presented intergranular and transgranular microcracks. The larger grains exceeded the critical size required to inhibit severe microcracking on cooling of Al2Mo3O12, and resulted in a linear CTE rather different (opposite sign) from the intrinsic one, underlining the importance of microstructure especially in these low CTE materials (Prisco et al., 2013).
A study of Al2W3O12 with different porosities showed the influence of porosity on Young’s modulus and hardness (Jardim et al., 2016), and this investigation provides further information concerning consolidation in the A2M3O12 family. Green bodies were prepared by uniaxially pressing Al2W3O12 powder at 177 MPa into cylinders without adding binder agents. Ranges of times and temperatures for conventional sintering were investigated for their influence on properties: 1123 K for 10 min, 1.5, 3, 6, 12, 24 or 48 h, or 1173 K for 1.5, 3 and 12 h, or 1273 K for 3, 4 or 12 h. The uniaxially pressed green compacts had a relative density of 67% TD. After 12 h of sintering, densities of 80%, 87 and 89% TD were obtained for sintering at 1123, 1173 and 1273 K, respectively. The grain size distribution of the initial Al2W3O12 powder was bimodal. The smaller grain sizes had diameters ranging from 100 to 200 nm, while the larger ones were plate-like and had thickness ranging from 300 to 700 nm and lengths varying from 1 to 5 µm. The body sintered at 1123 K maintained this feature, even after 24 h of sintering. The porosities of these samples ranged from 10 to 25%. In addition, except for the samples sintered at 1273 K, the relative densities increased with sintering time, while the 1273 K/12 h sintered body actually showed a decrease in density, attributed to pore formation due to incipient sublimation of WO3. A linear function was used to describe the variation of Young’s modulus with porosity, extrapolating to a Young’s modulus of 70 GPa at zero porosity, which is low, as expected for ceramic materials from the A2M3O12 family due to the flexibility of the framework structure. No clear dependence of CTE on porosity was found (Jardim et al., 2016).
In another study of Al2W3O12 (Prisco et al., 2016b), monolithic ceramics were prepared by mixing Al2W3O12 nanopowder with 1 mass% PEG and 1 mass% polyvinyl alcohol (PVA) as binders, while small amounts of distilled water were added until tacky. This mixture then was uniaxially pressed at 250 MPa for 3 min, resulting in green bodies with high relative densities, ∼ 73% TD. These samples were then sintered in a conventional pressureless manner for 10 h at 1273 K, resulting in sintered specimens of 91% TD. However, the sample was inhomogeneous, with some regions showing greater porosities and others exhibiting higher densities. The inhomogeneity was attributed to the strongly agglomerated starting powder. The more porous regions could be a consequence of inter-agglomerated porosity which requires higher sintering temperatures, or longer times, to lead to denser products. Furthermore, the overall microstructure was coarse, with grain sizes generally larger than 5 µm. This coarse-grained microstructure was accompanied by long intergranular and transgranular microcracks, as the critical grain size was exceeded. Such a coarse-grained microstructure leads to a reduction of mechanical strength.
In a study of highly consolidated (96% TD), single-phase orthorhombic Al2W3O12 the influences of two different sintering approaches on the microstructure and mechanical properties were investigated (Prisco et al., 2019). One approach was pressureless three-stage sintering (3SS), while the second was spark plasma sintering (SPS), a rapid consolidation method generally carried out at significantly lower temperatures than those usually applied in conventional sintering.
The 3SS is a method extended from the two-stage sintering method (Lin et al., 1997; Chen and Wang, 2000), proposed to suppress the rapid grain growth which accompanies the final stage of conventional sintering when the maximum densification is reached. This suppression is thought to be attained by exploiting the difference between the kinetics of grain boundary diffusion associated with densification (sintering) and the kinetics of grain boundary migration, associated with grain growth within a metastable microstructure (Chen and Wang, 2000). In the two-stage sintering carried out by Chen and Wang, the sample was heated to a high temperature to reach an intermediate density in a brief first stage and then cooled and kept at a lower temperature until it became nearly fully dense. Under these circumstances, sintering would not result in excessive grain growth, yet the densities would be high.
Another two-step sintering approach also had been proposed (Lin et al., 1997): a coarsening step at a lower temperature, before a densification step. In the coarsening step there is very little densification. This initial coarsening stage is responsible for improving of microstructural homogeneity prior to a subsequent sintering stage to avoid anomalous grain growth.
By joining these two approaches, 3SS was proposed to achieve sintered bodies with a more uniform microstructure, reduced grain growth and higher densities (Prisco et al., 2019). To prepare the green bodies, powdered orthorhombic Al2W3O12 was mixed with 3 mass% of PEG as binder and then uniaxially pressed at 250 MPa for 1 min, followed by isostatic pressing at 350 MPa for 2 min at room temperature (Prisco et al., 2019). The green bodies presented 58% TD. Three-stage sintering was carried out in air as shown schematically in Figure 13. The temperatures used for each stage were chosen based on the dilatometric curves of the as-prepared green bodies. The duration of the three stages, at 1173, 1348 and 1223 K, were 6, 1 and 6 h, respectively, and all ramps were 20 K min−1.
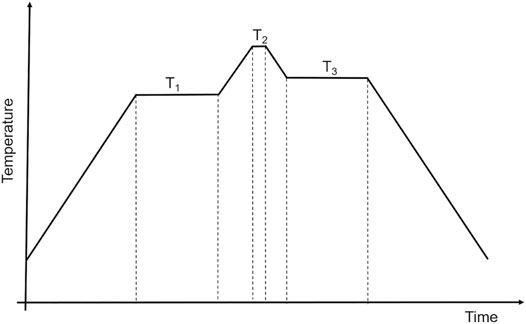
FIGURE 13. Schematic representation of the three-stage sintering (3SS) approach for consolidation of Al2W3O12 (Prisco et al., 2019).
In addition to 3SS, spark plasma sintering of orthorhombic Al2W3O12 was performed in vacuum, under 50 MPa of uniaxial pressure and at a temperature of 1273 K for 2 or 10 min. The heating ramp was 100 K min −1 (Prisco et al., 2019).
The microstructures, formed by 3SS and SPS, were quite different, although both sintered bodies showed 96% TD. The microstructure deriving from 3SS was homogeneous, with an average grain size of nearly 2 µm. The pellets obtained by spark plasma sintering were composed of nanometric grains, with grain size distribution in the same range as the starting powder particles (50–200 nm), indicating that only minor grain growth occurred during this sintering process (Prisco et al., 2019).
The mechanical properties of sintered bodies prepared by 3SS showed the same linear dependence on porosity encountered for conventionally sintered materials (Jardim et al., 2016). The average Young’s modulus was 62 GPa for 3SS bodies, while the Young’s moduli of compacts obtained from SPS were as high as 89 GPa (2 min) and 91 GPa (10 min), i.e., about 50% greater than those found for 3SS samples (Prisco et al., 2019), illustrating the significant beneficial impact of nanometric-grained microstructure on mechanical properties. The same conclusion was reached by comparing hardness which was improved from ∼500 VHN for 3SS to ∼800 VHN measured for SPS, where VHN is Vicker’s harness number (Prisco et al., 2019).
The influence of sintering on the microstructure and properties of ZrMgMo3O12 also has been investigated (Yang C. et al., 2019). ZrMgMo3O12 powder was first uniaxially pressed at ∼10 MPa for 3 min, then sintered in air for 5 h at 973 K. The microstructure obtained was not uniform, so, to improve the density and the uniformity of the ZrMgMo3O12 microstructure, the samples were sintered a second time, at 973 K for an additional 5, 24 or 72 h. The second sintering stage caused grain growth and increased the density of ZrMgMo3O12, and the densities increased with longer sintering times. This second sintering proved to be beneficial to eliminate internal porosity and to attain a more uniform grain size distribution. The hardness of samples increased as the duration of the second sintering increased, from 95 to 205 VHN, since the ceramics became denser and the hardness has an inverse relationship with porosity (Yang J. et al., 2019).
Furthermore, the CTE of ZrMgMo3O12 decreased as the duration of second sintering step was increased. The CTE after first sintering was 0.21 × 10–6 K−1, while after a second sintering stage of 5, 24 or 72 h the CTE decreased to 0.15 × 10–6, 0.10 × 10–6 and 0.04 × 10–6 K−1, respectively, as the second sintering led to a denser and more homogeneous microstructure (Yang C. et al., 2019).
The influence of different ball milling times (2, 12, 24, 48, 72 and 96 h) on Zr2WP2O12 powders and also on some physical properties of the sintered bodies has been reported (Shi et al., 2020). The milled powders were uniaxially cold pressed at 30 MPa and the green bodies were conventionally sintered for 4 h at temperatures as high as 1573 K. It was hypothesized that with increasing milling time, the powder mean particle size would diminish and the powder would become less agglomerated, leading to denser Zr2WP2O12 ceramics.
Indeed, the lowest density obtained after sintering was 81.5% TD for the powder milled for 2 h, and when the milling time was extended to 96 h, 95.4% TD was reached. The microstructures of ceramics obtained from powder milled for 2 h had larger grains and a higher proportion of pores, while those obtained from the powder milled for 96 h had a reduction in grain size, allowing for further densification (Shi et al., 2020).
The samples sintered from the powders milled for longer times had more negative values of the CTE: −2.6 × 10–6 K−1 (2 h) compared with −3.9 × 10–6 K−1 (96 h).
The hardness of samples increased as the samples became denser and had finer microstructure, ranging from approximately 90 HVN (at 81.5% TD) to 180 HVN (at 95.4% TD). In general terms, for a given material, higher density will lead to higher hardness (Shi et al., 2020).
Another study of Zr2WP2O12 examined the influence of added MgO as a sintering additive since Zr2WP2O12 powder has low sinterability (Isobe et al., 2009). The powder was mixed with MgO in the composition ranging from 0 to 0.5 mass%. Green bodies were prepared by pressing the Zr2WP2O12 powder at 50 MPa for 3 min and sintered at 1473 K for 4 h. The density of sintered body without the addition of MgO was ca. 60% TD, and the samples showed spherical grains and no densification. Samples that had additions of <0.1 mass% MgO presented similar densities to those with no addition of MgO. However, the addition of 0.5 mass% MgO gave rise to significant densification (95% TD). These samples had no large pores and a mean grain size of the samples of ∼1 μm, with a narrow grain size distribution (Isobe et al., 2009).
The same authors evaluated the extrinsic CTE of Zr2WP2O12 ceramics with 0.5 mass% MgO and found a value of - 3.4 × 10–6 K−1 from 303 to 873 K, which is close to the intrinsic CTE of Zr2WP2O12 without MgO addition as determined from diffraction data, −3 × 10–6 K−1 from ca. 40–470 K from a previous study (Evans et al., 1997). Mechanical properties were also measured for the samples with 0.5 mass% MgO: Vicker’s microhardness of 449 VHN, a three-point bend strength of 113 MPa, Young’s modulus of 74 GPa and Poisson ratio of 0.25. The authors concluded that Zr2WP2O12 ceramics can be used in engineering applications and are useful for preparation of materials of near zero thermal expansion (Isobe et al., 2009).
Another study (Shang et al., 2013) investigated the influence of MgO and PVA additives on the densities of Zr2WP2O12 ceramics. Zr2WP2O12 powder was cold pressed into cylinders with a uniaxial pressure of 390 MPa. The resulting pellets were sintered at 1473 K or 1573 K for 60, 120 or 180 min, and the densities obtained were ca. 73–76% TD. Rather than trying to enhance the density through increasing the sintering time or temperature, the authors investigated the influence of different quantities of MgO, as follows.
MgO was added to the Zr2WP2O12 powder at 0.5, 0.75, 1.0, 1.5, 2.2 or 2.5 mass%, and then the samples were uniaxially pressed at 390 MPa and sintered at 1573 K. The densities of the samples increased with increasing MgO content up to 1.0 mass% (reaching 92% TD) and then decreased with further MgO content (Shang et al., 2013).
The addition of MgO also influenced the Zr2WP2O12 microstructures (Shang et al., 2013). With no addition of MgO, the samples exhibited grains with petal-like shapes, which led to inefficient packing and high porosity. With the addition of 1 mass% MgO, the grains were smaller, more uniform and approximately spherical. Therefore, MgO led to the inhibition of secondary dendritic growth, allowing the particles to be more densely compacted (Shang et al., 2013).
The authors also examined the influence of re-sintering on the density of Zr2WP2O12. The samples were ground, pressed and sintered at 1573 K for an additional 60 min. Before re-sintering, 1 mass% of MgO and 2 mass% of PVA were added to the powder obtained by grinding of the sample without additives, and 2 mass% of PVA was added to the powder obtained by grinding of the sample with 1 mass% of MgO. Both re-sintered samples had increased densities, 98.6% TD and 99.8% TD, respectively.
However, their microstructures were quite different. The addition of MgO during re-sintering led to irregular, large-sized grains. This microstructure feature was due to the ground powder characteristics from the sample sintered without MgO, as this powder was prepared from a sintered body with large grains. When MgO was added in the first sintering, the grains obtained after re-sintering were even smaller than those seen in the first sintering stage with added MgO. According to the authors (Shang et al., 2013), this microstructure can be attributed to the regular grain size distribution obtained in the first sintering step, before re-sintering.
For conventional sintering, the addition of MgO provided a great increase in density, from 73% TD and 92% TD. Re-sintering resulted in even higher densities, up to 99.8% TD by re-sintering the powder ground from the 92 %TD sample (the powder made with 1 mass% MgO), mixed with 1 mass% of PVA (Shang et al., 2013).
The influence of sintering temperature on density and hardness of Y2W3O12 ceramics has been evaluated (Das et al., 2013). An aspect of this study was the use of two different starting powders, one synthesized by solid-state reaction in which Y2O3 and WO3 were mixed in stoichiometric proportions and the second prepared by milling of the previously synthesized powders in a planetary mill (10 h, with a ball-to-powder ratio of 10:1, milling speed 300 rpm). Both powders were uniaxially pressed at 500 MPa and then sintered at 1073, 1273, and 1473 K for an unspecified time interval.
The relative densities of the samples increased as the sintering temperature increased. However, the relative densities of samples from the milled powder were always higher. The 1073 K sintering resulted in 67.8% TD (as-synthesized powder) and 70.5% TD (milled powder). For 1273 K, the corresponding densities were 71% TD and 91% TD. The difference between the powders is likely due to the finer particles in the milled powder, which could lead to a better packing and hence to a higher densification. When the sintering was performed at the highest temperature, 1473 K, the relative densities were essentially the same for both powders: 95% TD (as-synthesized) and 95.6% (milled) (Das et al., 2013).
The sintered bodies obtained from the as-synthesized Y2W3O12 powder increased in hardness as the sintering temperature was increased. In contrast, the sintered bodies prepared from milled powder showed an increase of hardness between 1073 and 1273 K and then a slight decrease after 1473 K sintering. From 1273 to 1473 K the sintered bodies from as-synthesized powder presented a significant increase in density when compared with the increase of density within the sintered bodies obtained from milled Y2W3O12 powder. The main factor impacting increase of hardness in the ceramic bodies prepared from the as-synthesized powder was the densification, while the decrease in hardness observed for the sintered bodies obtained from the milled powder was due to excessive grain growth (Das et al., 2013). The highest hardness of ∼275 VHN was obtained for the milled powder sintered at 1273 K.
The transmittance of light can be attenuated by scattering, which, in turn, depends on grain size and grain packing in sintered ceramics. To investigate the relationship between microstructure and light scattering, Y2−x(ZnLi)xMo3O12 powders with x in the range 0–1.6 were prepared and pressed at 200 MPa followed by sintering for 5 h at 1073 K (Liu et al., 2019).
Investigation of the different microstructures obtained for the different contents of (ZnLi)3+ in Y2−x(ZnLi)xMo3O12 showed that for x = 0 the grains were spherical and separated from other grains by pores. As the amount of (ZnLi)3+ increased, the grains became larger and presented vertices and edges instead of circular arcs and, concomitantly, the presence of pores decreased. The (ZnLi)3+ content influenced grain shape, not grain size. Theoretically, increasing substitution of Y3+ for (ZnLi)3+ should lead to higher absolute densities, but the observed density was maximal at x = 1.0 (93 %TD) and then decreased at higher x (88% TD at x = 1.8). Laser light scattering was minimal (transmittance maximal) at x = 1.0 and 1.2; at those compositions, the samples exhibited grains that were regular in shape and size with low porosity. Furthermore, the materials were not hygroscopic. Samples with higher concentrations of (ZnLi)3+ presented more pores and consequently exhibited higher light scattering coefficients (Liu et al., 2019).
Consolidation and sintering methods have a great influence on the microstructure of monolithic ceramics and, as a consequence, on their mechanical, thermal, optical and other physical properties. The hurdle to obtaining ceramic bodies with good physical properties is the need to produce monoliths with homogeneous microstructure, with densities as close as possible to theoretical and with small grains, such that the critical grain size for crack propagation is not exceeded.
The features of the starting powder exert great influence on bulk ceramic properties. Powders with nanometric/submicronic particle size, more uniform particle size distribution and low agglomeration lead to more homogeneous microstructures with smaller mean grains and higher densities. In addition to soft-chemical routes for synthesis of the powders with these characteristics, ball-milling can be useful to achieve these goals. An alternative route for sintering of the powders would be 3SS, including a pre-coarsening step which enables improvement of microstructural homogeneity prior to densification.
In general, higher sintering temperatures and longer times promote higher grain growth. Therefore, SPS and HIP sintering methods that require lower temperatures and shorter sintering times to achieve good densification levels with smaller mean grain sizes are more useful since excessive grain growth has a negative influence on mechanical and optical properties of bulk ceramics.
The addition of sintering additives to the starting powder is also beneficial for reaching higher densities. Considering conventional sintering, such additions can promote densification of the ceramic material in shorter time intervals. Therefore, additives also positively influence the microstructure of the bulk ceramic.
Choice of appropriate starting powder along with consolidation/sintering methods and additives are crucial to achieve the desired final properties of the bulk ceramic.
In the past decade, the development of composites exhibiting controlled and reduced thermal expansion has triggered considerable research in several different areas (Lind, 2012; Sharma et al., 2012; Pontón et al., 2019a; Pontón et al., 2019b). A number of different ceramic fillers, including A2M3O12 and related families, have been used with the goal of counteracting the (usual) positive thermal expansion of ceramic, metal and polymer matrices.
However, the utilization of A2M3O12 and related families as composite fillers is constrained by the following factors: 1) phase transitions induced by temperature or pressure; 2) low stiffness; and 3) hygroscopic behavior (Pontón et al., 2018; Madrid et al., 2020). Ceramic fillers in the A2M3O12 family should be used in the temperature range of their orthorhombic phase to appropriately exploit their NTE and NZTE properties. Similarly, the pressure applied during manufacturing processes, especially in the case of ceramic and metal matrices, must not be beyond the stability range of the orthorhombic phase. In addition, because of their low stiffness, it is expected that adding these ceramics would decrease the Young’s modulus of conventional ceramic and metal matrices especially at high filler loadings, although this does not present a problem for more compliant polymer matrices (Pontón et al., 2019b). Lastly, the full release of structural water molecules that are accommodated within the crystal structure of some A2M3O12 phases, such as Y2Mo3O12, Y2W3O12 and Yb2W3O12, is mandatory for the preparation of reliable composites (Machado et al., 2021). In fact, a drying step prior to the composite manufacturing has become a common strategy (Yanase et al., 2009; Zhou et al., 2014; Zhou et al., 2015; Zhou et al., 2017; Pontón et al., 2018; Pontón et al., 2019b; Liu et al., 2020). However, studies of time-dependent water absorption of composites filled with hygroscopic A2M3O12 members should be carried out, particularly for ceramic and polymer matrices which can be sensitive to atmospheric moisture. Glazing of ceramic-based composites could be an alternative to resolve this issue (Sumithra and Umarji, 2005).
Another critical factor which is intrinsic to the synthesis methods of A2M3O12 and related ceramic families, is the degree of agglomeration in the as-synthesized powders. Hard agglomerates can be formed at high temperatures during solid-state reactions, or in the calcination stage of amorphous precursors obtained by co-precipitation and sol-gel routes, provoking necking between adjacent particles (Pontón et al., 2017; Marzano et al., 2019). Such filler agglomerates can act as stress concentrators in the matrix, especially at high filler loadings (Sharma et al., 2012). In addition, highly agglomerated fillers also are difficult to disperse in the matrix, which can then have a deleterious impact on the CTE and the mechanical properties of the composite (Pontón et al., 2019b).
Based on this context, the following sections provide an overview of ceramic-, metal-, and polymer-based composites reinforced with A2M3O12 and related materials. The influence of these thermomiotic fillers on the CTE and related thermal and mechanical properties are described in detail. The present methods for the manufacturing of these composites are also presented along with their respective advantages and challenges.
Ceramic matrix composites filled with A2M3O12 and related materials are attractive due to their potential for CTEs very close to zero, leading to enhanced thermal shock resistance. Such composites could be potential substitutes for traditional near-zero thermal expansion materials, such as Invar (Fe-Ni alloy) and lithium-aluminum-silicate glass-ceramics (Romao et al., 2015a).
There are several works describing the manufacturing of CMCs using A2M3O12 materials (Yanase et al., 2009; Liu et al., 2012; Koh et al., 2013; Romao et al., 2015a), CMCs with ABM3O12 (Yang J. et al., 2019; Yang et al., 2020) and CMCs with A2MX2O12 (Tani et al., 2010; Yanase et al., 2017; Zhang et al., 2017; Liu et al., 2018) prepared through solid-state routes, including in situ and ex situ approaches, as depicted in Figure 14. Other preparation methods, such as melt reaction (Tran et al., 2001) and co-precipitation followed by in situ solid-state reaction (Liu X. Z. et al., 2015), have also been reported. The manufacturing process conditions, linear CTE and potential applications of these composites are presented in Table 1.
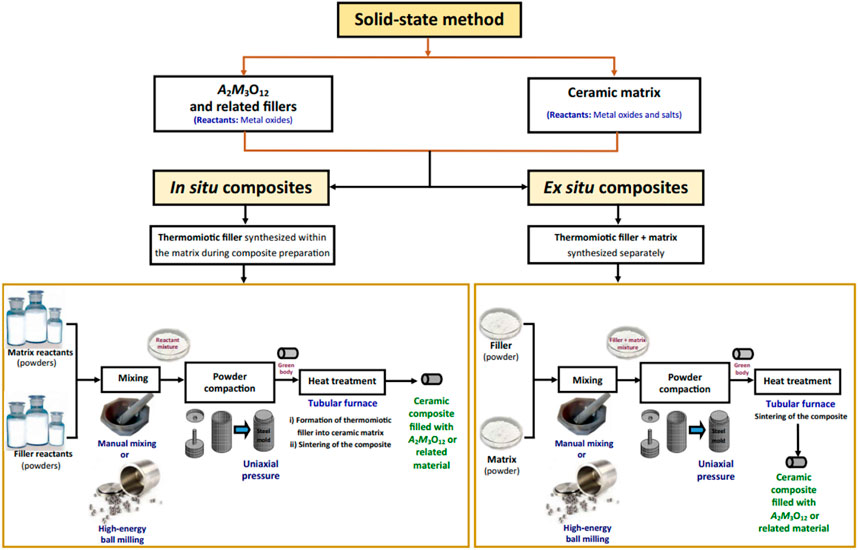
FIGURE 14. Scheme showing solid-state preparation and processing of ceramic matrix composites (CMCs) filled with A2M3O12 or related materials.
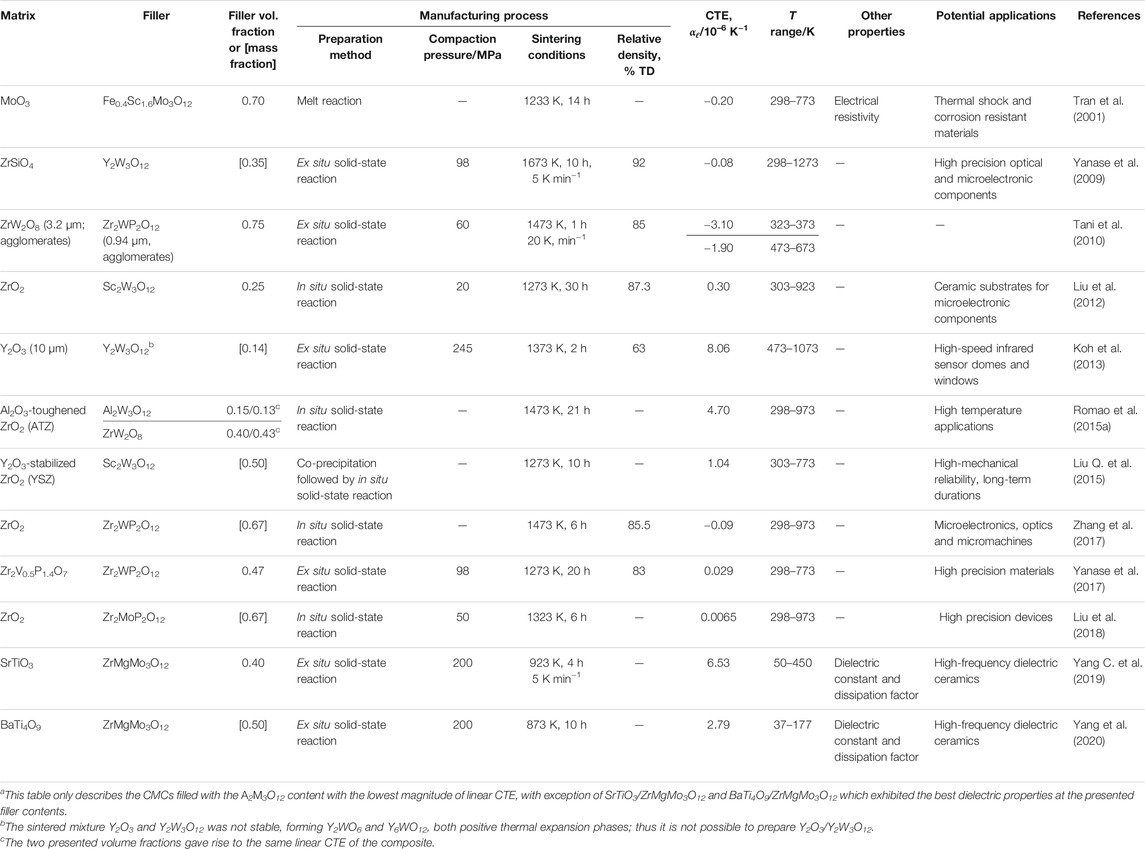
TABLE 1. Ceramic Matrix Composites (CMCs) filled with A2M3O12 and related families, their manufacturing conditions, linear CTE and potential applicationsa.
As can be seen in Table 1, CMCs with low-positive, negative and near-zero thermal expansion coefficients in a wide temperature range can be obtained by incorporating A2M3O12 (Y2W3O12, Sc2W3O12, Al2W3O12 and Fe0.4Sc1.6Mo3O12), ABM3O12 (ZrMgMo3O12) and A2MX2O12 (Zr2WP2O12 and Zr2MoP2O12) fillers. Although these composites are designed to exhibit improved thermal shock resistance, this property generally has not been experimentally determined or estimated, for instance, by the Hasselman figures of merit for severe heating conditions (Prisco et al., 2016b).
There are several other concerns associated with CMCs filled with A2M3O12 and related materials. One is the large CTE mismatch between the thermomiotic fillers and the positive thermal expansion of their ceramic matrices (Romao et al., 2015a), giving rise to residual thermal stresses after sintering of CMCs when cooled to ambient temperature, which leads to the formation of microcracks (Tran et al., 2001; Liu et al., 2012; Romao et al., 2015a). On subsequent heating, the microcracks could heal, influencing the bulk CTE and the mechanical properties of these CMCs (Prisco et al., 2013).
The thermal expansion mismatch stress, pCTE, inside a single spherical filler inclusion embedded into an infinite ceramic matrix can be calculated from (Selsing, 1961; Palmero, 2015):
where Δαℓ is the difference between the linear CTE of the matrix αℓ(m) and that of the thermomiotic-like filler αℓ(f) and ΔT is the difference between the processing and room temperatures, and Ym, Yf, νm and νf are the Young’s moduli and Poisson ratios of the matrix and filler, respectively.
Note that microcrack formation for a given maximum residual thermal stress can be reduced or even avoided during cooling if the filler inclusion is smaller than a critical size (Tran et al., 2001). As a first approach, the critical size can be predicted using a simple model (Davidge and Green, 1968). This model considers a single spherical inclusion embedded within an infinite ceramic matrix, with constant
with the surface formation energy, Us:
where r is the filler radius and γs is the effective surface energy of the matrix which is independent of the filler volume fraction. A necessary condition for microcrack growth is that the energy to create a new surface, Us, is less than Ut (Davidge and Green, 1968; Orellana et al., 2015; Luchini et al., 2017). Therefore, rc can be calculated when Ut = Us:
and microcrack formation can be avoided for r < rc.
This approach can be applied for low filler volume fractions since the mean distance between the filler particles is large enough to meet the criteria that their stress and strain fields are akin to those of the Davidge and Green model, with a single filler inclusion surrounded by an infinite ceramic matrix. However, Equation 12 would not apply for high filler volume fractions (≥0.30), and the assumption of a constant pCTE at the filler/matrix interface also would be invalid (Luchini et al., 2017). Finite element analysis (FEA) can be a useful tool to predict the critical filler radius at high volume fractions such as those commonly used to prepare CMCs/A2M3O12. The influence of the filler particle size on microcracking is a critical consideration. In this respect, microstructural engineering is essential to elucidate new synthesis routes for regulating the particle size of A2M3O12 and related fillers (Prisco et al., 2013). Optimization of the sintering conditions is another key factor that should be considered to control the filler and matrix grain growth (see also Section 6). In addition, the chemical stability of the ceramic matrix is important to restrict side reactions with the dispersed phase during sintering (Tran et al., 2001; Yanase et al., 2009; Zhang et al., 2017).
A2M3O12 and related fillers are more compliant than conventional ceramic matrices (for examples, see Table 1), such as ZrO2 (Liu et al., 2012; Zhang et al., 2017; Liu et al., 2018), Y2O3-doped ZrO2 (Liu X. Z. et al., 2015) and Al2O3-toughened ZrO2 (ATZ) (Romao et al., 2015a). As a result, the Young’s modulus of CMCs reinforced with these thermomiotic and NZTE fillers is expected to decrease with the incorporation of the dispersed phase, especially at high filler loadings (Romao et al., 2015a). Nevertheless, the assessment of the mechanical properties of these CMCs by flexural tests (modulus of rupture), ultrasonic measurements of the velocity of sound (Young’s modulus and other elastic constants) or microindentation tests (Young’s modulus and microhardness) is still scarce (Prisco et al., 2016b).
The low stiffness of A2M3O12 fillers also can have an impact on the CTE of CMCs, as demonstrated for ATZ composites reinforced with Al2W3O12/ZrW2O8 hybrid filler (Romao et al., 2015a). Two micromechanical models, the ROM and Turner model, as discussed in Section 5.1, were applied to predict their linear CTE (αℓ(c)). ROM, which only considers the CTE of the composite components and their volume fractions, predicted CTE values lower than those measured by dilatometry for ATZ/Al2W3O12/ZrW2O8. On the other hand, the experimental CTE values of these CMCs were well fit by the Turner model, revealing the strong influence of the filler bulk modulus, and therefore, the filler stiffness, on the effective CTE of these composites (Romao et al., 2015a). If pCTE is sufficiently large to initiate a pressure-induced phase transition, this will also act to reduce the effective stiffness of the affected component (Romao and White, 2016).
High volume fractions (up to 0.75, see Table 1) of A2M3O12 and related materials are required to provoke a substantial reduction on the CTE of ceramic matrices, which gives rise to an inhomogeneous filler distribution in the matrix and a porous microstructure (Yanase et al., 2017), compromising the relative density and, consequently, the mechanical performance of these CMCs. The highest relative density reached by these CMCs is ∼92% TD (Yanase et al., 2009); see Table 1. Hence, optimization of the sintering conditions can contribute to obtain fully dense CMCs. Note that A2M3O12 and related filler materials are frequently prone to pressure-induced transformation from the desired orthorhombic phase to the monoclinic phase at pressures <250 MPa (Varga et al., 2005), with some exceptions such as Zr2WP2O12 which is still orthorhombic at pressures as high as 300 MPa (Cetinkol and Wilkinson, 2009). Such transformation must be considered in selecting the compaction pressure value for the green CMCs prior sintering (Young et al., 2018). The compaction pressures reported for these CMCs (see Table 1), ranged between 50 and 245 MPa, and did not induce the unwanted phase transition.
Care also must be taken to avoid evaporation of the constituent oxides, such as MoO3 and WO3, at the sintering temperatures of the conventional ceramic matrices, as at 1773 K for ATZ (Esfahani et al., 2010) and 1673 K for ZrO2 (Zhang et al., 2017). Among the fillers presented in Table 1, Al2W3O12 and ZrMgMo3O12 decompose at temperatures higher than 1423 and 1073 K, respectively, due to WO3 and MoO3 evaporation (Romao et al., 2015b; Jardim et al., 2016; Madrid et al., 2020). The CMCs filled with A2M3O12 and related families should be sintered at lower temperatures, as in the case of SrTiO3/ZrMgMo3O12 and BaTi4O9/ZrMgMo3O12, processed at 923 and 873 K, respectively (Yang J. et al., 2019; Yang et al., 2020). Sintering aids such as TiO2 can reduce the sintering temperature of traditional ceramic matrices such as ATZ (Romao et al., 2015a). The use of covered Pt crucibles or Pt foils to contain the CMC pellets prior to sintering can suppress the volatilization of MoO3 and WO3 (Yang et al., 2007). If sintering of the composite occurs at temperatures near the decomposition of the filler, a quenching process can prevent filler decomposition (Tran et al., 2001; Tani et al., 2010; Romao et al., 2015a), but this can lead to problematic microcracks in the manufacture of large-sized CMCs (Yang C. et al., 2019).
Consequently, significant improvements in the preparation and processing of CMCs filled with A2M3O12 and related compounds are required for applications in microelectronics and high-precision optical devices with enhanced thermal shock resistance, high thermal stability, structural integrity and/or superior dielectric properties.
Metal matrices can be used with A2M3O2 and related materials to form cermets which overcome the shortcomings associated with brittleness, and low thermal and electrical conductivities of CMCs, while simultaneously allowing low-magnitude thermal expansion, high-temperature resistance and enhanced toughness (Liu et al., 2013; Zhou et al., 2017). These properties can be desirable for applications in microelectronics, and in the automotive and aerospace industries (Xiao et al., 2015). In this context, aluminum and its alloys, and also copper, have been selected as the preferred matrices for these cermets; see Table 2.
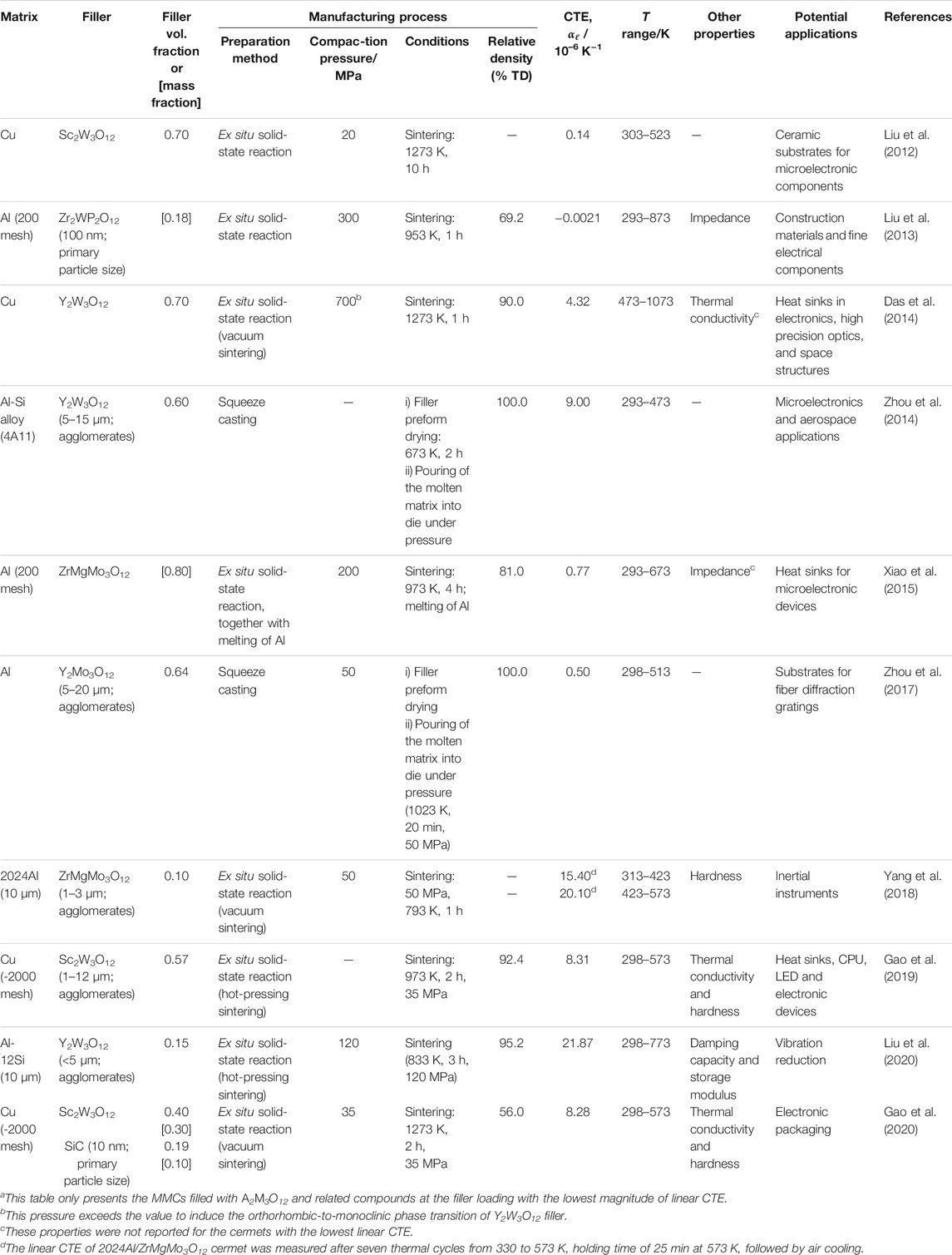
TABLE 2. Metal matrix composites (MMCs) filled with A2M3O12 and related materials, their manufacturing process, linear CTE and potential applicationsa.
The metal matrices have high thermal conductivities [κ(Al) = 237 W m−1 K−1, κ(Cu) = 400 W m−1 K−1] and low electrical resistivities [ρ(Al) = 2.43 × 10–8 Ω m−1, ρ(Cu) = 1.73 × 10–8 Ω m−1] (Uher, 2004), but high positive CTEs [αℓ(Al) = 23 × 10–6 K−1, αℓ(Cu) = 17 × 10–6 K−1] (Liu et al., 2012; Xiao et al., 2015). Therefore, a CTE mismatch with ceramic components can emerge, as in the case of chip substrates, which are made of silicon [αℓ(Si) = 2.6 × 10–6 K−1], gallium arsenide [αℓ(GaAs) = 5.8 × 10–6 K−1], germanium [αℓ(Ge) = 5.9 × 10–6 K−1] and indium phosphide [αℓ(InP) 4.6 × 10–6 K−1] (Yang et al., 2003; Gao et al., 2020). The main motivation to prepare metal matrix composites (MMCs) filled with A2M3O2 and related materials is to attain highly conductive cermets with CTEs as low as those of the ceramic substrates. However, significant CTE reductions of these cermets can only be achieved by extremely high-volume fractions of these fillers, typically in the range of 0.50–0.70 (see Table 2), which in turn decrease the thermal and electrical conductivities of the composites (Liu et al., 2012; Liu et al., 2013; Xiao et al., 2015). In addition, at a high filler loading the machinability and mechanical properties (tensile strength, ductility and toughness) of MMCs/A2M3O2 can be adversely affected, which leads to poor cermet performance (Yang et al., 2018), a critical issue for structural components in aerospace and electronic packaging applications.
The ex situ solid-state reaction is the most widespread approach to preparation of MMCs filled with A2M3O2 and related materials (Liu et al., 2012; Liu et al., 2013; Das et al., 2014; Xiao et al., 2015; Yang et al., 2018; Gao et al., 2019; Gao et al., 2020; Liu et al., 2020), while squeeze casting has been employed in a few works (Zhou et al., 2014; Zhou et al., 2017), as shown in Table 2.
Note that, depending on the heat treatment temperature and duration, and the chemical composition of the matrix, some elements in aluminum alloys can diffuse during sintering in ex situ solid-state reactions, precipitating undesirable compounds during quenching. For instance, Al2Cu precipitates were identified in 2024Al/ZrMgMo3O12 as a secondary phase, with volume contents up to 0.11; such precipitates act as an additional filler, influencing the CTE and the mechanical properties of the cermet (Yang et al., 2018). Furthermore, the chemical reaction between A2M3O12 fillers and metal matrices must be prevented during sintering. The sintering conditions and the chemical composition need to be carefully selected especially in the case of aluminum alloys.
Among the ex situ solid-state reactions, there are two variants of sintering: 1) hot pressing, including vacuum hot pressing, and 2) pressure-less processing (see Table 2). The first method requires limiting the pressure to prevent the orthorhombic-to-monoclinic phase transition for CMCs filled with A2M3O12 and related materials. However, high pressures are typically required to reach full densification and reduce porosity, which also influences the CTE and stiffness of the cermets (Yang et al., 2018). Furthermore, microstructural anisotropy can arise due to uniaxial hot pressing (Peng et al., 2014), a matter that should be considered for applications of these composites.
The focus in development of MMCs filled with A2M3O12 and related materials has been on their low thermal expansion, with only a few reports of their thermal conductivity and electrical response in terms of impedance. Actually, the cermets exhibiting the lowest thermal expansion are not those with the highest conductivity properties (Liu et al., 2012; Liu et al., 2013; Das et al., 2014; Xiao et al., 2015), as stated earlier.
A hybrid filler has been proposed in an attempt to prepare MMCs/A2M3O12 that satisfy the low CTE requirements for applications in electronic equipment without sacrificing the thermal conductivity of the metal matrices. This hybrid filler was composed of Sc2W3O12 submicronic particles and SiC nanoparticles as thermal expansion and heat spreading compensators, respectively. SiC has low thermal expansion [αℓ(SiC) = 4 × 10–6 K−1] and high thermal conductivity [κ(SiC) = 120 W m−1 K−1]. The resultant Cu/Sc2W3O12/SiC composite exhibited a linear CTE of 8 × 10–6 K−1 which is compatible with that of a GaAs substrate, thermal conductivity of 287 W m−1 K−1 which is higher than that of the aluminum, and a hardness of 120 HV, for Sc2W3O12 and SiC mass fractions of 0.30 and 0.10, respectively (Gao et al., 2020).
Studies assessing the mechanical properties of these cermets are still scarce, with hardness as the most reported property (Yang et al., 2018; Gao et al., 2019). For example, an increase on hardness of ∼24% compared with the neat matrix has been determined for 2024Al/ZrMgMo3O12, at a filler volume loading of 0.10 (Yang et al., 2018).
A recent study of the mechanical properties of MMCs/A2M3O12 was devoted to determination of the storage modulus and damping capacity through dynamic mechanical analysis (DMA), as exemplified by Al-12Si/Y2W3O12 (Liu et al., 2020). The storage modulus of this cermet gradually decreased with increasing Y2W3O12 filler content, owing to the low Young’s modulus of this filler, ca. 30 GPa (Pontón et al., 2018), compared with 69 GPa for the Al matrix (Liu et al., 2020). However, the damping capacity of Al-12Si/Y2W3O12 followed the opposite trend. These fillers can provoke high local strain at the filler/matrix interface because of the large CTE mismatch with the cermet’s matrix, resulting in a higher energy dissipation for Al-12Si/Y2W3O12, and consequently, an enhanced damping capacity, minimizing the vibration absorption, as quantified by the maximum loss factor obtained from DMA curves (Liu et al., 2020).
Another aspect that deserves special attention is related to the residual thermal stresses generated during cooling of MMCs/A2M3O12, from the fabrication temperature to the working conditions, due to the large CTE mismatch between the fillers and the metal matrix. Neutron and synchrotron diffraction have been used to measure the residual thermal stress in cermets (Peng et al., 2014), and it also can be estimated from a basic theoretical calculation (Lee et al., 1980; Krstic and Nicholson, 1981; Zhou et al., 2017), via the mismatch hydrostatic stress pCTE calculated with Equation 9. The matrix can endure plastic deformation at the filler-matrix interface when pCTE reaches 2/3 of the matrix yield strength, σy (Peng et al., 2014), i.e., approximately 200 MPa for Al and 220 MPa for Cu (Peng et al., 2014; Zhou et al., 2017). If pCTE > σy as in the case of Cu/Sc2W3O12 cooled from 973 to 298 K (pCTE = 850 MPa > σy), the matrix will be fully plastically deformed at room temperature (Gao et al., 2019). The residual thermal stress in excess of σy could be released through plastic deformation of the matrix at ambient temperature, increasing the dislocation density in the matrix (Arsenault and Shi, 1986), and increasing its yield strength (Delannay, 2017). On the other hand, residual thermal stress can remain in the cermet if pCTE < σy (Arsenault and Shi, 1986; Peng et al., 2014). Hence, the CTE and mechanical properties of MMCs/A2M3O12 depend on the relaxation extent of the thermal misfit stress. Thermal cycling could help eliminate the residual thermal stress: the CTE of 2024Al/ZrMgMo3O12 stabilized after seven thermal cycles at the conditions specified in Table 2, at values lower than before thermal cycling, revealing the intrinsic influence of ZrMgMo3O12 on this property after the relaxation of the residual thermal stress (Yang et al., 2018).
Finally, applications of these cermets in optics, metrology and high-precision engineering require the assessment of the thermal distortion parameter (TDP), a figure of merit defined as the temperature-induced distortion in a cermet (Subramaniam et al., 2014):
where, αℓ(c) and κ(c) are the linear CTE (expressed here in 10–6 K−1) and thermal conductivity (expressed in W m−1 K−1) of the cermet, respectively. Thus, a low TDP is an indicator of high dimensional thermal stability. TDP values of 0.034 and 0.028 have been reported for Cu/Sc2W3O12 and Cu/Sc2W3O12/SiC, respectively, which are similar to that of Si (0.020), demonstrating the wide-range applicability of these cermets (Gao et al., 2019; Gao et al., 2020).
The preparation of polymer matrix composites filled with A2M3O12 and related materials has been less explored than for ceramic and metal matrices, despite the expected significant reduction of CTE for compliant matrices at low filler contents (Pontón et al., 2019b). To date, only A2M3O12 (Al2Mo3O12, Al2W3O12, Y2W3O12 and Y2Mo3O12) and A2MX2O12 (Zr2WP2O12) fillers have been used to tailor the CTE of different polymer matrices (Soares et al., 2014; Zhou et al., 2015; Shi et al., 2016; Pontón et al., 2018; Ellis et al., 2019; Pontón et al., 2019b). Thermoplastics [medium and high-density polyethylene (MDPE and HDPE), and polymethyl methacrylate (PMMA)], thermosets [polyimide (PI)], and elastomers (silicone resin) have been employed; see Table 3.
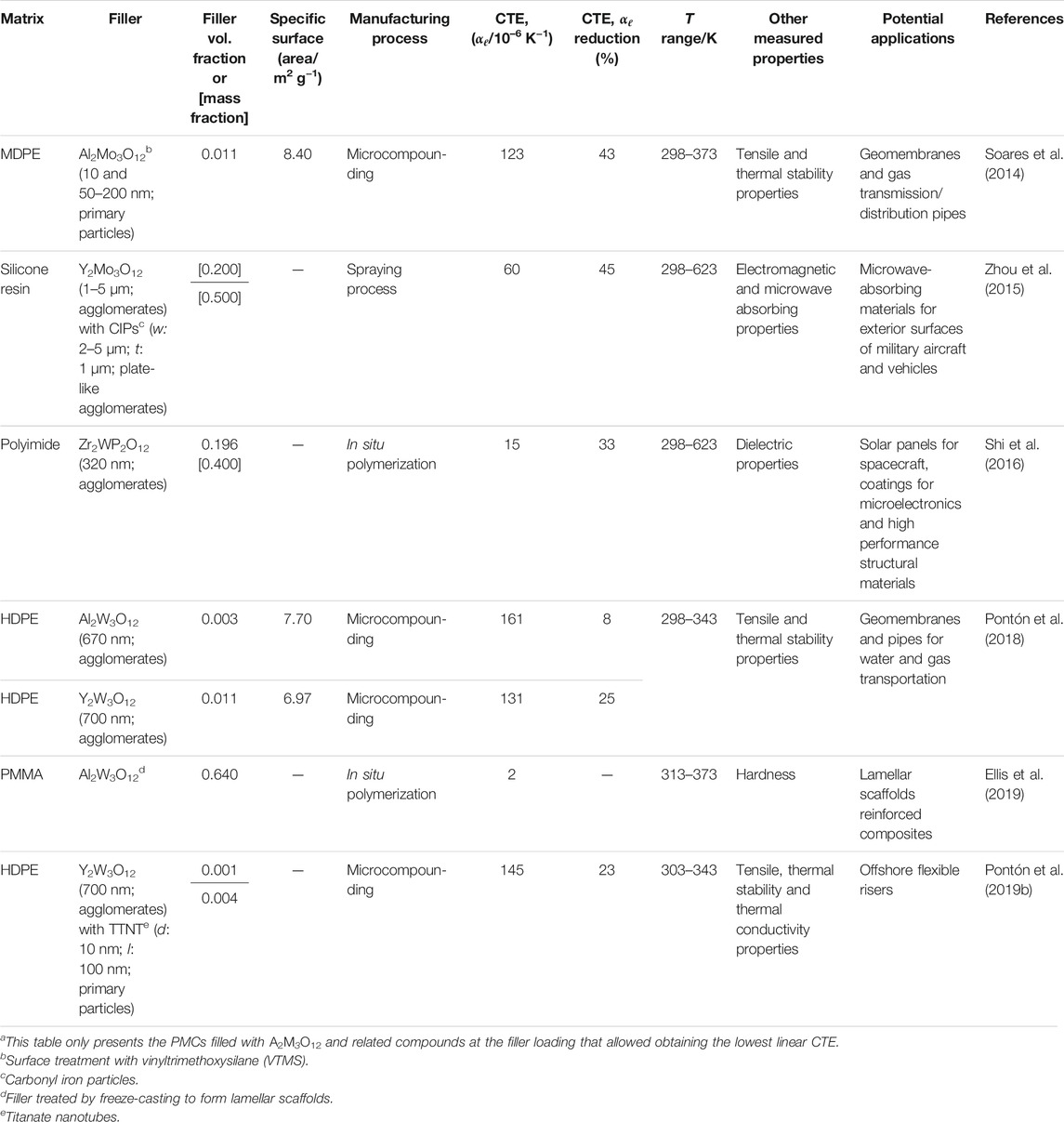
TABLE 3. Polymer matrix composites (PMCs) filled with A2M3O12 and related materials, their manufacturing process, linear CTE and potential applicationsa.
The preparation and processing of PMCs/A2M3O12, their filler volume fractions and anticipated applications are presented in Table 3. The filler volume fraction, the filler/matrix interactions at the interface and the dispersion state of the thermomiotic filler within the matrix are the fundamental factors that govern the thermal expansion and mechanical properties of these PMCs (Pontón et al., 2019b). Since most polymers are hydrophobic, and A2M3O12 and related fillers are hydrophilic (due to –OH surface groups), functionalization treatments have been proposed to increase the filler hydrophobicity, improving their wettability with the matrix and the filler/matrix adhesion. Silane coupling agents (vinyltrimethoxysilane, VTMS) and surfactants (cetyltrimethylammonium bromide, CTAB) are reported in the literature as functionalization agents that incorporate hydrophobic organic fragments on the filler surface through covalent or electrostatic interactions, respectively (Soares et al., 2014; Pontón et al., 2019b). These surface modifications also can contribute to better dispersion of the fillers into the matrix due to the compatible polarity of the components. One of the most inspiring achievements is 43% reduction in CTE for MDPE/Al2Mo3O12, at a remarkably low filler volume fraction of 0.011 (Table 3), despite the use of the (generally unfavorable) monoclinic phase for Al2Mo3O12 nanoparticles (Soares et al., 2014). This significant CTE reduction was attributed to the improved dispersion of this nanofiller as a result of the VTMS surface modification. Another strategy to enhance the filler/matrix interactions is to modify the polymer matrix, for instance by using polyethylene-grafted maleic anhydride (PE-g-MA), to render HDPE more hydrophilic. However, this treatment can negatively impact the CTE of these PMCs when heated, owing to the expansion of the PE-g-MA interfacial groups which are considerably longer than VTMS chains (Pontón et al., 2019b).
The simplest approach to manufacture PMCs/A2M3O12 is to add a pristine filler such that interfacial bonding can occur through mechanical interlocking because of filler roughness (Pontón et al., 2018). Furthermore, the dispersion of these fillers into the polymer matrix can be promoted by mixing methods, such as stirring during a spraying process (Zhou et al., 2015) and in situ polymerization (Shi et al., 2016; Ellis et al., 2019), as well as co-rotating extruder mixing in microcompounding (Soares et al., 2014; Pontón et al., 2018; Pontón et al., 2019b). In addition, the degree of dispersion of A2M3O12 fillers within polymer matrices strongly depends on their initial agglomeration state, derived from the selected synthesis route (vide supra).
Generally, engineered interfaces improve mechanical properties more than they reduce thermal expansion of PMCs/A2M3O12, as demonstrated for HDPE-based composites reinforced with Y2W3O12 and TTNT, at 0.001 and 0.004 volume fractions, respectively (Pontón et al., 2019b). Superior mechanical properties of these PMCs were obtained when the fillers were modified with CTAB. In contrast, the highest CTE reductions were achieved with pristine fillers, suggesting that the CTAB fragments on the filler surface could experience positive expansion during heating. Short-chain VTMS appears to be a more appropriate A2M3O12 modifier than CTAB for decreasing the composite CTE (Soares et al., 2014), probably due to its relatively minor expansion during heating. It is clear that different mechanisms control the thermal expansion and the mechanical properties of PMCs/A2M3O12 (Sharma et al., 2012; Pontón et al., 2019b).
Unlike CMCs/A2M3O12 and MMCs/A2M3O12 which are significantly influenced by residual thermal stresses that arise from the CTE discrepancy between the matrix and the filler during cooling, PMCs/A2M3O12 do not experience thermal stresses sufficient to compromise their structural integrity, as exemplified by composites with thermoplastic matrices. The thermal stresses of MDPE/Al2Mo3O12 were estimated through FEA, assuming 100 K temperature drop, near ambient temperature, and found to be below the yield strength of MDPE (Soares et al., 2014). Thus, the low stiffness of MDPE considerably decreased the thermal stresses, despite the large CTE mismatch between the composite components.
Note that A2M3O12 and related materials can be combined with other fillers, such as TTNT and CIPs to form hybrid fillers (see Table 3), improving the mechanical and microwave absorbing properties, respectively, while causing a substantial decrease in the CTE of the composites (Zhou et al., 2015; Pontón et al., 2019b). A detailed description of the micromechanical models that can be applied to predict the CTE of these ternary PMCs has been published (Pontón et al., 2019a).
Finally, to the best of our knowledge, the preparation of PMCs/A2M3O12 made with epoxy resin, a much-used matrix for several engineering fields, has not been reported yet in the literature, opening the possibility to embrace A2M3O12 and related families in applications dominated by this thermoset where a low CTE is essential, such as for encapsulated microelectronic devices.
The current interest in the A2M3O12 family is mainly due its potential applications, related principally to the thermal, optical and mechanical properties of its members (Table 4).
NTE and NZTE materials can be of critical importance to control thermal expansion and to avoid thermal shock (Yamamura et al., 2009). Since A2M3O12 ceramic materials can present NTE or NZTE in a wide range of temperatures, these can be used as components of composites to tune their overall CTE to a desired value, as detailed in Section 7. Such composites combine NTE or NZTE fillers and a ceramic, metallic or polymeric matrix with PTE to attain predetermined values of CTE (Fornasini et al., 2006; Peng et al., 2011; Miller et al., 2013; Truitt et al., 2015; Romao et al., 2015a; Wu et al., 2016; Young et al., 2016; Prisco et al., 2016a; Zhou et al., 2017).
Further thermal expansion applications include NZTE materials that can be used as substrates for fibers diffraction gratings, an application that is extremely sensitive to dimensional changes (Marinkovic et al., 2010; Zhou et al., 2017).
A2M3O12 ceramics are also good candidates for infrared transparent windows used in several applications including monitoring of industrial processes (Dasgupta et al., 2012; Prisco et al., 2016b). Infrared transparent windows also have military applications, including ceramic domes to protect the infrared tracker of high-speed missile from the harsh environment. This dome must survive the rapid heating to which the missile is subjected when launched and also must resist long-term erosion from raindrops and dust particles while the missile is carried beneath the wing of an aircraft. The materials for ceramic domes must have optimized high thermal shock resistance and infrared transparency, combined with good mechanical, thermal and optical properties (Harris, 2010).
In the field of optical applications, in addition to NTE behavior over a wide range of temperature, HfScMo2VO12, HfScW2PO12, ZrScMo2VO12 and ZrScW2PO12 present intense photoluminescence covering the visible-light region. (See also Section 5.3). These materials are therefore candidates for application in white light emitting diodes (wLEDs) and other emitting devices (Cheng et al., 2016; Ge et al., 2016a; Ge et al., 2016b; Cheng et al., 2017).
It was suggested that Dy3+ doped Y2W3O12 can also be utilized in wLEDs (Cao et al., 2020). Since Dy3+ simultaneously emits blue and yellow light, white emission is expected to be perceived from Dy3+ doped in a matrix such as Y2W3O12. On the other hand, tungstates, in general, are self-activated phosphors and can produce a broad band emission under UV excitation (see Section 5.3).
The application of A2M3O12 materials in optical thermometry is a recent research topic (Zou et al., 2019; Lv et al., 2021). Er3+/Yb3+ co-doped Y2Mo3O12 microparticles have been proposed for this purpose. The photon up-conversion emission (emission of higher-energy photons after absorbing lower-energy photons) in rare-earth doped Y2Mo3O12 is the key property for optical thermometry applications. Er3+/Yb3+ co-doped Y2Mo3O12 shows rapid response, high spatial resolution and can be read without contact, providing advantages over traditional thermometers. Er3+/Yb3+ co-doped Y2Mo3O12 microparticles irradiated at 980 nm can have bright green emission, which becomes more intense with increasing temperature, presenting a mechanism for optical thermometry (Lv et al., 2021).
Lanthanide-doped Yb2W3O12 also has been evaluated for optical thermometry (Zou et al., 2019). Yb2W3O12 was chosen due its thermal stability and NTE. Besides this, Yb3+ can harvest infrared excitation at 980 nm and subsequently sensitize up-conversion emissions in substitutional dopants such as Er3+, Tm3+ or Ho3+. Er3+-doped Yb2W3O12 exhibits characteristic green and red emissions of Er3+ under 980 nm excitation. As the temperature is increased, the green emission at 523 nm is significantly enhanced, as is the overall emission. The up-conversion emission intensity of this system returns to the original level on thermal cycling which indicates that there is no permanent change in the crystals during the heating and cooling. This is an important characteristic since the use of luminescent materials is commonly limited by the loss of emission with increased temperature due to thermal quenching. Thermal enhancement of up conversion offers significant opportunities for high-temperature thermometry (Zou et al., 2019).
However, the reversibility of the up-conversion emission intensity depends on the maximum temperature to which the system is subjected. Thermal luminescence is particle size dependent and overheating can induce sintering of the constituent particles. When A2M3O12 is lanthanide doped, A3+ acts as a sensitizer and Ln3+ acts as an activator. Thermal contraction in the host lattice can reduce the distance between the sensitizer and the activator, enhancing energy transfer efficiency and leading to an increase in Ln3+-activated up conversion luminescence. For this reason, matrices with low CTE can improve photon up conversion at high temperatures. However, A2M3O12 phases that are hygroscopic have their negative thermal expansion inhibited by the presence of water molecules, which also affects luminescence. Therefore, instead of using Yb2W3O12 as a host material in optical thermometers, Sc2Mo3O12 was recently proposed, since it is a non-hygroscopic material (Zhou et al., 2021).
Another possibility for optical thermometry combines PTE and NTE up-conversion luminescent phases (Zi et al., 2021). For rare-earth doped A2M3O12, the distance between the rare-earth ion and the A3+ ions decreases with increasing temperature, resulting in improved energy transfer from the A3+ ion to other rare-earth ions. A temperature sensor has been prepared based on the luminescence intensity of Y2Mo3O12:Yb3+, Er3+, which is an NTE phosphor, relative to that of Y2Ti2O7:Yb3+, Er3+, a PTE phosphor (Zi et al., 2021).
The optical properties of ceramics in the A2M3O12 family can also find use in biological applications. Rare-earth molybdates are excellent matrices for luminescent phosphor materials, and their well-defined micro-/nanoparticles are especially attractive for bioimaging applications owing to the low toxicity of molybdenum and rare-earth cations (Xu et al., 2019).
The potential application of ytterbium and erbium co-doped lanthanum molybdate for labeling biomolecules also has been reported (Yi et al., 2002). This material is an up-conversion phosphor, and as a fluorescent label it shows very low background signal and no photobleaching. Its use enables detection of multiple analytes since different colors of visible light can be obtained from different up-conversion phosphors excited by the same IR laser (Yi et al., 2002).
There are several other biological applications of rare-earth doped nanoparticles, again making use of their optical properties, along with photostability, absence of blinking, narrow or up-converted emission, large Stokes or anti-Stokes shifts, and long-lifetime excited states and absence of cytotoxicity. Among others, lanthanum molybdate was cited as a potential material for such applications. The features presented by this material makes it suitable to replace organic dyes or quantum dots in DNA assays, protein detection, nonspecific imaging, specific protein targeting, single-protein tracking and contrast agents for magnetic resonance imaging (Bouzigues et al., 2011).
In addition to the applications presented above, some members of A2M3O12 family have been investigated for their high ionic conductivity, which could potentially be important in solid electrolytes (Köhler et al., 1999; Imanaka, 2005; Zhou et al., 2008). See also Section 5.2.2.
For applications of composites with ceramics in the A2M3O12 family, as diverse as corrosion-resistant materials, high-frequency dielectrics, vibration reduction, electronic packaging, microwave absorption, and geomembranes, see Tables 1, 2, 3.
The thermal, optical and thermomechanical properties of the A2M3O12 materials make them attractive in many technological areas. The study of these potential applications is ongoing, and it is likely that in the future these materials will find real-life use on a large scale.
Almost 25 years since the discovery of NTE and NZTE in the A2M3O12 family, many advances in the area have been made, principally concerning understanding of the mechanism underlying the thermal expansion behavior. NTE and NZTE are rarely observed in materials, yet are widespread in the many possible compositions of the general formula A2M3O12 and related sub-families.
Following our thorough overview of the area, at the end of this review we now focus on the current challenges and opportunities encountered both in fundamental and applied aspects of the A2M3O12 family.
Foremost, rational design of linear CTE is still not fully operative. The octahedra volume distortion model currently proposed for rationalization of CTE variation in these families has to be investigated for more materials, especially solid solutions for which the CTE does not fall between the limits of the linear CTEs of the end-member phases. In addition, we still lack a complete understanding of the factors influencing the displacive monoclinic-to-orthorhombic phase transition, besides the electronegativity of the A3+ cation. Understanding the monoclinic-to-orthorhombic phase transition, as well as developing a procedure to eliminate or greatly decrease hygroscopicity of the materials with heavy rare-earths as A3+, are both critical factors for many potential applications. Further understanding of the thermoelastic, electrical and optical properties and their link with CTE present additional gaps in fundamental knowledge that will need to be addressed for future applications.
In the field of potential applications, more applied studies are needed to permit future inclusion of these extraordinary materials into useful advanced engineering ceramics. This will not be possible without major advances in the fields of powder synthesis, consolidation and sintering of monoliths. The field of composites presents many opportunities, especially for PMCs, however, uniform dispersion and well-designed interfaces are still major issues.
Novel potential applications are emerging every year, with the most recent cases being wLEDs and optical thermometry, where NZTE and NTE are fundamental advantages, permitting thermal stability and thermally enhanced up-conversion luminescence, respectively. Considering the unusual lattice dynamics, the vast number of available crystalline phases and compositions within the A2M3O12 family, and the consequent physical properties, new potential applications will continue to emerge.
All authors listed have made a substantial, direct, and intellectual contribution to the work by contributing to writing and editing, and approved it for publication.
BAM is grateful to CNPq (National Council for Scientific and Technological Development) for a Research Productivity Grant. PIP is thankful to Escuela Politécnica Nacional (Project PIE-EPN-PUC-RIO-2018). TM is grateful to CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil) for a doctoral degree scholarship. CPR acknowledges support by the European Union’s Horizon 2020 research and innovation programme through a Marie Skłodowska–Curie Fellowship, Grant Agreement No. 101030352. We also acknowledge NSERC Canada for support of MAW’s lab.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1See list of Abbreviations and Symbols at end of article.
Abrahams, S. C., and Bernstein, J. L. (1966). Crystal Structure of the Transition‐Metal Molybdates and Tungstates. III. Diamagnetic Sc2(WO4)3. J. Chem. Phys. 46, 2052–2063. doi:10.1063/1.1841001
Allred, A. L. (1961). Electronegativity Values from Thermochemical Data. J. Inorg. Nucl. Chem. 17, 215–221. doi:10.1016/0022-1902(61)80142-5
Andersen, H. L., Al Bahri, O. K., Tsarev, S., Johannessen, B., Schulz, B., Liu, J., et al. (2018). Structural Evolution and Stability of Sc2(WO4)3 after Discharge in a Sodium-Based Electrochemical Cell. Dalton Trans. 47, 1251–1260. doi:10.1039/c7dt04374k
Ari, M., Jardim, P. M., Marinkovic, B. A., Rizzo, F., and Ferreira, F. F. (2008). Thermal Expansion of Cr2xFe2−2xMo3O12, Al2xFe2−2xMo3O12 and Al2xCr2−2xMo3O12 Solid Solutions. J. Solid State. Chem. 181, 1472–1479. doi:10.1016/j.jssc.2008.03.015
Ari, M., Miller, K. J., Marinkovic, B. A., Jardim, P. M., De Avillez, R., Rizzo, F., et al. (2011). Rapid Synthesis of the Low Thermal Expansion Phase of Al2Mo3O12 via a Sol-Gel Method Using Polyvinyl Alcohol. J. Sol-gel Sci. Technol. 58, 121–125. doi:10.1007/s10971-010-2364-9
Arsenault, R. J., and Shi, N. (1986). Dislocation Generation Due to Differences between the Coefficients of Thermal Expansion. Mater. Sci. Eng. 81, 175–187. doi:10.1016/0025-5416(86)90261-2
Baiz, T. I., Gindhart, A. M., Kraemer, S. K., and Lind, C. (2008). Synthesis of MgHf(WO4)3 and MgZr(WO4)3 Using a Non-hydrolytic Sol-Gel Method. J. Sol-gel Sci. Technol. 47, 128–130. doi:10.1007/s10971-008-1765-5
Balashov, V. A., Vorona, G. I., Maier, A. A., and Proshina, O. P. (1975). Growth and Certain Properties of Sc2(WO4)3 Crystals. Neorg. Mater. 11, 1713–1714. doi:10.1007/bf01144752
Barker, R. E. (1963). An Approximate Relation between Elastic Moduli and Thermal Expansivities. J. Appl. Phys. 34, 107–116. doi:10.1063/1.1729049
Barron, T. H. K., and Munn, R. W. (1967). Analysis of the Thermal Expansion of Anisotropic Solids: Application to Zinc. Phil. Mag. 15, 85–103. doi:10.1080/14786436708230352
Blackman, M. (1957). On the Thermal Expansion of Solids. Proc. Phys. Soc. B 70, 827–832. doi:10.1080/1478643570824270610.1088/0370-1301/70/9/303
Blasse, G., and Ouwerkerk, M. (1980). Luminescence of Doped and Undoped Al2 (WO4)3, Sc2(WO4)3, and Lu2(WO4)3. J. Electrochem. Soc. 127, 429–434. doi:10.1149/1.2129682
Borchardt, H. J., and Bierstedt, P. E. (1966). Gd2(MoO4)3: A Ferroelectric Laser Host. Appl. Phys. Lett. 8, 50–52. doi:10.1063/1.1754477
Borchardt, H. J. (1963b). Rare‐Earth Tungstates and 1:1 Oxytungstates. J. Chem. Phys. 39, 504–511. doi:10.1063/1.1734285
Bouzigues, C., Gacoin, T., and Alexandrou, A. (2011). Biological Applications of Rare-Earth Based Nanoparticles. ACS Nano 5, 8488–8505. doi:10.1021/nn202378b
Brixner, L. H., Barkley, J. R., and Jeitschko, W. (1979). Chapter 30 Rare Earth Molybdates (VI). Handb. Phys. Chem. Rare Earths 3, 609–654. doi:10.1016/S0168-1273(79)03013-0
Brixner, L. H., Bierstedt, P. E., Sleight, A. W., and Licis, M. S. (1971). Precision Parameters of Some Ln2(MoO4)3-type Rare Earth Molybdates. Mater. Res. Bull. 6, 545–554. doi:10.1016/0025-5408(71)90003-1
Cao, C., Wei, S., Zhu, Y., Liu, T., Xie, A., Noh, H. M., et al. (2020). Synthesis, Optical Properties, and Packaging of Dy3+ Doped Y2WO6, Y2W3O12, and Y6WO12 Phosphors. Mater. Res. Bull. 126, 110846. doi:10.1016/j.materresbull.2020.110846
Cao, W., Li, Q., Lin, K., Liu, Z., Deng, J., Chen, J., et al. (2016). Phase Transition and Negative Thermal Expansion in Orthorhombic Dy2W3O12. RSC Adv. 6, 96275–96280. doi:10.1039/c6ra21136d
Cerón Cortés, A. E. C., Dosen, A., Blair, V. L., Johnson, M. B., White, M. A., and Marinkovic, B. A. (2021). Phase Transition and Coefficients of Thermal Expansion in Al2−xInxW3O12 (0.2 ≤ x ≤ 1). Materials 14, 4021. doi:10.3390/ma14144021
Cetinkol, M., Wilkinson, A. P., and Lee, P. L. (2009). Structural Changes Accompanying Negative Thermal Expansion in Zr2(MoO4)(PO4)2. J. Solid State. Chem. 182, 1304–1311. doi:10.1016/j.jssc.2009.02.029
Cetinkol, M., and Wilkinson, A. P. (2009). Pressure Dependence of Negative Thermal Expansion in Zr2(WO4)(PO4)2. Solid State. Commun. 149, 421–424. doi:10.1016/j.ssc.2009.01.002
Chen, D., Yuan, B., Cheng, Y., Ge, X., Jia, Y., Liang, E., et al. (2016). Phase Transition and Near-Zero Thermal Expansion in ZrFeMo2VO12. Phys. Lett. A 380, 4070–4074. doi:10.1016/j.physleta.2016.10.009
Chen, H.-Y. (1979). The Crystal Structure and Twinning Behavior of Ferric Molybdate, Fe2(MoO4)3. Mater. Res. Bull. 14, 1583–1590. doi:10.1016/0025-5408(72)90228-0
Chen, I.-W., and Wang, X.-H. (2000). Sintering Dense Nanocrystalline Ceramics without Final-Stage Grain Growth. Nature 404, 168–171. doi:10.1038/35004548
Cheng, Y., Liang, Y., Ge, X., Liu, X., Yuan, B., Guo, J., et al. (2016). A Novel Material of HfScMo2VO12 With Negative Thermal Expansion and Intense White-light Emission. RSC Adv. 6, 53657–53661. doi:10.1039/c6ra09666b
Cheng, Y., Liang, Y., Mao, Y., Ge, X., Yuan, B., Guo, J., et al. (2017). A Novel Material of HfScW2PO12 With Negative Thermal Expansion from 140 K to 1469 K and Intense Blue Photoluminescence. Mater. Res. Bull. 85, 176–180. doi:10.1016/j.materresbull.2016.09.008
Cheng, Y. Z., Wu, M. M., Peng, J., Xiao, X. L., Li, Z. X., Hu, Z. B., et al. (2007). Structures, Thermal Expansion Properties and Phase Transitions of ErxFe2−x(MoO4)3 (0.0≤x≤2.0). Solid State. Sci. 9, 693–698. doi:10.1016/j.solidstatesciences.2007.04.018
Costa, I. M., Blair, V. L., Paraguassu, W., and Marinkovic, B. A. (2019). Evaluating Al2-xGaxW3O12 System for Thermal Shock Resistance. J. Solid State. Chem. 277, 149–158. doi:10.1016/j.jssc.2019.05.041
Craig, D. C., and Stephenson, N. C. (1968). A Structural Study in the System Al2O3-WO3. Acta Crystallogr. Sect B 24, 1250–1255. doi:10.1107/s0567740868004061
Das, S., Das, S., and Das, K. (2013). Low Temperature Synthesis of Negative Thermal Expansion Y2W3O12. J. Materi Eng. Perform. 22, 3357–3363. doi:10.1007/s11665-013-0652-6
Das, S., Das, S., and Das, K. (2014). Synthesis and Thermal Behavior of Cu/Y2W3O12 Composite. Ceramics Int. 40, 6465–6472. doi:10.1016/j.ceramint.2013.11.097
Dasgupta, N., Sörge, E., Butler, B., Wen, T.-C., Shetty, D. K., Cambrea, L. R., et al. (2012). Synthesis and Characterization of Al2−x Scx (WO4)3 Ceramics for Low-Expansion Infrared-Transmitting Windows. J. Mater. Sci. 47, 6286–6296. doi:10.1007/s10853-012-6548-2
Davidge, R. W., and Green, T. J. (1968). The Strength of Two-Phase Ceramic/glass Materials. J. Mater. Sci. 3, 629–634. doi:10.1007/BF00757910
Delannay, F. (2018). 4.8 Thermal Stresses and Thermal Expansion in Metal Matrix Composites. Compr. Compos. Mater. 4, 213–241. doi:10.1016/B978-0-12-803581-8.03874-1
Dolabdjian, K., Kobald, A., Romao, C. P., and Meyer, H.-J. (2018). Synthesis and Thermoelastic Properties of Zr(CN2)2 and Hf(CN2)2. Dalton Trans. 47, 10249–10255. doi:10.1039/C8DT02001A
Drymiotis, F. R., Ledbetter, H., Betts, J. B., Kimura, T., Lashley, J. C., Migliori, A., et al. (2004). Monocrystal Elastic Constants of the Negative-Thermal-Expansion Compound Zirconium Tungstate (ZrW2O8). Phys. Rev. Lett. 93, 025502. doi:10.1103/PhysRevLett.93.025502
Ellis, S., Romao, C., and White, M. (2019). Near-Zero Thermal Expansion in Freeze-Cast Composite Materials. Ceramics 2, 112–125. doi:10.3390/ceramics2010011
Esfahani, H., Nemati, A., and Salahi, E. (2010). The Effects of Composition and Sintering Conditions on Zirconia Toughened Alumina (ZTA) Nanocomposites. Adv. Mater. Res. 93-94, 695–698. doi:10.4028/www.scientific.net/AMR10.4028/www.scientific.net/amr.93-94.695
Evans, J. S. O., Mary, T. A., and Sleight, A. W. (1995). Structure of Zr2(WO4)(PO4)2 from Powder X-Ray Data: Cation Ordering with No Superstructure. J. Solid State. Chem. 120, 101–104. doi:10.1006/jssc.1995.1383
Evans, J. S. O., Mary, T., and Sleight, A. W. (1997). Compressibility, Phase Transitions, and Oxygen Migration in Zirconium Tungstate, ZrW2O8. J. Solid State. Chem. 275, 61–65. doi:10.1126/science.275.5296.61
Evans, J. S. O., Mary, T. A., and Sleight, A. W. (1998a). Negative Thermal Expansion Materials. Phys. B 243, 311–316. doi:10.1016/S0921-4526(97)00571-1
Evans, J. S. O., Mary, T. A., and Sleight, A. W. (1998b). Negative Thermal Expansion in Sc2(WO4)3. J. Solid State. Chem. 137, 148–160. doi:10.1006/jssc.1998.7744
Evans, J. S. O. (1999). Negative Thermal Expansion Materials. J. Chem. Soc. Dalton Trans., 3317–3326. doi:10.1039/a904297k
Evans, J. S. O., and Mary, T. A. (2000). Structural Phase Transitions and Negative Thermal Expansion in Sc2(MoO4)3. Int. J. Inorg. Mater. 2, 143–151. doi:10.1016/S1466-6049(00)00012-X
Fang, H., Dove, M. T., and Phillips, A. E. (2014a). Common Origin of Negative Thermal Expansion and Other Exotic Properties in Ceramic and Hybrid Materials. Phys. Rev. B 89, 214103. doi:10.1103/PhysRevB.89.214103
Fang, H., and Dove, M. T. (2013b). Pressure-Induced Softening as a Common Feature of Framework Structures with Negative Thermal Expansion. Phys. Rev. B 87, 214109. doi:10.1103/PhysRevB.87.214109
Fang, H., Dove, M. T., and Refson, K. (2014b). Ag-Ag Dispersive Interaction and Physical Properties of Ag3Co(CN)6. Phys. Rev. B 90, 054302. doi:10.1103/PhysRevB.90.054302
Fang, H., Phillips, A. E., Dove, M. T., Tucker, M. G., and Goodwin, A. L. (2013a). Temperature-Dependent Pressure-Induced Softening in Zn(CN)2. Phys. Rev. B 88, 144103. doi:10.1103/PhysRevB.88.144103
Fornasini, P., Dalba, G., Grisenti, R., Purans, J., Vaccari, M., Rocca, F., et al. (2006). Local Behaviour of Negative Thermal Expansion Materials. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 246, 180–183. doi:10.1016/j.nimb.2005.12.062
Forster, P. M., and Sleight, A. W. (1999). Negative Thermal Expansion in Y2W3O12. Int. J. Inorg. Mater. 1, 123–127. doi:10.1016/S1466-6049(99)00021-5
Forster, P. M., Yokochi, A., and Sleight, A. W. (1998). Enhanced Negative Thermal Expansion in Lu2W3O12. J. Solid State. Chem. 140, 157–158. doi:10.1006/jssc.1998.7967
Gao, S., Nan, Z., Li, Y., Zhao, N., Liu, Q., Xu, G., et al. (2020). Copper Matrix Thermal Conductive Composites with Low Thermal Expansion for Electronic Packaging. Ceramics Int. 46, 18019–18025. doi:10.1016/j.ceramint.2020.04.117
Gao, S., Zhao, N., Liu, Q., Li, Y., Xu, G., Cheng, X., et al. (2019). Sc2W3O12/Cu Composites with Low Thermal Expansion Coefficient and High Thermal Conductivity for Efficient Cooling of Electronics. J. Alloys Comp. 779, 108–114. doi:10.1016/j.jallcom.2018.11.131
Gates, S. D., Colin, J. A., and Lind, C. (2006). Non-Hydrolytic Sol-Gel Synthesis, Properties, and High-Pressure Behavior of Gallium Molybdate. J. Mater. Chem. 16, 4214–4219. doi:10.1039/b608864c
Ge, X.-H., Mao, Y.-C., Li, L., Li, L.-P., Yuan, N., Cheng, Y.-G., et al. (2016a). Phase Transition and Negative Thermal Expansion Property of ZrMnMo3O12. Chin. Phys. Lett. 33, 046503. doi:10.1088/0256-307X/33/4/046503
Ge, X., Liu, X., Cheng, Y., Yuan, B., Chen, D., Chao, M., et al. (2016b). Negative Thermal Expansion and Photoluminescence Properties in a Novel Material ZrScW2PO12. J. Appl. Phys. 120, 205101. doi:10.1063/1.4968546
Ge, X., Mao, Y., Liu, X., Cheng, Y., Yuan, B., Chao, M., et al. (2016c). Negative Thermal Expansion and Broad Band Photoluminescence in a Novel Material of ZrScMo2VO12. Sci. Rep. 6, 1–8. doi:10.1038/srep24832
Giddy, A. P., Dove, M. T., Pawley, G. S., and Heine, V. (1993). The Determination of Rigid-Unit Modes as Potential Soft Modes for Displacive Phase Transitions in Framework crystal Structures. Acta Cryst. Sect A. 49, 697–703. doi:10.1107/S0108767393002545
Goodwin, A. L., Calleja, M., Conterio, M. J., Dove, M. T., Evans, J. S. O., Keen, D. A., et al. (2008). Colossal Positive and Negative Thermal Expansion in the Framework Material Ag3[Co(CN)6]. Science 319, 794–797. doi:10.1126/science.1151442
Grüneisen, E. (1912). Theorie des festen Zustandes einatomiger Elemente. Ann. Phys. 344, 257–306. doi:10.1002/andp.19123441202
Hammonds, K. D., Bosenick, A., Dove, M. T., and Heine, V. (1998). Rigid Unit Modes in Crystal Structures with Octahedrally Coordinated Atoms. Am. Mineral. 83, 476–479. doi:10.2138/am-1998-5-607
Hammonds, K. D., Dove, M. T., Giddy, A. P., Heine, V., and Winkler, B. (1996). Rigid-Unit Phonon Modes and Structural Phase Transitions in Framework Silicates. Am. Mineral. 81, 1057–1079. doi:10.2138/am-1996-9-1003
Harris, D. C. (2010). Optical Properties of Infrared Windows. Bellingham, Washington, USA: SPIE Optical Engineering Press, 63–83. doi:10.1117/3.349896.ch2
Hazen, R. M., and Prewitt, C. T. (1988). Effects of Temperature and Pressure on Interatomic Distances in Oxygen-Based Minerals. Am. Mineral. 62, 407–413. doi:10.1029/sp026p0407
Heinen, J., Ready, A. D., Bennett, T. D., Dubbeldam, D., Friddle, R. W., and Burtch, N. C. (2018). Elucidating the Variable-Temperature Mechanical Properties of a Negative Thermal Expansion Metal-Organic Framework. ACS Appl. Mater. Inter. 10, 21079–21083. doi:10.1021/acsami.8b06604
Hester, B. R., Hancock, J. C., Lapidus, S. H., and Wilkinson, A. P. (2017). Composition, Response to Pressure, and Negative Thermal Expansion in MIIBIVF6 (M = Ca, Mg; B = Zr, Nb). Chem. Mater. 29 (2), 823–831. doi:10.1021/acs.chemmater.6b04809
Hitchcock, F. R. M. (1895). The Tungstates and Molybdates of the Rare Earths. J. Am. Chem. Soc. 17, 520–537. doi:10.1021/ja02162a006
Hofmeister, A. M. (1991). Pressure Derivatives of the Bulk Modulus. J. Geophys. Res. 96, 21893–21907. doi:10.1029/91JB02157
Holzer, H., and Dunand, D. C. (1999). Phase Transformation and Thermal Expansion of Cu/ZrW2O8 Metal Matrix Composites. J. Mater. Res. 14, 780–789. doi:10.1557/JMR.1999.0104
Imanaka, N., Kobayashi, Y., Fujiwara, K., Asano, T., Okazaki, Y., and Adachi, G.-y. (1998). Trivalent Rare Earth Ion Conduction in the Rare Earth Tungstates With the Sc2(WO4)3-type Structure. Chem. Mater. 10, 2006–2012. 2006–2012. doi:10.1021/cm980157e
Imanaka, N. (2005). Novel Multivalent Cation Conducting Ceramics and Their Application. J. Ceram. Soc. Jpn. 113, 387–393. doi:10.2109/jcersj.113.387
Isobe, T., Hayakawa, Y., Adachi, Y., Uehara, R., Matsushita, S., and Nakajima, A. (2020). Negative Thermal Expansion in α-Zr2SP2O12 Based on Phase Transition- and Framework-type Mechanisms. NPG Asia Mater. 12, 80. doi:10.1038/s41427-020-00266-9
Isobe, T., Umezome, T., Kameshima, Y., Nakajima, A., and Okada, K. (2009). Preparation and Properties of Negative Thermal Expansion Zr2WP2O12 Ceramics. Mater. Res. Bull. 44, 2045–2049. doi:10.1016/j.materresbull.2009.07.020
Jakubinek, M. B., Whitman, C. A., and White, M. A. (2010). Negative Thermal Expansion Materials. J. Therm. Anal. Calorim. 99, 165–172. doi:10.1007/s10973-009-0458-9
Jardim, P. M., Garcia, E. S., and Marinkovic, B. A. (2016). Young׳s Modulus, Hardness and Thermal Expansion of Sintered Al2W3O12 with Different Porosity Fractions. Ceramics Int. 42, 5211–5217. doi:10.1016/j.ceramint.2015.12.045
Karmakar, S., Deb, S. K., Tyagi, A. K., and Sharma, S. M. (2004). Pressure-Induced Amorphization in Y2(WO4)3: In Situ X-ray Diffraction and Raman Studies. J. Solid State. Chem. 177, 4087–4092. doi:10.1016/j.jssc.2004.08.020
Karunarathne, A., Parajuli, P., Priyadarshan, G., Bhattacharya, S., Rao, R., Wei, P.-C., et al. (2021). Anisotropic Elasticity Drives Negative Thermal Expansion in Monocrystalline SnSe. Phys. Rev. B 103, 054108. doi:10.1103/PhysRevB.103.054108
Kennedy, C. A., and White, M. A. (2005). Unusual Thermal Conductivity of the Negative Thermal Expansion Material, ZrW2O8. Solid State. Commun. 134, 271–276. doi:10.1016/j.ssc.2005.01.031
Kennedy, C. A., White, M. A., Wilkinson, A. P., and Varga, T. (2007). Low thermal Conductivity of the Negative Thermal Expansion Material, HfMo2O8. Appl. Phys. Lett. 90, 151906. doi:10.1063/1.2721860
Keuter, P., Ravensburg, A. L., Hans, M., Karimi Aghda, S., Holzapfel, D. M., Primetzhofer, D., et al. (2020). A Proposal for a Composite with Temperature-independent Thermophysical Properties: HfV2-HfV2O7. Materials 13, 5021. doi:10.3390/ma13215021
Kochmann, D. M., and Bertoldi, K. (2017). Exploiting Microstructural Instabilities in Solids and Structures: from Metamaterials to Structural Transitions. Appl. Mech. Rev. 69, 050801. doi:10.1115/1.4037966
Koh, J.-H., Sorge, E., Wen, T.-C., and Shetty, D. K. (2013). Thermal Expansion Behaviors of Yttrium Tungstates in the WO3-Y2O3 System. Ceramics Int. 39, 8421–8427. doi:10.1016/j.ceramint.2013.04.024
Köhler, J., Imanaka, N., and Adachi, G.-y. (1999). New Cation Conducting Solid Electrolytes With the Sc2(WO4)3 Type Structure. J. Mater. Chem. 9, 1357–1362. doi:10.1039/a900999j
Kol’tsova, T. N. (2001). X-ray Diffraction Study of Y2W3O12·3H2O. Inorg. Mater. 37, 1375–1377. doi:10.1002/chin.201652004
Kreher, W. (1990). Residual Stresses and Stored Elastic Energy of Composites and Polycrystals. J. Mech. Phys. Sol. 38, 115–128. doi:10.1016/0022-5096(90)90023-w
Kreher, W. S. (1996). Modeling of Random Microstructural Stresses and Grain Boundary Damage in Polycrystals. Comput. Mater. Sci. 7, 147–153. doi:10.1016/S0927-0256(96)00073-0
Krstic, V. V., Nicholson, P. S., and Hoagland, R. G. (1981). Toughening of Glasses by Metallic Particles. J. Am. Ceram. Soc. 64, 499–504. doi:10.1111/j.1151-2916.1981.tb10313.x
Lee, J. K., Earmme, Y. Y., Aaronson, H. I., and Russell, K. C. (1980). Plastic Relaxation of the Transformation Strain Energy of a Misfitting Spherical Precipitate: Ideal Plastic Behavior. Metall. Trans. A. 11, 1837–1847. doi:10.1007/BF02655099
Li, Q.-J., Yuan, B.-H., Song, W.-B., Liang, E.-J., and Yuan, B. (2012). The Phase Transition, Hygroscopicity, and Thermal Expansion Properties of Yb2−XAlXMo3O12. Chin. Phys. B 21, 046501–046507. doi:10.1088/1674-1056/21/4/046501
Li, S., Ge, X., Yuan, H., Chen, D., Guo, J., Shen, R., et al. (2018). Near-Zero Thermal Expansion and Phase Transitions in HfMg1−xZnxMo3O12. Front. Chem. 6, 1–9. doi:10.3389/fchem.2018.00115
Li, T., Liu, X.-S., Cheng, Y.-G., Ge, X.-H., Zhang, M.-D., Lian, H., et al. (2017). Zero and Controllable Thermal Expansion in HfMgMo3-xWxO12. Chin. Phys. B 26, 016501–016507. doi:10.1088/1674-1056/26/1/016501
Li, X., Xu, H., Xia, X., Xie, F., Zhong, S., and Xu, D. (2019). One-step Synthesis of Sc2W3O12:Eu3+ Phosphors with Tunable Luminescence for WLED. Ceramics Int. 45, 10461–10467. doi:10.1016/j.ceramint.2019.02.107
Li, Z. Y., Song, W. B., and Liang, E. J. (2011). Structures, Phase Transition, and Crystal Water of Fe2-xYxMo3O12. J. Phys. Chem. C 115, 17806–17811. doi:10.1021/jp201962b
Liang, E., Huo, H., Wang, J., and Chao, M. (2008). Effect of Water Species on the Phonon Modes in Orthorhombic Y2(MoO4)3 Revealed by Raman Spectroscopy. J. Phys. Chem. C 112, 6577–6581. doi:10.1021/jp8013332
Liang, Y., Cheng, Y.-G., Ge, X.-H., Yuan, B.-H., Guo, J., Sun, Q., et al. (2017). Negative Thermal Expansion and Photoluminescence in Solid Solution (HfSc)0.83W2.25P0.83O12–δ. Chin. Phys. B 26, 106501. doi:10.1088/1674-1056/26/10/106501
Lim, T.-C. (2011). Coefficient of Thermal Expansion of Stacked Auxetic and Negative Thermal Expansion Laminates. Phys. Stat. Sol. (B) 248, 140–147. doi:10.1002/pssb.200983970
Lin, F. J. T., Jonghe, L. C., and Rahaman, M. N. (1997). Microstructure Refinement of Sintered Alumina by a Two-step Sintering Technique. J. Am. Ceram. Soc. 80, 2269–2277. doi:10.1111/j.1151-2916.1997.tb03117.x
Lind, C. (2012). Two Decades of Negative Thermal Expansion Research: Where Do We Stand? Materials 5, 1125–1154. doi:10.3390/ma5061125
Liu, C., Yu, L., Ma, Z., Liu, Y., Liu, C., Li, H., et al. (2020). Damping Capacity of Al-12Si Composites Effected by Negative Thermal Expansion of Y2W3O12 Particle Inclusions. J. Mater. Res. Tech. 9, 9985–9995. doi:10.1016/j.jmrt.2020.07.008
Liu, H., Sun, W., Xie, X., Yang, L., Zhang, Z., Zhou, M., et al. (2018). Adjustable Thermal Expansion Properties in Zr2MoP2O12/ZrO2 Ceramic Composites. Front. Chem. 6, 1–6. doi:10.3389/fchem.2018.00347
Liu, H., Sun, W., Zhang, Z., Lovings, L. N., and Lind, C. (2021). Thermal Expansion Behavior in the A2M3O12 Family of Materials. Solids 2, 87–107. doi:10.3390/solids2010005
Liu, J., Maynard-Casely, H. E., Brand, H. E. A., and Sharma, N. (2021). Sc1.5Al0.5W3O12 Exhibits Zero Thermal Expansion between 4 and 1400 K. Chem. Mater. 33, 3823–3831. doi:10.1021/acs.chemmater.1c01007
Liu, Q. Q., Cheng, X. N., and Yang, J. (2012). Development of Low Thermal Expansion Sc2(WO4)3 Containing Composites. Mater. Tech. 27, 388–392. doi:10.1179/1066785712Z.00000000094
Liu, X.-S., Cheng, F.-X., Wang, J.-Q., Song, W.-B., Yuan, B.-H., and Liang, E.-J. (2013). The Control of Thermal Expansion and Impedance of Al-Zr2(WO4)(PO4)2 Nano-Cermets for Near-Zero-Strain Al alloy and fine Electrical Components. J. Alloys Comp. 553, 1–7. doi:10.1016/j.jallcom.2012.11.010
Liu, X.-S., Cheng, Y.-G., Yuan, B.-H., Liang, E.-J., and Zhang, W.-F. (2019). Laser Scattering, Transmittance and Low Thermal Expansion Behaviors in Y2-x(ZnLi)xMo3O12 by Forming Regular Grains. Chin. Phys. B 28, 096501. doi:10.1088/1674-1056/ab3435
Liu, X., Yuan, B., Cheng, Y., Ge, X., Liang, E., and Zhang, W. (2017). Avoiding the Invasion of H2O into Y2Mo3O12 by Coating with C3N4 to Improve Negative Thermal Expansion Properties. Phys. Chem. Chem. Phys. 19, 13443–13448. doi:10.1039/c7cp02262j
Liu, X. Z., Hao, L. J., Wu, M. M., Ma, X. B., Chen, D. F., and Liu, Y. T. (2015). The Structure, Thermal Expansion and Phase Transition Properties of Ho2Mo3−xWxO12 (x=0, 1.0, 2.0) Solid Solutions. Mater. Res. Bull. 70, 640–644. doi:10.1016/j.materresbull.2015.05.021
Liu, Q., Fan, C., Wu, G., Zhao, Y., Sun, X., Cheng, X., et al. (2015). In-situ Synthesis of Sc2W3O12/YSZ Ceramic Composites with Controllable Thermal Expansion. Ceramics Int. 41, 8267–8271. doi:10.1016/j.ceramint.2015.03.021
Luchini, B., Sciuti, V. F., Angélico, R. A., Canto, R. B., and Pandolfelli, V. C. (2017). Critical Inclusion Size Prediction in Refractory Ceramics via Finite Element Simulations. J. Eur. Ceram. Soc. 37, 315–321. doi:10.1016/j.jeurceramsoc.2016.08.008
Lv, H., Du, P., Luo, L., and Li, W. (2021). Negative Thermal Expansion Triggered Anomalous Thermal Upconversion Luminescence Behaviors in Er3+/Yb3+-Codoped Y2Mo3O12 Microparticles for Highly Sensitive Thermometry. Mater. Adv. 2, 2642–2648. doi:10.1039/d1ma00072a
Machado, T. M., Muller Costa, I. L., Dosen, A., Lima de Faro Melo, G. S., Vasconcellos, L. E., and Marinkovic, B. A. (2021). Hygroscopicity, Phase Transition and Thermal Expansion in Yb2-xGaxW3O12 System. J. Alloys Comp. 854, 156643. doi:10.1016/j.jallcom.2020.156643
Madrid, A., Pontón, P. I., Garcia, F., Johnson, M. B., White, M. A., and Marinkovic, B. A. (2020). Solubility Limit of Zn2+ in Low Thermal Expansion ZrMgMo3O12 and its Influence on Phase Transition Temperature. Ceramics Int. 46, 3979–3983. doi:10.1016/j.ceramint.2019.09.252
Makovicky, E., and Balić-Žunić, T. (1998). New Measure of Distortion for Coordination Polyhedra. Acta Crystallogr. Sect B 54, 766–773. doi:10.1107/S0108768198003905
Marinkovic, B. A., Ari, M., de Avillez, R. R., Rizzo, F., Ferreira, F. F., Miller, K. J., et al. (2009). Correlation between AO6 Polyhedral Distortion and Negative Thermal Expansion in Orthorhombic Y2Mo3O12 and Related Materials. Chem. Mater. 21, 2886–2894. doi:10.1021/cm900650c
Marinkovic, B. A., Ari, M., Jardim, P. M., de Avillez, R. R., Rizzo, F., and Ferreira, F. F. (2010). In2Mo3O12: A Low Negative Thermal Expansion Compound. Thermochim. Acta 499, 48–53. doi:10.1016/j.tca.2009.10.021
Marinkovic, B. A., Jardim, P. M., Ari, M., Avillez, R. R. d., Rizzo, F., and Ferreira, F. F. (2008a). Low Positive Thermal Expansion in HfMgMo3O12. Phys. Stat. Sol. (B) 245, 2514–2519. doi:10.1002/pssb.200880262
Marinkovic, B. A., Jardim, P. M., De Avillez, R. R., and Rizzo, F. (2005). Negative Thermal Expansion in Y2Mo3O12. Solid State. Sci. 7, 1377–1383. doi:10.1016/j.solidstatesciences.2005.08.012
Marinkovic, B. A., Jardim, P. M., Rizzo, F., Saavedra, A., Lau, L. Y., and Suard, E. (2008b). Complex Thermal Expansion Properties of Al-Containing HZSM-5 Zeolite: A X-ray Diffraction, Neutron Diffraction and Thermogravimetry Study. Microporous Mesoporous Mater. 111, 110–116. doi:10.1016/j.micromeso.2007.07.015
Marinkovic, B. A., Jardim, P. M., Saavedra, A., Lau, L. Y., Baehtz, C., de Avillez, R. R., et al. (2004). Negative Thermal Expansion in Hydrated HZSM-5 Orthorhombic Zeolite. Microporous Mesoporous Mater. 71, 117–124. doi:10.1016/j.micromeso.2004.03.023
Marinkovic, B. A., Machado, T. M., de Avillez, R. R., Madrid, A., de Melo Toledo, P. H., and Andrade, G. F. S. (2021). Zero Thermal Expansion in ZrMg1-xZnxMo3O12. Ceramics Int. 47, 26567–26571. doi:10.1016/j.ceramint.2021.05.280
Mary, T. A., and Sleight, A. W. (1999). Bulk Thermal Expansion for Tungstate and Molybdates of the Type A2M3O12. J. Mater. Res. 14, 912–915. doi:10.1557/JMR.1999.0122
Marzano, M., Pontón, P. I., and Marinkovic, B. A. (2019). Co-precipitation of Low-Agglomerated Y2W3O12 Nanoparticles: The Effects of Aging Time, Calcination Temperature and Surfactant Addition. Ceramics Int. 45, 20189–20196. doi:10.1016/j.ceramint.2019.06.288
Miller, K. J., Johnson, M. B., White, M. A., and Marinkovic, B. A. (2012a). Low-Temperature Investigations of the Open-Framework Material HfMgMo3O12. Solid State. Commun. 152, 1748–1752. doi:10.1016/j.ssc.2012.06.022
Miller, K. J., Romao, C. P., Bieringer, M., Marinkovic, B. A., Prisco, L., and White, M. A. (2012b). Near-Zero Thermal Expansion in In(HfMg)0.5Mo3O12. J. Am. Ceram. Soc. 96 (2), 561–566. doi:10.1111/jace.12085],
Miller, K. J., Romao, C. P., Bieringer, M., Marinkovic, B. A., Prisco, L., and White, M. A. (2013). Near-Zero Thermal Expansion in In(HfMg)0.5Mo3O12. J. Am. Ceram. Soc. 96, 561–566. doi:10.1111/jace.12085
Miller, W., Smith, C. W., Dooling, P., Burgess, A. N., and Evans, K. E. (2010). Reduced Thermal Stress in Composites via Negative Thermal Expansion Particulate Fillers. Composites Sci. Tech. 70, 318–327. doi:10.1016/j.compscitech.2009.11.003
Nakamura, Y., Takenaka, K., Kishimoto, A., and Takagi, H. (2009). Mechanical Properties of Metallic Perovskite Mn3Cu0.5Ge0.5N:High-Stiffness Isotropic Negative Thermal Expansion Material. J. Am. Ceram. Soc. 92, 2999–3003. doi:10.1111/j.1551-2916.2009.03297.x
Nanthamathee, C., Ling, S., Slater, B., and Attfield, M. P. (2015). Contradistinct Thermoresponsive Behavior of Isostructural MIL-53 Type Metal-Organic Frameworks by Modifying the Framework Inorganic Anion. Chem. Mater. 27, 85–95. doi:10.1021/cm503311x
Nassau, K., Levinstein, H. J., and Loiacono, G. M. (1965). A Comprehensive Study of Trivalent Tungstates and Molybdates of the Type L2(MO4)3. J. Phys. Chem. Sol. 26, 1805–1816. doi:10.1016/0022-3697(65)90213-1
Nassau, K., Levinstein, H. J., and Loiacono, O. M. (1964). Trivalent Rare-Earth Tungstates of the Type M2(WO4)3. J. Am. Ceram. Soc. 47, 363–364. doi:10.1111/j.1151-2916.1964.tb13005.x
Occhialini, C. A., Guzmán-Verri, G. G., Handunkanda, S. U., and Hancock, J. N. (2018). Negative Thermal Expansion Near the Precipice of Structural Stability in Open Perovskites. Front. Chem. 6, 545. doi:10.3389/fchem.2018.00545
Omote, A., Yotsuhashi, S., Zenitani, Y., and Yamada, Y. (2011). High Ion Conductivity in MgHf(WO4)3 Solids with Ordered Structure: 1-D Alignments of Mg2+ and Hf4+ Ions. J. Am. Ceram. Soc. 94, 2285–2288. doi:10.1111/j.1551-2916.2011.04644.x
Orellana, T., Tejado, E. M., Funke, C., Fütterer, W., Riepe, S., Moller, H. J., et al. (2015). How Do Impurity Inclusions Influence the Mechanical Properties of Multicrystalline Silicon? Int. J. Metall. Mater. Eng. 1, 1–11. doi:10.15344/2455-2372/2015/101
Ortiz, A. U., Boutin, A., Fuchs, A. H., and Coudert, F.-X. (2012). Anisotropic Elastic Properties of Flexible Metal-Organic Frameworks: How Soft Are Soft Porous Crystals? Phys. Rev. Lett. 109, 195502. doi:10.1103/PhysRevLett.109.195502
Palmero, P. (2015). Structural Ceramic Nanocomposites: A Review of Properties and Powders' Synthesis Methods. Nanomaterials 5, 656–696. doi:10.3390/nano5020656
Pan, W., Phillpot, S. R., Wan, C., Chernatynskiy, A., and Qu, Z. (2012). Low Thermal Conductivity Oxides. MRS Bull. 37, 917–922. doi:10.1557/mrs.2012.234
Peng, J., Wu, M. M., Guo, F. L., Han, S. B., Liu, Y. T., Chen, D. F., et al. (2011). Crystal Structure and Negative Thermal Expansion of Solid Solution Y2W3−xMoxO12. J. Mater. Sci. 46, 5160–5164. doi:10.1007/s10853-011-5447-2
Peng, J., Wu, M. M., Wang, H., Hao, Y. M., Hu, Z., Yu, Z. X., et al. (2008). Structures and Negative Thermal Expansion Properties of Solid Solutions YxNd2−xW3O12 (x=0.0-1.0, 1.6-2.0). J. Alloys Comp. 453, 49–54. doi:10.1016/j.jallcom.2006.11.208
Peng, Z., Sun, Y. Z., and Peng, L. M. (2014). Hydrothermal Synthesis of ZrW2O8 Nanorods and its Application in ZrW2O8/Cu Composites with Controllable Thermal Expansion Coefficients. Mater. Des. 54, 989–994. doi:10.1016/j.matdes.2013.09.012
Petermann, K., and Mitzscherlich, P. (1987). Spectroscopic and Laser Properties of Cr3+-Doped Al2(WO4)3 and Sc2(WO4)3. IEEE J. Quan. Electron. 23, 1122–1126. doi:10.1109/JQE.1987.1073477
Piffard, Y., Verbaere, A., and Kinoshita, M. (1987). β-Zr2(PO4)2SO4: A Zirconium Phosphato-Sulfate with a Sc2(WO4)3 Structure. A Comparison between Garnet, Nasicon, and Sc2(WO4)3 Structure Types. J. Solid State. Chem. 71, 121–130. doi:10.1016/0022-4596(87)90150-2
Pley, M., and Wickleder, M. S. (2005). Two Crystalline Modifications of RuO4. J. Solid State. Chem. 178, 3206–3209. doi:10.1016/j.jssc.2005.07.021
Plyasova, L. M., Borisov, S. V., and Belov, N. V. (1967). The Garnet Pattern in the Structure of Iron Molybdate. Sov. Physics-crystallography 12, 25–27.
Pontón, P. I., Prisco, L. P., Dosen, A., Faro, G. S., de Abreu, M. A. S., and Marinkovic, B. A. (2017). Co-precipitation Synthesis of Y2W3O12 Submicronic Powder. Ceramics Int. 43, 4222–4228. doi:10.1016/j.ceramint.2016.12.055
Pontón, P. I., Prisco, L. P., and Marinkovic, B. A. (2018). Effects of Low Contents of A2M3O12 Submicronic Thermomiotic-like Fillers on Thermal Expansion and Mechanical Properties of HDPE-Based Composites. Polym. Compos. 39, E1821–E1833. doi:10.1002/pc.24811
Pontón, P. I., Yamada, K., Guamán, M. V., Johnson, M. B., White, M. A., and Marinkovic, B. A. (2019a). Data Supporting Micromechanical Models for the Estimation of Young's Modulus and Coefficient of Thermal Expansion of Titanate nanotube/Y2W3O12/HDPE Ternary Composites. Data in Brief 25, 104247. doi:10.1016/j.dib.2019.104247
Pontón, P. I., Yamada, K., Guamán, M. V., Johnson, M. B., White, M. A., Pandoli, O., et al. (2019b). The Effect of Titanate nanotube/Y2W3O12 Hybrid Fillers on Mechanical and Thermal Properties of HDPE-Based Composites. Mater. Today Commun. 18, 124–135. doi:10.1016/j.mtcomm.2018.11.014
Pourmortazavi, S. M., Rahimi-Nasrabadi, M., Aghazadeh, M., Ganjali, M. R., Karimi, M. S., and Norouzi, P. (2017). Synthesis of Sm2(WO4)3 Nanocrystals via a Statistically Optimized Route and Their Photocatalytic Behavior. Mater. Res. Express 4, 035012. doi:10.1088/2053-1591/4/3/035012
Prisco, L. P., Marzano, M., Pontón, P. I., Costa, A. M. L. M., da Costa Neto, C. A., Sweet, G., et al. (2019). Relationship between Sintering Methods and Physical Properties of the Low Positive Thermal Expansion Material Al2W3O12. Int. J. Appl. Ceram. Technol. 16, 346–356. doi:10.1111/ijac.13054
Prisco, L. P., Pontón, P. I., Guamán, M. V., Avillez, R. R., Romao, C. P., Johnson, M. B., et al. (2016b). Assessment of the Thermal Shock Resistance Figures of Merit of Al2W3O12, a Low Thermal Expansion Ceramic. J. Am. Ceram. Soc. 99, 1742–1748. doi:10.1111/jace.14160
Prisco, L. P., Pontón, P. I., Paraguassu, W., Romao, C. P., White, M. A., and Marinkovic, B. A. (2016a). Near-zero Thermal Expansion and Phase Transition in In0.5(ZrMg)0.75Mo3O12. J. Mater. Res. 31, 3240–3248. doi:10.1557/jmr.2016.329
Prisco, L. P., Romao, C. P., Rizzo, F., White, M. A., and Marinkovic, B. A. (2013). The Effect of Microstructure on Thermal Expansion Coefficients in Powder-Processed Al2Mo3O12. J. Mater. Sci. 48, 2986–2996. doi:10.1007/s10853-012-7076-9
Qiu, L., and White, M. A. (2001). The Constituent Additivity Method to Estimate Heat Capacities of Complex Inorganic Solids. J. Chem. Educ. 78, 1076. doi:10.1021/ed078p1076
Qu, J., Kadic, M., Naber, A., and Wegener, M. (2017). Micro-structured Two-Component 3D Metamaterials with Negative Thermal-expansion Coefficient from Positive Constituents. Sci. Rep. 7, 40643. doi:10.1038/srep40643
Ramachandran, V., and Srinivasan, R. (1972). Generalised Grüneisen Parameters of Elastic Waves in Calcite and its Thermal Expansion. J. Phys. Chem. Sol. 33, 1921–1926. doi:10.1016/S0022-3697(72)80491-8
Rao, K. V. K., Naidu, S. V. N., and Murthy, K. S. (1968). Precision Lattice Parameters and Thermal Expansion of Calcite. J. Phys. Chem. Sol. 29, 245–248. doi:10.1016/0022-3697(68)90068-1
Rao, R. R. (1974). Anderson-Grüneisen Parameter δ of Some Hexagonal Metals and MgO from Third-Order Elastic-Constant Data. Phys. Rev. B 10, 4173–4177. doi:10.1103/PhysRevB.10.4173
Rather, S. A., and Saha, B. K. (2021). Understanding the Elastic Bending Mechanism in a 9,10-Anthraquinone Crystal Through Thermal Expansion Study. CrystEngComm. In press in. doi:10.1039/D1CE00467K
Rimmer, L. H. N., and Dove, M. T. (2015). Simulation Study of Negative Thermal Expansion in Yttrium Tungstate Y2W3O12. J. Phys. Condens. Matter 27, 185401. doi:10.1088/0953-8984/27/18/185401
Romao, C. P. (2017). Anisotropic Thermal Expansion in Flexible Materials. Phys. Rev. B 96, 134113. doi:10.1103/PhysRevB.96.134113
Romao, C. P. (2019). Anomalous Thermal Expansion and Chiral Phonons in BiB3O6. Phys. Rev. B 100, 060302. doi:10.1103/PhysRevB.100.060302
Romao, C. P., Donegan, S. P., Zwanziger, J. W., and White, M. A. (2016). Relationships between Elastic Anisotropy and Thermal Expansion in A2Mo3O12 materials. Phys. Chem. Chem. Phys. 18, 30652–30661. doi:10.1039/C6CP06356J
Romao, C. P., Marinkovic, B. A., Werner-Zwanziger, U., and White, M. A. (2015a). Thermal Expansion Reduction in Alumina-Toughened Zirconia by Incorporation of Zirconium Tungstate and Aluminum Tungstate. J. Am. Ceram. Soc. 98, 2858–2865. doi:10.1111/jace.13675
Romao, C. P., Miller, K. J., Johnson, M. B., Zwanziger, J. W., Marinkovic, B. A., and White, M. A. (2014). Thermal, Vibrational, and Thermoelastic Properties of Y2Mo3O12 and Their Relations to Negative Thermal Expansion. Phys. Rev. B 90, 024305. doi:10.1103/PhysRevB.90.024305
Romao, C. P., Miller, K. J., Whitman, C. A., White, M. A., and Marinkovic, B. A. (2013). “Negative Thermal Expansion (Thermomiotic) Materials,” in Comprehensive Inorganic Chemistry II. Editors J. Reedijk, and K. Poeppelmeier (Oxford, UK: Elsevier), Vol. 2, 127–151. doi:10.1016/B978-0-08-097774-4.00425-3
Romao, C. P., Perras, F. A., Werner-Zwanziger, U., Lussier, J. A., Miller, K. J., Calahoo, C. M., et al. (2015b). Zero Thermal Expansion in ZrMgMo3O12: NMR Crystallography Reveals Origins of Thermoelastic Properties. Chem. Mater. 27, 2633–2646. doi:10.1021/acs.chemmater.5b00429
Romao, C. P., and White, M. A. (2016). Negative Stiffness in ZrW2O8 Inclusions as a Result of Thermal Stress. Appl. Phys. Lett. 109, 031902. doi:10.1063/1.4959094
Schapery, R. A. (1968). Thermal Expansion Coefficients of Composite Materials Based on Energy Principles. J. Compos. Mater. 2, 380–404. doi:10.1177/002199836800200308
Secco, R. A., Liu, H., Imanaka, N., and Adachi, G. (2001). Pressure-induced Amorphization in Negative Thermal Expansion Sc2(WO4)3. J. Mater. Sci. Lett. 20, 1339–1340. doi:10.1023/A:1010967021588
Selsing, J. (1961). Internal Stresses in Ceramics. J. Am. Ceram. Soc. 44, 419. doi:10.1111/j.1151-2916.1961.tb15475.x
Shang, R., Hu, Q., Liu, X., Liang, E., Yuan, B., and Chao, M. (2013). Effect of MgO and PVA on the Synthesis and Properties of Negative Thermal Expansion Ceramics of Zr2(WO4)(PO4)2. Int. J. Appl. Ceram. Technol. 10, 849–856. doi:10.1111/j.1744-7402.2012.02787.x
Sharma, G. R., Lind, C., and Coleman, M. R. (2012). Preparation and Properties of Polyimide Nanocomposites with Negative Thermal Expansion Nanoparticle Filler. Mater. Chem. Phys. 137, 448–457. doi:10.1016/j.matchemphys.2012.09.009
Shen, R., Yuan, B., Li, S., Ge, X., Guo, J., and Liang, E. (2018). Near-zero Thermal Expansion of ZrxHf1-xMgMo3O12 in a Larger Temperature Range. Optik 165, 1–6. doi:10.1016/j.ijleo.2018.03.035
Shi, X., Lian, H., Yan, X., Qi, R., Yao, N., and Li, T. (2016). Fabrication and Properties of Polyimide Composites Filled with Zirconium Tungsten Phosphate of Negative Thermal Expansion. Mater. Chem. Phys. 179, 72–79. doi:10.1016/j.matchemphys.2016.05.011
Shi, X., Zhou, Q., Yan, X., Li, X., and Zhu, B. (2020). Preparation and Properties of Zr2WP2O12 with Negative Thermal Expansion without Sintering Additives. Pac 14, 173–180. doi:10.2298/PAC2002173S
Shirasu, K., Nakamura, A., Yamamoto, G., Ogasawara, T., Shimamura, Y., Inoue, Y., et al. (2017). Potential Use of CNTs for Production of Zero Thermal Expansion Coefficient Composite Materials: An Experimental Evaluation of Axial Thermal Expansion Coefficient of CNTs Using a Combination of Thermal Expansion and Uniaxial Tensile Tests. Compos. Part. A. 95, 152–160. doi:10.1016/j.compositesa.2016.12.027
Sigmund, O., and Torquato, S. (1997). Design of Materials with Extreme Thermal Expansion Using a Three-phase Topology Optimization Method. J. Mech. Phys. Sol. 45 (6), 1037–1067. doi:10.1016/s0022-5096(96)00114-7
Sleight, A. W., and Brixner, L. H. (1973). A New Ferroelastic Transition in Some A2(MO4)3 Molybdates and Tungstates. J. Solid State. Chem. 7, 172–174. doi:10.1016/0022-4596(73)90152-7
Sleight, A. W. (1998). Compounds that Contract on Heating. Inorg. Chem. 37, 2854–2860. doi:10.1021/cen-v030n016.p162210.1021/ic980253h
Sleight, A. W. (2002). Negative Thermal Expansion. MRS Proc. 755, 381–391. doi:10.1557/proc-755-dd10.6
Soares, A. R., Pontón, P. I., Mancic, L., d’Almeida, J. R. M., Romao, C. P., White, M. A., et al. (2014). Al2Mo3O12/polyethylene Composites with Reduced Coefficient of Thermal Expansion. J. Mater. Sci. 49, 7870–7882. doi:10.1007/s10853-014-8498-3
Song, W.-B., Liang, E.-J., Liu, X.-S., Li, Z.-Y., Yuan, B.-H., and Wang, J.-Q. (2013). A Negative Thermal Expansion Material of ZrMgMo3O12. Chin. Phys. Lett. 30, 126502. doi:10.1088/0256-307X/30/12/126502
Song, W.-B., Wang, J.-Q., Li, Z.-Y., Liu, X.-S., Yuan, B.-H., and Liang, E.-J. (2014). Phase Transition and Thermal Expansion Property of Cr2−XZr0.5XMg0.5XMo3O12 Solid Solution. Chin. Phys. B 23, 066501. doi:10.1088/1674-1056/23/6/066501
Subramaniam, C., Yasuda, Y., Takeya, S., Ata, S., Nishizawa, A., Futaba, D., et al. (2014). Carbon Nanotube-Copper Exhibiting Metal-like Thermal Conductivity and Silicon-like Thermal Expansion for Efficient Cooling of Electronics. Nanoscale 6, 2669–2674. doi:10.1039/c3nr05290g
Sumithra, S., Tyagi, A. K., and Umarji, A. M. (2005). Negative Thermal Expansion in Er2W3O12 and Yb2W3O12 by High Temperature X-ray Diffraction. Mater. Sci. Eng. B 116, 14–18. doi:10.1016/j.mseb.2004.08.015
Sumithra, S., and Umarji, A. M. (2005). Hygroscopicity and Bulk Thermal Expansion in Y2W3O12. Mater. Res. Bull. 40, 167–176. doi:10.1016/j.materresbull.2004.09.009
Sumithra, S., and Umarji, A. M. (2006). Negative Thermal Expansion in Rare Earth Molybdates. Solid State. Sci. 8, 1453–1458. doi:10.1016/j.solidstatesciences.2006.03.010
Sumithra, S., and Umarji, A. M. (2004). Role of Crystal Structure on the Thermal Expansion of Ln2W3O12 (Ln = La, Nd, Dy, Y, Er and Yb). Solid State. Sci. 6, 1313–1319. doi:10.1016/j.solidstatesciences.2004.07.023
Suzuki, T., and Omote, A. (2004). Negative Thermal Expansion in (HfMg)(WO4)3. J. Am. Ceram. Soc. 87, 1365–1367. doi:10.1111/j.1151-2916.2004.tb07737.x
Swainson, I. P., and Dove, M. T. (1995). On the Thermal Expansion of β-cristobalite. Phys. Chem. Minerals 22, 61–65. doi:10.1007/BF00202681
Takenaka, K., and Ichigo, M. (2014). Thermal Expansion Adjustable Polymer Matrix Composites with Giant Negative Thermal Expansion Filler. Composites Sci. Tech. 104, 47–51. doi:10.1016/j.compscitech.2014.08.029
Takenaka, K., Okamoto, Y., Shinoda, T., Katayama, N., and Sakai, Y. (2017). Colossal Negative Thermal Expansion in Reduced Layered Ruthenate. Nat. Commun. 8, 1–7. doi:10.1038/ncomms14102
Takezawa, A., Takenaka, K., and Zhang, X. (2018). Inverse Analysis of Giant Macroscopic Negative Thermal Expansion of Ca2RuO4−y ceramics Based on Elasticity and Structural Topology Optimization. Appl. Phys. Express 11 (5), 055801. doi:10.7567/APEX.11.055801
Tani, J.-i., Takahashi, M., and Kido, H. (2010). Fabrication and Thermal Expansion Properties of ZrW2O8/Zr2WP2O12 Composites. J. Eur. Ceram. Soc. 30, 1483–1488. doi:10.1016/j.jeurceramsoc.2009.11.010
Templeton, D. H., and Zalkin, A. (1963). Crystal Structure of Europium Tungstate. Acta Cryst. 16, 762–766. doi:10.1107/s0365110x63001985
Tkachenko, A. V., and Zaliznyak, I. A. (2021). Empty Perovskites as Coulomb Floppy Networks: Entropic Elasticity and Negative Thermal Expansion. Phys. Rev. B 103 (13), 134106. doi:10.1103/PhysRevB.103.134106
Torres Dias, A. C., Luz Lima, C., Paraguassu, W., Pereira da Silva, K., Freire, P. T. C., Mendes Filho, J., et al. (2013). Pressure-induced Crystal-amorphous Transformation in Y2Mo3O12. Vibrational Spectrosc. 68, 251–256. doi:10.1016/j.vibspec.2013.08.004
Tran, K. D., Groshens, T. J., and Nelson, J. G. (2001). Fabrication of Near-Zero Thermal Expansion (FexSc1−x)2Mo3O12-MoO3 Ceramic Composite Using the Reaction Sintering Process. Mater. Sci. Eng. A 303, 234–240. doi:10.1016/S0921-5093(00)01906-7
Truitt, R., Hermes, I., Main, A., Sendecki, A., and Lind, C. (2015). Low Temperature Synthesis and Characterization of AlScMo3O12. Materials 8, 700–716. doi:10.3390/ma8020700
Tucker, M. G., Dove, M. T., and Keen, D. A. (2000). Direct Measurement of the Thermal Expansion of the Si-O Bond by Neutron Total Scattering. J. Phys. Condens. Matter 12, L425–L430. doi:10.1088/0953-8984/12/26/101
Uher, C. (2004). “Thermal Conductivity of Metals,” in In Thermal Conductivity. Physics of Solids and Liquids. Editor T. M. Tritt (Boston: Springer), 21–91. doi:10.1007/0-387-26017-X_2
Varga, T., Moats, J. L., Ushakov, S. V., and Navrotsky, A. (2007). Thermochemistry of A2M3O12 Negative Thermal Expansion Materials. J. Mater. Res. 22, 2512–2521. doi:10.1557/jmr.2007.0311
Varga, T., Wilkinson, A. P., Jorgensen, J. D., and Short, S. (2006). Neutron Powder Diffraction Study of the Orthorhombic to Monoclinic Transition in Sc2W3O12 on Compression. Solid State. Sci. 8, 289–295. doi:10.1016/j.solidstatesciences.2006.02.022
Varga, T., Wilkinson, A. P., Lind, C., Bassett, W. A., and Zha, C.-S. (2005). High Pressure Synchrotron X-ray Powder Diffraction Study of Sc2Mo3O12 and Al2W3O12. J. Phys. Condens. Matter 17, 4271–4283. doi:10.1088/0953-8984/17/27/004
Wang, J., Chen, Q., Chen, L., Ji, Y., Liu, Y., and Liang, E. (2021). Low Thermal Expansion, Phase Transition and Luminescence Properties of ZrxAl2-xMo3-xVxO12. Ceramics Int. 47, 2607–2614. doi:10.1016/j.ceramint.2020.09.107
Wang, Q., Jackson, J. A., Ge, Q., Hopkins, J. B., Spadaccini, C. M., and Fang, N. X. (2016). Lightweight Mechanical Metamaterials with Tunable Negative Thermal Expansion. Phys. Rev. Lett. 117, 175901. doi:10.1103/PhysRevLett.117.175901
Weck, P. F., Kim, E., Gordon, M. E., Greathouse, J. A., Dingreville, R., and Bryan, C. R. (2018). First-Principles Structural, Mechanical, and Thermodynamic Calculations of the Negative Thermal Expansion Compound Zr2(WO4)(PO4)2. ACS Omega 3, 15780–15788. doi:10.1021/acsomega.8b02456
Wei, Z., Tan, L., Cai, G., Phillips, A. E., da Silva, I., Kibble, M. G., et al. (2020). Colossal Pressure-Induced Softening in Scandium Fluoride. Phys. Rev. Lett. 124, 255502. doi:10.1103/PhysRevLett.124.255502
Wu, M.-M., Peng, J., Zu, Y., Liu, R.-D., Hu, Z.-B., Liu, Y.-T., et al. (2012). Thermal Expansion Properties of Lu2−XFeXMo3O12. Chin. Phys. B 21, 116102. doi:10.1088/1674-1056/21/11/116102
Wu, M.-Y., Jia, Y., and Sun, Q. (2016). Effects of A3+ Cations on Hydration in A2M3O12 Family Materials: A First-Principles Study. Comput. Mater. Sci. 111, 28–33. doi:10.1016/j.commatsci.2015.09.010
Wu, M. M., Cheng, Y. Z., Peng, J., Xiao, X. L., Chen, D. F., Kiyanagi, R., et al. (2007a). Synthesis of Solid Solution Er2−xCexW3O12 and Studies of Their Thermal Expansion Behavior. Mater. Res. Bull. 42, 2090–2098. doi:10.1016/j.materresbull.2007.01.015
Wu, M. M., Hu, Z. B., Liu, Y. T., and Chen, D. F. (2009a). Thermal Expansion Properties of Ln2−xCrxMo3O12 (Ln=Er and Y). Mater. Res. Bull. 44, 1943–1947. doi:10.1016/j.materresbull.2009.06.016
Wu, M. M., Peng, J., Cheng, Y. Z., Wang, H., Yu, Z. X., Chen, D. F., et al. (2006). Structure and Thermal Expansion Properties of Solid Solution Nd2−xErxW3O12 (0.0≤×≤0.6 and 1.5≤×≤2.0). Solid State. Sci. 8, 665–670. doi:10.1016/j.solidstatesciences.2006.02.030
Wu, M. M., Peng, J., Cheng, Y. Z., Xiao, X. L., Hao, Y. M., and Hu, Z. B. (2007b). Thermal Expansion in Solid Solution Er2−xSmxW3O12. Mater. Sci. Eng. B 137, 144–148. doi:10.1016/j.mseb.2006.11.004
Wu, M. M., Xiao, X. L., Hu, Z. B., Liu, Y. T., and Chen, D. F. (2009b). Controllable Thermal Expansion and Phase Transition in Yb2−xCrxMo3O12. Solid State. Sci. 11, 325–329. doi:10.1016/j.solidstatesciences.2008.08.002
Xiao, X. L., Cheng, Y. Z., Peng, J., Wu, M. M., Chen, D. F., Hu, Z. B., et al. (2008a). Thermal Expansion Properties of A2(MO4)3 (A=Ho and Tm; M=W and Mo). Solid State. Sci. 10, 321–325. doi:10.1016/j.solidstatesciences.2007.09.001
Xiao, X. L., Peng, J., Wu, M. M., Cheng, Y. Z., Chen, D. F., and Hu, Z. B. (2008b). The Crystal Structure and Thermal Expansion Properties of Solid Solutions Ln2−xDyxW3O12 (Ln=Er and Y). J. Alloys Comp. 465, 556–561. doi:10.1016/j.jallcom.2007.11.005
Xiao, X., Zhou, W., Liu, X., Chao, M., Li, Y., Zhang, N., et al. (2015). Electrical Properties of Al-ZrMgMo3O12 with Controllable Thermal Expansion. Ceramics Int. 41, 2361–2366. doi:10.1016/j.ceramint.2014.10.048
Xu, H., Liu, R., Zhang, S., Deng, M., Han, K., Xu, B., et al. (2019). Scandium Molybdate Microstructures with Tunable Phase and Morphology: Microwave Synthesis, Theoretical Calculations, and Photoluminescence Properties. Inorg. Chem. 58, 2491–2500. doi:10.1021/acs.inorgchem.8b03056
Yamamura, Y., Ikeuchi, S., and Saito, K. (2009). Characteristic Phonon Spectrum of Negative Thermal Expansion Materials with Framework Structure through Calorimetric Study of Sc2M3O12 (M = W and Mo). Chem. Mater. 21, 3008–3016. doi:10.1021/cm900965p
Yanase, I., Miyagi, M., and Kobayashi, H. (2009). Fabrication of Zero-Thermal-Expansion ZrSiO4/Y2W3O12 Sintered Body. J. Eur. Ceram. Soc. 29, 3129–3134. doi:10.1016/j.jeurceramsoc.2009.06.001
Yanase, I., Sakai, H., and Kobayashi, H. (2017). Fabrication of Zr2WP2O12/ZrV0.6P1.4O7 Composite with a Nearly Zero-Thermal-Expansion Property. Mater. Lett. 207, 221–224. doi:10.1016/j.matlet.2017.07.051
Yang, C., Li, J., Yang, D., Li, S., Qin, Y., Meng, S., et al. (2019). ZrW2O8 with Negative Thermal Expansion Fabricated at Ultralow Temperature: An Energy-Efficient Strategy for Metastable Material Fabrication. ACS Sust. Chem. Eng. 7, 14747–14755. doi:10.1021/acssuschemeng.9b02682
Yang, J., Liu, Z., Shi, Y., Li, M., Yang, M., and Liang, E. (2019). Investigation on the Synthesis and the Mechanical and Thermal Expansion Properties of ZrMgMo3O12 Ceramic Bodies. Ceramics Int. 45, 8750–8760. doi:10.1016/j.ceramint.2019.01.199
Yang, J., Wang, L., Tan, X., Zhi, Q., Yang, R., Zhang, G., et al. (2018). Effect of Sintering Temperature on the Thermal Expansion Behavior of ZrMgMo3O12p/2024Al Composite. Ceramics Int. 44, 10744–10752. doi:10.1016/j.ceramint.2018.03.110
Yang, M., Wei, S., Su, S.-l., Chao, M., Guo, J., Wang, H., et al. (2020). The Influence of ZrMgMo3O12 on the Dielectric Properties of BaTi4O9. Ceramics Int. 46, 10250–10255. doi:10.1016/j.ceramint.2020.01.017
Yang, V. K., Groenert, M., Leitz, C. W., Pitera, A. J., Currie, M. T., and Fitzgerald, E. A. (2003). Crack Formation in GaAs Heteroepitaxial Films on Si and SiGe Virtual Substrates. J. Appl. Phys. 93, 3859–3865. doi:10.1063/1.1558963
Yang, X., Cheng, X., Yan, X., Yang, J., Fu, T., and Qiu, J. (2007). Synthesis of ZrO2/ZrW2O8 Composites with Low Thermal Expansion. Composites Sci. Tech. 67, 1167–1171. doi:10.1016/j.compscitech.2006.05.012
Yi, G., Sun, B., Yang, F., Chen, D., Zhou, Y., and Cheng, J. (2002). Synthesis and Characterization of High-Efficiency Nanocrystal Up-Conversion Phosphors: Ytterbium and Erbium Codoped Lanthanum Molybdate. Chem. Mater. 14, 2910–2914. doi:10.1021/cm0115416
Yordanova, A., Koseva, I., Velichkova, N., Kovacheva, D., Rabadjieva, D., and Nikolov, V. (2012). Nanosized Pure and Cr Doped Al2−xScx(WO4)3 Solid Solutions. Mater. Res. Bull. 47, 1544–1549. doi:10.1016/j.materresbull.2012.02.023
Young, L., Alvarez, P. T., Liu, H., and Lind, C. (2016). Extremely Low Temperature Crystallization in the A2M3O12 Family of Negative Thermal Expansion Materials. Eur. J. Inorg. Chem. 2016, 1251–1256. doi:10.1002/ejic.2015014202016
Young, L., Gadient, J., and Lind, C. (2018). High Pressure Behavior of Chromium and Yttrium Molybdate (Cr2Mo3O12, Y2Mo3O12). Front. Chem. 6, 478. doi:10.3389/fchem.2018.00478
Yu, Z., Peng, J., Wang, H., Wu, M., Cheng, Y., Hu, Z., et al. (2008). Thermal Expansion Properties and Hygroscopicity of Y2−xSmXW3O12 (X = 0.0-0.4) Compounds. Sci. China Ser. E-technol. Sci. 51, 25–32. doi:10.1007/s11431-007-0040-2
Yuan, H., Wang, C., Gao, Q., Ge, X., Sun, H., Lapidus, S. H., et al. (2020). Structure and Negative Thermal Expansion in Zr0.3Sc1.7Mo2.7V0.3O12. Inorg. Chem. 59, 4090–4095. doi:10.1021/acs.inorgchem.0c00126
Zhang, H.-j., Zhang, Q., Jia, Q.-l., and Ye, G.-t. (2008). Preparation of Al2-xYxW3O12 Powders by Citrate Sol-Gel Process. Trans. Nonferrous Met. Soc. China 18, 1112–1116. doi:10.1016/S1003-6326(08)60190-9
Zhang, N., Zhou, W., Chao, M., Mao, Y., Guo, J., Li, Y., et al. (2015). Negative Thermal Expansion, Optical and Electrical Properties of HfMnMo2PO12−δ. Ceramics Int. 41, 15170–15175. doi:10.1016/j.ceramint.2015.08.090
Zhang, Z., Sun, W., Liu, H., Xie, G., Chen, X., and Zeng, X. (2017). Synthesis of Zr2WP2O12/ZrO2 Composites with Adjustable Thermal Expansion. Front. Chem. 5, 2–7. doi:10.3389/fchem.2017.00105
Zhou, C., Zhang, Q., Liu, S., Luo, B., Yi, E., Tian, E., et al. (2017). Thermal Mismatch Strain Induced Disorder of Y2Mo3O12 and its Effect on Thermal Expansion of Y2Mo3O12/Al Composites. Phys. Chem. Chem. Phys. 19, 11778–11785. doi:10.1039/C7CP00676D
Zhou, C., Zhang, Q., Liu, Y., Wu, G., and Liu, S. (2014). Thermal Expansion of Y2W3O12/Al Metal Matrix Composites. Mater. Res. Innov. 18, S4–S490. doi:10.1179/1432891714Z.000000000837
Zhou, Y., Adams, S., Rao, R. P., Edwards, D. D., Neiman, A., and Pestereva, N. (2008). Charge Transport by Polyatomic Anion Diffusion in Sc2(WO4)3. Chem. Mater. 20, 6335–6345. doi:10.1021/cm800466y
Zhou, Y., Cheng, Y., Huang, Q., Xu, J., Lin, H., and Wang, Y. (2021). Abnormal Thermally Enhanced Upconversion Luminescence of Lanthanide-Doped Phosphors: Proposed Mechanisms and Potential Applications. J. Mater. Chem. C 9, 2220–2230. doi:10.1039/d0tc05759b
Zhou, Y., Zhou, W., Wang, H., Luo, F., and Zhu, D. (2015). Preparation and Properties of Carbonyl Iron Particles (CIPs)/silicone Resin Composite with Negative Thermal Expansion Filler. J. Polym. Res. 22, 138. doi:10.1007/s10965-015-0775-6
Zi, Y., Yang, Z., Xu, Z., Bai, X., Ullah, A., Khan, I., et al. (2021). A Novel Upconversion Luminescence Temperature Sensing Material: Negative Thermal Expansion Y2Mo3O12:Yb3+, Er3+ and Positive Thermal Expansion Y2Ti2O7:Yb3+, Er3+ Mixed Phosphor. J. Alloys Comp. 880, 160156. doi:10.1016/j.jallcom.2021.160156
Zou, H., Yang, X., Chen, B., Du, Y., Ren, B., Sun, X., et al. (2019). Thermal Enhancement of Upconversion by Negative Lattice Expansion in Orthorhombic Yb2W3O12. Angew. Chem. Int. Ed. 58, 17255–17259. doi:10.1002/anie.201910277
Zuluaga, M. G., Dri, F. L., Zavattieri, P. D., and Moon, R. J. (2014). Anisotropy Calculator – 3D Visualization Toolkit. Available at: https://nanohub.org/tools/matrix2surface [accessed July 5, 2021]. doi:10.4231/D3JD4PQ2D
3SS 3-stage sintering
ATZ Al2O3-toughened ZrO2
CMC ceramic matrix composite
CTAB cetyltrimethylammonium bromide
CTE coefficient of thermal expansion
FEA finite element analysis
HDPE high-density polyethylene
HIP hot isostatic pressing
LED light-emitting diode
MDPE medium-density polyethylene
MMC metal matrix composites
NTE negative thermal expansion
NZTE near-zero thermal expansion
PE-g-MA polyethylene-grafted maleic anhydride
PEG polyethylene glycol
PI polyimide
PMMA polymethyl methacrylate
PMC polymer matrix composite
PTE positive thermal expansion
PVA polyvinyl alcohol
ROM rule of mixtures
SPS spark plasma sintering
TD theoretical density
TDP thermal distortion parameter
VHN Vicker’s hardness number
VTMS vinyltrimethoxysilane
wLED white light-emitting diode
XRD X-ray diffraction
XRPD X-ray powder diffraction
C e volumetric heat capacity at constant strain
C V heat capacity per unit volume
e elementary charge
E a attractive interaction energy
F a attractive ionic force
K bulk modulus
L 0 original length
p pressure
p CTE thermal expansion misfit stress
r interatomic distance, or atomic radius, or filler radius (depending on context)
r c critical filler radius
R sum of the cation and anion radii
R s thermal shock resistance coefficient
T temperature
U s surface formation energy
U t total energy stored during elastic deformation
V volume of unit cell
x variable describing chemical composition
Y Young’s modulus
Y ii directional Young’s modulus
Z 1 valence of the cation
Z 2 valence of the anion
α ℓ linear coefficient of thermal expansion
α V volume coefficient of thermal expansion
Δ αℓ difference between the linear CTE of a matrix, αℓ(m), and that of an NTE-like filler, αℓ(f)
ΔH enthalpy change
ΔL change in length
ε 0 electrical permittivity in vacuum
γ (overall) Grüneisen parameter
γ n Grüneisen parameter for vibrational mode n
γ s effective surface energy of the matrix
γ ii directional Grüneisen parameter
γ ii,n directional Grüneisen parameter for mode n
θ A−O−M bond angle
κ thermal conductivity
λ phonon mean free path
ν m Poisson ratio of matrix
ν f Poisson ratio of filler
ν s mean phonon speed (speed of sound)
ρ electrical resistivity
σ material strength
σ y matrix yield strength
ω n frequency of vibrational mode n
Keywords: thermal expansion, phase transition, hygroscopicity, physical properties, sintering, composite, applications
Citation: Marinkovic BA, Pontón PI, Romao CP, Moreira T and White MA (2021) Negative and Near-Zero Thermal Expansion in A2M3O12 and Related Ceramic Families: A Review. Front. Mater. 8:741560. doi: 10.3389/fmats.2021.741560
Received: 14 July 2021; Accepted: 09 August 2021;
Published: 17 September 2021.
Edited by:
Praveen Sekhar, Washington State University, United StatesReviewed by:
Renny Fernandez, Norfolk State University, United StatesCopyright © 2021 Marinkovic, Pontón, Romao, Moreira and White. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bojan A. Marinkovic, Ym9qYW5AcHVjLXJpby5icg==; Mary Anne White, bWFyeS5hbm5lLndoaXRlQGRhbC5jYQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.