Electromagnetic Response of Clustered Charged Particles

Electromagnetic response of clustered charged particles is the foundation of electromagnetic wave interaction with various natural phenomena, such as sandstorm, cloud, and volcano eruption. Previous studies usually employed assumption of independent charged particles, without considering the coupling between them. Here, we build up a general numerical model considering the multiple scattering effect, and test it with a charged two- and four-particle system. The numerical results show that independence assumption fails, while the number density of clustered charged particles is getting larger. This work may pave the way for deeper understanding on the electromagnetic interaction of clustered charged particles.

Introduction

Sand/dust storm is a natural phenomenon that may cause signals of remote sensing and telecommunication being worsened due to the attenuation of electromagnetic waves (EMWs) by sand particles. To understand the attenuation mechanism, much research has been conducted on the scattering of sand storm (Peterson and Strm, 1974; Ansari and Evans, 1982; Haddad et al., 1983; Ghobrial and Jervase, 1997; Islam et al., 2010) with the Lorenz–Mie theory. Notably, particles in the sand storm can be charged due to many reasons, such as friction and collision between particles (Gill, 1948;Gill and Alfrey, 1949; Lowell and Rose-Innes, 1980; Lacks and Mohan Sankaran, 2011; Xie et al., 2013a; Xie et al., 2013b). Existing research has shown that the scattering properties of charged particles are strikingly different from those of neutral ones (Klačka and Kocifaj, 2007; Zhou and Xie, 2011; Kocifaj, 2013; Klačka et al., 2015b; Kocifaj et al., 2015). For example, Klačka et al. found that scattering and absorption will be significantly enhanced by the surface charge for small particles with a size parameter less than 0.01 (Klačka and Kocifaj, 2007). In 1977, Bohren and Hunt put forward a model to solve the scattering problem of a charged particle through revising the boundary condition by introducing an excess charge surface conductivity (Bohren and Hunt, 1977; Bohren and Huffman, 1998). The Drude model that relates the surface conductivity of charged particles to the charge-to-mass ratio of the charge carriers and the driving frequency can be employed to understand the surface currents on the particles (Klačka and Kocifaj, 2007; Kocifaj, 2013; Klačka et al., 2015b).

However, although there is a large number of research conducted on the scattering properties of individual charged particles of different materials and shapes (Klačka and Kocifaj, 2010; Kocifaj et al., 2016; Liao et al., 2019; Yang et al., 2019; Xue et al., 2020), little attention was given on the interactions between charged particles in clusters. It is reported that conventional analytical methods, which assume the granular medium is homogeneous and neglect multiple scattering effects between particles, will lead to significant overestimation of the attenuation through the medium (Huang et al., 2020; Xie et al., 2020). Recently, Xie et al. improved the independent scattering approximation in conventional radiative transfer theory to deal with the multiple scattering effects in a charged granular system (Xie et al., 2020). In 2020, Chai J W et al. analytically studied the optical response of a symmetric circular array of metallic nanoparticles based on the eigen-decomposition method under the dipole approximation (Fung and Chan, 2008; Chai et al., 2020). In this article, we build up a fully analytical theoretical frame based on the T-matrix formulism (Tsang et al., 2001; Mishchenko et al., 2002, 2006; Huang et al., 2020) to study the electromagnetic response of multi-particle systems consisting of electrically charged spherical particles with multiple scattering effect considered. The article is organized as follows: In the Single charged particle section, before the discussion of the multiple scattering effect, we investigated the influence of various factors on the scattering of a single charged particle, such as the charge density, radius, and relative permittivity of the particle. We would like to state that our theoretical frame is under the assumption of uniform charge distribution on the particle surface. Uniform charge distribution is typical for particles of simple geometry such as spherical particles considered in this work, to which separation of variables method is applicable to find scattered electric and magnetic fields (Klačka et al., 2015a). In the Clustered charged particles section, the T-matrix formulism with modified boundary condition to calculate the electromagnetic response of clustered charged spherical particles is described. Then, in the Result section, the discussions on the numerical results of a single charged particle and clustered particles are presented, with comparison between different charge densities and inter-particle distances. Finally, the convergence performance of the proposed theoretical approach is investigated, and conclusions are given in the Conclusion section.

Single charged Particle

A charged spherical particle with radius $a$ is illuminated by x-polarized EMW propagating along the z-axis. The incident electric field can be expressed as ${\overrightarrow{E}}_{in}=e^{i(kz-\omega t)}\widehat{x}$, where $\omega =2\pi f$ and $f$ denotes the frequency of the EMW. Here, $\widehat{x}$ is the unit vector of the x-axis. The particle is assumed to be overall and uniformly charged. The material of the particle and ambient medium are set to be isotropic and homogeneous. Let ${\overrightarrow{E}}_1$ and ${\overrightarrow{H}}_1$ denote the field inside the particle, and ${\overrightarrow{E}}_2$ and ${\overrightarrow{H}}_2$ denote the field of the ambient. The electric field ${\overrightarrow{E}}_i$ (i = 1, 2) and magnetic field ${\overrightarrow{H}}_i$ (i = 1, 2) satisfy the following wave propagating equations:

$\begin{array}{c}\{\begin{array}{c}{\nabla }^2{\overrightarrow{E}}_2+k_2^2{\overrightarrow{E}}_2=0, {\nabla }^2{\overrightarrow{H}}_2+k_2^2{\overrightarrow{H}}_2=0\\ {\nabla }^2{\overrightarrow{E}}_1+k_1^2{\overrightarrow{E}}_1=0, {\nabla }^2{\overrightarrow{H}}_1+k_1^2{\overrightarrow{H}}_1=0\end{array}\end{array}(1)$

where k₁ and k₂ denote the wavenumber inside and outside the particle, which satisfy the dispersion relation:

$\begin{array}{c}{k}_i=\omega \sqrt{{\epsilon }_i{\mu }_i}\end{array}(2)$

where ${\mu }_i$ ($i=1, 2$) and ${\epsilon }_i$ ($i=1, 2$) are the permeability and permittivity of the particle and the ambient, respectively. We consider the medium outside the particle as a vacuum, i.e., ${\mu }_2={\mu }_0$ and ${\epsilon }_2={\epsilon }_0$. Here, ${\mu }_0=1.2566\times {10}^{-6} \mathrm{H}/\mathrm{m}$ and ${\epsilon }_0=8.8542\times {10}^{-12} \mathrm{F}/\mathrm{m}$ are the vacuum permeability and permittivity, respectively. ${\mu }_1={\mu }_r{\mu }_0$ and ${\epsilon }_1={\epsilon }_r{\epsilon }_0$ are the permeability and permittivity of the particle, respectively, where ${\mu }_r$ and ${\epsilon }_r$ are the relative permeability and relative permittivity, respectively. We begin with the Mie scattering theory, by which the problem of plane waves scattered by a spherical particle can be rigorously solved through matching the boundary conditions (Kong, 1986; Bohren and Huffman, 1998; Mishchenko et al., 2002; Lovat et al., 2020). The field outside the particle can be expressed as the superposition of the incident field and the scattered field,

$\begin{array}{c}\{\begin{array}{c}{\overrightarrow{E}}_2={\overrightarrow{E}}_{in}+{\overrightarrow{E}}_s\\ {\overrightarrow{H}}_2={\overrightarrow{H}}_{in}+{\overrightarrow{H}}_s\end{array}\end{array}(3)$

where ${\overrightarrow{E}}_s$ and ${\overrightarrow{H}}_s$ denote the scattered fields of the particle. It is commonly assumed in the Mie theory when studying the scattering of electromagnetic waves by spherical particles that the particle carries a zero charge. The boundary condition can be written as:

$\begin{array}{c}\{\begin{array}{c}\left({\overrightarrow{E}}_2-{\overrightarrow{E}}_1\right)\times \widehat{n}=0\\ \left({\overrightarrow{H}}_2-{\overrightarrow{H}}_1\right)\times \widehat{n}=0\end{array} atr=a\end{array}(4)$

where $\widehat{n}$ denotes the outward-directed unit vector normal to the surface of the particle.

However, when it comes to charged particles, the electrons on the surface will be driven by the electric field on the surface. Hence, there exist surface current $\overrightarrow{K}$ on the surface of the particle due to the movement of excess charge driven by the tangential electric field. The boundary condition is modified as:

$\begin{array}{c}\{\begin{array}{c}\left({\overrightarrow{E}}_2-{\overrightarrow{E}}_1\right)\times \widehat{n}=0\\ \left({\overrightarrow{H}}_2-{\overrightarrow{H}}_1\right)\times \widehat{n}=\overrightarrow{K}\end{array} atr=a\end{array}(5)$

The surface current can be expressed as:

$\begin{array}{c}\overrightarrow{K}={\sigma }_s{\overrightarrow{E}}_{\tau }\end{array}(6)$

where σ_s denotes the excess charge surface conductivity, and ${\overrightarrow{E}}_{\tau }$ stands for the tangential component of the electric field on the surface of the particle. σ_s is independent of position but may be complex and dependent on frequency. Under the assumption of free surface charges (i.e., not localized on the surface of the particle), we can adopt the Drude model and the equation of motion for a surface charge with mass m_s and charge q_s as

$m_s {\dot{\overrightarrow{u}}}_{\tau }=q_s{\overrightarrow{E}}_{\tau }-{\beta }_s{\overrightarrow{u}}_{\tau }(7)$

where ${\overrightarrow{u}}_{\tau }$ is the component of velocity tangential to the sphere, and ${\beta }_s$ is the damping coefficient. The oscillatory part of the solution of (Eq. 7) is

${\overrightarrow{u}}_{\tau }=\frac{q_s/m_s}{-i\omega +{\gamma }_s}{\overrightarrow{E}}_{\tau }(8)$

where ${\gamma }_s={\beta }_s/m_s$. Since $\overrightarrow{K}={\eta }_s{\overrightarrow{u}}_{\tau }$, where η_s is the density of charge, from (Eqs 6, 8), we have (Bohren and Hunt, 1977;Kocifaj, 2013;Klačka et al., 2015b;Holloway et al., 2019;zhang et al., 2020),

${\sigma }_s=\frac{{\eta }_s(q_s/m_s)}{-i\omega +{\gamma }_s}(9)$

where q_s/m_s is the charge-to-mass ratio of charge carriers. For electrons, we have $q_s/m_s=1.7587\times {10}^{11} \mathrm{C}/\mathrm{kg}$. The constant γ_s can be calculated as ${\gamma }_s=k_{B}T/\hslash$ (Klačka and Kocifaj, 2007), where k_B denotes the Boltzmann constant, and $\hslash$ denotes the Planck’s constant.

The problem of plane waves scattered by a charged particle can then be solved based on a T-matrix-based approach with modified boundary conditions, which is the generalized version of the Lorenz–Mie theory. The scattering of electromagnetic waves by homogeneous, isotropic sphere, which carries excess charge is tackled under the assumption that surface current is linearly related to the electric field parallel to the surface of the particle. The calculated scattering coefficients are, therefore, formally different from those of the standard Mie theory. We first expand the incident wave into spherical harmonics,

$\begin{array}{c}{\overrightarrow{E}}_{inc}=e^{i\left(kz-\omega t\right)}\widehat{x}\\ =e^{-i\omega t}\left\{-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m= -\mathrm{1,1}}{{\displaystyle i}}^n\frac{2n+1}{n\left(n+1\right)}}}\left[\frac{\widehat{x}\cdot {\overrightarrow{C}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}Rg{\overrightarrow{M}}_{mn}\left(kr,\theta ,\varphi \right)-i\frac{\widehat{x}\cdot {\overrightarrow{B}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}Rg{\overrightarrow{N}}_{mn}\left(kr,\theta ,\varphi \right)\right]\right\}\end{array}(10)$

where $i= \sqrt{-1}$. ${\overrightarrow{M}}_{mn}$ and ${\overrightarrow{N}}_{mn}$ are unit vectors of spherical waves, which can be written as

$\begin{array}{c}Rg{\overrightarrow{M}}_{mn}\left(kr,\theta ,\varphi \right)={\gamma }_{mn}{j}_n\left(kr\right){\overrightarrow{C}}_{mn}\left(\theta ,\varphi \right)\end{array}(11)$

$\begin{array}{c}Rg{\overrightarrow{N}}_{mn}\left(kr,\theta ,\varphi \right)=\frac{1}{k}\nabla \times Rg{\overrightarrow{M}}_{mn}\left(kr,\theta ,\varphi \right)={\gamma }_{mn}\left\{\frac{n\left(n+1\right)j_n\left(kr\right)}{kr}{\overrightarrow{P}}_{mn}\left(\theta ,\varphi \right)+\frac{{\left[kr{j}_n\left(kr\right)\right]}^{\prime }}{kr}{\overrightarrow{B}}_{mn}\left(\theta ,\varphi \right)\right\}\end{array}(12)$

where j_n and h_n are the first and third kinds of spherical Bessel function. Rg stands for the regular solution of the spherical harmonics, which means the solution is regular (finite) at the origin. The vector spherical waves without the prefix Rg are the expressions with j_n replaced by h_n. ${\gamma }_{mn}$ can be calculated as ${\gamma }_{mn}= \sqrt{\frac{\left(2n+1\right)\left(n-m\right)!}{4\pi nn\left(n+1\right)\left(n+m\right)!}}$. ${\overrightarrow{B}}_{mn}$, ${\overrightarrow{C}}_{mn}$, and ${\overrightarrow{P}}_{mn}$ can be written as (Tsang et al., 2000)

$\begin{array}{c}{\overrightarrow{B}}_{mn}=\left[\widehat{\theta }\frac{d}{d\theta }{P}_n^m\left(cos\theta \right)+\widehat{\varphi }\frac{im}{sin\theta }{P}_n^m\left(\cos \theta \right)\right]e^{im\varphi } \end{array}(13)$

$\begin{array}{c}{\overrightarrow{C}}_{mn}=\left[\widehat{\theta }\frac{im}{sin\theta }{P}_n^m\left(\cos \theta \right)-\widehat{\varphi }\frac{d}{d\theta }{P}_n^m\left(cos\theta \right)\right]e^{im\varphi }\end{array}(14)$

$\begin{array}{c}{\overrightarrow{P}}_{mn}= \widehat{r}{Y}_n^m\left(\text{θ},\mathrm{\varphi }\right)\end{array}(15)$

where $\widehat{r}$, $\widehat{\theta }$, and $\widehat{\varphi }$ are unit vectors under spherical coordinates. $P_n^m\left(cos\theta \right)$ is associated Legendre polynomials, and $Y_n^m\left(\theta ,\varphi \right)$ is spherical harmonics, which can be related by $Y_n^m\left(\theta ,\varphi \right)= P_n^m\left(cos\theta \right)e^{im\varphi }$.

The Scattered Field can Be Written as

${\overrightarrow{E}}_s=e^{-i\omega t}\left\{-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m= -\mathrm{1,1}}{{\displaystyle i}}^n\frac{2n+1}{n\left(n+1\right)}}}\left[-\frac{\widehat{x}\cdot {\overrightarrow{C}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}{b}_n{\overrightarrow{M}}_{mn}\left(kr,\theta ,\varphi \right)+i\frac{\widehat{x}\cdot {\overrightarrow{B}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}{a}_n{\overrightarrow{N}}_{mn}\left(kr,\theta ,\varphi \right)\right] \right\}(16)$

and the internal field of the particle can be written as

${\overrightarrow{E}}_1=e^{-i\omega t}\left\{-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle {\sum }_{m= -\mathrm{1,1}}{{\displaystyle i}}^n\frac{2n+1}{n\left(n+1\right)}}}\left[\frac{\widehat{x}\cdot {\overrightarrow{C}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}{d}_{n}Rg{\overrightarrow{M}}_{mn}\left(kr,\theta ,\varphi \right)-i\frac{\widehat{x}\cdot {\overrightarrow{B}}_{-m,n}\left(\mathrm{0,0}\right)}{{\gamma }_{mn}}{c}_{n}Rg{\overrightarrow{N}}_{mn}\left(kr,\theta ,\varphi \right)\right] \right\}(17)$

As mentioned above, ${\overrightarrow{E}}_2 = {\overrightarrow{E}}_{in} + {\overrightarrow{E}}_s$. Applying the boundary conditions (5) yields four linear equations of the expansion coefficients,

$\begin{array}{c}{h}_n\left(k_{2}a\right)b_n+j_n\left(k_{1}a\right)d_n=j_n\left(k_{2}a\right)\end{array}(18)$

$\begin{array}{c}{k}_1{\left[\left(k_{2}a\right)h_n\left(k_{2}a\right)\right]}^{\prime }{a}_n+k_2{\left[\left(k_{1}a\right)j_n\left(k_{1}a\right)\right]}^{\prime }{c}_n=k_1{\left[\left(k_{2}a\right)j_n\left(k_{2}a\right)\right]}^{\prime }\end{array}(19)$

$\left(\sqrt{{\mathit{ϵ}}_r}\left(k_{1}a\right)j_n\left(k_{1}a\right)+\frac{i\omega {\mu }_0{\sigma }_s}{k_2}{\left[\left(k_{1}a\right)j_n\left(k_{1}a\right)\right]}^{\prime }\right)c_n+k_{1}R{h}_n\left(k_{2}a\right)a_n= k_{1}a{j}_n\left(k_{2}a\right)(20)$

$\left(\frac{i\omega {\mu }_0{\sigma }_s}{k_2\sqrt{{\mathit{ϵ}}_r}}\left(k_{1}a\right)j_n\left(k_{1}a\right)-{\left[\left(k_{1}a\right)j_n\left(k_{1}a\right)\right]}^{\prime }\right)d_n-{\left[\left(k_{2}a\right)h_n\left(k_{2}a\right)\right]}^{\prime }{b}_n= -{\left[\left(k_{2}a\right)j_n\left(k_{2}a\right)\right]}^{\prime }(21)$

Solve the equations, and we can obtain scattering coefficients $\{a_n,b_n\}$ and, hence, the T-matrix:

$\begin{array}{c}{a}_n= -T_n^{\left(N\right)}=\frac{{{\psi }^{\prime }}_n\left(mx\right){\psi }_n\left(x\right)-m{{\psi }^{\prime }}_n\left(x\right){\psi }_n\left(mx\right)-\frac{i\omega {\sigma }_s{\mu }_0}{k_2}{{\psi }^{\prime }}_n\left(x\right){{\psi }^{\prime }}_n\left(mx\right)}{{\psi }_n^{\prime }\left(mx\right){\xi }_n\left(x\right)-m{{\xi }^{\prime }}_m\left(x\right){\psi }_n\left(mx\right)-\frac{i\omega {\sigma }_s{\mu }_0}{k_2}{{\xi }^{\prime }}_n\left(x\right){{\psi }^{\prime }}_n\left(mx\right)}\end{array}(22)$

$\begin{array}{c}{b}_n= -T_n^{\left(M\right)}=\frac{{\psi }_n\left(mx\right){{\psi }^{\prime }}_n\left(x\right)-m{\psi }_n\left(x\right){{\psi }^{\prime }}_n\left(mx\right)+\frac{i\omega {\sigma }_s{\mu }_0}{k_2}{\psi }_n\left(x\right){\psi }_n\left(mx\right)}{{\psi }_n\left(mx\right){\xi }_n^{\prime }\left(x\right)-m{\psi }_n\left(x\right){\psi }_n^{\prime }\left(mx\right)+\frac{i\omega {\sigma }_s{\mu }_0}{k_2}{\xi }_n\left(x\right){\psi }_n\left(mx\right)}\end{array}(23)$

where $m= \sqrt{{\mathit{ϵ}}_1}$, ${\psi }_n\left(x\right)=x{j}_n\left(x\right)$, ${\xi }_n\left(x\right)=x{h}_n\left(x\right)$, $x=k_{2}a$.

If we consider the surface charge density to be infinity, which will cause the conductivity ${\sigma }_s$ to be infinity (i.e., behaves like metal), the T-matrix can be reduced to the following:

$\begin{array}{c}{a}_n= -T_n^{\left(N\right)}=\frac{{{\psi }^{\prime }}_n\left(x\right){{\psi }^{\prime }}_n\left(mx\right)}{{{\xi }^{\prime }}_n\left(x\right){{\psi }^{\prime }}_n\left(mx\right)}\end{array}(24)$

$\begin{array}{c}{b}_n= -T_n^{\left(M\right)}=\frac{{\psi }_n\left(x\right){\psi }_n\left(mx\right)}{{\xi }_n\left(x\right){\psi }_n\left(mx\right)}\end{array}(25)$

Then, the scattering cross section can be expressed as

$\begin{array}{c}{C}_{sca}=\frac{2\pi }{k_2^2}{\displaystyle \sum _{n=1}^{\infty }\left(2n+1\right)\left({\left|a_n\right|}^2+{\left|b_n\right|}^2\right)}\end{array}(26)$

and the extinction cross section can be obtained by

$\begin{array}{c}{C}_{ext}= \frac{2\pi }{k_2^2}{\displaystyle \sum _{n=1}^{\infty }\left(2n+1\right)Re\left(a_n+b_n\right)}\end{array}(27)$

The scattering cross section implies the amount of energy removed by the scattering of the incidence wave, while the extinction cross section implies the amount of energy removed from the incident energy due to the sum of scattering and absorption by the particle. These cross sections of a single particle can be significantly altered by surface charges, material properties of the particle, and the environment (Wang et al., 2020).

Clustered Charged Particles

Under the classical assumption of independent scattering, the cross section of the multi-particle system can be written as $C_{sca}= {\displaystyle \sum }_i{C}_{sca}^i$, where $C_{sca}^i$ is the scattering cross section of the ith particle and can be calculated from the method mentioned in the Single charged particle section. However, in multi-particle systems, particles are electromagnetically coupled by the multiple scattering effect. The incident field of one particle can be expressed as the addition of the original incident field and scattered field from other particles [i.e., ${\overrightarrow{E}}_{ex}^{\left(l\right)}\left(\overrightarrow{r}\right)= {\overrightarrow{E}}_{inc}\left(\overrightarrow{r}\right)+{\displaystyle \sum }_{j\ne l}{\overrightarrow{E}}_s^{\left(j\right)}\left(\overrightarrow{r}\right)$].

A general theoretical frame to study the multiple scattering effect in a multi-particle system has been built in previous research (Tsang et al., 2001; Mishchenko et al., 2002, Mishchenko et al. 2006; Altuncu et al., 2019; Huang et al., 2020). Similar to the solid-state analogy, where waves are scattered by crystals lattice, here, lattice sums of spherical harmonic functions are adopted to model the scattering from discrete particles, and the center transformation is implemented with the T-matrix approach combined with the translational addition theorems, given the differences between the Schrödinger and Maxwell equations (Popov, 2012; Tan and Tsang, 2019). Consider N spherical particles with radii a₁, a₂, a₃, …, a_N, respectively. The ith particle has permittivity equal to ${\epsilon }_i$ and permeability equal to ${\mu }_i$. The incident field can be expanded into spherical harmonics with the center at origin as follows:

$\begin{array}{c}{\overrightarrow{E}}_{inc}={\displaystyle \sum _n{\displaystyle \sum _m\left[a_{mn}Rg{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r}\right)+b_{mn}Rg{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r}\right)\right]}} \end{array}(28)$

As mentioned above, for an incident EMW with electric field polarized in x-axis and propagating in z-axis, it has the form ${\overrightarrow{E}}_{in}=e^{i\left(kz-\omega t\right)}\widehat{x}$. We can then obtain the coefficients for the spherical harmonics for the incident waves:

$\begin{array}{c}{a}_{mn}=\{\begin{array}{c}{i}^{n+1}\frac{2n+1}{2{\gamma }_{-1,n}}, m= -1\\ i^{n+1}\frac{2n+1}{2n\left(n+1\right){\gamma }_{1,n}}, m=1\\ 0, else\end{array}\end{array}(29)$

$\begin{array}{c}{b}_{mn}=\{\begin{array}{c}-a_{-1,n}, m= -1\\ a_{1,n},m=1\\ 0, else\end{array}\end{array}(30)$

For an arbitrary particle, e.g., the lth particle, we assume the exciting field consisting of two parts: the first part is the original incident wave, and the other is the scattered wave from other particles. The expression for the exciting fields of the lth particle is

$\begin{array}{c}{\overrightarrow{E}}_{ex}^{\left(l\right)}={\displaystyle \sum _n{\displaystyle \sum _m\left[p_{mn}^{\left(l\right)}Rg{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r{r}_l}\right)+q_{mn}^{\left(l\right)}Rg{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r{r}_l}\right)\right]}}\end{array}(31)$

where $p_{mn}$ and $q_{mn}$ are unknown exciting field coefficients. $\overrightarrow{r{r}_l}$ equals $\overrightarrow{r}-\overrightarrow{r_l}$.

For the lth particle, the exciting field consists of the incidence wave, and the part that comes from the scattered field of other particles can be expressed as

$\begin{array}{c}{\overrightarrow{E}}_{ex}^{\left(l\right)}\left(\overrightarrow{r}\right)= {\overrightarrow{E}}_{inc}\left(\overrightarrow{r}\right)+{\displaystyle \sum _{j\ne l}{\overrightarrow{E}}_s^{\left(j\right)}\left(\overrightarrow{r}\right)}\end{array}(32)$

The electromagnetic field scattered by the jth particle$$can be calculated by multiplying the T-matrix by the total exciting field ${\overrightarrow{E}}_{ex}^{\left(j\right)}$ and replacing the first kind of spherical Bessel function j_n with third kind of spherical Bessel function h_n, which will give rise to scattered outward spherical waves.

$\begin{array}{c}{\overrightarrow{E}}_s^{\left(j\right)}={\displaystyle \sum _n{\displaystyle \sum _m\left[p_{mn}^{\left(l\right)}{T}_n^{\left(M\right)\left(j\right)}{\overrightarrow{M}}_{mn}\left(k{\overrightarrow{rr}}_j\right)+q_{mn}^{\left(l\right)}{T}_n^{\left(N\right)\left(j\right)}{\overrightarrow{N}}_{mn}\left(k{\overrightarrow{rr}}_j\right)\right]}}\end{array}(33)$

where $T_n^{\left(M\right)\left(j\right)}$ and $T_n^{\left(N\right)\left(j\right)}$ are T-matrices calculated in (Eqs 22–23). Substitute (Eqs 31, 33) into (Eq. 32), and we obtain,

${\displaystyle \sum }_n{\displaystyle \sum }_m\left[p_{mn}^{\left(l\right)}Rg{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r{r}_l}\right)+q_{mn}^{\left(l\right)}Rg{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r{r}_l}\right)\right]= {\displaystyle \sum _v{\displaystyle \sum _{\mu }\left[a_{\mu \nu }Rg{\overrightarrow{M}}_{\mu \nu }\left(k\overrightarrow{r}\right)+b_{\mu \nu }Rg{\overrightarrow{N}}_{\mu \nu }\left(k\overrightarrow{r}\right)\right]}}+{\displaystyle \sum }_{j\ne l}{\displaystyle \sum }_{\nu }{\displaystyle \sum }_{\mu }\left[p_{\mu \nu }^{\left(l\right)}{T}_{\nu }^{\left(M\right)\left(j\right)}{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)+q_{\mu \nu }^{\left(l\right)}{T}_{\nu }^{\left(N\right)\left(j\right)}{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)\right](34)$

In order to solve this equation, we need to transform all spherical waves on the right side to be centered at ${\overrightarrow{r}}_l$, i.e., transform ${\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)$ and $Rg{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)$ into linear combinations of ${\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_l\right)$, ${\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{rr}}_l\right)$, $Rg{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_l\right)$, and $Rg{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{rr}}_l\right)$. The addition theorem for spherical harmonics can be expressed as follows (Cruzan, 1962; Bruning and Yuen, 1971; Tsang and Kong, 1983; Stein, 1997). Let $\overrightarrow{r}= {\overrightarrow{r}}_0+\overrightarrow{r}\prime$, and we have

$\begin{array}{c}Rg{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r}\right)={\displaystyle \sum _v{\displaystyle \sum _{\mu }\left\{Rg{A}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{M}}_{\mu \nu }\left(k\overrightarrow{r^{\prime }}\right)+Rg{B}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(35)$

$\begin{array}{c}Rg{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r}\right)= {\displaystyle \sum _v{\displaystyle \sum _{\mu }\left\{Rg{B}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)+Rg{A}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(36)$

For $r_0>r\prime$,

$\begin{array}{c}{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r}\right)={\displaystyle \sum _v{\displaystyle \sum _{\mu }\left\{A_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)+Rg{B}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(37)$

$\begin{array}{c}{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r}\right)= {\displaystyle \sum _v{\displaystyle \sum _{\mu }\left\{B_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)+Rg{A}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right)Rg{\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(38)$

For $r_0<r\prime$,

$\begin{array}{c}{\overrightarrow{M}}_{mn}\left(k\overrightarrow{r}\right)= {\displaystyle \sum _v{\displaystyle \sum _{\mu }\left\{A_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right){\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)+Rg{B}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right){\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(39)$

$\begin{array}{c}{\overrightarrow{N}}_{mn}\left(k\overrightarrow{r}\right)={\displaystyle \sum _v{\displaystyle \sum _{\mu } \left\{B_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right){\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)+Rg{A}_{\mu \nu mn}\left(k{\overrightarrow{r}}_0\right){\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{r}}^{\prime }\right)\right\}}}\end{array}(40)$

The expressions of $A_{\mu \nu mn}\left(k\overrightarrow{r}\right)$ and $B_{\mu \nu mn}\left(k\overrightarrow{r}\right)$ were presented by Tsang and Kong (Tsang et al., 2001). We substitute these equations of translational additional theorem into (Eq. 34) by replacing terms of ${\overrightarrow{rr}}_j$ and $\overrightarrow{r}$ with ${\overrightarrow{r}}_l$. Balancing (Eq. 34) yields

$p_{mn}^{\left(l\right)}= {\displaystyle \sum _v{\displaystyle \sum _{\mu }\left[Rg{A}_{mn\mu \nu }\left(k{\overrightarrow{r}}_l\right)a_{\mu \nu }+Rg{B}_{mn\mu \nu }\left(k{\overrightarrow{r}}_l\right)b_{\mu \nu }\right]}}+{\displaystyle \sum _{j\ne l}{\displaystyle \sum _v{\displaystyle \sum _{\mu }\left[A_{mn\mu \nu }\left(k\overrightarrow{r_l{r}_j}\right)T_{\nu }^{\left(M\right)\left(j\right)}{p}_{mn}^{\left(j\right)}+B_{mn\mu \nu }\left(k\overrightarrow{r_l{r}_j}\right)T_{\nu }^{\left(N\right)\left(j\right)}{q}_{mn}^{\left(j\right)}\right]}}}(41)$

$q_{mn}^{\left(l\right)}={\displaystyle \sum _v{\displaystyle \sum _{\mu }\left[Rg{B}_{mn\mu \nu }\left(k{\overrightarrow{r}}_l\right)a_{\mu \nu }+Rg{A}_{mn\mu \nu }\left(k{\overrightarrow{r}}_l\right)b_{\mu \nu }\right]}}+{\displaystyle \sum _{j\ne l}{\displaystyle \sum _{\nu }{\displaystyle \sum _{\mu }\left[B_{mn\mu \nu }\left(k\overrightarrow{r_l{r}_j}\right)T_{\nu }^{\left(M\right)\left(j\right)}{p}_{mn}^{\left(j\right)}+A_{mn\mu \nu }\left(k\overrightarrow{r_l{r}_j}\right)T_{\nu }^{\left(N\right)\left(j\right)}{q}_{mn}^{\left(j\right)}\right]}}}(42)$

for l = 1, 2, 3, …N. These equations can be expressed in matrix form as follows:

$\begin{array}{c}{\overrightarrow{p}}^{\left(l\right)}={\displaystyle \sum _{j\ne l}\sigma ̿}\left(k{\overrightarrow{r_{l}r}}_j\right){T̿}^{\left(j\right)}{\overrightarrow{p}}^{\left(j\right)}+Rg\sigma ̿\left(k{\overrightarrow{r}}_l\right){\overrightarrow{a}}_{inc}\end{array}(43)$

$\begin{array}{c}{\overrightarrow{q}}^{\left(l\right)}= {\displaystyle \sum _{j\ne l}\sigma ̿}\left(k\overrightarrow{r_l{r}_j}\right){{\displaystyle T̿}}^{\left(j\right)}{\overrightarrow{q}}^{\left(j\right)}+Rg\sigma ̿\left(k{\overrightarrow{r}}_l\right){\overrightarrow{b}}_{inc}\end{array}(44)$

where ${\overrightarrow{a}}_{inc}$ and ${\overrightarrow{b}}_{inc}$ can be calculated through (Eqs 29, 30), $\sigma ̿\left(k\overrightarrow{r}\right)=\left[\begin{array}{cc}A̿\left(k\overrightarrow{r}\right)& B̿\left(k\overrightarrow{r}\right)\\ B̿\left(k\overrightarrow{r}\right)& A̿\left(k\overrightarrow{r}\right)\end{array}\right]$, $T̿=\left[\begin{array}{cc}{T̿}^{\left(M\right)}& 0\\ 0& {T̿}^{\left(N\right)}\end{array}\right].$

Considering the incident field as plane wave without loss of generality, the multiple scattering equations can be written as

$\begin{array}{c}{\overrightarrow{p}}^{\left(l\right)}= {\displaystyle \sum }_{j\ne l}\sigma ̿\left(k\overrightarrow{r_l{r}_j}\right){T̿}^{\left(j\right)}{\overrightarrow{p}}^{\left(j\right)}+e^{\overrightarrow{k}\cdot {\overrightarrow{r}}_l}{\overrightarrow{a}}_{inc}\end{array}(45)$

$\begin{array}{c}{\overrightarrow{q}}^{\left(l\right)}= {\displaystyle \sum }_{j\ne l}\sigma ̿\left(k{\overrightarrow{r_{l}r}}_j\right){T̿}^{\left(j\right)}{\overrightarrow{q}}^{\left(j\right)}+e^{\overrightarrow{k}\cdot {\overrightarrow{r}}_l}{\overrightarrow{b}}_{inc}\end{array}(46)$

The above equations can be solved by iteration. After solving for the exciting coefficients $\overrightarrow{p}$ and $\overrightarrow{q}$, we can get the scattering coefficients and the scattered waves

$\begin{array}{c}{\overrightarrow{a}}^{s\left(j\right)}={T̿}^{\left(j\right)}{{\displaystyle \overrightarrow{p}}}^{\left(j\right)}\end{array}(47)$

$\begin{array}{c}{\overrightarrow{b}}^{s\left(j\right)}={T̿}^{\left(j\right)}{\overrightarrow{q}}^{\left(j\right)}\end{array}(48)$

$\begin{array}{c}{\overrightarrow{E}}^{s\left(j\right)}={\displaystyle \sum _n{\displaystyle \sum _m\left[a_{mn}^{s\left(j\right)}{\overrightarrow{M}}_{mn}\left(k{\overrightarrow{rr}}_j\right)+b_{mn}^{s\left(j\right)}{\overrightarrow{N}}_{mn}\left(k{\overrightarrow{rr}}_j\right)\right]}} \end{array}(49)$

After obtaining all scattering coefficients of all particles, the scattered spherical waves centered at different particles should be transformed to be centered at one particular particle. Here, we set the particular center to be ${\overrightarrow{r}}_l$. By employing the addition theorems (35)–(40), we can obtain

${\overrightarrow{E}}^s={\overrightarrow{E}}^{s\left(l\right)}+{\displaystyle \sum _{j\ne l}{\displaystyle \sum _{n,m}{\displaystyle \sum _{\nu \mu }\left[\left(a_{mn}^{s\left(j\right)}{A}_{\mu \nu mn}\left(k\overrightarrow{r_l{r}_j}\right)+b_{mn}^{s\left(j\right)}{B}_{\mu \nu mn}\left(k{\overrightarrow{r_{l}r}}_j\right)\right){\overrightarrow{M}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)+\left(a_{mn}^{s\left(j\right)}Rg{B}_{\mu \nu mn}\left(k{\overrightarrow{r_{l}r}}_j\right)+b_{mn}^{s\left(j\right)}Rg{A}_{\mu \nu mn}\left(k\overrightarrow{r_l{r}_j}\right)\right){\overrightarrow{N}}_{\mu \nu }\left(k{\overrightarrow{rr}}_j\right)\right]}}}={\displaystyle \sum _{n,m}\left[a_{mn}^s{\overrightarrow{M}}_{mn}\left(k{\overrightarrow{rr}}_j\right)+b_{mn}^s{\overrightarrow{N}}_{mn}\left(k{\overrightarrow{rr}}_j\right)\right]}(50)$

Then, the scattering cross section in charged particle clusters considering the multiple scattering effects is given by

$\begin{array}{c}{C}_s=\frac{2\pi }{k_2^2}{\displaystyle \sum _{n=1}^{\infty }\left(2n+1\right)}\left(\frac{{{\displaystyle {\displaystyle {\sum }_m\left|a_{mn}^s\right|}}}^2}{{{\displaystyle {\displaystyle {\sum }_m\left|a_{mn}^s\right|}}}^2}+\frac{{{\displaystyle {\displaystyle {\sum }_m\left|b_{mn}^s\right|}}}^2}{{{\displaystyle {\displaystyle {\sum }_m\left|b_{mn}^s\right|}}}^2}\right)\end{array}(51)$

Result

For an incident EMW with frequency between 10 and 200 GHz with electric field polarized in the x direction and propagating in the z direction, EMW has the form ${\overrightarrow{E}}_{in}=e^{i\left(kz-\omega t\right)}\widehat{x}$, where k is the wavenumber. For typical particles with relative permittivity of 3.2 and a radius of 1 mm, the ratio of scattering cross section and extinction cross section of a charged particle to those of uncharged particle are plotted in Figures 1A,B, respectively. $C_{sca}$ and $C_{ext}$ are scattering cross section and extinction cross section for a charged particle, respectively. $C_{sca}^0$ and $C_{ext}^0$ are scattering cross section and extinction cross section for an uncharged particle, respectively. The surface charge density varies from 1 to 100 mC/m², which is consistent with the general level of net charges carried by particles in a sand/dust storm (Zhou et al., 2018). We also consider the extreme case that the surface charge density equals infinity, which will cause the surface conductivity to be infinite. In this case, the scattering properties of the particle will be equivalent to those of an ideal metal particle. It is illustrated in Figure 1A that with the increase in surface charge density, the scattering cross section will be enhanced in the low-frequency range where Rayleigh scattering is applicable. As shown in Figure 1A, as charge density increases, the curve of the scattering cross section gradually approaches the curve of the metal particle and finally reaches a saturated level as charges accumulated. The maximum enhancement of $C_{sca}$ for an ideal metal particle (i.e., particle with surface charge density to be infinite) is 6.983 times of $C_{sca}^0$ for an uncharged particle for frequencies below 10 GHz. On the contrary, the scattering cross section is reduced for charged particles in the higher-frequency range. For ideal metal particle or particles with surface charge density being infinite, $C_{sca}/C_{sca}^0$ reaches a minimum value 0.442 at $f=145.7 \mathrm{GHz}$. As the frequency gets much higher, that is, the wavelength is far less than the size of the particle, the influence of surface charges to the scattering cross section can be neglected. The reason for these totally different responses to surface charges is that the way free electrons oscillate in response to the applied electromagnetic field is highly dependent on the frequency of the incident waves. It is well known that metals are highly reflective, and electromagnetic waves are not allowed to penetrate through them in the low-frequency visible range, which can be attributed to the surface charges that screens the incident field. However, the free electrons have an intrinsic finite response time, above which they will not be fast enough to screen the penetration from incident fields, and therefore, the material is no longer strongly reflective and turns transparent. Here, the surface plasma frequency for dielectric charged particles, which are related to the electrostatic potential at the surface of the particle and the radius of the charged sphere, is much lower than that of metal since the carrier density for sand/dust particles are much lower compared with metal (Klačka and Kocifaj, 2007). However, a similar “reflective to transparent” transition can be inferred from the scattering and extinction cross sections presented in Figure 1. As illustrated in Figure 1B, the extinction cross section by a charged particle was enhanced. However, in the low-frequency range the enhancement of the extinction of EMWs did not increase monotonically with the increase in the surface charge density as for the scattering cross section. This is because the extinction by the particle is the sum of scattering and absorption. As the surface charge density increases from zero, at the first stage (corresponds to curves of $1$ and $10 \mathrm{mC}/{\mathrm{m}}^2$), the imaginary part of the effective complex permittivity, which accounts for energy loss, increases with the charge density, and therefore, the absorption by the particle increases. As the charge density further increases, at this stage (corresponds to curves from $10$ to $100 \mathrm{mC}/{\mathrm{m}}^2$), the charged particles were further “metalized” and exhibits highly reflective property, which shields the EMWs from penetrating through the particle. Consequently, the absorption cross section gets smaller as the surface charge density increases. For metallic particles, in the low-frequency range, the absorption is extremely low due to the screening effect to the incident field. This is the reason why the curve for the metallic particle (purple) shows the lowest extinction cross section in Figure 1B. In Figure 2, the electric field distributions (x component of the electric field) are plotted for a neutral particle, and a charged particle with surface current density equals 100 mC/m². As shown in Figures 2A,B at a lower frequency range ($f = 1 \mathrm{GHz}$), the field inside the charged particle is close to zero and is smaller compared with that of the neutral particle, which can be attributed to the screening effect of surface charges. As illustrated in Figures 2C,D, at a higher-frequency regime ($f = 100 \mathrm{GHz}$), for neutral and charged particles, the difference in the penetration of free electrons is not as pronounced as the screening effect in the lower-frequency range, which agrees with the smaller discrepancies in scattering cross sections at higher frequencies as depicted in Figure 1.

FIGURE 1

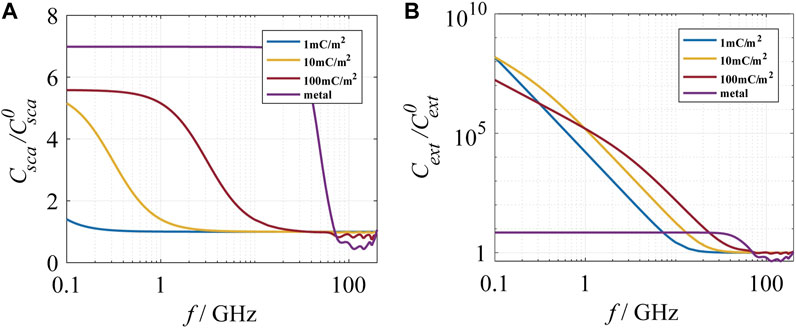
FIGURE 1. The influence of surface charge density on the scattering/extinction cross sections of a single particle. Surface charge densities are set to ${\eta }_s=1 , 10, 100,\infty \text{mC}/{\text{m}}^2$. (A) the ratio of scattering cross section of a charged particle to that of an uncharged one. $C_{sca}$ and $C_{sca}^0$ denote the scattering cross section of a charged particle and an uncharged one. (B) The ratio of extinction cross section of a charged particle to that of an uncharged one. $C_{ext}$ and $C_{ext}^0$ denote the extinction cross section of charged and uncharged particles.

FIGURE 2

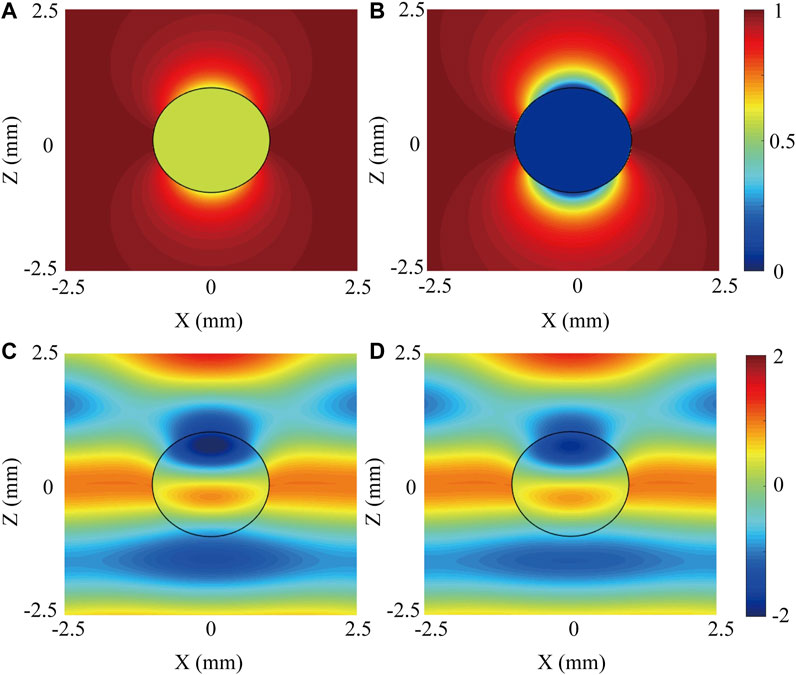
FIGURE 2. Field distributions of neutral and charged particles. The x component of the electric field at 1 GHz (upper panel) and 100 GHz (lower panel) for (A, C) a neutral particle and (B, D) a charged particle with surface charge density ${\eta }_s=100 \text{mC}/{\text{m}}^2$. The particle with a relative permittivity of 3.2 and a radius of 1 mm is illuminated by a plane wave polarized in the x direction and propagating in the z direction.

As shown in Figure 1B, compared with the scattering cross section, the extinction cross section is greatly enhanced by the surface charge in the low-frequency range, which satisfies the Rayleigh scattering limit. The enhancement increases when the frequency gets lower. For surface charge density equal to 10 mC/m², the enhancement of $C_{ext}$ reaches 1.5 × 10⁸ times of that of $C_{ext}^0$ at 0.1 GHz. If we consider a higher surface charge density, the enhancement will decrease and will be down to 1.7 × 10⁷ for surface charge density equal to 100 mC/m² and only 6.983 times the neutral extinction for ideal metal particles. For higher frequency, the extinction cross section is decreased by surface charges, but the effect is not strong as that of scattering cross section. $C_{ext}/C_{ext}^0$ has a minimum value of 0.441 at $f = 114.7 \mathrm{GHz}$ for ideal metal particles or particles with infinite surface charge density.

Next, the influence of the material of the particles on scattering and extinction properties is investigated. For particles with radius $a =$ 1 mm and surface charge density ${\eta }_s =$ 10 mC/m², the ratio of scattering cross section and extinction cross section of charged particles to those of the uncharged one are plotted in Figures 3A,B, respectively. The relative permittivities vary from 2 to 5. It can be seen that with the increase in the relative permittivity of particles, the enhancement effect by surface charges on the scattering cross section and extinction cross section is weakened in the low frequency, which satisfies the Rayleigh scattering limit. For a higher-frequency range above 50 GHz, as shown in the inset of Figure 3A, the decrease in the scattering cross section caused by the surface charges is enlarged by higher relative permittivity. In the higher frequency range, the extinction cross section remains unchanged for charged particles compared with uncharged particles.

FIGURE 3

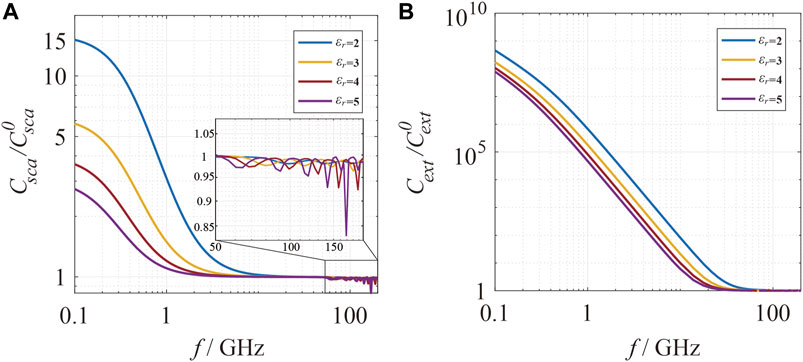
FIGURE 3. The influence of relative permittivity on the scattering/extinction cross sections of a single charged particle. Relative permittivity is set to ${\epsilon }_r=2, 3, 4, 5$. (A) The ratio of scattering cross section of a charged particle to that of an uncharged one. (B) The ratio of extinction cross section of a charged particle to that of an uncharged one.

The influence of the size of the particles on the scattering and extinction properties is also investigated. For a particle with relative permittivity equal to 3.2 and surface charge density equal to 10 mC/m², the ratio of scattering cross section and extinction cross section of charged particles to those of the uncharged one are plotted in Figures 4A,B, respectively. The radius of particles varies from 0.01 to 10 mm. It can be seen that for particles with smaller sizes, the enhancement effect by surface charges on the scattering cross section and extinction cross section is enlarged. This is because the enhancement effect is dependent on the bulk complex refractive index $m=\sqrt{{\epsilon }_r}$, and the imaginary part of $m$ represents the absorption of the particle. Since we mathematically assume the charge is confined to the surface layer of the particle, for larger particles, the surface-to-volume ratio is relatively low; therefore, the scattering/extinction caused by the surface charge is small compared with the distribution from the volume. On the other hand, as the frequency increases and goes beyond the Rayleigh scattering limit, the enhancement is reduced, and the ratio is approximate to unity.

FIGURE 4

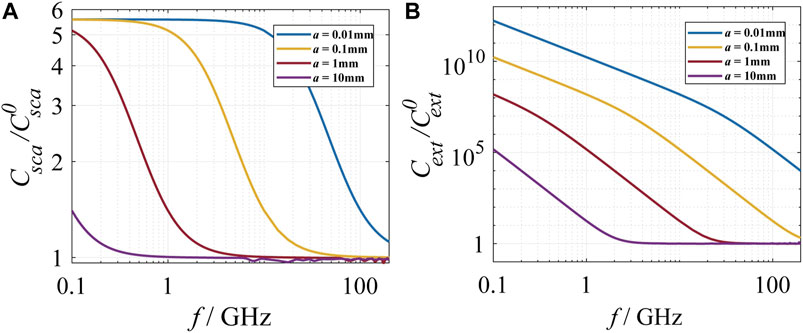
FIGURE 4. The influence of the size of the particles on the scattering/extinction cross sections of a single charged particle. The radii of particles are set to $a=0.01,0.1,1,10\text{ mm}$. (A) The ratio of scattering cross section of a charged particle to that of an uncharged one. (B) The ratio of extinction cross section of a charged particle to that of an uncharged one.

For a multi-particle system, the dependence of the scattering cross section on the number density and surface charge density of the particles is studied. Under the classical assumption of independent scattering, the scattering cross section can be expressed as $C_{sca}=N{C}_{sca}^{sig}$, where $C_{sca}^{sig}$ is the scattering cross section for a single particle, and N is the number of particles in the system. However, the practical scattering properties are different from the classical assumption due to the multiple scattering effect, and therefore, the scattering cross section is not linearly proportional to the number density of particles. First, we study the influence of the number density of the particles on the scattering cross section in a two-particle system. The number density is directly related to the distance between particles. A higher-number density is equivalent to a closer distance between two particles. Assume the incident EMW propagating in the z direction with frequency between 10 and 200 GHz, and the electric field is polarized in the x direction, which can be expressed as ${\overrightarrow{E}}_{in}=e^{i\left(kz-\omega t\right)}\widehat{x}$. For particles with a relative permittivity of 3.2 and a radius of 1 mm, the scattering cross section $C_{sca}$ of a two-particle system is calculated for different distances ($\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|=2.2$ and $3\text{ mm}$). The T-matrix calculation is based on the overall charged model described in the Single charged particle section. The scattering cross section of the two-particle system is calculated under three methods: the T-matrix-based multiple scattering model with the calculated scattering cross section denoted by $C_{sca}$, classical independent scattering model with results denoted by $C_{sca}^{Cla}$, and CST simulation with results denoted by $C_{sca}^{CST}$. Scattering spectrum with no surface charges and surface charge densities equal to 1 and 10 mC/m² are plotted in Figures 5A,D for different distances between two particles. The enlarged spectrum illustrated in the inset of Figures 5A,D shows that when the surface charge density increases from 0 to 1 and 10 mC/m², the scattering cross section is slightly reduced, and the deviation is amplified with higher surface current densities. This result is consistent with Figure 1A for a single charged particle where the scattering cross section is shown to be suppressed by surface charges in a higher-frequency range above 60 GHz.

FIGURE 5

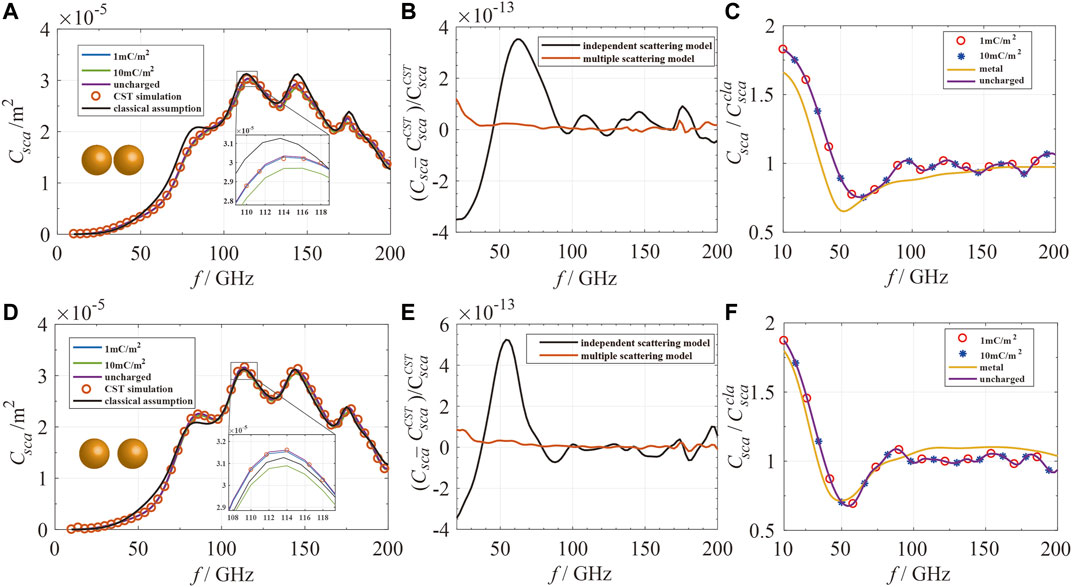
FIGURE 5. The scattering cross sections for two-particle systems with different separations and charge densities. First column: the scattering cross section of two-particle clusters calculated under the multiple scattering method (for uncharged particles charged particles), classical independent scattering assumption, and CST simulation (for uncharged particles) with the radius of particles equal to 1 mm; distances between two particles are (A) 2.2 mm and (D) 3 mm. Second column: the relative differences between the results calculated under classical assumption, multiple scattering model, and CST simulation for uncharged particles for distance equal to (B) 2.2 mm and (E) 3 mm. Third column: the ratio of scattering cross section calculated under the multiple scattering method to the results calculated with the classical assumption for distance equal to (C) 2.2 mm and (F) 3 mm.

There is an obvious difference between the result of multiple scattering method and classical independent scattering method. High accuracy of multiple scattering model can be seen when compared with CST simulation. Using the CST simulation as a benchmark, we calculated the relative difference between the two methods and the simulation to evaluate the accuracy of the multiple scattering model and classical assumption in Figures 5B,E. It can be seen that the multiple scattering model whose result is almost the same as simulation has higher accuracy compared with the classical assumption. As the distance between particles decreases from 3 to 2.2 mm, which is equivalent to increasing the number density, the maximum deviation between the calculated result under classical assumption and the simulation result increase from $2.2\times {10}^{-6}$ to $3.3\times {10}^{-6} {\mathrm{m}}^2$, and the mean absolute difference $E\left[\right|C_{sca}^{Cla}-C_{sca}^{CST}\left|\right]$ of the two results increases from $6.6\times {10}^{-7}$ to $9.3\times {10}^{-7} {\mathrm{m}}^2$ with a 40% increment. The mean relative differences are $1.26\times {10}^{-13}$ and $1.28\times {10}^{-13}$, respectively, while as shown in Figures 5B,E the mean relative differences between the results calculated by the multiple scattering model and the CST results are below $4\times {10}^{-14}$ for both separations. It reveals that a closer distance between particles or a higher-number density of particles will enhance the multiple scattering effect and make the result deviate further from the result calculated under the classical independent scattering assumption.

Next, to gain deeper insight into the electromagnetic response of clustered charged particles, we investigated the influence of surface charges on the multiple scattering effect. The ratio of the scattering cross section calculated under the multiple scattering model $C_{sca}$ and classical assumption $C_{sca}^{Cla}$ is plotted in Figures 5C,F for the two separations. Surface charge densities are set to 0, 1, 10 mC/m², and infinity (the same scattering properties with ideal metal), respectively. There is no observable influence of surface charges to the multiple scattering effect for surface charge density under 10 mC/m². For extreme situations, where we set the surface charge density to infinity, as illustrated in Figure 5C when the inter-particle distance is equal to 1.1 mm, the enhancement of scattering cross section by multiple scattering effect is weakened, and the weakened scattering cross section reaches the minimum when the frequency equals 54 GHz. As particles are getting closer, the deviation of the scattering cross section of metal particles with that of neutral particles is amplified.

We then increase the number of particles and validate the T-matrix-based multiple scattering model in a cluster composed of four particles. The pattern of the particle cluster is shown in the inset in Figures 6A,D. Because the distances between two of the particles in the cluster may be different, the distance R from each center of the particle to the center of the cluster is used to indicate the inter-particle distances. As illustrated in Figures 6A,D the scattering cross sections for four-particle clusters with R equals 1.5 and 2 mm, and the particle radius equals 1 mm are almost two times larger compared with the scattering cross section of the two-particle system since the number of particles is doubled. In the inset in Figures 6A,D the scattering spectrum is demonstrated to be suppressed by surface charges, which is in accordance with the results shown in Figures 1A, 5A,D. In Figures 6B,E when R decreases from 2 to 1.5 mm, the mean absolute difference $E\left[\right|C_{sca}^{Cla}-C_{sca}^{CST}\left|\right]$ between the results under classical independent scattering assumption and the CST simulation results increase from $1.5\times {10}^{-6}$ to $2.6\times {10}^{-6} {\mathrm{m}}^2$ with an 80% increment, which confirm the conclusion that the multiple scattering effect is amplified as the particles are getting closer to each other. The mean relative differences are $1.45\times {10}^{-6}$ and $3.36\times {10}^{-5}$, respectively. Compared with the results calculated under the multiple scattering model, as shown in Figures 6B,E the relative differences are several times larger, which validate the accuracy of the multiple scattering model.

FIGURE 6

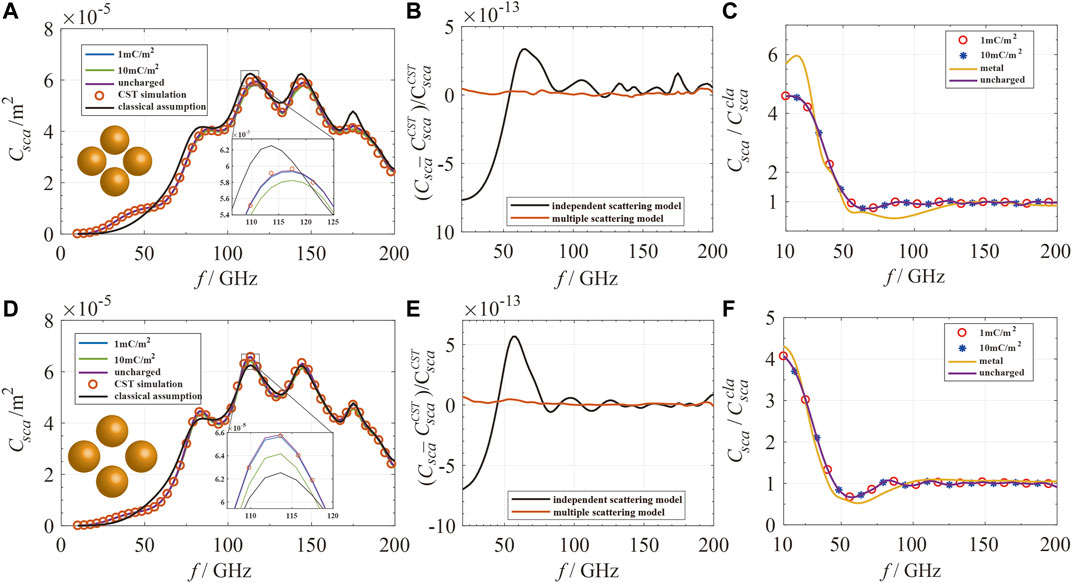
FIGURE 6. The scattering cross sections for four-particle clusters with different separations and charge densities. First column: the scattering cross section of four-particle clusters calculated under the multiple scattering method (for uncharged particles and charged particles), classical independent scattering assumption, and CST simulation (for uncharged particles) with radius of the particles equal to 1 mm, R equals (A) 1.5 mm and (D) 2 mm. Second column: the relative difference between the result calculated under classical assumption, multiple scattering model, and CST simulation for R equal to (A) 1.5 mm and (D) 2 mm. Third column: the ratio of scattering cross section calculated under the multiple scattering method to the results calculated with the classical assumption for R equal to (A) 1.5 mm and (D) 2 mm.

Finally, in Figure 7, we depict the ratio of the scattering cross section calculated under the multiple scattering model to the result under the classical assumption $C_{sca}/C_{sca}^{Cla}$ as a function of the maximum order Na in the formula of addition theorem and the number of iterations in solving Eqs 45, 46. Here, the frequency is set to 100 GHz, and the particles are set to be uncharged. The convergence is demonstrated to be closely related to the distance between particles. For consistency, different inter-particle distances are indicated by the distance R from the center point of the particle cluster to the center of individual spheres. As illustrated in Figure 7, for two and four particles, the results for four and six iterations are nearly identical, which means four times of iteration is enough for convergence while keeping relatively low computational costs. Therefore, in the former calculations, we adopted four times of iterations to ensure the accuracy of the calculation. As for the maximum order Na applied in the formula of addition theorem, for a two-particle system shown in Figure 7A, the result is convergent when Na is greater than 6 and 8 for R equals 1.1 and 1.5 mm, respectively. For four-particle clusters, the convergence condition is met for Na greater than 8 and 10 for R equals 1.5 and 2.0 mm, respectively. As demonstrated in Figure 7, the slope of the curve is higher, and the convergence condition is met at smaller Na for larger inter-particle distances.

FIGURE 7

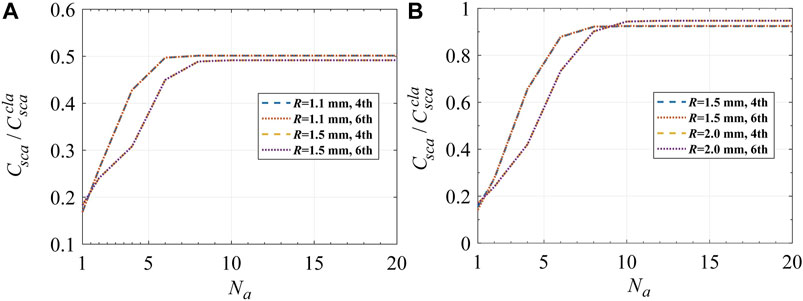
FIGURE 7. Convergence of the scattering cross section versus the number of iterations and N_a. The ratio of scattering cross section calculated under the multiple scattering method to the results calculated with the classical assumption for (A) two-particle clusters and (D) four-particle clusters with different separations between particles indicated by the distance R from the center point of the cluster to an individual particle.

Conclusion

Based on the T-matrix approach, the problem of electromagnetic waves scattered by a single-charged particle can be solved, and the influence of surface charged density and relative permittivity of the particle is investigated. For sizes of particles much smaller than the wavelength of the incident EMWs, the enhancement of extinction cross section by surface charge is enlarged with the higher surface charge density but reduced by higher permittivity of the particle. The enhancement of scattering cross section by surface charge is slightly enlarged by a higher surface charge density and reduced by a higher permittivity of the particle. For a higher-frequency range, the influence of surface charge and relative permittivity on the extinction cross section can be neglected, but the scattering cross section is slightly reduced by higher surface charge and larger relative permittivity of the particle. With the increase in the size of the particles, the enhancement of scattering/extinction cross sections due to the surface charges is smaller.

Next, exploiting the T-matrix approach based on the addition theorem and the iterative method, the multiple scattering problem of clustered charged particles can be solved. The influence of inter-particle distances and surface charge density on the multiple scattering effect is investigated. Scattering cross sections of two-particle systems and four-particle clusters are calculated via the multiple scattering method with varying inter-particle distances. The deviation from the result calculated under the classical independent scattering assumption is obvious when inter-particle distance is smaller than three times that of the particle radius and is further enlarged as particles are getting closer. Surface charge density has little influence on the multiple scattering effect within several hundred mC/m².

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WY did the calculation and implementation of the MATLAB program, XH, SZ and CW did the mathematical derivation, JJ, TY and FG did the simulation verification.

Funding

This work was supported by the National Natural Science Foundation of China(NNSFC) under Grants No. 51777213, National Key Laboratory Foundation No. 6142205200402, the Fundamental Research Funds for the Central Universities No. 2020XZZX002-15, Beijing Information science and technology university Research Grants No. 2025037.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altuncu, Y., Durukan, T., and Akdogan, R. E. (2019). Reconstruction of Two-Dimensional Objects Buried into Three-Part Space with Locally Rough Interfaces via Distorted Born Iterative Method. Pier 166, 23–41. doi:10.2528/PIER19072203

CrossRef Full Text | Google Scholar

Ansari, A. J., and Evans, B. G. (1982). Microwave Propagation in Sand and Dust Storms. IEE Proc. F Commun. Radar Signal. Process. UK 129, 315–322. doi:10.1049/ip-f-1.1982.0047

CrossRef Full Text | Google Scholar

Bohren, C. F., and Huffman, D. R. (1998). Absorption and Scattering of Light by Small Particles. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Bohren, C. F., and Hunt, A. J. (1977). Scattering of Electromagnetic Waves by a Charged Sphere. Can. J. Phys. 55, 1930–1935. doi:10.1139/p77-235

CrossRef Full Text | Google Scholar

Bruning, J., and Yuen Lo, L. (1971). Multiple Scattering of EM Waves by Spheres Part I--Multipole Expansion and ray-optical Solutions. IEEE Trans. Antennas Propagat. 19, 378–390. doi:10.1109/TAP.1971.1139944

CrossRef Full Text | Google Scholar

Chai, J., Ge, L., Hu, P., Xiang, H., and Han, D. (2020). Angle-dependent Optical Response of the Plasmonic Nanoparticle Clusters with Rotational Symmetry. Opt. Express 28, 10425–10437. doi:10.1364/OE.388590

PubMed Abstract | CrossRef Full Text | Google Scholar

Cruzan, O. R. (1962). Translational Addition Theorems for Spherical Vector Wave Functions. Quart. Appl. Math. 20, 33–40. doi:10.1090/qam/132851

CrossRef Full Text | Google Scholar

Fung, K. H., and Chan, C. T. (2008). Analytical Study of the Plasmonic Modes of a Metal Nanoparticle Circular Array. Phys. Rev. B 77, 205423. doi:10.1103/PhysRevB.77.205423

CrossRef Full Text | Google Scholar

Ghobrial, S. I., and Jervase, J. A. (1997). Microwave Propagation in Dust Storms at 10.5 GHz - A Case Study in Khartoum, Sudan, E80-B. Tokyo, Japan: IEICE Transactions on Communications., 1722–1727.

Google Scholar

Gill, E. W. B., and Alfrey, G. F. (1949). Frictional Electrification. Nature 163, 172. doi:10.1038/163172a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gill, E. W. B. (1948). Frictional Electrification of Sand. Nature 162, 568–569. doi:10.1038/162568b0

CrossRef Full Text | Google Scholar

Haddad, S., Salman, M. J. H., and Jha, R. K. (1983). Effects of Dust/sandstorm on Some Aspects of Microwave Propagation. Proc. ESA Spec. Publ. 194, 153–162.

Google Scholar

Holloway, C. L., Kuester, E. F., and Haddab, A. H. (2019). Retrieval Approach for Determining Surface Susceptibilities and Surface Porosities of a Symmetric Metascreen from Reflection and Transmission Coefficients. Pier 166, 1–22. doi:10.2528/PIER19022305

CrossRef Full Text | Google Scholar

Huang, H., Tsang, L., Colliander, A., Shah, R., Xu, X., and Yueh, S. (2020). Multiple Scattering of Waves by Complex Objects Using Hybrid Method of T-Matrix and Foldy-Lax Equations Using Vector Spherical Waves and Vector Spheroidal Waves. Pier 168, 87–111. doi:10.2528/PIER20080409

CrossRef Full Text | Google Scholar

Islam, M. R., Omer Elshaikh, Z. E., Khalifa, O. O., Alam, A. Z., Khan, S., and Naji, A. W. (2010). Prediction of Signal Attenuation Due to Duststorms Using Mie Scattering. Iiumej 11, 71–87. doi:10.31436/iiumej.v11i1.42

CrossRef Full Text | Google Scholar

Klačka, J., Kocifaj, M., Kundracik, F., Videen, G., and Kohút, I. (2015b). Generalization of Electromagnetic Scattering by Charged Grains through Incorporation of Interband and Intraband Effects. Opt. Lett. 40, 5070–5073. doi:10.1364/OL.40.005070

PubMed Abstract | CrossRef Full Text | Google Scholar

Klačka, J., Kocifaj, M., Kundracik, F., and Videen, G. (2015a). Optical Signatures of Electrically Charged Particles: Fundamental Problems and Solutions. J. Quantitative Spectrosc. Radiative Transfer 164, 45–53. doi:10.1016/j.jqsrt.2015.05.009

CrossRef Full Text | Google Scholar

Klacka, J., and Kocifaj, M. (2010). On the Scattering of Electromagnetic Waves by a Charged Sphere. Pier 109, 17–35. doi:10.2528/PIER10072708

CrossRef Full Text | Google Scholar

Klačka, J., and Kocifaj, M. (2007). Scattering of Electromagnetic Waves by Charged Spheres and Some Physical Consequences. J. Quantitative Spectrosc. Radiative Transfer 106, 170–183. doi:10.1016/j.jqsrt.2007.01.016

CrossRef Full Text | Google Scholar

Kocifaj, M., Klačka, J., Kundracik, F., and Videen, G. (2015). Charge-induced Electromagnetic Resonances in Nanoparticles. Annalen Der Physik 527, 765–769. doi:10.1002/andp.201500202

CrossRef Full Text | Google Scholar

Kocifaj, M., Kundracik, F., and Videen, G. (2016). Optical Characterization of Electrically Charged Particles Using Discrete Dipole Approximation. J. Quantitative Spectrosc. Radiative Transfer 184, 161–166. doi:10.1016/j.jqsrt.2016.07.010

CrossRef Full Text | Google Scholar

Kocifaj, M. (2013). Theoretical Conditions for Charge-Induced normal Modes in Spherical Particles. Laser Phys. Lett. 10, 055901. doi:10.1088/1612-2011/10/5/055901

CrossRef Full Text | Google Scholar

Kong, J. A. (1986). Electromagnetic Wave Theory. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Lacks, D. J., and Mohan Sankaran, R. (2011). Contact Electrification of Insulating Materials. J. Phys. D: Appl. Phys. 44, 453001. doi:10.1088/0022-3727/44/45/453001

CrossRef Full Text | Google Scholar

Liao, T.-H., Ding, K.-H., and Tsang, L. (2019). Broadband Green's Function with Higher Order Low Wavenumber Extractions for an Inhomogeneous Waveguide with Irregular Shape. Pier 164, 75–95. doi:10.2528/PIER18102903

CrossRef Full Text | Google Scholar

Lovat, G., Burghignoli, P., Araneo, R., Celozzi, S., Andreotti, A., Assante, D., et al. (2020). Shielding of an Imperfect Metallic Thin Circular Disk: Exact and Low-Frequency Analytical Solution. Pier 167, 1–10. doi:10.2528/PIER19090908

CrossRef Full Text | Google Scholar

Lowell, J., and Rose-Innes, A. C. (1980). Contact Electrification. Adv. Phys. 29, 947–1023. doi:10.1080/00018738000101466

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Travis, L. D., and Lacis, A. A. (2006). Multiple Scattering of Light by Particles: Radiative Transfer and Coherent Backscattering. Cambridge: Cambridge University Press.

Google Scholar

Mishchenko, M. I., Travis, L. D., and Lacis, A. A. (2002). Scattering, Absorption, and Emission of Light by Small Particles. Cambridge: Cambridge University Press.

Google Scholar

Peterson, B., and Strm, S. (1974). T-matrix Formulation of Electromagnetic Scattering from Multilayered Scatterers. Phys. Rev. D 10. doi:10.1103/physrevd.10.2670

CrossRef Full Text | Google Scholar

Popov, E. (2012). Gratings: Theory and Numeric Applications. France: Institut Fresnel, CNRS, AMU.

Google Scholar

Stein, S. (1997). Addition Theorems for Spherical Wave Functions. Quart. Appl. Math. 19, 15–24.

Google Scholar

Tan, S., and Tsang, L. (2019). Efficient Broadband Evaluations of Lattice Green's Functions via Imaginary Wavenumber Components Extractions. Pier 164, 63–74. doi:10.2528/PIER18102001

CrossRef Full Text | Google Scholar

Tsang, L., Kong, J. A., Ding, K. H., and Ao, C. O. (2001). Scattering of Electromagnetic Waves: Numerical Simulations. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Tsang, L., Kong, J. A., and Ding, K. H. (2000). Scattering of Electromagnetic Waves: Theories and Applications. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Tsang, L., and Kong, J. A. (1983). Scattering of Electromagnetic Waves from a Half Space of Densely Distributed Dielectric Scatterers. Radio Sci. 18, 1260–1272. doi:10.1029/RS018i006p01260

CrossRef Full Text | Google Scholar

Wang, C., Qian, C., Hu, H., Shen, L., Wang, Z., Wang, H., et al. (2020). Superscattering of Light in Refractive-Index Near-Zero Environments. Pier 168, 15–23. doi:10.2528/PIER20070401

CrossRef Full Text | Google Scholar

Xie, L., Han, K., Ma, Y., and Zhou, J. (2013a). An Electrification Mechanism of Sand Grains Based on the Diffuse Double Layer and Hertz Contact Theory. Appl. Phys. Lett. 103, 104103. doi:10.1063/1.4819948

CrossRef Full Text | Google Scholar

Xie, L., Li, G., Bao, N., and Zhou, J. (2013b). Contact Electrification by Collision of Homogenous Particles. J. Appl. Phys. 113, 184908. doi:10.1063/1.4804331

CrossRef Full Text | Google Scholar

Xie, L., Zhong, H., Du, Z., and Zhou, J. (2020). Monte Carlo Simulation of Electromagnetic Wave Transmittance in Charged Sand/dust Storms. J. Quantitative Spectrosc. Radiative Transfer 241, 106744. doi:10.1016/j.jqsrt.2019.106744

CrossRef Full Text | Google Scholar

Xue, Z., Wu, Y. M., Chew, W. C., Jin, Y.-Q., and Boag, A. (2020). The Multilevel Fast Physical Optics Method for Calculating High Frequency Scattered Fields. Pier 169, 1–15. doi:10.2528/PIER20071203

CrossRef Full Text | Google Scholar

Yang, P., Ding, J., Panetta, R. L., Liou, K.-N., Kattawar, G. W., and Mishchenko, M. I. (2019). On the Convergence of Numerical Computations for Both Exact and Approximate Solutions for Electromagnetic Scattering by Nonspherical Dielectric Particles (Invited Review). Pier 164, 27–61. doi:10.2528/PIER18112810

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Hu, X., Chen, H., and Gao, F. (2020). Designer Surface Plasmons Enable Terahertz Cherenkov Radiation (Invited). Pier 169, 25–32. doi:10.2528/PIER20102708

CrossRef Full Text | Google Scholar

Zhou, J., Dou, X., and Xie, L. (2018). Scattering and Attenuation of Electromagnetic Waves by Partly Charged Particles. J. Quantitative Spectrosc. Radiative Transfer 206, 55–62. doi:10.1016/j.jqsrt.2017.11.006

CrossRef Full Text | Google Scholar

Zhou, J., and Xie, L. (2011). Effect of Net Surface Charge on Particle Sizing and Material Recognition by Using Phase Doppler Anemometry. Appl. Opt. 50, 379–386. doi:10.1364/ao.50.000379

PubMed Abstract | CrossRef Full Text | Google Scholar