- 1School of Transportation, Civil Engineering and Architecture, Foshan University, Foshan, China
- 2College of Urban and Rural Construction, Zhongkai University of Agriculture and Engineering, Guangzhou, China
- 3Guangzhou University-Tamkang University Joint Research Centre for Engineering Structure Disaster Prevention and Control, Guangzhou University, Guangzhou, China
Functionally graded material (FGM) arches may be subjected to a locally radial load and have different material distributions leading to different nonlinear in-plane buckling behavior. Little studies is presented about effects of the type of material distributions on the nonlinear in-plane buckling of FGM arches under a locally radial load in the literature insofar. This paper focuses on investigating the nonlinear in-plane buckling behavior of fixed FGM arches under a locally uniformly distributed radial load and incorporating effects of the type of material distributions. New theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches under a locally uniformly distributed radial load that are subjected to three different types of material distributions are derived. The comparisons between theoretical and ANSYS results indicate that the theoretical solutions are accurate. In addition, the critical modified geometric slendernesses of FGM arches related to the switches of buckling modes are also derived. It is found that the type of material distributions of the fixed FGM arches affects the limit point buckling loads and bifurcation buckling loads as well as the nonlinear equilibrium path significantly. It is also found that the limit point buckling load and bifurcation buckling load increase with an increase of the modified geometric slenderness, the localized parameter and the proportional coefficient of homogeneous ceramic layer as well as a decrease of the power-law index p of material distributions of the FGM arches.
Introduction
Arch structure has been widely used in the practice, because of the unique characteristics about aesthetics and safety. Arch structure is often subjected to different forms of load and different boundary constraints in practical engineering, which may lead to structural damage of arches. (Timoshenko et al., 1962), (Schreyer, 1972) and (Plaut and Raymond, 1990) started the research of arches early. Then, (Bradford et al., 2002) researched the in-plane buckling behavior of symmetrical cross-section arches under a central point load. (Pi et al., 2002) used an energy method to build the nonlinear equilibrium equation and the buckling equilibrium equation of arches, and the analytical result of nonlinear buckling was obtained. (Pi et al., 2008) also presented a theoretical research on the nonlinear in-plane buckling of pin-ended circular arches subjected to a central point load with rotational restraints elastic end. (Pi and Bradford, 2009) developed the virtual work approach was used to establish post-buckling equilibrium differential equation and the nonlinear buckling, and the exact solution of the nonlinear bifurcations. (Cai and Feng, 2010) carried out the in-plane buckling of parabolic arches whose rotational stiffness of supports increases according to loaded. (Cai et al., 2012) carried out the buckling equations and nonlinear equilibrium by virtual work principal method. (Cai et al., 2013) also analyzed the buckling equilibrium path according to the bistable strut by using fixed arches subjected to a central point load. According to the principle of virtual work, (Han et al., 2016) studied the in-plane nonlinear buckling behavior of circular arches with elastic horizontal supports under a uniform radial load. (Yan et al., 2017) made an analytical study about the non-uniform shallow arch subjected to a central point load. (Pi et al., 2017) revealed in-plane buckling of fixed shallow circular arches with the arbitrary radial point load. (Lu et al., 2018) explored the nonlinear in-plane buckling and post-buckling behavior of the fixed arches subjected to a localized uniform radial load. (Lu et al., 2020) also explored effects of movement and rotation of supports on nonlinear instability of fixed shallow arches under a localized uniform radial load. (Hu et al., 2021) presented an analytical investigates for nonlinear buckling of pin-ended arch-beam structures. In addition to the optimization of the cross section can make the stability of the structure better (Chen and Young, 2021; Chen et al., 2021), the improvement of material engineering technology also can make the stability of the structure better.
Most of the arches studied in the above literatures are homogeneous solid materials, however, functionally graded material (FGM) has been widely used because their mechanical properties are better than those of homogeneous materials in recent years. FGM arches are usually composed of two or more materials, which can contribute to the superior performance of each material, but the stress and buckling of FGM arches become complicated. (Bateni and Eslami, 2015) conducted nonlinear buckling behavior of FG circular arches under the uniformly radial load using an analytical method. (Simsek, 2016) assumed the material properties of the beam vary as the power-law form in both axial and thickness directions. (Al-shujairi and Mollamahmutoğlu, 2018) concerned with the sandwich FG micro-beams is made of the ceramic-metal FG skin and homogenous ceramic core, based on the classical rule and the Mori-Tanaka homogenization scheme of composite material properties of the part of the FG sandwich size according to beam changes continuously by the thickness of the beam. For different boundary condition analysis, (Bateni and Eslami, 2014) explored the nonlinear in-plane buckling behavior of FGMs arches. Simply supported–simply supported and clamped–clamped boundary conditions are considered as two types of well-known symmetric boundary conditions for this analysis. (Simsek, 2016) investigated first two-dimensional FGM to research the buckling of beams with different boundary conditions, using adding auxiliary functions the boundary conditions are met. For different load form analysis, (Rastgo et al., 2005) explored the spatial buckling of pinned FGM arches being subjected to a thermal loading for using the Galerkin method. (Song and Li, 2008) using Kirchhoff” s assumption conducted nonlinear governing equations of FG arches under thermal and mechanical loads. (Asgari et al., 2014) focused the nonlinear thermo-elastic behavior of pin-ended FGM arches. The stability equation of the nonlinear primary equilibrium path was developed using adjacent equilibrium criterion. (Moita et al., 2018) studied the discrete model of the structural by the theory of high order shear deformation, and the finite element formulation is carried out to meet general FGM plate-shell type structures. (Yang et al., 2020a; Yang et al., 2020b; Yang et al., 2020c; Yang et al., 2021a; Yang et al., 2021b) have published a series of papers on in-plane buckling and free vibrations of functionally graded composite arches with graphene reinforcements. However, FGM arches may be subjected to a locally radial load and have different material distributions leading to different nonlinear in-plane buckling behavior. Little studies is presented about effects of the type of material distributions on the nonlinear in-plane buckling of FGM arches under a locally radial load in the literature.
This paper, therefore, aims at studying the in-plane buckling of a fixed functionally graded material arch under a locally uniformly distributed radial load incorporating effects of the type of material distributions. To illustrate the nonlinear in-plane buckling behavior of FGM arches, three types of material distributions containing functionally graded material layer and homogeneous material layer are considered. Theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches under a locally uniformly distributed radial load that are subjected to three different types of material distributions are derived. Comparisons with the ANSYS results present the theoretical solutions are enough accurate. The critical modified geometric slendernesses of FGM arches that are switches of buckling modes are also derived. In addition, the effects of the proportional coefficient of homogeneous ceramic layer, the type and power-law index p of material distributions on the buckling load and critical modified geometric slendernesses are discussed and examined.
Material Distribution of Functionally Graded material Arches
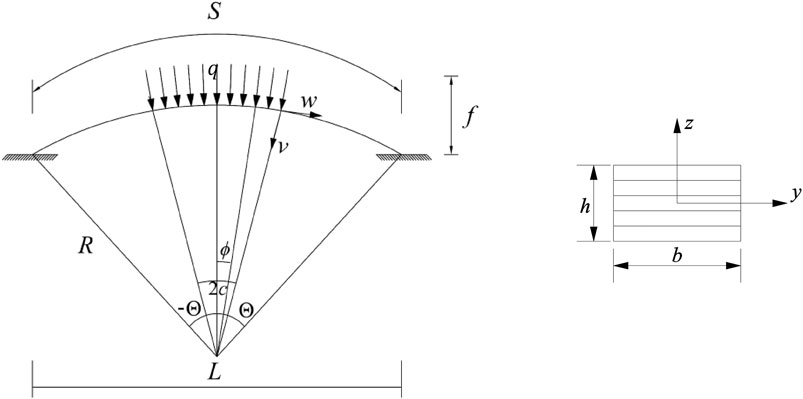
The FGM shallow arches under a locally uniformly distributed radial load q with a central angle
In this research, the metal-ceramic material Al-Al2O3 is adopted. According to power-law function, the FGM arch through the thickness are graded continuously as
where
In order to illustrate the nonlinear in-plane buckling behavior of FGM arches, three types of material distributions containing functionally graded material layer and homogeneous material layer are considered, including Type A, Type B, and Type C as shown in Figure 2. The cross-section of Type A represents that the top layer is the metal layer with the thickness
The volume fractions
and
where p is the power-law index of material distributions and
where
Nonlinear Equilibrium
The nonlinear in-plane buckling behavior of a fixed FGM arch subjected to a locally uniformly distributed radial load is investigated, which is shown in Figure 1. The potential energy Π of the FGM arch can then be given by
with the function
where
where
with
For nonlinear equilibrium of FGM arch using the principle of minimum total potential energy, the variation of the total potential energy obtained from Eq. 7 should vanish as
By substituting Eqs 10, 11 into Eq. 12, the Eq. 12 can then be rewritten as
where N and M are the axial and bending actions of the FGM arch, respectively, which can be given by
with
When material distributions of the FGM arch is subjected to Type A, the stiffness components of the FGM arch
When material distributions of the FGM arch is subjected to Type B, the stiffness components of the FGM arch
When material distributions of the FGM arch is subjected to Type C, the stiffness components of the FGM arch
Integrating Eq. 13 by parts, the differential equilibrium equations of a FGM arch under a locally uniformly distributed radial load can be derived as
By Substituting Eq. 14 into Eq. 15, the bending action of the FGM arch can be given by
By Substituting Eqs. 26, 28 into Eq. 27, Eq. 27 can then be rewritten as
where
with
Meanwhile, the essential boundary conditions at the both ends of FGM arch
also need to be satisfied. The non-dimensional radial displacement
where
and the
Equation 33 indicates that the non-dimensional radial displacement
Therefore, substituting Eq. 33 into Eq. 14, and integrating it along the arch length results in
Considering the essential boundary conditions obtained from Eq. 32, the Eq. 36 can be rewritten as
Subsequently, Calculating Eq. 37 leads to a quadratic equilibrium equation, as
where the coefficients
with λs being the modified geometric slenderness of the FGM arch, respectively, which can be express as
By solving Eq. 38, the relationship of the axial force with the locally uniformly distributed radial load can be obtained. Then, by substituting those relationship into Eq. 33, the non-dimensional radial displacement
Buckling Analysis
Limit Point Buckling and Bifurcation Buckling
The FGM arches under the locally uniformly distributed radial load may buckle in a limit point mode. According to the theory of (Lu et al., 2018) for an arches under the locally uniformly distributed radial load, the upper and lower limit point buckling loads can be derived using routine calculus, and the equation of equilibrium between
where
Therefore, the upper and lower limit point buckling loads can be obtained by solving Eqs 38, 43 simultaneously.
It can be found that the Eq. 43 for equilibrium of limit point buckling mode of the FGM arches are the same as those for the homogeneous arches (Lu et al., 2018). Similarly, refer to limit point buckling theory of the homogeneous arches under the locally uniformly distributed radial load, the axial force parameter
In addition, also refer to the above theory of homogeneous arch, the central displacement
with
The Eq. 46 has a real solution only when
from which the modified geometric slenderness
The FGM arches under the locally uniformly distributed radial load may buckle in a bifurcation mode. The equation of equilibrium of the FGM arch in the primary equilibrium path is obtained from Eq. 29. Similarly, the differential equation of equilibrium of the FGM arch in the case of infinitely close to the bifurcation equilibrium path can be given by
Therefore, the equation for equilibrium of bifurcation mode of the FGM arches can be built by substituting Eq. 29 into Eq. 49 as
It’s can be found that the equation for equilibrium of bifurcation mode of the FGM arches are the same as those for the homogeneous arches (Lu et al., 2018). Similarly, refer to bifurcation buckling theory of the homogeneous arches, the axial force parameter
In addition, the parameter
By substituting Eqs 51, 52 into Eq. 39, the equation of equilibrium between
where
with
The bifurcation buckling load of a FGM arch under a locally uniformly distributed radial load can be obtained once the localized parameter η is given.
Comparisons of Theoretical Solutions with ANSYS Results
According to Donnell’s shallow shell theory, in the ANSYS models of FGM arch, the geometry of the rectangular section was, the width b = 0.14 m, the total thickness h = 0.07 m, the power-law index p = 1 and the proportional coefficient of homogeneous ceramic layer
When a multilayer for metal-ceramic material Al-Al2O3 is used to simulate a continuous gradient properties, the accuracy of the FGM arch model increases with an increase of the number of layers of metal-ceramic material Al-Al2O3. As demonstrated in Figure 3, when material distributions of the FGM arch is subjected to Type A (Figure 3A), the cross-section of the FGM arch have 101 layers, the first layer is a homogeneous ceramic layer, and the second to the 101st layers are gradient layers from ceramic to metal. When material distributions of the FGM arch is subjected to Type B (Figure 3B), the cross-section of the FGM arch have 201 layers, the first to the 100st layers are gradient layers from metal to ceramic, the 101st is a homogeneous ceramic layer, and the 102st to the 201st layers are gradient layers from ceramic to metal. When material distributions of the FGM arch is subjected to Type C (Figure 3C), the cross-section of the FGM arch have 202 layers, the first layer is a homogeneous ceramic layer, the second to the 101st layers are gradient layers from ceramic to metal, the 102st to the 201st layers are gradient layers from metal to ceramic, the 101st is a homogeneous ceramic layer, and the last layer is a homogeneous ceramic layer.

FIGURE 3. ANSYS model of material distributions of FGM arch (A) Type A (B) Type B (C) Type C (D) ANSYS model with boundary conditions.
In addition, the proposed theoretical solution of the buckling equilibrium path, the limit point and bifurcation buckling load for the FGM arches under the locally uniformly distributed radial load are validated by ANSYS finite element results. Convergence researches for using the shell element shell181 of ANSYS show that 80 elements can produce convergent results. Therefore, 80 shell181 elements are chosen to simulate the FGM arches (Figure 3D).
Comparisons of the theoretical solutions of Eqs. 33, 38 for the limit point buckling equilibrium path and the limit point buckling load of the FGM arches with the corresponding ANSYS results are plotted in Figure 4. The variation curves of the dimensionless locally uniformly distributed radial load Q/(2NEc2Θ) with the dimensionless central displacement vc/f are plotted in Figure 4A for material distributions of the FGM arch being subjected to Type A, in Figure 4B for material distributions of the FGM arch being subjected to Type B, and in Figure 4C for material distributions of the FGM arch being subjected to Type C, where the locally uniformly distributed radial load with
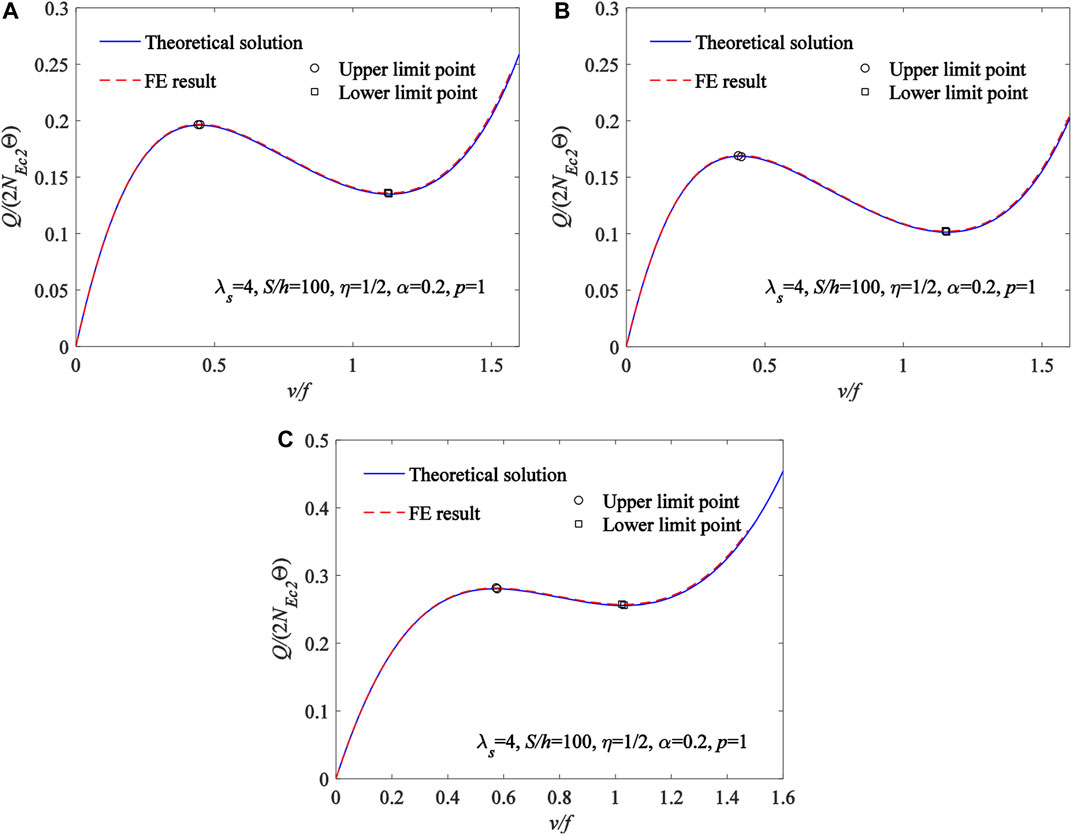
FIGURE 4. Comparisons of the theoretical solutions for the limit point buckling with the corresponding ANSYS results (A) Type A (B) Type B (C) Type C.
Comparisons of the theoretical solutions of Eqs 33, 53 for bifurcation buckling equilibrium path and the bifurcation buckling load of the FGM arches with the corresponding ANSYS results are plotted in Figure 5. The variation curves of the dimensionless locally uniformly distributed radial load Q/(2NEc2Θ) with the dimensionless central displacement vc/f are plotted in Figure 5A for material distributions of the FGM arch being subjected to Type A, in Figure 5B for material distributions of the FGM arch being subjected to Type B, and in Figure 5C for material distributions of the FGM arch being subjected to Type C, where the locally uniformly distributed radial load with
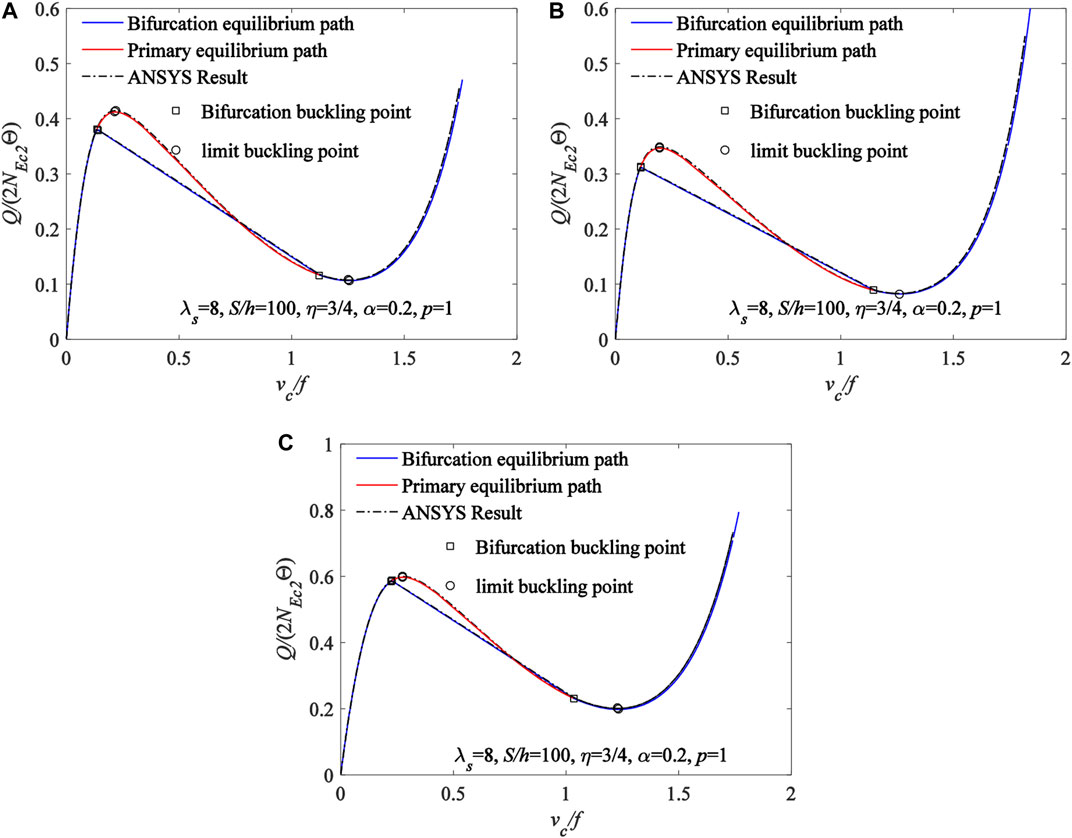
FIGURE 5. Comparisons of the theoretical solutions for the bifurcation buckling with the corresponding ANSYS results (A) Type A (B) Type B (C) Type C.
Hence, the theoretical solutions of Eqs 33, 38, 53 can be used to predict the buckling equilibrium path, the limit point and bifurcation buckling load for the FGM arches under the locally uniformly distributed radial load.
Limit Point Buckling Analysis
This section investigates the effects of the localized parameter η of locally uniformly distributed radial load, the type and the power-law index p of material distributions of the FGM arch on the limit point buckling equilibrium path and the limit point buckling load for FGM arches under a locally uniformly distributed radial load.
Under the locally uniformly distributed radial load, the limit point buckling equilibrium path obtained from Eqs 33, 38 for FGM arches having different localized parameter η are plotted in Figure 6A with the variation curves of vc/f vs Q/(2NEc2Θ), and in Figure 6B with the variation curves of N/NEc2vs Q/(2NEc2Θ), where the modified geometric slenderness
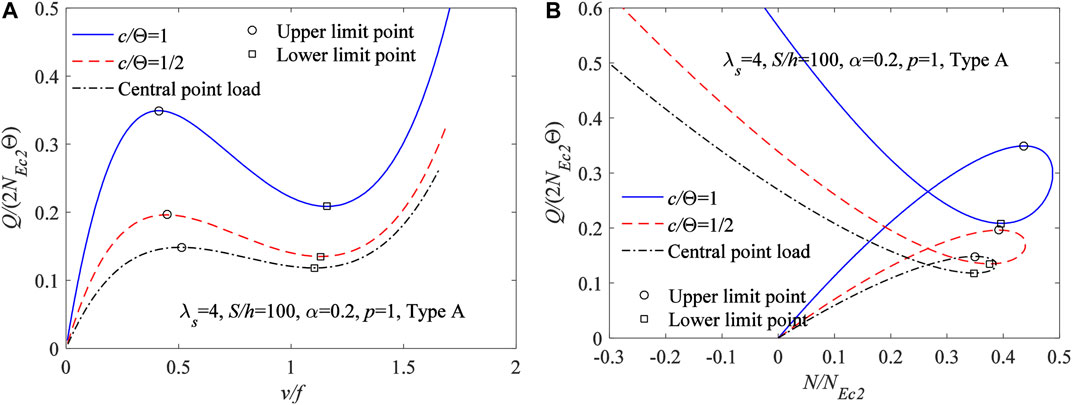
FIGURE 6. Limit point buckling equilibrium path for FGM arches having different localized parameter (A)vc/f vs Q/(2NEc2Θ) (B)N/NEc2vs Q/(2NEc2Θ).
In addition, the limit point buckling equilibrium path obtained from Eqs 33, 38 for FGM arches having different type of material distributions are plotted in Figure 7A with the variation curves of vc/f vs Q/(2NEc2Θ), and in Figure 7B with the variation curves of N/NEc2vs Q/(2NEc2Θ), where
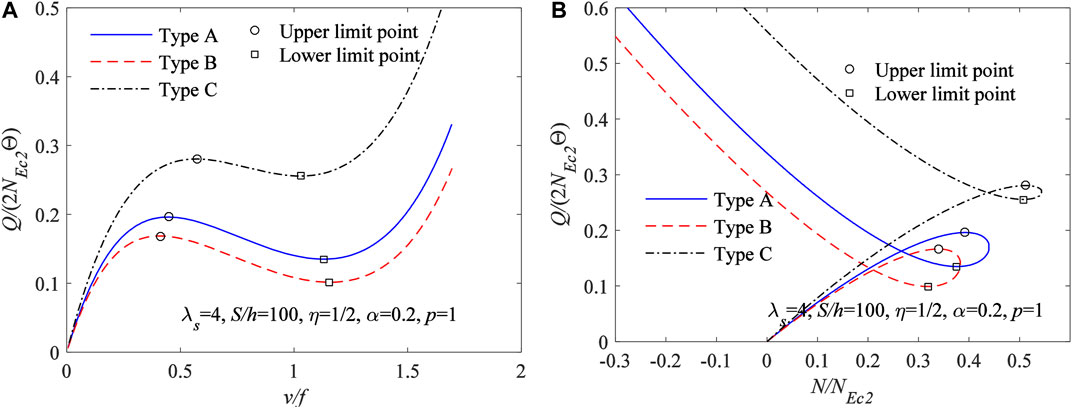
FIGURE 7. Limit point buckling equilibrium path for FGM arches having different type of material distributions (A)vc/f vs Q/(2NEc2Θ) (B)N/NEc2vs Q/(2NEc2Θ).
Similarly, Figure 8A plots the variation curves of vc/f vs Q/(2NEc2Θ) and Figure 8B plots the variation curves of N/NEc2vs Q/(2NEc2Θ) for FGM arches having different power-law index p, where
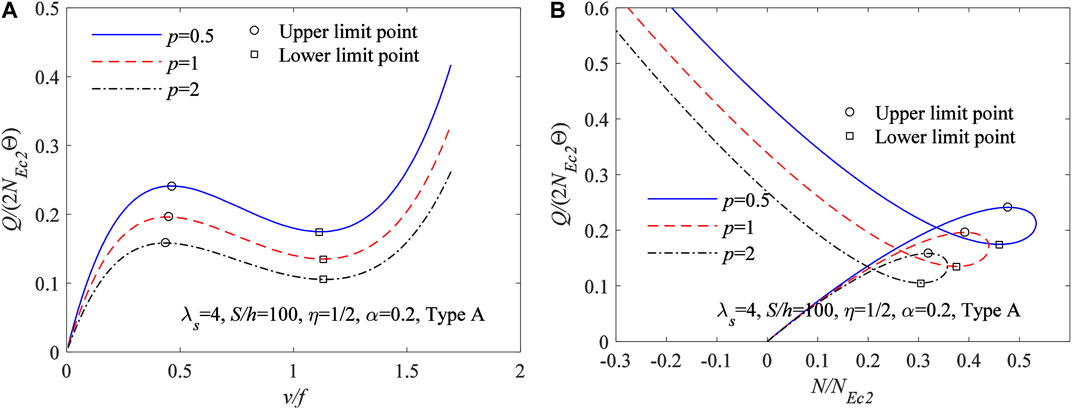
FIGURE 8. Limit point buckling equilibrium path for FGM arches having different power-law index of material distributions (A)vc/f vs Q/(2NEc2Θ) (B)N/NEc2vs Q/(2NEc2Θ).
Furthermore, the influences of the modified geometric slenderness
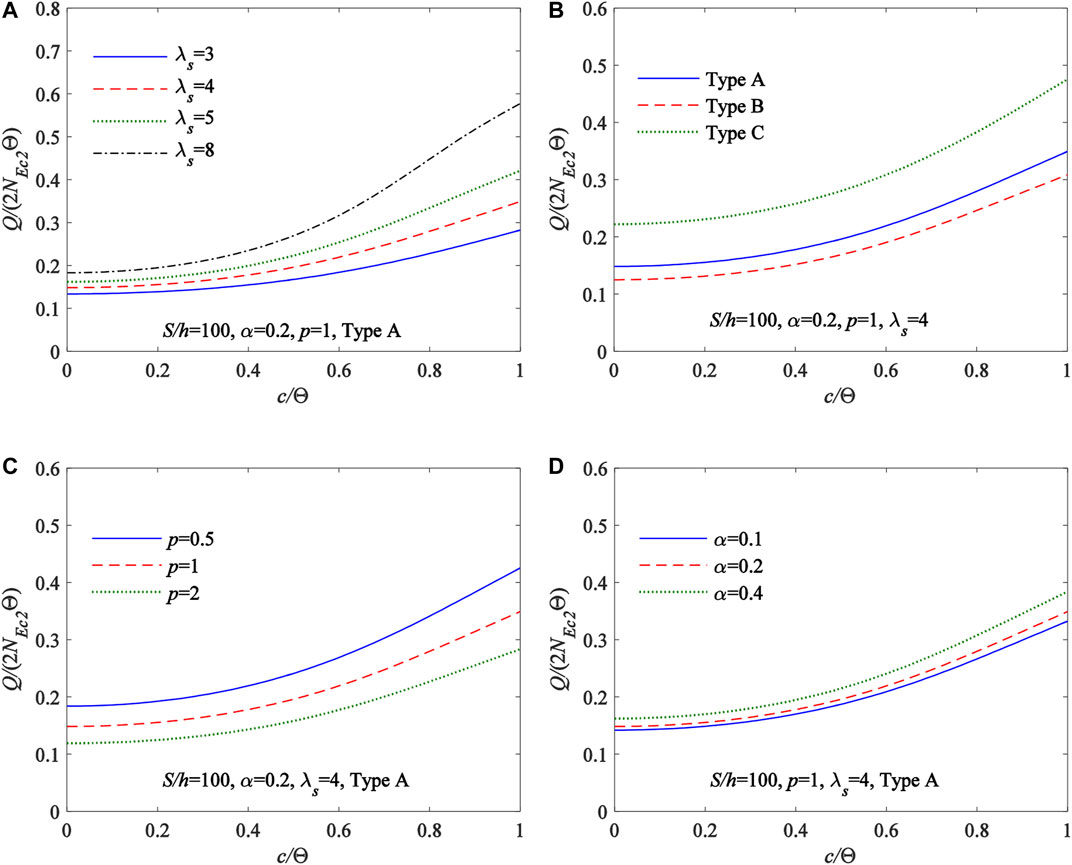
FIGURE 9. η vs Q/(2NEc2Θ) (A) different modified geometric slenderness (B) different type of material distributions (C) different power-law index p of material distributions (D) different proportional coefficient of homogeneous ceramic layer.
Bifurcation Buckling Analysis
This section investigates the effects of the localized parameter η of locally uniformly distributed radial load, the type of material distributions of the FGM arch on the bifurcation buckling equilibrium path and the bifurcation buckling load for FGM arches under a locally uniformly distributed radial load.
Under the locally uniformly distributed radial load, the bifurcation buckling equilibrium path obtained from Eqs 33, 53 for FGM arches having different localized parameter η are plotted in Figure 10A with the variation curves of vc/f vs Q/(2NEc2Θ), and in Figure 6B with the variation curves of N/NEc2vs Q/(2NEc2Θ), where the modified geometric slenderness
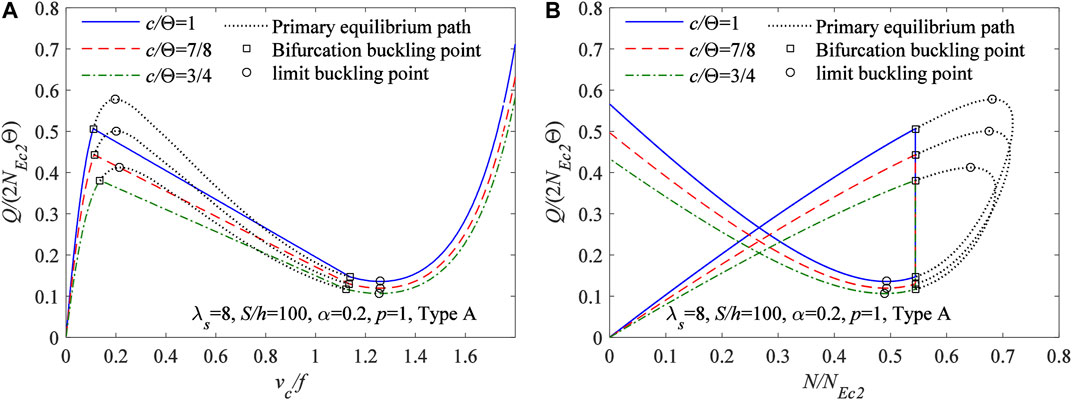
FIGURE 10. Bifurcation equilibrium path for FGM arches having different localized parameter (A)vc/f vs Q/(2NEc2Θ) (B)N/NEc2vs Q/(2NEc2Θ).
It can also be seen from Figure 10 that the localized parameter η has a significant effect on the bifurcation buckling equilibrium path and the bifurcation buckling load, the bifurcation buckling load increases with an increase of localized parameter η, which indicates that FGM arches having a larger length of the locally uniformly distributed radial loading segment are more prone to bifurcation buckling.
In addition, the bifurcation buckling equilibrium path obtained from Eqs 33, 53 for FGM arches having different type of material distributions are plotted in Figure 11A with the variation curves of vc/f vs Q/(2NEc2Θ), and in Figure 11B with the variation curves of N/NEc2vs Q/(2NEc2Θ), where
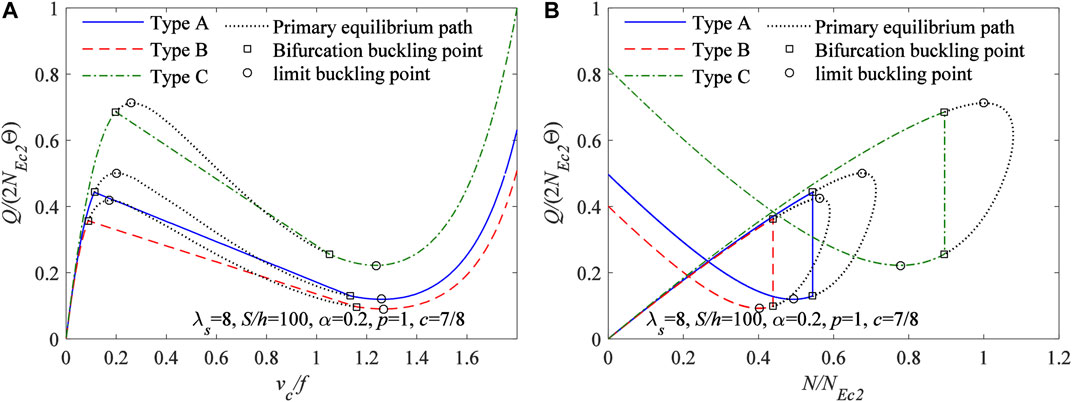
FIGURE 11. Bifurcation equilibrium path for FGM arches having different type of material distributions (A)vc/f vs Q/(2NEc2Θ) (B)N/NEc2vs Q/(2NEc2Θ).
Furthermore, the influences of the localized parameter η of locally uniformly distributed radial load, the type of material distributions and the modified geometric slenderness
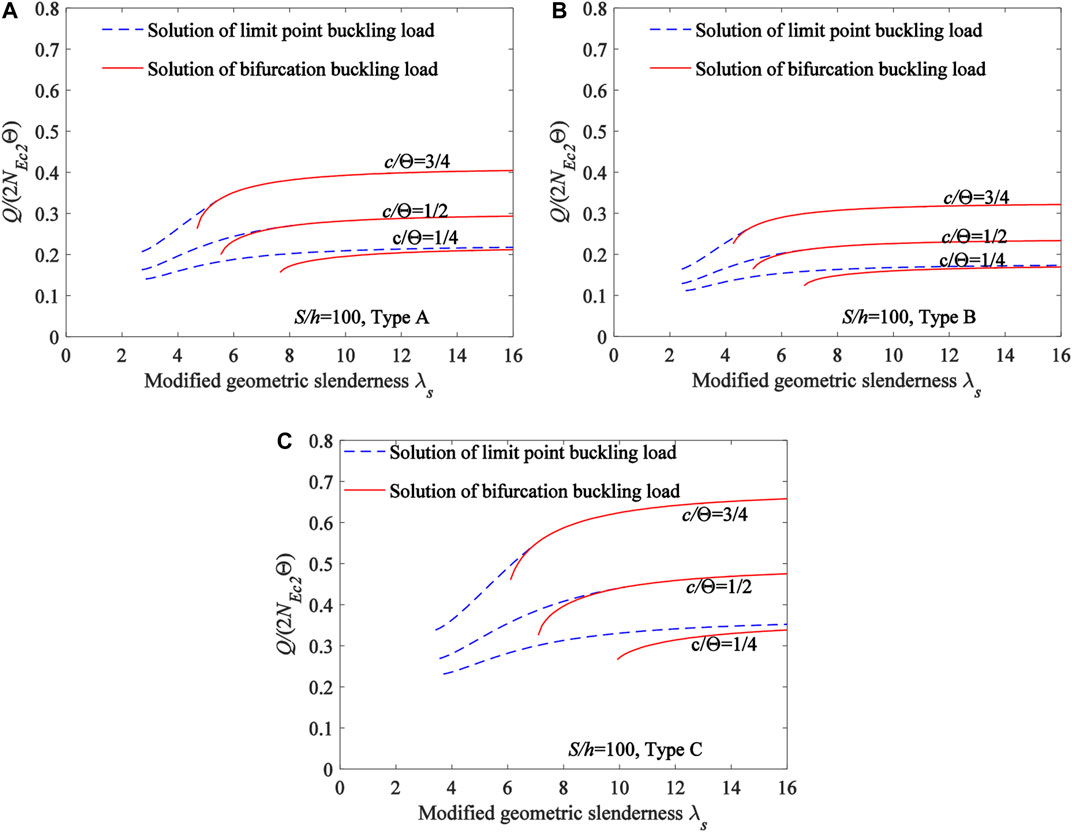
FIGURE 12. Limit point buckling load and bifurcation buckling load of the FGM arch (A) Type A (B) Type B (C) Type C.
Criteria for Switches of Buckling Mode of Functionally Graded Material Arch
It can be seen from the above research that fixed FGM arches under a locally uniformly distributed radial load may buckle in a limit point buckling mode or in a bifurcation buckling mode. The buckling equilibrium path for FGM arches having different modified geometric slenderness are plotted in Figure 13 with the variation curves of vc/f vs Q/(2NEc2Θ), where η = 0.75,
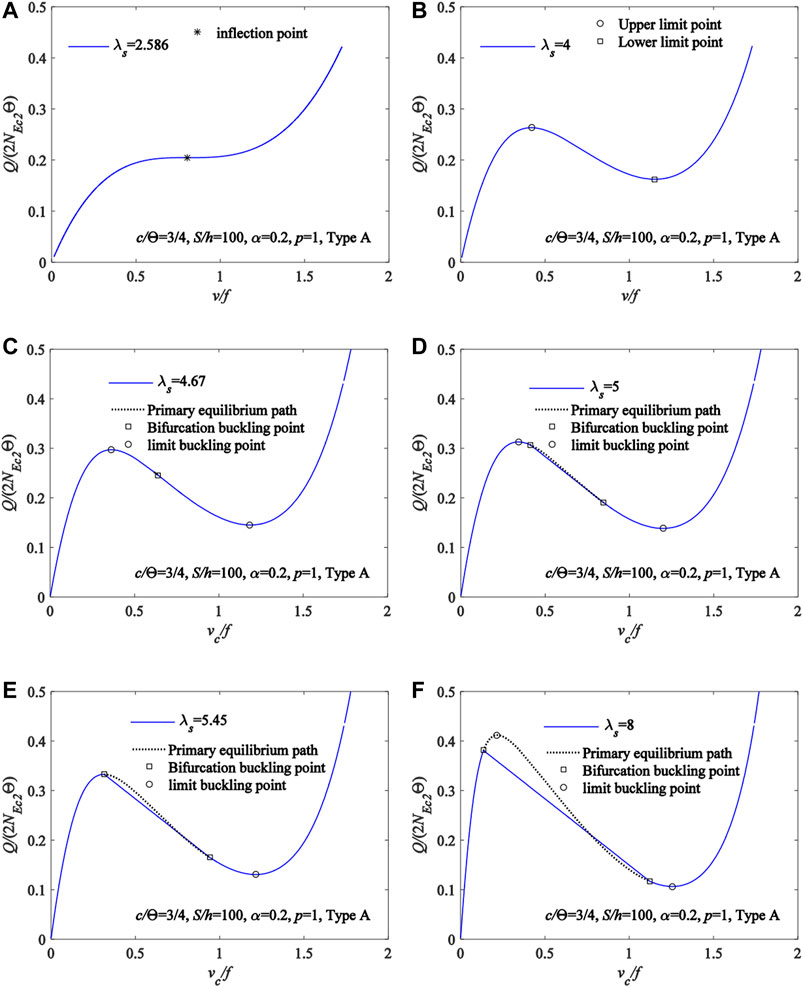
FIGURE 13. Buckling equilibrium path for FGM arches having different modified geometric slenderness (A)
The modified geometric slenderness λs obtained from Eq. 48 can make fixed FGM arches lose its stability in the lowest limit buckling mode. This modified geometric slenderness λsl can be expressed as
The modified geometric slenderness λs obtained from Eq. 53 can make fixed FGM arches lose its stability in the lowest bifurcation buckling mode. This modified geometric slenderness λsb1 can be expressed as
When the fixed FGM arches lose its stability in the lowest bifurcation buckling dominant mode, the modified geometric slenderness λsb2 corresponding to this mode can be obtained by equaling the upper bifurcation instability load to the upper limit point buckling load.
Typical variation curves of the localized parameter η vs the modified geometric slenderness λs are shown in Figure 14A for FGM arches having different type of material distributions, in Figure 14B for FGM arches having different power-law index p of material distributions and in Figure 14C for FGM arches having different proportional coefficient of homogeneous ceramic layer
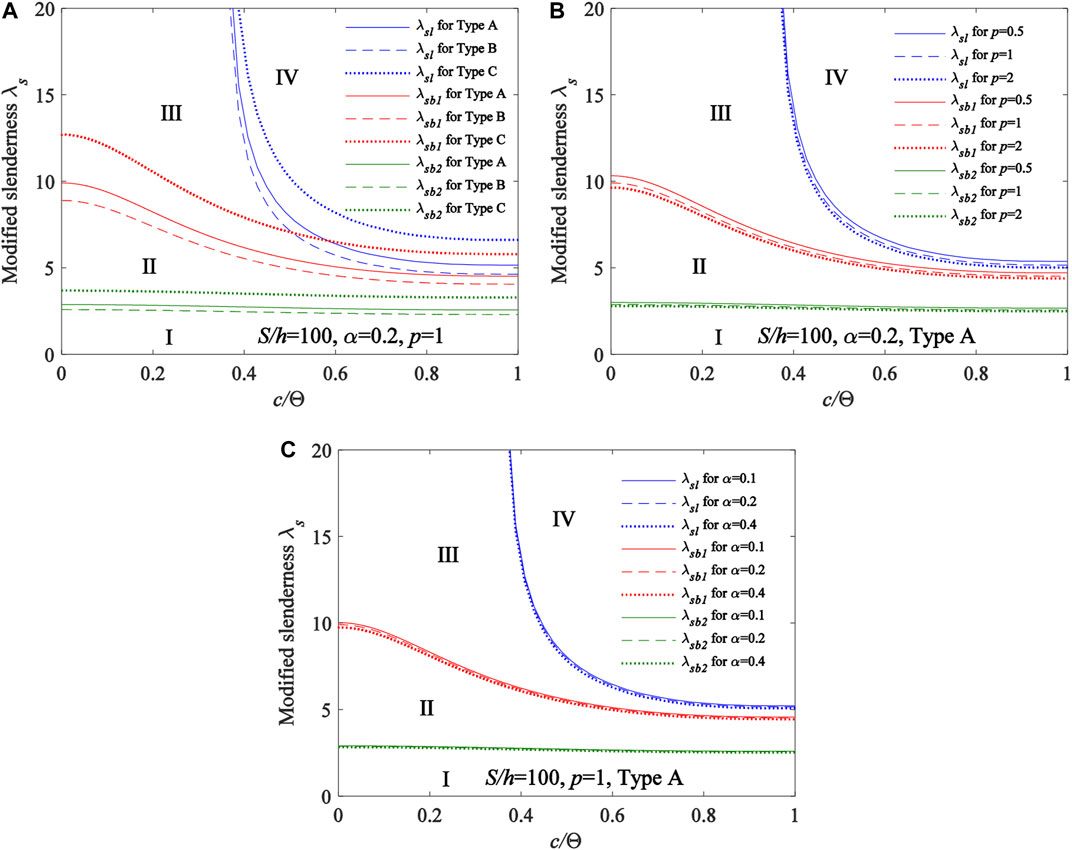
FIGURE 14. Localized parameter η vs Modified geometric slenderness λsl, λsb1, and λsb2(A) different type of material distributions (B) different power-law index p of material distributions (C) different proportional coefficient of homogeneous ceramic layer.
Conclusion
Theoretical studies of the nonlinear in-plane buckling of a fixed circular functionally graded material (FGM) arches under a locally uniformly distributed radial load have been explored in this paper. It was found that fixed FGM arches under a locally uniformly distributed radial load may buckle in a limit point buckling mode or in a bifurcation buckling mode. Theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches that are subjected to three different types of material distributions were obtained. It was found that the type of material distributions of the fixed FGM arches slight the limit point buckling loads and bifurcation buckling loads as well as the nonlinear equilibrium path significantly. Type C had a largest limit point buckling load and a largest bifurcation buckling load among Type A, Type B and Type C, it indicated that under the same proportion of metal and ceramic materials, the distribution of ceramics on the upper and lower surfaces of the cross-section can greatly improve the stability of the FGM arch. In addition, the limit point buckling load and bifurcation buckling load also increase with an increase of the modified geometric slenderness
The critical modified geometric slendernesses λsl, λsb1, and λsb2 that are switches of buckling modes were also derived. The localized parameter η has a significant effect on the modified geometric slenderness λsb1, λsb2, and limited effect on the modified geometric slenderness λsl, the modified geometric slenderness λsl, λsb1, and λsb2 increase with a decrease of the localized parameter η of the locally uniformly distributed radial load. It was found that Region I corresponding to FGM arches with λs < λsl is subjected to the no buckling mode, region II corresponding to FGM arches with λsl < λs < λsb1 is subjected to the limit point buckling mode, region III corresponding to FGM arches with λsb1 < λs < λsb2 is subjected to the bifurcation buckling mode, region IV corresponding to FGM arches with λs > λsb2 is subjected to the bifurcation buckling dominant mode. In addition, it was also found that the type of material distributions has a significant effect on the modified geometric slenderness λsl, λsb1 and λsb2, Type C has the largest modified geometric slenderness λsl, λsb1 and λsb2 among Type A, Type B and Type C, and the modified geometric slenderness λsl, λsb1 and λsb2 increase with an decrease of the power-law index p of material distributions and the proportional coefficient of homogeneous ceramic layer
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author Contributions
HL: Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing-review and editing. JZ: Formal analysis, Validation, Writing-review and editing. ZY: Formal analysis, Investigation, Methodology, Writing-original draft. AL: Data curation, funding acquisition. JZ: Project administration.
Funding
This work was funded by (Characteristic innovation projects of colleges and universities in Guangdong Province) with grant number (2019KTSCX190) and (National Natural Science Foundation of China) with grant number (51908146).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-shujairi, M., and Mollamahmutoğlu, C. (2018). Buckling and Free Vibration Analysis of Functionally Graded sandwich Microbeams Resting on Elastic Foundation by Using Non Local Strain Gradient Theory in Conjunction with Higher Order Shear Theories under thermal Effect. Compos. Part. B 154, 292–312. doi:10.1016/j.compositesb.2018.08.103
Asgari, H., Bateni, M., Kiani, Y., and Eslami, M. R. (2014). Non-linear Thermo-Elastic and Buckling Analysis of FGM Shallow Arches. Compos. Struct. 109, 75–85. doi:10.1016/j.compstruct.2013.10.045
Bateni, M., and Eslami, M. R. (2015). Non-linear In-Plane Stability Analysis of FG Circular Shallow Arches under Uniform Radial Pressure. Thin-Walled Structures 94, 302–313. doi:10.1016/j.tws.2015.04.019
Bateni, M., and Eslami, M. R. (2014). Non-linear In-Plane Stability Analysis of FGM Circular Shallow Arches under central Concentrated Force. Int. J. Non-Linear Mech. 60, 58–69. doi:10.1016/j.ijnonlinmec.2014.01.001
Bradford, M. A., Uy, B., and Pi, Y.-L. (2002). In-plane Elastic Stability of Arches under a central Concentrated Load. J. Eng. Mech. 128, 710–719. doi:10.1061/(asce)0733-9399(2002)128:7(710)
Cai, J., and Feng, J. (2010). Buckling of Parabolic Shallow Arches when Support Stiffens under Compression. Mech. Res. Commun. 37, 467–471. doi:10.1016/j.mechrescom.2010.05.004
Cai, J., Xu, Y., Feng, J., and Zhang, J. (2012). In-plane Elastic Buckling of Shallow Parabolic Arches under an External Load and Temperature Changes. J. Struct. Eng. 138, 1300–1309. doi:10.1061/(asce)st.1943-541x.0000570
Cai, J., Zhou, Y., and Feng, J. (2013). Post-buckling Behavior of a Fixed Arch for Variable Geometry Structures. Mech. Res. Commun. 52, 74–80. doi:10.1016/j.mechrescom.2013.07.002
Chen, M.-T., and Young, B. (2021). Beam-column Design of Cold-Formed Steel Semi-oval Hollow Non-slender Sections. Thin-walled Structures 162, 107376. doi:10.1016/j.tws.2020.107376
Chen, M.-T., Young, B., Martins, A. D., Camotim, D., and Dinis, P. B. (2021). Experimental Investigation on Cold-Formed Steel Lipped Channel Beams Affected by Local-Distortional Interaction under Non-uniform Bending. Thin-walled Structures 161, 107494. doi:10.1016/j.tws.2021.107494
Han, Q., Cheng, Y., Lu, Y., Li, T., and Lu, P. (2016). Nonlinear Buckling Analysis of Shallow Arches with Elastic Horizontal Supports. Thin-Walled Structures 109, 88–102. doi:10.1016/j.tws.2016.09.016
Hu, C.-F., Li, Z., and Hu, Q.-S. (2021). On Non-linear Behavior and Buckling of Arch-Beam Structures. Eng. Structures 239 (2), 112214. doi:10.1016/j.engstruct.2021.112214
Lu, H., Liu, A., Pi, Y.-L., Bradford, M. A., Fu, J., and Huang, Y. (2018). Localized Loading and Nonlinear Instability and post-instability of Fixed Arches. Thin-Walled Structures 131, 165–178. doi:10.1016/j.tws.2018.06.019
Lu, H. W., Liu, L. L., Liu, A. R., Pi, Y.-L., Bradford, M. A., and Huang, Y. H. (2020). Effects of Movement and Rotation of Supports on Nonlinear Instability of Fixed Shallow Arches. Thin-Walled Structures 122, 2020. doi:10.1016/j.tws.2020.106909
Moita, J. S., Araújo, A. L., Correia, V. F., Mota Soares, C. M., and Herskovits, J. (2018). Material Distribution and Sizing Optimization of Functionally Graded Plate-Shell Structures. Composites B: Eng. 142, 263–272. doi:10.1016/j.compositesb.2018.01.023
Pi, Y.-L., Bradford, M. A., and Liu, A. (2017). Nonlinear Equilibrium and Buckling of Fixed Shallow Arches Subjected to an Arbitrary Radial Concentrated Load. Int. J. Str. Stab. Dyn. 17 (8), 1750082. doi:10.1142/s0219455417500821
Pi, Y.-L., and Bradford, M. A. (2009). Non-linear In-Plane Postbuckling of Arches with Rotational End Restraints under Uniform Radial Loading. Int. J. Non-Linear Mech. 44 (9), 975–989. doi:10.1016/j.ijnonlinmec.2009.07.003
Pi, Y.-L., Bradford, M. A., and Tin-Loi, F. (2008). Non-linear In-Plane Buckling of Rotationally Restrained Shallow Arches under a central Concentrated Load. Int. J. Non-Linear Mech. 43 (1), 1–17. doi:10.1016/j.ijnonlinmec.2007.03.013
Pi, Y.-L., Bradford, M. A., and Uy, B. (2002). In-plane Stability of Arches. Int. J. Sol. Structures 39 (1), 105–125. doi:10.1016/s0020-7683(01)00209-8
Plaut, R. H., and Raymond, H. (1990). Buckling of Shallow Arches with Supports that Stiffen when Compressed. J. Eng. Mech. 116 (4), 973–976. doi:10.1061/(asce)0733-9399(1990)116:4(973)
Rastgo, A., Shafie, H., and Allahverdizadeh, A. (2005). Instability of Curved Beams Made of Functionally Graded Material under Thermal Loading. Int. J. Mech. Mater. Des. 2, 117–128. doi:10.1007/s10999-005-4446-3
Schreyer, H. L. (1972). The Effect of Initial Imperfections on the Buckling Load of Shallow Circular Arches. J. Appl. Mech. 39 (2), 445–450. doi:10.1115/1.3422698
Simsek, M. (2016). Buckling of Timoshenko Beams Composed of Two-Dimensional Functionally Graded Material (2D-FGM) Having Different Boundary Conditions. Compos. Struct. 49, 304–314. doi:10.1016/j.compstruct.2016.04.034
Song, X., and Li, S. R. (2008). Nonlinear Stability of Fixed-Fixed Fgm Arches Subjected to Mechanical and thermal Loads. Amr 33-37, 699–706. doi:10.4028/www.scientific.net/amr.33-37.699
Timoshenko, S. P., Gere, J. M., Prager, W., Gere, J. M., and Prager, W. (1962). Theory of Elastic Stability, Second Edition. J. Appl. Mech. 29 (1), 220–221. doi:10.1115/1.3636481
Yan, S.-t., Shen, X., Chen, Z., and Jin, Z. (2017). On Buckling of Non-uniform Shallow Arch under a central Concentrated Load. Int. J. Mech. Sci. 133, 330–343. doi:10.1016/j.ijmecsci.2017.08.046
Yang, Z., Feng, C., Yang, J., Wang, Y., Lv, J., Liu, A., et al. (2020a). Geometrically Nonlinear Buckling of Graphene Platelets Reinforced Dielectric Composite (GPLRDC) Arches with Rotational End Restraints. Aerospace Sci. Tech. 107, 106326. doi:10.1016/j.ast.2020.106326
Yang, Z., Zhao, S., Yang, J., Lv, J., Liu, A., and Fu, J. (2020b). In-plane and Out-Of-Plane Free Vibrations of Functionally Graded Composite Arches with Graphene Reinforcements. Mech. Adv. Mater. Structures, 1–11. doi:10.1080/15376494.2020.1716420
Yang, Z., Tam, M., Zhang, Y., Kitipornchai, S., Lv, J., and Yang, J. (2020c). Nonlinear Dynamic Response of FG Graphene Platelets Reinforced Composite Beam with Edge Cracks in thermal Environment. Int. J. Str. Stab. Dyn. 20, 2043005. doi:10.1142/s0219455420430051
Yang, Z., Liu, A., Yang, J., Lai, S.-K., Lv, J., and Fu, J. (2021a). Analytical Prediction for Nonlinear Buckling of Elastically Supported FG-GPLRC Arches under a central point Load. Materials 14 (8), 2026. doi:10.3390/ma14082026
Keywords: functionally graded material, fixed arch, limit point buckling, bifurcation buckling, critical modified geometric slenderness
Citation: Lu H, Zhou J, Yang Z, Liu A and Zhu J (2021) Nonlinear Buckling of Fixed Functionally Graded Material Arches Under a Locally Uniformly Distributed Radial Load. Front. Mater. 8:731627. doi: 10.3389/fmats.2021.731627
Received: 28 June 2021; Accepted: 27 July 2021;
Published: 09 August 2021.
Edited by:
Lin Xu, Jilin University, ChinaReviewed by:
Man-Tai Chen, Shanghai Jiao Tong University, ChinaQiang Feng, Shandong University of Science and Technology, China
Copyright © 2021 Lu, Zhou, Yang, Liu and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhicheng Yang, emhpY2hlbmcueWFuZ0B6aGt1LmVkdS5jbg==; Airong Liu, bGl1YXJAZ3podS5lZHUuY24=
 Hanwen Lu
Hanwen Lu Jinman Zhou
Jinman Zhou Zhicheng Yang
Zhicheng Yang Airong Liu
Airong Liu Jian Zhu
Jian Zhu