An Efficient Approach of Predicting the Elastic Property of Hydrating Cement Paste

Although elastic properties of hydrating cement paste are crucial in concrete engineering practice, there are only a few widely available models for engineers to predict the elastic behavior of hydrating cement paste. Therefore, in this paper, we derive an analytical model to efficiently predict the elastic properties (e.g., Young’s modulus) of hydrating cement paste. Notably, the proposed model provides the prediction of hydration, percolation, and homogenization of the cement paste, enabling the study of the early age elasticity evolution in cement paste. A hydration model considering the mineral composition and the initial w/c ratio was used, while the percolation threshold was calculated adopting a phenomenological semi-empirical method describing the effects of the solid volume fraction and the w/c ratio. An efficient mixing rule based on the degree of solid connectivity was then adopted to calculate the elastic properties of the hydrating cement paste. Moreover, for ordinary Portland cement, a simplified model was built using Powers’ hydration model. The obtained modeling results are following experimental data and other numerical results available in the literature.

Introduction

As a critical mechanical design parameter of concrete structures affecting their deformation and failure, the elastic modulus of cement pastes at early age constantly attracts engineering and scientific attention (Acker and Ulm, 2001; Bentur, 2002; Springenschmid, 2009). In general, as the main evolving cement component at an early age, hydrating cement paste critically affects the elastic modulus of cement paste. On the one hand, during the cement paste hydration process, the elastic modulus of cement paste is subjected to changes in the physical environment due to the microstructural development of the cement paste. On the other hand, the chemical composition of hydrating cement paste varies over time, so these physical and chemical changes make the prediction of elastic properties of cement pastes very challenging.

The literature on the experimental characterization of the elastic properties of cement-based materials during hardening is vast (Schutter and Taerwe, 1996; Boumiz et al., 1996; Princigallo et al., 2003; Constantinides and Ulm, 2004; Haecker et al., 2005; Voigt et al., 2005; Sun et al., 2005). Reinhardt and Grosse (2005) investigated cement-based samples during setting and hardening by adopting several testing methods based on the resonant frequency, ultra-sound wave propagation, impact echo, electric properties of concrete nuclear magnetic resonance, and acoustic emissions. Azenha et al. (2010, 2011) measured the elastic modulus of cement pastes and mortars using a novel method based on ambient vibration after casting and found that many factors affected the elastic modulus, especially the water-to-cement ratio (abbreviated as w/c). Irfan-ul-Hassan et al. (2016) characterized the elastic stiffness and creep properties of a series of ordinary Portland cement pastes at different aging stages. They found that the quasistatically determining elastic modulus agreed well with the ultrasonically determining elastic modulus for the same cement pastes. All these experiments indicated that the elasticity evolution of hydrating cement paste is closely related to the mineral composition and the w/c ratio of cement, and this relationship cannot be described as a simple mathematical correlation.

Besides the experimental studies, many analytical and numerical approaches have been proposed to predict the elastic properties of early-aged cement paste. Bernard et al. (2003) used Atkins’ model (Atkins, 1994) to simulate the hydration kinetics of ordinary Portland cement, demonstrating a multistep approach starting at the nano-level of the C-S-H matrix and predicting the elasticity evolution of cement-based materials with high accuracy. However, modeling may require an impractical number of specific model parameters to design the hydration kinetics. Using CEMHYD3D software to determine the cement paste microstructure numerically, Haecker et al. (2005) adopted a direct homogenization via the finite element method (FEM), exhibiting good results. They found better agreement with experimental results when the modeling resolution was increased. Applying the FEM and the Fast Fourier Transform elastic homogenization to the CEMHYD3D hydrating microstructure, Šmilauer et al. (2006) showed that this numerical homogenization was more accurate and versatile than Bernard’s method for the hydration kinetics simulation. The homogenization methods based on spherical particles provided too high percolation thresholds, while those established on non-spherical phases were successful in terms of providing exact percolation thresholds and strength upscaling (Pichler et al., 2009; Pichler et al., 2011; Pichler et al., 2013; Chu et al., 2018a; Chu et al., 2018b).

Sanahuja et al. (2007) adopted Powers’ hydration model (Powers and Brownyard, 1946) and modified the C–S–H bricks aspect ratio to obtain a proper percolation threshold. Their simulation results at a late age and the end of hydration were in good agreement with experimental data. Sun et al. (1999, 2005) investigated the early-age properties of the cement-based materials by ultrasonic waves and HYMOSTRUC3D simulation and revealed a dominant role of the connectivity of solid phases in the microstructure. Applying a combination of Powers’ hydration model, the self-consistent scheme (SCS), and a “burning” algorithm percolation method, Stefan et al. (2010) accurately predicted the early-age elastic properties of the cement-based materials. However, Powers’ model might be imprecise. Adopting CEMHYD3D to capture the hydration microstructure accurately, Zhao et al. (2013) studied the elastic properties of hydrating cement pastes with a method similar to Stefan et al. (2010). However, this model was inconsistent with the experimental evolution of the elastic properties with a low w/c ratio.

Although all the methods mentioned above are feasible and practical, they still exhibit some limitations. Moreover, an experimental approach is practical, but it requires more time and financial costs, and it does not yield a quantitative relationship or a transparent mechanism. Numerical simulations (adopting CEMHYD3D, HYMOSTRUC3D, or FEM) accurately generate microstructural properties but are related to high computational costs and sometimes depend on the model resolution or mesh (Haecker et al., 2005). Some analytical formulas used in the above works are highly accurate but too sophisticated and inconvenient for engineers (Bernard et al., 2003). Therefore, a more convenient and efficient method is needed to evaluate the development of the early-age elastic properties of cement pastes.

As already established, any prediction model has three indispensable parts: hydration model, percolation theory, and homogenization method. The present paper proposes new methods for all three parts; i.e., an efficient hydration method is proposed to consider the composition of the cement and the initial w/c ratio explicitly, the percolation threshold is calculated using a semi-empirical formula considering the effects of the solid volume fraction and the w/c ratio; and, an efficient mixing rule based on the degree of solid connectivity is used as a homogenization method to estimate elastic properties. Our efficient and convenient approach for engineers yields theoretical predictions of the early-age elastic properties of cement paste consistent with the experimental results.

Theoretical Framework

In this paper, a new set of hydration and percolation models, and a homogenization method, are proposed and combined to evaluate the evolution of the early-age elastic properties of cement paste. A detailed description of the framework is given in the following subsections.

Cement Hydration Model

The hydration model estimates the chemical composition of the hydrating cement paste and provides a volumetric prediction for the homogenization analysis. Powers’ model (Powers and Brownyard, 1946) was used by several researchers (Sanahuja et al., 2007; Stefan et al., 2010) for its timely implementation. However, the model might be imprecise and does not consider cement type (Stefan et al., 2010). It is important to note that some improvements to Powers’ classical model have already been proposed. In contrast to the single “hydrate” adopted by Powers, Muller et al. (2013) differentiated between C-S-H and calcium hydroxide and separated the interlayer water within C-S-H by nuclear magnetic resonance relaxometry, showing a nonlinear relationship between the mass fraction of bound water and the hydration degree. Based on these findings, Königsberger et al. (2016) developed a hydration model that could calculate the volumetric fractions of various components. The improved model yielded volumetric fractions more accurately, but it did not consider the type of cement. Atkins’s kinetic model used by Bernard et al. (2003) describes the hydration kinetics of each clinker X (where X = C₂S, C₃S, C₃A, C₄AF) according to nucleation, growth, and diffusion laws. The model is relatively accurate but introduces too many parameters for practical applications.

The Avrami equation was used to assess the reaction rates of four clinkers in Portland cement (Lin and Christian, 2007; Jennings and Tennis, 1994; Tennis and Jennings, 2000). The equation assumes that the clinkers react with similar rates:

${\alpha }_i=1-\exp \left[-a_i{\left(t-b_i\right)}^{c_i}\right](1)$

where α_i is the hydration degree of clinker I at time t (in days). a_i, b_i, and c_i are constants determined by a specific cement (Taylor, 1987), as shown in Table 1.

TABLE 1

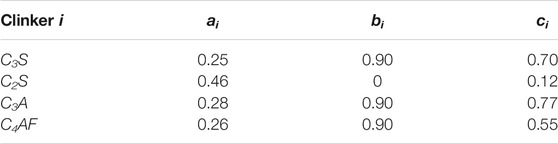
TABLE 1. Constants in the Avrami equations (Taylor, 1987).

The Avrami equation is suitable for nucleation and growth, but it cannot describe the reactions governed by diffusion. In addition, it can separate the reactions of different clinkers in Portland cement (Tennis and Jennings, 2000). However, it does not consider the effect of w/c.

Based on simple spatial considerations, Bentz (2006) developed a simple model of the Portland cement hydration kinetics:

$d\alpha /dt=k{\varphi }_w{\left(t\right)}^2\gamma \left(t\right)/{\varphi }_T\left(t\right),(2)$

where α is the hydration degree, and k is analogous to a first-order rate constant and varies with the specific cement composition, particle size distribution, and curing temperature. ${\varphi }_w\left(t\right)$, ${\varphi }_T\left(t\right)$ , and $\lambda \left(t\right)$ are the volume fractions of water-filled and unhydrated cement, and the total capillary porosity as functions of time t, respectively. The Bentz equation considers the influence of the w/c ratio and requires only one parameter. However, it assumes that the compounds react at the same rate.

In the present work, an efficient hydration kinetics model is proposed. The model combines the Avrami equation and Bentz’s model and shows the effects of w/c and mineralogical components of the cement. In this model, the Avrami equation is used to determine the initial reaction, while Bentz’s model describes the following hydration stage, explicitly expressed by:

$\{\begin{array}{c}{\alpha }_i=1-\exp \left[-k_0{a}_i{\left(t-b_i\right)}^{c_i}\right],t\le t_0\\ d{\alpha }_i/dt=k_i{\varphi }_w{\left(t\right)}^2{\gamma }_i\left(t\right)/{\varphi }_T\left(t\right),t\ge t_0\end{array}(3)$

where t₀ (in days) is the junction time of the two stages, k₀ and k_i are rate constants determined by the hydration degree of clinker i at time t₀, and ${\gamma }_i\left(t\right)$ denotes the volume fractions of four mineralogical components in the unhydrated cement. If there are no experimental data for the calibration of parameters, it is assumed that k₀= 1 and t₀ = 3.

Tennis and Jennings (1994) proposed two types of C-S-Hs in hydrating cement paste, i.e., one is high-density C-S-H (HD C-S-H), and another is low-density C-S-H (LD C-S-H). After drying, the mass fraction of LD C-S-H is:

${\mathrm{f}}_{\mathrm{LD}-\mathrm{C}-\mathrm{S}-\mathrm{H}/\mathrm{C}-\mathrm{S}-\mathrm{H}}=3.017\times \left(w/c\right)\times \alpha -1.347\alpha +\mathrm{0.538.}(4)$

The model results are compared quantitatively with experimental data of Danielson (1960) in Figure 1, which shows a reasonably good agreement. It can be seen that the present model is capable of describing the cement hydration.

FIGURE 1

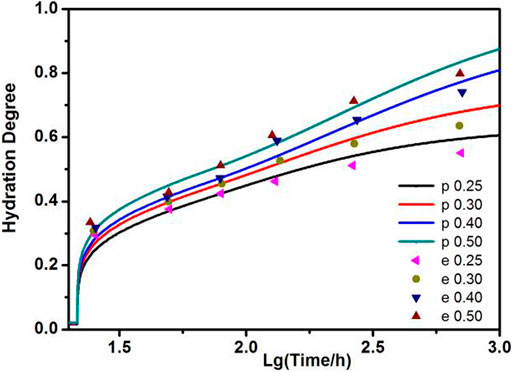
FIGURE 1. The present hydration model results (p) vs. experimental results (e) of Danielson (1960) with different w/c (t₀ = 3).

Percolation Theory

For the cement paste, the static elastic modulus exhibits a non-zero value only after a specific hydration degree α_s (equivalent to the set degree) has been reached, which is called a percolation threshold. The SCS was used by Bernard et al. to obtain the percolation threshold (Bernard et al., 2003), which relates to a solid volume fraction greater than 50% or a porosity lower than 50% (where the sum of the fractions of solid and porosity is 1). However, the SCS overestimates the percolation threshold. Sanahuja et al. (2007) improved it by modifying the slenderness ratio of C-S-H bricks based on experimental results, but they could not determine a fixed ratio fitting all situations.

Torrenti et al. (2005) and Zheng et al. (2012) introduced cohesion due to hydration products and particle agglomeration effects, and their predictions agreed with experimental results. Boumiz et al. (1996) obtained the percolation thresholds by measuring hydration heat and ultrasonic, showing that the percolation threshold, α_s, increased with the w/c ratio in cement pastes, being almost irrelevant to the w/c ratio in mortar or concrete. Additionally, for mortar, concrete, and cement pastes with a w/c ratio below a certain number (called the critical w/c ratio in the following sections), α_s was close to zero.

For a w/c value lower than critical, unhydrated cement particles are initially in contact, so the solid phase percolates once the hydration products are generated, yielding an almost zero α_s value. In an increasing w/c ratio, the cement particles are at the beginning mutually separated by water. As hydration proceeds, the solid volume, f_s, increases, and the hydrates glue the particles together. However, the microstructure has negligible stiffness until it reaches a sufficient solid phase to thread one side to the opposite, yielding an α_s increase with the w/c ratio.

Therefore, the question is how to determine the sufficient amount of solid. We here consider an extremely dispersed situation, in which the cement grains are supposed to be spherical particles uniformly distributed in the water, having the same diameter and hydration rate. When the solid volume fraction exceeds that of an inscribed sphere in the cube (the corresponding value is 0.5236), an interconnected solid phase forms, spanning the whole structure, so the sufficient amount of solid, f_ss, is 0.5236.

The above is a conservative estimation with an overestimated percolation threshold because the size, shape, hydration rate, and distribution of the cement grains are nonuniform. Moreover, the particle agglomeration effect considerably reduces the percolation threshold (Zheng et al., 2012).

In cement pastes with a low w/c ratio, the initial solid volume fraction, f_si, is larger than f_ss, resulting in a zero α_s value, similar to the prediction of Bernard et al. (2003). In the case of a high w/c ratio (>0.3), the solid phase percolates only if there are sufficient hydration products. In other words, the percolation threshold corresponds to a critical solid volume fraction, f_sc, which is smaller than f_ss and increases with the w/c ratio.

Based on the above analyses, we propose a semi-empirical formula considering the effects of the solid volume fraction and the w/c ratio to estimate the percolation threshold of a cement paste:

${\alpha }_s=\left\{\begin{array}{c}0,f_{si}\ge f_{ss}\\ \alpha \left(f_s=f_{sc}\right),f_{si}<f_{ss}\end{array}\right\}.(5)$

Here, the critical solid volume fraction, f_sc, is defined as follows:

$f_{sc}=\left\{\begin{array}{c}{f}_{si},f_{si}\ge f_{ss}\\ f_{si}+\beta \left(f_{ss}-f_{si}\right),f_{si}<f_{ss}\end{array}\right\},\beta =\beta \left(w/c\right)(6)$

where β is a function of the w/c ratio. According to a test conducted by Boumiz et al. (1996), β can be written as follows:

$\beta =\left\{\begin{array}{c}w/c,w/c<0.5\\ 0.5,w/c<0.5\end{array}\right\}.(7)$

It is noted that a high w/c ratio cannot be used in practice because of the associated high porosity and poor mechanical properties, and thus, we do not consider a w/c ratio larger than 0.6.

It is challenging to determine the accurate percolation threshold experimentally, and experimental values exhibit a specific measurement error and cannot provide a strict evaluation criterion; however, their trend can still provide a vital validation input (Maia et al., 2012). In Figure 2, the experimental values are taken from Boumiz et al. (1996). For the given cement, the percolation threshold, α_s, increases with the w/c ratio above a certain value, similar to the finding of Bernard et al. (2003). Moreover, the trend of our model is consistent with the experimental results.

FIGURE 2

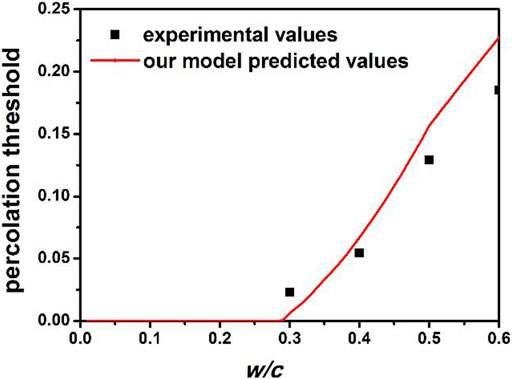
FIGURE 2. Percolation threshold predicted using our model and experimental results for different w/c ratios.

Homogenization Method

We now have the volumetric fractions of all phases and the percolation threshold as described above. A homogenization method is indispensable to determining the mechanical properties of the early-aged cement paste. Several homogenization methods have been used. As an example, the SCS scheme was used by Bernard et al. (2003), Sanahuja et al. (2007), and Zhao et al. (2013), while the FEM and Fast Fourier Transform elastic homogenization were applied by Šmilauer et al. (2006). Additionally, a burning algorithm was used by Stefan et al. (2010) and Zhao et al. (2013) to obtain the connected volume of solids.

Although the SCS can provide the percolation threshold and approximate elastic properties, it is an implicit algorithm and cannot be solved directly. Furthermore, it does not consider the gluing effect of the hydrated products and does not distinguish isolated clusters from the percolated solid phase so that the solid volume may be overestimated.

The isolated clusters (or non-percolated solid particles) do not contribute to shear stiffness. Their mechanical behavior is similar to that of water (Šmilauer et al., 2006; Zhao et al., 2013), so that we consider them as voids. Only percolated solid phase (or spanning clusters) contributes to the mechanical properties of the particular microstructure. Before the percolation threshold is reached, the volumetric fraction of the percolated solid phase is zero, and it can achieve a value of 100% if the solid phase fills out available space. Therefore, we write the volumetric fraction of the percolated solid phase, f_ps, as follows:

$f_{ps}=\left\{\begin{array}{c}0,f_s\le f_{sc}\\ \left(f_s-f_{sc}\right)/\left(1-f_{sc}\right),f_s>f_{sc}\end{array}\right\},(8)$

which shows that the hydrating cement paste does not exhibit stiffness when f_ps is zero. When f_ps equals 1, the elastic properties of the early-aged cement paste are equal to those of the solid phase. Thus, we propose that the elastic properties are the average volume values of the percolated solid phase and voids as expressed by:

$E_{cp}=f_{ps}{E}_s+\left(1-f_{ps}\right)E_v,(9)$

where E_cp, E_s, and E_v are elastic moduli of the cement paste, percolated solid phase, and voids, respectively. For simplicity, it is assumed that E_v = 0.

Elastic modulus, E_s, can be obtained from bulk modulus, K_s, and shear modulus, G_s, which are calculated adopting the Mori–Tanaka method, in which the LD C–S–H is chosen as a matrix phase. Supplementary Material briefly introduces the Mori–Tanaka method. The method represents a simple and useful approach for estimating the effective behavior of a composite material. The method has been described in detail by Budiansky (1965) and Mori et al. (1973). All the material properties used in the present study are given in Table 2.

TABLE 2

TABLE 2. Elastic parameters of components.

Results and Discussions

The modeling results are quantitatively compared with the experiments of Boumiz et al. (1996) for different w/c ratios ranging from 0.3 to 0.6, Figure 3, showing a reasonably good agreement and suggesting that the present model is capable of describing the elastic properties of a hydrating cement paste.

FIGURE 3

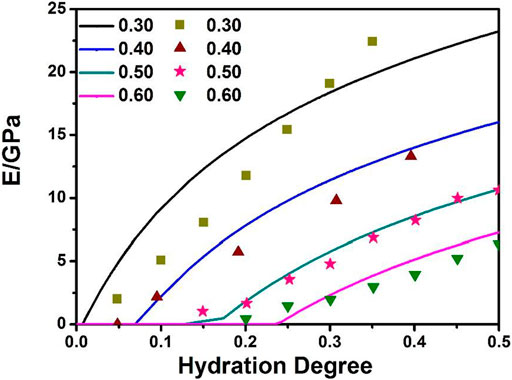
FIGURE 3. Elastic modulus (E) predicted using our model (continuous lines) and experimental results (points) for different w/c ratios.

Figure 3 indicates that the elastic modulus of cement pastes with a high w/c ratio is in good agreement with the experimental results. However, there is a discrepancy between the experiment and the model for cement paste having a low w/c ratio (e.g., 0.3), and the model exhibits a quasi-linear relationship between the elastic modulus trend with the hydration degree. This discrepancy was previously assigned to the measuring accuracy (Stefan et al., 2010; Zhao et al., 2013).

Figure 4 compares the present model results, experimental data of Boumiz et al. (1996), and numerical data of Zhao et al. (2013), who combined the CEMHYD3D hydration model, SCS, and a burning algorithm. The elastic modulus predicted by our modeling approximately coincides with that obtained by Zhao et al. (2013). Still, they overestimated the elastic modulus because the used burning algorithm and SCS gave a higher volumetric fraction of the percolated solid phase.

FIGURE 4

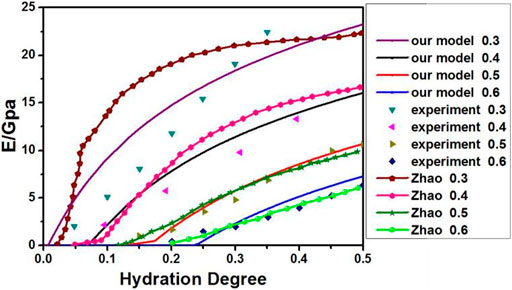
FIGURE 4. Comparison of results obtained in our model, the simulation results of Zhao et al. (2013), and experimental results of Boumiz et al. (1996) for different w/c ratios.

In the case of ordinary Portland cement, without considering the effects of the hydration rate and mineral composition, a more straightforward relationship between the elastic modulus and hydration degree can be derived by replacing the hydration model of Eq. 3 in Cement Hydration Model with Powers’s model, providing the volume fractions of the anhydrous phase (subscript a) and hydrates (h) as simple functions of the w/c ratio and the hydration degree, α:

$f_a=0.32\left(1-\alpha \right)/\left(w/c+0.32\right),f_h=0.68\alpha /\left(w/c+0.32\right)(10)$

Using the parameters from Table 3, the percolation threshold, α_s, and the elastic modulus of the hydrating cement paste, E_s, can be derived from Eqs 5–11 as follows:

$\alpha =\left\{\begin{array}{cc}0& w/c\le 0.2912\\ \left(1.1544\frac{w}{c}-0.423\right)w/c,& 0.5\ge w/c>0.2912\\ \mathrm{0.7272.}w/c-0.2117,& w/c>0.5\end{array}\right\},E_{cp}=f_{ps}{E}_s(11)$

where

$f_{ps}=\left\{\begin{array}{cc}\frac{0.36\alpha }{w/c},& w/c\le 0.2912\\ 1+\frac{1-0.36\alpha /w/c}{0.5236w/c-1.11524},& 0.5\ge w/c\ge 0.2912\\ \frac{0.4877\alpha -0.3546\cdot w/c+0.1033}{w/c+0.1033},& w/c>0.5\end{array}\right\}(12)$

$E_s=E_h\left[1+f_{ha}\frac{E_h/E_a-1}{1+0.5\left(1-f_{ha}\right)\left(E_h/E_a-1\right)}\right](13)$

$f_{ha}=f_h/\left(f_a+f_h\right)=\frac{1-\alpha }{1+1.125\alpha }(14)$

TABLE 3

TABLE 3. Mechanical properties of the cement paste phases obtained with the Powers model (Stefan et al., 2010).

Figures 5, 6 illustrate that the percolation threshold and the elastic modulus predicted using Powers’s model coincide with those obtained from experimental results and Eq. 3, validating our approach. Moreover, the equations based on Powers’s model are more straightforward for engineers.

FIGURE 5

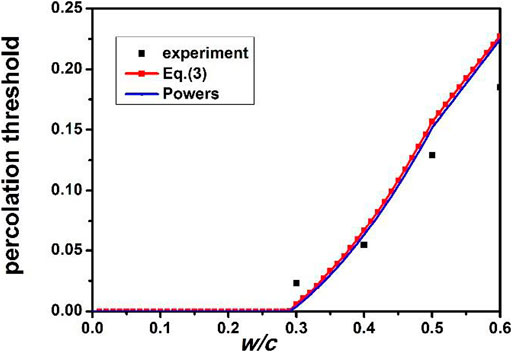
FIGURE 5. Percolation thresholds based on Powers’s model, Eq. 3, and experimental results of Boumiz et al. (1996) for different w/c ratios.

FIGURE 6

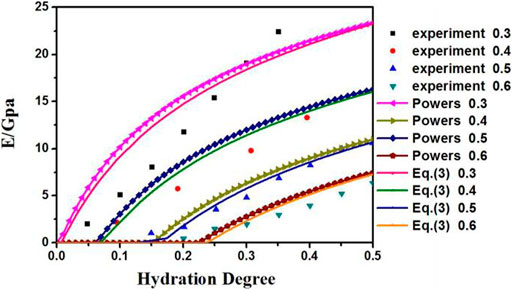
FIGURE 6. Elastic modulus based on Powers’s model, Eq. 3, and experimental results of Boumiz et al. (1996) for different w/c ratios.

The main advantage of our approach is its efficiency and practicability for engineering applications. The percolation threshold and elastic modulus were obtained using simple expressions instead of time-consuming computations, such as those of the SCS or a simulation with a burning algorithm.

The key to the modeling is an accurate description of the evolution of the volumetric fraction of the percolated solid phase. In this study, we adopted a simple phenomenological but rational assumption. The evolution of the volumetric fraction of the percolated solid phase can be precisely depicted using a combination of the burning algorithm and simulation (e.g., CEMHYD3D or HYMOSTRUC3D), but the calculations on the entire microstructure are very time-consuming. The percolation theory in our model simplifies the existing system and needs to be improved in future work.

Attention needs to be paid to the linear relationship between the elastic modulus evolution and the hydration degree, obtained experimentally by Boumiz et al. (1996). However, so far, for cement paste with a low w/c ratio (i.e., <0.3), all models (including our model) show that the elastic modulus is a convex function of the hydration degree. Excellent agreement with experimental results is observed at high w/c ratios. The discrepancy at the early age of hydration was previously assigned to the experimental measurements at this age. However, we argue that the discrepancy is more likely due to the tenuous and loose connectivity of the solid frame, along with the small volume fractions of hydrates at early ages. Therefore, the discrepancy needs to be investigated experimentally using a tool that effectively characterizes the tightness and strength of the solid frame connectivity.

The accurate predictions of the elastic modulus in the present work were limited to cement paste, but they can be extended to mortars and concretes if the effect of aggregate (or filler) on the percolated solid phase is reasonably considered. Ongoing research is expected to address this extension.

Conclusion

We proposed an efficient and straightforward approach for engineers to predict the early-age elastic properties of cement pastes. A hydration model considering the mineral composition and the initial w/c ratio was used, while the percolation threshold was calculated adopting a phenomenological semi-empirical method describing the effects of the solid volume fraction and the w/c ratio. An efficient mixing rule based on the degree of solid connectivity was then adopted to calculate the elastic properties of the hydrating cement paste. The predictive capability of the present model was validated by comparing the model predictions with other experimental and numerical studies. Moreover, for ordinary Portland cement, a simplified model was built using Powers’s hydration model, and it exhibited good consistency with experimental results.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BM and GD designed and prepared the frame, BY, CY, and QG collected data. ZJ, LQ, and JM helped on the touches. BM wrote the article with the help of all coauthors.

Funding

The work was supported by Yunnan Local Colleges Applied Basic Research Projects (No. 2018FH001-119, 202001BA070001-031), the Science Research Foundation of Yunnan Education Department of China (No. 2019J0734, No. 2019J0733), the Candidate Talents Training Fund of Yunnan Province (Project No. 2015HB064), and the National Natural Science Foundation of China (No. 11802265, No. 12063006). The authors (MBY and QLH) gratefully acknowledge financial support from the Hundred Talents Program of Yuxi (grants for 2019).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to express their gratitude to EditSprings (https://www.editsprings.com/) for the expert linguistic services provided.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.729644/full#supplementary-material

References

Acker, P., and Ulm, F.-J. (2001). Creep and Shrinkage of concrete: Physical Origins and Practical Measurements. Nucl. Eng. Des. 203, 143–158. doi:10.1016/S0029-5493(00)00304-6

CrossRef Full Text | Google Scholar

Atkins, P. W. (1994). Physical Chemistry. 5th ed. Oxford: Oxford Univ. Press.

Azenha, M., Faria, R., Magalhães, F., Ramos, L., and Cunha, Á. (2011). Measurement of the E-Modulus of Cement Pastes and Mortars since Casting, Using a Vibration Based Technique. Mater. Struct. 45 (1), 81–92. doi:10.1617/s11527-011-9750-9

CrossRef Full Text | Google Scholar

Azenha, M., Magalhães, F., Faria, R., and Cunha., Á. (2010). Measurement of concrete E-Modulus Evolution since Casting: a Novel Method Based on Ambient Vibration. Cement Concrete Res. 40, 1096–1105. doi:10.1016/j.cemconres.2010.02.014

CrossRef Full Text | Google Scholar

Bentur, A. (2002). Early Age Cracking in Cementitious Systems. State Of the Art Report Of the RILEM Technical Committee, (Haifa, RILEM, France: Early Age Cracking Tests), 241–255. doi:10.1617/2912143632.023

CrossRef Full Text | Google Scholar

Bentz, D. P. (2006). Influence of Water-To-Cement Ratio on Hydration Kinetics: Simple Models Based on Spatial Considerations. Cement Concrete Res. 36, 238–244. doi:10.1016/j.cemconres.2005.04.014

CrossRef Full Text | Google Scholar

Benvenist, Y. (1987) A New Approach to the Application of Mori–Tanaka’s Theory in Composite Materials. Mech. Mater. 6 (1), 147–157. doi:10.1016/0167-6636(87)90005-6

CrossRef Full Text | Google Scholar

Bernard, O., Ulm, F.-J., and Lemarchand, E. (2003). A Multiscale Micromechanics-Hydration Model for the Early-Age Elastic Properties of Cement-Based Materials. Cement Concrete Res. 33, 1293–1309. doi:10.1016/s0008-8846(03)00039-5

CrossRef Full Text | Google Scholar

Boumiz, A., Vernet, C., and Tenoudji, F. C. (1996). Mechanical Properties of Cement Pastes and Mortars at Early Ages. Adv. Cement Based Mater. 3, 94–106. doi:10.1016/S1065-7355(96)90042-5

CrossRef Full Text | Google Scholar

Budiansky, B. (1965). On the Elastic Moduli of Some Heterogeneous Materials. J. Mech. Phys. Sol. 13, 223–227. doi:10.1016/0022-5096(65)90011-6

CrossRef Full Text | Google Scholar

Chu, L., and Dui, G. (2018a). Exact Solutions for Functionally Graded Micro-cylinders in First Gradient Elasticity. Int. J. Mech. Sci. 148 (1), 366–373. doi:10.1016/j.ijmecsci.2018.09.011

CrossRef Full Text | Google Scholar

Chu, L., Dui, G., Yan, Z., and Zheng, Y. (2018b). Influence of Flexoelectricity on Electromechanical Properties of Functionally Graded Piezoelectric Nanobeams Based on Modified Couple Stress Theory. Int. J. Appl. Mech. 10 (9), 1850103. doi:10.1142/S175882511850103X

CrossRef Full Text | Google Scholar

Constantinides, G., and Ulm, F.-J. (2004). The Effect of Two Types of C-S-H on the Elasticity of Cement-Based Materials: Results from Nanoindentation and Micromechanical Modeling. Cement Concrete Res. 34 (1), 67–80. doi:10.1016/S0008-8846(03)00230-8

CrossRef Full Text | Google Scholar

Danielson, U. (1960). “Heat of Hydration of Cement as Affected by Water-Cement Ratio.” in Paper IV-S7, Proceedings of the 4th international symposium on the chemistry of cement, Washington DC, 4th International Congress on the Chemistry of Cement, 519–526.

Google Scholar

De Schutter, G., and Taerwe, L. (1996). Degree of Hydration-Based Description of Mechanical Properties of Early Age concrete. Mat. Struct. 29, 335–344. doi:10.1007/BF02486341

CrossRef Full Text | Google Scholar

Eshelby, J. D. (1957). The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lond. A. 241, 376–396. doi:10.1098/rspa.1957.0133

CrossRef Full Text | Google Scholar

Haecker, C.-J., Garboczi, E. J., Bullard, J. W., Bohn, R. B., Sun, Z., Shah, S. P., et al. (2005). Modeling the Linear Elastic Properties of portland Cement Paste. Cement Concrete Res. 35, 1948–1960. doi:10.1016/j.cemconres.2005.05.001

CrossRef Full Text | Google Scholar

Irfan-Ul-Hassan, M., Pichler, B., Reihsner, R., and Hellmich, C. (2016). Elastic and Creep Properties of Young Cement Paste, as Determined from Hourly Repeated Minute-Long Quasi-Static Tests. Cement Concrete Res. 82 (1), 36–49. doi:10.1016/j.cemconres.2015.11.007

CrossRef Full Text | Google Scholar

Jennings, H. M., and Tennis, P. D. (1994). Model for the Developing Microstructure in portland Cement Pastes. J. Am. Ceram. Soc. 77, 3161–3172. doi:10.1111/j.1151-2916.1994.tb04565.x

CrossRef Full Text | Google Scholar

Königsberger, M., Hellmich, C., and Pichler, B. (2016). Densification of C-S-H Is Mainly Driven by Available Precipitation Space, as Quantified through an Analytical Cement Hydration Model Based on NMR Data. Cement Concrete Res. 88 (1), 170–183. doi:10.1016/j.cemconres.2016.04.006

CrossRef Full Text | Google Scholar

Lin, F., and Christian, M. (2007). Micromechanics Model for the Effective Elastic Properties of Hardened Cement Pastes. Fuhe Cailiao Xuebao/acta Materiae Compositae Sinica 24 (2), 184–189. [in Chinese]. doi:10.3321/j.issn:1000-3851.2007.02.030

CrossRef Full Text | Google Scholar

Maia, L., Azenha, M., Faria, R., and Figueiras, J. (2012). Identification of the Percolation Threshold in Cementitious Pastes by Monitoring the E-Modulus Evolution. Cement and Concrete Composites 34 (6), 739–745. doi:10.1016/j.cemconcomp.2012.03.001

CrossRef Full Text | Google Scholar

Mori, T., and Tanaka, K. (1973). Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metallurgica 21, 571–574. doi:10.1016/0001-6160(73)90064-3

CrossRef Full Text | Google Scholar

Muller, A. C. A., Scrivener, K. L., Gajewicz, A. M., and McDonald, P. J. (2013). Densification of C-S-H Measured by 1H NMR Relaxometry. J. Phys. Chem. C 117 (1), 403–412. doi:10.1021/jp3102964

CrossRef Full Text | Google Scholar

Pichler, B., Hellmich, C., and Eberhardsteiner, J. (2009). Spherical and Acicular Representation of Hydrates in a Micromechanical Model for Cement Paste: Prediction of Early-Age Elasticity and Strength. Acta Mech. 203 (3), 137–162. doi:10.1007/s00707-008-0007-9

CrossRef Full Text | Google Scholar

Pichler, B., Hellmich, C., Eberhardsteiner, J., Wasserbauer, J., Termkhajornkit, P., Barbarulo, R., et al. (2013). Effect of Gel-Space Ratio and Microstructure on Strength of Hydrating Cementitious Materials: An Engineering Micromechanics Approach. Cement Concrete Res. 45 (1), 55–68. doi:10.1016/j.cemconres.2012.10.019

CrossRef Full Text | Google Scholar

Pichler, B., and Hellmich, C. (2011). Upscaling Quasi-Brittle Strength of Cement Paste and Mortar: A Multi-Scale Engineering Mechanics Model. Cement Concrete Res. 41 (5), 467–476. doi:10.1016/j.cemconres.2011.01.010

CrossRef Full Text | Google Scholar

Powers, T. C., and Brownyard, T. L. (1946). Studies of the Physical Properties of Hardened Portland Cement Paste. Jp 43, 469–504. doi:10.14359/15302

CrossRef Full Text | Google Scholar

Princigallo, A., Lura, P., van Breugel, K., and Levita, G. (2003). Early Development of Properties in a Cement Paste: a Numerical and Experimental Study. Cement Concrete Res. 33, 1013–1020. doi:10.1016/S0008-8846(03)00002-4

CrossRef Full Text | Google Scholar

Reinhardt, H. W., and Grosse, C. (2005). FInal Report of RILEM TC 185-ATC, 31. Bagneux: RILEM, 83–96. doi:10.1617/2912143705.004Basics

CrossRef Full Text | Google Scholar

R. Springenschmid (Editor) (2009). “Thermal Cracking in concrete at Early Ages,” in Proceedings no. 25 of the International RILEM Symposium, London, UK, Crc Press. doi:10.4324/9780203626528

CrossRef Full Text | Google Scholar

Sanahuja, J., Dormieux, L., and Chanvillard, G. (2007). Modelling Elasticity of a Hydrating Cement Paste. Cement Concrete Res. 37, 1427–1439. doi:10.1016/j.cemconres.2007.07.003

CrossRef Full Text | Google Scholar

Stefan, L., Benboudjema, F., Torrenti, J.-M., and Bissonnette, B. (2010). Prediction of Elastic Properties of Cement Pastes at Early Ages. Comput. Mater. Sci. 47, 775–784. doi:10.1016/j.commatsci.2009.11.003

CrossRef Full Text | Google Scholar

Sun, Z., Ye, G., and Shah, S. P. (2005). Microstructure and Early-Age Properties of Portland Cement Paste-Effects of Connectivity of Solid Phases. Aci Materials Journal. 102, 122–129. doi:10.14359/14306

CrossRef Full Text | Google Scholar

Sun, Z., Ye, G., Voigt, T., Shah, S. P., and van Breugel, K. (1999). Early Age Properties of portland Cement Pastes Investigated with Ultrasonic Shear Waves and Numerical Simulation. J. Nanjing Normal Univ. 1 (1), 1–10. doi:10.21985/N2W18Z

CrossRef Full Text | Google Scholar

S˘milauer, V., and Bittnar, Z. k. (2006). Microstructure-based Micromechanical Prediction of Elastic Properties in Hydrating Cement Paste. Cement Concrete Res. 36, 1708–1718. doi:10.1016/j.cemconres.2006.05.014

CrossRef Full Text | Google Scholar

Taylor, H. F. W. (1987). A Method for Predicting Alkazi Ion Concentrations in Cement Pore Solutions. Adv. Cement Res. 1 (1), 5–17. doi:10.1680/adcr.1987.1.1.5

CrossRef Full Text | Google Scholar

Tennis, P. D., and Jennings, H. M. (2000). A Model for Two Types of Calcium Silicate Hydrate in the Microstructure of portland Cement Pastes. Cement Concrete Res. 30, 855–863. doi:10.1016/S0008-8846(00)00257-X

CrossRef Full Text | Google Scholar

Torrenti, J. M., and Benboudjema, F. (2005). Mechanical Threshold of Cementitious Materials at Early Age. Mat. Struct. 38, 299–304. doi:10.1007/BF02479294

CrossRef Full Text | Google Scholar

Voigt, T., Ye, G., Sun, Z., Shah, S. P., and Breugel, K. V. (2005). Early Age Microstructure of Portland Cement Mortar Investigated by Ultrasonic Shear Waves and Numerical Simulation. Cement Concrete Res. 35 (5), 858–866. doi:10.1016/j.cemconres.2004.09.004

CrossRef Full Text | Google Scholar

Zhao, H., Wu, S., Huang, D., Chen, X., and Zhao, L. (2013). A Multi-Scale Percolation-Based Approach for the Prediction of Elasticity of Early-Age Cement Paste. Eur. J. Environ. Civil Eng. 17, s304–s320. doi:10.1080/19648189.2013.834602

CrossRef Full Text | Google Scholar

Zheng, J.-j., Zhang, J., and Scherer, G. W. (2012). Prediction of the Degree of Hydration at Initial Setting Time of Cement Paste with Particle Agglomeration. Cement Concrete Res. 42, 1280–1285. doi:10.1016/j.cemconres.2012.05.020

CrossRef Full Text | Google Scholar