
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 06 August 2021
Sec. Energy Materials
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.725219
This article is part of the Research Topic Development of Emerging Thermoelectric Materials View all 4 articles
Mg and Si as the typical dopants for p- and n-type gallium nitride (GaN), respectively, are widely used in GaN-based photoelectric devices. The thermal transport properties play a key role in the thermal stability and lifetime of photoelectric devices, which are of significant urgency to be studied, especially for the Mg- and Si-doped GaN. In this paper, the thermal conductivities of Mg- and Si-doped GaN were investigated based on first-principles calculations and phonon Boltzmann transport equation. The thermal conductivities of Mg-doped GaN are found to be 5.11 and 4.77 W/mK for in-plane and cross-plane directions, respectively. While for the Si-doped GaN, the thermal conductivity reaches the smaller value, which are 0.41 and 0.51 W/mK for in-plane and cross-plane directions, respectively. The decrease in thermal conductivity of Mg-doped GaN is attributed to the combined effect of low group velocities of optical phonon branches and small phonon relaxation time. In contrast, the sharp decrease of the thermal conductivity of Si-doped GaN is mainly attributed to the extremely small phonon relaxation time. Besides, the contribution of acoustic and optical phonon modes to the thermal conductivity has changed after GaN being doped with Mg and Si. Further analysis from the orbital projected electronic density of states and the electron localization function indicates that the strong polarization of Mg-N and Si-N bonds and the distortion of the local structures together lead to the low thermal conductivity. Our results would provide important information for the thermal management of GaN-based photoelectric devices.
Gallium nitride (GaN) has become one of the most potential basic materials for high power and high frequency electronic devices due to its wide band gap, high electron mobility and stability (Chang et al., 2008; Quah and Cheong, 2013). It is widely used in photoelectric and electronic fields and growth of materials, from light-emitting devices to high-power transistors (Pearton et al., 2001; Lee et al., 2008; Chung et al., 2010; Quah and Cheong, 2014; Quan et al., 2014; Li et al., 2016; Jiang et al., 2019). The p-type and n-type doping of GaN is the key to the preparation of optoelectronic devices (Wang et al., 2014; Krishna et al., 2019; Liu et al., 2021), because of providing the high carrier concentration and mobility. Among them, magnesium (Mg) is the only dopant to realize p-type conductivity (Lahourcade et al., 2009; Krishna et al., 2019), and silicon (Si) is the important dopant to realize n-type doping, which effectively enhances the luminous efficiency (Liu et al., 2021). In the practical application of GaN-based optoelectronic devices, the performance and lifetime of the devices mainly lie with the heat dissipation efficiency in the active region (Kamano et al., 2002; Liu et al., 2015). Thermal conductivity, an important character of materials, has attracted much attention due to its key role in determining the lifetime of electronic devices (Gillet et al., 2009). Experimentally, the thermal conductivity of GaN is significantly suppressed after doping with Mg and Si (Beechem et al., 2016; Paskov et al., 2017). For example, Beechem et al measured the thermal conductivity of GaN is 180 W/mK at room temperature, while the thermal conductivity of Mg-doped GaN reduces from 160 to 110 W/mK with the doping concentration increases from 2.8 × 1018 to 3 × 1019 cm−3. Paskov et al reported the thermal conductivity of GaN reduces from 245 to 210 W/mK with increasing the Si doping concentration from 1.6 × 1016 to 7 ×1 018 cm−3 at room temperature. Although the thermal conductivity of GaN doped with Mg and Si has been widely studied in experiments, its underlying physical mechanism is still ambiguous, which would limit the applications of GaN-based photoelectric devices and need to be further explored. Currently, the first-principles calculation of thermal conductivity of doped GaN is rare. The thermal conductivities of InGaN and AlGaN alloys were studied using the virtual crystal model, while the specific doping structures are ignored (Ma et al., 2016). Only the thermal transport properties of GaN doped with In and C have been studied based on the first-principles calculation with doping structures (Li and Wang, 2021). In fact, substitutional dopants introduce mass perturbations and extended bond perturbations (Fava et al., 2021), due to the difference in atomic masses of host and substituting atoms and the distortion produced by the dopant. Therefore, to further understand the thermal transport properties of GaN doped with Mg and Si, in-depth exploration is imperative.
In this work, the thermal conductivities of Mg- and Si-doped GaN are studied based on the first-principles method combined with the phonon Boltzmann transport equation. It is found that the thermal conductivities of Mg- and Si-doped GaN both reach the ultra-low values, the thermal conductivity of Si-doped GaN is even an order of magnitude lower than that of Mg-doped GaN. The phonon transport properties of GaN doped with Mg and Si are systematically analyzed based on the contribution of phonon branches, phonon group velocity, phonon relaxation time, phonon scattering phase space and Grüneisen parameter. Further electronic structures analyses are performed based on the projected electronic density of states (pDOS) and electron localization function (ELF) to provide deep insight into phonon transport in GaN doped with Mg and Si.
The thermal conductivity is obtained by solving the phonon Boltzmann transport equation (BTE) based on second order and third order interatomic force constants (IFCs) evaluated from first-principles calculations. At temperature T, the thermal conductivity can be expressed as (Li et al., 2014)
where kB, N and Ω are the Boltzmann constant, the number of q meshes in Brillouin zone and the volume of the unit cell, respectively. λ is the phonon mode composed of the branch index p and wave vector q,
Here,
where
First-principles calculations were performed based on density functional theory (DFT) using the Vienna ab-initio simulation package (VASP) (Kresse and Furthmuller, 1996) with the Perdew-Burke-Ernzerhof (PBE) (Perdew et al., 1997) of generalized gradient approximation (GGA) for the exchange-correlation functional. The kinetic energy cutoff of plane wave basis was set to be 600 eV and the Monkhorst-Pack (Monkhorst and Pack, 1976) k-mesh of 7
The harmonic and anharmonic IFCs were obtained using the real-space finite displacement difference method. Phonon harmonic properties including phonon dispersion relations and phonon density of states require the second order IFCs, while phonon anharmonic properties require the third order IFCs. The 2 × 2 × 2 supercells containing 32 atoms were used to calculate the second order and third order IFCs. We take the second order IFCs by using the density functional perturbation theory (DFPT) method as implemented in VASP and the Phonopy package (Togo and Tanaka, 2015). For the third order, we chose the cutoff interactions up to the 12th nearest neighbors and fifth nearest neighbors for GaN and GaN doped with Mg and Si, respectively, which were based on the carful convergence tests. With the second order and third order IFCs, the thermal conductivity can be obtained by solving the phonon Boltzmann transport equation as implemented in the ShengBTE package (Li et al., 2014) and the q-mesh of 9 × 9 × 9 was considered based on the thermal conductivity convergence test.
As shown in Figures 1A,C,E, the lattice structures of GaN, Mg- and Si-doped GaN with the hexagonal system and belong to the same P63mc space group. A 2 × 2 × 2 supercell of pristine GaN containing 8 unit cells is used to construct the doped GaN, and a Mg or Si atom is used to replace to a Ga atom in the center of the supercell to form Mg-doped or Si-doped GaN, respectively. The doping concentration is 6.25%. The optimized lattice constants of the three compounds are shown in Table 1. It is clearly seen that the lattice constants of GaN are consistent with the previous calculated values, and slightly larger than the experimental values, a = 3.190 Å and c = 5.189 Å (Schulz and Thiemann, 1977). The variations of the lattice parameters a, c and volume after Mg doping GaN are a bit larger than that of Si-doped GaN. Contrary to the Mg-doped GaN, the volume of GaN doping with Si becomes smaller, which may lie in the differences of the lattice parameters a and c between these two materials. Our results are consistent with others reports as listed in Table 1, which indicates the accuracy of our optimized structures.
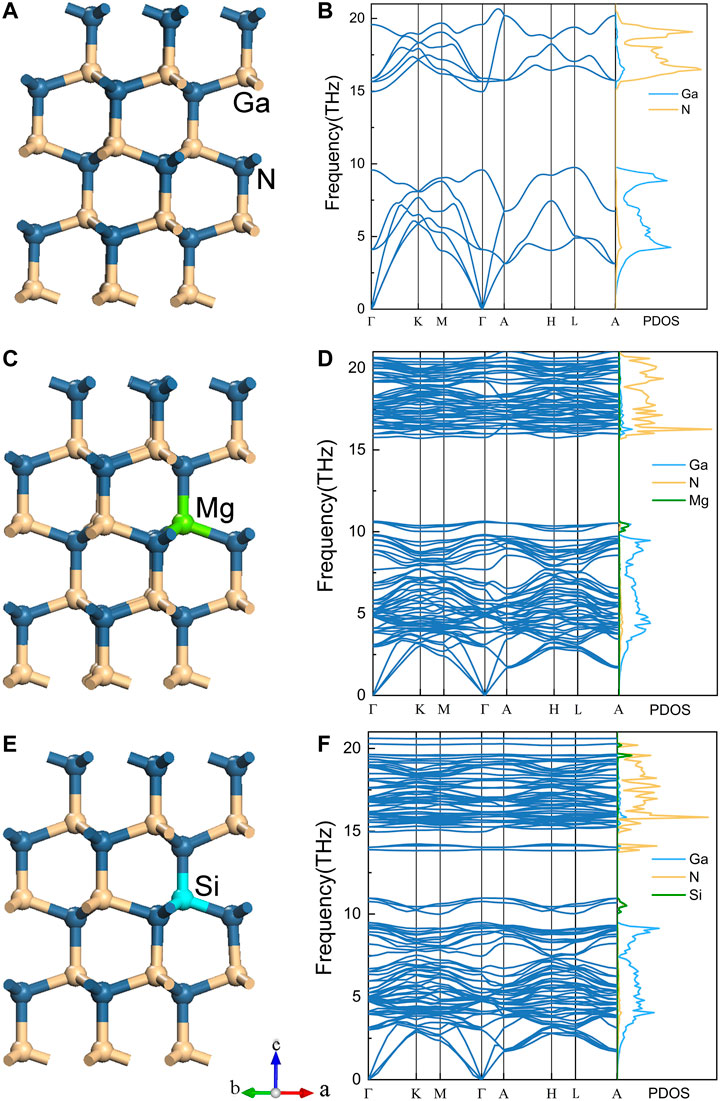
FIGURE 1. The crystal structure of wurtzite GaN (A), Mg-doped GaN (C), Si-doped GaN (E). The yellow, grey, green and light blue balls represent Ga, N, Mg and Si atoms, respectively. The phonon dispersion curves along the high-symmetry directions with corresponding projected phonon density of states of GaN (B), Mg-doped GaN (D), Si-doped GaN (F).
Lattice dynamic properties are investigated for indicating the thermodynamic stability of the materials and evaluating the lattice thermal conductivity. Based on the optimized structures, all phonon dispersions along the Γ-K-M-Γ-A-H-L-A path and corresponding projected phonon density of states (PDOS) of GaN, Mg-doped GaN and Si-doped GaN were calculated as shown in Figures 1B,D,F, which illustrate the structural stability of these compounds. As shown in Figure 1B, there exist 3 acoustic phonon branches and nine optical phonon branches in GaN (Bungaro et al., 2000). In addition, the optical phonon branches can be further divided into six high-frequency optical phonon branches above the gap and three low-frequency optical phonon branches below the gap. Obviously, the number of phonon branches in Mg-doped GaN and Si-doped GaN is much larger than that of GaN, which both have 96 phonon branches as illustrated in Figures 1D,F. Such phenomenon is consistent with previous reports of other doped materials, such as Bi-doped SnS, BiCuOch (ch = S, Se and Te), B- and N-doped graphene and N-Au co-doped graphene (Liu et al., 2016; Guan et al., 2020; Mann et al., 2020; Zhang et al., 2020), which can be put down to the 32-atom primitive cells of Mg-doped GaN and Si-doped GaN resulting in 96 independent vibration modes, including 3 acoustic modes and 93 optical modes. Further, the phonon bandgaps of GaN, Mg-doped GaN and Si-doped GaN can be obtained from their phonon dispersions, which are 5.38, 5.08, 2.87 THz, respectively. In general, the wide phonon bandgap can be attributed to the large mass difference (Gu and Yang, 2014; Wang et al., 2021). The atomic masses of Ga, Si, Mg and N are 69.72, 28.09, 24.31 and 14.01, respectively (Wieser and Berglund, 2009). In Si-doped GaN, due to the existence of the Si atom, the mass difference is the smallest, being 41.63. As for Mg-doped GaN, it has a slightly larger mass difference (45.41), but it is still lower than GaN (55.71). Further, the presence of several isolated phonon branches around 11 THz in the phonon dispersion of Mg-doped GaN results in the narrower bandgap, and the phonon bandgap of Si-doped GaN is the narrowest compared to GaN and Ga15Mg1N16 due to two separate parts of phonon branches around 11 THz and 14 THz in the phonon dispersion. As PDOS shows in Figures 1D,F, the isolated phonon branches above the low-frequency part are contributed by the Mg atom in Mg-doped GaN, and the isolated phonon branches above the low-frequency part and below the high-frequency part are mainly contributed by the Si and N atoms in Si-doped GaN, respectively.
The thermal conductivities of GaN, Mg-doped GaN and Si-doped GaN for in-plane and cross-plane directions in the temperature range from 200 to 1000 K are provided in Figure 2. It is shown that the thermal conductivities of Mg-doped GaN and Si-doped GaN are much lower than that of GaN in the whole temperature, especially the thermal conductivity of Si-doped GaN is even two orders of magnitude lower than that of GaN. It is noted that the thermal conductivity of GaN and Si-doped GaN along the in-plane direction is smaller than that along the cross-plane direction, and the anisotropy of thermal transport in wurtzite structures can be put down to the anisotropy of group velocity and has been well explained in literature reports (Ma et al., 2016; Wu et al., 2016). Moreover, the anisotropy of thermal conductivity in the three compounds decreases with the increasing temperature as shown in Figure 2A. As temperature increase from 200 to 1000 K, the anisotropy of thermal conductivity of GaN reduces monotonically from 33 to 9 W/mK, and for Mg- and Si-doped GaN, the anisotropy of thermal conductivity reduces monotonically from 0.52 to 0.10 W/mK and 0.13 to 0.03 W/mK, respectively. This change in anisotropy can be attributed to the enhancement of phonon-phonon scattering of acoustic phonons which mainly contribute to the anisotropy (Ma et al., 2016).
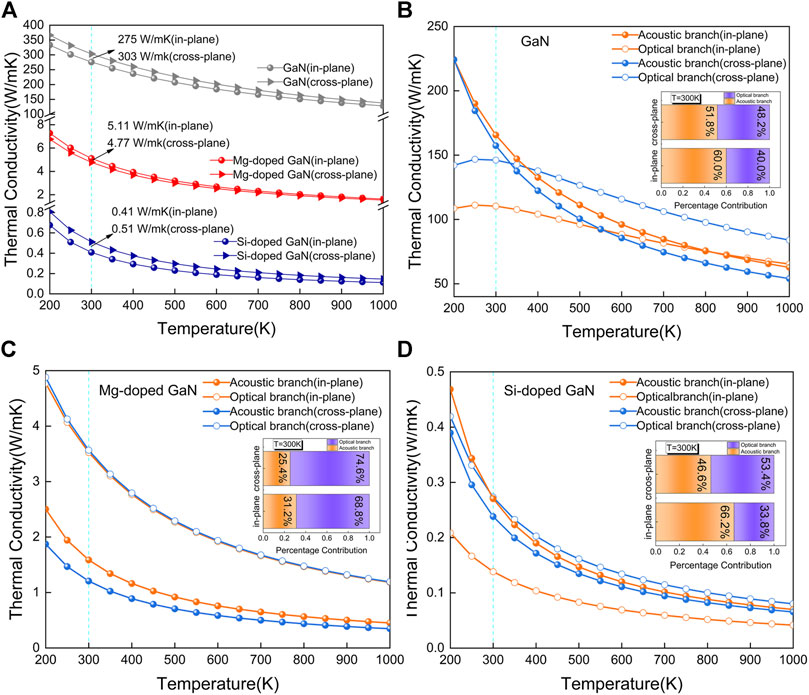
FIGURE 2. (A) Temperature (200–1000 K) dependent thermal conductivity of GaN, Mg-doped GaN and Si-doped GaN for in-plane and cross-plane directions. Temperature (200–1000 K) dependent contribution of acoustic and optical phonon branches to thermal conductivity along the in-plane and cross-plane directions for GaN (B), Mg-doped GaN (C), Si-doped GaN (D). Insets of (B-D): at 300 K, percentage contribution of acoustic and optical phonon branches to thermal conductivity along the in-plane and cross-plane directions for GaN, Mg-doped GaN and Si-doped GaN, respectively.
At 300 K, the thermal conductivity of GaN is calculated to be 275 and 303 W/mK for in-plane and cross-plane directions, respectively, which is in good agreement with the previous studies (Lindsay et al., 2012; Yang et al., 2016; Qin et al., 2017a). For Mg-doped GaN, the calculated thermal conductivity along the in-plane and cross-plane directions is 5.11 and 4.77 W/mK, respectively, while the thermal conductivity of Si-doped GaN reaches the minimum value, which is 0.41 and 0.51 W/mK for in-plane and cross-plane directions, respectively. Although the calculated results after GaN doping with Mg and Si are lower than the experimental values (Beechem et al., 2016; Choi et al., 2020), the decreasing trend of the thermal conductivity of GaN can still be well captured after doping. This phenomenon is consistent with the decrease in thermal conductivity calculated by the first-principles of other materials after doping (Ma et al., 2016; Mann et al., 2020). Thus, our results are useful to understand that the dopants lead to the decrease of thermal conductivity of GaN.
In order to study the underlying mechanism of phonon transport in Mg-doped GaN and Si-doped GaN, we first extracted the contribution from acoustic branches and optical branches. The insets of Figures 2B–D illustrate the percentage contribution of acoustic and optical phonon branches to thermal conductivity along the in-plane and cross-plane directions for GaN, Mg-doped GaN and Si-doped GaN at 300 K, respectively. It is found that the optical phonon branches contribute the most to the thermal conductivity along the in-plane and cross-plane directions of Mg-doped GaN, being 68.8 and 74.6%, respectively, which is contrary to that of GaN. For Si-doped GaN, the thermal conductivity along the in-plane direction is mainly contributed by the acoustic phonon branches, being 66.2%, while the percentage contribution of acoustic phonon branches to thermal conductivity along cross-plane direction drops to 46.6%. We can find that the contribution of optical phonon branches to the thermal conductivity increases after GaN doping with Mg and Si. This is expected as the phonon-phonon scattering of acoustic phonon modes becomes stronger because of the strong coupling of acoustic phonons with optical phonons, and may partly explain the sharp decrease in thermal conductivity. Moreover, the contribution of acoustic and optical phonon branches to the thermal conductivity along the in-plane and cross-plane directions changes with the temperature increasing as shown in Figures 2B–D. In the case of GaN, the contribution of acoustic phonon branches keeps decreasing as the temperature increase until the optical phonon branches become dominant. The reason can be explained by the thermal excitation (Qin et al., 2017a), the low frequency acoustic phonon modes are more easily thermally activated and saturated at lower temperature than the relevant temperature, while as for the high-frequency optical phonon modes, they are just beginning to be thermally activated near the relevant temperature, which mainly leads to the increase of heat capacity. By contrast, for Mg-doped GaN, the contribution among optical phonon branches and among acoustic phonon branches are clearly distinguishable, which the optical phonon mode always plays a key role in the thermal conductivity along the in-plane and cross-plane directions. Note that the contribution of optical phonon branches to the thermal conductivity along the in-plane direction for Si-doped GaN is lower than that of acoustic phonon branches in the whole temperature, which is different from the GaN and Mg-doped GaN.
In short, the magnitude of the decrease in thermal conductivity of GaN doped with Mg and Si is different, and the contribution of acoustic and optical branches to the thermal conductivity is also different. The underlying mechanisms will be explained through the following deep analysis.
To get insight into the low thermal conductivity of GaN doped with Mg and Si, comparative mode level at 300 K analysis among GaN, Mg-doped GaN and Si-doped GaN as plotted in Figure 3. First, from the phonon group velocity illustrated in Figure 3A, we can find that the group velocities of the low-frequency (below 3 THz) acoustic phonon branches with GaN, Mg-doped GaN and Si-doped GaN are almost same, which agree with the same slope of acoustic phonon branches in their phonon dispersions. Moreover, the group velocities of high-frequency (above 3 THz) optical phonon branches with Mg-doped GaN and Si-doped GaN are on the same scale, while both are smaller than that of GaN. Because of the thermal conductivities of Mg-doped GaN along the in-plane and cross-plane directions both are mainly contributed by the optical phonon branches, the lower group velocity of optical phonon branches partly contributes to the decrease of thermal conductivity of Mg-doped GaN. As for Si-doped GaN, the effect of the lower group velocity of optical phonon branches on its ultra-low thermal conductivity is negligible.
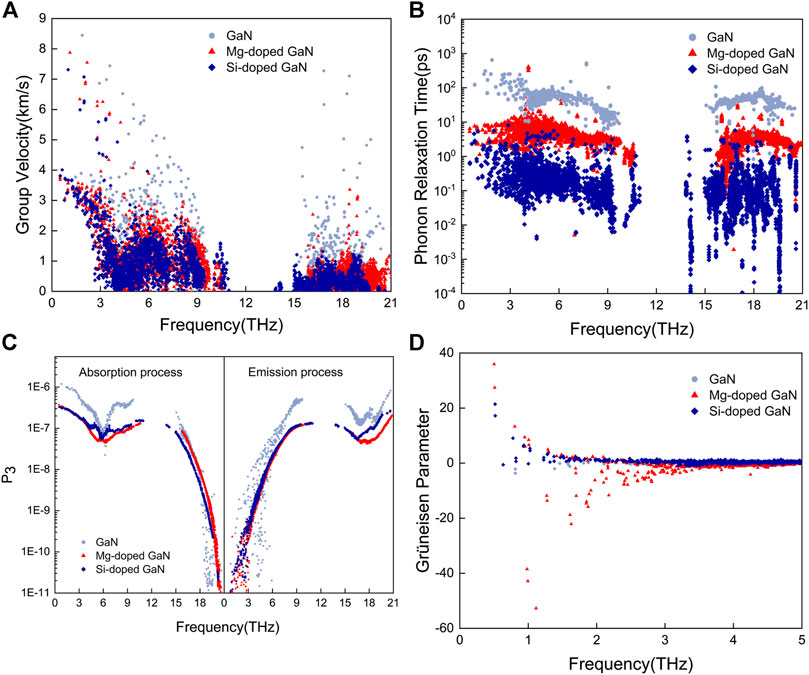
FIGURE 3. Phonon group velocity (A), phonon relaxation time (B), phonon scattering phase space (C) and Grüneisen parameter (D) as a function of frequency for GaN (gray), Mg-doped GaN (red) and Si-doped GaN (blue), respectively.
Further, the phonon relaxation time of the three compounds as shown in Figure 3B. It is found that the phonon relaxation time of Mg-doped GaN is an order of magnitude lower than that of GaN, and even the phonon relaxation time of Si-doped GaN is nearly three orders of magnitude lower than that of GaN. Based on the equation for calculating the thermal conductivity, the huge difference in phonon relaxation time directly explains the sharp decrease of thermal conductivity of GaN doped with Mg and Si. And the order of phonon relaxation time of GaN, Mg-doped GaN and Si-doped GaN exactly corresponds to the order of their thermal conductivity. In addition, the optical phonon branches contribute the most to the thermal conductivity along the in-plane and cross-plane directions of Mg-doped GaN, which can be attributed to the lifetime of the optical phonon branches around 5 THz is much larger than that of the low-frequency acoustic phonon branches as plotted in Figure 3B.
It is well known that the phonon relaxation time is inversely proportional to the scattering rate. In order to further clarify why the phonon relaxation time is reduced so dramatically, the phonon scattering phase space and phonon anharmonicity of the three compounds were compared and analyzed. The phonon scattering phase space is dominated by the phonon dispersion, which determines the scattering possibility (Lindsay and Broido, 2008; Qin et al., 2017b). We split the phonon scattering process into absorption and emission processes as shown in Figure 3C. According to the energy and momentum conservation of phonon scattering process, absorption process mainly occurs in the low-frequency phonon modes and emission process mainly occurs in the high-frequency phonon modes. From the overview of Figure 3C, it is unexpected found that the absorption and emission process of Mg-doped GaN and Si-doped GaN both are smaller than that of GaN, which may lie in the competitive effects in the scattering phase space result from the isolated optical phonon branches in their phonon dispersions. The competitive effect can be explained by the following analysis (Wang et al., 2021), on the one hand, the phonon-phonon scattering will be stronger due to the isolated phonon branches strengthen the coupling of the upper and lower phonon branches of the phonon bandgap. On the other hand, the phonon-phonon scattering will be weaker duo to the isolated phonon branches weaken the coupling of the upper and lower phonon branches of the phonon bandgap. Hence, the smaller scattering phase space of Mg-doped GaN and Si-doped GaN attribute to the effect of the isolated phonon branches around 10 THz in the phonon dispersions of Mg-doped GaN and Si-doped GaN on strengthening the coupling of the upper and lower phonon branches of the phonon bandgap is weaker than the effect on weakening the coupling of the upper and lower phonon branches of the phonon bandgap. However, such result is opposite to the phonon relaxation time of GaN, Mg-doped GaN and Si-doped GaN, which indicates phonon scattering phase space has no effect on the reduction of phonon relaxation time of GaN doped with Mg and Si. In addition, the phonon anharmonicity is characterized by the Grüneisen parameter (Wu et al., 2016), which determines the scattering strength. As shown in Figure 3D, the magnitude of the Grüneisen parameter for Mg-doped GaN and Si-doped GaN is obviously larger than that of GaN, indicating that stronger phonon anharmonicity in Mg-doped GaN and Si-doped GaN. The strong phonon anharmonicity can enhance the phonon-phonon scattering rate and further lead to a small phonon relaxation time. Therefore, the large Grüneisen parameter of Mg-doped GaN and Si-doped GaN is the fundamental reason for the decrease of their thermal conductivity. We noticed that the Grüneisen parameter of Mg-doped GaN is slightly larger than that of Si-doped GaN, which is consistent with the relative change of their volume.
To get an intuitive understanding of phonon transport in GaN doped with Mg and Si, we extracted the contribution of mode-level to the thermal conductivity, as shown in Figure 4A. The contribution of mode-level to the thermal conductivity of GaN after doping with Mg and Si is significantly different over the whole frequency rang. The mode level thermal conductivities of Mg- and Si-doped GaN are much lower than that of GaN, where the mode level thermal conductivity of Si-doped GaN is lower than that of Mg-doped GaN, which is consistent with the total thermal conductivity as shown in Figure 2A. Finally, we calculated the cumulative thermal conductivity in relative to the phonon mean free path (MFP). The MFP expresses the characteristic length of phonon travel on average before scattering (Fan et al., 2019). Figure 4B gives the MFP spectra of GaN, Mg- and Si-doped GaN. It is shown that the phonon with MFPs smaller 221.1, 8.9 and 2.4 nm contribute ∼50% of the thermal conductivity of GaN, Mg- and Si-doped GaN. In other words, after GaN being doped with Mg and Si, the phonons are more likely to be scattered during thermal transport, resulting in lower phonon lifetime, and further explaining the reason for the decrease in thermal conductivity.
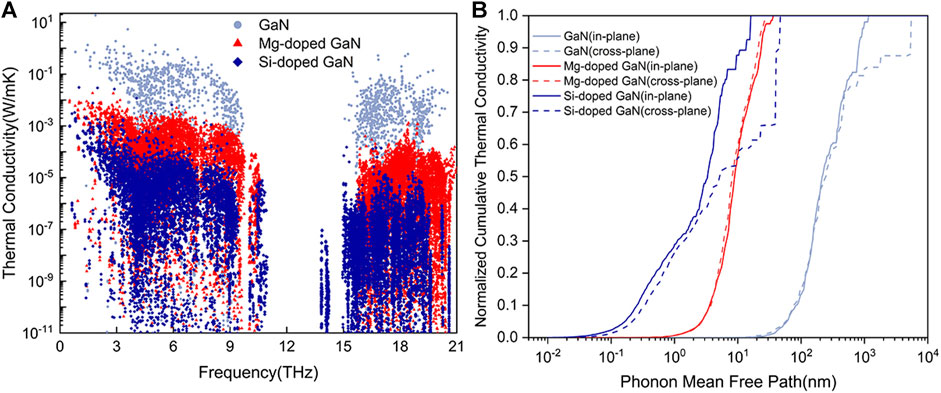
FIGURE 4. (A) Comparison of mode level thermal conductivity between GaN, Mg- and Si-doped GaN at 300 K. (B) Comparison of the cumulative thermal conductivity with respect to phonon mean free path of GaN, Mg- and Si-doped GaN at 300 K.
In brief, the decrease in thermal conductivity of Mg-doped GaN is due to both the low group velocities of optical phonon branches and small phonon relaxation time, while the sharp decrease of the thermal conductivity of Si-doped GaN is due to the extremely small phonon relaxation time. Further study found that the small phonon relaxation time of Mg-doped GaN and Si-doped GaN can be attributed to the strong phonon anharmonicity enhances the phonon-phonon scattering rate.
Considering that phonon transport is closely related to electronic behavior in atomic structure, we further analyzed it from the perspective of the electronic structures to understand the underlying mechanism of the decrease in thermal conductivity. In GaN, there exists the GaN4 tetrahedron formed by the bonding of the p orbitals of Ga and N atoms in the form of sp3 hybridization (Mishra et al., 2007), while the GaN4 tetrahedron will be broken down when Ga atom is substituted with Mg or Si atom. To this end, we extracted the orbital projected electronic density of states (pDOS) of the Mg, Si and be replaced Ga atoms and the electron localization function (ELF) of GaN, Mg-doped GaN and Si-doped GaN. As shown in Figure 5A, it is clearly seen that the contribution of the p orbitals of Mg and Si atoms to the sp3 hybridization is obviously decreased. In another words, the contribution to bonding from the p orbitals of Mg and Si atoms is decreased, which leads to the polarization of Mg-N and Si-N bonds is stronger than the Ga-N bond. This result is clearly shown by comparing the ELF of the three compounds. The strong polarization of the band will enhance the phonon-phonon scattering rate, resulting in low thermal conductivity. (Castro Neto et al., 2009). Besides, the length of Mg-N bond (2.017 Å) is slightly longer than that of Ga-N bond (1.968), while the length of Si-N bond (1.811) is much shorter than the Ga-N bond. Such phenomenon indicates the symmetry of the structures of Mg-doped GaN and Si-doped GaN are broken due to the distortion of the local structures, especially the structure of Si-doped GaN is even more distorted. The distortion of the geometric structure can affect the distribution of electrons in space, and it can be directly observed through the electronic local function in Figure 5. Obviously, after doping, the localized functions of electrons around Mg atoms and Si atoms deviate, causing the electron cloud to be unevenly distributed around it compared with GaN. This polarization environment promotes phonon-phonon scattering, which ultimately leads to ultra-low thermal conductivity. This difference indirectly explains the phonon relaxation time of Si-doped GaN is smaller than that of Mg-doped GaN results from the more severe distortion of the Si-doped GaN structure leads to the stronger phonon-phonon scattering.
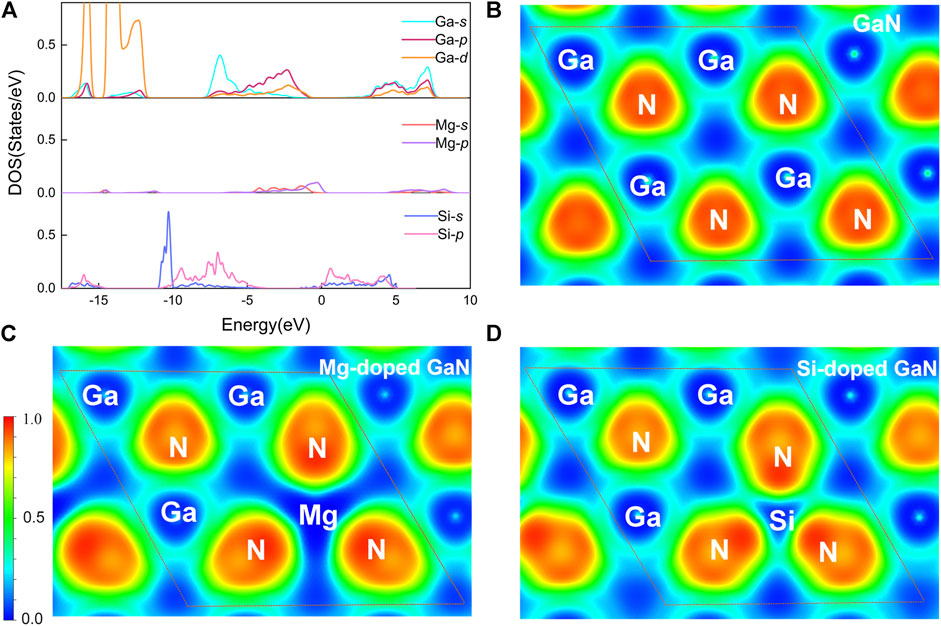
FIGURE 5. (A) The orbital projected electronic density of states (pDOS) of replaced-Ga, Mg and Si atoms. Top views of the electron localization function (ELF) for GaN (B), Mg-doped GaN (C) and Si-doped GaN (D).
In summary, the thermal conductivities of Mg and Si doped GaN are comparatively studied using first-principles calculations and phonon Boltzmann transport equation. The thermal conductivity of Mg-doped GaN is found to be 5.11 and 4.77 W/mK for in-plane and cross-plane directions, respectively, which is two orders of magnitude lower than that of GaN (275 and 303 W/mK), while the thermal conductivity of Si-doped GaN reaches the minimum value, which is 0.41 and 0.51 W/mK for in-plane and cross-plane directions, respectively. The decrease in thermal conductivity of GaN doped with Mg is due to both the low group velocities of optical phonon branches and small phonon relaxation time, by contrast, the sharp decrease of the thermal conductivity of Si-doped GaN is due to the extremely small phonon relaxation time. In addition, for GaN doped with Mg, the optical phonon mode plays a key role in the thermal conductivity along the in-plane and cross-plane directions, which is completely contrary to the fact that the thermal conductivity along the in-plane and cross-plane directions of GaN is mainly contributed by the acoustic phonon mode, while only the thermal conductivity along the cross-plane of Si-doped GaN is mainly contributed by the optical phonon mode. Further analysis from the electronic structures indicate that the strong polarization of Mg-N and Si-N bonds and the distortion of the local structures together lead to the low thermal conductivity. The fundamental mechanism revealed in our study would provide valuable insight for the thermal management of GaN-based photoelectric devices.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
SL: simulation, data analysis and manuscript writing. LY, CQ, KD and GQ: data analysis and discussion. ZX: conceiving the idea and discussion. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work was supported by the National Natural Science Foundation of China (Grant Nos. 61764006 and 52006057), Jiangxi Provincial Cultivation Program for Academic and Technical Leaders of Major Subjects (Grant No. 20194BCJ22025), Key Program of Jiangxi Provincial Natural Science Foundation (Grant No. 20202ACB202006), the Fundamental Research Funds for the Central Universities (Grant Nos. 531118010471 and 541109010001), and the Changsha Municipal Natural Science Foundation (Grant No. kq2014034), and the Scientific Innovation Team of Optoelectronic Information in Nanchang.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors acknowledge the computing facilities of the Center for Computing of Tsinghua University.
Beechem, T. E., McDonald, A. E., Fuller, E. J., Talin, A. A., Rost, C. M., Maria, J.-P., et al. (2016). Size dictated thermal conductivity of GaN. J. Appl. Phys. 120 (9), 095104. doi:10.1063/1.4962010
Bungaro, C., Rapcewicz, K., and Bernholc, J. (2000). Ab initiophonon dispersions of wurtzite AlN, GaN, and InN. Phys. Rev. B 61, 6720–6725. doi:10.1103/PhysRevB.61.6720
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. K. (2009). The electronic properties of graphene. Rev. Mod. Phys. 81 (1), 109–162. doi:10.1103/RevModPhys.81.109
Chang, Y. C., Chang, W. H., Chiu, H. C., Tung, L. T., Lee, C. H., Shiu, K. H., et al. (2008). Inversion-channel GaN metal-oxide-semiconductor field-effect transistor with atomic-layer-deposited Al2O3 as gate dielectric. Appl. Phys. Lett. 93 (5), 053504. doi:10.1063/1.2969282
Choi, S., Foley, B. M., Ryou, J. H., Chowdhury, S., Maria, J.-P., Ferri, K., et al. (2020). The Doping Dependence of the Thermal Conductivity of Bulk Gallium Nitride Substrates. J. Electron. Packaging 142 (4), 041112-1. doi:10.1115/1.4047578
Chung, K., Lee, C.-H., and Yi, G.-C. (2010). Transferable GaN layers grown on ZnO-coated graphene layers for optoelectronic devices. Science 330 (6004), 655–657. doi:10.1126/science.1195403
Du, Y., Chang, B., Zhang, J., Wang, H., Li, B., and Wang, M. (2011). Influence of Mg doping on the electronic structure and optical properties of GaN. Optoelectronics Adv. Meterials - Rapid Commun. 5, 1050–1055.
Fan, H., Wu, H., Lindsay, L., and Hu, Y. (2019). Ab initio investigation of single-layer high thermal conductivity boron compounds. Phys. Rev. B 100 (8), 085420. doi:10.1103/PhysRevB.100.085420
Fava, M., Protik, N. H., Li, C., Ravichandran, N. K., Carrete, J., van Roekeghem, A., et al. (2021). How dopants limit the ultrahigh thermal conductivity of boron arsenide: a first principles study. Npj Comput. Mater. 7 (1), 54. doi:10.1038/s41524-021-00519-3
Gillet, J.-N., Chalopin, Y., and Volz, S. (2009). Atomic-Scale Three-Dimensional Phononic Crystals with a Very Low Thermal Conductivity to Design Crystalline Thermoelectric Devices. J. Heat Transfer 131 (4), 043206-1. doi:10.1115/1.3072927
Gu, X., and Yang, R. (2014). Phonon transport in single-layer transition metal dichalcogenides: A first-principles study. Appl. Phys. Lett. 105 (13), 131903. doi:10.1063/1.4896685
Guan, J., Zhang, Z., Dou, M., Ji, J., Song, Y., Liu, J., et al. (2020). Thermoelectric properties of Bi-doped SnS: First-principle study. J. Phys. Chem. Sol. 137, 109182. doi:10.1016/j.jpcs.2019.109182
Ji, Y., Du, Y., and Wang, M. (2014). First-principles studies of electronic structure and optical properties of GaN surface doped with Si. Optik 125 (10), 2234–2238. doi:10.1016/j.ijleo.2013.10.028
Jiang, F., Zhang, J., Xu, L., Ding, J., Wang, G., Wu, X., et al. (2019). Efficient InGaN-based yellow-light-emitting diodes. Photon. Res. 7 (2), 144. doi:10.1364/prj.7.000144
Kamano, M., Haraguchi, M., Niwaki, T., Fukui, M., Kuwahara, M., Okamoto, T., et al. (2002). Temperature Dependence of the Thermal Conductivity and Phonon Scattering Time of a Bulk GaN Crystal. Jpn. J. Appl. Phys. 41 (Part 1, No. 8), 5034–5037. doi:10.1143/jjap.41.5034(
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Krishna, A., Raj, A., Hatui, N., Keller, S., and Mishra, U. K. (2019). Investigation of nitrogen polar p-type doped GaN/AlxGa(1-x)N superlattices for applications in wide-bandgap p-type field effect transistors. Appl. Phys. Lett. 115 (17), 172105. doi:10.1063/1.5124326
Kundu, A., Mingo, N., Broido, D. A., and Stewart, D. A. (2011). Role of light and heavy embedded nanoparticles on the thermal conductivity of SiGe alloys. Phys. Rev. B 84 (12), 125426. doi:10.1103/PhysRevB.84.125426
Lahourcade, L., Pernot, J., Wirthmüller, A., Chauvat, M. P., Ruterana, P., Laufer, A., et al. (2009). Mg doping and its effect on the semipolar GaN(112¯2) growth kinetics. Appl. Phys. Lett. 95 (17), 171908. doi:10.1063/1.3256189
Lee, S.-N., Paek, H. S., Kim, H., Jang, T., and Park, Y. (2008). Monolithic InGaN-based white light-emitting diodes with blue, green, and amber emissions. Appl. Phys. Lett. 92 (8), 081107. doi:10.1063/1.2887884
Li, C.-y., and Wang, J. (2021). The effect of atomistic substitution on thermal transport in large phonon bandgap GaN. Jpn. J. Appl. Phys. 60 (7), 071003. doi:10.35848/1347-4065/ac08ad
Li, G., Wang, W., Yang, W., Lin, Y., Wang, H., Lin, Z., et al. (2016). GaN-based light-emitting diodes on various substrates: a critical review. Rep. Prog. Phys. 79 (5), 056501. doi:10.1088/0034-4885/79/5/056501
Li, W., Carrete, J., Katcho, N. A., and Mingo, N. (2014). ShengBTE: A solver of the Boltzmann transport equation for phonons. Comp. Phys. Commun. 185 (6), 1747–1758. doi:10.1016/j.cpc.2014.02.015
Lindsay, L., Broido, D. A., and Reinecke, T. L. (2012). Thermal conductivity and large isotope effect in GaN from first principles. Phys. Rev. Lett. 109 (9), 095901. doi:10.1103/PhysRevLett.109.095901
Lindsay, L., and Broido, D. A. (2008). Three-phonon phase space and lattice thermal conductivity in semiconductors. J. Phys. Condens. Matter 20 (16), 165209. doi:10.1088/0953-8984/20/16/165209
Liu, G., Sun, H., Zhou, J., Li, Q., and Wan, X. G. (2016). Thermal properties of layered oxychalcogenides BiCuOCh (Ch = S, Se, and Te): A first-principles calculation. J. Appl. Phys. 119 (18), 185109. doi:10.1063/1.4949485
Liu, W. J., Hu, X. L., Ying, L. Y., Chen, S. Q., Zhang, J. Y., Akiyama, H., et al. (2015). On the importance of cavity-length and heat dissipation in GaN-based vertical-cavity surface-emitting lasers. Sci. Rep. 5, 9600. doi:10.1038/srep09600
Liu, W., Yuan, S., and Fan, X. (2021). Leakage of holes induced by Si doping in the AlGaN first barrier layer in GaN/AlGaN multiple-quantum-well ultraviolet light-emitting diodes. J. Lumin. 231, 117806. doi:10.1016/j.jlumin.2020.117806
Ma, J., Li, W., and Luo, X. (2016). Intrinsic thermal conductivities and size effect of alloys of wurtzite AlN, GaN, and InN from first-principles. J. Appl. Phys. 119 (12), 125702. doi:10.1063/1.4944809
Mann, S., Mudahar, I., Sharma, H., Jindal, V. K., Dubey, G. S., Gumbs, G., et al. (2020). Lattice thermal conductivity of pure and doped (B, N) Graphene. Mater. Res. Express 7 (9), 095003. doi:10.1088/2053-1591/abb2cd
Mishra, K. C., Schmidt, P. C., Laubach, S., and Johnson, K. H. (2007). Localization of oxygen donor states in gallium nitride from first-principles calculations. Phys. Rev. B 76 (3), 035127. doi:10.1103/PhysRevB.76.035127
Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/PhysRevB.13.5188
Omini, M., and Sparavigna, A. (1996). Beyond the isotropic-model approximation in the theory of thermal conductivity. Phys. Rev. B 53, 9064–9073. doi:10.1103/physrevb.53.9064
Paskov, P. P., Slomski, M., Leach, J. H., Muth, J. F., and Paskova, T. (2017). Effect of Si doping on the thermal conductivity of bulk GaN at elevated temperatures - theory and experiment. AIP Adv. 7 (9), 095302. doi:10.1063/1.4989626
Pearton, S. J., Ren, F., Zhang, A. P., Dang, G., Cao, X. A., Lee, K. P., et al. (2001). GaN electronics for high power, high temperature applications. Mater. Sci. Eng. B 82, 227–231. doi:10.1016/S0921-5107(00)00767-4
Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Qin, G., Qin, Z., Wang, H., and Hu, M. (2017b). Anomalously temperature-dependent thermal conductivity of monolayer GaN with large deviations from the traditional 1/T law. Phys. Rev. B 95 (19), 195416. doi:10.1103/PhysRevB.95.195416
Qin, Z., Qin, G., Zuo, X., Xiong, Z., and Hu, M. (2017a). Orbitally driven low thermal conductivity of monolayer gallium nitride (GaN) with planar honeycomb structure: a comparative study. Nanoscale 9 (12), 4295–4309. doi:10.1039/c7nr01271c
Quah, H. J., and Cheong, K. Y. (2014). Characterization of ultrathin Al 2 O 3 gate oxide deposited by RF-magnetron sputtering on gallium nitride epilayer on sapphire substrate. Mater. Chem. Phys. 148 (3), 592–604. doi:10.1016/j.matchemphys.2014.08.022
Quah, H. J., and Cheong, K. Y. (2013). Surface Passivation of Gallium Nitride by Ultrathin RF-Magnetron Sputtered Al2O3 Gate. ACS Appl. Mater. Inter. 5 (15), 6860–6863. doi:10.1021/am402333t
Quan, Z., Wang, L., Zheng, C., Liu, J., and Jiang, F. (2014). Roles of V-shaped pits on the improvement of quantum efficiency in InGaN/GaN multiple quantum well light-emitting diodes. J. Appl. Phys. 116 (18), 183107. doi:10.1063/1.4901828
Schulz, H., and Thiemann, K. H. (1977). Crystal structure refinement of AlN and GaN. Solid State. Commun. 23, 815–819. doi:10.1016/0038-1098(77)90959-0
Tamura, S.-i. (1983). Isotope scattering of dispersive phonons in Ge. Phys. Rev. B 27 (2), 858–866. doi:10.1103/PhysRevB.27.858
Tang, D.-S., Qin, G.-Z., Hu, M., and Cao, B.-Y. (2020). Thermal transport properties of GaN with biaxial strain and electron-phonon coupling. J. Appl. Phys. 127 (3), 035102. doi:10.1063/1.5133105
Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scripta Materialia 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021
Wang, B., Yu, P., Kucukgok, B., Melton, A. G., Lu, N., and Ferguson, I. T. (2014). Characterization of undoped and Si-doped bulk GaN fabricated by hydride vapor phase epitaxy. Phys. Status Solidi C 11 (3-4), 573–576. doi:10.1002/pssc.201300678
Wang, H., Wei, D., Duan, J., Qin, Z., Qin, G., Yao, Y., et al. (2021). The exceptionally high thermal conductivity after 'alloying' two-dimensional gallium nitride (GaN) and aluminum nitride (AlN). Nanotechnology 32 (13), 135401. doi:10.1088/1361-6528/abd20c
Ward, A., and Broido, D. A. (2010). Intrinsic phonon relaxation times from first-principles studies of the thermal conductivities of Si and Ge. Phys. Rev. B 81 (8), 085205. doi:10.1103/PhysRevB.81.085205
Ward, A., Broido, D. A., Stewart, D. A., and Deinzer, G. (2009). Ab initiotheory of the lattice thermal conductivity in diamond. Phys. Rev. B 80 (12), 125203. doi:10.1103/PhysRevB.80.125203
Wieser, M. E., and Berglund, M. (2009). Atomic weights of the elements 2007 (IUPAC Technical Report). Pure Appl. Chem. 81 (11), 2131–2156. doi:10.1351/pac-rep-09-08-03
Wu, X., Lee, J., Varshney, V., Wohlwend, J. L., Roy, A. K., and Luo, T. (2016). Thermal Conductivity of Wurtzite Zinc-Oxide from First-Principles Lattice Dynamics - a Comparative Study with Gallium Nitride. Sci. Rep. 6, 22504. doi:10.1038/srep22504
Yang, J.-Y., Qin, G., and Hu, M. (2016). Nontrivial contribution of Fröhlich electron-phonon interaction to lattice thermal conductivity of wurtzite GaN. Appl. Phys. Lett. 109 (24), 242103. doi:10.1063/1.4971985
Keywords: thermal conductivity, thermal contribution, phonon relaxation time, Mg-and Si-doped GaN, first-principles
Citation: Li S, Yu L, Qi C, Du K, Qin G and Xiong Z (2021) Different Effects of Mg and Si Doping on the Thermal Transport of Gallium Nitride. Front. Mater. 8:725219. doi: 10.3389/fmats.2021.725219
Received: 15 June 2021; Accepted: 29 July 2021;
Published: 06 August 2021.
Edited by:
Lorenzo Malavasi, University of Pavia, ItalyReviewed by:
Li Wang, Nanchang University, ChinaCopyright © 2021 Li, Yu, Qi, Du, Qin and Xiong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangzhao Qin, Z3pxaW5AaG51LmVkdS5jbg==; Zhihua Xiong, eGlvbmdfemhpaHVhQDEyNi5jb20=
†These authors have contributed equally to this work and share first authorship.
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.