Theoretical Study of Abnormal Thermal Expansion of CuSCN and Effect on Electronic Structure

CuSCN, as a new type of inorganic hole-transporting semiconductor with a wide bandgap (>3.4 eV), is attracting much attention in the fabrication of perovskite solar cells. In this article, by using first-principles density functional theory (DFT) and the quasi-harmonic approximation (QHA) approach, we have studied lattice dynamics and abnormal thermal expansion of the system, including α- and β-CuSCN phases. The influence of the abnormal thermal expansion of the lattice on the electronic structure, especially on the bandgap of the system, was explored and discussed. We found that due to the shearing modes and the three acoustic modes along the direction of the c-axis, the α- and β-CuSCN show a negative thermal expansion (NTE) in the direction of the c-axis. The torsion modes of the Cu–N–C–S atomic chains in the α-CuSCN may lead to an NTE in the directions of the a, b-axes of the α-phase. As a result, our theoretical results demonstrated that the α-CuSCN exhibits an anisotropic bulk NTE. While the β-CuSCN displays a strong uniaxial negative thermal expansion in the direction of the c-axis, in the directions of the a, b-axes, it exhibits positive thermal expansion. Our DFT calculations also predicted that the α-CuSCN has a direct bandgap, which increases slightly with increasing temperature. However, the β-CuSCN has an indirect bandgap at low temperature, which converts to a direct bandgap near the temperature of 375 K due to the strong positive expansion in the ab plane of the phase. Our work revealed the mechanisms of the abnormal thermal expansion of the two phases and a strong coupling between the anisotropic thermal expansion and the electronic structures of the system.

Introduction

Positive thermal expansion (PTE) is considered to be one of the basic properties of matter in nature. However, some materials have also been found to exhibit abnormal behavior, that is, negative thermal expansion (NTE), within a certain temperature range (Mary et al., 1996; Mittal et al., 2018). The NTE mechanisms could be divided into two categories: phonon-driven NTE or electronic origin NTE. The first is mainly contributed by some low-frequency phonons. This type of mechanism mainly occurs in compounds with framework structures (Gao et al., 2017; Liang et al., 2021), such as oxides (Khosrovani et al., 1997; Wei et al., 2020), fluorides (Greve et al., 2010), MOFs (Wei et al., 2013; Liu et al., 2018), and cyanide/Prussian blue analogs (Goodwin and Kepert, 2005; Gao et al., 2020a). The electronic origin NTE is mainly caused by the temperature dependence of charge transfer (Azuma et al., 2011), magnetic orders, and ferroelectric effects (Pan et al., 2019), such as in perovskite manganese nitride (Takenaka et al., 2008; Sun et al., 2010) and some alloys (Song et al., 2020).

Based on the crystal structure analysis of the NTE materials with framework structures, it is generally believed that the driving force of NTE is the transverse vibration of bridge chain atoms. A typical example is the transverse vibration of O atoms in the Zr–O–W chain of ZrW₂O₈ (Mary et al., 1996). The NTE of cyanide was first discovered by William et al. in 1997 in Zn(CN)₂ (Collings et al., 2013; Gao et al., 2020a). The NTE comes from the flexibility of the structure with a large number of low-frequency phonon modes, involving the transverse vibrations of the CN groups. In addition, for cyanides, such as AuCN, AgCN, and HT-CuCN, the atomic chains in their crystal structure are arranged in layers, and the thermal expansion shows strong anisotropy in low temperature ranges (Hibble et al., 2010).

Recently, Gao et al. suggested a simple rule based on the concept of average atomic volume (AAV) according to the statistical data of NTE materials, where they proposed a critical AAV of 16 Å³ for the framework compounds with NTE property, and they believed that the flexibility of the structure is the key factor for the NTE characteristics (Gao et al., 2020c). It provides a simple way to search for and discover new NTE materials. According to the AAV rule, we found that the layer of cyanide–copper thiocyanate (CuSCN), a transparent semiconductor with high hole mobility, has an AVV larger than the value of 16 Å³. Because the wide-bandgap semiconductor CuSCN is one of the most ideal inorganic hole transport materials used in perovskite photovoltaic devices and has received extensive attention in recent years (Wijeyasinghe and Anthopoulos, 2015; Arora et al., 2017), it is important and interesting to study the abnormal thermal expansion properties of the material, especially the effect of the abnormal thermal expansion on the electronic structures.

In this work, abnormal thermal expansion and the effect of the abnormal thermal expansion on the electronic structures were investigated for the two phases of the CuSCN, that is, α-CuSCN (Pbca) and β-CuSCN (P63mc), using the combined DFT and QHA approaches. The lattice dynamics calculations indicated that the α-CuSCN shows volume NTE behavior due to the shearing modes between the CuS layers, the acoustic modes, and the torsion modes of the Cu–N–C–S atomic chains, while for the β-CuSCN, the NTE only appears in the direction of the c-axis due to the shearing mode between the CuS layers, the acoustic modes, and the transverse vibration of cyanide (CN), but the lattice parameters in the directions of the a, b-axes show strong PTE and lead to the volume CTE being positive. The calculated electronic property shows that the α-CuSCN displays a direct bandgap semiconductor, while the β-CuSCN has an indirect bandgap at low temperatures. But interestingly, the indirect bandgap of the β-CuSCN converts to a direct bandgap when the temperature increases to 375 K. To our knowledge, the report about the effect of abnormal thermal expansion on the electronic property of CuSCN is yet to be published. The present results revealed the mechanisms of the abnormal thermal expansion of the materials and gave a hint to resolve the puzzle about the direct or indirect bandgap of the β-CuSCN.

Computation Methods

In this work, the calculations of the structural and the electronic properties were performed using the first-principles density functional theory (DFT), as implemented in the VASP code (Kresse and Furthmüller, 1996). In the calculations, the projector-augmented wave method (Kresse and Joubert, 1999), with the Perdew–Burke–Ernzerh (PBE) functional (Perdew et al., 1999), was used. The screened hybrid functional (HSE06) (Krukau et al., 2006) was also used to calculate band structures. The first Brillouin zone was integrated with a Monkhost–Pack (Monkhorst and Pack, 1976) k-point mesh (4 × 4 × 3 or 8 × 8 × 3) for the α- or β-CuSCN phase, respectively. The cutoff energy of the plane wave basis set is taken to be 500 eV. In the calculations, the atomic positions were relaxed until the force on an atom was smaller than 10⁻⁵ eV/Å and the total energy was converged to 10⁻⁹ eV/atom.

In our calculations, the α-CuSCN primitive cell contains 32 atoms, and the β-CuSCN primitive cell contains eight atoms. The density functional perturbation theory (DFPT) method is used to calculate the force constants of the systems (Baroni et al., 2001), and the phonon spectra are obtained using the PHONOPY code (Parlinski et al., 1997), which is a software package for the calculation of phonons and thermal expansion of crystals under harmonic and quasi-harmonic approximation (QHA). In QHA, the volume dependence of the phonon frequency, that is, part of the anharmonic effect, is considered. Detailed discussion of the QHA can be found in the references (Kuzkin and Krivtsov, 2015). In our previous work, the QHA provided a reasonable description of the dynamic properties of the compound (Liu et al., 2015; Chang et al., 2018; Li et al., 2020).

In order to obtain the coefficient of thermal expansion (CTE), 10 different volumes were taken to calculate the free energies of the 10 volumes around the equilibrium position of systems at a temperature of absolute zero. For each volume which was taken by altering lattice constants by a factor of 0.002, the shape of the unit cell was optimized while keeping the volume of the unit cell fixed, which was implemented by the VASP code. The Vinet equation of state (EOS) (Vinet et al., 1987) was employed to fit these data to get the volumetric CTE of the systems.

Results and Discussion

Structure and Thermal Expansion Properties

CuSCN is a member of the cyanide family and is a coordination compound formed by thiocyanate ions and Cu metal ions. It has a variety of different structures, including three-dimensional polycrystalline structures and two-dimensional (2D) polycrystalline structures (Tsetseris, 2016a), among which three-dimensional polycrystalline structures have received extensive attention as inorganic hole transport materials (Wijeyasinghe and Anthopoulos, 2015; Arora et al., 2017). The three-dimensional polycrystalline structure of CuSCN includes several phases, of which two phases, the α-CuSCN orthogonal phase (Pbca) and the β-CuSCN hexagonal phase (P63mc), are considered here. Constructed with an atomic chain of the Cu-N≡C-S module, through the twisting of the module and the bonding between the Cu and S atoms, one can achieve the orthogonal α-CuSCN, as shown in Figure 1A. The hexagonal β-CuSCN is obtained through the translation of the module and the connection between the Cu and S atoms, as shown in Figure 1B. For the two phases, each Cu has four coordination atoms, that is, three S and one N. Each S also has four coordination atoms, that is, three Cu and one C.

FIGURE 1

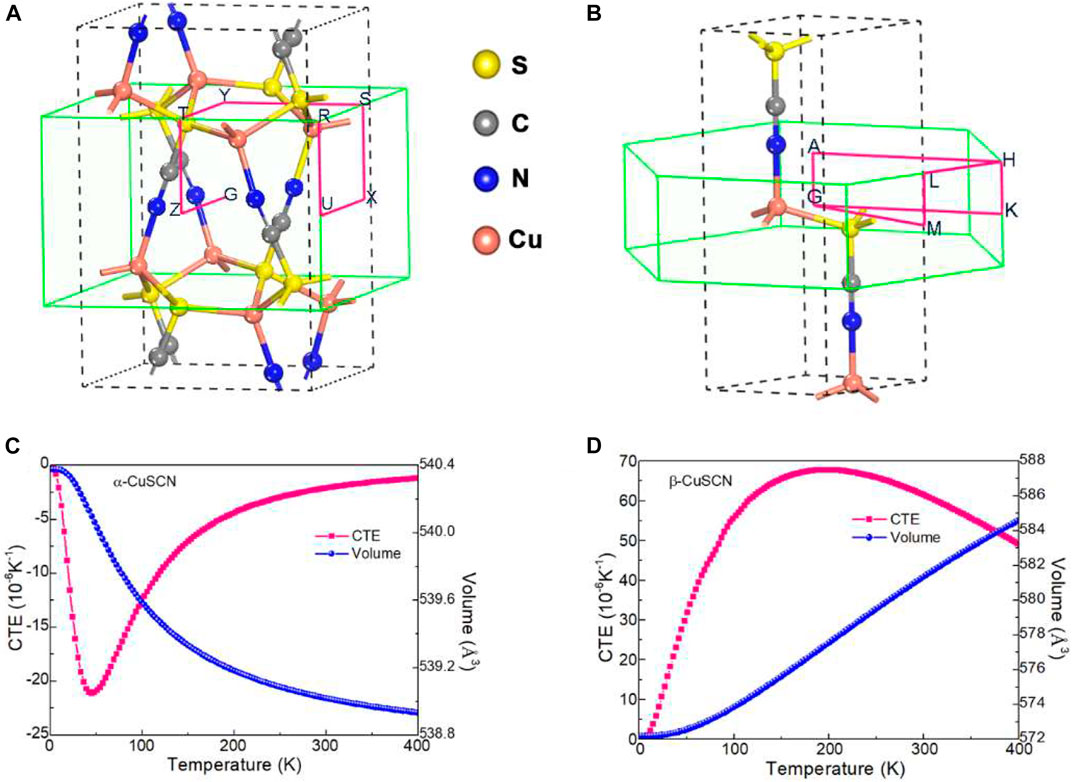
FIGURE 1. Crystal structure of (A) α-CuSCN and (B) β-CuSCN. The first Brillouin zone and the special k points used in band structure calculations are also presented. Temperature dependence of the cell volume and the CTE of (C) α-CuSCN and (D) β-CuSCN are given.

The optimized lattice parameters and the AAV of the two phases are shown in Table 1. Available experimental and theoretical results are also listed for comparison. Our theoretical calculations agree well with previous results and show that the β-CuSCN is more stable than the α-CuSCN by about 53 meV per CuSCN chemical unit, which agrees well with the previous theoretical result (Tsetseris, 2016b). The Gibbs free energies of the two phases vs. temperature were calculated and given in Supplementary Figure S1 in the electronic supplementary information (ESI), and they show that the β-CuSCN is more stable than the α-CuSCN in the whole temperature range (0−400 K).

TABLE 1

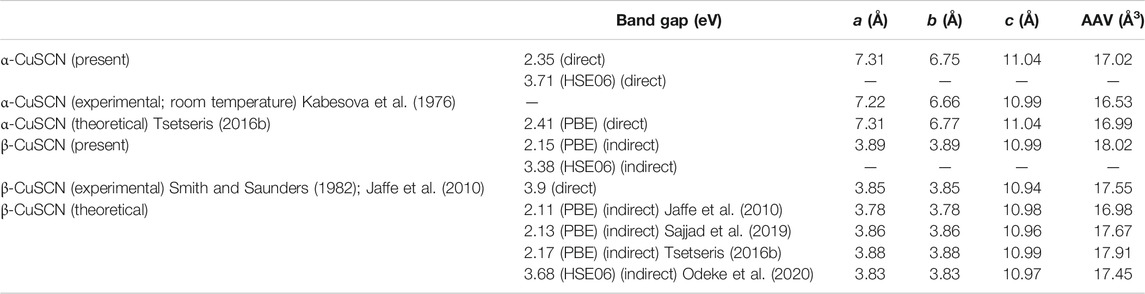
TABLE 1. Calculated lattice parameters a, b, and c, bandgaps, and AAV of α-CuSCN and β-CuSCN. Available experimental and theoretical (PBE and HSE06 functionals used) results were also listed for comparison.

The volume thermal expansion behavior of α-CuSCN and β-CuSCN was calculated, as shown in Figure 1C and Figure 1D, respectively. The α-CuSCN shows obvious volumetric NTE characteristics, and its average volumetric coefficient of thermal expansion (CTE) approaches −6.68 × 10⁻⁶ K⁻¹ (0−400 K), while the β-CuSCN shows strong volume PTE behavior (α_v = 42.09 × 10⁻⁶ K⁻¹, 0–400 K). It should be noted that though the β-CuSCN has a larger AAV than the α-CuSCN, only the α-CuSCN that was predicted to do so in our calculations exhibits NTE behavior. Seemingly, the criterion of NTE based on the AAV value is not strict, especially when comparing the thermal expansion behavior of two kinds of open-framework structures with different symmetry, because there are other factors, such as electronegativity, symmetry, chemical bond, and so on, to influence thermal expansion of materials. Anyhow, if the AAV of a system is larger than 16 Å³, it is very worth it to investigate its thermal expansion behavior and speed up to find new NTE compounds.

Phonon Dispersion and Grüneisen Parameters

In order to investigate the mechanisms of the abnormal thermal expansion of α-CuSCN and β-CuSCN, the phonon dispersion and Grüneisen parameters of different phonon modes were calculated. The phonon spectra and phonon density of states (PDOS) of the two phases are shown in Figures 2A,B, respectively. The phonon spectra of the two phases are roughly divided into four regions: two low-frequency regions (below 300 cm⁻¹), one intermediate-frequency region (400–430 cm⁻¹ and 740–760 cm⁻¹), and one high-frequency region (2130–2180cm⁻¹). It can be seen from the partial PDOS and the eigenvectors of the represented normal modes shown in Figure 3B (α-phase) and Figure 4B (β-phase) that the vibrations in the low-frequency region (below 300 cm⁻¹) are mainly contributed from the vibration of Cu, N, and S. In the intermediate-frequency region, the modes are originated from the opposite transverse movement of C and N (400–430 cm⁻¹) and the stretching vibration of the S and CN groups along the direction of the Cu-N≡C-S atomic chain (740–760 cm⁻¹). In the high-frequency region, it is caused by the stretching vibration of the C≡N triplet bond. These phonon frequency regions can be well explained by the structure and chemical bonds of the system (Liu et al., 2015). According to previous studies (Dove and Fang, 2016; Mittal et al., 2018; Gao et al., 2020b), we know that phonons in the low-frequency region have a great influence on the thermal expansion characteristics at low temperatures. Different from other cyanides, such as Prussian blue analogs, where the vibrations of metals are weak, the Cu atoms in CuSCN vibrate drastically at low frequencies, and then the vibrations of the S, N, and C atoms are dominated as the frequency increases.

FIGURE 2

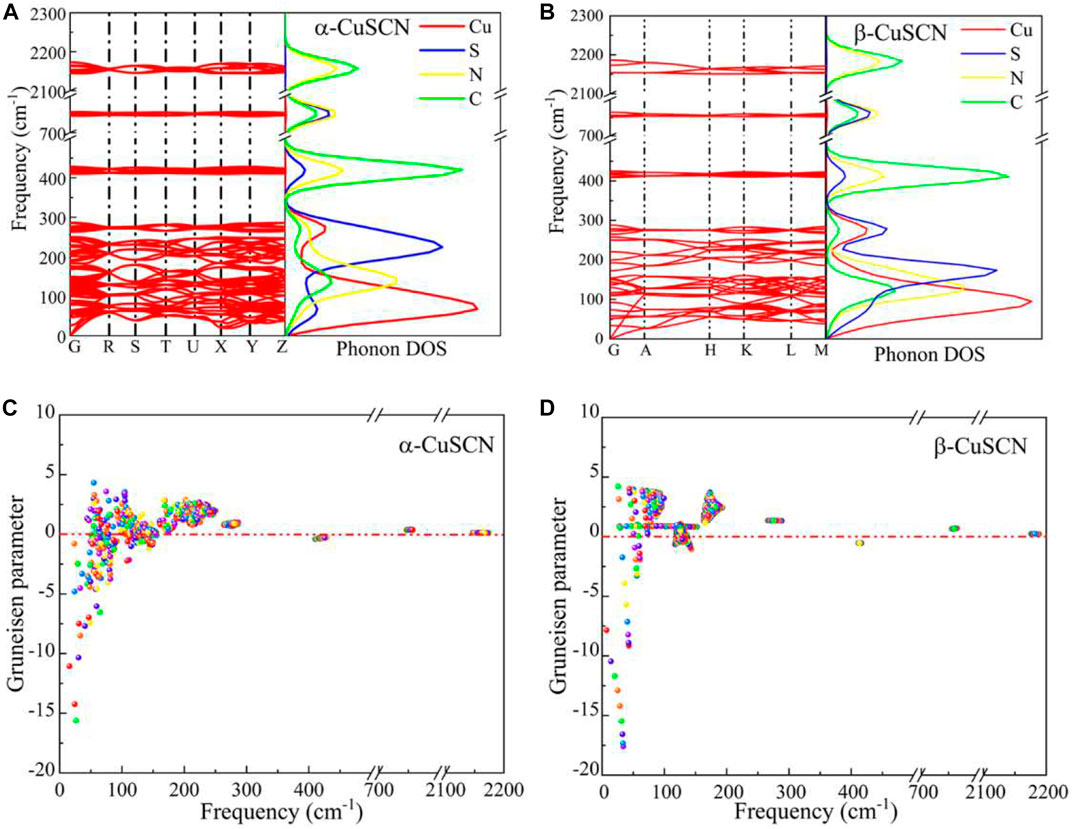
FIGURE 2. Phonon dispersion and PDOS for (A) α-CuSCN and (B) β-CuSCN. The mode Grüneisen parameters as a function of vibrational frequency for (C) α-CuSCN and (D) β-CuSCN.

FIGURE 3

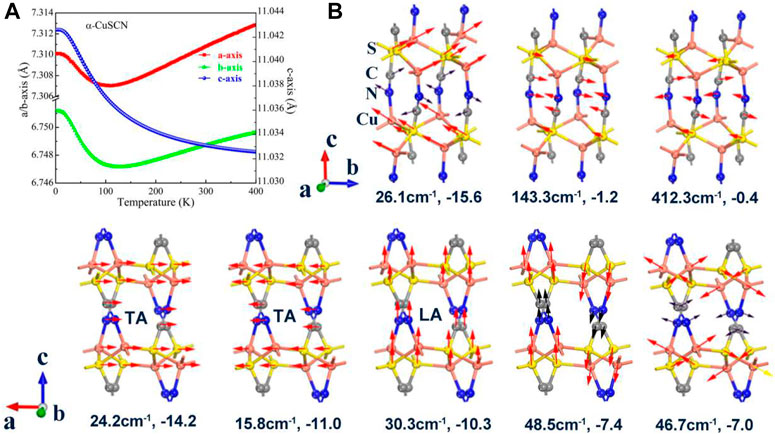
FIGURE 3. (A) Temperature dependence of lattice parameters in the temperature range of 0–400 K for α-CuSCN. (B) Eight representative low vibration modes with negative Grüneisen parameters of the phase. The frequency and the corresponding Grüneisen parameter are given for each mode.

FIGURE 4

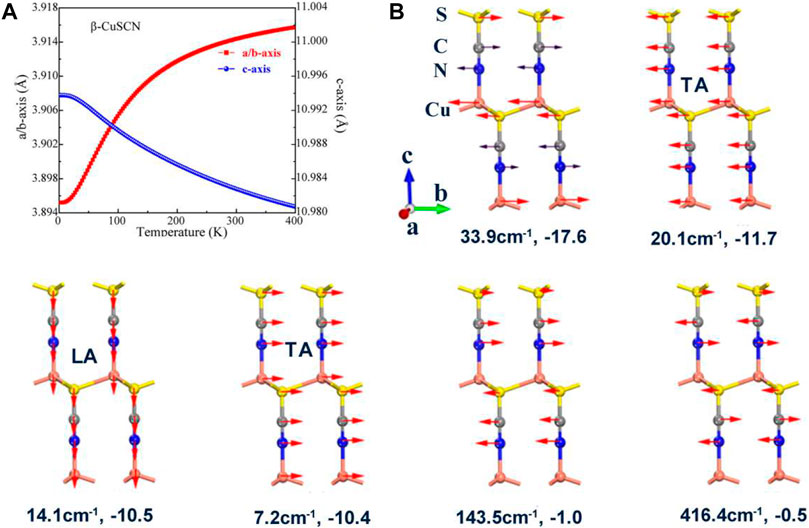
FIGURE 4. (A) Temperature dependence of lattice parameters in the temperature range of 0–400 K for β-CuSCN. (B) Six representative low vibration modes with negative Grüneisen parameters of the phase. The frequency and the corresponding Grüneisen parameter are given for each mode.

The Grüneisen parameters of the two phases were calculated to further understand the influence of phonons in the low-frequency region on NTE, as shown in Figures 2C,D. It can be clearly seen from the figures that the negative values of the Grüneisen parameters of the two phases appear mainly in the frequency range of less than 200 cm⁻¹. In the α-CuSCN, the number of phonon modes with negative values of Grüneisen parameters is greater than that of those with positive values; thus, it shows the volumetric NTE behavior. In contrast, in the β-CuSCN, it has relatively fewer negative values of Grüneisen parameters in the low-frequency region and a large number of positive values in a wide frequency range, so it displays PTE behavior. The difference in the Grüneisen parameters should be the reason for the obvious difference in the thermal expansion property of the two phases.

Analysis of Phonon Vibration Mode Based on Lattice Dynamics

In order to reveal the mechanism of the abnormal thermal expansion of the two phases derived using the low phonon modes, some representative low phonon modes with negative Grüneisen parameters are presented in Figures 3B, 4B. The lattice constants, as a function of temperature, are calculated and given in Figures 3A, 4A for the two phases, respectively. For the α-CuSCN, eight representative phonon modes (16 cm⁻¹–416 cm⁻¹) with negative Grüneisen parameters are shown in Figure 3B. The vibration mode (−26.1 cm⁻¹) with the largest negative Grüneisen parameter (−15.6) comes from the shearing motion between the CuS layers. The three acoustic modes [two transverse acoustic (TA) modes and one longitudinal acoustic (LA) mode] along the direction of the c-axis also have large negative Grüneisen parameters (−14.2, −11.0, and −10.3). These modes contribute NTE in the direction of the c-axis of the system. The torsion vibration modes (46.7 cm⁻¹ and 48.5 cm⁻¹) with negative Grüneisen parameters (−7.0 and −7.4) may lead to NTE in the ab plane, which may be the reason for the negative expansion of a ,b below 100 K shown in Figure 3A. The vibration modes for C and N (in a CN group) in phase (143.3 cm⁻¹) and opposite phase (412.3 cm⁻¹) also have negative Grüneisen parameters (−1.2 and −0.4), which also contribute to the NTE in the direction of the c-axis. For the β-CuSCN, six representative vibration modes (7 cm⁻¹–416 cm⁻¹) with negative Grüneisen parameters are shown in Figure 4B. Similar to the α-phase, the vibration mode (−33.9 cm⁻¹) with the largest negative Grüneisen parameter (−17.6) comes from the shearing motion between the CuS layers. The three acoustic modes [two transverse acoustic (TA) modes and one longitudinal acoustic (LA) mode] along the direction of the c-axis also have large negative Grüneisen parameters (−10.4, −11.7, and −10.5). These modes contribute to NTE in the direction of the c-axis of the system just like the case in the α-phase. The lack of the torsion vibration modes may be the reason for the positive expansion of a, b of the β-phase in the temperature range of 0–400 K, as shown in Figure 4A. The vibration modes for C and N (in a CN group) in phase (143.5 cm⁻¹) and opposite phase (416.4 cm⁻¹) also have negative Grüneisen parameters (−1.0 and −0.5), which also contribute to the NTE in the direction of the c-axis.

In conclusion, due to the shearing and acoustic phonon modes, both the α- and β-CuSCN exhibit NTE in the direction of the c-axis. For α-CuSCN, the a, b-axes also show negative thermal expansion in the low-temperature region, which may be due to the contributions from the torsion modes which are not found in the β-CuSCN. Therefore, the strong anisotropic thermal expansion is shown for the β-CuSCN, which is similar to the cyanide AuCN reported previously (Hibble et al., 2010). It should be pointed out that the acoustic modes play an important role in the NTE of the system. A more detailed discussion about the role of acoustic modes in NTE of materials can be found in the recent review of Liang et al. (2021).

Electronic Structure and Effect of Abnormal Thermal Expansion

In this section, we investigated the influence of the abnormal thermal expansion on the electronic structures of the two phases. First, we calculated the energy band structure and electronic partial density of states (EPDOS) of the α-CuSCN and β-CuSCN, as shown in Figures 5A,B. The calculated bandgap of the two phases is given in Table 1, and the previous theoretical and experimental results are also listed for comparison. It can be seen from the energy band structures and EPDOS that the α-CuSCN is a direct bandgap semiconductor with a bandgap of 2.35 eV. The valence band maximum (VBM) at the Г point is mainly contributed from Cu 3d orbitals, while the conduction band minimum (CBM) at the Г point is from C and N 2p orbitals. The bandgap of the β-CuSCN is 2.15 eV, which is an indirect bandgap where the VBM at the Г point is also mainly contributed from Cu 3d orbitals, but the CBM is located at the K point, which is originated from the antibonding molecular state of (CN)⁻¹ formed by 2p orbitals (Jaffe et al., 2010). If a screened hybrid functional (HSE06) was used to calculate the band structure of the β-CuSCN, the obtained bandgap can reach 3.38 eV (see Table 1), but it was still predicted to be an indirect bandgap. Our calculated band structures of the two phases are in good agreement with the previous theoretical results (Smith and Saunders, 1982; Jaffe et al., 2010; Tsetseris, 2016a; Ji et al., 2012). In fact, the previous theoretical calculations predict that the β-CuSCN is an indirect band semiconductor, which seems to disagree with the experimental observation (Ji et al., 2012; Pattanasattayavong et al., 2017). According to our following results about the effect of the abnormal thermal expansion on the band structure of the β-CuSCN, the disagreement may be explained by an indirect-to-direct band transition induced by the strong thermal expansion in the ab plane.

FIGURE 5

FIGURE 5. Band structures and EPDOS of (A) α-CuSCN and (B) β-CuSCN.

Due to the GGA, the bandgaps of the two phases were underestimated. Compared with the experimental values, the calculated gap values are smaller, but they are consistent with the previous theoretical results (Ji et al., 2012; Pattanasattayavong et al., 2017). If the screened hybrid functional (HSE06) were used, the calculated bandgap would be very close to the experiment, but it was still predicted to be an indirect bandgap.

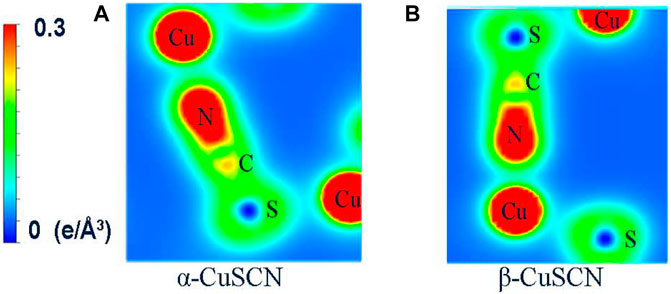
In order to clearly understand the bond properties between atoms in the two phases, we also calculated and plotted the total charge density in the plane involving the Cu-N≡C-S chain, as shown in Figures 6A,B, for the two phases, respectively. From the calculated total charge density, the bond features can be found, where C and N form a strong covalent bond, S and C form a weak covalent bond, N and Cu form a dative bond, and S and Cu form an ionic bond. These bond features are closely related to the character of different phonon modes. In order to further explain the bond nature, the calculated net charge of atoms was obtained according to the Bader analysis and is given in Supplementary Table S1 in the ESI. From the calculations, it can be seen that for both phases, the net charge of N, C, S, and Cu is −1.2|e|, 0.6|e|, 0.0|e|, and 0.6|e|, indicating that Cu and C lose electrons, while N gains electrons (|e| is charge of an electron). Born effective charges were also calculated by moving a small displacement (0.001 × c Å) of the atoms along the c direction, which are also listed in Supplementary Table S1. For the α-CuSCN, the calculated Born effective charges are Z_Cu^* = 0.12|e|, Z_S^* = −0.73|e|, Z_N^* = −0.32|e|, and Z_C^* = 0.95|e|. For the β-CuSCN, they are Z_Cu^* = 0.11|e|, Z_S^* = −0.39|e|, Z_N^* = −0.67|e|, and Z_C^* = 0.95|e|.

FIGURE 6

FIGURE 6. Charge density in the Cu-N≡C-S section of (A) α-CuSCN and (B) β-CuSCN.

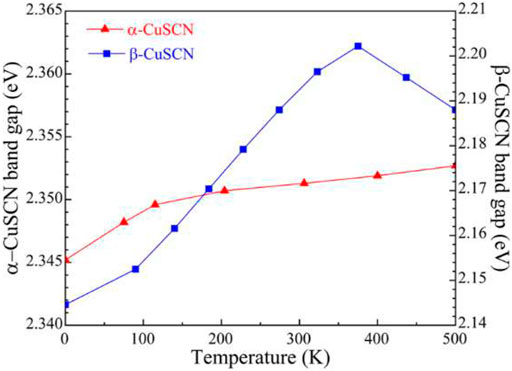
Thermal expansion alters the average distance of atoms in materials, and consequently, the electronic structure of materials is perturbed. Thermal expansion is one of the temperature effects. The electron–phonon coupling interactions due to atom displacement are another important temperature effect on the electronic structure (Zacharias et al., 2020). Here, only the effect of thermal expansion on the electronic structures was considered. According to the calculated lattice constants at different temperatures, the bandgaps at different temperatures have been calculated and are given in Figure 7 for the α- and β-CuSCN. The band structures of the β-CuSCN at 0 and 375 K are shown in Figure 8. The band structures of the α-CuSCN at different temperatures are given in Supplementary Figure S2 in the ESI. From the calculated temperature dependence of bandgaps, it can be found that for the α-CuSCN, the gap increases a little (Δ = 7 meV) as the temperature increases from 0 to 500 K. Meanwhile, for the β-CuSCN, the gap increases much more (Δ = 57 meV) as the temperature increases from 0 to 375 K and then decreases as the temperature further increases. It is interesting to find that for the β-CuSCN, the indirect band structure is converted to be a direct band structure as the temperature increases from 0 to 375 K (Figure 8). Comparing the band structure of the β-CuSCN at low temperature to that at high temperature, we can find the CBM at the K point shifts upward and becomes higher than the minima level of the conduct band at the G point at 375 K. The CBM at the K point is mainly derived from the antibonding states of C and N 2p orbitals (see Figure 5), and because the overlap of the antibonding states between neighboring cells becomes weaker as temperature increases (the distance between the Cu–N–C–S chains increases), the CBM at the K point shifts upward. From the viewpoint of total energy, the total energy of the β-CuSCN increases by about 0.04 eV/unit cell from the structure at 0 K (indirect bandgap) to the structure at 375 K (direct bandgap). This thermal expansion–induced indirect-to-direct bandgap transition may be similar to the indirect-to-direct band transition induced by element substitution, where Se substitution (CuSeCN) leads to the indirect bandgap of CuSCN converting to the direct bandgap of CuSeCN due to the larger lattice constants in the ab plane in CuSeCN (Smith and Saunders, 1982).

FIGURE 7

FIGURE 7. Thermal expansion–induced changes of the bandgaps in the α- and β-CuSCN.

FIGURE 8

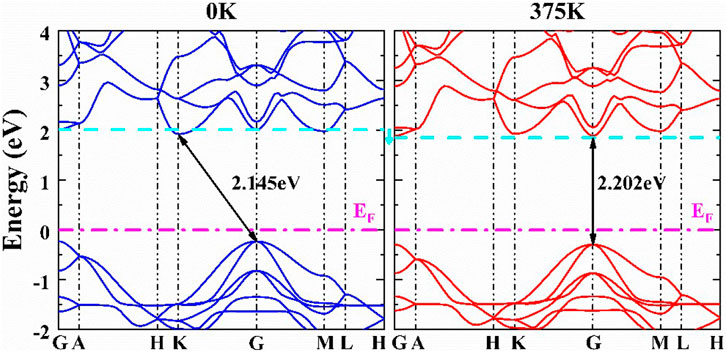
FIGURE 8. Electronic structures of the β-CuSCN at different volumes (the corresponding temperatures 0 and 375 K were labeled). The cyan dashed lines indicate the lowest unoccupied levels at the G point.

Conclusion

In this work, abnormal thermal expansion and its effect on the electronic structures of α- and β-CuSCN have been studied by combining the first-principles DFT and QHA approaches. Due to the different crystal structures of the two phases, the α-phase exhibits anisotropic volumetric NTE property and the β-phase shows strong anisotropic PTE property where the ab plane (CuS layer) exhibits strong PTE, while there is linear NTE in the direction of the c-axis (perpendicular to the CuS layer). The shearing mode of CuS layers and the acoustic modes play key roles in the anisotropic NTE of the two phases. The torsion modes of the α-CuSCN may be responsible for the NTE of the ab plane at low temperatures. Our results further demonstrated that the α-CuSCN is a direct bandgap semiconductor with a bandgap of 2.35 eV, and the gap becomes a little smaller as the temperature increases from 0 to 500 K. The β-CuSCN was predicted to be an indirect bandgap semiconductor with a bandgap of 2.15 eV at 0 K, where the CBM is at the K point. Due to the strong PTE in the ab plane, the distance between the parallel CN groups increases, which weakens the overlap interactions between the (CN)⁻¹ antibonding states and leads to the states shifting upward, and an indirect-to-direct band transition occurs. We predicted that the system converts to a direct band semiconductor at about 375 K. The present study revealed the mechanisms of the abnormal thermal expansion in the α-CuSCN and the β-CuSCN and shed light on the puzzle regarding the direct or indirect band structures of the β-CuSCN.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

QG and QS conceived the idea and designed the work. PS and JL performed density functional theory (DFT) calculations. All authors contributed to the discussions. PS, QG, and QS wrote the manuscript with help for the revision from all coauthors.

Funding

This work was supported by the National Natural Science Foundation of China (nos. 22071221, 21905252, and 11874328), the Natural Science Foundation of Henan (no. 212300410086), and the China Postdoctoral Science Foundation (2019M652558). All calculations were supported by the National Supercomputing Center in Zhengzhou.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.712395/full#supplementary-material

References

Arora, N., Dar, M. I., Hinderhofer, A., Pellet, N., Schreiber, F., Zakeeruddin, S. M., et al. (2017). Perovskite Solar Cells with CuSCN Hole Extraction Layers Yield Stabilized Efficiencies Greater Than 20%. Science. 358, 768–771. doi:10.1126/science.aam5655

PubMed Abstract | CrossRef Full Text | Google Scholar

Azuma, M., Chen, W.-t., Seki, H., Czapski, M., Olga, S., Oka, K., et al. (2011). Colossal Negative thermal Expansion in BiNiO3 Induced by Intermetallic Charge Transfer. Nat. Commun. 2, 347. doi:10.1038/ncomms1361

PubMed Abstract | CrossRef Full Text | Google Scholar

Baroni, S., de Gironcoli, S., Dal Corso, A., and Giannozzi, P. (2001). Phonons and Related crystal Properties from Density-Functional Perturbation Theory. Rev. Mod. Phys. 73, 515–562. doi:10.1103/RevModPhys.73.515

CrossRef Full Text | Google Scholar

Chang, D., Wang, C., Zeng, Z., Wang, C., Wang, F., Sun, Q., et al. (2018). Negative Thermal Expansion Properties and the Role of Guest Alkali Atoms in LnFe(CN)6 (Ln = Y, La) from ab Initio Calculations. J. Phys. Chem. C. 122, 12421–12427. doi:10.1021/acs.jpcc.8b01165

CrossRef Full Text | Google Scholar

Collings, I. E., Cairns, A. B., Thompson, A. L., Parker, J. E., Tang, C. C., Tucker, M. G., et al. (2013). Homologous Critical Behavior in the Molecular Frameworks Zn(CN)2 and Cd(imidazolate)2. J. Am. Chem. Soc. 135, 7610–7620. doi:10.1021/ja401268g

PubMed Abstract | CrossRef Full Text | Google Scholar

Dove, M. T., and Fang, H. (2016). Negative thermal Expansion and Associated Anomalous Physical Properties: Review of the Lattice Dynamics Theoretical Foundation. Rep. Prog. Phys. 79, 066503. doi:10.1088/0034-4885/79/6/066503

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., Chen, J., Sun, Q., Chang, D., Huang, Q., Wu, H., et al. (2017). Switching between Giant Positive and Negative Thermal Expansions of a YFe(CN)6 -based Prussian Blue Analogue Induced by Guest Species. Angew. Chem. Int. Ed. 56, 9023–9028. doi:10.1002/anie.201702955

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., Shi, X., Venier, A., Carnera, A., Huang, Q., Wu, H., et al. (2020a). Effect of H2O Molecules on Thermal Expansion of TiCo(CN)6. Inorg. Chem. 59, 14852–14855. doi:10.1021/acs.inorgchem.0c02029

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., Sun, Y., Shi, N., Milazzo, R., Pollastri, S., Olivi, L., et al. (2020b). Large Isotropic Negative thermal Expansion in Water-free Prussian Blue Analogues of ScCo(CN)6. Scripta Materialia. 187, 119–124. doi:10.1016/j.scriptamat.2020.05.041

CrossRef Full Text | Google Scholar

Gao, Q., Wang, J., Sanson, A., Sun, Q., Liang, E., Xing, X., et al. (2020c). Discovering Large Isotropic Negative Thermal Expansion in Framework Compound AgB(CN)4 via the Concept of Average Atomic Volume. J. Am. Chem. Soc. 142, 6935–6939. doi:10.1021/jacs.0c02188

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodwin, A. L., and Kepert, C. J. (2005). Negative thermal Expansion and Low-Frequency Modes in Cyanide-Bridged Framework Materials. Phys. Rev. B. 71, 140301. doi:10.1103/PhysRevB.71.140301

CrossRef Full Text | Google Scholar

Greve, B. K., Martin, K. L., Lee, P. L., Chupas, P. J., Chapman, K. W., and Wilkinson, A. P. (2010). Pronounced Negative Thermal Expansion from a Simple Structure: Cubic ScF3. J. Am. Chem. Soc. 132, 15496–15498. doi:10.1021/ja106711v

PubMed Abstract | CrossRef Full Text | Google Scholar

Hibble, S. J., Wood, G. B., Bilbé, E. J., Pohl, A. H., Tucker, M. G., Hannon, A. C., et al. (2010). Structures and Negative thermal Expansion Properties of the One-Dimensional Cyanides, CuCN, AgCN and AuCN. Z. Krist-cryst. Mater. 225, 457–462. doi:10.1524/zkri.2010.1314

CrossRef Full Text | Google Scholar

Jaffe, J. E., Kaspar, T. C., Droubay, T. C., Varga, T., Bowden, M. E., and Exarhos, G. J. (2010). Electronic and Defect Structures of CuSCN. J. Phys. Chem. C. 114, 9111–9117. doi:10.1021/jp101586q

CrossRef Full Text | Google Scholar

Ji, W., Yue, G.-Q., Ke, F.-S., Wu, S., Zhao, H.-B., Chen, L.-Y., et al. (2012). Electronic Structures and Optical Properties of CuSCN with Cu Vacancies. J. Korean Phys. Soc. 60, 1253–1257. doi:10.3938/jkps.60.1253

CrossRef Full Text | Google Scholar

Kabesova, M., Dunaj-Jurco, M., Serator, M., Gazo, J., and Garaj, J. (1976). The Crystal Structure of Copper(I) Thiocyanate and its Relation to the Crystal Structure of Copper(I1) Diammine Dithiocyanate Complex. Inorg. Chim. Acta. 17, 161–165. doi:10.1016/S0020-1693(00)81976-3

CrossRef Full Text | Google Scholar

Khosrovani, N., Sleight, A. W., and Vogt, T. (1997). Structure of ZrV2O7from −263 to 470°C. J. Solid State. Chem. 132, 355–360. doi:10.1006/jssc.1997.7474

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B. 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 125, 224106. doi:10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuzkin, V. A., and Krivtsov, A. M. (2015). Nonlinear Positive/negative thermal Expansion and Equations of State of a Chain with Longitudinal and Transverse Vibrations. Phys. Status Solidi B. 252, 1664–1670. doi:10.1002/pssb.201451618

CrossRef Full Text | Google Scholar

Li, Y., Gao, Q., Chang, D., Sun, P., Liu, J., Jia, Y., et al. (2020). Effect of Bond on Negative thermal Expansion of Prussian Blue Analogues MCo(CN)6 (M = Fe, Ti and Sc): a First-Principles Study. J. Phys. Condens. Matter. 32, 455703. doi:10.1088/1361-648X/aba777

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, E., Sun, Q., YuanWang, H. J., Wang, J., Zeng, G., and Gao, Q. (2021). Negative thermal Expansion: Mechanisms and Materials. Front. Phys. 16, 53302. doi:10.1007/s11467-021-1070-0

CrossRef Full Text | Google Scholar

Liu, Y., Jia, Y., Sun, Q., and Liang, E. (2015). Mechanism of Negative thermal Expansion in LaC2 from First-Principles Prediction. Phys. Lett. A. 379, 54–59. doi:10.1016/j.physleta.2014.10.041

CrossRef Full Text | Google Scholar

Liu, Z., Gao, Q., Chen, J., Deng, J., Lin, K., and Xing, X. (2018). Negative thermal Expansion in Molecular Materials. Chem. Commun. 54, 5164–5176. doi:10.1039/c8cc01153b

PubMed Abstract | CrossRef Full Text | Google Scholar

Mary, T. A., Evans, J. S. O., Vogt, T., and Sleight, A. W. (1996). Negative Thermal Expansion from 0.3 to 1050 Kelvin in ZrW2O8. Science 272, 90–92. doi:10.1126/science.272.5258.90

CrossRef Full Text | Google Scholar

Mittal, R., Gupta, M. K., and Chaplot, S. L. (2018). Phonons and Anomalous thermal Expansion Behaviour in Crystalline Solids. Prog. Mater. Sci. 92, 360–445. doi:10.1016/j.pmatsci.2017.10.002

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B. 13, 5188–5192. doi:10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Odeke, B. A., Chung, G. D., Fajemisin, J. A., Suraj, K. S., Tonui, D. K., Tobi, A. R., et al. (2020). Electronic Structure and Surface Properties of Copper Thiocyanate: A Promising Hole Transport Material for Organic Photovoltaic Cells. Materials. 13, 5765–65. doi:10.3390/ma13245765

CrossRef Full Text | Google Scholar

Pan, Z., Chen, J., Yu, R., Patra, L., Ravindran, P., Sanson, A., et al. (2019). Large Negative Thermal Expansion Induced by Synergistic Effects of Ferroelectrostriction and Spin Crossover in PbTiO3-Based Perovskites. Chem. Mater. 31, 1296–1303. doi:10.1021/acs.chemmater.8b04266

CrossRef Full Text | Google Scholar

Parlinski, K., Li, Z. Q., and Kawazoe, Y. (1997). First-Principles Determination of the Soft Mode in CubicZrO2. Phys. Rev. Lett. 78, 4063–4066. doi:10.1103/PhysRevLett.78.4063

CrossRef Full Text | Google Scholar

Pattanasattayavong, P., Promarak, V., and Anthopoulos, T. D. (2017). Electronic Properties of Copper(I) Thiocyanate (CuSCN). Adv. Electron. Mater. 3, 1600378. doi:10.1002/aelm.201600378

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1999). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865

CrossRef Full Text | Google Scholar

Sajjad, M., Singh, N., De Bastiani, M., De Wolf, S., and Schwingenschlögl, U. (2019). Copper Thiocyanate and Copper Selenocyanate Hole Transport Layers: Determination of Band Offsets with Silicon and Hybrid Perovskites from First Principles. Phys. Status Solidi RRL. 13, 1900328. doi:10.1002/pssr.201900328

CrossRef Full Text | Google Scholar

Smith, D. L., and Saunders, V. I. (1982). Preparation and Structure Refinement of the 2H Polytype of β-Copper(I) Thiocyanate. Acta Crystallogr. Sect B. 38, 907–909. doi:10.1107/S0567740882004361

CrossRef Full Text | Google Scholar

Song, Y., Sun, Q., Xu, M., Zhang, J., Hao, Y., Qiao, Y., et al. (2020). Negative thermal Expansion in (Sc,Ti)Fe2 Induced by an Unconventional Magnetovolume Effect. Mater. Horiz. 7, 275–281. doi:10.1039/C9MH01025D

CrossRef Full Text | Google Scholar

Sun, Y., Wang, C., Wen, Y., Chu, L., Pan, H., Nie, M., et al. (2010). Negative Thermal Expansion and Magnetic Transition in Anti-perovskite Structured Mn3Zn1−xSnxN Compounds. J. Am. Ceram.Soc. 93, 2178–2181. doi:10.1111/j.1551-2916.2010.03711.x

CrossRef Full Text | Google Scholar

Takenaka, K., Asano, K., Misawa, M., and Takagi, H. (2008). Negative thermal Expansion in Ge-free Antiperovskite Manganese Nitrides: Tin-Doping Effect. Appl. Phys. Lett. 92, 011927. doi:10.1063/1.2831715

CrossRef Full Text | Google Scholar

Tsetseris, L. (2016a). Two-dimensional Copper Thio- and Seleno-Cyanates. Phys. Chem. Chem. Phys. 18 (11), 7837–7840. doi:10.1039/c6cp00438e

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsetseris, L. (2016b). Copper Thiocyanate: Polytypes, Defects, Impurities, and Surfaces. J. Phys. Condens. Matter 28, 295801–295807. doi:10.1088/0953-8984/28/29/295801

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinet, P., Smith, J. R., Ferrante, J., and Rose, J. H. (1987). Temperature Effects on the Universal Equation of State of Solids. Phys. Rev. B 35, 1945–1953. doi:10.1103/PhysRevB.35.1945

CrossRef Full Text | Google Scholar

Wei, W., Gao, Q., Guo, J., Chao, M., He, L., Chen, J., et al. (2020). Realizing Isotropic Negative thermal Expansion Covering Room Temperature by Breaking the Superstructure of ZrV2O7. Appl. Phys. Lett. 116, 181902. doi:10.1063/1.5143691

CrossRef Full Text | Google Scholar

Wei, Y.-S., Chen, K.-J., Liao, P.-Q., Zhu, B.-Y., Lin, R.-B., Zhou, H.-L., et al. (2013). Turning on the Flexibility of Isoreticular Porous Coordination Frameworks for Drastically Tunable Framework Breathing and thermal Expansion. Chem. Sci. 4, 1539–1546. doi:10.1039/C3SC22222E

CrossRef Full Text | Google Scholar

Wijeyasinghe, N., and Anthopoulos, T. D. (2015). Copper(I) Thiocyanate (CuSCN) as a Hole-Transport Material for Large-Area Opto/electronics. Semicond. Sci. Technol. 30, 104002. doi:10.1088/0268-1242/30/10/104002

CrossRef Full Text | Google Scholar

Zacharias, M., Scheffler, M., and Carbogno, C. (2020). Fully Anharmonic Nonperturbative Theory of Vibronically Renormalized Electronic Band Structures. Phys. Rev. B. 102, 045126. doi:10.1103/PhysRevB.102.045126

CrossRef Full Text | Google Scholar