Seismic Performance of Ni-Ti SMA Wires Equipped in the Spatial Skeletal Structure

Nickel Titanium (Ni-Ti) Shape Memory Alloy (SMA) can be used to limit response of structure during external disturbances such as large seismic events. This paper presents a seismic performance study of Ni-Ti SMA wires equipped in the spatial skeletal structure. First, an improved Graesser-Cozzarelli (G-C) numerical constitutive model of the Austenitic phase of NiTi SMA wire is established. By contrast, the model based on uniaxial cyclic loading experimental tests is demonstrated as feasibility and validity. Next, a method consisting of a three-layer steel spatial skeletal structure model equipped with SMA wires is employed for simulation and experimental tests. According to the obtained constitutive numerical model, the simulation program of vibration control is written to simulate the effect of vibration control of seismic EL-centro wave. Furthermore, a shaking table experimental test was designed to verify the vibration control effect under the same action of seismic EL-centro wave. By comparison of the results of the numerical simulation and shaking table test, dynamic responses of the displacement and acceleration for different floors with control and without control was concluded. The superior superelastic properties of SMA wires used in passive control are investigated and the correctness of the constitutive numerical model are verified as well. The results show that such a comprehensive analysis integrates seismic-resistant behavior of Ni-Ti SMA wires in this type of structure. Besides, proposed method has broad application prospects to address the issues in passive control field of building structures.

Introduction

In recent years, more and more earthquake disasters have damaged various houses and buildings and their auxiliary facilities. Damaged construction projects of municipal facilities will threaten people’s lives, e.g., the Indian Ocean earthquake and tsunami (2004), Wenchuan earthquake (2008), etc. Spatial skeletal structure, the first barrier against earthquakes, is widely employed as the primary in building and bridge structures to undertake most of the external forces. Therefore, the mechanical properties of the spatial skeletal structure to seismic performance is especially crucial to building structures. Popular seismic design philosophy basically allows new materials to prevent or reduce seismic forces against earthquakes by civil engineers. However, the permanent residual deformation and damage makes it almost impossible for building structure to serve continuously, which has rendered huge economic losses. How to design and reconstruct structures to make them available to use continuously after repairs or adjustments has become one of the concentrations of seismic engineering. One strategy is to apply superelastic shape memory alloys (SMAs) in structures. (Ozbulut and Hurlebaus, 2010; Mertmann et al., 2011; Wang and Wu, 2011; Mohd Jani et al., 2014).

Shape memory alloy (SMA) is one of smart materials and contains Nickel Titanium (Ni-Ti) based alloys, Cu-based alloys, and FeMnSi-based alloys, etc. (Wang and Wu, 2011; Mertmann et al., 2011; Ozbulut et al., 2011; Gurubrahmam et al., 2019). SMAs have many superior properties, e.g., high hysteretic responses, excellent superelastic behavior, fine shape memory effect, good fatigue resistance, and well controllable mechanical properties. They have inspired interest from researchers for its recovery of inelastic deformations upon removing load applied. It is well known that such features are determined by its thermo-elastic martensite transformation, and martensite reorientation and detwinning (Yu et al., 2014; Liu et al., 2020). Theories and structural applications of SMAs have been studied and published. Brinson (1993) proposed a comprehensive one-dimensional constitutive law for SMAs, which introduced a separation of the martensite fraction internal variable into stress-induced and temperature-induced components into the model. Chausov et al. (2016) studied the processes of deformation and fracture of high-strength titanium alloys under impact-oscillatory loading and dynamic non-equilibrium, and the research revealed that significant microstructural refinement of the alloy was observed after the impact-oscillatory loading. Ren et al. (2007) studied the modeling of the hysteretic behavior of superelastic SMA wires using the improved Graesser’ model. Li et al. (2019) summarized an enormous number of constitutive models to describe the super-elastic effect and experimentally investigated the hysteretic behavior of super-elastic Ni-Ti SMA bars under quasi-static conditions. Mirzaeifar et al. (2013) proposed a closed-form solution for bending analysis of shape memory alloy (SMA) beams. Jung et al. (2013) investigated the deformation behavior of a composite panel as a function of the different composite geometric parameters of the shape memory alloy wire.

Recently, in order to explore all potential applications of SMAs, a reliable model that describes highly complex behavior of the material has been pursued by many researchers. Here Liu et al. (2020) proposed an improved 1D Graesser-Cozzarelli (G-C) model for predicting the hysteretic responses of the super-elastic SMAs at various strain rates and strain amplitudes. The simplified model is to improve efficiency and quality of SMA wires in structural vibration control. It is noted that in room temperature, the improved G-C model is fully focused on the loading conditions at a specified strain amplitude and strain rate. In previous studies, the superelastic SMAs have been widely employed in vibration control, structural strengthening and repair, and new damper devices (Graesser and Cozzarelli, 1992; Alam et al., 2007; Ozbulut and Hurlebaus, 2010; Ozbulut et al., 2011; Wang and Wu, 2011; Choi et al., 2018; Preciado et al., 2018; Hamdaoui et al., 2019; Mirzai et al., 2019). And the methods have been developed to dissipate the energy in structural engineering. Ghassemieh et al. (2012) verified a novel approach to reduce the vulnerability of reinforced concrete shear wall structures by using the SMA wires. Romano and Tannuri (2009) presented a developed cooling system actuator based on the Seebeck–Peltier effect to improve its dynamic response using a SMA wire. Boroschek et al. (2007) conducted a shaking table test that has a model of three-story structures that armed copper-based SMA dampers. Yan et al. (2013) designed a SMA wire energy dissipater. It is applied in a steel frame structure model to passively reduce dynamic responses of the steel frame structure. Parulekar et al. (2012) made an analytical study of a supporting steel structure of dump tanks with and without SMA dampers. Jia et al. (2019) proposed a new system including the advantage of SMA and inerter elements. In such cases, the SMA damping inerter is a robust system for mitigating structural vibration. Cladera et al. (2014) present a state of the knowledge of existing studies and applications of SMAs in distinguishing their properties: superelasticity, shape memory, and damping. Sayyaadi and Zakerzadeh (2012) studied the position control of shape memory alloy actuator which is based on the generalized Prandtl–Ishlinskii inverse model.

The superelastic properties of Ni-Ti SMA are the capacity of high hysteretic responses and excellent superelastic behavior under dynamic loading. They can be used to dissipate energy and reduce displacement of the structure. However, there are some challenges in that the prior vibration control research still lacks studies on relationship between SMA hysteresis response and passive control effect for shaking table test model experiments.

Given the fact that the mentioned studies have limitations, in this paper, a numerical constitutive model of the Austenitic phase of Ni-Ti SMA wire was established. It is based on the uniaxial cyclic loading experimental tests and the improved G-C constitutive model. In this research, simulation and experimental tests were included by a three-layer steel frame structure model equipped SMA wires. According to the obtained constitutive numerical model, the simulation program of vibration control is written to simulate the effect of vibration control of EL-centro wave (Niazi, 1986). Furthermore, a shaking table experimental test was designed to verify the vibration control effect of the assembled SMA wires. It is under the action of seismic EL-centro wave and the correctness of the simulated vibration control. The primary objective of this paper was to study the damping effect of SMA wires and the correctness of constitutive numerical model. By comparison, the superior superelastic properties of SMA wires used in passive control and the correctness of the constitutive numerical model is verified.

Methods for Modelling and Analyzing

Model of Super-Elastic SMA Wires

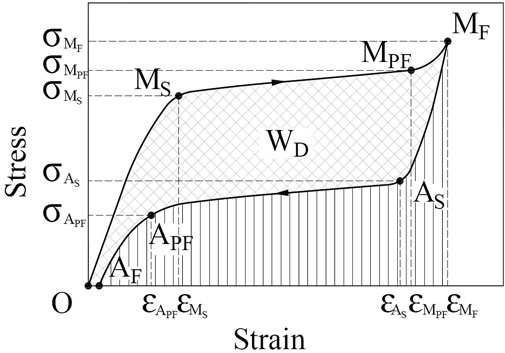
The superelasticity, which refers to the ability of undergoing large elastic deformation, is a unique property of SMAs. Under the condition of ambient temperature $\text{T}>{\text{T}}_{{\text{A}}_{\text{F}}}$(${\text{T}}_{{\text{A}}_{\text{F}}}$ is temperature above which the microstructure is fully austenitic), the stress-strain model of SMA wire is shown as the bold black solid curve in Figure 1 (Ozbulut and Hurlebaus, 2010; Liu et al., 2020). The material is initially in the austenitic phase as shown in the segment of O-M_S. When the SMA is under increasing tensile stress, the material enters into the phase of transformation from austenite to martensite. It is shown in the stress plateau segment of M_S-M_PF in the figure. Subsequently, the stress continues to increase beyond the M_PF point and enters the hardening martensite stage until it reaches the end of Point M_F. At this point, the stress and the strain both reach their maximum value and the SMA enters the unloading stress stage. The austenitic phase is shown in the segment of M_F-A_S. When the tensile stress continues to decrease, the material transforms from martensite to austenite, as shown in the stress plateau segment of A_S-A_PF in the figure. With the stress decreasing beyond the A_PF point to zero, it comes to the austenite stage until it reaches the end of point A_F. As Figure 1 shows, the area of a typical hysteretic stress-strain path curve is the dissipated energy per cycle (W_D). The parameter W_D is used to evaluate the energy-dissipation performance of the SMAs. In this study, only the phenomenological mechanical property is discussed in different uniaxial cyclic loading peak strain and loading speed in ambient temperature.

FIGURE 1

FIGURE 1. Typical hysteretic stress-strain curve of SMA wires.

Considering the significant influence of strain amplitude and strain rate, Liu et al. (2020) obtained a more accurate constitutive model based on G-C (Graesser-Cozzarelli) model with ambient temperature $\text{T}>{\text{T}}_{{\text{A}}_{\text{F}}}$ (${\text{T}}_{{\text{A}}_{\text{F}}}$ is temperature above which the microstructure is fully austenitic). For the loading stage, the equations that describe improved G-C model are as follows:

$\dot{\sigma }=\left(1-s\left(\epsilon \right)\right)E_{O{M}_s}\left[\dot{\epsilon }-\left|\dot{\epsilon }\right|{\left|\frac{\sigma -\beta }{{\sigma }_{M_S}}\right|}^{n-1}\left(\frac{\sigma -\beta }{{\sigma }_{M_S}}\right)\right]+s\left(\epsilon \right)E_{M_{PF}{M}_F}\dot{\epsilon }(1)$

$\beta =E_{O{M}_S}{h}_a\left(\epsilon -\frac{\sigma }{E_{O{M}_S}}\right)(2)$

$s\left(\epsilon \right)=\frac{\tanh \left(g(\left|\epsilon \right|-{\epsilon }_{M_{PF}})\right)+1}{2}(3)$

$h_a=\frac{E_{O{M}_S}}{E_{O{M}_S}-E_{M_S{M}_{PF}}}(4)$

For the unloading stage, the equations that describe improved G-C model are as follows:

$\dot{\sigma }=E_{M_F{A}_S}\left[\dot{\epsilon }-\left|\dot{\epsilon }\right|{\left|\frac{\sigma -\beta }{{\sigma }_{A_S}}\right|}^{n-1}\left(\frac{\sigma -\beta }{{\sigma }_{A_S}}\right)\right](5)$

$\beta =E_{M_F{A}_S}{h}_m(\epsilon -\frac{\sigma }{E_{M_F{A}_S}}+f_T\tanh \left(\overline{a}\epsilon \right))(6)$

$h_m=\frac{E_{M_F{A}_S}}{E_{M_F{A}_S}-E_{A_S{A}_{PF}}}(7)$

The tanh(x) is the error function expressed as:

$\tanh \left(x\right)=1-\frac{2}{1+e^{2x}}(8)$

where σ and ε are the uniaxial stress and the uniaxial strain respectively; ${\sigma }_{M_S}$ is the initiation stress for the forward transformation; ${\sigma }_{A_S}$ is the initiation stress for the reverse transformation; $E_{O{M}_S}$ is the deformation modulus of austenite; $E_{M_S{M}_{PF}}$ is the loading modulus of the mixed phase; $E_{M_{PF}{M}_F}$ is the deformation modulus of detwinned martensite; h_a is a coefficient that adjusts the stiffness of the stress plateau; $E_{M_F{A}_S}$ is the unloading modulus of the mixed phase; ${\epsilon }_{M_{PF}}$ is the completion strain for the forward transformation; n is the material coefficients that adjust the corner sharpness of the hysteretic curve; f_T is a coefficient that describes the phase state of SMAs at various temperatures; h_m is a coefficient that adjusts the stiffness of the stress plateau at the unloading stage; $\overline{a}$ is an adjustment coefficient.

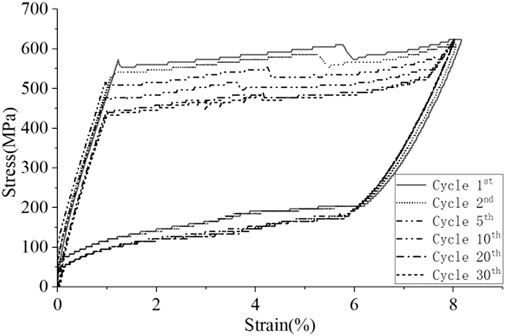
In previous studies, Binshan et al. (2017) conducted a uniaxial cyclic loading test on superelastic Ni-Ti SMA wire at laboratory temperature (20 ± 3°C). The diameter of specimens is 1.0 mm with composition Ti-51% at Ni and the phase-transition temperature is −13°C. To stabilize the material’s behavior and to eliminate the accumulation of residual strain, all specimens that were used in tests had been cyclically loaded 30 times at 3, 6, and 8% of peak strain with a strain rate at 4.5 × 10⁻³, 1.5 × 10⁻², 3.0 × 10⁻², and 4.5 × 10⁻²/sec respectively.

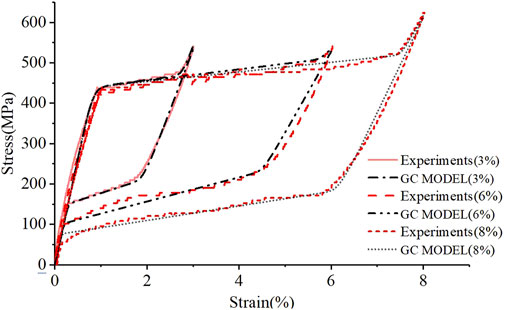
As Figure 2 shows, it is the hysteretic curves of various cycles from 1st to 30th under the condition of 8% strain amplitude with strain rate 4.5 × 10⁻³ s⁻¹. Figure 3 presents the comparison of the hysteretic curves between tests and improved G-C model of axial strain-amplitude-strain- rate-dependent model at 4.5 × 10⁻³ in austenitic phase for SMA wires. With the improved G-C model, the simulated parameters were shown in Table 1 under a different strain amplitude with strain rate 4.5 × 10⁻³ s⁻¹.

FIGURE 2

FIGURE 2. The hysteretic curves of various cycles.

FIGURE 3

FIGURE 3. Comparison between experiments and GC model with various strain amplitudes.

TABLE 1

TABLE 1. Simulation parameters of SMA wires.

To make further quantitative analysis, area surrounded by each stress-strain hysteresis loop (W_D) between the predictions of improved G-C model and the experimental test were compared. Table 2 shows the comparison results of different strain amplitudes. It shows that the improved model can substantially reduce the error percentage of the dissipated energy per cycle (W_D). The maximum error percentage of the improved G-C model is less than 3.10%, which can meet the demand of engineering calculating precision. By contrast, the improved model can accurately predict the actual energy dissipation at different strain rates.

TABLE 2

TABLE 2. Comparison results at various strain amplitudes.

Dynamic Equations of Seismic Control

According to Newton’s second law of motion and the basic principles of structural dynamics, the equation of motion for the structure equipped with austenite SMA wire passive control system shown in Figure 3 that is subjected to earthquake excitation was:

$\left[M\right]\left\{\ddot{u}\left(t\right)\right\}+\left[C\right]\left\{\dot{u}\left(t\right)\right\}+\left[K\right]\left\{u\left(t\right)\right\}=\left[G\right]\left[M\right]\left\{-{\ddot{u}}_g\left(t\right)\right\}+\left[L\right]\left\{F\left(t\right)\right\}(9)$

where [M], [C], and [K] are the structure’s mass matrix, damping matrix, and stiffness matrix respectively; $\left\{\ddot{u}\left(t\right)\right\}$, $\left\{\dot{u}\left(t\right)\right\}$, and $\left\{u\left(t\right)\right\}$ are respectively the acceleration, the velocity, and the displacement of the structure’s nodes relative to the ground motion; [G] is the position distribution matrix of earthquake excitation; $\left\{-{\ddot{u}}_g\left(t\right)\right\}$ is the acceleration of ground motion under earthquake excitation; [L] is cable node placement position matrix of the SMA wires; and [F(t)] is the passive control force imposed on the structure’s nodes by SMA wire cable. In the test, the direction of simulated seismic vibration was along the X axis. As a result, we can get the following formula:

$F\left(t\right)=\{\begin{array}{c}\sigma \cdot A\cdot \cos {\theta }_{ijk};\epsilon >0\\ 0;\epsilon \le 0\end{array}(10)$

where θ_ijk is the direction angle between the SMA wire inhaul cable ${\text{C}}_{{\text{J}}_{\text{XYZ}}^i{\text{J}}_{\text{XYZ}}^j}$ connecting the nodes and coordinate axis (X, Y, or Z); ${\text{C}}_{{\text{J}}_{\text{XYZ}}^i{\text{J}}_{\text{XYZ}}^j}$ is the cable that joins the nodes${\text{J}}_{XYZ}^i$ and ${\text{J}}_{XYZ}^j$, for example, in the study their four cables ${\text{C}}_{{\text{J}}_{001}{\text{J}}_{111}}$, ${\text{C}}_{{\text{J}}_{011}{\text{J}}_{121}}$, ${\text{C}}_{{\text{J}}_{110}{\text{J}}_{200}}$, ${\text{C}}_{{\text{J}}_{120}{\text{J}}_{210}}$ as shown in Figure 4B. J_XYZ represents node number of the frame structure, subscript x, y, and z, each letter represents the node’s position number on each axis respectively. σ, ε, and A are respectively the tensile stress, tensile strain, and area of section of the SMA wire inhaul cable connecting the structure node i as shown in Figure 4B. The number in the coordinate system represents the coordinate system number.

FIGURE 4

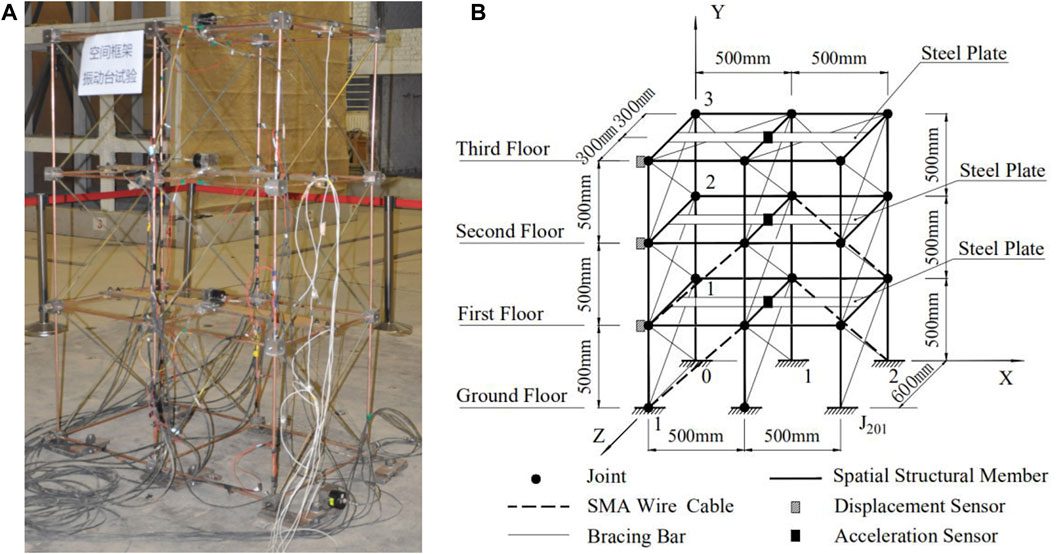
FIGURE 4. Experimental model of spatial skeletal structure: (A) real model, (B) schematic model and sensors.

Simulation and Experiment

Material and Test Model

In this study, the stresses were mainly considered in characteristic test at room temperature (20 ± 3°C). All SMA wire specimens were provided by Xi’an Saite Metal Materials Development Co., Ltd. The diameter of SMA wire is 1.0 mm with composition Ti-51% at Ni as mentioned in Model of Super-Elastic SMA Wires. The phase-transition temperature ${\text{T}}_{{\text{A}}_{\text{F}}}$ is −13°C provided by the manufacturer. Tests and optimized constitutive model of SMA wire were discussed in the previous sections. This section presents seismic control performance of optimization for improved G-C constitutive model. Here, numerical simulation experiment was used to study the control effects of a space frame structure model with the optimized model of SMA wire. Then a shaking table test was conducted to verify the correctness of the simulation. An experimental model is designed. It is a 2-span and 3-layer space frame structure with the shorter edge of 600 mm (Z direction), the longer edge of 1,000 mm (X direction), and the layer height h of 500 mm (Y direction) in plane dimension as shown in Figure 4. For installation convenience, each node was designed as installing and connecting holes with a 1 kg steel mass block. And a 12 kg steel plate is arranged on each floor as the floor weight. All spatial structural members adopt Q235B (ISO: Fe360D) steel pipes with an external diameter of 10 mm and wall thickness of 1.2 mm, the material elasticity modulus of 206 GPa, Poisson’s ratio of 0.3 and density of 7.85$\times$10³ kg/m³. In the shaking table test and the numerical simulation experiment, Wave of EL Centro earthquake (1940) was defined as earthquake simulate excitation as shown in Figure 5. Only horizontal seismic action was considered in this study with the direction of simulated seismic vibration along the X axis. By comparison, four austenite Ni-Ti SMA wire cables are selected to study the effect of the control simulation at last in the test model. The austenite Ni-Ti SMA wire cables as flexible supporting members were installed on the structure as shown in Figure 4. The joints J₀₀₁ J₀₁₁, and J₀₂₁ were armed with displacement sensors in the same vertical plane of the spatial skeletal structure. And acceleration sensors armed in the center of the plane of each floor are shown in Figure 4B.

FIGURE 5

FIGURE 5. Time-acceleration curve of El Centro earthquake.

Simulation

Dynamic time history analysis on the spatial skeletal structure equipped with SMA wire passive control system is conducted. Computation program based on Eqs 9, 10 prepared by MATLAB^® is used. Considering the vibration reduction efficiency and economy, four SMA wire inhaul cables were selected for comparison study between simulation and experiment under the same layout condition. The SMA wire inhaul cables arrangement are shown in Figure 4, and the corresponding cables are ${\text{C}}_{{\text{J}}_{001}{\text{J}}_{111}}$, ${\text{C}}_{{\text{J}}_{011}{\text{J}}_{121}}$, ${\text{C}}_{{\text{J}}_{110}{\text{J}}_{200}}$, and ${\text{C}}_{{\text{J}}_{120}{\text{J}}_{210}}$respectively.

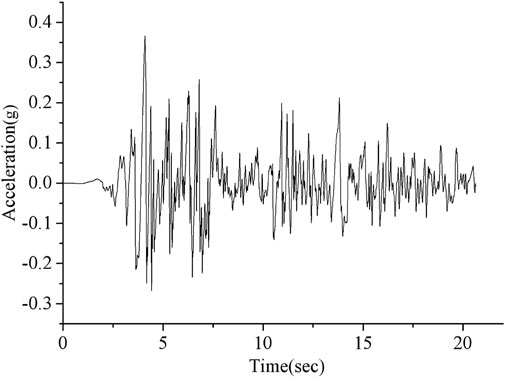
In this study, wave of EL Centro earthquake was selected as earthquake simulate excitation, using 20 s of time period, 0.02 s of step pace, and 200 gal of peak acceleration amplitude as shown in Figure 5.

Wave loading direction was uniaxial along direction X. The joints J₀₀₁ J₀₁₁, and J₀₂₁ were selected as monitoring points for displacement in the same vertical plane of the spatial skeletal structure. And each midpoint of spatial structural members was selected as monitoring points of acceleration.

As is show in Eq. 9, the dynamic analysis program of the structure was written by MATLAB^® language to vibration response of the structure. Firstly, results of improved G-C model were obtained. And the improved G-C model superelastic stress-strain models were saved in the form of data structure by using the save command. Stepwise integration method is a more effective dynamic analysis method in structural analysis. Here the newmark-β algorithm program (Krause and Walloth, 2012; Yuchuan et al., 2019) was used for dynamic analysis of spatial model structure with SMA wire passive control system to solve the dynamic equation. It is shown in Eq. 8, where the control force [F(t)] can be obtained by using the improved G-C model.

In numerical simulation, the following two hypotheses were made in calculating and analyzing the earthquake response. First, all the mass is concentrated at the nodes of each floor. Second, the change of temperature of SMA wire inhaul cable was ignored in the test, i.e., it was assumed that the initial working temperature of each inhaul cable T_0j will not change on the section of inhaul cable and the length direction, since it remains constant temperature T_0j ≥ ${\text{T}}_{{\text{A}}_{\text{F}}}$. Last, the seismic response, the acceleration response, and displacement response were obtained. Results were analyzed by simulation for no control and optimized control of the model structures.

Experimental Test Apparatus and Procedure

Experimental test apparatus. The shaking table test was carried out on a 4 m × 4 m simulated seismic vibration table designed and manufactured by MTS in the structural engineering and seismic laboratory of Xi’an University of Architecture and Technology in China. The data acquisition system was LMS SCADAS III data acquisition system made by LMS^® company. And PCB^® acceleration sensor and Harbin 891 displacement sensor were installed as shown in Figure 4B. Other main test equipments were chosen as dynamic resistance strain acquisition system, small dynamic strain recorder, and type 891 8-wire amplifier. Experimental model of spatial skeletal structure was shown in Figure 4 as the same as the model of emulation. Figure 4A is experimental model with SMA wire cable on the vibration table. Figure 4B is a schematic diagram of sensor layout including displacement sensors and acceleration sensors.

Experimental test procedure. In this test, the input direction of the seismic wave is still uniaxial along the X direction as Figure 4B shown by the MTS^® vibration table.

1) In the uncontrolled condition (there were no cables in J₀₀₁J₁₁₁, J₀₁₁J₁₂₁, J₁₁₀J₂₀₀, and J₁₂₀J₂₁₀ respectively):

First, the white noise excitation for a duration of 120 s was excited before the experimental test to estimate the dynamic properties of the model in the uncontrolled condition. Second, in the uncontrolled condition, 100 gal peak acceleration excitation was input respectively as shown in Figure 4. And after the excitation test, the white noise excitation was excited again. Then, 200 gal peak acceleration excitation was input. At the same time, the test data, the acceleration, and displacement response were detected and recorded.

2) In the controlled condition (there were SMA wires of cables in J₀₀₁J₁₁₁, J₁₁₀J₂₀₀, and J₁₂₀J₂₁₀ respectively):

All the experimental procedures are the same as the previous uncontrolled condition above. The white noise excitation, acceleration excitation was excited, and the data of acceleration and were detected and recorded.

Test Results and Discussion

Results of Simulation Dynamic Response

Under simulated ground motion load, acceleration and displacement values of each layer reflect the seismic performance of the structure. The characteristics of Ni-Ti SMA wire was tested and phase kinetics model was predicted in Methods for Modelling and Analyzing. This section discusses the effect of the strategy for position and force control realized for a three-floor space truss armed with Ni-Ti SMA wires, and the main results are shown in Figures 6, 7 with the EL Centro earthquake wave. For natural frequencies of the structure, the time history curves of acceleration were draw from the tests of the white noise excitation in shaking table test. Then the data were analyzed by the method of Fourier transform frequency response function. The natural frequencies of the structure was 2.4 Hz of every floor without control. The natural frequencies of the structure with control were respectively 4.16 Hz of first floor, 4.34 Hz of second floor, and 4.32 Hz of third floor. The natural frequencies of the structure were changed and the natural frequency of the structure increases. The stiffness of the structure increases after equipped Ni-Ti SMA wire as the bracing cable.

FIGURE 6

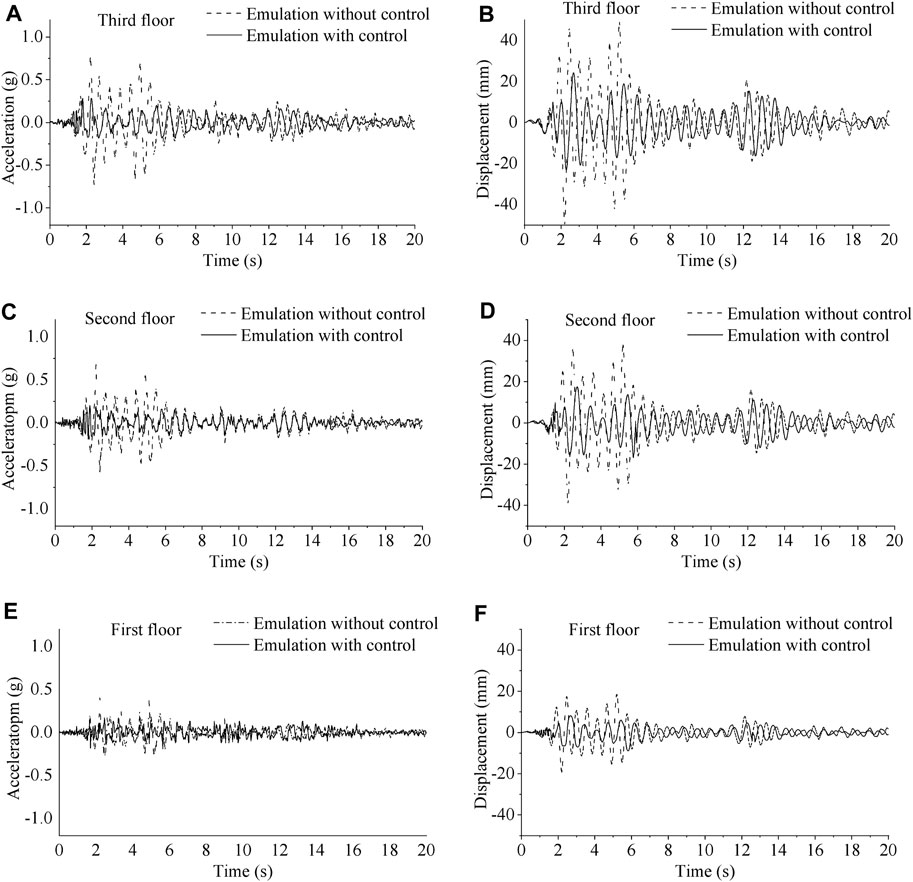
FIGURE 6. Time history curve of displacement response and acceleration response on model structure in emulation: (A) acceleration response on the third floor, (B) displacement response on the third floor, (C) acceleration response on the second floor, (D) displacement response on the second floor, (E) acceleration response on the first floor, and (F) displacement response on the first floor.

FIGURE 7

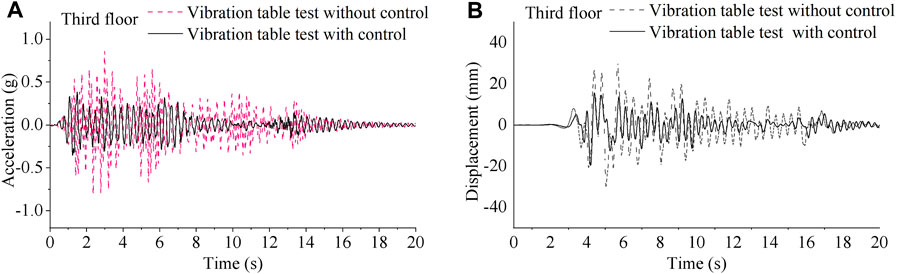
FIGURE 7. Time history curve of displacement response and acceleration response on experimental model structure in vibration table test: (A) acceleration response on the third floor, and (B) displacement response on the third floor.

The vibration displacement at the bottom of the base column was the same as that of the surface of the shaking table. The motion of the first floor was consistent with that of the shaking table. As shown in Figure 6, with the increase of floors, the corresponding acceleration and displacement becomes more obvious. As shown in Figures 6A–F were time history curve of emulated displacement response and acceleration response of the model structure for the 200 gal peak acceleration excitation. As shown in Figure 6, as the floors increase, the corresponding acceleration becomes more pronounced. As shown in Figure 6C, the time-history acceleration curves at the second floor. It shows that the acceleration amplitude of the spatial skeletal structure armed with Ni-Ti SMA wires was approximately 64% lower than that of no control. As shown in Figure 6D, the time-history displacement curves of second floor, the displacement amplitude of the spatial skeletal structure with control was approximately 53% lower than that of without control. Unlike the second floor, the acceleration amplitude decreased by 62% and the displacement amplitude decreased by 49% compared with the control and non-control in the third floor. It was deduced that the toughness of structure and the passive damping of Ni-Ti SMA wires both played an important role to reduce the vibration of the three floor frame structure. As Table 3 showns α₁ is control effect of peak displacement and α₂ control effect of peak acceleration between control and without control. The control effect of peak displacement and acceleration in 200 gal excited were better than 100 gal.

TABLE 3

TABLE 3. Comparison of displacement and peak acceleration with or without control.

Results of Vibration Table Test

With 100/200 gal EL Centro seismic wave input, the time-history curves of displacement and acceleration of each monitoring point in the frame structure equipped with SMA are shown in Figure 4B. As shown in Figure 7, vibration table test results of third floor for the 200 gal peak acceleration excitation was obtained. Figure 7A is third floor time-acceleration curve. In contrast, the model dissipates seismic energy mainly by the third floor. Figure 7B is third floor time-displacement curve. The displacement amplitude of third floor was approximately 30 mm without control, and 19 mm with control. The acceleration amplitude of third floor was approximately 0.72 g without control and 0.38 g with control.

Obviously, the SMA wire inhaul cables play a passive damping role under the vibration load. The inhaul cables bear the displacement movement of the position with the different strain amplitudes and strain rates in tests. They are stretched and unloaded to consumes energy and absorb vibration in the spatial skeletal structure.

By comparison of earthquake responses during simulation and vibration table test, it was obvious that the passive austenite Ni-Ti SMA wires worked better than the no-control one. The analysis results showed that the emulation and the experimental results of the structure’s earthquake response peak values are basically in agreement on the trend, indicating the feasibility of SMA wire passive control emulation by MATLAB^® and applicability of the improved G-C model.

The mechanical behavior of spatial skeletal structures made of Ni-Ti SMA alloys has been investigated. It shows reversible martensitic transformations and the associated effects of transformation plasticity and shape memory when simulating seismic loading modes.

Conclusion

This study focused on the mechanical properties and seismic performance of Ni-Ti SMA wire. A new numerical constitutive model of the Austenitic phase of Ni-Ti SMA wire was established. And the correctness of the model was verified by simulation and shaking table test. The following conclusions are reached:

1) The improved G-C models are stable and precise with a different strain amplitude and strain rate of Ni-Ti SMA wires in austenite state. The simulation parameters were calculated by the test data with different strain amplitudes and loading stages at room temperature. The improved model can accurately predict the actual energy dissipation at different strain rates.

2) The natural frequencies of the structure were changed with Ni-Ti SMA bracing cable. When the natural frequency of the structure increases, the stiffness of the structure increases after equipped Ni-Ti SMA wire as the bracing cable.

3) In emulation, the dynamic time history analysis on the spatial skeletal structure equipped with SMA wire passive control system showed that the control effect of peak displacement and acceleration in 200 gal excited performed better than 100 gal. The improved G-C model, a representative phenomenology-based model describing the deformation behavior of shape memory alloys under alternating loads, is stable and precise.

It is still noted that the improved G-C constitutive model for SMA bars is available to the uniaxial cyclic loading experimental tests at different strain amplitudes and loading rates. The study was the result of macroscopic representation at room temperature. In subsequent studies, the change factors such as temperature change, velocity, deformation rate, and the aging of the material will be fully considered.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YL, TY, BiL, WW, BoL, and SW contributed to conception and design of the study. YL and SW conceived and designed the method. TY and BiL conducted the tests and measured the data. BoL organized the database. YL and WW wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The work was financially supported by the Opening Fund of State Key Laboratory of Green Building in Western China (LSKF202116), key laboratory of well stability and fluid and rock mechanics in Oil and gas reservoir of Shaanxi Province, Xi’an Shiyou University (No. WSFRM20200102001), Science and Technology Plan Project of Yulin (CXY-2020-053), Innovation Capability Support Program of Shaanxi (NO.2020PT-038), Key Lab of Structural Engineering and Earthquake Resistance, Ministry of Education (XAUAT) (KL-SEER-ME -202003), and National Natural Science Foundation of China (No.51678480).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam, M. S., Youssef, M. A., and Nehdi, M. (2007). Utilizing shape memory alloys to enhance the performance and safety of civil infrastructure: a review. Can. J. Civ. Eng. 34, 1075–1086. doi:10.1139/l07-038

CrossRef Full Text | Google Scholar

Binshan, Y., Sheliang, W., Tao, Y., and Yujiang, F. (2017). BP Neural Netwok Constitutive Model Based on Optimization with Genetic Algorithm for SMA. ACTA METALLURGICA SINICA 53 (2), 248–256.

Google Scholar

Boroschek, R. L., Farias, G., Moroni, O., and Sarrazin, M. (2007). Effect of SMA Braces in a Steel Frame Building. J. Earthquake Eng. 11, 326–342. doi:10.1080/13632460601125763

CrossRef Full Text | Google Scholar

Brinson, L. C. (1993). One-Dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-constant Material Functions and Redefined Martensite Internal Variable. J. Intell. Mater. Syst. Structures 4 (2), 229–242. doi:10.1177/1045389x9300400213

CrossRef Full Text | Google Scholar

Chausov, M., Maruschak, P., Pylypenko, A., and Markashova, L. (2016). Enhancing plasticity of high-strength titanium alloys VT 22 under impact-oscillatory loading. Phil. Mag., 1–11. doi:10.1080/14786435.2016.1262973

CrossRef Full Text | Google Scholar

Choi, E., Mohammadzadeh, B., Kim, D., and Jeon, J.-S. (2018). A new experimental investigation into the effects of reinforcing mortar beams with superelastic SMA fibers on controlling and closing cracks. Composites B: Eng. 137, 140–152. doi:10.1016/j.compositesb.2017.11.017

CrossRef Full Text | Google Scholar

Cladera, A., Oller, E., and Ribas, C. (2014). Pilot Experiences in the Application of Shape Memory Alloys in Structural Concrete. J. Mater. Civil Eng. 26 (11), 1–10. doi:10.1061/(asce)mt.1943-5533.0000974

CrossRef Full Text | Google Scholar

Ghassemieh, M., Mostafazadeh, M., and Sadeh, M. S. (2012). Seismic control of concrete shear wall using shape memory alloys. J. Intell. Mater. Syst. Structures 23 (5), 535–543. doi:10.1177/1045389x12436731

CrossRef Full Text | Google Scholar

Graesser, E. J., and Cozzarelli, F. A. (1992). Shape-Memory Alloys as New Materials for Aseismic Isolation. J. Eng. Mech. 117 (11), 2590–2608.

Google Scholar

Hamdaoui, Karim., Benadla, Zahira., Chitaoui, H., and Benallal, M. E. (2019). Dynamic behavior of a seven century historical monument reinforced by shape memory alloy wires. Smart Structures Syst. 23 (4), 337–345.

Google Scholar

Jia, Y., Li, L., Wang, C., Lu, Z., and Zhang, R. (2019). A novel shape memory alloy damping inerter for vibration mitigation. Smart Mater. Structures (28), 1–12. doi:10.1088/1361-665x/ab3dc8

CrossRef Full Text | Google Scholar

Jung, B.-S., Kong, J.-P., Li, N., Kim, Y.-M., Kim, M.-S., Ahn, S.-H., et al. (2013). Numerical simulation and verification of a curved morphing composite structure with embedded shape memory alloy wire actuators. J. Intell. Mater. Syst. Structures 24 (1), 89–98. doi:10.1177/1045389x12459588

CrossRef Full Text | Google Scholar

Gurubrahmam, K., Baburam, K. G. e. a., Kumar, A., and Gara, D. K. (2019). A short review on constitutive modelling of the shape memory alloys-1. Ijmperd 9 (4), 849–858. doi:10.24247/ijmperdaug201987

CrossRef Full Text | Google Scholar

Krause, R., and Walloth, M. (2012). Presentation and comparison of selected algorithms for dynamic contact based on the Newmark scheme. Appl. Numer. Math. 62, 1393–1410. doi:10.1016/j.apnum.2012.06.014

CrossRef Full Text | Google Scholar

Li, C., Zhou, Z., and Zhu, Y. (2019). A uniaxial constitutive model for NiTi shape memory alloy bars considering the effect of residual strain. J. Intell. Mater. Syst. Structures 30 (8), 1163–1177. doi:10.1177/1045389x19835932

CrossRef Full Text | Google Scholar

Liu, B., Li, B., Wang, S., Liu, Y., Yang, T., and Zhou, Y. (2020). A 1D strain-amplitude- and strain-rate-dependent model of super-elastic shape memory alloys for structural vibration control. Structures 25, 426–435. doi:10.1016/j.istruc.2020.03.028

CrossRef Full Text | Google Scholar

Mertmann, M., Oswald, W., Steegmueller, R., and Schuessler, A. (2011). Study on Thermomechanical Treatment, Mechanical Properties and Fatigue of Nitinol Superelastic Thin Sheet. J. Mater. Eng. Perform. 20 (4-5), 787–792. doi:10.1007/s11665-011-9891-6

CrossRef Full Text | Google Scholar

Mirzaeifar, R., DesRoches, R., Yavari, A., and Gall, K. (2013). On superelastic bending of shape memory alloy beams. Int. J. Sol. Structures 50 (10), 1664–1680. doi:10.1016/j.ijsolstr.2013.01.035

CrossRef Full Text | Google Scholar

Mirzai, N. M., Attarnejad, R., and Hu, J. W. (2019). Enhancing the seismic performance of EBFs with vertical shear link using a new self-centering damper. INGEGNERIA SISMICA XXXV (4), 57–76.

Google Scholar

Mohd Jani, J., Leary, M., Subic, A., and Gibson, M. A. (2014). A review of shape memory alloy research, applications and opportunities. Mater. Des. (1980-2015) 56, 1078–1113. doi:10.1016/j.matdes.2013.11.084

CrossRef Full Text | Google Scholar

Niazi, M. (1986). Inferred displacements, velocities and rotations of a long rigid foundation located at el centro differential array site during the 1979 imperial valley, california, earthquake. Earthquake Engng. Struct. Dyn. 14, 531–542. doi:10.1002/eqe.4290140404

CrossRef Full Text | Google Scholar

Ozbulut, O. E., Hurlebaus, S., and Desroches, R. (2011). Seismic Response Control Using Shape Memory Alloys: A Review. J. Intell. Mater. Syst. Structures 22 (14), 1531–1549. doi:10.1177/1045389x11411220

CrossRef Full Text | Google Scholar

Ozbulut, O. E., and Hurlebaus, S. (2010). Neuro-fuzzy Modeling of Temperature- and Strain-rate-dependent Behavior of NiTi Shape Memory Alloys for Seismic Applications. J. Intell. Mater. Syst. Structures 21 (8), 837–849. doi:10.1177/1045389x10369720

CrossRef Full Text | Google Scholar

Parulekar, Y. M., Reddy, G. R., Vaze, K. K., Guha, S., Gupta, C., Muthumani, K., et al. (2012). Seismic response attenuation of structures using shape memory alloy dampers. Struct. Control. Health Monit. 19 (1), 102–119. doi:10.1002/stc.428

CrossRef Full Text | Google Scholar

Preciado, A., Ramirez-Gaytan, A., Gutierrez, N., Vargas, D., Manuel Falcon, J., and Ochoa, G. (2018). Nonlinear earthquake capacity of slender old masonry structures prestressed with steel. FRP NiTi SMA tendons, Steel Compos. Structures 26 (2), 213–226.

Google Scholar

Ren, W., Li, H., and Song, G. (2007). A one-dimensional strain-rate-dependent constitutive model for superelastic shape memory alloys. Smart Mater. Struct. 16 (1), 191–197. doi:10.1088/0964-1726/16/1/023

CrossRef Full Text | Google Scholar

Romano, R., and Tannuri, E. A. (2009). Modeling, control and experimental validation of a novel actuator based on shape memory alloys. Mechatronics 19, 1169–1177. doi:10.1016/j.mechatronics.2009.03.007

CrossRef Full Text | Google Scholar

Sayyaadi, H., and Zakerzadeh, M. R. (2012). Position control of shape memory alloy actuator based on the generalized Prandtl-Ishlinskii inverse model. Mechatronics 22 (7), 945–957. doi:10.1016/j.mechatronics.2012.06.003

CrossRef Full Text | Google Scholar

Wang, Q., and Wu, N. (2011). A review on structural enhancement and repair using piezoelectric materials and shape memory alloys. Smart Mater. Structures 21, 1–24. doi:10.1088/0964-1726/21/1/013001

CrossRef Full Text | Google Scholar

Yan, S., Niu, J., Mao, P., Song, G., and Wang, W. (2013). Experimental Research on Passive Control of Steel Frame Structure Using SMA Wires. Math. Probl. Eng. 2013, 1–13. doi:10.1155/2013/416282

CrossRef Full Text | Google Scholar

Yu, C., Kang, G., and Kan, Q. (2014). Crystal plasticity based constitutive model of NiTi shape memory alloy considering different mechanisms of inelastic deformation. Int. J. Plasticity 54, 132–162. doi:10.1016/j.ijplas.2013.08.012

CrossRef Full Text | Google Scholar

Yuchuan, F., Zhao, C., Hongye, Y., and Wen, B. (2019). Dynamic load identification algorithm based on Newmark-β and self-filtering. Proc. Inst. Mech. Eng. C: J. Mech. Eng. Sci. 234, 96–107. doi:10.1177/0954406219869981

CrossRef Full Text | Google Scholar

Nomenclature

$E_{O{M}_S}$ is the deformation modulus of austenite

$E_{M_S{M}_{PF}}$ is the loading modulus of the mixed phase

$E_{M_{PF}{M}_F}$ is the deformation modulus of detwinned martensite

$E_{M_F{A}_S}$ is the unloading modulus of the mixed phase

f_T is a coefficient that describes the phase state of SMAs at various temperatures

h_a is a coefficient that adjusts the stiffness of the stress plateau

h_m is a coefficient that adjusts the stiffness of the stress plateau at the unloading stage

n is the material coefficients that adjust the corner sharpness of the hysteretic curve

${\text{T}}_{{\text{A}}_{\text{F}}}$ (austenitic completion temperature at 0 stress) is temperature above which the microstructure is fully austenitic

${\text{T}}_{{\text{A}}_{\text{F}}}$ (austenitic completion temperature at 0 stress) is temperature above which the microstructure is fully austenitic

W_D is the dissipated energy per cycle

${\epsilon }_{M_{PF}}$ is the completion strain for the forward transformation

${\sigma }_{M_S}$ is the initiation stress for the forward transformation

${\sigma }_{A_S}$ is the initiation stress for the reverse transformation.