
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 17 May 2021
Sec. Energy Materials
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.683503
This article is part of the Research Topic Development of Emerging Thermoelectric Materials View all 4 articles
Two-dimensional (2D) pentagonal monolayer structures have shown promising characteristics and fascinating physical and chemical properties. The disparate strain-dependent thermal conductivity of two-dimensional penta-structures was reported, but the difference between the silicon-based pentagonal and hexagonal structures is barely researched. In this work, based on first-principles calculations, we studied the strain-modulated phonon transport behavior of two 2D pentagonal (penta-SiH and bilayer penta-Si) and one hexagonal silicene structures (H-silicene), of which the penta-SiH and H-silicene mean the structures are hydrogenated for the purpose of thermodynamical stability. We found that the silicon-based pentagonal structure also presented a different strain-dependent thermal conductivity from other pentagonal materials, such as penta-graphene, penta-SiC, or penta-SiN. Moreover, even with the similar strain-dependent thermal transport behavior in penta-SiH and bilayer penta-silicene, we find that the governing mechanism is still different. For both pentagonal silicene structures, the thermal conductivity presents a large improvement at first as the tensile strain increases from 0 to 10% and then stabilizes with a strain larger than 10%. A detailed analysis shows that the in-plane modes contributed the most part to the group velocity enhancement under strains in penta-SiH which is opposite from the bilayer penta-graphene, although the phonon group velocity and phonon lifetime of both structures increase with applied strain. On the other hand, a similarity was found in pentagonal silicene and hexagonal silicene despite the differences in geometry structures. Furthermore, based on the detailed analysis between the pentagonal (penta-SiH) and hexagonal silicene structures (H-silicene), the difference in out-of-plane phonon scattering cannot be ignored: different major scattering channels of the out-of-plane flexural modes result in different thermal conductivity sensitivity to strains, and the disparity in anharmonicity leads to different thermal conductivity under no strain.
Graphene is a very promising two-dimensional (2D) material due to its fantastic mechanical, electronic, and transport properties (Zhang et al., 2005; Balandin et al., 2008; Lindsay et al., 2010; Balandin, 2011; Liu et al., 2014). The discovery of graphene has generated extensive studies of 2D nanostructures, which have become a hot field of nanoscale materials and nanotechnology (Novoselov et al., 2004; Geim, 2009; Novoselov et al., 2012; Ferrari, 2014). While most of the monolayer structures share a similar hexagonal lattice structure, like graphene and boron nitride (BN) (Hu et al., 2014), recently, a new 2D carbon allotrope which is entirely composed of carbon pentagons and resembles the Cairo pentagonal tiling called penta-graphene was proposed from the first-principles calculation and was confirmed to be thermodynamically and mechanically stable (Zhang et al., 2015). Since the prediction of penta-graphene, lots of research studies on its properties have been conducted (Chen et al., 2016; Liu et al., 2016). Meanwhile, researchers also devoted efforts in finding other pentagonal monolayer structures, such as penta-SiC and penta-BN (Li et al., 2015; Lopez-Bezanilla and Littlewood, 2015; Zhang et al., 2016). Recently, some results of pentagonal silicene were published, which indicate its thermodynamic unstability (Ding and Wang, 2015). However, the H-decorated penta-silicene (penta-SiH) showed a stable structure and a great promise for excellent mechanical and electronic properties. Furthermore, a particular type of bilayer penta-silicene (penta-Si) is found to have even lower energy than all of the known hexagonal silicene bilayers, and therefore forms the most stable bilayer silicon material predicted so far (Aierken et al., 2016). On the other hand, experimental evidence of the existence of the pentagonal silicon monolayer structure was also published recently (Cerda et al., 2016). Thus, the pentagonal silicene could be a very important semiconductor material in the future for the materials community.
Among all the concerned physical properties of nanomaterials, thermal conductivity is always a very important property that is involved in various applications. However, the thermal property of the pentagonal silicene structure has still not been reported as well as the difference in the thermal behavior between hexagonal and pentagonal silicene structures. Motivated by the current situation, a first-principles study to investigate the thermal properties of both the monolayer penta-SiH and bilayer penta-Si structure is reported in this article. Beyond that, different thermal conductivity response to the tensile strain between hexagonal and pentagonal silicene is also discussed. We find that for pentagonal silicene, thermal conductivity increases under tensile strains (both monolayer and bilayer); meanwhile, for the hexagonal structure, the H-decorated silicene (H-silicene) presents a similar response to strains with the original silicene. We find a unified strain tuned thermal conductivity but with a different mechanism in pentagonal and hexagonal silicene.
By solving the phonon Boltzmann transport equation (BTE) with interatomic force constants evaluated from first-principles calculations, the intrinsic lattice thermal conductivity (κ) can be obtained. The lattice thermal conductivity is calculated from the solution of the BTE as below (Li et al., 2014):
where α and β denote the three directions (x, y, or z);
where
There are three dominant phonon-scattering mechanisms considered in our calculations, which are the intrinsic phonon–phonon scattering, the isotopic disorder, and the phonon boundary scattering. The intrinsic scattering rate from the three-phonon scattering processes is calculated as (Li et al., 2014)
where
where
All the first-principles calculations are performed based on the density functional theory (DFT) using the Vienna ab initio simulation package (VASP) (Kresse, 1996) with the projector augmented wave pseudopotentials (PAW) (Kresse, 1999). The Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1996) of generalized gradient approximation (GGA) is chosen as the exchange correlation functional, and the plane waves with a kinetic energy cutoff of 500 eV are used to expand the valance electron wave functions. This potential is also chosen by other researchers in many of the previous DFT calculations and is proved to be correct and accurate (Zhang et al., 2015; Chen et al., 2016; Li et al., 2015; Zhang et al., 2016). The electronic step and ionic step stop criteria are
Figure 1 illustrates the atomic structure of the H-decorated penta-silicene (penta-SiH) sheet (Figures 1A,B) and its phonon dispersion curve, as well as its phonon density of states (pDOS) (Figure 1C). The lattice constant is 5.31 Å, and the buckling height is 2.45 Å. Similar to penta-graphene, in original penta-silicene (no H-decorated), both
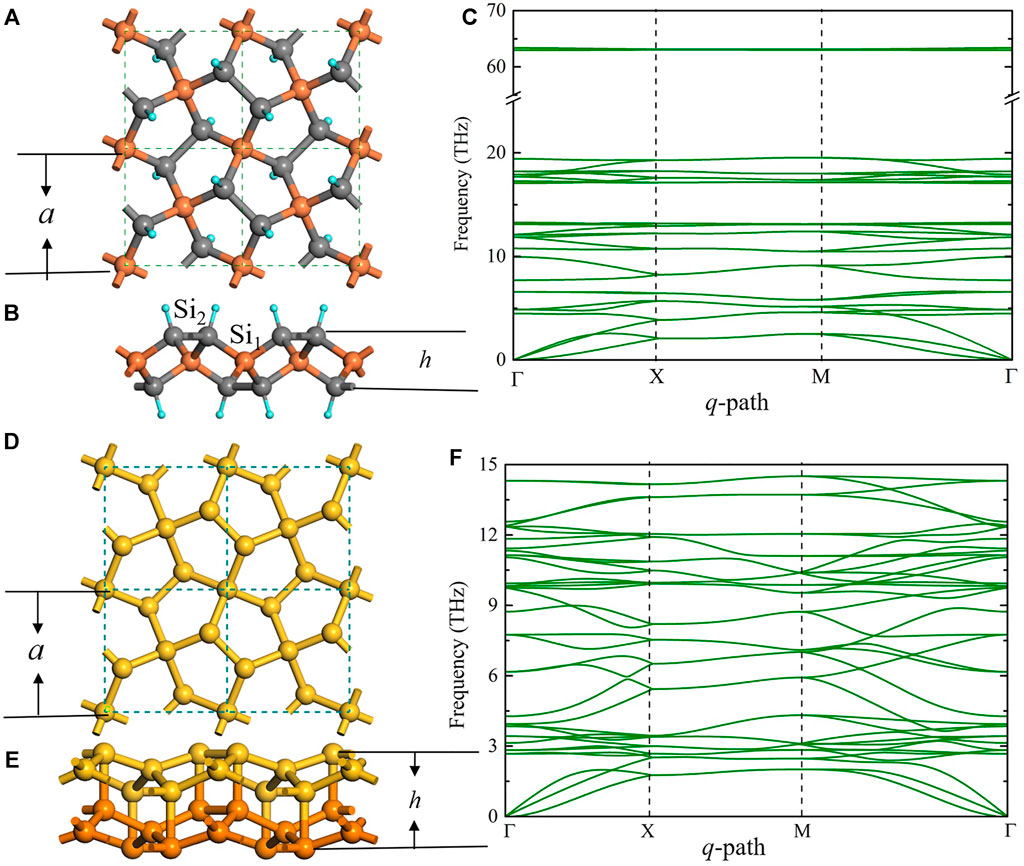
FIGURE 1. (A) Top view of the H-decorated silicene structure (penta-SiH). The smallest dashed square indicates the unit cell of the pentagonal structure. (B) The side view of the same structure, where a is the lattice constant and h is the buckling distance. Si1 (dark yellow) and Si2 (dark gray) represent the Si atom with and without H atom decoration, respectively. (C) Phonon dispersion curve and the phonon density of state (pDOS) of penta-SiH. (D) and (E) Top view and the side view of the bilayer penta-Si structure, respectively, where a is the lattice constant and h is the buckling distance. Yellow and orange atoms represent the different layers of the bilayer structure. (F) Phonon dispersion curve and the pDOS of the bilayer penta-Si structure.
As mentioned above, bilayer penta-Si is another stable pentagonal silicene structure. By directly stacking two monolayer pentagonal silicene together (AA-stacking), the Si2 atoms in each layer interact with each other and eliminate the unsaturated hanging bond, making the structure thermodynamically stable. Figures 1D,E show the crystal structure of the bilayer penta-Si, and the absence of imaginary frequency in the phonon dispersion as shown in Figure 1F illustrates the thermodynamical stability. For bilayer penta-Si, the lattice constant is 5.895 Å, and the buckling height is 3.43 Å. The bond length between all Si atoms is 2.46 Å (including the vertical bonds between two layers). From Figure 1C, we can see that all the phonon bands are below 15 THz, which yields the previous conclusion that in penta-SiH, the H atoms contribute to the high frequency bands (<15 THz), while Si atoms do the rest. In addition, phonon dispersion of bilayer penta-Si is very similar to that of penta-SiH for the low frequency part (15 THz), especially for acoustic phonon branches, implying the similarity in the thermal transport behavior, as we will see later.
In Figure 2, we demonstrate the strain-modulated lattice thermal conductivity of penta-SiH (Figure 2A) and bilayer penta-Si (Figure 2B), as well as the thermal conductivity under no strains with its phonon specific heat
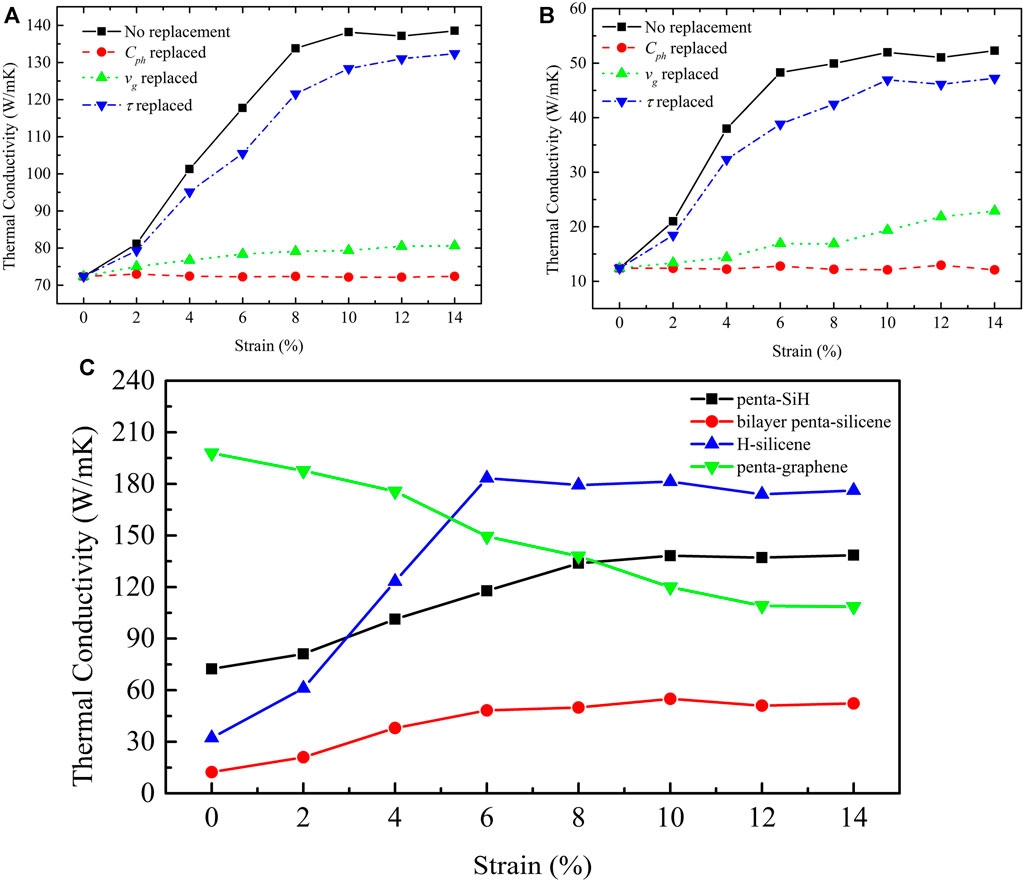
FIGURE 2. Intrinsic lattice thermal conductivity of penta-SiH (A) and bilayer penta-Si (B). “Replaced” means that the corresponding term was replaced by the value at certain strains and the other term stayed with non-strain values. (C) Comparison of the strain-dependent intrinsic lattice thermal conductivity among penta-SiH, bilayer penta-Si, H-silicene, and penta-graphene.
For bilayer penta-Si, the thermal conductivity presents a very similar trend as penta-SiH; that is, the thermal conductivity increases from 10 to 40
To further clarify how the strain tunes the thermal conductivity in penta-SiH and bilayer penta-Si, for both structures, we first compare the phonon dispersion curves under some typical strains, especially for the acoustic branches. Figure 3A shows the phonon dispersion of three acoustic phonon branches of penta-SiH, namely, the flexural acoustic (FA), longitudinal acoustic (LA), and transverse acoustic (TA) branches, along the q-path from
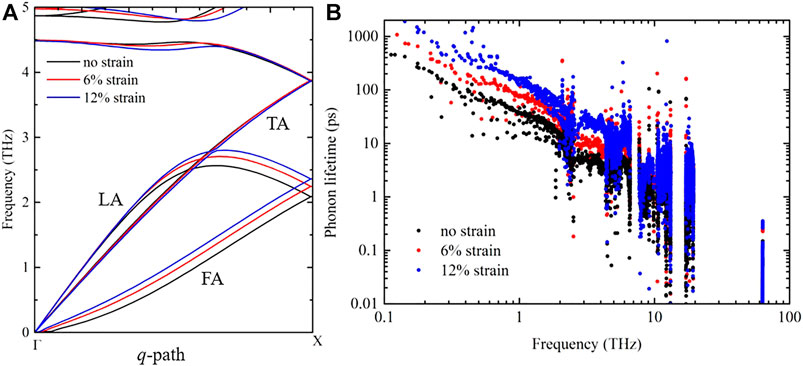
FIGURE 3. (A) Phonon dispersion curves of acoustic phonon branches of penta-SiH along the
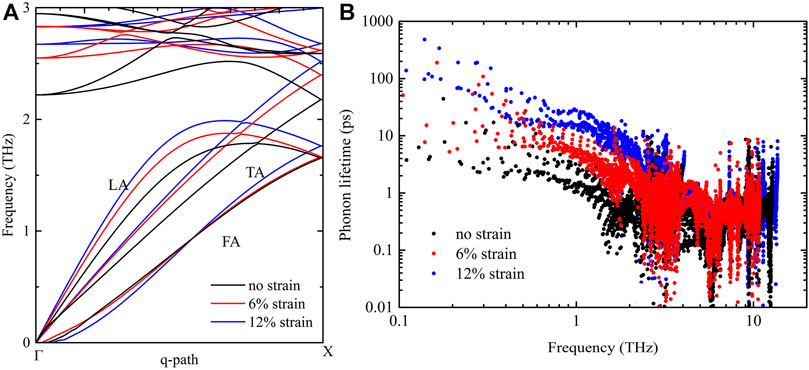
FIGURE 4. (A) Phonon dispersion curves of acoustic phonon branches of bilayer penta-Si along the
Although it is common that the thermal conductivity of the multilayer structure is much lower than that of the monolayer structure, we are still interested in digging out the fundamental reason. Figure 3B shows the phonon lifetime of penta-SiH under some typical strains, from which the phonon lifetime improvement under increased strains can be clearly observed. The lifetime of low-frequency phonons increases by about 10 times from 1
In addition, our earlier results (Xie et al., 2016) show that the thermal conductivity of monolayer silicene can also be largely tuned by the tensile strains, which present a similar tendency with the current pentagonal silicene structure. To further explore the mechanism of strain-tuned thermal conductivity in pentagonal and hexagonal silicene, we also calculated the thermal conductivity of H-decorated silicene (H-silicene) under strains. In Figure 2C, we compare the strain-dependent thermal conductivity among H-silicene, penta-SiH, and bilayer penta-Si. The thermal conductivity of the unstrained H-silicene is found to be lower than that of penta-SiH but higher than that of bilayer penta-Si. With the strain increasing, thermal conductivity of H-silicene increases most rapidly and becomes higher than that of penta-SiH when the strain is larger than 4%. The thermal conductivity reaches the highest value at 6% strain and then decreases slightly when the strain continuously increases. This trend is similar with that of the bare silicene (Xie et al., 2016). Comparing the absolute value with bare silicene (Xie et al., 2016), it is also worth noting that at large strains (<6%), the H decoration has little effect on the thermal conductivity of silicene.
To further investigate the mechanism of thermal conductivity changes under strains, the phonon dispersion curve and lifetime of H-silicene are also calculated. Figure 5A shows the acoustic phonon branches of H-silicene under typical strains. It is very interesting to find that even with the fundamentally different geometry structure, the phonon branches of pentagonal and hexagonal silicene still respond similarly to the tensile strains. The FA branch is stiffened when the strain is increased, indicating the enhancement of phonon group velocity of FA modes. While for TA and LA branches, although the changes are more obvious than penta-SiH, these changes still cannot result in the considerably large changes of group velocity. On the other hand, from the strain-modulated phonon lifetime as shown in Figure 5B, we know that the phonon lifetime of H-silicene increases rapidly with the strains. The lifetime of acoustic phonons increases by more than 10 times when the strain is increased from 0 to 8%. We believe this is the main reason responsible for the rapid increase of thermal conductivity upon tension. To make a short conclusion, the pentagonal H decorated silicene (penta-SiH) and hexagonal H-silicene share a very similar thermal transport behavior under tensile strains despite their different geometry structures. The mechanism underlying the strain-tuned thermal conductivity is also similar; that is, both the phonon group velocity and phonon lifetime increase under strain, except that the phonon lifetime increases more rapidly and obviously in the hexagonal H-silicene structure.
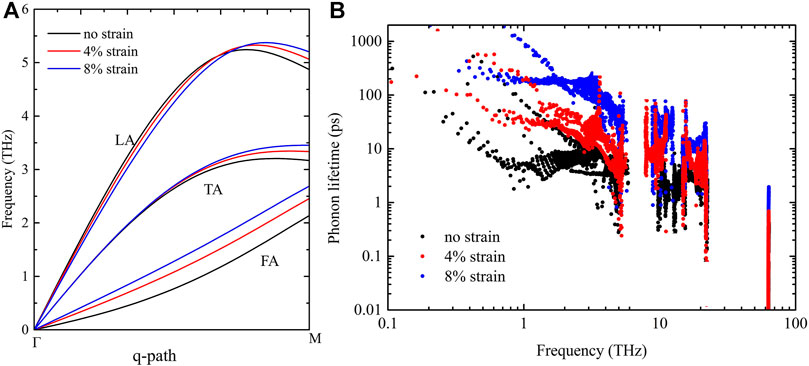
FIGURE 5. (A) Phonon dispersion curves of acoustic phonon branches of hexagonal H-silicene along the
Despite the similar mechanism and phenomenon between penta-SiH and H-silicene, it is very interesting to find that the thermal conductivity of H-silicene is smaller than that of penta-SiH when no strain is applied, but became higher when the strain is larger than 4%. Based on the above analysis, it is concluded that the difference is due to the rapid increasing of the phonon relaxation time. Nevertheless, a further investigation of its physical picture is also necessary. First of all, the thermal conductivity contribution from acoustic phonon branches is calculated. Figure 6 gives the thermal conductivity contribution from the in-plane modes (TA and LA) and the out-plane modes (FA), both the absolute value [(a) for penta-SiH and (b) for H-silicene] and percentage value [(c) for penta-SiH and (d) for H-silicene]. It is unexpected to find that the contribution of acoustic modes showed a very different tendency under strains. For penta-SiH, the out-plane mode (FA) plays a major role (contribution
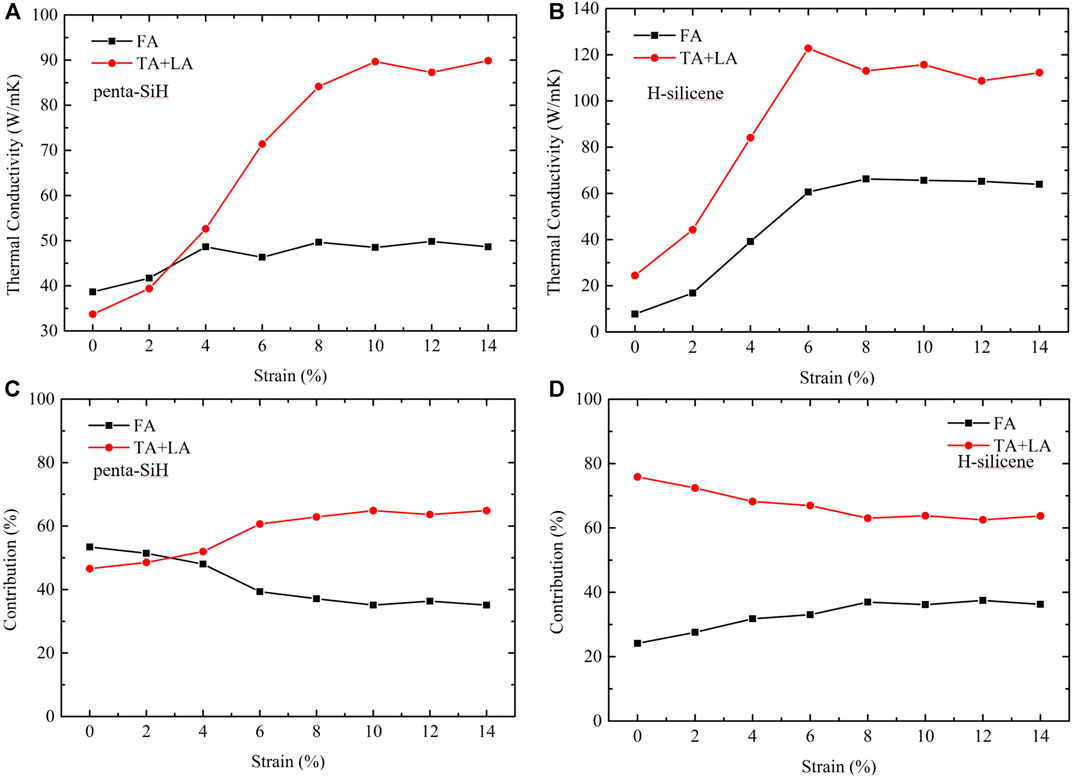
FIGURE 6. Thermal conductivity contribution from in-plane (TA and LA) and out-plane (FA) acoustic phonon modes of penta-SiH (a, c) and H-silicene (b, d). (A) and (B) The absolute value. (C) and (D) The percentage value.
However, the percentage results of H-silicene are very different from those of penta-SiH. Similar to the bare silicene, the in-plane modes contribute the most part of the thermal conductivity (nearly 80% under no strain). With the increasing strains, the contribution from the out-plane mode also increased (from 25 to 37%), but the out-plane modes always contribute the most part (more than 60%) of thermal conductivity. Considering our previous discussion about group velocity, the group velocity of FA modes showed a rather obvious increase under strains, which can be the reason of the contribution percentage change in H-silicene. However, the penta-SiH and H-silicene showed very similar group velocity changes under strains, but share very different contribution percentage changes from H-silicene.
Figure 7 gives the total phonon scattering rate of three acoustic phonon modes in penta-SiH (a) and H-silicene (b) under strains. For TA and LA modes, the scattering rate of both penta-SiH and H-silicene presented a significant drop under strains, but for FA modes, the difference cannot be ignored in the two materials. In penta-SiH, FA modes present a much more gentle decreasing tendency than TA and LA modes, while in H-silicene, the FA modes decreased as rapidly as the rest of the two phonon branches. This different scattering rate change tendency between FA modes and TA/LA modes in penta-SiH explains its contribution tendency in Figures 6A,C. On the other hand, due to the rapidly decreasing scattering rate of all three acoustic phonon modes, thermal conductivity of H-silicene increased more rapidly than that of penta-SiH under strains, which results in a higher value when the strain is larger than 4%. To further investigate the FA mode scattering differences between penta-SiH and H-silicene, we looked deeply into its scattering channels. Figures 7C,D display some typical scattering channel of FA modes in penta-SiH and H-silicene, respectively. From the results, it is obvious that the major scattering channel in the two structures is different. For penta-SiH, FA modes are more likely to scatter with the optical modes (
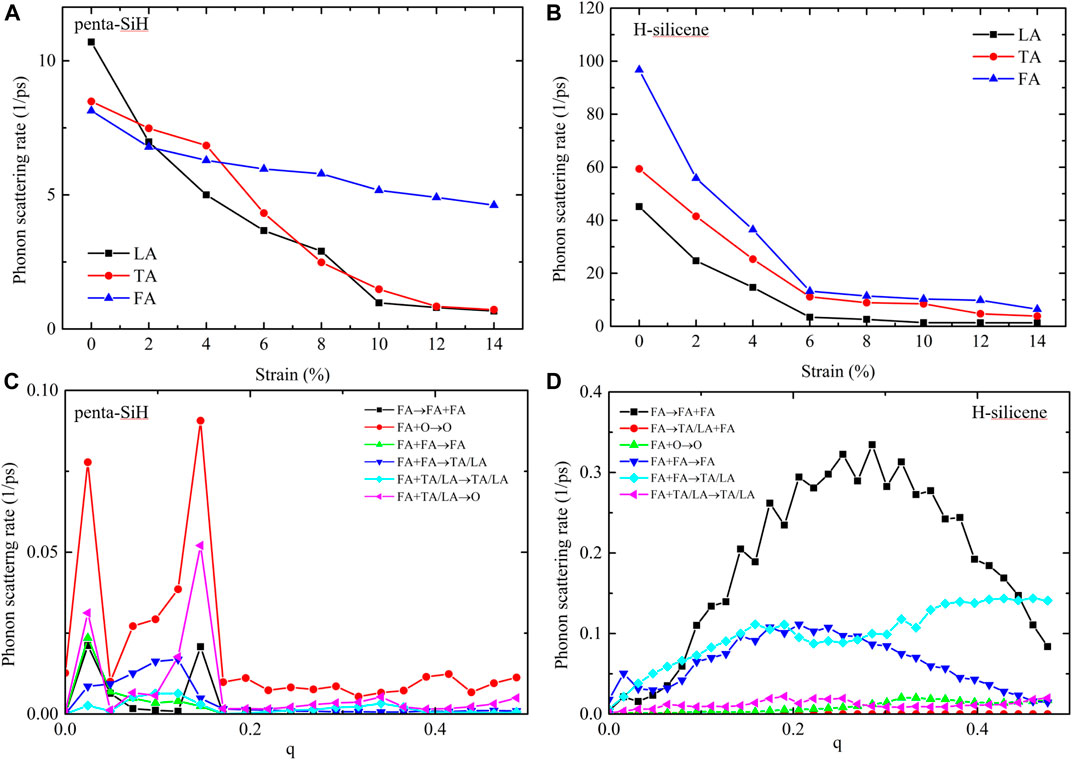
FIGURE 7. The total phonon scattering rates of FA, TA, and LA modes of penta-SiH (A) and H-silicene (B). (C) Some typical phonon scattering channels of FA modes in penta-SiH. (D) Some typical phonon scattering channels of FA modes in H-silicene.
On the other hand, we believe that the change of scattering channels is also connected with the system symmetry. Penta-SiH has the crystal symmetry of the space group
As we discussed above, different from the graphene/penta-graphene system, the similarity of thermal behavior between penta-SiH and H-silicene is obvious. To fundamentally understand this similarity from the atomic level, the orbital hybridization based on the projected electronic band structure and electron density of states (DOS) in the reciprocal space is shown in Figures 8A,B. In both H-silicene and penta-SiH, we only calculated the orbital hybridization of Si atoms. For H-silicene, as shown in Figure 8A, the
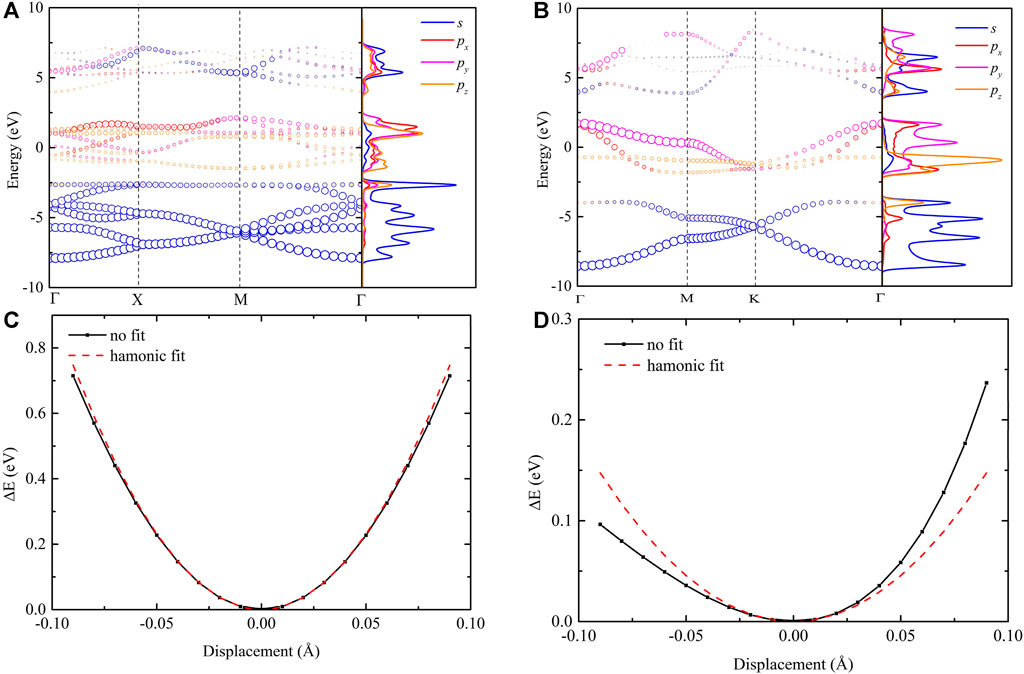
FIGURE 8. (Top) Orbital projected electronic structures projected on s,
To summarize, with first-principles calculations, we find that the lattice thermal conductivity of two 2D pentagonal silicene structures (penta-SiH and bilayer penta-Si) possesses strain dependence different from penta-graphene. Although both pentagonal silicene structures share a very similar thermal transport behavior under tensile strains, the governing mechanism is quite different. For both pentagonal silicene structures, the thermal conductivity first shows a large improvement (90% for penta-SiH and 400% for bilayer penta-Si) as tensile strain increases from 0 to 10% and then stabilizes with a strain larger than 10%. A detailed analysis shows that the phonon group velocity and phonon lifetime of both structures increase with applied strain, and the phonon lifetime plays the major role in the improvement of thermal conductivity. On the other hand, based on the detailed analysis between the pentagonal silicene structure (penta-SiH) and the hexagonal silicene structure (H-silicene), we find that despite their similarity in the thermal behavior under strains, their difference in out-of-plane phonon scattering cannot be ignored. Different major scattering channels of the out-of-plane flexural modes result in different thermal conductivity sensitivity to strains, and the disparity in anharmonicity leads to the different thermal conductivity under no strains. Through our calculations and analysis, we conclude that the pentagonal silicene structure shares very similar properties with the hexagonal silicene structure, which suggests that the pentagonal silicene structures might also be very promising for future nanoelectronic applications.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
HL appreciates the financial support from the National Natural Science Foundation of China (No. 11904296), Fundamental Research Funds for the Central Universities (No. SWU119002), and the Natural Science Foundation of Chongqing (cstc2020jcyj-msxm0803).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.683503/full#supplementary-material
Aierken, Y., Leenaerts, O., and Peeters, F. M. (2016). A First-Principles Study of Stable Few-Layer Penta-Silicene. Phys. Chem. Chem. Phys. 18, 18486–18492. doi:10.1039/c6cp03200a
Balandin, A. A. (2011). Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 10, 569–581. doi:10.1038/nmat3064
Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872
Cahangirov, S., Topsakal, M., Akturk, E., Sahin, H., and Ciraci, S. (2009). Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 102, 236804. doi:10.1103/PhysRevLett.102.236804
Cai, Y., Lan, J., Zhang, G., and Zhang, Y. W. (2014). Lattice Vibrational Modes and Phonon Thermal Conductivity of Monolayer Mos 2. Phys. Rev. B 89, 035438. doi:10.1103/physrevb.89.035438
Cerda, J. I., Slawinska, J., Le Lay, G., Marele, A. C., Gomez-Rodriguez, J. M., and Davila, M. E. (2016). Unveiling the pentagonal nature of perfectly aligned single-and double-strand si nano-ribbons on ag (110). Nat. Commun. 7. doi:10.1038/ncomms13076
Chen, J., Schusteritsch, G., Pickard, C. J., Salzmann, C. G., and Michaelides, A. (2016). Two Dimensional Ice from First Principles: Structures and Phase Transitions. Phys. Rev. Lett. 116, 025501. doi:10.1103/physrevlett.116.025501
Ding, Y., and Wang, Y. (2015). Hydrogen-induced Stabilization and Tunable Electronic Structures of Penta-Silicene: a Computational Study. J. Mater. Chem. C. 3, 11341–11348. doi:10.1039/C5TC02504D
Ferrari, A. C. (2014). Science and Technology Roadmap for Graphene, Related Two-Dimensional Crystals, and Hybrid Systems. Nanoscale 7, 4598–4810. doi:10.1039/C4NR01600A
Geim, A. K. (2009). Graphene: Status and Prospects. Science 324, 1530–1534. doi:10.1126/science.1158877
Hu, S., Lozada-Hidalgo, M., Wang, F. C., Mishchenko, A., Schedin, F., Nair, R. R., et al. (2014). Proton Transport through One-Atom-Thick Crystals. Nature 516, 227–230. doi:10.1038/nature14015
Kresse, G. (1996). Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kresse, G. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Li, F., Tu, K., Zhang, H., and Chen, Z. (2015). Flexible Structural and Electronic Properties of a Pentagonal B 2 C Monolayer via External Strain: A Computational Investigation. Phys. Chem. Chem. Phys. 17, 24151–24156. doi:10.1039/c5cp03885e
Li, W., Carrete, J., Katcho, A., and Mingo, N. (2014). Shengbte: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Li, W., Carrete, J., and Mingo, N. (2013). Thermal Conductivity and Phonon Linewidths of Monolayer Mos2 from First Principles. Appl. Phys. Lett. 103, 253103. doi:10.1063/1.4850995
Lindsay, L., Broido, D., and Mingo, N. (2010). Flexural Phonons and Thermal Transport in Graphene. Phys. Rev. B. 82, 115427. doi:10.1103/physrevb.82.115427
Liu, H., Qin, G., Lin, Y., and Hu, M. (2016). Disparate Strain Dependent Thermal Conductivity of Two-Dimensional Penta-Structures. Nano Lett. 16, 3831–3842. doi:10.1021/acs.nanolett.6b01311
Liu, H. K., Lin, Y., and Luo, S. N. (2014). Grain Boundary Energy and Grain Size Dependences of Thermal Conductivity of Polycrystalline Graphene. J. Phys. Chem. C. 118, 24797–24802. doi:10.1021/jp508035b
Lopez-Bezanilla, A., and Littlewood, P. B. (2015). σ–π-band Inversion in a Novel Two-Dimensional Material. J. Phys. Chem. C. 119, 19469–19474. doi:10.1021/acs.jpcc.5b04726
Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B. 13, 5188–5192. doi:10.1103/PhysRevB.13.5188
Novoselov, K. S., Fal’ko, V. I., Colombo, L., Gellert, P. R., Schwab, M. G., and Kim, K. (2015). A Roadmap for Graphene. Nature 490, 192–200. doi:10.1038/nature11458
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669. doi:10.1126/science.1102896
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Qin, Z., Qin, G., Zuo, X., Xiong, Z., and Hu, M. (2017). Orbitally Driven Low Thermal Conductivity of Monolayer Gallium Nitride (gan) with Planar Honeycomb Structure: a Comparative Study. Nanoscale 9, 4295–4309. doi:10.1039/c7nr01271c
Sahin, H., Cahangirov, S., Topsakal, M., Bekaroglu, E., Akturk, E., Senger, R. T., et al. (2009). Monolayer Honeycomb Structures of Group-Iv Elements and Iii-V Binary Compounds: First-Principles Calculations. Phys. Rev. B. 80, 155453. doi:10.1103/PhysRevB.80.155453
Tamura, S. (1983). Isotope Scattering of Dispersive Phonons in Ge. Phys. Rev. B. 27, 858. doi:10.1103/physrevb.27.858
Turney, J., Landry, E., McGaughey, A., and Amon, C. (2009). Predicting Phonon Properties and Thermal Conductivity from Anharmonic Lattice Dynamics Calculations and Molecular Dynamics Simulations. Phys. Rev. B. 79, 064301. doi:10.1103/physrevb.79.064301
Wei, X., Wang, Y., Shen, Y., Xie, G., Xiao, H., Zhong, J., et al. (2014). Phonon Thermal Conductivity of Monolayer Mos2: A Comparison with Single Layer Graphene. Appl. Phys. Lett. 105, 103902. doi:10.1063/1.4895344
Xie, H., Ouyang, T., Germaneau, E., Qin, G., Hu, M., and Bao, H. (2016). Large Tunability of Lattice Thermal Conductivity of Monolayer Silicene via Mechanical Strain. Phys. Rev. B. 93, 075404. doi:10.1103/physrevb.93.075404
Zhang, S., Zhou, J., Wang, Q., Chen, X., Kawazoe, Y., and Jena, P. (2015). Penta-graphene: A New Carbon Allotrope. Proc. Natl. Acad. Sci. 112, 2372–2377. doi:10.1073/pnas.1416591112
Zhang, S., Zhou, J., Wang, Q., and Jena, P. (2016). Beyond Graphitic Carbon Nitride: Nitrogen-Rich Penta-Cn2 Sheet. J. Phys. Chem. C. 120, 3993–3998. doi:10.1021/acs.jpcc.5b12510
Keywords: thermal conductivity, phonon, penta-structure, first principle calculation, silicene
Citation: Liu H, Qin G and Hu M (2021) Uniform Strain-Dependent Thermal Conductivity of Pentagonal and Hexagonal Silicene. Front. Mater. 8:683503. doi: 10.3389/fmats.2021.683503
Received: 21 March 2021; Accepted: 27 April 2021;
Published: 17 May 2021.
Edited by:
Zhenzhen Qin, Zhengzhou University, ChinaReviewed by:
Xuebin Wang, Nanjing University, ChinaCopyright © 2021 Liu, Qin and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huake Liu, aHVha2VsaXVAc3d1LmVkdS5jbg==; Ming Hu, aHVAc2MuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.