Creep Behavior of Near α High Temperature Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si Alloy

This study focuses on the microstructure characteristics and tensile and creep properties of a near α high temperature Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy. Microstructure characteristics were quantitatively investigated using optical microscopy, scanning electron microscope, and transmission electron microscopy. Tensile properties were carried out at room and high temperature. Creep properties were detected under applied stresses ranging from 100–350 MPa at 873–973 K, respectively. Results showed that Widmanstätten microstructure was obtained after hot forged and heat treatment. The strength decreases and the elongation rises with temperature increasing. The ultimate strength and elongation were 1010 MPa, 12% at room temperature, and 620 MPa, 20% at 923 K, respectively. The steady state creep rates rise correspondingly with stress and temperature. Stress exponents are measured within the range of 3.0–3.5. Thus, the creep mechanism is diffusion-controlled viscous glide of dislocation. Ti₃Al precipitates are observed. The boundaries and precipitates can obstruct dislocation movement to improve the creep properties. Fracture mechanism of creep is intergranular. The creep mechanism varied from climb of dislocation to sliding of dislocation solution.

Introduction

Titanium and its alloys exhibit many excellent properties, such as low density, good corrosion resistance, high modulus, and strength, allowing them to serve as competitive structural materials for aerospace components, aircraft engines, etc. (Hajari et al., 2017; Li et al., 2017; Xiong et al., 2020). The components of aeroengines operate in extreme environments of high temperature, high speed, and high pressure when the engine is running. High-temperature titanium alloys can meet the performance requirements of aeroengines due to their excellent high-temperature mechanical properties and high-temperature creep resistance. With the development of the aerospace manufacturing industry, the use temperature of components is getting higher and higher, so the high-temperature property requirements of materials are also getting higher and higher. And there is an urgent need to develop new high-temperature titanium alloys. The content of β-phase is relatively high in β and α-β titanium alloys. At high temperatures, the thermal stability and creep resistance of the β and α-β titanium alloys are greatly reduced. Near-α-type titanium alloys have good durability and creep resistance at high temperatures and are suitable for use in high-temperature working environments. In particular, near α titanium alloy has been developed to make various rotor and stator components for aeroengines (Jia et al., 2011; Balasundar et al., 2014; Su et al., 2018; Yang et al., 2020). In order to improve high temperature strength and creep-resistant stress for aerospace applications, effort has been devoted to the search for new near α titanium alloys or the development of existing alloys (Es-souni, 2001; Pan et al., 2009). Creep resistance is a time-dependent inelastic deformation often reported to occur at elevated temperatures and constant stresses, which is an important mechanical property for aeroengine materials (Balasundar et al., 2014).

Numerous studies have been carried out to understand the effect of various parameters on the creep resistance of the near α titanium alloy. For example, Hosseini et al. (Zheng et al., 2021) investigated the creep-rupture properties of near α titanium alloy with Widmanstätten, bimodal, and trimodal microstructure. Balasundar et al. (Balasundar et al., 2014) claimed that the creep strain increases with decreasing solution treatment temperature. In addition, Li et al. (Li et al., 2012) and Xiao et al. (Xiao et al., 2011) reported on the creep properties of near α high temperature titanium alloy with Widmanstätten microstructure and basketweave microstructure. The creep properties of Ti alloy with Widmanstätten microstructure and basketweave microstructure are superior to those of bimodal and trimodal microstructure. Ochonogor et al. (Ochonogor et al., 2017) explained that the temperature range at which creep deformation may occur at different levels is dependent on the response of material to deformation. Wang et al. (Pan et al., 2009) claimed that the creep mechanism of Ti alloy was divided into two types: non-pure metals controlled by viscous dislocation sliding, and pure metals controlled by climb of dislocation.

Since the chemical composition of near α Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy is different from the traditional near α titanium alloy, it is necessary to study and assess its high temperature creep behavior and application potentials. In the present work, the conventional Widmanstätten microstructures were prepared in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy. As a parametric study, creep properties as a function of testing temperatures and applied stresses were carefully investigated, with underlying mechanisms being discussed.

Experimental Procedure

The new near α Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy was designed and prepared in a vacuum consumable furnace according to a stoichiometric ratio. The ingot was melted three times to ensure composition uniform. The weight of the ingot was 150 kg. The Beta-transus temperature was 1303 K. In order to obtain Widmanstätten microstructure, first the billet with diameter of 230 mm was forged at 1403 K, and finally forged into bars ϕ 50 mm at 1273 K.

The Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy was heat-treated by solution treatment at 1323 K for 2 h, air cooled to room temperature, then annealed at 843 K for 2 h, and again air cooled to room temperature. Subsequently, samples were extracted for metallographic examination for the further preparation of tensile and creep specimens.

Microstructures of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy before and after creep deformation were observed by optical microscopy (OM), Philips-CM 200 transmission electron microscopy (TEM) and Philips FEI SIRION 200 scanning electron microscope (SEM). The specimens for microstructural observation were ground and polished, then etched by a solution of HF (1 ml), HNO₃ (3 ml), and water (10 ml) for 20 s. The TEM specimens were processed into (3 mm × 20 μm) by Dimple, then prepared by argon iron milling (Gatan).

Tensile properties were carried out by Zwick T1-Fr020 TN materials testing machine with a strain rate of 10⁻³ s⁻¹ at room temperature and high temperature (873 K, 923 K, and 973 K). Tensile specimens were machined along the parallel direction of hot forging. The gauge section’s size of tensile specimens is 15 mm × 4 mm × 1.5 mm. Creep specimens were machined along the parallel direction of hot forging. The creep specimens gauge section’s size is ϕ 5 mm × 25 mm. Creep properties of specimens were tested by CSS-3905 materials testing machine under a stress ranging from 100 to 350 MPa at 873 K, 923 K, and 973 K.

Results and Discussions

Microstructure and Tensile Properties

Figure 1 shows the microstructure of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy. The average size of β grain is about 80 μm, and some primary α phases are visible at the β grain boundaries. The microstructure consists of coarse colonies of similarly aligned Widmanstätten α + β phase. Size of both α lath and α + β colonies increase with the growth of β grain size. To be specific, the average size of α + β colonies in Figure 1 is about 28 μm and that of α lath is about 7.2 μm.

FIGURE 1

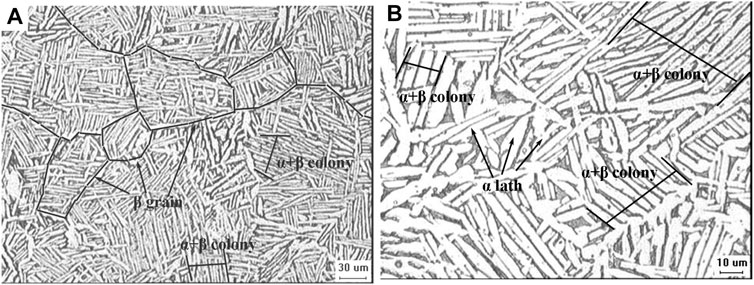
FIGURE 1. Optical microstructure of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after heat treatment with different magnification scales, (A) Widmanstätten, (B) higher magnification of Widmanstätten.

Microstructural characteristics (such as morphology and volume fraction of α and β phases, β grain size, etc.) are important factors that significantly influence the mechanical properties of Ti alloys (Ding et al., 2002; Jia et al., 2014; Li et al., 2018). The mentioned microstructural characteristics are determined by chemical composition, processing, and heat treatment method (Ding et al., 2002). The bimodal, Widmanstätten, and basket microstructures are often used in near α and α+β Ti alloys (Pan et al., 2009). Widmanstätten microstructure in Ti alloys has been reported to provide a better creep resistance compared with bimodal microstructure (Balasundar et al., 2014).

The room and high temperature tensile properties of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloys are listed in Table 1. At room temperature, yield strength, ultimate strength, elongation, and elastic modulus of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloys are 1,010 MPa, 1,150 MPa, 12%, and 118 GPa, respectively. The yield strength is higher than that of near α Ti-60 (∼982 MPa) (Li et al., 2017), Ti-6242s (931 MPa) (Hosseini et al., 2017), and IMI834 (∼931 MPa) (Balasundar et al., 2014). The high temperature tensile properties are affected greatly by temperature increasing. Ultimate strength and elongation of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb- 1.0Mo-0.32Si alloys are 698 MPa and 14% at 873 K. In comparison with those of 873 K, ultimate strength decreases about 10 and 20%, while elongation increases about 43 and 143% when tested at 923 K. The ultimate strength is about 13% higher than that of near α Ti-60 (∼617 MPa) at 873 K (Li et al., 2017).

TABLE 1

TABLE 1. Tensile properties of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloys.

Figure 2A,B show the SEM fractographies of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after room temperature and 973 K tensile, respectively. A large number of ductile dimples and a few stream-like patterns are observed in Figures 2A,B, which indicates that the fracture made of both room temperature and 973 K is ductility fracture. Dimples in Figure 2B are more common and deeper than those in Figure 2A, which would indicate better ductility of specimens tested at 973 K tensile than that of room temperature. The result is consistent with Table1.

FIGURE 2

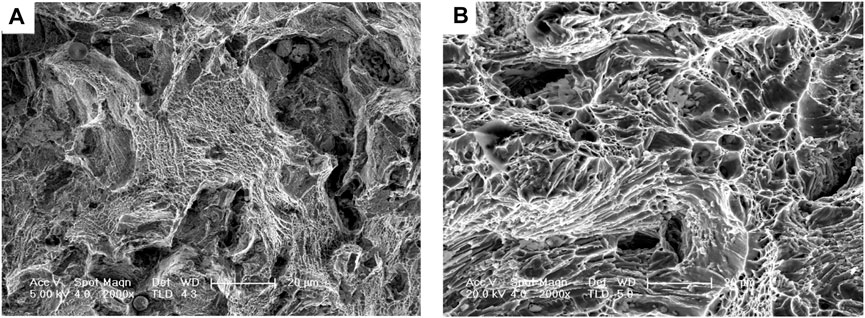
FIGURE 2. Fracture morphologies fractography of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after tensile, (A) room temperature, (B) 973 K.

Creep Behavior

The curves of logarithmic scale of creep strain vs. logarithmic scale of time are shown in Figure 3, which exhibit typical features of creep curves of Class-M solution alloy: the primary stage with a decreasing creep rate, the steady-state stage with steady creep rate, and the third stage with significantly increasing creep rate before creep rupture. The steady state creep stages last relatively longer at low temperatures or low stresses compared with those at high temperatures or high stresses. The steady stage lasts for a long time and the test is terminated after a constant creep rate obtained, when the temperature or stress is low. While, with a high the temperature or stress, the first and second stage are short, directly entering the third stage, and the minimum creep rate is determined as steady state creep rate.

FIGURE 3

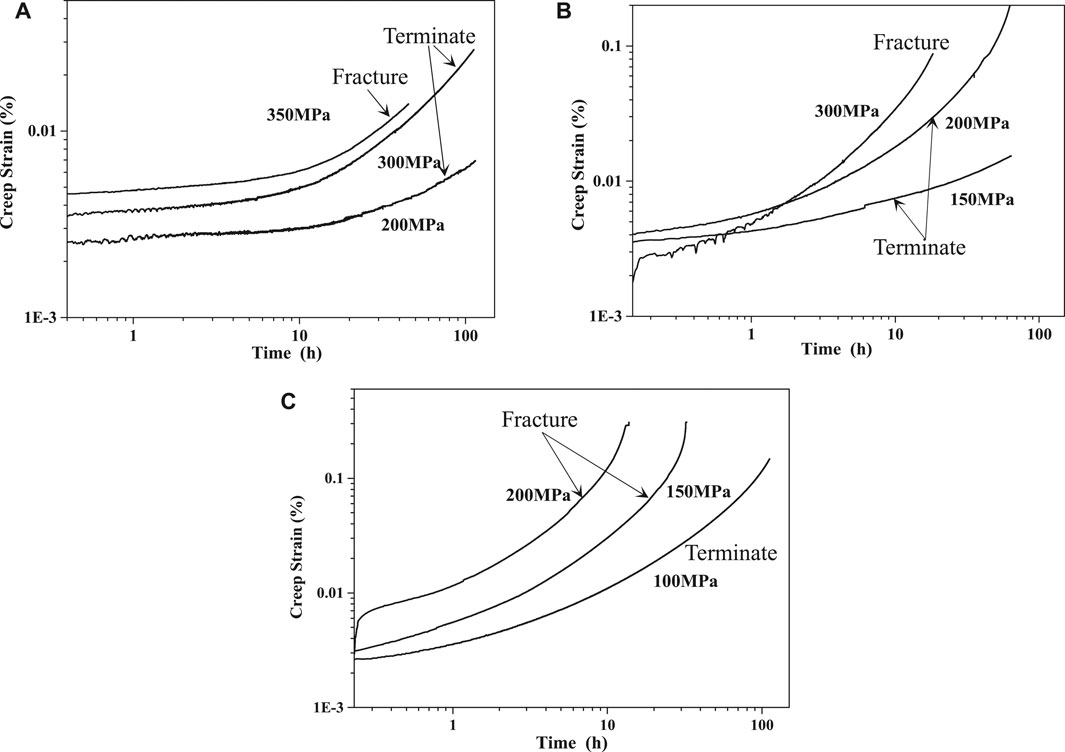
FIGURE 3. Logarithmic scale of creep strain vs. logarithmic scale of time at: (A) 873 K, (B) 923 K, (C) 973 K.

In general, the creep rate of this Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy can be obtained from the following Eq. 1 (Xiao et al., 2011):

$\epsilon =A{\sigma }^n\exp \left(-\frac{Q}{RT}\right)(1)$

where $\stackrel{•}{\epsilon }$ is steady state creep rates (creep rates), A is the material property constant, σ is the stress, n is the stress exponent, Q is the activation energy, R is the gas constant, and T is the temperature. Steady state creep rates of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy at different testing conditions are shown in Figure 4. The creep rate is found to increase with increasing temperature and stress. The creep strain of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy under 200 MPa is much smaller than that of IMI834 0.28% under 150 MPa at 873 K (Balasundar et al., 2014). Creep rate of near-α Ti alloy Ti-6Al-4Sn-4Zr-0.8Mo-1Nb-W-0.25Si is 3.35 × 10^–8 s⁻¹, 4.68 × 10^–7 s⁻¹, or 1.27 × 10^–6 s⁻¹ under 150, 200 MPa, or 250 MPa at 873 K (Zheng et al., 2021). Steady state creep rate of Ti-5Al-5Mo-5V-1Fe-1Cr alloy is 9.27 × 10^–8 s⁻¹ at 773 K, 200 MPa (Nie et al., 2014). The steady-state creep rate of TC18 samples with lamellar structure is 1.90 × 10^–8 s⁻¹ at 773 K, 200 MPa (Nie et al., 2016). The creep rate of near -α Ti alloy IMI834, IMI834 melt using high iron sponge, and IMI834 melt using low iron sponge with fully transformed β structure -lamellar α and retained β films is 5 × 10^–8∼1.5 × 10⁻⁷s⁻¹ at 923K, 220 MPa (Mishra et al., 2005). At 873K under an applied load of 210 MPa, the creep rate of Ti6242S is 5 × 10^–8 s⁻¹ after 60 h (Wimler et al., 2020). It can be concluded from the above report that the creep rate of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo -0.32Si alloy is significantly reduced.

FIGURE 4

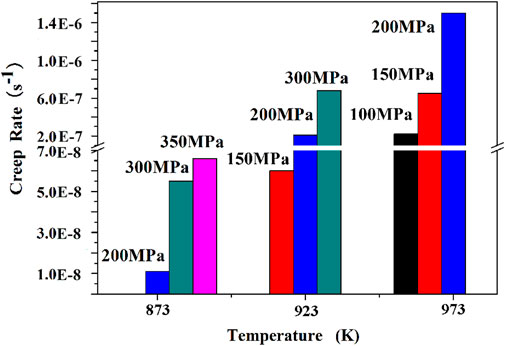
FIGURE 4. Creep rate of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy at different testing conditions.

The stress exponent (n) could be calculated by logarithmic interpolation of Eq. 1. Figure 5 shows the curves of stress - creep strain rate of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy on a double logarithmic scale. At 873 K, 923 K, and 973 K, the stress exponents are about 3.5, 3.5, and 3.1 in Figure 5. All the stress exponents locate within the range of solid solutions 3.0–3.5, so the creep mechanism is diffusion viscous-drag-controlled (Pan et al., 2009). When the stress exponent is 3.5, creep is dominated by dislocation sliding at low stress levels, but the stress exponent is 4.6 when creep is governed by climb of dislocation at higher stress level. If Al content in Ti alloy is high and temperature of creep test is high, the transition from climb of dislocation into glide of dislocation may occur (Pan et al., 2009).

FIGURE 5

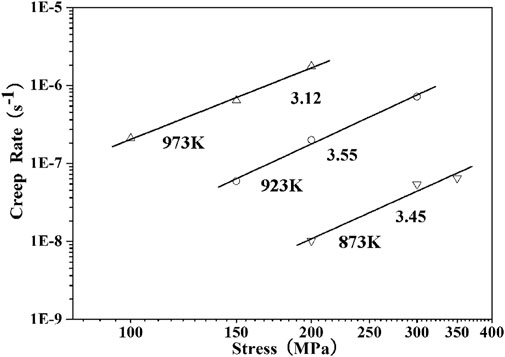
FIGURE 5. Relationship between stress and creep rate of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy on a double logarithmic scale.

The stress exponents of Ti alloy decrease with temperature increasing. If the shear modulus is added to Eq. 1, the steady-state creep rate can be deduced as follows (Es-souni, 2001):

$\dot{\text{ε}}=A\frac{Gb}{RT}{{\displaystyle \left(\frac{\text{σ}}{G}\right)}}^{n}D=A\frac{Gb}{RT}{{\displaystyle \left(\frac{\text{σ}}{G}\right)}}^n{D}_0\exp \left(-\frac{Q}{RT}\right)(2)$

$Q\left[\text{kJ/mol}\right]=-R\frac{d\ln \left(\dot{\text{ε}}T{G}^{n-1}\right)}{d\left(\frac{1000}{T}\right)}(3)$

where G is the shear modulus and D is the diffusion coefficient. The activation energy (Q) of Eq. 3 can be deduced from Eq. 2. According to Arrhenius equation, the activation energy can be calculated by the Arrhenius plot of logarithmic $\dot{\text{ε}}$ or $\dot{\text{ε}}T{G}^{\left(n-1\right)}$ vs. the reciprocal Kelvin temperature 1,000/T that provided constant stress.

The activation energies of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy under 150–300 MPa are calculated based on Eq. 3. The curve of logarithmic $\dot{\text{ε}}$ of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si vs. the reciprocal Kelvin temperature 1,000/T are shown in Figure 6. The activation energies of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy are 366 kJ/mol, 354 kJ/mol, and 337 kJ/mol under 150 MPa, 200 MPa, and 300 MPa, respectively, which is much higher than that of α Ti self-diffusion 240 kJ/mol (Malakondaiah and Rama Rao, 1981) and close to Al diffusion activation energy of α Ti (329 kJ/mol) (Köppers et al., 1997). The activation energy values fluctuate slightly with variation of stress.

FIGURE 6

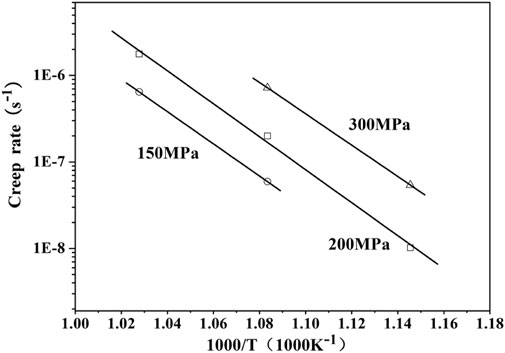
FIGURE 6. The activation energies of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy at different stress.

Creep rupture lives of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy were tested at 873 K, 923 K, and 973 K, respectively. Figure 7 shows the stress-creep rupture life of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy on a double logarithmic scale. The creep rupture life deceases with temperature or applied stress increasing. There is a linear correspondence between the logarithmic applied stress and the logarithmic creep rupture lifetime. An inverse linear relationship is found between the creep rupture life and the creep rate by Monkman and Grant, which is named as the Monkman-Grant relationship (Ali and Tamin, 2013). A constant (M ∼ 0.09) is obtained. A constant of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb- 1.0Mo-0.32Si alloy calculated by Eq. 4 is 0.75∼0.89. Creep rupture lives depends on the creep deformation rate, indicating that creep performance failure is controlled by strain (Evans et al., 1996).

$\text{tf}\times \stackrel{•}{\epsilon }=\text{M}\left(\sim 0.9\right)(4)$

Figure 8 shows the SEM microstructure near the fractography after tensile and after creep. A few circular micro cavities and intact continuous α phases on the grain boundaries are observed after tensile in Figure 8A. However, Figure 8B displays many circular micro cavities and few intact continuous α phases on the grain boundaries after creep. The fracture mechanism of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after creep is different from that after tensile. The circular microcavities on the grain boundaries grow and combine with each other to form cracks during creep, which indicates a typical intergranular fracture mechanism. The grain boundary strength decreases during high temperature creep.

FIGURE 7

FIGURE 7. The curve of applied stress-creep rupture life.

FIGURE 8

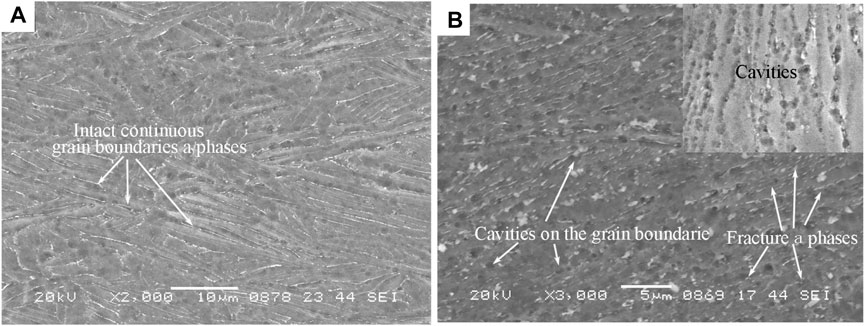
FIGURE 8. Scanning electron microscope (SEM) microstructure near the fractography, (A) after tensile, (B) after creep.

It is well known that creep mechanisms of near α titanium alloys include glide of dislocation and grain boundary sliding at high temperature (Pan et al., 2009). As the self and impurity diffusion in α Ti is lower than that in β Ti, deformation of α phase plays a dominant role in the process of creep. The dislocation motions are blocked in α phase. Figure 9 shows transmission electron microscopy (TEM) of dislocation motions in both grain boundaries (Figure 9A) and α lath (Figure 9B) after creep at 923 K with applied stress of 200 MPa. The microstructure of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after heat treatment is Widmanstätten microstructure with several colonies in β grains as shown in Figure 1. The α+β laths present an almost identical crystalline orientation with each other in α+β colonies, which has a great effect on the creep properties in Ti alloys. The Burgers orientation relationship is followed between α + β laths in Widmanstätten and basket microstructure, i.e., the (110) [111] slip system of β phase is coplanar with the (0001) [1,120] slip system of α phase (Miller et al., 1987; Zheng et al., 2021). The dislocation slip is not effectively blocked by interfaces of α+β laths in each colony, so dislocations can easily occur across the interfaces of α+β laths and the entire colony. However, each various colony has a unique relative orientation and the interface between colony can effectively prevent sliding transport (Bhattacharyya et al., 2003). Thus, the size of α+β colonies has a great influence on the creep properties of Ti alloy. The α+β colony size will be reduced with the decrease of β grain size, therefore, the α+β colony size can be effectively controlled by controlling the β crystal size (Yang et al., 2015). Moreover, small β grains can introduce more boundaries to serve as the barriers for dislocation transmission, which could influence the mechanical properties of Ti alloy (He et al., 2019). The creep rate becomes higher when the sizes of average grains become smaller.

FIGURE 9

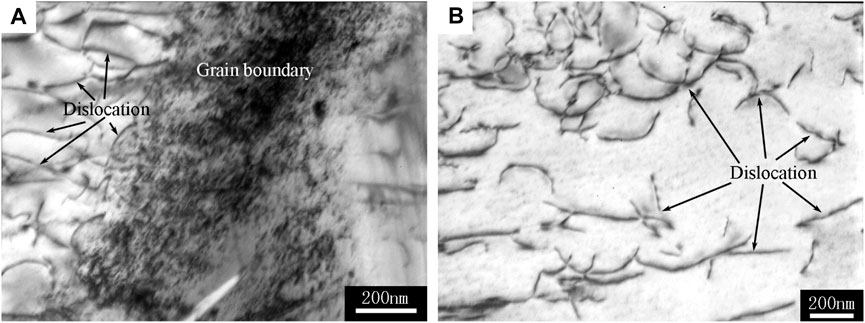
FIGURE 9. Transmission electron microscopy (TEM) of dislocation motions in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after creep at 923 K, 200 MPa, (A) in grain boundary, (B) in α lath.

The precipitated particles can also hinder dislocation slip and increase creep resistance. Figure 10 shows the precipitation of Ti₃Al in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after creep at 923 K with stress of 200 MPa. As shown in Figure 10, the Ti₃Al precipitates are small particles distributed uniformly in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy. The size of Ti₃Al particles becomes larger with increasing of creep temperature and time. The moving dislocations cut Ti₃Al particles in process of creep (Zheng et al., 2021), as shown in Figure 10. The shear stress along the active slip planes locally reduces as in process of deformation, which leads to planar slip. A large number of dislocations are concentrated at grain boundaries which will stop most of the dislocation from further transmission (Li et al., 2011a; Li et al., 2011b). Therefore, grain boundaries, interfaces, and precipitates are important influencing factors for creep properties.

FIGURE 10

FIGURE 10. Dark field TEM micrograph of Ti₃Al in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy after creep at 923 K, 200 MPa.

Conclusion

The tensile and creep properties of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si titanium alloy were investigated at 873, 923, and 973 K, respectively. The results can be summarized as follows:

1) At room temperature, yield strength and elongation of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo -0.32Si alloys are 1,010 MPa, 12%. Ultimate strength and elongation are 698 MPa and 14% at 873 K. All the stress exponents of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si locate within the range of solid solutions 3.0–3.5. The activation energies are 337–366 kJ/mol under 150–300 MPa. Under the same conditions, the tensile and creep properties of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si are better than those of IMI834 and Ti6242 alloy.

2) The creep fracture mechanism of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy is a typical intergranular fracture.

3) The Ti₃Al particles precipitate in the process of creep in Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb- 1.0Mo-0.32Si alloy. The boundaries and precipitates can obstruct dislocation movement, which improves the creep properties. Creep test of Ti-6.6Al-4.6Sn-4.6Zr-0.9Nb-1.0Mo-0.32Si alloy was implemented at high temperature; the transition from climb of dislocation to slide of dislocation may occur.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JL designed the experiment, answer questions and guided the arrangement during the whole thesis. DY processed the related experimental data and writed the paper. WT revised the paper and paid attention to the status of contribution. XZ and KS helped to inquire relevant information.

Funding

This work was supported by the National Nature Science Foundation of China (Grant Nos. 51504151, 51501112) and the Shanghai Science and Technology Committee Innovation Grant (17JC1400600, 17JC1400603).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ali, H. O., and Tamin, M. N. (2013). Modified Monkman–Grant Relationship for Austenitic Stainless Steel Foils. J. Nucl. Mater. 433, 74–79. doi:10.1016/j.jnucmat.2012.08.048

CrossRef Full Text | Google Scholar

Balasundar, I., Raghu, T., and Kashyap, B. P. (2014). Correlation between Microstructural Features and Creep Strain in a Near-α Titanium alloy Processed in the α+β Regime. Mater. Sci. Eng. A 609, 241–249. doi:10.1016/j.msea.2014.04.079

CrossRef Full Text | Google Scholar

Bhattacharyya, D., Viswanathan, G. B., Denkenberger, R., Furrer, D., and Fraser, H. L. (2003). The Role of Crystallographic and Geometrical Relationships between α and β Phases in an α/β Titanium alloy. Acta Materialia 51, 4679–4691. doi:10.1016/s1359-6454(03)00179-4

CrossRef Full Text | Google Scholar

Ding, R., Guo, Z. X., and Wilson, A. (2002). Microstructural Evolution of a Ti-6Al-4V alloy during Thermomechanical Processing. Mater. Sci. Eng. A 327, 233–245. doi:10.1016/s0921-5093(01)01531-3

CrossRef Full Text | Google Scholar

Es-souni, M. (2001). Creep Behaviour and Creep Microstructures of a High-Temperature Titanium alloy Ti-5.8Al-4.0Sn-3.5Zr-0.7Nb-0.35Si-0.06C (Timetal 834). Mater. Characterization 46, 365–379. doi:10.1016/s1044-5803(01)00136-x

CrossRef Full Text | Google Scholar

Evans, R. W., Hull, R. J., and Wilshire, B. (1996). The Effects of Alpha-Case Formation on the Creep Fracture Properties of the High-Temperature Titanium alloy IMI834. J. Mater. Process. Tech. 56, 492–501. doi:10.1016/0924-0136(96)85109-0

CrossRef Full Text | Google Scholar

Hajari, A., Morakabati, M., Abbasi, S. M., and Badri, H. (2017). Constitutive Modeling for High-Temperature Flow Behavior of Ti-6242S alloy. Mater. Sci. Eng. A 681, 103–113. doi:10.1016/j.msea.2016.11.002

CrossRef Full Text | Google Scholar

He, Y. S., Hu, R., Luo, W. Z., He, T., Lai, Y. J., Du, Y. J., et al. (2019). Microstructural Evolution and Creep Deformation Behavior of Novel Ti-22Al-25Nb-1Mo-1V-1Zr-0.2Si (at.%) Orthorhombic alloy. Trans. Nonfer Met. 29, 313–321. doi:10.1016/s1003-6326(19)64941-1

CrossRef Full Text | Google Scholar

Hosseini, R., Morakabati, M., Abbasi, S. M., and Hajari, A. (2017). Development of a Trimodal Microstructure with superior Combined Strength, Ductility and Creep-Rupture Properties in a Near Alpha Titanium alloy. Mater. Sci. Eng. A 696, 155–165. doi:10.1016/j.msea.2017.04.068

CrossRef Full Text | Google Scholar

Jia, W., Zeng, W., Liu, J., Zhou, Y., and Wang, Q. (2011). On the Influence of Processing Parameters on Microstructural Evolution of a Near Alpha Titanium alloy. Mater. Sci. Eng. A 530, 135–143. doi:10.1016/j.msea.2011.09.064

CrossRef Full Text | Google Scholar

Jia, W., Zeng, W., and Yu, H. (2014). Effect of Aging on the Tensile Properties and Microstructures of a Near-Alpha Titanium alloy. Mater. Des. 58, 108–115. doi:10.1016/j.matdes.2014.01.063

CrossRef Full Text | Google Scholar

Köppers, M., Herzig, C., Friesel, M., and Mishin, Y. (1997). Intrinsic Self-Diffusion and Substitutional Al Diffusion in α-Ti. Acta Materialia 45, 4181–4191. doi:10.1016/s1359-6454(97)00078-5

CrossRef Full Text | Google Scholar

Li, H., Zhao, Z., Ning, Y., Guo, H., and Yao, Z. (2018). Characterization of Microstructural Evolution for a Near-α Titanium Alloy with Different Initial Lamellar Microstructures. Metals 8, 1045. doi:10.3390/met8121045

CrossRef Full Text | Google Scholar

Li, J., Wang, L., Qin, J., Chen, Y., Lu, W., and Zhang, D. (2012). Effect of Microstructure on High Temperature Properties of In Situ Synthesized (TiB+La2O3)/Ti Composite. Mater. Characterization 66, 93–98. doi:10.1016/j.matchar.2012.02.010

CrossRef Full Text | Google Scholar

Li, J., Wang, L., Qin, J., Chen, Y., Lu, W., and Zhang, D. (2011). The Effect of Heat Treatment on thermal Stability of Ti Matrix Composite. J. Alloys Comp. 509, 52–56. doi:10.1016/j.jallcom.2010.09.005

CrossRef Full Text | Google Scholar

Li, J., Wang, L., Qin, J., Chen, Y., Lu, W., and Zhang, D. (2011). Thermal Stability of In Situ Synthesized (TiB+La2O3)/Ti Composite. Mater. Sci. Eng. A 528, 4883–4887. doi:10.1016/j.msea.2011.03.018

CrossRef Full Text | Google Scholar

Li, W., Chen, Z., Liu, J., Wang, Q., and Sui, G. (2017). Effect of Texture on Anisotropy at 600 °C in a Near-α Titanium alloy Ti60 Plate. Mater. Sci. Eng. A 688, 322–329. doi:10.1016/j.msea.2017.01.098

CrossRef Full Text | Google Scholar

Malakondaiah, G., and Rama Rao, P. (1981). Creep of Alpha-Titanium at Low Stresses. Acta Metallurgica 29, 1263–1275. doi:10.1016/0001-6160(81)90017-1

CrossRef Full Text | Google Scholar

Miller, W. H., Chen, R. T., and Starke, E. A. (1987). Microstructure, Creep, and Tensile Deformation in Ti-6Al-2Nb-1Ta-0.8Mo. Mta 18, 1451–1468. doi:10.1007/bf02646658

CrossRef Full Text | Google Scholar

Mishra, H., Ghosal, P., Nandy, T. K., and Sagar, P. K. (2005). Influence of Fe and Ni on Creep of Near α-Ti alloy IMI834. Mater. Sci. Eng. A 399, 222–231. doi:10.1016/j.msea.2005.03.027

CrossRef Full Text | Google Scholar

Nie, X.-A., Hu, Z., Liu, H.-Q., Yi, D.-Q., Chen, T.-Y., Wang, B.-f., et al. (2014). High Temperature Deformation and Creep Behavior of Ti-5Al-5Mo-5V-1Fe-1Cr alloy. Mater. Sci. Eng. A 613, 306–316. doi:10.1016/j.msea.2014.06.116

CrossRef Full Text | Google Scholar

Nie, X., Liu, H., Zhou, X., Yi, D., Huang, B., Hu, Z., et al. (2016). Creep of Ti-5Al-5Mo-5V-1Fe-1Cr alloy with Equiaxed and Lamellar Microstructures. Mater. Sci. Eng. A 651, 37–44. doi:10.1016/j.msea.2015.10.092

CrossRef Full Text | Google Scholar

Ochonogor, O. F., Akinlabi, E. T., and Nyembwe, D. (2017). A Review on the Effect of Creep and Microstructural Change under Elevated Temperature of Ti6Al4V alloy for Turbine Engine Application. Mater. Today Proc. 4, 250–256. doi:10.1016/j.matpr.2017.01.019

CrossRef Full Text | Google Scholar

Pan, W., Qin, J., N.W.J, Lu, and Chen, Y. F. (2009). Creep Behavior of In Situ Synthesized 7715D Titanium Matrix Composite. Mater. Trans. 50, 1411–1417. doi:10.2320/matertrans.mra2008425

CrossRef Full Text | Google Scholar

Su, C.-Y., Zhou, C.-Y., Lu, L., Li, J., Sun, P.-Y., and He, X.-H. (2018). Effect of Temperature and Dwell Time on Fatigue Crack Growth Behavior of CP-Ti. Metals 8, 1031. doi:10.3390/met8121031

CrossRef Full Text | Google Scholar

Wimler, D., Lindemann, J., Gammer, C., Spoerk-Erdely, P., Stark, A., Clemens, H., et al. (2020). Novel Intermetallic-Reinforced Near-α Ti Alloys Manufactured by Spark Plasma Sintering. Mater. Sci. Eng. A 792, 139798. doi:10.1016/j.msea.2020.139798

CrossRef Full Text | Google Scholar

Xiao, L., Tian, S. G., Bao, X. Y., and Chen, L. Q. (2011). Creep Properties and Effect Factors of Hot Continuous Rolled Ti-6Al-4V alloy. Mater. Sci. Eng. A. 529, 452–458. doi:10.1016/j.msea.2011.09.061

CrossRef Full Text | Google Scholar

Xiong, W., Luo, J., Wang, B., Li, X., and Chen, J. (2020). High Temperature Creep Behavior of Hydrogenated Ti-6Al-4V alloy. Int. J. Lightweight Mater. Manufacture 3, 298–304. doi:10.1016/j.ijlmm.2020.03.001

CrossRef Full Text | Google Scholar

Yang, D.-Y., Guo, S., Peng, H.-X., Cao, F.-Y., Liu, N., and Sun, J.-F. (2015). Size Dependent Phase Transformation in Atomized TiAl Powders. Intermetallics 61, 72–79. doi:10.1016/j.intermet.2015.02.017

CrossRef Full Text | Google Scholar

Yang, Y. L., Lin, Q. X., Chen, C. Y., Jen, Y. M., Wang, S. H., Chen, H. R., et al. (2020). Insight on Creep Behavior for Arrayed Interphase Nano-Precipitation in Ti-Microalloyed HSLA Steel. Mater. Chemis. 255, 123–125. doi:10.1016/j.matchemphys.2020.123553

CrossRef Full Text | Google Scholar

Zheng, Z. Z., Xiao, S. L., Wang, X. S., Guo, Y. F., Yang, J. H., Xu, L. J., et al. (2021). High Temperature Creep Behavior of an As-Cast Near-α Ti-6Al-4Sn-4Zr-0.8Mo-1Nb-1W-0.25Si alloy. Mater. Sci. Eng. A. 803, 140487. doi:10.1016/j.msea.2020.140487

CrossRef Full Text | Google Scholar