Microstructure-Dependent Rate Theory Model of Radiation-Induced Segregation in Binary Alloys

Conventional rate theory often uses the mean field concept to describe the effect of inhomogeneous microstructures on the evolution of radiation induced defect and solute/fission product segregation. However, the spatial and temporal evolution of defects and solutes determines the formation and spatial distribution of radiation-induced second phase such as precipitates and gas bubbles/voids, especially in materials with complicated microstructures and subject to high dose radiation. In this work, a microstructure-dependent model of radiation-induced segregation (RIS) has been developed to investigate the effect of inhomogeneous thermodynamic and kinetics properties of defects on diffusion and accumulations of solute A in AB binary alloys. Four independent concentrations: atom A, interstitial A, interstitial B, and vacancy on [A, B] sublattice are used as field variables to describe temporal and spatial distribution and evolution of defects and solute A. The independent concentrations of interstitial A and interstitial B allow to describe their different generation rates, thermodynamic and kinetic properties, and release the assumptions of interstitial generation and sink strength used in the conventional rate theory. Microstructure and concentration dependent chemical potentials of defects are used to calculate the driving forces of defect diffusions. With the model, the effects of defect chemical potentials and mobilities on the RIS in polycrystalline AB model alloys have been simulated. The results demonstrated the model capability in predicting defect evolution in materials with inhomogeneous thermodynamic and kinetic properties of defects. The model can be extended to materials with complicated microstructures such as a wide range of grain size distribution, coating structure and multiphases as well as radiation-induced precipitation subject to severe radiation damage.

Introduction

Radiation-induced segregation (RIS) and precipitation are important material property degradation mechanisms in irradiated materials (Lam et al., 1978; Odette and Lucas, 1986; Farrell et al., 1994; Akamatsu et al., 1995; Lu et al., 2008; Was et al., 2011; Hu et al., 2012; Nastar and Soisson, 2012; Field et al., 2013; Wharry and Was, 2013; Yang et al., 2016). In Ferritic/Martensitic (F/M) steels, experimental results suggested that the RIS of Cr at grain boundaries (GBs) enhances Cr precipitation, which not only led to embrittlement but also altered the corrosion resistance of grain boundaries (Bruemmer et al., 1999; Simonen and Bruemmer, 1999; Nastar and Soisson, 2012). Moreover, experimental data indicated that a number of factors such as temperature, grain boundary structure, and radiation rate might affect whether solutes segregate or deplete on grain boundaries (Damcott et al., 1995; Lu et al., 2008; Was et al., 2011). For instance, the RIS of Cr showed a bell-shape temperature dependence, changing from Cr enrichment to Cr depletion at grain boundaries with increasing temperatures (Wharry and Was, 2013). Low angle grain boundaries (LAGB) exhibited a suppressed RIS response when compared to relatively high angle grain boundaries (HAGB), and at the special Sigma coincident site lattice (CSL) boundaries, the RIS of Cr was also suppressed (Hu et al., 2012; Field et al., 2013).

In different length and time scales, theoretical models including rate theory (Woo and Singh, 1992; Grandjean et al., 1994; Allen and Was, 1998; Golubov et al., 2001; Was, 2016), cluster dynamics (CD) (Faney and Wirth, 2014; Jourdan et al., 2014; Ke et al., 2018), kinetic Monte Carlo (KMC) (Ortiz, 2007; Huang and Marian, 2016), atomistic kinetic Monte Carlo (AKMC) (Senninger et al., 2016; Soisson and Jourdan, 2016), Object kinetic Monte Carlo (OKMC) (Souidi et al., 2006; Dunn et al., 2013), and phase-field approaches (Badillo et al., 2015; Piochaud et al., 2016; Li et al., 2017) have been developed to describe defect evolution and RIS. AKMC takes into account all atoms in the system which could more accurately describe and calculate the effect of defect interaction on defect diffusion and clustering. But it is challenging to apply it in large simulation domains and high radiation doses. Coarse grained methods such as KMC and OKMC only consider defects in the system and are therefore computationally more efficient. However, to describe the complicated thermodynamic and kinetic properties of defects and defect clusters such as the elastic interaction, reaction, and anisotropic mobility requires a large set of model parameters which might be coupled and make the simulation difficult. The mean field approaches such as rate theory and CD treat structural defects such as dislocations, grain boundaries and second phase particle interfaces as sinks. With the effective sink strength of structural defects, the temporal evolution of average defect concentrations over the representative volume can be obtained efficiently by solving one dimensional rate theory (ODE). Spatially dependent rate theory has been developed to consider the effect of free surface on diffusion, trapping and detrapping kinetics of helium in BCC iron foils (Xu and Wirth, 2009; Xu and Wirth, 2010). It is well known that the thermodynamic and kinetic properties of defects on structural defects such as interface and grain boundaries are very different from those inside grains, which may result in inhomogeneous RIS and inhomogeneous precipitation of second phase. But the inhomogeneous thermodynamic and kinetics properties haven’t been considered in the existing rate theory models. Phase-field approach is good at describing spatial and temporal evolution of chemistry and microstructure in a system with inhomogeneous thermodynamic and kinetic properties. Current phase-field models of RIS (Piochaud et al., 2016; Xia et al., 2020) in bi-crystalline structure were extended from the rate theory. Like the rate theory, the sink strength of grain boundaries is derived by assuming that defects at sinks remain thermal equilibrium concentrations. However, this assumption might not be true for a system far from equilibrium. In nuclear materials, especially in materials with high irradiation dose and/or high dose rate, rich microstructure change such as recrystallization and gas bubble evolution can lead the system far from equilibrium.

In this work, we extended the rate theory to considers the effect of the inhomogeneous thermodynamic and kinetic properties of defects on RIS in polycrystalline structures. Defect diffusion is assumed to be driven by chemical potential gradient. The sink strength at grain boundaries that depends on local defect concentrations, diffusivity, and reaction rate, is replaced by local reaction. The model can release the assumptions discussed above. Because the same thermodynamic and kinetic models are used in phase-field models of phase transition the current model can be coupled with phase-field model to study radiation-induced precipitation.

Microstructure-Dependent Rate Theory Model

Description of Chemistry and Defects

We consider an AB binary model alloy and regard atom A as solute atom while atom B as solvent atom. In the conventional rate theory (Was, 2016), three independent variables, i.e., concentrations of atom A, interstitial (A and B) and vacancy (A and B) are used to describe spatial and temporal distributions of solute A and defects. Considering the fact that interstitials A and B might have 1) different generation rates during the cascade; 2) different chemical potentials on sinks, 3) different recombination rates with vacancies; 4) different binding energy with atom A and/or B, four independent variables, i.e., concentrations of atom A, interstitial A, interstitial B, and vacancy are used in the current model. They are denoted by $c_A(\mathit{r},t)$, $c_{Ai}(\mathit{r},t)$, $c_{Bi}(\mathit{r},t)$, and $c_V(\mathit{r},t)$, respectively. $\mathit{r}=\left(x_1,x_2,x_3\right)$ is the spatial coordinate and $t$ is time. It should be pointed out that $c_A(\mathit{r},t)$ is the total concentration including atom A in the lattice and the interstitial A which is also used in the rate equations (Was, 2016). Radiation generates the Frenkel pair such as interstitial A and vacancy A. When solute A has a low concentration, vacancy A has a low concentration as well. However, vacancies at atom A and atom B sites should have the similar local atomic configuration so that vacancy A and vacancy B have the same thermodynamic and kinetic properties. Therefore, it should be reasonable to use one variable $c_V(\mathit{r},t)$ describing the total vacancy concentration. Our model uses one sublattice i.e., sublattice [A, B, vacancy, Ai, or Bi] to describe the chemistry and defects, and uses one set of parameters ${\eta }_m\left(m=\mathrm{1,2},\cdots ,m_0\right)$ to describe the grain orientations in the polycrystalline structure where $m_0$ is the total number of grain orientations in the simulation cell. The order parameter ${\eta }_m$, which is obtained from phase-field modeling of grain growth, has the values of 1 inside the grain m, and 0 outside of the grain m, and continuously varies from 1 to 0 across the grain boundary. We define a shape function with the order parameters as $f\left(\eta \right)=2.0(1-{\displaystyle \sum }_{m=1}^{m_0}{\left({\eta }_m\right)}^2)$ that varies smoothly from 0 inside the grains to 1.0 at the centers of GBs. With the sets of concentration and order parameter variables, the inhomogeneous thermodynamic and kinetic properties of defects can be described.

Chemical Potentials

For a regular solution, the Gibbs free energy can be written as

$G=c_A{\mu }_A^0+c_B{\mu }_B^0+k_{B}T\left(c_{A}ln{\gamma }_A{c}_A+c_{B}ln{\gamma }_B{c}_B\right)(1)$

where $c_A$ and $c_B$ are the concentrations of atom A and B, ${\mu }_A^0 \text{and} {\mu }_B^0$ are the Gibbs free energies of pure A and B, ${\gamma }_j$ is the activity coefficient of species j, $k_B$ is the Boltzmann constant, and $T$ is the absolute temperature.

In irradiated materials, the vacancy and interstitial concentrations can be a few orders of magnitude higher than their thermal equilibrium concentrations although their concentrations are still lower compared with the concentrations of alloy atoms. The high defect concentrations affect not only the diffusivities of species, but also chemical potentials of species. If one assumes that 1) A and B form a regular solution; and 2) vacancy and interstitial A and B are dilute defects, the Gibbs free energy of the system can be written as

$G=\left[c_A{\mu }_A^0+c_B{\mu }_B^0+k_{B}T\left(c_A\text{ln}\left({\gamma }_A{c}_A\right)+c_B\text{ln}\left({\gamma }_B{c}_B\right)\right)\right]+{\displaystyle \sum }_m\left[c_m{\mu }_m^0+k_{B}T\left(c_{m}ln{c}_m\right)\right]m=V, Ai \text{and} Bi(2)$

The concentration $c_B$ of solvent atom B is a dependent variable and can be calculated by $c_B=1-c_A$ if defect concentrations are low (i.e., $c_{Ai}(\mathit{r},t)$, $c_{Bi}(\mathit{r},t)$ and $c_v(\mathit{r},t)$ <<1).

Chemical potentials of species at structural defects such as GBs, interfaces, and surfaces are usually different from those inside grains. The microstructure and/or spatial dependent chemical potential in the polycrystalline AB alloy cause an additional diffusion driving force that affects the fluxes of defects and species, hence, their segregation or depletion, and phase stability. To capture the effect of thermodynamic and kinetic properties of GBs on RIS, we extend the conventional rate theory to a microstructure-dependent rate theory model. The thermodynamic properties of the GBs are expected to closely correlate with the atomic density and composition. van der Waals (1979) showed that the energy of an interface can be described as a function of mass density and its variations within the interface region. Very recently, Kamachali et al. (2019) proposed a density-based thermodynamic model of GBs. The Gibbs free energy of GBs was described by the bulk free energy, atomic density, and gradient coefficient of atomic density. A Gaussian function was used to describe the atomic density change across a GB that evolves with composition. Atomic simulations (Kamachali et al., 2019) in alpha Fe showed that the atomic density of a GB with high symmetry has the Gaussian distribution. We use a shape function of ${\rho }_0+{\rho }^{GB}f\left(\eta \right)$ to express the atomic density of a GB, which is equal to ${\rho }_0$ inside the grain and smoothly varies to ${\rho }_0+{\rho }^{GB}$ at the center of the GB. ${\rho }_0$ is the density of a perfect crystal while ${\rho }^{GB}$ is the difference of atomic density between those inside a grain and on its grain boundary center due to free volumes at the center of the grain boundary. Similarly, other spatially dependent thermodynamic and kinetics properties such as chemical potential and diffusivity of species j can also be described as ${\text{Φ}}_j={\text{Φ}}_{0j}(\mathit{c},T)+{\text{Φ}}_j^{GB}(\mathit{c},T)f\left(\eta \right)$, $\mathit{c}=(c_A,c_{Ai},c_{Bi},c_V)$. ${\text{Φ}}_{0j}$($\mathit{c},T$) is the property of species $j$ inside a grain, and ${\text{Φ}}_j^{GB}(\mathit{c},T)f\left(\eta \right)$ is the difference of the property of species $j$ on the GB from those inside the grain. $j$ denotes any of the defects or solute A i.e., $j=Ai, Bi,V,\text{ or }A$. Therefore, the microstructure-dependent chemical potential of species j can be written as

${\mu }_j={\mu }_j^M+{\mu }_j^{GB}f\left(\eta \right)(3)$

where ${\mu }_j^M$ is the bulk chemical potential of species j, ${\mu }_j^{GB}$ is the difference of chemical potential of species j inside a grain and its grain boundary center. The diffusivity inhomogeneity can also be described by a similar expression as Eq. 3

$D_j=D_j^M+D_j^{GB}f\left(\eta \right)(4)$

where $D_j^M$ is the diffusivity of species j inside grains (also called bulk diffusivity) and $D_j^{GB}$ is the difference of diffusivity of species j between the bulk diffusivity and the diffusivity at the center of grain boundaries.

The spatial dependent chemical potential ${\mu }_j^{GB}f\left(\eta \right)$ of species j on grain boundaries can be expressed as ${\mu }_j^{GB}f\left(\eta \right)=\Delta H_j^{GB}-T\Delta S_j^{GB}$, where $\Delta H_j^{GB}$ and $\Delta S_j^{GB}$ are the difference of formation enthalpy and entropy due to the presence of grain boundaries, respectively. Low-angle symmetric tilt grain boundaries can be modeled by a wall of parallel edge dislocations (Hirth et al., 1968; Jiang et al., 2014; Xia et al., 2020). The elastic interaction between stress field associated with the dislocation array and point defects affect the formation (enthalpy) energy of species j near the grain boundaries. (Jiang et al., 2014) analyzed the effect of grain misorientation angles on the elastic interaction energy. Their results show that when the misorientation angle becomes greater than $10°\sim 15°$ the stress fields of dislocations overlap and cancel each other so that the elastic interaction is negligible. Therefore, ${\mu }_j^{GB}f\left(\eta \right)$ can also be written as ${\mu }_j^{GB}f\left(\eta \right)={\mu }_j^{GB0}+{\mu }_j^{GB\_elas}$, where ${\mu }_j^{GB0}$ and ${\mu }_j^{GB\_elas}$ are the effect of grain boundary atomic structures and elastic interaction on the chemical potential of species j, respectively. For a given grain boundary ${\mu }_j^{GB0}$ can be calculated by atomistic simulations (Tschopp et al., 2011). ${\mu }_j^{GB\_elas}$ can be assessed by analyzing the effect of the stress associated with the dislocation array on the formation enthalpy and entropy of species j. For symmetric tilt grain boundaries ${\mu }_j^{GB\_elas}$ can be expressed as Eqs 3, 4 by ignoring the effect of dislocation stresses on the formation entropy (Jiang et al., 2014). ${\mu }_j^{GB0}$ is not zero within grain boundaries about few lattice constant thickness (Tschopp et al., 2011). However, ${\mu }_j^{GB\_elas}$ reflects the elastic interaction which is a long-range interaction. For small angle grain boundaries the interaction region may reach tens of nanometers (Jiang et al., 2014). In this work, we focused on studying the effect of inhomogeneous chemical potentials ${\mu }_j^{GB}f\left(\eta \right)$ on RIS in model alloys. Chemical potentials ${\mu }_j^{GB}f\left(\eta \right)$ was constructed to reasonably capture the value and the length scale of elastic interaction by adjusting the shape function $f\left(\eta \right)$and the characteristic length $l_0$. Similarly, $D_j^{GB}f\left(\eta \right)$ could be constructed by the diffusivity data near grain boundaries from atomistic simulations and experiments.

Microstructure-Dependent Rate Theory

The rate theory model of RIS (Was, 2016) has been successfully used in predicting the effects of defect mobility, solute size, and defect-binding energies on solute segregation on surfaces and grain boundaries. However, the effects of grain morphology and inhomogeneous thermodynamic and kinetic properties of defects on RIS were ignored because most modeling was carried out in one dimension. In this work, we extend the rate theory model of RIS into polycrystalline structures. According to the rate theory, the evolution of chemical and defect concentrations is given by:

$\frac{\partial c_{\alpha }\left(\mathit{r},t\right)}{\partial t}=-\nabla \cdot J_{\alpha }\left(\mathit{r},t\right), \alpha =A \text{and} B(5)$

$\frac{\partial c_d\left(\mathit{r},t\right)}{\partial t}=-\nabla \cdot J_d\left(\mathit{r},t\right)+{\dot{g}}_d+{\dot{g}}_d^S+{\dot{g}}_d^R, d=V, Ai \text{and} Bi, (6)$

where $J_{\alpha }\left(\mathit{r},t\right)$ and $J_d\left(\mathit{r},t\right)$ are the fluxes of atom $\alpha$ and defect $d$, respectively. ${\dot{g}}_d$, ${\dot{g}}_d^S$, and ${\dot{g}}_d^R$ is the generation rate, sink rate, and recombination rate of defect $d$, respectively. The conservation principle requires the fluxes should satisfy the following equations (Piochaud et al., 2016):

$J_{\alpha }\left(\mathit{r},t\right)={\displaystyle \sum }_{d=V,Ai,Bi}{J}_{\alpha }^d(\mathit{r},t)(7)$

$J_d\left(\mathit{r},t\right)={\displaystyle \sum }_{\alpha =A,B}sign\left(d\right)J_{\alpha }^d(\mathit{r},t)(8)$

where $sign\left(d\right)=1$ for $d=Ai \text{or} Bi$ and $sign\left(d\right)=-1$ for $d=V$. In the framework of the thermodynamics of irreversible process (Onsager, 1931; Piochaud et al., 2016), the fluxes of chemical and defects driven by chemical potential gradient can be approximately calculated by,

$J_{\alpha }^d(\mathit{r},t)=-{\displaystyle \sum }_{\beta }\frac{L_{\alpha \beta }^d}{k_{B}T}(\nabla {\mu }_{\beta }+sign\left(d\right)\nabla {\mu }_d)(9)$

where $L_{\alpha \beta }$ is the Onsager kinetic coefficient. If we define the normalized Onsager coefficient as

$d_{\alpha \beta }^d=\frac{L_{\alpha \beta }^d}{c_d{c}_{\beta }}(10)$

the evolutions Eqs 5, 6 can be expressed as

$\frac{\partial c_{\alpha }(\mathit{r},t)}{\partial t}=\nabla \cdot {\displaystyle \sum }_d{\displaystyle \sum }_{\beta }\frac{d_{\alpha \beta }^d{c}_d{c}_{\beta }}{k_{B}T}(\nabla {\mu }_{\beta }+sign\left(d\right)\nabla {\mu }_d), \alpha =AandB(11)$

$\frac{\partial c_d(\mathit{r},t)}{\partial t}=\nabla \cdot {\displaystyle \sum }_{\alpha }{\displaystyle \sum }_{\beta }\frac{d_{\alpha \beta }^d{c}_d{c}_{\beta }}{k_{B}T}\left(sing\left(d\right)\nabla {\mu }_{\beta }+\nabla {\mu }_d\right)+{\dot{g}}_d+{\dot{g}}_d^S+{\dot{g}}_d^R, d=V, Ai \text{and } Bi. (12)$

In polycrystalline structures the inhomogeneous chemical potential ${\mu }_{\alpha }$ and ${\mu }_d$ are expressed as

${\mu }_{\alpha }(\mathit{r},t)={\mathit{\mu }}_{\alpha }^M+{\mu }_{\alpha }^{GB}f\left(\eta \right) ={\mu }_{\alpha }^0+k_{B}Tln\left({\gamma }_{\alpha }{c}_{\alpha }\right)+{\mu }_{\alpha }^{GB}f\left(\eta \right)(13)$

${\mu }_d(\mathit{r},t)={\mu }_d^0+k_{B}Tln\left(c_d\right)+{\mu }_d^{GB}f\left(\eta \right)(14)$

Assuming that 1) the chemical potentials ${\mu }_{\alpha }^M, (\alpha =A \text{and} B)$, satisfy the Gibbs-Duhem relationship ${\displaystyle \sum }{c}_{\alpha }\nabla {\mu }_{\alpha }^M=0$; 2) the defect concentration is low i.e., $c_d<<1$, then the chemical potential gradient can be calculated by

$\nabla {\mu }_{\alpha }=\frac{k_{B}T}{c_{\alpha }}\phi \nabla c_{\alpha }+{\mu }_{\alpha }^{GB}\nabla f\left(\eta \right),\varphi =(1+\frac{dln\left({\gamma }_{\alpha }\right)}{dln\left(c_{\alpha }\right)})(15)$

$\nabla {\mu }_d=\frac{k_{B}T}{c_d}\nabla c_d+{\mu }_d^{GB}\nabla f\left(\eta \right)(16)$

With the assumption of $L_{\alpha \beta }^d=0$ for $\alpha \ne \beta$ the evolution Eqs 11, 12 x are simplified as

$\begin{array}{l}\frac{\partial c_{Ai}\left(\mathit{r},t\right)}{\partial t}=\nabla (d_{AA}^{Ai}{c}_{Ai}\varphi \nabla c_A+d_{BB}^{Ai}{c}_{Ai}\varphi \nabla c_B+(d_{AA}^{Ai}{c}_A+d_{BB}^{Ai}{c}_B)\nabla c_{Ai}+{\kappa }_{Ai}^{GB}\nabla f\left(\eta \right)]\\ +{\dot{g}}_{Ai}+{\dot{g}}_{Ai}^S+{\dot{g}}_{Ai}^R, \end{array}(17)$

$\begin{array}{l}\frac{\partial c_{Bi}\left(\mathit{r},t\right)}{\partial t}=\nabla (d_{AA}^{Bi}{c}_{Bi}\varphi \nabla c_A+d_{BB}^{Bi}{c}_{Bi}\varphi \nabla c_B+(d_{AA}^{Bi}{c}_A+d_{BB}^{Bi}{c}_B)\nabla c_{Bi}+{\kappa }_{Bi}^{GB}\nabla f\left(\eta \right)]+{\dot{g}}_{Bi}+{\dot{g}}_{Bi}^S+{\dot{g}}_{Bi}^R, \end{array}(18)$

$\begin{array}{l}\frac{\partial c_V\left(\mathit{r},t\right)}{\partial t}=\nabla \left[-d_{AA}^V{c}_V\varphi \nabla c_A-d_{BB}^V{c}_V\varphi \nabla c_B+(d_{AA}^V{c}_A+d_{BB}^V{c}_B)\nabla c_V+{\kappa }_V^{GB}\nabla f\left(\eta \right)\right]\\ +{\dot{g}}_V+{\dot{g}}_V^S+{\dot{g}}_V^R, \end{array}(19)$

$\begin{array}{l}\frac{\partial c_A\left(\mathit{r},t\right)}{\partial t}=\nabla [\left(d_{AA}^V{c}_V+d_{AA}^{Ai}{c}_{Ai}+d_{AA}^{Bi}{c}_{Bi}\right)\varphi \nabla c_A-d_{AA}^V{c}_A\nabla c_V+d_{AA}^{Ai}{c}_A\nabla c_{Ai}+d_{AA}^{Bi}{c}_A\nabla c_{Bi}\\ +{\kappa }_A^{GB}\nabla f\left(\eta \right)], \end{array}(20)$

where ${\kappa }_i^{GB}, (i=A, Ai,Bi, \text{and} V)$ are functions of defect concentrations and chemical potentials on grain boundaries. They are given by

${\kappa }_{\alpha }^{GB}={\displaystyle \sum }_d{\displaystyle \sum }_{\beta }\frac{d_{\alpha \beta }^d{c}_d{c}_{\beta }}{k_B\text{T}}\left[{\mu }_{\beta }^{GB}+sign\left(d\right){\mu }_d^{GB}\right], \alpha =A \text{and} B(21)$

${\kappa }_d^{GB}={\displaystyle \sum }_{\alpha }{\displaystyle \sum }_{\beta }\frac{d_{\alpha \beta }^d{c}_d{c}_{\beta }}{k_B\text{T}}\left[\text{sign}\left(\text{d}\right){\mu }_{\beta }^{GB}+{\mu }_d^{GB}\right], d=V, Ai \text{and} Bi(22)$

If we further assume that $L_{\alpha \alpha }^d=L_{\beta \beta }^d$, the evolution Eqs 17–20 inside the grains (i.e., $f\left(\eta \right)=0$) become to the rate Eqs 6–20 of ref. (Was, 2016). The normalized Onsager coefficients $d_{\alpha \alpha }^d$ are the same as $d_{\alpha d}$ in Eqs 6–20 of ref. (Was, 2016) which is the diffusivity of atom $\alpha$ diffusing via exchanging with defect $d$ on a given neighboring site. The diffusivity coefficient $d_{ij}$ is given by

$d_{ij}=\frac{1}{6}{\lambda }_{i,j}^2{f}_{ij}{\nu }_{i,j}exp\left(\frac{-\text{Δ}{E}_m^{ij}}{k_{B}T}\right)(23)$

where ${\lambda }_{i,j}$ is the jump distance when atom $i$ and defect j exchange sites. $f_{ij}$ is the correlation factor (Wharry and Was, 2014). ${\nu }_{i,j}$ is the effective exchange-jump frequency of atom $i$ - defect $j$pair, and $\text{Δ}{E}_m^{ij}$ is the migration energy. In this work, $d_{\alpha \beta }^d=0, \alpha \ne \beta$ and $d_{\alpha \alpha }^d=d_{\alpha d}$.

In the conventional rate theory, the generation rate of defects ${\dot{g}}_d$ is assumed to be proportional to the alloy composition. Since interstitials A and B are treated as individual variables, more accurate interstitial generation rates from MD cascade simulations can be used when they satisfy the relationship of ${\dot{g}}_V={\dot{g}}_{Ai}+{\dot{g}}_{Bi}$. ${\dot{g}}_{Ai}$ and ${\dot{g}}_{Bi}$ are calculated by the equation of ${\dot{g}}_d=m_d\dot{K}$ where $\dot{K}$ is the dose rate and $m_d$ is the production efficiency of defect $d$. The recombination rate of Frenkel defects ${\dot{g}}_d^R=-{\alpha }_{dV}{c}_d{c}_V, d=Ai \text{and} Bi$. And ${\dot{g}}_V^R=-{\displaystyle \sum }_{d=Ai,Bi}{\alpha }_{dV}{c}_d{c}_V$. ${\alpha }_{dV}=z_{d,V}(D_d+D_V)/a^2$ is a rate constant, $a$ is the lattice constant, and ${\text{z}}_{d,V}$ is the combination factor of vacancies and interstitials. In polycrystalline structures, the main sinks of defects are dislocations and grain boundaries. The sink rate of defects on distributed dislocations can be calculated by ${\dot{g}}_d^S=z_{d,dis}{D}_d{\rho }_{dis}(c_d-c_d^{eq})$, where $z_{d,dis}$ is the sink strength constant of defect $d$ on dislocations.${\rho }_{dis}$ is the dislocation density. $D_d$ is the diffusivity of defect $d$. $c_d^{eq}$ is the thermal equilibrium concentration of defect $d$ at dislocations. Grain boundaries can be described by an array of dislocations such as small angle grain boundaries (Duh et al., 2001) and/or can be described as plane defects with high defect concentrations as discussed in Section 2.2. Defects (Ai, Bi, V) on grain boundaries may have different chemical potentials from those inside grains. Distributed dislocations on grain boundaries have elastic interaction with defects. Both the chemical potential and elastic interaction cause driving forces for defect diffusion. Conventional rate theory assumes that defects on grain boundaries remain their thermal equilibrium concentrations. It should be a reasonable assumption after the system reaches a steady state. However, for a system far from equilibrium, the assumption might be inappropriate. For example, if solute interstitials have much higher diffusivity than that of vacancies, the solute interstitials may accumulate on grain boundaries and form supper saturated solution. The excess interstitials might be emitted back to interior grains. But it is also possible that the super saturated solution or vacancies leads to the second phase formation or void formation on grain boundaries which are often observed in irradiated materials (Kuksenko et al., 2012; Zhao et al., 2018). In this work, the polycrystalline structure is naturally described in terms of inhomogeneous thermodynamic and kinetic properties. The sink of defects on grain boundaries is described by the local defect recombination enhanced by high defect concentrations and high defect mobility. Therefore, the assumption that defects on grain boundaries remain their thermal equilibrium concentrations in the conventional rate theory is released. A sink term $z_{d,GB}{D}_{d}f\left(\eta \right)(c_d-c_d^{eq})$ on grain boundaries is added in ${\dot{g}}_d^S$ to force defects having equilibrium concentrations on grain boundaries and study the effect of this sink term on the solute segregation.

Model Parameters

The normalized time $t^{\ast }=\frac{t{D}_0}{l_0^2}$, diffusivity $d_{ij}^{\ast }=\frac{d_{ij}}{D_0}$, gradient ${\nabla }^{\ast }=l_0\nabla$, and energy ${\mu }_j^{\ast }=\frac{{\mu }_j}{k_{B}T}$ are used for numerically solving Eqs 17–20. $l_0$ and $D_0=\text{max}\left\{d_{ij}\right\}$ are, respectively, the characteristic length and the largest partial diffusion coefficient of $d_{ij}$. Solving the equations, one has the spatial and temporal evolution of species concentration $c_i$. To simulate the effect of inhomogeneous thermodynamic and kinetic properties on RIS, parametric studies are carried out in model alloys. Table 1 lists the model parameters and thermodynamic and kinetic properties of defects used in the simulations.

TABLE 1

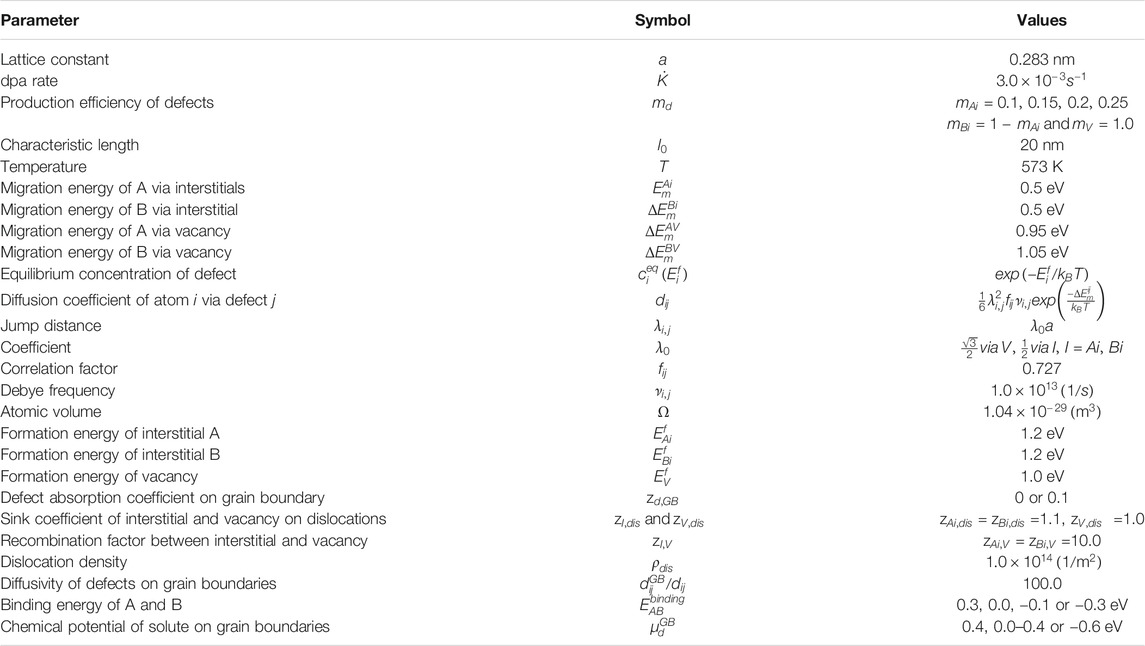
TABLE 1. Parameters for the ABVI model system named by Huang and Marian (2016) and Was (2016).

Results

We consider a model 10at % AB alloy. A denotes the solute atom while B the solvent atom. A phase field model of grain growth was used to generate a polycrystalline structure. The grain boundaries are defined by a shape function $f\left(\eta \right)=2(1-{\displaystyle \sum }_{m=1}^{m_0}{\left({\eta }_m\right)}^2)$ that has the value of 0 inside the grains and continuously varies to 1 at the center of the grain boundaries. Figure1A shows a two dimensional (2D) polycrystalline structure which has a dimension $256l_0\times l_0\times 256l_0$ and is used in the simulations. The average grain size is about $1.55\mu m$. From the 2D grain structure, we can see the microstructure features such as different sized grains, plate grain boundaries and triple points of grain boundaries. These features are like those in 3D grain structures. It is anticipated that the 2D simulations captured the physics of the effect of microstructures on RIS. Figure1B shows the distributions of the shape function $f\left(\eta \right)$ along the lines $A_1{A}_2$ and $B_1{B}_2$ respectively. The inhomogeneous thermodynamic and kinetic properties of species and defects in the polycrystalline structure are defined by $f\left(\eta \right)$ as described in Section 2.2.

FIGURE 1

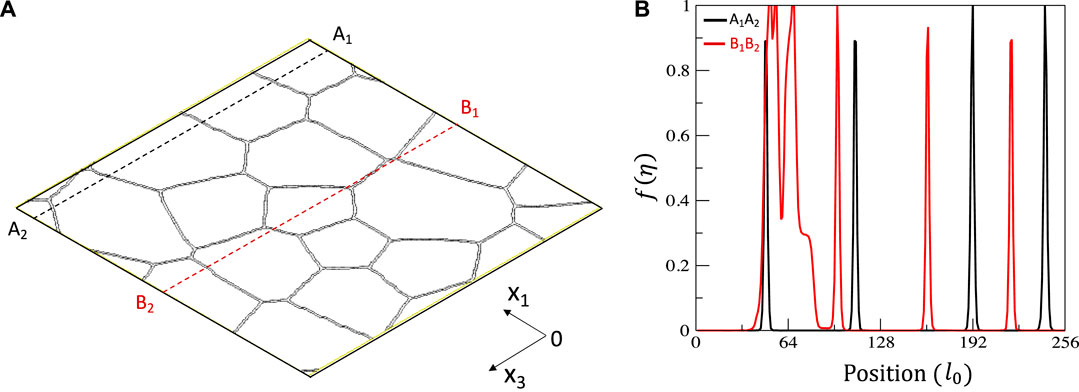
FIGURE 1. (A) the polycrystalline structure used in the simulations and (B) the shape function $f(\eta \left(x_3\right))$ along the lines $A_1{A}_2$ and $B_1{B}_2$ shown in (A).

Effect of Thermodynamic and Kinetic Properties of Grain Boundaries on Solute Segregation

In the conventional rate theory, the grain boundary is treated as a perfect sink of defects by assuming that defects have their thermal equilibrium concentrations. Current model releases this assumption and uses inhomogeneous chemical potentials (${\mu }_d^{GB}$) and diffusivity ($d_{ij}^{GB}$) of defects to describe the features of grain boundaries as sinks of defects. First, we consider the effect of solute atom’s chemical potential on RIS. In the simulations, the following model parameters are set up to be $m_{Ai}=0.1$, $d_{ij}^{GB}/d_{ij}=100$, ${\mu }_{Bi}^{GB}={\mu }_V^{GB}=0$, and $E_{AB}^{binding}=0.0$ thus $\varphi =1$. The other model parameters are listed in Table 1. ${\mu }_A^{GB}={\mu }_{Ai}^{GB}$ takes different values of 0.4, 0.0–0.4, and –0.6°[eV/atom], respectively, which means that the chemical potential of the solute A and self-interstitial on the grain boundaries is higher (positive value) or lower (negative value) than that inside grains by the value of ${\mu }_A^{GB}$. Figure 2 shows the distribution of the solute concentration change $\Delta c_A$at time $\text{t}=8.17\text{s}$. $\Delta c_A=c_A\left(\mathit{r}\right)-c_A^0$ where $c_A^0=0.10$ is the initial concentration of atom A and uniform in the simulation cell. The same color bar is used in the figures so that the color presents not only the effect of chemical potentials on the solute segregation or depletion but also the relative strength of RIS in the polycrystalline structure. To make more clear comparison, the distributions of the solute concentration change along the line $A_1{A}_2$ are plotted in Figure 3, where the dashed lines mark the locations of grain boundaries.

FIGURE 2

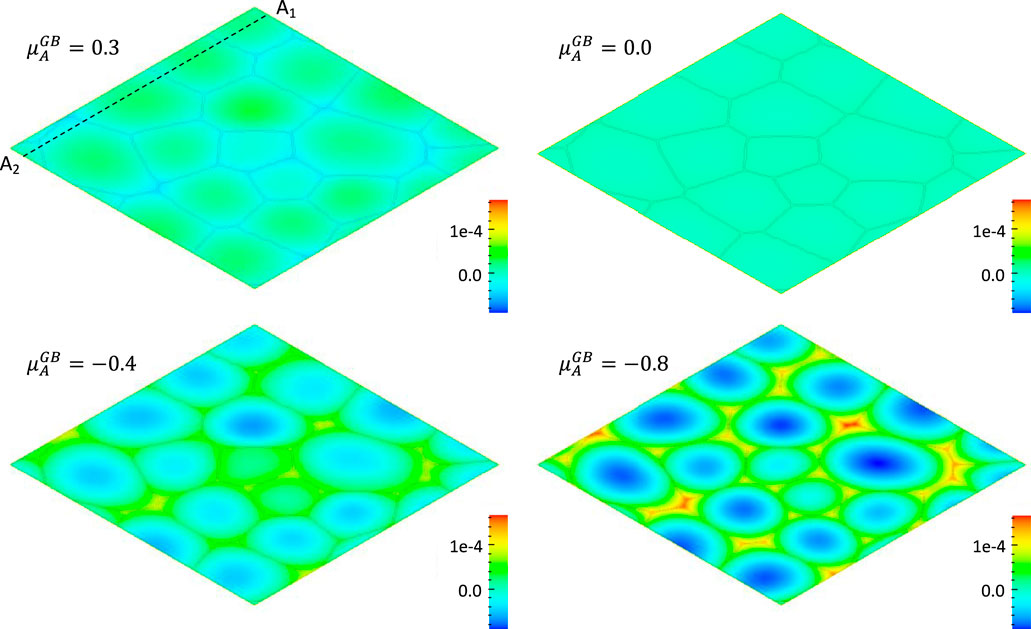
FIGURE 2. Effect of chemical potential ${\mu }_A^{GB}$ on the distribution of the solute A concentration change $\Delta c_A$. ${\mu }_A^{GB}$ has the unit of [eV/atom].

FIGURE 3

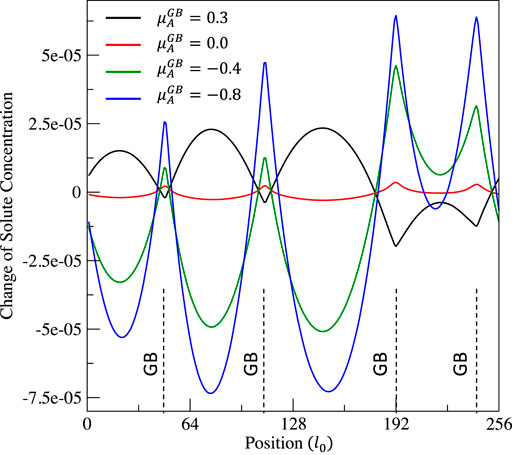
FIGURE 3. Distribution of solute concentration change $\Delta c_A$ along the line $A_1{A}_2$ shown Figure 1A for different chemical potential ${\mu }_A^{GB}$.

From Figures 2, 3, it can be clearly seen that 1) the solute A segregates on grain boundaries when ${\mu }_A^{GB}=0.0$ i.e., solute A has the same chemical potential on grain boundaries and inside grains. The solute segregation results from the inhomogeneous mobility of radiation defects. The larger diffusivity of defects on grain boundaries causes a faster defect recombination, hence, bigger defect concentration gradient, defect flux and RIS; 2) when solute A on grain boundaries has a higher chemical potential (${\mu }_A^{GB}=0.3$) than that inside grains the solute depletes on the grain boundaries. In this case, the chemical potential gradient of solute A dominates its flux; and 3) solute segregation increases with the decrease of the chemical potential (${\mu }_A^{GB}=-0.4, -0.6$). In this case, both chemical potential gradient and defect concentration gradient drive the solute diffusing to grain boundaries. The distributions of solute concentration on grain boundaries also show that the solute segregation or depletion on grain boundaries are not uniform. Solute concentration at triple points of grain boundaries is much higher or lower than that on straight grain boundaries. In addition, solute segregation on short grain boundaries is more uniform than that on large grain boundaries. The results imply more inhomogeneous RIS in polycrystalline structure with larger grains than that in polycrystalline structures with smaller grains. It should point out that a number of factors may cause the inhomogeneous RIS on grain boundaries. For example, from Figure 1B we can find that the shape function $f\left(\eta \right)$ which is defined by the order parameters obtained from phase-field modeling is not exactly equal to 1 on the grain boundaries. Consequently, the thermodynamic and kinetic properties of defects on grain boundaries are not the same. Actually, such a shape function naturally describes the inhomogeneous structures of grain boundaries at triple points i.e., curved boundaries connected different oriented grains. The inhomogeneous RIS on grain boundaries, which are often observed in experiments, confirms that the shape function can naturally describe the thermodynamic and kinetic properties of grain boundaries.

The equilibrium concentrations of interstitials ($c_{Ai}^{eq}, c_{Bi}^{eq}$) and vacancy ($c_V^{eq}$) on grain boundaries are setup to be $1.6\times {10}^{-7},1.6\times {10}^{-7}\text{ and }8.7\times {10}^{-13}$, respectively. The distributions of defect concentrations along the line $A_1{A}_2$are plotted in Figure 4. It can be seen that vacancies deplete on grain boundaries because the given defect diffusivity on grain boundaries is two order magnitude higher ($d_{ij}^{GB}/d_{ij}=100$) than that inside grains. Therefore, a fast defect recombination reduces the vacancy concentration. By the natural recombination, concentrations of vacancies closely reach to its thermal equilibrium concentration. However, the concentration of interstitial A increases with the decrease of chemical potential ${\mu }_{Ai}^{GB}$ because the flux of interstitial A toward grain boundaries increases. When ${\mu }_{Ai}^{GB}$is positive, the interstitial A depletes at grain boundaries. A negative ${\mu }_{Ai}^{GB}$ leads to a segregation of interstitial A at grain boundaries as shown in Figure 4B. This is because interstitial A has higher solubility (or equilibrium concentration) at grain boundaries with a negative ${\mu }_{Ai}^{GB}$. Concentration of interstitial B is much higher than its thermal equilibrium concentration and increases with the decrease of chemical potential ${\mu }_A^{GB}$. Besides the defect recombination on grain boundaries, other material processes may affect the defect concentrations as well. For example, interstitials can be absorbed by grain growth, and interstitials may diffuse to free surface through grain boundaries. Both processes reduce the interstitial concentration on grain boundaries. Current model uses the sink term “$z_{d,GB}$” to describe the absorption mechanisms of interstitials on grain boundaries. We can turn on or off this term to study the effect of sink on RIS which releases the assumption of perfect sink in the conventional rate theory. Increasing the $z_{d,GB}$ means more defects sinking on the grain boundaries. Figure 5A shows the solute concentration changes $\Delta c_A$ along $A_1{A}_2$ at time $\text{t}=8.17\text{s}$ for $z_{d,GB}=0 and 0.1$. The defect concentrations are plotted in Figures 5B,C. With the sink condition $z_{d,GB}=0.1$ the results indicate that 1) the concentrations of all defects reach their thermal equilibrium concentrations on grain boundaries 2) all defect concentrations inside grains decreases, and 3) the solute segregation on grain boundaries reduces. The reduction of RIS with the increase of sink strength ($z_{d,GB}$) is because the absorption of defects on grain boundaries lowers defect concentrations, hence the RIS kinetics. The results indicate that the assumption that all defects remain their thermal equilibrium concentrations in the rate theory is not necessarily correct unless the extra defects can be absorbed or emitted by grain boundaries. Grain boundaries acting as perfect sinks ($z_{d,GB}=0.1)$ reduces defect concentrations inside grain and the solute segregation kinetics on grain boundaries.

FIGURE 4

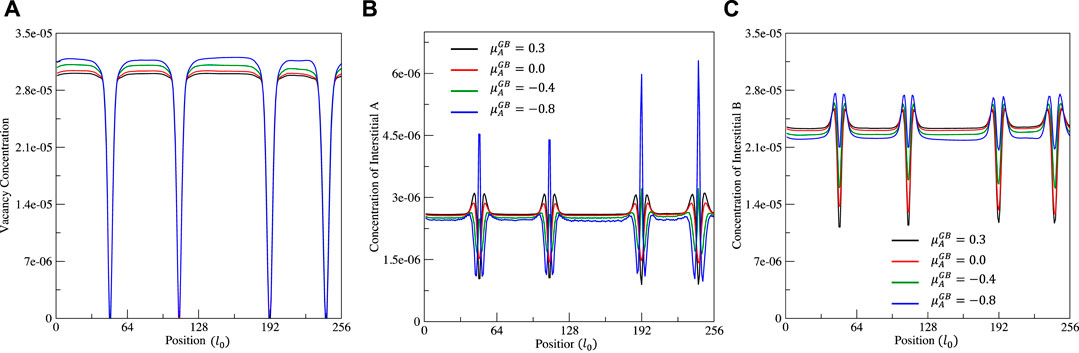
FIGURE 4. Effect of chemical potential ${\mu }_A^{GB}$ on defect concentrations along the line $A_1{A}_2$. (A) vacancy; (B) interstitial A; and (C) interstitial B at time $\text{t}=8.17\text{s}$. The legends in Figures (B) and (C) apply to (A).

FIGURE 5

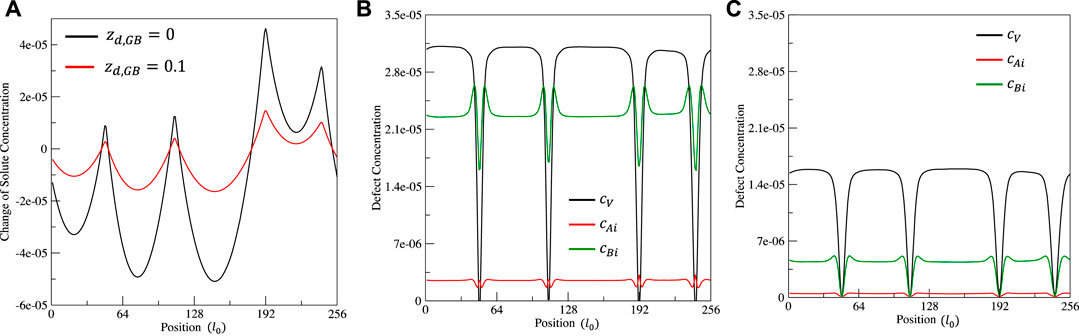
FIGURE 5. Effect of sink term $z_{d,GB}$ on RIS at time $\text{t}=8.17\text{s}$. (A) solute concentration change $\Delta c_A$, (B) defect concentrations along $A_1{A}_2$ for $z_{d,GB}=0$ and (C) defect concentrations along $A_1{A}_2$ for $z_{d,GB}=0.1$.

Effect of Binding Energy ${\mathit{E}}_{\mathit{ij}}^{\mathit{binding}}$ on Solute Segregation

For a regular solution AB, the mixing entropy can be approximated by the ideal solution mixing entropy:

$\Delta S_{mix}=-k_B\left(c_{A}ln{c}_A+c_{B}ln{c}_B\right)(24)$

The non-ideality of the solution is represented by the enthalpy of mixing, which, in the quasi-chemical approximation, is given by

$\Delta H_{mix}=c_A{c}_B{E}_{AB}^{binding}(25)$

where $E_{AB}^{binding}$ is defined as the binding energy of species A and B, and is given by

$E_{AB}^{binding}=z_{AB}\left[H_{AB}-(H_{AA}+H_{BB})/2\right](26)$

where $z_{AB}$ is the number of nearest neighbors, $H_{ij}$ is the bond enthalpy of the i − j bond. The free energy of mixing can be calculated by:

$\Delta G_{mix}=\Delta H_{mix}-\Delta S_{mix}T=c_A{c}_B{E}_{AB}^{binding}+k_{B}T\left(c_{A}ln{c}_A+c_{B}ln{c}_B\right)(27)$

The Gibbs free energy for a regular solution can be written as

$G=c_A{G}_A^0+c_B{G}_B^0+\Delta G_{mix}=c_A{\mu }_A^0+c_B{\mu }_B^0+k_{B}T\left(c_{A}ln{c}_A+c_{B}ln{c}_B\right)+c_A{c}_B{E}_{AB}^{binding}(28)$

where $G_A^0$ and $G_B^0$ are the Gibbs free energies of pure A and B, respectively. The first three terms in Eq. 28 describe the free energy of ideal solution, and the last term describes the mixing enthalpy of the regular solution. Equation 28 is an alternative expression of the Gibbs free energy described by Eq. 1. The thermodynamic factor $\varphi =1+\frac{dln\left({\gamma }_{\alpha }\right)}{dln\left(c_{\alpha }\right)}$ in Eq. 15 can be calculated by $\left[1-\frac{E_{AB}^{binding}{c}_A}{k_{B}T}\right]$ i.e., $\varphi =1-\frac{E_{AB}^{binding}{c}_A}{k_{B}T}$. With the same model parameters used in Section 4.1, but ${\mu }_A^{GB}={\mu }_{Ai}^{GB}=-0.4 \text{eV}/\text{atom}$ and $E_{AB}^{binding}=-0.3,0.0,0.1\text{ or }0.3\text{eV}/\text{atom}$, the effect of bonding energy $E_{AB}^{binding}$ on RIS is simulated and presented in Figure 6. From Eq. 15, a negative AB binding energy $E_{AB}^{binding}$ increases the thermodynamic factor $\varphi$. In contrast, a positive AB binding energy $E_{AB}^{binding}$ decreases the thermodynamic factor $\varphi$. Therefore, AB binding energy affects the fluxes driven by the concentration gradients of atom A and B. As a result, it affects the solute segregation. The results in Figure 6 demonstrate a clear tendency that a weaker AB binding energy ($E_{AB}^{binding}<0$) increases the RIS while a stronger AB binding energy ($E_{AB}^{binding}>0$) decreases the solute segregation.

FIGURE 6

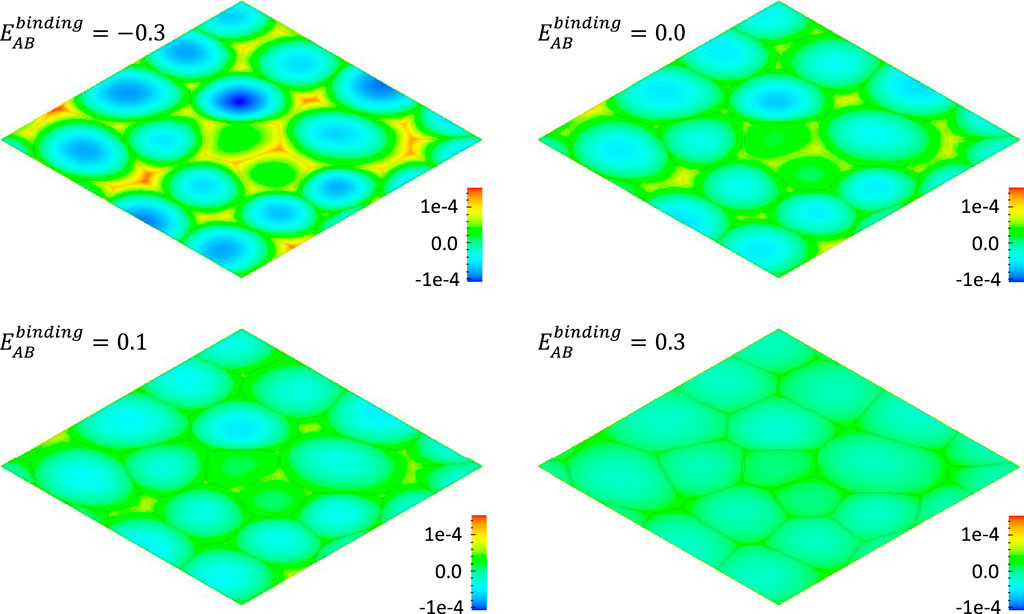
FIGURE 6. Effect of AB binding energy $E_{AB}^{binding}$ on the distribution of solute concentration change $\Delta c_A$at time $\text{t}=8.17\text{s}$. $E_{AB}^{binding}$ has the unit of [eV/atom].

If the binding among defects is strong, the faster diffusive defect has a drag effect on the slower diffusive defect. For instance, undersize solutes may tightly bind to interstitials forming interstitial-solute complexes that migrate as solute interstitials. In the rate theory (Was, 2016), the binding energy is used to scale the interstitial concentration of the solute which affect the partial diffusivity. The Gibbs free energy of the system with strong defect interaction can be generally written as

$G=\left[c_A{\mu }_A^0+c_B{\mu }_B^0+RT\left(c_A\text{ln}\left(c_A\right)+c_B\text{ln}\left(c_B\right)\right)\right] +{\displaystyle \sum }_m\left[c_m{\mu }_m^0+RT\left(c_{m}ln{c}_m\right)\right]+{\displaystyle \sum }_j\left[{\displaystyle \sum }_i{c}_i{c}_j{E}_{ij}^{binding}\right] m=Ai,Bi,\text{and} V; i,j=A,B,Ai, Bi, \text{and} V (29)$

The binding of defects $i$ and $j$ results in an additional flux $\frac{d_{ij}{E}_{ij}^{binding}{c}_i{c}_j}{k_{B}T}\nabla c_j$ on the flux of defect $i$ associated with the concentration gradient of defect $j$. The current model can consider the effect of defect binding on RIS once the binding energy $E_{ij}^{binding}$ is available.

Effect of Defect Generation Efficiency ${\mathit{m}}_{\mathit{d}}\mathit{ }$on Solute Segregation

In conventional rate theory, the generation rate of solute interstitials is assumed to be proportional to its concentration in the alloy i.e., ${\dot{g}}_A=c_A\dot{K}$ where $\dot{K}$ is the dpa rate. However, this generation rate may be only correct in the ideal alloy. MD simulations of cascades (Zhang et al., 2017) show that in Fe-Cr, the Cr interstitial fraction is much higher than the Cr solute concentration and the Cr interstitial production efficiency decreases with the increasing Cr concentration. In 10 at%CrFe, the fraction of the Cr interstitial is about 65–78% while the fraction of Fe interstitial is only about 35% or even lower. In contrast, in Fe-Cu, Cu interstitials are barely produced. In current model, the concentrations of interstitial A and B are treated as independent variables so that it can describe the effect of defect generation efficiency on RIS. With the same model parameters in Section 4.1, but ${\mu }_A^{GB}={\mu }_{Ai}^{GB}=-0.4\text{eV}/\text{atom}$ and $m_{Ai}=0.1,0.15,0.2$, and$0.25\text{eV}/\text{atom}$, the effect of production efficiency $m_{Ai}$ on RIS is simulated and displayed in Figures 7, 8. In the case of $m_{Ai}=0.1$, the solute segregate on grain boundaries as shown by the green line in Figure 8. This indicate that solutes have a flux toward grain boundaries. The results that increasing the generation rate of solute interstitials increase the RIS is expected. Therefore, in CrFe and CuFe alloys, it is important to consider the effect of solute interstitial production efficiency on RIS because their production efficiency is largely different from the concentration of solute.

FIGURE 7

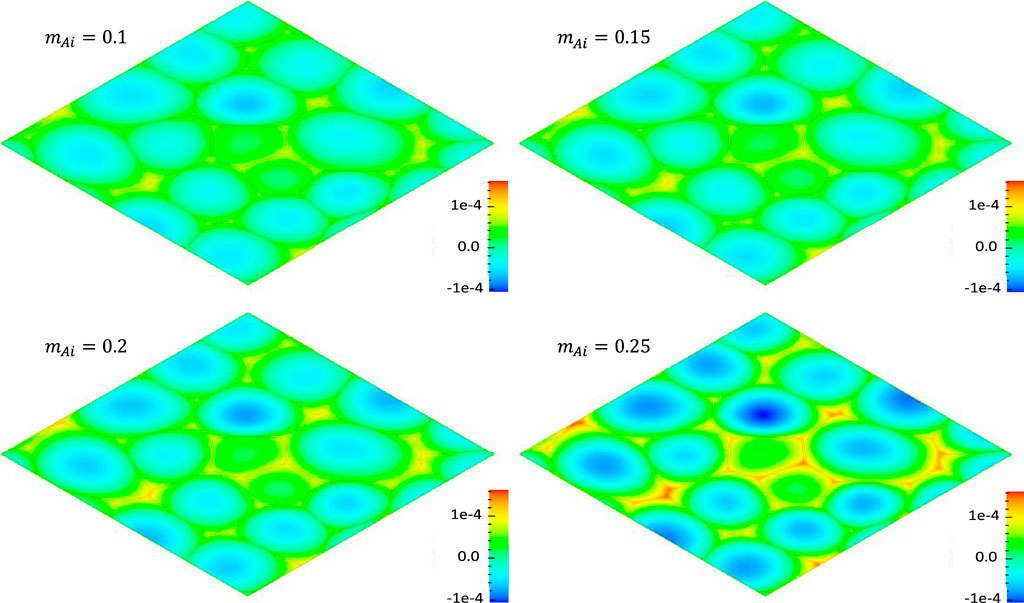
FIGURE 7. Effect of solute interstitial production efficiency $m_{Ai}$ on the distribution of solute concentration changes Δc_A at time $\text{t}=8.17\text{s}$.

FIGURE 8

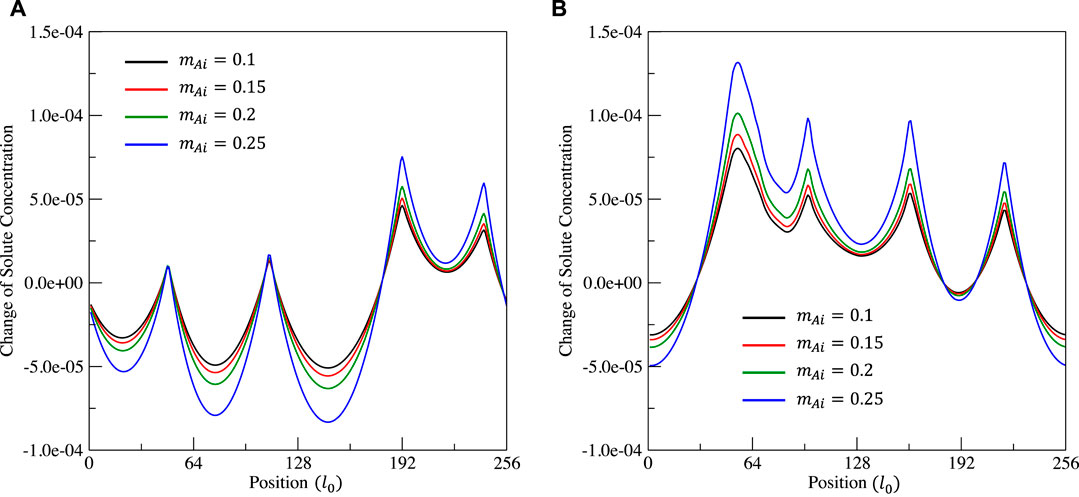
FIGURE 8. Distribution of the solute concentration change Δc_A at time $\text{t}=8.17\text{s}$ for different solute interstitial production efficiency $m_{Ai}$. (A) on the line $A_1{A}_2$ and (B) on the line BB′.

Effect of Defect Diffusivity on Solute Segregation

In the rate theory of RIS, the inhomogeneity of chemical potential in polycrystalline structures is ignored i.e., ${\mu }_d^{GB}=0.0$. At steady state the rate theory predicts that solute and vacancy concentration gradients have the relationship: $\nabla c_A\propto \left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)\nabla c_V$ (Was, 2016). With the migration energies and temperature listed in Table 1, we have the diffusivities of ${\text{d}}_{A,Ai}=1.6\times {10}^{-12}{\text{m}}^2/\text{s}; {\text{d}}_{A,V}=9.92\times {10}^{-14}{\text{m}}^2/\text{s}; {\text{d}}_{B,Bi}=1.6\times {10}^{-12}{\text{m}}^2/\text{s} \text{and} {\text{d}}_{B,V}=2.7\times {10}^{-13}{\text{m}}^2/\text{s}$, respectively. Thus, we have $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}=-0.63$. The negative value of $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}$ means $\nabla c_A\propto -\nabla c_V$. The solute segregation on grain boundaries shown by the red line in Figure 8 and the vacancy depletion on grain boundaries shown in the red line in Figure 10 indicate $\nabla c_A\propto -\nabla c_V$. Two other model systems with different values of $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}$ are considered to validate the model as well as the prediction of rate theory. In Model 1, the partial diffusivities (${\text{d}}_{A,Ai}=1.6\times {10}^{-14}{\text{m}}^2/\text{s}; {\text{d}}_{A,V}=4.8\times {10}^{-17}{\text{m}}^2/\text{s}; {\text{d}}_{B,Bi}=1.6\times {10}^{-16}{\text{m}}^2/\text{s and} {\text{d}}_{B,V}=7.2\times {10}^{-19}{\text{m}}^2/\text{s}$) are setup, which give $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}=-33.3$. In Model 3, the partial diffusivities (${\text{d}}_{A,Ai}=1.6\times {10}^{-16}{\text{m}}^2/\text{s}; {\text{d}}_{A,V}=4.8\times {10}^{-14}{\text{m}}^2/\text{s}; {\text{d}}_{B,Bi}=1.6\times {10}^{-14}{\text{m}}^2/\text{s and} {\text{d}}_{B,V}=4.8\times {10}^{-18}{\text{m}}^2/\text{s}$) are setup, which give $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}=10000$. The results in Figure 9 shows that effect of the relative partial diffusivity $\left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)$ on RIS. For Model 2, $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}$ is equal to be $-0.63$. It is clear that vacancy always deplete on grain boundaries shown in Figure 9B. Vacancy concentration inside grains increases with the decrease of $\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}$. Figure 9A demonstrates that the relationship $\nabla c_A\propto \left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)\nabla c_V$ hold which is in agreement with the rate theory’s prediction.

FIGURE 9

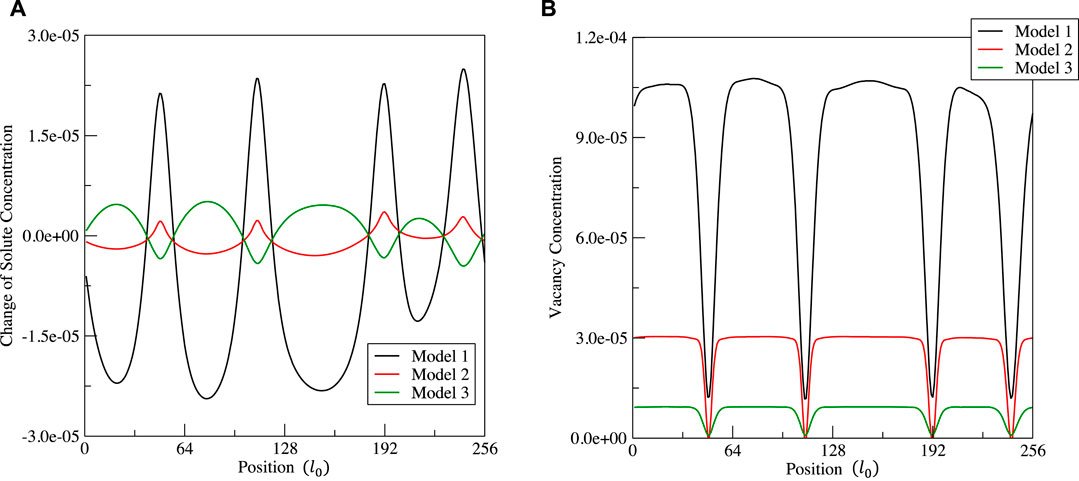
FIGURE 9. Distribution of the solute concentration change $\Delta c_A$ and vacancy concentration on the line $A_1{A}_2$ for different values of $\left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)$. (A) the solute concentration change and (B) the vacancy concentration.

FIGURE 10

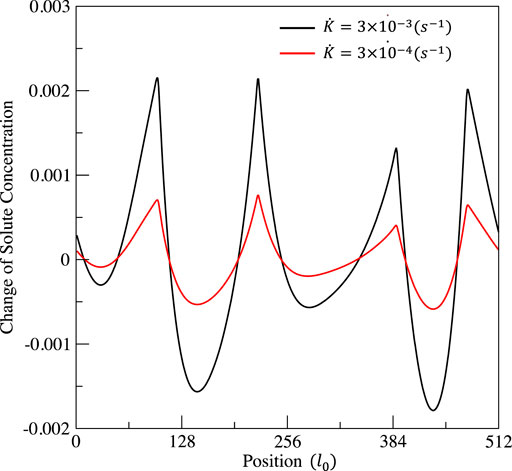
FIGURE 10. Distribution of the solute concentration change Δc_A at time $\text{t}=1816\text{s}$. Simulation cell: $512l_0\times l_0\times l_0$; dpa rate: $3.0\times {10}^{-3}$; sink strength $z_{d,GB}=0.005$; the rest model parameters are the same as that of the Model 1 described in Section 4.4.

Conclusion and Discussion

In this work the conventional rate theory of RIS has been extended by taking into account inhomogeneous thermodynamic and kinetics properties of defects. The developed model has the following features: 1) concentrations of solute and solvent interstitials are treated as independent variables. In conventional rate theory the total concentration of solute and solvent interstitials is treated as an independent variable and the fraction of the solute interstitial in the total interstitial concentration is assumed to be the same as the solute concentration in the alloy. The independent solute and solvent interstitial concentrations enable one to describe different thermodynamic and kinetic properties of solute and solvent interstitials including the chemical potentials and diffusivities on grain boundaries, production efficiency and binding energy among defects. 2) thermodynamic and kinetic properties of defects in a polycrystalline structure are expressed to be spatial or microstructure dependent, which enables one to examine the effect of thermodynamic and kinetic properties of defects on RIS at grain boundaries. 3) the assumption that grain boundaries are perfect sink of defects is released. Defect concentrations on grain boundaries are determined by their chemical potentials, recombination and absorption rates. The defect absorption refers to the scenario that defects are consumed by grain growth or migrate to free surface along grain boundaries. With the model, the effect of structural and concentration dependent thermodynamic and kinetic properties on RIS were simulated. For the given kinetic properties of defects inside grains and on grain boundaries, the results indicate that 1) vacancy depletion on grain boundaries is always observed and the relative kinetic property of $\left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)$ determines the solute flux i.e., $\nabla c_A\propto \left(\frac{d_{AV}}{d_{BV}}-\frac{d_{Ai}}{d_{Bi}}\right)\nabla c_V$ and segregation or depletion on grain boundaries, which is in agreement with the steady state solution predicted by the conventional rate theory; 2) RIS strongly depends on solute chemical potential on grain boundaries. Increasing the solute chemical potential on grain boundaries may change solute segregation to solute depletion, or vice versa; 3) solute segregation or depletion on grain boundaries is non-uniform. Solutes have strong segregation or depletion at triple points of grain boundaries. It implies that second phase may form first at the triple points which are, actually, often observed in materials. 4) the assumption that all defects remain their thermal equilibrium concentrations in the rate theory is not necessarily correct unless the extra defects can be absorbed or emitted by grain boundaries. Grain boundaries acting as perfect sinks $\left(z_{d,GB}=0.1\right)$ reduces defect concentrations inside grain and the solute segregation kinetics on grain boundaries. 5) the production efficiency of solute interstitials and the binding energy among defects are important parameters which affect the RIS.

The simulations demonstrate that developed model extends and strengthens the capability of the conventional rate theory of RIS. However, the inhomogeneous thermodynamic and kinetic properties add challenges in simulations. For example, to capture the thickness of grain boundaries about few nanometers we have to use a small grid size $l_0$ (Piochaud et al., 2016; Xia et al., 2020). As we know that the time step for solving the diffusion equations can be estimated by $dt=l_0^2/D_0$, where $D_0$ is the largest diffusivity of defects of interest. Decreasing $l_0$ and increasing $D_0$ reduce the time step and increase the computational cost. This is the reason why we presented the RIS at very early stage $\text{t}=8.17\text{s}$, and used a high dpa rate which can increase the defect concentration and speed up the RIS in this work. We can run a one dimensional (1D) model with larger grains, lower dpa rate and longer radiation time. Figure 10 shows the 1D result. It confirms that decreasing the dpa rate slows down the RIS kinetics, but doesn’t affect the RIS feature (depletion or segregation) for given thermodynamic and kinetics properties of defects. In irradiated materials, interstitials, which are dominant defects, usually have large and strong anisotropic diffusivity (such as one dimensional diffusion). The large and anisotropic diffusivity adds more difficulty in solving the diffusion equations. The model can be extended to use the first-passage approach (Hu and Henager, 2009; Hu et al., 2016) to describe the large and anisotropic diffusivity and to increase the time step and computational efficiency.

The characteristic length $l_0$ is an important model parameter. A larger $l_0$ allows to use a larger time step in the simulations. Two ways might be used to increase the $l_0$. One is to construct a shape function $f\left(\eta \right)$ which could describe an arrow or sharp grain boundaries. The other is to use an adaptive mesh to capture the thermodynamic and kinetic properties of defect on structural defects (Tonks et al., 2012; Chakraborty et al., 2016). Structural defects such as grain boundaries, second phase particles in ODS, and interfaces in coated cladding materials act as sinks of defects. The local chemistry change affects the phase stability, hence, microstructure change and material property degradation. The developed model is based on fundamental properties of defects such as the properties of grain boundaries (Admal et al., 2018) and interface, partial diffusivity (Messina et al., 2014) and binding energies. With the thermodynamic and kinetics properties of materials of interest, the model can be extended and applied in studying the effect of microstructure dependent thermodynamic and kinetic properties on defect evolution and RIS in materials with complicated microstructures.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SH: Conceptualization, Model development, Writing-original draft, review, and editing. YL: Code development, Simulation, Visualization, Writing-original draft, review, and editing. DB: Conceptualization, Review and editing, Project supervision. DS: Conceptualization, Review and editing, Funding acquisition, Project administration.

Funding

This research was supported by the National Nuclear Security Administration of the U.S. Department of Energy through the Tritium Technology Program at Pacific Northwest National Laboratory. Computation was performed using Environmental Molecular Sciences Laboratory (EMSL) computing resources at Pacific Northwest National Laboratory.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Admal, N. C., Po, G., and Marian, J. (2018). A Unified Framework for Polycrystal Plasticity with Grain Boundary Evolution. Int. J. Plasticity 106, 1–30. doi:10.1016/j.ijplas.2018.01.014

CrossRef Full Text | Google Scholar

Akamatsu, M., Van Duysen, J. C., Pareige, P., and Auger, P. (1995). Experimental Evidence of Several Contributions to the Radiation Damage in Ferritic Alloys. J. Nucl. Mater. 225, 192–195. doi:10.1016/0022-3115(95)00028-3

CrossRef Full Text | Google Scholar

Allen, T. R., and Was, G. S. (1998). Modeling Radiation-Induced Segregation in Austenitic Fe-Cr-Ni Alloys. Acta Materialia 46 (10), 3679–3691. doi:10.1016/s1359-6454(98)00019-6

CrossRef Full Text | Google Scholar

Badillo, A., Bellon, P., and Averback, R. S. (2015). A Phase Field Model for Segregation and Precipitation Induced by Irradiation in Alloys. Model. Simulation Mater. Sci. Eng. 23 (3). doi:10.1088/0965-0393/23/3/035008

CrossRef Full Text | Google Scholar

Bruemmer, S. M., Simonen, E. P., Scott, P. M., Andresen, P. L., Was, G. S., and Nelson, J. L. (1999). Radiation-induced Material Changes and Susceptibility to Intergranular Failure of Light-Water-Reactor Core Internals. J. Nucl. Mater. 274 (3), 299–314. doi:10.1016/s0022-3115(99)00075-6

CrossRef Full Text | Google Scholar

Chakraborty, P., Zhang, Y., and Tonks, M. R. (2016). Multi-scale Modeling of Microstructure Dependent Intergranular Brittle Fracture Using a Quantitative Phase-Field Based Method. Comput. Mater. Sci. 113, 38–52. doi:10.1016/j.commatsci.2015.11.010

CrossRef Full Text | Google Scholar

Damcott, D. L., Allen, T. R., and Was, G. S. (1995). Dependence of Radiation-Induced Segregation on Dose, Temperature and Alloy Composition in Austenitic Alloys. J. Nucl. Mater. 225, 97–107. doi:10.1016/0022-3115(94)00690-3

CrossRef Full Text | Google Scholar

Duh, T. S., Kai, J. J., Chen, F. R., and Wang, L. H. (2001). Numerical Simulation Modeling on the Effects of Grain Boundary Misorientation on Radiation-Induced Solute Segregation in 304 Austenitic Stainless Steels. J. Nucl. Mater. 294 (3), 267–273. doi:10.1016/s0022-3115(01)00493-7

CrossRef Full Text | Google Scholar

Dunn, A. Y., Capolungo, L., Martinez, E., and Cherkaoui, M. (2013). Spatially Resolved Stochastic Cluster Dynamics for Radiation Damage Evolution in Nanostructured Metals. J. Nucl. Mater. 443 (1-3), 128–139. doi:10.1016/j.jnucmat.2013.07.009

CrossRef Full Text | Google Scholar

Faney, T., and Wirth, B. D. (2014). Spatially Dependent Cluster Dynamics Modeling of Microstructure Evolution in Low Energy Helium Irradiated Tungsten. Model. Simulation Mater. Sci. Eng. 22 (6). doi:10.1088/0965-0393/22/6/065010

CrossRef Full Text | Google Scholar

Farrell, K., Mahmood, S. T., Stoller, R. E., and Mansur, L. K. (1994). An Evaluation of Low Temperature Radiation Embrittlement Mechanisms in Ferritic Alloys. J. Nucl. Mater. 210 (3), 268–281. doi:10.1016/0022-3115(94)90181-3

CrossRef Full Text | Google Scholar

Field, K. G., Barnard, L. M., Parish, C. M., Busby, J. T., Morgan, D., and Allen, T. R. (2013). Dependence on Grain Boundary Structure of Radiation Induced Segregation in a 9 wt.% Cr Model Ferritic/martensitic Steel. J. Nucl. Mater. 435 (1-3), 172–180. doi:10.1016/j.jnucmat.2012.12.026

Google Scholar

Golubov, S. I., Ovcharenko, A. M., Barashev, A. V., and Singh, B. N. (2001). Grouping Method for the Approximate Solution of a Kinetic Equation Describing the Evolution of Point-Defect Clusters. Philos. Mag. A 81 (3), 643–658. doi:10.1080/01418610108212164

CrossRef Full Text | Google Scholar

Grandjean, Y., Bellon, P., and Martin, G. (1994). Kinetic Model for Equilibrium and Nonequilibrium Segregation in Concentrated Alloys under Irradiation. Phys. Rev. B 50 (6), 4228–4231. doi:10.1103/physrevb.50.4228

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, R., Smith, G. D. W., and Marquis, E. A. (2012). Atom Probe Study of Radiation Induced Grain Boundary Segregation/depletion in a Fe-12%Cr Alloy. Prog. Nucl. Energ 57, 14–19. doi:10.1016/j.pnucene.2011.10.011

Google Scholar

Hu, S., Burkes, D. E., Lavender, C. A., Senor, D. J., Setyawan, W., and Xu, Z. (2016). Formation Mechanism of Gas Bubble Superlattice in UMo Metal Fuels: Phase-Field Modeling Investigation. J. Nucl. Mater. 479, 202–215. doi:10.1016/j.jnucmat.2016.07.012

CrossRef Full Text | Google Scholar

Hu, S., and Henager, C. H. (2009). Phase-field Modeling of Void Lattice Formation under Irradiation. J. Nucl. Mater. 394 (2), 155–159. doi:10.1016/j.jnucmat.2009.09.002

CrossRef Full Text | Google Scholar

Huang, C. H., and Marian, J. (2016). A Generalized Ising Model for Studying Alloy Evolution under Irradiation and its Use in Kinetic Monte Carlo Simulations. J. Phys-condens Mat 28 (42). doi:10.1088/0953-8984/28/42/425201

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, C., Swaminathan, N., Deng, J., Morgan, D., and Szlufarska, I. (2014). Effect of Grain Boundary Stresses on Sink Strength. Mater. Res. Lett. 2 (2), 100–106. doi:10.1080/21663831.2013.871588

CrossRef Full Text | Google Scholar

Jourdan, T., Bencteux, G., and Adjanor, G. (2014). Efficient Simulation of Kinetics of Radiation Induced Defects: A Cluster Dynamics Approach. J. Nucl. Mater. 444 (1-3), 298–313. doi:10.1016/j.jnucmat.2013.10.009

CrossRef Full Text | Google Scholar

Hirth, J. P., Lothe, J., and Anderson, P. M. (1968). Theory of Dislocation. New York: McGraw-Hill Book Company.

Kamachali, R. D., da Silva, A. K., McEniry, E., Ponge, D., Gault, B., Neugebauer, J., et al. (2019). Segregation–Assisted Spinodal and Transient Spinodal Phase Separation at Grain Boundaries. npj Comput Mater 6, 191 (2020). https://doi.org/10.1038/s41524-020-00456-7

Ke, J.-H., Ke, H., Odette, G. R., and Morgan, D. (2018). Cluster Dynamics Modeling of Mn-Ni-Si Precipitates in Ferritic-Martensitic Steel under Irradiation. J. Nucl. Mater. 498, 83–88. doi:10.1016/j.jnucmat.2017.10.008

CrossRef Full Text | Google Scholar

Kuksenko, V., Pareige, C., and Pareige, P. (2012). Intra Granular Precipitation and Grain Boundary Segregation under Neutron Irradiation in a Low Purity Fe-Cr Based Alloy. J. Nucl. Mater. 425 (1), 125–129. doi:10.1016/j.jnucmat.2011.10.031

CrossRef Full Text | Google Scholar

Lam, N. Q., Okamoto, P. R., Wiedersich, H., and Taylor, A. (1978). Radiation-Induced Solute Segregation and Precipitation in Alloys. Mta 9 (12), 1707–1714. doi:10.1007/bf02663400

CrossRef Full Text | Google Scholar

Li, B. Y., Hu, S. Y., Li, C. L., Li, Q. L., Chen, J., Shu, G. G., et al. (2017). Simulations of Irradiated-Enhanced Segregation and Phase Separation in Fe-Cu-Mn Alloys. Model. Simulation Mater. Sci. Eng. 25 (6). doi:10.1088/1361-651x/aa7197

CrossRef Full Text | Google Scholar

Lu, Z., Faulkner, R. G., Was, G., and Wirth, B. D. (2008). Irradiation-induced Grain Boundary Chromium Microchemistry in High Alloy Ferritic Steels. Scripta Materialia 58 (10), 878–881. doi:10.1016/j.scriptamat.2008.01.004

CrossRef Full Text | Google Scholar

Messina, L., Nastar, M., Garnier, T., Domain, C., and Olsson, P. (2014). Exact Ab Initio Transport Coefficients in Bcc Fe-X (X=Cr, Cu, Mn, Ni, P, Si) Dilute Alloys. Phys. Rev. B 90 (10). doi:10.1103/physrevb.90.104203

CrossRef Full Text | Google Scholar

Nastar, M., and Soisson, F. (2012). “Radiation-Induced Segregation,” in Comprehensive Nuclear Materials. Editor R. J. M. Konings (Oxford: Elsevier), 471–496. doi:10.1016/b978-0-08-056033-5.00035-5

CrossRef Full Text | Google Scholar

Odette, G. R., and Lucas, G. E. (1986). Irradiation Embrittlement of Reactor Pressure Vessel Steels: Mechanisms, Models, and Data Correlations. Editor L. E. Steele (West Conshohocken, PA: ASTM International), 206–241.

Onsager, L. (1931). Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 37 (4), 405–426. doi:10.1103/physrev.37.405

CrossRef Full Text | Google Scholar

Ortiz, M. J. C. C. J. (2007). Simulation of Defect Evolution in Irradiated Materials: Role of Intracascade Clustering and Correlated Recombination Phys. Rev. B 75, 184101. doi:10.1103/PhysRevB.75.184101

Piochaud, J. B., Nastar, M., Soisson, F., Thuinet, L., and Legris, A. (2016). Atomic-based Phase-Field Method for the Modeling of Radiation Induced Segregation in Fe-Cr. Comput. Mater. Sci. 122, 249–262. doi:10.1016/j.commatsci.2016.05.021

CrossRef Full Text | Google Scholar

Senninger, O., Soisson, F., Martínez, E., Nastar, M., Fu, C.-C., and Bréchet, Y. (2016). Modeling Radiation Induced Segregation in Iron-Chromium Alloys. Acta Materialia 103, 1–11. doi:10.1016/j.actamat.2015.09.058

CrossRef Full Text | Google Scholar

Simonen, E. P., and Bruemmer, S. M. (1999). Radiation-induced Grain Boundary Segregation in Austenitic Stainless Steels. Mater. Sci. Forum 294-2, 755–758. doi:10.4028/www.scientific.net/MSF.294-296.755

Google Scholar

Soisson, F., and Jourdan, T. (2016). Radiation-accelerated Precipitation in Fe-Cr Alloys. Acta Materialia 103, 870–881. doi:10.1016/j.actamat.2015.11.001

CrossRef Full Text | Google Scholar

Souidi, C. S. B. A., Domain, C., Terentyev, D., Malerba, L., Calder, A. F., Bacon, D. J., et al. (2006). Dependence of Radiation Damage Accumulation in Iron on Underlying Models of Displacement Cascades and Subsequent Defect Migration. J. Nucl. Mater. 355 (1–3), 89–103. doi:10.1016/j.jnucmat.2006.04.009

CrossRef Full Text | Google Scholar

Tonks, M. R., Gaston, D., Millett, P. C., Andrs, D., and Talbot, P. (2012). An Object-Oriented Finite Element Framework for Multiphysics Phase Field Simulations. Comput. Mater. Sci. 51 (1), 20–29. doi:10.1016/j.commatsci.2011.07.028

CrossRef Full Text | Google Scholar

Tschopp, M. A., Horstemeyer, M. F., Gao, F., Sun, X., and Khaleel, M. (2011). Energetic Driving Force for Preferential Binding of Self-Interstitial Atoms to Fe Grain Boundaries over Vacancies. Scripta Materialia 64 (9), 908–911. doi:10.1016/j.scriptamat.2011.01.031

CrossRef Full Text | Google Scholar

van der Waals, J. D. (1979). The Thermodynamic Theory of Capillarity under the Hypothesis of a Continuous Variation of Density. J. Stat. Phys. 20 (2), 200–244. doi:10.1007/bf01011514

CrossRef Full Text | Google Scholar

Was, G. S. (2016). Fundamentals of Radiation Materials Science: Metals and Alloys. Springer.

Was, G. S., Wharry, J. P., Frisbie, B., Wirth, B. D., Morgan, D., Tucker, J. D., et al. (2011). Assessment of Radiation-Induced Segregation Mechanisms in Austenitic and Ferritic-Martensitic Alloys. J. Nucl. Mater. 411 (1-3), 41–50. doi:10.1016/j.jnucmat.2011.01.031

CrossRef Full Text | Google Scholar

Wharry, J. P., and Was, G. S. (2013). A Systematic Study of Radiation-Induced Segregation in Ferritic-Martensitic Alloys. J. Nucl. Mater. 442 (1-3), 7–16. doi:10.1016/j.jnucmat.2013.07.071

CrossRef Full Text | Google Scholar

Wharry, J. P., and Was, G. S. (2014). The Mechanism of Radiation-Induced Segregation in Ferritic-Martensitic Alloys. Acta Materialia 65, 42–55. doi:10.1016/j.actamat.2013.09.049

CrossRef Full Text | Google Scholar

Woo, C. H., and Singh, B. N. (1992). Production Bias Due to Clustering of Point Defects in Irradiation-Induced Cascades. Philos. Mag. A 65 (4), 889–912. doi:10.1080/01418619208205596

CrossRef Full Text | Google Scholar

Xia, L. D., Ji, Y. Z., Liu, W. B., Chen, H., Yang, Z. G., Zhang, C., et al. (2020). Radiation Induced Grain Boundary Segregation in Ferritic/martensitic Steels. Nucl. Eng. Technol. 52 (1), 148–154. doi:10.1016/j.net.2019.07.009

CrossRef Full Text | Google Scholar

Xu, D. H., and Wirth, B. D. (2010). Modeling Spatially Dependent Kinetics of Helium Desorption in BCC Iron Following He Ion Implantation. J. Nucl. Mater. 403 (1-3), 184–190. doi:10.1016/j.jnucmat.2010.06.025

CrossRef Full Text | Google Scholar

Xu, D., and Wirth, B. D. (2009). Spatially Dependent Rate Theory Modeling of Thermal Desorption Spectrometry of Helium-Implanted Iron. Fusion Sci. Technol. 56 (2), 1064–1068. doi:10.13182/fst09-a9052

CrossRef Full Text | Google Scholar

Yang, Y., Field, K. G., Allen, T. R., and Busby, J. T. (2016). Roles of Vacancy/interstitial Diffusion and Segregation in the Microchemistry at Grain Boundaries of Irradiated Fe-Cr-Ni Alloys. J. Nucl. Mater. 473, 35–53. doi:10.1016/j.jnucmat.2016.02.007

CrossRef Full Text | Google Scholar

Zhang, Y. X., Schwen, D., and Bai, X. M. (2017). Molecular Dynamics Simulations of Concentration- Dependent Defect Production in Fe-Cr and Fe-Cu Alloys. J. Appl. Phys. 122 (22). doi:10.1063/1.5008757

CrossRef Full Text | Google Scholar

Zhao, H., De Geuser, F., Kwiatkowski da Silva, A., Szczepaniak, A., Gault, B., Ponge, D., et al. (2018). Segregation Assisted Grain Boundary Precipitation in a Model Al-Zn-Mg-Cu Alloy. Acta Materialia 156, 318–329. doi:10.1016/j.actamat.2018.07.003

CrossRef Full Text | Google Scholar