
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 05 July 2021
Sec. Computational Materials Science
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.678858
This article is part of the Research TopicComputational Defect PropertiesView all 7 articles
Tungsten (W) is a candidate for the plasma-facing components and divertor in future fusion applications. The material will be subject to a large particle influx (mainly helium and hydrogenic species) that will form bubbles. As bubbles grow, they compress the material, adding to thermal stresses, and eject self-interstitial atoms (SIAs—isolated or in clusters) to release internal pressure. These SIAs diffuse towards the surface in large stress/strain fields and on the surface are thought to act as precursors for nanotendril formation (also known as fuzz) that develops on the material surface modifying its morphology. In this work we analyze the effect of strain on the diffusion properties of both SIAs and adatoms. Relying on atomistic simulations, we compute the average time that a SIA created in the center of a tungsten slab takes to reach a (110) surface for different strains and temperatures. This time relates to the SIA diffusivity and allows to compute the activation energy and dipole tensor including surface effects. We observe a large strain effect that significantly modifies the propensity for SIAs to reach the surface and, hence, to cluster to form dislocation loops in the bulk crystal. Strain also alters the diffusivity of the adatom although to a lesser extent. Finally, we report on the resulting surface roughness evolution and its dependence on strain.
In fusion environments, plasma-facing components (PFCs) are exposed to stringent conditions as imposed by the plasma, required for the nuclear reaction to occur. Such PFCs must withstand extreme conditions of temperature and particle fluxes that modify the material microstructure, potentially leading to failure. (Knaster et al., 2016) Understanding the materials response upon such extreme environments is therefore crucial for the development of clean, safe and abundant fusion energy generation systems. Tungsten (W) is the main candidate as PFC due to its favorable properties, such as low sputtering yield, high sputtering threshold, high thermal conductivity and high melting point. (Suzuki et al., 2003; Ihli et al., 2006).
Despite these advantages, certain drawbacks have also been observed, such as the formation of a fuzz-like nanostructure in the W surface due to the helium (He) ash implantation, which leads to the formation of high-pressure bubbles that eject self-interstitial atoms (SIAs) to relax such high stresses, consequently generating vacancies in the bubbles. The diffusion of these SIAs, either individually or in clusters, towards the surface in the presence of stresses generated thermally and by the bubble distribution, seems to be an important mechanism contributing to the observed surface morphological evolution and nanotendril formation (Takamura et al., 2006; Baldwin et al., 2009; Yang et al., 2015; Wang et al., 2017). This fuzz nanostructure modifies the erosion propensity and potentially causes embrittlement of the divertor component, (Wirth et al., 2015) leading to particle sputtering that may disrupt the plasma. Fuzz forms under certain plasma conditions, when W is exposed to He and He-deuterium (D) mixed plasmas but not for pure D plasmas (Baldwin et al., 2009), at exposure temperatures in the range of 900–2000 K and incident ion energies around 20–100 eV with incoming fluxes on the order of 1024 m−2 s−1. (Kajita et al., 2009) Note that these incident energies are insufficient to generate radiation damage in the form of vacancies and self-interstitials, but lead to the formation of over-pressurized bubbles and subsequent trap mutation.
Many different models have been proposed in the literature to explain fuzz formation. (Krasheninnikov, 2011; Martynenko and Nagel’, 2012; Lasa et al., 2014; Fiflis et al., 2015; Ito et al., 2015; Ito et al., 2018; Dasgupta et al., 2019) Recently, Dasgupta et al. (Dasgupta et al., 2019; Dasgupta et al., 2020; Chen et al., 2021) have developed a continuum-scale model that tries to understand and predict the onset of fuzz formation depending on the exposure conditions. In this model, internal stresses due to the formation of highly over-pressurized bubbles is the main driving force for triggering surface instabilities leading to the formation of fuzz. Each bubble is modeled as an Eshelby inclusion acting as a source of hydrostatic compressive stress in the matrix. The model assumes a negligible contribution of particle sputtering to the surface morphology as the incident energies of the implanted He atoms are low. The model describes the change of a surface height function, h = h(x,y,t), in terms of transport of SIAs in one dimension toward the surface, as well as two-dimensional curvature-driven and stress-driven surface diffusion. In that model, the dependence of the process on strain/stress is included in the chemical potential of surface atoms. However, the fluxes also depend on the diffusion coefficient of the SIAs, both in the bulk and on the surface (after they reach the surface and become adatoms), and, in general, both of these diffusion coefficients are functions of the local strain fields. This dependence is still to be incorporated into larger-scale models. The purpose of this study is to better understand the effect of strain on the transport coefficients of SIAs in W in order to improve the predictive capabilities of the continuum-scale surface evolution model.
In this work we rely on atomistic simulations to systematically study the effect of strain on the diffusivities of SIAs and surface adatoms in W. We first describe the methodology that has been followed in this work in Section 2. We present the results in Section 3 where we show the significant effect of strain in the transport of SIAs in bulk W, with a less significant contribution to surface adatom diffusion. In Section 4 we discuss the implications of these results in the study of fuzz formation. Lastly, we draw the main conclusions of our study in Section 5.
We have used molecular dynamics (MD) simulations as implemented in the LAMMPS code (Plimpton, 1995) with an Embedded Atom Method (EAM) interatomic potential developed by Marinica et al. (Marinica et al., 2013) to model the behavior of body-centered cubic (bcc) W; this interatomic potential was designed specifically targeting defect properties in bcc W. We have used three different sets of simulations, with samples modeled by slab supercells oriented in the
The first set employs a sample of dimensions 61.5 × 76.1 × 86.6 Å3, with two free surfaces in the z direction and
The second set of simulations intended to compute the effect of strain on the diffusivity of adatoms on a W
The last simulation set aimed at analyzing the effect of biaxial strain on the morphological evolution of a W
To track the position of the SIA, we performed a common neighbor analysis (CNA) (Honeycutt and Andersen, 1987) to obtain the atoms that are not located in bcc lattice positions. For the first passage time simulations, a SIA is specified to reach the surface when all the atoms in the bulk crystal are arranged in bcc lattice sites.
According to the first passage time model, (Redner, 2001) the most probable time for a diffusing particle to reach a point in space from a given origin in 1D is given by
where Δx is the distance traveled by the walker (in this case a SIA) and DSIA is the SIA diffusivity. We have estimated this time running the first set of simulations described in Section 2. We have employed these results to fit a diffusion coefficient following transition state theory (TST) in the form
with D0 a diffusivity prefactor, ΔH the activation enthalpy, ΔE the activation energy, σa an activation stress tensor related to the difference of the stress tensor at the saddle point and at the initial configuration, ε the applied strain tensor and Ω the atomic volume as a reference constant volume for the system, which for W is Ω = 15.8 Å3. It should be mentioned that σa and ε in Eq. 2 denote the respective stress and strain tensors and the corresponding product is a double dot product (carried out through the contraction operator), which, multiplied by the atomic volume, gives a scalar quantity with units of energy. Fitting simultaneously the values gathered from MD we obtain D0 = 12.9 Å2 ps−1, ΔE = 0.19 eV, and σa = 110.6 GPa, considering tensile strains as positive. The large value of the activation stress highlights the strong effect of the biaxial strain on the SIA diffusivity in the bulk crystal. Furthermore, the positive sign of σa implies that the compressive strain leads to a decrease in the activation enthalpy, increasing the diffusivity, and hence, decreasing the first passage time. Note that ΔE is an effective activation energy in the
To better understand the role of the free surface, we have computed the diffusivity of a SIA in bulk W at ε = 0 and 700 K, 850 K and 1,000 K, respectively. We computed the mean-squared displacement tracking the center of mass of the non-bcc atoms obtained from CNA and used an Einstein relation to calculate the diffusivity. The effective activation energy following from this analysis resulted in a value of around 0.06 eV, which is significantly lower than the value obtained in the presence of the surface (0.19 eV). This value is fully consistent with recent experiments (Heikinheimo et al., 2019) that provide an upper bound for the SIA migration energy of 0.1 eV. To rationalize this result, we have computed the strain induced by the free surface relaxation, which generates a strain in the sample εs = 0.006 in the direction normal to the free surface at 1,000 K. Using σa = 110.6 GPa calculated from the first passage time and the same Ω as above, the increase in activation energy is ≈0.066 eV, resulting in an activation enthalpy of 0.126 eV, much closer to the value obtained from the first passage time computations.
Figure 1 shows the results from both MD (solid square symbols) and the theoretical model (solid lines). Figure 1A shows the dependence of the estimated first passage time on the applied strain for the three different temperatures studied, while Figure 1B presents the estimated time as a function of temperature. Fitting the MD results according to Eq. 2 clearly reproduces the trends computed from MD, where we observe a significant effect of strain on the first passage time, which may result in differences between the estimated times by almost two orders of magnitude. As we biaxially compress the material the time decreases as the diffusivity increases. The temperature effect seems to follow the usual Arrhenius relation for the cases studied in this work.
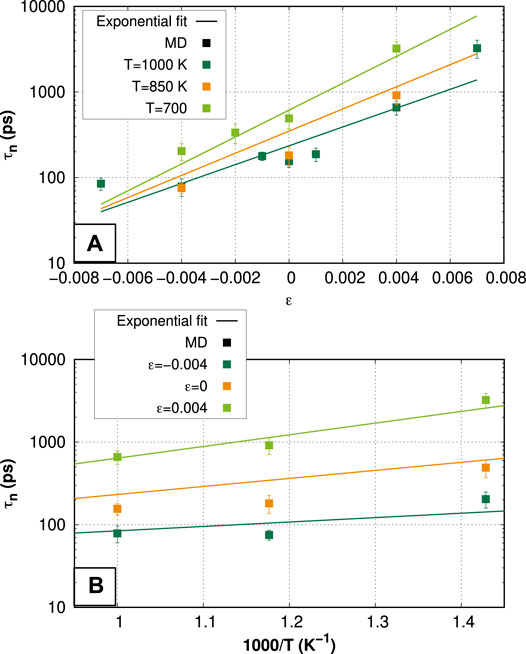
FIGURE 1. First passage time for a SIA to reach the free surface traveling a distance
Running MD simulations of the dynamics of the adatom on the W
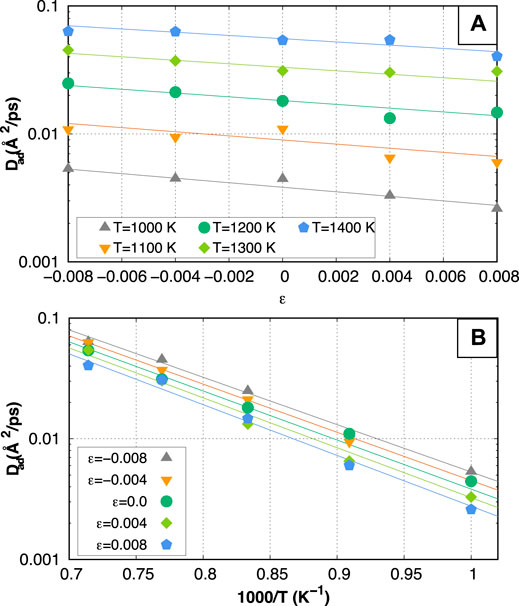
FIGURE 2. Diffusion coefficient of an adatom in a W
To rationalize the results obtained from the computation of the mean-squared displacement, we have performed NEB simulations to compute the MEPs and the respective activation barriers at various applied strain levels. Figure 3 shows the results, where we observe that indeed the compressive equibiaxial strain leads to a decrease in the activation enthalpy. The value of
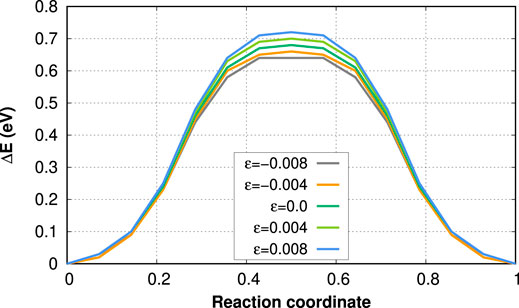
FIGURE 3. Minimum energy path for an adatom hopping along a
The third set of MD simulations examines the evolution of the surface morphology as added SIAs diffuse to the surface and migrate on it to form clusters and aggregates that lead to an increase in surface roughness depending on the applied equibiaxial strain. As shown in Section 3. One, strain has a profound effect on the SIA transport in the bulk material. The higher the tensile strain the longer the time the SIA spends inside the material, increasing the defect concentration, and hence, the propensity to react with incoming SIAs. Indeed, we see that the formation of SIA clusters and dislocation loops is more probable as the tensile strain increases. We have used the root mean squared surface roughness (SR), which is defined consistently with Ref. (Dasgupta et al., 2019)
with
We have run the MD simulations for 2 μs, adding a total of 10,000 SIAs to the W in the slab supercell. To compute the SR values, we have discretized the domain in x and y in small cells, with indices i and j, and found the atoms belonging to each of the surfaces. The size of the cells was chosen such that the minimum number of atoms per cell is one, with cell sizes ranging between 9 and 25 Å2. For each surface, the average value of the z coordinates of the atoms in each cell was computed and stored as h(i,j,t). The average SR of both surfaces was then calculated and it is shown in Figure 4, where we present a five-point average in time of the SR evolution.
Initially, we see that equibiaxial compression leads to a slightly larger SR since the SIAs travel fast to the surface. However, as we add more atoms, the SR at compressive strains plateaus. At this point, extra atoms create new bcc layers under compression and do not increase the SR, while under tension, the SR continues to grow, creating a crossover at around 1 μs. The same trend is followed by the number of atoms at the surface, the surface area and the distance between free surfaces as obtained by the alpha-shape algorithm (Stukowski, 2014) as implemented in the Ovito software (Stukowski, 2010) using 3 Å as the sphere probe radius. The latter is shown in Figure 5 after 2 μs, where we note that the average distance between free surfaces decays fairly linearly with the applied equibiaxial strain level. This indicates that the surface grows faster under compressive rather than tensile strain. It is also worth mentioning that the 2 μs reached by our MD simulations are too short compared with the experimental observations in which exposure times reach hundreds of minutes (i.e., several hours) and the surface roughness may reach values on the order of tens of nm.
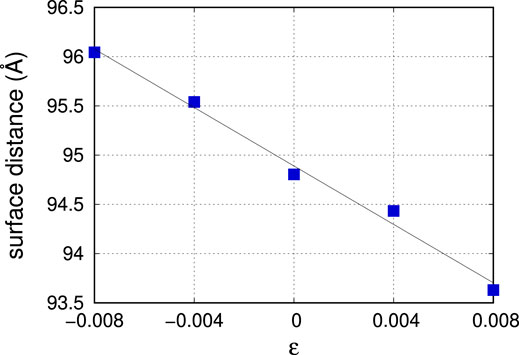
FIGURE 5. Average distance between free surfaces located by the alpha-shape algorithm (Stukowski, 2014) implemented in Ovito (Stukowski, 2010) using a sphere probe of 3 Å radius as a function of the applied equibiaxial strain level.
Figure 6 shows the time evolution of the W slab in the simulation supercell when an equibiaxial tensile strain
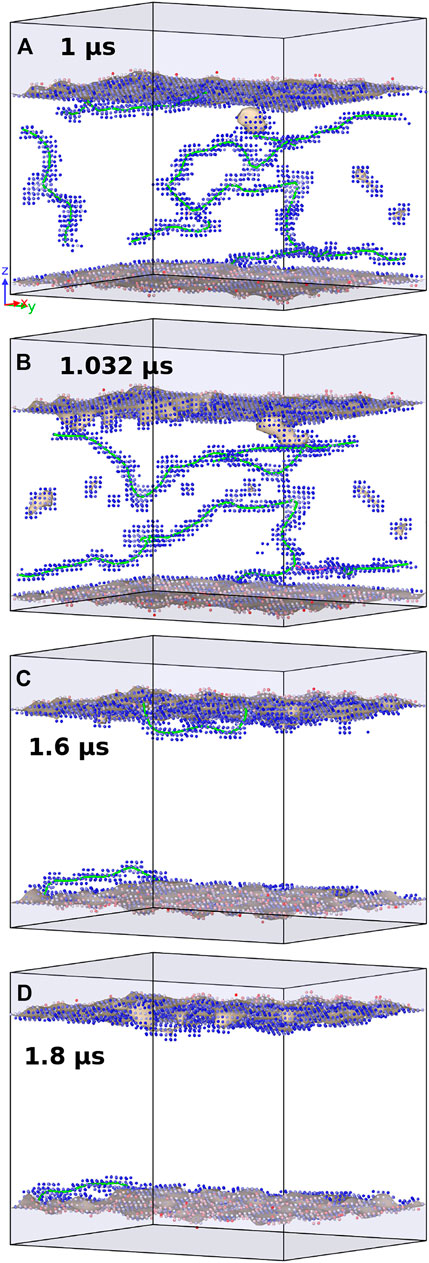
FIGURE 6. Evolution at different simulated times denoted in each subfigure, of a W slab with
The SIA concentration profile at steady state in the kinetic regime dominated by annihilation at the free surfaces is obtained from the diffusion equation
The former boundary condition implies that the free surface at z = 0 acts as a sink for SIAs while the latter one is a symmetry condition in the middle of the W slab. The steady-state concentration depends on strain as the diffusivity
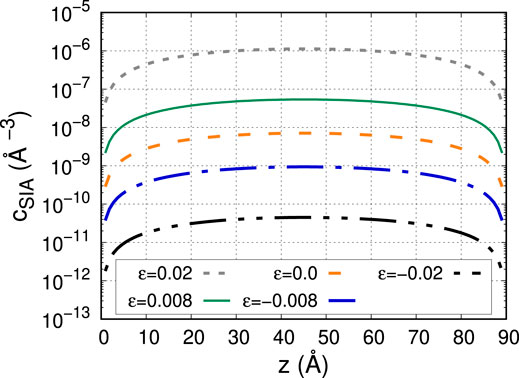
FIGURE 7. Steady-state concentration of SIAs in a material slab of 90 Å in thickness obtained by the solution to the diffusion equation given by Eq. 5 at different levels of biaxial strain.
It is important to note that under reactor operating conditions, a PFC is expected to be subject to compressive equibiaxial strains induced by the presence of over-pressurized He bubbles in the PFC near-surface region. However, the generation of a significant density of edge dislocations as a result of aggregation of SIAs or directly emitted by the bubbles, through the loop punching process, may lead to more complex scenarios, with local strain fields that can vary in character. Moreover, the strain state is likely to also change binding energies, which might modify the source terms, that we have however kept constant throughout this study, as we focus on the transport properties. Furthermore, surface growth and fuzz formation under biaxial compressive stress and promotion of surface roughness under biaxial tensile stress are not in contradiction with each other. We know that, due to the formation of over-pressurized helium bubbles, the near-surface region of PFC tungsten is under an equibiaxial compressive state of stress and, according to our surface morphological evolution models (see Refs. (Dasgupta et al., 2019; Dasgupta et al., 2020; Chen et al., 2021)), this is consistent with the formation and growth of nanotendrils emanating from the PFC surface, which is known to be the precursor to fuzz formation in PFC tungsten. In other words, the development of biaxial compressive stress is expected to promote fuzz formation. This is not at odds with the promotion of surface roughness by tensile stress. For example, it is well known that tensile stress (as well as compressive stress) can induce surface morphological instabilities, such as the Asaro-Tiller-Grinfeld instability (Maroudas, 2011) that promote surface roughness and may lead to surface cracking. The results presented here intend to convey a general picture of the effects of strain on the transport of SIAs and its effect on the morphological evolution of the free surface, in conjunction with providing activation parameters that can be readily used in larger-scale models, such as in cluster dynamics or reduced-order frameworks. (Blondel et al., 2018; Dasgupta et al., 2019)
As a matter of fact, the reduced-order (continuum-scale) model proposed by Dasgupta et al. (Dasgupta et al., 2019) describes the surface evolution in terms of the SIA fluxes towards the PFC surfaces and the adatom surface diffusion
with
At steady state,
The surface flux can be written as
In summary, we have analyzed the effect of equibiaxial strain on the transport of self-interstitial atoms towards a
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
EM: Conceptualization, Methodology, Software, Writing-Reviewing and Editing. BS: Methodology, Reviewing and Editing. BW: Reviewing and Editing. DM: Methodology, Writing-Reviewing and Editing.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
BS and EM thank support from the startup package at Clemson University. Clemson University is acknowledged for generous allotment of compute time on Palmetto cluster. EM (partial support), DM and BW acknowledge support from the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences and Office of Advanced Scientific Computing Research through the Scientific Discovery through Advanced Computing (SciDAC) project on Plasma Surface Interactions under Award Nos. DE-SC0008875 and DE-SC0018421.
Baldwin, M. J., Doerner, R. P., Nishijima, D., Tokunaga, K., and Ueda, Y. (2009). The Effects of High Fluence Mixed-Species (Deuterium, Helium, Beryllium) Plasma Interactions with Tungsten. J. Nucl. Mater. 390-391, 886–890. doi:10.1016/j.jnucmat.2009.01.247
Blondel, S., Bernholdt, D. E., Hammond, K. D., and Wirth, B. D. (2018). Continuum-scale Modeling of Helium Bubble Bursting under Plasma-Exposed Tungsten Surfaces. Nucl. Fusion 58 (12), 126034. doi:10.1088/1741-4326/aae8ef
Chen, C.-S., Dasgupta, D., Weerasinghe, A., Wirth, B. D., and Maroudas, D. (2021). Effects of Elastic Softening and Helium Accumulation Kinetics on Surface Morphological Evolution of Plasma-Facing Tungsten. Nucl. Fusion 61, 016016. doi:10.1088/1741-4326/abbf64
Chen, Z., and Ghoniem, N. (2013). Biaxial Strain Effects on Adatom Surface Diffusion on Tungsten from First Principles. Phys. Rev. B 88 (3), 035415. doi:10.1103/physrevb.88.035415
Dasgupta, D., Kolasinski, R. D., Friddle, R. W., Du, L., Maroudas, D., and Wirth, B. D. (2019). On the Origin of ‘fuzz’ Formation in Plasma-Facing Materials. Nucl. Fusion 59, 086057. doi:10.1088/1741-4326/ab22cb
Dasgupta, D., Maroudas, D., and Wirth, B. D. (2020). Prediction of Temperature Range for the Onset of Fuzz Formation in Helium-Plasma-Implanted Tungsten. Surf. Sci. 698, 121614. doi:10.1016/j.susc.2020.121614
Fiflis, P., Curreli, D., and Ruzic, D. N. (2015). Direct Time-Resolved Observation of Tungsten Nanostructured Growth Due to Helium Plasma Exposure. Nucl. Fusion 55 (3), 033020. doi:10.1088/0029-5515/55/3/033020
Heikinheimo, J., Mizohata, K., Räisänen, J., Ahlgren, T., Jalkanen, P., Lahtinen, A., et al. (2019). Direct Observation of Mono-Vacancy and Self-Interstitial Recovery in Tungsten. APL Mater. 7 (2), 021103. doi:10.1063/1.5082150
Henkelman, G., and Jónsson, H. (2000). Improved tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points. J. Chem. Phys. 113 (22), 9978–9985. doi:10.1063/1.1323224
Henkelman, G., Uberuaga, B. P., and Jónsson, H. (2000). A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 113 (22), 9901–9904. doi:10.1063/1.1329672
Honeycutt, J. D., and Andersen, H. C. (1987). Molecular Dynamics Study of Melting and Freezing of Small Lennard-Jones Clusters. J. Phys. Chem. 91, 4950–4963. doi:10.1021/j100303a014
Ihli, T., Hermsmeyer, S., Köhly, C., and Norajitra, P. (2006). Integration of an Advanced He-Cooled Divertor in a DEMO-Relevant Tokamak Geometry. Fusion Eng. Des. 81, 121–126. doi:10.1016/j.fusengdes.2005.05.002
Ito, A. M., Takayama, A., and Nakamura, H. (2018). Triple Hybrid Simulation Method for Tungsten Fuzzy Nanostructure Formation. Plasma Fusion Res. 13 (0), 3403061. doi:10.1585/pfr.13.3403061
Ito, A. M., Takayama, A., Oda, Y., Tamura, T., Kobayashi, R., Hattori, T., et al. (2015). Molecular Dynamics and Monte Carlo Hybrid Simulation for Fuzzy Tungsten Nanostructure Formation. Nucl. Fusion 55 (7), 073013. doi:10.1088/0029-5515/55/7/073013
Kajita, S., Sakaguchi, W., Ohno, N., Yoshida, N., and Saeki, T. (2009). Formation Process of Tungsten Nanostructure by the Exposure to Helium Plasma under Fusion Relevant Plasma Conditions. Nucl. Fusion 49 (9), 095005. doi:10.1088/0029-5515/49/9/095005
Knaster, J., Moeslang, A., and Muroga, T. (2016). Materials Research for Fusion. Nat. Phys 12 (5), 424–434. doi:10.1038/nphys3735
Krasheninnikov, S. I. (2011). Viscoelastic Model of Tungsten ‘fuzz’ Growth. Phys. Scr. T145, 014040. doi:10.1088/0031-8949/2011/t145/014040
Lasa, A., Tähtinen, S. K., and Nordlund, K. (2014). Loop Punching and Bubble Rupture Causing Surface Roughening -A Model for W Fuzz Growth. Epl 105 (2), 25002. doi:10.1209/0295-5075/105/25002
Marinica, M.-C., Ventelon, L., Gilbert, M. R., Proville, L., Dudarev, S. L., Marian, J., et al. (2013). Interatomic Potentials for Modelling Radiation Defects and Dislocations in Tungsten. J. Phys. Condens. Matter 25 (39), 395502. doi:10.1088/0953-8984/25/39/395502
Maroudas, D. (2011). Surface Morphological Response of Crystalline Solids to Mechanical Stresses and Electric Fields. Surf. Sci. Rep. 66, 299–346. doi:10.1016/j.surfrep.2011.05.001
Martynenko, Y. V., and Nagel’, M. Y. (2012). Model of Fuzz Formation on a Tungsten Surface. Plasma Phys. Rep. 38 (12), 996–999. doi:10.1134/s1063780x12110074
Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039
Stukowski, A., and Albe, K. (2010). Extracting Dislocations and Non-dislocation crystal Defects from Atomistic Simulation Data. Model. Simul. Mater. Sci. Eng. 18 (8), 085001. doi:10.1088/0965-0393/18/8/085001
Stukowski, A. (2014). Computational Analysis Methods in Atomistic Modeling of Crystals. JOM 66 (3), 399–407. doi:10.1007/s11837-013-0827-5
Stukowski, A. (2010). Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18 (1), 015012. doi:10.1088/0965-0393/18/1/015012
Suzuki, S., Ueda, Y., Tokunaga, K., Sato, K., and Akiba, M. (2003). Present Research Status on Divertor and Plasma Facing Components for Fusion Power Plants. Fusion Sci. Technol. 44, 41–48. doi:10.13182/fst03-a308
Takamura, S., Ohno, N., Nishijima, D., and Kajita, S. (2006). Formation of Nanostructured Tungsten with Arborescent Shape Due to Helium Plasma Irradiation. Plasma Fusion Res. 1, 051. doi:10.1585/pfr.1.051
Wang, K., Doerner, R. P., Baldwin, M. J., Meyer, F. W., Bannister, M. E., Darbal, A., et al. (2017). Morphologies of Tungsten Nanotendrils Grown under Helium Exposure. Sci. Rep. 7, 42315. doi:10.1038/srep42315
Wirth, B. D., Hammond, K. D., Krasheninnikov, S. I., and Maroudas, D. (2015). Challenges and Opportunities of Modeling Plasma-Surface Interactions in Tungsten Using High-Performance Computing. J. Nucl. Mater. 463, 30–38. doi:10.1016/j.jnucmat.2014.11.072
Woller, K. B., Whyte, D. G., and Wright, G. M. (2015). Dynamic Measurement of the Helium Concentration of Evolving Tungsten Nanostructures Using Elastic Recoil Detection during Plasma Exposure. J. Nucl. Mater. 463, 289–293. doi:10.1016/j.jnucmat.2014.11.126
Keywords: fusion, self-interstitial atoms, adatoms, transport, fuzz, plasma-facing components
Citation: Sun B, Maroudas D, Wirth BD and Martínez E (2021) Strain Effects on the Diffusion Properties of Near-Surface Self-Interstitial Atoms and Adatoms in Tungsten. Front. Mater. 8:678858. doi: 10.3389/fmats.2021.678858
Received: 10 March 2021; Accepted: 14 June 2021;
Published: 05 July 2021.
Edited by:
Yongfeng Zhang, University of Wisconsin-Madison, United StatesReviewed by:
Benjamin Beeler, North Carolina State University, United StatesCopyright © 2021 Sun, Maroudas, Wirth and Martínez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Enrique Martínez, ZW5yaXF1ZUBjbGVtc29uLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.