
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 17 June 2021
Sec. Ceramics and Glass
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.676764
This article is part of the Research Topic Nanostructured Glass: Properties and Applications View all 4 articles
In this work, the deformation behavior of as-prepared (AP) and structurally relaxed (SR) Cu–Zr–based nanoglasses (NGs) are investigated using nano- and micro-indentation. The NGs are subjected to structural relaxation by annealing them close to the glass transition temperature without altering their amorphous nature. The indentation load, p, vs. displacement, h, curves of SR samples are characterized by discrete displacement bursts, while the AP samples do not show any of them, suggesting that annealing has caused a local change in the amorphous structure. In both the samples, hardness (at nano- and micro-indentation) decreases with increasing p, demonstrating the indentation size effect. The micro-indentation imprints of SR NGs show evidence of shear bands at the periphery, indicating a heterogeneous plastic flow, while AP NG does not display any shear bands. Interestingly, the shear band density decreases with p, highlighting the fact that plastic strain is accommodated entirely by the shear bands in the subsurface deformation zone. The results are explained by the differences in the amorphous structure of the two NGs.
At room temperature, conventional amorphous alloys such as bulk metallic glasses and melt-spun ribbons (MSR) exhibit limited plasticity as deformation gets localized into one dominant shear band, leading to catastrophic failure (Schuh et al., 2007). While the same materials can show extensive plasticity at elevated temperatures (near and above the glass transition temperature) due to change in the plastic deformation mechanism from the shear band (SB) mediated to STZ-mediated flow (Prasad and Ramamurty, 2012). STZs are the fundamental carriers of plasticity (akin to dislocations in crystalline materials) in amorphous materials, comprising a cluster of atoms undergoing inelastic deformation beyond critical applied stress. STZs, unlike dislocations, are nearly impossible to observe directly using experiments, but the molecular dynamic studies show that they occur in the vicinity of regions containing high free volume. Consequently, it seems that one of the ways to increase the plasticity of amorphous alloys is to produce a structure containing areas of high free volume. With this motivation, Gleiter and coworkers (Jing et al., 1989; Gleiter, 2008; Gleiter, 2009; Gleiter, 2013; Gleiter, 2016) proposed the concept of nanoglasses (NGs) consisting of glassy grains (GGs) separated by glassy interfaces (GIs) of higher free volume, and later, several researchers have successfully fabricated NGs using different manufacturing routes (Gleiter et al., 2014; Nandam et al., 2017; Ivanisenko et al., 2018; Nandam et al., 2020). Extensive studies have been conducted on NGs to investigate their mechanical and functional properties using both experiments and simulations (Chen et al., 2011; Ritter et al., 2011; Sopu et al., 2011; Wang et al., 2011; Ritter and Albe, 2012; Adibi et al., 2013; Albe et al., 2013; Witte et al., 2013; Wang et al., 2014; Adjoud and Albe, 2016; Sniadecki et al., 2016; Nandam et al., 2017; Hirmukhe et al., 2019; Arnold et al., 2020; Singh et al., 2020a; Singh et al., 2020b; Hirmukhe et al., 2020; Katnagallu et al., 2020; Nandam et al., 2020). A series of MD simulation studies have been performed on NGs with different GG sizes and observed that the plasticity increases with the decreasing size of the GGs. The increase in plasticity is attributed to the increased number of GIs, which are the potential sites of STZs due to high free volume. Sopu et al. (2011) (Sopu and Albe, 2015) have shown that annealing of NGs causes a change in the deformation mechanism from STZ to shear band dominated due to the annihilation of free volume and increase in GG size. The simulations are complemented by the limited number of experimental studies (primarily using micro-compression or nano-indentation) using a small volume of materials (Fang et al., 2012; Wang et al., 2015; Wang et al., 2016). Wang et al. (2015), Wang et al. (2016) carried out in situ micro-compression of NGs and MSR and observed extensive plasticity in a binary Fe–Sc NG compared to MSR of identical composition.
The indentation (both micro- and nano-indentation) method is a viable technique to understand the deformation behavior of glasses as the deformation mechanisms taking place underneath the indenter gets reflected in the indentation load, p, vs. displacement, h, curves as well as the residual impression of the indentation imprint. Unlike MSR and BMGs, Cu–Zr-based NGs do not exhibit any noticeable displacement bursts (also known as pop-ins) in the loading portion of p vs. h curves, indicating that the flow is homogeneous (Pang et al., 2012; Nandam et al., 2017; Rauf et al., 2018) which is also supported by the absence of shear bands at the imprint edges of a micro-indent. The pop-ins in the loading curves correspond to nucleation and propagation of shear bands beneath the indentation (Singh et al., 2012; Singh et al., 2016). Recently, Sharma et al. (2021) have carried out bonded interface indentation experiments and observed that the subsurface deformation in a Pd–Si NG is accommodated by a large number of very fine secondary shear bands (SSBs) contrary to the few number of large primary shear bands (PSBs) in MSR of identical composition, suggesting that the absence of noticeable pop-ins in NGs could be due to the near homogeneous flow underneath the indentation. A good agreement is found between the experiments and simulations regarding the deformation mechanisms of the as-processed (AP) NGs. However, limited experimental studies are available in understanding the deformation of structurally relaxed (SR) NGs, despite several simulation studies, and there appears to be some discrepancy between the two. For example, Nandam et al., (2017) have reported the absence of pop-ins in the loading curves and SBs at the imprint edges of an annealed (at 0.9 Tg for 3 h) Cu–Zr NG, contrary to the MD results (though the exact annealing temperature is not well-described in the literature), which predicts SB-mediated plastic flow. So, it would be interesting to see if relaxing the NG at high temperatures (nearly at the Tg) has any effect on the nature of plastic flow. Apart from this, the role of p on the hardness, H; elastic modulus, E; and deformation mechanisms of AP and SR NGs is not studied in detail, at least experimentally. In the case of BMGs, it is observed that H decreases with increasing p, showing an indentation size effect (ISE). It would be interesting to examine the ISE on H and E in AP and SR NGs. Following this, the present work aims at 1) understanding the role of annealing (or structural relaxation) on the deformation behavior of NGs, 2) investigating the effect of indentation load/or size on H and E of AP and SR NGs, and 3) examining the evolution of shear bands with p around the indentation imprint.
Cu50Zr50 and Cu60Zr40 NGs are synthesized using magnetron sputtering in an inert gas condensation (IGC) system, and the processing details have been reported in detail by Nandam et al. (2017). Since the deformation behavior of both Cu50Zr50 and Cu60Zr40 NG is very similar in terms of plasticity, we have used AP Cu60Zr40 NG and SR Cu50Zr50 NG for our present evaluation. We will also make a comparison with the previously published results of Cu50Zr50 NG to give a more detailed analysis. Since the glass transition temperature, Tg , of the Cu50Zr50 NG is not clearly visible, we will consider the Tg of the MSR as the reference, that is, 410°C (Nandam et al., 2017). The AP NG was annealed at 400°C (about 0.98 Tg) for 90 min as the sub-Tg annealing promotes structural relaxation without crystallization. Both the AP and SR NGs are characterized using Mo Kα X-ray diffraction (XRD), as shown in Figure 1, which does not display any crystallization peaks in the diffraction spectrum of both the samples, confirming the amorphous nature of samples. In order to check the thermal stability, the NG samples are annealed slightly above the Tg (1.2 Tg) for 2 h and the XRD spectrum of which presented in Supplementary Figure S1. Supplementary Figure S1 shows small additional peaks in addition to the amorphous hump, suggesting that NGs are no longer fully amorphous, and the structural relaxation at this temperature leads to the formation of small crystallites. The sample surfaces for micro- and nano-indentation experiments are then polished to 0.25 μm surface finish using standard metallographic sample preparation. Nano-indentation was carried out at room temperature in a load-controlled mode using a Berkovich three-sided pyramidal shaped indenter tip. Before the experiment, the tip area function is calibrated using a standard quartz sample by making a series of indentations in the depth range of 80–200 nm. Nano-indentation experiments are conducted in the load range of 2–8 mN at a constant loading rate of 1 mN/s. For all the indentations, the thermal drift was kept under ± 0.05 nm/s. Micro-indentation experiments are carried out using a Vickers (four-sided) diamond indenter in the load range of 0.25–10 N with a loading and unloading segment of 10 s and a holding segment of 15 s at peak load. A minimum of ten indentations are performed at p to obtain statistically significant data. The indentation imprints and deformation morphology around the imprints are analyzed using scanning electron microscopy (SEM) and atomic force microscopy (AFM).
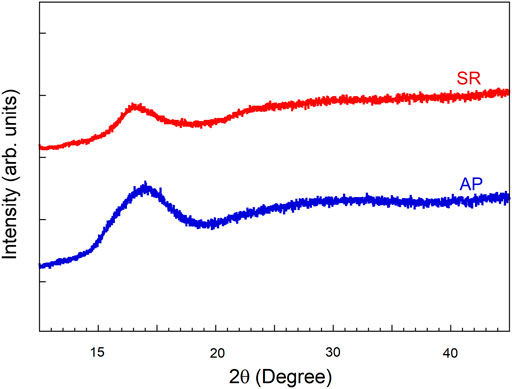
FIGURE 1. X-ray diffraction patterns of the SR and AP NGs displaying the amorphous nature of the samples.
Representative p vs. h curves of AP and SR NGs are shown in Figure 2. The loading curves of AP samples do not show any noticeable pop-ins, suggesting the homogeneous nature of plastic flow during the indentation, consistent with the literature (Pang et al., 2012; Nandam et al., 2017; Rauf et al., 2018). Unlike AP samples, the loading curves for the SR samples are characterized by a serrated flow, manifested by noticeable pop-ins (as indicated by the arrows). The serrations in the loading curves are attributed to nucleation and propagation of shear bands underneath the indentation, indicating that the plastic deformation is heterogeneous (Schuh and Nieh, 2003; Schuh et al., 2004; Greer et al., 2004; Yang et al., 2007a). Interestingly, Nandam and coworkers did not observe any pop-ins in SR NGs, annealed at 350°C (0.9 Tg) for 2 h, indicating that the deformation is still homogeneous. The indentation data were then analyzed using the Oliver and Pharr (O&P) method (Oliver and Pharr, 1992), according to which p and h are related for loading and unloading curves by Eq. 1 and Eq. 2, respectively:
where
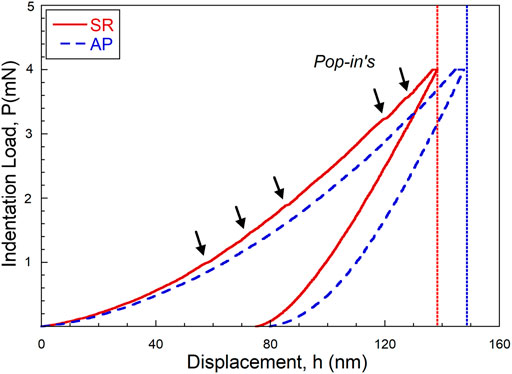
FIGURE 2. Representative indentation load, p, vs. penetration depth, h, curves of the SR and AP NGs obtained at a Pmax of 4 mN.
The variation in nanohardness, Hn, and elastic modulus, E, with the Pmax, plotted in Figure 3, clearly shows that both Hn and E decrease with increasing Pmax. The decrease in Hn with Pmax is referred to as the indentation size effect (ISE) and has been observed even in other metallic glasses, such as MSR and BMGs (Steenberge et al., 2007; Li et al., 2008; Li et al., 2009a; Huang et al., 2010; Jang et al., 2011; Xu et al., 2014; Xue et al., 2016). In the case of crystalline materials, the ISE is attributed to the presence of geometrically necessary dislocations (due to high plastic strain gradients) at low p (Nix and Gao, 1998; Pharr et al., 2010; Prasad and Ramesh., 2019; Kathavate et al., 2021). However, owing to the amorphous nature, the ISE in metallic glasses cannot be explained by the dislocation theory and is often attributed to the shear band nucleation and propagation characteristics underneath the indentation (Li et al., 2009b) and evolution of free volume during indentation (Yang and Nieh, 2007b). Huang et al. (2010) attributed the ISE in BMGs to the pileup of shear bands at the periphery of the imprint, which appears to be more pronounced at low indentation loads (due to the tip bluntness), thereby overestimation of hardness using the O&P method. However, the blunt tip theory cannot satisfactorily describe the ISE in NGs as the plastic flow under a blunt indenter is compressive in nature and transitions to cutting mechanism with a decreasing indenter angle. Therefore, pileup should be more pronounced for sharp indenters (or geometrically self-similar indenters) due to the large plastic strain gradients directly underneath the indenter. So, the blunt tip theory cannot definitely be used to explain the ISE, and the plastic flow characteristics of the material underneath the indenter will also contribute to the degree of pileup. Further, the pileup of shear bands does not appear to be the main reason for the ISE in AP NGs, at least as the imprint edges in SR NGs are free from shear bands (as shown in Figure 3, and Figure 4). Jang et al. (2011) also argued that the ISE in BMGs could be associated with the deformation mechanisms (rather than the overestimate in H), such as the occurrence of STZs in the subsurface indentation zone.
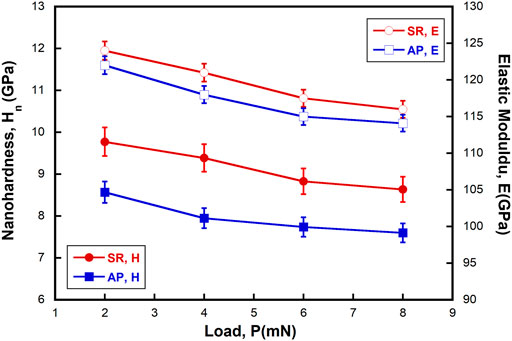
FIGURE 3. Variation of nanohardness, Hn , and elastic modulus, E, with maximum indentation load, Pmax, of both SR and AP NGs indicating the ISE.

FIGURE 4. Representative SEM images of Vickers indentation imprints of AP NGs maximum indentation load, Pmax, of (A) 0.5 N, (B) 1 N, (C) 2 N, and (D) 5 N.
To further understand the role of SR on deformation morphology and H, micro-indentation experiments are performed. The SEM images of micro-indentation imprints of AP and SR NGs are presented in Figure 4, and Figure 5, respectively. The imprints of AP NGs do not show any noticeable shear bands, while the SR NGs have profuse shear bands at the periphery of the imprint. The absence of shear bands at the imprint edges is generally attributed to homogeneous flow in metallic glasses, which is typically observed near the Tg (Prasad et al., 2007). Nandam et al. (2017) also did observe shear bands in NG samples annealed at 350°C for 2 h, consistent with the current results. The AFM images and the profilometry across the imprints of AP and SR samples (indented at Pmax ∼ 0.5 N), as shown in Figures 6A,B, respectively, further confirm the observations made by SEM. Interestingly, the pileup height (of the shear bands in SR NGs) at the imprint edges reaches as high as 310 nm (1/3rd of the penetration depth), suggesting that the plastic strain cannot be accommodated by the material in the subsurface deformation zone. The microhardness, Hm, of AP and SR samples is determined from the projected area of the impression and plotted against Pmax, as shown in Figure 7, which also clearly shows ISE. Similar observations were made by Ramamurty and coworkers (Jana et al., 2004; Ramamurty et al., 2005) in the case of BMGs who attributed the ISE in Hm to the roundness of the indenter at low indentation loads. The saturation Hm values of AP and SR NGs are 4.9 ± 0.03 and 5.9 ± 0.05 GPa, respectively, while for Hn, they were observed to be 7.6 and 8.6 GPa, respectively. A similar trend was observed in BMGs where the SR samples have shown higher Hm than the AP samples (Steenberge et al., 2007; Li et al., 2008; Xue et al., 2016). The number of SBs at the imprint edges (defined as SB density, ψ) is computed and plotted against Pmax, as shown in Figure 8. ψ is zero in AP NGs and independent of Pmax, while ψ decreases with increasing Pmax in SR NGs. The absence of SBs at high Pmax indicates that the plastic flow is fully accommodated by the subsurface deformation zone underneath the indentation without any pileup of SBs at the imprint edges. The indentation imprints of above-Tg annealed NGs, as presented in Supplementary Figure S2, also shows the presence of SBs at the periphery of the impression, indicating that the deformation in these samples is also mediated primarily by SBs but slightly to a lesser degree than that of sub-Tg annealed samples. The shear band density, ψ, of the above-Tg annealed samples along with the AP and sub-Tg annealed samples, as plotted in Supplementary Figure S3, confirms that ψ decreases in these samples.

FIGURE 5. Representative SEM images of Vickers indentation imprints of SR NGs at maximum indentation load, Pmax, of (A) 0.5 N, (B) 1 N, (C) 2 N, and (D) 5 N.
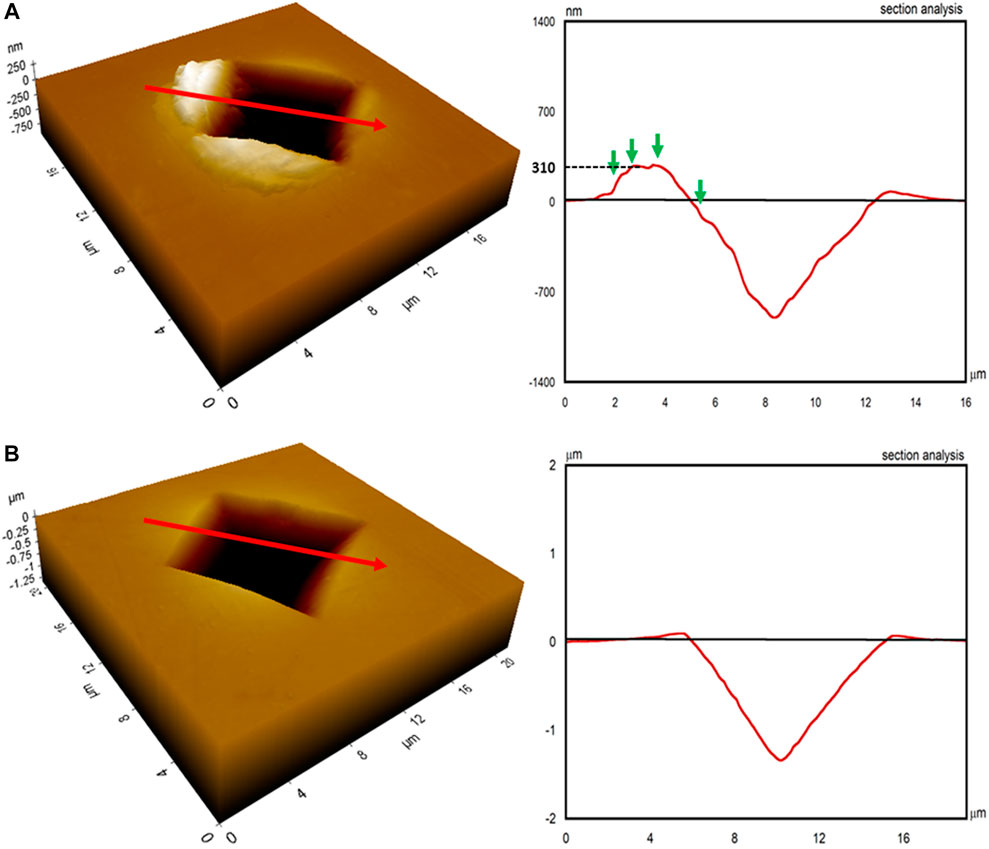
FIGURE 6. AFM images of the residual imprint along with the corresponding line scans taken across the edge of the imprint of (A) SR and (B) AP NGs obtained at a p of 0.5 N.
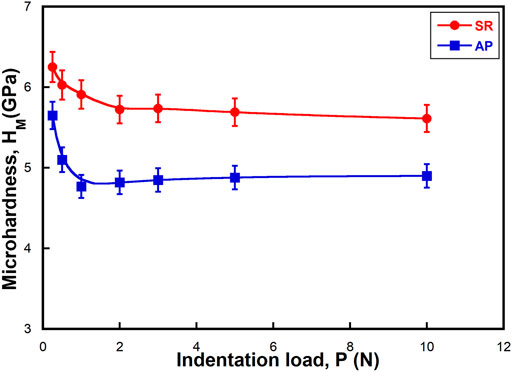
FIGURE 7. Plot showing the dependence of microhardness, Hm, on maximum indentation load, Pmax, for the SR and AP NGs.

FIGURE 8. Variation of the shear band density, ψ (number of shear bands on the indented surface), with maximum indentation load, Pmax, for both the SR and AP NGs.
It is well-established that sub-Tg annealing of BMGs leads to structural relaxation, thereby decreasing the free volume content of BMGs (Slipenyuk and Eckert, 2004). One of the consequences of this is the embrittlement of BMG, leading to an increase in H (Murali and Ramamurty, 2005; Ramamurty et al., 2005). In addition to the annihilation of free volume, the structural relaxation of NGs also promotes the formation of full icosahedron (FI) clusters, which may influence the mechanical properties. MD simulations of Cu–Zr NGs illustrate that structural relaxation causes an increase in the volume fraction of FI Cu
Furthermore, the free volume content and its evolution during plastic deformation influence H as per the following equation (Hey et al., 1998; Steenberge et al., 2007; Xue et al., 2016):
where constants A and B incorporate the activation volume of the flow event and material undergoing plastic shear,
where
where
Another possible reason for the ISE in SR-NGs could also be attributed to the overestimation of H at low indentation loads due to the pileup. The pileup is not significant in nano-indentation, and the differences in pileup are corrected, and Oliver–Pharr hardness is not substantial and differs by less than 5% (as shown in Supplementary Figure S4). Therefore, the ISE observed in SR NGs is indeed the response of the material not an experimental artifact. Unlike nanohardness, the microhardness values presented in Figure 7 are computed from the projected area of the impression and hence are corrected for pileup. It is also observed from Figure 7 that the ISE is more pronounced in microhardness than nanohardness. The ISE is mainly connected to the plastic zone size underneath the indentation, rather than the over- or underestimate of hardness due to the pileup. In the case of nano-indentation, the size of the plastic zone at the lowest and peak loads is not significant, and hence, the observed differences are smaller, while in the case of micro-indentation, the difference in indentation depths (and thus the size of the plastic zone sizes) between the smallest and highest loads is quite significant, thereby resulting in large ISE. A similar argument can be made to describe the ISE in AP NGs. The interesting question here is how does the increased plastic zone size lead to a reduction in hardness and increase pileup? We seek to explain this with the help of a model presented in Figures 10A–C. Figures 10A,B show the deformation morphology at low and high indentation loads for AP NGs, respectively, while Figures 10C,D represent the morphology of low and high indentation loads for SR NGs, respectively. We have considered the following facts while developing this model: 1) Structural relaxation leads to a decrease in free volume and STZ density, which is manifested in a reduction in the interface width and an increase in local atomic density inside the GGs (following MD simulations by Able and coworkers) and 2) the subsurface deformation volume increases with increasing indentation load (although the representative strain,
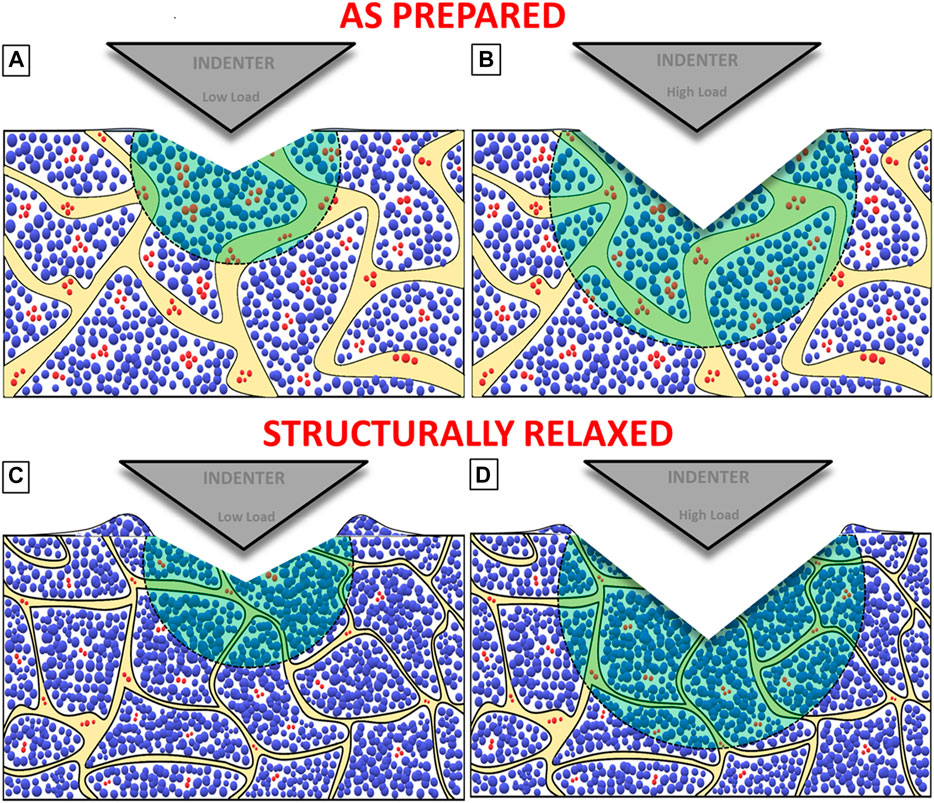
FIGURE 10. Schematic illustrating the differences in microstructure and deformation morphology between AP and SR NGs. (A, B) represents the deformation morphology at low and high indentation loads of AP NGs, respectively, while (C, D) for low and high indentation loads for SR NGs, respectively.
In the case of AP NGs, both at low and high indentation loads (Figures 10A,B), the plastic flow gets completely confined to subsurface deformation regions owing to the presence of a large number of STZs (displayed as red atoms) and high free volume present in the GG and GI which arrests the shear band pileup at the imprint edges. The increased contribution of free volume and STZs to the total deformation with an increase in indentation load also results in a decrease in H. In the case of SR NGs, at low indentation loads (Figure 10C), the plastic flow cannot be completely accommodated by the region underneath the indentation (owing to the low free volume and STZ density in the subsurface deformation zone), causing the upward flow of material (vis-à-vis shear bands) between the indenter and material, thereby leading to pileup of shear bands at the periphery of the imprint. On the other hand, the deformation volume increases with increasing indentation load (as shown Figure 10D), facilitating the increased contribution of free volume to the total plastic flow under the indentation arresting the pileup of shear bands. Another possibility that prevents the shear band pileup is the frictional forces between the indenter and specimen interface, which increases with increasing load leading to their flattening on the slanting faces of the impression. However, a detailed study is warranted to investigate the friction effects, the evolution of free volume, and shear band characteristics in the subsurface deformation zone.
In summary, the free volume has a marked influence on the deformation behavior of Cu–Zr NGs, with structurally relaxed (SR) NGs exhibiting a higher H than the as-prepared (AP) NGs. The loading curves of the SR NGs, in contrast to AP NGs, exhibit discrete displacement bursts, indicating that the plastic deformation is heterogeneous, which is also supported by the shear bands at the periphery of the imprint in the micro-indentation. The increase in H and serrated flow of the loading curves is attributed to the FI clusters and reduction in free volume due to the annealing, respectively. Further, the H decreases with increasing p in both the nano- and micro-indentation regimes, showing an indentation size effect. The increase in free volume generation in the subsurface deformation zone and the increase in deformation volume underneath the indentation with indentation load appear to be the reasons for the ISE.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
AS carried out the experiments, analyzed the data, and wrote the first draft of the manuscript. SN and HH generated the nanoglass material and gave their valuable inputs in the manuscript. KP supervised the whole work, reviewed, and edited the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
SN and HH would like to thank the DFG/SPP 1594 program for funding the project under HA1344/30-1. AS would like to thank MoE and IIT Indore for the fellowship and KP would like to thank the Science and Engineering Research Board, India, for supporting the work through the grant SRG/2019/002204.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.676764/full#supplementary-material
Adibi, S., Sha, Z.-D., Branicio, P. S., Joshi, S. P., Liu, Z.-S., and Zhang, Y.-W. (2013). A Transition from Localized Shear Banding to Homogeneous Superplastic Flow in Nanoglass. Appl. Phys. Lett. 103, 211905. doi:10.1063/1.4833018
Adjaoud, O., and Albe, K. (2016). Interfaces and Interphases in Nanoglasses: Surface Segregation Effects and Their Implications on Structural Properties. Acta Materialia 113, 284–292. doi:10.1016/j.actamat.2016.05.002
Adjaoud, O., and Albe, K. (2021). Nanoindentation of Nanoglasses Tested by Molecular Dynamics Simulations: Influence of Structural Relaxation and Chemical Segregation on the Mechanical Response. Front. Mater. 8, 95. doi:10.3389/fmats.2021.664220
Albe, K., Ritter, Y., and Şopu, D. (2013). Enhancing the Plasticity of Metallic Glasses: Shear Band Formation, Nanocomposites and Nanoglasses Investigated by Molecular Dynamics Simulations. Mech. Mater. 67, 94–103. doi:10.1016/j.mechmat.2013.06.004
Arnold, W., Birringer, R., Braun, C., Gleiter, H., Hahn, H., Nandam, S. H., et al. (2020). Elastic Moduli of Nanoglasses and Melt-Spun Metallic Glasses by Ultrasonic Time-Of-Flight Measurements. Trans. Indian Inst. Met. 73, 1363–1371. doi:10.1007/s12666-020-01969-x
Chen, N., Frank, R., Asao, N., Louzguine-Luzgin, D. V., Sharma, P., Wang, J. Q., et al. (2011). Formation and Properties of Au-Based Nanograined Metallic Glasses. Acta Materialia 59, 6433–6440. doi:10.1016/j.actamat.2011.07.007
Cheng, B., and Trelewicz, J. R. (2019). Interfacial Plasticity Governs Strain Delocalization in Metallic Nanoglasses. J. Mater. Res. 34, 2325–2336. doi:10.1557/JMR.2019.101
Cheng, Y. Q., Cao, A. J., Sheng, H. W., and Ma, E. (2008). Local Order Influences Initiation of Plastic Flow in Metallic Glass: Effects of alloy Composition and Sample Cooling History. Acta Materialia 56, 5263–5275. doi:10.1016/j.actamat.2008.07.011
Fang, J. X., Vainio, U., Puff, W., Würschum, R., Wang, X. L., Wang, D., et al. (2012). Atomic Structure and Structural Stability of Sc75Fe25 Nanoglasses. Nano Lett. 12, 458–463. doi:10.1021/nl2038216
Gleiter, H. (2016). Nanoglasses: a New Kind of Noncrystalline Material and the Way to an Age of New Technologies? Small 12, 2225–2233. doi:10.1002/smll.201500899
Gleiter, H. (2013). Nanoglasses: a New Kind of Noncrystalline Materials. Beilstein J. Nanotechnol. 4, 517–533. doi:10.3762/bjnano.4.61
Gleiter, H. (2008). Our Thoughts Are Ours, Their Ends None of Our Own: Are There Ways to Synthesize Materials beyond the Limitations of Today? Acta Materialia 56, 5875–5893. doi:10.1016/j.actamat.2008.08.028
Gleiter, H., Schimmel, T., and Hahn, H. (2014). Nanostructured Solids - from Nano-Glasses to Quantum Transistors. Nano Today 9, 17–68. doi:10.1016/j.nantod.2014.02.008
Glieter, H. (2009). Are There Ways to Synthesize Materials beyond the Limits of Today? Metall. Mater. Trans. A. Phys. Metall. Mater. Sci. 40, 1499–1509. doi:10.1007/s11661-009-9848-7
Greer, A. L., Castellero, A., Madge, S. V., Walker, I. T., and Wilde, J. R. (2004). Nanoindentation Studies of Shear Banding in Fully Amorphous and Partially Devitrified Metallic Alloys. Mater. Sci. Eng. A 375-377, 1182–1185. doi:10.1016/j.msea.2003.10.032
Hey, P. D., Sietsma, J., and Beukel, A. V. D. (1998). Structural Disordering in Amorphous Pd40Ni40P20 Induced by High Temperature Deformation. Acta Mater. 46, 5873–5882. doi:10.1016/S1359-6454(98)00234-1
Hirmukhe, S. S., Prasad, K. E., and Singh, I. (2019). Finite Element Analysis of Tensile Deformation of Nanoglass-Metallic Glass Laminate Composites. Comput. Mater. Sci. 161, 83–92. doi:10.1016/j.commatsci.2019.01.031
Hirmukhe, S. S., Prasad, K. E., and Singh, I. (2020). Investigation of Pressure Sensitive Plastic Flow in Nanoglasses from Finite Element Simulations. Scripta Materialia 180, 45–50. doi:10.1016/j.scriptamat.2020.01.022
Huang, Y., Shen, J., Sun, Y., and Sun, J. (2010). Indentation Size Effect of Hardness of Metallic Glasses. Mater. Des. 31, 1563–1566. doi:10.1016/j.matdes.2009.09.046
Ivanisenko, Y., Kübel, C., Nandam, S. H., Wang, C., Mu, X., Adjaoud, O., et al. (2018). Structure and Properties of Nanoglasses. Adv. Eng. Mater. 20, 1800404. doi:10.1002/adem.201800404
Jana, S., Bhowmick, R., Kawamura, Y., Chattopadhyay, K., and Ramamurty, U. (2004). Deformation Morphology Underneath the Vickers Indent in a Zr-Based Bulk Metallic Glass. Intermetallics 12, 1097–1102. doi:10.1016/j.intermet.2004.04.018
Jang, J.-i., Yoo, B.-G., Kim, Y.-J., Oh, J.-H., Choi, I.-C., and Bei, H. (2011). Indentation Size Effect in Bulk Metallic Glass. Scripta Materialia 64, 753–756. doi:10.1016/j.scriptamat.2010.12.036
Jing, J., Krämer, A., Birringer, R., Gleiter, H., and Gonser, U. (1989). Modified Atomic Structure in a PdFeSi Nanoglass. J. Non-Crystalline Sol. 113, 167–170. doi:10.1016/0022-3093(89)90007-0
Kathavate, V. S., Praveen Kumar, B., Singh, I., and Eswar Prasad, K. (2021). Analysis of Indentation Size Effect (ISE) in Nanoindentation Hardness in Polycrystalline PMN-PT Piezoceramics with Different Domain Configurations. Ceramics Int. 47, 11870–11877. doi:10.1016/j.ceramint.2021.01.027
Katnagallu, S., Wu, G., Singh, S. P., Nandam, S. H., Xia, W., Stephenson, L. T., et al. (2020). Nanoglass-Nanocrystal Composite-A Novel Material Class for Enhanced Strength-Plasticity Synergy. Small 16, 2004400. doi:10.1002/smll.202004400
Li, N., Chan, K. C., and Liu, L. (2008). The Indentation Size Effect in Pd40Cu30Ni10P20bulk Metallic Glass. J. Phys. D: Appl. Phys. 41, 155415. doi:10.1088/0022-3727/41/15/155415
Li, N., Liu, L., Chan, K. C., Chen, Q., and Pan, J. (2009a). Deformation Behavior and Indentation Size Effect of Au49Ag5.5Pd2.3Cu26.9Si16.3 Bulk Metallic Glass at Elevated Temperatures. Intermetallics 17, 227–230. doi:10.1016/j.intermet.2008.07.018
Li, N., Liu, L., and Chan, K. C. (2009b). Deformation Behavior and Indentation Size Effect in Amorphous and Crystallized Pd40Cu30Ni10P20 alloy. J. Mater. Res. 24, 1693–1699. doi:10.1557/jmr.2009.0222
Murali, P., and Ramamurty, U. (2005). Embrittlement of a Bulk Metallic Glass Due to Sub- Annealing. Acta Materialia 53, 1467–1478. doi:10.1016/j.actamat.2004.11.040
Nandam, S. H., Adjaoud, O., Schwaiger, R., Ivanisenko, Y., Chellali, M. R., Wang, D., et al. (2020). Influence of Topological Structure and Chemical Segregation on the thermal and Mechanical Properties of Pd-Si Nanoglasses. Acta Materialia 193, 252–260. doi:10.1016/j.actamat.2020.03.021
Nandam, S. H., Ivanisenko, Y., Schwaiger, R., Śniadecki, Z., Mu, X., Wang, D., et al. (2017). Cu-Zr Nanoglasses: Atomic Structure, thermal Stability and Indentation Properties. Acta Materialia 136, 181–189. doi:10.1016/j.actamat.2017.07.001
Nix, W. D., and Gao, H. (1998). Indentation Size Effects in Crystalline Materials: A Law for Strain Gradient Plasticity. J. Mech. Phys. Sol. 46, 411–425. doi:10.1016/S0022-5096(97)00086-0
Oliver, W. C., and Pharr, G. M. (1992). An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 7, 1564–1583. doi:10.1557/JMR.1992.1564
Pang, J.-J., Tan, M.-J., Liew, K. M., and Shearwood, C. (2012). Nanoindentation Study of Size Effect and Loading Rate Effect on Mechanical Properties of a Thin Film Metallic Glass Cu49.3Zr50.7. Physica B: Condensed Matter 407, 340–346. doi:10.1016/j.physb.2011.10.050
Park, K.-W., Jang, J.-i., Wakeda, M., Shibutani, Y., and Lee, J.-C. (2007). Atomic Packing Density and its Influence on the Properties of Cu-Zr Amorphous Alloys. Scripta Materialia 57, 805–808. doi:10.1016/j.scriptamat.2007.07.019
Pharr, G. M., Herbert, E. G., and Gao, Y. (2010). The Indentation Size Effect: A Critical Examination of Experimental Observations and Mechanistic Interpretations. Annu. Rev. Mater. Res. 40, 271–292. doi:10.1146/annurev-matsci-070909-104456
Prasad, K. E., Raghavan, R., and Ramamurty, U. (2007). Temperature Dependence of Pressure Sensitivity in a Metallic Glass. Scripta Mater. 57, 121–124. doi:10.1016/j.scriptamat.2007.03.033
Prasad, K. E., and Ramamurty, U. (2012). Effect of Temperature on the Plastic Zone Size and the Shear Band Density in a Bulk Metallic Glass. Mater. Sci. Eng. A. 535, 48–52. doi:10.1016/j.msea.2011.12.040
Prasad, K. E., and Ramesh, K. T. (2019). Hardness and Mechanical Anisotropy of Hexagonal SiC Single crystal Polytypes. J. Alloys. Comp. 770, 158–165. doi:10.1016/j.jallcom.2018.08.102
Ramamurty, U., Jana, S., Kawamura, Y., and Chattopadhyay, K. (2005). Hardness and Plastic Deformation in a Bulk Metallic Glass. Acta Materialia 53, 705–717. doi:10.1016/j.actamat.2004.10.023
Rauf, A., Guo, C. Y., Fang, Y. N., Yu, Z., Sun, B. A., and Feng, T. (2018). Binary Cu-Zr Thin Film Metallic Glasses with Tunable Nanoscale Structures and Properties. J. Non-Crystalline Sol. 498, 95–102. doi:10.1016/j.jnoncrysol.2018.06.015
Ritter, Y., and Albe, K. (2012). Chemical and Topological Order in Shear Bands of Cu64Zr36 and Cu36Zr64 Glasses. J. Appl. Phys. 111, 103527. doi:10.1063/1.471774810.1063/1.4717748
Ritter, Y., Şopu, D., Gleiter, H., and Albe, K. (2011). Structure, Stability and Mechanical Properties of Internal Interfaces in Cu64Zr36 Nanoglasses Studied by MD Simulations. Acta Materialia 59, 6588–6593. doi:10.1016/j.actamat.2011.07.013
Schuh, C. A., Lund, A. C., and Nieh, T. G. (2004). New Regime of Homogeneous Flow in the Deformation Map of Metallic Glasses: Elevated Temperature Nanoindentation Experiments and Mechanistic Modeling. Acta Materialia 52, 5879–5891. doi:10.1016/j.actamat.2004.09.005
Schuh, C. A., and Nieh, T. G. (2003). A Nanoindentation Study of Serrated Flow in Bulk Metallic Glasses. Acta Materialia 51, 87–99. doi:10.1016/s1359-6454(02)00303-8
Schuh, C., Hufnagel, T., and Ramamurty, U. (2007). Mechanical Behavior of Amorphous Alloys. Acta Materialia 55, 4067–4109. doi:10.1016/j.actamat.2007.01.052
Sharma, A., Nandam, S. H., Hahn, H., and Prasad, K. E. (2021). On the Differences in Shear Band Characteristics between a Binary Pd-Si Metallic and Nanoglass. Scripta Materialia 191, 17–22. doi:10.1016/j.scriptamat.2020.09.009
Singh, G., Narayan, R. L., Asiri, A. M., and Ramamurty, U. (2016). Discrete Drops in the Electrical Contact Resistance during Nanoindentation of a Bulk Metallic Glass. Appl. Phys. Lett. 108, 181903. doi:10.1063/1.4948540
Singh, P. S., Narayan, R. L., Sen, I., Hofmann, D. C., and Ramamurty, U. (2012). Effect of Strain Rate and Temperature on the Plastic Deformation Behaviour of a Bulk Metallic Glass Composite. Mater. Sci. Eng. A 534, 476–484. doi:10.1016/j.msea.2011.11.096
Singh, S. P., Chellali, M. R., Velasco, L., Ivanisenko, Y., Boltynjuk, E., Gleiter, H., et al. (2020a). Deformation-Induced Atomic Rearrangements and Crystallization in the Shear Bands of a Tb75Fe25 Nanoglass. J. Alloys Comp. 821, 153486. doi:10.1021/acsanm.0c0167410.1016/j.jallcom.2019.153486
Singh, S. P., Witte, R., Clemens, O., Sarkar, A., Velasco, L., Kruk, R., et al. (2020b). Magnetic Tb75Fe25 Nanoglass for Cryogenic Permanent Magnet Undulator. ACS Appl. Nano Mater. 3, 7281–7290. doi:10.1021/acsanm.0c01674
Slipenyuk, A., and Eckert, J. (2004). Correlation between Enthalpy Change and Free Volume Reduction during Structural Relaxation of Zr55Cu30Al10Ni5 Metallic Glass. Scripta Materialia. 50, 39–44. doi:10.1016/j.scriptamat.2003.09.038
Śniadecki, Z., Wang, D., Ivanisenko, Y., Chakravadhanula, V. S. K., Kübel, C., Hahn, H., et al. (2016). Nanoscale Morphology of Ni50Ti45Cu5 Nanoglass. Mater. Charact. 113, 26–33. doi:10.1016/j.matchar.2015.12.025
Sopu, D., and Albe, K. (2015). Enhancing the Plasticity of Metallic Glasses: Shear Band Formation, Nanocomposites and Nanoglasses Investigated by Molecular Dynamicssimulations. Mech. Mater. 67, 94–103. doi:10.1016/j.mechmat.2013.06.004
Sopu, D., Ritter, Y., Gleiter, H., and Albe, K. (2011). Deformation Behavior of Bulk and Nanostructured Metallic Glasses Studied via Molecular Dynamics Simulations. Phys. Rev. B 83, 100202. doi:10.1103/PhysRevB.83.100202
Spaepen, F. (1977). A Microscopic Mechanism for Steady State Inhomogeneous Flow in Metallic Glasses. Acta Metallurgica 25, 407–415. doi:10.1016/0001-6160(77)90232-2
Steenberge, N. V., Sort, J., Concustell, A., Das, J., Scudino, S., Surinach, S., et al. (2007). Dynamic Softening and Indentation Size Effect in a Zr-Based Bulk Glass-Forming alloy. Scripta Mater. 56, 605–608. doi:10.1016/j.scriptamat.2006.12.014
Wang, J. Q., Chen, N., Liu, P., Wang, Z., Louzguine-Luzgin, D. V., Chen, M. W., et al. (2014). The Ultrastable Kinetic Behavior of an Au-Based Nanoglass. Acta Materialia 79, 30–36. doi:10.1016/j.actamat.2014.07.015
Wang, J. Q., Wang, W. H., Liu, Y. H., and Bai, H. Y. (2011). Characterization of Activation Energy for Flow in Metallic Glasses. Phys. Rev. B 83, 012201. doi:10.1103/PhysRevB.83.012201
Wang, X., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2016). Sample Size Effects on Strength and Deformation Mechanism of Sc75Fe25 Nanoglass and Metallic Glass. Scripta Materialia 116, 95–99. doi:10.1016/j.scriptamat.2016.01.036
Wang, X. L., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2015). Plasticity of a Scandium-Based Nanoglass. Scripta Materialia 98, 40–43. doi:10.1016/j.scriptamat.2014.11.010
Witte, R., Feng, T., Fang, J. X., Fischer, A., Ghafari, M., Kruk, R., et al. (2013). Evidence for Enhanced Ferromagnetism in an Iron-Based Nanoglass. Appl. Phys. Lett. 103, 073106. doi:10.1063/1.4818493
Xu, F., Ding, Y. H., Deng, X. H., Zhang, P., and Long, Z. L. (2014). Indentation Size Effects in the Nano- and Micro-hardness of a Fe-Based Bulk Metallic Glass. Physica B: Condensed Matter 450, 84–89. doi:10.1016/j.physb.2014.05.057
Xue, F., Wang, F., Huang, P., Lu, T. J., and Xu, K. W. (2016). Structural Inhomogeneity and Strain Rate Dependent Indentation Size Effect in Zr-Based Metallic Glass. Mater. Sci. Eng. A 655, 373–378. doi:10.1016/j.msea.2015.12.083
Yang, B., and Nieh, T. (2007b). Effect of the Nanoindentation Rate on the Shear Band Formation in an Au-Based Bulk Metallic Glass. Acta Materialia 55, 295–300. doi:10.1016/j.actamat.2006.08.028
Keywords: nanoglass, amorphous, indentation size effect, micro-indentation, structural relaxation, plastic deformation, nano-indentation
Citation: Sharma A, Nandam SH, Hahn H and Prasad KE (2021) Effect of Structural Relaxation on the Indentation Size Effect and Deformation Behavior of Cu–Zr–Based Nanoglasses. Front. Mater. 8:676764. doi: 10.3389/fmats.2021.676764
Received: 06 March 2021; Accepted: 26 May 2021;
Published: 17 June 2021.
Edited by:
Shiv Prakash Singh, International Advanced Research Center for Powder Metallurgy and New Materials, IndiaReviewed by:
Na Chen, Tsinghua University, ChinaCopyright © 2021 Sharma, Nandam, Hahn and Prasad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: K. Eswar Prasad, ZXN3YXIucHJhc2FkQGdtYWlsLmNvbQ==; Sree Harsha Nandam, c3JlZS5uYW5kYW1Aa2l0LmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.