Optimization of the Indirect Extrusion Process of Copper-Clad Aluminum Rods by Methods of Statistical Experimental Designs and Numerical Analyses

The success of composite extrusion is influenced by multiple process parameters. In order to investigate the significance of specific parameters during indirect extrusion of copper-clad aluminum (CCA) rods, statistical methods were applied and a central composite experimental design was implemented. The runs of the experimental design were modeled with the finite element method based software DEFORM 2D and evaluated with respect to product quality, described by four response variables. Using variance and regression analyses, as well significant linear and quadratic effects of the five investigated process parameters as interactions between them were identified. Based on a statistical model, an overall optimum setting for the process parameters was predicted utilizing the response surface methodology with a desirability approach. By applying the output of the statistical analysis to an extrusion trial, the extrusion of a high quality CCA rod was achieved. Moreover, the results of the statistical analysis could be verified by comparing predicted and experimentally determined values of the investigated quality characteristics.

Introduction

Copper and aluminum are the most used materials for electrical conductors. Their high electrical conductivity predestinates them for this application. However, the high density and instable price of copper as well as the high contact resistance of the superficial aluminum oxide layer are downsides which must be coped with. Clad composites made of a copper sleeve and aluminum core synergize the benefits of both materials while neutralizing the disadvantages. Copper clad aluminum (CCA) composites are usually fabricated with a copper volume fraction of 10–30%. Due to the lower price and density of aluminum the material cost and weight of busbars can be reduced by up to 40 and 60%, respectively.

Copper clad aluminum rods, tubes, and wires are primarily produced by means of hydrostatic extrusion. The hydrostatic process conditions and excellent lubrication by the pressure medium enable a consistently homogeneous material flow which is substantial for sustaining a good product quality. But the handling of the pressure medium and billet preparation makes this a complex, cost and time intensive process. Thus, investigations on the extrusion of CCA rod by the much simpler processes of direct and indirect extrusion are of great interest. However, it was not possible to produce CCA rods of high quality and considerable length by means of these processes until now. To achieve an as homogeneous material flow as possible and prevent sleeve fracture during composite extrusion a manifold of process parameters must be considered. These are extrusion ratio, semi die angle, ram speed, lubrication, temperature control of the billet as well as flow stress ratio, volume fraction, and bonding of the billet components (Müller, 2004). The influence of extrusion ratio, semi die angle and friction on the extrusion force during indirect extrusion was investigated by Haghighat and Momeni-Khabisi (2014) using upper bound and finite element methods (FEMs). They found the optimal semi-die angle for minimal extrusion forces to be increasing with the extrusion ratio and friction factor. Kang and Kwon (2002) applied a fixed semi die angle of 30° when studying the extrudability of CCA in dependence of the extrusion ratio and lubrication by direct and indirect extrusion. They identified indirect extrusion and lower extrusion ratios to be beneficial for the extrudability due to lower strain rate differences between core and sleeve material. Amongst others, temperature control was analyzed by Kwon et al. (2004) using a semi die angle of 30° and an extrusion ratio of 21.4:1 during indirect extrusion. The upper limit for stable extrusion of CCA was found to be at around 350°C. Due to an increased flow stress ratio of the billet components, sleeve fractures occurred at higher temperatures. Jang and Hwang (2007) subjected the influence of interference bonding of the billet components to their numerical investigations. They stated a tight bonding to be essential for homogeneous material flow by analyzing the plastic flow behavior and velocity discontinuities during direct extrusion.

Literature regarding the indirect extrusion of CCA investigated mostly single or at most two or three process parameters influencing the general extrudability of CCA. An extensive investigation on multiple parameters and their interaction is missing. Therefore, a statistical investigation considering the influence of the five process parameters, extrusion ratio, semi die angle, ram speed, container temperature, and copper volume fraction on important characteristics of the extrusion process was conducted in this study. For optimizing this process, methods of statistical experimental designs were used, which is very uncommon in the field of extrusion research. To reduce the extensive experimental effort, which is necessary for the application of statistical experimental designs on investigations concerning hot extrusion, the necessary data for the investigation were gained by means of finite element analyses. Considering the results of the statistical investigation a successful extrusion trial was carried out to validate a suitable parameter set for sound CCA extrusion.

Materials and Methods

Numerical Investigations on CCA Extrusion by Means of Finite Element Analysis

The numerical investigations were performed using the FEM software DEFORM 2D. The code is based on the lagrangian approach and allows the description of transient material flow, as observed during extrusion of bimetallic rods. The investigated materials, cast aluminum alloy EN AW-1080A and extruded and annealed copper alloy CW004A, were modeled using the constitutive Hensel-Spittel equation as reported in Kuhnke et al. (2020b; Table 1). Friction was described with the shear model according to Tresca. Friction parameters and heat transfer coefficients (Table 1) were adopted from Sanabria et al. (2019) Klicken oder tippen Sie hier, um Text einzugeben. Numerical investigations performed with these parameter sets were in good agreement with experimental trials regarding material flow (Kuhnke et al., 2020b). Therefore, this parameter set was used to conduct the numerical investigations in this study.

TABLE 1

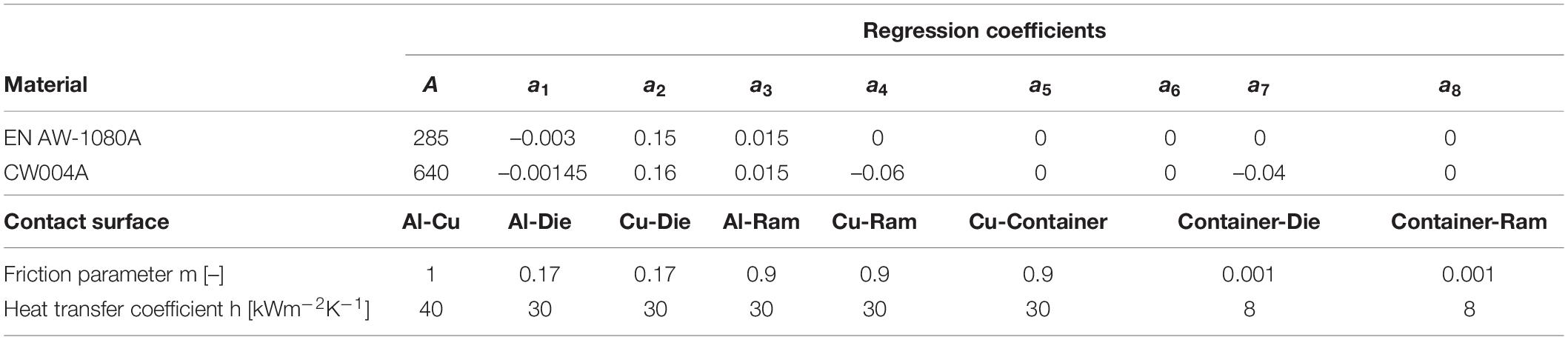
Table 1. Regression coefficients of the Hensel-Spittel equation for the billet materials as well as friction parameters and heat transfer coefficients for the FE-analysis of the indirect extrusion.

The axially symmetric model was built in correspondence to the setup of the available 8 MN extrusion press (Figure 1). The container bore is 95 mm in diameter and the billet dimensions are Ø93 × 200 mm. The copper sleeve was designed to be 20 mm longer than the aluminum core. This design benefits material flow during the unsteady beginning of the extrusion process and reduces the length of the full aluminum head (Kazanowski et al., 2004). Core and sleeve of the billet were set as plastic objects and meshed with 5,000 and 4,500 rectangular elements, respectively. Mesh windows were applied in the deformation zone to reduce the local element size and improve the accuracy of the calculations. For consideration of transient heat transfer between billet and tools, container, die, and ram were meshed with 1,000, 1,500, and 400 elements, respectively. All tools were set as rigid objects. Since different extrusion ratios, die angles, and copper volume fractions were investigated, die and billet geometry were varied according to these parameters. As in previous investigations only the container was heated (Kuhnke et al.,2020a,b). Billet and tools were set at room temperature. This reduces the flow stress ratio of copper and aluminum by heating and softening the copper sleeve, which is beneficial for the extrusion process. Ram and container movement was programmed to delay the beginning of the extrusion by 10 s. Thereby the necessary time for ram positioning in the extrusion process was reproduced. Due to long calculation times, the FE-analyses were stopped at a stroke of 80 mm.

FIGURE 1

Figure 1. FE-model for the extrusion of CCA rods.

No fracture model was available for the used material state of copper. In order to still be able to simulate sleeve fracture, findings of preliminary investigations were used. Sleeve necking was observed in FE-analyses (Figure 2) when axial tensile stresses in copper exceeded 200 MPa by far. Therefore, sleeve necking was used as indicator for material failure. Since high tensile stresses are assumed to be the cause for sleeve fracture (Kuhnke et al., 2020b), the fracture model according to (Cockcroft and Latham, 1968) was utilized as tool to generate sleeve fracture

FIGURE 2

Figure 2. Sleeve necking due to high tensile stresses.

where σ^∗ is the maximal principal stress, ε_f ist the fracture strain and C is a material constant. This model is also the default for damage calculation in DEFORM Scientific Forming Technologies Corporation (SFTC). When sleeve necking occurs, the damage value increases rapidly due to high strains and tensile stresses. Thus, DEFORM was configured to delete affected elements when a critical damage value of was 400 reached and thereby generate sleeve fracture.

Design of Experiments

Methods of experimental design are finding increasing use in manufacturing to optimize the production process. In some industrial fields as food industry, chemical industry, or pharmaceutical industry they are already standard methods. Statistical design of experiments (DoE) has been utilized to identify the most relevant process parameters (here also called process factors for differentiation from model parameters) with their linear, quadratic and interaction effects on response variables of interest with a minimal number of experiments. In industrial practice typically used designs are, e.g., Plackett–Burman screening designs (two-level, k > 6 factors), factorial designs of type 2^k or 2^(k–p) (two-level, 2 < k < 7 factors), central composite (or response surface designs), Latin square designs, and mixture designs. These designs are introduced in Box et al., 1978; Box and Draper, 1987; Mason et al., 1991; Coleman and Montgomery, 1993; Kleppmann, 2009; Montgomery, 2009, 2013. Considering the special case, that only three factors affecting a production process at two levels (low and high) the simplest full factorial design of type 2^k would require eight runs of the experiment, which are all possible combinations of settings. This full factorial design, visualized geometrically by the corner points of a cube, allows to estimate all three main and four interaction effects independently. The experimental error can be calculated on the base of additionally repeated runs of the experiment, e.g., in the center of that cube. For studying five factors the number of necessary runs in the experiment would increase to 2⁵ = 32. If the primary interest is in estimating all five main effects and merely the ten two-factor-interaction effects independently, only 16 runs would be necessary. That is why here a fractional design of type 2^(5–1) with 16 runs of the experiment would be sufficient. In the case where three- and more-factor interaction effects of the factors are also of interest, a full factorial design of type 2⁵ should be applied. In general, for more than five factors fractional factorial designs of type 2^(k–p) are the designs of choice.

Whereas fractional factorial designs of type 2^k–p are used for estimating the significant model parameters in linear models with interactions, based on only two-level settings (low and high) of the process factors, central composite designs (CCD) are preferred for estimating quadratic model parameters additionally. These CCD are developed from a 2^(k–p) fractional factorial design, which is augmented with n_c center points and n_s star points such that the number of level setting of the process factors is increasing to five levels. Using response surface models based on a CCD, a following multi-criteria optimization led to an overall optimum process parameter setting. All following analyses were carried out with the statistics software Statistica 12 (StatSoft Europa GmbH, 2013).

Assuming a quadratic model for the relationship between the five most relevant process factors in this study, that are extrusion ratio V, container temperature T_C, ram speed v_r, copper volume fraction φ_Cu and die angle 2α, and the response variables, the application of a CCD require a minimal necessary number of 2^(5–1)+3+10 = 29 runs. The levels of the process factors are shown in Table 2. The range of the individual factor levels was chosen in consideration of previous investigations and several other studies. This choice is important for identifying significant effects of the process parameters on the response variables of the extrusion process, that are length of full aluminum head, sleeve fracture, change in copper volume fraction, and fraction of CCA rod. These response variables play a decisive role for producing CCA rods of high quality.

TABLE 2

Table 2. Coded levels of the five process factors in the central composite design.

Copper clad aluminum rods have been successfully extruded with extrusion ratios between 7:1 and 21:1 (Kang et al., 2002; Kwon et al., 2004; Kuhnke et al.,2020a,b). Due to higher normal pressure in the deformation zone, higher extrusion ratios are expected to be advantageous for the formation of a flawless interface between copper and aluminum. Thus, the highest extrusion ratio tested in this study was 35:1. Kwon et al. (2004) also found 350°C to be the upper limit for the extrusion of CCA rod with an isothermal setup. As mentioned earlier, an anisothermal setup reduces the flow stress ratio of the billet materials. Therefore, the tested container temperature extends from room temperature to 430°C, covering the lowest possible flow stress ratio with an isothermal setup (Sanabria et al., 2019) and a high gradient anisothermal configuration. As both alloys revealed a low strain rate sensitivity in hot compression tests (Kang et al., 2002; Berski et al., 2006; Sanabria et al., 2019), only small influence of ram speed was expected and a wide range of ram speed (5–19 mm/s) was defined. The lower end of the investigated copper volume fraction, that is 0.15, was defined with regard to busbars commercially produced by means of hydrostatic extrusion (Bruker EST Hydrostatic Extrusions Limited, 2014). A value of 0.35 was assumed to be reasonable for the upper end since an excessive copper volume fraction compromises the benefits of the CCA rod. The tested die angles range from 60° to 180°. Conical dies with an angle of 60° are often used for investigations on bimetallic extrusions due to the favorable material flow. The largest investigated angle of 180° is represented by a flat die.

In a 2^5–1 design with 16 runs, the five main effects and all ten possible two-way interactions are not confounded with each other and can be estimated independently. In addition to these so-called corner points of a hypercube, a CCD includes several center points for estimating the experimental error and two axial points for every factor considered in the design. For each factor the latter are at a distance d to either side of the center, with all other factors held at the level of the center point. The CCD with all factor settings for the 29 runs can be found in Supplementary Table 1.

Results and Discussion

Numerical Results

The 29 runs of the CCD were carried out by means of numerical analysis. For this purpose, the presented FE-model was altered according to the corresponding process parameters of each run and run separately.

As described earlier, for all runs a constant friction parameter m = 0.17 was defined for the interaction between billet materials and die. This does not perfectly describe the actual conditions, where friction is a function of pressure, velocity and temperature (Sanabria et al., 2015). However, dependent friction parameters are not available yet and considering the good reproduction of material flow in Kuhnke et al. (2020b), constant friction parameters are sufficient to determine the influence of different process parameters.

For the statistical analysis of the extrusion process four different response variables were investigated. The first variable is the length of the full aluminum head, formed during the beginning of the extrusion. Two examples of different full aluminum heads are illustrated in Figure 3. For a sound composite extrusion this must be as short as possible. The more monolithic aluminum is extruded, the less is left for the formation of the composite and therefore, the copper volume fraction in the product increases.

FIGURE 3

Figure 3. Runs No. 12 (A) and 15 (B) with different lengths of the nose crop.

The second variable is the occurrence of sleeve fractures. This attribute provides a very elementary but effective parameter to characterize the rod quality. A binary yes/no criteria was applied to evaluate the rods. Examples of CCA rods with and without sleeve fractures are shown in Figure 4.

FIGURE 4

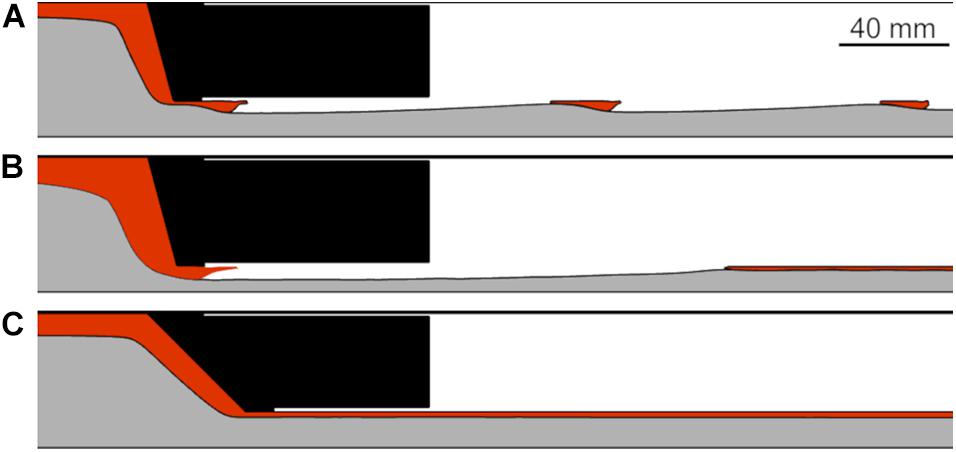
Figure 4. Different modes of sleeve fracture; (A) multiple sleeve fractures, (B) single sleeve fracture, and (C) no sleeve fracture.

The change in copper volume fraction was chosen as third response variable. Variations in copper volume fraction condition a change of sleeve thickness and thus impair the product quality. The measurement of the copper volume fraction was carried out by means of digital image processing and analysis. For this purpose, images of 5 cm long rod sections were exported from the FE-software and then processed with the freeware ImageJ. Using the particle analysis algorithm of ImageJ, the area share of aluminum and copper were determined and the copper volume fraction was calculated. Each a value of the tip and end of a CCA rod was allocated and the percentage change in copper volume fraction was calculated. Considering the bulging of copper during the formation of the full aluminum head, the measurement at the tip of the rod was actually taken 10 cm behind the tip of the CCA rod. If a sleeve fracture occurred, the value for the copper area share at end of the CCA rod was set to 0, which causes the change in copper volume fraction to be 100%. As no increase in copper volume fraction was measured in any run, the absolute value was used for better convenience.

Some CCA rods show multiple sleeve fractures (Figure 4A), others are characterized by a singular sleeve fracture (Figure 4B), and few show no sleeve fractures at all (Figure 4C). Therefore, a more robust criterion than yes/no for the characterization of the CCA rods was needed and a fourth response variable, fraction of CCA rod, was introduced. To determine this value, the length of all sections cladded with copper was added up and related to the total rod length. This variable considers not only sleeve fractures but also the length of the full aluminum head and therefore provides an overall criterion for the macroscopic product quality.

All numerical results of the four response variables, based on the CCD are listed in Supplementary Table 2.

Statistical Results

The statistical data analysis of the CCD realized by the statistics software Statistica, Vers. 12 included the following steps:

- Identification of the significant linear and quadratic effects of the five process factors and its interactions on the four response variables by methods of variance and regression analysis using a significance level of α = 0.05.

- Finding an optimum overall setting of these most influencing process factors using response surface methodology with a desirability approach as well for each response variable individually as for a combination of all response variables.

As a result of the variance analysis (ANOVA) all significant effects of the five process factors on the four response variables Y1–Y4 could be estimated and are presented together with their 95%- confidence intervals (they include the standard deviations of the random error) in Supplementary Table 3. Additionally, Supplementary Table 3 includes the coefficients of determination as a measure for the goodness of the relationship between process factors and response variables. The results for the response variable Y1 – Length of full aluminum head are presented here in more detail:

Significant linear and quadratic effects as well as interactions (P < 0.05), ordered by size on the response variable Y1 – Length of full aluminum head, have the process factors X₅, X₁, and X₃:

$$\begin{array}{c}{\text{X}}_5-\mathrm{Die}\mathrm{angle}\mathrm{\hspace{0.33em}2}\mathrm{\alpha }[{}^{\circ }].\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} }(\text{effect}\left({\text{X}}_5\right)=\mathrm{\hspace{0.33em}378.42}\text{mm})\hfill \\ {\text{X}}_1-\mathrm{Extrusion}\mathrm{Ratio}[-]\mathit{\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{1em}}(\text{effect}\left({\text{X}}_1\right)=\mathrm{\hspace{0.33em}224.75}\text{mm})\hfill \\ {\text{X}}_3-\mathrm{Ram}\mathrm{speed}[\text{mm}/\text{s}]\mathit{\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{1em}}(\text{effect}\left({\text{X}}_3\right)=-33.58\text{mm})\hfill \\ {\text{X}}_1{\text{X}}_5-\mathrm{the}\mathrm{interaction}\hfill \\ \mathrm{between}{\mathrm{X}}_1\mathrm{and}{\mathrm{X}}_5\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}(\text{effect}\left({\text{X}}_1^{*}{\text{X}}_5\right)=\mathrm{\hspace{0.33em}128.37}\text{mm})\hfill \\ {\text{X}}_5^2-\mathrm{quadratic}\mathrm{effect}\mathrm{of}{\mathrm{X}}_5\mathit{\hspace{1em}\hspace{1em}\hspace{1em}}(\text{effect}\left({\text{X}}_5^2\right)=\mathrm{\hspace{0.33em}147.31}\text{mm}).\hfill \end{array}$$

The largest influence on Y1 has the die angle X₅, in which the linear effect (X₅) = 378.47 mm means the average change of Y1 as a result of variations in the two factors’ level +1 and –1. The aim of a minimal length of full aluminum head then would require a low level of X₅ by taking into account, that as well the important quadratic effect of X₅ as the interaction between X₁ and X₅ must be considered. Figure 5 shows the main effect of the die angle as well as the interaction effect of extrusion ratio and die angle on the length of full aluminum head (Y1). The factors container temperature (X₂) and copper volume fraction (X₄) have no significant effects on this response variable.

FIGURE 5

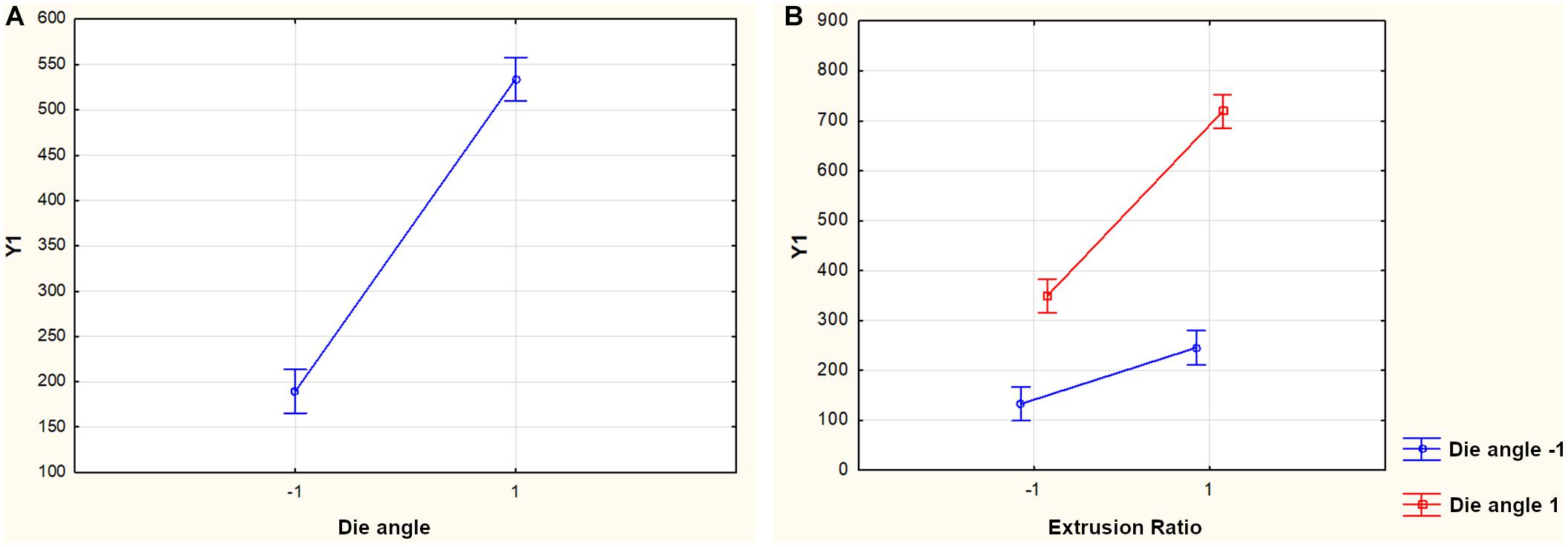
Figure 5. (A) Main effect (X₅) with respect to Y1 and (B) interaction effect (X1X5) with respect to Y1. Vertical bars denote 0.95 confidence intervals.

Whereas the pareto chart in Figure 6A graphically shows the significant standardized effects of the process variables, ordered by size, the chart in Figure 6B describes the goodness of the chosen regression model containing the linear effects of X₁, X₃, und X₅, the interaction between X₁ and X₅ and the quadratic effect of X₅. As well the chart in Figure 6B as the adjusted coefficient R² = 0,976 in Supplementary Table 3 show a very good fit of the model on the data. This adjusted R² is a measure of model fit, which relates the variance explained by the independent variables to the overall variance, adjusting for the number of effects used in the model.

FIGURE 6

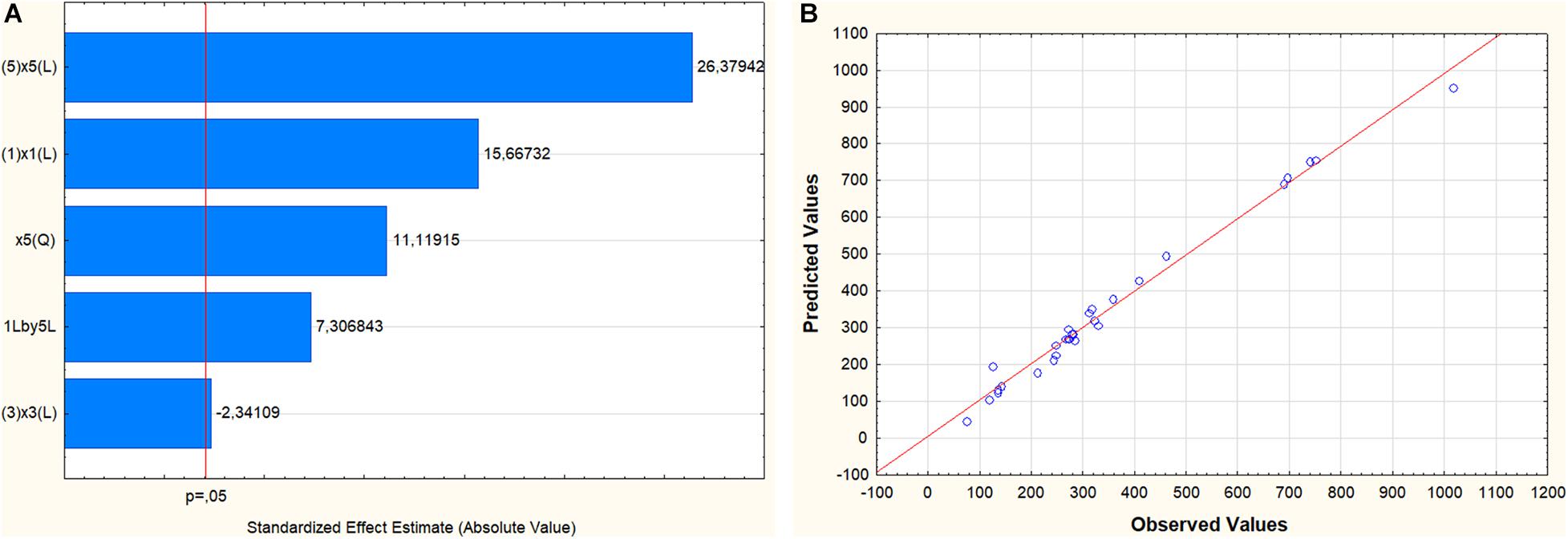
Figure 6. (A) Pareto chart with significant standardized effects with respect to Y1 and (B) a chart describing the relationship between observed and predicted model values with respect to Y1.

Based on the regression model Y₁ = 1196.5–20.62 x₁–4.80 x₃–19.75 x₅ + 0.31 x₁x₅ + 0.08 x₅² the aim of a minimal length of full aluminum head can be reached if the process factors have the following levels resp. levels within an interval:

$${\text{x}}_1=\mathrm{\hspace{0.33em}7};{\mathrm{x}}_2\in [30,\mathrm{\hspace{0.33em}430}]{}^{\circ }\text{C};{\mathrm{x}}_3=\mathrm{\hspace{0.33em}19}\text{mm}/\text{s};$$

$${\mathrm{x}}_4\in [0.15,0.35]\mathrm{and}{\mathrm{x}}_5=\mathrm{\hspace{0.33em}120}{}^{\circ }.$$

All significant effects on the further response variables Y2 – Y4 and the coefficients R² based on the estimated models can be found in Supplementary Table 3.

While the process factor X₅ – die angle 2α has a strong negative effect (p-value < 0,01) on the sleeve fracture (Y2), the smaller effects (p-value < 0,1) of ram speed (X₃), and copper volume fraction (X₄) are positive. Quite the contrary situation is the case for the variable change in copper volume fraction (| Y3|) with a strong positive effect of X₅ and smaller negative effects of X₃ and X₄.

In the case of fraction of CCA rod (Y4) the process factor X₅ is the most important factor with a negative effect, followed by the factors X₄ and X₃ with positive effects. As well linear as quadratic effects must be included in the model building process so that the following regression model can be fitted to the data:

$$\mathrm{Y4}=-1.44+0.017{\mathrm{x}}_3+13.09{\mathrm{x}}_4-\mathrm{\hspace{0.33em}22.80}{\mathrm{x}}_4^2-0,0001{\mathrm{x}}_5^2.$$

The aim of a maximal fraction of CCA rod can be reached if the factors have the following levels:

$${\text{x}}_1\in [7,\mathrm{\hspace{0.33em}35}];{\mathrm{x}}_2\in [30,\mathrm{\hspace{0.33em}430}]{}^{\circ }\text{C};$$

$${\mathrm{x}}_3=\mathrm{\hspace{0.33em}19}\text{mm}/\text{s};{\mathrm{x}}_4=\mathrm{\hspace{0.33em}0.3};\mathrm{and}{\mathrm{x}}_5=\mathrm{\hspace{0.33em}120}{}^{\circ }.$$

These optimal results for the responses Y1 and Y4 can be visualized by surface plots as presented in Figure 7.

FIGURE 7

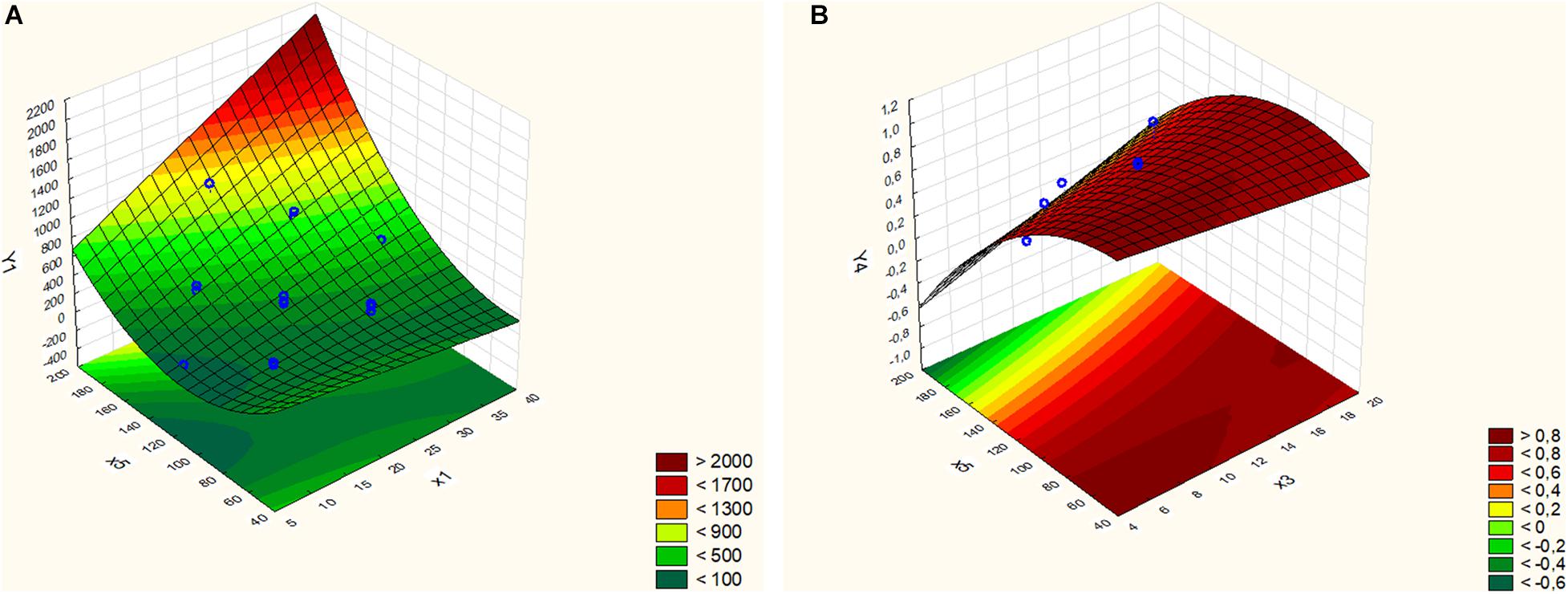
Figure 7. (A) Surface plot for Y1 – Length of full aluminum head [mm] and (B) surface plot for Y4 – Fraction of CCA rod [–].

In order to find an optimum overall setting of these most influencing process factors, response surface methods are applied by using desirability functions and the desirability index of Derringer (Derringer and Suich, 1980). Desirability functions allow to transfer each of the response variables into the interval [0;1] in order to make them comparable and to combine them into one common desirability index. Thereby, the desirability score 0 means undesirable (or unacceptable) and 1 stands for very desirable. The overall desirability then will be computed as the geometric mean of the individual desirabilities. Response/desirability profiling enables to inspect the response surface produced by fitting the observed responses using an equation based on levels of the process factors. A prediction profile as shown in Figure 8 for the four response variables consist of a series of graphs, one for each process factor and can show which levels of the factors produce the most desirable predicted response on the dependent variable. The last row contains the levels of the process factors, that optimize the overall desirability of the responses.

FIGURE 8

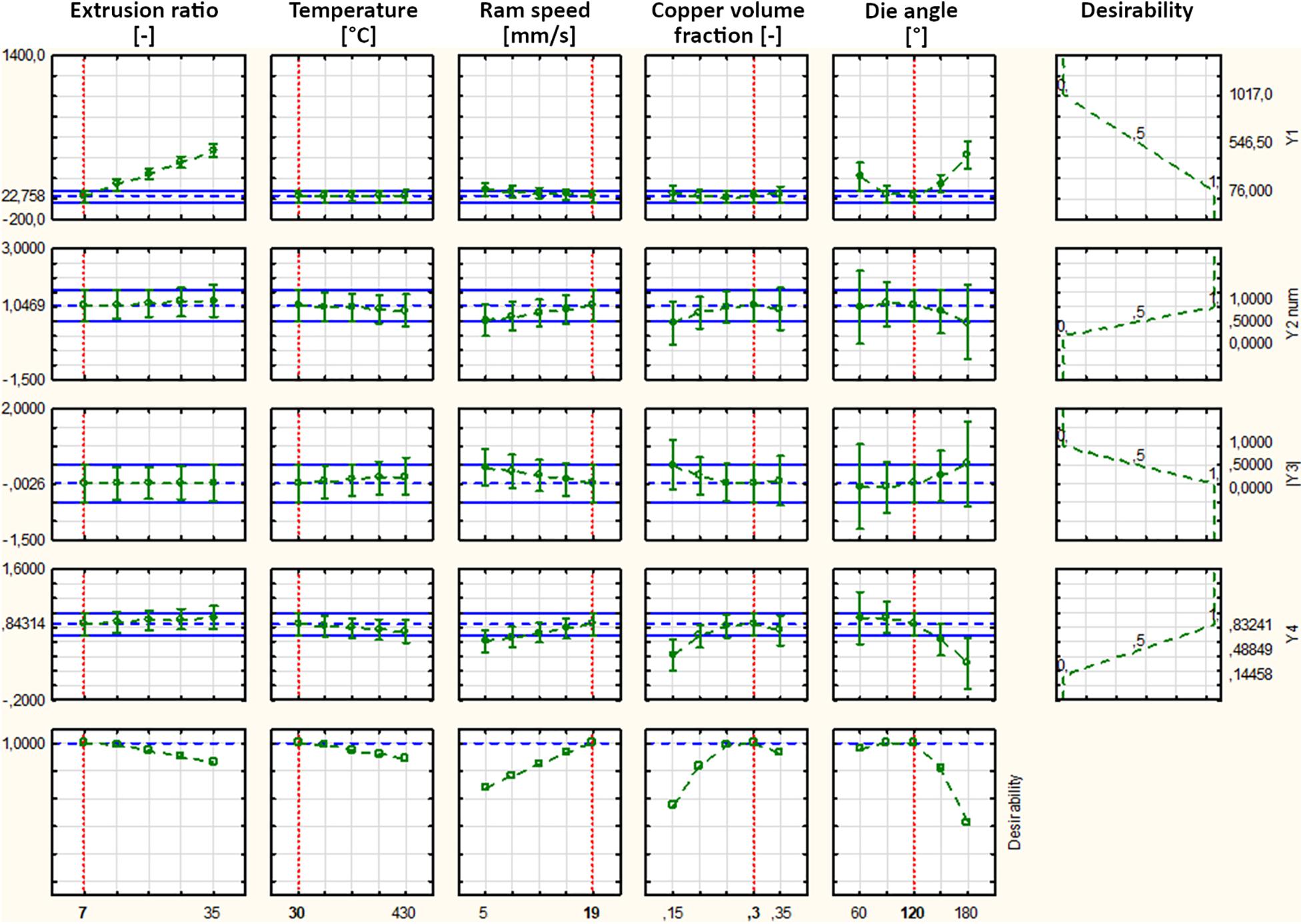
Figure 8. Plot of profiles for predicted values of all response variables Y1, Y2, | Y3|, and Y4 with confidence intervals and desirability function.

In order to optimize all four response variables in the following sense:

$$\mathrm{Y1}\to \text{min},\mathrm{Y2}\to \mathrm{\hspace{0.33em}1}\left(\text{no}\right),\left|\mathrm{Y3}\right|\to \min \mathrm{and}\mathrm{Y4}\to \max ,$$

the five process variables X₁ to X₅ should be set on the following levels:

$$\begin{array}{cccc}\hfill \text{Extrusin}\text{ratio}[-]& {\text{x}}_1\hfill & =\hfill & 7,\hfill \\ \hfill \text{Temperature}\left[°\text{C}\right]& \hfill {\text{x}}_2& =\hfill & 30,\hfill \\ \hfill \text{Ram}\text{speed}\left[\text{mm/s}\right]& {\text{x}}_3\hfill & =\hfill & 19,\hfill \\ \hfill \text{Copper}\text{volume}\text{fraction}\left[\text{−}\right]& {\text{x}}_4\hfill & =\hfill & 0.3\text{and}\hfill \\ \hfill \text{Die}\text{angle}\left[\text{°}\right]& {\text{x}}_5\hfill & =\hfill & 120.\hfill \end{array}$$

At these factor levels the overall desirability index would be equal 1 (very acceptable) and for the predicted response variables of the extrusion process of the CCA rods the following values, which are mean values in confidence intervals, would be expected:

$$\begin{array}{cccc}\hfill \text{Length}\text{of}\text{full}\text{aluminum}\text{head}\left[\text{mm}\right]& \hfill \text{Y1}& =\hfill & 22.76,\hfill \\ \hfill \text{Sleeve}\text{fracture}\left[\text{0/1}\right]& \hfill \text{Y2}& =\hfill & 1\text{(no)},\hfill \\ \hfill \text{Change}\text{in}\text{copper}\text{volume}\text{fraction}\left[\text{−}\right]& \hfill \left|\text{Y3}\right|& =\hfill & 0\text{and}\hfill \\ \hfill \text{Fraction}\text{of}\text{CCA}\text{rod}\left[\text{−}\right]\text{:}& \hfill \text{Y4}& =\hfill & \mathrm{0.84.}\hfill \end{array}$$

These optimal process conditions should lead to a good and stable quality of the CCA rod production.

Nevertheless, also small level changes, as, e.g., x₁ = 14 and x₅ = 90° would lead to an overall desirability index of 0.997, which is negligible less than 1,0 and allow as well a good CCA rod production. Expected values of the response variables in this case would be: Y1 = 84,70 mm; Y2 = 1 (no); | Y3| = 0,23; and Y4 = 1.0.

Extrusion Trial

The extrusion trial was carried out on an 8 MN extrusion press with a container diameter of 95 mm and integrated load cells. The DoE revealed a significant, but low influence of ram speed on the CCA extrusion process, which is in accordance with the low strain rate sensitivity of both billet materials. Hence, a ram speed of 5 mm/s was selected for better comparability with previous investigations (Sanabria et al., 2019; Kuhnke et al., 2020a). Comparability to that studies is also the reason for using an extrusion ratio of 14:1 and a die angle of 90° instead of 7:1 and 120°, respectively, as suggested by the results of the DoE. With multiple sleeve fractures at the last quarter of the composite extrusion, the trial conducted by Sanabria et al. was only partially successful. It is assumed that the sleeve fractures are induced firstly by an increased flow stress ratio as deformation heat is generated and secondly by high plastic strain in the copper sleeve. The container was deliberately kept at room temperature to achieve a minimal flow stress ratio with an isothermal setup. However, trials with the same process parameters, but increased container temperature, achieved sound extrusion of CCA rods (Kuhnke et al., 2020a). Therefore, the container temperature was set to 330°C in this trial. The anisothermal setup with a high container temperature should counteract the mentioned causes of sleeve fracture by heating the copper sleeve. Thus, the flow stress ratio is reduced, dynamic softening of the copper sleeve is facilitated and sleeve fractures are inhibited. Regarding these deviations from the optimal process conditions predicted by the statistical analysis, the overall desirability index is reduced to 0.864. The expected values of the response variables are: Y1 = 144 mm, Y2 = 1 (no), | Y3| = 0.24, and Y4 = 0.81. Considering the benefit of comparability to previous investigations, this minor disadvantage is accepted.

The die was designed with a bearing channel of 25 mm in diameter and 7.5 mm in length. To sustain good lubrication, which is essential to the process according to the findings of previous investigations (Sanabria et al., 2019; Kuhnke et al., 2020a), the die cone was ground with SiC-paper grid 80 and lubricated by applying Luprit SP19, a wax-graphite-based standard lubricant for hot extrusion. The billet (Figure 9A) was assembled with a sliding clearance fit by fitting an aluminum core made of the alloy EN AW-1080A into a sleeve machined out of extruded and annealed copper alloy CW004A. Length and diameter of the aluminum core were 180 mm and 77.8 mm, respectively. The front edge was fitted with a 10 mm radius to improve material flow during the beginning of the extrusion. The copper sleeve was 200 mm in length and lathed to a thickness of 7.6 mm, which is the smallest thickness that could be manufactured in-house. The resulting copper volume fraction and billet diameter are 0.30 and 93 mm, respectively. Core and sleeve were degreased with soap and ethanol before being joined. Additionally, the front quarter of the billet was wrapped in a layer of 250 μm thick graphite paper Grafoil GTB to enhance lubrication (Figure 9B). Tools and billet were applied at room temperature, while the container was heated to 330°C. During the extrusion, the extrusion force, profile exit temperature and billet temperature were recorded with the integrated load cells as well as thermocouples in the bearing channel and ram.

FIGURE 9

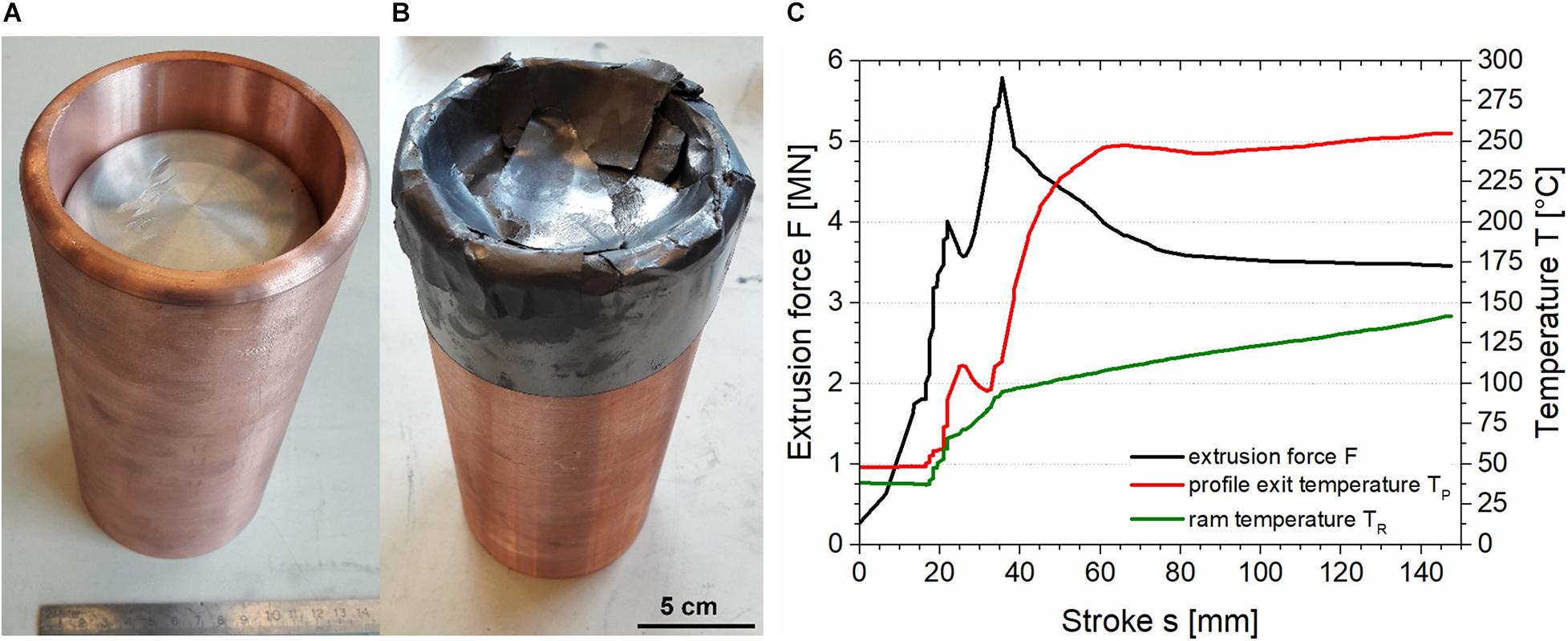
Figure 9. (A) Copper-aluminum composite billet, (B) billet with applied graphite foil, and (C) extrusiondiagram of the extrusion trial.

The extrusion diagram of the trial is illustrated in Figure 9C. The course of the extrusion force is characteristic for indirect extrusion. The global peak of 5.8 MN at a stroke of 35 mm represents the beginning of the extrusion and is followed by a plateau of 3.5 MN in the steady state. Due to the formation of a full aluminum head, a local peak is visible at a stroke of 22 mm. The profile exit temperature begins to increase as soon as the aluminum is in contact with the thermocouple in the bearing channel. Subsequent to the formation of the full aluminum head, the temperature decreases due to loss of contact to extruded material and measurement of the environment temperature (Kuhnke et al., 2020b). With the beginning of the composite extrusion contact is regained and the temperature increases to a nearly constant plateau at approximately 250°C. The ram temperature increases steadily due to the heat induced by the hot container.

The extruded CCA rod is displayed in Figure 10A. It is approximately 2 m in length and characterized by a 220 mm long full aluminum head and no sleeve fractures at all. The full aluminum head is 76 mm longer than predicted by the DoE, which is most likely due to an increased handling time during the loading phase of the extrusion. This was around 60 s instead of 10 s as assumed in the numerical analyses. Therefore, the billet is exposed to the containers heat for a longer time and heats up more. This causes the flow stress ratio to increase and more monolithic aluminum to be extruded.

FIGURE 10

Figure 10. (A) Extruded CCA rod and (B) evolution of the copper volume fraction.

Although the container temperature is identified as a factor with non-significant effect by the statistical analysis, an increase of that enabled an improvement of process stability and sleeve integrity compared to the trial of Sanabria et al. (2019). As mentioned before, a reduced flow stress ratio and dynamic softening of the copper sleeve is supposed to inhibit sleeve fractures. But as no fracture model was available for the numerical analyses and softening effects are not represented by the material models, these could not be taken into account by the statistical analysis and no effect was identified. However, since no sleeve fractures occurred in the experiment, this prediction was satisfactorily met.

To investigate the change in copper volume fraction, cross sections were taken in regular intervals of 20 cm, beginning 10 cm behind the tip of the CCA rod. These cross sections were ground and polished with SiC sandpaper and 6 μm/3 μm diamond suspension, respectively. The analysis was carried out by processing scans of the cross sections with the software GIMP and determining the copper volume fraction using the particle analysis algorithm of the software ImageJ. The results are illustrated in Figure 10B. For the first 30 cm the copper volume fraction is greatly elevated at around 0.43 but then drops to a constant level of 0.31–0.32 within another 40 cm. The increased copper volume fraction at the beginning of the extrusion is due to the non-steady processes, as described by Kuhnke et al. (2020b). When the steady state is reached, material flow becomes homogeneous and a constant copper volume fraction is generated. In the numerical analyses the measurement for the calculation of the copper volume fraction was made 10 cm behind the tip of the CCA rod and at a stroke of 80 mm. In the experiment the corresponding CCA rod length at a stroke of 80 mm is 85 cm. Therefore, the cross section taken at 90 cm was considered for the calculation of the change in copper volume. A reduction of copper volume fraction by 28% was determined. This little deviation from the predicted value of 24% is very acceptable and can be reasoned by the inaccurate modeling of the inhomogeneous material flow at the beginning of the extrusion (Kuhnke et al., 2020b).

With no sleeve fractures and a full aluminum head of 220 mm in length, the fraction of CCA rod for the whole rod is 0.89. For comparability with the results of the statistical analysis, the fraction of CCA rod was also determined by considering only a stroke of 80 mm and thus a rod length of 107 cm. The resulting fraction of CCA is 0.79, which is again in excellent agreement with the predicted value of 0.81, when taking into account the longer monolithic aluminum head.

Conclusion

In order to develop an optimal set of process parameters for the indirect extrusion of CCA rods, the process was modeled with the FEM-based software DEFORM 2D and analyzed using the methods of statistical DoE. Therefore, a CCD with 29 runs was applied.

Regression models, containing significant linear and quadratic effects and interactions of the five investigated process parameters, were the basis for the optimization of the indirect CCA extrusion process. All response variables were mostly influenced by the process parameter X5 – Die angle. Whereas the three process parameters X₁ – Extrusion ratio, X₃ – Ram speed, and X₅ – Die angle and the interaction between X1 and X5 were very important for a minimal length of full aluminum head (Y1), the other response variables Y2 – Sleeve fracture, Y3 – Change in copper volume fraction, and Y4 – Fraction of CCA rod were influenced especially by X₃ – Ram speed, X₄ – Copper volume fraction, and X₅ – Die angle. Response surface methods and desirability index were applied to find an optimum overall setting of these most influencing process factors.

For the purpose of validation, an extrusion trial was carried out using a near optimal parameter set suggested by the statistical analysis and the values of the response variables were compared. The experimental values are in great agreement with the predicted ones, which confirms the accuracy of the regression models. Furthermore, the application of a near optimal parameter set enabled the extrusion of a high quality CCA rod with considerable length by means of indirect extrusion. However, no significant effect of the container temperature was identified by the statistical analysis, although the trial revealed a great improvement of process stability and product quality by increasing the container temperature, compared to another trial conducted earlier.

Eventually, no change in copper volume fraction along the extrusion is predicted for the optimal set of process parameters. Considering the large part of the CCA rod with increased copper volume fraction, the realization of an extrusion with no change in copper volume fraction would further improve the product quality and allow for higher yields.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

SL, RN, FG, and SM contributed conception and design of the study. SL performed the numerical analysis. RN and SL interpreted the results of the numerical analysis. UR performed the statistical analysis. FG, RN, and SL carried out the extrusion trial. SL and UR wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

We are grateful for the financial support of the Deutsche Forschungsgemeinschaft (DFG; Grant No. MU 2963/14-1). We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.

Conflict of Interest

FG was employed by the company INGWERK GmbH.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.663306/full#supplementary-material

References

Berski, S., Dyja, H., Maranda, A., Nowaczewski, J., and Banaszek, G. (2006). Analysis of quality of bimetallic rod after extrusion process. J. Mater. Process. Tech. 177, 582–586.10.1016/j.jmatprotec.2006. 04.107

Google Scholar

Box, G. E. P., and Draper, N. R. (1987). Empirical Model-Building and Response Surfaces. New York, NY: Wiley.

Google Scholar

Box, G. E. P., Hunter, W. G., and Hunter, S. J. (1978). Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building. New York, NY: Wiley.

Google Scholar

Bruker EST Hydrostatic Extrusions Limited (2014). The Engineered Alternative to Copper Busbar: CUPONAL. Available online at: https://www.bruker.com/en/meta/fileadmin/_jcr_content/root/contentpar/search.download-asset.pdf/4894c4ef-44a9-46b2-9585-2ad704822d76/Busbar.pdf (Accessed January 28, 2021)

Google Scholar

Cockcroft, M. G., and Latham, D. J. (1968). Ductility and the workability of metals. J. Inst. Met. 96, 33–39.

Google Scholar

Coleman, D. E., and Montgomery, D. C. (1993). A systematic Approach to Planning for a Designed Industrial Experiment. Technometrics 35, 1–12. doi: 10.2307/1269280

CrossRef Full Text | Google Scholar

Derringer, G., and Suich, R. (1980). Simultaneous optimization of several response variables. J. Qual. Technol. 12, 214–219. doi: 10.1080/00224065.1980.11980968

CrossRef Full Text | Google Scholar

Haghighat, H., and Momeni-Khabisi, H. (2014). Analysis and finite element simulation of bimetallic backward rod extrusion. Aust. J. Mech. Eng. 12, 282–290. doi: 10.7158/M13-019.2014.12.3

CrossRef Full Text | Google Scholar

Jang, D. H., and Hwang, B. B. (2007). Deformation Analysis of co-extrusion process of aluminum alloy and copper alloy. Key Eng. Mater. 340-341, 645–648. doi: 10.4028/0-87849-433-2.645

CrossRef Full Text | Google Scholar

Kang, C. G., Jung, Y. J., and Kwon, H. C. (2002). Finite element simulation of die design for hot extrusion process of AL/Cu clad composite and its experimental investigation. J. Mater. Proc. Technol. 124, 49–56. doi: 10.1016/S0924-0136(02)00106-1

CrossRef Full Text | Google Scholar

Kang, C.-G., and Kwon, H. C. (2002). Finite element analysis considering fracture strain of sheath material and die lubricant in extrusion process of Al/Cu clad composites and its experimental investigation. Int. J. Mech. Sci. 44, 247–267. doi: 10.1016/S0020-7403(01)00102-3

CrossRef Full Text | Google Scholar

Kazanowski, P., Epler, M. E., and Misiolek, W. Z. (2004). Bi-metal rod extrusion – process and product optimization. Mater. Sci. Eng. A 369, 170–180. doi: 10.1016/j.msea.2003.11.002

CrossRef Full Text | Google Scholar

Kleppmann, W. (2009). Taschenbuch Versuchsplanung: Produkte und Prozesse optimieren. München: Hanser.

Google Scholar

Kuhnke, S., Gensch, F., Nitschke, R., Sanabria, V., and Mueller, S. (2020a). Influence of die surface topography and lubrication on the product quality during indirect extrusion of copper-clad aluminum rods. Metals 10:888. doi: 10.3390/met10070888

CrossRef Full Text | Google Scholar

Kuhnke, S., Sanabria, V., Gensch, F., Nitschke, R., and Mueller, S. (2020b). Numerical Investigations on material flow during indirect extrusion of copper-clad aluminum rods. Front. Mater. 7:157. doi: 10.3389/fmats.2020.00157

CrossRef Full Text | Google Scholar

Kwon, H. C., Jung, T. K., Lim, S. C., and Kim, M. S. (2004). Fabrication of Copper Clad Aluminum Wire(CCAW) by indirect extrusion and drawing. Mater. Sci. Forum 449-452, 317–320. doi: 10.4028/www.scientific.net/msf.449-452.317

CrossRef Full Text | Google Scholar

Mason, R. L., Gunst, R. F., and Hess, J. L. (1991). Statistical Design and Analysis of Experiments with Applications to Engineering and Science. New York, NY: Wiley.

Google Scholar

Montgomery, D. C. (2009). Statistical Quality Control, 6th Edn. New York, NY: Wiley.

Google Scholar

Montgomery, D. C. (2013). Design and Analysis of Experiments, 8th Edn. New York, NY: Wiley.

Google Scholar

Müller, K. (2004). Fundamentals of Extrusion Technology. Isernhagen: Giesel.

Google Scholar

Sanabria, V., Gall, S., Gensch, F., Nitschke, R., and Mueller, S. (2019). Backward extrusion of bimetallic aluminum-copper alloys at room temperature. AIP Conf. Proc. 2113:030001. doi: 10.1063/1.5112529

CrossRef Full Text | Google Scholar

Sanabria, V., Mueller, S., and Reimers, W. (2015). Friction Modelling in long bearing channels during multi-hole extrusion of aluminium alloy. Mater. Today Proc. 2, 4820–4828. doi: 10.1016/j.matpr.2015.10.021

CrossRef Full Text | Google Scholar

Scientific Forming Technologies Corporation (SFTC). Deform v11.3 System Documentation.

Google Scholar

StatSoft Europa GmbH (2013). Software Statistica, Vers.12. Germany: StatSoft Europa GmbH.

Google Scholar