
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 11 May 2021
Sec. Structural Materials
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.651435
This article is part of the Research Topic Advanced Nuclear Materials for Fission Reactors View all 8 articles
Due to the low neutron activity, the high thermal stability, and the good compression strength at elevated temperatures, medium-entropy Ta-Ti-V alloys have the application potential to be used in future nuclear engineering. According to experimental results, a special quasi-random structure (SQS) model and first-principles calculations are used to calculate the structural stability and the elasticity of the ternary single-phase body-centered cubic (BCC) Ta-Ti-V alloys with the compositions Ta24Ti14V16, Ta19Ti17V18, Ta16Ti21V17, Ta22Ti23V9, and Ta18Ti18V18. The mixing energy of five compositions is positive, which indicates that they are unstable at low temperature but stable at high temperature. Meanwhile, we predict the ability of elasticity in those five compositions, and the sequence of bulk modulus is Ta24Ti14V16 > Ta19Ti17V18 > Ta18Ti18V18 > Ta16Ti21V17 > Ta22Ti23V9 and ductility is Ta19Ti17V18 > Ta18Ti18V18 > Ta22Ti23V9 > Ta24Ti14V16 > Ta16Ti21V17. Additionally, the influence of the element content on elastic properties shows that the Ta content will increase the bulk modulus of the alloys, while Ti content decreases the bulk modulus. Higher V and Ti contents are beneficial to ductility, especially the V content. The higher Ta content will sharply reduce the ductility of the alloys. Our calculation has provided further theoretical mechanism for the Ta-Ti-V medium-entropy alloys (MEAs) preparation and development.
The recently developed novel concept of high-entropy alloys (HEAs), named by Yeh et al. (2004), has attracted an extensive attention in recent decades from both experimentalists and theoreticians. Initially, HEAs were loosely defined as single-phase solid solutions with at least five principal elements, each with an atomic percentage between 5 and 35% (Gao et al., 2016). These alloys owe their name to the assumption that the solid solution is stabilized by high configurational entropy of mixing. Meanwhile, the definition has been broadened to also include four-component alloys. Alloys with three and four principal elements are sometimes referred to as medium-entropy alloys (MEAs). Like HEAs, MEAs also exhibit good thermal stability (Wu et al., 2014; Sathiyamoorthi et al., 2017), high strength (Wu et al., 2014; Zhao et al., 2017), and excellent ductility (Gludovatz et al., 2016; Fu et al., 2018). Usually, HEAs can form a simple microstructure, e.g., body-centered cubic (BCC) or face-centered cubic (FCC), rather than complex intermetallic phases (Zhang et al., 2014).
In Ta-Ti-V MEAs (Jia et al., 2019), experimental results showed that they all exhibit BCC structures in their homogenized states. The four nominal compositions in this work are Ta40Ti27V33, Ta27Ti40V33, Ta35Ti45V20, and the equiatomic Ta33Ti33V34. They have examined their mechanical properties including ductility at room temperature and compression resistance at high temperature up to 800°C, and Ta35Ti45V20 exhibits the best compression resistance. Except for Ta40Ti27V33, the other three alloys have an acceptable tensile ductility of 7.6–13% fracture strain at room temperature. However, to date, the other elastic properties including shear modulus, Young’s modulus, and the influence of elemental content on elastic properties of Ta-Ti-V systems are still unknown. Fortunately, special quasi-random structures (SQSs) (Zunger et al., 1990) in combination with first-principles calculations (Perdew and Zunger, 1981) offer the possibility to study these properties. Theoretically, an infinite unit cell is needed to model random structures. The larger a unit cell is, the more first-principles calculations are needed. The SQS can effectively reduce the modeling size and provide reliable results (Wen et al., 2018).
In this study, we calculate the structural parameters, the stability, the elastic properties, and the influence of elemental content on elastic properties of Ta-Ti-V MEAs using first-principles calculations according to the SQS models. A series of useful results have been obtained including the elastic properties of different compositions for Ta-Ti-V MEAs and the influence of single element’s content on their ductility and deformation resistance.
The SQS method (Wei et al., 1990; Zunger et al., 1990) essentially finds small unit cell special structure, which can exactly reproduce the pair and multisite correlation functions of a random alloy between the first few nearest neighbors, deferring periodicity errors to more distant neighbors. In practice, convergence tests need to be performed in order to ensure that long-range interatomic interactions have negligible effects on the property of interest, such that the SQS method remains applicable. In the studies by Jiang et al. (2004) and Jiang (2009), rapid convergence of SQS calculated alloy properties (e.g., formation energy, lattice parameter, and band gap) with respect to the SQS size has been observed, which strongly indicates that those properties are indeed dominated by interactions between near neighbors. In such a case, even small SQSs are already sufficient to provide reliable results. In this study, according to the chemical compositions of the experimental samples (Jia et al., 2019), we generated various SQS-N structures (N is the atom number per SQS unit cell) with a high approximation atom percentage compositions of random BCC alloys. Our search criterion requires that the pair correlation functions of the SQS should be as close as those of the corresponding random alloys; it needs at least up to the 10th nearest neighbor; the second nearest neighbor for both ternary and quaternary correlation functions. We use the mcsqs code in the Alloy-Theoretic Automated Toolkit (ATAT) (van de Walle et al., 2002) to search SQSs.
All the first-principles calculations are employed by using VASP (Vienna ab initio simulation package) (Kresse and Furthmüller, 1996; Kresse and Furthüller, 1996). Projector-augmented wave (PAW) potentials (Blöchl, 1994) and Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) (Perdew et al., 1996) for the exchange–correlation function were performed. Plane-wave cutoff energy of 400 eV is used. A 3 × 3 × 3 BCC supercell containing 54 atoms is used, and the Brillouin zone is sampled with a 5 × 5 × 5 k-point mesh based on the Monkhorst-Pack scheme. The total energy convergence criterion of the self-consistent field (SCF) is set to be 1.0 × 10–5 eV/atom, and the first-order Methfessel-Paxton method with a width of 0.1 eV is implemented to fully relax the structures. Once the Hellmann–Feynman force acting on each atom is less than 0.01 eV/Å, the atoms are regarded as being fully relaxed.
The mixing and formation energy (Liu et al., 2005) of a random BCC alloy with compositions xTi and xV are obtained as:
where E(Ta), E(Ti), E(V), and E(SQS) are total energies (per atom) of the constituent elements Ta, Ti, and V from first-principles calculations and the corresponding SQS result. All the calculations are performed based on the full structural optimization. The pure elements BCC Ta, hexagonal close-packed (HCP) Ti, and BCC V structures are used as reference states in Eq. (1), noting that it takes BCC Ta for the mixing energy calculation in Eq. (2) for the SQS Ta-Ti-V MEAs with the BCC structure.
We can apply small strains to the equilibrium lattice, determine the resulting change in the total energy, and, from this information, deduce the elastic constant Cij. The elastic constants are identified as proportional to the second-order coefficient in a polynomial fit of the total energy as a function of the distortion parameter δ (Li, 2014). By using the elastic constant Cij, the mechanical stability of the cubic crystal can be estimated by the Born stable criterion [as Eq. (3)] (Ameri et al., 2014). Additionally, the polycrystalline elastic properties, including bulk modulus B, shear modulus G, and Young’s modulus E, are averaged by the Voigt-Reuss-Hill schemes [as Eq. (4)] (Hill, 1952). Here, B value is used to represent the ability of resistance of elastic deformation of the material, while it also uses Pugh ratio B/G value to represent the brittleness or ductility of the material (Push, 1954). According to Pugh’s classification, the critical value of B/G is 1.75. Meanwhile, the higher the B/G ratio, the better the ductility, otherwise more brittle.
In order to test the appropriate amount of atoms for the SQS-N structure, N is set as 24, 36, 54, and 120. To highly reflect the same proportion of concentration of each element in experiment (Jia et al., 2019), the same chemical compositions (in at.%) are set for Ta, Ti, and V, respectively, in this study. In Figure 1, the SQS calculated mixing energy ΔEmix (i.e., mixing enthalpies at 0 K) and equilibrium lattice constant (a) of BCC Ta-Ti-V alloys with equiatomic compositions, which are plotted as a function of N. This shows a rapid convergence of the SQS calculation with respect to N. Remarkably, our SQS-24 structure gives identical lattice constants as those given by the SQS-120 structure. For mixing energies, the difference between SQS-24 structure and SQS-120 structure is less than 0.5 kJ/mol, and the results from the SQS-54 structure is nearly equal to those obtained using SQS-120. In order to perform an efficient and economical calculation process, we considered SQS-54 in further elastic properties calculation, and it resulted in an accepted comparison for compositions with experiments. For example, the lattice constant a is from 3.184(9) Å when N = 120, which agrees with the parameter with 3.208 ± 0.005 Å of equiatomic Ta34Ti33V33 in experiment (Jia et al., 2019). The predicted structures with 54 atoms from SQS are given as Ta24Ti14V16, Ta19Ti17V18, Ta16Ti21V17, Ta22Ti23V9, and Ta18Ti18V18. Their crystalline structures are illustrated in Figure 2.
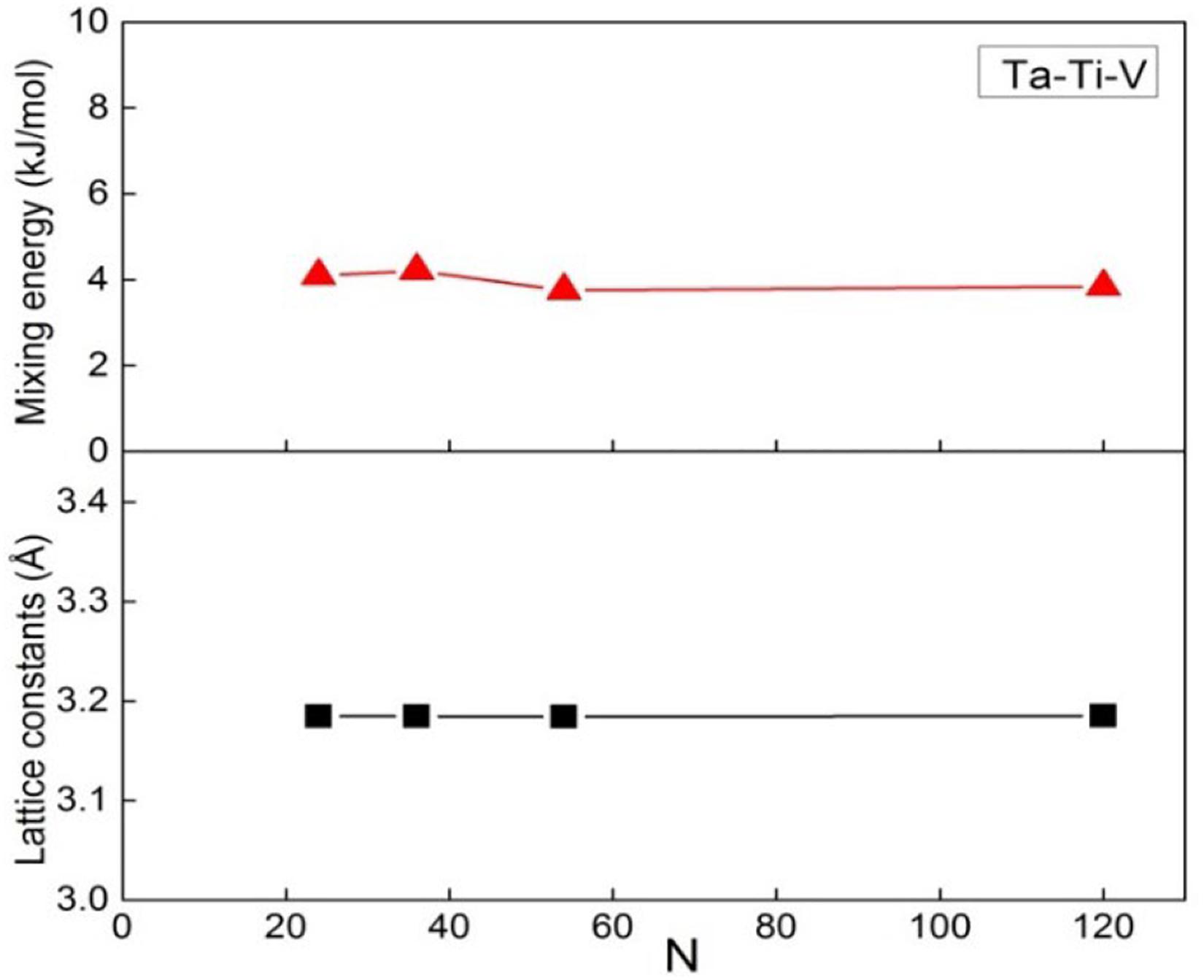
Figure 1. The calculated mixing energies from SQS (top) and equilibrium lattice constants of body-centered cubic (BCC) Ta-Ti-V medium-entropy alloy (MEA) as a function of the atom number N per unit (bottom).
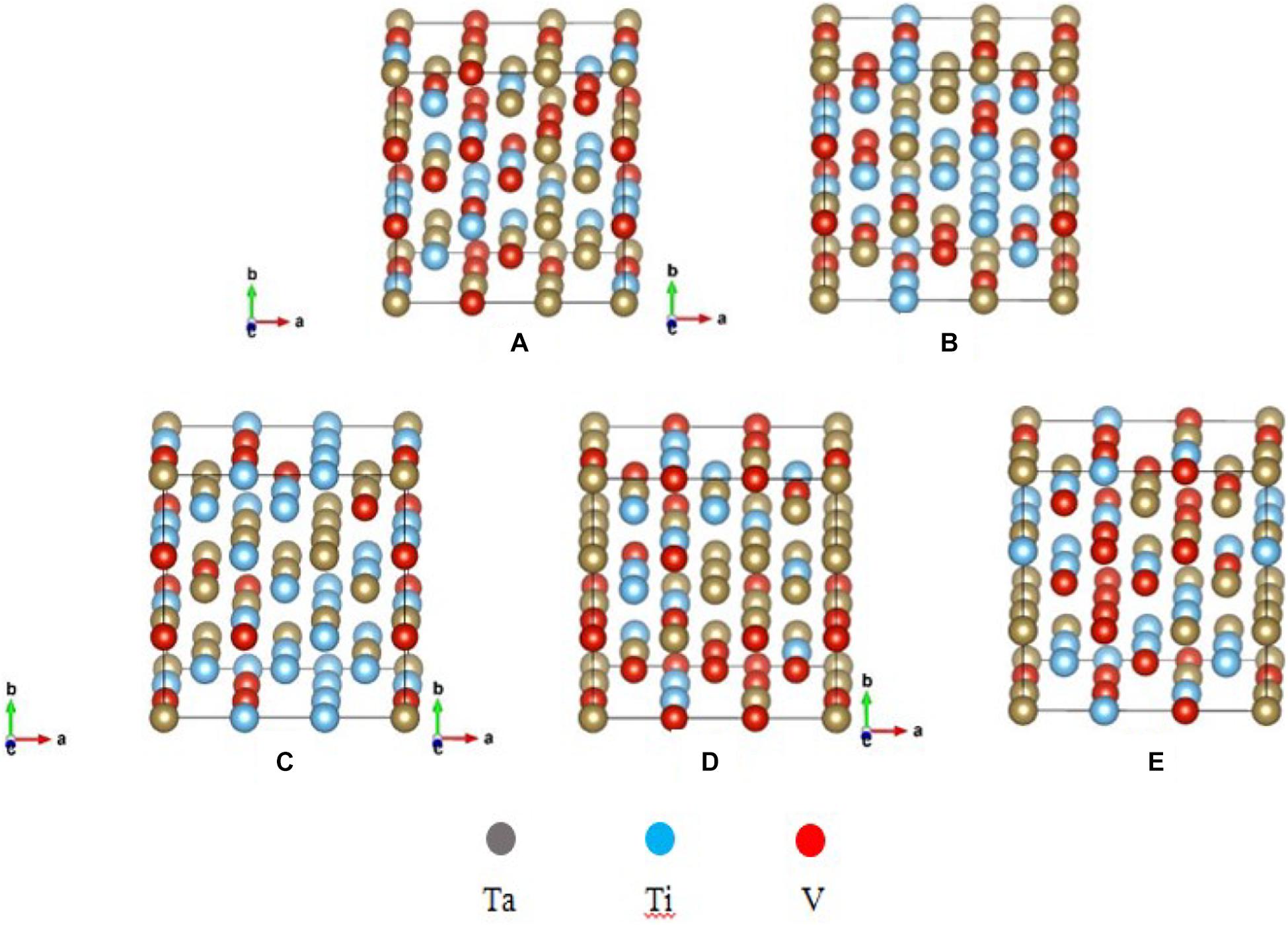
Figure 2. The crystallographic structure of ternary special quasi-random structures (SQSs) models. (A) Ta19Ti17V18, (B) Ta16Ti21V17, (C) Ta22Ti23V9, (D) Ta24Ti14V16, and (E) Ta18Ti18V18. The brown, blue, and red balls are Ta, Ti, and V atoms, respectively.
The calculated equilibrium lattice constants for pure BCC Ta, HCP Ti, and BCC V are given in Table 1. The relative error of the calculation value of the lattice constants of Ta, Ti, and V elements compared with experimental data (Martienssen and Warkimont, 2005) is less than 1.7%. The results reveal that our lattice constants calculations agree well with experimental values.
The calculated equilibrium lattice constant a, mixing energy ΔEmix, and formation energy ΔEform of Ta-Ti-V MEAs are summarized in Table 2. We note that Ta content can increase, but the V content can decrease the lattice constant of the alloy. This is mainly due to the higher Ta and the lower V lattice constant. The necessary requirement to form a single-phase solid solution is that the mixing energy should satisfy −16.25kJ/mol ≤ ΔEmix ≤ 5kJ/mol (Gao et al., 2017), and the mixing energy of all the predicted alloys’ compositions satisfies this condition. From Table 2, we can see that their mixing energies are all positive, which suggest they are unstable at a low temperature and stable at a high temperature. This phenomenon has also been observed from an experiment of the equiatomic composition (Jia et al., 2019). By using the formula G = HSQS−TSconf [G is Gibbs free energy and HSQS is formation enthalpy, which is equal to the formation energy at 0 K; in case of ternary equiatomic composition, Sconf = 1.1R,R = 8.314J/(mol⋅K) (Yeh et al., 2004)], it can be roughly estimated that BCC Ta18Ti18V18 can exist stably at T = 760 K, which is similar to the testing temperature (Jia et al., 2019).
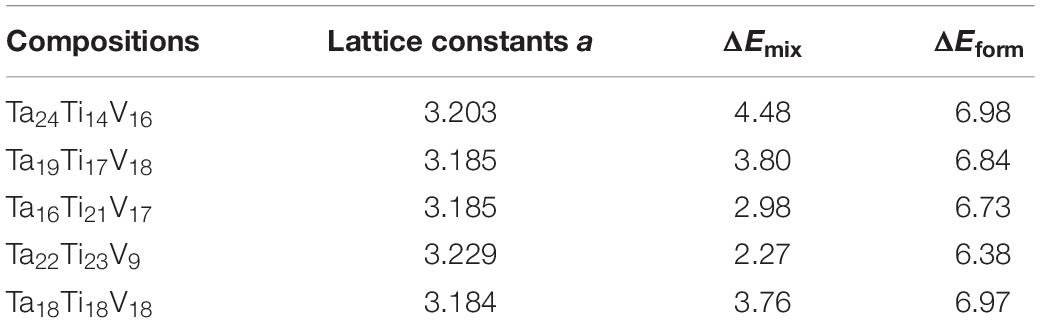
Table 2. Calculated equilibrium lattice constant a (Å), mixing energy ΔEmix (kJ/mol), and formation energy ΔEform (kJ/mol) for Ta-Ti-V MEAs.
The calculated single-crystal elastic constants, bulk modulus, shear modulus, Young’s modulus, and B/G ratio for pure BCC Ta, Ti, and V are listed in Table 3.
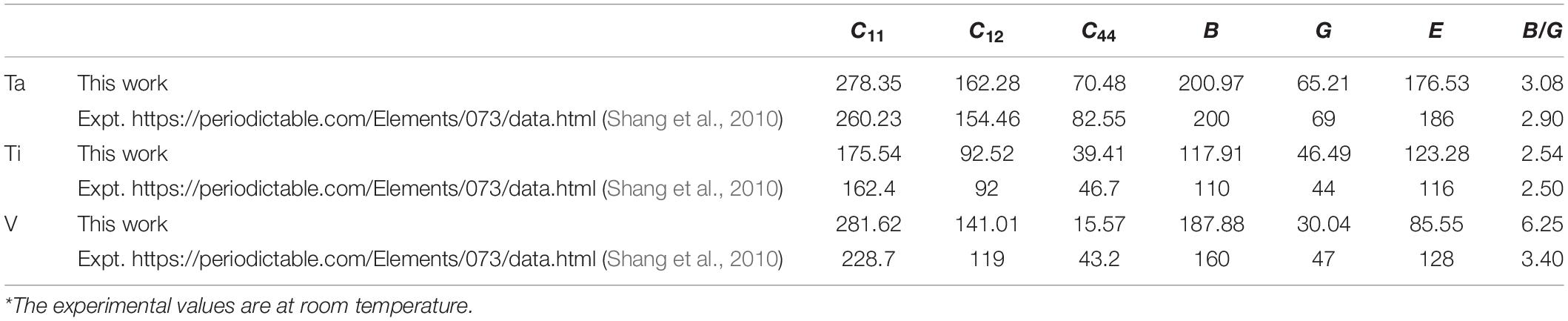
Table 3. Calculated elastic constant Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), and B/G ratio for pure elements, combined with experiment values*.
It can be obtained that the prediction of C44, B, G, and E of Ta and Ti elements are in line with the experimental values1 (Shang et al., 2010). However, for V atom, the difference between the calculated elastic constant values C44, B, G, E, and B/G and its experimental values1, (Shang et al., 2010) is relatively large, especially C44, which may be due to a deviation between V calculated lattice constant and its experimental value (Martienssen and Warkimont, 2005). This problem can be solved by treating semi-core 3p electrons of V as valence. We can see that Ta has the best material stiffness characterized by bulk modulus B = 200.97 GPa and Ti has the highest brittleness characterized by B/G ratio among the three elements. The calculated single-crystal elastic constants, bulk modulus, shear modulus, Young’s modulus, and B/G ratio for Ta-Ti-V MEAs are listed in Table 4.

Table 4. Calculated elastic constant Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), and B/G ratio for Ta-Ti-V MEAs.
The mechanical stability of the MEAs structure has a great significance in the manufacture and applications of the material. Regarding the Born stability criteria, the stability of cubic crystal is represented in Eq. (3). As the elastic strain energy is required to be positive, it can be seen from Table 4 that Ta24Ti14V16, Ta19Ti17V18, Ta16Ti21V17, Ta22Ti23V9, and Ta18Ti18V18 all meet the conditions of mechanical stability.
It is also known from Table 4 that Ta24Ti14V16 has the best bulk modulus and Ta19Ti17V18 has the best ductility. Meanwhile, B and B/G value of Ta18Ti18V18 are both smaller than Ta19Ti17V18, indicating that Ta19Ti17V18 has higher bulk stiffness and ductility than Ta18Ti18V18, which means that the equiatomic ratio composition may have the good thermal stability, while it is not necessary for the best mechanical performance. The elasticity for all predicted compositions has been compared, such as bulk modulus: Ta24Ti14V16 > Ta19Ti17V18 > Ta18Ti18V18 > Ta16Ti21V17 > Ta22Ti23V9 and ductility: Ta19Ti17V18 > Ta18Ti18V18 > Ta22Ti23V9 > Ta24Ti14V16 > Ta16Ti21V17. The trend is similar from the behavior of compression resistance in experiment (Jia et al., 2019), for example, increasing the Ta content can enhance the material strength. For the ductility, it can also be concluded that Ta is not favorable for the material ductility, while a relatively higher Ti can increase the ductility of the alloy, and the effect of V is between Ti and Ta.
The influence of element content on the elastic properties of Ta-Ti-V MEAs is also investigated. Considering that elastic properties are binary functions of the element content, we assume that the first variable is the ratio of random two elements’ contents and the other variable is the remaining one element’s content. The calculation is carried out by keeping one element’s content unchanged, then adjusting the ratio of the remaining two elements’ contents, and calculating the elastic constants of the system. Here, taking equal composition Ta18Ti18V18 as the benchmark, for example, the Ti content is fixed to 33.3 at.%, then the ratio of Ta and V content is adjusted from 0.385 to 2.6, and the elastic constants of the system are calculated. In this case, the relationship between the bulk modulus, shear modulus, Young’s modulus, and B/G with the ratio of different elements’ contents is shown in Figure 3.
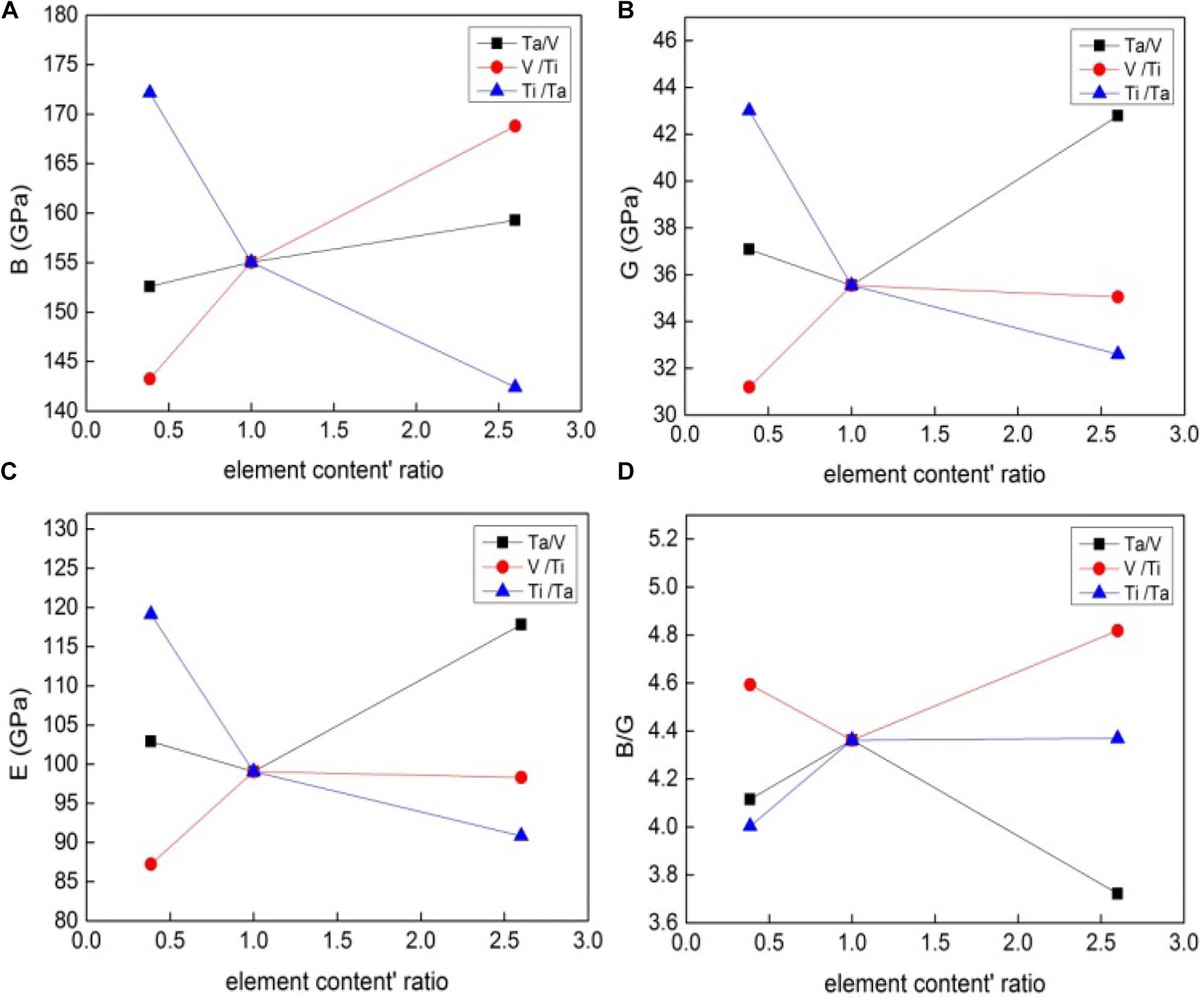
Figure 3. The relationship between the bulk modulus B (A), shear modulus G (B), Young’s modulus E (C), B/G (D), and element content ratio for Ta-Ti-V MEAs.
It can be seen that the elastic properties vary with the ratio of different elements’ contents. In Figure 3A, the bulk modulus shows a monotonous change. Specifically, the ratio of Ta and V content to V and Ti content can improve the material stiffness, while the ratio of Ti and Ta content is opposite. Consequently, Ta is the most favorable element to improve the material stiffness, while Ti content is the most unfavorable, which also confirms the data from the experimental. For the partial reason, Ta has the highest melting temperature of 3287 K, when compared to the temperatures 1943 K and 2199 K of Ti and V, respectively. Additionally, Ta has the highest elastic module among the three elements; it could make the alloy stiffness enhanced when the alloy reaches a high percentage of Ta atom.
Furthermore, in Figures 3B,C, G and E of the system firstly decrease and then increase with the increase of the Ta/V ratio, indicating that both higher Ta and V content will rise the material shear and the Young’s modulus. Additionally, both G and E obviously increase and then slightly decrease with the increase of V/Ti ratio, suggesting that the higher Ti content can reduce the shear and Young’s modulus. Finally, with the increase of Ti/Ta ratio, the trend of G and E decreases significantly, which is also consistent with the previous analysis. In general, the most favorable element for the material shear and Young’s modulus is Ta element, while the Ti content is the opposite. In the same way, according to Figure 3D, higher V and Ti content can improve the ductility, but the effect of V content is more obvious than the effect of Ti. The higher Ta content will sharply reduce the ductility of the alloys, which is proved by the fact in Reference (Jia et al., 2019), in which a lower lever Ti composition (Ta27Ti33V40) fractured before the elastic deformation stage.
However, the relationship between G, E, and B/G, and the effect of element content on the elastic constants of Ta-Ti-V MEAs are still need further investigations. For example, the study of more compounds with different atomic ratios, and the key factors that determine the mechanical properties of these compounds.
The first-principles calculations in combination with the SQS method are applied to calculate structural parameters, stability, elastic constants, elastic modulus, and the influence of element content on elastic properties for BCC Ta-Ti-V MEAs. According to experimental results, we used the mcsqs code to search SQS and obtained a series of compositions as Ta24Ti14V16, Ta19Ti17V18, Ta16Ti21V17, Ta22Ti23V9, and Ta18Ti18V18. Due to the mixing energy calculation, all compositions were estimated with a thermal stability at high temperature, which implies the application potentials for the high-temperature environment. The predicted Ta-Ti-V MEAs are mechanically stable since their elastic constants satisfy the mechanical stability conditions, and Ta24Ti14V16 has the best bulk module and Ta19Ti17V18 has the best ductility. Additionally, we calculated the elastic properties under the ratios of different elements’ contents. The influence of the element content on the elastic properties of the system shows that the enhancement of the Ta content will increase the bulk modulus of the alloys, while a higher Ti content can decrease the bulk modulus and their material stiffness as well. The higher V and Ti content are beneficial to ductility, especially V content. However, the higher Ta content will sharply reduce the ductility of the alloys. Our calculation has provided further theoretical mechanism basis for the Ta-Ti-V MEAs preparation and development.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
MP and WH: conception and design of the study. WH: acquisition of data and drafting the manuscript. MP, WH, ZH, HY, HW, LP, ZC, and YZ: analysis and interpretation of data. MP: revising the manuscript critically for important intellectual content. All authors contributed to the article and approved the submitted version.
This work was financially supported by the National MCF Energy R&D Program of China (2017YFE0301404) and the National Key R&D Program of China (2018YFE0308102).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors thank the National Supercomputing Center in Changsha for providing the computing resources.
Ameri, M., Arnel, S., Abidri, B., Ameri, I., Al-Douri, Y., Bouhafs, B., et al. (2014). Structural, elastic, electronic and thermodynamic properties of uranium filled skutterudites UFe4P12: first principle method. Mater. Sci. Semicand. Process. 27, 368–379. doi: 10.1016/j.mssp.2014.06.054
Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi: 10.1103/physrevb.50.17953
Fu, Z. Q., MacDonald, B. E., Zhang, D. L., Wu, B. Y., Chen, W. P., Ivanisenko, J., et al. (2018). Fcc nanostruc-tured TiFeCoNi alloy with multi-scale grains and enhanced plasticity. Scr. Mater. 143, 108–112. doi: 10.1016/j.scriptamat.2017.09.023
Gao, M. C., Gao, P., Hawk, J. A., Ouyang, L., Alman, D. E., and Widom, M. (2017). Computational modeling of high-entropy alloys: structures, thermodynamics and elasticity. J. Mater. Res. 32, 3627–3641. doi: 10.1557/jmr.2017.366
Gao, M. C., Yeh, J. W., Liaw, P. K., and Zhang, Y. (2016). High-Entropy Alloys: Fundamentals and Applications. Berlin: Springer.
Gludovatz, B., Hohenwarter, A., Thurston, K. V. S., Bei, H., Wu, Z., George, E. P., et al. (2016). Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat. Commun. 7, 10602–10609.
Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sec. 65, 349–354. doi: 10.1088/0370-1298/65/5/307
Jia, N. N., Li, Y. K., Liu, X., Zhang, Y., Wang, B. P., Wang, J. S., et al. (2019). Thermal stability and mechanical properties of low-activation single-phase Ti-V-Ta medium entropy alloys. JOM 71, 3490–3498. doi: 10.1007/s11837-019-03713-3
Jiang, C. (2009). First-principles study of ternary bcc alloys using special quasi-random structures. Acta Mater. 57, 4716–4726. doi: 10.1016/j.actamat.2009.06.026
Jiang, C., Wolverton, C., Sofo, J., Chen, L. Q., and Liu, Z. K. (2004). First-principles study of binary bcc alloys using special quasirandom structures. Phys. Rev. B 69, 214202–214211.
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi: 10.1103/physrevb.54.11169
Kresse, G., and Furthüller, J. (1996). Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi: 10.1016/0927-0256(96)00008-0
Li, X. Q. (2014). Mechanical Properties of Transition Metal Alloys from First-Principles Theory: Mechanical Properties of Materials. Sweden: Kungliga Tekniska Högskolan press.
Liu, J. Z., van de Walle, A., Ghosh, G., and Asta, M. (2005). Structure, energetics, and mechanical stability of Fe-Cu bcc alloys from first-principles calculations. Phys. Rev. B 72, 144109–144124.
Martienssen, W., and Warkimont, H. (2005). Springer Handbook Of Condensed Matter and Materials Data. Berlin: Springer.
Perdew, J. P., and Zunger, A. (1981). Self-interaction correction to density-functional approximations for many-electron sys-tems. Phys. Rev. B 23, 5048–5079. doi: 10.1103/physrevb.23.5048
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/physrevlett.77.3865
Push, S. F. (1954). Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 45, 823–843. doi: 10.1080/14786440808520496
Sathiyamoorthi, P., Basu, J., Kashyap, S., Pradeep, K. G., and Kottada, R. S. (2017). Thermal stability and grain boundary strengthening in ultrafine-grained CoCrFeNi high entropy alloy composite. Mater. Des. 134, 426–433. doi: 10.1016/j.matdes.2017.08.053
Shang, S. L., Saengdeejing, A., Mei, Z. G., Kim, D. E., Zhang, H., Ganeshan, S., et al. (2010). First-principles calculations of pure elements: equations of state and elastic stiffness constants. Comput. Mater. Sci. 48, 813–826.
van de Walle, A., Asta, M. D., and Ceder, G. (2002). The alloy-theoretic automated toolkit (ATAT): a user guide. Calphad 26, 539–553. doi: 10.1016/s0364-5916(02)80006-2
Wei, S. H., Ferreira, L. G., Bernard, J. E., and Zunger, A. (1990). Electronic properties of random alloys: special quasirandom structures. Phys. Rev. B 42, 9622–9650. doi: 10.1103/physrevb.42.9622
Wen, Z. Q., Zhao, Y. H., Tian, J. Z., Wang, S., Guo, Q. W., and Hou, H. (2018). Computation of stability, elasticity and thermodynamics in equiatomic AlCrFeNi medium-entropy alloys. J. Mater. Sci. 54, 2566–2576. doi: 10.1007/s10853-018-2943-7
Wu, Z., Bei, H., Pharr, G. M., and George, E. P. (2014). Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 81, 428–441.
Yeh, J. W., Chen, S. K., Lin, S. J., Gan, J. Y., Chin, T. S., Shun, T. T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303. doi: 10.1002/adem.200300567
Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93.
Zhao, Y. L., Yang, T., Tong, Y., Wang, J., Luan, J. H., Jiao, Z. B., et al. (2017). Heterogeneous precipitation behavior and stacking-fault-mediated deformation in a CoCrNi-based medium-entropy alloy. Acta Mater. 138, 72–82. doi: 10.1016/j.actamat.2017.07.029
Keywords: elasticity properties, stability, Ta-Ti-V, medium-entropy alloys, first-principles calculations
Citation: Hu W, Pan M, Huang Z, Yang H, Wu H, Pan L, Cao Z and Zhao Y (2021) The Stability and Elasticity in Ta-Ti-V Medium-Entropy Alloys Using First-Principles Calculations. Front. Mater. 8:651435. doi: 10.3389/fmats.2021.651435
Received: 25 January 2021; Accepted: 01 April 2021;
Published: 11 May 2021.
Edited by:
Huiqiu Deng, Hunan University, ChinaReviewed by:
Xuebang Wu, Institute of Solid State Physics, Hefei Institutes of Physical Science (CAS), ChinaCopyright © 2021 Hu, Pan, Huang, Yang, Wu, Pan, Cao and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Min Pan, bXBhbkBzd2p0dS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.