Experimental Study and Mechanism Analysis of Concrete-Filled Square Steel Tubular Columns Reinforced by Rhombic Stirrups Under Axial Compression

The square steel tube component has a beautiful appearance, simple joint connection, and it is widely available. However, the uneven distribution of effective constraints in the cross-section of a square steel tube hinders its application. A novel concrete-filled square steel tubular column was tested under axial compression. There were 11 specimens [10 concrete-filled square steel tube columns reinforced with rhombic stirrups with 90-degree internal angle (SSSC specimens) and 1 concrete-filled square steel tube column (SC specimen)]. The load-displacement curves, the law of failure process, failure mode, mechanism analysis, energy consumption, ductility, and stiffness degradation were described, we then investigated the influence of stirrup diameter, stirrup side length, stirrup spacing, steel tube thickness, aspect ratio, and steel ratio on the mechanical properties of the specimens. The results show that the failure process of the SSSC specimens was basically the same. The ultimate failure mode of the specimens with an aspect ratio of 4 was local buckling failure. The specimens with an aspect ratio of 5 and 6 failed due to bending failure in the plastic stage. The steel tube bulged out in different degrees in most of the debonding areas. The longitudinal bars also produced outward bending deformation in the larger bulging area of the steel tube. Some of the stirrups were broken in the later stage of loading. The characteristics of load-displacement curve changed with the changing of stirrup spacing. The strength of longitudinal constraint had an obvious influence on the bearing capacity. In a certain range of steel ratio (ρ_s = 8.97% ∼ 9.05%), the weakening of the lateral restraint of the stirrup cage had a greater adverse effect on the bearing capacity than the weakening of the effective restraint of the corner. In a certain range of steel ratio (ρ_s = 8.97% ∼ 9.49%), strengthening the effective corner constraint of stirrups improved the stiffness of the specimen, however, the ductility performance was reduced. The opposite was true for strengthening the lateral constraint of the stirrup cage.

Introduction

A concrete-filled steel tubular column is a vertical load-bearing member made of concrete fully injected into a thin-walled steel tube. According to the characteristics of its constituent materials, the concrete effectively supports the external thin-walled steel tube due to its large transverse deformation which appears in the process of loading; it not only avoids or alleviates the buckling of the steel tube to enhance the local stability but gives full play to the advantages of steel-bearing performance. At the same time, the steel tube provides the concrete with a hoop constraint, which gives the concrete a triaxial compression state, delays crack development, and improves the plasticity, toughness, and bearing capacity of it. Such a reasonable mechanism makes up for the defects of thin-walled steel compression stability and concrete brittleness. Therefore, many scholars hope to use the combined advantages of steel and concrete to find new combination materials for sustainable circulation. Tang et al. (2020) studied the axial compression performance of RAC-filled glass-fiber-reinforced polymer (GFRP)–steel composite tube columns (RACFCTs). The results showed that the compression behavior of the RACFCTs was adequate and the RACFCTs with a high RA replacement ratio and a high aspect ratio had a more ductile behavior. Meanwhile, the advantages of concrete-filled steel tubular columns, such as high strength, lightweight, good plasticity, fatigue resistance, and impact resistance enable convenient design and construction. In terms of design, the excellent ductility means that these columns are not limited by the axial compression ratio used in high-rise buildings, and only need to control the aspect ratio, which greatly widens the application range of concrete-filled steel tubes. Moreover, the regular shape can meet the appearance requirements of various building forms, which has been favored in many major engineering projects in recent years. In terms of construction, the cross-sectional area of concrete-filled steel tubular members is smaller than that of reinforced concrete members under the condition of bearing the same load, which saves a lot of construction materials. The steel tube can be used as the pouring formwork of components and the bearing support in the construction stage, which improves the construction conditions and speeds up the construction process (Zhao, 2001). Hence, concrete-filled steel tube structures have been widely used in modern high-rise, super high-rise, large-span heavy-duty, and innovative building structures because of their excellent mechanical performance, beautiful appearance, and relatively convenient construction technology.

According to the cross-section shape, concrete-filled steel tubular columns can be divided into circular concrete-filled steel tubular columns, square concrete-filled steel tubular columns, rectangular concrete-filled steel tubular columns, and polygonal concrete-filled steel tubular columns. Previous studies have shown that the circular steel tube concrete column had a higher bearing performance due to its uniform and stable constraint effect (Hu et al., 2003). Nowadays, research on the mechanical properties of concrete-filled circular steel tubular columns are well-established and relevant design regulations have been issued in different countries, including EC4 British Standards Institution (2004) of Europe, BS5400 British Standards Institution (2005) of the United Kingdom, AISC360-10 American Institute of Steel Construction (AISC) (2010) of the United States, Architectural Institute of Japan (AISC) (1997) of Japan, and China Construction Industry Press, 2014 of China, etc. For the current studied configuration, it is more convenient to utilize a square steel tube rather than a circular steel tube due to the straightforward fabrication and installation of beam-to-column joints for the outer column (Gardner et al., 2015). Thus, concrete-filled square steel tubular columns have the potential to be widely used in engineering. However, it has a weak section-constraint efficiency because of the section characteristics where the effective constraint weakens from the section diagonal to the section boundary. The middle area of the section side length can be regarded as the unconstrained area, as shown in Figure 1. Some study results showed that there was an “arch effect” in the constraint of the square steel tube section, and corresponding reinforcement measures were proposed (Sheikh and Uzumeri, 1980). Liang et al. (2017) investigated the effect of the stiffening arrangements on the properties of the concrete-filled steel tube columns with stiffeners of different geometric dimensions. The results showed that the local buckling of the steel tubes was delayed by the stiffener. The specimen with the four-sided stiffening arrangement possessed higher stiffness and better ductility as compared with the two-sided one. Gan et al. (2019) proposed a novel diagonal binding ribs-reinforced square concrete-filled steel tubular column. The results of an axial compression test showed that this method effectively delayed the local buckling of the steel tube and better confined the infilled concrete. Xu et al. (2020) combined this with the finite element software analysis method and carried out the study of straight rib and perforated rib-reinforced square concrete-filled steel tubular columns under axial compression. The results indicated that the bearing capacity of the stiffened specimens effectively improved, and the bearing capacity of the straight rib specimen was higher. The ductility of the perforated rib specimen was greater. Cai et al. (2014) and Wang et al. (2020) used constrained bars to strengthen concrete-filled square steel tubular columns and carried out systematic studies on the mechanical properties of this type of column. The results showed that the bearing capacity and ductility of the specimens with tie bars were the most obviously improved. The setting of stiffening belts of tie rods effectively delayed the local buckling of steel tubes. Feng et al. (2015) tested a novel composite column that had a square steel tube as the outer layer and a circular filament-wound FRP tube as the inner layer. Arid concrete was used to fill the internal space under axial compression. The results showed that this column had significant post-yield stiffness, ductile failure, and a stable residual bearing capacity. The influences of key design parameters on the mechanical characteristics were also clarified. Gardner et al. (2015) used a non-linear finite element (FE) to conduct parametric studies of concrete-filled double skin tubular columns with an outer square steel tube and an inner circular steel tube. The model was validated by available experimental data. Based on this, a new design pattern was proposed. It could provide a reliable prediction for the ultimate axial strength of double-skin tubular columns filled with short concrete. Yang et al. (2015) prepared sixteen double-skin steel tube specimens and only applied concrete between the layers. The results showed that the specimens had a high bearing capacity and a good deformation-resistant ability. The formulae of bearing capacity was proposed. Qian et al. (2014) studied the seismic behavior of high-strength concrete-filled double-tube (CFDT) columns with a square steel tube on the outside and a circular steel tube on the inside. The results showed that the lateral force-displacement hysteretic loops of all specimens were plump and stable. Ayough et al. (2020) performed a series of non-linear FE analyses of square concrete-filled double-skin steel tubular (CFDST) short columns with an inner circular steel tube and an outer square steel tube. A new design equation based on stress distribution over the concrete cross-section was proposed. The analysis results indicated that the thickness of the inner tube had great influence on its premature failure. The material properties and dimensions of composite columns highly affected the specimen’s performance. Ding et al. (2014) investigated the performance of the concrete-filled square steel tubular stub columns confined by internal loop, spiral stirrups, and inner stiffened under axial compression. The results showed that the mechanical performance of the stirrup-confined concrete-filled square steel tubular stub columns was better than inner-stiffened square concrete-filled steel tubular stub columns. The effects of different configurations of confinement, including internal stiffeners, hoops, and stirrups were explained. A simplified method for calculating the ultimate bearing capacity of concrete-filled steel tubular short columns confined by stirrups was proposed considering the constraint effect of a square steel tube and stirrup. Chen et al. (2017, 2018) and Jing et al. (2018) studied the axial mechanical properties of spiral reinforced concrete-filled square steel tubular columns. The results showed that the spiral reinforcement effectively improved the axial compression bearing capacity and deformation ductility of concrete-filled square steel tubular columns.

FIGURE 1

Figure 1. Section constraint diagram of a square steel tube.

Aiming at how to make up for the “arch effect” on the internal concrete constraint, the effective constraint mainly concentrates on the diagonal position of the square steel tube. A new type of reinforced concrete-filled square steel tube was proposed in which a rhombic stirrups cage with 90-degree internal angle was arranged with the diagonal line staggered with that of the steel tube by 45°. Eleven specimens were designed and manufactured for the axial compression loading test to reveal its mechanical mechanism and explore the new form of high-performance concrete-filled square steel tubes.

Experimental Programs

Specimens Details

Design Parameters

The outer square steel tube was a Q235 straight welded steel tube with a side length of 300 mm. The longitudinal reinforcement of the reinforcement cage was grade III steel with a diameter of 14 mm. The steel content of the longitudinal reinforcement of the specimen was 0.68%. Eleven specimens were designed, which considered parameters including thickness of the outer steel tube t (6 and 8 mm), stirrup diameter d (6, 8, and 10 mm), stirrup spacing S (50, 80, and 110 mm), stirrup side length b (160, 180, and 200 mm), and aspect ratio H/B (4, 5, 6). The specific design parameters of the specimen are shown in Table 1.

TABLE 1

Table 1. Design parameters of specimens.

Material Properties

Commercial concrete was used in this test and the measured strength China Architecture and Building Press, 2019 was 24.2 Mpa. The steel material performance indexes tested according to the standard test method Standards Press of China, 2010 are shown in Table 2.

TABLE 2

Table 2. Mechanical properties of steel.

The Manufacturing Processes

It must be ensured that the cross-section centroid of the stirrup cage coincides with that of the steel tube. First, the location line was drawn on the bottom steel plate. Then the stirrup cage was welded onto it. Second, the non-welded surface of the steel tube was opened, which only allowed the extension wire of the strain gauge of the inner stirrup cage to pass through. The largest volume opening hole damage rate and section damage rate were 0.05 and 1.4%. It can be confirmed from literature (Chen et al., 2014) that the influence on the bearing and deformation performance of square concrete-filled steel tubular specimens is not obvious on the condition of a volume opening hole damage rate of <0.7% and a section damage rate of <2.5%. After the extension wire was passed through the hole of the square steel tube from the inside to the outside, the stirrup cage and square steel pipe were placed vertically at the same time, then the square steel tube was welded onto the bottom plate after adjusting the position of it. Finally, concrete was poured into the vertical state of the specimen. After curing under natural conditions, the upper surface of the specimen was polished and leveled. Then the upper steel plate was welded and the grid lines were drawn after painting the steel tube. Photos of the production process are shown in Figures 2A–D.

FIGURE 2

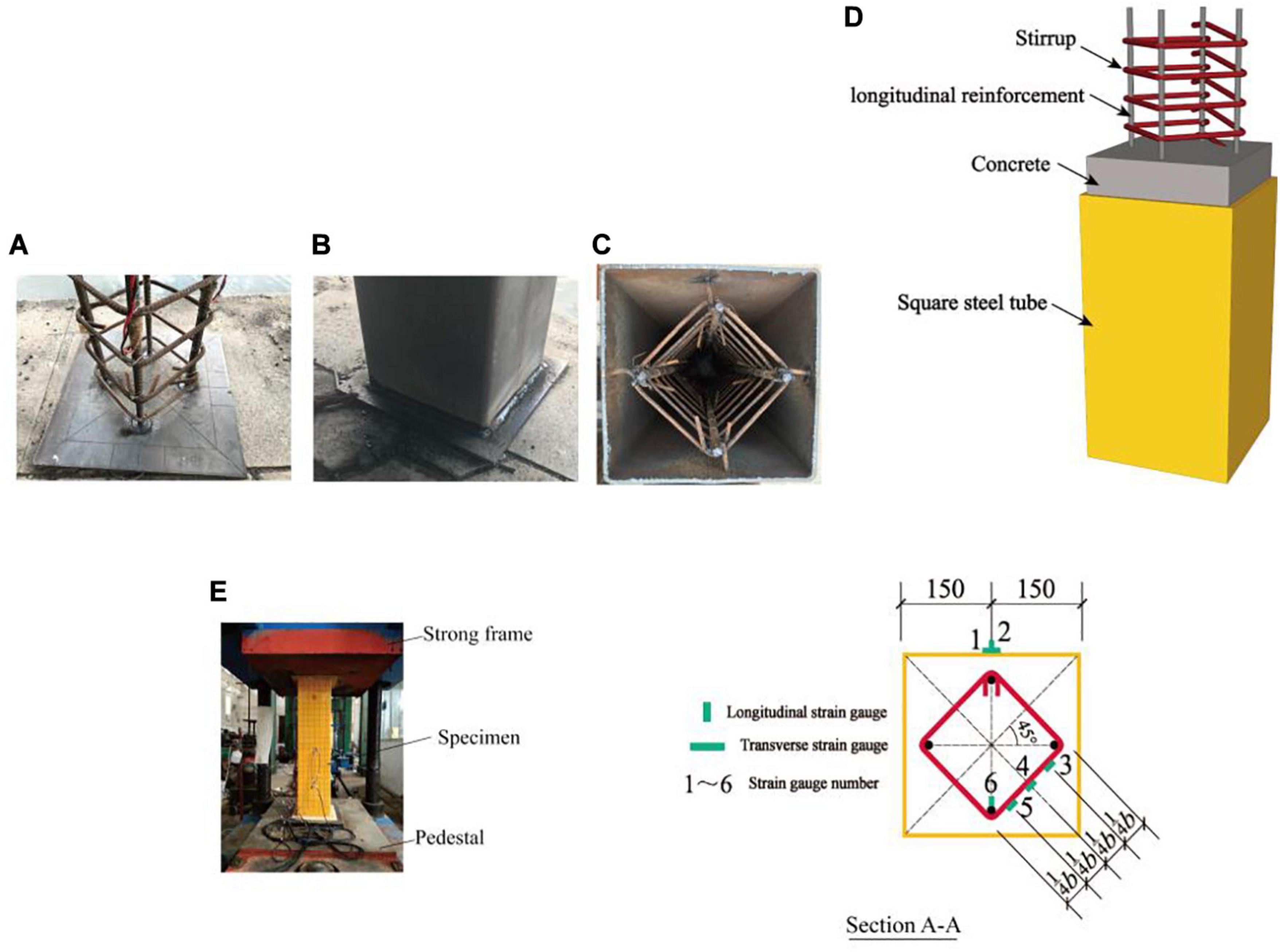
Figure 2. Specimen fabrication and test measuring facilities. (A) Welded stirrup cage. (B) Welded steel tube. (C) Section of specimen. (D) 3D diagram. (E) Test setup and arrangement of strain gauges.

Test Setup and Procedure

The test setup included a 10,000 kN electro-hydraulic servo-controlled press. The loading system was displacement-controlled and the loading rate was 2 mm/min. The load-displacement curve of the whole loading process was obtained by the acquisition system of the testing machine. When the axial displacement was 1/20 of the height of the specimen, the test concluded. The setup and strain gauge arrangement of the specimen are shown in Figure 2E.

Failure Modes

The failure process of the specimens was basically the same, according to the different aspect ratio. There were two different failure modes: local buckling failure (H/B = 4) and bending failure in the plastic stage (H/B = 5, H/B = 6). The final failure mode of each specimen is shown in Figure 3A.

FIGURE 3

Figure 3. Failure mode of specimens. (A) Final failure mode of specimens. (B) Damage of steel tube bulge area. (C) Tearing failure of steel tube. (D) Damage of stirrups and longitudinal bars.

Local Buckling Failure

The specimen (H/B = 4) presented local buckling failure. The specific process is as follows: there was no obvious change at the beginning of loading. After the peak point, the steel tube began to bulge outward gradually at the upper and lower ends. In the later stage of loading, a new bulging deformation developed from the upper or lower end to the middle of the specimen. The final failure mode of some of the specimens was local bulging, others had a large bulging deformation. The bulging on different surfaces were connected, forming an oblique bulge with a certain angle at the corner of the specimen. It should be noted that the SSSC3 specimen was damaged due to the corner of the steel tube tearing.

Bending Failure in Plastic Stage

The specimen (H/B = 5, H/B = 6) presented bending failure in the plastic stage. The specific process is as follows: there was no obvious deformation on the specimen at the initial stage of loading. While continuing loading, the bulging deformation of the middle part increased and gradually connected with the deformation of the adjacent surface due to the P-Δ effect at the plastic stage. The specimen was bent out of plane and the load of specimen decreased continuously.

Failure Characteristics

The pouring quality of the specimens was tested by the knocking method China Architecture and Building Press, 2010 at the beginning of the loading. It was found that most of the local debonding areas between the square steel tube and the concrete appeared at the end of the specimen, and some of the debonding areas appeared in the middle of it. In the process of loading, the steel tube bulged to a different degree at most of the local debonding areas, which indicated that the construction quality directly affected the performance of the components to a certain extent.

After the test, the steel tube was peeled off. Our findings were as follows: (1) The concrete was crushed in the large bulging deformation area (more than 3 cm outward). The concrete appeared to have compression cracks but was not crushed in the small bulging deformation area (less than 2 cm outward), which indicated that the steel tube bent first and then the concrete was crushed. The picture is shown in Figure 3B. The concrete was crushed into a needle shape in the tearing area at the corner of the SSSC3 specimen, which is shown in Figure 3C. (2) The concrete expanded outward in the process of loading. The longitudinal bars bent and some stirrups were broken at this position, which is shown in Figure 3D. This result indicated that the restrictive effect on concrete of the binding position of longitudinal reinforcement and the stirrup was stronger than the middle part of the stirrup side length and longitudinal reinforcement interval area.

Loading Process Analysis

Load-Strain Curve

The load-strain curves of the specimens obtained through the strain gauge are shown in Figure 4A. Where N and N_u are the axial pressure and the maximum axial pressure on the specimen and ε is the strain of the specimen. It should be noted that the steel tube of the SSSC2 specimen was not equipped with a strain gauge. The SSSC8 specimen did not have the corresponding strain gauge data due to a computer failure. And the No. 5 measuring point of the SSSC9 specimen was invalid.

FIGURE 4

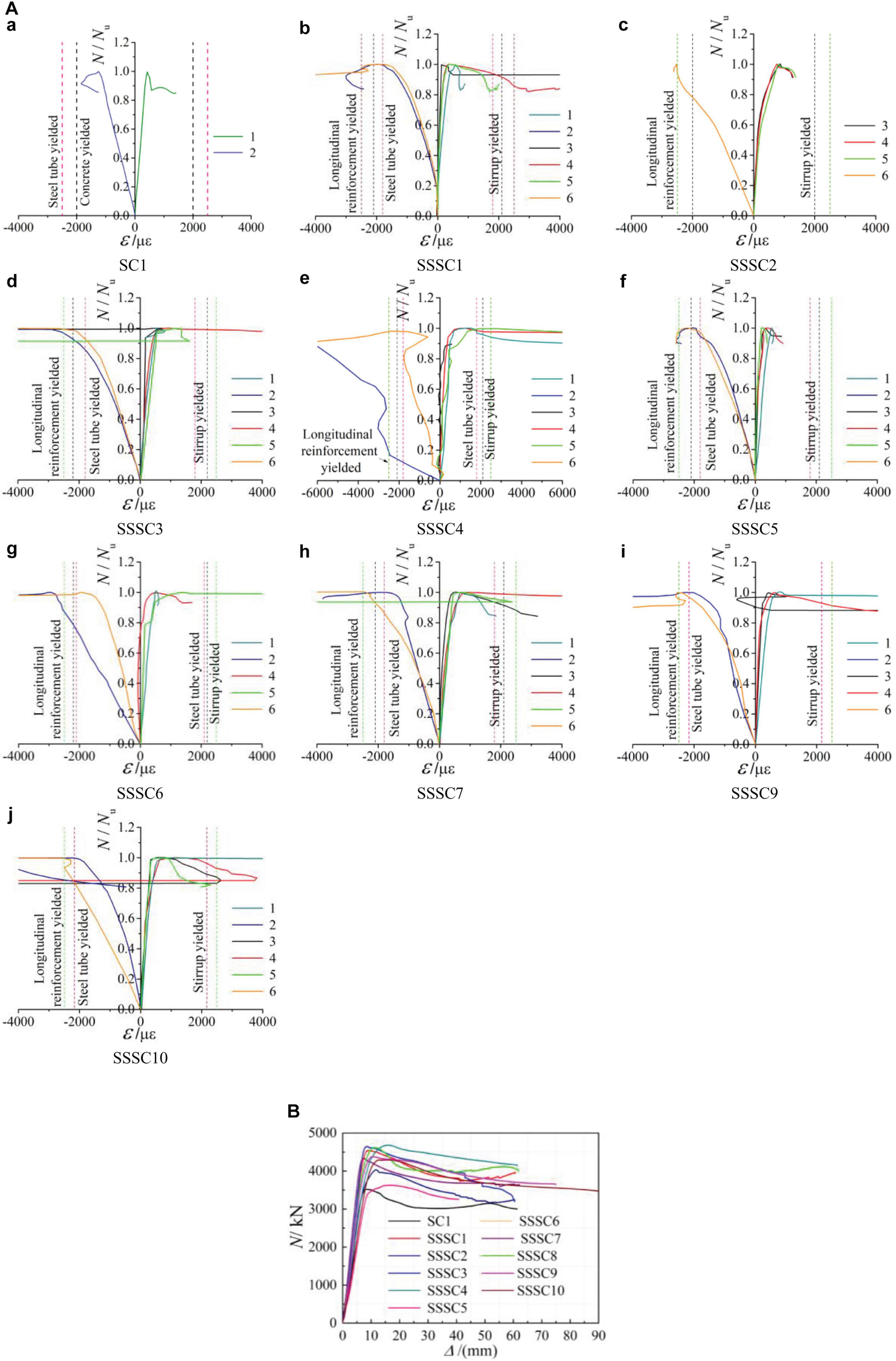
Figure 4. Load-strain curves and load-displacement curves. (A) Load-strain curves. (a) SC1, (b) SSSC1, (c) SSSC2, (d) SSSC3, (e) SSSC4, (f) SSSC5, (g) SSSC6, (h) SSSC7, (i) SSSC9, (j) SSSC10. (B) Load-displacement curves.

It can be found from Figure 4B that the stirrups of the SSSC specimens did not yield before the peak point, and the steel tube and longitudinal reinforcement had different degrees of longitudinal yield. The law of steel tube and longitudinal reinforcement yield was not consistent. Upon changing the stirrup diameter, the longitudinal strain of the steel tube was faster than that of longitudinal reinforcement. When the stirrup spacing was changed, the difference of strain development rate between longitudinal reinforcement and the steel tube was obvious, the steel tube yielded quickly. For the specimens with larger stirrup spacing, the strain development rate of longitudinal reinforcement was slightly faster than that of the steel tube. It can be concluded that different stirrup spacing had a certain effect on the steel yield order.

Load-Displacement Curve

The load-displacement (N-Δ) curves of the specimens obtained from the measuring system of the test device are shown in Figure 4B, where N is the axial pressure on the specimen and Δ is the axial displacement of the specimen.

It can be seen from Figure 4B that the peak load of the ordinary concrete-filled square steel tube column (SC1 specimen) was small, and the second peak point appeared at the later stage of the curve. It can be seen from Figure 4A,a that the compressive stress of the steel tube was greater than the tensile stress, indicating that the longitudinal compression of the steel was greater than the circumferential tension. In the loading process, with the increase of axial load, concrete cracks developed and expanded outward. The Poisson coefficient of concrete was greater than that of the steel tube, the steel tube had a lateral binding force on concrete. The strength of concrete increased because of the triaxial compression. However, steel provided a lateral constraint for concrete and bore axial pressure at the same time. Steel produced an outward bulge under the action of axial pressure, which weakened its lateral constraint on concrete. When the axial stress reached the ultimate compressive strength of concrete, the specimen reached the first peak value. After the test, no tearing was found in the steel tube. By observing the load-strain curve of the specimen (Figure 4A,a), it can be found that the longitudinal compressive strain of the steel tube decreased and the tensile strain increased at the later stage of loading, indicating that the lateral pressure on the steel tube increased. It can be inferred that the restraint effect of the steel tube on the concrete was increasing. And the bearing capacity of the specimen began to rise slowly until the second peak point. At that time, the axial deformation of the specimen was large and the bulge of the steel tube was obvious. The void space of the concrete with internal fragmentation expanded and the bearing capacity of the specimen decreased. Some curves of the SSSC specimens had an obvious descending section, some curves had the second peak point or load rising in the later stage, the possible reason is the redistribution of internal force caused by stirrup breaking or steel yielding during loading. And most curves had the phenomenon of sudden load drop due to the stirrup breaking. The bearing capacity and ductility of the SSSC specimens were improved to some extent, although the steel ratio was less than the SC1 specimen. This proves that the effective constraint at the corner of the stirrup cage improved the weak constraint in the middle of the side length of the steel tube section, and made the axial compression performance better than that of the ordinary concrete-filled square steel tube column.

Mechanism Analysis

The load-displacement (N-Δ) curve can be divided into two types due to the difference of constraint effect, as shown in Figures 5A,B.

FIGURE 5

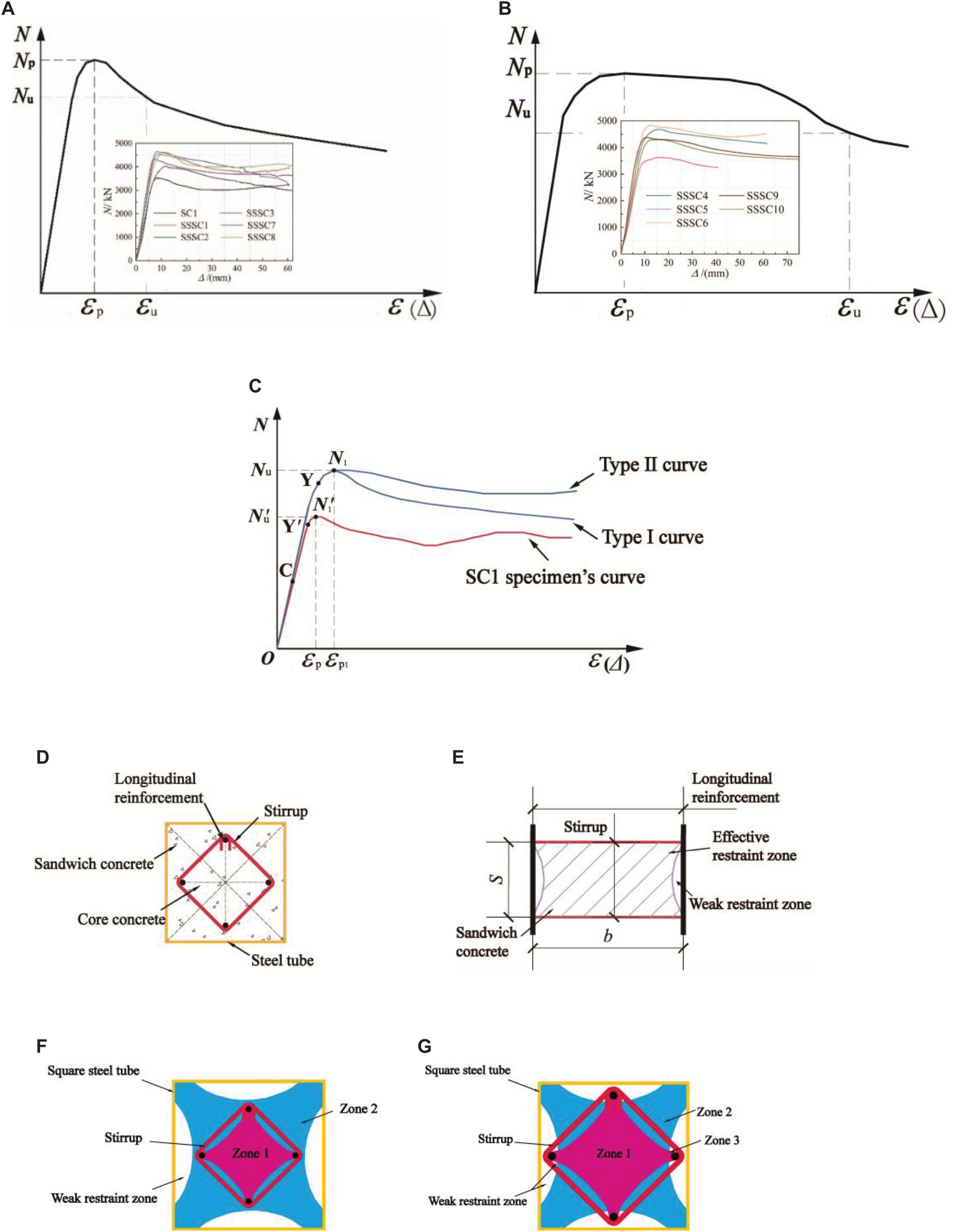
Figure 5. Mechanism analysis. (A) Type I curve. (B) Type II curve. (C) Comparison of load-displacement curves. (D) Sandwich concrete at cross-section. (E) Longitudinal sandwich concrete and its effective constraint distribution. (F) The first type of constraint mode. (G) The second type of constraint mode.

The load-displacement (N-Δ) curve of the specimens with a small steel ratio (ρ_s ≤ 9.47%) was a type I curve. It can be seen from Figure 5A that the type I curve showed an obvious peak at the peak point. The bearing capacity decreased with a large slope after it. When the load was reduced to N_u (0.85 N_p), the load of some specimens dropped due to the tensile fracture of stirrups. The load of some specimens increased slightly due to the reinforcement after steel yield.

The load-displacement (N-Δ) curve of the specimens with a large steel ratio (ρ_s ≥ 9.49%) was a type II curve. It can be seen from Figure 5B that the type II curve was smooth at the peak point. The bearing capacity was relatively stable. The ductility and energy dissipation capacity of this kind of specimen were excellent. It should be noted that the curve characteristics of the SSSC5 specimen (ρ_s = 9.05%, S = 110 mm) also conformed to the type II curve. Compared with SC1 (ρ_s = 10.67%, the type I curve), it was confirmed that the built-in rhombic stirrup can improve the axial compression behavior of concrete-filled square steel tubes. Compared with the SSSC1 specimen (ρ_s = 9.19%, S = 80 mm, type I curve), it showed that stirrup spacing had a great influence on the constraint effect of the specimen.

Figure 5C shows the comparison between SC1 specimen’s curve and SSSC specimen’s curve. It can be seen from the figure that the transverse deformation of concrete and tensile stress of the steel tube was quite small when the axial compression was small at the initial stage of loading. The constraint effect on the core concrete was not obvious. The initial development trend of the two types of curves was similar in the rising stage. The concrete in the unrestricted area appeared to have obvious cracks at the C point. As loading continued, the slope of bearing capacity of the SC1 specimen decreased gradually and began to yield. However, under the combined constraint of the stirrup cage and the steel tube, the bearing capacity of the SSSC specimen continued to rise. This indicated that the stirrup cage not only enhanced the constraint effect of the core constraint zone of the square steel tube, but also improved the stability of the unconstraint zone in the middle of the side length of the steel tube, delaying the development of the cracks in the sandwich concrete outside the stirrup cage. It should be noted that the sandwich concrete includes the concrete in the cross-section between the steel tube and the stirrup cage and the interlayer concrete between the two stirrups in the longitudinal direction, as shown in Figures 5D,E. The specimen with the steel tube and longitudinal reinforcement yielded, its bearing capacity decreased obviously after the peak point. The bearing capacity of the specimen where the longitudinal reinforcement yielded after the peak point decreased slightly with a platform area in the curve at the peak point. The results indicated that the rhombic stirrup cage not only improved the bearing capacity to a certain extent, but also had a favorable impact on the ductility and the descending section of the load-displacement curve.

The constraint distribution mode of the SSSC specimen under axial compression is shown in Figures 5F,G. Firstly, it is reasonable that the effective constraint of the rhombic stirrup with 90-degree internal angle is like that of the square steel tube. The constraint effect in the middle of side length is weakened by the “arch effect.” The difference is that the overall section constraint is far less than that of the square steel tube. According to the different design parameters of the rhombic stirrup cage, the cross-section will produce two different constraint effects. The first type constraint mode is where the rhombic stirrup cage is exactly in the effective constraint area of the steel tube (Figure 5F), and the b/B value is small. At this time, the strong constraint area, and weak constraint area (Figure 5E) of the rhombic stirrup cage are enhanced or improved. The effective constraint area of the cross-section of the specimen has not changed. The second type constraint mode is where the effective constraint area at the corner of the rhombic stirrup covers part of the weak constraint area of the steel tube, but there is still a weak constraint area inside the cage corner (Figure 5G), and the b/B value is large. At this time, the constraint area of the rhombic stirrup cage is only partially strengthened. The effective constraint area of the cross-section of the specimen increases.

In the first type of constraint mode, it can be seen from Figure 5F that there were two kinds of effective constraint regions and one weak constraint region when the SSSC specimen was under axial compression. Zone 1 was the area where the effective constraint of the stirrup cage was strengthened by the steel tube. The core concrete here was subjected to composite constraint. The bearing capacity was greatly improved under a triaxial stress state and reached the peak value after the longitudinal yield of the steel tube or longitudinal reinforcement. Zone 2 was the area where the effective constraint of the steel tube covered the sandwich concrete. The crack development and bearing capacity decline of the sandwich concrete were alleviated under the constraint of the steel tube. Zone 3 was the area where the effective constraint area of the stirrup covered the weak constraint area of the square steel tube in the second type of constraint mode (Figure 5G). There was an existent weak constraint zone near the corner of the stirrup. The weak constraint zone of the longitudinal sandwich concrete was not fully strengthened. Because the relative position of longitudinal reinforcement and the steel tube was too close, the concrete thickness here was thin. The possibility of full-length cracks in the middle of the side length of the steel tube was greater. The bearing capacity of the specimen after the peak value may decrease quickly. For the specimens with a small stirrup side length and meeting the first type of constraint mode, the stirrup constraint was far less than that of the steel tube. Even if the effective stirrup constraint was fully strengthened, there was no difference in the crack development speed of the sandwich concrete on the cross section. The bearing capacity of the specimen would still decline rapidly after the peak point.

According to the test results: the bearing capacity of the specimen increased with the increase of the side length of the rhombic stirrup. But the characteristics of the load-displacement curve had no obvious change, which belonged to type I. It can be inferred that the difference of constraint effect between the two types of constraint mode is mainly in the change of bearing capacity, but not in the development trend of load-displacement curve. In addition, the change of stirrup spacing made the trend of load-displacement curve different, which indicates that the bearing performance characteristics of the SSSC specimen largely depend on the stirrup cage longitudinal constraint effect on concrete in the later stage. Compared with the SC1 specimen (ρ_s = 10.67%, type I) and the SSSC5 specimen (ρ_s = 9.05%, S = 110 mm, type II), the built-in rhombic stirrup cage had a very favorable and obvious strengthening effect on the bearing capacity of the concrete-filled square steel tube under axial compression. Compared with the SSSC1 specimen (ρ_s = 9.19%, S = 80 mm, type I), the SC1 specimen (ρ_s = 10.67%, type I) and the SSSC5 specimen (ρ_s = 9.05%, S = 110 mm, type II), the results showed that the stirrup spacing decreased and the load-displacement curve characteristics changed. The longitudinal sandwich concrete height decreased, the constraint effect of the stirrup skeleton was enhanced, and the bearing capacity and initial stiffness increased. But the deformation performance was not improved compared with the SSSC5 specimen. Compared with the SSSC1 specimen (ρ_s = 9.19%, S = 80 mm, type I), the SC1 specimen (ρ_s = 10.67%, type I) and the SSSC4 (ρ_s = 9.49%, S = 50 mm, type II), the results showed that the great constraint of the longitudinal sandwich concrete made the bearing capacity and the later deformation performance of specimens effectively improve.

Characteristic Parameters

Table 3 gives the characteristic point parameters of each specimen, where the initial stiffness (K_e) is the secant stiffness corresponding to the 0.6 N_m in the ascending section of the load axial displacement curve. N_y, Δ_y, and E_y represent the load which is determined by the energy equivalent method, displacement, and energy dissipation at the yield point. N_m, Δ_m, and E_m represent the load, displacement, and energy dissipation at the peak point. N_3Δm, 3Δ_m, and E_3Δm represent the load, displacement, and energy dissipation at the point of three times peak displacement. μ is the ductility coefficient calculated from μ = E_3Δm/E_y (Tang, 1989). E is the total energy dissipation. It should be noted that the loading displacement of the SSSC5 specimen is less than 1/20 of the specimen height. Its three times peak displacement is greater than the total displacement, thus the discussion of energy dissipation and ductility performance does not include this specimen.

TABLE 3

Table 3. Parameters in feature points.

Results Analysis

Ductility and Energy Consumption

It can be seen from Table 3 and Figure 6A that: (1) the energy dissipation of each characteristic point of the SSSC specimen was greater than that of the SC1 specimen. Except that the energy dissipation at the yield point of the SSSC2 specimen was only increased by 6%. The energy dissipation of the remaining specimens was increased by 20% at least. The maximum energy dissipation was increased by 73%. (2) The ductility coefficient of the SSSC specimens was greater than that of the SC1 specimen, and the values were all greater than 5. (3) The results showed that the initial energy consumption was only 6%∼10% of the total energy consumption. The later energy consumption was more than 10 times of the previous energy consumption, which indicated that the concrete was in a triaxial compression state, and the bearing capacity did not drop sharply after the peak point. Moreover, the concrete played a supporting role when the steel tube had a large deformation, which effectively avoided the phenomenon that the bearing capacity of the steel tube decreased too fast due to excessive deformation. (4) For SSSC specimens with a steel ratio less than the SC1 specimen, the yield point energy consumption, total energy consumption, and ductility were 1.34, 1.06, and 1.15 times higher than those of the SC1 specimen. The results showed that the performance of concrete-filled square steel tubular columns can be strengthened by rhombic stirrup cages.

FIGURE 6

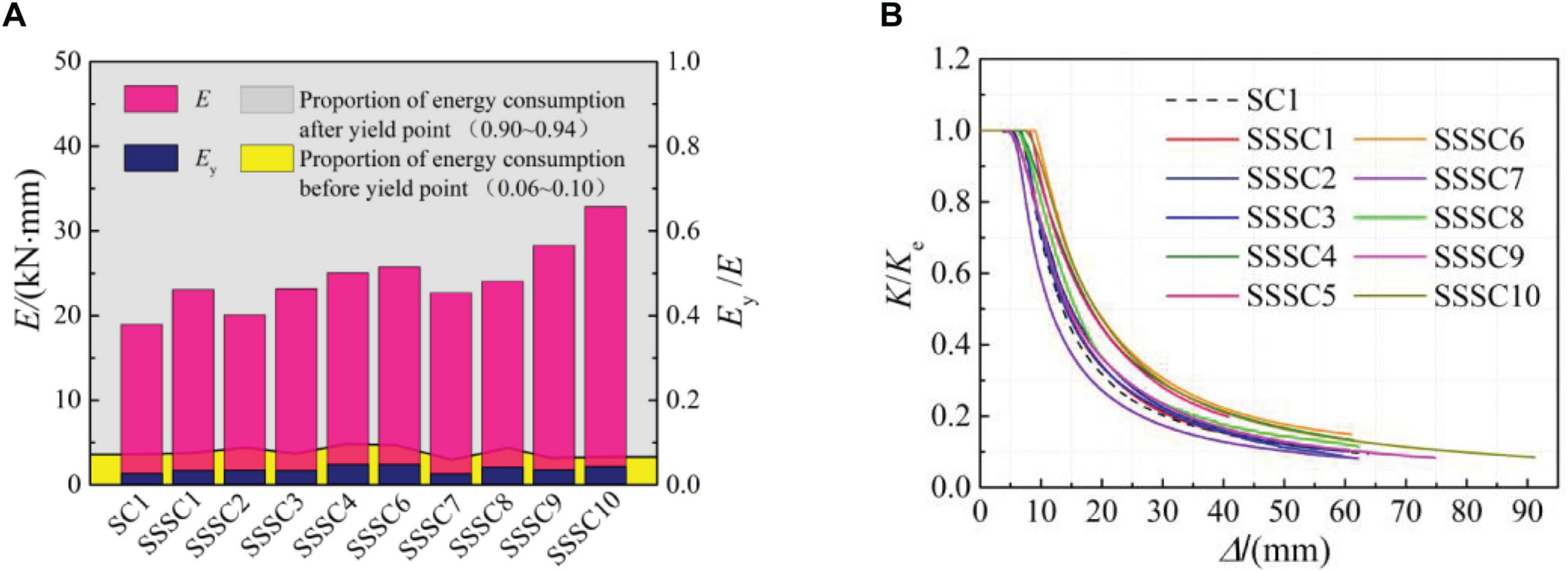
Figure 6. Ductility, energy Consumption and stiffness degradation. (A) The energy dissipation and proportion in feature points. (B) Stiffness degradation.

Stiffness Degradation

Figure 6B shows the stiffness degradation curve of the specimen. Taking K_e as the standard, the whole process of stiffness had a dimensionless treatment, where K represents the secant stiffness of the specimen. Compared with the contrast specimens, except for the SSSC7 specimen, the stiffness degradation trend of other specimens was moderate, especially for the SSSC6 specimen and SSSC10 specimen. This indicated that the built-in rhombic stirrup effectively alleviated the stiffness degradation.

Effect of Diameter of Stirrup

Figure 7 shows the influence of the stirrup diameter on the mechanical indexes of the specimen. It can be seen from Figure 7 that the initial stiffness, bearing capacity, and energy dissipation increased with the increase of the stirrup diameter. However, the peak strain and the ductility performance decreased. The load-displacement deformation curve type of the specimen was type I. For the specimen with a smaller stirrup diameter (the SSSC2 specimen), the longitudinal bars yielded earlier and the constraint effect of the stirrup cage on the core concrete was weak. With the increase of stirrup diameter, the steel ratio of the specimen increased, which had an obvious beneficial effect on the improvement of the bearing capacity and initial stiffness of the specimen. But for the specimen with a larger stirrup diameter (the SSSC3 specimen), the reinforcement effect was not obvious.

FIGURE 7

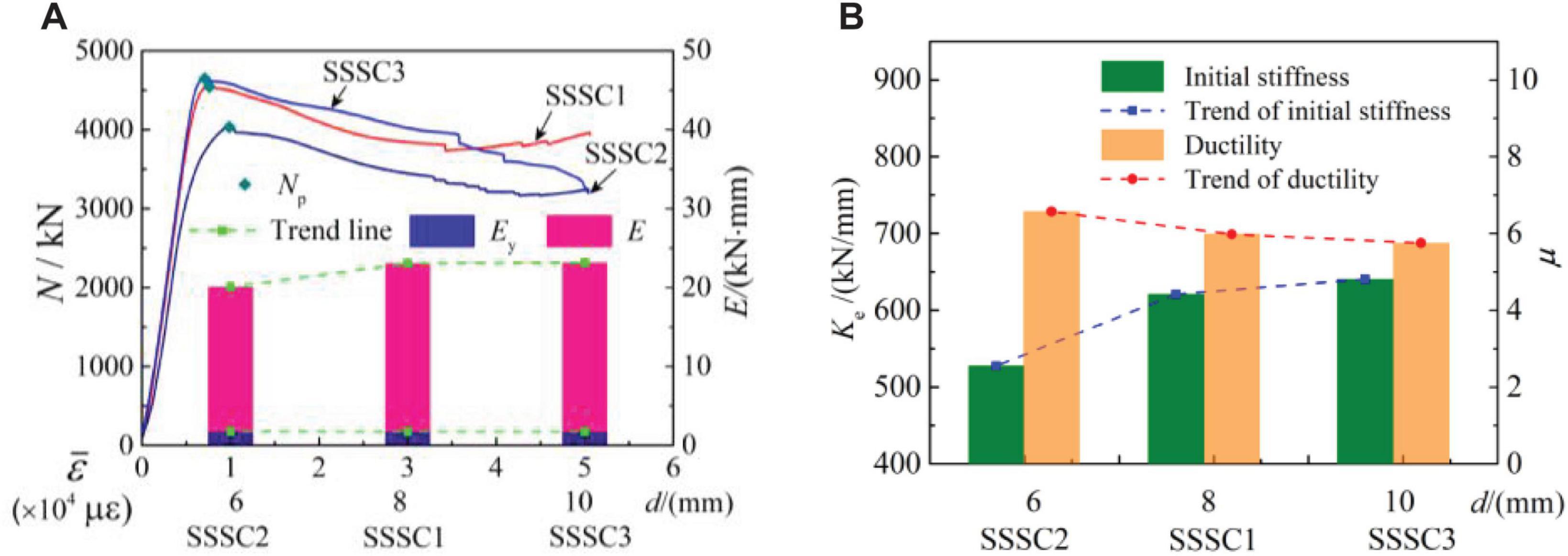
Figure 7. Effect of diameter of stirrup. (A) Variation of peak load, strain, and energy dissipation. (B) Stiffness degradation and ductility.

Effect of Stirrup Side Length

Figure 8 shows the influence of stirrup side length on the mechanical indexes of the specimens. It can be seen from Figure 8 that the bearing capacity, energy dissipation, and ductility of the specimens decreased, and the initial stiffness increased with the increase of stirrup side length. The load-displacement curve of the specimen is type I. For the SSSC8 specimen (b = 160 mm) with a small stirrup side length, the core columns of stirrups were concentrated. The effective constraints of the core concrete were more stable, which had a favorable influence on the development of the bearing capacity. However, sandwich concrete with a large area made the effective constraints on it smaller which led to the bearing capacity decreasing faster after the peak point. This phenomenon was alleviated when the stirrup side length increased to 180 mm (the SSSC1 specimen). When the side length increased to 200 mm (the SSSC7 specimen), the bearing capacity decreased quickly after the peak point due to the fact that the sandwich concrete between the corner of the stirrup and the steel tube was insufficient. Long cracks easily formed in the height direction of the specimen.

FIGURE 8

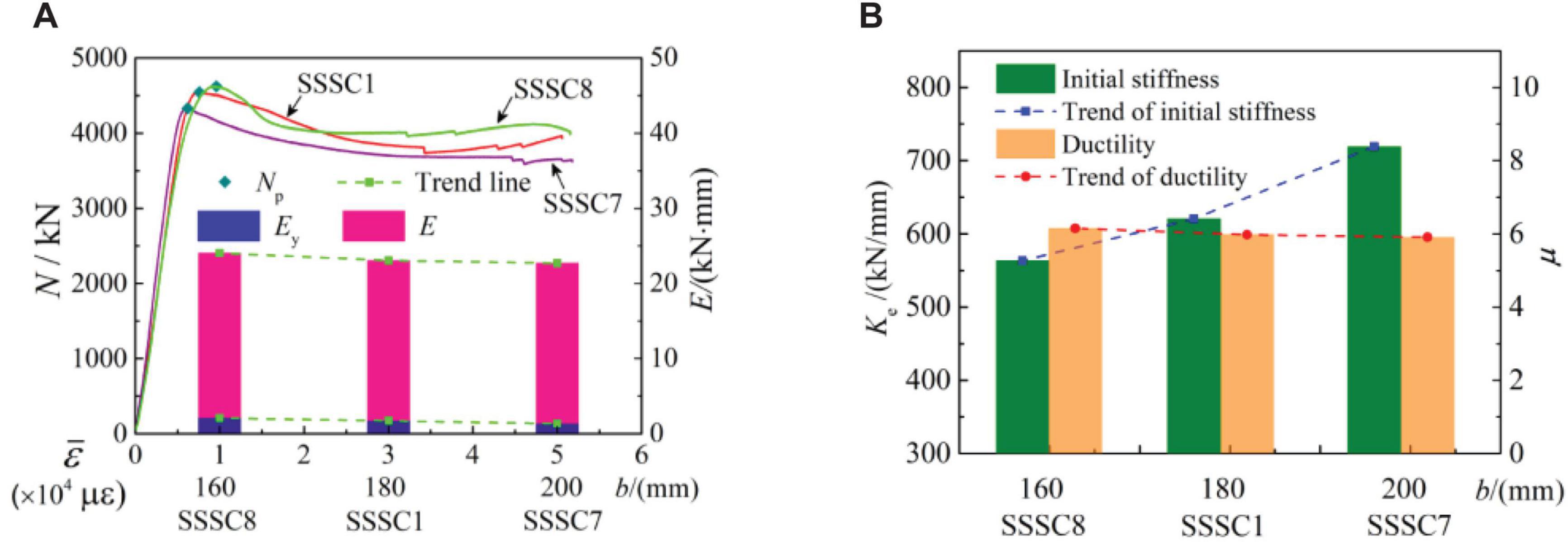
Figure 8. Effect of stirrup side length. (A) Variation of peak load, strain, and energy dissipation. (B) Stiffness degradation and ductility.

Effect of Stirrup Spacing

Figure 9 shows the influence of stirrup spacing on the mechanical properties of the specimen. It can be seen from Figure 9 that the bearing capacity, the energy dissipation, and ductility performance decreased, and the initial stiffness increased at first and then decreased with the increase of stirrup spacing. The change trend of the load-displacement curve type is: type II→ type I→ type II. The results showed that the steel ratio of the SSSC5 specimen with the largest stirrup spacing was smaller, and the constraint effect on the core concrete was weak. It affected the growth of its bearing capacity. At the beginning of loading, the longitudinal strain development of the longitudinal reinforcement was larger than that of the steel tube. The steel tube yielded and the longitudinal strain developed faster before the peak point meanwhile the longitudinal strain development speed of the longitudinal reinforcement slowed down, which delayed the excessive deformation of the steel tube and the rapid decline of the bearing capacity of the specimen. The load-displacement curve had a platform section at the peak point, which showed a good plastic deformation ability. Within a certain range, small stirrup spacing (110 mm∼80 mm) made the steel ratio increase, and the bearing capacity and initial stiffness of the specimens improve. For the specimen with stirrup spacing of 80 mm (the SSSC1 specimen), the longitudinal strain of the steel tube developed more than that of the longitudinal reinforcement in the early stage of loading. The steel tube yielded. Then the longitudinal reinforcement entered the plastic stage when the load was close to the peak point. The stress produced by the continuous loading remained unchanged, but the strain increased. The constraint effect of the stirrup cage on the core concrete was weakened. The load of the specimen decreased obviously. After the longitudinal bars yielded, the stirrups were broken one after another. It can be seen from the curve that the load dropped suddenly and then rose again. The bearing capacity of the specimen increased due to the strengthening of the steel in the later stage but the longitudinal deformation of the specimen was very large. When the stirrup spacing continued to decrease (80 mm∼50 mm), the reinforcement constraint effect of the stirrup cage on the core concrete was more obvious, increasing the bearing capacity and peak strain of the specimen. The energy dissipation and ductility performance were improved. And the situation where the bearing capacity of specimens decreased too fast after the peak point was alleviated.

FIGURE 9

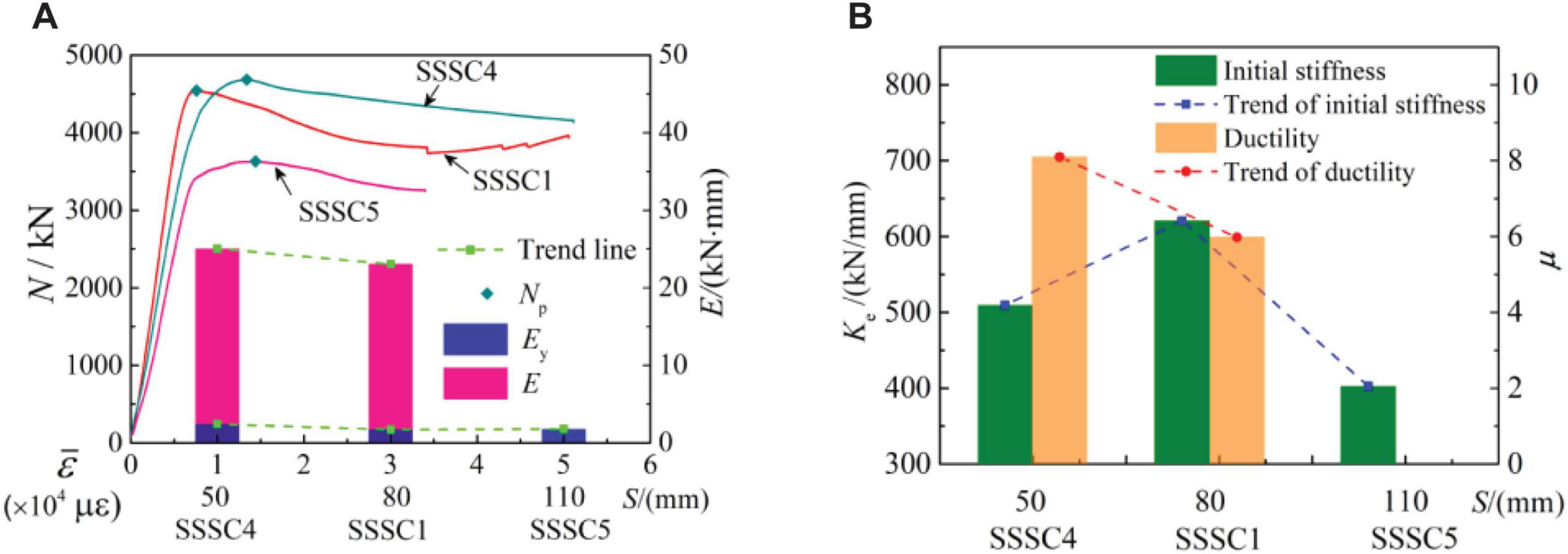
Figure 9. Effect of stirrup spacing. (A) Variation of peak load, strain, and energy dissipation. (B) Stiffness degradation and ductility.

Effect of Steel Tube Thickness

Figure 10 shows the influence of steel tube thickness on the mechanical properties of the specimen. It can be seen from Figure 10 that the bearing capacity, the energy dissipation, and ductility performance increased, peak strain and the initial stiffness decreased with the increase of steel tube thickness. The change trend of the load-displacement curve type is: type I→ type II. For the SSSC6 specimen with the increase of outer steel tube thickness, an increasing steel ratio had a favorable effect on the improvement of the bearing capacity of the specimen. At the initial stage of loading, the longitudinal strain of the steel tube developed rapidly and yielded before the peak point. There was a great difference in the longitudinal strain of the longitudinal reinforcement, which affected the initial stiffness of the specimen to a certain extent. After the peak point, the core concrete was still constrained by the steel tube and stirrup cage and the deformation of the steel was delayed, which made the bearing capacity decrease slowly. It effectively improved the working performance of the specimen in the later bearing period.

FIGURE 10

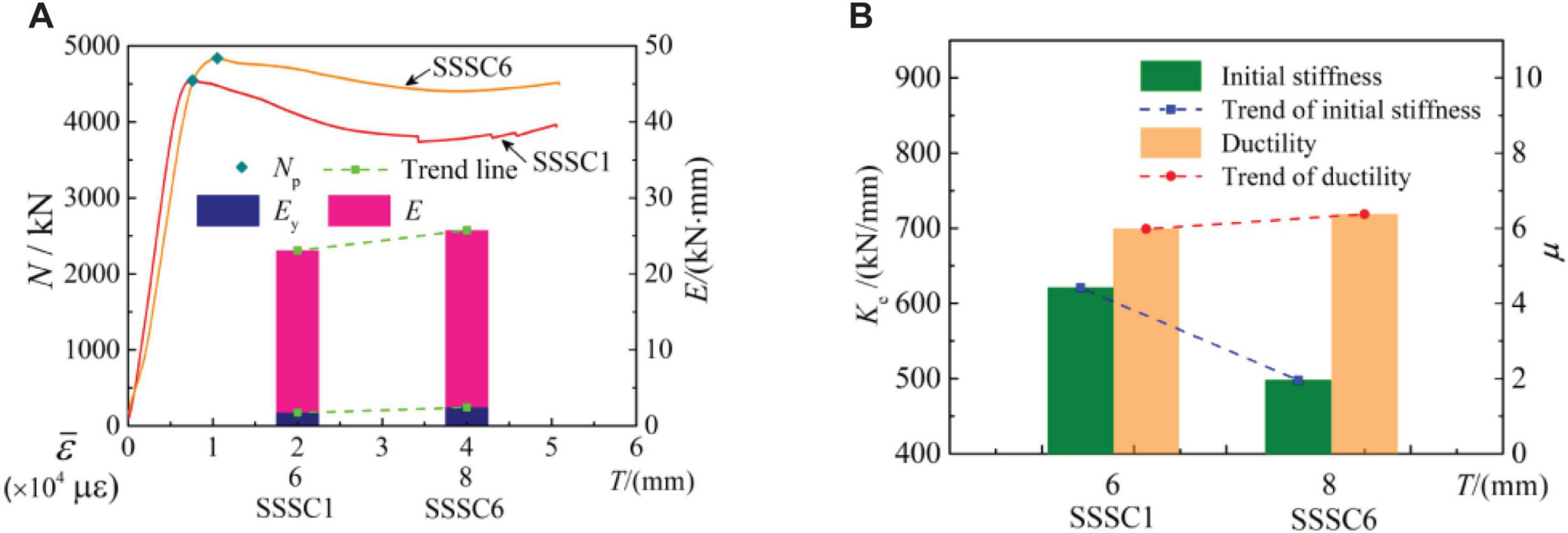
Figure 10. Effect of steel tube thickness. (A) Variation of peak load, strain, and energy dissipation. (B) Stiffness degradation and ductility.

Effect of Aspect Ratio

Figure 11 shows the influence of aspect ratio on the mechanical properties of the specimen. It can be seen from Figure 11 that the bearing capacity and peak strain of the specimen decreased, however, the total energy consumption increased, the initial stiffness and ductility performance increased at first and then decreased, and the yield energy consumption decreased at first and then increased with the increase of aspect ratio. The load-displacement curve of the specimen is type II. The results showed that a large aspect ratio made the bearing capacity decrease obviously due to the P-Δ effect. The bearing capacity of the specimens with an aspect ratio of 5∼6 had little difference, but the initial stiffness decreased significantly. The shape of the load-displacement deformation curve did not change with the change of the aspect ratio. At the end of the test, the SSSC6 and SSSC7 specimens had obvious overall bending deformation. The total energy consumption increased with the increase of aspect ratio. This may be due to the fact that the concrete with weak restraint in the middle of the side length of the square steel tube extruded outward and slid relative to the longitudinal reinforcement and stirrups, and section friction was produced on the interface between the concrete and stirrup cage during the loading process. The larger the aspect ratio the more friction accumulated in the longitudinal path, and the total energy consumption was greater.

FIGURE 11

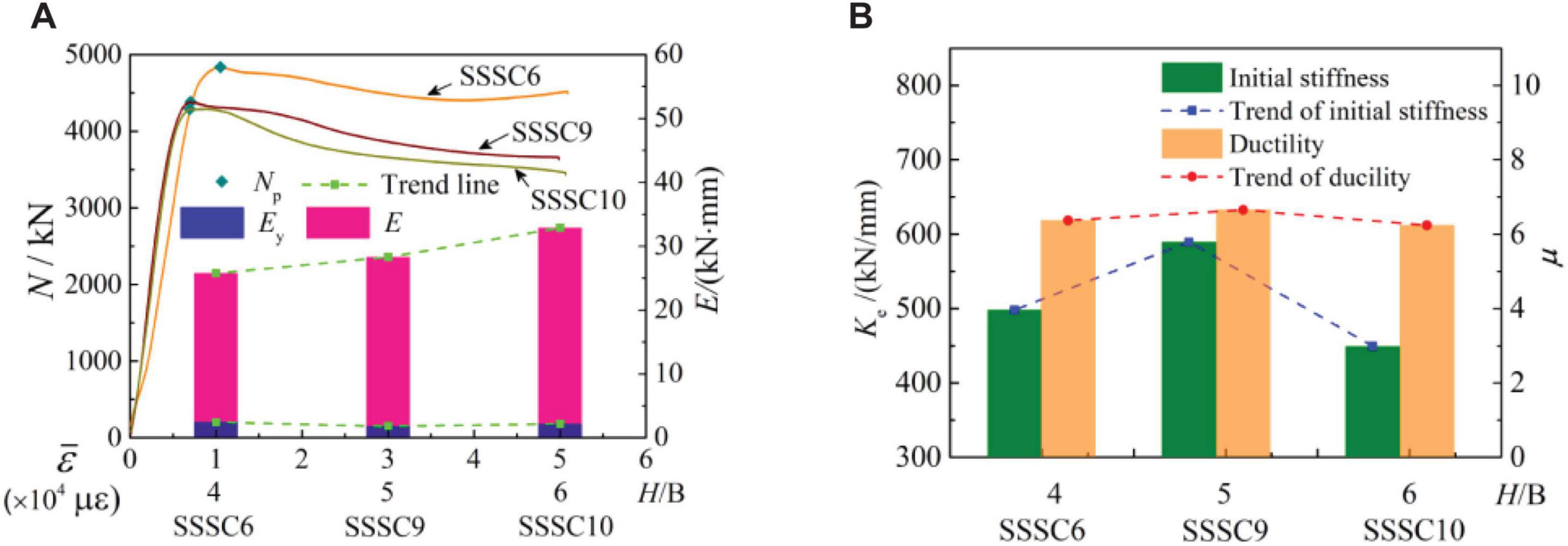
Figure 11. Effect of aspect ratio. (A) Variation of peak load, strain, and energy dissipation. (B) Stiffness degradation and ductility.

Effect of Steel Ratio

From the above analysis, the results showed that the change of stirrup size, steel tube thickness, and aspect ratio were related to the change of steel ratio. Combined with the influence of the steel ratio, the mechanical indexes of the specimens were treated in a unit according to it, comparing and analyzing the influencing factors.

Figure 12 shows the influence of steel ratio on the mechanical properties of the specimen. The number above the column chart shows the steel ratio of each specimen, and the unit is percentage (%). It can be seen from Figure 12A that the peak load of the specimen did not necessarily increase with the increase of steel ratio. Comparing the design parameters of the SSSC1, SSSC7, SSSC3, SSSC4, and SSSC6 specimens, the steel ratio of the specimens increased, only the unit bearing capacity of the SSSC4 specimen increased slightly. It should be noted that the steel tube thickness of the SSSC6 specimen was increased (T = 8 mm), and the unit bearing capacity of the specimen decreased a lot. The bearing capacity of the SSSC7 specimen with the maximum stirrup side length (b = 200 mm) decreased, but the initial stiffness and ductility improved (Figures 12B,C). In fact, increasing the side length of the stirrup was equivalent to expanding the area of the core concrete stirrup column, and the area of cross-section sandwich concrete was reduced. To a certain extent, it divided the cross-section wrapped with steel into small areas with the steel as the boundary, improving the stiffness of the specimen. Meanwhile, steel and concrete worked together well under the cross-section composite constraint. The ductility performance was enhanced. The SSSC3 (ρ_s = 9.47%) and SSSC4 (ρ_s = 9.49%) specimens with similar steel ratios had a large stirrup diameter and small stirrup spacing, respectively. The results showed that there was little difference in the increase of bearing capacity between them, the initial stiffness of the SSSC3 specimen increased. However, the ductility decreased. And the opposite was true for the SSSC4 specimen. It was pointed out that increasing the stirrup diameter (equivalent to increasing the corner constraint of the stirrup cage) and reducing the stirrup spacing (equivalent to strengthening the lateral constraint of the stirrup cage) were essentially enhancing the mechanical performance of the internal reinforcement cage. The results showed that the reinforcement of effective constraint at the corner of the stirrup cage improved the stiffness of the specimen, but weakened the ductility performance; the reinforcement of the lateral constraint of the stirrup cage made the ductility performance better, but the stiffness of the specimen decreased in a certain range of steel content (ρ_s = 8.97% 9.49%). Comparing the design parameters of the SSSC1, SSSC8, SSSC5, and SSSC2 specimens, the bearing capacity and initial stiffness decreased most with reduced stirrup spacing (SSSC5 specimen, S = 110 mm), followed by the reduction of stirrup diameter (SSSC2 specimen, d = 6 mm). It can be seen that the weakening of the lateral constraint of the stirrup cage had a more adverse effect on the bearing capacity than the weakening of the effective corner constraint in a certain range of steel content (ρ_s = 8.97% 9.05%). Except for SSSC4, a large steel ratio made the ductility decrease.

FIGURE 12

Figure 12. Effect of steel ratio. (A) Bearing capacity. (B) Stiffness. (C) Ductility.

Conclusion

Ten rhombic stirrups-reinforced concrete-filled square steel tubular columns (SSSC specimens) were tested. The failure process and mechanism of the SSSC specimens were analyzed and compared with the original concrete-filled square steel tube column (SC1 specimen). The influence rules of the different influencing factors on the mechanical properties of the specimens were discussed. The conclusions were as follows:

(1) The results showed that the failure process and final failure form of the SSSC specimens were like those of the SC1 specimen. The specimens with an aspect ratio of 4 displayed local buckling failure. The steel tube of the SSSC3 specimen was torn at the corner. The specimens with an aspect ratio of 5 and 6 (the SSSC9 and SSSC10 specimens) had bending failures in the plastic stage.

(2) The results showed that most of the debonding areas had different degrees of bulging. The longitudinal bars also had outward bending deformation in the larger bulging areas, and some of the stirrups were broken in the later stage of loading, which indicated that the binding position of the longitudinal reinforcement and stirrup had a stronger constraint effect on concrete. The constraint effect on concrete was weak at the middle part of the stirrup side length and longitudinal reinforcement interval area.

(3) The characteristics of the load-displacement curve changed with the changing of stirrup spacing, but the side length of the stirrup had little effect on it. This indicated that the strength of the longitudinal constraint had an obvious influence on the mechanic performance of the SSSC specimens.

(4) Compared with the SC1 specimen, the unit bearing capacity and ductility performance of the SSSC specimens (H/B = 4) were increased by at least 21% and 27%, respectively. In a certain range of steel ratio (ρ_s = 8.97% 9.05%), the weakening of the lateral constraint of the stirrup cage had a more adverse effect on the bearing capacity than the weakening of an effective corner constraint. In a certain range of steel content (ρ_s = 8.97% 9.49%), strengthening the effective corner constraint of the stirrup cage improved the stiffness, but reduced the ductility performance. And the opposite was true for strengthening the lateral constraint of the stirrup cage.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

ZC: funding acquisition, project administration, and supervision. FN: validation and writing – original draft. LM: writing – review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 51268004 and 51578163), Natural Science Foundation of Guangxi (project No: 2016GXNSFDA380032), and Bagui Scholar Program of Guangxi (No: [2019]79). This financial support was gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

American Institute of Steel Construction (AISC) (2010). ANSI/AISC 360-10. Specification for Structural Steel Buildings. Chicago, IL: AISC.

Google Scholar

Architectural Institute of Japan (AISC) (1997). Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures. Tokyo: AIJ.

Google Scholar

Ayough, P., Sulong, N.H. Ramli, Ibrahim, Z., and Hsiao, P.-C. (2020). Nonlinear analysis of square concrete-filled double-skin steel tubular columns under axial compression. Eng. Struct. 216:110678. doi: 10.1016/j.engstruct.2020.110678

CrossRef Full Text | Google Scholar

British Standards Institution (2004). Eurocode 4, EN 1994-1-1 Design of Composite Steel and Concrete Structures, Part 1.1. General Rules and Rules for Buildings. London: British Standards Institution.

Google Scholar

British Standards Institution (2005). BS 5400, Steel, Concrete, and Composite Bridges:Part5: Code of Practice for Design of Composite Bridges. London: British Standards Institution.

Google Scholar

Cai, J., Zheng, Z. X., Chen, Q. J., Zuo, Z. L., Yang, C., and Zheng, J. H. (2014). Experimental study on axial compression behavior of stiffened square section CFST short columns. J. Build. Struct. 35, 178–185.

Google Scholar

Chen, Z. P., Chen, Y. L., Zhong, M., and Xue, J. Y. (2014). Experimental study on axial compression capacity of concrete-filled square steel tubular columns with opening hole damage. Build. Struct. 09, 9–14. doi: 10.19701/j.jzjg.2014.09.002

CrossRef Full Text | Google Scholar

Chen, Z. P., Jing, C. G., and Ning, F. (2018). Axial compressive behavior and parametric analysis of spiral reinforcement concrete filled square steel tubular columns. China Civil Eng. J. 51, 13–57.

Google Scholar

Chen, Z. P., Jing, C. G., Xu, J. J., and Zhou, C. H. (2017). Mechanism and load-bearing capacity of square steel tubular and spiral stirrup composite confined-concrete stub columns under axial compression. China Civil Eng. J. 50, 47–56.

Google Scholar

China Architecture and Building Press (2010). GB50628-2010 Code for Quality Acceptance of the Concrete Filled Steel Tubular Engineering. Beijing: China Architecture and Building Press.

Google Scholar

China Architecture and Building Press (2019). GB/T 50081—2019 Standard for Test Method of Concrete Physical and Mechanical Properties. Beijing: China Architecture and Building Press.

Google Scholar

China Construction Industry Press (2014). GB 50936-2014 Technical Code for Concrete-Filled Steel Tubular Columns. Beijing: China Construction Industry Press.

Google Scholar

Ding, F. X., Fang, C. J., Bai, Y., and Gong, Y. Z. (2014). Mechanical performance of stirrup-confined concrete-filled steel tubular stub columns under axial loading. J. Construct. Steel Res. 98, 146–157. doi: 10.1016/j.jcsr.2014.03.005

CrossRef Full Text | Google Scholar

Feng, P., Cheng, S., Bai, Y., and Ye, L. P. (2015). Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Comp. Struct. 123, 312–324. doi: 10.1016/j.compstruct.2014.12.053

CrossRef Full Text | Google Scholar

Gan, D., Zhou, Z., and Zhou, X. (2019). Axially loaded thin-walled square concrete-filled steel tubes stiffened with diagonal binding ribs[J]. ACI Struct. J. 116:105848. doi: 10.14359/51718015

CrossRef Full Text | Google Scholar

Gardner, L., Hassanein, M. F., and Kharoob, O. F. (2015). Behaviour and design of square concrete-filled double skin tubular columns with inner circular tubes. Eng. Struct. 100, 410–424. doi: 10.1016/j.engstruct.2015.06.022

CrossRef Full Text | Google Scholar

Hu, H. T., Huang, C. S., Wu, M. H., and Wu, Y. M. (2003). Nonlinear analysis of axially loaded concrete-filled tube columns with confinement effect. J. Struct. Eng. 129, 1322–1329.

Google Scholar

Jing, C. G., Chen, Z. P., Zhou, S. W., and Xu, J. J. (2018). Experimental study on failure mechanism of square steel tube and spiral reinforcement multiple confined concrete stub columns under axial compression. J. Build. Struct. 39, 93–102. doi: 10.14006/j.jzjgxb.2018.03.012

CrossRef Full Text | Google Scholar

Tang, J.R. (1989). Seismic Resistance Of Joints In Reinforced Concrete Frames. Nanjing: Southeast University Press.

Google Scholar

Liang, W., Dong, J. F., Yuan, S. C., and Wang, Q. Y. (2017). Behavior of self-compacting concrete-filled steel tube columns with inclined stiffener ribs under axial compression. Strength Mater. 49, 125–132. doi: 10.1007/s11223-017-9850-z

CrossRef Full Text | Google Scholar

Qian, J. R., Li, N. B., Ji, X. D., and Zhao, Z. Z. (2014). Experimental study on the seismic behavior of high strength concrete filled double-tube columns. Earthquake Eng. Eng. Vibration 13, 47–57. doi: 10.1007/s11803-014-0211-7

CrossRef Full Text | Google Scholar

Sheikh, S. A., and Uzumeri, S. M. (1980). Strength and ductility of tied concrete columns [J]. J. Struct. Divis. 106, 1079–1102. doi: 10.1002/jps.2600671021

PubMed Abstract | CrossRef Full Text | Google Scholar

Standards Press of China (2010). GB/T 228. 1—2010 Metallic Materials: Tensile Testing: Part 1: Method of Test at Room Temperature. Beijing: Standards Press of China.

Google Scholar

Tang, Y., Fang, S., Chen, J., Ma, L., Li, L., and Wu, X. (2020). Axial compression behavior of recycled-aggregate-concrete-filled GFRP–steel composite tube columns. Eng. Struct. 216:110676. doi: 10.1016/j.engstruct.2020.110676

CrossRef Full Text | Google Scholar

Wang, Y. T., Cai, J., and Long, L. Y. (2020). Research on the restoring force model of square concrete-filled tubular columns with binding bars. Build. Sci. 6, 91–97. doi: 10.13614/j.cnki.11-1962/tu.2020.01.014

CrossRef Full Text | Google Scholar

Xu, B., Wu, F. H., Xu, G. Z., Kong, H. L., and Gu, G. Q. (2020). Study on impacts of straight ribs and perforated ribs on axial compressive performance of square CFST short columns. Build. Struct. 50, 71–75. doi: 10.19701/j.jzjg.2020.13.013

CrossRef Full Text | Google Scholar

Yang, Y. F., Hou, C., Meng, C. Y., and Han, L. H. (2015). Investigation on square concrete filled double-skin steel tube (CFDST) subjected to local bearing force: experiments. Thin Walled Struct. 94, 394–409. doi: 10.1016/j.tws.2015.04.026

CrossRef Full Text | Google Scholar

Zhao, H. T. (2001). Steel-Concrete Composite Structure. Beijing: Science Press.

Google Scholar