Geopolymer Concrete Compressive Strength via Artificial Neural Network, Adaptive Neuro Fuzzy Interface System, and Gene Expression Programming With K-Fold Cross Validation

The ultrafine fly ash (FA) is a hazardous material collected from coal productions, which has been proficiently employed for the manufacturing of geopolymer concrete (GPC). In this study, the three artificial intelligence (AI) techniques, namely, artificial neural network (ANN), adaptive neuro-fuzzy interface (ANFIS), and gene expression programming (GEP) are used to establish a reliable and accurate model to estimate the compressive strength $\left({f^{\prime }}_c\right)$ of fly ash–based geopolymer concrete (FGPC). A database of 298 instances is developed from the peer-reviewed published work. The database consists of the ten most prominent explanatory variables and ${f^{\prime }}_c$ of FGPC as a response parameter. The statistical error checks and criteria suggested in the literature are considered for the verification of the predictive strength of the models. The statistical measures considered in this study are MAE, RSE, RMSE, RRMSE, R, and performance index $\left(\rho \right)$. These checks verify that the ANFIS predictive model gives an outstanding performance followed by GEP and ANN predictive models. In the validation stage, the coefficient of correlation (R) for ANFIS, GEP, and ANN model is 0.9783, 0.9643, and 0.9314, respectively. All three models also fulfill the external verification criterion suggested in the literature. Generally, the GEP predictive model is ideal as it delivers a simplistic and easy mathematical equation for future use. The k-fold cross-validation (CV) of the GEP model is also conducted, which verifies the robustness of the GEP predictive model. Furthermore, the parametric study is carried via proposed GEP expression. This confirms that the GEP model accurately covers the influence of all the explanatory variables used for the prediction of ${f^{\prime }}_c$ of FGPC. Thus, the proposed GEP equation can be used in the preliminary design of FGPC.

Introduction

Fly ash is the unburned residual obtained from coal production and is taken out by the gases expelled from the boiler, which is then accumulated by means of mechanical or electrostatic precipitator (Rafieizonooz et al., 2016; Aprianti S, 2017; Akbar et al., 2021). Every year, about 375 million tons of FA is generated with a retention cost of $20–$40 per ton (Dwivedi and Jain, 2014). FA contains hazardous minerals like alumina, ferric oxide, and silica; putting to dump fill sites without sufficient treatment creates a destructive and harmful effect on the ecology (Carlson and Adriano, 1993; Kumar Tiwari et al., 2016; Nadesan and Dinakar, 2017; Ghazali et al., 2019). Virtuous waste management is needed for the sustainability of a healthy environment. Also, the ultrafine particles of FA, when reached to the respiratory system, cause different health issues like cancer, anemia, physiological disorder, dermatitis, and diarrhea. It also pollutes the ground water and alarms the aquatic life (Carlson and Adriano, 1993; Kumar Tiwari et al., 2016; Ghazali et al., 2019).

In the world, mostly, concrete is used for construction purposes and is the utmost desirable substance after water (Farooq et al., 2020a; Liew and Akbar, 2020). Around 3 tons of concrete is manufactured per person, which accumulates 25 billion tons of concrete production per year (Watts, 2019), which requires 2.6 billion tons of cement production every year and would be increased by 25 percent in the latter decade (Wongsa et al., 2020). However, the processing of cement has a detrimental role in polluting the environment. In manufacturing, 1 ton of cement and 1 ton of carbon dioxide are emitted into the atmosphere (Akbar and Liew, 2020). The cement utilizes limestone, and a serious deficiency of limestone may arise after 25–50 years (Farooq et al., 2020c; Sumanth Kumar et al., 2020). Thus, the production of green concrete is needed which leads to sustainable development and a healthy environment. FA acts as a supplementary cementitious material in the concrete mix and has been effectively used by researchers in the production of green concrete (Wang et al., 2017, Wang et al., 2019a; Chen et al., 2019). The consumption of FA in the construction is a better choice as it will not only reduce the malicious impact of its dumping into landfills but will also decrease the use of cement.

From the last 20 years, in the construction industry, the use of fly ash–dependent geopolymer concrete is increasing rapidly because it lessens the depletion of cement in geopolymer concrete (GPC) (Gülşan et al., 2019; Kondepudi and Subramaniam, 2019; Xie et al., 2019; Zhang et al., 2020a; Bajpai et al., 2020; Meesala et al., 2020; Noushini et al., 2020; Nuaklong et al., 2020). Because of the anomalous behavior of FA, its application in the construction industry is still limited (Jena et al., 2019; Nguyen et al., 2020; Sandanayake et al., 2020). FGPC is significantly used in the construction industry, but yet no method is available for the prediction of its compressive strength $\left({f^{\prime }}_c\right)$ based on the mix design parameters with maximal variables. The ${f^{\prime }}_c$ of FGPC fluctuates by numerous parameters such as temperature required for curing of the sample $\left(T\right)$, the time required for curing of the sample $\left(t\right)$, age of the sample $\left(A\right)$, the molarity $\left(M\right)$ of the sodium hydroxide (NaOH) solution used, the percentage of silicon dioxide (SiO₂) to the water ratio $\left(\text{\%}S/W\right)$ for preparing solution of sodium silicate (Na₂SiO₃), ratio between sodium silicate (Na₂SiO₃) solution to NaOH $\left(N_s{N}_s/N_o{N}_o\right)$, percentage by volume of total aggregates $\left(\% A_G\right)$, ratio between fine aggregate to total aggregates $\left(F/A_G\right)$, ratio between alkali to fly ash $\left(A_L/F_A\right)$, percentage of plasticizer $\left(\% P\right)$, and percentage of extra addition of water $\left(\% E_W\right)$ (Luhar et al., 2019; Tran et al., 2019; Van Dao et al., 2019; Wang et al., 2019b; Zhang et al., 2019, Zhang et al., 2020b; Prachasaree et al., 2020; Farooq et al., 2021). This raises uncertainty in the prediction of ${f^{\prime }}_c$ FGPC. Moreover, the rise in the use of supervised machine learning techniques for the development of an empirical model has been observed in recent times (Javed et al., 2020a).

Throughout the globe, AI techniques are being used to estimate concrete properties (Farooq et al., 2021). Various AI techniques are used by researchers such as fuzzy interface system (FIS), response surface methodology (RSM), adaptive neuro-fuzzy interface system (ANFIS), extreme machine learning (EML), artificial neural network (ANN), support vector machine (SVM), random forest (RF), particle swarm optimization algorithm (PSOA), backpropagation neural network (BPNN), genetic algorithm (GA), genetic programming (GP), and gene expression programming (GEP). Table 1 covers the recent research conducted for the prediction of concrete properties via AI techniques. The ANN and ANFIS techniques can detect and generalize the complicated patterns. Therefore, they can be effectively used to solve engineering complexities (Noori et al., 2010; Chou and Pham, 2013). The existence of enormous hidden neurons sometimes makes it difficult to develop the relationship between input and output variables. These models show a strong correlation between input and outputs but do not provide an empirical equation that can be further used in the field. This is due to the complex structure of ANN and ANFIS models, which limits the wide-scale adoption of these models (Noori et al., 2010; Sebaaly et al., 2018).

TABLE 1

TABLE 1. Application of artificial intelligence (AI) techniques in civil engineering materials.

Genetic programming (GP) is a worthy soft computing method as it ignores the prior developed relationship in the establishment of the model (Gandomi et al., 2012; Gandomi et al., 2013). Recently, in civil engineering, gene expression programming (GEP) is introduced which is an extension of GP. GEP uses a fixed-length linear chromosome and encodes a small program (Ferreira, 2006). It is advantageous as it provides a simple empirical equation for predicting the response, which can be used practically (Behnia et al., 2013; Beheshti Aval et al., 2017; Gholampour et al., 2017; Sadrossadat et al., 2018; Iqbal et al., 2020).

In the design and analysis of concrete, compressive strength $\left({f^{\prime }}_c\right)$ is the key factor (Akbar et al., 2020). Vast experimental research is carried to find the ${f^{\prime }}_c$ of FGPC. To avoid costly experimental procedures, to save time and to support the usage of FA in the building industry, the establishment of reliable, precise, and accurate mathematical equation is desirable, which can relate the maximum mix proportion variables and ${f^{\prime }}_c$ of FGPC. Alkaroosh et al. (Alkroosh and Sarker, 2019) established a GEP-based empirical relationship for the prediction of ${f^{\prime }}_c$ of FGPC, based on 56 instances saved from previous study (Hardjito and Rangan, 2005). The application of this model is limited to a confined database, that is, to the accompanying experimental results. Also, no variable was considered for the preparation of the Na₂SiO₃ solution. Furthermore, their model displays a strong increasing linear relation between the molarity of NaOH and ${f^{\prime }}_c$ of FGPC, which is contradictory to other studies, which confirms the decrease in the $\left({f^{\prime }}_c\right)$ of FGPC by increasing the molarity of the NaOH solution (Joseph and Mathew, 2012).

In this research, a comprehensive database of 298 instances has been established from the previous peer-reviewed published work which contains 101 cylindrical samples with a size of $\left(200 \times 100\right)\text{mm;}\text{height}\times \text{diameter}$, 31 cube samples with a size of $100\text{mm}$, and 166 cube samples with a size of $150\text{mm}$. The comprehensive database ensure the consistency of the AI models. As AI techniques involve complex programming and require excessive care and optimization. Therefore, three AI methods, that is, ANN, ANFIS, and GEP are employed to predict the ${f^{\prime }}_c$ of FGPC. The performance of these models is verified by k-fold cross-validation, statistical checks, and sensitivity and parametric study. Also, the performance of all these models is compared with each other to counter the complexity of programming.

Machine Learning Modeling Techniques

This study considers three different artificial intelligence (AI) algorithms, to establish a model for estimating the compressive strength of FGPC. The execution of these models does not need any prior knowledge of the experimental procedure. This section briefly describes the overview of the AI modeling techniques used in this research.

Gene Expression Programming

Koza suggested an artificial intelligence method, that is, genetic programming (GP), as a substitute for GA which works on fixed-size strings (Koza and Poli, 2005). GP is a flexible and adjustable programming method as it uses the nonlinear parse tree structure. It accepts the initial nonlinearity within the data. Such nonlinearity has been executed earlier (Koza and Poli, 2005; Alkroosh and Sarker, 2019). GP fails in considering the independent genome. GP deals with the nonlinear structure as both phenotype and genotype. This marks GP questionable in assembling the rudimentary and simple equation. To resolve the discrepancies in GP, Ferreira introduced a novel methodology called GEP (Koza and Poli, 2005). The noteworthy change in GEP is that it transfers the genome toward another generation. One more unique function is the formation of objects via chromosomes made up of genes, which are further expanded as tail and head (Saridemir, 2010). In GEP, every single gene is comprised of fitted length parameters, arithmetic operation as a set of functions, and terminal set of constants. In the operation of genetic code, there exists a one-to-one interaction between subsequent functions and the symbols of chromosomes. The essential figures and information needed for the establishment of an empirical equation are stored in the chromosomes. A novel language Karva is developed to deduce this information.

Figure 1 shows the flow diagram of the GEP technique. The first step is the fairly random distribution of fixed-size chromosomes for every instance. The same chromosomes are then represented as the expression trees (ET), and the fitness is calculated for every single individual. The mutation cycle keeps on with the addition of different individuals for several generations till the best model is achieved. To renovate the population, genetic operations like reproduction, mutations, and crossovers are carried out.

FIGURE 1

FIGURE 1. Architectural flowchart of GEP algorithm.

Artificial Neural Network

ANN analyzes the data by the artificial intelligence (AI) method. It uses the learning ability of the human brain. The extensively used form of ANN is the feed-forward backpropagation (FFBP) algorithm. Figure 2 illustrates that FFBP comprises of minimum three layers, that is, the input, the output, and the hidden layers. These layers are linked through nodes in an appropriate order along with approximated weights. The purpose of the input layer is to obtain the data from outside. Their nodes do not operate a single function on input data. The data become biased, weighted, and summed up in the hidden layer. The executed data are then transferred to the output layer (Alavi and Gandomi, 2011; Gandomi and Roke, 2015).

FIGURE 2

FIGURE 2. Architecture of the ANN model.

Two types of FFBP are generally used, that is, single-layer perceptron (SLP) and multiple layer perceptron (MLP). The SLP is easy and simple but cannot catch the nonlinear relationship, while the complex nature of MLP effectively handles the nonlinear relation between output and input variables. The steps involved in the mathematical operation of MLP are as following:

Step 1: In the first step, the input data is weighted and summed given as:

$S_j={\displaystyle \sum _{i=1}^n{\omega }_{ij}{I}_i+b_j};j=1, 2, 3, \dots \dots ,h,(1)$

where $n$, $I_i$, and ${\omega }_{ij}$ represent the total number of inputs, current input number, and the weight between the prior layer and the $j^{th}$ neuron, respectively, while “b” represents the process of termination.

Step 2: It involves an activation function. Different activation functions are used like a ramp, Gaussian, and sigmoid functions. However, the sigmoid function is utilized in this study which is stated as:

$S_j=\frac{1}{1+e^{-s_j}}; j=1, 2, 3, \dots \dots ,h.(2)$

Step 3: In this step, the final output is determined, which is dependent on the estimated outputs by hidden neurons. The ultimate output can be expressed as:

$O_k={\displaystyle \sum _{j=1}^h\left({\omega }_{jk}.S_j\right)+{b^{\prime }}_k};k=1, 2, 3, \dots \dots , m,(3)$

$O_k=sigmoid\left(O_k\right)=\frac{1}{1+e^{-O_k}} ;k=1, 2, 3, \dots \dots , m,(4)$

where ${\omega }_{jk}$ and $b_k{ }^{\prime }$ represent the weighted link between $j^{th}$ hidden node and $k^{th}$ output node, while $b_k{ }^{\prime }$ defines the biased outcome of the $k^{th}$ output node.

Artificial Neuro-Fuzzy Interface

ANFIS is another AI technique that combines the effect of fuzzy logic and ANN (Çaydaş et al., 2009). ANN is generally employed to lessen the probability of error in the outcome. Whereas the fuzzy logic is utilized to prove and demonstrate the practiced knowledge and is applied while mathematical modeling of the anticipated input and output data set (Jaafari et al., 2019). Generally, the ANFIS works on five layers. The description of these layers is as follows:

1st layer: It is the fuzzification layer that encompasses the functional members of the input parameters, which use the Gaussian function for the prediction of the outcome. The mathematical equation is given as:

${\mu }_{ui}\left(x\right)=\exp \left[-\frac{\left(x-a_i\right)}{2{\epsilon }_i^2}\right],(5)$

where ${\epsilon }_i$ and $a_i$ are the parameters used for the functional membership.

2nd layer: In this layer, nodes are utilized to send the output through the multiplication of the input with a particular weightage. This layer is worked on the fuzzy and logic via expression given below;

${\omega }_i={\mu }_{ui}\left(x\right)\times {\mu }_{vi}\left(y\right).(6)$

3rd layer: The aim of this layer is to normalize the functions of membership. The below-listed equation is used to estimate the ratio between various firing strengths.

$\overline{\omega }=\frac{{\omega }_i}{{\displaystyle {\sum }_i{\omega }_i}}.(7)$

4th layer: It is the defuzzification layer that utilizes the square nodes to conclude the rules of the fuzzy logic. The following expression shows the defuzzification process:

${\overline{\omega }}_i{f}_i={\omega }_i\times \left(m_{i}x+n_{i}y+r_i\right),(8)$

where $r_i$, $m_i$, and $n_i$ are all the linear parameters.

5th layer: This layer has the function to aggregate and sum up the previous layers and later on conclude the final output.

Acquisition of Data

For estimating the compressive strength $\left({f^{\prime }}_c\right)$ of FGPC, a comprehensive database file with 298 instances was compiled from the peer-reviewed published articles (Galvin et al., 1978; Hardjito and Rangan, 2005; Sumajouw and Rangan, 2006; Nuruddin et al., 2011a; Nuruddin et al., 2011b; Fareed Ahmed et al., 2011; Kusbiantoro et al., 2012; Olivia and Nikraz, 2012; Sujatha et al., 2012; Deb et al., 2013a; Deb et al., 2013b; Long et al., 2013; Patankar et al., 2013; Sarker et al., 2013; Vora and Dave, 2013; Albitar et al., 2015; Lavanya and Jegan, 2015; Okoye et al., 2015; Patankar et al., 2015; Shaikh and Vimonsatit, 2015; Thesis et al., 2015; Ganesan et al., 2015; Aliabdo et al., 2016; Nuaklong et al., 2016; Assi et al., 2016; Satpute et al., 2016; Shaikh, 2016; Shehab et al., 2016; Wongsa et al., 2016; Mehta and Siddique, 2017; Nath and Sarker, 2017; Ramujee and Potharaju, 2017; Sathanandam et al., 2017; Wardhono et al., 2017; Lokuge et al., 2018; Ishak et al., 2019). To carry out the more generalized study, both cylindrical shape samples and cubic samples with different sizes were considered in the dataset. It consists of 101 cylindrical samples $\left(200 \times 100\right)\text{mm};\text{height}\times \text{diameter}$, 31 cubic samples $\left(100 \text{mm}\right)$, and 166 cubic samples $\left(150 \text{mm}\right)$. The ${f^{\prime }}_c$ of concrete is size- and shape-dependent and varies with ratio between length and diameter (L/D) (del Viso et al., 2008; Hamad, 2017). The ${f^{\prime }}_c$ of $100\text{mm}$ cubic is 5% more than $150\text{mm}$ cubic samples. Also, the ${f^{\prime }}_c$ of $150\text{mm}$ cubic samples is 20% greater than cylindrical samples of size $\left(200 \times 100\right)\text{mm};\text{height}\times \text{diameter}$. Therefore, the compressive strength of both size of cubes is being normalized to cylinder compressive strength of size $\left(200\times 100\right)\text{mm};\text{height}\times \text{diameter}$.

The comprised dataset has ${f^{\prime }}_c$ as a response variable and has an explanatory variable such as temperature required for curing of the sample $\left(T\right)$, age of the sample $\left(A\right)$, the molarity $\left(M\right)$ of the sodium hydroxide (NaOH) solution used, the percentage of silicon dioxide (SiO₂) to the water ratio $\left(\% S/W\right)$ for preparing sodium silicate (Na₂SiO₃) solution, the ratio between sodium silicate (Na₂SiO₃) solution to NaOH $\left(N_s/N_o\right)$, the percentage by volume of total aggregates $\left(\% A_G\right)$, the ratio between fine aggregate to total aggregates $\left(F/A_G\right)$, the ratio between alkali to fly ash $\left(A_L/F_A\right)$, percentage of plasticizer $\left(\% P\right)$, and percentage of extra addition of water $\left(\% E_W\right)$. For all the collected samples, the time $\left(t\right)$ required for the initial curing of the sample is 24 h. It is true that ${f^{\prime }}_c$ rises with curing time $\left(t\right)$, but the rate of increment in ${f^{\prime }}_c$ of FGPC is quick till 24 h (Hardjito and Rangan, 2005). Moreover, some researchers stated that, due to quick geopolymerization, ${f^{\prime }}_c$ is not improved after 24 h (Van Jaarsveld et al., 2002). Therefore, limited study is conducted for prolonged curing time. The performance of every model relies on the distribution of input variables (Gandomi and Roke, 2015).

Figure 3 shows the cumulative percentage and frequency distribution for all the 10-input parameter used in the modeling of ${f^{\prime }}_c$ of FGPC. The data points of every input parameter are distributed over its range. Table 2 illustrates the range, variance, maximum, minimum, and mean values of the response and explanatory variables. To get accurate and precise results, it is suggested to utilize the projected models for the prediction ${f^{\prime }}_c$ of FGPC within the prescribed range.

FIGURE 3

FIGURE 3. Occurrence frequency and cumulative percentage of explanatory variables.

TABLE 2

TABLE 2. Mean value, standard deviation, and range of input and targeted parameters.

It must be noted that for the validation, consistency, and reliability of the dataset, many trials have been executed. The instances that deviate about 20% from the global norm were not counted in the development of the models. 298 data points were used to develop ANN, ANFIS, and GEP models for the prediction of ${f^{\prime }}_c$ of FGPC. The overall dataset is randomly subdivided into 2 statistically consistent subsets, that is, train subset (70%, 208 instances) and validation subset (30%, 90 instances) (Javed et al., 2020b). The train set has been utilized for training of the model, and the validation set was used to evaluate and verify the generalization capacity of models (Gholampour et al., 2017).

Development and Evaluation of Machine Learning Models

The first and foremost step in the establishment of the model using a machine learning algorithm is the selection of such input variables. To develop the generalized AI models, those input parameters are chosen, which greatly influence the properties of FGPC. To develop AI models for the compressive strength of FGPC, the most influential input variables considered in this study are shown in Eq. 9.

${f^{\prime }}_c=f\left(T,A,M,A_G,\%P,\%E_W,\%\left(S/W\right),\left(N_O/N_O\right),\left( A_L/F_A\right),\left( F/A_G\right)\right).(9)$

Development of Artificial Neural Network Model

The first step in the establishment of the ANN model is the adjustment of fitting parameters, which includes the numbers of the hidden layer, the hidden number of neurons in every layer, the function used for training of the neural network, the epochs, and the maximum number of repetitions. Table 3 displays the details of these parameters. MATLAB software is utilized for the execution of the ANN algorithm.

TABLE 3

TABLE 3. Setting of fitted parameters for ANN and ANFIS models.

Development of Artificial Neuro-Fuzzy Interface Model

Likewise, before the execution of the ANFIS algorithm, the fitting parameters were provided, which include the function used for the activation of the ANFIS algorithm, the number of epochs, and the maximum number of repetitions. Table 3 displays the detailed description of these parameters. Similarly, for the execution of the ANFIS algorithm, MATLAB software is utilized.

Development of Gene Expression Programming Model

The three groups of fitting parameters are used in the development of the GEP model. These are the ordinary model parameters, the numerical constants, and the genetic operators. The ordinary parameters include the population size, that is, the number of chromosomes, the number of genes, the connecting function, the head size, and the set of functions. The numerical constants cover the number of constants used per each gene, the type of data, and its lower and upper bound. The genetic operators involve the mutation rate, transposition function for root insertion sequence (RIS) and insertion sequence (IS), and rate of recombination for combining and splitting two chromosomes. To achieve a generous algorithm, the setting parameter setting suggested in the previous study has been utilized (Iqbal et al., 2020). Table 4 shows the detailed description of GEP setting parameters. GeneXproTool has been utilized to run the GEP-based algorithm.

TABLE 4

TABLE 4. Setting of fitted parameters for the GEP model.

Model Performance Evaluation Criteria

Generally, the coefficient of correlation (R) is utilized to study the performance and operation of the models. Because of the insensitivity of R in relation to division and multiplication of response to the constants, it cannot be exclusively chosen to judge the accuracy and precision of the model (Babanajad et al., 2017). Thus, this research study also considers the evaluation of the models via various statistical error parameters, that is, the relative squared error (RSE), root mean squared error (RMSE), mean absolute error (MSE), relative root mean squared error (RRMSE), and the performance index $\left(\rho \right)$. The performance index $\left(\rho \right)$ evaluates the model using the function of both RRMSE and R (Gandomi and Roke, 2015). Equations 10–15 show the mathematical expressions of these statical error parameters.

$\text{MAE}=\frac{{\displaystyle {\sum }_{i=1}^n\left|x_i-y_i\right|}}{n},(10)$

$\text{RSE}=\frac{{\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{y}}_{\mathit{i }}-{\mathit{x}}_{\mathit{i}}\right)}^2}}{{\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}}{\left(\overline{\mathit{x}}-{\mathit{x}}_{\mathit{i}}\right)}^2}},(11)$

$\text{RMSE}=\sqrt{\frac{{\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{x}}_{\mathit{i}}-{\mathit{y}}_{\mathit{i}}\right)}^2}}{\mathit{n}}},(12)$

$R=\frac{{\displaystyle {\sum }_{i=1}^n\left(x_i-{\overline{x}}_i\right)\left(y_i-{\overline{y}}_i\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(x_i-{\overline{x}}_i\right)}^2}{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2}}},(13)$

$\text{RRMSE}=\frac{1}{\left|\overline{x}\right|}\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-y_i\right)}^2}}{n}},(14)$

$\rho =\frac{\text{RRMSE}}{1+\text{R}}.(15)$

In the above expressions, here, $y_i$, $x_i$, ${\overline{y}}_i$, and ${\overline{x}}_i$ are the $i^{th}$ model output, experimental output, average model outcome, and average experimental output, respectively. While n shows the number of instances in the dataset. The best calibrated model is the one that yields lower error statistics and a higher value of R. The researchers reported that for a strongly correlated model, the value of R must be greater than 0.8, and for an ideal model, it should be 1 (Gandomi et al., 2011). The value of the performance index $\left(\rho \right)$ generally ranges from zero to positive infinity. Moreover, for the better model performance, $\left(\rho \right)$ should be approximately equal to zero.

K-Fold Cross-Validation Model

Cross-validation (CV) is the technique generally considered for the judgment of the performance and flexibility of the machine learning model, while statistical analysis generalizes to an independent dataset. There are various types of CV techniques, for example, bootstrapping, Jack Knife test, disjoint sets test, three-way split test, and Monte Carlo test. (Saud et al., 2020). The k-fold cross-validation (CV) is carried out to minimize the sampling bias and overfitting issue.

In this research k-fold, CV algorithm is used which is Jack Knife’s test part. The k-fold CV is the technique used to judge the working of the model, which splits the whole dataset into “k” equal subsets. In which, k-1 subsets are used for data training and one subset is hold out which is used for validation or testing with other datasets (Saud et al., 2020). In the k-fold CV technique, the entire procedure is recurring k-times through varying the testing and training data samples. Furthermore, the finest model is chosen via finding minimal error based on different error approximation statistics. The effectiveness of CV is that the entire instances are utilized for training and validation of the model, and every instance is once utilized for the validation purpose. The steps involved in the k-fold CV are as follows:

• Splitting the whole dataset into “k” number of equal parts, known as folds.

• Among “k” folds, one-fold is chosen for testing purposes and “k-1” folds are saved for training purposes.

• The model is fitted upon train folds and predicted upon test fold. This recurs for all the folds.

• For the prediction of the best model, the error is estimated via statistical checks like correlation coefficient (R) and root mean squared error (RMSE). Further, the best coefficient value that corresponds to lesser error is selected.

Kohavi (Kohavi, 1995) reported that the ten-fold CV algorithm provides reliable variance with reduced computational complexity. The whole dataset comprises of 298 instances that are divided into ten-folds. Nine-folds are utilized for training various models. One-fold is held to test against the best coefficient value provided by nine-folds. The entire process is recurred 10 times as the validation is to be executed the number of generations the data are divided. Among the 10 coefficient values, the best coefficient which displays minimal RMSE value is chosen. The flow diagram of the whole k-fold CV is shown in Figure 4.

FIGURE 4

FIGURE 4. Flow diagram of K-fold cross-validation.

Results and Discussion

Performance Assessment of Artificial Neural Network Model

The ANN has its importance in resolving a complex engineering problem. It is initially developed for predicting the models for complicated procedures that are nonlinear in nature. The simulation of the process requires input parameters (garbage in) to predict the output (garbage out). The ultimate results of the ANN predictive model are presented in Figure 5, which shows the slope of the regression lines for training and validation data points, that is, 0.9715 and 0.9762, respectively, (see Figures 5A,B) displays the dispersion of absolute error for the whole dataset utilized in ANN modeling. The percentage of average error and maximum percentage of error come out to be 9.83 and 14.67%, respectively. Nearly 80% of the data points have error values less than 10%. The hidden layers of ANN are like a black box, and it is very hard to find a proposed equation.

FIGURE 5

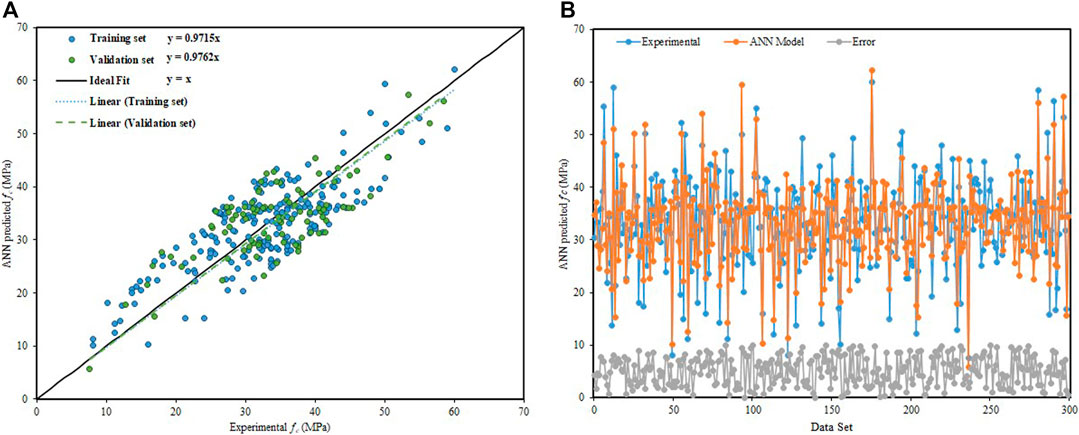
FIGURE 5. ANN model predictive results. (A) Regression line slope of the ANN model. (B) Dispersion of absolute error values of the ANN model.

Performance Assessment of Artificial Neuro-Fuzzy Interface Model

In fuzzy system works on fuzzy reasoning and IF–THEN rules, ANFIS is a more powerful tool which is a combination of fuzzy logic and neural network. Figure 6A depicts that the slope of the regression line in the training and validation stage is 0.9949 and 1.000, respectively, which defines a strong correlation between ANFIS predicted outcome values and experimental outputs of ${f^{\prime }}_c$ of FGPC. Figure 6B displays the outburst performance of the ANFIS predictive model. The average and maximum percent deviation between predictive ANFIS values and experimental values is quite lesser, that is, 2.58 and 6.09%. 95% data points show lesser error than 5%, which proves the superiority of the ANFIS model over the ANN model. Furthermore, the frequency of maximum absolute error is very less.

FIGURE 6

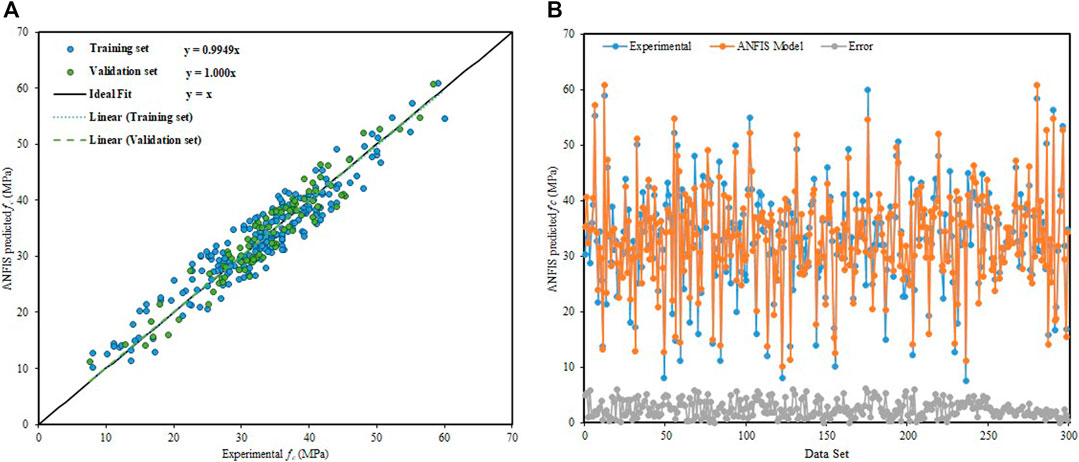
FIGURE 6. ANFIS model predictive results. (A) Regression line slope of the ANFIS model. (B) Dispersion of absolute error values of the ANFIS model.

Gene Expression Programming–Based Empirical Equation

As presented in Figure 7, GEP provides an expression tree (ET) with four sub-ETs, which is translated to have empirical relation for the prediction of compressive strength $\left({f^{\prime }}_c\right)$ of FGPC. Table 5 shows the description of indicators used in the expression tree of the GEP model. Eq. 16 is the final form of GEP’s empirical equation that can be used for the prediction of ${f^{\prime }}_c$ of FGPC in MPa. The variables A, B, C, and D are shown as Eqs 17–20 are the four variables that have been derived from sub-ET-1, sub-ET-2, sub-ET-3, and sub-ET-4, respectively.

$\text{Compressive }\text{strength}\text{of}\text{FGPC}={f^{\prime }}_c\left(\text{MPa}\right)=A\times B\times C\times D,(16)$

$A=\sqrt[3]{\%\left(S/W\right)}-\%P+\left(M\times \left(F/A_G\right)\times \left(A_L/F_A\right)\times 6.61\right)+\%E_W-\%A_G,(17)$

$B=-\sqrt[3]{\frac{A+80}{0.083\left(T-17.9\right)}+M+\left(N_S/N_O\right)},(18)$

$C=\frac{F}{A_G}-\left(\%E_W\times M-\frac{0.0003}{\left(N_S/N_O\right)-\%E_W}\right)-0.0003,(19)$

$D=\sqrt[3]{\frac{(\%P-\%\left(S/W\right)1.160}{T}}+\sqrt[3]{\frac{0.170}{\left(F/A_G\right)}}+\mathrm{0.770.}(20)$

FIGURE 7

FIGURE 7. Expression trees (ETs) of the GEP model.

TABLE 5

TABLE 5. Description of indicators used in expression tree of the GEP model.

Performance Assessment of Gene Expression Programming Model

Figure 8A presents a strong correlation via the slope of the regression line between the predicted results of the GEP model and experimental values. From the training instances and validation instances, the regression line slope is calculated as 1.000 and 0.9892, respectively. The distribution of absolute error values between experimental and targeted outcomes is shown in Figure 8B. The maximum error percentage and the average percentage of absolute error are quite closer, that is, 8.32 and 6.47%, respectively. In comparison with ANN, the occurrence of maximum absolute error values is quite lesser. In the validation stage, 90% of data points of GEP predicted values have an error lower than 10%, with an average percent error lesser than 5.560%. ANFIS gives an outstanding performance as compared to GEP, but it fails in providing a flexible and simplistic empirical equation for future use.

FIGURE 8

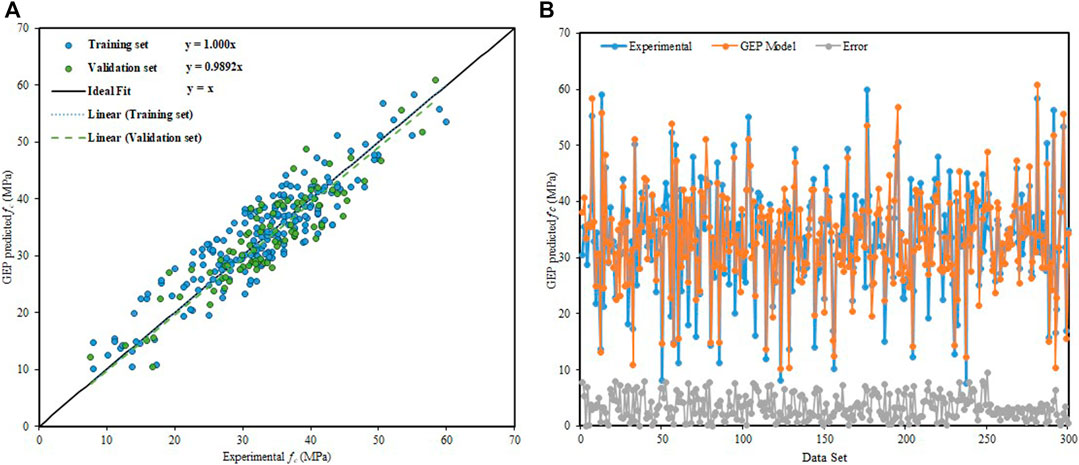
FIGURE 8. GEP model predictive results. (A) Regression line slope of the GEP model. (B) Dispersion of absolute error values of the GEP model.

Statistics and External Verification of Artificial Neural Network, Artificial Neuro-Fuzzy Interface, and Gene Expression Programming Models

The statistics considered in this study for the error analysis of training and validation sets of ANN, ANFIS, and GEP models are shown in Table 6. The results indicate that all three models performed effectively, giving lesser error values. This shows the robust correlation between models predicted outcomes and experimental values. Among all the three models, ANFIS gives an outstanding performance followed by GEP and ANN models. In ANFIS, for the training instances, the MAE, RMSE, RSE, and R equal 3.286, 4.086, 0.294, and 0.9256, respectively, and measured as 2.084, 2.593, 0.0493, and 0.9783 for the validation instances. While for GEP, these values come out to be 5.823, 5.971, 0.325, and 0.8586 for the training instances, respectively, and 2.057, 2.643, 0.0675, and 0.9643 for the validation instances. The consistency of the GEP model is dependent on the number of data points in the dataset. The literature reveals that for the development of a reliable and consistent GEP model, the minimum value of the ratio between total number of instances and the total input variable must 3 (Gandomi and Roke, 2015). This study uses a higher value equal to 30 which comes from 298 data points and 10 input variables. Thus, as compared to ANN, an accurate and reliable GEP predictive model has been accomplished. In general, GEP modeling is preferred over ANFIS and ANN as it provides an empirical relation between the input variables and the response. However, ANN and ANFIS fail in providing an empirical relationship due to its complex architecture. As presented in Table 6, the performance index $\left(\rho \right)$ for all the predictive models is nearly equal to zero. Thus, the developed GEP equation is reliable and accurate and can be utilized for the prediction of fresh data lying within the range provided in Table 2.

TABLE 6

TABLE 6. Statistics of ANN, ANFIS, and GEP models.

The predicted results of all three models are also verified through the statistical checks suggested in the literature. The inclination (slope) of the regression line, that is, $m^{\prime }or m$ (crossing through an origin) must be near to 1 (Aslam et al., 2020). The authors also endorsed that the squared coefficient of correlation (crossing an origin) between the experimental outputs and predictive model results, that is, $R_o^2$ or between the model predictive results and experimental outputs, that is, $R_o^2$ must be near to 1 (Alavi et al., 2011). These external verification checks are summarized in Table 7. This replicates that all the predictive models are correct and accurate and not just work as a correlation but have a predicting capability.

TABLE 7

TABLE 7. Verification of ANN, ANFIS, and GEP models via criteria suggested in the literature.

Comparison Between Artificial Neural Network, Artificial Neuro-Fuzzy Interface, and Gene Expression Programming Models

Figure 9 illustrates the comparison of the output proposed via ANN, ANFIS, and GEP models, for both the training and validation phases. It shows that all the models can capture the output precisely within an acceptable range of error. The performance index $\left(\rho \right)$ and RMSE for the ANFIS model are lesser than ANN and GEP model in both training and validation phases. However, GEP performed better than the ANN model. The ${\rho }_{training}$ and ${\text{RMSE}}_{training}$ for the ANFIS model are 49% and 32% better than the GEP model, respectively; and 51% and 32% better than the ANN model. While in the validation stage, ${\rho }_{validation}$ and ${\text{RMSE}}_{validation}$ are 22% and 2% better than GEP, respectively; and 55% and 48% better than the ANN model. ANFIS is a combination of ANN and fuzzy logic and thus gives an outburst performance in both the validation and training phase. Generally, the GEP predictive model is ideal as it delivers a simplistic and easy mathematical equation for future use.

FIGURE 9

FIGURE 9. Comparison between the predicted compressive strength via ANN, ANFIS, and GEP models.

K-Fold Cross-Validation of the Gene Expression Programming Model

Validation of the model is of great importance in machine learning, to test the performance and generalization ability of the model and to assure the optimal accuracy of the model. CV is conducted via k-fold CV algorithm, to improve the robustness, reliability, and effectiveness of the developed GEP model. The fluctuation in the selected statistical performance, that is, R and RMSE are shown in Figure 10. The maximum, minimum, and mean values of R for the predictive model are 0.9723, 0.8706, and 0.9239, respectively, and 9.5031, 4.4537, and 6.9605 for RMSE, respectively. While the standard deviations of R and RMSE are 0.0328 and 1.5173, respectively. Based on the mentioned statistical indicators, the results of k-fold cross-validation confirm the generalization capacity and accurateness of the predictive model.

FIGURE 10

FIGURE 10. K-fold cross-validation results for the GEP model. (A) Coefficient of correlation (R). (B) Root mean square error (RMSE).

Sensitivity and Parametric Analysis

In this study, sensitivity analysis (SA) is conducted using GEP model outputs. The purpose is to assess the comparative contribution of all the ten explanatory variables utilized for the estimation of compressive strength $\left({f^{\prime }}_c\right)$ of FGPC (Iqbal et al., 2020). The SA explains the dependence of the model outputs upon the explanatory parameters via Eqs 21, 22.

$N_k=f_{\text{max}}\left(x_k\right)-f_{\min }\left(x_k\right),(21)$

$\text{SA}=\frac{N_k}{{\displaystyle {\sum }_n^{i=1}{N}_i}}.(22)$

Here, $x_k$ is the $k^{th}$ input dominion. While $f_{\text{min}}\left(x_k\right)$ and $f_{\text{max}}\left(x_k\right)$ display the minimum and maximum output values, respectively, subjected to $k^{th}$ input dominion keeping the other explanatory variables at their mean values. The $N_k$ represents the range of the $k^{th}$ dominion, which is calculated by taking the difference between $f_{\text{max}}\left(x_k\right)$ and $f_{\text{min}}\left(x_k\right)$. Both, the SA as well as the parametric study were performed only via train instances because both the validation and training set data are consistent. (Gandomi et al., 2011; Iqbal et al., 2020). Figure 11 displays the results of SA for the ${f^{\prime }}_c$ of FGPC (Iqbal et al., 2020).

FIGURE 11

FIGURE 11. Percentage of the comparative contribution of input variables.

In this research, a parametric study is also conducted via GEP model outcomes (using Equation 16), to assess the trend of predicted ${f^{\prime }}_c$ of FGPC with the single explanatory variables. The fluctuation in ${f^{\prime }}_c$ is determined just by varying only one explanatory variable from maximum to minimum, and the rest all are kept constant at their mean values. The ultimate results of the parametric study of ${f^{\prime }}_c$ of the GEP model is shown in Figure 12.

FIGURE 12

FIGURE 12. Change in compressive strength by changing input variables.

In working with GPC, the initial temperature $\left(T\right)$ for curing of samples is the utmost problematic parameter. Figure 11 depicts similar results and shows that $T$ relatively contributes 25.30% in the ${f^{\prime }}_c$ of FGPC. Figure 12 illustrates the trend between the explanatory variables and the response. It shows a linearly decreasing trend between ${f^{\prime }}_c$ and $\left(\%S/W\right)$, $\% E_W$, $M$, and $\left(A_L/F_A\right)$. While the trend of ${f^{\prime }}_c$ with $T$, $\left(N_s/N_o\right)$, $\% A_G$, $\left(F/A_G\right)$, and $A$ is increasing with a different rate.

In the production of FGPC, alkaline solution releases hydroxides and silicates, which creates polymers of alumina silicates. Extra heat is required to expedite its reaction with the source substance and to enhance the ${f^{\prime }}_c$ of FGPC. Figure 12 depicts a rise in ${f^{\prime }}_c$ till curing temperature rises to 100°C. The authors reported that curing of FGPC at higher temperatures results in the loss of moisture content, even if it is sealed properly (Joseph and Mathew, 2012). The ${f^{\prime }}_c$ reduces after 240 days because the gel fills up the voids, resulting in the development of compressed and semi-homogenous structure (Wardhono et al., 2017). Figure 12 displays that ${f^{\prime }}_c$ improves with increase in the volume of total aggregates; however, the volume of total aggregates is directly interlinked with the ration between fine aggregates to total aggregates.

The effect of molarity $\left(M\right)$ of NaOH solution, the $A_L/F_A$ ratio, and $N_s/N_o$ ratio on the ${f^{\prime }}_c$ of FGPC is linked with each other. However, the amount of Na₂SiO₃ alters the microstructure and significantly affects ${f^{\prime }}_c$ of FGPC. So, in the formulation of Na₂SiO₃ solution, the ratio between the percentage of silica $\left(\%S/W\right)$ ratio needs to be greater, to achieve greater ${f^{\prime }}_c$. The lesser $A_L/F_A$ the ratio in connection with the lesser molar solution of NaOH and greater $N_s/N_o$ ratio ensure the high ${f^{\prime }}_c$ of FGPC. However, NaOH solution must be an adequate amount for the completion of dissolution of geopolymers. The same results have also been studied in the previous study (Lokuge et al., 2018).

To accomplish a high workable FGPC mix and to prevent cracking, the addition of extra water and plasticizer is required (Nuruddin et al., 2011a). Figure 11 displays that the inclusion of plasticizers or extra addition of water $\left(E_W\right)$ affects ${f^{\prime }}_c$ 6.71 and 18.85% separately as compared to other input variables. As evident from Figure 12 that ${f^{\prime }}_c$ rises with the inclusion of plasticizers and reduces by adding $E_W$. Because the $E_W$ may cause segregation and bleeding in green concrete, if exceed a certain limit.

The parametric and sensitivity analysis accurately capture the effect of all input parameters considered in the establishment of machine learning models for the prediction of ${f^{\prime }}_c$ of FGPC. Furthermore, results similar to Figure 12 have also been reported by different authors (Nuruddin et al., 2011a; Lokuge et al., 2018).

Conclusion

In this study, the three AI techniques, namely, ANN, ANFIS, and GEP are used for estimating the compressive strength $\left({f^{\prime }}_c\right)$ of FGPC. Ten influential and prominent parameters are used as explanatory variables for the accurate prediction of ${f^{\prime }}_c$ of FGPC. The k-fold CV, statistical error checks, and criterion suggested in the literature are considered for the verification of the predictive tendency of the models. The statistical measure considered in this study is MAE, RSE, RMSE, RRMSE, R, and performance index $\left(\rho \right)$. These checks verify that the ANFIS predictive model gives an outstanding performance followed by GEP and ANN predictive models. In the validation stage, the coefficient of correlation (R) for ANFIS, GEP, and ANN models is 0.9783, 0.9643, and 0.9314, respectively. All three models also accurately fulfill the external verification criterion suggested in the literature. Generally, the GEP predictive model is ideal as it delivers a simplistic and easy mathematical equation for future use. Furthermore, the k-fold CV of the GEP model is also conducted, which verifies the accurateness and robustness of the GEP predictive model. The parametric study is carried via the proposed GEP expression. This confirms that the GEP model accurately covers the influence of all the explanatory variables used for the prediction of ${f^{\prime }}_c$ of FGPC. Thus, the proposed GEP equation can be used in the preliminary design of FGPC.

However, it is highly suggested to conduct the leachate study, before the addition of fly ash (FA) as geopolymer material. This study offers a practical and effective base for the use of hazardous FA in concrete, as a substitute for discarding into landfills. This would eventually step toward viable, sustainable, and efficient construction with reduced greenhouse gases and lesser utilization of energy. In terms of disposal cost of FA and carbon credit, it would increase the economy of a country.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

MAK: methodology, software, data curation, and writing –original draft; AZ: supervision, funding acquisition and project administration; FF: investigation, writing –review and editing; MFJ: conceptualization, software, writing –review and editing; RA: resources and validation; HA: visualization and resources; MIK: resources and formal analysis.

Funding

This research was supported by the deanship of scientific research at Prince Sattam Bin Abdulaziz University under the research project number 2020/01/16810 and was also followed by the National University of science and technology (NUST), Islamabad, Pakistan.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmadi-Nedushan, B. (2012). Prediction of elastic modulus of normal and high strength concrete using ANFIS and optimal nonlinear regression models. Construction Building Mater. 36, 665–673. doi:10.1016/j.conbuildmat.2012.06.002

CrossRef Full Text | Google Scholar

Akande, O., Owolabi, K., O. T., Twaha, S., and Olatunji, S. O. (2014). Performance comparison of SVM and ANN in predicting compressive strength of concrete. IOSR J. Comput. Eng. 16, 88–94. doi:10.9790/0661-16518894

CrossRef Full Text | Google Scholar

Akbar, A., Farooq, F., Shafique, M., Aslam, F., Alyousef, R., and Alabduljabbar, H. (2021). Sugarcane bagasse ash-based engineered geopolymer mortar incorporating propylene fibers. J. Building Eng. 33, 101492. doi:10.1016/j.jobe.2020.101492

CrossRef Full Text | Google Scholar

Akbar, A., and Liew, K. M. (2020). Assessing recycling potential of carbon fiber reinforced plastic waste in production of eco-efficient cement-based materials. J. Clean. Prod. 274, 123001. doi:10.1016/j.jclepro.2020.123001

CrossRef Full Text | Google Scholar

Akbar, A., Liew, K. M., Farooq, F., and Khushnood, R. A. (2020). Exploring mechanical performance of hybrid MWCNT and GNMP reinforced cementitious composites. Constr. Build. Mater. 267, 120721. doi:10.1016/j.conbuildmat.2020.120721

CrossRef Full Text | Google Scholar

Alavi, A. H., Ameri, M., Gandomi, A. H., and Mirzahosseini, M. R. (2011). Formulation of flow number of asphalt mixes using a hybrid computational method. Construction Building Mater. 25, 1338–1355. doi:10.1016/j.conbuildmat.2010.09.010

CrossRef Full Text | Google Scholar

Alavi, A. H., and Gandomi, A. H. (2011). Prediction of principal ground-motion parameters using a hybrid method coupling artificial neural networks and simulated annealing. Comput. Structures 89, 2176–2194. doi:10.1016/j.compstruc.2011.08.019

CrossRef Full Text | Google Scholar

Albitar, M., Visintin, P., Mohamed Ali, M. S., and Drechsler, M. (2015). Assessing behaviour of fresh and hardened geopolymer concrete mixed with class-F fly ash. KSCE J. Civ. Eng. 19, 1445–1455. doi:10.1007/s12205-014-1254-z

CrossRef Full Text | Google Scholar

Aliabdo, A. A., Abd Elmoaty, A. E. M., and Salem, H. A. (2016). Effect of cement addition, solution resting time and curing characteristics on fly ash based geopolymer concrete performance. Construction Building Mater. 123, 581–593. doi:10.1016/j.conbuildmat.2016.07.043

CrossRef Full Text | Google Scholar

Alkroosh, I. S., and Sarker, P. K. (2019). Prediction of the compressive strength of fly ash geopolymer concrete using gene expression programming. Comput. Concr. 24, 295–302. doi:10.12989/cac.2019.24.4.295

CrossRef Full Text | Google Scholar

Aprianti S, E. (2017). A huge number of artificial waste material can be supplementary cementitious material (SCM) for concrete production - a review part II. J. Clean. Prod. 142, 4178–4194. doi:10.1016/j.jclepro.2015.12.115

CrossRef Full Text | Google Scholar

Aslam, F., Farooq, F., Amin, M. N., Khan, K., Waheed, A., Akbar, A., et al. (2020). Applications of gene expression programming for estimating compressive strength of high-strength concrete. Adv. Civil Eng. 2020, 1–23. doi:10.1155/2020/8850535

CrossRef Full Text | Google Scholar

Assi, L. N., Deaver, E., Elbatanouny, M. K., and Ziehl, P. (2016). Investigation of early compressive strength of fly ash-based geopolymer concrete. Construction Building Mater. 112, 807–815. doi:10.1016/j.conbuildmat.2016.03.008

CrossRef Full Text | Google Scholar

Babanajad, S. K., Gandomi, A. H., and Alavi, A. H. (2017). New prediction models for concrete ultimate strength under true-triaxial stress states: an evolutionary approach. Adv. Eng. Softw. 110, 55–68. doi:10.1016/j.advengsoft.2017.03.011

CrossRef Full Text | Google Scholar

Bachir, R., Sidi Mohammed, A. M., and Habib, T. (2018). Using artificial neural networks approach to estimate compressive strength for rubberized concrete. Period. Polytech. Civil Eng. 62, 858–865. doi:10.3311/PPci.11928

CrossRef Full Text | Google Scholar

Bajpai, R., Choudhary, K., Srivastava, A., Sangwan, K. S., and Singh, M. (2020). Environmental impact assessment of fly ash and silica fume based geopolymer concrete. J. Clean. Prod. 254, 120147. doi:10.1016/j.jclepro.2020.120147

CrossRef Full Text | Google Scholar

Beheshti Aval, S. B., Ketabdari, H., and Asil Gharebaghi, S. (2017). Estimating shear strength of short rectangular reinforced concrete columns using nonlinear regression and gene expression programming. Structures 12, 13–23. doi:10.1016/j.istruc.2017.07.002

CrossRef Full Text | Google Scholar

Behnia, D., Ahangari, K., Noorzad, A., and Moeinossadat, S. R. (2013). Predicting crest settlement in concrete face rockfill dams using adaptive neuro-fuzzy inference system and gene expression programming intelligent methods. J. Zhejiang Univ. Sci. A. 14, 589–602. doi:10.1631/jzus.A1200301

CrossRef Full Text | Google Scholar

Carlson, C. L., and Adriano, D. C. (1993). Environmental impacts of coal combustion residues. J. Environ. Qual. 22, 227–247. doi:10.2134/jeq1993.00472425002200020002x

CrossRef Full Text | Google Scholar

Çaydaş, U., Hasçalik, A., Ekici, S., Hasçalık, A., and Ekici, S. (2009). An adaptive neuro-fuzzy inference system (ANFIS) model for wire-EDM. Expert Syst. Appl. 36, 6135–6139. doi:10.1016/j.eswa.2008.07.019

CrossRef Full Text | Google Scholar

Chen, L., Wang, L., Cho, D.-W., Tsang, D. C. W., Tong, L., Zhou, Y., et al. (2019). Sustainable stabilization/solidification of municipal solid waste incinerator fly ash by incorporation of green materials. J. Clean. Prod. 222, 335–343. doi:10.1016/j.jclepro.2019.03.057

CrossRef Full Text | Google Scholar

Chou, J.-S., and Pham, A.-D. (2013). Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Construction Building Mater. 49, 554–563. doi:10.1016/j.conbuildmat.2013.08.078

CrossRef Full Text | Google Scholar

Dao, D., Ly, H.-B., Trinh, S., Le, T.-T., and Pham, B. (2019). Artificial intelligence approaches for prediction of compressive strength of geopolymer concrete. Materials 12, 983. doi:10.3390/ma12060983

CrossRef Full Text | Google Scholar

Deb, P. S., Nath, P., and Sarker, P. K. (2013a). Properties of fly ash and slag blended geopolymer concrete cured at ambient temperature, In S. Yazdani, and A. Singh (ed) ISEC 2013 - 7th International Structural Engineering and Construction Conference, Manoa, Honolulu, Jun 18-23 2013, 571–576. doi:10.3850/978-981-07-5354-2-M-55-433

CrossRef Full Text | Google Scholar

Deb, P. S., Sarker, P. K., and Nath, P. (2013b). Sulphate resistance of slag blended fly ash based geopolymer concrete, In V. Dao, and P. Dux (ed) Proceedings of the 26th Biennial National Conference of the Concrete Institute Australia: Understanding Concrete, Gold Coast, QLD, Australia, Oct 16-18 2013

Google Scholar

del Viso, J. R., Carmona, J. R., and Ruiz, G. (2008). Shape and size effects on the compressive strength of high-strength concrete. Cement Concrete Res. 38, 386–395. doi:10.1016/j.cemconres.2007.09.020

CrossRef Full Text | Google Scholar

Dwivedi, A., and Jain, M. K. (2014). Fly ash – waste management and overview : a Review. Recent Res. Sci. Technol. 6, 30–35.

Google Scholar

Emamian, S. A., and Eskandari-Naddaf, H. (2019). Effect of porosity on predicting compressive and flexural strength of cement mortar containing micro and nano-silica by ANN and GEP. Construction Building Mater. 218, 8–27. doi:10.1016/j.conbuildmat.2019.05.092

CrossRef Full Text | Google Scholar

Fareed Ahmed, M., Fadhil Nuruddin, M., and Shafiq, N. (2011). Compressive strength and workability characteristics of low-calcium fly ash-based self-compacting geopolymer concrete. World Acad. Sci. Eng. Technol. 74, 8–14.

Google Scholar

Farooq, F., Ahmed, W., Akbar, A., Aslam, F., and Alyousef, R. (2021). Predictive modeling for sustainable high-performance concrete from industrial wastes: a comparison and optimization of models using ensemble learners. J. Clean. Prod. 292, 126032. doi:10.1016/j.jclepro.2021.126032

CrossRef Full Text | Google Scholar

Farooq, F., Akbar, A., Khushnood, R. A., Muhammad, W. L. B., Rehman, S. K. U., and Javed, M. F. (2020a). Experimental investigation of hybrid carbon nanotubes and graphite nanoplatelets on rheology, shrinkage, mechanical, and microstructure of SCCM. Materials 13, 230. doi:10.3390/ma13010230

CrossRef Full Text | Google Scholar

Farooq, F., Nasir Amin, M., Khan, K., Rehan Sadiq, M., Faisal Javed, M. F., Aslam, F., et al. (2020b). A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC). Appl. Sci. 10, 7330–7418. doi:10.3390/app10207330

CrossRef Full Text | Google Scholar

Farooq, F., Rahman, S. K. U., Akbar, A., Khushnood, R. A., Javed, M. F., alyousef, R., et al. (2020c). A comparative study on performance evaluation of hybrid GNPs/CNTs in conventional and self-compacting mortar. Alexandria Eng. J. 59, 369–379. doi:10.1016/j.aej.2019.12.048

CrossRef Full Text | Google Scholar

Ferreira, C. (2006). Gene expression programming mathematical modeling by an artificial intelligence, Berlin, Heidelberg: Springer.

Galvin, B., Lloyd, N., and Lecturer, S. (1978). Fly ash based geopolymer concrete with recycled concrete aggregate, Perth, Australia: Curtin University.

Gandomi, A. H., Alavi, A. H., Mirzahosseini, M. R., and Nejad, F. M. (2011). Nonlinear genetic-based models for prediction of flow number of asphalt mixtures. J. Mater. Civ. Eng. 23, 248–263. doi:10.1061/(ASCE)MT.1943-5533.0000154

CrossRef Full Text | Google Scholar

Gandomi, A. H., Babanajad, S. K., Alavi, A. H., and Farnam, Y. (2012). Novel approach to strength modeling of concrete under triaxial compression. J. Mater. Civ. Eng. 24, 1132–1143. doi:10.1061/(ASCE)MT.1943-5533.0000494

CrossRef Full Text | Google Scholar

Gandomi, A. H., and Roke, D. A. (2015). Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 88, 63–72. doi:10.1016/j.advengsoft.2015.05.007

CrossRef Full Text | Google Scholar

Gandomi, A. H., Yun, G. J., and Alavi, A. H. (2013). An evolutionary approach for modeling of shear strength of RC deep beams. Mater. Struct. 46, 2109–2119. doi:10.1617/s11527-013-0039-z

CrossRef Full Text | Google Scholar

Ganesan, N., Abraham, R., and Deepa Raj, S. (2015). Durability characteristics of steel fibre reinforced geopolymer concrete. Construction Building Mater. 93, 471–476. doi:10.1016/j.conbuildmat.2015.06.014

CrossRef Full Text | Google Scholar

Getahun, M. A., Shitote, S. M., and Abiero Gariy, Z. C. (2018). Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Construction Building Mater. 190, 517–525. doi:10.1016/j.conbuildmat.2018.09.097

CrossRef Full Text | Google Scholar

Ghazali, N., Muthusamy, K., and Wan Ahmad, S. (2019). Utilization of fly ash in construction, in IOP conference series: materials science and engineering. Bristol, UK: Institute of Physics Publishing. doi:10.1088/1757-899X/601/1/012023

CrossRef Full Text | Google Scholar

Gholampour, A., Gandomi, A. H., and Ozbakkaloglu, T. (2017). New formulations for mechanical properties of recycled aggregate concrete using gene expression programming. Construction Building Mater. 130, 122–145. doi:10.1016/j.conbuildmat.2016.10.114

CrossRef Full Text | Google Scholar

Gülşan, M. E., Alzeebaree, R., Rasheed, A. A., Niş, A., and Kurtoğlu, A. E. (2019). Development of fly ash/slag based self-compacting geopolymer concrete using nano-silica and steel fiber. Constr. Build. Mater. 211, 271–283. doi:10.1016/j.conbuildmat.2019.03.228

CrossRef Full Text | Google Scholar

Hamad, A. J. (2017). Size and shape effect of specimen on the compressive strength of HPLWFC reinforced with glass fibres. J. King Saud Univ. - Eng. Sci. 29, 373–380. doi:10.1016/j.jksues.2015.09.003

CrossRef Full Text | Google Scholar

Hammoudi, A., Moussaceb, K., Belebchouche, C., and Dahmoune, F. (2019). Comparison of artificial neural network (ANN) and response surface methodology (RSM) prediction in compressive strength of recycled concrete aggregates. Construction Building Mater. 209, 425–436. doi:10.1016/j.conbuildmat.2019.03.119

CrossRef Full Text | Google Scholar

Hardjito, D., and Rangan, B. V. (2005). Development and properties of low-calcium fly ash-based geopolymer concrete, Perth, Australia: Curtin University of Technology

Iqbal, M. F., Liufeng, Q.-f., Azim, I., Azim, X., Yang, J., Javed, M. F., et al. (2020). Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 384, 121322. doi:10.1016/j.jhazmat.2019.121322

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishak, S., Lee, H. S., Singh, J. K., Ariffin, M. A. M., Lim, N. H. A. S., and Yang, H. M. (2019). Performance of fly ash geopolymer concrete incorporating bamboo ash at elevated temperature. Materials 12, 3404. doi:10.3390/ma12203404

CrossRef Full Text | Google Scholar

Jaafari, A., Panahi, M., Pham, B. T., Shahabi, H., Bui, D. T., Rezaie, F., et al. (2019). Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 175, 430–445. doi:10.1016/j.catena.2018.12.033

CrossRef Full Text | Google Scholar

Javed, M. F., Amin, M. N., Shah, M. I., Khan, K., Iftikhar, B., Farooq, F., et al. (2020a). Applications of gene expression programming and regression techniques for estimating compressive strength of bagasse ash based concrete. Crystals 10, 737–817. doi:10.3390/cryst10090737

CrossRef Full Text | Google Scholar

Javed, M. F., Farooq, F., Memon, S. A., Akbar, A., Khan, M. A., Aslam, F., et al. (2020b). New prediction model for the ultimate axial capacity of concrete-filled steel tubes: an evolutionary approach. Crystals 10, 741. doi:10.3390/cryst10090741

CrossRef Full Text | Google Scholar

Jena, S., Panigrahi, R., and Sahu, P. (2019). Mechanical and durability properties of fly ash geopolymer concrete with silica fume. J. Inst. Eng. India Ser. A. 100, 697–705. doi:10.1007/s40030-019-00400-z

CrossRef Full Text | Google Scholar

Joseph, B., and Mathew, G. (2012). Influence of aggregate content on the behavior of fly ash based geopolymer concrete. Scientia Iranica 19, 1188–1194. doi:10.1016/j.scient.2012.07.006

CrossRef Full Text | Google Scholar

Kohavi, R. (1995). A study of cross-validation and bootstrap for accuracy estimation and model selection. Int. Jt. Conf. Artif. Intell. Available at: http://robotics.stanford.edu/∼ronnyk (Accessed January 2, 2021)

Google Scholar

Kondepudi, K., and Subramaniam, K. V. L. (2019). Rheological characterization of low-calcium fly ash suspensions in alkaline silicate colloidal solutions for geopolymer concrete production. J. Clean. Prod. 234, 690–701. doi:10.1016/j.jclepro.2019.06.124

CrossRef Full Text | Google Scholar

Koza, J. R., and Poli, R. (2005). Genetic programming. Search methodologies: introductory tutorials in optimization and decision support techniques (Boston, MA: Springer), 127–164. doi:10.1007/0-387-28356-0_5

CrossRef Full Text | Google Scholar

Kumar Tiwari, M., Bajpai, S., and Kumar Dewangan, U. (2016). Fly ash utilization: a brief review in Indian context. Int. Res. J. Eng. Technol. 3, 949-956.

Google Scholar

Kusbiantoro, A., Nuruddin, M. F., Shafiq, N., and Qazi, S. A. (2012). The effect of microwave incinerated rice husk ash on the compressive and bond strength of fly ash based geopolymer concrete. Construction Building Mater. 36, 695–703. doi:10.1016/j.conbuildmat.2012.06.064

CrossRef Full Text | Google Scholar

Lavanya, G., and Jegan, J. (2015). Evaluation of relationship between split tensile strength and compressive strength for geopolymer concrete of varying grades and molarity. Int. J. Appl. Eng. Res. 10, 35523–35529. http://www.ripublication.com.

Google Scholar

Liew, K. M., and Akbar, A. (2020). The recent progress of recycled steel fiber reinforced concrete. Construction Building Mater. 232, 117232. doi:10.1016/j.conbuildmat.2019.117232

CrossRef Full Text | Google Scholar

Lokuge, W., Wilson, A., Gunasekara, C., Law, D. W., and Setunge, S. (2018). Design of fly ash geopolymer concrete mix proportions using Multivariate Adaptive Regression Spline model. Construction Building Mater. 166, 472–481. doi:10.1016/j.conbuildmat.2018.01.175

CrossRef Full Text | Google Scholar

Long, T., Shi, X. S., Wang, Q. Y., and Li, L. (2013). Mechanical properties and microstructure of fly ash based geopolymeric polymer recycled concrete. Sichuan Daxue Xuebao (Gongcheng Kexue Ban)/journal Sichuan Univ. (Engineering Sci. Ed. 45, 43–47.

Google Scholar

Luhar, S., Chaudhary, S., and Luhar, I. (2019). Development of rubberized geopolymer concrete: strength and durability studies. Construction Building Mater. 204, 740–753. doi:10.1016/j.conbuildmat.2019.01.185

CrossRef Full Text | Google Scholar

Ly, H. B., Pham, B. T., Dao, D., Le, V. M., Le, L. M., and Le, T. T. (2019). Improvement of ANFIS model for prediction of compressive strength of manufactured sand concrete. Appl. Sci. 9, 3841. doi:10.3390/app9183841

CrossRef Full Text | Google Scholar

Mashhadban, H., Kutanaei, S. S., and Sayarinejad, M. A. (2016). Prediction and modeling of mechanical properties in fiber reinforced self-compacting concrete using particle swarm optimization algorithm and artificial neural network. Construction Building Mater. 119, 277–287. doi:10.1016/j.conbuildmat.2016.05.034

CrossRef Full Text | Google Scholar

Meesala, C. R., Verma, N. K., and Kumar, S. (2020). Critical review on fly‐ash based geopolymer concrete. Struct. Concrete 21, 1013–1028. doi:10.1002/suco.201900326

CrossRef Full Text | Google Scholar

Mehta, A., and Siddique, R. (2017). Properties of low-calcium fly ash based geopolymer concrete incorporating OPC as partial replacement of fly ash. Construction Building Mater. 150, 792–807. doi:10.1016/j.conbuildmat.2017.06.067

CrossRef Full Text | Google Scholar

Nadesan, M. S., and Dinakar, P. (2017). Mix design and properties of fly ash waste lightweight aggregates in structural lightweight concrete. Case Stud. Construction Mater. 7, 336–347. doi:10.1016/j.cscm.2017.09.005

CrossRef Full Text | Google Scholar

Nath, P., and Sarker, P. K. (2017). Flexural strength and elastic modulus of ambient-cured blended low-calcium fly ash geopolymer concrete. Construction Building Mater. 130, 22–31. doi:10.1016/j.conbuildmat.2016.11.034

CrossRef Full Text | Google Scholar

Nguyen, K. T., Nguyen, Q. D., Le, T. A., Shin, J., and Lee, K. (2020). Analyzing the compressive strength of green fly ash based geopolymer concrete using experiment and machine learning approaches. Construction Building Mater. 247, 118581. doi:10.1016/j.conbuildmat.2020.118581

CrossRef Full Text | Google Scholar

Noori, R., Hoshyaripour, G., Ashrafi, K., and Araabi, B. N. (2010). Uncertainty analysis of developed ANN and ANFIS models in prediction of carbon monoxide daily concentration. Atmos. Environ. 44, 476–482. doi:10.1016/j.atmosenv.2009.11.005

CrossRef Full Text | Google Scholar

Noushini, A., Castel, A., Aldred, J., and Rawal, A. (2020). Chloride diffusion resistance and chloride binding capacity of fly ash-based geopolymer concrete. Cement and Concrete Composites 105, 103290. doi:10.1016/j.cemconcomp.2019.04.006

CrossRef Full Text | Google Scholar

Nuaklong, P., Jongvivatsakul, P., Pothisiri, T., Sata, V., and Chindaprasirt, P. (2020). Influence of rice husk ash on mechanical properties and fire resistance of recycled aggregate high-calcium fly ash geopolymer concrete. J. Clean. Prod. 252, 119797. doi:10.1016/j.jclepro.2019.119797

CrossRef Full Text | Google Scholar

Nuaklong, P., Sata, V., and Chindaprasirt, P. (2016). Influence of recycled aggregate on fly ash geopolymer concrete properties. J. Clean. Prod. 112, 2300–2307. doi:10.1016/j.jclepro.2015.10.109

CrossRef Full Text | Google Scholar

Nuruddin, M. F., Demie, S., and Shafiq, N. (2011a). Effect of mix composition on workability and compressive strength of self-compacting geopolymer concrete. Can. J. Civ. Eng. 38, 1196–1203. doi:10.1139/l11-077

CrossRef Full Text | Google Scholar

Nuruddin, M. F., Qazi, S. A., Kusbiantoro, A., and Shafiq, N. (2011b). Utilisation of waste material in geopolymeric concrete. Proc. Inst. Civil Eng. - Construction Mater. 164, 315–327. doi:10.1680/coma.2011.164.6.315

CrossRef Full Text | Google Scholar

Okoye, F. N., Durgaprasad, J., and Singh, N. B. (2015). Mechanical properties of alkali activated flyash/Kaolin based geopolymer concrete. Construction Building Mater. 98, 685–691. doi:10.1016/j.conbuildmat.2015.08.009

CrossRef Full Text | Google Scholar

Olivia, M., and Nikraz, H. (2012). Properties of fly ash geopolymer concrete designed by Taguchi method. Mater. Des. (1980-2015) 36, 191–198. doi:10.1016/j.matdes.2011.10.036

CrossRef Full Text | Google Scholar

Patankar, S. V., Ghugal, Y. M., and Jamkar, S. S. (2015). Mix design of fly ash based geopolymer concrete, in Advances in structural engineering: materials, New Delhi: Springer India, Vol 3, 1619–1634. doi:10.1007/978-81-322-2187-6_123

CrossRef Full Text | Google Scholar

Patankar, S. V., Jamkar, S. S., and Ghugal, Y. M. (2013). Effect of water-to-geopolymer binder ratio on the production of fly ash based geopolymer concrete. Int. J. Adv. Technol. Civ. Eng., 79–83. doi:10.13140/2.1.4792.1284

CrossRef Full Text | Google Scholar

Paulson, A. J., Prabhavathy, R. A., Rekh, S., and Brindha, E. (2019). Application of neural network for prediction of compressive strength of silica fume concrete. Int. J. Civ. Eng. Technol. 10, 1859 Available at: http://www.iaeme.com/IJCIET/index.asp1859http://www.iaeme.com/ijmet/issues.asp?JType=IJCIET&VType=10&IType=2. http://www.iaeme.com/IJMET/index.asp1860http://www.iaeme.com/IJCIET/issues.asp?JType=IJCIET&VType=10&IType=2 (Accessed January 31, 2021)

Google Scholar

Prachasaree, W., Limkatanyu, S., Hawa, A., Sukontasukkul, P., and Chindaprasirt, P. (2020). Manuscript title: development of strength prediction models for fly ash based geopolymer concrete. J. Building Eng. 32, 101704. doi:10.1016/j.jobe.2020.101704

CrossRef Full Text | Google Scholar

Rafieizonooz, M., Mirza, J., Salim, M. R., Hussin, M. W., and Khankhaje, E. (2016). Investigation of coal bottom ash and fly ash in concrete as replacement for sand and cement. Construction Building Mater. 116, 15–24. doi:10.1016/j.conbuildmat.2016.04.080

CrossRef Full Text | Google Scholar

Ramujee, K., and Potharaju, M. (2017). Mechanical properties of geopolymer concrete composites. in Materials today: proceedings. Amsterdam, Netherlands: Elsevier Ltd, 2937–2945. doi:10.1016/j.matpr.2017.02.175

CrossRef Full Text | Google Scholar

Sadrmomtazi, A., Sobhani, J., and Mirgozar, M. A. (2013). Modeling compressive strength of EPS lightweight concrete using regression, neural network and ANFIS. Construction Building Mater. 42, 205–216. doi:10.1016/j.conbuildmat.2013.01.016

CrossRef Full Text | Google Scholar

Sadrossadat, E., Ghorbani, B., Hamooni, M., and Moradpoor Sheikhkanloo, M. H. (2018). Numerical formulation of confined compressive strength and strain of circular reinforced concrete columns using gene expression programming approach. Struct. Concrete 19, 783–794. doi:10.1002/suco.201700131

CrossRef Full Text | Google Scholar

Safiuddin, M., Raman, S., Abdus Salam, M., and Jumaat, M. (2016). Modeling of compressive strength for self-consolidating high-strength concrete incorporating palm oil fuel ash. Materials 9, 396. doi:10.3390/ma9050396

CrossRef Full Text | Google Scholar

Sandanayake, M., Gunasekara, C., Law, D., Zhang, G., Setunge, S., and Wanijuru, D. (2020). Sustainable criterion selection framework for green building materials - an optimisation based study of fly-ash Geopolymer concrete. Sustainable Mater. Tech. 25, e00178. doi:10.1016/j.susmat.2020.e00178

CrossRef Full Text | Google Scholar

Saridemir, M. (2010). Genetic programming approach for prediction of compressive strength of concretes containing rice husk ash. Constr. Build. Mater. 24, 1911–1919. doi:10.1016/j.conbuildmat.2010.04.011

CrossRef Full Text | Google Scholar

Sarker, P. K., Haque, R., and Ramgolam, K. V. (2013). Fracture behaviour of heat cured fly ash based geopolymer concrete. Mater. Des. 44, 580–586. doi:10.1016/j.matdes.2012.08.005

CrossRef Full Text | Google Scholar

Sathanandam, T., Awoyera, P. O., Vijayan, V., and Sathishkumar, K. (2017). Low carbon building: experimental insight on the use of fly ash and glass fibre for making geopolymer concrete. Sustainable Environ. Res. 27, 146–153. doi:10.1016/j.serj.2017.03.005

CrossRef Full Text | Google Scholar

Satpute, S., Shirasath, M., and Hake, S. (2016). Investigation of alkaline activators for fly-ash based geo-polymer concrete. Int. J. Adv. Res. Innov. Ideas Educ., 2 (5), 2395–4396.

Saud, S., Jamil, B., Upadhyay, Y., and Irshad, K. (2020). Performance improvement of empirical models for estimation of global solar radiation in India: a k-fold cross-validation approach. Sustainable Energ. Tech. Assessments 40, 100768. doi:10.1016/j.seta.2020.100768

CrossRef Full Text | Google Scholar

Sebaaly, H., Varma, S., and Maina, J. W. (2018). Optimizing asphalt mix design process using artificial neural network and genetic algorithm. Construction Building Mater. 168, 660–670. doi:10.1016/j.conbuildmat.2018.02.118

CrossRef Full Text | Google Scholar

Shaikh, F. U. A. (2016). Mechanical and durability properties of fly ash geopolymer concrete containing recycled coarse aggregates. Int. J. Sustainable Built Environ. 5, 277–287. doi:10.1016/j.ijsbe.2016.05.009

CrossRef Full Text | Google Scholar

Shaikh, F. U. A., and Vimonsatit, V. (2015). Compressive strength of fly-ash-based geopolymer concrete at elevated temperatures. Fire Mater. 39, 174–188. doi:10.1002/fam.2240

CrossRef Full Text | Google Scholar

Shehab, H. K., Eisa, A. S., and Wahba, A. M. (2016). Mechanical properties of fly ash based geopolymer concrete with full and partial cement replacement. Construction Building Mater. 126, 560–565. doi:10.1016/j.conbuildmat.2016.09.059

CrossRef Full Text | Google Scholar

Sujatha, T., Kannapiran, K., and Nagan, S. (2012). Strength assessment of heat cured geopolymer concrete slender column. Asian J. Civ. Eng. 13, 635–646.

Google Scholar

Sumajouw, M. D. J., and Rangan, . B. V. (2006). Low-Calcium fly ash-based geopolymer Concrete : reinforced beams and columns. Perth, Australia: Curtin University of Technology, 1–120.

Sumanth Kumar, B., Sen, A., and Rama Seshu, D. (2020). Shear strength of fly ash and GGBS based geopolymer concrete, in Lecture notes in civil engineering. Berlin, Germany: Springer, 105–117. doi:10.1007/978-981-15-3361-7_8

CrossRef Full Text | Google Scholar

Thesis, A., Joseph, B., and Philosophy, D. O. F. (2015). Behaviour of geopolymer concrete exposed to elevated temperatures school of engineering, Kochi, India: Cochin University of Science and Technology, 682022

Tran, T. T., Pham, T. M., and Hao, H. (2019). Rectangular stress-block parameters for fly-ash and slag based geopolymer concrete. Structures 19, 143–155. doi:10.1016/j.istruc.2019.01.006

CrossRef Full Text | Google Scholar

Van Jaarsveld, J. G. S., Van Deventer, J. S. J., and Lukey, G. C. (2002). The effect of composition and temperature on the properties of fly ash- and kaolinite-based geopolymers. Chem. Eng. J. 89, 63–73. doi:10.1016/S1385-8947(02)00025-6

CrossRef Full Text | Google Scholar

Vora, P. R., and Dave, U. V. (2013). Parametric studies on compressive strength of geopolymer concrete. Proced. Eng. 51, 210–219. doi:10.1016/j.proeng.2013.01.030

CrossRef Full Text | Google Scholar

Wang, L., Chen, L., Cho, D.-W., Tsang, D. C. W., Yang, J., Hou, D., et al. (2019a). Novel synergy of Si-rich minerals and reactive MgO for stabilisation/solidification of contaminated sediment. J. Hazard. Mater. 365, 695–706. doi:10.1016/j.jhazmat.2018.11.067

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Wang, D., and Chen, H. (2017). The role of fly ash microsphere in the microstructure and macroscopic properties of high-strength concrete. Cement and Concrete Composites 83, 125–137. doi:10.1016/j.cemconcomp.2017.07.021

CrossRef Full Text | Google Scholar

Wang, Y., Hu, S., and He, Z. (2019b). Mechanical and fracture properties of fly ash geopolymer concrete addictive with calcium aluminate cement. Materials 12, 2982. doi:10.3390/ma12182982

CrossRef Full Text | Google Scholar

Wardhono, A., Gunasekara, C., Law, D. W., and Setunge, S. (2017). Comparison of long term performance between alkali activated slag and fly ash geopolymer concretes. Construction Building Mater. 143, 272–279. doi:10.1016/j.conbuildmat.2017.03.153

CrossRef Full Text | Google Scholar

Watts, J. (2019). Concrete: the most destructive material on Earth. Guard, 1–11, February 25, 2019.

Google Scholar

Wongsa, A., Siriwattanakarn, A., Nuaklong, P., Sata, V., Sukontasukkul, P., Chindaprasirt, P., et al. (2020). Use of recycled aggregates in pressed fly ash geopolymer concrete. Environ. Prog. Sustainable Energ. 39. doi:10.1002/ep.13327

CrossRef Full Text | Google Scholar

Wongsa, A., Zaetang, Y., Sata, V., and Chindaprasirt, P. (2016). Properties of lightweight fly ash geopolymer concrete containing bottom ash as aggregates. Construction Building Mater. 111, 637–643. doi:10.1016/j.conbuildmat.2016.02.135

CrossRef Full Text | Google Scholar

Xie, J., Wang, J., Rao, R., Wang, C., and Fang, C. (2019). Effects of combined usage of GGBS and fly ash on workability and mechanical properties of alkali activated geopolymer concrete with recycled aggregate. Composites B: Eng. 164, 179–190. doi:10.1016/j.compositesb.2018.11.067

CrossRef Full Text | Google Scholar

Yaseen, Z. M., Deo, R. C., Hilal, A., Abd, A. M., Bueno, L. C., Salcedo-Sanz, S., et al. (2018). Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 115, 112–125. doi:10.1016/j.advengsoft.2017.09.004

CrossRef Full Text | Google Scholar

Zhang, H., Li, L., Sarker, P. K., Long, T., Shi, X., Wang, Q., et al. (2019). Investigating various factors affecting the long-term compressive strength of heat-cured fly ash geopolymer concrete and the use of orthogonal experimental design method. Int. J. Concr. Struct. Mater. 13. doi:10.1186/s40069-019-0375-7

CrossRef Full Text | Google Scholar

Zhang, H. Y., Qiu, G. H., Kodur, V., and Yuan, Z. S. (2020a). Spalling behavior of metakaolin-fly ash based geopolymer concrete under elevated temperature exposure. Cement and Concrete Composites 106, 103483. doi:10.1016/j.cemconcomp.2019.103483

CrossRef Full Text | Google Scholar

Zhang, P., Gao, Z., Wang, J., Guo, J., Hu, S., and Ling, Y. (2020b). Properties of fresh and hardened fly ash/slag based geopolymer concrete: a review. J. Clean. Prod. 270, 122389. doi:10.1016/j.jclepro.2020.122389

CrossRef Full Text | Google Scholar