BIC-Based Data-Driven Rail Track Deterioration Adaptive Piecewise Modeling Framework

The records of maintenance activities are required for modeling the track irregularity deterioration process. However, it is hard to guarantee the completeness and accuracy of the maintenance records. To tackle this problem, an adaptive piecewise modeling framework for the rail track deterioration process driven by historical measurement data from the comprehensive inspection train (referred to as CIT) is proposed. The identification of when maintenance activities occurred is reformulated as a model selection optimization problem based on Bayesian Information Criterion. An efficient solution algorithm utilizing adaptive thresholding and dynamic programming is proposed for solving this optimization problem. This framework’s validity and practicability are illustrated by the measurement data from the CIT inspection of the mileage section of K21 + 184 to K220 + 308 on the Nanchang-Fuzhou railway track from 2014 to 2019. The results indicate that this framework can overcome the disturbance of contaminated measurement data and accurately estimate when maintenance activities were undertaken without any historical maintenance records. What is more, the adaptive piecewise fitting model provided by this framework can describe the irregular deterioration process of corresponding rail track sections.

Introduction

Track irregularity directly impacts the running stability and safety of trains. Maintaining tracks in an acceptable condition is essential, but it consumes many physical and staff resources. In order to develop cost-effective and rational maintenance plans under limited resources, prior information about track irregularity is required. Thus, this study on predicting the deterioration of track irregularity is critical to railway operation. Many kinds of research have been carried out to forecast track irregularity. Meier-Hirmer et al., (2006) modeled the changes in standard deviation of longitudinal level within a maintenance cycle using the Gamma process. Veit and Marsching, 2010 developed an exponential function to model the behavior of track quality deterioration between two adjacent maintenance events and discussed the interrelations between deterioration rate and the initial quality. Zhu et al., (2013) applied a Gaussian random process to model track irregularities of profile and alignment and studied their power spectral densities. Considering that the evolution of track irregularity is periodic, exponential, and has multiple stages, Xu et al., (2012) employed a multi-stage linear fitting model to describe the track irregularity deterioration process between two adjacent maintenance actions. Lee et al., (2018) combined an artificial neural network (ANN) and support vector regression (SVR) to better represent the deterioration phenomena of track segments for optimizing the maintenance plans in terms of time and cost. In their experiments, at least two years of maintenance records were required to obtain a stable prediction of track deterioration. Mercier et al., (2012) conjointly utilized longitudinal and transversal leveling indicators using a bivariate Gamma process to predict track quality. Vale and Lurdes (2013) developed a stochastic model based on the Dagum distribution for longitudinal level.

Considering that maintenance activities, including tamping, grinding, and others obviously recover track irregularity and have an effect on the deterioration modes (Quiroga and Schnieder, 2010), the aforementioned studies mainly focus on the deterioration process between adjacent maintenance activities. Some studies for multiple maintenance periods have been developed under the following two main assumptions. One is that maintenance records are accessible for modeling; the other is that deterministic mathematical models can express the relationship between deterioration rates and initial qualities right after maintenance actions. Accordingly, segmenting the deterioration process of track irregularity according to maintenance activities is fundamental for exploring the deterioration rules based on historical measurement data. However, the complete and accurate records of maintenance activities are unobtainable because most of the previous records have been lost. Thus, it has become an urgent task to establish an algorithm to automatically identify when maintenance activities were carried out in the process of deterioration (referred to as maintenance-points). Each maintenance-point is tagged by the detection date, which is right after the maintenance activities.

Identification of maintenance-points in the process of track irregularity deterioration is equivalent to making inferences about unknown multiple change-points in the field of applied statistics. There are vast amounts of studies on multiple change-points analysis in different applied contexts, for example, in econometrics (Dias, 2004), in biology (Xi et al., 2011), in climatology (Reeves et al., 2007; Lu et al., 2010), and in hydrology (Perreault et al., 2000). It has also been introduced to traffic flow data for freeway incident detection. Yang et al., (2014) proposed the coupled Bayesian RPCA by extending the Bayesian robust principal component analysis (RPCA) approach for detecting unusual traffic events. The traffic events were localized based on coupling the multiple traffic data streams. Liu et al., (2008) developed an automated traffic incidents detection algorithm on the basis of the cumulative sum (CUSUM). Moreover, in order to achieve real-time defect detection of high-speed train wheels, Wang et al., (2020) utilized the Bayesian dynamic linear model (DLM) to detect change-points in strain monitoring data from high-speed train bogies. Many effective methods have been developed and verified, such as maximum likelihood, Bayes-type, cumulative sum, and others (Jandhyala et al., 2013). Among them, information criteria provides a method for multiple change-points estimation without any priori information on their locations and number (Hall et al., 2013). Bayesian Information Criterion (referred to as BIC) is popularly applied (Watanabe, 2012; Hall et al., 2015). BIC was proposed by Schwarz (1978) and is widely applied as a model selection criterion. Regarding the number of change-points as the dimension of the model, Yao (1988) applied BIC for making inferences about the change-points when the means of observations on different time periods were distinct. However, Zhang and Siegmund (2007) found that the classic BIC had poor performance when applied to irregular statistical models. Thus, Zhang proposed a modified BIC that differently penalized the model dimension components of BIC’s objective function. Hannart and Naveau (2012) improved BIC for multiple change-points analysis by introducing priori information on the relative positions and amplitude of change-points and deriving a closed-form mathematical expression of the criterion based on Laplace approximation. Successes in applying BIC to other practical problems such as detecting change in acoustics have been widely reported in the literature (Chen and Gopalakrishnan, 1998; Kotti et al., 2006).

The major contribution of this paper is to propose an adaptive piecewise modeling framework that is driven by historical measurement data from CIT and enables us to describe the rail track deterioration process. This framework is capable of tolerating contaminated measurement data and automatically identifying maintenance-points in the process of deterioration. This problem is reformulated as a model selection optimization problem by taking advantage of BIC. Linear regression (referred to as LR) is applied to model each subsequence individually divided by maintenance-points. Then the objective function is derived according to the framework of BIC and is modified by incorporating an optimized weight for the model complexity component. Based on the effect of maintenance activities on deterioration rate, an efficient solution algorithm for minimizing the objective function is developed by comprehensively utilizing the adaptive thresholding and dynamic programming. The proposed framework is validated by the measurement data for the Nanchang-Fuzhou railway track through CIT collection from 2014 to 2019.

The rest of the article is organized as follows. In Modeling framework based on Bayesian Information Criterion Section, we derive an objective function based on BIC and modify it by incorporating a weight coefficient. In Solution algorithm Section, we develop a solution algorithm based on adaptive thresholding and dynamic programming. Then, we discuss the optimal value of weight coefficient. In Empirical analysis Section, the performance of the proposed framework is evaluated by practical measurement data. Finally, we summarize the research and discuss our ongoing work related to this article.

Modeling Framework Based on Bayesian Information Criterion

For Chinese railways, the track quality index (TQI) is employed to quantify track irregularity. It is the sum of standard deviations of seven geometrical parameters for a 200 m-long track section (Xu et al., 2011). The standard deviation for each geometrical parameter is calculated from measurement data collected by CIT. Among the seven geometrical parameters, track profile irregularity is particularly related to mechanized maintenance activities. Thus, the inference about maintenance-points is studied on the basis of track profile irregularity (referred to as $TQ{I}_p$).

The inference of change-points based on BIC is a model selection procedure that minimizes a constrained function based on the maximum likelihood method defined by BIC (Gang and Ghosh, 2011). Accordingly, we reformulate the inference on the number and locations of maintenance-points in the deterioration process of $TQ{I}_p$ into a model selection problem based on BIC. Denoting the set of all piecewise LR models as $\Omega$ and each model in it as ${\rm M}\in \Omega$. BIC defines the optimal fitting model from $\Omega$ as the one that minimizes Eq. 1.

$BIC=-2\ln \left(L\right)+K\ln \left(N\right)(1)$

wherein $N$ is the sample size, $L$ is the maximized likelihood of fitting model $M$, and $K$ is the number of parameters to be estimated.

In a certain time period, suppose that $n$ inspections have been accomplished for a 200 m-long track section, the set of difference in days between the $i^{th}$ detection date and the first detection date are denoted by $t=\left(t_1,t_2,\cdots ,t_n\right)$ while the set of corresponding detection values of $TQ{I}_p$ by $y=\left(y_1,y_2,\cdots ,y_n\right)$. And there are $m$ maintenance-points in $y=\left(y_1,y_2,\cdots ,y_n\right)$. The maintenance-points split $y=\left(y_1,y_2,\cdots ,y_n\right)$ into $m+1$ independent subsequences. Denoting ${\tau }_k(0\le k\le m+1)$ as the maintenance-point that splits the $k^{th}$ and the ${(k+1)}^{st}$ subsequences and ${\tau }_0=0$, ${\tau }_{m+1}=t_n$. Each subsequence is modeled by LR. Thus, the LR model ${\widehat{M}}_k$ for the $k^{th}$ subsequence is denoted as

$y_i={\beta }_{k0}+{\beta }_{k1}{t}_i+{\epsilon }_k({\tau }_{k-1}\le t_i<{\tau }_k)(2)$

where ${\beta }_k=\left({\beta }_{k0},{\beta }_{k1}\right)$ is the corresponding parameter vector for ${\widehat{M}}_k$ and the random error term ${\mathit{\epsilon }}_{\mathit{k}}$ is iid. Denoting the variance of ${\epsilon }_k$ as ${\sigma }_k^2$, we obtain that ${\epsilon }_k\sim N\left(0,{\sigma }_k^2\right)$. Based on the assumption on the distribution of ${\epsilon }_k$, for ${\tau }_{k-1}\le t_i<{\tau }_k$, we obtain that $y_i\sim N({\beta }_{k0}+{\beta }_{k1}{t}_i,{\sigma }_k^2)$. Denoting the value of $TQ{I}_p$ in the $i^{th}(0<i\le n)$ detection as $y_i$ and the probability density function of $y_i$ is expressed as

$P\left(y_i\right)=\frac{1}{{\sigma }_k\sqrt{2\pi }}{e}^{-\frac{1}{2{\sigma }_k^2}{\left(y_i-{\beta }_{k0}-{\beta }_{k1}{t}_i\right)}^2}(3)$

the maximum likelihood estimation of ${\widehat{M}}_k$ is

$L\left({\widehat{M}}_k|{\beta }_k,{\sigma }_k^2\right)=\frac{1}{{\left(2\pi {\sigma }_k^2\right)}^{\frac{{\tau }_k-{\tau }_{k-1}}{2}}}{e}^{-\frac{1}{2{\sigma }_k^2}{\displaystyle \sum }_{t_i={\tau }_{k-1}}^{{\tau }_k}{\left(y_i-{\beta }_{k0}-{\beta }_{k1}{t}_i\right)}^2}(4)$

${\sigma }_k^2=\frac{1}{{\tau }_k-{\tau }_{k-1}}{\displaystyle \sum }_{t_i={\tau }_{k-1}}^{{\tau }_k}{(y_i-{\beta }_{k0}-{\beta }_{k1}{t}_i)}^2(5)$

Suppose that $\widehat{M}=\left\{{\widehat{M}}_1,{\widehat{M}}_2,\cdots ,{\widehat{M}}_{m+1}\right\}$,$\beta =\left\{{\beta }_1,{\beta }_2,\cdots ,{\beta }_{m+1}\right\}$, the maximum likelihood estimation of$\widehat{M}$ is

$L\left(\widehat{M}|\beta ,{\sigma }^2\right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{\sigma }^2}{e}^{-\frac{{{\displaystyle \sum }}_{k=1}^{m+1}\left({\tau }_k-{\tau }_{k-1}\right)}{2}}(6)$

${\sigma }^2={\displaystyle \prod }_{k=1}^{m+1}{\left({\sigma }_k^2\right)}^{\frac{{\tau }_k-{\tau }_{k-1}}{2}}(7)$

The number of parameters to be estimated, including $\left[\left({\beta }_{10},{\beta }_{11}\right),\cdots ,\left({\beta }_{(m+1)0},{\beta }_{(m+1)1}\right)\right]$, $\left({\tau }_1,\cdots ,{\tau }_m\right)$, and ${\sigma }^2$ is $3m$. Based on Eq. 1, we obtain

$BIC\left(\widehat{M}\right)=n\left(\ln 2\pi +1\right)+\ln {\sigma }^2+3m\ln \left(n\right)(8)$

$n\left(\ln 2\pi +1\right)$ in Eq. 8 is fixed when the series is given. Accordingly, the objective function of $BIC\left(\widehat{M}\right)$ is redefined as

$BIC\left(\widehat{M}\right)=\ln {\sigma }^2+3m\ln \left(n\right)(9)$

where $\ln {\sigma }^2$ is the sum of squared residuals that reflects the precision of the model and $3m\ln \left(n\right)$ is the penalty term of model complexity. We denote $\zeta \left(0<\zeta \le 1\right)$ as a weight coefficient for the complexity of the fitting model. The weight coefficient is determined according to a guideline which will be introduced in The optimal value of the weight coefficient Section. Thus, the object function is

$BIC\left(\widehat{M}\right)=\ln {\sigma }^2+\zeta \times 3m\ln \left(n\right)(10)$

The optimal fitting model $\widehat{M}$ for the deterioration process is defined as the one that minimizes Eq. 10. And we consider that the change-points of $\widehat{M}$ are the maintenance-points which will be identified in the deterioration process.

Solution Algorithm

Since the number of maintenance-points is unknown, a large amount of computation is needed for attaining the optimal fitting model based on Eq. 10. In order to reduce computation load and to make the algorithm practical, we propose an efficient solution algorithm based on the characteristics of maintenance-points.

The Different Characteristics of Maintenance-Points and Contaminated Measurement Data

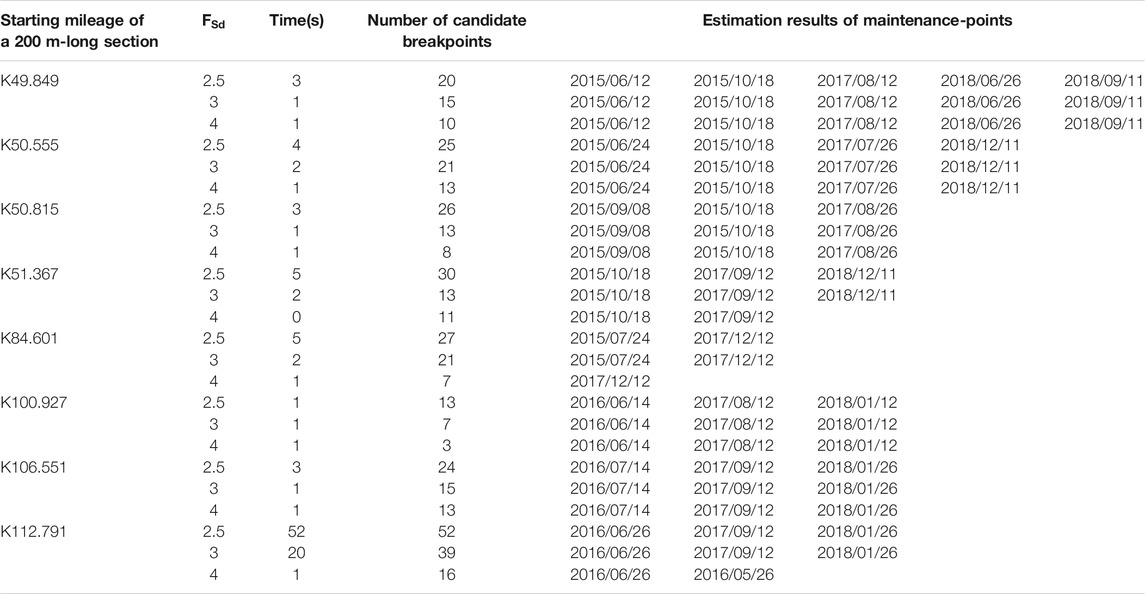
This paper is targeted to automatically identify the maintenance-points in the deterioration process of $TQ{I}_p$ for exploring the deterioration rules of track irregularity. However, outliers in the deterioration process caused by contaminated measurement data might interfere with the identification of maintenance-points. Each outlier is tagged by the corresponding detection date. Maintenance-points and outliers are characterized as follows.

The deterioration process of $TQ{I}_p$ of a 200 m-long track section on the Nanchang-Fuzhou railway from 2014 to 2019 is shown in Figure 1. As shown in Figure 1, the value of $TQ{I}_p$ drops obviously after maintenance activities. Denoting the first order difference of $y=\left(y_1,y_2,\cdots ,y_n\right)$ as $d=\left(d_1,d_2,\cdots ,d_n\right)$ where $d_1=0$ and $d_i=y_i-y_{i-1}$. $d_i$ is much greater/smaller than the neighboring values if maintenance activities were carried out at $t_i$. The outliers caused by contaminated measurement data display the same characteristics. The difference between the maintenance-points and outliers is their different impact on the current deterioration process. The maintenance-points terminate the current deterioration cycle, reduce the value of $TQ{I}_p$ to a specified scope, and start a new deterioration cycle. Outliers show significant deviations from the current deterioration process but have no impact on the current deterioration rate.

FIGURE 1

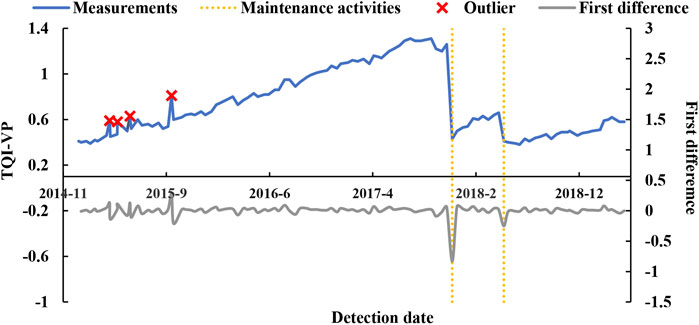
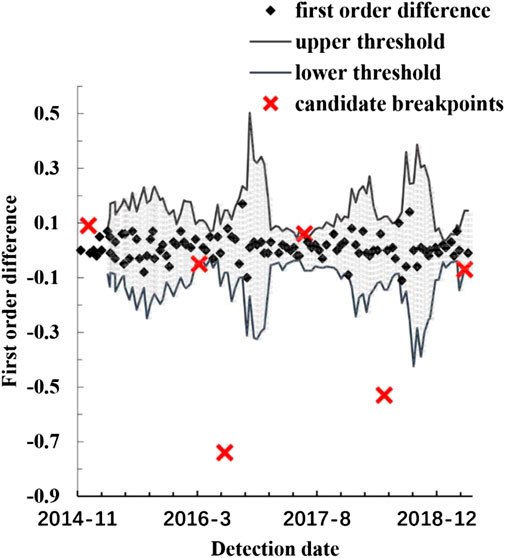
FIGURE 1. The different characteristics of maintenance activities and contaminated measurement data.

Candidate Breakpoints Identified by Adaptive Thresholding Method

The maintenance-points and outliers in the deterioration process are collectively referred to as “candidate breakpoints”. Distinguishing the maintenance-points from outliers within candidate breakpoints will greatly reduce computation load. Accordingly, we develop a method for identifying candidate breakpoints in the deterioration process based on the aforementioned characteristics of maintenance-points and outliers. Constant thresholding is not feasible since track irregularity recovers at different degrees after maintenance among track sections. What is more, outliers cannot be within a predetermined range. Adaptive thresholding provides a solution to this problem (Breier and Branišová, 2015; Wang, 2015). On the basis of adaptive thresholding, we develop a method combining the autoregressive model (referred to as AR) to identify candidate breakpoints in the deterioration process.

Candidate breakpoints are localized by applying this method to the first order difference $d=(d_1,d_2,\cdots ,d_n)$ of $TQ{I}_p$. The values of $(d_1,d_2,\cdots ,d_n)$ are dynamically stable within a small range if there is no candidate breakpoint, while the similarity in the distribution of $(d_1,d_2,\cdots ,d_n)$ is destroyed if there is a candidate breakpoint. Thus, we define a sliding window, and the value at the current moment is predicated based on the historical values which are selected into the sliding window. AR is applied to predicate the value at the current moment based on the historical values. The values of the upper threshold and lower threshold are adjusted via the predicated value and variance of historical values in the sliding window. The difference between predicated value and actual value at the current moment decides whether there is a candidate breakpoint or not. We consider $t_i$ as a candidate breakpoint if $d_i$ exceeds the preset thresholds. The method is divided into five steps as follows.

Step one: calculate the first order difference $d=(d_1,d_2,\cdots ,d_n)$ of $TQ{I}_p$.

Step two: denote the sliding window as $w=(w_1,w_2,\cdots ,w_l)$ where $l$ is the window size and the absolute value of every element in $d$ as $d_{abs}=\left(\left|d_1\right|,\left|d_2\right|,\cdots ,\left|d_n\right|\right)$. $q_{90}$ is defined as the 90%-quantile of $d_{abs}$. Starting with the first element in $d_{abs}$, $d_i$ is added into $w$ if $\left|d_i\right|\le q_{90}$ while $t_i$ is tagged as a candidate breakpoint if $\left|d_i\right|>q_{90}$, then the remaining elements are recursively checked in sequence until the sliding window is full.

Step three: fit $w$ with $AR\left(p\right)$ through the Yule-Walker method (Brockwell et al., 1987), where $p$ is the order of the AR model. Denote the predicated value at the current moment by $AR\left(p\right)$ as ${\tilde{d}}_i$.

Step four: according to the Pauta criterion ($3\sigma$ criterion), the proportion of outliers in a series is less than $0.3\mathit{\%}$ under the constraint of $3\sigma$ (Li et al., 2016). We denote the upper threshold as $T_{upper}$ and the lower threshold as $T_{lower}$, then

$T_{upper}={\tilde{d}}_i+3\times Sd(11)$

$T_{lower}={\tilde{d}}_i-3\times Sd(12)$

where $Sd$ is the standard deviation of historical values in $w$.

Step five: if $d_i\notin \left[T_{lower},T_{upper}\right]$, $t_i$ is tagged as a candidate breakpoint, and $w$ is not changed. Otherwise, $d_i$ is added into $w$ while the earliest element in $w$ is removed. Return to Step three until all of the elements in $d$ have been detected.

The candidate breakpoints identified by the aforementioned method are denoted by ${\tau }_c=\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_{\tilde{m}}\right)$ where $\tilde{m}$ is the number of candidate breakpoints. The composite diagram of a typical realization is shown in Figure 2, in which dots represent the first order difference of $TQ{I}_p$, the shaded part represents the limitation range of thresholds, and red crosses represent the identified candidate breakpoints. Moreover, the pseudocode of the adaptive thresholding method is provided in Figure 3.

FIGURE 2

FIGURE 2. A typical realization of the adaptive thresholding method.

FIGURE 3

FIGURE 3. Pseudo code for the adaptive thresholding method.

Dynamic Programming for Finding Optimal Fitting Model

Dynamic programming is a multi-stage optimization method and is applicable to various practical problems (Bellman and Dreyfus, 1962). We now consider a method based on the principle of dynamic programming to find an optimal fitting model that achieves the minimum of Eq. 10. Suppose that $r\left(1\le r\le \tilde{m}\right)$ breakpoints are selected from all the candidate breakpoints ${\tau }_c=\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_{\tilde{m}}\right)$ and then the series $y=\left(y_1,y_2,\cdots ,y_n\right)$ is divided into $r+1$ subsequences. To find the optimal fitting model, LR is employed to fit each subsequence by the least-square method, independently. Then, $BIC\left(\widehat{M}\right)$ is calculated according to Eq. 10. Finally, the optimal fitting model is acquired by iterating to the minimum. Let $\mathrm{Min}\left(z\right)$ be the minimum of object $z$. When the number of the selected breakpoints is $r$, $\mathrm{Min}\left[BIC\left(\widehat{M}|r\right)\right]$ is equal to $\mathrm{Min}\left[S\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_r\right)\right]$ where

$S\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_r\right)=In\left({\sigma }^2\right)={\displaystyle \sum }_{k=1}^{r+1}\left[\frac{{\tau }_k-{\tau }_{k-1}}{2}In\left({\sigma }_k^2\right)\right](13)$

$c\left({\tau }_{k-1},{\tau }_k\right)$ is defined as the sum of squared residuals for the subsequence, which is constrained in $\left({\tau }_{k-1},{\tau }_k\right)$. We obtain

$c\left({\tau }_{k-1},{\tau }_k\right) =\frac{{\tau }_k-{\tau }_{k-1}}{2}In\left({\sigma }_k^2\right)(14)$

$S\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_r\right)={\displaystyle \sum }_{k=1}^{r+1}c\left({\tau }_{k-1},{\tau }_k\right)(15)$

For $0\le j\le r$, defining $b_{r-j}\left({\tau }_j\right)$ as the minimum of $S\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_r\right)$ on the basis that the first $j$ breakpoints are confirmed, we obtain

$b_{r-j}\left({\tau }_j\right)=\underset{{\tau }_{j+1},\cdots ,{\tau }_r}{\mathrm{Min}}\left[{\displaystyle \sum }_{k=j+1}^{r+1}c\left({\tau }_{k-1},{\tau }_k\right)\right](16)$

Considering the tamping will not be operated for a rail track section twice in a month, we set the constraint that ${\tau }_{j+1}-{\tau }_j>30$ and suppose that ${\tau }_0=t_0,{\tau }_{r+1}=t_n$. Searching the optimal combination of candidate breakpoints is equivalent to solving the following recursive problem:

$\begin{array}{l}{b}_{r-j}\left({\tau }_j\right)=\underset{{\tau }_j+30<{\tau }_{j+1}<{\tau }_{j+1}-30\times \left(r-j-1\right)}{\mathrm{Min}}\left\{c\left({\tau }_j,{\tau }_{j+1}\right)+\underset{{\tau }_{j+2},\cdots ,{\tau }_r}{\mathrm{Min}}\left[{\displaystyle \sum }_{k=j+2}^{r+1}c\left({\tau }_{k-1},{\tau }_k\right)\right]\right\}\\ =\underset{{\tau }_j+30<{\tau }_{j+1}<{\tau }_{j+1}-30\times \left(r-j-1\right)}{\mathrm{Min}}\left\{c\left({\tau }_j,{\tau }_{j+1}\right)+b_{r-j-1}\left({\tau }_{j+1}\right)\right\}\end{array}(17)$

To sum up, the recurrence formulas are

$\{\begin{array}{c}{b}_0\left({\tau }_r\right)=c\left({\tau }_r,{\tau }_{r+1}\right)\\ b_{r-j}\left({\tau }_j\right)=\underset{{\tau }_j+30<{\tau }_{j+1}<{\tau }_{j+1}-30\times \left(r-j-1\right)}{\mathrm{Min}}\left\{c\left({\tau }_j,{\tau }_{j+1}\right)+b_{r-j-1}\left({\tau }_{j+1}\right)\right\}\left(0\le j<r\right)\end{array}(18)$

From the previous, it is concluded that $\mathrm{Min}\left[BIC\left(\widehat{M}|r\right)\right]=b_r\left({\tau }_0\right)$. What is more, $\mathrm{Min}\left[BIC\left(\widehat{M}|r+1\right)\right]$ can be calculated based on the intermediate results for computing $b_r\left({\tau }_0\right)$. Denoting $f_r\left({\tau }_z\right)$ as the optimal results for the subsequence which begins at ${\tau }_z$ under the circumstance that the number of selected candidate breakpoints is $r$, then the recurrence formulas of $f_r\left({\tau }_z\right)$ are

$\{\begin{array}{c}{f}_0\left({\tau }_z\right)=c\left({\tau }_z,{\tau }_{r+1}\right)\\ f_r\left({\tau }_z\right)=\underset{{\tau }_z+30<{\tau }_1<{\tau }_{r+1}-30\times \left(r-1\right)}{\mathrm{Min}}\left\{c\left({\tau }_z,{\tau }_1\right)+f_{r-1}\left({\tau }_1\right)\right\}\left(1\le r\le \tilde{m}\right)\end{array}(19)$

Searching the optimal results under the assumption that there are $r$ maintenance-points in the deterioration process of $TQ{I}_p$ is equivalent to calculating $f_r\left({\tau }_0\right)$. The iteration is terminated if the aforementioned constraint cannot be satisfied. For $1\le r\le \tilde{m}$, the set of optimal results with a different number of selected candidate breakpoints is denoted by $f\left({\tau }_0\right)=\left[f_1\left({\tau }_0\right),f_2\left({\tau }_0\right),\cdots f_{\tilde{m}}\left({\tau }_0\right)\right]$ and the optimal piecewise fitting model is the one that achieves $\mathrm{Min}\left[f\left({\tau }_0\right)\right]$. The change-points of this model which are selected from the set of candidate breakpoints, are the maintenance-points, while others are outliers.

The Optimal Value of the Weight Coefficient

The value of the weight coefficient $\zeta$ in Eq. 10 has a significant impact on the accuracy and reliability of the results identified by the aforementioned framework. Relying on the historical measurement data from 2014 to 2019 for the nearly 200 km-long track sections of the Nanchang-Fuzhou rail line (as shown in Figure 4), we obtain the optimal value of $\zeta$ which enables the identified maintenance-points to almost correspond with the actual ones. The measurement data are acquired from CIT, which inspects the railways twice a month on average in China. In particular, the preprocessing and transforming of measurement data, which include mileage correction, historical waveform data alignment, and the TQI calculation of each geometric parameter, have been completed relying on the system developed by our team (Xu et al., 2015). Thus, we consider that the data are complete and reliable. Meanwhile, we obtain a set of actual maintenance-points of each track section via manual analysis. They were considered as correctly identified maintenance-points if they were also included in the set of the actual ones.

FIGURE 4

FIGURE 4. Location of the Nanchang-Fuzhou rail line.

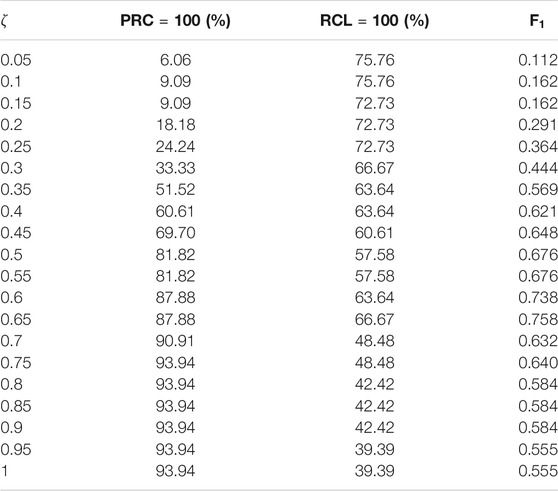
To assess the performance of the proposed framework with different values of $\zeta$, we employ the precision (referred to as PRC) and recall rates (referred to as RCL) given by:

$PRC=\frac{T_{est}}{T_{est}+F_{est}}\times 100\%(20)$

$RCL=\frac{T_{est}}{M_{man}}\times 100\% (21)$

where $T_{est}$ denotes the number of correctly identified maintenance-points from candidate breakpoints , $F_{est}$ is the number of erroneous ones, and $M_{man}$ is the number of actual maintenance-points from manual analysis. $F_1$ defined by Eq. 22 is also considered. The higher the value of $F_1$, better performance is obtained.

$F_1=\frac{2\times PRC\times RCL}{PRC+RCL}(22)$

To find the optimal value of $\zeta$, the maintenance-points of each rail track section are estimated by the proposed framework, whose $\zeta$ gradually increases by 0.05. By contrast, using the estimated maintenance-points to the actual ones, we obtain the PRC and RCL of each section. For each $\zeta$, the proportion of sections whose PRC = 100% and sections whose RCL = 100% are counted separately, while the results are tabulated in Table 1. From Table 1, it is concluded that RCL is getting smaller while PRC is getting larger with the increase of $\zeta$. Based on $F_1$, the optimal value of $\zeta$ is determined as 0.65.

TABLE 1

TABLE 1. The statistic results for different values of weight coefficient.

Empirical Analysis

In this section, 33 track sections of 200 m in length are further analyzed to demonstrate the performance of the presented framework with $\zeta =0.65$. Then, the calculation procedure of this framework is displayed through two track sections in detail.

Performance Analysis

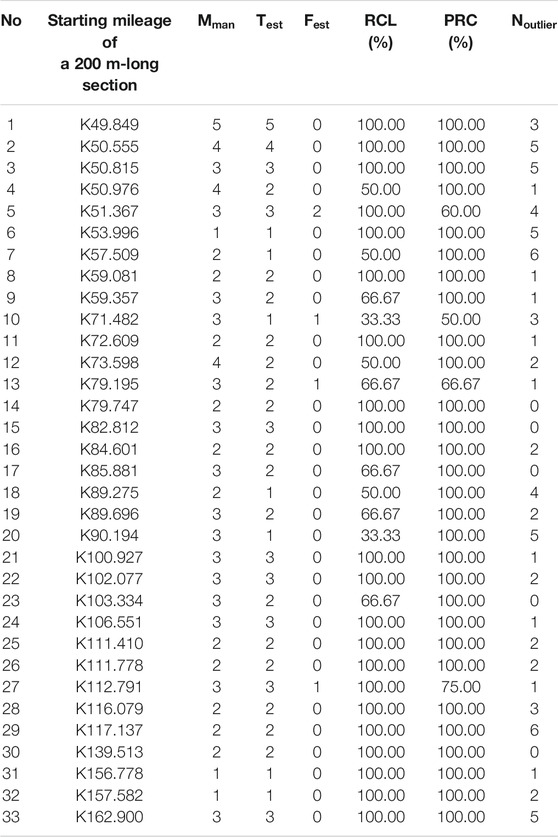
PRC and RCL for each track section are calculated based on the comparison between the estimated maintenance-points and the actual ones. To evaluate the accuracy of the presented framework with the interference of contaminated measurement data, we have investigated the outliers due to the contaminated measurement data of each track section. $N_{outlier}$ is denoted as the number of outliers. The results of the metrics are tabulated in Table 2. Based on that, we obtain the distributions of PRC and RCL, which are tabulated in Table 3.

TABLE 2

TABLE 2. The evaluation for the identification results of different rail track sections.

TABLE 3

TABLE 3. The distributions of PRC and RCL.

From Table 3, we obtain that the proposed framework owns a high PRC and RCL for most rail track sections. It indicates that this framework is capable of overcoming the disturbance of contaminated measurement data and accurately distinguishing the maintenance-points from outliers within candidate breakpoints. Meanwhile, the RCL of a few sections are not satisfactory. Through analyzing further, we find that it has resulted from the fact that not all maintenance-points are included in the set of candidate breakpoints.

Sensitivity Analysis

A large range of thresholds in Candidate Breakpoints Identified by the Adaptive Thresholding Method Section leads to an excessive number of candidate breakpoints, requiring more time to obtain the minimum of Eq. 10. However, the actual maintenance-points might be left out if the range of thresholds is too small. Accordingly, the sensitivity of this framework to the range of thresholds is discussed in this section. According to Eqs 11, 12, we find that the range of thresholds is significantly affected by the times of $Sd$ (the standard deviation of historical values selected into the sliding window), which is denoted by $F_{Sd}$. To access the sensitivity, we apply this framework to some of the sections in Table 2 for each $F_{Sd}\in \left\{2.5,\mathrm{3,4}\right\}$. The other values of parameters in the implementation of this framework are kept consistent with those in Performance Analysis Section. The comparison results among different values of $F_{Sd}$ are tabulated in Table 4. The computation time in seconds and the number of candidate breakpoints are given in column 3, 4, while the estimated maintenance-points of each section with different values of $F_{Sd}$ are given in column 5.

TABLE 4

TABLE 4. The comparison results among different values of $F_{Sd}$.

From Table 4, we obtain that compared with $F_{Sd}=3$, the computation time is increased by 145% on average for $F_{Sd}=2.5$. What is more, the estimated maintenance-points are the same between $F_{Sd}=3$ and $F_{Sd}=2.5$. Although it requires less computation time when $F_{Sd}=4$, some of the actual maintenance-points are left out as the estimation results of the sections starting at K51.367, K84.601, and K112.791 indicate. Thus, it is reasonable that $F_{Sd}=3$ in Candidate Breakpoints Identified by the Adaptive Thresholding Method Section.

Section One: K117 + 137–K117 + 337

This section is on a tangent track. The candidate breakpoints identified by the adaptive thresholding method are shown in Figure 5A. The value of $\mathrm{Min}\left[BIC\left(\widehat{M}|r\right)\right]$ for a different number of selected candidate breakpoints are shown in Figure 5B and $BIC\left(\widehat{M}\right)$ obtains the minimum when the number is 2. The identified maintenance-points are 2016-05-26 and 2018-04-13. The estimated maintenance-points and piecewise fitting model are shown in Figure 5C. The maintenance-points estimated by the proposed framework are exactly as the actual ones. The deterioration process is divided into three subprocesses. Although there are lots of outliers caused by contaminated measurement data in the first subprocess, the maintenance-points are accurately identified.

FIGURE 5

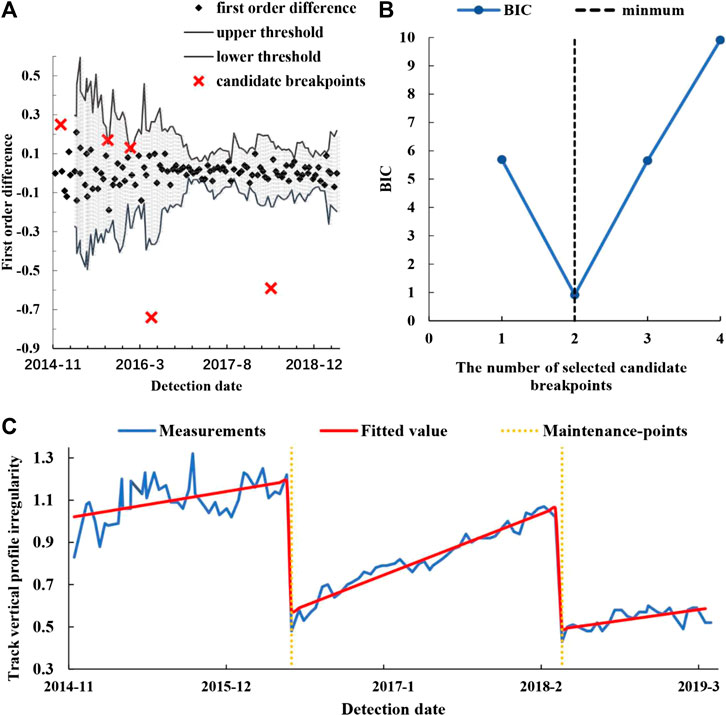
FIGURE 5. The identified maintenance-points and piecewise fitting model of section one: (A) the candidate breakpoints identified by the adaptive thresholding method; (B) the value of BIC for a different number of selected candidate breakpoints; (C) the piecewise fitting model.

Section Two: K162 + 900–K163 + 100

This section is on a curved track. The candidate breakpoints identified by the adaptive thresholding method are shown in Figure 6A, and the value of $\mathrm{Min}\left[BIC\left(\widehat{M}\right|r)\right]$ for this section are shown in Figure 6B. The number of selected candidate breakpoints corresponding to the optimal result is 3. The estimated maintenance-points and piecewise fitting model are shown in Figure 6C. The identified maintenance-points are 2016-3-14, 2018-01-12, and 2018-06-26. The outliers caused by contaminated measurement data are mainly located in the first subprocess. The slope of the fitting model for each subprocess reflects its deterioration rate. It is obvious that the deterioration rates are different before and after maintenance activities. Thus, we believe that the deterioration rates might be affected by maintenance activities.

FIGURE 6

FIGURE 6. The identified maintenance-points and piecewise fitting model of section two: (A) the candidate breakpoints identified by adaptive thresholding method; (B) the value of BIC for a different number of selected candidate breakpoints; (C) the piecewise fitting model.

Conclusion

In this paper, a rail track deterioration modeling framework driven by historical measurement data from CIT is proposed. The modeling framework requires no historical maintenance records and does not assume the quality of track measurement data. The proposed framework formulates the identification of maintenance activities with a model selection optimization problem, based on a modified Bayesian Information Criterion by incorporating an optimized weight for the model complexity component into the objective function. An efficient solution algorithm utilizing adaptive thresholding and dynamic programming is proposed for the model selection problem, taking the characteristics of the effect of maintenance on track deterioration trend.

The proposed track deterioration modeling framework is applied to the historical measurement data from 2014 to 2019 for the nearly 200 km-long track sections of the Nanchang-Fuzhou rail line. Based on that application, the optimal value of the weight coefficient which is incorporated for the model complexity is discussed in The Optimal Value of the Weight Coefficient Section. Moreover, the assessment indicators are calculated based on 33 200 m-long track sections. As the assessment indicators indicate, the proposed framework is capable of accurately identifying the maintenance-points and creating an adaptive piecewise model of the deterioration process.

However, for a few track sections, the estimated maintenance-points are less than the actual ones, which resulted from the fact that not all maintenance-points were included in the set of candidate breakpoints. Therefore, one of the emphases for the next step will be on improving the algorithm to ensure that the set of candidate breakpoints contains all of the maintenance-points.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation

Author Contributions

YY: model-establishment and paper-writing. PX, GY, and JL: theoretical-guidance, paper-review and editing. LC: data preprocessing. All authors contributed to the article and approved the submitted version

Funding

This research is supported by the Science and Technology Research and Development Program of China Railway’s “Intelligent Operation and Maintenance Technology for Beijing-Zhangjiakou HSR (Grand No. P2018G051)” project.

Conflict of Interest

GY was employed by China State Railway Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bellman, R. E., and Dreyfus, S. E. (1962). Applied dynamic programming. J. Am. Stat. Assoc. 59, 366. doi:10.2307/2282884

Google Scholar

Breier, J., and Branišová, J. (2015). A dynamic rule creation based anomaly detection method for identifying security breaches in log records. Wireless Pers. Commun. 94, 1–15. doi:10.1007/s11277-015-3128-1

CrossRef Full Text | Google Scholar

Brockwell, P. J., Davis, R. A., Berger, J. O., Fienberg, S. E., and Singer, B. (1987). Time series: theory and methods. Berlin, Germany: Springer-Verlag.

CrossRef Full Text

Chen, S. S., and Gopalakrishnan, P. S. (1998). “Clustering via the Bayesian information criterion with applications in speech recognition,” in IEEE international Conference on acoustics, speech and signal processing, Seattle, WA, May 15–15, 1998 (IEEE).

Google Scholar

Dias, A. (2004). Change-point Analysis for dependence structures in finance and insurance. Risk Measures for the 21st Century. 321–335. Available at SSRN: https://ssrn.com/abstract=2464242

Gang, S., and Ghosh, J. K. (2011). Developing a new BIC for detecting change-points. J. Stat. Plann. Inference 141, 1436–1447. doi:10.1016/j.jspi.2010.10.017

CrossRef Full Text | Google Scholar

Hall, A. R., Osborn, D. R., and Sakkas, N. (2013). Inference on structural breaks using information criteria. The Manchester School 81, 54–81. doi:10.1111/manc.12017

CrossRef Full Text | Google Scholar

Hall, A. R., Osborn, D. R., and Sakkas, N. (2015). Structural break inference using information criteria in models estimated by two‐stage least squares. J. Time Ser. Anal. 36, 741–762. doi:10.1111/jtsa.12107

CrossRef Full Text | Google Scholar

Hannart, A., and Naveau, P. (2012). An improved bayesian information criterion for multiple change-point models. Technometrics 54, 256–268. doi:10.1080/00401706.2012.694780

CrossRef Full Text | Google Scholar

Jandhyala, V., Fotopoulos, S., Macneill, I., and Liu, P. (2013). Inference for single and multiple change-points in time series. J. Time Ser. Anal. 34 (4), 423–446. doi:10.1111/jtsa.12035

CrossRef Full Text | Google Scholar

Kotti, M., Benetos, E., Kotropoulos, C., Gustavo, L., and Martins, P. M. (2006). Speaker Change Detection using BIC: a comparison on two datasets. Int. Symp. Commun. Available at at: http://hdl.handle.net/10044/1/12249

Google Scholar

Lee, J. S., Hwang, S. H., Choi, Y., and Kim, I. K. (2018). Prediction of track deterioration using maintenance data and machine learning schemes. J. Transport. Eng. 144, 04018045. doi:10.1061/jtepbs.0000173

CrossRef Full Text | Google Scholar

Li, L., Wen, Z., and Wang, Z. (2016). Outlier detection and correction during the process of groundwater lever monitoring base on Pauta criterion with self-learning and smooth processing,” in Asian simulation conference SCS autumn simulation multi-conference. October 8–11, 2016.

Google Scholar

Liu, Y. U., Lei, Y. U., Yi, Q. I., Wang, J., and Wen, H. (2008). Traffic incident detection algorithm for urban expressways based on probe vehicle data. J. Transp. Syst. Eng. Inf. Technol. 8, 36–41. doi:10.1016/s1570-6672(09)60001-5

CrossRef Full Text | Google Scholar

Lu, Q., Lund, R., and Lee, T. C. M. (2010). AN MDL approach to the climate segmentation problem. Ann. Appl. Stat. 4, 299–319. doi:10.1214/09-aoas289

CrossRef Full Text | Google Scholar

Meier-Hirmer, C., Senee, A., Riboulet, G., Sourget, F., and Roussignol, M. (2006). “A decision support system for track maintenance,” in Computers in railways X: computer system design and operation in the railway and other transit systems. Editors J. Allan, C. A. Brebbia, A. F. Rumsey, G. Sciutto, S. Sone, and C. J. Goodman (Southampton: Computational Mechanics Publication Ltd), 217.

Google Scholar

Mercier, S., Meier-Hirmer, C., and Roussignol, M. (2012). Bivariate Gamma wear processes for track geometry modelling, with application to intervention scheduling. Struct. Infrastruct Eng. 8, 357–366. doi:10.1080/15732479.2011.563090

CrossRef Full Text | Google Scholar

Perreault, L., Parent, É., Bernier, J., Bobée, B., and Slivitzky, M. (2000). Retrospective multivariate Bayesian change-point analysis: a simultaneous single change in the mean of several hydrological sequences. Stoch. Environ. Res. Risk Assess. 14, 0243–0261. doi:10.1007/s004770000051

CrossRef Full Text | Google Scholar

Quiroga, L. M., and Schnieder, E. (2010). A heuristic approach to railway track maintenance scheduling. COMPRAIL 2010 114. doi:10.2495/cr100631

CrossRef Full Text | Google Scholar

Reeves, J., Chen, J., Wang, X. L., Lund, R., and Lu, Q. Q. (2007). A review and comparison of changepoint detection techniques for climate data. J. Appl. Meteorol. Climatol. 46, 900. doi:10.1175/jam2493.1

CrossRef Full Text | Google Scholar

Schwarz, G. (1978). Estimating the dimension of a model. Ann. Stat. 6, 461–464. doi:10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Vale, C., and Lurdes, S. M. (2013). Stochastic model for the geometrical rail track degradation process in the Portuguese railway Northern Line. Reliab. Eng. Syst. Saf. 116, 91–98. doi:10.1016/j.ress.2013.02.010

CrossRef Full Text | Google Scholar

Veit, P., and Marschnig, S. (2010). “Sustainability IN track - a precondition for high speed traffic,” in ASEM 2010 joint rail conference AMER SOC MECHANICAL ENGINEERS, Urbana, Illinois, April 27–29, 2010, 349–355.

Google Scholar

Wang, H. (2015). Anomaly detection of network traffic based on prediction and self-adaptive threshold. Int. J Future Gener. Commun. Networking 8, 205–214. doi:10.14257/ijfgcn.2015.8.6.20

CrossRef Full Text | Google Scholar

Wang, Y. W., Ni, Y. Q., and Wang, X. (2020). Real-time defect detection of high-speed train wheels by using Bayesian forecasting and dynamic model. Mech. Syst. Signal Process. 139. doi:10.1016/j.ymssp.2020.106654

CrossRef Full Text | Google Scholar

Watanabe, S. (2012). A widely applicable bayesian information criterion. J. Mach. Learn. Res. 14, 867–897. doi:10.1002/cem.2494

Google Scholar

Xi, R., Hadjipanayis, A. G., Luquette, L. J., Kim, T. M., Lee, E., Zhang, J., et al. (2011). Copy number variation detection in whole-genome sequencing data using the Bayesian information criterion. Proc. Natl. Acad. Sci. U.S.A. 108, E1128–E1136. doi:10.1073/pnas.1110574108 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, P., Liu, R.-K., Wang, F.-T., and Sun, Q.-X. (2012). A novel description method for track irregularity evolution. Int. J. Comput. Intell. Syst. 4, 1358–1366. doi:10.1080/18756891.2011.9727886

CrossRef Full Text | Google Scholar

Xu, P., Sun, Q., Liu, R., Souleyrette, R. R., and Wang, F. (2015). Optimizing the alignment of inspection data from track geometry cars. Comput. Aided Civ. Infrastruct. Eng. 30, 19–35. doi:10.1111/mice.12067

CrossRef Full Text | Google Scholar

Xu, P., Sun, Q., Liu, R., and Wang, F. (2011). A short-range prediction model for track quality index. Proc. Inst. Mech. Eng.—F J. Rail Rapid Transit 225, 277–285. doi:10.1177/2041301710392477

CrossRef Full Text | Google Scholar

Yang, S., Kalpakis, K., and Biem, A. (2014). Detecting road traffic events by coupling multiple timeseries with a nonparametric bayesian method. IEEE Trans. Intell. Transp. Syst. 15, 1936–1946. doi:10.1109/tits.2014.2305334

CrossRef Full Text | Google Scholar

Yao, Y.-C. (1988). Estimating the number of change-points via Schwarz’ criterion. Stat. Probab. Lett. 6, 181–189. doi:10.1016/0167-7152(88)90118-6

CrossRef Full Text | Google Scholar

Zhang, N. R., and Siegmund, D. O. (2007). A modified Bayes information criterion with applications to the analysis of comparative genomic hybridization data. Biometrics 63, 22–32. doi:10.1111/j.1541-0420.2006.00662.x |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, M., Cheng, X., Miao, L., Sun, X., and Wang, S. (2013). Advanced stochastic modeling of railway track irregularities. Adv. Mech. Eng. 5. doi:10.1155/2013/401637

CrossRef Full Text | Google Scholar