Insight Into the Strengthening Mechanism of the Al-Induced Cross-Linked Calcium Aluminosilicate Hydrate Gel: A Molecular Dynamics Study

Understanding and controlling the mechanical properties of calcium aluminosilicate hydrate (C-A-S-H) gel is essential to the performance improvement of cementing materials. This study characterizes the mechanical properties and failure mechanism of cross-linked C-A-S-H that have Al/Si ratios ranging from 0 to 0.20 by employing the reactive molecular dynamics simulation. In these constructed C-A-S-H models, the Al-induced cross-linking effect on the aluminosilicate chains is well reproduced. With the incorporation of aluminate species, layered C-S-H structure gradually transforms into three-dimensional C-A-S-H. The uniaxial tensile tests show that Al-induced cross-links significantly increase the cohesive force and stiffness of C-A-S-H along both y- and z-directions. In the C-A-S-H model with the Al/Si ratio equal to 0.2, in which all the bridging sites are cross-linked, the toughness along y-direction significantly improves the interlayer mechanical properties compared to those within the layers. The deformation mechanism of the C-A-S-H structure is also studied. Results show that the depolymerization of the calcium aluminosilicate skeleton is the main route to uptake the loading energy. Both the increase of y- and z-directional strength of the structure can be related to the increasing polymerization of aluminosilicate chains along that direction. This demonstrates the important role of aluminosilicate chains in resisting the external tensile loading. Besides, during the failure process in C-A-S-H elongation, the hydrolysis reactions of calcium silicate skeleton are caused by the coupling effect of loading and interlayer water “attack.” While the Al-O-Si bond breakage results from the protonation of bridging oxygen atom, the hydrolytic reaction of Si-O-Si is initiated by five-coordinate silicon formation. Both pathways weaken the bridging bond and thus result in the breakage of T-O-Si, where T is Al or Si.

Introduction

Cement manufacture is estimated to produce approximately 6–8% of the yearly man-made global CO₂ emissions (Mir and Nehme, 2017). Moreover, due to the increasing demand for concrete materials, this part of carbon emission is still increasing (Scrivener, 2008). In order to lower the environmental impact of the construction industry, people have used industrial wastes or byproducts to develop alternative binders (Mikulčić et al., 2016). The wide usage of some supplementary cementitious materials (SCMs), including fly ash (FA) and blast furnace slag (BFS) (Lothenbach et al., 2011), has not only reduced CO₂ emission (Sethy et al., 2016) (Huntzinger and Eatmon, 2009) but also prepared blended cement pastes that exhibit better performance than pure cement paste in some aspects, such as resistance in sulfate attack (Juenger et al., 2011) and alkali-aggregate reaction (ASR) (Shehata and Thomas, 2002; Duchesne and Bérubé, 1994). The Portland cement (PC) production results in about 0.85 tonnes/tonne of CO₂ emission (Feiz et al., 2015), while the CO₂ emissions by FA and BFS production are only 1/94 and 1/43 of the amount CO₂ emitted during cement manufacture, respectively (Chen et al., 2010).

High-volume SCM blended cement is often richer in Si and Al element than the PC (Lothenbach et al., 2011). This changes the stoichiometry of calcium silicate hydrate (C-S-H) gel, the main hydration product of cement-based materials. The Ca/Si ratio of the C-S-H gel is lowered and aluminum is incorporated into its structure (Lothenbach et al., 2011), leading to the formation of calcium aluminosilicate hydrate (C-A-S-H). Since C-A-S-H gel is the phase that gives strength to the hardened cement blend, it is necessary to study its mechanical properties. One of the cases is the mechanical properties of cross-linked C-A-S-H. C-S-H is structurally similar to tobermorite (Hamid, 1981; Merlino et al., 2001), which has principal layers composed of pseudooctahedrally coordinated calcium sheets sandwiched on both sides by silicate chains in the form of “drierkette.” In the interlayer regions, there are water molecules and calcium ions that connect the adjacent main layers. Hence, the C-S-H structure is weak in the interlayer direction (Hou et al., 2014b). When aluminum is included in the C-S-H structure, it resides on the silicate chains and heals the broken silicate chains. In these chains, Al occupancy in the bridging position is preferred over the pairing position (Manzano et al., 2009a; Pegado et al., 2014). The branched (alumino)silicate chains are more easily formed in the C-A-S-H gel than in the C-S-H gel (Myers et al., 2015; Bernal et al., 2013; Myers et al., 2013). It is found that calcium-poor and aluminum-rich cementitious environment and high temperature (up to 80°C) can promote the cross-linked C-A-S-H formation. Structurally, the branch chains bridge the neighboring principal layers with covalent bonds, which improve the interlayer interaction in the C-A-S-H structure. This was experimentally proved by recent studies from (Geng et al., 2017a; Geng et al., 2017b). They have investigated the compressibility of the crystal lattice of both non-cross- and cross-linked C-(A-)S-H under hydrostatic pressure, utilizing the synchrotron radiation-based high-pressure X-ray diffraction (XRD) technique. The results showed that the stiffness of non-cross-linked C-A-S-H is lower in the z-axis than in the xy-plane (the readers can see the stacked main layers along z-direction for C-A-S-H molecular structure in Figure 1A), and the cross-links can stiffen the C-A-S-H gel along the interlayer direction. However, the strengthening mechanism of cross-links remains not fully understood, owing to the experimental limit in accessing smaller length scales.

FIGURE 1

FIGURE 1. Atomistic representation of the C-(A-)S-H models with Al/Si ratios of 0, 0.10, and 0.20.

This article aims to study the mechanical properties of cross-linked C-A-S-H gel through molecular dynamics (MD) simulation. MD can give insight into the properties of materials at the molecular scale level and provide a complementary understanding of the experimental findings. Its wide application in the C-S-H studies renders the research length scale down to nanometers. The mechanical properties of mineral analogues of C-S-H, tobermorite and jennite, were calculated and the results match well with experimental data (Shahsavari et al., 2009) (Manzano et al., 2009b; Murray et al., 2010). Pellenq (Pellenq et al., 2009) proposed a “realistic C-S-H model” of the Ca/Si ratio of 1.7, which can accurately predict the experimentally obtained structure and strength properties (Allen et al., 2007; Constantinides and Ulm, 2007; Ulm et al., 2007). After that, the C-S-H model with various Ca/Si ratios was also constructed (Abdolhosseini Qomi et al., 2014) (Hou et al., 2015b) and its mechanical properties were in good agreement with the experimental results. The C-A-S-H (Ca/Si ratio = 1.7) with various Al/Ca ratios was also simulated by (Qomi et al., 2012) and (Hou et al., 2015a). The results show that the aluminum substitution for interlayer calcium improves the polymerization of aluminosilicate chains as well as the mechanical properties of C-A-S-H. Based on the MD simulation, cement/aggregate/fiber interface characterization (Zhou et al., 2019) and aggregate radiation failure (Zhou and Ju, 2020) were also investigated. The above studies provided an excellent basis for the implementation of our work.

In this article, the mechanical response and constitutive relationships of C-A-S-H with different cross-linking degrees are investigated by simulating uniaxial tension. Note that the branch structure in our constructed model is different from those in Qomi’s (Qomi et al., 2012) and Hou’s model (Hou et al., 2015a). In our models, cross-links occurred through the bond formation between the bridging silicate and aluminate sites in aluminosilicate chains of two adjacent primary layers, where the bridging sites can only bind to each other by pairs. This cross-linking mode is more related to the existing C-A-S-H structure models (Manzano et al., 2009a) (Pegado et al., 2014) and can characterize the mechanical responses more accurately. Relying on the ability to couple chemical reaction with the mechanical response provided by ReaxFF (Duin et al., 2001), the morphology transformation and hydrolytic reactions of calcium aluminosilicate skeleton in the C-A-S-H model during its structural deformation are also studied. This study can help elucidate the influence mechanisms of Al substitution on the performance of C-S-H gel and guide the design of sustainable concrete in engineering practice.

Computational Method

Reactive Force Field

The atomic interaction within the models was defined by the reactive force field (ReaxFF). ReaxFF was initially developed to simulate hydrocarbons (Duin et al., 2001). Since then, it has been successfully applied in many fields, including combustion, catalysis, material failure, and surface chemistry. The ReaxFF force field is equipped with the ability to describe the bond formation, bond breakage, and charge polarization (Fogarty et al., 2010), without recourse to a predefined and invariable covalent bond state. Furthermore, the bond order concept in the ReaxFF allows the energy to change smoothly during an energy-conserving simulation. Previous studies have been performed to study the Si/SiO₂ interfaces (Leroch and Wendland, 2012), dynamics of gel water in the C-S-H (Manzano et al., 2012a) (Hou et al., 2015b), and the restriction of C-S-H structure on guest ions (Hou et al., 2017). These applications demonstrate that ReaxFF can capture the structure, reactivity, and mechanical features of C-A-S-H/water interfaces with great accuracy. The ReaxFF parameters for the elements in this work were taken from previously published literature (Duin et al., 2003; Manzano, et al., 2012b; Liu et al., 2012).

Model Construction

The molecular structure of C-A-S-H is constructed using the method performed in previous simulations (Pellenq et al., 2009; Yang et al., 2018). Merlino’s cross-linked 11 Å tobermorite [Ca_4.5Si₆O₁₆(OH)·5H₂O] (Merlino et al., 2001) was utilized as the starting configuration. Firstly, a supercell containing 2 × 2 × 1 crystallographic tobermorite unit cells was constructed and the interlayer water within the cells was totally removed. Then, half of the bridging silicate tetrahedra in the supercell were substituted with aluminate tetrahedra. It is worth noting that only one of the two given adjacent bridging silicate tetrahedra is substituted to avoid the negative charge repulsion of aluminate species. Secondly, bridging aluminate tetrahedra were randomly deleted to create five calcium aluminosilicate skeletons of Al/Si ratios of 0, 0.05, 0.10, 0.15, and 0.20. An equivalent amount of hydrogen atoms was added to balance the negative charges induced by Al-Si substitution. Note that the upper limit Al/Si ratio is close to the maximum experimental findings of Al/Si ratio in C-A-S-H from Faucon et al. (Faucon et al., 1999) and Sun et al. (Sun et al., 2006). And this value is also the upper limit for the C-A-S-H model following the Lowenstein rule (Lowenstein, 1954). Thirdly, the structures of anhydrous calcium aluminosilicate were relaxed at 0 K. After the relaxation, water adsorption in the dry C-A-S-H model is performed by the Grand Canonical Monte Carlo (GCMC) method in the GULP package (Gale and Rohl, 2003). Adsorbent molecules were repeatedly inserted into and deleted from the simulation system until the system reaches equilibrium with the surrounding imaginary water reservoir. The adsorption was taken place with chemical potential of water of 0 eV under 300 K. The chemical potential in GCMC method was calculated following the regulation of the CSH-FF force field (Shahsavari et al., 2011). Finally, the LAMMPS software (Plimpton, 1995) (Aktulga et al., 2012) was utilized to carry out the MD. The Verlet algorithm was used to integrate the atomic trajectories in the system, with a time step of 0.25 fs. First, 250 ps of MD run was employed under constant pressure and temperature (NPT ensemble) (T = 298 K and P = 1 atom) to equilibrate the system. After 250 ps of MD run, 1000 ps of MD run was performed to average the system properties.

Uniaxial Tensile Loading

Given the anisotropic mechanical behavior of C-S-H gel (Hou et al., 2014b), uniaxial tensions along three dimensions were separately performed on the C-A-S-H models.

Before the tension test, the supercell of the obtained C-A-S-H models was periodically replicated along three dimensions to create cells of the size of about 4 × 4 × 4 nm³. Note that including a massive number of atoms can ensure the simulation stability of the system and its failure mode in particular. The uniaxial tension test of the structures was set to a strain rate of 0.08 per picosecond. For the purpose of anisotropic relaxation of the system, during the tension along one direction, the target pressure in directions normal to this direction was set to zero. The stress-strain evolution curves obtained in the uniaxial tension processes are plotted to analyze the mechanical properties of C-A-S-H. In addition, configurations were recorded for every 100 steps for the analysis of failure mode.

Results and Discussion

Structure of C-A-S-H Models

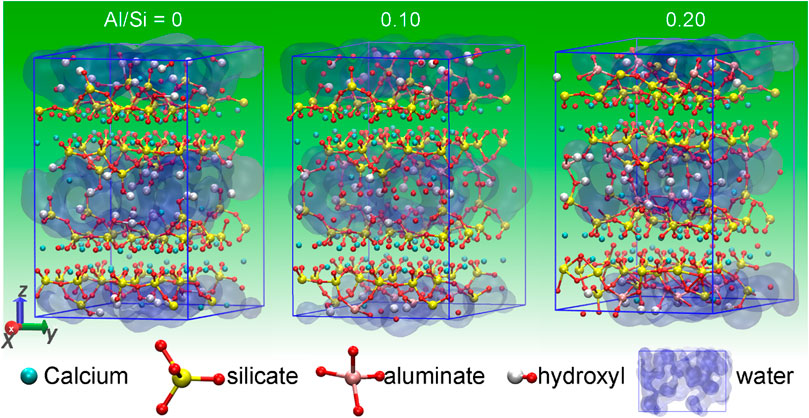
The obtained molecular structures of C-A-S-H models after the MD simulation are presented in Figure 1. For the C-S-H model (see Figure 1A), it can be observed that the Cas (calcium) and the Os (oxygen) atoms are bonded together to form the Cas-Os sheets, with defective “dreierketten” silicate chains flanking on each side. The negative charges of the calcium silicate layers were neutralized via the presence of interlaminar Ca²⁺ ions. In addition, there are also some water molecules in the interlaminar region. In the cross-linked C-A-S-H models (Figures 1B,C), aluminum in the defective bridging position of the chains not only links the broken silicate chains but also cross-links the silicate chain of the neighboring main layers. With the increase of Al/Si ratio, more aluminum atoms enter the bridging sites and cross-link the neighboring aluminosilicate chains. At the Al/Si ratio of 0.2, all bridging sites in the aluminosilicate chains are cross-linked (Figure 1C). In the cavities among the cross-linked aluminosilicate chains, there is zeolitic content (interlayer water molecules and Ca²⁺ ions). Figure 2 provides a schematic diagram that describes the bridging effect of aluminum on the adjacent primary layers in C-A-S-H gel. The three 2D pictures correspond to the C-A-S-H molecular structures in Figure 1, respectively.

FIGURE 2

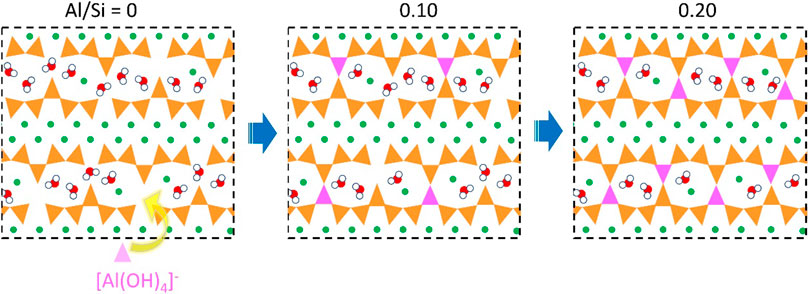
FIGURE 2. Schematic diagram of aluminum-induced bridging effect in C-(A-)S-H, where orange and pink triangles denote silicate and aluminate tetrahedra, green circles denote calcium atoms, and red-white circles denote water molecules.

The polymerization degree of silicate tetrahedra is an important parameter that influences the mechanical response of the C-A-S-H structure. Hence, the distribution of Qⁿ(mAl) species in the C-A-S-H model is calculated. Qⁿ(mAl) represents the connectivity factor of silicate tetrahedra. The increase of n from 0 to four denotes the transformation of silicate from monomer to network structures, while m ranging from 0 to n denotes the number of neighboring aluminate species for the given silicate tetrahedron. As shown in Figure 3A, there are 40% of Q¹ species and 60% of Q² species in the Al-free C-S-H model, indicating that the silicate tetrahedra are presented in linear silicate chain structures. As aluminum gradually enters the structure, the percentages of Q¹ and Q² species decrease, while those of Q²(1Al) and Q³(1Al) increase. This suggests that silicate tetrahedra are transformed from linear to branched chain structure. As shown in Figure 3B, the aluminate tetrahedron heals the broken silicate chains, thereby producing two Q²(1Al). Meanwhile, the cross-linking of the aluminate tetrahedron with the neighboring silicate chain results in a Q³(1Al) formation.

FIGURE 3

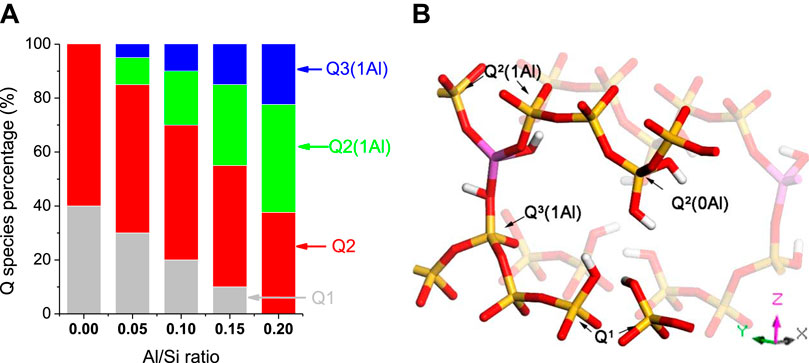
FIGURE 3. (A) Q species distribution of the C-A-S-H models (adapted from Manzano et al., (2012b)); (B) atomistic representation of the Q species in the models. Yellow and red sticks denote silicate chain (Si-O); magenta and red sticks denote aluminate chain (Al-O); the green and gray spheres indicate intra- and interlayer calcium atoms; red and white ball-sticks are water molecules and hydroxyl groups.

Stress-Strain Relationship

The stress-strain relation is a common way to characterize the constitutive relationship of materials. Figure 4 portrays the stress-strain evolution of C-A-S-H models as they are elongated along x-, y-, and z-directions, respectively. Take the C-A-S-H model of Al/Si ratio of 0.10, for example (Figure 4A). With the increase of the strain along x-direction, the stress firstly increases. This indicates the deformation of the C-A-S-H structure to take the tensile loading. At the strain of 0.19 Å/Å, the stress gets its maximum value of 10.66 GPa, which is the tensile strength of the structure. Then, the stress drops fast and it reduces to 4.83 GPa at the strain of 0.27 Å/Å. During this stage, cracks are formed in the C-A-S-H model and grow rapidly. After the strain of 0.27 Å/Å, the stress declines slowly until the end of the elongation process. This is because the C-A-S-H structure is destroyed after that strain level and hence cannot uptake tensile loading. The stress-strain relationship along y-direction shows a ladder-like pattern (Figure 4B). After the initial increase, there is an increase of stress, which reaches its first maximum of 10.43 GPa at the strain of 0.13 Å/Å, followed by a rapid reduction, which is down to 6.75 GPa at the strain of 0.17 Å/Å. After the first minimum, the stress again increases and reaches a second maximum of 9.67 GPa at a strain of 0.36 Å/Å. After this strain level, the stress-strain curve turns to a monotonic decrease. The secondary increase of stress resembles the work hardening effect of the tensioned steel material (Kocks and Mecking, 2003). It is worth mentioning that the ladder-like curve in y-direction presents in all the models, which suggests that the C-A-S-H structure has good plasticity along this direction. It worth noting that the cohesion force of C-A-S-H along x-direction originated from the connection between silicate chains and CaO sheets, whereas the cohesion force along y-direction originated not only from the Ca-O-Si bonds but also from the Si-O-Si bonds within silicate chains. Finally, the structural difference in x- and y-directions for C-A-S-H gel results in distinct different mechanical results. On the other hand, compared with the stress-strain relationships in x- and y-directions, their counterpart in z-direction shows a brittle nature. As shown in Figure 4C, the stress increases to 6.53 GPa when the strain is 0.16 Å/Å. Then, the stress continuously decreases and gets zero at the strain of 0.28 Å/Å.

FIGURE 4

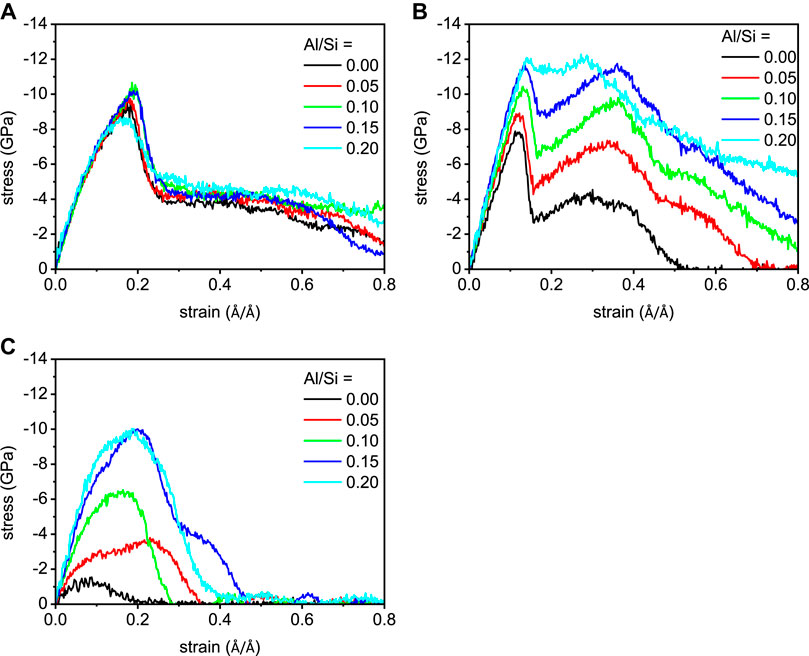
FIGURE 4. The stress-strain relationships of the C-(A-)S-H models along (A) x-, (B) y-, and (C) z-directions.

Mechanical Properties

The tensile strength and Young’s modulus can more intuitionally display the evolution of mechanical properties of the structure. As shown in Figure 5, the x- and y-directional tensile strengths of the non-cross-linked C-S-H are 9.58 GPa and 7.88 GPa, respectively. But their z-directional counterpart is 1.54 GPa. A similar trend can be observed in its Young’s modulus. This demonstrates the mechanical feature of C-S-H gel, that is, with strong interaction in xy-plane but very weak cohesion between the layers. As the Al/Si ratio increases from 0 to 0.20, the z-directional tensile strength of the C-(A-)S-H displays a substantial increase from 1.54 GPa to 10.03 GPa. The Young’s modulus along z-direction also increases from 24.32 GPa to 96.32 GPa. This reflects that the cross-linking of aluminosilicate chains greatly improves the interlayer interaction in the C-A-S-H. Furthermore, the Al incorporation also strengthens the C-A-S-H structure along y-direction. As the Al/Si ratio rises from 0 to 0.20, the tensile strength in y-direction increases from 7.88 GPa to 12.27 GPa and Young’s modulus increases from 71.48 GPa to 91.64 GPa. The tensile strength and Young’s modulus along x-direction appear to vary in relatively small ranges. With the aluminum incorporation into the structure, their values first increase and then decrease. The x-directional tensile strength and Young’s modulus approach their maxima at the Al/Si ratio of 0.10 and 0.15, respectively. With the cross-linking of the C-A-S-H model, the difference between interlayer strength and xy planar strength is significantly narrowed. At Al/Si ratio of 0.20, the z-directional strength even compares well with the xy-plane cohesion. The mechanical behavior of the C-A-S-H model transforms gradually from one featured by layered structure to one by glass-like materials. This finding is consistent with previous research (Geng et al., 2017a). They have tested the compressibility of lattice parameters of the unit cell under hydrostatic pressure. The results show that, for the non-cross-linked C-S-H, the compliance is about 3.3% per 10 GPa along the x- and y-directions (a and b unit cell decrease by 3.3% relative to the values at atmospheric pressure at an external hydrostatic pressure of 10 GPa) and 7–11% per 10 GPa along z-direction. For the cross-linked C-A-S-H sample with Al/Si ratio of 0.10, the compressibility of c parameter is largely improved (compliance ≈4% per 10 GPa) and close to that of a and b parameters, while the compressibility of a and b parameters is almost the same as that of non-cross-linked one.

FIGURE 5

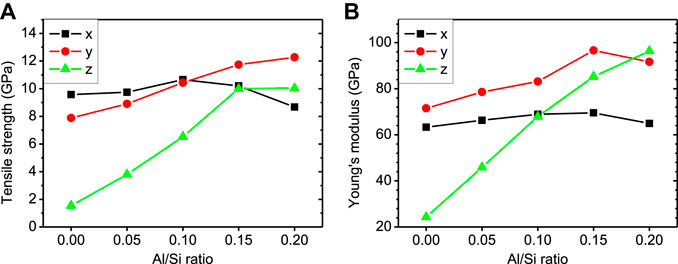
FIGURE 5. (A) Tensile strength and (B) Young’s modulus along three directions for C-A-S-H structures of various Al/Si ratios.

Molecular Structure Evolution

In order to gain an in-depth knowledge of the underlying mechanisms of the mechanical behavior, the molecular structure evolution of C-A-S-H models under tensile loading is investigated. Since the aluminosilicate chains are essential to the loading resistance of the structure, their morphology evolution under tension process is analyzed. Furthermore, as suggested in a previous study, water molecules’ intrusion will “attack” bridging bonds in the structure and weaken their bond strength (Hou et al., 2014a). This process consumes the interlayer water molecule and forms various hydroxyl groups; thus, the numbers of water molecules and hydroxyls are recorded to investigate the hydrolytic reaction during tensile loading.

Tensile Loading Along x-Direction

The deformed molecular structures for the C-S-H and C-A-S-H model (Al/Si = 0 and 0.20, respectively) from the strain of 0.0 Å/Å to 0.8 Å/Å during tension along x-direction are shown in Figure 6. For the C-S-H gel (Figure 6A), when strain is within 0.4 Å/Å, the ionic bonds between silicate chains and principal layer Ca are prolonged to take the loading. At the strain of 0.4 Å/Å, cracks can be clearly observed in the structure. Meanwhile, the silicate chains are displaced and rotated due to the tensile loading. As a result, the arrangement of calcium silicate layers becomes disordered. As the strain increases from 0.4 Å/Å to 0.8 Å/Å, the defective regions extend rapidly and connect with one another. The C-S-H structure is fractured at the strain of 0.8 Å/Å. With respect to the C-A-S-H model (Al/Si = 0.2), the structure appears to be more rigid. As shown in Figure 6B, the elongation initially leads to the extending distances between silicate chains and intralayer calcium. At the strain of 0.4 Å/Å, there is a hole amid the C-A-S-H structure. However, the aluminosilicate chains around the hole appear not to be twisted and still have their linear chain structures. The calcium aluminosilicate substrate also maintains its ordered structure to some extent. With the increase of strain from 0.4 Å/Å to 0.8 Å/Å, the hole rapidly grows and causes the fracture of the C-A-S-H structure, but the layered structure remains ambiguously visible in the fractured model. This can be attributed to the highly polymerized double aluminosilicate chains that show high stiffness and less deformation under tensile loading. Overall, it can be concluded that the x-directional cohesive property originates from the ionic bonds between main layer calcium atoms and silicate clusters (Hou et al., 2014b). Al incorporation does not change the nature of interacting bonds, which can explain why the x-directional strength exhibits little variation for the different models. The slight changes in tensile strength and Young’s modulus may be related to the change in the rigidity of the structure.

FIGURE 6

FIGURE 6. Molecular structure evolution (view along y-direction) of C-A-S-H with Al/Si ratio of (A) 0 and (B) 0.2. From top to bottom, the tensile strains along x-direction are 0.0 Å/Å, 0.2 Å/Å, 0.4 Å/Å, and 0.8 Å/Å, respectively.

It can be noted from Figure 7 that there is almost no Q species variation in any of the five models, demonstrating the stability of the aluminosilicate chains during x-directional elongation. The number evolution of water molecules and hydroxyl groups are shown in Figure 8. It can be noted that the main variation in the models is the water dissociation and Si-OH and Ca-OH formation. This corresponds to the hydrolytic reaction of Si-O-Ca bonds (Hou et al., 2015b), as depicted in Figure 9A. Firstly, the ionic bond between silicate tetrahedron and the main layer Ca atom is extended due to the tensile loading. The water molecule moves to silicate tetrahedron and forms a hydrogen bond with the nonbridging oxygen atom (Onb). The strong Coulomb attraction from Onb atom promotes the dissociation of water molecule to form H⁺ and OH⁻ ions. While hydrogen ion is bonded to Onb to form Si-OH group, the remaining OH⁻ is coordinated to interlayer Ca²⁺ ion to form a Ca-OH group. Therefore, the water molecule dissociation screens the interaction of the silicate cluster and the Ca²⁺ ion. Moreover, in the Al-containing models, there are also some Al-OH and Al-O(H)-Si groups production, in addition to the Ca-OH and Si-OH formation. This is due to the protonation of Ob atom in Al-O-Si bonds. As portrayed in Figure 9B, when the aluminate tetrahedron is distorted owing to the tensile loading, two water molecules diffuse close to the Al atom and adsorb on it. Then, one adsorbed water molecule transfers one of its hydrogen atoms to the Ob atom of the Al-O-Si bond. The water dissociation results in an Al-OH and an Al-O(H)-Si formation. It is worth noting that the Al-O(H)-Si tri-clusters are also observed in previous simulations of silicate-aluminate glasses (Benoit et al., 2001) (Cormier et al., 2000). This shows the reactivity of the Al-O-Si bond, which is different from the chemically inert Si-O-Si bond (Manzano et al., 2012a). In our work, the reactivity of Ob in Al-O-Si bonds is activated by the external loading. As proposed by Zhu et al., (2005), the energy barrier for the dissociation of water molecules can be reduced by the external loading. The loading also activates the distorted aluminate tetrahedron and leads to its transformation to octahedron. It can be noticed that hydrolytic reactions start at the strain level of about 0.2 Å/Å for all five models, which corresponds to the failure strain of C-A-S-H. The number of hydroxyls increases even at the end of the tension test, indicating the continuous hydrolytic reactions during the breakage of the C-A-S-H molecular structure.

FIGURE 7

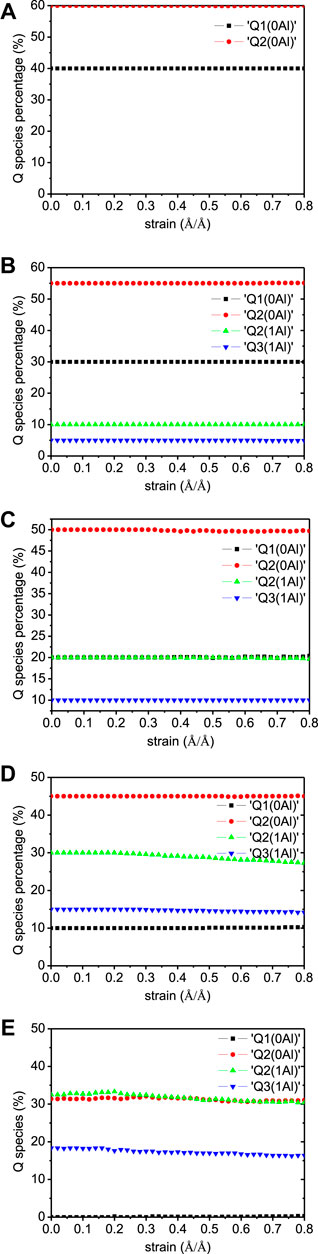
FIGURE 7. Q species variation in C-A-S-H model under x-directional elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20.

FIGURE 8

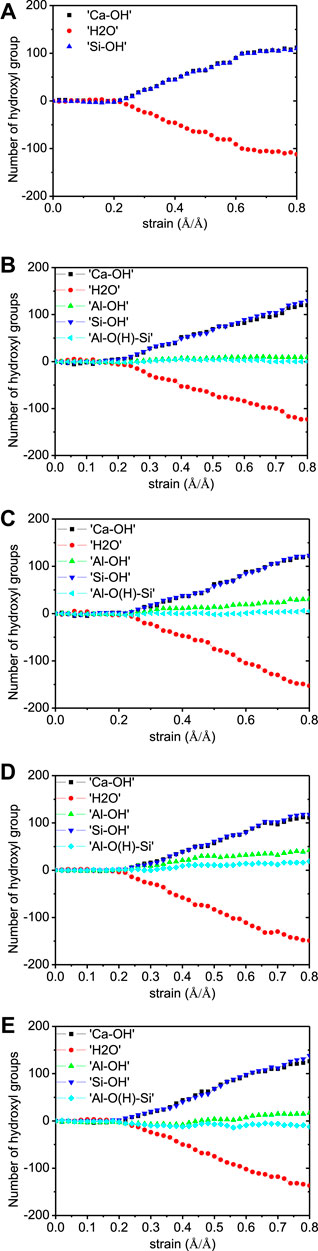
FIGURE 8. Number evolution of Ca-OH, Si-OH, Al-OH, Al-O(H)-Si, and H₂O in C-A-S-H model during x-directional elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20.

FIGURE 9

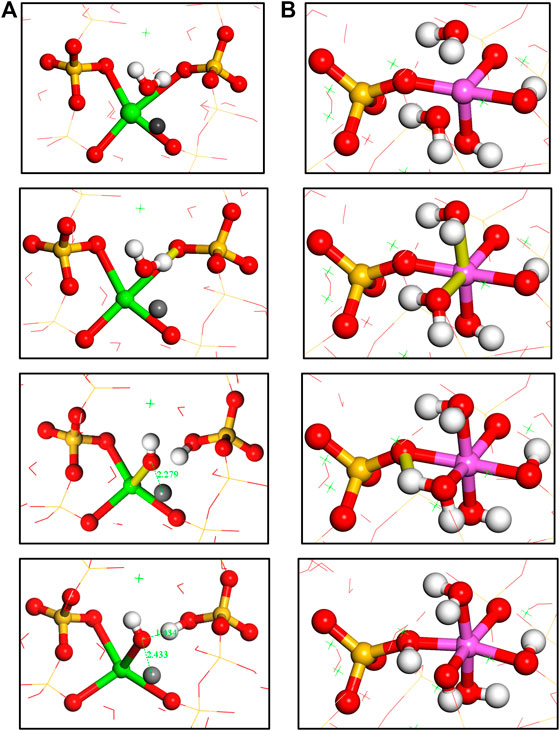
FIGURE 9. (A) Hydrolytic reaction pathway of Si-O-Ca bond; (B) two water molecules association on the aluminum atom and one water molecule dissociation to form an Al-OH and Al-O(H)-Si bonds.

When comparing the five models, it can be observed that the number of produced Al-OH groups first increases and then decreases with the increasing number of Al-Si substitutions. The number of Al-OH formation reaches its maximum at the Al/Si ratio of 0.15. It can be noted from Figure 10A that the relatively short silicate chains are easy to translate and rotate by the loading in the C-S-H model. With the increase of Al/Si ratio, aluminosilicate chains became longer and branched. These longer chains are hard to translate or rotate and are more likely to be twisted under tensile loading. Thus, the increasing Al content in the twisted chains results in more Al-OH formation. However, the polymerization of silicate/aluminate species and the formation of branch structures also stiffen the chains. At the Al/Si ratio of 0.2, the long double chains are rigid and show less extent of twist during the elongation, as illustrated in Figure 10C. In that situation, the number of Al-hydrolytic reactions decreases. It is widely believed that bond distortion and breakage are ways for materials to uptake external loading. Tensile test results show that Young’s modulus and tensile strength of C-A-S-H also show decreases at Al/Si ratio of 0.20. Therefore, the variation in x-directional mechanical properties is also correlated with the twist of aluminosilicate chains. As shown in Figure 10, the flexible branch chains in C-A-S-H with Al/Si ratio of 0.1 show a larger extent of twist than those of Al/Si ratio of 0 and 0.2. These chains (Figure 10B) play a more important role in binding together the surrounding principal layer calcium atoms.

FIGURE 10

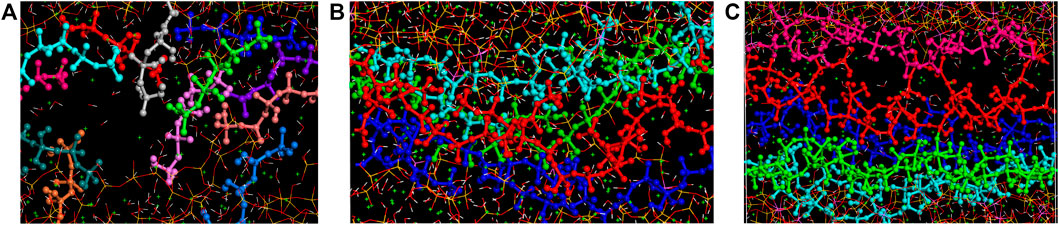
FIGURE 10. The morphology of (alumino)silicate chains (view along z-axis) in C-A-S-H model of Al/Si ratio of (A) 0, (B) 0.10, and (C) 0.20 at x-directional tensile strain of 0.8 Å/Å.

Tensile Loading Along y-Direction

The structure deformation of the C-A-S-H models from strain of 0.0 Å/Å to 0.6 Å/Å during tension along y-direction is presented in Figure 11. In the C-S-H gel (Figure 11A), the silicate chains are defective, limiting their ability to resist the loading. At the strain of 0.2 Å/Å, some cracks are formed in the defective silicate sites. As the strain increase, the cracks grow rapidly and connect together, until the final fracture of the model. It can be concluded that the y-directional cohesion force of the model comes from the ionic bonds between silicate clusters and calcium ions. This is akin to the interaction of C-S-H along the x-axis. Consequently, the Al-free C-S-H model has similar mechanical properties in x- and y-directions (see Figure 5). The mechanical properties in y-direction are higher than those in x-direction for the C-A-S-H model of Al/Si ratio of 0.2. This is because the prolonged aluminosilicate chains can help resist the tension. It can be noted from Figure 11B that the failure process of the C-A-S-H model is greatly delayed owing to the toughness of the highly polymerized aluminosilicate tetrahedra. No large cracks are observed in the C-A-S-H structure, even at the strain of 0.6 Å/Å. It is worth noting that the breakage of one bridging bond in the branch structure would not lead to the rupture of the double aluminosilicate chain. As is shown in the inset of Figure 11B, the neighboring chains can still resist the loading through the cross-linking connection, which can interpret the secondary increase in the stress-strain curves.

FIGURE 11

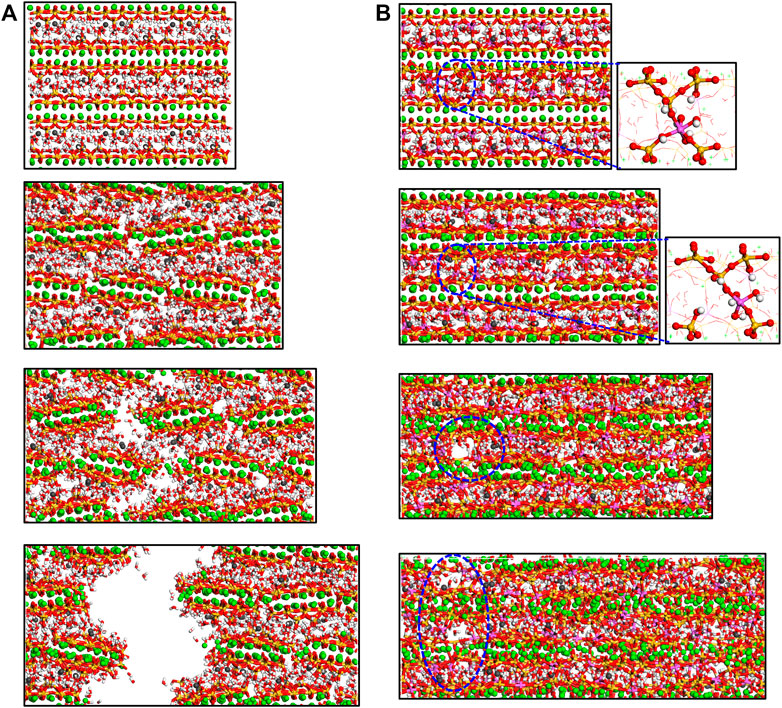
FIGURE 11. Molecular structure evolution (view along x-direction) of C-A-S-H with Al/Si ratio of (A) 0 and (B) 0.20. From top to bottom, the tensile strains along z-direction are 0.0 Å/Å, 0.2 Å/Å, 0.4 Å/Å, and 0.6 Å/Å, respectively.

The Q species variation in the C-A-S-H during their elongation along y-direction is given in Figure 12. As depicted in Figure 12A, the proportions of Q species in the C-S-H structure are constant during the tensile process. This is consistent with the above observation that the C-S-H model is fractured across the defective sites in silicate chains. On the other hand, all the Al-containing models show a reduction of Q² and Q³ and an increase of Q¹, implying the breakage of longer chains and production of chain ends. The C-A-S-H model with Al/Si ratio of 0.1 is taken as an example to demonstrate the Q species evolution. When the strain is lower than 0.18 Å/Å, the Q species percentages remain constant. This corresponds to the extension of the aluminosilicate chains. At the strain of 0.18 Å/Å, the connections between aluminate and silicate species start to break, resulting in the reduction of Q²(1Al) and the increase of Q¹(0Al). When the strain approaches 0.34 Å/Å, the siloxane bonds also begin to break, leading to the reduction of Q²(0Al) and formation of Q¹(0Al). There is also a small reduction in Q³(1Al) species, suggesting a small proportion of branch structure breakage during y axial tension. After the strain of 0.7 Å/Å, the model is totally fractured and the transformation of aluminosilicate chains morphology stops. It is worth noting that the Al-O-Si bonds are broken at lower strain values than the Si-O-Si bonds, denoting that the Al-O-Si bonds are weaker than the Si-O-Si bonds. This corroborated the simulation results from Qomi et al., (2012), who found that aluminosilicate chains show lower mechanical strength than silicate chains. Overall, as Al/Si ratio increases, the change of Q species content becomes more pronounced. This reflects that the longer aluminosilicate chains play more important roles in resisting the external tension.

FIGURE 12

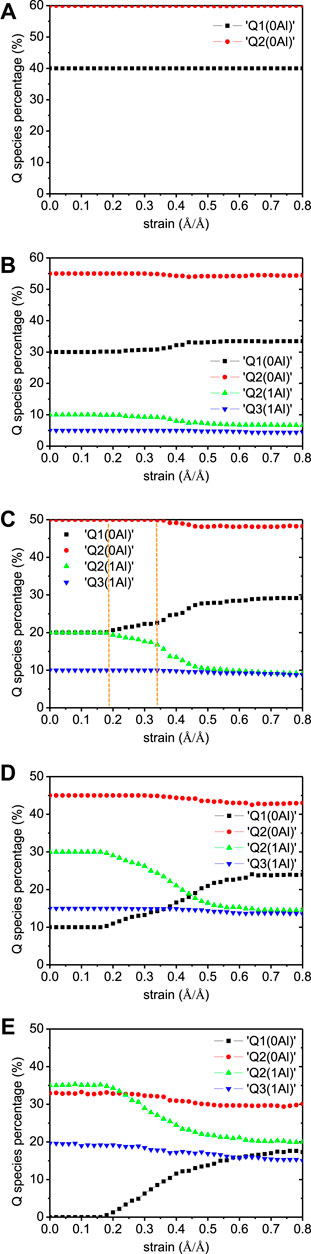
FIGURE 12. Q species variation in C-A-S-H model under y-directional elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20.

Figure 13 shows the number of water dissociation and hydroxyls formation during the elongation process. The fracture of the C-S-H model only observes the hydrolytic reaction of Si-O-Ca ionic bonds. This is because that the presence of a large number of defective sites weakens the ability of the aluminosilicate chains to resist the loading. When the Al-incorporated models are prolonged, there are Al-OH and Al-O(H)-Si groups apart from the Ca-OH and Si-OH formation. Take the case of the C-A-S-H model of Al/Si ratio of 0.1 (see Figure 13C). As the strain increases from 0 Å/Å to 0.18 Å/Å (aluminosilicate chain extension stage), there are water reduction and a small amount of Al-OH and Al-O(H)-Si formation. This corresponds to the coordinate structure change of aluminum and protonation of Ob in Al-O-Si bonds (see Figure 9B). When the strain ranges from 0.18 Å/Å to 0.34 Å/Å, there are Si-OH, Ca-OH, Al-OH, and Al-O(H)-Si formations. This involves the breakage of both Si-O-Ca and Al-O-Si bonds. While the hydrolytic reaction of the Si-O-Ca is direct (Figure 9A), the breakage of Al-O-Si bond is complex, which can be described with Eqs. 1.Eqs. 2

${\text{Al}‐\text{O}‐\text{Si }+\text{ H}}_2\text{O }\to \text{ HO}‐\text{Al}‐\text{O}\left(\text{H}\right)‐\text{Si }\to \text{Al}‐\text{OH }+\text{ Si}‐\text{OH}(1)$

${\text{Al}‐\text{O}‐\text{Si }+\text{ H}}_2\text{O}\to {\text{Al}‐\text{O}\left(\text{H}\right)‐\text{Si }+\text{ OH}}^{\mathrm{-}}\to \text{Al}‐\text{OH }+\text{ Si}‐\text{OH}(2)$

It should be noted that the hydrolytic reaction of the Al-O-Si bond is a two-stage reaction. The reaction intermediates are Ca-OH, Al-OH, and Al-O(H)-Si, and the final hydrolytic reaction products are Al-OH and Si-OH. The reaction pathways are discussed in the following section. After the strain of 0.34 Å/Å, the number of Al-O(H)-Si groups drops and that of Si-OH groups increases. This is caused by the hydrolytic reaction of Al-O and Si-O bonds. Since the hydrolytic reaction of Si-O-Si only produces Si-OH groups [Eq. 3; Hou et al., 2015b], the number of Si-OH groups increases more rapidly at this stage.

${\text{Si}‐\text{O}‐\text{Si }+\text{ H}}_2\text{O}\to \text{Si}‐\text{OH }+\text{ Si}‐\text{OH}(3)$

The producing rate of Si-OH and Al-OH groups under tensile loading increases with increasing Al/Si ratio of C-A-S-H, illustrating that more aluminate/silicate bonds are broken in the cross-linked C-A-S-H model with higher Al/Si ratios. This matches well with the Q species percentages evolution, implying that the C-A-S-H is strengthened along y-direction by the polymerization of aluminosilicate chains.

FIGURE 13

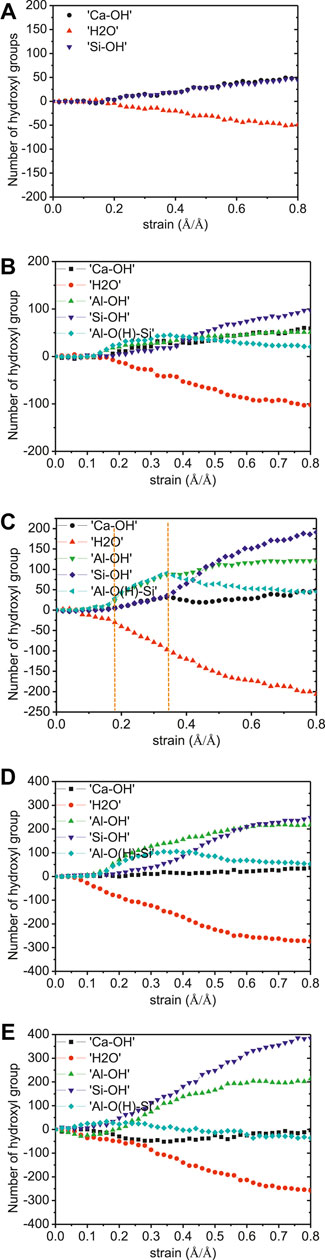
FIGURE 13. Number evolution of Ca-OH, Si-OH, Al-OH, Al-O(H)-Si, and H₂O in C-A-S-H gel during y-directional elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20.

Tensile Loading Along z-Direction

The tension process of C-(A-)S-H along z-direction was illustrated in Yang et al., (2018) in detail. Here, the tension failure of C-(A-)S-H along the z-direction is briefly represented, in order to give a comparison between the tensile loading process along different dimensions. The molecular structure of the C-A-S-H with Al/Si ratio of 0 and 0.2 as a function of tensile strain along z-direction is illustrated in Figure 14. It can be noted from Figure 14A that the calcium silicate sheets in non-cross-linked C-S-H can be easily taken apart. With increasing tensile strain, the crack is created and grown fast. When the structure is stretch-fractured, no evident deformation in calcium silicate sheets is observed. This is due to that the interlayer interacting bonds are too weak to resist the loading. On the contrary, the cross-linked C-A-S-H is stronger along the interlayer direction. As shown in Figure 14B, the fracture of the C-A-S-H model is slighter than that of the C-S-H model at the same strain level. At the strain of 0.3 Å/Å, the model is fractured, with the calcium aluminosilicate substrate deformed and the structure turns disordered. This indicates that the principal layers act as an integral to resist the loads and deformation. Hence, the cross-linked C-A-S-H model shows higher mechanical strength than the non-cross-linked C-S-H model.

FIGURE 14

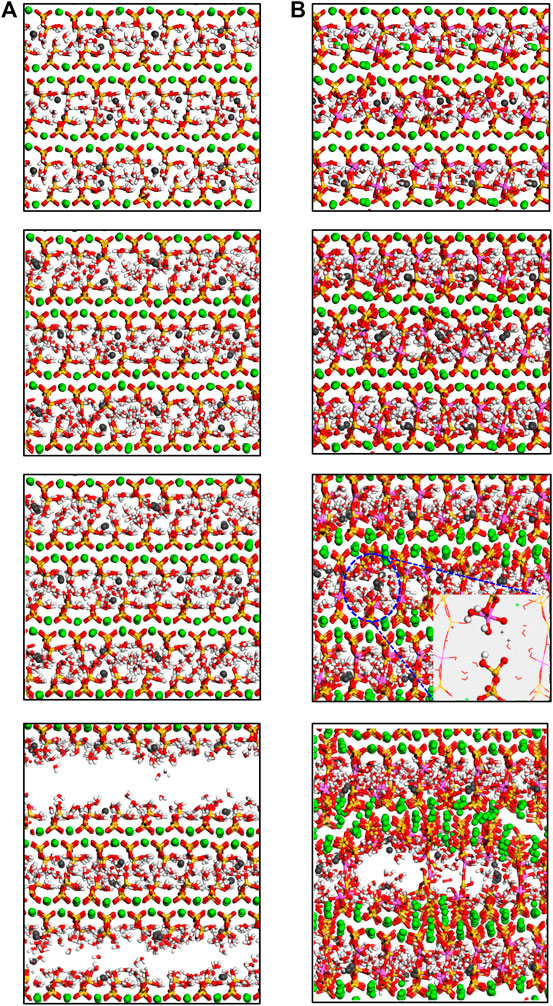
FIGURE 14. Molecular structure evolution (view along y-direction) of C-A-S-H with Al/Si ratio of (A) 0 and (B) 0.20. From top to bottom, the tensile strains along z-direction are 0.0 Å/Å, 0.1 Å/Å, 0.2 Å/Å, and 0.3 Å/Å, respectively (adapted from Yang et al., (2018)).

The Q species percentages evolution during the tensile loading along z-direction is given in Figure 15. Expectedly, the Q species percentages are constant during the tensile process of non-cross-linked C-S-H model (Figure 15A). The Q species evolution is found in the Al-substituted models and becomes more pronounced with the increase of Al/Si ratio. The main change is the decrease of Q³(1Al) and the increase of Q²(0Al) species, indicating the breakage of branch structures. This means that an increasing number of cross-links participated in the elongation process of the structure, thereby leading to a higher mechanical strength along z-direction. The number evolution of water molecules and hydroxyl groups is illustrated in Figure 16. There are no hydrolytic reactions in the non-cross-linked model because the elongation process involves no change in the silicate chain morphology. From another perspective, no hydrolytic reactions to take up the loading energy also denote the lower strength. In the cross-linked models, there are Al-OH and Si-OH increases and water molecules reduction, which indicates the hydrolytic reaction of Al-O-Si bonds, as described in Eqs. 1.Eqs. 2 When comparing the five models, it can be observed that the number of hydrolytic reactions increases as the Al/Si ratio of C-A-S-H increases. This proves that the enhanced interlayer strength is correlated with the cross-links between neighboring layers.

FIGURE 15

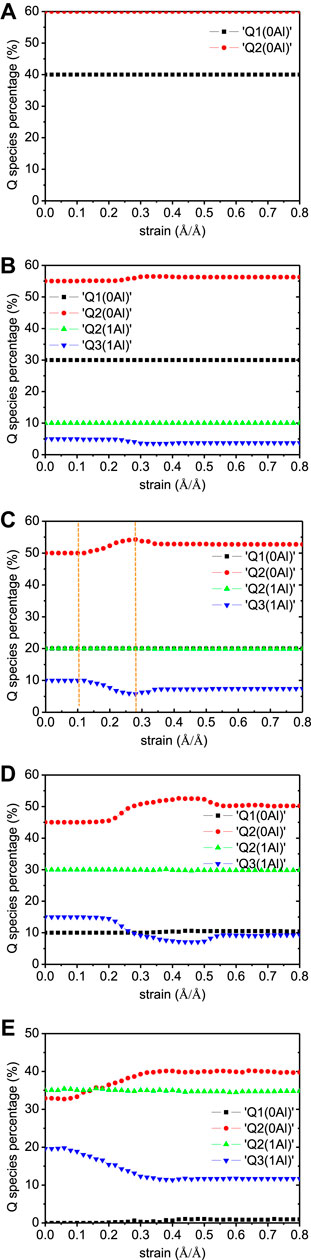
FIGURE 15. Q species evolution of C-A-S-H model under z-directional elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20 (adapted from Yang et al., (2018)).

FIGURE 16

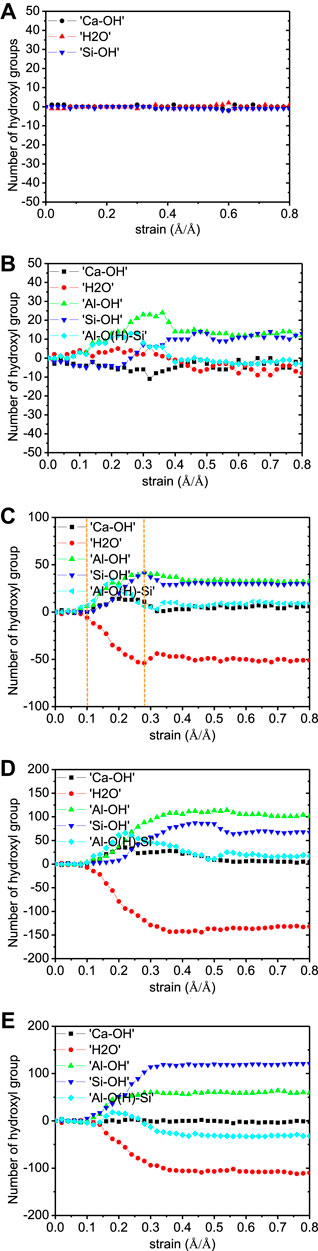
FIGURE 16. Number of Ca-OH, Si-OH, Al-OH, Al-O(H)-Si, and H₂O evolution of C-A-S-H model under z-direction elongation. The Al/Si ratios of the model are (A) 0.00, (B) 0.05, (C) 0.10, (D) 0.15, and (E) 0.20 (adapted from Yang et al., (2018)).

Hydrolytic Reaction Pathways of Al-O-Si and Si-O-Si Bonds

It can be concluded that the breakage of Al-O-Si and Si-O-Si bonds in our work is the result of combined tensile loading and water “attack.” This can be compared to the well-documented mechanisms found in the dissolution of aluminosilicate glasses, quartz, and feldspar, which involve the reaction of Al-O-Si and Si-O-Si under sole water “attack.” The hydrolytic reaction pathways of the Al-O-Si bond are illustrated in Figures 17A,B. In the first pathway, the water molecule is first adsorbed on the distorted aluminate tetrahedron. Then, the water molecule dissociates into H⁺ and OH⁻. While the OH⁻ remains connected to the aluminum atom, the H⁺ ion binds to the neighboring bridging oxygen atom to form an oxygen tricluster. With further increase of the strain, the Al-O bond is broken in the Al-O(H)-Si. As a result, one Si-OH group is produced. In the second pathway, the Ob atom is protonated by the hydrogen atom from the neighboring water molecule. Correspondingly, the water molecule turns into a free hydroxyl group. After the breakage of Al-O bond, the hydrogen atom in the adsorbed water molecule is transferred to the free hydroxyl to form a water molecule, as depicted in Figure 17B. The proton transfer resembles the “hydrogen hopping” process described by Manzano et al., (2015). The difference between the first and second hydrolytic reaction pathway is the types of reaction intermediates, which are Al-O(H)-Si and Al-OH for the first pathway but Al-O(H)-Si and Ca-OH for the second pathway. The hydrolytic reaction pathway of the Si-O-Si bond is depicted in Figure 14C, which is also described in Mahadevan and Garofalini (2008) (Hou et al., 2015b). Firstly, the silicate tetrahedra are distorted due to the external loading. One water molecule diffuses to the silicon atom and binds to it. Subsequently, the bridging Si-O bond in the five-coordinated silicon structure is broken, which makes the silicon atom returns to a four-coordinated structure. The adsorbed water molecule immediately gives one of its hydrogen atoms to the nonbridging oxygen atom, leading to the formation of two Si-OH groups.

FIGURE 17

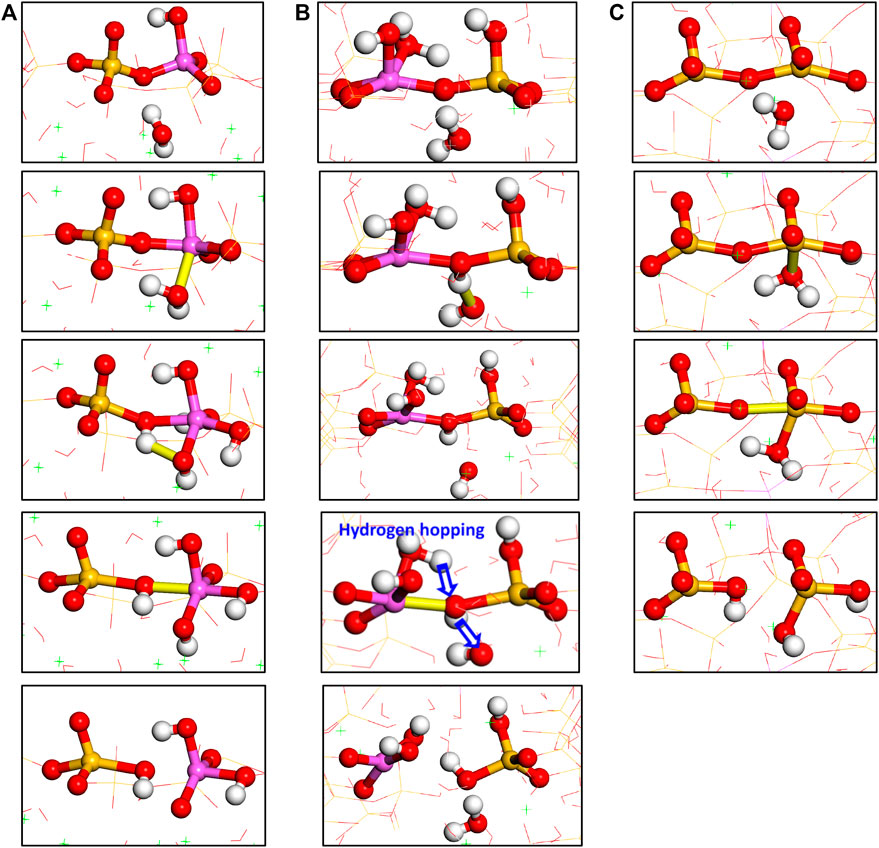
FIGURE 17. Hydrolytic reaction pathways of Al-O-Si bonds through (A) Pathway 1 and (B) Pathway 2 (adapted from Yang et al., (2018)); (C) hydrolytic reaction pathway of Si-O-Si bonds.

According to the hydrolytic reaction pathways, the differences between Al-O-Si and Si-O-Si bonds breakage can be concluded as follows:

The hydrolytic reaction of the Al-O-Si bond is a two-stage reaction, where the reaction intermediate five-/six-coordinated aluminum atom and Al-O(H)-Si groups can linger for a relatively long time until the Al-O bond breaks at high strain levels. During the Si-O-Si breakage, however, the water adsorption, Si-O bond breakage, and water dissociation almost happen simultaneously, implying the five-coordinated silicon atom and adsorbed water are thermodynamically unstable. Tsomaia (Tsomaia et al., 2003) studied the dissolution of albite crystal and glass and detected the six-coordinated Al in the surface of the samples. In those dissolution samples, the Al and Si atoms are originally tetracoordinated in aluminosilicate networks. This can corroborate our simulation results that the reaction intermediates during the breakage of the Al-O-Si bond are relatively stable. With respect to the hydrolytic reaction of the Si-O-Si bond, since most of the Si⁴⁺ species are four-coordinated at atmospheric pressure (Schindler and Stumm, 1987) (Bensted, 1999), it is reasonable that the five-coordinated Si is unstable. Ab initio calculations (Kubicki et al., 1996) demonstrated that the proton affinity of Si-OH is weak, which has ruled out the existence of Si-OH₂ at a neutral or basic solution. The flexible coordination change of the aluminum atom decreases the hydrolysis activation energy of the Al-O-Si linkages (Criscenti et al., 2005), which can help explain the lower strength of the Al-O-Si bond than that of the Si-O-Si bond.

The dissolution of aluminosilicate glass, feldspar, or quartz is influenced by the environmental pH. It found that both the Si-O-Si and Al-O-Si bonds can be broken in either an acidic or alkali environment. In an acidic solution, the hydronium ion attacks the bridging site and protonates the bridging oxygen atom. This significantly weakens the bridging bonds in Si-O-Si and Si-O-Al and leads to the bonds’ breakage (Xiao and Lasaga, 1994). On the other hand, in a basic environment, the hydroxyl first deprotonates the Si-OH group and turns into a water molecule. Then, the water molecule bonds to one of the silicon atoms to produce a pentacoordinated silicate species, which weakens the bridging Si-O bond and finally leads to the breakage of the Si-O-Si bond (Xiao and Lasaga, 1996). In our simulation, the protonation of bridging oxygen atom plays a role in weakening the Al-O connection, which resembles the T-O bond (T = Al or Si) attacked by hydronium ions, while the breakage of Si-O bond is facilitated by the pentacoordinated Si formation, similar to T-O bond attacked by OH⁻ ions. Therefore, the hydrolytic reactions of Al-O-Si and Si-O-Si bonds in our work approximately correspond to acidic dissolution and alkali dissolution, respectively. Furthermore, the low reactivity of Ob atom in Si-O-Si reduces the possibility of Si-O breakage due to proton “attack.” This indicates that a higher acidic environment is needed to dissolve the Si-O-Si bond, as compared with the Al-O-Si bond (Kubicki et al., 1996).

Conclusion

In this work, the mechanical properties of cross-linked C-A-S-H of Al/Si ratios ranging from 0 to 0.2 were studied by MD simulating uniaxial test. Based on the ReaxFF coupled with chemical reaction and mechanical response, the failure mechanism of the C-A-S-H structure was also investigated. Several conclusions can be drawn as follows:

The presence of aluminate species can heal the broken silicate clusters and cross-link the silicate chains of neighboring calcium silicate sheet. The branch structure formation significantly increases the polymerization of aluminosilicate chains, leading to the transformation from a two-to a three-dimensional C-A-S-H structure.

The uniaxial tensile testing shows that, by bridging the defective silicate chains and forming branch structures, Al-induced cross-links significantly increase the tensile strength and Young’s modulus of C-A-S-H structure both along y- and z-directions, where the latter undergoes a larger extent of increase. When all the bridging sites are cross-linked at Al/Si ratio of 0.2, the mechanical properties of the C-A-S-H structure along z-direction almost match those in the xy-plane.

During the elongation process, the tensile loading is taken up mainly by the depolymerization of the calcium aluminosilicate skeleton, which demonstrates the backbone role of calcium aluminosilicate sheets in the C-A-S-H structure. The strengthening of the C-A-S-H structure can be achieved by the polymerization of aluminosilicate chains, which can replace weaker ionic or hydrogen bonds with stronger covalent bonds.

During the failure process of the structure, the combined effect of loading and water “attack” is responsible for the bond breakage. As compared with Si-O-Si bond, the reaction intermediates during the hydrolytic reaction of the Al-O-Si bond are relatively stable, making the hydrolytic reaction process of Al-O-Si bond slower. In addition, the bridging bonds breaking in Al-O-Si and Si-O-Si are induced by different ions’ “attack.” While the bond breakage in Al-O-Si results from the protonation of the bridging oxygen atom, the bridging bond breakage in Si-O-Si is a consequence of the pentacoordinated silicon formation. The ions’ attack weakens the bridging bond (Al-O or Si-O) and results in its rupture.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

GZ was involved in writing of the original draft, formal analysis, and methodology. YL was involved in investigation and data curation. JY was involved in conceptualization and writing, review, and editing. QD was involved in supervision and validation. DS was involved in funding acquisition.

Funding

Financial support from the National Natural Science Foundation of China (Grant Nos. 51878003 and 52008002), Natural Science Research Project of Higher School of Anhui Province (Grant No. KJ2019ZD55), Excellent Young Talent Support Project of Anhui Province (Grant No. gxyqZD2019055), and Doctoral Scientific Research Startup Foundation of Anhui Jianzhu University (Grant No. 2019QDZ66) is gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abdolhosseini Qomi, M. J., Krakowiak, K. J., Bauchy, M., Stewart, K. L., Shahsavari, R., Jagannathan, D., et al. (2014). Combinatorial molecular optimization of cement hydrates. Nat. Commun. 5, 4960. doi:10.1038/ncomms5960

PubMed Abstract | CrossRef Full Text | Google Scholar

Aktulga, H. M., Fogarty, J. C., Pandit, S. A., and Grama, A. Y. (2012). Parallel reactive molecular dynamics: numerical methods and algorithmic techniques. Parallel Comput. 38 (4–5), 245–259. doi:10.1016/j.parco.2011.08.005

CrossRef Full Text | Google Scholar

Allen, A. J., Thomas, J. J., and Jennings, H. M. (2007). Composition and density of nanoscale calcium-silicate-hydrate in cement. Nat. Mater. 6 (4), 311–316. doi:10.1038/nmat1871

PubMed Abstract | CrossRef Full Text | Google Scholar

Benoit, M., Ispas, S., and Tuckerman, M. E. (2001). Structural properties of molten silicates from ab initio, molecular-dynamics simulations: comparison between CAO-Al2O3-SiO2, and SiO2. Phys. Rev. B. 64 (22), 224205. doi:10.1103/physrevb.64.224205

CrossRef Full Text | Google Scholar

Bensted, J. (1999). Thaumasite – background and nature in deterioration of cements, mortars and concretes. Cement Concr. Compos. 21 (2), 117–121. doi:10.1016/s0958-9465(97)00076-0

CrossRef Full Text | Google Scholar

Bernal, S. A., Provis, J. L., Walkley, B., Nicolas, R. S., Gehman, J. D., and Brice, D. G. (2013). Gel nanostructure in alkali-activated binders based on slag and fly ash, and effects of accelerated carbonation. Cement Concr. Res. 53 (2), 127–144. doi:10.1016/j.cemconres.2013.06.007

CrossRef Full Text | Google Scholar

Chen, C., Habert, G., Bouzidi, Y., Jullien, A., and Ventura, A. (2010). Lca allocation procedure used as an incitative method for waste recycling: an application to mineral additions in concrete. Resour. Conserv. Recycl. 54 (12), 1231–1240. doi:10.1016/j.resconrec.2010.04.001

CrossRef Full Text | Google Scholar

Constantinides, G., and Ulm, F.-J. (2007). The nanogranular nature of C-S-H. J. Mech. Phys. Solid. 55 (1), 64–90. doi:10.1016/j.jmps.2006.06.003

CrossRef Full Text | Google Scholar

Cormier, L., Neuville, D. R., and Calas, G. (2000). Structure and properties of low-silica calcium aluminosilicate glasses. J. Non-Cryst. Solids 274 (1), 110–114. doi:10.1016/s0022-3093(00)00209-x

CrossRef Full Text | Google Scholar

Criscenti, L. J., Brantley, S. L., Mueller, K. T., Tsomaia, N., and Kubicki, J. D. (2005). Theoretical and 27Al CPMAS NMR investigation of aluminum coordination changes during aluminosilicate dissolution. Geochem. Cosmochim. Acta 69 (9), 2205–2220. doi:10.1016/j.gca.2004.10.020

CrossRef Full Text | Google Scholar

Duchesne, J., and Bérubé, M. A. (1994). Evaluation of the validity of the pore solution expression method from hardened cement pastes and mortars. Cement Concr. Res. 24 (3), 456–462. doi:10.1016/0008-8846(94)90132-5

CrossRef Full Text | Google Scholar

Duin, V. A. C., Dasgupta, S., Lorant, F., and Goddard, W. A. (2001). Reaxff: a reactive force field for hydrocarbons. J. Phys. Chem. 105 (41), 9396–9409. doi:10.1021/jp004368u

CrossRef Full Text | Google Scholar

Duin, V. A. C., Strachan, A., Stewman, S., Zhang, Q., Xu, X., and Goddard, W. (2003). ReaxFF SiO reactive force field for silicon and silicon oxide systems. J. Phys. Chem. 107 (19), 3803–3811. doi:10.1021/jp0276303

CrossRef Full Text | Google Scholar

Faucon, P., Delagrave, A., Richet, C., Marchand, J. M., Zanni, H., and Zanni, H. (1999). Aluminum incorporation in calcium silicate hydrates (C−S−H) depending on their Ca/Si ratio. J. Phys. Chem. B. 103 (37), 7796–7802. doi:10.1021/jp990609q

CrossRef Full Text | Google Scholar

Feiz, R., Ammenberg, J., Baas, L., Eklund, M., Helgstrand, A., and Marshall, R. (2015). Improving the CO2 performance of cement, part I: utilizing life-cycle assessment and key performance indicators to assess development within the cement industry. J. Clean. Prod. 98, 272–281. doi:10.1016/j.jclepro.2014.01.083

CrossRef Full Text | Google Scholar

Fogarty, J. C., Aktulga, H. M., Grama, A. Y., van Duin, A. C., and Pandit, S. A. (2010). A reactive molecular dynamics simulation of the silica-water interface. J. Chem. Phys. 132 (17), 174704. doi:10.1063/1.3407433

PubMed Abstract | CrossRef Full Text | Google Scholar

Gale, J. D., and Rohl, A. L. (2003). The general utility lattice program (gulp). Mol. Simulat. 29 (5), 291–341. doi:10.1080/0892702031000104887

CrossRef Full Text | Google Scholar

Geng, G., Myers, R. J., Li, J., Maboudian, R., Carraro, C., Shapiro, D. A., et al. (2017a). Aluminum-induced dreierketten chain cross-links increase the mechanical properties of nanocrystalline calcium aluminosilicate hydrate. Sci. Rep. 7, 44032. doi:10.1038/srep44032

PubMed Abstract | CrossRef Full Text | Google Scholar

Geng, G., Myers, R. J., Qomi, M. J. A., and Monteiro, P. J. M. (2017b). Densification of the interlayer spacing governs the nanomechanical properties of calcium-silicate-hydrate. Sci. Rep. 7 (1), 10986. doi:10.1038/s41598-017-11146-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamid, S. Α. (1981). The crystal structure of the 11 Ä natural tobermorite Ca2. 25 [Si3O7. 5 (OH) 1.5]⋅ 1H2O. Z. Kristallogr.-Cryst. Mat. 154 (1–4), 189–198. doi:10.1524/zkri.1981.154.14.189

CrossRef Full Text | Google Scholar

Hou, D., Hu, C., and Li, Z. (2017). Molecular simulation of the ions ultraconfined in the nanometer-channel of calcium silicate hydrate: hydration mechanism, dynamic properties, and influence on the cohesive strength. Inorg. Chem. 56 (4), 1881–1896. doi:10.1021/acs.inorgchem.6b02456

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., Li, Z., and Zhao, T. (2015a). Reactive force field simulation on polymerization and hydrolytic reactions in calcium aluminate silicate hydrate (C-A-S-H) gel: structure, dynamics and mechanical properties. RSC Adv. 5 (1), 448–461. doi:10.1039/c4ra10645h

CrossRef Full Text | Google Scholar

Hou, D., Ma, H., Li, Z., and Jin, Z. (2014a). Molecular simulation of “hydrolytic weakening”: a case study on silica. Acta Mater. 80, 264–277. doi:10.1016/j.actamat.2014.07.059

CrossRef Full Text | Google Scholar

Hou, D., Zhao, T., Ma, H., and Li, Z. (2015b). Reactive molecular simulation on water confined in the nanopores of the calcium silicate hydrate gel: structure, reactivity, and mechanical properties. J. Phys. Chem. C, 119(3), 1346–1358. doi:10.1021/jp509292q

CrossRef Full Text | Google Scholar

Hou, D., Zhu, Y., Lu, Y., and Li, Z. 2014b). Mechanical properties of calcium silicate hydrate (C-S-H) at nano-scale: a molecular dynamics study. Mater. Chem. Phys. 146 (3), 503–511. doi:10.1016/j.matchemphys.2014.04.001

CrossRef Full Text | Google Scholar

Huntzinger, D. N., and Eatmon, T. D. (2009). A life-cycle assessment of Portland cement manufacturing: comparing the traditional process with alternative technologies. J. Clean. Prod. 17 (7), 668–675. doi:10.1016/j.jclepro.2008.04.007

CrossRef Full Text | Google Scholar

Juenger, M. C. G., Winnefeld, F., Provis, J. L., and Ideker, J. H. (2011). Advances in alternative cementitious binders. Cement Concr. Res. 41 (12), 1232–1243. doi:10.1016/j.cemconres.2010.11.012

CrossRef Full Text | Google Scholar

Kocks, U. F., and Mecking, H. (2003). Physics and phenomenology of strain hardening: the fcc case. Prog. Mater. Sci. 48 (3), 171–273. doi:10.1016/s0079-6425(02)00003-8

CrossRef Full Text | Google Scholar

Kubicki, J. D., Blake, G. A., and Apitz, S. E. (1996). Ab initio calculations on aluminosilicate q3 species: implications for atomic structures of mineral surfaces and dissolution mechanisms of feldspars. Am. Mineral. 81 (7–8), 789–799. doi:10.2138/am-1996-7-801

CrossRef Full Text | Google Scholar

Leroch, S., and Wendland, M. (2012). Simulation of forces between humid amorphous silica surfaces: a comparison of empirical atomistic force fields. J. Phys. Chem. C Nanomater Interfaces 116 (50), 26247. doi:10.1021/jp302428b

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Jaramillo-Botero, A., Goddard, W. A., and Sun, H. (2012). Development of a reaxff reactive force field for ettringite and study of its mechanical failure modes from reactive dynamics simulations. J. Phys. Chem. 116 (15), 3918–3925. doi:10.1021/jp210135j

CrossRef Full Text | Google Scholar

Lothenbach, B., Scrivener, K., and Hooton, R. D. (2011). Supplementary cementitious materials. Cement Concr. Res. 41 (12), 1244–1256. doi:10.1016/j.cemconres.2010.12.001

CrossRef Full Text | Google Scholar

Lowenstein, W. (1954). The distribution of aluminum in The Tetrahedra of silicates and aluminates. Am. Mineral. 39, 92–96.

Google Scholar

Mahadevan, T. S., and Garofalini, S. H. (2008). Dissociative chemisorption of water onto silica surfaces and formation of hydronium ions. J. Phys. Chem. C. 112 (5), 1507–1515. doi:10.1021/jp076936c

CrossRef Full Text | Google Scholar

Manzano, H., Dolado, J. S., and Ayuela, A. 2009a). Aluminum incorporation to dreierketten silicate chains. J. Phys. Chem. B. 113 (9), 2832–2839. doi:10.1021/jp804867u

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzano, H., Durgun, E., López-Arbeloa, I., and Grossman, J. C. (2015). Insight on tricalcium silicate hydration and dissolution mechanism from molecular simulations. ACS Appl. Mater. Interfaces 7 (27), 14726–14733. doi:10.1021/acsami.5b02505

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzano, H., Moeini, S., Marinelli, F., van Duin, A. C., Ulm, F. J., and Pellenq, R. J. (2012a). Confined water dissociation in microporous defective silicates: mechanism, dipole distribution, and impact on substrate properties. J. Am. Chem. Soc. 134 (4), 2208–2215. doi:10.1021/ja209152n

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzano, H., Pellenq, R. J., Ulm, F. J., Buehler, M. J., and van Duin, A. C. (2012b). Hydration of calcium oxide surface predicted by reactive force field molecular dynamics. Langmuir 28 (9), 4187–4197. doi:10.1021/la204338m

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzano, H., Dolado, J. S., and Ayuela, A. (2009b). Elastic properties of the main species present in Portland cement pastes. Acta Mater. 57 (5), 1666–1674. doi:10.1016/j.actamat.2008.12.007

CrossRef Full Text | Google Scholar

Merlino, S., Bonaccorsi, E., and Armbruster, T. (2001). The real structure of tobermorite 11 Å: normal and annomalous forms. Eur. J. Mineral. 13 (3), 65–80. doi:10.1127/0935-1221/2001/0013-0577

CrossRef Full Text | Google Scholar

Mikulčić, H., Klemeš, J. J., Vujanović, M., Urbaniec, K., and Duić, N. (2016). Reducing greenhouse gasses emissions by fostering the deployment of alternative raw materials and energy sources in the cleaner cement manufacturing process. J. Clean. Prod. 136, 119–132. doi:10.1016/j.jclepro.2016.04.145

CrossRef Full Text | Google Scholar

Mir, A. E., and Nehme, S. G. (2017). Utilization of industrial waste perlite powder in self-compacting concrete. J. Clean. Prod. 157, 507–517. doi:10.1016/j.jclepro.2017.04.103

CrossRef Full Text | Google Scholar

Murray, S. J., Subramani, V. J., Selvam, R. P., and Hall, K. D. 2010). Molecular dynamics to understand the mechanical behavior of cement paste. Transport. Res. Rec. 2142, 75–82. doi:10.3141/2142-11

CrossRef Full Text | Google Scholar

Myers, R. J., Bernal, S. A., San Nicolas, R., and Provis, J. L. (2013). Generalized structural description of calcium-sodium aluminosilicate hydrate gels: the cross-linked substituted tobermorite model. Langmuir 29 (17), 5294–5306. doi:10.1021/la4000473

PubMed Abstract | CrossRef Full Text | Google Scholar

Myers, R. J., L’Hôpital, E., Provis, J. L., and Lothenbach, B. (2015). Effect of temperature and aluminium on calcium (alumino)silicate hydrate chemistry under equilibrium conditions. Cement Concr. Res. 68, 83–93. doi:10.1016/j.cemconres.2014.10.015

CrossRef Full Text | Google Scholar

Pegado, L., Labbez, C., and Churakov, S. V. (2014). Mechanism of aluminium incorporation into c-s-h from ab initio calculations. J. Mater. Chem. 2 (10), 3477–3483. doi:10.1039/c3ta14597b

CrossRef Full Text | Google Scholar

Pellenq, R. J., Kushima, A., Shahsavari, R., Van Vliet, K. J., Buehler, M. J., Yip, S., et al. 2009). A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. U.S.A. 106 (38), 16102–16107. doi:10.1073/pnas.0902180106

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117 (1), 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Qomi, M. J., Ulm, F., and Pellenq, J. (2012). Evidence on the dual nature of aluminum in the calcium-silicate-hydrates based on atomistic simulations. J. Am. Ceram. Soc. 95 (3), 1128–1137. doi:10.1111/j.1551-2916.2011.05058.x

CrossRef Full Text | Google Scholar

Schindler, P. W., and Stumm, W. (1987). “The surface chemistry of oxides, hydroxides, and oxide minerals,” in Aquatic surface chemistry: chemical processes at the particle-water interface. Editor W. Stumm (New York: Wiley), 83–100.

Google Scholar

Scrivener, K. (2008). The concrete conundrum. Chem. World, 62–66.

Google Scholar

Sethy, K. P., Pasla, D., and Chandra Sahoo, U. (2016). Utilization of high volume of industrial slag in self compacting concrete. J. Clean. Prod. 112 (5), 581–587. doi:10.1016/j.jclepro.2015.08.039

CrossRef Full Text | Google Scholar

Shahsavari, R., Pellenq, R. J., and Ulm, F. J. (2011). Empirical force fields for complex hydrated calcio-silicate layered materials. Phys. Chem. Chem. Phys. 13 (3), 1002–1011. doi:10.1039/c0cp00516a

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahsavari, R., Buehler, M. J., Pellenq, R. J.-M., and Ulm, F.-J. (2009). First-principles study of elastic constants and interlayer interactions of complex hydrated oxides: case study of tobermorite and jennite. J. Am. Ceram. Soc. 92 (10), 2323–2330. doi:10.1111/j.1551-2916.2009.03199.x

CrossRef Full Text | Google Scholar

Shehata, M. H., and Thomas, M. D. A. (2002). Use of ternary blends containing silica fume and fly ash to suppress expansion due to alkali-silica reaction in concrete. Cement Concr. Res. 32 (3), 341–349. doi:10.1016/s0008-8846(01)00680-9

CrossRef Full Text | Google Scholar

Sun, G. K., Young, J. F., and Kirkpatrick, R. J. (2006). The role of Al in C-S-H: NMR, XRD, and compositional results for precipitated samples. Cement Concr. Res. 36 (1), 18–29. doi:10.1016/j.cemconres.2005.03.002

CrossRef Full Text | Google Scholar

Tsomaia, N., Brantley, S. L., Hamilton, J. P., Pantano, C. G., and Mueller, K. T. (2003). NMR evidence for formation of octahedral and tetrahedral al and repolymerization of the si network during dissolution of aluminosilicate glass and crystal. Am. Mineral. 88 (1), 54–67. doi:10.2138/am-2003-0107

CrossRef Full Text | Google Scholar

Ulm, F.-J., Vandamme, M., Bobko, C., Alberto Ortega, J., Tai, K., and Ortiz, C. (2007). Statistical indentation techniques for hydrated nanocomposites: concrete, bone, and shale. J. Am. Ceram. Soc. 90 (9), 2677–2692. doi:10.1111/j.1551-2916.2007.02012.x

CrossRef Full Text | Google Scholar

Xiao, Y., and Lasaga, A. C. (1996). Ab initio quantum mechanical studies of the kinetics and mechanisms of quartz dissolution: OH− catalysis. Geochem. Cosmochim. Acta 60 (13), 2283–2295. doi:10.1016/0016-7037(96)00101-9

CrossRef Full Text | Google Scholar

Xiao, Y., and Lasaga, A. C. (1994). Ab initio quantum mechanical studies of the kinetics and mechanisms of silicate dissolution: h + (h 3 o + ) catalysis. Geochem. Cosmochim. Acta 60 (13), 2283–2295. doi:10.1016/0016-7037(96)00101-9

CrossRef Full Text | Google Scholar

Yang, J., Hou, D., and Ding, Q. (2018). Structure, dynamics, and mechanical properties of cross-linked calcium aluminosilicate hydrate: a molecular dynamics study. ACS Sustain. Chem. Eng. 6, 9403–9417. doi:10.1021/acssuschemeng.8b01749

CrossRef Full Text | Google Scholar

Zhou, S., and Ju, J. W. (2020). The damage and healing of quartz under radiation at high temperatures. Int. J. Damage Mech. 29, 923–942. doi:10.1177/1056789519894547

CrossRef Full Text | Google Scholar

Zhou, S., Vu-Bac, N., Arash, B., Zhu, H., and Zhuang, X. (2019). Interface characterization between polyethylene/silica in engineered cementitious composites by molecular dynamics simulation. Molecules 24 (8), 1497. doi:10.3390/molecules24081497

CrossRef Full Text | Google Scholar

Zhu, T., Li, J., Lin, X., and Yip, S. (2005). Stress-dependent molecular pathways of silica-water reaction. J. Mech. Phys. Solid. 53 (7), 1597–1623. doi:10.1016/j.jmps.2005.02.002

CrossRef Full Text | Google Scholar