Numerical Assessment of the Performance of Elastic Cloaks for Transient Flexural Waves

Introduction

State of the Art and Research Challenges

The control of elastic waves to cloak a region of the ambient space has been shown achievable by transformation elastodynamics, which provides the mechanical properties of the material surrounding the region (Milton et al., 2006; Brun et al., 2009; Norris and Shuvalov, 2011). A relevant application of this broad area is the control of transverse waves in plates, for which solutions have been proposed mainly based on two approaches: a “passive” one, where the features of the cloak are achieved by a given microstructure (Farhat et al., 2009a; Farhat et al., 2009b; Brun et al., 2014; Colquitt et al., 2014; Climente et al., 2016; Zareei and Alam, 2017; Liu and Zhu, 2019; Misseroni et al., 2019) and an “active” one, in which tunable quantities depending on the actual mechanical input are employed for the same goal (see e.g., Futhazar et al., 2015; O’Neill et al., 2015; Chen et al., 2016; Ning et al., 2020). Experiments have been also proposed to validate some of the previous theoretical proposals (Stenger et al., 2012; Misseroni et al., 2016; Darabi et al., 2018; Misseroni et al., 2019). Most of these investigations show that this technique can be feasible and likely to be employed in centimetre-size real-life systems with wave frequencies in the order of a few kHz.

Within the set of attempts based on the “passive” approach, Colquitt et al. (2014) proposed a transformation to conceive a Kirchhoff-Love plate theory for cloaking flexural waves. The resulting governing equations for the thin plate in the transformed domain involve the presence of variable (in space) bending and torsional stiffnesses, and density, in addition to the presence of in-plane body forces and prestresses in the plate. In the same paper, the general framework was specialised to the case of a square cloak composed of four trapezoidal elements (see Figure 1) embedded in an isotropic, homogeneous domain. For this geometry, a set of relationships was established to provide explicit expressions of the quantities concerned in each part of the cloak. The broadband effectiveness of the meta-material plate cloak was then assessed by means of numerical tests.

FIGURE 1

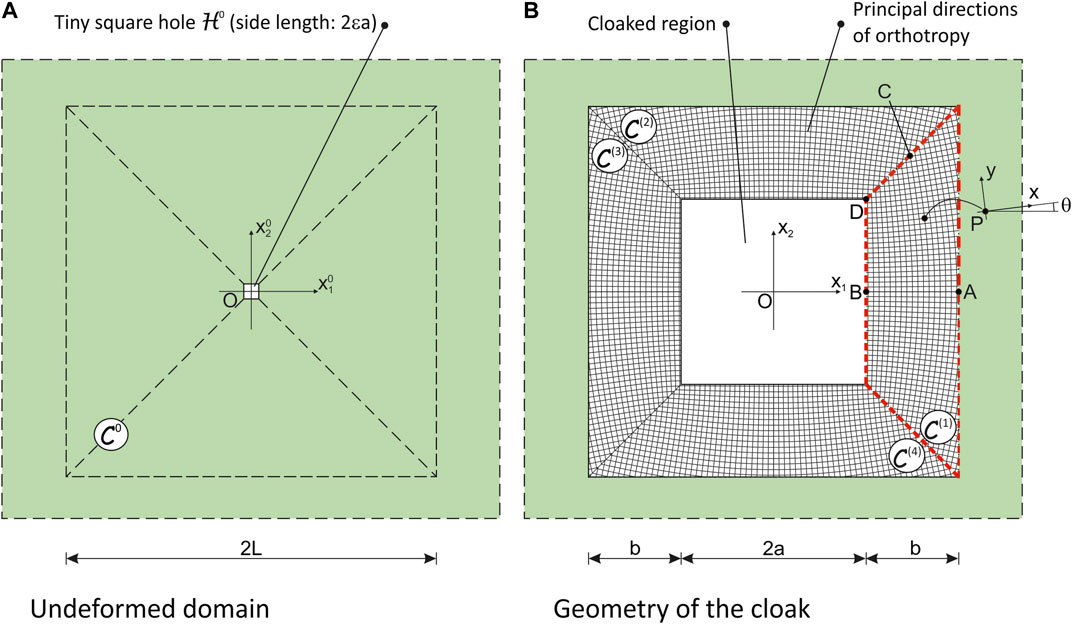
FIGURE 1. Sketch of a square meta-structural cloak studied by Colquitt et al. (2014): (A) initial, undeformed domain ${\mathcal{C}}^0$ where the plate is isotropic and homogeneous; (B) transformed domain $\mathcal{C}$ where the four trapezoids composing the cloak are numbered. The principal directions of orthotropy are represented with thin lines (the local axes at a generic point P are labelled x and y as depicted). The perimeter of trapezoid ${\mathcal{C}}^{\left(1\right)}$ is marked with a dashed red line.

The features of the suggested meta-structure can be summarised as follows:

(1) the cloak is locally an orthotropic thin plate with principal directions varying point-to-point. These directions obey the geometric symmetries of the domain (see, e.g., trapezoid displayed in Figure 1B, where the principal directions are sketched with thin lines). In the same figure, the increase of the out-of-alignment of the local principal system with the axis of symmetry towards the diagonals of the cloak can be noticed;

(2) by investigating how the stiffnesses of the plate in the orthotropic principal system depend on the position and thinking to construct the plate with a homogeneous material, it turns out that the thickness of the plate must assure an increase in bending stiffness along the direction parallel to the inner boundary of the cloak moving away the axis of symmetry of each trapezoid and a decrease of the bending stiffness along the “radial” direction moving towards the centre of the cloak. These two requirements are apparently in contradiction, but they must be addressed in an effective design;

(3) the twisting stiffness in the principal system of orthotropy vanishes at each point of the domain;

(4) the mass density of the cloak is not constant and varies with the Jacobian of the transformation; in particular, this quantity decreases by approaching the inner boundary of the cloak;

(5) in-plane body forces and prestresses in the interior of the domain as well as forces per unit length applied along the diagonals of the cloak are necessary to warrant equilibrium. The predicted prestress is compressive in a large part of the domain with values that are likely to exceed the buckling threshold for the thin structure.

The set of listed properties demonstrates that the design and engineering of an effective cloak for flexural waves based on transformation elastodynamics of Kirchhoff-Love plates is an exceptional challenge. Actually, the presence of severe compressive prestresses leads to the conclusion that it is impossible to construct a stable, ideal cloak. Therefore, an approach based on carefully considered approximations are required to achieve the goal. In the experimental test conducted by Misseroni et al. (2016), for instance, the design of the approximated cloak has focused mainly on the match of bending stiffnesses along the directions of orthotropy.

Moving from the points raised in the just edited list, the goal of the paper is four-fold:

(1) the first aim is to design and implement a fully open in-house FE code, based on a subparametric technique, to simulate transient wave propagation in locally orthotropic Kirchhoff-Love plates;

(2) the numerical tool is then exploited to assess the performance of meta-structural square cloaks designed by assuming reasonable approximations (prestress free, local twisting stiffness as limited as possible, cross sections of the plate ensuring the required local bending stiffnesses, non-constant mass density);

(3) the same tool is employed to investigate the role of certain stiffness parameters, i.e., twisting and coupling bending stiffnesses;

(4) in addition, a non-secondary purpose of the paper is to propose an extension of the theory to encompass interaction of the cloak with an elastic substrate modelled with a Winkler foundation and assess its effectiveness.

Background

The definition of the flexural cloak is based on a transformation, say $\mathit{\chi }$, that maps a two-dimensional subdomain ${\mathcal{C}}^0\subset \mathcal{K}$ occupied by a homogeneous, isotropic Kirchhoff-Love plate, to the domain $\mathcal{C}$ where the meta-plate is to be constructed, i.e., ${\chi }_k:{\mathcal{C}}^0\to \mathcal{C},x_K^0\to x_k={\chi }_k\left(x_K^0\right)$.¹ The map is such that the transformed equation in the latter is still the governing equation for flexural waves supported by a Kirchhoff-Love plate. In our case, ${\mathcal{C}}^0$ is a square deprived of a tiny hole ${\mathcal{H}}^0$ in the centre (Figure 1A) that is mapped to a collection of four trapezoids ${\mathcal{C}}^{\left(i\right)}\left(i=1,\dots ,4\right)$ (Figure 1B), such that $\mathcal{C}=\cup {\mathcal{C}}^{\left(i\right)}$. The length of one side of the external boundary of both ${\mathcal{C}}^0$ and $\mathcal{C}$ is equal to $2L$ whereas that of ${\mathcal{H}}^0$ is equal to $2\mathit{\epsilon }a$, where ε is a small parameter.²

In both configurations, the exterior domain $\mathcal{K\setminus }{\mathcal{C}}^0=\mathcal{K}\setminus \mathcal{C}$ is occupied by the initial, homogeneous structure that possesses constant thickness H, mass density per unit volume ${\rho }^0$ and bending stiffness $D^0=E{H}^3/\left[12\left(1-{\nu }^2\right)\right]$, where E is the Young’s modulus of the material and ν its Poisson’s ratio. When free-standing, the governing equation of the plate under harmonic vibrations takes the form

$D^0{\nabla }_0^{4}w+{\sigma }^0\ddot{w}=0,(1)$

where $w\left(x_K^0,t\right)$ is the transverse displacement, ${\nabla }_0^4$ is the biharmonic operator in ${\mathcal{C}}^0$ and ${\sigma }^0={\rho }^{0}H$ is the mass density per unit area. For the relevant case of a plate resting on a homogeneous substrate modelled as a bed of independent linear springs (Winkler model), a term $k_W^0$ is to be added on the left-hand side of Eq. 1, where $k_W^0$ is the subgrade coefficient. We emphasise that in Eq. 1, $D^0$ and ${\sigma }^0$ are independent of the position.

The function ${\chi }_k\left(x_K^0\right)$ is assumed to be invertible, a requisite that is met if its evaluation in the inner boundary of the cloak is non-singular as in the case under study, After having recalled that uppercase indices refer to points belonging to ${\mathcal{C}}^0$ and that a comma indicates partial differentiation, the gradient of the transformation $x_{i,K}$, its Jacobian $J\left(x_p\right)=\text{det}{x}_{i,K}$ and the tensor³

$g_{ij}\left(x_p\right)=x_{i,P}{x}_{j,P}/J$

are instrumental in defining the properties of the cloak as shown by Colquitt et al. (2014).

In order to have a complete overview on the established theory of meta-plate cloaks, we remind that the local governing equation of a Kirchhoff-Love plate takes the form (Timoshenko and Woinowsky-Krieger, 1959; Lekhnitskii et al., 1968)

$m_{ij,ij}+n_{ij}{w}_{,ij}-s_i{w}_{,i}=\sigma \ddot{w},(2)$

where σ is the mass density per unit area, $m_{ij}$ represents the set of moments per unit length whilst $n_{ij}$ and $s_i$ denote membrane forces and in-plane body forces per unit length, respectively, in equilibrium through fulfillment of the condition

$n_{ij,j}+s_i=0.(3)$

The next step is to substitute the constitutive equations that connect $m_{ij}$ to the generalised curvature $w_{,kl}$ as $m_{ij}=-D_{ijkl}\left(x_p\right)w_{,kl}$, where $D_{ijkl}$ is the stiffness tensor which may depend on the position. The substitution in Eq. 2 yields

$D_{ijkl}{w}_{,ijkl}+2D_{ijkl,i}{w}_{,jkl}+\left(D_{ijkl,ij}-n_{kl}\right)w_{,kl}+s_l{w}_{,l}=-\sigma \ddot{w},(4)$

an equation used by Colquitt et al. (2014) to identify the different terms corresponding to the transformation and confirm that the flexural displacement of a Kirchhoff-Love plate under an arbitrary coordinate mapping may be interpreted as a generalised plate.

The identification of terms shows that the stiffness tensor of the transformed plate corresponds to

$D_{ijkl}\left(x_p\right)=D^{0}J{g}_{ij}{g}_{kl},(5)$

the in-plane body forces to

$s_l\left(x_p\right)=D^0{\left[g_{rs}{\left(J{g}_{ql,q}\right)}_{,r}\right]}_{,s},(6)$

and the transformed density per unit area turns out to be $\sigma \left(x_p\right)={\rho }^{0}H/J.$

When the Winkler foundation is involved, the subgrade coefficient transforms similarly to the density, i.e.,

$k_W\left(x_p\right)=k_W^0/J,(7)$

a quantity that is now dependent on the position.

Focusing now on the square cloak transformation sketched in Figure 1 and, in particular, on trapezoid ${\mathcal{C}}^{\left(1\right)}$, ${\chi }^{\left(1\right)}\left(x_K^0{\mathit{e}}_K\right)=\left(\alpha x_1^0+c\right){\mathit{e}}_1+\left(\alpha x_2^0+c{x}_2^0/x_1^0\right){\mathit{e}}_2$,

$x_{i,K}^{\left(1\right)}=\left(\begin{array}{cc}\alpha & 0\\ \frac{x_2\alpha c}{x_1\left(c-x_1\right)}& \frac{x_1\alpha }{x_1-c}\end{array}\right),$

and $J^{\left(1\right)}=x_1{\alpha }^2/\left(x_1-c\right)$, where

$\alpha =\frac{b/L}{1-\mathit{\epsilon }a/L},c=\frac{a-\mathit{\epsilon }a}{1-\mathit{\epsilon }a/L},$

and $\left\{{\mathit{e}}_1,{\mathit{e}}_2\right\}$ is the orthonormal basis associated with both co-ordinate systems $O{x}_1^0{x}_2^0$ and $O{x}_1{x}_2$; a is the half-length of the side of the square hole to be cloaked and $b=L-a$ is the “cloak thickness”. This information defines the six independent components of the stiffness tensor $D_{ijkl}$, the prestress $n_{ij}$ and the in-plane body forces $s_i$ in the four subdomains. For trapezoid ${\mathcal{C}}^{\left(1\right)}$, all these quantities are reported in Appendix A. For the other parts of the cloak, they can be easily inferred by taking into account the relevant symmetries. Note that α is dimensionless while $\left[c\right]=$[L].

For the same trapezoid ${\mathcal{C}}^{\left(1\right)}$, to reach the orthotropic principal directions at a point P, the angle $\theta \left(x_1,x_2\right)$ (anticlockwise in the domain $x_2>0$, see Figure 1B) is now introduced. In particular, this angle identifies the principal axis x (respectively y) moving from $x_1$ (respectively $x_2$). Its value is

$\theta =\frac{1}{4}\text{arccos}\left[-\frac{Q}{Q+2\left(D_{1111}-D_{2222}\right)\left(D_{2221}-D_{1112}\right)}\right],(8)$

where

$Q=\left(D_{1111}+D_{2222}-2D_{1122}-4D_{1212}\right)\left(D_{1112}+D_{2221}\right).(9)$

In the new local system $Pxy$, the constitutive relationships assume the form

$m_{xx}=-D_{xxxx}{w}_{,xx}-D_{xxyy}{w}_{,yy},m_{yy}=-D_{xxyy}{w}_{,xx}-D_{yyyy}{w}_{,yy},m_{xy}=-D_{xyxy}{w}_{,xy},(10)$

where the new stiffness moduli contained therein are provided in terms of $D_{ijkl}$ in Appendix A.

Interestingly, as shown by Colquitt et al. (2014), the twisting stiffness $D_{xyxy}$ brought about by the transformation vanishes in all points of the transformed domain. This is a particular feature of the cloak under investigation that must be properly addressed in a meaningful design. It is worth recalling that in an isotropic plate with compact cross section, $D_{xyxy}=D^0\left(1-\nu \right)$.

The cloak is subjected to traction-free boundary conditions in the inner free boundary and to continuity conditions at the interface between itself and the outer homogeneous plate.

Numerical Model and Implementation in a In-House Finite Element Code

With the aim of performing numerical simulations via the Finite Element Method (FEM) of the transient dynamic behaviour of a square cloak, a weak form of the governing equations is now obtained. The formulation can be derived by multiplying Eq. 4 by the test function $v\left(x_1,x_2\right)$ and using the Galerkin method (Zienkiewicz and Taylor, 2005; Reddy, 1993). After the application of the divergence theorem to the generic sub-domain $\text{Ω}$ of the entire plate and use of the equilibrium Eq. 3, the final expression becomes

$\begin{array}{l}\underset{\text{Ω}}{{\displaystyle \int }}{v}_{,ij}{D}_{ijkl}{w}_{,kl}d\text{Ω}-\underset{\text{Ω}}{{\displaystyle \int }}{v}_{,l}{n}_{kl}{w}_{,k}d\text{Ω}+\underset{\text{Ω}}{{\displaystyle \int }}\sigma v\ddot{w}d\text{Ω}+\underset{\text{Ω}}{{\displaystyle \int }}{k}_{W}vwd\text{Ω}\\ -\underset{\text{Γ}}{{\displaystyle \int }}\left\{m_{\widehat{n}}{v}_{,\widehat{n}}-v\left(t_{\widehat{n}}+m_{\widehat{n}\widehat{s},\widehat{s}}\right)\right\}ds+\underset{\text{Γ}}{{\displaystyle \int }}\left\{n_{\widehat{n}\widehat{s}}v{w}_{,\widehat{n}}+n_{\widehat{n}}v{w}_{,\widehat{s}}\right\}ds=0,\forall v\in H_0^2\left(\text{Ω}\right),\end{array}(11)$

where the term involving $k_W$ is now taken into account. In expression Eq. 11, ${(\cdot )}_{,\widehat{n}}$ and ${(\cdot )}_{,\widehat{s}}$ are the directional derivatives along the normal unit vector $\widehat{\mathit{n}}$ and tangent unit vector $\widehat{\mathit{s}}$ of the boundary $\text{Γ}$ of $\text{Ω}$; $m_{\widehat{n}}$, $m_{\widehat{n}\widehat{s}}$ are the bending and twisting moments per unit length along $\text{Γ}$, respectively, whereas $n_{\widehat{n}}$, $n_{\widehat{n}\widehat{s}}$ describe the in-plane internal actions along the normal and tangent unit vectors; $t_{\widehat{n}}$ is the specific shear force on the boundary and $H_0^2\left(\text{Ω}\right)$ is the suitable Sobolev space. It should be noted that in the standard procedure leading to the weak form Eq. 11, the terms $D_{ijkl,i}$ and $D_{ijkl,ij}$ naturally disappear by integrating by part. The analysed plate is composed of various subdomains with different stiffness properties represented by the terms $D_{ijkl}$: the uncloaked region $\mathcal{K}\setminus \mathcal{C}$ possesses a homogeneous stiffness $D^0$ whereas the cloak is described by the parameters $D_{ijkl}$ given in Eq. 5.

Geometric and analytical approximations are performed to achieve the discretised formulation by dividing the entire domain into a finite subset of elements, i.e., $\text{Ω}\approx {\cup }_{e=1}^{n_e}{\text{Ω}}_e$, where $n_e$ is the number of the elements, and substituting unknown and test functions with the linear combinations

$w\left(x_1,x_2,t\right)=N_p\left(x_1,x_2,t\right)u_p\left(t\right),v\left(x_1,x_2,t\right)=N_q\left(x_1,x_2,t\right)v_q,(12)$

respectively, where $N_k\left(x_1,x_2,t\right)$, $k=\left\{p,q\right\}$, are shape functions defined on the spatial domain ${\text{Ω}}_e$ and indices $p,q$ range within a suitable interval as specified later. For each Finite Element, the final discretised formulation can be written as

$\begin{array}{l}{\displaystyle \sum _{p=1}^{n_p}{\displaystyle \sum _{q=1}^{n_q}{v}_q}}\{{\displaystyle {\int }_{{\Omega }_e}{N}_{q,ij}}{D}_{ijkl}{N}_{p,kl}{u}_{p}d\Omega +{\displaystyle {\int }_{{\Omega }_e}\sigma }{N}_q{N}_p{\ddot{u}}_{p}d\Omega +{\displaystyle {\int }_{{\Omega }_e}{k}_W}{N}_q{N}_p{u}_{p}d\Omega \\ -{\displaystyle {\int }_{{\Gamma }_e}\left[m_{\widehat{n}}{N}_{q,\widehat{n}}-N_q\left(t_{\widehat{n}}+m_{\widehat{n}\widehat{s},\widehat{s}}\right)\right]}ds\}=0,\forall v_q,\end{array}(13)$

where $n_p$ and $n_q$ are the number of the shape functions that discretise w and v, respectively, and all the terms related to the in-plane prestress have been neglected.

A parametric representation is implemented in the code: the shape functions are defined in the local coordinate system $O\xi \eta$ of the master element ${\widehat{\text{Ω}}}_e=\{\left(\xi ,\eta \right)\subseteq {\mathrm{ℝ}}^2:-1\le \xi \le 1,$$-1\le \eta \le 1\}$, which is mapped into each element of the mesh using appropriate coordinate transformations. Since an isoparametric representation is not possible for thin-plate elements unless a previous distortion of the mesh (see for example Petera and Pittman, 1994), a subparametric representation has been adopted, so the bilinear shape functions that are used for the transformation of the master element are different from the hermitian ones used for the analytical approximation of the unknown.

The structured mesh employed in the numerical analyses is composed of quadrangular elements with four nodes in the corner of each element whose generalised displacements are

$\left\{w^{\left(k\right)}{w}_{,\xi }^{\left(k\right)}{w}_{,\eta }^{\left(k\right)}{w}_{,\xi \eta }^{\left(k\right)}\right\},k=\mathrm{1,2,3,4},(14)$

leading to ($n_p=n_q=$) 16 degrees of freedom for the element (Imbert, 1979; Petyt, 1990; Reddy, 1993; Zienkiewicz and Taylor, 2005).

Finally, after substitution and integration of the aforementioned shape functions in Eq. 1 and the assembly operation over all the Finite Elements of the mesh, the set of algebraic equations used for the spatial approximation of this problem can be written as

$\mathit{M}\ddot{\mathit{u}}\left(t\right)+\mathit{Ku}\left(t\right)=\mathit{f}\left(t\right),(15)$

where $\mathit{M}$ and $\mathit{K}$ are the mass matrix and the stiffness matrix, respectively; $\mathit{u}\left(t\right)$ is the vector of the degrees of freedom whereas $\mathit{f}\left(t\right)$ is the vector of generalised external loads.

The approximation in the time domain is performed with the single-step time-integration algorithm Generalized-α method (Chung and Hulbert, 1993; Chung and Hulbert, 1994) which is an evolution of the well-known Newmark method that is frequently used for transient dynamical analysis in mechanics (see Imbert, 1979; Hughes, 1987; Petyt, 1990; Zienkiewicz and Taylor, 2005). According to this method, Eq. 15 is written as

$\mathit{M}\ddot{\mathit{u}}\left(t_n\right)+\mathit{C}\dot{\mathit{u}}\left(t_n\right)+\mathit{Ku}\left(t_n\right)=\mathit{f}\left(t_n\right),(16)$

where a generic damping matrix $\mathit{C}$ comes into play and the time-domain discretisation

$\mathit{T}=\left\{0,t_1,t_2,\dots ,t_n,\dots ,t_N=T_{\text{max}}\right\},t_{n+1}=t_n+\text{Δ}{t}_n,(17)$

is performed with respect to the time-domain $T=\left[0,T_{\text{max}}\right]$.

The Taylor’s expansions of the solution $\mathit{u}\left(t_{n+1}\right)\equiv {\mathit{u}}_{n+1}$ and its first time derivative $\dot{\mathit{u}}\left(t_{n+1}\right)\equiv {\dot{\mathit{u}}}_{n+1}$ are given by

$\begin{array}{c}{\mathit{u}}_{n+1}={\mathit{u}}_n+\text{Δ}{t}_n{\dot{\mathit{u}}}_n+\left(1-{\theta }_2\right)\frac{\text{Δ}{t}_n^2}{2}{\ddot{\mathit{u}}}_n+{\theta }_2\frac{\text{Δ}{t}_n^2}{2}{\ddot{\mathit{u}}}_{n+1},\\ {\dot{\mathit{u}}}_{n+1}={\dot{\mathit{u}}}_n+\left(1-{\theta }_1\right)\text{Δ}{t}_n{\ddot{\mathit{u}}}_n+{\theta }_1\text{Δ}{t}_n{\ddot{\mathit{u}}}_{n+1},\end{array}(18)$

where ${\theta }_1$ and ${\theta }_2$ are positive real parameters that define the integration scheme. Eq. 18 are substituted into Eq. 16 calculated in the intermediate time value $t_{n+1-{\alpha }_f}=\left(1-{\alpha }_f\right)t_{n+1}+{\alpha }_f{t}_n$, thus obtaining

$\mathit{M}\left[\left(1-{\alpha }_m\right){\ddot{\mathit{u}}}_{n+1}+{\alpha }_m{\ddot{\mathit{u}}}_n]+\mathit{C}[\left(1-{\alpha }_f\right){\dot{\mathit{u}}}_{n+1}+{\alpha }_f{\dot{\mathit{u}}}_n]+\mathit{K}[\left(1-{\alpha }_f\right){\mathit{u}}_{n+1}+{\alpha }_f{\mathit{u}}_n\right]={\mathit{f}}_{n+1-{\alpha }_f},(19)$

where ${\alpha }_f$ and ${\alpha }_m$ are two additional parameters that will be specified later. The following implicit scheme can be used to achieve the solution ${\ddot{\mathit{u}}}_{n+1}$, namely

${\ddot{\mathit{u}}}_{n+1}={\mathcal{A}}^{-1}\left[{\mathit{f}}_{n+1-{\alpha }_f}-\mathit{K}{\mathit{u}}_n-\left(\mathit{C}+\mathit{K}\left(1-{\alpha }_f\right)\text{Δ}{t}_n\right){\dot{\mathit{u}}}_n-\left(\mathit{M}{\alpha }_m+\mathit{C}\left(1-{\alpha }_f\right)\left(1-{\theta }_1\right)\text{Δ}{t}_n+\mathit{K}\left(1-{\alpha }_f\right)\left(1-{\theta }_2\right)\frac{\text{Δ}{t}_n^2}{2}\right){\ddot{\mathit{u}}}_n\right],(20)$

where $\mathcal{A}=\left[\mathit{M}\left(1-{\alpha }_m\right)+\mathit{C}\left(1-{\alpha }_f\right){\theta }_1\text{Δ}{t}_n+\mathit{K}\left(1-{\alpha }_f\right){\theta }_2\frac{\text{Δ}{t}_n^2}{2}\right]$. Equations 18 and 20 are employed to calculate the complete solution at each time step $t_n$.

The Generalized-α method is completely described by the four parameters ${\alpha }_m$, ${\alpha }_f$, ${\theta }_1$, ${\theta }_2$ that define the stability and the convergence properties of the time-integration scheme. They can be written as a function of the asymptotic spectral radius ${\rho }_{\infty }\in \left[\mathrm{0,1}\right]$ which is related to the numerical damping in the high-frequency limit as

${\alpha }_m=\frac{2{\rho }_{\infty }-1}{{\rho }_{\infty }+1},{\alpha }_f=\frac{{\rho }_{\infty }}{{\rho }_{\infty }+1},{\theta }_1=\frac{1}{2}-{\alpha }_m+{\alpha }_f,{\theta }_2=\frac{1}{2}{\left(1-{\alpha }_m+{\alpha }_f\right)}^2.(21)$

It is worth mentioning that Eq. 15 can be profitably employed to perform time-harmonic simulations once a harmonic form for $\mathit{u}\left(t\right)$ and $\mathit{f}\left(t\right)$ is introduced.

The mass matrix can generally be computed in different ways: the consistent mass matrix ${\mathit{M}}_C$ is obtained directly from the weak Eq. 13, so the inertia contribution is assigned to each node via the shape function; the lumped mass matrix ${\mathit{M}}_L$ is a diagonal matrix obtained condensing the mass of each element in its nodes via equilibrium. In the ensuing simulations we considered a mixed mass matrix $\mathit{M}=\left(1-{\alpha }_l\right){\mathit{M}}_C+{\alpha }_l{\mathit{M}}_L$, where ${\alpha }_l\in \left[\mathrm{0,1}\right]$ [see Hughes (1987) and Zienkiewicz and Taylor (2005)].

We implemented this numerical model in a Finite Element code, written using the software Matlab. The program deals with anisotropic and inhomogeneous thin elastic plates with different possible shapes of the domain and various kind of boundary and loading conditions. Using this code, it is also possible to perform static and modal analyses.

Numerical Simulations and Performance of the Cloak

Using the code described above, we studied the transient propagation of flexural waves in a simply-supported square plate in which a square hole is cloaked with respect to out-of-plane vibration generated by a point force varying sinusoidally. With reference to Figure 2, the homogeneous plate in ${\mathcal{C}}^0$ is a steel one ($E=210$ GPa, $\nu =0.3$, ${\rho }^0=\mathrm{7,800}$ kg/m) with thickness $H=1$ mm and bending stiffness $D^0=19.23$ Nm. The outer side of the cloak is such that $L=0.75$ m while $a=0.1923$ m, $b=0.5577$ m and $\mathit{\epsilon }a=0.025$ m.⁴ When a Winkler-like soil comes into play in the analysis, the stiffness of the elastic substratum is represented by $k_W^0=0.5\cdot {10}^6$ N/m, qualitatively corresponding to that of a silicone material (Bigoni et al., 2008; Gei, 2008).

FIGURE 2

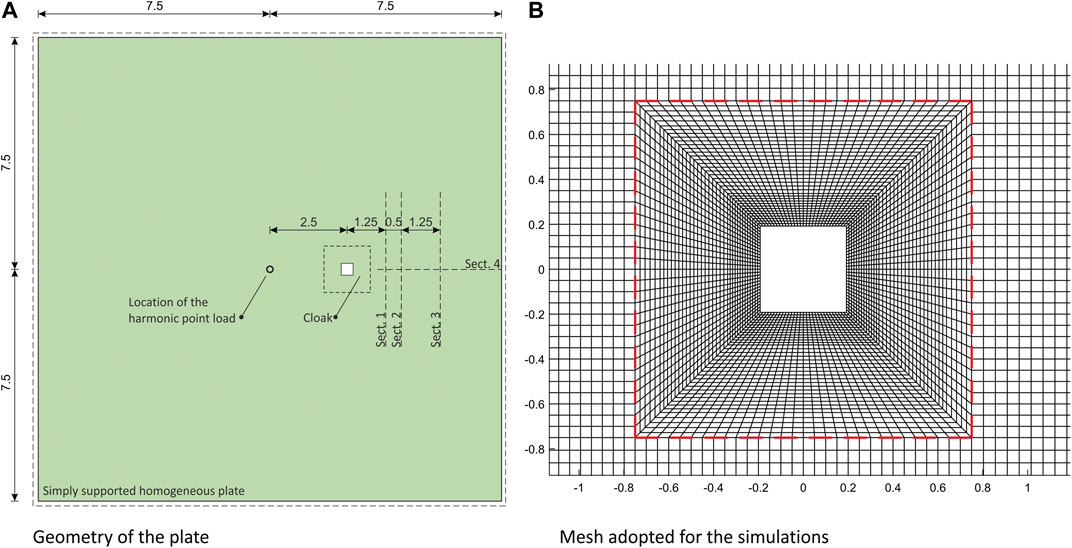
FIGURE 2. A) Geometry of the studied plate where it is visible the point where the time-varying force is enforced (dimensions in m) and the sections considered in Figure 4; (B) detail of the mesh, the external boundary of the cloak is marked with a dashed red line.

The boundary conditions on the outer perimeter are those of a simply supported plate, namely null transversal displacement $w{|}_{\partial \mathcal{K}}=0$, null rotation $w_{,\widehat{s}}{|}_{\partial \mathcal{K}}=0$ and null bending moment $m_{\widehat{n}}{|}_{\partial \mathcal{K}}=0$. The distance between the centre of the plate and the centre of the cloaked square hole is equal to 2.5 m. A harmonic transversal point force $F\left(t\right)=\overline{F}\text{cos}\left(\omega t\right)$ is applied at the centre of the plate where we assumed $\overline{F}=100$ N and ω varying from 50 to 600 rad/s. The information of the point load is contained in the vector load $\mathit{f}\left(t\right)$ in the right-hand-side of Eqs. 15 and 16.

The mesh that we used for the transient analysis is composed of ($n_e=$) 83,340 quadrangular elements with 335,864 total degrees of freedom; the elements are rectangular and regular outside the area of the cloak whereas the mesh is refined and composed of trapezoidal elements inside the area of the cloak. Each trapezoid of the cloak ${\mathcal{C}}^{\left(i\right)}$ is composed of 1,080 Finite Elements.

We performed a transient dynamical analysis with the Generalized-α method (see above) for which we chose ${\rho }_{\infty }=1$ to neglect numerical damping, therefore the method reduced to a second order and unconditionally stable algorithm with ${\alpha }_m={\alpha }_f={\theta }_1={\theta }_2=1/2,$ which is equivalent to the constant-average acceleration method (Reddy, 1993). This choice of the parameters of the numerical algorithm leads to a stable scheme for any time interval, so we considered a time domain $T=[\mathrm{0,200}$ ms$]$ with $\text{Δ}{t}_n=1$ ms. We assumed homogeneous initial condition, so $\mathit{u}\left(t=0\right)={\mathit{u}}_0=\mathit{0}$ and $\dot{\mathit{u}}\left(t=0\right)={\dot{\mathit{u}}}_0=\mathit{0}$. The initial value of ${\ddot{\mathit{u}}}_0$ (necessary in the first step) has been calculated assuming the initial condition on ${\mathit{u}}_0$ and ${\dot{\mathit{u}}}_0$ and solving Eq. 16 for $t=0$. In the time-domain integration we neglected the contribution of the damping matrix, i.e., $\mathit{C}=\mathit{0}$, and we assumed ${\alpha }_l=0.5$.

The performance of the cloak is now assessed with reference to the following case studies:

(1) a cloak possessing all properties of the Theoretical Transformation Without Prestress (TTWP) is analysed first. As recalled in the Introduction, the prestress is ruled out as it is not realistic to assume the distribution of initial stress $n_{ij}$ and in-plane body forces foreseen by the transformation. For this cloak, however, the local twisting stiffness $D_{xyxy}$ vanishes in the whole domain $\mathcal{C}$;

(2) a cloak possessing all properties of the TTWP–but with a different amount of torsional stiffness $D_{xyxy}$ to evaluate the influence of this parameter–is investigated. This case is significant as every constructed meta-plate cloak would be equipped with a certain amount of twisting stiffness;

(3) same as 2), but with the goal of estimating the role of the coupling bending stiffness $D_{xxyy}$;

(4) a cloak with the properties predicted by the TTWP is then studied, but resting on a substrate modelled as a Winkler foundation whose position-dependent subgrade modulus obeys relationship Eq. 7.

For all case studies, the displacement maps and the other relevant quantities that are illustrated are computed at a time t compatible with a propagation of the wavefront located downline of the region of the cloak, but not significantly disturbed by secondary waves reflected at the boundary of the plate.

Performance of the Cloak

The displacement map of a TTWP cloak computed at $t=155$ ms for $\omega =300$ rad$/$s is displayed in Figure 3B, to be compared with that reported in Figure 3A for a plate with an uncloaked hole. In the latter diagram, a wake is evident just on the right-hand side of the hole as well as a perturbed wave pattern on the left-hand side due to reflection caused by the hole. Those two features have been eliminated by the cloak that is able to regularise the wavefront emerging from the device into the expected circular pattern and minimise back scattering. A cloak following the transformation with prestress (Eqs. 5 and 6) would have produced a circular wavefront matching that of a homogeneous plate as presented by Colquitt et al. (2014).

FIGURE 3

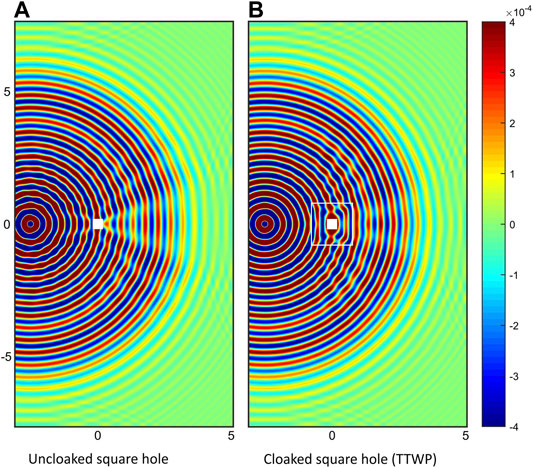
FIGURE 3. Displacement map w (in m) computed numerically at $t=155$ ms for $\omega =300$ rad$/$s: (A) uncloaked square hole; (B) performance of a cloak obtained through the Theoretical Transformation Without Prestress (TTWP). The square-shaped white contour sketched in (B) indicates the external boundary of the cloak.

In order to appraise more in detail the quality of the cloaking, Figure 4 reports the out-of-plane displacement w for the four sections sketched in Figure 2; the first three sections are transverse with respect to the propagation of the wave, at a distance from the centre of the hole of 1.25 m (Section no. 1), 1.75 m (Section no. 2) and 3 m (Section no. 3); the fourth one runs longitudinally from a point at 0.25 m just outside the right-hand boundary of the cloak to the external side of the plate. In all plots, the red line, which describes the displacements of the TTWP cloak, follows quite well the dashed line representing the response of the square, hole-less, homogeneous plate $\mathcal{K}$. Figure 4D shows that the approximate cloak is able to reproduce quite satisfactorily the phase of the wave of the homogeneous plate/perfect cloak at points in the region just after the cloaked region, to confirm the remark on Figure 3B that the TTWP cloak is able to reconstruct the circular wavefront.

FIGURE 4

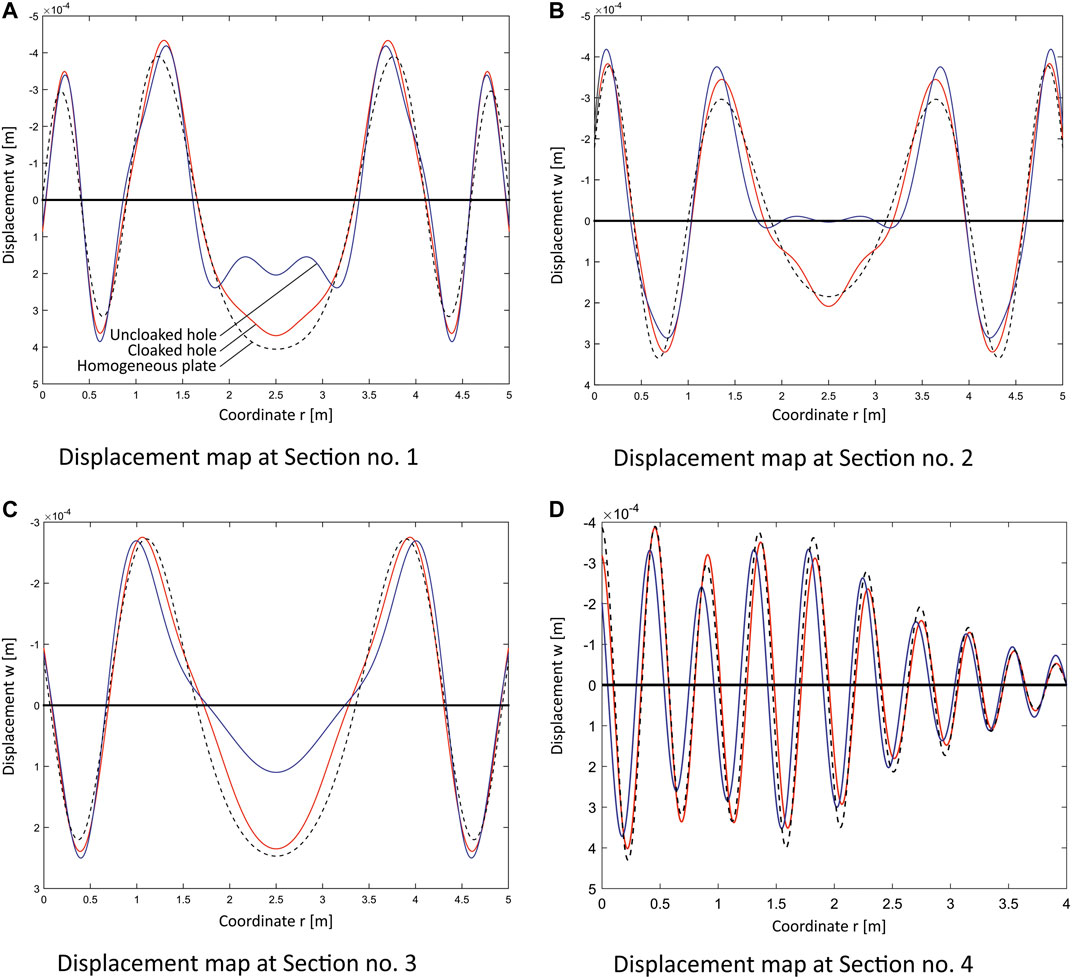
FIGURE 4. Displacement map w (in m) computed at $t=155$ ms for $\omega =300$ rad$/$s along the four Sections sketched in Figure 2. Comparison between solutions for a cloaked (TTWP–red line) and an uncloaked (blue line) hole. The dashed line represents the response of a homogeneous plate without the hole.

In order to measure quantitatively the quality of the cloak we adopt the index (Colquitt et al., 2014)

$\mathcal{Q}=\frac{{{\displaystyle \int }}_{\varsigma }|w^{\text{FE}}\left(r\right)-w^{\text{Hom}}\left(r\right){|}^{2}dr}{{{\displaystyle \int }}_{\varsigma }|w^{\text{Hom}}\left(r\right){|}^{2}dr},(22)$

that is computed along the relevant section ς that is described by the co-ordinate r. Perfection corresponds to $\mathcal{Q}=0$. In Eq. 22, $w^{\text{FE}}$ are the displacements computed by the numerical model for the non-homogeneous case under investigation and $w^{\text{Hom}}$ corresponds to the solution for the homogeneous plate. With reference to the four sections displayed in Figure 4, it turns out that the quality indices are those reported in Table 1, showing that the cloaked solutions are in average 5.95 times more effective than the uncloaked ones, therefore a good result is in any case obtained.

TABLE 1

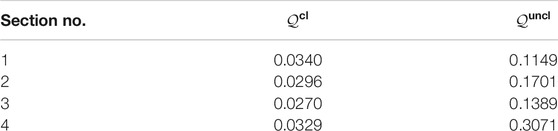
TABLE 1. Quality index for the four sections reported in Figure 4.

The effect of an amount of twisting stiffness on the displacement map of a cloak TTWP is displayed in Figure 5 where several increasing values of the parameter $D_{xyxy}$ are analysed. The plot on the far left is the one reported in Figure 3B. The detrimental effect of this parameter is readily observed. A quality factor can also be computed for the displayed cases. For Section no. 2, $\mathcal{Q}$ increases from 0.1241 (second panel) to 1.348 (far right panel) showing a constant worsening in the response of the meta-plate. In Appendix B, a strategy to minimise the twisting stiffness of a fibre-composite micro-structured plate is illustrated.

FIGURE 5

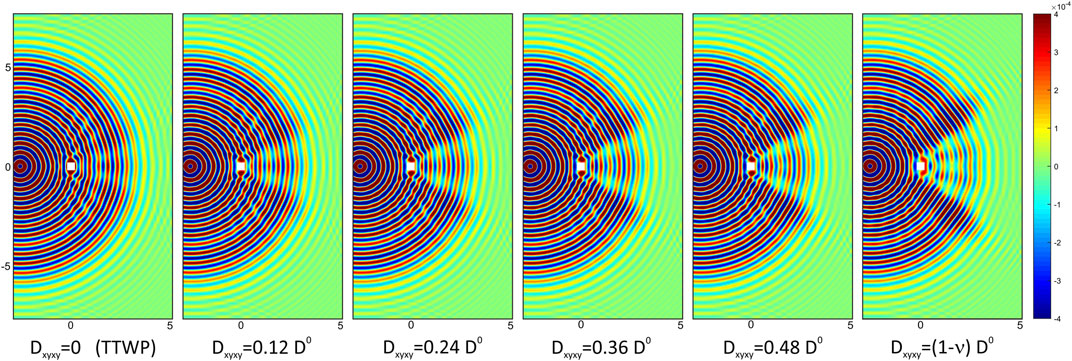
FIGURE 5. Displacement map w (in m) computed numerically at $t=155$ ms for $\omega =300$ rad$/$s carried out for increasing twisting stiffness $D_{xyxy}$. The detrimental effect on the cloaking performance of an increase in this parameter is clearly evident.

A similar analysis can be reiterated for the coupling stiffness $D_{xxyy}$. This term plays an unexpected important role as revealed by the simulations reported in Figure 6 where TTWP meta-plates are implemented, but possessing a $D_{xxyy}$ whose point-wise value corresponds to 90, 50, and 10$\text{\%}$ of the theoretical one. Unexpected because, on the one hand, in a rational microstructured plate design where the principal bending stiffnesses $D_{xxxx}$ and $D_{yyyy}$ are matched first, the coupling term simply results as an outcome of the choices made previously; on the other hand, the mathematical transformation generally predicts values of this parameter that are remarkably larger than those that can be reasonably reachable for an orthotropic plate (see Appendix B, where the list of theoretical stiffnesses are reported for two selected cases). The three panels displayed in the figure clearly demonstrate the relevance of the coupling bending stiffness in assuring an accurate behaviour of the cloak.

FIGURE 6

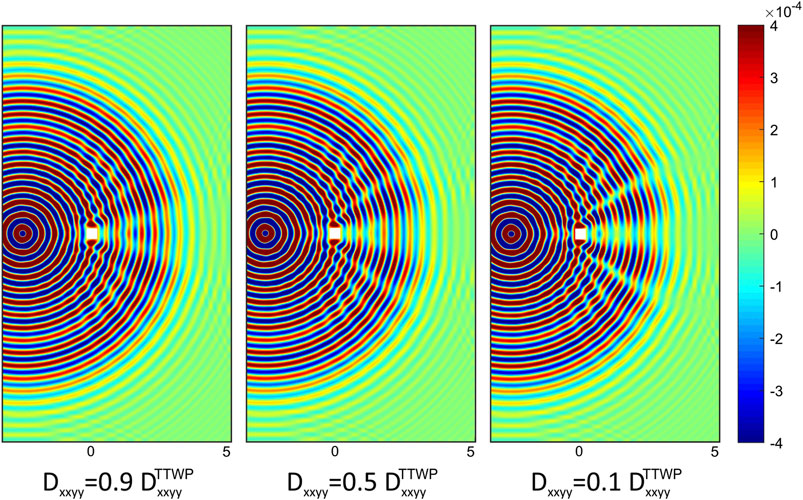
FIGURE 6. Displacement map w (in m) computed numerically at $t=140$ ms for $\omega =300$ rad$/$s carried out for decreasing coupling bending stiffness $D_{xxyy}$. $D_{xxyy}^{\text{TTWP}}$ indicates the value of the variable predicted by the theoretical transformation. The damaging effect on the cloaking performance of a decrease in this parameter is clearly evident.

The last picture of this subsection (Figure 7) refers to a TTWP cloak subjected to point-loads pulsating at different ω, to show that the approximate model is behaving well for a quite broad range of frequencies. The time of computation t differs from one picture to the other in order to compare a similar displacement pattern. For all displayed cases, the meta-plate is able to reconstruct satisfactorily the circular wavefront.

FIGURE 7

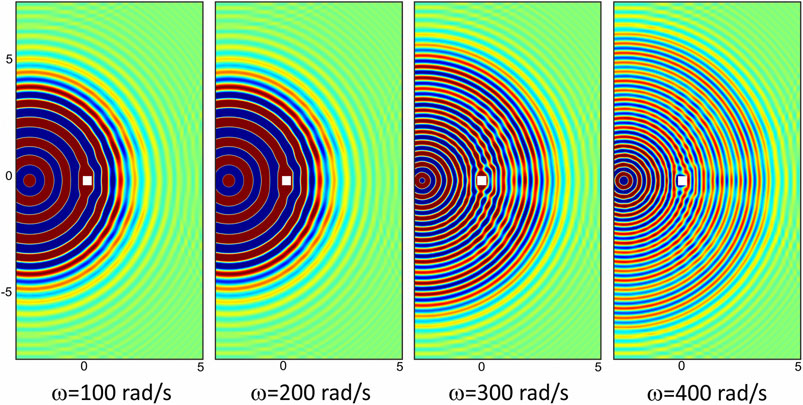
FIGURE 7. Displacement maps w (in m) computed numerically at frequencies 100, 200, 300 and 400 rad/s (at different times t in order to compare a similar displacement pattern) for a TTWP cloak.

Flexural Cloaks on Winkler Substrates

In real applications, cloaks are likely grounded to a substrate which also provides the support of the object to hide. The cloaking features of a plate resting on a Winkler foundation is analysed in Figure 8 for $\omega =300$ rad$/$s at $t=145$ ms. In part b), the TTWP cloak rests on a bed of springs whose subgrade modulus is constant ($k_W=k_W^0$). This assumption clearly worsens the performance of the device with respect to the uncloaked hole case (Figure 8A). Conversely, the position dependent stiffness $k_W\left(x_p\right)$, whose value in $\mathcal{C}$ follows Eq. 7, guarantees a satisfactory behaviour of the device, as it can be noted that the wavefront reconstructs correctly after the transformed domain. Similarly to the simply-supported plate, solutions along two sections (i.e. no. 2 and no. 4 in Figure 2A) are studied in Figure 9. The quality index for the two sections are ${\mathcal{Q}}_2^{\text{cl}}=0.0134$, ${\mathcal{Q}}_2^{\text{uncl}}=0.1719$ and ${\mathcal{Q}}_4^{\text{cl}}=0.0164$, ${\mathcal{Q}}_4^{\text{uncl}}=0.3304$, respectively. Again, the behaviour of the perfect cloak, both in phase and amplitude, is captured remarkably well by the approximate one with position dependent subgrade modulus. This shows that a correct design of a flexural cloak resting on a substrate requires the presence of a variable subgrade modulus that follows the provision of the theoretical transformation.

FIGURE 8

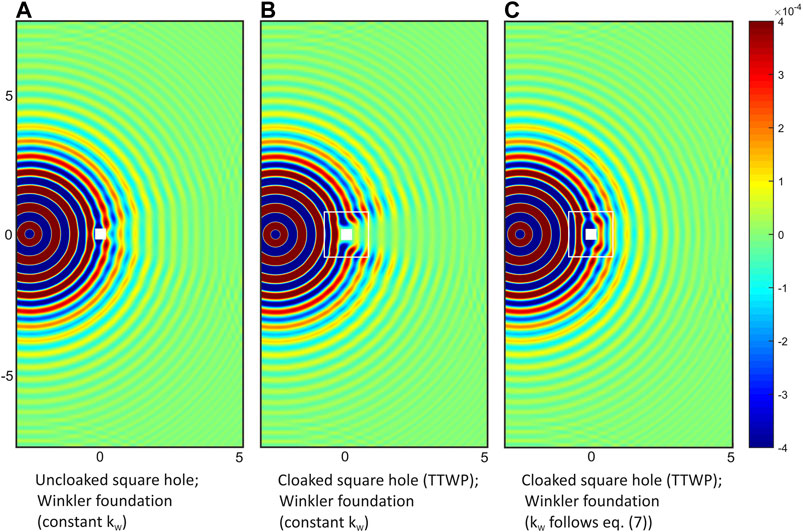
FIGURE 8. Displacement maps w (in m) computed numerically at $t=145$ ms for $\omega =300$ rad$/$s. (A) Uncloaked square hole where the plate rests on a Winkler foundation with $k_W^0=0.5\cdot {10}^6$ N/m; (B) hole cloaked by a plate obtained through the TTWP resting on a Winkler foundation with a constant $k_W=k_W^0$; (C) same as (B), but with a position-dependent subgrade module whose value follows Eq. 7. The square-shaped white contour indicates the external boundary of the cloak.

FIGURE 9

FIGURE 9. Displacement map w (in m) computed at $t=145$ ms for $\omega =300$ rad$/$s along Sections no. 2 (A) and no. 4 (B) in Figure 2 for a plate resting on a Winkler foundation with $k_W^0=0.5\cdot {10}^6$ N/m. Comparison between solutions for a cloaked hole (TTWP with position-dependent subgrade module (see Eq. 7 and Figure 8) –red line) and an uncloaked one (constant subgrade module–blue line). The dashed line represents the response of a homogeneous plate without the hole.

As a final remark of this section, one must note that the employed geometrical, elastic and loading conditions correspond to a chosen prototype geometry, but the scale of the dimensions, and the load intensity and frequency can be changed to obtain an identical behaviour on a different scaled structure subjected to different load conditions.

Concluding Remarks

The engineering of a meta-structural cloak for elastic flexural waves based on transformation elastodynamics is an exceptional challenge which theoretically would require the implementation of unfeasible compressive prestresses and in-plane body forces to warrant equilibrium. Therefore, reasonable assumptions should be adopted that are however grounded on the following main points: 1) the meta-plate has a locally orthotropic response with 2) an almost vanishing twisting stiffness, 3) spatially-varying bending stiffnesses and 4) density. In addition, the structure invariably would interact with a substrate.

With the aim of dealing with a fully open simulation tool, a FE code is developed and implemented with the specific purpose of studying transient wave propagation in locally orthotropic Kirchhoff-Love plates. A subparametric technique is adopted for spatial discretization, whereas the approximation in the time domain is performed with the single-step time-integration algorithm Generalized-α method.

The performance of a prototype meta-plate square cloak based on the approximate assumption of null prestress is then assessed parametrically by focusing specially on the role of the twisting stiffness and the coupling bending stiffness. The reason is that while the local principal bending rigidities can be matched quite easily in a microstructured plate, for those two parameters the process is much more difficult.

The simulations show that for an effective cloaking response, the twisting stiffness should be lower than 10$\text{\%}$ of the bending one for the homogeneous plate, while for the coupling bending stiffness a departure of 10$\text{\%}$ from the theoretical value already worsens with some evidence the performance of the meta-plate.

A second contribution of this work consists in the extension of the general theory of thin-plate cloaks to comprise interaction of the meta-structure with an elastic substrate via Winkler-foundation model. The conclusion is that the subgrade modulus transforms similarly to the mass density of the plate. The numerical simulations confirm this finding and clearly show that a constant modulus beneath the cloak jeopardizes dramatically the functionality of the structure.

The FE tool can be further expanded to embed inelastic responses of plate and substrate, thus enabling simulations of approximate supported meta-plates subjected to transient waves arising from seismic shocks.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation

Author Contributions

DV and MG conceived the idea. MR and DV developed and implemented the numerical tool. MR performed the simulations. MR, DV, and MG wrote the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MR acknowledges Italian Ministry of Education, University and Research (MIUR) for supporting their research under grant PRIN no. 2015LYYXA8. MG acknowledges support from EU-H2020-Marie Curie-Sklodowska Action-COFUND grant SIRCIW (agreement no. 663830).

Appendix A: Material Parameters and Pre-Stress for the Cloak

The six independent flexural stiffnesses for trapezoid ${\mathcal{C}}^{\left(1\right)}$ of the cloak are

$D_{1111}^{\left(1\right)}={\alpha }^2\left(1-\frac{c}{x_1}\right)D^0,D_{2222}^{\left(1\right)}=\frac{{\alpha }^2{\left(c^2{x}_2^2+x_1^4\right)}^2}{{\left(x_1-c\right)}^3{x}_1^5}{D}^0,D_{2211}^{\left(1\right)}=\frac{{\alpha }^2\left(c^2{x}_2^2+x_1^4\right)}{\left(x_1-c\right)x_1^3}{D}^0,$

$D_{1212}^{\left(1\right)}=\frac{{\alpha }^2{c}^2{x}_2^2}{\left(x_1-c\right)x_1^3}{D}^0,D_{1112}^{\left(1\right)}=-{\alpha }^{2}c\frac{x_2}{x_1^2}{D}^0,D_{2212}^{\left(1\right)}=-\frac{{\alpha }^{2}c{x}_2\left(c^2{x}_2^2+x_1^4\right)}{{\left(x_1-c\right)}^2{x}_1^4}{D}^0.$

The remaining components can be deduced from the major and minor symmetries of $D_{ijkl}$. The membrane forces and in-plane body forces are

$n_{11}^{\left(1\right)}=\frac{2{\alpha }^{2}c}{x_1^2\left(x_1-c\right)}{D}^0,n_{22}^{\left(1\right)}=-\frac{2{\alpha }^{2}c\left(x_1^4+8c{x}_2^2{x}_1-3c^2{x}_2^2\right)}{x_1^4{\left(x_1-c\right)}^3}{D}^0,$

$n_{12}^{\left(1\right)}=\frac{2{\alpha }^{2}c{x}_2\left(3x_1-2c\right)}{{\left(x_1-c\right)}^2{x}_1^3}{D}^0,s_1^{\left(1\right)}=0,s_2^{\left(1\right)}=\frac{24{\alpha }^{2}c{x}_2}{{\left(x_1-c\right)}^3{x}_1^2}{D}^0.$

Stiffnesses transform locally as follows:

$D_{xxxx}=D_{1111}{\text{cos}}^4\theta +2\left(D_{1122}+2D_{1212}\right){\text{sin}}^2\theta {\text{cos}}^2\theta +D_{2222}{\text{sin}}^4\theta +2\left(D_{1112}{\text{cos}}^2\theta +D_{2221}{\text{sin}}^2\theta \right)\text{sin}2\theta ,$

$D_{yyyy}=D_{1111}{\text{sin}}^4\theta +2\left(D_{1122}+2D_{1212}\right){\text{sin}}^2\theta {\text{cos}}^2\theta +D_{2222}{\text{cos}}^4\theta -2\left(D_{1112}{\text{sin}}^2\theta +D_{2221}{\text{cos}}^2\theta \right)\text{sin}2\theta ,$

$D_1=D_{1122}+\left(D_{1111}+D_{2222}-2\left(D_{1122}+2D_{1212}\right)\right){\text{sin}}^2\theta {\text{cos}}^2\theta +\left(D_{2221}-D_{1112}\right)\text{cos}2\theta \text{sin}2\theta ,$

$D_{xyxy}=D_{1212}+\left(D_{1111}+D_{2222}-2\left(D_{1122}+2D_{1212}\right)\right){\text{sin}}^2\theta {\text{\hspace{0.17em}cos}}^2\theta +\left(D_{2221}-D_{1112}\right)\text{cos}2\theta \text{sin}2\theta .$

Appendix B: An Example of a Micro-Structured Plate Cloak

A design based on a micro-structured meta-plate is here proposed with the aim of matching locally the principal bending stiffnesses $D_{xxxx}$ and $D_{yyyy}$, and limiting the twisting stiffness $D_{xyxy}$. The exercise is conducted by assuming a high-performance fibre-reinforced material whose epoxy matrix (shortened as “ep”; material parameters: $E_{\text{ep}}=3.4$ GPa, ${\nu }_{\text{ep}}=0.3$, ${\rho }_{\text{ep}}=\mathrm{1,200}$ kg/m) is stiffened by long boron fibres (shortened as “B”; material parameters: $E_{\text{B}}=380$ GPa, ${\nu }_{\text{B}}=0.13$, ${\rho }_{\text{B}}=\mathrm{2,600}$ kg/m) (Kaw, 2006; Mroz, 2011). The meta-plate is such that the cross section orthogonal to axis x is compact (and corresponds to the “core”, indicated with “c”) with its thickness matching the height H and fibres aligned along axis x. That orthogonal to axis y features a set of tiny rectangular appendices, in the number of n over a length equal to H, on both the outer sides called “teeth” (shortened as “t”). The total height of core and teeth is $H_y$ (Figure 10). The reason of selecting rectangular appendices lies in the stringent requirement of limiting the twisting stiffness. The slenderness of the teeth may lead to instability on the side of the plate in compression, however this issue is not further addressed here. Fibres are here aligned along axis y only in the teeth. Along both directions, fibres are locally measured out (their volume fractions are spatially-varying design variables that are however capped at 0.8) to allow the relevant cross section to reach the needed bending stiffness.

In the spirit of the Kirchhoff-Love theory for plates, the core material is subjected to a plane-stress state, therefore the linear elastic constitutive equations read

${\sigma }_{xx}=\frac{E_{\text{c}1}}{1-{\nu }_{xy}^{\text{c}}{\nu }_{yx}^{\text{c}}}{\epsilon }_{xx}+\frac{{\nu }_{xy}^{\text{c}}{E}_{\text{c}2}}{1-{\nu }_{xy}^{\text{c}}{\nu }_{yx}^{\text{c}}}{\epsilon }_{yy},{\sigma }_{yy}=\frac{E_{\text{c}2}}{1-{\nu }_{xy}^{\text{c}}{\nu }_{yx}^{\text{c}}}{\epsilon }_{yy}+\frac{{\nu }_{xy}^{\text{c}}{E}_{\text{c}2}}{1-{\nu }_{xy}^{\text{c}}{\nu }_{yx}^{\text{c}}}{\epsilon }_{xx},$

${\tau }_{xy}=G_{\text{c}}{\gamma }_{xy},(23)$

whereas the teeth undergo a uniaxial stress (i.e., ${\sigma }_{yy}^{\text{t}}=E_{\text{t}}{\mathit{\epsilon }}_{yy}$). All constitutive parameters of the composite in both core and teeth follow the rule of mixtures applied to composite materials,⁵ however more sophisticated models [e.g., Halpin-Tsai model, Halpin and Kardos (1976)] can be adopted for their estimation.

The effective stiffnesses $D_{ijkl}^{\text{clk}}$ appearing in the cloak moment/curvature constitutive equations (cf. Eq. 10)

$m_{xx}=-D_{xxxx}^{\text{clk}}{w}_{,xx}-D_{xxyy}^{\text{clk}}{w}_{,yy},m_{yy}=-D_{yyyy}^{\text{clk}}{w}_{,yy}-D_{xxyy}^{\text{clk}}{w}_{,xx},(24)$

$m_{xy}=-D_{xyxy}^{\text{clk}}{w}_{,xy}$

can be calculated by applying the standard methodology of integrating locally stresses across the plate thickness. The integration leads to

$D_{xxxx}^{\text{clk}}=D^{0}R\frac{E_{\text{c}1}}{E_{\text{c}2}},D_{xxyy}^{\text{clk}}=D^{0}R{\nu }_{xy}^{\text{c}},D_{xyxy}^{\text{clk}}=G_{\text{c}}\frac{H^3}{6}+G_{\text{t}}\frac{H_y-H}{6}{\left(\frac{H}{n}\right)}^2,$

$D_{yyyy}^{\text{clk}}=D^0\left[R+\left(1-{\nu }^2\right)\frac{E_{\text{t}}}{E}\left[{\left(\frac{H_y}{H}\right)}^3-1\right]\right],(25)$

where $R=\left(E_{\text{c}2}/E\right)\left(1-{\nu }^2\right)/\left(1-{\nu }_{xy}^{\text{c}}{\nu }_{yx}^{\text{c}}\right)$.

With reference to the square transformation displayed in Figure 1B, the properties of the two cross sections of the micro-structured plate can be defined as follows:

1) the function $c_{\text{B}}^{\text{c}}\left(x_1,x_2\right)$ is computed through Eq. 25 in which $D_{xxxx}\left(x_1,x_2\right)$ replaces the current entry on the left-hand side of the equation. The resulting expression is a cubic in the unknown. For the typical involved parameter $D_{xxxx}\left(x_1,x_2\right)$, there is always a solution in the range $0<c_{\text{B}}^{\text{c}}\le 0.8$;

2) Equation 25 can now be employed to compute $H_y$ or alternatively $c_{\text{B}}^{\text{t}}\left(x_1,x_2\right)$) in which $D_{yyyy}\left(x_1,x_2\right)$ appears on the left-hand side of the equation. In a practical case, the usual choice is to set $c_{\text{B}}^{\text{t}}=0.8$ and then $H_y$ is to be calculated;

3) the teeth density $n/H$ should be selected so that the twisting stiffness can be estimated via Eq. 25.

Eventually, the coupling term $D_{xxyy}^{\text{clk}}$ can be computed through Eq 25.

The outcome of the design is shown in Tables 2 and 3 with reference to two transformations whose parameters are (both with $L=0.75$ m): 1) $a=0.1$ m, $b=0.65$ m and $\mathit{\epsilon }a=0.025$ m, and 2) $a=0.1923$ m, $b=0.5577$ m and $\mathit{\epsilon }a=0.025$ m (i.e., the one studied in the numerical simulations). It can be noted that in all control points listed in the tables, the value of $D_{xxyy}^{\text{clk}}$ is orders of magnitude smaller than the theoretical one.

FIGURE 10

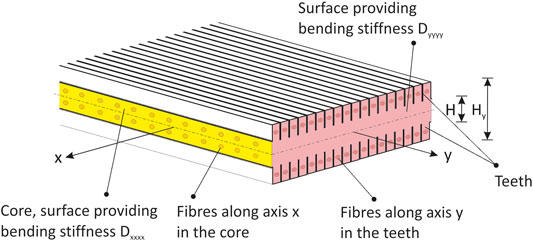
FIGURE 10. Local micro-structure of the meta-plate for cloaking flexural waves. The yellow (resp. pink) cross section provides the bending stiffness $D_{xxxx}$ (resp. $D_{yyyy}$). Axes x and y correspond to the local principal directions of orthotropy. The teeth density is $n/H$.

TABLE 2

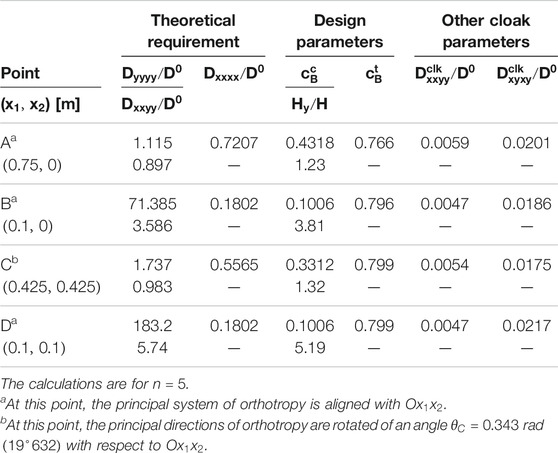
TABLE 2. Microstructural parameters of the boron/epoxy cloak for the transformation whose parameters are $a=0.1$ m, $b=0.65$ m, $\mathit{\epsilon }a=0.025$ m, $L=0.75$ m.

TABLE 3

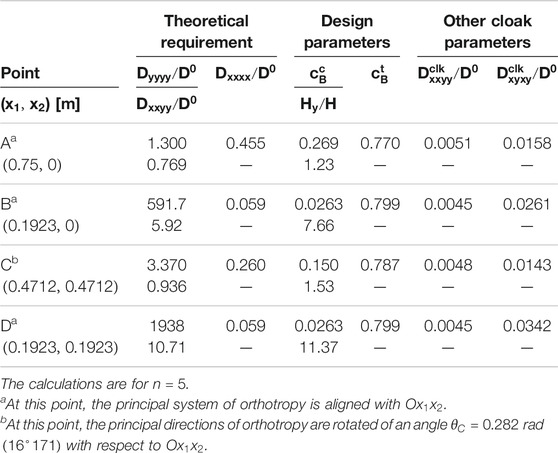
TABLE 3. Microstructural parameters of the boron/epoxy cloak for the transformation whose parameters are $a=0.1923$ m, $b=0.5577$ m, $\mathit{\epsilon }a=0.025$ m, $L=0.75$ m.

Footnotes

¹Uppercase and lowercase indices, both ranging between 1 and 2, are referred to reference and transformed domains, respectively, whereas a 0 in either super- or sub-script position indicates that the quantity concerned is evaluated in the reference configuration.

²ϵ plays the role of regularisation parameter for the construction of a near cloak (Kohn et al., 2008) in which the material properties at the inner boundary of the cloak are not singular.

³The summation over the repeated index is implied throughout the paper.

⁴With this set of parameters, it turns out that for the trapezoid ${\mathcal{C}}^{\left(1\right)}$ the stiffnesses for the four representative points sketched in Figure 1B are displayed in Table 3. The minimum value $D_{1111}$ is achieved along the whole inner boundary whereas the maximum $D_{2222}$ is at point D.

⁵In particular, $E_{\text{c}1}$, ${\nu }_{xy}^{\text{c}}$ follow the weighted average ${(\cdot )}_{\xi }={(\cdot )}_{\text{B}}{c}_{\text{B}}^{\xi }+{(\cdot )}_{\text{ep}}{c}_{\text{ep}}^{\xi }$, whereas $E_{\text{c}2}$, $G_{\text{c}}$, and $G_{\text{t}}$ obey the harmonic average $1/{(\cdot )}_{\xi }=c_{\text{B}}^{\xi }/{(\cdot )}_{\text{B}}+c_{\text{ep}}^{\xi }/{(\cdot )}_{\text{ep}}$, with $\xi \in \left\{\text{c},\text{t}\right\}$; ${\nu }_{yx}^{\text{c}}={\nu }_{xy}^{\text{c}}{E}_{\text{c}2}/E_{\text{c}1}$.

References

Bigoni, D., Gei, M., and Movchan, A. B. (2008). Dynamics of a prestressed stiff layer on an elastic half space: filtering and band gap characteristics of periodic structural models derived from long-wave asymptotics. J. Mech. Phys. Solid. 56, 2494–2520. doi:10.1016/j.jmps.2008.02.007

CrossRef Full Text | Google Scholar

Brun, M., Colquitt, D. J., Jones, I. S., Movchan, A. B., and Movchan, N. V. (2014). Transformation cloaking and radial approximations for flexural waves in elastic plates. New J. Phys. 16, 093020. doi:10.1088/1367-2630/16/9/093020

CrossRef Full Text | Google Scholar

Brun, M., Guenneau, S., and Movchan, A. B. (2009). Achieving control of in-plane elastic waves. Appl. Phys. Lett. 94, 061903. doi:10.1063/1.3068491

CrossRef Full Text | Google Scholar

Chen, Y., Hu, J., and Huang, G. (2016). A design of active elastic metamaterials for control of flexural waves using the transformation method. J. Intell. Mater. Syst. Struct. 27, 1337–1347. doi:10.1177/1045389x15590273

CrossRef Full Text | Google Scholar

Chung, J., and Hulbert, G. M. (1993). A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-α method. J. Appl. Mech. 60, 371–375. doi:10.1115/1.2900803

CrossRef Full Text | Google Scholar

Chung, J., and Hulbert, G. M. (1994). A family of single-step houbolt time integration algorithms for structural dynamics. Comput. Methods Appl. Mech. Eng. 118, 1–11. doi:10.1016/0045-7825(94)90103-1

CrossRef Full Text | Google Scholar

Climente, A., Torrent, D., and Sánchez-Dehesa, J. (2016). Analysis of flexural wave cloaks. AIP Adv. 6, 121704. doi:10.1063/1.4968611

CrossRef Full Text | Google Scholar

Colquitt, D. J., Brun, M., Gei, M., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2014). Transformation elastodynamics and cloaking for flexural waves. J. Mech. Phys. Solid. 72, 131–143. doi:10.1016/j.jmps.2014.07.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Darabi, A., Zareei, A., Alam, M.-R., and Leamy, M. J. (2018). Experimental demonstration of an ultrabroadband nonlinear cloak for flexural waves. Phys. Rev. Lett. 121, 174301. doi:10.1103/physrevlett.121.174301

PubMed Abstract | CrossRef Full Text | Google Scholar

Farhat, M., Guenneau, S., and Enoch, S. (2009a). Ultrabroadband elastic cloaking in thin plates. Phys. Rev. Lett. 103, 024301. doi:10.1103/PhysRevLett.103.024301

PubMed Abstract |CrossRef Full Text | Google Scholar

Farhat, M., Guenneau, S., Enoch, S., and Movchan, A. B. (2009b). Cloaking bending waves propagating in thin elastic plates. Phys. Rev. B 79, 033102. doi:10.1103/PhysRevB.79.033102

CrossRef Full Text | Google Scholar

Futhazar, G., Parnell, W. J., and Norris, A. N. (2015). Active cloaking of flexural waves in thin plates. J. Sound Vib. 356, 1–19. doi:10.1016/j.jsv.2015.06.023

CrossRef Full Text | Google Scholar

Gei, M. (2008). Elastic waves guided by a material interface. Eur. J. Mech. Solid. 27, 328–345. doi:10.1016/j.euromechsol.2007.10.002

CrossRef Full Text | Google Scholar

Halpin, J. C., and Kardos, J. L. (1976). Halpin-tsai equations: a review. Polym. Eng. Sci. 16, 344–352. doi:10.1002/pen.760160512

CrossRef Full Text | Google Scholar

Hughes, T. (1987). The finite element method - linear static and dynamic finite element analysis. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

Imbert, F. (1979). Analyse des structures par elements finis. Paris, France: Cepadues editions.

Google Scholar

Kaw, A. (2006). Mechanics of composite materials. Boca Raton, FL: Taylor & Francis Group.

Google Scholar

Kohn, R. V., Shen, H., Vogelius, M. S., and Weinstein, M. I. (2008). Cloaking via change of variables in electric impedance tomography. Inverse Probl. 24, 015016. doi:10.1088/0266-5611/24/1/015016

CrossRef Full Text | Google Scholar

Lekhnitskii, S., Tsai, S., and Cheron, T. (1968). Anisotropic plates. New York, NY: Gordon and Breach.

Google Scholar

Liu, M., and Zhu, W. D. (2019). Nonlinear transformation-based broadband cloaking for flexural waves in elastic thin plates. J. Sound Vib. 445, 270–287. doi:10.1016/j.jsv.2018.12.025

CrossRef Full Text | Google Scholar

Milton, G. W., Briane, M., and Willis, J. R. (2006). On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 8, 248. doi:10.1088/1367-2630/8/10/248

PubMed Abstract | CrossRef Full Text | Google Scholar

Misseroni, D., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2016). Cymatics for the cloaking of flexural vibrations in a structures plate. Sci. Rep. 6, 23929. doi:10.1038/srep23929

PubMed Abstract | CrossRef Full Text | Google Scholar

Misseroni, D., Movchan, A. B., and Bigoni, D. (2019). Omnidirectional flexural invisibility of multiple interacting voids in vibrating elastic plates. Proc. R. Soc. A 475, 2229. doi:10.1098/rspa.2019.0283

PubMed Abstract | CrossRef Full Text | Google Scholar

Mroz, A. (2011). Stability analysis of a plane, rectangular, boron-epoxy laminated plate basing on strength properties determined by different methods. Mech. Mech. Eng. 15, 161–181.

Google Scholar

Ning, L., Wang, Y.-Z., and Wang, Y.-S. (2020). Active control cloak of the elastic wave metamaterial. Int. J. Solid Struct. 202, 126–135. doi:10.1016/j.ijsolstr.2020.06.009

CrossRef Full Text | Google Scholar

Norris, A. N., and Shuvalov, A. L. (2011). Elastic cloaking theory. Wave Motion. 48, 525–538. doi:10.1016/j.wavemoti.2011.03.002

CrossRef Full Text | Google Scholar

O’Neill, J., Selsil, O., McPhedran, R. C., Movchan, A. B., and Movchan, N. V. (2015). Active cloaking of inclusions for flexural waves in thin elastic plates. Q. J. Mech. Appl. Math. 68, 263–288. doi:10.1093/qjmam/hbv007

CrossRef Full Text | Google Scholar

Petera, J., and Pittman, J. F. T. (1994). Isoparametric hermite elements. Int. J. Numer. Meth. Engng. 37, 3489–3519. doi:10.1002/nme.1620372006

CrossRef Full Text | Google Scholar

Petyt, M. (1990). An introduction to the finite element method. Cambridge, UK: Cambridge University Press.

Google Scholar

Reddy, J. (1993). An introduction to the finite element method. 2nd Edn. New York, NY: McGraw-Hill.

Google Scholar

Stenger, N., Wilhelm, M., and Wegener, M. (2012). Experiments on elastic cloaking in thin plates. Phys. Rev. Lett. 108, 014301. doi:10.1103/PhysRevLett.108.014301

PubMed Abstract | CrossRef Full Text | Google Scholar

Timoshenko, S., and Woinowsky-Krieger, S. (1959). Theory of plates and shells. New York, NY: McGraw-Hill.

Google Scholar

Zareei, A., and Alam, M.-R. (2017). Broadband cloaking of flexural waves. Phys. Rev. E 95, 063002. doi:10.1103/PhysRevE.95.063002

PubMed Abstract | CrossRef Full Text | Google Scholar

Zienkiewicz, O., and Taylor, R. (2005). The finite element method. 6th Edn. Amsterdam, Netherlands: Elsevier.

Google Scholar