How Severe Plastic Deformation Changes the Mechanical Properties of Thermoelectric Skutterudites and Half Heusler Alloys

Introduction

In the midst of climate change, we are urged to find sustainable, cheap and fast methods to produce green energy. Thermoelectric (TE) materials can convert any form of waste heat directly into electricity without any moving parts (Snyder and Toberer, 2008). The quality of a TE material is judged by the figure of merit, ZT = (S²T)/(ρλ) where S is the Seebeck coefficient, T is the temperature, ρ is the electrical resistivity, λ = λ_e + λ_ph is the thermal conductivity, consisting of the electronic, λ_e, and the phonon part, λ_ph. Besides silicides (Sadia et al., 2016), Bi-tellurides (Ma et al., 2008; Poudel et al., 2008; Yu et al., 2009; Ashida et al., 2012), PbTe (Cohen et al., 2015; Guttmann et al., 2015; Komisarchik et al., 2016) or Zintl phases [(Kauzlarich, 2019) and references therein], just to point out some important TE materials, skutterudites [review articles (Snyder and Toberer, 2008), (Nolas et al., 1999; Uher, 2001; Rowe, 2006; Rull-Bravo et al., 2015; Schierning et al., 2015; Rogl and Rogl, 2017b; Rogl et al., 2019; Rogl and Rogl, 2019; Hasan et al., 2020) and references therein] and half-Heusler alloys [(Sakurada and Shutoh, 2005; Gelbstein et al., 2011; Poon et al., 2011; Xie et al., 2012; Fu et al., 2013; Schwall and Balke, 2013; Appel and Gelbstein, 2014; Fu et al., 2015; Gürth et al., 2016; Li et al., 2016; Rogl et al., 2017b; Tavassoli et al., 2017; Tavassoli et al., 2018; Zhu et al., 2019) and review articles (Casper et al., 2012; Poon, 2018) and references therein] are the most promising candidates, exhibiting not only a high ZT value, but they are easy to fabricate and the starting materials can generally be chosen from those available and cheap. In addition, skutterudites as well as half-Heusler alloys are suitable for heat sources at moderate temperatures (300 –900 K) such as in automobile exhaust or industrial waste heat. Still, it is a goal of researchers to further increase ZT. Besides other routes, an efficient technique is to decrease λ_ph via a drastic reduction of the grain size, and in parallel to enhance the phonon boundary scattering at interfaces and crystal defects, such as point, line and volume defects (Kim et al., 2015; Zhang et al., 2017).

One possibility covers “bottom-up” methods like ball-milling (BM) or high-energy ball milling (HBM), which decrease the grain size to micrometers or even below hundred nanometers and increase the defect density (Rogl et al., 2014b), but during solidification in a hot press or via spark plasma sintering, the grains partially re-grow, and the defect density decreases.

Another possibility is severe plastic deformation (SPD), a “bottom-down” method, which produces materials with grains down to nanometer range and in addition introduces vacancies, dislocations, grain boundaries with high angles of misorientation and other defects (Zehetbauer and Estrin, 2009; Rogl et al., 2012a; Rogl et al., 2012c; Valiev et al., 2012; Rogl et al., 2013b; Valiev et al., 2016; Ivanisenko et al., 2016; Rogl et al., 2020a).

SPD, actually dating back to 200 BC, when repetitive forging and folding was used to strengthen the steel for swords (Langdon, 2011; Segal, 2018), is one of the major techniques to produce materials with ultra fine grains. In the 1930s Nobel laureate P.W. Bridgman used a combination of compression and torsional straining on metals (Bridgman, 1952), but the method, then called intensive plastic deformation, became scientifically important in the 1990ies when Valiev et al. published a clear evidence of ultra fine grains (Valiev et al., 1991). Musalimov introduced the term SPD (Musalimov and Valiev, 1992).

Nowadays, besides high pressure torsion (HPT) there are several other methods to introduce SPD like equal channel angular extrusion/pressing (ECAP), continuous extrusion forming (CONFORM), accumulated roll bonding (ARB), multi directional forging (MDF), cyclic extrusion, and compression (CEC), repetitive corrugation and straightening (RCS), twist extrusion (TE), hot area reduction extrusion (HARE), the cone-cone method (CCM), just to name the most important ones. All these methods have advantages and disadvantages. Using forging, extrusion and rolling, the cross section is limited, they need very high loads and result in anisotropic substructures, but the advantage is that the length of the produced material is almost unlimited. Continuous extrusion forming, e.g., is applied for wire and tube manufacturing. ARB accumulates a large strain in the sheet and a very fine structure, however, not three-dimensionally equiaxed. For details on these techniques see the overview articles by Valiev et al. (2016) (Valiev et al., 1993; Valiev et al., 2006).

ECAP and HPT are the most commonly used methods (Valiev et al., 1993; Sanusi et al., 2012; Valiev et al., 2016; Ivanisenko et al., 2016; Suwas and Mondal, 2019). They have both the advantage that the cross sectional area of the sample remains nearly unchanged by deformation; the result is the formation of a finer grain structure while damage and fracture are suppressed. Using ECAP, the sample can be extruded several times, reaching an ultrafine grain structure, but with ECAP, using back pressure, only 2 GPa at the most can be achieved, whereas with HPT it is possible to reach 10 GPa.

Various research groups used the ECAP process on Bi-Te alloys (for a summary see (Rogl et al., 2013b)) and found grain refinement and as consequence enhanced TE properties and higher hardness but also in some cases higher bending strength and/or reduced texture.

Why in our case HPT was used, is explained as follows: HPT infers severe torsional strains into a disk-shaped sample, placed between two anvils, one rotating against the other while applying a large uniaxial compressive stress, usually in the range of 1–10 GPa (Figure 1). With this technique very high strains can be imposed and thus produce bulk nanocrystalline materials with a high concentration of defects, not only high-angle grain boundaries but also numerous point defects and dislocations. Applied on hand-ground (HM) or BM and hot-pressed (HP) samples, this method leads to an enhancement of the figure of merit ZT of a TE material, because after HPT-processing—although the electrical resistivity is enhanced and the Seebeck coefficient remains basically unchanged—the thermal conductivity is significantly lower. ZTs of filled and unfilled skutterudites, half-Heusler or Heusler alloys increase by up to 30%, as was shown by the authors (Zhang et al., 2010a; Rogl et al., 2011c; Rogl et al., 2012a; Rogl et al., 2012b; Rogl et al., 2012c; Rogl et al., 2013a; Rogl et al., 2013b; Rogl et al., 2014b; Rogl et al., 2015; Rogl et al., 2020a), Anbalagan et al. (Anbalagan et al., 2014), Masuda et al. (Masuda et al., 2018), and other groups as listed in Refs. (Rogl et al., 2013b; Rogl et al., 2019b; Rogl and Rogl, 2019; Rogl et al., 2020a).

FIGURE 1

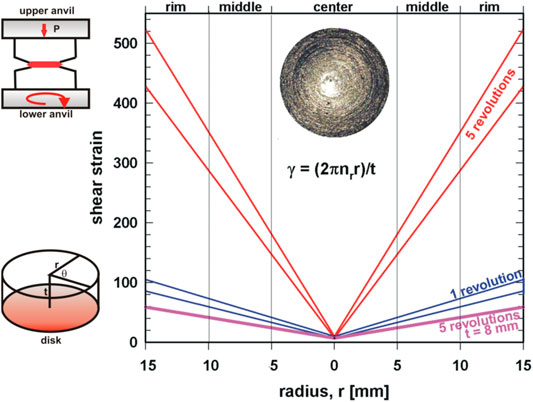
FIGURE 1. Left: schematic view of the HPT setup and of the sample dimension and the parameters used to determine the imposed strain in HPT. Right: Shear strain, γ, vs. radius, r. Data are valid for samples with thickness 0.9 mm < t < 1.1 mm, unless indicated otherwise. Photo: HPT processed disk.

Recently the authors used HPT at moderate temperatures as a new route to directly consolidate and plastically deform commercially produced p- and n-type skutterudite powders (TIAG, Austria) into a dense solid (Rogl et al., 2018; Rogl et al., 2019a). Thereby the time and energy consuming hot-pressing step with its concomitant significant grain growth can be avoided. Cold pressing (CP) prior to HPT was used to compact the powder so that it could be placed easily as a solid disc on the anvil of the HPT equipment. ZT-values for p-type DD_0.6Fe₃CoSb₁₂ reached ZT = 1.3 at 773 K and for n-type (Sm,Mm)_0.15CoSb₁₂ ZT = 1.45 at 823 K, and the whole procedure takes less than half an hour. To produce these samples via HPT, in contrast to ECAP, has additionally the advantage that the metal tube, which is necessary to confine the powder, already breaks and falls off during pre-pressing so no contamination of the sample occurs, which may not be the case when using ECAP because the filled metal tube must be extruded as well.

In an additional step this sustainable and fast method has been scaled up to produce bulk p- and n-type skutterudites of larger sizes (disks with a diameter of 30 mm and a height of 1 or even 8 mm). ZTs were in about the same range or even higher than for the small samples, the production time was between 30 and 50 min and the big samples with a weight of about 50 g turned out to be homogeneous and could therefore directly be used to cut legs for TE modules (Rogl et al., 2020b). A further upscale of this fast and sustainable production method (disks with a diameter of 10 cm and various heights), using commercial p- and n-type skutterudite powder is planned.

Also other research groups like Han et al. (2020) or Ikoma (2019) used HPT. Han et al. synthesized hybrid nanocrystalline alloys by mechanical bonding through HPT. This procedure decreased the density of the lightweight alloys but due to grain refinement improved the hardness, leading to an exceptional specific strength especially at the disk edges. Ikoma highlighted HPT for application on crystalline semiconducting materials, which were transformed to metallic high-pressure phases, developing noble electrical and optical properties.

The adaptation of TE materials to industrial applications requires not only an in-depth knowledge of their TE but also of their mechanical properties, because a prerequisite for commercial use is mechanical robustness to undergo repetitive thermo-cycling, but also to resist cracking or failure from vibrations. For a flawless long-term and cyclic performance of TE devices it is essential that the thermal expansion coefficients of p- and n-legs be chosen as similar as possible. Therefore, it is equally important to consider possible changes after SPD. Although mechanical properties, including thermal expansion, of hot-pressed skutterudites and half-Heusler alloys have been published in review articles [(Rogl et al., 2010b; Zhang et al., 2010b; Rogl et al., 2011b; Rogl and Rogl, 2011; Rogl et al., 2016)], so far no overview of the mechanical properties of HPT consolidated skutterudites and half-Heusler alloys exists.

For HPT samples one must consider two main arguments: 1) the shear strain of HPT samples is directly proportional to the number of revolutions and to the radius of the specimen but is inversely proportional to the thickness, therefore HPT samples are inhomogeneous in respect to grain size and defect density, and as a consequence they are also inhomogeneous in respect to micro-structural, physical and, to some extent, to mechanical properties, i.e., mechanical properties of a specimen of the rim area might differ from those of the center area; 2) as during annealing grains grow and defects partially anneal out, the above-mentioned properties change to some extent. In most cases after one heating and cooling cycle the sample is thermally stable in respect to TE properties, however, considering mechanical properties, particularly thermal expansion, this is not always the case.

HPT consolidated specimens, stemming from HP or CP samples or powder undergo changes during heating, which are reflected in the temperature dependent thermal conductivity but much more in the temperature dependent electrical resistivity and thermal expansion, exhibiting curves with anomalies when measured in a first heating cycle (Rogl et al., 2020c). For thermally stable samples the temperature-dependent thermal expansion curve becomes linear.

Accordingly, the present paper evaluates the effect of HPT processing of p- and n-type skutterudites and half-Heusler alloys on the hardness, elastic moduli, fracture indentation toughness, and thermal expansion in comparison to a HP reference sample. We thereby focus on the influence of the applied shear strain (Vorhauer and Pippan, 2004; Pippan et al., 2008) as well as on the changes after annealing (usually measurement induced heating from 300 to 850 K within several hours).

Experimental Techniques

Sample Preparation

Skutterudites

a. Samples hot pressed prior to densification via HPT (HP + HPT):

The DD-filled as well as the multi-filled p-type bulk skutterudites (DD stands for didymium, a natural rare earth double filler consisting of ∼95% of Nd and ∼5% of Pr) were prepared via an optimized reaction-melting technique (for details see Refs. (Rogl et al., 2010a; Rogl et al., 2011a; Rogl et al., 2012b; Rogl et al., 2012c; Rogl et al., 2013b)). The multi-filled n-type skutterudites were synthesized from arc-melted master alloys YbSb₂, SrSb₂, BaSb₃ and Co₄Sb₁₂ (for details see Ref. (Rogl et al., 2012a; Rogl et al., 2014b)). After grinding by hand (using a WC-mortar and pestle (HM)) or BM (BM; Vario Planetenmühle, Pulverisette4, WC-containers/balls), the densification of the material was accomplished by HP in a graphite die in an argon atmosphere at 600°C under a pressure of 50 MPa employing a uniaxial hot press system (HP W 200/250-2200-200-KS, FCT Systeme GmbH). The so gained cylinders of 10 mm in diameter and about 10 mm height were cut into discs of about 1 mm height to measure various physical and mechanical properties, labeled as HP. At least two of these discs were used for SPD experiments via HPT, as described in detail below, further on referred to as HP + HPT.

b. Samples cold pressed prior to densification via high-pressure torsion (CP + HPT):

For the CP + HPT samples commercially produced p- and n-type skutterudite powders, DD_0.7Fe₃CoSb₁₂ and (Sm,Mm)_0.15CoSb₁₂ (from TIAG, Austria), were used. About 1 g of the original powder was cold pressed, a step only necessary to place the right amount of powder on the anvil of the high-pressure torsion equipment. These cold pressed pellets were HPT processed, as described below, and are further referred to as CP + HPT. As reference sample the commercial powder was hot pressed, as described in (a), named HP.

c. “Big” samples (powder + HPT):

For samples having a diameter of 30 mm and a height of 1 mm or 8 mm, the same commercial skutterudite powders, as used for CP + HPT, were directly HPT processed (powder + HPT).

Half-Heusler Alloys

P- and n-type half-Heusler alloys were prepared using an optimized arc melting technique followed by a treatment in a high frequency furnace, long time BM and an advanced hot-pressing technique (for details see Refs. (Gürth et al., 2016; Rogl et al., 2017b; Tavassoli et al., 2017; Tavassoli et al., 2018)). The HP samples were then HPT processed (HP + HPT).

Severe Plastic Deformation via High Pressure Torsion

The HPT technique used here is based on the Bridgman anvil-type device where a thin, disc-shaped sample is subjected to torsional strain under a high pressure between two anvils (Figure 1). On the sample disc, placed between the two anvils, a hydrostatic pressure, P, in the order of several GPa is applied (1–10 GPa) and at the same time plastic torsial straining is achieved by rotation of one of the anvils. In constrained HPT, samples are placed into the cavity of the lower anvil, preventing an outward flow of material and this way avoiding a reduction of the thickness.

The shear strain, γ, is dependent on the number of revolutions, n_r, the radius, r and the thickness, t, of the specimen in the following way: γ = (2πn_rr)/t (with the rotation angle θ = 2πn_r) as illustrated in Figure 1. After Pippan et al. (2008) even at the center point (r = 0) the shear strain γ > 0.

For all samples, except for the “big” ones, HPT was performed in a hot-processing equipment from W. Klement, Austria, with inductive heating controlled by an infrared pyrometer. Sample dimensions were: r = 5 mm, t ∼ 1 mm and process parameters were: 4 GPa; one, four or eight revolutions; 0.2 rpm; about 300°C; in some cases protective Ar atmosphere was used.

The “big” samples were processed in a custom-built equipment from Klement, Austria, outfitted with an induction heating system from IEW Corporation. The powder was filled into a hollow copper cylinder (wall thickness 1 mm) with an inner diameter of 30 mm and a height of 2, 3 or 16.5 mm (placed on the lower anvil) and subsequently compacted under a nominal pressure of 5 GPa, heated to 250°C or 300°C (15 min holding time) before the pellet was deformed at a rotational speed of 0.2 rpm for 0.13, one or five revolutions (details are given in references (Rogl et al., 2020b)).

For all HPT samples the shear strain is increasing from the center to the rim as can be seen in Figure 1. For discs with r = 5 mm and t ∼1 mm the shear strain increases from ∼5 to ∼31 for one revolution and to ∼155 for five revolutions. This increase at the rim is even bigger for the samples with r = 15 mm and t ∼ 1 mm, namely ∼476. In contrast to all these thin samples, the shear strain for the samples with r = 15 mm and a height of 8 mm reaches, even for five revolutions, only ∼60 at the rim.

Measurement Techniques

Density—Porosity

The relative density (in %) d_rel compares the measured density d_A from Archimedes' principle with the X-ray density d_X: d_rel = (d_A/d_X)×100; the X-ray-density d_X is given by d_X = MZ/VL, where Z is the number of formula units within the unit cell, M is the molar mass in [g/mol], V is the volume and L is Loschmidt’s number. The relative porosity, por (in %), is given by por = 100 – d_rel.

Crystallite Size and Dislocation Density

The crystallite size and its distribution as well as the dislocation density were evaluated from heavily exposed XRD patterns applying the modified Williamson-Hall method developed by Ungar et al. (2009). For this purpose, the convolutional multiple whole profile-fitting algorithm (CMWP) was used, as given in detail by Ribarik et al. (2004) (Schafler, 2011; Lohmiller et al., 2013).

Hardness

Prior to hardness tests the samples were polished with a 0.3 μm alumina paste to produce an optical finish before testing. Hardness was determined with two different equipments. For static hardness measurements a microhardness tester was used, AD PAAR-MHT-4, mounted within a Zeiss Axioplan optical microscope employing a load of 1 N, a rate of 0.1 N/s and a loading time of 10 s (referred to as HV0.1).

For all indentation data the hardness HV is

$HV=\frac{0.102\times 2F\sin \frac{136°}{2}}{{\left(2\ell \right)}^2}=1\text{.}891\frac{\text{F}}{{(2\ell )}^2}(1)$

with the diagonal length 2ℓ of the indent and F the indentation load. At least 10 different impresses were applied to obtain minimum standard deviations.

For dynamic hardness measurements a micro-indenter MHT4 and a Zeiss microscope was employed. With this indenter the load is decreased until relaxation of the sample occurs, which is also the reason why the dynamic hardness usually is slightly lower than the static hardness, as for static hardness measurements the diagonals of the imprints are measured after the force was released and the imprint has shrunk slightly.

Indentation Fracture Toughness

Fracture toughness is a measure of the resistance of a material to crack propagation. There are various methods to determine the fracture toughness like by the introduction of a pre-crack into the test sample e.g., the Chevron Notched Flexure Specimen method, the Single-Edge Pre-cracked Beam method or the sharp “V” Notch Beam method. All these methods do not qualify for rather brittle HPT-processed samples; however, it is possible to determine the Vickers indentation fracture toughness (also named Vickers fracture resistance) (Lawn et al., 1980; Sakai and Bradt, 1993; Clement et al., 1999), K_IC from the relation (Shetty et al., 1985; Ponton and Rawlings, 1989)

${\text{K}}_{\text{IC}}=\beta {\left(\frac{\text{E}}{\text{HV}}\right)}^{1/2}\frac{\text{F}}{{\text{c}}^{3\text{/}2}}(2)$

where E is the Young’s modulus, HV is the hardness, F is the indentation load, c is the radial crack length from the center of the Vickers indentation to the tip and β is a function of the indenter angle, which for Vickers indentation is: ß = 0.016(4).

As not in all cases E was measured, a second method was chosen to determine the indentation fracture toughness, i.e. by applying the Shetty-Wright-Mincer-Clauer equation (Shetty et al., 1985; Ponton and Rawlings, 1989)

${\text{K}}_{\text{I}\text{C}}=\text{ 0}\text{.}0319\frac{\text{F}}{\text{a }{\ell }^{1\text{/}2}},(3)$

where a is half of the indentation diagonal and ℓ (ℓ = c – a) is the length of the crack measured from the corner of the indent to the tip. This equation requests that according to Madeiros et al. (Madeiros and Dias, 2013) the cracks can be classified as of Palmqvist type, which is the case, if c/a ≤2.5.

Elastic Properties and Fracture Strength

Resonant ultrasound spectroscopy (RUS), based on Migliori’s method (Migliori et al., 1993), was used to determine elastic properties via the eigenfrequencies of the sample with the knowledge of samples' mass and dimensions. Cylindrical samples are mounted “edge-to-edge” between two piezo-transducers and are excited via a network analyzer (HP 8751A) in the frequency range from 100 to 500 kHz (Migliori and Maynard, 2005). Elastic properties, Young’s modulus (E) and Poisson’s ratio (ν), can be derived via a least-squares fit program, comparing the measured and calculated eigenfrequencies.

RUS measurements require ideally a spherical or at least a cubic shape of the sample, therefore, only HP samples qualified to be measured with RUS, because HP + HPT and CP + HPT samples are very thin in comparison to their diameter. As a consequence, for HPT compacted samples, the Young’s modulus was determined in parallel with dynamic hardness measurements with a micro-indenter (MI) MHT4. The software of the MI evaluates the Young’s modulus, E, for a given Poisson’s ratio, ν. For all HPT samples, ν of RUS measurements of the HP sample were used for the respective determination of E with the MI and for the calculation of other elastic moduli, as slight changes of ν hardy influence E. Even though the same ν was used, differences between E values from RUS and MI measurements may occur because with RUS the whole sample is measured, whereas the MI indenter touches only a very small area of the sample’s surface.

$\text{B}=\frac{\text{E}}{3\left(1-2\text{ν}\right)}(4)$

$\text{G}=\frac{\text{E}}{2\left(\text{ν}+1\right)}(5)$

While the hardness is a measure for the strength of a material, the elastic modulus not only characterizes the elasticity of a material but also affects the thermal shock resistance and fracture strength, σ (σ ≈ E^1/2).

The error for mechanical properties’ data is generally about 5% or less. More details about mechanical properties measurements can be found from a series of publications on the subject [(Zhang et al., 2010a), (Rogl and Rogl, 2011), (Rogl et al., 2016), (Zhang et al., 2010b; Dahal et al., 2015; He et al., 2015; Rogl and Rogl, 2017a) and references therein].

Thermal Expansion

Thermal expansion was measured with two different types of equipment. From 4.2 K to room temperature a miniature capacitance dilatometer was used, above room temperature a dynamic mechanical analyser DMA7 (Perkin Elmer Inc.) was applied (for details see (Rotter et al., 1998; Rogl and Rogl, 2011; Rogl et al., 2016)). The thermal expansion coefficient α follows from a temperature derivative of the length change Δ$\ell$, i.e.,

$\text{α }=\left(\frac{\partial \mathrm{ }\text{Δ}\ell }{\partial \mathrm{ }\text{T}}\right)\frac{1}{{\ell }_{\text{0}}}(6)$

Results and Discussion

Mechanical properties are dependent on the specimens’ composition and additional phases in the sample, on the density and temperature. Therefore, in this work, all densities have been given and values are valid for room temperature if not stated otherwise. As SPD has an enormous influence on grain size, defect density and density of a material, these parameters must be discussed before going into details about changes in mechanical properties.

Microstructure and Density

Figure 2A compares the crystallite size, derived from the XRD data, of the HP processed skutterudite samples to those of HPT compacted ones before and after heat treatments. Although the domain size of the HP reference samples varies between 55 and 155 nm, it is significantly reduced in case of the respective HPT specimens. The crystallite size does neither differ significantly among the HPT samples, with about 30–50 nm, nor among positions, center or rim, within the sample. Also, the history of the sample, HP, CP or powder, has hardly an influence. During measurement induced annealing the crystallites grow, but still remain smaller than those of the HP sample.

FIGURE 2

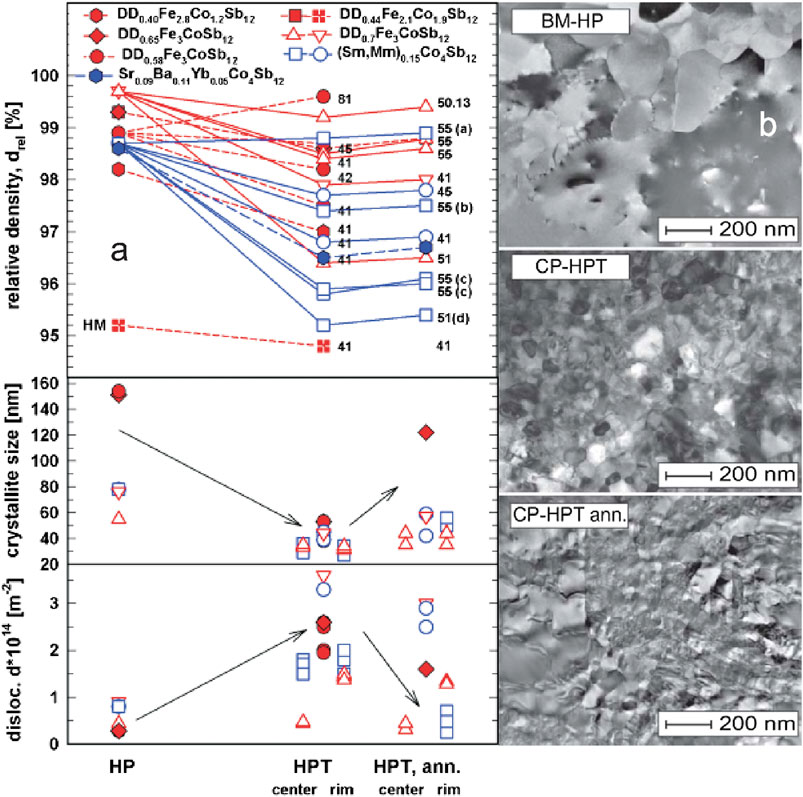
FIGURE 2. (A) Skutterudites: relative density, d_rel(upper panel), crystallite size (middle panel) and dislocation density (lower panel) vs. various treatments: HP, HPT (after HP) and after annealing the HP + HPT sample. Full symbols indicate HP + HPT samples, open symbols indicate CP + HPT or powder + HPT (big) samples (Note: The numbers indicate the applied pressure in GPa followed by the number of revolutions. (a), (b), (c) and (d) denote differently processed specimens of the same sample). (B) TEM images of p-type DD_0.7Fe₃CoSb₁₂ (from top to bottom) of a HP, a CP + HPT and a CP + HPT annealed sample.

The dislocation density, (Figure 2A), appears mirror-inverted to the crystallite size, being larger in case of the HPT processed specimens. Annealing reduces the dislocation density, in some cases to the same level found for the HP samples.

TEM images (Figure 2B), exemplarily shown for p-type DD_0.7Fe₃CoSb₁₂, highlight the difference in grain size between the HP, CP + HPT and the annealed CP + HPT samples. The HP sample reveals a distribution of grains in the range of 200 nm, whereas the CP + HPT sample exhibits a mixture of grains of various sizes, but all of them smaller than 100 nm. After annealing, most of the very small grains have grown and therefore the size distribution becomes more homogeneous.

Figure 2A also represents the relative densities of various p- and n-type skutterudites after HP, which is the reference value, after HP + HPT (full symbols) or after CP + HPT (open symbols) and in some cases also after annealing. All data refer to an average value of the whole sample. The two numbers, xy in Figure 2 indicate the applied pressure in GPa, x, and the number of revolutions, y. One can see that for almost all HPT samples (HP or CP prior to SPD) the relative density is lower in comparison to the HP reference sample. Due to the fact, that besides the introduction of various defects also very small holes occur, the density decreases. Additional thermal treatments cause only a marginal densification because during annealing mini-cracks anneal out completely or fuse together to smaller holes. Whereas the relative density of HPT samples, processed with a pressure of p = 1–5 GPa, is decreased by 0.5%–1.9%, the increase after annealing is usually only in the range of 0.1% to maximal 0.3%, which means that also after annealing the density of the HP sample is not reached.

Two samples in Figure 2 catch special attention: 1) the HM sample, DD_0.44Fe_2.1Co_1.9Sb₁₂, which has, due to the fact that the bulk was ground by hand, a much lower density already before SPD, and which additionally decreases after HPT processing, 2) DD_0.58Fe₃CoSb₁₂, consolidated with a pressure of 8 GPa and one revolution, which exhibited after HPT a higher density than the respective HP specimen. Due to an extraordinary high pressure (p = 8 GPa) hardly any holes could develop and the sample was firmly compacted. From Figure 2 we can learn even more: although three specimens of a sample of n-type (Sm,Mm)_0.15Co₄Sb₁₂ with a diameter of 30 mm were consolidated with 5 GPa and five revolutions (labeled as 55), the densities of 55(a), 55(b) and 55(c) turned out to be different. As sample 55(a) was processed at 300°C, and sample 55(b) was processed at only 250°C, we can conclude that the higher the processing temperature is, the higher is the density. In case of sample 55(a) the applied pressure of 5 GPa together with five turns at 300°C yielded a sample with a density in the range of the HP one, which, like a HP sample, was practically not influenced by annealing at all. 55(c) shows that the density for two specimens from a sample with a height of 8 mm, cut in two perpendicular directions is, within the error bar alike (For more details about sample preparation see (Rogl et al., 2016)). Finally sample 51(d) is processed with only one revolution and consequently owns a lower density. The same trend also becomes noticeable for the big p-type skutterudite DD_0.6Fe₃CoSb₁₂, i.e. the density is higher for sample 55 than for sample 51. One big DD_0.6Fe₃CoSb₁₂ sample (50.13) displays another phenomenon. As the sample was processed with less than one eight of a full revolution hardly any defects and cracks were introduced; its behavior is thus closer to an HP than to an HPT consolidated sample. As a consequence, the density is higher than for the sample processed with one full revolution.

Archimedes measurements with specimens of very low masses are usually not accurate enough to reliably distinguish the density between center and rim area of a sample with a diameter of 10 mm and a height of 1 mm, however, with the big samples with a diameter of 30 mm such density measurements were performed. It turned out that the samples are more porous (by about 0.5% or even less) in the rim than in the center area. Most likely this is a consequence of voids and/or cracks created by the higher shear strains at the rim.

All half-Heusler alloys (Figure 3) generally show the same density behavior as the skutterudites: a decrease of density after HPT and a slight increase after one or more heat treatments.

FIGURE 3

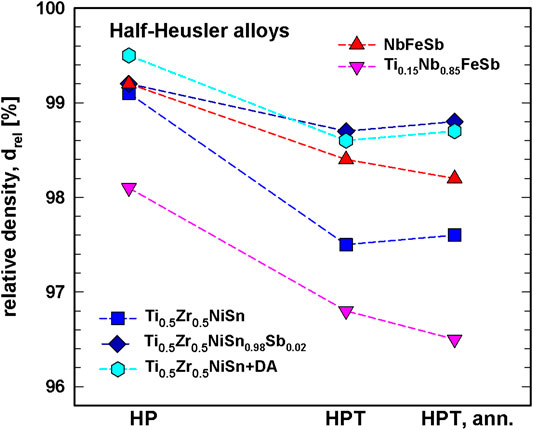
FIGURE 3. Half Heusler alloys: relative density, d_rel, vs. various treatments, HP, HPT (after HP) and after annealing the HP + HPT sample.

Hardness

Hardness of HPT compacted samples is affected by three separate factors: 1) the fine grain size, 2) the specific texture and 3) the high dislocation density, which is an inherent feature of the SPD-processed microstructure.

Figure 4 (upper panel) presents the correlation between Vickers hardness, HV and the relative density of selected HP and HPT compacted skutterudites before, and in some cases, after annealing. The data of the HP samples (open symbols) were linearly fitted; therefore, it is easy to see that all hardness values of the corresponding HPT samples (full symbols) have a much higher hardness, although their density is lower. As expected, both, densities as well as the hardness increase slightly after annealing. The same behavior is valid for p- and n-type half-Heusler alloys, as can be seen in Figure 4 (lower panel). Figure 4, in addition, shows that half Heuslers generally are harder than skutterudites.

FIGURE 4

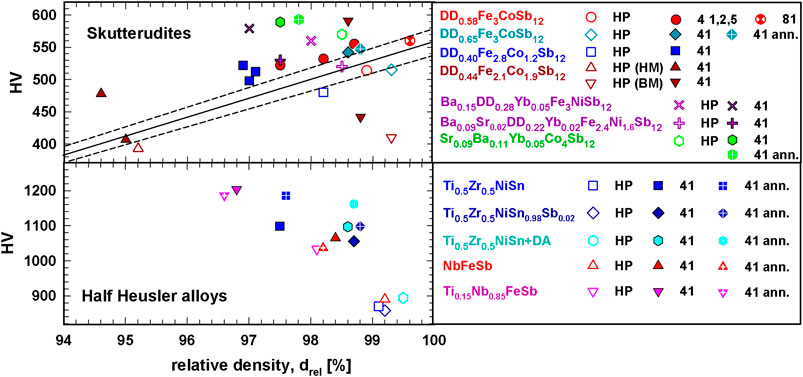
FIGURE 4. Skutterudites (upper panel) and half Heusler alloys (lower panel): Vickers hardness, HV, vs. relative density, d_rel.

To explain this contradictory behavior, lower density—higher hardness, one has to consider that for a constant temperature two parameters affect the measured hardness of these materials, i.e., the relative density and grain size coupled with the defect density. A lower relative density of powder compacts results in lower hardness values; therefore, the HPT samples are expected to reveal lower hardness values. On the other hand, for a given density a decrease of grain size (Hall-Petch relation) together with an increase of the defect density drives higher hardness values, which generally applies to the HPT processed samples, as all measured values after HPT are larger than those of the HP reference sample. This means that the increase of hardness in HPT samples is mainly governed by grain refinement and the introduction of defects.

Figures 5, 6 display the dependence of static hardness on the shear strain for HP + HPT skutterudite and half-Heusler samples. For both groups of TE materials hardness is increasing with increasing shear strain. For some samples the hardness was measured in the center and rim area (not shown), with the result that the hardness is increasing from the center to the rim in accordance with Zhilyaev et al. (2003), who found that for a material where recovery is slow the hardness is initially lower in the center than at the rim. Vorhauer and Pippan (2004) and Pippan et al. (2008) among others reported that the microhardness varies significantly along the radius of disks processed by HPT at the early stages of deformation but that the hardness becomes homogeneous with a high level of deformation. Basically, the same results were found in various other investigations of simple metals [e.g., (Valiev et al., 2010; Song et al., 2012; Borodachenkova et al., 2017; Rijal et al., 2020)]; unfortunately, no distribution of density is given in these publications.

FIGURE 5

FIGURE 5. Skutterudites, HP, HP + HPT, HP + HPT annealed: Vickers hardness, HV, vs. shear strain.

FIGURE 6

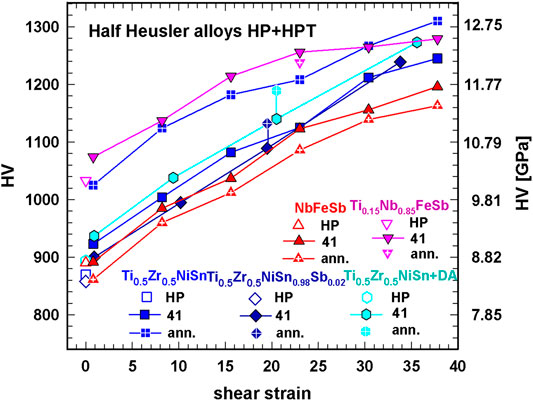
FIGURE 6. Half Heusler alloys, HP, HP + HPT, HP + HPT annealed: Vickers hardness HV, vs. shear strain.

For three CP + HPT samples static hardness was measured along the radius of the disk from the innermost point to the rim; results are shown in Figure 7. For the p-type DD_0.7Fe₃CoSb₁₂ the difference between the hardness value of the HP sample (HV = 510) and the center of the CP + HPT sample (HV = 524) seems to vanish, but considering a lower relative density of 2% (see Figure 4) of the CP + HPT sample, the hardness is increased, as it was found by the authors (Rogl and Rogl, 2011) that in case of skutterudites generally a change of 1% in relative density equals a change of ∼40 in HV. For DD_0.7Fe₃CoSb₁₂ the increase in hardness from the center to rim with only 4% is low. For n-type (Sm,Mm)_0.15Co₄Sb₁₂ the difference in hardness between the center of the CP + HPT samples, is bigger than for the p-type skutterudite: for the sample processed with 4 GPa and one revolution the increase in hardness is about 50%. Whereas the increase from the center to the rim for the CP + HPT sample, consolidated with one revolution is more or less linear, the sample, processed with five turns, displays a linear increase, followed by a plateau-like behavior in the middle section and an even steeper linear increase toward the rim. This observation is also backed by the work of Das et al. (2012) reporting for HPT treated aluminum samples that not only hardness gradually increases with distance from the center to edge but additionally with the number of turns.

FIGURE 7

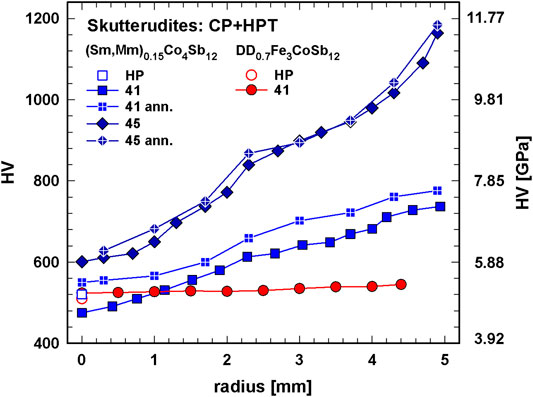
FIGURE 7. Skutterudites, CP + HPT, CP + HPT annealed: Vickers hardness, HV, vs. radius of the sample.

After annealing the change in hardness is marginal throughout the whole measured range, although it appears slightly enhanced for the n-type CP + HPT sample processed with one revolution.

Figure 8 illustrates the dependence of static hardness on the applied shear strain of big p- and n-type skutterudite samples (diameter of the disk is 30 mm), compacted directly from powder via HPT. In general, all hardness values of the big HPT samples are higher than those of the HP counterparts. Grain refinement with the introduction of defects influences this mechanical property stronger than the lower density. For both, p- and n-type hardness is higher for the specimens produced with five turns in comparison to those, produced with one turn: this was also observed for the samples with 10 mm diameter. Furthermore, in both cases samples with a thickness of about 8 mm, due to generally lower shear strain, have lower hardness values than those with a thickness of only about 1 mm. The difference in hardness, measured on specimens cut perpendicular to each other from one sample, is insignificant. It is interesting to note that the DD_0.7Fe₃CoSb₁₂ sample, which due to only 0.13 turns appears closer to a hot pressed than to an HPT processed sample (300°C, 5 GPa), reveals a spectacular high density and as a result also a high hardness. After annealing, and a slightly higher density also hardness is marginally enhanced.

FIGURE 8

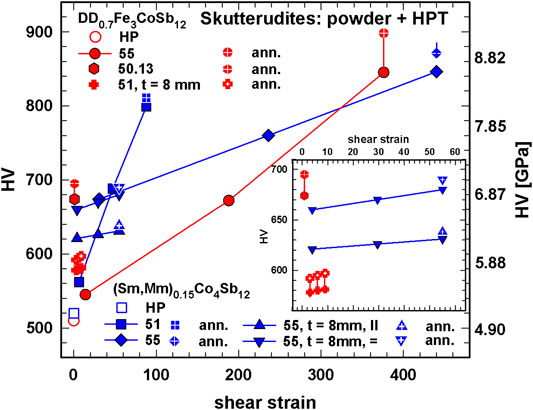
FIGURE 8. Skutterudites, powder + HPT, powder + HPT annealed: Vickers hardness, HV, vs. shear strain. Insert: enlargement for a shear strain of 0–64.

Indentation Fracture Toughness

Resistance against crack growth, often being characterized by the fracture toughness, K_IC, is another mechanical property, which is important for the practical use of a TE material. Theoretically K_IC should decrease with increasing strength and hardness. Unfortunately, no data about TE SPD treated materials are available and only a few specimens, HP, HP + HPT and CP + HPT, revealed crack propagation during hardness measurements. This is the reason why it is hard to draw a universal conclusion from the current results for all HPT processed skutterudites and half-Heusler alloys. With almost no change of the Young's modulus for HP + HPT and CP + HPT samples after HPT, not much change in fracture indentation toughness, K_IC, can be expected; still it should be found out whether or not it is easy for cracks to spread after HPT (for details also see (Hohenwarter et al., 2009; Hohenwarter et al., 2011; Hohenwarter and Pippan, 2011)). The values of fracture indentation toughness of various HP skutterudites with 1.1 MPa m^1/2 < K_IC < 2.2 MPa m^1/2 (Rogl and Rogl, 2011) and of various HP half-Heusler alloys with 1.8 MPa m^1/2 < K_IC < 2.3 MPa m^1/2 (Rogl et al., 2016) indicate, even considering an error bar of 10%, that K_IC of half-Heusler alloys is higher than that of skutterudites. For CP + HPT DD_0.7Fe₃CoSb₁₂ K_IC was calculated with Eq. 2 and revealed K_IC = 1.36 ± 0.14 MPa m^1/2, for CP + HPT (Sm,Mm)_0.15Co₄Sb₁₂ K_IC = 1.23 ± 0.12 MPa m^1/2 for the sample 41 and 1.26 ± 0.13 MPa m^1/2 for the sample 45.

For half-Heusler HP-Ti_0.5Zr_0.5NiSn fracture indentation toughness was determined in a previous work of the authors yielding K_IC = 1.9 ± 0.2 MPa m^1/2 (Rogl et al., 2016). As the Youngs modulus was not measured for HP + HPT Ti_0.5Zr_0.5NiSn, Eq. 3 was applied for the calculation of K_IC, with c/a = 1.8 satisfying the Palmqvist criterion. The resulting K_IC = 1.3 ± 0.13 MPa m^1/2 is, even considering the error bar, lower than that of the HP sample.

Lower fracture indentation toughness values after SPD were also found for steel (Pippan and Hohenwarter, 2016; Schwarz et al., 2017) or iron (Hohenwarter and Pippan, 2010). The reason given was the higher hardness coupled with an enhanced defect density (especially dislocations), an explanation, which also makes sense for the here-discussed TE materials.

Elasticity and Debye Temperature

Figure 9 gives an overview of all measured elastic properties of HP and HPT processed skutterudites. Measurements performed with the micro-indenter, MI, where the Young’s modulus, E, is determined from imprints, yield somewhat higher values (1–3%, for DD_0.58Fe₃CoSb₁₂ even a little bit more) than those measured on the entire sample with RUS.

FIGURE 9

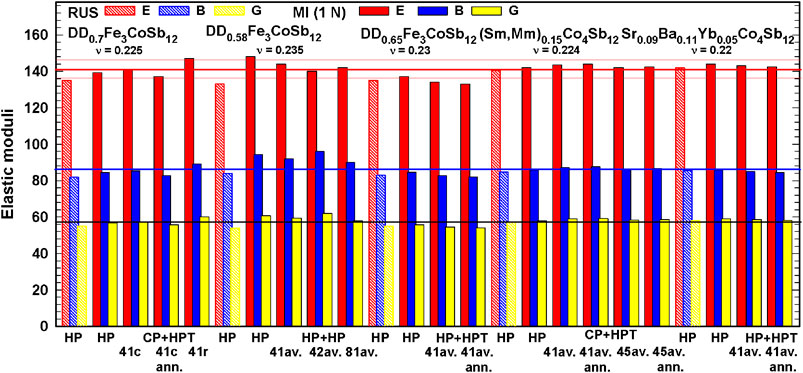
FIGURE 9. Elastic moduli of p- and n-type skutterudites, after various treatments. Thick lines depict the average values, thin lines the standard deviation.

Comparing the rather accurate RUS measurements of the p- and n-type skutterudites and taking into account that the relative density is higher than 98.5% for all of them, one can see that the Young’s moduli, E, of the n-type skutterudites are on average slightly higher than those of the p-type and that DD_0.58Fe₃CoSb₁₂ with the lowest filling level and the lowest density among the p-type skutterudites has the lowest E. These observations confirm earlier findings of the authors (Rogl and Rogl, 2011). As E decreases almost linearly with decreasing density (for details see (Rogl and Rogl, 2011)) and all HPT samples have a lower density than the HP ones, lower E values are expected, which indeed is the case for almost all HPT samples (see the values gained with the micro indenter). In this context it is interesting to note that Li et al. (2018) demonstrated that plastic deformation decreased the elastic moduli for brass, aluminum, and low carbon steel by 10–20%.

Bulk modulus, B, and shear modulus, G, were evaluated with Eqs 4, 5, respectively; the values are also presented in Figure 9.

The average Young’s modulus, E, of all depicted values resulted in E_av = 141.3 GPa with a standard deviation of ς_E = 4.9 GPa, which is lower than the error of 5% occurring during measurements. As the average E for all HP samples is 142 GPa and for all HPT samples is 141 GPa, one can conclude that the Young’s moduli and as a consequence the shear and bulk moduli are practically unaffected by SPD.

Pugh’s relation (Pugh, 1954), i.e., a material is considered as brittle if B/G < 1.75, defines all discussed skutterudites as brittle (all exhibit values 1.4 < B/G < 1.6).

The fracture or breaking strength, i.e., the stress at which a specimen fails via fracture, can be roughly estimated with σ ∼ E^1/2, which would be about 12 GPa for the specimens discussed above.

Figure 10 is dedicated to the relation between Vickers hardness and Young’s modulus (HV-E) of skutterudites. The plots HV-E of the various HP skutterudites (full symbols) are fitted linearly, revealing the relation HV = 3.75(16) E. Almost all HP skutterudites have data on the fit line or at least between the two error bars of the fit. In a recent article (Rogl et al., 2017a) and a review article ((Rogl and Rogl, 2017a) and references therein) the authors also presented the influence of nanoparticles, dispersed in the skutterudites matrix, on ZT and on mechanical properties. These data are plotted in Figure 10 with partially filled symbols: almost all skutterudites with dispersed nanoparticles have values not only above the fit line but mainly also above the upper error line; n-type skutterudites with Ta_0.8Zr_0.2B particles reveal especially high HV and E values. Interestingly all data points for HPT samples (big symbols) appear above the upper error line, in some cases the data are even above those with dispersed nanoparticles and for all n-type skutterudites they are higher than those of the p-type. The CP + HPT sample of (Sm,Mm)_yCo₄Sb₁₂ exhibits already a high value after one revolution, but for the specimen processed with five revolutions this value is extraordinary high, indicating once more that, applying the same pressure, more HPT-revolutions yield higher strength.

FIGURE 10

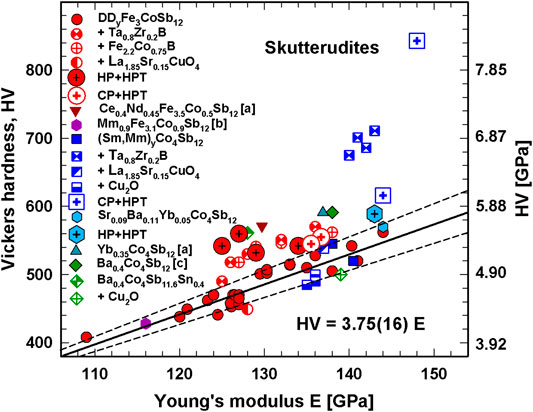
FIGURE 10. Vickers hardness, HV, vs. Youngs modulus, E; the solid line is the fit for all HP skutterudites, the dashed lines stand for the 10% error bar. [a] = (He et al., 2015), b = (Dahal et al., 2015), [c] = (Battabyal et al., 2015).

Elastic moduli have been measured and evaluated for two half-Heusler alloys, namely for p-type Ti_0.15Nb_0.85FeSb and for n-type Ti_0.5Zr_0.5NiSn (see Figure 11). Whereas the elastic moduli of p- and n-type skutterudites are very close to each other (Figure 9), for p- and n-type half-Heusler alloys they differ significantly. RUS reveals for p-type Ti_0.15Nb_0.85FeSb a Young’s modulus of E = 192.3 GPa, while E = 164.0 for n-type Ti_0.5Zr_0.5NiSn, which is about 15% lower. Consequently, these lower values infer also lower shear and bulk moduli. RUS data and those gained from micro indentation hardly differ. While there is almost no difference between the elastic moduli of the HP sample and the values at the center of the HPT half-Heusler alloys, there is a slight increase toward the rim. But hardly any change was observed after annealing. Whereas Pugh’s relation (Pugh, 1954), applied on all skutterudites discussed, characterized them as brittle, for both half-Heusler alloys, HP or HP + HPT, center or rim, 1.84 < B/G < 1.95, and therefore they may be considered as “ductile”.

FIGURE 11

FIGURE 11. Elastic moduli of p- and n-type half-Heusler alloys, after various treatments.

Debye temperatures are of importance to define the vibrational spectra of TE materials: any change in the Debye temperature suggests an alteration of the dynamic properties of atoms. There are various methods to extract the Debye temperature θ_D. Isotropic compounds, being compacted via HP or HPT into a dense bulk are suitable for determining θ_D from the sound velocity, using Anderson’s equation (Anderson, 1963):

$\text{θ}{}_{\text{D}}=\frac{\text{h}}{{\text{k}}_{\text{B}}}{\left(\frac{{3\text{nLd}}_{\text{A}}}{4\text{Mπ}}\right)}^{1\text{/}3}{\text{v}}_{\text{m}}(7)$

where h is the Plank’s constant, k_B is the Boltzmann’s constant, L is Loschmidt’s number, d_A is the measured density, M is the molecular weight, and n is the number of atoms in the asymmetric unit cell. In isotropic polycrystalline materials the mean sound velocity v_m follows from

$\text{v}{}_{\text{m}}={\left[\frac{1}{3}\left(\frac{2}{{\text{v}}_{\text{T}}^3}+\frac{1}{{\text{v}}_{\text{L}}^3}\right)\right]}^{-1/3}\text{with}\text{v}{}_{\text{L}}={\left(\frac{3\text{B }+4\text{G}}{3\text{d}}\right)}^{1/2}\text{and}\text{v}{}_{\text{T}}={\left(\frac{\text{G}}{\text{d}}\right)}^{1\text{/}2}(8)$

where v_L and v_T are the longitudinal and transversal sound velocities, respectively (Schreiber et al., 1973).

For most p- and n-type skutterudites the Debye temperature of the HP sample is in the range of θ_D ∼ 320 K, for the multi-filled Fe/Ni substituted skutterudites a bit lower with θ_D ∼ 275 K, whereas the two investigated half-Heusler alloys with their more rigid lattice structure have distinctly higher Debye temperatures (for Ti_0.15Nb_0.85FeSb θ_D = 430 K and for Ti_0.5Zr_0.5NiSn θ_D = 419 K). Common to all compounds, skutterudites and half Heuslers, p- and n-type, is that the Debye temperature after SPD is lower, although in some cases only less than 2%. The lower Debye temperature for HPT samples compared to the HP ones can be attributed to an increased amplitude of thermal vibrations of atoms at the grain boundaries and a higher concentration of point defects near the grain boundary regions. The reduction in the Debye temperature after SPD is much more pronounced for metals e.g., with a decrease of 23% for copper, 22% for nickel or even 48% for iron (Goyal, 2018).

Thermal Expansion

Before discussing the changes in thermal expansion after SPD, some basics, found by the authors (Rogl et al., 2010) should be stated. Thermal expansion of Sb-based skutterudites is increasing with an increasing amount of fillers and/or an increasing amount of iron content, which explains why Co-based n-type skutterudites basically have a smaller thermal expansion coefficient, α, than Fe-based p-type skutterudites. Furthermore, it could be shown that grain size and density have only a marginal influence on the thermal expansion coefficient (Rogl et al., 2010b).

In Figure 12 the thermal expansion of p-type skutterudite DD_0.58Fe₃CoSb₁₂ and n-type skutterudite Sr_0.07Ba_0.07Yb_0.07Co₄Sb₁₂ are displayed in the temperature range from 4.2 to 300 K and from 300 to 700 K, respectively. The thermal expansion coefficient, α, in the temperature range of 150–270 K for HP DD_0.58Fe₃CoSb₁₂ is α = 12.0 (2)×10⁻⁶ K⁻¹ and for HP Sr_0.07Ba_0.07Yb_0.07Co₄Sb₁₂ is α = 11.8 (2)×10⁻⁶ K⁻¹. Below room temperature the temperature dependent Δℓ/ℓ₀ curves do not show any anomalies (Figure 12). For both samples α is lower after HPT; this reduction in α is more pronounced for Sr_0.07Ba_0.07Yb_0.07Co₄Sb₁₂ (16%) than for DD_0.58Fe₃CoSb₁₂ (4%).

FIGURE 12

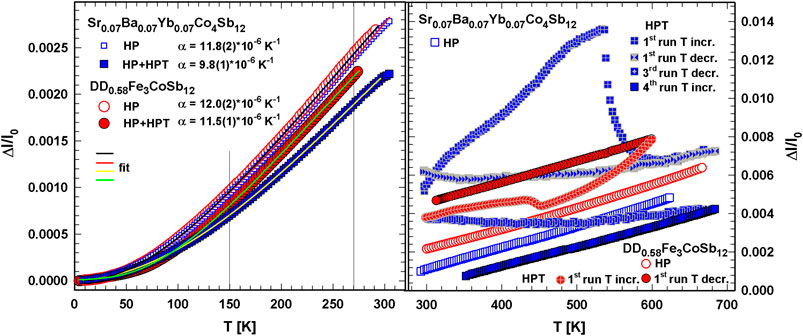
FIGURE 12. Length change, Δℓ/ℓ₀ vs. temperature, T, of HP and HP + HPT DD_0.58Fe₃CoSb₁₂ and Sr_0.07Ba_0.07Yb_0.07Co₄Sb₁₂ below room temperature with fits (see text) (left) and above room temperature (right). Some curves are shifted for a better view.

To analyze the thermal expansion as a function of temperature, the semi-classical model of Mukherjee et al. (1996) has been successfully used to quantitatively describe the thermal expansion coefficient in terms of the phonon spectrum including Debye and Einstein phonon modes. The Debye and Einstein temperatures, θ_D and θ_E were obtained from least squares fits to the experimental data (for equations and details see Refs (Rogl et al., 2010b). and (Mukherjee et al., 1996)). For HP DD_0.58Fe₃CoSb₁₂ θ_D = 325 K and θ_E = 63 K; after HPT, the Debye temperature with θ_D = 318 K has not changed as much as the Einstein temperature dropping to θ_E = 35 K. The same behavior occurs for Sr_0.07Ba_0.07Yb_0.07Co₄Sb₁₂ with θ_D = 309 K and θ_E = 61 K before and with θ_D = 302 K and θ_E = 32 K after HPT, indicating that after SPD the phonon vibrations of the atomic framework (Debye modes) are not much affected, whereas the frequencies of the rattlers (Einstein modes) tend toward lower energy modes.

It should furthermore be mentioned that the Debye temperatures of both samples are in the same range as those extracted with Anderson’s equations (Eqs 7, 8) from the elastic moduli.

For n-type Sr_0.07Ba_0.07Yb_0.07 Co₄Sb₁₂ the shrinking in the Δℓ/ℓ₀ vs. T curve is much more drastic than for the p-type skutterudites and occurs at 530 K followed by only a weak increase (Figure 12). The heating and cooling curve of the second and third run (not shown) exhibited a hysteresis, which was slimmer for the third run than for the second one. Finally the temperature dependent Δℓ/ℓ₀ was linear at the fourth run during heating and cooling (the latter is not shown), revealing α = 9.9 (1) × 10⁻⁶ K⁻¹ in the temperature regime 350–700 K, which fits perfectly well to the value of α below room temperature.

The temperature dependent Δℓ/ℓ₀—T curves of CP + HPT p-type DD_0.7Fe₃CoSb₁₂ and n-type (Sm,Mm)_0.15Co₄Sb₁₂, as shown in Figure 13, have a lot in common but differ quite much from their HP + HPT counterparts. In both cases during the first heating run, from 300 to 400 K, the samples shrink drastically, followed by a further very slight decrease till 800 K. This shrinking of a sample, HPT-consolidated with a pressure of 4 GPa at almost 600 K, is astonishing and can be only explained with an annealing out of vacancies and fusing together of mini-cracks mainly during the first temperature increase of only hundred degrees (300–400 K). This explanation is backed by the fact that after annealing the density of the samples is enhanced. Both samples contract during the first run with decreasing temperature and exhibit a linear Δℓ/ℓ₀—T behavior for in- and decreasing temperature (the latter is not shown in Figure 13) during the second circle. In the temperature range 300–800 K for HP DD_0.7Fe₃CoSb₁₂α = 10.9 (1) × 10⁻⁶ K⁻¹ and for the CP + HPT sample α = 7.0 (1) × 10⁻⁶ K⁻¹; for (Sm,Mm)_0.15Co₄Sb₁₂ the respective values are α = 9.8 (2) × 10⁻⁶ K⁻¹ and α = 5.6 (2) × 10⁻⁶ K⁻¹, indicating for both skutterudites that the thermal expansion coefficient of CP + HPT samples is roughly only two thirds of those of the corresponding HP samples.

FIGURE 13

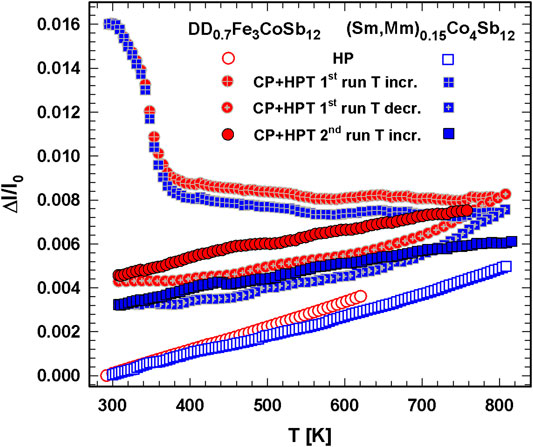
FIGURE 13. Length change, Δℓ/ℓ₀ vs. temperature, T, of HP DD_0.7Fe₃CoSb₁₂ and (Sm,Mm)_0.15Co₄Sb₁₂ in comparison to the CP + HPT processed samples. Some curves are shifted for a better view.

For the big samples (∼50 g), directly compacted from skutterudite powder, the results are almost the same, having also lower thermal expansion coefficients for the stable HPT samples in comparison to the HP ones.

A decrease in thermal expansion after SPD was also reported for the Fe-36%Ni invar alloy by Voroshilov et al. (1973) and Bitkulov et al. (2006), whereas Zhang and Alexandrov (1998) published a higher thermal expansion coefficient of Ni after SPD, attributed to nonequilibrium dislocations that disturb grain boundaries leading to large atomic displacements near interfaces.

Recently the authors have systematically compared the temperature dependent thermal expansion with the temperature dependent electrical resistivity, ρ (Rogl et al., 2020), especially between 300 and 800 K of HP samples and those after SPD. Whereas for HP samples both, the ρ(T)-curve as well as the Δℓ/ℓ₀—T curve are linear for in- and decreasing temperatures without a hysteresis, the micro-structural changes of HPT samples during measurement induced heating influence the thermal expansion and electrical resistivity more or less simultaneously. In both cases at the first run with increasing temperature the crystallites grow and in parallel the defect density becomes lower but also micro or nano cracks fuse together or anneal out completely. For HP + HPT samples after expanding linearly, with the electrical resistivity increasing, a severe change takes place around 400 K, when the sample shrinks and further on expands again (Figure 12 (right)). At the same temperature, 400 K, the electrical resistivity exhibits a plateau-like maximum followed by an almost linear decrease. For CP + HPT samples a decrease of thermal expansion occurs between 300 and 400 K and a slight anomaly around 650 K where indeed also one exists for the electrical resistivity. After several measurement runs the samples arrive at a thermally stable behavior, i.e., they exhibit a less steep but linear Δℓ/ℓ₀ – T curve. The ρ(T)-curve curve runs parallel to the one of the HP sample but at higher values, indicating that the grains are still smaller and the defect density is higher than for the HP samples. Rijal et al. (2020) also found such an anomaly in electrical resistivity after HPT of commercial pure copper, but did not measure thermal expansion. Kourov et al. (2007) investigated the effect of plastic deformation on physical properties and structure of the shape memory alloy Ti_49.5Ni_50.5. They found after SPD due to the transition from the microcrystalline to the amorphous/nanocrystalline state an increase in the electrical resistivity with an irreversible temperature hysteresis, which they also found for the Δℓ/ℓ₀—T curve. They also report a shape of the Δℓ/ℓ₀—T curve anomalous for metal alloys. For the annealed Ti_49.5Ni_50.5 alloy the ρ(T)-curve has the typical shape of polycrystalline stoichiometric TiNi alloys.

The thermal expansion behavior of the two half-Heusler alloys, p-type Ti_0.15Nb_0.85FeSb and n-type Ti_0.5Zr_0.5NiSn are displayed in Figure 14 and revealed for the HP samples α = 12.8 (1) × 10⁻⁶ K⁻¹ and α = 11.3 (1) × 10⁻⁶ K⁻¹ between 300 and 880 K. The Δℓ/ℓ₀—T curves of the HP + HPT samples show almost the same behavior of Ti_0.15Nb_0.85FeSb and Ti_0.5Zr_0.5NiSn. During the first heating, both samples contract till 550 K, because of annealing out of holes, followed by an increase, which is more pronounced for the p-type than for the n-type sample. The first run with decreasing temperature shows linear behavior, though with the slope less steep below 550 K. With further cycling (not displayed) in both cases the hysteresis between heating and cooling becomes smaller. Finally, after four cycles the condition is stable, but still the “kink” at 550 K remains, indicating a changing thermal expansion coefficient. Between 550 and 880 K α = 12.3 (2) × 10⁻⁶ K⁻¹ for Ti_0.15Nb_0.85FeSb and α = 11.0 (2) × 10⁻⁶ K⁻¹ Ti_0.5Zr_0.5NiSn, whereas below 550 K the value is only about one third.

FIGURE 14

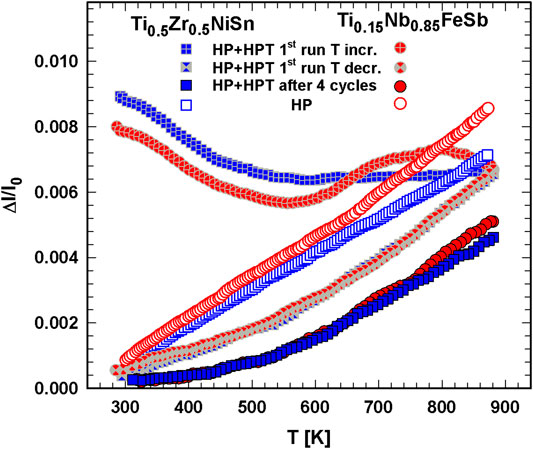
FIGURE 14. Length change, Δℓ/ℓ₀ vs. temperature, T, of HP Ti_0.5Zr_0.5NiSn and Ti_0.15Nb_0.85FeSb in comparison to the HP + HPT processed samples. Some curves are shifted for a better view.

Thermal Shock Resistance

The thermal shock resistance is the ability of a solid to withstand sudden changes in temperature either on heating or cooling (Lu, 1998). The magnitude of the thermal shock resistance is an important parameter for the operation of a TE device in a cyclic temperature gradient. Due to the temperature gradient between the hot and cold ends of the device’s legs, mechanical failure can arise from the stress within the leg. Assuming that the rate of change of temperature is such as to allow time for heat conduction between the hot and cold end of the TE leg, then the thermal shock resistance parameter P_T can be calculated with

$P_T=\frac{\sigma (\text{1}-\nu )\lambda }{\alpha \text{E}}(9)$

where σ is the tensile fracture strength, ν is the Poison’s ratio, λ is the thermal conductivity, α is the coefficient of thermal expansion and E is Young’ modulus.

Usually decreasing grain size and increasing density can improve the thermal shock resistance; additionally, reducing the material’s coefficient of thermal expansion and increasing the strength and thermal conductivity can prevent a failure due to thermal shock. As after SPD the grain size is lower but also the density, and due to the fact, that after HPT thermal conductivity is lower but also the coefficient of thermal expansion, not much change in the thermal shock resistance is expected. Taking an average value of σ from the literature for the p- and n-type skutterudites (σ = 37 MPa and σ = 86 MPa, respectively (Snyder, 2008) (Ravi, 2008)), a rough estimation can be presented for P_T. For the p-type skutterudites P_T ∼ 36–42 W/m, is lower than for the n-type with P_T ∼ 150–170 W/m.

Internal Stress

The internal stress, τ_int, dealing with the forces and stresses inside a leg material, can be estimated from Eq. 10:

${\text{τ}}_{\text{int}}=\mathrm{G}\alpha (\text{w}/\text{2}\ell )\Delta \mathrm{T}(10)$

where G is the shear modulus, α is the coefficient of thermal expansion, w is the width and ℓ is the length of the leg.

The internal stresses were calculated for TE legs with w = 2 mm and ℓ = 5 mm. As can be seen in Figure 15, due to higher shear moduli and slightly higher coefficients of thermal expansion, the internal stresses of HP p- and n-type skutterudites (thick lines) are higher than those of the corresponding HP + HPT and CP + HPT processed skutterudites (thin lines). The difference between the HP and HP + HPT is maximal 13%, whereas it is more than 30% between HP and CP + HPT. Similarly, for the p- and n-type half-Heusler alloys (not shown in Figure 15) the internal stress of HP p-type Ti_0.15Nb_0.85FeSb (122 MPa at ΔT/ℓ = 140 K/mm) and of the n-type Ti_0.5Zr_0.5NiSn (99 MPa at ΔT/ℓ = 140 K/mm) is about 5% higher than that of the HP + HPT processed counterparts.

FIGURE 15

FIGURE 15. Internal stress of skutterudites, HP, HP + HPT and CP + HPT vs. ΔT/ℓ.

Conclusion

Even though skutterudites and half-Heusler alloys have a lower density after SPD, hardness is higher, governed mainly by grain refinement and enhanced defect density. Hardness is dependent on the shear strain introduced during HPT processing: hardness is the higher the more revolutions are applied and in addition hardness increases along the radius from the center to the rim of the HPT-processed cylindrical sample. After annealing, the density and hardness of HPT samples appear slightly enhanced. However, higher hardness coupled with an enhanced defect density results in lower indentation fracture toughness.

All elastic moduli for p- or n-type skutterudites as well as for half-Heusler alloys are within the error bar the same for HP and HP + HPT as well as for CP + HPT samples. Pugh’s relation classifies skutterudites as brittle, half-Heuslers as “ductile”.

Like metals, skutterudites and half-Heusler alloys have a lower Debye temperature after SPD even though in case of the latter two the difference is only in the range of about 2%. For skutterudites it was found that the Einstein temperature is roughly only half after HPT, indicating that after SPD the vibrations of the atomic lattice are not as much affected as the frequencies of the rattlers are.

Whereas Δℓ/ℓ₀—T curves of HPT processed skutterudites below room temperature do not exhibit any anomalies, above 300 K they do. Dependent on the treatment (i.e., HP or CP before HPT) and on the composition, it might take several temperature cycles till most of the defects and micro holes are annealed out and the Δℓ/ℓ₀—T curve becomes stable with respect to temperature cycling. In all cases, however, the thermal expansion coefficient after SPD is lower than before.

Generally, one can conclude that HPT consolidated samples have two advantages in comparison to HP ones: the TE figure of merit is higher, and the material appears mechanically strengthened.

Author Contributions

Both authors contributed equally to the work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors want to thank V. Soprunyuk and Prof. W. Schranz for thermal expansion measurements of half-Heusler alloys and Prof. J. Bursik (IPM, Brno) for providing TEM images.

References

Anbalagan, R., Rogl, G., Zehetbauer, M., Sharma, A., Rogl, P., Suwas, S., et al. (2014). Effect of high-pressure torsion on texture, microstructure, and Raman spectroscopy: case study of Fe and Te-substituted CoSb₃. J. Electron. Mater. 43 (10), 3817–3823. doi:10.1007/s11664-014-3179-1

CrossRef Full Text | Google Scholar

Anderson, O. L. (1963). A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solid. 24, 909–917. doi:10.1016/0022-3697(63)90067-2

CrossRef Full Text | Google Scholar

Appel, O., and Gelbstein, Y. (2014). A comparison between the effects of Sb and Bi doping on the thermoelectric properties of the Ti0.3Zr0.35Hf0.35NiSn half-heusler alloy. J. Electron. Mater. 43 (6), 1976–1982. doi:10.1007/s11664-013-2930-3

CrossRef Full Text | Google Scholar

Ashida, M., Sumida, N., Hasezaki, K., Matsunoshita, H., and Horita, Z. (2012). Effects of low rotational speed on crystal orientation of Bi. Mater. Trans. 53, 588–591. doi:10.2320/matertrans.me201101

CrossRef Full Text | Google Scholar

Battabyal, R., Priyadarshini, B., Sivaprahasam, D., Karthiselva, N. S., and Gopalan, R. (2015). The effect of CuO₂ nanoparticle dispersion on the thermoelectric properties of n-type skutterudites. J. Phys. D Appl. Phys. 48, 455309–455317. doi:10.1088/0022-3727/48/45/455309

CrossRef Full Text | Google Scholar

Bitkulov, I. K., Burkhanov, A. M., Kazantsev, V. A., Mulyukov, R. R., Mulyukov Ya, K., and Safarov, I. M. (2006). Effect of severe plastic deformation on the properties of the Fe36% Ni invar alloy. Phys. Met. Metallogr. 102 (1), 91–96. doi:10.1134/S0031918X06070131

CrossRef Full Text | Google Scholar

Borodachenkova, M., Wen, W., and de Bastos Pereira, A. M. (2017). “High‐Pressure torsion: experiments and modeling,” in Severe plastic deformation techniques. Editor M. Cabbio, (London, UK: Intech Open 69173 4, 93–112

Google Scholar

Bridgman, P. W. (Editor) (1952). Studies in large scale plastic flow and fracture. New York, NY:McGraw-Hill

Google Scholar

Casper, F., Graf, T., Chadov, S., Balke, B., and Felser, C. (2012). Half-Heusler compounds: novel materials for energy and spintronic applications. Semicond. Sci. Technol. 27, 063001. doi:10.1088/0268-1242/27/6/063001

CrossRef Full Text | Google Scholar

Clement, J., Torres, P., Gil, F. J., and Planell, J. A. (1999). Evaluation by Vickers indentation of fracture toughness of a phosphate biodegradable glass. J. Mat. Sci.: Mat. in Medicine 10, 437–441. doi:10.1023/A:1008935316741

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, I., Kaller, M., Komisarchik, G., Fuks, D., and Gelbstein, Y. (2015). Enhancement of the thermoelectric properties of n-type PbTe by Na and Cl co-doping. J. Mater. Chem. C 3, 9559–9564. doi:10.1039/c5tc01781e

CrossRef Full Text | Google Scholar

Dahal, T., Gahlawat, S., Jie, Q., Dahal, K., Lan, Y., White, K., et al. (2015). Thermoelectric and mechanical properties on mischmetal filled p-type skutterudites Mm_0.9Fe_4-xCo_xSb₁₂. J. Appl. Phys. 117, 055101–055108. doi:10.1063/1.4906954

CrossRef Full Text | Google Scholar

Das, M., Das, G., Ghosh, M., Wegner, M., Rajnikant, V., Ghosh-Chowdhury, S., et al. (2012). Microstructures and mechanical properties of HPT processed 6063 Al alloy. Mater Sci Eng A 558, 525–532. doi:10.1016/j.msea.2012.08.040

CrossRef Full Text | Google Scholar

Fu, C., Liu, Y., Xie, H., Liu, X., Zhao, X., Snyder, G. J., et al. (2013). Electron and phonon transport in Co-doped V_0.6Nb_0.4FeSb half-Heusler thermoelectric materials. J. Appl. Phys. 114 (13), 134905. doi:10.1063/1.4823859

CrossRef Full Text | Google Scholar

Fu, C., Zhu, T., Liu, Y., Xie, H., and Zhao, X. (2015). Band engineering of high-performance p-type NbFeSb based half-Heusler thermoelectric materials for figure of merit ZT > 1. Energy Environ. Sci. 8, 216–220. doi:10.1039/c4ee03042g

CrossRef Full Text | Google Scholar

Gelbstein, Y., Tal, N., Yarmek, A., Rosenberg, Y., Dariel, M. P., Ouardi, S., et al. (2011). Thermoelectric properties of spark plasma sintered composites based on TiNiSn half-Heusler alloys. J. Mater. Res. 26 (15), 1919–1923. doi:10.1557/jmr.2011.107

PubMed Abstract | CrossRef Full Text | Google Scholar

Goyal, R. K. (2018). Nanomaterials and nanocomposites: Synthesis, properties, characterization techniques and applications, Boca Raton, FL: CRC Press Taylor and Francis, 41–43

Google Scholar

Gürth, M., Rogl, G., Romaka, V. V., Grytsiv, A., Bauer, E., and Rogl, P. (2016). Thermoelectric high ZT half-Heusler alloys Ti_1-x-yZr_xHf_yNiSn. Acta Mater. 104, 210–222. doi:10.1016/j.actamat.2015.11.022

CrossRef Full Text | Google Scholar

Guttmann, G. M., Dadon, D., and Gelbstein, Y. (2015). Electronic tuning of the transport properties of off-stoichiometric Pb_xSn_1-xTe thermoelectric alloys by Bi₂Te₃ doping. J. Appl. Phys. 11, 065102. doi:10.1063/1.4928459

CrossRef Full Text | Google Scholar

Han, J-K., Herndon, T., Jang, J., Langdon, T. G., and Kawasaki, M. (2020). Synthesis of hybrid nanocrystalline alloys by mechanical bonding through high-pressure torsion. Adv. Eng. Mater. 22, 1901289. doi:10.1002/adem.201901289

CrossRef Full Text | Google Scholar

Hasan, Md. N., Wahid, H., Nayan, N., and Ali, M. S. M. (2020). Inorganic thermoelectric materials: a review. Int. J. Energy Res. 44 (8), 6170–6222. doi:10.1002/er.5313

CrossRef Full Text | Google Scholar

He, R., Gahlawat, S., Guo, C., Chen, S., Dahal, T., Zhang, H., et al. (2015). Studies on mechanical properties of thermoelectric materials by nanoindentation. Phys. Status Solidi 212 (10), 2191–2195. doi:10.1002/pssa.201532045

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenwarter, A., Bachmaier, A., Gludovatz, B., Scheriau, S., and Pippan, R. (2009). Technical parameters affecting grain refinement by high pressure torsion. Int. J. Mater. Res. 100, 1653–1661. doi:10.3139/146.110224

CrossRef Full Text | Google Scholar

Hohenwarter, A., and Pippan, R. (2010). Anisotropic fracture behavior of ultrafine-grained iron. Mater. Sci. Eng. A 527, 2649–2656. doi:10.1016/j.msea.2009.12.033

CrossRef Full Text | Google Scholar

Hohenwarter, A., and Pippan, R. (2011). Fracture toughness evaluation of ultrafine-grained nickel. Scripta Mater. 64, 982–985. doi:10.1016/j.scriptamat.2011.02.007

CrossRef Full Text | Google Scholar

Hohenwarter, A., Taylor, A., Stock, R., and Pippan, R. (2011). Effect of large shear deformations on the fracture behavior of a fully pearlitic steel. Metall. Mater. Trans. 42 (6), 1609–1618. doi:10.1007/s11661-010-0541-7

CrossRef Full Text | Google Scholar

Ikoma, Y. (2019). Severe plastic deformation of semiconductor materials using high-pressure torsion. Mater. Trans. 60 (7), 1168–1176. doi:10.2320/matertrans.mf201907

CrossRef Full Text | Google Scholar

Ivanisenko, Yu., Kulagin, R., Fedorov, V., Mazilkin, A., Scherer, T., and Baretzky, B. (2016). High pressure torsion extrusion as a new severe plastic deformation process. Mater Sci. Eng. A 664, 247–256. doi:10.1016/j.msea.2016.04.008

CrossRef Full Text | Google Scholar

Kauzlarich, S. M. (2019). Special advances in Zintl phases. Materials 12 (6), 2554. doi:10.3390/ma12162554

CrossRef Full Text | Google Scholar

Kim, S., Lee, K. H., Mun, H. A., Kim, H. S., Hwang, S. W., Roh, J. W., et al. (2015). Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 348 (6230), 109–113. doi:10.1126/science.aaa4166

PubMed Abstract | CrossRef Full Text | Google Scholar

Komisarchik, G., Fuks, D., and Gelbstein, Y. (2016). High thermoelectric potential of n-type Pb_1-xTi_xTe alloys. J. Appl. Phys. 120 (5), 055104. doi:10.1063/1.4960573

CrossRef Full Text | Google Scholar

Kourov, N. I., Pushin, V. G., Korolev, A. V., Kazantsev, V. A., Marchenkova, E. B., and Uksusnikov, A. N. (2007). Effect of severe plastic deformation on the structure and properties of the Ni_2.16Mn_0.84Ga alloy. Phys. Met. Metallogr. 103, 270–277. doi:10.1134/S0031918X07030076

CrossRef Full Text | Google Scholar

Langdon, T. G. (2011). Processing by severe plastic deformation: historical developments and current input. Mater. Sci. Forum 667-669, 9–14. doi:10.4028/www.scientific.net/MSF.667-669.9

CrossRef Full Text | Google Scholar

Lawn, B. R., Evans, A. G., and Marshall, D. B. (1980). Elastic/plastic indentation damage in ceramics: the median/radial crack system. J. Am. Ceram. Soc. 63, 574–581. doi:10.1111/j.1151-2916.1980.tb10768.x

CrossRef Full Text | Google Scholar

Li, G., An, Q., Aydemir, U., Goddard, W. A., Wood, M., Zhai, P., et al. (2016). Enhanced ideal strength of thermoelectric half-Heusler TiNiSn by sub-structure engineering. J. Mater. Chem. 4, 14625–14636. doi:10.1039/c6ta04123j

CrossRef Full Text | Google Scholar

Li, Q., Hua, G., Lu, H., Yu, B., and Li, D. Y. (2018). Understanding the effect of plastic deformation on elastic modulus of metals based on a percolation model with electron work function. JOM 70 (7), 1130–1135. doi:10.1007/s11837-018-2891-3

CrossRef Full Text | Google Scholar

Lohmiller, J., Baumbusch, R., Kerber, M., Castrup, A., Hahn, H., Schafler, E., et al. (2013). Following the deformation behavior of nanocrystalline Pd films on polyimide substrates using in situ synchrotron XR. Mech. Mater. 67, 65–73. doi:10.1016/j.mechmat.2013.04.010

CrossRef Full Text | Google Scholar

Lu, T. J, and Fleck, N. A. (1998). The thermal shock resistance of solids. Acta Mater. 46 (13), 4755–4768. doi:10.1016/s1359-6454(98)00127-x

CrossRef Full Text | Google Scholar

Ma, Y., Hao, Q., Poudel, B., Lan, Y. C., Yu, B., and Wang, D. C. (2008). High thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Nano Lett. 8, 2580–2584. doi:10.1021/nl8009928

CrossRef Full Text | Google Scholar

Madeiros, E. E., and Dias, A. M. S. (2013). Experimental and numerical analysis of Vickers hardness testing. Int. J. Res. Rev. Appl. Sci. 17, 9–18

Google Scholar

Masuda, S., Tsuchiya, K., Qiang, J., Miyazaki, H., and Nishino, Y. (2018). Effect of high-pressure torsion on the microstructure and thermoelectric properties of Fe₂VAl-based compounds. J. Appl. Phys. 124, 035106–035109. doi:10.1063/1.5034390

CrossRef Full Text | Google Scholar

Migliori, A., and Maynard, J. D. (2005). Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev. Sci. Instrum. 76, 121301–121307. doi:10.1063/1.2140494

CrossRef Full Text | Google Scholar

Migliori, A., Sarrao, J., Visscher, W. M., Bell, T. M., Lei, M., Fisk, Z., et al. (1993). Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Physica B 183, 1–24. doi:10.1016/0921-4526(93)90048-b

CrossRef Full Text | Google Scholar

Mukherjee, G. D., Bansal, C., and Chatterjee, A. (1996). Thermal expansion study of ordered and disordered Fe₃Al: an effective approach for the determination of vibrational entropy. Phys. Rev. Lett. 76 (11), 1876–1879. doi:10.1103/physrevlett.76.1876

CrossRef Full Text | Google Scholar

Musalimov, R. S., and Valiev, R. Z. (1992). Dilatometric studies of aliminium alloy with submicrograin structure. Scripta Metall. Mater. 27, 1685. doi:10.1016/0956-716x(92)90002-v

CrossRef Full Text | Google Scholar

Nolas, G. S., Morelli, D. T., and Tritt, T. M. (1999). Skutterudites: a phonon-glass-electron crystal approach to advanced thermoelectric energy conversion applications. Annu. Rev. Mater. Sci. 29, 89–116. doi:10.1146/annurev.matsci.29.1.89

CrossRef Full Text | Google Scholar

Pippan, R., and Hohenwarter, A. (2016). The importance of fracture toughness in ultrafine and nanocrystalline bulk materials. Mater Res Lett 4, 127–136. doi:10.1080/21663831.2016.1166403

PubMed Abstract | CrossRef Full Text | Google Scholar

Pippan, R., Scheriau, S., Hohenwarter, A., and Hafok, M. (2008). Advantages and limitations of HPT: a review. Mater. Sci. Forum 16 584–586.

PubMed Abstract | Google Scholar

Ponton, C. B., and Rawlings, R. D. (1989). Vickers indentation fracture toughness test, Part 1, Review of literature and formulation of standardised indentation toughness equations. Mater. Sci. Technol. 5, 865–872. doi:10.1179/mst.1989.5.9.865

CrossRef Full Text | Google Scholar

Poon, S. J. (2018). Recent advances in thermoelectric performance of half-Heusler compounds. Metals 8, 989–999. doi:10.3390/met8120989

CrossRef Full Text | Google Scholar

Poon, S. J., Wu, D., Zhu, S., Xie, W., Tritt, T. M., Thomas, P., et al. (2011). Half-Heusler phases and nanocomposites as emerging high-ZT thermoelectric materials. J. Mater. Res. 26 (22), 2795–2802. doi:10.1557/jmr.2011.329

CrossRef Full Text | Google Scholar

Poudel, B., Hao, Q., Ma, Y., Lan, Y. C., Minnich, A., Yu, B., et al. (2008). High thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638. doi:10.1126/science.1156446

CrossRef Full Text | Google Scholar

Pugh, S. F. (1954). XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Phil. Magazine and J. of Sci. 45, 823–843. doi:10.1080/14786440808520496

CrossRef Full Text | Google Scholar

Ravi, V., Firdosy, S., Caillat, T., Lerch, B., Calamino, A., Pawlik, R., et al. (2008). Mechanical properties of thermoelectric skutterudites. AIP Conf. Proceedings 969, 656. doi:10.1063/1.2845027

CrossRef Full Text | Google Scholar

Ribarik, G., Ungar, T., and Gubicza, J. (2004). Correlation between strength and microstructure of ball-milled Al–Mg alloys determined by X-ray diffraction. J. Mater. Sci. Eng. 387-389, 343–347. doi:10.1016/j.msea.2004.01.089

CrossRef Full Text | Google Scholar

Rijal, A., Singh, S. P., Han, J.-K., Kawasaki, M., and Kumar, P. (2020). Effect of High-pressure torsion on hardness and electrical resistivity of commercial pure Cu. Adv. Eng. Mater. 22, 1900547–1900558. doi:10.1002/adem.201900547

CrossRef Full Text | Google Scholar

Rogl, G., Ghosh, S., Wang, L., Bursik, J., Grytsiv, A., Kerber, M., et al. (2020a). Half-Heusler alloys: enhancement of ZT after severe plastic deformation (ultra-low thermal conductivity). Acta Mater. 183, 285–300. doi:10.1016/j.actamat.2019.11.010

CrossRef Full Text | Google Scholar

Rogl, G., Gosh, S., Renk, O., Yubuta, K., Grytsiv, A., Schafler, E., et al. (2020b). HPT production of large bulk skutterudites. J. Alloys Compd. 854, 156678. doi:10.1016/j.jallcom.2020.156678

CrossRef Full Text | Google Scholar

Rogl, G., Soprunyuk, V., Schranz, W., Zehetbauer, M. J., Bauer, E., and Rogl, P. (2020c). Resistivity and thermal expansion (4.2 – 820 K) of skutterudites after severe plastic deformation (via HPT). Z. Anorg. Allg. Chem. 646, 1267–1272. doi:10.1002/zaac.202000040

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Anbalagan, R., Bursik, J., Kerber, M., Schafler, E., et al. (2018). Direct SPD-processing to achieve high-ZT skutterudites. Acta Mater. 159, 352–363. doi:10.1016/j.actamat.2018.08.020

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Bauer, E., and Rogl, P. (2019). “Thermoelectric Sb-based skutterudites for medium temperatures,” in Advanced thermoelectrics: materials, contacts, devices and systems. Editors Z Ren, Y Lan, and Q Zhang, (Boca Raton, FL: CRC Press), 193–230

Google Scholar

Rogl, G., Grytsiv, A., Failamani, F., Hochenhofer, M., Bauer, E., and Rogl, P. (2017a). Attempts to further enhance ZT in skutterudites via nano-composites. J. Alloys Compd. 695:682–696. doi:10.1016/j.jallcom.2016.10.114

CrossRef Full Text | Google Scholar

Rogl, G., Sauerschnig, P., Rykavets, Z., Romaka, V. V., Heinrich, P., Hinterleitner, B., et al. (2017b). (V,Nb)-doped half Heusler alloys based on {Ti,Zr,Hf}NiSn with high ZT. Acta Mater. 131, 336–348. doi:10.1016/j.actamat.2017.03.071

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Gürth, M., Tavassoli, A., Ebner, C., Wünschek, A., et al. (2016). Mechanical properties of half-Heusler alloys. Acta Mater. 107, 178–195. doi:10.1016/j.actamat.2016.01.031

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Horky, J., Anbalagan, R., Bauer, E., and Mallik, R. C. (2015). Changes in microstructure and physical properties of skutterudites after severe plastic deformation. Phys. Chem. Chem. Phys. 17, 3715–3722. doi:10.1039/c4cp05230g

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Rogl, P., Bauer, E., Hochenhofer, M., Anbalagan, R., et al. (2014a). Nanostructuring of p- and n-type skutterudites reaching figures of merit of approximately 1.3 and 1.6, respectively. Acta Mater. 76, 434–448. doi:10.1016/j.actamat.2014.05.051

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Rogl, P., Peranio, N., Bauer, E., Zehetbauer, M., et al. (2014b). N-type skutterudites (R,Ba,Yb)_yCo₄Sb₁₂ (R = Sr, La, Mm, DD, SrMm, SrDD) approaching ZT∼2.0. Acta Mater. 63, 30–43. doi:10.1016/j.actamat.2013.09.039

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Rogl, P., Bauer, E., Kerber, M. B., Zehetbauer, M., et al. (2010a). Multi-filled nanocrystalline p-type didymium – skutterudites with ZT>1.2. Intermetallics 18, 2435–2444. doi:10.1016/j.intermet.2010.08.041

CrossRef Full Text | Google Scholar

Rogl, G., Zhang, L., Rogl, P., Grytsiv, A., Falmbigl, M., Rajs, D., et al. (2010b). Thermal expansion of skutterudites. J. Appl. Phys. 107, 043507–043517. doi:10.1063/1.3284088

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Rogl, P., Bauer, E., and Zehetbauer, M. (2011a). A new generation of p-type didymium skutterudites with high ZT. Intermetallics 19, 546–555. doi:10.1016/j.intermet.2010.12.001

CrossRef Full Text | Google Scholar

Rogl, G., Puchegger, S., Zehetbauer, M., and Grytsiv, A. (2011b). Dependence of the elastic moduli of skutterudites on density and temperature. Mater. Res. Soc. Symp. Proc. 1325. doi:10.1557/opl.2011.845

CrossRef Full Text | Google Scholar

Rogl, G., Zehetbauer, M., Kerber, M., Rogl, P., and Bauer, E. (2011c). Impact of ball milling and high-pressure torsion on the microstructure and thermoelectric properties of p- and n-type Sb-based skutterudites. Mater. Sci. Forum 667-669, 1089–1094. doi:10.4028/www.scientific.net/MSF.667-669.1089

CrossRef Full Text | Google Scholar

Rogl, G., Grytsiv, A., Rogl, P., Royanian, E., Bauer, E., Horky, J., et al. (2013a). Dependence of thermoelectric behavior on severe plastic deformation parameters: a case study on p-type skutterudite DD_0.60Fe₃CoSb₁₂. Acta Mater. 61, 6778–6788. doi:10.1016/j.actamat.2013.07.052

CrossRef Full Text | Google Scholar

Rogl, G., Rogl, P., Bauer, E., and Zehetbauer, M. (2013b). “Severe plastic deformation, a tool to enhance thermoelectric performance,” in Thermoelectric nanomaterials. Editors K. Kuomoto, and T. Mori, (Heidelberg, Germany: Springer Series in Materials Science), 182, 193–254

Google Scholar

Rogl, G., and Rogl, P. (2017a). How nanoparticles can change the figure of merit, ZT, and mechanical properties of skutterudites. Mater Today Phys 3, 48–69. doi:10.1016/j.mtphys.2017.12.004

CrossRef Full Text | Google Scholar

Rogl, G., and Rogl, P. (2017b). “Skutterudites, a most promising group of thermoelectric materials,” in Current opinion in green and sustainable chemistry. Editor S. Schorr, (Amsterdam, Netherlands: Elsevier), 4, 50–57

Google Scholar

Rogl, G., and Rogl, P. (2011). Mechanical properties of skutterudites. Sci. Adv. Mater. 3, 517–538. doi:10.1166/sam.2011.1181

CrossRef Full Text | Google Scholar

Rogl, G., and Rogl, P. (2019). “Skutterudites: progress and challenges,” in Novel thermoelectric materials and device design concepts. Editors S. Skipidarov, and M. Nikitin, (Switzerland: Springer Nature Switzerland), 177–2001

Google Scholar

Rogl, G., Aabdin, Z., Schafler, E., Horky, J., Setman, D., Zehetbauer, M., et al. (2012a). Effect of HPT processing on the structure, thermoelectric and mechanical properties of Sr0.07Ba0.07Yb0.07Co4Sb12. J. Alloys Compds. 537, 183–189. doi:10.1016/j.jallcom.2012.05.011

CrossRef Full Text | Google Scholar

Rogl, G., Setman, D., Schafler, E., Horky, J., Kerber, M., Zehetbauer, M., et al. (2012b). “Changes of thermoelectric properties and hardness after HPT processing of micro- and nanostructured skutterudites,” in NATO science for piece and security series B: physics and biophysics. Editors V. Zlatic, , and A. Hewson, (Berlin, Germany: Springer Science and Business Media BV) Vol. 7, 81–91

Google Scholar

Rogl, G., Setman, D., Schafler, E., Horky, J., Kerber, M., Zehetbauer, M., et al. (2012c). High pressure torsion, a new processing route for thermoelectrics of high ZTs by means of severe plastic deformation. Acta Mater. 60, 2146–2157. doi:10.1016/j.actamat.2011.12.023

CrossRef Full Text | Google Scholar

Rogl, G., Yubuta, K., Kerber, M., Grytsiv, A., Zehetbauer, M., Bauer, E., et al. (2019a). Sustainable and simple processing technique for n-type skutterudites with high ZT and their analysis. Acta Mater. 173, 9–19. doi:10.1016/j.actamat.2019.04.025

CrossRef Full Text | Google Scholar

Rogl, G., Zehetbauer, M. J., and Rogl, P. F. (2019b). The effect of severe plastic deformation on the thermoelectric performance of skutterudites, half-Heuslers and Bi-Tellurides. Mater. Trans. 60 (10), 2071–2085. doi:10.2320/matertrans.mf201941

CrossRef Full Text | Google Scholar

Rotter, M., Müller, H., Gratz, E., Dörr, M., and Löwenhaupt, M. (1998). A miniature capacitance dilatometer for thermal expansion and magnetostriction. Rev. Sci. Instrum. 69, 2742–2746. doi:10.1063/1.1149009

CrossRef Full Text | Google Scholar

Rowe, D. M. (2006). Thermoelectrics handbook macro to nano. Boca Raton, Fl: CRC Taylor&Francis.

Google Scholar

Rull-Bravo, M., Moure, A., Fernández, J. F., and Martín-González, S. (2015). Skutterudites as thermoelectric material: revisited. RSC Adv. 5, 41653–41667. doi:10.1039/c5ra03942h

CrossRef Full Text | Google Scholar

Sadia, Y., Aminov, Z., Mogilyansky, D., and Gelbstein, Y. (2016). Texture anisotropy of higher manganese silicide following arc-melting and hot-pressing. Intermetallics 68, 71–77. doi:10.1016/j.intermet.2015.08.009

CrossRef Full Text | Google Scholar

Sakai, M., and Bradt, R. C. (1993). Fracture toughness testing of brittle materials. Int. Mater. Rev. 38, 53–78. doi:10.1179/imr.1993.38.2.53

CrossRef Full Text | Google Scholar

Sakurada, S., and Shutoh, N. (2005). Effect of Ti substitution on the thermoelectric properties of (Zr,Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 86, 082105–082108. doi:10.1063/1.1868063

CrossRef Full Text | Google Scholar

Sanusi, K. O., Makinde, O. D., and Oliver, G. J. (2012). Equal channel angular pressing technique for the formation of ultra-fine grained structures. South Afr. J. Sci. 108 (9/10), 212. doi:10.4102/sajs.v108i9/10.212

CrossRef Full Text | Google Scholar

Schafler, E. (2011). Strength response upon pressure release after high-pressure torsion deformation. Scripta Mater. 64, 130–132. doi:10.1016/j.scriptamat.2010.09.026

CrossRef Full Text | Google Scholar

Schierning, G., Chavez, R., Schmechel, R., Balke, B., Rogl, G., and Rogl, P. (2015). Concepts for medium-high to high temperature thermoelectric heat-to-electricity conversion: a review of selected materials and basic considerations of module design. Transl. Mater. Res. 2, 025001–025026. doi:10.1088/2053-1613/2/2/025001

CrossRef Full Text | Google Scholar

Schreiber, E., Anderson, O. L., and Soga, N. (1973). Elastic constants and their measurements. New York, NY: McGraw-Hill Companies, Inc New York

Google Scholar

Schwall, M., and Balke, B. (2013). Phase separation as a key to a thermoelectric high efficiency. Phys. Chem. Chem. Phys. 15 (6), 1868–1872. doi:10.1039/c2cp43946h

CrossRef Full Text | Google Scholar

Schwarz, K. T., Kormout, K. S., Pippan, R., and Hohenwarter, A. (2017). Impact of severe plastic deformation on microstructure and fracture toughness evolution of a duplex-steel. Mater. Sci. Eng. A 703, 173–179. doi:10.1016/j.msea.2017.07.062

CrossRef Full Text | Google Scholar

Segal, V. (2018). Review: modes and processes of severe plastic deformation (SPD). Materials (Basel) 11, 1175. doi:10.3390/ma11071175

CrossRef Full Text | Google Scholar

Shetty, D. K., Wright, I. G., Mincer, P. N., and Clauer, A. H. (1985). Indentation fracture of WC-Co cements. J. Mater. Sci. 20, 1873–1882. doi:10.1007/bf00555296

CrossRef Full Text | Google Scholar

Snyder, G. J., and Toberer, E. S. (2008). Complex thermoelectric materials. Nat. Mater. 7, 105–114. doi:10.1038/nmat2090

CrossRef Full Text | Google Scholar

Song, Y., Wang, W., Gao, D., Kim, H-S., Yoon, E-Y., Lee, D-J., et al. (2012). Inhomogeneous hardness distribution of high-pressure torsion processed IF steel disks. Mater. Sci. Appl. 3, 234–239. doi:10.4236/msa.2012.34034

CrossRef Full Text | Google Scholar

Suwas, S., and Mondal, S. (2019). Texture evolution in severe plastic deformation processes. Mater. Trans. 60 (8), 1457–1471. doi:10.2320/matertrans.mf201933

CrossRef Full Text | Google Scholar

Tavassoli, A., Failamani, F., Grytsiv, A., Rogl, G., Heinrich, P., Müller, H., et al. (2017). On the half-Heusler compounds Nb_1-x{Ti,Zr,Hf}_xFeSb: phase relations, thermoelectric properties at low and high temperature, and mechanical properties. Acta Mater. 135, 263–276. doi:10.1016/j.actamat.2017.06.011

CrossRef Full Text | Google Scholar

Tavassoli, A., Grytsiv, A., Rogl, G., Romaka, V. V., Michor, H., Reissner, M., et al. (2018). The half Heusler system Ti_1+xFe_1.33−xSb – TiCoSb with Sb/Sn substitution: phase relations, crystal structures and thermoelectric properties. Dalton Trans. 47, 879–897. doi:10.1039/c7dt03787b

CrossRef Full Text | Google Scholar

Uher, C. (2001). Skutterudites: prospective novel thermoelectrics, Semiconduct. Semimet. 69 (5), 139–253. doi:10.1016/s0080-8784(01)80151-4

CrossRef Full Text | Google Scholar

Ungar, T., Schafler, E., and Gubicza, J. (2009). “Microstructure of bulk nanomaterials determined by X-Ray line profile analysis,” in Bulk nanostructured materials. Editors M. J. Zehetbauer, and Y. T. Zhu, (New York, NY: VCH Wiley), 361–396

Google Scholar

Valiev, R., Estrin, Y., Horita, Z., Langdon, T. G., Zehetbauer, M. J., and Zhu, Y. T. (2016). Producing bulk ultrafine-grained materials by severe plastic deformation: ten years later. JOM 68 (4), 1216–1226. doi:10.1007/s11837-016-1820-6

CrossRef Full Text | Google Scholar

Valiev, R. Z., Enikeev, N. A., Murashkin, Yu M., Kazykhanov, V. U., and Sauvage, X. (2010). On the origin of the extremely high strength of ultrafine-grained Al alloys produced by severe plastic deformation. Scripta Mater. 63, 949–952. doi:10.1016/j.scriptamat.2010.07.014

CrossRef Full Text | Google Scholar

Valiev, R. Z., Estrin, Y., Horita, Z., Langdon, T. G., Zehetbauer, M. J., and Zhu, Y. T. (2006). Producing bulk ultrafine-grained materials by severe plastic deformation. J. Met. 58, 33–39. doi:10.1007/s11837-006-0213-7

CrossRef Full Text | Google Scholar

Valiev, R. Z., Murashkin, Yu M., Ganeev, A. V., and Enikeev, N. A. (2012). Superstrength of nanostructured metals and alloys produced by severe plastic deformation. Phys. Met. Metallogr. 113 (13), 1193–1201. doi:10.1134/s0031918x12130042

CrossRef Full Text | Google Scholar

Valiev, R. Z., Kasilnikov, N. A., and Tsenev, N. K. (1991). Plastic deformation of alloys with submicron-grained structure. Mater. Sci. Eng. A 137, 35–40. doi:10.1016/0921-5093(91)90316-f

CrossRef Full Text | Google Scholar

Valiev, R. Z., Korznikov, A. V., and Mulyukov, R. R. (1993). Structure and properties of ultrafine-grained materials produced by severe plastic deformation. Mater. Sci. Eng. A 168, 141–148. doi:10.1016/0921-5093(93)90717-s

CrossRef Full Text | Google Scholar

Vorhauer, A., and Pippan, R. (2004). On the homogeneity of deformation by high pressure torsion. Scripta Mater. 51, 921–925. doi:10.1016/j.scriptamat.2004.04.025

CrossRef Full Text | Google Scholar

Voroshilov, V. P., Zakharov, A. I., Kalinin, V. M., and Uralov, A. S. (1973). Effect of plastic deformation and heat treatment on the temperature coefficient of linear expansion and magnetic properties of iron-nickel invar alloys. Fiz. Met. Metalloved. 35 (5), 953–958

Google Scholar

Xie, W., Weidenkaff, A., Tang, X., Zhang, Q., Poon, J., and Tritt, T. M. (2012). Recent Advances in nanostructured thermoelectric half-Heusler compounds. Nanomaterials 2, 379–412. doi:10.3390/nano2040379

CrossRef Full Text | Google Scholar

Yu, F., Zhang, J., Yu, D., He, J., Liu, Z., Xu, B., et al. (2009). Enhanced thermoelectric figure of merit in nanocrystalline Bi₂Te₃ bulk. J. Appl. Phys. 105, 094303. doi:10.1063/1.3120865

CrossRef Full Text | Google Scholar

Zehetbauer, M. J., and Estrin, Y. (2009). “Modeling of strength and strain hardening of bulk nanostructured materials,” in Bulk nanostructured materials. Editors Zehetbauer, M. J., and Zhu, Y. T. (Weinheim, Germany: Wiley VCH), 109–135

Google Scholar

Zhang, K., Alexandrov, I. V., and Valiev, R. Z. (1998). The thermal behavior of atoms in ultrafine-grained Ni processed by severe plastic deformation. J. Appl. Phys. 84 (4), 1924–1927. doi:10.1063/1.368320

CrossRef Full Text | Google Scholar

Zhang, L., Grytsiv, A., Bonarski, B., Kerber, M., Setman, D., Schafler, E., et al. (2010a). Impact of high-pressure torsion on the microstructure and physical properties of Pr_0.67Fe₃CoSb₁₂, Pr_0.71Fe_3.5Ni_0.5Sb₁₂, and Ba_0.06Co₄Sb₁₂. J. Alloys Compd. 494, 78–83. doi:10.1016/j.jallcom.2010.01.042

CrossRef Full Text | Google Scholar

Zhang, L., Rogl, G., Grytsiv, A., Puchegger, S., Koppensteiner, J., and Spieckermann, F. (2010b). Mechanical properties of filled antimonide skutterudites. Mater. Sci. Eng. B 170, 26–31. doi:10.1016/j.mseb.2010.02.022

CrossRef Full Text | Google Scholar

Zhang, Q., Zhou, Z., Dylla, M., Agne, M. T., Peid, Y., Wang, L., et al. (2017). Realizing high-performance thermoelectric power generation through grain boundary engineering of skutterudite-based nanocomposites. Nanomater. Energy 41, 501–510. doi:10.1016/j.nanoen.2017.10.003

CrossRef Full Text | Google Scholar

Zhilyaev, A. P., Nurislamova, G. V., Kim, B. K., Baró, M. D., Szpunar, J. A., and Langdon, T. G. (2003). Experimental parameters influencing grain refinement and microstructural evolution during high pressure torsion. Acta Mater. 51, 753–765. doi:10.1016/s1359-6454(02)00466-4

CrossRef Full Text | Google Scholar

Zhu, H., Mao, J., Li, Y., Sun, J., Wang, Y., Zhu, Q., et al. (2019). Discovery of TaFeSb-based half-Heuslers with high thermoelectric performance. Nat. Commun. 10 (270), 1–9. doi:10.1038/s41467-018-08223-5

CrossRef Full Text | Google Scholar