Mechanical Properties and Microstructure of Reinforced Passivation Film: A Reactive Molecular Dynamics Study

Reinforced concrete is one of the most critical composite materials in the modern civil engineering and can improve the tensile resistance of concrete. Its passivation film plays an important role in the durability of concrete and the steel corrosion. But, due to the size limitations, the destruction of micro-scale steel bars has not been well studied. In this work, the reactive molecular dynamics simulation was employed to studying the mechanical properties of the steel and its passivation film. The uniaxial stretching of different compounds of γ-FeOOH, γ-Fe₂O₃ and Fe was performed. We found that the oxidation can reduce the tensile strength of steel. For the three compounds of γ-FeOOH, γ-Fe₂O₃ and Fe, the order of tensile strength from high to low is Fe > γ-Fe₂O₃ > γ-FeOOH. But, the ductility of γ-FeOOH under x direction is increased. The detail microstructure analysis shown that the difference of tensile strength is origin from the coordination in the materials. The two kinds of stretching processes of whole system stretching (in the Fe phase and x direction of γ-FeOOH phase) and partly area stretching (in the Fe₂O₃ phase and z direction of γ-FeOOH phase) were clarified. The external force is dispersed in whole system stretching but opposite in partly area stretching. This investigation leads to possible new direction for studying the tensile strength of materials, and the strategy of evaluating materials tensile strength can supply valuable information in evaluating and improving the mechanical properties of reinforced concrete.

Introduction

Reinforced concrete can effectively improve the tensile strength of ordinary Portland concrete (Alexander, 1959; Song and Hwang, 2004; Song et al., 2005; Park et al., 2012), which is widely used in high-rise buildings, bridges and other construction projects (Horvath, 2004; Scrivener and Kirkpatrick, 2008; Anandavalli, 2012; Allen and Iano, 2019). But the rebar failure caused by cyclic loading (Psycharis et al., 2018) great limits the application of reinforced concrete. The studies of mechanical properties of rebar have attracted extensive attention (Kanaev et al., 2018; Bandyopadhyay et al., 2019). In general, the rebar contains two components which are the steel phase and its passivation film. In the alkaline environment of concrete, the passivation film is formed and locates on the surface of the steel (Luo et al., 2015). Reinforced passivation film plays an important role for improving the durability of concrete and preventing corrosion. Therefore, the study on the mechanical properties of steel and its’ passivation film is facilitated to further using and developing the reinforced concrete.

Many researches effort to study the mechanical properties of steel bars at the macroscopic scale (Tuutti, 1982; MacGregor et al., 1997; Angst et al., 2017; Gong and Maekawa, 2018; Gong and Maekawa, 2019). Thomas and Ramaswamy (2007) have studied the mechanical properties of steel fiber-reinforced concrete and proposed a model that predicted the experimental test data quite accurately. Further, the mechanical properties for different effects of temperature (Düğenci et al., 2015), craft (Seo et al., 2016) and strength (Iqbal et al., 2015) fiber-reinforced concrete were investigated. These studies have played a crucial role for understanding the relationship among the mechanical properties of steel bars, structure, and environment. However, due to the size limitations, the destructions of steel bars in micro-scale have not been well clarified (Zhang et al., 2016; Boscato et al., 2018; Saha et al., 2018; Nykyforchyn et al., 2019; Sienko et al., 2019). The fiber in reinforced concrete can be regarded as a layered structure in which the surface is composed by γ-FeOOH, γ-Fe₂O_3, and iron from outside to inside. The iron phase is covered by the passivation film. The mechanical properties of the passivation film can significantly affect the mechanical properties of fiber. The investigation of mechanical properties of passivation film needs micro-scale perspective, due to the fine structure of passivation film on steel surface.

Recently, the molecular dynamics (MD) simulation is considered as an effective means to study the molecular behavior in nanoscale (Abdolhosseini Qomi et al., 2012; Hou et al., 2018; Wang et al., 2019; Fogg et al., 2019; Hou et al., 2019; Hou et al., 2020; Wang et al., 2020a; Wang et al., 2020b; Wang et al., 2020c), which can also reveal the micro-structural changes of materials under force loading (Hou et al., 2014; Hou et al., 2015; Hou, 2019; Hou et al., 2019). There are many precedents for the study of crystal mechanical behavior using MD simulation. Li et al. (2019) study the tension behaviors of nanopolycrystalline Cu–Ta alloys through MD simulations, and the influences of several important factors on the mechanical properties of the materials are considered. Wu et al. (2015) used MD methods to study the effects of vacancies and dislocations on the mechanical properties for interfacial deformation processes of methane hydrates. The results show dislocation-free brittle failure in monocrystalline hydrates and an unexpected crossover from strengthening to weakening in polycrystals. Lin et al. (2017) used parallel MD to simulate the mechanical properties of graphene reinforced polymer nanocomposites with temperature dependent. These researches confirm that MD is an effective way to study the mechanical properties of materials. But, for many metallic materials, the breaking process often involves the breaking of the main valence bond. Many traditional force-fields cannot accurately descript the internal interaction during the breaking process of materials. In the process of steel bar destruction, the molecular bonding changes are very complicated, and the traditional MD force field cannot describe the process correctly. Van Duin et al. (2001) have proposed a useful reactive force field that can accurately descript the atomic interaction (Manzano et al., 2012a; Manzano et al., 2012b; Pitman and Van Duin, 2012; Hou et al., 2017; Soria et al., 2018; Ponomarev et al., 2019; Hou et al., 2020), which can be used in studying the destruction process of steel and its’ passivation film.

Thus, in this work, the reactive MD method was employed for studying the mechanical properties of steel and its’ passivation film. The uniaxial stretching processes of different compounds (γ-FeOOH, γ-Fe₂O₃, and iron) were performed. We found that oxidation can reduce the strength of iron, but increased ductility under certain condition. The strength evolutions of micro-scale structure in the destruction process of each compounds were clarified. The detail analysis reveals the relationship between internal bonding and mechanical properties of steel. This study presented can supply valuable information in evaluating and improving the mechanical properties of reinforced concrete.

Simulation Method

Models

The structure used for the simulation was obtained by amplifying the initial lattice cell (The corresponding Fe, γ-Fe₂O₃, and γ-FeOOH.cif is shown in Supplementary Material or the link: https://doi.org/10.5281/zenodo.3957278. https://doi.org/10.5281/zenodo.3961152) for the Fe, γ-Fe₂O₃, and γ-FeOOH as shown in Figure 1. The box size was controlled to approximately 20 Å in x/y direction and 50 Å in z direction. The box parameters of the expanded Fe were a × b × c = 20.04 Å × 20.04 Å × 48.72 Å, α = β = γ = 90°, which is containing 1,666 iron atoms. The box parameters of the expanded γ-Fe₂O₃ were a × b × c = 17.44 Å × 20.14 Å × 54.88 Å, α = β = γ = 90°, which is containing 944 Fe atoms and 1,184 O atoms. The box parameters of the expanded γ-FeOOH were a × b × c = 49.28 Å × 25 Å × 19.35 Å,α = β = γ = 90°, which is containing 640 Fe atoms and 1,280 O atoms and 640 H atoms. The three types of models employed the same simulation conditions to ensure the accuracy of simulation results. The temperature was maintained at 300 K and used the Nose–Hoover thermostat (Nosé, 1984). The atomic trajectories were calculated by using the Verlet algorithm and the simulation time step was set to 0.25 fs.

FIGURE 1

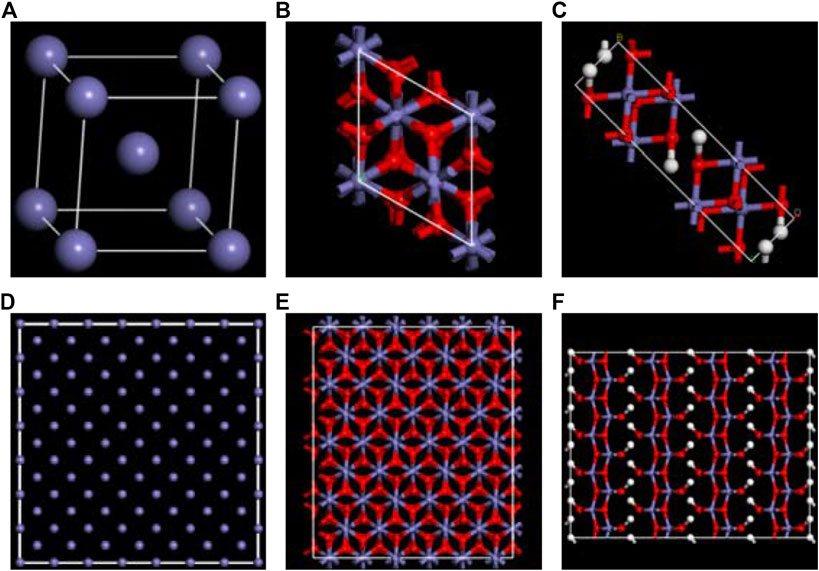
FIGURE 1. The configuration of original unit of (A) Fe, (B) γ-Fe₂O₃, (C) γ-FeOOH. And the supercell structures of (D) Fe, (E) γ-Fe₂O₃, and (F) γ-FeOOH. The purple, red and white balls represent iron, oxygen, and hydrogen atoms, respectively.

FIGURE 2

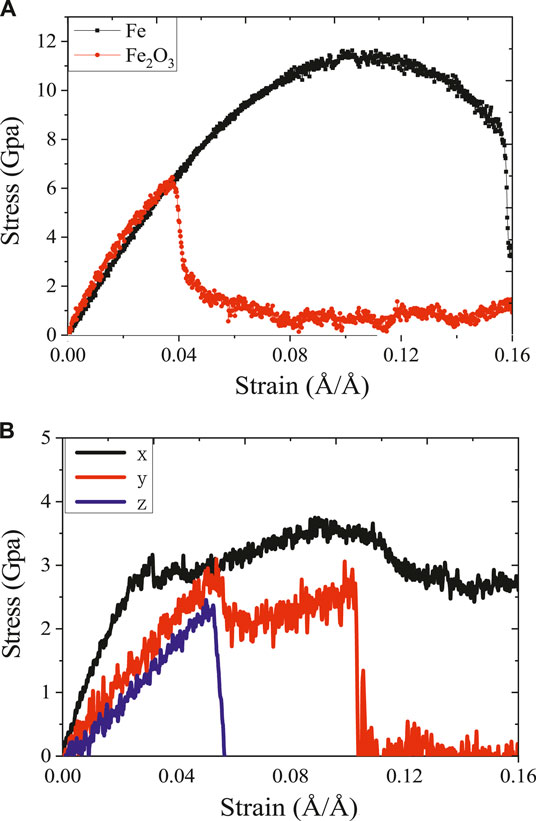
FIGURE 2. The stress–strain curve of (A) Fe, γ-Fe₂O₃ along the z direction, (B) stress–strain curve of γ-FeOOH along the x/y/z direction.

Simulation Details

The LAMMPS software (Plimpton, 1995) was employed to perform the MD simulations. The reactive force field force field was employed for Fe, γ-Fe₂O₃, and γ-FeOOH model, which is widely used to study the strength process of materials. The force field parameters were modeled by using the work of Aryanpour et al. (2010). And the relevant force field parameters can be free acquire in their supporting information. The force field parameters are able to reproduce chemical reactions and examined by quantum calculations and experimental measurements in Aryanpour’s work. Periodic boundary conditions were employed. Firstly, energy minimization was achieved to the transport simulation to eliminate high energy regions during model construction. Secondly, all atoms in the model relaxed 10 ps under the NPT ensemble. Finally, 800 ps stretched process was performed at a constant rate of 0.0008 Å/ps in the z direction, and the stretching rate is not set in the x and y directions. It should be noted that a large number of atomic trajectories will be used for later statistical analysis. The configuration is recorded every 100 steps to ensure the statistical stability of the data analysis.

Results and Discussion

Stress–Strain Curve

The stress–strain curve can be used to analyze the mechanical behavior of the layered structure during stretching and helps to understand the constitutive relationship between stress and strain. In the process of uniaxial stretching simulation, the mechanical properties of Fe, γ-Fe₂O₃ and γ-FeOOH were evaluated by calculating the stress–strain curve at the tensile rate of 0.0008 Å/ps and running at 800 ps. As shown in Figure 2, the stress–strain curves of the three types of structures were plotted. Since the γ-FeOOH structure has significant anisotropy, thus it is stretched in both three directions of x, y and z, and the stress–strain relationship in three directions is compared. For Fe and γ-Fe₂O₃, as shown in Figure 2A, during the tensile process, stress first increases linearly in the elastic stage and subsequently slowly increases to a maximum of 11 Gpa at a strain of 0.1 Å/Å. As the strain increases, the stress drops to 8 Gpa gradually and has a longer yield behavior, which means that Fe has good toughness in the z direction. Although the γ-Fe₂O₃ structure cannot be completely destroyed by the stretching in the simulation time, it showed a slightly complete destruction process. For γ-Fe₂O₃, at strains up to 0.04 Å/Å, the stress reaches the elastic limit (about 6 Gpa). After the strain reaches 0.04 Å/Å, the material stress drops sharply without obvious yield behavior. Even at a strain of 0.16 Å/Å, the stress does not drop to zero, implying good plasticity along the z direction. As shown in Figure 2B, γ-FeOOH exhibits different stress–strain relationships of tensile loading in the x, y, and z direction. Since the y direction mainly depends on the interlayer non-bonding interaction between the interlayer iron and hydroxyl groups, the intermolecular force is weaker than the covalent bond, so the elastic in the y direction is significant lower than that in the x or z direction. The y-direction layers are separated from each other after that the tensile load is applied along z direction. Such performance of stress–strain curve indicates that the oxidation can reduce the tensile strength of steel. For the three compounds of γ-FeOOH, γ-Fe₂O₃, and Fe, the order of tensile strength from high to low is Fe > γ-Fe₂O₃ > γ-FeOOH. But, the ductility under x direction is increased, which indicates that the surficial γ-FeOOH facilitates to resist bends.

FIGURE 3

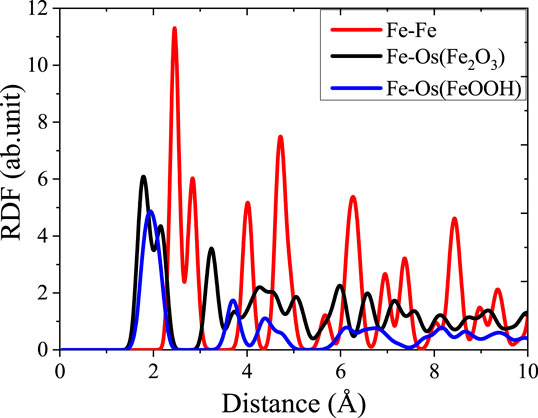
FIGURE 3. Radial distribution function image of the bond in the three types of structures before simulation.

It is observed through the stress–strain curves of γ-FeOOH in three directions that the stress–strain curves in the x and y direction have a complete failure process. When stretched in the x direction and the strain is 0.02 Å/Å, the structure reaches the elastic limit and then enters the yielding stage. During the yield phase, the structure loses its ability to resist deformation. As the simulation progresses, the strain continues to increase. When the strain reaches 0.04 Å/Å, the structure enters the strengthening phase. During this period, because of the dislocations, slips, twins and other line defects caused by stress load, the material has the significantly effects on dislocation strengthening, so the stress increases slightly. When the strain reaches 0.09 Å/Å, the material enters the local necking behavior and defects increase, resulting in a sharp drop in stress. The structure reaches the elastic limit when the tensile strain in the y direction reaches 0.05. Then there is a small stage of the yield behavior and the strengthening behavior. Unlike stretching in the x direction, when stretching in the y direction, there is no significant local necking behavior. This is due to the weak hydrogen bonding effect, which cause the interlayer separation process is weak by the contraction of the bond.

For further analyzing the influence of local variation on mechanical properties when the material is subjected to load, we calculated relevant parameters of the radial distribution function (RDF), time correlation function and coordination number.

Microstructural Parameter

The RDF is usually used to evaluate the degree of disorder of the structure, reflecting the atomic aggregation state of the material. The atomic arrangement of initial models are explained by calculating the RDF of Fe, γ-Fe₂O₃, and γ-FeOOH before stretching. Fe structure contains only iron atom, and adjacent iron atoms are bonding to surrounding atoms by forming the metal bonds. As shown in Figure 3, there is a multi-peak distribution of the RDF curve of Fe–Fe. The valley is located at 2.44 Å, which determines the number of coordination atoms of the central Fe atom in this range, while the valley at 3.2 Å contains the remaining two atoms around the central Fe atoms that are not bonded to the central Fe atoms. The primary bonding in γ-Fe₂O₃ structure is the Fe–O_s (O_s is a bridging oxygen atom in the structure) bond and Fe–Fe bond. In the steady state before stretching, there is a small valley at 1.97 Å and a large valley at 2.6 Å between the RDF curve of Fe–O_s. The locations of two valleys are the distances of the bonding length of Fe–O_s bond that does not form a regular tetrahedron centered on Fe atoms exhibited the anisotropy. In the structure of γ-FeOOH, Fe–O_s and Fe–O_h rely on the covalent bond with strong interaction. γ-FeOOH exhibits a distinct layered distribution in the y direction, and the interaction of layers is mainly driven by the intermolecular force: Van der Waals force and H-bond that results the relatively weak interactions.

As shown in Figure 4, the change in atomic and local environment during stretching is revealed by calculating the RDF curve changes corresponding to different stretching stages. In the Fe structure, before the strain is 0.04 Å/Å, the RDF curve of Fe–Fe showed the same tendency as the steady state before stretching: there are two valleys at the distance of 2.44 and 3.2 Å. However, as the strain increases, the depth of the first valley in the curve becomes shallower. When the strain reaches 0.12 Å/Å, the first valley disappears completely. At the same time, the first peak width in the RDF curve of Fe–Fe is gradually widened during the stretching process, indicating that the structure tends to be disordered by the relatively regular crystal during the stretching process. The bond between Fe–Fe at 2.44 Å during stretching is first elongated, while the covalent bond with a bond length of 3.2 Å is more stable.

FIGURE 4

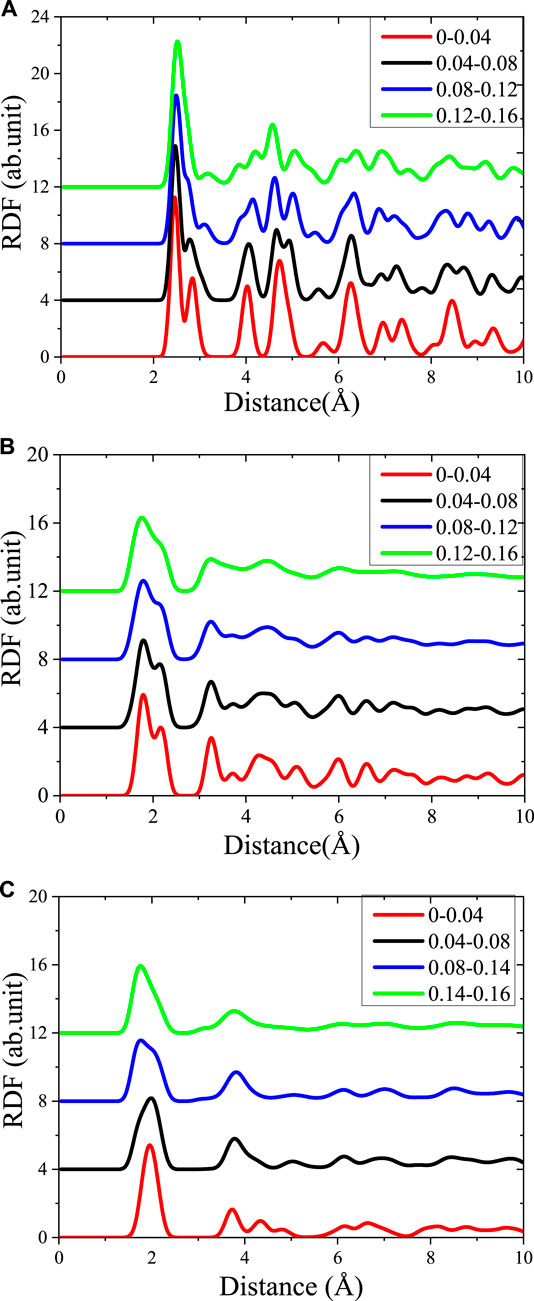
FIGURE 4. The Radial distribution function (RDF) curve of the different stages in the stretching process (A) Fe–Fe in Fe structure, (B) Fe–O_s in γ-Fe₂O₃ structure, and (C) Fe-O_s in γ-FeOOH structure.

Similarly, in the γ-Fe₂O₃ structure, the location of first valley of RDF gradually decreases during the process of strecthing. The bond with the bond length of 1.98 Å are gradually elongated, while local environments with 2.5 Å are more stable. As the simulation progresses, the RDF curve is tended to flat and the numbers of peaks is reduced, which means that the structure changes from crystal to amorphous form in the stretching progresses. On the contrary, as the stretching progresses, the RDF curve of Fe–O_s in the γ-FeOOH structure does not change much. However, as the width of the first peak gradually increase as the stretching proceeds, meaning that the structure tends to be disordered. In γ-FeOOH, the first peak (1.98 Å) indicates the most stable bond distance between Fe–O_s, and the second peak (3.2 Å) indicates the strong spatial correlation between neighboring Fe atoms.

The different RDFs in the stretching process proof that the orderly of all the three materials are decreased after stretching. But the ability of maintaining the initial ordering of Fe phase is better than that of γ-Fe₂O₃ and γ-FeOOH phase, which indicates the highest tensile strength appeared on Fe phase. The RDF of γ-Fe₂O₃ phase has the largest change, exhibiting the lowest ductility. We can conclude that the stretching of steel primary affects the structural ordering. But, the first peak of RDF seems little changes, which indicates that the lattice is less affected in the directions where a stretching rate is not set.

Strain and Coordination

For exploring the origin of different tensile strength in three model, Figure 5 shows the change in atomic coordination number of Fe during simulation. The time evolution of microstructure is consistent with the RDF analysis. By analyzing the changes of coordination number, reveal the change of the local environment of the atom and the structural during the stretching process. During the simulation, the atoms inside the crystal are arranged and deformed, and slip or twining occurs between the atomic structures. Through deforming the arrangement of atoms in lattices, the coordination number of the central atom changes. Since the crystal distribution in the Fe structure is isotropic, the coordination changes regions are also randomly distributed during the simulation. It can be seen from Figure 5 that the number of 14-coordinate and 13-coordinate atoms gradually increased during the simulation. Due to the formation of defects, such as dislocations, some iron atoms form a 16-position coordination. The specific structure of different coordination numbers is shown in Figure 6. We can deduce that with the stretching process, the coordination number of Fe in the entire system will change. Therefore, the Fe phase is not easily broken and shows high tensile strength. In addition, we discussed the relationship between strain and number of coordinates.

FIGURE 5

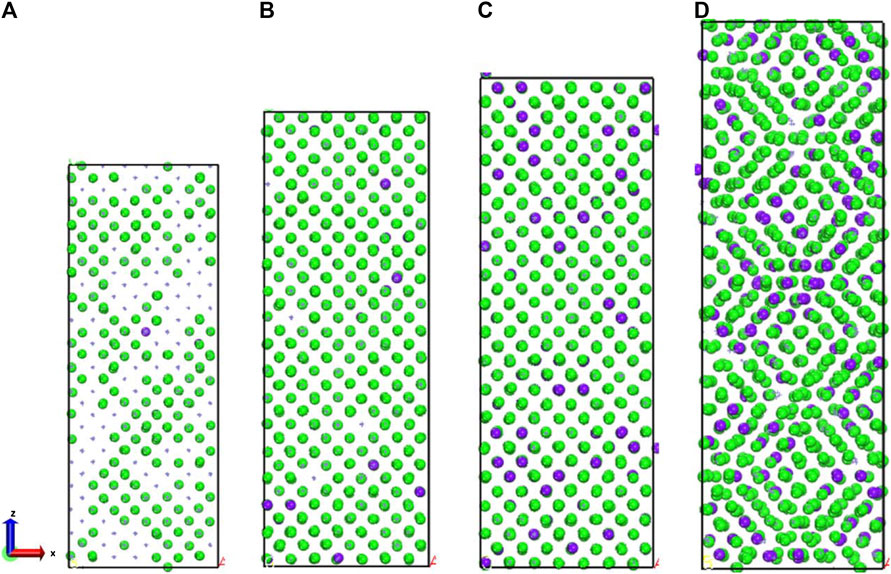
FIGURE 5. (A) 400 ps, (B) 500 ps, (C) 600 ps, and (D) 700 ps atomic coordination local diagram. The green sphere represents iron with 14 coordination Fe atoms, the purple sphere represents iron with 13 coordination Fe atoms.

FIGURE 6

FIGURE 6. Fe local structure diagrams with different coordination numbers. Color scheme: purple = Fe; orange = central Fe.

When the strain reaches 0.04 Å/Å, the stress reaches the elastic limit. As shown in Figure 7, the coordination number does not change significantly until the strain reached 0.04 Å/Å. In elastic behavior, when the material is under load, the flexibility between the metal bonds does not cause a significant change in the coordination number. At the macro level, the material will not suffer substantial damage during elastic deformation. After entering the yield stage, the coordination number decreased significantly. After the strain reached 0.08 Å/Å, the coordination number showed a small upward trend, which is mainly because of dislocation strengthening in the yield stage. After entering the yield stage, the material undergoes yield strengthening and the mechanical properties will gradually increase. This discipline is consistent with macroscopic phenomena. In the elastic phase, the coordination number maintains constant. In the yielding stage, the coordination number decreased. After breaking, the coordination partial recovery. Therefore, the stretching process is essentially breaking the coordination of atoms in materials. The similar analysis is taken for γ-Fe₂O₃ phase and γ-FeOOH phase.

FIGURE 7

FIGURE 7. Strain–coordination map of iron atoms in Fe structure.

As shown in Figure 8, for the structure of γ-Fe₂O₃, the coordination number curve showed a significant decrease when the strain reached 0.08 Å/Å. Corresponding to the stress–strain curve, the material passes the elastic limit and reaches the yielding stage after the strain reaches 0.08 Å/Å. It can be observed from Figure 10 that the tensile failure of γ-Fe₂O₃ starts form both ends and gradually moves toward the middle of the structure as the simulation time extends. The phenomenon is caused by periodic boundary conditions set during the simulation. During the stretching process, the Fe–O_s bond (as shown in Figure 9) evolved from the initial stable 6 coordination to the 5, 4 coordination, and a small amount evolved to the 3 coordinates. Where the damage occurred, the coordination is much lower than the average. As the damage progresses further, the distribution of atomic coordination changes gradually becomes disordered. Comparing to the Fe phase, in the γ-Fe₂O₃ phase system, the coordination structure is only changed in a part of region. The external force can’t be dispersed throughout the whole system. After the breaking, the coordination number will not be recovered. Therefore, the oxidation can increase the brittleness of Fe phase. For explaining the different stretching process of γ-FeOOH at difference direction, we further studied the structural evolutions of γ-FeOOH stretching.

FIGURE 8

FIGURE 8. Coordination–strain diagram of Fe atom in γ-Fe₂O₃ structure.

FIGURE 9

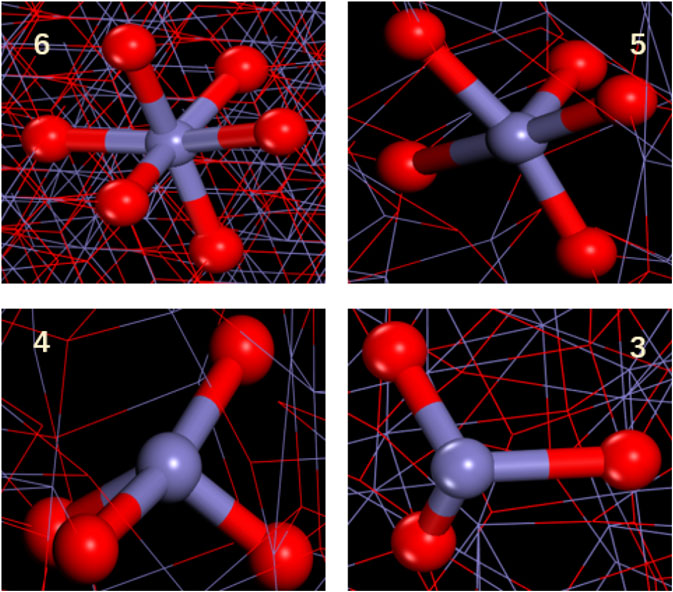
FIGURE 9. Local structure diagram of Fe with different coordination in γ-Fe₂O₃. Color scheme: purple = Fe; red = O.

FIGURE 10

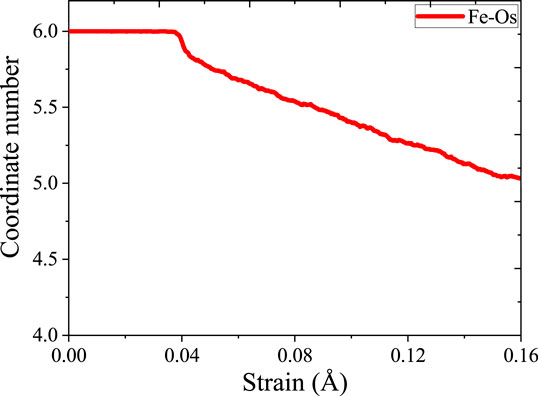
FIGURE 10. (A) 100 ps, (B) 190 ps, (C) 200 ps, and (D) 400 ps γ-Fe₂O₃ structure Fe atom coordination map. Among them, green represents iron with a coordination number of 5, purple represents iron with a coordination number of 4, and pink represents iron with a coordination number of 3.

When these materials are stretched at the same tensile rate, the mechanical properties exhibited by γ-FeOOH are greatly different when stretched in different directions, as shown in Figures 11, 12. The tensile strength at x direction is stronger than that at z or y direction, which means the mechanical properties of FeOOH is stronger in this direction. Destruction of the bond of Fe–O_s in the x direction results in the crack of material. The coordination number indicates that the coordination distribution of Fe–O_s in γ-FeOOH is relatively uniform. When stretched along the y direction, material damage is primarily achieved by breaking the H bonds formed by the hydroxyl groups between the layers and the layers. This phenomenon proof that γ-FeOOH performed different stretching properties at certain directions. In the x direction, the evolution of coordination is like the Fe phase according to the Figure 13. With the stretching process, the coordination number is changed in whole system. The external force is dispersed throughout the whole system. But, in the z direction, the evolution of coordination is like the γ-Fe₂O₃ phase. The coordination structure is only changed in a part of region. The external force is not dispersed throughout the whole system. Therefore, the brittleness of γ-FeOOH phase is increased in z direction.

FIGURE 11

FIGURE 11. (A) 100 ps, (B) 400 ps, (C) 600 ps, (D) 700 ps γ-FeOOH structure in the x-direction of stretching when the Fe atom coordination local variation. The green sphere represents iron with a coordination number of 4, and the purple sphere represents iron with a coordination number of 2.

FIGURE 12

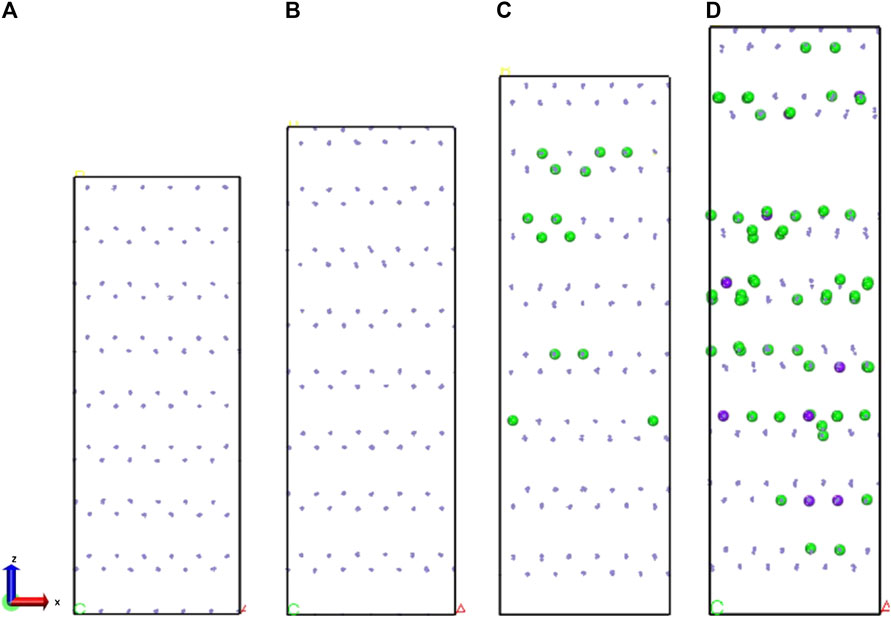
FIGURE 12. (A) 100 ps, (B) 200 ps, (C) 400 ps, and (D) 600 ps γ-FeOOH structure in the z-direction stretching when the Fe atom coordination local variation. The green sphere represents iron with a coordination number of 4, and the purple sphere represents iron with a coordination number of 2.

FIGURE 13

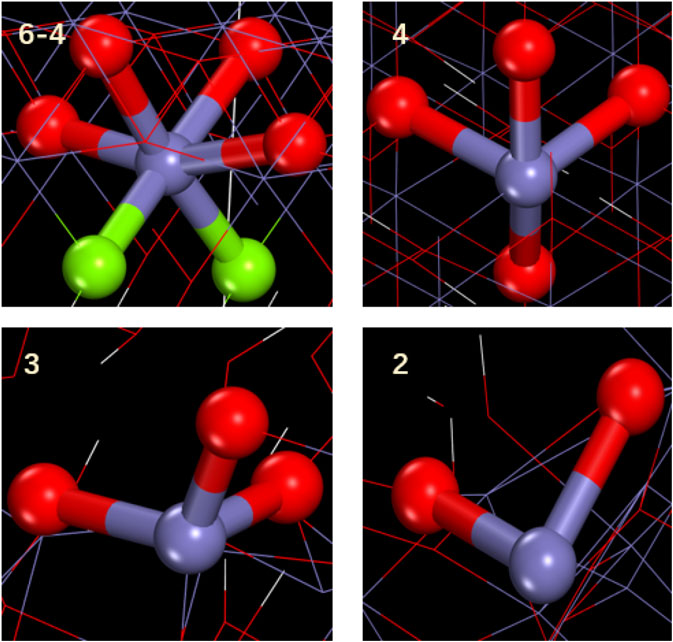
FIGURE 13. Partial structure of Fe with different coordination in γ-FeOOH. Green balls represent oxygen on the hydroxyl group, and red balls represent oxygen atoms connecting two iron atoms.

Conclusion

In this work, the reactive MD simulation was employed to studying the mechanical properties of steel and its’ passivation film. The uniaxial stretching of different compounds (γ-FeOOH, γ-Fe₂O₃, and iron) was performed. We found that oxidation can reduce the strength of iron, but increased ductility under certain conditions. The evolutions of micro-scale structure in the destruction process of each compounds were clarified. The detail analysis revealing the relationship of internal bonding and mechanical properties of steel. The detail conclusion is as follow: Firstly, the oxidation can reduce the tensile strength of steel. For the three compounds of γ-FeOOH, γ-Fe₂O_3, and Fe, the order of tensile strength from high to low is Fe > γ-Fe₂O₃ > γ-FeOOH. But, the ductility of γ-FeOOH under x direction is increased. Moreover, in the stretching process, the Fe and γ-Fe₂O₃ phase resist the stretching by the metal bonds or covalent bonds among atoms. But the γ-FeOOH resist the stretching by the chemical bonds and intermolecular interaction at x and z direction, respectively. The force between the layers of γ-FeOOH is weak and more susceptible to damage. Finally, the tensile strength is origin from the coordination in the materials. There are two kinds of stretching process. One is in the Fe phase and x direction of γ-FeOOH phase, in which the coordination number is changed in whole system with stretching. The external force is dispersed throughout the whole system. Other is in the Fe₂O₃ phase and z direction of γ-FeOOH phase. The coordination structure is only changed in a part of region. The external force is not dispersed throughout the whole system. The difference of stretching process result in large difference of tensile strength.

This investigation leads to possible new direction for studying the tensile strength of materials. In the future, it will be desirable to reveal the fracture process of steel with composite structure of Fe, γ-Fe₂O₃, and γ-FeOOH in which there are different environmental conditions. These works of the reactive MD simulations provide an excellent approach for observing and revealing the stretching process of solid materials. This strategy of evaluating materials tensile strength can supply valuable information in evaluating and improving the mechanical properties of reinforced concrete.

Data Availability Statement

All datasets generated for this study are included in the manuscript/Supplementary Material.

Author Contributions

ZL, XX, and MW performed this work and are the primary contributors in this work. MW primarily wrote the manuscript. PW, XH, YZ, and XW performed this work in details and assisted in making the picture. All authors of this manuscript have reviewed the manuscript and approved it for publication.

Funding

Financial support from National Natural science foundation of China under Grant 51678317, 51978352, 51908308; Natural science foundation of Shandong Province under Grant ZR2017JL024; The Fok Ying-Tong Education Foundation for Young Teachers in the Higher Education Institutions of China (Grant No. 161069); China Postdoctoral Science Foundation under Grant 2019M652345.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.523126/full#supplementary-material

References

Abdolhosseini Qomi, M. J., Ulm, F.-J., and Pellenq, R. J.-M. (2012). Evidence on the dual nature of aluminum in the calcium-silicate-hydrates based on atomistic simulations. J. Am. Ceram. Soc. 95 (3), 1128–1137. doi:10.1111/j.1551-2916.2011.05058.x

CrossRef Full Text | Google Scholar

Alexander, K. M. (1959). Strength of the cement aggregate bond. ACI J. Proc. 56, 377–390.

https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&ID=8102.Google Scholar

Allen, E., and Iano, J. (2019). Fundamentals of building construction: materials and methods. New Jersey, USA: John Wiley and Sons.

Google Scholar

Anandavalli, N. (2012). Experimental and analytical studies on laced reinforced concrete and laced steel-concrete composite elements.

http://hdl.handle.net/10603/15646.Google Scholar

Angst, U. M., Geiker, M. R., Michel, A., Gehlen, C., Wong, H., Isgor, O. B., et al. (2017). The steel-concrete interface. Mater. Struct. 50 (2), 143. doi:10.1617/s11527-017-1010-1

CrossRef Full Text | Google Scholar

Aryanpour, M., Van Duin, A. C. T., and Kubicki, J. D. (2010). Development of a reactive force field for iron- oxyhydroxide systems. J. Phys. Chem. 114 (21), 6298–6307. doi:10.1021/jp101332k

CrossRef Full Text | Google Scholar

Bandyopadhyay, K., Lee, J., Shim, J.-H., Hwang, B., and Lee, M.-G. (2019). Modeling and experiment on microstructure evolutions and mechanical properties in grade 600 MPa reinforcing steel rebar subjected to temp core process. Mater. Sci. Eng. A 745, 39–52. doi:10.1016/j.msea.2018.12.079

CrossRef Full Text | Google Scholar

Boscato, G., Reccia, E., and Cecchi, A. (2018). Non-destructive experimentation: dynamic identification of multi-leaf masonry walls damaged and consolidated. Compos. B Eng. 133, 145–165. doi:10.1016/j.compositesb.2017.08.022

CrossRef Full Text | Google Scholar

Düğenci, O., Haktanir, T., and Altun, F. (2015). Experimental research for the effect of high temperature on the mechanical properties of steel fiber-reinforced concrete. Construct. Build. Mater. 75, 82–88. doi:10.1016/j.conbuildmat.2014.11.005

CrossRef Full Text | Google Scholar

Fogg, J. L., Aghajamali, A., Hinks, J. A., Donnelly, S. E., Shiryaev, A. A., et al. (2019). Modification of nanodiamonds by xenon implantation: a molecular dynamics study. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 453, 32–40. doi:10.1016/j.nimb.2019.05.062

CrossRef Full Text | Google Scholar

Gong, F., and Maekawa, K. (2018). Multi-scale simulation of freeze-thaw damage to RC column and its restoring force characteristics. Eng. Struct. 156, 522–536. doi:10.1016/j.engstruct.2017.11.066

CrossRef Full Text | Google Scholar

Gong, F., and Maekawa, K. (2019). Proposal of poro-mechanical coupling among ASR, corrosion and frost action for damage assessment of structural concrete with water. Eng. Struct. 188, 418–429. doi:10.1016/j.engstruct.2019.03.036

CrossRef Full Text | Google Scholar

Horvath, A. (2004). Construction materials and the environment. Annu. Rev. Environ. Resour. 29, 181–204. doi:10.1146/annurev.energy.29.062403.102215

CrossRef Full Text | Google Scholar

Hou, D. (2019). Molecular simulation on cement-based materials. Singapore: Springer.

Google Scholar

Hou, D., Ma, H., Zhu, Y., and Li, Z. (2014). Calcium silicate hydrate from dry to saturated state: structure, dynamics and mechanical properties. Acta Mater. 67, 81–94. doi:10.1016/j.actamat.2013.12.016CrossRef Full Text |

Google Scholar

Hou, D., Li, T., and Wang, P. (2018). Molecular dynamics study on the structure and dynamics of NaCl solution transport in the nanometer channel of CASH gel. ACS Sustain. Chem. Eng. 6 (7), 9498–9509. doi:10.1021/acssuschemeng.8b02126CrossRef Full Text |

Google Scholar

Hou, D., Lu, Z., Li, X., Ma, H., and Li, Z. (2017). Reactive molecular dynamics and experimental study of graphene-cement composites: structure, dynamics and reinforcement mechanisms. Carbon N. Y. 115, 188–208. doi:10.1016/j.carbon.2017.01.013

CrossRef Full Text | Google Scholar

Hou, D., Xu, J., Zhang, Y., and Sun, G. (2019). Insights into the molecular structure and reinforcement mechanism of the hydrogel-cement nanocomposite: an experimental and molecular dynamics study. Compos. B Eng. 177, 107421. doi:10.1016/j.compositesb.2019.107421

CrossRef Full Text | Google Scholar

Hou, D., Yu, J., and Wang, P. (2019). Molecular dynamics modeling of the structure, dynamics, energetics and mechanical properties of cement-polymer nanocomposite. Compos. B Eng. 162, 433–444. doi:10.1016/j.compositesb.2018.12.142

CrossRef Full Text | Google Scholar

Hou, D., Zhang, J., Pan, W., Zhang, Y., and Zhang, Z. (2020). Nanoscale mechanism of ions immobilized by the geopolymer: a molecular dynamics study. J. Nucl. Mater. 528, 151841. doi:10.1016/j.jnucmat.2019.151841

CrossRef Full Text | Google Scholar

Hou, D., Zhang, W., Sun, M., Wang, P., Wang, M., Zhang, J., et al. ( 2020). Modified lucas-washburn function of capillary transport in the calcium silicate hydrate gel pore: a coarse-grained molecular dynamics study. Cement Concr. Res. 136, 106166. doi:10.1016/j.cemconres.2020.106166

CrossRef Full Text | Google Scholar

Hou, D., Zhao, T., Ma, H., and Li, Z. (2015). Reactive molecular simulation on water confined in the nanopores of the calcium silicate hydrate gel: structure, reactivity, and mechanical properties. J. Phys. Chem. C 119 (3), 1346–1358. doi:10.1021/jp509292q

CrossRef Full Text | Google Scholar

Iqbal, S., Ali, A., Holschemacher, K., and Bier, T. A. (2015). Mechanical properties of steel fiber reinforced high strength lightweight self-compacting concrete (SHLSCC). Construct. Build. Mater. 98, 325–333. doi:10.1016/j.conbuildmat.2015.08.112

CrossRef Full Text | Google Scholar

Kanaev, A. T., Bogomolov, A. V., Kanaev, A. A., and Reshotkina, E. N. (2018). Influence of intermittent quenching and self-tempering on the mechanical properties of rebar steel. Steel Translat. 48 (2), 130–134. doi:10.3103/s0967091218020079

CrossRef Full Text | Google Scholar

Li, W., Wang, X., Gao, L., Lu, Y., and Wang, W. (2019). Atomic study on tension behaviors of sub-10 Nm nanopolycrystalline Cu–Ta alloy. Materials 12 (23), 3913. doi:10.3390/ma12233913

CrossRef Full Text | Google Scholar

Lin, F., Xiang, Y., and Shen, H.-S. (2017). Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites-a molecular dynamics simulation. Compos. B Eng. 111, 261–269. doi:10.1016/j.compositesb.2016.12.004

CrossRef Full Text | Google Scholar

Luo, H., Su, H., Dong, C., Xiao, K., and Li, X. (2015). Electrochemical and passivation behavior investigation of ferritic stainless steel in alkaline environment. Construct. Build. Mater. 96, 502–507. doi:10.1016/j.conbuildmat.2015.08.052

CrossRef Full Text | Google Scholar

MacGregor, J. G., Wight, J. K., Teng, S., and Irawan, P. (1997). Reinforced concrete: mechanics and design. Saddle River, NJ: Prentice Hall Upper, Vol. 3.

Google Scholar

Manzano, H., Moeini, S., Marinelli, F., Van Duin, A. C. T., Ulm, F.-J., and Pellenq, R. J.-M. (2012a). Confined water dissociation in microporous defective silicates: mechanism, dipole distribution, and impact on substrate properties. J. Am. Chem. Soc. 134 (4), 2208–2215. doi:10.1021/ja209152n

CrossRef Full Text | Google Scholar

Manzano, H., Pellenq, R. J. M., Ulm, F.-J., Buehler, M. J., and Van Duin, A. C. T. (2012b). Hydration of calcium oxide surface predicted by reactive force field molecular dynamics. Langmuir 28 (9), 4187–4197. doi:10.1021/la204338m

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81 (1), 511–519. doi:10.1063/1.447334

CrossRef Full Text | Google Scholar

Nykyforchyn, H., Tsyrulnyk, O., Zvirko, O., and Krechkovska, H. (2019). Non-destructive evaluation of brittle fracture resistance of operated gas pipeline steel using electrochemical fracture surface analysis. Eng. Fail. Anal. 104, 617–625. doi:10.1016/j.engfailanal.2019.06.037

CrossRef Full Text | Google Scholar

Park, S. H., Kim, D. J., Ryu, G. S., and Koh, K. T. (2012). Tensile behavior of ultra high performance hybrid fiber reinforced concrete. Cement Concr. Compos. 34 (2), 172–184. doi:10.1016/j.cemconcomp.2011.09.009

CrossRef Full Text | Google Scholar

Pitman, M. C., and Van Duin, A. C. T. (2012). Dynamics of confined reactive water in smectite clay-zeolite composites. J. Am. Chem. Soc. 134 (6), 3042–3053. doi:10.1021/ja208894m

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117 (1), 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Ponomarev, I., van Duin, A. C. T., and Kroll, P. (2019). Reactive force field for simulations of the pyrolysis of polysiloxanes into silicon oxycarbide ceramics. J. Phys. Chem. C 123 (27), 16804–16812. doi:10.1021/acs.jpcc.9b03810

CrossRef Full Text | Google Scholar

Psycharis, I. N., Kalyviotis, I. M., and Mouzakis, H. P. (2018). Experimental investigation of the response of precast concrete cladding panels with integrated connections under monotonic and cyclic loading. Eng. Struct. 159, 75–88. doi:10.1016/j.engstruct.2017.12.036

CrossRef Full Text | Google Scholar

Saha, S. K., Uphaus, T. M., Cuadra, J. A., Divin, C., Ladner, I. S., Enstrom, K. G., et al. (2018). Kinematic fixtures to enable multi-material printing and rapid non-destructive inspection during two-photon lithography. Precis. Eng. 54, 131–137. doi:10.1016/j.precisioneng.2018.05.009

CrossRef Full Text | Google Scholar

Scrivener, K. L., and Kirkpatrick, R. J. (2008). Innovation in use and research on cementitious. Material. Cem. Concr. Res. 38 (2), 128–136. doi:10.1016/j.cemconres.2007.09.025

CrossRef Full Text | Google Scholar

Seo, E. J., Cho, L., Estrin, Y., and De Cooman, B. C. (2016). Microstructure-mechanical properties relationships for quenching and partitioning (Q&P) processed steel. Acta Mater. 113, 124–139. doi:10.1016/j.actamat.2016.04.048

CrossRef Full Text | Google Scholar

Sienko, R., Bednarski, L., and Howiacki, T. (2019). “About distributed internal and surface strain measurements within prestressed concrete truck scale platforms,” in IOP conference series: materials science and engineering, Vol. 471, 52074.

https://iopscience.iop.org/article/10.1088/1757-899X/471/5/052074/pdf.Google Scholar

Song, P. S., and Hwang, S. (2004). Mechanical properties of high-strength steel fiber-reinforced concrete. Construct. Build. Mater. 18 (9), 669–673. doi:10.1016/j.conbuildmat.2004.04.027

CrossRef Full Text | Google Scholar

Song, P. S., Hwang, S., and Sheu, B. C. (2005). Strength properties of nylon-and polypropylene-fiber-reinforced concretes. Cement Concr. Res. 35 (8), 1546–1550. doi:10.1016/j.cemconres.2004.06.033

CrossRef Full Text | Google Scholar

Soria, F. A., Zhang, W., Paredes-Olivera, P. A., Van Duin, A. C. T., and Patrito, E. M. (2018). Si/C/H ReaxFF reactive potential for silicon surfaces grafted with organic molecules. J. Phys. Chem. C 122 (41), 23515–23527. doi:10.1021/acs.jpcc.8b07075

CrossRef Full Text | Google Scholar

Thomas, J., and Ramaswamy, A. (2007). Mechanical properties of steel fiber-reinforced concrete. J. Mater. Civ. Eng. 19 (5), 385–392. doi:10.1061/(asce)0899-1561(2007)19:5(385)

CrossRef Full Text | Google Scholar

Tuutti, K. (1982). Corrosion of steel in concrete. Stockholm: Cement-och betonginst.

Google Scholar

Van Duin, A. C. T., Dasgupta, S., Lorant, F., and Goddard, W. A. (2001). ReaxFF: a reactive force field for hydrocarbon. J. Phys. Chem. 105 (41), 9396–9409. doi:10.1021/jp004368uCrossRef Full Text | Google Scholar

Wang, M., Fang, T., Zhong, H., Li, J., Yan, Y., and Zhang, J. (2019). Optimal aggregation number of reverse micelles in supercritical carbon dioxide: a theoretical perspective. Soft Matter 15 (16), 3323–3329. doi:10.1039/c8sm02299b

CrossRef Full Text | Google Scholar

Wang, P., Qiao, G., Guo, Y., Zhang, Y., Hou, D., Jin, Z., et al. (2020a). Molecular dynamics simulation of the interfacial bonding properties between graphene oxide and calcium silicate hydrate. Construct. Build. Mater. 260, 119927. doi:10.1016/j.conbuildmat.2020.119927

CrossRef Full Text | Google Scholar

Wang, P., Qiao, G., Zhang, Y., Hou, D., Zhang, J., Wang, M., et al. (2020b). Molecular dynamics simulation study on interfacial shear strength between calcium-silicate-hydrate and polymer fibers. Construct. Build. Mater. 257, 119557. doi:10.1016/j.conbuildmat.2020.119557

CrossRef Full Text | Google Scholar

Wang, P., Yang, Q., Wang, M., Hou, D., Jin, Z., Wang, P., et al. (2020c). Theoretical investigation of epoxy detachment from CSH interface under aggressive environment. Construct. Build. Mater. 264, 120232. doi:10.1016/j.conbuildmat.2020.120232

CrossRef Full Text | Google Scholar

Wu, J., Ning, F., Trinh, T. T., Kjelstrup, S., Vlugt, T. J. H., He, J., et al. (2015). Mechanical instability of monocrystalline and polycrystalline methane hydrates. Nat. Commun. 6, 8743. doi:10.1038/ncomms9743

CrossRef Full Text | Google Scholar

Zhang, J., Ma, H., Pei, H., and Li, Z. (2016). Steel corrosion in magnesia-phosphate cement concrete beams. Mag. Concr. Res. 69 (1), 35–45. doi:10.1680/jmacr.15.00496

CrossRef Full Text | Google Scholar