Theoretical Design for the Non-Toxic and Earth-Abundant Perovskite Solar Cell Absorber Materials

Though perovskite solar cells have good prospects, they also have some disadvantages, especially the impact of Pb on the environment and the use of expensive elements, which makes their production difficult to industrialize. Using first-principle density functional theory, we have investigated the geometric structures, electronic structures, and optical absorption coefficients of non-toxic and earth-abundant 1B-based perovskite solar cell absorbers. Our results show that Cs₂AgAuI₆, a toxin-free and inexpensive AgAu-based perovskite solar cell absorber, is suitable for use. It has a suitable HSE bandgap (1.289 eV) and a sharp absorption coefficient (~10⁵ cm⁻¹). Meanwhile, it is beneficial to the average electron and hole effective masses are 0.346 and 0.316 m₀ respectively. The phonon spectra show that it is stable. Because the d-orbital energy of Cu is higher than those of Ag and Au, CuAu-based perovskite is not stable. This can be seen from the phonon spectra. Therefore, our calculations could provide strong evidence for the experimental synthesis of lead-free and low-cost perovskite solar cell absorber materials.

Introduction

In the space of <10 years, Perovskite solar cell (PSCs) material has gradually become a star material in the field of solar photovoltaic conversion. It has excellent photoelectric conversion efficiency (PCE), which has grown from 3.8 to 25.2% (Kojima et al., 2009; NREL Efficiency Chart Vol, 2019). The structural formula of a perovskite solar cell is AM^IVX^VII₃. Nowadays, A can be not only a small organic molecule [A¹ = CH₃${\text{NH}}_3^{+}$, CH(NH₂)${}_2^{+}$] but also a low-valent group-IA metal cation (A² = Cs⁺, Na⁺, and Rb⁺), M^IV represents a divalent group-IVA metal cation (M^IV = Pb²⁺, Sn²⁺), and X is a halogen (X = Cl, Br, and I). This tremendous progress is because of its superior optoelectronic properties: suitable band gaps, a high tolerance factor (Gao et al., 2019), long carrier diffusion length (Stranks et al., 2013), low exciton binding energy (Lee et al., 2012; Burschka et al., 2013), and balanced electron and hole mobility (Stoumpos et al., 2013; Ponseca et al., 2014). These advantages make us more confident in researching and exploring perovskite solar cell materials.

Although the current perovskite solar cells have seen great success in theoretical research, there are still some great challenges in their practical application and large-scale commercial production. The first urgent problem to be solved is the stability of devices using perovskite material, especially devices that are under high temperature or a humid environment. This may be due to the loose chemical bonds between the organic cations and their inherent instability (Kulbak et al., 2015; Niu et al., 2015; Sutton et al., 2016). Recently, studies have shown that partial replacement of MA by FA can significantly improve the thermal stability of hybrid perovskite (Hu et al., 2014; Pellet et al., 2014; Binek et al., 2015). Therefore, in this paper, we will use the element Cs to replace the organic cation and research the various properties of the resulting perovskite solar cell materials. The second is the use of Pb in the perovskite materials, because it is a toxic element and is very harmful to our living environment. Therefore, we need to replace it but without affecting the photovoltaic conversion efficiency. Many researchers have used Sn to replace Pb, but Sn²⁺ is easily oxidized in air to Sn⁴⁺, and compared with lead-containing perovskite solar cells, devices with Sn-based perovskite materials have lower PCEs, e.g., that of MASnI₃ is only about 6% and that of CsSnI₃ is only about 3.5% (Hao et al., 2014; Noel et al., 2014). Therefore, researchers have considered converting two Pb²⁺ into IB group (Ag⁺, Au ⁺, and Cu⁺) and IIIA group (In³⁺, Bi³⁺, and Ga³⁺) elements to keep the same valence number at M^IV sites (Du et al., 2017; Meng et al., 2017; Slavney et al., 2017; Volonakis et al., 2017; Wei et al., 2017; Zhao et al., 2017) and design lead-free halide double-perovskite A₂M⁺M³⁺${\text{X}}_6^{\text{VII}}$. This work provides us with an idea to guide our exploration of inorganic non-toxic halide double-perovskite solar cells.

Recently, research has focused on the non-toxic inorganic mixed-valence double-perovskite solar cell absorption layer material Cs₂Au₂I₆ (Matsushita et al., 2005; Castro-Castro and Guloy, 2010; Debbichi et al., 2018; Giorgi et al., 2018), where the Au element has a mixed valency of +1 and +3 (Liu et al., 1999). This material has a direct bandgap (~1.3 eV) and good stability and photoelectric conversion efficiency. However, a disadvantage is that Au is an expensive metal element, so this material is difficult to commercialize and industrialize.

In this paper, our results show that Cs₂AgAuI₆, a non-toxic and inexpensive AgAu-based perovskite solar cell absorber, is a suitable alternative. It has a suitable HSE bandgap (1.289 eV) and a sharp absorption coefficient (~10⁵ cm⁻¹). Meanwhile, it is beneficial to the average effective masses of electron and hole carriers, 0.346 and 0.316 m₀, respectively. This is almost the same as that of MAPbI₃. The phonon spectra show that it is stable. Because the d-orbital energy of Cu is higher than those of Ag and Au, CuAu-based perovskite is not stable. This can be seen from the phonon spectra. Therefore, our calculations could provide strong evidence for the experimental synthesis of lead-free and low-cost perovskite solar cell absorber materials.

Computational Methods

Our first-principles calculations were performed on the basis of density-functional theory (DFT) methods by using the Vienna Ab Initio Simulation Package (VASP) code (Kresse and Furthmüller, 1996) and the standard frozen-core projector augmented-wave (PAW) methods (Kresse and Joubert, 1999). In the calculation, we used the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE) (Perdew et al., 1996) as the exchange-correlation functional to optimize the structures and calculate band gaps. In order to reduce the self-interaction error of DFT in bandgap calculation, we used the Heyd-Scuseria-Ernzerhof (HSE) of the standard hybrid density functional with 25% exact Fock exchange (Krukau et al., 2006). The cutoff energy for the plane wave function was 400 eV. The structures are relaxed until total energies are converged to 10⁻⁸ eV, and the k-point meshes have a grid spacing of 2π × 0.02 Å⁻¹. The force on all atoms was <3 × 10⁻³ eV·Å⁻¹. The 6 × 6 × 6 k-grid was used for density of states (DOS) and optical absorption coefficient calculation of halide perovskite. For the calculation of the phonon spectrum, the finite difference method was implemented in Phonopy code (Togo and Tanaka, 2015), and we constructed a 2 × 2 × 2 supercell of perovskite structures. The force constant was obtained by considering phonon-phonon interaction with the calculation of VASP. The phonon spectrum was acquired by processing the data in Phonopy. MD simulations of a 3 × 3 × 3 supercell with 270 atoms were implemented at room temperature (300 K) with VASP code using the canonical ensemble with a Nose–Hoover thermostat (Hoover, 1985) under an energy cutoff of 300 eV with 1,000 steps under a time step of 1.0 fs. The properties of the electronic structure and optics were obtained using the VASPKIT program (Wang et al., 2019).

Results and Discussion

Firstly, we established the most stable crystal structure. Here, we choose ABX₃ of four different crystal structures belonging to the space groups Pm-3m, I4/mmm, P63/mmc, and Pnma, respectively. The different total energies referring to the most stable configuration (I4/mmm) are 0.376, 0, 0.671, and 0.110 eV. In our DFT calculation, we thus use the structure with the I4/mmm space group, shown in Figure 1a. The most stable one, with the cell parameter 8.647 Å, is consistent with the previous experimental result (Debbichi et al., 2018).

FIGURE 1

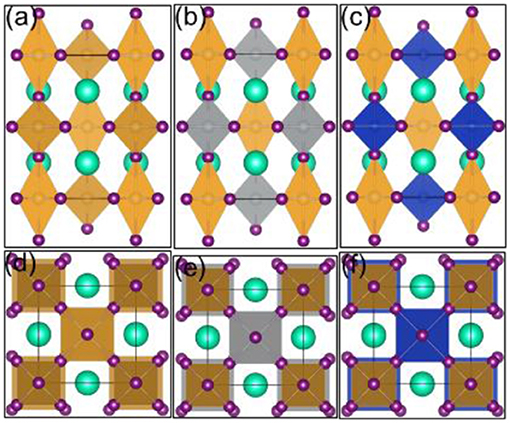
Figure 1. 1B-based perovskite solar cell absorber crystal structures: (a) Cs₂Au(I)Au(III)I₆, (b) Cs₂Ag(I)Au(III)I₆, (c) Cs₂Cu(I)Au(III)I₆: side view; (d) Cs₂Au(I)Au(III)I₆, (e) Cs₂Ag(I)Au(III)I₆, (f) Cs₂Cu(I)Au(III)I₆: top view. Yellow, gray, and blue shapes represent Au, Ag, and Cu atoms, respectively. Visualization was performed with VESTA (Momma and Izumi, 2008).

Then, we established a suitable double perovskite crystal structure. We see that Cs₂M⁺M³⁺${\text{X}}_6^{\text{VII}}$ has four different crystal structures because there are four different cation sites in Au-based perovskite. In our calculation, the most stable ones can be seen in Figures 1b,c. Both of them have the same perovskite structure symmetry and it should be easier to form for junctions with low non-radiative recombination.

The Goldschmidt tolerance factor (t) can be used as an empirical index to evaluate the structural stability of the perovskite (Kieslich et al., 2015; Shi et al., 2016; Travis et al., 2016), and for AM^IVX^VII₃ perovskite, t is defined as:

$\begin{array}{l}t=\frac{R_A+R_X}{\sqrt{2}(R_M+R_X)}\end{array}$

where R_A, R_M, and R_X represent the effective ion radii of the A, M site cation and X site anion, respectively. For double perovskite A₂M⁺M³⁺${\text{X}}_{6,}^{\text{VII}}$ the Goldschmidt tolerance factor t for the M site $R_M=\frac{R_M^{+}+R_M^{3+}}{2}$. Generally speaking, the lower the symmetry index of the structure, the lower the Goldschmidt tolerance factor t. When t = 1, it is an ideal cubic perovskite structure; the range 0.9 ≤ t ≤ 1 is generally considered to be very suitable of perovskite, indicating the possibility of a cubic structure; in the range of 0.71 ≤ t ≤ 0.9, it indicates that due to the inclination of the MX₆ octahedron, a rhombohedral or orthorhombic structure may be formed; when t < 0.71, it will change the unstable perovskite structure. In our results, the tolerance factor is 0.827, 0.906, and 0.932 for Cs₂Au₂I₆, Cs₂AgAuI₆, and Cs₂CuAuI₆, respectively. This means that it is possible to form the cubic perovskite structure for all of them. This is consistent with our calculation, as shown in Figure 1. In addition, we performed ab initio molecular dynamics (AIMD) simulations to evaluate the thermal stability of Cs₂AgAuI₆. As shown in Figure S1, the structures during 1.0ps AIMD simulation maintain the perovskite structure, indicating that Cs₂AgAuI₆ is thermally stable.

As we know, the thermodynamic stability of photovoltaic materials should be stable under all possible decomposition pathways. The decomposition pathways of Cs₂Au₂I₆, Cs₂AgAuI₆, and Cs₂CuAuI₆ can be seen in Table S1. The enthalpy of decomposition (ΔH_d) is the amount of energy that a substance gains during a reaction, which is the difference between the sum of the energies of each substance that is obtained after the reaction and the energies of the reactants themselves. A positive ΔH means that the reaction is endothermic; it means that the reactant itself is very stable and needs to absorb energy from the outside to react, which results in suppressed decomposition of Cs₂Au₂I₆, Cs₂AgAuI₆, and Cs₂CuAuI₆ and shows that the structure is stable.

As can be seen in Table S1, we would be able to synthesize Cs₂Au₂I₆ much more easily than MAPbI₃ because the dissociation energy of the former is larger than that of the latter (Yin et al., 2014a; Debbichi et al., 2018). We also find that we should avoid forming the secondary phase AuI₃ by carefully controlling the growth conditions. Although some of the decomposition enthalpies of Cs₂CuAuI₆ are larger than that of Cs₂AgAuI₆, it would be difficult to form the former if we found the secondary phases (for example CuI₂, CsCuI₃) in the experiment. Meanwhile, we should also be much more careful to control the experimental conditions to form Cs₂CuAuI₆ and Cs₂AgAuI₆ so as to avoid any of the secondary phases (for example, CuI, AgI, CsCu₂I₃, CsAg₂I₃, CsCuI₃, and CsAuI₃) forming. Also, it is more important to avoid the secondary phase Cs₂Au₂I₆ forming in the experiment if we would want to synthesize Cs₂CuAuI₆ and Cs₂AgAuI₆.

In solar cell devices, the photo-generated carriers can be effectively collected along the electrodes. The effective mass of carriers is one of the important factors that determine the carrier mobility. Therefore, we choose the ideal semiconductor materials, which should have light effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$). The effective mass of the photo-generated carrier can be approximately fitted around the band edge by:

$\begin{array}{l}{\text{m}}^{\text{*}}={\hslash }^2{\left[\frac{{\partial }^2\epsilon (\text{k})}{\partial {\text{k}}^2}\right]}^{\text{-}1},\end{array}$

where k represents the wave vector along different directions and ε(k) represents the eigenvalue of energy on the band.

From our results, the effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$) are clearly comparable among various semiconductor materials. Cs₂Au₂I₆ is more suitable as a perovskite solar cell material, as it has heavy effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$) at point N in Figure 2 of 0.362m₀ and 0.371m₀. In previous research, MAPbI₃ perovskite solar cells have been shown to have good electronic and optical properties. It was found that the effective mass of its electron (${\text{m}}_{\text{e}}^{*}$) is 0.32 m₀ and of the hole (${\text{m}}_{\text{h}}^{*}$) is 0.36 m₀ (Giorgi et al., 2013; Yin et al., 2014b). This further indicates that when perovskite solar cells have lower effective masses of electrons and holes, their photo-generated carriers will be better collected by the electrodes and have higher photoelectric conversion efficiency. For Cs₂AgAuI₆, the heavy effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$) are 0.548 and 0.494 m₀, while for Cs₂CuAuI₆, the effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$) are heavier, 0.754 and 0.572 m₀. It is clear that the effective masses of the electron and hole in Cs₂AgAuI₆ and Cs₂CuAuI₆ are much larger than those in CsAuI₃. This is because the d orbital of Ag and Cu is higher than that of Au, so the VBM is much more localized in Cs₂AgAuI₆ and Cs₂CuAuI₆ than in Cs₂Au₂I₆, and the VBM is much more dispersive in Cs₂Au₂I₆ than in Cs₂AgAuI₆ and Cs₂CuAuI₆. This can be seen in Figure 2.

FIGURE 2

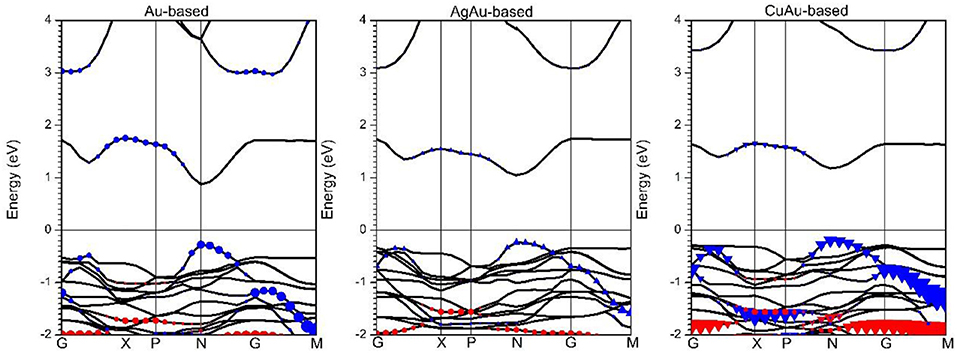
Figure 2. The HSE band structures of 1B-based perovskite solar cell absorbers. Blue and red shapes indicate the dz² and dx²-y² orbitals of 1B atoms, respectively. Circles, triangles, and inverted triangles represent Au, Ag, and Cu atoms contributions, respectively.

FIGURE 3

Figure 3. The HSE optical absorption coefficients of 1B-based perovskite solar cell absorbers.

Although PBE or HSE+SOC calculations sometimes give a bandgap result that approaches experimental values (Yin et al., 2014a; Du, 2015), the most recent calculation shows that the HSE calculation of the Cs₂Au₂I₆ system approaches the experiment results. As shown in Figure S2, the relative band gap between PBE and PBE+SOC calculations is only around 0.1 eV. From Figure 2, the bandgap of Cs₂Au₂I₆ obtained with HSE calculation is 1.167 eV; this is consistent with recent theoretical reports (~1.3 eV) (Giorgi et al., 2018) and is close to a previous experimental result, which gave a value of 1.31 eV (Debbichi et al., 2018). This indicates that Cs₂Au₂I₆ lacks strong exciton binding energy, so it is easier to produce a free election and hole after photoexcitation; at the same time, the G → M band gap is relatively flat, which indicates that Cs₂Au₂I₆ has two-dimensional or one-dimensional properties (Saparov et al., 2016; Xiao et al., 2016). At the same time, Figure 2 shows that the HSE band gaps of Cs₂AgAuI₆ and Cs₂CuAuI₆ are 1.289 and 1.344 eV, respectively. It is clearly seen that the band edge of Cs₂Au₂I₆ is the d-orbital of the Au atom, while the band edge of Cs₂AgAuI₆ and Cs₂CuAuI₆ is the d-orbital of the Ag and Cu atoms, respectively. This is because the d electron energy of Ag and Cu atoms is higher than the d electron energy of an Au atom (Kojima and Kitagawa, 1994). This was also confirmed by the PDOS in Figure S3. In Figure 2, it can be seen at band edges along the G → M direction have flat conduction and valance bands, and the possibility of carrier mobility has huge anisotropy along out-of-plane and in-plane direction; this is due to Cs₂Au₂I₆ having different 5d-orbital splitting of elongated Au³⁺(d⁸)I₆ octahedra and compressed Au⁺(d¹⁰)I₆ octahedra (Liu et al., 1999; Tang et al., 2019), and Cs₂AgAuI₆ at the band edge also has two different d metal cations, indicating that Cs₂Au₂I₆ and Cs₂AgAuI₆ have 2D electronic properties in 3D materials (Tang et al., 2019). Meanwhile, the bandgap edges of the N → P direction shows an obvious dispersion band edge. We calculated that Cs₂Au₂I₆ has light effective masses of the electron (${\text{m}}_{\text{e}}^{*}$) and hole (${\text{m}}_{\text{h}}^{*}$) of 0.145 and 0.137 m₀ and that those of Cs₂AgAuI₆ are 0.310 and 0.218 m₀, indicating that the carriers are easier to move. This is due to the Au and I orbitals forming an anti-bonding overlap so that there is larger dispersion. We found that the band gap of Cs₂Au₂I₆ is almost the same as that of Cs₂AgAuI₆ is the ideal material that we were looking for.

It should be noted that the optimal solar cell absorbers should have a direct bandgap and high optical absorption with p-p optical transition (Yin et al., 2014b). Although 1B-based perovskites have d-d optical transition, they also have comparatively high optical absorption (~10⁵ cm⁻¹) (Figure 3). This is consistent with previous research on semiconductors with d-d transitions (Heo et al., 2017). From our results, we found that the optical absorption of the 1B-based perovskites has strongly anisotropic properties. There is different optical absorption for the directions parallel and perpendicular to the z-axis. This is in good agreement with previous experimental and theoretical results (Debbichi et al., 2018; Giorgi et al., 2018). Our results show that the optical absorptions of Cs₂Au₂I₆ and Cs₂AgAuI₆ are very similar. This is because both of them have a similar band structure. Meanwhile, we found that the optical absorption along the zz direction of Cs₂AgAuI₆ is stronger than that of Cs₂Au₂I₆. This is because the bond length between the cation and I became longer when we use Ag atom substitution of an Au atom in Cs₂Au₂I₆. As can be seen from Table 1, the lattice constant of Cs₂AgAuI₆ is a little larger than that of Cs₂Au₂I₆. Then, the d-d transition became weaker in Cs₂AgAuI₆, so the optical absorption coefficient will become stronger in Cs₂AgAuI₆.

TABLE 1

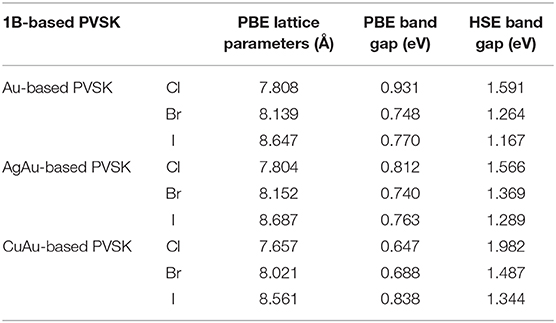
Table 1. The structural parameters (Å), PBE band gap (eV), and HSE band gap (eV) of 1B-based perovskite solar cell absorbers.

Through Figure 4, we can clearly see that Cs₂Au₂I₆ and Cs₂AgAuI₆ are stable, even if the system of Cs₂Au₂I₆ and Cs₂AgAuI₆ has a lower virtual frequency; this may be due to the strong Coulomb interaction between metal elements, and the virtual frequency is within reasonable limits. In this study, we tried to dope with other elements the reduce the amount of Au needed. The phonon spectra calculation from our research indicates that Cs₂AgAuI₆ is very stable, contrary to Cs₂CuAuI₆, and so a Cu-based perovskite solar cell absorber would be difficult to synthesize. This is clearly shown in Figure 2 the d band energy of the Cu atom is higher than that of the Ag and Au atoms. This result is consistent with the previous calculation (Xiao et al., 2017).

FIGURE 4

Figure 4. Calculated phonon spectra of Cs₂Au₂I₆, Cs₂AgAuI₆, and Cs₂CuAuI₆, respectively.

The calculated bandgaps and the geometric parameters are summarized in Table 1. The picture painted by our results could provide practical guidance for choosing the appropriate compositions to harvest good solar-to-solar cell absorbers. For example, for a two-junction tandem solar cell configuration that obtains the best conversion efficiency, the top and bottom cell should be made of semiconductors with bandgaps of 1.9 and 1.0 eV. Table 1 suggests that Cs₂CuAuCl₆ could be chosen for the top cell and Cs₂Au₂I₆ could be chosen for the bottom cell. For a three-junction configuration, the semiconductors for the top, middle, and bottom cells should have bandgaps of 2.3, 1.4, and 0.8 eV, respectively. Accordingly, Table 1 suggests Cs₂Au₂(Br_1−xCl_x)₆ and Cs₂AgAu(Br_1−xCl_x)₆ for the middle cell and Cs₂Au₂I₆ for the bottom cell, though there is no optimal composition for the top cell. Our results show that all of the compositions in Table 1 with the same perovskite structure should be easier to form for junctions with low non-radiative recombination.

Conclusions

In the paper, we researched the crystal structures, electronic structures, and optical properties of 1B-based perovskite solar cell absorbers by using the density-functional theory. Our results show that Cs₂AgAuI₆, a non-toxic and inexpensive AgAu-based perovskite solar cell absorber, may be a good choice. It has a suitable HSE band gap (1.289 eV) and a sharp absorption coefficient (~10⁵ cm⁻¹). Meanwhile, it is beneficial to the average effective masses of the electron and hole carrier, 0.346 and 0.316 m₀, respectively. The phonon spectra show that it is stable. Because the d-orbital energy of Cu is higher than those of Ag and Au, CuAu-based perovskite is not stable. This can be seen from the phonon spectra. Therefore, our calculations could provide strong evidence for experimental synthesis of lead-free and low-cost perovskite solar cell absorber materials.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

CF conceived the idea and performed the calculations. All authors analyzed the results and wrote the paper.

Funding

This work was supported by funding from the National Natural Science Foundation of China (under Grant No. 11604035).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00168/full#supplementary-material

References

Binek, A., Hanusch, F. C., Docampo, P., and Bein, T. (2015). Stabilization of the trigonal high-temperature phase of formamidinium lead iodide. J. Phys. Chem. Lett. 6, 1249–1253. doi: 10.1021/acs.jpclett.5b00380

PubMed Abstract | CrossRef Full Text | Google Scholar

Burschka, J., Pellet, N., Moon, S.-J., Humphry-Baker, R., Gao, P., Nazeeruddin, M. K., et al. (2013). Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–319. doi: 10.1038/nature12340

PubMed Abstract | CrossRef Full Text | Google Scholar

Castro-Castro, L. M., and Guloy, A. M. (2010). Organic-based layered perovskites of mixed-valent gold(I)/gold(III) iodides. Angew. Chem. Int. Ed. 115, 2877–2880. doi: 10.1002/ange.200350929

PubMed Abstract | CrossRef Full Text | Google Scholar

Debbichi, L., Lee, S., Cho, H., Rappe, A. M., Hong, K.-H., Jang, M. S., et al. (2018). Mixed valence perovskite Cs₂Au₂I₆: a potential material for thin-film pb-free photovoltaic cells with ultrahigh efficiency. Adv. Mater. 30:1707001. doi: 10.1002/adma.201707001

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, K.-Z., Wang, X. M., Han, Q. W., Yan, Y. F., and Mitzi, D. B. (2017). Heterovalent B-site Co-alloying approach for halide perovskite bandgap engineering. ACS Energy Lett. 2, 2486–2490. doi: 10.1021/acsenergylett.7b00824

CrossRef Full Text | Google Scholar

Du, M.-H. (2015). Density functional calculations of native defects in CH₃NH₃PbI₃: effects of spin–orbit coupling and self-interaction error. J. Phys. Chem. Lett. 68, 1461–1466. doi: 10.1021/acs.jpclett.5b00199

CrossRef Full Text | Google Scholar

Gao, F., Zhao, Y., Zhang, X., and You, J. (2019). Recent progresses on defect passivation toward efficient perovskite solar cells. Adv. Energy Mater. 10:1902650. doi: 10.1002/aenm.201902650

CrossRef Full Text | Google Scholar

Giorgi, G., Fujisawa, J.-I., Fujisawa, H., and Yamashita, K. J. (2013). Small photocarrier effective masses featuring ambipolar transport in methylammonium lead iodide perovskite: a density functional analysis. Phys. Chem. Lett. 4, 4213–4216. doi: 10.1021/jz4023865

PubMed Abstract | CrossRef Full Text | Google Scholar

Giorgi, G., Yamashita, K., and Palummo, M. (2018). Two-dimensional optical excitations in the mixed-valence Cs₂Au₂I₆ fully inorganic double perovskite. J. Mater. Chem. C. 6, 10197–10201. doi: 10.1039/C8TC03496F

CrossRef Full Text | Google Scholar

Hao, F., Stoumpos, C. C., Cao, D. H., Chang, R. P. H., and Kanatzidis, M. G. (2014). Lead-free solid-state organic–inorganic halide perovskite solar cells. Nat. Photonics 8, 489–494. doi: 10.1038/nphoton.2014.82

CrossRef Full Text | Google Scholar

Heo, J., Yu, L., Altschul, E., Waters, B. E., Wager, J. F., Zunger, A., et al. (2017). CuTaS₃: intermetal d-d Transitions Enable High Solar Absorption. Chem. Mater. 29, 2594–2598. doi: 10.1021/acs.chemmater.6b04730

CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31:1695. doi: 10.1103/PhysRevA.31.1695

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, M., Liu, L., Mei, A., Yang, Y., Liu, T., and Han, H. (2014). Efficient hole-conductor-free, fully printable mesoscopic perovskite solar cells with a broad light harvester NH₂CH=NH₂PbI₃. J. Mater. Chem. A 2, 17115–17121. doi: 10.1039/C4TA03741C

CrossRef Full Text | Google Scholar

Kieslich, G., Sun, S., and Cheetham, A. (2015). An extended Tolerance Factor approach for organic–inorganic perovskites. Chem. Sci. 6, 3430–3433. doi: 10.1039/C5SC00961H

PubMed Abstract | CrossRef Full Text | Google Scholar

Kojima, A., Teshima, K., Teshima, Y., and Miyasaka, T. (2009). Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051. doi: 10.1021/ja809598r.

PubMed Abstract | CrossRef Full Text | Google Scholar

Kojima, N., and Kitagawa, H. (1994). Optical investigation of the intervalence charge-transfer interactions in the three-dimensional gold mixed-valence compounds Cs₂AuX₆ (X = Cl, Br or I). J. Chem. Soc. Dalton Trans. 3, 327–331. doi: 10.1039/dt9940000327

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi: 10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 59:1758. doi: 10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125:224106. doi: 10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulbak, M., Cahen, D., and Hodes, G. (2015). How important is the organic part of lead halide perovskite photovoltaic cells? efficient cspbbr₃ cells. J. Phys. Chem. Lett. 6, 2452–2456. doi: 10.1021/acs.jpclett.5b00968

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M. M., Teuscher, J., Miyasaka, T., Murakami, T. N., and Snaith, H. J. (2012). Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 338, 643–647. doi: 10.1126/science.1228604

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X. J., Matsuda, K., Moritomo, Y., Nakamura, A., and Kojima, N. (1999). Electronic structure of the gold complexes Cs₂Au₂X₆ (X=I, Br, and Cl). Phys. Rev. B. 59, 7925. doi: 10.1103/PhysRevB.59.7925

CrossRef Full Text | Google Scholar

Matsushita, N., Fukuhara, F., and Kojima, N. (2005). A three-dimensional bromo-bridged mixed-valence gold(I,III) compound, Cs₂Au(I)Au(III)Br₆. Acta. Crystallogr. E. 61, i123–i125. doi: 10.1107/S1600536805016594

CrossRef Full Text | Google Scholar

Meng, W. W., Wang, X. M., Xiao, Z. W., Wang, J. B., Mitzi, D. B., and Yan, Y. F. (2017). Parity-forbidden transitions and their impact on the optical absorption properties of lead-free metal halide perovskites and double perovskites. J. Phys. Chem. Lett. 8, 2999–3007. doi: 10.1021/acs.jpclett.7b01042

PubMed Abstract | CrossRef Full Text | Google Scholar

Momma, K., and Izumi, F. (2008). VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658. doi: 10.1107/S0021889808012016

CrossRef Full Text | Google Scholar

Niu, G., Guo, X., and Wang, L. (2015). Review of recent progress in chemical stability of perovskite solar cells. J. Mater. Chem. A 3, 8970–8980. doi: 10.1039/C4TA04994B

CrossRef Full Text | Google Scholar

Noel, N. K., Stranks, S. D., Abate, A., Wehrenfennig, C., Guarnera, S., Haghighirad, A.-A., et al. (2014). Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 7, 3061–3068. doi: 10.1039/C4EE01076K

CrossRef Full Text | Google Scholar

NREL Efficiency Chart Vol (2019) https://www.nrel.gov/pv/cell-efficiency.html.

Google Scholar

Pellet, N., Gao, P., Gregori, G., Yang, T.-Y., Nazeeruddin, M. K., Maier, J., et al. (2014). Mixed-organic-cation perovskite photovoltaics for enhanced solar-light harvesting. Angew. Chem. Int. Ed. 126, 3215–3221. doi: 10.1002/ange.201309361

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Ponseca, C. S. Jr., Savenije, T. J., Abdellah, M., Zheng, K., Yartsev, A., Pascher, T., et al. (2014). Organometal halide perovskite solar cell materials rationalized: ultrafast charge generation, high and microsecond-long balanced mobilities, and slow recombination. J. Am. Chem. Soc. 136, 5189–5192. doi: 10.1021/ja412583t

PubMed Abstract | CrossRef Full Text | Google Scholar

Saparov, B., Sun, J.-P., Meng, W. W., Xiao, Z. W., Duan, H.-S., Gunawan, O., et al. (2016). Thin-film deposition and characterization of a Sn-deficient perovskite derivative Cs₂SnI₆. Chem. Mater. 28, 2315–2322. doi: 10.1021/acs.chemmater.6b00433

CrossRef Full Text | Google Scholar

Shi, C., Yu, C.-H., and Zhang, W. (2016). Predicting and screening dielectric transitions in a series of hybrid organic–inorganic double perovskites via an extended tolerance factor approach. Angew. Chem, Int. Ed. 128, 5892–5896. doi: 10.1002/ange.201602028

CrossRef Full Text | Google Scholar

Slavney, A. H., Leppert, L., Bartesaghi, D., Gold-Parker, A., Toney, M. F., Savenije, T. J., et al. (2017). Defect-induced band-edge reconstruction of a bismuth-halide double perovskite for visible-light absorption. J. Am. Chem. Soc. 139, 5015–5018. doi: 10.1021/jacs.7b01629

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoumpos, C. C., Malliakas, C. D., and Kanatzidis, M. G. (2013). Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 52, 9019–9038. doi: 10.1021/ic401215x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stranks, S. D., Eperon, G. E., Grancini, G., Menelaou, C., Alcocer, M. J. P., Leijtens, T., et al. (2013). Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344. doi: 10.1126/science.1243982

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutton, R. J., Eperon, G. E., Miranda, L., Parrott, E. S., Kamino, B. A., Patel, J. B., et al. (2016). Bandgap-tunable cesium lead halide perovskites with high thermal stability for efficient solar cells. Adv. Energy Mater. 6, 1502458. doi: 10.1002/aenm.201502458

CrossRef Full Text | Google Scholar

Tang, G., Xiao, Z., and Hong, J. (2019). Designing two dimensional properties in there dimensional halide perovskite via orbital engineering. J. Phys. Chem. Lett. 10, 6688–6694. doi: 10.1021/acs.jpclett.9b02530

PubMed Abstract | CrossRef Full Text | Google Scholar

Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scr. Mater. 108, 1–5. doi: 10.1016/j.scriptamat.2015.07.021

CrossRef Full Text | Google Scholar

Travis, W., Glover, E. N. K., Bronstein, H., Scanlon, D. O., and Palgrave, R. G. (2016). On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system. Chem. Sci. 7, 4548–4556. doi: 10.1039/c5sc04845a

PubMed Abstract | CrossRef Full Text | Google Scholar

Volonakis, G., Haghighirad, A. A., Milot, R. L., Sio, W. H., Filip, M. R., Wenger, B., et al. (2017). Cs₂InAgCl₆: a new lead-free halide double perovskite with direct band gap. J. Phys. Chem. Lett. 8, 772–778. doi: 10.1021/acs.jpclett.6b02682

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, V., Xu, N., Liu, J.-C., Tang, G., and Geng, W. (2019). VASPKIT: a pre- and post- processing program for VASP code. arXiv preprint arXiv:1908.08269.

Google Scholar

Wei, F. X., Deng, Z. Y., Sun, S. J., Zhang, F. H., Evans, D. M., Kieslich, G., et al. (2017). Synthesis and properties of a lead-free hybrid double perovskite: (CH₃NH₃)₂AgBiBr₆. Chem. Mater. 29, 1089–1094. doi: 10.1021/acs.chemmater.6b03944

CrossRef Full Text | Google Scholar

Xiao, Z. W., Du, K.-Z., Meng, W. W., Mitzi, D. B., and Yan, Y. F. (2017). Chemical origin of the stability difference between copper(I)- and silver(I)- based halide double perovskites. Angew. Chem. Int. Ed. 129, 12275–12279. doi: 10.1002/anie.201705113

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, Z. W., Meng, W. W., Saparov, B., Duan, H.-S., Wang, C. L., Feng, C. B., et al. (2016). photovoltaic properties of two-dimensional (CH₃NH₃)₂Pb(SCN)₂I₂ perovskite: a combined experimental and density functional theory study. J. Phys. Chem. Lett. 7, 1213–1218. doi: 10.1021/acs.jpclett.6b00248

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, W.-J., Shi, T. T., and Yan, Y. F. (2014a). Unusual defect physics in CH₃NH₃PbI₃ perovskite solar cell absorber. Appl. Phys. Lett. 104:063903. doi: 10.1063/1.4864778

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, W.-J., Shi, T. T., and Yan, Y. F. (2014b). Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 26, 4653–4658. doi: 10.1002/adma.201306281

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, X. G., Yang, D. W., Sun, Y. H., Li, T. S., Zang, L. J., Yu, L. P., et al. (2017). Cu-In Halide Perovskite (CIHP) solar absorbers. J. Am. Chem. Soc. 139, 6718–6725. doi: 10.1021/jacs.7b02120

PubMed Abstract | CrossRef Full Text | Google Scholar