An Optimal NARX Neural Network Identification Model for a Magnetorheological Damper With Force-Distortion Behavior

This paper presents an optimal NARX neural network identification model for a magnetorheological (MR) damper with the force-distortion behavior. An intensive experimental study is conducted for designing the NARX network architecture to enhance modeling accuracy and availability, and the activation function selection, weights, and biases of the selected network are optimized by differential evolution algorithm. Different experimental training and validation samples are used for network training. The prediction capability of the optimal NARX model is verified by new measured test data. The test and comparative results show that the optimal NARX network model can satisfactorily emulate the dynamic behavior of MR damper and effectively capture its distortion behavior occurred with the increased current. The developed inverse NARX network model can effectively estimate the required current and track desired damping force. Moreover, the effects of different noise disturbance on the NARX network model performance are analyzed, and the model error varies slightly with a small noise disturbance. The accuracy of the results supports the use of this modeling technique for identifying irregular non-linear models of MR damper and similar devices.

Introduction

Magnetorheological (MR) damper has emerged as an effective semiactive control device used to attenuate the undesired vibrations. The characteristics of a MR damper may vary between viscous liquid and semisolid under different damping coefficients according to the applied strength of a magnetic field controlled by a voltage or current (Metered et al., 2010). MR dampers offer several advantages such as quick response time, easy design, low power consumption, and large dynamic range, which are used in a wide range of applications such as vehicle suspension system (Oh and Choi, 2019), seismic protection (Christie et al., 2019), and weapon shock resistance (Li and Wang, 2012). As the dynamic characteristics of a MR damper are obtained in advance when it is applied in semiactive vibration control, it is necessary to establish an accurate MR damper model for identifying its dynamics to guarantee a relatively good vibration reduction effect. From the measured hysteretic mechanical features of various MR dampers, it can be found that their dynamic forces exhibit a strong non-linear property due to the viscoplastic behavior of MR fluids and uncertainty of external magnetic field and excitation (Song et al., 2005; Tu et al., 2019). Besides the accurate prediction of dynamic behaviors, the relevant inverse dynamic model is also required to produce reasonable current that can track the desired control force when the MR damper applied in this situation (Hu et al., 2017).

Various mechanical models of MR dampers used for mechanical analysis and vibration control can be classified as parametric and non-parametric models. The parametric model is commonly used for the forward dynamics of a MR damper attributed to its simple physical structure. Its mechanical behavior is physically modeled using a combination of different damping, elasticity, and friction elements, which can well-describe the constitutive physical features of the damper (Sahin et al., 2010). These parametric models mainly include the Bingham model, hysteretic biviscous model, Bouc–Wen model, hyperbolic tangent model, and their corresponding modified and improved types (Wang and Liao, 2011; Rossi et al., 2018). Among them, the phenomenological model has been widely adopted, which can accurately represent the non-linear hysteresis of a typical MR damper over a wide range of operating conditions. However, this method is required to identify too many parameters, which increases model complexity and is difficult to identify inverse model (Chang et al., 2016).

An alternative non-parametric model can simulate the dynamics of a MR damper by the non-linear fitting and training methods with various intelligent algorithms. In this modeling process, several input variables, such as the piston displacement, velocity, current, and temperature of MR damper, are required to be obtained for further training (Zapateiro and Luo, 2007). Owing to its flexibility and self-learning ability, neural networks can be combined with many training algorithms in MR damper modeling to provide a desired identification performance. Du et al. presented an approach to approximate the forward and inverse dynamic behaviors of MR damper using evolving radial basis function network (Du et al., 2006). Tudón-Martínez et al. developed a feed forward artificial neural network to model the two commercial MR dampers in detail, which was based on experimental damping force, as well as different input current, piston rod displacement, and velocity (Tudón-Martínez et al., 2012). A recursive lazy learning method based on neural networks was considered to describe the hysteretic characteristics of MR damper (Boada et al., 2011). To determine the input control current for vehicle suspension, Zong et al. established an inverse MR damper model using adaptive neuro-fuzzy inference system technique so as to gain the desired damping force (Zong et al., 2012). Khalid et al. proposed a dynamic recurrent neural network modeling approach to reproduce the hysteretic non-linear behavior for a small-scale MR damper, and the modified Bouc–Wen model was employed as the reference model to provide the comprehensive training data (Khalid et al., 2014). Although the above neural network models could describe the full mechanical behaviors of MR damper, they failed to consider the distorted hysteresis phenomenon caused by fluid compressibility and vacuum. Moreover, the train and test data sets of many network models were consistently derived from the same operating excitation condition with the random divide ratio, which reduced the generalization capability of the model.

Recently, the optimal neural network models were successful developed in MR dampers. Priyandoko et al. incorporated a particle swarm optimization method for the non-parametric modeling of MR dampers using adaptive neuro-fuzzy technique (Priyandoko and Baharom, 2013). To enhance the forecast capacity of the artificial neural network model, Yu et al. applied the ant colony algorithm in model training to obtain the optimal network model based on the data sampled from the MR elastomer isolator (Yu et al., 2015). Xu et al. investigated a back propagation (BP) neural network model with artificial bee colony algorithm, which was used to obtain the required voltage for semiactive control of MR damper simulated by phenomenological model (Xu et al., 2017). It is found that the neural network optimization used in these studies aims to optimize the weights and biases.

The non-linear autoregressive network with exogenous inputs (NARX) was widely used in various vibration damper modeling. It is a very general and powerful black-box model due to its capability of capturing a wide variety of non-linear dynamic behavior. Alghafir et al. developed a computationally NARX-type neural network model to characterize highly non-linear frequency-dependent thermally sensitive hydraulic dampers for use in the virtual tuning of passive suspension systems (Alghafir and Dunne, 2012). Ni et al. used the NARX network technique within a Bayesian inference framework to present the forward and inverse dynamic modeling of a self-sensing MR damper (Ni et al., 2015). Fu et al. designed a NARX neural network with three-layer structure to approximate the dynamics of MR elastomer isolator (Fu et al., 2016). Overall, these previous studies indicated that the NARX network model precisely captures the non-linear behavior of the target vibration damper.

In this paper, the dynamic response characteristics of the MR damper under different loading conditions (variable excitations and applied currents) are obtained. Based on this, the NARX network architectures are designed by the trial-and-error method to guarantee the good modeling accuracy. The activation functions, weights, and biases of selected network are optimized by differential evolution algorithm (DEA). For better prediction, new measured test data, which are not available in the training process, are used to verify the prediction capability of the optimal NARX model. The effect of noise disturbance on the modeling error is also investigated. The rest of this paper is organized as follows. In MR Damper and Test Environment, the dynamic mechanical characteristic experiment of the shear-valve mode MR damper is presented. NARX Neural Network Identification Modeling of MR Damper describes the NARX network employed for characterizing the non-linear dynamics of a MR damper with a force-distortion behavior. Inverse Tracking Identification of MR Damper deploys an optimal inverse NARX network model to emulate the required current and track desired damping force. Finally, a brief conclusion is given in Conclusion.

Mr Damper and Test Environment

Figure 1 shows the mechanical test system used for this investigation, which mainly consists of INSTRON tensile machine, WYK-301 DC-regulated power supply, control monitor, and MR damper with shear-valve mode. The structure size of MR damper is mainly determined by 72 mm in cylinder inner diameter, 20 mm in piston rod diameter, and 220 mm in cylinder height, and the damping gap is 1 mm. The MR fluid of the damper is mainly composed of carbonyl iron powder (25%), synthetic hydrocarbon oil, and additives. The material properties of MR fluid are given in Table S1. The lower end of MR damper is fixed on the lower gripper of test bench, which remains motionless. Meanwhile, the upper end of MR damper is excited by simulated vibration. In the experiment, MR damper is clamped on the gripper of INSTRON tensile machine after connecting its coil lead wire to the power supply. The tensile machine is then operated in a harmonic displacement mode with various combinations of amplitude and frequency by setting the stretching times, which provides a reciprocating work motion for MR damper at different input currents. Finally, the response damping force is detected by force sensor and recorded in the control monitor. The piston velocity signal of MR damper is derived by the finite differential procedure of the measured displacement.

FIGURE 1

Figure 1. Mechanical test system. (A) Tensile machine. (B) MR damper used for testing.

To make the identified model fully represent the dynamics of MR damper, different amplitudes are selected for the tests under various loading frequencies (0.5–1 Hz). For each loading case, different currents (0–2 A) are used to examine the performance of the MR damper under different magnetic fields. Figure S1 shows measured force–displacement and force–velocity responses of the MR damper working in a 15 mm amplitude with a frequency of 1 Hz under different currents. It is observed that the damping force of MR damper increases with the applied current, and the obvious force-distortion behaviors are shown in the initial compress and rebound stroke. As the current increases, the force lag is more obvious. The major reason for this behavior is the reciprocal compensation interference between the piston and floating piston of MR damper. The floating piston performs a volume compensation for the compression of the MR fluids and trapped air in the compress and rebound stroke. When the MR damper is subjected to the larger current at small piston velocity range, the MR fluids will gradually change from the viscous liquid to semisolid state in the damping gap, which blocks the flow of MR fluids between the upper and lower cylinder chambers. This results in the floating piston unable to perform effective volume compensation and further exhibiting the stroke distortion phenomenon before the vacuum in the cylinder chamber is compensated. Such volume compensation anomalies may be caused by various specific MR damper structures, such as the poor sealing, low compensation stiffness, and insufficient filling of MR fluids. In addition, the clearance between the MR damper and grippers of the tensile testing machine should be compensated by the displacement, which also results in the damping force lag. Therefore, MR damper with force distortion exhibits strong non-linear dynamic characteristics in the measured force–displacement and force–velocity responses.

NARX Neural Network Identification Modeling of MR Damper

The NARX neural network model can realize an overall input/output black-box mapping by the multilayer perceptron incorporating time delay unit and output feedback in the input layer (Chan et al., 2015). As shown in Figure 2, the NARX model is expressed in terms of the discrete-time input–output equation as:

$\begin{array}{r}\widehat{y}(t)=f{\displaystyle [}u(t),u(t-1),\cdots ,u(t-n_u),y(t-1),\cdots ,\\ y(t-n_y)]+e(t)& (1)\end{array}$

where y(t) and $\widehat{y}$(t) are the target and predicted output variables, respectively; u(t) is the input variable of the network; n_u and n_y are the time delays of input and output variable; and e(t) is the model error between the target and prediction.

FIGURE 2

Figure 2. NARX neural network structure with s outputs.

According to the input variable u(t), the hidden layer output at time t is obtained as

$\begin{array}{ll}{H}_i(t)=f_1{\displaystyle [}{\displaystyle \sum _{r=0}^{n_u}}{w}_{ir}u(t-r)+{\displaystyle \sum _{l=1}^{n_y}}{w}_{il}y(t-l)+a_i]& (2)\end{array}$

where w_ir is the connection weight between the input neuron u(t–r) and ith hidden neuron. w_il is the connection weight between the ith hidden neuron and output feedback neuron y(t–l); a_i is the bias of the ith hidden neuron; and f ₁(·) is the hidden layer activation function.

Combining the hidden layer output, the final prediction can be given by

$\begin{array}{ll}{\widehat{y}}_j(t)=f_2\left[{\displaystyle \sum _{i=1}^{n_h}}{w}_{ji}{H}_i(t)+b_j\right]& (3)\end{array}$

where w_ji is the connection weight between the ith hidden neuron and jth predicted output n_h; b_j is the bias of the jth predicted output; n_h is the number of hidden neurons; and f ₂(·) is the output layer activation function.

Table 1 lists the training, validation, and test data sets used for NARX network modeling from the measured experimental dynamic damping force of MR damper, which combines different working excitations under various frequencies and amplitudes, and the training samples are illustrated in Figure 3. The training samples are used for the network learning process to update the weights and biases in real time. The network model can realize a more accurate stop iteration to prevent data overfitting by setting validation samples, and its generalization performance is verified by untrained test samples. The model prediction performance is evaluated by the root mean square error (RMSE) between the measured and predicted damping force, which is given by

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left[\widehat{F}(i)-F(i)\right]}^2}& (4)\end{array}$

TABLE 1

Table 1. Training, validation, and test samples of NARX model.

FIGURE 3

Figure 3. Training samples.

where F(i) and $\widehat{\mathit{\text{F}}}$(i) are the measured and predicted damping force; N is the total number of data.

NARX Neural Network Architecture

Generally, the piston displacement, piston velocity, current, and past damping force are selected as input variables in the network modeling of MR damper. In terms of Formula (1), the NARX network model of MR damper can be expressed as

$\begin{array}{r}\widehat{F}(t)=f[x(t),\cdots ,x(t-n_x),v(t),\cdots ,v(t-n_v),\\ I(t),\cdots ,I(t-n_I),F(t-1),\cdots ,F(t-n_F)]& (5)\end{array}$

where x(t), v(t), and I(t) are the piston displacement, piston velocity, and current of MR damper at time t, respectively; F(t) and $\widehat{\mathit{\text{F}}}$(i) are the measured and predicted damping force at time t, respectively; n_x, n_v, n_I, and n_F are the time delays of the piston displacement, piston velocity, current, and past damping force.

To reduce model redundant and improve its accuracy in real-time applications, it is necessary to select a simplified network architecture with suitable hidden layer parameters, input variables, and time delays. Figure 4 shows the modeling error index RMSE under different time delays and input variables. In this preliminary analysis, the number of hidden neuron is set at 15 for each network configuration. When the network input variable is (x, v, F), poor model performance is evident due to the fact that damping force is current dependent. Similarly, the model performance is also unsatisfactory when (x, v, I) is considered as input variables. Hence, it is essential to consider the current and past damping force into the network inputs. By comparing the RMSE results from the input variables (x, I, F) and (x, v, I, F), it is also necessary to make the piston velocity as an input. Moreover, a comparison, as shown in the RMSE errors of the input combinations (v, I, F) and (x, v, I, F), indicates that the contribution of piston displacement for improving the prediction performance is negligible, and even increases the model error after the time delay increases to a certain range. In addition, the model error is significantly reduced when the time delay increases but has an increasing trend when the time delay is larger than two. As a result, we select the piston velocity, current, and past damping force (v, I, F) as the input variables of NARX network model, and the time delay is chosen at two to obtain a better prediction result.

FIGURE 4

Figure 4. The root mean square error (RMSE) under different input combinations.

Once the network inputs and time delays were defined, different numbers of hidden neurons and layers are evaluated. Figure 5 shows the modeling error index RMSE under different hidden layer parameters. It can be seen that if the number of hidden neurons and layers is increased in this structure, the modeling performance is improved under a stronger learning ability in the network. However, this will also result in a complex training network toward the undesirable overfitting. The modeling error RMSE of network model with a three-layer hidden structure presents a unstable oscillation state when the hidden neuron is beyond eight. However, there is no significant difference after the hidden neuron reaches 14. Considering the model simplicity and comparable accuracy, we choose a one-hidden-layer network with 14 hidden neurons according to the minimal dimensions criterion.

FIGURE 5

Figure 5. The root mean square error (RMSE) under different hidden layer parameters.

Optimal NARX Neural Network Modeling

In general, the weights and biases of NARX network are randomly chosen, and the activation functions for hidden and output layers are set by default to hyperbolic tangent function (tansig) and linear function (purelin) in most network training, respectively. As a result, the network is prone to the local optimization, resulting in a poorly performing training result. Therefore, the genetic algorithm and particle swarm optimization, characterized by random global search capability, are often used to optimize the connection weights and biases of BP neural network, and obtain better model prediction performance (Zhang et al., 2015; Liu et al., 2017). To further improve the prediction performance of the selected NARX network model, the DEA with stronger robustness is used to simultaneously optimize the activation function selection, weights, and biases. The corresponding parameters of the DEA are set as follows: evolutionary iterations is 100, population size is 40, mutation weight is 0.6, crossover probability is 0.85, and five activation functions (logsig, purelin, tansig, satlins, and radbas) are selected for the optimization process in this study. Figure 6 describes the optimization procedure of DEA for NARX network model, which is mainly composed of the optimization algorithm iteration and network update prediction. The detailed process is given as follows.

FIGURE 6

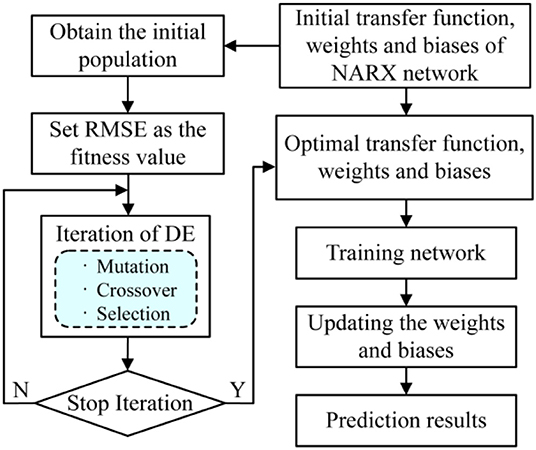
Figure 6. The optimization procedure of differential evolution algorithm (DEA) for NARX network model.

Step 1. The above-obtained network architecture is first established, and the initial population of the activation function, weights, and biases are randomly generated within the set certain range. In this operation, several parameters are configured, including the population size, mutation weight, and crossover probability. The population is randomly initialized by

$\begin{array}{ll}{x}_{ij}=U_{min}+rand\times (U_{max}-U_{min})& (6)\end{array}$

where x_ij is the initial individual, i = 1, 2,…, P, j = 1, 2,…, D; P and D are the population size and number of the objective parameters, respectively; The rand is a random number with a uniform probability distribution in [0, 1]; U_max and U_min are the upper and lower bounds of initial population, respectively.

Step 2. To obtain the better generalization ability with small training error in the network model, the RMSE calculated by all samples is regarded as the fitness function. The objective fitness function value corresponding to every reshaped population is recorded.

Step 3. A differential variable is generated by subtracting two different random objective individuals, and both the mutation and crossover operations are conducted to generate new experimental individuals in the search space by updating the differential variables. For each objective individual, the corresponding differential mutation is expressed by

$\begin{array}{ll}{v}_i^{G+1}=x_{r1}^G+{\eta }_r(x_{r2}^G-x_{r3}^G)& (7)\end{array}$

$\begin{array}{ll}{\eta }_r=(1-\eta )\times rand+\eta & (8)\end{array}$

where $v_i^G$⁺¹ is the (G + 1)th generation mutation individual; the individual serial numbers r₁, r₂, and r₃ are different and randomly generated. η is the mutation weight within the range of [0, 2]; η_r is a robust mutation factor.

To enhance the diversity of the population, a crossover operation is also performed as follows

$\begin{array}{ll}{u}_{ij}^{G+1}=\{\begin{array}{cc}{v}_{ij}^{G+1},\hfill & \text{if }rand\le CRorj=rd\hfill \\ x_{ij}^G,\hfill & \text{ otherwise}\hfill \end{array}\hfill & (9)\end{array}$

where u_ij is the new experimental individual; CR is the crossover probability within the range of [0, 1]; and rd is a randomly generated integral number in [1,2,…, D].

Step 4. The fitness of each individual in the updated population is evaluated. The experimental individual is chosen as the offspring when its fitness value is better than that of the objective individual. Otherwise, the objective individual remain becomes the offspring. The evolution process will repeat for a fixed iteration or be ended when the search process converges with a given accuracy. The best individual will be used to determine the optimal network parameters. The selection method is given as follows, where f is the fitness function.

$\begin{array}{ll}{x}_i^{G+1}=\{\begin{array}{cc}{u}_i^{G+1},\hfill & \text{if }f\left(u_i^{G+1}\right)<f\left(x_i^G\right)\hfill \\ x_i^G,\hfill & \text{otherwise}\hfill \end{array}\hfill & (10)\end{array}$

Step 5. The NARX network is trained with the optimal activation function, weights, and biases. Then the predicted results are output by updating these parameters.

Figure 7 presents the iteration process of the fitness and activation function in the network model optimized by DEA. As the evolutionary iteration increases, the population fitness RMSE decreases gradually. The best and worst finesses are reduced by 21.2 and 45.7%, respectively. After continuous iterative optimization, the activation function of the hidden layer is optimized from radbas to tansig, and the activation function of the output layer is optimized from purein to tansig. According to the above design issues, the NARX network identification model of MR damper with 8 input neurons, 14 hidden neurons, and 1 output neuron is eventually established.

FIGURE 7

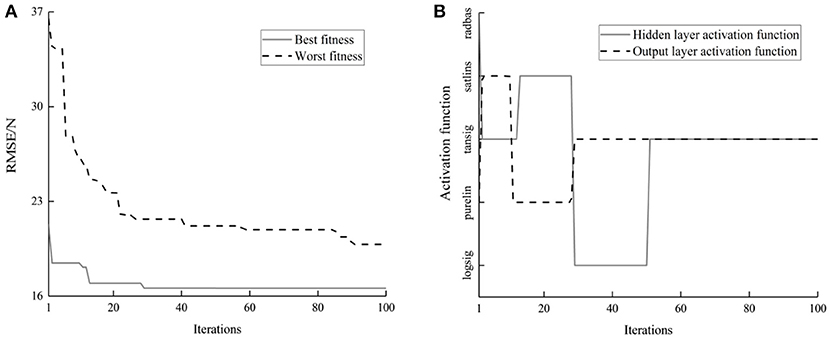
Figure 7. The iteration process of the fitness and activation function in the network model. (A) The fitness. (B) The activation function.

Figure 8 illustrates the comparisons of the measured and predicted results about the force–displacement and force–velocity curves under different test conditions given in Table 1. It can be observed that the force–displacement and force–velocity hysteretic loops predicted by the optimal NARX network model match the measured results and effectively capture the force-distortion behavior of the damper. Therefore, the network model has accurate prediction generalization ability for other untrained samples. It is noted that there exist obvious error in peak region of piston velocity in the force–velocity loops. This can be explained that the sample points are rarely distributed, and there are a jump behavior for loading the next set of data sample in these regions. According to the prediction results, the error distribution of the original and optimal network model at the limits is shown in Figure 9. The count shown in this distribution is dependent on the bin size of 2 N. Table S2 summarizes the prediction errors (RMSE) of the original and optimal network model under different test data sets. It is apparent that the error distribution of the optimal network model is concentrated in the vicinity of zero and less distributed in the range of larger errors than that of the original network model. Furthermore, the optimal network model obtains smaller prediction error than the original model under each test set. These results suggest that the optimal NARX network model with DEA is, in this case, able to achieve a higher degree of model fidelity than the original model.

FIGURE 8

Figure 8. Comparisons of the measured and predicted force–displacement and force–velocity results. (A) Test 1. (B) Test 2. (C) Test 3.

FIGURE 9

Figure 9. Error distribution of the original and optimal network model.

To further elaborate the effectiveness of the proposed model for identifying irregular non-linear behavior compared with other models, a comparative analysis under the obtained experimental data (15 mm−0.75 Hz) is established with other parametric and non-parametric models: algebraic model and BP neural network model (Yu et al., 2015; Kanarachos et al., 2018). The DEA is also used for model optimal identification under the same parameter settings. Figure 10 gives the comparisons between the measured and predicted results for other two models. Owing to the limitation of the higher-degree non-linear differential equations in the parametric model, the force-distortion behavior cannot be well-described by the algebraic model, which leads to its poor accuracy. The prediction result of BP neural network model without internal memory appears the unsteady fluctuation response. Figure 11 presents the relative error distribution boxplots between the measured and predicted results from the proposed model and contrasting models. Clearly, the relative error distribution found in the proposed model is much smaller than that of other models. Thus, the effectiveness and superiority of the proposed model are further illustrated.

FIGURE 10

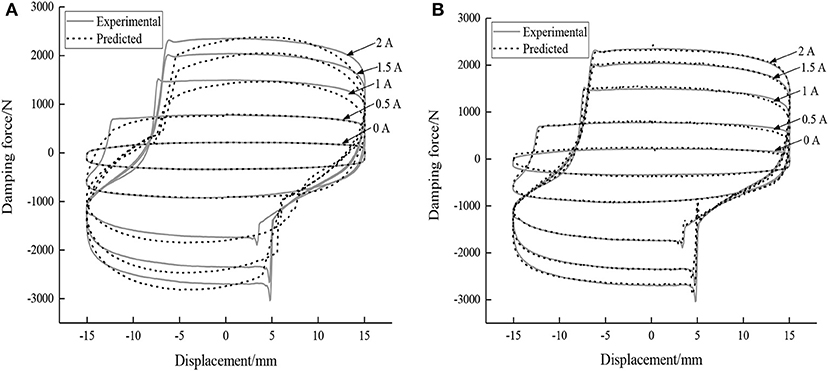
Figure 10. Comparisons between the measured and predicted results for other two models. (A) Algebraic model. (B) Back propagation (BP) neural network model.

FIGURE 11

Figure 11. The relative error boxplots for the proposed model and contrasting models.

It is clear that noise disturbance in the measured inputs and output is unavoidable in a real system and generating unfavorable effect on control performance. Therefore, it is necessary to analyze the impact of noise disturbance on the network model performance. Since the noise ranges existed in the piston velocity, current and past damping force are completely inconsistent; these inputs are uniformly normalized before the noise analysis. It is assumed that the white noise is loaded into the normalized inputs, and the effect of the added disturbance with different signal-to-noise ratio on the model error is shown in Figure S2, where the larger signal-to-noise ratio reflects the less noise disturbance present in the inputs. Although the small noise disturbance has little influence on the modeling performance of NARX network, there is a rapidly increasing model error as the noise disturbances continue to increase. It is noted that each input has different effect on the model error. Among them, the past damping force has the greatest influence on the modeling performance than other inputs include the current and piston velocity. Therefore, it is necessary to strengthen the noise reduction of input signal to minimize the disturbance effect on the accurate network model of MR damper in practical systems.

Inverse Tracking Identification of MR Damper

To effectively estimate the required current for tracking the desired damping force generated from some optimal control algorithms, an inverse dynamic identification model for this irregular MR damper is established using the NARX network. This model can continuously adjust the control current to fully utilize the intelligent damping characteristics of MR damper. Based on the above forward model of MR damper, an inverse NARX network dynamic model can be formulated as

$\begin{array}{r}\widehat{I}(t)=f[x(t),\cdots ,x(t-n_x),v(t),\cdots ,v(t-n_v),\\ F(t),\cdots ,F(t-n_F),I(t-1),\cdots ,I(t-n_I)]& (11)\end{array}$

where $\widehat{I}$(t) is the predicted current of MR damper.

Like the forward model, the network inputs of this inverse dynamic model are selected as the piston velocity, damping force, and past current with the time delay n_v = n_F = n_I = 2. Subsequently, the disorder test distribution data sets under the different excitations and currents are used for configuring the inverse model to assess its prediction performance. Figure 12 shows the iteration process when DEA is used to optimize the activation function selection, weights, and biases of the inverse dynamic model. The prediction error of the inverse dynamic model is also continuously optimized. The best and worst finesses are reduced by 23.4 and 45.2%, respectively. The optimal activation functions for the hidden and output layers are obtained as satlins and purelin, respectively.

FIGURE 12

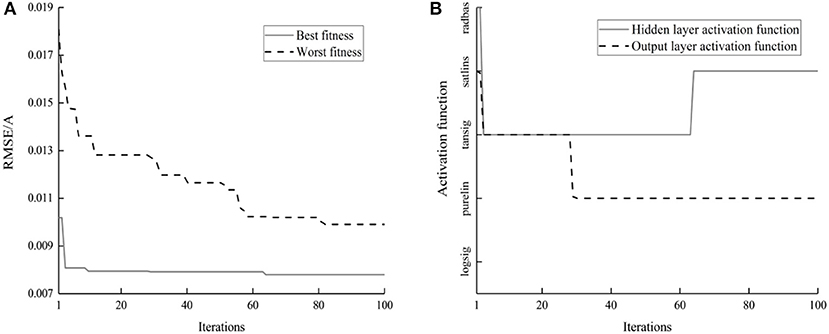
Figure 12. The iteration process of the fitness and activation function in the inverse model. (A) The fitness. (B) The activation function.

Figure 13 shows the predicted results from the inverse dynamic model in comparison with the measured ones. It can be concluded that the measured currents applied to the MR damper are matched well with the predicted results. The measured damping force can be tracked precisely when the predicted currents of the inverse dynamic model applied to the corresponding forward model. This means that the input current is effectively evaluated by the optimal inverse dynamic model. Figure 14 shows the error distribution of the original and optimal inverse models at the limits, which shows the significant smaller error concentration range in the optimal inverse dynamic model. Table S3 shows the modeling error RMSE for the predicted current and tracking damping force compared with the measured ones. It is apparent that the smaller prediction errors of the required current and tracked damping force are simultaneously obtained in the optimal inverse dynamic model. These verification results demonstrate that the developed inverse dynamic model accurately emulates the required current to track desired damping force.

FIGURE 13

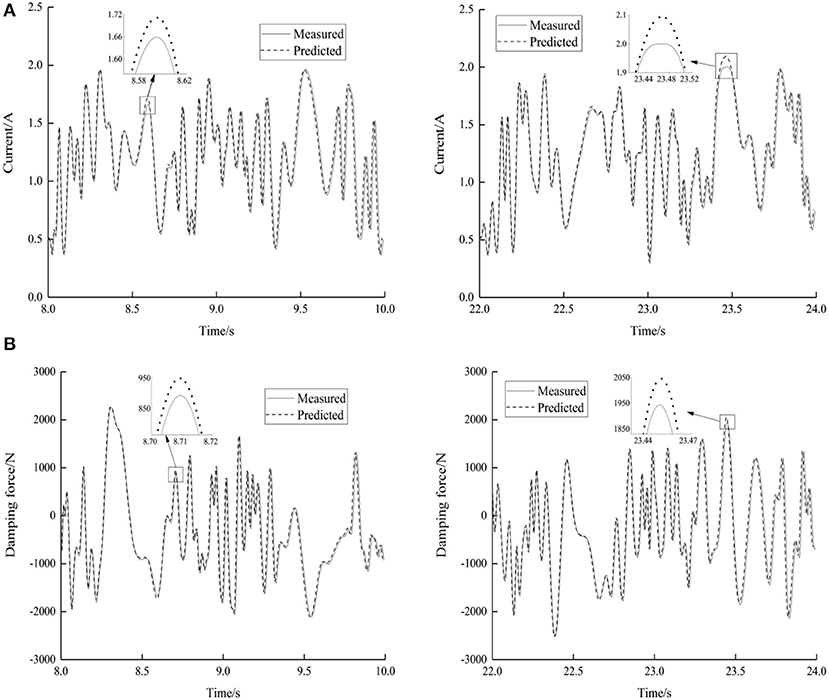
Figure 13. The predicted results from the inverse dynamic model in comparison with the measured ones. (A) Predicted current. (B) Tracked damping force.

FIGURE 14

Figure 14. Error distribution of the original and optimal inverse model.

Considering the influence of noise disturbance on the inverse dynamic model performance, the modeling error caused by the noise disturbance of different signal-to-noise ratio in each normalized input is given in Figure S3. The graph shows that there is a slow increase under the relatively small noise disturbance in the modeling error. Therefore, it can be concluded that the proposed NARX network model can provide reliable robustness. The damping force disturbance with noise still has the most prominent influence on the model performance compared with other inputs, which leads to more obvious modeling error.

Conclusion

In this paper, an optimal NARX neural network identification model was developed for a MR damper with the force-distortion behavior. The intensive train results showed that the selected NARX network architecture with 8–14–1 neurons and 2 input delays can obtain good prediction capability. In addition, the activation function selection, weights, and biases of the selected network were optimized by DEA. It is certified that the optimal NARX network model could emulate the dynamic behavior of the MR damper more satisfactorily than the original one and other models by comparing the RMSE and error distribution and also effectively captures the distortion behavior of MR damper. Meanwhile, the developed inverse NARX network model was able to effectively estimate the required current to track desired damping force. Moreover, the effect of different noise disturbance on the model performance was analyzed. The model error was varied slightly with a small noise disturbance. It is noted that the damping force with noise disturbance has a big influence on the model predictive capability. A possible way to deal with this problem is performing the enhanced filtering and noise reduction on the acquired measurement data to reduce its adverse effect on the real system. As a result, the optimal NARX network modeling technique could be effective in formulating the non-linear dynamics of MR dampers and adequate for the mechanical analysis of MR damper and semiactive control system.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

QL initiated the research and carried out the modeling and computation work. WC and QZ investigated the technical background. HH and QZ helped with the proofreading and writing of the article. QL and ZX designed the experiments.

Funding

This work was supported by the National Natural Science Foundation of China (grant nos. 51575463 and 51975495) and the Key Project in Science and Technology Plan of Xiamen (grant no. 3502Z20191019).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00010/full#supplementary-material

References

Alghafir, M. N., and Dunne, J. F. (2012). A NARX damper model for virtual tuning of automotive suspension systems with high-frequency loading. Vehicle Syst. Dyn. 50, 167–197. doi: 10.1080/00423114.2011.575946

CrossRef Full Text | Google Scholar

Boada, M. J. L., Calvo, J. A., Boada, B. L., and Díaz, V. (2011). Modeling of a magnetorheological damper by recursive lazy learning. Int. J. Non-Linear Mech. 46, 479–485. doi: 10.1016/j.ijnonlinmec.2008.11.019

CrossRef Full Text | Google Scholar

Chan, R. W. K., Yuen, J. K. K., Lee, E. W. M., and Arashpour, M. (2015). Application of Non-linear-Autoregressive-Exogenous model to predict the hysteretic behavior of passive control systems. Eng Struct. 85, 1–10. doi: 10.1016/j.engstruct.2014.12.007

CrossRef Full Text | Google Scholar

Chang, C. M., Strano, S., and Terzo, M. (2016). modeling of hysteresis in vibration control systems by means of the Bouc-Wen model. Shock Vib. 2016:3424191. doi: 10.1155/2016/3424191

CrossRef Full Text | Google Scholar

Christie, M. D., Sun, S., Deng, L., Ning, D. H., Du, H., Zhang, S. W., et al. (2019). A variable resonance magnetorheological-fluid-based pendulum tuned mass damper for seismic vibration suppression. Mech. Syst. Signal Process. 116, 530–544. doi: 10.1016/j.ymssp.2018.07.007

CrossRef Full Text | Google Scholar

Du, H. P., Lam, J., and Zhang, N. (2006). modeling of a magneto-rheological damper by evolving radial basis function networks. Eng. Appl. Artif Intell. 19, 869–881. doi: 10.1016/j.engappai.2006.02.005

CrossRef Full Text | Google Scholar

Fu, J., Liao, G. Y., Yu, M., Li, P. D., and Lai, J. J. (2016). NARX neural network modeling and robustness analysis of magnetorheological elastomer isolator. Smart Mater. Struct. 25:125019. doi: 10.1088/0964-1726/25/12/125019

CrossRef Full Text | Google Scholar

Hu, G. L., Liu, Q. J., Ding, R. Q., and Li, G. (2017). Vibration control of semi-active suspension system with magnetorheological damper based on hyperbolic tangent model. Adv. Mech. Eng. 9, 1–15. doi: 10.1177/1687814017694581

CrossRef Full Text | Google Scholar

Kanarachos, S., Savitski, D., Lagaros, N., and Fitzpatrick, M. E. (2018). Automotive magnetorheological dampers: modelling and parameter identification using contrast-based fruit fly optimisation. Soft Comput. 22, 8131–8149. doi: 10.1007/s00500-017-2757-6

CrossRef Full Text | Google Scholar

Khalid, M., Yusof, R., Joshani, M., and Selamat, H. (2014). Non-linear identification of a magneto-rheological damper based on dynamic neural networks. Comput. Aided Civ. Infrastruct. Eng. 29, 221–233. doi: 10.1111/mice.12005

CrossRef Full Text | Google Scholar

Li, Z. C., and Wang, J. (2012). A gun recoil system employing a magnetorheological fluid damper. Smart Mater. Struct. 21:105003. doi: 10.1088/0964-1726/21/10/105003

CrossRef Full Text | Google Scholar

Liu, C. J., Ding, W. F., Li, Z., and Yang, C. Y. (2017). Prediction of high-speed grinding temperature of titanium matrix composites using BP neural network based on PSO algorithm. Int. J. Adv. Manuf. Technol. 89, 2277–2285. doi: 10.1007/s00170-016-9267-z

CrossRef Full Text | Google Scholar

Metered, H., Bonello, P., and Oyadiji, S. O. (2010). The experimental identification of magnetorheological dampers and evaluation of their controllers. Mech. Syst. Signal Process. 24, 976–994. doi: 10.1016/j.ymssp.2009.09.005

CrossRef Full Text | Google Scholar

Ni, Y. Q., Chen, Z. H., and Or, S. W. (2015). Experimental identification of a self-sensing magnetorheological damper using soft computing. J. Eng. Mech. 141:04015001. doi: 10.1061/(ASCE)EM.1943-7889.0000930

CrossRef Full Text | Google Scholar

Oh, J. S., and Choi, S. B. (2019). Ride quality control of a full vehicle suspension system featuring magnetorheological dampers with multiple orifice holes. Front. Mater. 6:8. doi: 10.3389/fmats.2019.00008

CrossRef Full Text | Google Scholar

Priyandoko, G., and Baharom, M. Z. (2013). PSO-optimised adaptive neuro-fuzzy system for magneto-rheological damper modeling. Int. J. Appl. Electromagnet. Mech. 41, 301–312. doi: 10.3233/JAE-121615

CrossRef Full Text | Google Scholar

Rossi, A., Orsini, F., Scorza, A., Botta, F., Belfiore, N. P., and Sciuto, S. A. (2018). A review on parametric dynamic models of magnetorheological dampers and their characterization methods. Actuators 7:16. doi: 10.3390/act7020016

CrossRef Full Text | Google Scholar

Sahin, I., Engin, T., and Çeşmeci, S. (2010). Comparison of some existing parametric models for magnetorheological fluid dampers. Smart Mater. Struct. 19:035012. doi: 10.1088/0964-1726/19/3/035012

CrossRef Full Text | Google Scholar

Song, X. B., Ahmadian, M., and Southward, S. C. (2005). Modeling magnetorheological dampers with application of non-parametric approach. J. Intell. Mater. Syst. Struct. 16, 421–432. doi: 10.1177/1045389X05051071

CrossRef Full Text | Google Scholar

Tu, J. W., Li, Z., Zhang, J. R., Gao, K., Liao, J. P., and Gao, J. W. (2019). Development, test and mechanical model of the leak-proof magnetorheological damper. Front. Mater. 6:118. doi: 10.3389/fmats.2019.00118

CrossRef Full Text | Google Scholar

Tudón-Martínez, J. C., Lozoya-Santos, J. J., Morales-Menendez, R., and Ramirez-Mendoza, R. A. (2012). An experimental artificial-neural-network-based modeling of magneto-rheological fluid dampers. Smart Mater. Struct. 21:085007. doi: 10.1088/0964-1726/21/8/085007

CrossRef Full Text | Google Scholar

Wang, D. H., and Liao, W. H. (2011). Magnetorheological fluid dampers: a review of parametric modeling. Smart Mater. Struct. 20:023001. doi: 10.1088/0964-1726/20/2/023001

CrossRef Full Text | Google Scholar

Xu, Q., Chen, J. Y., Liu, X. P., Li, J., and Yuan, C. Y. (2017). An ABC-BP-ANN algorithm for semi-active control for magnetorheological damper. KSCE J. Civ. Eng. 21, 2310–2321. doi: 10.1007/s12205-016-0680-5

CrossRef Full Text | Google Scholar

Yu, Y., Li, Y. C., and Li, J. C. (2015). Non-parametric modeling of magnetorheological elastomer base isolator based on artificial neural network optimized by ant colony algorithm. J. Intell. Mater. Syst. Struct. 26, 1789–1798. doi: 10.1177/1045389X15577649

CrossRef Full Text | Google Scholar

Zapateiro, M., and Luo, N. S. (2007). Parametric and non parametric characterization of a shear mode magnetorheological damper. J. Vibro Eng. 9, 14–18.

Google Scholar

Zhang, Y. X., Gao, X. D., and Katayama, S. (2015). Weld appearance prediction with BP neural network improved by genetic algorithm during disk laser welding. J. Manufact. Syst. 34, 53–59. doi: 10.1016/j.jmsy.2014.10.005

CrossRef Full Text | Google Scholar

Zong, L. H., Gong, X. L., Guo, C. Y., and Xuan, S. H. (2012). Inverse neuro-fuzzy MR damper model and its application in vibration control of vehicle suspension system. Vehicle Syst. Dyn. 50, 1025–1041. doi: 10.1080/00423114.2011.645489

CrossRef Full Text | Google Scholar