Optimizing Vibration Attenuation Performance of a Magnetorheological Damper-Based Semi-active Seat Suspension Using Artificial Intelligence

This paper aims to improve control performance for a magnetorheological damper (MRD)-based semi-active seat suspension system. The vibration of the suspension is isolated by controlling the stiffness of the MRD using a proportion integration differentiation (PID) controller. A new intelligent method for optimizing the PID parameters is proposed in this work. This new method appropriately incorporates particle swarm optimization (PSO) into the PID-parameter searching processing of an improved fruit fly optimization algorithm (IFOA). Thus, the PSO-IFOA method possesses better optimization ability than IFOA and is able to find a globally optimal PID-parameter set. The performance of the PID controller optimized by the proposed PSO-IFOA for attenuating the vibration of the MRD suspension was evaluated using a numerical model and an experimental platform. The results of both simulation and experimental analysis demonstrate that the proposed PSO-IFOA is able to optimize the PID parameters for controlling the MRD semi-active seat suspension. The control performance of the PSO-IFOA-based PID is superior to that of individual PSO-, FOA-, or IFOA-based methods.

Introduction

Engineers often work in a high vibration environment, which seriously affects their health (Maikala and Bhambhani, 2013). Seat suspension is widely used as a buffer unit to solve the hostile vibration problem. Compared to other existing seat suspension systems, semi-active seat suspension based on a magnetorheological damper (MRD) has the advantages of a simple structure, low power consumption, strong damping force-adjustment capability, and fast response speed. Moreover, the natural frequency and damping characteristics of the semi-active seat suspension can be adjusted according to the excitation frequency, which can improve damping performance. However, it is difficult to obtain the proper natural frequency and damping performance in the absence of an effective control strategy. For this reason, achieving high performance control for semi-active seat suspension systems has become an essential research topic in recent years.

Proportion integration differentiation (PID) controllers have been widely used in industrial contexts because of their advantageous characteristics of having a simple structure, strong robustness, high cost-benefit ratio, and high reliability (Kuntanapreeda, 2016; Zamani et al., 2017; Pan et al., 2018). PID controllers have found application in process control (Mukherjee and Ghoshal, 2007), flight control (Savran et al., 2006), motor driving control (Hernandez-Guzman and Carrillo-Serrano, 2011), and instrumentation (Feng et al., 2014). The most important factor that affects the performance of a PID controller is the determination of the PID parameters (Ang et al., 2005; Ramezanian et al., 2013). Because of the strong non-linearity and time delay that is in the nature of an engineered system such as a semi-active seat suspension system (Zhou et al., 2011; Lu et al., 2015), it is necessary to optimize the parameters of the PID controller. The fruit fly optimization algorithm (FOA) (Shi et al., 2015), which has been developed according to the foraging behavior of fruit flies, is able to address the problem of PID parameter optimization (Wang and Liu, 2014; Han et al., 2016; Wang et al., 2016). However, due to the fixed flight distance and blind search direction in individual fruit flies, the optimization performance of the FOA is not always satisfactory due to the fact that some individual fruit flies cannot escape from a local optimum (Pan et al., 2014). Particle swarm optimization (PSO), which is based on the feeding behavior of flocks, is another method for optimizing the PID parameters (Meissner et al., 2006). However, it is easy to fall into a local optimum, and a particle cannot jump out of its own cycle (Srivastava and Agarwal, 2010). The improved fruit fly optimization algorithm (IFOA) is an optimization of the FOA with increased global search capability for optimizing the PID parameters. However, its control accuracy is still not ideal (Liu et al., 2017). To solve this problem, this paper develops a new method based on particle swarm optimization and the improved fruit fly optimization algorithm (PSO-IFOA) to optimize the PID parameters for the vibration control of semi-active seat suspension and shows that it possesses better dynamic response characteristics and control accuracy compared with FOA, PSO, and IFOA. The control performance of the PID controller optimized by PSO-IFOA is evaluated using simulations and experimental tests.

The rest of this paper is organized as follows. In section Literature Review, a literature review is performed. In section Proposed Method, the basic theories of PID parameter optimization and FOA are presented, the PSO-IFOA is proposed. In section Vibration Control Performance, Simulation and experimental tests are carried out to evaluate the PSO-IFOA method. Conclusions and future work are summarized in section Conclusions and Future Work.

Literature Review

The most recent publications relevant to this paper have mainly been concerned with two research streams: PID parameter optimization and FOA. In this section, we try to summarize the relevant literature.

PID Parameter Optimization

The parameter adjustment of a traditional PID mainly relies on working experience. In Xu (2015), the leapfrog algorithm was used to improve the global search capability of the FOA and optimize the PID parameters, and the relevant experimental results indicated that the performance of the PID controller had been optimized significantly. Fuzzy logic, genetic algorithms, and neural networks were used to tune the PID parameters, and the results indicated that a controller with a combination of these algorithms was better than the conventional controller (Alkamachi and Erçelebi, 2017; Eduardo et al., 2018; Eltag et al., 2019). Vijayakumar and Manigandan (2016) proposed an ant colony optimization algorithm to optimize the genetic algorithm and PID parameters and found through experimental study that a non-linear PID-based on the enhanced genetic algorithm was more suitable for servo control and supervisory operation. Liu et al. (2018) proposed a parameter adjustment approach for PIDs based on iterative learning control. The relevant simulation and experimental results indicated that the proposed approach could intelligently adjust the PID parameters of an atomic force microscope. Bhambhani and Shah (2016) adjusted the parameters of a PID controller by a novel optimization approach called queue intelligence, and it proved to present a better response than the genetic algorithm. Mei and Luo (2017) proposed a parameter optimization approach for PID controllers based on improved coevolution and found that this approach had better convergence speed, adaptability, and precision and wider application prospects.

Fruit Fly Optimization Algorithm

In recent years, many researchers have started to focus on the FOA. In Yu et al. (2015), an IFOA was proposed to identify the parameters for an improved LuGre friction model used in the modeling for MRD. The IFOA was shown to be able to enhance the convergence rate of the algorithm and to avoid local optima. Yu et al. (2014, 2016) used an IFOA based on a self-adaptive step update strategy (SSFFOA) to characterize a magnetorheological elastomer (MRE) base isolator, and an enhanced PSO was used to identify the model parameters for the MRE base isolator. Meanwhile, the superiority and feasibility of the proposed algorithms were verified. Ahmet et al. (2017) proposed an improved version of FOA and showed through experiment that the improved version of FOA was more equal and fairer in terms of screening the solution space. Xu et al. (2016) proposed an IFOA and illustrated its effectiveness and superiority through a comprehensive comparison among five typical algorithms. Han et al. (2017) developed a novel FOA with trend search and coevolution and showed experimentally that the novel FOA had higher robustness. Lei et al. (2016) proposed a novel fruit fly optimization clustering algorithm to identify dynamic protein complexes by combining FOA and gene expression profiles. Zheng and Wang (2016) proposed a knowledge-guided FOA to deal with the dual resource-constrained flexible job-shop scheduling problem and experimentally verified the effectiveness of the proposed algorithm.

Discussion

Many PID parameter optimization approaches have been proposed in the above literature and have been applied in recent decades, but these also have some shortcomings. Firstly, PID controllers designed by different intelligent algorithms have diverse control effects on the same system. Secondly, conventional PID controllers have a worse control effect than PID controllers designed with an intelligent algorithm. Thirdly, due to the large non-linearily and hysteresis of semi-active seat suspension, it is necessary to design a control system with a faster response, more accurate control, and less overshoot to address these problems. Lastly, FOA has great advantages in terms of iteration rate and encoding efficiency but still has the potential to fall into a local optimum.

Therefore, a PSO-IFOA is proposed to adjust the parameters for the PID controller of an MRD-based semi-active seat suspension. The velocity formula of PSO is utilized to redefine the flight distance and direction of IFOA to reduce the possibility of blind search of individual fruit flies. The convergence precision of IFOA can be enhanced, and local optima can be avoided. Both a simulation model and an experimental system of the MRD-based semi-active seat suspension are established to evaluate the effectiveness and correctness of the proposed PSO-IFOA-PID method.

Proposed Method

Proposed PSO-IFOA Method

FOA is a global intelligent optimization algorithm that is established by simulating the foraging behavior of the fruit fly. The FOA can be implemented via the following steps (Liu et al., 2017).

Step 1: Determine the population amount (PA), the maximum iteration number (IN_max), flying distance range (FR), group location range (LR), and initial location (X_−axis, Y_−axis) of the fruit fly population.

Step 2: Calculate the random flight direction and distance to search for the food of the individual fruit fly.

$\begin{array}{ll}\{\begin{array}{l}{X}_i=X_{\_axis}+2FR\times Ran{d}_i-FR\\ Y_i=Y_{\_axis}+2FR\times Ran{d}_i-FR\end{array}& (1)\end{array}$

Step 3: Calculate the distance between the individual fruit fly and the origin, and then calculate the flavor concentration parameter, which is the reciprocal of the distance.

$\begin{array}{ll}\text{Distance}:Dis{t}_i=\sqrt{{X_i}^2+{Y_i}^2},& (2)\end{array}$

$\begin{array}{ll}\text{Concentrationparameter}:S_i=1/Dis{t}_i.& (3)\end{array}$

Step 4: Substitute S_i into the fitness function, calculate the value of the flavor concentration function Smell_i, and find the best flavor concentration in the fruit fly population. In this paper, the minimum value is taken as the best flavor concentration.

$\begin{array}{ll}Smel{l}_i=Function(S_i),& (4)\end{array}$

$\begin{array}{ll}\left[bestSmell,bestindex\right]=min(Smell).& (5)\end{array}$

Step 5: Obtain the best flavor value and the coordinates of (X_−axis, Y_−axis).

$\begin{array}{ll}Smellbest=bestSmell,& (6)\end{array}$

$\begin{array}{ll}\{\begin{array}{l}{X}_{\_axis}=X(bsetindex)\\ Y_{\_axis}=Y(bsetindex)\end{array}& (7)\end{array}$

Step 6: When the smell concentration reaches the preset precision value or the iteration number reaches the maximal IN_max, the search stops. Otherwise, repeat Steps 2–5.

Because the flight distance of an individual fruit fly in FOA is within a fixed interval and the search direction is blind, the probability of individual fruit fly falls into a local optimum greatly increases. In order to enhance the capacity of global and local search, the FR should be optimized.

The position of particles in PSO is affected by the current speed, memory, and optimal location of the population. The search direction of an individual fruit fly could be guided by PSO. The velocity equation of PSO can be used to replace the random flight distance of FOA to improve the search capability; this is described as follows:

$\begin{array}{ll}\{\begin{array}{l}{X}_i=X_{\_axis}+(w{V}_{xi}+c_{x1}{r}_1(X_{\_axis}-X_i)\\ +c_{x2}{r}_2(X_{best}-X_i))\\ Y_i=Y_{\_axis}+(w{V}_{yi}+c_{y1}{r}_1(Y_{\_axis}-Y_i)\\ +c_{y2}{r}_2(Y_{best}-Y_i))\end{array},& (8)\end{array}$

where w is the inertia weight and c_x1, c_x2, c_y1, and c_y2 are the learning factors; the random constants r₁ and r₂ are within [0, 1]; V_xi and V_yi are the flying speed of an individual fruit fly along the X and Y directions. The increase of the inertia weight can enhance the global search capability but decrease the local search capability and vice versa. Therefore, in order to achieve a good trade-off between global and local search capabilities, the inertia weight w should maintain a large value in the early stage of operation and a small value in the later stage of operation. In this paper, the normal distribution formula is used as the prototype, and the difference x between the individual's position and the global optimum position is used as an independent variable to update the inertia weight w, as follows:

$\begin{array}{ll}x=k_1(smell(i)-smellbest),& (9)\end{array}$

$\begin{array}{ll}f(x)=\frac{k_2}{\sqrt{2\pi }}{e}^{(-\frac{x^2}{2})},& (10)\end{array}$

$\begin{array}{ll}w=k_3{e}^{(-f(x))}+k_4,& (11)\end{array}$

where k₁ = 100, k₂ = 16, k₃ = 1, k₄ = 0.2, k₁, k₂, and k₃ are used to control the change rate of the inertial weight and the upper limit of the control parameters, and k₄ is used to control the upper and lower limits of the inertia weight. In this method, when the gap between the individual and the global optimum positions is large, the calculated inertia weight is large, which increases the individual's global search capability. Meanwhile, when the gap between the individual and the global optimum positions is small, the calculated inertia weight is small, which can accelerate toward the optimal point. Figure 1 shows the change rule of inertia weight with iteration number in the calculation, which indicates that the inertia weight maintains a large value in the early stage of operation and a small value in the later stage of operation and that the parameter values of k₁-k₄ can meet our requirements in the calculation. The flowchart of the proposed PSO-IFOA is illustrated in Figure 2.

FIGURE 1

Figure 1. The change rule of inertia weight with iteration number.

FIGURE 2

Figure 2. Flowchart of PSO-IFOA.

Feasibility Verification of Search Capability of PSO-IFOA

In order to verify the search capability of the PSO-IFOA, four tests were conducted using four popular functions (i.e., Ackely, Rastrigin, Schewell, and Matyas) (Xu et al., 2016). The convergence trend and optimization precision of the tests were compared using FOA, PSO, IFOA, and PSO-IFOA. Table 1 shows the optimal solutions of the four test functions. The initialization conditions were the same for the four algorithms; that is, the population quantity was 30, and the iteration number was 100. Figure 3 shows the convergence curves of the test functions.

TABLE 1

Table 1. The optimal solution of the four test functions.

FIGURE 3

Figure 3. Convergence curves of the test functions.

As can be seen in Table 1, the smallest optimal solution of the four test functions is produced by the proposed PSO-IFOA method. Figure 3 shows that the proposed PSO-IFOA has a fast convergence speed and a higher convergence precision than the other three methods.

Feasibility Verification of PSO-IFOA for Optimizing PID Parameters

The feasibility of PSO-IFOA for optimizing PID parameters was investigated using a numerical model of a semi-active seat suspension system. Modeling of the semi-active seat suspension system mainly included two aspects, which were human body dynamics modeling and seat dynamics modeling. The research in this paper is mainly concerned with the vibration absorption performance of semi-active seat suspension, which is the vibration attenuation transmitted from a cab to a human body. In this situation, the human body can be considered to a mass block without considering its internal vibration characteristics. In the actual seat suspension, the cushion also possesses vibration damping performance due to its characteristics of stiffness and damping. Therefore, the vibration damping characteristics of the cushion should be considered in establishing the semi-active seat suspension model. A shear suspension structure was adopted in this research due to its good lubrication at the turning structure, and the friction resistance at the rotating structure was then ignored. In order to simplify the calculation process, a 2-DOF semi-active seat suspension model was established. The human body was simplified as a mass block with equivalent mass of m₁, the cushion was simplified as a spring and a damper, with a massless elastic coefficient and a damping coefficient of k₁ and c₁, respectively. The suspension was regarded as a subsystem with equivalent mass of m₂, equivalent stiffness of k₂, and variable damping coefficient of c₂. The kinematics equation was established according to the 2-DOF semi-active seat suspension model, as shown in Equation (12).

$\begin{array}{ll}\{\begin{array}{c}{m}_1{\ddot{x}}_1+c_1({\dot{x}}_1-{\dot{x}}_2)+k_1(x_1-x_2)=0\\ m_2{\ddot{x}}_2-c_1({\dot{x}}_1-{\dot{x}}_2)-k_1(x_1-x_2)-c_2(\dot{u}-{\dot{x}}_2)\\ -k_2(u-x_2)=0\end{array}& (12)\end{array}$

where u is the vibration excitation transmitted from the cab to the seat suspension, x₂ is the displacement response of the top plate of the seat suspension, and x₁ is the displacement response of the human body; ẋ₁ and ẍ₁ are the first and second derivatives of x₁, ẋ₂, and ẍ₂ are the first and second derivatives of x₂, and $\stackrel{.}{u}$ is the first derivative of u. In this study, k₁ = 19,496 N/m, k₂ = 150,261 N/m, c₁ = 2,165 Ns/m, c₂ = 1,600 Ns/m, m₁ = 18 kg, m₂ = 70 kg.

The kinematic Equation (12) was transformed in Laplace transform, and the transfer function of human displacement response x₁ and vibration excitation u could be obtained as follows:

$\begin{array}{l}G(s)=\frac{x_1}{u}=\frac{(c_{1}s+k_1)(c_{2}s+k_2)}{(m_1{s}^2+c_{1}s+k_1)(m_2{s}^2+c_{1}s+c_{2}s+k_1+k_2)}\\ -{(c_{1}s+k_1)}^2.& (13)\end{array}$

The parameters of the PSO-IFOA, IFOA, PSO, and FOA were set as: PA = 50, IN_max = 100, (X_−axis, Y_−axis)∈ (0, 5), FR = 0.5, ω₁ = 0.999, ω₂ = 0.001, ω₃ = 2.0, and ω₄ = 100.

In the simulation, a step command signal was input into the control system. The simulation time was 0.4 s. The convergence curves of the comprehensive performance index function J for the different control methods are shown in Figure 4A, and the step response curves of each controller are shown in Figure 4B. Table 2 provides the control performance evaluation indicators. It can be seen in Figure 4A that the convergence speed and precision of the PSO-IFOA controller are superior to those of the FOA, PSO, and IFOA controllers. This is because the proposed PSO-IFOA method possesses a stronger global search capability than the others. One can observe in Figure 4B and Table 2 that the PSO-IFOA-optimized PID controller produces the best overshoot and adjustment time of the four methods. The proposed PSO-IFOA PID controller outperforms the other three methods in terms of dynamic characteristics.

FIGURE 4

Figure 4. (A) Convergence curves of Best J and (B) step response curves of the controllers.

TABLE 2

Table 2. Control performance evaluation indicators of the controllers.

Vibration Control Performance

Simulation Results

In order to evaluate the effectiveness of the PSO-IFOA-optimized PID controller, an MRD-based semi-active seat suspension system was established using Matlab/Simulink. The MRD damping effect was considered in this model. The displacement and acceleration responses of the human body were measured under different excitations such as collision and harmonic and random vibrations that were imposed on the seat model. The vibration control performances of the FOA-PID, PSO-PID, IFOA-PID, and PSO-IFOA-PID methods are shown in Figures 5–7. The root-mean-square (RMS), peak-to-peak (PTP), and vibration-dose-value (VDV) of the acceleration response were adopted as the criteria with which to evaluate the random vibration effect.

FIGURE 5

Figure 5. Acceleration and displacement responses under collision vibration.

The displacement and acceleration responses of the human body in the condition of collision vibration are shown in Figure 5. As can be seen in the figure, compared to the other three controllers, the peak values of human acceleration at the first four waves were smallest with the proposed PSO-IFOA method, the overshoot of the proposed method was, respectively, reduced by 16.29, 6.04, 2.35, and 0.43%, and the stabilizing time was, respectively, decreased by 35.6, 20.6%, 12.99, and 2.5% compared to the other methods.

The displacement and acceleration responses of the human body in the condition of harmonic vibration are shown in Figure 6. As can be seen in the figure, compared to the other three controllers, the proposed PSO-IFOA method has the smallest peak values of human acceleration at the first four waves, and its overshoot was, respectively, reduced by 71.2, 47.6, 28.7, and 3.7% compared to the other methods.

FIGURE 6

Figure 6. Acceleration and displacement responses under harmonic vibration.

Figure 7 depicts the displacement and acceleration responses of the human body in the condition of random vibration. As can be seen in the figures, compared to the other three controllers, the displacement and acceleration amplitudes are smallest with the proposed PSO-IFOA method. Thus, the damping effect of the MRD can be better controlled by the proposed method.

FIGURE 7

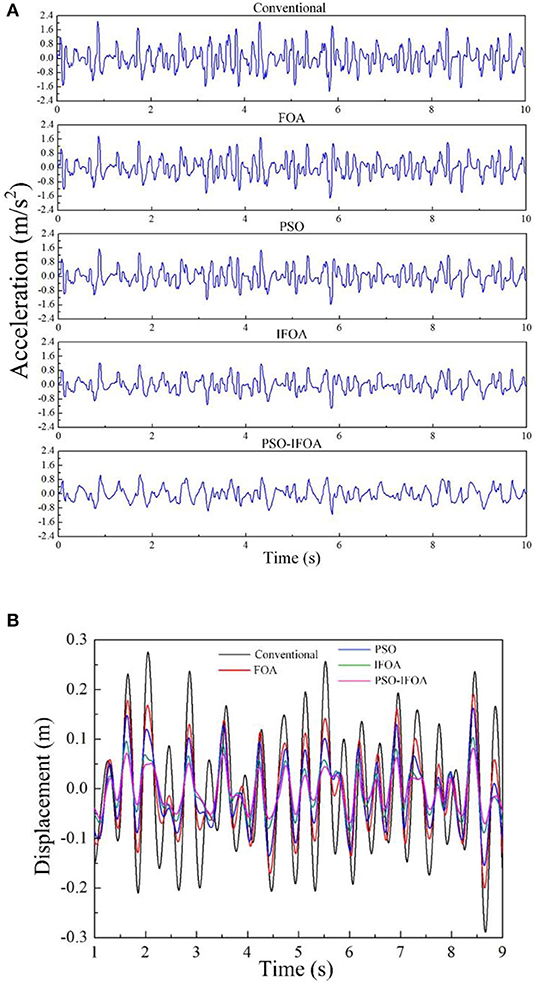
Figure 7. (A) Acceleration responses under random vibration, and (B) displacement responses under random vibration.

Table 3 compares the RMS, PTP, and VDV of the acceleration amplitude using different controllers. One can note that the proposed PSO-IFOA-PID controller decreased the RMS values by 60.26, 46.25, 33.06, and 9.17%, respectively, when compared with the other four methods; the PTP was, respectively, decreased by 43.74, 36.85, 28.95, and 13.06%, and the VDV was, respectively, reduced by 39.93, 29.87, 17.37, and 7.08%. As a result, the control performance of the proposed method is superior to those of the other methods in the simulations.

TABLE 3

Table 3. Acceleration response characteristics under random vibration.

Experiments

Introduction to MRD

The design principle of MRD is that the curing degree of magnetorheological fluid (MRF) is controlled in real time by changing the magnetic field intensity at the damping channel so as to achieve the purpose of controllable damping force. The structure of the MRD is shown in Figure 8. When uneven road excitation occurs, relative motion will appear in the vehicle body and seats, which results in variation in displacement on either side of the MRD. The MRD will then be stretched or compressed, and the MRF will be pushed from one working space to another. In this process, the friction between the MRF and the pore wall and the internal friction between liquid molecules cause the generation of damping force, which causes the vibration energy of the whole suspension system to be converted into thermal energy and consumed to achieve the aim of reducing vibration.

FIGURE 8

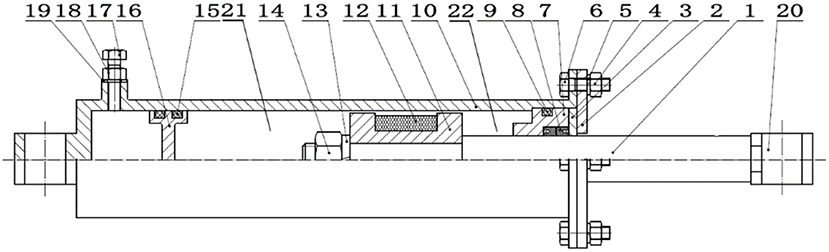
Figure 8. Structural diagram of MRD. One to twenty-two are the piston rod, end cover, pressing plate, nut-M5, washer, screw-M5, guide holder, seal ring, O-ring (41.2 × 3.55A), cylinder block, piston, coil, spring washer, nut-M12, O-ring (38.7 × 3.55G), floating piston, screw-M5, nut-M5, sealing washer, joint, working space 1, and working space 2, respectively.

In order to make the design of MRD more reasonable, the key sizes of the MRD are optimized by the genetic multi-objective optimization algorithm, which possesses better accuracy in achieving multi-objective optimization. The implementation of the optimization processes can be achieved through the following steps.

Step 1: Define the damping force equation and the adjustable multiple calculation model of the MRD, which is as follows:

$\begin{array}{llll}{F}_v& =& F_{\eta }+F_{\tau }=\frac{12\eta L{A_p}^{2}v}{\pi D{h}^3}+\frac{3L{A}_p\tau }{h},& (14)\end{array}$

$\begin{array}{llll}{\beta }_v& =& \frac{F_{\tau }}{F_{\eta }}=\frac{\pi D\tau h^2}{4\eta A_{p}v},& (15)\end{array}$

where F_η is the non-adjustable viscous damping force, F_τ is the adjusted coulomb damping force, η, τ, and v are the dynamic viscosity, shear yield stress, and flow velocity of MRF, respectively. L, A_p, D, and h indicate the effective length, effective area of the inner ring, inner diameter, and clearance thickness of the damped channel, respectively.

Step 2: Establish the mathematical model of the optimized objective function, which as follows:

$\begin{array}{ll}G(x)=m\frac{F_v}{F_{vmax}}+n\frac{{\beta }_v}{{\beta }_{vmax}},& (16)\end{array}$

where m and n are the weighting coefficients, and the sum of m and n is 1.

Step 3: Set the optimization variables and the corresponding value range. These are shown in Equations (17) and (18).

$\begin{array}{ll}X={\left[L,h,D,d\right]}^T,& (17)\end{array}$

$\begin{array}{ll}\{\begin{array}{c}0.01m\le L\le 0.04m\\ 0.0005m\le h\le 0.003m\\ 0.025m\le D\le 0.045m\\ 0.015m\le d\le 0.025m\end{array}.& (18)\end{array}$

where d is the diameter of a coil. In this study, the optimized parameters were set as L = 0.026 m, h = 0.001 m, D = 0.03 m, and d = 0.022 m and the turns of coil as N = 240. A photograph of the physical MRD developed is shown in Figure 9.

FIGURE 9

Figure 9. Photograph of the developed MRD.

The MRF for this experiment is MRF-250, purchased from Zhang Dongnan intelligent materials studio. It is comprised of soft magnetic carbonyl iron particles (average diameter: 8 μm, density: 7.86 g/cm³; Beijing DK Nano Technology Co., Ltd.), dimethyl silicone oil (viscosity: 100 cSt at 25°C, density: 0.965 g/cm³; Shin-Etsu, Japan), sodium dodecylbenzenesulfonate, oleic acid (purity 90%), graphite, and diatomite powder. The zero-field viscosity, saturation yield stress, and working temperature of MRF-250 are 242.5 mPa•s, 55.25 kPa, and −40 to 150°C, respectively.

Introduction of the Experimental System

Vibration experiments were performed on the semi-active seat suspension with MRD to evaluate the actual control performance of the proposed control method. The experimental system consists of a 6-DOF vibration table (model 6ZYD, rated load: 500 kg, frequency: 50 Hz, maximum displacement and acceleration: ±400 mm and 50 m/s²), a semi-active seat suspension with MRD, two acceleration sensors (model CT1005L, sensitivity: 50 mv/g, frequency range: 0.5–800 Hz, measuring range: 0–100 g, maximum impedance and linearity: 100 Ω and 1%), a constant current adapter (model CT5204, maximum frequency, output amplitude, accuracy, and noise: 0.31 KHz, 10 VP, 1.5%, and 1 mVrms), a data acquisition card (model PCI8735, measuring range: 0–10 V, accuracy: 0.0001, non-linearity: ±1 LSB, sampling rate: 500 KHz), a programmable current source (model DP811A, voltage range: 0–40 V, current range: 0–5 A, maximum response speed: 50 μs, resolution: 1/0.5 mV), and a digital signal processor (model TMS320F28335). The main performance parameters of the digital signal processor are shown in Table 4. An Figure S1 has been provided as a Supplementary Material to describe the experimental system.

TABLE 4

Table 4. Main technical indicators of the TMS320F28335 development board.

The 6-DOF vibration table consists of a foundation platform, a top platform, and six hydraulic cylinders, which can realize shock vibration, simple harmonic vibration, random vibration, and path spectrum reappearance. One acceleration sensor is used to measure the acceleration response of the human body, and another acceleration sensor is used to measure the excitation acceleration of the seat suspension. The constant current adapter is used to provide appropriate working voltage for the acceleration sensors, meanwhile, which can amplify the signal detected by the sensors and de-noise the measured signal. The data acquisition card is used to collect data and transmit the collected data to the controller and computer. The digital signal processor is the core of the whole control system and is employed as the controller for the semi-active seat suspension with MRD. Semi-active seat suspension with MRD is a kind of suspension system that uses MRF as a damping medium and is designed by using the rheological effect of MRF. The damping force of the suspension can be adjusted in real time according to the vibration state of the automobile cab. Compared to other suspension systems, semi-active seat suspension with MRD possesses the strengths of a simple structure, controllable performance, fast response, strong adaptability, and continuously adjustable damping force.

Experimental Results

Figures 10A,B present the acceleration and displacement responses of the semi-active seat suspension with MRD under random vibration by using the control methods of traditional PID, FOA-PID, PSO-PID, IFOA-PID, and PSO-IFOA-PID. Figure 10C presents the power spectral densities (PSD) of the acceleration response under random vibration by using the same control methods. The RMS, VDV, and VDV values for the acceleration response are presented in Table 5. Figure 10A indicates that the lowest acceleration amplitude is generated under the PSO-IPOA-PID control method during the entire time history. Figure 10B indicates that the maximum displacements under the control methods of traditional PID, FOA-PID, PSO-PID, IFOA-PID, and PSO-IFOA-PID are 0.0343, 0.0294, 0.0258, 0.0231, and 0.0197 m, respectively; thus, the maximum displacement in the PSO-IFOA-PID is significantly lower than with the other methods. Figures 10A,B prove that the best damping effect is achieved by using the PSO-IFOA-PID control method. Figure 10C indicates that the largest peak value of the PSD of acceleration appears at 6.7 Hz under the PSO-IPOA-PID control method, which is lower than with the other methods. This result proves that the PSO-IFOA-PID can effectively reduce the PSD of acceleration response. Table 5 shows that, compared to the control methods of traditional PID, FOA-PID, PSO-PID, and IFOA-PID, the RMS of the acceleration response in PSO-IFOA-PID is, respectively, decreased by 65.58, 52.93, 43.27, and 20.63%, the PTP of the acceleration response is, respectively, decreased by 47.53, 38.34, 33.67, and 18.3%, the VDV of the acceleration response is, respectively, decreased by 42.65, 32.88, 26.65, and 12.36%. Table 5 also indicates that only under the PSO-IFOA-PID control method can the damping effect meet the ISO2361-1 comfort evaluation standard (RMS ≤ 0.315 m/s²). The experiments verify the effectiveness and superiority of the purposed PSO-IFOA-PID control method.

FIGURE 10

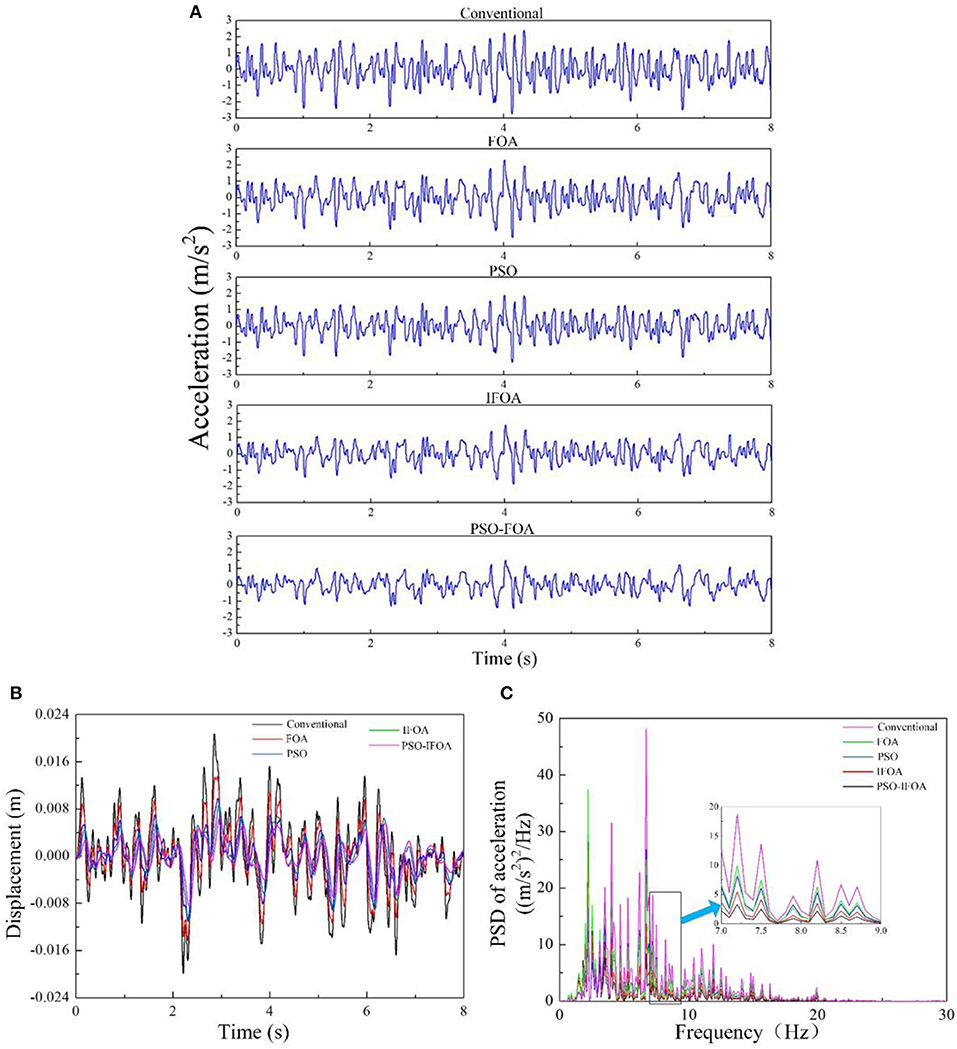
Figure 10. (A) Acceleration responses under random vibration, (B) displacement responses under random vibration, and (C) human vibration magnitude under random vibration.

TABLE 5

Table 5. Evaluation indices of the acceleration response.

Conclusions and future work

This paper proposed a PSO-IFOA-PID control method to improve the control performance for an MRD based semi-active seat suspension system. In order to verify the feasibility and superiority of the PSO-IFOA-PID, the search and control parameter optimization ability of traditional PID, FOA-PID, PSO-PID, IFOA-PID, and PSO-IFOA-PID were compared. The results indicated that the PSO-IFOA-PID had better optimization accuracy, faster convergence speed, and higher convergence precision in solving four test functions. Meanwhile, the PSO-IFOA-PID exhibited the advantages of adjusting the control parameters with better convergence speed and precision, and a shorter adjustment time, without overshoot, and having better steady and dynamic response characteristics. Furthermore, example simulations and experiments using the traditional PID, FOA-PID, PSO-PID, IFOA-PID, and PSO-IFOA-PID were carried out, and the results of both the simulations and experiments indicated that PSO-IFOA-PID control was the most ideal method.

In future work, new intelligent algorithms should be researched to achieve better response characteristics for the control performance of the semi-active controller of MRD seat suspension. Moreover, the temperature of MRD rises when it has been working for a long time, which will increase the internal pressure of the cylinder and result in the leakage of MRF. This adversely affects the damping characteristics of MRD, so further study is needed on how to improve the damping characteristics by controlling the temperature, and relevant experiments will also need to be carried out.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

NW, XL, and KW: conceptualization, methodology, and formal analysis. NW, KW, ZL, and HH: software. WL, NW, and TS-G: validation. NW, WL, and HH: investigation. XL and ZL: resource and data curation. NW and KW: writing–original draft preparation and visualization. HH, TS-G, and WL: writing–review and editing. XL: supervision and project administration.

Funding

This research was funded by the National Science Foundation of China (No. 51975568), National Natural Science Foundation of Jiangsu Province (No. BK20191341), Key Laboratory of Fluid Power and Intelligent Electro-Hydraulic Control (Fuzhou University), Taishan Scholar (tsqn201812025), and Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and Australia ARC DECRA (No. DE190100931).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank the reviewers for their contributions to this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00269/full#supplementary-material

Figure S1. Experimental system.

References

Ahmet, B., Hazim, I., and Ismail, B. (2017). An improvement in fruit fly optimization algorithm by using sign parameters[J]. Soft Comput. 22, 1–17. doi: 10.1007/s00500-017-2733-1

CrossRef Full Text | Google Scholar

Alkamachi, A., and Erçelebi, E. (2017). Modelling and genetic algorithm based-PID control of h-shaped racing quadcopter. Arab. J. Sci. Eng. 42, 1–10. doi: 10.1007/s13369-017-2433-2

CrossRef Full Text | Google Scholar

Ang, K. H., Chong, G., and Li, Y. (2005). PID control system analysis, design, and technology. IEEE Trans. Contr. Syst. Technol. 13, 559–576. doi: 10.1109/TCST.2005.847331

CrossRef Full Text | Google Scholar

Bhambhani, A., and Shah, P. (2016). “PID parameter optimization using cohort intelligence technique for D.C motor control system,” in 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT 2016) (Pune). doi: 10.1109/ICACDOT.2016.7877629

CrossRef Full Text | Google Scholar

Eduardo, F. O., Rossomando, F. G., and Soria, C. M. (2018). Self-tuning of a neuro-adaptive PID controller for a SCARA robot based on neural network. IEEE Lat. Am. Trans. 16, 1364–1374. doi: 10.1109/TLA.2018.8408429

CrossRef Full Text | Google Scholar

Eltag, K., Aslamx, M. S., and Ullah, R. (2019). Dynamic stability enhancement using fuzzy PID control technology for power system. Int. J. Control Autom. Syst. 17, 234–242. doi: 10.1007/s12555-018-0109-7

CrossRef Full Text | Google Scholar

Feng, G. D., Liu, M., and Wang, G. L. (2014). Genetic algorithm based optimal placement of PIR sensors for human motion localization. Optim. Eng. 15, 643–656. doi: 10.1007/s11081-012-9209-z

CrossRef Full Text | Google Scholar

Han, X. M., Liu, Q. M., and Wang, H. Z. (2017). Novel fruit fly optimization algorithm with trend search and co-evolution. Knowl. Based Syst. 11, 16–27. doi: 10.1016/j.knosys.2017.11.001

CrossRef Full Text | Google Scholar

Han, Y. Y., Gong, D. W., Li, J. Q., and Zhang, Y. (2016). Solving the blocking flow shop scheduling problem with makespan using a modified fruit fly optimisation algorithm. Int. J. Prod. Res. 54, 6782–6797. doi: 10.1080/00207543.2016.1177671

CrossRef Full Text | Google Scholar

Hernandez-Guzman, V. M., and Carrillo-Serrano, R. V. (2011). Global PID position control of PM stepper motors and PM synchronous motors. Int. J. Control 84, 1807–1816. doi: 10.1080/00207179.2011.626457

CrossRef Full Text | Google Scholar

Kuntanapreeda, S. (2016). Adaptive control of fractional-order unified chaotic systems using a passivity-based control approach. Nonlinear Dyn. 84, 2505–2515. doi: 10.1007/s11071-016-2661-0

CrossRef Full Text | Google Scholar

Lei, X. J., Ding, Y. L., and Fujita, H. (2016). Identification of dynamic protein complexes based on fruit fly optimization algorithm. Knowl. Based Syst. 105, 270–277. doi: 10.1016/j.knosys.2016.05.019

CrossRef Full Text | Google Scholar

Liu, H., Li, Y. Z., Zhang, Y., Chen, Y., Song, Z., Wang, Z., et al. (2018). Intelligent tuning method of PID parameters based on iterative learning control for atomic force microscopy. Micron 104, 26–37. doi: 10.1016/j.micron.2017.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X. H., Shi, Y., and Xu, J. (2017). Parameters tuning approach for proportion integration differentiation controller of magnetorheological fluids brake based on improved fruit fly optimization algorithm. Symmetry 9, 109–121. doi: 10.3390/sym9070109

CrossRef Full Text | Google Scholar

Lu, Y. Z., Yan, D. P., Zhang, J. Y., and Levy, D. (2015). A variant with a time varying PID controller of particle swarm optimizers. Inform. Sci. 297, 21–49. doi: 10.1016/j.ins.2014.11.017

CrossRef Full Text | Google Scholar

Maikala, R. V., and Bhambhani, Y. N. (2013). Estimating reduced oxygenation levels in the erector spinae lumbar muscle region during seated whole-body vibration. Int. J. Ind. Ergonom. 43, 121–128. doi: 10.1016/j.ergon.2012.11.006

CrossRef Full Text | Google Scholar

Mei, L., and Luo, J. (2017). PID Parameters optimization with improved cooperative coevolution algorithm. Comput. Tech. Dev. 27, 37–42. doi: 10.3969/j.issn.1673-629X.2017.08.008

CrossRef Full Text | Google Scholar

Meissner, M., Schmuker, M., and Schneider, G. (2006). Optimized particle swarm optimization (OPSO) and its application to artificial neural network training. BMC Bioinformatics 7:125. doi: 10.1186/1471-2105-7-125

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukherjee, V., and Ghoshal, S. P. (2007). Intelligent particle swarm optimized fuzzy PID controller for AVR system. Electr. Pow. Syst. Res. 77, 1689–1698. doi: 10.1016/j.epsr.2006.12.004

CrossRef Full Text | Google Scholar

Pan, Q. K., Sang, H. Y., Duan, J. H., and Gao, L. (2014). An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 62, 69–83. doi: 10.1016/j.knosys.2014.02.021

CrossRef Full Text | Google Scholar

Pan, W., Lyu, M. Y., Hwang, K. S., Ju, M. Y., and Shi, H. B. (2018). A neuro-fuzzy visual servoing controller for an articulated manipulator. IEEE Access. 99, 3346–3357. doi: 10.1109/ACCESS.2017.2787738

CrossRef Full Text | Google Scholar

Ramezanian, H., Balochian, S., and Zare, A. (2013). Design of optimal fractional-order PID controllers using particle swarm optimization algorithm for automatic voltage regulator (AVR) system. J. Control Autom. Electr. Syst. 24, 601–611. doi: 10.1007/s40313-013-0057-7

CrossRef Full Text | Google Scholar

Savran, A., Tasaltin, R., and Becerikli, Y. (2006). Intelligent adaptive nonlinear flight control for a high performance aircraft with neural networks. ISA Trans. 45, 225–247. doi: 10.1016/S0019-0578(07)60192-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, H. S., San, Y., and Zhu, Y. (2015). An improved fruit fly optimization algorithm and its application. Expert Syst. Appl. 42, 4310–4323. doi: 10.1016/j.eswa.2015.01.048

CrossRef Full Text | Google Scholar

Srivastava, S., and Agarwal, B. N. P. (2010). Inversion of the amplitude of the two-dimensional analytic signal of the magnetic anomaly by the particle swarm optimization technique. Geophys. J. Int. 182, 652–662. doi: 10.1111/j.1365-246X.2010.04631.x

CrossRef Full Text | Google Scholar

Vijayakumar, K., and Manigandan, T. (2016). Nonlinear PID controller parameter optimization using enhanced genetic algorithm for nonlinear control system. Control Eng. Appl. Inf. 18, 3–10.

Google Scholar

Wang, L., Liu, R., and Liu, S. (2016). An effective and efficient fruit fly optimization algorithm with level probability policy and its applications. Knowl. Based Syst. 97, 158–174. doi: 10.1016/j.knosys.2016.01.006

CrossRef Full Text | Google Scholar

Wang, W. C., and Liu, X. G. (2014). Melt index prediction by least squares support vector machines with an adaptive mutation fruit fly optimization algorithm. Chemometr. Intell. Lab. 141, 79–87. doi: 10.1016/j.chemolab.2014.12.007

CrossRef Full Text | Google Scholar

Xu, C. (2015). An improved fruit fly optimization algorithm and its application of PID parameters tuning. J. Inf. Comput. Sci. 12, 3647–3654. doi: 10.12733/jics20105957

CrossRef Full Text | Google Scholar

Xu, J., Wang, Z. B., Tan, C., and Si, L. (2016). Adaptive wavelet threshold denoising method for machinery sound based on improved fruit fly optimization algorithm. Appl. Sci. 6, 199–208. doi: 10.3390/app6070199

CrossRef Full Text | Google Scholar

Yu, Y., Li, Y. C., and Li, J. C. (2014). Parameter identification of a novel strain stiffening model for magnetorheological elastomer base isolator utilizing enhanced particle swarm optimization. J. Intel. Mat. Syst. Str. 26, 2446–2462. doi: 10.1177/1045389X14556166

CrossRef Full Text | Google Scholar

Yu, Y., Li, Y. C., and Li, J. C. (2015). Parameter identification and sensitivity analysis of an improved LuGre friction model for magnetorheological elastomer base isolator. Meccanica 50, 2691–2707. doi: 10.1007/s11012-015-0179-z

CrossRef Full Text | Google Scholar

Yu, Y., Li, Y. C., Li, J. C., and Gu, X. Y. (2016). Self-adaptive step fruit fly algorithm optimized support vector regression model for dynamic response prediction of magnetorheological elastomer base isolator. Neurocomputing 211, 41–52. doi: 10.1016/j.neucom.2016.02.074

CrossRef Full Text | Google Scholar

Zamani, A. A., Tavakoli, S., and Etedali, S. (2017). Fractional order PID control design for semi-active control of smart base-isolated structures: a multi-objective cuckoo search approach. ISA Trans. 67, 222–232. doi: 10.1016/j.isatra.2017.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, X. L., and Wang, L. (2016). A knowledge-guided fruit fly optimization algorithm for dual resource constrained flexible job-shop scheduling problem. Int. J. Prod. Res. 54, 1–13. doi: 10.1080/00207543.2016.1170226

CrossRef Full Text | Google Scholar

Zhou, D. W., Gao, X., Liu, G. H., Mei, C. L., Jiang, D., and Liu, Y. (2011). Randomization in particle swarm optimization for global search ability. Expert Syst. Appl. 38, 15356–15364. doi: 10.1016/j.eswa.2011.06.029

CrossRef Full Text | Google Scholar