From the Buffer Layer to Graphene on Silicon Carbide: Exploring Morphologies by Computer Modeling

Epitaxial graphene grown by thermal Si decomposition of Silicon Carbide appears in different morphological variants, depending on the production conditions: the strongly rugged buffer layer, retaining a considerable amount of sp³ hybridized buffer layer, the softly corrugated graphene monolayer and the rather flat quasi free standing monolayer with sparse small pits pinned to localized electronic states. Therefore, graphene on SiC is not a single material, but a set of materials with different morphologies depending on the environmental conditions during the synthesis. In all cases the distortion from the ideal flat structure seem to follow to some extent specific symmetries, which appear to preserve some memory of the interaction with the SiC bulk, even in the cases in which the sheet is substantially decoupled from it. Defects bear interesting properties, e.g., localized hot spots of reactivity and localized electronic states with specific energy depending on their nature and morphology, while their possible symmetric location is an added value for applications. Therefore, being capable of controlling the morphology, concentration, symmetry and location of the defects would allow tailoring this material for specific applications. Based on ab initio calculations and simulations, we first describe in detail the morphology of the different systems, and subsequently, we formulate hypotheses on the relationship between morphology and the formation process. We finally suggest future simulation studies capable of revealing the still unclear steps. These should give indication on how to tune the environmental conditions to control the final morphology of the sample and specifically design this material.

Carbon Layers on SiC: Not Simply “Graphene”

The thermal decomposition of silicon carbide (SiC) is a widely used technique to produce high quality epitaxial graphene (Norimatsu and Kusunoki, 2014). The morphology and properties of resulting carbon sheets, however, depend on the exposed surface: while C-rich (Bouhafs et al., 2017) or non-polar (Ostler et al., 2013) surfaces give rise to rather decoupled sheets, upon selective silicon evaporation from the hexagonal Si rich surfaces [e.g., 6H-SiC(0001)], excess carbon reconstruction produces in the first instance an hexagonal carbon layer partially bound to the substrate called the buffer layer (Goler et al., 2013a) (BL), which retains a considerable amount of sp³ hybridized sites (see Figure 1A). “Real” graphene (completely sp² hybridized) can subsequently be obtained either by continuing Si evaporation, which leads to the formation of a second buffer layer and detachment of the first one (becoming the monolayer graphene, MLG) or by intercalating hydrogen (Riedl et al., 2010) or metals (Fiori et al., 2017) underneath the buffer layer, leading to the formation of the so-called Quasi Free-standing MonoLayer Graphene (QFMLG) (Riedl et al., 2009) (see Figure 1A). The morphology of the three types of carbon layer is very different: The BL is strongly rippled (Bouhafs et al., 2017; Cavallucci and Tozzini, 2018), with peaked crests following a moiré pattern induced by the covalent interaction with the substrate (see Figures 1B,C); these in turn induce a (much less pronounced) corrugation in the overlying MLG, whose exact conformation (concave or convex), however, seems to depend on the environmental conditions influencing the weak BL-MLG van der Waals (vdW) interaction (Mallet et al., 2007; Telychko et al., 2015; Cavallucci and Tozzini, 2016). Finally, the QFMLG is very weakly interacting with the substrate and is basically flat, except in correspondence of defects (vacancies) of the H (or metal) intercalating layer, where it increasingly bends inward as the vacancy size increases (Figure 1B, bottom). Additionally, localized electronic states form in correspondence of the vacant sites, whose energy and “shape” (as observed by scanning tunneling microscopy—STM—experiments) depend on the number and relative location of the vacant sites (Figure 1C) (Cavallucci et al., 2018; Murata et al., 2018). This variety of morphologies suggests a number of interesting applications: the buffer layer sharp crests are areas in which the regularity of the delocalized π system is locally destroyed or at least disturbed, and therefore likely to be highly reactive sites, prone to adhesion of atomic species [e.g., hydrogen (Goler et al., 2013b)] or other chemicals for functionalization. The effect of selective adhesion of H is also possible—to a minor extent—on the MLG, where, additionally, one might exploit the multi-stability and possibility of changing the curvature to control the adsorption/desorption of hydrogen (Tozzini and Pellegrini, 2011) for H-storage applications (Tozzini and Pellegrini, 2013). Finally, QFMLG is a promising system for electronics: besides a better mobility with respect to MLG (Speck et al., 2011), it also displays a Schottky type graphene/SiC interface (Sonde et al., 2009) offering the possibility of tailoring the ohomic/non-homic properties of the system (Hertel et al., 2012); in addition in the presence of H vacancies, the tunable energy of the filled (and empty) states associated with the dangling bonds, located within the SiC electronic band gap and near the Dirac point of graphene suggest applications in nano-opto-electronics (Telychko et al., 2015).

FIGURE 1

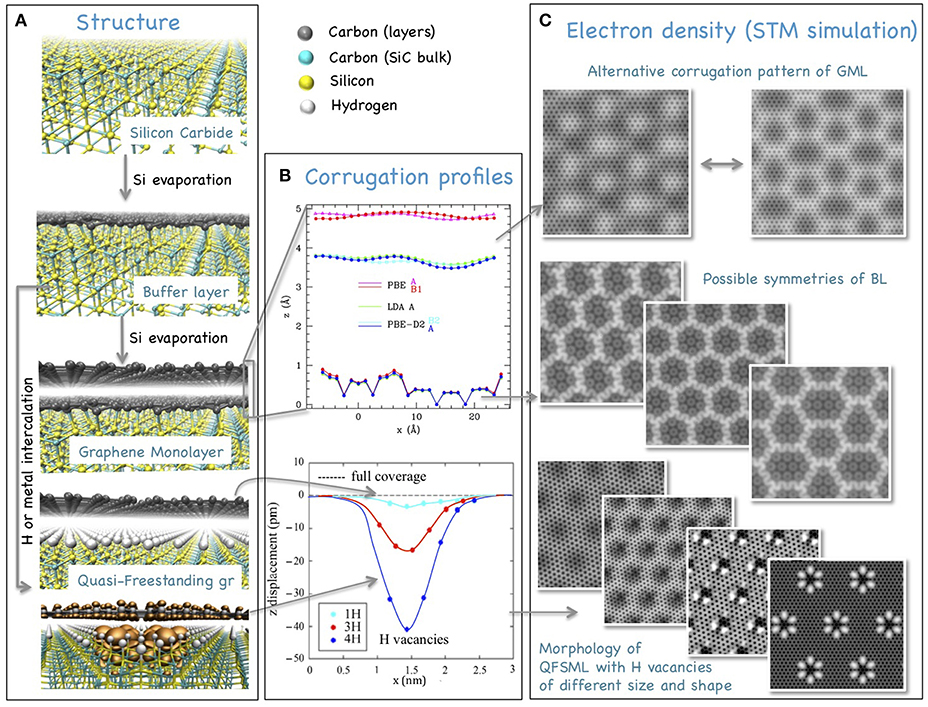
Figure 1. A summary of the features of the SiC supported “graphenes.” (A) A scheme of the sheets formation: From top to bottom the pictures report the bulk SiC, the buffer layer, the graphene monolayer detaching upon formation of a subsequent buffer layer, and the quasi-freestanding forming upon intercalation of H underneath the buffer layer; the latter is also represented with vacancies in the H intercalating layer: the localized electronic states due to dangling Si bonds are represented as iso-charge-density surfaces in orange; arrows indicate the evolution flow and a legend for the atom color is reported aside. (B) Corrugation profiles of graphene sheet and buffer in the MLG system (upper plot, different colors correspond to different density functionals used for the calculation and/or different corrugation pattern, indicated) and of the quasi freestanding layer in the presence of H vacancies of increasing size (as reported, lower plot); arrows connect the corresponding parts of the structures. (C) Simulated STM images of the different systems. From top to bottom: two alternative corrugation patterns of the graphene monolayer; possible different symmetries of the moiré pattern of bonding/corrugation of the buffer layer; localized states produced by H vacancies of different shape and size. The calculations of MLG (top) and the last one of the QFMLG (bottom, foreground) are obtained with the 6√3 × 6√3 R30_SiC/13 × 13_gr supercell, the others with the √31 × √31R8.95_SiC 7 × 7 R21.787_gr. Plots and pictures of (B,C) are reproduced with permission for adapting or using data from Cavallucci and Tozzini (2016, 2018), Cavallucci et al. (2018), Murata et al. (2018).

What makes these morphologies even more interesting for applications (Quesnel et al., 2015) is the fact that the distortions from ideal graphene (corrugations or pits and localized states) follow a regular pattern. This is more evident in the BL and MLG, where the moiré pattern reflects a super periodicity, which was initially recognized as “quasi” 6 × 6 of SiC, and attributed to the mismatch between the SiC and graphene lattice parameters. Interestingly, a similar symmetry can be observed also in QFMLG, especially if obtained under slow hydrogenation conditions: vacancies seems to prefer locating on an hexagonal super-lattice of size ~1.8 nm (still corresponding to 6 × 6), although not all the sites are occupied (the concentration and shape of vacancies is very variable, depending on the temperature and pressure of hydrogen during the process) (Murata et al., 2014; Cavallucci and Tozzini, 2016). This indicates that, in spite of the decoupling operated by the intercalating layer, the QFMLG preserves some memory of the interaction with the substrate. In order to understand this subtle aspect of the structural features of the system, one must go through the details of the formation processes.

The Moiré Pattern: Unique or Not Unique?

Moiré patterns of structural distortion generally arise from a mismatch between two periodic 2D lattices coming into contact. In this case, these are the hexagonal faces of SiC (with lattice parameter ~3.07 Å) and the hexagonal carbon layer. As the lattice parameter of the latter, one usually considers the ideal graphene value 2.46 Å, leading to a consensus supercell of ~3.2 nm side, corresponding to 6√3 × 6√3 R30 of SiC and 13 × 13 of graphene (see Figure 2A). This symmetry and the corresponding supercell are considered the standard model system (Mallet et al., 2007; Kim et al., 2008; Sforzini et al., 2015) for calculations, and are compatible with the experimental observations of MLG¹ (Varchon et al., 2008). The picture is consistent, considering that the level of residual mismatch of graphene in this supercell is very small, compatible with the soft corrugation observed in MLG. DFT calculations show that the sharp crests of the BL form a “tessellation” of the plane including three different types of irregular hexagonal “tiles” (see Figure 1C, central part, the forefront). The irregularity is due to the fact that the crests are formed by harmchair lines and the 13 × 13 supercell is not compatible with a set of them forming a regular hexagon. This conformation, however, seems somehow regularized in room temperature observations of the BL, in which the hexagonal tiles appear more smeared and regular hexagonal (Nair et al., 2017; Cavallucci et al., 2018). In addition, in the low temperature determinations, the pattern does not seem unique (Ostler et al., 2013; Yagyu et al., 2014): During the early stages of the Si evaporation other simpler and more regular symmetries are observed for the BL (Riedl, 2010; Hu et al., 2013). This behavior might be explained by considering that, due to the large amount of sp³ hybridization, the “natural” lattice parameter of the BL might differ substantially from the 2.46 Å of the ideal graphene, and therefore different consensus supercells might be possible.

FIGURE 2

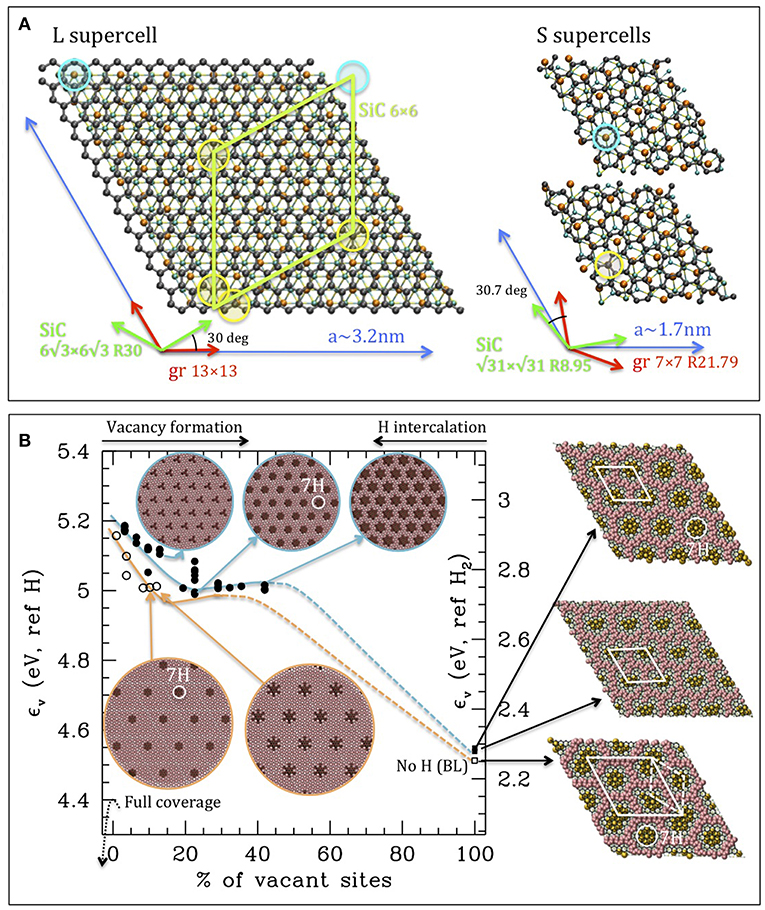
Figure 2. (A) L and S supercells of the graphene on SiC systems. Two S cells with different relative translations of graphene with respect to SiC are reported. In all cases hollow type sites (with Si lying under the hexagon center) and top type sites (with Si under a carbon) are circled in cyan and yellow, respectively. Supercell lattice vectors, SiC and graphene lattice vectors are reported in blue, green and red, respectively (with sizes, and notations reported in the same color). The relative rotation of lattices is reported in black. In the L model, the 6 × 6 supercell of SiC is also reported, in green. Atom color coding: Black = C in the carbon sheet; orange = location of H in the full coverage or of Si of the upper layer; cyan and yellow = C and Si in the bulk. (B) Main plot: energy of the system per vacant Si site as a function of the concentration of vacant sites referred to the system with full coverage. The scale on the left consider the extraction of H in atomic form, that on the right the extraction in molecular form (the two differ by a rigid shift corresponding to half of the H₂ formation energy. The completely hydrogenated system—QFMLG—is out of scale below the x axis). The filled dots correspond to vacancies located in sites with the √31 × √31 R8.95 periodicity (~6 × 6), empty dots to vacancies located in 6√3 × 6√3 R30 (nearly 1/3 dense). Analogously, filled and empty squares correspond to the buffer layer (no H) with the two periodicities (The blue and orange lines are eye-guides for the two sets of points). The circular insets report representation of the system with vacancies of different size in the two symmetries as indicated by the arrows. The completely dehydrogenated systems (BL) are reported on the right, with the following color code: the C atoms of the “crest” are represented in pink as large spheres, while the Si sites more strongly bound to the buffer layer are in orange. The hexagonal lattice is superimposed in black. 7H type vacancies are circled in white. Data are taken with permission from Cavallucci and Tozzini (2016), Cavallucci et al. (2018), Murata et al. (2018) and recast in different form.

Following this idea, we recently explored different supercells by means of DFT calculations. We focused in particular on one obtained by allowing a small relative rotation of the two lattices (Sclauzero and Pasquarello, 2012), namely the 7 × 7 R21.787 of graphene and √31 × √31 R8.95 for SiC (Figure 2A). In this supercell graphene and SiC lattice display a relative rotation of <1°, and a lattice parameter very similar to the 6 × 6 (~1.7Å). Having about 1/3 of the volume, this supercell it is named S (small) as opposed to standard 13 × 13 (large, L), and it is about one order of magnitude less expensive in calculations. Furthermore, the pattern of buffer layer crests evaluated in S (Fiori et al., 2017) display a more regular hexagonal symmetry (see Figure 2B right side images and Figure 1C, central images), more similar in this respect to the high temperature determinations and to the hexagonal phases of occurring during the buffer formation.

The DFT calculations of QFMLG bring further insights on the interplay between symmetry and substrate interaction. The electronic structures of the localized states of vacancies evaluated in S and L differ very little, indicating that the very small relative rotation of the two lattices does not affect the local properties (Cavallucci et al., 2018). Conversely, S allows for the placing of vacancies on a regular hexagonal lattice, while L does not, unless vacancies are located in different relative position with respect to graphene, e.g., some of them centered under a carbon site (named top) and some of them centered under a graphene hexagon (named hollow) (see Figure 2A). Because equal size top and hollow vacancies have energies differing by several tens of meV (Cavallucci et al., 2018), it appears that symmetry and energy optimization conflict in the L supercell. In S supercell, conversely, a regular hexagonal lattice of nm size comparable to the observed one can be occupied by all equal vacancies.

Insight Into the Formation Processes

Further insight can be gained from energetic considerations. One can evaluate the energy of vacancies (per vacant site) by using

$\begin{array}{ll}{\epsilon }_v=\frac{(E_{vac}+N{\epsilon }_H)-E_{full}}{N}& (1)\end{array}$

i.e., considering the hydrogen extraction process (E_full being the energy of the fully hydrogenated system, E_vac the energy of the system with the vacancy and ε_H the energy of the extracted hydrogen). This process turns out endothermic, requiring ~5 eV per H if extraction is operated in atomic form, or ~2.8 eV if the recombination to H₂ after extraction is considered (Figure 2B). Interestingly enough, however, the extraction energy decreases as H is extracted, indicating that states with larger number of vacant sites are more stable, down to the fully dehydrogenated state (the BL) where the energy per vacant site is ~2.3 eV (with respect to H₂, Figure 2B). Furthermore, vacant sites show a clear tendency to aggregate; at the same level of hydrogenation, the states with larger (and fewer) vacancies are energetically favored with respect to states with smaller (and nearer) vacancies (empty and filled dots in Figure 2B, respectively). Indeed, the H extraction process is not “linear.” The plot of Figure 2B reports two energy profiles (eye guiding colored lines) corresponding to creation of vacancies of increasing size at two different concentrations, namely on the ~6 × 6 lattice, blue line, and on the 6√3 × 6√3, orange. The profiles show a shallow well located at two different hydrogenation levels, corresponding however to vacancies of the same size and shape, namely the round shaped one, with 7 Si vacant sites (circled in white in Figure 2B). The question naturally arises: why, in spite of the fact that the QFMLG is basically decoupled from the SiC substrate, do vacancies tend to form in specific locations and to have a preferential size?

This can be understood by considering that normally, the vacancies form by the opposite process, i.e., by a partial hydrogenation starting from the buffer layer. Therefore, the right question to ask is which are the sites that hydrogenate last. Assuming that the hydrogenation occurs slowly and in controlled low pressure conditions, one can hypothesize that H can penetrate more easily under the crests of the buffer layer, and saturate first the Si sites located under them, which are already detached from the buffer. In the three representation of the buffer layer (in Figure 2B, right side, for L, Sh, and St supercell, respectively) crests are represented in pink. In the same images, the Si sites farther from crests are colored in orange, and are those likely to be hydrogenated last. As it can be seen, in the L model (bottom) they are of three different shapes, one corresponding to the round 7H vacancy, one “elliptical” and one “egg-shaped.” In total, they occupy all the sites of a 6 × 6 lattice, while each of them occupy a 6√3 × 6√3 lattice. Again, having the same shape vacancy with a fully occupied 6 × 6 lattice seems unlikely, therefore one must either abandon the full symmetry, or the shape homogeneity or the full occupation of the superlattice. Conversely, in the S supercell one can have all same shape vacancies located on an ~6 × 6 lattice (precisely the √31 × √31 R8.95) fully occupied; in addition, in the case of Sh system the vacancies have the shape of the most stable 7H vacancy.

Conclusions and Perspectives

In conclusion, this analysis suggests that, in spite of the effective decoupling between the QFMLG and the substrate, the vacancies and the localized electronic states produced by them both in the buffer and in the graphene layer preserve a strong memory of the parent buffer layer: the preferred location of the vacancies will be in the center of the “tiles” defined by the system of crests of the BL. Therefore, the hydrogenation appears to be driven by different forces, in partial conflict among each other: the starting (somehow ambiguous) symmetry of the buffer layer; the tendency of vacancies to aggregate and prefer given shapes; the final conformation of the system, which appears to follow a 6 × 6 periodicity. This explains the variability of the QFMLG samples: conflicting forces tend to stabilize one or the other conformation depending on the specific environmental condition during the process and resulting in incomplete or irregular occupation of the 6 × 6 lattice. Of course, uncontrolled or extreme hydrogenation conditions can also produce less stable vacancy conformation, i.e., different sizes and shapes (Murata et al., 2018), increasing the sample diversity.

Advanced molecular simulations of the H-intercalation process including e.g., Meta-Dynamics (Barducci et al., 2011), Gran Canonical Monte Carlo (Andersen et al., 2019), or Kinetic-Monte Carlo (Frenkel and Smit, 2002) could give an insight into the acting mechanisms, and indications on how to tune the environmental condition in order to control, e.g., the concentration, site occupation, and size of the vacancies in the final sample. This would be of outmost importance, considering that these parameters influence the electronic properties of the sample. However, we remark that these simulations should be done without imposing a specific symmetry on the system, which should be left free of choosing and changing it during the process, and of following several possible routes for the hydrogen intercalation. Therefore, very large simulation supercells must be used, which excludes the possibility of addressing the problem with ab initio techniques. The problem would be addressable with empirical force fields (FF), provided they can take into account accurately enough the breaking and formation of the C-Si and Si-H bonds, of the partial sp²-sp³ hybridization state of the carbon layer, and at the same time of the vdW interaction between the detached part of the layer and the partially hydrogenated substrate. A few FF exist that can perform one or more of these tasks (Tersoff, 1988; Los and Fasolino, 2003; Dittner et al., 2015; O'Connor et al., 2015; Harrison et al., 2018) and the evaluation of their performances and, possibly, their modification to cope with this very complex system is currently in the course.

Data Availability

All datasets generated for this study are included in the manuscript and/or the supplementary files.

Author Contributions

LB and TC provided the data, performed the data analysis, and participated in the writing of the paper. VT checked the data, prepared the figures, organized, and wrote the manuscript.

Funding

This work was supported by EU-H2020, Graphene-Core1 (agreement No 696656) and Core2 (agreement No 75219), MCSA (agreement No 657070), by CINECA awards IsB11_flexogra (2015), IsC36_ElMaGRe (2015), IsC44_QFSGvac (2016), IsC44_ReIMCGr (2016), IsC61_MGchpDFA (2018), and PRACE Tier0 award Pra13_2016143310 (2016).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Stefan Heun, Prof. Paolo Giannozzi, Dr. Camilla Coletti, Dr. Yuya Murata, and Dr. Vittorio Pellegrini for useful discussions. We aknowledge CINECA staff for technical support.

Footnotes

1. ^The 6√3 × 6√3 R30 periodicity includes the 6 × 6.

References

Andersen, M., Panosetti, C., and Reuter, K. A. (2019). Practical guide to surface kinetic Monte Carlo simulations. Front. Chem. 7:202. doi: 10.3389/fchem.2019.00202

PubMed Abstract | CrossRef Full Text | Google Scholar

Barducci, A., Bonomi, M., and Parrinello, M. (2011). Metadynamics. Interdiscip. Rev. Comput. Mol. Sci. 1, 826–843. doi: 10.1002/wcms.31

CrossRef Full Text | Google Scholar

Bouhafs, C., Zakharov, A. A., Ivanov, I. G., Giannazzo, F., Eriksson, J., Stanishev, V., et al. (2017). Multi-scale investigation of interface properties, stacking order and decoupling of few layer graphene on C-face 4H-SiC. Carbon 116, 722–732. doi: 10.1016/j.carbon.2017.02.026

CrossRef Full Text | Google Scholar

Cavallucci, T., Murata, Y., Takamura, M., Hibino, H., Heun, S., and Tozzini, V. (2018). Unraveling localized states in quasi free standing monolayer graphene by means of density functional theory. Carbon 130, 466–474. doi: 10.1016/j.carbon.2018.01.027

CrossRef Full Text | Google Scholar

Cavallucci, T., and Tozzini, V. (2016). Multistable rippling of graphene on SiC: a density functional theory study. J. Phys. Chem. C 120, 7670–7677. doi: 10.1021/acs.jpcc.6b01356

CrossRef Full Text | Google Scholar

Cavallucci, T., and Tozzini, V. (2018). Intrinsic structural and electronic properties of the buffer layer on silicon carbide unraveled by density functional theory. Sci. Rep. 8:13097. doi: 10.1038/s41598-018-31490-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Dittner, M., Müller, J., Metin Aktulga, H., and Hartke, B. (2015). Efficient global optimization of reactive force-field parameters. J. Comp. Chem. 36, 1550–1561. doi: 10.1002/jcc.23966

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiori, S., Murata, Y., Veronesi, S., Rossi, A., Coletti, C., and Heun, S. (2017). Li-intercalated graphene on SiC (0001): an STM study. Phys. Rev. B 96:125429. doi: 10.1103/PhysRevB.96.125429

CrossRef Full Text | Google Scholar

Frenkel, D., and Smit, B. (2002). Understanding Molecular Simulation. London: Academic Press.

Google Scholar

Goler, S., Coletti, C., Piazza, V., Pingue, P., Colangelo, F., Pellegrini, V., et al. (2013a). Revealing the atomic structure of the buffer layer between SiC (0001) and epitaxial graphene. Carbon 51, 249–254. doi: 10.1016/j.carbon.2012.08.050

CrossRef Full Text | Google Scholar

Goler, S., Coletti, C., Tozzini, V., Piazza, V., Mashoff, T., Beltram, F., et al. (2013b). Influence of graphene curvature on hydrogen adsorption: toward hydrogen storage devices. J. Phys. Chem. C, 117, 11506–11513. doi: 10.1021/jp4017536

CrossRef Full Text | Google Scholar

Harrison, J. A., Schall, J. D., Maskey, S., Mikulski, P. T., Knippenberg, M. T., and Morrow, B. H. (2018). Review of force fields and intermolecular potentials used in atomistic computational materials research. Appl. Phys. Rev. 5:031104. doi: 10.1063/1.5020808

CrossRef Full Text | Google Scholar

Hertel, S., Waldmann, D., Jobst, J., Albert, A., Albrecht, M., Reshanov, S., et al. (2012). Tailoring the graphene/silicon carbide interface for monolithic wafer-scale electronics Nat. Comm. 3:957. doi: 10.1038/ncomms1955

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, T. W., Ma, F., Ma, D. Y., Yang, D., Liu, X. T., Xu, K. W., et al. (2013). Evidence of atomically resolved 6 × 6 buffer layer with long-range orderand short-range disorder during formation of graphene on 6H-SiC by thermal decomposition. Appl. Phys. Lett. 102:171910. doi: 10.1063/1.4804290

CrossRef Full Text | Google Scholar

Kim, S., Ihm, J., Choi, H. J., and Son, Y.-W. (2008). Origin of anomalous electronic structures of epitaxial graphene on silicon carbide. Phys. Rev. Lett. 100:176802. doi: 10.1103/PhysRevLett.100.176802

PubMed Abstract | CrossRef Full Text | Google Scholar

Los, J. H., and Fasolino, A. (2003). Intrinsic long-range bond-order potential for carbon: performance in Monte Carlo simulations of graphitization. Phys. Rev. B 68:024107. doi: 10.1103/PhysRevB.68.024107

CrossRef Full Text | Google Scholar

Mallet, P., Varchon, F., Naud, C., Magaud, L., Berger, C., and Veuillen, J. Y. (2007). Electron states of mono- and bilayer graphene on si probed by scanning-tunneling microscopy. Phys. Rev. B 76:041403. doi: 10.1103/PhysRevB.76.041403

CrossRef Full Text | Google Scholar

Murata, Y., Cavallucci, T., Tozzini, V., Pavliček, N., Gross, L., Meyer, G., et al. (2018). Atomic and electronic structure of Si dangling bonds in quasi-free-standing monolayer graphene. Nano Res. 11, 864–873. doi: 10.1007/s12274-017-1697-x

CrossRef Full Text | Google Scholar

Murata, Y., Mashoff, T., Takamura, M. S., Tanabe, S., Hibino, H., et al. (2014). Correlation between morphology and transport properties of quasi-free-standing monolayer graphene. App. Phys. Lett. 105:221604. doi: 10.1063/1.4902988

CrossRef Full Text | Google Scholar

Nair, M. N., Palacio, I., Celis, A., Zobelli, A., Gloter, A., Kubsky, S., et al. (2017). Band gap opening induced by the structural periodicity in epitaxial graphene buffer layer. Nano Lett. 17, 2681–2689. doi: 10.1021/acs.nanolett.7b00509

CrossRef Full Text | Google Scholar

Norimatsu, W., and Kusunoki, M. (2014). Epitaxial graphene on SiC{0001}: advances and perspectives. Phys. Chem. Chem. Phys. 16:3501. doi: 10.1039/C3CP54523G

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Connor, T. C., Andzelm, J., and Robbins, M. O. (2015). AIREBO-M: a reactive model for hydrocarbons at extreme pressures. J. Chem. Phys. 142:024903. doi: 10.1063/1.4905549

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostler, M., Deretzis, I., Mammadov, S., Giannazzo, F., Nicotra, G., Spinella, C., et al. (2013). Direct growth of quasi-free-standing epitaxial graphene on nonpolar SiC surfaces. Phys. Rev. B 88:085408. doi: 10.1103/PhysRevB.88.085408

CrossRef Full Text | Google Scholar

Quesnel, E., Roux, F., Emieux, F., Faucherand, P., Kymakis, E., Volonakis, G., et al. (2015). Graphene-based technologies for energy applications, challenges and perspectives. 2D Mater. 2:030204. doi: 10.1088/2053-1583/2/3/030204

CrossRef Full Text | Google Scholar

Riedl, C. (2010). Epitaxial grapheneon silicon carbide surfaces: growth, characterization, doping and hydrogen intercalation (PhD thesis), Fridrich Alexander Universität Erlangen, Nurberg, Germany.

Google Scholar

Riedl, C., Coletti, C., Iwasaki, T., Zakharov, A. A., and Starke, U. (2009). Quasi-free-standing epitaxial graphene on SiC obtained by hydrogen intercalation. Phys. Rev. Lett. 103:246804. doi: 10.1103/PhysRevLett.103.246804

PubMed Abstract | CrossRef Full Text | Google Scholar

Riedl, C., Coletti, C., and Starke, U. (2010). Structural and electronic properties of epitaxial graphene on SiC(0001): a review of growth, characterization, transfer doping and hydrogen intercalation. J. Phys. D Appl. Phys. 43:374009. doi: 10.1088/0022-3727/43/37/374009

CrossRef Full Text | Google Scholar

Sclauzero, G., and Pasquarello, A. (2012). Low-strain interface models for epitaxial graphene on SiC(0001). Diam. Rel. Mater. 23, 178–183. doi: 10.1016/j.diamond.2011.11.001

CrossRef Full Text | Google Scholar

Sforzini, J., Nemec, L., Denig, T., Stadtmüller, B., Lee, T.-L., Kumpf, C., et al. (2015). Approaching truly freestanding graphene: the structure of hydrogen-intercalated graphene on 6H-SiC(0001). Phys. Rev. Lett. 114:106804. doi: 10.1103/PhysRevLett.114.106804

PubMed Abstract | CrossRef Full Text | Google Scholar

Sonde, S., Giannazzo, F., Raineri, V., Yakimova, R., Huntzinger, J.-R., Tiberj, A., et al. (2009). Electrical properties of the graphene/4H-SiC (0001) interface probed by scanning current spectroscopy. Phys. Rev. B 80:241406. doi: 10.1103/PhysRevB.80.241406

CrossRef Full Text | Google Scholar

Speck, F., Jobst, J., Fromm, F., Ostler, M., Waldmann, D., Hundhausen, M., et al. (2011). The quasi-free-standing nature of graphene on H-saturated SiC(0001). Appl. Phys. Lett. 99:122106. doi: 10.1063/1.3643034

CrossRef Full Text | Google Scholar

Telychko, M., Berger, J., Majzik, Z., Jelínek, P., and Švec, M. (2015). Graphene on SiC(0001) inspected by synamic atomic force microscopy at room temperature. Beilstein. J. Nanotechnol. 6, 901–906. doi: 10.3762/bjnano.6.93

CrossRef Full Text | Google Scholar

Tersoff, J. (1988). Empirical interatomic potential for silicon with improved elastic properties. Phys. Rev. B 38:9902. doi: 10.1103/PhysRevB.38.9902

PubMed Abstract | CrossRef Full Text | Google Scholar

Tozzini, V., and Pellegrini, V. (2011). Reversible hydrogen storage by controlled buckling of graphene layers. J. Phys. Chem. C 115, 25523–25528. doi: 10.1021/jp208262r

CrossRef Full Text | Google Scholar

Tozzini, V., and Pellegrini, V. (2013). Prospects for hydrogen storage in graphene. Phys. Chem. Chem. Phys. 15, 80–89. doi: 10.1039/C2CP42538F

PubMed Abstract | CrossRef Full Text | Google Scholar

Varchon, F., Mallet, P., Veuillen, J.-Y., and Magaud, L. (2008). Ripples in epitaxial graphene on the Si-terminated SiC(0001) surface. Phys. Rev. B 77:235412. doi: 10.1103/PhysRevB.77.235412

CrossRef Full Text | Google Scholar

Yagyu, K., Tajiri, K., Kohno, A., Takahashi, K., Tochihara, H., Tomokage, H., et al. (2014). Fabrication of a single layer graphene by copper intercalation on a SiC(0001) surface. Appl. Phys. Lett. 104:053115. doi: 10.1063/1.4864155

CrossRef Full Text | Google Scholar