
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 03 May 2019
Sec. Carbon-Based Materials
Volume 6 - 2019 | https://doi.org/10.3389/fmats.2019.00093
This article is part of the Research Topic Frontiers in Materials: Rising Stars View all 56 articles
Mechanical strain sensing is ubiquitous, found in applications such as heart rate monitoring, analysis of body part motion, vibration of machines, dilatation in buildings and large infrastructure, and so forth. Piezoresistive materials and sensors based on those offer versatile and robust solutions to measure strains and displacements and can be implemented even in acceleration and pressure analyses. In this paper, we overview the most prominent piezoresistive materials, and present a case study on carbon foams as well as on their hierarchical hybrid structures with carbon nanotubes/nanofibers. Our results show highly non-linear electrical resistance and mechanical stress dependence on uniaxial strain in both types of materials up to 50% compression. The Young's moduli increase with compressive strain between 1–65 and 0.1–92 kPa for the foam and hierarchical structure, respectively. The foams have giant gauge factors (up to −1000) with large differential gauge factors (on the scale of −10) and differential pressure sensitivity of 0.016 Pa−1 (at 10% strain) making them suitable for detecting both small and large displacements with excellent accuracy of electrical readout as we demonstrate in detecting building wall displacement as well as in monitoring heart rate and flexing of fingers.
Electrically conductive and semiconducting materials change their conductivity upon mechanical deformation. The effect is known as piezoresistivity, and can be described by the gauge factor (GF), which shows the relative change of resistance with the applied strain. In a first order approximation, , where ΔR/R0 and Δρ/ρ0 are the relative change of resistance and resistivity, respectively, ε is the mechanical strain and ν is the Poisson's ratio of the material.
In most of the bulk metals (e.g., Al, Au, Cu) and in many crystalline alloys and metallic glass compositions (e.g., constantan, Cu60Ni40, Ni68Si15B17, Ni80Cr20, Pd40Cu30Ni10P20), GF is typically ~2 (Hu et al., 2000; Schweizer, 2005; Yi et al., 2011; Jiang et al., 2015) and thus piezoresistivity may be accounted mainly for the change of geometry (viz. the Poisson's ratio is ~0.5). However, some metals such as Pt and Ni display much larger GF values (4 and −12, respectively; Schmid et al., 2014 and Yi et al., 2011), which indicates that the deformation-induced change in resistivity has also a role in the piezoresistive effect and shall be taken into account.
In semiconductors, GF can be several orders of magnitude higher than in metals, as piezoresistivity is mainly governed by the strong variation of the materials' resistivity with strain, and thus the geometrical effects may be neglected. When deforming a semiconducting solid, the band structure and the effective mass of carriers also change, which result in their increased or decreased concentration and mobility (depending on the type of majority carriers and whether the strain is compressive or tensile; Bardeen and Shockley, 1950; Kanda, 1991). In the case of common crystalline semiconductors such as p-type Si or Ge, GF has a value of ~100. Interestingly, for Si nanowires even higher GFs (up to 30-fold, compared to bulk Si) were reported and explained by strain induced carrier mobility change and surface effects (He and Yang, 2006). However, as it was demonstrated later using time-dependent electromechanical measurements, the increased apparent piezoresistive coefficients were actually due to charge trapping and detrapping on the surface of depleted Si, whereas the intrinsic piezoresistvity of the nanostructured material is essentially the same as that of bulk (Milne et al., 2010). Recent studies on semiconducting metal oxide thin films and nanostructures, e.g., on TiO2 (Fraga et al., 2012), MoO3 (Wen et al., 2014), and ZnO (Kaps et al., 2017); as well as on layered transition metal dichalcogenides, e.g., MoS2 (Nayak et al., 2014; Manzeli et al., 2015), MoSe2, WSe2 (Hosseini et al., 2015), and PtSe2 (Li et al., 2016; Wagner et al., 2018) showed highly strain dependent electronic properties, giving rise to quite high GFs comparable to those of Si and Ge (e.g. 441 for MoO3 nanobelts, −148 for MoS2 monolayers or −85 for PtSe2 thin films).
Piezoresistivity in powders of conductive materials has been also studied for quite long time. For instance, the first carbon microphones made nearly 150 years ago exploited the pressure sensitivity of electrical resistance in carbon powders placed between an electrically conductive metal diaphragm and a back-side electrode plate (Hope, 1978). The pressure waves of sound induce vibrations of the thin diaphragm, which then transfers the vibrations to the carbon powder thus varying the intimacy of contacts between the conductive particles resulting in a variation of its overall resistance in synchrony with the waves of the sound. In the compressed carbon powder, the distance between the particles decrease giving rise to a better percolation and higher tunneling probability of electrons thus inducing an apparent piezoresistivity with gauge factors of around 20 (Cunningham and Bibby, 1993). In a similar fashion, powders, films and woven-like fabrics of 1 and 2-dimensional (1D and 2D, respectively) carbon nanoparticles, i.e., single (Gilshteyn and Nasibulin, 2015) and multi-walled nanotubes (Feng et al., 2010; Tadakaluru et al., 2014; Chun et al., 2018), graphene (Bae et al., 2013; Smith et al., 2013; Zhao et al., 2015; Liu X. et al., 2017) and reduced graphene oxide (Kuang et al., 2013; Mi et al., 2017; Xu et al., 2018) show piezoresistive properties. The great benefits of the low dimensional carbon nanostructures are easy formation of entangled thin films and simple transfer onto elastomers enabling excellent strain sensor devices to monitor heart rate, motion of body parts (Chang et al., 2018; Gilshteyn, 2018; Liu Y. et al., 2018; Park et al., 2018) and dilatation/vibrations of buildings as well as other large infrastructure (Schumacher and Thostenson, 2014; Augustin, 2018) among many others (Amjadi et al., 2016).
In contrast to bulk or thin film Au, quite large gauge factors (from 33 to 109) were measured for very thin films (assembled 2–3 particle layers) of monodisperse (12 nm in diameter) 3-mercaptopropionic acid and 6-mercaptohexanoic acid functionalized Au nanoparticles. The unprecedented gauge factors are explained by the easy change of inter-particle distances in the soft mercaptocarboxylic matrix causing considerable variation of tunneling resistances and current paths in the nanoparticle network (Jiang et al., 2015). In fact, percolation and tunneling play crucial roles in the overall piezoresisive behavior of composites with conductive fillers (e.g., carbon or metal nanomaterials) embedded in polymer matrices (Stassi et al., 2014). A large variety of organic as well as inorganic polymer composites with highly diverse mechanical properties was demonstrated in the past years, such as CNTs, carbon filaments, graphene and MXenes e.g., in poly(methyl methacrylate) (Kang et al., 2006), polysulfone (Oliva-Aviles et al., 2011), poly(dimethylsiloxane) (Liu and Choi, 2010; Hou et al., 2013) epoxy (Chiacchiarelli et al., 2013), polyimide (Ma et al., 2017), poly(styrene-butadienestyrene) (Wang et al., 2018), or even in concrete (Chung, 2002). Also polymer blends of conductive and insulating phases were proved as useful strain gauge materials. For instance, solution cast films of polyaniline and styrene-ethylene/butylene-styrene SEBS copolymer were found to bear with piezoresistive character with moderate GFs of ~2 (Costa et al., 2018); however, electrospun fibers of poly(3,4-ethylenedioxythiophene) poly(styrenesulfonate) and polyvinyl alcohol showed GF up to ~400 (Liu et al., 2011). Foams of intrinsically conductive materials as well as their polymer composites enrich even further the palette of piezoresistive materials providing new degrees of freedom (e.g., porosity, pore structure) to tune the mechanical and electromechanical properties (Pham et al., 2014; Liu H. et al., 2017; Ke et al., 2018; Liu W. et al., 2018; Yang et al., 2018). Such a good mechanical diversity is particularly important since the optimal transfer of strain or displacement from the object to the sensor device requires soft (or stiff) matrices for large (small) displacements or deformations of soft (stiff) objects. The gauge factors of soft composites is typically low or moderate (between 1 and 10) but allow good analysis of large strains of up to several tens of percentages, whereas hard composites such as those of epoxy or cement have GF values even above 50 (Chiacchiarelli et al., 2013; Yoo et al., 2018) which can be exploited in low strain regimes.
Here, we present and compare soft piezoresistive foams of pyrolyzed polymer foams and their hierarchical structures with carbon nanotubes (CNTs) and nanofibers (CNFs), which display high gauge factors in a large strain window. The fascinating properties pave the road for versatile strain sensing in very different fields that we also demonstrate here. In addition, in an attempt to explain the underlying mechanism of piezoresistive behavior, we analyze the strain dependent conductivity data and highlight the shortcomings of the percolation model for the foam-type 3-dimensional conductive networks.
Pyrolysis of the melamine foams results in a significant weight loss (~90%) and volumetric shrinkage (~90%), while the open-pore structure remains unchanged. After impregnating nickel acetylacetonate and reducing that in H2 to form Ni nanoparticles in the foams, we grow CNTs/CNFs at 770°C on the catalyst nanoparticles along the skeletal structure by chemical vapor deposition from acetylene precursor. The dimensions of the as-synthesized hierarchical hybrid structures do not decrease any further compared to the parent carbon foams. The CNTs are multi-walled with high concentration of defects as indicated by their curled microstructure. Apart from CNTs, we can also find some CNFs, which emerge from larger Ni catalyst nanoparticle upon the CVD process (Figures 1A–I).

Figure 1. (a,d,g) Schematic drawings of the original open pore structure melamine foam, carbon foam and hierarchical carbon foam and carbon nanotube hybrid, respectively. Panels (b,e,h) show low magnification scanning electron micrographs of the corresponding structures. In panels (c,f,i) magnified images of the samples are shown as indicated by the corresponding white rectangular selected areas in images (b,e,g).
Resistance and stress measurements vs. mechanical strain show both the carbon foam and its hierarchical structures with CNTs/CNFs have highly non-linear behavior (Figures 2A–D). The Young's moduli of the materials increase with compression between 1–65 kPa and 0.1–92 kPa for the foam and hierarchical structure, respectively. The enormous decrease of resistances being approximately 3-orders of magnitude upon 50% compressive strain for both types of materials make up giant gauge factors |GF| > 1000. Even the differential gauge factors calculated as are having values as high as −10 in the low strain regime (0 < ε < 0.2). The differential pressure sensitivity values are 0.002 and 0.016 Pa−1 (at ε = 0.1) for the carbon foam and hierarchical structures, respectively making these materials as promising choices for detecting both small and large displacements with excellent accuracy of electrical resistance readout. The hierarchical structures display pressure sensitivities close those measured for highly complicated laminated multilayer thin films structures of polypyrrole, polyvinyl alcohol nanowires, polyethylene terephthalate, and indium-doped tin oxide (Luo et al., 2017).
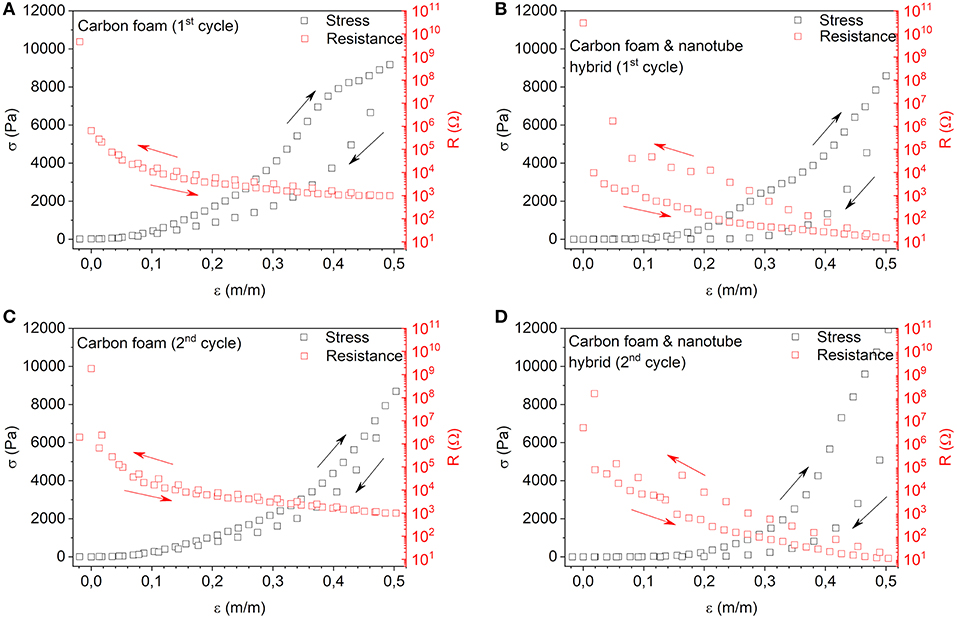
Figure 2. Electrical resistance and mechanical stress as a function of strain for (A) carbon foam and (B) hierarchical carbon foam and carbon nanotube hybrid structures measured in the first deformation cycle up to ~50%strain and back to the starting position. Panels (C,D) display the measured data obtained in the second deformation cycle for the corresponding specimens. The original dimensions (width × length × height) of the samples are 11.1 × 9.0 × 2.0 mm3 (carbon foam) and 9.6 × 9.3 × 2.0 mm3 (carbon foam and nanotube hybrid). The first resistance data point in each plot below 0% strain indicates insufficient contact with the electrodes in the experimental jig.
To assess the piezoresistive functionality of the carbon foams in the practice, we mounted their small pieces in three very different environments: between two structurally separate walls in our laboratory building as well as on a human index finger joint and over the radial artery of a wrist (Figure 3). In each experiment, the applied foams were simply sandwiched between aluminum packaging foil slices (acting as electrical contacts) and then pre-stressed to ensure firm fixture of the sensors for the experiments to detect relative motion of the adjacent walls as well as to analyze flexing of the finger and to monitor heart rate, respectively.
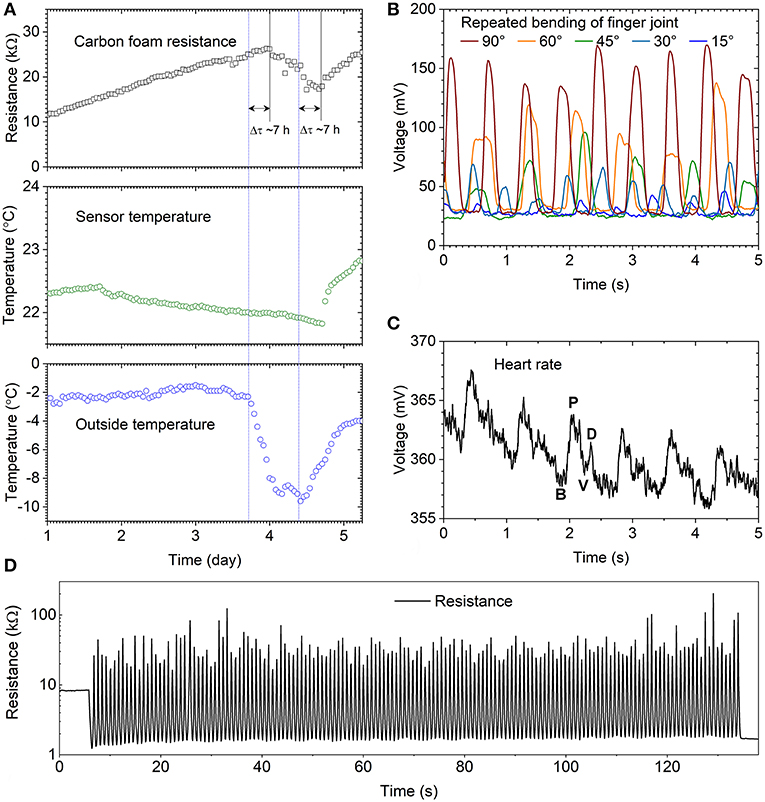
Figure 3. Carbon foam based sensors monitoring displacements with highly diverse nature: (A) relative displacement of adjacent building walls constructed on separate concrete foundations, (B) repeated flexing of the index finger joint between the middle and proximal phalanges, and (C) heart rate monitored on the radial artery (B: base point, P: percussion wave, V: valley and D: dicrotic wave). (D) Resistance of a cube shaped foam under mechanical compression cycling (160 repetitions at 30% strain).
The electrical resistance of the carbon foam placed between the two separate building walls (Figure 3A) shows a continuous drift, which seems to be independent from the temperature of the sensor (monitored with a thermocouple placed next to it). This is not surprising, since the temperature coefficient of resistance at near room temperature for the foam is about−0.02 deg−1 that we calculated from the temperature dependent resistance data published earlier (Pham et al., 2014). On day 4, the monotonic increase of resistance is broken by a significant drop (ΔR/R~-0.4) that occurred within a period of 16 h, suggesting a slow but well defined compressive deformation of the sensor. The relative change of resistance corresponds to ~4% decrease of the length of the sensor from ~5.0 mm to ~4.8 mm corresponding to a relative lateral displacement of ~0.2 mm of the two walls. Motion of buildings is a known phenomenon (Lenczner, 1981), which may be caused by several reasons, including the change of the environment moisture and temperature as well as subsequent variation of the temperature gradients in the ground and building parts. To see whether the change of weather conditions could be responsible for the lateral movement of the two separate walls detected by the sensor, we checked the official outside air temperature measured by a meteorological station ~5 km from our laboratory. The records show that the outside air temperature has started to drop from −2°C to −10°C about 7 h before the sensor detected the displacement. When the temperature has started to increase again (after ~16 h), the resistance of the sensor followed that, again with ~7 h of delay indicating the possible correlation between the outside air temperature and building motion data.
Carbon foams mounted on an index finger and on the radial artery also proved to be feasible for monitoring the corresponding physiological functions. In the former case, the higher degree the finger is flexed, the higher the measured voltage drop is measured over the resistor connected in series with the sensor (Figure 3B). This is logical since flexing of the finger compresses the sensor making it more conductive, thus allowing higher currents in the circuit. Even without any particular optimization, already ~15° flexing angle can be detected well. As for the pulse monitoring sensor, we can clearly follow up the heart beats by simply pressing the foam against the radial artery (Figure 3C). Considering the voltage signal variation, measured over a series resistor of 330 Ω, the change of the current in the circuit is ~2%, which corresponds to ~3% decrease of the sensor device resistance being sufficient to resolve the typical waveform (Chang, 2013) including the percussion wave, dicrotic notch (valley) and dicrotic wave in each pulse.
The foams are not only easy to integrate into very different environments to perform sensing but they also show reliable operation over long period of time as demonstrated in the building wall displacement measurements (Figure 3A) and they can stand repeated deformations very well (Figures 3B–D). These properties are particularly important in the practice and make the carbon based foams a good challenger of other soft piezoresistive composites of polymers and conductive fillers.
In 2 or 3-dimensional (2D or 3D) networks of nanomaterials, the conduction mechanism has been shown to obey the percolation-tunneling model described by the power function , where κ is the conductivity, c is the volumetric concentration or areal density of the conductive filler, c0 is the corresponding critical concentration or density, and α is the critical exponent having a typical (universal) value of around 2 for 3D (Hou et al., 2013) and 1.33 for 2D networks (Hu et al., 2004), respectively. Furthermore, even conductivity of cellular and reticulated vitreous carbon foams derived from self-similar polymer foams (e.g., phenolic-furanic foams, polyurethane templates resorcinol-formaldehyde) have been shown to have power function dependence on the density of structures (Letellier et al., 2017).
To plot our data and see whether it is in line with the percolation model, we first transform the R resistance values to conductivity taking into account the deformation of the foam as: , where l and A are the original sample thickness and cross-section area, ε is the applied strain and ν is the Poisson's ratio considered as 0.3, typical for foams. Similarly, we also transform the strain axes to concentration by taking it as unity at ε = 0 and dividing that with the volume of the deformed sample as: . After having κ and c, in a double logarithmic plot, a linear fit gives the critical exponent, α. We find that none of the plots may be fitted with a single linear. In the case of the carbon foam, we cannot make any sort of reasonable fit because of the continuously changing slope as shown in Figure 4A. For the hybrid sample in Figure 4B, we find the data scatters around two linear slopes giving critical exponents 31.0 ± 2.3 (low strain regime 0 < ε < 0.2) and 3.7 ± 0.2 (high strains 0.2 < ε < 0.5), both being rather high in reference to the universal value of 2 supposed to be valid for random networks of percolating conductors. Accordingly, the very steep function of resistance vs. strain in our carbon foams and hierarchical structures cannot be explained by a simple percolation-tunneling model of conductors placed randomly in a volume. This is actually not completely surprising, since percolated foams are not fulfilling entirely the conditions of the model. Instead of having randomly placed conductors in 3D, the carbon foam made by the pyrolysis of melamine foam is a macroscopically continuous 3D skeleton of a carbon material with poorly ordered sp2 and sp3 content, which is likely to follow the multi-phonon hopping transport model as we concluded earlier from temperature dependent electrical conductivity measurements (Pham et al., 2014). Here, we speculate that upon deformation, the stresses in certain volumes of the carbon skeleton change the electronic band structure locally (e.g., by introducing new energy states in the insulating domains of the material and/or changing the Fermi level in the conductive phase) and alter not only the heights of tunneling gaps but also the distances between adjacent conductive regions thus giving rise to a highly complex strain dependent conduction. We have to emphasize here, that stress dependent conduction is not only seen for ordinary semiconducting crystals, but has been shown both theoretically and experimentally for various form of carbon nanomaterials. In the case of carbon nanotubes, band gap opening is common under stress (Martel et al., 1998; Yang and Han, 2000). Further, as it was concluded for sputter deposited amorphous carbon films with both sp2 and sp3 carbon content, the piezoresistivity of such material is due to hopping between conductive sp2 grains in an insulating sp3 surrounding (Grimaldi et al., 2000; Peiner et al., 2006).
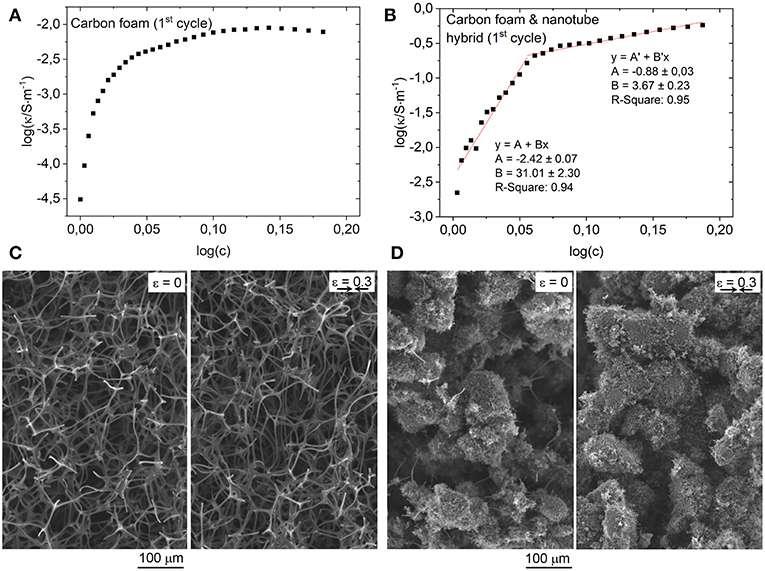
Figure 4. Double logarithmic plots of the electrical conductivity and concentration (strain dependent inverse volume) for (A) carbon foam and (B) carbon foam and carbon nanotube hybrid structures. The plots are derived from the first compression cycle data of electrical resistance vs. mechanical stress in Figures 2A,B. Scanning electron micrographs of (C) carbon foam and (D) composite foam without and with uniaxial strain.
On the other hand, in the case of the carbon foam and nanotube hybrid structure, electrical transport via the CNT network superposes on the one of the skeletal structure, and plays also a role in the overall conduction process. At low strains, the CNT network on the skeleton of the foam is already forming an entangled layer, which is reflected by the relatively high conductivity of the hybrid foam in reference to the carbon foam (~10−2 vs. ~10−4 S/m). Increasing the strain in the hybrid structure until ε~20% is improving the conduction in the skeleton as described for the carbon foam. Over ~20% strain, we find a change of the conduction mechanism with a critical exponent of 3.7 ± 0.2 (in contrast to the low strain exponent being 31.0 ± 2.3). Considering the microstructure of the hierarchically structured foam, it is a physically realistic scenario that strains above ~20% result in new contacts between the CNT networks located at the adjacent skeletal wires of the carbon foam. To visualize such a phenomenon, we use electron microscopy imaging to analyze how the skeleton structure of the carbon foam as well as the hierarchical structure of the composite foam change under mechanical strain (ε = 0.3). As shown in Figure 4C, the skeleton of the carbon foam only deforms without significantly changing the density of the interconnects. On the other hand, upon compression of the carbon nanotube coated composite foam, a more compact structure seems to form, in which the nanotube layers on adjacent skeleton wires can make direct contacts (Figure 4D). As such, we can eventually talk about percolation and tunneling in the foam despite the slightly higher critical exponent than the anticipated universal value for 3D network of conductive particles.
In fact, the critical exponent may show non-universal values, usually exceeding the value of 2, as found in carbon-polymer composites and granular metal-oxide networks (Vionnet-Menot et al., 2005; Bauhofer and Kovacs, 2008). The origin of such behavior has been extensively studied during the past years and has been attributed to anisotropy (Celzard and Marêché, 2003) as well as to the statistical distribution of the electrical transport properties of the contacts (Kogut and Straley, 1979; Halperin et al., 1985; Feng et al., 1987). For instance, according to the inverted random-void model (Balberg, 1987, 1998), in which tunneling current flows between conducting spheres placed in an insulating matrix, the critical exponent may be dependent on the mean tunneling distance and can be much higher than 2, if the distribution function of the tunneling distances decays slower than the tunneling decay (Vionnet-Menot et al., 2005). Therefore, these models may give a reasonable explanation why the non-ideal network of contacts between the CNT coated parts of the hybrid foam show the slightly higher critical exponent than the universal value.
In closing, we studied the piezoresistive behavior of two different types of carbon foam structures, one made by the pyrolysis of an open pore structure melamine foam, and another obtained by growing carbon nanotubes/nanofibers in pores of the first. Both kinds of foams show giant piezoresistive gauge factors (GF < −1000) and withstand very large compressive deformations (ε ~0.5) that are reversible after the first compression cycle thus enabling versatile strain gauge applications for displacement, deformation, and pressure sensing. The giant piezoresistive gauge factors cannot be explained solely by the classical percolation-tunneling model. The results suggest a more complex mechanism, in which a local variation of the electrical transport behavior in the sp2-sp3 hybridized carbon skeleton of the foam takes place due to local stresses upon mechanical deformation.
The carbon foams were obtained by pyrolyzing melamine foam (BASF, Basotect® W) at 800°C for 60 min in 150 mL/min flow of N2 similar to that we described earlier (Pham et al., 2014). Heating rates of 15°C/min until 300°C, and 2°C/min from 300 to 800°C were applied. The obtained carbon foams were rinsed and sonicated in de-ionized water and then dried at 70°C overnight to remove any Na+ impurities enriched on the surface of the skeletal structure we found by XPS in our previous work (Pham et al., 2014). To grow carbon nanotubes in the pores of the foams, the samples were cut into 30 × 10 × 5 mm3 pieces, impregnated with a solution of nickel acetylacetonate (0.8 g/L in acetone), and then dried in a box furnace at 70°C for 1 h. After decomposing and reducing the Ni precursor to metallic Ni nanoparticles in 2 L/min 15% H2/Ar flow at 770°C for 6 min, the gas flow was switched for a mixture of C2H2 (80 mL/min) and 15% H2/Ar (70 mL/min, bubbled through a water container) for 30 min.
For the mechanical strain dependent stress and electrical resistance measurements, the synthesized foams were cut into pieces of ~10 × 10 × 2 mm3 size and then were placed between two parallel copper plates. The lower plate was fixed on a tray of a computer connected weighting scale (Precisa LS 620M), whereas the upper plate was mounted on a computer controlled vertical translation stage. The pressing force was calculated from the measured weight upon compression adjusted by the vertical displacement of the upper copper electrode plate. The as formed circuit was sourced with 5 V DC and the current was measured using a Keithley 2636A SourceMeter.
A rectangular foam cut to a size of 23 × 5 × 7 mm3 was brought in mechanical contact with Al packaging foil sheets and after being pressed along the 7 mm long side, it was placed in a gap of ~5 mm between two walls in our laboratory. One of the walls is an ordinary wall of the building, whereas the other one is a part of a vibration-free structure built on a separate and more robust concrete foundation. The resistance of the pre-strained foam was measured with a Fluke 2635A Hydra Series II Data Bucket for over several days. A thermocouple was placed in the proximity of the sensor to monitor the actual temperature of the sensor. For the local temperature outside the building we use the weather data of the Finnish Meteorological Institute collected at a station located ~5 km from our laboratory building.
A piece of carbon foam with dimensions of 15 × 5 × 3 mm3 was equipped with two Al foil slices and then fixed over the joint of proximal and middle phalanges of the index finger using a rubber ring. A resistor of 330 Ω was connected in series to the sensor and the circuit was sourced with 1 V (Agilent E3630A), while the voltage drop over the resistor was using an oscilloscope (Agilent DSO-X 3024A).
The measurement setup is similar to that used in the analysis of finger joint bending but the carbon foam (size of 5 × 5 × 5 mm3) sandwiched between Al foil pieces was manually pressed against the radial artery with a pressure of ~15 kPa.
OP designed and performed the experiments. KK and OP analyzed the data and wrote the paper.
The authors acknowledge funding received from the EU H2020 (NewPack), Business Finland (Grelectronics), Academy of Finland (Suplacat), Interreg Nord–Lapin liitto (Flexibla Transparenta Ledande Filmer som Electroder), University of Oulu (more-than-Moore RC and Entity), and Infotech Oulu.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Technical help of Dr. Jussi Putaala and Topias Järvinen are acknowledged. We also thank the support received from the Micro- and Nanotechnology Center, University of Oulu.
Amjadi, M., Kyung, K. U., Park, I., and Sitti, M. (2016). Stretchable, skin-mountable, and wearable strain sensors and their potential applications: a review. Adv. Funct. Mater. 26, 1678–1698. doi: 10.1002/adfm.201504755
Augustin, T. (2018). Structural Health Monitoring of Carbon Fiber Reinforced Polymers and Carbon Nanotube Modified Adhesive Joints via Electrical Resistance Measurement. Doctoral thesis, Hamburg University of Technology, Germany.
Bae, S.-H., Lee, Y., Sharma, B. K., Lee, H.-J., kim, J.-H., and Ahn, J.-H. (2013). Graphene-based transparent strain sensor, Carbon 51, 236–242. doi: 10.1016/j.carbon.2012.08.048
Balberg, I. (1987). Tunneling and nonuniversal conductivity in composite materials. Phys. Rev. Lett. 59, 1305–1308. doi: 10.1103/PhysRevLett.59.1305
Balberg, I. (1998). Limits on the continuum-percolation transport exponents. Phys. Rev. B 57, 13351–13354. doi: 10.1103/PhysRevB.57.13351.
Bardeen, J., and Shockley, W. (1950). Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 80:72. doi: 10.1103/PhysRev.80.72
Bauhofer, W., and Kovacs, J. Z. (2008). A review and analysis of electrical percolation in carbon nanotube polymer composites. Comp. Sci. Technol. 69, 1486–1498. doi: 10.1016/j.compscitech.2008.06.018
Celzard, A., and Marêché, J. F. (2003). Non-universal conductivity critical exponents in anisotropic percolating media: a new interpretation. Phys. A 317 305–312. doi: 10.1016/S0378-4371(02)01367-5
Chang, H., Kim, S., Jin, S., Lee, S. W., Yang, G. T., Lee, K. Y., et al. (2018). Ultrasensitive and highly stable resistive pressure sensors with biomaterial-incorporated interfacial layers for wearable health-monitoring and human-machine interfaces. ACS. Appl. Mater. Interf. 10, 1067–1076. doi: 10.1021/acsami.7b14048
Chang, S. (2013). The meridian system and mechanism of acupuncture–a comparative review. Part 2: mechanism of acupuncture analgesia. Taiwan J. Obstet. Gynecol. 52, 14–24. doi: 10.1016/j.tjog.2013.01.004
Chiacchiarelli, L. M., Rallini, M., Monti, M., Puglia, D., Kenny, J. M., and Torre, L. (2013). The role of irreversible and reversible phenomena in the piezoresistive behavior of graphene epoxy nanocomposites applied to structural health monitoring. Composite Sci. Technol. 80, 73–79. doi: 10.1016/j.compscitech.2013.03.009
Chun, S., Son, W., and Choi, C. (2018). Flexible pressure sensors using highly-oriented and free-standing carbon nanotube sheets. Carbon 139, 586–592. doi: 10.1016/j.carbon.2018.07.005
Chung, D. D. L. (2002). Piezoresistive cement-based materials for strain sensing. J. Intell. Mater. Syst. Struct. 13, 599–609. doi: 10.1106/104538902031861
Costa, P., Oliveira, J., Horta-Romarís, L., Abad, M.-J., Moreira, J. A., Zapiráin, I., et al. (2018). Piezoresistive polymer blends for electromechanical sensor applications. Comp. Sci. Technol. 168, 353–362. doi: 10.1016/j.compscitech.2018.10.022
Cunningham, M. J., and Bibby, G. L. (1993). “Measurement and instrumentation,” in Electrical Engineer's Reference Book, ed G. R. Jones (Oxford: Butterworth-Heinemann Ltd.), 3/39.
Feng, C., Liu, K., Wu, J.-S., Liu, L., Cheng, J.-S., Zhang, Y., et al. (2010). Flexible, stretchable, transparent conducting films made from superaligned carbon nanotubes. Adv. Funct. Mater. 20, 885–891. doi: 10.1002/adfm.200901960
Feng, S., Halperin, B. I., and Sen, P. N. (1987). Transport properties of continuum systems near the percolation threshold. Phys. Rev. B 35, 197–214. doi: 10.1103/PhysRevB.35.197
Fraga, M. A., Furlan, H., Pessoa, R. S., Rasia, L. A., and Mateus, C. F. R. (2012). Studies on SiC, DLC and TiO2 thin films as piezoresistive sensor materials for high temperature application. Microsyst. Technol. 18, 1027–1033. doi: 10.1007/s00542-012-1435-y
Gilshteyn, E. (2018). Components for Stretchable Electronics Based on Single-Walled Carbon Nanotubes. Doctoral thesis, Skolkovo Institute of Science and Technology, Russia.
Gilshteyn, E., and Nasibulin, A. G. (2015). “Aerosol synthesized carbon nanotube films for stretchable electronic applications,”in IEEE 15th International Conference on Nanotechnology (IEEE-NANO) 27-30 July 2015, Rome, 893–896. doi: 10.1109/NANO.2015.7388758
Grimaldi, C., Ryser, P., and Strässler, S. (2000). Gauge factor of thick film resistors: outcomes of the variable range hopping model. J. Appl. Phys. 88, 4164–4169. doi: 10.1063/1.1290738
Halperin, B. I., Feng, S., and Sen, P. N. (1985). Differences between lattice and continuum percolation transport exponents. Phys. Rev. Lett. 54, 2391–2394. doi: 10.1103/PhysRevLett.54.2391
He, R., and Yang, P. (2006). Giant piezoresistance effect in silicon nanowires. Nat. Nanotechnol. 1, 42–46. doi: 10.1038/nnano.2006.53
Hosseini, M., Elahi, M., Pourfath, M., and Esseni, D. (2015). Very large strain gauges based on single layer MoSe2 and WSe2 for sensing applications. Appl. Phys. Lett. 107:253503. doi: 10.1063/1.4937438
Hou, Y., Wang, D. R., Zhang, X. M., Zhao, H., Zha, J. W., and Dang, Z. M. (2013). Positive piezoresistive behavior of electrically conductive alkyl-functionalized graphene/polydimethylsilicone nanocomposites. J. Mater. Chem. C 1, 515–521. doi: 10.1039/c2tc00114d
Hu, C., Gao, Y., and Sheng, Z. (2000). The piezoresistance coefficients of copper and copper-nickel alloys. J. Mater. Sci. 35, 381–386. doi: 10.1023/A:1004755014553
Hu, L., Hecht, D. S., and Grüner, G. (2004). Percolation in transparent and conducting carbon nanotube networks. Phys. Rev. B 4, 2513–2517. doi: 10.1021/nl048435y
Jiang, C. H., Ni, I.-C., Tzeng, S.-D., and Kuo, W. (2015). Nearly isotropic piezoresistive response due to charge detour conduction in nanoparticle thin films. Sci. Rep. 5:11939. doi: 10.1038/srep11939
Kanda, Y. (1991). Piezoresistance effect of silicon. Sens. Actuat. A 28, 83–91. doi: 10.1016/0924-4247(91)85017-I
Kang, I., Schulz, M. J., Kim, J. H., Shanov, V., and Shi, D. (2006). A carbon nanotube strain sensor for structural health monitoring. Smart Mater. Struct. 15, 737–748. doi: 10.1088/0964-1726/15/3/009
Kaps, S., Bhowmick, S., Gröttrup, J., Hrkac, V., Stauffer, D., Guo, H., et al. (2017). Piezoresistive response of quasi-one-dimensional ZnO nanowires using an in situ electromechanical device. ACS Omega 2, 2985–2993. doi: 10.1021/acsomega.7b00041
Ke, K., Bonab, V. S., Yuan, D., and Manas-Zloczower, I. (2018). Piezoresistive thermoplastic polyurethane nanocomposites with carbon nanostructures. Carbon 139, 52–58. doi: 10.1016/j.carbon.2018.06.037
Kogut, P. M., and Straley, J. P. (1979). Distribution-induced non-universality of the percolation conductivity exponents. J. Phys. C 12:2151. doi: 10.1088/0022-3719/12/11/023
Kuang, J., Liu, L., Gao, Y., Zhou, D., Chen, Z., Han, B., et al. (2013). A hierarchically structured graphene foam and its potential as a large-scale strain-gauge sensor. Nanoscale 5, 12171–12177. doi: 10.1039/c3nr03379a
Lenczner, D. (1981). Movements in Buildings, 2nd Edn (Oxford: Pergamon Press), 1–108. doi: 10.1016/C2009-0-06788-9
Letellier, M., Macutkecic, J., Kuzhir, P., Banys, J., Fierro, V., and Celzard, A. (2017). Electromagnetic properties of model vitreous carbon foams. Carbon 122, 217–227. doi: 10.1016/j.carbon.2017.06.080
Li, P., Li, L., and Zeng, X. C. (2016). Tuning the electronic properties of monolayer and bilayer PtSe2 via strain engineering. J. Mater. Chem. A 4:18922. doi: 10.1039/C6TA08032D
Liu, C. X., and Choi, J. W. (2010). Strain-dependent resistance of PDMS and carbon nanotubes composite microstructures. IEEE Trans. Nanotechnol. 9, 590–595. doi: 10.1109/TNANO.2010.2060350
Liu, H., Dong, M., Huang, W., Gao, J., Dai, K., Guo, J., et al. (2017). Lightweight conductive graphene/thermoplastic polyurethane foams with ultrahigh compressibility for piezoresistive sensing. J. Mater. Chem. C 5:73. doi: 10.1039/c6tc03713e
Liu, N., Fang, G., Wan, J., Zhou, H., Long, H., and Zhao, X. (2011). Electrospun PEDOT:PSS–PVA nanofiber based ultrahigh-strain sensors with controllable electrical conductivity. J. Mater. Chem. 21, 18962–18966. doi: 10.1039/c1jm14491j
Liu, W., Liu, N., Yue, Y., Rao, J., Luo, C., Zhang, H., et al. (2018). A flexible and highly sensitive pressure sensor based on elastic carbon foam. J. Mater. Chem. C, 1451–1458. doi: 10.1039/c7tc05228f
Liu, X., Tang, C., Du, X., Xiong, S., Xi, S., Liu, Y., et al. (2017). A highly sensitive graphene woven fabric strain sensor for wearable wireless musical instruments. Mater. Horiz. 4, 477–486. doi: 10.1039/c7mh00104e
Liu, Y., Wang, H., Zhao, W., Zhang, M., Qin, H., and Xie, Y. (2018). Flexible, stretchable sensors for wearable health monitoring: sensing mechanisms, materials, fabrication strategies and features. Sensors 18:645. doi: 10.3390/s18020645
Luo, C., Liu, N., Zhang, H., Liu, W., Yue, Y., Wang, S., et al. (2017). A new approach for ultrahigh-performance piezoresistive sensor based on wrinkled PPy film with electrospun PVA nanowires as spacer. Nano Energy 41, 527–534. doi: 10.1016/j.nanoen.2017.10.007
Ma, Y., Liu, N., Li, L., Hu, X., Zou, Z., Wang, J., et al. (2017). A highly flexible and sensitive piezoresistive sensor based on MXene with greatly changed interlayer distances. Nat. Comm. 8:1207. doi: 10.1038/s41467-017-01136-9
Manzeli, S., Allain, A., Ghadimi, A., and Kis, A. (2015). Piezoresistivity and strain-induced band gap tuning in atomically thin MoS2. Nano Lett. 15, 5330–5335. doi: 10.1021/acs.nanolett.5b01689
Martel, R., Schmidt, T., Shea, H. R., Hertel, T., and Avouris, P. H. (1998). Single- and multi-wall carbon nanotube field-effect transistors. Appl. Phys. Lett. 73, 2447–2449. doi: 10.1063/1.122477
Mi, Q, Wang, Q., Zang, S., Mao, G., Zhang, J., and Ren, X. (2017). RGO-coated elastic fibres as wearable strain sensors for full-scale detection of human motions. Smart Mater. Struct. 27:015014. doi: 10.1088/1361-665X/aa9aff
Milne, J. S., Rowe, A. C. H., Arscott, S., and Renner, C. H. (2010). Giant piezoresistance effects in silicon nanowires and microwires. Phys. Rev. Lett. 105:226802. doi: 10.1103/PhysRevLett.105.226802.
Nayak, A. P., Bhattacharyya, S., Zhu, J., Liu, J., Wu, X., Pandey, T., et al. (2014). Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun. 5:3731. doi: 10.1038/ncomms4731
Oliva-Aviles, A. I., Aviles, F., and Sosa, V. (2011). Electrical and piezoresistive properties of multi-walled carbon nanotube/polymer composite films aligned by an electric field. Carbon 49, 2989–2997. doi: 10.1016/j.carbon.2011.03.017
Park, S.-J., Kim, J., Chu, M., and Khine, M. (2018). Flexible piezoresistive pressure sensor using wrinkled carbon nanotube thin films for human physiological signals. Adv. Mater. Technol. 3:1700158. doi: 10.1002/admt.201700158
Peiner, E., Tibrewala, A., Bandorf, R., Biehl, S., Lüthje, H., and Doering, L. (2006). Micro force sensor with piezoresistive amorphous carbon strain gauge. Sens. Actuat. A 130–131, 75–82. doi: 10.1016/j.sna.2005.11.059
Pham, T. N., Samikannu, A., Kukkola, J., Rautio, A.-R., Pitkänen, O., Dombovari, A., et al. (2014). Industrially benign super-compressible piezoresistive carbon foams with predefined wetting properties: from environmental to electrical applications. Sci. Rep. 4:6933. doi: 10.1038/srep06933
Schmid, P., Zarfl, C., Balogh, G., and Schmid, U. (2014). Gauge factor of titanium/platinum thin films up to 350°C. Proc. Eng. 87, 172–175. doi: 10.1016/j.proeng.2014.11.611
Schumacher, T., and Thostenson, E. T. (2014). Development of structural carbon nanotube–based sensing composites for concrete structures. J. Intellig. Mater. Syst. Struct. 25, 1331–1339. doi: 10.1177/1045389X13505252
Schweizer, T. M. (2005). Electrical Characterization and Investigation of the Piezoresistive E?ect of PEDOT:PSS Thin films. Master's thesis, Georgia Institute of Technology, US.
Smith, A. D., Niklaus, F., Paussa, A., Vaziri, S., Fischer, A. C., Sterner, M., et al. (2013). Electromechanical piezoresistive sensing in suspended graphene membranes. Nano Lett. 13, 3237–3242. doi: 10.1021/nl401352k
Stassi, S., Cauda, V., Canavese, G., and Pirri, C. F. (2014). Flexible tactile sensing based on piezoresistive composites: a review. Sensors 14, 5296–5332. doi: 10.3390/s140305296
Tadakaluru, S., Thongsuwan, W., and Singjai, P. (2014). Stretchable and flexible high-strain sensors made using carbon nanotubes and graphite films on natural rubber. Sensors 14, 868–876. doi: 10.3390/s140100868
Vionnet-Menot, S., Grimaldi, C., Maeder, T., Strässler, S., and Ryser, P. (2005). Tunneling-percolation origin of nonuniversality: theory and experiments. Phys. Rev. B 71:064201. doi: 10.1103/PhysRevB.71.064201.
Wagner, S., Yim, C., McEvoy, N., Kataria, S., Yokaribas, V., Kuc, A., et al. (2018). Highly sensitive electromechanical piezoresistive pressure sensors based on large-area layered PtSe2 films. Nano Lett. 18, 3738–3745. doi: 10.1021/acs.nanolett.8b00928
Wang, X., Meng, S., Tebyetekerwa, M., Li, Y., Pionteck, J., Sun, B., et al. (2018). Highly sensitive and stretchable piezoresistive strain sensor based on conductive poly(styrene-butadiene-styrene)/few layer graphene composite fiber. Compos. A 105, 291–299. doi: 10.1016/j.compositesa.2017.11.027
Wen, X., Yang, W., Ding, Y., Niu, S., and Wang, Z. L. (2014). Piezoresistive effect in MoO3 nanobelts and its application in strain-enhanced oxygen sensors. Nano Res. 7, 180–189. doi: 10.1007/s12274-013-0385-8
Xu, M., Qi, J., Li, F., and Zhang, Y. (2018). Highly stretchable strain sensors with reduced graphene oxide sensing liquids for wearable electronics. Nanoscale 10, 5264–5271. doi: 10.1039/c7nr09022f
Yang, J., Ye, Y., Li, X., Lü, X., and Checn, R. (2018). Flexible, conductive, and highly pressure-sensitive graphene-polyimide foam for pressure sensor application. Compos. Sci. Technol. 164, 187–197. doi: 10.1016/j.compscitech.2018.05.044
Yang, L., and Han, J. (2000). Electronic structure of deformed carbon nanotubes. Phys. Rev. Lett. 85, 154–157. doi: 10.1103/PhysRevLett.85.154
Yi, J., Bai, H. Y., Zhao, D. Q., Pan, M. X., and Wang, W. H. (2011). Piezoresistance effect of metallic glassy fibers. Appl. Phys. Lett. 98:241917. doi: 10.1063/1.3599843
Yoo, D.-Y., You, I., Youn, H., and Lee, S.-J. (2018). Electrical and piezoresistive properties of cement composites with carbon nanomaterials. J. Compos. Mater. 52, 3325–3340. doi: 10.1177/0021998318764809
Keywords: carbon foams, carbon nanotubes, hybrid structures, piezoresistivity, non-universal conductivity critical exponent, percolation, strain gauges
Citation: Kordas K and Pitkänen O (2019) Piezoresistive Carbon Foams in Sensing Applications. Front. Mater. 6:93. doi: 10.3389/fmats.2019.00093
Received: 30 December 2018; Accepted: 12 April 2019;
Published: 03 May 2019.
Edited by:
Federico Cesano, University of Turin, ItalyReviewed by:
Senentxu Lanceros-Mendez, University of Minho, PortugalCopyright © 2019 Kordas and Pitkänen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Krisztian Kordas, a3Jpc3p0aWFuLmtvcmRhc0BvdWx1LmZp
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.