The Structure of Amorphous and Deeply Supercooled Liquid Alumina

Shi, Caijuan; Alderman, Oliver L. G.; Berman, Diana; Du, Jincheng; Neuefeind, Joerg; Tamalonis, Anthony; Weber, J. K. Richard; You, Jinglin; Benmore, Chris J.

doi:10.3389/fmats.2019.00038

ORIGINAL RESEARCH article

Front. Mater., 19 March 2019

Sec. Ceramics and Glass

Volume 6 - 2019 | https://doi.org/10.3389/fmats.2019.00038

The Structure of Amorphous and Deeply Supercooled Liquid Alumina

$\r\nCaijuan Shi,$ Caijuan Shi^1,2

Oliver L. G. Alderman³

Diana Berman⁴

Jincheng Du⁴

Joerg Neuefeind⁵

Anthony Tamalonis³

J. K. Richard Weber^2,3

Jinglin You¹

Chris J. Benmore²^*

¹State Key Laboratory of Advanced Special Steel, Shanghai Key Laboratory of Advanced Ferrometallurgy, School of Materials Science and Engineering, Shanghai University, Shanghai, China
²Argonne National Laboratory, X-Ray Science Division, Advanced Photon Source, Argonne, IL, United States
³Materials Development, Inc., Arlington Heights, IL, United States
⁴Materials Science and Engineering, University of North Texas, Denton, TX, United States
⁵Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, United States

Liquid Al₂O₃ has been supercooled more than 500 K below its melting point (T_m = 2,327 K) using aerodynamic levitation and laser heating techniques. High energy synchrotron x-ray measurements were performed over a temperature range of 1,817 ≤ T (K) ≤ 2,700 and stroboscopic neutron diffraction at 1,984 and 2,587 K. The diffraction patterns have been fitted with Empirical Potential Structure Refinement (EPSR) models and compared to classical Molecular Dynamics (MD) simulation results. Both sets of models show similar trends, indicating the presence of high populations of AlO₄ and AlO₅ polyhedral units predominantly linked by triply shared oxygen atoms. EPSR reveals that the mean Al–O coordination number changes linearly with temperature with n_AlO = 4.41 – [1.25 × 10⁻⁴] (T – T_m), with a 2.5 Å cutoff. Both EPSR and MD simulations reveal a direction of the temperature dependence of the aluminate network structure which moves further away from the glass forming ideal (n_AlO = 3) during supercooling. Furthermore, we provide new experimental data and models for amorphous alumina grown by sequential infiltration synthesis of a polymer template. The amorphous solid form likely has a larger Al-O coordination number than the liquid, consistent with expectations for the hypothetical glass.

Introduction

In the deeply entrenched terminology of glass science, Al₂O₃ is classified as an intermediate oxide, because it can function as both a “network former” (tetrahedral Al-O species) or a “network modifier” (5- or 6-fold Al) depending on the multi-component glass composition (McMillan and Piriou, 1983; Risbud et al., 1987; Stebbins et al., 2000; Benmore et al., 2003; Mei et al., 2006, 2008; Neuville et al., 2006; Weber et al., 2008; Wilding et al., 2010). In the stable corundum crystalline form (α-Al₂O₃), Al occupies octahedral sites within a hexagonal close-packed arrangement of oxygen such that n_AlO = 6. However, in the disordered molten state, the Al-O coordination number decreases substantially from 6, to form a predominantly corner-shared network of 4-fold tetrahedra mixed with some more highly coordinated Al (Neuville et al., 2009; Skinner et al., 2013). Nonetheless, pure Al₂O₃ cannot be obtained as a bulk glass, even under very fast cooling conditions (Sun, 1949; Rosenflanz et al., 2004), despite the fact that the liquid can be supercooled several hundred degrees below its melting point (Krishnan et al., 2005). Alumina can, however, be produced in amorphous forms by anodic oxidation (Lamparter and Kniep, 1997), magnetron sputtering (Lee et al., 2009, 2010; Lee and Ryu, 2017) and sequential infiltration synthesis (Berman et al., 2017).

Amorphous Al₂O₃ thin films have numerous applications in semiconductor, space and energy technologies, and their unique chemical durability and mechanical strength make them effective as protective films (Stierle et al., 2004; Kresse et al., 2005). Amorphous alumina has also been considered to contribute to dust around stars (Onaka et al., 1989; Miyata et al., 2000). Molten alumina is used for the controlled growth of large sapphire single crystals as laser hosts and optical materials (Cockayne et al., 1967; LaBelle, 1971; Fejer et al., 1984; Nubling and Harrington, 1997), and is important in governing the behavior of aluminum-fueled rocket motor effluents (Plastinin et al., 2001; Burt and Boyd, 2007). Knowledge of the atomic-scale structure is essential for understanding chemical and physical properties, and various experiments (Coutures et al., 1990; Massiot et al., 1990; Florian et al., 1995; Waseda et al., 1995; Ansell et al., 1997; Krishnan et al., 2005; Neuville et al., 2009; Skinner et al., 2013) and simulations (Ahuja et al., 1998; Belonoshko, 1998; Gutiérrez et al., 2000; Van Hoang, 2004, 2005; Van Hoang and Oh, 2004, 2005; Hung and Vinh, 2006; Verma et al., 2011) have been conducted to explore the structure of pure liquid alumina. The consensus indicates that the average Al-O coordination number falls in the range of 4–5, with a dominant proportion of AlO₄ tetrahedra (Coutures et al., 1990; Massiot et al., 1990; Florian et al., 1995; San Miguel et al., 1998; Van Hoang, 2004; Neuville et al., 2009; Skinner et al., 2013). Interpretations of NMR (Florian et al., 1995) and XANES (Neuville et al., 2009) experiments on the one hand have suggested that liquid alumina comprises of a mixture of 4- and 6-fold coordinated Al sites undergoing rapid exchange, resulting in the average coordination number 4.5. This has led to a heterogeneous structural model (Neuville et al., 2009), in which liquid alumina is supposed to comprise of a quasi-diphasic structure composed of dense corundum clusters and a less dense AlO₄ structure surrounded by octahedral vacancies. On the other hand, molecular dynamics simulations (Hemmati et al., 1999) indicate that liquid alumina consists of predominantly 5-fold coordination, with appreciable 4- and 6-fold polyhedra present. More recent work (Skinner et al., 2013) proposed an intermediate scenario, using both x-ray and neutron diffraction combined with molecular dynamics (MD) simulations, whereby liquid alumina contains mostly AlO₄, but with a significant fraction of AlO₅ units, and only minor fractions of AlO₃ and AlO₆. It is interesting to compare Skinner et al.'s model of the structure of liquid alumina with that of solid amorphous alumina, which has also been studied by x-ray, neutron diffraction (Lamparter and Kniep, 1997) and NMR (Lee et al., 2009, 2010; Lee and Ryu, 2017). In this study we find that in the amorphous forms AlO₄ tetrahedra still dominate the structure, but with even more AlO₅ units than in the liquid, and slightly more AlO₆ octahedra.

Previous attempts to extract information on the temperature-dependent structure of molten Al₂O₃ are limited. Some studies (Ansell et al., 1997; Krishnan et al., 2005) measured the x-ray structure factor of normal and supercooled liquid alumina, in the temperature range of 2,000 ≤ T (K) ≤ 2,700 over a momentum transfer range 0.5 ≤ Q (Å⁻¹) ≤ 16.0 but the results were inconclusive. To enhance the supercooling of liquid alumina, the presence of a solid container can be eliminated, which prevents heterogeneous crystal nucleation at the solid-liquid interface. In this work, aerodynamic levitation with laser heating has been combined with high-energy x-ray diffraction and stroboscopic neutron diffraction to enable measurements over extensive Q and temperature ranges, with good statistical accuracy. Empirical potential structure refinement (EPSR) (Soper, 1996, 2005) modeling is used to obtain structural models of amorphous and supercooled liquid alumina that are consistent with the neutron and x-ray measurements and to explore in detail the structural evolution with temperature. Classical molecular dynamics simulations are performed and found to provide similar results, revealing a weak but distinct structural temperature dependence of alumina in the supercooled and equilibrium liquid regimes.

Theory

In an x-ray diffraction experiment, the total structure factor S(Q) is related to the scattered intensity, I(Q), through (Keen, 2001),

\begin{matrix} \begin{array}{l} S (Q) - 1 = \frac{I (Q) - (\sum_{i} {f_{i}}^{2} (Q)) - C (Q)}{{[\sum_{i}^{} c_{i} f_{i} (Q)]}^{2}}, \end{array} & (1) \end{matrix}

where c_i is the atomic fraction of element i, and f_i(Q) represent independent atom (atomic) x-ray scatting form factors. C(Q) is the Compton scattering. A similar equation can be written for the case of neutrons in terms of the Q-independent coherent neutron scattering lengths. The measured S(Q) is most commonly expressed using the Faber–Ziman formalism (Faber and Ziman, 1965) as the sum of the x-ray weighted elemental partial structure factors S_ij(Q) whereby,

\begin{matrix} \begin{array}{l} S (Q) - 1 = \frac{\sum_{i, j} c_{i} c_{j} f_{i} (Q) f_{j} (Q) [S_{i j} (Q) - 1]}{{[\sum_{i} c_{i} f_{i} (Q)]}^{2}} . \end{array} & (2) \end{matrix}

The total pair distribution function G(r) is obtained via a sine Fourier transformation of Q.(S(Q)-1) using

\begin{matrix} G^{X / N} (r) - 1 = \frac{1}{2 π^{2} r ρ} \int_{Q_{\min}}^{Q_{\max}} Q [S^{X / N} (Q) - 1] M (Q) \sin (Q r) d Q, & (3) \end{matrix}

where ρ is the atomic number density in atoms Å⁻³. A Lorch (Lorch, 1969) or other modification function M(Q) is often used to minimize the truncation oscillations generated during the Fourier transform over a finite Q-range (defined by the Q_max limit). To emphasize the longer-r correlations, the real space differential distribution function, D(r) = 4 πρr [G(r)–1] is also defined and used in this work (Susman et al., 1991).

The partial pair distribution functions, g_ij(r) provide the average coordination number n_ij(r) between distances r₁ and r₂ by radial integration according to Keen (2001),

\begin{matrix} n_{i j} = \int_{r_{1}}^{r_{2}} 4 π r^{2} c_{i} ρ g_{i j} (r) d r . & (4) \end{matrix}

Methods

Sample Synthesis

In this study, the amorphous alumina samples were grown by sequential infiltration synthesis, which involves diffusion-controlled penetration and subsequent chemisorption of inorganic molecules inside a polymer template (Berman et al., 2017; She et al., 2017). Alumina samples were grown on a silicon substrate and subsequently removed for the measurements. The film growth procedure initially involved deposition of a 1 μm thick polystyrene-b-poly-4-vinyl pyridine (PS-p4VP) block-copolymer film with 75 k-b-25 k composition, on a substrate. After swelling at 75°C for 1 h in ethanol solution, the sample was placed in an atomic layer deposition chamber. Stepwise exposure of the polymer film to vapors of trimethylaluminum (TMA) and water results in the growth of aluminum oxide structure inside the polar domain, vinyl pyridine, of the polymer matrix. The structure of the aluminum oxide, after removal of the polymer template in an oxygen atmosphere at an elevated temperature (400°C) is amorphous (She et al., 2018). For the liquid levitation experiments, single crystal corundum (Al₂O₃) beads of 3mm diameter and 99.99% purity were used as starting material.

High-Energy X-Ray Diffraction

X-ray diffraction measurements were made at beamline 6-ID-D of the Advanced Photon Source (Argonne, IL, USA) using an incident x-ray beam of wavelength 0.123675 Å (100.25 keV). A Perkin Elmer XRD1621 area detector was placed ~400 mm downstream of the sample. It was calibrated using a polystyrene ball coated with a CeO₂ powder standard to give a Q range of 0.5–22.5 Å⁻¹. An aerodynamic levitation and laser heating system was employed to eliminate heterogeneous nucleation at the melt-container interface and thus increasing the propensity for supercooling (Alderman et al., 2016). A droplet was obtained by melting a levitated spherical alumina bead above a conical nozzle (Nordine et al., 2000; Hennet et al., 2006) in a high purity Ar or O₂ atmosphere using a 400W CO2 laser (Synrad Firestar). Diffraction patterns were collected by isothermal 120 s duration measurements, repeated in ~100 K steps cooling from 2,700 to 1,817 K. The mass of sample changed from 56.35(1) to 56.16(1) mg (a loss of 0.34%) after the series of x-ray measurements were completed. The droplet surface temperature was measured using 0.9 μm wavelength optical pyrometer (Chino IR-CAS). The pyrometer readings assumed a constant emissivity ε_λ of 0.92 for the wavelength range of 0.7–1.1 μm. The accuracy rating of the pyrometer is ~2% in the temperature range > 2,000°C and ~1% for temperatures 1,500–2,000°C. The x-ray beam was centered on the top 200 μm of the sample to align with the pyrometry measurement, avoid scattering from the conical levitation nozzle and minimize attenuation effects from the sample (Benmore et al., 2019). Only data from the top half of the Debye–Scherrer cone were used for analysis to avoid complex attenuation corrections of the scattered beam through the nozzle (Benmore and Weber, 2017). The diffraction data were corrected for detector dark currents using the data acquisition software QXRD (Jennings, 1997). The two-dimensional images were then corrected (Skinner et al., 2012) for polarization using Fit2D (Hammersley et al., 1996). The absorption, geometry, detector effects, and the normalization procedure were carried out using PDFgetX2 (Qiu et al., 2004).

Neutron Diffraction

X-ray and neutron diffraction measurements are sensitive to different aspects of the same structure owing to their differing scattering mechanisms. For liquid alumina, the x-ray diffraction data are more sensitive to the heavier Al correlations, while neutrons are scattered more strongly by the oxygen nuclei. To obtain more information from the three contributing pair terms Al-Al, Al-O, and O-O, both neutron and x-ray data were combined in this study. Neutron-diffraction measurements were made at the NOMAD beamline of the Spallation Neutron Source (SNS), Oak Ridge, TN, USA. Event-based stroboscopic data acquisition was carried out using the NOMAD diffractometer (Neuefeind et al., 2012) to study supercooled Al₂O₃. A spheroid of Al₂O₃ with a mass of ~30 mg and nominally 3 mm in diameter was laser heated in an aerodynamic levitator and the measured data normalized to a vanadium standard of approximately the same size and geometry at the same position. A pyrometer provided surface temperature data in a similar set up to x-ray measurements (Weber et al., 2014). The stroboscopic measurements were made during a stable and reproducible temperature cycle established between the equilibrium and the supercooled liquid (Granroth et al., 2018). The structure of liquid alumina was measured over the temperature range 1,984–2,587 K, cycling for 1 h, during which time no crystallization of alumina was observed.

Empirical Potential Structure Refinement

Structural models of supercooled liquid Al₂O₃ were derived from diffraction data using EPSR simulations (Soper, 1996, 2005). EPSR is a fixed-volume method which generates a disordered material structure in agreement with diffraction experiments, by employing variable interaction potentials to drive the model toward agreement with the measured scattering data. ND and XRD data were used at the temperatures 1,974 and 2,583 K, which are the mean values of ND and X-ray experiment temperature, whilst XRD data alone were used over the wider T range of those measurements 1,817–2,700 K. Initial Monte Carlo simulations were performed on 6,400 atoms within a cubic box. Temperature dependent densities are fixed by using equation 2 in (Paradis et al., 2004). These also provided reasonable starting configurations for MD simulations (section Classical Molecular Dynamics). Atoms interacted via a Lennard-Jones (12–6) potential and partial (0.5 e) charge Coulomb term, as described by Soper (Soper, 1996). The L-J parameters for O and Al were taken from Weigel et al. (2008): ε_O = 0.1,625 kJ mol⁻¹, σ_O = 3.6 Å, q_O = −e, ε_Al = 0.26 kJ mol⁻¹, σ_Al = 1.26 Å, q_Al = 1.5 e. After the initial simulation, the empirical potential term was refined to improve agreement with the scattering data, and the maximum allowed energy amplitude was set to ~30% of initial model energy. Once the goodness-of-fit parameter was minimized, structural data were collected over ensembles of more than 2,000 configurations.

It is important to note the variation in densities between amorphous alumina films obtained by different production methods, which have been found to cover a wide range between 2.66 and 3.40 g cm⁻³ as discussed in section Density. Given the strong correspondence between structure and density, we conducted EPSR simulations with different mass densities (see Table 3).

Classical Molecular Dynamics

To help understand the physics that underpin mechanisms of structural changes in supercooled liquid alumina, classical MD simulations were performed. Pair potentials for Al₂O₃ have been developed by many authors (Winkler et al., 2004; Van Hoang and Oh, 2005; Hung et al., 2006; Du and Corrales, 2007; Du et al., 2009). Of these, Du and Corrales (Du and Corrales, 2007) have reported a partial-charge model that has previously been determined to be in very good agreement with the measured x-ray and neutron diffraction results (Skinner et al., 2013). We therefore employ the Du and Corrales pair potentials in this study, which take the Buckingham form (Du and Corrales, 2007)

\begin{matrix} \begin{array}{l} U_{α β} (r) = \frac{z_{α} z_{β} e^{2}}{r} + A_{α β} exp (- r / B_{α β}) - \frac{C_{α β}}{r^{6}}, \end{array} & (5) \end{matrix}

where r is the separation of atom pairs, z_α is the charge on an ion of type α, e is the elementary charge, and A_αβ, B_αβ, and C_αβ are parameters determined by simultaneous fitting to structures and physical properties of a wide range of related crystalline materials (Massobrio et al., 2015). It has previously been noted that a problem with these pair potentials is that they can lead to unphysical attractive forces at small atomic separations (the Buckingham catastrophe) (Winkler et al., 2004; Du et al., 2009). To solve this problem, a D_αβ/r¹² repulsive term was added (Skinner et al., 2013), but this has been neglected in our simulations since the differences in structure and properties introduced by it were determined to be negligible. This would not necessarily remain the case at extremes of pressure and temperature.

Classical MD simulations were performed using the DL_POLY package (Smith and Forester, 1996) on a system containing N = 6,400 atoms. The 3-dimensional models obtained from Monte Carlo simulations (see section Empirical Potential Structure Refinement) were used as starting configurations for the MD simulations, which were conducted either in the canonical (NVT) or the isothermal-isobaric (NPT) ensemble, using a Hoover-Nose thermostat or thermostat-barostat, at P = 1 atm and various temperatures. A time step of 1.0 fs was selected, with the first 25,000 steps used for equilibration, and particle trajectories typically integrated over a further 50,000 steps. Amorphous alumina was simulated by quenching from 2,700 to 300 K stepwise, in 100K steps, with an average cooling rate of 2 × 10¹² K s⁻¹.

Density

Using an electrostatic levitation method Paradis et al. (Paradis et al., 2004) obtained a linear relation between the density and temperature of the liquid and supercooled alumina over the range 2,175 ≤ T (K) ≤ 2,435 whereby ρ(T) = 2.93 – (0.12 × 10⁻³)(T – T_m) in g cm⁻³ (Figure 1) with T_m = 2,327 K. The density of liquid alumina has also been determined using aerodynamic levitation to be ρ(T) = 2.79 – (0.118 × 10⁻³)(T − 2,500) (g cm⁻³), over the wider temperature range 2,000–3,100 K (Glorieux et al., 1999). It can be seen that the density values obtained from electrostatic levitation are systematically higher than the aerodynamic levitation measurements and are in better agreement with the values obtained from modeling neutron and x-ray diffraction data, see (Skinner et al., 2013) for further discussion. In this work we therefore chose to extend the linear relation provided by Paradis et al. (2004) to lower temperatures to analyze our experimental data.

FIGURE 1

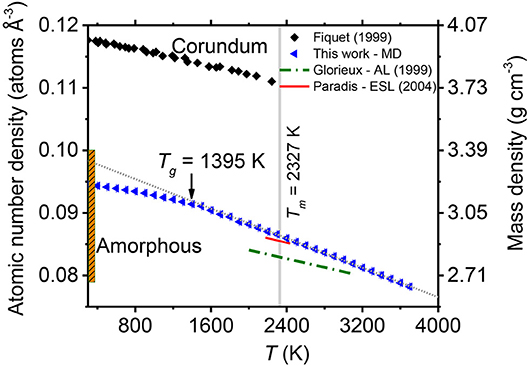
Figure 1. The temperature dependence of the density of corundum and liquid alumina. The densities of liquid and amorphous Al₂O₃ obtained by MD modeling in this paper are shown as blue triangles. The intersection of linear extrapolations of the density for the amorphous solid and the liquid yield the glass transition temperature of the model shown. The red (solid) and green (broken) lines show the experimental densities obtained by Paradis et al. (2004) and Glorieux et al. (1999), respectively. The experimental temperature-dependent densities of corundum are plotted as black diamonds (Fiquet et al., 1999). The vertical orange bar plots the range of room temperature densities of amorphous Al₂O₃ thin films (see text).

The density of amorphous alumina has been reported by several groups (Oka et al., 1979; Kniep et al., 1989; Lee et al., 1995; Wang et al., 1997; Momida et al., 2006; Gorham et al., 2014). Kniep et al. (1989) suggested that the density of pure amorphous alumina was 3.3 g cm⁻³. Lee et al. (1995) reported the density of alumina film deposited by magnetron techniques was 3.4 g cm⁻³. Momida et al. (2006) calculated the density of the amorphous structures to range from 3.02 to 3.38 g cm⁻³ using first-principles calculations. More recently, Gorham et al. (2014) synthesized a-Al₂O₃ thin films with densities ranging from 2.66 to 3.07 g cm⁻³. Wang et al. (1997) have calculated alumina film densities between 3.28 and 3.84 g cm⁻³ (with AlCl₃, H₂, and CO₂ as the reactants), which is much denser than found by other studies in the literature. This could be attributed to heavy contaminants, such as Cl. Both due to the non-equilibrium nature, and the variable porosities and impurities of the samples, the density of amorphous alumina is not unique but ranges from 2.66 to 3.4 g cm⁻³, see Figure 1.

Results

The densities of supercooled and quenched Al₂O₃ obtained by molecular dynamics simulations in this study are compared to experimental literature values in Figure 1. The liquid structure factors and pair distribution functions obtained from the diffraction and simulation methods described above are shown for the highest and lowest temperature points in Figure 2. The temperature-dependent changes in structure are highlighted in Figures 3, 4 through the use of difference functions. Results for amorphous alumina are shown in Figures 5, 6 and 7.

FIGURE 2

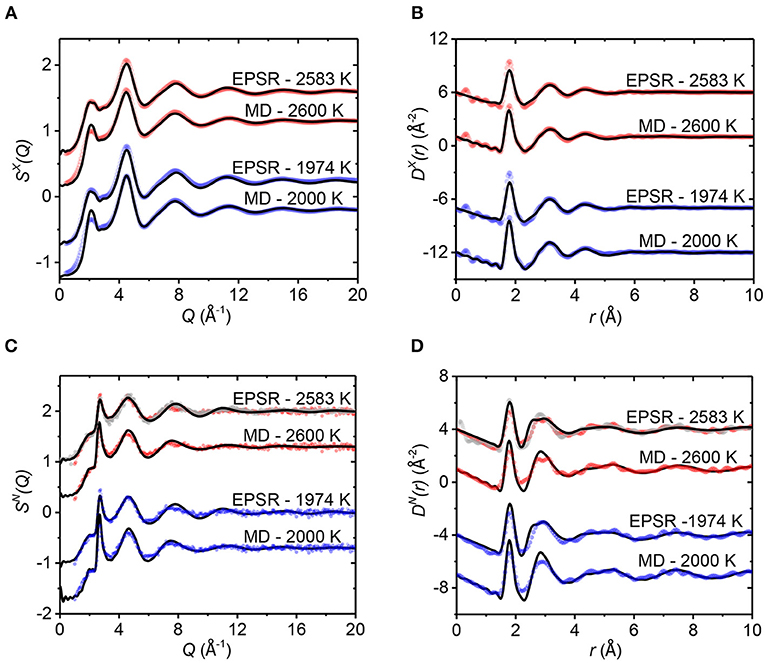
Figure 2. The x-ray (A,B) and neutron (C,D) total structure factors S(Q) (A,C) and total distribution functions D(r) (B,D), obtained with a Q_max of 20.0 Å⁻¹. In each panel, the measured data (points) are compared to the EPSR and MD simulation results (solid black lines). Skinner et al. (2013) neutron data are plotted as gray circles for comparison. Vertical offsets have been applied for clarity.

FIGURE 3

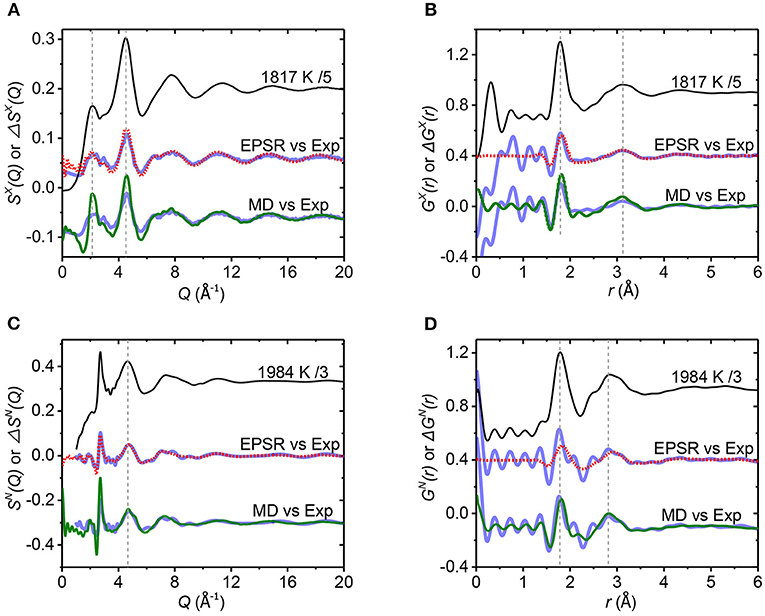
Figure 3. (A,C) show the total structure factor S(Q) at the lowest temperature measured by both x-rays (scaled by 1/5) and neutrons (scaled by 1/3), of 1,817 and 1,984 K, compared to differences, ΔS^X(Q) and ΔS^N(Q), between different temperatures. The total structure factors are shown as solid black lines, x-ray, and neutron difference data is shown as blue circles for 1,964–2,580 K and 1,984–2,587 K, respectively. EPSR results are displayed as dotted red lines using 1,974–2,583 K. Similarly, for the MD simulation solid green lines represent 2,000–2,600 K. (B,D) show the corresponding experimental pair distribution functions G^X(r) at 1,817 K (scaled by 1/5) and G^N(r) at 1,984 K (scaled by 1/3) compared to the differences ΔG^X(r) and ΔG^N(r). Vertical offsets have been applied for clarity.

FIGURE 4

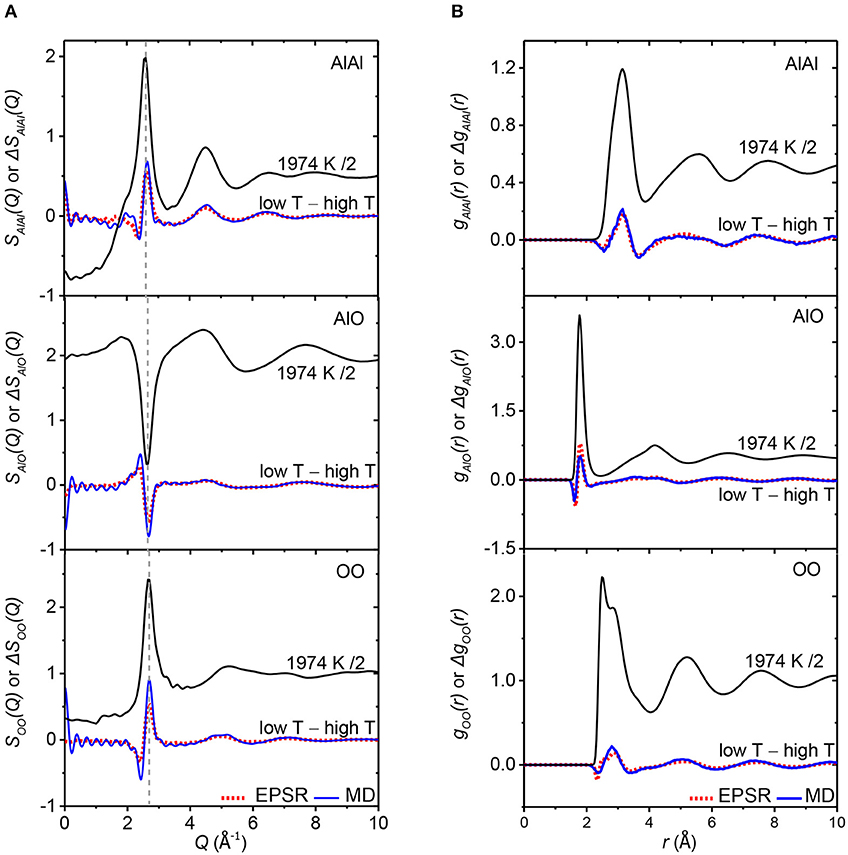
Figure 4. (A) Shows the partial structure factors S_ij(Q) for the EPSR model at a temperature of 1,974 K, compared to the temperature dependent changes (cold minus hot). The difference functions for the MD model are given by the solid blue lines (2,000–2,600 K) and the EPSR models by the dotted red lines (1,974–2,583 K). Vertical offsets have been applied for clarity. Similarly, (B) shows the corresponding partial pair-distributions functions g_ij(r) for the 1,974 K EPSR model, compared to the temperature-dependent changes, Δg_ij(r).

FIGURE 5

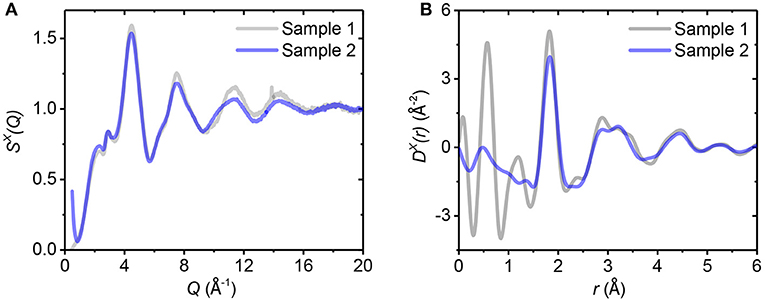
Figure 5. The (A) x-ray total structure factor S(Q) and (B) total differential distribution function D(r) for two amorphous alumina samples.

FIGURE 6

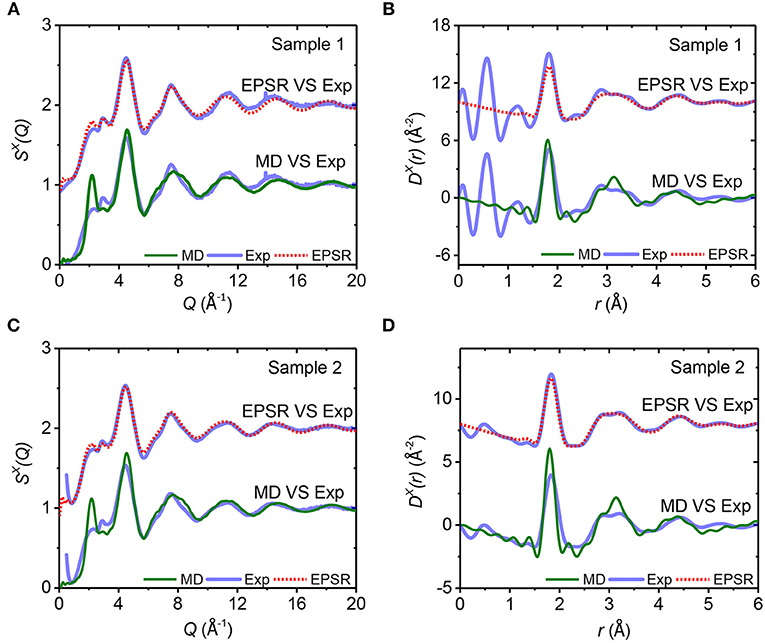
Figure 6. The x-ray total structure factors S(Q) (A,C) and total distribution functions D(r) (B,D) for amorphous alumina, obtained with a Q_max of 20.0 Å⁻¹. In each panel, the measured data (solid blue lines) are compared to the EPSR (dotted red lines) and MD simulation results (solid green lines).

FIGURE 7

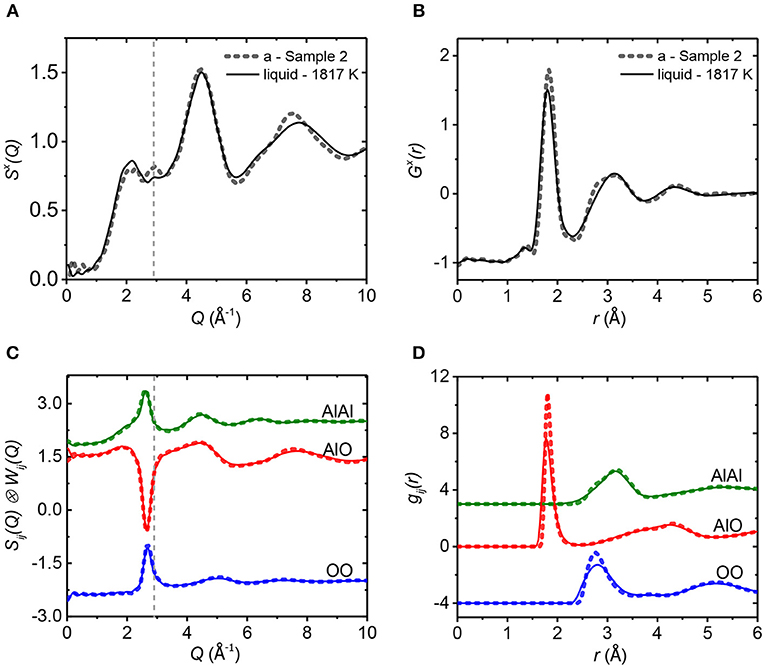
Figure 7. Comparison of amorphous Al₂O₃ (Sample 2, dotted lines) to supercooled liquid Al₂O₃ at 1,817 K (solid lines). The total (A,B) and partial (C,D) x-ray structure factors S(Q) (A,C) and pair distribution functions G(r) (B,D) from EPSR are shown. Note that the S_ij(Q) in part (C) have been multiplied by the x-ray pair weighting factors, W_ij(Q). Vertical offsets have been applied for clarity.

Diffraction Data and Simulations

For the EPSR models, the agreement with the x-ray S(Q)'s is within the experimental error. However, there is some slight disagreement in the region 6 < Q < 10 Å⁻¹ with the neutron data, and correspondingly in the 2 < r < 4 Å range in real space. The MD simulation results obtained using Du and Corrales (2007) potentials are largely consistent with the measured x-ray diffraction data (see Figure 2A) except for a small difference in the x-ray first diffraction peak at 2.12 Å⁻¹, which contains contributions from all three partials but is most pronounced in S_AlAl(Q).

Figures 2A,C show the measured and modeled structure factors S^X(Q) and S^N(Q) for liquid alumina. The data here were measured over a wider temperature range and with an improved signal-to-noise ratio compared to previous experiments (Landron et al., 2001; Krishnan et al., 2005). The first three peak positions listed in Table 1 are in good agreement with other studies (Ansell et al., 1997; Skinner et al., 2013). The real space differential distribution functions D^X(r) and D^N(r), measured for liquid alumina at the temperatures of 1,974 and 2,583 K are plotted in Figures 2B,D. There is a single asymmetric peak at 1.78 Å in both D^X(r) and D^N(r) functions, which represents the Al-O bond length distribution.

TABLE 1

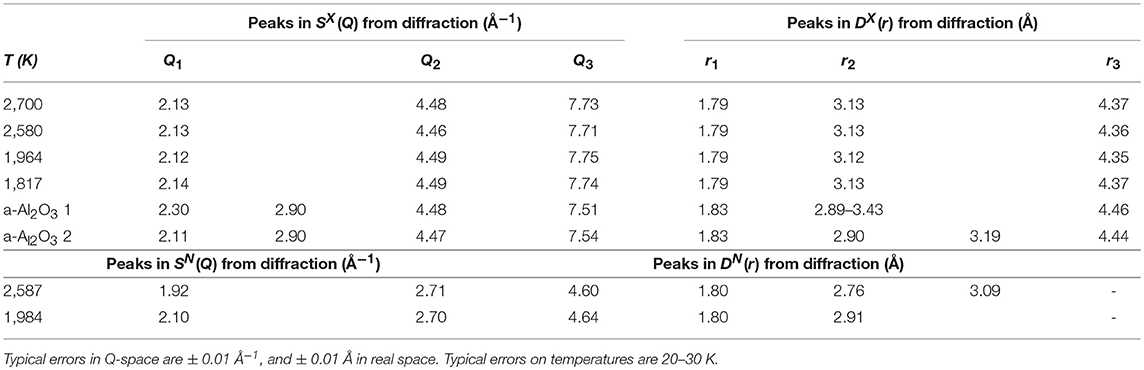
Table 1. Peak positions in both reciprocal and real space from x-ray and neutron diffraction on supercooled liquid alumina.

As the temperature decreases, the first peak sharpens and increases in intensity in real space without a significant change in position. The first Al-O peak is well-reproduced in our MD simulations of D^X(r) (see Figure 2B), while the EPSR peak is slightly higher than observed in the experiment. The broad second peak in D^X(r) and D^N(r) represents a combination of the Al-Al and O-O correlations at 2.8 and 3.13 Å, respectively, (we refer the reader to the partial pair distribution functions shown in Figure 4). A comparison of x-ray diffraction measurements made in pure oxygen and argon atmospheres (see Figure S1) reveals negligible differences, indicating the change in oxygen partial pressure has very little effect on the bulk structure of liquid alumina. However, the Ar gas atmosphere appeared to favor deeper supercooling, down to 1,817 K, compared to only 2,148 K in pure O₂ gas.

The numerical values of the peak positions from our diffraction measurements are given in Table 1. There is generally a very good agreement between our experiments, our MD simulations and with previous studies (Krishnan et al., 2005). The peak positions in real space and reciprocal space show subtle, if any, changes during cooling.

Deeply Supercooled Alumina

In order to explore the structural changes upon supercooling from the stable melt, the difference functions ΔS(Q) and ΔG(r) are plotted in Figure 3 using ΔS(Q) = S_cold(Q) – S_hot(Q) and ΔG(r) = G_cold(r) – G_hot(r). Analogous functions obtained from EPSR and MD simulation at the temperatures closest to the experimental ones are shown for comparison. The difference functions obtained are in good agreement, indicating that both of our models capture the same underlying structural changes upon supercooling.

To resolve the origin of the temperature-dependent differences, we plot the partial pair contributions from EPSR compared to the simulated (cold minus hot) difference functions ΔS_ij(Q) and ΔG_ij(r) in Figures 4A,B. We note that the change in the total structure factors arises from a mixture of changes in all three partial factors. A key observation is that changes occur in the Al-O partial pair distribution function, Δg_AlO(r), which corresponds to the first peak in both ΔG^X(r) and ΔG^N(r) at ~1.8 Å. Peaks at 3.08 and 2.88 Å in Δg_AlAl(r) and Δg_OO(r) jointly give rise to the second broad peak of ΔG^X(r) and ΔG^N(r).

Amorphous vs. Supercooled Liquid Alumina

Two amorphous samples were measured by x-ray diffraction and the x-ray structure factors are compared in Figure 5. There are small structural differences between the two samples, which are most likely caused by differences in sample synthesis procedure, or inhomogeneity in the thin film.

It is worth noting that the small but clearly apparent peak at Q = 2.9 Å⁻¹ of S^X(Q), which stands out in both of the amorphous samples (Figure 5A), is a feature which is barely distinguishable in the high temperature liquid (Figure 2A), but becomes increasingly apparent as a subtle feature in the supercooled liquid (Figures 2A, 3A). EPSR model fits and MD quench results for glassy alumina are compared to the experimental data in Figure 6. EPSR yields good fits which are similar for both samples. The MD model for glassy alumina has a much larger first sharp diffraction peak compared to the experimental data, a magnification of the differences seen in Figure 2A for liquid alumina.

Figure 7 compares the EPSR results for amorphous sample 2 with the supercooled liquid at 1,817 K. Figure 7C indicates that the enhanced peak at Q = 2.9 Å⁻¹ in the amorphous solid mainly arises from a sharpening of the oxygen-related correlations Al-O and O-O. From Figure 7D, the Al-O peak at 1.8 Å shifts to higher r in amorphous alumina, which means a longer Al-O bond length and likely a larger coordination number. The O-O peak also sharpens, leading to the more pronounced shoulder of the 2nd peak in G^X(r), Figure 7B. Similar results are obtained by comparison of amorphous sample 1 and the supercooled liquid at 1,817 K (see Figure S2).

Discussion

Mean Coordination Numbers

The average Al-O coordination number was obtained from the partial radial distribution functions using Equation (4) with a high-r cut off of r₂ = 2.5 Å, which corresponds to the first minimum in g_AlO(r). Both the MD and EPSR simulation results show that the average Al-O coordination number increases gradually with decreasing temperature (see Figure 8). The EPSR model obtained using both neutron and x-ray data as constraints, is in good agreement with the MD simulation results, while the EPSR model obtained using x-ray data alone gives a slightly lower Al-O coordination number, but within the estimated error bar of the fitted models of ± 1%.

FIGURE 8

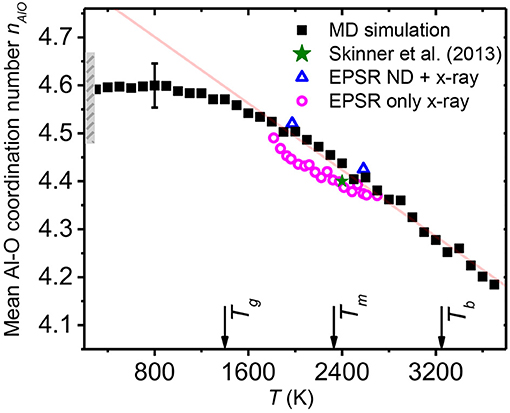
Figure 8. Temperature dependence of the average Al-O coordination numbers obtained from the MD and EPSR models with a cutoff distance r₂ = 2.5 Å. The range of Al-O coordination numbers of amorphous alumina obtained from EPSR models at 300 K are plotted as a gray bar, with densities ranging from 2.99 to 3.22 g cm⁻³. The arrows indicate the model glass transition temperature T_g = 1,395 K and the experimental melting and boiling points, T_m = 2,327 K and T_b = 3,250 K, respectively.

EPSR and MD simulations both reveal that the mean Al-O coordination number changes linearly with temperature as n_AlO = 4.41 – [1.25 × 10⁻⁴] (T – T_m) for the range 1,817 ≤ T (K) ≤ 2,700, and n_AlO = 4.44 – [1.73 × 10⁻⁴] (T – T_m) for the range 1,500 ≤ T (K) ≤ 3,700, for EPSR and MD respectively. From the EPSR results, the mean Al-O coordination number n_AlO changes from 4.37 at 2,700 K to 4.49 at 1,817 K, about a 2.8% variation over the experimental temperature range. At 2,378 K, the average Al-O coordination number from EPSR is 4.40, consistent with the values reported from previous diffraction work (Ansell et al., 1997; Landron et al., 2001; Hennet et al., 2002; Skinner et al., 2013). The subtlety of the changes with temperature are a clear reason why they have not been detected in previous studies covering smaller temperature ranges. It is worth mentioning that the mean coordination number shows a linear correlation with the liquid density. This is similar to titanium dioxide melts reported by Alderman et al. (2014) where it has been suggested that coordination change provides an important mechanism of thermal expansion.

Glass Transition, Density, and Thermal Expansion

The hypothetical glass transition temperature, T_g, for the Al₂O₃ system can be extracted from the MD simulation. Obtaining T_g from the intersection of linear extrapolations of the amorphous solid and liquid densities (Figure 1) yields T_g ≃ 1,395 K. No experimental value for T_g is available, because pure Al₂O₃ cannot be obtained as a bulk glass, even under fast cooling conditions (Sun, 1949; Rosenflanz et al., 2004). However, MD simulations by Van Hoang (2004) have previously reported the glass transition to be at the much higher temperature of 2,000 K. Such a high T_g is not observed in our experiments, since we have obtained a deeply supercooled liquid at 1,817 K. Nonetheless, our value for T_g ≃ 1,395 K is consistent with our experimental observations, and with the relatively large T_g values observed for high-alumina rare earth aluminate glasses (Johnson et al., 2005; Watanabe et al., 2012) (T_g > 1,100 K). Note however, that by heating a crystalline supercell to 3,700 K, a melting point of 2,800 K is found (see Figure S3), which is around 500 K higher than the experimental value of 2,327 K (Schneider, 1970). Although this method of melting point determination is subject to overestimation due to superheating, it is likely that at least part of the difference arises from the pair potentials used. This, along with the extremely rapid MD quench rate, likely both lead to overestimation of the glass transition temperature by MD.

It is worth noting that the liquid thermal expansion coefficient predicted from our MD simulations is ~65% larger than observed experimentally (Figure S4). In order to check this result we simulated the corundum (α-alumina) crystal structure and subjected it to stepwise heating to obtain the volume expansion coefficient (α_V). Again α_V is larger than measured experimentally by 43% at 300 K up to 64% at 2,400 K. This suggests that this is a feature of the Du and Corrales pair potentials used. Given the strong correlation between density and coordination numbers, the enhanced α_V of the MD models could lead to exaggeration of the observed structural changes. This is indeed evident in the slightly smaller slope, dn_AlO/dT, observed in Figure 8 for the EPSR derived models, which had densities fixed at those given by the Paradis et al. (2004) relation, with lower α_V than the MD model. It is also interesting to note that our MD simulations predict a smaller α_V for amorphous (glassy) alumina, as compared to crystalline corundum.

Coordination Number Distributions

The relative fractions of AlO_x species (where x = 3, 4, 5, 6) and OAl_y species (where y = 2, 3, 4) were obtained from the EPSR and MD models. Both models show that AlO₄ and AlO₅ are the predominant polyhedral units in the stable melt and supercooled liquid. Figure 9A indicates the main change in structure is from the exchange of the population of AlO₄ and AlO₅ units upon cooling. AlO₃ and AlO₆ units only make up a small proportion (<10%) for the liquid below 2,700 K, which is the highest temperature probed in our diffraction measurements. The majority of oxygen atoms are found to be triply shared by these AlO_x units, Figure 9B, and the number of OAl₃ increases with decreasing temperature, at the expense of OAl₂ bridging oxygen species. This represents a primary reason why alumina does not form a glass despite the propensity to deeply supercool. Although the Al-O coordination remains low, triply shared oxygen atoms violate Zachariasens's rule (Zachariasen, 1932) of glass formation since they reduce the flexibility of Al-O-Al bond angles and encourage denser, edge shared polyhedral structures that are prone to crystallization.

FIGURE 9

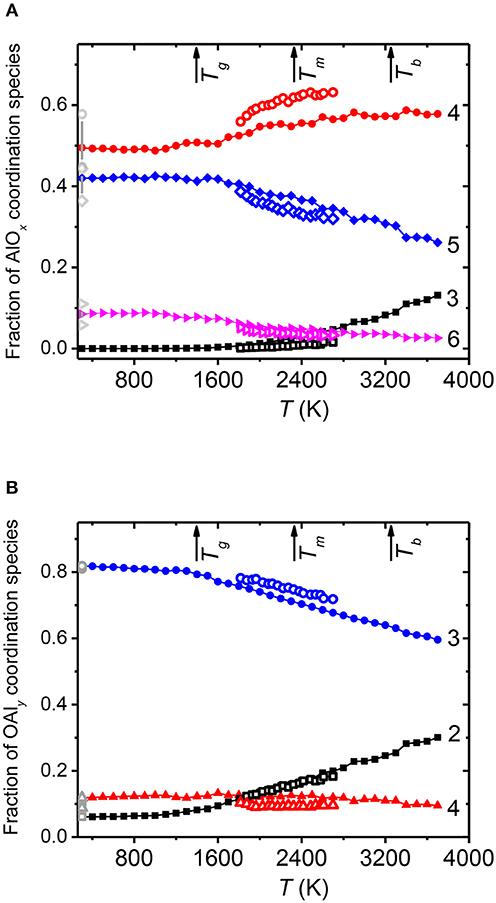
Figure 9. The temperature dependence of the distribution of (A) AlO_x units (where x = 3, 4, 5, 6) and (B) OAl_y units (where y = 2, 3, 4) from the MD simulation (solid symbols) and EPSR models (open symbols) obtained using r₂ = 2.5 Å. The corresponding AlO_x and OAl_y distributions in amorphous alumina from EPSR models at 300 K are plotted as gray symbols, with densities of 2.99 and 3.22 g cm⁻³ leading to the ranges shown. The arrows indicate the glass transition temperature, T_g = 1,395 K, from the MD simulation, together with the experimental melting point, T_m = 2,327 K, and boiling point T_b = 3,250 K of Al₂O₃ (Taylor et al., 1992). We note that the MD model remains liquid up to the highest temperatures studied.

A pioneering study by Landron et al. (2001) measured the structure of liquid alumina at 2,500 K using neutron diffraction and EPSR was used to obtain a structural model. The authors reported a mean Al-O coordination number of 4.2(3) with a distribution given in Table 2. However, the errors on this speciation distribution are expected to be large, due to the low signal-to-noise of the neutron data, and lack of any constraints provided by x-ray diffraction. Skinner et al. (2013) reported high-quality neutron and x-ray data on liquid alumina at ~2,400 K. A simultaneous fit using Reverse Monte Carlo (RMC) yielded a structure with a mean Al-O coordination number of 4.40 (with r₂ = 2.5 Å). Our EPSR model at 2,416 K gives a structure in good agreement with Skinner's model at 2,400 K (Table 2).

TABLE 2

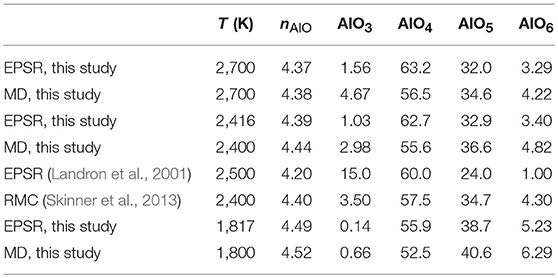
Table 2. Summary of average Al-O coordination number and speciation (%) of liquid alumina obtained using r₂ = 2.5 Å.

For amorphous alumina sample 2, the structure factor obtained yielded a relatively flat low r region in D(r) below the first physical peak (due to Al-O bonds). The slope in this region of D(r) was used to estimate the sample density at 3.05(15) g cm⁻³ (atomic number density 0.09 Å⁻³) which was used during EPSR modeling. Amorphous sample 1 was modeled by EPSR using slightly lower quality x-ray diffraction data, so three different densities of 3.10 (12) g cm⁻³ were assumed to evaluate the errors associated with this assumption (Table 3). The result from EPSR for sample 2 using this density gives an average Al-O coordination number of 4.62, which is close to the value for glassy alumina from our classical MD simulation (density of 3.21 g cm⁻³). Our MD simulation result at 300 K is expected to provide an indication of how an alumina glass structure (could it be made) might look, with 49.5% AlO₄, 42.0% AlO₅, and 8.5% AlO₆ units (Table 3), which is consistent with the results of ab initio MD simulation reported by Davis and Gutiérrez (2011). Also, both EPSR and MD simulation results of this work are similar to those measured by ²⁷Al NMR for amorphous alumina made by sputtering techniques (Lee et al., 2009, 2010; Lee and Ryu, 2017). Lamparter and Kniep (1997) reported a much lower average Al-O coordination number than others using the RMC method, but this may be due to the considerable sulfur and H₂O content of the sample, among other possible reasons.

TABLE 3

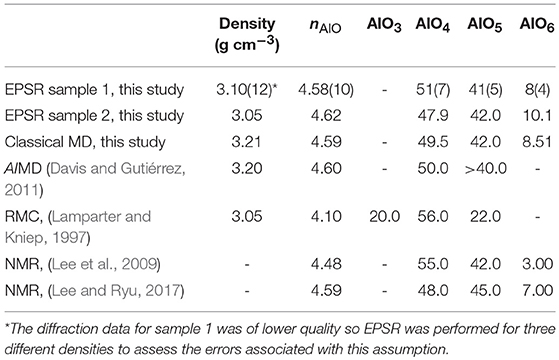
Table 3. Summary of average Al-O coordination number and speciation (%) of amorphous alumina thin films obtained using r₂ = 2.5 Å.

The Al-O coordination number distributions in liquid and amorphous alumina summarized in Tables 2, 3, indicate the general conclusion that amorphous alumina has a larger mean Al-O coordination, which is consistent with the observed shift of the Al-O peak in G(r) to longer distances in the solid, see Figure 7D. The difference is mainly caused by a larger faction of AlO₅, and a smaller faction of AlO₄, in amorphous alumina, as compared to the liquid.

Bond Angle Distributions

Bond angle distributions play an essential role in describing the polyhedral shape and packing within the liquid structure. The Al-O-Al and O-Al-O bond angle distributions provide information on the inter- and intra-polyhedral connectivity, respectively. In Figure 10, we plot the probability B(θ)/ sinθ as a function of bond angle for both the EPSR and MD simulations using Al-O, O-O and Al-Al cutoff distances of 2.5, 3.8, and 4.1 Å, respectively. Dividing the true distributions, B(θ), by the random distribution, sinθ, accounts for the diminishing probability of 180° (or 0°) bond angles. Individual bond angle distributions corresponding to the linkages of Al₅-O₃-Al₅, Al₄-O₃-Al₄, Al₄-O₂-Al₄, O₃-Al₅-O₃, O₃-Al₄-O₃, and O₂-Al₄-O₂ have been described in detail in previous work by Skinner et al. (2013) and their results are applied to our analysis below.

FIGURE 10

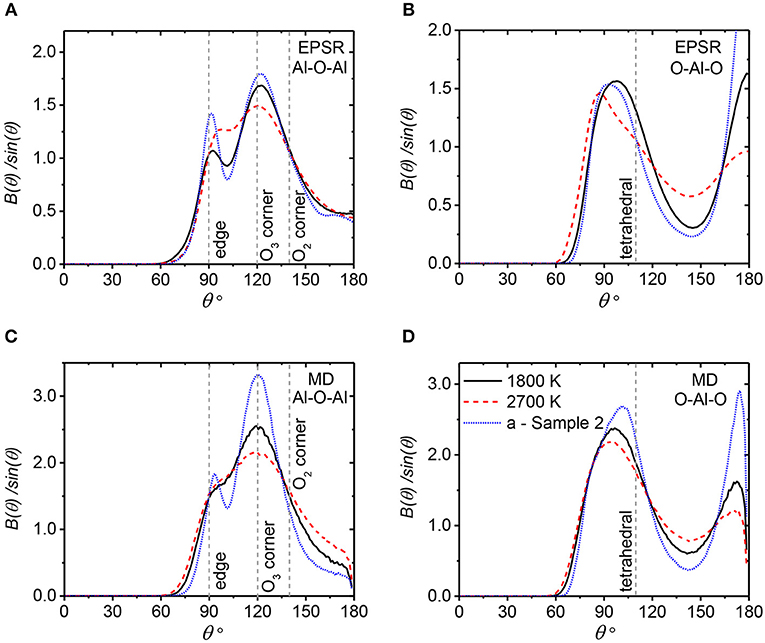
Figure 10. The bond angle distributions for amorphous alumina sample 2, and liquid alumina at the highest and lowest experimental temperatures of 2,700 and 1,817 K. EPSR results using a density of 3.05 g cm⁻³ (A,B) and MD models (C,D). (A,C) show the Al-O-Al angle distribution; (B,D) display the O-Al-O angle distribution. The dashed lines denote bond angles for some typical polyhedral arrangements (Skinner et al., 2013).

The Al-O-Al bond angle distributions from our EPSR and MD simulations are shown in Figures 10A,C. The main peak at 120° corresponds to Al₄-O₃-Al₄ linkages and these become better defined at lower temperatures, indicating that slightly more AlO₄ units are linked by 3-fold coordinated oxygens; namely AlO₄ oxygen triclusters. The broad tail extending to 180° is associated with a large fraction of AlO₄ units connected by 2-fold coordinated oxygen atoms. The peak at ~96° is attributed to Al₅-O₃-Al₅ linkages and represents the formation of edge-sharing AlO₅ units. This peak becomes slightly sharper with decreasing temperature indicating that better defined Al₅-O₃-Al₅ form and connect by edge sharing with supercooling. This is in line with the more pronounced tail in the O-Al-O distribution at ~170° at the lower temperature, which derives from the O₃-Al₅-O₃ units. The O-Al-O bond angle distributions in Figures 10B,D show generally similar trends but the features are sharper in the EPSR model. The broad peak comprises two main components: the O₃-Al₅-O₃ around 80° and O₃-Al₄-O₃ around 109.5°. The peak at ~100° sharpens and shifts to higher angles upon supercooling.

Glass Forming Ability

Liquid alumina is unlike any of the single oxide glass formers, such as SiO₂ or B₂O₃, because it has an average cation-oxygen coordination number n_M_O > V_M, the cation valence. This means that it violates Zachariasen's first rule of network glass formation, namely that the inequality n_OM = (c_M/c_O)n_M_O = (V_O/V_M)n_M_O ≤ 2 = V_O should hold. Indeed, experimentally, while it is found that alumina can be deeply supercooled, it not only cannot form glass but has properties vastly different from those of the single oxide glass formers, including much lower viscosities (Doremus, 2002). This can be understood qualitatively by the local structure. The predominance of OAl₃ units limits the range of Al-O-Al angles and hence the flexibility to form a disordered network. The very same structural feature also lowers the single bond strength and hence viscous flow via bond breaking and reforming events is promoted, something which is further facilitated by a distribution of coordination environments (unlike e.g., SiO₂ or B₂O₃). It is interesting to note that, as liquid alumina is supercooled, the coordination numbers increase such that the structure moves further away from the glass forming ideal of n_AlO = 3. This is the opposite of observations in the case of some modified glass-forming aluminates such as CaAl₂O₄ (Liška et al., 2008; Drewitt et al., 2012). In-situ Al-27 NMR measurements on liquid alumina and calcium aluminates support this finding (Capron et al., 2001; Massiot et al., 2008), because the temperature dependence of the isotropic chemical shift changes sign from positive for liquid alumina, to negative for molten CaAl₂O₄. In the case of CaAl₂O₄, the Al-O coordination decreases during cooling, and tends toward 4, leading to a structure which promotes open network glass formation, with n_OAl close to 2, which is enabled by charge balance from the modifying Ca²⁺ cations and the smaller Al /O ratio.

Conclusions

The structure of deeply supercooled liquid Al₂O₃ has been investigated using a combination of high energy x-ray diffraction and neutron diffraction, revealing a weak but continuous dependence of the local structure on temperature. The structure of amorphous alumina has also been investigated using x-ray diffraction. Atomistic models based on empirical potential structure refinement to the diffraction data, and classical molecular dynamics simulations using the inter-atomic potentials of Du and Corrales (2007) lead to similar pictures. Namely,

1. The mean Al-O coordination number increases gradually under supercooling. AlO₄ and AlO₅ are the predominant motifs in normal and supercooled liquid alumina. The number of AlO₅ units increases by 21% during supercooling from 2,700 to 1,817 K. The oxygen atoms are mainly linked to three AlOx polyhedra, and the number of OAl₃ increases by 9% over the same experimentally accessed temperature range, at the expense of OAl₂ bridging oxygens.

2. Oxygen triclusters Al_{4, 5}-O₃-Al_{4, 5} dominate the linkages found in both the stable melt and supercooled liquid. As the liquid is supercooled, a growth in the population of Al₅-O₃-Al₅ groups is observed, and these tend to share edges.

3. Compared to the liquid, amorphous alumina has a smaller fraction of AlO₄ and a larger number of AlO₅ motifs, leading to a larger mean Al-O coordination number. Given the observed increase in coordination numbers during supercooling, the local structure of amorphous alumina is consistent with expectations for the hypothetical glass.

4. Nonetheless, the temperature dependence of the structure of liquid alumina is such that glass formation becomes less and less likely during supercooling. This is because larger coordination numbers and edge-sharing polyhedra tend to reduce network flexibility and promote crystallization.

Data Availability

The full datasets generated for this study are available on request to the corresponding author. Exemplary x-ray and neutron structure factors are available in the Supplementary Material, Table S1.

Author Contributions

CB conceived the work. DB fabricated the samples. CS, OA, JN, AT, JW, and CB performed the experiments. CS, OA, and JD performed the simulations. CS, OA, JY, and CB wrote the paper.

Funding

This research used resources of the Advanced Photon Source, the U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357 and by the Spallation Neutron Source, Oak Ridge National Laboratory under Contract No. DE-AC05-00OR22725. This work was partially funded under DOE grant number DE-SC0015241.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

CS gratefully acknowledges financial support from the China Scholarship Council (CSC No. 201706890053).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00038/full#supplementary-material

References

Ahuja, R., Belonoshko, A. B., and Johansson, B. (1998). Melting and liquid structure of aluminum oxide using a molecular-dynamics simulation. Phys. Rev. E 57:1673. doi: 10.1103/PhysRevE.57.1673