A Novel Approach for Preparation and In Situ Tensile Testing of Silica Glass Membranes in the Transmission Electron Microscope

The mechanical behavior of glasses in the micro- and nanometer regime increasingly gains importance in nowadays modern technology. However, suitable small-scale preparation and mechanical testing approaches for a reliable assessment of the mechanical properties of glasses still remain a big challenge. In the present work, a novel approach for site-specific preparation and quantitative in situ tensile testing of thin silica glass membranes in the transmission electron microscope (TEM) is presented. Thereby, advanced focused ion beam techniques are used for the preparation of nanoscale dog bone-shaped silica glass specimens suitable for in situ tensile testing. Small amounts of gallium are detected on the surface of the membranes resulting from redeposition effects during the focused ion beam preparation procedure. Possible structural changes of silica glass upon irradiation with electrons and gallium ions are investigated by controlled irradiation experiments, followed by a structural analysis using Raman spectroscopy. While moderate electron beam irradiation does not alter the structure of silica glass, ion beam irradiation results in minor densification of the silica glass membranes. In situ tensile testing of membranes under electron beam irradiation results in distinctive elongations without fracture confirming the phenomenon of superplasticity. In contrast, in situ tensile testing in the absence of the electron beam reveals an elastic/plastic deformation behavior and finally leads to fracture of the membranes. The Young’s moduli of the glass membranes pulled at beam-off conditions in the TEM are comparable with values known for bulk fused silica, while the tensile strength is in the range of values reported for silica glass fibers with comparable dimensions. The impact of electron beam irradiation on the mechanical properties of silica glass membranes is further discussed. The results of the present work open new avenues for dedicated preparation and nanomechanical characterization of silica glass and further contribute to a fundamental understanding of the mechanical behavior of such glasses when being scaled down to the nanometer regime.

Introduction

Increasing research efforts on the improvement of the mechanical reliability of glasses clearly evidence their importance in today’s and future modern nanotechnology (Wondraczek et al., 2011). As a well-established material in complex optical and electronic applications (Murata, 1996; Yamane and Asahara, 2000) and due to the increasing tendency of device miniaturization, silica glass nowadays has to fulfill functionality and mechanical reliability simultaneously. Hence, a broader knowledge and classification of its mechanical behavior occurring on smaller scales is of particular interest and importance. Despite its well-known brittleness on macroscopic scale, several approaches have proven that silica glass can exhibit a certain amount of plasticity when scaled down to the micro- and/or nanometer regime (Zheng et al., 2010; Nomura et al., 2011; Lacroix et al., 2012a,b; Kermouche et al., 2016; Luo et al., 2016). In addition to volume conservative plastic flow (Kermouche et al., 2016), plastic deformation in silica glass relies on densification, a mechanism which is related to permanent volumetric changes of the glassy lattice (Ernsberger, 1968; Grimsditch, 1984; Lambropoulos et al., 1996; Perriot et al., 2006; Wondraczek et al., 2007; Wakabayashi et al., 2011; Lacroix et al., 2012b). Moreover, Yamaguchi et al. (2004) have shown that the brittleness of silica glass can be reduced (on macroscopic scale) by dedicated irradiation with high energy electrons. Subsequent mechanical tests have shown that the brittleness is reduced by stress relaxation, which is induced by an increase in free volume related to dangling bonds. Iwata and Nishi (2008) demonstrated that irradiation of silica glass with electrons results in an increased impact value (obtained from standard Charpy impact tests) due to an increase in the bonding energy for the silicon–oxygen atomic pairs in the atomic network structure of silica glass. Several approaches have demonstrated that sol-gel-derived nanoscale silica spheres exhibit an enormous ductility if compressed under moderate electron beam (e-beam) irradiation inside the transmission electron microscope (TEM) (Zheng et al., 2010; Mačković et al., 2014, 2016) and scanning electron microscope (SEM) (Romeis et al., 2012; Stauffer et al., 2014; Bhowmick et al., 2015). In contrast, nanoscale vitreous silica spheres (heat-treated Stöber-Fink-Bohn (SFB)-type silica (Stöber et al., 1968; Hanisch et al., 2012)) fracture in brittle manner if compressed in the absence of e-beam irradiation inside the SEM and TEM (Romeis et al., 2014, 2015; Paul et al., 2015). Zheng et al. (2010) performed in situ tensile experiments of amorphous silica fibers under moderate e-beam irradiation in the TEM, by using a method reported by Han et al. (2007a,b). The fibers are prepared on standard TEM grids coated with a holy carbon support film. By irradiating the carbon support film with the e-beam, an extension of the holes in the carbon film was achieved, and, hence, a tensile force was generated and transferred on the silica fibers. By using this approach, superplastic deformations of more than 200% were observed inside the TEM (Zheng et al., 2010). The high energy e-beam generates structural and bonding defects and facilitates the bond-switching mechanism, which favors the rotation and migration of atomic clusters to accommodate plastic flow in the amorphous network (Zheng et al., 2010). However, high energy e-beam irradiation can also result in structural changes, such as densification in case of vitreous silica (Primak and Kampwirth, 1968; Dellin et al., 1977) and local deformations in case of amorphous silica films (Storm et al., 2005). These examples altogether indicate that under certain circumstances the conventionally brittle silica glass in general can exhibit enormous ductility and/or superplasticity.

Dedicated preparation of small scale specimens and testing approaches increasingly come to the fore, as they represent one way to avoid and/or minimize surface defects, which in general control the strength of brittle materials. The probably most widespread method for fabrication of silica glass fibers in the micro- and nanometer regime is the so-called flame brushing technique (Bilodeau et al., 1988). Thereby, a gas burner is used to locally heat up a section of an optical fiber while simultaneously stretching it and achieving silica tapers with a locally reduced diameter. Starting from standard telecom optical fibers with a diameter of 125 μm, Brambilla and Payne (2009) used a modified flame brushing technique for fabrication of amorphous silica nanowires with diameters ranging from 60 to 300 nm and performed ex situ tensile experiments. In the size range of 100–300 nm in diameter, the silica glass fibers showed tensile strengths ranging from 9 to 13 GPa. However, in case of diameters ≤100 nm, the silica fibers showed a strong scatter in their tensile strength ranging from 9 to 27 GPa. Tong et al. (2003) used a two-step drawing process to fabricate long free-standing silica wires with uniform diameters down to 50 nm and a surface roughness at atomic level, while no information of their mechanical behavior is reported. However, Silva et al. (2006) used the method proposed by Tong et al. (2003) for fabrication of silica fibers with diameters ranging from 280 to 1950 nm and performed bending experiments with a cantilever probe implemented in a scanning probe microscope. The authors reported that silica fibers with diameters ranging from 280 to 1950 nm exhibited stiffness values of bulk silica (Silva et al., 2006). Just recently, Luo et al. (2016) used a two-step in situ process (modulated taper-drawing, followed by drawing inside the TEM) to prepare silica glass fibers with diameters below 50 nm. In situ tensile experiments performed in the absence of e-beam irradiation inside the TEM showed a brittle-to-ductile transition of silica glass nanofibers at room temperature when the fiber diameter is reduced below 18 nm. Moreover, in case of fibers with diameters <20 nm, a strong scatter in their fracture stress (σ_f) values ranging from 1 to 13 GPa is observed, depending on the used strain rate during the in situ tensile experiments (Luo et al., 2016).

Advanced scale-bridging mechanical testing is nowadays increasingly focusing on in situ approaches in the TEM and SEM, as they offer the possibility for direct visual observation of deformation events (occurring on micro- and/or nanoscale) and simultaneous acquisition of quantitative (nano-)mechanical data (Legros et al., 2010). Moreover, the commercial availability of advanced preparation techniques, such as the focused ion beam (FIB), and their application in the field of materials science and engineering have opened new opportunities for dedicated preparation of micro- and nanoscale specimens (Giannuzzi and Stevie, 2005). Even though FIB instruments nowadays have excellent imaging and micro-/nanomachining capabilities, one well-known issue is the ion irradiation-induced damage and change of the specimen material (Volkert and Minor, 2007). Most reports are based on experiences from FIB preparation and its impact on the structure and mechanical properties of crystalline materials (Uchic et al., 2004; Biener et al., 2006; Volkert and Lilleodden, 2006; Kiener et al., 2012). As for instance emphasized by Kiener et al. (2007), Ga⁺ irradiation-induced damage can significantly influence the mechanical behavior of submicron-sized Cu. In the review by Kato (2004), several damage reduction techniques are suggested, such as usage of gas-assisted etching, low-energy FIB, cleaning of FIB-fabricated cross sections by wet or dry etching and cleaning by broad ion beam milling. Very recently, Lee et al. (2016) demonstrated for FIB-prepared Al pillars that in situ annealing inside the TEM can be employed for removing defects below the surface introduced by FIB milling.

As a standard method for fabrication of silica glass pillars, which are suitable for mechanical testing in the SEM, the reactive ion etching method was reported (Lacroix et al., 2012a,b; Kermouche et al., 2016). However, currently, there is no FIB-based approach available for fabrication of silica glass specimens for in situ mechanical testing on micro- and/or nanoscale. Studies are available in literature which focus on FIB preparation of metallic glasses suitable for mechanical testing (Guo et al., 2007; Tian et al., 2012) and even report on the effect of FIB preparation on the structure of metallic glasses (Zhang et al., 2016). Reports exist in which amorphous silica and silica glass specimens are irradiated with high energy ions from external sources, followed by a structural analysis of the irradiated material. In this context, Primak and Kampwirth (1968) showed that irradiation of vitreous silica with 140 keV He⁺ results in densification of the material, which possesses an equal contribution from ionization compaction and that caused by energy transfer to atomic vibrations. Snoeks et al. (1994) showed that irradiation of thermally grown silica thin films with heavy Xe ions results in local deformations, densification, and plastic flow of the material. However, so far, little is known about the impact of FIB preparation on the structure of silicate glasses in the micro/nanometer regime. This indicates that a reliable preparation of micro- and/or nanoscale silica glass specimens, which are suitable for in situ mechanical testing inside the TEM and SEM, still remains a big challenge.

Within the scope of aspects introduced above, the aim of the present work was to develop a reliable method for the preparation of small scale glass tensile specimens and to establish a way to assess the mechanical properties of glasses when being scaled down to the micro-/nanometer regime. By following this concept, the present work introduces a novel approach for the site-specific preparation and quantitative in situ tensile testing of nanoscale silica glass membranes inside the TEM, which so far is lacking in the mechanical testing community. Silica glass was chosen as a model system due to its relevance in today’s modern nanotechnology. By using advanced FIB techniques, nanoscale silica glass specimens are prepared in dog bone geometry, suitable for in situ tensile testing in the TEM. Raman spectroscopy is used to evaluate the structural integrity of the glass network in the silica membranes and identify possible damage induced by ion and/or e-beam irradiation during FIB preparation and/or in situ tensile testing. Characteristics for FIB-based preparation of nanoscale glass specimens are further emphasized. In situ tensile tests of silica glass membranes in the TEM are carried out under e-beam irradiation as well as in the absence of the e-beam. Depending on the experimental conditions, the silica glass membranes exhibit clear differences in their mechanical behavior. We further believe that the present work will contribute to a generalized understanding of the mechanical behavior of other, more complex glassy systems as well, and possibly also can be applied to crystalline materials.

Materials and Methods

Sample Preparation

Optically transparent Pelco^® membranes from pure and amorphous, thermally deposited silicon dioxide (50 μm × 50 μm windows in a silicon nitride frame) are purchased from Plano GmbH (Germany), which closely resembles the structure of silica glass (see section Impact of Ion- and e-beam Irradiation on the Structure of Silica Glass). The site-specific preparation of silica glass tensile specimens was carried out using a Helios NanoLab 660 DualBeam SEM/FIB system from FEI Company (Netherlands). The SEM/FIB is equipped with an ultra high-resolution Elstar™ e-beam column with a monochromator system and a resolution of ~1 nm at 1–30 kV, a high-resolution Tomahawk™ ion beam column, a gas injection system for C deposition, an EasyLift™ micromanipulator, and an Oxford X-Max^N detector for energy dispersive X-ray (EDX) spectroscopy. More details on the preparation procedure of tensile specimens on push-to-pull (PTP) devices for in situ tensile experiments inside the TEM are given in Sections “Workflow for In Situ Tensile Testing of Silica Glass Membranes in the TEM” and “Site-Specific Preparation of Silica Glass Tensile Specimens.”

In Situ Tensile Testing in the TEM

Transmission electron microscopy was performed by using a Titan³ Themis 300 (FEI Company, Netherlands) operated at 300 keV acceleration voltage. The microscope is equipped with a high-brightness field-emission gun (X-FEG), a monochromator system, two C_s-correctors (probe and image side) from Corrected Electron Optical Systems (CEOS GmbH, Germany), a Super-X detector for EDX spectroscopy, a Gatan Imaging Filter Quantum for electron energy loss spectroscopy (EELS), a high-angle annular dark-field (HAADF) detector for atomic number contrast imaging, and a 4K CMOS (complementary metal-oxide semiconductor) camera. In situ tensile testing was performed with the PI95 TEM Picoindenter^® (Hysitron, Inc., USA) and PTP devices inside of the Titan³ Themis 300. Comparable experimental setups have been recently used for in situ tensile testing of individual Ag nanowires (Kobler et al., 2015) and in situ tensile experiments of Au and alloyed Cu thin (Liebig et al., 2016). In the present study, the PI95 holder was operated under displacement control, while experiments are carried out with and without e-beam irradiation. In our previous studies on nanoscale silica spheres, we noticed a strong impact of e-beam irradiation on their mechanical behavior inside the TEM (Mačković et al., 2014, 2016) and SEM (Romeis et al., 2012). Similarly, in the present work, the impact of e-beam irradiation was investigated in case of silica glass. Quantitative nanomechanical data obtained from the tensile experiments are then directly correlated with in situ movie data recorded with the CMOS camera of the TEM.

Raman Spectroscopy

Raman spectroscopy was performed using a LabRAM HR—Evolution (Horiba Scientific, USA) micro Raman setup. The excitation wavelength was 532 nm (frequency-doubled Nd-YAG laser source). Grating, slit, and confocal hole were 1,800 l mm⁻¹, 100 μm, and 100 μm, respectively. The spectral resolution was ~0.5 cm⁻¹. The laser power in plane of the samples was 20 mW.

Atomic Force Microscopy

The membrane thickness was measured with an atomic force microscope (AFM, NanoWizard3, JPK Instruments, Berlin, Germany) in the intermittent contact mode using a NSC15/AlBS cantilever tip (MikroMasch^®, Bulgaria; resonance frequency 325 kHz, spring constant 46 N m⁻¹, nominal tip radius <10 nm). Measurements were performed with the fast scanning direction perpendicular to the membrane edge for three different membranes that have been prepared on PTP devices. For image processing and thickness determination, the software JPKSPM Data Processing was used. After background subtraction and inclination correction, a histogram-based approach was used for thickness evaluation.

Results and Discussion

Workflow for In Situ Tensile Testing of Silica Glass Membranes in the TEM

In the present work, silica glass was chosen as a model system, in order to get more insights on the intrinsic strength, deformation behavior, and elastic properties of amorphous materials. Furthermore, nanoscale specimens and nanomechanical testing approaches are one way to avoid/minimize the general problem of surface defects, which control the strength of brittle materials and usually prevent the exploration of intrinsic effects. Hence, the aim of the present work was to develop a workflow for the site-specific preparation of thin, nanoscale silica glass specimens suitable for quantitative in situ tensile testing inside the TEM and get insights on the mechanical properties occurring on micro-/nanoscale. Figure 1 schematically demonstrates this workflow. In the first step, a piece of a thin silica glass membrane is extracted from a Pelco^® membrane (also see section Sample Preparation) by using the FIB. In the following step, the extracted silica glass membrane is transferred onto a PTP device. Next, a tensile specimen with dog bone geometry is prepared by careful FIB cutting. The PTP device together with the FIB-prepared silica glass tensile specimen is then mounted into the Hysitron PI95 TEM Picoindenter^®, and in situ tensile testing is performed inside the TEM. As a result, in situ TEM movie data of the deformation event and nanomechanical data are obtained simultaneously and can be directly correlated. In the following chapters, the single steps of the workflow are described in more detail, whereby characteristics and challenges are emphasized.

FIGURE 1

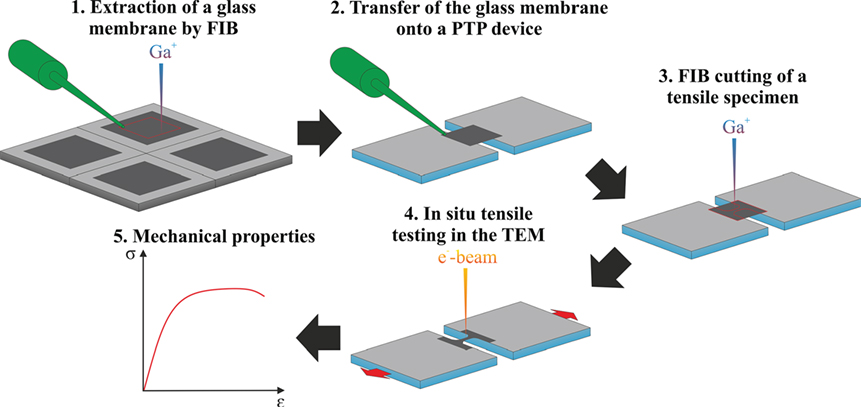
Figure 1. Scheme demonstrating the workflow for the site-specific preparation and quantitative in situ tensile testing of thin silica glass membranes inside the transmission electron microscope (TEM).

Impact of Ion- and e-beam Irradiation on the Structure of Silica Glass

As introduced above, structural changes of amorphous silica (Primak and Kampwirth, 1968; Snoeks et al., 1994) are reported in literature upon irradiation with heavy ions. Moreover, structural changes and changes in the mechanical properties of vitreous silica (Primak and Kampwirth, 1968; Dellin et al., 1977; Storm et al., 2005) and silica glass (Yamaguchi et al., 2004; Iwata and Nishi, 2008) are reported upon irradiation with electrons on the macroscopic and microscopic scale. To account for this, we carried out a systematic analysis of the impact of Ga⁺ irradiation (during FIB preparation) and e-beam irradiation (during experiments in the TEM) on the structure of silica glass membranes. Targeted irradiation experiments are carried out with electrons (parallel illumination in the TEM) according to our previous approach (Mačković et al., 2014) and Ga⁺ (in scanning mode in FIB) with beam current densities of ~10⁻³ and ~10⁻⁶ A cm⁻² in the TEM and FIB, respectively. Identical beam current densities are also used later on during the preparation routine of silica glass membranes in the FIB and in situ tensile testing in the TEM. Raman spectroscopy is used to evaluate the structural integrity of the glass network in the silica glass membranes and to investigate possible damage induced by Ga⁺ and/or electron irradiation.

In addition and for direct comparison with the irradiated material, Raman spectra are obtained from pristine (non-irradiated) silica glass membranes. Figure 2 exemplarily shows the results from Raman spectroscopy, while in general good data reproducibility was given. The non-irradiated silica glass membranes exhibit typical Raman spectra with well-known characteristics of vitreous silica on micro- (Perriot et al., 2006) and nanoscale (Paul et al., 2015; Romeis et al., 2015). The intense band at 440 cm⁻¹ occurs due to stretching of bridging oxygen atoms between two Si atoms. As observed by Sharma et al. (1981) for vitreous silica, this intense band can also be observed at 437 cm⁻¹. The two defect lines D₁ and D₂, which are located at 495 and 606 cm⁻¹, are attributed to breathing modes of the four- and three-membered Si–O rings in vitreous silica (Galeener, 1982). The broad band at 795 cm⁻¹ is a ω3 mode with little transverse optical-linear optical splitting (Galeener, 1979). The band at 1055 cm⁻¹ can be attributed either to the high frequency antisymmetric Si-O stretching mode (McMillan et al., 1984) or to a transverse optical mode (Galeener, 1979) occurring in vitreous silica. In case of all three Raman spectra, a relatively weak signal is detected at ~1,060 cm⁻¹, which might arise from sp³-type vibrations of hydrogen-free carbons (Ferrari and Robertson, 2001). The Raman spectrum of the e-beam irradiated silica glass membrane is comparable to the one of the non-irradiated membrane, which indicates that no major structural changes occur upon e-beam irradiation. In our previous work (Paul et al., 2015), targeted e-beam irradiation experiments inside the TEM and subsequent Raman spectroscopy was performed on 200-nm diameter vitreous silica spheres (heat-treated SFB-type silica spheres (Romeis et al., 2014; Paul et al., 2015)). It was found that e-beam irradiation does not significantly alter the structure of vitreous silica spheres [only minor densification ≤2 vol.% (Paul et al., 2015) was observed], even though higher beam current densities of ~10⁻² A cm⁻² were used during irradiation, compared to beam current densities of ~10⁻³ A cm⁻² used for irradiation of the glass membranes in the present study. In this context, Luo et al. (2016) irradiated silica glass fibers with electrons inside the TEM by using a beam current density of 2.5 × 10⁻³ A cm⁻² for 1 min, and subsequently performed EELS measurements on the irradiated material. No differences in the chemical composition and electronic structure (or bonding characteristics) are noticed upon irradiation with the e-beam, in comparison to the non-irradiated silica glass fibers. These results confirm that moderate e-beam irradiation in the TEM does not significantly change the structure and chemistry of silica glass. In contrast, in the case of Ga⁺ irradiated membranes, we observed that the intense band, which in the case of pristine silica glass is usually located at 440 cm⁻¹, shifts to higher wavenumbers (see Figure 2). This phenomenon can be attributed to a densification of the silica glass network structure. Similar features are observed in the Raman spectra by Perriot et al. (2006) in indentation-densified amorphous silica and by Romeis et al. (2015) in compression-densified vitreous silica spheres. Previously, compression-induced densification of silica glass was observed by Tomozawa et al. (1998) in uniaxial compression experiments and infrared spectroscopy measurements and by Mochizuki and Kawai (1972) in pressure-densified vitreous silica. It has been explained to be accommodated by a decrease of the bond angles of inter-tetrahedral Si-O-Si bonds of the silica glass network structure (Mochizuki and Kawai, 1972; Tomozawa et al., 1998). In an earlier work, densification induced by heavy Xe⁺ irradiation was reported for 1.85 μm thick amorphous silica films (Snoeks et al., 1994). However, Ga⁺ irradiation-induced densification of nanoscale silica glass, which we observe here by Raman spectroscopy, has so far not been reported in literature.

FIGURE 2

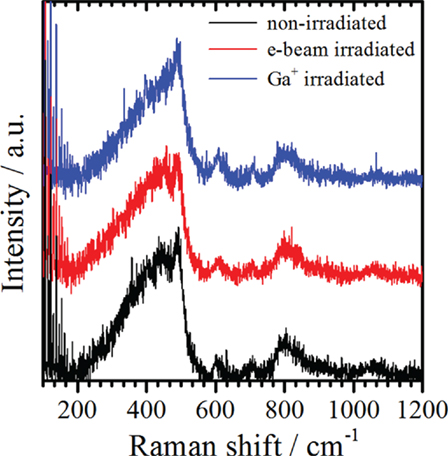
Figure 2. Representative (baseline corrected) Raman spectra of a pristine (non-irradiated), an e-beam, and a Ga⁺ irradiated silica glass membrane.

In the next step, dog bone-shaped tensile specimens are prepared directly on the silica glass film of the Pelco^® membrane (see Figures 3A,B). During preparation of the silica glass membrane with the Ga⁺ beam redeposition of Ga in form of particles on the silica glass membrane occurred, which is evident from scanning TEM (STEM)-EDX measurements shown in Figures 3C–F. Furthermore, during FIB preparation, the silica glass membranes are cut “blindly,” meaning that direct irradiation of the dog bone-shaped tensile specimen was prevented during the full preparation procedure, which avoids/minimizes FIB-induced preparation artifacts. By using STEM-EDX analysis, we evaluated the Ga content after a typical FIB preparation of the glass membranes. The results are shown in Figures 3C–F. Measurements are performed in the middle and edge regions of the membranes, as exemplarily shown in Figures 3C,D and Figures 3E,F, respectively. In general, in the middle region of the membranes, a higher Ga content is observed. Furthermore, tilting experiments of the membranes by ±45° in the TEM showed that the Ga-enriched particles are mainly located on the bottom side of the membranes (see Figures 3G–J).

FIGURE 3

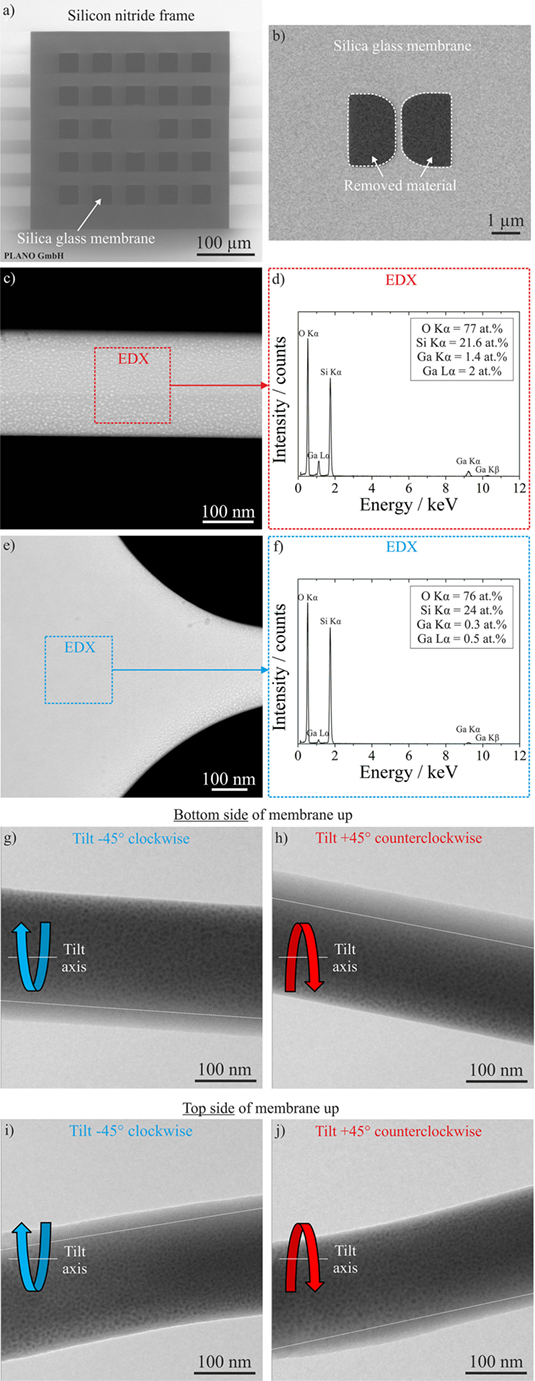
Figure 3. Direct observation of Ga-enriched particle redeposition on the silica glass membranes upon focused ion beam (FIB) preparation. (A) SEM image of a Pelco membrane; (B) SEM image of a silica glass membrane, in which a tensile specimen with dog bone geometry is prepared by FIB; (C,E) HAADF-STEM images of a silica glass tensile specimen (middle and edge region, respectively); (D,F) EDX spectra recorded in regions indicated in (C,E), respectively; (G-J) bright-field TEM images of a silica glass membrane obtained in different tilting conditions.

Thickness Determination of Silica Glass Membranes

The specimen thickness is one of the crucial dimensions needed for the evaluation of the mechanical properties from in situ tensile experiments. In order to determine the membrane thickness, TEM and complementary (tapping mode) AFM measurements are performed. For the TEM measurement, silica glass membranes are transferred from a Pelco^® grid onto a silicon wafer, a Pt protective layer is deposited and cross-sections are prepared by FIB lift-out (see Figure 4A).

FIGURE 4

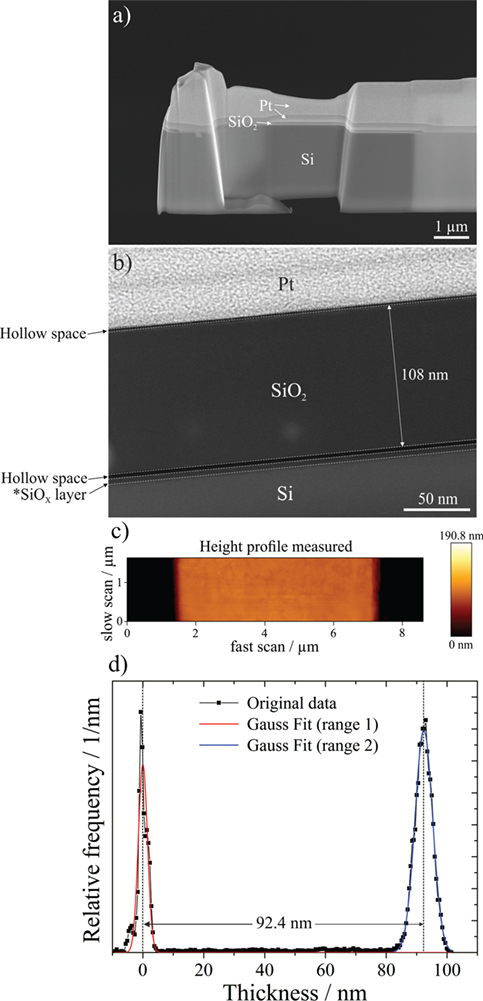
Figure 4. Thickness determination of silica glass membranes: (A) scanning electron microscope (SEM) image of focused ion beam (FIB)-prepared cross-section; (B) scanning TEM (STEM) image of a part of the FIB cross-section shown in (A); (C,D) atomic force microscopy (AFM) data of one silica glass membrane measured directly on the push-to-pull (PTP) device.

Multiple STEM-EDX line scans are performed perpendicular to the Pt–SiO₂–Si interfaces along the length of the FIB cross-section, which show an average thickness of 107.15 ± 1.05 nm. Figure 4B exemplarily shows a silica glass membrane with a thickness of 108 nm. In the case of AFM measurements, the thickness is directly measured on silica glass membranes that were already prepared on PTP devices. Figure 4C shows exemplarily a height profile of a section of a silica glass membrane viewed from top. In order to evaluate the thickness, Gauss fits are applied to the original experimental data in the ranges indicated in the intensity—thickness diagram shown in Figure 4D. The thickness of the membrane shown in Figure 4D is 92.4 nm. For two other membranes thickness values of 99.3 and 103.6 nm are obtained by AFM. Based on AFM and FIB cross-section measurements, an average thickness value of 100.6 ± 6.35 nm is obtained and used for further calculations. For more accuracy in future experiments, it is essential to determine the membrane thickness of each individual membrane before the tensile experiments.

Site-Specific Preparation of Silica Glass Tensile Specimens

For in situ tensile experiments in the TEM, the silica glass membranes are prepared from Pelco^® membranes (see section Sample Preparation and SEM image in Figure 3A) on PTP devices. Figure 5 shows an overview SEM image of a PTP device. The region where the specimen can be prepared is localized between a mobile and fixed part of the PTP device. By pushing with the indenter on the mobile part of the PTP device, the springs are deflected and a tensile force is applied to the specimen. Figure 6 exemplarily shows the site-specific preparation procedure of a silica glass membrane on the PTP device for in situ tensile testing in the TEM. A piece of the silica glass membrane is first cut out of the Pelco^® membrane using the FIB and is further on transferred onto the PTP device with the micromanipulator.

FIGURE 5

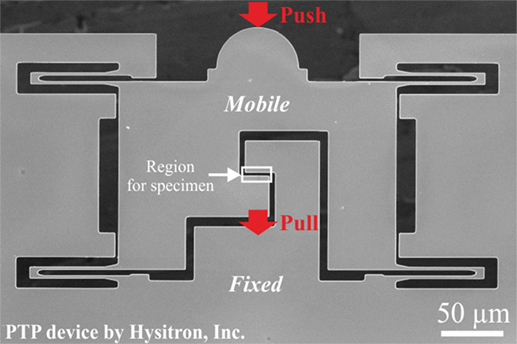
Figure 5. Scanning electron microscope (SEM) image showing a push-to-pull (PTP) device for in situ tensile experiments in the transmission electron microscope (TEM).

FIGURE 6

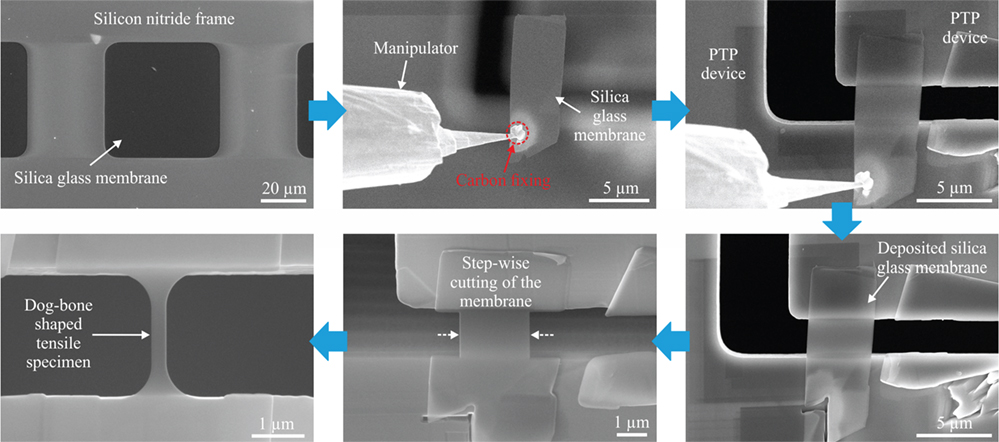
Figure 6. Scanning electron microscope (SEM) images showing the site-specific preparation of a thin dog bone-shaped silica glass tensile specimen on a push-to-pull (PTP) device suitable for in situ tensile testing in the transmission electron microscope (TEM).

Carbon is used to attach the membrane to the manipulator and pure adhesion is used to fix the membrane to the PTP device. After placing the membrane onto the PTP device, the Ga⁺ beam is used to separate the membrane from the manipulator. From the practical point of view, it should be noted that in some case the silica glass membrane lifted up when detached from the manipulator and the transfer failed. The deposited silica glass membrane is cut step-wise starting from the outer and going to the inner part of the membrane. Finally, by using a self-designed mask for cutting (8-bit gray scale image), the tensile specimen is milled in a single step to the final dog bone-shaped geometry.

In Situ Tensile Testing of Silica Glass Membranes in the TEM

As proof of principle, in situ tensile experiments of silica glass membranes are performed at beam-on and beam-off conditions inside the TEM. Figure 7 shows in situ movie frames of a tensile experiment performed interruptedly under moderate e-beam irradiation (beam current density ~10⁻³ A cm⁻²) in the TEM. The corresponding in situ Movies S1–S3 (Video S1–S3) in Supplementary Material show the first, second, and third cycle of tensile experiments, respectively, performed on the same silica glass membrane. As can be seen in Figure 7 and the in situ TEM movies, large strains up to 41% are achieved without fracture of the glass membrane. At the end of the third run, a crack was initiated in the upper edge region of the membrane (see left side in the necked region of the silica glass membrane in Movie S3 (Video S3) in Supplementary Material) and would most probably have caused the failure of the membrane upon further tension. Moreover, the glass membrane is deformed relatively uniformly along the gauge length indicated with the dashed rectangles, showing only minor necking (see left side of the membrane in Figures 7B–D). So far, no quantitative nanomechanical data are reported in literature for nanoscale silica glass pulled under e-beam irradiation inside the TEM. In the present work, the glass membrane (average diameter ~221 nm, thickness ~100 nm) that was pulled under moderate e-beam irradiation in the TEM, exhibits a yield stress (σ_y) of 1.9 GPa measured at 0.2% plastic strain. After the first pulling cycle (at a strain of 25%), a tensile stress of 6.8 GPa is observed. The Young’s modulus (E) of 49 GPa, which is evaluated from the linear fit in the low deformation regime of the engineering stress-strain curve, is clearly below values known for bulk fused silica (72–76 GPa) (Adachi and Sakka, 1990), most probably caused by the e-beam. Moreover, this E value of 49 GPa has to be interpreted with care, since e-beam irradiation in principle could induce plastic flow of silica glass already in the early stages of deformation. Hence, in future, loading-unloading experiments need to be exploited under e-beam irradiation in order to determine the elastic deformation regime. It is well known from literature (Zheng et al., 2010; Yue and Zheng, 2014) that tensile testing of amorphous silica fibers under e-beam irradiation in the TEM can lead to superplastic deformations (more than 200% (Zheng et al., 2010)). In our previous works (Mačković et al., 2014, 2016), we observed the E of as-synthesized SFB-type nanoscale silica spheres (sol-gel-derived silica) to be strongly dependent on the e-beam irradiation dose used before compression of the spheres inside the TEM. An E value of ~21 GPa is observed in case of low dose e-beam irradiation (beam current density of ~10⁻⁴ A cm⁻²), while at e-beam irradiation with higher dose (beam current density of ~10⁻² A cm⁻²) an E of ~ 45 GPa is observed (Mačković et al., 2014). Also in this case, the E values of 21 and 45 GPa are significantly lower than the value known for bulk fused silica (72–76 GPa) (Adachi and Sakka, 1990). However, they are typical for such SFB-type silica particles, as reported for sol-gel-derived hollow silica spheres and silica microcapsules by Zhang et al. (2009, 2010) and submicron-sized silica spheres by Romeis et al. (2012, 2014) and Paul et al. (2015), respectively. In difference to this, Romeis et al. (2014) and Paul et al. (2015) reported E values of 71 ± 1.4 GPa for heat-treated SFB-type silica spheres approaching the values known for bulk fused silica (72-76 GPa) (Adachi and Sakka, 1990). Similar values of the E are observed by Paul et al. (2015) from in situ compression experiments for 200 nm-sized vitreous silica spheres in the SEM and TEM with the e-beam blanked.

FIGURE 7

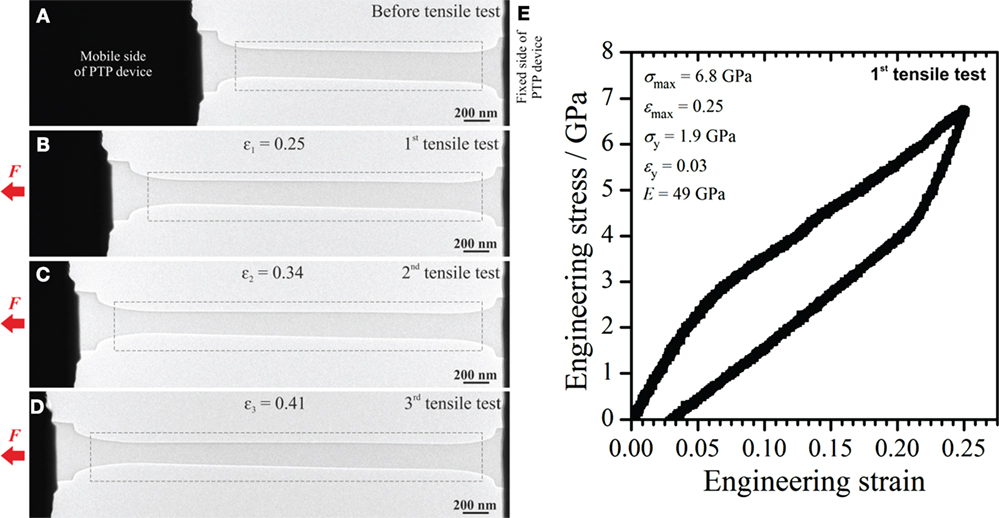
Figure 7. In situ tensile testing of a silica glass membrane under moderate e-beam irradiation in the transmission electron microscope (TEM). The specimen is pulled interruptedly to different strains, as indicated in (B–D). (E) The mechanical response of the silica glass membrane from the first tensile test is shown. The dashed rectangles in (A–D) indicate the regions in which the deformation was concentrated. The tensile experiment is carried out with a strain rate of 2.3 × 10⁻³ s⁻¹.

As introduced above, the high energy e-beam generates structural and bonding defects in the amorphous lattice and facilitates the bond-switching mechanism, which favors the rotation and migration of atomic clusters to accommodate plastic flow in silica (Zheng et al., 2010). Hence, the e-beam irradiation causes a softening of the silica network structure both reducing its rigidity and promoting plastic flow. This could explain the lower E that we observed in case of in situ tensile testing of a silica glass membrane under e-beam irradiation, in comparison to the tensile test performed at beam-off conditions.

In contrast, in situ tensile testing of a silica glass membrane (diameter ~351 nm, thickness ~100 nm) at beam-off conditions inside the TEM (see Figure 8) results in a high amount of elastic deformation, followed by brittle fracture at a fracture strain of ~ 8%. To obtain this value, the initial slip of the membrane is subtracted, as indicated in Figure 8E. The slip off of the membrane is also confirmed by SEM analyses after the tensile experiment. The fracture surface of the membrane appears to be relatively smooth, as can be seen in Figures 8C,D. The particle and/or island-like dark contrasts visible in Figures 8C,D are Ga-enriched particles redeposited during FIB preparation. In contrast to the tensile experiment performed at beam-on conditions (see Figure 7), here the deformation took place almost over the whole length of the tensile specimen (see the red dashed lines in Figure 8B), which indicate the initial shape of the membrane. The σ_f of 5.4 GPa is slightly below values reported for silica glass fibers with comparable dimensions (Brambilla and Payne, 2009), but clearly exceeds tensile strength values reported for microscale silica fibers with E-glass (ranging from ~2.1 to 3.4 GPa) and basaltic glass compositions (ranging from ~1 to 4 GPa) (Lund and Yue, 2010). The E of 76 GPa is in the range of values known for bulk fused silica (Adachi and Sakka, 1990). Silva et al. (2006) performed bending experiments on silica nanowires with diameters ranging from 280 to 1950 nm and observed values of E similar to ours (measured at beam-off conditions). Just recently, Luo et al. (2016) performed in situ tensile experiments with nanoscale silica glass fibers (with diameters well below 50 nm) at beam-off conditions in the TEM and performed complementary molecular dynamics simulations. The authors noticed plasticity at length scales of 10 nm and a significant brittle-to-ductile transition upon reducing the fiber diameter below 18 nm (Luo et al., 2016).

FIGURE 8

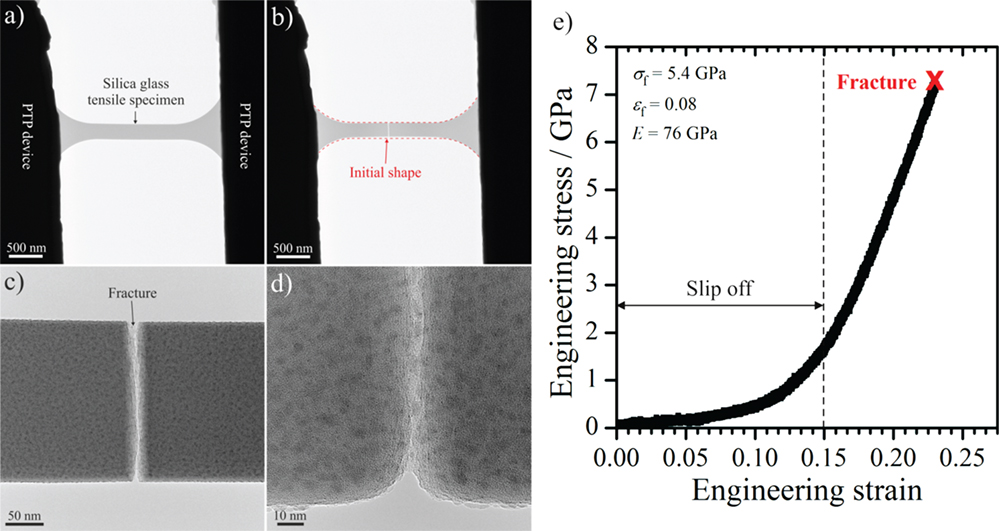
Figure 8. In situ tensile testing of a silica glass membrane at beam-off conditions in the transmission electron microscope (TEM). (A,B) TEM images show the silica glass tensile specimen before and after tensile testing, respectively. (C,D) Higher magnification TEM images show the fractured region of the glass membrane. (E) The mechanical properties of the glass membrane are shown. The tensile experiment is carried out with a strain rate of 2.3 × 10⁻³ s⁻¹.

In a third experiment (see Figure 9), a silica glass membrane was pulled under e-beam irradiation (beam current density of ~10⁻² A cm⁻²), while during elongation the e-beam is switched off at a strain of ~20%. This kind of experiment directly evidences the impact of e-beam irradiation on the deformation behavior of silica glass inside the TEM. The corresponding in situ TEM Movie S4 (Video S4) is available in the Supplementary Material. As can be seen in the Movie S4 (Video S4) in Supplementary Material and in Figure 9D, during the elongation under e-beam irradiation, the silica glass membrane exhibits an elastic/plastic deformation behavior. After an initial elastic deformation regime, it yields at a strain of ~6%, while reaching a σ_y of ~2.2 GPa. The following plastic deformation regime suddenly ends at the point where the e-beam is switched off (see Figure 9D), where a stress of 4.5 GPa is reached. The absence of the e-beam is directly correlated with an instantaneous change in the mechanical response of silica glass. Starting from the point where the e-beam is blanked, the stress (and the force signal in the Movie S4 (Video S4) in Supplementary Material) increases in a linear manner, indicating a purely elastic behavior, finally reaching a value of 13.8 GPa where the membrane fractures. After subtracting the fraction of the initial e-beam-assisted deformation regime, a σ_f ~9.4 GPa (at ~0.12 fracture strain) and an E value of 78 GPa are observed for the silica glass membrane at beam-off conditions. The σ_f is in the range of values of silica glass fibers with comparable dimensions reported by Brambilla and Payne (2009) and again clearly exceeds values reported for microscale silica fibers by Lund and Yue (2010). The E of 78 GPa is in the range of values known for bulk fused silica (Adachi and Sakka, 1990) and also in the range of values reported by Silva et al. (2006) for silica nanowires with comparable dimensions. Moreover, the E value also agrees well with the one observed for the silica glass membrane pulled at beam-off conditions in the TEM (see Figure 8 and text above). This experiment directly demonstrates in situ how the e-beam irradiation in the TEM can be used to control the mechanical behavior of silica glass. Just recently, we observed a similar behavior in case of in situ compression experiments of nanoscale SFB-type silica spheres in the TEM (Mačković et al., 2016). Upon switching off the e-beam during in situ compression in the TEM, the deformation behavior of silica spheres switched from elastic/plastic to completely elastic (Mačković et al., 2016), similar to what we observed here for silica glass membranes. It has to be noted that the σ_max value of 4.5 GPa obtained at ε_max ≈ 0.2 during the beam-on deformation regime of the tensile experiment shown in Figure 9 is slightly lower in comparison to the stress value of ~5.4 GPa observed at a comparable plastic strain in the beam-on tensile test shown in Figure 7. The slight differences in the stress values are possibly caused by the variation of the membrane thickness, as we observed by AFM measurements and TEM analysis of the FIB cross-section.

FIGURE 9

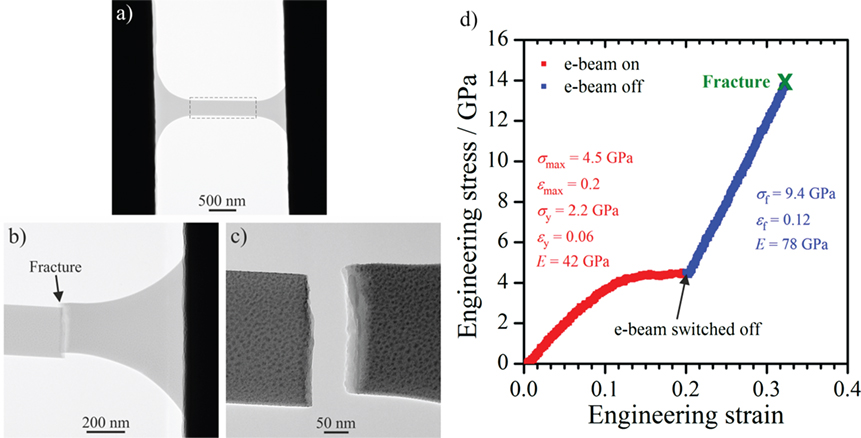
Figure 9. In situ tensile testing of a silica glass membrane under initial e-beam irradiation and at beam-off conditions. The transmission electron microscope (TEM) image in (A) shows the membrane before the tensile test, while the TEM images in (B,C) show the membrane after fracture. The dotted rectangle in (A) indicates the region in which the deformation was concentrated. The stress–strain curve and mechanical properties of the silica glass membrane for beam-on and beam-off conditions are shown in (D). The tensile experiment is carried out with a strain rate of 2.3 × 10⁻³ s⁻¹.

Even though in the present work, based on the experimental setup, e-beam irradiation is not expected to cause significant heating of the silica glass specimens, future work is planned to check this systematically as a case study. As shown just recently by Niekiel et al. (2016), parallel beam electron diffraction can be used in situ in the TEM to perform local temperature measurements with high precision. A similar experimental setup is currently being developed to assess quantitative data of a possible temperature increase upon irradiation with electrons in the TEM. Furthermore, it is expected that silica glass shows an e-beam dose-dependent mechanical response during tensile testing in the TEM, similarly to our observations discussed in the text above for nanoscale SFB-type silica spheres in the TEM (Mačković et al., 2014, 2016). To account for this, in situ tensile experiments carried out at different e-beam conditions in the TEM are planned in near future.

As a final remark, it should be noted that all in situ tensile experiments showed good reproducibility.

Summary and Outlook

In conclusion, we have presented a novel approach combining site-specific FIB preparation with quantitative in situ tensile testing of nanoscale silica glass membranes inside the TEM. Following this approach, valuable insights into the nanomechanical behavior of silica glass are obtained. Moreover, the impact of Ga⁺ irradiation on the structure of silica glass during preparation in the FIB is reported and discussed. The Ga⁺ irradiation causes a slight densification of the silica glass network structure, accompanied with redeposition of Ga-enriched particles onto the surface of the silica glass membranes. In contrast, moderate e-beam irradiation in the TEM is found not to alter the structure of silica glass. In situ tensile testing of silica glass membranes under moderate e-beam irradiation inside the TEM results in large plastic strains without fracture. In contrast, in situ tensile testing of silica glass membranes in the absence of the e-beam leads to elastic/plastic deformations followed by brittle fracture. At beam-off conditions, the silica glass membranes exhibit Young’s moduli, which are comparable with values known for bulk fused silica. In case of in situ tensile testing under moderate e-beam irradiation in the TEM, the silica glass membranes exhibit a lowered Young’s moduli. In the absence of e-beam irradiation, the silica glass membranes exhibit fracture stress values, which are in the range of those known for silica glass fibers with comparable dimensions.

Further aspects that need to be addressed and improved in future are given in the following. One effect that obviously occurs during tensile testing of the membranes is a change of specimen thickness, which is not considered in the present work. Currently, work is under way to track thickness changes by in situ EELS measurements during tensile testing. Moreover, in order to make more precise statements about the specimen thickness of each pulled silica glass membrane, thickness measurements by EELS and AFM need to be performed before each tensile test. Furthermore, for a better comparability between the single tensile experiments, uniform tensile specimen geometry needs to be implemented.

The approach presented in the present work is likely applicable also to other glass systems and may also be suitable for crystalline materials.

Author Contributions

ES and MM conceived the project. TP, CD, and HS elaborated the FIB transfer. MM and NS carried out the in situ TEM experiments. PH, SR, and WP contributed AFM measurements and Raman spectroscopy data. MM, TP, and ES designed the manuscript. All authors discussed the results and implications and commented on the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Financial support by the DFG is gratefully acknowledged.

Funding

Funding was provided by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) through the SPP1594 “Topological Engineering of Ultra-Strong Glasses” (project SP648/6-1), the Research Training Group GRK1896 “In situ microscopy with electrons, X-rays, and scanning probes” and the Cluster of Excellence EXC315 “Engineering of Advanced Materials” (EAM).

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fmats.2017.00010/full#supplementary-material.

Movies S1–S4 (Videos S1–S4) show in situ tensile tests of silica glass membranes performed inside the Titan³ Themis 300 with the Hysitron PI95 TEM Picoindenter^®. The Movies S1–S3 (Videos S1–S3) show in situ tensile tests performed on the same silica glass membrane interruptedly with different maximum strains.

Movie S1 (Video S1). In situ tensile test of a silica glass membrane under moderate e-beam irradiation in the transmission electron microscope (TEM) (maximum strain ~25%). The movie speed is increased 10×.

Movie S2 (Video S2). In situ tensile test of a silica glass membrane under moderate e-beam irradiation in the transmission electron microscope (TEM) (maximum strain ~34%). The movie speed is increased 10×.

Movie S3 (Video S3). In situ tensile test of a silica glass membrane under moderate e-beam irradiation in the transmission electron microscope (TEM) (maximum strain ~41%). The movie speed is increased 10×.

Movie S4 (Video S4). In situ tensile test of a silica glass membrane under initial e-beam irradiation and beam-off conditions in the transmission electron microscope (TEM). The movie speed is increased 10×.

References

Adachi, T., and Sakka, S. (1990). Dependence of the elastic moduli of porous silica gel prepared by the sol-gel method on heat-treatment. J. Mater. Sci. 25, 4732–4737. doi: 10.1007/BF01129933

CrossRef Full Text | Google Scholar

Bhowmick, S., Stauffer, D., Major, R., Warren, O., and Asif, S. A. S. (2015). A combined effect of electron beam and stress on plastic flow of amorphous silica microparticles. Microsc. Microanal. 21, 1015–1016. doi:10.1017/S1431927615005875

CrossRef Full Text | Google Scholar

Biener, J., Hodge, A. M., Hayes, J. R., Volkert, C. A., Zepeda-Ruiz, L. A., Hamza, A. V., et al. (2006). Sie effects on the mechanical beahvior of nanoporous Au. Nano Lett. 6, 2379–2382. doi:10.1021/nl061978i

CrossRef Full Text | Google Scholar

Bilodeau, F., Hill, K. O., Faucher, S., and Johnson, D. C. (1988). Low-loss highly overcoupled fused couplers: fabrication and sensitivity to external pressure. J. Lightwave Tech. 6, 1476–1482. doi:10.1109/50.7904

CrossRef Full Text | Google Scholar

Brambilla, G., and Payne, D. N. (2009). The ultimate strength of glass silica nanowires. Nano Lett. 9, 831–835. doi:10.1021/nl803581r

PubMed Abstract | CrossRef Full Text | Google Scholar

Dellin, T. A., Tichenor, D. A., and Barsis, E. H. (1977). Volume, index-of-refraction, and stress changes in electron-irradiated vitreous silica. J. Appl. Phys. 48, 1131–1138. doi:10.1063/1.323791

CrossRef Full Text | Google Scholar

Ernsberger, F. M. (1968). Role of densification in deformation of glasses under point loading. J. Am. Ceram. Soc. 51, 545–547. doi:10.1111/j.1151-2916.1968.tb13318.x

CrossRef Full Text | Google Scholar

Ferrari, A. C., and Robertson, J. (2001). Resonant Raman spectroscopy of disordered, amorphous, and diamond like carbon. Phys. Rev. B Condens. Matter Mater. Phys. 64, 075414. doi:10.1103/PhysRevB.64.075414

CrossRef Full Text | Google Scholar

Galeener, F. L. (1979). Band limits and the vibrational spectra of tetrahedral glasses. Phys. Rev. B Condens. Matter Mater. Phys. 19, 4292–4297. doi:10.1103/PhysRevB.19.4292

CrossRef Full Text | Google Scholar

Galeener, F. L. (1982). Planar rings in glasses. Solid State Commun. 44, 1037–1040. doi:10.1016/0038-1098(82)90329-5

CrossRef Full Text | Google Scholar

Giannuzzi, L. A., and Stevie, F. A. (eds) (2005). Introduction to Focused Ion Beams: Instrumentation, Theory, Techniques and Practise. USA: Springer-Verlag

Google Scholar

Grimsditch, M. (1984). Polymorphism in amorphous SiO2. Phys. Rev. Lett. 52, 2379–2381. doi:10.1103/PhysRevLett.52.2379

CrossRef Full Text | Google Scholar

Guo, H., Yan, P. F., Wang, Y. B., Tan, J., Zhang, Z. F., Sui, M. L., et al. (2007). Tensile ductility and necking of metallic glass. Nat. Mater. 6, 735–739. doi:10.1038/nmat1984

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, X. D., Zhang, Z., Zhang, Y. F., Zheng, K., Zhang, X. N., Hao, Y. J., et al. (2007a). Low-temperature in situ large strain plasticity of ceramic SiC nanowires and its atomic-scale mechanism. Nano Lett. 7, 452–457. doi:10.1021/nl0627689

CrossRef Full Text | Google Scholar

Han, X., Zheng, K., Zhang, Y., Zhang, X., Zhang, Z., and Wang, Z. L. (2007b). Low-temperature in situ large-strain plasticity of silicon nanowires. Adv. Mater. 19, 2112–2118. doi:10.1002/adma.200602705

CrossRef Full Text | Google Scholar

Hanisch, M., Mačković, M., Taccardi, N., Spiecker, E., and Klupp Taylor, R. N. (2012). Synthesis of silver nanoparticle necklaces without explicit addition of reducing or templating agents. Chem. Commun. 48, 4287–4289. doi:10.1039/c2cc30671a

CrossRef Full Text | Google Scholar

Iwata, K., and Nishi, Y. (2008). Effect of electron-beam irradiation on impact value of silica glass. Mater. Trans. 49, 2058–2062. doi:10.2320/matertrans.MRA2008605

CrossRef Full Text | Google Scholar

Kato, N. I. (2004). Reducing focused ion beam damage to transmission electron microscopy samples. J. Electron Microsc. (Tokyo) 53, 451–458. doi:10.1093/jmicro/dfh080

PubMed Abstract | CrossRef Full Text | Google Scholar

Kermouche, G., Guillonneau, G., Michler, J., Teisseire, J., and Barthel, E. (2016). Perfectly plastic flow in silica glass. Acta Mater. 114, 146–153. doi:10.1016/j.actamat.2016.05.027

CrossRef Full Text | Google Scholar

Kiener, D., Motz, C., Rester, M., Jenko, M., and Dehm, G. (2007). FIB damage of Cu and possible consequences for miniaturized mechanical tests. Mater. Sci. Eng. A Struct. Mater. 459, 262–272. doi:10.1016/j.msea.2007.01.046

CrossRef Full Text | Google Scholar

Kiener, D., Zhang, Z., Sturm, S., Cazzotes, S., Imrich, P. J., Kirchlechner, C., et al. (2012). Advanced nanomechanics in the TEM: effects of thermal annealing on FIB prepared Cu samples. Philos. Mag. 92, 3269–3289. doi:10.1080/14786435.2012.685966

CrossRef Full Text | Google Scholar

Kobler, A., Beuth, T., Klöffel, T., Prang, R., Moosmann, M., Scherer, T., et al. (2015). Nanotwinned silver nanowires: structure and mechanical properties. Acta Mater. 92, 299–308. doi:10.1016/j.actamat.2015.02.041

CrossRef Full Text | Google Scholar

Lacroix, R., Chomienne, V., Kermouche, G., Teisseire, J., Barthel, E., and Queste, S. (2012a). Micropillar testing of amorphous silica. Int. J. Appl. Glass Sci. 3, 36–43. doi:10.1111/j.2041-1294.2011.00075.x

CrossRef Full Text | Google Scholar

Lacroix, R., Kermouche, G., Teisseire, J., and Barthel, E. (2012b). Plastic deformation and residual stresses in amorphous silica pillars under uniaxial loading. Acta Mater. 60, 5555–5566. doi:10.1016/j.actamat.2012.07.016

CrossRef Full Text | Google Scholar

Lambropoulos, J. C., Xu, S., and Fang, T. (1996). Constitutive law for the densification of fused silica, with applications in polishing and microgrinding. J. Am. Ceram. Soc. 79, 1441–1452. doi:10.1111/j.1151-2916.1996.tb08748.x

CrossRef Full Text | Google Scholar

Lee, S., Jeong, J., Kim, Y., Han, S. M., Kiener, D., and Oh, S. H. (2016). FIB-induced dislocations in Al submicron pillars: annihilation by thermal annealing and effects on deformation behavior. Acta Mater. 110, 283–294. doi:10.1016/j.actamat.2016.03.017

CrossRef Full Text | Google Scholar

Legros, M., Gianola, D. S., and Motz, C. (2010). Quantitative in situ mechanical testing in electron microscopes. MRS Bull. 35, 354–360. doi:10.1557/mrs2010.567

CrossRef Full Text | Google Scholar

Liebig, J. P., Göken, M., Richter, G., Mačković, M., Przybilla, T., Spiecker, E., et al. (2016). A flexible method for the preparation of thin film samples for in situ TEM characterization combining shadow-FIB milling and electron-beam-assisted etching. Ultramicroscopy 171, 82–88. doi:10.1016/j.ultramic.2016.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lund, M. D., and Yue, Y. (2010). Impact of drawing stress on the tensile strength of oxide glass fibers. J. Am. Ceram. Soc. 93, 3236–3243. doi:10.1111/j.1551-2916.2010.03879.x

CrossRef Full Text | Google Scholar

Luo, J., Wang, J., Bitzek, E., Huang, J. Y., Zheng, H., Tong, L., et al. (2016). Size-dependent brittle-to-ductile transition in silica glass nanofibers. Nano Lett. 16, 105–113. doi:10.1021/acs.nanolett.5b03070

PubMed Abstract | CrossRef Full Text | Google Scholar

Mačković, M., Niekiel, F., Wondraczek, L., Bitzek, E., and Spiecker, E. (2016). In situ mechanical quenching of nanoscale silica spheres in the transmission electron microscope. Scr. Mater. 121, 70–74. doi:10.1016/j.scriptamat.2016.04.019

CrossRef Full Text | Google Scholar

Mačković, M., Niekiel, F., Wondraczek, L., and Spiecker, E. (2014). Direct observation of electron-beam-induced densification and hardening of silica nanoballs by in situ transmission electron microscopy and finite element method simulations. Acta Mater. 79, 363–373. doi:10.1016/j.actamat.2014.05.046

CrossRef Full Text | Google Scholar

McMillan, P., Piriou, B., and Couty, R. (1984). A Raman study of pressure-densified vitreous silica. J. Chem. Phys. 81, 4234–4236. doi:10.1063/1.447455

CrossRef Full Text | Google Scholar

Mochizuki, S.-S., and Kawai, N. (1972). Lattice vibrational spectra of vitreous silica densified by pressure. Solid State Commun. 11, 763–765. doi:10.1016/0038-1098(72)90265-7

CrossRef Full Text | Google Scholar

Murata, H. (1996). Handbook of Optical Fibers and Cables, New York: Marcel Dekker, Inc.

Google Scholar

Niekiel, F., Kraschewski, S. M., Müller, J., Butz, B., and Spiecker, E. (2016). Local temperature measurement in the TEM by parallel beam electron diffraction. Ultramicroscopy doi:10.1016/j.ultramic.2016.11.028

CrossRef Full Text | Google Scholar

Nomura, K., Chen, Y.-C., Kalia, R. K., Nakano, A., and Vashishta, P. (2011). Defect migration and recombination in nanoindentation of silica glass. Appl. Phys. Lett. 99, 111906. doi:10.1063/1.3637052

CrossRef Full Text | Google Scholar

Paul, J., Romeis, S., Mačković, M., Marthala, V. R. R., Herre, P., Przybilla, T., et al. (2015). In situ cracking of silica beads in the SEM and TEM – effect of particle size on structure–property correlations. Powder Technol. 270, 337–347. doi:10.1016/j.powtec.2014.10.026

CrossRef Full Text | Google Scholar

Perriot, A., Vandembroucq, D., Barthel, E., Martinez, V., Grosvalet, L., Martinet, C., et al. (2006). Raman microspectroscopic characterization of amorphous silica plastic behavior. J. Am. Ceram. Soc. 89, 596–601. doi:10.1111/j.1551-2916.2005.00747.x

CrossRef Full Text | Google Scholar

Primak, W., and Kampwirth, R. (1968). The radiation compaction of vitreous silica. J. Appl. Phys. 39, 5651–5658. doi:10.1063/1.1656029

CrossRef Full Text | Google Scholar

Romeis, S., Paul, J., Hanisch, M., Marthala, V. R. R., Hartmann, M., Taylor, R. N. K., et al. (2014). Correlation of enhanced strength and internal structure for heat-treated submicron Stöber silica particles. Part. Part. Syst. Charact. 31, 664. doi:10.1002/ppsc.201300306

CrossRef Full Text | Google Scholar

Romeis, S., Paul, J., Herre, P., De Ligny, D., Schmidt, J., and Peukert, W. (2015). Local densification of a single micron sized silica sphere by uniaxial compression. Scr. Mater. 108, 84–87. doi:10.1016/j.scriptamat.2015.06.023

CrossRef Full Text | Google Scholar

Romeis, S., Paul, J., Ziener, M., and Peukert, W. (2012). A novel apparatus for in situ compression of submicron structures and particles in a high resolution SEM. Rev. Sci. Instrum. 83, 95105. doi:10.1063/1.4749256

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, S. K., Mammone, J. F., and Nicol, M. F. (1981). Raman investigation of ring configurations in vitreous silica. Nature 292, 140–141. doi:10.1038/292140a0

CrossRef Full Text | Google Scholar

Silva, E. C. C. M., Tong, L., Yip, S., and Van Vliet, K. J. (2006). Size effects on the stiffness of silica nanowires. Small 2, 239–243. doi:10.1002/smll.200500311

CrossRef Full Text | Google Scholar

Snoeks, E., Polman, A., and Volkert, C. A. (1994). Densification, anisotropic deformation, and plastic flow of SiO2 during MeV heavy ion irradiation. Appl. Phys. Lett. 65, 2487–2489. doi:10.1063/1.112646

CrossRef Full Text | Google Scholar

Stauffer, D., Bhowmick, S., Major, R., Warren, O. L., and Syed Asif, S. A. (2014). High plastic strain of silica microparticles under electron beam irradiation. Microsc. Microanal. 20, 1544–1545. doi:10.1017/S1431927614009453

CrossRef Full Text | Google Scholar

Stöber, W., Fink, A., and Bohn, E. (1968). Controlled growth of monodisperse silica spheres in the micron size range. J. Colloid Interface Sci. 26, 62–69. doi:10.1016/0021-9797(68)90272-5

CrossRef Full Text | Google Scholar

Storm, A. J., Chen, J. H., Ling, X. S., Zandbergen, H. W., and Dekker, C. (2005). Electron-beam-induced deformations of SiO₂ nanostructures. J. Appl. Phys. 98, 014307-1-8. doi:10.1063/1.1947391

CrossRef Full Text | Google Scholar

Tian, L., Cheng, Y.-Q., Shan, Z.-W., Li, J., Wang, C.-C., Han, X.-D., et al. (2012). Approaching the ideal elastic limit of metallic glasses. Nat. Commun. 3, 609. doi:10.1038/ncomms1619

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomozawa, M., Lee, Y.-K., and Peng, Y.-L. (1998). Effect of uniaxial stresses on silica glass structure investigated by IR spectroscopy. J. Non. Cryst. Solids 242, 104–109. doi:10.1016/S0022-3093(98)00780-7

CrossRef Full Text | Google Scholar

Tong, L. M., Gattass, R. R., Ashcom, J. B., He, S. L., Lou, J. Y., Shen, M. Y., et al. (2003). Subwavelength-diameter silica wires for low-loss optical wave guiding. Nature 426, 816–819. doi:10.1038/nature02193

PubMed Abstract | CrossRef Full Text | Google Scholar

Uchic, M. D., Dimiduk, D. M., Florando, J. N., and Nix, W. D. (2004). Sample dimensions influence strength and crystal plasticity. Science 305, 986–989. doi:10.1126/science.1098993

PubMed Abstract | CrossRef Full Text | Google Scholar

Volkert, C. A., and Lilleodden, E. T. (2006). Size effects in the deformation of sub-micron Au columns. Philos. Mag. (Abingdon) 86, 5567–5579. doi:10.1080/14786430600567739

CrossRef Full Text | Google Scholar

Volkert, C. A., and Minor, A. M. (2007). Focused ion beam microscopy and micromachining. MRS Bull. 32, 389–399. doi:10.1557/mrs2007.62

CrossRef Full Text | Google Scholar

Wakabayashi, D., Funamori, N., Sato, T., and Taniguchi, T. (2011). Compression behavior of densified SiO2 glass. Phys. Rev. B Condens. Matter Mater. Phys. 84, 144103–144101. doi:10.1103/PhysRevB.84.144103

CrossRef Full Text | Google Scholar

Wondraczek, L., Mauro, J. C., Eckert, J., Kühn, U., Horbach, J., Deubener, J., et al. (2011). Towards ultrastrong glasses. Adv. Mater. 23, 4578–4586. doi:10.1002/adma.201102795

PubMed Abstract | CrossRef Full Text | Google Scholar

Wondraczek, L., Sen, S., Behrens, H., and Youngman, R. (2007). Structure-energy map of alkali borosilicate glasses: effects of pressure and temperature. Phys. Rev. B Condens. Matter Mater. Phys. 76, 014202. doi:10.1103/PhysRevB.76.014202

CrossRef Full Text | Google Scholar

Yamaguchi, N., Oguri, K., Tonegawa, A., and Nishi, Y. (2004). Brittleness control of silica glass surface irradiated by sheet electron beam. J. Japan Inst. Met. 68, 198–201. doi:10.2320/jinstmet.68.198

CrossRef Full Text | Google Scholar

Yamane, M., and Asahara, Y. (2000). Glasses for Photonics. Cambridge University Press.

Google Scholar

Yue, Y., and Zheng, K. (2014). Strong strain rate effect on the plasticity of amorphous silica nanowires. Appl. Phys. Lett. 104, 231906. doi:10.1063/1.4882420

CrossRef Full Text | Google Scholar

Zhang, L., D’Acunzi, M., Kappl, M., Auernhammer, G. K., Vollmer, D., van Kats, C. M., et al. (2009). Hollow silica spheres: synthesis and mechanical properties. Langmuir 25, 2711–2717. doi:10.1021/la803546r

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., D’Acunzi, M., Kappl, M., Imhof, A., van Blaaderen, A., Butt, H.-J., et al. (2010). Tuning the mechanical properties of silica microcapsules. Phys. Chem. Chem. Phys. 12, 15392–15398. doi:10.1039/c0cp00871k

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Pauly, S., Zhu, Z. W., Gemming, T., Fu, H. M., Eckert, J., et al. (2016). Ion milling-induced micrometer-sized heterogeneities and partial crystallization in a TiZrCuFeBe bulk metallic glass. Intermetallics 73, 5–11. doi:10.1016/j.intermet.2016.02.002

CrossRef Full Text | Google Scholar

Zheng, K., Wang, C., Cheng, Y.-Q., Yue, Y., Han, X., Zhang, Z., et al. (2010). Electron-beam-assisted superplastic shaping of nanoscale amorphous silica. Nat. Commun. 1, 24. doi:10.1038/ncomms1021

PubMed Abstract | CrossRef Full Text | Google Scholar