Experimental and Theoretical Investigation of the Elastic Moduli of Silicate Glasses and Crystals

A combined quantum mechanical and thermodynamic approach to the mechanical properties of multicomponent silicate glasses is presented. Quantum chemical calculations based on density functional theory on various silicate systems were performed to explore the crystalline polymorphs existing for a given chemical composition. These calculations reproduced the properties of known polymorphs even in systems with extensive polymorphism, like MgSiO₃. Properties resting on the atomic and electronic structure, i.e., molar volumes (densities) and bulk moduli were predicted correctly. The theoretical data (molar equilibrium volumes, bulk moduli) were then used to complement the available experimental data. In a phenomenological evaluation, experimental data of bulk moduli, a macroscopic property resting on phononic structure, were found to linearly scale with the ratios of atomic space demand to actual molar volume in a universal way. Silicates ranging from high-pressure polymorphs to glasses were represented by a single master line. This suggests that above the Debye limit (in practice: above room temperature), the elastic waves probe the short range order coordination polyhedra and their next neighbor linkage only, while the presence or absence of an extended translational symmetry is irrelevant. As a result, glasses can be treated—with respect to the properties investigated—as commensurable members of polymorphic series. Binary glasses fit the very same line as their one-component end members, again both in the crystalline and glassy state. Finally, it is shown that the macroscopic properties of multicomponent glasses are also linear superpositions of the properties of their constitutional phases (as determined from phase diagrams or by thermochemical calculations) taken in their respective glassy states. This is verified experimentally for heat capacities and Young’s moduli of industrial glass compositions. It can be concluded that the combined quantum mechanical and thermochemical approach is a quantitative approach for the design of glasses with desired mechanical properties, e.g., for the development of high-modulus glasses.

Introduction

Elastic properties of glasses have gained great importance during the last years. Especially for reinforcement applications it is essential to develop glass compositions with targeted elastic moduli. Calculation and prediction of elastic moduli of silicate glasses is still a great challenge. Models based on oxide increments (e.g., Makishima and Mackenzie, 1973; Rocherulle et al., 1989) have been very successful in general, but are applicable to very limited compositional regions only. This is due to the fact that glasses typically are extremely non-ideal mixtures if described on the basis of their oxide components j. However, as previously shown (Conradt, 2004), glasses can be treated as nearly ideal mixtures of components reflecting the stoichiometries of their coexisting constitutional compounds k. In this description frame, heats of mixing and (due to the number of atoms comprised in each k) even entropies of mixing may be neglected. The macroscopic properties P of glasses are approximated very well by weighted sums of the individual properties P_k of components k, taken in their glassy state (Conradt, 2010). The additivity of macroscopic properties of multicomponent glasses is well substantiated for heat capacities, entropies, enthalpies, and Gibbs energies. The close relation of this stoichiometric concept to structural reality has been demonstrated by NMR and neutron scattering experiments (Vedishcheva et al., 2001; Wright et al., 2001).

It is the aim of the present paper to extend the above concept to the elastic properties. For this purpose, we first focus on understanding the relation between the structure and elastic properties in polymorphic one-component series (MgSiO₃), always comprising the isochemical glasses. This step is supported by density functional theory (DFT) calculations verifying structures, molar volumes, and bulk moduli of known crystalline polymorphs as well as hypothetical low-density polymorphs. Then, we show that the elastic moduli of binary and multicomponent glasses, like the heat capacities, etc., mentioned above, are indeed given by linear superpositions of the properties of the individual constitutional compounds. By this approach, elastic moduli are predicted, which underestimate the experimental values by less than 5 GPa.

Experimental Methods and Data Acquisition

Density functional theoretical calculations were carried out in the framework of the projector augmented-wave method (Blöchl, 1994) using the Vienna Ab Initio Simulation Package (Kresse and Furthmüller, 1996; Kresse and Joubert, 1999). Plane wave basis sets with kinetic energies up to 500 eV were used. Exchange and correlation were approximated by the parametrization proposed by Perdew et al. (1996). Brillouin zone sampling was carried out on a dense k-point grid in reciprocal space, and it was made sure to have at least 1,000 k-point⋅atoms. Theoretical bulk moduli and equilibrium molar volumes were obtained by fitting the electronic energies at several well-chosen volumes to Murnaghan’s equation of state (Murnaghan, 1937). The starting structures were taken from the literature and the molar volume was varied and the structure was optimized with fixed volume and symmetry. Additionally, other equations of states (Birch, 1947; Vinet et al., 1987) were tested in order to verify the results; no significant change in bulk modulus and molar volume was found.

Experimental data for glasses and crystals were on one hand collected from literature (Carmichael, 1984; Bass, 1995; Rouxel, 2007) and on the other hand measured by impulse excitation method. This method is based on the relation between elastic moduli and geometry, mass, and specific mechanical resonant frequencies of suitable samples of the tested material. Therefore, glasses were melted from pure chemicals in an electrical furnace at temperatures between 1,400 and 1,550°C in Pt/Rh crucibles; dwell time at maximum temperature was minimum 4 h. The melts were cast into graphite molds; the blocks were annealed at approx. T_g + 50 K for about 24 h and then cooled to room temperature at 2 K/min. Bar-shaped samples (65 mm × 10 mm × 5 mm) with smooth plane-parallel faces were prepared by cutting, grinding, and polishing. Young’s modulus was measured by impulse excitation technique (equipment by Lemmens B.V., Belgium) at ambient pressure and 25°C. Samples were excited to transverse oscillation and the resulting resonant frequency in flexural mode was measured. Young’s modulus E was calculated according to ASTM E1876 (ASTM, 2002):

$E=\frac{m\cdot {\mathrm{\omega }}_{\text{flex}}^2\cdot l^3}{w\cdot h^3}\cdot f_{\text{korr}}$ (1)

where m is the sample mass, l, w, and h are the geometrical dimensions length, width, and height, respectively, ω_flex is the resonant frequency in the first flexural mode of vibration, and f_korr is a correction term.

Results and Discussion

Quantum Chemical Calculations

Several polymorphs of magnesium silicate (MgSiO₃) were investigated using the abovementioned DFT methodology. These polymorphs included three enstatite type structures together with the high-pressure polymorphs adopting the ilmenite and perovskite structure, respectively.

The calculated volume-dependent electronic ground state energy for each of the polymorphs is presented in Figure 1. The pyroxene-structured polymorphs proto-, ortho-, and clinoenstatite show a second energetic minimum at higher volumes. The deviations between these three energy curves are significantly smaller than their differences to the high-pressure polymorphs. The energy levels for the high-pressure polymorphs, ilmenite and perovskite, are much higher. As expected, only at quite small molar volumes, which correspond to higher pressure, these modifications become energetically favorable.

FIGURE 1

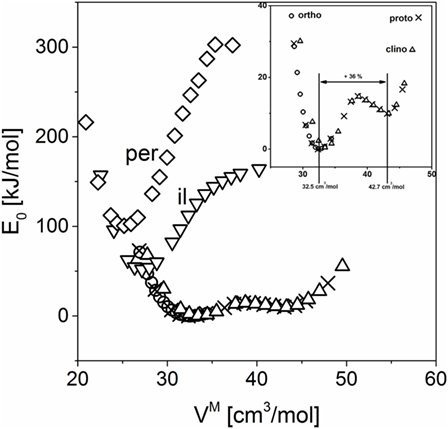
Figure 1. Relative electronic ground state energy for MgSiO₃ polymorphs calculated by density functional theory. per, perovskite structure; il, ilmenite structure; ortho, orthoenstatite; proto, protoenstatite; clino, clinoenstatite.

A similar observation as for the enstatite polymorphs has recently been made for the case of jadeite (Stoffel et al., 2016) where such a low-density polymorph was found to be similar to the isochemical glass phase with jadeite composition in terms of its macroscopic properties.

The first minimum in the energy curve corresponded to the naturally occurring phase of jadeite, which has an experimentally determined molar volume of 60.5 cm³/mol for the formula unit NaAlSi₂O₆.

The comparison of the bulk moduli and the molar volumes calculated by DFT of these two stable structures showed an increase in molar volume of about 38% (experiment 37%) and a strong decrease of the bulk modulus. This coincides very well with the experimentally determined differences in elastic moduli between jadeite crystal and glass. So there exists a hypothetical crystalline structure with a short range order very close to the local structure of the glass and with nearly the same mechanical properties.

For comparison, the zeolithe analcime NaAlSi₂O₆⋅H₂O has a molar volume of 96.94 cm³/mol. Using Helgeson’s (Helgeson and Kirkham, 1976) value of the partial molar volume of H₂O of approximately 8 cm³/mol, this yields a molar volume for dehydrated analcime of approximately 88.9 cm³/mol, which is in fair agreement with the value of the hypothetical structure identified; this also matches with the experimentally determined molar volume of the isochemical glass. Previous DFT calculations (Stoffel et al., 2016) as well as calorimetric values showed that both dehydrated analcime and the isochemical glass display nearly identical heat capacity c_p.

Turning back to magnesium silicate, the second minimum in the energy curves shows a molar volume of 42.7 cm³/mol, which is much larger than the experimental value of the glass, 36.36 cm³/mol (Figure 1). In contrast to the jadeite case, the glass seems not to locally adopt this low-density structure but possibly, as concluded from the molar volume, a structure in between the hypothetical low-density structure and the enstatite polymorphs.

The structural differences between the MgSiO₃ polymorphs can be seen in Figure 2. The enstatite structures (Figure 2A) are built of corner-linked silica tetrahedra forming chains. These chains are arranged in layers where in between the magnesium ions can be found on octahedral sites. Protoenstatite and orthoenstatite have an orthorhombic crystal structure, while clinoenstatite is tilted and therefore monoclinic. The ilmenite structure (Figure 2B) consists of silica octahedra that are edge-linked and form layers, the structure has a trigonal space group. The second high-pressure polymorph of the perovskite type has an orthorhombic crystal structure (Figure 2C); it is built of corner-linked silica octahedra. DFT calculations of MgSiO₃ garnet have not been carried out because of mixed occupancy of magnesium and silicon ions. A comparison of calculated and measured values for the molar volume and the bulk modulus is shown in Table 1.

FIGURE 2

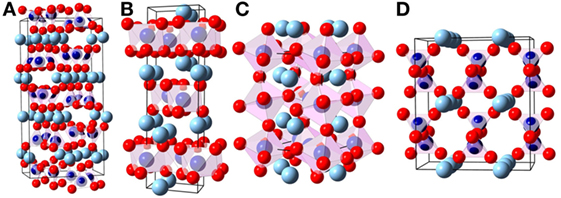
Figure 2. Atomic structures of MgSiO₃ (A: protoenstatite Murakami et al., 1984, B: ilmenite Yamanaka, 2005, C: perovskite Dobson and Jacobsen, 2004, D: hypothetical high-V phase [own work]). Dark blue, silicon; light blue, magnesium; red, oxygen; graphically presented by the use of (Ozawa and Kang, 2004); see Table 1 for density and bulk moduli.

TABLE 1

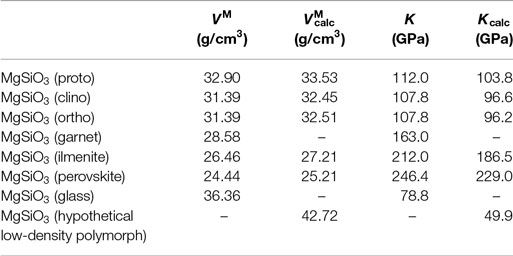
Table 1. Comparison of DFT-calculated and experimentally determined molar volumes V^M and bulk moduli K of MgSiO₃ polymorphs (Carmichael, 1984; Bass, 1995; Gwanmesia et al., 2000; Kavner et al., 2000).

The calculated values agree quite well with the experimental data within the possible precision frame; small deviations are results of different environmental parameters and mainly on limitations of DFT calculations. All experiments were carried out at ambient conditions (25°C, 1 bar) while the calculations do not include temperature effects.

Phenomenological Approach to the Bulk Moduli of Crystals and Glasses

The bulk modulus of a stoichiometric entity k is, by dimensional analysis, proportional to the quotient of its internal bond energy $U_k^0$ and its molar volume $V_k^{\text{M}}$,

$K\propto \frac{U_k^0}{V_k^{\text{M}}}.$ (2)

This correlation can be derived by taking an interatomic potential U of the form

$U=\frac{A}{r^m}+\frac{B}{r^n}$ (3)

or of the form

$U=\frac{e^2}{4\cdot \mathrm{\pi }\cdot {\mathrm{\epsilon }}_0}\cdot \frac{z_1\cdot z_2}{r}+B\cdot \text{exp}\left(\frac{-r}{r_{\text{A}}}\right)$ (4)

where A, B, m, n, and r_A are constants, r is the distance between ions, e is the elementary charge, ε₀ is the electric constant, z₁ and z₂ are the charges of the involved ions and r₀ is the equilibrium distance, respectively. The first derivative of U is the force, in the vicinity of U₀. The elastic moduli, K as one example, are then given by:

$K=\frac{1}{r_0}\cdot \frac{\mathit{dF}}{\mathit{dr}}\propto \frac{1}{r_0}\cdot \frac{d^{2}U}{{\mathit{dr}}^2}\propto \frac{U_0}{r_0^3}\propto \frac{U_0}{V^{\text{M}}}.$ (5)

$V_k^{\text{M}}$ is readily assessed by the molar mass of the stoichiometric formula, M_k, and the density ρ_k as determined by experiment,

$V_k^{\text{M}}=\frac{M_k}{{\mathrm{\rho }}_k}.$ (6)

The bond energy $U_k^0$ is derived from the difference of the internal energies of formation (from the elements in the sense of thermodynamic normalization) of compounds k and the sum of internal energies of formation of the constituting monoatomic gases; all substances are taken at P = 1 bar and 25°C. At ambient pressure, the difference Δ between internal energies U and enthalpies of formation H amounts to less than 0.2%, corresponding to Δ = P ⋅ V^M. Thus, for the calculation, tabulated heats of formation of gaseous species are used to assess the values of $U_k^0$,

$U^0=H^0-\mathit{pV}\approx H^0$ (7)

with

$H^0=H_k^0-{\displaystyle \sum _g}{\mathrm{\nu }}_g{H}_g^0,$ (8)

where ν is the stoichiometric coefficient of each gaseous species g. $U_k^0$ comprises the energetics of real structures reflecting the stoichiometries of coexisting phases (even of unknown topology), whereas $V_k^{\text{M}}$ is based on the real space demand of such structures. As shown later, the proportionality factor in equation 5 is approximately constant for silicates. In Table 2, the heats of formation mentioned above are compiled for different silicates, both in their crystalline and glassy state, and the resulting $U_k^0$ and $V_k^{\text{M}}$ for crystals and glasses, respectively, are compiled. While the normalized difference of bond energies

$\frac{U^0\left(X\right)-U^0\left(\mathit{GL}\right)}{U^0\left(X\right)}\approx 0.01\pm 0.005$ (9)

displays minor changes between isochemical glasses and crystals only, the corresponding value of molar volumes

$\frac{V^{\text{M}}\left(\mathit{GL}\right)-V^{\text{M}}\left(X\right)}{V^{\text{M}}\left(X\right)}\approx 0.1\pm 0.08$ (10)

is one order of magnitude higher. Thus, we conclude that the difference of bulk moduli of crystals and their isochemical glasses is essentially determined by the atomic space demand and to a lesser extent only by the bond energies involved. In addition, it can also be seen in Table 2 that the bond energies of different glassy compounds only differ marginally. Therefore, in a next step, we evaluate the bulk moduli of series of crystalline polymorphs comprising the respective glasses as disordered polymorphs, according to their atomic space demand.

TABLE 2

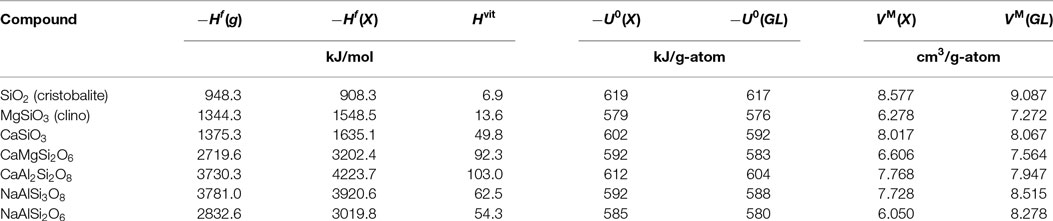
Table 2. Heat of formation H, internal energy U, and molar volume V^M of different silicates in gaseous (g), crystalline (X), or glassy (GL) state; g-atom is mol divided by the number of atoms in one formula unit; the heats of formation of the monoatomic gases Si, Al, Mg, Ca, Na, and O amount to +450.0, +329.6, +146.8, +177.8, +108.0, +249.2 kJ/mol, respectively (Kubaschewski et al., 1993).

The theoretical space demand is presented in terms of a normalized molar volume

$p=\frac{V^0}{V^{\text{M}}},$ (11)

where

$V^0=\frac{\mathrm{4\pi }}{3}{N}_{\text{A}}\sum \left(x_i{r}_i^3\right),$ (12)

and

$V^{\text{M}}=\frac{M}{\mathrm{\rho }}$ (13)

with N_A, Avogadro number; x_i, molar fraction; r_i, ionic radius. The following ionic radii were used: r_Si = 0.026 nm, r_Al = 0.039 nm, r_Na = 0.098 nm, r_Ca = 0.106 nm, r_Mg = 0.057 nm, and r_O = 0.14 nm (Shannon and Prewitt, 1969, 1970; Shannon, 1976). Note that the normalized molar volume p is proportional to the density ρ for a given chemical composition like MgSiO₃.

This is in accordance with former publications (Rouxel, 2007) showing also that the elastic properties scale with the atomic packing density C_pack. It is true that the assessment of atomic space demand via the packing of spherical ions (Eq. 12) is a crude approach only. The following evaluation will, however, show that the macroscopic elastic properties of crystals and glasses alike are essentially grasped by this simple approach.

An investigation was made for the series of polymorphs with the composition MgSiO₃. This naturally occurring magnesium silicate has at least three different modifications at ambient pressure and two high-pressure polymorphs as mentioned above; in addition, a garnet structure is here taken into account. These different modifications are varying in bulk modulus from 108 to 246 GPa (Carmichael, 1984; Bass, 1995; Gwanmesia et al., 2000; Kavner et al., 2000). The corresponding value measured for glassy samples is around 79 GPa (Bass, 1995). To demonstrate the predominant influence of V^M within a series of (isochemical) polymorphs with strongly varying bulk moduli; a plot bulk modulus versus the normalized molar volume p is done (Figure 3, left). The graph shows the data for six crystalline and the glassy polymorph of MgSiO₃. A regression leads to the linear correlation shown. Note that the bulk modulus of glassy MgSiO₃ aligns very well with the crystalline polymorphs. Thus, numerically, the bulk modulus K of a series of polymorphs is given by

$K=b\cdot \left(p-p_c\right).$ (14)

FIGURE 3

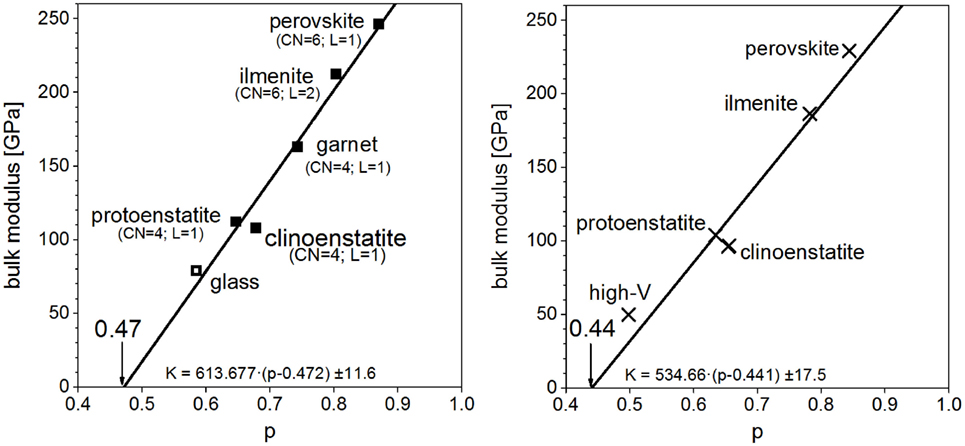
Figure 3. Bulk moduli of MgSiO₃ polymorphs (CN, coordination number; L = 1 corner-linked; L = 2 edge-linked), left: experimental data (Carmichael, 1984; Bass, 1995; Gwanmesia et al., 2000; Kavner et al., 2000), right: density functional theory calculations.

Here, p_c denotes the intercept at zero bulk modulus. This is the point where the structure loses the resistance against any compression. It amounts to p_c = 0.47 ± 0.02 in this case, which is quite close to the percolation threshold of corner-linked tetrahedral structures, e.g., diamond structure, which is 0.43 (Frisch et al., 1961; Sykes and Essam, 1964). For the interpretation of the slope b, let us recall the proportionality between K and the normalized molar volume p, and the proportionality between p and density ρ; this implies K ∝ ρ. Hence, the slope of the straight line reflects K/ρ, i.e., the squared velocity v² of an elastic wave:

$\frac{K\cdot M}{V^0}\cdot \frac{1}{\mathrm{\rho }}\propto \frac{K}{\mathrm{\rho }}=v^2.$ (15)

Coming from the upper right corner in the graph, the structural motifs of the polymorphs are changing from corner-sharing silicon octahedra (perovskite) to edge-sharing silicon octahedra (ilmenite) to tetrahedral structures in the pyroxenes and the glass. At the intercept with the abscissa, the bulk modulus assumes zero. The p value at this point corresponds to the percolation limit, i.e., the widest volume packing still permitting the form of a dense (Euclidean) material. Indeed, the value read, p_c = 0.47, corresponds to the theoretically calculated percolation limit (Frisch et al., 1961; Sykes and Essam, 1964) of corner-linked tetrahedra. It can be concluded that elastic properties are determined by structural motifs (i.e., the oxygen coordination polyhedra of the cations and the nature of linkage of adjacent polyhedra), which are similar in glasses and isochemical crystals. The right graph in Figure 3 shows the same analysis on the DFT-calculated data. Although the data are deviating from experimental values, both, the experimental data and the calculated data, yield very similar regression lines. It can be seen that the correlation between molar volume and bulk modulus is the same for the calculations; discrepancies mainly stem from differences of calculated molar volumes. An example of a binary series of glasses is shown in Figure 4. Data for the abovementioned series between jadeite and diopside is plotted together with the data of the two crystalline phases. Again, a common linear context for both, glasses and crystals, is obtained. Jadeite glass has the lowest normalized molar volume and the lowest bulk modulus of this glassy series. At contrast, the jadeite crystal has a higher normalized molar volume and bulk modulus than the diopside crystal. The changes in short range order between glassy and crystalline diopside are much smaller than the changes occurring in the jadeite system. This leads to a comparatively smaller deviation in the elastic moduli. The DFT-calculated bulk moduli for diopside and jadeite crystal, as mentioned above for magnesium silicate, are about 10–17% lower than the measured ones. DFT calculations give a good assessment of the elastic moduli but no hard predictions. Analysis of the intercept at zero bulk modulus leads to 0.445 ± 0.005. This is nearly the same value as for the magnesium silicates and again coincides very well with the percolation limit of corner-linked tetrahedral structures. From Figure 4, a further conclusion is drawn: the elastic moduli of the binary glasses are equal to the linear compositional superposition of the elastic moduli of the one-component end-member glasses.

FIGURE 4

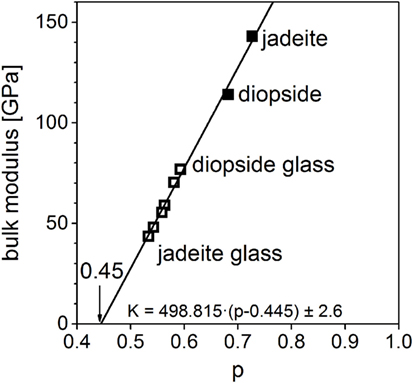
Figure 4. Bulk moduli of jadeite–diopside series (filled: crystalline, open: glassy), standard error δK = ± 2.6 GPa (Jindal et al., 2011).

The same correlation was found between normalized molar volume and Young’s modulus in this case. It is obtained for another series of glasses; in this case, it was between enstatite, MgSiO₃, and anorthite, CaAl₂Si₂O₈, as it is depicted in Figure 5. The changes in bulk modulus between crystal and glass for anorthite are rather small, Young’s modulus decreases by 9%, whereas for enstatite, these changes are quite big, Young’s modulus decreases by 42%. Anorthite has a much lower Young’s modulus than enstatite. Corresponding to this, glassy anorthite has the lowest modulus of the glassy series and glassy MgSiO₃ the highest one. Structural changes between glassy and crystalline phase are greater for MgSiO₃ but not that great to reverse the order. The intercept of the regression line at zero Young’s modulus corresponds with a normalized molar volume of 0.452 ± 0.003 just as the percolation threshold mentioned above.

FIGURE 5

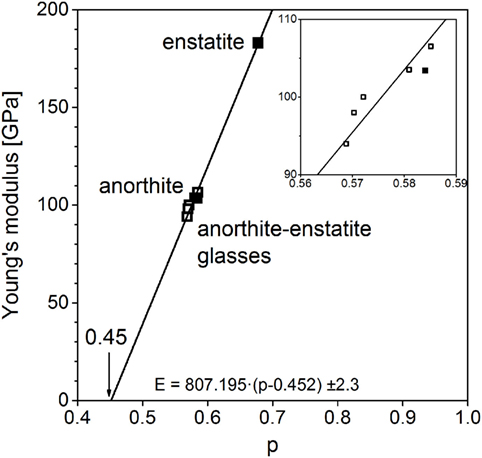
Figure 5. Young’s moduli of anorthite–enstatite series (filled: crystalline, open: glassy), standard error δK = ± 2.3 GPa (Bass, 1995).

The previous experimental data sets are assembled to gain one master regression line for crystalline and glassy silicates and alumosilicates (Figure 6) that can be used for all abovementioned examples instead of the individual ones:

$K\text{ in GPa}=579.3\cdot \left(p-0.46\right)\pm 10.38.$ (16)

FIGURE 6

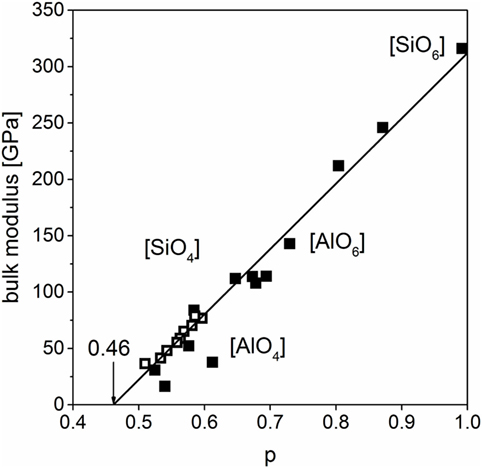
Figure 6. Bulk moduli of different crystalline and glassy silicates including SiO₂ (filled: crystalline, open: glassy), fit without SiO₂ polymorphs, standard error δK = ± 10.4 GPa (Carmichael, 1984; Bass, 1995).

Structures with octahedrally coordinated silicon atoms exhibit the highest bulk moduli. With increasing molar volume structural motifs change. First, a section with a mixture of silica tetrahedra and alumina octahedra is passed and then tetrahedrally dominated structures with the lowest moduli occur. Bulk moduli of glassy silicates can also be found in this region. Data for pure silica, SiO₂, were also analyzed in regard of this behavior; crystalline and glassy structures were added to the master curve (Figure 6). The crystalline polymorphs have a great variety in molar volume and bulk modulus due to the existence of a great number of phases at ambient pressure and also some high-pressure polymorphs. The highest values are tabulated for the high-pressure phase stishovite (silica octahedra). The polymorphs on the left side of the graph are high- and low-quartz and high- and low-cristobalite. Glassy silica has a marginally larger modulus than these phases.

The data obtained by DFT calculations, molar volume and bulk moduli, show a good correlation to the master line (Figure 7). That gives the possibility to calculate data by DFT and use them for further calculations or predictions instead of experimental data in those cases where the synthesis is complicated, although hard predictions by DFT are not possible. Our use of DFT calculations is mainly to identify stable structures and possible glassy structures in the hypothetical low-density polymorphs.

FIGURE 7

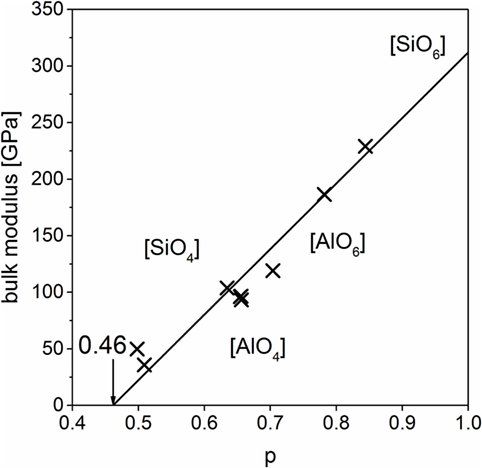
Figure 7. Density functional theory-calculated bulk moduli of different crystalline and glassy silicates with master line from Figure 6.

It can be concluded that the mechanisms responsible for elastic properties are the same for crystalline and glassy silicates. Short range order and near medium-range order, namely, nature and linkage of adjacent coordination polyhedra, have significant influence, whereas the translational symmetry on long range order is irrelevant. This offers the opportunity to apply models developed for multicrystalline materials also to multicomponent glassy materials. Attention is drawn in this context to a recent paper pointing out the similar nature of elastic waves in ordered and disordered solids (Brazhkin and Trachenko, 2014). We can also state that macroscopic elastic properties of binary mixtures can be obtained by the superposition of the properties of the two end members in glassy state, which was shown by the analysis of two-component systems (jadeite–diopside and anorthite–enstatite).

Calculation of Elastic Moduli for Multicomponent Glasses

Availability of data concerning glass properties is significantly worse than for crystalline phases. Calculating glass properties is therefore always a big challenge.

The most applied model for the calculation of Young’s moduli of oxide glasses was developed by Makishima and Mackenzie (1973). The model rests on partial molar bonding energies and volumes of each oxide; it works well for glass compositions in the range of soda-lime-silicate glasses but in the case of glasses containing elevated amounts of magnesium oxide, the accuracy of the model is decreasing up to underestimations of the experimental values by approximately 10%.

It has been shown (Conradt, 2004, 2010) that the macroscopic thermodynamic properties Z of multicomponent glasses, Z = c_p, H, S, G, are calculated in a fully quantitative way by linearly superimposing the corresponding properties Z_k of the constitutional end members k as taken from the (multidimensional) phase diagrams:

$Z={\displaystyle \sum _k}{n}_k\cdot Z_k,$ (17)

where n_k is the molar amount of k. H_k and S_k of the glasses differ from the values of their isochemical crystalline counterparts by vitrification enthalpies H^vit and vitrification entropies S^vit, respectively (Gutzow and Schmelzer, 2013), whereas the heat capacities of isochemical crystalline and glassy components k below T_g are nearly identical. Figure 4 suggests that the same type of superposition principle is valid for the elastic properties.

After all, the elastic properties are based on the nature of elastic waves like the c_p function. The possibility of superposition of macroscopic properties (shown for jadeite–diopside mixtures) was extended to multicomponent systems. For this purpose, the phase composition corresponding to the glass composition has to be calculated; the elastic moduli of these phases in a glassy state have to be taken to calculate moduli of the glasses.

For polycrystalline materials, different ways of superposition to gain elastic moduli have been proposed. Two of them were analyzed, namely, Voigt (1889), considering constant strain over all components, leading to a linear average for Young’s modulus on the one hand and Reuß (1929), proposing constant stresses over all components, leading to a reciprocal average on the other hand. The weighting of elastic moduli of components can be realized with volume or density. Originally, the volume fractions were used by Voigt, which leads to a weighting by molar fractions. The above results on elastic moduli suggest the weighting by densities, since elastic moduli scale linearly with p ∝ ρ, which yields mass fractions as weighting factors. This is also achieved by summing up the partial energy contributions of the elastic waves (Eq. 15). From these, we get two possible ways to calculate cumulative Young’s modulus:

$E={\displaystyle \sum _k}{y}_k\cdot E_k$ (18)

with y_k, mass fraction of component k; E_k, Young’s modulus of component k in glassy state, and:

$E=\frac{1}{{\displaystyle \sum _k}\frac{y_k}{E_k}}.$ (19)

Calculated values using both models with mass fractions and molar fractions as weighting factors were compared with experimentally determined values for a great number of glass compositions.

Some of the investigated glass compositions are given in Table 3. Three glass compositions are mixtures of anorthite (CAS₂) and enstatite (MS), which were already mentioned above (Figure 5), in varying molar amount; these glasses were melted and elastic moduli were measured in our labs. The data for the two float glasses are taken from literature (Rouxel, 2007). Table 4 shows the comparison of calculated and measured Young’s moduli for these glasses and additionally for two industrial E-CR-glasses. The appropriated values of Young’s moduli of the constituent phases for the calculations are shown in Table 5.

TABLE 3

Table 3. Oxide compositions, measured by XRF, of studied glasses regarding Young’s moduli in wt%.

TABLE 4

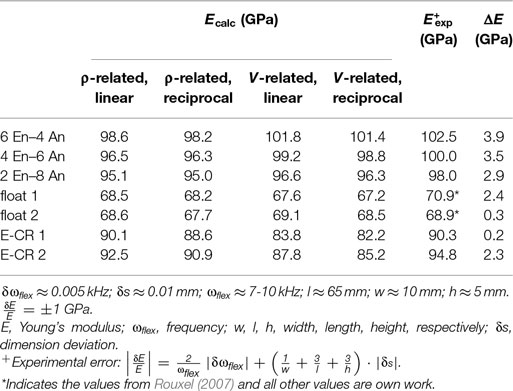
Table 4. Comparison of Young’s moduli, calculated (via superposition of glassy constituents) versus measured values; calculations: density and volume related with linear and reciprocal average, respectively; experimental data: this work except * from Rouxel (2007).

TABLE 5

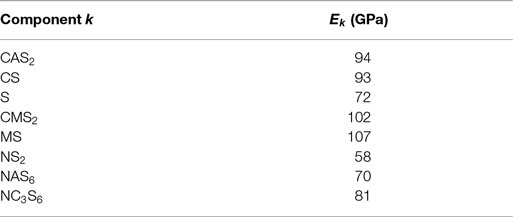
Table 5. Glassy components k and their Young’s moduli; S, SiO₂; A, Al₂O₃; C, CaO; M, MgO; N, Na₂O (Bansal and Doremus, 1986; Bass, 1995).

For materials having density fluctuations but no phase boundaries, like glasses, the Voigt average using mass fractions was found to represent the conditions responsible for elastic moduli very well. Although we see that volume-based weighting predicts some values quite precisely, in general, density-based weighting is preferred because of the significant better match for the industrial E-CR-glasses. The deviations between calculated (using Eq. 18) and measured values are smaller than 4%. This quite high precision can be found for a great number of examples.

The tool shown here provides the opportunity to design glass compositions with desired elastic properties in a simple and easy way. It enables us to do systematic development of high-modulus glasses.

Conclusion

Quantum mechanical calculations based on DFT were performed on the systems MgSiO₃ and NaAlSi₂O₆. The calculations reproduced well the structures of all known crystalline polymorphs as well as their molar volumes and bulk moduli. The agreement with experimental data was better than 5 and 15%, respectively.

Beyond this, the calculations also yielded hypothetical low-density polymorphic equilibrium structures for which no real crystals have been found so far. However, as judged from molar volume and bulk modulus, these hypothetical structures reflect local structural entities of isochemical glasses.

Phenomenologically, experimental data of elastic moduli were found to linearly scale with the ratios of atomic space demand to actual molar volume. Silicates ranging from crystalline high-pressure polymorphs to glasses were represented by a single master line. In other words, glasses can be treated—with respect to the properties investigated—as commensurable members of polymorphic series. This goes together well with earlier observations that heat capacities of crystalline low-pressure polymorphs and their isochemical glasses are identical within experimental error. These observations are interpreted by the fact that, at temperatures above room temperature, elastic waves probe the short range order coordination polyhedra and their next neighbor linkage only, but are “blind” to the presence or absence of an extended translational symmetry. The master line is valid for silicate and alumosilicate crystals and glasses; other glass families, e.g., borates, follow their own common straight line with different intercept p_c and different slope due to different structural units and different U₀, respectively.

The elastic properties of binary and multicomponent glasses were precisely represented by linear compositional superimpositions of the properties of their corresponding constitutional end members, taken in their respective glassy states. This goes together well with earlier observations showing that the very same superposition principle is valid for the thermodynamic functions of enthalpy and entropy. These observations suggest that multicomponent glasses are composed of local structural entities reflecting the topologies of their constitutional end members. The elastic properties of multicomponent glasses predicted by this principle of additivity agreed with experimental data by better than 5%. Thus, in turn, the approach to the elastic properties of multicomponent glasses via their constitutional end members may serve as a powerful tool for the development of novel glass compositions with high elastic moduli.

Author Contributions

This manuscript was written through the contributions of all authors.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was financially supported by the German Science Foundation through its priority program SPP 1594 (Project No. CO 249/11-1). This support and allocation of super computing resources by RWTH Aachen IT Center are gratefully acknowledged.

References

ASTM. (2002). Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration. ASTM E 1876-01.

Google Scholar

Bansal, N. P., and Doremus, R. H. (1986). Handbook of Glass Properties. Orlando: Academic Press.

Google Scholar

Bass, J. D. (1995). “Elasticity of minerals, glasses, and melts,” in Mineral Physics & Crystallography: A Handbook of Physical Constants, ed. T. J. Ahrens (Washington, DC: American Geophysical Union), 45–63.

Google Scholar

Birch, F. (1947). Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824. doi:10.1103/PhysRev.71.809

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Brazhkin, V. V., and Trachenko, K. (2014). Collective excitations and thermodynamics of disordered state: new insights into an old problem. J. Phys. Chem. B 118, 11417–11427. doi:10.1021/jp503647s

PubMed Abstract | CrossRef Full Text | Google Scholar

Carmichael, R. S. (1984). CRC Handbook of Physical Properties of Rocks. Boca Raton, FL: CRC Press.

Google Scholar

Conradt, R. (2004). Chemical structure, medium range order, and crystalline reference state of multicomponent oxide liquids and glasses. J. Non Cryst. Solids 345–346, 16–23. doi:10.1016/j.jnoncrysol.2004.07.038

CrossRef Full Text | Google Scholar

Conradt, R. (2010). “Thermodynamics of glass melting,” in Fiberglass and Glass Technology, eds F. T. Wallenberger and P. A. Bingham (Boston, MA: Springer), 385–412.

Google Scholar

Dobson, D. P., and Jacobsen, S. D. (2004). The flux growth of magnesium silicate perovskite single crystals. Am. Mineral. 89, 807–811. doi:10.2138/am-2004-5-615

CrossRef Full Text | Google Scholar

Frisch, H. L., Sonnenblick, E., Vyssotsky, V. A., and Hammersley, J. M. (1961). Critical percolation probabilities (site problem). Phys. Rev. 124, 1021–1022. doi:10.1103/PhysRev.124.1021

CrossRef Full Text | Google Scholar

Gutzow, I., and Schmelzer, J. (2013). The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization. Berlin, New York: Springer.

Google Scholar

Gwanmesia, G. D., Liu, J., Chen, G., Kesson, S., Rigden, S. M., and Liebermann, R. C. (2000). Elasticity of the pyrope (Mg 3 Al 2 Si 3 O 12)-majorite (MgSiO 3) garnets solid solution. Phys. Chem. Miner. 27, 445–452. doi:10.1007/s002699900054

CrossRef Full Text | Google Scholar

Helgeson, H. C., and Kirkham, D. H. (1976). Theoretical prediction of the thermodynamic properties of aqueous electrolytes at high pressures and temperatures. III. Equation of state for aqueous species at infinite dilution. Am. J. Sci. 276, 97–240. doi:10.2475/ajs.276.2.97

CrossRef Full Text | Google Scholar

Jindal, R., Jayaganthan, R., Singh, I. V., and Conradt, R. (2011). Synthesis and characterization of clinopyroxene based glasses and glass-ceramics along diopside (CaMgSi2O6)–jadeite (NaAlSi2O6) join. Ceram. Int. 37, 741–748. doi:10.1016/j.ceramint.2010.09.049

CrossRef Full Text | Google Scholar

Kavner, A., Sinogeikin, S. V., Jeanloz, R., and Bass, J. D. (2000). Equation of state and strength of natural majorite. J. Geophys. Res. 105, 5963–5971. doi:10.1029/1999JB900374

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Kubaschewski, O., Alcock, C. B., and Spencer, P. J. (1993). Materials Thermochemistry. Oxford, New York: Pergamon Press.

Google Scholar

Makishima, A., and Mackenzie, J. D. (1973). Direct calculation of Young’s Modulus of glass. J. Non Cryst. Solids 12, 35–45. doi:10.1016/0022-3093(73)90053-7

CrossRef Full Text | Google Scholar

Murakami, T., Takéuchi, Y., and Yamanaka, T. (1984). X-ray studies on protoenstatite. Z. Kristallogr. Cryst. Mater. 166, 263–275. doi:10.1524/zkri.1984.166.14.263

CrossRef Full Text | Google Scholar

Murnaghan, F. D. (1937). Finite deformations of an elastic solid. Am. J. Math. 59, 235. doi:10.2307/2371405

CrossRef Full Text | Google Scholar

Ozawa, T. C., and Kang, S. J. (2004). Balls&Sticks: easy-to-use structure visualization and animation program. J. Appl. Crystallogr. 37, 679. doi:10.1107/S0021889804015456

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865

CrossRef Full Text | Google Scholar

Reuß, A. (1929). Berechnung der Fließgrenze von Mischkristallen auf Grund der Platizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 9, 49–58. doi:10.1002/zamm.19290090104

CrossRef Full Text | Google Scholar

Rocherulle, J., Ecolivet, C., Poulain, M., Verdier, P., and Laurent, Y. (1989). Elastic moduli of oxynitride glasses. J. Non Cryst. Solids 108, 187–193. doi:10.1016/0022-3093(89)90582-6

CrossRef Full Text | Google Scholar

Rouxel, T. (2007). Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 90, 3019–3039. doi:10.1111/j.1551-2916.2007.01945.x

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 32, 751–767. doi:10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Shannon, R. D., and Prewitt, C. T. (1969). Effective ionic radii in oxides and fluorides. Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem. 25, 925–946. doi:10.1107/S0567740869003220

CrossRef Full Text | Google Scholar

Shannon, R. D., and Prewitt, C. T. (1970). Revised values of effective ionic radii. Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem. 26, 1046–1048. doi:10.1107/S0567740870003576

CrossRef Full Text | Google Scholar

Stoffel, R. P., Philipps, K., Conradt, R., and Dronskowski, R. (2016). A first-principles study on the electronic, vibrational, and thermodynamic properties of jadeite and its tentative low-density polymorph. Z. Anorg. Allg. Chem. 642, 590–596. doi:10.1002/zaac.201600071

CrossRef Full Text | Google Scholar

Sykes, M. F., and Essam, J. W. (1964). Critical percolation probabilities by series methods. Phys. Rev. 133, A310–A315. doi:10.1103/PhysRev.133.A310

CrossRef Full Text | Google Scholar

Vedishcheva, N. M., Shakhmatkin, B. A., and Wright, A. C. (2001). Thermodynamic modelling of the structure of glasses and melts: single-component, binary and ternary systems. J. Non Cryst. Solids 293–295, 312–317. doi:10.1016/S0022-3093(01)00683-4

CrossRef Full Text | Google Scholar

Vinet, P., Smith, J. R., Ferrante, J., and Rose, J. H. (1987). Temperature effects on the universal equation of state of solids. Phys. Rev. B 35, 1945–1953. doi:10.1103/PhysRevB.35.1945

CrossRef Full Text | Google Scholar

Voigt, W. (1889). Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 274, 573–587. doi:10.1002/andp.18892741206

CrossRef Full Text | Google Scholar

Wright, A. C., Shakhmatkin, B. A., and Vedishcheva, N. M. (2001). The chemical structure of oxide glasses: a concept consistent with neutron scattering studies? Glass Phys. Chem. 27, 97–113. doi:10.1023/A:1011366508857

CrossRef Full Text | Google Scholar

Yamanaka, T. (2005). Structure change of MgSiO3, MgGeO3, and MgTiO3 ilmenites under compression. Am. Mineral. 90, 1301–1307. doi:10.2138/am.2005.1621

CrossRef Full Text | Google Scholar