Mermin differential inverse inelastic mean free path of electrons in polymethylmethacrylate

Introduction

Electrons continually interact with the matter around us. We use electron beams for our purposes, either on the side of production of materials or on that of their characterization. Let us think to the many applications such as the processing of materials with plasma and to the local melting of materials for joining large components. We use electron beams also in the electron lithography, an important technique utilized for the production of the microelectronics devices. Let us consider the importance of the beams of electrons in the characterization of the materials, performed using techniques such as the electron microscopy and all the electron spectroscopies. Electrons interact with the surfaces of the space-crafts. The plasma–wall interaction in the fusion reactors also involves electron–matter interaction. Electrons play a role also in the cancer proton therapy, where cascades of secondary electrons are produced. These electrons of very low energy are toxic for the human body cells, since they produce damage to the biomolecules due to ionizations/excitations and the resulting break of chemical bonds. Also the secondary electrons which have ultra-low energies – and which, for a long time, were thought to be relatively harmless – are dangerous for the biomolecules due to the so-called “dissociative electron attachment.” And, of course, we wish to minimize the effects of the irradiation on the healthy tissues near to the diseased cells.

In all the mentioned cases, the modeling of the interaction of the electrons with the matter is very important, as it can be used to provide a solid theoretical interpretation of the experimental evidences.

The interpretation of the experimental results is often based on the Monte Carlo method (MC). The doping contrast in secondary-electron emission of pn-junctions was investigated by the use of the MC method (Dapor et al., 2008; Rodenburg et al., 2010). The modeling of electron interaction with polymers, and in particular with the polymethylmethacrylate, has been demonstrated to be very important in nano-metrology. Line-scan of resist materials with given geometrical cross-sections deposited on silicon or silicon dioxide, and the corresponding linewidth measurements, obtained with the secondary electrons in the Critical-Dimension Scanning Electron Microscope (CD SEM), require an interpretation that can be performed using MC calculations (Dapor et al., 2010).

The MC method, in turn, requires an accurate description of the differential inverse inelastic mean free path (DIIMFP), in order to calculate the inelastic mean free path (IMFP) and the distribution function for inelastic collisions of electrons causing energy losses less than or equal to given values.

Mermin Theory

The Mermin dielectric function (Mermin, 1970) is given by

${\epsilon }_{\mathrm{M}}\left(\mathit{\text{q}},\omega \right)=1+\frac{\left(1+i/\mathrm{\omega \tau }\right)\left[{\epsilon }^0\left(\mathit{\text{q}},\omega +i/\tau \right)-1\right]}{1+\left(i/\mathrm{\omega \tau }\right)\left[{\epsilon }^0\left(\mathit{\text{q}},\omega +i/\tau \right)-1\right]/\left[{\epsilon }^0\left(\mathit{\text{q}},0\right)-1\right]},$ (1)

where q is the momentum, ω the frequency, τ the relaxation time, and ε⁰(q, ω) the Lindhard dielectric constant (Lindhard, 1954)

${\mathrm{\epsilon }}^0\left(\mathit{\text{q}},\mathrm{\omega }\right)=1+\frac{\mathrm{4\pi }{e}^2}{q^2}B\left(\mathit{\text{q}},\mathrm{\omega }\right),$ (2)

$B\left(\mathit{\text{q}},\mathrm{\omega }\right)=\int \frac{d\mathit{\text{p}}}{4{\mathrm{\pi }}^3}\frac{f_{\mathit{\text{p}}+\mathit{\text{q}}/2}-f_{\mathit{\text{p}}-\mathit{\text{q}}/2}}{\mathrm{\omega }-\left({\mathrm{ϵ}}_{\mathit{\text{p}}+\mathit{\text{q}}/2}-{\mathrm{ϵ}}_{\mathit{\text{p}}-\mathit{\text{q}}/2}\right)/\hslash }.$ (3)

In these equations e is the electron charge, f_p is the Fermi–Dirac distribution, and ϵ_p the free electron energy.

Energy Loss Function

Let us now consider a superposition of free and bound oscillators. For any oscillator, the energy loss function (ELF) is given by the opposite of the imaginary part of the inverse of the Mermin dielectric function:

$\text{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_{\mathrm{M}}\left({\mathrm{\omega }}_{\mathrm{i}}\mathrm{,}{\mathrm{\gamma }}_{\mathrm{i}};\mathit{\text{q}},\mathrm{\omega }\right)}\right]=\frac{{{\mathrm{\epsilon }}_{\mathrm{M}}}_{\mathrm{2}}}{{{\mathrm{\epsilon }}_{\mathrm{M}}}_{\mathrm{1}}^{\mathrm{2}}+{{\mathrm{\epsilon }}_{\mathrm{M}}}_{\mathrm{2}}^{\mathrm{2}}}.$ (4)

where

${\mathrm{\epsilon }}_M={\mathrm{\epsilon }}_{M_1}+i{\mathrm{\epsilon }}_{M_2}$ (5)

and ω_i, and γ_i are, respectively, the frequency and the damping constant associated to each specific oscillator. A linear combination of Mermin-type ELFs, one per oscillator, allows to calculate the electron ELF for q = 0, for any specific material (Planes et al., 1996; Abril et al., 1998; de Vera et al., 2011)

$\text{Im}\left[\frac{-1}{\mathrm{\epsilon }\left(q=0,\mathrm{\omega }\right)}\right]={\displaystyle \sum _{\mathrm{i}}}{A}_{\mathrm{i}}\mathrm{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_{\mathrm{M}}\left({\mathrm{\omega }}_{\mathrm{i}}\mathrm{,}{\mathrm{\gamma }}_{\mathrm{i}}\mathrm{;}q=0,\mathrm{\omega }\right)}\right].$ (6)

In this equation, A_i, ω_i, and γ_i are determined looking for the best fit of the available experimental optical ELF. Actually, as both Mermin and Drude–Lorentz oscillators converge on the same values in the optical limit (i.e., for q = 0) (de la Cruz and Yubero, 2007),

$\text{Im}\left[\frac{-1}{\mathrm{\epsilon }\left(q=0,\mathrm{\omega }\right)}\right]={\displaystyle \sum _{\mathrm{i}}}{A}_{\mathrm{i}}\mathrm{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_{\mathrm{M}}\left({\mathrm{\omega }}_{\mathrm{i}}\mathrm{,}{\mathrm{\gamma }}_{\mathrm{i}}\mathrm{;}q=0,\mathrm{\omega }\right)}\right]={\displaystyle \sum _{\mathrm{i}}}{A}_{\mathrm{i}}\mathrm{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_{\mathrm{D}}\left({\mathrm{\omega }}_{\mathrm{i}}\mathrm{,}{\mathrm{\gamma }}_{\mathrm{i}}\mathrm{;}q=0,\mathrm{\omega }\right)}\right],$ (7)

where the Drude–Lorenz functions are given by (Ritchie and Howie, 1977)

$\text{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_D\left({\mathrm{\omega }}_i,{\mathrm{\gamma }}_i;q=0,\mathrm{\omega }\right)}\right]=\frac{{\mathrm{\gamma }}_i\mathrm{\omega }}{{\left({\mathrm{\omega }}_i^2-{\mathrm{\omega }}^2\right)}^2+{\left({\mathrm{\gamma }}_i\mathrm{\omega }\right)}^2},$ (8)

the best fit can also be performed using a linear combination of Drude–Lorentz functions, instead of Mermin functions.

For the present work, the parameters provided by de Vera et al. (2011) obtained by calculating the best fit of the Ritsko et al. (1978) experimental optical data, were used.

Once the values of the best fit parameters have been established, the extension out of the optical domain (q ≠ 0) can be obtained by (Planes et al., 1996; Abril et al., 1998; de Vera et al., 2011)

$\mathrm{Im}\left[\frac{-1}{\mathrm{\epsilon }\left(q,\mathrm{\omega }\right)}\right]={\sum }_i{A}_{\mathrm{i}}\mathrm{Im}\left[\frac{-1}{{\mathrm{\epsilon }}_{\mathrm{M}}\left({\mathrm{\omega }}_{\mathrm{i}},{\mathrm{\gamma }}_{\mathrm{i}};q,\mathrm{\omega }\right)}\right].$ (9)

Differential Inverse Inelastic Mean Free Path and Inelastic Mean Free Path

The ELF allows, in turn, the computation of the DIIMFP, given by

$\frac{d{\mathrm{\lambda }}_{\text{inel}}^{-1}}{\mathrm{d\hslash }\mathrm{\omega }}=\frac{1}{\mathrm{\pi }{a}_{0}T}{\int }_{q-}^{q+}\frac{\mathit{dq}}{q}\text{Im}\left[\frac{-1}{\mathrm{\epsilon }\left(q,\mathrm{\omega }\right)}\right],$ (10)

where a₀ is the Bohr radius, T is the kinetic energy of the incident electrons and

$q_{\pm }=\sqrt{\frac{2m}{{\hslash }^2}}\left(\sqrt{T}\pm \sqrt{T-\hslash \mathrm{\omega }}\right).$ (11)

The Mermin DIIMFP of electrons in PMMA is represented in Figure 1, for kinetic energies of the incident electrons in the range from 10 to 1000 eV.

FIGURE 1

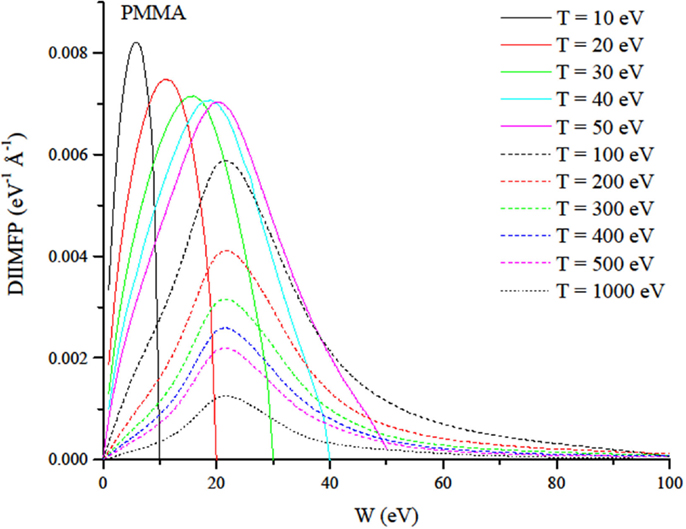
Figure 1. Mermin DIIMFP of electrons in PMMA for selected values of the incident electron kinetic energy T in the range 10–1000 eV.

The inverse of the integral of every curve presented in Figure 1 provides, for each kinetic energy T, the IMFP. According to de la Cruz and Yubero (2007), the values of the IMFP calculated using the Tanuma, Powell, and Penn (TPP) empirical predictive formula (Tanuma et al., 1994) are systematically higher than the corresponding values calculated within the Mermin theory. For PMMA, according to our calculation, when T = 100 eV, the Mermin IMFP is equal to 6.3 Å while when T = 1000 eV, it is equal to 27.6 Å. According to TPP, the IMFP of PMMA is equal to 7.9 Å for T = 100 eV and to 33.7 Å for T = 1000 eV (Tanuma et al., 1994). Also approaches based on the Drude–Lorentz theory (Emfietzoglou et al., 2013; Dapor, 2014a,b; Dapor et al., 2015) provide values of the IMFP systematically higher than those obtained using the Mermin theory. The IMFP of PMMA calculated according to the Drude–Lorentz theory is equal to 10.1 Å for T = 100 eV and to 33.5 Å for T = 1000 eV (Dapor, 2014a).

It is not simple to express an opinion about the different approaches used today to calculate the DIIMFP, and hence the IMFP, due to the lack of experimental data and their quite large uncertainty (Dapor et al., 2015). Roberts et al. (1980) provided the experimental values of 29 ± 4 Å for 1196 eV electrons and 33 ± 5 Å for 1328 eV electrons in PMMA. On the one hand, also taking into account of the experimental uncertainty, de Vera et al. (2011) have shown that these values are closer to those predicted by the Mermin theory than to those predicted by the TPP formula, usually taken as a reference and provided, among other IMFP data, by the NIST database. On the other hand, the number of experimental data about electron IMFP in PMMA seems to be definitely too small to judge. Since Mermin theory is much more accurate it is preferable, even if we conclude that, at the moment, both Mermin theory and TTP empirical predictive formula are compatible with the available experimental data about IMFP in PMMA.

Conclusion

Calculations of the DIIMFP of electron in materials are of paramount importance for modeling the transport of electrons in solid targets. In this paper, we presented the calculations of the DIIMFP of electrons in PMMA based on the Mermin theory (Mermin, 1970) and on the de Vera et al. (2011) best fit of the Ritsko et al. (1978) optical data.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author wishes to express his gratitude to Isabel Abril, Pablo de Vera, and Rafael Garcia-Molina for their invaluable suggestions. This work was supported by Istituto Nazionale di Fisica Nucleare (INFN) through the Supercalcolo agreement with FBK.

References

Abril, I., Garcia-Molina, R., Denton, C. D., érez-Pérez, F. J. P., and Arista, N. R. (1998). Dielectric description of wakes and stopping powers in solids. Phys. Rev. A 58, 357. doi: 10.1103/PhysRevA.58.357

CrossRef Full Text | Google Scholar

Dapor, M. (2014a). Energy loss of fast electrons impinging upon polymethylmethacrylate. Nucl. Instrum. Methods Phys. Res. B doi:10.1016/j.nimb.2014.11.101

CrossRef Full Text | Google Scholar

Dapor, M. (2014b). Transport of Energetic Electrons in Solids, Springer Tracts in Modern Physics, Vol. 257. Berlin: Springer.

Google Scholar

Dapor, M., Ciappa, M., and Fichtenr, W. (2010). Monte Carlo modeling in the low-energy domain of the secondary electron emission of polymethylmethacrylate for critical-dimension scanning electron microscopy. J. Micro/Nanolith. MEMS MOEMS. 9, 023001. doi:10.1117/1.3373517

CrossRef Full Text | Google Scholar

Dapor, M., Garberoglio, G., and Calliari, L. (2015). Energy loss of electrons impinging upon glassy carbon, amorphous carbon, and diamond: comparison between two different dispersion laws. Nucl. Instrum. Methods Phys. Res. B doi:10.1016/j.nimb.2014.11.115

CrossRef Full Text | Google Scholar

Dapor, M., Inkson, B. J., Rodenburg, C., and Rodenburg, J. M. (2008). A comprehensive Monte Carlo calculation of dopant contrast in secondary-electron imaging, Europhys. Europhys. Lett. 82, 30006. doi:10.1209/0295-5075/82/30006

CrossRef Full Text | Google Scholar

de la Cruz, W., and Yubero, F. (2007). Electron inelastic mean free paths: influence of the modelling energy-loss function. Surf. Interface Anal. 39, 460. doi:10.1002/sia.2545

CrossRef Full Text | Google Scholar

de Vera, P., Abril, I., and Garcia-Molina, R. (2011). Inelastic scattering of electron and light ion beams in organic polymers. J. Appl. Phys. 109, 094901. doi:10.1063/1.3581120

CrossRef Full Text | Google Scholar

Emfietzoglou, D., Kyriakou, I., Garcia-Molina, R., and Abril, I. (2013). The effect of static many-body local-field corrections to inelastic electron scattering in condensed media. J. Appl. Phys. 114, 144907. doi:10.1063/1.4824541

CrossRef Full Text | Google Scholar

Lindhard, J. (1954). On the properties of a gas of charged particles. Kgl. Danske Videnskab. Selskab Mat.-fys. Medd. 28, 8.

Google Scholar

Mermin, N. D. (1970). Lindhard dielectric function in the relaxation-time approximation. Phys. Rev. B 1, 2362. doi:10.1103/PhysRevB.1.2362

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Planes, D. J., Garcia-Molina, R., Abril, I., and Arista, N. R. (1996). Wavenumber dependence of the energy loss function of graphite and aluminium. J. Electron Spectros. Relat. Phenomena 82, 23. doi:10.1016/S0368-2048(96)03043-5

CrossRef Full Text | Google Scholar

Ritchie, R. H., and Howie, A. (1977). Electron excitation and the optical potential in electron microscopy. Philos. Mag. 36, 463. doi:10.1080/14786437708244948

CrossRef Full Text | Google Scholar

Ritsko, J. J., Brillson, L. J., Bigelow, R. W., and Fabish, T. J. (1978). Electron energy loss spectroscopy and the optical properties of polymethylmethacrylate from 1 to 300 eV. J. Chem. Phys. 69, 3931. doi:10.1063/1.437131

CrossRef Full Text | Google Scholar

Roberts, R. F., Allara, D. L., Pryde, C. A., Buchanan, D. N. E., and Hobbins, N. D. (1980). Mean free path for inelastic scattering of 1.2 kev electrons in thin poly(methylmethacrylate) films. Surf. Interface Anal. 2, 5. doi:10.1002/sia.740020103

CrossRef Full Text | Google Scholar

Rodenburg, C., Jepson, M. A. E., Bosch, E. G. T., and Dapor, M. (2010). Energy selective scanning electron microscopy to reduce the effect of contamination layers on scanning electron microscope dopant mapping. Ultramicroscopy 110, 1185. doi:10.1016/j.ultramic.2010.04.008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Tanuma, S., Powell, C. J., and Penn, D. R. (1994). Calculations of electron inelastic mean free paths. V. Data for 14 organic compounds over the 50–2000 eV range. Surf. Interface Anal. 21, 165. doi:10.1002/sia.740210302

CrossRef Full Text | Google Scholar