Numerical modelling of the impact of coral reef degradation and sea level rise on coastal protection at The Buccoo Reef, Tobago: implications for reef restoration and management strategies

Coral reefs provide natural coastal protection through depth-induced wave breaking and frictional dissipation on the fore reef, the reef crest, and the back reef. The coral reef roughness is a significant factor in wave attenuation through frictional dissipation and is directly linked to the reef’s health. The influence of reef roughness on frictional dissipation under representative conditions, and the extent to which coral reef degradation and Sea Level Rise (SLR) reduces this coastal protection service remains underexplored, especially at coastal sites in Caribbean Small Island Developing States. A numerical modelling approach using a coupled depth-averaged (2DH) hydrodynamic and spectral wave model in Delft3D was used to evaluate the coastal protection effectiveness of a fringing reef under varying scenarios of coral reef degradation and SLR at The Buccoo Reef, Tobago. Using near present day conditions as the baseline scenario, assessed wave conditions showed 100% and 96.45% reductions at low and high tides respectively. Under modelled degraded reef conditions on the reef flat, wave heights increased by an average of 21.74% compared to baseline conditions, while for modelled healthier reefs, there was an 18.9% decrease in wave heights from the baseline scenario. Using various SLR scenarios, wave heights showed increases over baseline conditions between 160.5% and 388.4% for increases in sea level from 0.25 m to 1.00 m. The results highlight the importance of the frictional dissipation provided by healthy coral reefs, with degraded corals and rising sea levels leading to substantial increases in nearshore wave heights which could exacerbate issues such as coastal erosion and flooding. Management strategies such as Integrated Coastal Zone Management (ICZM) and innovative approaches such as the deployment of artificial reefs which are specifically designed to replicate the complex structure and roughness of natural reefs can contribute to wave attenuation by frictional dissipation.

1 Introduction

Coral reefs provide natural coastal protection against coastal hazards such as storm surges and coastal flooding and erosion, through a reduction in wave energy by an average of 97% (Costa et al., 2016; Elliff and Silva, 2017; Ferrario et al., 2014; Lugo-Fernández et al., 1998). Reefs dissipate wave energy mainly by depth-induced wave breaking along the reef crest as well as frictional dissipation as a result of the coral reef roughness (Keyzer et al., 2020; Quataert et al., 2015; Baldock et al., 2020; Osorio-Cano et al., 2019; Baldock et al., 2014). The effectiveness of coral reefs as coastal protection, however, depends on several factors such as (i) the reef geometry and morphology (Baldock et al., 2020; Costa et al., 2016; Masselink et al., 2019; Quataert et al., 2015), (ii) water levels on the reef, (iii) incident wave characteristics (Costa et al., 2016; Quataert et al., 2015; Péquignet et al., 2011; Lentz et al., 2016), (iv) coral reef roughness which is affected by coral reef degradation (Baldock et al., 2020; Monismith et al., 2015; Osorio-Cano et al., 2019; Quataert et al., 2015), and (v) climate change including Sea Level Rise (SLR) (Beetham and Kench, 2018; Elliff and Silva, 2017; Keyzer et al., 2020; Villanoy et al., 2012).

While depth-induced wave breaking on the reef crest is a crucial mechanism of wave energy dissipation, frictional dissipation as a result of coral reef roughness is found to be dominant on the reef flat. Meta-analyses and synthesis of global literature on coral reefs and wave attenuation conducted by Ferrario et al. (2014) have shown that the reef crest dissipates an average of 86% of the wave energy and the reef flats were responsible for dissipating 65% of the remaining wave energy as a result of frictional dissipation, highlighting the importance of frictional dissipation in wave attenuation. Despite this crucial role in wave attenuation, there have been limited studies on the frictional dissipation provided by coral reefs and how coastal protection provided by coral reefs is affected by continued coral reef degradation and SLR. The reason for the lack of studies on frictional dissipation may be in part due to the fact that there is no standard method for parameterising reef roughness in numerical modelling studies (Osorio-Cano et al., 2019). Traditionally, coral reefs are represented in hydrodynamic and spectral wave models, such as Delft3D and MIKE21, as friction coefficients (Baldock et al., 2020; Osorio-Cano et al., 2019; Quataert et al., 2015; Baldock et al., 2014) which are calibrated and validated using field measurements. Further, in Caribbean Small Island Developing States (SIDS), studies such as these are rare largely due to the paucity of comprehensive field-scale data. Regardless, these types of scientific investigations are crucial for coastal zone management in Caribbean SIDS as the high concentration of persons and economic assets in coastal regions are extremely susceptible to natural hazards (such as hurricanes) and climate changes like SLR (Marchitto et al., 2023).

Coral reef degradation results in a decrease in the frictional dissipation provided by the coral reefs. Healthy coral communities provide a geometrical complexity, and this helps to dissipate wave energy by surface roughness. The mortality and degradation of coral reefs mean that dead reefs become smoother, contribute less to dissipation through bottom friction and result in an increase in depth due to the removal of coral skeletons (Baldock et al., 2020; Ferrario et al., 2014; Keyzer et al., 2020). Assuming that widespread coral reef degradation continues, and the rate of vertical accretion cannot keep pace with SLR, there may be an increase in the water depth on reefs of +1.0m by the year 2100 (Storlazzi et al., 2011; Jevrejeva et al., 2010).

Studies such as Storlazzi et al. (2011) and Grady et al. (2013) have investigated the impact of SLR and changes in morphology on coral reef hydrodynamics and sediment transport through a coupled depth-averaged hydrodynamic, spectral wave and sediment transport model using Delft3D. However, reef accretion changes and reef roughness were not represented in the model. Instead, the coral reef degradation in these scenarios were represented as a lack of vertical accretion by assuming that reef accretion rates could not keep up with SLR. Conversely, Keyzer et al. (2020) used Delft3D to investigate the potential of coastal ecosystems to mitigate SLR and represented the coral reefs in the model bathymetry by increased bottom friction for three scenarios of reef development: keep up, catch up and give up scenarios. This Keyzer et al. (2020) study, however, did not specifically investigate the effectiveness of the coral reefs as coastal protection and the reef roughness was not captured in the model. While Baldock et al. (2014) investigated the wave dynamics on idealised reef profiles under various SLR scenarios and reef roughness conditions using a one dimensional wave transformation model, a calibrated and validated field-based model would provide insight into influence of coral reef roughness on frictional dissipation under realistic conditions and how coral reef degradation reduces this coastal protection service. Recent advancements in coral reef restoration have expanded to include both transplantation initiatives and the incorporation of artificial reefs. However, there remains a significant gap in our understanding of how to implement these strategies effectively for successful restoration outcomes (Hein et al., 2019; Higgins et al., 2022). To the authors’ knowledge the selected site, Buccoo Reef in Tobago, has not undergone a similar detailed investigation to ascertain the future impact of the reef degradation. This knowledge can be influential in guiding management strategies regarding coral reefs such as conservation and reef restoration efforts on the island, which is one part of the twin-island republic of Trinidad and Tobago; the southern-most of the Caribbean Island nations. While the Buccoo Reef provides a critical coastal protection function, the reef has experienced extreme coral reef mortality and degradation over the past couple decades due to climate change as well as anthropogenic stresses (Lapointe et al., 2010; Laydoo et al., 1998; Mallela and Crabbe, 2009), making the Buccoo Reef ideally suited for investigating the impact of coral reef degradation.

As such, the objectives of this study are (i) to investigate the impact of coral reef degradation and SLR on wave conditions of the fringing reef at Buccoo Bay, Tobago and its effectiveness at coastal protection and (ii) to identify potential implications for reef restoration and future management strategies. For the present study, a numerical modelling approach is used through the development of a coupled depth-averaged (2DH) hydrodynamic and spectral wave model using Delft3D which is calibrated and validated using field collected data from Buccoo Reef, Tobago. This model is used to investigate the effect of coral reef degradation and SLR on wave conditions by varying friction factors and water depths on the reef to represent various scenarios.

The paper will first briefly describe the study area, and then discuss the numerical methods used for assessment of the study site. The results of the investigation will then be presented and discussed, highlighting any limitations of the study. The paper will conclude while emphasizing possible mechanisms for improvement of the study, and potential applications of the output.

2 Methods

2.1 Study area and climatology

The Buccoo Reef is located at the low energy, leeward south-western edge of Tobago in the Southern Caribbean (between latitudes 11°08’N to 11°12’N and longitudes 60°40’W to 60°51’W) and forms an inter-related complex with the Bon Accord Lagoon. The reef is approximately 7 km² and was classified by Laydoo et al. (1998) as a fringing reef in which there are five emergent reef platforms which arc seaward of the reef lagoon from Sheerbird’s Point in the east to Pigeon Point in the west. These five emergent reef platforms are known as the Eastern Reef, Outer Reef, Northern Reef, Western Reef and the Pigeon Point Reef (Figure 1A).

Figure 1

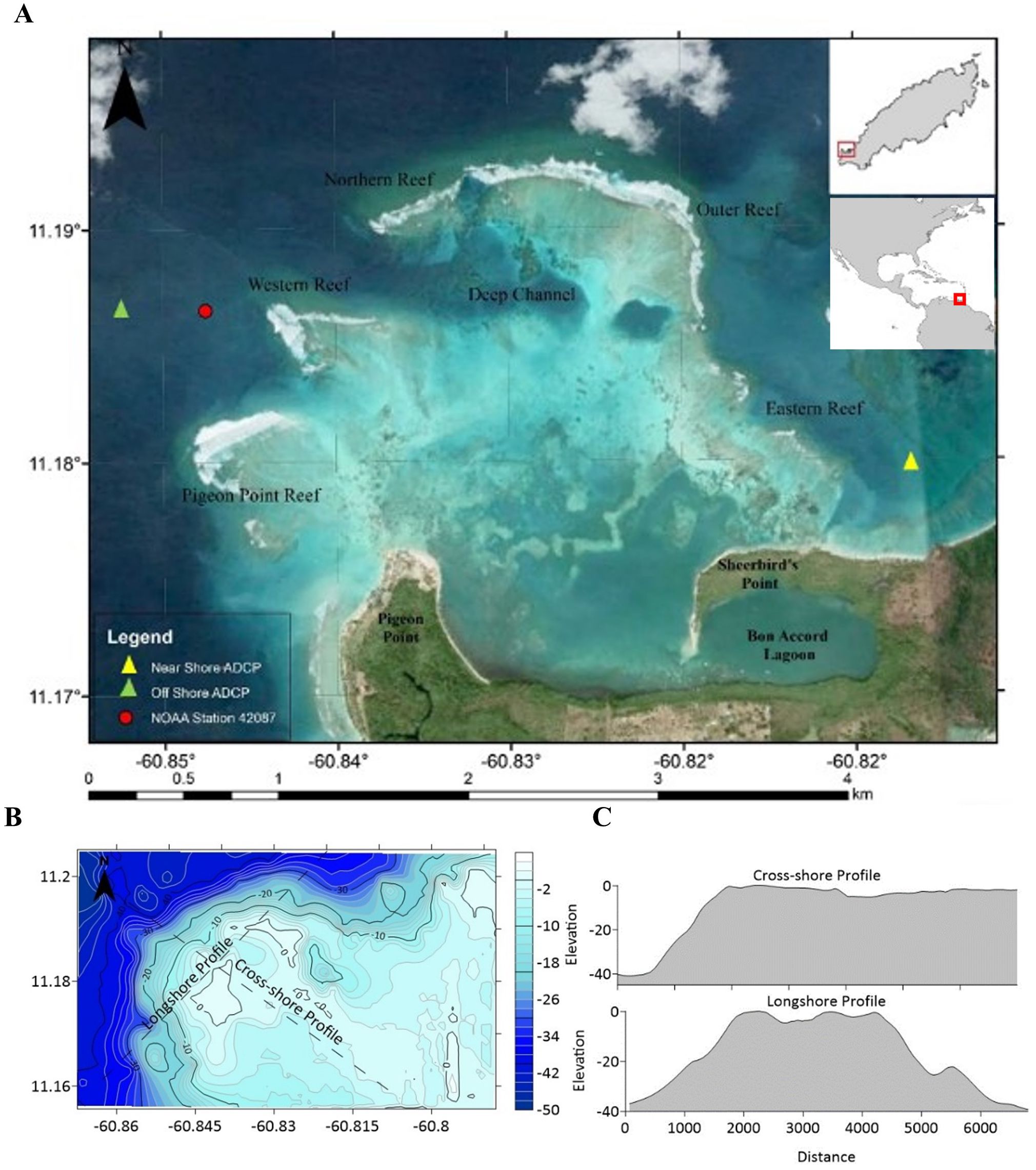
Figure 1. (A) Location of study area, offshore and nearshore ADCPs and NOAA station 42087), (B) Bathymetric of the Buccoo Reef with water depths (m), (C) cross-shore and Longshore bathymetric profiles on the reef.

There are several sandy channels located between the reef flats with the Deep Channel located between the Western and Northern Reef being the deepest and widest (refer to Figure 1A). Landward of the reef, there is a shallow sandy lagoon which consists mainly of patch coral communities. The reef platforms consist generally of a very narrow seaward reef crest, followed by a wider, more extensive backreef which consists mainly of coral rubble. The reef crests induce wave breaking and consist of an easily recognized breaker zone (Laydoo et al., 1998). To the north of the reef system, the forereef is the most extensive, sloping to depths up to 40 m as seen in Figures 1B, C. The forereef consists of mainly of wave-resistant corals such as elkhorn and large colonies of stony corals (Laydoo et al., 1998). The forereefs on the western reef flats, however, slope to a depth of about 20 m and the eastern forereefs slope to a depth of about 15 m showing differences in geometry and morphology among the various platforms.

Ganase and Lochan (2022) used a rugosity measure to determine the three-dimensional structural complexity of 10 coral reef locations in Tobago: Buccoo Western and Outer Reef, Culloden Western and Eastern Reef, Castara, Plymouth, Charlotteville, Angel Reef, Blackjack Hole and Flying Reef. Of these observed coral reefs, Booby Island in Charlotteville had the highest structural complexity (~0.41), with the Buccoo Outer and Western Reefs having rugosities of approximately 0.33 and 0.21 respectively.

While the Buccoo Reef is located on the leeward, low energy side of Tobago, it is still exposed to the northeast trade winds throughout the year (Laydoo et al., 1998). During the wet season, typically from June to December, the predominant wind direction is from the North-East. During the dry season from January to May, however, there are generally stronger winds from a westerly direction. Wave energy was also found to be high during the Northern Hemisphere winter months, i.e., between November and December, due to Mid-Atlantic storms in the North Atlantic Ocean generating swell waves in the nearshore (Laydoo et al., 1998). The tide in this area is classified as semi-diurnal with a significant diurnal inequality, having an average spring tidal range of 0.78 m and an average neap tidal range of 0.4 m.

The waves at Buccoo Bay predominantly approach from the west or southwest with significant wave heights between 0.10 m to 0.60 m (Darsan et al., 2013). While the site does experience the impacts of higher energy events, such as tropical waves, tropical depressions, storms and hurricanes, Trinidad and Tobago is located at the southern border of the Tropical Atlantic Hurricane Belt and is not as frequently impacted by passing tropical disturbances or cyclonic activity when compared to other SIDS in the Eastern Caribbean (Clarke et al., 2019). Regardless, the tracks of 10 tropical storms and 5 hurricanes have either passed proximal to or made direct landfall in Trinidad and Tobago between 1933 and 2024 with Hurricanes Flora (1963), Ivan (2004), Emily (2005) and Beryl (2024) being notable events that impacted Tobago (National Hurricane Center, 2024; Clarke et al., 2019; National Hurricane, 2024).

2.2 Model description – Delft3D

Delft3D has been successfully used in previous studies to simulate the hydrodynamic processes taking place on coral reefs (Grady et al., 2013; Green et al., 2018; Keyzer et al., 2020; Storlazzi et al., 2011). The present study makes use of a two-way coupled depth-averaged (2DH) hydrodynamic and wave model through the Delft3D-FLOW and Delft3D-WAVE modules respectively.

The hydrodynamic model, Delft3D-FLOW, solves the unsteady Shallow Water Equations (SWE) consisting of the horizontal equations of motion and the continuity equation as well as transport equations under the shallow water assumption using a structured grid and finite difference scheme (Lesser et al., 2004). The model is forced at the open boundaries by tidal and meteorological forcing, being widely used for predicting flows in shallow seas and coastal areas.

The wave model, Delft3D-WAVE, incorporates the third generation SWAN Model (Simulating WAves Nearshore) and has been extensively used to simulate the propagation of random, short-crested wind waves in coastal areas. The model solves the discrete spectral action balance equation Equation 1) on a structured grid which accounts for processes such as the generation of waves by wind as well as dissipation by bottom friction and depth-induced wave breaking among other processes; the latter two being particularly important for this study.

$\begin{array}{ll}\frac{\partial N}{\partial t}+{\nabla }_{\overrightarrow{x}}·[(\overrightarrow{c_g}+\overrightarrow{u}\nabla )N]+\frac{\partial c_{\text{σ}}N}{\partial \text{σ}}+\frac{\partial c_{\text{θ}}N}{\partial \text{θ}}=\frac{S_{\text{tot}}}{\text{σ}}& (1)\end{array}$

The first term in Equation 1 represents the local rate of change of the action density, $N$, reflecting how the wave spectrum evolves at a specific location over time, t. The second term involves the spatial gradient, ${\nabla }_{\overrightarrow{x}}$, and accounts for the movement of the action density propelled by the group velocity of the waves, $\overrightarrow{c_g}$, along with the effects of currents, $\overrightarrow{u}$. The third term pertains to the propagation speed in spectral space, $c_{\sigma }$, and describes how the action density varies with the relative frequency, σ. This third term considers the redistribution of energy across the frequency spectrum due to factors like depth changes and current velocities. The fourth term addresses the rate of change in action density concerning the wave direction, $\text{θ}$, incorporating the propagation speed from directional shifts, $c_{\theta }$. The fourth term is crucial for understanding modifications in wave direction caused by refraction as waves move through areas of differing depths and currents. On the equation’s right-hand side, $S_{tot}$ represents the source term, normalized by frequency. The right-hand side of the equation encompasses all energy sources and sinks within the system, such as wind input, wave breaking, bottom friction, and non-linear wave interactions, each affecting the accumulation or dissipation of wave energy.

The process of depth-induced wave-breaking is represented in SWAN as the spectral version of the bore model of Battjes and Janssen (1978) and the bottom friction models within SWAN consist of the JONSWAP by Hasselmann et al. (1973), drag law model of Collins (1972) and the eddy viscosity model of Madsen et al. (1988).

An online coupling of Delft-WAVE with Delft3D-FLOW was used such that the Delft-WAVE module has a dynamic interaction with the Delft-FLOW module. The results of the computations from the Delft-FLOW module are used as input for the Delft-WAVE module and vice versa. This online coupling is crucial, in this instance, to investigate the effect of tidal variations and water levels on the wave characteristics on the reef.

2.3 Model set-up

The development of the coupled 2DH hydrodynamic and spectral wave model involved the creation of a model grid, interpolation of bathymetry as well as the input of initial and boundary conditions and various model parameters such as bottom friction. The model domain covered an area of 8 km x 4 km, from the western edge of the island extending beyond the Buccoo Bay headland to capture the entire Buccoo Reef system and its effect on the nearshore areas as seen in Figure 2.

Figure 2

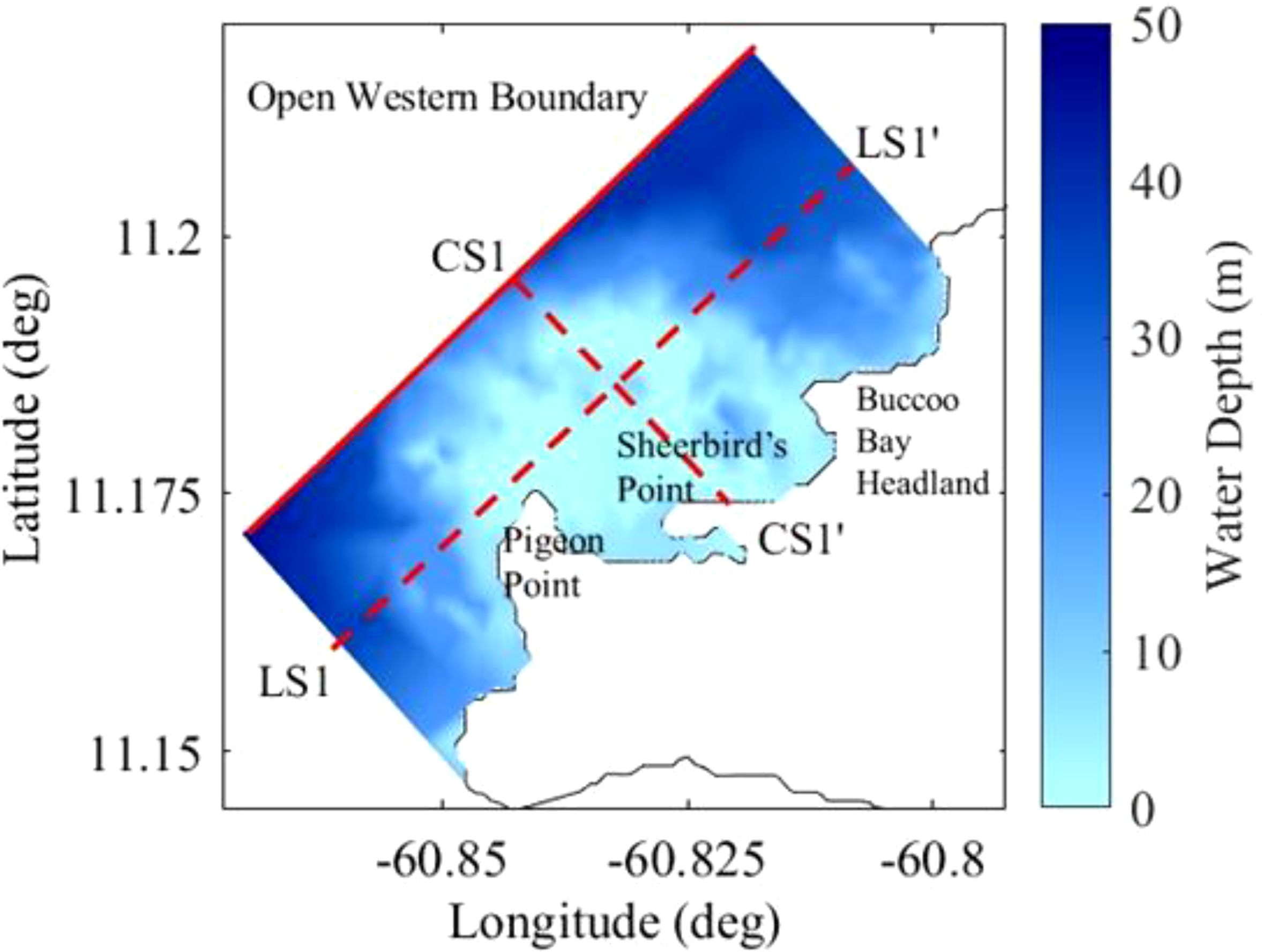
Figure 2. Model domain, interpolated bathymetry, open western boundary (red line) and cross-sections CS1-CS1’ and LS1-LS1’.

There were a total of 65 grid cells in the cross-shore direction and 126 grid cells in the long-shore direction with a total of 6627 grid elements. Each grid cell had a horizontal resolution of 60 m which was deemed sufficient to capture the key geomorphic features of the reef while maintaining computational efficiency. This structured grid and resolution was used for the model simulations to ensure that the SWAN model within Delft-WAVE functioned efficiently as well as to capture the complex processes taking place along the reef profile. The depth within each cell was obtained by interpolating bathymetry obtained from GEBCO (General Bathymetric Chart of the Oceans) bathymetry data. The bathymetry for the Buccoo Reef area was sourced from the GEBCO dataset, which provides global coverage at a resolution of 15 arc-seconds. While high resolution local bathymetric surveys would improve the spatial resolution of the data inputs, the bathymetric data used for this study was sufficient to capture the significant features and changes along the reef profile (Figure 1C).

The model boundary conditions were imposed only on the open western boundary (as this boundary represents the primary location by which wave energy enters the domain) and the two lateral boundaries consisted of Neumann boundary conditions to enable water to move through freely. The boundary conditions for the hydrodynamic model were generated from tidal constituents obtained from the TPXO7.2 global tide solution using 14 constituents A0, M2, S2, N2, K2, K1, O1, P1, Q1, MF, MM, M4, MS4 and MN4 at the Western boundary. Hourly wind data from ERA5 Reanalysis data was applied to the western boundary of the Delft-Flow model domain. The ERA5 data consisted of wind speed and wind direction at 10 m above sea level for the simulation time period. The spectral wave model was forced at the Western boundary using time series wave data obtained from an offshore deployed Acoustic Doppler Current Profiler (ADCP); location seen in Figure 1A. Model results were extracted from cross-sections CS1-CS1’ and LS1-LS1 (Figure 2).

Bottom friction in the model was represented using the formulation by Madsen et al. (1988). In the Madsen et al. (1988) formulation, the bottom friction coefficient (Equation 2) is a function of the bottom roughness height as well as the actual wave conditions.

$\begin{array}{ll}{C}_{\text{bottom}}=f_w\frac{g}{\sqrt{2}}{U}_{\text{rms}}& (2)\end{array}$

where $g$ represents acceleration due to gravity, $U_{\text{rms}}$ represents the root mean square of the wave orbital velocities near the seabed and $f_w$ is a non-dimensional friction factor bottom friction factor, estimated using the Jonsson (1966) formulation (Equation 3):

$\begin{array}{ll}\frac{1}{4\sqrt{f_w}}+{10}_{\log }\left(\frac{1}{4\sqrt{f_w}}\right)=m_f+{10}_{\log }\left(\frac{a_b}{K_N}\right)& (3)\end{array}$

In Equation 3, $a_b$ is a representative near-bottom excursion amplitude and K_N is the bottom roughness length scale which accounts for the effect of bed roughness on energy dissipation. Baldock et al. (2014) used the Madsen et al. (1988) bottom friction formulation, choosing a $K_N$ of 0.04 m and 0.1 m for model input for a smooth and rough reef respectively. This is equivalent to friction factors (f_w) of 0.1 for smooth reefs and 0.2 for rough reefs; values which are consistent with previous studies (Lowe et al., 2005; Sheppard et al., 2005). As such, a $K_N$ value of 0.08 m was chosen for initial model runs but was finetuned during calibration of the model. It was assumed that the roughness was uniform over the entire coral reef. In reality, the reef roughness would vary spatially over the reef, but detailed studies would be required to delineate distinct areas and as such the reef roughness is assumed to be homogenous over the reef. A similar approach has been adopted in previous studies (Baldock et al., 2014, 2020; Keyzer et al., 2020).

2.4 Model calibration and validation

Data from two ADCPs (RDI Teledyne Workhorses) comprised the hydrodynamic dataset used for this study. The previously mentioned ADCP (600kHz device) was deployed offshore in about 20.6m water depth and collected data from 13:00hrs on 02 May to 14:00hrs on 31 May 2016. The second ADCP (1200kHz) was deployed in the nearshore area in a water depth of approximately 5.2m and collected data from 14:00hrs on 02 May to 13:50hrs on 31 May 2016. The wave data consisted of hourly significant wave heights, peak wave periods and peak wave directions. Hourly water level variations were extracted from the ADCP data and used to validate the modelled water levels against observed measurements. The calibration and validation dataset for the model consisted of twenty-nine (29) days of available data using the offshore and nearshore deployed ADCPs. The model was initially run from 02-May-2016 to 09-May-2016, and this initial 7-day period was used both as a spin-up phase and a calibration phase. During this time, the modelled conditions were well-established over the small domain, ensuring an adequate transition from the initial to the boundary conditions within the system. The model was calibrated by varying the bottom friction factors, wave breaking coefficient and wind drag coefficients as well as the Manning’s roughness until there was an acceptable agreement between the predicted $(X_{model})$ and the observed $(X_{Obs})$ significant wave heights. The results of the 7-day simulation were then used as initial conditions for the subsequent 22-day analysis period, ensuring that the model started the main analysis from a stable and accurately calibrated state. For the validation simulation, the model was then run for a period of twenty-two (22) days from 09-May-2016 to 30-May-2016. Given the relatively small size of the model domain, this 22-day period was sufficient to investigate the wave conditions on the reef as well as the effects of water levels and tides. This approach aligns with previous studies (Quataert et al., 2015; Keyzer et al., 2020). The model was calibrated and validated by comparing the modelled significant wave heights and water levels to the observed significant wave heights and water levels. The model performance was quantitatively assessed by calculating the model Bias, Root Mean Square Error (RMSE), Coefficient of Determination R², the Scatter Index (SI) and the Skill Score (Equations 4–8).

$\begin{array}{ll}B\text{i}as= \frac{1}{N}{\sum }^{ }(X_{model}-X_{Obs})& (4)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{N}{\sum }^{ }{(X_{model }-X_{Obs})}^2}& (5)\end{array}$

$\begin{array}{ll}Scatter Index= \frac{RMSE}{X_{\text{obs}}}& (6)\end{array}$

$\begin{array}{ll}{R}^2=1-\frac{{\sum }_{i=1}^n{(X_{Obs}-X_{model})}^2}{{\sum }_{i=1}^n{(X_{Obs}-{\overline{X}}_{Obs})}^2}& (7)\end{array}$

$\begin{array}{ll}\text{Skill Score}=1-\frac{{\sum }_{i=1}^n{(X_{\text{mod}el}-X_{\text{obs}})}^2}{{\sum }_{i=1}^n{(\left|X_{\text{mod}el}-X_{\text{obs}}\right|+\left|X_{\text{obs}}-{\overline{X}}_{\text{obs}}\right|)}^2}& (8)\end{array}$

2.5 Model scenarios

After successful calibration and validation of the model, the sensitivity of the wave conditions on the reef to coral reef degradation was determined by varying the friction factors on the reef to represent healthy corals and smooth, dead corals. Carlot et al. (2023) used field measurements to show that the median Nikuradse roughness of healthy reefs at Mo’orea, French Polynesia was about 0.42 m, within a range of 0.34 to 0.52 m. Li et al. (2024) used logarithmic profile analysis to determine that the mean Nikuradse roughness at three reef flats in the Nansha Islands, South China Sea were in the range of 0.11 to 0.28 m. This study follows the approach of Baldock et al. (2014), where a Nikuradse roughness (K_N) of 0.1 m was used for rough reefs and 0.04 m for smooth reefs. Again, it was assumed that this roughness value was constant over the entire coral reef, depicting scenarios that show no spatial variation in coral health changes.

In order to simulate the effect of SLR on wave conditions over the reef, the ‘Give-Up’ scenario for coral reefs by Neumann (1985) is assumed where the already stressed and degraded reefs cannot keep pace with SLR, vertical accretion stops, and the reef erodes. As such, the friction factor representing degraded reefs is kept constant and the depths on the reef are increased. Projected estimates of sea-level rise (SLR) from the Intergovernmental Panel on Climate Change (IPCC) AR6 report indicate a likely increase in global mean sea level of 0.28–1.01 m by the year 2100 (Fox-Kemper et al., 2021). Therefore, the depths on the reef are increased in intervals of +0.25, +0.50 and +1.00 m, following the work of Storlazzi et al. (2011), to represent the increases in sea level by the year 2100.

The various model scenarios used the same 22-day measured offshore wave data from the validation step as representative of the high occurrence wave conditions at the Buccoo site. The focus on these high probability conditions, rather than the low probability events, would provide valuable insights into the prevalent wave conditions in nearshore areas and guide studies on prevailing sediment regimes and morphological response. In these scenarios, it is assumed that there are no changes in the future wave, tidal and wind conditions as SLR and coral reef degradation progresses and as such, the model was run using the same boundary conditions and model data.

3 Results

3.1 Model calibration and validation

Model calibration was conducted to achieve an acceptable level of agreement with the observed significant wave heights and water levels. Typically, for standard models, performance during calibration and validation is deemed acceptable if the modelled values are within 10% of the observed values (Williams and Esteves, 2017). However, due to the complexities inherent in coral reef hydrodynamics, lower agreements with observed wave heights have been reported in prior studies. For instance, Quataert et al. (2015) observed Scatter Index (SI) values of 0.170 for calibration and 0.115 for validation on the inner reef flat. Similarly, Masria et al. (2023) reported an SI of 0.419 and an RMSE of 0.06 m. Consequently, this model was calibrated to achieve SI values approximately $\pm$ 0.4 and RMSE values $\pm$ 0.06 m. The wave directions were also included in the calibration and validation of the model, and these are included for completeness. Figure 3 shows the offshore and nearshore measured and modelled wave heights for the simulation period during model validation and Figure 4 shows the nearshore measured and modelled water levels. Figure 5 shows a comparison between the measured and modelled parameters of significant wave heights, wave directions and water levels.

Figure 3

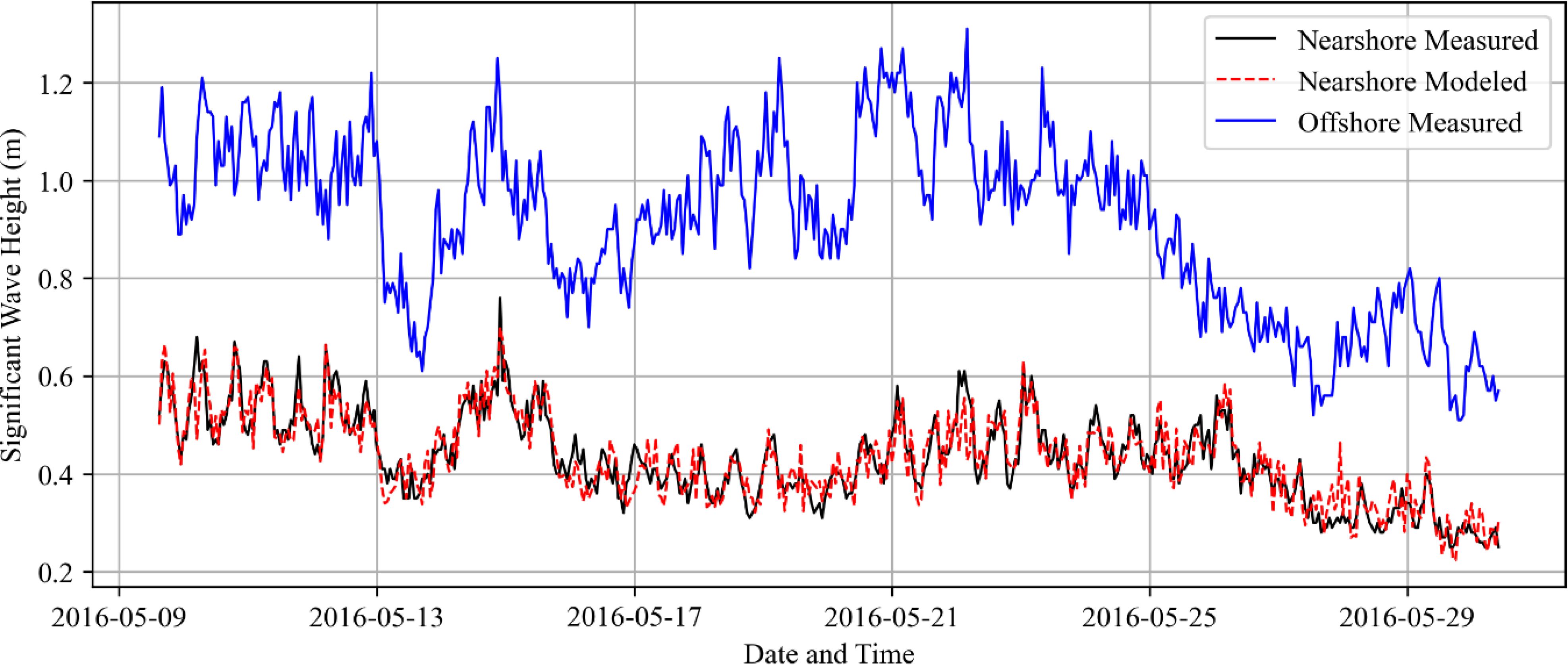
Figure 3. Nearshore measured wave heights, nearshore modelled wave heights and offshore measured wave heights during the validation period of the model simulation.

Figure 4

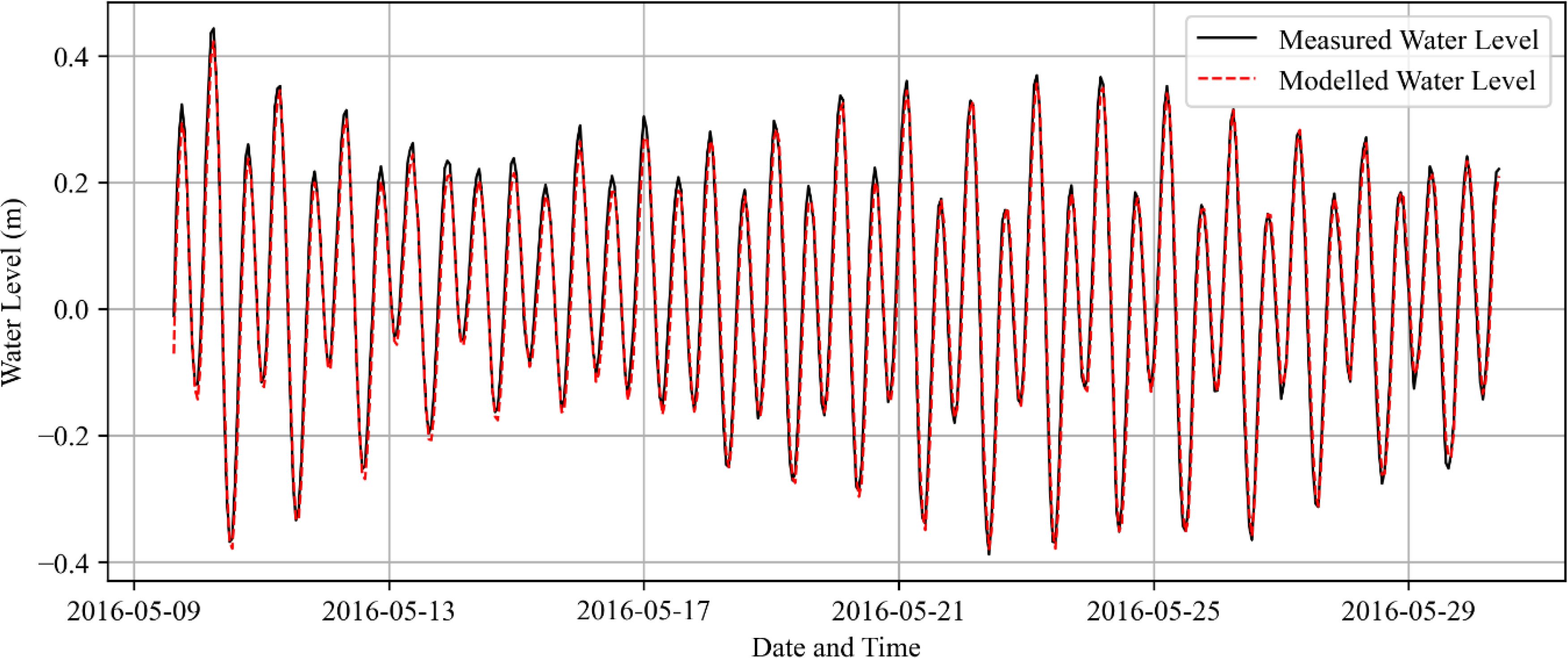
Figure 4. Nearshore measured and modeled water levels during the validation period of the model simulation.

Figure 5

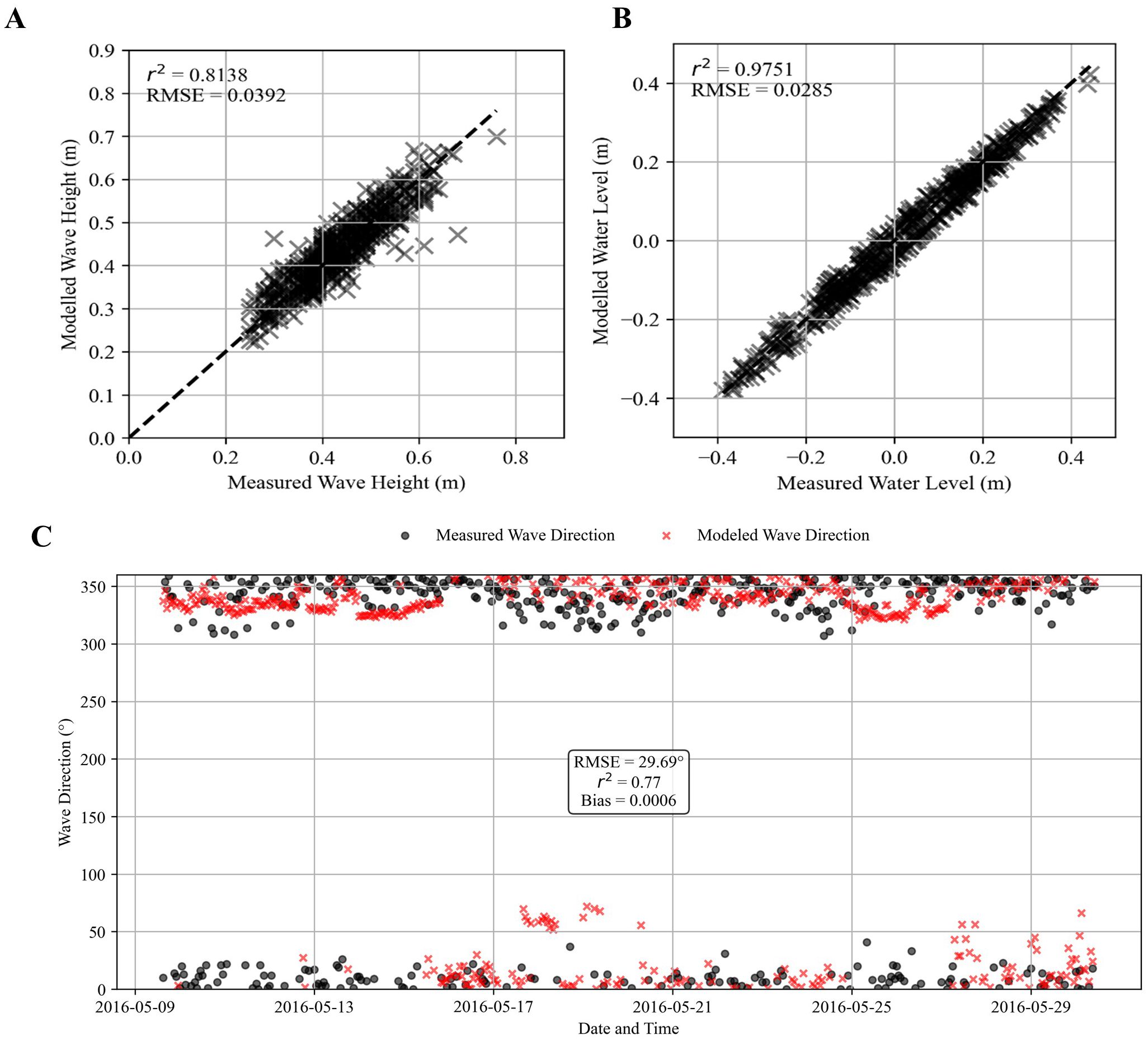
Figure 5. Comparison of measured and modelled (A) significant wave heights (B) water levels and (C) wave directions.

Model calibration showed that a $K_N$ of 0.07 m, Manning’s roughness of 0.05, a wave breaking coefficient of 0.78 and default wind drag coefficients provided the best agreement with observed significant wave heights and water levels. A summary of the calibration and validation statistics is seen in Table 1.

Table 1

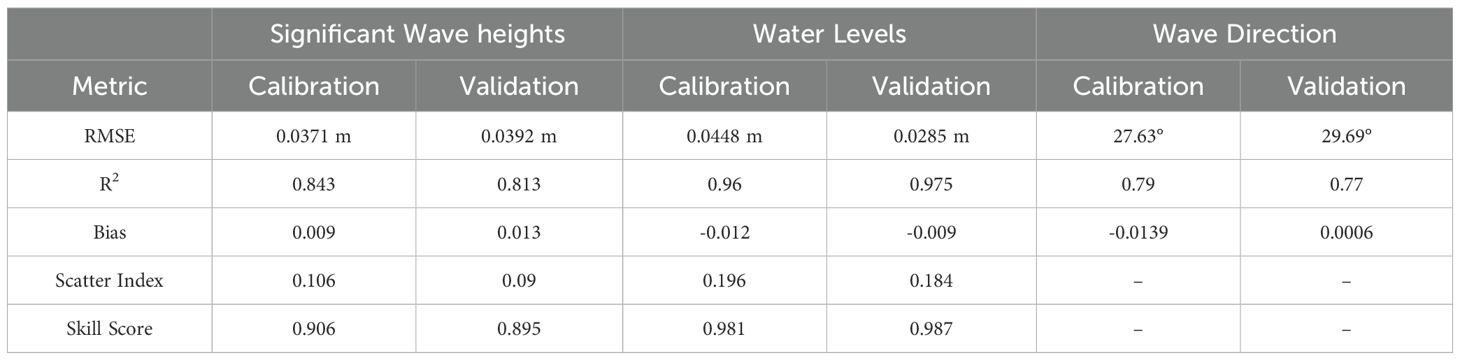
Table 1. Calibration and validation metrics for significant wave heights, water levels and wave directions.

For significant wave heights, the RMSE values during calibration and validation are 0.0371 m and 0.0392 m, respectively, indicating low average deviations between modeled and observed values. The R² remains consistently high at 0.843 during calibration and 0.813 during validation, suggesting that the model captures over 80% of the variance in wave heights. The Bias values, at 0.009 m (calibration) and 0.013 m (validation), reveal a slight overprediction of wave heights, but these values are small enough to be negligible in practical terms. The Scatter Index (SI), at 0.106 during calibration and 0.09 during validation, further highlights the model’s accuracy, as these values are well below the commonly accepted threshold of 0.2 for good performance. The Skill Score values, 0.906 and 0.895 for calibration and validation respectively, confirm the model’s reliability in reproducing wave heights under both sets of conditions.

For water levels, the RMSE decreases from 0.0448 m during calibration to 0.0285 m during validation, indicating an improvement in model accuracy after calibration. The R² values are exceptionally high, at 0.96 for calibration and 0.975 for validation, demonstrating that the model captures nearly all the variance in the observed water levels. The Bias values are minimal, with a slight underprediction of -0.012 m during calibration and -0.009 m during validation. The SI values for water levels, at 0.196 (calibration) and 0.184 (validation), indicate slightly higher relative errors compared to wave heights, but these values are still within an acceptable range for hydrodynamic modeling. The Skill Score values, 0.981 during calibration and 0.987 during validation, highlight the model’s ability to reproduce observed water levels.

3.2 Significant wave heights on the reef

The base scenario in the simulations represents near-present-day wave conditions on the reef, influenced by tides without changes to the friction factors or water levels. This base scenario serves as a control for assessing the impact of varying conditions on the coastal protection efficacy provided by the reef. The times 21-05-2016 at 05:00 and 11:00 were selected to represent High Tide and Low Tide Levels respectively, to effectively capture the tidal modulation of wave heights on the reef. Figures 6A, B show the significant wave heights on the reef with the arrows representing wave directions. Simulations reveal that wave heights are lower on the reef platform during Low Tide (21-05-2016 11:00) and higher during High Tide (21-05-2016 at 05:00). In this scenario, offshore wave heights are 1.07 m during Low Tide and 0.96 m during High Tide Levels. Throughout both tidal conditions, incident waves undergo depth-induced wave breaking at the reef crest, dissipating wave energy, and resulting in reduced wave energy conditions on the landward side of the reef.

Figure 6

Figure 6. Significant wave heights at (A) the low tide level, (B) the high tide level.

Specifically, during low tide, the reef becomes exposed, rendering wave heights on the reef minimal, as illustrated in Figure 7A along the Northern Reef. Additionally, waves are reformed by wind where they propagate shoreward, albeit at a significantly reduced magnitude but which may be more pronounced at high tide than at low tide.

Figure 7

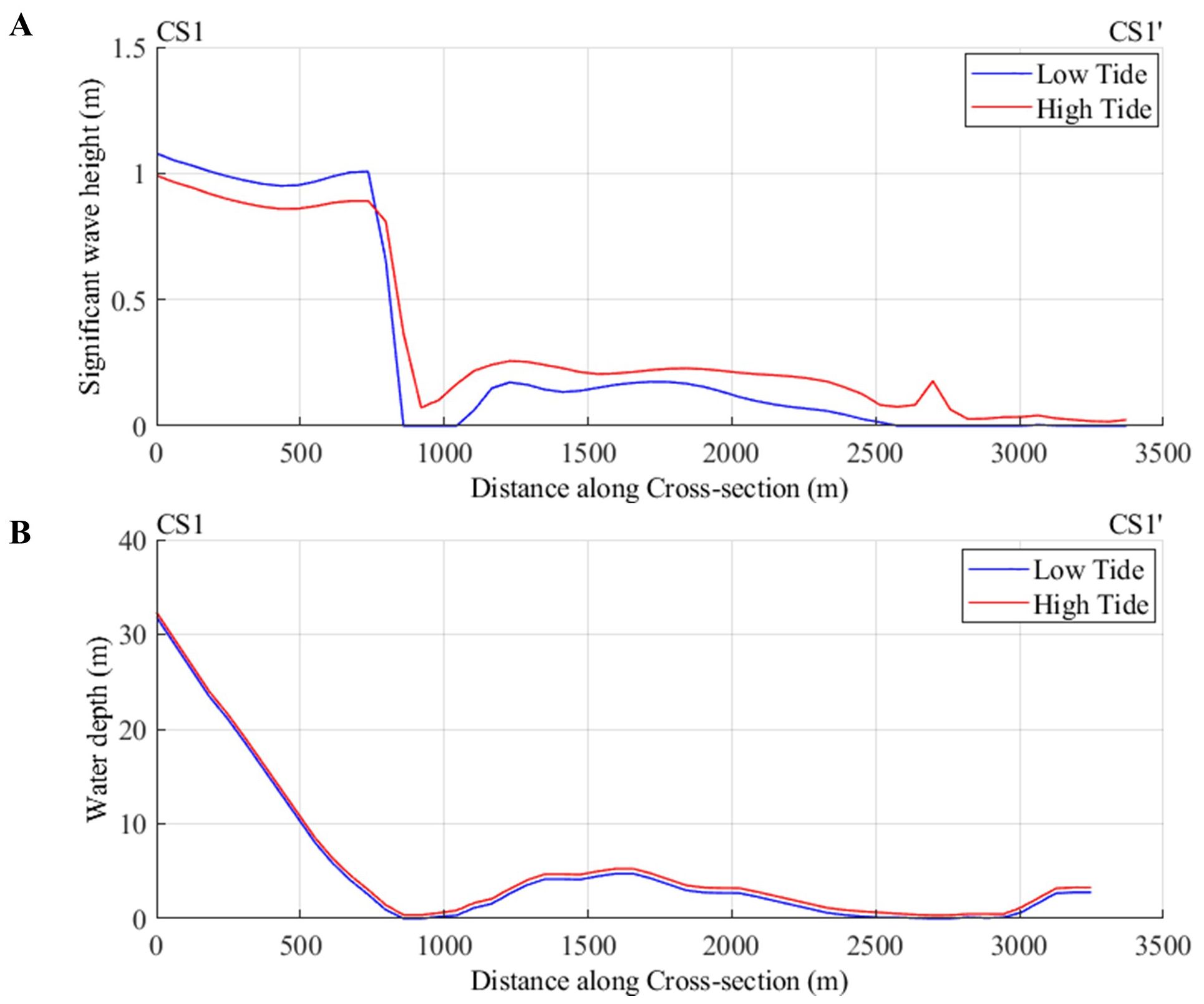
Figure 7. (A) Significant wave heights at low tide and high tide along cross-section CS1-CS1’ and (B) water depths at low tide and high tide along cross-section CS1-CS1’.

Further attenuation of wave heights occurs through frictional dissipation, influenced by the coral reef’s roughness. Notably, along cross-section CS1-CS1’ (Figure 7A) during low tide, wave height at breaking was approximately 0.98 m, leading to a complete (100%) reduction in significant wave height. At high tide, the breaking wave height was approximately 0.87 m, with a subsequent 96.45% reduction due to depth-induced wave breaking. Beyond this point, on the reef flat, wave heights experience a 93% decrease as a result of frictional dissipation due to coral reef roughness. There was an overall wave height reduction of approximately 97.39% during the high tide by the reef which is consistent with previous field-based studies (Costa et al., 2016; Ferrario et al., 2014; Péquignet et al., 2011).

Depth-induced wave breaking on the reef crest was also found to be a function of incident wave characteristics as well as the steepness of the reef. Figure 8A shows the significant wave height along cross-section LS1-LS1’. The Outer Reef, near LS1’, with slightly higher incident wave heights and steeper slopes result in much higher breaking wave heights, leading to a significant portion of the wave energy being dissipated over a shorter distance. Conversely, the gentler slopes of the Pigeon Point reef (approximately located at 2500 m along the LS1-LS1’ cross-section) show much lower breaking wave heights and a more gradual breaking of waves, spreading the energy dissipation over a longer distance.

Figure 8

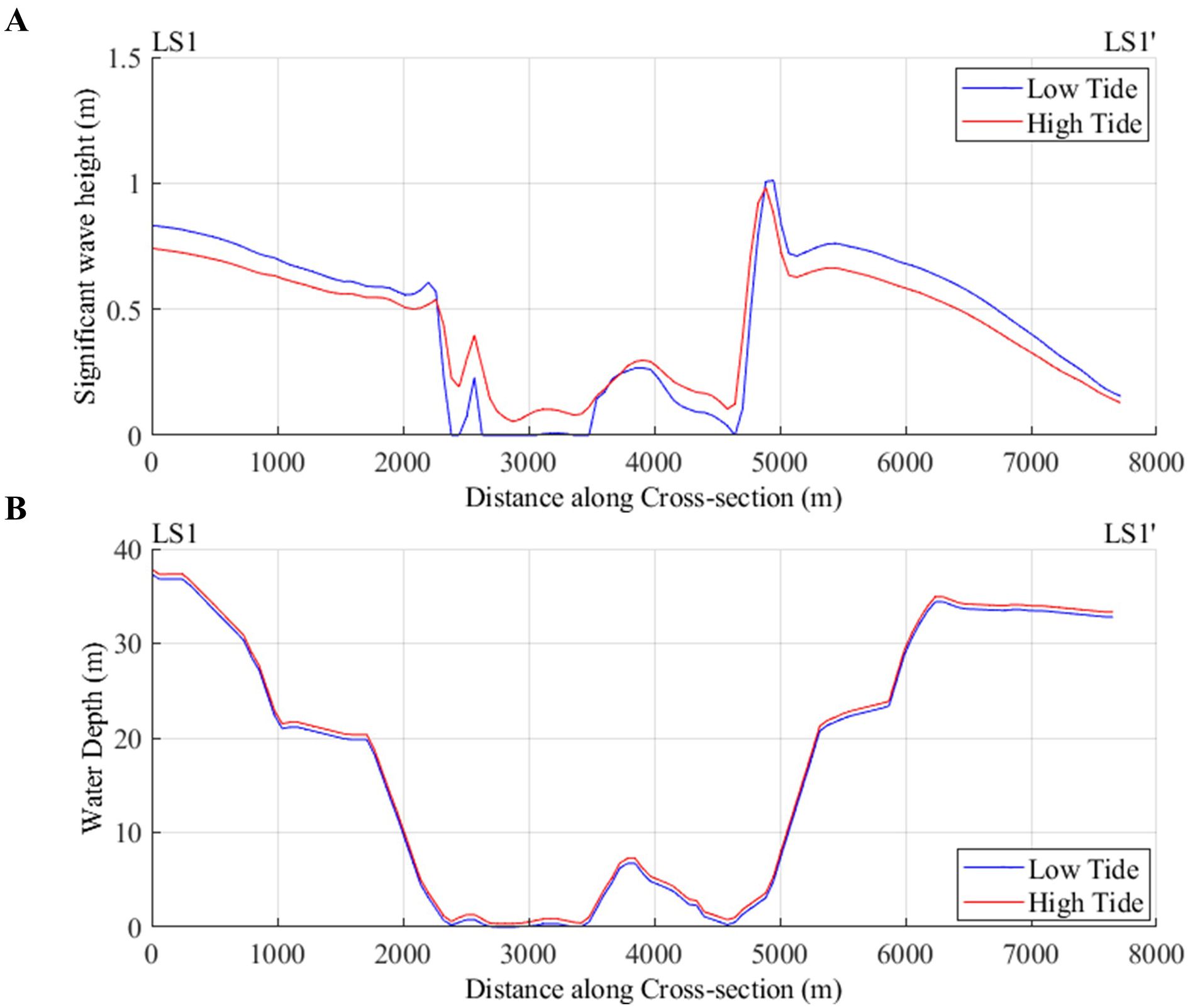
Figure 8. (A) Significant wave heights at low tide and high tide along cross-section LS1-LS1’ and (B) Water depths at low tide and high tide along cross-section LS1-LS1’.

3.3 Impact of coral reef degradation on wave conditions

The friction factors were varied to represent healthy coral reefs (high friction factor, $K_N$ = 0.1 m) and degraded and smooth coral reefs (low friction factor, $K_N$ = 0.04 m). Figure 9 illustrates the significant wave heights across cross-sections CS1-CS1’ and LS1-LS1’during the high tide level under the varying friction factor scenarios. For the Low Friction Scenario, representing degraded, smooth coral reefs, there was an average increase in significant wave heights on the reef flat by 21.74% along cross-section CS1-CS1’, indicating a notable reduction in the frictional dissipation provided by the coral reef compared to the baseline scenario. Similarly, along cross-section LS1-LS1’, there was an average increase in wave heights by 5.54%, suggesting that frictional dissipation plays a role in wave attenuation on both reef crests and platforms. Conversely, in the High Friction Factor Scenario, representing healthy coral reefs, there was an average decrease in significant wave heights by 18.9% from the Base Scenario for the cross-section CS1-CS1’. Figure 9 also shows that the changes in friction factors do not affect the occurrence of depth-induced wave breaking or the location of depth-induced wave breaking.

Figure 9

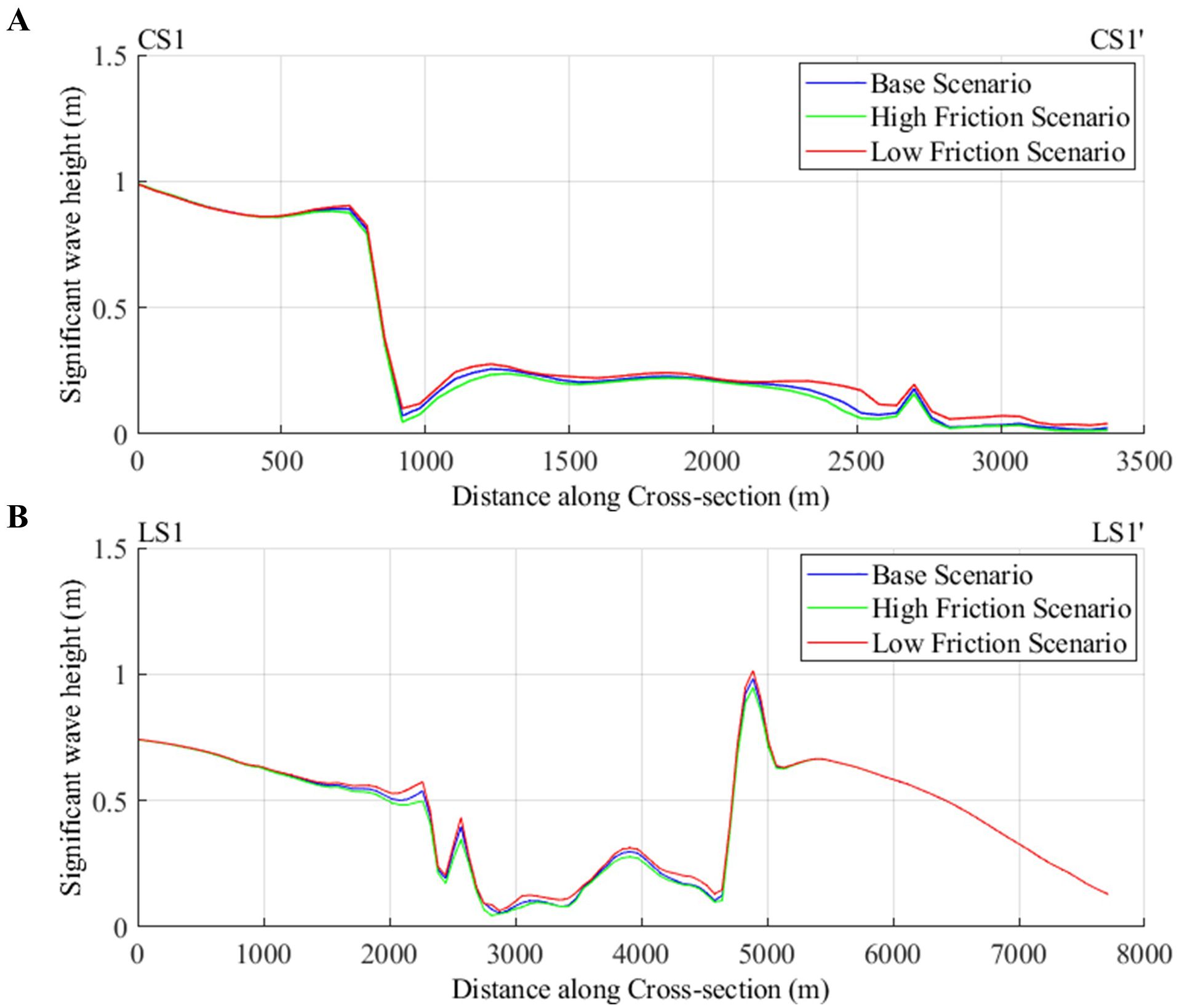
Figure 9. Significant wave heights under base scenario, low friction scenario and high friction scenario along (A) cross-section CS1-CS’ and (B) cross-section LS1-LS1’.

3.4 Impact of sea level rise on wave conditions

The model simulations for the different SLR scenarios were conducted by increasing water levels in increments of +0.25 m, +0.50 m, and +1.00 m above the baseline, reflecting the SLR projections for the year 2100 by Fox-Kemper et al. (2021). Figure 10 shows the significant wave heights on the reef for each increment. As sea level rises, there is a clear increase in wave heights on the reef platform as well as nearshore wave heights, showing a substantial decrease in the effectiveness of the reef at coastal protection through depth-induced wave breaking and frictional dissipation.

Figure 10

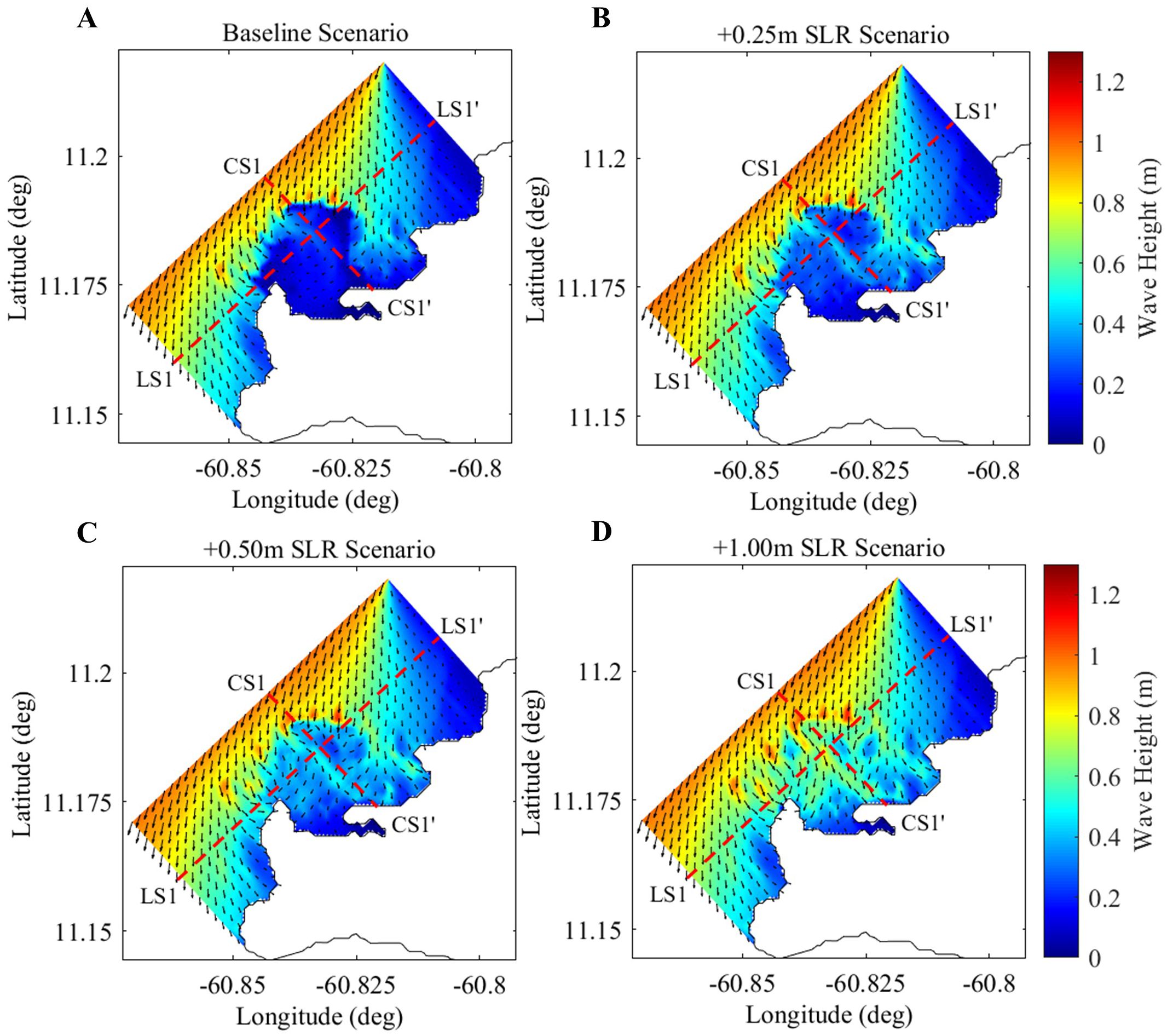
Figure 10. Significant wave heights on the reef for the (A) baseline SLR scenario, (B) +0.25m SLR scenario, (C) +0.50m SLR scenario and (D) +1.00m SLR scenario.

Figure 11 illustrates the changes in significant wave heights across cross-sections CS1-CS1’ and LS1-LS1’ under different SLR scenarios. Specifically, for cross-section CS1-CS1’ (Figure 11A), the results show an average rise in significant wave heights of 160.5% under the +0.25 m SLR scenario, a 235.56% increase for the +0.50 m SLR scenario, and a substantial 388.44% increase for the +1.00 m SLR scenario. Along cross-section LS1-LS1’ (Figure 11B), there was an average increase in significant wave heights by 58.04% for the +0.25 m SLR Scenario, 86.66% for the 0.50m SLR Scenario and 154.45% for the 1.00 m SLR Scenario. Along both cross-sections, the location of depth-induced wave breaking moves slightly landward with substantial increases in nearshore wave heights due to the significant reduction of the frictional dissipation provided by the coral reefs.

Figure 11

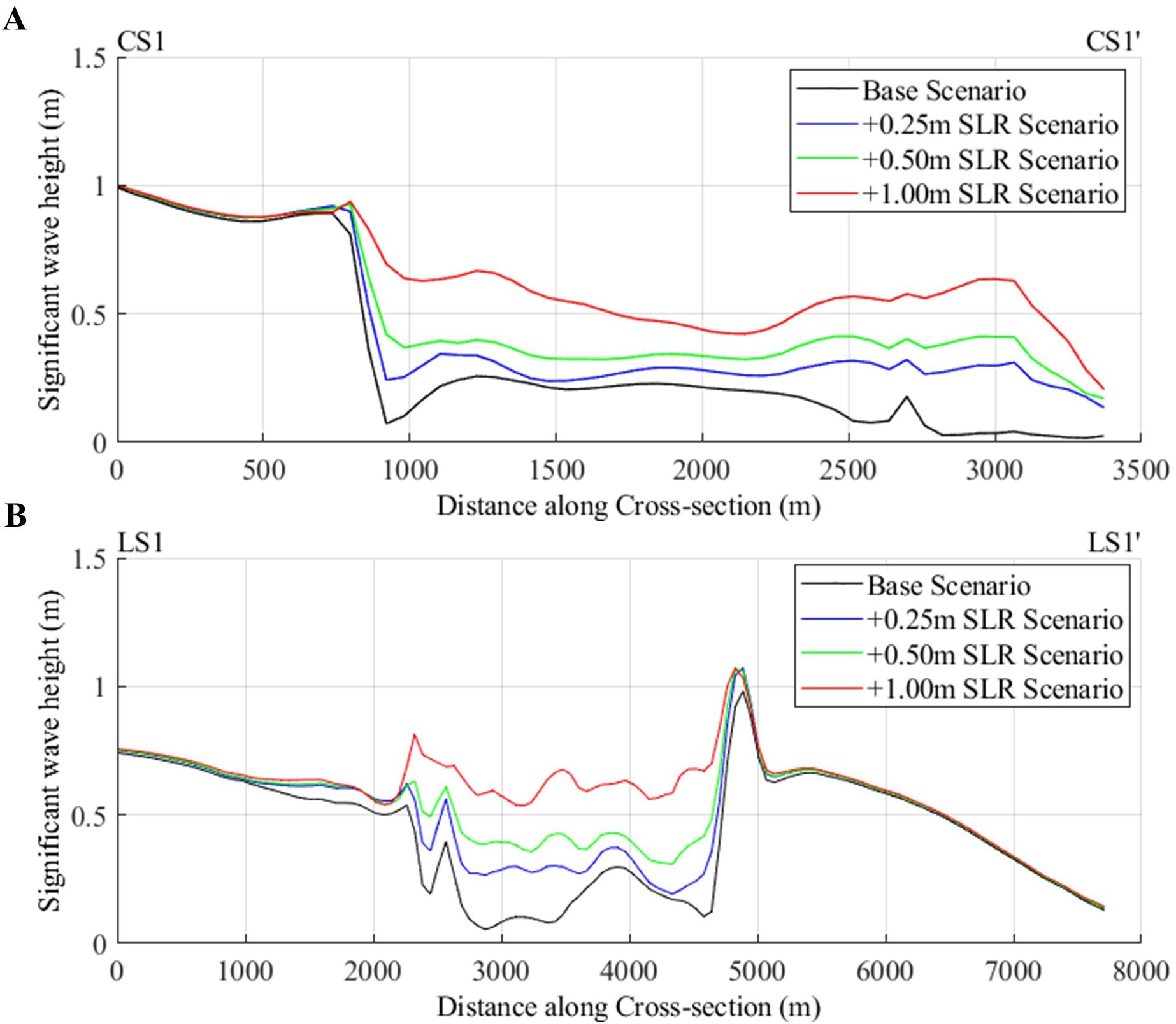
Figure 11. Significant wave heights for the baseline, +0.25m, +0.50m and 1.00m SLR scenarios along (A) cross-section CS1-CS1’ and (B) cross-section LS1-LS1’.

4 Discussion

4.1 Numerical modelling of the effectiveness of the reef at coastal protection

The numerical modelling approach used in the study provided valuable insights into the effectiveness of coral reefs as coastal protection through depth-induced wave breaking and frictional dissipation at the study site of Buccoo Bay in Tobago under high-probability wave conditions. After successful calibration of the model, a $K_N$ = 0.07 m was used for model simulations to represent the baseline scenario, suggesting that the reef has already undergone some level of coral reef degradation, loss of roughness and decrease in frictional dissipation. While there was a good agreement between modelled and measured wave heights and water levels (Figure 5) and the model performance was similar to previous studies (Masria et al., 2023; Quataert et al., 2015), there is a critical need for species-specific friction factors for coral reefs to enhance the accuracy of the model predictions, as well as the application of these spatially varying factors across the reef. Currently, there are no standardized methods for parameterizing reef roughness in numerical models (Osorio-Cano et al., 2019). However, adopting an interdisciplinary approach that includes ecological indices, such as the rugosity index, could significantly enhance the accuracy of modelling coral reef hydrodynamics and provide a more focused approach to reef restoration/management strategies.

The simulations representing the baseline scenario highlight the importance of incident wave characteristics, water levels, reef geometry and frictional dissipation on the coastal protection effectiveness of the reef through wave attenuation and dissipation. The wave heights on the reef were tidally modulated with a complete reduction in significant wave heights at the low tide level, primarily due to the reef being exposed, and a 96.45% reduction during the high tide level as a result of wave breaking on the reef crest (Figure 7). The variations in reef geometry between Pigeon Point Reef and the steeper Outer Reef show that the steeper reefs induce wave breaking over shorter distances with higher breaking wave heights. The gentler sloping Pigeon Point reef can allow unbroken waves into the reef lagoon, increasing the nearshore wave energy.

The significance of frictional dissipation in reducing wave height was evidenced by a substantial 93% decrease in wave heights and the importance of coral reefs in coastal protection was highlighted by an overall significant wave height reduction of approximately 97.39% during the high tide by the reef which is consistent with previous field-based studies (Costa et al., 2016; Ferrario et al., 2014; Péquignet et al., 2011).

4.2 The impact of coral reef degradation and SLR

The health of the coral reefs affects the reef roughness and subsequent frictional dissipation provided by the reef. Healthy coral reefs are more geometrically complex and provide greater frictional dissipation than smooth, dead corals. This phenomenon is especially seen in the model scenarios in which the friction factors were varied (Figure 9). For the High Friction Scenario ($K_N$= 0.1 m), representing healthy coral reefs, there was an average decrease in significant wave heights of 18.9%. In the case of the Low Friction Scenario (K_N = 0.04 m), which represented dead, smooth corals, there was an average increase in significant wave heights of 21.74% from the base scenario and a 40.64% increase from the High Friction Scenario. These results underscore the importance of the health of coral reefs and their role in coastal protection.

For the SLR Scenarios, the Neumann (1985) ‘Give-Up’ scenario was assumed, suggesting that coral reefs did not keep up with SLR. This assumption was reasonable since rates of accretion for exposed fringing reefs vary between 1-4mm year^-1 (Buddemeier and Smith, 1988; Montaggioni, 2005). The SLR Scenarios show substantial increases in nearshore wave heights with an average increase in significant wave heights by 160.5% under the +0.25m SLR scenario, a 235.56% increase for the +0.50m SLR scenario, and a substantial 388.44% increase for the +1.00m. These increases in wave heights are a result of the decrease in depth-induced wave breaking taking place on the reef crest and frictional dissipation as sea level rises, with substantially higher wave heights in the nearshore area. The combination of coral reef degradation and SLR can lead to substantial increases in nearshore wave heights which can exacerbate existing coastal hazards such as coastal erosion and flooding and negatively impact coastal ecosystems and diminish the valuable ecosystem services that they provide.

The Buccoo Reef was designated a Marine Protected Area (MPA) in 1973 (Laydoo et al., 1998) and a Ramsar site in 2006 (Peters et al., 2023). While ongoing monitoring efforts by the Institute of Marine Affairs (IMA) have provided valuable baseline data on reef conditions and degradation trends and there are several technical reports (Darsan et al., 2013; Alemu and Amoroso, 2015; Ganase and Lochan, 2022), little has been implemented to address the coral reef degradation due to anthropogenic influence and adaptations to climate change and sea level rise. Consequently, it is imperative to develop and implement effective management strategies and solutions to address the challenges posed by coral reef degradation and rising sea levels.

4.3 Implications for reef restoration and future management strategies

The results of this study underscore the critical role of coral reef health and their adaptability to sea level rise in sustaining their coastal protection functions. Preserving the effectiveness of this natural defence requires ongoing efforts to maintain reef health and enhance their resilience. Two key approaches to achieve this, supported by the results of the study, are Integrated Coastal Zone Management (ICZM) and the implementation of artificial reefs.

Although ICZM is a well-established concept, its effective implementation remains crucial for managing coral reef ecosystems, as it directly affects their health and, in turn, their coastal protection capabilities in Caribbean SIDS. Our study demonstrated that healthy coral reefs, characterized by increased roughness, provide greater wave attenuation. Therefore, management strategies that reduce reef degradation and focus on enhancing reef health are essential for maintaining and improving their coastal protection function. ICZM offers a comprehensive approach to address these anthropogenic impacts, aiming to mitigate ongoing degradation. For coral reefs, effective ICZM involves managing land-based pollution sources, regulating coastal development, promoting sustainable tourism, enforcing protective regulations, and integrating community involvement (Gibson et al., 1998). While this study primarily focuses on wave dynamics and the role of the Buccoo Reef in dissipating wave energy, future research should incorporate an assessment of potential coastal impacts, such as damage to infrastructure, erosion, and effects on local populations. Such analyses would complement the findings of this study and provide actionable insights into coastal management strategies. ICZM efforts promote reef preservation and natural reef restoration which will assure healthy reefs to afford vital coastal protection services for present and future generations.

The results of the study have also shown that both frictional dissipation and depth-induced wave breaking are key processes involved in coastal protection by coral reefs. Healthy coral reefs with a high roughness and high friction factor of $K_N$ = 0.1 m contributed significantly to wave attenuation. Artificial reefs designed to replicate this level of roughness can achieve similar protective effects, particularly over extended distances, as demonstrated in Figure 9. Durable substances such as concrete and ceramics, which have been shown to effectively support marine life, can be used but any adverse short-, medium- or long-term impacts of these should be carefully assessed (Baine, 2001). To the authors’ knowledge, current artificial reef execution efforts have not fully considered the role of frictional dissipation, and incorporating this factor into their design and deployment could greatly enhance their effectiveness in dissipating wave energy.

The SLR scenarios revealed that increased depth on the reef crest reduces depth-induced wave breaking, leading to significant increases in nearshore wave energy (Figure 10). Artificial reefs strategically positioned to account for rising sea levels can help maintain the coastal protection benefits traditionally provided by natural reefs through depth-induced wave breaking, achieving a level of coastal protection comparable to the base scenario (Figure 11A). This approach allows artificial reefs to continue to provide this essential coastal protection as well as support the growth and survival of coral reefs across coastal areas in Caribbean SIDS to adopt more climate-resilient strategies.

5 Conclusion

A numerical modelling approach using a coupled depth-averaged hydrodynamic and spectral wave model in Delft3D was employed to evaluate the coastal protection effectiveness of a fringing reef at Buccoo Bay, Tobago through depth-induced wave breaking and frictional dissipation under scenarios of reef degradation and SLR. The study results emphasize the importance of factors such as water levels and reef geometry in wave energy dissipation, with 100% and 96.45% reduction in wave heights at low and high tides, respectively. The model scenarios for degraded reef conditions showed a 21.74% mean increase in wave heights over baseline, whereas the model scenarios for healthier reefs showed a decrease in wave heights by 18.9% from the baseline. The modelled SLR scenarios showed increases in wave heights ranging from 160.5% and 388.4% as SLR progressed.

The findings underscore the importance of the frictional dissipation provided by healthy coral reefs, with degraded corals and rising sea levels leading to increased nearshore wave heights which could exacerbate issues such as coastal erosion and flooding. While this research primarily analyzed these factors independently, future studies should investigate their combined impacts to provide a more holistic understanding of coastal resilience challenges. Integrating dynamic reef degradation scenarios with SLR projections would enable a deeper evaluation of their compounded effects on wave dynamics, sediment transport, and shoreline stability. Such efforts would offer valuable insights for developing adaptive coastal management strategies in the face of climate change. The simulations also reveal a significant need for species-specific friction factors to improve model accuracy, as well as the application of these spatially varying factors across the reef.

Considering the critical role of reef health in coastal protection through processes like frictional dissipation and depth-induced wave breaking, management strategies such as ICZM are essential. ICZM can effectively address key anthropogenic stresses, thereby enhancing the resilience of coral reefs and preserving their coastal protection functions. The strategic deployment of climate-resilient solutions like artificial reefs, designed to mimic the complex structures and roughness of natural reefs, can significantly enhance wave attenuation through frictional dissipation and depth-induced wave breaking. When appropriately placed, these artificial reefs offer a pragmatic approach to maintaining the ecological and protective functions of coral reefs in the face of ongoing environmental and climate changes in Caribbean SIDS.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AB: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. DV-L: Conceptualization, Data curation, Formal analysis, Investigation, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The publication of this article was funded by the Open Access (OA) Acceleration Project, implemented by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.

Acknowledgments

The first author would like to acknowledge the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT) for financial support through the MEXT Scholarship for graduate studies. The kind support of the Department of Life Sciences at the University of the West Indies, St. Augustine Campus in sharing the hydrodynamic data for Buccoo Reef is very much appreciated.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alemu J., Amoroso R. (2015). Coral Reef Monitoring for Tobago: Status of the Coral Reefs of Tobago – 2013 and Summary Report 2010–2013 (Chaguaramas, Trinidad and Tobago: Institute of Marine Affairs). Available online at: https://www.ima.gov.tt/wp-content/uploads/2023/09/2010-Coral_Reef_Monitoring_Status_Report_Tobago_2010-2013-2015.pdf (Accessed December 31, 2024).

Google Scholar

Baine M. (2001). Artificial reefs: a review of their design, application, management and performance. Ocean Coast. Manage. 44, 241–259. doi: 10.1016/S0964-5691(01)00048-5

Crossref Full Text | Google Scholar

Baldock T. E., Golshani A., Callaghan D. P., Saunders M. I., Mumby P. J. (2014). Impact of sea-level rise and coral mortality on the wave dynamics and wave forces on barrier reefs. Mar. pollut. Bull. 83, 155–164. doi: 10.1016/j.marpolbul.2014.03.058

PubMed Abstract | Crossref Full Text | Google Scholar

Baldock T. E., Shabani B., Callaghan D. P., Hu Z., Mumby P. J. (2020). Two-dimensional modelling of wave dynamics and wave forces on fringing coral reefs. Coast. Eng. 155, 103594. doi: 10.1016/j.coastaleng.2019.103594

Crossref Full Text | Google Scholar

Battjes J. A., Janssen J. P. F. M. (1978). “Energy loss and set-up due to breaking of random waves,” in Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany. (Reston, VA: American Society of Civil Engineers (ASCE)) 1978, 569–587. doi: 10.1061/9780872621909.034

Crossref Full Text | Google Scholar

Beetham E., Kench P. S. (2018). Predicting wave overtopping thresholds on coral reef-island shorelines with future sea-level rise. Nat. Commun. 9, 3997. doi: 10.1038/s41467-018-06550-1

PubMed Abstract | Crossref Full Text | Google Scholar

Buddemeier R. W., Smith S. V. (1988). Coral reef growth in an era of rapidly rising sea level: predictions and suggestions for long-term research. Coral Reefs 7, 51–56. doi: 10.1007/BF00301982

Crossref Full Text | Google Scholar

Carlot J., Vousdoukas M., Rovere A., Karambas T., Lenihan H. S., Kayal M., et al. (2023). Coral reef structural complexity loss exposes coastlines to waves. Sci. Rep. 13, 16835. doi: 10.1038/s41598-023-28945-x

PubMed Abstract | Crossref Full Text | Google Scholar

Clarke J., de Berdt Romilly G., McCue J., Pinder S., Pounder C., Campbell D., et al. (2019). Vulnerability and Capacity Assessment (VCA) Report. Technical Assistance for the Environment Programme. (Port of Spain, Trinidad and Tobago: Ministry of Planning and Development). Available online at: https://www.planning.gov.tt/sites/default/files/Final_TAEP_Vulnerability_and_Capacity_Assessment_Report_Trinidad_and_Tobago_Jan_2019.pdf (Accessed December 31, 2024).

Google Scholar

Collins J. I. (1972). Prediction of shallow-water spectra. J. Geophys. Res. (1896-1977) 77, 2693–2707. doi: 10.1029/JC077i015p02693

Crossref Full Text | Google Scholar

Costa M. B. S. F., Araújo M., Araújo T. C.M., Siegle E. (2016). Influence of reef geometry on wave attenuation on a Brazilian coral reef. Geomorphology 253, 318–327. doi: 10.1016/j.geomorph.2015.11.001

Crossref Full Text | Google Scholar

Darsan J., Alexis C., Barton J. (2013). Coastal Conservation Project: Status of Beaches and Bays in Tobago, (2004–2008) (Chaguaramas, Trinidad and Tobago: Institute of Marine Affairs). Available online at: https://www.ima.gov.tt/wp-content/uploads/2018/04/Coastal-Con-Sept-2013-Status-Beaches-Bay-Tobago-2004-08-Final-Dec2016.pdf (Accessed December 31, 2024).

Google Scholar

Elliff C. I., Silva I. R. (2017). Coral reefs as the first line of defense: Shoreline protection in face of climate change. Mar. Environ. Res. 127, 148–154. doi: 10.1016/j.marenvres.2017.03.007

PubMed Abstract | Crossref Full Text | Google Scholar

Ferrario F., Beck M. W., Storlazzi C. D., Micheli F., Shepard C. C., Airoldi L. (2014). The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat. Commun. 5, 37945. doi: 10.1038/ncomms4794

PubMed Abstract | Crossref Full Text | Google Scholar

Fox-Kemper B., Hewitt H. T., Xiao C., Aðalgeirsdóttir G., Drijfhout S. S., Edwards T. L., et al. (2021). “Ocean, Cryosphere and Sea Level Change,” in Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Eds. Masson-Delmotte V., Zhai P., Pirani A., Connors S. L., Péan C., Berger S., Caud N., Chen Y., Goldfarb L., Gomis M. I., Huang M., Leitzell K., Lonnoy E., Matthews J. B. R., Maycock T. K., Waterfield T., Yelekçi O., Yu and B. Zhou R. (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA), 1211–1362.

Google Scholar

Ganase A., Lochan H. (2022). The Status of Coral Reefs in Tobago (Chaguaramas, Trinidad and Tobago: Institute of Marine Affairs). Available online at: https://www.ima.gov.tt/wp-content/uploads/2023/09/Status-of-Coral-Reef-of-Tobago-2020-Ganase-Lochan-20231.pdf (Accessed December 31, 2024).

Google Scholar

Gibson J., McField M., Wells S. (1998). Coral reef management in Belize: an approach through integrated coastal zone management. Ocean Coast. Manage. 39, 229–244. doi: 10.1016/S0964-5691(98)00007-6

Crossref Full Text | Google Scholar

Grady A. E., Moore L. J., Storlazzi C. D., Elias E., Reidenbach M. A. (2013). The influence of sea level rise and changes in fringing reef morphology on gradients in alongshore sediment transport. Geophys. Res. Lett. 40, 3096–3101. doi: 10.1002/grl.50577

Crossref Full Text | Google Scholar

Green R. H., Lowe R. J., Buckley M. L. (2018). Hydrodynamics of a tidally forced coral reef atoll. J. Geophys. Res.: Oceans 123, 7084–71015. doi: 10.1029/2018jc013946

Crossref Full Text | Google Scholar

Hasselmann K., Barnett T. P., Bouws E., Carlson H., Cartwright D. E., Enke K., et al. (1973). Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Technical Report. (Hamburg, Germany: Deutches Hydrographisches Institut).

Google Scholar

Hein M. Y., Birtles A., Willis B. L., Gardiner N., Beeden R., Marshall N. A. (2019). Coral restoration: Socio-ecological perspectives of benefits and limitations. Biol. Conserv. 229, 14–25. doi: 10.1016/j.biocon.2018.11.014

Crossref Full Text | Google Scholar

Higgins E., Metaxas A., Scheibling R. E. (2022). [amp]]ldquo;A systematic review of artificial reefs as platforms for coral reef research and conservation. PloS One 17, e02619645. doi: 10.1371/journal.pone.0261964

PubMed Abstract | Crossref Full Text | Google Scholar

Jevrejeva S., Moore J. C., Grinsted A. (2010). How will sea level respond to changes in natural and anthropogenic forcings by 2100? Geophys Res Lett. 37 (7). doi: 10.1029/2010GL042947

Crossref Full Text | Google Scholar

Jonsson I. G. (1966). “Wave boundary layers and friction factors.” In Proceedings of the 10th International Conference on Coastal Engineering, Tokyo, Japan. 1966, 127–148. Reston, VA: American Society of Civil Engineers (ASCE).

Google Scholar

Keyzer L. M., Herman P. M. J., Smits B. P., Pietrzak J. D., James R. K., Candy A. S., et al. (2020). The potential of coastal ecosystems to mitigate the impact of sea-level rise in shallow tropical bays. Estuarine Coast. Shelf Sci. 246, 107050. doi: 10.1016/j.ecss.2020.107050

Crossref Full Text | Google Scholar

Lapointe B. E., Langton R., Bedford B. J., Potts A. C., Day O., Hu C. (2010). Land-based nutrient enrichment of the Buccoo Reef Complex and fringing coral reefs of Tobago, West Indies. Mar. pollut. Bull. 60, 334–3435. doi: 10.1016/j.marpolbul.2009.10.020

PubMed Abstract | Crossref Full Text | Google Scholar

Laydoo R. S., Bonair K., Alleng G. (1998). “Buccoo reef and bon accord Lagoon, Tobago, Republic of Trinidad & Tobago,” in CARICOMP–Caribbean Coral Reef, Seagrass and Mangrove Sites. Ed. Kjerfve B. (UNESCO, Paris), 171–176.

Google Scholar

Lentz S. J., Churchill J. H., Davis K. A., Farrar J. T. (2016). Surface gravity wave transformation across a platform coral reef in the Red Sea. J. Geophys. Res.: Oceans 121, 693–705. doi: 10.1002/2015jc011142

Crossref Full Text | Google Scholar

Lesser G. R., Roelvink J. A., van Kester J. A. T. M., Stelling G. S. (2004). Development and validation of a three-dimensional morphological model. Coast. Eng. 51, 883–915. doi: 10.1016/j.coastaleng.2004.07.014

Crossref Full Text | Google Scholar

Li J., Wang Ya P., Gao S. (2024). In situ hydrodynamic observations on three reef flats in the Nansha Islands, South China Sea. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1375301

Crossref Full Text | Google Scholar

Lowe R. J., Falter J. L., Bandet M. D., Pawlak G., Atkinson M. J., Monismith S. G., et al. (2005). Spectral wave dissipation over a barrier reef. J. Geophys. Res.: Oceans 110. doi: 10.1029/2004JC002711

Crossref Full Text | Google Scholar

Lugo-Fernández A., Roberts H. H., Suhayda J. N. (1998). Wave transformations across a Caribbean fringing-barrier Coral Reef. Continent. Shelf Res. 18, 1099–11245. doi: 10.1016/S0278-4343(97)00020-4

Crossref Full Text | Google Scholar

Madsen O., Poon Y.-K., Graber H. C. (1988). “Spectral wave attenuation by bottom friction: theory,” in Proceedings of the 21st International Conference on Coastal Engineering, March 20–25, 1988, Torremolinos, Spain, 492–504. Reston, VA: American Society of Civil Engineers (ASCE).

Google Scholar

Mallela J., Crabbe M. J. C. (2009). [amp]]ldquo;Hurricanes and coral bleaching linked to changes in coral recruitment in Tobago. Mar. Environ. Res. 68, 158–1625. doi: 10.1016/j.marenvres.2009.06.001

PubMed Abstract | Crossref Full Text | Google Scholar

Marchitto B., Conde J., Santos R., de Nicola C., Ferrazzi M., Baldini A., et al. (2023). Climate Risks for Latin America and the Caribbean: Are Banks Ready for the Green Transition? Luxembourg: European Investment Bank. Available online at: https://www.eib.org/attachments/lucalli/20230142_climate_risks_for_latin_america_and_the_caribbean_en.pdf (Accessed December 31, 2024).

Google Scholar

Masria A., Omara H., Diab R., Nassar K. (2023). Hydromorphological management of a lengthy coastal strip in the presence of natural coral reefs flocs in the red sea. Ocean Coast. Manage. 232, 106424. doi: 10.1016/j.ocecoaman.2022.106424

Crossref Full Text | Google Scholar

Masselink G., Tuck M., McCall R., Dongeren Ap v., Ford M., Kench P. (2019). Physical and numerical modeling of infragravity wave generation and transformation on coral reef platforms. J. Geophys. Res.: Oceans 124, 1410–14335. doi: 10.1029/2018JC014411

Crossref Full Text | Google Scholar

Monismith S. G., Rogers J. S., Koweek D., Dunbar R. B. (2015). Frictional wave dissipation on a remarkably rough reef. Geophys. Res. Lett. 42, 4063–40715. doi: 10.1002/2015GL063804

Crossref Full Text | Google Scholar

Montaggioni L. F. (2005). History of Indo-Pacific coral reef systems since the last glaciation: Development patterns and controlling factors. Earth-Science Rev. 71, 1–75. doi: 10.1016/j.earscirev.2005.01.002

Crossref Full Text | Google Scholar

National Hurricane Center (2024). NHC Data Archive (Washington, DC: National Oceanic and Atmospheric Administration (NOAA)). Available online at: https://www.nhc.noaa.gov/data/ (Accessed December 31, 2024).

Google Scholar

Neumann A. C., Macintyre I. G. (1985). “Reef response to sea-level rise: keep-up, catch-up, or give-up,” in Proceedings of the fifth international coral reef congress Tahiti. (Moorea, French Polynesia: Antenne Museum–EPHE). 3, 105–110.

Google Scholar

Osorio-Cano J. D., Alcérreca-Huerta J. C., Mariño-Tapia I., Osorio AndrésF., Acevedo-Ramírez C., Enriquez C., et al. (2019). [amp]]ldquo;Effects of roughness loss on reef hydrodynamics and coastal protection: approaches in Latin America. Estuaries Coasts 42, 1742–17605. doi: 10.1007/s12237-019-00584-4

Crossref Full Text | Google Scholar

Peters S. M., Guppy R., Ramsewak D., Potts A. (2023). Socioeconomic dimensions of the Buccoo Reef Marine Park, an assessment of stakeholder perceptions towards enhanced management through MSP. ICES J. Mar. Sci. 80, 1399–1409. doi: 10.1093/icesjms/fsad066

Crossref Full Text | Google Scholar

Péquignet A. C., Becker J. M., Merrifield M. A., Boc S. J. (2011). The dissipation of wind wave energy across a fringing reef at Ipan, Guam. Coral Reefs 30, 71–82. doi: 10.1007/s00338-011-0719-5

Crossref Full Text | Google Scholar

Quataert E., Storlazzi C., Rooijen A. v., Cheriton O., Dongeren Ap v. (2015). The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines. Geophys. Res. Lett. 42, 6407–64155. doi: 10.1002/2015GL064861

Crossref Full Text | Google Scholar

Sheppard C., Dixon D. J., Gourlay M., Sheppard A., Payet R. (2005). Coral mortality increases wave energy reaching shores protected by reef flats: Examples from the Seychelles. Estuarine Coast. Shelf Sci. 64, 223–2345. doi: 10.1016/j.ecss.2005.02.016

Crossref Full Text | Google Scholar

Storlazzi C. D., Elias E., Field M. E., Presto M. K. (2011). Numerical modeling of the impact of sea-level rise on fringing coral reef hydrodynamics and sediment transport. Coral Reefs 30, 83–96. doi: 10.1007/s00338-011-0723-9

Crossref Full Text | Google Scholar

Villanoy C., David L., Cabrera O., Atrigenio M., Siringan F., Aliño P., et al. (2012). Coral reef ecosystems protect shore from high-energy waves under climate change scenarios. Climatic Change 112, 493–5055. doi: 10.1007/s10584-012-0399-3

Crossref Full Text | Google Scholar

Williams J. J., Esteves L. S. (2017). Guidance on setup, calibration, and validation of hydrodynamic, wave, and sediment models for shelf seas and estuaries. Adv. Civil Eng. 2017, 5251902. doi: 10.1155/2017/5251902

Crossref Full Text | Google Scholar