Spatio-temporal variations of the heat fluxes at the ice-ocean interface in the Bohai Sea

Thermodynamic process between the ice and the ocean plays a critical role in the evolution of sea-ice growth and melting in marginal seas. At the ice-ocean interface, the oceanic heat flux and the conductive heat flux transmitted through the ice layer jointly determine the latent heat flux driving the phase change (i.e., ice freezing/melting). In this study, the determination of two important thermal parameters in the ice module of the HAMSOM ice-ocean coupled model, namely the mixed layer thickness and the heat exchange coefficient at the ice-ocean interface, has been adjusted to improve the model performance. Spatio-temporal variations of heat fluxes at the ice-ocean interface in the Bohai Sea are investigated, based on the validated sea ice simulation in the 2011/2012 ice season. The relationships between the interfacial heat fluxes and oceanic and atmospheric conditioning factors are identified. We found that the surface conductive heat flux through ice shows short-term fluctuations corresponding to the atmospheric conditions, the magnitude of these fluctuations decreases with depth in the ice layer, likely due to reduced influence from atmospheric conditions at greater depths. Atmospheric conditions are the key controlling factors of the conductive heat flux through ice, while the oceanic heat flux is mainly controlled by the oceanic conditions (i.e., mixed layer temperature). Spatially, the value of the oceanic heat flux is larger in the marginal ice zone with relatively thin ice than in the inner ice zone with relatively thick ice. In the Bohai Sea, when ice is growing, heat within the ice layer is transferred upward from the ice base, and the heat is losing at the ice-ocean interface. This heat loss in the inner ice zone is obviously greater than that in the marginal ice zone. Whereas when ice is melting, the opposite is true.

1 Introduction

The Bohai Sea is a semi-enclosed shallow marginal sea in the western Pacific Ocean off northern China. The water depth of its three bays (Liaodong Bay, Bohai Bay, and Laizhou Bay) typically does not exceed 30 m (see Figure 1). The Bohai Sea is one of the lowest-latitude marginal seas where ice can form in winter (Wang et al., 2000). The ice season often starts at the beginning or middle of December and ends at the middle or end of March in the following year (Bai and Wu, 1998). On one hand, sea ice, as a disaster, affects the engineering and shipping, offshore oil and gas production to varying degrees in the Bohai Sea, e.g., ships are besieged by ice fields, transportation is interrupted, and offshore structures are often seriously threatened by sea ice encroachment. The Bohai Sea and its coastal areas are an important economic development zone for China. Improvements in sea ice forecasting/modeling contributed by the adjustments of model parameters and mastery of ice dynamic and thermodynamic characteristics, can effectively assist the early warning, disaster mitigation and resource utilization of sea ice, as well as the planning, designing, and building offshore structures in the Bohai Sea (Li et al., 1999; Yang, 2000; Zhao et al., 2022). On the other hand, offshore climate anomalies in northern China are correlated with global atmospheric circulation changes, governed by the East Asian atmospheric circulation system during the same period, therefore the Bohai Sea ice conditions are also a response to the global and polar climate change (Liu et al., 2013; Luo et al., 2017; Collins et al., 2018; Screen et al., 2018).

Figure 1

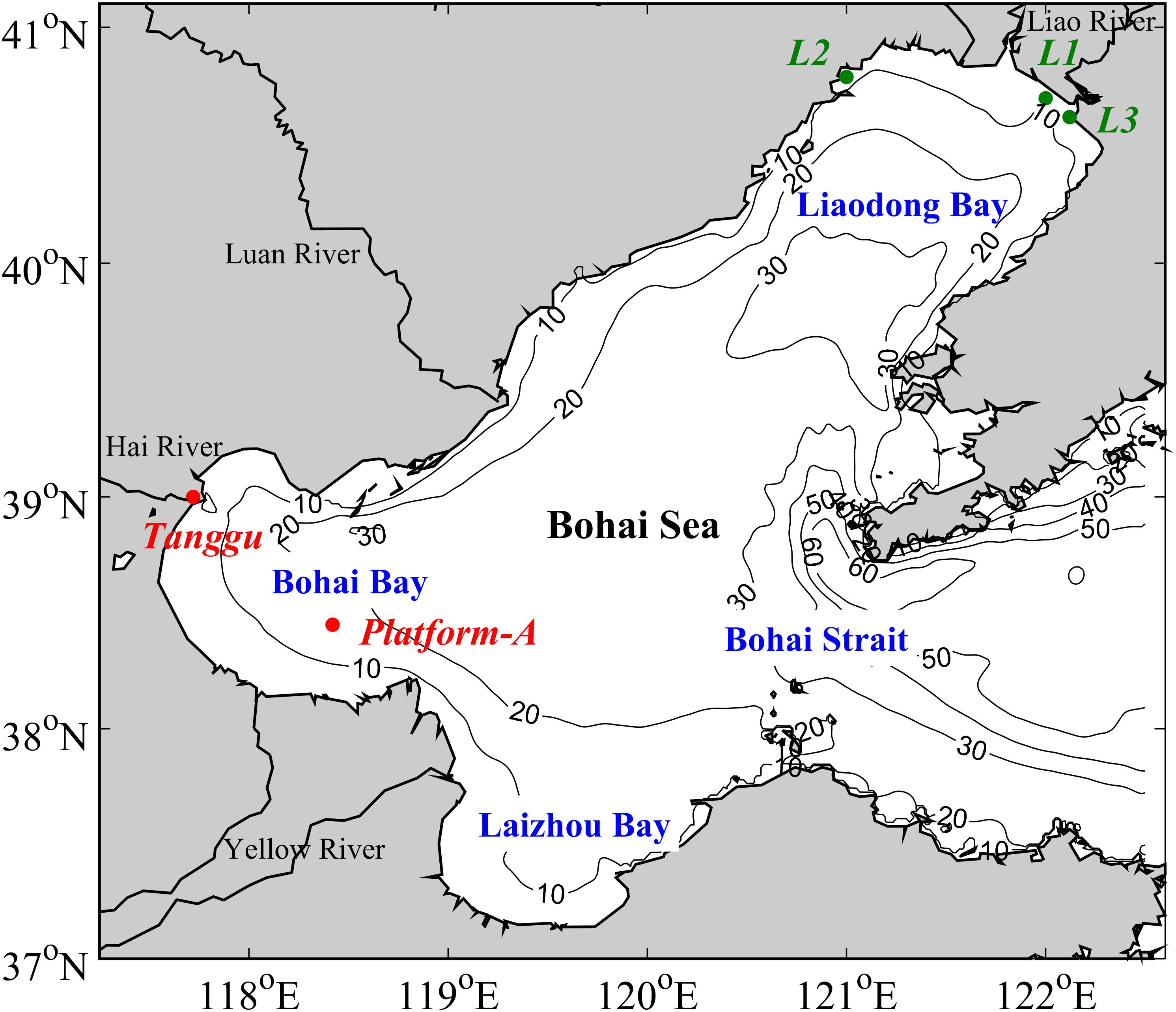
Figure 1. Bathymetry of the Bohai Sea (m). The Liaodong Bay, Bohai Bay, Laizhou Bay, and the Bohai Strait are marked in blue on the map. The positions of the two observation stations (Tanggu and Platform-A) are marked in red points. The positions of the three local waters [Erjiegou water (L1), Dabijiashan water (L2) and Xipaotai water (L3)] on the top of Liaodong bay are marked in green points.

Sea ice thermodynamics reflects the ice freezing/melting caused by the thermal forces, measured by various heat fluxes at the air-ice-ocean interfaces. Since a prototype of the sea ice growth and melting process can be obtained by purely thermal calculations without considering the dynamical effects (Wang et al., 1984; Yang, 2015; Wang et al., 2017), the ice freezing/melting in the Bohai Sea is mainly controlled by its thermal processes. Moreover, phase change (i.e., ice freezing/melting) occurs mainly at the ice base (i.e., the ice-ocean interface), implying that the thermal processes at the ice-ocean interface are key to the overall sea ice thermodynamics (Yu et al., 2022). An inter-comparison among the CMIP6 models also showed that basal growth and melting are the main processes in the modeled annual circle of the Arctic sea ice mass budget, in which the amounts of annual mean ice mass increasing from basal growth are ten times as large as those from frazil ice formation (Keen et al., 2021). As shown in Figure 2, at the ice-ocean interface, the oceanic heat flux which represents the heat transferred from the mixed layer to the ice base, and the conductive heat fluxes transmitted upward through the ice layer (including which near-surface ice layer and near-bottom ice layer), jointly determine the latent heat flux driving the phase change. These interfacial heat fluxes which measure the heat exchange between the ocean and ice layer determine the evolution of basal sea ice growth and ablation in the Bohai Sea (Liu, 2013).

Figure 2

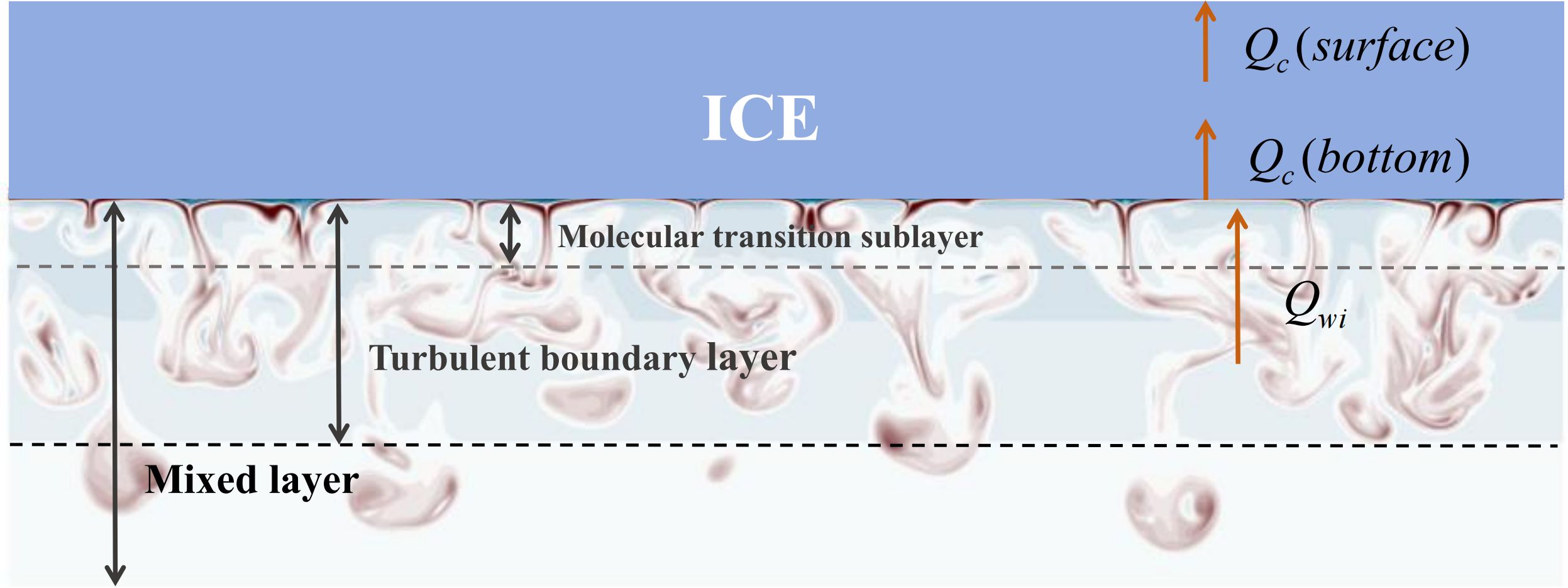
Figure 2. Schematic representation of the ice layer, turbulent boundary layer (including the molecular transition sublayer), and the mixed layer. The orange arrows represent the surface and bottom conductive heat flux through ice, $Q_c(surface)$, $Q_c(bottom)$, and the oceanic heat flux $Q_{wi}$, respectively. Picture background quoted from Keitzl et al. (2016).

Leppäranta and Shirasawa (2007) indicated that the oceanic heat flux plays an active role in controlling ice thickness and mass change based on an ice thermodynamic model and the Saroma-ko ice station data. They pointed out that an important feature of oceanic heat flux is that it affects not only the total thickness of the ice, but also the stratification of the ice sheet, as it melts the congelation ice at the base, thus providing the potential for more ice formation. Lin and Zhao (2019) showed that oceanic heat flux in the Arctic Ocean has large seasonal and spatial variability based on the observations from 28 buoys, as do the conductive heat flux through ice (Fan et al., 2017). The seasonal variability of the oceanic heat flux in the Arctic Ocean may reach one order of magnitude (Lei et al., 2014). Ha et al. (2016) found that the under-ice oceanic heat flux responds to the cyclic oscillations of the under-ice Pacific Summer Water (PSW) flow rate based on measurement data within 15 m under the Arctic ice. Similar result was also found in the Antarctic region, showing that the sea ice freezing and melting is influenced by the ice-ocean stress exerted by the Southern Ocean convection current (Ma et al., 2020). Therefore, the hydrographic characteristics of the mixed layer are critical factors in the ice mass change at the ice-ocean interface.

In the Bohai Sea, because of its thin seasonal sea ice, it is technically challenging to deploy marine instruments under the ice and obtain turbulence-scale observations of marine fields in the ice-ocean boundary layer. Most of the thermodynamic studies of the Bohai Sea ice focus on the air-ice and air-ocean interfaces, whereas few studies focus on the ice-ocean interface, with most of them relying largely on numerical simulations. Currently, researches on the ice-ocean thermodynamics in the Bohai Sea have mainly focused on the oceanic heat flux. In the initial numerical studies of the Bohai Sea ice, the oceanic heat flux was set as an empirical constant (Wang et al., 1984; Wang and Wu, 1994). Later, Wang et al. (1999) established an empirical relationship between the oceanic heat flux and water depth. Then Ji et al. (2002) introduced a more sophisticated parameterization scheme proposed by McPhee (1992) in which the oceanic heat flux is calculated by the temperature difference and the friction velocity between ice and ocean. Su et al. (2005) simulated the Bohai Sea ice in the 2000/2001 ice season based on the POM ice-ocean coupled model using the above parameterization scheme of the oceanic heat flux, and found that the seasonal variation of oceanic heat flux in the Bohai Sea is quite pronounced, which is influenced by the Yellow Sea warm current in winter. It is worth noting that most existing sea ice simulations for the Bohai Sea are based on parameterization schemes originally derived from modeling polar sea ice. However, the Bohai Sea is one of the world’s lowest natural freezing latitudes, and its seasonal thin sea ice has obvious unique characteristics. Unlike the polar sea ice, the thickness of the Bohai sea ice is thin, usually less than 40 cm. The ice conditions change drastically due to the frequent passage of cold fronts in winter. The numerical simulation of the Bohai Sea ice therefore requires more elaborate physical parameterizations than that of polar sea ice. Therefore, the establishment of more suitable calculation schemes for key parameters for the Bohai Sea is one of the research motivations of this study.

The main research motivation of this study is to fill the knowledge gap in understanding the spatio-temporal variations of heat fluxes at the ice-ocean interface. Our results indicate that seasonal thin ice evolution in the Bohai Sea is very sensitive to oceanic and atmospheric environmental conditions, and the interfacial heat fluxes measuring the ice-ocean heat exchange usually have significant temporal and spatial variations. In addition to the oceanic heat flux, the conductive heat flux through ice is equally important in controlling the basal ice freezing/melting. Further studies and analyses for the temporal and spatial variations of ice-ocean interfacial fluxes, and their relationships with oceanic and atmospheric conditioning factors are warranted to better understand the ice thermodynamic processes in the Bohai Sea.

This work is organized as follows. In section 2, the methods and data used in this study are described. Section 3 introduces the modeling work to reproduce sea ice results that are close to observation. The spatio-temporal variations and mechanisms of the ice-ocean interfacial heat fluxes are investigated in section 4. The applicability of the adjustments for two model parameters, as well as the advances in ice-ocean thermal interactions compared to prior researches are discussed in section 5. Finally, section 6 summarizes the main outcomes of this study.

2 Materials and methods

2.1 The ice-ocean coupled model

The Hamburg Shelf Ocean Model (HAMSOM) used in this work is a full-fledged three-dimensional primitive equation model with a free surface. The Cartesian coordinates are used with an Arakawa C-grid and a semi-implicit numerical scheme. The numerical framework of the ocean model was described by Backhaus (1985). The sea-ice model presented here is a two-class (ice and open water) model that takes into account both the ice dynamics and ice thermodynamics properties. It is a modification of the viscous-plastic model suggested by Hibler (1979) with three-layer thermodynamics according to Semtner (1976). The fundamental sea ice equations, thermodynamic properties, and rheology were introduced in detail by Ólason and Harms (2010) and Olason (2016).

The simulated area in this study is the Bohai Sea (see Figure 1), covering the latitude and longitude of 37°N~41.25°N and 117.25°E~122.5°E, respectively. The simulation period for an ice season covers from Nov. 1 to Mar. 31 on the next year, with a time step of 60 seconds and a horizontal grid resolution of 1’×1’ (1/60 arc degree, approximately 1.8 km in the meridional direction and 1.5 km in the zonal direction). There are 12 z-level grids used in vertical plane.

2.2 The forcing data

Bathymetry for the model domain is interpolated from the high-precision data provided by the Beihai Branch of the Ministry of Natural Resources of China. The model is initialized with monthly climatological salinity data from the OGCM for Earth Simulator (OFES) datasets (Sasaki et al., 2008) and a fused temperature data constructed by the Simple Ocean Data Assimilation (SODA) datasets (Carton et al., 2018) and a high-resolution satellite remote sensing assimilation SST (Group for High Resolution Sea Surface Temperature, GHRSST) (Donlon et al., 2012) using the “vertical projecting” assimilation method (Jia et al., 2022a). Due to the shallow depth of the Bohai Sea and the strong vertical mixing of seawater under the influence of energetic winds in winter, the dynamical steady state can be reached just a few tens of hours after the simulation starts (Liu, 2013), which means that after the simulation starts, the current velocity field in the Bohai Sea quickly adapts to the forcing of surface wind and open-boundary tides, and there is very little dependence on the initial current velocity and the initial elevation fields. Therefore, the initial current velocity and the initial elevation fields are set to zero. The harmonic constants of eight main tidal constituents at the open boundary are provided by The Oregon State University (OSU) Tidal Databases (Erofeeva et al., 2020).

The hourly meteorological data obtained from the global Climate Forecast System Reanalysis (CFSR) produced by the US Center for Environmental Prediction (NCEP) above the sea surface, including the 2 m air temperature, wind speed, cloud cover, precipitation rate, and specific humidity (Saha et al., 2011), are interpolated for the atmospheric forcing. Figure 3 displays the 2 m air temperature at the observation stations Tanggu and Platform-A (the positions of the two stations are labeled in Figure 1) during the winter of 2011/2012 and the corresponding values extracted from the NCEP dataset. The mean absolute errors at the two stations are 0.26°C and 0.25°C, respectively. This indicates that NCEP data can realistically reflect the weather system variations in the Bohai Sea during winter when large-scale cold air fronts occur.

Figure 3

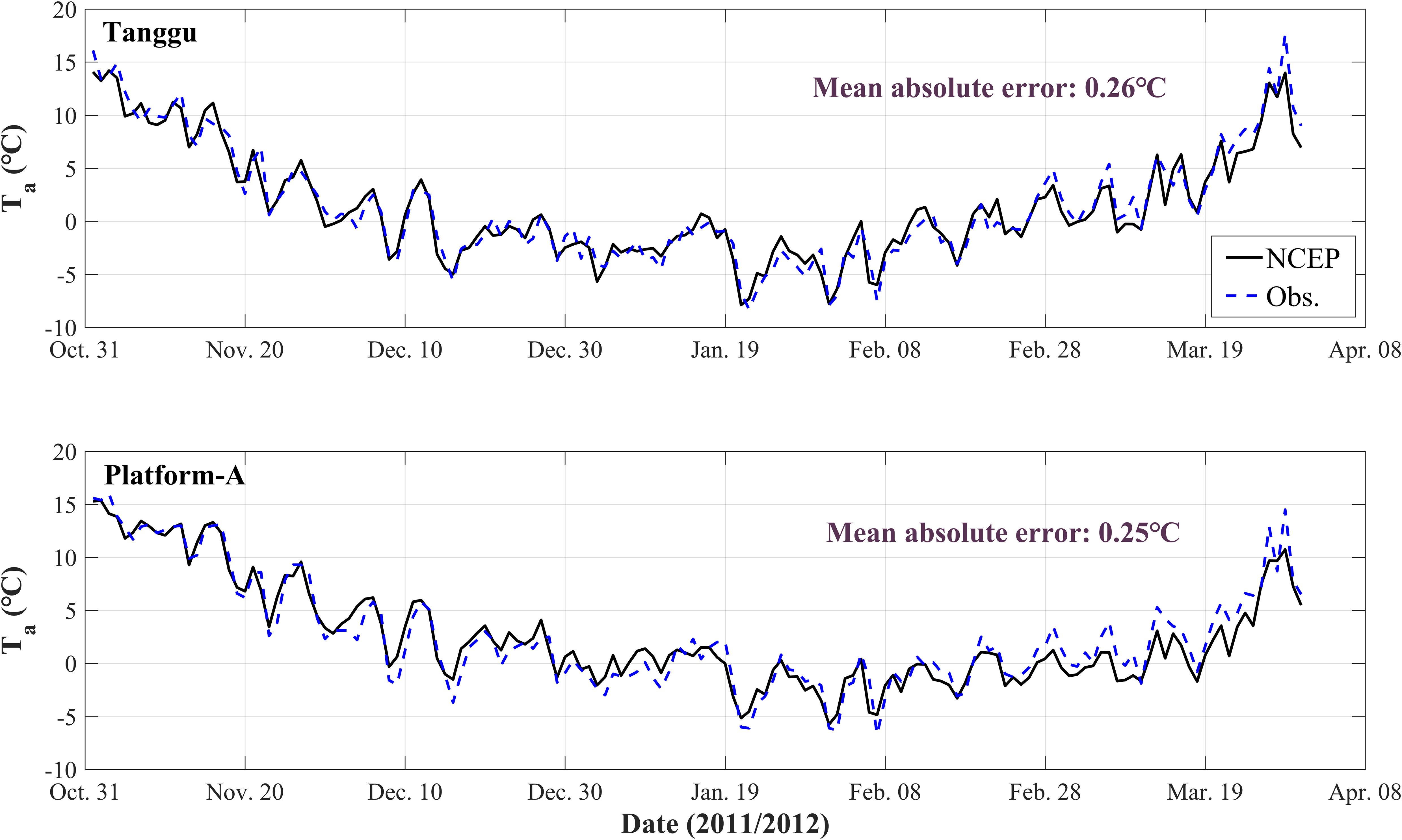
Figure 3. Comparison of the NCEP 2m air temperature (solid black line) and the corresponding observations (blue dashed line) at the Tanggu station (top) and Platform-A station (bottom) during the winter of 2011/2012. The mean absolute error of each station is indicated in the respective graph.

Compared with coastal observation, sea survey, radar, and other observation methods, satellite remote sensing has the ability of large-scale, rapid, synchronous, and long-term continuous observation, and has unparalleled advantages in economy. In this study, the ice edge distance (i.e., the distance between the intersection of the central axis of Liaodong Bay and the ice edge line and the axis apex, see Figure 4A) and the ice area observations from the satellite inversion, as well as the observed information for ice thickness and ice concentration in the three local waters (Erjiegou water (L1), Dabijiashan water (L2) and Xipaotai water (L3), the locations are shown in Figure 1) shown in Table 1 are obtained from the North China Sea Marine Forecasting Center of the Ministry of Natural Resources and its annual winter Sea Ice Land and Coastal Monitoring Report in the Bohai Sea. The satellite images that appeared in this paper are extracted from the NASA Worldview application (https://worldview.earthdata.nasa.gov), part of the NASA Earth Observing System Data and Information System (EOSDIS). The inversion data for ice thickness from GOCI ocean color remote sensing satellite shown in Figure 5 is obtained from Yan et al. (2024).

Figure 4

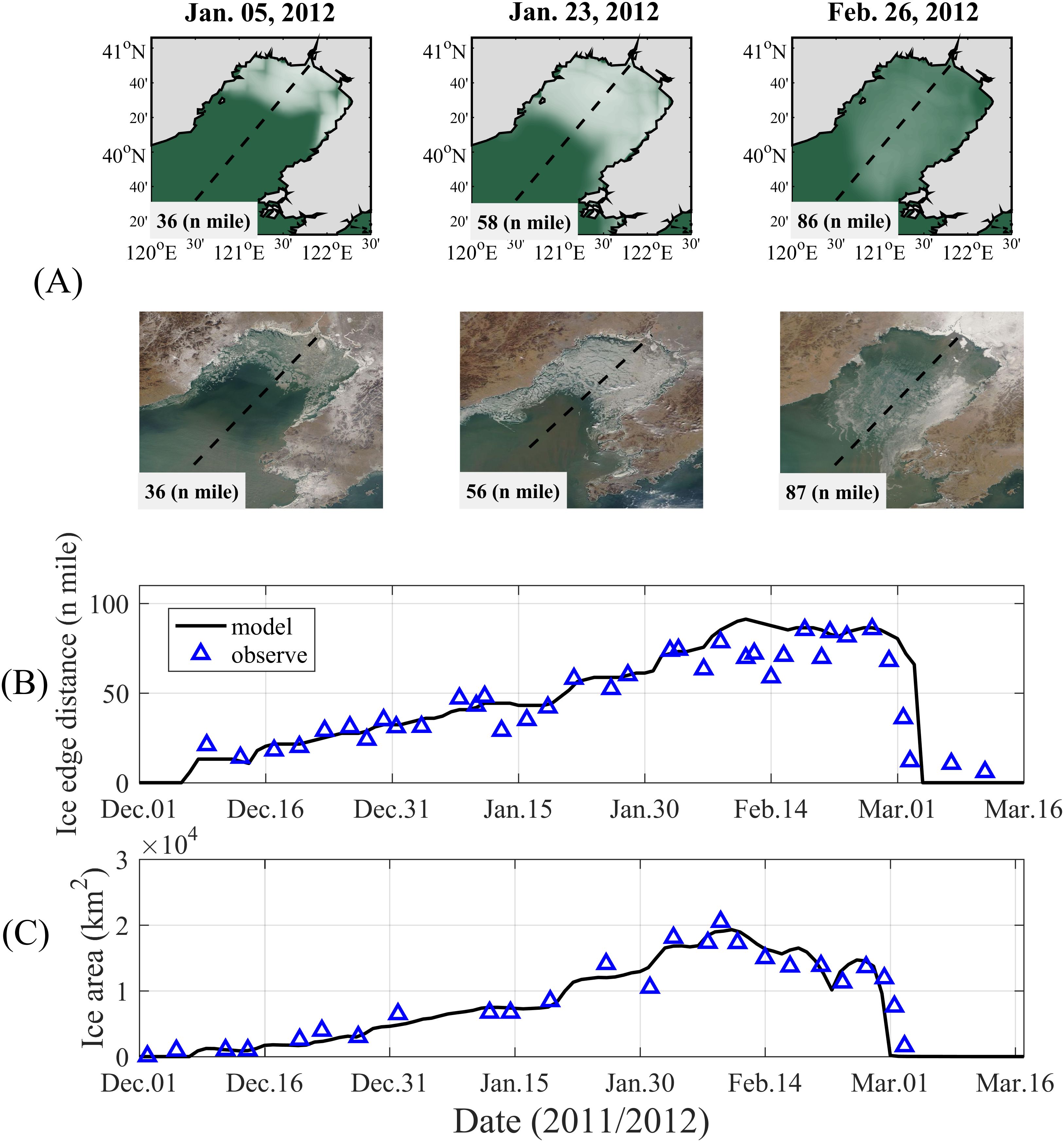
Figure 4. (A) Simulated ice extent (first line) and the corresponding satellite images (second line) in Liaodong Bay on Jan. 05, 2012, Jan. 23, 2012 and Feb. 26, 2012, the dashed lines are the central axis of Liaodong Bay, and the values of ice edge distances are indicated in the lower left corner. (B) Time series of the simulated ice edge distance, the blue triangles are the observation data from the satellite inversion. (C) Time series of the simulated ice area which has a total ice concentration area higher than 15%, the blue triangles are the observation data from the satellite inversion.

Table 1

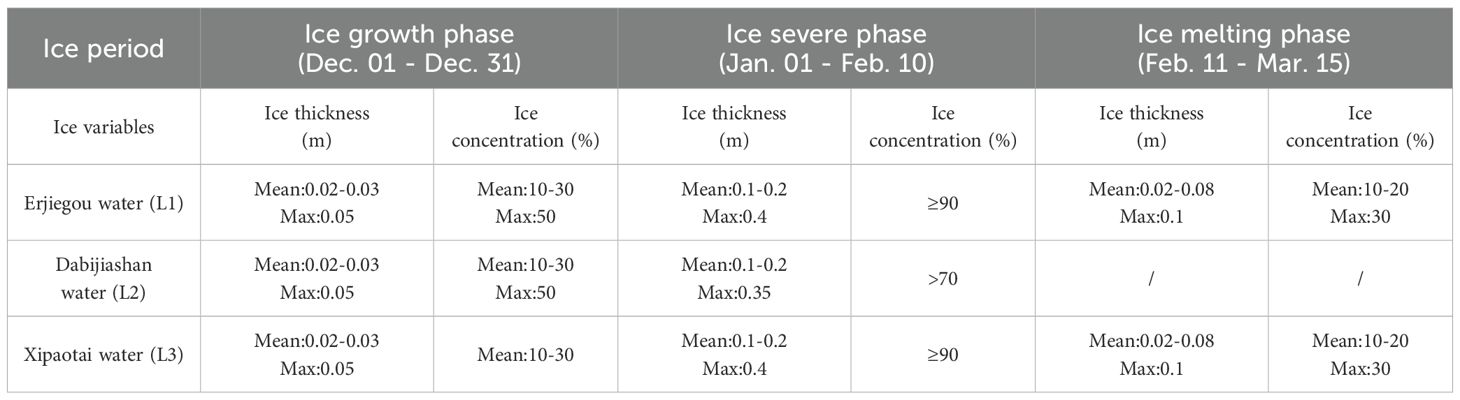
Table 1. Observed information of the ice thickness and ice concentration of the three local waters [Erjiegou water (L1), Dabijiashan water (L2) and Xipaotai water (L3)] during the ice growth phase, ice severe phase and the ice melting phase of the 2011/2012 ice season.

Figure 5

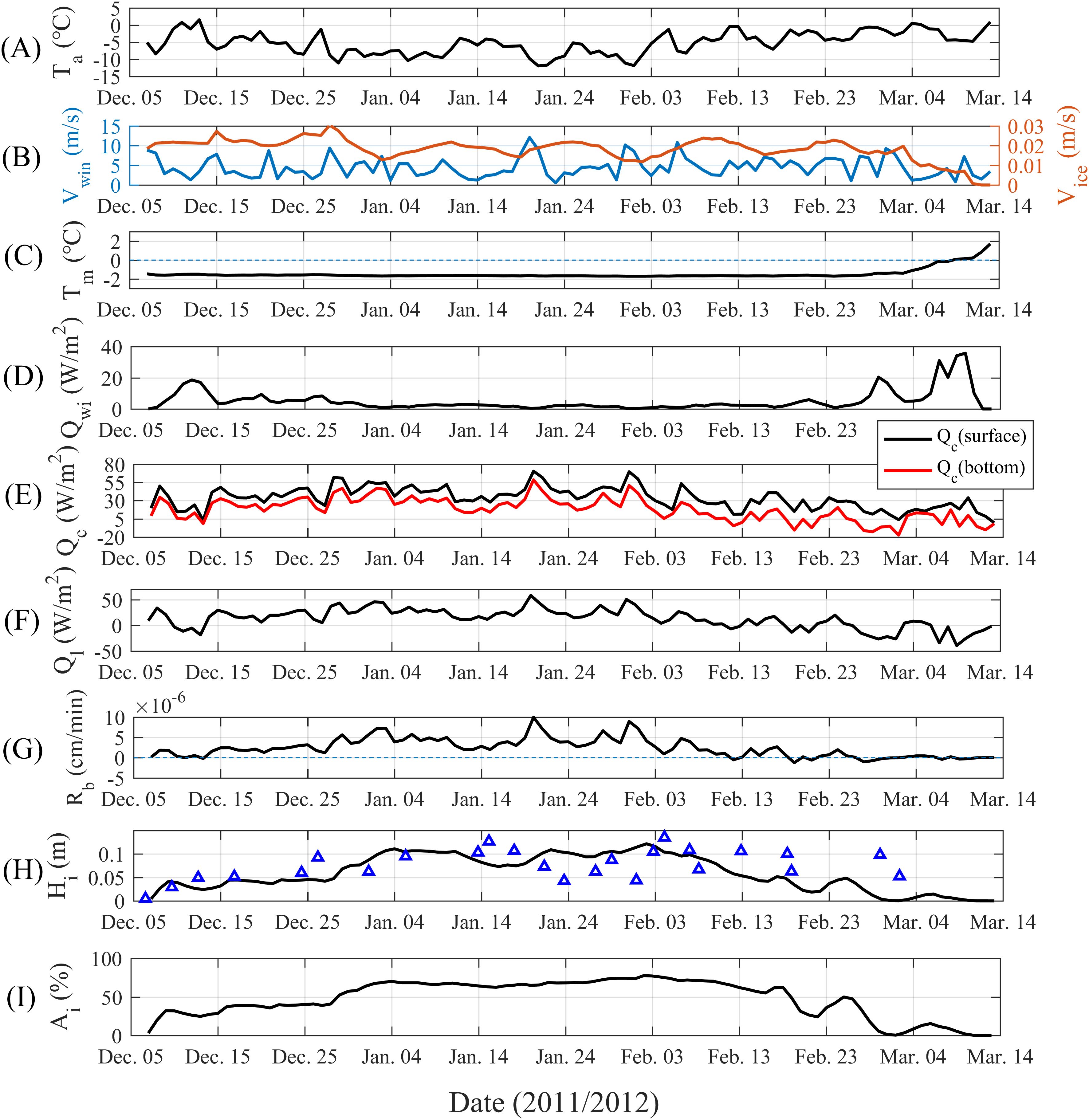
Figure 5. The time series of ice coverage-averaged variables [including sea surface air temperature T_a (A), sea surface wind speed Vwin and ice drift velocity  V_ice (B), the mixed layer temperature T_m (C), the oceanic heat flux Q_wi (D), the conductive heat flux through ice Q_c (E), the latent heat flux Q_l (F), freezing/melting rate of ice base R_b (G), ice thickness H_i (H) and ice concentration A_i (I)] during the 2011/2012 ice season. The blue triangles in graph (H) are the inversion data for ice thickness from GOCI ocean color remote sensing satellite.

3 Modeling Work

As mentioned before, numerical simulations of the Bohai Sea ice need to consider its unique characteristics, more detailed descriptions of the key sea-ice physical processes, and appropriate parameters need to be taken into consideration. Therefore, to improve the applicability and accuracy of the HAMSOM ice-ocean coupled model for sea ice simulations in the Bohai Sea, we adjust two key thermal parameters of the ice module, which is the mixed layer thickness and the heat exchange coefficient (HEC) at the ice-ocean interface.

3.1 Mixed layer thickness

Mixed layer thickness determines the amount of heat content of the mixed layer, which in turn has an important influence on the hydrographic properties of the mixed layer (Wang et al., 2000). In the ice model, mixed layer thickness can influence the amount of sea ice freezing/melting at the ice-ocean interface by participating in the calculation of the variation rates of mixed layer temperature and salinity and the freezing rate of new-formed ice. In existing sea-ice simulations, the mixed layer thickness in the ice thermodynamics module is set to the thickness of the first water layer (Arthun and Schrum, 2010; Ólason and Harms, 2010; Olason, 2016; Lin and Zhao, 2019). This should be based on the premise that there is little difference between the first water layer thickness and the actual mixed layer thickness. Whereas the Bohai Sea is shallow, the vertical mixing of the water column is outright under the influence of high winds in winter, so the hydrographic properties of the water column are in vertical homogeneity from the sea surface to the seabed in the Bohai Sea (Liu, 2013; Yan et al., 2022). In other words, setting the mixed layer thickness to the first water layer thickness would cause a serious underestimation for the mixed layer thickness in the Bohai Sea during the ice season. In order to investigate the sensitivity of the ice simulations in the Bohai Sea to the mixed layer thickness, ice simulations in 2009/2010 ice season and 2011/2012 ice season are modeled using three different mixed layer thickness settings, including the first water layer thickness (default setting, 6 m), half of the water depth and the entire water depth.

The ice area results, defined here as the area of grid cells with at least a 15% sea ice concentration, of the above simulations are shown in Figure 6, the time-averaged absolute errors of different cases (shown in the legend) are also calculated. It can be found that for both ice seasons, the simulated ice area obtained by setting mixed layer thickness to the entire water depth are overall increased and closer to the satellite observations than the other two cases, and the calculated time-averaged absolute errors are reduced in both ice seasons. It is calculated that for the 2009/2010 ice season, setting mixed layer thickness to entire water depth leads to a 10% improvement in the ice area simulations, compared to the default setting. While for the 2011/2012 ice season, 17% improvement is made.

Figure 6

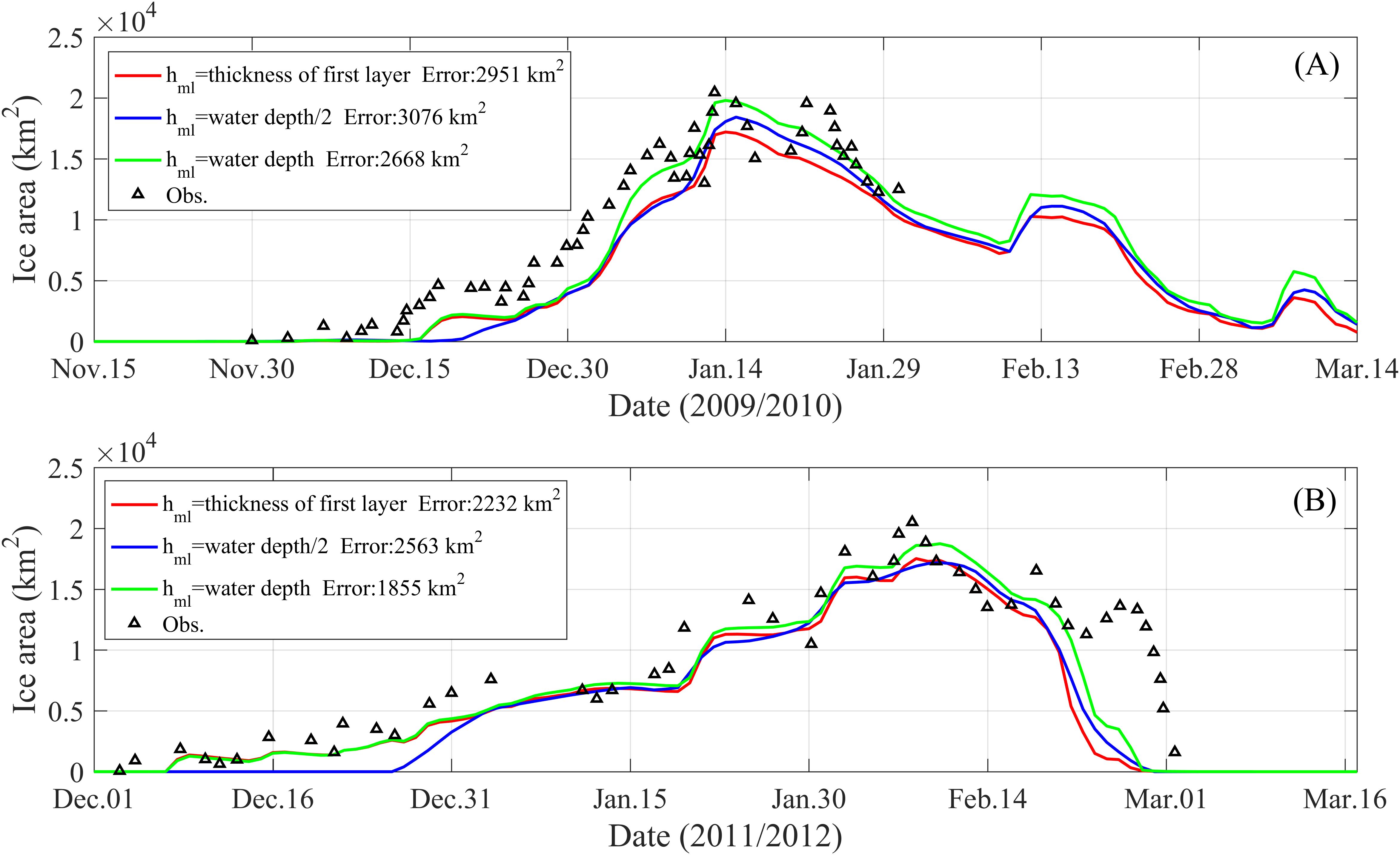
Figure 6. (A) Time series of the simulated ice area obtained by setting mixed layer thickness to the first water layer thickness (default setting, red line), half of the water depth (blue line) and entire water depth (green line) in 2009/2010 ice season. The triangles are the observation data from the satellite inversion. The time-averaged absolute errors of the three simulations are labeled in the legend. (B) Same as graph (A), but for the 2011/2012 ice season.

To further clarify the effect mechanism of the mixed layer thickness to the sea ice variables, we present the time series of the ice coverage-averaged interfacial thermal parameters (including oceanic heat flux, conductive heat flux through ice, freezing/melting rate of the ice base (positive values represent ice freezing rates and negative values represent ice melting rates) and ice concentration) obtained by setting mixed layer thickness to the first water layer thickness and the entire water depth in the 2009/2010 ice season as shown in Figure 7. It can be noticed that compared to setting mixed layer thickness as the first water layer thickness (blue lines), there is a significant decrease in the oceanic heat flux especially in the ice melting phase when setting it to the entire water depth (red lines), while the conductive heat flux through ice remains essentially unchanged, and the freezing/melting rate of the ice base grows slightly, as well as the ice concentration.

Figure 7

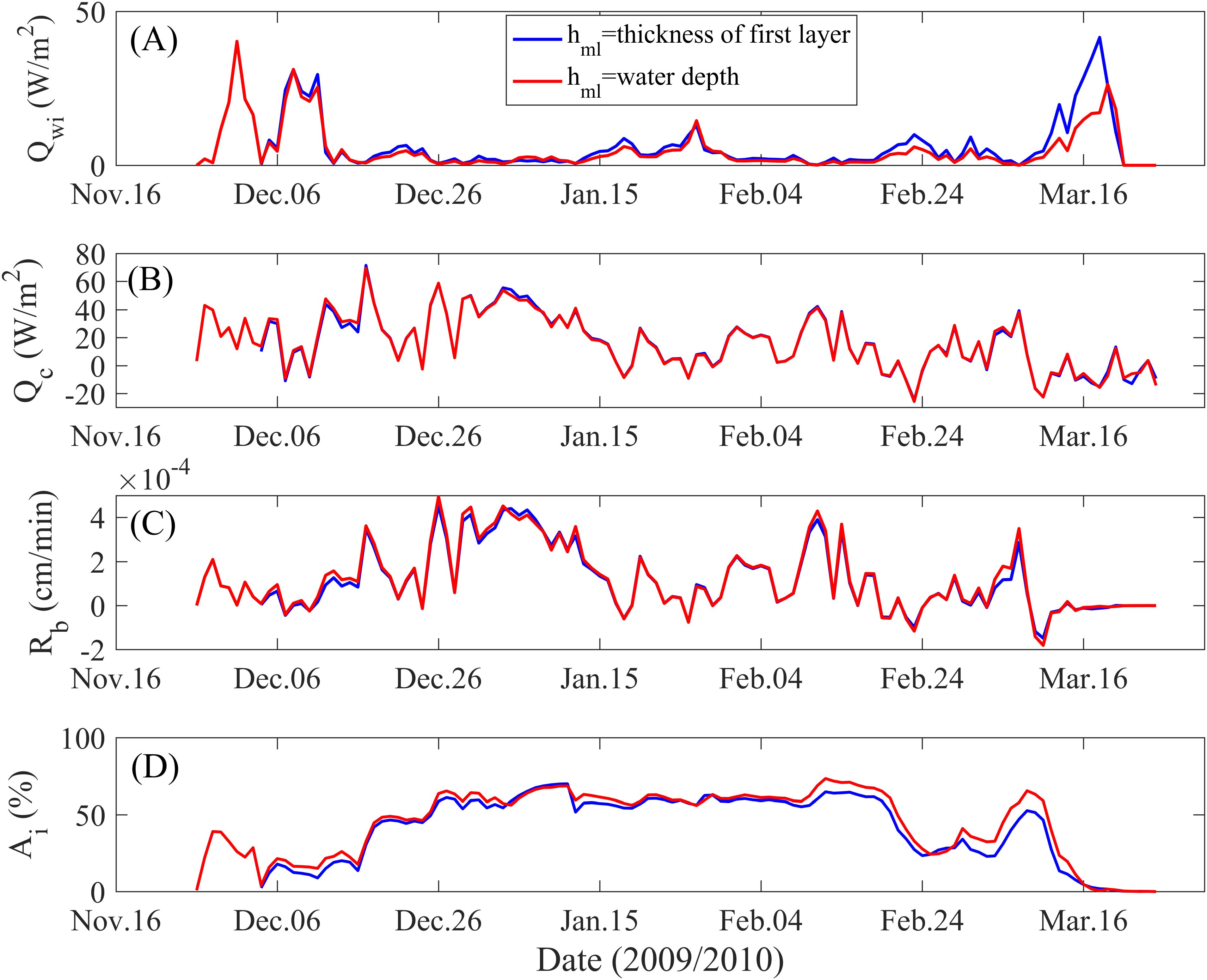
Figure 7. Time series of the ice coverage-averaged oceanic heat flux (A), conductive heat flux through ice (B), freezing/melting rate of the ice base (C), and the ice concentration (D) obtained by setting mixed layer thickness to the first water layer thickness (blue lines) and the entire water depth (red lines) in the 2009/2010 ice season.

The effect mechanism of the mixed layer thickness on sea ice variables can be preliminary sorted out, based on the variations of the above parameters. For all grids except for those where the water depth equals the first water layer thickness, the mixed layer thickness setting to the entire water depth is deepened compared to the first water layer thickness. The deepening of the mixed layer thickness implies an increase in the total heat content of the mixed layer. This also means that when the mixed layer is changed by the same amount of heat, the magnitude of the change in the mixed layer temperature is reduced, i.e., the variation rate of the mixed layer temperature is reduced. As a result, the warming of the mixed layer due to the heating effect of solar radiation decreases during the ice melting phase, leading to a decrease in the positive deviation of the mixed layer temperature from the ice base temperature ($T_m-T_f$ in Equation 1), and a consequent decrease in the oceanic heat flux (Figure 7A) as measured by this temperature deviation. The oceanic heat flux and the conductive heat flux through ice jointly determine the heat budget at the ice-ocean interface. Since the conductive heat flux through ice is calculated from the vertical temperature gradient within the ice layer and is not directly constrained by the mixing layer temperature, the effect of the mixing layer thickness on the conductive heat flux through ice is negligible (Figure 7B). Therefore, the decrease in oceanic heat flux to the ice base implies a decrease in the amount of heat gained, manifesting net heat loss, resulting in an increase in the freezing rate of the ice base (Figure 7C), which ultimately leads to an increase in sea ice variables such as ice concentration (Figure 7D), ice thickness (same trend with the ice concentration, picture omitted) and ice area (Figure 6A). The corresponding mechanism schematic is shown in Figure 8.

Figure 8

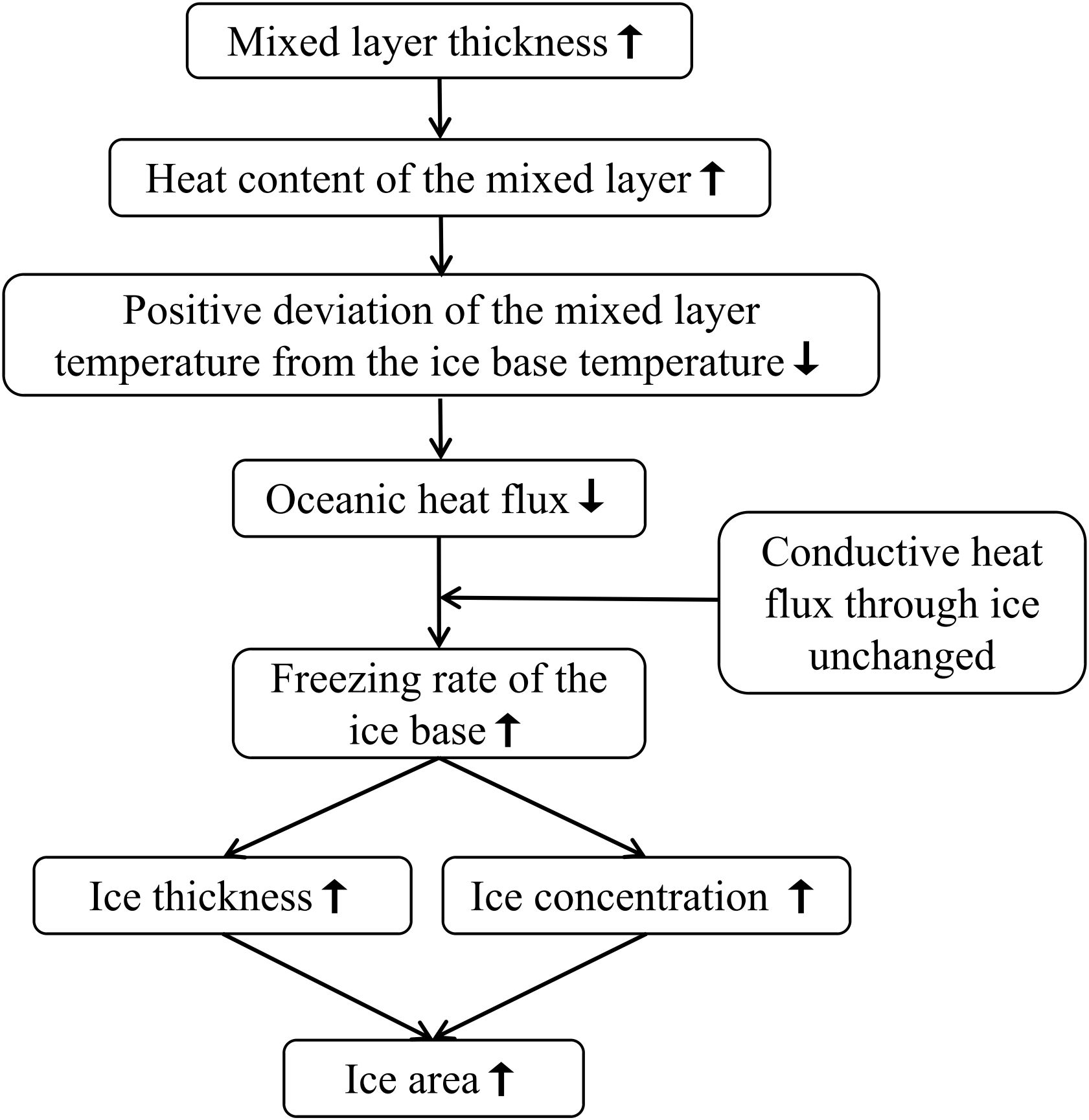
Figure 8. Schematic for the mechanism of the influence of the mixed layer thickness on sea ice variables.

In summary, the deepening of the mixed layer somewhat corrects the heat content of the mixed layer, and hence the variation rates of the hydrographic properties within the mixed layer, and ultimately brings corrections to the sea ice variables in the Bohai Sea.

3.2 Heat exchange coefficient at the ice-ocean interface

The oceanic heat flux is the key factor determining the heat balance at the ice-ocean interface (Wettlaufer, 1991). The oceanic heat flux $Q_{wi}$ can be estimated by the following bulk formula (McPhee, 1992):

$\begin{array}{ll}{Q}_{wi}={\rho }_w{c}_p{C}_h{u}_{*}(T_m-T_f),& (1)\end{array}$

where the ${\rho }_w$ is sea water density, $c_p$ is the specific heat capacity of sea water, $u_{*}$ is the ice-ocean friction velocity. $T_m$ is the mixed layer temperature and $T_f$ is the local freezing point (i.e., the temperature of ice base). $C_h$ is the HEC at the ice-ocean interface.

Although the well-established formulation scheme (Equation 1) of oceanic heat flux has been introduced in many ice models applied to the Bohai Sea, the HEC at the ice-ocean interface is still set as an empirical constant. This parameter characterizes the efficiency of heat transfer between the ice and the ocean and is related to turbulent and molecular motions within the ice-ocean boundary layer (McPhee, 1992; Sirevaag, 2009; Dansereau et al., 2014; Ha et al., 2016). Ji et al. (2002) surmised that the HEC varies with ice thickness and the hydraulic roughness of the ice under-surface based on the atmospheric, hydrographic and sea-ice observations from point stations in the JZ20-2 Sea Area of Liaodong Bay, 1997-1998. More specific physical processes involved in ice-ocean heat transmission could be ignored if setting the HEC to a constant (McPhee, 1992). Therefore, the relationship between the HEC and ice thickness and the ice-ocean friction velocity based on the parameterization proposed by McPhee (1992) was introduced into our model to obtain the time and space-varying HEC in our previous study (Jia et al., 2022b). The HEC parameterization formulas are as follows:

$\begin{array}{ll}{C}_h=\frac{1}{{\varphi }_{turb}+{\varphi }_{mol}}& (2)\end{array}$

$\begin{array}{ll}{\varphi }_{turb}=\frac{1}{k}log(\frac{u_{*}{\xi }_N{\eta }_{*}}{f{z}_0})+\frac{1}{2{\xi }_N{\eta }_{*}}-\frac{1}{k}& (3)\end{array}$

$\begin{array}{ll}{\varphi }_{mol}=b{R}_e^{1/2}{P}_r^{2/3}& (4)\end{array}$

Here, the ${\varphi }_{turb}$ and ${\varphi }_{mol}$ are the non-dimensional temperature changes across the turbulent boundary layer and the molecular transition sublayer embedded within the turbulent boundary layer (see Figure 2), respectively. Turbulent motions caused by shear forces of ocean currents under ice dominate in the turbulent boundary layer, while molecular viscosity and diffusivity motions dominate in the molecular transition sublayer. The Von-Karman’s constant k is 0.4. ${\xi }_N$ is a constant, was approximated to 0.05 by McPhee (1992) at the time the parameterization was proposed which applied in the Arctic Ocean. Dansereau et al. (2014) also set it to 0.052 in the ice simulations of the Pine Island ice shelf, West Antarctica. In this paper, it is taken to be 0.05. ${\eta }_{*}$ is a buoyancy factor, equal to 1 when the stratification is neutrally stable (McPhee, 1992). f is the Coriolis parameter. $z_0$ is the hydraulic roughness of the ice under-surface, $u_{*}$ is the ice-ocean friction velocity. The used calculation schemes of both $z_0$ and $u_{*}$ were proposed by Mellor and Kantha (1989) (see Equations 5, 8 in the following content, respectively). b is an empirical constant, 0.6, taken as the approximation to the laboratory result of Yaglom and Kader (1974), following McPhee (1992). $R_e$ is the Reynolds number, $R_e=\frac{u_{*}{h}_{mol}}{\nu }$, where $h_{mol}$ is the thickness of molecular transition sublayer, $h_{mol}=30z_0$ (Yaglom and Kader, 1974), v is the kinematic molecular viscosity (v= $1.8\times {10}^{-6}$). The molecular Prandtl number $P_r$ is 12.9.

Our previous findings indicated that the ice simulation accuracy was effectively improved when using the above parameterized HEC than using constant HEC, especially for the ice melting phase. After HEC parameterization, the time-averaged absolute error of the simulated ice area reduced from 1855 km² (HEC=0.001, default setting) to 1154 km². More detailed descriptions of the difference in the results between using the HEC parameterization and constant values were provided in Jia et al. (2022b).

To further improve the applicability of the above HEC parameterization to the Bohai Sea ice simulations, the new work in this study over our previous work (Jia et al., 2022b) lies in evaluating the calculation schemes for the two core parameters, the hydraulic roughness of the ice under-surface $z_0$ and the ice-ocean friction velocity $u_{*}$. For the hydraulic roughness of the ice under-surface, in addition to the previously used Mellor and Kantha (1989) scheme, another two schemes proposed by McPhee (1992) and Dansereau et al. (2014), respectively, are also induced here to detect the model performance of the Bohai Sea ice. The formulas of the three schemes assessed in this study are:

$\begin{array}{ll}{z}_0=\frac{0.05}{3}{h}_i& (5)\end{array}$

(Mellor and Kantha, 1989),

$\begin{array}{ll}{z}_0=h_1{e}^{-k\frac{\left|\overrightarrow{v_i}-\overrightarrow{v_w}\right|}{u_{*}}}& (6)\end{array}$

(McPhee, 1992),

$\begin{array}{ll}{z}_0=5\frac{\nu }{u_{*}}& (7)\end{array}$

(Dansereau et al., 2014),

where $h_i$ is the ice thickness, $h_1$ is the depth at which the first water layer located. $\overrightarrow{v_i}$ is the ice velocity, and $\overrightarrow{v_w}$ is the mixed layer velocity under the ice.

For the ice-ocean friction velocity, two calculation schemes proposed by Mellor and Kantha (1989) (used previously) and McPhee et al. (2016) are assessed here. The two schemes formulas are:

$\begin{array}{ll}{u}_{*}=\sqrt{C_{dw}\left|\overrightarrow{v_i}-\overrightarrow{v_w}\right|}& (8)\end{array}$

(Mellor and Kantha, 1989)

$\begin{array}{ll}{u}_{*}=\sqrt{C_{dw}}\left|\overrightarrow{v_w}\right|& (9)\end{array}$

(McPhee et al., 2016),

where $C_{dw}$ is the ice-ocean drag coefficient, which is set as 0.0055 following Fujisaki et al. (2011).

The simulated ice area using different hydraulic roughness calculation schemes and different friction velocity calculation schemes are compared respectively in Figure 9.

Figure 9

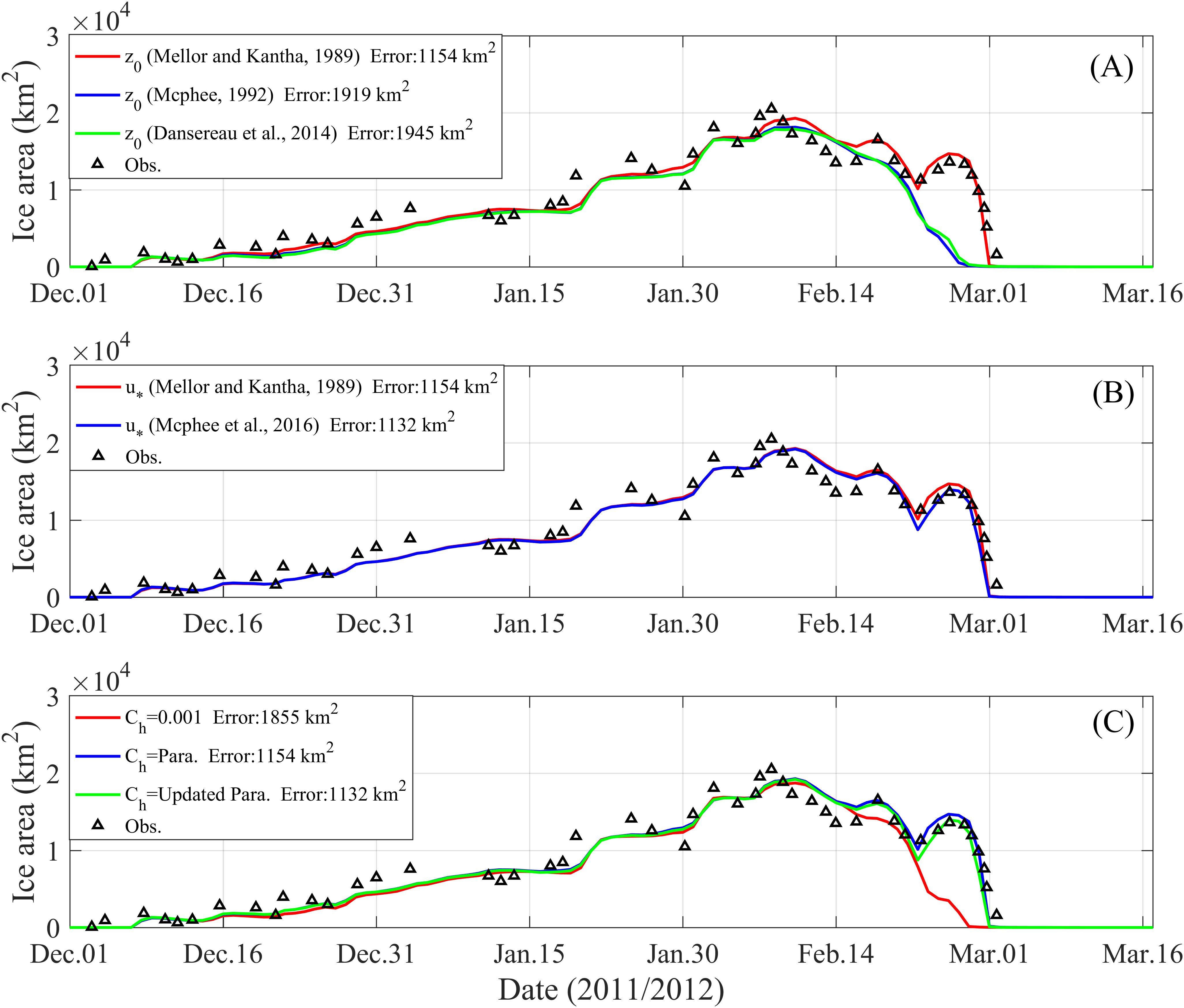
Figure 9. (A) Time series of the simulated ice area obtained by using the hydraulic roughness of the ice under-surface calculation schemes proposed by Mellor and Kantha (1989) (red line), McPhee (1992) (blue line) and Dansereau et al. (2014) (green line) in 2011/2012 ice season. The triangles are the observation data from the satellite inversion. The time-averaged absolute errors of the three simulations are labeled in the legend. (B) Same as graph (A), but for the simulations using the ice-ocean friction velocity calculation schemes proposed by Mellor and Kantha (1989) (red line) and McPhee et al. (2016) (blue line). (C) Same as graph (A), but for the simulations obtained by setting HEC as the model default value 0.001 (red line), using the previously HEC parameterization (blue line), and using the updated HEC parameterization with new ice-ocean friction velocity calculation scheme (green line).

As we can see from Figure 9A, the hydraulic roughness calculation scheme proposed by Mellor and Kantha (1989) give the best model performance, the two fluctuations occurred from Feb. 16 to 20 and Feb. 22 to Mar. 1, 2012 are well reflected, however, the other two schemes not captured. And Figure 9B shows that the friction velocity calculation scheme proposed by McPhee et al. (2016) has slightly better model performance than the other scheme. Thus, the hydraulic roughness of the ice under-surface $z_0$ calculation scheme still use the scheme proposed by Mellor and Kantha (1989), and the ice-ocean friction velocity $u_{*}$ calculation scheme proposed by McPhee et al. (2016) is selected to apply in the HEC parameterization.

In order to check the effectiveness of the updated HEC parameterization with new ice-ocean friction velocity calculation scheme in improving the model performance, the simulated ice area obtained by a constant HEC (0.001, model default setting), using the previously HEC parameterization in Jia et al. (2022b), and using the updated HEC parameterization, respectively, are compared in Figure 9C. Our simulations suggest that the HEC parameterizations can improve the accuracy of ice simulations to a large extent compared with the simulation using constant HEC value (0.001). Significant improvement is seen during the ice melting phase, with two notable fluctuations satisfactorily captured using the parameterized HEC. And the updated HEC parameterization with new ice-ocean friction velocity calculation scheme leads to the best performance, with its time-averaged absolute error decreasing further from the previously HEC parameterization, from 1154 km² to 1132 km². Therefore, the updated HEC parameterization is applied in the subsequent numerical simulations of the Bohai Sea ice in this study.

3.3 Verification of simulated ice results

To comprehensive verify the ice simulations in the 2011/2012 ice season obtained after the adjustments of the two key parameters in the ice thermodynamics module, firstly, the simulated ice thickness and ice concentration in three local waters [Erjiegou water (L1), Dabijiashan water (L2) and Xipaotai water (L3)] on the top of Liaodong bay (Figure 10) are validated by the corresponding observed information during the ice growth, severe, and melting phases (Table 1) collected from the Bohai Sea Ice Land and Coastal Monitoring Report in the 2011/2012 ice season. It can be seen that the ice thickness time series during the whole ice season at the three waters basically experienced multiple fluctuations with varying magnitude. Compared with the observed information, the simulated ice thickness and ice concentration in the three local waters are generally within reasonable limits, however, the ice concentration in Xipaotai water during the ice severe phase was underestimated by about 30%.

Figure 10

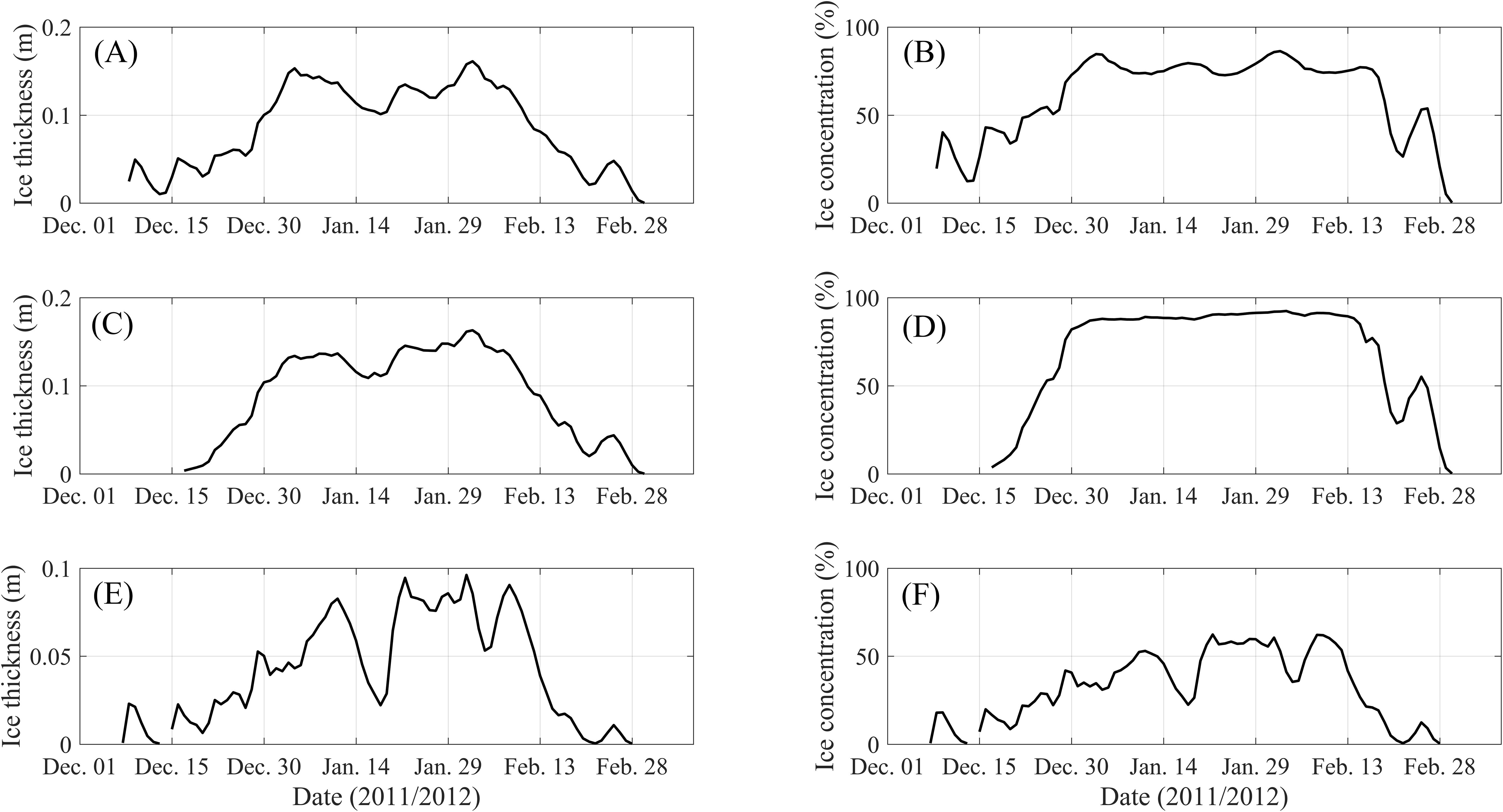
Figure 10. Simulated time series of ice thickness and ice concentration of three local waters [Erjiegou water (L1), Dabijiashan water (L2) and Xipaotai water (L3)] located at the top of Liaodong bay in the 2011/2012 ice season. (A, B) show the ice thickness and ice concentration of Erjiegou water; (C, D) correspond to the Dabijiashan water; (E, F) correspond to the Xipaotai water.

Then, three model days (Jan. 05, Jan. 23, and Feb. 26 in 2012) are selected to compare the simulated ice extent and the corresponding satellite images (Figure 4A), the calculated ice edge distances are also labeled in the lower left corner of each graph. Since sea ice mainly exists in Liaodong Bay in the 2011/2012 ice season, only the Liaodong Bay area is shown in the figure. Our results indicate that both the simulated ice extent and ice edge distance are basically consistent with the satellite data, the errors of the simulated ice edge distances on all three days did not exceed 2 nautical miles. A comparison of the time series of the simulated ice edge distance (Figure 4B) and ice area (Figure 4C) with the observations from the satellite inversion, as well as their error analysis (Table 2) also suggest that the temporal trend of ice variables is in good agreement with the satellite inversion observations. Quite significant correlations are found between the simulated ice edge distance (Pearson’s correlation coefficient r=0.92) and ice area (Pearson’s correlation coefficient r=0.98) with the corresponding satellite observations. In summary, the satisfactory model performance in 2011/2012 ice season allows to perform in-depth thermodynamic analysis of the ice-ocean interface.

Table 2

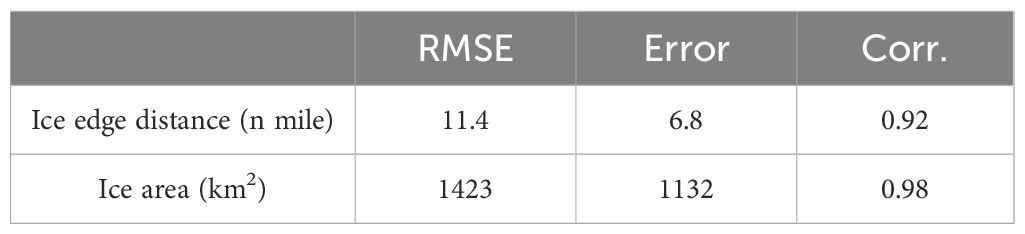
Table 2. Root mean square errors (RMSE), time-averaged absolute errors (abbreviated as Error), and the correlation coefficients of the ice edge distance and ice area results during the entire ice season compared with the satellite inversion observations.

4 Variations of the heat fluxes at the ice-ocean interface

4.1 Temporal variations

To interpret the temporal variation characteristics of the heat fluxes at the ice-ocean interface in the Bohai Sea, the time series of the atmospheric conditioning factors (including sea surface air temperature and wind speed), the oceanic conditioning factor (i.e., mixed layer temperature), the ice variables (including ice drift velocity, ice thickness, ice concentration, and the freezing/melting rate of ice base), and the interfacial heat fluxes (including the conductive heat flux through ice, oceanic heat flux, and the latent heat flux) during the 2011/2012 ice season are shown in Figure 5. The correlation coefficients between the heat fluxes with the atmospheric, oceanic and ice conditioning factors are also calculated and listed in Table 3.

Table 3

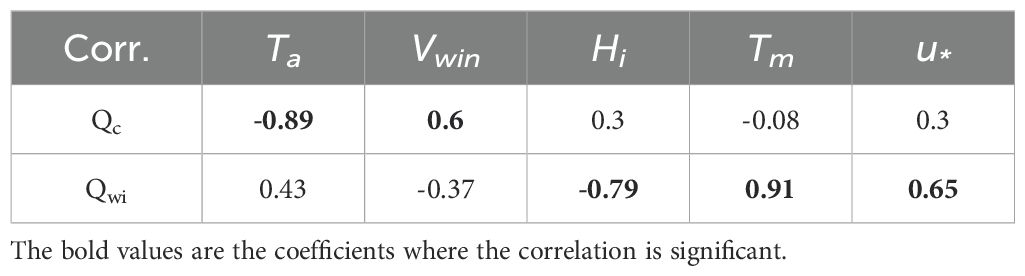
Table 3. Correlation coefficients between the interfacial heat fluxes (including conductive heat flux through ice Q_c and oceanic heat flux Q_wi) with the atmospheric, ice and oceanic conditioning factors (including sea surface air temperature T_a and sea surface wind velocity V_win, and ice thickness H_i, mixed layer temperature T_m, and the ice-ocean friction velocity u_*).

4.1.1 Environmental Conditions

Controlled by the Asian continental high pressure, and the atmospheric conditions in the Bohai Sea have obvious continental characteristics. Cold fronts accompanied by strong winds and cooling occur frequently during winter. Sea surface air temperature (Figure 5A) and wind speed (Figure 5B) fluctuate widely, and show short-term fluctuations. During the winter of 2011/2012, the sea surface air temperature dropped below -5°C on Dec. 6, 2011. The lowest air temperature appeared on Jan. 22, 2012, then gradually warmed up amidst ups and downs (Figure 5A). Correspondingly, the mixed layer temperature dropped to the freezing point (approx. -1.67°C) by early December 2011 due to the atmospheric conditions and remained around the freezing point until the end of February, then gradually increased (Figure 5C).

4.1.2 Conductive heat flux through ice

In the HAMSOM ice module, the surface conductive heat flux through ice Q_c(surface) is calculated by the temperature gradient within the ice layer close to the surface interface:

$\begin{array}{ll}{Q}_c(surface)=k_i\frac{\partial T_i}{{\partial }_z}|s_{,}& (10)\end{array}$

while the bottom conductive heat flux through ice Q_c(bottom) is calculated by the temperature gradient in the ice layer close to the ice base:

$\begin{array}{ll}{Q}_c(bottom)=k_i\frac{\partial T_i}{{\partial }_z}|b_{,}& (11)\end{array}$

where k_i is the thermal conductivity of sea ice, T_i is the ice temperature.

In the Bohai Sea, the conductive heat flux through ice Q_c (Figure 5E) exhibits the short-term fluctuations consistent with the atmospheric forcing (i.e., sea surface air temperature and wind speed) (Figures 5A, B), and the fluctuation patterns of both the surface and the bottom conductive heat flux are fairly synchronous. The magnitude of the conductive heat flux rises significantly during the occurrence of cold fronts with decreasing air temperature and increasing wind speed at sea surface, suggesting that the fluctuations of the conductive heat flux are very likely driven by the weather system. The magnitude of the bottom conductive heat flux is overall smaller than the surface conductive heat flux, implying that the atmospheric conditions have a weaker influence on the lower ice layer than the upper layer.

To test this hypothesis, we examine the relationships between the heat fluxes and the environmental conditions (shown in Table 3). Here, the heat fluxes include the conductive heat flux through ice Q_c [the average of Q_c(surface) and Q_c (bottom)] and the oceanic heat flux Q_wi, the atmospheric factors include sea surface air temperature T_a and sea surface wind velocity V_win, and the ice and oceanic factors include ice thickness H_i, mixed layer temperature T_m, and the ice-ocean friction velocity u_*. The results show a strong negative correlation between the conductive heat flux through ice and sea surface air temperature (Pearson’s correlation coefficient r=-0.89), and a strong positive correlation with the sea surface wind speed (r=0.60), indicating that the atmospheric conditions are the key controlling factors of the conductive heat flux through ice. By contrast, the correlations between the conductive heat flux through ice and ice conditions such as ice thickness, oceanic conditions including mixed layer temperature and ice-ocean friction velocity are relatively weak.

4.1.3 Oceanic heat flux

Figure 5D shows that the temporal variation of the oceanic heat flux is remarkable in the Bohai Sea. High values (10~40 W/m²) were found during the beginning (Dec. 07 ~ 30, 2011) and the end (Feb. 24 ~ Mar. 13, 2012) of the ice season, low values (<10 W/m²) appeared during the middle period (January to Mid-February) of the ice season. Influenced by the frequent cold fronts during the middle period of the ice season (January to Mid-February), the mixed layer temperature (Figure 5C) maintained near the local freezing point, i.e., the mixed layer temperature elevation above freezing calculated only when the mixing layer temperature is larger than the freezing point is maintained near zero. Consequently, the values of the oceanic heat flux remain positive and close to zero during the middle period of the ice season. The oceanic heat flux here can reach a maximum value of ~40 W/m², and the values ranging from 1 to 7 W/m² in the middle ice season. This is relatively consistent with the oceanic heat flux values under the Beaufort Sea, a marginal shelf sea in western Canadian Arctic, where also experience strong seasonal ice controlled by its surface water mass which nearly 90 m thick and ranges in temperature from -1.4°C in late summer to -1.8°C in winter. Maykut and McPhee (1995) used daily CTD data from 5 AIDJEX camps in the Beaufort Sea to estimate the oceanic heat flux and found maximum values reached 40~60 W/m² in August (ice melting phase), for an annual-average of 5.1 W/m². The annual-average value calculated based on 10 platforms with observations through the summer in the Beaufort Gyre was 6.6 W/m², ranging from 4 to 9 W/m² during the low-value period (Krishfield and Perovich, 2005).

As shown in Table 3, there are three main factors affecting the oceanic heat flux, which are the mixed layer temperature, ice thickness and the ice-ocean friction velocity. Among them, the most significant positive correlation (r=0.91) occurs between mixed layer temperature and oceanic heat flux. The time series of oceanic heat flux and mixed layer temperature elevation above freezing calculated from Arctic ice platforms observations by Krishfield and Perovich (2005) also showed that the annual variability characteristics of the two are very close to each other. Strong positive correlation (r=0.65) also occurs between the ice-ocean friction velocity and oceanic heat flux. The ice-ocean friction velocity time series shows periodic fluctuation under the influence of tidal current, implying that the oceanic heat flux is also affected by tide. Therefore, the variation trend of oceanic heat flux during the ice season reflects the characteristics of hydrological conditions to a large extent. In addition, there is also a strong negative correlation (r=-0.79) between ice thickness and the oceanic heat flux. A possible explanation is that, ice thickness can affect the hydraulic roughness of the ice under-surface (Mellor and Kantha, 1989), which determines the efficiency of heat exchange at the ice-ocean interface, and thus the oceanic heat flux.

In summary, different from the conductive heat flux through ice, the correlations between the oceanic heat flux with the oceanic and ice conditioning factors are greater than that with the atmospheric conditioning factors.

4.1.4 Ice conditions

The temporal trend of the freezing/melting rate of the ice base (Figure 5G) is highly consistent with the latent heat flux (Figure 5F). During the winter of 2011/2012, the Bohai Sea began to freeze on Dec. 7, 2011, and completely melted on Mar. 13, 2012. The ice regimes first grew and then declined, accompanied by several fluctuations during the process, reaching its peak on Feb. 2, 2012 (Figures 5H, I). Throughout the ice season, the ice coverage-averaged ice thickness reached a maximum of about 13 cm, and the ice coverage-averaged ice concentration reached a maximum of about 80%. The inversion data for ice thickness from GOCI ocean color remote sensing satellite (Yan et al., 2024) was compared with our simulations here, shown in Figure 5H. As we can see, the simulated ice thickness during the ice growth phase is generally in line with the inversion data, while the fluctuations of the simulated ice thickness trend during the ice severe phase are more gentle than the inversion data, and the values for the ice melting phase are lower than the inversion data. The time-averaged absolute deviation of these two data is 0.03 m.

4.2 Spatial variations

To investigate the spatial variation characteristics of the heat fluxes at the ice-ocean interface and compare their differences between ice growth state and ice melting state, the distributions of the key interfacial thermal parameters on two representative days, with one day in the ice growth phase and the other in the ice melting phase, are illustrated in Figures 11, 12, respectively.

Figure 11

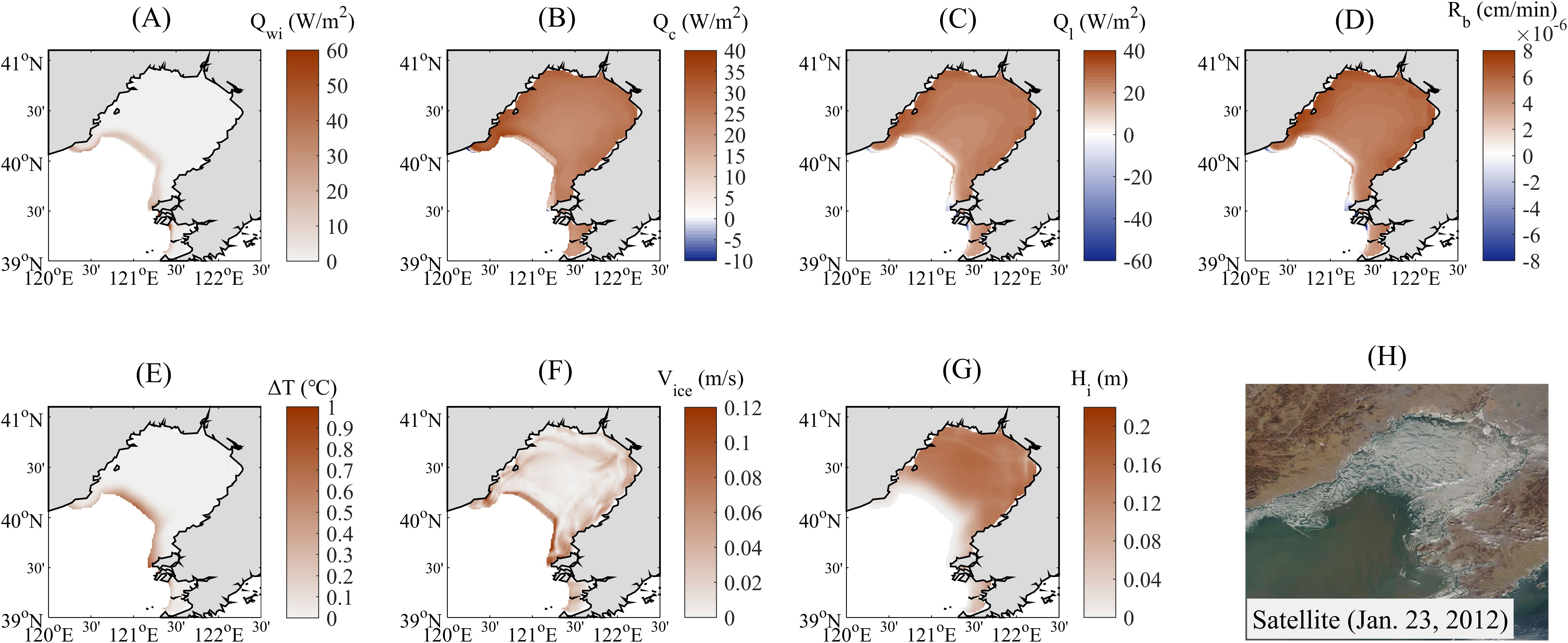
Figure 11. Distributions of the simulated ice thermal parameters [including the oceanic heat flux Q_wi (A), the conductive heat flux through ice Q_c (B), the latent heat flux Q_l (C), freezing/melting rate of ice base R_b (D), the mixed layer temperature elevation above freezing ΔT (E), ice drift velocity V_ice (F) and the ice thickness H_i (G)] and the satellite image (H) on Jan. 23, 2012, the day in the ice growth phase. (The positive value represents the upward direction and the negative represents downward).

Figure 12

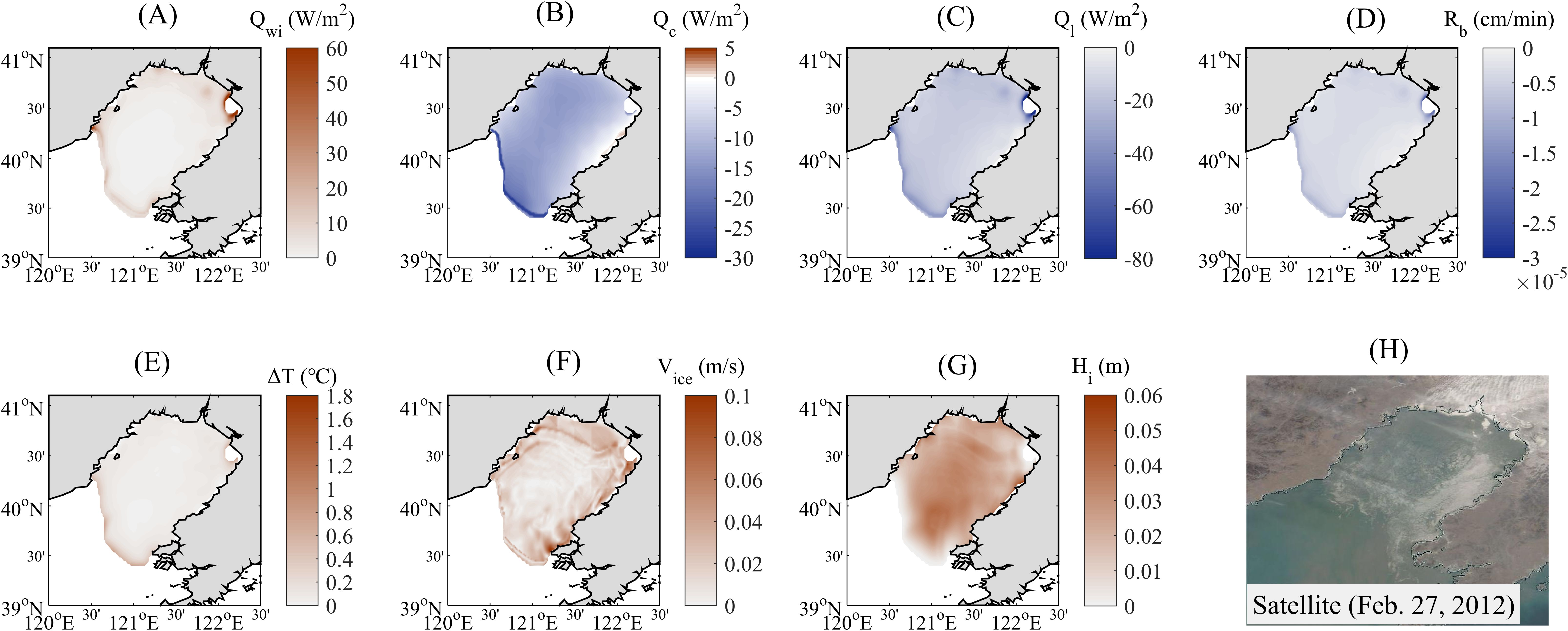
Figure 12. Same as Figure 11, but on Feb. 27, 2012, the day in the ice-melt phase.

Firstly, the result shows that the oceanic heat flux is always positive both in ice growth state and ice melting state. This is because the oceanic heat flux represents the unidirectional heat transfer from the mixed layer to the ice base and is measured by the mixed layer temperature elevation above freezing (calculated only when the mixing layer temperature is greater than the freezing point). The value of the oceanic heat flux is larger in the marginal ice zone (MIZ) (about 20~80 W/m²) with relatively thin ice than in the inner ice zone (IIZ) (< 20 W/m²) with relatively thick ice, and the value in the nearshore area in the northern especially northeastern part of Liaodong Bay is also relatively large when in the ice-melt phase (shown in Figures 11A, 12A). This phenomenon can be explained from both dynamic and thermodynamic aspects. From the aspect of dynamics, the mixed layer under the MIZ with lower ice concentration (i.e., more polynyas) is more susceptible to the wind energy input, which strengthens the ice drift velocity (shown in Figures 11F, 12F) and turbulent mixing, further promoting heat exchange within the ice-ocean boundary layer. From the aspect of thermodynamics, the polynyas in the MIZ make the underlying mixed layer more susceptible to atmospheric thermal driven, and the mixed layer temperature can be heated above freezing by more solar radiation (shown in Figures 11E, 12E).

We can also see that in the ice growth state, the value of the conductive heat flux through ice in the whole field is mostly positive (shown in Figure 11B), which means that the heat is transferred upward from the ice base. The magnitude in MIZ (about 10~18 W/m²) is smaller than in the IIZ (about 20~40 W/m²). While in the ice melting state, the value of the conductive heat flux through ice in the whole field is mostly negative (shown in Figure 12B), which means that heat is being transferred downward. The magnitude in MIZ (about 22~28 W/m²) is larger than in the IIZ (<20 W/m²). The simulated value range here is relatively consistent with that in the Arctic ocean. Fan et al. (2017) computed the conductive heat flux through ice in the Arctic Ocean in the four winter months (November–February) for a long period of 36 years (1979–2014) based on monthly mean Pan-Arctic Ice Ocean Modeling and Assimilation System (PIOMAS) sea ice thickness fields, and found that the value range is about 10~30 W/m², most values fall in the 15~25 W/m².

The change of latent heat flux is the result of competition between the conductive heat flux through ice and oceanic heat flux, characterizing the heat gain or loss at the ice-ocean interface. During the growth of the ice, the latent heat flux in the whole field is almost positive (shown in Figure 11C), indicating that the heat is transmitting upward from the ice base, and the ice-ocean interface is losing heat. The degree of this heat loss in the IIZ is obviously greater than that in the MIZ. During the ice melting phase, the latent heat flux in the whole field is negative (shown in Figure 12C), indicating that the heat is transmitting downward to the ice base, and the ice-ocean interface is gaining heat. The degree of this heat gain in the MIZ and nearshore area is greater than that in the IIZ.

As for the freezing/melting rate of ice base, its spatial distribution closely resembles the latent heat flux (shown in Figures 11D, 12D). During ice growing and melting, the whole field is positive (freezing) and negative (melting), respectively. As shown in Figures 11G, 12G, the ice thickness in the MIZ is thinner than the IIZ. The simulated ice coverage and ice edge line are generally confirmed by satellite images. The simulated spatial distribution characteristics of ice thickness in the ice growth state are also consistent with the satellite image, while in the ice melting state, the simulated ice thickness in Liaodong Bay is not well characterized by thick in the east side and thin in the west side. Since the spatial distribution of ice thickness in the Liaodong Bay is highly influenced by its clockwise circulation field (Wu et al., 2005), the ice dynamic process including mixed layer currents, the ice velocity needs to be further studied and improved in the future.

5 Discussion

5.1 Applicability of the proposed parameter adjustments

As stated the influence mechanism of mixed layer thickness on ice variables described in section 3.1, the mixed layer thickness can effectively affect the heat budget at the ice-ocean interface by determining the variation rates of hydrographic properties within the mixed layer (Wang et al., 2000). Therefore, it is important to define reasonable values for the mixed layer thickness in the sea ice module that meets the environmental conditions of the local area. For sea ice simulations in the areas with significant mixed layer seasonal or spatial variation, setting mixed layer thickness as the thickness of the first water layer (the default setting) in the ice model would bias the calculation of the variation rates of the hydrographic properties of the mixed layer, especially in z-level height coordinate models. Due to the vertical mixing homogenization of the water column during winter, the mixed layer thickness at each grid determined using the temperature difference threshold method (the difference between the temperature at the depth and the surface temperature is less than 0.2°C) in the Bohai Sea is almost equal to its water depth (figure omitted). So we directly make the mixed layer thickness the entire water depth in the Bohai Sea ice simulations, which is a reflection of the special atmospheric and oceanic environmental conditions of the Bohai Sea. Wang et al. (2000) indicated that the hydrographic properties under ice as well as the oceanic heat flux at the ice-ocean interface are modulated by bathymetry in the Bohai Sea. A consistency of the sea ice edge line with the isobath contour line in the Bohai Sea provides support for this finding (Li et al., 2020; Yan et al., 2022). For other marginal seas such as the Baltic Sea and Sea of Okhotsk, they also experience strong seasonal sea ice with different bathymetry, atmospheric and oceanic environmental conditions. The mixed layer thickness in the Sea of Okhotsk is characterized by significant seasonal and spatial variations, a mixed layer of uniform temperature nearly at the freezing point extending down to a depth of about 300 m was observed in winter of the southwestern of the Okhotsk Sea (Ohshima et al., 2001), which is far deeper than the first water layer thickness in general models. Seasonal variations are also a major feature of mixed layer thickness in the Baltic Sea, about half of the water column in the Baltic Sea is dominated by the seasonal signal directly because mixed layer thickness varies in the range of 20-30 m at a mean water depth of only 52 m (Meier et al., 2003). Considering the unique oceanographic characteristics of these seas, we suggest to use a temperature difference threshold method to determine the mixed layer thickness at each grid in order to more accurately determine the extent of the hydrodynamic mixing of the water column under the ice.

An updated parameterization of the heat exchange efficiency (i.e., HEC) between the ice and the ocean is applied in the Bohai Sea ice simulations in this study. Here, the HEC at the ice-ocean interface is defined as the non-dimensional temperature changes across the turbulent boundary layer and the molecular transition sublayer, considering the impact of the ice-ocean friction velocity and the hydraulic roughness of the ice under-surface. The values of oceanic heat flux modeled by Su et al. (2005) using the constant HEC (2.2×10^-5) in the MIZ of the Liaodong Bay range from 30 W/m² to 100 W/m², which are relatively larger than our values (about 20~80 W/m²) using the parameterized HEC. Using the oceanic heat (about 20 W/m² to 50 W/m²) provided by the Yellow Sea warm current in winter (Wang et al., 1984) as a reference (Wang et al., 2000), the oceanic heat flux modeled in this study has a more reasonable value. Many ice models for simulating ice shelf in polar regions have adopted this HEC parameterization (e.g., Little et al., 2009 [HIM]; Holland et al., 2010 [MICOM/POLAIR]; Makinson et al., 2011 [MICOM]; Timmermann et al., 2012 [FESOM] and Galton-Fenzi et al., 2012 [ROMS]). Nevertheless, constant HEC is still adopted in some ice models. From the simulations shown in Figure 9C, the HEC parameterization scheme has a better performance and is able to capture more detailed ice fluctuations during the ice melting phase. Dansereau et al. (2014) also found that important differences appeared in the ice melting rate distribution under the Pine Island ice shelf, West Antarctica between simulations using constant HEC and parameterized HEC. They indicated that the regions of largest melting coincide with strong outflow plumes and fast mixed layer currents when using the parameterized HEC, which cannot be simulated using constant HEC. The role of the ice-ocean friction velocity is highlighted, they also pointed that the turbulence measured by friction velocity dominate over temperature gradient in setting oceanic heat flux through the ice-ocean boundary layer. Therefore, a careful evaluation of the calculation scheme for ice-ocean friction velocity is necessary. We propose that a dynamic HEC should be used in modeling marginal ice zones where melting occurs frequently.

5.2 Advances in ice-ocean thermal interactions compared to prior researches

To our knowledge, the existing studies of ice-ocean interfacial heat fluxes in the Bohai Sea mainly focus on the oceanic heat flux. The main conclusions from existing studies include: 1) the evolution of the Bohai Sea ice is more dominated by ocean heat content (i.e., oceanic heat flux) of the mixed layer than salt (Yan et al., 2022); 2) the oceanic heat flux in the Bohai Sea has large value at the beginning of the ice season and then decreases as the ice season progresses (Ji et al., 2002; Su et al., 2005), and 3) the oceanic heat flux is controlled by the mixed layer thickness and mixed layer temperature (Wang et al., 2000).

These findings are also reflected in our results. Further, we found that the oceanic heat flux in the Bohai Sea rises again at the end of the ice season after reaching a minimum (close to zero) during the middle ice season. Su et al. (2005) obtained the similar result based on their numerical results of the Bohai Sea ice in the 2000/2001 ice season using the POM ice-ocean coupled model. The main difference between our results and theirs, however, is that values of the oceanic heat flux we modeled are larger at the end of the ice season than at the beginning. The stronger rebound of the oceanic heat flux at the end of the ice season is due to the stronger rewarming of air temperatures at this period (Figure 5A), causing a greater increase in the mixed layer temperature elevation above freezing (Figure 5C) and thus the heat transferred from the ocean to the ice (Figure 5D). Yang (2015) obtained an optimal solution for the oceanic heat flux in the Arctic Ocean based on an optimal identification model for the ice base sublayer energy balance system, using an improved genetic mathematical algorithm. Their results show that the oceanic heat flux generally declines from the early stage of ice growth, and increases when entering the ice melt period, until reaching the maximum value when the ice melts completely. This finding is consistent with our simulation results.

In addition, the new outcomes in this study which haven’t been reported in existing studies for the Bohai Sea include:

1. Besides the mixed layer thickness and mixed layer temperature, the oceanic heat flux in the Bohai Sea is also dominated by the ice-ocean friction velocity and the ice thickness. Current velocity in the mixed layer drives out shear forces that form the background field for turbulent mixing (Toole et al., 2010). Ice-ocean friction velocity can be considered as a surrogate for turbulent mixing (Lei et al., 2014), and ice thickness can affect the efficiency of the heat transfer between ice and ocean (i.e., HEC) by controlling the hydraulic roughness of the ice under-surface. Therefore, both the ice-ocean friction velocity and the ice thickness largely influence the heat budget at the ice-ocean interface. Same as our results, Lei et al. (2014) pointed out that the heat budget at the ice-ocean interface (i.e., the oceanic heat flux) was strongly dependent on ice thickness utilizing an ice mass balance buoy (IMB) deployed in the Arctic Ocean. Toole et al. (2010) also indicated that the oceanic heat flux in the central Canada Basin is proportional to the ice-ocean stress calculated by the ice-ocean friction velocity, and the mixed layer temperature elevation above freezing.

2. In the Bohai Sea, values of the oceanic heat flux are larger in the marginal ice zone (MIZ) with relatively thin ice than in the inner ice zone (IIZ) with relatively thick ice. Su et al. (2005) also found the oceanic heat flux is much larger in the MIZ than in the IIZ in their simulations based on the time series at two single points (one located in the IIZ and the other located in the MIZ). We also find that when ice is melting, in addition to the MIZ, large values of the oceanic heat flux occurred at the nearshore area in the northern especially northeastern part of Liaodong Bay. And, we add a preliminary mechanistic explanation for this phenomenon in section 4.2.

3. Our simulation indicates that the temporal trend of the freezing/melting rate of the ice base (Figure 5G) is highly consistent with the conductive heat flux through ice (Figure 5E). So in addition to the oceanic heat flux, another ice-ocean interfacial heat flux (i.e., the conductive heat flux through ice) is also worth studying in the Bohai Sea. We find that the sea surface air temperature and wind speed are the key controlling factors of the conductive heat flux through ice. The conductive heat flux through ice exhibits the short-term fluctuations consistent with the frequent attacks of the winter cold fronts. And the atmospheric conditions have a weaker influence on the lower ice layer than the upper ice layer. In addition, other possible impact factors such as cloud cover, the roughness on the ice surface and the threshold effects for the short-term variability of atmospheric conditions are also worth exploring.

4. In the ice growth state, heat within the ice layer is transferred upward from the ice base, and the heat is losing at the ice-ocean interface. This heat loss in the IIZ is obviously greater than that in the MIZ. While in the ice melting state, heat within the ice layer is being transferred downward, and the heat is gaining at the ice-ocean interface. This heat gain in the MIZ is greater than that in the IIZ. Lin and Zhao (2018) also indicated that during the melting period (summer) in the Arctic Ocean, heat is transferred from ice surface to ice base within the ice layer. Until September, when entering the freezing period, the heat within the ice layer changes to a bottom-up transfer.

The model parameter adjustments and simulations analysis in this study only focus on the ice-ocean thermal process. Ice dynamic processes need to be evaluated or improved in the future. In particular, the value/calculation of the ice-ocean drag coefficient (C_dw) needs to be further evaluated as it affects both ice thermodynamic and dynamic processes. Constant ice-ocean drag coefficient is usually employed in sea ice simulations (Dansereau et al., 2014). Holland and Feltham (2006) set C_dw to 0.0015 at the ice shelf base to account for smoothing effects by melting and ice pumping. Dansereau et al. (2014) found that reasonable cavity-averaged melt rate under PIIS can be matched when using C_dw in the range of 0.005-0.01. In this study, a C_dw value of 0.0055 following Fujisaki et al. (2011) is adopted in the HEC parameterization. The ice-ocean drag coefficient is a highly uncertain parameter, related sensitivity studies for this coefficient will be followed up in the future.

6 Conclusions

In this study, we perform numerical modeling of the Bohai sea ice using the HAMSOM ice-ocean coupled model to investigate the spatio-temporal variations of the heat fluxes at the ice-ocean interface. Driven by the frequent cold fronts during the winter in the Bohai Sea, both the surface and the bottom conductive heat flux through ice show short-term fluctuations, and the magnitude of these fluctuations are weakened from the top to the lower ice layer. The oceanic heat flux has large value at the beginning and end of the ice season, and remained below 10 W/m² in the middle ice period. Ice thickness, ice-ocean friction velocity and mixed layer temperature are the three main control factors of the oceanic heat flux. Overall, the atmospheric conditions are the key control factors of the conductive heat flux through ice, while the oceanic conditions have much weaker influence. In contrast, the temporal variation of oceanic heat flux is more controlled by oceanic conditions than by atmospheric conditions. As for the spatial variations of the interfacial heat fluxes, the value of oceanic heat flux is larger in the MIZ with thin ice than in the IIZ with thick ice. In the ice growth state, the conductive heat flux through ice and the latent heat flux is mostly positive, indicating that the heat is transmitting upward from the ice base and the ice-ocean interface is losing heat. And the heat loss in the IIZ is greater than that in the MIZ. While in the ice melting state, these two heat fluxes are mostly negative, which means that the heat is transmitting downward in the ice layer, and the ice-ocean interface is gaining heat. The degree of the heat gain in the MIZ is greater than that in the IIZ.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

BJ: Writing – original draft, Visualization, Methodology, Formal analysis, Conceptualization. LX: Writing – review & editing, Validation, Methodology, Data curation. XC: Writing – review & editing, Supervision, Project administration. WZ: Writing – review & editing, Project administration.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Sino-German Mobility Program: CHESS-Chinese and European Coastal Shelf Seas Ecosystem Dynamics-A Comparative Assessment (M-0053) and a contribution to the Helmholtz PoF program “The Changing Earth – Sustaining our Future” on its Topic 4: Coastal zones at a time of global change.

Acknowledgments

Thanks are given to the North China Sea Marine Forecasting Center of the Ministry of Natural Resources for their observation data support, and to Ms. LIU Xin at the National Super Computing Center in Jinan, China for their support in configuring the super-computing environment. We thank Dr. Thomas Pohlmann from the University of Hamburg, Germany, for providing the HAMSOM codes as well as for his helpful suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arthun M., Schrum C. (2010). Ocean surface heat flux variability in the Barents Sea. J. Mar. Syst. 83, 88–98. doi: 10.1016/j.jmarsys.2010.07.003

Crossref Full Text | Google Scholar

Backhaus J. O. A. (1985). three-dimensional model for the simulation of shelf sea dynamics. Deutsche Hydrografische Z. 38, 165–187. doi: 10.1007/BF02328975

Crossref Full Text | Google Scholar

Bai S., Wu H. (1998). Numerical sea ice forecast for the Bohai Sea. Acta Meteorologica Sin. 56, 139–153.

Google Scholar

Carton J. A., Chepurin G. A., Chen L. (2018). SODA3: A new ocean climate reanalysis. J. Climate 31, 6967–6983. doi: 10.1175/JCLI-D-18-0149.1

Crossref Full Text | Google Scholar

Collins M., Minobe S., Barreiro M., Bordoni S., Kaspi Y., Yoshida A. K., et al. (2018). Challenges and opportunities for improved understanding of regional climate dynamics. Nat. Climate Change 8, 101–108. doi: 10.1038/s41558-017-0059-8

Crossref Full Text | Google Scholar

Dansereau V., Heimbach P., Losch M. (2014). Simulation of subice shelf melt rates in a general circulation model: Velocity-dependent transfer and the role of friction. J. Geophysical Res. Oceans 119, 1765–1790. doi: 10.1002/2013JC008846

Crossref Full Text | Google Scholar

Donlon C. J., Martin M., Stark J., Jones J. R., Fiedler E., Wimmer W. (2012). The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 116, 140–158. doi: 10.1016/j.rse.2010.10.017

Crossref Full Text | Google Scholar

Erofeeva S., Padman L., Howard S. L. (2020). Tide Model Driver (TMD) version 2.5, Toolbox for Matlab. Available online at: https://www.github.com/EarthAndSpaceResearch/TMD_Matlab_Toolbox_v2.5. (Accessed June 16, 2017)

Google Scholar

Fan X., Bi H., Wang Y., Fu M., Zhou X., Xu X., et al. (2017). Increasing winter conductive heat transfer in the arctic sea-ice-covered areas: 1979–2014. J. Ocean Univ. China (Oceanic Coast. Sea Research) 16, 1061–1071. doi: 10.1007/s11802-017-3359-8

Crossref Full Text | Google Scholar

Fujisaki A., Mitsudera H., Yamaguchi H. (2011). Dense shelf water formation process in the Sea of Okhotsk based on an ice-ocean coupled model. J. Geophysical Research: Oceans 116, C03005. doi: 10.1029/2009JC006007

Crossref Full Text | Google Scholar

Galton-Fenzi B. K., Hunter J. R., Coleman R., Marsland SJ and Warner R. C. (2012). Modeling the basal melting and marine ice accretion of the Amery Ice Shelf. J. Geophysical Res. 117, C09031. doi: 10.1029/2012JC008214

Crossref Full Text | Google Scholar

Ha H. K., Yae S. E., Park J. H., Cole S., Park K., Hyoung S. L. (2016). “Observation of oceanic heat flux to the sea ice using ice-tethered moorings: Canada Basin, Arctic Ocean,” in EGU General Assembly 2016 Conference. Geophysical Research Abstracts, Vienna Austria, held 17-22 April, 2016, Vol. 18. EGU2016–5436.

Google Scholar

Hibler W. D. A. (1979). Dynamic thermodynamic sea ice model. J. Phys. Oceanography 9, 815–846. doi: 10.1175/1520-0485(1979)009<0815:ADTSIM>2.0.CO;2

Crossref Full Text | Google Scholar

Holland P. R., Feltham D. L. (2006). The effects of rotation and ice shelf topography on frazil-laden ice shelf water plumes. J. Phys. Oceanography 36, 2312–2327. doi: 10.1175/JPO2970.1

Crossref Full Text | Google Scholar

Holland P. R., Jenkins A., Holland D. M. (2010). Ice and ocean processes in the Bellingshausen Sea, Antarctica. J. Geophysical Res. 115, C05020. doi: 10.1029/2008JC005219

Crossref Full Text | Google Scholar

Ji S., Yue Q., Bi X. (2002). Heat transfer coefficient between ice cover and water in the Bohai Sea. Mar. Sci. Bull. 21, 9–15.

Google Scholar

Jia B., Chen X., Zheng P. (2022b). The role of the heat exchange coefficient at the ice/ocean interface in Bohai Sea ice modeling. Continental Shelf Res. 241, 104735. doi: 10.1016/j.csr.2022.104735

Crossref Full Text | Google Scholar

Jia B., Chen X., Zheng P., Su J. (2022a). The influence of the initial temperature field on sea ice simulations in the Bohai Sea in winter of 2015/2016. Mar. Sci. Bull. 24, 1–18.

Google Scholar

Keen A., Blockley E., Bailey D. A., Debernard J. B., Bushuk M., Delhaye S., et al. (2021). An inter-comparison of the mass budget of the Arctic sea ice in CMIP6 models. Cryosphere 15, 951–982. doi: 10.5194/tc-15-951-2021

Crossref Full Text | Google Scholar

Keitzl T., Mellado J. P., Notz D. (2016). Reconciling estimates of the ratio of heat and salt fluxes at the ice–ocean interface. J. Geophysical Research: Oceans 121, 8419–8433. doi: 10.1002/2016JC012018

Crossref Full Text | Google Scholar

Krishfield R. A., Perovich D. K. (2005). Spatial and temporal variability of oceanic heat flux to the Arctic ice pack. J. Geophysical Res. 110, C07021. doi: 10.1029/2004JC002293

Crossref Full Text | Google Scholar

Lei R., Li N., Heil P., Cheng B., Zhang Z., Sun B. (2014). Multiyear sea-ice thermal regimes and oceanic heat flux derived from an ice mass balance buoy in the Arctic Ocean. J. Geophysical Research: Oceans 119, 537–547. doi: 10.1002/2012JC008731

Crossref Full Text | Google Scholar

Leppäranta M., Shirasawa K. (2007). “Influence of the ice-ocean heat flux on the ice thickness evolution in Saroma-ko lagoon, Hokkaido, Japan”, in Proceedings of the 16th International Northern Research Basins Symposium and Workshop, 27 August - 2 September, 2007, Petrozavodsk, Russia.

Google Scholar

Li H., Bai S., Zhang Z., Wu H. (1999). Numerical simulation of tidal effects on ice for the Bohai Sea. Mar. Forecasts 16, 39–47.

Google Scholar

Li R., Lu Y., Hu X., Guo D., Zhao P., Wang N., et al. (2020). Space–time variations of sea ice in bohai sea in the winter of 2009–2010 simulated with a coupled ocean and ice model. J. Oceanography 77, 243–258. doi: 10.1007/s10872-020-00566-2

Crossref Full Text | Google Scholar

Lin L., Zhao J. (2018). Studies of the thermal conductivity of snow and conductive heat flux on Arctic perennial sea ice. Haiyangxuebao 40, 23–32. doi: 10.3969/j.issn.0253-4193.2018.11.003

Crossref Full Text | Google Scholar

Lin L., Zhao J. (2019). Estimation of oceanic heat flux under sea ice in the Arctic Ocean. J. Ocean Univ. China (Oceanic Coast. Sea Research) 18, 605–614. doi: 10.1007/s11802-019-3877-7

Crossref Full Text | Google Scholar

Little C. M., Gnanadesikan A., Oppenheimer M. (2009). How ice shelf morphology controls basal melting. J. Geophysical Res. 114, C12007. doi: 10.1029/2008JC005197

Crossref Full Text | Google Scholar

Liu Y. (2013). Key technologies research and application of sea ice numerical forecast in the Bohai Sea (Qingdao: Ocean University of China).

Google Scholar

Liu Y., Liu Q., Sui J., Song J., Bai S. (2013). The respond of ice for the Bohai Sea and the Huanghai Sea with the general circulation and the climate change in winters. Acta Oceanologica Sin. 35, 18–27.

Google Scholar

Luo D., Yao Y., Dai A., Simmonds I. (2017). Increased quasi stationarity and persistence of winter Ural blocking and Eurasian extreme cold events in response to arctic warming. Part II: Theor. explanation. J. Climate 30, 3569–3587. doi: 10.1175/JCLI-D-16-0262.1

Crossref Full Text | Google Scholar

Ma L., Wang B., Cao J. (2020). Impacts of atmosphere–sea ice–ocean interaction on Southern Ocean deep convection in a climate system model. Climate Dynamics 54, 4075–4093. doi: 10.1007/s00382-020-05218-1

Crossref Full Text | Google Scholar

Makinson K., Holland P. R., Jenkins A., Nicholls K. W. (2011). Influence of tides on melting and freezing beneath Filchner-Ronne Ice Shelf, Antarctica. Geophysical Res. Lett. 38, L06601. doi: 10.1029/2010GL046462

Crossref Full Text | Google Scholar

Maykut G. A., McPhee M. G. (1995). Solar heating of the Arctic mixed layer. J. Geophysical Res. 100, 24691–24703. doi: 10.1029/95JC02554

Crossref Full Text | Google Scholar

McPhee M. G. (1992). Turbulent heat flux in the upper ocean under sea ice (Journal of Geophysical Research97(C4): 5365–5379.

Google Scholar

McPhee M. G., Stevens C. L., Smith I. J., Robinson N. J. (2016). Turbulent heat transfer as a control of platelet ice growth in supercooled under-ice ocean boundary layers. Ocean Sci. 12, 507–515. doi: 10.5194/os-12-507-2016

Crossref Full Text | Google Scholar

Meier H. E. M., Dscher R., Torgny F. (2003). A multiprocessor coupled ice-ocean model for the Baltic Sea: Application to salt inflow. J. Geophysical Res. Oceans 108(C8), 3273. doi: 10.1029/2000JC000521

Crossref Full Text | Google Scholar

Mellor G. L., Kantha L. (1989). An ice-ocean coupled model. J. Geophysical Res. 94, 10937–10954. doi: 10.1029/JC094iC08p10937

Crossref Full Text | Google Scholar

Ohshima K. I., Mizuta G., Itoh M., Fukamachi Y., Watanabe T., Nabae Y., et al. (2001). Winter oceanographic conditions in the Southwestern part of the Okhotsk sea and their relation to sea ice. J. Oceanography 57, 451–460. doi: 10.1023/A:1021225303621

Crossref Full Text | Google Scholar

Olason E. (2016). A dynamical model of Kara Sea land-fast ice. J. Geophysical Res. 121, 3141–3158. doi: 10.1002/2016JC011638

Crossref Full Text | Google Scholar

Ólason E. Ö., Harms I. (2010). Polynyas in a dynamic thermodynamic sea-ice model. Cryosphere 4, 147–160. doi: 10.5194/tc-4-147-2010

Crossref Full Text | Google Scholar

Saha S., Moorthi S., Wu X., Wang J., Nadiga S., Tripp P., et al. (2011). Updated Monthly. NCEP Climate Forecast System Version 2 (CFSv2) Selected Hourly Time-Series Products (Research data archive at the national center for atmospheric research, computational and information systems laboratory) (Accessed 2016-08-10).

Google Scholar

Sasaki H., Nonaka M., Masumoto Y., Sasai Y., Uehara H., Sakuma H. (2008). “An eddy-resolving hindcast simulation of the quasi-global ocean from 1950 to 2003 on the Earth Simulator,” in High resolution numerical modelling of the atmosphere and ocean. Eds. Ohfuchi W., Hamilton K. (NY: Springer New York), p157–p185. doi: 10.1007/978-0-387-49791-4_10

Crossref Full Text | Google Scholar

Screen J. A., Bracegirdle T. J., Simmonds I. (2018). Polar climate change as manifest in atmospheric circulation. Curr. Climate Change Rep. 4, 383–395. doi: 10.1007/s40641-018-0111-4

PubMed Abstract | Crossref Full Text | Google Scholar

Semtner A. (1976). Model for thermodynamic growth of sea ice in numerical investigations of climate. J. Phys. Oceanography 6, 379–389. doi: 10.1175/1520-0485(1976)006<0379:AMFTTG>2.0.CO;2

Crossref Full Text | Google Scholar

Sirevaag A. (2009). Turbulent exchange coefficients for the ice/ocean interface in case of rapid melting. Geophysical Res. Lett. 36, 144–155. doi: 10.1029/2008GL036587

Crossref Full Text | Google Scholar

Su J., Wu H., Liu Q., Zhang Y., Bai S. (2005). A coupled ice-ocean model for the Bohai Sea I. Study Model. parameter. Acta Oceanologica Sin. 27, 19–26.

Google Scholar

Timmermann R., Wang Q., Hellmer H. H. (2012). Ice-shelf basal melting in a global finite-element sea-ice/ice-shelf/ocean model. Ann. Glaciology 53, 303–304. doi: 10.3189/2012AoG60A156

Crossref Full Text | Google Scholar

Toole J. M., Timmermans M.-L., Perovich D. K., Krishfield R. A., Proshutinsky A., Richter-Menge J. A. (2010). Influences of the ocean surface mixed layer and thermohaline stratification on Arctic Sea ice in the central Canada Basin. J. Geophysical Res. 115, C10018. doi: 10.1029/2009JC005660

Crossref Full Text | Google Scholar

Wang K., Liu P., Jin S., Wang N., Yu Z. (2017). Sea-ice growth and decay model of Bohai Sea based on thermodynamic process. Adv. Water Sci. 28, 116–123. doi: 10.14042/j.cnki.32.1309.2017.01.013

Crossref Full Text | Google Scholar

Wang R., Liu X., Zhang L. (1984). Numerical tests on sea ice in the Bohai Sea. Acta Oceanologica Sin. 6, 572–580.

Google Scholar

Wang K., Wang C., Wu H. (2000). A solution of sea ice thermodynamic process for the Bohai Sea. Mar. Sci. Bull. 19, 1–11.

Google Scholar

Wang Z., Wu H. (1994). Sea ice thermal processes and simulation of their coupling with the dynamic process. Oceanologia Limnologia Sin. 25, 408–415.

Google Scholar

Wang K., Wu H., Wang C., Wu S. (1999). A study of basic hydrologic and meteorological parameters in the ice-covered Bohai Sea. Mar. Sci. Bull. 18, 17–28.

Google Scholar

Wettlaufer J. S. (1991). Heat flux at the ice-ocean interface. J. Geophysical Research: Oceans 96, 7215–7236. doi: 10.1029/90JC00081

Crossref Full Text | Google Scholar

Wu L., Wu H., Li W., Liu Q., Zhang Y., Liu Y., et al. (2005). Sea ice drifts in response to winds and tide in the Bohai Sea. Acta Oceanologica Sin. 27, 15–21. doi: 10.3321/j.issn

Crossref Full Text | Google Scholar

Yaglom A. M., Kader B. A. (1974). Heat and mass transfer between a rough wall and turbulent flow at high Reynolds and Peclet numbers. J. Fluid Mechanics 62, 601–623. doi: 10.1017/S0022112074000838

Crossref Full Text | Google Scholar

Yan Y., Gu W., Gierisch A. M. U., Xu Y., Uotila P. (2022). NEMO-Bohai 1.0: a high-resolution ocean and sea ice modelling system for the Bohai Sea, China. Geoscientific Model. Dev. 15, 1269–1288. doi: 10.5194/gmd-15-1269-2022

Crossref Full Text | Google Scholar

Yan R., Zhang X., Bi W., Wang N., Zhao Y., Bi L., et al. (2024). Extraction and analysis of the sea ice parameter dataset of the Bohai Sea from 2011 to 2021 based on GOCI. Front. Mar. Science. 11, 1364889. doi: 10.3389/fmars.2024.1364889

Crossref Full Text | Google Scholar

Yang G. (2000). Bohai sea ice conditions. J. Cold Regions Eng. 14, 54–67. doi: 10.1061/(ASCE)0887-381X(2000)14:2(54)

Crossref Full Text | Google Scholar

Yang Y. (2015). Parameter identification system of the oceanic heat flux between ice and water. Mathematics Pract. Theory 45, 78–88. doi: CNKI:SUN:SSJS.0.2015-03-011

Google Scholar

Yu L., Liu J., Gao Y., Shu Q. (2022). A sensitivity study of Arctic ice-ocean heat exchanges to the three-equation boundary condition parametrization in CICE6. Adv. Atmospheric Sci. 39, 1398–1416. doi: 10.1007/s00376-022-1316-y

Crossref Full Text | Google Scholar

Zhao F., Dong R., Wu L., Song J., Jiang J., Zhang D. (2022). Analysis of ice conditions in JZ20-2 sea area in Liaodong Bay, Bohai Sea during the winter of 2012/2022. Appl. Sci. Technol. 49, 141–146. doi: 10.11991/yykj.202209021

Crossref Full Text | Google Scholar