Spatiotemporal similarity of relative dispersion in the Gulf of Mexico

How a pair of pollutant parcels deviates from each other with an initial separation distance r₀, known as relative dispersion or Richardson dispersion, is relevant in many circumstances. This study examines the spatiotemporal similarity of the Richardson relative dispersion in the Gulf of Mexico by reanalyzing the Lagrangian trajectory of the surface drifter provided by two famous field experiments, that is, the Grand Lagrangian Deployment and the Lagrangian Submesoscale Experiment. The experimental dispersion curve indicates a critical separation time. When above this critical time, the dispersion shows an asymptotic power law growth independent of the initial separation distance r₀. Below it, the dispersion curve shows a strong spatiotemporal dependence with two spatiotemporal similarity regimes that can be identified for both experiments by looking at the isoline of the normalized dispersion curve. A new similarity variable is introduced to successfully collapse measured dispersion curves. However, the observed spatiotemporal similarity cannot be reproduced by the submesoscale preserved model. Thus, our results suggest that small-scale fluctuations play a crucial role in the relative dispersion of oceanic flows.

1 Introduction

The dispersion in the ocean and atmosphere is primarily controlled by the presence of various scales of motion, including small-scale turbulence (ranging from a few millimeters to hundreds of meters), submesoscale eddies (ranging from a few hundred meters to a few kilometers), mesoscale eddies (from a few to several dozen kilometers), and large-scale circulations (ranging from a few hundred to thousands of kilometers), among others (Thorpe, 2005; Vallis, 2017). To characterize the dispersion of fluid parcels or other scalars, such as temperature, salinity, nutrients, and biological and pollutant concentrations, to name a few, the single-particle dispersion (also known as absolute dispersion or Taylor dispersion) or the pair dispersion (also known as relative dispersion or Richardson dispersion) in the Lagrangian framework is often taken into account (Taylor, 1922; Richardson, 1926; Batchelor, 1950). In practice, relative dispersion is typically quantified using the mean squared displacement (MSD) $D_R(r_0,\tau )$ between two particles as a function of separation time τ and initial separation distance r₀ to see how they separate from each other; see the definition in Section 2.2. Theoretical consideration of three-dimensional homogeneous and isotropic turbulence suggests an asymptotic cubic growth of the MSD for a large separation time scale t, known as Richardson’s law of dispersion (Richardson, 1926; Batchelor, 1950). However, observing Richardson’s dispersion law in laboratory or field experiments is challenging due to the need for a significant separation of scales between the dissipative length, the initial separation distances of the tracers, the maximum observation range and the integral scale of the flow (Sawford, 2001; Salazar and Collins, 2009), and the influence of small-scale intermittency (Tan and Ni, 2022). Alternatively, other methods have been deployed to study the dispersion, for example, the finite-size Lyapunov exponent (FSLE) (Berti et al., 2011; Zavala Sansón, 2015; Berti and dos Santos, 2016; Sansón et al., 2017; Essink et al., 2019; Meyerjürgens et al., 2020; Balwada et al., 2021; Berti and Lapeyre, 2021; Meunier et al., 2021), pair separation probability density function (PDF) (Sansón et al., 2017; Essink et al., 2019; Balwada et al., 2021; Meunier et al., 2021), and structure functions (Poje et al., 2014; Callies et al., 2019; Essink et al., 2019; Balwada et al., 2021; Spydell et al., 2021), to name a few. These methods can characterize spatial and temporal variations in particle motion and can also provide information on the collective behavior of groups of particles and additional information on the chaotic nature of geophysical flows and associated turbulence. Despite the limitation mentioned above in direct calculation of the MSD of the relative dispersion, it is still widely used; for example, experimental evidence of both the ballistic and cubic regimes of the MSD predicted by dispersion theory has been reported (Bourgoin et al., 2006; Ni and Xia, 2013; Thalabard et al., 2014; Bourgoin, 2015; Sansón et al., 2017; Essink et al., 2019; Xia et al., 2019; Meyerjürgens et al., 2020; Balwada et al., 2021; Berti and Lapeyre, 2021; Spydell et al., 2021; Tan and Ni, 2022; Shnapp et al., 2023, 2024). However, Richardson’s dispersion law has not yet been fully validated, due to several limitations. For example, the time scale range τ or initial separation distance r₀ of the cubic growth of $D_R(r_0,\tau )$ is shorter than expected by theory; as a consequence of the finite size of the system or observation area or intermittency correction, the scaling exponent of the MSD has also shown an r₀ dependence (Xia et al., 2019; Tan and Ni, 2022; Shnapp et al., 2023).

Instead of verifying the ballistic and cubic regimes of the MSD, in this work, a spatiotemporal similarity implicated by dispersion theory is pursued using data from two surface drifter datasets in the Gulf of Mexico (GoM). With the observed similarity parameters, we introduce a new variable to successfully collapse the normalized dispersion curve. The new normalized dispersion curve shows the generalized exponential growth and is then followed by power law growth with scaling exponents coincidentally agreeing with the ballistic or cubic law. The remainder of this work is structured as follows. Section 2.1 provides a description of the datasets used in the study. Section 2.2 briefly discusses the theoretical consideration. Moreover, OceanParcels is introduced in Section 2.3. The experimental results are presented in Section 3. Finally, we provide a discussion and a summary of this study in Section 4.

2 Data and method

2.1 Field experiments in Gulf of Mexico

After the Deepwater Horizon oil spill disaster in April 2010, extensive field observations were conducted to gain a deeper understanding of the region dynamics in the GoM. The Grand Lagrangian Deployment (GLAD) in 2012 and the Lagrangian Submesoscale Experiment (LASER) in 2016, conducted by the Consortium for Advanced Research on Transport of Hydrocarbon in the Environment (CARTHE), are the two largest field experiments, deploying more than 300 and 1,000 drifters, respectively. These experiments were carried out in the northern GoM near the Deepwater Horizon site, the Louisiana coast, and the DeSoto Canyon, as shown in Supplementary Figure S1. The GLAD experiment, conducted from July 2012 to January 2013, utilized Global Positioning System (GPS) technology for a detailed time series analysis of drifter positions, revealing complex and non-Gaussian statistical parameters of the velocity field (Mariano et al., 2016). The LASER experiment, which ran from January to April 2016, provided high-resolution observations of the surface velocity field, significantly improving our understanding of submesoscale velocity fields and geostrophic circulation (Gonçalves et al., 2019). The lifetimes of each drifter are depicted in Supplementary Text S1 and Supplementary Figure S2.

In the GLAD experiment, drifters were deployed following the design principles of the Coastal Ocean Dynamics Experiment (CODE) (Davis, 1985). These drifters, which are depicted in Supplementary Figure S3A, had drogues set at a depth of 1 m. The Globalstar satellite network was used to track their positions, updating every 5 min with an estimated accuracy of 7 m. Challenges such as intermittent satellite signals, data losses, and issues with drifter recovery were addressed (Yaremchuk and Coelho, 2015). The final dataset comprised 297 drifters, with tracking periods ranging from 4 to 94 days. The average tracking duration was 56 days, with a standard deviation of 28 days. Analyses were performed on this dataset to assess relative dispersion, highlighting submesoscale eddy effects (Poje et al., 2014), and to evaluate Lagrangian intermittency (Lin et al., 2017).

In the LASER experiment, CARTHE designed biodegradable drifters, illustrated in Supplementary Figure S3B, with drogues positioned 0.4 m below the surface to track near-surface currents. These drifters utilized Spot GPS technology to report their positions every 5 min, achieving location accuracy within 10 m (Novelli et al., 2017). However, challenges such as adverse weather conditions or interactions with marine life sometimes caused drogue loss, reducing the number of GPS records and increasing wind sensitivity, thus impacting tracking precision (Haza et al., 2018). Undrogued drifters exhibited significantly higher mobility compared to their drogued counterparts, leading to data discrepancies. To align with data from the GLAD experiment and to minimize data from undrogued units, only drogued drifters were analyzed in the LASER dataset, which underwent rigorous quality checks including 15-min interpolation and verification of drogue status (D’Asaro et al., 2017). The dataset included 959 drifters, with trajectory durations varying from 5 h to 89 days. The average duration was 25 days, with a standard deviation of 20 days.

2.2 Relative dispersion of two particles

Two-particle dispersion, also known as relative dispersion or Richardson dispersion, is a crucial phenomenon in turbulent flows, with relevance in a wide range of applications, including ocean pollution, passive scalar advection, and rescue missions (Falkovich et al., 2001; Sawford, 2001; Salazar and Collins, 2009; Corrado et al., 2017). The prediction of superdiffusivity in pair dispersion dates back to 1926 when Richardson (1926) suggested that for a large time separation τ, the MSD should be independent of the initial separation distance r₀ and should increase with time as ${\tau }^3$ when $r_0$ is in the inertial range (Salazar and Collins, 2009), which is written as follows:

$\begin{array}{ll}{D}_R(r_0,\tau )=\langle r_{ij}{(r_0,t+\tau )}^2{\rangle }_t=gϵ{\tau }^3& (1)\end{array}$

in which $r_{ij}(r_0,t+\tau ) = \left|{\overrightarrow{x}}_i(t+\tau ) -{\overrightarrow{x}}_j(t+\tau )\right|$ is the great circle distance between the chance pair of the ith and jth drifters at time $t+\tau$ and $r_0=r_{ij}(r_0,t+\tau ){|}_{\tau }{}_{=0}$ is the initial separation distance when they were paired; τ is the separation time after they were paired (LaCasce and Bower, 2000; LaCasce and Ohlmann, 2003; LaCasce, 2008); $ϵ$ is the mean energy dissipation rate of the flow, and g is the Richardson constant (Sawford, 2001; Salazar and Collins, 2009) (see the diagram of relative dispersion in Supplementary Figure S4); and ${\langle ·\rangle }_t$ means average over time t. Later, Batchelor (1950) refined Richardson’s dispersion relation within Kolmogorov’s theory of three-dimensional hydrodynamic turbulence (Kolmogorov, 1941; Obukhov, 1941). When the separation time $\tau \ll t_B$, a so-called Batchelor regime is written as

$\begin{array}{ll}{D}_B(r_0,\tau )=\langle {(r_{ij}(r_0,\tau )-r_0)}^2{\rangle }_t=\frac{11}{3}{C}_B{(r_0ϵ)}^{2/3}{\tau }^2,\tau \ll t_B& (2)\end{array}$

where $t_B=r_0^{2/3}{ϵ}^{-1/3}$ is the so-called Batchelor time scale (Sawford, 2001; Bourgoin et al., 2006; Salazar and Collins, 2009); $C_B$ is the Kolmogorov constant for the longitudinal second-order velocity structure function (Sawford, 2001). For a long separation time τ, that is, $\tau \gg t_B,D_B(r_0,\tau )$ is expected to have an asymptotic approach to the Richardson dispersion law above.

Now, we consider normalized MSDs by their initial separation distance $r_0$, i.e., $M_R(r_0,\tau )=D_R(r_0,\tau )/r_0^2$ and $M_B(r_0,\tau )=D_B(r_0,\tau )/r_0^2$. Both Equations 1 and 2 can be rewritten as functions of a dimensionless time variable $\tau /t_B=\tau r_0^{-2/3}{ϵ}^{1/3}$. This implies a spatiotemporal similarity for the case of three-dimensional hydrodynamic turbulence. In real oceanic flows, owing to the presence of other motions, such as mesoscale eddies, waves, and tides, to name a few, both ballistic and cubic regimes may not be well defined, and the energy dissipation rate ϵ is difficult to retrieve or varies greatly with space and time due to the non-stationarity of the flow. Therefore, the spatiotemporal similarity may not follow the one indicated by the Batchelor time scale. Thus, we introduce a new variable $\mathcal{T}=\tau r_0^{-\text{γ}}$ to characterize spatiotemporal similarity in the normalized relative dispersion $M_R(r_0,\tau )$. The experimental scaling exponent of γ was then extracted from the field experiment data. Note that the spatiotemporal similarity by Batchelor’s theory is recovered when γ = 2/3.

2.3 OceanParcels virtual drifters tracking

In this work, we also compared our results with the output from the MITgcm LLC4320 model. We use OceanParcels, a cutting-edge tool for simulating particle movement in marine environments due to its flexibility and efficiency (Delandmeter and Van Sebille, 2019; Kehl et al., 2023). This package excels at modeling the transport of various particles, such as biogeochemical elements, plastics, and marine life, through the ocean by simulating their paths in three-dimensional water currents, based on modeled and observed data. Its ability to perform large-scale simulations involving millions of particles is supported by advanced computational methods, making it invaluable for detailed studies on particle dispersion under various oceanic conditions. Here, we use the surface velocity field data from the first layer (e.g., 0.5 m below the surface) of the MITgcm LLC4320 model (Marshall et al., 1997; Forget et al., 2015; Arbic et al., 2018), which has a vertical resolution of 90 levels and a spatial resolution 1/48 degree, ≃ 2 km, with a simulation time step of 25 s. The instantaneous results are stored at 1-h intervals. Tidal processes are incorporated to effectively model the interactions between continental shelves and slopes, as well as the alteration of water masses, which influence the overall global ocean circulation (Flexas et al., 2015). The surface conditions are based on atmospheric data from the European Centre for Medium-Range Weather Forecasts (ECMWF) operational model at a 0.14° resolution, starting from the year 2011. The simulation period is divided into Autumn–Winter and Spring–Summer, corresponding to the months of the GLAD and LASER experiments, respectively. Two sets of numerical experiments were performed to track virtual particles released in the same position as those of the actual field experiments (see Supplementary Figure S1). To ensure the accuracy and stability of the simulation, the fourth-order Runge–Kutta time advance is used with a time step of 20 min. Previous studies have demonstrated that this model is capable of preserving submesoscale features (Lin et al., 2020; Yang et al., 2021), thereby providing a reliable framework for our particle tracking experiments.

3 Results

In the calculation of MSD $D_R(r_0,\tau )$, different initial separation scales r₀ are considered on a logarithmic scale from 10 m to 10 km where 2/3 power law of the second-order structure function roughly holds with a width of 20% for each value (see Supplementary Text S2, Supplementary Figure S5 for detailed reason for selecting initial separation scales). These spatial scales r₀ are in the three-dimensional and submesoscale range (Poje et al., 2014, 2017). Figures 1A, C present the experimental relative dispersion $D_R(r_0,\tau )$ of the GLAD and LASER drifters, in which the increase in r₀ is indicated by the vertical arrow. The number of drifter pairs is plotted in Supplementary Figure S6, and the statistical MSD data for sample sizes less than 1,000 are excluded. At first glance, they show a strong dependence on r₀. For the GLAD case, different from the prediction of the Richardson dispersion theory, the dispersion curve of the smallest r₀ = 10 m shows three different regimes of $D_R(r_0,\tau )\propto {\tau }^{\alpha }$ with scaling exponents roughly from 2 to ≃3.5 and to ≃1.6 when τ ≥ 16 days. Note that the first two regimes are separated by a time scale of approximately 1 day, which could be the effect of the strong diurnal tide (Lin et al., 2017). With increasing r₀, the scaling exponent α, evaluated over the interval 2 ≤ τ ≤ 16 days, appears to remain constant at approximately 3.5 in the range 10 ≤ r₀ ≤ 200 m and then declines linearly to 2 for r₀ ≥ 200 m. Refer to the inset in Figure 1A, which shows that the 95% confidence interval provided by the least squares fitting method is too narrow to be visible. The Richardson law holds true at approximately r₀ = 1,100 m. It is notable that in homogeneous and isotropic turbulence, a value of approximately r₀/η ≃ 3 has been observed, where η is known as the Kolmogorov scale (Tan and Ni, 2022). Moreover, an asymptotic behavior is evident when the separation time above a critical time scale t_c ≃ 16 days: all dispersion curves collapse with each other with a slope α ≃ 1.58. It appears to be an effect of the finite size of the flow system, e.g., $\mathcal{O}$ (1,000) km, since for a long-time evolution, the MSD should reach the same destination. In other words, for a smaller r₀, it moves faster than a larger r₀ to reach the same endpoint at the same time, resulting in a decrease of α for a median separation time τ, as observed in other literature (Tan and Ni, 2022; Shnapp et al., 2023).

Figure 1

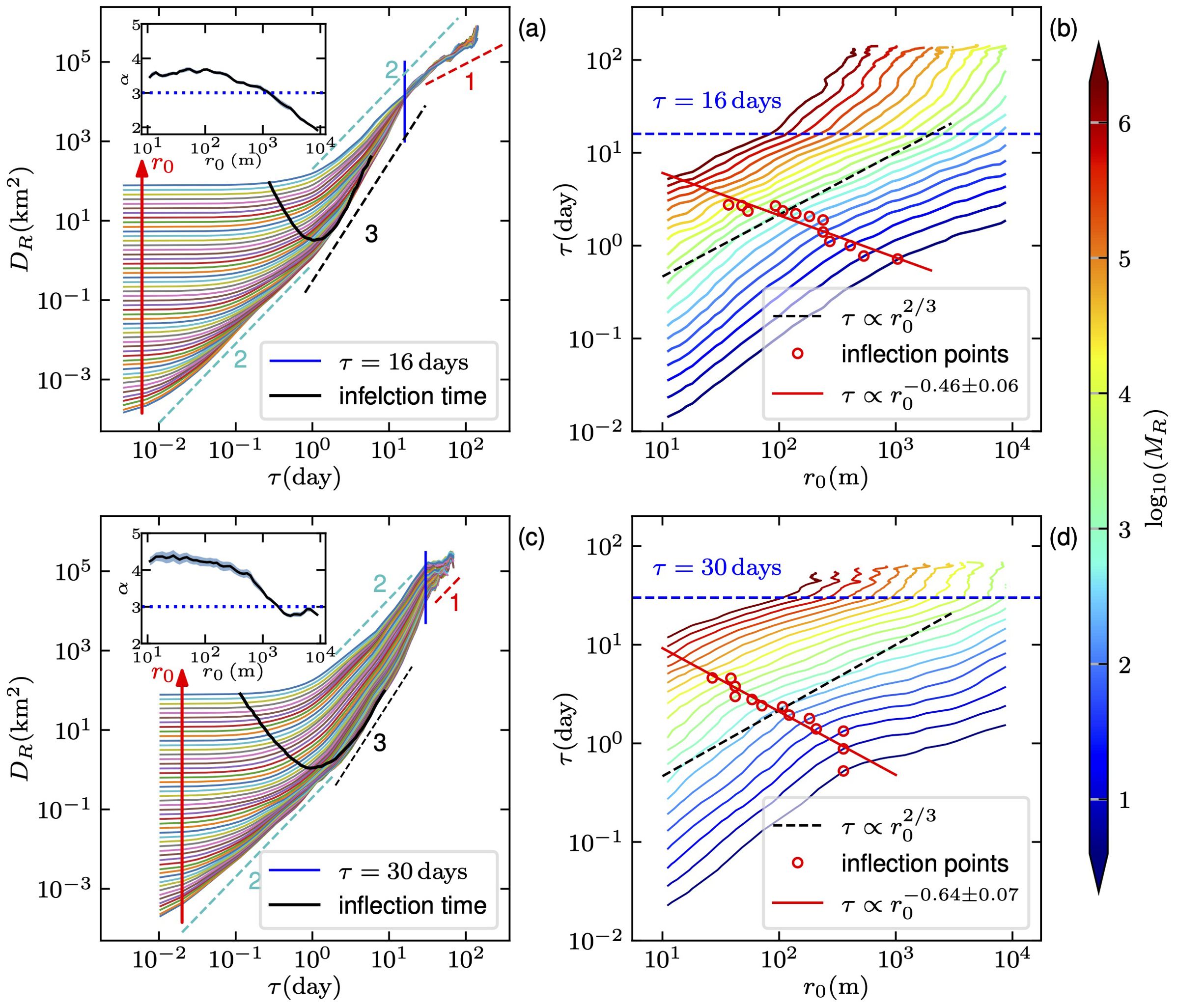
Figure 1. (A, C) show the relative dispersion curve $D_R(r_0,\tau )$ for the GLAD and LASER experiments, respectively. Each curve represents a different initial separation distance r₀, increasing on a logarithmic scale from 10 m to 10 km. Dashed lines with labeled slopes represent power law relationships for reference. (B, D) feature contour plots of normalized MSD $M_R(r_0,\tau )$ for the GLAD and LASER experiments, respectively. The red circles indicate inflection points on each isoline, and the red straight lines are power law fits of these points. The thick black lines in (A, C) depict the measured $D_R(r_0,\tau )$ at the experimental inflection points. The insets in (A, C) show the measured scaling exponent $\alpha (r_0)$, respectively, on the range 2 ≤ τ ≤ 16 days and 10 ≤ τ ≤ 30 days for GLAD and LASER experiments, where the blue band indicates a 95% fitting confidence level.

In the LASER case, a similar evolution pattern is observed; see also the scaling exponent α estimated on the range 10 ≤ τ ≤ 30 days in the inset of Figure 1C. For example, for the case r₀ = 10 m, three scaling regimes of MSDs are also observed, and the separation time scale of first two regimes is 1 day. However, the asymptotic behavior observed here is different from that of the GLAD case due to the seasonal variation of the flow pattern. For example, beyond the critical time scale t_c ≃ 30 days, the experimental dispersion curves tend to reach the same distance. It could be expected that if we have a long enough observation, the dispersion curve might reach the same asymptotic behavior as observed for the GLAD experiment.

Figures 1B, D show the isoline levels of the corresponding normalized MSDs $M_R(r_0,\tau )$ in a log–log view, in which the spatiotemporal 2/3 scaling indicated by Batchelor theory is illustrated as a dashed line. For the GLAD case, when τ ≤ 16 days, the dual power law behavior of small $M_R(r_0,\tau )$ is evident, with scaling exponents below and above the 2/3 value, respectively. As r₀ and τ increase, this dual power law behavior gradually transitions to a single power law. The inflection point is then identified using a search algorithm; see details in Supplementary Text S3. These inflection points follow a power law trend that decays $\tau \propto r_0^{-\beta }$ with β ≃ 0.46 ± 0.06. Beyond τ = 16 days, the isoline follows a power law behavior with a scaling exponent 1.28 ± 0.04, where the uncertainty corresponds to the standard deviation of the calculated scaling exponents for the isolines. The observed triple power law behavior implies a different spatiotemporal similarity for different initial separation distance r₀ and separation time τ.

For the LASER case, we observe a similar pattern as in the GLAD case. Similarly with the GLAD case, when τ ≤ 30 days, a dual power law behavior with the inflection point satisfies the power law relation $t\propto r_0^{-0.64\pm 0.07}$. It is interesting to note that if the MSD $D_R(r_0,\tau )$ at the inflection point is shown against the separation time τ, the LASER one seems to parallel the GLAD one, showing a similarity between these two experiments; see Figures 1A, C; see also the reproduced plot in Supplementary Figure S7. When τ ≥ 30 days, the third power law regime is clearly evident with a scaling exponent 1.21 ± 0.04; see Figure 1D. Inspired by these observations, we introduce a new variable $\mathcal{T}=\tau r_0^{-\text{γ}}$ as mentioned above, in which γ is a spatiotemporal similarity parameter experimentally determined. Note that except for the case γ = 2/3, $\mathcal{T}$ cannot be normalized by ϵ as a dimensionless variable.

The experimental scaling exponent γ was calculated as the mean value of the scaling exponent for each regime’s isoline for values 0.6 ≤ log₁₀(M_R) ≤ 6.5 in steps of 0.3, and the standard deviation indicates the uncertainty. For the GLAD experiment, the values are γ = 0.90 ± 0.09, 0.50 ± 0.04, and 1.28 ± 0.04, while for the LASER experiment, they are γ = 0.91 ± 0.10, 0.37 ± 0.04, and 1.21 ± 0.04, respectively. It is noteworthy that, with the exception of the second regime, the experimental γ values are quite similar between the GLAD and LASER experiments. Figure 2 shows the scatter points of the normalized MSD $M_R(\mathcal{T})$ using experimental γ to emphasize the spatiotemporal similarity. Visually, they collapse well with each other for all three regimes. In the following, we provide the details of each regime.

Figure 2

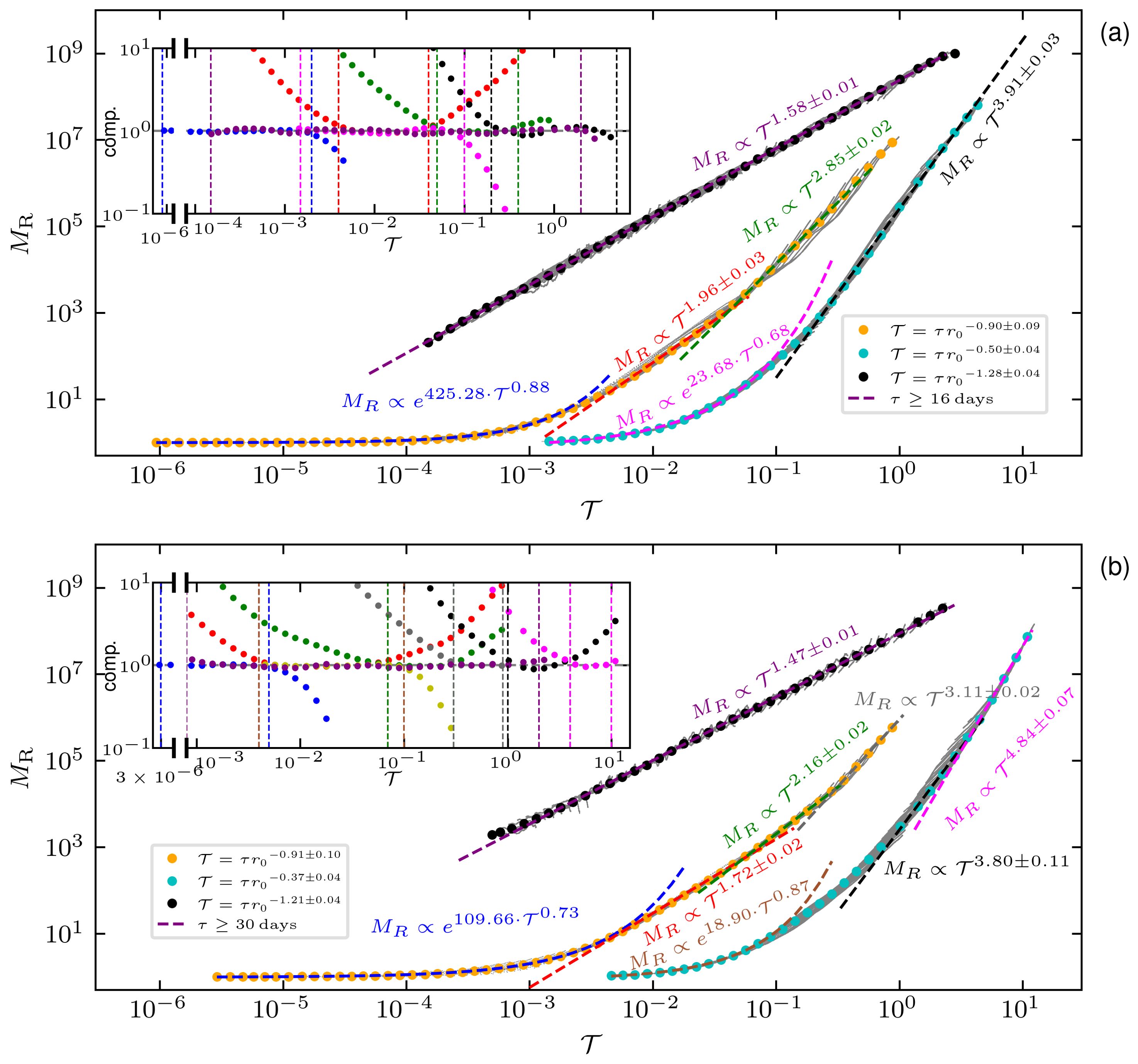
Figure 2. The normalized dispersion curve $M_R(\mathcal{T})$ for the (A) GLAD and (B) LASER experiments using the new similarity variable $\mathcal{T}$. The gray scatter dots illustrate the curve, mostly obscured by the data points. Colored symbols denote mean values of $M_R(\mathcal{T})$, aggregated by 10 points per order of magnitude. Colored dashed lines represent generalized exponential and power law fits of these means. Insets show the compensated curves with fit ranges highlighted by vertical colored lines for clarity.

i) The first spatiotemporal similarity regime: For the initial stage of the first regime, the rescaled dispersion curve can be fitted using a generalized exponential function, that is $M_R(\mathcal{T})\propto e^a{}^{{\mathcal{T}}^{\zeta }}$, with ζ = 0.88 ± 0.03 and 0.73 ± 0.02, respectively, in the range 9×10⁻⁷ ≤ $\mathcal{T}$ ≤ 0.002 and 3×10⁻⁶ ≤ T ≤ 0.005 for the cases GLAD and LASER, for more than three orders of $\mathcal{T}$; see Figure 2. To emphasize the observed generalized exponential law, the compensated curves are shown in the inset. Above the initial stage, the dispersion curve transits to the power law behavior, that is, $M_R(\mathcal{T})\propto {\mathcal{T}}^{\xi }$, with more than one order of $\mathcal{T}$. For the GLAD case, a Batchelor-like ballistic regime is found in the range 0.004 ≤ $\mathcal{T}$ ≤ 0.04 with a scaling exponent 1.96 ± 0.03. Then, it is followed by a Richardson-like cubic regime in the range 0.05 ≤ $\mathcal{T}$ ≤ 0.4 with a scaling exponent 2.85 ± 0.02. However, for the LASER case, three distinct power law regimes are observed: the first within 0.004 ≤ $\mathcal{T}$ ≤ 0.07 with a scaling exponent of 1.72 ± 0.02, which is lower than that typically associated with the Batchelor regime; the second within 0.07 ≤ $\mathcal{T}$ ≤ 0.3 with a scaling exponent of 2.16 ± 0.02, slightly above the Batchelor range; and the third within 0.3 ≤ $\mathcal{T}$ ≤ 1, followed by a scaling exponent of 3.11 ± 0.02, approaching the cubic growth described by the Richardson law.

ii) The second spatiotemporal similarity regime: The scatter plot of the second spatiotemporal similarity regime is also shown in Figure 2. Visually, they first obey a generalized exponential growth with a scaling exponent ζ = 0.68 ± 0.06 for the GLAD and 0.87 ± 0.10 for the LASER, within the range 0.0015 ≤ $\mathcal{T}$ ≤ 0.1 for GLAD and 0.004 ≤ $\mathcal{T}$ ≤ 0.1 for LASER. Subsequently, a transition to power law behavior is observed. For the GLAD, a single power law behavior is used to fit the data in the range 0.2 ≤ $\mathcal{T}$ ≤ 5 with a scaling exponent ξ = 3.91 ± 0.03. It is more complex for the LASER case; for instance, three different power laws may be identified for at least half the order of $\mathcal{T}$, e.g., five points on a logarithmic scale. The corresponding scaling exponents are ξ = 3.80 ± 0.11 and 4.84 ± 0.07, respectively, in the range 1 ≤ $\mathcal{T}$ ≤ 4 and 4 ≤ $\mathcal{T}$ ≤ 10. Note that these scaling exponents are significantly different from the theoretical prediction of the ballistic or cubic laws.

iii) The third spatiotemporal similarity regime: For large time evolution, e.g., τ ≥ 16 days and τ ≥ 30 days for the GLAD and LASER experiments, the experimental dispersion curves $D_R(r_0,\tau )$ tend to be independent of the initial separation distance r₀ with a scaling exponent α = 1.50 ± 0.01 for the GLAD, while it is not obvious for the LASER experiment. A scaling relation between $D_R(r_0,\tau )$ and $M_R(\mathcal{T})$ in this regime indicates a scaling relation αβ = 2 and ξ = α (Supplementary Text S4 contains the derivation of the formulas), which is validated by the experimental values α ≃ 1.50, β ≃ 1.28, and ξ ≃ 1.58 for the GLAD experiment for more than four orders of $\mathcal{T}$, that is, in the range 0.00015 ≤ $\mathcal{T}$ ≤ 2; see Figures 1A, B, 2A. For the LASER experiment, the third spatiotemporal similarity regime is short; see Figures 1C, D. However, the power law behavior of $M_R(\mathcal{T})$ is observed for more than three orders of $\mathcal{T}$, that is, in the range 0.0008 ≤ $\mathcal{T}$ ≤ 2 with a scaling exponent 1.47 ± 0.01; see Figure 2B. This provides an opportunity to extract the scaling exponent α in a more accurate way with a significant extended power law behavior.

Supplementary Tables S1, S2 summarize the symbols as well as the previously mentioned scaling exponents and their respective scale ranges.

4 Discussion and conclusions

Note that for the field experiment, the drifter can feel all size of oceanic motions, e.g., small-scale three-dimensional turbulence, waves, tides, submesoscale and mesoscale eddies, and loop current, to list a few. If we consider the finite-size effect of the drifter, some of the small-scale motions will be filtered out (Bec et al., 2010). On the other hand, the relative dispersion is believed to be the result of the accumulation effect of small-scale fluctuations (Thalabard et al., 2014; Bourgoin, 2015). Despite the very high Reynolds number, the Richardson law, that is, the cubic growth of the dispersion curve, is not expected in the real oceanic experiment for a range of the initial separation distance r₀. As we show above, the spatiotemporal similarity still holds. To see the capability of the ocean model, two numerical experiments are performed using the hourly data from the MITgcm LLC4320 with a spatial resolution Δx ≃ 2 km. Note that the submesoscale feature is expected to be preserved in this model (Lin et al., 2020). The virtual drifter was released at the same location as the GLAD and LASER experiments (see Supplementary Figure S1). Dispersion curves of these two virtual experiments are shown in Supplementary Figures S8A, S8B. Figures 3A, B show the contour plot of the normalized dispersion curve $M_R(r_0,\tau )$. For comparison, the normalized relative dispersion curve $M_R(r_0,\tau )$ of the three-dimensional hydrodynamic turbulence was calculated using Lagrangian data from the direct numerical simulation with a Reynolds number $R{e}_{\lambda }= 400$ (Bec et al., 2010). Figure 3C shows the experimental $M_R(r_0,\tau )$ with the initial separation distance in the range 11 ≤ r₀/η ≤ 500, where η is the so-called Kolmogorov scale. It confirms in the inertial range the existence of the spatiotemporal similarity $t\propto r_0^{2/3}$ presented in Section 2.2. However, visually, this spatiotemporal similarity is not evident in the simulations, likely due to the model’s inability to capture small-scale fluctuations. As noted by Poje et al. (2014), owing to the absence of submesoscale fluctuation, the long-time evolution of the dispersion from the geostrophic velocity produced by the AVISO altimeter data is significantly underestimated. Their results suggested that the submesoscale dynamics is critical for the model. Moreover, Supplementary Figure S8C shows that dispersion in real experiments is a little bit faster than in virtual experiments.

Figure 3

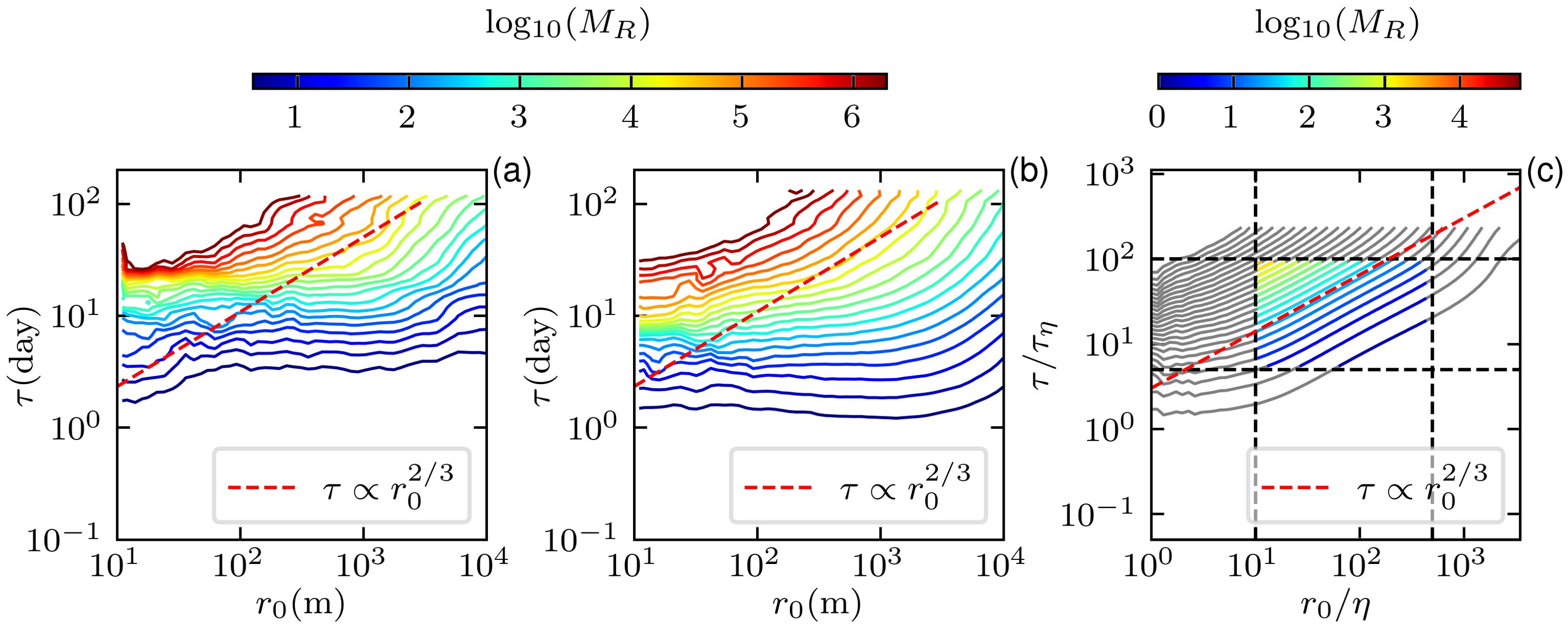
Figure 3. The normalized MSD $M_R(r_0,\tau )$ from MITgcm LLC4320 experiments: (A, B) correspond to the seasons of the GLAD and LASER experiments; (C) the direct numerical simulation of 3D hydrodynamic turbulence. The 2/3 scaling, implied by the dispersion theory, is depicted as a red dashed line. The dashed line in (C) denotes the inertial range 5 ≤ τ/τ_η ≤ 100 and 10 ≤ r₀/η ≤ 500.

Our results here suggest that small-scale fluctuation is also relevant when the relative dispersion is considered. Note that the scale separation in the real oceanic flow and the models is very different. For example, it is safe to estimate the Kolmogorov scale as η ≃ 1 mm (Thorpe, 2005). In the MITgcm LLC4320 model, the scale ratio between spatial resolution Δx and the Kolmogorov scale η is roughly of the order $\mathcal{O}$(10⁶). Therefore, at least six orders of the spatial scale of motion are missed. It seems that an additional parameter should be introduced in the dispersion model to represent the effect of the missed three-dimensional small-scale fluctuation (van Sebille et al., 2018). A systematic test might be performed in the near future using the high-resolution Surface Quasi-Geostrophic (SQG) model (Berti and Lapeyre, 2021) or the direct numerical simulation of the two-dimensional Kolmogorov flow (Fylladitakis et al., 2018) to see the filter effect of the spatial resolution.

Additionally, we observe that the relative dispersion processes of GLAD and LASER drifters have notable differences. Seasonal velocities and vorticity differences are evident; that is, the GLAD experiment was conducted in Winter and Spring, while the LASER experiment was conducted in Summer and Autumn. Such seasonal variations in circulation and eddy kinetic energy are known to significantly influence the relative dispersion of drifters in oceanographic studies. See more details of seasonal velocity and vorticity in GoM during GLAD and LASER experiments in Supplementary Figures S9–S13; for the description, see Supplementary Text S5.

In summary, here we consider the relative dispersion with a different initial separation distance from two field experiments in GoM. Instead of checking Richardson’s law, we study the spatiotemporal similarity implied by the dispersion theory. The raw dispersion curve $D_R(r_0,\tau )$ shows an asymptotic trend when the separation time is larger than a critical time t_c, e.g., 16 days and 30 days, respectively, for GLAD and LASER experiments. When the separation time τ is smaller than t_c, a dual power law behavior can be identified for the isoline of the normalized relative dispersion curve $M_R(r_0,\tau )$. The corresponding inflection point follows a power law decaying in spatiotemporal space. Moreover, the isolines of $M_R(r_0,\tau )$ seem to be in parallel with each other, confirming the existence of spatiotemporal similarity. Then, a new similarity variable $\mathcal{T} =\tau r_0^{-\gamma }$ is introduced to take into account the spatiotemporal similarity. When $M_R(r_0,\tau )$ is rewritten using $\mathcal{T}$, that is, $M_R(\mathcal{T})$, they collapse well with each other and show generalized exponential growths or power law growths. When the separation time is larger than t_c, the power law scaling exponent of $M_R(\mathcal{T})$ can be analytically related to their raw asymptotic scaling trend. Thus, it provides an alternative way to estimate the asymptotic scaling exponent with more precision. We also show that the experimental spatiotemporal similarity is not reproduced by the high-resolution model. Our results suggest that small-scale fluctuations play a crucial role in the relative dispersion, which poses a challenge to the existence dispersion model.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

YM: Formal analysis, Writing – original draft, Writing – review & editing. YH: Conceptualization, Investigation, Writing – original draft, Writing – review & editing. JH: Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is sponsored by the National Natural Science Foundation of China (No. U22A20579).

Acknowledgments

We would like to thank the Consortium for Advanced Research on Transport of Hydrocarbon in the Environment (CARTHE) for providing the valuable data used in this research. Their efforts in making the data accessible and maintaining its quality are greatly appreciated. We also thank the valuable comments and the nice suggestions from the Editor and two reviewers that help improve the article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1446297/full#supplementary-material

References

Arbic B. K., Alford M. H., Ansong J. K., Buijsman M. C., Ciotti R. B., Farrar J. T., et al. (2018). A primer on global internal tide and internal gravity wave continuum modeling in HYCOM and MITgcm. New Front. operat. oceanogr. 13, 307–392. doi: 10.17125/gov2018.ch13

Crossref Full Text | Google Scholar

Balwada D., Lacasce J. H., Speer K. G., Ferrari R. (2021). Relative dispersion in the Antarctic circumpolar current. J. Phys. Oceanogr. 51, 553–574. doi: 10.1175/jpo-d-19-0243.1

Crossref Full Text | Google Scholar

Batchelor G. K. (1950). The application of the similarity theory of turbulence to atmospheric diffusion. Q. J. R. Meteorol. Soc. 76, 133–146. doi: 10.1002/qj.49707632804

Crossref Full Text | Google Scholar

Bec J., Biferale L., Lanotte A., Scagliarini A., Toschi F. (2010). Turbulent pair dispersion of inertial particles. J. Fluid Mechan. 645, 497–528. doi: 10.1017/S0022112009992783

Crossref Full Text | Google Scholar

Berti S., dos Santos F. A. (2016). Relative dispersion and turbulence in the Southwestern Atlantic Ocean from drifter’s data. Chaotic Model. Simul. 1, 9–20.

Google Scholar

Berti S., Lapeyre G. (2021). Lagrangian pair dispersion in upper-ocean turbulence in the presence of mixed-layer instabilities. Phys. Fluids 33, 036603. doi: 10.1063/5.0041036

Crossref Full Text | Google Scholar

Berti S., Santos F. A. D., Lacorata G., Vulpiani A. (2011). Lagrangian drifter dispersion in the Southwestern Atlantic Ocean. J. Phys. Oceanogr. 41, 1659–1672. doi: 10.1175/2011jpo4541.1

Crossref Full Text | Google Scholar

Bourgoin M. (2015). Turbulent pair dispersion as a ballistic cascade phenomenology. J. Fluid Mechan. 772, 678–704. doi: 10.1017/jfm.2015.206

Crossref Full Text | Google Scholar

Bourgoin M., Ouellette N. T., Xu H., Berg J., Bodenschatz E. (2006). The role of pair dispersion in turbulent flow. Science 311, 835–838. doi: 10.1126/science.1121726

PubMed Abstract | Crossref Full Text | Google Scholar

Callies U., Carrasco R., Floeter J., Horstmann J., Quante M. (2019). Submesoscale dispersion of surface drifters in a coastal sea near offshore wind farms. Ocean Sci. 15, 865–889. doi: 10.5194/os-15-865-2019

Crossref Full Text | Google Scholar

Corrado R., Lacorata G., Palatella L., Santoleri R., Zambianchi E. (2017). General characteristics of relative dispersion in the ocean. Sci. Rep. 7, 46291. doi: 10.1038/srep46291

PubMed Abstract | Crossref Full Text | Google Scholar

D’Asaro E., Guigand C., Haza A., Huntley H., Novelli G., Özgökmen T., et al. (2017). Lagrangian Submesoscale Experiment (LASER) surface drifters, interpolated to 15-minute intervals (Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC), Harte Research Institute, Texas A&M University–Corpus Christi). doi: 10.7266/N7W0940J

Crossref Full Text | Google Scholar

Davis R. E. (1985). Drifter observations of coastal surface currents during CODE: the method and descriptive view. J. Geophys. Res.: Oceans 90, 4741–4755. doi: 10.1029/JC090iC03p04741

Crossref Full Text | Google Scholar

Delandmeter P., Van Sebille E. (2019). The Parcels V2.0 Lagrangian framework: New field interpolation schemes. Geosci. Model. Dev. 12, 3571–3584. doi: 10.5194/gmd-12-3571-2019

Crossref Full Text | Google Scholar

Essink S., Hormann V., Centurioni L. R., Mahadevan A. (2019). Can we detect submesoscale motions in drifter pair dispersion? J. Phys. Oceanogr. 49, 2237–2254. doi: 10.1175/jpo-d-18-0181.1

Crossref Full Text | Google Scholar

Falkovich G., Gawędzki K., Vergassola M. (2001). Particles and fields in fluid turbulence. Rev. Modern Phys. 73, 913–975. doi: 10.1103/RevModPhys.73.913

Crossref Full Text | Google Scholar

Flexas M., d. M., Schodlok M. P., Padman L., Menemenlis D., Orsi A. H. (2015). Role of tides on the formation of the Antarctic Slope Front at the Weddell-Scotia Confluence. J. Geophys. Res.: Oceans 120, 3658–3680. doi: 10.1002/2014JC010372

Crossref Full Text | Google Scholar

Forget G., Campin J.-M., Heimbach P., Hill C., Ponte R., Wunsch C. (2015). ECCO version 4: An integrated framework for non-linear inverse modeling and global ocean state estimation. Geosci. Model. Dev. 8, 3071–3104. doi: 10.5194/gmd-8-3071-2015

Crossref Full Text | Google Scholar

Fylladitakis E. D. (2018). Kolmogorov flow: Seven decades of history. J. Appl. Math. Phys. 6(11), 2227. doi: 10.4236/jamp.2018.611187

Crossref Full Text | Google Scholar

Gonçalves R. C., Iskandarani M., Özgökmen T., Thacker W. C. (2019). Reconstruction of submesoscale velocity field from surface drifters. J. Phys. Oceanogr. 49, 941–958. doi: 10.1175/jpo-d-18-0025.1

Crossref Full Text | Google Scholar

Haza A. C., D’Asaro E., Chang H., Chen S., Curcic M., Guigand C., et al. (2018). Drogue-loss detection for surface drifters during the Lagrangian Submesoscale Experiment (LASER). J. Atmos. Ocean. Technol. 35, 705–725. doi: 10.1175/jtech-d-17-0143.1

Crossref Full Text | Google Scholar

Kehl C., Nooteboom P. D., Kaandorp M. L. A., van Sebille E. (2023). Efficiently simulating Lagrangian particles in large-scale ocean flows — Data structures and their impact on geophysical applications. Comput. Geosci. 175, 105322. doi: 10.1016/j.cageo.2023.105322

Crossref Full Text | Google Scholar

Kolmogorov A. N. (1941). Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Doklady Akademii Nauk SSSR 30, 301. doi: 10.1098/rspa.1991.0075

Crossref Full Text | Google Scholar

LaCasce J. H. (2008). Statistics from lagrangian observations. Prog. Oceanogr. 77, 1–29. doi: 10.1016/j.pocean.2008.02.002

Crossref Full Text | Google Scholar

LaCasce J. H., Bower A. (2000). Relative dispersion in the subsurface North Atlantic. J. Mar. Res. 58, 863–894. doi: 10.1357/002224000763485737

Crossref Full Text | Google Scholar

LaCasce J. H., Ohlmann C. (2003). Relative dispersion at the surface of the Gulf of Mexico. J. Mar. Res. 61, 285–312. doi: 10.1357/002224003322201205

Crossref Full Text | Google Scholar

Lin H., Liu Z., Hu J., Menemenlis D., Huang Y. (2020). Characterizing meso- to submesoscale features in the South China Sea. Prog. Oceanogr. 188, 102420. doi: 10.1016/j.pocean.2020.102420

Crossref Full Text | Google Scholar

Lin L., Zhuang W., Huang Y. (2017). Lagrangian statistics and intermittency in Gulf of Mexico. Sci. Rep. 7, 17463. doi: 10.1038/s41598-017-17513-9

PubMed Abstract | Crossref Full Text | Google Scholar

Mariano A. J., Ryan E. H., Huntley H. S., Laurindo L. C., Coelho E., Griffa A., et al. (2016). Statistical properties of the surface velocity field in the northern Gulf of Mexico sampled by GALD drifters. J. Geophys. Res.: Oceans 121, 5193–5216. doi: 10.1002/2015jc011569

Crossref Full Text | Google Scholar

Marshall J., Adcroft A., Hill C., Perelman L., Heisey C. (1997). A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res.: Oceans 102, 5753–5766. doi: 10.1029/96jc02775

Crossref Full Text | Google Scholar

Meunier T., Pérez Brunius P., Rodríguez Outerelo J., García Carrillo P., Ronquillo A., Furey H., et al. (2021). A deep water dispersion experiment in the Gulf of Mexico. J. Geophys. Res.: Oceans 126, e2021JC017375. doi: 10.1029/2021jc017375

Crossref Full Text | Google Scholar

Meyerjürgens J., Ricker M., Schakau V., Badewien T. H., Stanev E. V. (2020). Relative dispersion of surface drifters in the North Sea: The effect of tides on mesoscale diffusivity. J. Geophys. Res.: Oceans 125. doi: 10.1029/2019jc015925

Crossref Full Text | Google Scholar

Ni R., Xia K.-Q. (2013). Experimental investigation of pair dispersion with small initial separation in convective turbulent flows. Phys. Rev. E 87, 63006. doi: 10.1103/PhysRevE.87.063006

PubMed Abstract | Crossref Full Text | Google Scholar

Novelli G., Guigand C. M., Cousin C., Ryan E. H., Laxague N. J. M., Dai H., et al. (2017). A biodegradable surface drifter for ocean sampling on a massive scale. J. Atmos. Ocean. Technol. 34, 2509–2532. doi: 10.1175/jtech-d-17-0055.1

Crossref Full Text | Google Scholar

Obukhov A. (1941). On the distribution of energy in the spectrum of turbulent flow. Doklady Akademii Nauk SSSR 5, 453–466.

Google Scholar

Poje A. C., Özgökmen T. M., Bogucki D. J., Kirwan A. (2017). Evidence of a forward energy cascade and Kolmogorov self-similarity in submesoscale ocean surface drifter observations. Phys. Fluids 29, 020701. doi: 10.1063/1.4974331

Crossref Full Text | Google Scholar

Poje A. C., Özgökmen T. M., Lipphardt J., Haus B. K., Ryan E. H., Haza A. C., et al. (2014). Submesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Natl. Acad. Sci. 111, 12693–12698. doi: 10.1073/pnas.1402452111

PubMed Abstract | Crossref Full Text | Google Scholar

Richardson L. F. (1926). Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. London Ser. A 110, 709–737. doi: 10.1098/rspa.1926.0043

Crossref Full Text | Google Scholar

Salazar J. P. L. C., Collins L. R. (2009). Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mechan. 41, 405–432. doi: 10.1146/annurev.fluid.40.111406.102224

Crossref Full Text | Google Scholar

Sansón L. Z., Pérez-Brunius P., Sheinbaum J. (2017). Surface relative dispersion in the Southwestern Gulf of Mexico. J. Phys. Oceanogr. 47, 387–403. doi: 10.1175/jpo-d-16-0105.1

Crossref Full Text | Google Scholar

Sawford B. (2001). Turbulent relative dispersion. Annu. Rev. Fluid Mechan. 33, 289–317. doi: 10.1146/annurev.fluid.33.1.289

Crossref Full Text | Google Scholar

Shnapp R., Brizzolara S., Neamtu-Halic M. M., Gambino A., Holzner M. (2023). Universal alignment in turbulent pair dispersion. Nat. Commun. 14, 4195. doi: 10.1038/s41467-023-39903-6

PubMed Abstract | Crossref Full Text | Google Scholar

Shnapp R., Liberzon A., Bohbot-Raviv Y., Fattal E. (2024). On local isotropy and scale dependence of pair dispersion in turbulent canopy flows. J. Fluid Mechan. 978, A3. doi: 10.1017/jfm.2023.1001

Crossref Full Text | Google Scholar

Spydell M. S., Feddersen F., Macmahan J. (2021). Relative dispersion on the inner shelf: Evidence of a batchelor regime. J. Phys. Oceanogr. 51, 519–536. doi: 10.1175/jpo-d-20-0170.1

Crossref Full Text | Google Scholar

Tan S., Ni R. (2022). Universality and intermittency of pair dispersion in turbulence. Phys. Rev. Lett. 128, 114502. doi: 10.1103/PhysRevLett.128.114502

PubMed Abstract | Crossref Full Text | Google Scholar

Taylor G. I. (1922). Diffusion by continuous movements. Proc. London Math. Soc. 2, 196–212. doi: 10.1112/plms/s2-20.1.196

Crossref Full Text | Google Scholar

Thalabard S., Krstulovic G., Bec J. (2014). Turbulent pair dispersion as a continuous-time random walk. J. Fluid Mechan. 755, R4. doi: 10.1017/jfm.2014.445

Crossref Full Text | Google Scholar

Thorpe S. A. (2005). The turbulent ocean (Cambridge, UK: Cambridge University Press). doi: 10.1017/CBO9780511819933

Crossref Full Text | Google Scholar

Vallis G. K. (2017). Atmospheric and oceanic fluid dynamics (Cambridge, UK: Cambridge University Press). doi: 10.1017/9781107588417

Crossref Full Text | Google Scholar

van Sebille E., Griffies S. M., Abernathey R., Adams T. P., Berloff P., Biastoch A., et al. (2018). Lagrangian ocean analysis: Fundamentals and practices. Ocean Model. 121, 49–75. doi: 10.1016/j.ocemod.2017.11.008

Crossref Full Text | Google Scholar

Xia H., Francois N., Faber B., Punzmann H., Shats M. (2019). Local anisotropy of laboratory two-dimensional turbulence affects pair dispersion. Phys. Fluids 31, 025111. doi: 10.1063/1.5082851

Crossref Full Text | Google Scholar

Yang Y., McWilliams J. C., San Liang X., Zhang H., Weisberg R. H., Liu Y., et al. (2021). Spatial and temporal characteristics of the submesoscale energetics in the Gulf of Mexico. J. Phys. Oceanogr. 51, 475–489. doi: 10.1175/jpo-d-20-0247.1

Crossref Full Text | Google Scholar

Yaremchuk M., Coelho E. F. (2015). Filtering drifter trajectories sampled at submesoscale resolution. IEEE J. Ocean. Eng. 40, 497–505. doi: 10.1109/joe.2014.2353472

Crossref Full Text | Google Scholar

Zavala Sansón L. (2015). Surface dispersion in the gulf of California. Prog. Oceanogr. 137, 24–37. doi: 10.1016/j.pocean.2015.04.008

Crossref Full Text | Google Scholar