Oxygen optodes on oceanographic moorings: recommendations for deployment and in situ calibration

Miller, Una Kim; Fogaren, Kristen E.; Atamanchuk, Dariia; Johnson, Clare; Koelling, Jannes; Le Bras, Isabela; Lindeman, Margaret; Nagao, Hiroki; Nicholson, David P.; Palevsky, Hilary; Park, Ellen; Yoder, Meg; Palter, Jaime B.

doi:10.3389/fmars.2024.1441976

METHODS article

Front. Mar. Sci., 15 November 2024

Sec. Ocean Observation

Volume 11 - 2024 | https://doi.org/10.3389/fmars.2024.1441976

This article is part of the Research Topic Best Practices in Ocean Observing View all 82 articles

Oxygen optodes on oceanographic moorings: recommendations for deployment and in situ calibration

Jannes Koelling^3†

Ellen Park⁷

¹Graduate School of Oceanography, University of Rhode Island, Narragansett, RI, United States
²Department of Earth and Environmental Sciences, Boston College, Chestnut Hill, PA, United States
³Department of Oceanography, Dalhousie University, Halifax, NS, Canada
⁴Scottish Association for Marine Science, Oban, United Kingdom
⁵Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA, United States
⁶School of Ocean & Earth Science, University of Southampton, Southampton, United Kingdom
⁷Massachusetts Institute of Technology - Woods Hole Oceanographic Institution Joint Program in Oceanography, Cambridge and Woods Hole, Woods Hole, MA, United States
⁸Department of Marine Chemistry and Geochemistry, Woods Hole Oceanographic Institution, Woods Hole, MA, United States

Increasing interest in the deployment of optical oxygen sensors, or optodes, on oceanographic moorings reflects the value of dissolved oxygen (DO) measurements in studies of physical and biogeochemical processes. Optodes are well-suited for moored applications but require careful, multi-step calibrations in the field to ensure data accuracy. Without a standardized set of protocols, this can be an obstacle for science teams lacking expertise in optode data processing and calibration. Here, we provide a set of recommendations for the deployment and in situ calibration of data from moored optodes, developed from our experience working with a set of 60 optodes deployed as part of the Gases in the Overturning and Horizontal circulation of the Subpolar North Atlantic Program (GOHSNAP). In particular, we detail the correction of drift in moored optodes, which occurs in two forms: (i) an irreversible, time-dependent drift that occurs during both optode storage and deployment and (ii) a reversible and pressure-and-time-dependent drift that is detectable in some optodes deployed at depths greater than 1,000 m. The latter is virtually unidentified in the literature yet appears to cause a low-bias in measured DO on the order of 1 to 3 µmol kg⁻¹ per 1,000 m of depth, appearing as an exponential decay over the first days to months of deployment. Comparisons of our calibrated DO time series against serendipitous mid-deployment conductivity-temperature-depth (CTD)-DO profiles, as well as biogeochemical (BGC)-ARGO float profiles, suggest the protocols described here yield an accuracy in optode-DO of ∼1%, or approximately 2.5 to 3 µmol kg⁻¹. We intend this paper to serve as both documentation of the current best practices in the deployment of moored optodes as well as a guide for science teams seeking to collect high-quality moored oxygen data, regardless of expertise.

1 Introduction

Measurements of dissolved oxygen (DO) concentrations in the ocean can provide valuable information on a number of physical and biogeochemical processes, including the ventilation and circulation of saturated surface waters, respiration and productivity, and temperature-driven changes in gas solubility (Thomas and Joyce, 2010; Stendardo and Gruber, 2012; Oschlies et al., 2018; Palter and Trossman, 2018; Wolf et al., 2018; Dove et al., 2021; Lévy et al., 2022). Furthermore, the ongoing and widespread decline in DO concentrations across the world’s oceans (Diaz and Rosenberg, 2008; Ito et al., 2017; Lévy et al., 2022) poses a significant threat to organisms already living near the edge of their metabolic oxygen demand (Diaz and Rosenberg, 2008; Cheung et al., 2013; Deutsch et al., 2015). For these reasons, measuring DO has become a priority in oceanographic research, prompting the creation of international working groups that promote the collection and dissemination of DO measurements, such as the Global Ocean Oxygen Network (GO2NE), the Scientific Community on Ocean Research (SCOR) Working Group 142 “Quality Control Procedures for Oxygen and Other Biogeochemical Sensors on Floats and Gliders” (Bittig et al., 2018a), and the International Association for the Physical Sciences of the Oceans (IAPSO) Best Practice Study Group on “Ship-based CTD/O2 operations, calibration, and processing procedures”. A key data stream comes in the form of sustained, autonomous time series made possible by the deployment of oxygen sensors on oceanographic moorings (Emerson et al., 2008; Emerson and Stump, 2010; Atamanchuk et al., 2020; Koelling et al., 2022).

Optical oxygen sensors, called optodes, are more stable over time than the electro-chemical sensors (“electrodes”; Clark et al., 1953) commonly incorporated into shipboard conductivity-temperature-depth (CTD) packages, making them the preferred sensor for long-term deployments on floats, gliders, and moorings. However, optodes are still known to drift substantially from factory calibration over their lifetime, requiring additional, periodic calibrations by the user. While a growing body of literature seeks to characterize the nature of optode drift (e.g., Bushinsky and Emerson, 2013; D’Asaro and McNeil, 2013; Bittig and Körtzinger, 2015; Bittig et al., 2015; Johnson et al., 2015; Bushinsky et al., 2016; Bittig et al., 2018b; Ren et al., 2023), its mechanisms are not fully understood (SeaBird Electronics, 2023), and no universal drift correction exists. Each optode must therefore be individually calibrated, following protocols that vary depending on the mode of deployment and optode design. As moored optode deployments are still uncommon relative to float- and glider-based deployments, no such standardized procedures exist in the context of moorings. This paper responds to the need to document the current best practices for the deployment and in situ calibration of fixed-depth optodes on moorings and additionally aims to serve as a step-by-step guide for science teams seeking to collect high-quality, moored DO measurements. By focusing on moorings, we complement the existing general guide to the principles and applications of optodes in Bittig et al., 2018b, which centered on profiling platforms such as Argo floats.

The protocols for acquiring and calibrating optode data recommended in this paper (Figure 1) were developed from our experience working with 60 moored optodes deployed over a 2-year period on sections of the Overturning in the Subpolar North Atlantic Program (OSNAP; Lozier et al., 2019) mooring array at depths ranging from approximately 50 m to 3,400 m. As such, they are intended to apply to optodes deployed at depths ranging from the near-surface to depths of several thousand meters. This effort was part of the Gases in the Overturning and Horizontal circulation of the Subpolar North Atlantic Program (GOHSNAP) (Atamanchuk et al., 2021 and Figure 1 therein).

Figure 1

Figure 1. Flowchart summarizing the key protocols described in this paper, which are color-coded and grouped as follows: (blue) the deployment and recovery of the moored optodes, along with the collection of necessary CTD-DO profiles, (orange) the calibration of CTD-DO profiles using Winkler-analyzed bottle samples, and (green) the post-cruise processing and calibration of optode data, which includes conversion of raw optode outputs to DO concentrations and the correction of drift using Winkler-calibrated CTD-DO. Term definitions can be found in Table 1.

The main body of this text provides both a conceptual and practical understanding of the protocols, with actionable steps summarized in a “quick-start” guide found in the Supplementary Materials, a step-by-step list meant to be referenced by the science team throughout the cruise preparation, mooring deployment, mooring recovery, and post-cruise data processing stages. Key terminology used in the main body text and quick-start guide is summarized in the glossary (Table 1). Section 2 orients the reader to the physical principles behind optode measurements and provides a basic understanding of the conversion of unprocessed optode outputs to DO and the nature of moored optode drift that helps rationalize the many calibration steps that follow. Section 3 offers advice on optode selection and other considerations for mooring instrumentation. Section 4 describes procedures to be followed while onboard the mooring deployment and recovery cruises, which include preparation of the optodes for deployment (Section 4.1) and the collection of shipboard DO casts (Section 4.2), termed CTD-DO, that provide crucial in situ calibration points for the optode DO measurements. These CTD-DO casts must be calibrated against Winkler-titrations of discrete seawater samples, or “Winklers” (Winkler, 1888; Langdon, 2010), and Sections 4.3 and 4.4 describe the collection and shipboard analysis of Niskin water samples for Winklers. Section 5 covers all post-cruise data processing and calibration steps for producing calibrated optode-DO time series, which includes the calibration of the CTD-DO needed to derive the optode-DO calibration points (Section 5.1, see also Supplementary Materials), the conversion of unprocessed optode outputs (phase measurements) to DO concentrations (Section 5.2), and the removal of reversible and irreversible drift from the optode-DO time series (Sections 5.3 and 5.4). Section 6 discusses sources of uncertainty in the resulting, calibrated optode-DO time series and presents a validation of 11 calibrated DO time series against fortuitous mid-deployment Winkler-calibrated CTD-DO profiles external to the calibration process, as well as available biogeochemical(BGC)-Argo float DO (BGC-Argo-DO) profiles. Section 7 outlines aspects of Findable, Accessible, Interoperable, and Reusable (FAIR; Wilkinson et al., 2016) data archiving in the context of moored optode-DOs. Finally, Section 8 summarizes the key concepts and protocols introduced in the text.

Table 1

Table 1. Glossary.

2 Overview

The basic physical principles of oxygen sensing with optodes provide helpful context for the protocols described in this paper and are briefly described here; readers interested in a deeper technical understanding are referred to Lakowicz, 1999 and Bittig et al., 2018b. Optodes are based on the principle of luminescence quenching, which is the reduction of fluorescent intensity in the presence of a specified substance, in this case, oxygen. The optode repeatedly excites a luminescent substance, or luminophore, immobilized within a flexible, oxygen-permeable substrate, referred to as a sensing foil (see Figure 1 in Tengberg et al., 2006 for a diagram of optode parts). The intensity and lifetime of the emitted light is “quenched” (reduced) in the presence of oxygen, which the optode registers as a phase shift between the modulated luminophore excitation and light emission signals (see Figure 2 in Bittig et al., 2018b for a conceptual illustration). This phase shift can be related to DO concentration $([O_{2}])$ with a modified version (Uchida et al., 2008) of the classic Stern-Volmer relationship,

\begin{array}{l} [O_{2}] = \frac{(ϕ_{0} / ϕ - 1)}{K_{s v}} S_{c o r r} P_{c o r r} & (1) \end{array}

Here, $ϕ_{0}$ is the phase shift in the absence of oxygen, $ϕ$ is the phase shift recorded by the optode, and $K_{s v}$ is the Stern-Volmer constant. $ϕ_{0}$ and $K_{s v}$ are calculated using in situ temperature measurements and manufacturer-determined coefficients from a “multi-point” factory calibration, in which the response of the optode’s sensing foil to DO in a range of temperatures and DO concentrations is characterized (Bushinsky and Emerson, 2013). This response, and therefore the calculation of Equation 1 (later detailed in Section 5.2), is specific to each individual sensing foil/optode. $S_{c o r r}$ and $P_{c o r r}$ are correction factors that compensate for the virtually instantaneous effects of salinity and pressure, respectively, on the phase equilibrium between the sensing foil and DO in the ambient seawater. $S_{c o r r}$ is calculated from in situ salinity measurements and manufacturer-determined coefficients. $P_{c o r r}$ corrects what is known as the “instantaneous pressure response” in optodes (Bittig et al., 2018b) and is calculated from in situ pressure measurements and a user-determined coefficient. Pressure, in particular, causes substantial error in measured DO (order 1-3 µmol kg⁻¹ per 1,000 m) at depths of more than several hundred meters due to its compounding effects on the optode’s luminophore, DO activity within the sensing foil, and luminescence quenching (Bittig et al., 2018b). In Figure 2, the instantaneous pressure response is made apparent with data from a “cal-dip”, a CTD cast in which optodes are affixed to the ship’s CTD profiler frame, providing simultaneous and co-located optode-DO and CTD-DO profiles: the optode-DO profile without any pressure correction (i.e., $P_{c o r r}$ ), the solid black line, exhibits increasing bias with depth relative to the Winkler-calibrated CTD-DO profile, the solid blue line. This depth-dependent bias is removed by the application of $P_{c o r r}$ , shown in the corrected profile as a dashed black line. Note that the application of $P_{c o r r}$ does not remove the depth-independent bias in the optode-DO profile, that is, the optode-DO profile still appears offset from the Winkler-calibrated CTD-DO profile. This remaining discrepancy arises from instrument drift and is handled in a separate step, described below and in Section 5.4.

Figure 2

Figure 2. An example cal-dip profile illustrating the instantaneous pressure response seen in uncorrected optode-DO (solid black line) relative to Winkler-calibrated CTD-DO (blue line). Application of $P_{c o r r}$ in Equation 1 removes only the instantaneous pressure response, with the dotted black line showing the result of its removal. The inset photo shows an example of a cal-dip, where the optodes are strapped to the frame of the CTD profiler.

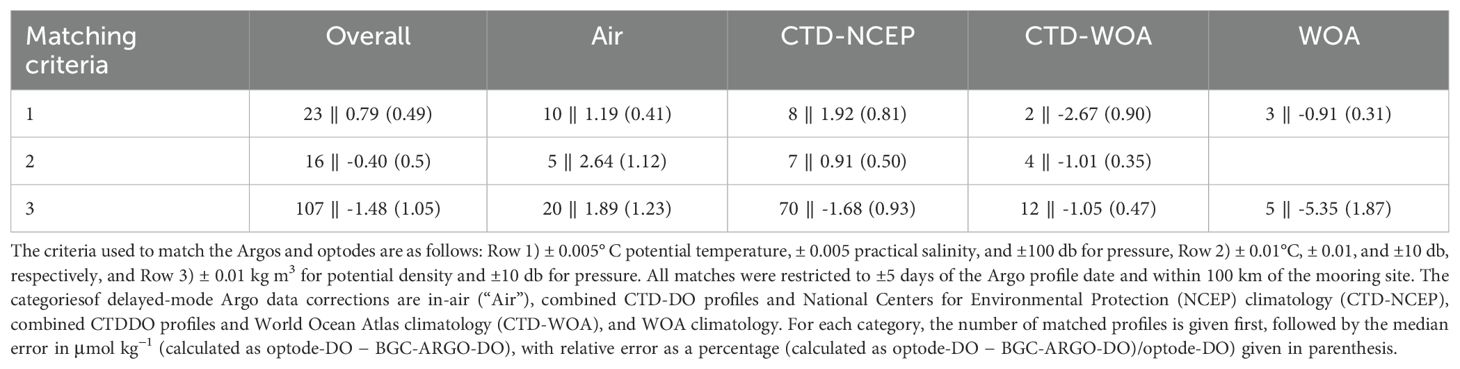
The user must be aware of two types of time-dependent optode drift in the context of moored deployments, one irreversible in nature and the other reversible. The “irreversible drift”, so-called here because its effects stay with the optode for its lifetime (i.e., do not reverse), has been widely observed in float-based optode deployments (D’Asaro and McNeil, 2013; Johnson et al., 2015; Bushinsky et al., 2016; Bittig and Körtzinger, 2017; Bittig et al., 2018b; Ren et al., 2023) and manifests in virtually all optodes as measurements of DO that read lower than the actual DO concentration of the sampled water mass. This low-bias has been shown to change exponentially with time, with rapid drift occurring within several years of initial factory calibration before leveling out to a constant bias (D’Asaro and McNeil, 2013; Bittig et al., 2018b; Ren et al., 2023). Because of this, older optodes can generally be considered more stable than newer optodes. The time dependence of irreversible drift is augmented by sampling intensity, which is why manufacturers subject optodes to extensive sampling (“burn-in” or “pre-maturation”) prior to factory calibration (Bittig et al., 2018b). While irreversible drift changes exponentially over the lifetime of the optode, the years-long time scale of its exponential character results in in situ drift appearing in moored time series as a quasi-linear decrease in optode-DO (e.g., Figure 3A).

Figure 3

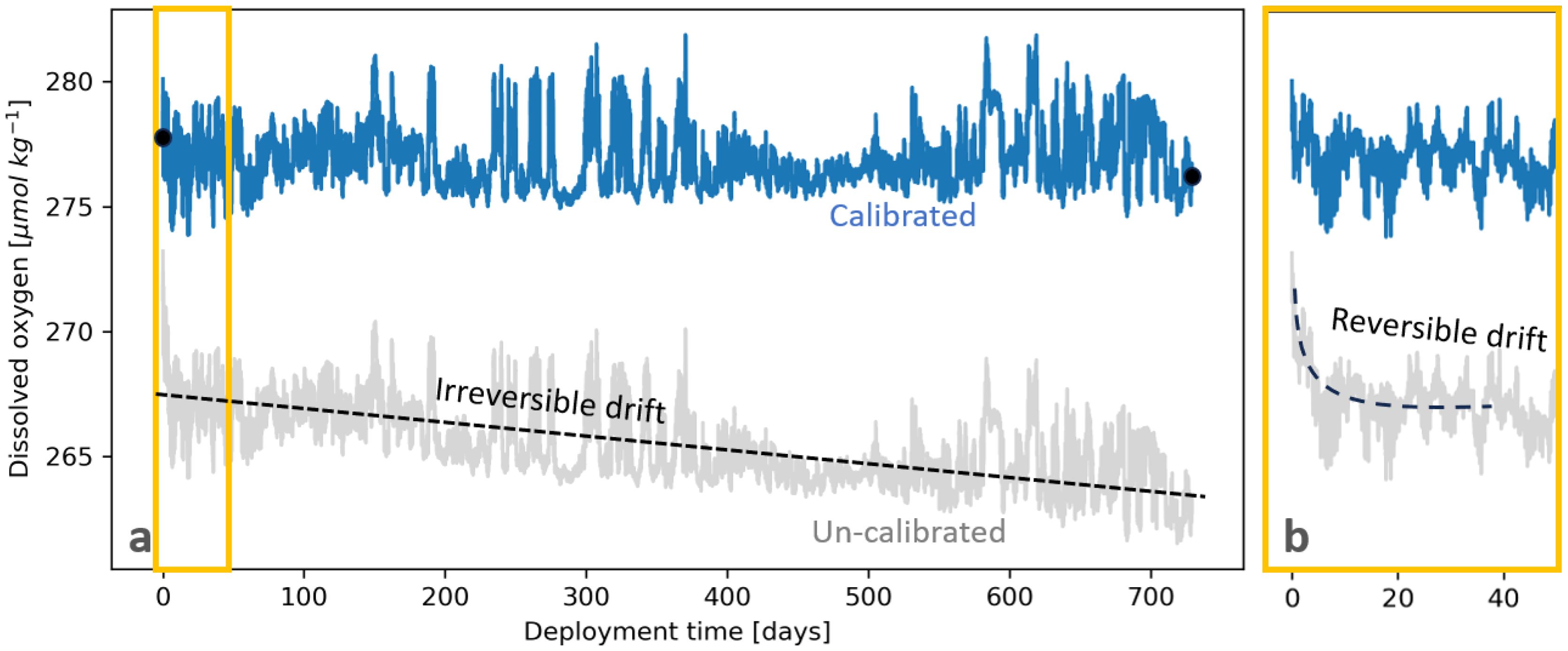
Figure 3. Examples of how (A) irreversible and (B) reversible drift appear in moored optode-DO time series. Uncalibrated data are shown in grey and calibrated data in blue. The data shown here were collected from an optode at 2,022 m depth at OSNAP Station K10. (B) zooms in on the first 50 days of the full 2-year dataset, corresponding to the period of time outlined in the yellow box in (A). The black dots near the start and end of the time series in panel (A) indicate the calibration points derived from CTD-DO.

The “reversible” drift is also exponential in nature, and its characteristic exponential decay occurs on a much shorter time scale, making it readily evident in uncalibrated moored optode-DO time series (e.g., Figure 3B). The reversible drift is both pressure- and time-dependent, increasing with pressure (depth) and occurring on time scales of days to months (Berx et al., 2019). The defining characteristic of reversible drift is that, unlike irreversible drift, its effects reverse once the optode is recovered to the surface. It can therefore only be quantified in situ before the optode has been recovered from the depth at which it was deployed (Berx et al., 2019). Its cause is unknown, but its dependence on pressure suggests that it may be a time-dependent expression of the same mechanisms causing the instantaneous pressure response seen in Figure 2 and corrected for with $P_{c o r r}$ . We found that reversible drift was detectable in some, but not all, of the moored GOHSNAP optodes deployed at depths of greater than 1,000 m (further discussed in Section 5.3).

Any optodes deployed below 1,000 m should therefore be checked for reversible drift. If present, we recommend that reversible drift is removed by fitting and subtracting an exponential function of the form $y = a e^{- b x} + c$ fitted to the trace of the drift (Section 5.3). This is a heuristic means of handling reversible drift based on the present understanding of its nature (Berx et al., 2019 and our own dataset) and will likely evolve as more deep-moored optodes are deployed and observations of reversible drift are amassed.

All optodes, regardless of deployment depth, must be corrected for irreversible drift by applying a time-dependent gain correction factor, $G (t)$ , to the uncalibrated DO measurements,

\begin{array}{l} [O_{2}]_{c a l i b r a t e d} = G (t) [O_{2}] & (2) \end{array}

Here, $G (t)$ is a linear function fitted to two or more calibration points in time, e.g., $G (t_{1})$ and $G (t_{2})$ , calculated via comparison with shipboard CTD-DO collected upon mooring deployment and recovery (See Figure 4 and Sections 4.2 and 5.4). The use of two or more calibration points to derive $G (t)$ , rather than the application of a single gain-correction at either the start or end of the time series, is supported by an average in situ drift of 2% observed in the 60 GOHSNAP optodes over the ∼2-year deployment period. This suggests that moored optode-DO are capable of incurring errors on the order of 1% (∼3 µmol kg⁻¹) per year of in situ deployment, making the derivation of a time-dependent gain-correction factor from at least two calibration points in time necessary. As a note, some optode manuals recommend that in addition to factory calibrations, the user performs calibrations onboard the ship using a 100% oxygen saturation reference point. This typically involves having the optode log in free air for several hours before or after deployment, or for several days while immersed in a water tank aerated using an aquarium bubbler. We do not recommend that the user performs these “saturation-calibration” procedures, as they do not provide calibration points as robust as those derived from the Winkler-calibration CTD-DO profiles described in this paper. In addition to the fact that only in situ DO measurements can reveal bias in optode-DO time series incurred from reversible drift, which reverses once the optode is recovered to the ship, calibration with CTD-DO profiles is advantageous over saturation-calibrations because it enables calibration to a range of temperatures, DO, and pressures and avoids issues of sensitivity of in-air optode behavior to humidity and temperature stability, and of accidental supersaturation of aerated water baths (Bittig et al., 2018b).

Figure 4

Figure 4. The removal of irreversible drift from optode-DO. (A) Calculation of $G (t_{1})$ (Equation 5) from cal-dip profiles of optode-DO and Winkler-calibrated CTD-DO. Blue shading indicates the depth range over which the ratio is calculated; data shallower than 500 m are excluded due to high upper-ocean variability and possible hysteresis in the optode relative to the electrode. (B) Calculation of $G (t_{1})$ or $G (t_{2})$ from cal-cast data (Equation 5). Oxygen measurements from the cal-cast and the moored optodes are matched within ±5 days of one another using potential temperature, practical salinity, and pressure measured by the cal-cast CTD and moored microCATs. Cal-cast and mooring data points that match within specified temperature, salinity, and pressure thresholds are shown in blue and black, respectively. Unpaired data points that do not match within these criteria are shown in grey and light blue, respectively. (C) A conceptual depiction of how $G (t_{1})$ and $G (t_{2})$ essentially “pin” the two ends of the calibrated optode-DO time series. To produce the calibrated time series, the uncalibrated optode-DO is multiplied by $G (t)$ (Equation 2), a linear fit between $G (t_{1})$ and $G (t_{2})$ . The light blue shading indicates that the full optode-DO time series is multiplied by $G (t)$ .

There are two types of CTD-DO profiles that must be collected in order to calibrate optode-DO. The first is the aforementioned “cal-dip,” in which the optodes are affixed to the CTD profiler frame and dual optode-DO and CTD-DO profiles are obtained, not necessarily at the mooring site. Cal-dip casts are used to both correct the instantaneous pressure response (Figure 2) as well as to derive $G (t_{1})$ . The second is a “cal-cast,” in which a CTD-DO cast is performed as close as possible to the mooring site where the optodes are deployed and actively sampling in situ. Cal-casts provide $G (t_{2})$ and in cases where reversible drift is present, $G (t_{1})$ as well (discussed further in Section 5.3). CTD-DO from cal-casts is matched to the moored optode-DO using temperature and salinity (collected by a sensor co-located with the optode on the mooring), since cal-cast data at the pressure level of the optode might sample a different water mass due to heaving or spatial gradients. Details on protocols for the collection of both cal-dips and cal-casts are described in Sections 4.2 and 4.3, which include the collection of Niskin bottle samples at strategic depths along each profile. This is because all collected CTD-DO profiles must be calibrated using Winklers (Sections 4.4 and Section 5.1 and Supplementary Material). It should be noted that because the quality of Winklers is highly dependent on the skill of those collecting and analyzing the bottle samples, it is assumed that the science team either already includes, or will hire, a Winkler specialist who will participate in the mooring deployment and recovery cruises. Handling of bottle samples and Winkler analysis by those without prior experience will risk the quality of CTD-DO, and therefore the calibration of the optode-DO.

In short, the major aspects of optode deployment and calibration, summarized in Figure 1, are: a) the deployment and recovery of the moored optodes, along with the collection of necessary CTD-DO profiles (blue boxes), b) the calibration of CTD-DO profiles using Winkler-analyzed bottle samples (orange boxes), and c) the post-cruise processing and calibration of optode data, which includes conversion of raw optode outputs to DO concentrations and the correction of drift using Winkler-calibrated CTD-DO profiles (green boxes).

3 Instrument considerations

The most widely used optodes in the oceanographic community are those with a silicone-based membrane, such as the Sea-Bird Electronics (SBE) 63, Aanderaa 3830/4330, and the slow variant of RBRcoda T.ODO. JFE Rinko optodes are also used, though their luminophores are suspended in a PMMA coating rather than a silicone membrane (Bittig et al., 2014). The behavior and drift characteristics of silicone membranes are better documented and characterized in the literature (e.g., Bittig and Körtzinger, 2017; Bushinsky and Emerson, 2013; D’Asaro and McNeil, 2013; Johnson et al., 2015; Bushinsky et al., 2016; Ren et al., 2023) than other materials due to their widespread usage for nearly two decades, and the protocols for optode calibration described in this paper were developed based on the analysis of data from moored Aanderaa 4330 optodes and existing literature on the performance of SBE 63 and Aanderaa 3830/4330 optodes. Therefore, we recommend the use of optodes with a standard silicone membrane, specifically a PreSens PSt3 membrane, until differences, if any, in the behavior of alternative sensing foil materials become better characterized.

When purchasing optodes, the science team should ensure that they have been multi-point factory calibrated and subjected to the aforementioned pre-conditioning procedure known as “burn-in” or “pre-maturation” to increase stability. Because the parameters in Equation 1 are sensing-foil-specific, and therefore, optode-specific, multi-point factory calibrations for each optode will allow for higher accuracy than the alternative of “batch” factory calibrations, in which the results of the multi-point calibrations of a subset of foils are extrapolated to an entire batch (Bittig et al., 2018b). Most optodes can be procured with an integrated data logger, or else a compatible logger must be acquired separately. The sensor/logger system should be powered by a high-quality lithium-metal/ion battery pack intended for long-duration deployments. The design of the sensor-logger system should enable easy battery pack service while at sea.

It is important that each optode on the mooring line is deployed with a co-located CTD sensor in order to provide the temperature, salinity, and pressure measurements necessary for calibration, processing, and interpretation. Temperature and salinity are used for matching water masses between the mooring and cal-casts, and pressure is used for the optimization of $P_{c o r r}$ in Equation 1. Salinity is also used in the calculation of $S_{c o r r}$ . The optode itself measures temperature close to its sensing foil, as temperature is required to calculate $ϕ_{0}$ , $K_{s v}$ , and $S_{c o r r}$ in Equation 1. Because the factory coefficients for these terms were developed using the optode’s temperature probe readings, and because these readings are located as close as possible to the sensing foil, the optode temperature should be used in these calculations. However, for water mass matching, we recommend using temperature from a co-located CTD, as these measurements are typically well-calibrated and come with specifications on accuracy and precision.

Finally, the electrodes on shipboard CTD profilers should be calibrated once yearly. This is the responsibility of the ship operator, but we recommend that the science team confirm the date of the last calibration with the ship operator during cruise planning.

4 Cruise protocols

4.1 Optode handling and preparation

When handling the optode, care should be taken to avoid touching the optode sensing foil or exposing it to sunlight for extended periods. A pre-soak for at least 24-48 hours prior to any data collection—cal-dip or deployment—is required for all optodes. This is due to the so-called “wetting” effect: the optode foil sometimes dries out during transport or improper storage, which can affect oxygen measurements by 1%-2% until the foil fully re-hydrates over the course of hours or days (Aanderaa Data Instruments, 2018). This makes a pre-soak especially crucial for the quality of optode data collected on cal-dips, which take place over the course of only several hours. This soak should be performed in a covered bucket to prevent sunlight from degrading the optode foil (Palevsky et al., 2023).

Several measures can be taken during optode deployment preparation to ensure the quality and ease of processing of the collected oxygen data, such as clock synchronization and synchronization of the sample intervals with co-located instruments. Where applicable, the salinity setting in the optode deployment software should always be set to 0, otherwise the software will apply a salinity correction to the oxygen measurements using a default salinity of 35. Best practice entails performing this salinity correction ( $S_{c o r r}$ in Equation 1) using measured salinity from the co-located CTD sensor (Section 5.2). Finally, for non-pumped optodes set to be deployed to depths of 1,000 m or greater, sampling should be scheduled to begin before or during the mooring’s descent through the water column in order to ensure that reversible drift is fully captured, as it can begin to take effect in a matter of hours after deployment. However, if the optode is connected to a pump (e.g., SBE63), the science team should not risk sampling while still in the air on deck.

4.2 Cal-dips and Cal-casts

Every optode must be deployed on a cal-dip cast prior to its deployment on the mooring. Multiple optodes can be “cal-dipped” on a single cal-dip cast, limited only by how many optodes can be reasonably attached to the frame of the CTD profiler. To set up a cal-dip, optodes should be securely attached to the frame of the shipboard CTD profiler with their sensing foils facing downward and away from the frame; this avoids particles settling on the foils. One method for attaching optodes to the frame is to secure ratchet straps between the top and bottom rungs of the frame and affix the optodes to the straps using hose clamps and zip ties, as in Figure 5. The cal-dip cast does not need to be close to the mooring site and can be performed anywhere in the region with a similar water mass structure, provided that it is done a) within days of the mooring deployment and b) to depths greater than 1,000 m and to at least the same depth as the planned mooring deployment. The first requirement aims to minimize the amount of irreversible drift that can occur between the cal-dip and optode deployment, therefore preserving the accuracy of $G (t_{1})$ derived from the cal-dip. We found that $G (t_{1})$ derived from cal-dips performed within 10 days prior to mooring deployment generally agreed with $G (t_{1})$ derived from cal-casts collected on the same mooring deployment cruise to within 1%. The second requirement ensures adequate characterization of $P_{c o r r}$ in Equation 1. It also allows for greater confidence in $G (t_{1})$ derived from the ratio of the CTD-DO and optode-DO profiles by capturing more stable, deep water masses; a portion of the profile in the upper ocean is typically excluded from this calculation due to high variability and the differing response times of the CTD profiler electrode and the optode.

Figure 5

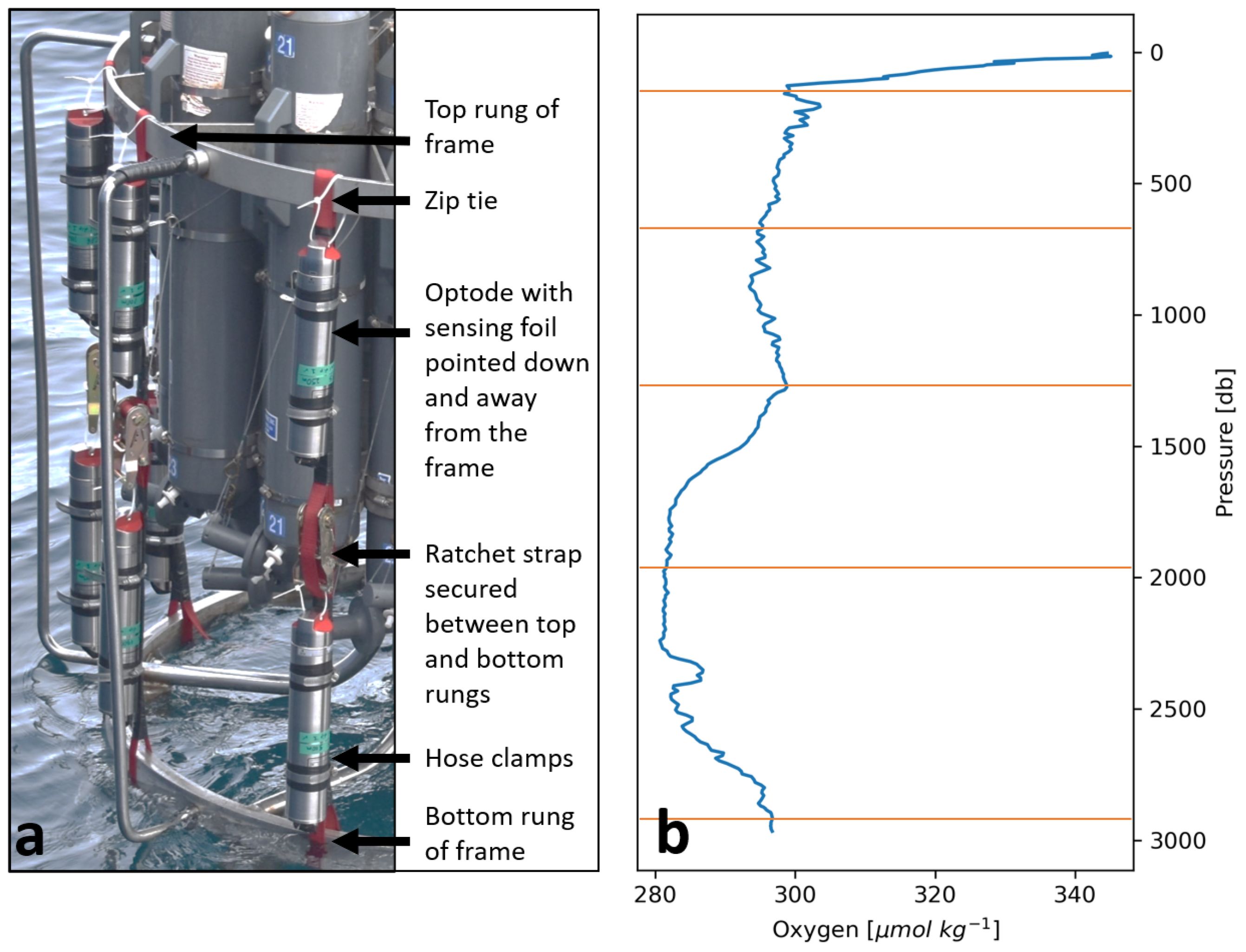
Figure 5. (A) An example of how optodes are strapped to the frame of the CTD profiler in order to perform a calibration “dip” cast, or “cal-dip”. (B) An example of a CTD-DO profile with depths (orange lines) selected for upcast Niskin bottle sampling for Winkler analysis.

Cal-casts should be performed at each mooring site on the deployment cruise, and again on the recovery cruise. As cal-casts are meant to provide concurrent CTD-DO with the moored optode measurements, they are ideally performed after the mooring has been deployed on the deployment cruise, and before the mooring has been recovered on the recovery cruise, while the optodes are actively sampling in situ. In practice, the order of operations on a complex mooring cruise can depend on many factors; it is imperative that cal-casts are collected at each mooring site even if they do not adhere to these strict criteria on timing. The depth of the cal-cast should exceed the deepest optode by at least 100 m to ensure matchups of sampled CTD-DO and optode DO in the temperature-salinity space in the event of heave or lateral variability between the mooring and cal-cast sites.

4.3 Niskin sampling

The CTD-DO profiles collected on cal-dips and cal-casts are calibrated using Winkler samples from Niskin bottles. To ensure optimal CTD-DO calibration for these critical casts (see Supplementary Material), we recommend that bottle samples be collected for every cal-dip and cal-cast. Here, we provide recommendations to help determine optimal points for Niskin sampling.

The downcast profile should be examined during collection to identify the depths at which to collect bottle samples for Winkler analysis during the upcast, with the goal of prioritizing samples from:

1. Stable water masses, as this increases confidence that the CTD and the Niskin bottle will sample the same water masses. Ideally, all sampling depths will be within a well-mixed layer in which CTD-DO readings are constant for at least several tens of meters.

2. Extrema, as this provides the broadest possible range of oxygen concentrations to use for calibration. We note that while the oxygen maximum is a useful point for calibration, it is often near the surface, which is not typically a stable water mass. If this is the case, prioritize sampling of deeper local maxima and only sample the near-surface if the capacity for sample analysis allows.

3. A range of depths. We recommend sampling the deepest stable water mass on each cal-dip and cal-cast if resources allow, as this will improve the calibration of the pressure correction factor, E, in Equation S1 (in Supplementary Material) used to convert the raw electrode output to DO.

An example CTD-DO downcast profile is shown with suitable bottle-sampling depths highlighted in Figure 5B. The CTD cast operator should stop fully at each Niskin sampling depth to ensure that the DO sensors have stabilized before firing the Niskin. Optodes have a longer response time than CTD-DO sensors; we have found that a stop time of at least 2 minutes allows for both electrode and optode stabilization. Allowing the extra time for the optodes to stabilize during these stops allows for Winklers to be used directly in their calibration in the event that the CTD-DO profile is deemed unusable.

Once a cal-dip or cal-cast has been completed and the CTD profiler has been secured on the deck, Niskin bottles should be immediately prepared for sampling. Replicate bottle samples should be collected from each Niskin.

4.4 Considerations for Winkler analysis

Winkler analysis of the Niskin bottle samples should begin as soon as possible following collection. Decisions as to the number of Winkler samples to collect from each cast will depend on the capacity and priorities of the science team. Ideally, time and resources would allow for Winkler measurements from at least 4-5 depths on every cal-dip and cal-cast on the cruise, with depths chosen to capture the full range of stable water masses on each cast. We caution that it is possible to experience unexpected shifts in SBE43 calibration (e.g. due to fouling) even if attention is given to regular sensor cleaning on the CTD package, and therefore recommend collecting Winkler samples from all key casts to ensure that it will be possible to produce usable CTD-DO data. Furthermore, as stated in the previous section, these Winkler samples will become crucial for optode calibration in the case of SBE43 sensor failure on a cal-dip or cal-cast. We also recommend collecting duplicate Winkler samples from the same Niskin bottle from at least one depth per cast, and more if possible, to verify the precision of the Winkler measurements.

We again emphasize the importance of having an individual with substantial Winkler experience onboard to perform the analyses. This cruise-dedicated Winkler specialist will already be familiar with reagent preparation, bottle sample collection, titration instrumentation and software, and the fundamentals of the chemical reactions, all of which have been thoroughly covered in the GO-SHIP Repeat Hydrography Manual (Langdon, 2010). In brief, the key aspects for ensuring high-quality Winkler measurements are as follows: Winkler measurements should produce replicates that agree to within 0.1%; anywhere between 0.1%- 0.2% should be flagged as suspect but may still be used for calibration, and those with over 0.2% error should be discarded, as greater disagreement generally indicates sample contamination during collection and/or analysis. The median of replicate data should be reported, consistent with Best Practice Data Standards for Discrete Chemical Oceanographic Observations (Jiang et al., 2022). For the highest accuracy, the concentration of the titrant used in the Winkler determination needs to be calculated using a reference standard. A high-quality standard, such as the potassium iodate standard produced by Ocean Scientific International Ltd (OSIL), should be measured, at minimum, once at the beginning of the cruise and a second time at the end of the cruise. At the beginning of each titration session, an internal standard that has been referenced to the OSIL standard could be used.

Given the time-intensive nature of completing Winkler titrations onboard the ship, collection and preservation of discrete water samples for Winkler analysis is frequently delegated to multiple members of the science team, possibly including those without prior experience. If this is the case, we recommend planning opportunities for training and practice prior to the collection of the Niskin samples. Furthermore, since novice samplers may introduce air contamination (bubbles) more often than experienced samplers, it will be especially critical to prioritize the collection of replicate samples from each Niskin.

Every effort should be made to ensure that Winkler measurements are performed onboard by a trained Winkler specialist in order to avoid contamination and sample loss. In the event that onboard titrations are not possible during the mooring deployment or recovery cruises (e.g., personnel constraints during the COVID-19 pandemic), the collection and preservation of oxygen samples for subsequent laboratory analysis on land is necessary. Best practices for the storage of bottle samples are described in Zhang et al. (2002). As this method deviates from the well-established best practice of performing the Winkler analysis onboard the ship, all samples to be stored for delayed analysis should be collected in duplicate, or even triplicate, as an additional quality control measure. We recommend consulting with an experienced Winkler analyst prior to the cruise to ensure that proper collection and storage techniques are understood. We also caution that issues in stored bottle samples cannot be discovered until the post-cruise Winkler analysis, when no further samples can be collected, potentially jeopardizing the calibration of CTD-DO and, therefore, of optode-DO.

5 Post-cruise data processing and calibrations

5.1 Calibration of CTD-DO with Winklers

While Section 5 primarily focuses on optode calibration protocols, we include here a brief background and description of electrode calibration, as well-calibrated CTD-DO profiles are crucial for optode calibration. Detailed protocols for science teams performing the electrode calibrations themselves may be found in the Supplementary Materials, with code for a worked example available at https://github.com/fogaren/CTD-DO-Calibration-Example. The recommendations given in this paper apply to SBE 43 electrodes, the sensor found on most shipboard CTD packages.

Oxygen electrodes measure a voltage proportional to the flux of oxygen molecules across a polarographic membrane. Oxygen-dependent voltages are converted to oxygen concentrations using a calibration equation (Owens and Millard, 1985; Uchida et al., 2010) calculated with sensor-specific factory calibration coefficients. However, to produce the best possible oxygen measurements, the user must re-calibrate the oxygen profiles with Winkler samples in order to 1) reflect changes in membrane permeability that have occurred since factory calibration as a result of electro-chemical drift and fouling (e.g., by oil or jellyfish), and 2) optimize coefficients that were not factory-calibrated under pressure.

Historically, these in situ calibrations were performed for each CTD-DO profile on a cruise using non-linear least squares fits of Winkler data to a calibration equation typically containing 5 to 8 calibration coefficients (Uchida et al., 2010 and references therein). Given the large scope of tasks required on mooring cruises, it is often infeasible to collect the number of Winklers required to robustly constrain a calibration equation with this many coefficients for every single CTD-DO profile. Instead, we offer an alternative workflow for calibrating CTD-DO sensors that relies on the Sea-Bird oxygen calibration equation (Equation S2 in Supplementary Material), which incorporates temperature corrections from an updated sensor design and includes physically motivated pressure and temperature corrections (Atkinson et al., 1996; Edwards et al., 2010). Using our recommended workflow and Sea-Bird calibration equation, the number of calibration coefficients that require optimization using Winkler samples is reduced to two, which reduces the number of Winklers needed to robustly constrain the coefficients. We note these recommendations were developed in the absence of a clear community consensus on instructions for researchers needing CTD-DO data for this type of mooring calibration work, and encourage readers to consult forthcoming recommendations from the ongoing IAPSO Best Practice Study Group on ship-based CTD/O2 operations, calibration, and processing procedures for additional guidance.

5.2 Conversion of optode phase reading to DO concentration

The first step in processing optode data is to convert the phase shift registered by the optode in units of degrees or volts to DO concentration using the modified Stern-Volmer Equation, Equation 1 (Uchida et al., 2008). The exact form of Equation 1 differs slightly across manufacturers depending on the factory-determined coefficients provided and the user should therefore consult the instrument manual for the appropriate calculation of the terms $K_{s v}$ , $ϕ_{0}$ , and $S_{c o r r}$ . Regardless of its form, the calculation of $S_{c o r r}$ should be done with the in situ salinity measurements made by the co-located CTD rather than a default constant salinity value. We do not recommend following the manufacturer-provided $P_{c o r r}$ formula, as the pressure-compensation factor $(p_{f a c})$ that defines the magnitude of the instantaneous pressure effect per 1,000 dbar is typically given as a generic value of 3.2% or 4% per 1,000 m when in reality, it is specific to each optode. Variation in the reported $p_{f a c}$ values for individual optodes (Tengberg et al., 2006; Uchida et al., 2008; Bittig et al., 2015) suggests that the use of a generic $p_{f a c}$ value could result in an error on the order of 1% per 1,000 m for any given optode. Indeed, our analysis of the 60 GOHSNAP pairs of cal-dip optode-DO and Winkler-calibrated CTD-DO profiles show a range of $p_{f a c}$ values from 2.4% to 4.3% per 1,000 m (Figure 6A). Instead, $P_{c o r r}$ should be calculated as:

Figure 6

Figure 6. (A) A histogram of individually-determined $p_{f a c}$ values for the GOHSNAP optodes shows substantial variability. (B) An example of the root-square-mean (RMS) error between the cal-dip CTD-DO and optode-DO profiles using values of $p_{f a c}$ in Equation 3 ranging from 0.01 to 0.05. The value of $p_{f a c}$ that minimizes RMS error (here, $p_{f a c}$ = 0.0349) is the optimal $p_{f a c}$ for a particular optode.

\begin{array}{l} P_{c o r r} = 1 + \frac{p_{f a c} p}{1000}, & (3) \end{array}

where $p_{f a c}$ is individually determined for each optode. Here, p is pressure in dbars. Bittig et al., 2018b suggested a two-step pressure correction that empirically models variation in the pressure effect across optodes using temperature and pressure measurements. It was developed based on BGC-ARGO data as deep as 2,000 m and has a reported uncertainty of 0.3% per 1,000 dbar (Bittig et al., 2015). However, given the shipboard capability for cal-dips with moored optode deployments, we recommend the most accurate method of accounting for the instantaneous pressure response, which is to directly determine $p_{f a c}$ for each optode using cal-dip profiles.

The optimal $p_{f a c}$ for an individual optode is determined through a comparison of the cal-dip optode-DO, calculated from Equation 1 by omitting the $P_{c o r r}$ term, with the corresponding cal-dip Winkler-calibrated CTD-DO profile. Equation 1 is calculated iteratively with values of $p_{f a c}$ in $P_{c o r r}$ from 0.01 to 0.05 (i.e., 1%-5% per 1,000 m). The value of $p_{f a c}$ that minimizes the root-mean-square error (RMSE) between the pressure-corrected optode-DO profile and its paired CTD-DO profile is the optimal $p_{f a c}$ for that optode (e.g., Figure 6B). In our calculations, data above 500 m were excluded due to potential hysteresis between the optode-DO and CTD-DO that can occur in the strong oxygen gradients encountered in near-surface waters. Users may need to adapt this approach to remove other sections of their profiles collected in strong oxygen gradients. Once the optimal $p_{f a c}$ is determined for an individual optode, the full Equation 1 including $P_{c o r r}$ can then be calculated for all optode data, that is, both the cal-dip profile and the time series collected for the duration of the moored deployment. Hereafter, all references to optode-DO assume a calculation using optode-specific values of $p_{f a c}$ .

Optode-DO calculated from Equation 1 is in units of µmol L⁻¹ and can be converted to µmol kg⁻¹ by multiplication with 1000/ $ρ_{0}$ , where $ρ_{0}$ is the potential density of water referenced to the sea surface (Bittig et al., 2018a). Units of µmol kg⁻¹ are preferred when oxygen is used as a passive tracer because oxygen concentration per unit mass is independent of changes in temperature and pressure.

5.3 Detection and removal of reversible drift

Optodes deployed at depths below 1,000 m must be examined for reversible drift. If no optodes were deployed at these depths, the user may skip to Section 5.4.

Observations of reversible drift are limited compared to those of irreversible drift, but our own observations and those reported in Berx et al., 2019 allow us to define a working definition of reversible drift as an exponential decay at the start of an optode-DO time series from deeper than 1,000 m that occurs in the absence of a similar decay in the co-located potential temperature time series. We recommend that the reversible drift be removed only when there is no corresponding change in potential temperature, in order to avoid the inadvertent removal of real DO changes associated with changes in temperature-dependent solubility or movement of different water masses past the mooring site. The user may wish to also consider the salinity time series in regions where salinity provides additional information on dynamic processes. The exponential decrease in DO associated with reversible drift can appear on multiple time scales, loosely categorized as “fast drift” (time scales on the order of days) and “slow drift” (time scales on the order of weeks to months) (Berx et al., 2019). A single optode can exhibit reversible drift on both time scales. The observed reversible drift is most pronounced in the optodes deployed below 1,000 m; above 1,000 m, the reversible drift—if present—is indistinguishable from the sensor noise and natural variability.

One way to separate natural variability in DO from the exponential decline characteristic of reversible drift is as in Berx et al., 2019, where temperature-driven variability was removed from each DO time series prior to examination for drift. This was done by fitting a relationship between temperature anomalies and DO anomalies for each optode-DO time series. This can be helpful in cases where the temperature-DO relationship has low variability; however, in the relatively variable GOHSNAP optode-DO time series, the fitted relationships had high RMS error and were not suitable for this approach. Instead, we suggest the following steps to identify and remove reversible drift, which are based on the characteristics of reversible drift observed here and reported by Berx et al., 2019. These should be applied to every optode-DO time series deployed at depths greater than 1,000 m.

1. Evaluate optode-DO time series for fast reversible drift.

a. Fit an exponential of the form of Equation 4 to the first 15 days of the optode-DO time series, where a, b, and c are determined via least-squares and t is in units of elapsed time (e.g., days). Calculate the exponential time constant, τ, as 1/b, taking care to account for the sampling interval when interpreting the resulting units of time.

\begin{array}{l} y = a e^{- b t} + c & (4) \end{array}

b. Repeat Step 1a for the first 15 days of potential temperature from the CTD co-located with the optode.

c. The optode-DO time series likely exhibits fast drift if the following are true:

i. A fit of the form of Equation 4 is found for the first 15 days of the optode-DO time series by the least-squares curve fitting function.

ii. Either no optimal exponential fit is found for the first 15 days of potential temperature, or if an optimal fit is found, τ of the temperature fit is not within several days of τ of the optode-DO fit.

iii. The magnitude (a) of the exponential function fit to the optode-DO is greater than twice the standard deviation of the first 15 days of optode-DO. This criterion helps to distinguish drift from natural variability.

2. If the optode-DO time series is determined to exhibit fast drift, remove the drift by subtracting $a e^{- b t}$ from the first 15 days (e.g, Figure 7).

Figure 7

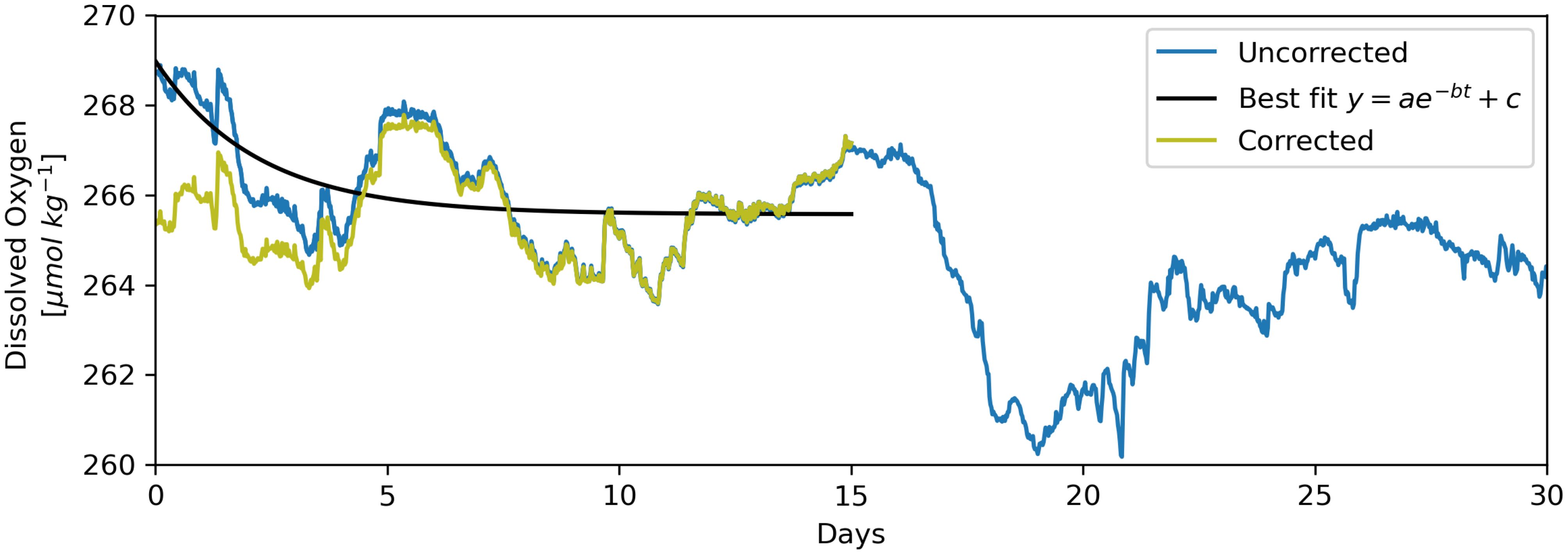
Figure 7. Removal of reversible drift via fitting and subtraction of an exponential function. The “corrected” (yellow) time series results from the subtraction of the least-squares fit exponential function (without the constant, c, i.e., $y = a e^{- b t}$ ) from the “uncorrected” (blue) time series. This example from the K9 mooring (western Labrador Sea) at a depth of 2,878 m exhibits “fast” reversible drift, which occurs in the first days to weeks of deployment (also shown in right-most panel of the middle row in Figure 8).

3. Evaluate the optode-DO time series for slow reversible drift. If fast drift was identified in the previous step, use the fast-drift-corrected time series for the following steps:

a. Detrend the full optode-DO time series. This isolates potential reversible drift from any quasi-linear trends present due to long-term natural variability or irreversible drift.

b. Fit Equation 4 to the first 300 days of the optode-DO time series, or the full optode-DO time series, whichever is shorter. Limiting the time period over which Equation 4 is fit to 300 days or less helps to constrain the fit to the time scales at which slow reversible drift has been observed, typically with decay time constants on the order of weeks (Table 2), and avoid fitting to longer-term variability unrelated to reversible drift.

c. Repeat Steps 3a and 3b for the co-located potential temperature time series.

d. The optode-DO time series likely exhibits slow reversible drift if the following are true:

Table 2

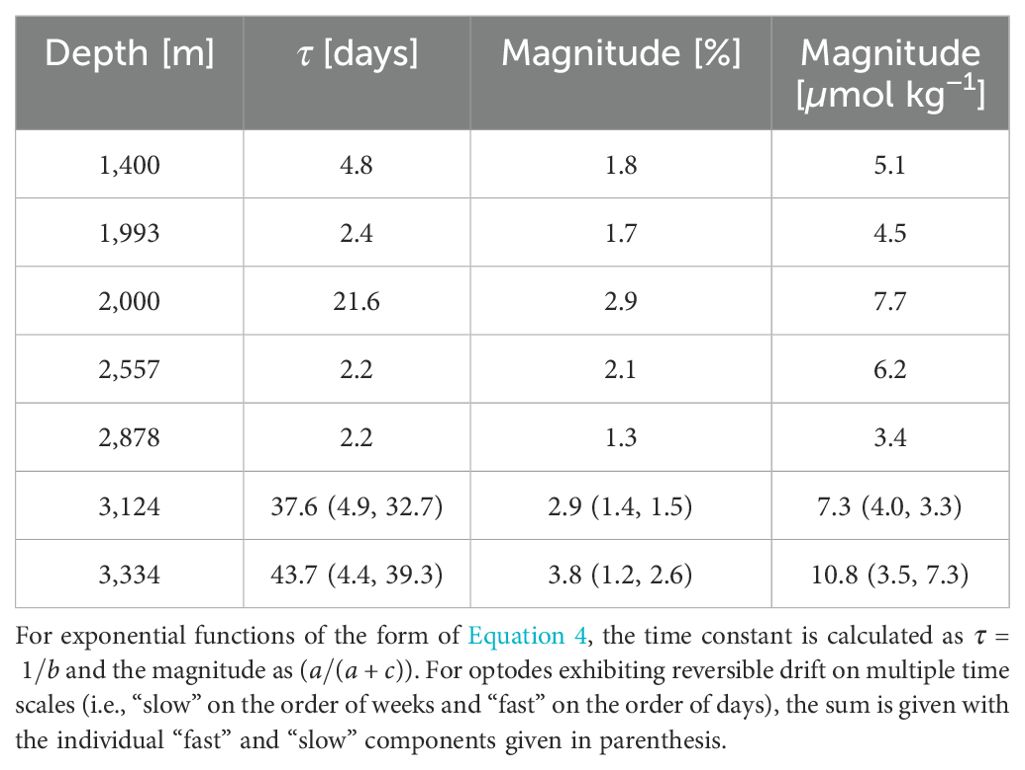
Table 2. Characteristics of best-fit exponential for an optode-DO determined to exhibit reversible drift.

i. An optimal fit of the form of Equation 4 is found for the first 300 days of the optode-DO time series by the least-squares curve fitting function.

ii. Either no exponential fit is found for the first 300 days of potential temperature, or if a fit is found, τ of the temperature fit is not within approximately 20 days of τ of the optode-DO fit.

iii. The magnitude (a) of the exponential function fit to the optode-DO is greater than twice the standard deviation calculated across the full time series. On this time scale, seasonal variability can cause large variations in dissolved oxygen that may be mistaken for reversible drift if sampling begins during a seasonal decline in oxygen.

e. If the optode-DO time series is determined to exhibit slow drift, remove the drift by subtracting $a e^{- b t}$ from the time period over which Equation 4 was fit.

Of the 24 optodes on the OSNAP array that were deployed at depths greater than 1,000 m, we diagnosed reversible drift in seven (Figure 8) using these criteria. Of these seven optodes, six exhibited fast decay with exponential time constants (τ) ranging from 2 to 5 days and magnitudes from 1.5% to 2.1%, and three exhibited slow decay, with magnitudes of 1.2%-2.9% and time constants of 21-40 days (Table 2). Two of these seven exhibited both slow and fast decay. Figures 9A, B show an example optode-DO time series with a clear exponential decay that is absent in the paired potential temperature time series, suggesting (slow) reversible drift based on the criteria above. Figures 9C, D show an example in which both the optode-DO and potential temperature time series exhibit exponential behavior with similar time constants, suggesting the decline in DO is a real physical occurrence rather than an artifact of reversible drift. Figure 9E is an example of where a fit to Equation 4 was found over the first 300 days of the optode-DO but not in the potential temperature time series (latter not shown). However, we decided that this exponential decline should not be attributed to reversible drift because (a) the fit does not appear representative of the visual trace data over which it was calculated and (b) the magnitude of the fit does not exceed the standard deviation calculated across the full time series (criteria 1(c)iii and 3(d)iii). Furthermore, the initial decay in question appears to be the declining portion of a regular seasonal cycle in which DO increases in the spring and summer months and declines through fall and winter, i.e., the context suggests that the initial decay could be a real decrease rather than a result of drift. This case highlights the necessary role of subjective analysis when applying the suggested criteria. While the use of least-squares fitting and calculation of standard deviations provide some measure of objectivity, at present, the determination of whether an optode-DO time series exhibits reversible drift ultimately rests on the analyst’s judgment of how reasonably the exponential fit represents the time series as well consideration of local hydrography and variability at the mooring site. As more in situ data from moored oxygen optodes are obtained and analyzed, we anticipate that lessons from those results will enable future refinements to these steps that will reduce the need for subjective analysis.

Figure 8

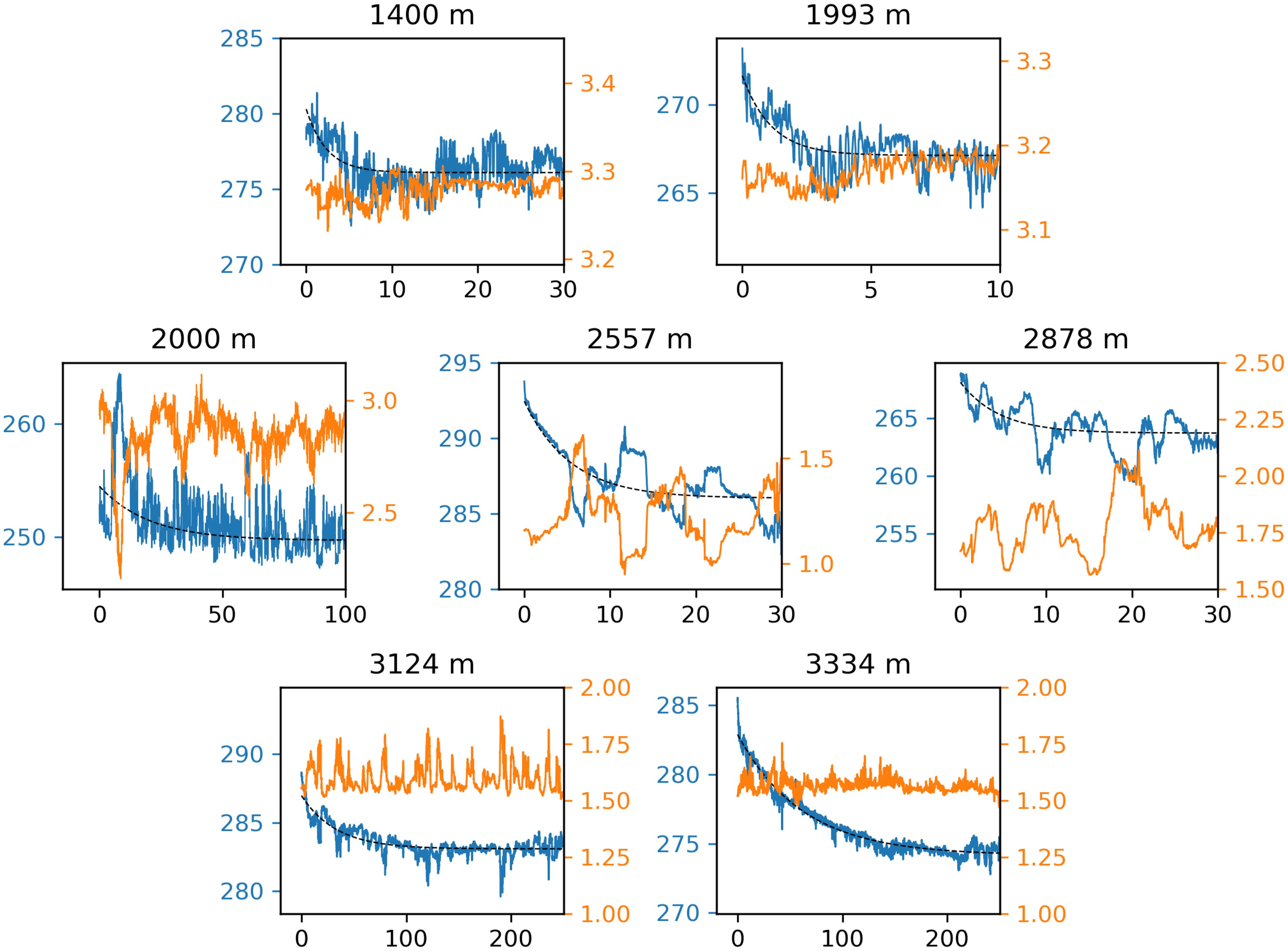
Figure 8. Reversible drift in 7 of 24 GOHSNAP optodes deployed at depths greater than 1,000 m. In all subplots, the horizontal axis is time in days since deployment, the left vertical axis is dissolved oxygen (DO) in µmol kg⁻¹ in blue, and the right vertical axis is potential temperature in °C in orange. In each panel, exponential decay is clear in the optode-DO time series but not in the co-located temperature time series. The dashed lines show the least-squares fit to the optode-DO. For time constants and the magnitudes of the fitted drifts, see Table 2.

Figure 9

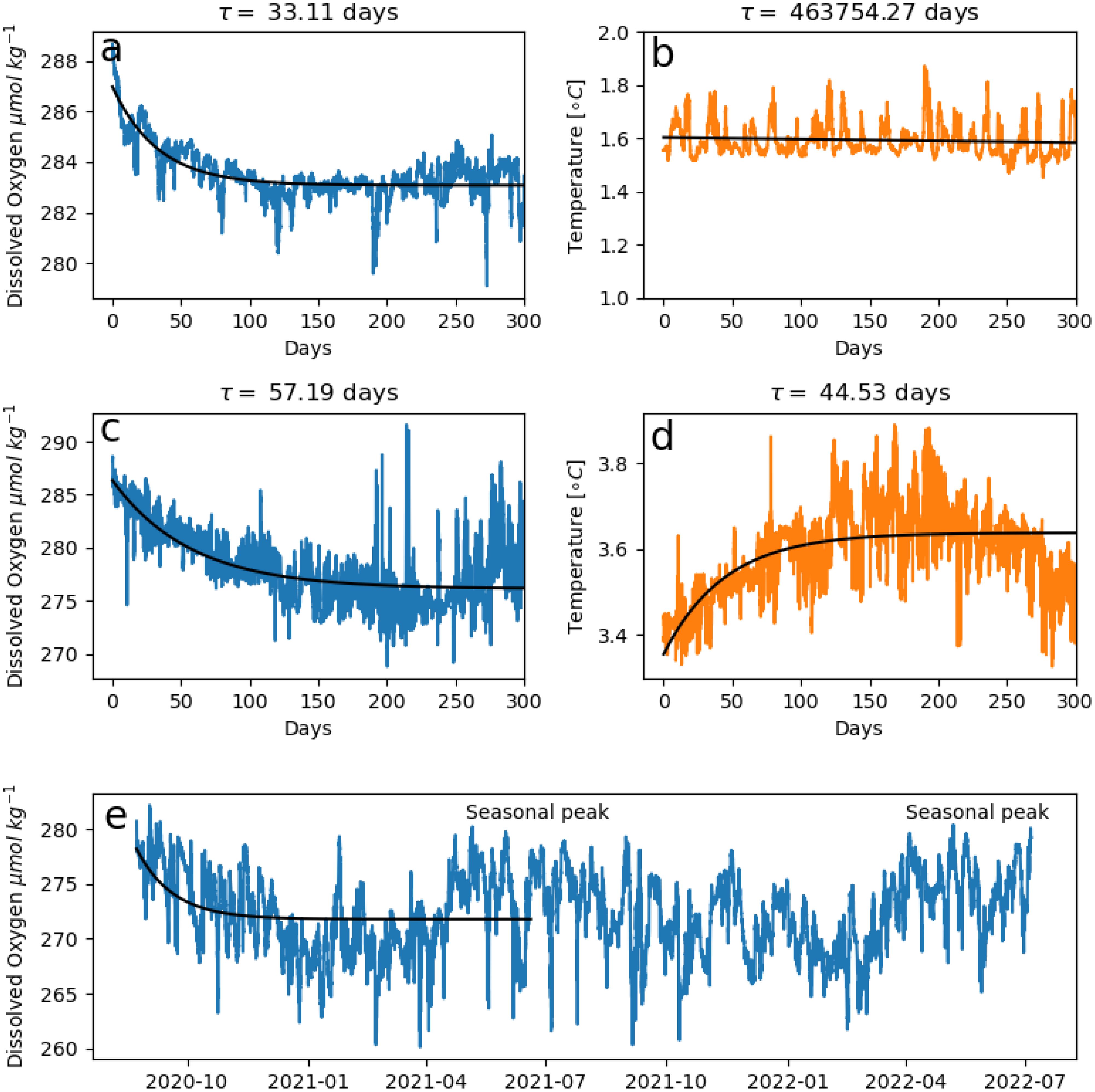
Figure 9. The determination of the presence or absence of reversible drift in three example optodes following the criteria outlined in Section 5.3. In the first example, from the same optode at 3,124 m shown in Figure 8, an optimal fit is found for (A) the dissolved oxygen (DO) time series but not the (B) co-located potential temperature time series, suggesting reversible drift is present. In the second example, from an optode at 597 m (above the 1,000 m depth at which we believe reversible drift to be detectable), an optimal fit is found for both the (C) DO and (D) temperature time series, and their similar exponential decay time constants (τ) suggest that reversible drift is not present. (E) shows an example of an optode-DO time series at 2,025 m depth that was determined not to exhibit reversible drift even though a fit was found for the optode-DO time series and not in the potential temperature time series (latter not shown). In addition to failing criterion 3(d)iii for reversible drift, the initial decay here appears to be a real decline in DO that is part of a regular seasonal cycle of peaks and declines at this site.

5.4 Removal of irreversible drift

At this step in the processing of optode-DO, raw optode phase readings have been converted to DO concentrations, the optimal $p_{f a c}$ for each optode has been determined and applied to both the optode-DO cal-dip profile and deployment time series, and any optodes deployed at depths greater than 1,000 m have been examined, and if applicable, corrected, for reversible drift. The final step is to correct for irreversible drift, i.e., to calibrate each optode-DO time series against deployment and recovery CTD-DO profiles. As outlined in Section 2, this is done by multiplication of the optode-DO time series with a time-dependent gain correction, $G (t)$ , a linear fit between two calibration points, $G (t_{1})$ and $G (t_{2})$ (Equation 2). These calibration points are calculated at the beginning and end of the optode-DO time series as a ratio of optode-DO to Winkler-calibrated CTD-DO:

\begin{array}{l} G (t_{i}) = m e a n (C T D ‐ D O / o p t o d e ‐ D O) & (5) \end{array}

For the initial calibration point, $G (t_{1})$ , this ratio is most robustly calculated from co-located and concurrent water column profiles of optode-DO and CTD-DO; that is, cal-dip profiles. This is additionally advantageous because it leaves the deployment cruise cal-cast profile as a means of independent validation. However, in cases where reversible drift has been detected and removed, $G (t_{1})$ should be calculated from the deployment cruise cal-cast CTD-DO matched in temperature and salinity space to the moored optode-DO instead. This avoids uncertainty in accounting for the discrepancy between the cal-dip optode-DO and the optode-DO time series with the trace of reversible drift subtracted out. The final calibration point, $G (t_{2})$ , is calculated using cal-cast CTD-DO, regardless of whether reversible drift was identified in the optode-DO time series or not; this ensures that any undetected reversible drift that has accumulated over the deployment period is captured.

When calculating $G (t_{1})$ from Equation 5 using cal-dip profiles, the profiles should exclude the highly-variable surface layer, which can cause hysteresis between the oxygen profiles. In our calculations, Equation 5 was evaluated for the profiles from 500 m to the deepest point of the profile (e.g., Figure 4A). When calculating either $G (t_{1})$ or $G (t_{2})$ from cal-cast data, Equation 5 is evaluated using CTD-DO from the cal-cast and optode-DO from ± 5 days of the date of the cal-cast that have been matched within a chosen threshold of potential temperature, practical salinity, and pressure. This ensures a comparison of DO from the same water mass. A “good” match between the water masses sampled by the optode and by the CTD should result in a standard deviation in the ratio of CTD-DO to optode-DO of less than 0.01. This is because a difference of ± 0.01 in $G (t_{i})$ yields differences in calibrated optode-DO on the order of ± 1%, which is within the accuracy specification reported by manufacturers for multi-point factory calibrations (Aanderaa Data Instruments, 2018; SeaBird Electronics, 2023). For the GOHSNAP dataset, a potential temperature threshold of 0.005°C, a practical salinity threshold of 0.005, and a pressure threshold of ± 100 dbar yielded suitable standard deviations in $G (t_{i})$ (Figure 4B). The science team will need to adjust these thresholds according to their data and can additionally choose to narrow the ± 5 day time threshold.

Once $G (t_{1})$ and $G (t_{2})$ are determined, $G (t)$ is calculated as a linear relationship between these two points.

\begin{array}{l} G (t) = m t + b & (6) \end{array}

where $m = \frac{G (t_{2}) - G (t_{1})}{t_{2} - t_{1}}$ and t is in the same unit of elapsed time as in Equation 4. $G (t)$ may then be used in Equation 2 to obtain the final, calibrated optode-DO time series (Figure 4C). Code examples of the step-by-step processing and calibration of optode-DO with and without the reversible drift are available at https://github.com/unamiller/optode_processing_examples.

6 Uncertainties and validation

The steps described in Section 5 aim to reduce uncertainties and achieve the most accurate moored optode-DO time series possible. As with any data product, however, uncertainties remain in the final calibrated optode-DO time series. The largest source of uncertainty is from the drift correction process, in which both the trend and magnitude of the calibrated optode-DO time series are essentially set by two calibration points, $G (t_{1})$ and $G (t_{2})$ . Inaccurate $G (t_{1})$ or $G (t_{2})$ can therefore introduce bias and artificial trends in the calibrated optode-DO time series, underscoring the necessity of proper Winkler calibration of CTD-DO and the careful matching of water masses between cal-casts and mooring sites.

As $G (t_{1})$ and $G (t_{2})$ are calculated from the mean ratio of CTD-DO to optode-DO (Equation 5), the standard deviation of the ratio reflects error in the oxygen measurements or in the matching of their respective water masses. If the optode and CTD electrode are accurate and sampling precisely the same water mass at the same time, their ratio should be consistent across each data point, i.e., low variance about the mean. This is exemplified by cal-dips, where the typical RMS error between the two profiles is less than 1 µmol kg⁻¹ (e.g., Figure 6B), equivalent to uncertainty of less than 0.3% in the resulting calculation of Equation 5. $G (t_{1})$ or $G (t_{2})$ derived from cal-casts, however, will take on greater error due to spatial and temporal variability in DO between the mooring site and the cast site, as well as any error in the accuracy of the temperature and salinity measurements used to match water masses. The use of a 0.01 limit for the standard deviation of the ratio of CTD-DO to optode-DO (Equation 5) when matching water masses is an attempt to limit uncertainty in $G (t_{1})$ or $G (t_{2})$ , such that uncertainty in the resulting calibrated optode-DO is approximately 1% (Section 3). Because cal-casts are used to calculate both $G (t_{1})$ and $G (t_{2})$ in optode-DO time series corrected for reversible drift, these time series will have higher uncertainty related to their calibration than time series without reversible drift, which use cal-dips for the calculation of $G (t_{1})$ . This is in addition to any uncertainty in least-squares fit of the exponential function to the reversible drift trace.

Serendipitous CTD-DO casts taken at three of the OSNAP array mooring sites mid-way through the optode deployment period allow us to assess uncertainty in the calibrated optode-DO time series using data fully independent of the calibration process (Figures 10–12). These CTD-DO were matched to each of the 11 optodes at the three mooring sites using the same potential temperature, practical salinity, and pressure thresholds described in Section 5.4. The average error between the optode-DO and these mid-deployment CTD-DO casts ranged from 0.26 to 8.87 µmol kg⁻¹ with a median of 2.40 µmol kg⁻¹ and a mean of 2.67 µmol kg⁻¹. The two highest average errors, 8.87 and 4.55 µmol kg⁻¹, were found in the two shallowest optodes at 77 and 530 db (Figures 10A, B), where spatial and temporal variability in dissolved oxygen, and therefore error, between the serendipitous cal-cast and mooring site are likely elevated due to patchiness in biological activity and convective processes.

Figure 10

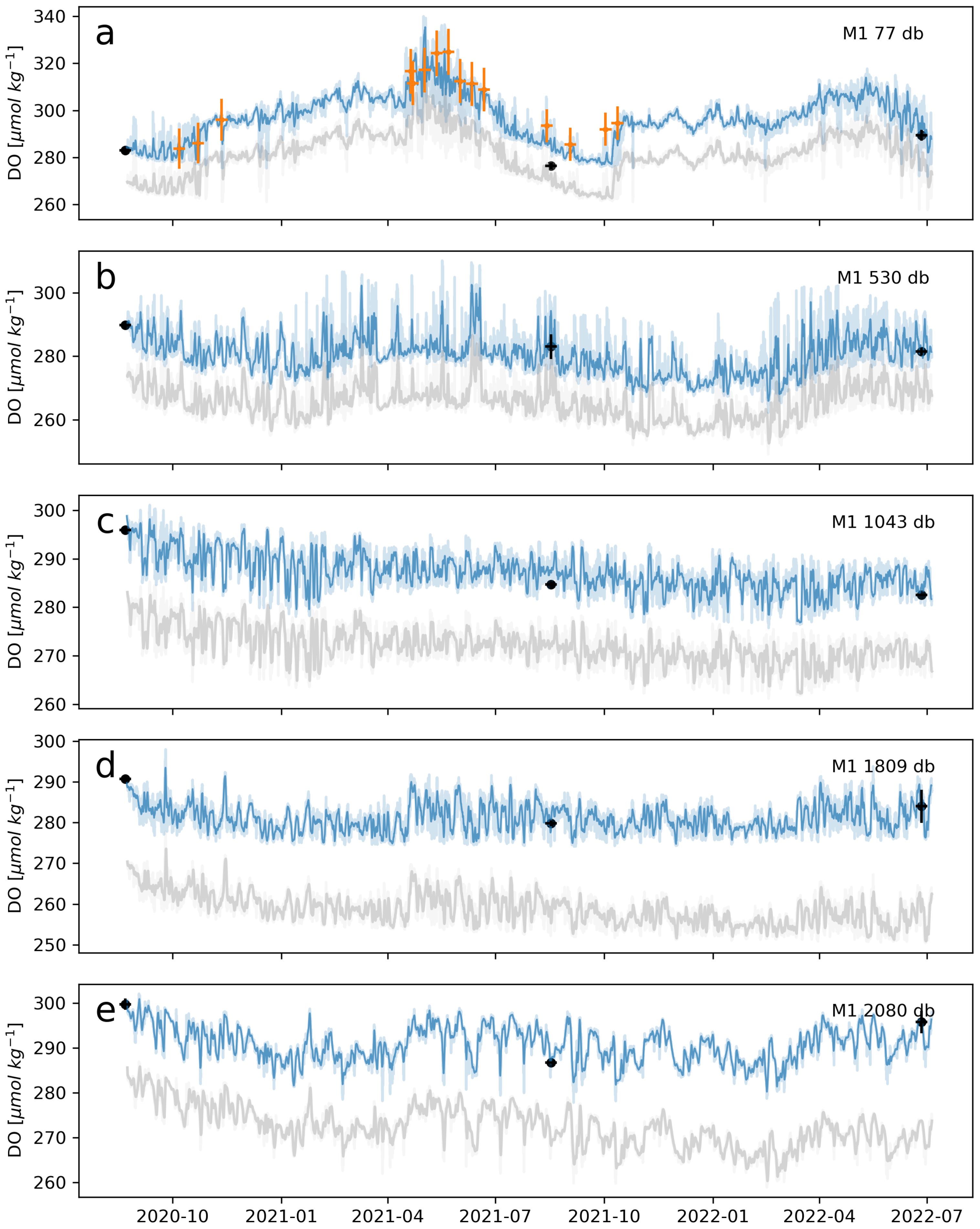
Figure 10. Comparison of delayed-mode BGC-Argo-DO (orange) and Winkler-calibrated CTD-DO (black) to 1-day averaged calibrated (blue) optode-DO time series at OSNAP Mooring M1. Uncalibrated optode-DO is shown in grey. Panels (A–E) show data at increasing depths along the mooring line. Data were matched in practical salinity, potential temperature, pressure, and time, and for the BGC-Argo-DO, a 100 km radius surrounding the mooring site was used to collate argo profiles. Underlaid light blue and light grey time series show the full un-averaged calibrated and uncalibrated time series, respectively. The CTD-DO data points at the start and end of each time series are from the deployment and recovery cruise cal-casts. In most optode-DO time series (those without reversible drift), the deployment cruise cal-cast is not used in the calibration and therefore serves as an external validation point. The mid-deployment CTD-DO data points shown here were not used in the calibration and also serve as external validation points. Each BGC-Argo-DO data point represents an individual profile. Clusters of data points are usually from the same Argo float. Horizontal error bars on all CTD-DO and BGC-Argo-DO data points indicate the +- 5-day period over which the water mass matchup was performed. Vertical error bars on the cal-cast are the standard deviation of the CTD-DO within the water mass matching criteria. Vertical error bars on the BGC-ARGO-DO indicate the error reported within the data file.

Figure 11

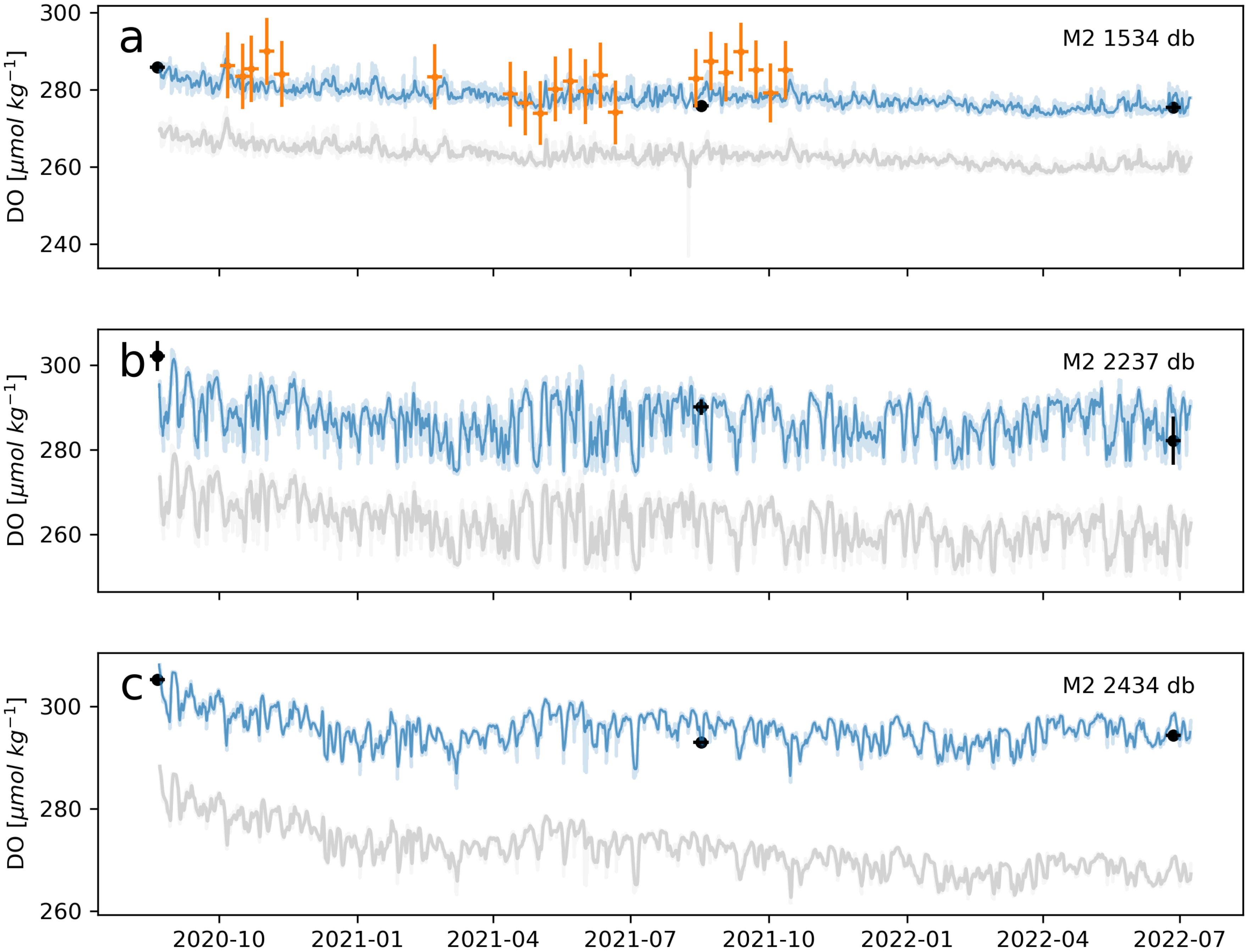
Figure 11. Same as in Figure 10 but for optodes on OSNAP Mooring M2.

Figure 12

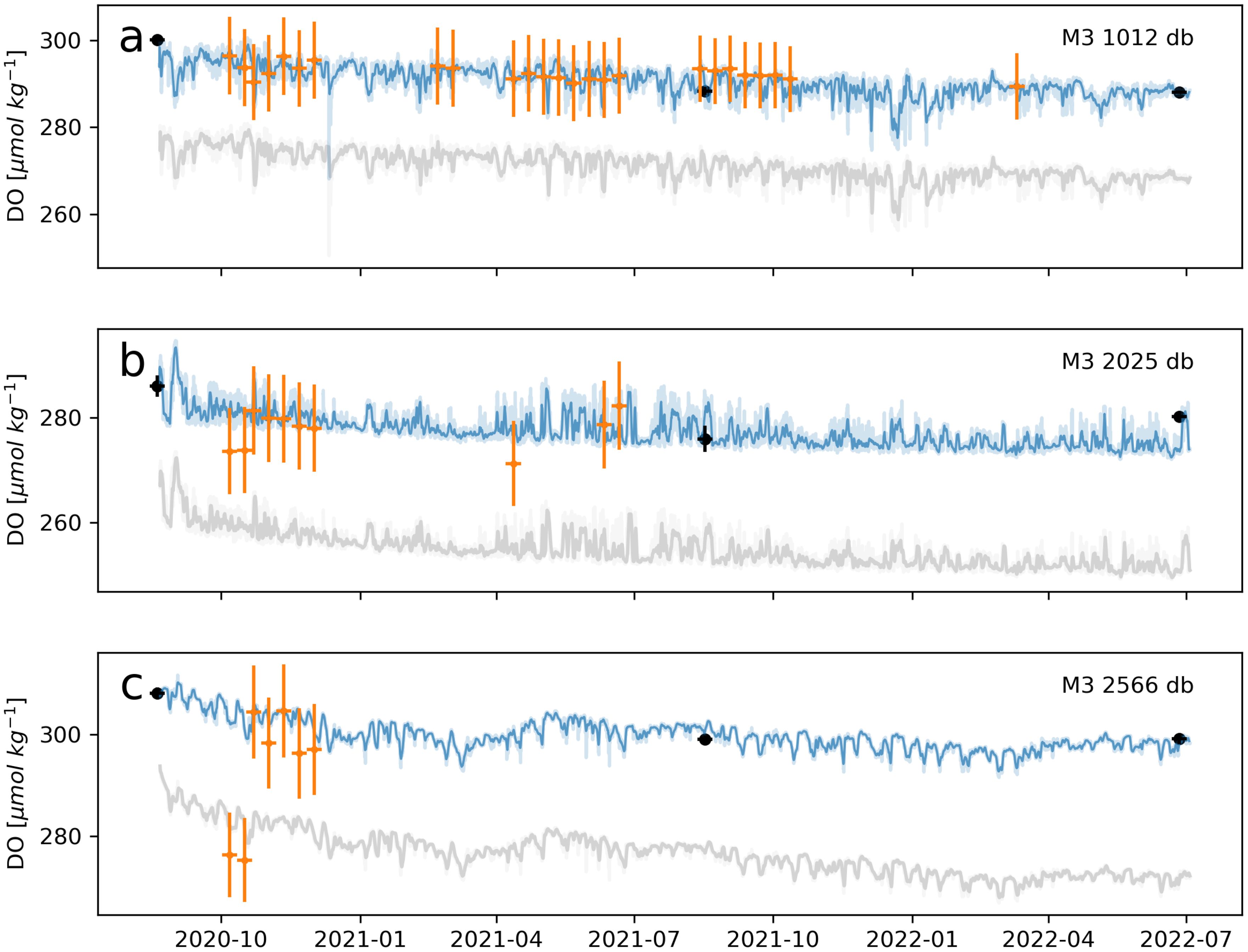
Figure 12. (A–C) Same as in Figure 10 but for optodes on OSNAP Mooring M3. Note that Argos typically sample only to depths less than 2,000 m, but data shown at greater depths here were collected by a “Deep-Arvor float”, capable of sampling as deep as 4,000 m. In (C), the two BGC-Argo-DO points that appear much lower than the other cluster of points were from a separate float with a separate calibration procedure. As values of ∼250 µmol kg⁻¹ are anomalously low for this region, the discrepancy likely indicates an issue with the calibration of this particular float.

Notably, despite the larger uncertainties associated with the correction of optode-DO with reversible drift, the three optodes with reversible drift did not have errors that were systematically higher than those without. Errors in these three optodes were 2.81, 3.23, and 1.53 µmol kg⁻¹ at 1,993 db, 2,000 db, and 2,557 db, respectively, compared to the average error across all 11 optodes of 2.67 µmol kg⁻¹. Overall, the average error of 2.67 µmol kg⁻¹ is roughly 1% of calibrated optode-DO and consistent with the estimated 1% uncertainty associated with the use of cal-casts to derive $G (t_{1})$ and $G (t_{2})$ . This suggests that uncertainty in the calibrated optode-DO time series is broadly ∼1% across the deployment period and that the leading source of uncertainty is from the matching of water masses between the cal-cast and mooring site, even for time series that were corrected for reversible drift.

DO profiles from optodes on BGC-Argo floats (BGC-Argo-DO; Thierry et al., 2021) provide an alternative and more accessible means of validation for optode-DO calibrations than mid-deployment Winker-calibrated CTD-DO casts. It should be noted, however, that BGC-Argo have their own uncertainties associated with “delayed-mode” correction protocols that are reported in the range of 1% - 3% (±∼3 - 9 µmol kg⁻¹) (Takeshita et al., 2013; Johnson et al., 2015; Mignot et al., 2019; Maurer et al., 2021). Some may also lack correction for the instantaneous pressure response, as is suspected for the anomalous BGC-Argo-DO data points in Figures 12B and C that appear low relative to the moored time series as well as to other Argo data points. These low-biased data are from the same float, suggesting an issue in data processing. Overall, we found the median error between BGC-Argo-DO and GOHSNAP optode-DO to be near or below 1% (Table 3). BGC-Argo-DO profiles can be matched to moored optode-DO using the same time, potential temperature, practical salinity, and pressure criteria used to match cal-cast profiles to the moored optodes, though we found more relaxed criteria yielded similarly low errors. Only “delayed-mode” BGC-Argo-DO profiles should be used in comparison with calibrated optode-DO, as these have undergone a greater degree of quality control and data correction than “adjusted-mode” or “real-time” profiles. We found that a relatively large search radius (100 km, centered at each mooring site) for BGC-Argo-DO profiles in the OSNAP study region still yielded helpful comparisons when filtered using strict temperature and salinity criteria, though some regions may require a smaller search radius. Code for accessing the BGC-ARGO repository and matching with the OSNAP moorings can be found at https://github.com/ellenrpark/bgcargo_floatmatchups.

Table 3

Table 3. Error between BGC-ARGO-DO and GOHSNAP moored optode-DO.

As an example of the value of comparison with BGC-Argo profiles, we used BGC-Argo-DO to verify a steady decline in optode-DO observed across the deployment period at mooring sites “M2” and “M3” (Figures 11, 12). A potential concern in interpreting this trend was that rather than reflecting a real physical process, these results might instead be indicative of a systematic error in the Winkler calibrations of CTD-DO at these two sites. However, both BGC-Argo profiles and the mid-deployment cal-casts validate the calibrated optode-DO, suggesting that the decline is a real phenomenon. In particular, BGC-Argo-DO available across the full deployment period at 1,012 db at M3 independently shows the same decline (Figure 12A). Cross-validation of optode-DO against CTD-DO, BGC-Argo-DO, and other platforms, such as gliders, holds the additional benefit of promoting the cohesion and interoperability of DO datasets across the oceanographic community.

7 FAIR data archiving

To maximize the impact and future use of DO measurements from moorings, we recommend applying the Findability, Accessibility, Interoperability and Reuse (FAIR) Data Principles when organizing data products (Wilkinson et al., 2016). The international Climate and Ocean Variability, Predictability and Change (CLIVAR) program outlines a data policy that includes principles of free and unrestricted exchange, metadata, quality control, data preservation, reusability, and easy access. Ideally, this should include the whole chain of data required to reproduce final products, including shipboard discrete sample (e.g., Winkler) and CTD data, optode and CTD measurements from cal-dips, raw moored optode data, and final calibrated versions.

For discrete bottle data, current best practices (Jiang et al., 2022) outline standards for column headers, units, quality flags, etc. in accordance with practices of the Carbon Hydrographic Data Office (CCHDO) at Scripps Institution of Oceanography.

Moored data is best reported using a format that includes data and metadata, such as NetCDF. The data model should follow existing exemplars such as the Climate and Forecast (CF) conventions (Hassell et al., 2017) and the Argo data manual (Thierry et al., 2022). Quality-controlled moored oxygen data is best presented alongside aligned time series of temperature, pressure, and salinity, which allows for calculations of related derived parameters such as the equilibrium saturation concentration and apparent oxygen utilization (AOU). We also recommend including the following data attributes: optode serial number, manufacturer and model, mooring ID, nominal depth, median pressure, latitude, longitude, reversible pressure correction flag (true/false), $p_{f a c}$ , $G (t_{1})$ , $G (t_{2})$ , and a brief description of the calibration methods. Example NetCDFs containing calibrated optode-DO data can be found at https://github.com/unamiller/optode_processing_examples/tree/main/FAIR-format NetCDF examples.

Finally, we note that best practices for moored biogeochemical data are actively evolving and the science team should consult the latest publications and community consensus to inform decisions on data model and format.

8 Summary

In this paper, we have described protocols for moored optode deployment, data processing, and data calibration, with recommendations intended to achieve the collection of high-quality optode-DO measurements. The major points are reiterated here, and the reader is again referred to the quick-start guide and worked examples made available in the Supplementary Material and on GitHub.

1. Optodes are known to drift from factory calibration, requiring calibration against CTD-DO collected on the mooring deployment and recovery cruises. This drift occurs as a time-dependent “irreversible drift” and a pressure-and-time-dependent “reversible drift”, which is identified in some optodes deployed at depths below 1,000 m. Analysis of the 60 GOHSNAP optodes over 2 years of deployment showed irreversible drift occurring at an average rate of ∼1% per year of in situ deployment. Reversible drift was detected in 7 of the 24 optodes deployed at depths greater than 1,000 m and ranged in magnitude from 0.85% to 3.3% per 1,000 m (Table 2).

2. Reversible drift in optodes has not been widely characterized outside of the present study. Our observations of the 60 GOHSNAP optodes and those of Berx et al., 2019 suggest that for moored optodes below depths of 1,000 m, reversible drift can be identified as an exponential decay in dissolved oxygen occurring within the first days (“fast reversible drift”) or weeks to months (“slow reversible drift”) of deployment in the absence of a similar change in the co-located potential temperature time series. We provide a heuristic protocol for the identification and removal of reversible drift and emphasize the role of expert judgment in assessing and correcting for this drift. As more deep-moored optode data are collected and analyzed by the community, we expect its characterization, and thus protocols for removal, will evolve.

3. The two types of CTD casts required to calibrate moored optode-DO are 1) cal-dips, casts on which optodes are strapped to the CTD profiler and dual optode-DO and CTD-DO profiles are obtained, and 2) cal-casts, CTD-DO profiles taken as close to the mooring site as possible while the optodes are sampling in situ. These CTD casts are used to derive $G (t_{1})$ and $G (t_{2})$ , the two gain-correction factors used to calculate the linear calibration function $G (t)$ used in Equation 2.

4. Cal-dips also serve as a means of determining the optode-specific pressure correction factor, $p_{f a c}$ , in the $P_{c o r r}$ term of Equation 1, which corrects the instantaneous pressure response. Our analysis of the 60 GOHSNAP optodes shows values of $p_{f a c}$ to range from 2.4% to 4.3% per 1,000m, suggesting that use of a default constant value of $p_{f a c}$ could result in error on the order of 1% per 1,000 m in an individual optode.

5. The accuracy of calibrated optode-DO depends directly on the quality of shipboard CTD-DO, which itself must be calibrated using Winklers. Because Winkler titrations are highly sensitive and require a skilled analyst, any science team planning to deploy moored optodes must also plan for the collection and analysis of Winklers on both the deployment and recovery cruises. On-board titrations by a skilled analyst yield the highest-quality Winklers.

6. The calibration of moored optode-DO can be validated through cross-platform comparisons, such as with mid-deployment CTD-DO profiles (calibrated with Winklers) and/or BGC-Argo-DO and DO from optode-equipped gliders. Comparison of BGC-Argo-DO profiles to the GOHSNAP optode-DO matched using potential temperature, practical salinity, pressure, and time thresholds yielded median relative errors of ∼1% or less.

Data availability statement

BGC-Argo data can be obtained from https://data-argo.ifremer.fr/. CTD-DO data are published as Fogaren and Palevsky (2023). GOHSNAP mooring data are forthcoming on BCO-DMO. All other data inquiries may be directed to the corresponding author.

Author contributions

UM: Writing – original draft, Writing – review & editing, Investigation, Data Curation, Formal analysis, Methodology, Visualization, Software, Validation, Project administration. KF: Writing – original draft, Writing – review & editing, Investigation, Data Curation, Software, Formal analysis, Methodology, Visualization. DA: Writing – original draft, Writing – review & editing, Investigation, Methodology, Formal analysis, Resources, Conceptualization, Funding acquisition, Project administration. CJ: Writing – review & editing, Investigation, Methodology. JK: Writing – review & editing, Methodology, Investigation. IL: Writing – original draft, Writing – review & editing, Investigation, Funding acquisition, Project administration, Data curation, Resources. ML: Writing – review & editing, Data curation. HN: Writing – review & editing, Data curation. DN: Writing – original draft, Writing – review & editing, Data curation, Software, Project administration, Investigation, Funding acquisition. HP: Writing – original draft, Writing – review & editing, Funding acquisition, Formal analysis, Investigation, Data curation, Resources, Project administration, Conceptualization. EP: Writing – review & editing, Formal analysis, Investigation, Data curation, Software, Validation. MY: Writing – review & editing, Data curation. JP: Writing – original draft, Writing – review & editing, Funding acquisition, Formal analysis, Investigation, Methodology, Supervision, Conceptualization, Project administration, Resources.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. UM and JP were supported by National Science Foundation (NSF) award 1947829. HP, KF, and MY were supported by NSF award 1947970. IL and HN were supported by NSF awards OCE-2038481 and OCE-2122579. DA and JK were supported by the Canada Excellence Research Chair (CERC) in Ocean Science and Technology, the Canada First Research Excellence Fund (Ocean Frontier Institute grant, Module B), and the CERC.Ocean group led by Prof. Douglas Wallace at Dalhousie University. EP was supported by OCE-2023080 and OCE-1947567. DN was supported by OCE-1947567. BGC-Argo is supported by the Global Ocean Biogeochemistry Array (GO-BGC) Project under the NSF Award 1946578 with operational support from NSF Award 2110258.

Acknowledgments

We thank Overturning in the Subpolar North Atlantic Program (OSNAP), and in particular, Dr. Johannes Karstensen, Dr. Dave Hebert, Dr. Marc Ringuette, Dr. Susan Lozier, Dr. Fiamma Straneo, Dr. Amy Bower, and Dr. Robert Pickart for supporting us in deploying optodes on the mooring array and thereby enabling the Gases in the Overturning and Horizontal circulation of the Subpolar North Atlantic Program (GOHSNAP). We also thank the crew and scientists aboard the 2019-2020 OSNAP mooring cruises: AM2001, AR45, AR46, MSM94-01, AT48-05, AR69-03, and M184, as well as the two reviewers for their insightful comments and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1441976/full#supplementary-material

References

Aanderaa Data Instruments (2018). Aanderaa oxygen optodes: best practices for maintaining high data quality (Bergen, Norway: Aanderaa Data Instruments AS). doi: 10.25607/OBP-868

Crossref Full Text | Google Scholar

Atamanchuk D., Koelling J., Send U., Wallace D. W. R. (2020). “Rapid transfer of oxygen to the deep ocean mediated by bubbles,” in Nature geoscience 13.3. Publisher (London, U.K.: Nature Publishing Group), 232–237. doi: 10.1038/s41561-020-0532-2

Crossref Full Text | Google Scholar

Atamanchuk D., Palter J., Palevsky H., Le Bras I., Koelling J., Nicholson D. (2021). “Linking oxygen and carbon uptake with the meridional overturning circulation using a transport mooring array,” in Oceanography, (Oceanography, Rockville, MD) 9–9. doi: 10.5670/oceanog.2021.supplement.02-03

Crossref Full Text | Google Scholar

Atkinson M. J., Thomas F. I. M., Larson N. (1996). Effects of pressure on oxygen sensors. J. Atmos. Ocean. Technol. 13, 1267–1274. doi: 10.1175/1520-0426(1996)013<1267:EOPOOS>2.0.CO;2

Crossref Full Text | Google Scholar

Berx B., Cunningham S., von Appen W.-J., Atamanchuk D., Brown P., Fraser N., et al. (2019). Report on the observational potential of the TMAs. en (Kiel, Germany: AtlantOS). 35. doi: 10.3289/atlantos_d3.18

Crossref Full Text | Google Scholar

Bittig H. C., Fiedler B., Fietzek P., Körtzinger A. (2015). Pressure Response of Aanderaa and Sea-Bird Oxygen Optodes. J. Atmos. Ocean. Technol. (Ifremer. Brest, Franc) 32, 2305–2317. doi: 10.1175/JTECH-D-15-0108.1

Crossref Full Text | Google Scholar

Bittig H. C., Fiedler B., Scholz R., Krahmann G., Körtzinger A. (2014). Time response of oxygen optodes on profiling platforms and its dependence on flow speed and temperature. Limnol. Oceanogr.: Methods 12, 617–636. doi: 10.4319/lom.2014.12.617

Crossref Full Text | Google Scholar

Bittig H. C., Körtzinger A. (2015). Tackling oxygen optode drift: near-surface and in-air oxygen optode measurements on a float provide an accurate in situ reference. J. Atmos. Ocean. Technol. 32, 1536–1543. doi: 10.1175/JTECH-D-14-00162.1

Crossref Full Text | Google Scholar

Bittig H. C., Körtzinger A. (2017). Technical note: Update on response times, in-air measurements, and in situ drift for oxygen optodes on profiling platforms. Ocean Sci. 13, 1–11. doi: 10.5194/os-13-1-2017

Crossref Full Text | Google Scholar

Bittig H. C., Körtzinger A., Johnson K., Claustre H., Emerson S., Fennel K., et al. (2018a). SCOR WG 142: Quality Control Procedures for Oxygen and Other Biogeochemical Sensors on Floats and Gliders. Recommendations on the conversion between oxygen quantities for Bio-Argo floats and other autonomous sensor platforms.

Google Scholar

Bittig H. C., Körtzinger A., Neill C., van Ooijen E., Plant J. N., Hahn J., et al. (2018b). Oxygen optode sensors: principle, characterization, calibration, and application in the ocean. Front. Mar. Sci. 4. doi: 10.3389/fmars.2017.00429

Crossref Full Text | Google Scholar

Bushinsky S. M., Emerson S. (2013). A method for in-situ calibration of Aanderaa oxygen sensors on surface moorings. Mar. Chem. 155, 22–28. doi: 10.1016/j.marchem.2013.05.001

Crossref Full Text | Google Scholar

Bushinsky S. M., Emerson S. R., Riser S. C., Swift D. D. (2016). Accurate oxygen measurements on modified Argo floats using in situ air calibrations. Limnol. Oceanogr.: Methods. 14, 491–505. doi: 10.1002/lom3.10107

Crossref Full Text | Google Scholar

Cheung W. W.L., Sarmiento J. L., Dunne J., Frölicher T. L., Lam V. W.Y., Deng Palomares M. L., et al. (2013). Shrinking of fishes exacerbates impacts of global ocean changes on marine ecosystems. Nat. Climate Change. 3, 254-258. doi: 10.1038/nclimate1691

Crossref Full Text | Google Scholar

Clark L. C., Wolf R., Granger D., Taylor Z. (1953). Continuous recording of blood oxygen tensions by polarography. J. Appl. Physiol. 6, 189–193. doi: 10.1152/jappl.1953.6.3.189

PubMed Abstract | Crossref Full Text | Google Scholar

D’Asaro E. A., McNeil C. (2013). Calibration and stability of oxygen sensors on autonomous floats. J. Atmos. Ocean. Technol. 30, 1896–1906. doi: 10.1175/JTECH-D-12-00222.1

Crossref Full Text | Google Scholar

Deutsch C., Ferrel A., Seibel B., Pörtner H.-O., Huey R. B. (2015). Climate change tightens a metabolic constraint on marine habitats. Science 348, 1132–1135. doi: 10.1126/science.aaa1605

PubMed Abstract | Crossref Full Text | Google Scholar

Diaz R. J., Rosenberg R. (2008). “Spreading dead zones and consequences for marine ecosystems,” in Science 321.5891 (Washington, DC: American Association for the Advancement of Science), 926–929. doi: 10.1126/science.1156401

PubMed Abstract | Crossref Full Text | Google Scholar

Dove L. A., Thompson A. F., Balwada D., Gray A. R. (2021). Observational evidence of ventilation hotspots in the southern ocean. J. Geophys. Res.: Oceans 26, e2021JC017178. doi: 10.1029/2021JC017178

Crossref Full Text | Google Scholar

Edwards B., Murphy D., Janzen C., Larson N. (2010). Calibration, response, and hysteresis in deep-sea dissolved oxygen measurements. J. Atmos. Ocean. Technol. 27, 920–931. doi: 10.1175/2009JTECHO693.1

Crossref Full Text | Google Scholar

Emerson S., Stump C. (2010). Net biological oxygen production in the ocean—II: Remote in situ measurements of O2 and N2 in subarctic pacific surface waters. Deep Sea Res. Part I: Oceanogr. Res. Papers 57, 1255–1265. doi: 10.1016/j.dsr.2010.06.001

Crossref Full Text | Google Scholar

Emerson S., Stump C., Nicholson D. (2008). Net biological oxygen production in the ocean: Remote in situ measurements of O2 and N2 in surface waters. Global Biogeochem. Cycles. 22. doi: 10.1029/2007GB003095

Crossref Full Text | Google Scholar

Fogaren K. E., Palevsky H. (2023). Bottle-calibrated dissolved oxygen profiles from yearly turn-around cruises for the Ocean Observations Initiative (OOI) Irminger Sea Array 2014–2022 (Biological and Chemical Oceanography Data Management Office (BCO-DMO). Woods Hole, MA). doi: 10.26008/1912/BCO-DMO.904721.1

Crossref Full Text | Google Scholar

Hassell D., Gregory J., Blower J., Lawrence B. N., Taylor K. E. (2017). A data model of the Climate and Forecast metadata conventions (CF-1.6) with a software implementation (cf-python v2.1). Geosci. Model. Dev. 10, 4619–4646. doi: 10.5194/gmd-10-4619-2017

Crossref Full Text | Google Scholar

Ito T., Minobe S., Long M. C., Deutsch C. (2017). Upper ocean O2 trends: 1958–2015. Geophys. Res. Lett. 44, 4214-4223. doi: 10.1002/2017GL073613

Crossref Full Text | Google Scholar

Jiang L.-Q., Pierrot D., Wanninkhof R., Feely R. A., Tilbrook B., Alin S., et al. (2022). Best practice data standards for discrete chemical oceanographic observations. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.705638

Crossref Full Text | Google Scholar

Johnson K. S., Plant J. N., Riser S. C., Gilbert D. (2015). Air oxygen calibration of oxygen optodes on a profiling float array. J. Atmos. Ocean. Technol. 32, 2160–2172. doi: 10.1175/JTECH-D-15-0101.1

Crossref Full Text | Google Scholar

Koelling J., Atamanchuk D., Karstensen J., Handmann P., Wallace D. W.R. (2022). Oxygen export to the deep ocean following Labrador Sea Water formation. Biogeosciences 19, 437–454. doi: 10.5194/bg-19-437-2022

Crossref Full Text | Google Scholar

Lakowicz J. R. (1999). Principles of fluorescence spectroscopy (Boston, MA: Springer US). doi: 10.1007/978-1-4757-3061-6

Crossref Full Text | Google Scholar

Langdon C. (2010). Determination of dissolved oxygen in seawater by winkler titration using the amperometric technique (International Ocean Carbon Coordinating Project. Sopot, Poland). doi: 10.25607/OBP-1350

Crossref Full Text | Google Scholar

Lévy M., Resplandy L., Palter J. B., Couespel D., Lachkar Z. (2022). “Chapter 13 - The crucial contribution of mixing to present and future ocean oxygen distribution,” in Ocean mixing. Eds. Meredith M., Naveira Garabato A. (Amsterdam, Netherlands: Elsevier), 329–344. doi: 10.1016/B978-0-12-821512-8.00020-7

Crossref Full Text | Google Scholar

Lozier M. S., Li F., Bacon S., Bahr F., Bower A. S., Cunningham S. A., et al. (2019). A sea change in our view of overturning in the subpolar North Atlantic. Science 393, 516–521. doi: 10.1126/science.aau6592

PubMed Abstract | Crossref Full Text | Google Scholar

Maurer T. L., Plant J. N., Johnson K. S. (2021). Delayed-mode quality control of oxygen, nitrate, and pH data on SOCCOM biogeochemical profiling floats. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.683207

Crossref Full Text | Google Scholar

Mignot A., D’Ortenzio F., Taillandier V., Cossarini G., Salon S. (2019). Quantifying observational errors in biogeochemical-argo oxygen, nitrate, and chlorophyll a concentrations. Geophys. Res. Lett. 46, 4330–4337. doi: 10.1029/2018GL080541

Crossref Full Text | Google Scholar

Oschlies A., Brandt P., Stramma L., Schmidtko S. (2018). “Drivers and mechanisms of ocean deoxygenation,” in Nature Geoscience (London U.K.: Nature Publishing Group), 467–473. doi: 10.1038/s41561-018-0152-2

Crossref Full Text | Google Scholar

Owens W.B., Millard R. C. (1985). A New Algorithm for CTD Oxygen Calibration. J. Phys. Oceanogr. 15, 621–631. doi: 10.1175/1520-0485(1985)015<0621:ANAFCO>2.0.CO;2

Crossref Full Text | Google Scholar

Palevsky H., Clayton S., Atamanchuk D., Battisti R., Batryn J., Bourbonnais A., et al. (2023). OOI biogeochemical sensor data best practices and user guide. Version 1.1.1 (Ocean Observatories Initiative, Biogeochemical Sensor Data Working Group). doi: 10.25607/OBP-1865.2

Crossref Full Text | Google Scholar

Palter J. B., Trossman D. S. (2018). The sensitivity of future ocean oxygen to changes in ocean circulation. Global Biogeochem. Cycles 32, 738–751. doi: 10.1002/2017GB005777

Crossref Full Text | Google Scholar

Ren A. S., Rudnick D. L., Twombly A. (2023). Drift characteristics of sea-bird dissolved oxygen optode sensors. J. Atmos. Ocean. Technol. 40, 1645–1656. doi: 10.1175/JTECH-D-22-0103.1

Crossref Full Text | Google Scholar

SeaBird Electronics (2023). SBE 63 optical dissolved oxygen sensor user manual (Sea-Bird Scientific. Bellevue, WA).

Google Scholar

Stendardo I., Gruber N. (2012). Oxygen trends over five decades in the North Atlantic. J. Geophys. Res.: Oceans. 117. doi: 10.1029/2012JC007909

Crossref Full Text | Google Scholar

Takeshita Y., Martz T. R., Johnson K. S., Plant J. N., Gilbert D., Riser S. C., et al. (2013). A climatology-based quality control procedure for profiling float oxygen data. J. Geophys. Res.: Oceans 118, 5640–5650. doi: 10.1002/jgrc.20399

Crossref Full Text | Google Scholar

Tengberg A., Hovdenes J., Andersson H. J., Brocandel O., Diaz R., Hebert D., et al. (2006). Evaluation of a lifetime-based optode to measure oxygen in aquatic systems. Limnol. Oceanogr.: Methods 4, 7–17. doi: 10.4319/lom.2006.4.7

Crossref Full Text | Google Scholar

Thierry V., Bittig H. C., Gilbert D., Kobayashi T., Kanako S., Schmid C. (2022). Processing Argo oxygen data at the DAC level (Ifremer. Brest, Franc).

Google Scholar

Thierry V., Bittig H. C., The Argo-Bgc Team (2021). Argo quality control manual for dissolved oxygen concentration (Ifremer. Brest, Franc).

Google Scholar

Thomas L. N., Joyce T. M. (2010). Subduction on the northern and southern flanks of the gulf stream. J. Phys. Oceanogr. 10, 429–438. doi: 10.1175/2009JPO4187.1

Crossref Full Text | Google Scholar

Uchida H., Johnson G. C., McTaggart K. E. (2010). CTD oxygen sensor calibration procedures. In, (eds Hood E. M., Sabine C. L., Sloyan B. M.), 17pp. (IOCCP Report Number 14; ICPO Publication Series Number 134). doi: 10.25607/OBP-1344

Crossref Full Text | Google Scholar

Uchida H., Kawano T., Kaneko I., Fukasawa M. (2008). In situ calibration of optode-based oxygen sensors. J. Atmos. Ocean. Technol., 2271–2281. doi: 10.1175/2008JTECHO549.1

Crossref Full Text | Google Scholar

Wilkinson M. D., Dumontier M., Aalbersberg I. J., Appleton G., Axton M., Baak A., et al. (2016). The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 3, 160018. doi: 10.1038/sdata.2016.18

PubMed Abstract | Crossref Full Text | Google Scholar

Winkler (1888). The determination of dissolved oxygen. Ber. Dtsch. Chem. Ges 21, 843–842.

Google Scholar

Wolf M. K., Hamme R. C., Gilbert D., Yashayaev I., Thierry V. (2018). Oxygen saturation surrounding deep water formation events in the labrador sea from argo-O2 data. Global Biogeochem. Cycles 32, 635–653. doi: 10.1002/2017GB005829

Crossref Full Text | Google Scholar

Zhang J.-Z., Berberian G., Wanninkhof R. (2002). Long-term storage of natural water samples for dissolved oxygen determination. Water Res. 36, 4165–4168. doi: 10.1016/S0043-1354(02)00093-3

PubMed Abstract | Crossref Full Text | Google Scholar

Keywords: biogeochemical sensors, BGC-Argo, dissolved oxygen, ocean best practices, oceanographic mooring, optode calibration

Citation: Miller UK, Fogaren KE, Atamanchuk D, Johnson C, Koelling J, Le Bras I, Lindeman M, Nagao H, Nicholson DP, Palevsky H, Park E, Yoder M and Palter JB (2024) Oxygen optodes on oceanographic moorings: recommendations for deployment and in situ calibration. Front. Mar. Sci. 11:1441976. doi: 10.3389/fmars.2024.1441976

Received: 31 May 2024; Accepted: 09 October 2024;
Published: 15 November 2024.

Edited by:

Virginie Van Dongen-vogels, Australian Institute of Marine Science (AIMS), Australia

Reviewed by:

Dominique Lefevre, UMR7294 Institut Méditerranéen d’océanographie (MIO), France
Laurent Coppola, UMR7093 Laboratoire d’océanographie de Villefranche (LOV), France

Copyright © 2024 Miller, Fogaren, Atamanchuk, Johnson, Koelling, Le Bras, Lindeman, Nagao, Nicholson, Palevsky, Park, Yoder and Palter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Una Kim Miller, dW5hLm1pbGxlckB1cmkuZWR1

^†Present address: Jannes Koelling, Cooperative Institute for Climate, Ocean, and Ecosystems Studies, University of Washington, Seattle, WA, United States

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.