Parameterization scheme of the sea surface drag coefficient considering the influence of wave states and sea spray stress

The drag coefficient of the sea surface is crucial for the exchange of momentum between the ocean and atmosphere. The wave state significantly influences the variability of the drag coefficient. In the past, researchers commonly employed single-parameterization methods to describe this influence. However, the influence of wave conditions on drag coefficient is complex and variable, and it is difficult to accurately describe it with a single parameter alone. Wave age represents the ability of wind-induced waves to input energy, while wave steepness reflects the stability of the waves. By simultaneously considering wave age and wave steepness, a more accurate characterization of the dynamic nature of waves can be achieved. Additionally, the presence of sea spray profoundly impacts the distribution of the momentum flux between the ocean and atmosphere, thereby influencing the drag coefficient of the sea surface. In this study, we established a novel sea spray generation function that bases on both the wind speed and wave states (wave steepness and wave age). Considering this function, the momentum flux of sea spray droplets was analyzed under different wave states. Moreover, with increasing wave age or wave steepness, the effective sea surface drag coefficient is attenuated at low to moderate wind speeds. Considering the challenge of simultaneously obtaining wave age and wave steepness data, this paper proposes a relationship equation between the two wave state parameters. When the wave age is greater than 0.4, the correlation between the wave age and the wave steepness is strong. As the wind speed increases from low to high, there is a noticeable decrease in the effective sea surface drag coefficient with the corresponding increase in wave age. When the wave age is less than 0.4, the wave steepness reaches a maximum value, and the effective sea surface drag coefficient increases with the increase of the wave age at medium and low wind speed. With further increases in wind speed, the momentum flux derived from the air also increases. Simultaneously, the effective sea surface drag coefficient exhibits a decrease as wave age increases.

1 Introduction

The investigation of the fundamental characteristics of typhoons, one of the most intense and catastrophic weather phenomena occurring over the ocean, and their accurate forecasting have long been significant topics and research hotspots in the fields of oceanography and atmospheric science. The sea surface drag coefficient serves as a key factor in accurately representing the interaction between the atmosphere and the ocean, influencing the transfer of momentum across their interface. Therefore, the selection of an appropriate drag coefficient value directly influences the precision of typhoon numerical predictions.

Within the interaction between the ocean and atmosphere, the momentum flux at the sea surface is one of the primary driving forces of wave generation. The momentum flux between the ocean and atmosphere is typically characterized by the sea surface drag coefficient. Hence, investigating the aforementioned aspects is crucial for enhancing our understanding of typhoons and accurately predicting their behavior, thereby aiding in the effective mitigation of the impacts of these severe weather events. Moreover, comprehending the dynamic interactions between the ocean and atmosphere, including the sea surface drag coefficient, is vital for improving numerical modeling and forecasting capabilities pertaining to typhoon activity.

Initially, it was commonly assumed that the sea surface drag coefficient remained constant. However, with further advancements in research based on initial atmospheric boundary layer theory, researchers have gradually discovered a mathematical relationship between the sea surface drag coefficient and wind speed, leading to the parameterization of the sea surface drag coefficient based on wind speed (Large and Pond, 1981; Geernaert et al., 1986; Yelland and Taylor, 1996).

In recent years, mounting evidence has highlighted the crucial role of sea wave conditions in investigating the interaction between the ocean and atmosphere (Donelan et al., 1990; Toba et al., 1990; Shi et al., 2011). According to Guan and Xie (2004), the drag coefficient and the wind speed have a linear relationship with respect to the wave slope parameter (δ). Shi et al. (2019) parameterized the drag coefficient using wave age (β). The R_B parameter, as opposed to the 10-m wind speed or friction velocity, was proposed to provide a better characterization of the variability of the sea surface drag coefficient (Toba and Koga, 1986). Originally utilized as an indicator of the wave breaking intensity on the sea surface, R_B has been extensively applied in the study of the ocean-atmosphere boundary layer, encompassing investigations into air-sea gas exchange, momentum transfer, and sea spray generation (Rizza et al., 2018). Recently, researchers elucidated that both the wave age and wave steepness impact the air-sea momentum flux (Zhao and Li, 2019). The wave steepness is an internal parameter denoting the wave stability. The wave age is an external parameter representing the ability of wind to input energy into waves.

As research has advanced, it has been revealed that the sea surface drag coefficient does not exhibit linear growth at high wind speeds. Instead, its increase becomes suppressed or even attenuated beyond a certain threshold (Powell et al., 2003). Laboratory observations have further confirmed the occurrence of this phenomenon (Donelan et al., 2004; Takagaki et al., 2012). However, discrepancies in the attenuation level of the drag coefficient at high wind speeds exist among different studies. One key contributing factor to this variation is the unclear identification of the underlying mechanisms of the observed attenuation. Moon et al. (2007) proposed that wave presence leads to drag coefficient attenuation at high wind speeds. However, in reality, the sea surface comprises not only waves but also spray droplets that are generated from wave breaking and remain suspended above the sea surface with increasing wind speed. At high wind speeds, sea spray droplets significantly affect momentum exchange at the sea surface, identifying them as one of the primary causes for drag coefficient attenuation (Andreas and Emanuel, 2001; Xu et al., 2021). Observations and experiments have provided evidence supporting the role of sea spray droplets in the attenuation of the sea surface drag coefficient at high wind speeds (Donelan et al., 1990; Powell et al., 2003).

With increasing wind speed, waves under high-wind conditions experience breaking, resulting in the generation of numerous small spray droplets. These droplets, which are abundant and remain suspended above the sea surface, contribute to a significant momentum flux referred to as the sea spray flux. The considerable impact of the sea spray flux originating from sea surface spray at high wind speeds on the overall momentum exchange at the ocean–atmosphere interface was also highlighted (Shi et al., 2009). As described above, it is clear that sea spray droplets play a role in attenuating the sea surface drag coefficient at high wind speeds in the ocean-atmosphere boundary layer.

Andreas (2004) proposed an explanation, suggesting that the attenuation of the sea surface drag coefficient at high wind speeds can be attributed to the presence of the sea spray flux. As sea sprays enter the air, they undergo immediate acceleration by local winds, a process referring to the movement of air on a small scale within a specific region or localized area. Consequently, there is a decrease in the wind speed due to the dissipation of this energy. Upon re-impacting the sea surface, spray droplets transfer their momentum back to the water, thereby facilitating momentum redistribution between the atmosphere and ocean at the air–sea interface. This phenomenon is referred to as momentum transfer induced by spray droplets (Munk, 1955). Near the sea surface, when wind speeds exceed 30-35 m/s, the momentum flux from sea spray becomes comparable to the total momentum flux at the air–sea interface. At wind speeds exceeding 60 m/s, the atmospheric momentum flux is completely transformed into the momentum flux from sea spray (Andreas, 2004). Previous drag coefficient derivations at high wind speeds corresponded to the wind-induced total momentum flux. However, the analysis of Andreas (1998) demonstrated that the momentum flux from sea spray functions as a correction term to the total momentum flux generated by wind. Consequently, the drag coefficient at high wind speeds cannot be derived solely from the total momentum flux, and the correction of the momentum flux from sea spray should be considered. There are already analytical expressions for the drag coefficient at high wind speeds that can describe this attenuation phenomenon (Andreas, 2004; Makin, 2005). The correction effect of the momentum flux from sea spray on the total momentum flux at the air–sea interface was considered in deriving the drag coefficient at high wind speeds, explicitly incorporating the representation of the sea spray flux in the drag coefficient relationship (Andreas, 2004). Ultimately, it was concluded that the drag coefficient at high wind speeds ceases to increase with increasing wind speed and eventually becomes attenuated. Consequently, it was recommended to investigate the influence of sea spray droplets on the drag coefficient at high wind speeds.

The assertion that sea spray droplets cause attenuation of the drag coefficient at high wind speeds is well established. However, there has been ongoing debate regarding the formulation of the sea spray generation function (SSGF), which quantifies the production rate of spray droplets per unit area and time (Wu, 1973; Monahan, 1986; Andreas, 1992; Wu, 1993; Fairall et al., 1994; Lafon et al., 2004). This ambiguity causes difficulty in determining the precise degree to which sea spray droplets contribute to the attenuation of the drag coefficient. After analyzing previously proposed SSGFs, the SSGF calculation results should approximately exhibit a fourth-power dependence on the friction velocity (Andreas et al., 1995; Andreas and Decosmo, 2002). They identified the order of magnitude for the various SSGFs and identified three potential functions (Andreas, 1992, Fairall et al., 1994; Andreas and Decosmo, 2002) that conform with the observed characteristics of sea spray generation. However, it is important to highlight that these three functions do not account for the influence of waves. Waves are a ubiquitous phenomenon at the ocean–atmosphere interface and significantly impact the energy exchange between these two media. Meanwhile, the generation of sea spray droplets is not only related to the wind, the wave states also play a close role (Nilsson et al., 2021; Xu et al., 2021). At sufficiently high wind speeds, the energy of breaking waves increases, resulting in the generation of sea spray droplets. These droplets are forcefully ejected from the wave crests, while the crashing breakers produce spray as they collide with the surface below (Lenain and Melville, 2017; Song et al., 2023). Consequently, SSGFs that neglect wave effects are incomplete. Adopting a parameterization approach, Zhao et al. (2006) introduced wave information into the SSGF, partitioning it into two components: the generation rate of spray droplets dependent on wave conditions and the spray size spectrum. Through empirical data fitting, they derived an SSGF that yielded results consistent with the magnitude range proposed by Andreas et al. (1995) for the three previously identified functions conforming with sea spray generation characteristics. However, it should be noted that the formulation of Zhao et al. (2006) is valid for spray droplets with a certain radius range. Building upon the work of it, Shi et al. (2009) presented a novel SSGF that incorporates the impact of wave conditions on the flux of spray. They emphasized the significance of considering wave conditions when calculating the momentum flux generated by sea spray, underscoring their nonnegligible impact. In summary, existing SSGFs do not fully consider the combined effect of wind and waves in the process of sea spray generation. Further refinement of these functions is necessary to encompass a broader range of spray droplet radii under the combined influence of wind and waves.

The wave age β (β*), wave steepness δ, and wind-wave Reynolds number R_B are all referred to as wind-wave parameters. The relationship between wave conditions and drag coefficients is intricate and diverse, making it challenging to capture their complexity solely with a single parameter. Wave age represents the capacity of wind to transmit energy, while wave steepness indicates the stability of the wave itself. Both factors effectively capture wave characteristics. In this study, we propose utilizing the wind-wave Reynolds number R_B as a metric and develop a novel sea spray generation function based on the wave age and wave steepness. By considering various growth relationships among these wind-wave parameters, we aim to derive a comprehensive parameterization scheme that incorporates the influences of wave age, wave steepness and sea spray on the sea surface drag coefficient.

2 Data and methods

2.1 Relationship between the wave states and the growth of wind waves

To validate the growth relationship of wind waves indicated by observation data (Hamada, 1963; Kunishi, 1963; Kunishi and Imasato, 1966; Toba, 1972; Kawai et al., 1977; Katsaros and Ataktürk, 1992; Dobson et al., 1994; Janssen, 1997; Johnson et al., 1998), we determined the mutual relationship between the dimensionless wave height and wave age, as shown in Figure 1. By employing the least squares method, the optimal fitting equation for the data can be expressed as:

Figure 1

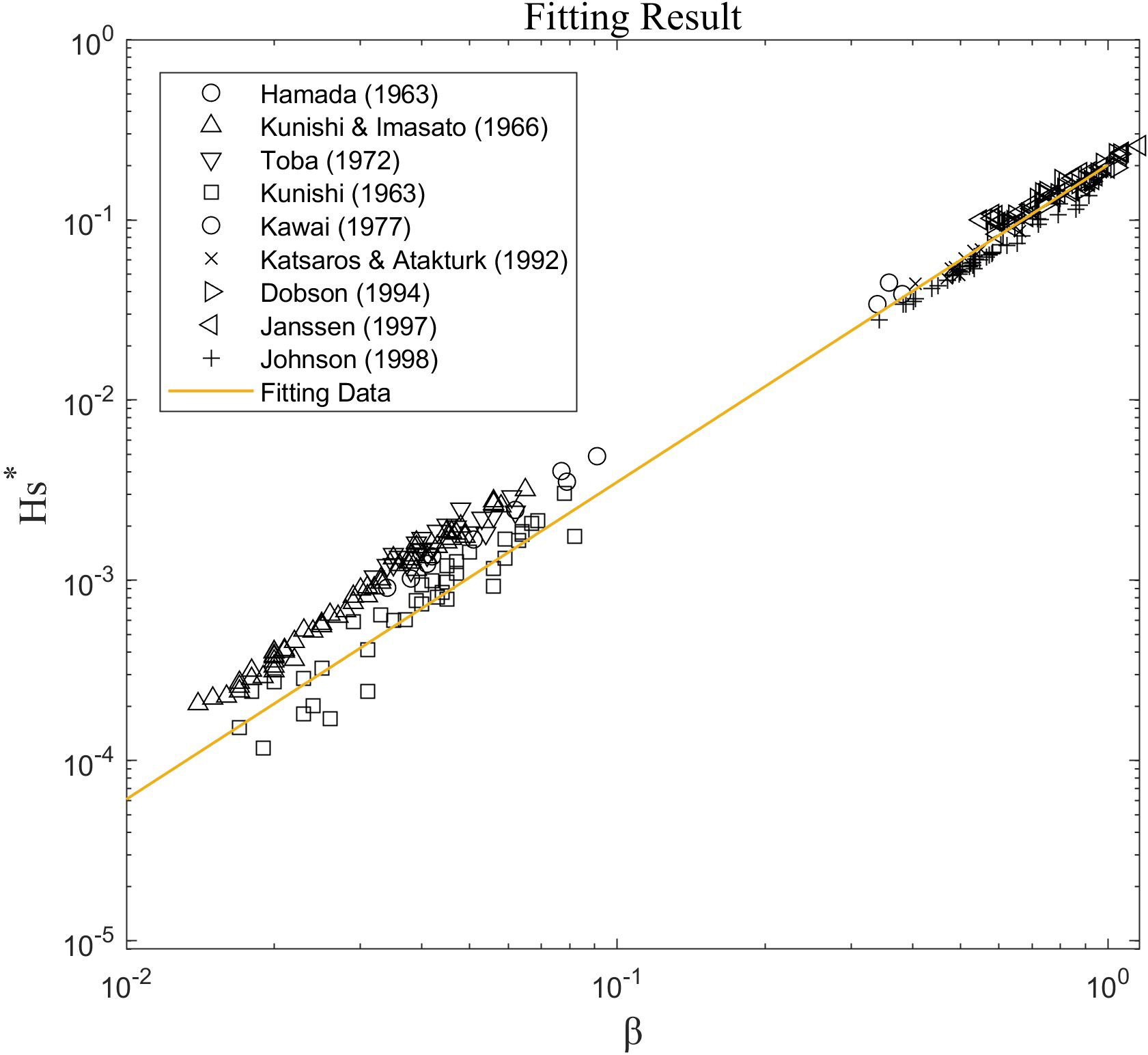
Figure 1 Relationship between the dimensionless wave height and wave age. The scatter points in this figure are laboratory and offshore observation data, and the orange solid line is the least squares fitting result. Hs* is the expression of dimensionless wave height.

$\begin{array}{ll}{H}_S^{*}=2.02\times {10}^{-1}\times {\beta }^{1.76},r=0.99& (1)\end{array}$

The correlation coefficient (r) is 0.99, which is close to 1.0. The growth relationship of waves can be obtained through measurements made in the field and in the laboratory. A significant correlation has been observed between the wind-wave parameter and wave height, which aligns with the widely recognized 3/2 power law (Toba, 1972). This relationship is attributed to the local equilibrium that exists between wind and waves.

2.2 Calculation of the drag coefficient

The evaporative layer of sea spray droplets, with a thickness approximately equal to one significant wave height, is where momentum exchange between droplets and the surrounding environment primarily happens (Andreas and Decosmo, 2002). The sea spray droplets in the evaporative layer absorb momentum from the surrounding air, resulting in a reduction of momentum transfer at the air-sea interface compared with the situation of without sea spray. That is, considering the effects of sea spray, the “effective” momentum flux τ_eff should be:

$\begin{array}{ll}{\tau }_{\text{eff}}={\tau }_T-{\tau }_{\text{sp}}& (2)\end{array}$

where τ_T is the total momentum flux and τ_sp is the sea spray momentum flux.

τ_T can generally be obtained as follows:

$\begin{array}{ll}{\tau }_T={\rho }_a{u}_{*}^2={\rho }_a{C}_D{U}_{10}^2& (3)\end{array}$

where ρ_a represents the air density and u_* represents the friction velocity. Meanwhile, C_D represents the sea surface drag coefficient and U₁₀ represents the wind speed at a height of 10m above the sea surface. Based on Equation (3), the expression for the effective momentum flux at the air-sea interface τ_eff is also given as follows:

$\begin{array}{ll}{\tau }_{eff}={\rho }_a{C}_{D,eff}{U}_{10}^2& (4)\end{array}$

where τ_eff depends on the effective drag coefficient C_D,eff that takes the impact of sea spray into account.

By combining Equations (2) and (4), we can get:

$\begin{array}{ll}{C}_{D,eff}=C_D-\frac{{\tau }_{sp}}{{\rho }_a{U}_{10}^2}& (5)\end{array}$

The given equation above represents the expression of C_D,eff, that considers the influence of sea spray droplets. It indicates that the C_D,eff is influenced by sea spray. The impact of sea spray droplets causes a decrease in the sea surface drag coefficient as the sea spray droplet effect increases. The effect of sea spray droplets is primarily reflected in the ratio of the sea spray momentum flux to the square of the sea surface wind speed. Therefore, accurate estimation of the sea spray momentum flux is crucial for the appropriate utilization of Equation (5) in calculating the effective sea surface drag coefficient.

2.3 Calculation of the sea spray momentum flux

The sea spray momentum flux τ_sp can be calculated using the scheme as follows (Andreas, 2004):

$\begin{array}{ll}{\tau }_{sp}=\frac{4\pi }{3}{\rho }_w\underset{r_{lo}}{\overset{r_{hi}}{\int }}{u}_{sp}(r_0)r_0^3\frac{dF}{d{r}_0}d{r}_0& (6)\end{array}$

where $\frac{dF}{d{r}_0}$ represents the sea spray generation function and ρ_w represents the density of seawater. Meanwhile, r_lo and r_hi represents the minimum and maximum droplet radii respectively. r₀ is the formation radii of the droplet, and u_sp(r₀) denotes the horizontal velocity of a specific sea spray droplet before it returns to the sea surface.

The sea surface wind speed can be represented by the following expression:

$\begin{array}{ll}{u}_{\text{z}}=\frac{u_{*}}{\kappa }\text{ln} (\frac{z}{z_0})& (7)\end{array}$

where u_z indicates the wind speed above the sea surface, κ is the von Karman constant (κ = 0.4) and z₀ represents the length of sea surface roughness. All droplets are supposed to be subjected to local winds during the brief flight over the sea surface before falling back. Hence, u_sp(r₀) is independent of the formation radii and instead relies on the height of the droplet z_s (Andreas, 2004). According to Equation (7), the relationship can be represented as follows:

$\begin{array}{ll}{u}_{z_s}=u_{sp}(r_0)=\frac{u_{*}}{\kappa }\text{ln} (\frac{z_s}{z_0})& (8)\end{array}$

where $u_{z_s}$ is the wind speed at z_s above the sea surface. Therefore, Equation (8) can be used to calculate the horizontal velocity of a specific sea spray droplet before it returns to the sea surface. According to Iida et al. (1992), the relationship between z_s and H_s can be expressed as z_s = 0.635H_s, where H_s represents the significant wave height. This empirical relationship provides a parameterization method for estimating H_s (Toba, 1972; Hanson and Phillips, 1999):

$\begin{array}{ll}{H}_s=0.018U_{10}^2{\beta }^{3/2}& (9)\end{array}$

z₀ can be calculated as follows (Zhao and Li, 2019):

$\begin{array}{ll}{z}_0=\{\begin{array}{cc}3.5153\times {10}^{-5}{\beta }^{-0.42}{U}_{10}^2/g& \text{ for }\beta >0.4\\ 2.1583\times {10}^{-4}{\beta }^{1.56}{U}_{10}^2/g& \text{for }\beta \le 0.4\end{array}& (10)\end{array}$

2.4 Sea spray generation function

Based on Equation (6), the SSGF is commonly regarded as a function of the formation radii r₀ and the wind speed U₁₀, as shown in Equation (11). If the scale spectrum of sea spray droplets is not influenced by the wind speed, the SSGF can be separated into two distinct components. One component solely depends on the wind speed, while the other component exclusively relates to the droplet size. This can be expressed as follows:

$\begin{array}{ll}\frac{dF}{d{r}_0}=f_1(U_{10})f_2(r_0)& (11)\end{array}$

where f_i and f₂ represent distinct functions that are independent of each other within the SSGF.

Andreas (2004) made simplifications to the calculation of sea spray momentum flux and proposed an assumption shown as follows:

$\begin{array}{ll}{\tau }_{sp}\sim u_{*}^4& (12)\end{array}$

It has been demonstrated that different SSGFs exhibit varying relationships with wind speed, showing significant differences in magnitude (Cavaleri et al., 2007). It is important to note that wind does not solely impact the formation of sea spray droplets; the presence of waves also plays a crucial role. Waves influence the exchange of air-sea fluxes. Researchers have pointed out that neglecting the influence of wave conditions leads to uncertainties in calculating the spray momentum flux. They suggest that the droplet generation function should incorporate both wind and wave conditions (Zhao et al., 2006). By assuming that the influence of droplet radius and wave state remains independent, the sea spray generation function can be divided into two distinct functions:

$\begin{array}{ll}\frac{dF}{d{r}_0}=f_1(R_B)f_2(r_0)& (13)\end{array}$

where $R_B=\frac{u_{*}^2}{{\omega }_p\nu }$ is the wind-wave Reynolds number, v is the air viscosity coefficient, at 1.5×10^-5m²/s and ω_p = 2π/T_s represents the circular frequency that corresponds to the peak of the wave spectrum. The air-sea boundary layer commonly employs the wind-wave Reynolds number to investigate the impact of wave conditions on gas and momentum transfer at the ocean surface. Combined with Equations (3), R_B can also be expressed in the following form:

$\begin{array}{ll}{R}_B=\frac{U_{10}^3}{g\nu }{C}_D\beta & (14)\end{array}$

It was indicated that the drag coefficient can be represented as a linear function of the wind speed with the slope being associated with δ (Guan and Xie, 2004):

$\begin{array}{ll}{C}_D\times {10}^3=0.78+0.475{\delta }^{1/2}{U}_{10} & (15)\end{array}$

Equation (15) performs well within the commonly measured range of drag coefficients (1.0-2.3×10^-3) (Guan and Xie, 2004). Substituting Equation (15) into Equation (14), the expression of R_B that depends on both the wave age and wave steepness can be written as follows:

$\begin{array}{ll}{R}_B=\frac{U_{10}^3}{g\nu }(0.78+0.475{\delta }^{1/2}{U}_{10})\beta \times {10}^{-3} & (16)\end{array}$

Applying this theory to measured laboratory data, Equation (13) can be expressed by (Zhao et al., 2006):

$\begin{array}{ll}dF/d{r}_0=\{\begin{array}{cc}7.84\times {10}^{-3}{R}_B^{1.5}{r}_0^{-1},& 30\le r_0<75\mu m\\ 4.41\times {10}^1{R}_B^{1.5}{r}_0^{-3},& 75\le r_0<200\mu m\\ 1.41\times {10}^{13}{R}_B^{1.5}{r}_0^{-8},& 200\le r_0\le 500\mu m\end{array}& (17)\end{array}$

The results obtained from Equation (17) adequately encompass the calculated values range of mainstream droplet generation functions (Zhao et al., 2006). However, it should be noted that this equation is limited to sea spray droplets with a radius ranging from 30 ≤ r₀ ≤ 500μm, and thus does not account for droplets generated by bubbles.

Monahan (1986) developed an SSGF specifically designed for droplets generated by bubbles, based on the whitecap coverage rate(W). This particular SSGF is applicable to sea spray droplets within a relative humidity range of 80% with radii ranging from 0.8-10μm:

$\begin{array}{ll}\frac{dF}{d{r}_{80}}=\frac{W}{{\tau }_d}\frac{dE}{d{r}_{80}}=W\frac{1}{{\tau }_d}\frac{dE}{d{r}_{80}}& (18)\end{array}$

where r₈₀ represents the sea spray droplet radius at a reference relative humidity of 80%, τ_d = 3.53 s denotes the typical decay time of whitecap. It is suggested that W is solely dependent on the wind speed. Meanwhile $\frac{dE}{d{r}_{80}}$ signifies the number of droplets generated per unit whitecap area and unit time during the decay stage, within the increment range of the unit radius corresponding to r₈₀.

The source function of $\frac{dE}{d{r}_{80}}$ is given by (Monahan, 1986):

$\begin{array}{ll}\begin{array}{l}\frac{dE}{d{r}_{80}}=1.262\times {10}^6{r}_{80}^{-3}\times {10}^{1.19\text{exp}(-B^2)}\\ \frac{dE}{d{r}_{80}}=1.262\times {10}^6{r}_{80}^{-3}(1+0.057r_{80}^{1.05})\times {10}^{1.19\exp (-B^2)}\\ B=(0.380-\log r_{80})/0.650\end{array}& (19)\end{array}$

The SSGF developed by Equation (19) has been extensively validated as highly useful in subsequent research (Stramska, 1987; Gong, 2003). Then, the SSGF was revised based on simulated observations from a wave tank experiment that aimed to simulate whitecap events (Woolf et al., 1988). They specifically focused on improving the representation of foam droplets generated by bubbles and obtained the following revision result:

$\begin{array}{ll}\frac{dE}{d{r}_{80}}=\exp [16.1-3.43\text{log}{r}_{80}-2.49{(\text{log}{r}_{80})}^2+1.21{(\text{log}{r}_{80})}^3]& (20)\end{array}$

Myrhaug et al. (2016) estimated long-term Marine aerosol flux based on long-term changes in wind statistics from the northern North Sea to obtain a new SSGF:

$\begin{array}{ll}\frac{dE}{d(\log r_{80})}=29419(1+0.057r_{80}{}^{3.45})\text{exp}\{3.68\text{exp}[-5.33{(0.433-\text{log}{r}_{80})}^2]-4.7\text{ln}r{[1+30r_{80}]}^{-0.017r_{80}{}^{-1.44}}\}& (21)\end{array}$

Subsequently, we performed a least square fitting analysis of Equations (19–21), resulting in a simplified expression of $\frac{dE}{d{r}_{80}}$:

$\begin{array}{ll}\frac{dE}{d{r}_{80}}=6.11\times {10}^6{r}_{80}^{-3.5} r=0.98& (22)\end{array}$

Additionally, accounting for the relationship between r₈₀ and r₀, the following applies (Andreas, 1992):

$\begin{array}{ll}{r}_{80}=0.518r_0^{0.976}& (23)\end{array}$

Accounting for Equations (18), (22) and (23), the sea spray droplet size spectrum mentioned above (Andreas, 1998) and SSGF continuity, Equation (17) was modified, resulting in the following revised expression:

$\begin{array}{ll}dF/d{r}_0=\{\begin{array}{cc}1.40\times {10}^1{R}_B^{1.5}{r}_0^{-3.5},& 2\le r_0<20 \text{μm}\\ 7.84\times {10}^{-3}{R}_B^{1.5}{r}_0^{-1},& 20\le r_0<75 \text{μm}\\ 4.41\times {10}^1{R}_B^{1.5}{r}_0^{-3},& 75\le r_0<200 \text{μm}\\ 1.41\times {10}^{13}{R}_B^{1.5}{r}_0^{-8},& 200\le r_0\le 500 \text{μm}\end{array}& (24)\end{array}$

By incorporating Equations (16, 24), we can derive the SSGF that accounts for both wind speed and wave conditions (wave age and wave steepness):

$\begin{array}{ll}dF/d{r}_0=\{\begin{array}{cc}1.40\times {10}^1{(6.67U_{10}^3\beta (0.78+0.475{\delta }^{1/2}{U}_{10}))}^{1.5}{r}_0^{-3.5},& 2\le r_0<20\mu m\\ 7.84\times {10}^{-3}{(6.67U_{10}^3\beta (0.78+0.475{\delta }^{1/2}{U}_{10}))}^{1.5}{r}_0^{-1},& 20\le r_0<75\mu m\\ 4.41\times {10}^1{(6.67U_{10}^3\beta (0.78+0.475{\delta }^{1/2}{U}_{10}))}^{1.5}{r}_0^{-3},& 75\le r_0<200\mu m\\ 1.41\times {10}^{13}{(6.67U_{10}^3\beta (0.78+0.475{\delta }^{1/2}{U}_{10}))}^{1.5}{r}_0^{-8},& 200\le r_0<500\mu m\end{array}& (25)\end{array}$

The above SSGF illustrates the dynamic characteristics of spray generation in the marine environment. Based on physical principles and empirical observations, we incorporated wave parameters, including the wave age and wave steepness, to establish the relationship between the wind speed, wave conditions, and sea spray momentum flux. Primarily, the spray generation function encompasses rate coefficients that vary with spray radius, reflecting the varying influences of the droplet size. Smaller droplets are more susceptible to wind forcing and wave effects in the generation process, while larger droplets exhibit increased resistance to both wind and wave forces. Additionally, the wave state, as represented by the wave age and wave steepness, plays an important role in spray generation. According to Equation (25), this suggests that under similar wind and wave conditions, a higher wave age and a greater wave steepness contribute to enhanced spray production. Furthermore, the wind speed (U₁₀) constitutes another key factor in the spray generation function. Strong wind causes high air turbulence above the waves, leading to fluctuating vertical velocities that facilitate droplet detachment from wave crests, thereby promoting spray formation.

In conclusion, the spray generation function integrates wave parameters such as wave age, wave steepness, and wind speed to describe the dynamic characteristics of spray generation in the marine environment. This mathematical model offers insights into the underlying physical mechanisms governing spray generation at the ocean surface and can be employed for predicting and investigating the spray distribution and evolution in marine environments.

3 Result

The calculation of the sea spray momentum flux, based on Equation (6), critically depends on the SSGF. However, the influence of waves has often been neglected in prior SSGFs. After comparatively analyzing laboratory and field observation data, the wave steepness primarily ranged from 0.01 to 0.14 when considering the application of Stokes wave theory (Zhao and Li, 2019). As shown in Figure 2 (Monahan, 1986; Iida et al., 1992; Fairall et al., 1994; Clark et al., 2006; Demoisson et al., 2013; Zhu et al., 2014; Myrhaug et al., 2016), the proposed SSGF [Equation (25)] exhibits distinct values under different wave ages and wave steepness conditions. This further emphasizes the importance of considering the impact of wave conditions in the SSGF.

Figure 2

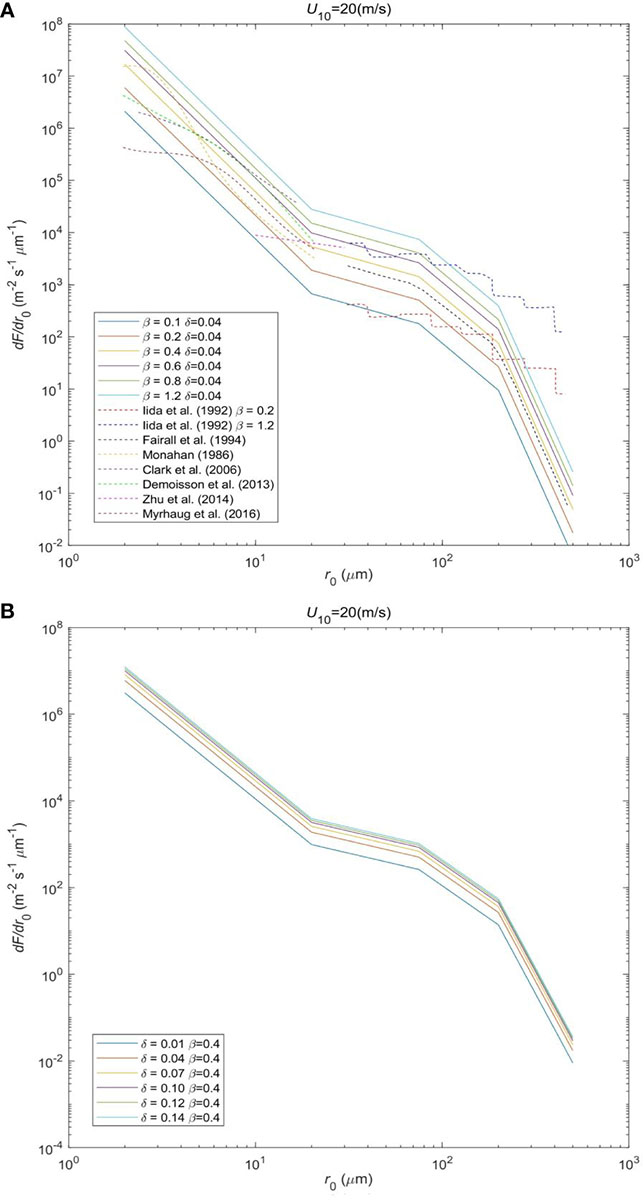
Figure 2 (A, B) SSGF under different wave states. The solid lines in this figure show the variation trend of the droplet generation function derived in this paper with the formation radius under different wave states, and the dashed lines are the result of previous studies.

Figure 2A illustrates that the SSGF displays an increasing trend with increasing wave age, deviating from the variation pattern of the surface roughness described by Equation (10). The change in the SSGF varies across the different wave age ranges. This divergence occurs because the effective wave height, as described by Equation (9), increases with increasing wave age, resulting in an overall increase in the SSGF. Notably, the SSGF demonstrates a more rapid increase for wave ages below 0.4, while the increase rate declines for wave ages above 0.4. Figure 2B reveals that the SSGF exhibits an increasing trend with increasing wave steepness. Simultaneously, with increasing wave steepness, the magnitude of the increase in the SSGF gradually decreases. This can be attributed to the fact that under high-wind conditions, intense wave breaking reaches a saturation point where the wave steepness attains its maximum limit, impeding further development of wind waves.

The influence of wind on sea spray droplets results in their movement above the sea surface for a certain period. In this process, the spray droplets interact with the surrounding environment, exchanging momentum and the change in momentum transfer between the air and sea caused by sea spray (Andreas, 2004). According to his explanation, close to the sea surface, the acceleration of spray droplets by wind leads to partial loss of the air-sea momentum flux. This lost momentum is converted into the spray momentum flux, thereby causing a deceleration in the wind speed.

Figure 3A shows the variations in the spray momentum flux and the total momentum flux with wind speed under various wave age conditions. The spray momentum flux differences can exceed several orders of magnitude. Furthermore, with increasing wave age, the spray momentum flux shows an increase. This indicates a significant impact of wave conditions on the spray momentum flux. In comparison, the changes in the total momentum flux with wind speed are less pronounced. At wind speeds ranging from approximately 25-55 m/s, the spray momentum flux under the different wave age conditions can even reach the same order of magnitude as the total momentum flux. This highlights the substantial influence of wave conditions on the magnitude of the spray momentum flux. Higher wave ages lead to earlier attainment of comparable levels between the spray momentum flux and the total momentum flux. Figure 3B shows the variation in the spray momentum flux with wind speed under different wave steepness conditions. Overall, a higher wave steepness tends to result in a higher spray momentum flux. However, compared to Figure 3A, the changes in the spray momentum flux caused by the wave steepness are smaller, particularly at low to moderate wind speeds. At high wind speeds, the increase in the spray momentum flux becomes relatively limited with increasing wave steepness. This phenomenon can be attributed to the fact that the wave age, which describes the ability of wind to transfer energy into waves and is directly related to the wind speed, exerts a more notable influence. In contrast, the wave steepness is controlled by wave breaking and is directly related to the wave stability.

Figure 3

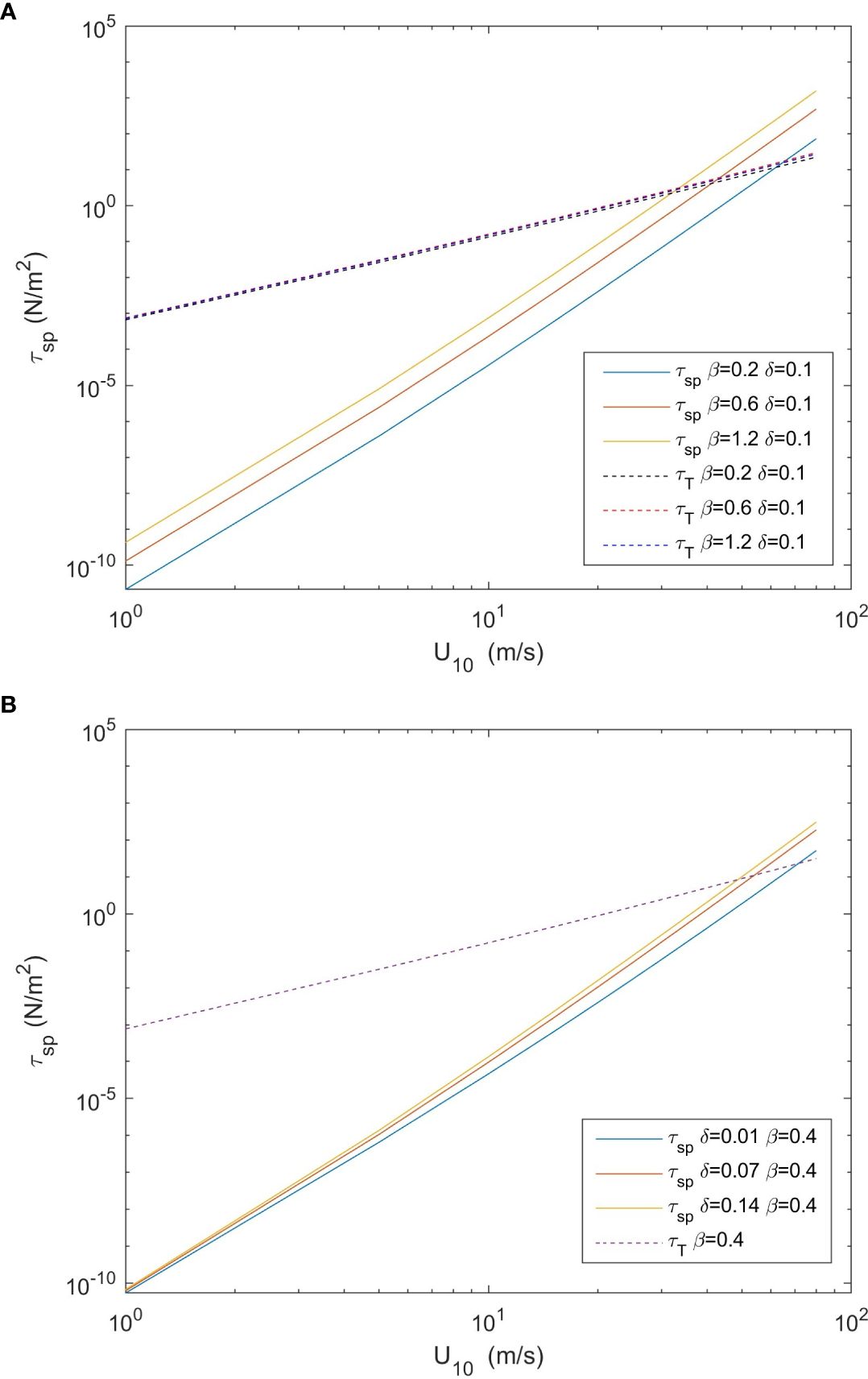
Figure 3 (A, B) Variations in the sea spray momentum flux and total momentum flux under different wave states. The solid lines in the figure show the change trend of sea spray stress with wind speed under different wave states, and the dashed lines show the change trend of total stress with wind speed under different wave states.

Figure 4 shows the variation in the spray momentum flux under different wave states, providing further insights into the relationship between wave conditions and the spray momentum flux. Consistent with the findings in Figure 3, it is clear that with increasing wave age and wave steepness, the spray momentum flux also increases. By parameterizing the spray momentum flux using the wave age, Figure 4A demonstrates that with increasing wave steepness, the magnitude of the difference in the spray momentum flux between the different wave steepness conditions gradually decreases. Figure 4B shows the parameterization process of the spray momentum flux using the wave steepness. Similar to Figure 4A, with increasing wave age, the magnitude of the difference in the spray momentum flux between the different wave ages also gradually decreases. Moreover, the magnitude of the difference in the spray momentum flux between the different wave age conditions is notably larger than that depicted in Figure 4A. This observation indicates that both the wave age and wave steepness notably impact the spray momentum flux. Therefore, integrating wave state information with wind speed measurements could enhance our comprehension of the intricate dynamics involved in air-sea momentum exchange mediated by spray.

Figure 4

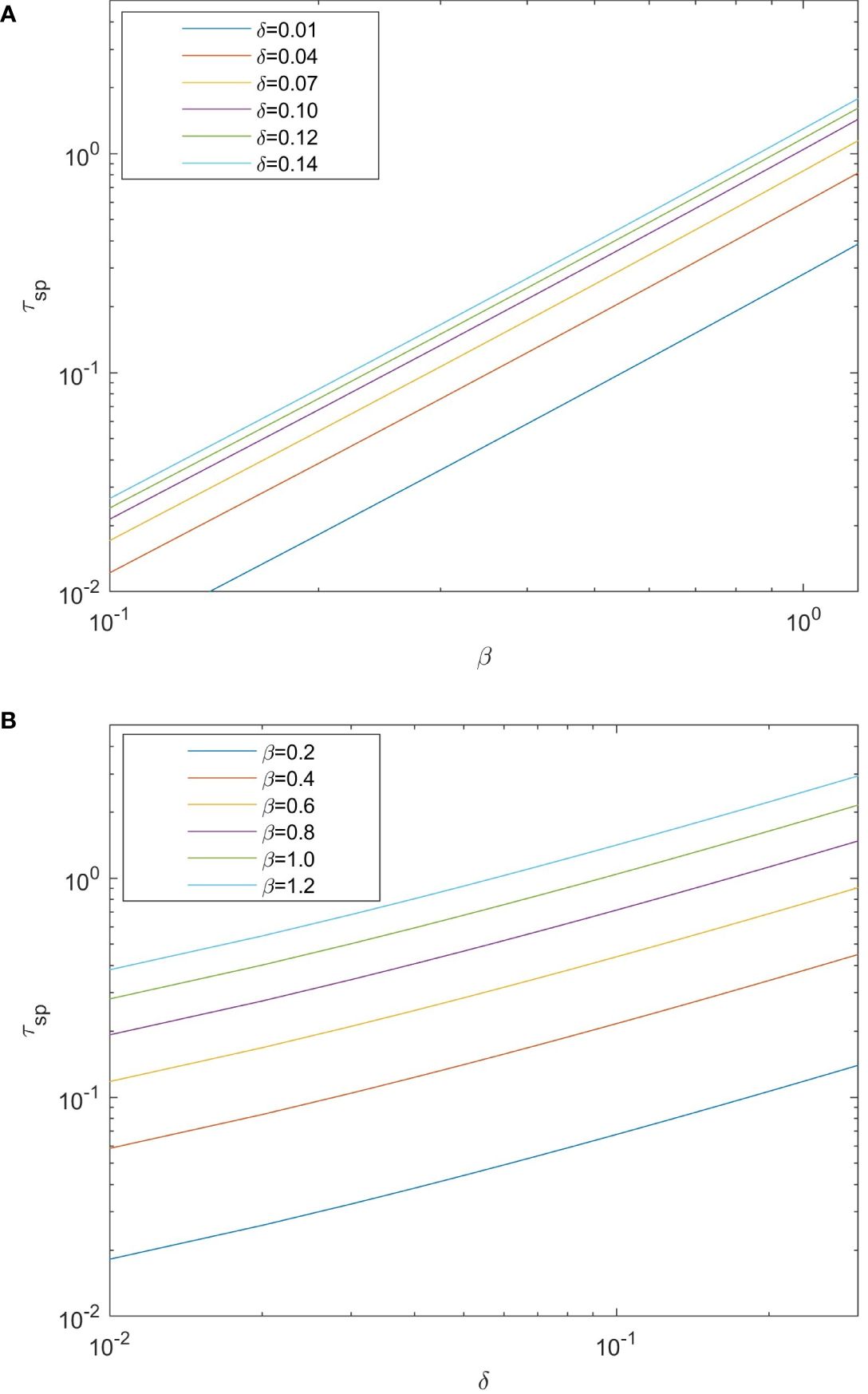
Figure 4 Variations in the sea spray droplets momentum flux under different wave states. The solid lines in (A) respectively represent the variation trend of sea spray stress with wave age under different wave steepness conditions, and the solid lines in (B) respectively represent the variation trend of sea spray stress with wave steepness under different wave age conditions.

Figure 5 shows the variation in the ratio of the droplet momentum flux to the total momentum flux under different wave conditions. The findings indicate that given the same wave steepness (wave age), with increasing wave age (wave steepness), a higher ratio of the droplet momentum flux to the total momentum flux is observed. At a wind speed of 30 m/s, as both the wave age and wave steepness approach 1, the ratio of the droplet momentum flux to the total momentum flux approaches 1, suggesting comparable magnitudes. Furthermore, with further increase in the wave age or wave steepness, the flux ratio gradually increases.

Figure 5

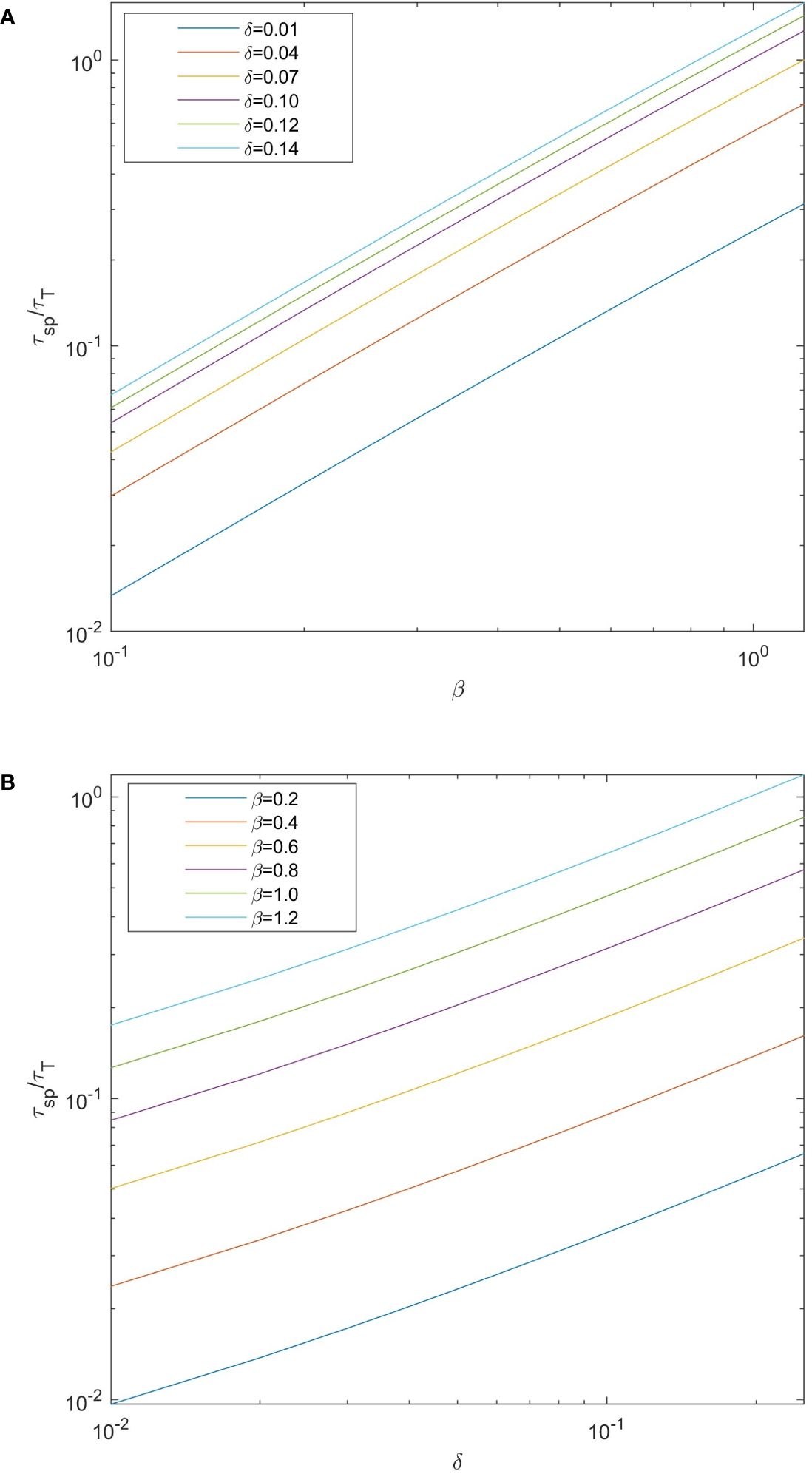
Figure 5 Variations in the ratio of the sea spray droplets momentum flux to the total momentum flux under different wave states. The solid lines in (A) respectively represent the changing trend of the ratio of droplet stress to total stress with wave age under different wave steepness, and the solid lines in (B) respectively represent the changing trend of the ratio of droplet stress to total stress with wave steepness under different wave age.

The above analysis demonstrates that considering the wave state provides a better characterization of the droplet momentum flux. As previously mentioned in Equation (12), the droplet stress should be proportional to the fourth power of the friction velocity (Andreas, 2004). The calculation of the droplet momentum flux was simplified and obtained the following equation:

$\begin{array}{ll}{\tau }_{sp}=6.2\times {10}^{-5}{\rho }_w{u}_{*}^4& (26)\end{array}$

According to Figures 6, 7, it has been observed that the sea spray generation function proposed in this study [Equation (25)] successfully encompasses and accounts for the results obtained from Equation (26) and previous results (Fairall et al., 1994; Andreas, 2004; Clark et al., 2006; Shi et al., 2021). This finding serves to validate the accuracy of Equation (25) while also demonstrating the influence of wave age on sea spray momentum flux. Moreover, it unequivocally demonstrates the substantial impact of wave conditions on the droplet momentum flux. By explicitly considering the wave state in the calculation of the droplet momentum flux, the proposed model captures the intricate interplay between wave characteristics and droplet dynamics, providing a more comprehensive and accurate representation of this phenomenon. Neglecting the wave state in such calculations could lead to an incomplete understanding of the underlying processes and potentially result in erroneous estimations. Therefore, incorporating the characterization of wave conditions is crucial for more robust and precise assessment of the spray momentum flux.

Figure 6

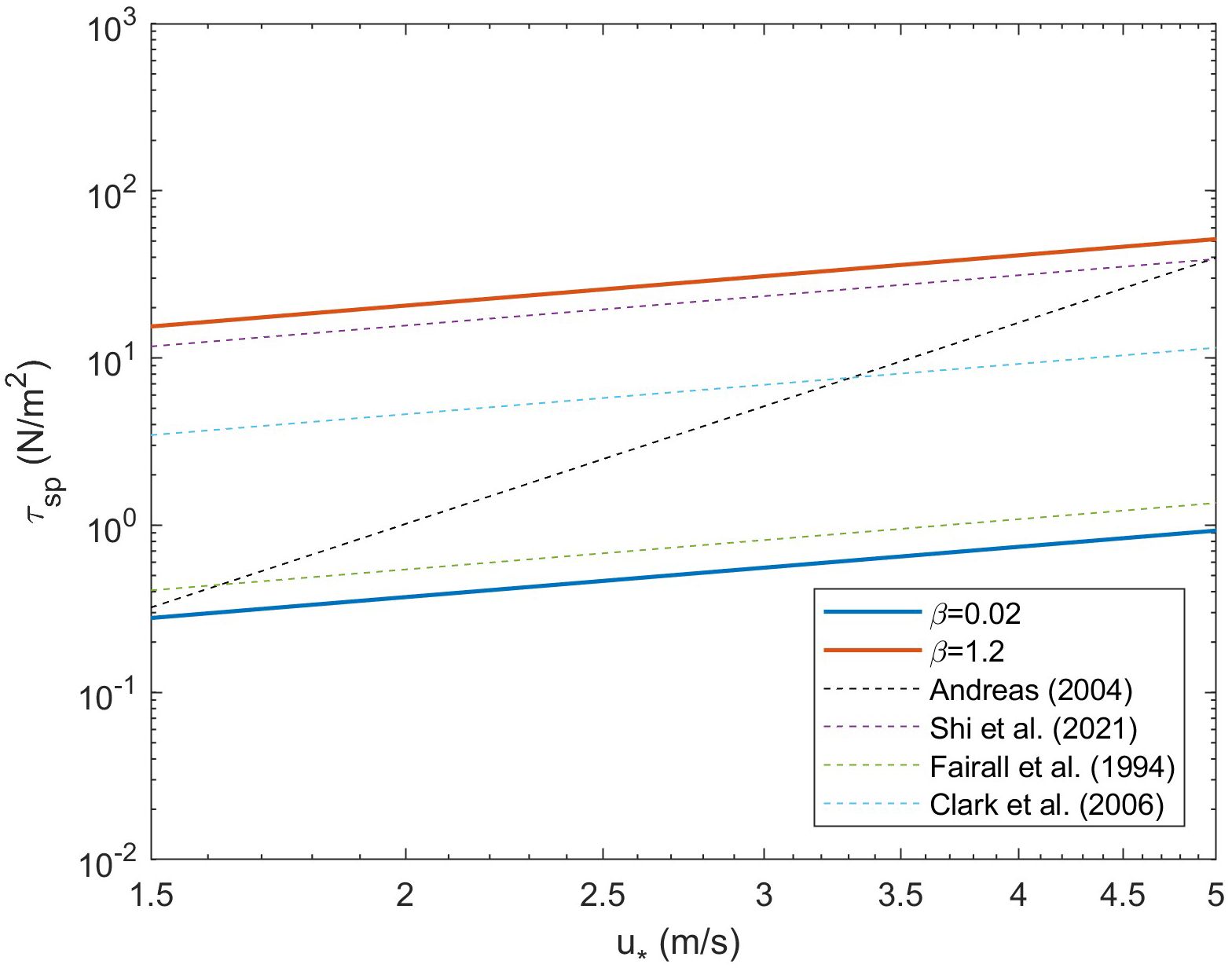
Figure 6 Spray momentum flux under different wave ages compared to Equation (28). The solid lines in the figure show the variation trend of sea spray stress with friction velocity under different wave age, and the dashed lines show the previous research results.

Figure 7

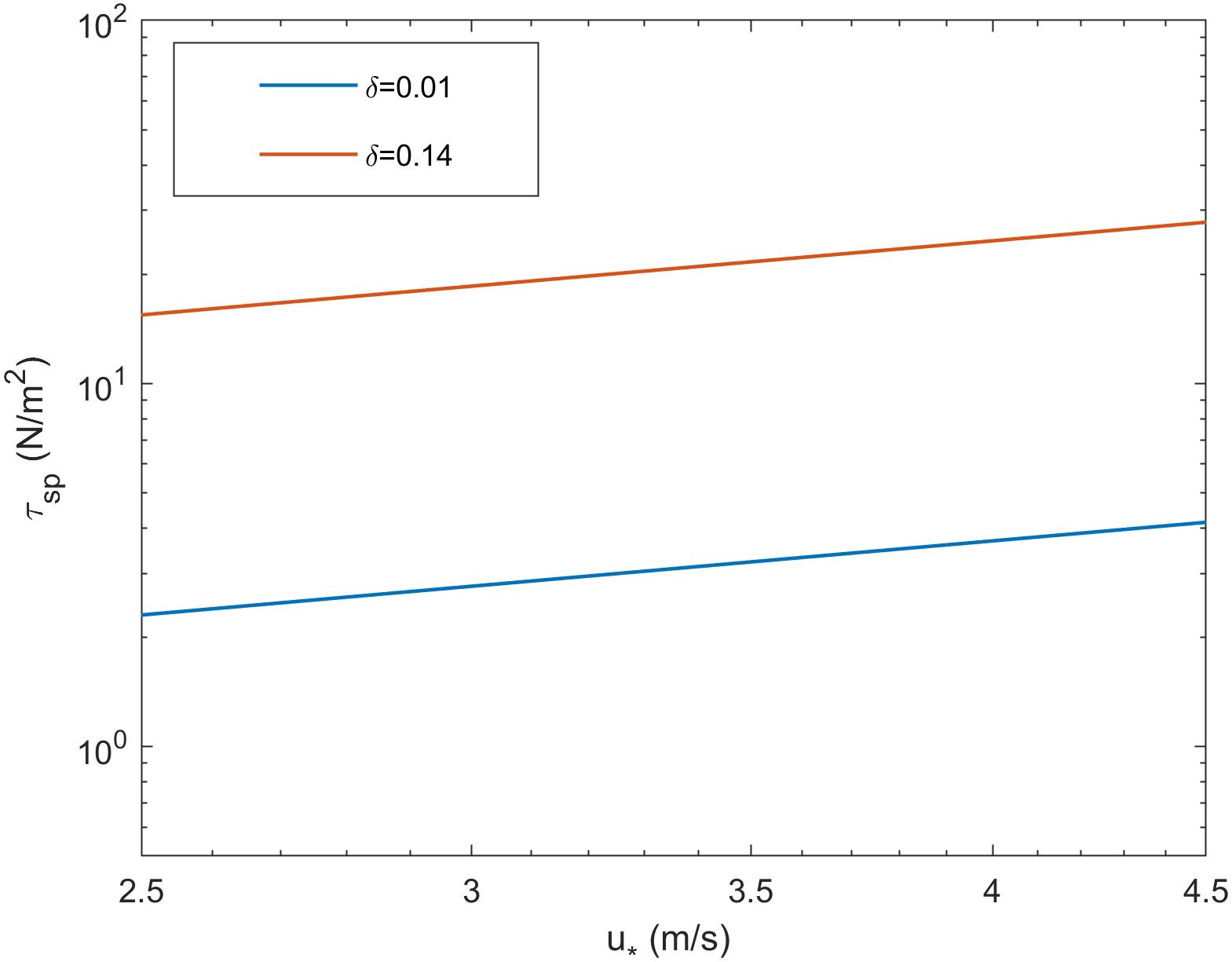
Figure 7 Spray momentum flux under different wave steepness values. The solid lines in the figure show the variation trend of sea spray stress with friction velocity under different wave slope.

4 Discussion

4.1 Variation in the drag coefficient with wind speed without the effect of sea spray

To examine the impact of droplets on the drag coefficient at high wind speeds, we initially explored the relationship between the drag coefficient and wind speed in the absence of droplet influence. According to Makin (2005), the sea surface drag coefficient can be calculated by:

$\begin{array}{ll}{C}_D={(\frac{\kappa }{\ln (10/z_0)})}^2& (27)\end{array}$

Figure 8 shows the variation in the surface drag coefficient with wind speed under different wave conditions, assuming no influence from oceanic droplets. The black line indicates the linear relationship between the drag coefficient and wind speed proposed by Wu (1980). Figure 8 shows that there exists a positive correlation between the drag coefficient and wind speed. When considering the effect of the wave age, it is observed that for wave ages less than 0.4, the drag coefficient increases with increasing wave age. However, for wave ages greater than 0.4, the drag coefficient decreases with increasing wave age. This trend agrees with the changes in wave age.

Figure 8

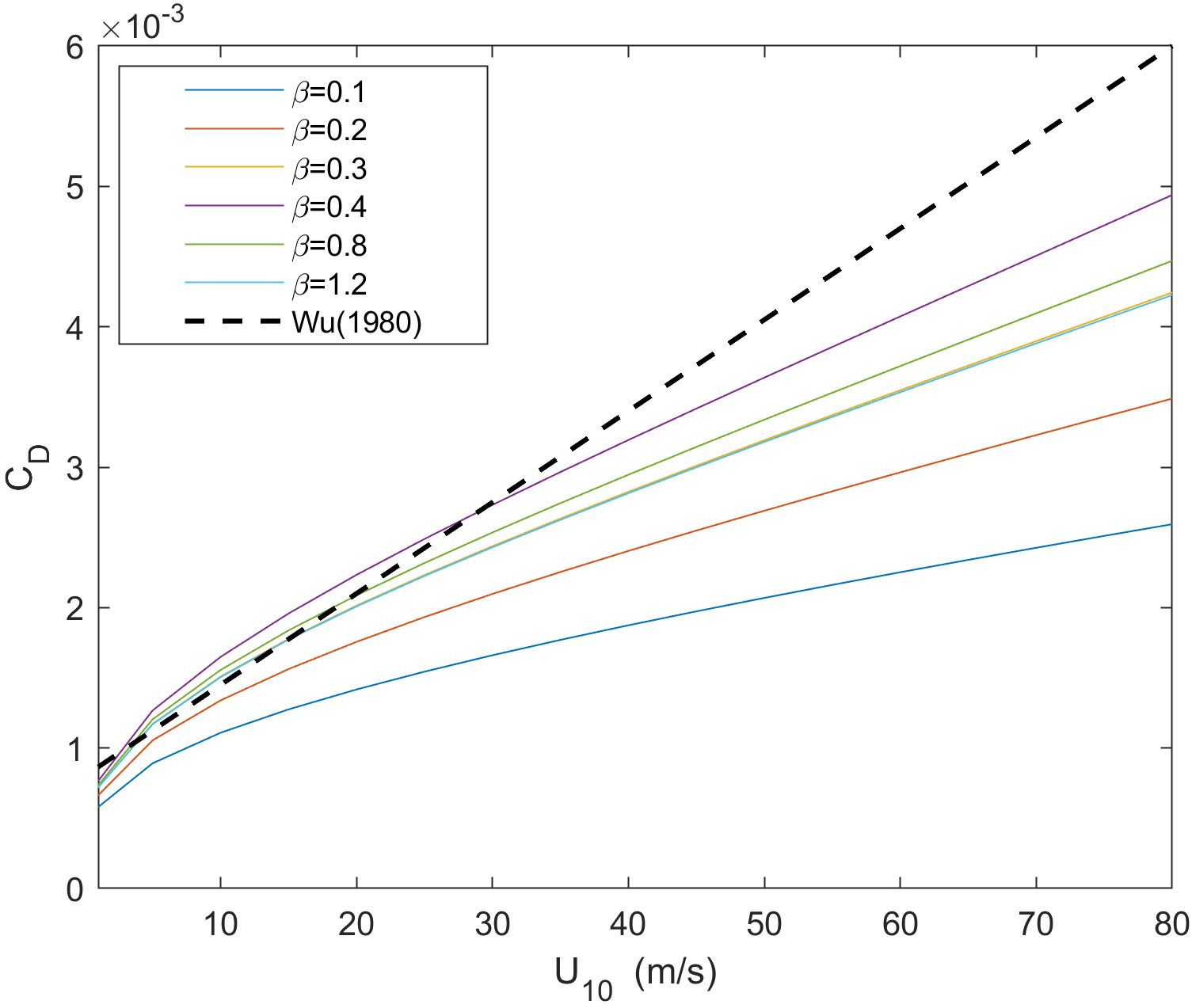
Figure 8 Changes in the drag coefficient with wind speed without considering the influence of sea spray droplets. The solid lines in the figure shows the change curve of drag coefficient with wind speed under different wave ages, and the dashed line shows the calculation of Wu (1980).

At low to moderate wind speeds, specifically at wind speeds below 25 m/s, the calculated values of the surface drag coefficient adequately capture the results obtained by Wu (1980). This indicates the validity of this calculation method at low to moderate wind speeds. As the wind speed is further increased, the calculation results gradually fall down. This discrepancy occurs because the linear relationship of the surface drag coefficient with the wind speed proposed by Wu (1980) overestimates the drag coefficient at high wind speeds (Moon et al., 2003). Recent studies have indicated a decay in the surface drag coefficient at high wind speeds (Chen et al., 2022; Kuznetsova et al., 2023). To elucidate the attenuation mechanism of the sea surface drag coefficient influenced by droplets at high wind speeds, an analysis was conducted based on Equation (5), considering the influence of droplets on the surface drag coefficient.

4.2 Variation in the drag coefficient with wind speed under the effect of sea spray

By employing Equation (5), we can analyze the impact of droplets on the surface drag coefficient, denoted as C_D,eff. As shown in Figure 9A, the drag coefficient under the different wave states exhibits attenuation with increasing wind speed, which is the same as the results obtained by previous studies (Andreas, 2004). Based on Equation (24), a large number of sea spray droplets generated at high wind speed are considered to reduce the drag coefficient (Wan et al., 2017). However, the wind speed at which the drag coefficient initially decays varies depending on the wave conditions. Generally, at higher wave ages, the surface drag coefficient tends to attenuate at lower wind speeds. At wave ages below 0.4 and low to moderate wind speeds, the surface drag coefficient increases with both wave age and wind speed. Nevertheless, as the wind speed is further increased, the surface drag coefficient gradually decreases with increasing wave age. This observation can be attributed to the fact that, based on Figure 3A, only under high-wind speed conditions can droplets acquire a higher momentum flux from the atmosphere. At wave ages surpassing 0.4, irrespective of the wind speed conditions, the surface drag coefficient decreases with increasing wave age. According to Figure 4A, the droplet momentum flux increases with the increase of wave age, making it more obvious that the effective sea surface drag coefficient decreases with the increase of wave age.

Figure 9

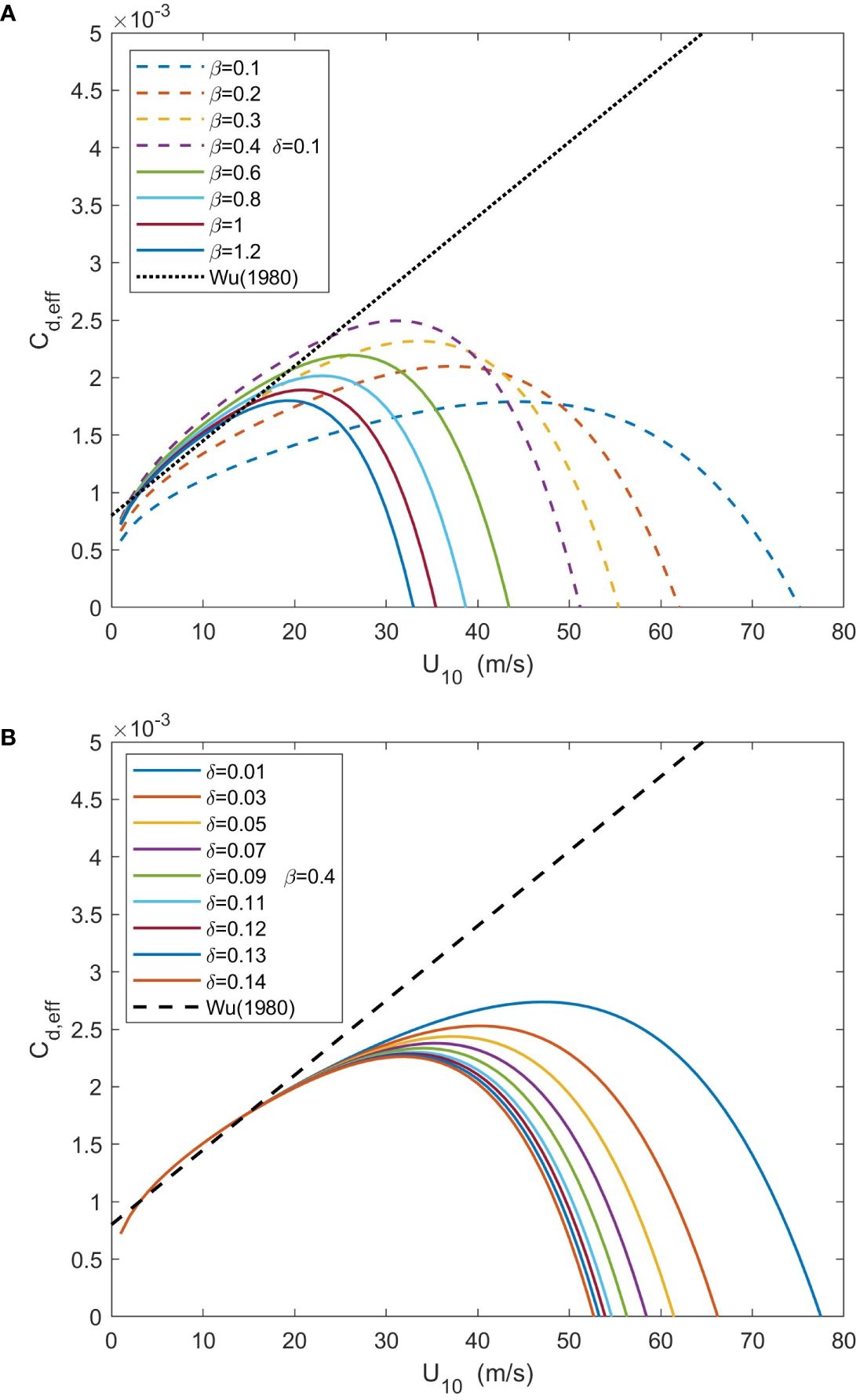
Figure 9 Variation in the sea surface drag coefficient influenced by sea spray with wind speed. The dashed lines in (A) represent the variations of effective drag coefficient with wind speed under different wave age states when the wave age is less than or equal to 0.4. The solid lines represent the variations of effective drag coefficient with wind speed at different wave age states when the wave age is greater than 0.4. The dotted line represents the calculation of Wu (1980). The dashed lines in (B) represent the variations of effective drag coefficient with wind speed under different wave steepness states when the wave steepness is less than or equal to 0.1. The solid lines represent the variations of effective drag coefficient with wind speed under different wave steepness states when the wave steepness is greater than 0.1. The dotted line represents the calculation of Wu (1980).

Figure 9B shows the relationship between the sea surface drag coefficient and wind speed under varying wave steepness conditions. At low to moderate wind speeds, a positive correlation can be observed between the sea surface drag coefficient and wind speed. With increasing wind speed, the sea surface drag coefficient demonstrates a certain level of attenuation under the different wave steepness conditions, which is particularly evident at high wind speeds. Moreover, larger wave steepness values amplify the susceptibility of the sea surface drag coefficient to decay at lower wind speeds, exhibiting a higher attenuation rate. According to Figures 3B, 4B, this is because under different wind and wave conditions, the increase of wave steepness can increase the droplet flux (Xu et al., 2023), that is, the momentum flux obtained from the air increases with the increase of wind speed at high wind speed. Importantly, it should be noted that once the wave steepness reaches a relatively high value, a further increase in the wave steepness exerts a negligible impact on the attenuation of the sea surface drag coefficient.

4.3 Variation in the drag coefficient with wind speed considering the interrelation between wave age, wave steepness, and effect of droplet transmission at high wind speeds

According to the dispersion relationship of surface waves in deep water, the relationship between β and δ can be given as:

$\begin{array}{ll}\delta =\frac{1}{2\pi }{\beta }^{-2}\frac{g{H}_s}{U_{10}^2}& (28)\end{array}$

The mature wind waves correspond to β_* > 14.29 (Hara and Belcher, 2004), which is roughly equivalent to β = 0.4. By substituting Equation (1) into Equation (28), we can obtain the following:

$\begin{array}{ll}\begin{array}{l}\delta =\{\begin{array}{cc}3.21\times {10}^{-2}{\beta }^{-0.24}& \text{for }\beta >0.4\\ 0.040& \text{for }\beta \le 0.4\end{array}\\ \end{array}& (29)\end{array}$

The value of δ decreases as β increases in situations with β > 0.4. If the growth relationships of wind waves are valid at low and moderate wind speeds, the two parameters can be interchanged. It is emphasized that at high wind speeds, δ cannot continuously increases as β decreases. This limitation exists due to the intense wave breaking, which sets an upper limit on the value of δ. According to Stokes wave theory, the maximum theoretical value of δ is 1/7 However, according to the calculation results of Equation (29) and the integration of laboratory and outer sea wave steepness data by Zhao and Li (2019), only the ideal wind wave prepared in the laboratory can reach the theoretical maximum of wave steepness, and the change range of actual measured wave steepness in outer sea is between 0.01 and 0.05, which further proves the rationality of Equation (29). In general, we may lack wave steepness data. As such, Equation (29) can be used to calculate the wave steepness from the wave age.

Figure 10 shows the variation of effective drag coefficient with wind speed considering the relationship between wave age and wave steepness. The observed trend of drag coefficient attenuation in this figure resembles that depicted in Figure 9. The notable difference is the fact that under the same wave age conditions, the wind speed corresponding to the onset of drag coefficient reduction varies. Accounting for the interplay between the wave age and wave steepness at high wind speeds, it can also be observed that the continuous increase in the wave steepness declines. Consequently, the influence of the wave steepness on the spray momentum flux gradually stabilizes, leading to an overall higher wind speed at which the drag coefficient begins to decline. Notably, under high-wave age conditions, the drag coefficient starts declining at approximately 25 m/s, a finding that better conforms with real-world conditions and corroborates the research outcomes reported by Troitskaya et al. (2012) and Powell et al. (2003).

Figure 10

Figure 10 Drag coefficient obtained by considering the changes in the wave age and wave steepness at high wind speeds. The dashed lines in Figure 10 represent the variations of effective drag coefficient with wind speed under different wave age states when the wave age is less than or equal to 0.4. The solid lines represent the variations of effective drag coefficient with wind speed at different wave age states when the wave age is greater than 0.4. The dotted line represents the calculation of Wu (1980).

5 Conclusion

In this research, we mainly investigated the influence of wave states on the sea spray generation function and the drag coefficient under high-wind conditions. With experimentation and computation, it was found that the SSGF varies in magnitude under different wave age and wave steepness conditions, indicating that the influence of wave states should be considered in the SSGF. The SSGF increased with wave age and showed an upward trend with increasing wave steepness. Wave states substantially influence the spray momentum flux, which gradually increases as waves develop and can ultimately attain a comparable magnitude to that of the total momentum flux. At high wind speeds, the influence of sea spray on the sea surface drag coefficient should also be considered. A new sea surface drag coefficient under high-wind conditions was established with a SSGF considering the influence of wave states. We revealed that the sea surface drag coefficient under the different wave conditions exhibits attenuation at high wind speeds. Moreover, it was found that with increasing wave age or wave steepness, the sea surface drag coefficient is more prone to decay at low to moderate wind speeds. Finally, considering the interrelation between the wave age and wave steepness at high wind speeds, the obtained relationship between the drag coefficient and wind speed yielded a more realistic decay pattern.

In summary, this research emphasizes the notable influences of the wave age and wave steepness on the spray generation function and the drag coefficient, providing a new perspective to better understand the complex dynamics of air-sea momentum exchange. When studying the changes in the spray momentum flux, the effects of wave states and wind speed should be comprehensively considered. Furthermore, combining wave state information with wind speed measurements could enhance our understanding of the complex dynamic process of air-sea momentum exchange. Additionally, in this paper, we proposed equations for calculating the spray generation function and describing the drag coefficient, and we verified their accuracy. We reveal the effect of wave age and wave steepness on the attenuation of drag coefficient at high wind speed, and the influence of wave state on drag coefficient cannot be ignored. Although wave age and wave steepness both have an effect on the attenuation of the drag coefficient at high wind speed, the attenuation of the drag coefficient at high wind speed is dominated by wave age because wave steepness cannot continue to increase under actual conditions due to the limitation of wave stability. The research results are important for further exploring aerosol transport and air–sea interactions in marine environments.

The study of sea spray droplets has encountered significant challenges due to the lack of laboratory and offshore observation data in high wind speeds. To overcome this hurdle, the next step involves conducting droplet measurements in both laboratory and marine settings to gain a deeper understanding of the droplet generation process. In this study, novel advancements have been made in the generation function of droplets within the 2 ≤ r₀< 20μm. Moving forward, our attention will be directed towards deducing a comprehensive droplet generation function that encompasses all the typical particle size range, thereby ensuring a smoother curve for the droplet generation function. Between the ocean and the atmosphere, it is crucial to highlight that the drag coefficient of the sea surface has a significant influence not only on the momentum flux but also on the heat exchange. The exchange of momentum and heat at the air-sea interface plays a vital role in the genesis and evolution of typhoons. These processes serve as crucial energy sources, driving the intense convective activity and vertical motion within typhoon systems. Consequently, our future endeavors will incorporate the examination of droplet dynamics and using the ocean-atmosphere coupling model to investigate the impact of the sea spray droplets on the simulation of typhoon waves.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: The reader can ask for all the related data from the first author (emhhb3plcWkyMkBudWR0LmVkdS5jbg==). Requests to access these datasets should be directed to Zeqi Zhao, (emhhb3plcWkyMkBudWR0LmVkdS5jbg==).

Author contributions

ZZ: Writing – review & editing, Writing – original draft, Visualization, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. JS: Writing – review & editing, Writing – original draft, Supervision, Resources, Methodology, Funding acquisition, Conceptualization. HW: Writing – review & editing, Validation, Supervision, Investigation. ZY: Writing – review & editing, Visualization, Supervision, Methodology, Investigation. WZ: Writing – review & editing, Supervision, Methodology, Investigation, Funding acquisition. XZ: Writing – review & editing, Supervision, Resources, Methodology, Investigation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Science Foundation of China (Grant Nos.42192552).

Acknowledgments

The authors would like to express their gratitude to all researchers for providing observational data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andreas E. L. (1992). Sea spray and the turbulent air-sea heat fluxes. J. Geophys. Res. Oceans. 97, 11429–11441. doi: 10.1029/92JC00876

CrossRef Full Text | Google Scholar

Andreas E. L. (1998). A New Sea Spray Generation Function for Wind Speeds up to 32 m s–1. J. Phys. Oceanogr. 28, 2175–2184. doi: 10.1175/1520-0485(1998)028<2175:ANSSGF>2.0.CO;2

CrossRef Full Text | Google Scholar

Andreas E. L. (2004). Spray stress revisited. J. Phys. Oceanogr. 34, 1429–1440. doi: 10.1175/1520-0485(2004)034<1429:SSR>2.0.CO;2

CrossRef Full Text | Google Scholar

Andreas E. L., Decosmo J. (2002). The signature of sea spray in the hexos turbulent heat flux data. Boundary-Layer. Meteorol. 103, 303–333. doi: 10.1023/A:1014564513650

CrossRef Full Text | Google Scholar

Andreas E. L., Edson J. B., Monahan E. C., Rouault M. P., Smith S. D. (1995). The spray contribution to net evaporation from the sea: A review of recent progress. Boundary-Layer. Meteorol. 72, 3–52. doi: 10.1007/BF00712389

CrossRef Full Text | Google Scholar

Andreas E. L., Emanuel K. A. (2001). Effects of sea spray on tropical cyclone intensity. J. Atmos. Sci. 58, 3741–3751. doi: 10.1175/1520-0469(2001)058<3741:EOSSOT>2.0.CO;2

CrossRef Full Text | Google Scholar

Cavaleri L., Alves J. H. G. M., Ardhuin F., Babanin A., Banner M., Belibassakis K., et al. (2007). Wave modelling – The state of the art. Prog. Oceanogr. 75, 603–674. doi: 10.1016/j.pocean.2007.05.005

CrossRef Full Text | Google Scholar

Chen S., Qiao F., Zhang J. A., Xue Y., Ma H., Chen S. (2022). Observed drag coefficient asymmetry in a tropical cyclone. J. Geophys. Res.: Oceans. 127, e2021JC018360. doi: 10.1029/2021JC018360

CrossRef Full Text | Google Scholar

Clarke A., Owens S., Zhou J. (2006). An ultrafine sea-salt flux from breaking waves: Implications for cloud condensation nuclei in the remote marine atmosphere. J. Geophys. Res. 111, D06202. doi: 10.1029/2005JD006565

CrossRef Full Text | Google Scholar

Demoisson A., Tedeschi G., Piazzola J. (2013). A model for the atmospheric transport of sea-salt particles in coastal areas. Atmospheric Research 132–133, 144–153. doi: 10.1016/j.atmosres.2013.04.002

CrossRef Full Text | Google Scholar

Dobson F. W., Smith S. D., Anderson R. J. (1994). Measuring the relationship between wind stress and sea state in the open ocean in the presence of swell. Atmos. Ocean. 32, 237–256. doi: 10.1080/07055900.1994.9649497

CrossRef Full Text | Google Scholar

Donelan M. A., Haus B. K., Reul N., Plant W. J., Stiassnie M., Graber H. C., et al. (2004). On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 31, (18). doi: 10.1029/2004GL019460

CrossRef Full Text | Google Scholar

Donelan M. A., Le Méhauté B., Hanes. D. M. (1990). Air-sea interaction. The sea: ocean engineering science. J. Wiley. 9, 239–292.

Google Scholar

Fairall C., Jeffrey K., Greg H. (1994). The effect of sea spray on surface energy transports over the ocean. Global Atmosphere. Ocean. System. 2, 121–142.

Google Scholar

Geernaert G. L., Katsaros K. B., Karl R. (1986). Variation of the drag coefficient and its dependence on sea state. J. Geophys. Res. Oceans. 91, 7667–7679. doi: 10.1029/JC091iC06p07667

CrossRef Full Text | Google Scholar

Gong S. L. (2003). A parameterization of sea-salt aerosol source function for sub- and super-micron particles. Global Biogeochem. Cycles. 17, (4). doi: 10.1029/2003GB002079

CrossRef Full Text | Google Scholar

Guan C., Xie L. (2004). On the linear parameterization of drag coefficient over sea surface. J. Phys. Oceanogr. 34, 2847–2851. doi: 10.1175/JPO2664.1

CrossRef Full Text | Google Scholar

Hamada T. (1963). An experimental study of development of wind waves Vol. 2 (Yokosuka, Japan: Report of Port and Harbour Research Institute), 1–41.

Google Scholar

Hanson J. L., Phillips O. M. (1999). Wind sea growth and dissipation in the open ocean. J. Phys. Oceanogr. 29, 1633–1648. doi: 10.1175/1520-0485(1999)029<1633:WSGADI>2.0.CO;2

CrossRef Full Text | Google Scholar

Hara T., Belcher S. E. (2004). Wind profile and drag coefficient over mature ocean surface wave spectra. J. Phys. Oceanogr. 34, 2345–2358. doi: 10.1175/JPO2633.1

CrossRef Full Text | Google Scholar

Iida N., Toba Y., Masaaki C. (1992). A new expression for the production rate of sea water droplets on the sea surface. J. Oceanogr. 48, 439–460. doi: 10.1007/BF02234020

CrossRef Full Text | Google Scholar

Janssen J. A. M. (1997). DOES WIND STRESS DEPEND ON SEA-STATE OR NOT? – A STATISTICAL ERROR ANALYSIS OF HEXMAX DATA. Boundary-Layer. Meteorol. 83, 479–503. doi: 10.1023/A:1000336814021

CrossRef Full Text | Google Scholar

Johnson H. K., Højstrup J., Vested H. J., Larsen. S. E. (1998). On the dependence of sea surface roughness on wind waves. J. Phys. Oceanogr. 28, 1702–1716. doi: 10.1175/1520-0485(1998)028<1702:OTDOSS>2.0.CO;2

CrossRef Full Text | Google Scholar

Katsaros K. B., Ataktürk S. S. (1992). Dependence of Wave-Breaking Statistics on Wind Stress and Wave Development (Berlin, Heidelberg: Springer).

Google Scholar

Kawai S., Kozo O., Toba Y. (1977). Field data support of three-seconds power law and gu*σ–4-spectral form for growing wind waves. J. Oceanographical. Soc. Japan. 33, 137–150. doi: 10.1007/BF02109685

CrossRef Full Text | Google Scholar

Kunishi H. (1963). An Experimental Study on the Generation and Growth of Wind Waves Vol. 61 (Kyoto, Japan: Bulletins - Disaster Prevention Research Institute, Kyoto University), 1–41.

Google Scholar

Kunishi H., Imasato N. (1966). ON THE GROWTH OF WIND WAVES BY HIGH-SPEED WIND FLUME. Disaster. Prev. Res. Inst. Annuals. 9, 667–676.

Google Scholar

Kuznetsova A., Baydakov G., Dosaev A., Troitskaya Y. (2023). Drag coefficient parameterization under hurricane wind conditions. Water 15, 1830. doi: 10.3390/w15101830

CrossRef Full Text | Google Scholar

Lafon C., Piazzola J., Forget P., Le Calve O., Despiau. S. (2004). Analysis of the variations of the whitecap fraction as measured in a coastal zone. Boundary-Layer. Meteorol. 111, 339–360. doi: 10.1023/B:BOUN.0000016490.83880.63

CrossRef Full Text | Google Scholar

Large W. G., Pond S. (1981). Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Oceanogr. 11, 324–336. doi: 10.1175/1520-0485(1981)011<0324:OOMFMI>2.0.CO;2

CrossRef Full Text | Google Scholar

Lenain L., Melville W. K. (2017). Evidence of sea-state dependence of aerosol concentration in the marine atmospheric boundary layer. J. Phys. Oceanogr. 47, 69–84. doi: 10.1175/JPO-D-16-0058.1

CrossRef Full Text | Google Scholar

Makin V. K. (2005). A note on the drag of the sea surface at hurricane winds. Boundary-Layer. Meteorol. 115, 169–176. doi: 10.1007/s10546-004-3647-x

CrossRef Full Text | Google Scholar

Monahan E. C. (1986). “The Ocean as a Source for Atmospheric Particles,” in The Role of Air-Sea Exchange in Geochemical Cycling. Ed. Buat-Ménard P. (Springer Netherlands, Dordrecht), 129–163.

Google Scholar

Moon I.-J., Ginis I., Hara T., Thomas B. (2007). A physics-based parameterization of air–sea momentum flux at high wind speeds and its impact on hurricane intensity predictions. Monthly. Weather. Rev. 135, 2869–2878. doi: 10.1175/MWR3432.1

CrossRef Full Text | Google Scholar

Moon I.-J., Ginis I., Hara T., Tolman H. L., Wright C. W., Walsh E. J. (2003). Numerical simulation of sea surface directional wave spectra under hurricane wind forcing. J. Phys. Oceanogr. 33, 1680–1706. doi: 10.1175/2410.1

CrossRef Full Text | Google Scholar

Munk W. H. (1955). Wind stress on water: An hypothesis. Q. J. R. Meteorol. Soc. 81, 320–332. doi: 10.1002/qj.49708134903

CrossRef Full Text | Google Scholar

Myrhaug D., Wang H., Holmedal L. E. (2016). Addendum to “Sea spray aerosol flux estimation based on long-term variation of wave statistics”: estimation based on long-term variation of wind statistics. Oceanologia 58, 150–153. doi: 10.1016/j.oceano.2015.11.003

CrossRef Full Text | Google Scholar

Nilsson E. D., Hultin K. A. H., Mårtensson E. M., Markuszewski P., Rosman K., Krejci R. (2021). Baltic sea spray emissions: in situ eddy covariance fluxes vs. Simulated tank sea spray. Atmosphere 12, 274. doi: 10.3390/atmos12020274

CrossRef Full Text | Google Scholar

Powell M. D., Vickery P. J., Reinhold T. A. (2003). Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 422, 279–283. doi: 10.1038/nature01481

PubMed Abstract | CrossRef Full Text | Google Scholar

Rizza U., Canepa E., Ricchi A., Bonaldo D., Carniel S., Morichetti M., et al. (2018). Influence of wave state and sea spray on the roughness length: feedback on medicanes atmosphere. Atmosphere 9, 8, 301. doi: 10.3390/atmos9080301

CrossRef Full Text | Google Scholar

Shi J., Feng Z., Sun Y., Zhang X., Zhang W., Yu Y. (2021). Relationship between sea surface drag coefficient and wave state. J. Mar. Sci. Eng. 9, 1248. doi: 10.3390/jmse9111248

CrossRef Full Text | Google Scholar

Shi J., Zhao D., Li X., Zhong Z. (2009). New wave-dependent formulae for sea spray flux at air-sea interface. J. Hydrodynamics. Ser. B. 21, 573–581. doi: 10.1016/S1001-6058(08)60186-9

CrossRef Full Text | Google Scholar

Shi J., Zhong Z., Li R., Li. Y., Sha W. (2011). Dependence of sea surface drag coefficient on wind-wave parameters. Acta Oceanol. Sin. 30, 14–24. doi: 10.1007/s13131-011-0101-z

CrossRef Full Text | Google Scholar

Song A., Li J., Tsona N., Du L. (2023). Parameterizations for sea spray aerosol production flux. Appl. Geochem. 157, 105776. doi: 10.1016/j.apgeochem.2023.105776

CrossRef Full Text | Google Scholar

Stramska M. (1987). Vertical profiles of sea salt aerosol in the atmospheric surface layer: a numerical model. Acta Geophys. Polonica. 35, 87–100.

Google Scholar

Takagaki N., Komori S., Suzuki N., Iwano K., Kuramoto T., Shimada S., et al. (2012). Strong correlation between the drag coefficient and the shape of the wind sea spectrum over a broad range of wind speeds. Geophys. Res. Lett. 39, (23). doi: 10.1029/2012GL053988

CrossRef Full Text | Google Scholar

Toba Y. (1972). Local balance in the air-sea boundary processes. J. Oceanogr. 28, 109–120. doi: 10.1007/BF02109772

CrossRef Full Text | Google Scholar

Toba Y., Iida N., Kawamura H., Ebuchi N., Jones I. S.F. (1990). Wave dependence of sea-surface wind stress. J. Phys. Oceanogr. 20, 705–721. doi: 10.1175/1520-0485(1990)020<0705:WDOSSW>2.0.CO;2

CrossRef Full Text | Google Scholar

Toba Y., Koga M. (1986). “A parameter describing overall conditions of wave breaking, whitecapping, sea-spray production and wind stress,” in Oceanic Whitecaps: And Their Role in Air-Sea Exchange Processes. Eds. Monahan E. C., Mac Niocaill G (Springer Netherlands, Dordrecht), 37–47.

Google Scholar

Troitskaya Y. I., Sergeev D. A., Kandaurov A. A., Baidakov G. A., Vdovin M. A., Kazakov. V. I. (2012). Laboratory and theoretical modeling of air-sea momentum transfer under severe wind conditions. J. Geophys. Res. Oceans. 117, C00J21. doi: 10.1029/2011JC007778

CrossRef Full Text | Google Scholar

Wan Z., Zhu J., Sun K., Zhou K. (2017). An integrated turbulent simulation and parameter modeling study on sea-spray dynamics and fluxes. Ocean. Eng. 130, 64–71. doi: 10.1016/j.oceaneng.2016.11.041

CrossRef Full Text | Google Scholar

Woolf D. K., Monahan E. C., Spiel. D. E. (1988). “Quantification of the marine aerosol produced by whitecaps,” in Preprints, seventh conference on ocean-atmosphere interaction, anaheim meteorological society, Boston, USA. 182–185.

Google Scholar

Wu J. (1973). Spray in the atmospheric surface layer: Laboratory study. J. Geophys. Res. 1896-1977) 78, 511–519. doi: 10.1029/JC078i003p00511

CrossRef Full Text | Google Scholar

Wu J. (1980). Wind-Stress coefficients over Sea surface near Neutral Conditions—A Revisit. J. Phys. Oceanogr. 10, 727–740. doi: 10.1175/1520-0485(1980)010<0727:WSCOSS>2.0.CO;2

CrossRef Full Text | Google Scholar

Wu J. (1993). Production of spume drops by the wind tearing of wave crests: The search for quantification. J. Geophys. Res. Oceans. 98, 18221–18227. doi: 10.1029/93JC01834

CrossRef Full Text | Google Scholar

Xu X., Voermans J. J., Guan C., Babanin A. V. (2023). Sea spray induced air-sea heat and salt fluxes based on the wave-steepness-dependent sea spray model. Acta Oceanol. Sin. 42, 35–41. doi: 10.1007/s13131-022-2073-6

CrossRef Full Text | Google Scholar

Xu X., Voermans J. J., Ma H., Guan C., Babanin A. V. (2021). A wind–wave-dependent sea spray volume flux model based on field experiments. J. Mar. Sci. Eng. 9, 1168. doi: 10.3390/jmse9111168

CrossRef Full Text | Google Scholar

Yelland M., Taylor P. K. (1996). Wind stress measurements from the open ocean. J. Phys. Oceanogr. 26, 541–558. doi: 10.1175/1520-0485(1996)026<0541:WSMFTO>2.0.CO;2

CrossRef Full Text | Google Scholar

Zhao D., Li M. (2019). Dependence of wind stress across an air–sea interface on wave states. J. Oceanogr. 75, 207–223. doi: 10.1007/s10872-018-0494-9

CrossRef Full Text | Google Scholar

Zhao D., Toba Y., Sugioka K., Komori S. (2006). New sea spray generation function for spume droplets. J. Geophys. Res. Oceans. 111, C02007. doi: 10.1029/2005JC002960

CrossRef Full Text | Google Scholar

Zhu J., Wan Z., Wang X., Lü L. (2014). Modeling of sea spray droplets in the ocean. Thermal. Sci. 18, 1577–1582. doi: 10.2298/TSCI1405577Z

CrossRef Full Text | Google Scholar