Sivaji Patra1*
Charan Kumar Basuri1,2*
Pradipta R. Muduli1,3
Vishnu Vardhan Kanuri1,4
Robin R. S.1,5
Ganguly Dipnarayan1,5
Abhilash K. R.1,5
Lovaraju Avvari2
Uma Sankar Panda1Dash S. K.1Ramana Murthy M. V.1- 1National Center for Coastal Research, Ministry of Earth Sciences, Chennai, India
- 2Marine Biological Laboratory, Department of Zoology, Andhra University, Visakhapatnam, India
- 3Wetland Research and Training Centre, Chilika Development Authority, Balugaon, India
- 4Central Pollution Control Board, Ministry of Environment, Forest and Climate Change, Kolkata, India
- 5National Centre for Sustainable Coastal Management, Ministry of Environment, Forest and Climate Change, Chennai, India
Introduction
Coastal lagoons are the most productive systems in the world because these environments are susceptible to significant nutrient influxes via runoff and direct human waste, which give rise to intricate and unpredictable variations in both spatial and temporal biogeochemical dynamics (Roselli et al., 2009; Tagliapietra et al., 2009). These variations are caused by fluctuations in salinity and temperature gradients, shallow depth, benthic–pelagic interface processes, and restricted connections with the adjacent sea (Torréton et al., 2007). Conversely, shallow-water lagoons exhibit significantly higher ecological diversity than fully marine water bodies due to their diverse biological communities that include freshwater, brackish water, and marine water (Dube et al., 2010). Given these factors, a quantitative mathematical methodology is essential for determining impacts developing solutions to improve water quality, and predicting potential nutrient loads (Jayaraman et al., 2007). This method allows for the assessment of primary, secondary, and tertiary production by anticipating potential outcomes and understanding the impact of local management strategies (Giusti et al., 2010). Understanding ecologically significant processes requires comprehending transformative mechanisms, which necessitate modeling and describing altered biogeochemical cycles.
Previous studies used coefficients derived from field experiments in temperate regions, which have distinct water quality and ecological characteristics compared to tropical areas, such as higher annual solar irradiation, water temperatures exceeding 18°C, and increased primary production (Lewis, 1987; Prasad et al., 2014; Panda et al., 2015). Therefore, the mathematical models employed to predict water quality in tropical water bodies cannot directly adopt the chemical and biological parameters linked to climatic zones (Lin et al., 2001). This limitation stems from variations in local physicochemical properties, diverse tropical biological processes, and models calibrated to specific environmental regimes (Dunlop et al., 2008). Given this context, it becomes imperative to establish a comprehensive modeling framework tailored to tropical coastal water systems.
The present study embodies the culmination of the “Chilika Lake Ecosystem Modeling” project, which provides crucial insights into the prediction of biogeochemical events. In the realm of tropical ecosystems, it is worth noting that there is a significant dearth of research in this area, especially when it comes to the Indian sub-continent. Considering this, a set of objectives has been devised to confront this deficiency in understanding.
i. The determination of rate constants in Chilika Lake holds significant value in terms of predicting and understanding its sustainable biogeochemical processes.
ii. Validation of predictions from a mathematical model on primary and secondary production, which strongly correlate with ecosystem water quality, using in situ monitored data.
Sampling and analysis
Study area
Chilika Lagoon, a designated Ramsar site in India, features a distinctive pear-shaped, shallow water body with a longitudinal stretch of 64.3 km and an average width of 20.1 km (Pattnaik, 1998) (Figure 1A). Its seasonal variability in total area, ranging from approximately 704 km² in summer to 1,020 km² during the monsoon, is influenced by the confluence of three key tributaries of the Mahanadi River, namely, Daya, Bhargavi, and Nuna. These tributaries play a crucial role in regulating the lagoon’s hydrography, along with the 52 streams from the western catchment regions contributing a substantial volume of freshwater (3.1 × 106 m3 d−1 and 166.8 × 106 m3 d−1 during pre-monsoon and monsoon, respectively) (Gupta et al., 2008). A significant hydrological intervention in September 2000, involving the creation of a new mouth, successfully addressed ecological challenges such as low salinity and macrophyte overgrowth observed in 1996–1997 (Satyanarayana, 1999). Seawater exchange primarily occurs through the Outer channel, supplemented by a discreet connection via the Palur canal in Rambha Bay, resulting in a dynamic interplay of marine water, brackish water, and freshwater ecosystems. Hydrographically, the lagoon is classified into four sectors: the Southern sector, connected to the sea through the Palur canal; the Northern sector, receiving the maximum discharge through rivers; the Outer channel, connected directly to the sea; and the Central sector, serving as the mixing zone of the Northern sector and the Outer channel. The present study was conducted during January 2009 and December 2011 in the lagoon’s southern and central sectors, characterized by minimal salinity changes, aimed to derive major coefficients for a comprehensive understanding of its ecological dynamics (Gupta et al., 2008; Muduli et al., 2013) (Figure 1B).
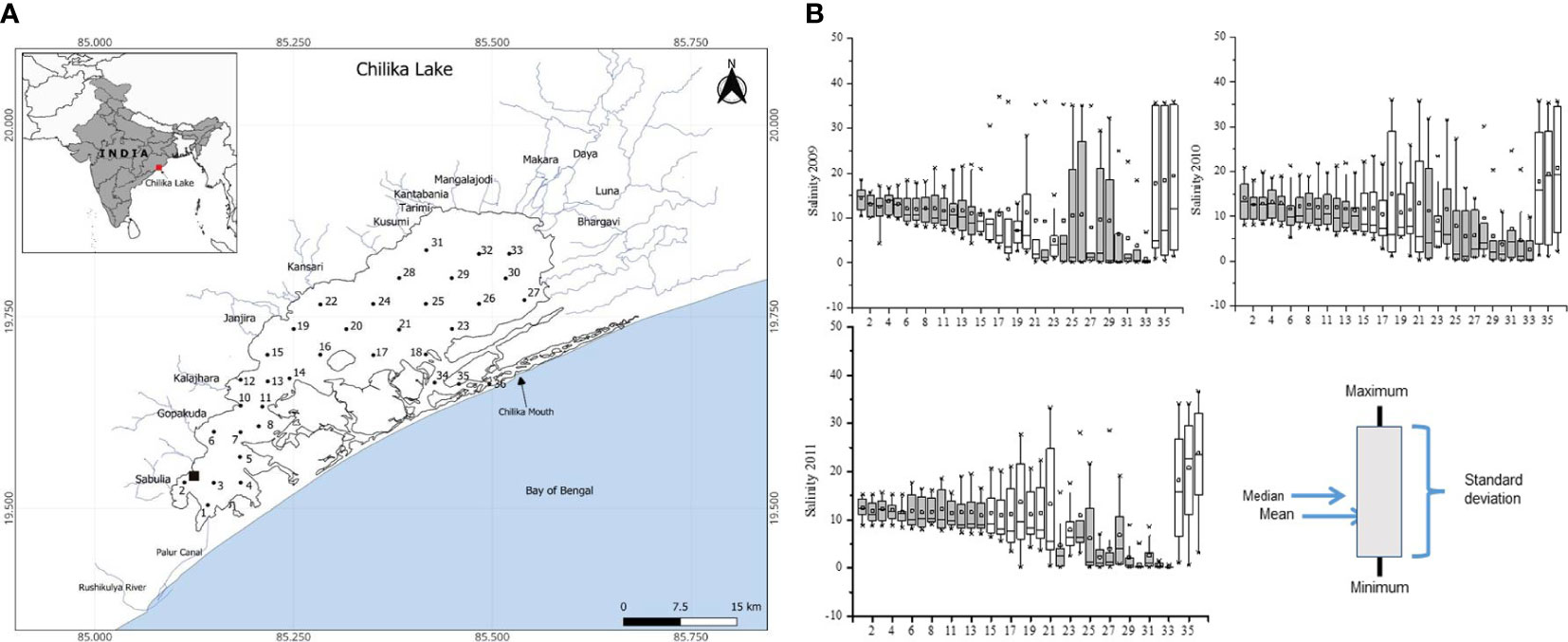
Figure 1 (A) Map of Chilika lagoon with study locations. The black solid square near station (St.) 2 shows the benthic chamber experiment location. Southern sector: St. no. 1–14; Central sector: St. no. 15–23; Northern sector: St. no. 24–32; and Outer channel: St. no. 34–36. (B) Salinity variations across the sampling locations and four sectors of Chilika Lake during the study periods from 2009 to 2011.
Biogeochemical parameters and experimental methods
Dissolved inorganic nutrients (NH4, NO2, NO3, and PO4) were estimated using protocols from Grasshoff et al. (1999). The determination of carbonaceous biological oxygen demand (CBOD) was conducted by employing the dissolved oxygen (DO) method with a 5-day incubation period (APHA, 23rd Edition). The MIKE-21 Manual was used to calculate the first-order decay rate at 20°C, temperature coefficient for decay rate, and half-saturation oxygen concentration. Moreover, the concentrations of ammonia and phosphorus were estimated from the BOD incubated bottles to assess the production of ammonia and phosphorus during the organic matter degradation (i.e., carbonaceous BOD) and their content was calculated following the DHI Manual for WQ-2003. The ammonia in sediments was extracted using the potassium chloride technique (Riley and Vitousek, 1995) and analyzed using the hypochlorite method (Grasshoff et al., 1999). The H14CO32 incorporation method was used to measure nitrification rates (Brion and Billen, 1998, 2000), while oxygen demand during nitrification was determined using conversation factors from NH4 to NO2 and NO3 to NO2 (Wezernak and Gannon, 1967).
For new carbon production estimation, the Chlorophyll-a (Chl-a) measurement before and after 12 h, along with the radioactive carbon (C14) technique, is used under in situ incubation conditions. Microzooplankton (MZP) grazing experiments were conducted to analyze grazing rates, phytoplankton growth rate, and daily turnover using the dilution technique (Landry and Hassett, 1982). The mass of zooplankton was measured in carbon (C) by filtering 20 ml of culture using a pre-combusted (at 450°C for 4H) 25-mm Whatman GF/F filter (0.7 μm). Similarly, phytoplankton samples were oven dried at 60°C and their organic carbon (de-carbonated by HCl fumes) content was measured using an elemental analyzer on alternate days (Thermo Finnigan, Flash EA1112) (Redalje, 1983). L-Cystine was used as standard and precision of analysis was checked against NIST 1941b and found to be at ±0.1%.
Sediment oxygen demand (SOD) was measured using laboratory-based and in situ field methods, using sediment core samples and a submersible benthic chamber where the depth is ~1.5 m, to minimize sediment manipulation and reflect ambient field conditions. The benthic chamber used in this experiment is made up of a height of 30 cm and a diameter of 29 cm, with indigenous fabrication employing a translucent acrylic sheet of 1.3 cm thickness (Abhilash et al., 2012; Muduli et al., 2013). The chamber was equipped with a leakproof design and provisions to replace withdrawn sample volume through side ports. To prevent excessive penetration into sediment, emplacement flanges were attached to two opposite outer walls, with a maximum depth of 15 cm. The chamber was incubated with an artificial bottom current created by generating a mechanical stirring every 10 min to simulate natural processes. DO samples from the chamber water were collected at 3-h intervals for 24 h via Tygon tubing, using a peristaltic pump. Care was taken in avoiding air bubbles and entrapped water in Tygon tube before sampling. For further experiment details, refer to Muduli et al. (2013).
The experiments were conducted during the stable post-monsoon (November to January) and pre-monsoon (March to June) seasons covering all the 3 years (January 2009 and December 2011), and the mean results were used to calculate coefficient derivations, with each experiment performed five times.
Model formulations
All the model equations, units, and nomenclatures for hydro-chemical, biological, and sediment processes for model requirements were adopted from MIKE 21 Water Quality Temples 2003 in tandem with Hang et al. (2009).
Results and discussion
BOD is a crucial factor in the aerobic metabolism of various organisms, including pelagic and benthic ones (APHA, 1992; Bhateria and Jain, 2016). In Chilika Lake, the CBOD decay rate constant was measured as 0.24 d−1. In general, temperature, hydraulic parameters, and in situ processes significantly influence BOD decay rate, with micro-/macro-organisms playing a direct role in governing overall BOD rates within the water column. Despite this, the BOD sources include mass debris, decreased flora and fauna, and mass zooplankton detritus. The dynamics of water quality are exemplified by the difference between clean waters with low BOD values and high organic content with elevated BOD values, which can lead to severe DO depletion and potential fish kills (Penn et al., 2003). This study investigates various BOD processes, the CBOD decay temperature correction factor (1.048 θ), the ratio of ammonium released by BOD decay (0.28 g NH4-N/g BOD), half-saturation concentrations of DO for organic matter degradation (0.38 mg O2/L), and phosphorus content in dissolved BOD (0.6 ± 0.035 g P/g BOD) (Table 1).
Table 1 Comparison of biogeochemical rate constants of Chilika Lagoon with other areas.
In riverine systems, the decomposition of organic matter often hinges on the bacterial populations. For example, in Malaysian river water, CBOD decay rates were found to be higher than BOD decay rates observed during different seawater dilutions, attributed to the suppression of nitrifying bacteria, resulting in reduced oxygen consumption (Nuruzzaman et al., 2018). Our study found that CBOD decay rates in experimental sites were comparable to those in San Francisco Bay Estuary (Chen, 1970), James River (O’Connor, 1981), and Patuxent River Estuary (Lung and Bai, 2003), indicating distinctly brackish waters. The study found that the NH4 release ratio during BOD decay was consistent with Venice Lagoon (Melaku Canu et al., 2001) and Chesapeake Bay (Cerco and Cole, 1994) studies, and the phosphate content in dissolved BOD was lower than Savannah Harbor (NATIONAL BOARD OF WATERS, 1982), indicating that algal growth played a significant role as a regulating factor.
Estimating DO concentrations is crucial for understanding oxidation and reduction processes, nutrient release, and gas production. Oxygen enters water through direct absorption from the atmosphere and photosynthesis, which consumes carbon from the atmosphere by phytoplankton and submerged aquatic vegetation (e.g., Potamogeton pectinatus, Halophila sp., and Vallinaria sp.). This understanding is essential for considerate nutrient release and gas production. Consequently, DO is a helpful indicator of environmental health due to its correlation with phytoplankton biomass (Bhateria and Jain, 2016). DO is also linked to the nutrient cycle through microbial mineralization and demineralization mechanisms. In Chilika Lake, maximum oxygen production at noon was 7.99 ± 0.011m2/d, with submerged plants acting as a major sink for DO at 191.6 m2/d.
Carbon-based primary production measures can be compared to oxygen-based measures, with adjustments based on the photosynthetic quotient (PQ), which represents the molar ratio of oxygen and carbon production. PQ can vary depending on inorganic nitrogen source, with higher values used for nitrate utilization. The carbon-to-oxygen ratio at primary production in the lagoon was 0.31 ± 0.006 mg C/mg O. The study determined the DO-to-Chl-a ratio, DO-to-mass detritus ratio, and DO-to-mass zooplankton ratios in all lagoon sectors and mean values are 0.1391 ± 0.202 g DO/mg Chl, 0.0174 ± 0.004 mg DO/mg D, and 0.2708 ± 0.11 mg DO/mg Z, respectively (Table 1). The mean water to air oxygen flux rate was calculated as 0.0008 mM/m2/d. These results indicate that the fluctuations in water quality are linked to algal growth. For instance, during peak photosynthetic production, Chl-a concentrations coincide with DO and pH values (Lindenberg et al., 2008), making the DO-to-Chl-a ratio crucial for estimating ecosystem health. DO-to-detritus and mass zooplankton ratios indicate the lagoon’s biological stability.
The non-humic dissolved organic matter production can be related to chlorophyll-a as well as bacteria–chlorophyll concentrations (Khan and McKnight, 2010; Harvey et al., 2015; del Giorgio and Peters, 1993). The bacterial degradation of organic matter results in the production of inorganic molecules, including NH4 in sediment, which is an important indicator of organic load and its conversion into an inorganic state. The NH4 concentration in lagoon sediment was quantified as 284.6 mg/m3, providing valuable insights into nutrient regeneration from the bottom sediment. The study measured the increase in dissolved NH4 concentration in a lagoon using benthic chamber experiments, which revealed a mean value of 0.0041 mM/m2/d (Table 1), where the variations in chlorophyll content were linked to the dissolved organic nitrogen and NH4, especially in the northern part, due to active in situ mineralization of POC-rich SPM (Patra et al., 2016). Additionally, the re-suspension of bottom sediment during the pre-monsoon period due to high wind action increased SPM levels, which could also affect the lagoon’s NH4 concentration (Ganguly et al., 2015).
The nitrification process involves the microbial transformation of NH4 to NO2 and NO3 is important in the nitrogen (N) cycle. The nitrification rate was observed as 3.001 (k Ni NH) and is comparable to the South China Sea (0–5.2 kNiNH) (Dai et al., 2008). In the Mediterranean Lagoon and Ria de Aveiro (temperate lagoon), the nitrification rates were reported as 0.011 kNiNH and 0.05 kNiNH (at 20°C) (Chapelle et al., 2000; Lopes et al., 2010), and the nitrification and de-nitrification processes are subject to the distinctive environmental parameters prevailing in the local context. The N-to-mass detritus ratio and N-to-Chl-a ratio were shown as 0.12 yN/D and 0.019 yN/Chl, respectively, which are in agreement with other studies (Cugier et al., 2005; Hang et al., 2009).
Phosphorus is a key nutrient in ecosystem dynamics, limiting algal development. Sediment in shallow water systems regulates P levels in the water column. The complex processes of P transformation, preservation, and recycling at the sediment–water interface are influenced by the reactivity of P forms and diverse biological, physical, and geochemical factors, with estuarine and coastal environments serving as vital P sinks and filters (Liu et al., 2016). Furthermore, previous studies suggested that the mineralization of organic matter and the reduction of iron oxide affect P release into the water column (Ruttenberg, 1992). The P cycle in turbid waters is still unknown due to its reliance on other elements. Studies using spatiotemporal data from lagoon ecosystems aim to understand phosphate involvement and its relationship with primary producers, consumers, and detritus. The estimated mean sediment to water of PO4-P flux rate was recorded as 0.00437 mM/m2/d. The mean ratios of P to Chl-a, mass detritus, and mass zooplankton in Chilika Lake were measured as 0.0036 ± 0.001 g P/mg Chl, 0.000321 ± 0.00001 mg P/mg D, and 100.94 ± 52.7 mg P/mg Z, respectively. These results are comparable (Table 1) with the previous studies conducted elsewhere (Chen et al., 2002; Nobre et al., 2010); however, the P-to-mass zooplankton ratio showed a high value, which may be due to the high productivity nature of Chilika Lake.
The complex and non-linear relationship between phytoplankton carbon biomass and chlorophyll concentration is influenced by light, nutrients, and temperature within the euphotic zone, as documented in various studies (Brown et al., 2003; Le Bouteiller et al., 2003; Armstrong, 2006). Under nutrient-rich conditions, the phytoplankton carbon-to-chlorophyll (C:Chl) ratio decreases as light levels decrease, a phenomenon known as “photoacclimation” (Dubinsky and Stambler, 2009). The natural death rate of Chl-a in laboratory conditions is 0.7 d−1 (Table 1), indicating that chlorophyll concentrations, which are indicators of phytoplankton populations, are influenced by nutrient availability. In general, nitrogenous nutrients enter through oxygen-demanding processes like nitrification, while phosphorus is released through cellular processes, excretions, and river runoff. Conversely, total suspended matter (TSM) includes all living, non-living, organic, and inorganic materials, including chlorophylls and suspended planktons, and is significantly related to chlorophyll concentrations, highlighting the interconnectedness of environmental factors.
MZP are primarily composed of ciliates, are the primary consumer of nanoplankton, and serve as an important link between small primary producers and larger consumers in aquatic feed webs (Burkill et al., 1993). The lagoon has a mean grazing rate of 0.305 d−1, and the mean mass of zooplankton to Chl-a was calculated to be 0.341g Z/mg Chl, based on extensive spatiotemporal data collection. The decline in phytoplankton biomass is influenced by factors like water quality, zooplankton grazing, and their life cycle, while zooplankton abundance is regulated through secondary grazing and natural mortality mechanisms (Ger et al., 2014). Greater grazing values indicate higher rates of zooplankton domination, possibly measured by zooplankton-to-chlorophyll ratios.
Oxygen depletion in aquatic ecosystems is primarily caused by sediment organic material oxidation and invertebrate anaerobic respiration, affecting a significant portion of water column oxygen consumption, thus making measuring the rate of change in DO concentration essential for understanding oxygen flux changes (Akomeah and Lindenschmidt, 2017). Consequently, the study estimated the change in column DO concentration in a chamber-entrapped water volume and analyzed the SOD, revealing that temperature, water flow velocity, residence time, and sediment composition are key factors influencing SOD (Zeledon-Kelly, 2009).
The designed experiment calculated the temperature coefficient for SOD, the half-saturation concentration for SOD, and the DO sediment exchange rates. The results showed a temperature coefficient of 0.87 g O2/m2/d and a half-saturation concentration of 0.46 mg/L, with a mean SOD of 1.45 mg/m2/d (Table 1). The mean DO exchange rate between water column and sediment is 1.082 mg/L, which controls the benthic community and nutrient leaching from sedimentary pore water, but has a significant impact on shallow-water aquatic bodies. The high SOD of 5.01 μmol/m2/h in Chilika Lake may be attributed to the high benthic primary production resulting in increased benthic oxygen demand. Algae usually consume oxygen during nighttime respiration, while during daylight photosynthesis, they generate and release oxygen (Akomeah and Lindenschmidt, 2017).
Conclusion
The findings from this study indicate that the lagoonal ecosystem possesses a noteworthy level of resilience in the face of environmental fluctuations, comparable to other tropical shallow ecosystems worldwide. These determined rate constants mark a significant step towards establishing an ecosystem model tailored to the lagoon. Such a model would be instrumental in forecasting ecosystem alterations in response to variations in chemical and biological elements. In the northern part of the lagoon, where nutrient, SPM (suspended particulate matter), and chlorophyll-a levels are notably high, it is apparent that this region exerts a dominant influence over the entire lagoon. Further investigations into this northern region are necessary. It is worth noting that the derived rate constants may exhibit variations contingent upon species composition, abundance, decomposition processes, and evolving environmental conditions. It is important to note that although this study was conducted in saline to semi-saline conditions, the insights obtained may be applicable to the vast majority of tropical brackish water lagoons.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SP: Conceptualization, Supervision, Writing – original draft, Writing – review & editing. BK: Data curation, Validation, Writing – review & editing. PM: Data curation, Methodology, Writing – review & editing, Validation. KV: Data curation, Methodology, Writing – review & editing, Validation. RR: Data curation, Investigation, Methodology, Writing – review & editing, Validation. DG: Data curation, Investigation, Writing – review & editing. AK: Data curation, Methodology, Writing – review & editing. AL: Data curation, Methodology, Writing – review & editing. UP: Validation, Writing – review & editing. SD: Writing – review & editing, Validation. MR: Project administration, Supervision, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors thank Secretary, Ministry of Earth Sciences, Indian Navy (INS Chilika) and Dr. B.R Subramanian, former Director of ICMAM-PD for the support. This manuscript is dedicated to late Prof. A.V. Raman, Andhra University for his invaluable support. This study is a part of MoES-ICMAM, presently known as the National Center for Coastal Research (NCCR) project “Ecosystem Modeling for Chilika Lagoon”. This is NCCR manuscript contribution number 382.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abhilash K. R., Raveendran T. V., Limna Mol V. P., Deepak M. P. (2012). Sediment Oxygen Demand in Cochin backwaters, a tropical estuarine system in the south-west coast of India. Mar. Environ. Res. 79, 160–166.
Akomeah E., Lindenschmidt K. E. (2017). Seasonal variation in sediment oxygen demand in a northern chained river-lake system. Water 9, 254. doi: 10.3390/w9040254.
Aminot A., Guillaud J. F., Kerouel R. (1997). La baie de Seine: hydrologie, nutriments et chlorophylle 1978–1994. Edition IFREMER Reperes Ocean 14, 148.
Antonopoulos V. Z., Gianniou S. K. (2003). Simulation of water temperature and dissolved oxygen distribution in Lake Vegoritis, Greece. Ecol. Model. 160, 39–53.
APHA (1992). “Standard methods for the examination of water and wastewater,” in 18th Edition, American Public Health Association (APHA), American Water Works Association (AWWA) and Water Pollution Control Federation (WPCF), Washington DC.
Armstrong R. A. (2006). Optimality-based modeling of nitrogen allocation and photoacclimation in photosynthesis. Deep-Sea Res. Pt. II 53, 513–531. doi: 10.1016/j.dsr2.2006.01.020.
Bhateria R., Jain D. (2016). Water quality assessment of lake water: a review. Sustain. Water Resour. Manage. 2, 161–173. doi: 10.1007/s40899-015-0014-7.
Brion N., Billen G. (1998). A reassessment of the H14CO3- incorporation method for measuring autotrophic nitrification and its use to estimate nitrifying biomass of nitrifying bacteria. Rev. Des. Sci. l’Eau 11, 283–302.
Brion N., Billen G. (2000). Wastewater as a source of nitrifying bacteria in river systems: the case of the river Seine downstream from Paris. Water Res. 34, 3213–3221. doi: 10.1016/S0043-1354(00)00075-0.
Brown S. L., Landry M. R., Neveux J., Dupouy C. (2003). Microbial community abundance and biomass along a 180° transect in the equatorial Pacific during an El Nino-SouthernOscillation cold phase. J. Geophys. Res. 108, 8139.
Burkill P. H., Edwards E. S., John A. W. G., Sleigh M. A. (1993). Microzooplankton and their herbivorous activity in the Northeastern Atlantic Ocean. DeepSea Res. Part II: Topical Stud. Oceanogr. 40, 479–493.
Cerco C. F., Cole T. M. (1994). Three-dimensional eutrophication model of Chesapeake Bay, Main Report. Tech. Rep. EL-94-4 (Vicksburg, MS) 1.
Chapelle A., Menesguen A., Deslous-Paoli J. M., Souchu P., Mazouni N., Vaquer A., et al. (2000). Modelling nitrogen, primary production and oxygen in a Mediterranean lagoon. Impact oysters farming inputs watershed. Ecol. Model. 127, 161–181.
Chen C. W. (1970). Concepts and utilities of ecological model. J. San. Engr. Div. ASCE. 96, 1085–1097.
Chen C., Schwab D. J., Beletsky D., Fahnenstiel G. L., Jiang M., et al. (2002). A model study of the coupled biological and physical dynamics in Lake Michigan. Ecol. Model. 152, 145–168.
Cloern J. E., Grenz C., Vidergar-Lucas L. (1995). An empirical model of the phytoplankton chlorophyll:carbon ratio - the conversion factor between productivity and growth rate. Limnol. Oceanogr. 40, 1313–1321.
Cugier P., Menesguen A., Guillaud J. F. (2005). Three-dimensional (3D) ecological modelling of the Bay of Seine (English Channel, France). J. Sea. Res. 54, 104–124.
Dai M., Zhai W., Cai W.-J., Callahan J., Huang B., Shang S., et al. (2008). Effects of an estuarine plume-associated bloom on the carbonate system in the lower reaches of the Pearl River estuary and the coastal zone of the northern South China Sea. Cont. Shelf Res. 28, 1416–1423.
del Giorgio P. A., Peters R. H. (1993). “The influence of DOC on the bacteria-chlorophyll relationship in lakes,” in Internationale Vereinigung für theoretische und angewandte Limnologie: Verhandlungen. (Stuttgart, Germany), 25 (1), 359–362.
Dube A., Jayaraman G., Rani R. (2010). Modelling the effects of variable salinity on the temporal distribution of plankton in shallow coastal lagoons. J. Hydro-Environ. Res. 4, 199–209. doi: 10.1016/j.jher.2010.03.003.
Dubinsky Z., Stambler N. (2009). Photoacclimation processes in phytoplankton: mechanisms, consequences, and applications. Aquat. Microb. Ecol. 56, 163–176. doi: 10.3354/ame01345.
Dunlop J. E., Kefford B. J., McNeil V. H., McGregor G. B., Choy S., Nugegoda D. (2008). A Review of guideline development for suspended solids and salinity in tropical rivers of Queensland, Australia. Australas. J. Ecotoxicol. 14, 129–142.
Gamier J., Blanc P., Benest D. (1989). Estimating a carbon/ chlorophyll ratio in nannoplankton (Creteil Lake, S.-E. Paris, France). Water Res. Bull. 25, 751–754.
Ganguly D., Patra S., Muduli P. R., Vishnu Vardhan K., Abhilash K. R., Robin R. S., et al. (2015). Influence of nutrient input on the trophic state of a tropical brackish water lagoon. J. Earth Sys. Sci. 124, 1005–1017. doi: 10.1007/s12040-015-0582-9.
Ger K. A., Hansson L. A., Lürling M. (2014). Understanding cyanobacteria-zooplankton interactions in a more eutrophic world. Freshw. Biol. 59, 1783–1798. doi: 10.1111/fwb.12393.
Geider R. J., Maclntyre H. L., Kana T. M. (1998). A dynamic regulatory model of phytoplanktonic acclimation to light, nutrients, and temperature. Limnol. Oceanogr. 43 (4), 679–694.
Giusti E., Marsili-Libelli S., Renzib M., Focardi S. (2010). Assessment of spatial distribution of submerged vegetation in the Orbetello lagoon by means of a mathematical model. Ecol. Model. 221, 1484–1493. doi: 10.1016/j.ecolmodel.2010.02.019.
Grasshoff K., Ehrdardt M., Kremling K., Anderson L. G. (1999). Methods of seawater analysis (Germany: Wiley). doi: 10.1002/9783527613984.
Gupta G. V. M., Sarma V. V. S. S., Robin R. S., Raman A. V., Jaikumar M., Rakesh M., et al. (2008). Influence of net ecosystem metabolism in transferring riverine organic carbon to atmospheric CO2 in a tropical coastal lagoon (Chilika lake, India). Biogeochemistry 87, 265–285. doi: 10.1007/s10533-008-9183-x.
Hang M. T. H., Don N. C., Araki H., Yamanishi H., Koga K. (2009). Applications of a new ecosystem model to study the dynamics of phytoplankton and nutrients in the Ariake Sea, west coast of Kyushu, Japan. J. Mar. Syst. 75, 1–16. doi: 10.1016/j.jmarsys.2008.07.006.
Harvey E. T., Kratzer S., Andersson A. (2015). Relationships between colored dissolved organic matter and dissolved organic carbon in different coastal gradients of the Baltic Sea. Ambio 44, 392–401. doi: 10.1007/s13280-015-0658-4.
Hessen D. O., Lyche A. (1991). Inter and intra-specific variations in zooplankton element composition. Arch. Hydrobiol. 121, 343–353.
Irwin B. (1991). Coulometric measurement of primary production, with comparison against dissolved oxygen and 14C methods in a seasonal study. Mar. Ecol. Prog. Ser. 71, 97–102.
Jayaraman G., Rao A. D., Dube A., Mohant P. K. (2007). Numerical simulation of circulation and salinity structure in Chilika lagoon. J. Coast. Res. 23, 861–877. doi: 10.2112/04-0225R.1.
Jørgensen S. E., Bendoricchio G. (2001). Fundamentals of ecological modelling, Third ed (The Netherlands: Elsevier).
Khan A. L., McKnight D. M. (2010). Evaluation of the relationship between dissolved organic material, chlorophyll-a and algal species in lakes and drinking water reservoirs throughout the State of Colorado. AGU Fall Meet. Abs. 2010, B11I–B105.
Kitajima K., Hogan K. P. (2003). Increases of chlorophyll a/b ratios during acclimation of tropical woody seedlings to nitrogen limitation and high light. Plant Cell Environ. 26, 857–865.
Landry M. R., Hassett R. P. (1982). Estimating the grazing impact of marine microzooplankton. Mar. Biol. 67, 283–288. doi: 10.1007/BF00397668.
Le Bouteiller A., Leynaert A., Landry M. R., Le Borgne R., Neveux J., Rodier M., et al. (2003). Primary production, new production, and growth rate in the equatorial Pacific: Changes from mesotrophic to oligotrophic regime. J. Geophys. Res. 108, 8141. doi: 10.1029/2001JC000914.
Lewis W. M. Jr. (1987). Tropical limnology. Ann. Rev. Ecol. Syst. 18, 159–184. doi: 10.1146/annurev.es.18.110187.001111.
Lin H. J., Hung J. J., Shao K. T., Kuo F. (2001). Trophic functioning and nutrient flux in a highly productive tropical lagoon. Oecologia 129, 395–406. doi: 10.1007/s004420100730.
Lindenberg M. K., Hoilman G., Wood T. M. (2008). Water quality conditions in Upper Klamath and Agency lakes, Oregon 2006. U.S. Geol. Survey Sci. Investig. Rep., 2008–5201. doi: 10.3133/sir20085201.
Liu J., Zang J., Zhao C., Yu Z., Xu B., Li J. (2016). Phosphorus speciation, transformation, and preservation in the coastal area of Rushan Bay. Sci. Total Environ. 565, 258–270. doi: 10.1016/j.scitotenv.2016.04.177.
Ling T.-Y., Ng C.-S., Lee N., Buda D. (2009). Oxygen Demand of the Sediment from the Semariang Batu River, Malaysia. World Appl. Sci. J. 7, 440–447.
Muduli P. R., Vardhan Kanuri V., Robin R. S., Charan Kumar B., Patra S., Raman A. V., et al. (2013). Distribution of dissolved inorganic carbon and net ecosystem production in a tropical brackish water lagoon, India. Cont. Shelf Res. 64, 75–87. doi: 10.1016/j.csr.2013.05.014.
Lopes J. F., Almeida M. A., Cunha M. A. (2010). Modelling the ecological patterns of a temperate lagoon in a very wet spring season. Ecol. Model. 221, 2302–2322.
Lung W. S., Bai S. (2003). A water quality model for the Patuxent estuary: Current conditions and predictions under changing land-use scenarios. Estuaries 26, 267–279.
Lung W., Hwang B. G. (1994). Water Quality Modeling of the St. Martin River, Assawoman and Isle of Wight Bays (Charlottesville: Maryland Department of the Environment, Environmental and Water Resources Engineering Research Report, No. 15, School of Engineering and Applied Science, University of Virginia), 1994.
Melaku Canu D., Umgiesser G., Solidoro C. (2001). Short-term simulations under winter conditions in the Lagoon of Venice: A contribution to the environmental impact assessment of temporary closure of the inlets. Ecol. Modell. 138, 215–230.
National Board of Waters (1982). Vesiviranomaisennäytteenottomenetelmät. (The sampling methods of water investigation used by water authorities). Vesihallituksenjulkaisuja 40, 1–52.
Nobre A. M., Ferreira J. G., Nunes J. P., Yan X., Bricker S., Corner R., et al. (2010). Assessment of coastal management options by means of multilayered ecosystem models. Estuar. Coast. Shelf Sci. 87, 43–62.
Nuruzzaman Md., Al-Mamun A., Noor Bin Salleh Md. (2018). Experimenting biochemical oxygen demand decay rates of Malaysian river water in a laboratory flume. Environ. Eng. Res. 23, 99–106. doi: 10.4491/eer.2017.048.
O’Connor D. J. (1981). “Modeling of Eutrophication in Estuaries,” in Estuaries and Nutrients. Contemporary Issues in Science and Societyz. Eds. Neilson B. J., Cronin L. E. (Humana Press).
Panda U. S., Mahanty M. M., Ranga Rao V., Patra S., Mishra. P. (2015). Hydrodynamics and water quality in Chilika lagoon- A modelling approach. Proc. Eng. 116, 639–646. doi: 10.1016/j.proeng.2015.08.337.
Patra S., Raman A. V., Ganguly D., Robin R. S., Muduli P. R., Kanuri V., et al. (2016). Influence of suspended particulate matter on nutrient biogeochemistry of a tropical shallow lagoon, Chilika, India. Limnology 17, 223–238. doi: 10.1007/s10201-015-0475-2.
Pattnaik S. S. (1998). “Estimation of sediment flow into the Chilika lake,” in Abstracts of the Workshop on Sustainable Development of Chilika Lake, Orissa (Bhubaneswar, India) (Chilika Development Authority, Bhubaneshwar, India), 32.
Penn M. R., Pauer J. J., Miheleie J. R. (2003). “Biochemical oxygen demand,” in Environmental and Ecological Chemistry, vol. 2 . Ed. Sabjic A. (UNESCOEOLSS, Isle of Man, UK), 278.
Prasad B. S. R. V., Srinivasu P. D. N., Varma P. S., Raman A. V., Ray S. (2014). Dynamics of dissolved oxygen in relation to saturation and health of an aquatic body: A case for Chilka Lagoon, India. J. Ecosyst., 1–17.
Qian P., Franks P. J. S., Landry M. R. (2011). Microzooplankton grazing dynamics: parameterizing grazing models with dilution experiment data from the California Current Ecosystem. Mar. Ecol. Prog. Ser. 438, 59–69.
Qian P., Franks P. J. S., Landry M. R., Goericke R., Taylor A. G. (2010). Modeling phytoplankton growth rates and chlorophyll to carbon ratios in California coastal and pelagic ecosystems. J. Geophys. Res. 115, G04003.
Redalje (1983). Phytoplankton carbon biomass and specific growth rates determined with the labeled chlorophyll a technique. Mar. Ecol. Prog. Ser. 11, 217–225. doi: 10.3354/meps011217.
Reichert P., Borchardt D., Henze M., Rauch W., Shanahan P., Somlyody L., et al. (2001). River Water Quality Model no. 1 (RWQM1): II. Biochemical process equations. Water Sci. Technol. 43, 11–30.
Riley R. H., Vitousek P. M. (1995). Nutrient dynamics and nitrogen trace gas flux during ecosystem development in montne rain forest. Ecology 76, 292–304. doi: 10.2307/1940650.
Rohit Goyal (2011). Modelling Hydrodynamics for Water Quality of the Dwarka Region (Gujarat). 2nd International Conference on Environmental Science and Development IPCBEE vol.4 (2011) © (2011) (Singapore: IACSIT Press).
Roselli L., Fabbrocini A., Manzo C., D’Adamo R. (2009). Hydrological heterogeneity, nutrient dynamics and water quality of a non-tidal lentic ecosystem (Lesina Lagoon, Italy). Estuar. Coast. Shelf Sci. 84, 539–552. doi: 10.1016/j.ecss.2009.07.023.
Ruttenberg K. C. (1992). Development of a sequential extraction method for different forms of phosphorus in marine sediments. Limnol. Oceanogr. 37, 1460–1482. doi: 10.4319/lo.1992.37.7.1460.
Satyanarayana C. H. (1999). Hydrographic and phytoplankton characteristics of Chilka Lake, a brackish water lagoon, on the east coast of India, Ph.D. Andhra University, Visakhapatnam, India.
Seiki T., Izawa H., Date E., Sunahara H. (1994). Sediment Oxygen Demand in Hiroshima Bay. Water Res. 28, 385–393.
Soetaert K., Herman P. M. J. (1995). Carbon flows in the Westerschelde estuary (The Netherlands) evaluated by means of an ecosystem model (MOSES). Hydrobiologia 311, 247–266.
Sterner R. W., Elser J. J., Hessen D. O. (1992). Stoichiometric relationships among producers, consumers, and nutrient cycling in pelagic ecosystems. Biogeochemistry 17, 49–67.
Sullivan A. B., Snyder D. M., Rounds S. A. (2010). Controls on biochemical oxygen demand in the upper Klamath River, Oregon. Chem. Geol. 269, 12–21. doi: 10.1016/j.chemgeo.2009.08.007.
Tagliapietra D., Sigovini M., Volpi Ghirardini A. (2009). A review of terms and definitions to categorise estuaries, lagoons and associated environments. Mar. Freshw. Res. 60, 497–509. doi: 10.1071/MF08088.
Torréton J. P., Rochelle-Newall E., Jouon A., Faure V., Jacquet S., Douillet P. (2007). Correspondence between the distribution of hydrodynamic time parameters and the distribution of biological and chemical variables in a semi-enclosed coral reef lagoon. Estuar. Coast. Shelf Sci. 74, 766–776. doi: 10.1016/j.ecss.2007.05.018.
USACE (2006). Development of the hydrodynamic and water quality models for the Savannah Harbour Expansion Project. 62–74.
Wezernak C. T., Gannon J. J. (1967). Oxygen-Nitrogen relationships in autotrophic nitrification. Appl. Microbiol. 15, 1211–1215. doi: 10.1128/am.15.5.1211-1215.1967.
Keywords: ecosystem models, Chilika lagoon, coefficients, biogeochemistry, eutrophication, rate constant
Citation: Patra S, Basuri CK, Muduli PR, Kanuri VV, R. S. R, Dipnarayan G, K. R. A, Avvari L, Panda US, S. K. D and M. V. RM (2024) Determination of biogeochemical rate constants for Chilika Lake, a tropical brackish water lagoon on the east coast of India. Front. Mar. Sci. 11:1323229. doi: 10.3389/fmars.2024.1323229
Received: 17 October 2023; Accepted: 29 January 2024;
Published: 26 February 2024.
Edited by:
Angel Pérez-Ruzafa, University of Murcia, SpainReviewed by:
Dilip Kumar Jha, National Institute of Ocean Technology, IndiaAli Ertürk, Istanbul University, Türkiye
Copyright © 2024 Patra, Basuri, Muduli, Kanuri, R. S., Dipnarayan, K. R., Avvari, Panda, S. K. and M. V.. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sivaji Patra, c2l2YWppcGF0cmFAZ21haWwuY29t; Charan Kumar Basuri, YmNoYXJhbmt1bWFyOUBnbWFpbC5jb20=