Marine heatwaves (MHWs) are warm sea surface temperature (SST) anomalies with substantial ecological and economic consequences. Observations of MHWs are based on relatively short instrumental records, which limit the ability to forecast these events on decadal and longer timescales. Paleoclimate reconstructions can extend the observational record and help to evaluate model performance under near future conditions, but paleo-MHW reconstructions have received little attention, primarily because marine sediments lack the temporal resolution to record short-lived events. Individual foraminifera analysis (IFA) of paleotemperature proxies presents an intriguing opportunity to reconstruct past MHW variability if strong relationships exist between SST distributions and MHW metrics. Here, we describe a method to test this idea by systematically evaluating relationships between MHW metrics and SST distributions that mimic IFA data using a 2000-member linear inverse model (LIM) ensemble. Our approach is adaptable and allows users to define MHWs based on multiple duration and intensity thresholds and to model seasonal biases in five different foraminifera species. It also allows uncertainty in MHW reconstructions to be calculated for a given number of IFA measurements. An example application of our method at 12 north Pacific locations suggests that the cumulative intensity of short-duration, low-intensity MHWs is the strongest target for reconstruction, but that the error on reconstructions will rely heavily on sedimentation rate and the number of foraminifera analyzed. This is evident when a robust transfer function is applied to new core-top oxygen isotope data from 37 individual Globigerina bulloides at a site with typical marine sedimentation rates. In this example application, paleo-MHW reconstructions have large uncertainties that hamper comparisons to observational data. However, additional tests demonstrate that our approach has considerable potential to reconstruct past MHW variability at high sedimentation rate sites where hundreds of foraminifera can be analyzed.

1 Introduction

Marine heatwaves (MHWs) are prolonged periods of anomalously warm ocean temperature relative to local climatologies that can have considerable socioeconomic impacts (von Biela et al., 2019; Free et al., 2023; Leggat et al., 2019; Oliver et al., 2021; Rogers-Bennett and Catton, 2019; Smith et al., 2023, 2021). MHWs can occur throughout the global ocean as evidenced by recent events in the northeast Pacific, East China Sea, Tasman Sea, Mediterranean Sea, northwest Atlantic, southwest Atlantic and Benguela current region (Oliver et al., 2021). Observational data suggest that MHW frequency, duration and spatial extent have increased in recent decades (Frölicher et al., 2018; Holbrook et al., 2020; Oliver et al., 2018; Yao et al., 2022), and a prominent north Pacific event from 2014-2016 may be the most ecologically and economically impactful ever recorded (Bond et al., 2015; Cheung and Frölicher, 2020; Di Lorenzo and Mantua, 2016). Nicknamed the “Blob,” this event caused major shifts in the geographic range of organisms from copepods to sunfish, closed commercially-important fisheries, initiated an unprecedented harmful algal bloom and contributed to mass strandings of birds and marine mammals (Cavole et al., 2016; Jones et al., 2018; McCabe et al., 2016). Recent trends in MHW behavior are due at least in part to anthropogenic global warming (Barkhordarian et al., 2022; Laufkötter et al., 2020), and forecasts based on general circulation model (GCM) ensembles such as phases 5 and 6 of the Coupled Model Intercomparison Project (i.e. CMIP5 and CMIP6, Eyring et al., 2016; Taylor et al., 2012) generally predict these trends will continue (Frölicher et al., 2018; Oliver et al., 2019). However, comparisons of these GCM ensembles to observed MHWs show significant biases that can both overestimate and underestimate various measures of MHW behavior (Hirsch et al., 2021; Plecha et al., 2021), thereby raising concern regarding the accuracy of decadal to centennial forecasts.

MHW variability reflects the combined influence of temperature changes due to external radiative forcing and internal modes (Holbrook et al., 2019; Oliver et al., 2021). Both internal and external forcings operate on decadal timescales that are relatively well captured by instrumental data, and longer centennial to millennial timescales that are not resolved by observations. Accordingly, MHW forecasts exhibit considerable skill on sub-annual timescales (Holbrook et al., 2020; Jacox et al., 2022), but not on longer timescales over which the models are uncalibrated and unvalidated. Furthermore, observational data reflect the recent, relatively low CO₂ climate, which may not accurately record the breadth and magnitude of feedbacks expected in the high CO₂ climate of future centuries (Tierney et al., 2020). Both processes likely contribute to the biases in CMIP forecasts of future MHW activity, and point to a need for new strategies to validate MHW behavior in models over a larger dynamic range.

Paleoclimate data offer the potential to extend the observational record and thus evaluate model performance under boundary conditions different than those recorded during the observational era. For example, climates such as those of the Pliocene and Eocene have been identified as good analogs for future warming (Burke et al., 2018), and can serve as benchmarks against which to calibrate and validate models. Despite this, few studies have approached MHWs from a paleoclimate perspective, likely because most paleoceanographic archives lack the high temporal resolution necessary to characterize individual MHWs. Massive hermatypic corals may be an exception (Zinke et al., 2015), but this archive is primarily limited to low-latitude ocean regions during the latest Quaternary period. In contrast, marine sediments can record ocean variability across millions of years in diverse oceanographic settings, and preserve proxies like foraminifera that are sensitive to MHWs (Lane et al., 2023). Unfortunately, most marine sedimentary archives have low sediment accumulation rates and experience bioturbation, which leads to temporal resolutions of centuries to millennia that are far too coarse to record monthly to annual MHWs.

Individual foraminifera analysis (IFA) offers a potential solution to this temporal averaging problem in marine sediments. Unlike traditional paleoceanographic applications of foraminifera, which pool individuals to estimate mean conditions, IFA measures geochemical proxies in many single foraminifera and then interprets the shape of the resulting distribution (Ford et al., 2018, 2015; Groeneveld et al., 2019; Khider et al., 2011; Koutavas et al., 2006; Koutavas and Joanides, 2012; Leduc et al., 2009; Rongstad et al., 2020; Rustic et al., 2020; Thirumalai et al., 2019; White et al., 2018). Given the ~4 week lifespan of most mixed layer planktonic foraminifera (Spero, 1998) due to a lunar-pacing of reproduction (Erez et al., 1991; Jonkers et al., 2015), each measured shell approximates a monthly snapshot of ocean conditions. The collective distribution of these snapshots then represents changes in the statistical properties of both mean climate and extremes over a time interval that is dictated by sedimentation rate, bioturbation and sampling interval. For example, IFA has been used to reconstruct the El Niño Southern Oscillation (ENSO) in the tropical Pacific based on the expectation that increased ENSO variability will broaden the distribution of reconstructed SST relative to the seasonal cycle, which manifests itself as an increase in standard deviation (Ford et al., 2015; Khider et al., 2011; Koutavas et al., 2006; Koutavas and Joanides, 2012; Rustic et al., 2020; White et al., 2018). Like ENSO variability, MHWs are also characterized by relatively short-lived sea surface temperature (SST) anomalies, and changes in their mean behavior between time periods could produce distinct changes in IFA-based SST distributions.

In practice, there are a number of complications that make it challenging to identify how an IFA-based SST distribution might be altered by changes in MHWs. For example, traditional approaches to calibrating foraminifera proxies using global core-top sediment (Elderfield and Ganssen, 2000; Malevich et al., 2019; Saenger and Evans, 2019; Tierney et al., 2019) or sediment traps (Anand et al., 2003; Gray et al., 2018; Huang et al., 2008) would be extremely costly because orders of magnitude more analyses would be necessary to generate IFA-based SST distributions for each site or time interval. Furthermore, it is not yet obvious how the accuracy of IFA-based SST distributions vary with the number of geochemical proxy measurements made, which makes it difficult to know how many foraminifera would need to be sampled to make meaningful MHW reconstructions. Variations in the seasonality of different foraminifera species is also a complicating factor, and it is likely that relationships between IFA-based SST distributions and MHWs are specific to both individual species and sites. Finally, the numerous ways of describing both MHWs and SST distributions create a large pool of potential relationships, which may make it challenging to identify those that are most useful.

In light of these complications, it is attractive to evaluate relationships between IFA-based SST distributions and MHWs in a pseudoproxy framework. Pseudoproxies (Mann and Rutherford, 2002) are realistic approximations of actual proxy data that are generated by passing the output of physically consistent climate simulations through a proxy system model (Dee et al., 2016; Evans et al., 2013) that mimics complicating factors such as variations in seasonality. This approach obviously avoids the cost and labor of true geochemical proxy measurements and allows relationships between IFA-based SST distributions and MHWs to be explored quickly and efficiently. Furthermore, generating pseudoproxies from large ensembles of climate model simulations allows many realistic climate states to be sampled, thereby providing the large sample size necessary for robust measures of skill and error. Because pseudoproxies are generated from a known signal, they also provide valuable opportunities for validation and a testbed for evaluating how the accuracy of a relationship might change due to choices such as the MHW definition assumed, the foraminifera species considered, the sedimentation rate at a site or the number of proxy measurements used to generate an IFA-based SST distribution. Finally, because climate model simulations are spatially complete, a pseudoproxy approach allows relationships to be compared across large regions to identify sites where they have the greatest potential to generate meaningful MHW reconstructions.

Here we describe a method for evaluating quantitative relationships between SST distributions similar to those that could be generated via IFA and various measures of MHW variability with the goal of identifying which have the greatest potential to yield paleo-MHW reconstructions. We adopt a pseudoproxy approach in which a 2000-member linear inverse model (LIM) ensemble is used to compare MHW behavior to SST distribution statistics that mimic IFA measurements. Our approach is adaptable and allows users to evaluate five different foraminifera species, numerous MHW definitions and a number of realistic complications. While we are motivated by the desire to eventually reconstruct paleo-MHWs, the goal of this study is simply to define a framework for identifying the most robust quantitative transfer functions between IFA-based SST distributions and MHWs. Below, we first describe the data sources, construction and validation of an algorithm that can evaluate transfer functions based on different foraminifera species and MHW definitions. We then demonstrate the utility of our approach through the example application of identifying the most promising targets for paleo-MHW reconstructions in the northeast Pacific. Finally, we demonstrate how our approach can be integrated with IFA data using new high-precision oxygen isotope (δ¹⁸O) analyses of individual Globigerina bulloides from core-top sediments. We focus on the northeast Pacific domain with the goal of generating transfer functions that could eventually be used to generate paleo-MHW reconstructions that place events like the 2014-2016 “Blob” MHW (Bond et al., 2015) into context. However, the approach we describe is also valid for other species and ocean regions, thereby providing a framework for developing additional transfer functions and paving the way toward an improved understanding of the spatiotemporal behavior of MHWs.

2 Methods

2.1 Overview of the algorithm design

A simplified design of our method and its basic order of operations are summarized in Figure 1, while more specific information is presented in later subsections. The primary input to our algorithm is an ensemble of monthly SST timeseries. Monthly data is required since this is the approximate lifespan of an individual foraminifera (Spero, 1998), and each SST value can be considered analogous to what might be reconstructed from the measurement of a paleotemperature proxy in a single foraminifer. Multiple timeseries are required because each timeseries is ultimately reduced to a single SST distribution, and thus effectively contributes only a single data point to a given transfer function. We note that we use the phrase “transfer function” throughout the remainder of the text to describe the quantitative relationships between IFA pseudoproxy SST distributions and MHWs.

Figure 1

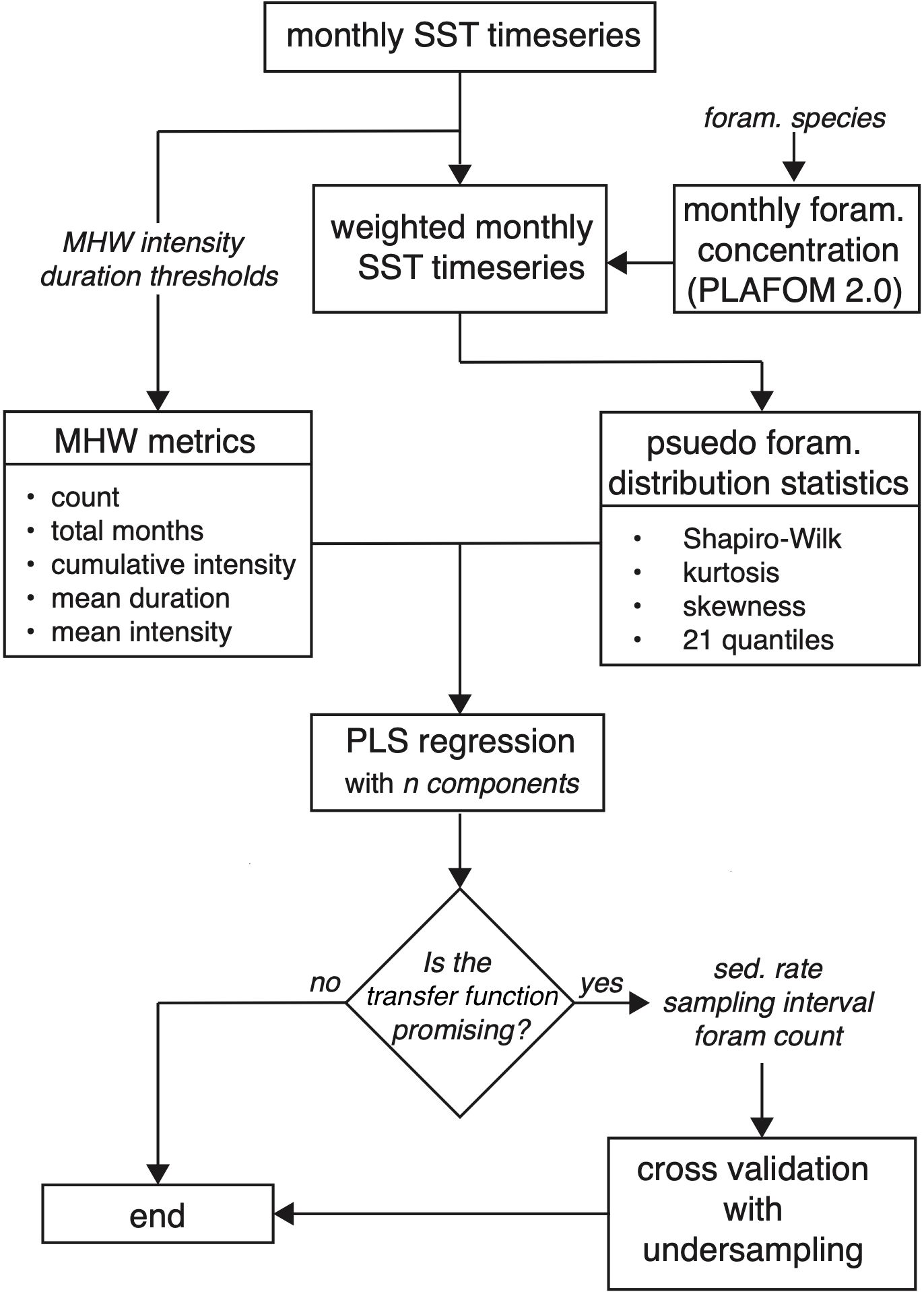
Figure 1. Schematic of our workflow for generating transfer functions between pseudoproxy SST distribution statistics and MHW metrics, and evaluating their skill. Italicized text indicates a user-defined choice. Monthly SST timeseries derive from COBEv2, ERSSTv5, HadISST or the LIM ensemble. MHW intensity and duration thresholds refer to the minimum intensity and duration necessary for a warm anomaly to be defined as a MHW, and metrics represent various measures of these MHWs. Monthly foraminifera concentrations, based on the PLAFOM2.0 model of Kretschmer et al. (2018), are used to generate a weighted monthly SST timeseries that represents the seasonal bias of a defined species. Distribution statistics summarize these seasonally-weighted pseudoproxy SST timeseries. Partial least squares (PLS) regression is used to develop transfer functions between distribution statistics and MHW metrics. If a user chooses to do so, the error on a reconstruction for a given number of individual foraminifera can be evaluated.

The algorithm then allows a user to specify how a MHW is defined and this information is used to calculate MHWs for each SST timeseries within the ensemble. One of five foraminifera species (Neogloboquadrina pachyderma, Neogloboquadrina incompta, Globigerina bulloides, Trilobatus sacculifer or Globigerinoides ruber) is also specified, and used to weight the monthly SST timeseries based on the seasonal concentration of that species as calculated by the proxy system model of Kretschmer et al. (2018). Statistics that summarize the shape of weighted SST distributions are then regressed against MHW measures using partial least squares regression (Mehmood et al., 2012) to develop initial transfer functions. If regression statistics and comparisons to observed MHWs suggest that a transfer function is promising, the user can perform additional cross validation to evaluate how a transfer function might perform in a paleoclimate context. For example, realistic sedimentation rates and sampling intervals can be specified to estimate how many foraminifera will be required to achieve a desired accuracy in a MHW reconstruction. This can be compared against the number of foraminifera actually present or the analytical budget available to provide a feasibility check before committing to a laborious and costly study.

2.2 Monthly SST from a linear inverse model (LIM) ensemble and observations

As noted previously, implementing our method requires an ensemble of monthly SST data. For the purposes of calibration, data should span a wide range of MHW states while still being physically realistic. Here, we achieve this using a 2,000 member LIM ensemble that has previously been used to explore Pacific MHWs (Xu et al., 2021).

LIMs are stochastically-forced linear dynamical models that are empirically determined. That is, the predictable dynamics of the climate system are inferred from auto covariance and lagged covariance of the coarse-grained climate variables, whereas the remaining unresolved fast-decaying and rapid nonlinear processes associated with weather are parameterized as spatially-coherent Gaussian white noise. The underlying assumption of a LIM construction is that the coarse-grained climate evolution acts as an integrated response to the rapid weather variability (Hasselmann, 1976), resulting in a system in which its predictable dynamics can be represented to a reasonable approximation linearly and deterministically. The unpredictable stochastic forcing, on the other hand, contributes to energizing the climate system. A LIM simulation obtained by integrating the stochastic forcing forward in time thus represents a climate system that can be diagnosed in the same manner as simulations from coupled GCMs, but with the advantage that many realizations of the simulated timeseries can be generated relatively easily (e.g. Ault et al., 2013; Newman et al., 2011). This general approach has been used extensively to explore Pacific SST on sub-annual to multidecadal timescales using LIMs (Alexander et al., 2008; Capotondi et al., 2022; Penland and Matrosova, 1994; Penland and Sardeshmukh, 1995; Xu et al., 2022, 2021).

The LIM ensemble in this study is based on Extended Reconstructed Sea Surface Temperature data set version 3 (ERSSTv3; Smith et al., 2008) in the tropical and north Pacific (110°E–60°W and 20°S–60°N) from 1950-2019 (Xu et al., 2021). It is gridded at 2° x 2° and consists of 2,000 physically-realistic timeseries of monthly SST that are 70 years each. This ensemble represents a large number of “alternate histories” of north Pacific SST that drastically increases the data available for generating transfer functions and allows for the large sample size necessary for robust statistics. Furthermore, this large ensemble is more likely to span the range of variability that could have existed in the geologic past, thereby making our transfer functions more relevant to paleo-MHW reconstructions.

To validate LIM-based transfer functions, we also evaluate MHWs in monthly SST timeseries from three additional gridded observational products. ERSST version 5 (ERSSTv5) is gridded at 2° x 2° and was analyzed for the period from 1854-2023 A.D (Huang et al., 2017). Version two of the Centennial in situ Observation-Based Estimates of SST (COBEv2) is gridded at 1° x 1° and was analyzed for the period from 1850-2023 (Hirahara et al., 2014). Finally, the Hadley Centre Sea Ice and Sea Surface Temperature data set HadISST is gridded at 1° x 1° and was analyzed for the period from 1870-2022 (Rayner et al., 2003).

2.3 MHW definitions and their detection in observations and LIMs

While MHWs are broadly defined as periods when SSTs exceed climatology by some amount for some period of time, there is no strict consensus on these values. For example, observational studies based on daily satellite SST data commonly define a MHW to be a thermal anomaly that exceeds the 90^th percentile for at least five days (Hobday et al., 2016), but model-based studies have considered intervals that exceed climatological SST by at least one standard deviation for at least five months to be MHWs (Xu et al., 2021). While the daily MHW definition is clearly outside the bounds of what our approach can resolve, we see no need to make further a priori assumptions about what magnitude of warming or duration constitutes a MHWs. We therefore allow the user to define an intensity threshold and duration for considering a warm anomaly to be a MHW. Intensity thresholds are formulated in terms of the number of standard deviations above monthly climatology (e.g. across all Januarys) within a single timeseries. Duration thresholds are simply an integer number of consecutive months. We use the term “definition” throughout the remainder of the text to refer to these various ways of defining MHWs. For example, a low intensity, short duration definition may specify MHWs to be times when monthly SST exceeds the climatological value by at least one standard deviation for at least one month, while a high intensity, long duration definition might require SST to exceed climatology by at least two standard deviations for at least four months.

For a given definition, MHWs are calculated across the entire length of a SST timeseries, but each monthly timeseries in the ensemble is considered separately. In the case of LIM data, this means MHWs are identified within each 70-year realization, but the 2,000 ensemble members are considered independently. Thus, the LIM ensemble provides 2,000 separate estimates of MHW behavior for each definition considered.

To account for global warming trends, a 30-year high pass filter is applied to ERSSTv5, COBEv2 and HadISST timeseries prior to calculating climatologies (Figure 2A). This is equivalent to a shifting (as opposed to fixed) baseline approach and is consistent with the idea that a MHW should be an exceptional event above a background state that is distinct from lower frequency anthropogenic warming (Amaya et al., 2023). LIM simulations do not have a global warming trend so do not require filtering.

Figure 2

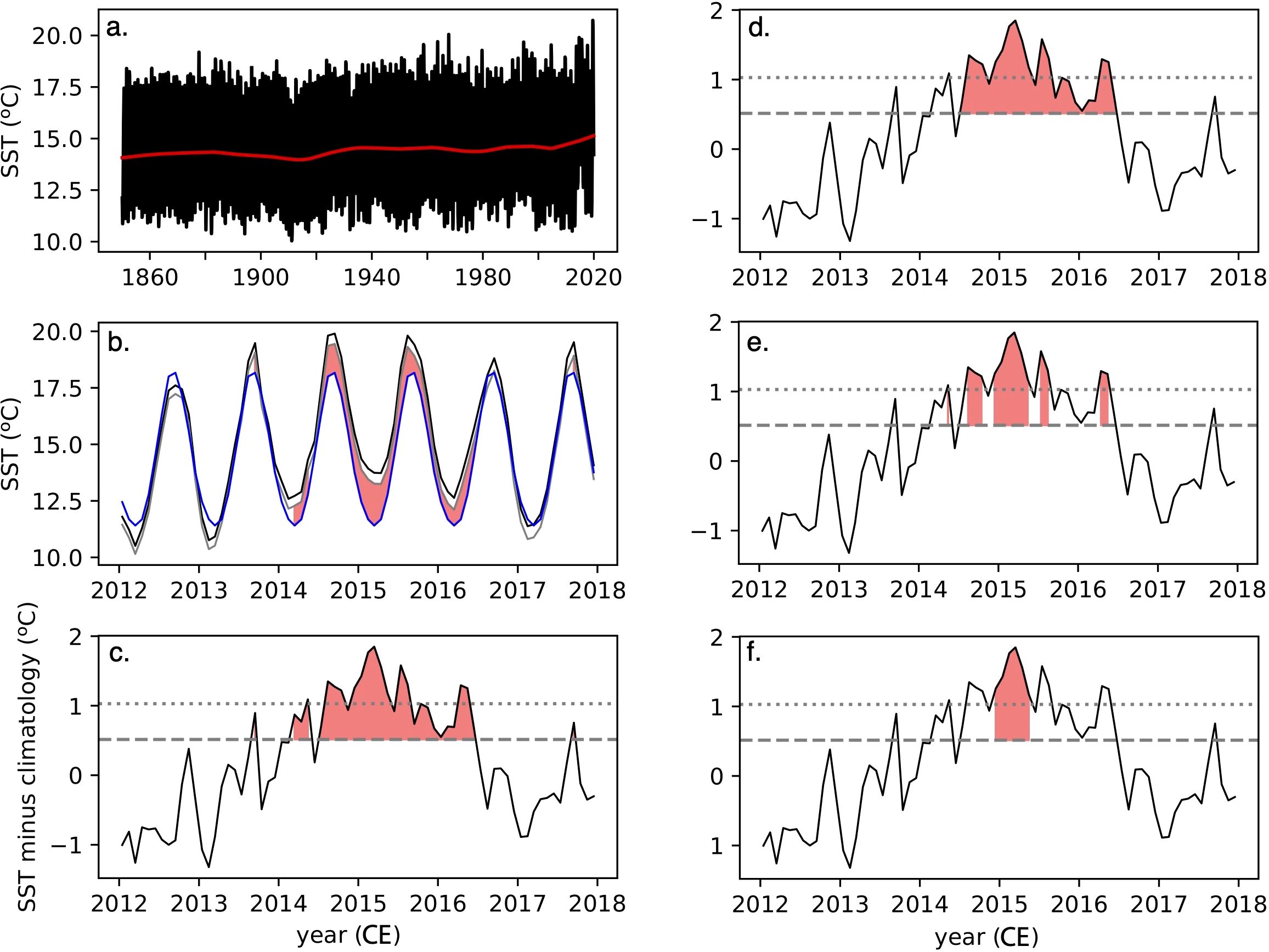
Figure 2. (A) COBEv2 SST at DSDP Site 36 (black) and the low frequency trend associated with the 30-year high pass filter (red). This filter is used to remove the global warming trend from observational data when calculating MHW metrics (B) Subset of COBEv2 SST for the years from 2012-2018 spanning the “Blob” MHW (black) and the same signal after removing the low frequency trend (grey). The climatology plus one standard deviation (blue) marks a threshold above which a MHW could be defined (red shading) (C) SST with the low frequency trend and climatology removed (black) relative to the upper bound of one standard deviation (grey dashed line) and two standard deviations (grey dotted line). Times exceeding one standard deviation provide an equivalent definition (red shading) that are identical to panel (B). (D) As in panel (C) for intensity and duration thresholds of one standard deviation and five months (E) As in panel (C) for intensity and duration thresholds of two standard deviations and one month (F) As in panel (C) for intensity and duration thresholds of two standard deviations and five months.

Once MHWs are identified, they are further characterized based on five metrics (Figure 2). In some cases metrics are normalized to a decade to account for the different lengths of ERSSTv5, COBEv2, HadISST and LIM timeseries. We use the term “metric” throughout the remainder of the text to refer to the following five ways of characterizing MHW behavior:

● Count (n/decade): Total MHW events, normalized to a decade

● Total months (n/decade): Total number of months in a timeseries that meet the assigned MHW definition, normalized to a decade.

● Cumulative intensity (°C/decade): Sum of monthly intensities in a timeseries that meet the assigned MHW definition, normalized to a decade.

● Mean duration (months): Average length of all MHWs in a timeseries

● Mean intensity (°C): Average intensity of all MHWs in a timeseries.

The values for these metrics can vary considerably with the choice of MHW definition, and increases or decreases in one metric do not necessarily cause equivalent changes in other metrics. An example using COBEv2 data from the northeast Pacific gridbox closest to Deep Sea Drilling Project (DSDP) Site 36 (Table 1) and spanning the 2012-2018 interval that includes the “Blob” MHW is shown in Figure 2. Using one standard deviation and one month as intensity and duration thresholds, respectively, four MHW events are identified (Figure 2C). Two events have a duration of a single month and intensities of 0.89°C and 0.75°C, respectively, which both exceed one standard deviation (0.51°C), but not two (1.02°C). Because these events are a single month, their cumulative intensities are identical to their mean intensities. A third event has a duration of three months, a mean intensity of 0.91°C and a cumulative intensity of 2.73°C. A fourth event represents the “Blob” event and has a duration of 24 months, a mean intensity of 1.12°C and cumulative intensity of 26.87°C. If the MHW definition is changed to have a duration threshold of five months, the three shorter events are no longer considered MHWs and only the “Blob” event remains with identical metrics (Figure 2D). Using two standard deviations and one month thresholds to define MHWs excludes most of the three shorter events, but also splits the “Blob” event into four (Figure 2E). Thus, the count of MHWs actually increases to five, which have durations of one to six months and mean intensities of 1.09 to 1.50°C. Using two standard deviations and five month thresholds, eliminates all but one high intensity MHW that represents the most intense portion of the “Blob” event (Figure 2F).

Table 1

Table 1. Locations and sedimentation rates of north Pacific sites.

2.4 Accounting for seasonality in foraminifera abundance

Planktonic foraminifera live in near-surface ocean environments around the globe and have long been recognized as valuable tools for reconstructing past SST (Anand et al., 2003; Bemis et al., 1998; Elderfield and Ganssen, 2000; Emiliani, 1955; Lea et al., 2000, 1999). Given their lifespan, measuring established paleotemperature proxies such as δ¹⁸O (Bemis et al., 1998) or magnesium to calcium ratios (Mg/Ca; Lea et al., 1999) in individual foraminifera allows for distributions of monthly SST to be generated (Ford et al., 2015; Koutavas et al., 2006; Rongstad et al., 2020; Rustic et al., 2020). These distributions are approximately equivalent to those based on monthly LIM and observational SST data, and therefore provide a means to use LIM-based transfer functions to reconstruct past MHW behavior.

However, planktonic foraminifera preferentially live at depths and during seasons when optimal growth conditions exist, and are therefore seasonally-biased recorders of SST (Jonkers et al., 2013, 2010; Jonkers and Kučera, 2015; Ortiz et al., 1995; Sautter and Thunell, 1989; Taylor et al., 2018; Tolderlund et al., 1971). To account for seasonality, monthly LIM ensemble data must be weighted to generate pseudoproxy SST timeseries that mimic the information that can be reconstructed from IFA. We achieve this using an existing planktonic foraminifera proxy system model (PLAFOM2.0), which is a global model of foraminifera abundance that predicts the monthly concentration (in mmol C m^-3) of five species: N. pachyderma, N. incompta, G. bulloides, T. sacculifer and G. ruber (Fraile et al., 2008; Kretschmer et al., 2018). PLAFOM2.0 uses a marine ecosystem model that predicts foraminifera food sources (Moore et al., 2001) to calculate species-specific rates of growth and mortality (Fraile et al., 2008). PLAFOM2.0 has recently been integrated with the biogeochemically-active ocean component of the Community Earth System Model (Hurrell et al., 2013) to calculate global estimates of foraminifera concentration in each month of the year and at 24 vertical levels between 0 and 250 meters (Kretschmer et al., 2018).

Our approach extracts PLAFOM2.0 concentrations for the user-defined foraminifera species from the grid-box closest to monthly SST data. Monthly foraminifer concentrations are summed across the model’s entire 250 m depth domain, thereby removing the user from a priori assumptions regarding depth habitat. The total annual foraminifer concentration is then used to convert monthly concentrations into proportions. Values greater than 0.083 (i.e. 1/12) reflect some degree of foraminifera seasonal preference. An example based on G. bulloides from DSDP Site 36 is shown in Figure 3. Monthly proportions are used as weights to resample the original SST timeseries and generate a new SST record that mimics the seasonal bias of the selected foraminifera species.

Figure 3

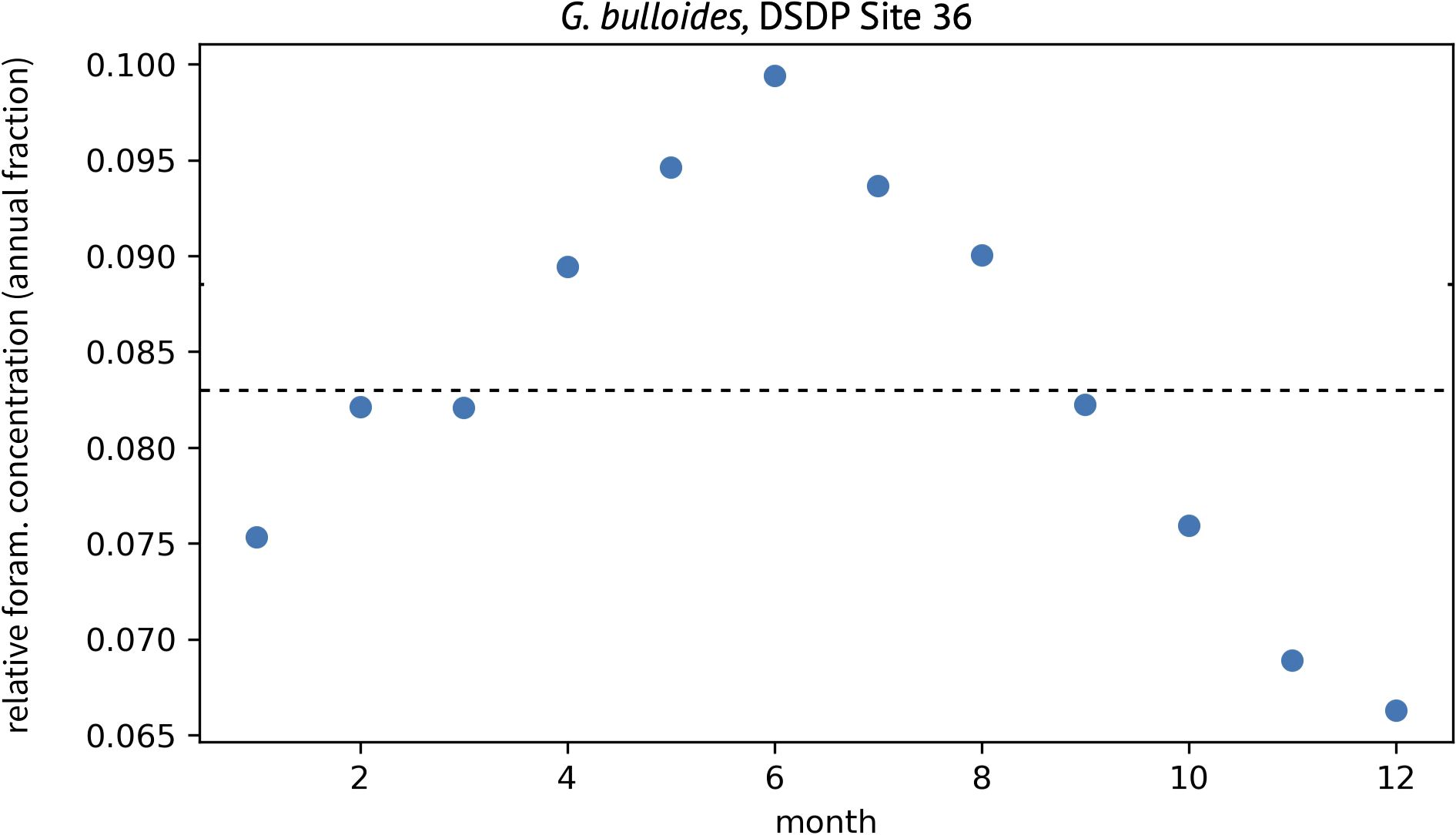
Figure 3. Example of the modeled seasonal change in the relative concentration of G. bulloides at DSDP Site 36. Values greater than 0.083 (dashed line) represent some degree of seasonal preference.

2.5 Summary statistics of SST distributions

A number of statistical values have been developed to summarize the shape of a distribution. These statistics are attractive for establishing transfer functions because they condense the large amount of data in a SST distribution into a single value. For each of the monthly-weighted SST timeseries described above, we calculate a series of statistics that summarize the shape of their distributions. We use the term “statistic” throughout the remainder of the text to refer to the following measures of distributions that are plausible predictors of MHW metrics:

● Shapiro-Wilk test: A statistical test evaluating the null hypothesis that data are Gaussian (Shapiro and Wilk, 1965). Test statistic values range from 0 to 1, with higher values representing closer agreement with a Gaussian distribution.

● Kurtosis: A measure of how often outliers occur or the “tailedness” of a distribution

● Skewness: A measure of a distribution’s asymmetry

● Quantiles 1-21: Values dividing a distribution into 21 continuous intervals of equal probability.

Statistics are calculated from standardized SST anomalies by subtracting means and dividing by standard deviations, and after 30-year high pass filtering in the case of ERSSTv5, COBEv2 and HadISST. Standardizing has no effect on Shapiro-Wilk, kurtosis and skewness values, and changes quantiles by a fixed proportion that varies between sites. The latter is helpful when comparing sites with different amplitude climatologies as it forces the total range of quantiles to be approximately equal. Standardizing also eliminates the need to select a specific proxy-temperature calibration for cases that calibrations are linear. That is, if δ¹⁸O values of foraminifera were used to estimate SST using a linear calibration (e.g. Bemis et al., 1998), the standardized anomalies of those δ¹⁸O values would have the same distribution statistics as δ¹⁸O-based SST estimates (for some statistics, the inverse relationship between δ¹⁸O and temperature would need to be accounted for by multiplying by -1).

2.6 Constructing transfer functions between pseudoproxy SST distribution statistics and MHW metrics

Our method next uses partial least squares regression (PLSR) to evaluate if pseudoproxy SST distribution statistics (section 2.5) are useful predictors of any MHW metric (section 2.3). PLSR is an attractive alternative to more traditional ordinary least squares regression for this application because it allows information from all distribution statistics to contribute to a transfer function despite considerable collinearity among them (Mehmood et al., 2012). Pseudoproxy SST distribution statistics are transformed into a new set of orthogonal components and a transfer function is generated using only a subset of these components. The dimensionality reduction of PLSR is therefore similar to principal components regression (PCR) with the difference that PLSR maximizes covariance between independent and dependent variables when selecting components while PCR only considers the variance of independent variables. Thus, PCR can inadvertently eliminate components with considerable predictive power if they have low variance, while PLSR is less prone to this effect.

We implement PLSR separately for each of the five MHW metrics using the scikit-learn Python module (Pedregosa et al., 2011). The number of components to include in the PLSR is chosen by first randomly selecting 30 pseudoproxy SST timeseries from the ensemble along with their corresponding MHW metrics. Subsets of 70% of each pseudoproxy SST timeseries are then used to generate PLSR-based transfer functions with 1 to 10 components that are each capable of predicting a MHW metric. Applying each transfer function to the withheld 30% of data allows the differences between the predicted and observed MHW metrics to be used to calculate root mean square errors (RMSE):

$$\text{RMSE}=\sqrt{\frac{{\sum }_i^N{(MH{W}_i- {\widehat{MHW}}_i)}^2}{N}}$$

where MHW_i-hat is the predicted MHW metric for ensemble member i, MHW_i is the true MHW metric for that ensemble member and N is the number of ensemble members considered. The change in RMSE with additional components allows the user to identify an appropriate number of components to include in the PLSR (Figure 4). To guide users toward transfer functions that balance lower RMSE with complexity, we highlight two values: 1) the number of components that yield the overall lowest RMSE and 2) the number of components at which RMSE ceases to improve by at least 1%. After the user selects a number of components, a new PLSR transfer function is generated using all pseudoproxy SST timeseries within the ensemble.

Figure 4

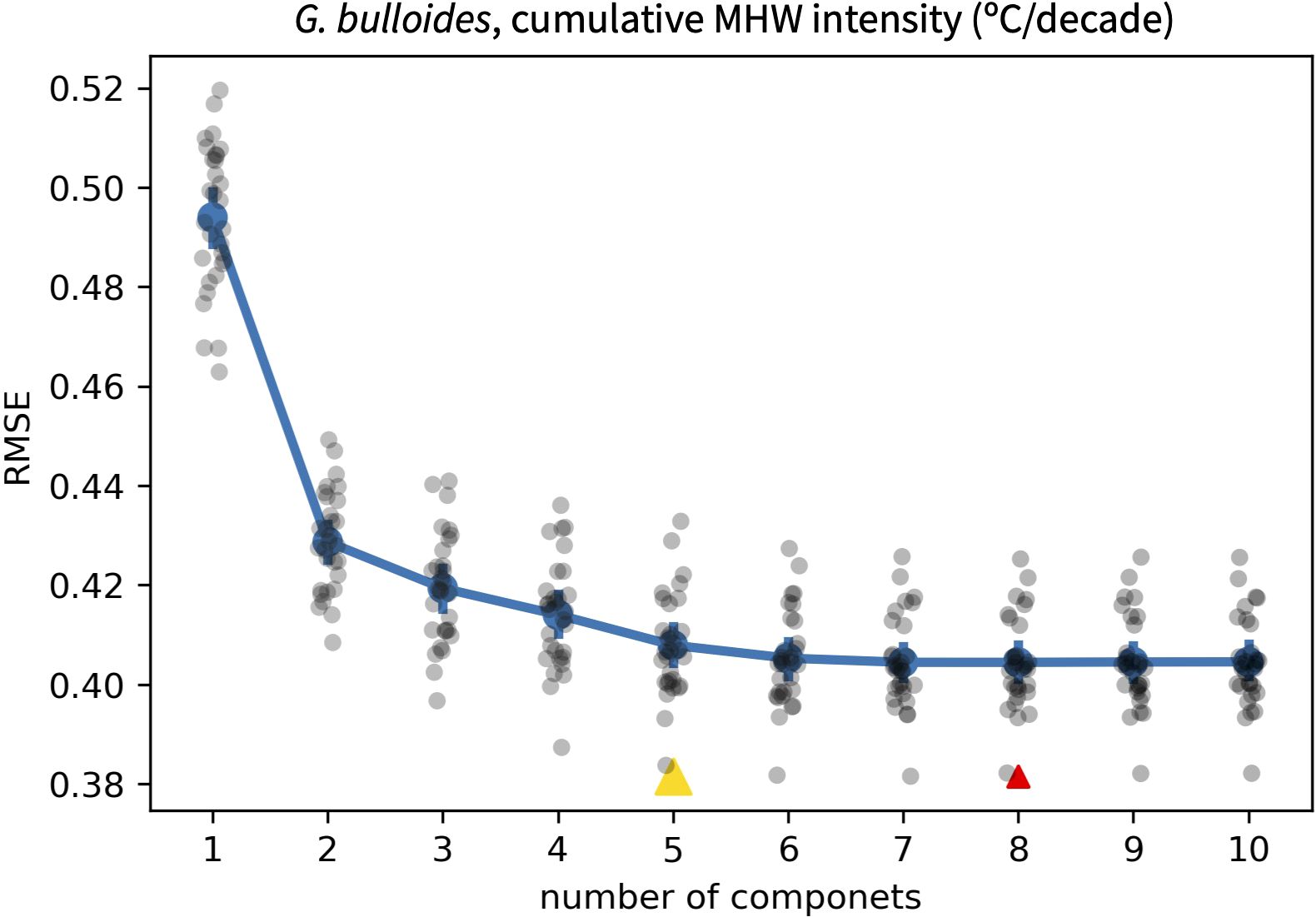
Figure 4. Example of how regression RMSE (RMSE_reg) changes with the number of components included in the partial least squares regression. In this case, the cumulative intensity of MHWs, defined using intensity and duration thresholds of one standard deviation and one month, are related to the statistics of a pseudoproxy SST distribution based on G. bulloides seasonality at DSDP Site 36. While the user is ultimately left to select the number of components to use in a PLSR, the values at which RMSE_reg is at its minimum (red triangle) and ceases to improve by at least 1% (yellow triangle) are provided to inform this choice.

The performance of a transfer function is initially evaluated using its correlation coefficient (r²), the standard deviation of regression residuals (RMSE_reg) and the RMSE relative to observations (RMSE_obs). The latter value is calculated by applying the distribution statistics for ERSSTv5, COBEv2 and HadISST monthly SST data to the LIM-based transfer function and comparing the calculated MHW metric to each record’s true value (Figure 5). This out of sample validation provides an important check on how well a LIM-based transfer function reflects reality. If the user deems a transfer function to be sufficiently promising, the influence of under-sampling can then be evaluated.

Figure 5

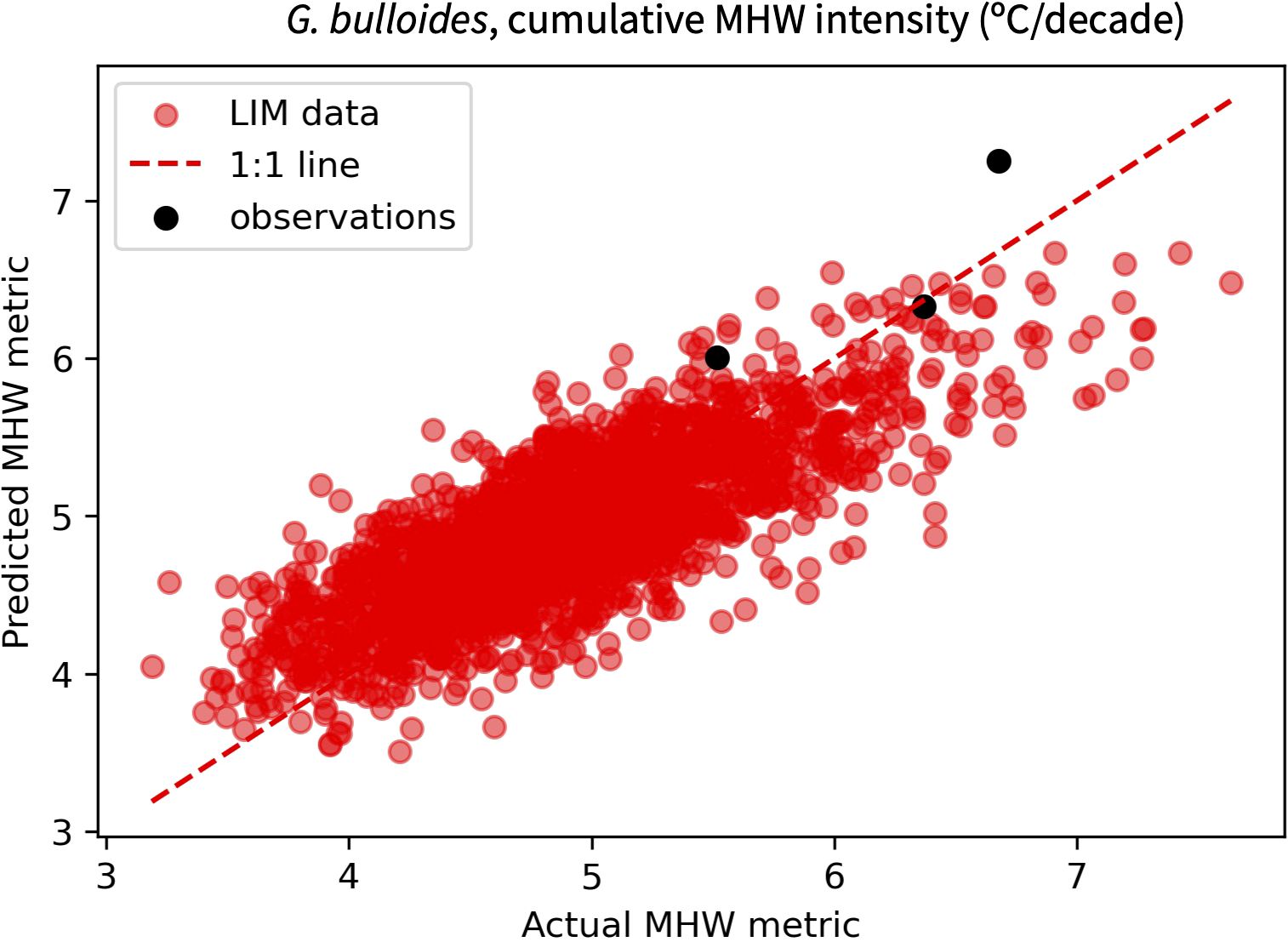
Figure 5. Example comparison of MHW cumulative intensity at DSDP Site 36 predicted from a PLSR-based transfer function versus that observed in the LIM ensemble (red) or observational SST products (black). MHWs are defined using intensity and duration thresholds of one standard deviation and one month and distribution statistics derive from a pseudoproxy SST distribution that is based on G. bulloides seasonality at DSDP Site 36. The consistency with which the LIM-based transfer function estimates independent observations supports the validity of our approach.

In practice, IFA will always under-sample past SST because only tens or hundreds of monthly values will be reconstructed from foraminifera within a sedimentary interval that represents decades to millennia. To evaluate how sensitive transfer functions are to this effect, our approach considers a series of scenarios in which 50 to 800 foraminifera tests are picked from a sedimentary interval. Because the number of foraminifera measured is equivalent to the number of months sampled, the amount of time represented in a sedimentary interval (derived from sedimentation rate) can be used to calculate what fraction of all months will be recorded by a given number of IFA measurements. For example, if 200 foraminifera are measured from a sedimentary interval representing 500 years (equivalent to 6,000 months), 3.3% of all months are sampled. Using a randomly selected ensemble member, we randomly draw the fraction of values equivalent to each number of picked foraminifera. This yields an under-sampled pseudoproxy SST record that mimics what would be generated from IFA in marine sediments. The distribution statistics from the under-sampled, pseudoproxy IFA data are then applied to the transfer function and the resulting reconstructed MHW metric is compared with the true value. This is repeated 500 times to quantify the RMSE associated with sampling each number of foraminifera (RMSE_samp). A fit through a range of possible IFA measurements gives an estimate of RMSE_samp for any number of foraminifera (Figure 6) and is valuable for evaluating what level of accuracy can be expected from a sample prior to geochemical analyses.

Figure 6

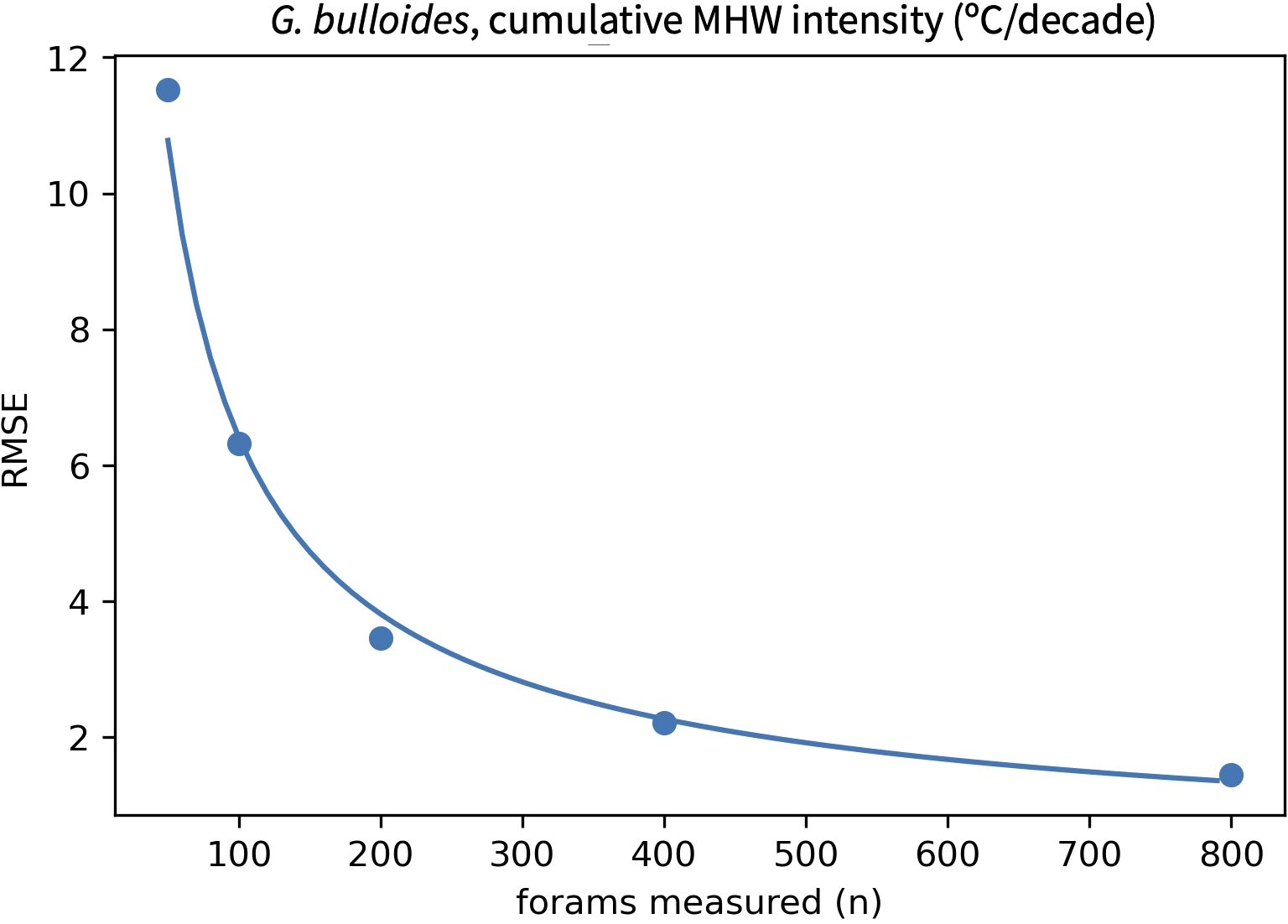
Figure 6. Example result demonstrating how the RMSE of a reconstructed MHW metric will vary with the number of foraminifera measured. Results vary based on the strength of a transfer function’s fit and the sedimentation rate at a site. Here, the transfer function in Figure 5 is applied to scenarios in which 50, 100, 200, 400 or 800 G. bulloides are measured at DSDP site 36. This suggests that the cumulative intensity of MHWs at this site would be reconstructed with an error of approximately ±6°C/decade if 100 G. bulloides were measured. A fit through the five points allows RMSE_samp to be calculated for any number of foraminifera, which in this case is: ln(RMSE_samp) = 5.385 - 0.753 * ln(n forams).

A disadvantage of PLSR is that the transformation of distribution statistics into new orthogonal variables can complicate the interpretation of regression coefficients in terms of actual physical properties. Our algorithm produces two resources that give some insight into how distribution statistics vary with changes in a MHW metric. The first gives the loadings for each distribution statistic and component (Figure 7A). Larger loadings indicate that a particular distribution statistic has a greater influence on a given component, while loadings of the same sign indicate which distribution statistics covary in the same direction. The second resource presents the difference in distribution statistics between ensemble members with the highest and lowest 10% of a MHW metric (Figure 7B). This allows the user to see which distribution statistics change the most between extreme values of MHW metrics.

Figure 7

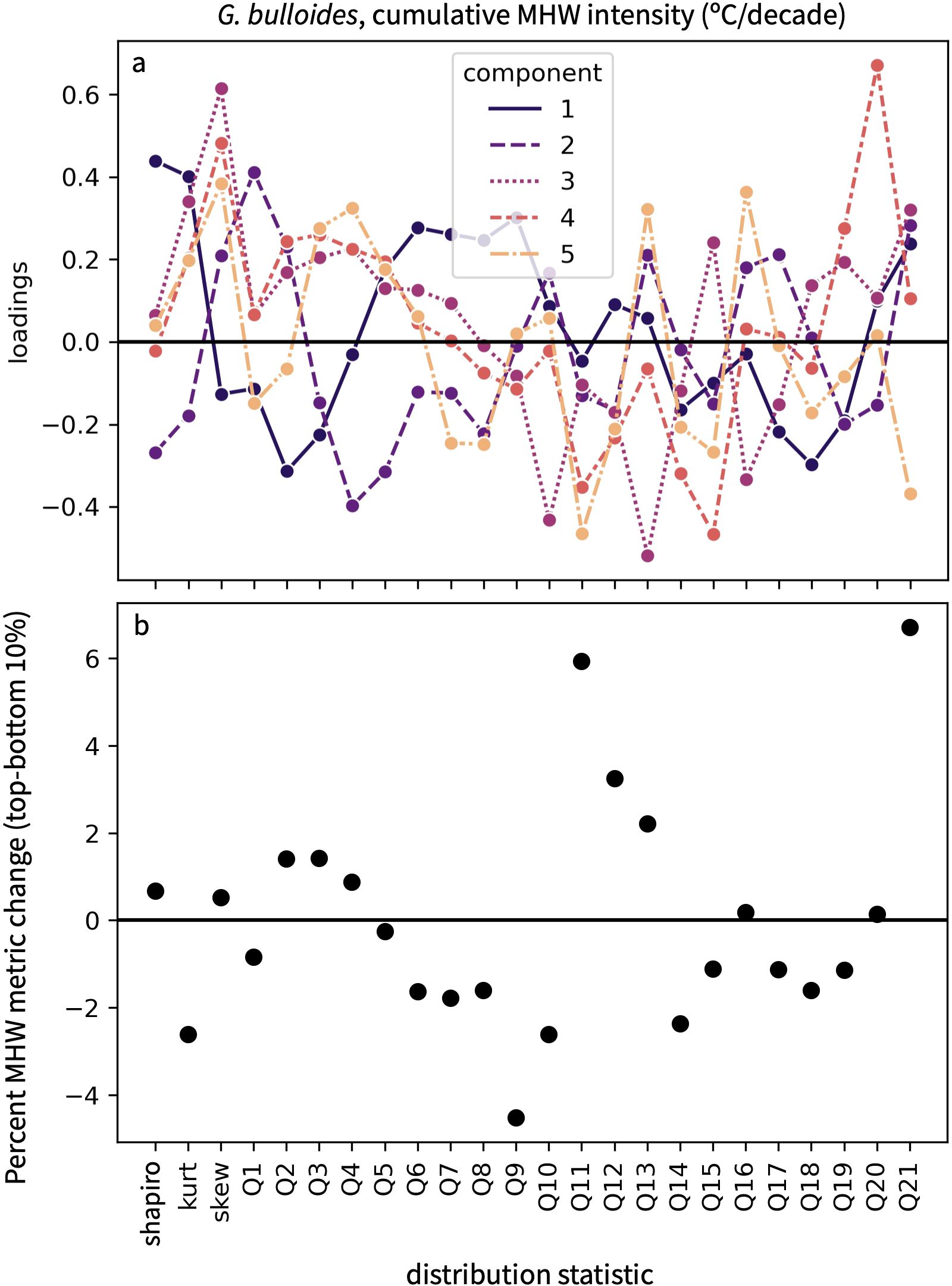
Figure 7. Information to aid in the physical interpretation of a transfer function (A) The loadings on each component of the PLSR allow the user to visualize how distribution statistics vary relative to one another. (B) The percent difference in each distribution statistic between the LIM ensemble members with the highest and lowest 10% of a MHW metric. This example uses the regression from Figure 5 to plot the difference between LIM ensemble members at DSDP Site 36 with the highest and lowest cumulative intensities.

2.7 Example application at northeast Pacific sites

To demonstrate a potential application of our method we apply it at 12 northeast Pacific locations (Figure 8; Table 1) with the goal of identifying sites where IFA-based SST distributions have the greatest potential to reconstruct paleo-MHW variability. We consider a domain from about 40-60°N and 130-160°W that approximates the area influenced by the 2014-2016 “Blob” MHW (Bond et al., 2015). Of the 12 sites, seven locations (noted with site numbers from the Deep Sea Drilling Program or Ocean Drilling Program (ODP)) represent sediment cores that have been recovered, while the remaining five locations (labeled A-E) represent locations at which cores could potentially be collected in the future. These five sites are exemplary, and selected only to fill gaps in the spatial distribution of existing cores without considering the type or thickness of sediment at specific coordinates. Sedimentation rates at each site are taken from previously published age models when possible, and estimated from adjacent cores (Costa et al., 2024) when such data is unavailable (Table 1).

Figure 8

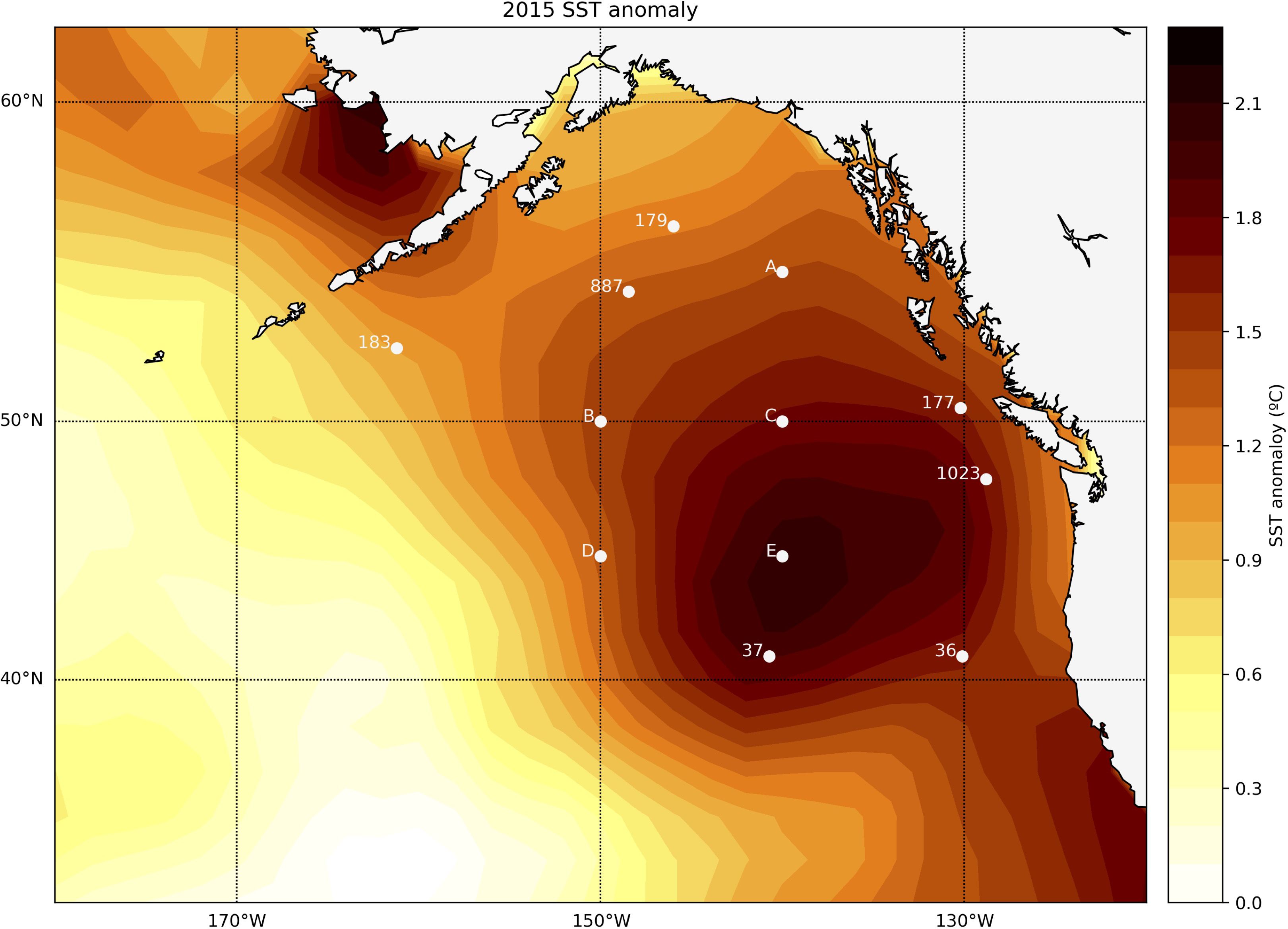
Figure 8. Locations of the northeast Pacific sites considered in this study relative to the 2015 SST anomaly associated with the “Blob” MHW. Numeric values represent the locations of existing DSDP and ODP marine sediment cores. Letters represent hypothetical locations at which cores could be collected within the geographic range of the 2015 MHW event.

At each site we consider a series of MHW definitions that include duration thresholds of 1, 2 and 4 months and intensity thresholds of 1 or 2 standard deviations. We model the seasonal abundance of G. bulloides and N. incompta since they are common in the modern northeast Pacific (Ortiz and Mix, 1992; Sautter and Thunell, 1989; Taylor et al., 2018) and in sediment cores (Davies et al., 2011; Praetorius et al., 2015; Taylor et al., 2014). We consistently select the number of components included in the PLSR based on the value at which RMSE ceases to improve by at least 1% (section 2.6; Figure 4). We perform additional evaluation of under-sampling only when a transfer function’s correlation coefficient exceeds 0.5. This value is selected somewhat arbitrarily to increase efficiency by not considering the influence of under-sampling for transfer functions with seemingly little promise. Other users may make alternative decisions. When under-sampling is evaluated, we use our best-estimates of sedimentation rate at each site (Table 1) and assume a 1 cm sampling interval. In total we evaluate 60 potential transfer functions at each of the 12 sites to identify which MHW metrics, based on which MHW definitions, are mostly likely to be reconstructed by which foraminifera species at each location.

2.8 Stable isotope analyses of individual G. bulloides

To demonstrate how a transfer function may be applied to actual IFA data to reconstruct paleo-MHWs we also measured δ¹⁸O in individual G. bulloides from core-top (0-1 cm) sediments at DSDP Site 36. Core-top sediments are commonly assumed to approximate recent oceanographic conditions, and have been widely used to calibrate and validate paleoceanographic proxies (Quintana Krupinski et al., 2017; Rongstad et al., 2020; Saenger and Evans, 2019; Tierney et al., 2019). Core-top sediments were first wet sieved at 63 μm and dried. All G. bulloides were then picked from the 150-250 μm and >250 μm size fractions. Forty-five individuals from the larger size fraction were briefly sonicated in water and methanol before being transferred to Kiel device vials. δ¹⁸O was measured at the Oregon State University Stable Isotope Laboratory using a Thermo-Fisher Kiel IV carbonate device coupled to a custom Thermo-Fisher MAT253+ isotope ratio mass spectrometer that has been optimized to analyze small volumes of carbon dioxide. For example, each ion beam has a factor of ~3 greater than stock amplification for m/z 44, 45, and 46, and a modified pressure-adjust routine that minimizes sample versus standard pressure imbalances in small samples. This roughly doubles the instrument’s signal to noise ratio at low beam intensities (typically near 1000 mV with the greater amplification; Supplementary Table S3), at the cost of a slight increase in nonlinearity with sample size. Modifications prevent running high mass samples without saturating the detectors, or requiring expansions, which can be problematic with such small amounts of CO₂ gas. Loading small volumes of reference gas reproducibly can also be a challenge, and requires extra analyses of carbonate standards for the purpose of isotope calibration relative to Vienna Pee Dee Belemnite (VPDB). In this study, small (up to 0.1 to 0.2 permil) linear corrections were made for source nonlinearity as a function of major beam intensity. Specifically, 8-9 analyses of an in-house standard (Wiley Marble) within each run were used to constrain linear relationships for raw δ¹⁸O and δ¹³C versus m/z 44, and then used to correct source nonlinearity in all other analyses from that run using their measured m/z 44 intensity. An additional small correction for reference gas depletion during each run was applied based on trends in the same Wiley Marble standards versus analysis time. This gas depletion correction has since been eliminated by increasing the size of the reference gas reservoir. The weights of the individual shells were calculated from the relationship between initial gas pressures (the Kiel VM1 gauge) and measured weights of standards ranging from about 3 to 17 μg, measured on a Sartorius SE2 ultramicrobalance (Supplementary Table S3). The uncertainty in the calcite weight associated with each shell analysis estimated from initial gas pressures is about 1 μg. Comparing measured to calculated mass for standards in this study yields a RMSE of 2 μg (Supplementary Table S3). Multiple analyses of NBS19 bracketed samples to evaluate precision and normalized data to the VPDB scale.

3 Results

The primary result of this work is the methodology described above, which identifies and quantifies robust transfer functions between pseudoproxy IFA-based SST distributions and MHW metrics. However, our application of it in the northeast Pacific provides an important example of the information it generates, how those results might be used, and the characteristics of sites with the greatest potential to reconstruct MHWs.

3.1 Locations and characteristics of the best transfer functions

Transfer function correlation coefficients vary significantly depending on site, MHW metric and MHW definition. The best fits occur at proposed locations B and C in the central part of the domain (50°N, 140-150°W) where r² values can exceed 0.8 (Figure 9A). Robust transfer functions with r² >0.7 are still found at many other locations including ODP Site 887, DSDP Site 183, ODP Site 1023 and proposed location E, but sites further south and west (e.g. DSDP Site 37 and proposed location D) have weaker best fits with maximum r² values below 0.6. Best fits consistently come from transfer functions that target the cumulative intensity of MHWs, while transfer functions that target other MHW metrics rarely have correlation coefficients above 0.5 (Figure 9B). Fits are typically best when MHWs are defined based on a duration of one month, but the decline in r² values for duration thresholds of two and four months is modest (Figure 9C). Fits are also highest when MHWs are defined using an intensity threshold of one standard deviation, but often decrease considerably when the threshold is changed to two standard deviations (Figure 9D). In comparison, differences between species are minor and transfer functions based on G. bulloides are often similar to those based on N. incompta without evidence for once species consistently outperforming the other.

Figure 9

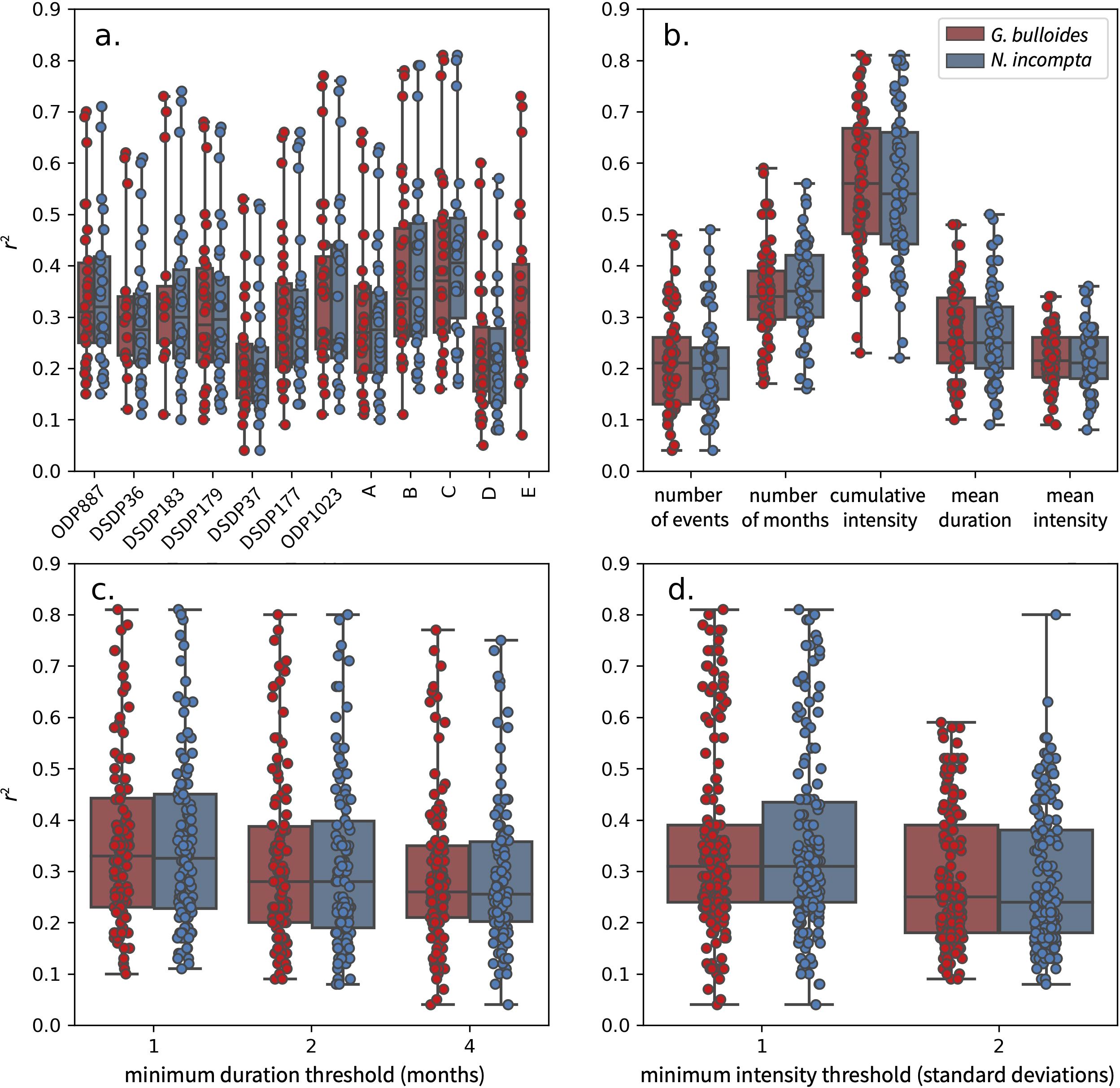
Figure 9. Summary of correlation coefficients for all 720 transfer functions considered. (A) differences between transfer functions based on G. bulloides (red) and N. incompta (blue) at the 12 northeast Pacific sites (B) differences between transfer functions targeting each of the five MHW metrics (C) differences between transfer functions for each of the three duration thresholds considered when defining MHWs (D) differences between transfer functions for the two intensity thresholds considered when defining MHWs.

However, high correlation coefficients do not guarantee a transfer function can accurately reconstruct MHWs. While our evaluation of under-sampling does show that RMSE_samp decreases in transfer functions with higher r² values (Figure 10A), sedimentation rate appears to be a more important control on accuracy (Figure 10B). For example, a transfer function that targets the cumulative intensity of short duration, low intensity MHWs using G. bulloides at proposed location C has a very high correlation coefficient of 0.81, but applying this transfer function to a SST distribution based on 200 foraminifera would reconstruct MHW cumulative intensity with an error of ±351% due to the location’s low sedimentation rate of 0.14 cm/kyr. In contrast, applying transfer functions with weaker fits (r² 0.66-0.71) to SST distributions based on 200 foraminifera at sites with higher sedimentation rates of ~7 cm/kyr (i.e. ODP Site 887, DSDP Site 179) would reconstruct MHW cumulative intensity with an error of only about ±45% (Figure 10B).

Figure 10

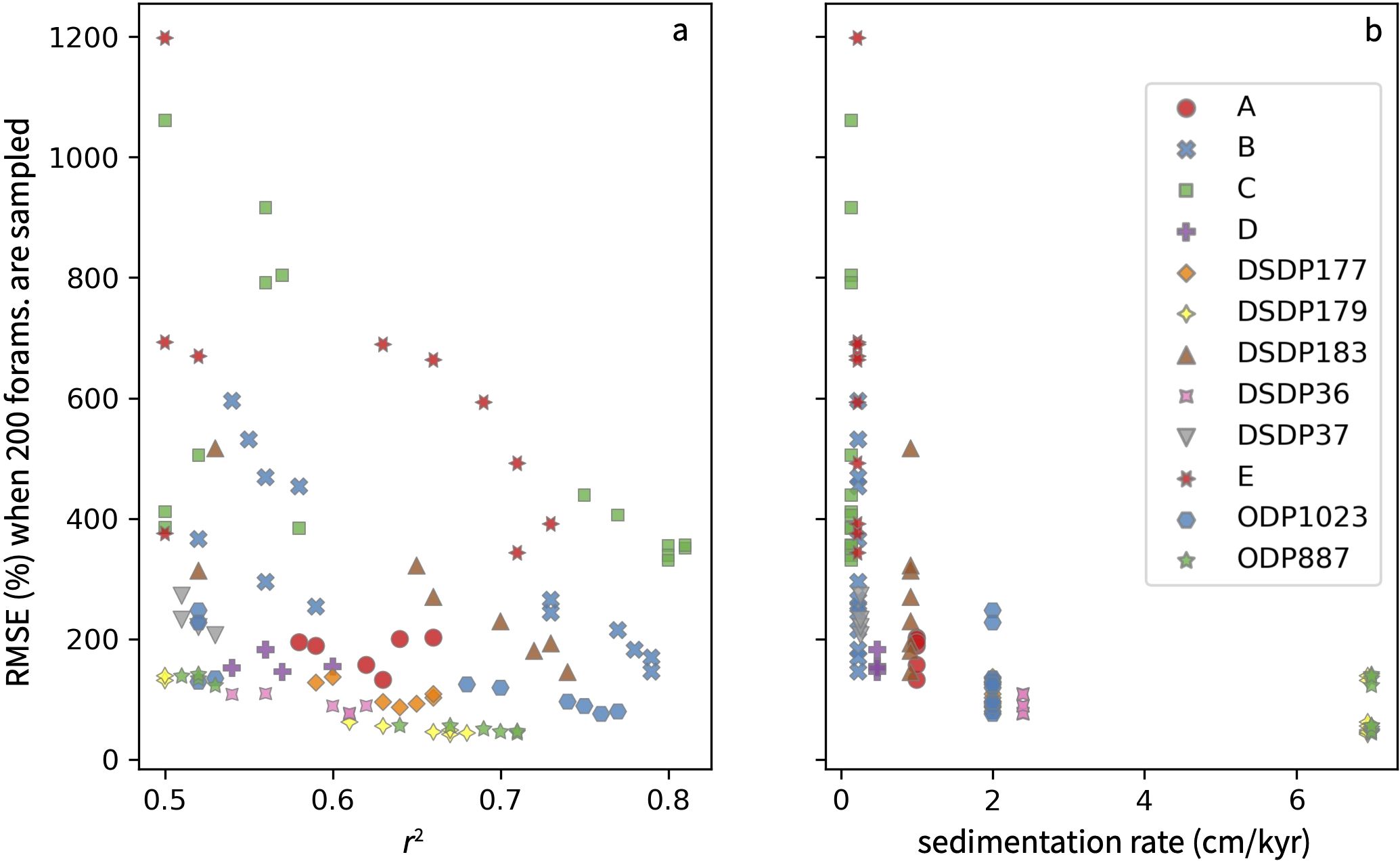
Figure 10. The RMSE expected for MHW reconstructions when only 200 foraminifera are measured. (A) versus the correlation coefficient of the transfer function and (B) versus the sedimentation rate of each site. The lowest RMSE values occur at the highest sedimentation rates, not the highest correlation coefficients. RMSE is expressed as a percent of the LIM ensemble mean to accommodate the differing units of MHW metrics. Under-sampling was only evaluated in transfer functions with a r² > 0.5.

3.2 Individual G. bulloides stable isotopes

Of the 45 individual foraminifera analyzed from site DSDP Site 36, 37 were large enough (calcite weight 3-15 μg) for the dual inlet pressure adjustment required for high precision analysis (Supplementary Table S3). External precision was 0.03‰ and 0.09‰ for NBS19 δ¹³C and δ¹⁸O, respectively (1σ, n = 6) and 0.02‰ and 0.07‰ for in-house standard Wiley Marble (1σ, n = 13). Average δ¹⁸O internal precision for standards with masses >3 μg was 0.05‰ (0.03‰ for masses 10-15 μg, 0.04‰ for 6-10 μg, and 0.07‰ for 3-6 μg). Average δ¹⁸O for all G. bulloides was 1.84 ± 0.78‰ with a total range of 0.39 - 3.15‰. While G. bulloides with masses of 3-6 μg had a somewhat higher mean δ¹⁸O of 2.1 ± 0.76 (n=14) than those with masses of 6-10 μg (δ¹⁸O = 1.66 ± 0.71; n=11) and 10-15 μg (δ¹⁸O = 1.69 ± 0.83; n=12), the slope of -0.06‰/μg observed for all data was not significant (p = 0.06) and we treated the data as a single population. The standard deviation of the individual shell data is a factor of 20 greater than internal precision, and a factor of 10 greater than external analytical precision, so the variability in foraminiferal data can reliably be interpreted to reflect the environment of their habitat. The distribution of proxy data is shown in Figure 11 and complete distribution statistics are given in Supplementary Table S4, acknowledging that the relatively small number of foraminifera analyzed may not accurately capture the true underlying distribution.

Figure 11

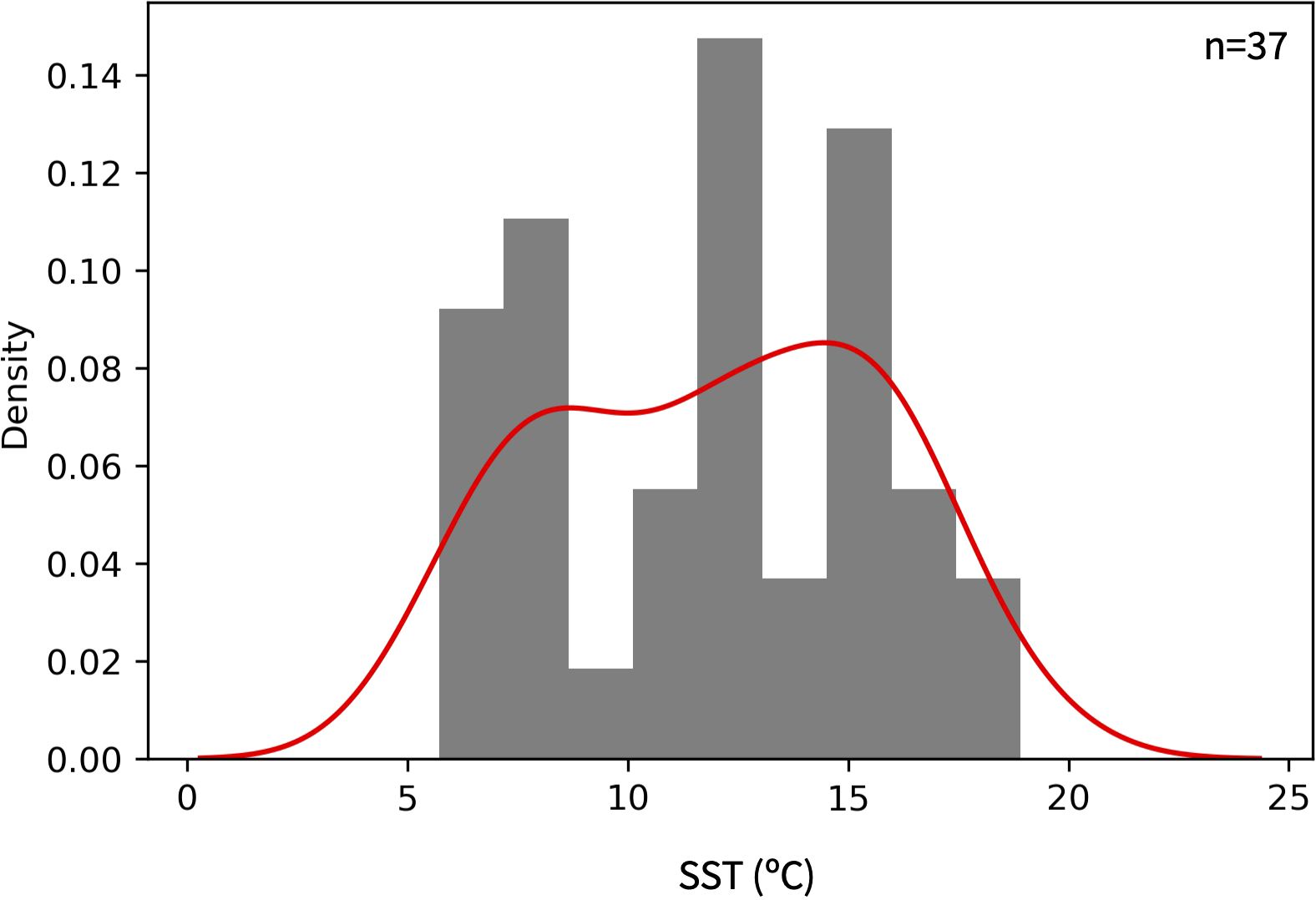
Figure 11. Histogram of SST estimates based on the δ¹⁸O of 37 individual G. bulloides (grey) and the kernel density estimation of the population (red). Oxygen isotopic values were converted to temperature using the calibration of Bemis et al. (1998). The Shapiro-Wilk statistic, kurtosis and skewness of the distribution are 0.95, -1.18 and -0.075, respectively. Complete statistics are given in Supplementary Table S4.

We applied these IFA-based distribution statistics to a transfer function that predicts the cumulative intensity of MHWs at DSDP Site 36. The transfer function accounts for the seasonal ecology of G. bulloides, and defines MHWs using intensity and duration thresholds of one standard deviation and one month, respectively. Applying a transfer function that defines MHWs using a two month duration threshold yielded similar results (not shown). IFA-based distribution statistics calculated a cumulative intensity of 10.63°C/decade in core-top sediments, which is appreciably higher than values of 6.68°C/decade, 6.37°C/decade and 5.52°C/decade in ERSSTv5, COBEv2 and HadISST data, respectively. However, because only 37 individuals are measured, the influence of under-sampling is severe and we calculate the error on reconstructed cumulative intensity to be ±14.38°C/decade.

4 Discussion

This study provides a framework for developing transfer functions that can reconstruct past MHW variability from IFA paleotemperature distributions. Our systematic application of this approach at a series of northeast Pacific sites suggests that promising transfer functions can be generated from multiple species in most regions, and that the cumulative intensity of short duration, low intensity MHWs is the metric that can be reconstructed with the greatest skill. It is not immediately clear why transfer functions that target cumulative intensity consistently outperform others, but we speculate that it may relate to the metric’s reliance on both duration and intensity. That is, variations in MHW duration or intensity alone may cause only modest changes to a SST distribution, while their combined influence in the cumulative intensity metric may be larger and more detectable. Similarly, we speculate that using duration and intensity thresholds of one month and one standard deviation, respectively, to define MHWs yields stronger transfer functions because of the greater number of these low intensity, short duration events within each LIM ensemble member. A thorough evaluation of the mechanisms responsible for these observations and the degree to which they occur outside the north Pacific domain is left for future work.

In contrast, the relationship between transfer function skill and sedimentation rate is more straightforward. One centimeter of marine sediment in the central gyres can typically reflect many thousand years of time for sedimentation rates <0.25 cm/kyr (Table 1). Transfer function correlation coefficients at proposed location C are the highest of any location we consider, but one centimeter of sediment corresponds to about 7,000 years, or equivalently, 84,000 months. In this case, 200 foraminifera only represent about 0.25% of all months, leading to a severely under-sampled SST distribution and MHW reconstructions with errors exceeding ±350% (Figure 10B). Despite a higher sedimentation rate at DSDP Site 36, the influence of under-sampling on the individual foraminifera δ¹⁸O data we generate is similar. Our 37 analyses represent only about 0.75% of the approximately 5000 months recorded by a centimeter of sediment at the site, making it unlikely that the resulting SST distribution (Figure 11) is representative of the larger population. While it is possible to generate a cumulative intensity estimate from these 37 analyses, the error on this value is too large to compare to observed modern values in a meaningful way. It is regrettable that our δ¹⁸O data was generated in parallel with the development of our method, and we therefore missed an opportunity to evaluate how the relative paucity of G. bulloides at DSDP Site 36 would impact the accuracy of MHW reconstructions. Fortunately, similar situations should be avoidable in the future by using our method to calculate the expected accuracy of a MHW reconstruction prior to conducting geochemical analyses.

Given the sensitivity of our method to sedimentation rate, it is not surprising that the most accurate MHW reconstructions occur at ODP Site 887 and DSDP Site 179 where sedimentation rates are ~7 cm/kyr. At these locations, one centimeter of sediment reflects about 150 years, or 1800 months, and measuring 200 foraminifera would represent about 11% of all months. In these cases, the SST distribution is less dramatically under-sampled and RMSE_samp decreases to about ±45%. While obviously an improvement, it seems likely that errors of this magnitude would still limit the practical application of our approach to only major shifts in MHW behavior.

The best path to reducing uncertainty in MHW reconstructions when applying our approach is to minimize the degree of under-sampling, which can be achieved in two ways. First, more foraminifera can be measured to increase the fraction of all months sampled. For example, we calculate that the error on MHW cumulative intensity reconstructed from N. incompta at DSDP Site 179 can be reduced from ±42% when 200 foraminifera are sampled to ±21% when 800 are sampled. These sample sizes may seem unreasonably large given that IFA studies typically measure only 50-100 individuals (Ford et al., 2015; Koutavas et al., 2006; Rongstad et al., 2020; Rustic et al., 2020). However, previous studies have not rigorously evaluated the sensitivity of their results to under-sampling and may have similar sample requirements. The likelihood that large sample requirements will be necessary to address many hypotheses will favor analytical approaches that achieve high throughput measurements of geochemical proxies without significantly sacrificing analytical precision. Even with analytical advances, the degree to which errors can be reduced by increasing sample sizes will ultimately be determined by the number of foraminifera present in a sample, and it may not always be possible to achieve a desired level of skill simply by making more measurements.

A second way to decrease the errors caused by under-sampling is to reduce the number of months recorded in a sampling interval by targeting high sedimentation rate sites. Continental margins sites, such as those in the Gulf of Alaska (Walczak et al., 2020) or the Santa Barbara Basin (Hendy et al., 2002), can have sedimentation rates in excess of 100 cm/kyr and minimal bioturbation, which allow a 1 cm sample to achieve near decadal resolution. Application of our method at these locations shows strong transfer functions similar to other north Pacific sites (not shown), and can reconstruct MHW cumulative intensity with an error below ±20% when 100 foraminifera are sampled, and below ±15% when 200 are analyzed. In comparison to reducing errors by increasing sample sizes, targeting high sedimentation rate sites has the advantage of improving accuracy while also minimizing analytical time and expense. These variables are obviously not exclusive however, and sites with both high sedimentation rates and abundant foraminifera are currently the best candidates for applying our method to generate paleo-MHW reconstructions.

Such reconstructions have the potential to significantly expand upon existing paleo-MHW research, which, to our knowledge, consists only of a single study of bi-monthly to annual coral data in western Australia (Zinke et al., 2015). Evidence that foraminifera assemblages vary with MHWs on short timescales (Lane et al., 2023) is an important result, but it will be difficult to attribute assemblage changes to past MHW variability as opposed to changes in the mean state. Additionally, it is not yet clear if changes in assemblages primarily reflect a response to MHW duration, frequency, intensity or some combination of these metrics. On the other hand, our transfer functions target specific MHW metrics in a quantitative way that facilitates statistical analyses and comparisons to independent model simulations. While we highlight a northeast Pacific application, the framework we describe can be applied to other foraminifera species in other ocean domains to significantly advance knowledge of spatiotemporal MHW variability.

Despite promise, the accuracy with which MHWs can be reconstructed using our approach relies on a number of assumptions that should be carefully considered when interpreting results. In many cases these same assumptions also apply to traditional foraminifera-based reconstructions and are an inherent complication of paleoceanography. For example, changes in the seasonality of G. bulloides or N. incompta growth have the potential to alter mean SST reconstructions (Jonkers and Kučera, 2015), but would also likely change paleotemperature distributions independently of MHW behavior. Applying our transfer functions in the distant past would therefore require demonstrating that seasonality had not changed significantly, or generating new transfer functions with alternate modeled seasonalities that account for any changes. These alternate seasonalities could be generated for modern species by rerunning foraminifera ecology models (Fraile et al., 2008; Kretschmer et al., 2018; Moore et al., 2001) under the boundary conditions of past climates, but may be challenging for extinct species.

It may also be important that PLAFOM2.0 (Kretschmer et al., 2018) calculates seasonal trends in foraminifera concentrations, which could differ from trends in calcification. The rate of planktic foraminifera chamber formation and calcification is known to vary throughout their life (de Nooijer et al., 2014; Lea et al., 1995; Ter Kuile and Erez, 1984), causing geochemical proxies such as Mg/Ca or δ¹⁸O to vary with shell size (Elderfield et al., 2002). To minimize this effect, paleoceanographic reconstructions typically target foraminifer tests within narrow size fractions. However, seasonal biases can also differ between size fractions (Jonkers et al., 2013; Thunell et al., 1983) and aren’t accounted for by PLAFOM2.0. This could cause the true seasonal bias of actual IFA data to differ from that modeled in IFA pseudoproxies when only narrow size fractions are considered. While additional work is necessary to characterize the scope of this potential complication, solutions seem possible if it proves to be a concern. For example, seasonal biases of specific size fractions could be incorporated into proxy system models like PLAFOM2.0 or shell size could be added as an independent variable when predicting paleotemperatures, thereby allowing all foraminifera to be measured regardless of size fraction.

It is also plausible that the seasonal distributions generated by PLAFOAM2.0 (Kretschmer et al., 2018) do not account for ecological responses that are unique to MHWs. For example, stratification during a MHW could isolate foraminifera from the nutrient-rich subsurface, possibly ending their growing season and ability to record MHWs if they could not alter their habitat depth. While this possibility will ultimately have to be evaluated on a case by case basis, the best data available to evaluate it in the north Pacific is the 4-year sediment trap study of Sautter and Thunell (1989). These data overlap with multiple MHWs, with the initial 2 years being characterized by a long duration, low intensity MHW associated with the 1982/83 El Niño, and a shorter duration MHW occurring during the winter of 1984-85. During this interval G. bulloides exhibited a seasonal flux from March-July, while N. incompta was most abundant from August-November. Both trends agree with the modeled distributions of Kretschmer et al. (2018), but are inconsistent with the possibility that the growing season of either species ends abruptly with the onset of a MHW. Support for this comes from the observation that G. bulloides were found in Santa Barbara Basin sediment traps throughout the 2014-2016 “Blob” MHW (Cherry et al., 2023), although these organisms may be a distinct genotype from those in more subpolar environments and therefore may respond to MHWs differently. Additional monitoring of how foraminifera assemblages and abundance change across a range of MHW intensities and durations (e.g. Lane et al., 2023) is certainly warranted since available data are limited, but current knowledge suggests that G. bulloides and N. incompta remain present and with similar seasonality during many MHWs.

If future work should demonstrate that certain species exhibit ecological biases that make them unsuitable for MHW reconstructions, it is encouraging that our method predicts robust transfer functions across multiple species. The framework we describe accommodates five different foraminifera species, and will allow reconstructions to target only the species whose ecology is minimally impacted by MHWs. Alternatively, if multiple species are found to have uncorrelated ecological biases, it may be advantageous to generate multiple independent MHW reconstructions from different species in the same sedimentary interval. These reconstructions could then be combined to maximize their mutual MHW information and minimize species-specific effects.

Moving forward, our approach could be improved by further refining our proxy system model, which could consider bioturbation more realistically. When calculating the fraction of months sampled by a given number of IFA measurements, we currently assume that sedimentation rate is the only variable determining the amount of time represented by one centimeter of sediment. While this assumption may be valid at sites with anoxic bottom waters void of benthic organisms, bioturbation could significantly increase the amount of time represented in a sedimentary interval because of mixing over depths of 10 or more centimeters (Dolman et al., 2021). Fortunately, tools exist to rigorously evaluate bioturbation in sedimentary archives (Dolman and Laepple, 2018) and can be incorporated into future versions of our algorithm.

Species specific paleotemperature calibrations will not be a major concern as long as they are linear, which is often true for δ¹⁸O (Bemis et al., 1998; Mulitza et al., 2003). In these cases, transformations do not change the distribution statistics between raw geochemical data and reconstructed temperature. The same is not true for exponential paleotemperature calibrations (Anand et al., 2003; Lea et al., 1999; Saenger and Evans, 2019), and Mg/Ca data would need to be transformed to temperature to apply our transfer functions. In either case, changes in the δ¹⁸O or Mg/Ca of seawater between time intervals would not influence distributions as long as these values remained relatively constant within each IFA time interval.

Finally, we stress that any paleo-MHW reconstructions based on our approach should be interpreted only in the context within which they are calibrated. Reconstructed MHWs will follow the definition in Section 2.3, and will not necessarily reflect trends based on the daily definitions commonly used when studying modern MHWs. Furthermore, changes in one metric should not be assumed to be representative of other metrics or MHW definitions. That is, a reconstructed increase in MHW cumulative intensity should not be taken to mean there were also increases in the number or duration of events. Similarly, a transfer function based on short duration, low intensity MHWs should not be used to suggest changes in higher intensity or longer duration events. While there are undoubtedly other ways to generate transfer functions between IFA distributions and MHW metrics, reconstructions from this study should only be interpreted for the region, metric and definition for which they are calibrated and validated.

5 Conclusions

We describe a framework to evaluate how well SST distributions can predict MHW metrics, with the goal of generating transfer functions that can be applied to monthly paleotemperature distributions derived from IFA. Results reveal that the cumulative intensity of short duration, low intensity MHWs is the most promising target for reconstruction, and can likely be calculated with an error of less than 15% at continental margin sites with sedimentation rates in excess of 100 cm/kyr. Our approach is a major advance in the nascent field of paleo-MHW research that allows specific MHW metrics and their uncertainty to be quantified from individual foraminifera in marine sediments. While we present an example application from the northeast Pacific, our approach is valid in other ocean domains and for other foraminifera species. Application of our method in broader contexts therefore has considerable potential to advance knowledge surrounding the spatiotemporal variability of MHWs prior to the observational era. Future paleo-MHW reconstructions will provide valuable context for interpreting modern trends as well as out-of-sample validation targets for climate models, both of which should help improve forecasts of MHW behavior on decadal-centennial timescales.

Data availability statement

The datasets presented in this study can be found online at https://github.com/caseysaengerWWU/mhw_calibration.

Author contributions

CS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. CJ-D: Investigation, Writing – review & editing. AG: Funding acquisition, Writing – review & editing. AM: Investigation, Methodology, Writing – review & editing. AR: Methodology, Writing – review & editing. TX: Writing – original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. We thank the National Science Foundation Division of Ocean Sciences for funding this work through Marine Geology and Geophysics award 2202543 to CS, AG and CJ-D. AM also acknowledges support from Oregon State University, and from NSF Marine Geology and Geophysics awards 1850083 and 2149564.

Acknowledgments

We thank Jennifer Fehrenbacher for valuable discussion of foraminifera ecology and Mike Evans and Andy Bunn for insight regarding regression techniques. We also acknowledge the support of Jennifer McKay for her oversight of OSU’s Stable Isotope Laboratory. We thank Johan Schijf and Edmund Hathorne for editorial oversight, the reviewers named on the cover page for thoughtful feedback and additional comments from reviewers.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1321254/full#supplementary-material

References

Alexander M. A., Matrosova L., Penland C., Scott J. D., Chang P. (2008). Forecasting pacific SSTs: linear inverse model predictions of the PDO. J. Clim. 21, 385–402. doi: 10.1175/2007JCLI1849.1

Crossref Full Text | Google Scholar

Amaya D. J., Jacox M. G., Fewings M. R., Saba V. S., Stuecker M. F., Rykaczewski R. R., et al. (2023). Marine heatwaves need clear definitions so coastal communities can adapt. Nature 616, 29–32. doi: 10.1038/d41586-023-00924-2

PubMed Abstract | Crossref Full Text | Google Scholar

Anand P., Elderfield H., Conte M. H. (2003). Calibration of Mg/Ca thermometry in planktonic foraminifera from a sediment trap time series. Paleoceanography 18. doi: 10.1029/2002PA000846

Crossref Full Text | Google Scholar

Ault T. R., Deser C., Newman M., Emile-Geay J. (2013). Characterizing decadal to centennial variability in the equatorial Pacific during the last millennium. Geophys. Res. Lett. 40, 3450–3456. doi: 10.1002/grl.50647

Crossref Full Text | Google Scholar

Barkhordarian A., Nielsen D. M., Baehr J. (2022). Recent marine heatwaves in the North Pacific warming pool can be attributed to rising atmospheric levels of greenhouse gases. Commun. Earth Environ. 3, 1–12. doi: 10.1038/s43247-022-00461-2

Crossref Full Text | Google Scholar

Bemis B. E., Spero H. J., Bijma J., Lea D. W. (1998). Reevaluation of the oxygen isotopic composition of planktonic foraminifera: Experimental results and revised paleotemperature equations. Paleoceanography 13, 150–160. doi: 10.1029/98PA00070

Crossref Full Text | Google Scholar

Bond N. A., Cronin M. F., Freeland H., Mantua N. (2015). Causes and impacts of the 2014 warm anomaly in the NE Pacific. Geophys. Res. Lett. 42, 3414–3420. doi: 10.1002/2015GL063306

Crossref Full Text | Google Scholar

Brennan P. R., Bhattacharya T., Feng R., Tierney J. E., Jorgensen E. M. (2022). Patterns and mechanisms of northeast pacific temperature response to pliocene boundary conditions. Paleoceanogr. Paleoclimatology 37, e2021PA004370. doi: 10.1029/2021PA004370

Crossref Full Text | Google Scholar

Burke K. D., Williams J. W., Chandler M. A., Haywood A. M., Lunt D. J., Otto-Bliesner B. L. (2018). Pliocene and Eocene provide best analogs for near-future climates. Proc. Natl. Acad. Sci. 115, 13288–13293. doi: 10.1073/pnas.1809600115

Crossref Full Text | Google Scholar

Capotondi A., Newman M., Xu T., Di Lorenzo E. (2022). An optimal precursor of northeast pacific marine heatwaves and central pacific el niño events. Geophys. Res. Lett. 49, e2021GL097350. doi: 10.1029/2021GL097350

Crossref Full Text | Google Scholar

Cavole L. M., Demko A. M., Diner R. E., Giddings A., Koester I. (2016). Biological impacts of the 2013–2015 warm-water anomaly in the northeast pacific: winners, losers, and the future. Oceanography 29, 273–285. doi: 10.5670/oceanog.2016.32

Crossref Full Text | Google Scholar

Cherry K., Havard E., Benitez-Nelson C., Tappa E., Davis C. V. (2023). Planktic Foraminiferal Response to the 2014-2015 Marine Heatwave in the Santa Barbara Basin (San Francisco: Presented at the AGU Fall Meeting).

Google Scholar

Cheung W. W. L., Frölicher T. L. (2020). Marine heatwaves exacerbate climate change impacts for fisheries in the northeast Pacific. Sci. Rep. 10, 6678. doi: 10.1038/s41598-020-63650-z

PubMed Abstract | Crossref Full Text | Google Scholar

Costa K. M., Pavia F. J., Piecuch C. G., McManus J. F., Weinstein G. A. (2024). Pelagic sedimentation rates in the North Pacific using Thorium-230 depth profiling. Geochim. Cosmochim. Acta 369, 126–140. doi: 10.1016/j.gca.2023.11.020

Crossref Full Text | Google Scholar

Davies M. H., Mix A. C., Stoner J. S., Addison J. A., Jaeger J., Finney B., et al. (2011). The deglacial transition on the southeastern Alaska Margin: Meltwater input, sea level rise, marine productivity, and sedimentary anoxia. Paleoceanography 26. doi: 10.1029/2010PA002051

Crossref Full Text | Google Scholar

Dee S. G., Steiger N. J., Emile-Geay J., Hakim G. J. (2016). On the utility of proxy system models for estimating climate states over the common era. J. Adv. Model. Earth Syst. 8, 1164–1179. doi: 10.1002/2016MS000677

Crossref Full Text | Google Scholar

de Nooijer L. J., Spero H. J., Erez J., Bijma J., Reichart G. J. (2014). Biomineralization in perforate foraminifera. Earth-Sci. Rev. 135, 48–58. doi: 10.1016/j.earscirev.2014.03.013

Crossref Full Text | Google Scholar

Di Lorenzo E., Mantua N. (2016). Multi-year persistence of the 2014/15 North Pacific marine heatwave. Nat. Clim. Change 6, 1042–1047. doi: 10.1038/nclimate3082

Crossref Full Text | Google Scholar

Dolman A. M., Groeneveld J., Mollenhauer G., Ho S. L., Laepple T. (2021). Estimating bioturbation from replicated small-sample radiocarbon ages. Paleoceanogr. Paleoclimatology 36, e2020PA004142. doi: 10.1029/2020PA004142

Crossref Full Text | Google Scholar

Dolman A. M., Laepple T. (2018). Sedproxy: a forward model for sediment-archived climate proxies. Clim. Past 14, 1851–1868. doi: 10.5194/cp-14-1851-2018

Crossref Full Text | Google Scholar

Donahue J. G. (1970). “Pleistocene diatoms as climatic indicators in North Pacific sediments,” in Geological Investigations of the North Pacific. Ed. Hays J. D. (Boulder, Colorado: Geological Society of America). doi: 10.1130/MEM126-p121

Crossref Full Text | Google Scholar

Elderfield H., Ganssen G. (2000). Past temperature and δ18O of surface ocean waters inferred from foraminiferal Mg/Ca ratios. Nature 405, 442–445. doi: 10.1038/35013033

PubMed Abstract | Crossref Full Text | Google Scholar

Elderfield H., Vautravers M., Cooper M. (2002). The relationship between shell size and Mg/Ca, Sr/Ca, δ18O, and δ13C of species of planktonic foraminifera. Geochem. Geophys. Geosystems 3, 1–13. doi: 10.1029/2001GC000194

Crossref Full Text | Google Scholar

Emiliani C. (1955). Pleistocene temperatures. J. Geol. 63, 538–578. doi: 10.1086/626295

Crossref Full Text | Google Scholar

Erez J., Almogi-Labin A., Avraham S. (1991). On the life history of planktonic foraminifera: lunar reproduction cycle in globigerinoides sacculifer (Brady). Paleoceanography 6, 295–306. doi: 10.1029/90PA02731

Crossref Full Text | Google Scholar

Evans M. N., Tolwinski-Ward S. E., Thompson D. M., Anchukaitis K. J. (2013). Applications of proxy system modeling in high resolution paleoclimatology. Quat. Sci. Rev. 76, 16–28. doi: 10.1016/j.quascirev.2013.05.024

Crossref Full Text | Google Scholar

Eyring V., Bony S., Meehl G. A., Senior C. A., Stevens B., Stouffer R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016

Crossref Full Text | Google Scholar

Ford H. L., McChesney C. L., Hertzberg J. E., McManus J. F. (2018). A deep eastern equatorial pacific thermocline during the last glacial maximum. Geophys. Res. Lett. 45, 11,806–11,816. doi: 10.1029/2018GL079710

Crossref Full Text | Google Scholar

Ford H. L., Ravelo A. C., Polissar P. J. (2015). Reduced el niño–southern oscillation during the last glacial maximum. Science 347, 255–258. doi: 10.1126/science.1258437

PubMed Abstract | Crossref Full Text | Google Scholar

Fraile I., Schulz M., Mulitza S., Kucera M. (2008). Predicting the global distribution of planktonic foraminifera using a dynamic ecosystem model. Biogeosciences 5, 891–911. doi: 10.5194/bg-5-891-2008

Crossref Full Text | Google Scholar

Free C. M., Anderson S. C., Hellmers E. A., Muhling B. A., Navarro M. O., Richerson K., et al. (2023). Impact of the 2014–2016 marine heatwave on US and Canada West Coast fisheries: Surprises and lessons from key case studies. Fish Fish. 24, 652–674. doi: 10.1111/faf.12753

Crossref Full Text | Google Scholar

Frölicher T. L., Fischer E. M., Gruber N. (2018). Marine heatwaves under global warming. Nature 560, 360–364. doi: 10.1038/s41586-018-0383-9

PubMed Abstract | Crossref Full Text | Google Scholar

Galbraith E. D., Jaccard S. L., Pedersen T. F., Sigman D. M., Haug G. H., Cook M., et al. (2007). Carbon dioxide release from the North Pacific abyss during the last deglaciation. Nature 449, 890–893. doi: 10.1038/nature06227

PubMed Abstract | Crossref Full Text | Google Scholar

Gray W. R., Weldeab S., Lea D. W., Rosenthal Y., Gruber N., Donner B., et al. (2018). The effects of temperature, salinity, and the carbonate system on Mg/Ca in Globigerinoides ruber (white): A global sediment trap calibration. Earth Planet. Sci. Lett. 482, 607–620. doi: 10.1016/j.epsl.2017.11.026

Crossref Full Text | Google Scholar

Groeneveld J., Ho S. L., Mackensen A., Mohtadi M., Laepple T. (2019). Deciphering the variability in mg/ca and stable oxygen isotopes of individual foraminifera. Paleoceanogr. Paleoclimatology 34, 755–773. doi: 10.1029/2018PA003533

Crossref Full Text | Google Scholar

Hasselmann K. (1976). Stochastic climate models Part I. Theory. Tellus 28, 473–485. doi: 10.1111/j.2153-3490.1976.tb00696.x

Crossref Full Text | Google Scholar

Hendy I. L., Kennett J. P., Roark E. B., Ingram B. L. (2002). Apparent synchroneity of submillennial scale climate events between Greenland and Santa Barbara Basin, California from 30–10ka. Quat. Sci. Rev. 21, 1167–1184. doi: 10.1016/S0277-3791(01)00138-X

Crossref Full Text | Google Scholar

Hirahara S., Ishii M., Fukuda Y. (2014). Centennial-scale sea surface temperature analysis and its uncertainty. J. Clim. 27, 57–75. doi: 10.1175/JCLI-D-12-00837.1

Crossref Full Text | Google Scholar

Hirsch A. L., Ridder N. N., Perkins-Kirkpatrick S. E., Ukkola A. (2021). CMIP6 multiModel evaluation of present-day heatwave attributes. Geophys. Res. Lett. 48, e2021GL095161. doi: 10.1029/2021GL095161

Crossref Full Text | Google Scholar

Hobday A. J., Alexander L. V., Perkins S. E., Smale D. A., Straub S. C., Oliver E. C. J., et al. (2016). A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 141, 227–238. doi: 10.1016/j.pocean.2015.12.014

Crossref Full Text | Google Scholar

Holbrook N. J., Scannell H. A., Sen Gupta A., Benthuysen J. A., Feng M., Oliver E. C. J., et al. (2019). A global assessment of marine heatwaves and their drivers. Nat. Commun. 10, 2624. doi: 10.1038/s41467-019-10206-z

PubMed Abstract | Crossref Full Text | Google Scholar

Holbrook N. J., Sen Gupta A., Oliver E. C. J., Hobday A. J., Benthuysen J. A., Scannell H. A., et al. (2020). Keeping pace with marine heatwaves. Nat. Rev. Earth Environ. 1, 482–493. doi: 10.1038/s43017-020-0068-4

Crossref Full Text | Google Scholar

Huang B., Thorne P. W., Banzon V. F., Boyer T., Chepurin G., Lawrimore J. H., et al. (2017). NOAA extended reconstructed sea surface temperature (ERSST), version 5. doi: 10.7289/V5T72FNM

Crossref Full Text | Google Scholar

Huang K.-F., You C.-F., Lin H.-L., Shieh Y.-T. (2008). In situ calibration of Mg/Ca ratio in planktonic foraminiferal shell using time series sediment trap: A case study of intense dissolution artifact in the South China Sea. Geochem. Geophys. Geosystems 9. Available at: https://psl.noaa.gov/data/gridded/data.noaa.ersst.v5.html.

Google Scholar

Hurrell J. W., Holland M. M., Gent P. R., Ghan S., Kay J. E., Kushner P. J., et al. (2013). The community earth system model: A framework for collaborative research. Bull. Am. Meteorol. Soc 94, 1339–1360. doi: 10.1175/BAMS-D-12-00121.1

Crossref Full Text | Google Scholar

Jacox M. G., Alexander M. A., Amaya D., Becker E., Bograd S. J., Brodie S., et al. (2022). Global seasonal forecasts of marine heatwaves. Nature 604, 486–490. doi: 10.1038/s41586-022-04573-9

PubMed Abstract | Crossref Full Text | Google Scholar

Jaeger J. M., Gulick S. P. S., LeVay L. J., Asahi H., Bahlburg H., Belanger C. L., et al. (2014). Proceedings of the Integrated Ocean Drilling Program Vol. 341: Expedition reports Southern Alaska margin (Technical Report) (College Station, Texas: Integrated Ocean Drilling Program).

Google Scholar

Jones T., Parrish J. K., Peterson W. T., Bjorkstedt E. P., Bond N. A., Ballance L. T., et al. (2018). Massive mortality of a planktivorous seabird in response to a marine heatwave. Geophys. Res. Lett. 45, 3193–3202. doi: 10.1002/2017GL076164

Crossref Full Text | Google Scholar

Jonkers L., Brummer G.-J. A., Peeters F. J. C., Van Aken H. M., De Jong M. F. (2010). Seasonal stratification, shell flux, and oxygen isotope dynamics of left-coiling N. pachyderma and T. quinqueloba in the western subpolar North Atlantic: Sseasonal foraminiferal fluxes and δ¹⁸ O. Paleoceanography 25. doi: 10.1029/2009PA001849

Crossref Full Text | Google Scholar

Jonkers L., Kučera M. (2015). Global analysis of seasonality in the shell flux of extant planktonic Foraminifera. Biogeosciences 12, 2207–2226. doi: 10.5194/bg-12-2207-2015

Crossref Full Text | Google Scholar

Jonkers L., Reynolds C. E., Richey J., Hall I. R. (2015). Lunar periodicity in the shell flux of planktonic foraminifera in the Gulf of Mexico. Biogeosciences 12, 3061–3070. doi: 10.5194/bg-12-3061-2015

Crossref Full Text | Google Scholar

Jonkers L., Van Heuven S., Zahn R., Peeters F. J. C. (2013). Seasonal patterns of shell flux, δ ¹⁸ O and δ ¹³ C of small and large N. pachyderma (s) and G. bulloides in the subpolar North Atlantic. Paleoceanography 28, 164–174. doi: 10.1002/palo.20018

Crossref Full Text | Google Scholar

Kemnitz N., Hammond D. E., Henderson P., Le Roy E., Charette M., Moore W., et al. (2023). Actinium and radium fluxes from the seabed in the northeast Pacific Basin. Mar. Chem. 250, 104180. doi: 10.1016/j.marchem.2022.104180

Crossref Full Text | Google Scholar

Khider D., Stott L. D., Emile-Geay J., Thunell R., Hammond D. E. (2011). Assessing El Niño Southern Oscillation variability during the past millennium. Paleoceanography 26. doi: 10.1029/2011PA002139

Crossref Full Text | Google Scholar

Koutavas A., deMenocal P. B., Olive G. C., Lynch-Stieglitz J. (2006). Mid-Holocene El Niño–Southern Oscillation (ENSO) attenuation revealed by individual foraminifera in eastern tropical Pacific sediments. Geology 34, 993–996. doi: 10.1130/G22810A.1

Crossref Full Text | Google Scholar

Koutavas A., Joanides S. (2012). El niño–southern oscillation extrema in the holocene and last glacial maximum. Paleoceanography 27. doi: 10.1029/2012PA002378

Crossref Full Text | Google Scholar

Kretschmer K., Jonkers L., Kucera M., Schulz M. (2018). Modeling seasonal and vertical habitats of planktonic foraminifera on a global scale. Biogeosciences 15, 4405–4429. doi: 10.5194/bg-15-4405-2018

Crossref Full Text | Google Scholar

Lane M. K., Fehrenbacher J. S., Fisher J. L., Fewings M. R., Crump B. C., Risien C. M., et al. (2023). Planktonic foraminiferal assemblages reflect warming during two recent mid-latitude marine heatwaves. Front. Mar. Sci. 10. doi: 10.3389/fmars.2023.1155761

Crossref Full Text | Google Scholar

Laufkötter C., Zscheischler J., Frölicher T. L. (2020). High-impact marine heatwaves attributable to human-induced global warming. Science 369, 1621–1625. doi: 10.1126/science.aba0690

PubMed Abstract | Crossref Full Text | Google Scholar

Lea D. W., Martin P. A., Chan D. A., Spero H. J. (1995). Calcium uptake and calcification rate in the planktonic foraminifer Orbulina universa. J. Foraminifer. Res. 25, 14–23. doi: 10.2113/gsjfr.25.1.14

Crossref Full Text | Google Scholar

Lea D. W., Mashiotta T. A., Spero H. J. (1999). Controls on magnesium and strontium uptake in planktonic foraminifera determined by live culturing. Geochim. Cosmochim. Acta 63, 2369–2379. doi: 10.1016/S0016-7037(99)00197-0

Crossref Full Text | Google Scholar

Lea D. W., Pak D. K., Spero H. J. (2000). Climate impact of late quaternary equatorial pacific sea surface temperature variations. Science 289, 1719–1724. doi: 10.1126/science.289.5485.1719

PubMed Abstract | Crossref Full Text | Google Scholar

Leduc G., Vidal L., Cartapanis O., Bard E. (2009). Modes of eastern equatorial Pacific thermocline variability: Implications for ENSO dynamics over the last glacial period. Paleoceanography 24. doi: 10.1029/2008PA001701

Crossref Full Text | Google Scholar

Leggat W. P., Camp E. F., Suggett D. J., Heron S. F., Fordyce A. J., Gardner S., et al. (2019). Rapid coral decay is associated with marine heatwave mortality events on reefs. Curr. Biol. 29, 2723–2730.e4. doi: 10.1016/j.cub.2019.06.077

PubMed Abstract | Crossref Full Text | Google Scholar

Malevich S. B., Vetter L., Tierney J. E. (2019). Global core top calibration of δ18O in planktic foraminifera to sea surface temperature. Paleoceanogr. Paleoclimatology 34, 1292–1315. doi: 10.1029/2019PA003576

Crossref Full Text | Google Scholar

Mann M. E., Rutherford S. (2002). Climate reconstruction using ‘Pseudoproxies.’. Geophys. Res. Lett. 29. doi: 10.1029/2001GL014554

Crossref Full Text | Google Scholar

McCabe R. M., Hickey B. M., Kudela R. M., Lefebvre K. A., Adams N. G., Bill B. D., et al. (2016). An unprecedented coastwide toxic algal bloom linked to anomalous ocean conditions. Geophys. Res. Lett. 43, 10,366–10,376. doi: 10.1002/2016GL070023

Crossref Full Text | Google Scholar

McManus D. A., Burns R. E., Weser O., Valuer T., von der Borch C. V., Olsson R. K., et al. (1970). “Initial reports of the deep sea drilling project, 5,” in Initial Reports of the Deep Sea Drilling Project (Washington DC: U.S. Government Printing Office). doi: 10.2973/dsdp.proc.5.1970

Crossref Full Text | Google Scholar

Mehmood T., Liland K. H., Snipen L., Sæbø S. (2012). A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 118, 62–69. doi: 10.1016/j.chemolab.2012.07.010

Crossref Full Text | Google Scholar

Moore J. K., Doney S. C., Kleypas J. A., Glover D. M., Fung I. Y. (2001). An intermediate complexity marine ecosystem model for the global domain. Deep Sea Res. Part II Top. Stud. Oceanogr. 49, 403–462. doi: 10.1016/S0967-0645(01)00108-4

Crossref Full Text | Google Scholar

Mulitza S., Boltovskoy D., Donner B., Meggers H., Paul A., Wefer G. (2003). Temperature:δ18O relationships of planktonic foraminifera collected from surface waters. Palaeogeogr. Palaeoclimatol. Palaeoecol. 202, 143–152. doi: 10.1016/S0031-0182(03)00633-3

Crossref Full Text | Google Scholar

Newman M., Alexander M. A., Scott J. D. (2011). An empirical model of tropical ocean dynamics. Clim. Dyn. 37, 1823–1841. doi: 10.1007/s00382-011-1034-0

Crossref Full Text | Google Scholar

Oliver E. C. J., Benthuysen J. A., Darmaraki S., Donat M. G., Hobday A. J., Holbrook N. J., et al. (2021). Marine heatwaves. Annu. Rev. Mar. Sci. 13, 313–342. doi: 10.1146/annurev-marine-032720-095144

Crossref Full Text | Google Scholar

Oliver E. C. J., Burrows M. T., Donat M. G., Sen Gupta A., Alexander L. V., Perkins-Kirkpatrick S. E., et al. (2019). Projected marine heatwaves in the 21st century and the potential for ecological impact. Front. Mar. Sci. 6. doi: 10.3389/fmars.2019.00734

Crossref Full Text | Google Scholar

Oliver E. C. J., Donat M. G., Burrows M. T., Moore P. J., Smale D. A., Alexander L. V., et al. (2018). Longer and more frequent marine heatwaves over the past century. Nat. Commun. 9, 1324. doi: 10.1038/s41467-018-03732-9

PubMed Abstract | Crossref Full Text | Google Scholar

Opdyke N. D., Foster J. H. (1970). “Paleomagnetism of cores from the North Pacific,” in Geological Investigations of the North Pacific. Ed. Hays J. D. (Boulder, Colorado: Geological Society of America). doi: 10.1130/MEM126-p83

Crossref Full Text | Google Scholar

Ortiz J. D., Mix A. C. (1992). The spatial distribution and seasonal succession of planktonic foraminifera in the California Current off Oregon, September 1987 – September 1988. Geol. Soc Lond. Spec. Publ. 64, 197–213. doi: 10.1144/GSL.SP.1992.064.01.13

Crossref Full Text | Google Scholar

Ortiz J. D., Mix A. C., Collier R. W. (1995). Environmental control of living symbiotic and asymbiotic foraminifera of the California Current. Paleoceanography 10, 987–1009. doi: 10.1029/95PA02088

Crossref Full Text | Google Scholar

Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., et al. (2011). Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830. doi: 10.5555/1953048.2078195

Crossref Full Text | Google Scholar

Penland C., Matrosova L. (1994). A balance condition for stochastic numerical models with application to the El Niño-Southern Oscillation. J. Clim. 7, 1352–1372. doi: 10.1175/1520-0442(1994)007<1352:ABCFSN>2.0.CO;2

Crossref Full Text | Google Scholar

Penland C., Sardeshmukh P. D. (1995). The optimal growth of tropical sea surface temperature anomalies. J. Clim. 8, 1999–2024. doi: 10.1175/1520-0442(1995)008<1999:TOGOTS>2.0.CO;2

Crossref Full Text | Google Scholar

Plecha S. M., Soares P. M. M., Silva-Fernandes S. M., Cabos W. (2021). On the uncertainty of future projections of Marine Heatwave events in the North Atlantic Ocean. Clim. Dyn. 56, 2027–2056. doi: 10.1007/s00382-020-05529-3

Crossref Full Text | Google Scholar

Praetorius S. K., Mix A. C., Walczak M. H., Wolhowe M. D., Addison J. A., Prahl F. G. (2015). North Pacific deglacial hypoxic events linked to abrupt ocean warming. Nature 527, 362–366. doi: 10.1038/nature15753

PubMed Abstract | Crossref Full Text | Google Scholar

Quintana Krupinski N. B., Russell A. D., Pak D. K., Paytan A. (2017). Core-top calibration of B/Ca in Pacific Ocean Neogloboquadrina incompta and Globigerina bulloides as a surface water carbonate system proxy. Earth Planet. Sci. Lett. 466, 139–151. doi: 10.1016/j.epsl.2017.03.007

Crossref Full Text | Google Scholar

Rayner N. A., Parker D. E., Horton E. B., Folland C. K., Alexander L. V., Rowell D. P., et al. (2003). Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmospheres 108, 2002JD002670. doi: 10.1029/2002JD002670

Crossref Full Text | Google Scholar

Rea D. K. (1994). The paleoclimatic record provided by eolian deposition in the deep sea: The geologic history of wind. Rev. Geophys. 32, 159–195. doi: 10.1029/93RG03257

Crossref Full Text | Google Scholar

Rogers-Bennett L., Catton C. A. (2019). Marine heat wave and multiple stressors tip bull kelp forest to sea urchin barrens. Sci. Rep. 9, 15050. doi: 10.1038/s41598-019-51114-y

PubMed Abstract | Crossref Full Text | Google Scholar

Rongstad B. L., Marchitto T. M., Serrato Marks G., Koutavas A., Mekik F., Ravelo A. C. (2020). Investigating ENSO-related temperature variability in equatorial pacific core-tops using mg/ca in individual planktic foraminifera. Paleoceanogr. Paleoclimatology 35, e2019PA003774. doi: 10.1029/2019PA003774

Crossref Full Text | Google Scholar

Rustic G. T., Polissar P. J., Ravelo A. C., White S. M. (2020). Modulation of late Pleistocene ENSO strength by the tropical Pacific thermocline. Nat. Commun. 11, 5377. doi: 10.1038/s41467-020-19161-6

PubMed Abstract | Crossref Full Text | Google Scholar

Saenger C. P., Evans M. N. (2019). Calibration and validation of environmental controls on planktic foraminifera mg/ca using global core-top data. Paleoceanogr. Paleoclimatology 34, 1249–1270. doi: 10.1029/2018PA003507

Crossref Full Text | Google Scholar

Sautter L. R., Thunell R. C. (1989). Seasonal succession of planktonic foraminifera; results from a four-year time-series sediment trap experiment in the Northeast Pacific. J. Foraminifer. Res. 19, 253–267. doi: 10.2113/gsjfr.19.4.253

Crossref Full Text | Google Scholar

Shapiro S. S., Wilk M. B. (1965). An analysis of variance test for normality (complete samples)†. Biometrika 52, 591–611. doi: 10.1093/biomet/52.3-4.591

Crossref Full Text | Google Scholar

Smith K. E., Burrows M. T., Hobday A. J., King N. G., Moore P. J., Sen Gupta A., et al. (2023). Biological impacts of marine heatwaves. Annu. Rev. Mar. Sci. 15, 119–145. doi: 10.1146/annurev-marine-032122-121437

Crossref Full Text | Google Scholar

Smith K. E., Burrows M. T., Hobday A. J., Sen Gupta A., Moore P. J., Thomsen M., et al. (2021). Socioeconomic impacts of marine heatwaves: Global issues and opportunities. Science 374, eabj3593. doi: 10.1126/science.abj3593

PubMed Abstract | Crossref Full Text | Google Scholar

Smith T. M., Reynolds R. W., Peterson T. C., Lawrimore J. (2008). Improvements to NOAA’s historical merged land–ocean surface temperature analysis, (1880–2006). J. Clim. 21, 2283–2296. doi: 10.1175/2007JCLI2100.1

Crossref Full Text | Google Scholar

Spero H. J. (1998). Life history and stable isotope geochemistry of planktonic foraminifera. Paleontol. Soc Pap. 4, 7–36. doi: 10.1017/S1089332600000383

Crossref Full Text | Google Scholar

Taylor M. A., Hendy I. L., Pak D. K. (2014). Deglacial ocean warming and marine margin retreat of the Cordilleran Ice Sheet in the North Pacific Ocean. Earth Planet. Sci. Lett. 403, 89–98. doi: 10.1016/j.epsl.2014.06.026

Crossref Full Text | Google Scholar

Taylor B. J., Rae J. W. B., Gray W. R., Darling K. F., Burke A., Gersonde R., et al. (2018). Distribution and ecology of planktic foraminifera in the North Pacific: Implications for paleo-reconstructions. Quat. Sci. Rev. 191, 256–274. doi: 10.1016/j.quascirev.2018.05.006

Crossref Full Text | Google Scholar

Taylor K. E., Stouffer R. J., Meehl G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1

Crossref Full Text | Google Scholar

Ter Kuile B., Erez J. (1984). In situ growth rate experiments on the symbiont-bearing foraminifera Amphistegina lobifera and Amphisorus hemprichii. J. Foraminifer. Res. 14, 262–276. doi: 10.2113/gsjfr.14.4.262

Crossref Full Text | Google Scholar

Thirumalai K., DiNezio P. N., Tierney J. E., Puy M., Mohtadi M. (2019). An el niño mode in the glacial Indian Ocean? Paleoceanogr. Paleoclimatology 34, 1316–1327. doi: 10.1029/2019PA003669

Crossref Full Text | Google Scholar

Thunell R. C., Curry W. B., Honjo S. (1983). Seasonal variation in the flux of planktonic foraminifera: time series sediment trap results from the Panama Basin. Earth Planet. Sci. Lett. 64, 44–55. doi: 10.1016/0012-821X(83)90051-1

Crossref Full Text | Google Scholar

Tierney J. E., Malevich S. B., Gray W., Vetter L., Thirumalai K. (2019). Bayesian calibration of the mg/ca paleothermometer in planktic foraminifera. Paleoceanogr. Paleoclimatology 34, 2005–2030. doi: 10.1029/2019PA003744

Crossref Full Text | Google Scholar

Tierney J. E., Poulsen C. J., Montañez I. P., Bhattacharya T., Feng R., Ford H. L., et al. (2020). Past climates inform our future. Science 370, eaay3701. doi: 10.1126/science.aay3701

PubMed Abstract | Crossref Full Text | Google Scholar

Tolderlund D. S., Bé A. W. H., Be A. W. H. (1971). Seasonal distribution of planktonic foraminifera in the Western North Atlantic. Micropaleontology 17, 297. doi: 10.2307/1485143

Crossref Full Text | Google Scholar

von Biela V. R., Arimitsu M. L., Piatt J. F., Heflin B., Schoen S. K., Trowbridge J. L., et al. (2019). Extreme reduction in nutritional value of a key forage fish during the Pacific marine heatwave of 2014-2016. Mar. Ecol. Prog. Ser. 613, 171–182. doi: 10.3354/meps12891

Crossref Full Text | Google Scholar

Walczak M. H., Mix A. C., Cowan E. A., Fallon S., Fifield L. K., Alder J. R., et al. (2020). Phasing of millennial-scale climate variability in the Pacific and Atlantic Oceans. Science 370, 716–720. doi: 10.1126/science.aba7096

PubMed Abstract | Crossref Full Text | Google Scholar

White S. M., Ravelo A. C., Polissar P. J. (2018). Dampened El Niño in the early and mid-holocene due to insolation-forced warming/deepening of the thermocline. Geophys. Res. Lett. 45, 316–326. doi: 10.1002/2017GL075433

Crossref Full Text | Google Scholar

Xu T., Newman M., Capotondi A., Di Lorenzo E. (2021). The continuum of northeast pacific marine heatwaves and their relationship to the tropical pacific. Geophys. Res. Lett. 48, 2020GL090661. doi: 10.1029/2020GL090661

Crossref Full Text | Google Scholar

Xu T., Newman M., Capotondi A., Stevenson S., Di Lorenzo E., Alexander M. A. (2022). An increase in marine heatwaves without significant changes in surface ocean temperature variability. Nat. Commun. 13, 7396. doi: 10.1038/s41467-022-34934-x

PubMed Abstract | Crossref Full Text | Google Scholar

Yao Y., Wang C., Fu Y. (2022). Global marine heatwaves and cold-spells in present climate to future projections. Earths Future 10, e2022EF002787. doi: 10.1029/2022EF002787

Crossref Full Text | Google Scholar

Zinke J., Hoell A., Lough J. M., Feng M., Kuret A. J., Clarke H., et al. (2015). Coral record of southeast Indian Ocean marine heatwaves with intensified Western Pacific temperature gradient. Nat. Commun. 6, 8562. doi: 10.1038/ncomms9562

PubMed Abstract | Crossref Full Text | Google Scholar