Swimming and acoustic calling behavior attributed to Bryde’s whales in the central North Pacific

1 Introduction

Bryde’s whales (Balaenoptera edeni) are a species of baleen whale found primarily in the tropics and subtropics with relatively little known about their ecology. Their migration patterns and population structure are largely unknown. The definition of this species itself is debated with some suggesting that it is a single species and others suggesting that it should be categorized as two species (e.g. Constantine et al., 2018). Much of the current knowledge about Bryde’s whales has been collected in the past 20 years from visual, tagging, and passive acoustic data, all with relatively small sample sizes.

Bryde’s whales make a variety of call types across their geographic range; here we will focus on call types recorded in the Pacific. In the Eastern Tropical Pacific, six call types were described by Oleson et al. (2003) and their nomenclature for the call types has been largely adopted. Heimlich et al. (2005) recorded similar calls to Oleson et al. (2003), also in the Eastern Tropical Pacific, but used descriptive names instead of numerical names. Both Oleson et al. (2003) and Heimlich et al. (2005) observed that the calls were not distributed uniformly throughout the study area and certain calls seemed to be more common in certain areas. In the Gulf of California, three new call types and one previously described call type (Be4) from the Eastern Tropical Pacific have been recorded, with some individuals producing multiple call types (Viloria-Gómora et al., 2015). In the eastern North Pacific in the Southern California Bight, the Be4 call type has also been detected seasonally from August–December over multiple years (Kerosky et al., 2012). Different call types have been recorded in the western North Pacific off Japan and China (Oleson et al., 2003; Wang et al., 2022) and a potential Bryde’s whale pulsed call has been detected in the Mariana Archipelago (Szesciorka et al., 2023). In the western South Pacific, calls similar to Be3 and the low burst tonal described by Oleson et al. (2003) and Heimlich et al. (2005), respectively, were recorded year-round near New Zealand and in the Lau Basin, near Fiji and Tonga (McDonald, 2006; Brodie and Dunn, 2015). Finally, in the central North Pacific, call types similar to the Be3 were recorded and individual calling whales were tracked over the U.S. Navy’s Pacific Missile Range Facility (PMRF) off the coast of Kaua‘i, Hawai‘i (Helble et al., 2016). The call types recorded in the Eastern Tropical Pacific, central North Pacific, and western South Pacific had average inter-call intervals (ICIs) of 0.3–6.3 min, with all but one call type ICI greater than 1 min (Oleson et al., 2003; Heimlich et al., 2005; Brodie and Dunn, 2015; Helble et al., 2016), while those in the western North Pacific had considerably shorter ICIs of 2–17 s (Oleson et al., 2003; Wang et al., 2022). It is unknown if these various call types correspond to different populations of Bryde’s whales or if individual Bryde’s whales produce a variety of call types throughout their range or at different times of the year. The purpose of these call types is also unknown with a lack of information about sex of the vocalizers or behavioral context. While there may be slight differences between the calls recorded in Hawaiian waters and those recorded in other parts of the Pacific, we determined that the calls recorded for this paper are the Be3 call type which has an impulsive broadband start followed by a low-frequency tone or slight downsweep with a duration in the North Pacific of approximately 1.7 s (calls may be longer in the western South Pacific) and a frequency range of about 10–200 Hz with a peak frequency of 25.6–33 Hz (Oleson et al., 2003; McDonald, 2006; Brodie and Dunn, 2015; Helble et al., 2016, and shown in Figure 1). Although there are no corresponding visual sightings with the calls described in this paper, for the remainder of this paper we will be attributing these calls to Bryde's whales due to the similarities of similar verified calls recorded elsewhere.

Figure 1

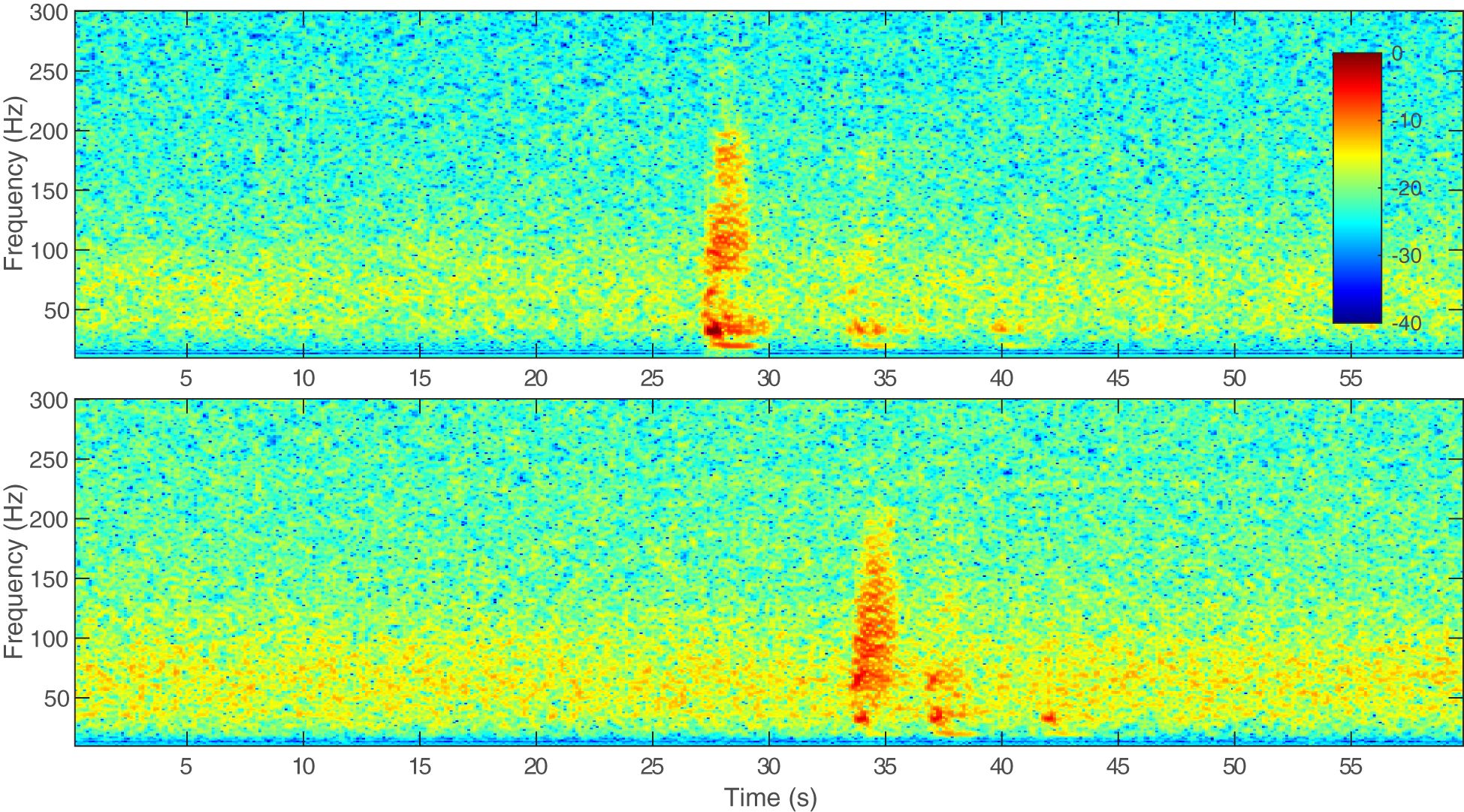
Figure 1 Example spectrograms of the same Bryde’s whale call recorded on a hydrophone nearer to the whale (upper) and a hydrophone farther from the whale (lower), on 25 August 2015. The call was recorded at a 6 kHz sampling rate. A 1,000-point fast Fourier transform (FFT) with a Hanning window and 75% overlap was used to create the spectrogram. Acoustic data were recorded with a high-pass filter at 50 Hz, as evidenced by significant roll-off in the signal. The colorbar indicates relative decibel (dB) levels normalized to the peak frequency of the call in the upper plot. The second and third multipath arrivals can be seen in both spectrograms.

A few studies have provided some insight into Bryde’s whale swimming and diving behavior. Two closely associated individuals were tagged in June 2006 near Portugal (Alves et al., 2009). Most commonly this pair dove to relatively shallow depths (less than 40 m), but they also dove deeper and sometimes lunged on those deeper dives, which were most common within an hour of sunset and during the nighttime hours after midnight (Alves et al., 2009). During the limited tagging period, the average dive duration was 5 min (Alves et al., 2009). In contrast, four Bryde’s whales tagged in New Zealand in August 2011 (austral winter) displayed resting behavior at night with a mostly horizontal body orientation, slower breathing rate, and lower fluking rate, and deeper, highly variable dives during the day (Izadi et al., 2018). In Hawaiian waters in late summer and fall, Bryde’s whales have been tracked using passive acoustic monitoring (PAM) (n=17) and followed with a vessel (n=1) and have been observed swimming at an average velocity of 1.6–2.5 m/s (Smultea et al., 2010; Helble et al., 2016). The Bryde’s whales tracked around Hawai’i have been observed in relatively deep water (∼3000–5000 m) (Smultea et al., 2010; Helble et al., 2016) and those on PMRF swam along very straight paths, primarily towards the west, and often parallel but separated by several kilometers to other vocalizing Bryde’s whales (Helble et al., 2016).

The goal of this study was to expand on the initial work done by Helble et al. (2016) to investigate Bryde’s whale behavior at PMRF over twelve years. The population size of Bryde’s whales in Hawaiian waters between July and December was estimated to be approximately 602 whales in 2017 (Becker et al., 2021), but there have been very few published visual (41 sightings) or acoustic observations (17 PAM tracks) (Helble et al., 2016; Becker et al., 2021). We report both the calling rate and kinematic behavior of vocalizing Bryde’s whales. Calling rate is an important metric for estimating abundance using PAM (e.g. Marques et al., 2009), which is a goal for current marine mammal monitoring efforts as PAM is more cost-effective, more easily automated, can have a longer monitoring duration, and is better for detection of visually cryptic species than visual observations (Fleishman et al., 2023). Baseline (undisturbed) kinematic behavior is critical for understanding if and how anthropogenic activity impacts animals. Here we report Bryde’s whale kinematic behavior and how it changes as a function of a variety of temporal variables (calendar year, day of the year, season, hour of day), an environmental variable (wind speed), and the individual’s calling rate.

2 Methods

2.1 Study area and data description

Acoustic data were collected over 1465 recording days at PMRF off the coast of Kaua‘i, Hawai‘i from January 2011 to December 2022 (Figure 2). The recordings originated from 47 broadband bottom-mounted hydrophones spanning a grid approximately 20 km to the east-west and 58 km to the north-south (Figure 3), with depths ranging from 650 m to 4,700 m. The recording period between January 2011 and July 2017 made use of all 47 hydrophones, while the period from August 2017 to December 2022 used a subset of hydrophones (37 hydrophones until February 2018, then 36 from then on) due to hydrophone outages. Only calls localized within a 1,160 km² study area (white rectangle in Figure 3) were included in this study so that the probability of detection, localization, and tracking of Bryde’s whales remained as consistent as possible through changing noise conditions (Guazzo et al., 2020; Helble et al., 2020b) and hydrophone availability. Full bandwidth data were recorded every month during this recording period (with the exception of February–June 2021) at a 96 kHz sampling rate with 16-bit samples, typically to their maximum duration of 1.9 days. Data were recorded about twice a month as permitted by the range schedule. To increase the monitoring effort while retaining the frequency bands needed for baleen whale detection, additional recordings were made at a 6 kHz sampling rate starting in August 2014. These recordings had a maximum duration of 16.2 days and a mean duration of 2.6 days. When a new recorder was installed in June 2021, the maximum duration of 96 kHz data increased to 5.6 days, precluding the need for the lower sampled data going forward. No recordings during U.S. Navy training activities were included in this analysis, but training could have occurred before or after a recording.

Figure 2

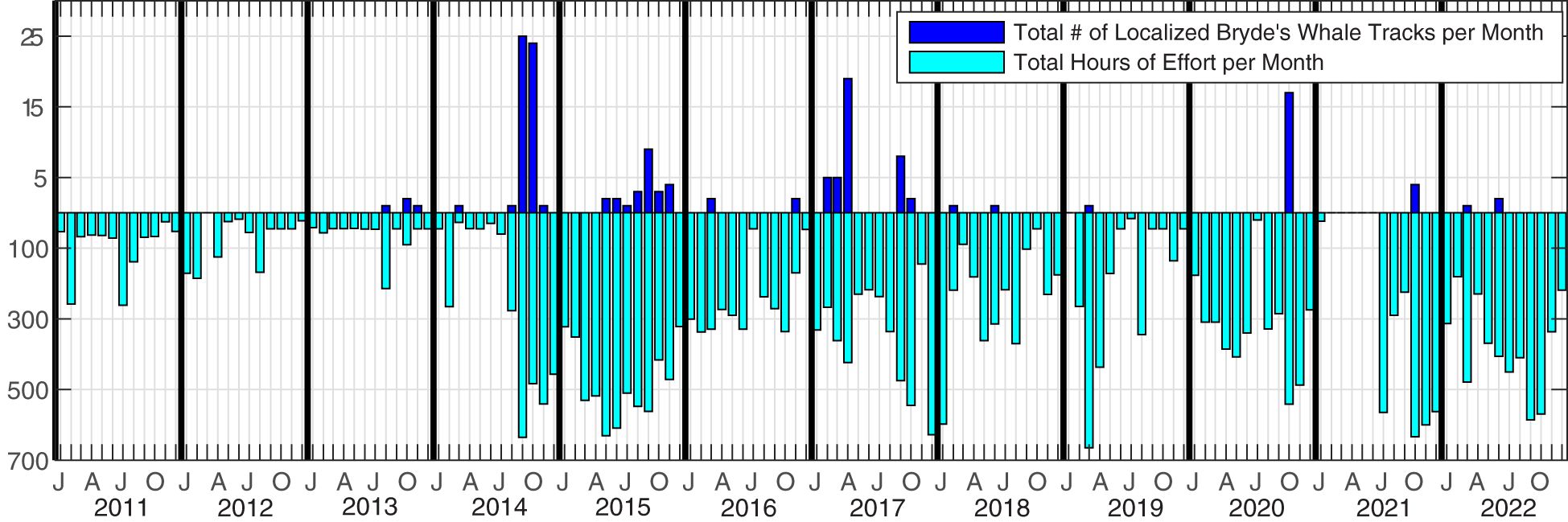
Figure 2 Recording effort in hours per month (light blue) and number of Bryde’s whale tracks per month (dark blue). Tracks were included if at least 12 calls occurred within the study area and met the tracking parameters.

Figure 3

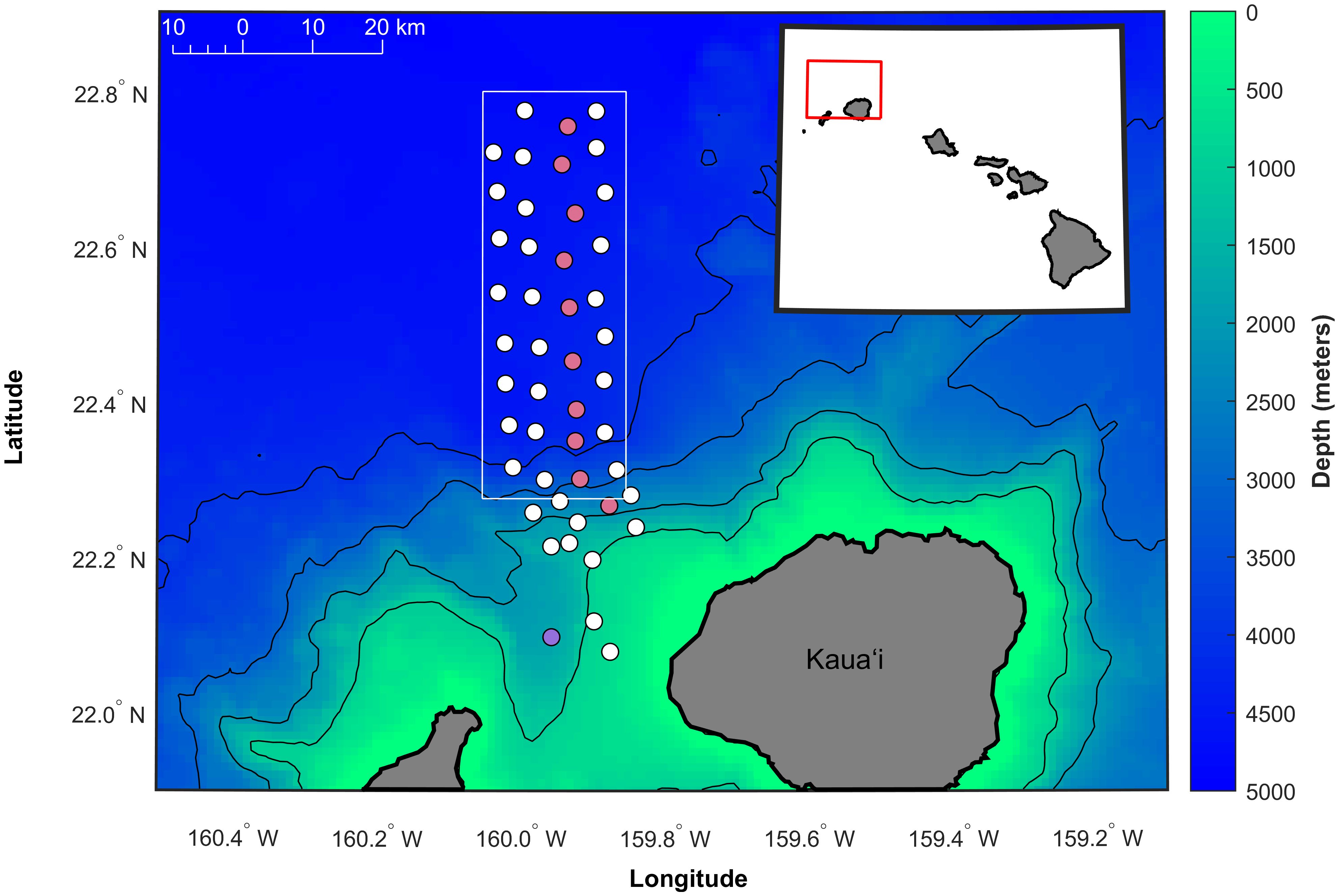
Figure 3 Map of the approximate locations of the 47 hydrophones used in this analysis (circles) at the Pacific Missile Range Facility (PMRF) off Kaua‘i, Hawai‘i, as shown by the red box in the inset map. Two different system outages resulted in a loss of 11 hydrophones (colored pink and purple corresponding to outages in August 2017 and February 2018, respectively). The study area of the array extends approximately 20 km to the east-west and 58 km to the north-south (boundaries shown by solid white box). Depth contours are every 1,000 m (1 km spatial resolution, Hawai‘i Mapping Research Group, The School of Ocean and Earth Science and Technology, the University of Hawai‘i at Mānoa http://www.soest.hawaii.edu/hmrg/multibeam/bathymetry.php).

2.2 Detection, classification, localization, and tracking

PMRF recordings were used to detect, classify, localize, and track central North Pacific Bryde’s whale calls. The methods used to obtain the Bryde’s whale tracks are described in detail for minke whale (Balaenoptera acutorostrata) calls in Section 2 of Martin et al. (2022), and thus are only briefly described here.

The Bryde’s whale detection algorithm (which is part of a larger suite of algorithms detecting multiple whale species) can operate on both 96 kHz data and 6 kHz data. A 16384-point fast-Fourier transform (FFT) with a 1024-point advance is applied to 96 kHz data, and a 1024-point FFT with 64-point advance is used on 6 kHz data. Both processing schemes use Hanning windows. Standard alpha-beta filtering is applied to each of the instantaneous FFT data bins for a long-term noise background estimate with alpha=1 and beta=999. The instantaneous FFT is divided over the long-term background FFT from 11.7 Hz to 82.0 Hz (a frequency range chosen to detect the dominant signal component for multiple low-frequency whale calls) to get the signal-to-noise ratio (SNR) for each frequency bin in that range. The signal duration is measured by accumulating consecutive time bins in which the SNR in any frequency bin is above 12 dB. A detection is logged (as the time of the first bin with an SNR over 12 dB) if the max SNR occurs below 70.3 Hz, is greater than 20 dB, and corresponds to a continuous signal in which the pitch starts higher and ends lower, and is at least 0.27 sec in length. These parameters have been used over the last decade to detect low-frequency baleen calls such that the probability of missed detection is near zero within the defined study area and under most noise conditions (Guazzo et al., 2020; Helble et al., 2020b; Martin et al., 2023). In practice, the sensitivity of the detected calls to these specific parameters is low as the calls detected are limited to high SNR calls in the study area of the PMRF range. This scenario is very different than most single-hydrophone studies that cannot confine their study area and as a result are much more sensitive to changes in ocean noise (explored in detail by Helble et al., 2013).

Times of arrival (TOAs) across multiple hydrophones were used to localize Bryde’s whale calls. The measured TOAs of the same call on pairs of hydrophones were subtracted from each other to calculate measured time difference of arrivals (TDOAs). Modeled TDOAs based on direct path transmission and average sound speed of 1516 m/s were calculated from theoretical source locations across the study area. The weighted (based on the proximity of the hydrophone to the theoretical location) least square error between measured and modeled TDOAs was minimized to calculate the position of the calling whale, such that only localizations with a weighted least square error value of less than or equal to 0.15 s were used in this analysis. This threshold was chosen to optimize the balance between retaining localizations from detections with imprecise detection times and excluding spurious localizations due to e.g., detections of multi-paths or times of high calling density. In practice, true localizations were well below this threshold while spurious localizations tended to be well above, leading to little ambiguity between the two.

An automatic tracking algorithm recursively examined distance and time between successive localized calls to group them into tracks (Klay et al., 2015). The parameters used for tracking are specific to the species being tracked and the following values were specified for Bryde’s whale tracks: each track needed at least 12 call localizations, each localization needed to be detected on at least 6 hydrophones, and the spacing between subsequent localizations could not be more than 0.06° in both latitude and longitude (∼6.7 km) or 40 minutes in time. Without the ability to compare acoustic localizations with GPS tags or focal follows, these parameters were empirically chosen to consistently link high-quality localizations that are likely to belong to the same animal based on average calling rate and physical limitations (i.e., maximum swimming speed) and assure that the track contains enough observations to assess swimming behavior.

2.3 Categorizing swimming behavior

Bryde’s whale swimming behavior was then categorized into two states – a faster, more directed state (Faster State) and a slower, less directed state (Slow State) – using hidden Markov models (HMMs). Because HMMs require inputs from equally-spaced time steps, the tracks were first resampled to generate a position every 5 minutes using the crawlWrap function of the R package momentuHMM (McClintock and Michelot, 2018), a wrapper for the continuous-time random walk (CRAWL) model of Johnson et al. (2008). The estimated localization accuracy at PMRF within the study area has a standard deviation of approximately 60 m in the x and y direction so this value was applied to all call localizations (Helble et al., 2015; Martin et al., 2015; Harris et al., 2019; Helble et al., 2020b). We used CRAWL to generate a best-fitting track for each Bryde’s whale track with a single imputation and extracted speed and turning angle from each 5 min interval. A single imputation was chosen because the track step lengths (distance traveled within the 5 min interval) were typically much larger than the measurement errors associated with the CRAWL location outputs, which resulted in little degradation of the HMM results when using a single imputation versus multiple. These methods were similar to those used for minke whales by Helble et al. (2023) and Durbach et al. (2021) and for fin whales (Balaenoptera physalus) by Guazzo et al. (2021).

To understand the general kinematic behavior of vocalizing Bryde’s whales before applying HMMs, we calculated mean speed, average heading, and directivity index from the smoothed tracks. Mean speed is equal to the average of the 5 min interval speeds for each track. Average heading is equal to the heading of the average of the unit vectors for each interval. Directivity index is equal to the net distance traveled divided by the cumulative distance between each 5 min position. To calculate straight-line distance and heading, the shape of Earth was approximated with the WGS-84 reference ellipsoid (Decker, 1986). Similar methods were used for both minke whales (Durbach et al., 2021; Helble et al., 2023), and fin whales (Guazzo et al., 2021), allowing for direct comparisons of swim kinematics between these species on PMRF.

The step length and turning angle values from the smoothed CRAWL tracks were used to classify each interval into kinematic state with the Viterbi algorithm (Langrock et al., 2012; McClintock and Michelot, 2018). The number of states and the sampling interval were chosen based on prior knowledge of Bryde’s whales in Hawaiian waters (Helble et al., 2016) as well as other baleen whale behavior on the range (Guazzo et al., 2021; Helble et al., 2023). Though it is possible that there are more than two kinematic states, given the low sample size, two states was a good starting point to avoid overfitting the model. Step length was modeled using a gamma distribution with initial values of 246 m and 738 m (standard deviations of 159 m and 390 m) and turning angle was modeled as a wrapped Cauchy distribution centered around 0° with initial concentration parameters of 0.7 and 0.9 for the Slow and Faster States, respectively (where a concentration parameter of 0 would indicate random turning and 1 would indicate traveling in a straight line, Bacheler et al., 2019). These initial step length values were chosen to coincide with the average speed found for Bryde’s whales in Helble et al. (2016) ± 50%, and the initial turning angles were determined by examining the range of turning angles for Bryde’s whales in Helble et al. (2016) along with the range of turning angles found for other baleen whale species on PMRF (Durbach et al., 2021; Guazzo et al., 2021; Helble et al., 2023). However, the final results were not sensitive to initial value selection (initial values were adjusted by ±25% in all combinations and the state parameters did not change). Because the sample size precluded estimating random effects due to individual variation, the track data were pooled and modeled together rather than allowing the HMM model parameters to vary between individual tracks. HMMs were fitted by numerical maximization of the likelihood with step length and turning angles modeled as state variables and the probability of transitioning between states modeled as a function of predictor variables hypothesized to influence Bryde’s whale swimming behavior. The Akaike information criterion (AIC) (Akaike, 1974) and similarly the AIC weights (Burnham and Anderson, 2002) were used to rank the models. Model fitting and model comparisons were done using the momentuHMM package (v 1.4.3, McClintock and Michelot, 2018) in R (v 4.0.3, R Core Team, 2020).

2.4 Relationship between swimming behavior and independent variables

The predictor variables that were tested as potential indicators of Bryde’s whale swimming behavior included year, day of the year, season, hour of day, wind speed, and the number of calls in the last 15 minutes. In addition to running each variable on its own as a univariate model, a multivariate model with all variables represented was tested against those with iteratively eliminated predictor variables.

To test the effect of various temporal variables, transition probabilities between kinematic behavioral states were modeled as a function of year, days since January 1 of each year (reset each year), season, and hour of day. Season was defined as three distinct four-month time periods within a year: January–April, May–August, and September–December. The three seasons were chosen based on initial observations that the Bryde’s whales had unique acoustic abundance and swimming behaviors within these seasons. Hour of the day was evaluated both as a continuous cosinor function with a period of 24 hours and as a categorical variable (night, dawn, day, and dusk) with dawn and dusk periods of two hours each centered around the time of sunrise and sunset, respectively.

To test the effect of wind speed, which could increase ambient noise levels, sea state, or otherwise impact swimming capabilities, transition probabilities between kinematic behavioral states were modeled as a function of estimated wind speed. These values were derived from modeled ocean surface wind speeds (at 10 m elevation) with 4.5 km spatial grid resolution and 1 hour time resolution (Hitzl et al., 2014, 2020) from 2011–2021 (values were not available for 2022). We averaged the modeled wind speeds within the PMRF area and used the hourly wind speed closest in time to each 5 min interval. We hypothesized that Bryde’s whales might respond to the resulting changes in wave height and sea state caused by earlier wind speeds, so to test this hypothesis, we incorporated wind speeds with 0–24 hours delay into the HMM models.

To test for an association between calling rate and swimming behavior, transitions between kinematic behavioral states were modeled as a function of the number of calls along the track from the last 15 min. Because Bryde’s whales usually call approximately once per 5 min interval, tabulating the number of calls within the 5 min intervals used for track analysis provides a coarse resolution for the calling behavior. Therefore, call tabulations were determined over longer 15 min windows in order to have a larger sample size of calls. We expect that these longer, overlapping windows would result in more conservative relationships between swimming behavior and calling rate because our ability to detect a change in calling behavior would be delayed and calling rate changes that were not sustained would not be captured.

2.5 Bryde’s whale calling analysis

When measuring calling rates, it is important to ensure that all call detections are valid and missed detections are minimized. Recordings from the hydrophones running through the center of the array were loaded into the Raven Pro software package (Center for Conservation Bioacoustics, 2019) for each Bryde’s whale track. Analysts manually validated the automatic call detections in each track by adding missed calls and removing false detections. This process was similar to that described in more detail by Helble et al. (2020a). In practice, the automated detection, localization, and classification process performed well, and few adjustments were needed by the analysts (missed detections and false detections were each less than 1%, and missed localizations – where the call was not detected on enough hydrophones – were less than 14%). In the cases where multiple whales were vocalizing simultaneously, the pattern of signal arrival times across the hydrophones was used to associate missed calls with the correct whale. If it was not possible to reliably associate the missed calls with the correct whale, the track was removed from the calling analysis portion of the study (but was still used for the kinematic portion). The sensitivity of our kinematic results to these missed calls was analyzed and is discussed further in Section 3.

The ICIs between successive calls in a track were calculated by subtracting their time of call emissions (TOEs). These TOEs were estimated using the relative positions of the receiving hydrophone and the vocalizing whale. However whale positions were not available for calls that were manually added during the validation process described above. Instead the TOE for each missed call was calculated using the position of the most recent localized call. In practice, Bryde’s whales vocalize often and few successive calls were missed by the automated software, so estimated TOEs for the missed calls are likely well within one second of the true TOE. To determine whether the observed ICIs for Bryde’s whales changed over time, the median ICI for each track was first calculated. A linear model was then fit to those median ICIs for each track as a function of the dates of the tracks.

Along-track cue rates were calculated for each track by dividing the total number of calls in a track by the total elapsed time. The along-track cue rate is the vocalization rate of an individual whale while it is vocally active and is in units of calls/hour. Because the response variable in this case could be modeled as a count variable, a quasi-Poisson generalized linear model (GLM) with a log link function was used to model the number of calls in a track over time, with an offset term to account for varying track durations (a quasi-Poisson model was used rather than a typical Poisson to account for apparent overdispersion in the typical Poisson model residuals). It is important to note the along-track cue rate is not the total population cue rate which would include non-calling whales and times when whales were not vocally active.

3 Results

Between January 2011 and December 2022, 150 individual Bryde’s whale tracks were observed in the PMRF study area. These tracks contained a total of 6042 automatically detected and tracked Bryde’s whale calls, from 1465 days of acoustic recording effort on PMRF. All of these tracks were used for swimming behavior categorization, but because wind data was only available through December 2021, the HMM analysis relating swimming behavior to independent variables excluded the three tracks that occurred in 2022.

A manual review of all 150 tracks was completed by analysts, and 118 tracks were deemed suitable for examining the along-track acoustic cue rate. The remaining 32 tracks were not used for the acoustic cue rate portion of the study because it was difficult to determine whether the missed calls along the track originated from the focal animal or a nearby conspecific. A sensitivity test was conducted by randomly dropping 40% of the calls localized along the tracks. After re-running the model with these dropped localizations, the HMM parameter estimates and the model selection findings were unchanged, signifying that the missed localization rate of 14% would not meaningfully affect the swimming behavior statistics from the CRAWL model or the HMM results.

3.1 Categorizing swimming behavior

Overall, based on track kinematics for all 150 tracks, vocalizing Bryde’s whales on PMRF traveled along fairly direct paths with little turning (Figure 4). The whales favored traveling toward the southwest (circular mean of average track headings = 224.3°). The mean of the mean track speeds was 1.7 m/s with a standard deviation of 0.7 m/s. The median directivity index was 0.74 and the mode was between 0.9 and 1 (data bin width of 0.1 units, see Figure 4).

Figure 4

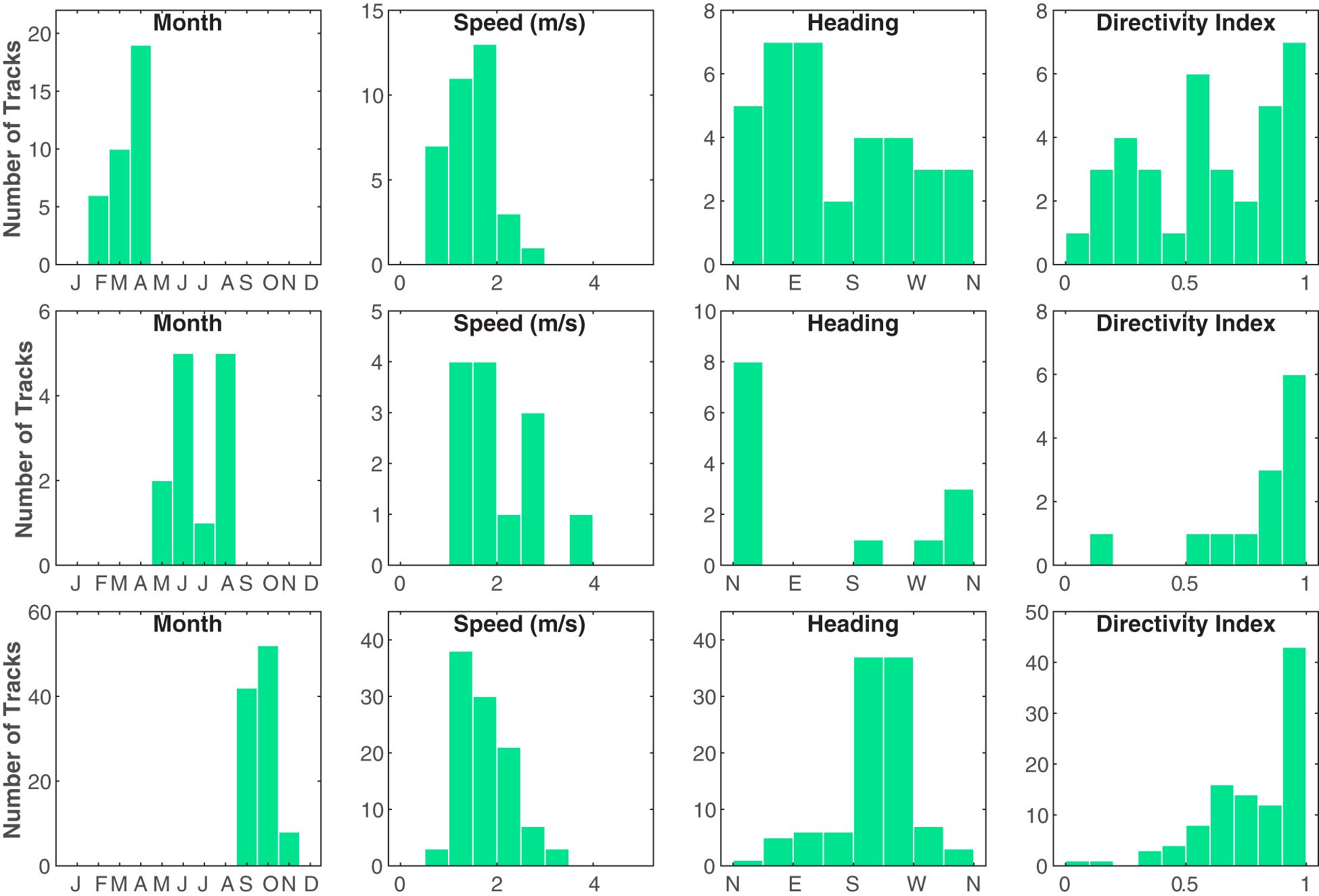
Figure 4 Histograms of the average speed (m/s), average heading, and directivity index (straight-line distance traveled divided by the total distance traveled) for each Bryde’s whale track. The first row contains tracks from the January–April season (n = 35), the second row contains tracks from the May–August season (n = 13), and the third row contains tracks from the September–December season (n = 102) (January and December had no Bryde’s whale tracks). Note the differences in y-axes limits between the plots. These groupings might indicate three distinct seasonal behaviors on the PMRF range.

Speed, heading, and directivity index varied as functions of days since January 1 (Figure 4), with distinct differences between the three defined seasons of January–April, May–August, and September–December (January and December had no Bryde’s whale tracks). Most of the tracks occurred in the September– December season (68%), while 23% occurred in the January–April Season, and only 9% occurred in the May–August season. The January–April season had the least directional travel, slowest speeds, and most variable headings. Though there were few tracks, the May–August season showed highly directional travel to the north, while the majority of tracks that occurred in the September–December season exhibited directional travel to the southwest. The relationship between whale swimming behavior and time was also analyzed further with the HMMs.

The CRAWL tracks, spaced at even 5 min intervals, fit the original tracks well and, while infrequent, helped eliminate spurious localizations (Figure 5). Each of the 5 min intervals was categorized into kinematic behavioral state using the Viterbi algorithm, with 66% of the intervals categorized as the Slow State and 34% of the intervals categorized as the Faster State. The average speed for whales in the Slow State was 1.0 m/s and the average speed for whales in the Faster State was 2.1 m/s (Table 1; Figure 6). The distinction between the two states seems to have been largely driven by the differences in speed rather than by turning angle (0.88 in the Faster State versus 0.82 in the Slower State). These values were stable across all fitted models (less than 2% variability). Three example tracks are shown in Figure 5, containing the original localizations (black dots) and the CRAWL-modeled positions with colored circles or triangles marking the two behavioral states (Slow and Faster). Because Bryde’s whale swimming behavior is complex, no three tracks can summarize the trends from all 150 tracks.

Figure 5

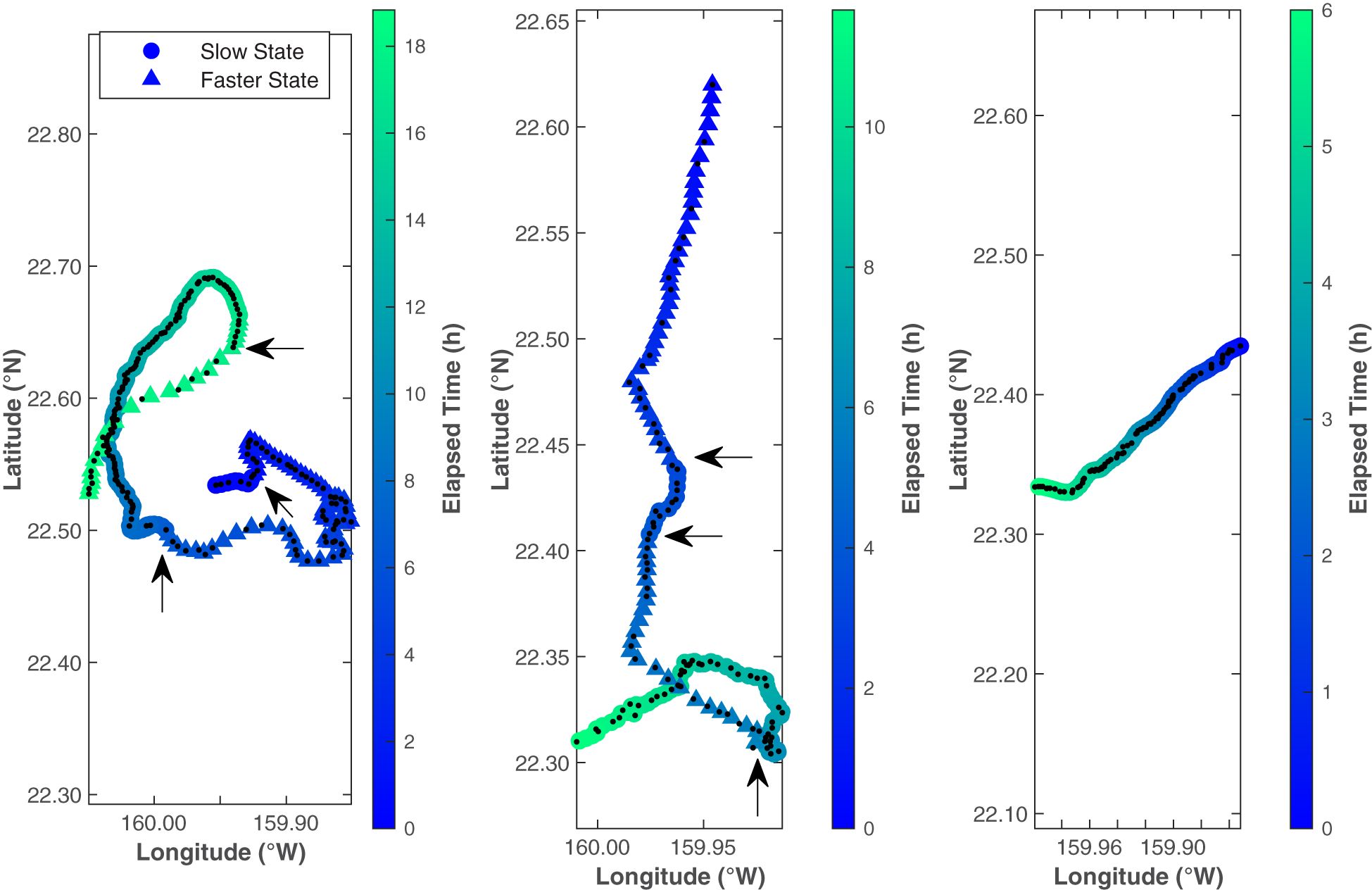
Figure 5 These three example Bryde’s whale tracks show one black dot at the position of every localized call. Colored circles and triangles show the estimated whale locations on 5 min intervals with circles representing the Slow State and triangles representing the Faster State. The states were determined by hidden Markov models. Arrows indicate the locations of state changes. Color indicates time since the start of the track. Note that the elapsed time is different for each track. From left to right, these tracks started at 25 August 2014 11:47, 24 October 2014 13:46, and 24 October 2014 23:21 HST. The first two tracks were selected to illustrate the performance of the CRAWL model locations compared to the original call locations, as well as illustrating state switching along a track. The third track was chosen to represent a typical Bryde’s track from the dataset, with most tracks transiting in a fairly straight directional movement towards the southwest.

Table 1

Table 1 Model parameters with 5 min steps for continuous Hour of Day (highest ranking AIC for univariate models).

Figure 6

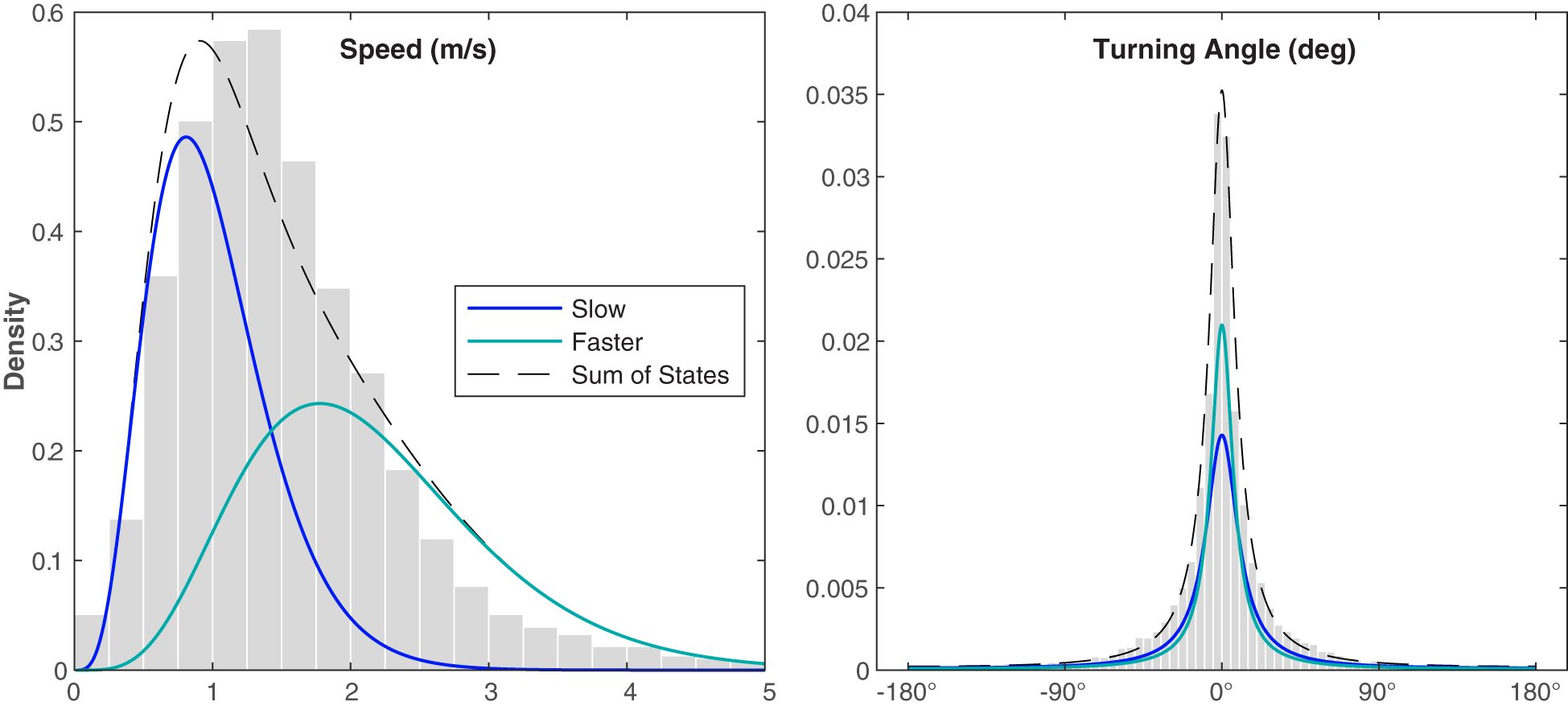
Figure 6 Distributions of the observed variables measured in 5 min intervals for the Bryde’s whale CRAWL tracks normalized by the probability density function. The gray histograms show the observed values normalized by the area of each bar, the blue curves show the probability density function of the Slow State, the teal curves show the probability density function of the Faster State, and the black dashed lines show the sum of the two states. The kinematic states were estimated using a hidden Markov model.

3.2 Relationship between swimming behavior and independent variables

Six different independent variables were tested (with one variable tested two different ways) that we hypothesized might influence Bryde’s whale swimming behavior (Figure 7). The covariates, in increasing order of the AIC of each univariate model tested, were hour of day (continuous and categorical), season, days since Jan 1, wind speed, calling rate, and year (Table 2). The stationary state probability models for six of the univariate models tested can be seen in Figure 8. Similar figures for the multivariate models are not included due to the difficulty of fully representing the various combinations of variables, particularly the categorical variables, which cannot be represented by a mean for the purposes of displaying other predictors.

Figure 7

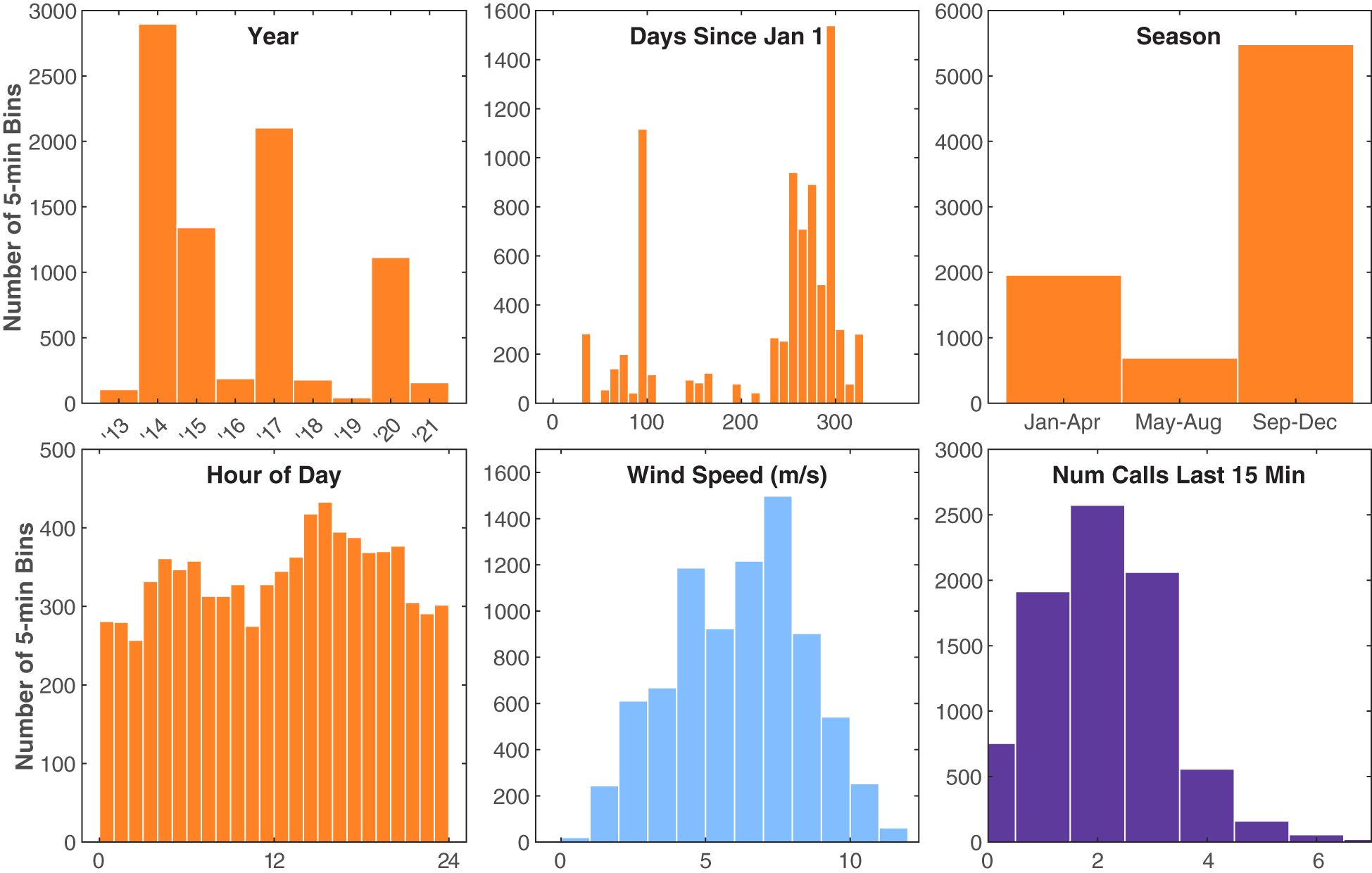
Figure 7 Histograms of the independent variables observed during Bryde’s whale tracks. The y-axis counts are the number of 5 min bins. Time variables are shown in orange, the environmental variable is shown in blue, and the Bryde’s acoustic behavioral variable (number of calls in the last 15 min) is shown in purple. Hour of day is in local Hawaii Standard Time and was tested both as a continuous and a categorical variable.

Table 2

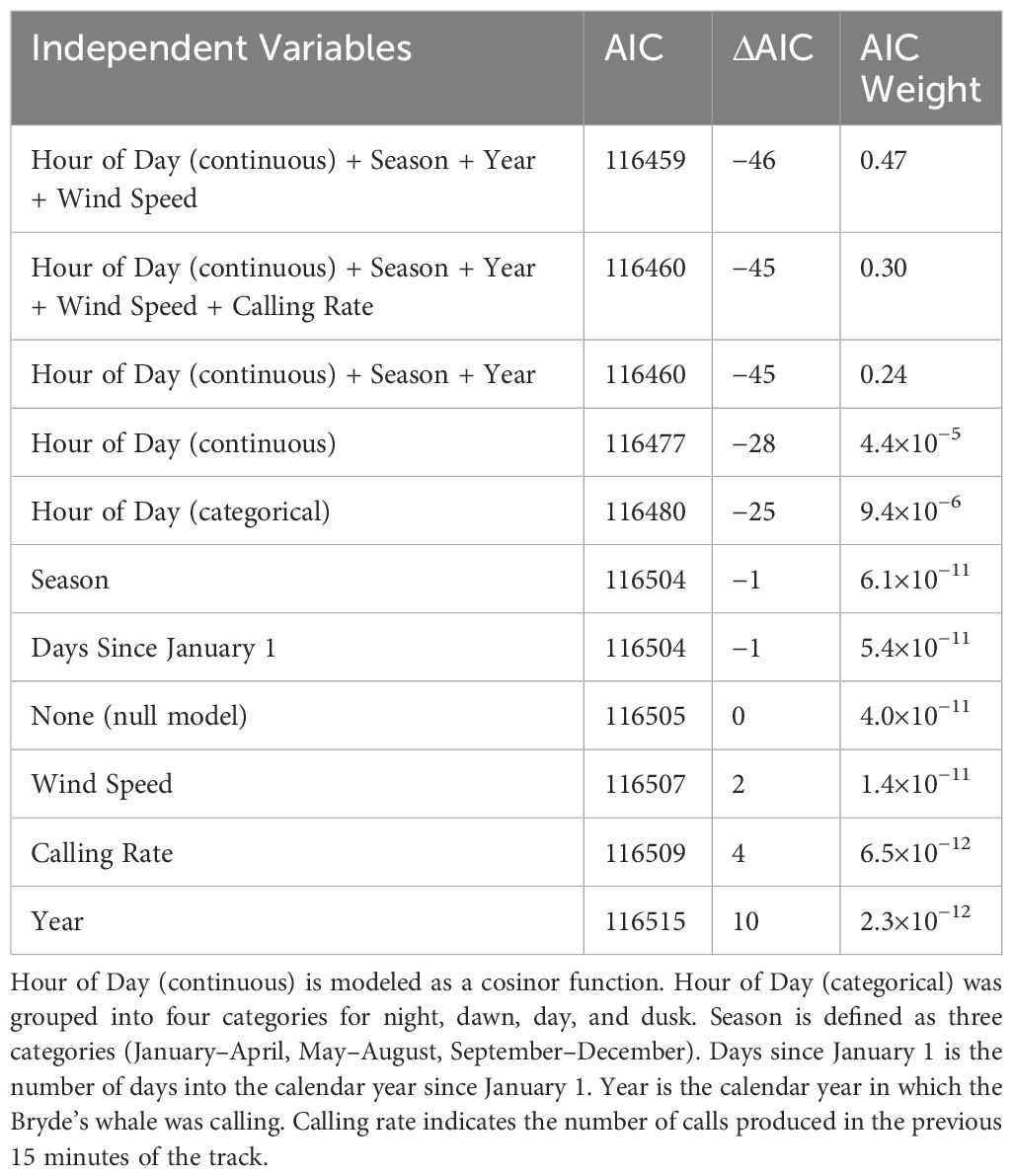
Table 2 Models used to explain vocalizing Bryde’s whale swimming behavior, ranked by the Akaike information criterion (AIC) and AIC weights.

Figure 8

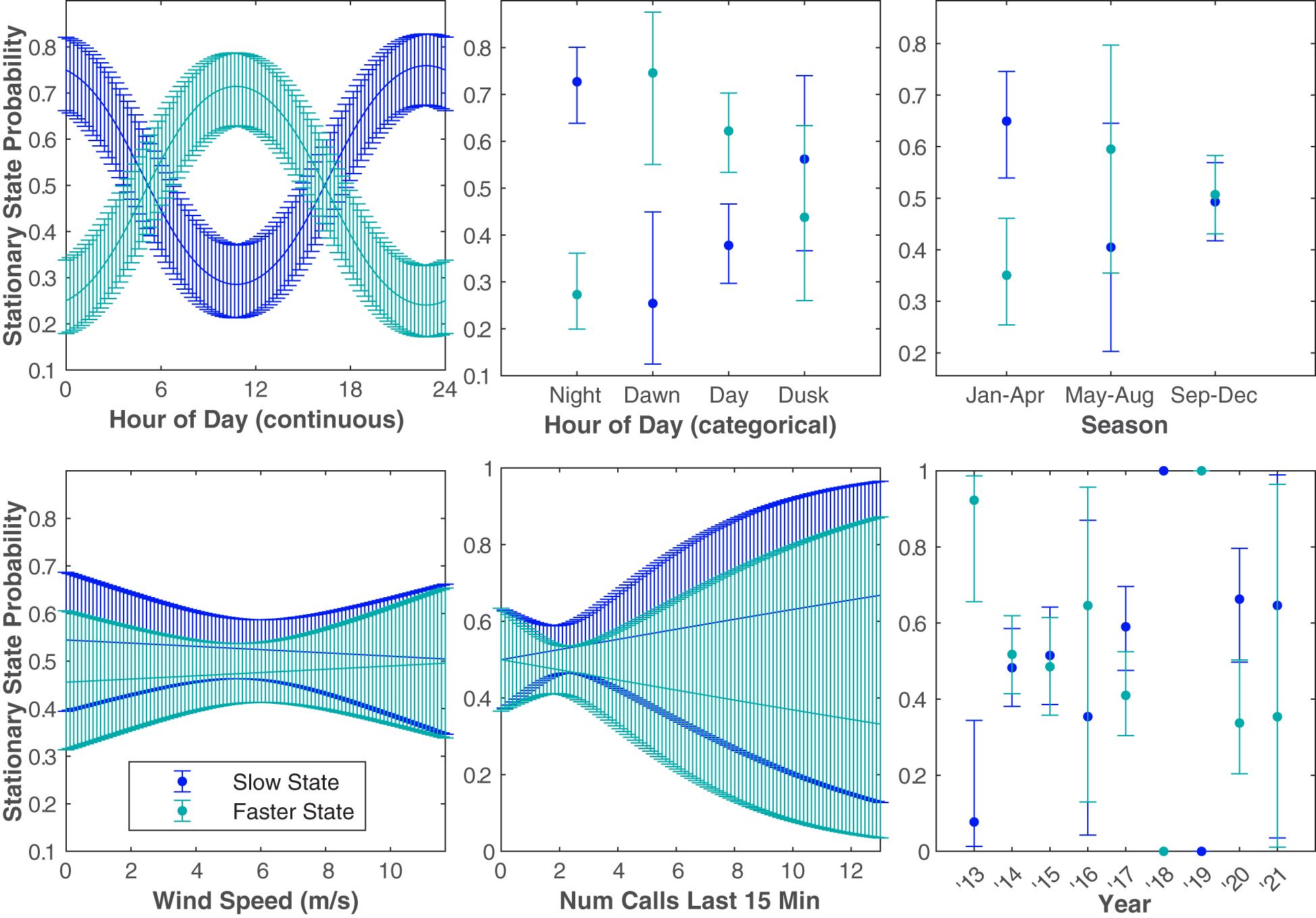
Figure 8 The probability of a 5 min observation being in the Slow State or the Faster State based on the independent variable tested. The blue and teal curves show the stationary state probabilities of the Slow State and the Faster State, respectively. The error bounds show the 95% confidence intervals. Plots are shown in order of AIC score from best (upper left) to worst (lower right). Wind speed, number of calls in the last 15 min, and year ranked lower than the null model. Days since January 1 is not shown because grouping the time of year variable categorically (season) was a better predictor variable for the model.

The change in the stationary state probabilities as a function of each covariate in isolation indicated that temporal variables were generally the strongest predictors of swimming state (Figure 8). Wind speed and calling rate alone both resulted in models that ranked lower than the null. However, multivariate models that included the best predictors of time of year (season) and time of day (hour, continuous) did better than any univariate model, and the best of those models included some variables that did poorly on their own. The model with the lowest AIC score included season, hour (continuous), year, and wind speed, indicating that this combination of covariates is the best predictor of Bryde’s whale swimming state of those tested. Only the top three multivariate models are included in Table 2, as their AIC weights were orders of magnitude above the rest but their AIC scores were within 1 point of each other.

Based on both the continuous and categorical hour of day predictor variables, there is a strong indication that Bryde’s whales were more likely to swim slower at night. Because it was a slightly better predictor variable for the model (i.e., its univariate model had a slightly lower AIC score) and was visibly easier to intuit patterns in the modeling results, season was favored over days since January 1 for exploring intra-annual patterns. Bryde’s whales were more likely to be in the Slow State during the January–April season. They were more likely to be in a Faster State in the May–August season, although there was considerable uncertainty in the model due to the low number of samples within that time period. The probability of kinematic state was approximately equal during the September–December season. The year univariate model ranked lower than the null model, with no clear patterns in kinematic behavior based on the year. Some years contained very few tracks, making it difficult to see trends in kinematic behavior based on the year. Year was likely included in the best model due to the high variation in number of tracks between years, though it is also possible that interannual variability in climate, food, etc. does contribute to likely swimming state in a given year (though not enough for year to perform well as a covariate on its own without accounting for variability due to other factors).

The change in the stationary state probability as a function of the environmental covariate tested (wind speed) tested worse than the null model. Delaying the wind speed up to 24 hours did not improve the AIC score. Despite this, wind speed does seem to account for some variability in swimming state in the multivariate models, though it is possible that some of these final covariates in the best model are somewhat collinear and therefore overrepresented (e.g., if wind speed varies in a predictably seasonal way).

The number of calls in the last 15 minutes did not show any clear patterns in relation to the Bryde’s whale kinematic behavior, and the univariate model ranked worse than the null model.

3.3 Bryde’s whale calling analysis

The ICIs were measured between all calls for 118 of the 150 Bryde’s whale tracks that were verified in Raven Pro. The overall median ICI between all the tracked calls was 306 s (5.1 min) and the overall mean ICI was 361 s (6.0 min). The median ICIs within tracks increased over time at a rate of 13.1 s/year (95% CI[6.3,19.9]) (Figure 9).

Figure 9

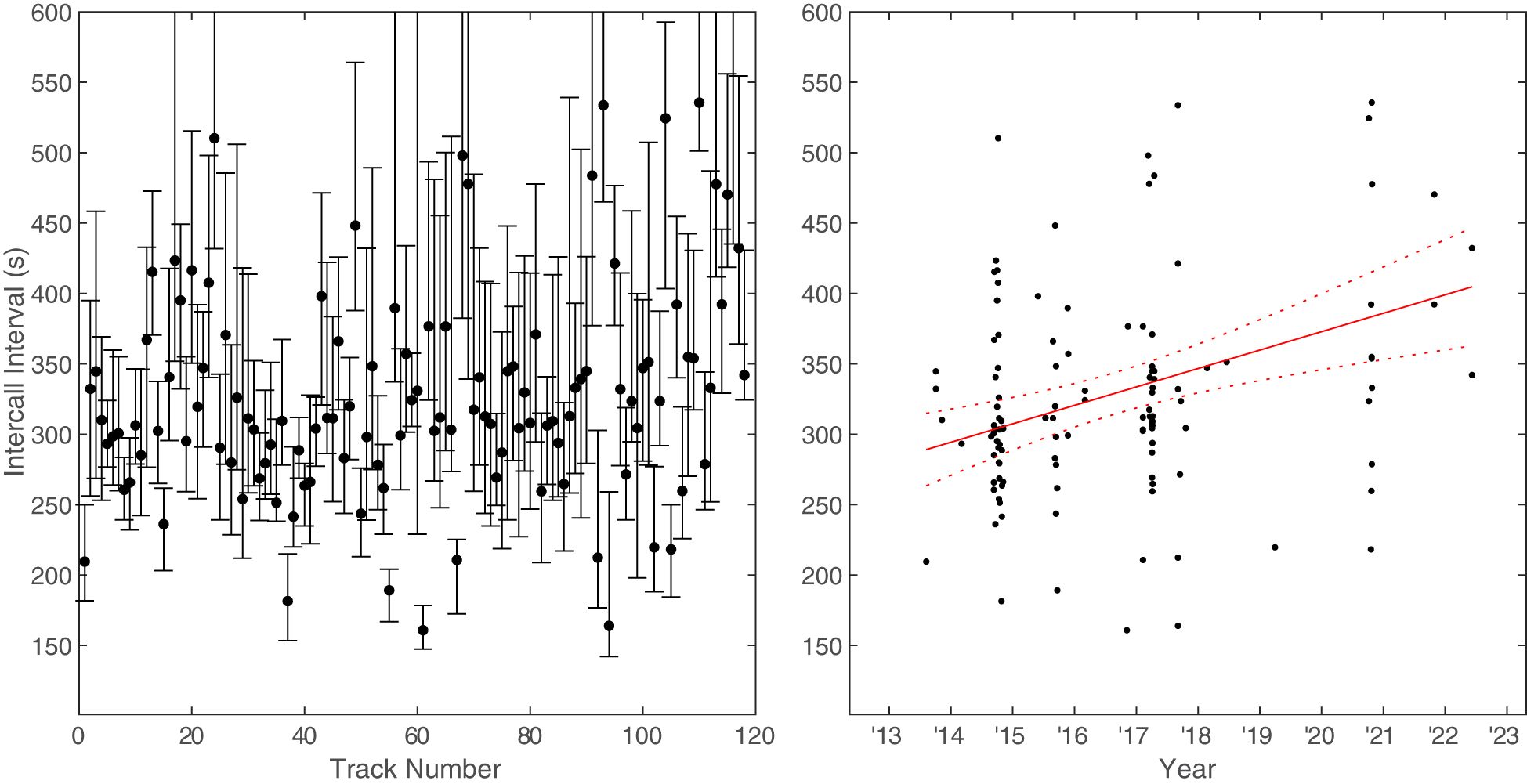
Figure 9 Bryde’s whale median inter-call interval (ICI) for each track plotted both as a function of track number (left) and as a function of time (right). The vertical bars in the left plot extend between the 25th and 75th percentiles. A linear model was fit to the data points on the right. Dashed lines represent the 95% confidence intervals.

The along-track cue rate was calculated for 118 of the 150 tracks by summing the calls along a track and dividing the total calls by the total amount of elapsed time for the track (Figure 10). The median along-track cue rate for the 118 tracks was 22 calls/hour (Q1 = 15, Q3 = 39), and the mean along-track cue rate was 29 calls/hour. The overall predicted trend from the quasi-Poisson model was slightly negative, but with confidence intervals that suggest no clear evidence of a trend in cue rate over time (year parameter estimate: -0.05, 95% CI[-0.14 to 0.03]). The differences between cue rate and ICI (as metrics and the resulting implications) are explored further in Section 4.

Figure 10

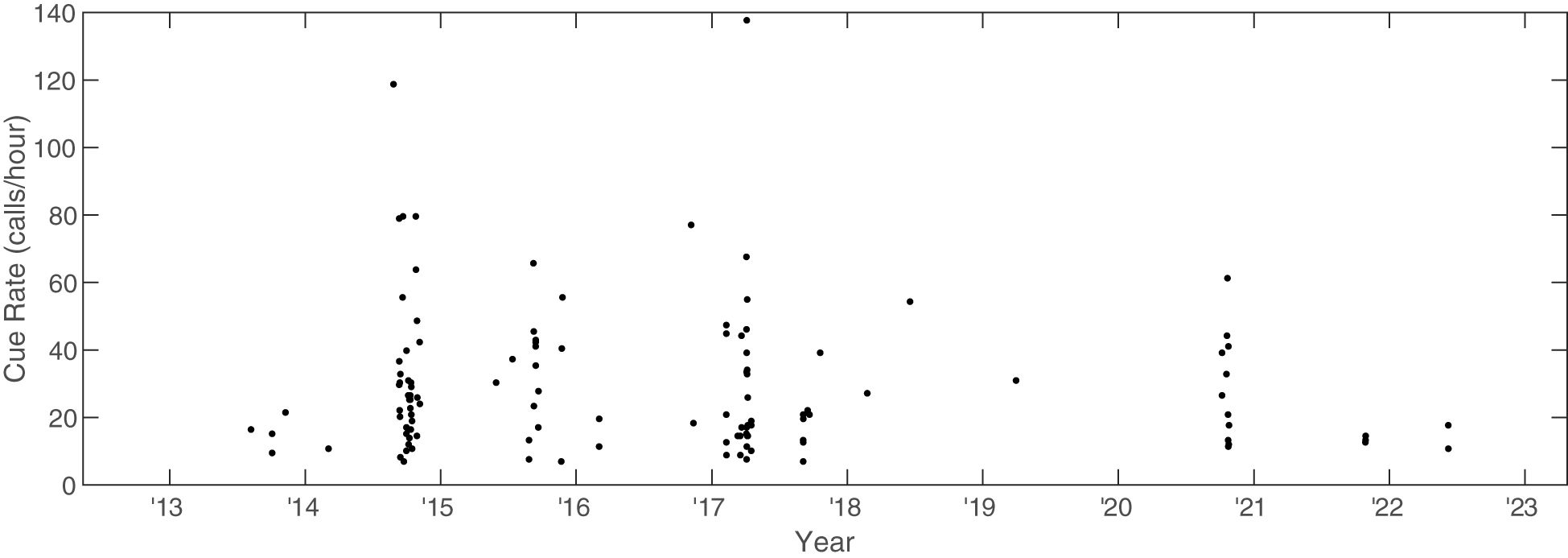
Figure 10 Along-track cue rate for Bryde’s whales on PMRF as a function of time. Cue rate was calculated as number of calls along a track divided by the total elapsed time of the track and is in units of calls/hour.

4 Discussion

This study adds important knowledge about Bryde’s whale seasonal behavior in Hawaiian waters. Previous studies have only measured Bryde’s whale movement over short time periods (e.g., Alves et al., 2009; Helble et al., 2016; Izadi et al., 2018) and so whether and how Bryde’s whale behavior changes within and between years had not been investigated. We observed three distinct seasonal movement patterns on PMRF with whales swimming slowly in all directions in the January–April season, quickly and toward the north in the May–August season, and with a mixture of speeds and toward the southwest in the September–December season. Although compass headings were not included in the HMM analysis due to sample size, speed and turning angle as represented in the HMMs also supported these general observations. These patterns may provide some insight into Bryde’s whale large-scale movement behavior.

Over these 12 years, no Bryde’s whales were tracked in December or January. Either Bryde’s whales during these months were producing different vocalizations or Bryde’s whales were absent or not consistently vocalizing during these times. Since the Bryde’s whales tracked during the rest of the year never produced any other call types within their calling sequences, it seems most likely that December and January are times when this population of Bryde’s whales is absent from the area and adds support that the January–April and September–December seasons are separate from each other. In addition, the abundance of tracks generated by actively vocalizing Bryde’s whales is the greatest at PMRF in the September–December season, however their acoustic presence shows high interannual variability and is much less predictable than the annual timings of other baleen whales on PMRF such as humpback whales (Megaptera novaeangliae) (Henderson et al., 2018; Guazzo et al., 2020), fin whales (Helble et al., 2020a), and minke whales (Martin et al., 2022). The other large baleen whales are driven by annual migrations between northern feeding grounds and more tropical breeding grounds, but it is unknown how Bryde’s whales are using the tropical and sub-tropical waters they occupy year-round or what drives their movements and when. Furthermore, because their acoustic presence is so sporadic and data recordings are intermittent, it is possible that there simply has not been adequate recording effort to capture their full presence in certain months, and seasonal trends may be heavily influenced by months with unusually high numbers of vocalizing Bryde’s whales transiting the range, such as in September and October 2014.

Despite this new information, many more questions remain. For example, are the whales that seasonally pass through PMRF the same population or three separate populations? The tracks captured here only have a single call type along them, which is similar to the Be3 call type recorded in the Eastern Tropical Pacific and western South Pacific (Oleson et al., 2003; Heimlich et al., 2005; McDonald, 2006; Brodie and Dunn, 2015). Could these whales spend part of the year in other parts of the Pacific, or are those separate populations? Although there are slight differences in these calls compared to what has been described elsewhere, some of these differences could be due to recording equipment and local sound propagation and not significant differences in the calls being produced. At the least, since similar calls have been recorded across such a wide spread of the Pacific, these Bryde’s whales may be more connected than others that produce different call types. We recommend that more effort be dedicated to recording this call type again in other areas of the Pacific. Although Bryde’s whales have rarely been visually sighted in Hawaiian waters, if possible, long-duration satellite tagging might allow us to answer more questions about their Hawaiian water residency patterns.

Of the four baleen whale species that we have been able to track on PMRF, Bryde’s whales have been observed swimming with the fastest average speeds (1.7 m/s in this study; range of 1.6–2.5 m/s in Hawaiian waters in Smultea et al., 2010; Helble et al., 2016). In contrast, vocalizing minke whales swam at an average speed of 1.3 m/s (Helble et al., 2023), fin whales at an average speed of 1.1 m/s (Guazzo et al., 2021), and humpback whales at an average speed of 1.0 m/s (Henderson et al., 2018). Bryde’s whales also seemed to have more directional travel regardless of kinematic state, with 0.82 and 0.88 concentrations in turning angle in the Slow and Faster States, respectively, versus 0.68 and 0.85 for minke whales (Helble et al., 2023) and 0.68 and 0.88 for fin whales (Guazzo et al., 2021). Humpback whales were modeled differently but had directivity indices that ranged between 0.81 and 1.00, depending on state (Henderson et al., 2018). However, all of these speed and directivity measures are for actively vocalizing individuals and non-vocalizing individuals might travel differently. In addition, since the other species are in Hawaiian waters primarily in the winter and are therefore likely engaging in mating behavior, the whale behavioral state might be influencing the observed kinematics. Fin and humpback whale vocalizations detected on PMRF are male song, while minke whale calls might be used to establish territory (Martin et al., 2022), but the significance of Bryde’s whale calls and the type of behavior they are engaging in are unknown. Finally, these were all measured during times without Navy mid-frequency active sonar (MFAS), which, along with other anthropogenic activity, may cause changes in swimming speed and directionality. For example, during times when Navy sonar was active, minke whales on PMRF swam in a fast movement state 75% of the time with average speeds of 2.4 m/s (Durbach et al., 2021). These baseline behaviors are important to capture in order to understand potential impacts of anthropogenic activity.

The kinematic behavior of these Bryde’s whales had the strongest relationship with time of day and time of year. Bryde’s whales were most likely to be in the Slow State and display slow speeds and less directed swimming at night. This pattern may indicate resting behavior at night and is similar to what was observed for Bryde’s whales in New Zealand (Izadi et al., 2018), but different from what was observed in Portugal (Alves et al., 2009). However, both of these other studies were done with very small sample sizes (n=2 and n=4, respectively) and analyzing behavior over a larger portion of the population might reveal different patterns. Bryde’s whales at PMRF were also most likely to be in the Slow State in the January–April season, with less differentiation between the probability of the two kinematic states the rest of the year, which adds confidence to the seasonal pattern observed without the HMM. In contrast to other baleen whales at PMRF, Bryde’s whale kinematic behavior was not strongly related to calling rate. For example, minke whales were more likely to swim faster when calling rapidly (Helble et al., 2023) and fin whales were more likely to swim slower when they were singing continuously (Guazzo et al., 2021).

The ICIs of Bryde’s whales tracked at PMRF were more similar to the longer ICIs of Bryde’s whale Be3 calls recorded in the Eastern Tropical Pacific and western South Pacific than the shorter ICIs of Be3 calls recorded in the western North Pacific (Oleson et al., 2003; Heimlich et al., 2005; Brodie and Dunn, 2015; Wang et al., 2022). Along with similar call types, this finding could indicate that these Bryde’s whales in the central North Pacific are more closely related to the Bryde’s whales in the Eastern Tropical Pacific and western South Pacific than to those in the western North Pacific.

There is some indication that the median ICI is lengthening over time for Bryde’s whales. The median drift of 13.1 s/year amounts to a 3.4% drift when compared to the median for all Bryde’s whale tracks over the study period. Interestingly, some fin whale notes also exhibited a lengthening of inter-note intervals (INIs) at PMRF, with fin whale note pairings of B-A and A-B notes lengthening at approximately 5% a year (Helble et al., 2020a). Fin whales have been known to change INIs both gradually and suddenly, so it is unclear if the lengthening in fin whales will continue or eventually be replaced with a new dominant note pairing and/or INIs (Helble et al., 2020a). So far, only one Bryde’s whale call type has been identified on PMRF, and no rapid shifts in ICIs have been observed.

The Bryde’s whale along-track cue rate, which is the number of total calls along a track divided by the track length, has remained more stable than the median ICI. While there is some indication of lengthening of the median ICI, the along-track cue rate can remain stable if there are fewer or shorter calling breaks (such as those due to surfacing) along the track as the ICIs lengthen, which seems to be the case in this study. It is also possible that the median ICI may be driven in large part by the higher number of vocalizing Bryde’s whale tracks in 2015, 2016, and 2018. Both the along-track cue rate and the median ICI could be density-dependent, which could impact the perception of long-term trends. Adding additional tracks and years would be helpful to confirm any long-term changes in ICI and the relative stability of the along-track cue rate. Despite these uncertainties, Bryde’s whale calling behavior – regardless of metric – seems far more stable than other baleen whale vocalizations in the area, such as minke whale calls, which occur more rapidly when conspecifics are nearby, and fin whale song, which can change abruptly mid-track and also exhibits a clearer long-term INI lengthening. This stability may make Bryde’s whales a more promising candidate for pursuing cue-rate-based measures of density estimation.

For single hydrophone recording systems, it is typically not possible to localize and track Bryde’s whales, so the number of tracks cannot be used as a cue for density estimation. In theory, counting the number of calls on a single hydrophone system could be used to estimate the number of animals in the area, but the proportion of time an animal is in a calling state and the number of vocally active whales within the population would need to be known. The results provided in this study show that when a Bryde’s whale in Hawaiian waters is in a calling state, the cue rate is relatively stable. However, there is considerable cue rate variability between tracks, and so enough calls would need to be counted (enough unique animals sampled) on a single hydrophone system to account for this variability. Despite these obstacles, it is encouraging to see that there were no sudden shifts in call types or along-track cue rates for the duration of the study.

In conclusion, this study expands on the initial study by Helble et al. (2016) in which 17 Bryde’s whale tracks were described based on acoustic recordings from a single season off the coast of Kaua‘i, Hawai‘i. Here, 150 Bryde’s whale tracks were identified in data spanning more than a decade, with recording effort in nearly every month of the study period. Distinct differences in speed, heading, and directivity were noted in three defined seasons (January–April, May–August, and September–December), and Bryde’s whale acoustic presence shows high interannual variability, with less predictable presence than other baleen whales in the area. Bryde’s whale large-scale movement behavior (and whether they engage in annual migrations) has been understudied, and this seasonality observed at PMRF adds important knowledge about their annual patterns. Two kinematic states were identified (slower, less directional movement and faster, more directional movement), which were most related to the season and the hour of the day in univariate models. Although track kinematics and whale presence were limited to acoustically active whales in this study, detailed movements were collected on 150 Bryde’s whale tracks and their patterns compared over daily and annual timescales, which is an order of magnitude greater than the number of individuals whose swimming behavior has been studied in the past. Very little is known about how Bryde’s whale vocalization behavior changes over time within a given region, which this study investigates in Hawaiian waters. Notably, only a single call type has been identified, with some indication that the median ICI is lengthening over time. Additional data are needed to confirm this trend, and more combined visual and acoustic studies should be conducted to explore if Bryde’s whales in the region produce other call types. While this study contributes significant insights into Bryde’s whale swimming and acoustic behavior in Hawaiian waters, many questions still remain. We encourage other researchers to collect long-term visual, acoustic, and genetic data about Bryde’s whales across their range to further investigate the behavior, life history, population distribution, and abundance of this under-studied species.

Data availability statement

The dataset presented in this study can be found in an online repository: https://seamap.env.duke.edu/dataset/2284.

Ethics statement

Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements because the study used passive acoustic monitoring, therefore, no part of the study disturbed any of the animals’ natural behavior.

Author contributions

TH: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. GA: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. RG: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing. DA: Investigation, Validation, Writing – review & editing. CM: Data curation, Software, Writing – review & editing. SM: Data curation, Methodology, Software, Writing – review & editing. ID: Formal analysis, Methodology, Software, Writing – review & editing. EH: Data curation, Project administration, Supervision, Writing – review & editing, Funding acquisition.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the U.S. Navy’s Living Marine Resources Program (Award Number N0002523WR0051R), Commander, U.S. Pacific Fleet (Code N465JR, Award Number N0007023WR0EP8F), and tool development necessary for this analysis was supported by the Office of Naval Research (Code 322, Award Number N0001422WX01263).

Acknowledgments

The authors would like to thank Yi-Leng Chen and Feng Hsiao who provided the modeled wind speeds. The authors thank the personnel at PMRF, especially Eliseo Boloson, Bruce Comisap, Mike Dick, Jim Hager, Robin Higuchi, Bryson Kurokawa, Jon Winsley, and Jeffrey Yates, for obtaining recordings of acoustic data, as without the acoustic data this type of analysis would not be possible.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akaike H. (1974). A new look at the statistical model identification. IEEE Trans. Auto. Control 19, 716–723. doi: 10.1109/TAC.1974.1100705

CrossRef Full Text | Google Scholar

Alves F., Dinis A., Cascão I., Freitas L. (2009). Bryde’s whale (Balaenoptera brydei) stable associations and dive profiles: new insights into foraging behavior. Mar. Mamm. Sci. 26, 202–212. doi: 10.1111/j.1748-7692.2009.00333.x

CrossRef Full Text | Google Scholar

Bacheler N. M., Michelot T., Cheshire R. T., Shertzer K. W. (2019). Fine-scale movement patterns and behavioral states of gray triggerfish Balistes capriscus determined from acoustic telemetry and hidden Markov models. Fish Res. 215, 76–89. doi: 10.1016/j.fishres.2019.02.014

CrossRef Full Text | Google Scholar

Becker E. A., Forney K. A., Oleson E. M., Bradford A. L., Moore J. E., Barlow J. (2021). Habitat-based density estimates for cetaceans within the waters of the U.S. Exclusive Economic Zone around the Hawaiian Archipelago (NOAA Technical Memorandum NMFS-PIFSC-116, U.S. Department of Commerce). doi: 10.25923/X9Q9-RD73

CrossRef Full Text | Google Scholar

Brodie D. C., Dunn R. A. (2015). Low frequency baleen whale calls detected on ocean-bottom seismometers in the Lau basin, southwest Pacific Ocean. J. Acoustic. Soc. America 137, 53–62. doi: 10.1121/1.4904556

CrossRef Full Text | Google Scholar

Burnham K. P., Anderson D. R. (2002). Model selection and multimodal inference. 2 edn (175 Fifth Avenue, New York, NY 10010: Springer-Verlag New York). doi: 10.1007/b97636

CrossRef Full Text | Google Scholar

Center for Conservation Bioacoustics. (2019). Raven Pro: Interactive Sound Analysis Software (Version 1.6.1) (Ithaca, NY: The Cornell Lab of Ornithology). Available at: http://ravensoundsoftware.com/.

Google Scholar

Constantine R., Iwata T., Nieukirk S. L., Penry G. S. (2018). Future directions in research on Bryde’s whales. Front. Mar. Sci. 5. doi: 10.3389/fmars.2018.00333

CrossRef Full Text | Google Scholar

Decker B. L. (1986). “World geodetic system 1984,” in Presented at Fourth International Geodetic Symposium on Satellite Positioning, Austin, Texas.

Google Scholar

Durbach I. N., Harris C. M., Martin C., Helble T. A., Henderson E. E., Ierley G., et al. (2021). Changes in the movement and calling behaviour of minke whales (Balaenoptera acutorostrata) in response to navy training. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.660122

CrossRef Full Text | Google Scholar

Fleishman E., Cholewiak D., Gillespie D., Helble T., Klinck H., Nosal E.-M., et al. (2023). Ecological inferences about marine mammals from passive acoustic data. Biol. Rev. 98, 1633–1647. doi: 10.1111/brv.12969

CrossRef Full Text | Google Scholar

Guazzo R. A., Durbach I. N., Helble T. A., Alongi G. C., Martin C. R., Martin S. W., et al. (2021). Singing fin whale swimming behavior in the central North Pacific. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.696002

CrossRef Full Text | Google Scholar

Guazzo R. A., Helble T. A., Alongi G. C., Durbach I. N., Martin C. R., Martin S. W., et al. (2020). Lombard effect: humpback whale song source levels increase as ambient ocean noise levels increase. J. Acoust. Soc Am. 148, 542–555. doi: 10.1121/10.0001669

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris C. M., Martin S. W., Martin C., Helble T. A., Henderson E. E., Paxton C. G. M., et al. (2019). Changes in the spatial distribution of acoustically derived minke whale (Balaenoptera acutorostrata) tracks in response to Navy training. Aquat. Mamm. 45, 661–674. doi: 10.1578/AM.45.6.2019.661

CrossRef Full Text | Google Scholar

Heimlich S. L., Mellinger D. K., Nieukirk S. L., Fox C. G. (2005). Types, distribution, and seasonal occurrence of sounds attributed to Bryde’s whales (Balaenoptera edeni) recorded in the eastern tropical Pacific 1999–2001. J. Acoustic. Soc. America 118, 1830–1837. doi: 10.1121/1.1992674

CrossRef Full Text | Google Scholar

Helble T. A., D’Spain G. L., Hildebrand J. A., Campbell G. S., Campbell R. L., Heaney K. D. (2013). Site specific probability of passive acoustic detection of humpback whale calls from single fixed hydrophones. J. Acoust. Soc Am. 134, 2556–2570. doi: 10.1121/1.4816581

PubMed Abstract | CrossRef Full Text | Google Scholar

Helble T. A., Guazzo R. A., Alongi G. C., Martin C. R., Martin S. W., Henderson E. E. (2020a). Fin whale song patterns shift over time in the central North Pacific. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.587110

CrossRef Full Text | Google Scholar

Helble T. A., Guazzo R. A., Durbach I. N., Martin C. R., Alongi G. C., Martin S. W., et al. (2023). Minke whales change their swimming behavior with respect to their calling behavior, nearby conspecifics, and the environment in the central North Pacific. Front. Mar. Sci. 10. doi: 10.3389/fmars.2023.1148987

CrossRef Full Text | Google Scholar

Helble T. A., Guazzo R. A., Martin C. R., Durbach I. N., Alongi G. C., Martin S. W., et al. (2020b). Lombard effect: minke whale call source levels vary with natural variations in ocean noise. J. Acoust. Soc Am. 147, 698–712. doi: 10.1121/10.0000596

PubMed Abstract | CrossRef Full Text | Google Scholar

Helble T. A., Henderson E. E., Ierley G. R., Martin S. W. (2016). Swim track kinematics and calling behavior attributed to Bryde’s whales on the Navy’s Pacific Missile Range Facility. J. Acoust. Soc Am. 140, 4170–4177. doi: 10.1121/1.4967754

PubMed Abstract | CrossRef Full Text | Google Scholar

Helble T. A., Ierley G. R., D’Spain G. L., Martin S. W. (2015). Automated acoustic localization and call association for vocalizing humpback whales on the Navy’s Pacific Missile Range Facility. J. Acoust. Soc Am. 137, 11–21. doi: 10.1121/1.4904505

PubMed Abstract | CrossRef Full Text | Google Scholar

Henderson E. E., Helble T. A., Ierley G., Martin S. (2018). Identifying behavioral states and habitat use of acoustically tracked humpback whales in Hawaii. Mar. Mamm. Sci. 34, 701–717. doi: 10.1111/mms.12475

CrossRef Full Text | Google Scholar

Hitzl D. E., Chen Y.-L., Hsiao F. (2020). Wintertime easterly and southeasterly airflow in the ‘Alenuihāhā Channel, Hawaii. Mon Wea Rev. 148, 1337–1362. doi: 10.1175/MWR-D-19-0042.1

CrossRef Full Text | Google Scholar

Hitzl D. E., Chen Y.-L., Nguyen H. V. (2014). Numerical simulations and observations of airflow through the ‘Alenuihāhā Channel, Hawaii. Mon Wea Rev. 142, 4696–4718. doi: 10.1175/MWR-D-13-00312.1

CrossRef Full Text | Google Scholar

Izadi S., Johnson M., de Soto N. A., Constantine R. (2018). Night-life of Bryde’s whales: ecological implications of resting in a baleen whale. Behav. Ecol. Sociobiol. 72, 78. doi: 10.1007/s00265-018-2492-8

CrossRef Full Text | Google Scholar

Johnson D. S., London J. M., Lea M.-A., Durban J. W. (2008). Continuous-time correlated random walk model for animal telemetry data. Ecology 89, 1208–1215. doi: 10.1890/07-1032.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerosky S. M., Širović A., Roche L. K., Baumann-Pickering S., Wiggins S. M., Hildebrand J. A. (2012). Bryde’s whale seasonal range expansion and increasing presence in the Southern California Bight from 2000 to 2010. Deep Sea Res. Part I 65, 125–132. doi: 10.1016/j.dsr.2012.03.013

CrossRef Full Text | Google Scholar

Klay J., Mellinger D. K., Moretti D. J., Martin S. W., Roch M. A. (2015). Advanced methods for passive acoustic detection, classification, and localization of marine mammals (Arlington, VA: Office of Naval Research). Available online at: https://www.onr.navy.mil/reports/FY15/mbklay.pdf (Accessed 22 January 2020).

Google Scholar

Langrock R., King R., Matthiopoulos J., Thomas L., Fortin D., Morales J. M. (2012). Flexible and practical modeling of animal telemetry data: hidden Markov models and extensions. Ecology 93, 2336–2342. doi: 10.1890/11-2241.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Marques T. A., Thomas L., Ward J., DiMarzio N., Tyack P. L. (2009). Estimating cetacean population density using fixed passive acoustic sensors: an example with Blainville’s beaked whales. J. Acoust. Soc Am. 125, 1982–1994. doi: 10.1121/1.3089590

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin C. R., Guazzo R. A., Helble T. A., Alongi G. C., Durbach I. N., Martin S. W., et al. (2022). Minke whales call rapidly when calling conspecifics are nearby. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.897298

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin C. R., Henderson E. E., Martin S. W., Alongi G. A., Guazzo R. A., Helble T. A., et al. (2023). FY22 annual report on Pacific Missile Range Facility marine mammal monitoring (San Diego, CA: Naval Information Warfare Center Pacific).

Google Scholar

Martin S. W., Martin C. R., Matsuyama B. M., Henderson E. E. (2015). Minke whales (Balaenoptera acutorostrata) respond to navy training. J. Acoust. Soc Am. 137, 2533–2541. doi: 10.1121/1.4919319

PubMed Abstract | CrossRef Full Text | Google Scholar

McClintock B. T., Michelot T. (2018). momentuHMM: R package for generalized hidden Markov models of animal movement. Methods Ecol. Evol. 9, 1518–1530. doi: 10.1111/2041-210X.12995

CrossRef Full Text | Google Scholar

McDonald M. A. (2006). An acoustic survey of baleen whales off Great Barrier Island, New Zealand. New Z. J. Mar. Freshw. Res. 40, 519–529. doi: 10.1080/00288330.2006.9517442

CrossRef Full Text | Google Scholar

Oleson E. M., Barlow J., Gordon J., Rankin S., Hildebrand J. A. (2003). Low frequency calls of Bryde’s whales. Mar. Mamm. Sci. 19, 407–419. doi: 10.1111/j.1748-7692.2003.tb01119.x

CrossRef Full Text | Google Scholar

R Core Team. (2020). R: A Language and Environment for Statistical Computing (Vienna, Austria: R Foundation for Statistical Computing). Available at: https://www.R-project.org/.

Google Scholar

Smultea M. A., Jefferson T. A., Zoidis A. M. (2010). Rare sightings of a Bryde’s whale (Balaenoptera edeni) and sei whales (B. Borealis) (Cetacea: Balaenopteridae) northeast of O’ahu, Hawai’i. Pac Sci. 64, 449–457. doi: 10.2984/64.3.449

CrossRef Full Text | Google Scholar

Szesciorka A. R., McCullough J. L. K., Oleson E. M. (2023). An unknown nocturnal call type in the Mariana Archipelago. JASA Express Lett. 3, 011201. doi: 10.1121/10.0017068

PubMed Abstract | CrossRef Full Text | Google Scholar

Viloria-Gómora L., Romero-Vivas E., Urbán R. J. (2015). Calls of Bryde’s whale (Balaenoptera edeni) recorded in the Gulf of California. J. Acoust. Soc Am. 138, 2722–2725. doi: 10.1121/1.4932032

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang Z.-T., Duan P.-X., Chen M., Mei Z.-G., Sun X.-D., Nong Z.-W., et al. (2022). Vocalization of Bryde’s whales (Balaenoptera edeni) in the Beibu Gulf, China. Mar. Mamm. Sci. 38, 1118–1139. doi: 10.1111/mms.12917

CrossRef Full Text | Google Scholar