- Merchant Marine College, Shanghai Maritime University, Shanghai, China
The significant uncertainty and complexity of vessels at sea poses challenges for regulatory bodies in the fishing industry. This paper presents a method for identifying fishing vessel trajectory characteristics involving the Fourier series transform. The model utilizes the Fourier series and Gaussian mixture clustering to address the complexity and uncertainty issues in fishing vessel trajectories. First, the vessel trajectories undergo a process of dimensionality expansion and projection along the temporal axis. The relationship between trajectories and complex plane projection was elucidated in this process. Second, a vessel trajectory identification model involving Fourier transformation was constructed. Subsequently, the phase spectrum was assigned binary values using differentiation, and the phase spectrum characteristics of the transformed trajectories through Fourier transformation were analyzed. Finally, six encoding formats for fishing vessel motion trajectories in phase spectrum encoding are introduced, along with the determination of uncertain vessel motion range through mixed Gaussian clustering. This method has been validated using a dataset comprising 7,000 fishing vessel trajectories collected from the Beidou satellite positioning system. The results demonstrate that the range of uncertain vessel motion was able to be obtained with the assistance of Gaussian mixture clustering, with an 80% probability position of approximately 1,000 m and a 50% probability position of around 2,000 m. Effective identification of fishing vessel operating and navigational states was achieved, leading to the determination of a safety distance for fishing vessels in the range of 1,000m–2,000 m. This research holds important reference value for fishery regulatory agencies in terms of supervising fishing vessels and maintaining a safe navigational distance.
1 Introduction
The Earth’s surface is covered by oceans, accounting for 71% of its total area. Oceanic fisheries play a crucial role in local, national, and global economies (Yan et al., 2022; Hong and Chun, 2023). Fishing vessel activities have consistently accounted for a significant proportion of the global maritime fleet. With the advancement of the Chinese Belt and Road Initiative and its policies on becoming a maritime power, the density of vessels in coastal waters has been steadily increasing (Yang et al., 2023). Additionally, China possesses abundant fisheries resources, with numerous fishing grounds scattered along its coast. Presently, China has a fleet of 73,100 fishing vessels, and its fishery production has increased from 5,219,850 t in 2005 to 80,420,190 t in 2019 (Sun et al., 2023). However, fishing vessel operations were characterized by complexity and variability. Not only do collisions between fishing vessels and other vessels occur frequently, leading to severe human casualties, but also they pose challenges in terms of regulating and supervising fishing activities (Obeng et al., 2022). Hence, identifying the behavioral characteristics of fishing vessels has become a key topic of concern for maritime regulatory agencies and fishery management departments, aiming to minimize collision accidents between commercial and fishing vessels.
Normally, ship trajectories, speed, and heading were considered key factors in studying ship behavior characteristics (Rong et al., 2019; Zhou et al., 2019). With the increasing deployment of AIS devices and Beidou navigation systems on fishing vessels, research on ship behavior characteristics based on big data has become a focal point for scholars (Gao and Shi, 2019; Wei et al., 2020; Murray and Perera, 2021). Trajectory prediction and anomaly detection were the mainstream research directions in studying ship trajectory characteristics. Extracting ship behavior characteristics and monitoring abnormal behavior through classification and clustering methods were the prevalent approaches in this research field (Naftel and Khalid, 2006; Espindle and Kochenderfer, 2009). As early as the emergence of AIS data, Suo et al. (2022) started to explore establishing mathematical models to classify the navigation behavior of different ships based on historical trajectory records. The support vector machine (SVM) was the most commonly used classification method due to its simplicity and robustness, which makes it favored by many scholars. Moreno-Salinas et al. (2013) utilized SVM for regression analysis to identify ship behavior characteristics and monitor abnormal behavior based on ship rudder angle, speed, and trajectory. In the research direction of classification, clustering was considered the foundation and prerequisite (Wei et al., 2022). However, sometimes the two were parallel. Zhou Yan proposed a two-step approach: first clustering the vessels and then classifying them based on their characteristics. The clustering results obtained through unsupervised learning can be used to describe the behavioral features of the vessels (Zhou et al., 2019). Among unsupervised clustering methods, k-means was a classic approach known for its fast convergence. Unfortunately, k-means were sensitive to complex noise points, which can result in inaccurate clustering. To address this limitation, Mingyang Zhang combined two big data clustering methods, DBSCAN and k-means, with CPA to effectively handle hydrological and meteorological information (Zhang et al., 2023b). These two methods belong to hard clustering, and in contrast, there was also a soft clustering method that performed well when the boundaries between clusters were not clearly defined. Gaussian mixture clustering represents a notable example of soft clustering. It reflects clusters through probabilities, where points closer to the center have higher probabilities (Hong and Chun, 2023). This aligns with potential collision points surrounding vessels. To identify the spatiotemporal features of ship trajectories, Gao Ming has improved the sliding window algorithm for extracting trajectory feature points, resulting in enhanced accuracy and efficiency of feature extraction (Gao and Shi, 2019). Currently, interdisciplinary research and the adoption of technical approaches from neighboring disciplines have received significant attention in the study of ship behavior characteristics. Inspired by the automotive industry, artificial intelligence algorithms have been widely applied to ship trajectory prediction (Papageorgiou et al., 2022; Zhu et al., 2022; Chen et al., 2023a). Many scholars utilize machine learning, deep learning, neural networks, and other artificial intelligence algorithms to integrate AIS, radar, electronic charts, VTs, and other data sources for real-time prediction of ship trajectories based on their past behavior patterns (Espindle and Kochenderfer, 2009; Moreno-Salinas et al., 2013; Zhao and Roh, 2019; Perera, 2020). These methods were effective in extracting ship behavior characteristics from speed and heading features.
Ship motion was influenced by various factors such as vessel performance, hydrological characteristics, and meteorological conditions. Analyzing the impact of these environmental factors from the perspective of ship motion dynamics can reveal the mechanisms behind ship trajectory. Ship motion involves six degrees of freedom, making the trajectory characteristics inherently complex (Zhang et al., 2023c). However, fishing vessels have a lower tolerance to natural environments compared with general cargo vessels. Moreover, fishing vessels were influenced by fishing operations and fish movement, resulting in complex and highly uncertain trajectories. This poses a significant challenge in determining the characteristics of fishing vessel motion (Wang et al., 2023). Interestingly, in the field of information technology, mathematical methods were often employed to simplify and establish patterns in the processing of complex signals. Fortunately, in the field of information processing research, signals often exhibit highly complex characteristics. For example, through methods such as Fourier transform, wavelet transform, ST (singular transformation), and W-V (Wigner-Ville) transform, these complex signals could be transformed into regular and traceable patterns (Neild et al., 2003; Khalid, 2010; Bhat and Dar, 2023; Li et al., 2023). The Fourier series has wide applications in various industries including industrial, optics, chemistry, materials, and information technology. It allows for the conversion of complex information into simpler, regular patterns (Ricaud et al., 2019). This technique has also been applied and adapted in research areas such as video trajectory recognition and identification of object motion features. When it comes to extracting spatial trajectory features, least squares polynomial fitting was suitable for modeling simple motion trajectories in the spatial domain. Vehicles moving uniformly along a highway serve as the best example. Furthermore, it can also be used to smooth the x–y projection of more complex spatiotemporal trajectories (Nanayakkara and Abayaratne, 2003). In highly complex spatiotemporal trajectory research, the Chebyshev and Fourier series were highly compatible (Cui and Ng, 2004). The aforementioned studies have shown that the Fourier series has demonstrated good performance in video motion target detection and spatiotemporal trajectory classification (Naftel and Khalid, 2006; Khalid, 2010). The trajectory of a fishing vessel was a three-dimensional trajectory consisting of both the temporal dimension and the two-dimensional plane motion. From a physical perspective, the trajectory of a fishing vessel can be seen as the projection of the three-dimensional trajectory onto the time axis. Mathematically, this two-dimensional coordinate can be regarded as the projection of complex numbers onto the complex function plane. Therefore, to identify the trajectory features of fishing vessels, this paper proposes a complex trajectory identification model involving the Fourier transform. The idea of addressing the complexity of fishing vessel motion trajectories by processing complex information into simpler signals was rare in the research field of ship trajectory complexity characteristics. Moreover, accounting for the uncertainty of vessel motion was a prominent topic in studying ship trajectory characteristics (Zhang et al., 2023a). The current mainstream approach involves probabilistic descriptions of this uncertainty. As previously mentioned, Gaussian mixture clustering, which utilizes probability to describe clustering features, aligns well with the potential collision probabilities of vessels. It can be effectively employed to characterize the uncertainty in fishing vessel motion trajectories.
This paper makes a dual contribution. On the one hand, it proposes a novel method for fishing vessel trajectory identification by utilizing the Fourier series to address the complexity of fishing vessel trajectories. On the other hand, it explores the compatibility between Gaussian mixture clustering and collision probabilities to address the uncertainty in fishing vessel motion. The organization of the remaining sections was as follows: Section 2 provides the workflow and describes the data sources and formats. It also explains the mapping relationship between fishing vessel trajectories and the complex plane and provides relevant theoretical knowledge of the Fourier transform. Section 3 presents the analysis of the results obtained from applying the proposed method. Section 4 discussed the characteristics of the phase spectrum of fishing vessel trajectories under different operating modes and the issue of uncertain motion range of trajectories. Finally, the research findings of this article are presented in Section 5.
2 Data and methods
2.1 Methods framework
In the field of fishing vessel behavior characterization, the extraction of trajectory features was a critical research area. However, due to the influence of fish schools and fishing patterns, the behavior characteristics of fishing vessels vary with different operation modes. This results in significant uncertainty and complexity in fishing vessel trajectories (Li et al., 2022; Gao et al., 2023). Undoubtedly, this adds to the difficulty of fishing vessel identification. Therefore, this paper aims to find a method to identify simple motion features from complex trajectories.
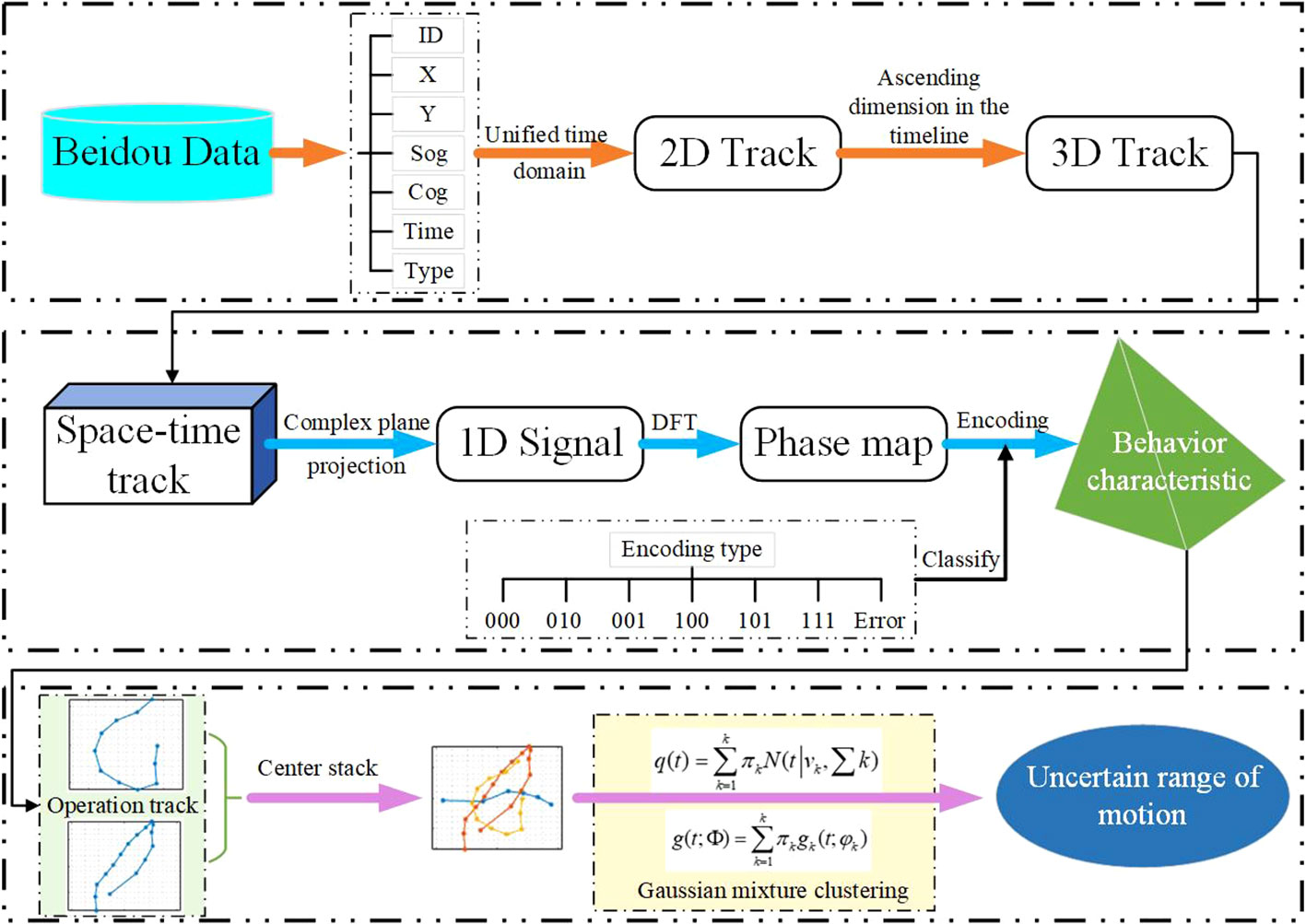
Fundamentally, fishing vessel trajectories consist of two-dimensional information. By employing mathematical methods, complex trajectories can be abstracted as information- processing problems and multidimensional fishing vessel motion trajectories were able to reduce to one-dimensional information. Thus, this paper proposed a fishing vessel complex trajectory identification model based on the Fourier series. Firstly, AIS data and Beidou data were filtered, cleaned, and interpolated to obtain continuous AIS and Beidou data for fishing vessels. Secondly, the data were divided into different operation modes based on vessel identification numbers. Then, the Fourier series was introduced to process the complex motion trajectories of fishing vessels and extract motion features. Ultimate, operation trajectories were identified based on the encoded features, thereby obtaining the range of uncertain motion. The specific workflow is illustrated in Figure 1.
The first step involves preprocessing the Beidou data to ensure data reliability. This process includes obtaining continuous ship data with equal temporal intervals. Relevant information such as time, position, speed, and heading would be selected and saved. Subsequently, a ship trajectory dataset was generated, which serves as the foundation for subsequent work. The 2D motion trajectory of the fishing vessel was reconstructed, while also increasing the dimensionality of the trajectory on the time axis.
Second, to analyze the spatiotemporal motion characteristics of the fishing vessel trajectory, a trajectory transformation model involving the Fourier series was constructed. The spatiotemporal characteristics of the trajectory were analyzed in the XOZ and YOZ projection planes under the three-dimensional motion trajectory. The mapping relationship of the trajectory in the complex plane was analyzed in the XOY plane. Based on this mapping relationship, the Fourier transform was applied to obtain the phase spectrum of the motion trajectory. The phase spectrum information was processed into a binary encoding (0–1) form. The original classification in the encoded form was obtained. The trajectory features of the ship were analyzed based on the encoding characteristics, while also discussing the feature variations caused by different operation modes.
In the third step, to explore the uncertainty of the fishing vessel’s motion, the trajectory abnormal region was extracted based on the encoding content. At last, the central positions onto the abnormal trajectory section, and the Gaussian mixture clustering was employed to obtain the uncertain motion range of the fishing vessel.
2.2 Data description
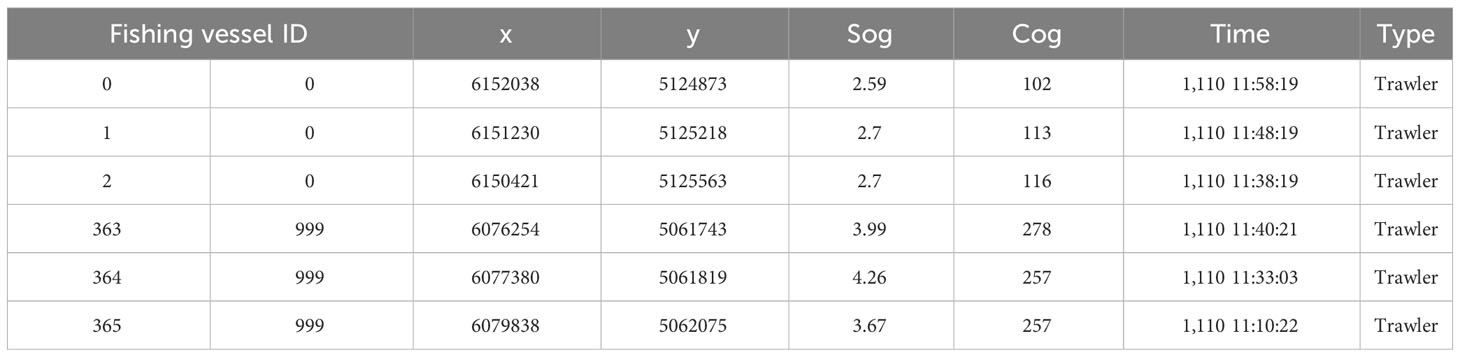
Chinese coastal areas were rich in fisheries resources, spanning the entire coastal region (Yang et al., 2023). Shanghai Port was the world’s largest port in terms of container throughput. During the fishing season, a large number of fishing vessels enter the waterway and navigate near commercial ships. The Beidou data from Shanghai Port was the most representative data for this study. The Beidou data were in the X–Y Cartesian coordinate system. However, the initial format of the Beidou data varies, necessitating preprocessing before experimental analysis was able to be conducted. The collection and preprocessing of the Beidou data were described in this section. This study used Beidou data to describe the behavior of ships. The Beidou Satellite Navigation System was a globally operated satellite navigation system built and operated by China, with a focus on national security and socioeconomic development needs. It provided users worldwide with all-weather, all-time, high-precision positioning, navigation, and timing services (Sun et al., 2022a). In recent years, the Beidou satellite positioning and navigation system has been widely applied in the field of fisheries production. This article’s data were sourced from Alibaba Cloud (https://tianchi.aliyun.com/dataset/50009). The data indicate that fishing vessels are distributed along the southeastern coast of China. This study was based on 11,000 fishing vessels, and the data were stored in CSV format, with each CSV file containing 300–600 records. Each record includes six pieces of information, which were fishing vessel ID, position (x, y), velocity, direction, time, and type, as shown in Table 1. The fishing vessels were divided into three operational modes, which were called trawler, gill netter, and purse seiner, based on the labeled fishing vessel types in the table. The classification results were then used for the analysis of fishing vessel operational mode characteristics. Heading, speed, and position were considered effective attributes for recording ship behavior. This study focused on the analysis of fishing vessel behavior characteristics in the context of uncertain and complex motion trajectories. Therefore, only the positional points of fishing vessels were considered in this study.
2.3 Problem description
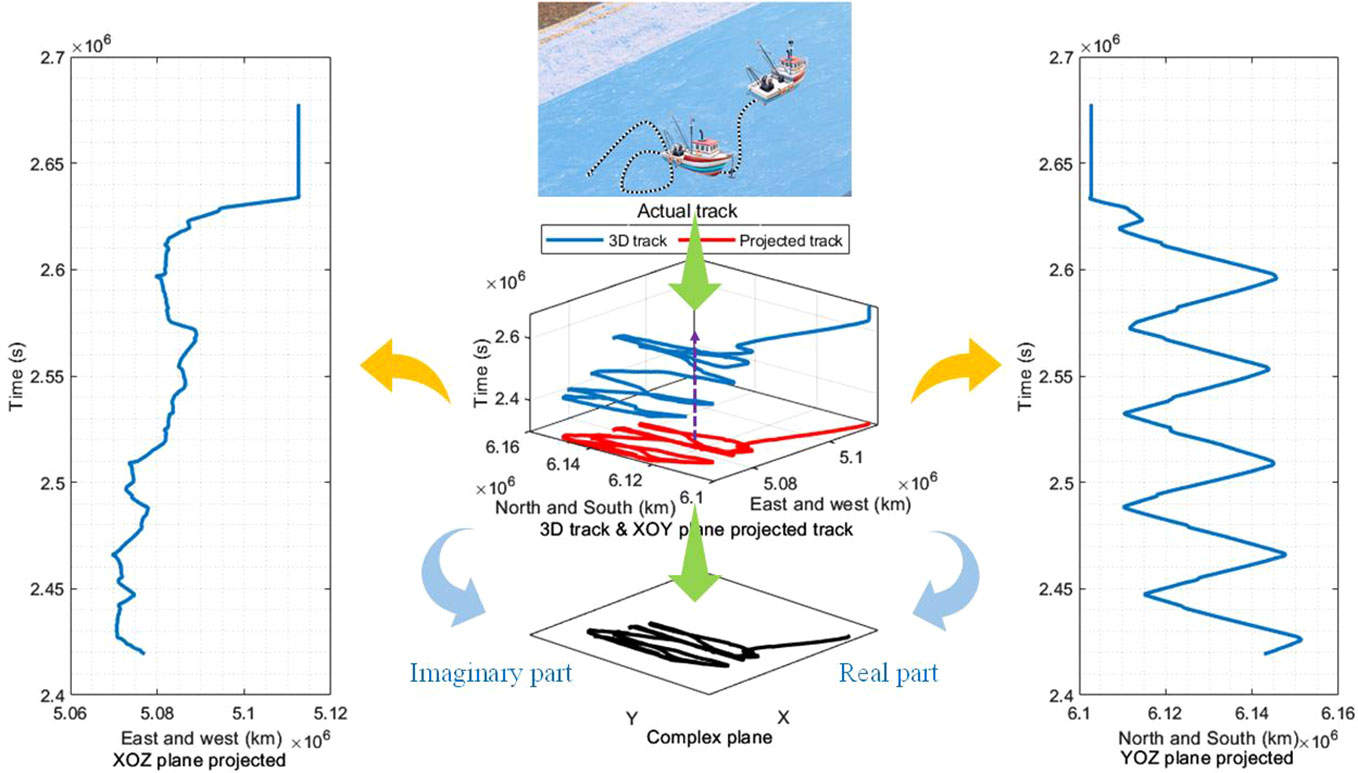
Currently, the trajectories of fishing vessels are influenced by various factors such as operational patterns, sea conditions, and fish movement. The entire trajectory of fishing vessels exhibited significant uncertainty, resulting in complex characteristics of their motion (Li et al., 2022). Research has found that the motion trajectory of fishing vessels tends to become more complex during fishing activities. However, apart from that, their motion characteristics were relatively simple. By elevating the dimensionality of a specific fishing vessel’s motion trajectory in the temporal dimension, this study aims to obtain the XOY projection, which represents the actual motion trajectory. The XOZ projection represents the motion trajectory of the y-axis in the time dimension, and the YOZ projection represents the motion trajectory of the x-axis in the time dimension. Hence, we can interpret the motion along these two axes as signal features. Fourier transform was then introduced for signal processing of the trajectory data (Khalid, 2010). If the projection of the XOY trajectory was mapped onto the complex plane, the real and imaginary parts in the complex plane correspond to the x and y motion trajectories (Nanayakkara and Abayaratne, 2003). Under this mapping relationship, the Fourier transform was utilized for fishing vessel trajectory identification. Figure 2 illustrates the above process in detail.
2.4 Modeling
2.4.1 Discrete Fourier series transformation
Every seemingly chaotic appearance in the world was an irregular curve on a timeline, and in fact, these curves are composed of infinite sinusoidal waves. The Fourier series perfectly explained this law. This study recorded the movement trajectory of fishing vessels on nautical charts, with each position embodying a time attribute. We abstracted it into a mathematical concept by considering the projection of the moving object O in the (x, y) plane of the image. O records its position in the (x, y, t) space at each moment in time. Therefore, we can define the movement trajectory of the fishing vessel (Naftel and Khalid, 2006; Khalid, 2010):
The equation, , represents the set of fishing vessel movement positions in space. By considering the trajectory as a motion under a time series, let k denote the length of the time series.
If we decomposed the fishing vessel movement trajectory into two separate one-dimensional time series for the horizontal and vertical displacements as and , respectively, where , then we can establish a complex motion trajectory identification model using the Fourier series.
If a condition was met, let us say the condition , then the spatiotemporal trajectory of the fishing vessel can be represented by , in terms of one-dimensional time. The k-point discrete Fourier transform (DFT) of was defined as the sequence of k complex numbers , as given by Equation (2). Similarly, an expression for , can be provided in Equation (3).
where . Generally, the DFT sequence was truncated after n terms, . Here, and signify real values. In this scenario, the motion trajectory feature vectors and consist of 2n+2 entries for each time series, encompassing both the real and imaginary parts.
It was commonly understood that there exists a mapping relationship between the complex plane and the real plane, which can be represented as
The mapping transforms points on the plane into complex number form, where the real part represents the horizontal coordinate on the plane, and the imaginary part represents the vertical coordinate on the plane.
2.4.2 Gaussian mixture clustering based on location relation
The movement of a fishing vessel was a stochastic process, and its positional distribution can often be described using a probability distribution. The Gaussian mixture model (GMM) was a probabilistic model composed of multiple Gaussian distributions weighted and combined. Each Gaussian model represents a class, so the number of models needs to be determined before training the model (Zhao et al., 2012; Hong and Chun, 2023). Assuming we have sample data , if the data follow a Gaussian distribution, the probability density function is given by
In the context where v represents the model expectation, it was commonly approximated using the sample mean. Similarly, , which represents the model variance, was typically approximated using the sample variance. Assuming there are k Gaussian distributions mixed with certain probabilities, we obtained a Gaussian mixture model composed of k Gaussian distributions. Mathematically, it can be represented as
This equation, , represents the mean of the kth class of sample data, and represents the covariance matrix of the kth class of sample data
In the given equation, represents the distribution density of the kth component, whereas represents the mixing probability for the kth component, with its parameters denoted as . The unknown parameters in the equation were collectively denoted as .
3 Results
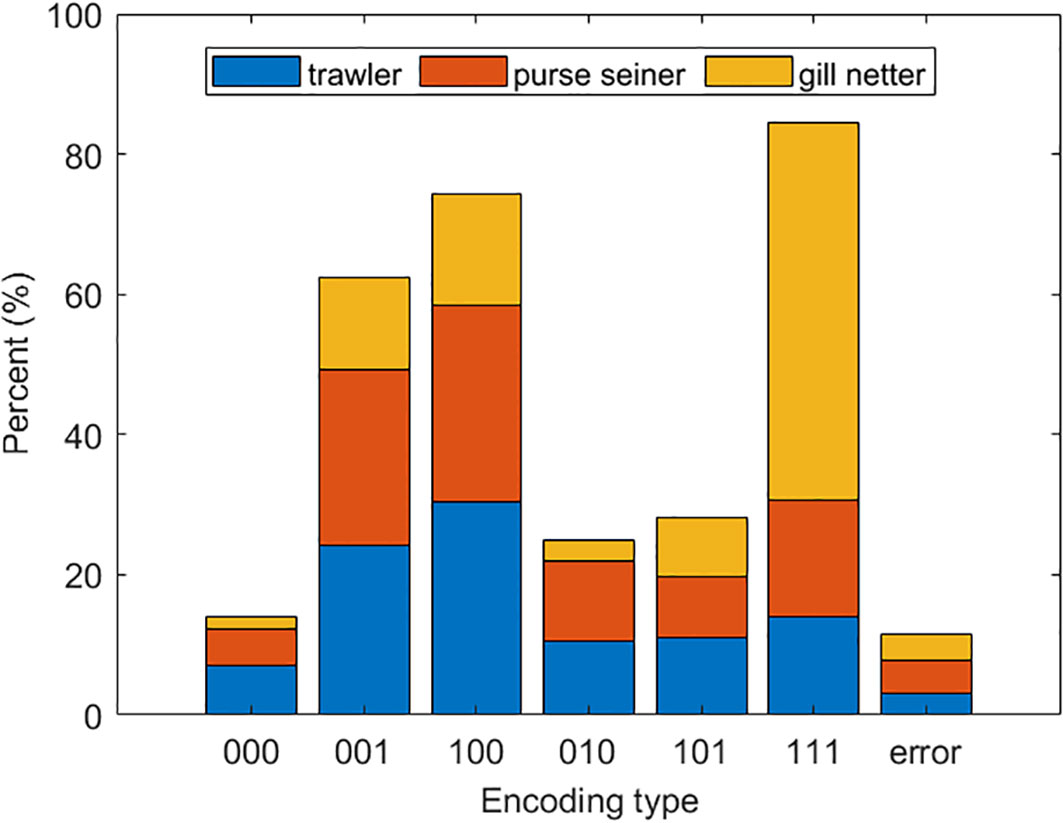
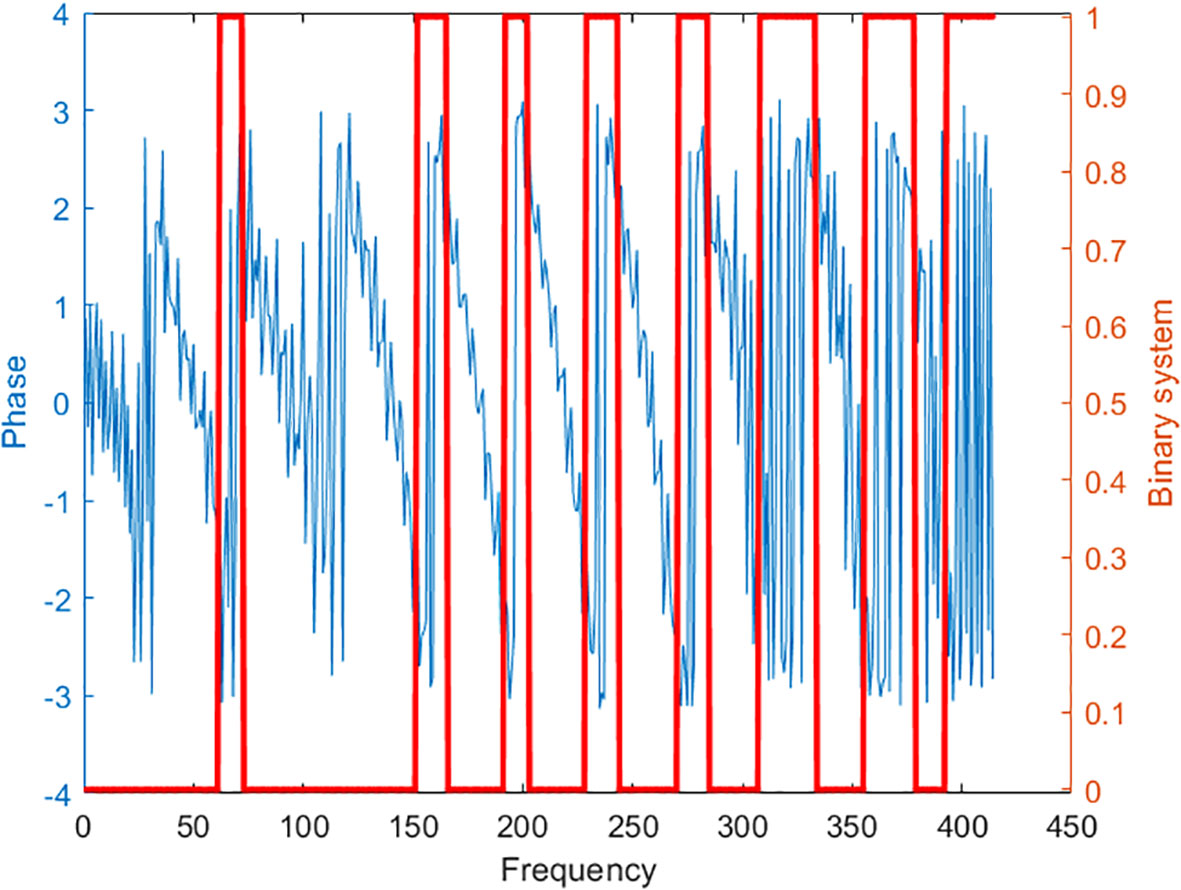
To investigate the spatiotemporal characteristics of fishing vessel trajectories, an analysis of the phase spectrum features based on the Fourier transform results was required. In this section, the phase spectrum was subjected to derivative processing, resulting in a transformation into a binary coding pattern of 0 and 1. However, after encoding the phase spectrum of 7,000 fishing vessel trajectories, it was observed that the phase spectra can be roughly classified into six encoding patterns. Figure 3 illustrates the composition of the six encoded patterns and their corresponding phase spectra. Through this encoded scheme, the seemingly chaotic phase spectra were categorized, which can facilitate the identification of fishing vessel motion states.
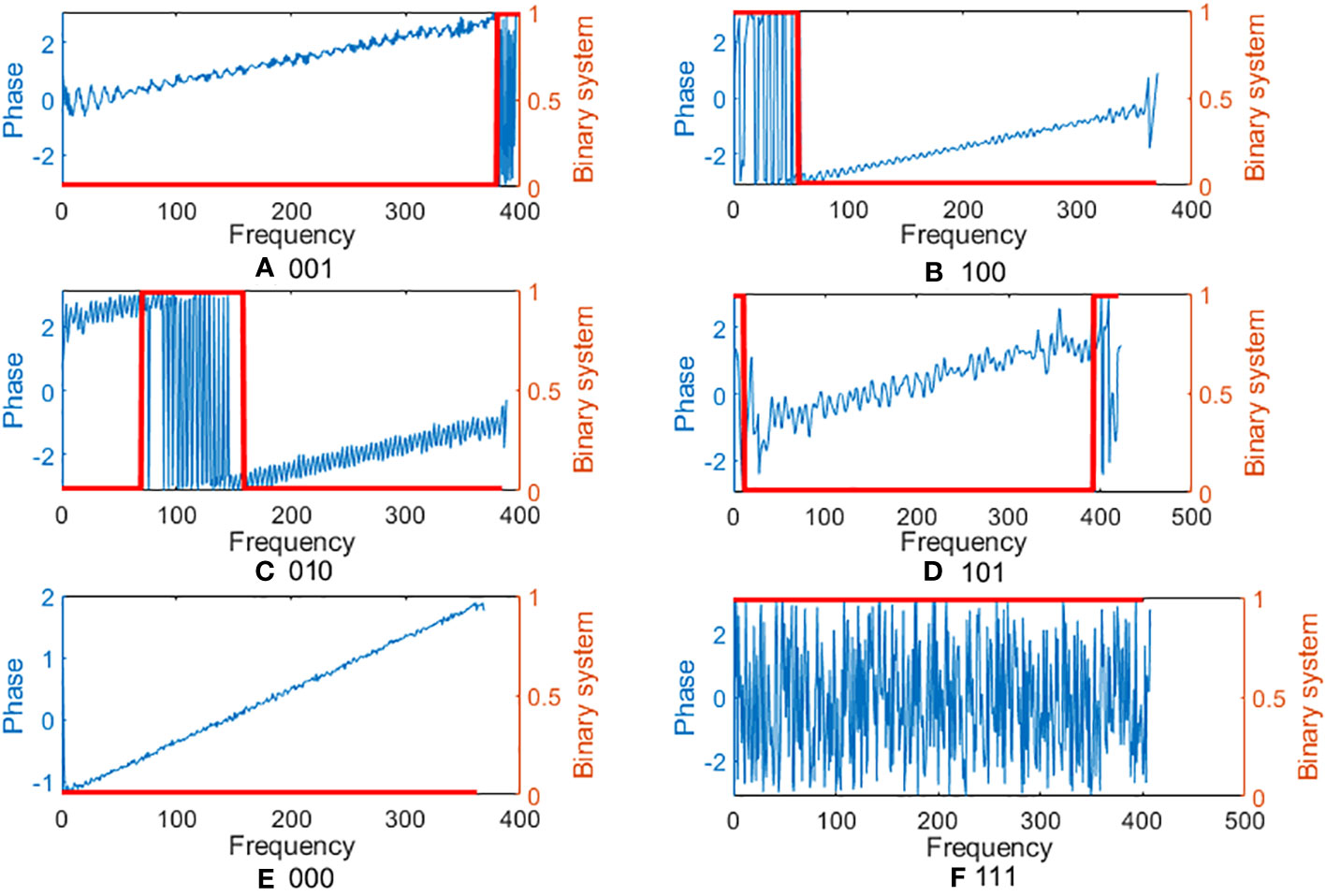
Figure 3 Phase spectrum characteristics of fishing vessel track. The six encoding formats: (A) 001, (B) 100, (C) 010, (D) 101, (E) 000, (F) 111.
3.1 Operation mode recognition based on fishing boat trajectory
According to the International Regulations for Preventing Collisions at Sea (COLREGs), a fishing vessel was defined as any vessel that was engaged in fishing activities using fishing gear such as a trawler, gill netter, and purse seiner, or any other equipment that restricts its maneuverability (Domeh et al., 2023). However, it did not include vessels that were fishing using trolling gear or any gear that did not restrict their maneuverability. The regulations clearly state that there were different responsibilities between powered vessels and fishing vessels. Therefore, based on the responsibilities they undertake, fishing vessels can be categorized into three states during their maritime navigation: underway (not engaged in fishing operations), underway fishing (engaged in fishing operations), and at anchor. To identify the underway and fishing operation patterns of fishing vessels, this section used the projection relationship of fishing vessel positions onto the complex plane mentioned before. After performing the Fourier transform on the vessel trajectories, it was observed that the Fourier transform phase spectrum of the vessel trajectories consists of long waves and short waves. In this study, the long waves were represented as 1, whereas the short waves were represented as 0, as shown in Figure 4A. Figure 4B illustrates that each trajectory’s phase spectrum was composed of 0 and 1, with 1 representing the long wave component corresponding to the anomalous positions in the trajectory shown in Figure 4C. In Figure 4C, the two-dimensional trajectory of the fishing vessel was presented below the time axis, forming a three-dimensional positional relationship to analyze the relationship between vessel trajectory changes, phase spectrum, and velocity. In the vessel’s motion trajectory, the directly relevant factor was the vessel’s velocity. In Figure 4D, the influence of velocity on anomalous trajectories can be observed. This provides sufficient evidence to verify the accuracy of detecting anomalous vessel actions using relatively common long waves. Here, anomalous vessel actions refer to irregular variations in speed and heading during fishing operations. Therefore, the detected anomalous vessel actions correspond to the fishing vessel’s operational periods.
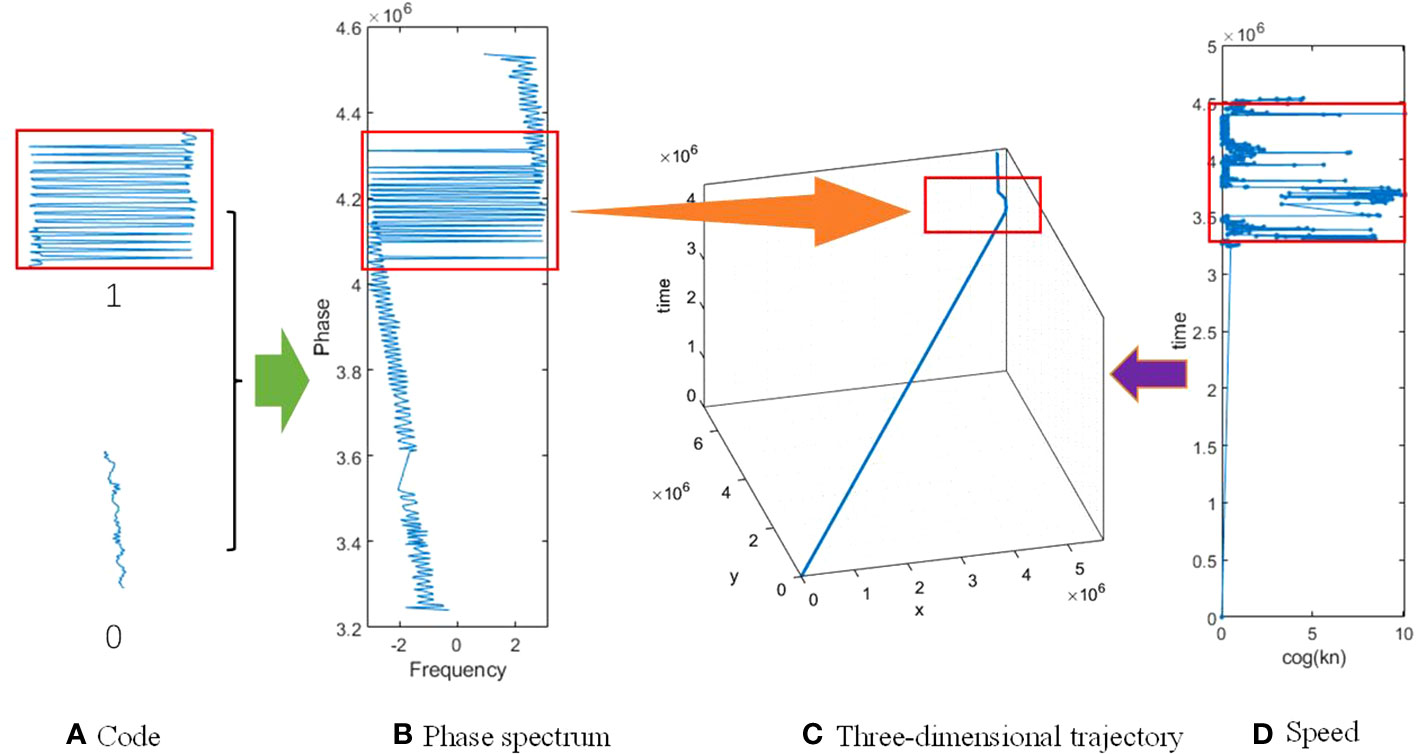
Figure 4 Identification of fishing vessels in navigation state and operation. (A) Code, (B) Phase spectrum, (C) Three-dimensional trajectory, (D) Speed.
3.2 Motion track characteristics of fishing vessels
To study the spatiotemporal motion characteristics of fishing vessel trajectories, signal processing methods can be applied to transform the trajectories. The phase spectrum, which was the result of the Fourier transform of the fishing vessel trajectory, exhibits distinct features. It was composed of 0 and 1. As mentioned earlier, coding 1 corresponded to the state of anomalous vessel actions, whereas 0 corresponded to the state of normal vessel heading. With the presence of this coding, it became easy to identify the behavioral state of the fishing vessel during its navigation process. Thus, in Figure 3, 001, 100, 010, 101, and 111 can be interpreted as instances of abnormal fishing vessel behavior, whereas 000 can be interpreted as the vessel being in a normal navigation state with regular motion patterns. Table 2 describes the classification results of the fishing vessels using six coding formats. However, there were still 4% of cases that were not included. From the coding distribution, it can be concluded that fishing vessels rarely exhibit regular navigation states. Therefore, identifying the uncertain motion of fishing vessels has always been a focal point of research. Furthermore, the presence of 111 indicated that even in a considerable length of time, nearly 21% of fishing vessels exhibit abnormal behavior. Meanwhile, the classification results of 001, 101, 100, and 010 indicated that fishing vessel motion trajectories were complex and highly uncertain. They can transition from navigating to conducted fishing operations for a certain period and then revert to normal navigation. This made it challenging to predict the future motion trajectories and states of fishing vessels at any specific time interval.
3.3 Analysis of differences in fishing vessel operation patterns
Different fishing operations were able to classify into trawler, gill netter, and purse seiner (Darasi and Aksissou, 2019). In the dataset, there happen to be samples representing these three categories. To explore the distribution of different fishing modes under the six coding states, this study classified the vessels according to their operation modes. In Figure 5, it was evident that gill netter occupied a relatively large proportion within the entire 111 coding format. This finding was closely related to the operational characteristics of gill netter fishing vessels. In practice, during the process of deploying gill netter, fishing vessels need to move slowly or remain stationary on the sea surface to fully spread the nets in the designated fishing area. Once the nets were successfully deployed, the vessels initiated the dragged operation. Due to the strong water flow and the inertia of vessel motion during gill netter dragging, the vessels often undergo rotational movements (Kim et al., 2014). As a result, the motion trajectories of gill netter vessels frequently change. Compared with the regular motion pattern represented by the 000 coding mode, the proportion of 111 coding modes in gill netter vessels was particularly low. This aligns with the unique operational characteristics of gill netter vessels. Regarding purse seining operations, after selecting the fishing area, purse seine fishing vessels need to deploy the nets, and they may remain static or move slowly to accomplish this task (Granado et al., 2023). During purse seining operations, the motion of fishing vessels was relatively stable. After successfully deploying the nets, the vessels need to operate by hauling the nets. This process was generally intense and required the cooperation of fishermen. They collected the nets from all sides using lifting and closing techniques, based on the shape and size of the purse seine. Similarly, in trawler operations, fishing vessels tow the trawl nets at a constant or variable speed on the sea surface. The propulsion generated by the vessel was transmitted to the trawl nets through the towing cables, causing lateral and vertical displacement of the nets. At the same time, the trawl nets exert a certain drag force on the vessel, resulting in lateral and vertical displacement motions of the vessel. These motions were regular. However, in trawling operations, the resistance and friction generated by the nets in the seawater caused a decrease in the vessel’s speed. Moreover, during trawler operations, factors such as wind direction, water currents, and vessel speed frequently lead to rotational movements of the fishing vessels (Obeng et al., 2022). The motion patterns of vessels during trawler and purse seiner operations precisely reflected the combination of operational and navigational patterns. This aligns well with the coding patterns of 010, 001, 100, and 101 obtained in this study.
3.4 Trajectory anomaly monitor and analysis
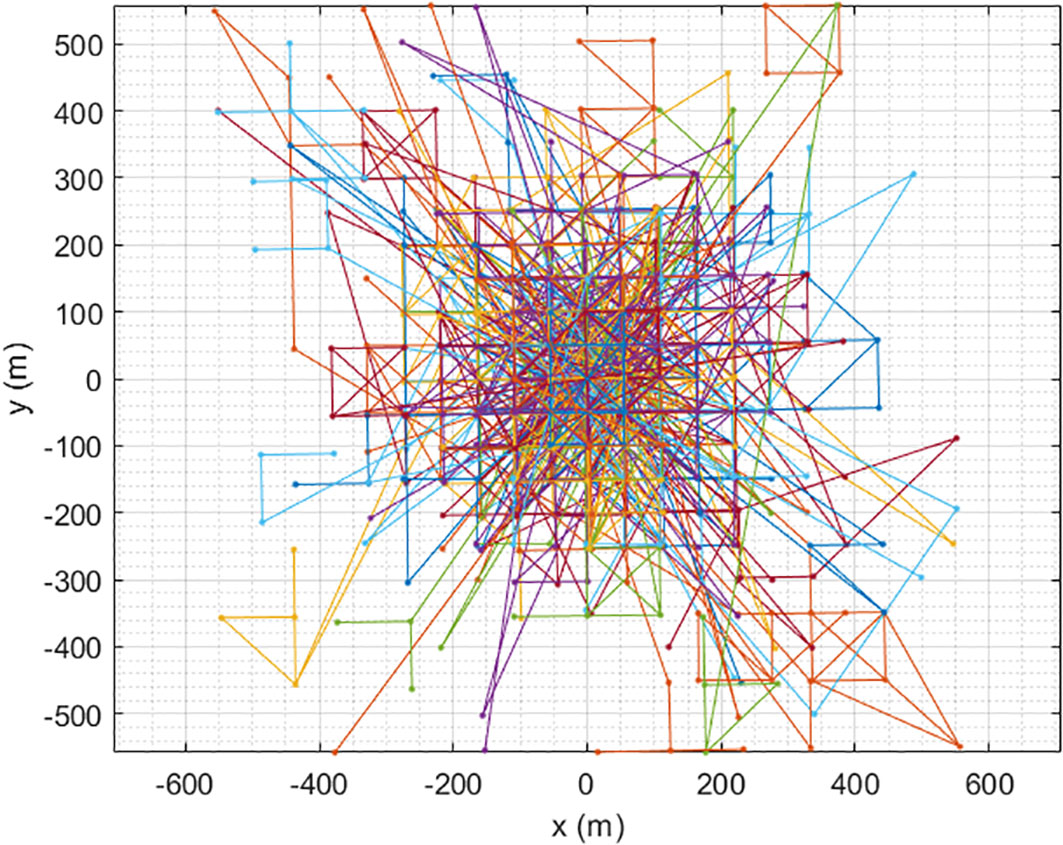
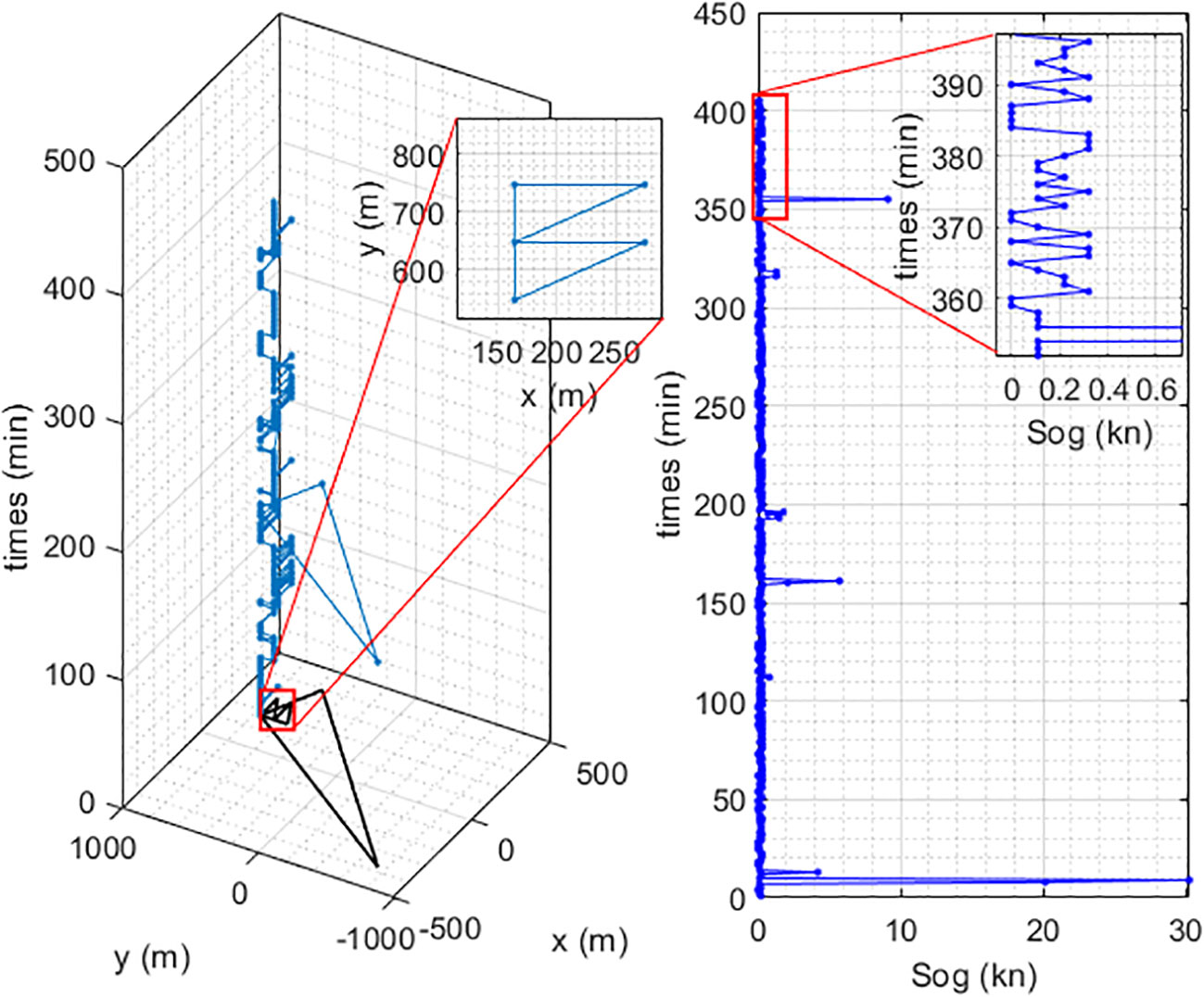
In the trajectory observations of the classified results, it was found that there was a certain type of anomalous vessel behavior in the seventh coding category, which cannot be categorized into the six coding formats, as shown in Figure 6. In this coding format, 0 and 1 cross each other. Therefore, based on the results of the anomalous coding, this study traced back to the trajectory states of the fishing vessels. It was found that fishing vessels in this coding state exhibit two characteristics in Figure 7. On the one hand, the range of vessel trajectory movement was limited to a radius of around 500 m. On the other hand, the distance between adjacent jump points was between 100 and 300 m. Since the time interval used in this study was 10 min, considering that even if a fishing vessel anchors, it would still be influenced by the water currents. Previous studies that used Beidou data to investigate fishing vessel operation characteristics had suggested that vessel speeds in anchored situations were around 0.3 m/s, influenced by water currents (Li et al., 2021). To analyze the reasons for the positional jumps, Figure 8 illustrates a single trajectory and the corresponding relationship between the trajectory and velocity. The left-magnified image shows the projection of the trajectory on the XOY plane. It can be determined that the fishing vessel’s position jumps between 100 and 200 m. The right magnified image illustrates the variation in the vessel’s speed during a certain period. It can be determined that the vessel is not in a completely stationary state. Instead, it was moving at a speed of 0.2 knots. Therefore, it can be concluded that the jumps in the fishing vessel’s position are due to this speed variation. This speed variation was closely related to the dynamics of vessel motion (Zhang et al., 2023c). As far as we were concerned, speed changes may be influenced by two behaviors. On the one hand, vessel drift occurs due to water currents, resulting in a migration of approximately 100 m within 10 min. On the other hand, to keep the vessel stable in a specific position, the operator applies a certain speed to counteract the water current and return to a relatively stable position. It was generally understood that within a 10-min time interval, the vessel moves approximately 100 m during this process.
3.5 Analysis of an uncertain range of motion of fishing vessels
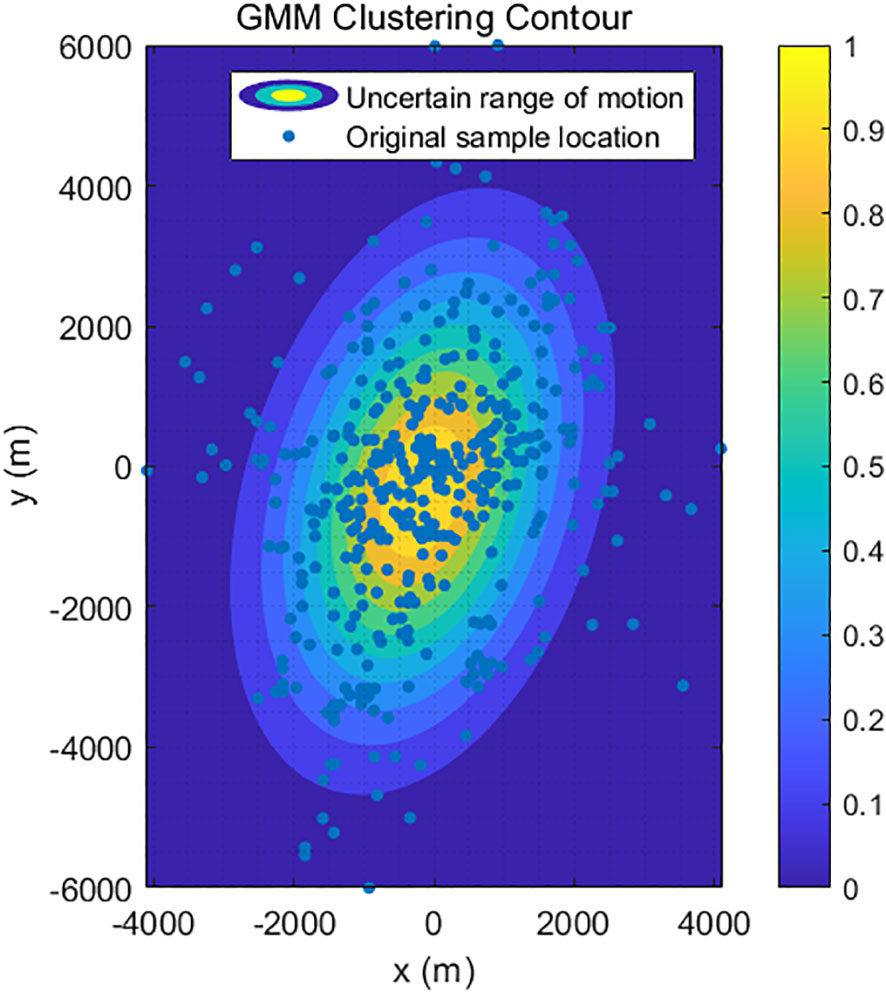
The abovementioned research confirmed the existence of uncertainty in fishing vessel motion trajectories. To address the uncertainty associated with complex vessel motion, this study analyzed the motion characteristics of fishing vessels in different operation modes. It was found that the coding feature of 1 in the phase spectrum is closely related to fishing vessel operations and exhibits a strong correspondence. Moreover, this study interpreted abnormal vessel behavior in terms of turning, looping, and circling movements. By extracting the positions during the segments with coding 1, the study effectively obtains the periods of fishing vessel operations, especially during periods of complex trajectory changes. From a God’s-eye view, the motion of these fishing vessels with complex movements will always be uncertain. Other vessels cannot predict the future motion states of fishing vessels through conventional means. However, it can be imagined that fishing vessels move within a certain range of uncertainty. If this uncertain range of motion can be identified, it means that the safe zone of the fishing vessel has been identified. Based on this idea, the study applies relative range processing to the extracted operation trajectories and then superimposes the trajectory segments of each vessel to obtain the distribution of fishing vessel motion positions within a certain range. As shown in Figure 9, this study applied Gaussian mixture clustering to the position features and processed them accordingly. The uncertainty range was represented by the probabilities of the Gaussian mixture model. The corresponding range with a probability of 0.8 was approximately 1,000 m, whereas the range with a probability of 0.5 is around 2,000 m. Fishing vessel distribution beyond 4,000 m was relatively rare.
4 Discussion
4.1 Advantages and limitations
The proposed method in this paper takes into consideration the complex nature and uncertainties associated with the motion trajectories of fishing vessels during navigation. Unlike most existing methods, this approach employs mathematical reasoning to study the characteristic patterns of complex vessel trajectories. By projecting the trajectories onto the complex plane and introducing the Fourier transform, the complex trajectories were made regular and predictable. This approach was considered cutting-edge and uncommon in the research of vessel trajectory characteristics. Furthermore, coding methods from signal processing are adapted to encode the results of the Fourier transform. The encoded results not only enable the classification of trajectory characteristics and identification of habitual motion patterns of different fishing vessels but also facilitate the extraction of operational feature segments from complex trajectories. In similar studies, SVM and LSTM were considered state-of-the-art methods in ship trajectory classification research, with accuracy rates typically ranging from 70% to 80% (Sun et al., 2022b). In the research of using satellite images for detecting target vessels, the AirSAR ship was a highly accurate technique, with an accuracy level of approximately 91.11% (Yasir et al., 2023). CNN and deep learning were considered advanced and mainstream methods, achieving an accuracy of 92.5% (Xie et al., 2023). By simplifying the ship’s motion trajectory, Chen was able to increase the recognition rate to 95.5% (Chen et al., 2023b). The indirect results in Table 2 indicate a correct classification rate of approximately 96% for the proposed method. The observed results demonstrate a significant improvement in the overall performance. Finally, Probability was considered an effective descriptor for ship collision point detection (Hong and Chun, 2023). Similarly, we observe a high level of compatibility between the uncertainty of fishing vessel motion trajectories and Gaussian mixture clustering. Gaussian mixture clustering was applied to these operational feature segments to obtain the uncertain motion range of fishing vessel trajectories. Unlike the traditional approaches based on extreme distances for motion and boundary determination, the clustering results demonstrate robust timeliness and comprehensiveness. This not only allows for the delineation of uncertain motion boundaries based on probabilities but also presents the probability-based representation of any potential motion in the surrounding area to other vessels.
This study proposes, for the first time, the use of the Fourier series to analyze ship motion trajectories. Although the results have shown promising outcomes, there is still ample room for improvement in this area of research. In Section 3.3, an analysis of the identification capability of the codes in different operational modes is presented. For instance, the gill netter can be well identified using the coding of 111. However, in terms of identification coverage, there were limitations. It was not possible to include all operational modes within the six codes. For example, although the coding of 111 includes a large number of gill netter operational modes, approximately 30% still come from the other two modes. In the case of the 000 code, it can effectively identify cases that do not belong to the gill netter. However, there was a possibility of 5% of cases being mixed with the other two modes. Furthermore, in the coding identification results, there remain approximately 4% of cases that cannot be covered by the six codes, leading to the occurrence of the cross-interference of 0 and 1 codes mentioned in Section 3.4. This paper has downplayed the role of ship kinematics, which may serve as a crucial focus for future research. Exploring the influence of ship motion dynamics could provide valuable insights and contribute to further advancements in this field.
4.2 Relationships among trajectory, complex plane, and Fourier series
As is widely known, the motion trajectory of a vessel was, in fact, the projection of the vessel’s temporal movement on the XOY plane. For complex numbers, their geometric interpretation was in the two-dimensional plane as vectors. Specifically, complex numbers were regarded as linear mappings on the complex plane. Mathematical theorems informed us that linear mappings inevitably transform straight lines into straight lines and circles into Fourier series. Hence, it was understood that the vessel’s motion trajectory could be represented in the complex plane using complex numbers through linear mappings. Fourier series revealed that any periodic function could be expressed as an infinite series composed of sine and cosine functions. In this context, Euler’s formula played a crucial role as it facilitated the transformation of the trigonometric form of the Fourier transform into a complex number form. However, Fourier series could only transform periodic time domains into non-periodic frequency domains, which means it could express waveforms of periodic transformations as simple superpositions of sub-waveforms. It was capable of decomposing complex signals into simpler ones for separation. Nonetheless, its limitations resided in its support solely for periodic time domains. Unfortunately, real-world trajectories exhibited seemingly chaotic non-periodic motions. Fourier transforms precisely expressed non-periodic time domains in non-periodic frequency domains. Therefore, the motion trajectory of a fishing vessel could be associated with Fourier series, linearly mapping the complex motion trajectory onto the complex plane. In fact, the application of Fourier series found widespread use, particularly in signal processing where it proved to be highly effective. It offered the means to extract periodic components from complex signals. This line of reasoning remained equally applicable in trajectory motion analysis. Based on time-frequency distribution, multiple periodic motions could be extracted to address complex motion problems (Briassouli and Ahuja, 2007).
4.3 Applications
Fishery regulation has always been a topic of great significance within the fishery administration. The sustainable development of the fishery industry, the practice of rational fishing, and the reinforcement of regulatory efforts have garnered strong attention from regulatory authorities. Identifying fishing behavior patterns was an effective way to combat illegal fishing and monitor excessive fishing. In the past, the concealment of fishing vessel data posed the greatest challenge to identifying fishing behavior patterns. Nevertheless, with the continuous release of AIS (Automatic Identification System) and BeiDou data, a foundation has been laid for using big data to study fishing vessel behavior patterns. Previous studies based on AIS data have shown significant differences in operational trajectories among different types of fishing vessels. The proposed fishing vessel trajectory identification model involving the Fourier transform can effectively identify the operational patterns of fishing vessels from BeiDou data. The identification results can provide a strong basis for regulatory enforcement by fisheries authorities.
Furthermore, situational awareness was the first step in ship collision avoidance. Howbeit, fishing vessels may not always adhere to COLREGs and often exhibit complex motion during navigation (Zhang et al., 2021b). The issue of uncertainty in fishing vessel motion trajectories due to their complex behavior was a focal topic in the study of automatic collision avoidance. The ability of merchant ships to accurately assess the actions of fishing vessels during navigation was crucial for successful avoidance. Assigning specific codes to fishing vessel trajectories can effectively identify their operational behavior patterns. The Gaussian mixture clustering model can be used to cluster operational trajectory segments, addressing the issue of uncertainty in fishing vessel motion. The uncertain motion range described in Section 3.5, ranging from 1,000 to 2,000 m, can serve as a reference for merchant ships to navigate around fishing vessels. In maritime navigation, there was a consensus that collision risks already exist within a range of 1–2 nautical miles (Zhang et al., 2021a). In the field of fishing vessel research, some scholars have defined the safe distance for fishing vessels as 1 nautical mile (1,852 m) (Fukuto and Imazu, 2013). Sheng-Long Kao’s fishing vessel safe avoidance zone defines the safe areas for nine operation modes, including single-line, longline, trawler, gill netter, and purse seiner. He suggested that a range of 1.5–1.6 nautical miles was considered safe (Kao and Chang, 2017). The Chinese fishing vessel guidelines stipulate that fishing vessels should maintain a distance of 1 nautical mile when navigating through fishing zones (MSA, 2021). According to the safety operation distance and rules for Chinese and Korean fishing vessels, both sides of trawler vessels should not pass within 2,000 m ahead of the vessel that was currently trawling, which could hinder its operations. It is generally accepted in ship-to-ship encounters between merchant vessels and fishing vessels that the probability of collision within a distance of 1 nm is approximately 70% (Zhu et al., 2023). This finding confirms the reasonableness of considering a fishing vessel’s uncertain movement range to be around 1 nm. Hence, the uncertain motion range of fishing vessels in this study roughly aligns with the established safe distances in China. Compared with other countries, the range was relatively larger, indicating a safer distance.
5 Conclusions and future work
The present study discussed the identification issue of complex fishing vessel trajectories and their uncertain motion range. The implemented fishing vessel trajectory identification model in this research is capable of effectively discerning the operational types of fishing vessels and providing a secure estimation of the uncertain movement range of the vessels.
First of all, a fishing vessel trajectory identification model involving the Fourier transform was constructed. The phase spectrum was encoded with a 0–1 format by taking the derivative of the phase spectrum. The operational states of the fishing vessel were represented by six valid encoding formats: 000, 001, 010, 100, 101, and 111. Among these formats, 0 corresponded to regular fishing vessel trajectories, whereas 1 corresponded to complex fishing vessel trajectories. Comparative analysis and discussions were carried out on three different operational modes, revealing that the obtained encoding formats effectively interpreted the operational states of different fishing vessels.
Next, in this study, the complex trajectories were extracted and overlaid using a center-to-center superposition approach. The uncertain motion range of the fishing vessel trajectories was obtained through Gaussian mixture clustering. The results showed that the probabilities of the fishing vessel trajectories were distributed around 1,000 m with an 80% confidence level and around 2,000 m with a 50% confidence level. The study demonstrated the consistency between the obtained uncertain motion range of the fishing vessels and the safety distances for fishing vessels in different countries, which was broader and safer.
Last but not least, this research not only contributes to the identification and control of fishing vessels by fisheries regulatory authorities but also provides effective reference safety distances for commercial vessels to ensure safe navigation with fishing vessels. Furthermore, the final uncertain motion range will be used in the avoidance process of encounters between commercial and fishing vessels in complex water areas. This method will provide commercial vessels with the uncertain motion range of fishing vessels, assisting them in avoiding the dangerous moving range of fishing vessels. The next phase of research will primarily focus on developing an automated collision avoidance system based on uncertain fishing vessel motion range and enhancing identification accuracy by considering ship kinematics.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
QZ: Formal Analysis, Investigation, Methodology, Software, Writing – original draft. YX: Funding acquisition, Validation, Writing – review & editing, Supervision. SH: Funding acquisition, Validation, Writing – review & editing, Conceptualization. YC: Formal Analysis, Investigation, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by funding from the National Key Research and Development Program of China (Grant No. 2021YFC2801005). The project is also supported by the National Natural Science Foundation of China (Grant No. 52272353).
Acknowledgments
The authors would like to thank the reviewers and editors for their comments which helped improve the paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bhat M. Y., Dar A. H. (2023). The two-sided short-time quaternionic offset linear canonical transform and associated convolution and correlation. Math. Methods Appl. Sci. 18, 8478–8495. doi: 10.1002/mma.8994
Briassouli A., Ahuja N. (2007). Extraction and analysis of multiple periodic motions in video sequences. IEEE Trans. Pattern Anal. Mach. Intell. 29, 1244–1261. doi: 10.1109/tpami.2007.1042
Chen X. Q., Wang Z. C., Hua Q. Z., Shang W. L., Luo Q., Yu K. P. (2023a). AI-empowered speed extraction via port-like videos for vehicular trajectory analysis. IEEE Trans. Intelligent Transportation Syst. 24, 4541–4552. doi: 10.1109/tits.2022.3167650
Chen X. Q., Wu H., Han B., Liu W., Montewka J., Liu R. W. (2023b). Orientation-aware ship detection via a rotation feature decoupling supported deep learning approach. Eng. Appl. Artif. Intell. 125. doi: 10.1016/j.engappai.2023.106686
Cui Y., Ng R. (2004). Indexing spatio-temporal trajectories with Chebyshev polynomials. Proc. ACM SIGMOD Conf. 18, 599–610. doi: 10.1145/1007568.1007636
Darasi F., Aksissou M. (2019). Longline, trawl, and purse seine in coastal fishing of Tangier port in North-West of Morocco. Egyptian J. Aquat. Res. 45, 381–388. doi: 10.1016/j.ejar.2019.11.005
Domeh V., Obeng F., Khan F., Bose N., Sanli E. (2023). An operational risk awareness tool for small fishing vessels operating in harsh environment. Reliability Eng. System Saf. 234. doi: 10.1016/j.ress.2023.109139
Espindle L. P., Kochenderfer M. J. (2009). Classification of primary radar tracks using Gaussian mixture models. Iet Radar Sonar Navigation 3, 559–568. doi: 10.1049/iet-rsn.2008.0182
Fukuto J., Imazu H. (2013). New collision alarm algorithm using obstacle zone by target (OZT). IFAC Proc. Volumes 46, 91–96. doi: 10.3182/20130918-4-jp-3022.00044
Gao D., Zhu Y., Guedes Soares C. (2023). Uncertainty modelling and dynamic risk assessment for long-sequence AIS trajectory based on multivariate Gaussian Process. Reliability Eng. System Saf. 230. doi: 10.1016/j.ress.2022.108963
Gao M., Shi G. Y. (2019). Ship spatiotemporal key feature point online extraction based on AIS multi-sensor data using an improved sliding window algorithm. Sensors 19, 17. doi: 10.3390/s19122706
Granado I., Hernando L., Uriondo Z., Fernandes-Salvador J. A. (2023). A Fishing Route Optimization Decision Support System: The case of the tuna purse seiner. Eur. J. Operational Res. 312, 718–732. doi: 10.1016/j.ejor.2023.07.009
Hong J., Chun H. (2023). A prediction model for healthcare time-series data with a mixture of deep mixed effect models using Gaussian processes. Biomed. Signal Process. Control 84. doi: 10.1016/j.bspc.2023.104753
Kao S.-L., Chang K.-Y. (2017). Study on fuzzy GIS for navigation safety of fishing boats. J. Mar. Eng. Technol. 16, 84–93. doi: 10.1080/20464177.2017.1291191
Khalid S. (2010). Motion-based behaviour learning, profiling and classification in the presence of anomalies. Pattern Recognition 43, 173–186. doi: 10.1016/j.patcog.2009.04.025
Kim S.-G., Lee W.-I. L., Yuseok M. (2014). The estimation of derelict fishing gear in the coastal waters of South Korea: Trap and gill-net fisheries. Mar. Policy 46, 119–122. doi: 10.1016/j.marpol.2014.01.006
Li H. S., Li G. Q., Xia H. Y. (2023). Three-dimensional quantum wavelet transforms. Front. Comput. Sci. 17, 14. doi: 10.1007/s11704-022-1639-y
Li M., Mou J., Chen P., Rong H., Chen L., Van Gelder P. (2022). Towards real-time ship collision risk analysis: An improved R-TCR model considering target ship motion uncertainty. Reliability Eng. System Saf. 226. doi: 10.1016/j.ress.2022.108650
Li J., Zhang P., Cai Y., Zhang Q., Zhang K., Jing Z., et al. (2021). Performance of VMS and nightly satellite in monitoring light fishing vessels in the open South China Sea. Fisheries Res. 243. doi: 10.1016/j.fishres.2021.106100
Moreno-Salinas D., Chaos D., de la Cruz J. M., Aranda J. (2013). Identification of a surface marine vessel using LS-SVM. J. Appl. Mathematics 11. doi: 10.1155/2013/803548
MSA. (2021). Safety guidelines for the prevention of collisions between merchant vessels and fishing vessels in Chinese Coastal Waters. Available at: https://info.chineseshipping.com.cn/cninfo/News/202105/t20210510_1352400.shtml?msclkid=ee19c2e8c78f11ec878c7edeefd81e2a.
Murray B., Perera L. P. (2021). An AIS-based deep learning framework for regional ship behavior prediction. Reliability Eng. System Saf. 215, 14. doi: 10.1016/j.ress.2021.107819
Naftel A., Khalid S. (2006). Classifying spatiotemporal object trajectories using unsupervised learning in the coefficient feature space. Multimedia Syst. 12, 227–238. doi: 10.1007/s00530-006-0058-5
Nanayakkara A., Abayaratne C. (2003). Identification of semiclassical chaos in two-dimensional PT-symmetric systems. Can. J. Phys. 81, 835–846. doi: 10.1139/p03-052
Neild S. A., Mcfadden P. D., Williams M. S. (2003). A review of time-frequency methods for structural vibration analysis. Eng. Structures 25, 713–728. doi: 10.1016/s0141-0296(02)00194-3
Obeng F., Domeh V., Khan F., Bose N., Sanli E. (2022). Capsizing accident scenario model for small fishing trawler. Saf. Sci. 145, 13. doi: 10.1016/j.ssci.2021.105500
Papageorgiou D., Hansen P. N., Dittmann K., Blanke M. (2022). Anticipation of ship behaviours in multi-vessel scenarios. Ocean Eng. 266, 15. doi: 10.1016/j.oceaneng.2022.112777
Perera L. P. (2020). Deep learning toward autonomous ship navigation and possible COLREGs failures. J. Offshore Mechanics Arctic Engineering-Transactions Asme 142, 10. doi: 10.1115/1.4045372
Ricaud B., Borgnat P., Tremblay N., Goncalves P., Vandergheynst P. (2019). Fourier could be a data scientist: From graph Fourier transform to signal processing on graphs. Comptes Rendus Physique 20, 474–488. doi: 10.1016/j.crhy.2019.08.003
Rong H., Teixeira A. P., Guedes Soares C. (2019). Ship trajectory uncertainty prediction based on a Gaussian Process model. Ocean Eng. 182, 499–511. doi: 10.1016/j.oceaneng.2019.04.024
Sun Y., Lian F., Yang Z. (2023). Analysis of the activities of high sea fishing vessels from China, Japan, and Korea via AIS data mining. Ocean Coast. Manage. 242. doi: 10.1016/j.ocecoaman.2023.106690
Sun B., Nie L., Wang W., Sun Y., Li H. (2022a). Dynamic identification of logistics critical roads based on BeiDou trajectory data. IET Intelligent Transport Systems 17, 1467–1481. doi: 10.1049/itr2.12329
Sun T., Xu Y., Zhang Z., Wu L., Wang F. (2022b). A hierarchical spatial-temporal embedding method based on enhanced trajectory features for ship type classification. Sensors 22. doi: 10.3390/s22030711
Suo Y. F., Ji Y. X., Zhang Z. Y., Chen J. H., Claramunt C. (2022). A formal and visual data-mining model for complex ship behaviors and patterns. Sensors 22, 21. doi: 10.3390/s22145281
Wang C., Zhang X., Yang Z., Bashir M., Lee K. (2023). Collision avoidance for autonomous ship using deep reinforcement learning and prior-knowledge-based approximate representation. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1084763
Wei Z., Xie X., Zhang X. (2020). AIS trajectory simplification algorithm considering ship behaviours. Ocean Eng. 216. doi: 10.1016/j.oceaneng.2020.108086
Wei Z. K., Xie X. L., Zhang X. J. (2022). Maritime anomaly detection based on a support vector machine. Soft Computing 26, 11553–11566. doi: 10.1007/s00500-022-07409-w
Xie Z., Lin R., Wang L., Zhang A., Lin J., Tang X. (2023). Data augmentation and deep neural network classification based on ship radiated noise. Front. Mar. Sci. 10. doi: 10.3389/fmars.2023.1113224
Yan Z., He R., Ruan X., Yang H. (2022). Footprints of fishing vessels in Chinese waters based on automatic identification system data. J. Sea Res. 187. doi: 10.1016/j.seares.2022.102255
Yang J. X., Sun Y., Song Q. Y., Ma L. Q. (2023). Laws and preventive methods of collision accidents between merchant and fishing vessels in coastal area of China. Ocean Coast. Manage. 231, 13. doi: 10.1016/j.ocecoaman.2022.106404
Yasir M., Shanwei L., Mingming X., Hui S., Hossain M. S., Colak A. T. I., et al. (2023). Multi-scale ship target detection using SAR images based on improved Yolov5. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1086140
Zhang M. Y., Kujala P., Hirdaris S. (2023a). A machine learning method for the evaluation of probabilistic grounding risk reflecting ship motion uncertainties. Adv. Collision Grounding Ships Offshore Structures 12, 28–29. doi: 10.1201/9781003462170-15
Zhang M. Y., Kujala P., Musharraf M., Zhang J. F., Hirdaris S. (2023b). A machine learning method for the prediction of ship motion trajectories in real operational conditions. Ocean Eng. 283. doi: 10.1016/j.oceaneng.2023.114905
Zhang M. Y., Montewka J., Manderbacka T., Kujala P., Hirdaris S. (2021a). A big data analytics method for the evaluation of ship - ship collision risk reflecting hydrometeorological conditions. Reliability Eng. System Saf. 213. doi: 10.1016/j.ress.2021.107674
Zhang M. Y., Taimuri G., Zhang J. F., Hirdaris S. (2023c). A deep learning method for the prediction of 6-DoF ship motions in real conditions. Proc. Institution Mechanical Engineers Part M-Journal Eng. Maritime Environment. doi: 10.1177/14750902231157852
Zhang X., Wang C., Jiang L., An L., Yang R. (2021b). Collision-avoidance navigation systems for Maritime Autonomous Surface Ships: A state of the art survey. Ocean Eng. 235. doi: 10.1016/j.oceaneng.2021.109380
Zhao Q., Hautamäki V., Kärkkäinen I., Fränti P. (2012). Random swap EM algorithm for Gaussian mixture models. Pattern Recognition Lett. 33, 2120–2126. doi: 10.1016/j.patrec.2012.06.017
Zhao L. M., Roh M. I. (2019). COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean Eng. 191, 15. doi: 10.1016/j.oceaneng.2019.106436
Zhou Y., Daamen W., Vellinga T., Hoogendoorn S. P. (2019). Ship classification based on ship behavior clustering from AIS data. Ocean Eng. 175, 176–187. doi: 10.1016/j.oceaneng.2019.02.005
Zhu S. X., Li C. Y., Fang K. X., Peng Y. C., Jiang Y. M., Zou Y. J. (2022). An optimized algorithm for dangerous driving behavior identification based on unbalanced data. Electronics 11, 15. doi: 10.3390/electronics11101557
Keywords: vessel behavior feature, uncertainty and complexity, Fourier transform, Gaussian mixture clustering, fishing vessel
Citation: Zhu Q, Xi Y, Hu S and Chen Y (2023) Exploring the behavior feature of complex trajectories of ships with Fourier transform processing: a case from fishing vessels. Front. Mar. Sci. 10:1271930. doi: 10.3389/fmars.2023.1271930
Received: 11 August 2023; Accepted: 25 September 2023;
Published: 20 October 2023.
Edited by:
Agnieszka Lazarowska, Gdynia Maritime University, PolandReviewed by:
Tien Anh Tran, Seoul National University, Republic of KoreaSpyros Hirdaris, Aalto University, Finland
Copyright © 2023 Zhu, Xi, Hu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yongtao Xi, eGl5dEBzaG10dS5lZHUuY24=
 Qinghua Zhu
Qinghua Zhu Yongtao Xi
Yongtao Xi Shenping Hu
Shenping Hu Yan Chen
Yan Chen