Application of nonlinear stiffness mechanism on energy harvesting from vortex-induced vibrations

This study investigates the potential of vortex-induced vibration (VIV) as a renewable energy source, achieved when fluid flow interacts with a bluff body, inducing self-sustained oscillations through vortex shedding in the wake. While VIV research has traditionally focused on understanding its mechanisms and mitigating detrimental effects, interest in VIV energy harvesting has surged as a means to convert marine hydrokinetic (MHK) energy into usable electrical power. The nonlinear effects of two linear oblique springs on VIV energy harvesting are explored using the wake oscillator model, encompassing bistable and Duffing hardening stiffness. The study examines the response and energy harvesting performance while considering the impact of undeformed spring length, structural damping, and initial conditions on VIV energy conversion. Findings show that nonlinear stiffness application in the VIV system can broaden the synchronization bandwidth or reduce the VIV initiation flow speed. Bistable stiffness may broaden the synchronization velocity range, while Duffing hardening stiffness efficiently reduces the VIV initiation speed with small energy harvesting loss. Combining both stiffness types with appropriate control strategies presents a promising approach for achieving a broad synchronization VIV bandwidth and low initiation flow speed. Key parameters, such as the nondimensional parameter defining spring system obliquity and the ratio between undeformed spring length and cylinder diameter, significantly influence VIV response and energy harvesting. Moreover, optimal structural damping is vital to maximize energy harvesting efficiency, and understanding and controlling initial conditions are crucial for optimizing VIV synchronization bandwidth and energy harvesting efficiency for both bistable and Duffing hardening stiffness. This study provides valuable insights into VIV system dynamics and energy conversion potential with nonlinear springs, offering promising avenues for enhancing energy harvesting efficiency and inspiring further applications of nonlinear effects in VIV energy converters.

1 Introduction

Vortex-induced vibration (VIV), which occurs when a fluid flow interacts with a bluff body, induces self-sustained oscillations resulting from the periodic shedding of vortices in the wake. Due to the adverse consequences of VIV including fatigue damage and compromised integrity of structures in many engineering disciplines such as ocean, civil and aerospace engineering, extensive research efforts have been dedicated to comprehending the underlying mechanisms of VIV (Sarpkaya, 2004; Williamson and Govardhan, 2008; Bearman, 2011) and developing strategies to mitigate its detrimental effects on engineering structures (Zhu et al., 2015; Gao et al., 2021). However, in recent years, the increasing demand for renewable energy sources has fueled the recognition of the potential for VIV to be harnessed as a valuable source of renewable energy. The marine hydrokinetic (MHK) energy, which is abundant in steady current flows, such as those in rivers, tides, and ocean currents have sparked significant interest in exploring the concept of VIV energy harvesting, which aims to convert the MHK energy to usable electrical energy through VIV (Bernitsas, 2016). The concept of VIV-based energy converter was earlier proposed by (Bernitsas et al., 2008) and the first vortex induced vibration for aquatic clean energy (VIVACE) converter was developed and following generations of VIVACE converters are continuously developed (Kim et al., 2021).

The efficiency of the VIV energy converter depends on the lock-in region, where synchronization occurs when the vortex shedding frequency is close to the natural period of the structure. When the incoming flow velocity is out of the lock-in region, the amplitude decreases sharply, leading to reduced energy conversion efficiency or even complete energy loss (Wang et al., 2020; Lv et al., 2021). Thus, broadening the operating bandwidth becomes a key factor in enhancing the power capture efficiency. Equally crucial is the VIV initiation speed, which significantly impacts the VIV energy converter’s design. A low-speed VIV initiation with broad synchronization bandwidth can substantially improve the converter’s efficiency and scalability in practical applications. Numerous studies have explored diverse aspects of the VIV energy converter to enhance power capture efficiency. For instance, Azadeh-Ranjbar et al. (2018) investigated the influence of the cylinder’s aspect ratio on the response of the VIV, finding increasing the aspect ratio amplifies the cylinder’s amplitude and expands the lock-in frequency region of VIV. Zhang et al. (2017) examined the impact of the bluff body cross sections on VIV energy harvesting in tandem arrangements and concluded that the Cir-Tria prism has better performance on energy harvesting. Chang et al. (2011) applied passive turbulence control through selectively distributed surface roughness to enhance the VIV’s synchronization range and amplitude. In addition to investigating the influence of the cylinder parameters, systemic parameters of the VIV setup have attracted attentions as well. Sun et al. (2016) studied the effect of mass-ratio, damping and stiffness on optimal hydrokinetic energy conversion of a rough cylinder, discovering that increasing the spring stiffness can shift the VIV synchronization range to higher flow velocity region. Further, Sun et al. (2018) introduced adaptive piecewise-linear springs in the hydrokinetic energy converter, revealing that the nonlinear springs can lower the VIV initiation speed and improve the energy harvesting efficiency.

In addition to the nonlinearity based on the piecewise-linear springs, the nonlinearity from the bistable or Duffing hardening springs can be a potential way to improve the energy harvesting efficiency (Ramlan et al., 2010). By selecting suitable spring nonlinearity, the theoretical energy harvester can achieve high performance across a significantly broader range of Reynolds numbers compared to a conventional system (Mackowski and Williamson, 2013). The bistable springs were applied in a VIV system by Huynh and Tjahjowidodo (2017) and experiments shown that the chaotic vibrations may occur, control strategy may be needed to prevent the VIV energy converter operating in chaotic regions (Huynh et al., 2018). Recently, the lock-in regime for VIV of a cylinder attached to a bistable spring was investigated by Badhurshah et al. (2019) with an Equilibrium Constraint approach proposed and compared to the wake oscillator model. While these studies have enhanced our understanding of the bistable VIV system’s mechanism, a successful implementation of bistable springs in the VIV energy converter remains to be explored.

In the present study, the effect of nonlinearity, specifically from the nonlinear springs composed of two linear oblique springs, on the VIV energy harvesting is investigated. The nonlinearity effect includes not only the bistable effect but also the Duffing hardening effect as both effects can be easily achieved by the setup of two linear oblique springs. Through the wake oscillator model, the VIV response and the energy harvesting efficiency are examined, while the influence of the undeformed spring length, structural damping and initial condition on the VIV energy harvesting has been evaluated as well.

The rest of the paper is organized as follows. Following this introduction, the VIV energy harvesting model is presented in Section 2, including the wake oscillator model, nonlinear spring system and the state space model for solving the governing equations. In Section 3, the energy harvesting performance and dynamic responses for the VIV system with nonlinear springs are analyzed. In Section 4, the influence of undeformed spring length, structural damping and initial condition on the VIV energy harness is investigated. Finally, the conclusions are drawn in Section 5.

2 VIV modelling for energy harvesting

This section presents the governing equations for VIV modelling based on the wake oscillator model and introduces the numerical simulation method for solving the coupled equations between the VIV structure and the wake oscillator utilizing the state space model. The reliability of numerical model is verified by comparing it with the experimental results with the same parameters.

2.1 Governing equations for VIV based on wake oscillator model

A typical VIV system with linear springs is illustrated in Figure 1A. The system comprises a circular cylinder equipped with two sets of linear springs and dampers positioned at both ends. Under the influence of a steady current, the cylinder experiences oscillatory motion, which is constrained exclusively in the $y$ direction. This oscillation converts the MHK energy to mechanical energy of the cylinder. Through the implementation of the power take-off system, the mechanical energy is further converted to electricity. In the present analysis, the power take-off system is simplified by considering it as a damping element incorporated into the structure. Moreover, we assume that the structural damping solely arises from the presence of the power take-off system.

FIGURE 1

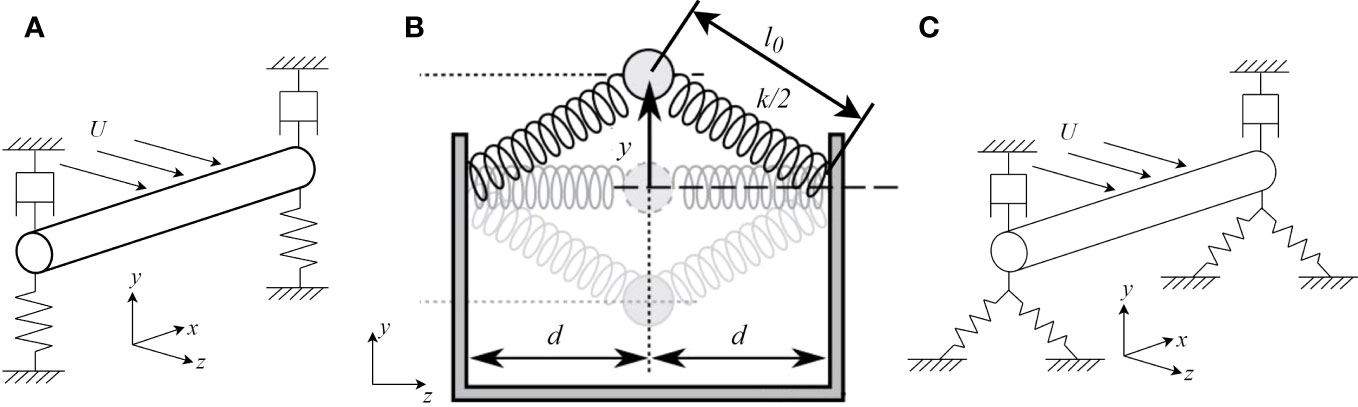
Figure 1 Schematic of (A) a VIV energy harvester with linear springs (Huynh and Tjahjowidodo, 2017), (B) a nonlinear spring system (Wang and Harne, 2017), and (C) a VIV energy harvester with nonlinear springs.

The wake oscillator model, which was proposed by Facchinetti et al. (2004) and subsequently refined by Farshidianfar and Dolatabadi (2013), is employed to simulate the fluid dynamics. This model enables the simulation of the intricate fluid-structure interactions inherent in the VIV phenomenon. The coupling equations between the structure and the wake oscillator are expressed as follows:

$\begin{array}{ll}\left(m_s+\frac{1}{4}\pi C_a\rho D^2\right)\ddot{y}+\left[r_s+\gamma \left(\frac{2\text{πSt}U}{D}\right)\rho D^2\right]\dot{y}+F(y)=\frac{1}{4}\rho U^{2}D{C}_{L0}q& (1)\end{array}$

$\begin{array}{ll}\ddot{q}+ϵ\left(\frac{2\pi \text{St}U}{D}\right)(1-\beta q^2+\lambda q^4)\dot{q}+{\left(\frac{2\pi \text{St}U}{D}\right)}^{2}q=\frac{A}{D}\ddot{y}& (2)\end{array}$

where $m_s$ is the structural mass of the cylinder per unit length; $C_a\rho D^2\pi /4$ is the fluid added mass, in which $C_a$ is the added mass coefficient, $D$ is the cylinder diameter and $\rho$ is the water density; $r_s$ is the structural damping; $\gamma$ is the stall parameter, which is given as $\gamma =C_d/(4\pi \text{St})$ where $C_d$ denotes the drag coefficient; $\text{St}$ is the Strouhal number; $U$ is the current velocity; $F(y)$ is the restoring force from the spring system; $C_{L0}$ is the reference lift coefficient; $q$ is the wake variable; $ϵ$ is the coefficient of nonlinearity for the wake oscillator; $\beta$ and $\text{λ}$ are the damping coefficients of the second-order and the fourth-order term over $ϵ$, respectively; $A$ is the force coefficient for the coupling of the wake oscillator.

2.2 Nonlinear spring system

For nonlinear spring system as shown in Figure 1B, the two identical springs of undeformed lengths $l_0$ with the stiffness of $k/2$ connect a lumped mass to a surrounding frame of span $2d$. It is assumed that the displacements of the mass are in a vertical direction, i.e., along the y-axis only.

$\begin{array}{ll}F(y)=ky\left[1-l_0/\sqrt{y^2+d^2}\right]& (3)\end{array}$

Define the spring system obliquity as $\alpha =d/l_0$, the non-dimensional force can be written as

$\begin{array}{ll}{F}^{*}(y^{*})=\left(1-\frac{1}{\sqrt{y^{*2}+{\alpha }^2}}\right)y^{*}& (4)\end{array}$

where $F^{*}(y^{*})=F(y)/(k{l}_0)$, $y^{*}=y/l_0$. For the present setup, $\alpha >0$. When $\alpha <1$, i.e., $l_0>d$, the mass cannot be easily maintained in the central configuration, i.e., the zero-displacement position, $y =0$, is not stable, while the two symmetric stable positions are adjacent to the central unstable state. Thus, it is a bistable system. When $\alpha \ge 1$, i.e., $l_0\le d$, the nonlinear system can be seen as a Duffing hardening system (Wang and Harne, 2017), the mass will come to rest at the zero-displacement position, $y=0$, and it is a monstable system.

The dimensional potential energy of the nonlinear spring system is determined by

$\begin{array}{ll}{E}^{*}(y^{*})={\left(\sqrt{y^{*2}+{\alpha }^2}-1\right)}^2& (5)\end{array}$

where $E^{*}(y^{*})=E(y)/(0.5k{l}_0^2)$.

The nondimensional equivalent stiffness of the nonlinear spring system is given as

$\begin{array}{ll}\frac{d{F}^{*}(y^{*})}{d{y}^{*}}=1-\frac{{\alpha }^2}{{(y^{*2}+{\alpha }^2)}^{3/2}}& (6)\end{array}$

The nondimensional force-displacement curves for different $\alpha$ values are demonstrated in Figure 2A, illustrating the nonlinear characteristics of the system. Notably, a distinct jump in the resultant force from the two springs is observed as the mass passes through the symmetric stable positions. It is seen that the smaller value of $\alpha$ results in sharper jumps. Combining the nondimensional equivalent stiffness curves shown in Figure 2B, it is evident that the system exhibits negative stiffness within the regions between the two stable positions when $\alpha$< 1. Furthermore, absolute value of the equivalent stiffness at the central position increases as $\alpha$ value decreases. Conversely, when $\alpha$> 1, the equivalent stiffness becomes positive, signifying a transition to a monostable system. For the potential energy depicted in Figure 2C, two potential energy wells are apparent and an energy peak exists at the central unstable position when $\alpha$< 1. Smaller values of $\alpha$ correspond to higher central energy peaks, which results in increased difficulty for the mass to cross the central position and form inter-well oscillation. As $\alpha$ increases, the central energy peaks diminish. When $\alpha$> 1, the central energy peak vanishes entirely, indicating a monstable configuration.

FIGURE 2

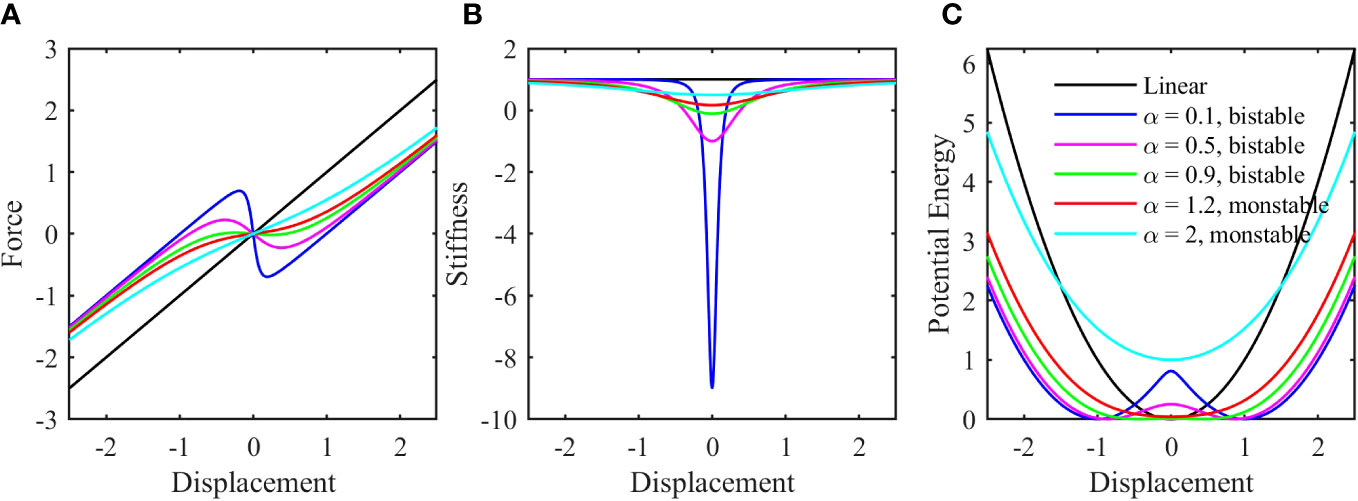
Figure 2 The characteristics of the nonlinear spring system with different $\alpha$ values: (A) The force-displacement curve; (B) The equivalent stiffness; (C) The potential energy.

2.3 State space model for solving governing equations

A state space model is adopted to solve the coupled equations of the structure and the wake oscillator. Define the following state vector:

$\begin{array}{ll}x={[x_1,x_2,x_3,x_4]}^{\text{T}}={[y,\dot{y},q,\dot{q}]}^{\text{T}}& (7)\end{array}$

For the VIV energy converter with a linear spring system as shown in Figure 1A, $F(y)=ky$, the governing equations (Eqs. (1) and (2)) can be written in a state-space form as:

$\begin{array}{ll}\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\left\{\frac{1}{4}\rho U^{2}D{C}_{L0}{x}_3-[r_s+\gamma (\frac{2\pi \text{St}U}{D})\rho D^2]x_2-k{x}_1\right\}\left(\frac{4}{4m_s+\pi C_M\rho D^2}\right)\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4=\frac{A}{D}\left\{\frac{1}{4}\rho U^{2}D{C}_{L0}{x}_3-[r_s+\gamma (\frac{2\pi \text{St}U}{D})\rho D^2]x_2-k{x}_1\right\}\left(\frac{4}{4m_s+\pi C_M\rho D^2}\right)\\ -ϵ(\frac{2\pi \text{St}U}{D})(1-\beta x_3^2+\lambda x_3^4)x_4-{\left(\frac{2\pi \text{St}U}{D}\right)}^2{x}_3\end{array}& (8)\end{array}$

For the VIV energy converter with a nonlinear spring system as shown in Figure 1C, $F(y)=ky\left\{1-{[{(y/l_0)}^2+{\alpha }^2]}^{-1/2}\right\}$, Eqs. (1) and (2) are rewritten in a state-space form as:

$\begin{array}{ll}\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\left\{\frac{1}{4}\rho U^{2}D{C}_{L0}{x}_3-[r_s+\gamma (\frac{2\pi \text{St}U}{D})\rho D^2]x_2-k\left[1-\frac{1}{\sqrt{{(x_1/l_0)}^2+{\alpha }^2}}\right]\right\}\left(\frac{4}{4m_s+\pi C_a\rho D^2}\right)\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4=\frac{A}{D}\left\{\frac{1}{4}\rho U^{2}D{C}_{L0}{x}_3-[r_s+\gamma (\frac{2\pi \text{St}U}{D})\rho D^2]x_2-k\left[1-\frac{1}{\sqrt{{(x_1/l_0)}^2+{\alpha }^2}}\right]\right\}\left(\frac{4}{4m_s+\pi C_a\rho D^2}\right)\\ -ϵ\left(\frac{2\pi \text{St}U}{D}\right)(1-\beta x_3^2+\lambda x_3^4)x_4-{\left(\frac{2\pi \text{St}U}{D}\right)}^2{x}_3\end{array}& (9)\end{array}$

Based on the state space model, the displacement and velocity of the VIV system with linear and nonlinear spring systems can be numerically achieved for discrete time by solving Eqs. (8) and (9) using the 4^th order Runge-Kutta method. By obtaining the cylinder velocity, the time-averaged power harvested by the VIV system can be determined. For the sake of analysis simplification, the harnessed power per unit cylinder length is calculated based on the damping component $r_s$, which is given as:

$\begin{array}{ll}P=\frac{r_s}{t_2-t_1}\underset{t_1}{\overset{t_2}{\int }}\dot{y^2}dt& (10)\end{array}$

where $t_1$ and $t_2$ are the starting and ending time for the power generation, respectively. In the present analysis, $t_1$ is selected as 1000s to avoid the initial transient effect from the numerical simulation and $t_2$ is selected to be 10000s.

The power conversion efficiency is defined as:

$\begin{array}{ll}\eta (\%)=\frac{P}{P_{\text{fluid }}\times \text{ Betz limit }}\times 100& (11)\end{array}$

where the Betz limit serves as a commonly employed metric for assessing the power efficiency of wind turbines. It represents the theoretical upper bound of power efficiency (59.26%) that can be attained by any energy converter extracting power from an open flow (Kim et al., 2021);

$P_{\text{fluid }}$ is the power in a fluid flowing through the area swept by the cylinder with unit length, which is define as:

$\begin{array}{ll}{P}_{\text{fluid }}=\frac{1}{2}\rho U^3(2A_m+D)& (12)\end{array}$

where $A_m$ is the motion amplitude of the cylinder.

2.4 Model parameters and verification of numerical model

The parameters of the VIV structure and the wake oscillator model are listed in Table 1. In the present study, the circular cylinder is assumed to be 1.0 m long.

TABLE 1

Table 1 Parameters of the VIV structure and the wake oscillator model.

To verify the numerical model, typical parameters of a VIV system presented by Khalak and Williamson (1999), i.e., $m^{*}=m_s/(0.25\pi \rho D^2)=$ 10.1, $\text{ξ}=r_s/2\sqrt{k(m_s+0.25\text{πρ}{D}^2)}=$ 0.00129, are used. In the experiments conducted by Khalak and Williamson (1999), a rigid cylinder was elastically mounted with linear springs, and its transverse oscillations were measured across a range of reduced velocities, considering both low and high mass-damping conditions. Though the parameters selected in the present study may not represent an optimistic design for a VIV energy harvester, they serve well for the verification of the numerical model since the primary objective of this study is to investigate the influence of nonlinear springs on the VIV system.

The nondimensional motion amplitude is plotted against the reduced velocity in Figure 3, where the reduced velocity, $U_r$, is defined as $U_r=U/(f_{n}D)$, with $f_n$ is representing the natural frequency of the VIV system. The comparison between the numerical model results and the experimental data reveals a good agreement for the VIV upper branch measured points. However, it should be noted that the lower branch from the experiments cannot be accurately captured by the wake oscillator employed in this study. This limitation stems from the wake oscillator model’s half-empirical nature, which involves fixed empirical parameters to simplify the intricate fluid-structure interaction. Thus, the inherent inability of the wake oscillator model to capture certain nonlinear behaviors, including the response seen in the lower branch, should be recognized (Han et al., 2023). Given that the primary focus of this study is to investigate the impact of nonlinear stiffness on the maximum responses of the VIV system, the omission of the upper-lower-branch transition in VIV can be considered reasonable. While the model may not fully capture the entire range of VIV behavior, it remains suitable for examining the specific objective of assessing the influence of nonlinear stiffness.

FIGURE 3

Figure 3 Verification of the numerical model with linear spring system.

3 Energy harvesting performance and dynamic responses for VIV system with nonlinear springs

In this section, the energy harvesting performance and the dynamic responses of the VIV system with linear and nonlinear springs are investigated. In the numerical simulations, the structural damping ratio is selected as $\xi$= 0.0129, which corresponds to a damping coefficient of $r_s$=24.73 N/s. The remaining parameters are kept consistent with those used in the verification case. For the nonlinear springs, the length of the undeformed spring is $l_0$= 0.5 m, resulting a nondimensional undeformed spring length of $l_0/D$= 1.0. The $\text{α}$ value varies from 0.1 to 2.0 to study the dynamic characteristics of the nonlinear system.

3.1 Energy harvesting performance

The harnessed power and the power conversion efficiency of the VIV system with nonlinear springs are presented in Figure 4, alongside the corresponding values obtained from the VIV system with linear springs. This comparison is conducted to showcase the energy harvesting performance of the VIV system, considering various $\text{α}$ values associated with the nonlinear springs.

FIGURE 4

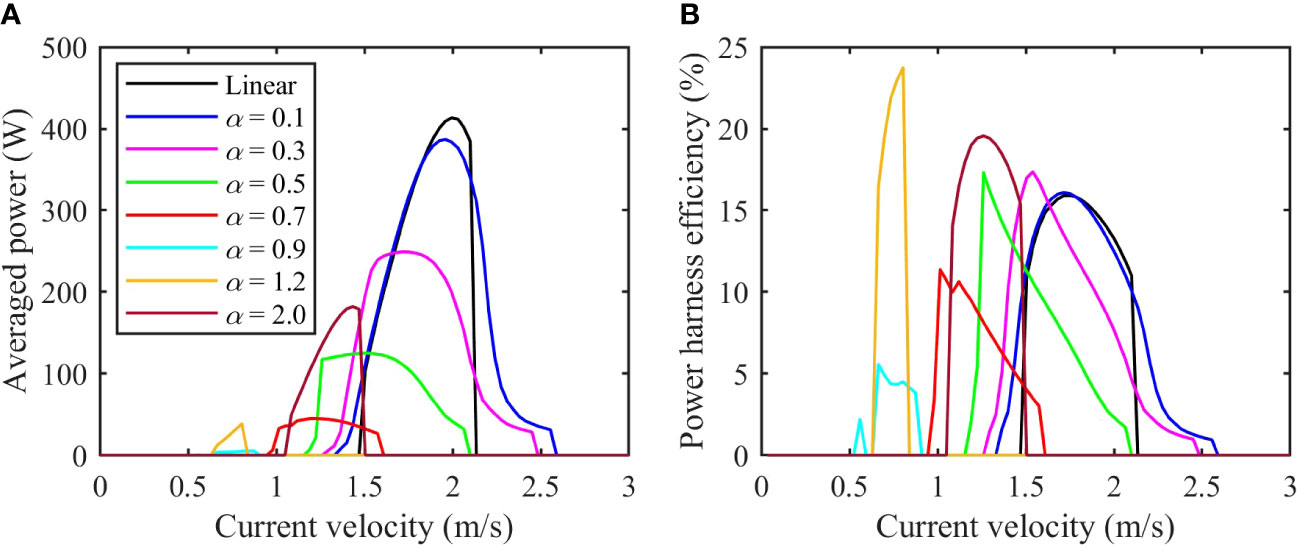
Figure 4 The power (A) and power efficiency (B) harvested by the VIV system with nonlinear spring stiffness l₀/D = 1.0, y₀ = 0, where y₀ is the initial displacement of the cylinder).

As shown in Figure 4A, the harnessed power by the VIV system with linear springs come from current velocity range from 1.5 m/s to 2.2 m/s, indicating the VIV harvesting device works only in this current velocity region. With the nonlinear springs utilized in the VIV system, the velocity range where the fluid energy can be harvested expands or shifts. For small $\text{α}$ values (say 0.1 and 0.3) of the nonlinear springs, the range of the current velocity amenable to power extraction expand to both the larger and smaller velocity regions. Additionally, the averaged power peak shifts towards the lower velocity region, accompanied by a reduction of the peak magnitude.

Continuing with increasing $\text{α}$ values (e.g., 0.5 and 0.7), the velocity range favorable for energy harvesting gradually shifts towards to lower velocity regions gradually and the power peak becomes flatter and lower. When the $\text{α}$ approaches 0.9, the range of velocities suitable for power extraction shifts to a significantly lower region, spanning from 0.7m/s to 0.9 m/s, which is considerably lower than the range observed with linear springs. As $\text{α}$ surpasses 1.0 (e.g., 1.2 and 2.0), the velocity range at which the VIV system operates effectively reverts back to the large velocity region with increasing $\text{α}$ values and the peak power increases again.

In Figure 4B, it is as expected that the power harness efficiency, which is derived from the averaged power, exhibits a similar expansion or shift of the velocity range as observed Figure 4A. However, our attention is drawn to the peaks of the power harness efficiency curves. While the averaged power peaks obtained from the nonlinear springs with different α values consistently remain lower than those from the linear springs, the efficiency peak shows a distinct trend.

For small α values (e.g., 0.1 – 0.5), the efficiency peak undergoes minimal change as α increases, despite the decrease in peak power. This behavior can be attributed to the shift towards lower current velocity regions, where the fluid power flowing through the VIV device decreases due to the reduced velocity. As α continues to increase while remaining smaller than 1.0, the efficiency peak gradually diminishes. However, when α exceeds 1.0, an interesting observation emerges: the efficiency peak experiences a sharp increase, even though the working velocity remains low (as seen in the curve with α = 1.2). Further increasing α results in a decrease in the efficiency peak but still larger than that from the linear springs.

It is seen that the utilization of bistable stiffness, characterized by small α values (0.1 – 0.5), demonstrates the capability to expand the working velocity range for energy harvesting without compromising the efficiency, in comparison to the VIV system equipped with linear springs. However, it is important to note that bistable stiffness with larger α values (> 0.5) leads to a decrease in energy harness efficiency, despite enabling the utilization of the lower current velocity range. On the other hand, when the nonlinear spring system becomes monstable (α > 1.0), a favorable shifting of the current velocity range can still be achieved, accompanied by a significant increase in the energy harness efficiency beyond what the linear springs system can achieve.

3.2 Dynamic responses of VIV system with nonlinear springs

To investigate the underlying reasons for the power harvesting performance of the VIV system, a comprehensive analysis of the motion characteristics is conducted and presented in Figures 5–9. Figure 5 specifically focuses on the VIV system equipped with linear springs, revealing the presence of regular motion in the displacement and velocity time histories (see Figures 5A, B). Moreover, the phase portrait shown in Figure 5C illustrates the formation of elliptical trajectories. Power spectral density analysis in Figure 5D further confirms the occurrence of synchronization between the fluid represented by the wake oscillator and the circular cylinder, with the cylinder’s response predominantly exhibiting a single frequency.

FIGURE 5

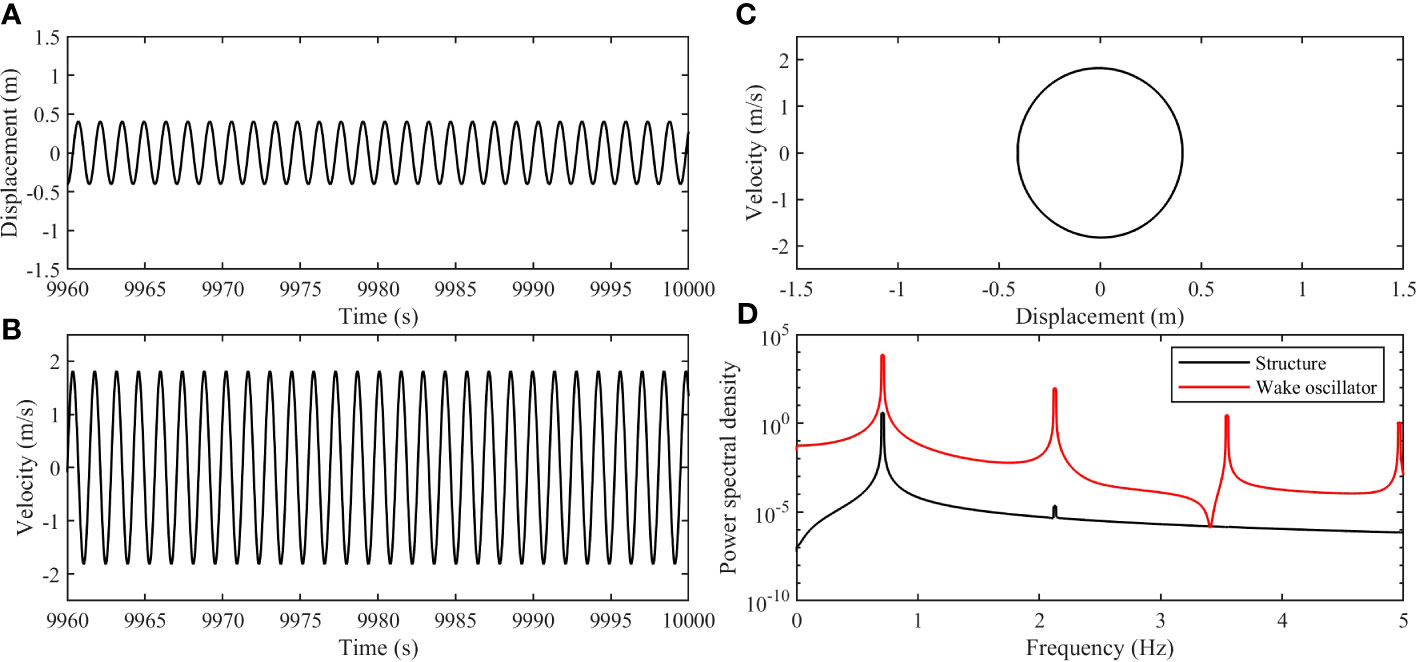
Figure 5 The dynamic responses of the cylinder with linear springs ($y_0=0$, $U=2.0\text{ m}/\text{s}$): (A) The displacement time history; (B) The velocity time history; (C) The phase portrait from the displacement and the velocity; (D) Power spectral density of the displacement for the cylinder and the wake oscillator.

FIGURE 6

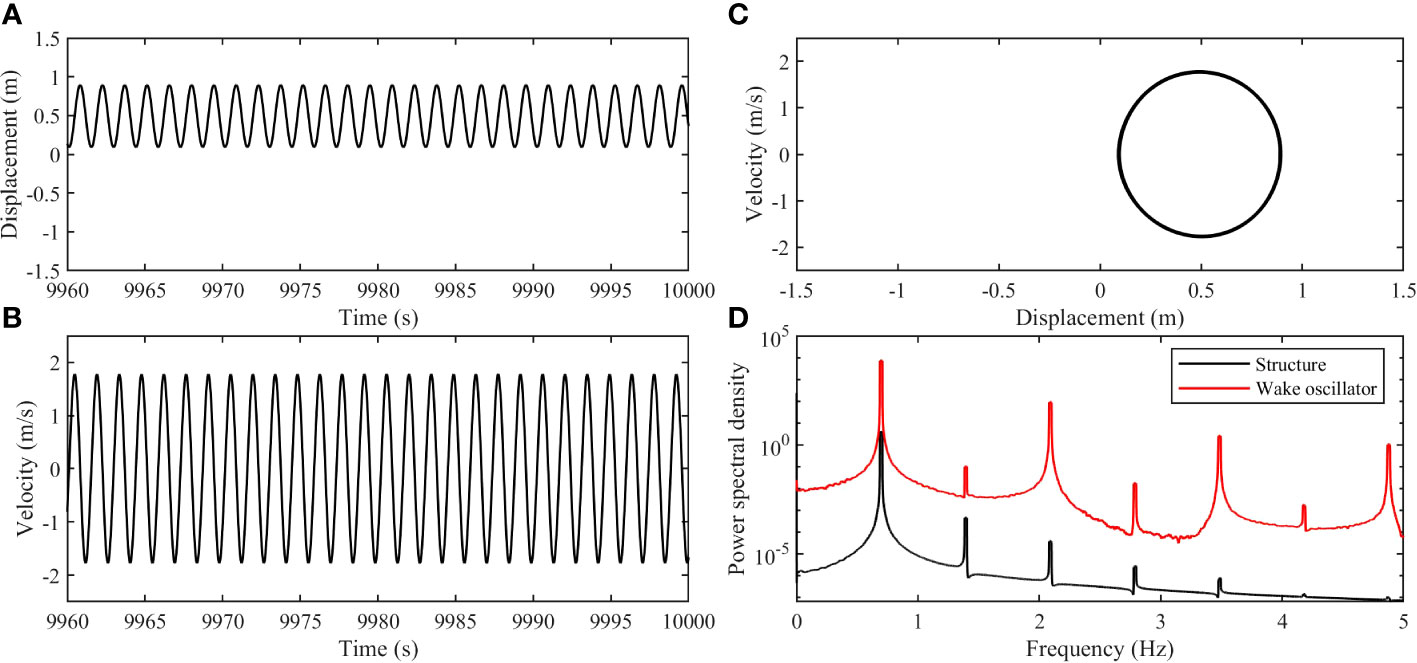
Figure 6 The dynamic responses of the cylinder with $\alpha = 0.1$ ($l_0/D=1.0$, $y_0=0$, $U=1.9\text{ m}/\text{s}$): (A) The displacement time history; (B) The velocity time history; (C) The phase portrait from the displacement and the velocity; (D) Power spectral density of the displacement for the cylinder and the wake oscillator.

Figure 6 illustrates the dynamic responses of the VIV system equipped with nonlinear springs with a value of $\text{α}$= 0.1. The displacement and velocity time histories displayed in Figures 6A, B showcase the cylinder’s oscillation around the equilibrium position at y = 0.5, indicating an intra-well oscillation due to presence of the bistable stiffness. This observation is further substantiated by the phase portrait in Figure 6C, where the centre of the elliptical trajectory aligns with a displacement of 0.5 m. In addition, the symmetry observed in the phase portrait indicates the intra-well oscillation of the cylinder closely resembles that of a linear system. This can be explained by examining the equivalent stiffness curves shown in Figure 2B. Specifically, for the case $\alpha$= 0.1, the curve demonstrates a narrow region of highly negative stiffness. However, outside this region, the equivalent stiffness at the stable equilibrium tends to be linear. Consequently, when the cylinder undergoes intra-well oscillations with small amplitudes, it remains within the linear stiffness region and does not enter the nonlinear regime. Notably, Figure 6D reveals the persistence of synchronization between the fluid and the circular cylinder as evidenced by the alignment of the frequency peaks between the structure and the wake oscillator. The dominated frequency of the structure motion is the lowest frequency peak, and the displacement and velocity time histories appear regular though some minor higher frequency peaks are observed in the power spectral density curve of the cylinder.

Upon increasing $\text{α}$ to 0.5 for the nonlinear springs, the dynamic responses of the VIV system are presented in Figure 7 Notably, the steady oscillation of the cylinder remains intra-well. However, a distinct change can be seen in the displacement and velocity time histories depicted in Figures 7A, B, where asymmetry in the crests and troughs is evident, unlike the case of $\text{α}$= 0.1. This asymmetry is further manifested in the phase portrait shown in Figure 7C, which resembles the shape of a water droplet. The emergence of this asymmetry can be attributed to the increased $\text{α}$ value, which expands the nonlinear stiffness region, as illustrated in Figure 2B. During an oscillation period, the cylinder traverses both the linear stiffness region, which lies far from the central position and the nonlinear negative stiffness region near the central position y = 0 without crossing it. Consequently, an asymmetric oscillation pattern is formed around the stable equilibrium position. Moreover, Figure 7D confirms the synchronization between the cylinder and the wake oscillator, reinforcing the influence of the fluid on the cylinder’s response.

FIGURE 7

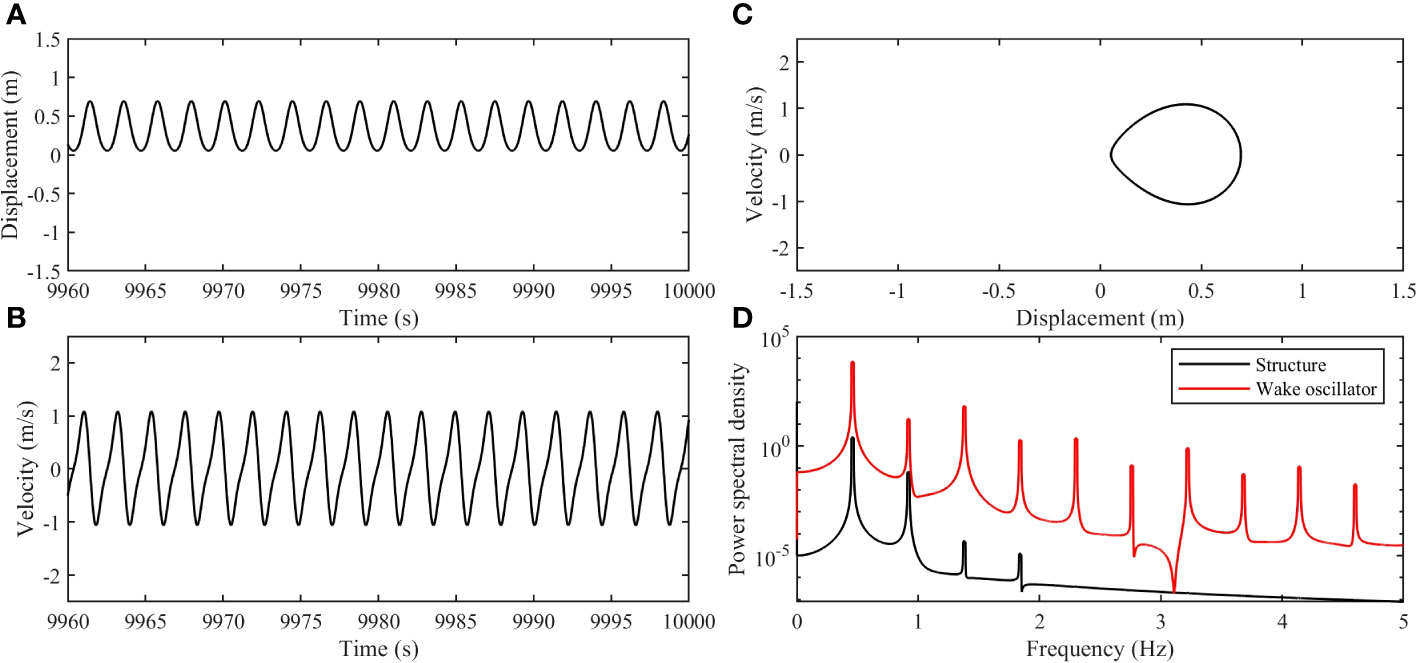
Figure 7 The dynamic responses of the cylinder with $\alpha =0.5$ ($l_0/D=1.0$, $y_0=0$, $U=1.3\text{ m}/\text{s}$): (A) The displacement time history; (B) The velocity time history; (C) The phase portrait from the displacement and the velocity; (D) Power spectral density of the displacement for the cylinder and the wake oscillator.

As $\alpha$ further increases to 0.9 for the nonlinear springs, the cylinder demonstrates distinct dynamic responses, as depicted in Figure 8 Notably, the displacement and velocity time histories in Figures 8A, B exhibit irregular features, and the cylinder crosses the central position y = 0, indicating the occurrence of inter-well oscillation. This behavior can be attributed to the significant reduction of the potential barrier at the central position as $\alpha$ reaches 0.9, facilitating the cylinder’s movement across the central position and the formation of the inter-well oscillation. However, Figure 8C reveals that the phase portrait fails to form a closed shape, indicating the emergency of chaotic oscillations in the cylinder’s motion. Moreover, the power spectral density curves depicted in Figure 8D confirm the absence of synchronization between the cylinder and the wake oscillator, as no dominating frequency peak is observed in the cylinder motion. These findings suggest that the cylinder undergoes chaotic motion under the influence of the nonlinear springs with $\alpha$= 0.9.

FIGURE 8

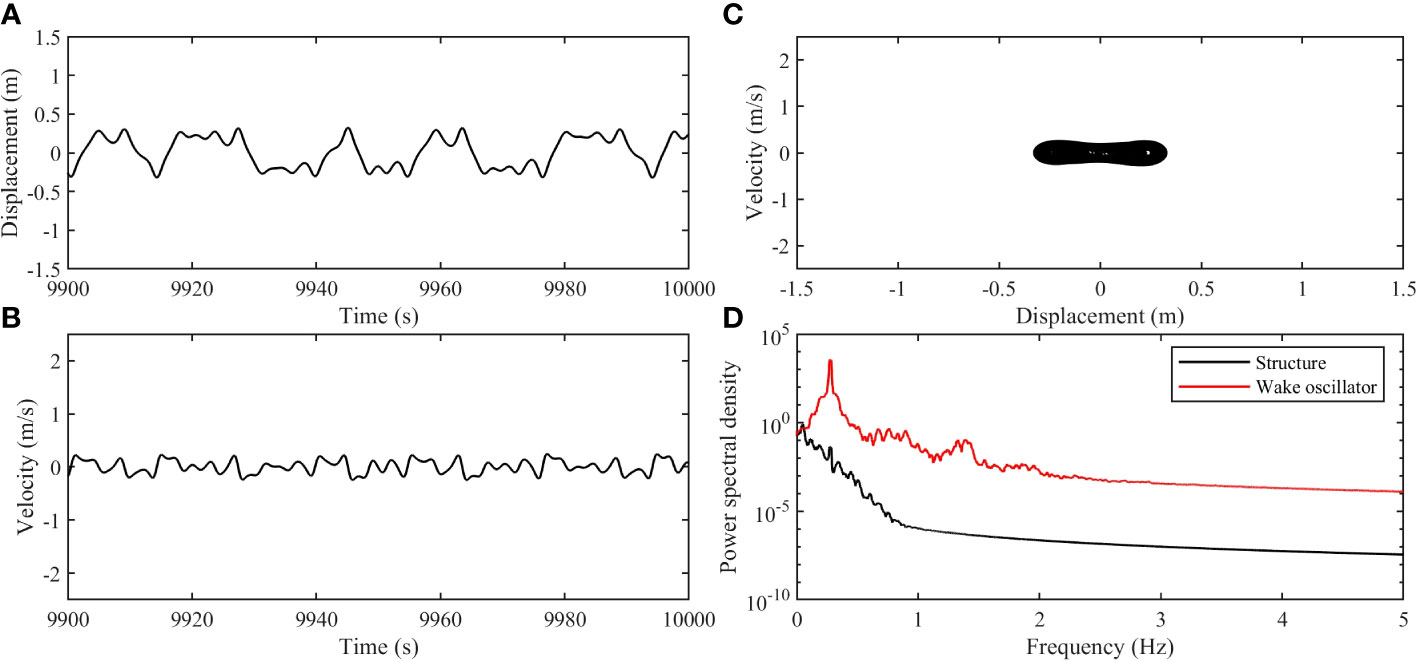
Figure 8 The dynamic responses of the cylinder with $\alpha =0.9$ ($l_0/D=1.0$, $y_0=0$, $U=0.7\text{ m}/\text{s}$): (A) The displacement time history; (B) The velocity time history; (C) The phase portrait from the displacement and the velocity; (D) Power spectral density of the displacement for the cylinder and the wake oscillator.

The subsequent increase of $\alpha$ to 1.2 signifies the transition of the VIV system with nonlinear spring system to a monstable state. This monstable characteristic is evident in the dynamic responses of the cylinder, as depicted in Figure 9 Notably, the displacement and velocity time histories displayed in Figures 9A, B exhibit steady regular shapes with a mean displacement of 0, indicative of a stable oscillatory behavior. Furthermore, Figure 9C demonstrates the formation of an elliptical trajectory in the phase portrait, further confirming the monstable nature of the system. Additionally, the synchronization between the cylinder and the wake oscillator is observed, as evidenced by the power density curves presented in Figure 9D. These findings illustrate the distinct dynamic responses of the VIV system with nonlinear springs in the monostable regime, characterized by stable oscillations and synchronization with the wake oscillator.

FIGURE 9

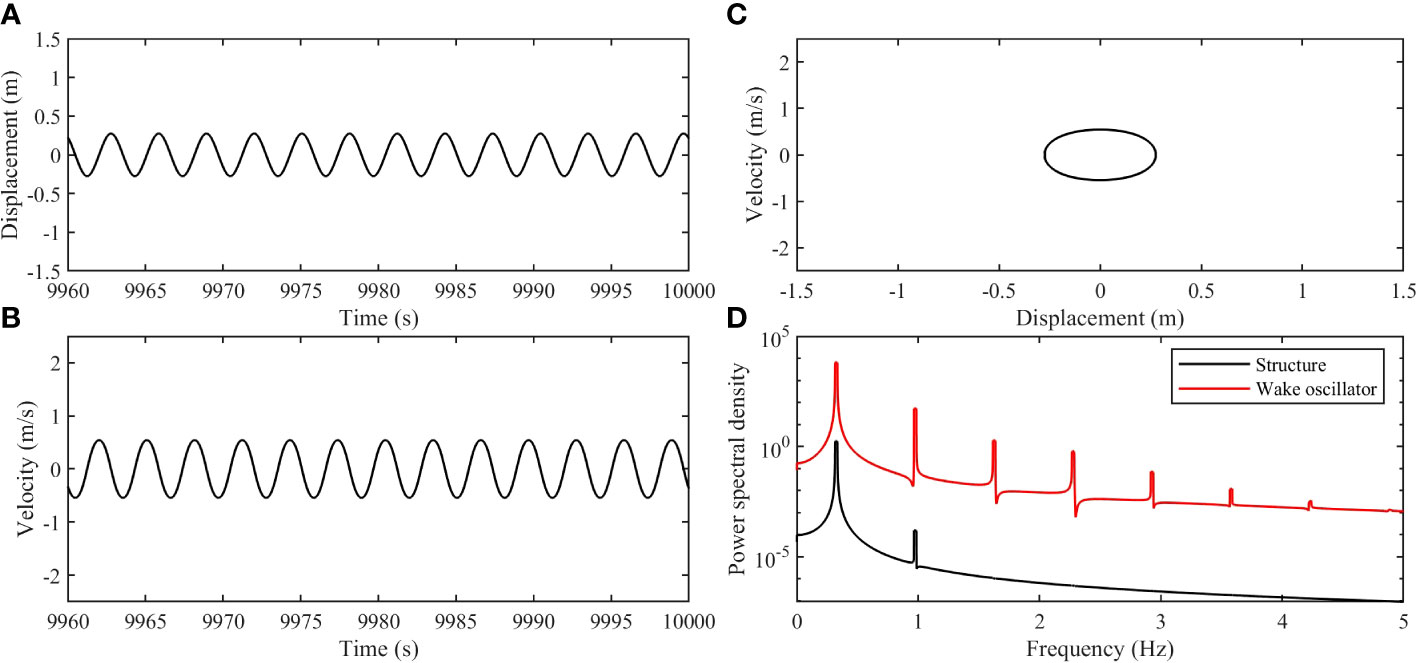
Figure 9 The dynamic responses of the cylinder with $\alpha =1.2$ ($l_0/D=1.0$, $y_0=0$, $U=0.8 \text{m}/\text{s}$): (A) The displacement time history; (B) The velocity time history; (C) The phase portrait from the displacement and the velocity; (D) Power spectral density of the displacement for the cylinder and the wake oscillator.

4 Key parameters for VIV system with nonlinear springs

4.1 Nondimensional undeformed spring length

While the nondimensional parameter $\text{α}$ determines the dynamic characteristics of the nonlinear spring system itself, the nondimensional undeformed spring length, which is the ratio between the dimensional undeformed spring length to the cylinder diameter, may influence the dynamic responses of the cylinder when the nonlinear springs are coupled to the VIV system. This nondimensional parameter serves as an indicator of the compatibility between the nonlinear springs and the VIV system.

To investigate this influence, four cases with different nondimensional undeformed spring length ratios (0.6, 1.0, 2.0 and 5.0) are considered while the other parameters are kept unchanged from Section 3. The value of $\text{α}$ for all three cases is from 0.1 to 2.0. Figure 10 illustrates the power conversion efficiency for each case. It is observed that for bistable nonlinear spring system, varying the $l_0/D$ values has a significant impact on the power conversion efficiency magnitude while the range of current velocities that can be harvested is not remarkably changed. For example, when $\text{α}$= 0.1, the power efficiency peaks of the case with $l_0/D$= 0.6 demonstrate a significant drop compared to those of cases with $l_0/D$= 1.0, 2.0 and 5.0. For cases with $\text{α}$= 0.5, a remarkable increase of the power conversion efficiency is observed when the $l_0/D$ value increases from 0.6 to 5. On the other hand, for the monstable nonlinear spring system (i.e., $\text{α}$= 1.2 and 2), the influence of different $l_0/D$ values is relatively small.

FIGURE 10

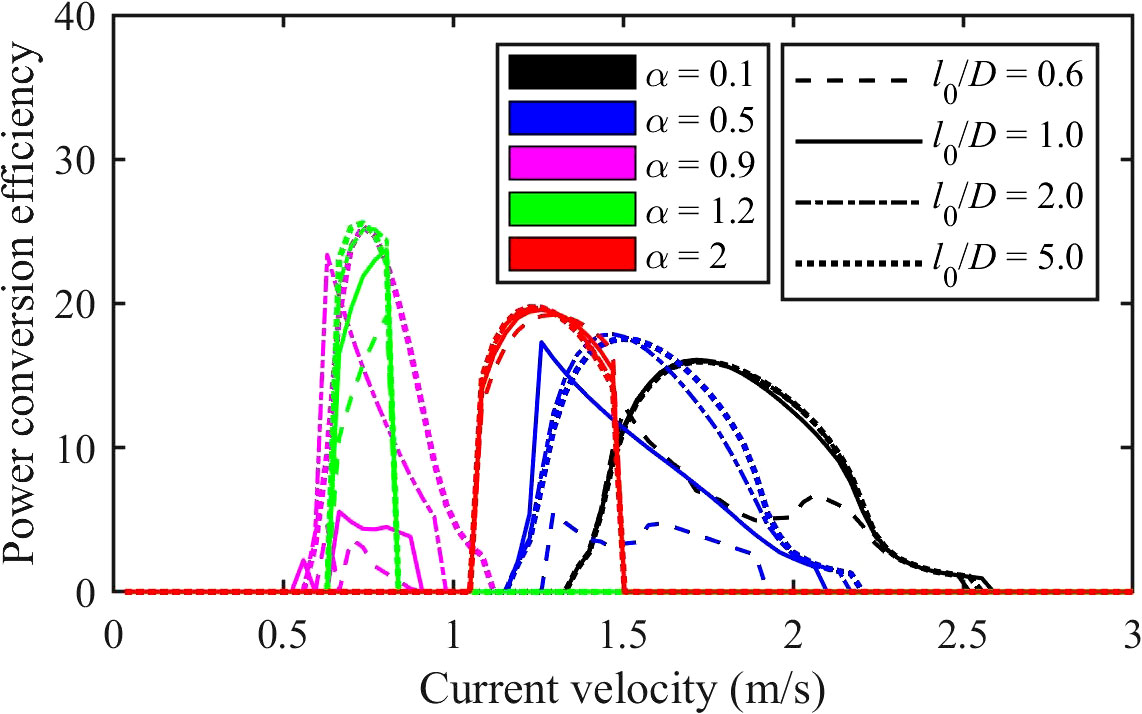
Figure 10 The power conversion efficiency of the VIV energy converter equipped with nonlinear springs with different $l_0/D$ values.

The dynamic responses of the cylinder for cases with different $l_0/D$ values are examined, as depicted in Figures 11 and 12. For cases with $\alpha$= 0.1, the displacement time histories for the cases with $l_0/D$= 1.0, 2.0 and 5.0 exhibit intra-well oscillations, with the equilibrium positions shift farther away from the central position ($y$= 0) as $l_0/D$ increases. However, in the case with $l_0/D$= 0.6, the cylinder displacement shows a combination of inter-well and intra-well oscillations. The phase portrait curves of $l_0/D$= 1.0, 2.0 and 5.0 show similar closed shapes with different center locations, indicating the regular oscillations with different equilibrium positions. In contrast, the phase portrait curve for $l_0/D$= 0.6 demonstrates that the cylinder motions tend to be chaotic. For cases with $\alpha$= 0.5 as shown in Figure 12, all the four cases with different $l_0/D$ values show stable intra-well oscillations, and motion amplitude increases with the increasing $l_0/D$ value. The equilibrium position shifts further away from the central position ($y$= 0) as the $l_0/D$ value increases as well.

FIGURE 11

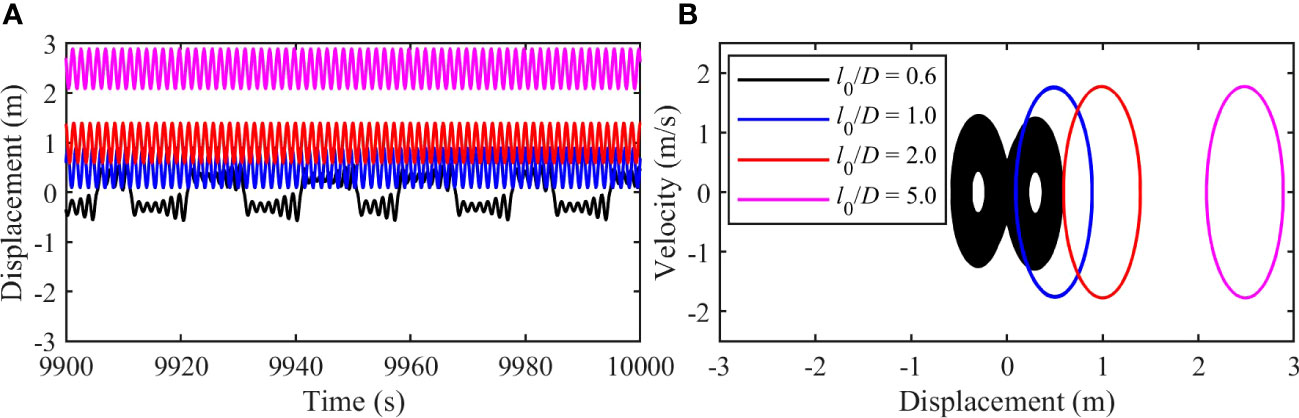
Figure 11 The dynamic responses of the cylinder with different $l_0/D$ values ($\alpha =0.1$, $y_0=0$, $U=1.89\text{ m}/\text{s}$): (A) The displacement time history; (B) The phase portrait from the displacement and the velocity.

FIGURE 12

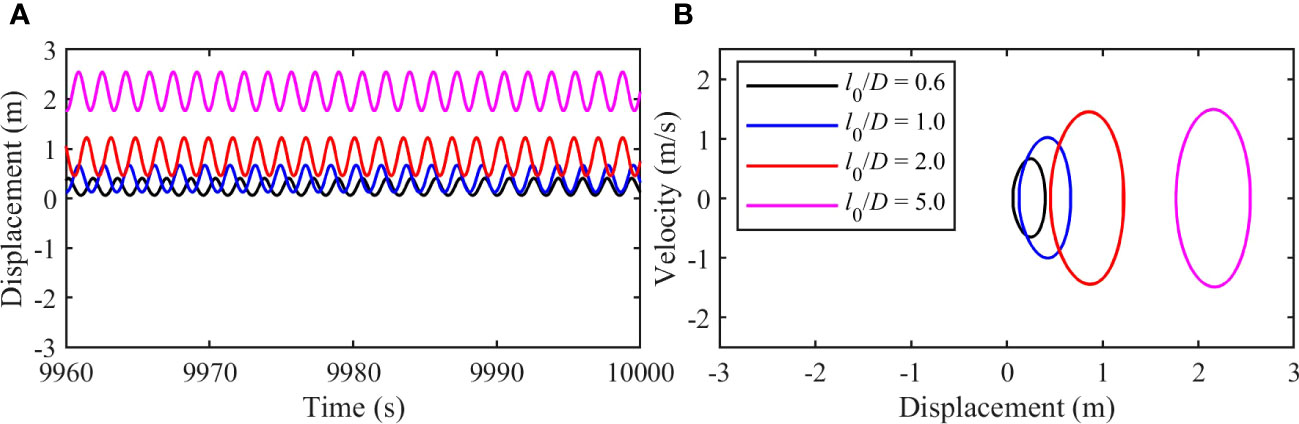
Figure 12 The dynamic responses of the cylinder with different $l_0/D$ values ($\alpha =0.5$, $y_0=0$, $U=1.65\text{ m}/\text{s}$): (A) The displacement time history; (B) The phase portrait from the displacement and the velocity.

4.2 Structural damping

The structural damping, which is assumed from the power take off system only in the present study, is a key design parameter in the VIV energy harvesting device. Small structural damping may lead to suboptimal energy conversion efficiency from the mechanical energy to electricity, while excessive structural damping may impede cylinder motions, resulting in reduced energy conversion efficiency from the fluid energy to mechanical energy.

The influence of the structural damping on the power conversion efficiency is investigated by varying the damping ratio $\text{ξ}$ while all the other parameters in the simulations are kept the same with those from Section 3. The power conversion efficiency curves are shown in Figure 13. It is evident that if the damping ratio is small, i.e., $\xi$= 0.0013, the power conversion efficiency is very low for all the $\alpha$ values, indicating that the bottle-neck of the VIV system is on the damping ratio. When $\xi$ increases from 0.0013 to 0.013, the power conversion efficiency increases significantly for all the $\text{α}$ values, though the different increase magnitudes are observed for different $\text{α}$ values. A further increase of the $\xi$ value from 0.013 to 0.13 demonstrate distinct influences on the power conversion efficiency for different $\text{α}$ values. For small $\alpha$ values, i.e., 0.1 and 0.5, a further remarkable increase of the power conversion efficiency is observed, while for $\alpha$ values of 0.9, 1.2 and 2.0, the cylinder motions are suppressed due to the increased damping ratios. Thus, striking the right balance in structural damping is essential for achieving optimal energy conversion efficiency in the design of VIV energy harvesting device.

FIGURE 13

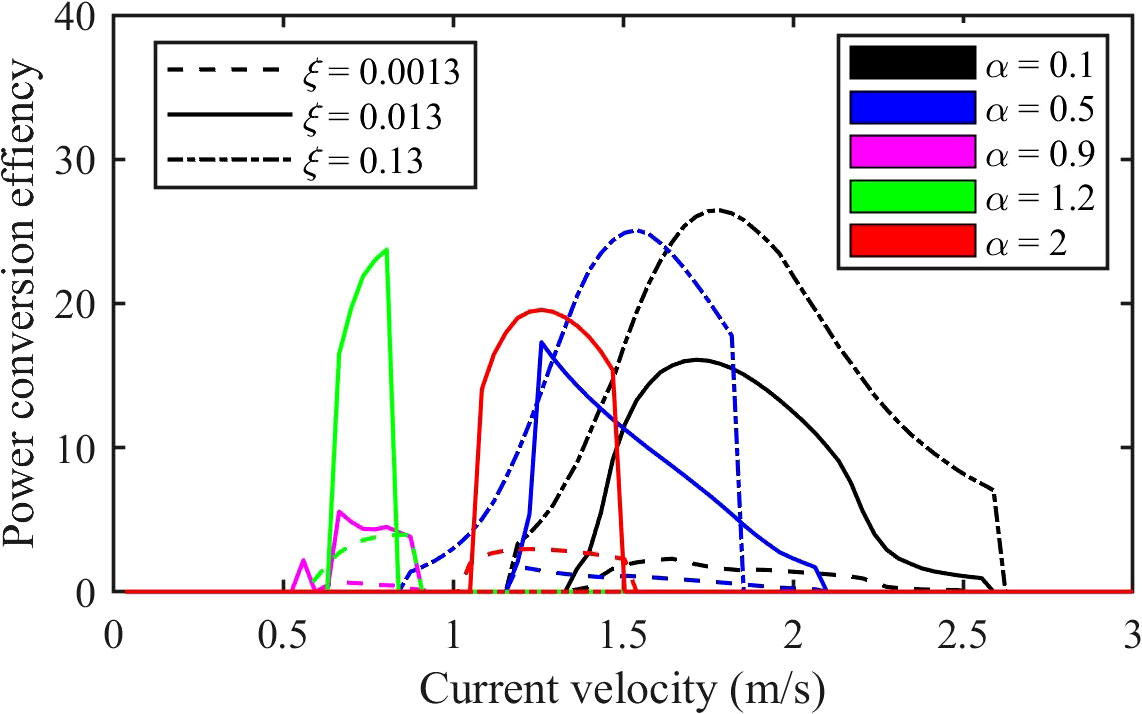
Figure 13 The power conversion efficiency of the VIV energy converter equipped with nonlinear springs with different damping ratios.

4.3 Initial conditions

The sensitivity of dynamic responses to the initial conditions is well-documented in bistable system (Wang and Harne, 2017). In the context of this study, where the bistable springs are coupled with the wake oscillator model representing the fluid, it is essential to investigate where the coupled VIV system with bistable springs retains sensitivity to the initial conditions.

The impact of different initial conditions on the power conversion efficiency is analysed by investigating various scenarios, as depicted in Figure 14. The results reveal that the initial displacements of the cylinder play a role in determining the range of current velocities that the VIV system can effectively utilize, particularly affecting the maximum current velocity that can be harnessed. In the case of $\alpha$= 0.1, which indicates the system is bistable, the utilizable current velocity range experiences a slight initial increase, followed by a decrease with higher initial displacements. Conversely, for the system with $\alpha$= 2.0, the maximum utilizable current velocity initially increases with higher initial displacements, but eventually becomes bounded. Both bistable and monostable nonlinear VIV systems are influenced by the initial conditions, with the primary impact being on the range of utilizable flow velocities, as certain initial conditions may prevent the VIV system from being excited.

FIGURE 14

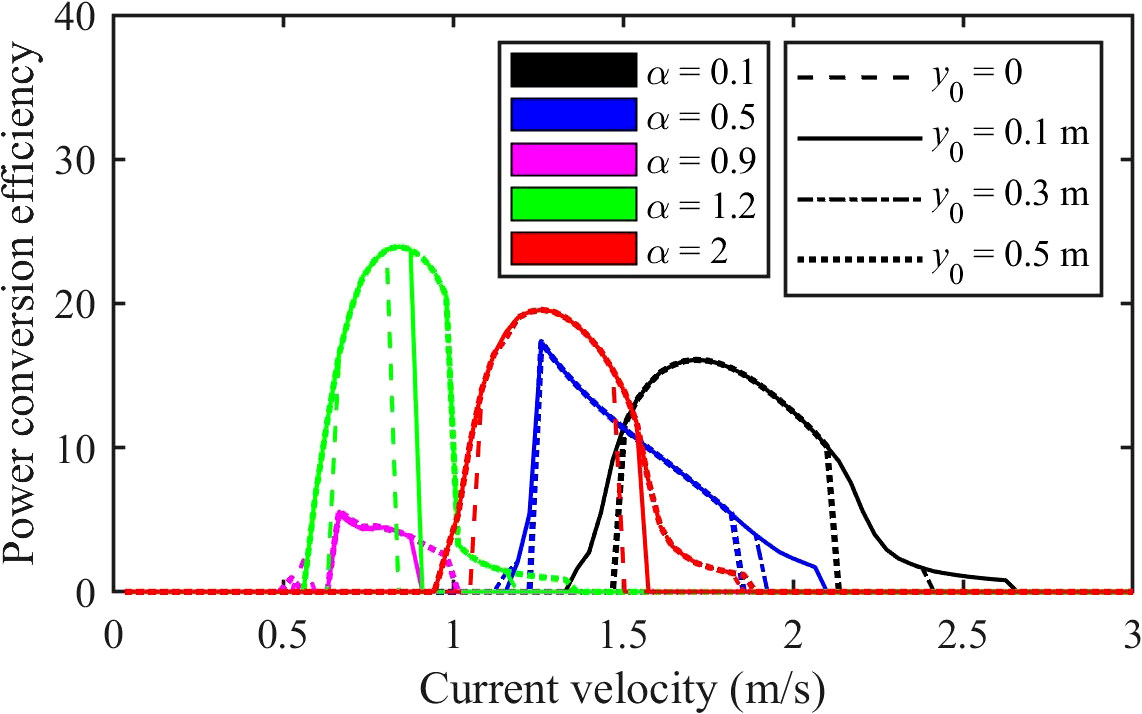
Figure 14 The power conversion efficiency of the VIV energy converter equipped with nonlinear springs with different initial conditions.

5 Conclusions

The nonlinear effect from two linear oblique springs on the VIV energy harvesting is investigated based on the wake oscillator model. The bistable stiffness and the Duffing hardening stiffness are both considered and their effects on the system’s response and energy harvesting performance are studied. Notably, the application of nonlinear stiffness in the VIV system shows promising outcomes in terms of expanding the synchronization bandwidth of VIV or lowering the VIV initiation flow speed.

The bistable stiffness with small $\alpha$ values demonstrates a capacity to broaden the synchronization velocity range, while large $\alpha$ values lower the VIV initiation flow speed. However, the VIV response under bistable stiffness with large $\alpha$ values tends to become chaotic. In contrast, the system with Duffing hardening stiffness exhibits a monstable behavior and proves more efficient in lowering the VIV initiation flow speed without significant energy harvesting efficiency loss. This may enlighten the combination of the bistable stiffness and Duffing hardening stiffness in a single VIV setup with two oblique springs by employing appropriate control strategies to adjust $\alpha$ values, thus achieving a broad synchronization VIV bandwidth with a low initiation flow speed.

For the nonlinear spring system composed of two linear oblique springs, the nondimensional parameter $\alpha$, which defines the obliquity of the spring system in undeformed state, is a key parameter influencing the nonlinearity. When this nonlinear spring system is applied in a VIV system, the ration between the undeformed spring length to the cylinder diameter serves as an essential indicator of the compatibility between the nonlinear springs and the VIV system. Both parameters significantly influence the VIV response and energy harvesting performance, calling for careful consideration in the design and optimization process.

Regarding structural damping, which is assumed to be all from the PTO system, it is evident that small damping results in larger VIV response but lower power conversion efficiency. Conversely, higher structural damping may lead to smaller VIV motion amplitudes. The optimal structural damping is a key factor to achieve the highest energy harvesting efficiency from VIV.

Lastly, the initial condition of the VIV is found to exert a considerable influence on the VIV response and corresponding energy harvesting, regardless of whether bistable or Duffing hardening stiffness is at play. Understanding and controlling the initial condition can thus contribute significantly to optimizing the VIV synchronization bandwidth and energy harvesting performance.

It’s important to recognize that the introduction of nonlinearities can also introduce complexities, such as the potential for chaotic behavior within the VIV system. As a result, optimizing the performance of a nonlinear VIV system demands intricate design strategies, significantly more involved than those applied in linear systems. Moreover, the implementation of nonlinear VIV systems might necessitate more sophisticated control mechanisms to sustain optimal working conditions. Thus, further studies on the optimization and control of the VIV energy harvesting with nonlinear springs are needed.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZG: Conceptualization, Formal Analysis, Software, Writing – original draft. ZL: Funding acquisition, Writing – review & editing. JN: Data curation, Methodology, Writing – review & editing. QY: Visualization, Writing – review & editing. KL: Project administration, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research is supported by the National Natural Science Foundation of China (Grant No. 52271279 and Grant No. 52071162) and the Research Start-Up Funds of Jiangsu University of Science and Technology (Grant No. 1012932104).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azadeh-Ranjbar V., Elvin N., Andreopoulos Y. (2018). Vortex-induced vibration of finite-length circular cylinders with spanwise free-ends: Broadening the lock-in envelope. Phys. Fluids 30, 105104. doi: 10.1063/1.5042774

CrossRef Full Text | Google Scholar

Badhurshah R., Bhardwaj R., Bhattacharya A. (2019). Lock-in regimes for Vortex-Induced Vibrations of a cylinder attached to a bistable spring. J. Fluids Struct. 91, 102697. doi: 10.1016/j.jfluidstructs.2019.102697

CrossRef Full Text | Google Scholar

Bearman P. W. (2011). Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658. doi: 10.1016/j.jfluidstructs.2011.03.021

CrossRef Full Text | Google Scholar

Bernitsas M. M. (2016). Harvesting energy by flow included motions BT - springer handbook of ocean engineering. Eds. Dhanak M. R., Xiros N. I. (Cham: Springer International Publishing). doi: 10.1007/978-3-319-16649-0_47

CrossRef Full Text | Google Scholar

Bernitsas M. M., Raghavan K., Ben-Simon Y., Garcia E. M. H. (2008). VIVACE (Vortex induced vibration aquatic clean energy): A new concept in generation of clean and renewable energy from fluid flow. J. Offshore Mech. Arct. Eng. 130. doi: 10.1115/1.2957913

CrossRef Full Text | Google Scholar

Chang C.-C., Ajith Kumar R., Bernitsas M. M. (2011). VIV and galloping of single circular cylinder with surface roughness at 3.0×104≤Re≤1.2×105. Ocean Eng. 38, 1713–1732. doi: 10.1016/j.oceaneng.2011.07.013

CrossRef Full Text | Google Scholar

Facchinetti M. L., de Langre E., Biolley F. (2004). Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 19, 123–140. doi: 10.1016/j.jfluidstructs.2003.12.004

CrossRef Full Text | Google Scholar

Farshidianfar A., Dolatabadi N. (2013). Modified higher-order wake oscillator model for vortex-induced vibration of circular cylinders. Acta Mech. 224, 1441–1456. doi: 10.1007/s00707-013-0819-0

CrossRef Full Text | Google Scholar

Gao Z., Efthymiou M., Cheng L., Zhou T., Minguez M., Zhao W. (2021). Towards a model of hydrodynamic damping for a circular cylinder with helical strakes at low KC. Mar. Struct. 78, 103025. doi: 10.1016/j.marstruc.2021.103025

CrossRef Full Text | Google Scholar

Han P., Langre E., Thompson M. C., Hourigan K. (2023). Vortex-induced vibration forever even with high structural damping. (Cambridge University Press: The Journal of Fluid Mechanics). 962, 1–16. doi: 10.1017/jfm.2023.268

CrossRef Full Text | Google Scholar

Huynh B. H., Tjahjowidodo T. (2017). Experimental chaotic quantification in bistable vortex induced vibration systems. Mech. Syst. Signal Process. 85, 1005–1019. doi: 10.1016/j.ymssp.2016.09.025

CrossRef Full Text | Google Scholar

Huynh B. H., Tjahjowidodo T., Zhong Z. W., Wang Y., Srikanth N. (2018). Design and experiment of controlled bistable vortex induced vibration energy harvesting systems operating in chaotic regions. Mech. Syst. Signal Process. 98, 1097–1115. doi: 10.1016/j.ymssp.2017.06.002

CrossRef Full Text | Google Scholar

Khalak A., Williamson C. H. K. (1999). Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851. doi: 10.1006/jfls.1999.0236

CrossRef Full Text | Google Scholar

Kim E. S., Sun H., Park H., Shin S., Chae E. J., Ouderkirk R., et al. (2021). Development of an alternating lift converter utilizing flow-induced oscillations to harness horizontal hydrokinetic energy. Renew. Sustain. Energy Rev. 145, 111094. doi: 10.1016/j.rser.2021.111094

CrossRef Full Text | Google Scholar

Lv Y., Sun L., Bernitsas M. M., Sun H. (2021). A comprehensive review of nonlinear oscillators in hydrokinetic energy harnessing using flow-induced vibrations. Renew. Sustain. Energy Rev. 150, 111388. doi: 10.1016/j.rser.2021.111388

CrossRef Full Text | Google Scholar

Mackowski A. W., Williamson C. H. K. (2013). An experimental investigation of vortex-induced vibration with nonlinear restoring forces. Phys. Fluids 25. doi: 10.1063/1.4819082

CrossRef Full Text | Google Scholar

Ramlan R., Brennan M. J., Mace B. R., Kovacic I. (2010). Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 59, 545–558. doi: 10.1007/s11071-009-9561-5

CrossRef Full Text | Google Scholar

Sarpkaya T. (2004). A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447. doi: 10.1016/j.jfluidstructs.2004.02.005

CrossRef Full Text | Google Scholar

Sun H., Kim E. S., Nowakowski G., Mauer E., Bernitsas M. M. (2016). Effect of mass-ratio, damping, and stiffness on optimal hydrokinetic energy conversion of a single, rough cylinder in flow induced motions. Renew. Energy 99, 936–959. doi: 10.1016/j.renene.2016.07.024

CrossRef Full Text | Google Scholar

Sun H., Ma C., Bernitsas M. M. (2018). Hydrokinetic power conversion using Flow Induced Vibrations with nonlinear (adaptive piecewise-linear) springs. Energy 143, 1085–1106. doi: 10.1016/j.energy.2017.10.140

CrossRef Full Text | Google Scholar

Wang J., Geng L., Ding L., Zhu H., Yurchenko D. (2020). The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 267, 114902. doi: 10.1016/j.apenergy.2020.114902

CrossRef Full Text | Google Scholar

Wang K. W., Harne R. L. (2017). Harnessing bistable structural dynamics: for vibration control, energy harvesting and sensing (Hoboken, New Jersey: John Wiley & Sons).

Google Scholar

Williamson C. H. K., Govardhan R. (2008). A brief review of recent results in vortex-induced vibrations. J. Wind Eng. Ind. Aerodyn. 96, 713–735. doi: 10.1016/j.jweia.2007.06.019

CrossRef Full Text | Google Scholar

Zhang B., Song B., Mao Z., Tian W., Li B. (2017). Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 133, 723–736. doi: 10.1016/j.energy.2017.05.051

CrossRef Full Text | Google Scholar

Zhu H., Yao J., Ma Y., Zhao H., Tang Y. (2015). Simultaneous CFD evaluation of VIV suppression using smaller control cylinders. J. Fluids Struct. 57, 66–80. doi: 10.1016/j.jfluidstructs.2015.05.011

CrossRef Full Text | Google Scholar