A residual network with geographical and meteorological attention for multi-year ENSO forecasts

Introduction: As global temperatures continue to rise, extreme weather phenomena such as El Niño and the Southern Oscillation (ENSO) near the equatorial Pacific Ocean are occurring more frequently and leading to tropical cyclones, droughts, and a series of extreme weather disasters. Accurately predicting ENSO in advance can greatly reduce the serious damage to human society, economy, and ecological environment. However, existing methods often neglect the data relation between geographical regions and meteorological factors, hindering the accuracy of ENSO prediction.

Methods: To overcome this problem, we propose a residual network with geographical and meteorological attention to capture important geographical information and explore the spatio-temporal correlation of different meteorological factors. Specifically, we propose two main attention modules: (1) the Geographical Semantic Information Enhancement Module (GSIEM), which selectively attends to important geographical regions and filters out irrelevant noise through a spatial-axis attention map, and (2) the Meteorological Factors Discriminating Enhancement Module (MFDEM), which aims to learn the spatio-temporal dependency of different meteorological factors using a learnable channel-axis weight map. We then integrate our proposed two attention modules into the backbone using residual connection, enhancing the model's prediction ability.

Results: We conducted extensive experimental comparisons and ablation studies to evaluate the performance of our proposed method. The results show that our method outperforms existing state-of-the-art methods in ENSO prediction, with a significant improvement in prediction accuracy.

Discussion: Our proposed method effectively captures geographical and meteorological information, facilitating accurate ENSO prediction. The attention modules we proposed can effectively filter out irrelevant noise and learn the spatio-temporal dependency of different meteorological factors, contributing to the superior performance of our model. Overall, our study provides a novel approach for ENSO prediction and has great potential for practical applications.

1 Introduction

ENSO is a phenomenon characterized by a persistent rise in sea surface temperature (SST) in the equatorial eastern Pacific Ocean, representing an anomaly in the earth’s climate system. As the global climate continues to warm, ENSO are becoming more frequent, drawing increasing attention. These occurrences often cause extreme weather disasters in most regions of the world, including tropical cyclones (Timmermann et al., 2018), droughts (Cai et al., 2020), floods (Takahashi and Martínez, 2019) and heavy rains (Wang, 2021). Therefore, there is a strong impetus to precisely predict these events ahead of time.

In recent years, several indicators have been proposed for monitoring ENSO, such as Nino 3.4 index (Ye et al., 2021), oceanic nino index (Glantz and Ramírez, 2020), southern oscillation index (Raj and Geetha, 2021) and SST index (Yan et al., 2020). These indicators can be predicted using SST anomalies or heat content (HC, vertical mean ocean temperature above 300 m). Among these indicators, the Nino 3.4 index is the most popular and important indicator, calculated as the three-month sliding mean of the SST anomaly over 5 °S -5 °N and 170°W -120°W on the global map. When the Nino3.4 index remains above 0.5 °C for a minimum of five months, it is considered that an ENSO event has occurred.

Forecasting ENSO remains a challenging task due to the nonlinear nature of ENSO and its interactions with other climate modes (Ren et al., 2022). Existing ENSO forecasting methods can be broadly categorized into two groups: traditional forecasting methods and deep learning-based forecasting methods. Traditional forecasting methods usually utilize the physics of ocean-atmosphere interactions to forecast ENSO. Specially, Zebiak and Cane (1987) proposed a coupled prediction model to forecast ENSO by imitating perturbations in the average state of the monthly climate specified from observed data. Based on this model (Zebiak and Cane, 1987), various improved coupled models such as the intermediate coupled model (Wang et al., 2017) and the coupled general circulation model (Luo, 2007) have been proposed to solve predictions of ENSO. There are other traditional works (Knaff and Landsea, 1997; Xue and Leetmaa, 2000; Alexander et al., 2008) that utilized statistical theory to infer the evolution of ENSO from a large amount of historical data. These statistical methods can be roughly divided into two categories (Ye et al., 2021): Holt-Winters (HW) methods (Holt, 2004; So and Chung, 2014) and autoregressive integrated moving average (ARIMA) methods (Siswanto, 2010; Rosmiati et al., 2021). For example, Holt (2004) proposed a Holt-Winters (HW) method to adapt the model parameters to the variation of the observed data curve and predict Eino 3.4 index by the exponential moving average (EMA). Based on HM methods, So and Chung (2014) considered both the mean and variance in the historical data and proposed a forecasting method to statistically infers dynamic seasonality in heteroskedastic time series models. Rosmiati et al. (2021) proposed an autoregressive integrated moving average (ARIMA) model to complete the ocean climate prediction and achieve the ideal prediction results of ENSO. However, these traditional methods (So and Chung, 2014; Rosmiati et al., 2021) can only achieve satisfactory prediction results in the short-term forecasting problem but perform poorly in long-term prediction results due to the uncertainty of initial conditions and the cognitive limitations of empirical models (Ye et al., 2021). Besides, ENSO forecasts is a complex nonlinear problem involving several meteorological factors, traditional methods using the physics of ocean-atmosphere interaction or statistical theory cannot fully understand the evolution of ENSO.

Recently, deep learning technology has advanced significantly, and several deep neural networks have been proposed (Aguilar-Martinez and Hsieh, 2009; Shukla et al., 2011; McDermott and Wikle, 2017; Ham et al., 2019; Ye et al., 2021) for predicting ENSO by exploring complex correlations with historical data. For instance, Shukla et al. (2011) utilized artificial neural network (ANN) models to study the correlation between Indian summer monsoon rainfall and Nino indexes, and the results illustrated that the performance of the ANN model far exceeded that of other nonlinear models. Aguilar-Martinez and Hsieh (2009) were the first to use Bayesian neural network (BNN) and support vector regression model (SVR) to forecast the tropical Pacific SST anomalies at lead times ranging from 3 to 15 months. Additionally, there are also some methods (McDermott and Wikle, 2017; McDermott and Wikle, 2019) that utilize recurrent neural networks (RNN) to achieve long-term ENSO forecasts by taking into account short-term prediction results. McDermott and Wikle (2017) introduced the quadratic echo state network (QESN), which uses an embedded input and a quadratic reservoir output interaction to make highly accurate forecasts of SST in the tropical Pacific. Zhang et al. (2017) first used long short-term memory (LSTM) to predict changes in SST in the coastal seas of China. Broni-Bedaiko et al. (2019) used various complex network metrics extracted from climate networks, combined with LSTM, to forecast ENSO. To improve the spatial correlation of SST, Shi et al. (2015) proposed the ConvLSTM architecture for precipitation prediction, which incorporates convolution layers into the LSTM model to capture spatial features. However, RNN-based methods train a single model for all prediction tasks from short-to-long term, which inevitably encounters the problem of error accumulation, and consequently the inaccuracy of long-term prediction. To address this issue, Ham et al. (2019) proposed a CNN-based parallel model to avoid the error accumulation by assigning data to different forecast periods, or lead-months. Specifically, they trained multiple individual prediction models, each related to a specific lead-month, which can improve the accuracy of the predictions and can lead to more reliable forecasts.

Although numerous methods have been proposed to address ENSO forecasts, they still suffer from weak performance due to the following critical challenges: (1) ENSO exhibits intricate spatial and temporal complexities (Timmermann et al., 2018; Fang and Chen, 2023), the predictors in different regions have varying degrees of influence on it. For example, the SST anomalies in the western North Atlantic and western South Atlantic, as well as western and southern Pacific, have a more significant effect on ocean circulation anomalies, which is one of the primary drivers of ENSO. However, previous CNN-based methods treated all regions equally, overlooking essential geographical information and introducing irrelevant geographical noise. (2) Due to the characteristics of the fast change rate and high frequency noise in the meteorological data, it is a challenging task to forecast ENSO based solely on SST data. While some methods (Ham et al., 2019; Ye et al., 2021) have utilized both SST and HC to predict ENSO and achieved effective performance improvements, they considered SST and HC as two independent variables and assigned equal importance in the training process. We argue that SST and HC are correlated variables with spatio-temporal associations and should have different weights at different times.

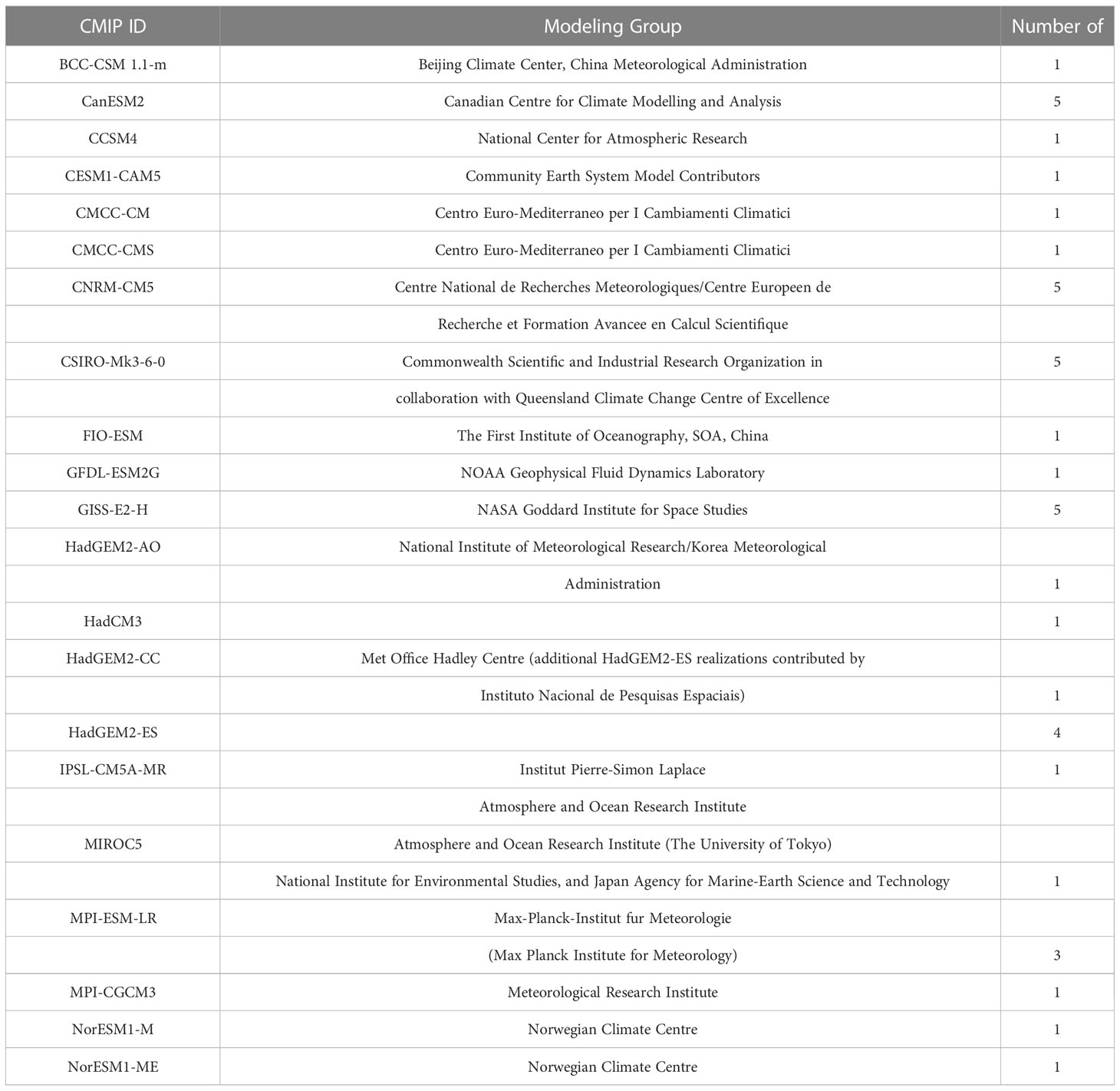
To cope with above issues, we propose a residual network with geographical and meteorological attention for multi-year ENSO forecasts, which named GM-CNN. As illustrated in Figure 1, we first concatenate three consecutive months of SST and HC data as network inputs, and use the input layer with kernel size of 4 × 8 to obtain the initial feature map. To capture important geographical information and filter out irrelevant noise, we propose a geographical semantic information enhancement module (GSIEM) to output the geographical semantic weight map by the attention mechanism consists of two channel-oriented pooling layers and a convolutional layer. In addition, we also propose a meteorological factors discriminating enhancement module (MFDEM) to adaptively assign different weights to two meteorological factors (SST and HC) by two pooling layers along the spatial axis and two convolutional layers. Moreover, we fuse the hierarchical attention mechanism into the backbone through the residual connection to enhance the representative ability of the encoder. In summary, the main contributions of this work can be summarized as follows:

● We propose a residual network with geographical and meteorological attention for multi-year ENSO forecasts, which can adaptively monitor the evolution of ENSO based on two meteorological factors (SST and HC).

● We introduce two attention modules with distinct dimensions: the geographical semantic information enhancement module, which enables the model to selectively attend to different geographical regions, and the meteorological factors discriminating enhancement module, which explores the interplay between SST and HC.

● The experimental results for the period between 1982 and 2017 indicate that our proposed method outperforms state-of-the-art methods, highlighting the effectiveness of our approach.

FIGURE 1

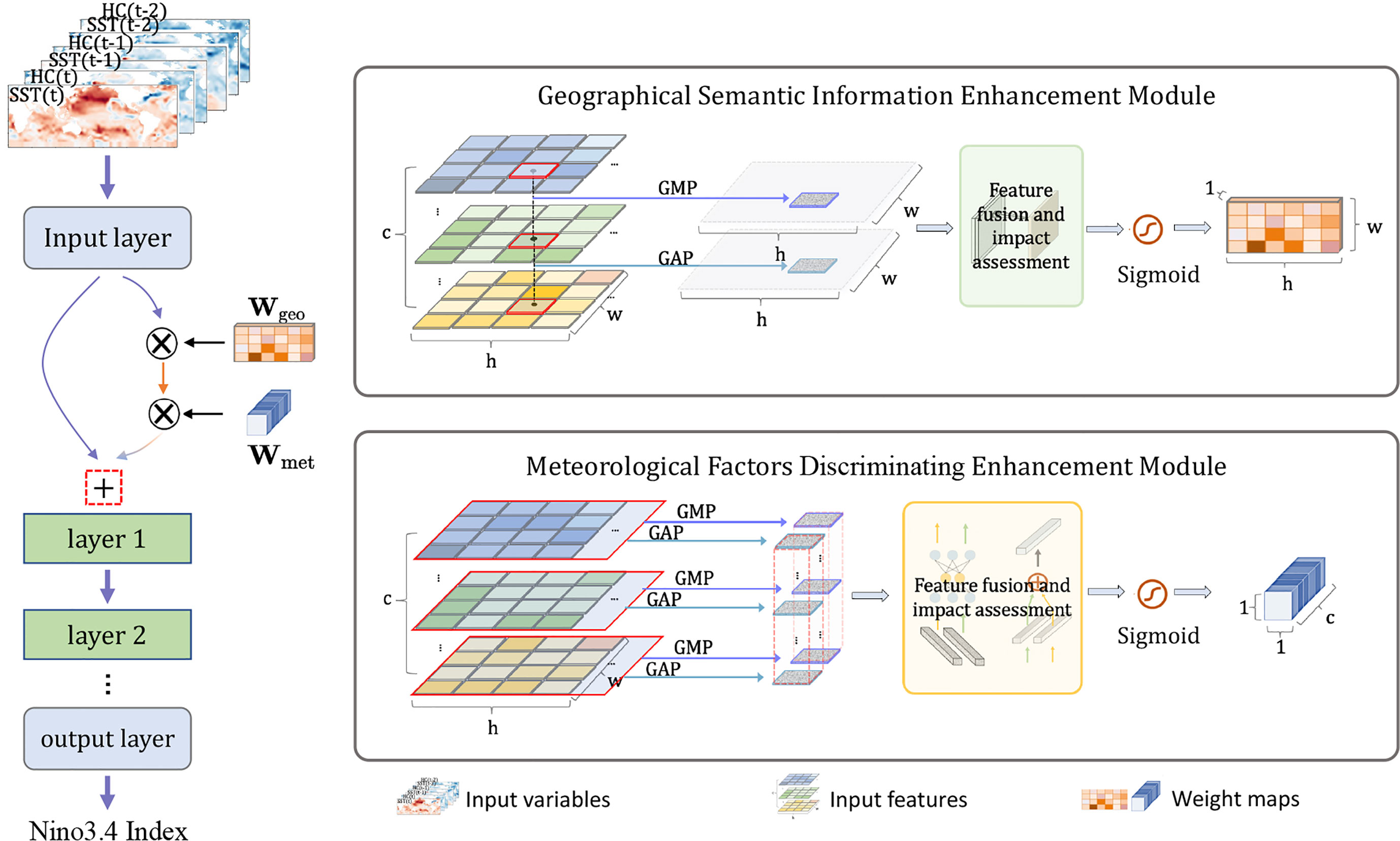
Figure 1 Flowchart of the proposed GM-CNN. The model structure is shown on the left, and the two key module structures are shown on the right. Two meteorological factors for three consecutive months are fed into the neural network, then the embeddings out from the input layer are assigned to study a multi-layered attention relationship. Afterwards, this attention relationship are propagated to the original embeddings by the addition device.

2 Method

We present a novel approach for multi-year ENSO forecasts, called Residual Network with Geographical and Meteorological Attention, as illustrated in Figure 1. In Sec. 2.1, we provide an overview of multi-year ENSO forecasts. We then introduce the Geographical Semantic Information Enhancement Module in Sec. 2.2, which enables the network to assign attention to different geographical regions. Finally, in Sec. 2.3, we describe the Meteorological Factors Discriminating Enhancement Module, which enhances the representation of meteorological properties in the input data.

2.1 Preliminary

In recent works (Ham et al., 2019; Ye et al., 2021), multi-year EI Nino forecasts have been defined as a spatio-temporal prediction problem. Concretely, we aim to predict the Nino3.4 indexes for the next l months using two types of meteorological data (SST and HC) of three consecutive months, which can be formulated as:

$\begin{array}{ll}\left\{P_t,P_{t+1}\dots P_{t+l}\right\}=\varphi (\left\{X_t,X_{t-1},X_{t-2}\right\})& (1)\end{array}$

where $X_t\in R^{C_0\times W_0\times H_0}$, $W_0=24$ and $H_0=72$ represents 24*72 meteorological data in the $0^{\circ }$ – ${360}^{\circ }$ E and ${55}^{\circ }$ S– ${60}^{\circ }$ N, and $C_0=2$ represents two types of meteorological data (SST and HC). $\varphi$ is the predicted model. $P=\left\{P_t,P_{t+1}\dots P_{t+l}\right\}$ is the predicted Niño3.4 indexes of the next $l$ months and $l\in \left\{1,2\dots 20\right\}$. In this work, we adopt a CNN-based parallel network (Ham et al., 2019) as the backbone for encoding input features and generating the predicted indexes. To minimize the discrepancy between the predicted value and ground truth, we employ the mean squared error (MSE) loss function given below:

$\begin{array}{ll}L(P,Y)=\frac{1}{n}\sum _{i=1}^n{\left|p^i-y^i\right|}^2& (2)\end{array}$

The aforementioned operations serve as the general paradigm for multi-year ENSO forecasts. However, there are two issues outlined in the introduction that impede the effectiveness of this paradigm: 1) ignoring the impact of distinct geographical regions. 2) ignoring the influence of different meteorological factors over time. It is prone to give trivial solutions when we equally treat both meteorological data (SST and HC) and regions of all latitude and longitude. Therefore, we propose geographical semantic information enhancement module to adaptively focus on different geographical regions as described in Sec. 2.2 and a meteorological factors discriminating enhancement module to explore the relationship between two types of meteorological data (SST and HC) under different months in Sec. 2.3. Finally, we integrate our proposed two attention modules into the original backbone using the residual connection, which can enhance the representative ability of the encoder and is formulated as follows:

$\begin{array}{ll}{X}_{i,j,k}^1=f_{\text{in}}(X_{i,j,k})+f_{\text{in}}(X_{i,j,k})\odot {\mathbf{\text{W}}}_{\text{geo}}^{1,j,k}\odot {\mathbf{\text{W}}}_{\text{met}}^{i,1,1}& (3)\end{array}$

where $X$ is the input data containing both SST and HC for three consecutive months, $f_{\text{in}}$ is the input layer containing kernel size $4\times 8$ for obtaining the initial feature map. ${\mathbf{\text{W}}}_{\text{reg}\hspace{0.17em}}$ represents the geographical semantic weight map to tap the importance of different geographical regions for ENSO prediction, ${\mathbf{\text{W}}}_{\text{met}}$ is the meteorological factors weight map to explore the relationship between two types of meteorological data. $\odot$ denotes the multiplication of matrix elements, $+$denotes the matrix elements wise addition. $X^1$, the feature combining geographical attention and meteorological attention, is further fed into the subsequent network to extract high-dimensional features.

2.2 Geographical semantic information enhancement module

To comprehensively explore the complex interactions among spatial and temporal dependencies, we investigate the interplay between SST and HC for ENSO across various geographical regions through an attention mechanism along the channel axis. Generally, the shallow features of the input data carry more original structural information, that is, spatio-temporal information. As the network layers become deeper, more abstract information is extracted, but the amount of raw information is reduced. Therefore, we mine the initial features after the input layer to capture significant geographical information. Specifically, we utilize global average-pooling and max-pooling operations along the channel to learn the feature distribution and salient features related to SST and HC over three consecutive months in different geographical regions. As shown in Figure 2, the entire process is described as follows:

FIGURE 2

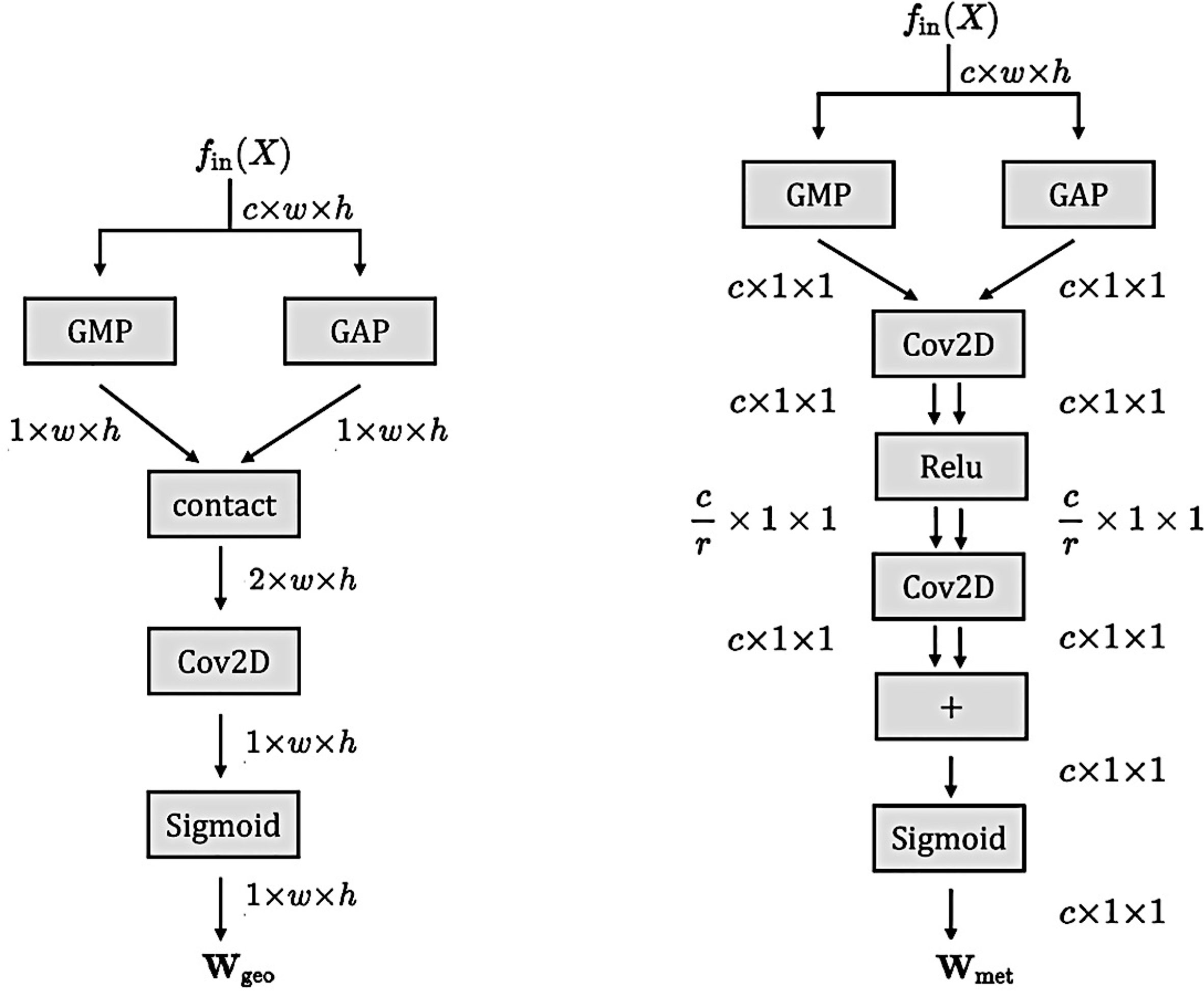
Figure 2 The specific network structures to respectively congregate W_geo and W_met, which share the similar learning procedure while in the quite different completion ways. Next to the line is marked the dimensional change throughout the process, and it is worth noting that “GMP” and “GAP” are carried out on different dimensions for the computation of W_geo and W_met. During the processing of W_met, the structure from “Cov2D” to the next “Cov2D” is actually a multilayer perceptron for cross-communication, “r” is the channel compression ratio.

To extract meaningful spatial features from the input data $X$, we employ an input layer with a kernel size of 4 $\times$ 8 to obtain the initial feature map $f_{\text{in}}(X)$. Next, we use a global average-pooling GAP($·$) and a global max-pooling GMP($·$) operations along the channel axis to obtain the average feature distribution GAP($f_{\text{in}}(X)$) and the salient feature map GMP($f_{\text{in}}(X)$) in different geographical regions. In order to fully consider the characteristics of both feature maps, we then contact GAP($f_{\text{in}}(X)$) and GMP($f_{\text{in}}(X)$) along the channel axis into the final geographical feature map $W_{\text{geo}}^{\text{c}}\in R^{2\times w\times h}$. Subsequently, a convolutional layer and a sigmoid $\delta (·)$ function are used to model the interaction between two types of feature maps and quantify their contribution to the prediction of ENSO. Formally,

$\begin{array}{ll}{W}_{\text{geo}}=\delta [Cov2D(W_{\text{geo}}^{\text{c}})]& (4)\end{array}$

By incorporating the geographical semantic information enhancement module, we propagate the learned geographical weight to the global feature maps through the utilization of $f_{\text{in}}(X_{i,j,k})\odot W_{\text{geo}}^{1,\text{j},\text{k}}$, which allows for the dynamic allocation of attention to various geographical regions.

2.3 Meteorological factors discriminating enhancement module

Existing methods treat SST and HC equally, limiting the prediction ability. However, it has been demonstrated that SST and HC are two distinct variables with different variability characteristics (Levitus et al., 2000; Trenberth and Fasullo, 2013). For exploring the spatio-temporal associations between SST and HC, we propose a meteorological factors discriminating enhancement module.

To obtain the data characteristics of different meteorological factors of three consecutive months, we first embed the input data to the initial feature map using the input layer. Then, we collect statistical information by utilizing global average-pooling and global max-pooling operations along the spatial axis. Specifically, we obtain ${\mathit{\text{W}}}_{\text{me} \text{t}}^{avg}=GAP(f_{\text{in}}(X))\in R^{c\times 1\times 1}$ and ${\mathit{\text{W}}}_{\text{met}}^{max}=GMP(f_{\text{in}}(X))\in R^{c\times 1\times 1}$ from all geographical regions. Next, we propose a bottleneck structure with two convolutional layers to explore the impact of different meteorological factors in different months. Finally, we add the two statistical information and obtain the final meteorological factor weight map $W_{\text{met}}$ using a sigmoid function $\delta (·)$. The entire process can be formulated as follows:

$\begin{array}{ll}{W}_{\text{met}}=\delta (Bottleneck(GMP(f_{\text{in}}(X)))+Bottleneck(GAP(f_{\text{in}}(X))))& (5)\end{array}$

In a similar fashion to the geographical semantic weight map, the acquired meteorological factors weight map is disseminated to the $c$ global feature maps through matrix multiplication $\odot$, which allows for the adaptive assignment of weights for both meteorological factors across various months. By utilizing both the geographical semantic weight map $W_{\text{geo}}$ and the meteorological factor weight map $W_{\text{met}}$, we can assess the significance of meteorological factors at different months and locations for accurate ENSO forecasts. Furthermore, this enables us to identify the most relevant data and filter out redundant noise in the input data, thereby improving the encoder’s representational capacity and achieving higher precision predictions.

3 Experiment

To validate the performance of the proposed method, we conduct comprehensive evaluations in this section. We start by describing the dataset, implementation details, and evaluation metrics used in our experiments. Next, we showcase the forecast performance of the proposed framework and provide visualizations of some predicted simulations. We also compare the proposed method with several state-of-the-art methods for ENSO forecasts. Additionally, we conduct ablation studies to further explore the contribution of key modules to the overall performance.

3.1 Dataset

We evaluate our approach using three widely-used datasets presented in Figure 3: CMIP5 (Bellenger et al., 2014), SODA (Giese and Ray, 2011) and GODAS (Behringer and Xue, 2004). The CMIP5 dataset, which is the achievement of the Coupled Model Intercomparison Project phase5, contains historical simulation data from 1861 to 2004, with 21 different patterns per year, for a total of 2961 samples. Here, the “pattern” refers to the data provided by various institutions and organizations in the CMIP5 program. These data essentially represent different climate assumptions and parameters used to study and simulate global climate and climate change. Table 1 lists the patterns and specific members used for training. The SODA dataset, provided by American Simple Ocean Data Assimilation, contains 100 historical observation data samples from 1871 to 1973. The GODAS dataset, collected by the Global Ocean Data Assimilation System, includes 36 years of historical observation data from 1982 to 2017. In line with previous research (Ham et al., 2019; Ye et al., 2021), our approach begins by pre-training the model on the CMIP5 dataset, fine-tuning it on the SODA dataset, and finally testing it on the GODAS dataset. The datasets include two types of data: SST anomalies and HC (Heat Content) anomalies, where SST represents the ocean surface temperature and HC here is the upper 300 meters of vertical mean ocean temperature. Both the SST and HC inputs are three-dimensional array $x\in R^{M\times la\times lo}$, where $x_{i,j,k}$ represents the value of a meteorological factor in the $i^{th}$ month, $j^{th}$ latitude and $k^{th}$ longitude. It is noteworthy that the latitude range is $0^{\circ }$ – ${360}^{\circ }$ E and the longitude range is ${55}^{\circ }$ S– ${60}^{\circ }$ N, with a spatial resolution of $5^{\circ }\times 5^{\circ }$. Therefore, the input shape is $R^{6\times 72\times 24}$.

FIGURE 3

Figure 3 The dataset for training and testing the model. CMIP5 and SODA are datasets used for training, while GODAS serves as the testing dataset to verify performance.

TABLE 1

Table 1 The list of CMIP5 patterns used to train the GM-CNN model.

3.2 Implementation details

We adopt a CNN-based parallel network as our baseline architecture, which comprises three convolution layers, two pooling layers, and a fully connected layer. We use a $4\times 8$ kernel size for the input layer with an output channel of 50. The kernel size for the geographical semantic information enhancement module is set to $6\times 6$, and the channel compression ratio for the bottleneck structure in the meteorological factors discriminating enhancement module is set to 2. We trained the entire framework in an end-to-end manner using stochastic gradient descent (SGD) with a momentum of 0.9, and a batch size of 400. We empirically set the learning rate to 0.01. During the training phase, we first load the CMIP5 dataset to pre-train the network and save the trained weigtht parameters, then initialize these parameters when importing the SODA dataset for further training.

3.3 Evaluation metrics

To evaluate the forecast performance of the proposed framework, we employ two commonly used evaluation metrics: Correlation Coefficient Skill (Corr) and Root Mean Square Error (RMSE).

* Corr is a metric that evaluates the linear correlation between the predicted indexes and ground truth. It can be computed using the following equation:

$\begin{array}{ll}\underset{l}{\text{Corr}}=\frac{1}{12}\sum _{m=1}^{12}\frac{{\sum }_{t=s}^e\left(Y_{t,m}-{\stackrel{-}{Y}}_m\right)\left(P_{t,m,l}-{\stackrel{-}{P}}_{m,l}\right)}{\sqrt{{\sum }_{t=s}^e{\left(Y_{t,m}-{\stackrel{-}{Y}}_m\right)}^2{\sum }_{t=s}^e{\left(P_{t,m,l}-{\stackrel{-}{P}}_{m,l}\right)}^2}}& (6)\end{array}$

Here, $P$ and $Y$ represent the predicted and actual values, respectively. $Y_m$and $P_{m,l}$ are temporal climatologies corresponding to the calendar month $m$ (from 1 to 12), and $l$ denotes the forecast month-ahead. The variable $t$ represents the year being forecasted, $s$ and $e$ indicate the earliest (1984) and latest year (2017) of the validation dataset, and ${\overline{Y}}_m$ and ${\overline{P}}_{m,l}$ indicate the multi-year average of the corresponding variable. A higher Corr value indicates better accuracy in predicting the evolution of the events.

* The Root Mean Square Error (RMSE) is a commonly used evaluation metric that measures the prediction error in terms of the standard deviation of the residual. It is calculated as follows:

$\begin{array}{ll}\underset{l}{\text{RMSE}}=\frac{1}{12}\sum _{m=1}^{12}\sqrt{\frac{{\sum }_{t=s}^e{(Y_{t,m}-P_{t,m,l})}^2}{\left|e-s\right|}}& (7)\end{array}$

A smaller value of RMSE indicates better predictive performance of the model as it reflects the heterogeneity between the predicted and actual values.

3.4 Results of the proposed GM-CNN

Figure 4 illustrates the all-season Corr and RMSE of the 3-month moving-averaged Niño3.4 index from 1982 to 2017, with forecasting conducted from 1 to 20 months in advance. The Corr index decreases while RMSE increases as the forecast horizon increases, indicating that the network’s predictive ability deteriorates with longer forecast periods due to the complexity of oscillation mechanisms and climate change chaos within ocean-atmosphere systems. Nonetheless, we can observe that corrstill remains above 0.5 with a lead time of 16 months, which demonstrates the superior forecasting ability of our model.

FIGURE 4

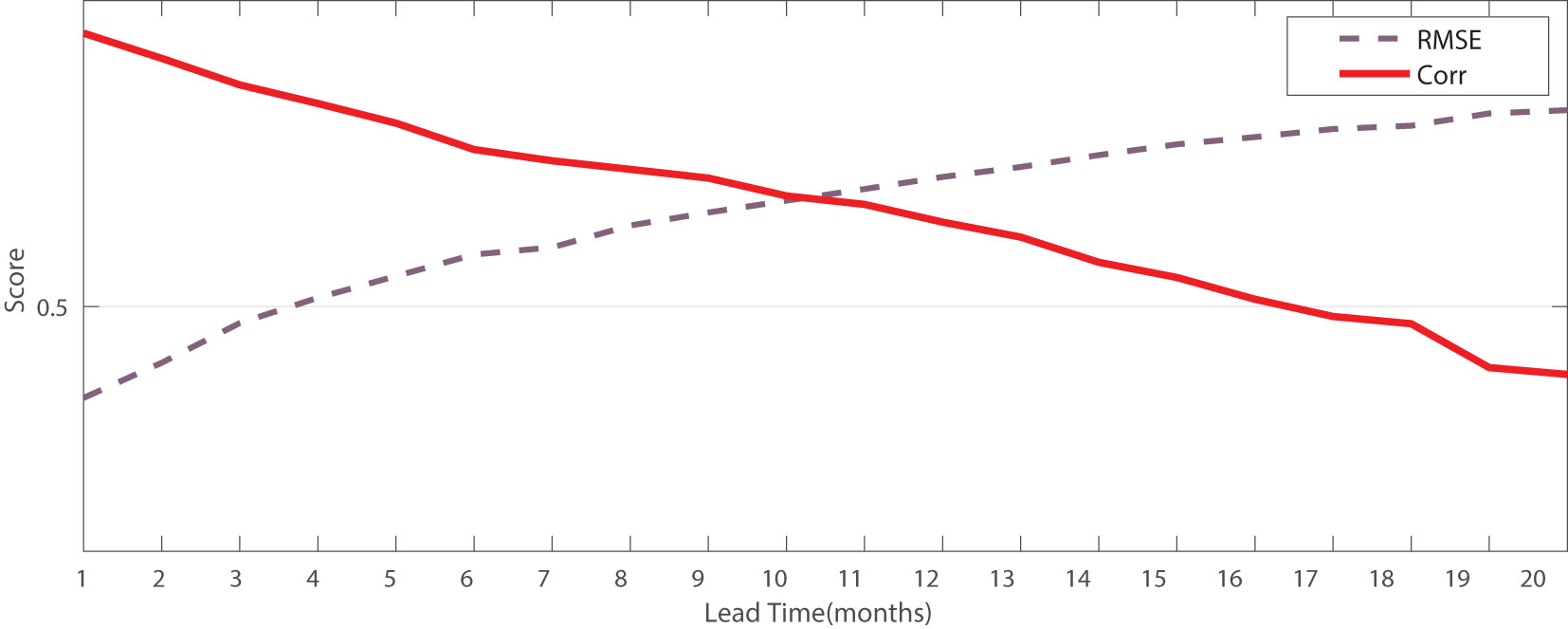
Figure 4 The Corr and RMSE between the real observed value and the predicted value output by the trained model. The abscissa locates the leading months from 1 to 20, and the ordinate indicates the prediction ability of the corresponding preceding month.

To intuitively show the difference between the Nino 3.4 index predicted by our trained model and the ground truth from 1982 to 2017, we visualize the predicted results for 1-,6-,12-, and 18-lead month ahead in Figure 5. The forecast curve and the observation curve exhibit a similar trend at 1-month and 6-month lead times, indicating that the proposed network can effectively extrapolate the evolution of ENSO for short-term forecasts. Despite the high difficulties in long-term predictions, our model’s results maintain an approximate trend with the observed values, demonstrating its robustness.

FIGURE 5

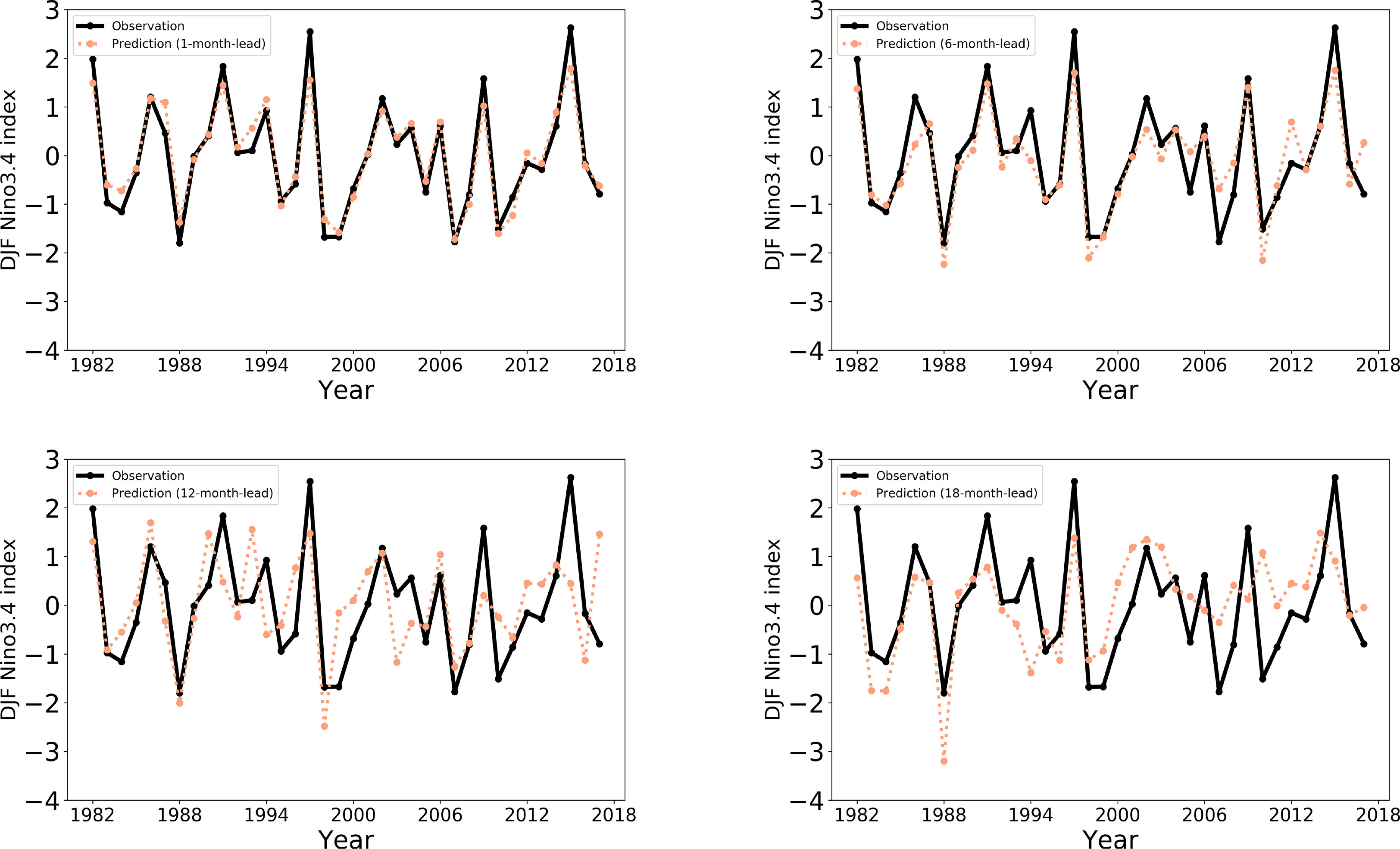
Figure 5 Prediction and observation curves of the Nino 3.4 index at different lead-months (1, 6, 12, 18). The abscissa represents specific interannual years, and the ordinate depicts the DJF seasonal Niño 3.4 index (obtained from the calculation of 3 consecutive monthly changes) of the corresponding year.

3.5 Performance comparison with previous methods

In this section, we compare the proposed GM-CNN with existing representative deep learning-based approaches to validate the superiority of our network.

● UNET (Ronneberger et al., 2015). UNET is well-known in the field of image segmentation for its simplicity and efficiency, utilizing a U-shaped structure composed of a contracting path for context capture and a symmetric expanding path for accurate localization.

● LSTM-FC (Zhao et al., 2019). LSTM-FC combines an LSTM-based temporal simulator and a neural network-based spatial module to effectively capture the characteristics of historical data.

● ZG-PSDL (Zheng et al., 2020). ZG-PSDL is a DNN-based network that utilizes four stacked composite layers to deduce the evolution of SST.

● HAM-CNN (Ham et al., 2019). The HAM-CNN framework is a popular method for predicting ENSO, which uses a parallel network of only three convolutional layers, two pooling layers, and a fully connected layer to prevent error accumulation.

● MS-CNN (Ye et al., 2021). Based on HAM-CNN, MS-CNN incorporates adaptive arrangement of different receptive fields for distinct prediction terms in order to capture more specific features.

The comparison work above was demonstrated in Ye et al. (2021), where they replicated these methods using the same dataset and experimental conditions. Figure 6 provides the all-season correlation results of the proposed method and other state-of-the-art methods on GODAS dataset, where “Ours” indicates the approach proposed in this paper. It can be observed that the proposed method outperforms other methods in most cases, except slightly lower than MS-CNN for the lead time between 1 to 3 months. Based on the results of the comparative experiments, the following observations and analyses can be made.

FIGURE 6

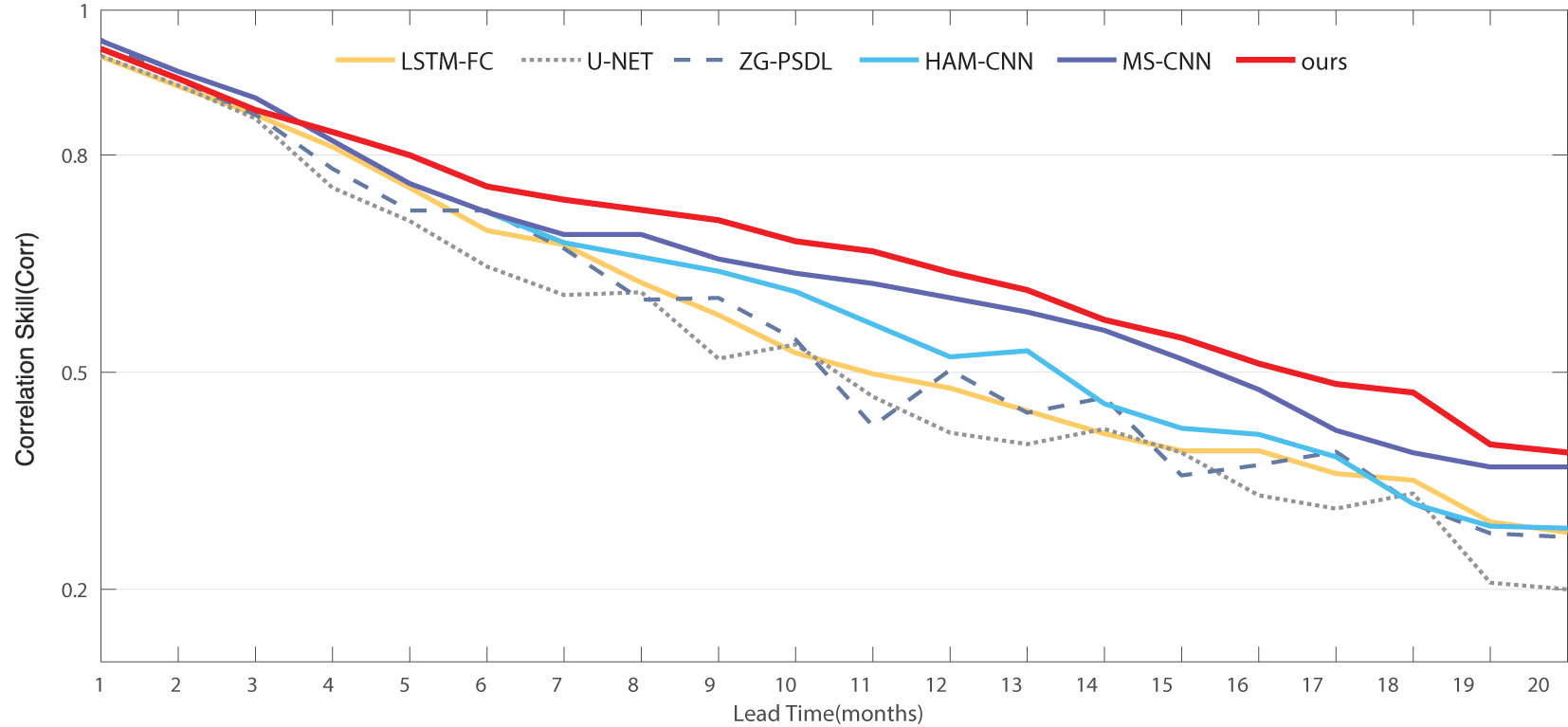
Figure 6 Comparison for the Corr of predictions and observations on Nino 3.4 index obtained using different deep learning based models. The ordinate represents the correlation coefficient between the predicted values and the true values for each model on the test set.

3.5.1 Comparison between Parallel-network methods and Single-model methods

The parallel-network methods, such as HAM-CNN, MS-CNN, and our proposed method (OURS), exhibit superior performance compared to the single-model methods (U-NET, LSTM-FC, ZG-PSDL), particularly in long-term forecast settings. This result indicates that the parallel framework is effective in preventing cumulative errors that may arise when predicting different lead times using a single model. Moreover, the indexes predicted by U-NET and ZG-PSGL fluctuate continuously as the lead time increases, indicating that deep networks with large parameters may overfit the insufficient training data. In contrast, parallel networks (HAM-CNN, MS-CNN, OURS) with shallow network architectures and fewer parameters tend to maintain more stable training and develop more robust models for meteorological data.

3.5.2 Comparison between proposed method and Parallel-network methods

The results show that our proposed method outperforms the state-of-the-art HAM-CNN and MS-CNN, highlighting the advantages of our approach. HAM-CNN and MS-CNN employ parallel convolutional networks to capture spatio-temporal features from input data, but overlook the enhancement of important information as well as filtering noise. In contrast, our proposed method, which incorporates two attention modules, can effectively assign weights to meteorological factors at different months and locations, leading to more accurate ENSO forecasts.

For a more detailed comparison with the best methods and to study the effect of seasons on ENSO, we compared the seasonal correlation coefficients with MS-CNN, which performs best among the existing deep learning methods, as shown in Figure 7. The results demonstrate that our proposed model achieves better performance than MS-CNN (Ye et al., 2021) in most seasons, validating the advantage of our approach. Both methods exhibit weaker performance in three target months: May, June, and July, which can be attributed to the Spring Predictability Barrier (Meng et al., 2020). However, our proposed method outperforms MS-CNN in the ‘JFM’, ‘FMA’, ‘MAM’, and ‘AMJ’ settings, with higher relevance in short term forecasts and more robust performance in long-term forecasts. This highlights that larger receptive fields can capture more information but may introduce more noise. In contrast, our method explores the contribution of data from different meteorological factors and geographical regions, effectively filtering out noise and improving performance.

FIGURE 7

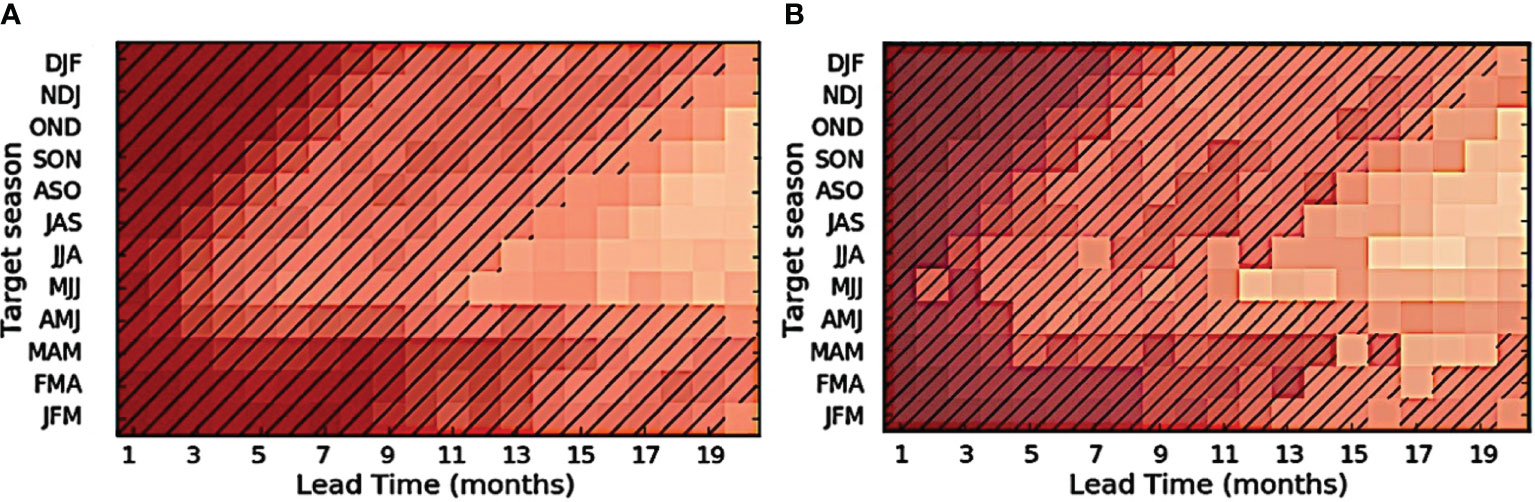
Figure 7 Seasonal corr comparison between (A) ours GM_CNN and (B) the sates of the arts MS-CNN. Darker colors indicate higher relevance and results marked by {black slashes} indicate that the correlation coefficient exceeds 0.5. “target season” denotes the month to be predicted, “JFM” denotes the Nino 3.4 index which {is} obtained from the calculation of 3 consecutive monthly changes.

3.6 Ablation studies

In order to comprehensively investigate the contribution and effectiveness of the key modules, we conducted ablation studies on the proposed two attention designs. As illustrated in Figure 8, the ‘Baseline’ represents the basic parallel-CNN network without the hierarchical attention. ‘Baseline+GSIEM’ and ‘Baseline+MFDEM’ represent adding only one attention module to the basic model, while ‘Baseline+GSIEM+MFDEM’ is the proposed design that combines both modules. As observed from Figures 8A, B ‘Baseline+GSIEM’ outperforms ‘Baseline’ in all lead times, indicating our geographical attention can capture the important regions which plays an essential role in ENSO and suppresses noise in irrelevant areas. ‘Baseline+MFDEM’ can enhance the model’s ability to predict ENSO compared to the basic model, demonstrating that our meteorological attention can explore the interaction relation between SST and HC in different months, improving the fitting ability of the model to meteorological factors. Moreover, Figure 8C shows that ‘Baseline+GSIEM’ and ‘Baseline+MFDEM’ achieve comparable scores, and the combination of the two modules, ‘Baseline+GSIEM+MFDEM’, yields the best performance in most cases, further verifying the effectiveness of our proposed method.

FIGURE 8

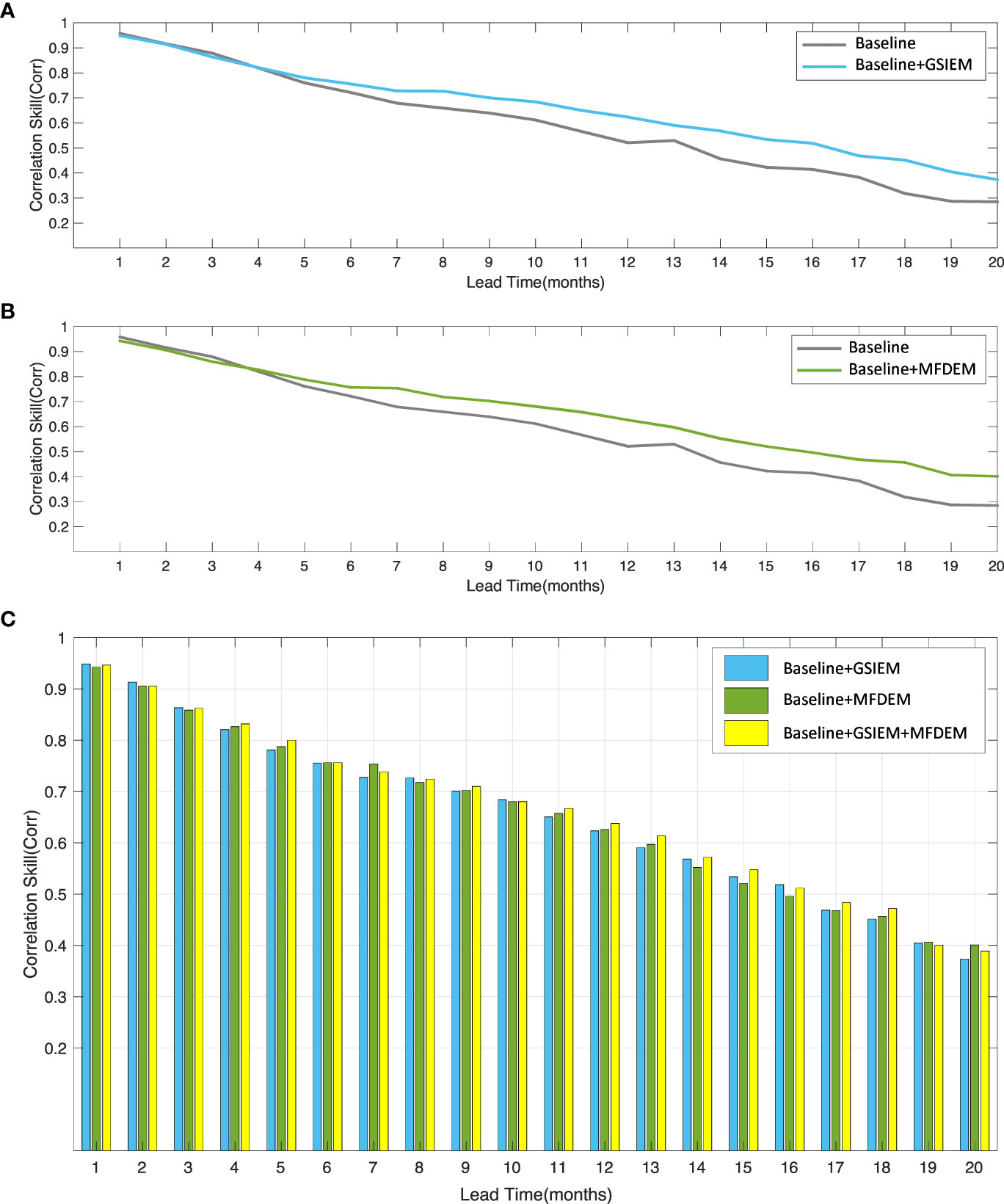
Figure 8 Ablation studies for the proposed two key modules. A and B show the effect of one single module, and the C compares the effects of separate modules and the simultaneous use of two modules.

4 Conclusion

ENSO is a powerful interannual climate indicator with global significance, making precise forecasts of its occurrences can aid individuals in gaining a better perception of and reacting to climate changes. This paper presents an end to end residual network with geographical and meteorological attention for multi-year ENSO forecasts. The proposed design inovatively incorporates two attention modes (from the geographical semantic information enhancement module and the meteorological factors discriminating enhancement module) to improve the accuracy of predictions. The feasibility and superiority of the proposed design have been confirmed through correlation coefficient experiments conducted on historical observation and simulation datasets. Furthermore, ablation experiments conducted on key modules reveal that various regions and meteorological factors have distinct impacts on ENSO predictions. Considering the intricacy of the ENSO event and its variations, future research could leverage a combination of multiple indicators to delve deeper into the multifaceted characteristics (Chen et al., 2022) inherent in such phenomena. As the ENSO event prediction network exhibits versatility, we also plan to broaden its application in the future by exploring its potential for predicting other meteorological factors, such as radar echoes, tropical cyclones, and tropical unstable waves.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of therepository/repositories and accession number(s) can be found below: https://zenodo.org/record/3244463#.ZCPsD3bMKUk.

Author contributions

DS, YL and TH contributed to conception and design of the study. DS, YL and WHL wrote the first draft of the manuscript. TH, ZW organized the database. A-AL, WL, WHL, YL performed the statistical analysis. TH, A-AL, WL wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Key Research and Development Program of China (2021YFF0704000) and the National Natural Science Foundation of China (U22A2068, 31770904).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguilar-Martinez S., Hsieh W. W. (2009). Forecasts of tropical pacific sea surface temperatures by neural networks and support vector regression. Int. J. Oceanog. 2009, 167239. doi: 10.1155/2009/167239

CrossRef Full Text | Google Scholar

Alexander M. A., Matrosova L., Penland C., Scott J. D., Chang P. (2008). Forecasting pacific ssts: linear inverse model predictions of the pdo. J. Climate 21, 385–402. doi: 10.1175/2007JCLI1849.1

CrossRef Full Text | Google Scholar

Behringer D., Xue Y. (2004)Evaluation of the global ocean data assimilation system at ncep: the pacific ocean (Seattle) (Accessed Proc. Eighth Symp. on Integrated Observing and Assimilation Systems for Atmosphere, Oceans, and Land Surface), 11–15.

Google Scholar

Bellenger H., Guilyardi É., Leloup J., Lengaigne M., Vialard J. (2014). Enso representation in climate models: from cmip3 to cmip5. Climate Dynam. 42, 1999–2018. doi: 10.1007/s00382-013-1783-z

CrossRef Full Text | Google Scholar

Broni-Bedaiko C., Katsriku F. A., Unemi T., Atsumi M., Abdulai J.-D., Shinomiya N., et al. (2019). El Niño-southern oscillation forecasting using complex networks analysis of lstm neural networks. Artif. Life Robot. 24, 445–451. doi: 10.1007/s10015-019-00540-2

CrossRef Full Text | Google Scholar

Cai W., McPhaden M. J., Grimm A. M., Rodrigues R. R., Taschetto A. S., Garreaud R. D., et al. (2020). Climate impacts of the el niño–southern oscillation on south america. Nat. Rev. Earth Environ 1, 215–231. doi: 10.1038/s43017-020-0040-3

CrossRef Full Text | Google Scholar

Chen N., Fang X., Yu J. Y.. (2022). A multiscale model for El Niño complexity. npj Clim Atmos Sci 5, 16. doi: 10.1038/s41612-022-00241-x

CrossRef Full Text | Google Scholar

Fang X., Chen N. (2023). Quantifying the predictability of enso complexity using a statistically accurate multiscale stochastic model and information theory. J. Climate 36, 2681–2702. doi: 10.1175/JCLI-D-22-0151.1

CrossRef Full Text | Google Scholar

Giese B. S., Ray S. (2011). El Niño variability in simple ocean data assimilation (soda), 1871–2008. J. Geophys. Res.: Ocean. 116, giese2011nino.

Google Scholar

Glantz M. H., Ramírez I. J. (2020). Reviewing the oceanic niño index (oni) to enhance societal readiness for el niño’s impacts. Int. J. Dis. Risk Sci 11, 394–403. doi: 10.1029/2010JC006695

CrossRef Full Text | Google Scholar

Ham Y.-G., Kim J.-H., Luo J.-J. (2019). Deep learning for multi-year enso forecasts. Nature 573, 568–572. doi: 10.1038/s41586-019-1559-7

CrossRef Full Text | Google Scholar

Holt C. C. (2004). Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast 20 (1), 5–10. doi: 10.1016/j.ijforecast.2003.09.015

CrossRef Full Text | Google Scholar

Luo J.J. (2007). Extended enso predictions using a fully coupled ocean–atmosphere model. Journal of Climate 21.1, 84–93 doi: 10.1175/2007JCLI1412.1

CrossRef Full Text | Google Scholar

Knaff J. A., Landsea C. W. (1997). An el niño–southern oscillation climatology and persistence (cliper) forecasting scheme. Weather forecast. 12, 633–652. doi: 10.1175/1520-0434(1997)012<0633:AENOSO>2.0.CO;2

CrossRef Full Text | Google Scholar

Levitus S., Antonov J. I., Boyer T. P., Stephens C. (2000). Warming of the world ocean. Science 287, 2225–2229. doi: 10.1126/science.287.5461.2225

CrossRef Full Text | Google Scholar

McDermott P. L., Wikle C. K. (2017). An ensemble quadratic echo state network for non-linear spatio-temporal forecasting. Stat 6, 315–330. doi: 10.1002/sta4.160

CrossRef Full Text | Google Scholar

McDermott P. L., Wikle C. K. (2019). Bayesian Recurrent neural network models for forecasting and quantifying uncertainty in spatial-temporal data. Entropy 21, 184. doi: 10.3390/e21020184

CrossRef Full Text | Google Scholar

Meng J., Fan J., Ludescher J., Agarwal A., Chen X., Bunde A., et al. (2020). Complexity-based approach for el niño magnitude forecasting before the spring predictability barrier. Proc. Natl. Acad. Sci. 117, 177–183. doi: 10.1073/pnas.1917007117

CrossRef Full Text | Google Scholar

Raj Y. E. A., Geetha B. (2021). Relation between southern oscillation index and indian northeast monsoon as revealed in antecedent and concurrent modes. Mausam 59.1, 15–34. doi: 10.54302/mausam.v59i1.1129

CrossRef Full Text | Google Scholar

Ren H., Zhang W., Lian T., Xie R., Hayashi M. (2022). Editorial: enso nonlinearity and complexity: features, mechanisms, impacts and prediction. in. Front. Earth Sci 10, 967362. doi: 10.3389/feart.2022.967362

CrossRef Full Text | Google Scholar

Ronneberger O., Fischer P., Brox T. (2015) U-Net: convolutional networks for biomedical image segmentation In: Navab N., Hornegger J., Wells W., Frangi A Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. MICCAI 2015. Lecture Notes in Computer Science (Springer, Cham) 9351. doi: 10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Rosmiati R., Liliasari S., Tjasyono B., Ramalis T. (2021)Development of arima technique in determining the ocean climate prediction skills for pre-service teacher. Journal of Physics: Conference Series IOP Publishing 1731 (1), 012072. doi: 10.1088/1742-6596/1731/1/012072

CrossRef Full Text | Google Scholar

Shi X., Chen Z., Wang H., Yeung D.-Y., kin Wong W., chun Woo W. (2015). Convolutional lstm network: a machine learning approach for precipitation nowcasting. NIPS 2015, 802–810. doi: 10.48550/arXiv.1506.0421

CrossRef Full Text | Google Scholar

Shukla R. P., Tripathi K. C., Pandey A. C., Das I. (2011). Prediction of indian summer monsoon rainfall using niño indices: a neural network approach. Atmospheric Res. 102, 99–109. doi: 10.1016/j.atmosres.2011.06.013

CrossRef Full Text | Google Scholar

Siswanto B. (2010). Simulasi fenomena enso berbasis model sirkulasi global Vol. 1 (Warta LAPAN) 1 (3).

Google Scholar

So M. K., Chung R. S. (2014). Dynamic seasonality in time series. Comput. Stat Data Anal. 70, 212–226. doi: 10.1016/j.csda.2013.09.010

CrossRef Full Text | Google Scholar

Takahashi K., Martínez A. G. (2019). The very strong coastal el niño in 1925 in the far-eastern pacific. Climate Dynam 52 (12), 7389–7415. doi: 10.1007/s00382-017-3702-1

CrossRef Full Text | Google Scholar

Timmermann A., An S. I., Kug J.-S., Jin F.-F., Cai W., Capotondi A., et al. (2018). El Niño–southern oscillation complexity. Nature 559 (7715), 535–545. doi: 10.1038/s41586-018-0252-6

CrossRef Full Text | Google Scholar

Trenberth K. E., Fasullo J. T. (2013). An apparent hiatus in global warming? Earth’s Future 1, 19–32. doi: 10.1002/2013EF000165

CrossRef Full Text | Google Scholar

Wang T. (2021). Spatiotemporal model based on deep learning for enso forecasts. Atmosphere 12 (7), 810. doi: 10.3390/atmos12070810

CrossRef Full Text | Google Scholar

Wang Y., Jiang J., Zhang H., Dong X., Wang L., Ranjan R., et al. (2017). A scalable parallel algorithm for atmospheric general circulation models on a multi-core cluster. Future Generation Comput. Syst 72, 1–10. doi: 10.1016/j.future.2017.02.008

CrossRef Full Text | Google Scholar

Xue Y., Leetmaa A. (2000). Forecasts of tropical pacific sst and sea level using a markov model. Geophys. Res. Lett. 27, 2701–2704. doi: 10.1029/1999GL011107

CrossRef Full Text | Google Scholar

Yan J., Mu L., Wang L., Ranjan R., Zomaya A. Y. (2020). Temporal convolutional networks for the advance prediction of enso. Sci. Rep 10, 8055. doi: 10.1038/s41598-020-65070-5

CrossRef Full Text | Google Scholar

Ye M., Nie J., Liu A., Wang Z., Huang L., Tian H., et al. (2021). Multi-year enso forecasts using parallel convolutional neural networks with heterogeneous architecture. Front. Mar. Sci. 1092. doi: 10.3389/fmars.2021.717184

CrossRef Full Text | Google Scholar

Zebiak S. E., Cane M. A. (1987). A model el niñ–southern oscillation. Monthly Weather Rev. 115, 2262–2278. doi: 10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2

CrossRef Full Text | Google Scholar

Zhang Q., Wang H., Dong J., Zhong G., Sun X. (2017). Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 14, 1745–1749. doi: 10.1109/LGRS.2017.2733548

CrossRef Full Text | Google Scholar

Zhao J., Deng F., Cai Y., Chen J. (2019). Long short-term memory-fully connected (lstm-fc) neural network for pm2. 5 concentration prediction. Chemosphere 220, 486–492. doi: 10.1016/j.chemosphere.2018.12.128

CrossRef Full Text | Google Scholar

Zheng G., Li X., Zhang R., Liu B. (2020). Purely satellite data–driven deep learning forecast of complicated tropical instability waves. Sci. Adv. 6, eaba1482. doi: 10.1126/sciadv.aba1482

CrossRef Full Text | Google Scholar