Cyclic threshold shear strain for pore water pressure generation and stiffness degradation in marine clays at Yangtze estuary

Cyclic threshold shear strain is a fundamental property of saturated soils under cyclic loading. To investigate the cyclic threshold shear strain for pore water pressure generation (γ_tp) and stiffness degradation (γ_td), a series of strain-controlled multistage undrained cyclic triaxial tests were carried out on in-situ saturated marine clay in the Yangtze estuary with different plasticity index I_p. The test results show that both γ_tp and γ_td increase with increasing I_p, and γ_tp is larger than γ_td for the same marine clay tested under the same conditions, with γ_tp = 0.017 ~ 0.019%, γ_td = 0.008 ~ 0.012% for I_p of 17, γ_tp = 0.033 ~ 0.039%, γ_td = 0.020 ~ 0.025% for I_p of 32, and γ_tp = 0.040 ~ 0.048%, γ_td = 0.031 ~ 0.036% for I_p of 40. Moreover, the development of stiffness degradation may not necessarily require the generation of pore water pressure but can be aggravated by it. Furthermore, the γ_tp and γ_td of marine clay are compared with terrestrial soils and marine clays cited from the published literature, the results indicate that the special marine sedimentary environment and the combined action of flow and tidal wave system cause the γ_tp and γ_td of marine clay in the Yangtze estuary to be smaller than that of the terrestrial clays and marine clays in other sea areas.

1 Introduction

With the global intensive exploitations of marine resources and strategic spaces, offshore and coastal engineering, such as wind power platforms, oil drilling platforms, subsea pipelines and tunnels, and anchors, thrives in marine environments where soft clays form the bulk of the seabed (Li et al., 2012; Shi et al., 2018). However, when the soft clays are subjected to periodic marine geology disasters (e.g. typhoons, storms, tsunamis, and earthquakes), they may suffer cyclic degradation, which will trigger stability problems of marine structures and reduce their service life. Hence the dynamic properties of marine clays under marine geology disasters have received extensive attention from the scientific and engineering communities (Fattah and Mustafa, 2016; Fattah et al., 2017; Yang et al., 2018; Zhu et al., 2020; Fattah et al., 2021; Pan et al., 2021; Jin et al., 2022; Lei et al., 2022; Tsai, 2022; Wu et al., 2023). The cyclic threshold shear strain for pore water pressure generation (γ_tp) [when the cyclic shear strain amplitude (γ_c) is below γ_tp, negligible pore water pressure generated, and while γ_c > γ_tp, pore water pressure accumulates significantly.] and stiffness degradation (γ_td) [when γ_c< γ_td, negligible stiffness degradation occurred, and while γ_c > γ_td, apparent stiffness degradation occurred.] are the foundation parameters of the dynamic disaster properties of saturated soils (Dobry et al., 1982; Tabata and Vucetic, 2010). The γ_tp and γ_td can divide the cyclic behavior of the soil into two distinct parts, leading to adopting different methods to investigate the cyclic soil behavior. Therefore, the γ_tp and γ_td are two crucial parameters for analyzing and solving the problems of pore water pressure generation and stiffness degradation caused by marine geology disasters.

Many experimental studies have been performed on γ_tp or γ_td of saturated sands (Dobry et al., 1982; Chen et al., 2019; Vucetic et al., 2021; Saathoff and Achmus, 2022) and terrestrial clays (Ohara and Matsuda, 1988; Hsu and Vucetic, 2004; Hsu and Vucetic, 2006; Mortezaie and Vucetic, 2016; Soralump and Prasomsri, 2016; Ichii and Mikami, 2018; Parsa et al., 2022) by conducting cyclic triaxial tests (CTX), cyclic hollow cylinder torsional shear tests (CHCTS), and cyclic direct simple shear tests (CDSS), and the values of γ_tp and γ_td are listed in Table 1. The results of these studies reveal that the values of γ_tp and γ_td of a given saturated sand are almost the same, while γ_tp is larger than γ_td in a given saturated terrestrial clay. The variation of γ_tp and γ_td of saturated terrestrial clay has a relation with several factors and can be categorized into two types: (1) soil properties, such as plasticity index (I_p), over-consolidation ratio (OCR), and soil structure; and (2) loading conditions, such as initial effective consolidation pressure (${{\sigma }^{\prime }}_0$) and loading frequency. Previous investigations revealed that I_p and OCR are the primary factors affecting γ_tp and γ_td of saturated terrestrial clays. The γ_tp and γ_td both increase substantially with I_p and OCR. However, the effect of loading conditions is not sufficiently clear and needs further study.

TABLE 1

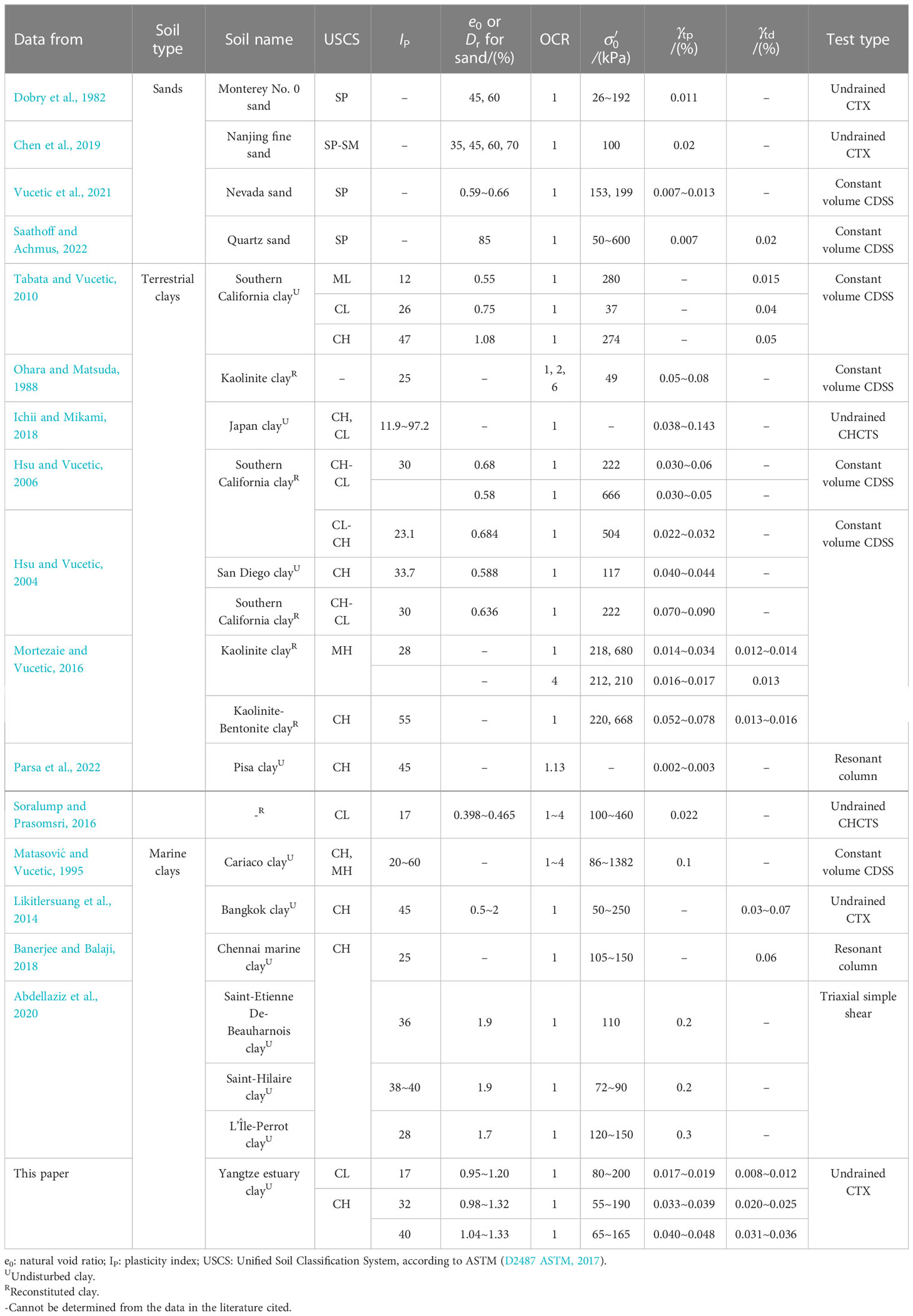
Table 1 Summary of the threshold shear strain for pore water pressure generation (γ_tp) and stiffness degradation (γ_td) for sands, terrestrial clays, and marine clays reported in the literature and this paper.

Due to the particularity of the marine sedimentary environments, the basic dynamic characteristics between marine clays and terrestrial clays were significantly different. Hence the results of terrestrial clays cannot be indiscriminately adapted to marine clays. Unfortunately, limited studies were performed on γ_tp and γ_td of undisturbed marine clays. Matasović and Vucetic (1995) summarized the published data and found that the γ_tp of Cariaco undisturbed marine clays was 0.1%. Abdellaziz et al. (2020) investigated the γ_tp of three types of Eastern Canada clays and concluded that the γ_tp for the clays with I_p =36 and 38 ~ 40 was 0.2%, while it was 0.3% for the clays with I_p =28. It was noted that the variation pattern of γ_tp in Abdellaziz et al. (2020) is contrary to previous studies but was not explained in detail. Likitlersuang et al. (2014) observed that the γ_td of Bangkok clays ranged from 0.03% to 0.07%, which was defined as the shear strain at G/G_max = 0.7 within the normalized shear modulus versus shear strain curves. Banerjee and Balaji (2018) reported that the γ_td of Chennai clays was 0.06% under isotropic consolidation conditions, and γ_td decreased with the consolidation stress ratio (ratio of minor principal stress to major principal stress). The values of γ_tp and γ_td in the above four literature are also listed in Table 1. As can be seen in Table 1, the γ_tp of undisturbed marine clays is approximately one order of magnitude larger than that of terrestrial clays, and the γ_tp is also slightly larger. It should be mentioned that the above studies were carried out in specific regions and under particular conditions, which are not completely appropriate for different types of marine clays in different regions, and the results of previous studies are not entirely consistent. Therefore, further research on γ_tp and γ_td of undisturbed marine clays is still crucial.

In this study, a series of multistage strain-controlled undrained cyclic triaxial tests were performed on marine clays in the Yangtze estuary to investigate the variation characteristics of the cyclic threshold shear strain for pore water pressure generation (γ_tp) and stiffness degradation (γ_td). Consequently, a linkage of γ_tp and γ_td with three different values of plasticity index (I_p ≈ 17, 32, and 40) was found, and the differences between γ_tp and γ_td were analyzed. In addition, the differences between the values of γ_tp and γ_td for marine clays in the Yangtze estuary and those of sands, terrestrial clays, and marine clays in other regions in the published literature were compared. The work in this paper can contribute to further understanding and analysis of dynamic properties problems of marine clays during marine geology disasters.

2 Materials and experimental methods

2.1 Description of sites and soil samples

The marine clays were obtained from two boreholes (J12 and J7) of an offshore wind power project at the Yangtze estuary in Qidong city, Nantong (Figure 1). The site is located at the intersection of the Jiangsu coast and the Yangtze River coastline, with strong interaction between the sea and the river. It is about 200 m from the shore, and the lowest elevation of the seabed with the slight undulation of topography is about -13 m, with an elevation difference amplitude of 6.55 m. According to the meteorological and hydrological survey, this site is permanently subjected to the cyclic action of two tidal systems: the tidal progressive system in the East China Sea and the tidal amphidromic system in the Yellow Sea, in which the tidal progressive system in the East China Sea plays a dominant role. The tidal pattern of this site is irregular semidiurnal tidal waves, with a tidal amplitude ranging from 0.06 m to 5.84 m. The maximum surficial tidal-current velocity is 2.20 m/s (ebb) and 3.30 m/s (flood). Tidal asymmetry is obvious with a ratio of 1.4:1 between ebb and flood duration, causing a strong impact on soil sedimentation. Moreover, it will occasionally encounter earthquakes, as well as storms caused by typhoons.

FIGURE 1

Figure 1 Geographical locations of the sampling (Base map data ^© 2023 Google).

The marine clays were retrieved using a thin-wall sampler with a maximum drilling depth below the seabed of approximately 29 m. The distance between the J12 borehole (with a water depth of 12.6 m) and the J7 borehole (with a water depth of 10.3 m) is about 150 m. The upper 8 m of the J12 borehole and the upper 7 m of the J7 borehole were flow plastic sludge, which makes it difficult to form samples and is not contained in this study. All retrieved marine clays were trimmed to solid cylindrical samples with a diameter of 100 mm and a height of 200 mm. Subsequently, the samples were packed into metal cylinders of the same size as the samples and consequently sealed with wax. The sealed samples were wrapped in foam board to minimize disturbance during transportation to the laboratory.

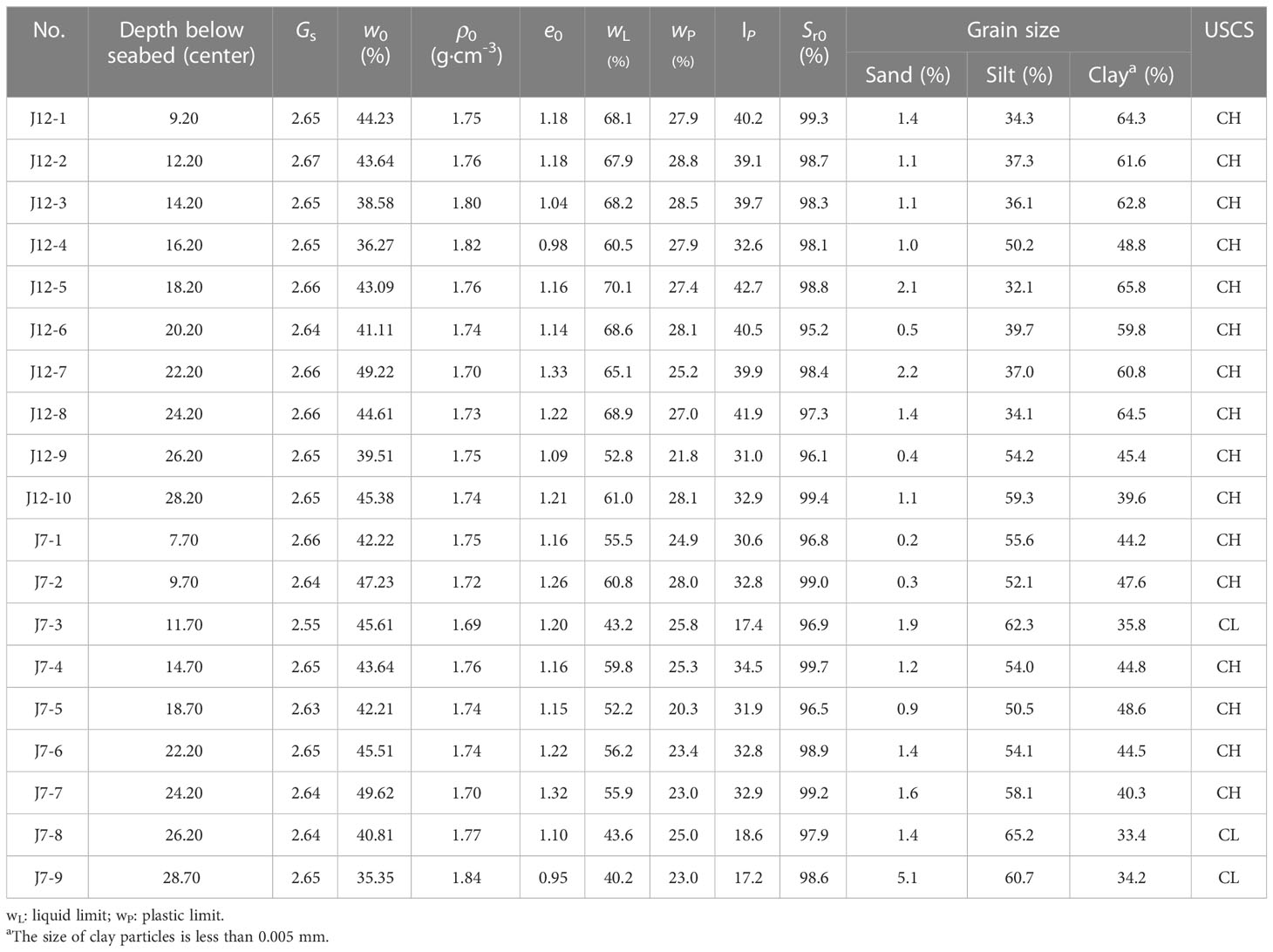
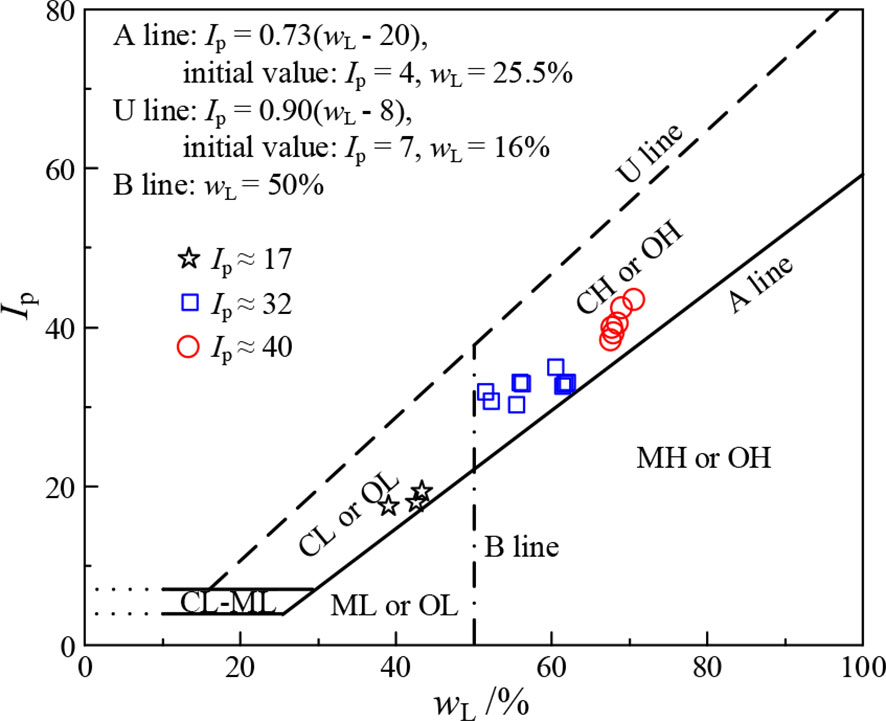
Table 2 lists the basic physical properties of the used marine clays. The tests of the particle-size analysis, special gravity (G_s), natural water content (w₀), natural wet density (${\rho }_0$), and Atterberg limits were determined according to ASTM D422 (ASTM, 2007), D2216 (ASTM, 2019), D854 (ASTM, 2014), D1556/D1556M (ASTM, 2015), and (D4318 ASTM, 2017), respectively. The natural void ratio ($e_0$) and the degree of saturation (S_r0) were calculated based on the basic physical properties. It was found that the used marine clays in the Yangtze estuary have approximately three values of $I_{\text{P}}$ (17, 32, 40), and high $e_0$ and S_r0 with values ranging from 0.95 to 1.33 and 95.2% to 99.7%, respectively. Figure 2 illustrates the classification of the used marine soils in the Unified Soil Classification System (USCS) chart according to ASTM (D2487 ASTM, 2017). It reveals that the used marine soils can be categorized as CL (clay of low plasticity) and CH (clay of high plasticity).

TABLE 2

Table 2 Basic physical properties of marine clays in the Yangtze estuary.

FIGURE 2

Figure 2 Positions of the tested marine soils in the plasticity chart.

2.2 Test apparatus

The multistage strain-controlled undrained cyclic triaxial tests were carried out using a dynamic triaxial apparatus manufactured by GDS Instruments Ltd., UK. This apparatus can measure the cyclic axial stress (σ_d) and the cyclic axial strain (ϵ_a) of soil samples subjected to cyclic loading with an accuracy of 0.1 kPa and 0.004%. More information about this apparatus was described exhaustively in Chen et al. (2020) and Ma et al. (2023). The cyclic shear stress (τ) and cyclic shear strain (γ) can be determined by the following equation (Rollins et al., 1998; Chen et al., 2022):

$\begin{array}{ll}\{\begin{array}{l}\tau \text{ = }{\sigma }_{\text{d}}\mathrm{/2}\\ \gamma =(1+\nu ){ϵ}_{\text{a}}\end{array}& (1)\end{array}$

where the ν is the dynamic Poisson’s ratio. The saturated specimens will not generate volumetric strain, which typically occurs in soils in undrained conditions during cyclic loading, hence the ν can be assumed to be 0.5 (Fahoum et al., 1996; Chen et al., 2022). During the multistage strain-controlled undrained cyclic triaxial tests, the dynamic shear modulus at the i^th stage and the N^th cycle (G_si,_N) can be calculated as follow (Idriss et al., 1978):

$\begin{array}{ll}{G}_{\text{s}i,N}=\frac{{\tau }_{\text{c}i,N}}{{\gamma }_{\text{c}i}}& (2)\end{array}$

where the τ_ci,_N is the cyclic shear stress amplitude at the i^th stage and the N^th cycle, and the γ_ci is the cyclic shear strain amplitude at the i^th stage.

2.3 Test procedures

The cylindrical specimens for running triaxial tests with a diameter of 50 mm and a height of 100 mm were cut from the center of the large marine samples. After weighing, the specimen was covered by eight vertical filter paper strips (with a width of 8 mm and a length of 75mm) on the lateral side to facilitate drainage. Consequently, the specimen was wrapped by a rubber membrane with a thickness of 0.3 mm and was then installed in the triaxial pressure chamber. It was noted that under the condition of artificially undisturbing the specimen, the time of sticking the filter papers and installing should be as short as possible to reduce water loss. The specimen was saturated by the backpressure method with degassed water until Skempton’s B-value (Skempton, 1954) was larger than 0.97, the financial back pressure was 400 kPa and the duration of this process was about 10 h. After saturation, each specimen was isotropically consolidated to the initial effective confining pressure (${{\sigma }^{\prime }}_{\text{c}0}$), which was determined based on the sampling depth below the seabed, and the consolidation took about 2 ~ 3 days until the drainage volume was less than 60 mm³/h.

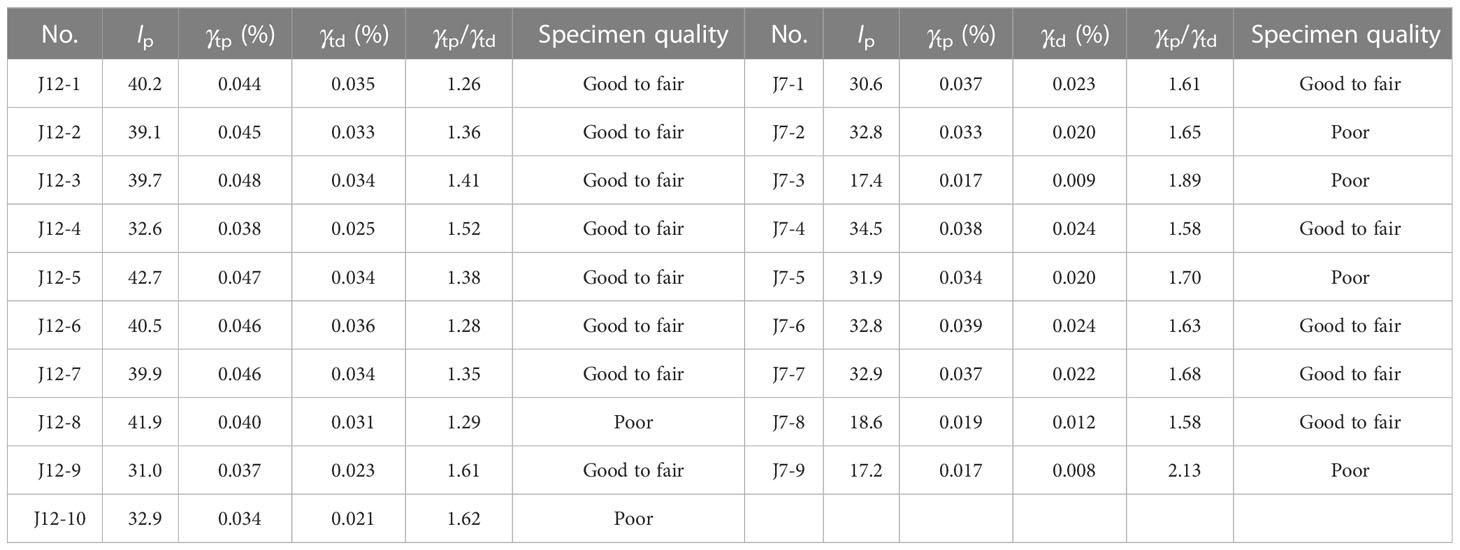
After sufficient consolidation, the multistage strain-controlled undrained cyclic triaxial tests were performed on each specimen in seven multistage with each stage having 10 cycles according to ASTM D3999 (ASTM, 2011). The loading frequency (f) was 0.1 Hz. The γ_ci varied from 0.015 to 3%. The test schemes were listed in Table 3. Lunne et al. (1997); Lunne et al. (2006) proposed a quantification of specimen disturbance based on the ratio of the difference of the void ratio before and after consolidation (Δe) with e₀, as shown in Table 4. The sample quality of the tested marine specimens in this paper was shown in Table 3. It illustrates that the quality of thirteen specimens was good to poor and six specimens were poor.

TABLE 3

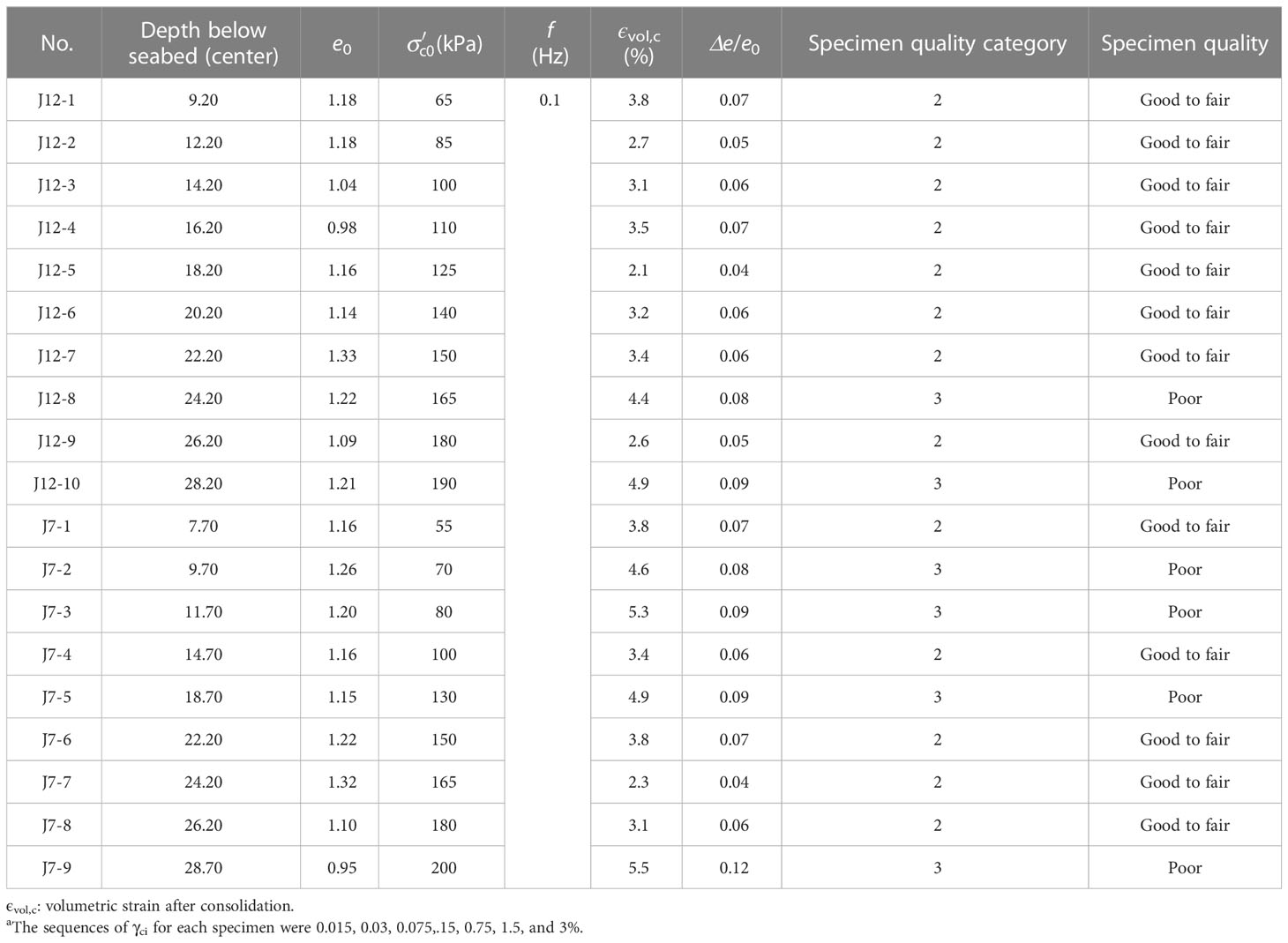
Table 3 Test program for multistage strain-controlled undrained cyclic triaxial tests^a.

TABLE 4

Table 4 Criteria for evaluation of sample disturbance based on Δe/e₀ proposed by Lunne et al. (1997); Lunne et al. (2006).

3 Typical results of multistage strain-controlled undrained cyclic triaxial tests

Three specimens with different I_p [J7-3 (I_p = 17.4), J7-4 (I_p = 34.5), and J12-1 (I_p = 40.2)] are taken as examples. Figure 3 presents the typical results for the variations of cyclic shear strain (γ), cyclic shear stress (τ), dynamic shear modulus (G_si,_N), and pore water pressure (Δu) with cycles (N) for the three specimens. The Δu of the three specimens did not develop with the increasing N during the 1^st stage, and whether there is an increase could not be observed intuitively during the 2^nd stage, but a significant increase appeared during the 3^rd ~ 7^th stages. Therefore, there is a cyclic threshold shear strain for pore water pressure generation (γ_tp) of marine clays in the Yangtze estuary, that is, there exists a γ_tp so that when the cyclic shear strain amplitude (γ_c) is below γ_tp, negligible Δu generated, and while γ_c > γ_tp, Δu accumulates significantly. It can be estimated that the γ_tp for the tested specimens ranged from 0.015% to 0.075%. Likewise, The $G_{\text{s}i,N}$ of specimen J7-3 decreased with N from the 1^st stage, while that of specimens J7-4 and J12-1 decreased from the 2^nd and 3^rd stages, respectively. The decrease of G_si,_N with N can reflect the stiffness degradation of soils (Pan et al., 2021; Jin et al., 2022). Hence there is a cyclic threshold shear strain for stiffness degradation (γ_td) of marine clays in the Yangtze estuary, that is, there exists a γ_td so that when γ_c< γ_td, there is no noticeable stiffness degradation and the microstructure of the soils hardly changes at this stage, and while γ_c > γ_td, the microstructure is destroyed causing the apparent stiffness degradation. It can be tentatively determined that the γ_td for the tested specimens should be less than 0.075%. How to accurately identify the values of γ_tp and γ_td will be discussed in detail in the following section.

FIGURE 3

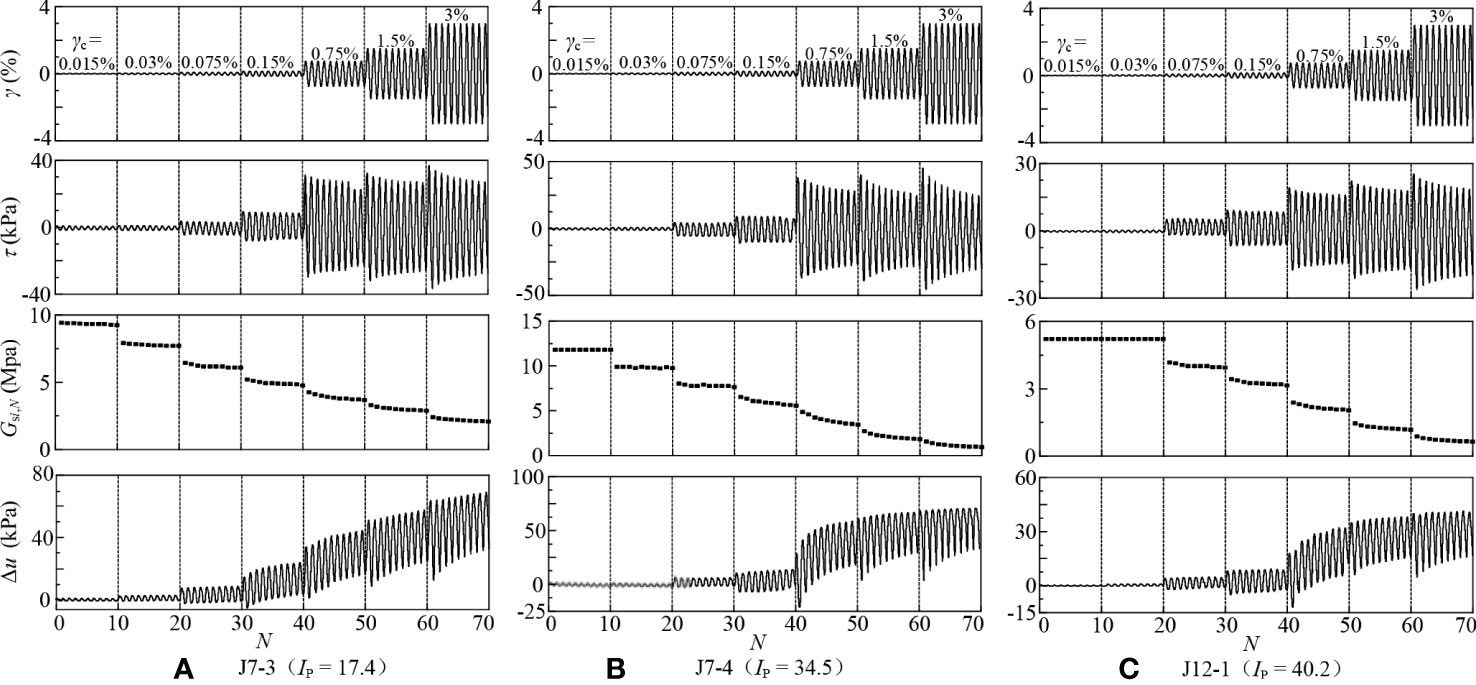
Figure 3 Variation of shear strain, shear stress, dynamic shear modulus, and pore pressure with cycles for different I_p: (A) J7-3 (I_p = 17.4); (B) J7-4 (I_p = 34.5); (C) J12-1 (I_p = 40.2).

4 Results and discussions

4.1 Cyclic threshold shear strain for pore water pressure generation, γ_tp

For accurately identifying the values of γ_tp, each cyclic stage was regarded as an individual stage, so the effective confining pressure at the i^th stage (${{\sigma }^{\prime }}_{\text{c}i}$) and the modified pore water pressure at the i^th stage and the N^th cycle ($\Delta u_{i,N}^{\ast }$) can be estimated by Eqs. (3) and (4), respectively:

$\begin{array}{ll}{{\sigma }^{\prime }}_{\text{c}i}={{\sigma }^{\prime }}_{\text{c}0}-\Delta u_{i-1}\text{'}(i=1,2,\cdots ,7)& (3)\end{array}$

$\begin{array}{ll}\Delta u_{i,N}^{\ast }=\Delta u_{i,N}-\Delta u_{i-1}\text{'}(i=1,2,\cdots ,7)& (4)\end{array}$

where $\Delta u_{i-1}$ is the pore water pressure at the (i-1)^th stage and $\Delta u_0=0$; $\Delta u_{i,N}$ is the pore water pressure at the i^th stage and the N^th cycle. Consequently, the normalized pore water pressure ratio at the N^th cycle during each stage ( $r_{\text{u}i,N}^{\ast }$) can be determined by Eq. (5):

$\begin{array}{ll}{r}_{\text{u}i,N}^{\ast }=\Delta u_{i,N}^{\ast }/{{\sigma }^{\prime }}_{\text{c}i}\text{'}(i=1,2,\cdots ,7)& (5)\end{array}$

The relationships between $r_{\text{u}i,N}^{\ast }$ and γ_c for six representative specimens at different stages and Ns are shown in Figure 4. The points in the same column represent the $r_{\text{u}i,N}^{\ast }$ at different cycles of the same stage. To obtain a more accurate value of γ_tp, only the cyclic stages below and the 3 ~ 4 cyclic stages above γ_tp are taken into account. Combining Figures 3 and 4, after the generation of Δu, the development pattern of Δu showed remarkable differences among specimens J7-3 and J7-9 with lower I_p ≈ 17, specimens J7-6 and J12-9 with higher I_p ≈ 32, and specimens J12-1 and J12-6 with I_p ≈ 40 within the range of γ_c applied in this paper. For specimens with I_p ≈ 17 (Figures 4A–C), the Δu increased linearly with γ_c. While for specimens with I_p ≈ 32 and 40 (Figures 4E–I), when γ_c< 0.15%, the Δu increased slowly with γ_c, when γ_c > 0.15%, the Δu increased significantly with γ_c, but the rate of increment decreased and the value of Δu tend to be stable. For given γ_c and N, the larger values of I_p of the specimens, the smaller Δu was, that is, the development rate of Δu for marine clays with smaller I_p was greater than that with larger I_p. This change law of Δu with I_p is in accordance with the observation in Nhan et al. (2022) and Kantesaria and Sachan (2021).

FIGURE 4

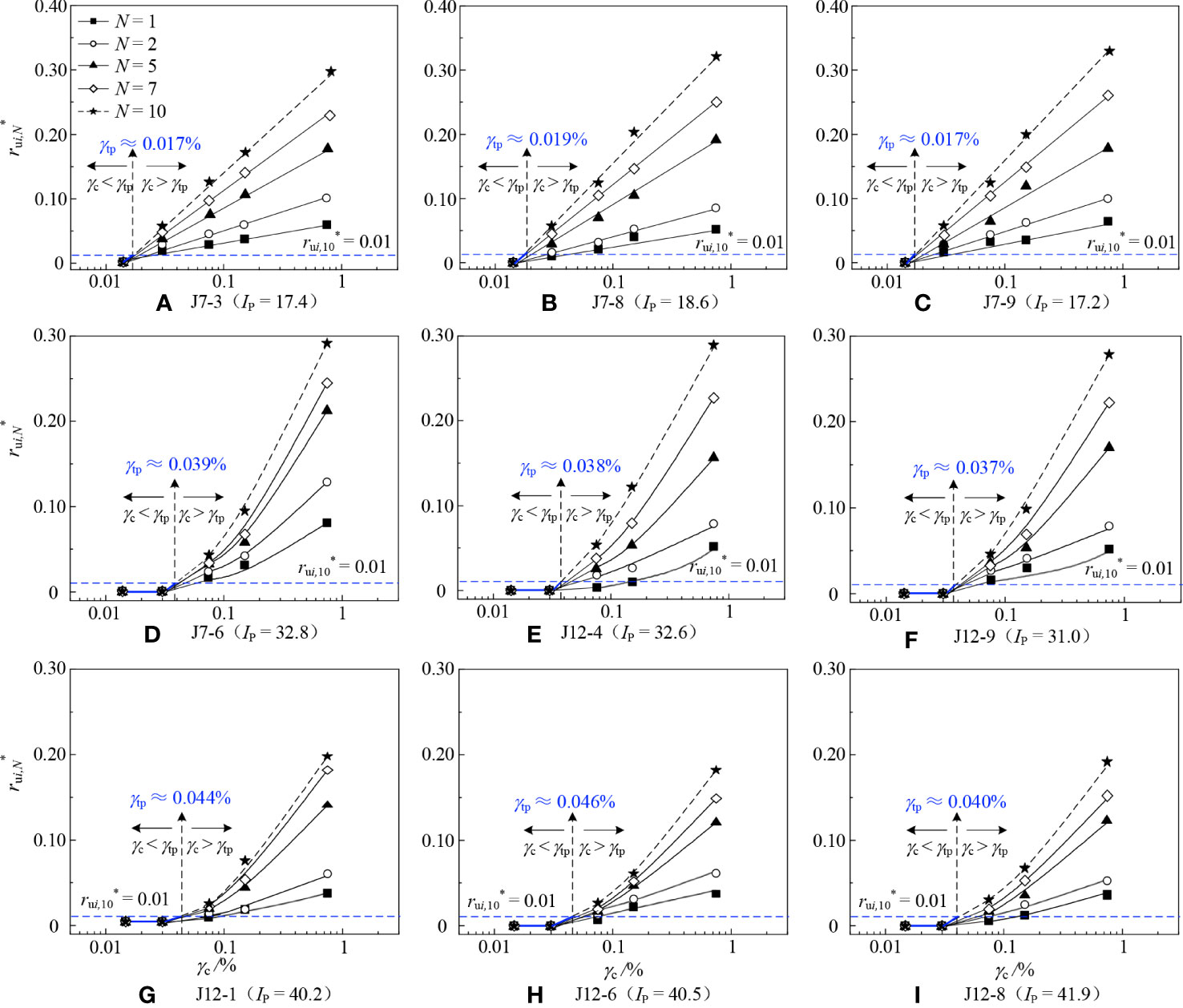
Figure 4 The relationship curves between $r_{\text{u}i,N}^{\ast }$ and γ_c for marine clay at different N. (A) J7-3 (Ip = 17.4); (B) J7-8 (Ip = 18.6); (C) J7-9 (Ip = 17.2); (D) J7-6 (Ip = 32.8); (E) J12-4 (Ip = 32.6); (F) J12-9(Ip = 31.0); (G) J12-1 (Ip = 40.2); (H) J12-6 (Ip = 40.5); (I) J12-8 (Ip=41.9).

In this paper, the values of γ_tp were determined as that of γ_c when Δu reaches 1% of ${{\sigma }^{\prime }}_{\text{c}i}$ for the first time, i.e., the $r_{\text{u}i,N}^{\ast }$ reaches 0.01 for the first time. The blue dotted lines represent the $r_{\text{u}i,N}^{\ast }$ = 0.01. For specimens with I_p ≈ 17 (Figures 4A–C), the values of $r_{\text{u}i,N}^{\ast }$ kept zero during the whole 1^st stage (γ_c = 0.015%). While during the 2^nd stage, $r_{\text{u}i,N}^{\ast }$ increased obviously with N. According to the development trend of $r_{\text{u}i,10}^{\ast }$, the γ_tp is about 0.018%, 0.017%, and 0.019% for specimens J7-3, J7-8, and J7-9, respectively. While specimens with I_p ≈ 32 and 40 (Figures 4E–I), $r_{\text{u}i,N}^{\ast }$ maintained zero during the first two stages and increased from the 3^rd stage. Similarly, the γ_tp of specimens J7-6, J12-4, J12-9, J12-1, J12-6, and J12-8 is about 0.039%, 0.038%, 0.037%, 0.044%, 0.046%, and 0.048%, respectively. The γ_tp for each tested specimen is summarized in Table 5. It presents that γ_tp of marine clay in the Yangtze estuary increased with I_p, and this trend was also obtained in Hsu and Vucetic (2006). This may be due to that the larger the I_p, the stronger the ability of the soils to combine with water, and the weaker the ability of water to transmit pore water pressure, leading to the less susceptible generation of pore water pressure. Hence the γ_tp of specimens with larger I_p was larger.

TABLE 5

Table 5 Summary table of γ_tp and γ_td of tested marine clay.

4.2 Cyclic threshold shear strain for stiffness degradation, γ_td

The stiffness degradation characteristics of the soil under cyclic loading can be quantitatively characterized by the degradation index δ and the degradation parameter t, which reflect the degree and rate of soil stiffness degradation, respectively. In strain-controlled tests, the δ and t can be expressed as follow:

$\begin{array}{ll}\delta =\frac{G_{\text{s}i,N}}{G_{\text{s}i,1}}=\frac{{\tau }_{\text{c}i,N}/{\gamma }_{\text{c}i}}{{\tau }_{\text{c}i,1}/{\gamma }_{\text{c}i}}=\frac{{\tau }_{\text{c}i,N}}{{\tau }_{\text{c}i,1}}& (6)\end{array}$

$\begin{array}{ll}t=-\frac{\log \delta }{\log N}\text{ or }\delta \text{ = }{N}^{-t}& (7)\end{array}$

where $G_{\text{s}i,1}$ is the dynamic shear modulus at the i^th stage and the 1^st cycle, ${\tau }_{\text{c}i,1}$ is the shear stress amplitude at the i^th stage and the 1^st cycle.

Taking 9 specimens with different I_p as an example, Figure 5 demonstrates the relationship between δ and N under different γ_c. As can be seen from Figure 5, with increasing γ_c, both the δ and t increased significantly for the same N, indicating that the degree and the rate of stiffness degradation will intensify with increasing deformation of soils. For a given γ_c, the δ decreased linearly with N in the log-log scale coordinates system, i.e., the t kept constant, reflecting that once the stiffness degradation is presented, the stiffness degradation degree will continue to accumulate even if the γ_c no longer developed. Moreover, the t decreased with the increasing I_p. This variation law of t with I_p is in accordance with the observation in Kantesaria and Sachan (2021). Figure 5 also reveals that specimens with I_p ≈ 17 (Figures 5A–C) experienced stiffness degradation from the 1^st stage, hence their γ_td was less than 0.015%, specimens with I_p ≈ 32 (Figures 5D–F) experienced that from the 2^nd stage with γ_td varies between 0.015% and 0.030%, and specimens with I_p ≈ 40 (Figures 5G–I) showed that from the 3^rd stage with γ_td ranged from 0.030% and 0.075%. The relationship between δ and t can be fitted by the following equation:

FIGURE 5

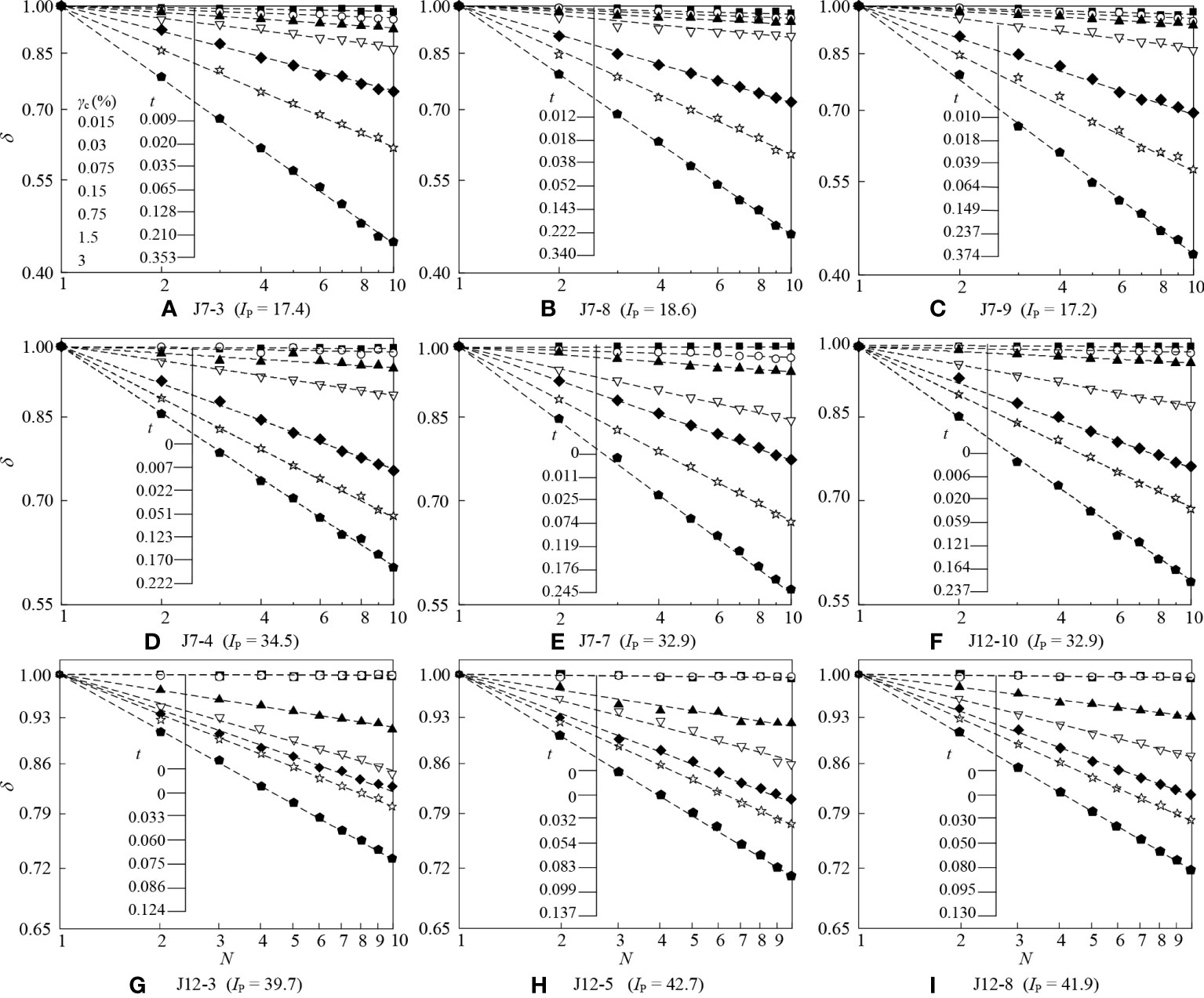
Figure 5 The relationship curves between δ and N for marine clay at different γ_c. (A) J7-3 (Ip = 17.4); (B) J7-8 (Ip = 18.6); (C) J7-9 (Ip = 17.2); (D) J7-4 (Ip = 34.5); (E) J7-7 (Ip = 32.9); (F) J7-10(Ip = 32.9); (G) J12-3 (Ip = 39.7); (H) J12-5 (Ip = 42.7); (I) J12-8 (Ip=41.9).

$\begin{array}{ll}t=a·{({\gamma }_{\text{c}}-{\gamma }_{\text{td}})}^b& (8)\end{array}$

where a and b are the fitting parameters. The fitting results are shown in Figure 6. It can be found that the values of γ_td for three specimens with I_p ≈ 17 ranged from 0.010% to 0.012% (Figure 6A), those for three specimens with I_p ≈ 32 ranged from 0.022% to 0.026% (Figure 6B), and for three specimens with I_p ≈ 17 ranged from 0.030% to 0.034% (Figure 6C). The γ_td for each tested specimen is summarized in Table 5. This table indicates that γ_td of marine clay in the Yangtze estuary increased with I_p, and this trend was also obtained in Hsu and Vucetic (2004); Hsu and Vucetic (2006) and Tabata and Vucetic (2010). This may be due to that the larger the I_p, the stronger the ability of the soils to combine with water, and under the adsorption of bound water, the soil particles are resistant to sliding subjected to external loading and the structure is less likely to be damaged. Hence the γ_td of specimens with larger I_p was larger.

FIGURE 6

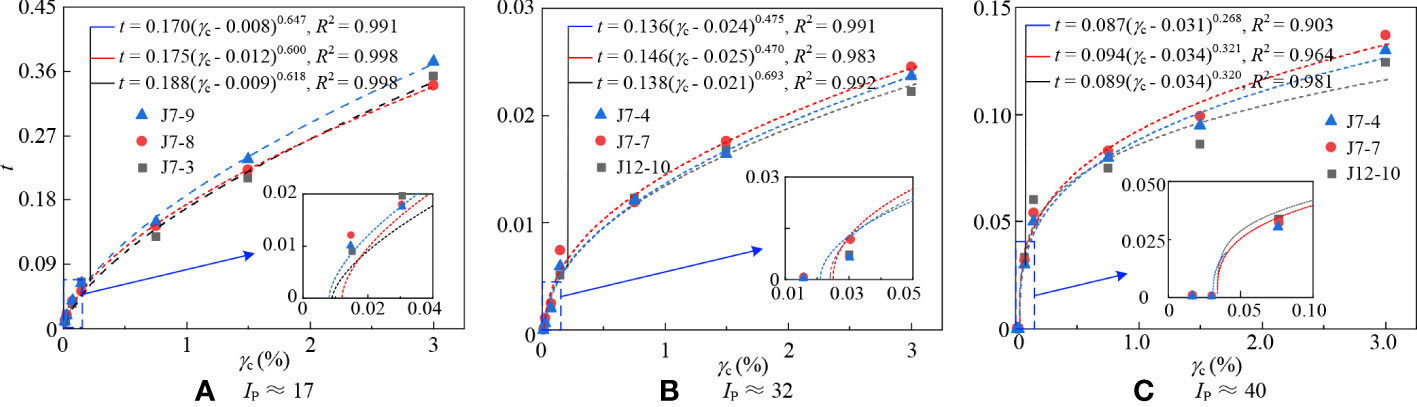
Figure 6 The relationship curves between t and γ_c for marine clay. (A) Ip ≈ 17; (B) Ip ≈ 32; (C) Ip ≈ 40.

4.3 Analysis of the differences between γ_tp and γ_td

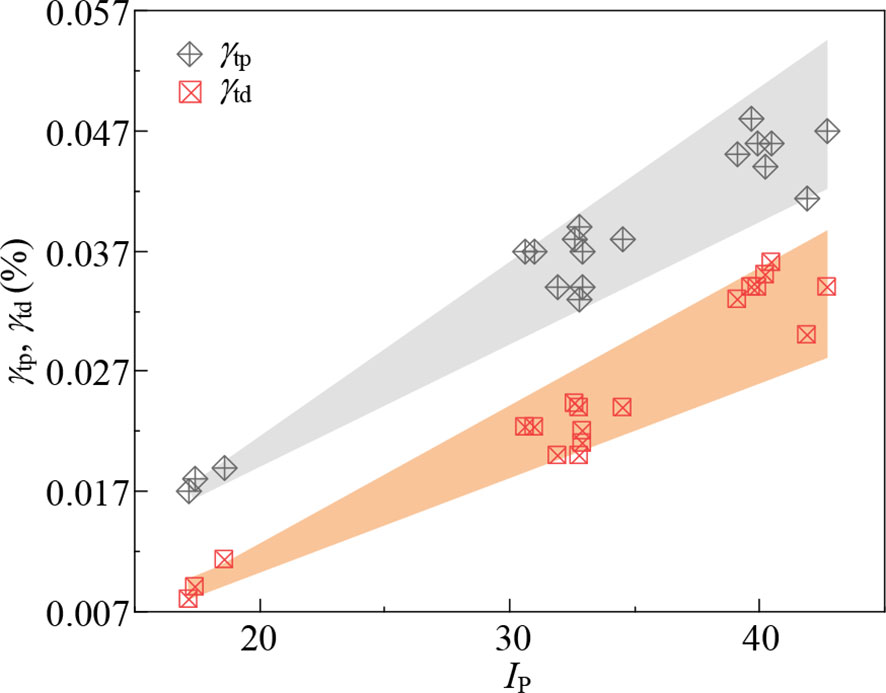
Figure 7 illustrates the differences between γ_tp and γ_td. It can be seen that both γ_tp and γ_td were distributed within a narrow range. For a given marine clay, the value of γ_tp was always larger than that of γ_td, with the minimum γ_tp/γ_td ratio of 1.26 obtained from specimen J12-1 and the maximum γ_tp/γ_td ratio of 2.13 obtained from specimen J7-9 (listed in Table 5). The dispersion degree of γ_tp and γ_td increased with increasing I_P. Figures 8A–F presents the variation of $r_{\text{u}i,N}^{\ast }$ and t with γ_c for six specimens with good to poor and poor qualities. Specimen J7-3 was taken as an example (Figure 8A), its γ_tp was 0.017% and γ_td was 0.009%. Combining with Figure 5A, when γ_c< γ_td, neither pore water pressure nor stiffness degradation was generated; when γ_c varied from γ_td to γ_tp, the pore water pressure was small to negligible, which will not lead to effective stress reduction, but a slight degree of stiffness degradation occurred, as shown in the orange zone of Figure 8A; however, when γ_c > γ_tp, the pore pressure began to accumulate and the degree and rate of stiffness degradation increased significantly with increasing N under the same γ_c. Similar phenomena are also observed in Tabata and Vucetic (2010) and Mortezaie and Vucetic (2016). Therefore, it can be preliminarily considered that the kinetic energy input by the cyclic loading will lead to the gradual destruction of the inherent microstructure of the marine clay, and the consequent stiffness degradation. When the kinetic energy exceeds the range that the inherent structure can bear, part of the kinetic energy will be converted into pore water potential energy, contributing to the generation of pore water pressure, which will aggravate stiffness degradation. In summary, the development of stiffness degradation of marine clay does not necessarily require the increase of pore water pressure, but the increase of pore water pressure will further damage the soil structure and make the stiffness more seriously decay.

FIGURE 7

Figure 7 Comparison of γ_tp and γ_td.

FIGURE 8

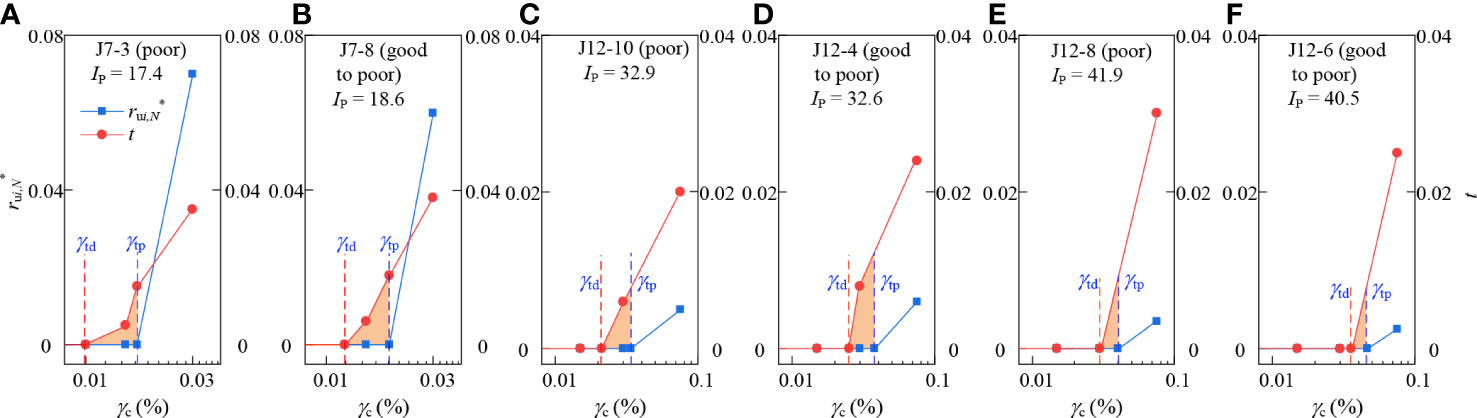
Figure 8 Variation of $r_{\text{u}i,N}^{\ast }$ and t with γ_c for six specimens. (A) J7-3; (B) J7-8; (C) J12-10; (D) J12-4; (E) J12-8; (F) J12-6.

4.4 Comparison to published data in the previous literature

The comparison of γ_tp and γ_td between marine clays in the Yangtze estuary and published data in the previous literature is shown in Figure 9. The gray area is the distribution range of γ_tp and γ_td proposed by Vucetic (1994) and Tabata and Vucetic (2010), respectively, based on CTX, CHCTS, CDSS, resonant column tests, and cyclic torsional shear tests. It can be seen that the γ_tp and γ_td generally increase with the increasing I_p. Moreover, the γ_tp and γ_td of undisturbed terrestrial clays distribute uniformly in the gray area, while the γ_tp and γ_td of reconstituted terrestrial clays are apparently smaller than those of undisturbed terrestrial clays. This occurs because the remolding process destroys the microstructure of undisturbed clays, forming weak structures and cement, which will further lead to reconstituted clays being more likely damaged than undisturbed clays subjected to cyclic loading.

FIGURE 9

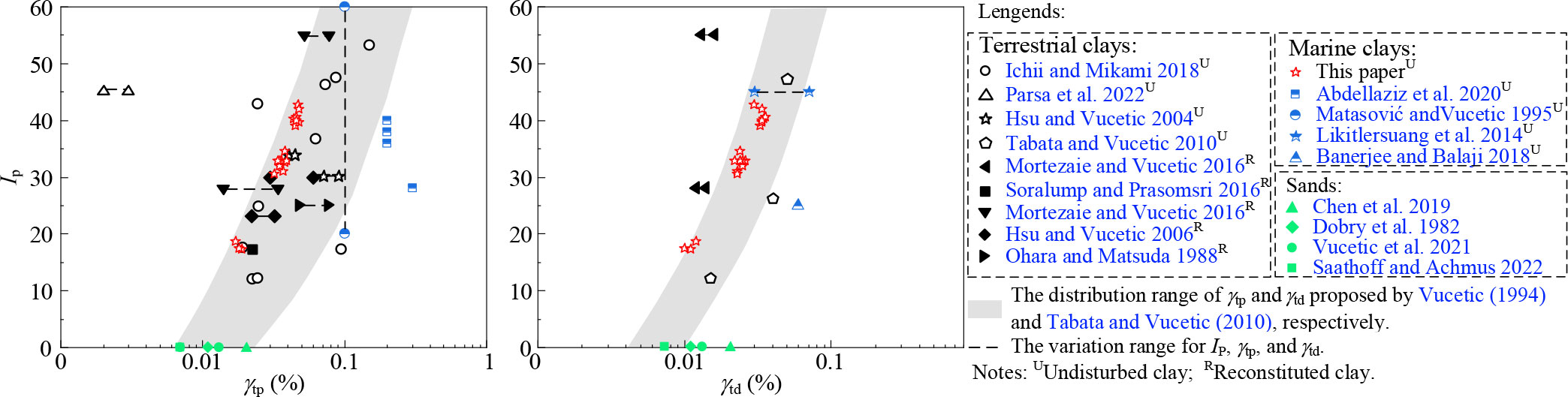
Figure 9 Relationship between the γ_tp and γ_td and I_P obtained in this paper and the previous literature.

A more interesting phenomenon is that the γ_tp and γ_td of marine clays in the Yangtze estuary are basically distributed along the left boundary of the gray area, and the marine clay with I_p ≈ 17 was more obvious, furthermore, the γ_tp and γ_td were much smaller than those of marine clays in the cited literature. The reason may be that the sedimentary environments of marine clays were significantly different from those of terrestrial clays. Under the influence of high salt content, low-temperature seawater environment, and special cementitious materials, marine clays exhibit many flocculated structures and form a loose and porous interior (Sun et al., 2020; Wang et al., 2021). Hence marine clays have high porosity and high water content. However, internal closed pores without hydraulic conductivity occupy the majority of the total pores, leading to the low permeability of marine clays. In addition, due to the enlarged section of the Yangtze estuary at the sampling site, the Yangtze River water flow speed is abruptly reduced and the transported debris and sediments are rapidly deposited here, resulting in the soil particles being unable to adjust to the best position in time to form the fragile structure and cementation. Additionally, the marine clays at this sampling site are permanently subjected to the combined action of the water flow of the Yangtze River and the tidal wave system in the East China Sea and the Yellow Sea, which further affects their sediment dynamics (Su et al., 2022; Zhang et al., 2020) and destroys its structure and cementation. These reasons collectively result in the differences between the γ_tp and γ_td of marine clays in the Yangtze estuary and those of terrestrial clays and marine clays in other sea areas.

5 Conclusions

In this paper, a series of multistage strain-controlled undrained cyclic triaxial tests were performed on the marine clays at the Yangtze estuary in Qidong city, Nantong. The cyclic threshold shear strain for pore water pressure generation (γ_tp) and stiffness degradation (γ_td) of marine clays having plasticity index I_p ≈ 17, 32, and 40 were investigated, and the conclusions are as follows:

(1) The larger the I_p, the stronger the ability of the soils to combine with water, the weaker the ability of water to transmit pore water pressure. Furthermore, under the adsorption of bound water, the soil particles are resistant to sliding subjected to external loading. Therefore, the pore water pressure is less susceptible to generate and the structure is less likely to be damaged, leading to γ_tp and γ_td for marine clays at the Yangtze estuary increase with the increasing I_p. For marine clays having I_p ≈ 17, γ_tp = 0.017 ~ 0.019% and γ_td = 0.008 ~ 0.012%. For marine clays having I_p ≈ 32, γ_tp = 0.033 ~ 0.039% and γ_td = 0.020 ~ 0.025%. For marine clays having I_p ≈ 40, γ_tp = 0.040 ~ 0.048% and γ_td = 0.031~ 0.036%.

(2) Under the same test conditions, γ_tp is larger than γ_td for the same specimen, and γ_tp/γ_td ranges between 1.2 and 1.8. This confirmed that under cyclic loading, the stiffness degradation and pore water pressure generation of marine clays have a sequence with the development of stiffness degradation preceding pore water pressure generation. The development of soil stiffness degradation does not necessarily require the increase of pore water pressure, but the increase of pore water pressure will aggravate the stiffness degradation.

(3) Due to the fragile structure, the γ_tp and γ_td of reconstituted clays are relatively low. Both γ_tp and γ_td of marine clays in the Yangtze River estuary are less than those of terrestrial clays and marine clays in other sea areas, which is because the marine clays in the Yangtze estuary have a lower inter-particle cementation strength affected by the special marine sedimentary environment and the combined action of flow and tidal wave system, which makes it more vulnerable to damage subjected to cyclic loading.

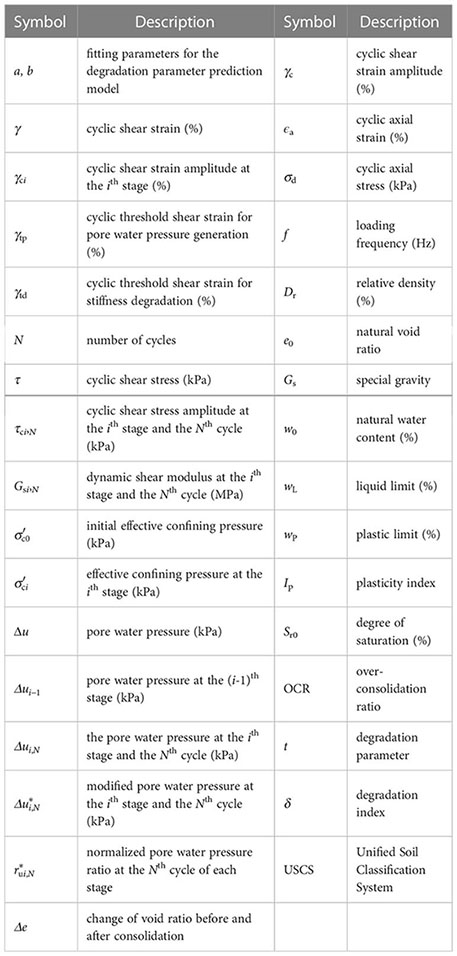
Notation

The following symbols are used in this paper:

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

XX: Investigation, Writing – review and editing, Methodology, Validation, Data curation. D-WJ: Writing- review and editing, Validation. T-ZH: Methodology, Writing – review and editing, Validation. Z-YC: Resources, Methodology; LZ: Validation, Modification; QW: Conceptualization, Methodology, Validation. Supervision, G-XC: Resources, Funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China under grant no 51978334.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdellaziz M., Karray M., Chekired M., Delisle M. C. (2020). Shear modulus and damping ratio of sensitive Eastern Canada clays. Can. Geotech. J. 58 (5), 1118–1133. doi: 10.1139/cgj-2020-0254

CrossRef Full Text | Google Scholar

ASTM (2007). Standard test method for particle-size analysis of soils (West Conshohocken, PA: ASTM International). doi: 10.1520/D422-63(2007)E02

CrossRef Full Text | Google Scholar

ASTM (2011). Standard test methods for the determination of the modulus and damping properties of soils using the cyclic triaxial apparatus (West Conshohocken, PA: ASTM International). doi: 10.1520/D3999_D3999M-11E01

CrossRef Full Text | Google Scholar

ASTM (2014). Standard test methods for specific gravity of soil solids by water pycnometer (West Conshohocken, PA: ASTM International). doi: 10.1520/D0854-14

CrossRef Full Text | Google Scholar

ASTM (2015). Standard test method for density and unit weight of soil in place by sand-cone method (West Conshohocken, PA: ASTM International). doi: 10.1520/D1556_D1556M-15E01

CrossRef Full Text | Google Scholar

ASTM D2487 (2017). Standard practice for classification of soils for engineering purposes (Unified soil classification system) (West Conshohocken, PA: ASTM International). doi: 10.1520/D2487-17E01

CrossRef Full Text | Google Scholar

ASTM D4318 (2017). Standard test method for sand content by volume of bentonitic slurries (West Conshohocken, PA: ASTM International). doi: 10.1520/D4318-17E01

CrossRef Full Text | Google Scholar

ASTM (2019). Standard test method for laboratory determination of water (moisture) content of soil and rock by mass (West Conshohocken, PA: ASTM International). doi: 10.1520/D2216-19

CrossRef Full Text | Google Scholar

Banerjee S., Balaji P. (2018). Effect of anisotropy on cyclic properties of chennai marine clay. Int. J. Geosynth. Groun. Eng. 4, 27. doi: 10.1007/s40891-018-0144-8

CrossRef Full Text | Google Scholar

Chen G. X., Liang K., Zhao K., Yang J. (2022). Shear modulus and damping ratio of saturated coral sand under generalised cyclic loadings. Géotechnique 1–18. doi: 10.1680/jgeot.21.00181

CrossRef Full Text | Google Scholar

Chen G. X., Wu Q., Zhao K., Shen Z. F. (2020). A binary packing material-based procedure for evaluating soil liquefaction triggering during earthquakes. J. Geotech. Geoenviron. Eng. 146 (6), 04020040. doi: 10.1061/(ASCE)GT.1943-5606.0002263

CrossRef Full Text | Google Scholar

Chen G. X., Zhao D. F., Chen W. Y., Juang C. H. (2019). Excess pore-water pressure generation in cyclic undrained testing. J. Geotech. Geoenviron. Eng. 145 (7), 04019022. doi: 10.1061/(ASCE)GT.1943-5606.0002057

CrossRef Full Text | Google Scholar

Dobry R., Ladd R. S., Yokel F. Y., Chung R., Powell D. J. (1982). Prediction of pore water pressure buildup and liquefaction of sands during earthquakes by the cyclic strain method. NBS Build. Sci. Ser. 138, 150. doi: 10.6028/NBS.BSS.138

CrossRef Full Text | Google Scholar

Fahoum K., Aggour M. S., Amini F. (1996). Dynamic properties of cohesive soils treated with lime. J. Geotech. Eng. 122 (5), 382–389. doi: 10.1061/(ASCE)0733-9410(1996)122:5(382

CrossRef Full Text | Google Scholar

Fattah M. Y., Al-Mosawi M. J., Al-Ameri A. F. I. (2017). Stresses and pore water pressure induced by machine foundation on saturated sand. Ocean Eng. 146, 268–281. doi: 10.1016/j.oceaneng.2017.09.055

CrossRef Full Text | Google Scholar

Fattah M. Y., Al-Omari R. R., Hameedi M. K. (2021). Tracing of stresses and pore water pressure changes during a multistage modified relaxation test model on organic soil. Arab. J. Geosci. 14, 1976:1-9. doi: 10.1007/s12517-021-08321-7

CrossRef Full Text | Google Scholar

Fattah M. Y., Mustafa F. S. (2016). Development of excess pore water pressure around piles excited by pure vertical vibration. Int. J. Civ. Eng. 15 (6), 907–920. doi: 10.1007/s40999-016-0073-7

CrossRef Full Text | Google Scholar

Hsu C. C., Vucetic M. (2004). Volumetric threshold shear strain for cyclic settlement. J. Geotech. Geoenviron. Eng. 130, 58–70. doi: 10.1061/(ASCE)1090-0241(2004)130:1(58

CrossRef Full Text | Google Scholar

Hsu C. C., Vucetic M. (2006). Threshold shear strain for cyclic pore-water pressure in cohesive soils. J. Geotech. Geoenviron. Eng. 132 (10), 1325–1335. doi: 10.1061/(ASCE)1090-0241(2006)132:10(1325

CrossRef Full Text | Google Scholar

Ichii K., Mikami T. (2018). Cyclic threshold shear strain in pore water pressure generation in clay in situ samples. Soil. Found. 58 (3), 756–765. doi: 10.1016/j.sandf.2018.01.005

CrossRef Full Text | Google Scholar

Idriss I. M., Dobry R., Singh R. D. (1978). Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div 104 (GT12), 1427–1447. doi: 10.1061/AJGEB6.0000727

CrossRef Full Text | Google Scholar

Jin H. X., Guo L., Sun H. L., Shi L., Cai Y. Q. (2022). Undrained cyclic shear strength and stiffness degradation of overconsolidated soft marine clay in simple shear tests. Ocean Eng. 262, 112270. doi: 10.1016/j.oceaneng.2022.112270

CrossRef Full Text | Google Scholar

Kantesaria N., Sachan A. (2021). Cyclic degradation and pore-water pressure response of high-plasticity compacted clay. J. Geotech. Geoenviron. Eng. 147 (11), 04021113. doi: 10.1061/(ASCE)GT.1943-5606.0002630

CrossRef Full Text | Google Scholar

Lei J. C., Wang Y. Z., Zhang B. H., Li F., Liu C. X. (2022). Cyclic and post-cyclic characteristics of marine silty clay under the multistage cycling-reconsolidation conditions. Ocean Eng. 258, 111803. doi: 10.1016/j.oceaneng.2022.111803

CrossRef Full Text | Google Scholar

Li J., Gao J. H., Wang Y. P. (2012). Distribution and dispersal pattern of clay minerals in surface sediments, eastern beibu gulf, south China Sea. Acta Oceanol. Sin. 2), 78–87. doi: 10.1007/s13131-012-0194-z

CrossRef Full Text | Google Scholar

Likitlersuang S., Teachavorasinskun S., Surarak C. (2014). Small strain stiffness and stiffness degradation curve of Bangkok clays. Soil. Found. 53 (4), 498–509. doi: 10.1016/j.sandf.2013.06.003

CrossRef Full Text | Google Scholar

Lunne T., Berre T., Andersen K. H., Strandvik S., Sjursen M. (2006). Effects of sample disturbance and consolidation procedures on measured shear strength of soft marine Norwegian clay. Can. Geotech. J. 43 (7), 726–750. doi: 10.1139/t06-040

CrossRef Full Text | Google Scholar

Lunne T., Berre T., Strandvik S. (1997). “Sample disturbance effects in soft low plastic Norwegian clay,” in Proceedings of the Conference on Recent Developments in Soil and Pavement Mechanics, Rio de Janeiro, Brazil, 25–27 June. 81–102 (Balkema, Rotterdam: Norwegian Geotechnical Institute).

Google Scholar

Ma W. J., Qin Y., Wu Q., Zhang G. K., Chen G. X. (2023). Cyclic failure mechanisms of saturated marine coral sand under various consolidations. Appl. Ocean Res. 131, 103450. doi: 10.1016/j.apor.2022.103450

CrossRef Full Text | Google Scholar

Matasović N., Vucetic M. (1995). Generalized cyclic-degradation-pore-pressure generation model for clays. J. Geotech. Eng. 121 (1), 33–42. doi: 10.1061/(ASCE)0733-9410(1995)121:1(33

CrossRef Full Text | Google Scholar

Mortezaie A., Vucetic M. (2016). Threshold shear strains for cyclic degradation and cyclic pore water pressure generation in two clays. J. Geotech. Geoenviron. Eng. 142 (5), 04016007. doi: 10.1061/(ASCE)GT.1943-5606.0001461

CrossRef Full Text | Google Scholar

Nhan T. T., Matsuda H., Sato H., Thien D. Q. (2022). Pore water pressure and settlement of clays under cyclic shear: effects of soil plasticity and cyclic shear direction. J. Geotech. Geoenviron. Eng. 148 (2), 04021185. doi: 10.1061/(ASCE)GT.1943-5606.0002734

CrossRef Full Text | Google Scholar

Ohara S., Matsuda H. (1988). Study on the settlement of saturated clay layer induced by cyclic shear. Soil. Found. 28 (3), 103–113. doi: 10.3208/sandf1972.28.3_103

CrossRef Full Text | Google Scholar

Pan K., Yuan Z. H., Zhao C. F., Tong J. H., Yang Z. X. (2021). Undrained shear and stiffness degradation of intact marine clay under monotonic and cyclic loading. Eng. Geol. 297, 106502. doi: 10.1016/j.enggeo.2021.106502

CrossRef Full Text | Google Scholar

Parsa M., Bagheripour M. H., Presti D. C. F. L. (2022). Experimental and simulation study on dynamic properties of two historical soils in Italy. Int. J. Civ. Eng. 1–18. doi: 10.1007/s40999-022-00781-6

CrossRef Full Text | Google Scholar

Rollins K. M., Evans M. D., Diehl N. B., Daily W. D. (1998). Shear modulus and damping relationships for gravels. J. Geotech. Geoenviron. Eng. 124 (5), 396–405. doi: 10.1061/(ASCE)1090-0241(1998)124:5(396

CrossRef Full Text | Google Scholar

Saathoff J. E., Achmus A. (2022). “Excess pore pressure estimation based on cyclic laboratory tests,” in Proceedings of the 7th International Young Geotechnical Engineers Conference, Sydney Australia. 451–456 (Australian Geomechanics Society).

Google Scholar

Shi F. D., Shi X. F., Su X., Fang X. S., Wu Y. H., Cheng Z. B., et al. (2018). Clay minerals in Arctic kongsfjorden surface sediments and their implications on provenance and paleoenvironmental change. Acta Oceanol. Sin. 37 (5), 29–38. doi: 10.1007/s13131\-018-1220-6

CrossRef Full Text | Google Scholar

Skempton A. W. (1954). The pore-pressure coefficients a and b. Géotechnique 4 (4), 143–147. doi: 10.1680/geot.1954.4.4.143

CrossRef Full Text | Google Scholar

Soralump S., Prasomsri J. (2016). Cyclic pore water pressure generation and stiffness degradation in compacted clays. J. Geotech. Geoenviron. Eng. 142 (1), 04015060. doi: 10.1061/(ASCE)GT.1943-5606.0001364

CrossRef Full Text | Google Scholar

Su J. F., Fan D. D., Liu J. P., Wu J. Y. (2022). Anatomy of the transgressive depositional system in a sediment-rich tide-dominated estuary: the paleo-Yangtze estuary, China. Mar. Petrol. Geol. 121, 104588. doi: 10.1016/j.marpetgeo.2020.104588

CrossRef Full Text | Google Scholar

Sun H., Hou M. X., Chen C., Ge X. R. (2020). Microstructure investigation of soft clay subjected to triaxial loading. Eng. Geol. 274 (1), 105735. doi: 10.1016/j.enggeo.2020.105735

CrossRef Full Text | Google Scholar

Tabata K., Vucetic M. (2010). “Threshold shear strain for cyclic degradation of three clays,” in Proceeding of 5th International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego (Missouri Univ. of Science and Technology).

Google Scholar

Tsai C. C. (2022). Generalized simple model for predicting the modulus degradation and strain accumulation of clay subject to long-term undrained cyclic loading. Ocean Eng. 254, 111412. doi: 10.1016/j.oceaneng.2022.111412

CrossRef Full Text | Google Scholar

Vucetic M. (1994). Cyclic threshold shear strains in soils. J. Geotech. Eng. 120 (12), 2208–2228. doi: 10.1061/(ASCE)0733-9410(1994)120:12(2208)

CrossRef Full Text | Google Scholar

Vucetic M., Thangavel H., Mortezaie A. (2021). Cyclic secant shear modulus and pore water pressure change in sands at small cyclic strains. J. Geotech. Geoenviron. Eng. 147 (5), 04021018. doi: 10.1061/(ASCE)GT.1943-5606.0002490

CrossRef Full Text | Google Scholar

Wang H. L., Sun H., Huang Z. X., Ge X. R. (2021). A microstructural investigation on hydraulic conductivity of soft clay. B. Eng. Geol. Environ. 80, 4067–4078. doi: 10.1007/s10064-021-02176-8

CrossRef Full Text | Google Scholar

Wu Q., Wang Z. F., Qin Y., Yang W. B. (2023). Intelligent model for dynamic shear modulus and damping ratio of undisturbed marine clay based on back-propagation neural network. J. Mar. Sci.Eng. 11 (2), 249. doi: 10.3390/jmse11020249

CrossRef Full Text | Google Scholar

Yang Q., Ren Y. B., Niu J. L., Cheng K., Hu Y. X., Wang Y. (2018). Characteristics of soft marine clay under cyclic loading: a review. B. Eng. Geol. Environ. 77 (3), 1027–1046. doi: 10.1007/s10064-017-1078-4

CrossRef Full Text | Google Scholar

Zhang Q., Su M., Yao P., Chen Y. P., Stive M. J. F., Zhang Z. B. (2020). Dynamics of a tidal current system in a marginal sea: a case study of the yellow sea, China. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.596388

CrossRef Full Text | Google Scholar

Zhu J. F., Zhao H., Luo Z. Y., Liu H. X. (2020). Investigation of the mechanical behavior of soft clay under combined shield construction and ocean waves. Ocean Eng. 206, 107250. doi: 10.1016/j.oceaneng.2020.107250

CrossRef Full Text | Google Scholar