DCC-GAN-based channel emulator for underwater wireless optical communication systems

The complex and variable oceanic environment challenges channel modeling of Underwater Wireless Optical Communication (UWOC) systems. Most of the classical modeling methods focus mainly on the water environment and ignore the effect of communication equipment on signal transmission, thus making it difficult to model the UWOC channel’s complicated characteristics comprehensively. In this work, a UWOC channel emulator based on Deep Convolutional Conditional Generative Adversarial Networks is established and verified to address the challenge, which can effectively learn the characteristics of channel response and generate emulated signals with randomness like a real UWOC system in a practical application environment. Compared with the approaches based on multi-layer perceptron and convolutional neural network, the experimental results of the proposed method indicate outstanding performances in time domain, frequency domain and universality with different turbidity levels, respectively. This approach provides a new idea for applying deep learning techniques to the field of UWOC channel modeling.

1 Introduction

Nowadays, with the gradual deepening of marine research, there has been a significant increase in underwater activities such as marine environment monitoring, offshore oil exploration, underwater archaeology, and underwater experimental data collection, so a reliable and high transmission rate underwater wireless communication technique is urgently needed (Zeng et al., 2017). Acoustic communication can no longer meet the growing demand for high-speed rates due to its low bandwidth and high transmission delay. Additionally the transmission distance of underwater radio frequency (RF) communication is suppressed because of the skin effect of radio waves (Kaushal and Kaddoum, 2016; Miramirkhani and Uysal, 2018). While utilizing the Underwater Wireless Optical Communication (UWOC) technique, which features high bandwidth, fast transmission rate, good confidentiality and low cost, is gaining more and more attention and has broad application prospects (Chi et al., 2015).

When light propagates through seawater, photons will randomly collide with water molecules or other particles in seawater and deviate from the original propagation direction, leading to a phenomenon of beam divergence, thus causing a loss of optical power at the receiving end. Meanwhile, the farther the distance of light transmission, the more severe the beam divergence becomes, while the loss of the received optical signal directly affects the communication distance and transmission rate of the UWOC system (Mobley, 1994; Gabriel et al., 2013). Furthermore, the attenuation characteristics of the UWOC channel to the optical signal vary with different marine environmental parameters, such as depth and water quality. The complicated absorption and scattering characteristics of the same channel for various wavelengths of light also vary greatly (Zeng et al., 2017). Therefore, the complexity of the UWOC channel poses considerable difficulties for channel modeling.

In recent years, with the development of theory, optoelectronic technology and the improvement of computer performance, the research on UWOC channels has made remarkable progress. Sermsak Jaruwatanadilok modeled the impulse response of the UWOC channel using vector radiative transfer theory which includes multiple scattering effects and polarization. And the scattering effects were quantified as a function of distance and bit error rate (BER) (Jaruwatanadilok, 2008). Brandon M. Cochenour et al. proposed the Beam-Spread Function (BSF) to estimate the impact of scattering effects on the received signal power in the underwater light propagation process (Cochenour et al., 2008). Chadi Gabriel et al. quantified the UWOC channel impulse response for different water types and link distances using the Monte Carlo approach (Gabriel et al., 2013). Shijian Tang et al. presented a closed-form expression of double Gamma functions to model the UWOC channel impulse response, which fits well with the Monte Carlo simulation results (Tang et al., 2014). Also using numerical Monte Carlo simulations, Sanjay Kumar Sahu and Palanisamy Shanmugam obtained a more accurate UWOC channel model by improving the scattering phase function(Sahu and Shanmugam, 2018).

The aforementioned studies mainly focus on the loss of optical signals during the propagation in different water types. Actually, in the process of signal transmission, it is inappropriate to ignore the effect of optical and electrical devices at the transmitter and receiver ends, such as the dark current noise of the photomultiplier tube (PMT), the impulse response of the electronic amplifier, the nonlinear response of the laser, the errors in digital-to-analog (D/A) or analog-to-digital (A/D) conversion and so on. Therefore, a realistic and reliable UWOC channel model is required to completely capture the effects of all parts of the communication system on signal transmission, which is a complex process that neural networks are ideally suited to emulate. Yiheng Zhao et al. proved the feasibility of utilizing neural networks for UWOC channel modeling by proposing a channel emulator called two tributaries heterogeneous neural network (TTHnet) (Zhao et al., 2019), which is based on a combined design of multi-layer perceptron (MLP) and convolutional neural network (CNN). The 1.2m saltwater channel experiments verified the TTHnet regarding both spectrum and BER mismatch, realizing more accurate performance than other channel emulators.

Generative Adversarial Networks (GAN) (Goodfellow et al., 2014), composed of a generator and a discriminator, is one of the most critical research directions in deep learning. Owing to its outstanding data generation capability, GAN has been widely used in computer vision and natural language processing (Pan et al., 2019). In order to generate samples with specific properties, Mhdi Mirza and Simon Osindero proposed a Conditional Generative Adversarial Network (CGAN), where conditional information is added to guide the GAN generator to generate samples (Mirza and Osindero, 2014). The content and structure of the conditional information can be flexibly changed according to the application scenario. For instance, CGAN has been utilized for image resolution enhancement (Ledig et al., 2017) and semantic segmentation of images (Souly et al., 2017), as well as for generating images from text descriptions (Reed et al., 2016; Liang et al., 2017). Apart from applications in computer vision, previous studies in the field of communication have proved that GAN is an effective approach for channel modeling. Davide Righini et al. proposed an approach to generate channel transfer functions for power line communication using Mixture Generative Adversarial Nets (Hoang et al., 2018), which outperforms traditional modeling methods (Righini et al., 2019). In Ref. (Ye et al., 2020), CGAN was employed to model channel effects in end-to-end wireless communication system, and simulation results show that the CGAN approach is effective in additive white Gaussian noise (AWGN) channels, Rayleigh fading channels, and frequency-selective channels. Yudi Dong et al. also developed a CGAN-based channel estimation method for multiple-input multiple-output (MIMO) mmWave wireless communication systems, which has better robustness and reliability compared with conventional methods and other deep learning methods (Dong et al., 2021).

In this article, a Deep Convolutional Conditional Generative Adversarial Networks (DCC-GAN) method for modeling UWOC channels is developed and experimentally tested at different turbidity waters and various transmission rates. The performance is evaluated by spectrum mismatch, BER mismatch and correlation coefficient. The experimental results show that the generator can generate emulated signals with randomness like the real UWOC channel, proving that our proposed model can learn and analyze the characteristics of the channel well. To the best of our knowledge, this is the first study to apply GAN to emulate UWOC channels, which has great potential for exploration in channel modeling.

The rest of the paper is organized as follows. In Section 2, the theoretical principle of the proposed channel emulator is presented, and then the architecture of DCC-GAN is described in detail. In Section 3, the experimental setup for making UWOC datasets is introduced. In Section 4, a series of experiments are carried out to demonstrate the effectiveness of the proposed method. Finally, a brief conclusion is given in Section 5.

2 The proposed channel emulator based on DCC-GAN

2.1 GAN and CGAN

GAN, as its name implies, is a generative network model for learning data distribution in the way of adversarial training, where the aim is to learn a model that can produce samples close to the target distribution. In this article, the DCC-GAN is applied to model the distribution of the UWOC channel output based on a GAN.

The GAN system consists of two parts, namely the generator G and the discriminator D. The input to the generator is a noise sample z which is subject to a specific prior distribution p_z, e.g., Gaussian distribution. Then, the generator transforms the noise sample z into a generated sample G(z). The discriminator takes either a real sample x from the target distribution p_data or a generated sample as input and returns the probability that the input comes from the target distribution rather than the generator. During the training stage, the objective of the discriminator is to learn to distinguish whether the current sample is from the real dataset or the data generated by the generator, while the objective of the generator is to generate fake samples that are as similar as possible to the real samples to fool the discriminator. If the discriminator can successfully distinguish between the two types of samples, then this information is fed back to the generator so that the generator can learn to generate samples more like the real samples. As the number of adversarial training epoch increases, the learning ability of the generator and the discriminating ability of the discriminator become stronger and stronger. Finally, the training progress ends when the discriminator can no longer discriminate between the real samples and the generated fake ones better than random guessing.

Generally, denote the parameter sets of the generator and discriminator as θ_G and θ_D, respectively, the objective functions of the generator and discriminator can be mathematically expressed as follows:

$\begin{array}{ll}{L}_G=\underset{{\theta }_G}{\min }{E}_{z\sim p_z(z)}[\log (1-D(G(z)))]& (1)\end{array}$

$\begin{array}{ll}{L}_D=\underset{{\theta }_D}{\max }{E}_{x\sim p_{data}(x)}[\log D(x)]+E_{z\sim p_z(z)}[\log (1-D(G(z)))]& (2)\end{array}$

The objective of G is to maximize the output of D when the input to D is G(z), while the objective of D is to return a high value when the input is a real sample x and a low one when the input is G(z), thus forming an adversarial training mechanism.

As shown in Figure 1, the GAN can be extended to a CGAN model if a conditional information y is imposed on the generator and discriminator. The conditional information attaches constraints to the original GAN so that the generator can generate data under the guidance of the conditional information, which addresses the issue of uncontrollable sample categories generated by the original GAN. Then, the optimization functions of the generator and discriminator become:

FIGURE 1

Figure 1 Structure of CGAN.

$\begin{array}{ll}{L}_G=\underset{{\theta }_G}{\min }{E}_{\tilde{x}\sim p_g(\tilde{x})}[\log (1-D(\tilde{x}|y))]& (3)\end{array}$

$\begin{array}{ll}{L}_D=\underset{{\theta }_D}{\max }{E}_{x\sim p_{data}(x)}[\log D(x|y)]+E_{\tilde{x}\sim p_g(\tilde{x})}[\log (1-D(\tilde{x}|y))]& (4)\end{array}$

Where, p_g is the generator model distribution implicitly defined by $\tilde{x}=G(z|y)$, $z\sim p_z(z)$.

CGAN is employed in the proposed UWOC channel emulator to simulate the output signal with the given conditioning information on the transmitted signal.

2.2 Architecture of DCC-GAN

Although the original GAN is a powerful generative model, it always suffers from difficulties in training and poor quality of the generated results. By combining GAN with CNN, Deep Convolutional Generative Adversarial Networks (DCGAN)(Radford et al., 2016) can significantly improve the quality of the generated results by exploiting the powerful feature extraction ability of two-dimensional convolutional layer and also find an appropriate network structure for stable training by improving CNN, thus remarkably overcoming the shortcomings of the original GAN. In this work, the hierarchical one-dimensional convolutional layers are used to replace the original MLP. Therefore, the proposed method is called “Deep Convolutional Conditional GAN”. It is appropriate to employ convolutional layers since convolutional operations between signals can represent the channel response. The specific parameters of DCC-GAN are shown in Table 1, where K denotes the batch size, and the dimension of the noise sample z is 8. Every 100 adjacent signals are sequentially input to the network, with each signal containing 20 sampling points.

TABLE 1

Table 1 Model parameters of DCC-GAN.

2.3 Improvement of the objective function

According to Ref. (Goodfellow et al., 2014), minimizing the original GAN’s loss function is equivalent to minimizing the Jensen–Shannon (JS) divergence between the target distribution p_data and the generator model distribution p_g, which tends to cause the gradients to vanish when the discriminator saturates. This training difficulty arises because the JS divergence is potentially not continuous for the generator’s parameters (Arjovsky et al., 2017). So, the Earth-Mover (also called Wasserstein-1) distance W(q, p) is introduced to replace JS divergence in Wasserstein GAN(Arjovsky et al., 2017), where the discriminator is also called a critic. Using the Kantorovich-Rubinstein duality, the critic loss function can be obtained as Eq. (5) where ℤ is the set of 1-Lipschitz functions.

$\begin{array}{ll}\underset{{\theta }_D\in \mathbb{Z}}{\min }{L}_{critic}=\underset{{\theta }_D\in \mathbb{Z}}{\min }\{E_{\tilde{x}\sim p_g(\tilde{x})}[D(\tilde{x}|y)]-E_{x\sim p_{data}(x)}[D(x|y)]\}& (5)\end{array}$

In this case, minimizing L_critic is equivalent to minimizing the Wasserstein-1 distance W(p_data, p_g) by optimizing the generator’s parameters. Nevertheless, to enforce the Lipschitz constraint on the critic, Wasserstein GAN suggests clipping the weights of the critic to a compact space, which may result in either vanishing or exploding gradients when the clipping threshold is not tuned carefully. To avoid undesirable behaviors, a soft version of the constraint called the Wasserstein GAN Gradient Penalty (WGAN-GP) algorithm (Gulrajani et al., 2017) is proposed as an alternative way to enforce the Lipschitz constraint, and the gradient penalty metric L_gp is defined as:

$\begin{array}{ll}{L}_{gp}=\lambda E_{\widehat{x}\sim p_{\widehat{x}}(\widehat{x})}[{({\nabla }_{\widehat{x}}D{(\widehat{x}|y)}_2-1)}^2]& (6)\end{array}$

Where, $p_{\widehat{x}}$ is defined as sampling uniformly along straight lines between pairs of points sampled from p_data and p_g, λ denotes penalty coefficient.

In this article, the WGAN-GP algorithm is introduced to improve the training instability of DCC-GAN. The objective function of D is then reformulated as a combination of critic loss and gradient penalty metric, which is described as:

$\begin{array}{ll}{L}_D=\underset{{\theta }_D}{\min }\left\{L_{critic}+L_{gp}\right\}& (7)\end{array}$

And the objective function of G is modified as:

$\begin{array}{ll}{L}_G=\underset{{\theta }_G}{\min }{E}_{\tilde{x}\sim p_g(\tilde{x})}[-D(\tilde{x}|y)]& (8)\end{array}$

In the experiments, λ is set to 5, which works well on the proposed DCC-GAN and the UWOC datasets.

2.4 Training details of DCC-GAN

The improvement in training instability not only allows us to enhance sample quality by experimenting with a broader range of network architectures but also requires little hyperparameter tuning. The training procedure of DCC-GAN is illustrated in Algorithm 1 in detail. The training process aims to obtain an ideal generator architecture, which can model the distribution of the UWOC channel output, that is, to realize the function of the channel emulator. In each iteration, the generator and discriminator training processes are carried out alternately. When one model is trained, the other one is fixed. The real data can be obtained from the transmitted signal through the real channel, while the fake data is obtained from the transmitted signal through the generator. The loss function of Eq. (8) is utilized to update the generator’s parameters. The real, fake, and true-fake joint distribution data are fed into the discriminator, respectively, with the transmitted signal as conditional information. The parameters of the discriminator are updated according to the loss function of Eq. (7). Both models are optimized by the Adam optimizer using stochastic gradient descent, with an initial learning rate α of 0.0002. The initial hyperparameter values in Algorithm 1 are derived from a previous study on RF channel modeling(Ye et al., 2020). In order to ensure that the algorithm can handle a wide range of input data while still converging within a reasonable number of epochs, extensive experimentation is carried out to fine-tune these values. Ultimately, experimental results indicate that setting λ to 5 and using a batch size m of 20 yield the best performance. Assuming that k represents the number of discriminator iterations per generator iteration, the optimal convergence can be obtained in the experiments when k is set to 6. The number of training epochs is set to at least 200.

ALGORITHM 1 MINIBATCH STOCHASTIC GRADIENT DESCENT TRAINING OF DCC-GAN. ASSUME THE GENERATOR PARAMETER ΘG AND THE DISCRIMINATOR PARAMETER ΘD. THE DEFAULT VALUES OF K=6, M=20, Λ=5 AND Α=0.0002 ARE USED.

Algorithm 1 Minibatch stochastic gradient descent training of DCC-GAN. Assume the generator parameter θG and the discriminator parameter θD. The default values of k=6, m=20, λ=5 and α=0.0002 are used..

3 Experimental setup and details

This section describes the experimental procedure for making the UWOC dataset in detail. To simulate the characteristics of the UWOC channels, a 35 meters underwater laser communication system was built. The entire experimental setup of the UWOC system is shown in Figure 2. The main components of the UWOC system are shown in Figure 3.

FIGURE 2

Figure 2 Experimental setup and block diagram of the UWOC system and channel emulator.

FIGURE 3

Figure 3 Components of the UWOC system. (A) Water tank. (B) Transmitter: 488nm laser. (C) Receiver: photomultiplier tube (PMT), amplifier unit (AMP), oscilloscope (OSC), DC power supply and high voltage power supply. (D) 35 m blue-green light reflection paths.

3.1 Experimental setup

3.1.1 Transmitter

As shown in Figure 3B, a semiconductor laser (OXXIUS, LaserBoxx-488) with an emission peak wavelength of 488 nm is employed at the transmitter end, which meets the requirements of blue-green light in the 450 nm to 550 nm band where the attenuation of seawater is much less than that of other wavelengths(Duntley, 1963). The laser has built-in driver circuitry, which can accept analog signal input directly and adjust the emitted optical power according to the application scenario.

3.1.2 Establishment of UWOC channel

The underwater channel for light transmission is built in a 5 m × 1 m × 1 m water tank, shown in Figure 3A, which is filled with clear tap water or artificial turbid water. The communication distance of 35 m is achieved by using six reflective mirrors fixed to the tank’s inner walls on both sides by cardan joints. The reflection of each 5 m light path is realized by fine-tuning the angle of the mirrors. A total propagation distance of 35 m (5 m × 7) can be obtained, through six reflections, as shown in Figure 3D.

3.1.3 Receiver

As shown in Figure 3C, a PMT (Hamamatsu, R1527) is employed at the receiver end, which has a spectral response in the range 185 nm-680 nm, with an optimal spectral response of about 400 nm, and works well with the 488 nm laser. Although the PMT has the advantages of low noise and high gain, the output current is still shallow, so a signal amplifier unit (AMP) (Hamamatsu, C11184) is needed. They are powered by high voltage and DC power, respectively.

3.2 Experimental procedure

An integral experimental setup is demonstrated in Figure 2. At first, the non-return-to-zero on-off-keying (NRZ-OOK) modulated signals are loaded into an arbitrary waveform generator (AWG) as the transmitted signal. Then, the AWG performs D/A conversion of the signals and outputs analog electrical signals to drive the laser for intensity modulation. Thus, optical signals for underwater transmission can be generated. After passing through a 35m underwater channel, the PMT detects and the AMP amplifies the optical signals, and then the received photons are converted back into electrical signals. Afterward, a memory oscilloscope (OSC) is employed to sample and record the corresponding digital signals. Finally, the offline processing operations are performed, including synchronization, demodulation, and the BER calculation. Meanwhile, the synchronized signals are adopted as the received signal, and the received signal and the corresponding transmitted signal are collected to make the UWOC dataset.

According to the setup of the network architecture in Figure 2, the received and the corresponding transmitted signals are combined to train the proposed DCC-GAN. In detail, as conditional information, the transmitted signal is fed into the generator along with a noise sample. Then, the generator outputs a fake received signal, and the discriminator will decide whether the input signal is a real signal or a fake one from the generator under the guidance of the transmitted signal. The generator and discriminator can find their optimal parameters individually according to the training strategy in Algorithm 1. When the training process finishes, the function of emulating the UWOC channel is realized. Finally, to evaluate the model’s generalization ability, independent samples from the test set are employed to estimate the trained channel emulator.

This work produces a series of datasets under different experimental conditions, and the experiment parameters are shown in Table 2. Besides the tap water channel, two artificial turbid water channels are also created by adding a specific quantity of Aluminum Hydroxide (Al(OH)₃), which is commonly used as a scattering agent. The attenuation coefficient at wavelength 488 nm is measured to be 0.1169 m^-1 (tap water), 0.2318 m^-1 and 0.471 m^-1 in three types of water, respectively. Correspondingly, the transmitting optical powers are also finely adjusted to obtain the optimal received signal.

TABLE 2

Table 2 Experimental parameters.

4 Experiment results and analysis

In this section, the performance of the proposed channel emulator is demonstrated and analyzed concerning different types of water and various transmission rates. In detail, metrics such as the absolute amplitude spectrum mismatch, Pearson correlation coefficient, and the BER mismatch between each emulated received signal and real received signal are calculated and compared.

Suppose a real received signal and its emulated signal are denoted as X and $\tilde{X}$, respectively. The calculation of absolute amplitude spectrum mismatch is described as:

$\begin{array}{ll}spectrummismatch(X,\tilde{X})=abs(FFT(X)-FFT(\tilde{X}))& (9)\end{array}$

The BER mismatch can be computed as:

$\begin{array}{ll}BERmismatch(X,\tilde{X})=abs(BER(X)-BER(\tilde{X}))& (10)\end{array}$

And the correlation coefficient is defined as:

$\begin{array}{ll}Corr(X,\tilde{X})=\frac{Cov(X,\tilde{X})}{\sqrt{Var(X)Var(\tilde{X})}}& (11)\end{array}$

Where, $Var(·)$ is the variance, $Cov(X,\tilde{X})$ represents the covariance of X and $\tilde{X}$.

The BER directly reflects the noise intensity of the UWOC channel, so three typical channels with different orders of magnitude of BER, shown in Table 3, are selected to test the performance of DCC-GAN. To compare with conventional neural networks and demonstrate the superiority of the generative adversarial approach, a CNN model is designed with similar complexity. Its specific structure and parameters are shown in Table 4. Furthermore, an MLP model is also introduced from a previous study (Ye et al., 2017) related to wireless channel estimation, which contains five layers and neurons in each layer are 200,500,250,120 and 200, respectively. The activation function of each layer is ReLU, except for no activation function in the last layer. In both models, the Adam optimizer updates the weights and the loss function is Mean Square Error (MSE), the batch size for training is 20 and the learning rate is 0.001.

TABLE 3

Table 3 Parameters of three typical channels.

TABLE 4

Table 4 Model Parameters of CNN.

4.1 Performance comparison in the time domain

In engineering applications, the Pearson correlation coefficient is often used to measure the similarity between signal sequences (Ahmed, 2015). The correlation coefficient value lies from -1 to 1, where 1 represents perfect correlation, while -1 shows a negative correlation and 0 indicates no correlation. Figure 4 shows the comparison of correlation coefficients of the signals generated by the three neural network-based channel emulators in channel-1, channel-2 and channel-3, respectively. During the training process, the convergence rate of DCC-GAN is similar to CNN and faster than MLP. After 200 training epochs, the correlation coefficient of DCC-GAN is 0.99 in all cases, while the values of CNN and MLP are 0.95, 0.96, 0.95 and 0.83, 0.86, 0.84 in channel-1, channel-2 and channel-3, respectively. Figure 5 shows the BER mismatch performance comparison of the three network models in three channels. From the figure, the BER mismatch performance of DCC-GAN is much better than MLP and CNN, where the BER mismatches of DCC-GAN-based channel emulator are 6.7%, 10.4%, 9.3% of the CNN-based method and only 0.03%, 0.16%, 0.82% of the MLP-based method in channel-1, channel-2 and channel-3, respectively. It indicates that the signal waveform generated by the DCC-GAN-based channel emulator is the closest to the real signal.

FIGURE 4

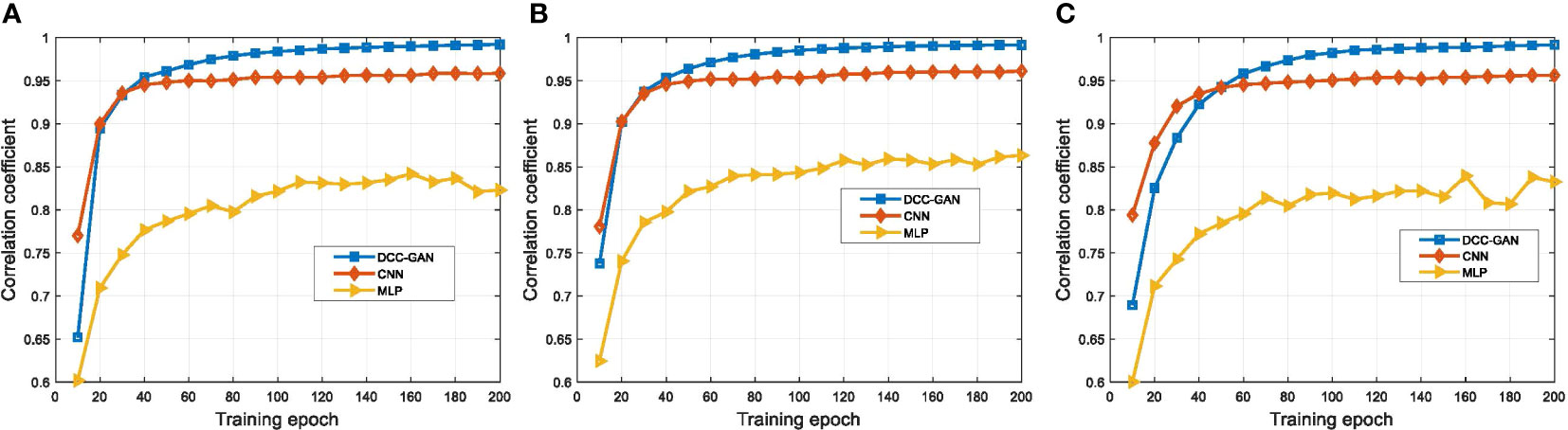
Figure 4 The performance of correlation coefficient for different channel emulators on the test set after 200 training epochs in (A) channel-1, (B) channel-2 and (C) channel-3.

FIGURE 5

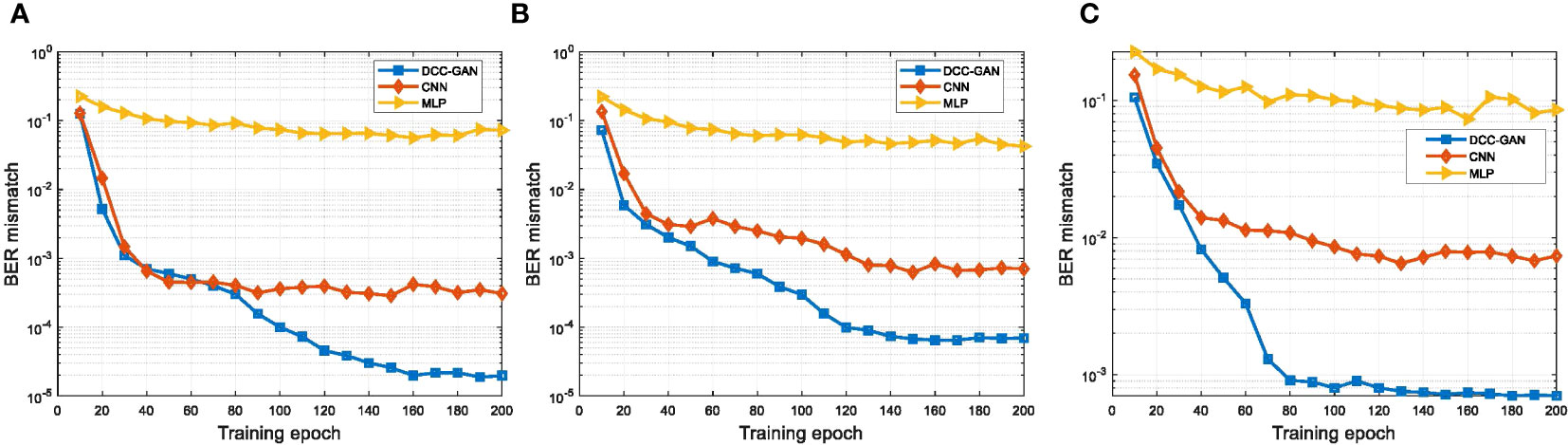
Figure 5 The performance of BER mismatch for different channel emulators on the test set after 200 training epochs in (A) channel-1, (B) channel-2 and (C) channel-3.

Due to the bandwidth limitation of the electro-optical devices, the nonlinear distortion of the UWOC system increases with the transmission rate. To estimate the proposed method at various transmission rates, the BER versus transmission rate curves are demonstrated in Figure 6A. When the transmission rate increases, the BER curves of the emulated and real received signals exhibit a same trend towards a specific increase. The maximum BER mismatch of the DCC-GAN-based channel emulator is 0.4 dB at various transmission rates. Hence the proposed channel emulator is generally applicable to the variation of transmission rate.

FIGURE 6

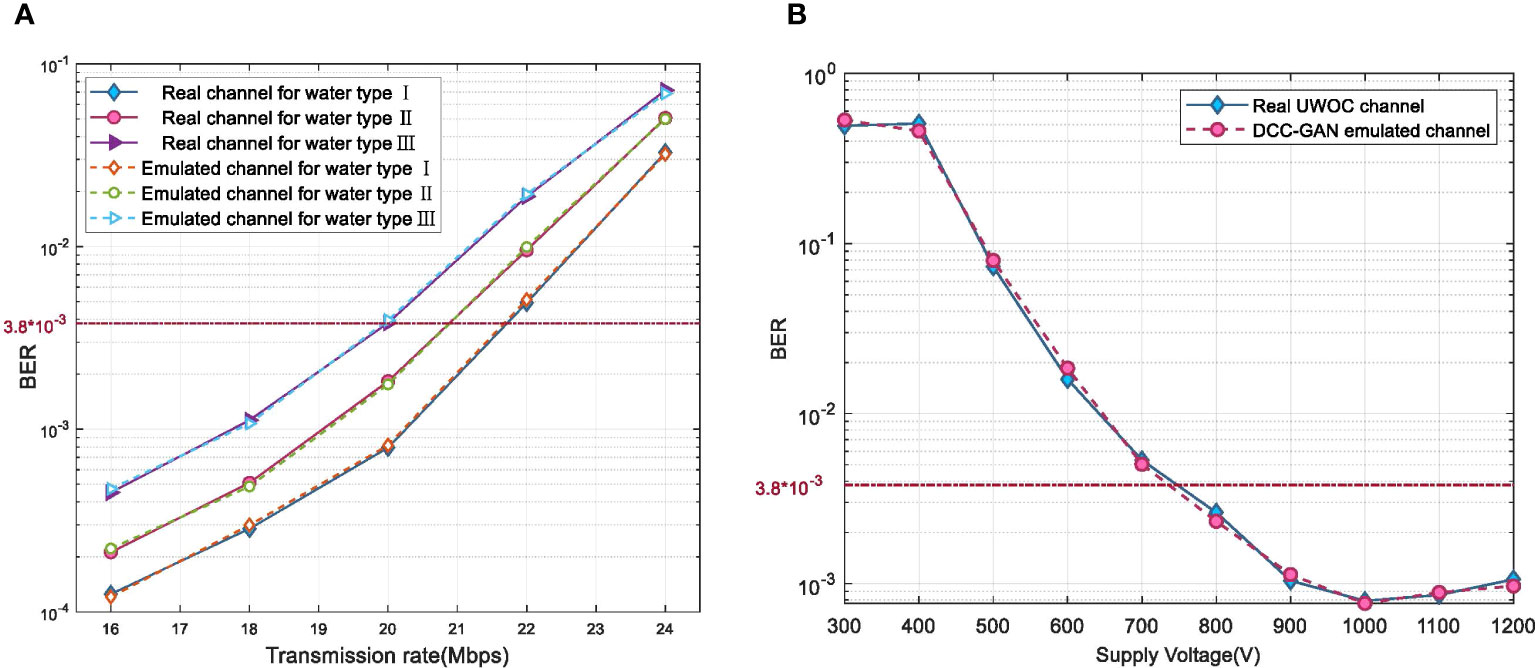
Figure 6 BER comparison of real received signal and emulated signal at various (A) transmission rates and (B) PMT working points.

In addition to bandwidth limitation, inappropriate working point settings of optoelectronic devices can also cause system errors. At the receiver, the supply voltage directly affects the PMT’s dark current noise and gain performance, prompting the need for an appropriate working point to optimize the output signal-to-noise ratio for each application scenario. Figure 6B displays a comparison of BER between the real signal of the UWOC system and the emulated signal generated by DCC-GAN at various PMT working points. Results show that as the supply voltage gradually increases, the BER trend of the simulated signal aligns well with that of the real signal, with the optimal voltage being around 1000 V. When the voltage exceeds 700 V, the BER mismatch does not surpass 0.72 dB, which signifies the capability of DCC-GAN to effectively capture changes in the channel state due to the nonlinear response of optoelectronic devices.

4.2 Comparison in the frequency domain

Features in the frequency domain can show some phenomena that cannot be found in the time domain, so some experiments are carried out to compare the spectrum of the signals. The results generated by three neural network-based channel emulators and the real received signal in channel-1 are shown in Figure 7A. The absolute mismatches of magnitude between each emulated spectrum and the real one are shown in Figure 7B for a more transparent demonstration, where the average mismatches of MLP, CNN and DCC-GAN are 2.56, 1.14 and 0.25 dB, respectively. Figures 8, 9 show the comparison of the spectrum performance for three channel emulators in channel-2 and channel-3, respectively. The average spectrum mismatches are 2.38, 0.89 and 0.24 dB in channel-2, 2.53, 0.97 and 0.34 dB in channel-3, respectively. From the mismatch curves in Figures 7B, 8B, and 9B, it can be noticed that the mismatch of MLP is high at all frequency bands, the mismatch of CNN is mainly clustered in the higher frequency bands, while the mismatch of DCC-GAN is lower than the others in all bands, and inevitable the lowest average spectrum mismatch. Obviously, the spectrum generated by the proposed emulator is the closest one to the real signal in all experimental channels. Therefore, the DCC-GAN-based channel emulator can more accurately capture the characteristics of different channels in the frequency domain.

FIGURE 7

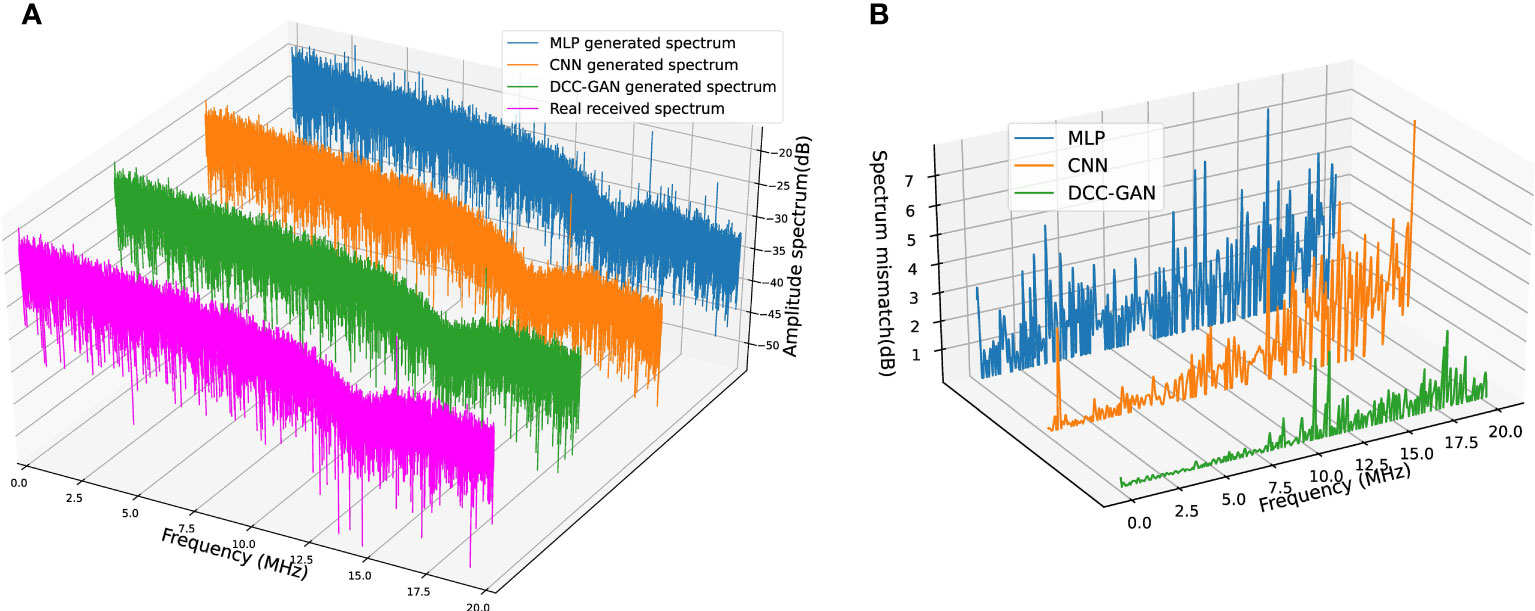
Figure 7 (A) Spectrum comparison of real received signal and signals generated by three channel emulators in channel-1. (B) Corresponding spectrum mismatch between the real spectrum and the generated spectrum.

FIGURE 8

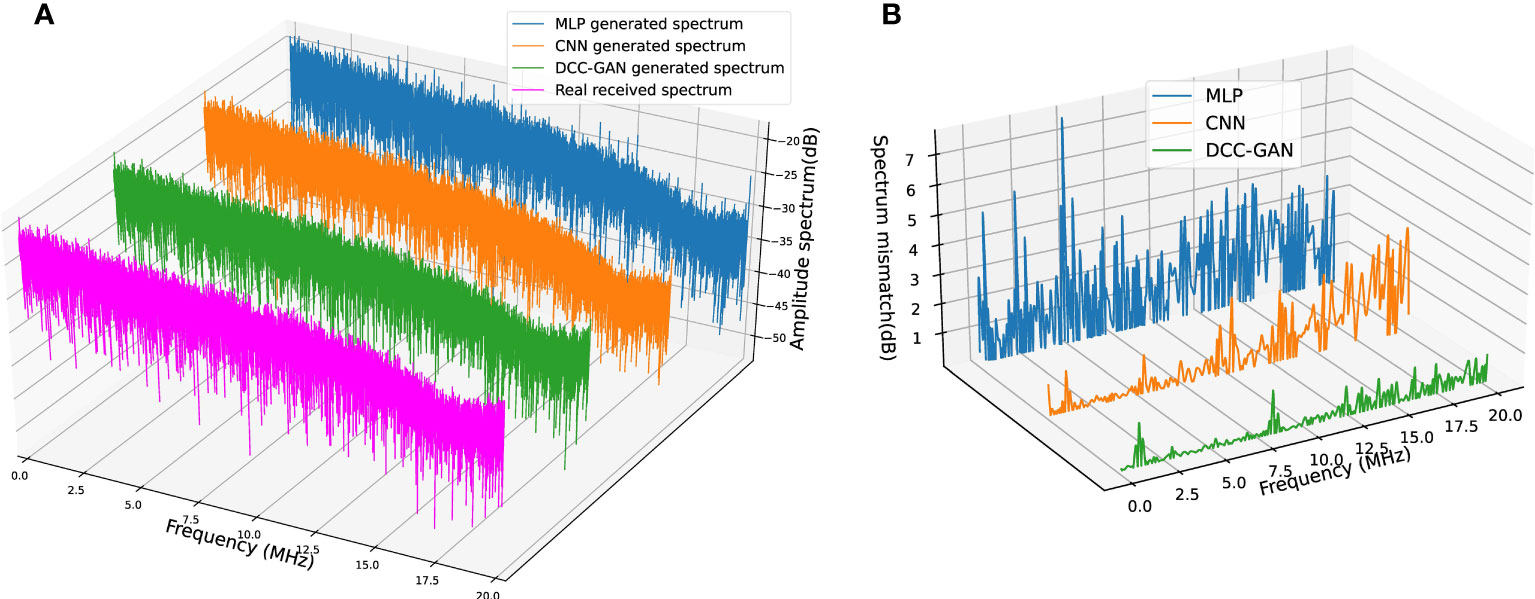
Figure 8 (A) Spectrum comparison of real received signal and signals generated by three channel emulators in channel-2. (B) Corresponding spectrum mismatch between the real spectrum and the generated spectrum.

FIGURE 9

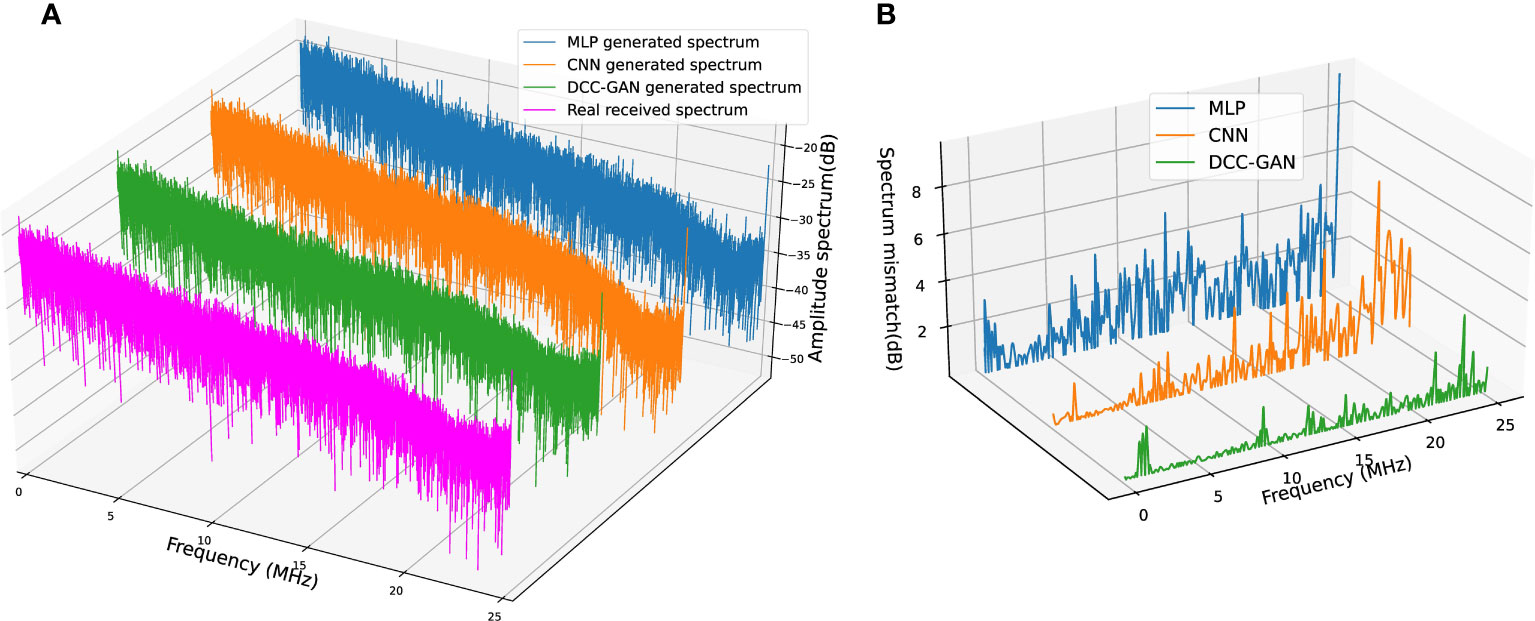
Figure 9 (A) Spectrum comparison of real received signal and signals generated by three channel emulators in channel-3. (B) Corresponding spectrum mismatch between the real spectrum and the generated spectrum.

4.3 Discussion on other advantages of DCC-GAN

Benefiting from the diversity of samples generated by GAN, the DCC-GAN-based channel emulator has the additional capability to simulate the randomness of the received signal. This means that the emulated signal generated by the proposed model will not be identical each time for the same input signal, just like an actual receive procedure. For example, if a certain digital sequence is transmitted twice, two signals with slight random differences will be received. In Figure 10, these two real signals are named true signal 1 and true signal 2. Then, the same signal is fed into the channel emulator multiple times to check the differences. Two signals of simulations are selected to compare with the two real received signals. For better visualization, the relative errors of each signal to the true signal 1 are also displayed, and the average error are 0.0302, 0.0309 and 0.0296 V, respectively. The three error curves are not identical to each other, and the average error between the generated signal and the real signal is quite close to the average error between the real signals, indicating that the generated signals have similar random characteristics to the real signal.

FIGURE 10

Figure 10 Comparison of DCC-GAN generated samples and real samples.

Kernel density estimation (KDE) is a non-parametric estimation method which is commonly used in statistics to estimate the probability density function of a random variable(O’Brien et al., 2016). Based on the KDE approach, the comparisons of the data distribution generated by MLP, CNN and DCC-GAN with the real signal are shown in Figures 11A–C, respectively. The real data satisfies a bimodal distribution with a peak-to-peak distance of 0.956 and two half-peak widths of 0.117 and 0.125. For the above three properties, the errors of the data distribution generated by DCC-GAN are only 0.001, 0.001 and 0.002, respectively, while the values of CNN and MLP are 0.039, 0.128, 0.096 and 0.381, 0.483, 0.542, respectively. So it can be clearly observed that the distribution generated by DCC-GAN converges most approximately to the real distribution.

FIGURE 11

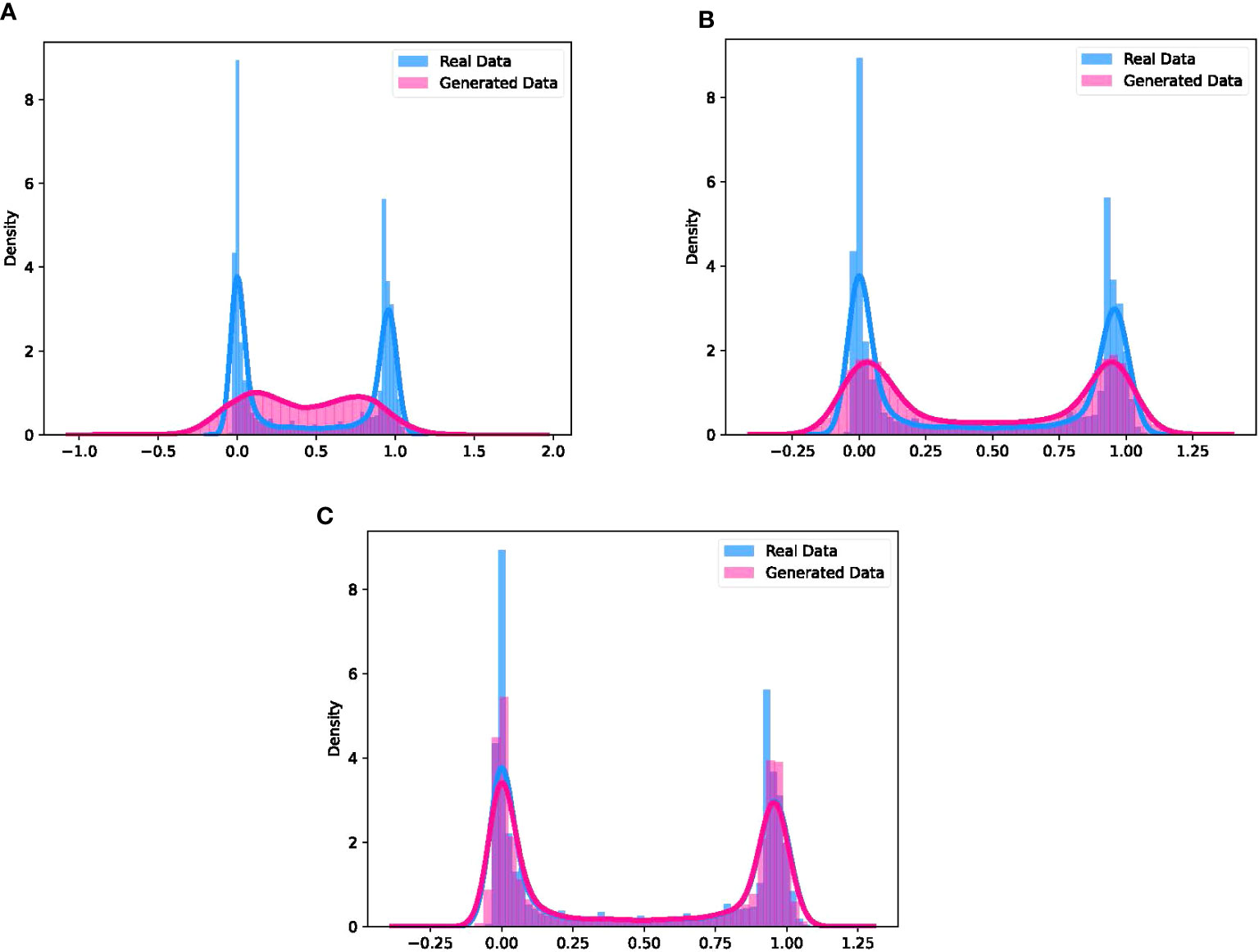
Figure 11 Comparison between the real distribution of UWOC channel and the distribution of data generated by (A) MLP, (B) CNN and (C) DCC-GAN.

The above experimental results reveal that the emulated signal and the real signal share highly similar characteristics, the DCC-GAN-based channel emulator can not only learn the channel distribution accurately, but also output the emulated signal with randomness to restore the UWOC channel more realistically.

5 Conclusion

This paper proposes a novel DCC-GAN-based model to emulate the UWOC channel more realistically, which combines the advantages of CGAN, DCGAN and WGAN-GP algorithms to achieve high-quality generated results and stable training. A series of evaluation experiments regarding the spectrum, correlation coefficient and BER have verified the universality of the proposed channel emulator on different water channels and various transmission rates. The results indicate the effectiveness of DCC-GAN by demonstrating superior performance in both time and frequency domains compared with MLP and CNN-based approaches. Besides, the proposed model can learn the distribution of channel output more realistically to restore the underwater communication signal. The trained model can be used offline to generate diverse signal samples for subsequent experimental analysis, which will offer significant savings on experimental costs and effectively expedite the research advance of the UWOC systems. Therefore, this study opens a promising way to apply deep learning techniques in the UWOC channel modeling field.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HH and MF contributed to conception and design of the study. HH performed the experimental analysis and wrote the first draft of the manuscript. MF contributed to the manuscript revision. MF, XL, and BZ provided guidance and funding for this research. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Key Research and Development Project of Hainan Province (No.ZDYF2022GXJS001), Shandong Provincial Natural Science Foundation Grant (ZR2020MF011) and a grant from the National Natural Science Foundation of China (No.61971253).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed S. N. (2015). “9 - essential statistics for data analysis,” in Physics and engineering of radiation detection, 2nd ed. Ed. Ahmed S. N. (Amsterdam, The Netherlands: Elsevier), 541–593. doi: 10.1016/B978-0-12-801363-2.00009-7

CrossRef Full Text | Google Scholar

Arjovsky M., Chintala S., Bottou L. (2017). “Wasserstein generative adversarial networks,” in INTERNATIONAL CONFERENCE ON MACHINE LEARNING, VOL 70, eds. D. Precup and Y. Teh (1269 LAW ST, SAN DIEGO, CA, UNITED STATES: JMLR-JOURNAL MACHINE LEARNING RESEARCH), vol. 70 of Proceedings of Machine Learning Research. 34th International Conference on Machine Learning, Sydney, AUSTRALIA, AUG 06-11, 2017.

Google Scholar

Chi N., Haas H., Kavehrad M., Little T. D., Huang X.-L. (2015). Visible light communications: demand factors, benefits and opportunities [guest editorial]. IEEE Wireless Commun. 22, 5–7. doi: 10.1109/MWC.2015.7096278

CrossRef Full Text | Google Scholar

Cochenour B. M., Mullen L. J., Laux A. E. (2008). Characterization of the beam-spread function for underwater wireless optical communications links. IEEE J. Oceanic Eng. 33, 513–521. doi: 10.1109/JOE.2008.2005341

CrossRef Full Text | Google Scholar

Dong Y., Wang H., Yao Y.-D. (2021). Channel estimation for one-bit multiuser massive mimo using conditional gan. IEEE Commun. Lett. 25, 854–858. doi: 10.1109/LCOMM.2020.3035326

CrossRef Full Text | Google Scholar

Duntley S. Q. (1963). Light in the sea*. J. Opt. Soc Am. 53, 214–233. doi: 10.1364/JOSA.53.000214

CrossRef Full Text | Google Scholar

Gabriel C., Khalighi M.-A., Bourennane S., Léon P., Rigaud V. (2013). Monte-Carlo-based channel characterization for underwater optical communication systems. J. Opt. Commun. Netw. 5, 1–12. doi: 10.1364/JOCN.5.000001

CrossRef Full Text | Google Scholar

Goodfellow I. J., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., et al. (2014). “Generative adversarial nets,” in ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 27 (NIPS 2014), vol. 27 . Eds. Ghahramani Z., Welling M., Cortes C., Lawrence N., Weinberger K. (10010 NORTH TORREY PINES RD, LA JOLLA, CALIFORNIA 92037 USA: NEURAL INFORMATION PROCESSING SYSTEMS (NIPS), 2672–2680.

Google Scholar

Gulrajani I., Ahmed F., Arjovsky M., Dumoulin V., Courville A. (2017). “Improved training of wasserstein gans,” in Proceedings of the 31st international conference on neural information processing systems (Red Hook, NY, USA: Curran Associates Inc), 5769–5779. NIPS’17.

Google Scholar

Hoang Q. M., Nguyen T. D., Le T., Phung D. Q. (2018). “Mgan: training generative adversarial nets with multiple generators,” in International Conference on Learning Representations.

Google Scholar

Jaruwatanadilok S. (2008). Underwater wireless optical communication channel modeling and performance evaluation using vector radiative transfer theory. IEEE J. Selected Areas Commun. 26, 1620–1627. doi: 10.1109/JSAC.2008.081202

CrossRef Full Text | Google Scholar

Kaushal H., Kaddoum G. (2016). Underwater optical wireless communication. IEEE Access 4, 1518–1547. doi: 10.1109/ACCESS.2016.2552538

CrossRef Full Text | Google Scholar

Ledig C., Theis L., Huszár F., Caballero J., Cunningham A., Acosta A., et al. (2017). “Photo-realistic single image super-resolution using a generative adversarial network,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 105–114. doi: 10.1109/CVPR.2017.19

CrossRef Full Text | Google Scholar

Liang X., Hu Z., Zhang H., Gan C., Xing E. P. (2017). “Recurrent topic-transition gan for visual paragraph generation,” in 2017 IEEE International Conference on Computer Vision (ICCV). 3382–3391. doi: 10.1109/ICCV.2017.364

CrossRef Full Text | Google Scholar

Miramirkhani F., Uysal M. (2018). Visible light communication channel modeling for underwater environments with blocking and shadowing. IEEE Access 6, 1082–1090. doi: 10.1109/ACCESS.2017.2777883

CrossRef Full Text | Google Scholar

Mirza M., Osindero S. (2014). Conditional generative adversarial nets. ArXiv. doi: 10.48550/arXiv.1411.1784

CrossRef Full Text | Google Scholar

Mobley C. (1994). Light and water: radiative transfer in natural waters.

Google Scholar

O’Brien T. A., Kashinath K., Cavanaugh N. R., Collins W. D., O’Brien J. P. (2016). A fast and objective multidimensional kernel density estimation method: fastkde. Comput. Stat Data Anal. 101, 148–160. doi: 10.1016/j.csda.2016.02.014

CrossRef Full Text | Google Scholar

Pan Z., Yu W., Yi X., Khan A., Yuan F., Zheng Y. (2019). Recent progress on generative adversarial networks (gans): a survey. IEEE Access 7, 36322–36333. doi: 10.1109/ACCESS.2019.2905015

CrossRef Full Text | Google Scholar

Radford A., Metz L., Chintala S. (2016). Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR. doi: 10.48550/arXiv.1511.06434

CrossRef Full Text | Google Scholar

Reed S., Akata Z., Mohan S., Tenka S., Schiele B., Lee H. (2016). “Learning what and where to draw,” in Proceedings of the 30th international conference on neural information processing systems (Red Hook, NY, USA: Curran Associates Inc), 217–225. NIPS’16.

Google Scholar

Righini D., Letizia N. A., Tonello A. M. (2019). “Synthetic power line communications channel generation with autoencoders and gans,” in 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm). 1–6. doi: 10.1109/SmartGridComm.2019.8909700

CrossRef Full Text | Google Scholar

Sahu S. K., Shanmugam P. (2018). A theoretical study on the impact of particle scattering on the channel characteristics of underwater optical communication system. Optics Commun. 408, 3–14. doi: 10.1016/j.optcom.2017.06.030

CrossRef Full Text | Google Scholar

Souly N., Spampinato C., Shah M. (2017). “Semi supervised semantic segmentation using generative adversarial network,” in 2017 IEEE International Conference on Computer Vision (ICCV). 5689–5697. doi: 10.1109/ICCV.2017.606

CrossRef Full Text | Google Scholar

Tang S., Dong Y., Zhang X. (2014). Impulse response modeling for underwater wireless optical communication links. IEEE Trans. Commun. 62, 226–234. doi: 10.1109/TCOMM.2013.120713.130199

CrossRef Full Text | Google Scholar

Ye H., Li G. Y., Juang B. (2017). Power of deep learning for channel estimation and signal detection in ofdm systems. IEEE Wireless Communication Lett. PP, 114–117. doi: 10.1109/LWC.2017.2757490

CrossRef Full Text | Google Scholar

Ye H., Liang L., Li G. Y., Juang B.-H. (2020). Deep learning-based end-to-end wireless communication systems with conditional gans as unknown channels. IEEE Trans. Wireless Commun. 19, 3133–3143. doi: 10.1109/TWC.2020.2970707

CrossRef Full Text | Google Scholar

Zeng Z., Fu S., Zhang H., Dong Y., Cheng J. (2017). A survey of underwater optical wireless communications. IEEE Commun. Surveys Tutorials 19, 204–238. doi: 10.1109/COMST.2016.2618841

CrossRef Full Text | Google Scholar

Zhao Y., Zou P., Yu W., Chi N. (2019). Two tributaries heterogeneous neural network based channel emulator for underwater visible light communication systems. Opt. Express 27, 22532–22541. doi: 10.1364/OE.27.02253211

PubMed Abstract | CrossRef Full Text | Google Scholar