Sea level anomalies in the southeastern tropical Indian Ocean as a potential predictor of La Niña beyond one-year lead

1 Introduction

ENSO is one of the most important climate phenomena on interannual time scales, involving variations in sea surface temperature (SST) in the central and eastern tropical Pacific Ocean, influencing temperature and precipitation globally through variations in atmospheric circulation. Substantial efforts have been dedicated to predicting its onset and development because of its extensive repercussions worldwide. The ENSO has been shown to be predictable with one- to two-year lead times in certain numerical hindcast experiments (Kirtman and Schopf, 1998; Fedorov and Philander, 2000; Chen et al., 2004; Luo et al., 2008). However, considerable uncertainties still exist in real-time forecasts (Chen and Cane, 2008; Jin et al., 2008; Duan and Wei, 2012; Tang et al., 2018), and practical prediction skills are currently limited to six months (Latif et al., 1998; Barnston et al., 1999; Kirtman et al., 2002; Barnston et al., 2012; Mu and Ren, 2017; Barnston et al., 2019). The largest forecasting errors are associated with the prediction of ENSO across boreal spring (Tippett et al., 2012; Timmermann et al., 2018; Ham et al., 2019), the so-called spring predictability barrier (SPB), which is a major source of uncertainty in long-lead ENSO forecasting.

El Niño and La Niña are the warm and cool phases of the ENSO cycle, respectively. La Niña events occur when the SST in the cold tongue of the eastern equatorial Pacific is below average, inducing climate anomalies globally, including droughts in the southern United States and South America and floods in Australia, Indonesia, and the Philippines (Ropelewski and Halpert, 1987; Kiladis and Diaz, 1989; Nicholson and Selato, 2000; Cole et al., 2002; Cook et al., 2007; Hoyos et al., 2013; Chikamoto et al., 2015; Yoon and Leung, 2015; Fasullo et al., 2018; Jong et al., 2020). Cold winters induced by La Niña in the Northern Hemisphere increase the global demand for energy such as coal, natural gas, and oil. In the past, ENSO prediction efforts have focused on El Niño prediction, with less attention given to La Niña prediction (Zhang et al., 2013; DiNezio et al., 2017; Luo et al., 2017; Hu et al., 2019a). Therefore, it is important to explore the possibility and feasibility of transpiring SPB in La Niña prediction.

The latest extreme La Niña event took place in September 2020 and persisted for two years, with the center of the maximum negative SST anomalies (SSTA) located over the central-eastern equatorial Pacific Ocean. Most models from the International Research Institute for Climate and Society (IRI) failed to forecast the outburst of this event before May 2020, with the majority of the model plumes favoring a neutral or weak El Niño state (Niño 3.4 index between -0.5 °C and +0.5 °C). The historical La Niña events (1995/1996, 1998/1999, 2007/2008, and 2010/2011) were also failed to be predicted at the 1-year lead (Zhang et al., 2013; Luo et al., 2017). Thus, La Niña long-lead forecasting remains challenging to date.

Internal oceanic dynamics in the tropical Pacific associated with the recharge oscillator (Wyrtki, 1985; Jin, 1997) is considered a key ENSO mechanism. The most widely used index, the ocean heat content (OHC, Wyrtki, 1985) or warm water volume (WWV, Meinen and McPhaden, 2000) indices, have proven to provide a long-lead precursor for the occurrence of La Niña (Planton et al., 2018; Planton et al., 2021). However, the weak WWV anomalies prove to be ineffective in predicting the 2010/2011 and 2020/2021 La Niña events following weak-to-moderate El Niños. Lately, inter-basin interactions over the tropical Indo-Pacific Ocean and Atlantic-Pacific Ocean are suggested to play important roles in ENSO variability and predictability (Webster, 1995; Clarke and Van Gorder, 2003; Izumo et al., 2010; Ham et al., 2013; Cai et al., 2019; Wang, 2019; Capotondi et al., 2020). Some studies, therefore, have suggested that SSTA in the Atlantic and Indian Ocean may initiate the onset of these two La Niña events (Luo et al., 2017; Hasan et al., 2022).

Prediction of ENSO using the Indian Ocean Dipole (IOD, Saji et al., 1999; Webster et al., 1999) index as a precursor has the potential to increase the lead times of successful prediction to as long as one year across the spring barrier. Existing studies have focused on atmospheric teleconnection via the Walker circulation (Kug and Kang, 2006; Izumo et al., 2010; Ha et al., 2017). Other studies suggest that the “oceanic channel” of the Indonesian Throughflow (ITF) may provide an important connection between the Indian and Pacific Ocean climate variabilities (Yuan et al., 2011; Yuan et al., 2013; Mayer et al., 2018; Yuan et al., 2018; Wang et al., 2022; Xu et al., 2022; Yuan et al., 2022). The cold tongue SSTA were found to correlate significantly with sea level anomalies (SLA) in the southeastern tropical Indian Ocean (SETIO), the eastern pole of the IOD, one year before. The dynamics are through Kelvin wave propagation from the equatorial Indian Ocean into the western Pacific Ocean via the Indonesian seas. ENSO is characterized by asymmetry in amplitude, duration and transitions (Okumura and Deser, 2010). El Niño tend to decay rapidly followed by La Niña, whereas La Niña sometimes last for two years (Ohba and Ueda, 2009; Hu et al., 2014, 2016; DiNezio et al., 2017; Okumura et al., 2017; Iwakiri and Watanabe, 2020). So far, the role of the Indo-Pacific “oceanic channel” dynamics in the asymmetric predictability of El Niño and La Niña has not been investigated.

In this study, a simple linear regression model is developed to apply the “oceanic channel” dynamics to ENSO prediction, in which only the SLA in the SETIO are used as a precursor. Compared to the WWV in the western Pacific in fall, which could not transpire the spring barrier in general, the upwelling anomalies (negative SLA) in the SETIO is a more effective and longer-lead predictor of La Niña. The model predicts essentially all of the La Niña events following the outbursts of the positive IOD (pIOD) events successfully at the lead time of one year, including the 2020/2021 cold event. These results underline the importance of the “oceanic channel” dynamics in the predictability of one type of La Niña event preceded by pIOD.

The remainder of this paper is organized as follows. Section 2 introduces the observational dataset and methods used in this study. Section 3 presents the asymmetry in the lead relationship between the SETIO SLA and Niño 3.4 SSTA, which suggests that the negative SETIO SLA in the boreal fall is a better long-lead precursor for one type of La Niña event (those preceded by pIODs) at a lead time of one year. The paper closes with conclusions and discussions in Section 4.

2 Data and method

2.1 Data

2.1.1 Reanalysis and observation data

The sea level data from 1993 to 2021 was obtained from the Aviso satellite altimeter. The SST data included the ERSST v5 (Huang et al., 2017). Wind data were obtained from NCEP data (Kalnay et al., 1996). Other wind data were obtained from the ERA5 reanalysis, which have been regridded to a regular lat-lon grid of 0.25 degrees (Hersbach et al., 2020). The surface current data is provided by the Estimating the Circulation and Climate of the Ocean, Phase II (ECCO2) reanalysis. The horizontal resolution is 1/4-deg. ORA-S5 was not used here because data after 2019 were not available. The annual cycle of each variable was removed by subtracting the monthly climatological means. Subsurface temperature anomalies from the global gridded Argo dataset are used, which has a 1°×1° horizontal resolution and 58 vertical layers from the surface to 1975 dbar (Roemmich and Gilson, 2009). The WWV index was derived from the ocean analyses of the Bureau National Operations Centre (BNOC) at the Australian Bureau of Meteorology (Smith, 1995), which are based on Tropical Atmosphere Ocean (TAO) array, Argo floats and XBT measurements. It is well known that the sea level rise in the tropical Indian Ocean in the last two decades has been significantly higher than before (Unnikrishnan et al., 2015). The SLA was detrended as we focused on interannual variability.

2.1.2 ENSO forecast data

The 2020/2021 ENSO forecast results were provided by the International Research Institute (IRI)/Climate Prediction Center (CPC) (Blumenthal et al., 2014) [https://iri.columbia.edu/our-expertise/climate/enso/]. The multi-model forecasts during 1995/96, 1998/99, and 2007/08 La Niña were obtained from the North American Multi-Model Ensemble (NMME) seasonal predictions system (Kirtman et al., 2014) [http://iridl.ldeo.columbia.edu/SOURCES/.Models/.NMME/], which consists of coupled models from US modeling centers including NOAA/NCEP, NOAA/GFDL, IRI, NCAR, and NASA, and Canada’s CMC. NMME hindcast (1982–2010) was used in the current work. Hindcasts of Niño 3.4 SSTA for fall (September-November) initialized in the previous fall (11.5-month lead) were considered. This criterion resulted in the selection of 12 models: CanCM4i, CanSIPSv2, CMC1-CanCM3, CMC2-CanCM4, COLA-RSMAS-CCSM3, COLA-RSMAS-CCSM4, GEM-NEMO, GFDL-CM2p1, GFDL-CM2p1-aer04, GFDL-CM2p5-FLORA06, GFDL-CM2p5-FLOR-B01, and NCAR-CESM1.

2.2 Method

2.2.1 Linear regression model of La Niña prediction

The La Niña prediction model was built as follows:

$\begin{array}{ll}SSTA\_Nino3.4 (t)=a+b*SLA\_SETIO(t-1)& (1)\end{array}$

SLA_SETIO(t − 1) is the SLA over SETIO during the boreal fall when pIOD occurs. SSTA_Nino3.4 (t)  is the SSTA over the Niño 3.4 region during the next fall. b is the regression coefficient and a is a constant term. The data during 1993-2019 were used to calculate and b and to make the 2020/2021 La Niña prediction using the negative SETIO SLA during the fall of 2019.

2.2.2 Cross-validation method

To test the predictive capability of the linear regression model in La Niña prediction, the cross-validation method (Michaelsen, 1987) was used to hindcast the Niño 3.4 index during La Niña events. We chose the leaving-one-out strategy. This strategy systematically deletes one year from 1993 to 2021, builds a forecast model from the remaining years, and tests the prediction on the deleted case. For example, for the 2020/21 case, the 2020 data were deleted, and a forecast model was built from the remaining years to predict the 2020/2021 La Niña event. The assessment of the prediction was evaluated using the correlation between the linear regression model prediction (using the cross-validation method) and observed data from 1993 to 2021.

2.2.3 SETIO SLA calculated from the wind-forced Kelvin wave for the longer period

A linear coastal-trapped Kelvin wave model (Hu et al., 2019b) was used to calculate the Indian Ocean SLA since 1950. This model is based on an analytical Kelvin wave model (Gill, 1982; Sprintall et al., 2000), in which wind-forced Kelvin wave propagation along the Kelvin wave pathway from the western Indian Ocean (0°, 45°E) to the Maluku Channel (2 °N, 126.5 °E). The model use the momentum equation in the alongshore direction:

$\begin{array}{ll}\frac{d{A}_k}{dt}+c\frac{d{A}_k}{dx}=\frac{cX}{g}& (2)\end{array}$

where A_k is the SLA along the Kelvin wave characteristics, g is the acceleration due to gravity, X is the projection of alongshore wind stress onto each baroclinic mode, and c is the wave speed (2.71 m/s for the first baroclinic mode). Equation (2) is integrated along the Kelvin wave characteristics to get the solution of A_k (Hu et al., 2019b).

2.2.4 Definition of indices

In this study, we defined the SLA index over the SETIO as the average SLA in the area of 10 °S–0 °N, 90 °E–110 °E. The Niño 3.4 index was calculated as the average SSTA in the area of 5 °S–5 °N, 170 °W–120 °W. The Indian Ocean dipole mode index (DMI) was constructed by the differences in SSTA in the western tropical Indian Ocean (50 °E–70 °E, 10 °S–10 °N) and southeastern tropical Indian Ocean (90 °E–110 °E, 0 °–10 °S). The WWV index is defined as the volume of water above the 20 °C isotherm in the equatorial Pacific (120 °E–80 °W, 5 °N–5 °S). The WWV_w index is defined as the WWV in the western equatorial Pacific (155 °E–120 °E, 5 °N–5 °S).

3 Results

3.1 A better long-lead precursor of the La Niña: negative SETIO SLA at the lead time of one year

Figure 1A shows the lead relation between SLA in the SETIO (10 °S–0 °, 90 °E–110 °E) in the boreal fall (September to November) and SSTA in the Niño 3.4 region (5 °S–5 °N, 170 °W–120 °W) one-year later. Only the relationship after 1993 is indicated because of the short time series of AVISO SLA data. Tide gauge sea level data along the Sumatra-Java Island chain are extremely rare and are unable to expand the time coverage of the SLA-Niño 3.4 relationship much longer in history.

FIGURE 1

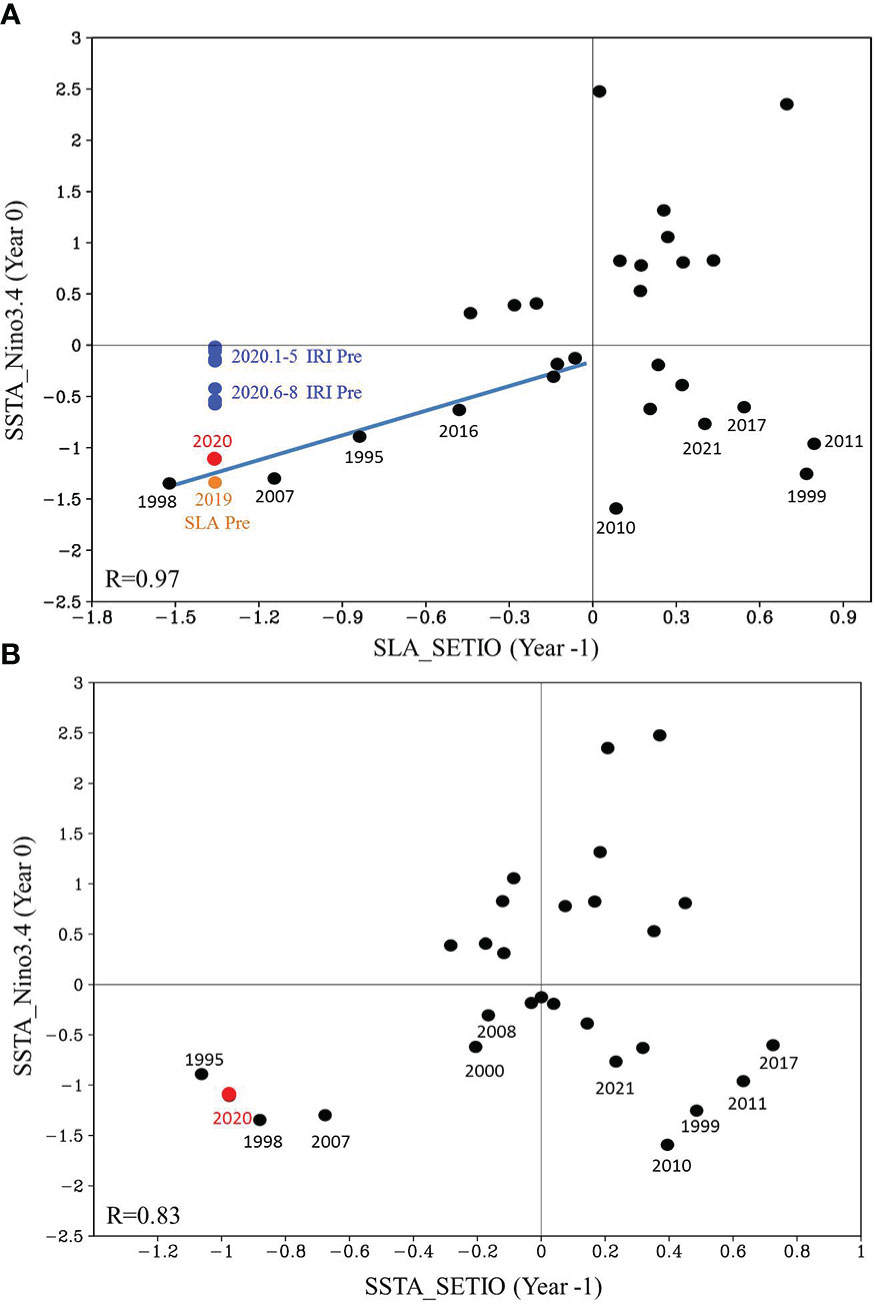
Figure 1 Relationship of the SETIO SLA (A) and SSTA (B) in fall with the Niño3.4 index one year later, respectively. Units are °C for Niño3.4 index and decimeter for SLA. Black dots stand for the annual observations, with the year 2020 highlighted in red. Blue dots denote IRI prediction of the fall 2020 Niño3.4 index made from the initial conditions in January through August of 2020. Blue line denotes regressed linear relation between the SLA and the Niño3.4 index one year later in the third quadrant. Orange dot denotes the prediction of the fall 2020 Niño3.4 index using the linear regression model with the fall 2019 SLA in the SETIO as the predictor. Correlation coefficients in the third quadrant are shown in the lower left of each panel.

A noteworthy feature is an asymmetry in the lead relationship between the SETIO SLA and Niño 3.4 SSTA. For a pIOD event, following the upwelling anomalies (negative SLA) off Java in the fall, a La Niña event will occur in the next fall (in the third quadrant of Figure 1A). Their correlation coefficient is 0.97 (exceeding the 99% confidence level according to Student’s t-test), which is much greater than the correlation coefficient of 0.39 (exceed the 95% confidence level) for the whole dataset. The relationship between the negative SETIO SLA and La Niña one year later is one-to-one since no strong warm events in the equatorial Pacific were found following pIOD events (no points far away from the origin in the second quadrant, Figure 1A). In contrast, for the negative phase of the IOD (nIOD), following the downwelling anomalies (positive SLA) off Java in the fall, the Niño 3.4 SSTA may be either positive (in the first quadrant) or negative (in the fourth quadrant) in the following year, suggesting either an El Niño or La Niña event following the nIOD. This result reveals an asymmetric lead relation between the SETIO SLA and Niño 3.4 SSTA, with negative SLA (upwelling anomalies) in the SETIO in the fall being a better predictor of La Niña one year later.

When strong upwelling anomalies (negative SLA) occurred over the SETIO during the boreal fall, strong La Niña events occurred in the following year. Since 1993, 1995/1996, 1998/1999, 2007/2008, 2016/2017, and 2020/2021 La Niña events followed the strong pIOD events in 1994, 1997, 2006, 2015, and 2019 (Figure 1A). Among them, three events are the multi-year lingering La Niña events, 1998/99/2000, 2016/17/18, and 2020/21/22. Notably, the relationship between the SETIO SLA in fall and the Niño 3.4 index a year later was different in the first and second years of the 2-year La Niña. La Niña in the first year was preceded by the pIOD (in the third quadrant of Figure 1A), whereas the SETIO SLA is positive in the previous year for the La Niña in the second year for the 1999/2000, 2017/18, and 2021/22 La Niña events (in the fourth quadrant of Figure 1A). This means that one type of La Niña events (those are preceded by pIODs) could be predicted at a lead time of one year based on the negative SETIO SLA during the pIOD events, whereas predictability of another type of La Niña events, the 2-year La Niña in the second year, does not arise from the factor in the Indian Ocean in the previous year. Anyway, the negative SLA in SETIO is a better precursor for most strong La Niña events, including the 2-year La Niña evens in the first year. Here, 2-year La Niña event on 2010/11/12 is a special case. The SETIO SLA are both positive in the previous first and second years.

The above lead relation was found to be not as good between SETIO SSTA and Niño 3.4 SSTA as between SETIO SLA and Niño 3.4 SSTA (Figure 1B). The correlation coefficient between the negative SETIO SSTA and Niño 3.4 SSTA one year later was 0.83. This is expected because the SSTA are a less direct representation of upwelling anomalies off Sumatra-Java than the SLA. The use of SSTA in SETIO as the precursor generally does not lead to successful La Niña predictions as SLA used as a precursor. Moreover, an asymmetric lead relation with Niño 3.4 SSTA does not exist for the SETIO SSTA in the longer dataset (see Section3.5), although the relationship between the negative SETIO SSTA in fall and La Niña one year later is one-to-one after 1993. Hasan et al. (2022) indicated that the Indian Ocean may contribute to the initiation and predictability of the 2020/21/22 La Niña, but they did not find that the negative SLA in the SETIO was a better long-lead precursor for a strong La Niña event.

The ENSO phase transition is asymmetric (Kessler, 2002; Larkin and Harrison, 2002; Okumura and Deser, 2010). La Niña often follows El Niño, but the reverse is not always true. Furthermore, El Niño often forces a response in the Indian Ocean in the form of IOD (Wang et al., 2019; Xue et al., 2022). Does the good relationship between La Niña and negative SETIO SLA at the lead time of one-year result from the preceding El Niño? As shown in Figure 2A, the asymmetry in the ENSO phase transition was also found in the relationship between the Niño 3.4 SSTA in the previous and following years. However, the correlation between positive Niño 3.4 SSTA in the previous fall and negative Niño 3.4 SSTA in the following year was not significant (-0.23). Thus, the Niño 3.4 SSTA in the fall is not a good precursor for La Niña events one year later.

FIGURE 2

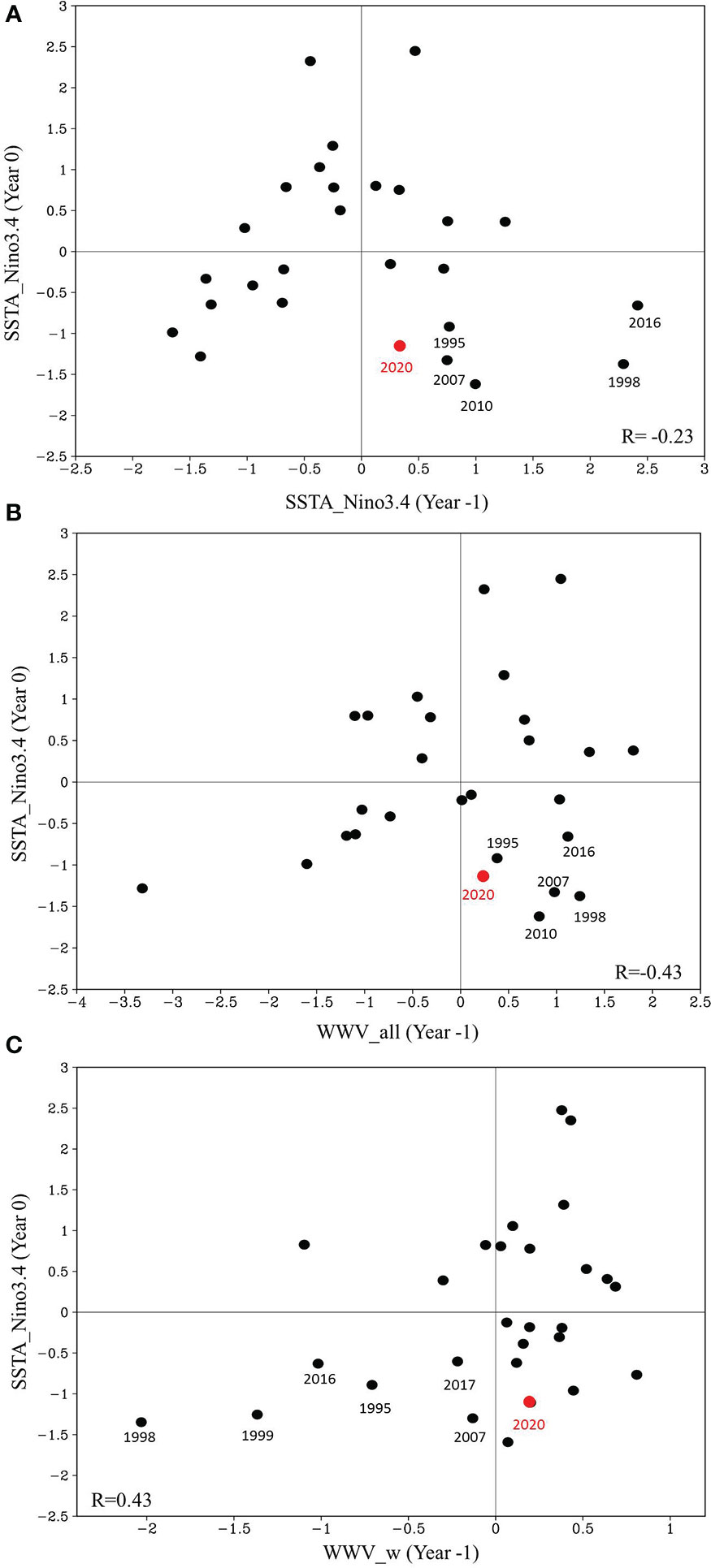
Figure 2 Relationship of the (A) Niño3.4, (B) WWV in the equatorial Pacific (WWV_all) and (C) WWV in the western equatorial Pacific (WWV_w) in fall with the Niño3.4 index one year later. Correlation coefficients in the fourth quadrant are shown in the lower right of (A, B), correlation coefficient in the third quadrant is shown in the lower left of (C).

Furthermore, according to the ENSO recharge oscillator (Jin, 1997), ENSO events tend to be preceded by anomalous WWV in the equatorial Pacific. The release of WWV in the equatorial Pacific can lead to La Niña events in the following year (Meinen and McPhaden, 2000). The negative WWV index in fall, especially the WWV in the western equatorial Pacific (WWV_w), has been consistently considered the best precursor of La Niña one-year before (Planton et al., 2018). As shown in Figures 2B, C, for the type of the La Niña events preceded by pIOD, 1995/96, 1998/99, 2007/08, and 2016/17 La Niña events, negative WWV anomalies in the western equatorial Pacific (in the third quadrant in Figure 2C) occurred in the previous fall but with positive WWV anomalies across the entire equatorial Pacific (in the fourth quadrant in Figure 2B). Although the correlation of the negative Niño 3.4 index with the discharged WWV_w one year before (0.43) was higher than that with the positive Niño 3.4 SSTA at the one-year lead time (-0.23), it was still not significant and far less than that with the negative SETIO SLA at a lead time of one year (0.97, with 99% confidence level). This result suggests that, at longer lead times, before the spring predictability barrier, the WWV or Niño 3.4 index is not a good predictor of the type of La Niña events preceded by the pIOD. Especially for the 2020/21 La Niña, WWV_w is not negative, meaning that the equatorial western Pacific is not in a discharge state.

Therefore, although the negative SLA in the SETIO in the fall may not be an independent predictor of La Niña (which is partly correlated with preceding El Niño), it is a better long-lead precursor for the type of La Niña events (preceded by pIOD) than the positive SSTA in Niño 3.4 and discharge WWV in the western Pacific as a predictor.

3.2 Prediction of the 2020/21 La Niña event

We noticed this long-lead relationship between SETIO SLA and Niño 3.4 SSTA in 2019 and applied it to the 2020/21 ENSO forecasting as soon as the 2019 pIOD was in a mature phase. We constructed a simple linear regression model based on the negative SETIO SLA in the fall and the Niño 3.4 index one year later during 1993–2019 (see section 2.2.1). Then, using the negative SETIO SLA during the fall of 2019 already observed as a precursor, we predicted the Niño 3.4 SSTA in the coming fall of 2020 to be -1.34°C (orange color dot in Figure 1A) with 95% confidence interval (-1.56°C, -1.12°C). One year later, the observed Niño 3.4 index (-1.11°C, red dot in Figure 1A) was very close to our prediction made one year earlier (with only 0.23°C difference), suggesting the success of the simple linear regression model in predicting the 2020/2021 La Niña beyond the lead time of 1 year. Our prediction is evidently much better than the real-time forecasts of the IRI models using initial conditions in earlymid-2020 (blue dots in Figure 1A), which were made much later than our prediction and were much weaker than the observation (red dot in Figure 1A) in approximately six months. The IRI forecasts made in January through May 2020 had predicted the Niño 3.4 SSTA to be near zero in the coming fall of 2020, while forecasts made in June through August of the majority of the models in the IRI plume continue to favor an ENSO-neutral state (Niño 3.4 index near 0.5°C) in the coming fall. Therefore, the 2020/21 La Niña event was not successfully predicted by the IRI models at lead times of one to three seasons.

3.3 Dynamics of the 2020/21 La Niña predictability

The 2020/21 La Niña followed a weak El Niño; thus, the discharge process in the tropical Pacific was not strong enough to energize the event (Figure 2). In the summer-fall of 2019, associated with the climax of the 2019 super pIOD, the anomalous easterly winds were strong to the west over the equatorial Indian Ocean, forcing the SSTA and SLA in the southeastern basin to grow quickly into a strong pIOD state (Figure 3). The equatorial Indian Ocean easterly wind anomalies in late 2019 forced strong upwelling Kelvin waves to propagate to the east along the Sumatra-Java island chain, which induces negative SLA in the SETIO and alters the pressure gradient across the Indonesian Seas. ITF transport increased significantly during the summer-fall of 2019 in response to pIOD forcing. Shortly thereafter, the SLA in the western equatorial Pacific Ocean began to propagate eastward along the equator around January 2020 (Figures 3, 4). The upwelling Indian Ocean Kelvin waves forced by easterly wind anomalies during the 2019 pIOD are thus suggested to propagate eastward through the Indonesian seas and reach the western equatorial Pacific, which triggered or enhanced the development of a strong La Niña in 2020. These results underscore the importance of inter-basin dynamic interactions between the Indian and Pacific Oceans through the “oceanic channel” in forcing the 2020/21 La Niña. None of the IRI dynamical coupled climate models can predict the 2020/21 La Niña one year in advance probably because they do not simulate the Indo-Pacific “oceanic channel” dynamics well although they include this oceanic channel.

FIGURE 3

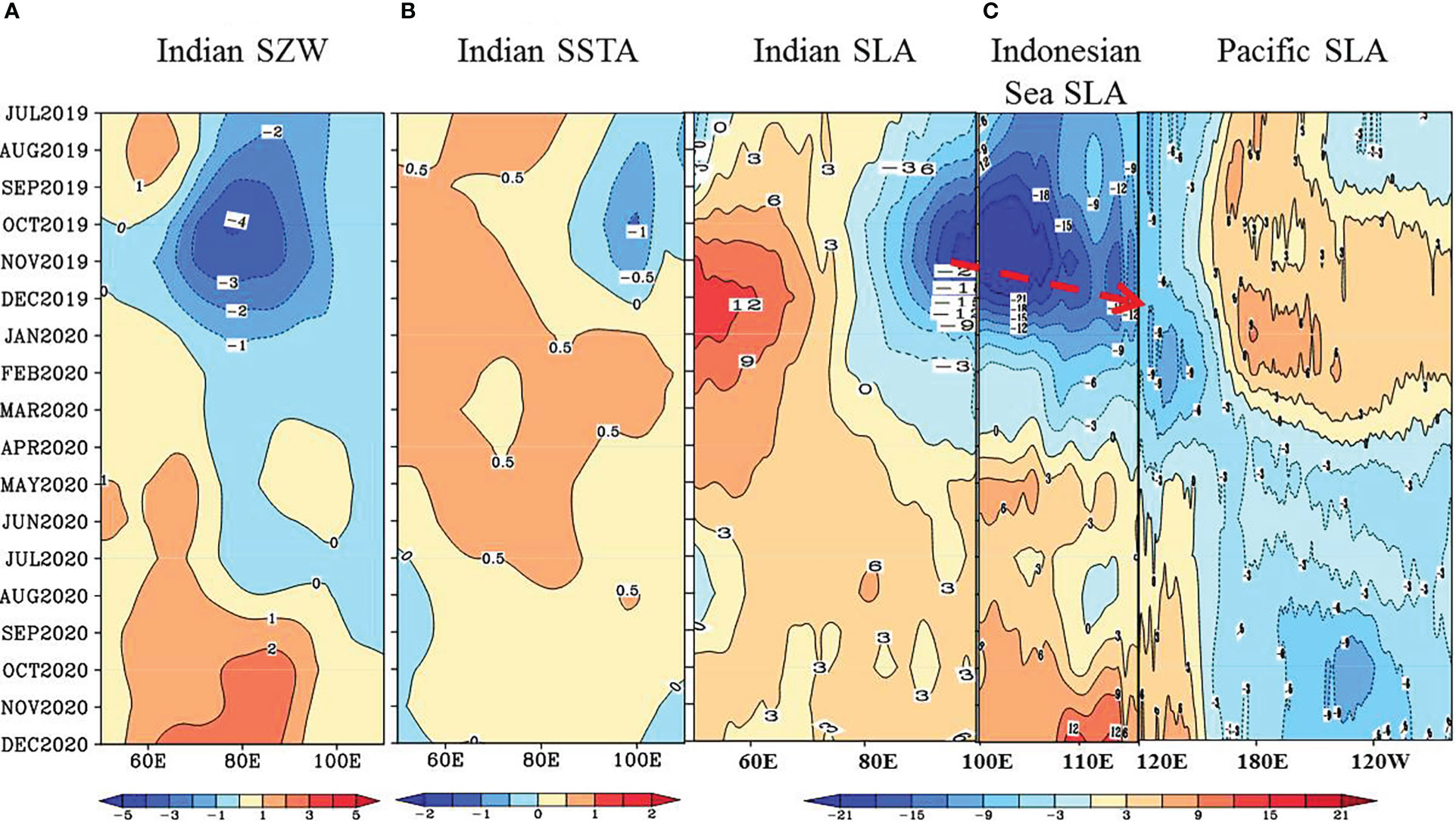
Figure 3 The “oceanic channel” dynamics of the 2020/21 La Nina predictability. Longitude-time plots of observed monthly anomalies of (A) surface zonal wind (SZW, m/s), (B) SSTA (°C) over the equatorial Indian and Pacific Ocean (5°S-5°N), and (C) SLA (cm) over the equatorial Indian and Pacific Ocean (1°S-1°N) and alongshore the Sumatra-Java island chain during the 2019 pIOD. The red dashed arrow indicates the eastward-propagating Kelvin wave.

FIGURE 4

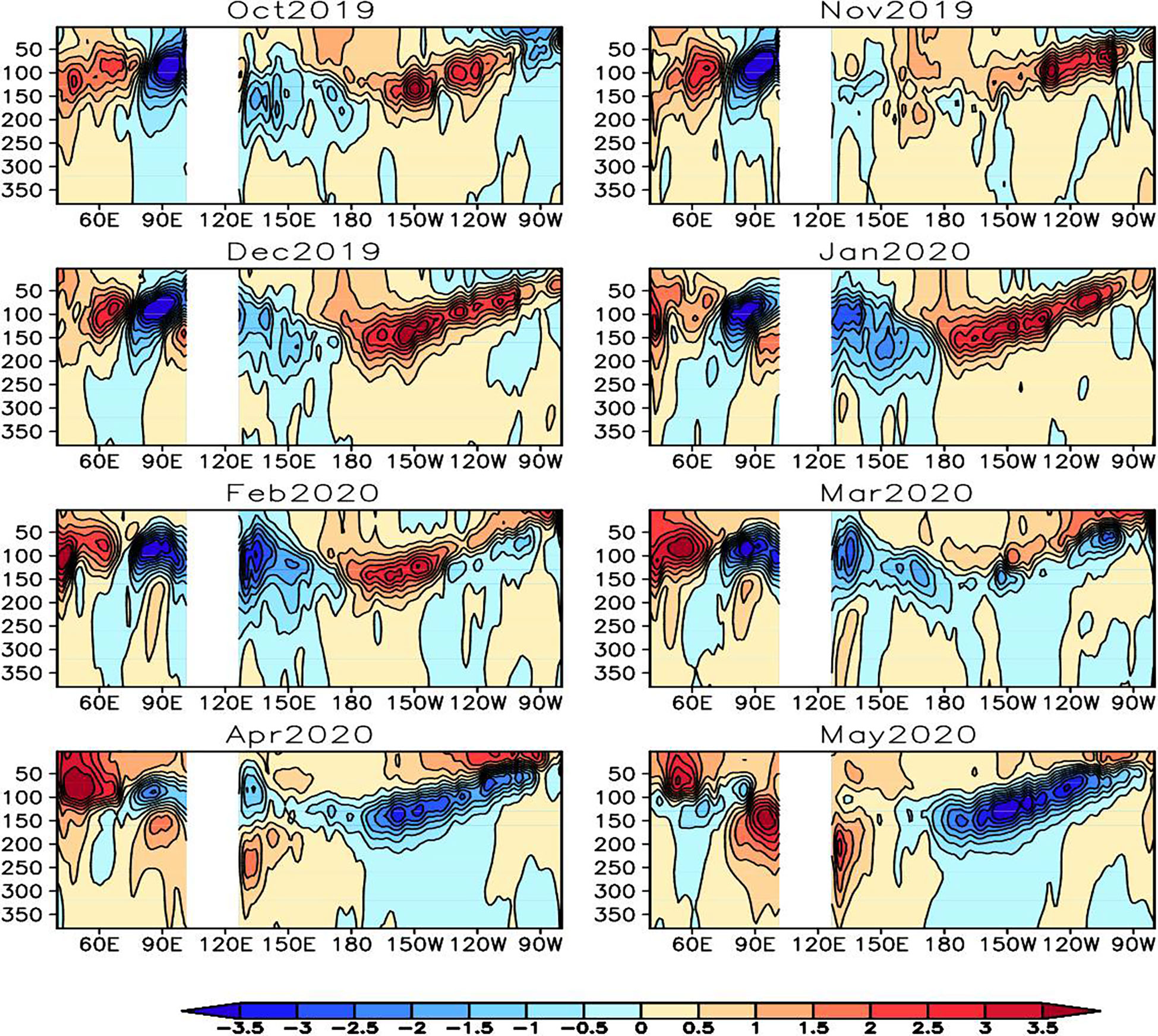
Figure 4 The propagation of the Kelvin waves over the Indo-Pacific Ocean during 2019-2020. Monthly Argo temperature anomalies (°C) over the equatorial Indian and Pacific Ocean (5°S-5°N) during 2019-2020.

The propagation of Kelvin waves into the Indonesian seas has been demonstrated by in situ direct mooring observations and ocean reanalysis data. Using moored current observations in the Makassar Strait and the Maluku Channel combined with high-resolution ocean modeling validated with satellite data, it has been shown that Indian Ocean Kelvin waves propagated into the Makassar Strait and arrived at the northeastern Indonesian seas during 2015–2016 (Hu et al., 2019b; Pujiana et al., 2019). The propagation of the strong upwelling equatorial Kelvin waves forced by the Indian Ocean easterly anomalies during the 2019 pIOD was simulated successfully by Estimating the Circulation and Climate of the Ocean Phase II (ECCO2) reanalysis (Figure 5), showing strong southward current anomalies in the Makassar Strait from October 2019 through February 2020. The currents and SLA in the Makassar Strait were evidently not forced by local winds, because the surface wind anomalies were southeasterlies (hollow arrow in Figure 5). The high resolution of ECCO2 simulations has resolved the channels and straits in the Indonesian seas well, showing a negative SLA propagating into the Indonesian seas along the south Java coasts in the winter of 2019 in agreement with the altimeter sea level anomalies. This suggests the propagation of Indian Ocean upwelling Kelvin waves through the Indonesian seas.

FIGURE 5

Figure 5 The propagation of the Kelvin waves through the Indonesian seas during 2019-2020. SLA (cm, shading) and surface current anomalies (m s^-1, vectors) from ECCO2 from October 2019 to February 2020. The hollow arrow indicates the direction of the surface wind anomalies over Indonesian Sea.

The upwelling Kelvin waves arrived in the western Pacific Ocean, as suggested by the strong westward current anomalies in the Sulawesi Sea in December 2019, coincides with the southward current anomalies in the Makassar Strait. The upwelling equatorial Kelvin waves propagated further eastward along the equator (Figure 4). From April to May, upwelling Kelvin waves induced negative subsurface temperature anomalies in the eastern equatorial Pacific, which moved to the surface associated with the shoaling thermocline in the eastern equatorial Pacific. These anomalies are suggested to trigger Bjerknes positive feedback, leading to an outburst of the 2020/21 La Niña event.

It is known that interbasin interaction between the tropical Indian and Pacific also involves an atmospheric bridge. The easterly wind anomalies in the western Pacific persist from spring to winter, triggering the cold SSTA in the eastern Pacific. Previous studies demonstrated that the pIOD can generate easterly wind anomalies in the western Pacific through the Indo-Pacific atmospheric bridge (e.g., Hasan et al., 2022). However, the lead relation between the SETIO SLA in fall and the easterly wind anomalies in the western equatorial Pacific during the following summer is not significant with the lag correlation coefficient of 0.4 (Figure 6), indicating that the atmospheric bridge is not the dominant process contributing to the long-lead good predictor of La Niña events preceded by pIOD. Moreover, Wang et al. (2022) compared the relative roles of the atmospheric bridge and the oceanic channel between the Indian and Pacific in ENSO forecasts through pacemaker experiments. Their model results suggested that the “oceanic channel” dynamics is dominant, whereas the 2020/21 La Niña cannot be generated by the atmospheric bridge alone. They demonstrated that La Niña event is induced by subsurface temperature anomalies in the tropical Indian Ocean propagating to the eastern equatorial Pacific Ocean at the end of 2020.

FIGURE 6

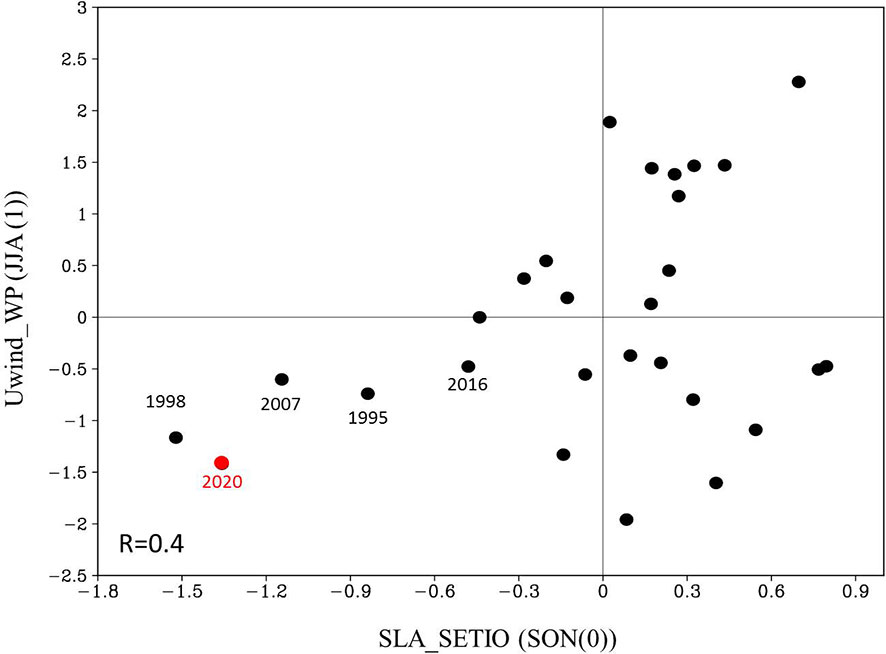
Figure 6 The relationship between the SETIO SLA in fall and the surface zonal wind anomalies in the western equatorial Pacific (130°E -180°E, 5°N-5°S) in the following summer. Correlation coefficient in the third quadrant is shown in the lower left of this Figure.

The westerly anomalies in the western equatorial Pacific also forced upwelling Rossby waves with negative SLA in the far western Pacific Ocean from November 2019 to February 2020 (Figures 7A, B). The Rossby waves propagated westward and were reflected into upwelling Kelvin waves at the western boundary. This process may have contributed to the onset of the 2020/21 La Niña event (Figure 7C). However, the SLA off the east coasts of Mindanao (5 °N–8 °N, 127 °E–135 °E), representing the equatorial Rossby waves before reflection at the Pacific western boundary, shows poor correlation with the Niño 3.4 index at the one-year time lag (Figure 8), suggesting low predictability of long-lead La Niña using the western boundary reflection as a precursor. The variability of the western boundary reflection and the Niño 3.4 index are significantly correlated within approximately eight months, which does not break through the SPB in general (figure not shown). We emphasize the role of the Indo-Pacific “oceanic channel” dynamics in La Niña prediction at longer lead times, before the SPB.

FIGURE 7

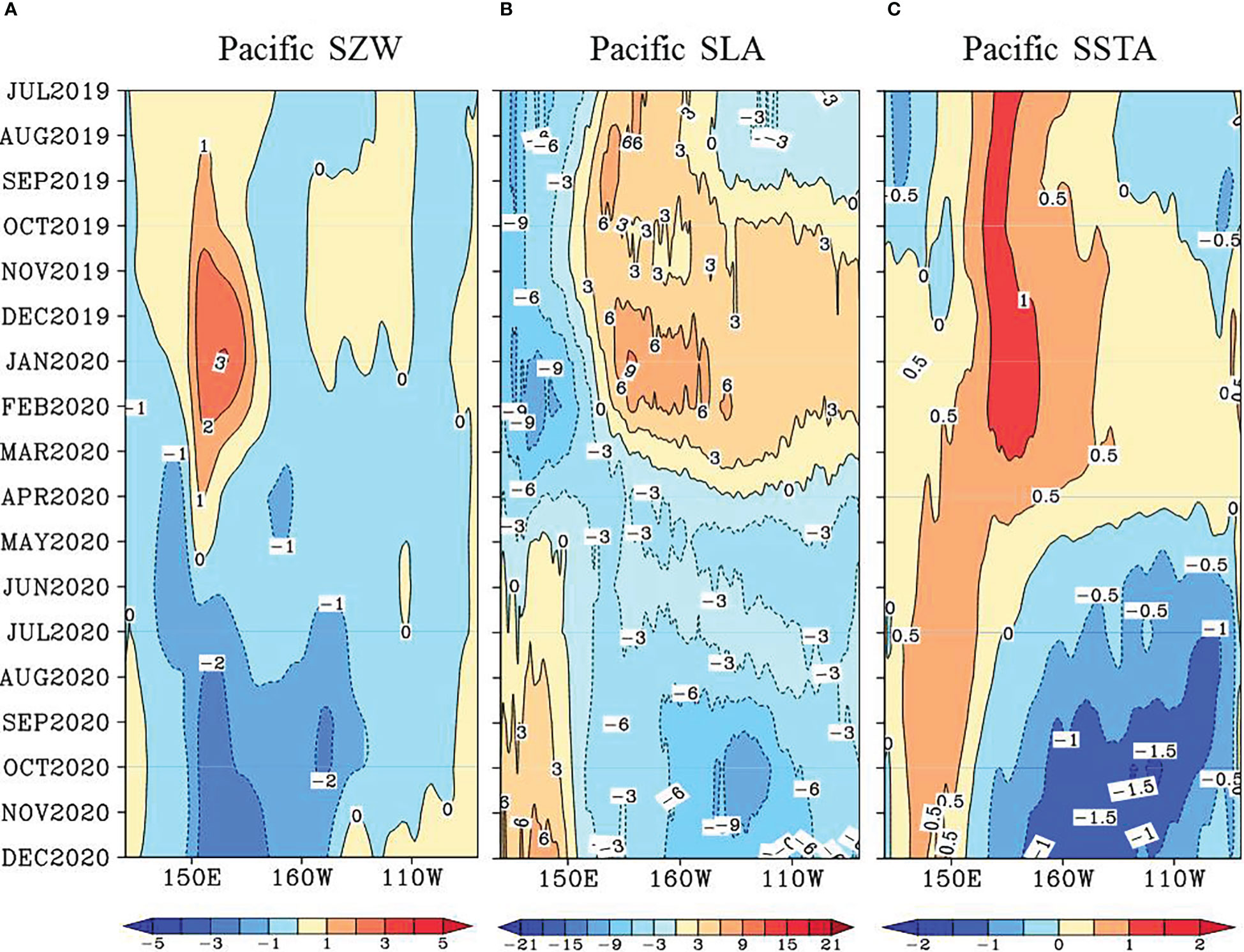
Figure 7 Evolution characteristics of 2020/2021 La Niña event. Longitude-time plots of observed monthly anomalies of (A) SZW (ms^-1) over the equatorial Pacific Ocean (5°S-5°N), (B) SLA (cm) over the equatorial Pacific Ocean (1°S-1°N), and (C) SSTA (°C) over the equatorial Pacific Ocean (5°S-5°N).

FIGURE 8

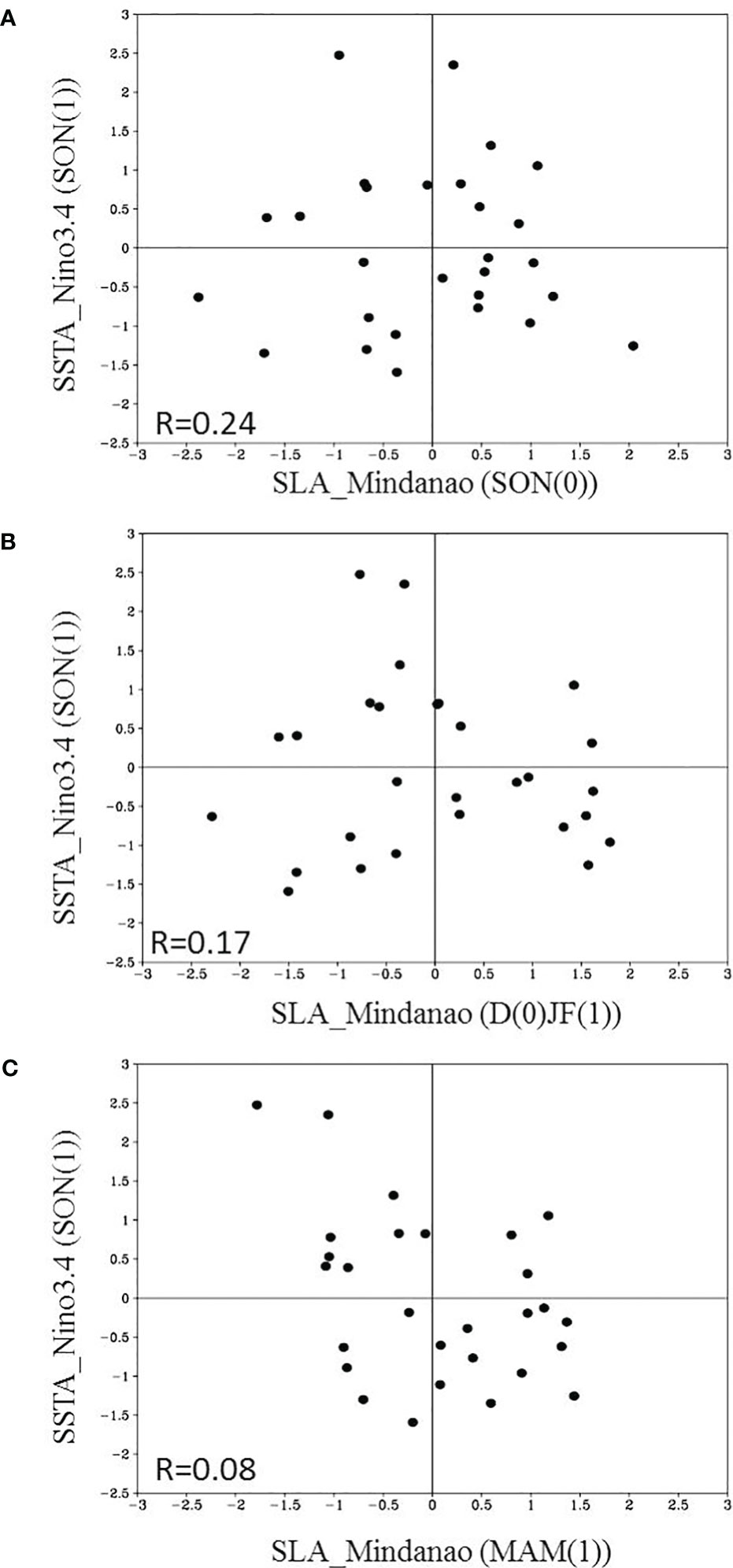
Figure 8 The relationship between equatorial Rossby waves at the Pacific Ocean western boundary and the Niño3.4 index one year later. Scatter plot of the fall Niño3.4 index (°C) with the preceding (A) SON, (B) DJF, and (C) MAM SLA (decimeter) off the east coasts Mindanao (127°E-135°E, 5°N-8°N) during 1993-2020. Correlation coefficients in the third quadrant are shown in the lower left of each panel.

3.4 1995/96, 1998/99, 2007/08 La Niña events preceded by the 1994, 1997, 2006 pIOD

Similar to the prediction of 2020/21 La Niña event, 1995/1996, 1998/1999, 2007/2008, and 2010/2011 La Niña events were not successfully predicted by the NMME models at one-year lead (Figure 9). A simple linear regression model, based on the lead relation between the negative SETIO SLA in fall and Niño 3.4 one year later, has been tested for its predictive capability to hindcast the historical La Niña events preceded by pIOD since 1993 (eight cases in the third quadrant of Figure 1A). Here, the cross-validation method (see section 2.2.2) was used to hindcast these La Niña events. Finally, for the eight La Niña events preceded by pIOD, the correlation between the predicted and observed Niño 3.4 indices is 0.95, above the 99% significance level. The small root-mean-square-error (RMSE) of 0.14°C suggests successful predictions of the La Niña events at a lead time of at least 12 months.

FIGURE 9

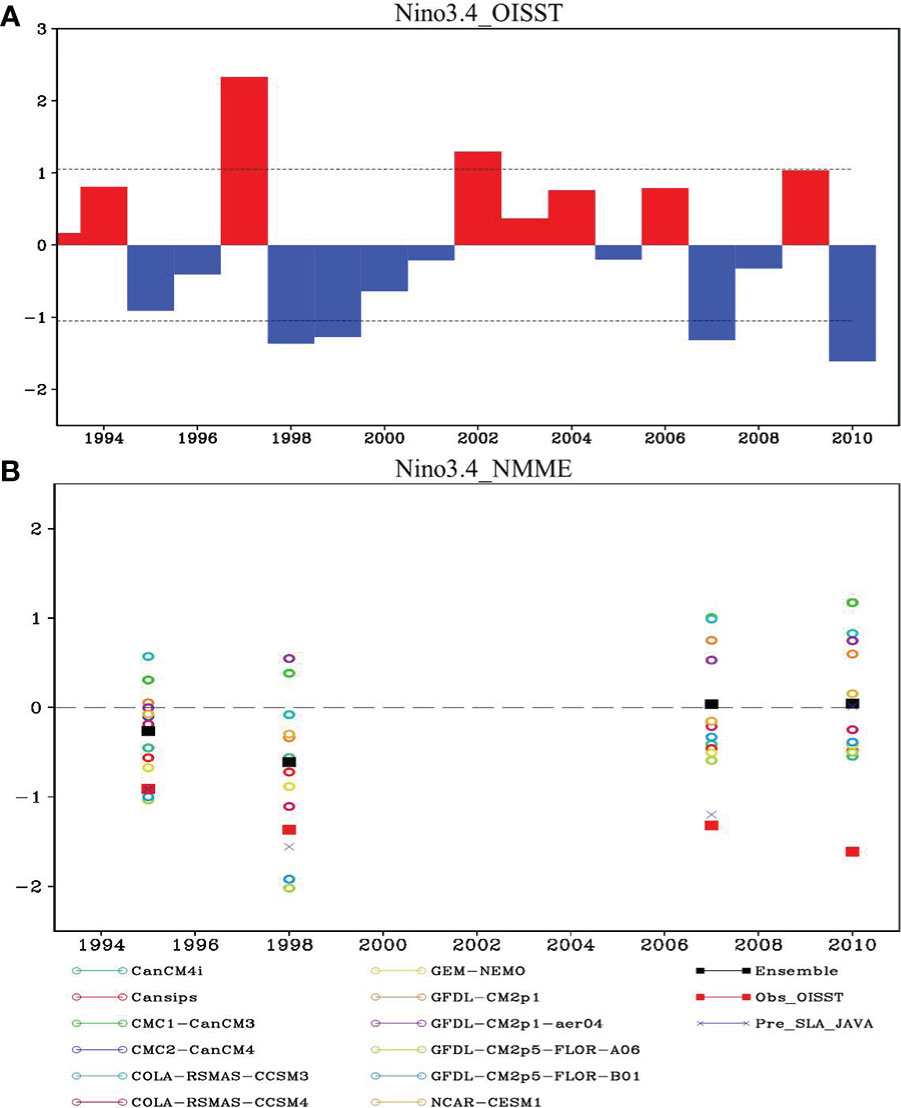
Figure 9 Forecasts of the historical strong La Niña events from 1993. (A) The fall Niño3.4 index (°C) from the OISST data for the 1993-2010 period. (B) The fall Niño3.4 index of NMME model and multi-model mean forecasts (at lead 11.5 months) for 1993-2010. The Niño3.4 index based on observations is also shown for reference (red squares). Blue crosses denote the predictions of the fall Niño3.4 index using the linear regression model with the fall SLA in the SETIO as the precursor.

The forecasts of our linear regression model are not only good for the mature phase, but also for the evolution of strong La Niña since 1993. Figure 10 shows the predicted results of the 1995/96, 1998/99, 2007/08, and 2020/21 events preceded by the 1994, 1997, 2006 and 2019 pIOD. Using the linear regression between the SETIO SLA in the fall and the Niño 3.4 indices from June through March of the third year, the initial cold SSTA in the equatorial eastern Pacific in June are predicted successfully, which are strengthened gradually in the summer through winter owing to the Bjerknes positive feedback induced by the upwelling Kelvin waves. After reaching the mature state in winter, the La Niña anomalies begin to decay, presumably due to the arrival of negative feedbacks, including reflected Kelvin waves from the western boundary. The time evolution of La Niña predicted by our linear regression model was in reasonable agreement with the observations.

FIGURE 10

Figure 10 Forecasts of linear regression model at the evolution of the strong La Niña events. Niño3.4 index during 2020/2021, 2007/2008, 1998/1999, 1995/1996 La Niña events from the observation (solid lines) and prediction (dot lines) using the SLA in the SETIO in fall of 2019, 2006, 1997, 1994. Grey columns indicate the root mean square error (RMSE).

The Indo-Pacific “oceanic channel” dynamics still work to trigger/enhance the development of a strong La Niña preceded by 1994, 1997, and 2006 pIOD events, because 1) it can been seen that, from the SLA evolution (Figure 11), the upwelling Kelvin wave propagate eastward through the Indonesian seas and reach the western equatorial Pacific, and 2) the Makassar Strait southward currents is also identified during the pIOD events of 1994, 1997, and 2006 (Figure 12), suggesting the propagation of Indian Ocean upwelling Kelvin waves through the Indonesian seas.

FIGURE 11

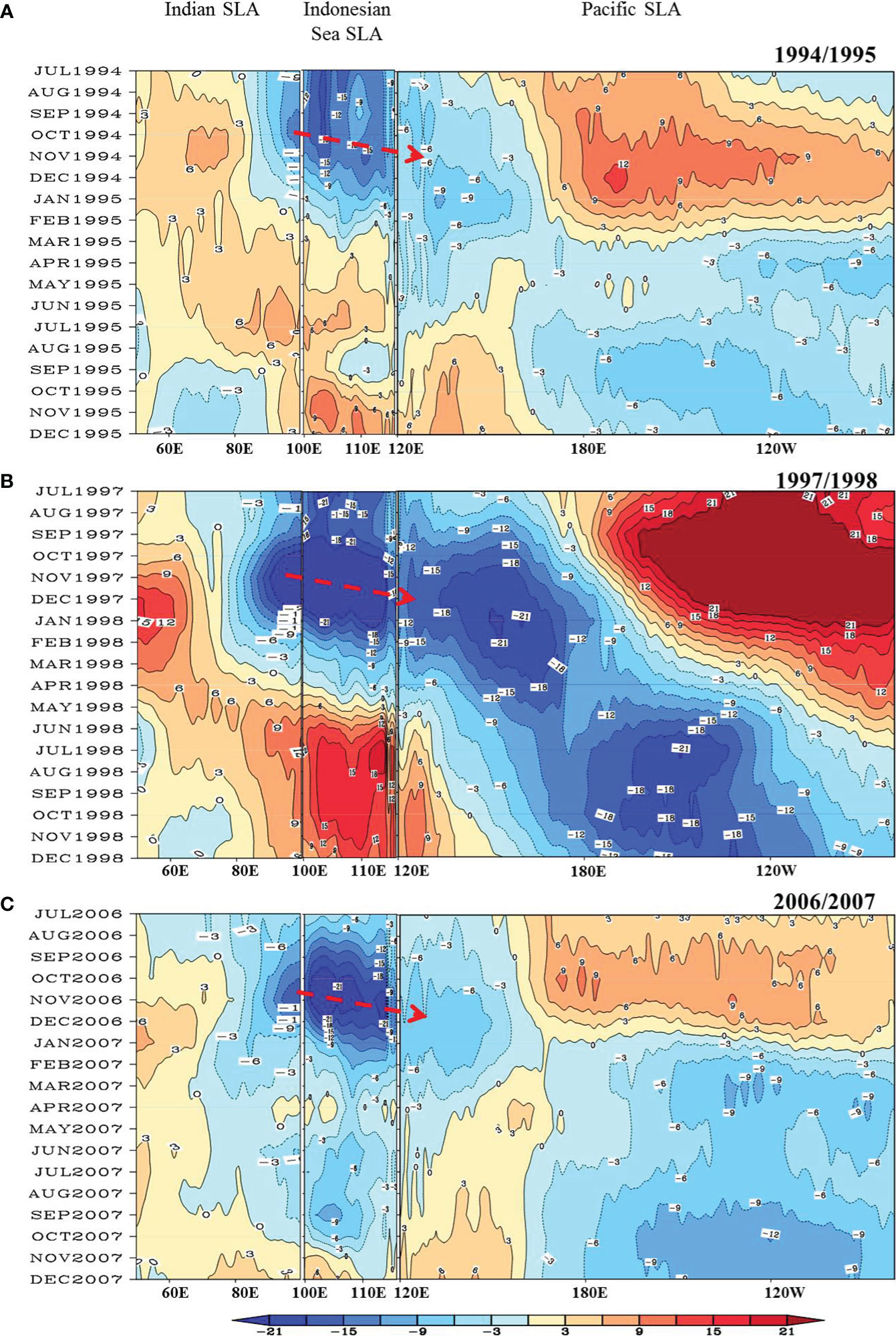
Figure 11 The “oceanic channel” dynamics during the historical La Niña events. SLA (cm) over the equatorial Indian and Pacific Ocean (1°S-1°N) and alongshore the Sumatra-Java island chain during the 1994(A), 1997(B), 2007(C) pIOD. The red dashed arrows indicate the eastward-propagating Kelvin wave.

FIGURE 12

Figure 12 The propagation of the Kelvin waves through the Indonesian seas during the historical pIOD events. SLA (color shading, cm) and surface current anomalies (vectors, ms^-1) from ECCO2 during October and December of the (A) 1994, (B) 1997, (C) 2006 pIOD events.

Although easterly wind anomalies in the western Pacific followed the 1994, 1997, and 2006 pIOD (Figure 6), the lead relationship between the SETIO SLA in fall and the surface zonal wind anomalies in the western Pacific in the following summer is not significant. Thus, the atmospheric bridge is not the dominant process contributing to the long-lead good predictor of La Niña events in 1995/96, 1998/99, and 2007/08.

Similar to the 2020/21 La Niña event, the 1995/96 and 2007/08 La Niña events followed weak El Niño events in 1994/95 and 2006/07, respectively, which were insufficient to produce significant discharge processes (Figures 2A, C). The Indo-Pacific interaction potentially plausibly energized these La Niña events through “ocean channel”. However, the 1998/99 La Niña event was preceded by a strong El Niño event in 1997/98, which may be controlled by the discharge process. Meantime, the Indo-Pacific interaction may also play an important role, in which “ocean channel” dynamics potentially contribute to the La Niña event. The combined contributions of the discharge process in the tropical Pacific and remote forcing from the Indian Ocean may enhance the prediction of La Niña events.

3.5 Application the statistical model to longer time series in history

The statistical model above using oceanic signals from the Indian Ocean can be used to make La Niña forecasts back in history. To overcome the short time series of AVISO SLA data, wind data from a much longer time series were used to estimate the Kelvin wave SLA (Equation 2), which represent the Indo-Pacific “oceanic channel” connection through the Indonesian seas. Here, wind data from the ERA5 reanalysis of the ECMWF were used. Consistent results were obtained for the NCEP product (figures not shown). The Kelvin wave SLA, represented by integrating the wind stress anomalies along the characteristic line starting from the western Indian Ocean to the Maluku Channel, has shown a relationship with the Niño 3.4 index at a one-year time lag similar to that of AVISA SLA during 1993–2020 (Figure 13A).

FIGURE 13

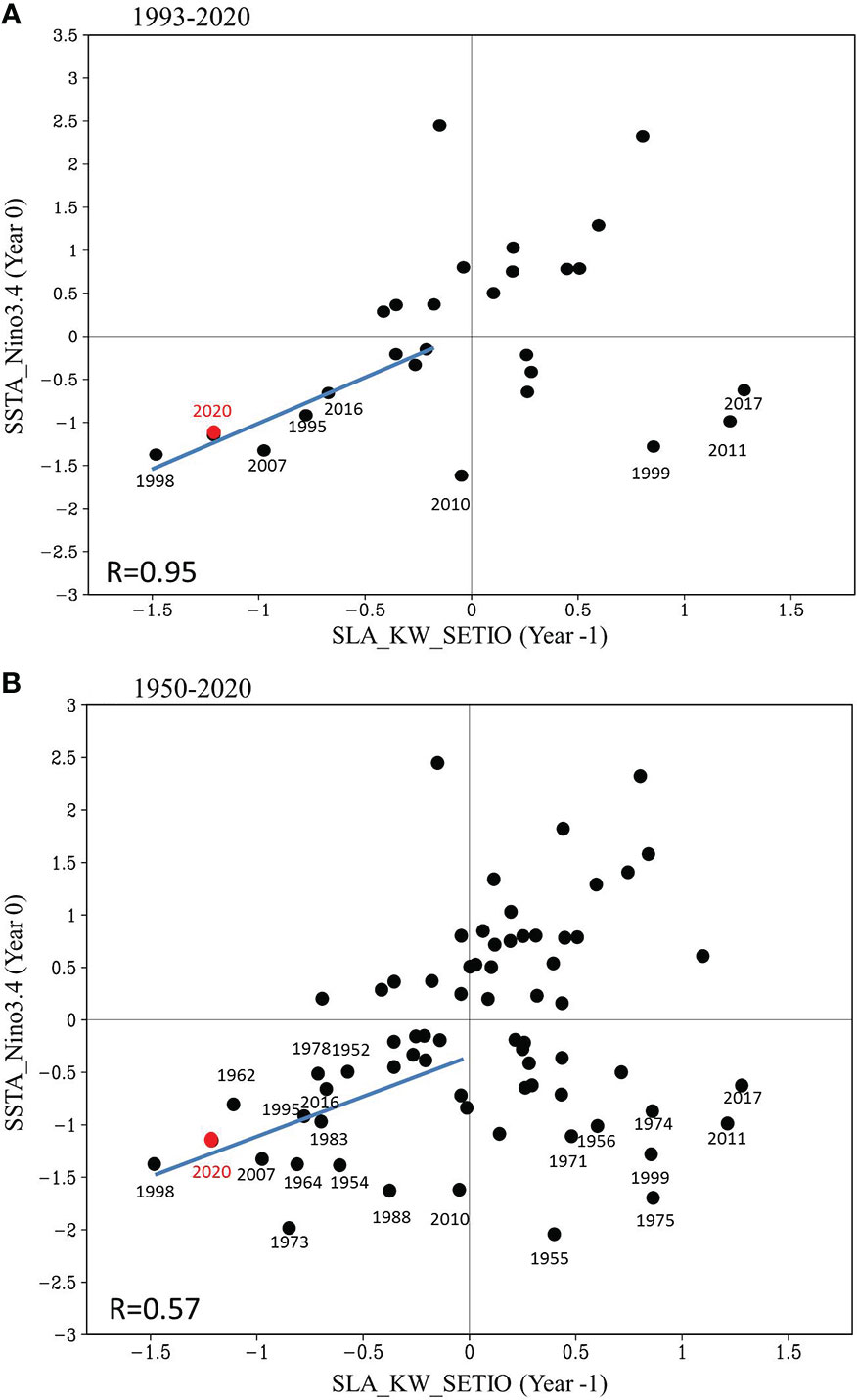
Figure 13 Application of the statistical model to longer SLA time series. (A) Scatter plot of the fall Niño3.4 index (°C) as a function of the fall SLA (decimeter) calculated from the wind-forced Kelvin wave (SLA_KW_SETIO) integrated along the pathway one year before during 1993-2020. Blue line denotes regressed linear relation between the fall SLA_KW_SETIO and the fall Niño3.4 index one year later. The value of 2010 is not included in calculating the blue line. (B) Same as in (A), but for the period of 1950-2020. Correlation coefficients in the third quadrant are shown in the lower left of each panel.

The high predictability based on the SETIO SLA also holds for the La Niña events back in history. For the longer period since 1950, the asymmetric relationship between the SETIO SLA and Niño 3.4 index at a one-year lag basically holds (Figure 13B). In particular, the linear relation between the negative SETIO SLA and Niño 3.4 SSTA one year later still exists for the longer data, suggesting that strong upwelling anomalies in the SETIO precede strong La Niña in the following year. The negative SLA (upwelling anomalies) clearly favored the occurrence of La Niña one year later with a correlation coefficient of 0.57 exceeding the 99% confidence level. The much larger number of samples in the longer time series (72 years in ERA5 versus 29 years in AVISO data) yielded a considerably smaller correlation coefficient still above the statistical significance. In addition, when downwelling anomalies dominate the SETIO, the Niño 3.4 index one year later may be either positive or negative, which is similar to the uncertainty during 1993–2021. The above analysis suggests that the simple linear regression model of La Niña prediction at a lead time of one year, based on Indo-Pacific “oceanic channel” dynamics, is likely useful notwithstanding the decadal variability of the Indo-Pacific Ocean and climate.

Historical SLA from oceanic data assimilation products extending back to 1950 is also examined for the IOD-ENSO predictability. The correlation coefficient between the negative SETIO SLA and Niño 3.4 SSTA one year later is 0.51 for the ECMWF Ocean Reanalysis System 4 (ORA4), but is only 0.37 for the German contribution to the Estimating the Circulation and Climate of the Ocean project 3 (GECCO3) (figures not shown). We speculate that the differences are caused by the coarse resolution of the ocean model in resolving the narrow channels of the Indonesian seas and topography, which could induce artificial eastern boundary reflection in the eastern Indian Ocean to contaminate the SLA signals.

The linear relationship between the negative SETIO SSTA and Niño 3.4 SSTA since 1950 (correlation coefficient is 0.34 in Figure 14) is not as good as between the negative SETIO SLA and the Niño 3.4 index (correlation coefficient is 0.57, Figure 13B). Although the correlation coefficient between the negative SETIO SSTA and Niño 3.4 SSTA exceeded the 99% significance level, it did not capture the one-to-one relationship between the negative SETIO SLA and Niño 3.4 SSTA one year later. When a strong negative SSTA occur over the SETIO during boreal fall, the Niño 3.4 SSTA can be either positive or negative in the following year, suggesting that La Niña prediction based on the SSTA in the Indian Ocean contains large uncertainties.

FIGURE 14

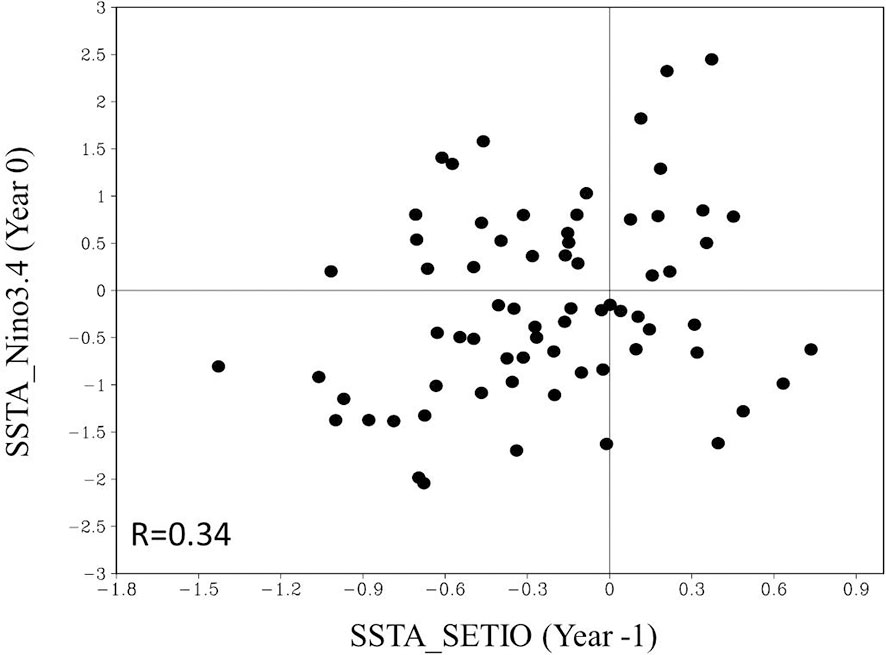
Figure 14 Application of the statistical model to longer SSTA time series. Scatter plot of the fall Niño3.4 index with the SETIO SSTA in the preceding fall for the period of 1950-2020. Correlation coefficient in the third quadrant is shown in the lower left of this figure.

4 Conclusion and discussion

ENSO predictors used in most exiting statistical forecasts are variables in the tropical Pacific Ocean, especially WWV indices, which have proven to provide a precursor for the onset of La Niña. Other factors, including inter-basin interactions over the tropical Indo-Pacific Ocean, have been shown to play important roles in ENSO predictability. The previous studies have demonstrated that SSTA in the Indian Ocean may initiate the onset and contribute to the predictability of the 2010/2012 and 2020/2021 La Niña events (Luo et al., 2017; Hasan et al., 2022), which follow weak-to-moderate El Niño without large discharged WWV anomalies. These studies have only focused on atmospheric teleconnection via Walker circulation. The present study emphasizes that the upwelling anomalies in the STEIO provide a better predictor beyond the one-year lead for La Niña events preceded by the pIOD. The dynamics are suggested to occur through the “oceanic channel” of the ITF.

Our analysis suggests a clear asymmetry in the lead correlation between the SETIO SLA in boreal fall and Niño 3.4 SSTA one year later: negative SETIO SLA lead to La Niña, while positive SLA lead to either La Niña or El Niño. The negative SLA (upwelling anomalies) in the SETIO in boreal fall is a better long-lead precursor for one type of La Niña events (which are preceded by pIODs) at the lead time of one year, with a correlation coefficient of 0.97 (exceed the 99% confidence level) since 1993. This relationship is applicable to longer time series in history since 1950, with a correlation coefficient of 0.57 (exceed the 99% confidence level).

It is worth mentioning that some studies, e.g. Jiang et al. (2021), have argued that the IOD-ENSO link is a result of ENSO cycling and, therefore, “adds no additional information to ENSO prediction”. However, the auto-correlation of Niño3.4 at one year time lag is only -0.12 during 1950-2020, way below the statistical significance level. Moreover, the auto-correlation at one year lag is not statistical significant in any decade after 1970 (figure not shown). In contrast, the IOD-ENSO lag correlation is strong during the 1990s (Yuan et al., 2022). Clearly, the ENSO autocorrelation is not the major cause of the IOD-ENSO lead-lag relationship. Furthermore, the correlation of the negative Niño 3.4 index with the discharged WWV in the previous fall is insignificant. These results suggest that, at longer lead times across the SPB, the WWV or Niño3.4 index could not be good predictors of La Niña. The negative SLA in SETIO, which are partly correlated with the preceding El Niño, is mainly produced by the strong ocean-atmosphere coupling over the tropical Indian Ocean with intrinsic nonlinearity. The model of Jiang et al. (2021) does not include this process nor the IOD feedback on ENSO.

Here, we emphasize that the dynamics behind this long-lead predictability are the Indo-Pacific “oceanic channel” connection (Figure 15). When a pIOD occurs during fall, anomalous upwelling Kelvin waves propagate from the eastern Indian Ocean to the western Pacific through the Indonesian Seas and further to the eastern equatorial Pacific Ocean, elevating the thermocline and forcing a La Niña event to develop during the following year. However, the atmospheric bridge was not the dominant process contributing to the high long-lead predictability of strong La Niña events in 1995/96, 1998/99, 2007/08, and 2020/21. Although easterly wind anomalies in the western Pacific followed the 1994, 1997, 2006 and 2019 pIOD events, the lead correlation between the negative SETIO SLA in fall and the easterly wind anomalies in the western Pacific during the following summer was not significant. Recently, pacemaker experiments (Wang et al., 2022) depicted that the Indo-Pacific “oceanic channel” are dominantly important in ENSO forecasts, whereas the atmospheric bridge is secondary to the generation of 2020/21 La Niña. The present analysis emphasizes that the “oceanic channel” is likely to influence the predictive skill of La Niña.

FIGURE 15

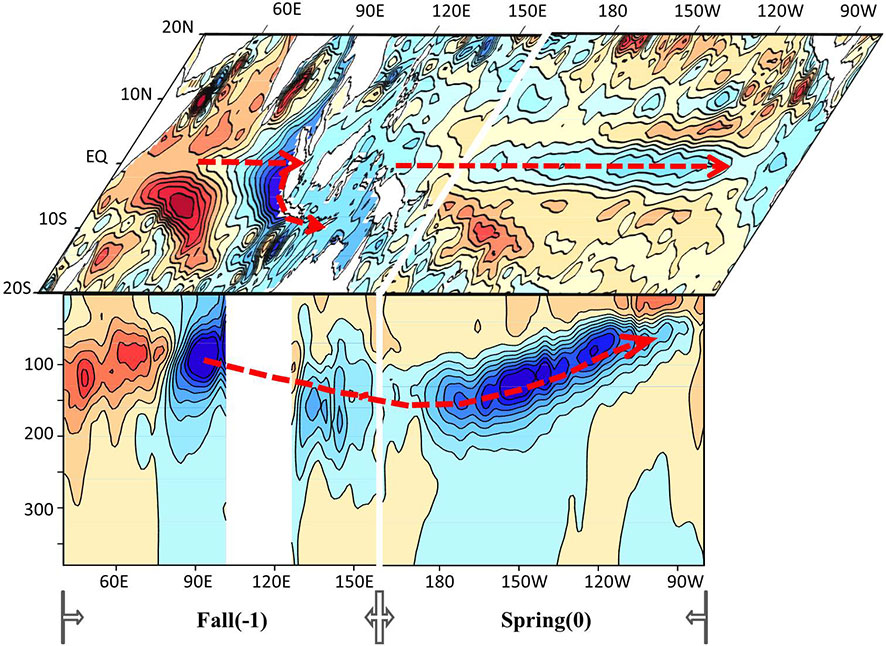
Figure 15 Schematic illustration for the negative SETIO SLA as a predictor of the La Niña events based on the tropical Indo-Pacific “ocean channel” dynamics. The upper (lower) part of this figure shows the SLA (subsurface temperature anomalies). The left (right) part of this figure shows the condition during the peak of pIOD (following spring). The red dashed arrows indicate the eastward-propagating Kelvin wave.

Our results suggest that the lead relationship between SETIO SLA and Niño 3.4 SSTA one year later is asymmetric between El Niño and La Niña. A strong pIOD event triggered the onset of a La Niña event in the following year. A warm event in the eastern equatorial Pacific in the year following a pIOD event does not exist. In contrast, after a nIOD event the tropical Pacific may evolve into either an El Niño or La Niña event or a neutral state. The predictability of this type of La Niña events, including the 2-year La Niña in the second year (1999/2000, 2017/18, 2021/22), did not result from the Indian Ocean in the previous year. The Indo-Pacific interaction, especially the “oceanic channel” dynamics, may partly explain the asymmetry of the warm and cold phases of ENSO predictability.

The asymmetry in predictive skills of negative and positive SETIO SLA may be due to the stronger coupling between the cold tongue SSTA and the eastern equatorial Pacific thermocline depth anomalies during La Niña than during El Niño (Yuan and Rienecker, 2003; Yuan, 2009; Tang et al., 2015). It is known that the surface heat balance is dependent on the depth of the surface mixed layer in the eastern equatorial Pacific. Upwelling currents elevate thermocline and mixed layer in the eastern equatorial Pacific, making the cold tongue SSTA more sensitive to vertical advection. In contrast, downwelling currents depress the thermocline and mixed layer in the eastern equatorial Pacific, resulting in the cold tongue SSTA de-coupled from the thermocline anomalies. Thus, stronger cooling anomalies occur following the pIOD than the warming anomalies produced by the downwelling of the same amplitudes following the nIOD. In addition, some of the La Niña events, such as the 2-year La Niña in the second year, are independent of the Indian Ocean interannual variations. For this type of La Niña events, the cold tongue SSTA are largely controlled by the internal dynamics in the Pacific basin, which explains the events in the fourth quadrant in Figure 1A. The physical mechanisms leading to the asymmetry in the lead correlation between the SETIO SLA and Niño 3.4 SSTA one year later deserve further investigations.

From the previous and current works, it can be observed that ENSO predictability results from a combination of the internal oceanic processes in the Pacific and interbasin interactions through the atmospheric bridge and oceanic channel. For some ENSO events, oceanic channels between the tropical Indian and Pacific Ocean were not the dominant process for the onset of El Niño/La Niña one year later. In any case, the present study emphasizes that an early upwelling anomalies (negative SLA) in the SETIO is an effective and long-lead predictor of La Niña onset timing and amplitude, especially for the 1995/96, 2007/08, and 2020/21 La Niña events following strong pIOD events with weak concurrent El Niño events.

Because of the limited number of La Niña events in the observational record, our statistical results still have some uncertainties. Model result of Wang et al. (2022) has demonstrated the dominate role of “oceanic channel” in the generation of 2020/21 La Niña event. Numerical model experiments are needed in the next step to test the relative roles of the “oceanic channel” and the atmospheric bridge between the tropical Indian and Pacific Ocean for the 1995/96, 1998/99, 2007/08 and 2016/17 La Niña events.

Data availability statement

The 2020 La Niña forecast were obtained from the IRI/CPC [https://iri.columbia.edu/our-expertise/climate/enso/]. The OISST, ERSST, and NCEP data were provided by NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, through their website [https://www.esrl.noaa.gov/psd/]. Satellite altimeter sea level data were obtained from the Aviso project web page [http://www.aviso.altimetry.fr]. ECCO2 data were downloaded from the Asia-Pacific Data-Research Center (APDRC) [http://apdrc.soest.hawaii.edu/data/data.php].

Author contributions

DY developed the scientific hypotheses, directed the research, and attracted fundings to support the study. XZ conducted the analysis. XZ and DY wrote the manuscript. JW worked on the reanalysis data, helped interpret the “oceanic channel” dynamics. All authors contributed to the article and approved the submitted version.

Funding

This work is jointly supported by the National Key R&D Program of China (2019YFA0606702, 2020YFA0608801), CAS (XDB42010000), NSFC (42175027, 41720104008, 91858204), and Shandong Natural Science Foundation Project (ZR2019ZD12). DY is supported by the National Key R&D Program of China (2019YFC1509102) project, “Taishan Scholar Program” of Shandong province and the “Kunpeng outstanding Scholar of MNR/FIO of China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barnston A. G., Glantz M. H., He Y. (1999). Predictive skill of statistical and dynamical climate models in SST forecasts during the 1997-98 El niño episode and the 1998 la niña onset. Bull. Am. Meteorol. Soc 80, 217–243. doi: 10.1175/1520-0477(1999)080<0217:PSOSAD>2.0.CO;2

CrossRef Full Text | Google Scholar

Barnston A. G., Tippett M. K., L’Heureux M. L., Li S., Dewitt D. G. (2012). Skill of real-time seasonal ENSO model predictions during 2002– 11: Is our capability increasing? Bull. Am. Meteorol. Soc 93, 631–651. doi: 10.1175/BAMS-D-11-00111.1

CrossRef Full Text | Google Scholar

Barnston A. G., Tippett M. K., Ranganathan M., L’Heureux M. L. (2019). Deterministic skill of ENSO predictions from the north American multimodel ensemble. Climate Dynamics 53, 7215–7234. doi: 10.1007/s00382-017-3603-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Blumenthal M. B., Bell M., del Corral J., Cousin R., Khomyakov I. (2014). IRI data library: enhancing accessibility of climate knowledge. Earth Perspect. 1 (1), 1–12. doi: 10.1186/2194-6434-1-19

CrossRef Full Text | Google Scholar

Cai W., Wu L., Lengaigne M., Li T., McGregor S., Kug J. S., et al. (2019). Pantropical climate interactions. Science 363, 944–944. doi: 10.1126/science.aav4236

CrossRef Full Text | Google Scholar

Capotondi A., Wittenberg A. T., Kug J.S., Takahashi K., McPhaden M. J. (2020). ENSO Diversity. Geophysical Monograph. In 2021 American Geophysical Union. John Wiley & Sons, Inc. 253, 65–86.

Google Scholar

Chen D., Cane M. A. (2008). El Niño prediction and predictability. J. Comput. Phys. 227, 3625–3640. doi: 10.1016/j.jcp.2007.05.014

CrossRef Full Text | Google Scholar

Chen D., Cane M. A., Kaplan A., Zebiak S. E., Huang D. (2004). Predictability of El niño over the past 148 years. Nature 428, 733–736. doi: 10.1038/nature02439

PubMed Abstract | CrossRef Full Text | Google Scholar

Chikamoto Y., Timmermann A., Luo J.-J., Mochizuki T., Kimoto M., Watanabe M., et al. (2015). Skilful multi-year predictions of tropical trans-basin climate variability. Nat. Commun. 6, 1–7. doi: 10.1038/ncomms7869

CrossRef Full Text | Google Scholar

Clarke A. J., Van Gorder S. (2003). Improving El niño prediction using a space-time integration of indo-pacific winds and equatorial pacific upper ocean heat content. Geophysical Res. Lett. 30, 1399. doi: 10.1029/2002GL016673

CrossRef Full Text | Google Scholar

Cole J. E., Overpeck J. T., Cook E. R. (2002). Multiyear la niña events and persistent drought in the contiguous united states. Geophysical Res. Lett. 29, 25-1–25-4. doi: 10.1029/2001GL013561

CrossRef Full Text | Google Scholar

Cook E. R., Seager R., Cane M. A., Stahle D. W. (2007). North American drought: Reconstructions, causes, and consequences. Earth.-Sci. Rev. 81, 93–134. doi: 10.1016/j.earscirev.2006.12.002

CrossRef Full Text | Google Scholar

DiNezio P. N., Deser C., Okumura Y., Karspeck A. (2017). Predictability of 2-year la niña events in a coupled general circulation model. Climate dynamics 49 (11), 4237–4261. doi: 10.1007/s00382-017-3575-3

CrossRef Full Text | Google Scholar

Duan W. S., Wei C. (2012). The “spring predictability barrier” for ENSO predictions and its possible mechanism: Results from a fully coupled model. Int. J. Climatology 33, 1280–1292. doi: 10.1002/joc.3513

CrossRef Full Text | Google Scholar

Fasullo J., Otto-Bliesner B., Stevenson S. (2018). Enso’s changing influence on temperature, precipitation, and wildfire in a warming climate. Geophys. Res. Lett. 45, 9216–9225. doi: 10.1029/2018GL079022

CrossRef Full Text | Google Scholar

Fedorov A. V., Philander S. G. (2000). Is El niño changing? Science 288, 1997–2002. doi: 10.1126/science.288.5473.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Gill A. E. (1982). Atmosphere-ocean dynamics (San Diego, CA: Academic Press).

Google Scholar

Ha K. J., Chu J. E., Lee J. Y., Yun K. S. (2017). Interbasin coupling between the tropical Indian and pacific ocean on interannual timescale: Observation and CMIP5 reproduction. Climate Dynamics 48, 459–475. doi: 10.1007/s00382-016-3087-6

CrossRef Full Text | Google Scholar

Ham Y. G., Kug J. S., Park J. Y., Jin F. F. (2013). Sea surface temperature in the north tropical Atlantic as a trigger for El Niño/Southern Oscillation events. Nat. Geosci. 6 (2), 112–116. doi: 10.1038/ngeo1686

CrossRef Full Text | Google Scholar

Ham Y. G., Kim J. H., Luo J. J. (2019). Deep learning for multi-year ENSO forecasts. Nature 573 (7775), 568–572. doi: 10.1038/s41586-019-1559-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasan N. A., Chikamoto Y., McPhaden M. J. (2022). The influence of tropical basin interactions on the 2020ical basin interactiNiño. Front. Clim. 4. doi: 10.3389/fclim.2022.1001174

CrossRef Full Text | Google Scholar

Hersbach H., Bell B., Berrisford P., Hirahara S., Horányi A., Muñoz-Sabater J., et al. (2020). The era5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hoyos N., Escobar J., Restrepo J. C., Arango A. M., Ortiz J. C. (2013). Impact of the 2010–2011 la niña phenomenon in Colombia, south America: The human toll of an extreme weather event. Appl. Geogr. 39, 16–25. doi: 10.1016/j.apgeog.2012.11.018

CrossRef Full Text | Google Scholar

Hu J., Duan W., Zhou Q. (2019a). Season-dependent predictability and error growth dynamics for la niña predictions. Climate Dynamics 53, 1063–1076. doi: 10.1007/s00382-019-04631-5

CrossRef Full Text | Google Scholar

Hu X., Sprintall J., Yuan D., Tranchant B., Gaspar P., Koch-Larrouy A., et al. (2019b). Interannual variability of the sulawesi Sea circulation forced by indo-pacific planetary waves. J. Geophysical Res. 124, 1616–1633. doi: 10.1029/2018JC014356

CrossRef Full Text | Google Scholar

Hu Z. Z., Kumar A., Xue Y., Jha B. (2014). Why were some La Niñios followed by another La Niña. Clim. Dyn. 42, 1029–1042.

Google Scholar

Hu Z. Z., Kumar A., Huang B., Zhu J., Zhang R. H., Jin F. F. (2016). Asymmetric evolution of El Niño and La Niña: The recharge/discharge processes and role of the off-equatorial sea surface height anomaly. Clim. Dyn. 49 (7-8), 1–12.

Google Scholar

Huang B., Thorne P. W., Banzon V. F., Boyer T., Chepurin G., Lawrimore J. H., et al. (2017). Extended reconstructed Sea surface temperature version 5 (ERSSTv5), upgrades, validations, and intercomparisons. J. Climate 30, 8179–8205. doi: 10.1175/JCLI-D-16-0836.1

CrossRef Full Text | Google Scholar

Iwakiri T., Watanabe M. (2020). Mechanisms linking multi-year la niña with preceding extreme El niño. Sci. Rep. 11, 17465. doi: 10.21203/rs.3.rs-123982/v1

CrossRef Full Text | Google Scholar

Izumo T., Vialard J., Lengaigne M., de boyer Montegut C., Behera S. K., Luo J. J., et al. (2010). Influence of the state of the Indian ocean dipole on following year’s El niño. Nat. Geosci. 3, 168–172. doi: 10.1038/ngeo760

CrossRef Full Text | Google Scholar

Jiang F., Zhang W., Jin F.-F., Stuecker M. F., Allan R. (2021). El Niño pacing orchestrates inter-basin pacific-Indian ocean interannual connections. Geophys. Res. Lett. 48, e2021GL095242. doi: 10.1029/2021GL095242

CrossRef Full Text | Google Scholar

Jin F. F. (1997). An equatorial ocean recharge paradigm for ENSO. Part I: conceptual model. J. Atmos. Sci. 54 (7), 811–829.

Google Scholar

Jin E. K., Kinter J. L., Wang B., Park C. K., Kang I.-S., Kirtmanet B. P., et al. (2008). Current status of ENSO prediction skill in coupled ocean-atmosphere models. Climate Dynamics 31, 647–664. doi: 10.1007/s00382-008-0397-3

CrossRef Full Text | Google Scholar

Jong B.-T., Ting M., Seager R., Anderson W. B. (2020). Enso teleconnections and impacts on us summertime temperature during a multiyear la niña life cycle. J. Climate 33, 6009–6024. doi: 10.1175/JCLI-D-19-0701.1

CrossRef Full Text | Google Scholar

Kalnay E., Kanamitsu M., Kistler R., Collins W., Deaven D., Gandin L., et al. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc 77, 437–471. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2

CrossRef Full Text | Google Scholar

Kessler W. S. (2002). Is ENSO a cycle or a series of events? Geophys. Res. Lett. 29, 2125. doi: 10.1029/2002GL015924

CrossRef Full Text | Google Scholar

Kiladis G. N., Diaz H. F. (1989). Global climate anomalies associated with extremes in the southern oscillation. J. Climate 2, 1069–1090. doi: 10.1175/1520-0442(1989)002<1069:GCAAWE>2.0.CO;2

CrossRef Full Text | Google Scholar

Kirtman B. P., Min D., Infanti J. M., Kinter J. L., Paolino D. A., Zhang Q., et al. (2014). The north American multi-model ensemble (NMME): Phase-1 seasonal to interannual prediction, phase-2 toward developing intra-seasonal prediction. Bull. Am. Meteorol. Soc 95, 585–601. doi: 10.1175/BAMS-D-12-00050.1

CrossRef Full Text | Google Scholar

Kirtman B. P., Schopf P. S. (1998). Decadal variability in ENSO predictability and prediction. J. Climate 11, 2804–2822. doi: 10.1175/1520-0442(1998)011<2804:DVIEPA>2.0.CO;2

CrossRef Full Text | Google Scholar

Kirtman B. P., Shukla J., Balmaseda M., Graham N., Penland C., Xue Y., et al. (2002). “Current status of ENSO forecast skill: A report to the climate variability and predictability numerical experimentation group,” in CLIVAR working group on seasonal to interannual prediction (International CLIVAR Project Office: CLIVAR Publication Series No. 56), 26.

Google Scholar

Kug J.-S., Kang I.-S. (2006). Interactive feedback between ENSO and the Indian ocean. J. Climate 19, 1784–1801. doi: 10.1175/JCLI3660.1

CrossRef Full Text | Google Scholar

Larkin N. K., Harrison D. E. (2002). ENSO warm (El niño) and cold (La niña) event life cycles: Ocean surface anomaly patterns, their symmetries, asymmetries, and implications. J. Clim. 15, 1118–1140. doi: 10.1175/1520-0442(2002)015<1118:EWENOA>2.0.CO;2

CrossRef Full Text | Google Scholar

Latif M., Anderson D., Barnett T., Cane M., Kleeman R., Leetmaa A., et al. (1998). A review of the predictability and prediction of ENSO. J. Geophysical Res. 103, 14375–14393. doi: 10.1029/97JC03413

CrossRef Full Text | Google Scholar

Luo J.-J., Liu G., Hendon H., Alves O., Yamagata T. (2017). Inter-basin sources for two-year predictability of themulti-year la niña event in 2010-2012. Sci. Rep. 7, 1–7. doi: 10.1038/s41598-017-01479-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo J. J., Masson S., Behera S. K., Yamagata T. (2008). Extended ENSO predictions using a fully coupled ocean atmosphere model. J. Climate 21, 84–93. doi: 10.1175/2007JCLI1412.1

CrossRef Full Text | Google Scholar

Mayer M., Balmaseda M. A., Haimberger L. (2018). Unprecedented 2015/2016 indo-pacific heat transfer speeds up tropical pacific heat recharge. Geophysical Res. Lett. 45 (7), 3274–3284. doi: 10.1002/2018gl077106

CrossRef Full Text | Google Scholar

Meinen C. S., McPhaden M. J. (2000). Observations of warm water volume changes in the equatorial Pacific and their relationship to El Niño and La Nina. J. Climate 13, 3551–3559. doi: 10.1175/1520-0442(2000)013,3551:OOWWVC.2.0.CO;2

CrossRef Full Text | Google Scholar

Michaelsen J. (1987). Cross-validation in statistical climate forecast model. J. Appl. Meteorol. Clim. 26, 1589–1600. doi: 10.1175/1520-0450(1987)026<1589:CVISCF>2.0.CO;2

CrossRef Full Text | Google Scholar

Mu M., Ren H. L. (2017). Enlightenments from researches and predictions of 2014–2016 super El niño event. Sci. China-Earth Sci. 60, 1569–1571. doi: 10.1007/s11430-017-9094-5

CrossRef Full Text | Google Scholar

Nicholson S. E., Selato J. C. (2000). The influence of la niña on African rainfall. Int. J. Climatology 20, 1761–1776. doi: 10.1002/1097-0088(20001130)20:14<1761::AID-JOC580>3.0.CO;2-W

CrossRef Full Text | Google Scholar

Ohba M., Ueda H. (2009). Role of nonlinear atmospheric response to SST on the asymmetric transition process of ENSO. J. Climate 22, 177–192.

Google Scholar

Okumura Y. M., Deser C. (2010). Asymmetry in the duration of El niño and la niña. J. Climate 23, 5826–5843. doi: 10.1175/2010JCLI3592.1

CrossRef Full Text | Google Scholar

Okumura Y. M., DiNezio P., Deser C. (2017). Evolving impacts of multiyear la niña events on atmospheric circulation and us drought. Geophys. Res. Lett. 44, 11–614. doi: 10.1002/2017GL075034

CrossRef Full Text | Google Scholar

Planton Y. Y., Vialard J., Guilyardi E., Lengaigne M., Izumo T. (2018). Western Pacific oceanic heat content: A better predictor of La Niña than of El Niño. Geophys. Res. Lett. 45, 9824–9833. doi: 10.1029/2018GL079341

CrossRef Full Text | Google Scholar

Planton Y. Y., Vialard J., Guilyardi E., Lengaigne M., Mcphaden M. J. (2021). The asymmetric influence of ocean heat content on ENSO predictability in the CNRM-CM5 coupled general circulation model. J. Climate 34 (14), 5775–5793. doi: 10.1175/JCLI-D-20-0633.1

CrossRef Full Text | Google Scholar

Pujiana K., McPhaden M. J., Gordon A. L., Napitu A. M. (2019). Unprecedented response of Indonesian throughflow to anomalous indo-pacific climatic forcing in 2016. J. Geophysical Res. 124, 3737–3754. doi: 10.1029/2018JC014574

CrossRef Full Text | Google Scholar

Roemmich D., Gilson J. (2009). The 2004-2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the argo program. Prog. Oceanogr. 82 (2), 81–100. doi: 10.1016/j.pocean.2009.03.004

CrossRef Full Text | Google Scholar

Ropelewski C. F., Halpert M. S. (1987). Global and regional scale precipitation patterns associated with the El Niño/Southern oscillation. Mon. Weather Rev. 115, 1606–1626. doi: 10.1175/1520-0493(1987)115<1606:GARSPP>2.0.CO;2

CrossRef Full Text | Google Scholar

Saji N. H., Goswami B. N., Vinayachandran P. N., Yamagata T. (1999). A dipole mode in the tropical Indian ocean. Nature 401, 360–363. doi: 10.1038/43854

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith N. R. (1995). The BMRC ocean thermal analysis system, aust. Met. Mag. 44, 93–110.

Google Scholar

Sprintall J., Gordon A. L., Murtugudde R., Susanto R. D. (2000). A semiannual Indian ocean forced kelvin wave observed in the Indonesian seas in may 1997. J. Geophysical Res. 105 (C7), 17217–17, 230. doi: 10.1029/2000JC900065

CrossRef Full Text | Google Scholar

Tang Y., Zhang R. H., Liu T., Duan W., Yang D., Zheng F., et al. (2018). Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 5, 826–839. doi: 10.1093/nsr/nwy105

CrossRef Full Text | Google Scholar

Tang Y., Kleeman R., Miller S. (2015). Enso predictability of a fully coupled gcm model using singular vector analysis. J. Climate 19 (14), 3361–3377. doi: 10.1175/JCLI3771.1

CrossRef Full Text | Google Scholar

Timmermann A., An S., Kug J. S., Jin F. F., Cai W., Capotondi A., et al. (2018). El Niño–southern oscillation complexity. Nature 559, 535. doi: 10.1038/s41586-018-0252-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Tippett M. K., Barnston A. G., Li S. (2012). Performance of recent multimodel ENSO forecasts. J. Appl. Meteorol. Clim. 51 (3), 637–654. doi: 10.1175/JAMC-D-11-093.1

CrossRef Full Text | Google Scholar

Unnikrishnan A. S., Nidheesh A. G., Lengaigne M. (2015). Sea Level rise trends off the Indian coasts during the last two decades. Curr. Sci. 108 (5), 966–971. Available at: https://www.jstor.org/stable/24216526.

Google Scholar

Wang C. (2019). Three-ocean interactions and climate variability: a review and perspective. Climate Dynamics 53, 5119–5136. doi: 10.1007/s00382-019-04930-x

CrossRef Full Text | Google Scholar

Wang H., Kumar A., Murtugudde R., Narapusetty B., Seip K. L. (2019). Covariations between the Indian ocean dipole and ENSO: A modeling study. Climate Dynamics 53 (9-10), 5743–5761. doi: 10.1007/s00382-019-04895-x

CrossRef Full Text | Google Scholar

Wang J., Zhang S., Jiang H., Yuan D. (2022). Effects of 2019 subsurface Indian ocean initialization on the forecast of the 2020/2021 la niña event. Climate Dynamics. doi: 10.1007/s00382-022-06442-7

CrossRef Full Text | Google Scholar

Webster P. J. (1995). The annual cycle and the predictability of the tropical coupled ocean atmosphere system. Meteoeal. Atmos. Phys. 56, 33–55. doi: 10.1007/BF01022520

CrossRef Full Text | Google Scholar

Webster P. J., Moore A. M., Loschnigg J. P., Leben R. R. (1999). Coupled ocean–atmosphere dynamics in the Indian ocean during 1997–98. Nature 401, 356–360. doi: 10.1038/43848

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu T., Yuan D., Wang J. (2022). Assessment of the oceanic channeldynamics responsible for the IOD-ENSO precursory teleconnection in CMIP5 climate models. Front. Clim. 4. doi: 10.3389/fclim.2022.996343

CrossRef Full Text | Google Scholar

Xue J., Luo J.-J., Zhang W., Yamagata T. (2022). ENSO-IOD inter-basin connection is controlled by the Atlantic multidecadal oscillation. Geophys. Res. Lett. 49, e2022GL101571. doi: 10.1029/2022GL101571

CrossRef Full Text | Google Scholar

Yoon J.-H., Leung L. R. (2015). Assessing the relative influence of surface soil moisture and enso sst on precipitation predictability over the contiguous united states. Geophysical. Res. Lett. 42, 5005–5013. doi: 10.1002/2015GL064139

CrossRef Full Text | Google Scholar

Yuan D., Rienecker M. M. (2003). Inverse estimation of sea surface heat fluxes over the equatorial pacific ocean: seasonal cycle. J. Geophysical Res. 108 (C8), 3247. doi: 10.10239/2002JC001367

CrossRef Full Text | Google Scholar

Yuan D. (2009). Interannual horizontal heat advection in the surface mixed layer over the equatorial pacific ocean: Assimilation versus TAO analysis. Theor. Appl. Climatol. 97 (1-2), 3–15. doi: 10.1007/s00704-008-0068-7

CrossRef Full Text | Google Scholar

Yuan D., Wang J., Xu T., Xu P., Zhou H., Zhao X., et al. (2011). Forcing of the Indian ocean dipole on the interannual variations of the tropical pacific ocean: Roles of the Indonesian throughflow. J. Climate 24 (14), 3593–3608. doi: 10.1175/2011JCLI3649.1

CrossRef Full Text | Google Scholar

Yuan D., Zhou H., Zhao X. (2013). Interannual climate variability over the tropical pacific ocean induced by the Indian ocean dipole through the Indonesian throughflow. J. Climate 26 (9), 2845–2861. doi: 10.1175/JCLI-D-12-00117.1

CrossRef Full Text | Google Scholar

Yuan D., Hu X., Xu P., Zhao X., Yukio M., Han W. (2018). The IOD-ENSO precursory teleconnection over the tropical indo-pacific ocean: Dynamics and long-term trends under global warming. J. Oceanol. Limnol. 36 (1), 4–19. doi: 10.1007/s00343-018-6252-4

CrossRef Full Text | Google Scholar

Yuan D., Xu P., Xu T., Zhao X. (2022). Decadal variability of the interannual climate predictability associated with the indo-pacific oceanic channel dynamics in CCSM4. Front. Clim. 4. doi: 10.3389/fclim.2022.1043305

CrossRef Full Text | Google Scholar

Zhang R.-H., Zheng F., Zhu J., Wang Z. (2013). A successful real-time forecast of the 2010–11 la niño event. Sci. Rep. 3, 1108. doi: 10.1038/srep01108

CrossRef Full Text | Google Scholar