Seasonal variations of tidal currents in the deep Timor Passage

Exact knowledge on the seasonal variations of main tidal constituents is beneficial for improving tidal prediction. The semi-annual cycles in K₁ and S₂ tides are abnormally exaggerated by astronomical P₁ and K₂ tides, which interferes with our understanding on tidal seasonality. The widely-used tidal inference method in previous studies cannot fully separate astronomical P₁ and K₂ tides from seasonal P₁ and K₂ tides due to inaccurate inference relationship. In this study, on the basis of the ‘credo of smoothness’ which indicates that tidal admittances are smooth functions of tidal frequencies, we develop a novel but simple method to address this intractable issue and applied this method to explore the seasonality of tidal currents observed in the deep Timor Passage at the depth of 1800m. We find that the timing and range of seasonal modulations of M₂, S₂, K₁, and O₁ tides are distinct. Annual variations in tidal currents are much stronger than semi-annual variations in tidal currents. The annual and semi-annual ranges of M₂ tide can reach 2.69 cm/s and 1.51 cm/s, which are largest among main constituents. Although the annual range of K₁ tide is only 1.85 cm/s, considering the relatively small amplitude of time-averaged K₁ tide (2.87cm/s), K₁ the most affected tide by the annual cycle. The seasonal cycles of semi-diurnal tides (M₂ and S₂) are basically synchronous while those of diurnal tides (K₁ and O₁) are generally out-of-phase. As a general method, the proposed method can be widely applied to other sea areas to explore local tidal seasonality.

1 Introduction

Originated from astronomical forcing, tides and tidal currents are omnipresent in the global ocean and fundamental for ocean activities such as maritime logistics and ocean engineering (Amin, 1985; Pan et al., 2022a; Pan et al., 2022b; Wei et al., 2022). The interplay of barotropic tides with rough topography in the stratified ocean can generate baroclinic tides (Wunsch, 1975; Zhao et al., 2019). As an indispensable intermediate process in tide-to-turbulence cascade, baroclinic tides play a vital role in ocean mixing processes (Munk and Wunsch, 1998; Egbert and Ray, 2000; Li et al., 2021). Egbert and Ray (2000) indicated that deep sea mixing needs ~2TW energy to maintain deep-water circulation and at least 1TW energy is provided by baroclinic tides. As a result of seasonal changes in ocean environment (such as river flow, ocean stratification and sea ice), tides and tidal currents display significant seasonal variations which have been explored in the global ocean (Corkan, 1934; Foreman et al., 1995; Kang et al., 2002; St-Laurent et al., 2008; Kagan and Sofina, 2010; Georgas, 2012; Müller, 2012; Devlin et al., 2018; Wang et al., 2020; Du and Yu, 2021; Ray, 2022).

The seasonality of tidal currents in the deep sea are mainly derived from ocean stratification and astronomical factors (Xu et al., 2014; Cao et al., 2017; Li et al., 2021). The frequency of K₂ (P₁) tide is equal to that of the S₂ (K₁) tide add (minus) 2 cycle per year. Therefore, the semi-annual cycles of K₁ and S₂ tides are significantly enhanced due to the existence of astronomical P₁ and K₂ tides. To keep pace with the seasonal variations of M₂ and O₁ tides which are not influenced by nearby astronomical tides, nearly all researches applied tidal inference method to infer and eliminate the contribution of astronomical P₁ and K₂ tides when discussing the seasonal variations of K₁ and S₂ tides. The inference relationship between K₂ (P₁) and S₂ (K₁) tides can be determined based on the actual tidal constants from observed time series longer than half a year. It should be noted that the observed K₁ tide is nearly astronomical while the observed P₁ tide has two major energy sources: One is the astronomical P₁ tide, the another is the real seasonal variations of K₁ tide originated from semi-annual variations in ocean environment (labeled as the seasonal P₁ tide). Although the astronomical P₁ tide and the seasonal P₁ tide have same tidal period, their amplitudes and phases are totally different because they are forced by distinct physical processes (see section 3 for details). It is well known that astronomical P₁ and K₁ tidal waves have similar physical properties, thus, the astronomical P₁ tide can be simply inferred from the astronomical K₁ tide while the seasonal P₁ tide cannot. The observed P₁ tide is the vectorial synthesis of the seasonal P₁ tide and the astronomical P₁ tide. Similarly, the observed K₂ tide is the vectorial synthesis of the seasonal K₂ tide and the astronomical K₂ tide. Hence, the inference relationship derived from the observed P₁ (K₂) and observed K₁ (S₂) tide may be problematic due to the interference of the seasonal P₁ (K₂) tide.

To the best of our knowledge, there are no valid methods to take the place of the potentially problematic inference method to fully remove astronomical P₁ and K₂ tides from observed P₁ and K₂ tides. The aim of this research is to revisit this noteworthy issue and propose a new method according to the ‘credo of smoothness’ (Munk and Cartwright, 1966) to solve the problem. The new method is applied to the deep Timor Passage to explore the seasonality of local tidal currents. Our paper is organized as follows. Study area and tidal current observations are introduced in section 2. Section 3 displays the methods and results, followed by the discussions and conclusions in section 4 and section 5, respectively.

2 Study area and data

As a long, deep and narrow trench between the Australian continental shelf and the Timor Island with average depth of ~2000m (Figure 1), the Timor Passage is one of the major corridors for the Indonesian Throughflow (ITF). Fresh and warm sea waters from the western Pacific Ocean are transported to the tropical Indian Ocean via the Timor Passage and the Lombok and Ombai Straits, which are important and essential for maintaining the thermohaline balance in the global ocean (Sprintall et al., 2009). The deep current transport through the Timor Passage shows significant semi-annual and annual variations, which are related to remote Kelvin waves from the Indican Ocean and local monsoonal forcing, respectively (Wang et al., 2022).

FIGURE 1

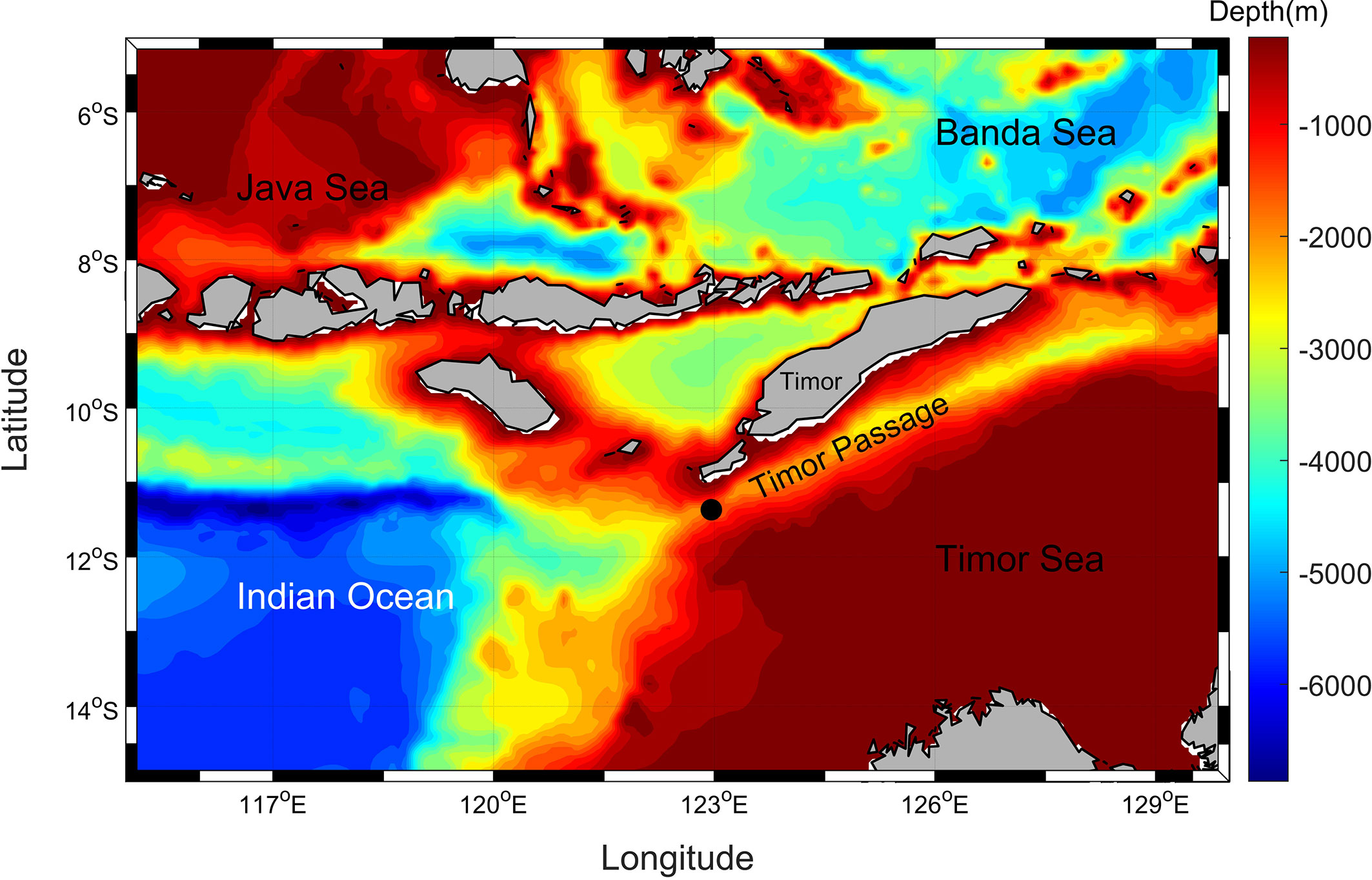
Figure 1 The location of the mooring (black dot). Water depths are from ETOPO1 dataset (Amante and Eakins, 2009).

Due to complex coastlines and topography, tides and tidal currents near the Indonesian archipelago are among the most complicated in the global ocean (Ray et al., 2005; Robertson, 2010). The mixing induced by tides has significant influences on ocean ecology and climate system (Sprintall and Révelard, 2014; Katavouta et al., 2022). Based on EOT20 tidal model (Hart-Davis et al., 2021) derived from multi-satellite altimeters, at the observation point, M₂ tide has the largest amplitude (88.39cm), followed by S₂ (48.78cm), K₁ (27.33cm), and O₁(17.00cm). Local tidal form factor, which is defined by the ratio of the sum of O₁ and K₁ tidal amplitudes to the sum of S₂ and M₂ tidal amplitudes (Pan et al., 2023a), is only 0.32, indicating that local tides are dominated by semi-diurnal tides.

Hourly current observations at depth of 1800m from the mooring (black dot in Figure 1) located in the southeast of the Timor Passage (122.9598°E, 11.3683°S) as part of the INSTANT program are analyzed. The Timor Passage mooring observations cover the period from January 1, 2004 to December 20, 2006. However, there are numerous missing values during January 1, 2004 to June 25, 2005. Thus, we only use 18 months observations from June 25, 2005 to December 20, 2006 to ensure the robustness and reliability of the results. The completeness of studied current data can reach 98.55%. More details of mooring observations can be found in Sprintall et al. (2009).

As shown in Figure 2, eastward tidal currents are significantly stronger than northward tidal currents due to the direction of the Timor Passage. Thus, we decompose eastward and northward currents into currents along and perpendicular to the trench. Only currents along the trench are focused and harmonically analyzed using S_TIDE toolbox (Pan et al., 2018a). It should be noted that to avoid the interference of strong non-tidal background currents on tidal estimation, we use Iteratively Reweighted Least Squares (IRLS) regression (Huber, 1996; Leffler and Jay, 2009) to take place of widely-used ordinary least squares (OLS) regression in the course of harmonic analysis. IRLS regression is much complicated than OLS regression and readers can refer Leffler and Jay (2009) for details. The effectiveness and accuracy of IRLS regression in tidal estimation have been verified by numerous studies (Leffler and Jay, 2009; Matte et al., 2013; Matte et al., 2014; Pan and Lv, 2021; Pan et al., 2022a; Pan et al., 2023a). Local tidal currents are highly non-stationary, with strong intraseasonal vairiability (Figure 2), which deserves further investigation. Table 1 displays tidal constants of major tidal constituents in the deep Timor Passage. Ssa tide with a period of half a year has the largest amplitude (21.65cm/s). which is consistent with Wang et al. (2022). Sa tide with a period of a year has an amplitude of 4.27cm/s. Among semi-diurnal and diurnal tides, M₂ has the largest amplitude (9.05cm/s), followed by S₂ (4.38cm/s), K₁(2.87cm/s), and O₁(2.31cm/s).

FIGURE 2

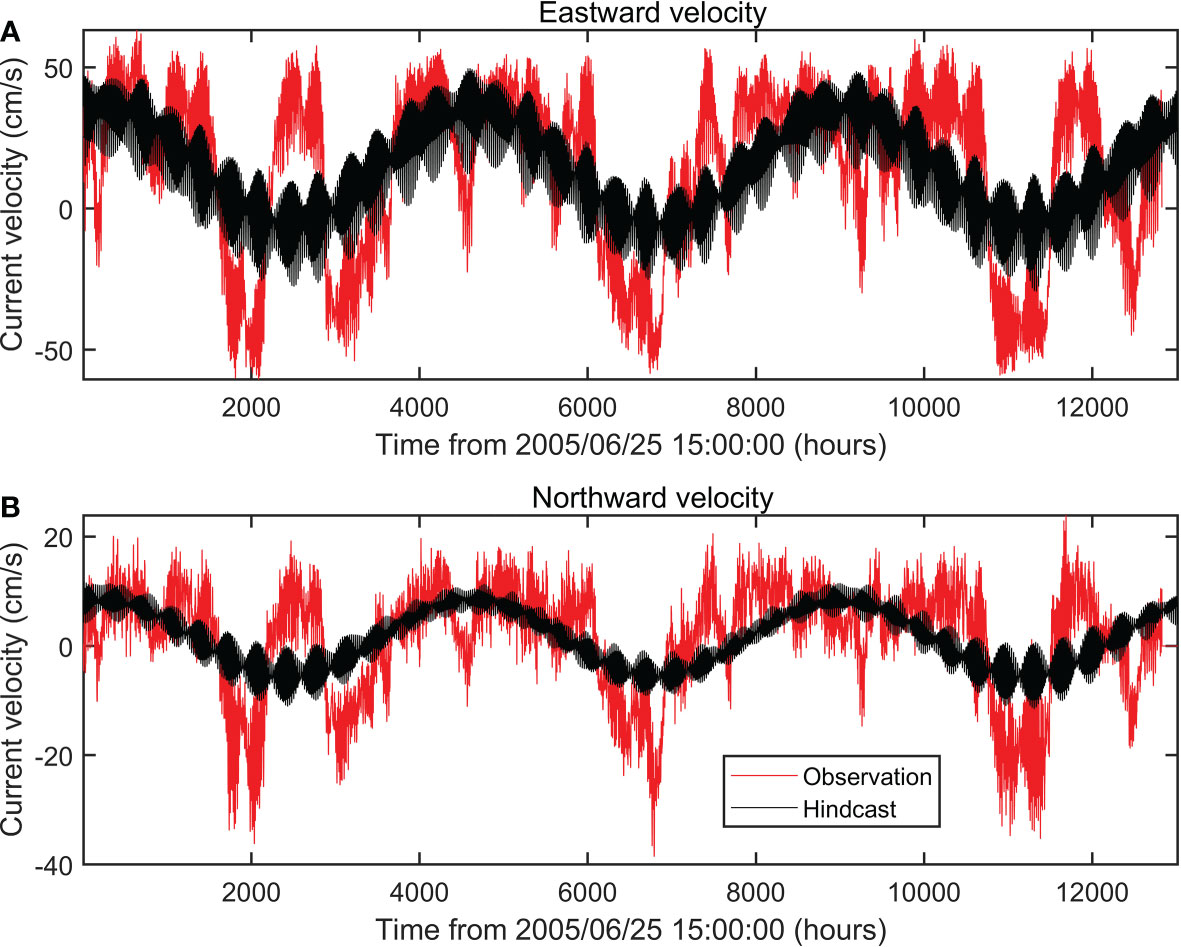
Figure 2 (A) Eastward current velocities (red line) and their hindcast (black line) via harmonic analysis. (B) Northward current velocities (red line) and their hindcast (black line) via harmonic analysis.

TABLE 1

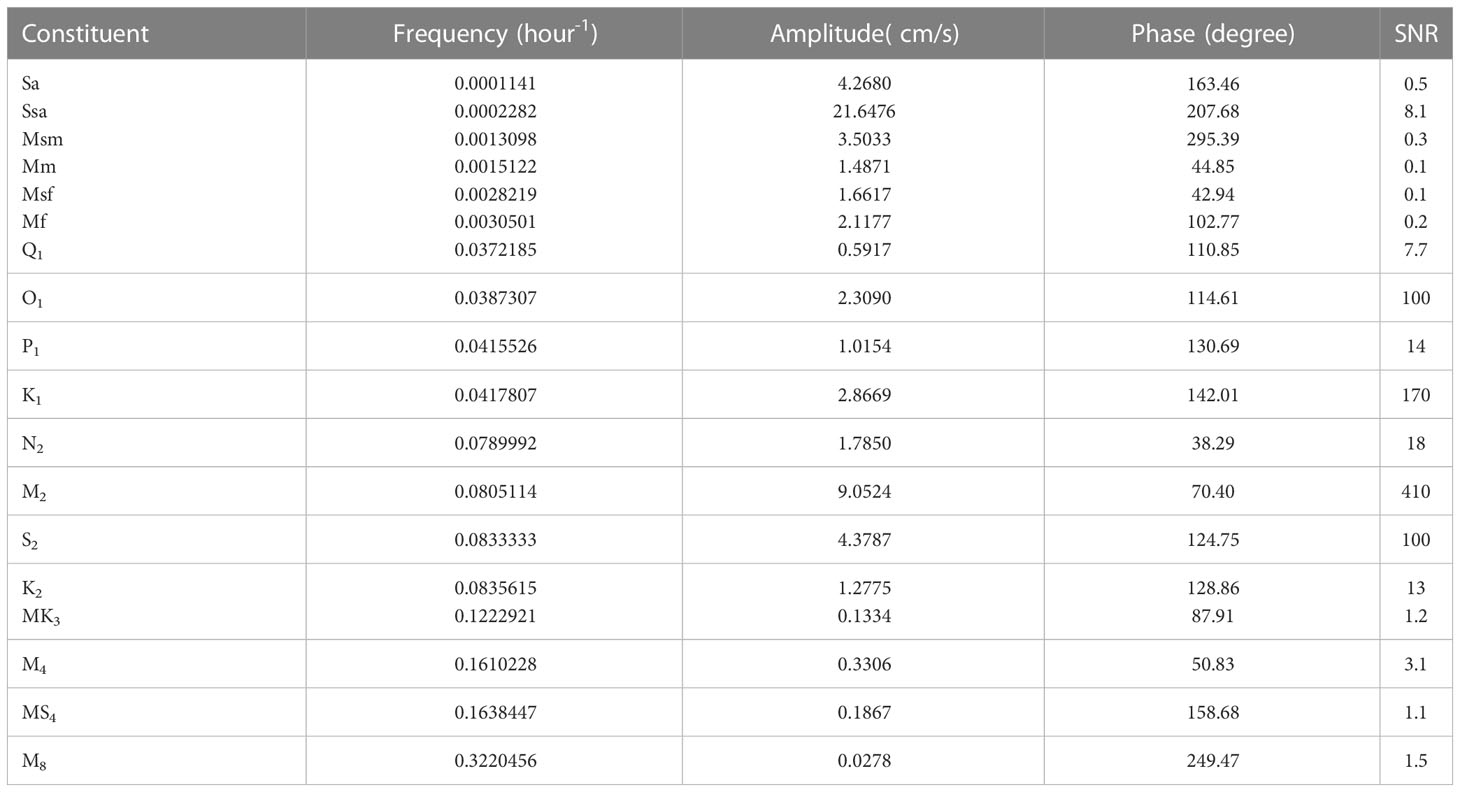
Table 1 Amplitudes and phase lags of major diurnal, semi-diurnal, and shallow water tides estimated from long-term current observations along the trench. SNR means signal-to-noise ratio.

Although long-period tides like Sa, Msm and Mf have large amplitudes, they are not significant due to low signal-to-noise ratios (SNRs). Generally, the SNR of a significant constituent should be no less than two (Pawlowicz et al., 2002). M₄ tide is the strongest shallow water constituent, with an amplitude of only 0.33cm/s. Figure 3A shows the combination of observed K₁, O₁, and P₁ tides. The sum of K₁ and O₁ tides can induce semi-monthly variations (13.66 days) of high tide. Note that P₁ tide can semi-annually modulate K₁ tide, thus, fortnightly variations of high tides (Figure 3A) are not stationary but modulated by semi-annual cycles. The combination of observed M₂, S₂, and K₂ tides also has semi-annually modulated fortnightly cycles (Figure 3B).

FIGURE 3

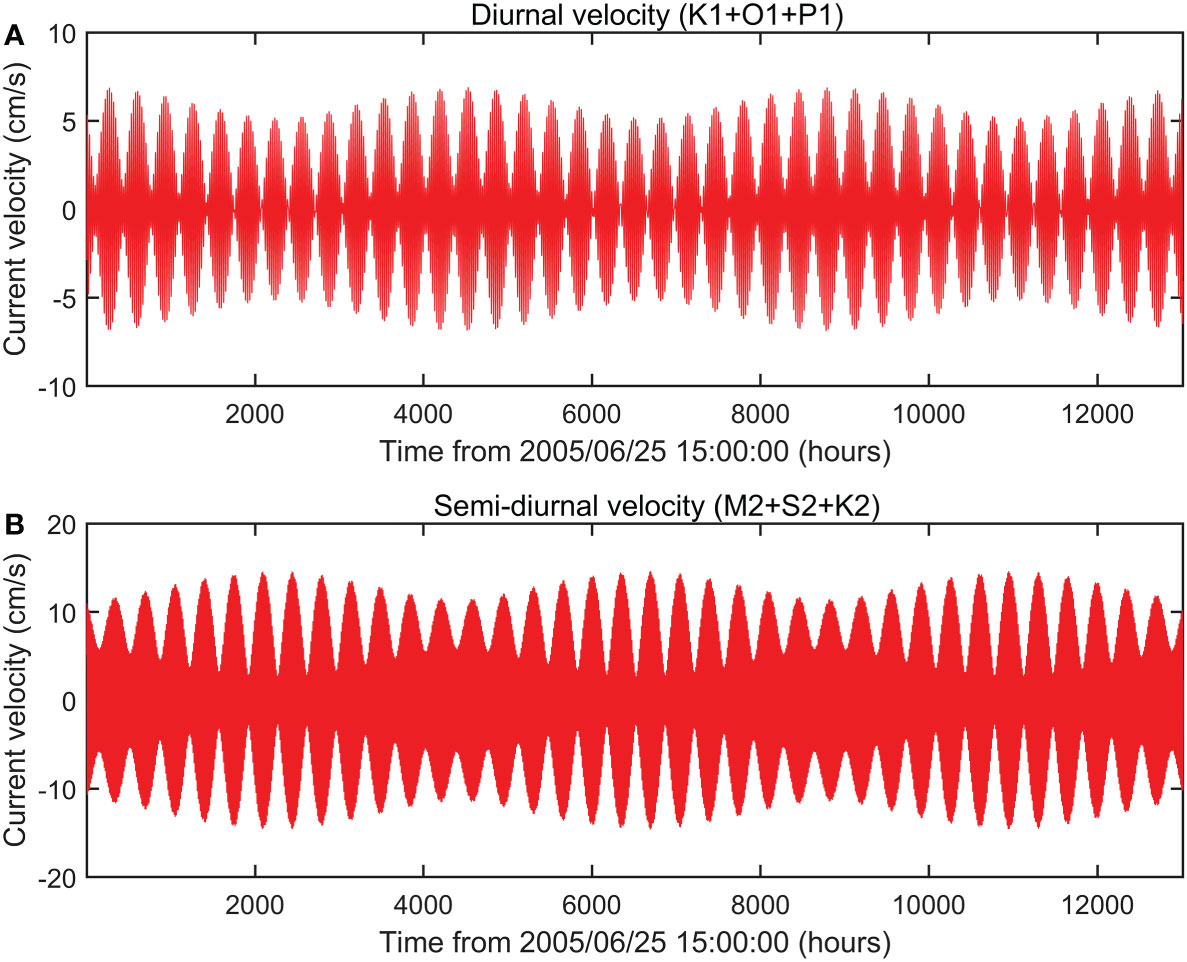
Figure 3 (A) The combination of observed K₁, O₁, and P₁ tidal currents. (B) The combination of observed M₂, S₂, and K₂ tidal currents. Note that the results are estimated from currents along the trench.

O₁ and Q₁ tidal frequencies are close, which means that O₁ and Q₁ tides have similar physical properties. As a result, tidal phase lags of O₁ and Q₁ tides are very close, and the difference of O₁ and Q₁ tidal phase lags is only 3.76° (Table 1). The difference of K₁ and P₁ frequencies is much smaller than that of O₁ and Q₁ frequencies, which means that the difference of K₁ and P₁ phase lags should be smaller than 3.76°. However, the observed difference of K₁ and P₁ phase lags is as high as 11.32°, which clearly indicates that the observed P₁ tide is not purely astronomical, but contains a non-negligible contribution of K₁ seasonality. In the next section, we will introduce a novel method which can fully separate the seasonal P₁(K₂) tide from the astronomical P₁ (K₂) tide.

3 Methodology and results

3.1 Methodology

The proposed method is based on the ‘credo of smoothness’ (Munk and Cartwright, 1966) which implies that tidal admittances are smooth functions of tidal frequencies (Feng et al., 2015; Pan et al., 2023b). Defined by the ratios of observed amplitudes to equilibrium amplitudes (normalized amplitude) and phase differences of observed phases and equilibrium phases, tidal admittances represent the response of astronomical forcing to local topography and coastlines. In general, tidal waves with close periods always have similar responses which means that their admittances should also be close. Note that such smoothness is built on the premise that tides are purely astronomical. The existence of non-astronomical tides may destroy the nature of smoothness, but also provides an opportunity to eliminate non-astronomical tides.

Equilibrium tidal amplitudes are obtained via s_equilibrium_tide function in S_TIDE toolbox. Phase differences of observed phases and equilibrium phases (i.e. phase lags) are directly estimated via classical harmonic analysis. The admittances of minor tidal constituents such as J₁, 2Q₁, 2N₂, L₂ are not used because their SNRs are too small (generally less than 0.5) which means that they may be contaminated by strong non-tidal background noises. As shown in Figure 4A, normalized diurnal amplitudes are parabolic functions of tidal frequencies (dash line). Unknown coefficients (i.e. a, b, c) in Eq.(1) can be estimated by ordinary least squares. f is tidal frequency. Cubic polynomials or higher-order polynomials are not recommended to avoid over-fitting(Feng et al., 2015; Pan et al., 2023b).

FIGURE 4

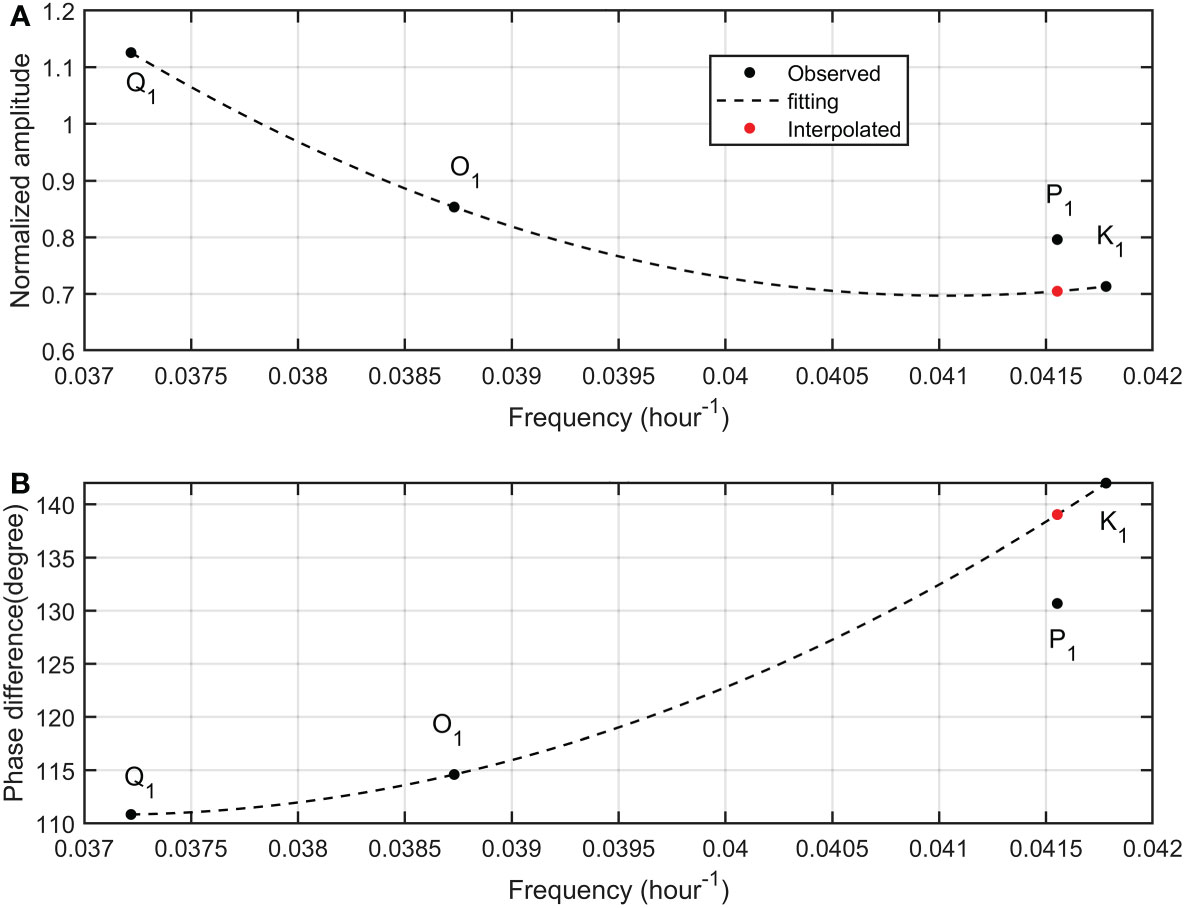
Figure 4 Normalized tidal amplitudes (A) and phase differences (B) for main diurnal tides at depth of 1800m from the mooring. Black dots are observed tidal admittances while red dots are interpolated admittances. Dash lines are determined via ordinary least squares.

$\begin{array}{ll}y=a+bf+c{f}^2& (1)\end{array}$

Due to the interfere of non-astronomical contributions, normalized observed P₁ amplitude significantly deviates from the fitting curve. Similarly, phase differences are also quadratic functions of frequencies (Figure 4B). The observed P₁ phase difference noticeably deviates from the quadratic curve. By the quadratic interpolation, the normalized astronomical P₁ amplitude and astronomical P₁ phase difference can be calculated (red dots in Figure 4). Based on known equilibrium amplitudes, the astronomical P₁ amplitude (0.90 cm/s) and phase lag (139.04°) are calculated. The astronomical P₁ phase lag (139.04°) is very close to the astronomical K₁ phase lag (142.01°). The ratio of the astronomical P₁ amplitude (0.90 cm/s) to the astronomical K₁ amplitude (2.87cm/s) is 0.314 which is slightly smaller than the equilibrium theoretical value (0.331). At last, subtracting the astronomical P₁ tide vectorially from the observed P₁ tide generates the seasonal P₁ tide (Figure 5A). The amplitude and phase of the seasonal P₁ tide is 0.181cm/s and 84.4°, respectively.

FIGURE 5

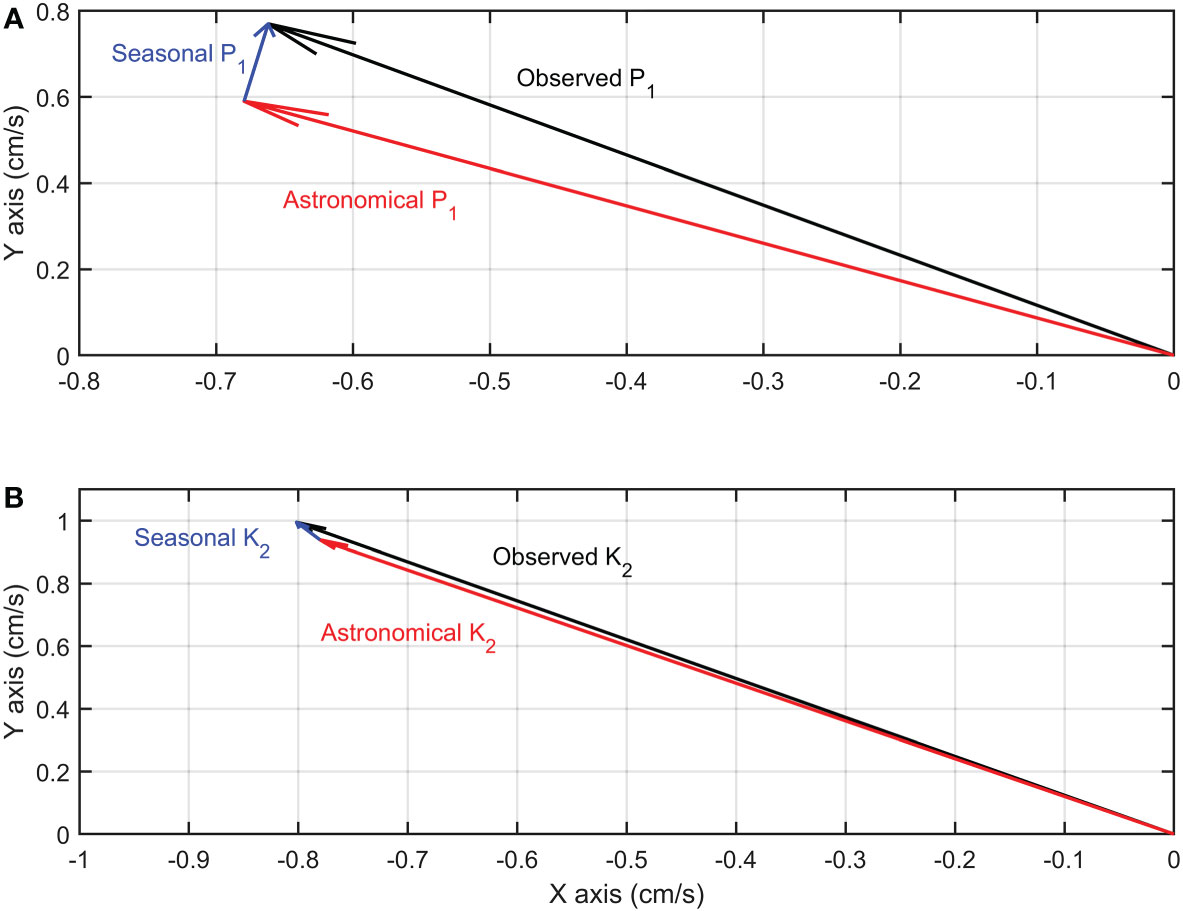
Figure 5 (A) The vectorial synthesis of the seasonal P₁ tide (blue arrow) and the astronomical P₁ tide (red arrow) generates the observed P₁ tide (black arrow). (B) Same as A, but for K₂ tide.

As displayed in Figure 6A, normalized semi-diurnal amplitudes range from 0.55 to 0.6 except K₂. Phase differences for semi-diurnal tides are nearly linear (Figure 6B). Based on the fitting curve and equilibrium amplitudes, the astronomical K₂ amplitude (1.221cm/s) and phase lag (129.72°) are calculated. Via vector operation, the seasonal K₂ amplitude (0.06cm/s) and phase lag (110.93°) are derived. Because the seasonal K₂ tide is very weak, therefore, the observed K₂ tide is nearly same to the astronomical K₂ tide (Figure 5B).

FIGURE 6

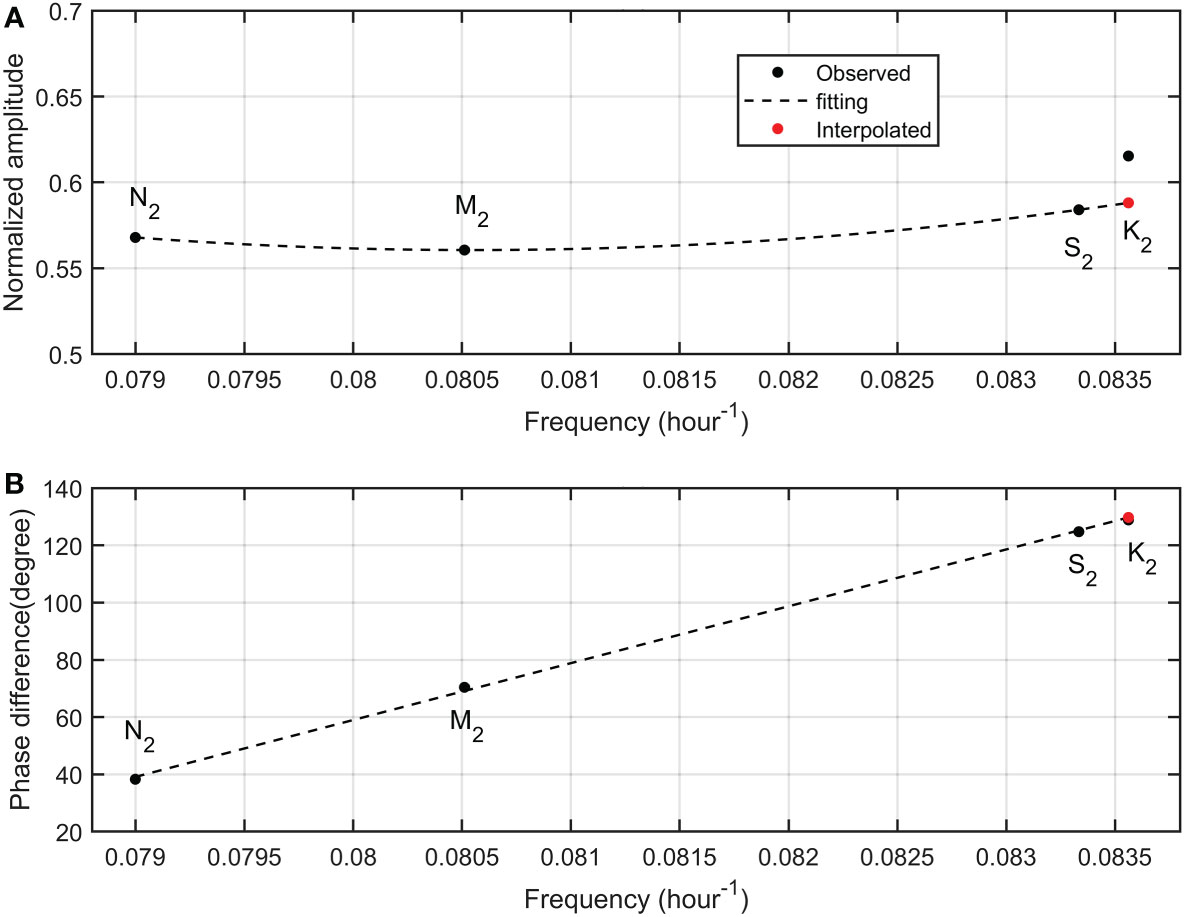
Figure 6 Same as Figure 4, but for semi-diurnal tides.

3.2 Seasonal variations of main tidal constituents

The seasonality of main tidal constituents can induce minor constituents whose frequencies are near main constituents. For example, the annual modulation of K₁ tide can induce S₁ and PSI₁ tides, whose frequencies are w_K1-w_Sa and w_K1+w_Sa, where w_K1 and w_Sa mean the frequencies of K₁ and Sa tides, respectively. The semi-annual modulation of K₁ tide can induce P₁ and PHI₁ tides, whose frequencies are w_K1-2*w_Sa and w_K1+2*w_Sa. The annual modulation of S₂ tide can induce T₂ and R₂ tides, whose frequencies are w_S2-w_Sa and w_S2+w_Sa. Like P₁ and K₂, T₂ tide can also directly obtain considerable energy from astronomical forcing. According to the fitting curve in Figure 6, the astronomical T₂ amplitude (0.256cm/s) and phase lag (122.93°) can be calculated. The observed T₂ amplitude and phase lag are 0.578cm/s and 182.03°, respectively. Through vectorial operation, the seasonal T₂ amplitude (0.498cm/s) and phase lag (208.22°) are obtained.

The combination of S₁ and PSI₁ tides represents the annual cycle of K₁ tide while the combination of P₁ (astronomical contribution removed) and PHI₁ tides represents the semi-annual cycle of K₁ tide (Figure 7). The seasonal variations of M₂, S₂, and O₁ tides can be obtained in similar ways (Figures 7, 8). As shown in Figures 7, 8, seasonal variations of four main constituents are significant and their features are distinct. M₂ tide has the largest annual range (2.69cm/s), followed by S₂ (1.85cm/s), K₁ (1.85cm/s), and O₁ (0.93cm/s). Considering the relatively small amplitude of K₁ tide (2.87cm/s), it is the greatest affected tide by the annual cycle. The range of the semi-annual cycle is much smaller than that of the annual cycle. M₂ tide has the largest semi-annual range (1.51cm/s), followed by S₂ (0.72cm/s), O₁ (0.45cm/s), and K₁ (0.27cm/s). Among four major tidal constituents, O₁ tide has the largest ratio of the range of the semi-annual cycle to tidal amplitude (0.195), which means that the semi-annual cycle has the strongest influence on O₁ tide.

FIGURE 7

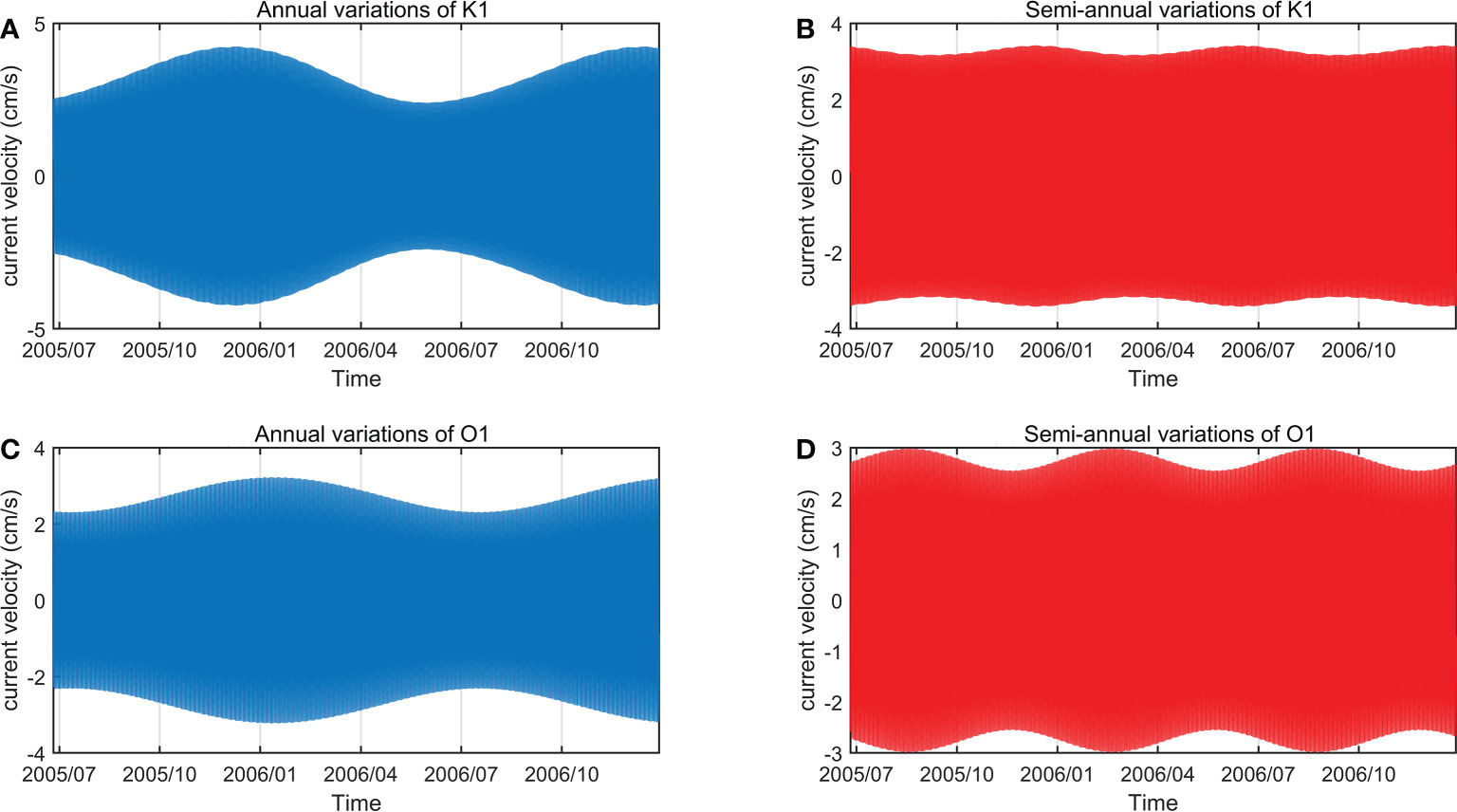
Figure 7 Annual (A) and semi-annual (B) variations of K₁ tidal currents. Annual (C) and semi-annual (D) variations of O₁ tidal currents.

FIGURE 8

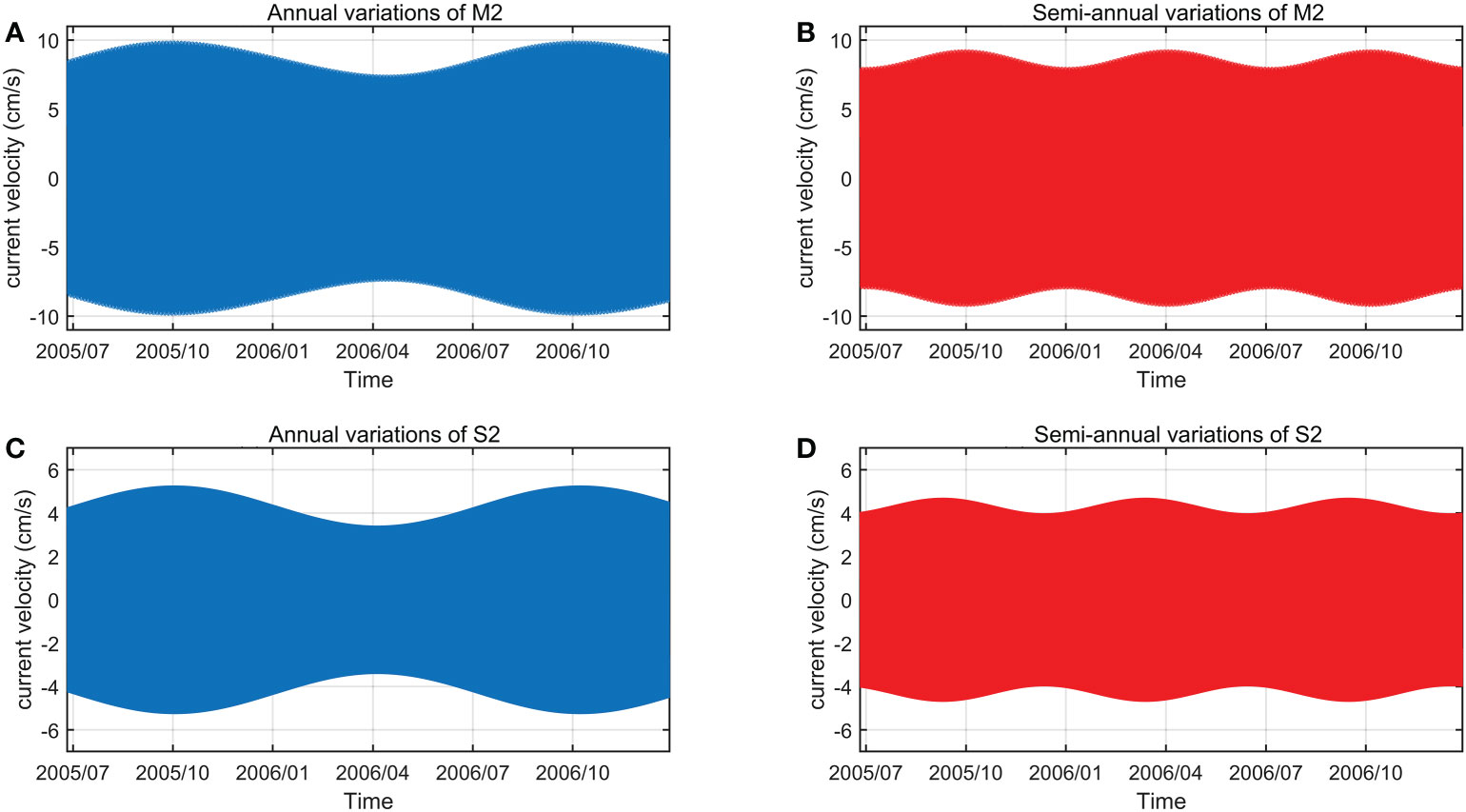
Figure 8 Annual (A) and semi-annual (B) variations of M₂ tidal currents. Annual (C) and semi-annual (D) variations of S₂ tidal currents.

The annual variations of M₂ and S₂ tides are precisely synchronous (Figure 8). Both of them peak at the end of September while reach the minimum value in early April. Compared to semi-diurnal tides, the annual variations of K₁ and O₁ tides are basically synchronous (Figure 7). K₁ tide peaks in early December while reach the minimum value at the end of May. The annual variation of O₁ tide has a delay of about one month compared to that of K₁ tide.

The semi-annual variations of K₁ and O₁ tides are generally opposite. The semi-annual variation of K₁ reaches the minimum value at the end of August and peaks in early December while that of O₁ peaks in mid-August and reaches the minimum value in mid-December (Figure 7). The semi-annual variations of M₂ and S₂ tides are generally synchronous while a delay of about 20 days exists (Figure 8). The semi-annual variation of M₂ reaches the minimum value at the end of December and peaks at the end of September while that of S₂ peaks in early September and reaches the minimum value in early December. Figures 7, 8 indicate that tidal response to seasonal changes in ocean environment is frequency-dependent.

4 Discussions

4.1 Application to surface tides

The proposed method is not limited to deep currents but can also be applied to surface tides because the principle of smoothness is generally credible for all tidal signals. Surface tides at the mooring also have noticeable seasonal variations. Figures 9, 10 display tidal admittances for main semi-diurnal and diurnal tides which are totally different. Tidal admittances for diurnal tides are parabolic functions of tidal frequencies while those for semi-diurnal tides are nearly linear functions. The structure of functions should be related to the local topography and coastline which can influence tidal propagation, reflection, refraction, and dissipation. It is obvious that diurnal tides and semi-diurnal tides which have vastly different periods and wave lengths must show distinct tidal responses to the astronomical forcing in the same sea areas.

FIGURE 9

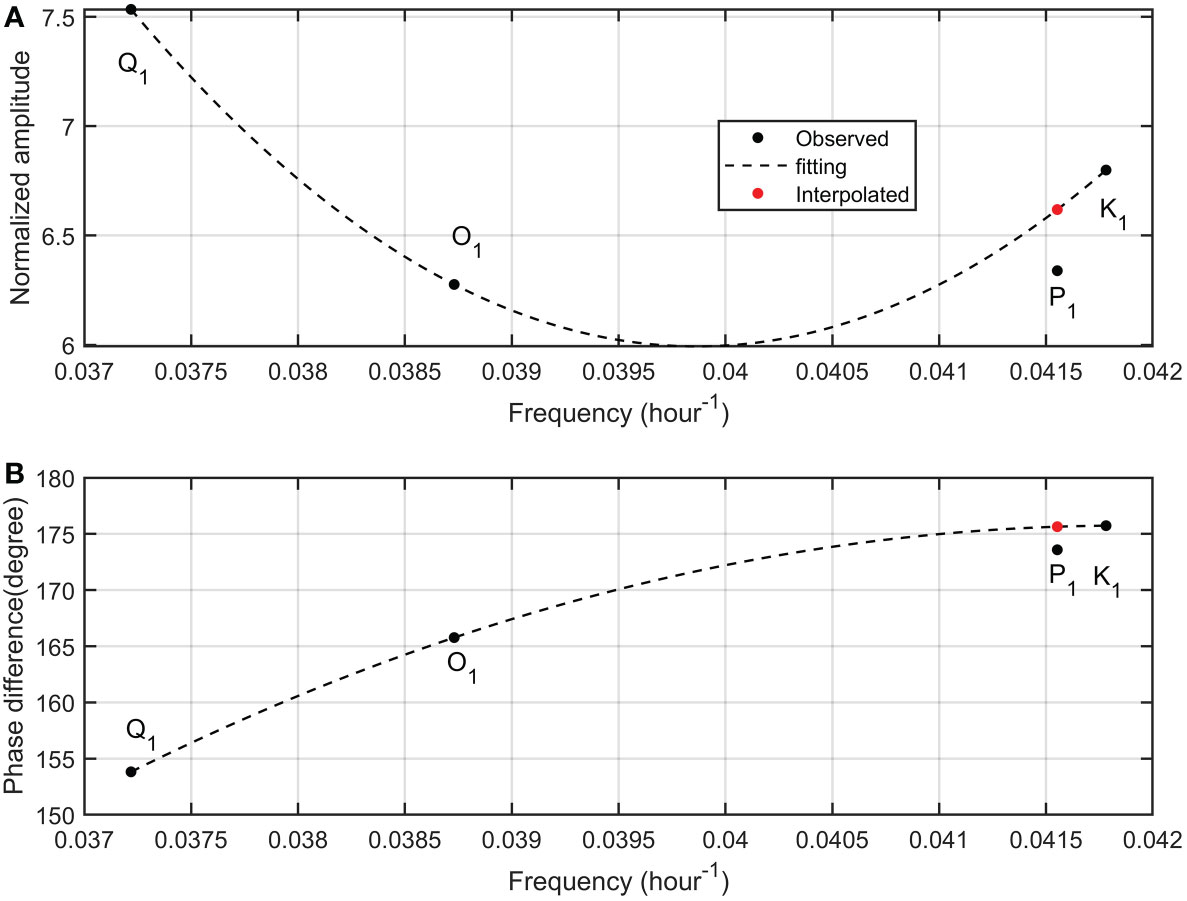
Figure 9 Same as Figure 4, but for surface tides at the mooring. Tidal constants are derived from EOT20 model.

FIGURE 10

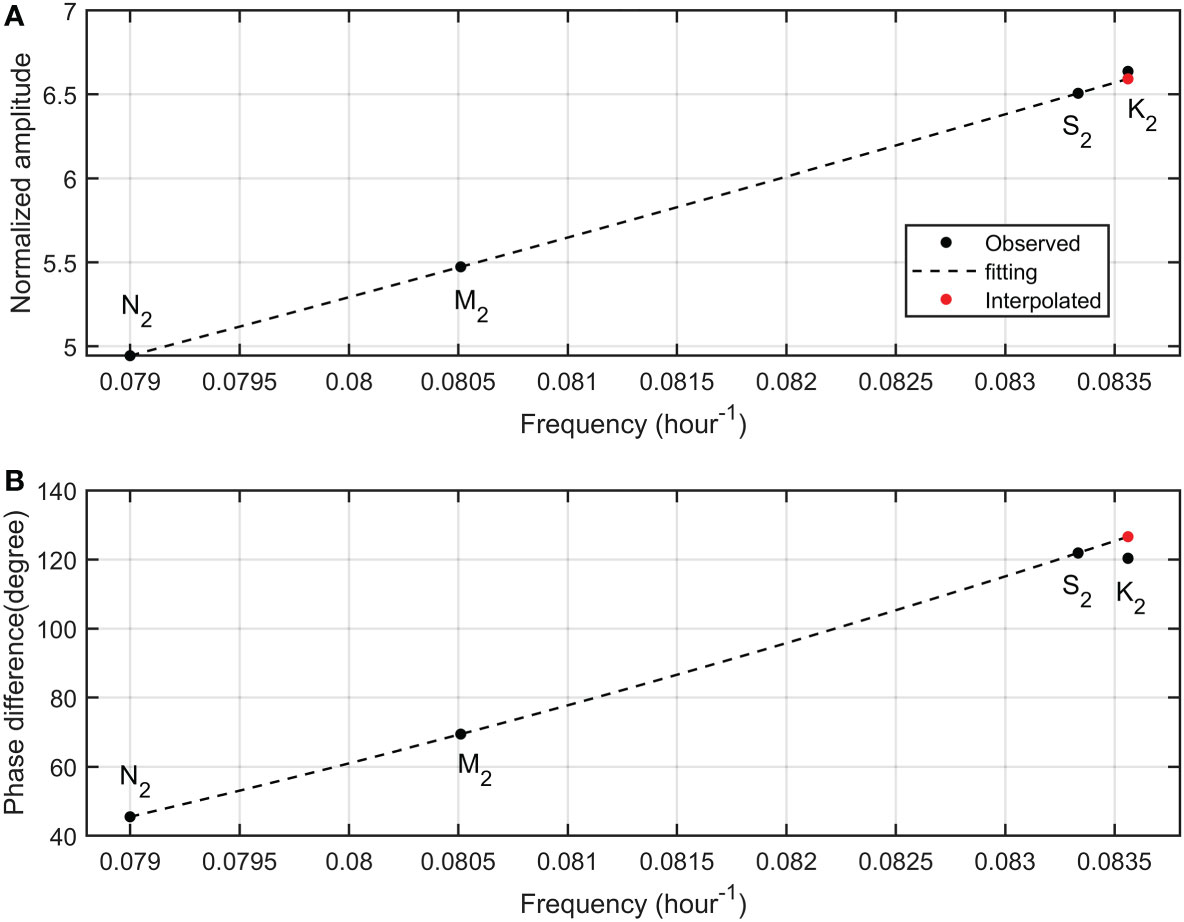
Figure 10 Same as Figure 6, but for surface tides at the mooring. Tidal constants are derived from EOT20 model.

Like tidal currents, the seasonality of surface tides makes P₁ and K₂ tidal admittances deviate from the fitted curves. Based on the method described above, the seasonal P₁ (K₂) tide can be separated from the astronomical P₁ (K₂) tide. The seasonal (astronomical) P₁ tide has an amplitude of 0.46 (8.44) cm and a phase lag of 34.32° (175.64°) while the seasonal (astronomical) K₂ tide has an amplitude of 1.49 (13.69) cm and a phase lag of 37.02° (126.56°). The ratio of the astronomical P₁ amplitude (8.44cm) to the astronomical K₁ amplitude (27.33cm) is 0.309 which indicates that tidal inference using the equilibrium theoretical value (0.331) may be not accurate enough even in the deep sea.

4.2 Limitation of the proposed method

Near-inertial currents are generated by ubiquitous changing wind stress (Munk and Wunsch, 1998; Hu et al., 2023). The frequency of near-inertial currents is near F (i.e. Coriolis frequency), which can be expressed as following:

$\begin{array}{ll}F=2w\sin (\text{L)}& (2)\end{array}$

Where L is latitude while w is the angular velocity of the earth rotation. It is obvious that the period of near-inertial currents changes with latitude. At 26.45°N/S, 27.61°N/S, 29.82°N/S, 30.00°N/S, the periods of near-inertial currents are same to the periods of Q₁, O₁, P₁, and K₁ tides, respectively. Also, at 70.98°N/S, 74.48°N/S. 85.78°N/S, the periods of near-inertial currents are same to the periods of N₂, M₂ and S₂ tides. Therefore, at these latitudes, near-inertial motions can contribute to semi-diurnal and diurnal tides, and the credo of smoothness may be interfered. Note that no near-inertial motions can contribute to K₂ tide.

In addition, in the development of the principle of smoothness, Munk and Cartwright (1966) did not consider the potential influence of tidal resonance which may influence the smoothness of tidal admittances. Hence, care must be taken when applying the proposed method to resonant sea areas, such as the Gulf of Tonkin in the South China Sea, which is well-known for strong diurnal resonance (Pan et al., 2022a; Pan et al., 2023a).

5 Conclusions and summary

Tides and tidal currents display noticeable seasonal variability in numerous sea areas especially in the river estuaries and polar regions. Knowledge on tidal seasonality is fundamental for accurate tidal prediction which is beneficial for substantial human activities in the ocean like navigation and ocean engineering (Müller et al., 2014; Pan et al., 2018a; Pan et al., 2018b; Gan et al., 2021; Pan and Lv, 2021; Wei et al., 2022). Due to different tidal periods and wave lengths, the seasonal variations of main tidal constituents are distinct. The existence of astronomical P₁ and K₂ tides anomalously exaggerate the semi-annual cycles in K₁ and S₂ tides. The method of tidal inference which is widely used in previous studies cannot fully separate astronomical P₁ and K₂ tides from seasonal P₁ and K₂ tides. In this research, a novel but simple method based on the ‘credo of smoothness’ is developed to solve this nettlesome problem. Since tidal admittances are smooth functions of frequencies, astronomical P₁ and K₂ tides can be obtained via the interpolation. The seasonal P₁ (K₂) tide has totally different amplitude and phase compared to the astronomical P₁ (K₂) tide.

We applied the proposed method to explore the seasonality of tidal currents observed in the deep Timor Passage at the depth of 1800m. It is found that the timing and range of seasonal variations of four main constituents are discrepant. The annual and semi-annual ranges of M₂ tide are largest among main constituents. O₁ tide has the smallest annual range while K₁ has the smallest semi-annual range. The peak times of seasonal variations of M₂ and S₂ tides are generally consistent while those of K₁ and O₁ tides are basically not synchronous. Except tidal currents in the deep sea, our method is also suitable for surface tides. It is expected that the proposed method can be widely used in the exploration of tidal seasonality in the global ocean.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HP: Data curation, Conceptualization, Methodology, Visualization, Writing – original draft, Writing – review & editing. JS, TX, FT: Writing – review & editing. ZW: Writing – review & editing, Supervision, Resources, Funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

This study is jointly supported by the Laoshan Laboratory (No. LSKJ202202700), the National Natural Science Foundation of China (NSFC) Projects (42206022, 42076024, 42076023), the Global Change and Air-Sea Interaction II (Contact No.GASI-01-ATP-STwin), the China Postdoctoral Science Foundation (2022M713677) and the Qingdao postdoctoral application research project (QDBSH202108).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amante C., Eakins B. W. (2009). ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis. NOAA Tech. Memorandum NESDIS NGDC-24, 19.

Google Scholar

Amin M. (1985). Temporal variations of tides on the west coast of great Britain. Geophys. J. R. Astron. Soc. 82, 279–299. doi: 10.1111/j.1365-246X.1985.tb05138.x

CrossRef Full Text | Google Scholar

Cao A., Guo Z., Lv X., Song J., Zhang J. (2017). Coherent and incoherent features, seasonal behaviors and spatial variations of internal tides in the northern south China Sea. J. Mar. Syst. 172, 75–83. doi: 10.1016/j.jmarsys.2017.03.005

CrossRef Full Text | Google Scholar

Corkan R. H. (1934). An annual perturbation in the range of tide. P. R. Soc London 144, 537–559. doi: 10.2307/2935543

CrossRef Full Text | Google Scholar

Devlin A. T., Zaron E. D., Jay D. A., Talke S. (2018). Seasonality of tides in southeast Asian waters. J. Phys. Oceanogr. 48 (2), 1169–1190. doi: 10.1175/JPO-D-17-0119.1

CrossRef Full Text | Google Scholar

Du Z., Yu Q. (2021). Comment on “seasonal and nodal variations of predominant tidal constituents in the global ocean”. Cont. Shelf Res. 227, 104524. doi: 10.1016/j.csr.2021.104524

CrossRef Full Text | Google Scholar

Egbert G. D., Ray R. D. (2000). Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405, 775–778. doi: 10.1038/35015531

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng X., Tsimplis M. N., Woodworth P. L. (2015). Nodal variations and long-term changes in the main tides on the coasts of China. J. Geophys. Res. Oceans 120, 1215–1232. doi: 10.1002/2014JC010312

CrossRef Full Text | Google Scholar

Foreman M. G. G., Walters R. A., Henry R. F., Keller C. P., Dolling A. G. (1995). A tidal model for eastern Juan de fuca strait and the southern strait of Georgia. J. Geophys. Res. Oceans 100, 721–740. doi: 10.1029/94JC02721

CrossRef Full Text | Google Scholar

Gan M., Pan H., Chen Y., Pan S. (2021). Application of the variational mode decomposition (VMD) method to river tides. Estuar. Coast. Shelf Sci. 261, 107570. doi: 10.1016/j.ecss.2021.107570

CrossRef Full Text | Google Scholar

Georgas N. (2012). Large Seasonal modulation of tides due to ice cover friction in a midlatitude estuary. J. Phys. Oceanogr. 42, 352–369. doi: 10.1175/JPO-D-11-063.1

CrossRef Full Text | Google Scholar

Hart-Davis M. G., Piccioni G., Dettmering D., Schwatke C., Passaro M., Seitz F. (2021). EOT20: a global ocean tide model from multi-mission satellite altimetry, earth syst. Sci. Data 13, 3869–3884. doi: 10.5194/essd-13-3869-2021

CrossRef Full Text | Google Scholar

Hu Y., Yu F., Chen Z., Si G., Liu X., F and Ren Q. (2023). Two near-inertial peaks in antiphase controlled by stratification and tides in the yellow Sea. Front. Mar. Sci. 9, 1081869. doi: 10.3389/fmars.2022.1081869

CrossRef Full Text | Google Scholar

Huber P. J. (1996). Robust statistical procedures, CBMS-NSF regional conference series in applied mathematics, vol. 68, 2nd ed. Soc. Ind. Appl. Mathematics, 67.

Google Scholar

Kagan B., Sofina E. (2010). Ice-induced seasonal variability of tidal constants in the Arctic ocean. Cont. Shelf Res. 30, 643–647. doi: 10.1016/j.csr.2009.05.010

CrossRef Full Text | Google Scholar

Kang S. K., Foreman M. G. G., Lie H.-J., Lee J.-H., Cherniawsky J., Yum K.-D. (2002). Two-layer tidal modeling of the yellow and East China seas with application to seasonal variability of the M₂ tide. J. Geophys. Res. 107 (C3), 3020. doi: 10.1029/2001JC000838

CrossRef Full Text | Google Scholar

Katavouta A., Polton J. A., Harle J. D., Holt J. T. (2022). Effect of tides on the Indonesian seas circulation and their role on the volume, heat and salt transports of the Indonesian throughflow. J. Geophys. Res. Oceans 127, e2022JC018524. doi: 10.1029/2022JC018524

CrossRef Full Text | Google Scholar

Leffler K. E., Jay D. A. (2009). Enhancing tidal harmonic analysis: Robust (hybrid L1/L2) solutions. Cont. Shelf Res. 29 (1), 78–88. doi: 10.1016/j.csr.2008.04.011

CrossRef Full Text | Google Scholar

Li B., Wei Z., Wang Y., Guo X., Xu T., Lv X. (2021). Application of S_TIDE in exploration of seasonal variations of internal tidal amplitudes in the northern south China Sea. J. Atmos. Oceanic Technol. 38, 1425–1438. doi: 10.1175/JTECH-D-20-0119.1

CrossRef Full Text | Google Scholar

Matte P., Jay D. A., Zaron E. D. (2013). Adaptation of classical tidal harmonic analysis to nonstationary tides, with application to river tides. J. Atmos. Ocean. Technol. 30, 569–589. doi: 10.1175/JTECH-D-12-00016.1

CrossRef Full Text | Google Scholar

Matte P., Secretan Y., Morin J. (2014). Temporal and spatial variability of tidal-fluvial dynamics in the st. Lawrence fluvial estuary: An application of nonstationary tidal harmonic analysis. J. Geophys. Res. Oceans 119, 5724–5744. doi: 10.1002/2014JC009791

CrossRef Full Text | Google Scholar

Müller M. (2012). The influence of changing stratification conditions on barotropic tidal transport and its implications for seasonal and secular changes of tides, cont. Shelf Res. 47, 107–118. doi: 10.1016/j.csr.2012.07.003

CrossRef Full Text | Google Scholar

Müller M., Cherniawsky J. Y., Foreman M. G., von Storch J.-S. (2014). Seasonal variation of the M₂ tide. Ocean Dynam. 64, 159–177. doi: 10.1007/s10236-013-0679-0

CrossRef Full Text | Google Scholar

Munk W. H., Cartwright D. E. (1966). Tidal spectroscopy and prediction. Philos. Trans. R. Soc London A 259, 533–581. doi: 10.1098/rsta.1966.0024

CrossRef Full Text | Google Scholar

Munk W., Wunsch C. (1998). Abyssal recipes II: Energetics of tidal and wind mixing. Deep-Sea Res. Part I-Oceanogr Res. Pap 45, 1977–2010. doi: 10.1016/S0967-0637(98)00070-3

CrossRef Full Text | Google Scholar

Pan H., Devlin A. T., Xu T., Lv X., Wei Z. (2022a). Anomalous 18.61-year nodal cycles in the gulf of tonkin revealed by tide gauges and satellite altimeter records. Remote Sens. 14, 3672. doi: 10.3390/rs14153672

CrossRef Full Text | Google Scholar

Pan H., Guo Z., Wang Y., Lv X. (2018b). Application of the EMD method to river tides. J. Atmos. Oceanic Technol. 35 (4), 809–819. doi: 10.1175/JTECH-D-17-0185.1

CrossRef Full Text | Google Scholar

Pan H., Jiao S., Xu T., Lv X., Wei Z. (2022b). Investigation of tidal evolution in the bohai Sea using the combination of satellite altimeter records and numerical models. Estuar. Coast. Shelf Sci. 279, 108140. doi: 10.1016/j.ecss.2022.108140

CrossRef Full Text | Google Scholar

Pan H., Li B., Xu T., Wei Z. (2023a). Subseasonal tidal variability in the gulf of tonkin observed by multi-satellite altimeters and tide gauges. Remote Sens. 15, 466. doi: 10.3390/rs15020466

CrossRef Full Text | Google Scholar

Pan H., Lv X. (2021). Is there a quasi 60-year oscillation in global tides? Cont. Shelf Res. 222, 104433. doi: 10.1016/j.csr.2021.104433

CrossRef Full Text | Google Scholar

Pan H., Lv X., Wang Y., Matte P., Chen H., Jin G. (2018a). Exploration of tidal-fluvial interaction in the Columbia river estuary using S_TIDE. J. Geophys. Res. Oceans 123, 6598–6619. doi: 10.1029/2018JC014146

CrossRef Full Text | Google Scholar

Pan H., Xu T., Wei Z. (2023b). Anomalously large seasonal modulations of shallow water tides at lamu, Kenya. Estuar. Coast. Shelf Sci. 281, 108203. doi: 10.1016/j.ecss.2022.108203

CrossRef Full Text | Google Scholar

Pawlowicz R., Beardsley B., Lentz S. (2002). Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 28 (8), 929–937. doi: 10.1016/S0098-3004(02)00013-4

CrossRef Full Text | Google Scholar

Ray R. D. (2022). Technical note: On seasonal variability of the M₂ tide. Ocean Sci. 18, 1073–1079. doi: 10.5194/os-18-1073-2022

CrossRef Full Text | Google Scholar

Ray R. D., Egbert G. D., Erofeeva S. Y. (2005). A brief overview of tides in the Indonesian seas. Oceanography 18, 74–79. doi: 10.5670/oceanog.2005.07

CrossRef Full Text | Google Scholar

Robertson R. (2010). Tidal currents and mixing at the INSTANT mooring locations. Dynam. Atmos. Oceans 50, 331–373. doi: 10.1016/j.dynatmoce.2010.02.004

CrossRef Full Text | Google Scholar

Sprintall J., Révelard A. (2014). The Indonesian throughflow response to indo-pacific climate variability. J. Geophys. Res. Oceans 119 (2), 1161–1175. doi: 10.1002/2013JC009533

CrossRef Full Text | Google Scholar

Sprintall J., Wijffels S. E., Molcard R., Jaya I. (2009). Direct estimates of the Indonesian throughflow entering the Indian ocean: 2004-2006. J. Geophys. Res. 114, C07001. doi: 10.1029/2008JC005257

CrossRef Full Text | Google Scholar

St-Laurent P., Saucier F. J., Dumais J.-F. (2008). On the modification of tides in a seasonally ice-covered sea. J. Geophys. Res. 113, C11014. doi: 10.1029/2007JC004614

CrossRef Full Text | Google Scholar

Wang D., Pan H., Jin G., Lv X. (2020). Seasonal variation of the main tidal constituents in the bohai bay. Ocean Sci. 16, 1–14. doi: 10.5194/os-16-1-2020

CrossRef Full Text | Google Scholar

Wang J., Zhang Z., Li X., Wang Z., Li Y., Hao J., et al. (2022). Moored observations of the timor passage currents in the Indonesian seas. J. Geophys. Res. Oceans 127, e2022JC018694. doi: 10.1029/2022JC018694

CrossRef Full Text | Google Scholar

Wei Z., Pan H., Xu T., Wang Y., Wang J. (2022). Development history of the numerical simulation of tides in the East Asian marginal seas: An overview. J. Mar. Sci. Eng. 10, 984. doi: 10.3390/jmse10070984

CrossRef Full Text | Google Scholar

Wunsch C. (1975). Internal tides in the ocean. Rev. Geophys. 13, 167–182. doi: 10.1029/RG013i001p00167

CrossRef Full Text | Google Scholar

Xu Z., Yin B., Hou Y., Liu A. K. (2014). Seasonal variability and north-south asymmetry of internal tides in the deep basin west of the Luzon strait. J. Mar. Syst. 134, 101–112. doi: 10.1016/j.jmarsys.2014.03.002

CrossRef Full Text | Google Scholar

Zhao J., Zhang Y., Liu Z., Zhao Y., Wang M. (2019). Seasonal variability of tides in the deep northern south China Sea. Sci. China Earth Sci. 62, 671–783. doi: 10.1007/s11430-017-9315-7

CrossRef Full Text | Google Scholar