Underwater ice adaptive mapping and reconstruction using autonomous underwater vehicles

The undersides of floating ice shelves and sea ice in the Antarctic and Arctic are among the least accessible environments on Earth. The interactions between ice shelves, sea ice, and the ocean are of considerable scientific interest. In order to fully understand the complex picture of sea ice, and not just its surface, it is quite necessary to map the underside to comprehend the full context of its growth and decay patterns. Autonomous Underwater Vehicles (AUVs) are rapidly becoming the desired platform of choice for mapping the underside of sea ice to provide high-resolution 3D views of sea ice topography. To increase the efficiency and accuracy of AUV sampling behaviors is significant for the under-ice observation mission given its limited endurance. In this paper, we present a low-cost underwater ice mapping framework for small-sized AUVs using adaptive sampling and map reconstruction methods. A small-sized AUV is cost-effective and convenient for operation in polar regions; however, due to its limited loading capacity and energy, it is more applicable for the vehicle to carry single-beam sonar for ice bottom mapping but not multi-beam. Thus, the essential issue in this application is how to obtain the key information of ice topography and how to reconstruct the map of ice draft (namely underwater ice thickness) with AUV sparse mapping swathes. To address this, we propose a graphics-based adaptive mapping method to densify the measuring of ice bottom surface with ‘noticeable’ variations; moreover, we also present a sparse approximation method for ice draft map reconstruction using the sparse mapping swathes from a single-beam sonar. Our efforts are to introduce an effective and efficient approach for underwater ice mapping using low-cost small-sized AUVs. Our proposed adaptive mapping and reconstruction methods are validated in the under-ice scenario created using the field data.

1 Introduction

The polar regions remain some of the least explored parts of the planet’s oceans, despite their central role in understanding climatic processes and change (Singh et al., 2017). The undersides of floating ice shelves and sea ice in the Antarctic and Arctic are among the least accessible environments on Earth (Dowdeswell et al., 2008). The interactions between ice shelves, sea ice, and the ocean are of considerable scientific interest, as the nature and rate of freezing and melting processes that take place are of wider significance to the global environmental system (Broecker, 1991).

Limitations of access have long restricted exploration and investigation of the cavities beneath ice shelves and the underside of sea ice to a limited number of drill holes and scientific utilization of submarines (Dowdeswell et al., 2008). However, the results were statistically weak and said little about the shape of the ice bottom, the distribution of pressure ridge depths or the difference between the roughness levels of ridged and level ice, or between first-year and multi-year ice. All these aspects are important to understand the multifaceted concept of sea ice and its effect on the surrounding climate. In order to fully understand the complex picture of sea ice, and not just its surface, it is quite necessary to map the underside to comprehend the full context of its growth and decay patterns (Wadhams and Krogh, 2019). The topography of sea ice is also important for such diverse applications as evaluating its containment potential for oil blowouts, its role as a substrate for a sea ice ecosystem, its impact on icebreaker design, and its scattering potential for under-ice acoustic propagation (Wadhams, 2012).

The use of emerging technologies like unmanned underwater vehicles provides an effective approach by which these very inaccessible and inhospitable parts of the global ocean and cryosphere can be investigated safely. The development of free-flying autonomous underwater vehicles (AUVs) with ranges of tens to hundreds of kilometres enables extensive missions to take place beneath sea ice and floating ice shelves (Dowdeswell et al., 2008). They are rapidly becoming the desired platform of choice for mapping the underside of sea ice to provide a high-resolution 3D view of sea ice topography.

The earliest AUV surveys under ice were carried in the Beaufort Sea in 1972 using a vehicle called the Unmanned Arctic Research Submersible (UARS), equipped with three narrow-beam upward sonars (Francois and Nodland, 1972). The observations of under-ice topography were collected by UARS (Francois, 1977). The International Submarine Engineering Company (ISE) together with the Canadian Defence Research Establishment (Atlantic) developed a large AUV called Theseus for laying optical fiber cables in ice-covered waters in the Arctic in 1996, but not for scientific data collection purposes (Ferguson et al., 1999). In 2001, the UK Autosub vehicle successfully used a single-beam upward sonar for underwater ice observation in the Antarctic (Brierley et al., 2002). Similarly, an ice profiling sonar was applied in the ALTEX AUV, developed by Monterey Bay Aquarium Research Institute, in an Arctic test cruise (Tervalon and Henthorn, 2002). The research team at the University of Cambridge pioneered the collection of 3D ice underside mapping data using a multibeam sonar with the Autosub II AUV off NE Greenland in 2004 (Wadhams et al., 2006). Since then, a systematic measure of the shape of the sea ice underside has been conducted worldwide. The same vehicle later collected multibeam sonar data under the Fimbul ice shelf in the Antarctic (Nicholls et al., 2006).

The SeaBed class twin-hulled AUV developed by WHOI has conducted a dozen research expeditions to polar regions in the last decade, including missions in support of biological and geological mapping, as well as sea ice studies in both the Arctic and Antarctic (Singh et al., 2017). Ten floe-scale maps of sea-ice draft were collected by SeaBed AUV missions undertaken during two recent early spring voyages (IceBell and SIPEX-2) in three regional sectors around Antarctica. These maps reveal heavy deformation in all three near-coastal regions, producing a mean sea ice draft well in excess of that typically observed from drilling data (Williams et al., 2015). The University of Tasmania used an ISE Explorer class AUV (named nupiri muka) to collect data from beneath both sea ice and ice shelves to understand how the oceans interact with Antarctic ice shelves (King et al., 2018). This powerful vehicle was deployed to the Sørsdal ice shelf in East Antarctica in 2019. With the valuable data collected by the nupiri muka AUV, it was found that cold and salty water present beneath the ice shelf with a deep seafloor trough at the entrance to the ice shelf, indicative of a cold ocean environment with low melt rates (Gwyther et al., 2020).

For ease of AUV launch and recovery, such as from holes in the ice or from boats alongside a sea ice edge, small AUVs were welcome in the polar missions. The Icelandic Gavia AUV was deployed in the Beaufort Sea in 2007 and in the Lincoln Sea in 2008 to obtain valuable under-ice sonar images using a GeoSwath multi-beam sonar system (Wadhams and Doble, 2008; Doble et al., 2009). The vehicle operated at a 50m depth in order to not collide with the multi-year ice ridging, at a 30m depth in areas with first-year ice, and in melt regions at a 20m depth (Wadhams and Krogh, 2019). A REMUS AUV was deployed beneath coastal sea ice offshore of Barrow, AK, to obtain cross-shore hydrographic transects (temperature, salinity, and velocity versus depth) that would provide estimates of the transport of relatively dense, salty water from the Chukchi Sea to the Arctic Ocean in winter (Plueddemann et al., 2012). An echosounder was pointed vertically and used as an upside-down altimeter to record the distance from the vehicle to underside of the ice for ice keel avoidance, but not for underwater ice observation.

It can be assumed that operating an AUV under ice will bring about many challenges in terms of reliable communication, localization, obstacle avoidance, and so on. In such a situation, to increase the efficiency and accuracy of AUV sampling behaviors is significant for the under-ice observation mission given its limited endurance. However, the existing studies usually applied the AUVs for under ice data collection by designing the fixed sampling trajectory beforehand and offline, which means the vehicle just followed the fixed trajectory to complete the mission, and was not able to change its sampling behavior adaptively online for increased sampling accuracy and efficiency.

Adaptive ocean observation refers to fixed or mobile observing platforms being able to autonomously adjust measurement/operational parameters based on the oceanographic environment and signals, aiming at acquiring key information of the observed oceanographic processes (Zhang, 2013). Adaptive detection and sampling by AUVs have achieved unprecedented accuracy and efficiency in studies of thermoclines (Cruz and Matos, 2010; Petillo et al., 2010; Zhang et al., 2012a), upwelling fronts (Zhang et al., 2012b; Zhang et al., 2012c), internal waves (Cazenave et al., 2011; Petillo and Schmidt, 2014), and other ocean dynamic phenomena (Zhang et al., 2010; Zhang et al., 2011). However, adaptive observation techniques have been less considered in underwater ice mapping missions so far. To the best of our knowledge, this paper presents the first study on the adaptive mapping of underwater ice using AUVs.

In our study, we present a low-cost underwater ice mapping framework for small-sized AUVs using adaptive sampling and map reconstruction methods. A small-sized AUV is cost-effective and convenient for operation in polar regions; however, due to its limited loading capacity and energy, it is more applicable for the vehicle to carry single-beam sonar for ice bottom mapping but not multi-beam. Thus, the essential issue in this application is how to obtain the key information of ice topography and how to reconstruct the map of ice bottom with AUV sparse mapping swathes. To address this, we propose a graphics-based adaptive mapping method to densify the measurements of ice bottom surface with ‘noticeable’ variations; moreover, we also present a sparse approximation method for ice map reconstruction using the sparse mapping swathes of single-beam sonar. Our efforts are to introduce an effective and efficient approach for underwater ice mapping using low-cost small-sized AUVs; however, not all the aspects of the field work are taken into account in our current study, such as the impact of AUV navigation and sampling errors on the mapping and reconstruction results.

The rest of this paper is organized as follows. Section 2 presents the vehicle and sensors we apply for the underwater ice mapping mission. In Section 3, we introduce the framework of this study as well as our proposed methods on AUV adaptive mapping and reconstruction of the regional ice draft. The proposed framework and methods are validated in Section 4; the applicability analysis is conducted as well. Section 5 summarizes the main findings and describes some additional avenues for continuing research.

2 Platform and sensors

In this section, the platform and sensors we apply for underwater ice adaptive mapping are presented. As we mentioned above, for ease of operation, a small-sized AUV is considered; see Figure 1. The vehicle is 1.8m length and has a diameter of 0.2m. The maximum working depth is 120m and the nominal forward running speed is 1m/s (with the maximum speed of 2m/s). In order to conduct the mission safely and effectively under ice, the vehicle is equipped with a variety of sensors and sonars, such as the Conductivity-Temperature-Depth (CTD) sensor and the Doppler Velocity Log (DVL, including altimeter function) for hydrological measurements, the forward looking sonar for obstacle avoidance, the side-scan sonar and the single-beam sonar (altimeter) for bottom mapping, the acoustic modem for underwater communication, and the USBL beacon for underwater localization. The observation section at the bow of the vehicle can turn 180° to make the sonar scan either upward or downward. In our application, the underwater ice thickness (namely ice draft) can be measured by the difference between the pressure sensor and the altimeter readings, when the altimeter scans upward.

FIGURE 1

Figure 1 AUV for underwater ice mapping.

The CTD is from Sea & Sun Technology GmbH. The working range of the pressure sensor is 20bar, while the accuracy is up to 0.05% full scale in the given temperature range. A Teledyne RD Instruments Pathfinder 600kHz Phased Array DVL is adopted. The DVL has both bottom tracking and water tracking capabilities, so it can tell both the vehicle velocity and current velocity within its working range, as well as the altitude with respect to the bottom. The maximum bottom tracking altitude is 150m; the one-way beam width is 2.2°. A 120kHz Echo Sounder from IMAGENEX is used as an independent altimeter as well. The beam width of its transducer is 20°, while its working range is up to 300m. The resolution of the measured altitude is within 0.1% of the working range. The sampling rates of both the altimeter and the pressure sensor are set as 5Hz. Thus, the ice draft measurements are collected sparsely along AUV trajectory. So, it is challenging to obtain the key variation information of the underwater ice topography with the sparse measurements of ice draft efficiently; it is also essential to reconstruct the ice draft map using the sparse ice draft samplings effectively. In this work, we will focus on the study of adaptive mapping and map reconstruction methods using our AUV to address the above two issues (namely increasing the efficiency and the effectiveness of the mapping mission). Note that the actual specifications of our AUV and the equipped sensors mentioned here will be considered in our later simulations for the proposed methods validation in Section 4.

3 Methods

In this section, the framework of our study on adaptive mapping and reconstruction of underwater ice is firstly introduced; then the details of our proposed adaptive mapping and reconstruction methods are presented, respectively.

3.1 Framework for adaptive mapping and reconstruction of underwater ice

Given the endurance limitation of the vehicle, and also for safety consideration, the total mapping area is usually divided into several blocks in the real mapping mission; the vehicle will map each block one by one. To make the mission controllable, the mapping area of each block is set as 500m×500m in our study. The selection of this scale is reasonable because the sea ice draft measurements within this range are fine enough to calibrate the estimated sea ice draft using satellite remote sensing image, such as MODIS data with a pixel size of 250m.

As shown in Figure 2, in our study the framework for the generation of underwater ice map starts from AUV rough mapping of the given block globally along a predetermined trajectory below the ice surface; then the collected ice draft data is used to reconstruct the ice map online using interpolation method initially; with this rough global ice map, the AUV will further identify the regions with ‘noticeable’ ice draft variation based on certain graphical criteria and conduct intensive mapping of these regions locally along an optimized trajectory, which is designed by a trajectory planner; finally, both the rough global measurements and the refined local measurements will be applied together to reconstruct the final ice map using sparse approximation method.

FIGURE 2

Figure 2 Framework for underwater ice adaptive mapping and reconstruction. The mapping and reconstruction results are shown in the right subplots: (A) Rough mapping, (B) Rough reconstruction, (C) Intensive mapping, and (D) Refined reconstruction.

The main intention of this proposed framework is to develop AUV intelligence to improve the efficiency of underwater ice mapping. It is worth mentioning that this framework is applicable to the AUV equipped with either a single-beam sonar or a multi-beam sonar. Moreover, there are two rounds of ice map reconstruction: the first one is for rough map reconstruction and happens before intensive mapping, for which some well-known linear interpolation method is applied due to its rapidness and convenience; the second one aims for the final refined map reconstruction and occurs after intensive mapping, and we use our proposed sparse approximation method to complete this.

3.2 Rough mapping and reconstruction

The purpose of rough mapping and rough map reconstruction is to collect and present the ice draft information in the observation area globally but roughly. In rough mapping, the AUV maps the observation area at a constant depth along a predetermined trajectory, which could be zig-zag or lawnmower patterns. Before running in a zig-zag or lawnmower trajectory, the vehicle will go around the observation area once to map the ice bottom along the boundary of the target block. The constant depth for mapping is decided considering the working range of the pressure sensor and the altimeter as well as the possible variation range of the ice draft in that area, according to the available historic information. The spacing between the trajectory segments is determined by general estimation before the mission, depending on the size of the observation area, the endurance of the vehicle, and the expected resolution of the rough map.

The rough mapping data is sampled sparsely in space. In order to generate the global rough ice draft map of the observation area in situ, we use the well-developed Kriging method to reconstruct the rough map online, due to its low demand on the computing power of AUV processor. Kriging is a method of spatial interpolation that originated in the field of mining geology. It is one of several interpolation methods that use a limited set of sampled data points to estimate the value of a variable over a continuous spatial field (Le and Zidek, 2006; Bivand et al., 2013). It differs from simpler interpolation methods, such as Inverse Distance Weighted Interpolation, Linear Regression, or Gaussian decays, which use the spatial correlation between sampled points to interpolate the values in the spatial field. The interpolation of Kriging is based on the spatial arrangement of the empirical observations, rather than on a presumed model of spatial distribution. It can be a helpful method to preserve spatial variability that would be lost using a simpler method if there is at least moderate spatial autocorrelation (Auchincloss et al., 2007).

3.3 Adaptive mapping

Based on the roughly reconstructed global ice draft map after the predetermined sampling along the zig-zag trajectory, further adaptive mapping can be conducted. The principle for adaptive mapping is to firstly identify and extract the local regions of interest for intensive mapping as these regions present the key variation of the ice topography in the given area; then, the vehicle will be guided to cover these regions along an optimized trajectory, considering the maneuverability of the vehicle and the efficiency of completing the mission. The methods for the identification and extraction of the interested regions as well as the trajectory planner for intensive mapping will be introduced, respectively.

3.3.1 Identification of interested regions

To identify the regions of interest autonomously from the roughly reconstructed ice map, we need to define the identification rules quantitatively. As we mentioned before, the interested regions are the areas that present remarkable topographic variations; here, we propose three criteria to identify those regions: the ice draft, the ice draft gradient, and the ice draft entropy methods.

(1) Ice draft method

It is the simplest method that involves defining a certain threshold of ice draft for thicker ice regions’ identification, and regions with larger ice draft than the defined threshold are the interested regions for intensive mapping. The ice draft method can be described as below:

$\begin{array}{ll}\begin{array}{c}d\ge D_{thrd,}\end{array}& (1)\end{array}$

where d denotes the ice draft variable; D_thrd is the defined ice draft threshold, the value of which can be assigned based on the average of the roughly mapped ice draft measurements, like this

$\begin{array}{ll}\begin{array}{c}{D}_{thrd}=\frac{K}{N}{\displaystyle \sum _{n=1}^N}{D}_n,\end{array}& (2)\end{array}$

where N is the number of ice draft measurements in rough mapping; K is a proportional coefficient, which can be defined as either a constant or a variable. If the coefficient K is set as a constant, its value is usually chosen to be larger than 1, in order to identify a limited number of interested regions for further intensive mapping within the AUV’s endurance limit. In the latter case, its value could be adjusted according to the total numbers or the area of the interested regions adaptively. Or, for simplicity, we can easily take the value at a certain percentile of the ice draft measurements as the threshold based on experience.

(2) Ice draft gradient method

The second method is to solve the gradient of the ice draft in the roughly reconstructed map. The ice draft gradient method detects the edges of thicker ice regions by looking for the maximum and minimum in the first derivative of the ice draft in two perpendicular directions of the roughly reconstructed ice draft map, which can help to identify the regions of interest with large absolute values of ice draft gradient for further intensive mapping.

There are many edge detection methods by gradient operators such as the Sobel, Roberts, and Laplace operators, many of which are used to clarify the local transformation (for example, sharp edges) in the optical metrology. Taking the Sobel operator as an example, it performs a 2-D spatial gradient operation on an image to enhance the edges. The operator consists of a pair of 3-by-3 convolution kernels, S_x and S_y respectively for the two perpendicular directions, while the second kernel is simply a rotation of the first (Jiang and Scott, 2020):

$\begin{array}{ll}\begin{array}{c}{S}_x=\left[\begin{array}{ccc}1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right], S_y=\left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]\end{array}& (3)\end{array}$

The above convolution kernels are separately applied to the ice draft map to produce the approximate G_x and G_y gradients for each pixel to detect edges in vertical and horizontal directions.

$\begin{array}{ll}\begin{array}{c}{G}_x=S_{x}T, G_y=S_{y}T\end{array}& (4)\end{array}$

These can then be combined to find the absolute magnitude of the gradient at each point:

$\begin{array}{ll}\begin{array}{c}{G}_a=\sqrt{G_x^2+G_y^2}\end{array}& (5)\end{array}$

Edges in the map are emphasized because the gradients at the edges are usually larger than those in the homogeneous region. In the application of the Sobel operator, coefficients of the convolution kernels can be adjusted according to our requirement provided the kernel honors the properties of derivative masks. An increase in the coefficients of the middle row or column in the 3-by-3 convolution kernels increases the number of detected edges (Misra and Wu, 2020).

With the solved ice draft gradient map, the ice draft gradient method can be described as this:

$\begin{array}{ll}\begin{array}{c}g\ge G_{thrd,}\end{array}& (6)\end{array}$

where g denotes the ice draft gradient variable; G_thrd is the defined ice draft gradient threshold, the value of which can be assigned based on the average or certain percentile of the ice draft gradient in the map, similar to the one determined in the ice draft method.

(3) Ice draft entropy method

The last method is to calculate the entropy of the ice draft in the roughly reconstructed ice map, which is called the ice draft entropy method. Entropy is a measure of uncertainty or randomness in an image (Dey, 2018). Local entropy is related to the complexity contained in a given neighborhood, typically defined by a structuring element. The entropy filter can detect subtle variations in the local gray level distribution (scikit-image, 2022). In our case, the area in the ice map with relatively large values of local entropy presents the regions of interest with significant ice draft variation.

In information theory, information entropy is the log-base-2 of the number of possible outcomes for a message. To calculate the entropy of the ice draft map, the ice draft measurements should be converted to the gray image format; then the entropy value of the 9-by-9 neighborhood around the corresponding pixel can be calculated to compute the local entropy of the map:

$\begin{array}{ll}\begin{array}{c}e=-{\displaystyle \sum _{i=0}^{255}}{P}_i{\log }_2{P}_{i,}\end{array}& (7)\end{array}$

where e denotes the ice draft entropy variable; P_i is the probability (obtained from the normalized histogram of the gray image) associated with the gray-level, i. For pixels on the borders of the map, the symmetric padding method is applied, in which the values of padding pixels are a mirror reflection of the border pixels in the map (entropyfilt, MathWorks, 2022).

With the solved ice draft entropy map, the ice draft entropy method can be described as this:

$\begin{array}{ll}\begin{array}{c}e\ge E_{thrd,}\end{array}& (8)\end{array}$

where E_thrd is the defined ice draft entropy threshold, the value of which can be assigned based on the average or certain percentile of the ice draft entropy in the map, similar to the one determined in the above methods.

Thus, with the above proposed methods, the interested regions for further intensive mapping can be identified and compared, which will be discussed in the later section.

3.3.2 Shape extraction of interested regions

Actually, the identified regions of interest are outlined by spatial point sets, while the boundaries of the interested regions should be further generalized using shape extraction algorithm. We use Alpha shape algorithm to generalize the boundaries of the interested regions, which is an approach to formalize the intuitive notion of “shape” for spatial point sets. The Alpha shape is a concrete geometric concept which is mathematically well defined: it is a generalization of the convex hull and a subgraph of the Delaunay triangulation. Given a finite point set, a family of shapes can be derived from the Delaunay triangulation of the point set; a real parameter, “alpha,” controls the desired level of detail (François, 2022).

Since some of the extracted regions are large and some small, we choose to calculate the area of the Alpha shapes to sort the scale of the regions, and abandon the small ones by defining a certain threshold. Considering the limitation of AUV maneuverability, we neglect the extracted Alpha shapes with areas less than 1% of the total mission area.

The identified regions of interest usually have irregular boundaries and random distribution, which is less convenient for following AUV trajectory planning for intensive mapping. Hence, it is necessary to extract the regions of interest using regularized shapes, such as rectangle, circle, or ellipse, to envelope the boundary of the interested region. For the sake of simplicity, in our study we use a rectangle to envelop each region of interest; thus, the shape extraction problem turns into finding the minimum area bounding rectangle of the interested region.

In general, the minimum area bounding rectangle method could find the minimum area rectangle of the target graph by gradually rotating the graph and projecting it into the coordinate axis (D'Errico, 2022). The rotation method has the disadvantage that the accuracy of the solved minimum area bounding rectangle depends on the size of the rotation interval. In our study, the rotation interval is tuned for the acceptable accuracy and calculation time. We also set a certain area threshold to filter the minimum area bounding rectangles with small areas, given the limitation of AUV maneuverability.

3.3.3 Trajectory planning for intensive mapping

Once the regularized shapes of the interested regions are extracted, the trajectory planner will plan an optimal trajectory for the vehicle to cover the interested regions for intensive sampling. The trajectory planning is not only to intensively cover each individual interested region but also to connect the total regions of interest together to generate one executable and optimal trajectory.

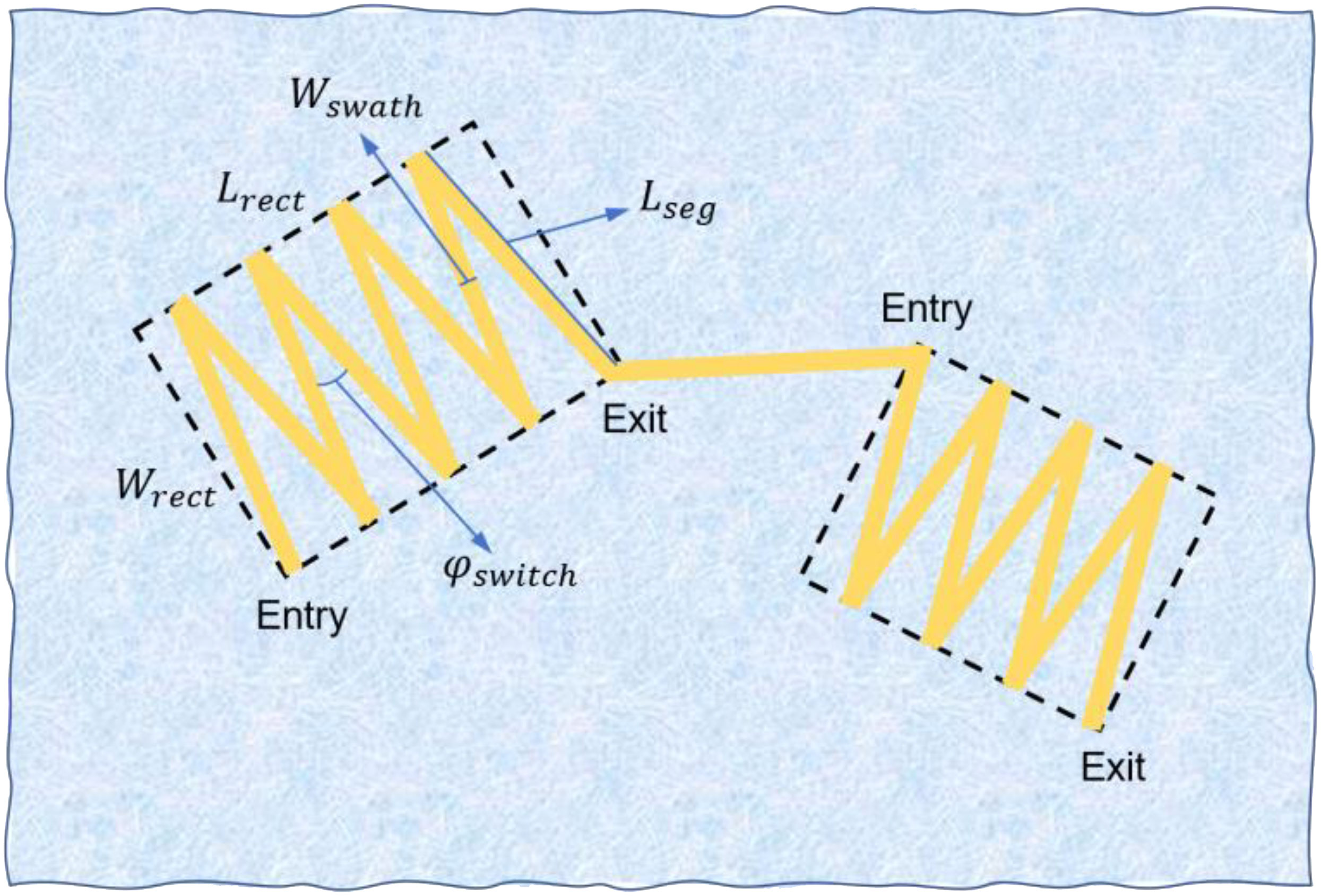
The coverage for the intensive mapping of each individual region of interest also uses a zig-zag trajectory in the horizontal plane below the ice bottom. The heading switch angle is controlled according to the aspect ratio and the area of the interested rectangular regions adaptively, also considering AUV heading maneuverability limitation. For trajectory planning, we define a coverage ratio to determine the spacing of the zig-zag segments within each rectangle:

$\begin{array}{ll}\begin{array}{c}R=\frac{W_{swath}{N}_{seg}{L}_{seg}}{L_{rect}{W}_{rect}},\end{array}& (9)\end{array}$

where L_rect and W_rect are respectively the length and width of the extracted rectangular region; W_swath indicates the swath width of the single-beam sonar; N_seg is the segment number of the zig-zag trajectory within one rectangle; and L_seg is the length of each segment in zig-zag trajectories and can be calculated by the following expression:

$\begin{array}{ll}\begin{array}{c}{L}_{seg}=\sqrt{W_{rect}^2+{\left(\frac{L_{rect}}{N_{seg}}\right)}^2}& .\end{array}& (10)\end{array}$

The swath width of the sonar will vary with the varied vertical distance between the vehicle and the ice bottom if the vehicle runs at a given water depth constantly. We assume the vehicle maintains level flight with the pitch angle fixed at 0, so that the sonar performance will not be affected by the attitude adjustment of the vehicle. N_seg can be tuned if the values of L_rect and W_rect are known, in order to make the value of the coverage ratio R within a certain range (like between 30% and 40%). This range is chosen considering both the efficiency of the mapping mission and AUV heading maneuverability limitation, based on our existing experience. The heading switch angle of zig-zag trajectory should satisfy:

$\begin{array}{ll}\begin{array}{c}{\phi }_{switch}=2*arctan\frac{L_{rect}}{N_{seg}{W}_{rect}}\ge {\phi }_{limit.}\end{array}& (11)\end{array}$

where ${\phi }_{limit}$ is decided upon the heading maneuverability limit of our vehicle, and is set as 10° in our study. Moreover, we can choose whether to use an even number or an odd number for N_seg to control the location of the entry and exit of the zig-zag trajectory within the rectangular region, so as to facilitate the connection between the interested regions. The definitions of the symbols mentioned above are illustrated in Figure 3.

FIGURE 3

Figure 3 AUV trajectory for intensive mapping in the minimum area bounding rectangles (Top view).

As for the planning of the global trajectory that connects all the interested regions, the total running time is considered as the optimization objective, while the maneuverability of the vehicle is taken as the boundary condition. For simplicity, we consider that the total AUV trajectory is composed by straight running lines and heading switch arcs. The total AUV trajectory for intensive mapping can be optimized by solving the following formula:

$\begin{array}{ll}\text{min}(T)=\min (k_{line}\frac{L_{line}}{v}+k_{arc}\frac{{\phi }_{arc}}{\omega }),s.t. {\phi }_{switch}\ge {\phi }_{limit}& (12)\end{array}$

where T is the total running time; L_line denotes the total length of the straight lines; ${\phi }_{arc}$ presents the total arc for heading switch; v is the velocity of straight running and $\omega$ is the angular rate of heading switch, while both v and $\omega$ can be solved from AUV dynamic model. Here, k_line and k_arc are respectively the weights of straight running time and heading switch time.

In our study, the AUV trajectory is planned on an AUV dynamics level; that means both the translational and the angular velocities are solved from AUV dynamic model in the trajectory planner. Thus, the cost of both straight running and turning motion can be taken into account in AUV trajectory planning. Generally, a longer trajectory will consume more running time, and more turning motion will take more running time as well. Therefore, we use the running time as the metric to evaluate the trajectory planning results.

3.4 Refined reconstruction

In our previous work (Zeng et al., 2021), we proposed a sparse approximation method to solve the Doppler smearing and aliasing problems when AUV samples and reconstructs ocean dynamic fields with temporal and spatial variation, such as gravity plume or internal waves. Sparse approximation is a technique to reconstruct a function by using a small number of basis functions chosen from a large set of basis functions (Girosi, 1998). A sparse signal means that it can be represented on a basis where most basis coefficients are zero. As fields of ocean phenomena are generally continuous and smooth, one could safely assume that they have sparse representations on an appropriate basis, either in the spatial dimensions or in the time dimension (Candes and Wakin, 2008; Mitra et al., 2015).

For our underwater ice mapping mission, the sea ice bottom is a frozen topographic field with slow temporal variation and unpredictable spatial variation during the mission duration (of several hours). So, in our current study we propose a sparse approximation method to reconstruct a spatially varying underwater ice field using AUV mapping data, while the temporal variation of the ice bottom in a much larger time scale will be considered in our future work. As we explained above, the sparse approximation method is applied for the final refined reconstruction of the ice draft map using both the rough and the intensive mapping data. Usually, this is conducted by data post-processing offline given its higher computing power requirements.

3.4.1 Theory of method

The sparse approximation method for ice bottom map reconstruction is mainly based on the general theory of Adcock (2017). Assume that a spatially varying ice draft field of sea ice in a horizontal section can be sparsely represented by a function f in a 2-dimensional bounded domain D = [-1,1]², and

$\begin{array}{ll}\begin{array}{c}f={ }_{i\in \mathbb{N}02}^{\sum }{c}_i\varphi i_{,}\end{array}& (13)\end{array}$

where i denotes a 2-dimensional multi-index $i=(i_1,i_2)\in {\mathbb{N}}_0^2$, ${\left\{{\varphi }_i\right\}}_{i\in {\mathbb{N}}_0^2}$ presents the 2-dimensional Legendre Polynomials (LP) basis, and ${(c_i)}_{i\in {\mathbb{N}}_0^2 }\in {\ell }^2({\mathbb{N}}_0^2)$ are the sparse coefficients of the basis. The dimensions of i are orderly representing the two spatial dimensions in the horizontal plane. The basis ${\left\{{\varphi }_i\right\}}_{i\in {\mathbb{N}}_0^2}$ is the tensor product of the univariate LP basis in each direction,

$\begin{array}{ll}\begin{array}{c}{\varphi }_i={\varphi }_{i_1}\otimes {\varphi }_{i_2}\end{array}& (14)\end{array}$

Note that the basis ${\left\{{\varphi }_i\right\}}_{i\in {\mathbb{N}}_0^2}$ consists of infinite modes and is not numerically computable. For the sake of computability, the basis ${\left\{{\varphi }_i\right\}}_{i\in {\mathbb{N}}_0^2}$ is truncated by a truncation parameter matrix $K\in {\mathbb{N}}^{2\times 2}.$. For simplicity, we let K be a symmetric matrix, where all diagonal elements are set to be K_L and others are set to be K_S. K_L and K_S are chosen to be positive integers, and ${\kappa }_L\ge {\kappa }_S$. Larger K_L and K_S increase the potential of the reconstructions for representing higher frequency and larger wavenumber components of the field. However, larger K_L and K_S will increase the problem scale as well as the solving time, so they are usually set to be as large as possible, as long as the computational power allows. The selection of K_L and K_S is discussed in detail in (Zeng et al., 2021). Define a subset $\text{Λ} \subset {\mathbb{N}}_0^2$:

$\begin{array}{ll}\begin{array}{c}\Lambda = {\displaystyle \underset{m=1}{\overset{2}{\cup }}\left\{k\in {\mathbb{N}}_0^2:k_d\le K_{d,m}-1,d=1,2\right\}.}\end{array}& (15)\end{array}$

where k denotes the element of the matrix K. Thus, the truncated LP basis is denoted by ${\left\{{\varphi }_i\right\}}_{i\in \text{Λ}}$, in which only the lower modes of the basis are retained.

In this way, the truncated approximation to f can be represented by

$\begin{array}{ll}\begin{array}{c}\tilde{f}={ }_{i\in \text{Λ }}^{\sum }{\widehat{c}}_i\varphi i_{,}\end{array}& (16)\end{array}$

where ${({\widehat{c}}_i)}_{i\in {\mathbb{N}}_0^2 }$ denotes the sparse coefficients of the truncated LP basis to be estimated.

It is assumed that the AUV collects N normalized ice draft measurements ${\left\{y_n\right\}}_{n=1}^N\in {[-1,1]}^N$ at dispersed spatial points of ${\left\{q_n\right\}}_{n=1}^N$, $q_n\in D$ when sampling the observation area. To exploit the information of all AUV sampling data and reconstruct the ice bottom map, one can estimate $\widehat{c}$ and find the sparse approximation of the ice draft distribution $\tilde{f}$ from N AUV measurements by solving the following Least Absolute Shrinkage and Selection Operator (LASSO) problem:

$\begin{array}{ll}\min \frac{1}{2N}{\Vert \begin{array}{c}\\ y_n-\tilde{f}(q_n)\\ \end{array}\Vert }_2+\lambda {\Vert \begin{array}{c}\\ \widehat{c}\\ \end{array}\Vert }_1,n=1,\text{...},N,& (17)\end{array}$

where λ is the nonnegative regularization parameter. In this paper, the value of λ is typically in the range of 10^-6 to 10^-5. ${\widehat{c}}_1$ is the ${\ell }^1$ -norm of $\widehat{c}$, $\parallel ·{\parallel }_2$ denotes the ${\ell }^2$ -norm. Once the LASSO problem Equation (17) is solved, the ice bottom map can be reconstructed by Equation (16) with the estimated $\widehat{c}$ and presented by substituting a grid to $\tilde{f}(x)$.

Furthermore, since the sparse approximation method is not sensitive to the spatial rotation of the field, we can smooth the reconstruction results by using average value method. We firstly rotate the sample points at multiple angles to calculate the corresponding reconstructed ice bottom map, then reverse the rotation of the reconstructed maps back to the original angle, and finally superimpose the multiple reconstructions to obtain the final ice bottom map by averaging. The proposed rotation and averaging method can effectively improve the quality of the reconstructed results, which benefits from the rotation-insensitivity characteristics of the sparse approximation method.

The LASSO problem given in Equation (17) is coded and solved using MATLAB. All the computation in our study is executed on a PC with a 16-core Ryzen9 5950X CPU and 128G of RAM.

3.4.2 Performance metrics

The performance of reconstructions can be evaluated by comparing the reconstructed underwater ice field $\tilde{f}$with the actual field f in the mapping area. Two metrics are adopted to assess the performance of reconstruction: Peak Signal-to-Noise Ratio (PSNR) (Huynh-Thu and Ghanbari, 2008) and Structural Similarity Index (SSIM) (Wang et al., 2004). They are commonly used as quantitative indexes for image or video quality evaluation.

● PSNR is a logarithmic ratio of the power of maximum possible value of the actual field f to the power of Root Mean Square Error (RMSE) between the actual field f and the reconstructed field $\tilde{f}$. A larger PSNR value means relatively less corruption in the reconstruction. The RMSE is defined as

$\begin{array}{ll}\text{RMSE}=\sqrt{\begin{array}{c}\frac{1}{I\times J}{\displaystyle \sum _{i,j=1}^{I,J}}{\left(f_{i,j}-{\tilde{f}}_{i,j}\right)}^2.\end{array}}& (18)\end{array}$

where I and J are the resolutions of each dimension of rasterized f and $\tilde{f}$. And the PSNR is formulated as

$\begin{array}{ll}\begin{array}{c}PSNR=20{\log }_{10}\left(\frac{\text{max}(f)}{\text{RMSE}(f,\tilde{f})}\right),\end{array}& (19)\end{array}$

where max (f) is the peak value of f.

● SSIM is a perceptual metric used to quantify the similarity of images or videos. A higher SSIM value indicates a greater degree of similarity between the actual and the reconstructed fields. The formulation of SSIM is

$\begin{array}{ll}\begin{array}{c}\text{SSIM}=\frac{\left(2{\mu }_f{\mu }_{\tilde{f}}+C_1\right)\left(2{\sigma }_{f\tilde{f}}+C_2\right)}{\left({\mu }_f^2+{\mu }_{\tilde{f}}^2+C_1\right)\left({\sigma }_f^2+{\sigma }_{\tilde{f}}^2+C_2\right)},\end{array}& (20)\end{array}$

where ${\mu }_f$, ${\mu }_{\tilde{f}}$, ${\sigma }_f, {\sigma }_{\tilde{f}}$, and ${\sigma }_{f\tilde{f}}$ are respectively the local means, standard deviations, and cross-covariance of the actual and reconstructed fields f and $\tilde{f}$; $C_1={(k_{1}L)}^2$ and $C_2={(k_{2}L)}^2$ are constants for stabilization, preventing the denominator from being zero, where k₁ << 1, k₂ << 1 and L is equal to 2^B − 1, determined by the bit depth B of f.

With the above sparse approximation method, the ice draft measurements from both rough and intensive mappings can be used to reconstruct a refined map of the ice bottom in the given observation area.

4 Method validation

Currently, our own vehicle is still under general tests and the available polar mission is under planning. In order to validate the above proposed framework and methods for AUV adaptive mapping and ice map reconstruction, we construct the testing scenario using the available ice bottom mapping data from other polar missions, so that our proposed algorithms could be tested by numerical simulations before the field tests. The actual specifications of our AUV and the equipped sensors mentioned in Section 2 are considered in our simulations here. Moreover, we also conduct the applicability analysis to briefly discuss the applicability of our proposed adaptive mapping method by classifying underwater ice scenarios.

4.1 Simulation scenario setup

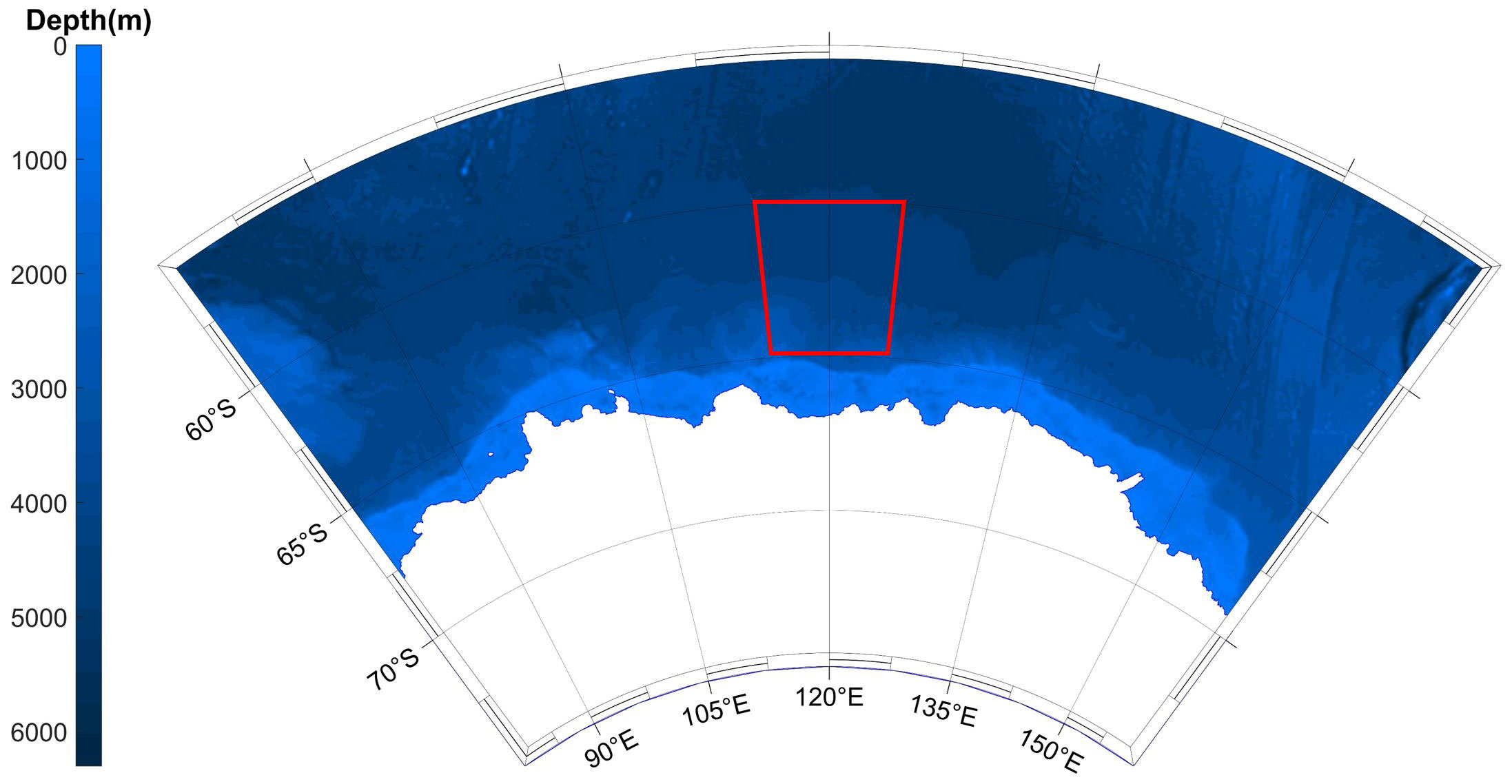
We apply floe-scale 3-D mapping data of sea ice draft to generate our test scenario. The dataset was collected using a multibeam sonar mounted on an AUV, from the SIPEX II voyage of the Aurora Australis, 2012-2013 season, and the AUV utilized was the ‘JAGUAR’ Seabed-class vehicle from the Deep Submergence Laboratory at the Woods Hole Oceanographic Institution (Williams et al., 2017).

There were in total four missions conducted beneath sea ice during the SIPEX-II voyage, in the region of (60.0 ~ 65.0°S, 115.0 ~ 125.0°E); see Figure 4. Apart from the multibeam sonar data, the CTD, ADCP, and hyperspectral data were also collected by the AUV.

FIGURE 4

Figure 4 Mission area of JAGUAR AUV during SIPEX II voyage.

Although the multibeam sonar was used in the mapping mission, the field data was still sampled sparsely in space. Here, we use the Kriging method to generate a sea ice draft map within the given mapping area, which is taken as the “real” map of the testing scenario. The interpolated sea ice draft map is shown in Figure 5A. Since the available field data is limited, we rotate and splice the pieces of interpolated images, to generate our testing scenario with desired size and interested distribution of ice features. As a result, the obvious symmetrical patterns can be found in the generated map. The total area of the generated sea ice draft map is 500m × 500m. We can see that the sea ice draft in the map has remarkable variation in the three-dimensional space. Most of the ice draft is less than 8m, but there are several isolated regions with larger ice draft. They will be taken as the regions of interest in this study, which will be identified and sampled intensively using our proposed adaptive mapping methods. The ice draft surface in 2D is presented in Figure 5B, which is a filled contour plot containing ice draft isolines every 0.5m interval.

FIGURE 5

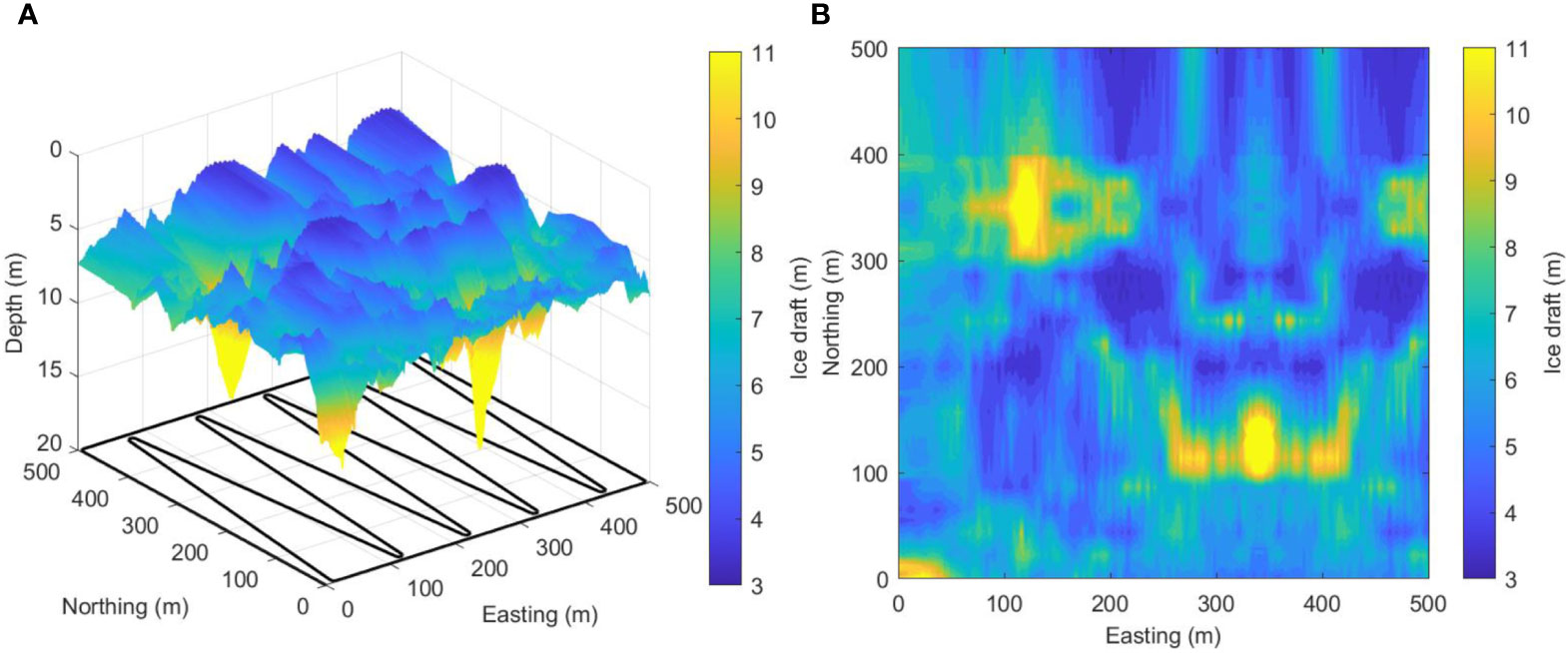
Figure 5 Ice draft map of testing scenario (Black solid lines present the predetermined trajectory for rough mapping). (A) 3D mapping of ice draft. (B) Underwater ice thickness surface in 2D.

4.2 Results and discussion

In this section, we present the simulation results of our proposed framework and methods for underwater ice mapping and reconstruction. The proposed AUV adaptive sampling algorithms have been validated, including autonomous identification and shape extraction of the interested regions, and trajectory planning for intensive mapping. In addition, the reconstruction results of ice draft map are compared and discussed.

4.2.1 Identification of interested regions

In the given observation area, the AUV first moves underwater at the speed of 1m/s at a constant depth of 20m along a predetermined zig-zag trajectory to map the ice bottom very roughly, while the heading switch angle of the zig-zag trajectory is 12°. With the roughly collected mapping data, the global ice draft map is reconstructed online in real time using the Kriging interpolation method. The roughly reconstructed map is shown in Figure 6A. It can be imagined that the rough map only presents the very general features of the observation area and loses the fine details. The accuracy of the roughly reconstructed map is evaluated; Figure 7 gives the deviation error of the ice draft between the reconstructed and the real map, which varies between -4.16m and 7.33m. It is obvious that the spacing of AUV zig-zag trajectory segments will affect the reconstruction accuracy as large reconstruction errors appear beyond the AUV trajectory. Globally, the reconstruction errors distribute uniformly within the observation area with RMSE=0.8689m, while the values of the performance metrics of the rough reconstruction are PSNR=19.4895 and SSIM=0.7834, which can be taken as the baseline for further comparison. In our study, we find if RMSE is smaller than 1m, PSNR is larger than 17, and SSIM is larger than 0.7, then the accuracy of the roughly reconstructed map is acceptable for further adaptive mapping.

FIGURE 6

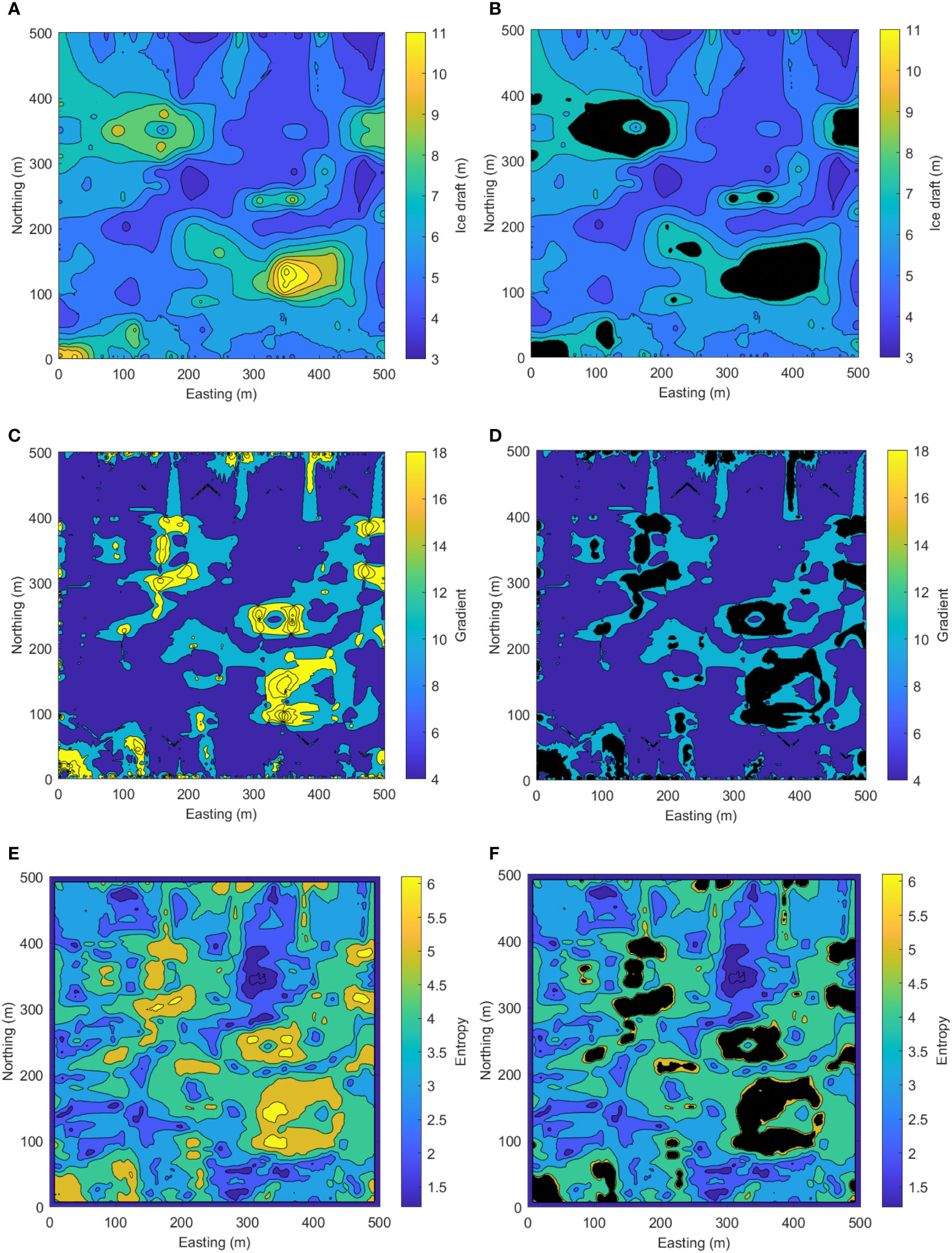
Figure 6 Roughly reconstructed ice draft results and interested regions identified by different criteria. (A) Rough reconstruction of ice draft map. (B) Interested regions identified by ice draft criterion. (C) Ice draft gradient of the roughly reconstructed map. (D) Interested regions identified by ice draft gradient criterion. (E) Ice draft entropy of the roughly reconstructed map. (F) Interested regions identified by ice draft entropy criterion.

FIGURE 7

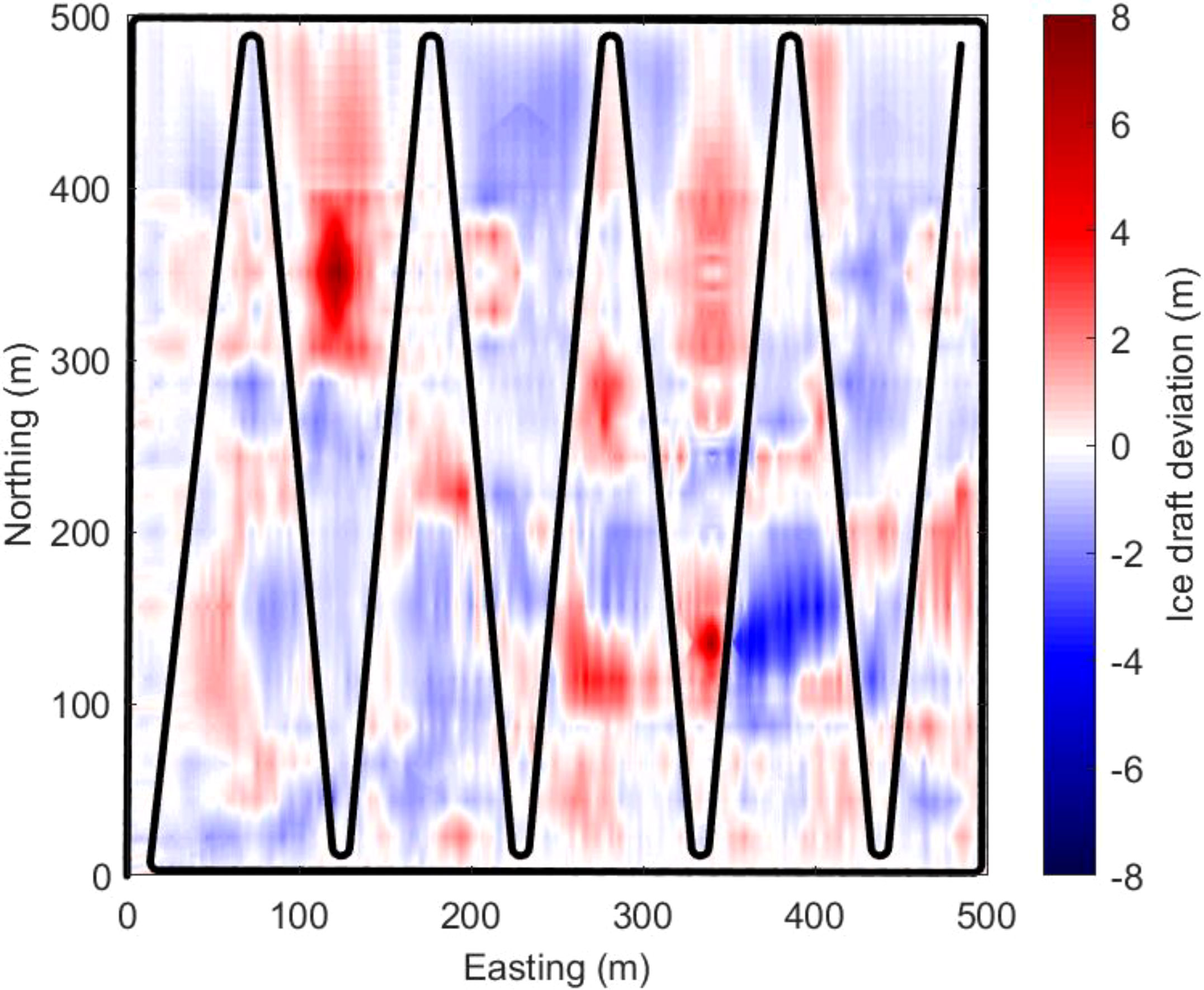
Figure 7 Deviation error between reconstructed and actual ice draft (Black solid track presents the predetermined trajectory for rough mapping).

Figures 6C, E respectively present ice draft gradient and entropy in the roughly reconstructed ice map. We can see the regions of interest respectively identified by the three identification criteria are shown in the right-column subplots of Figure 6. The interested regions identified by ice draft in Figure 6B seem more focused in large scale, while the ones identified by ice draft gradient and entropy coincide with each other generally, which look more scattered in relatively small scale in Figures 6D, F. This indicates that these two criteria are more sensitive to represent the variation of ice draft, although the difference in the threshold selection of the three criteria will influence the identified results. In our study, we take the value of the ice draft parameters at the 90% percentile as the threshold of each criterion for the interested region identification. It is also found that the ice draft gradient around the edge of the map looks more cluttered and broken, which is caused by the inherent defect of the algorithm on the solving of feature gradient at the edge of the image.

4.2.2 Shape extraction of interested regions

Figure 8 presents the extracted areas for intensive mapping by the three different criteria for further intensive mapping. The white dotted contours indicate the interested regions extracted by Alpha shape algorithm with areas larger than 1% of the total observation area; we refer to this percentage as the area ratio for Alpha shape extraction in our study. The identified regions are enveloped by the red rectangles, using the minimum area bounding rectangle method. Note that the number and the size of the extracted bounding rectangles can be tuned by adjusting the threshold of each identification criterion as well as the area ratio for Alpha shape extraction, by which the fineness of the intensive mapping as well as the maneuverability of the vehicle could be balanced.

FIGURE 8

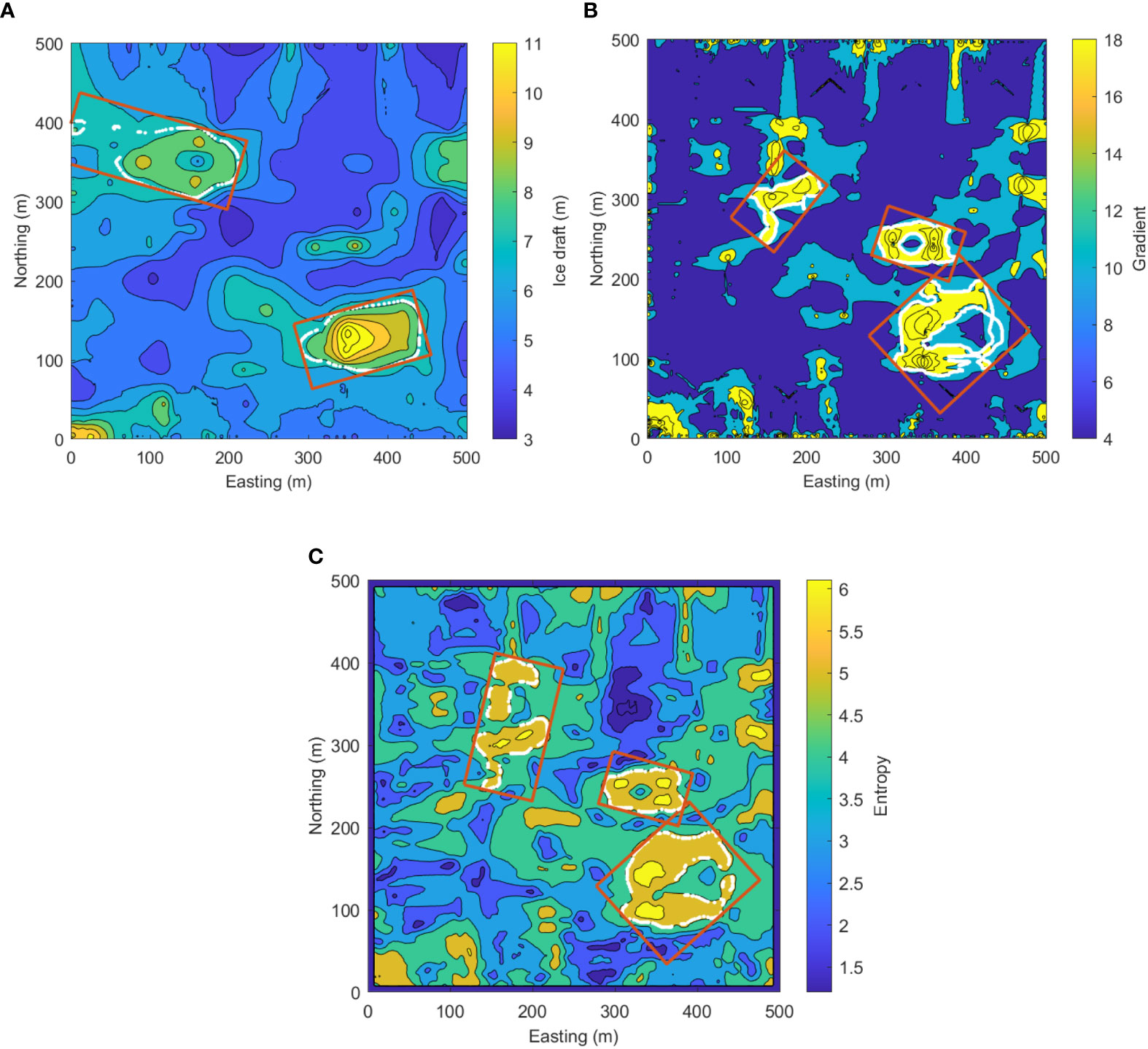
Figure 8 Extracted rectangles for intensive mapping by different criteria (White dash-dotted contours indicate the extracted regions of interest. Red rectangular boxes show the minimum area bounding rectangles of the interested regions). (A) Interested area extracted by ice draft criterion. (B) Interested area extracted by ice draft gradient criterion. (C) Interested area extracted by ice draft entropy criterion.

The areas extracted by ice draft criterion seem continuous and gathered in blocks in Figure 8A, while the ones extracted by either ice draft gradient or entropy look patchy and scattered in irregular stripes or donut shapes in Figures 8B, C. From the results in Figure 8, we can see the distribution of the extracted rectangles is different among the three cases, which is due to the principle and the threshold selection in the three criteria. It seems that the ones extracted by ice draft entropy include most of the regions identified by the other two criteria.

Figure 8 also reveals that some minimum area bounding rectangles may exceed the mission area; however, in the trajectory planning for AUV intensive mapping, if the vehicle touches the boundary of the observation area, it will switch its heading to run away from the boundary, which will be illustrated in the later subsection.

4.2.3 Trajectory planning for intensive mapping

The trajectory for intensive mapping is planned based on the rough mapping results, and in the real application the vehicle performs the rough and the intensive mappings one by one continuously in one running round within the given observation area. From Figure 9, it can be found that the vehicle both starts and ends at the same point (in the left bottom corner) of the mapping area. It firstly runs around the rectangular mission area and then moves in the predetermined zig-zag trajectory to roughly map the given area. With the reconstructed rough ice draft map online, the vehicle continues to map the regions of interest adaptively one by one in an optimal trajectory generated by the trajectory planner. As we mentioned before, the trajectory is optimized by minimizing the total running time under the constraint of vehicle maneuverability. We can see that the trajectory of the vehicle is restricted within the given mission area even if the extracted rectangle exceeds the boundary of the area and only the inside parts are mapped. This indicates that the trajectory planner is able to adapt to the scenarios with irregular boundaries.

FIGURE 9

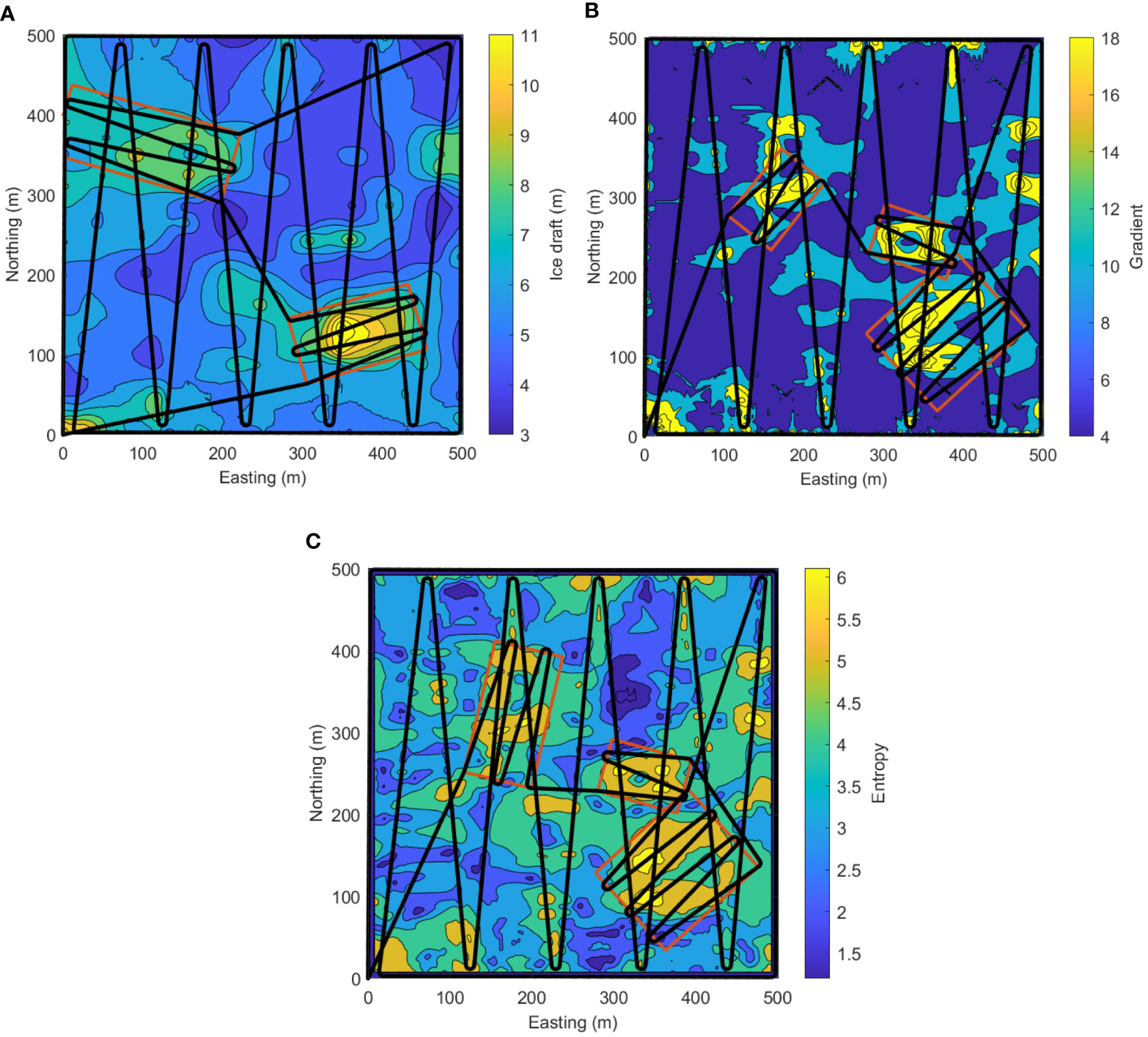
Figure 9 Planned trajectory for adaptive mapping under different criteria (Black solid track presents the optimized trajectory for both rough and intensive mapping). (A) Planned trajectory under ice draft criterion. (B) Planned trajectory under ice draft gradient criterion. (C) Planned trajectory under ice draft entropy criterion.

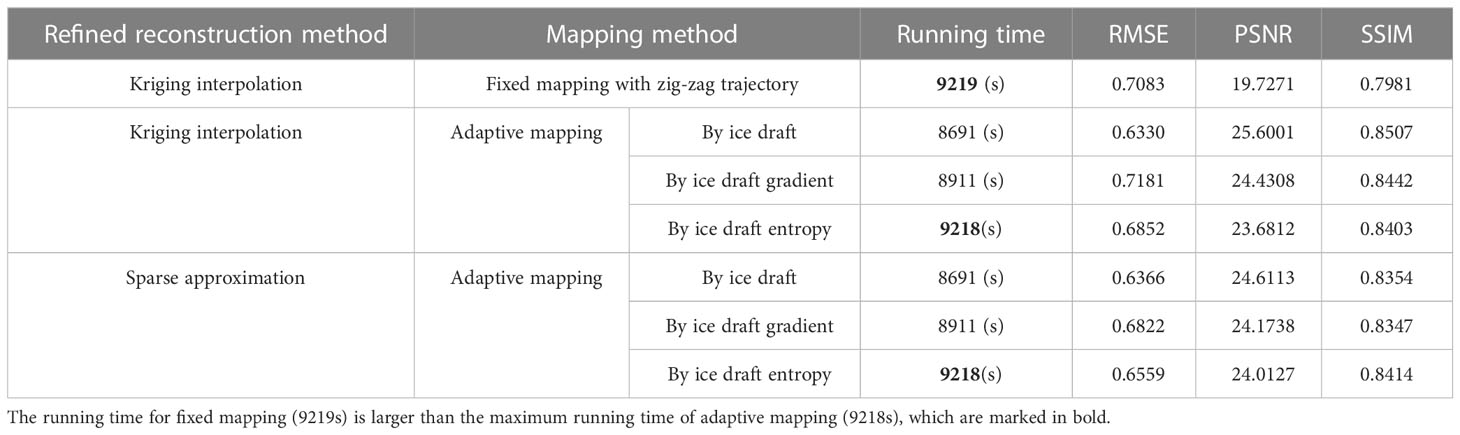
The total running time for adaptive mapping (including both rough and intensive mapping) under the three different criteria are respectively 8691s, 8911s, and 9218s. It shows that the total running time varied a little bit for the three cases and the variation is within several minutes. The planned trajectory under ice draft entropy criterion takes the longest time as the total area of the interested regions extracted by this criterion is the largest, which is mentioned above.

4.2.4 Underwater ice map reconstruction

With the above rough and intensive mapping data, the refined sea ice draft map can be further reconstructed. For comparison, the refined maps are respectively reconstructed by Kriging interpolation method and our proposed sparse approximation method. Besides, we also compare the effect of the three criteria for interested region identification on the reconstructed results.

Figure 10 presents the reconstructed ice draft maps by Kriging interpolation and sparse approximation under different adaptive mapping criteria. In general, the reconstructed maps both look sketchy and smooth compared with the ‘real’ map. That is because our purpose is to map the main variation and key features of underwater ice topography and generate a sea ice draft map in a cost-effective and efficient way, while the very detailed features are not our focus. This is especially true since the vehicle has limited energy, and the underwater ice topography varies with the surrounding environment, so it is better for the vehicle to complete the mapping mission as soon as possible.

FIGURE 10

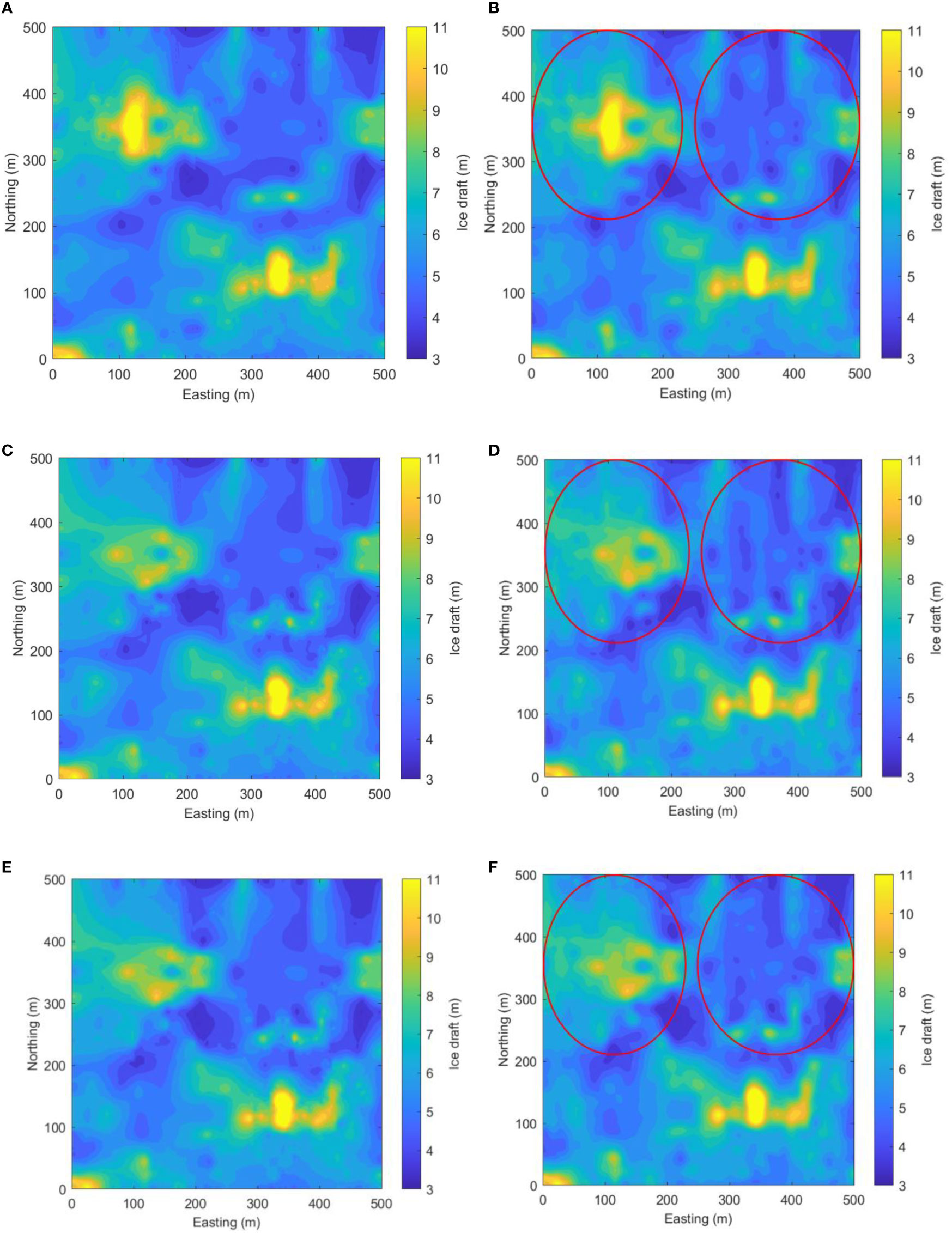
Figure 10 Reconstructed ice draft map by different adaptive mapping and reconstruction methods (Red ellipses indicate the area for performance comparison). (A) Kriging interpolation under ice draft criterion. (B) Sparse approximation under ice draft criterion. (C) Kriging interpolation under ice draft gradient criterion. (D) Sparse approximation under ice draft gradient criterion. (E) Kriging interpolation under ice draft entropy criterion. (F) Sparse approximation under ice draft entropy criterion.

In Figure 10, we can see that the refined reconstruction results by both Kriging interpolation and sparse approximation are able to reflect most of the features of the regions with large ice draft or obvious ice draft variation in Figure 5 (real map). In total, five regions with ice draft larger than 8m can be identified and reconstructed. However, the reconstructed maps by sparse approximation seem more stratified than the ones reconstructed by Kriging interpolation comparing the regions marked by red ellipses in Figure 10. Note that all the reconstructed maps are presented as filled contour plots containing ice draft isolines of every 0.5m interval, so the more stratified map indicates that more detailed features are captured.

The deviation errors of the ice draft reconstruction results by Kriging interpolation and sparse approximation under different adaptive mapping criteria are shown in Figure 11. It shows that the reconstruction results by ice draft criterion have the smallest variation range of deviation error, which is between -2.51m and 4.49m, while the ones by the other two adaptive mapping criterion have relatively large variation range of deviation error from -2.60m to 7.33m, as the thicker region at the upper left of the real map is not fully recognized by either ice draft gradient or entropy criterion with given threshold values for interested region identification and extraction. The difference of deviation error between Kriging interpolation and sparse approximation is obvious if comparing the shade and texture of the two sets of deviation error images; we can see that the deviation errors by sparse approximation look lighter and smoother in color than the ones by Kriging interpolation, which indicate smaller and steadier deviation errors, especially in the regions marked with red ellipses in Figure 11.

FIGURE 11

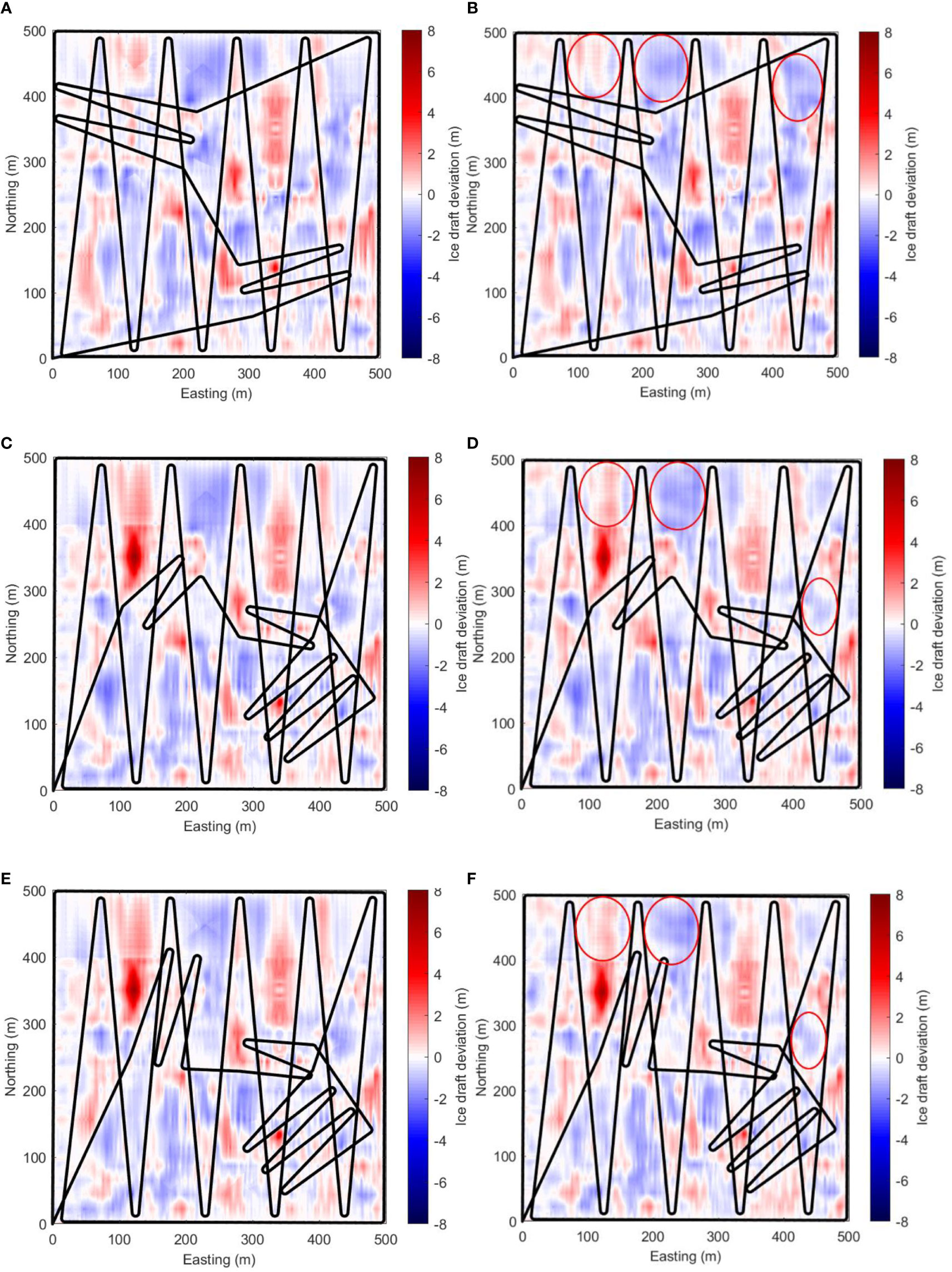
Figure 11 Deviation errors of different adaptive mapping and reconstruction methods (Red ellipses indicate the area for performance comparison). (A) Kriging interpolation under ice draft criterion. (B) Sparse approximation under ice draft criterion. (C) Kriging interpolation under ice draft gradient criterion. (D) Sparse approximation under ice draft gradient criterion. (E) Kriging interpolation under ice draft entropy criterion. (F) Sparse approximation under ice draft entropy criterion.

To demonstrate the performance advantage of adaptive mapping, we also conducted benchmark mapping using a fixed zig-zag trajectory. The fixed trajectory is similar to the rough mapping trajectory as illustrated in Figure 5 but with denser zig-zag segments. To make the comparisons fair, the total fixed but denser zig-zag trajectory takes the comparative running time, which is no less than the maximum running time of adaptive mapping (including rough and intensive mapping, which is in total 9218s). In our simulation, the total running time for fixed mapping is set as 9219s. With the measurements along the fixed but denser zig-zag trajectory, the ice draft map is reconstructed using Kriging interpolation, as shown in Figure 12.

FIGURE 12

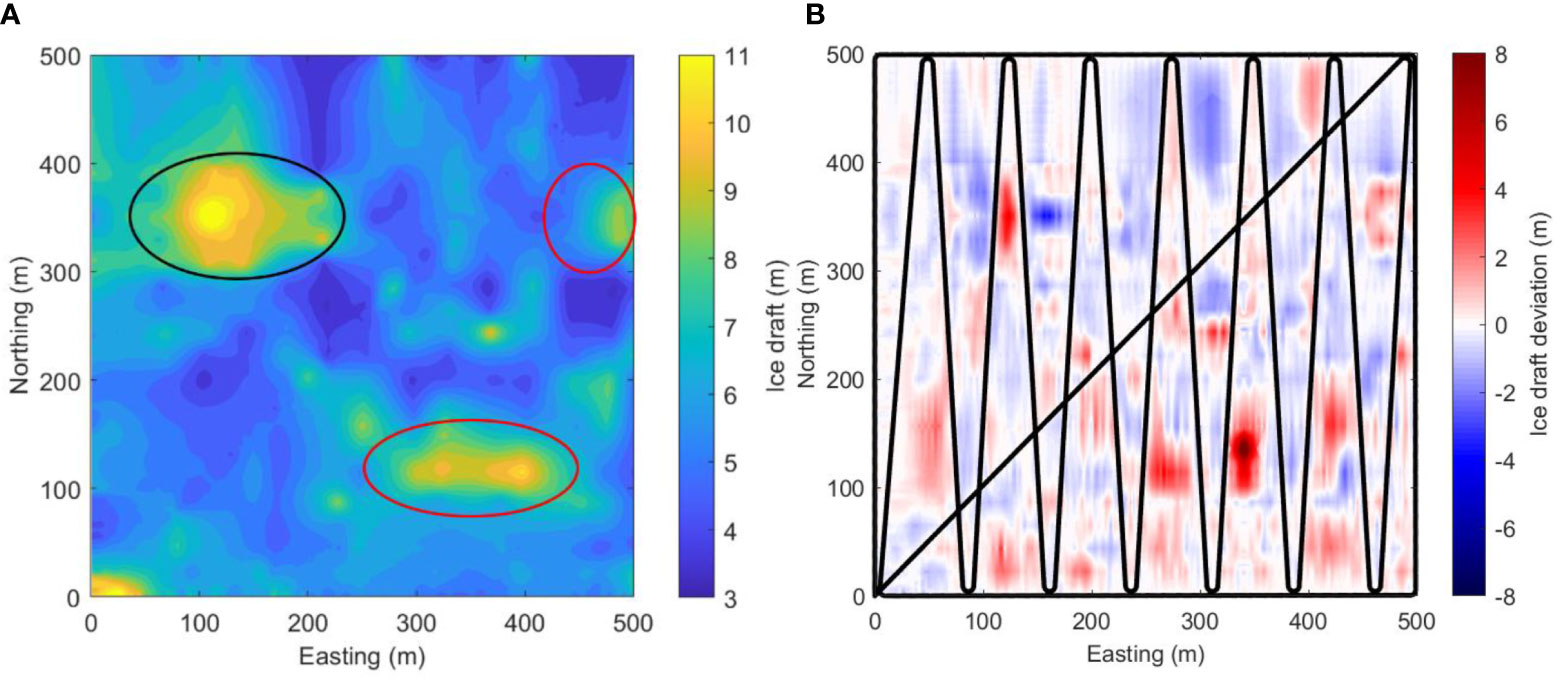
Figure 12 Reconstruction results by Kriging interpolation with fixed trajectory (Red and black ellipses indicate the area for performance comparison). (A) Reconstructed ice draft map. (B) Deviation error between reconstructed and actual ice draft.

The deviation error of the reconstruction result varies from -3.94m to 9.19m; the variation range is even larger than the one of rough mapping in Figure 7. That is because some thicker regions happen to locate in the spacing area of the fixed but denser zig-zag trajectory, and cannot be sampled and reconstructed accurately. So, the performance of fixed mapping tends to be random in nature depending on the ice draft feature distribution in the given observation area. In spite of this, the color of the deviation error image in Figure 12B is generally lighter than the one in Figure 7. Since the spacing of the fixed zig-zag trajectory becomes denser than the rough mapping, the reconstructed map contains more detailed features and looks more stratified, if comparing Figure 12A with Figure 6A. Moreover, as the vehicle moving in fixed but denser zig-zag trajectory maps the observation area uniformly, the general variation characteristics of the ice draft can be captured, and we can see that the total five regions with obvious ice draft variation are reflected in Figure 12A. However, some reconstructed features are still too rough to present the real features in Figure 5B, see the red ellipses marked regions in Figure 12A; besides, some reconstructed features seem less accurate, see the black ellipse-marked region in Figure 12A.

Apart from the above qualitative analysis, we also conducted quantitative comparison among different mapping and reconstruction results, using the performance metrics defined in Section 3.4.2. The comparison results are summarized in Table 1. We can see that generally the reconstruction results by adaptive mapping are better than the fixed mapping one given the comparative running time of the AUV, as smaller RMSE, larger PSNR, and larger SSIM are achieved. In the given mapping scenario, adaptive mapping using the ice draft method for interested region identification takes the minimum running time, but can generate the best reconstruction results, while the ones using the other two identification methods produce similar reconstruction performances to each other, if evaluated by the defined performance metrics. We guess the proposed three identification methods may be more competent in their individual preferable mapping scenarios, which will be further discussed in the following subsection.

TABLE 1

Table 1 Comparison of reconstruction results.

From the results in Table 1, it can be found that in the adaptive mapping missions, there are only slight differences between the refined reconstruction results by Kriging interpolation and sparse approximation, respectively. For the adaptive mapping using ice draft method, the reconstruction by Kriging interpolation performs a little bit better; for the adaptive mapping using ice draft entropy method, the reconstruction result by sparse approximation looks slightly better; for the adaptive mapping using ice draft gradient method, each reconstruction method has its own superiority in performance metrics. Overall, it can be concluded that the advantage of sparse approximation in the reconstruction of a static ice draft field is not that obvious from the defined performance metrics; from our previous qualitative analysis, however, we know that the sparse approximation can reconstruct more detailed features in the ice draft map (in shade and texture) than the Kriging interpolation. Sparse approximation is also capable of reconstructing the temporally dynamic field which will be key to reconstructing the time variation of the ice draft field. To save the length of this paper, the reconstruction of the time-varied ice draft field will be considered and discussed in our future work.

4.3 Applicability analysis

Based on our discussion above, it is noticed that our proposed adaptive mapping and reconstruction methods may be more competent in their individual preferable under-ice mapping scenarios. So, it is necessary to discuss the distribution characteristics of ice draft features and the applicability of our proposed methods.

From the IPCC the Fifth Assessment Report (IPCC, 2013), we know that two relatively thin floes (pieces of ice) colliding with each other can ‘raft’, stacking one on top of the other and thickening the ice. When thicker floes collide, thick ridges may be built from broken pieces, with a height above the surface (ridge sail) of 2 m or more, and a much greater thickness (~10 m) and width below the ocean surface (ridge keel). The ridge keel is caused by deformed ice, which is exposed to be the dominant features of sea ice in polar regions. The existing surveys indicate that the floes are much thicker and more deformed than reported by most drilling and ship-based measurements of Antarctic sea ice (Williams et al., 2015). It is also suggested that thick ice in the near-coastal and interior pack may be under-represented in existing in situ assessments of Antarctic sea ice and hence, on average, Antarctic sea ice may be thicker than previously thought. As a result, the area of the deformed thicker ice is taken as the regions of interest for intensive mapping in our observation missions.

As is shown in Figure 13, the variation of regional ice draft can be generally classified into four categories: flat or gradual feature, uniformly distributed small-scaled coarse feature, uniformly distributed large-scaled sharp feature, as well as separated or clustered large-scaled sharp feature. Here, the small-scaled feature means the maximum fluctuation of ice draft is less than 2m, while the large-scaled feature indicates the maximum fluctuation of ice draft is more than 5m. It can be imaged that our proposed adaptive method is less applicable to the first two categories of underwater ice scenarios as few regions of interest can be identified there with moderate varied features. As for the third category, if the deformed ice regions are distributed dispersedly and densely in the observation area, the interested region for adaptive mapping will be identified as a large whole area, even filling up the observation area; such a situation is similar to the first two categories. If the deformed thicker ice regions are distributed separately or clustered in the field, it is more appliable for our proposed adaptive mapping method to identify and intensively map a limited number of interested regions.

FIGURE 13

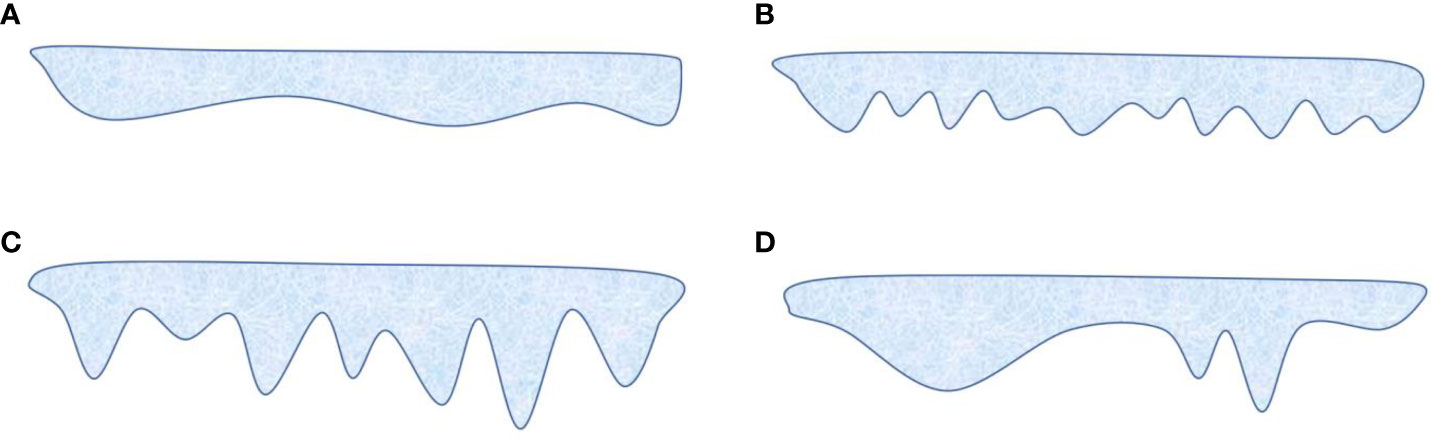
Figure 13 Underwater ice scenario comparisons (2D profile of ice draft). (A) Flat or gradual feature. (B) Uniformly distributed coarse feature. (C) Uniformly distributed sharp feature. (D) Separated or clustered feature with different ice draft gradient.

Moreover, the selection of the thresholds in the identification methods will affect the adaptive mapping performance and heavily depend on the ice draft variation of the individual interested region, the values of which are currently assigned based on the average or certain percentile of the ice draft parameters. From the interested region identification results in Section 4.2, we can see that if the ice draft variation of the interested region is slow with a gentle slope (like the left feature in Figure 13D), the ice draft method for the interested region identification may be more applicable as the deformed ice regions could be identified as large blocks, while the ice draft gradient and entropy methods are more sensitive to ice draft variation and suitable for the scenario where the ice draft variation of the interested region is sharp with a steep slope (see the right feature in Figure 13D), and the deformed ice regions could be identified as patchy stripes or donuts. Moreover, the identification performances of the ice draft gradient and entropy methods are similar as the identified regions of interest by the two methods coincide in general. Besides, the selection of the area ratio for Alpha shape extraction will also influence the accuracy and the efficiency of the mapping and reconstruction results. Based on the above findings, we notice that it is necessary to apply some more intelligent mapping methods, such as self-learning of the ice draft features from online measurements, which will be considered in our future study.

5 Conclusions

This paper presented a low-cost underwater ice mapping framework for small-sized AUVs using adaptive sampling and reconstruction methods. The goal of our study is to adaptively obtain the key information of ice topography and reconstruct the map of ice draft efficiently, given the limited AUV endurance and the sparse mapping measurements. A graphics-based adaptive mapping method was proposed to densify the measuring of ice draft in the regions with ‘noticeable’ variations. Three criteria were proposed to identify the interested regions with remarkable variation of ice draft (namely the deformed ice regions) based on the roughly reconstructed ice draft map. The Alpha shape algorithm was used to extract the boundaries of the interested regions. To make it convenient for AUV trajectory planning for intensive mapping, the regions of interest were further enveloped by the minimum area bounding rectangles. Moreover, a trajectory planner was designed to generate an optimal trajectory for the vehicle to map all the interested regions intensively, by minimizing the total running time under the constraint of vehicle maneuverability. The sparse approximation method was proposed to reconstruct the slowly varied ice draft map with the limited sparse mapping swathes. We also defined the quantitative indexes to assess the performance of reconstruction, which are Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM).

In order to validate the above proposed framework and methods for AUV adaptive mapping and reconstruction of underwater ice topography, the testing scenario was created using the available ice bottom mapping data from the field, and our proposed algorithms were tested and compared by a set of numerical simulations. For comparison, the refined ice draft maps are reconstructed both by Kriging interpolation method and our proposed sparse approximation method. In general, the reconstructed maps by both methods looked sketchy and smooth compared with the ‘real’ map, while the ones reconstructed by sparse approximation seemed more stratified than the ones reconstructed by Kriging interpolation, which indicated that more detailed features were captured. The difference of deviation error of ice draft between Kriging interpolation and sparse approximation was obvious if comparing the shade and texture of the two sets of deviation error images. We could see that the deviation errors by sparse approximation looked lighter and smoother in color, which denoted smaller and steadier deviation errors.

Apart from the qualitative analysis, we also conducted quantitative comparison among different mapping and reconstruction results, using the defined performance metrics. It was found that the reconstruction results by adaptive mapping were generally better than the fixed mapping one given the comparative running time of the AUV, as smaller RMSE, larger PSNR, and larger SSIM were achieved. In the given mapping scenario, adaptive mapping using the ice draft method for interested region identification took the minimum running time, but could generate the best reconstruction results, while the ones using the other two identification methods produced similar reconstruction performances to each other. It revealed that the proposed three identification methods for adaptive mapping may be more competent in their individual preferable mapping scenarios. There were only slight differences between the refined reconstruction results by Kriging interpolation and sparse approximation in the values of the performance metrics. In the end, the applicability analysis was conducted to discuss the applicability of the proposed adaptive mapping method by classifying the underwater ice scenarios. It was concluded that our proposed method was more applicable to the underwater ice scenarios where the deformed thicker ice regions were distributed separately or clustered.

Since the selection of the thresholds in the identification and extraction methods will affect the adaptive mapping and reconstruction performance heavily depending on the ice draft variation in the individual interested region, some more intelligent mapping methods based on self-learning of the ice draft features from the online measurements will be considered in our future study. Moreover, only the reconstruction of the spatial variation of the ice draft was considered in our current work; as sparse approximation is also capable of reconstructing the temporally dynamic field, we will consider reconstructing the temporal variation of the ice draft field in the future. There are also some key practical issues that should be carefully addressed, such as the impact of AUV navigation and sampling errors on the adaptive mapping and reconstruction results, to ensure the performance of our proposed methods in the future field applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

SF and XC supported the conceptualization of this research. XZ, GZ, and SF developed the adaptive mapping and reconstruction methods. XZ and SF processed and analyzed the data. SF and XC drafted the manuscript and provided project management. All authors contributed to editing the manuscript and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 52001338), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA22000000), and the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) (Grant No. SML311021012).

Acknowledgments

The authors would like to thank Australian Antarctic Data Centre and the relevant researchers (Williams, G.D., Junz, C., Kimball, P., Frost, R. and Alexander, P.) for generously provide the 3-D mapping data of sea ice draft using an autonomous underwater vehicle in the Antarctic (doi: 10.4225/15/59ffe1ed02df1). The authors are grateful to the reviewers for their insightful comments and suggestions, which helped to improve the quality of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adcock B. (2017). Infinite-dimensional l1 minimization and function approximation from pointwise data. Constructive Approximation 45 (3), 345–390. doi: 10.1007/s00365-017-9369-3

CrossRef Full Text | Google Scholar

Auchincloss A. H., Diez Roux A. V., Brown D. G., Raghunathan T. E., Erdmann C. A. (2007). Filling the gaps: Spatial interpolation of residential survey data in the estimation of neighborhood characteristics. Epidemiology 18, 469–478. doi: 10.1097/EDE.0b013e3180646320

PubMed Abstract | CrossRef Full Text | Google Scholar

Bivand R. S., Pebesma E. J., Gómez-Rubio V. (2013). Applied spatial data analysis with r (Ch. 8 “Interpolation and geostatistics”) (New York: Springer). doi: 10.1007/978-1-4614-7618-4?

CrossRef Full Text | Google Scholar

Brierley A. S., Millard N. W., McPhail S. D., Stevenson P., Pebody M., Perrett J., et al. (2002). Antarctic Krill under sea ice: elevated abundance in a narrow band just south of ice edge. Science 295, 1890–1892. doi: 10.1126/SCIENCE.1068574

PubMed Abstract | CrossRef Full Text | Google Scholar

Broecker W. S. (1991). The great ocean conveyor. Oceanography 4 (2), 79–89. doi: 10.5670/oceanog.1991.07

CrossRef Full Text | Google Scholar

Candes E. J., Wakin M. B. (2008). An introduction to compressive sampling. IEEE Signal Process. Magazine 25 (2), 21–30. doi: 10.1109/MSP.2007.914731

CrossRef Full Text | Google Scholar

Cazenave F., Zhang Y., McPhee-Shaw E., Bellingham J. G., Stanton T. P. (2011). High-resolution surveys of internal tidal waves in Monterey bay, California, using an autonomous underwater vehicle. Limnol. Oceanography: Methods 9, 571–581. doi: 10.4319/lom.2011.9.571

CrossRef Full Text | Google Scholar

Cruz N. A., Matos A. C. (2010). “Adaptive sampling of thermoclines with autonomous underwater vehicles,” in Proceedings of the 2010 IEEE/OES OCEANS Sydney, Sydney, Australia. 1–6. doi: 10.1109/OCEANS.2010.5663903

CrossRef Full Text | Google Scholar

D'Errico J. (2022). A suite of minimal bounding objects, MATLAB central file exchange 23, 2022. Available at: https://www.mathworks.com/matlabcentral/fileexchange/34767-a-suite-of-minimal-bounding-objects.

Google Scholar

Dey S. (2018). Hands-On Image Processing with Python, Chapter 5, Image Enhancement using Derivatives (Birmingham, UK: Packt Publishing Limited), 1–492.

Google Scholar

Doble M. J., Forrest A. L., Wadhams P., Laval B. E. (2009). Through-ice AUV deployment: operational and technical experience from two seasons of Arctic fieldwork. Cold Regions Sci. Technol. 56, 90–97. doi: 10.1016/j.coldregions.2008.11.006

CrossRef Full Text | Google Scholar

Dowdeswell J., Evans J., Mugford R., Griffiths G., McPhail S., Millard N., et al. (2008). Autonomous underwater vehicles (AUVs) and investigations of the ice–ocean interface in Antarctic and Arctic waters. J. Glaciol. 54 (187), 661–672. doi: 10.3189/002214308786570773

CrossRef Full Text | Google Scholar

entropyfilt, MathWorks (2022). Available at: https://www.mathworks.com/help/images/ref/entropyfilt.html#d123e95589.

Google Scholar

Ferguson J., Pope A., Butler B., Verrall R. I. (1999). Theseus AUV: Two record breaking missions. Sea Technol. 40 (2), 65–70. doi: 64611/0093-3651/4504533

Google Scholar

Francois R. E. (1977). High resolution observations of under-ice morphology (Seattle, WA, USA: Applied Physics Laboratory, University of Washington,) Technical Report, APL-UW 7712, p. 30. Accession Number: ADA039753.

Google Scholar

François B. (2022). Available at: http://cgm.cs.mcgill.ca/~godfried/teaching/projects97/belair/alpha.html.

Google Scholar

Francois R. E., Nodland W. K. (1972). Unmanned Arctic Research Submersible (UARS) system development and test report (Seattle, WA, USA: Applied Physics Laboratory, University of Washington), Technical Report, APL-UW 7219, p. 88. Accession Number: 00043944.

Google Scholar

Girosi F. (1998). An equivalence between sparse approximation and support vector machines. Neural Comput. 10 (6), 1455–1480. doi: 10.1162/089976698300017269

PubMed Abstract | CrossRef Full Text | Google Scholar

Gwyther D. E., Spain E., King P., Guihen D., Williams G. D., Evans E., et al. (2020). Cold ocean cavity and weak basal melting of the sørsdal ice shelf revealed by surveys using autonomous platforms. J. Geophysical Res.: Oceans 125 (6), e2019JC015882. doi: 10.1029/2019JC015882

CrossRef Full Text | Google Scholar

Huynh-Thu Q., Ghanbari M. (2008). Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 44 (13), 800–801. doi: 10.1049/el:20080522

CrossRef Full Text | Google Scholar

IPCC (2013). “Climate change 2013: The physical science basis. contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change,” in Chapter 4 observations: Cryosphere. Stocker T. F., Qin D., Plattner G.-K., Tignor M., Allen S. K., Boschung J., Nauels A., Xia Y., Bex V., Midgley P. M. (Eds.) (Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press), 1535 pp.

Google Scholar

Jiang X. J., Scott P. J. (2020). Advanced metrology, chapter 11: Characterization of free-form structured surfaces (San Diego, CA, USA: Academic Press), 281–317.

Google Scholar

King P., Williams G., Coleman R., Zürcher K., Bowden-Floyd I., Ronan A., et al. (2018). ““Deploying an AUV beneath the sørsdal ice shelf: Recommendations from an expert-panel workshop,”,” in 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal. 1–6, November. doi: 10.1109/AUV.2018.8729786

CrossRef Full Text | Google Scholar

Le N. D., Zidek J. V. (2006). Statistical analysis of environmental space-time processes (Ch. 7, “Spatial prediction: Classical approaches”) (New York: Springer). doi: 10.1007/0-387-35429-8

CrossRef Full Text | Google Scholar

Misra S., Wu Y. (2020). Machine Learning for Subsurface Characterization, Chapter 10: Machine learning assisted segmentation of scanning electron microscopy images of organic-rich shales with feature extraction and feature ranking (Houston, Texas, USA: Gulf Professional Publishing), 289–314.

Google Scholar

Mitra U., Choudhary S., Hover F., Hummel R., Kumar N., Naryanan S., et al. (2015). Structured sparse methods for active ocean observation systems with communication constraints. IEEE Commun. Magazine 53 (11), 88–96. doi: 10.1109/MCOM.2015.7321976

CrossRef Full Text | Google Scholar

Nicholls K. W., Abrahamsen E. P., Buck J. J. H., Dodd P. A., Goldblatt C., Griffiths G., et al. (2006). Measurements beneath an Antarctic ice shelf using an autonomous underwater vehicle. Geophysical Res. Lett. 33, L08612. doi: 10.1029/2006GL025998

CrossRef Full Text | Google Scholar

Petillo S., Balasuriya A., Schmidt H. (2010). “Autonomous adaptive environmental assessment and feature tracking via autonomous underwater vehicles,” in Proceedings of the 2010 IEEE/OES OCEANS Sydney, Sydney, Australia. 1–9. doi: 10.1109/OCEANSSYD.2010.5603513

CrossRef Full Text | Google Scholar

Petillo S., Schmidt H. (2014). Exploiting adaptive and collaborative AUV autonomy for detection and characterization of internal waves. IEEE J. Oceanic Eng. 39 (1), 150–164. doi: 10.1109/JOE.2013.2243251

CrossRef Full Text | Google Scholar

Plueddemann A. J., Kukulya A. L., Stokey R., Freitag L. (2012). Autonomous underwater vehicle operations beneath coastal Sea ice. IEEE/ASME Trans. Mechatronics 17 (1), 54–64. doi: 10.1109/TMECH.2011.2174798

CrossRef Full Text | Google Scholar

scikit-image (2022). Available at: https://scikit-image.org/docs/stable/auto_examples/filters/plot_entropy.html.

Google Scholar

Singh H., Maksym T., Wilkinson J., Williams G. (2017). Inexpensive, small auvs for studying ice-covered polar environments. Sci. Robotics 2 (7), eaan4809. doi: 10.1126/scirobotics.aan4809

CrossRef Full Text | Google Scholar

Tervalon N. S., Henthorn R. (2002). “Ice profiling sonar for an AUV: experience in the Arctic,” in Proceedings of the 2002 MTS/IEEE OCEANS Biloxi (Biloxi), MI, USA. Vol. 1. 305–310. doi: 10.1109/OCEANS.2002.1193288

CrossRef Full Text | Google Scholar

Wadhams P. (2012). The use of autonomous underwater vehicles to map the variability of under-ice topography. Ocean Dynamics 62 (3), 439–447. doi: 10.1007/s10236-011-0509-1

CrossRef Full Text | Google Scholar

Wadhams P., Doble M. J. (2008). Digital terrain mapping of the underside of sea ice from a small AUV. Geophysical Res. Lett. 35, L01501. doi: 10.1029/2007GL031921

CrossRef Full Text | Google Scholar

Wadhams P., Krogh B. (2019). Operational history and development plans for the use of AUVs and UAVs to map sea ice topography. Polar Sci. 21 (2019), 195–203. doi: 10.1016/J.POLAR.2019.07.004

CrossRef Full Text | Google Scholar

Wadhams P., Wilkinson J. P., McPhail S. D. (2006). A new view of the underside of Arctic sea ice. Geophysical Res. Lett. 33, L04501. doi: 10.1029/2005GL025131

CrossRef Full Text | Google Scholar

Wang Z., Bovik A. C., Sheikh H. R., Simoncelli E. P. (2004). ). image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13 (4), 600–612. doi: 10.1109/TIP.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams G. D., Junz C., Kimball P., Frost R., Alexander P. (2017) 3-D mapping of sea ice draft with an autonomous underwater vehicle, Ver. 1, Australian Antarctic Data Centre (Accessed 2022-10-26). doi: 10.4225/15/59ffe1ed02df1

CrossRef Full Text | Google Scholar

Williams G., Maksym T., Wilkinson J., Kunz C., Singh H. (2015). Thick and deformed Antarctic sea ice mapped with autonomous underwater vehicles. Nat. Geosci. 8 (1), 61–67. doi: 10.1038/ngeo2299

CrossRef Full Text | Google Scholar

Zeng G., Fan S., Cao Y., Peng C. (2021). “Sparse reconstruction of gravity plume using autonomous underwater vehicles,” in Proceedings of the 2021 ACM International Conference on Underwater Networks & Systems (WUWNet'21), Shenzhen, China. 1–8. doi: 10.1145/3491315.3491320

CrossRef Full Text | Google Scholar

Zhang Y. (2013). Adaptive ocean observation. Adv. Earth Sci. 28 (5), 537–541. (Chinese journal with English abstracts).

Google Scholar

Zhang Y., Bellingham J. G., Godin M. A., Ryan J. P. (2012a). Using an autonomous underwater vehicle to track the thermocline based on peak-gradient detection. IEEE J. Oceanic Eng. 37 (3), 544–553. doi: 10.1109/JOE.2012.2192340

CrossRef Full Text | Google Scholar

Zhang Y., Godin M. A., Bellingham J. G., Ryan J. P. (2012b). Using an autonomous underwater vehicle to track a coastal upwelling front. IEEE J. Oceanic Eng. 37 (3), 338–347. doi: 10.1109/JOE.2012.2197272

CrossRef Full Text | Google Scholar

Zhang Y., McEwen R. S., Ryan J. P., Bellingham J. G. (2010). Design and tests of an adaptive triggering method for capturing peak samples in a thin phytoplankton layer by an autonomous underwater vehicle. IEEE J. Oceanic Eng. 35 (4), 785–796. doi: 10.1109/JOE.2010.2081031

CrossRef Full Text | Google Scholar

Zhang Y., Mcewen R. S., Ryan J. P., Bellingham J. G., Thomas H., Thompson C. H., et al. (2011). A peak-capture algorithm used on an autonomous underwater vehicle in the gulf of Mexico oil spill response scientific survey. J. Field Robotics 28 (4), 484–496. doi: 10.1002/rob.20399

CrossRef Full Text | Google Scholar

Zhang Y., Ryan J. P., Bellingham J. G., Harvey J. B. J., McEwen R. S. (2012c). Autonomous detection and sampling of water types and fronts in a coastal upwelling system by an autonomous underwater vehicle. Limnol. Oceanography: Methods 10, 934–951. doi: 10.4319/lom.2012.10.934

CrossRef Full Text | Google Scholar