Numerical study on the internal fluid mixing and its influencing mechanisms of the wave-driven floating photobioreactor for microalgae production

The wave-driven floating photobioreactors (PBRs) with advantages of easy in scaling-up, low energy inputs and low fabricating cost, hold great potential for massive and cost-energy effective microalgae production. However, their applications may be seriously challenged by intermittent waves that could produce very poor mixing under poor wave conditions, leading to a significant reduction of biomass productivity or even collapse of the cultures. To improve the utilization efficiency of waves for efficient and stable microalgae production in the floating PBRs, this work aims at numerically studying the fluid-dynamics of the floating PBRs, as well as the effects from wave conditions, culture depth and three different PBRs’ structures of square, rectangular and circular types. The results showed that the liquid inside the floating PBRs follow a periodic sinusoidal and reciprocating flow, and the square PBR had aggressive mixing characteristics at high wave excitation frequency, while the rectangular PBR produced more intense mixing at low wave excitation frequency. Regarding the culture depth, the dependence of liquid mixing on the culture depth showed a decreasing trend. Moreover, the results indicated that the PBRs with a high culture depth had several dead zones, although there was apparent upward flow at the high excitation frequency. This work provides valuable insight into increasing the utilization efficiency of wave energy for mixing enhancement in the floating PBRs and their design.

1 Introduction

The aquaculture industry plays important role in supplying sustainable food for human society, but its green and sustainable development is seriously challenged by the increasing deterioration of aquaculture water bodies and the shortage of aquaculture feed such as fishmeal and fish oil (Froehlich et al., 2022). As a promising approach, microalgae with abundant nutrients are great candidate substitutes for fishmeal and fish oil (Carvalho et al., 2020), and are also indispensable food for filter-feeding animals such as shellfish (Wang et al., 2022). Moreover, microalgae are also promising for the ecological remediation of aquaculture wastewater due to their rapid growth rate and high uptake rate of N and P (Zhao and Huang, 2021; Feng et al., 2022). Owing to these advantages, the global demand of using microalgae for the aquaculture industry is rapidly increasing.

Currently, there are two common systems for phototrophic microalgal cultivation: the open ponds and closed photobioreactors (PBRs) (Kumar and Jain, 2014). The open ponds have been widely used for most of commercial microalgal productions due to their advantages of low capital costs, low energy inputs, and easing in scaling-up (Zhu et al., 2022). However, the open ponds are also featured with disadvantages of low cell density, high evaporative rates, difficult in controlling of cultivation conditions, and high risks of contaminations (Hoffman et al., 2017), resulting in unstable production, and low biomass productivity and low quality of microalgae-based products. Compared with the open ponds, the PBRs such as flat plate PBRs, bubble tubular PBRs, and bubble column PBRs (Lehr and Posten, 2009), can have much higher cell density and biomass productivity, and advantage of controlling the cultivation conditions. Although the PBRs have these much better cultivation performances than the open pond, the PBRs are now only used for the high value-added microalgal products such as astaxanthin (Borowitzka, 2013), owing to their high fabricating costs, high energy inputs and high costs of maintenance and operation. Also, the PBRs are challenged by the problems of scaling-up, which makes it difficult to meet the rapid and massive requirements of microalgae feeds for aquaculture industry.

In recent year, the floating PBRs on the water surface by using wave energy for culture mixing, have received considerable attention for potential application on microalgal biomass production for aquaculture industry, due to their advantages of low capital costs, easy in scaling-up, low energy inputs, and high biomass productivity (Dogaris et al., 2015; Huang et al., 2016; Park et al., 2018). For instance, the Isochrysis zhangjiangensis were successfully cultured in a 1000 L floating PBR, and it produced the same cultivation performance as the flat panel PBR (100 L) at even a scale ten times greater (Zhu et al., 2019b), providing a massive and efficient algae feed production approach. More importantly, the floating PBRs can be deployed on the water surface of the aquaculture bodies, in which the PBRs can utilize aquaculture wastewater on site to culture microalgae consequently, and then supply microalgae in situ for use as fresh feed without biomass treatments and nutrient loss references (Figure 1). Moreover, the microalgae can be inoculated to the aquaculture bodies as seeds for their rapid proliferation, contributing to the twin goal of aquaculture wastewater treatments and supplying of microalgal feeds on site (Viegas et al., 2021).

FIGURE 1

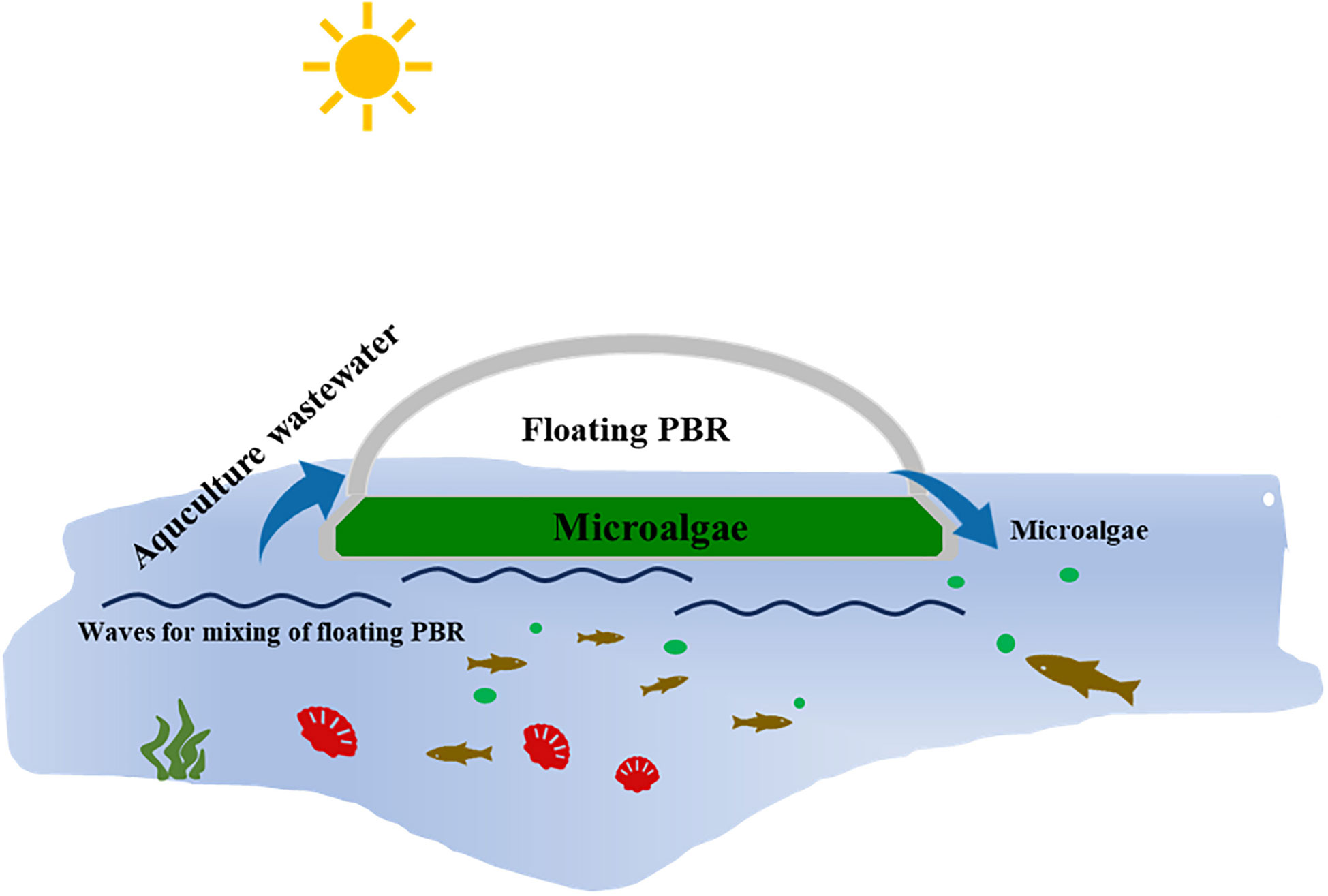
Figure 1 Diagram of the application of floating PBR on aquaculture for microalgae feed production and aquaculture wastewater treatments in situ.

However, applications of the floating PBRs that use waves as the sole energy for culture mixing may be seriously challenged by the intermittent waves, which could produce very poor mixing under poor wave conditions (Yew et al., 2019). Since sufficient mixing could reduce cell settling, facilitate efficient mass transfer and improve the light-dark cycle frequency of algal cells for their efficient cultivation (Gao et al., 2015), the poor mixing from low wave conditions would significantly reduce the biomass productivity of the floating PBRs and even cause the collapse of their cultures (Bitog et al., 2011). Hence, how to efficiently use wave energy for efficient and stable microalgae production is significant for the floating PBRs, especially for improving the utilization efficiency of the poor waves to enhance mixing efficiency. To reach this goal, a number of research groups preliminarily studied the liquid mixing (liquid sloshing) in the floating PBRs (Kim et al., 2016; Cheng et al., 2018; Cho and Pott, 2019; Zhu et al., 2019a; Guler et al., 2020; Khor et al., 2020). Most of them focused on the studies of the hydrodynamic behaviors, wave excitations, culture depth, and baffles structures by physical experiments or numerical simulations. Their studies greatly facilitated the hydrodynamic understanding of PBRs under wave excitation, and showed that the controllable parameters including baffles structures, PBR configurations (rectangular, circular and square types), and culture depths are the fundamental factors affecting the movement responses and mixing performances of floating PBRs. Still, several issues need to be resolved as below:

● As the most important influencing factor, the effect of wave conditions on the liquid mixing have not been thoroughly understood, neither their synergic effect with the above-mentioned controllable parameters.

● Compared with uncontrollable wave conditions, the controllable parameters play much more important roles in increasing utilization efficiency of waves. However, their effects on the liquid mixing are also not explicit, neither their influencing mechanisms.

Given these issues, this present work focuses on investigating fluid dynamics in the wave-driven floating PBRs without mixing devices, especially the influences of wave conditions, the PBR geometry, and the culture depth on fluid dynamics, as well as their synergic influences. Firstly, a CFD-based numerical simulation model was established to study fluid dynamics, and the validity of the developed model was verified by comparing its simulated results with the experimental results. Then, the effects of different configurations, excitation frequencies, and culture depths on fluid hydrodynamics were studied via the developed numerical model. In this present study, the fluid hydrodynamics were analyzed regarding flow characteristics, the average velocity of culture fluid, and dead zone fraction (DZF). This study provides an effective reference to improve wave energy utilization for mixing enhancement and valuable insights for the optimum design and commercial scaling-up of the floating PBRs, holding great potential in producing massive and low cost microalgal biomass for the sustainable and green development of aquaculture industry.

2 Methods

2.1 Model description

Most of the existing floating PBR structures are mainly square and rectangular, and their motion responses are significantly different. Zhu et al. found through physical experiments that the square PBR experienced more intense movement than the rectangular PBR, but also little mooring force (Zhu et al., 2018). For cylindrical PBRs, the main research focuses on land culture, while the floating PBR applied in Marine culture is rarely studied. The tanks with the three structures mentioned above are also common objects in the sloshing research, so it is applicable to the structural research of floating PBRs.

In this study, three types of floating PBRs (i.e., square, rectangular, and cylindrical) were used for numerical simulations (Figure 2), and all have an effective culture area of 1.0 m². As shown in Figure 2, the dimension of the square PBR is 1.0 m×1.0 m×0.3 m (length × width × height), the dimension of the rectangular PBR is 1.7 m×0.6 m×0.3 m (length × width × height), whereas the cylindrical PBR has a dimension of 1.12 m×0.3 m (diameter × height).

FIGURE 2

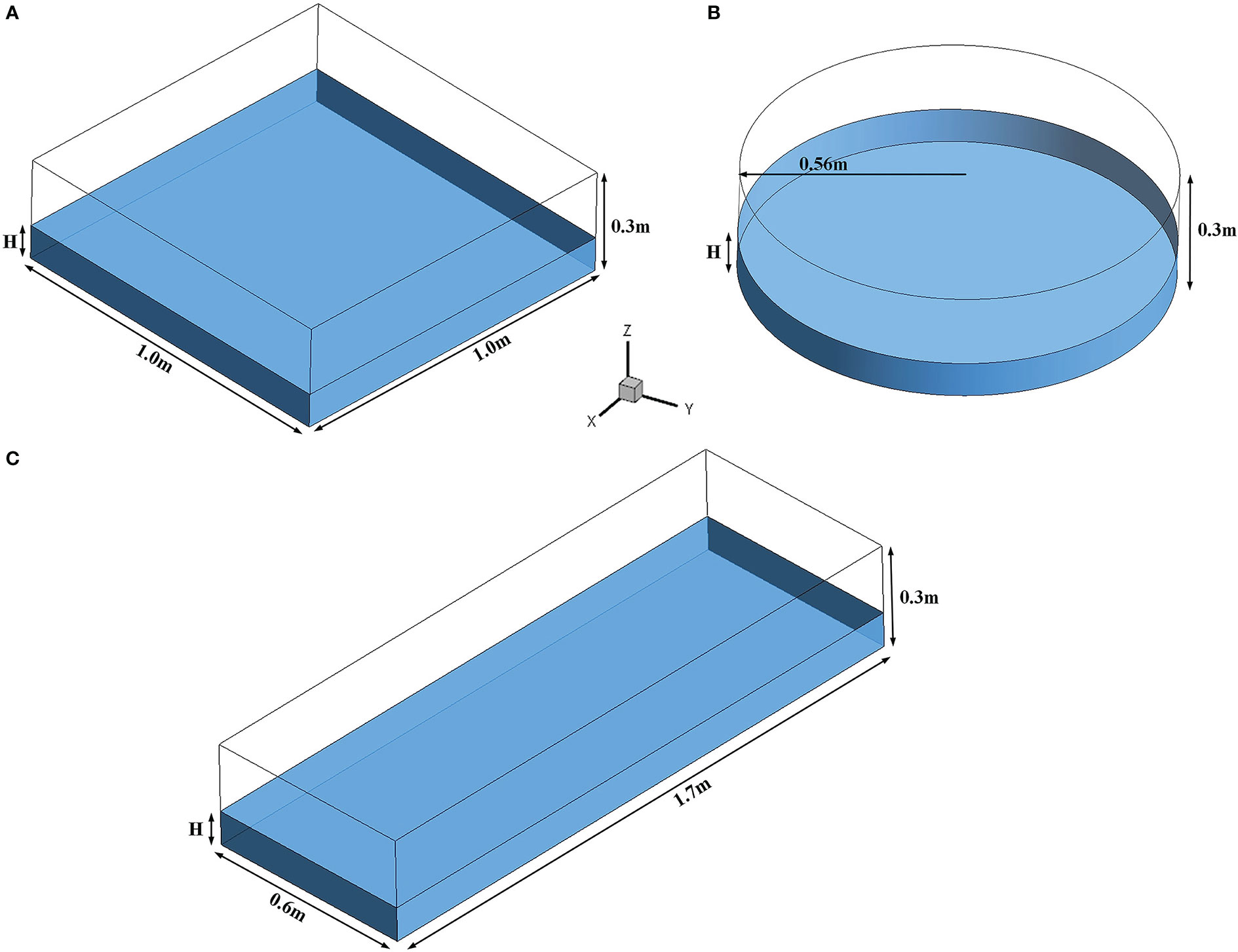
Figure 2 Configurations of the floating PBRs. (A) Square PBR (B) Cylindrical PBR (C) Rectangular PBR.

As a floating object, the floating PBR experiences liquid sloshing due to its forced sinusoidal hydrodynamic movement (Eq. 1) under external wave excitation (Zhu et al., 2018).

$\begin{array}{ll}S(t)=S_0\text{cos}\theta \text{sin}\omega t& (1)\end{array}$

where S₀ is the motion amplitude of floating PBR, and S_{0 =} 0.01 _m is selected for the numerical simulations of these three PBR models according to a previous study (Zhu et al., 2019a); θ is the amplitude of the roll movement, and θ =10° is selected for the numerical simulations; t is the time; ω represents the frequencies of external wave excitations, which are significantly affected by the configuration and liquid depth of the floating PBRs, and the excitation conditions are described by Eq. (2).

$\begin{array}{ll}{\omega }_{mn}^2=\sqrt{{\left(\frac{m\pi g}{L}\right)}^2+{\left(\frac{n\pi g}{W}\right)}^2}\times tanh\sqrt{{\left(\frac{m\pi H}{L}\right)}^2+{\left(\frac{n\pi H}{W}\right)}^2}& (2)\end{array}$

where L is the length of the tank, W is the width of the tank, H is the liquid depth, as illustrated in Table 1. m and n can be taken as 1, 2, 3, etc. In this study, the n^th order theoretical formula of free sloshing liquid was adopted to calculate the natural frequency of free sloshing liquid inside PBRs, which has been widely used in the study of liquid sloshing inside the floating objects (Zhu et al., 2018). According to the first-order natural frequency theory of free sloshing liquid, the natural frequency of the free sloshing liquid for the square and rectangular floating PBR is 3.06 rad/s and 1.84 rad/s, respectively, when only considering the lateral shaking of the reactor (m=1, n=0). For the circular floating PBR, since the natural frequency cannot be solved directly by theoretical formula, the lateral shaking of the reactors and their heaving were both considered in this present work.

TABLE 1

Table 1 The culture depth used for numerical simulation of liquid sloshing.

Hence, this study investigated the effect of the PBRs’ configuration and liquid depth, and the wave conditions on the liquid sloshing inside the floating PBRs, where three configurations of PBRs as described in Section 2, and five culture depths (H) of 0.05, 0.10, 0.15, 0.20 and 0.25 m are considered (Table 1). For the effect of wave conditions, the incident wave with different excitation frequencies (Table 2).

TABLE 2

Table 2 The excitation frequencies used for numerical simulation of the liquid sloshing inside square PBRs with a culture depth of 0.1 m.

2.2 Numerical descriptions

The flow in the floating PBRs was assumed to be incompressible with constant density and molecular viscosity. The unsteady Reynolds-averaged Navier-Stokes (URANS) simulations of gas-liquid two-phase flow were conducted by using the VOF model to track the volume fraction of each of the fluids throughout the domain. First, the pre-processing software (ICEM CFD 18.2) was used to complete the grid division of the floating PBRs. Then, dynamic mesh and 6 DOF body were used to simulate the movement process of PBR, and the user-defined function (UDF) was used to define the movement of the PBRs. Finally, the CFD code Fluent v18.2 was used to solve the URANS equations. The computation time of numerical method validation is 5 s, and the calculation time for the statistical analysis section is 15 s.

2.3 Governing equations

The Navier-Stokes equations with turbulence model are solved to model the three-dimensional flow field and acquire the velocity and pressure variables. The URANS equations regarding the conservation of mass and momentum in a Cartesian form are shown as below:

$\begin{array}{ll}\frac{\partial \rho }{\partial \text{t}}+\frac{\partial }{\partial x_i}(\rho u_{\text{i}})=0& (3)\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial t}(\rho u_i)+\frac{\partial }{\partial x_j}(\rho u_i{u}_j)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_j}-\frac{2}{3}{\delta }_{ij}\frac{\partial u_k}{\partial x_k}\right)\right]-\frac{\partial }{\partial x_i}\left(\overline{\rho u_i^{\text{'}}{u}_j^{\text{'}}}\right)& (4)\end{array}$

where ρ is the fluid density, u_i is the velocity component in the Cartesian coordinates, and μ is the mixture dynamic viscosity. $\overline{\rho u_i^{\text{'}}{u}_j^{\text{'}}}$ is Reynolds stress that needs be resolved to close Eq. (4).

The standard k-ϵ model is selected to describe the turbulent flow in this study. This model is based on model transport equations for the turbulence kinetic energy and its dissipation rate (Launder and Spalding, 1972). The turbulence kinetic energy, k, and its rate of dissipation, ϵ, can be obtained from the following transport equations:

$\begin{array}{ll}\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\partial k{u}_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho ϵ-Y_M+S_k& (5)\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial t}\left(\rho ϵ\right)+\frac{\partial }{\partial x_i}\left(\partial ϵu_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{ϵ}}\right)\frac{\partial ϵ}{\partial x_j}\right]+G_{1ϵ}\frac{ϵ}{k}\left(G_k+G_{3ϵ}{G}_b\right)+G_{2ϵ}\rho \frac{{ϵ}^2}{k}+S_{ϵ}& (6)\end{array}$

where G_k represents the generation of turbulence kinetic energy due to the mean velocity gradients. G_b is the generation of turbulence kinetic energy due to buoyancy. Y_M represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate. C_1ϵ, C_2ϵ, and C_3ϵ are constants. σ_k and σ_ϵ are the turbulent Prandtl numbers for k and ϵ, respectively. S_k and Sϵ are source terms.

The VOF model can describe the free flow surface coupled by the interaction of two or more insoluble fluids, which is carried out by solving a single set of equations (Eq. 3, 4) and tracking the volume fraction of each of the fluids throughout the domain (Eq. 7, 8, 9).

$\begin{array}{ll}\rho ={\rho }_l{a}_l+{\rho }_g{a}_g& (7)\end{array}$

$\begin{array}{ll}\mu ={\mu }_l{a}_l+{\mu }_g{a}_g& (8)\end{array}$

$\begin{array}{ll}{a}_l+a_g=1& (9)\end{array}$

where ρ_l and ρ_g are the densities of water and air. μ_l and μ_g are the viscosities of water and air. a_l and α_g are the volume fractions of water and air, respectively.

2.4 Computational domain and mesh generation

The governing equations in this study are a set of partial differential equations (PDEs). The PDEs can be discretized using the finite volume method (FVM) with structured grids. The computational domain is represented by numerical grids at which the variables can be transferred and calculated. The computational domains are three simple geometric bodies that include a rectangular body, a square body, and a cylindrical body respectively. And the upper part of the area is filled with air and the lower part is filled with water. As shown in Figure 3, the computational domains are meshed with orthogonal hexahedral grids and the mesh size is 10^-3 m. Furthermore, the grid independence study will be addressed in section 3.4 of this paper. To ensure the grid orthogonality, the cylindrical domain for 3D simulations utilizes an O-grid. In addition, the stability and convergence of the computation need to be introduced to assure by using Courant-Friedrichs-Lewy (CFL) number to define the convergence condition of the numerical simulation. The Courant number is defined as follow:

FIGURE 3

Figure 3 Mesh model (A) Square PBR (B) Cylindrical PBR (C) Rectangular PBR.

$\begin{array}{ll}{C}_0=\frac{\left|U_{Max}\right|\Delta t}{\Delta x_{Min}}& (9)\end{array}$

where U_Max is the maximum flow velocity, U_Max=0.5m·s^-1 ; the Δx_Min is the minimum grid size, Δx_Min=10^-3 ; Δt is time step, Δt=10^-4 . To ensure the stability and convergence of the computation, Courant number should be controlled less than 1.

2.5 Boundary conditions and discretization

Considering floating PBR is a closed structure, all the boundaries of the PBR are defined by moving wall boundary conditions with no slip. The water free surface is captured by using VOF model.

The discretization is to convert the PDEs into non-linear algebraic equations. For unsteady flows, an elliptic problem has to be solved at each time step. Unsteady flows are solved by an equivalent iteration scheme, and then problems turn out to be solutions of linear equation systems. Firstly, utilizing the finite volume method (FVM) with structured grids to discretize these PDEs, as shown in Figure 3. The coupled scheme is implemented for pressure-velocity coupling, where the discretization of the convective terms is conducted by the semi-implicit method for the pressure-linked equations (SIMPLE) scheme. Then, the spatial discretization of the pressure and momentum is conducted through second-order upwind differencing schemes, respectively. The temporal discretization is conducted using a second-order implicit differencing scheme. Finally, the algebraic equations are solved by the Gauss–Seidel iterative method with the Algebraic Multigrid (AMG) solver. The convergence criteria for the inner iterations are set as 10^-6 for the discretized continuity, momentum, and energy equations. And the time step is set as 10^-3 for unsteady conditions.

2.6 Measurements of DZF

The flow velocity should be higher than 0.1 m·s^-1 to circulate the microalgae culture to avoid cell settling (Zhang et al., 2015), and this value has been widely used as the threshold of the dead zone. However, since the liquid inside the floating PBRs followed a periodic sinusoidal and reciprocating flow, the DZF for the floating PBRs was specially defined and calculated as follows:

$\begin{array}{ll}\text{DZF}=\frac{{\displaystyle \sum _i^n{V}_i}}{n{V}_{FBP}}\times 100\%& (10)\end{array}$

where DZF represents the dead zone volume fraction, n is the total number of calculated samples, V_i represents the fluid volume of instantaneous velocity< 0.1 m·s^-1 at the time i, V_FBP is the total fluid volume in floating PBR.

3 Results and discussion

3.1 Model validation

To validate the numerical method developed in this work, the liquid sloshing experiments conducted by Delorme et al. were selected (Delorme et al., 2009), in which three different cases were used for the validation. As shown in Figure 4, the numerical interface shapes of all three cases were almost the same as their corresponding experimental photos, and the trends of the visible wave were also constant with their corresponding experimental results. These results indicated that the developed numerical model could well predict the fluid sloshing, and it was then adopted for the sequent simulations.

FIGURE 4

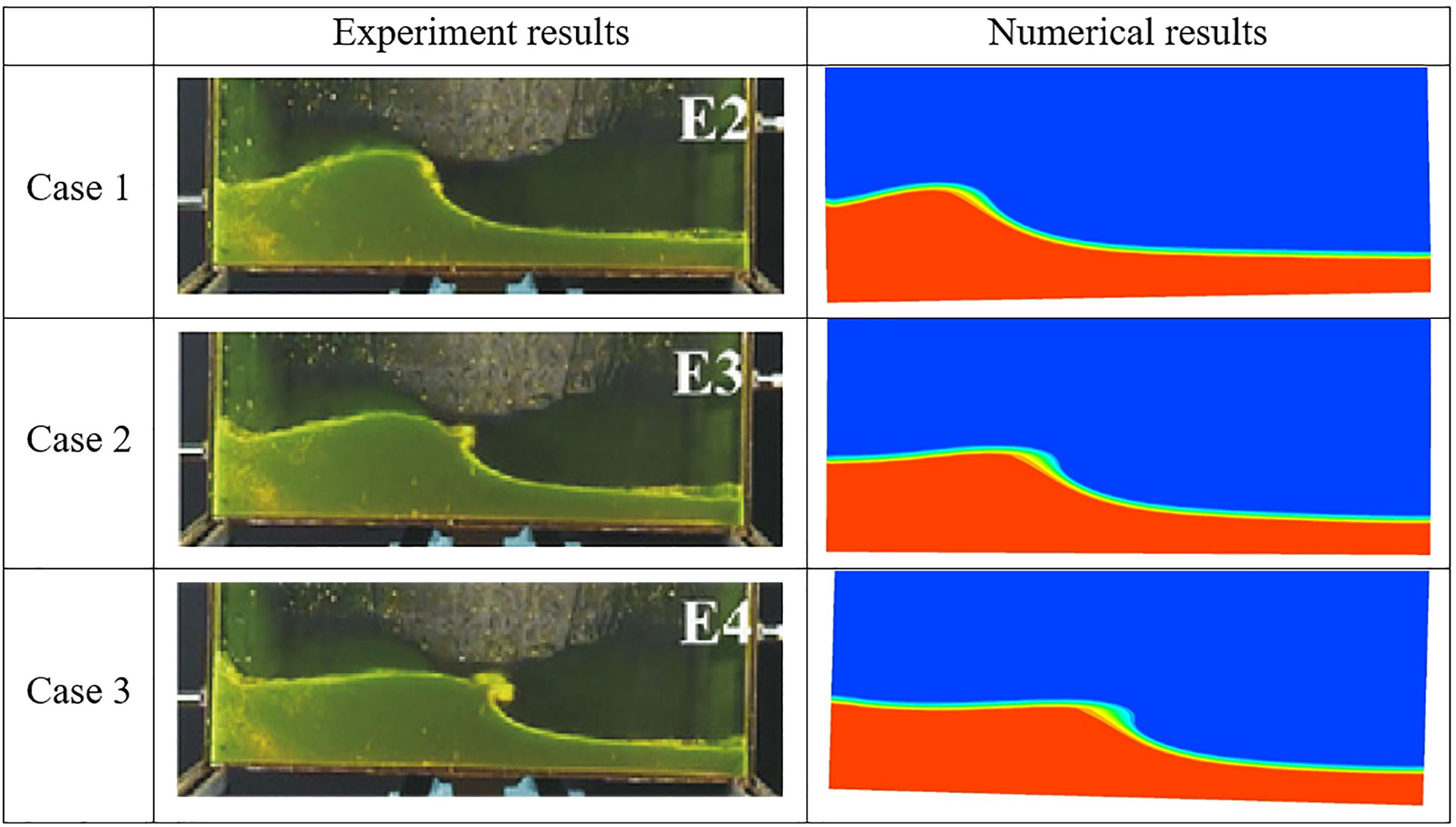
Figure 4 Gas-liquid phase diagram of liquid sloshing in tank. (A) Experimental results from (Delorme et al., 2009) and (B) the numerical simulation results from the CFD model developed in this study.

The grid size has been established as one of the most significant factors affecting the accuracy of numerical results (Jiang et al., 2015). Hence, to further scrutinize the accuracy of the developed model, the effect of grid sizes on the accuracy of the numerical results was investigated. In this present work, three grid sizes, namely mesh-1 (5.0×10^-4 m), mesh-2 (1.0×10^-3 m) and mesh-3 (5.0×10^-3 m), were selected for the grid-independent verification. As shown in Figure 5, the numerical simulation results of these three meshes almost coincided with their corresponding experimental results, indicating they are sufficient to obtain the convergent results. Therefore, to reach the twin goals of reducing computational resources and maintaining high calculation accuracy, the mesh with a grid size of 1.0×10^-3 m was selected in the sequent numerical simulations.

FIGURE 5

Figure 5 Time histories of pressure with three different grid levels.

3.2 Effect of floating PBR’s configurations

As shown in Figure 6, the internal fluid of the floating PBRs under continuous wave excitations, experienced a periodic sinusoidal and reciprocating flow at high wave excitation conditions due to the forced sinusoidal hydrodynamic movement of the floating PBRs. This is different from the unidirectional flow of the liquid generated in conventional microalgal cultivation systems, such as open ponds and tubular PBRs. Notably, the flow velocities of the liquid inside the square and cylindrical floating PBRs were enhanced with the increasing of the wave excitation conditions, where the average highest velocity (ranged from 0.035 to 0.43 m·s^-1) increased with the increasing of the wave excitation frequencies, and their sloshing periods were also significantly decreased (ranged from 4.1 to 1.37 s). However, the fluids followed un-regular sinusoidal flows at the low wave excitation frequencies, which have low highest average velocity and long sloshing periods, indicating that the poor wave conditions are insufficient to generate efficient liquid mixing. Generally, the average fluid velocity of the square and cylindrical floating PBRs increased with the increasing of wave excitation frequencies, resulting in their more violent liquid mixing than the rectangular floating PBR under high excitation frequency. Compared with these two floating PBRs, the wave excitation frequency had no significant effect on the average fluid velocity of the rectangular floating PBR.

FIGURE 6

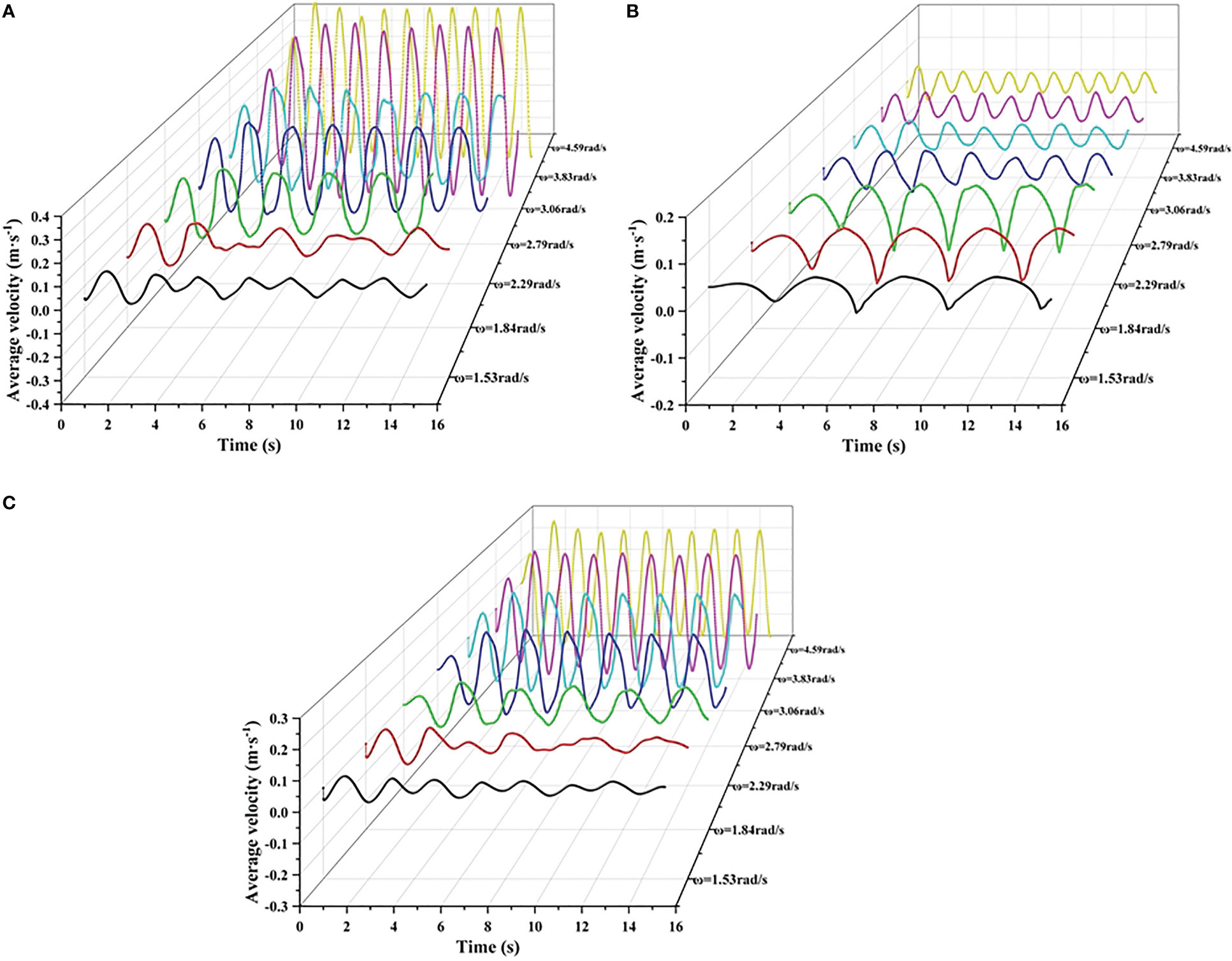
Figure 6 The average velocity of liquid inside the floating PBRs under continuous wave excitations. (A) Square PBR (B) Rectangular PBR (C) Cylindrical PBR. (Culture depth: 0.1 m).

The DZFs of the floating PBRs under continuous wave excitation are shown in Figure 7. Briefly, the DZFs of square and cylindrical PBR were increased with the increasing of the wave excitation frequencies, where the lowest DZFs of 1.5% and 0.3% were achieved in the square and rectangular PBR at the highest wave excitation frequency of 4.59 rad/s, respectively. The corresponding DZFs for these two PBRs were up to 39% and 36% at the lowest wave excitation frequency of 1.53 rad/s, respectively. However, it interesting is that the rectangular floating PBR had about two times lower DZF than the other two PBRs under the low excitation frequencies (1.56 and 1.84 rad/s), indicating it had more efficient liquid mixing under poor wave conditions. As calculated, the excitation frequencies of the rectangular floating PBR are close to its resonant frequency (1.84 rad/s), while there are significant differences for that between the square and cylindrical floating PBRs. Consequently, the resonant oscillation occurred in the rectangular floating PBR under the low excitation frequencies of 1.56 and 1.84 rad/s, which is the crucial reason why the rectangular floating PBR had so more efficient liquid mixing under these excitation frequencies.

FIGURE 7

Figure 7 The dead zone volume fractions for the floating PBRs (Culture depth:0.1 m).

As shown in Figure 13, under the continuous wave excitations, the floating PBR can produce the same mixing performance as the open pond and bubble column PBR in terms of DZFs, and even better in the low culture depth of 0.1 m (Hadiyanto et al., 2013). However, the DZF of the floating PBRs could be much high under natural waves due to their intermittence, and there is even no fluid flow or mixing. In this case, a high level of dissolved oxygen and culture temperature may be accumulated, resulting in a decrease in algal biomass productivity and even the collapse of the cultures (Zhu et al., 2019c), which has been considered one of the biggest challenges for the commercial applications of the floating PBRs. A promising method to solve this problem is using renewable energy such as wind energy and solar energy to supply supplementary mixing for the floating PBRs under poor waves. For instance, the solar panel can be installed with the floating PBRs to supply mixing when the low culture velocity, high culture temperature or high concentration of dissolved oxygen are detected. More importantly, this operation can be completely achieved using artificial intelligence technology (Wang et al., 2021). This provides a promising approach to reduce the decrease of algal biomass productivity and increase the net energy ratio (NERs) of microalgal biofuels. Due to these advantages, a related study on this proposed technology should be intensively required in the future.

Since the upward flow of fluids along the light propagation direction could enhance the light-dark cycle frequency of cells, promoting the upward flows have been considered a promising method to increase microalgal biomass productivity (Yang et al., 2016; Nzayisenga et al., 2020). However, as exemplified by the square PBR (Figure 8), the flows inside it mainly followed a horizontal flow, and this phenomenon is more aggressive under low wave excitation frequencies. This phenomenon is more typical for the square PBR and cylindrical PBR under high wave excitation frequencies of 3.06, 3.89, and 4.56 rad/s (Figure 9). Due to the longer length of the rectangular PBR in the direction of wave motion than the other two PBRs, the excitation waves have changed its move direction before the transverse impacts wall (Figure 10). Consequently, the velocity of the transverse wave in the rectangular PBR was significantly reduced due to the force from the reversed excitation waves, resulting in much poor wave roll-over than the other two reactors (Figure 10). Based on these results, it is promising to install the ‘walls’ (or termed as flow deflectors or baffles) inside the floating PBRs to enhance their upward fluid flow, and the similar methods have been reported and proposed in other studies (Zhu et al., 2018).

FIGURE 8

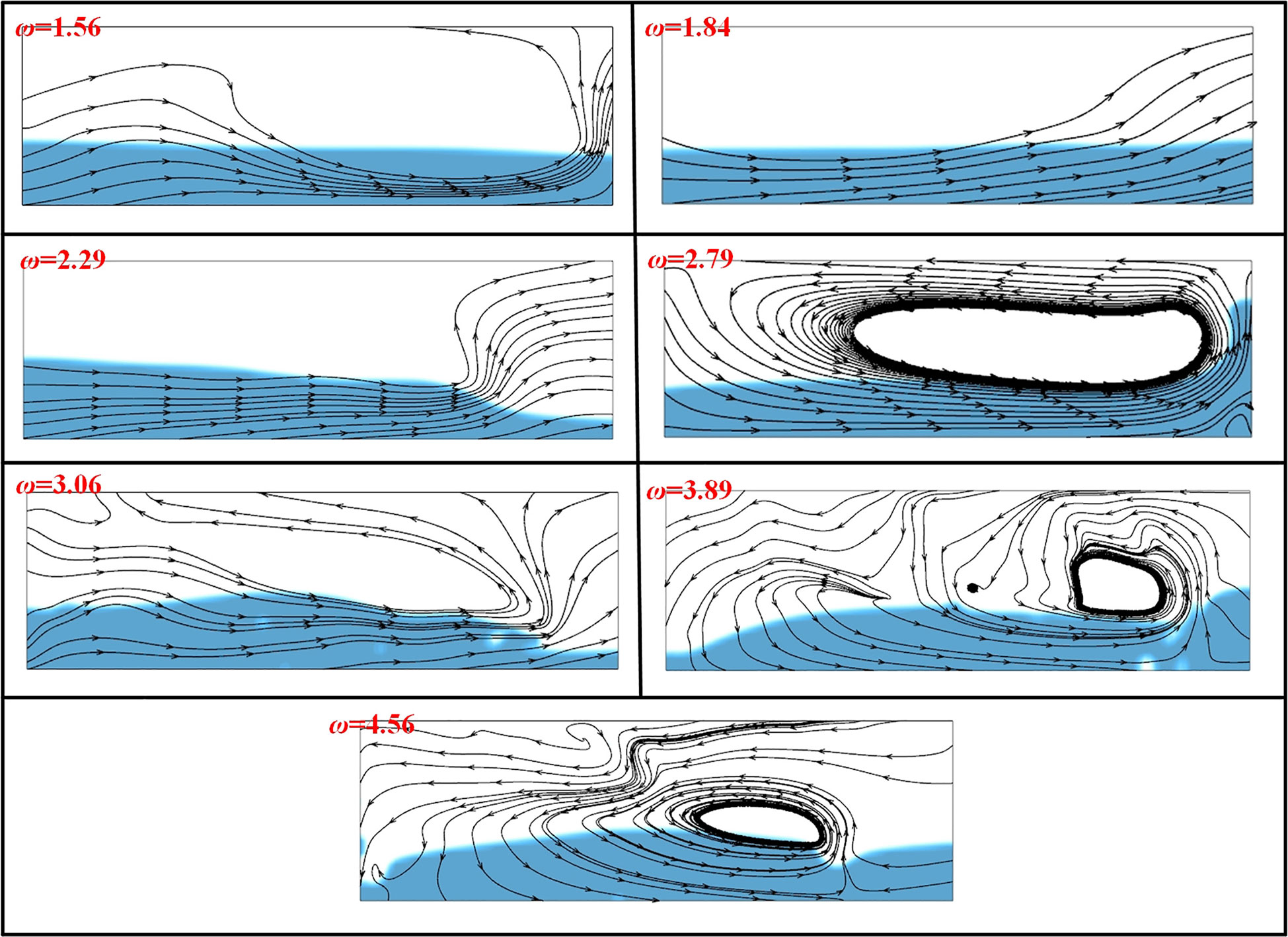
Figure 8 Streamline diagram of square PBR at t₅ under different excitation frequencies (Culture depth: 10 cm, t_{5 =} 5T). t₅ represents the moment at the fifth cycle, T represents sloshing period.

FIGURE 9

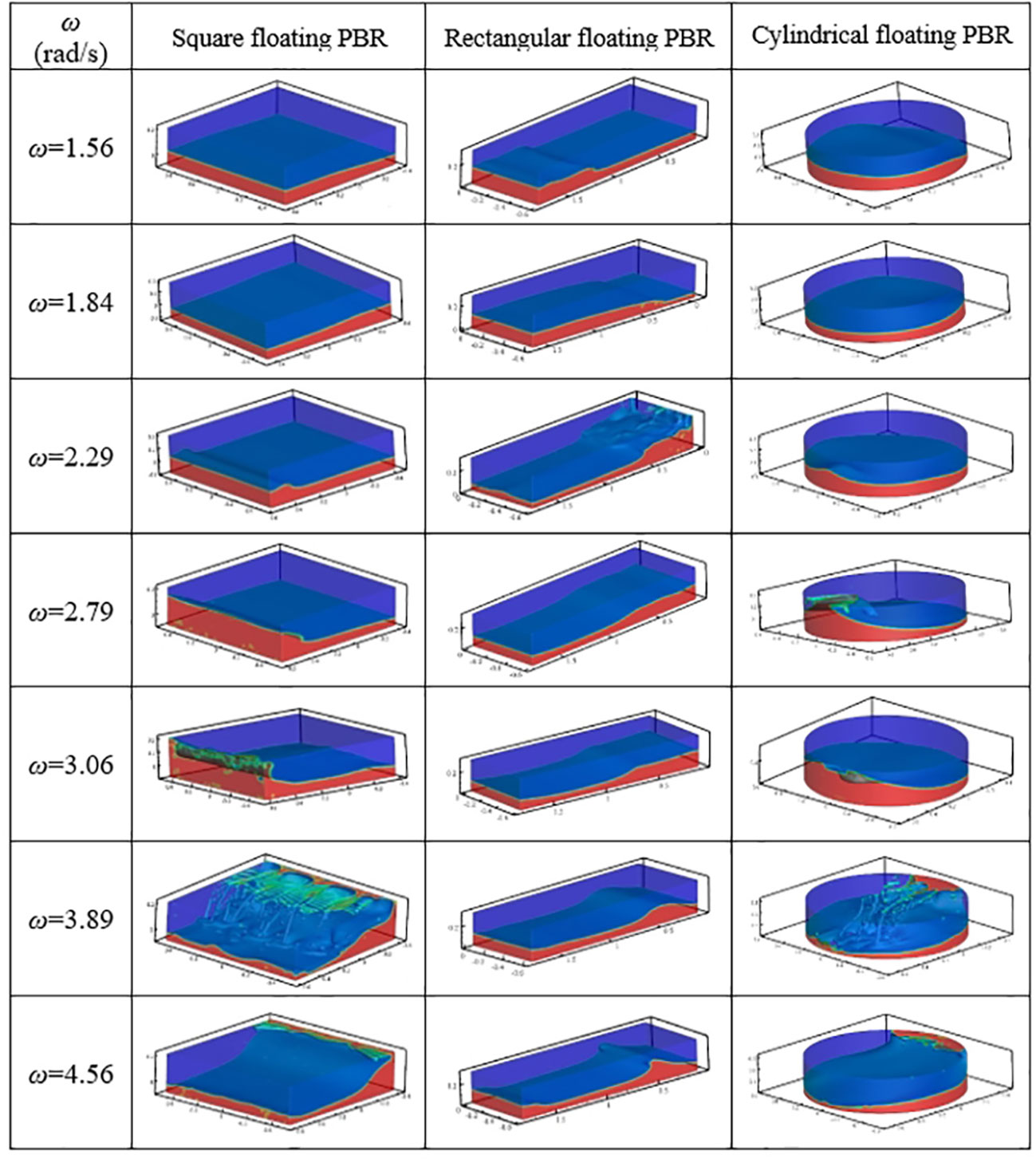
Figure 9 Gas-liquid phase diagram of floating PBRs at t_4.25. (t_{4.25 =} 4T+0.25T, culture depth: 0.1 m). t_4.25 represents the moment at a quarter of the fifth cycle, T represents sloshing period.

FIGURE 10

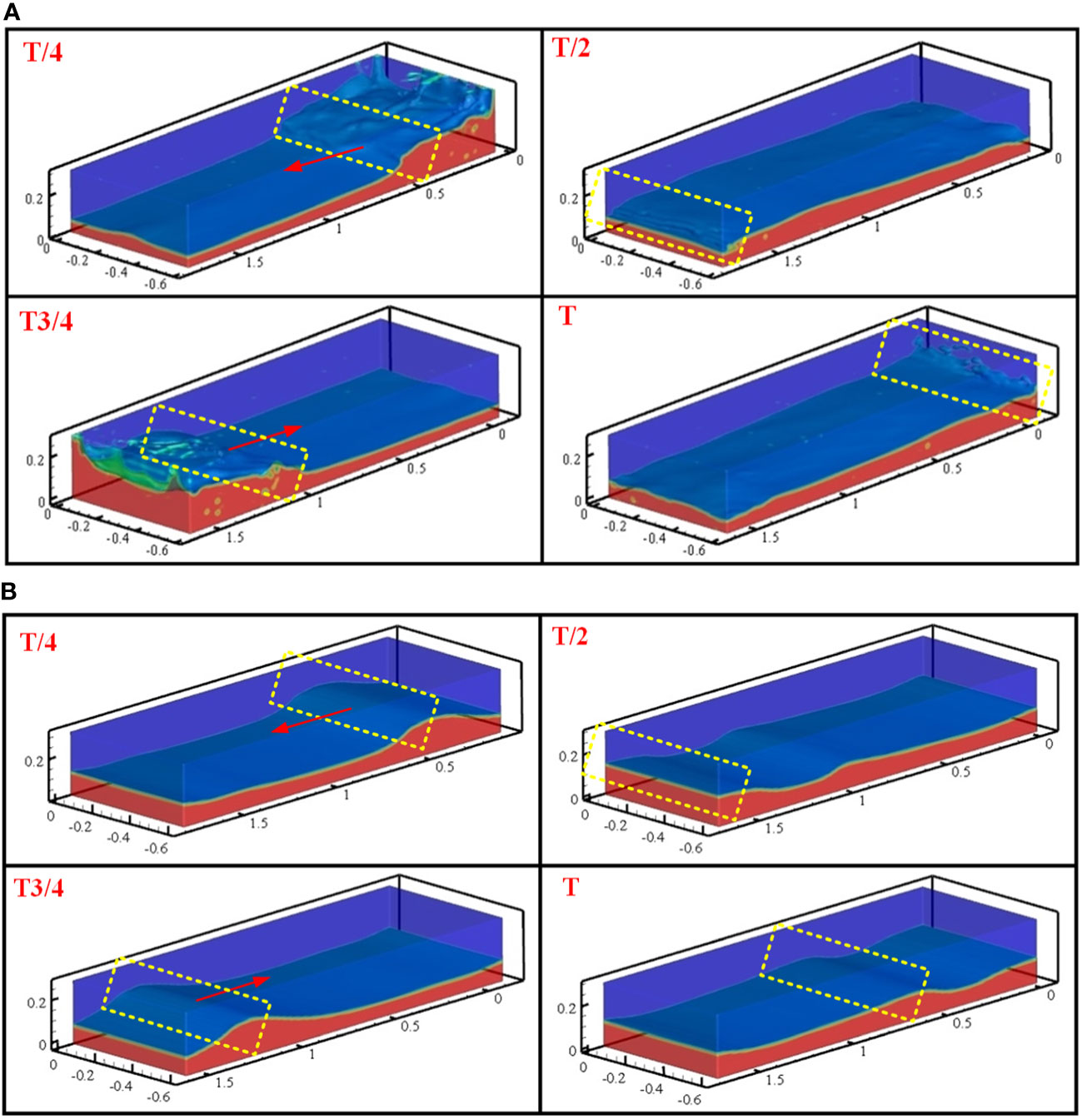
Figure 10 Gas-liquid phase diagram of the rectangular PBR at t₅ (A) ω=2.29 rad/s (B) ω=3.89 rad/s. (t_{5 =} 5T, culture depth: 0.1 m). t₅ represents the moment at the fifth cycle, T represents sloshing period.

The previous study has confirmed that the square floating PBR experienced more intense hydrodynamic movement than the rectangular PBR (Zhu et al., 2019a), while this present study revealed that the square floating PBR also produced more efficient liquid mixing. These results indicate that the square PBR is more suitable for microalgae cultivation, but its application may be limited due to its poor mixing performance under the low wave excitation frequency. More seriously, the poor mixing can become severer with the increasing of its scale-up even under the high wave frequency (Zhu et al., 2019c), presenting a great obstacle for the application of the floating PBRs. As shown in this study, the structure of reactor has an important influence on its mixing performance, especially for the length of the reactor along the wave propagating direction. Hence, the length of the floating PBRs along the wave direction should be controlled and optimized to successfully scale up the floating PBR and maintain efficient mixing in it, and optimizing the combination of the length and the flow deflectors would be a promising method for the purpose, which should be intensively studied in future.

3.3 Effect of culture depth

Figure 11 shows the fluid dynamic of the floating PBRs with different culture depths. For the square and circular PBR, the flows inside them mainly followed horizontal flow under low culture depth (H=0.05 m, Figures 12A, C), and then followed an upward flow under high culture depth (H≥0.1 m, Figures 11A, C). This is because the friction between the bottom wall and the fluid can significantly suppress liquid sloshing when a thinner liquid layer appears, and similar results were also reported in another study (Chen and Xue, 2018). However, compared with these two PBRs, the flows inside the rectangular floating PBR mainly followed horizontal flow even with the increase of culture depth (Figure 11B). Notably, there is no significant difference in the fluid dynamics between the different culture depths under low-frequency waves for these three PBRs. For instance, as shown in Figure 12, the flows inside the square PBR mainly followed similar horizontal flows.

FIGURE 11

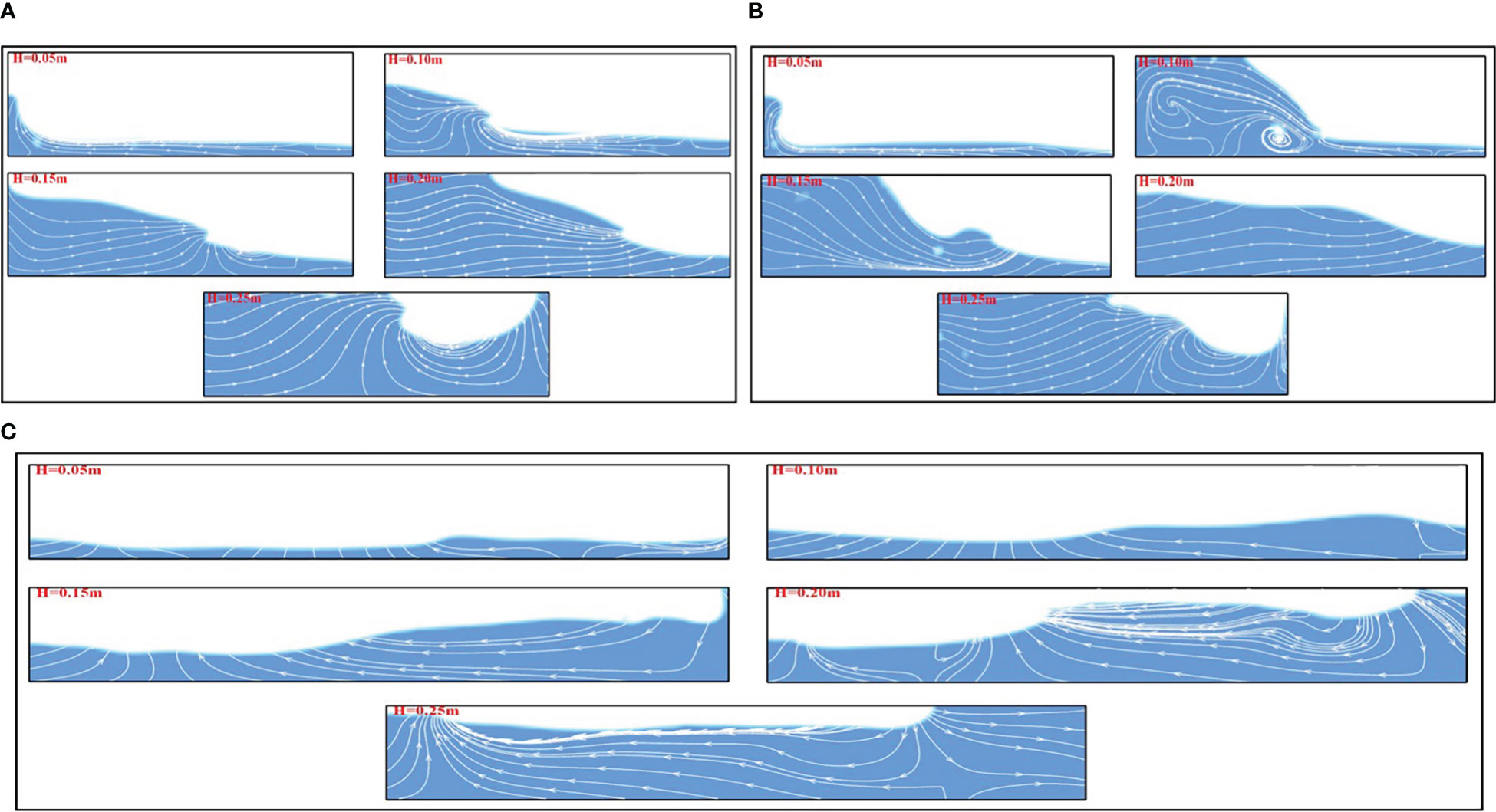
Figure 11 Streamline diagram of floating PBRs with different culture depth at t₅: (A) Square PBR, (B) Rectangle PBR and (C) Cylindrical PBR (ω=3.06 rad/s, t_{5 =} 5T). t₅ represents the moment at the fifth cycle, T represents sloshing period.

FIGURE 12

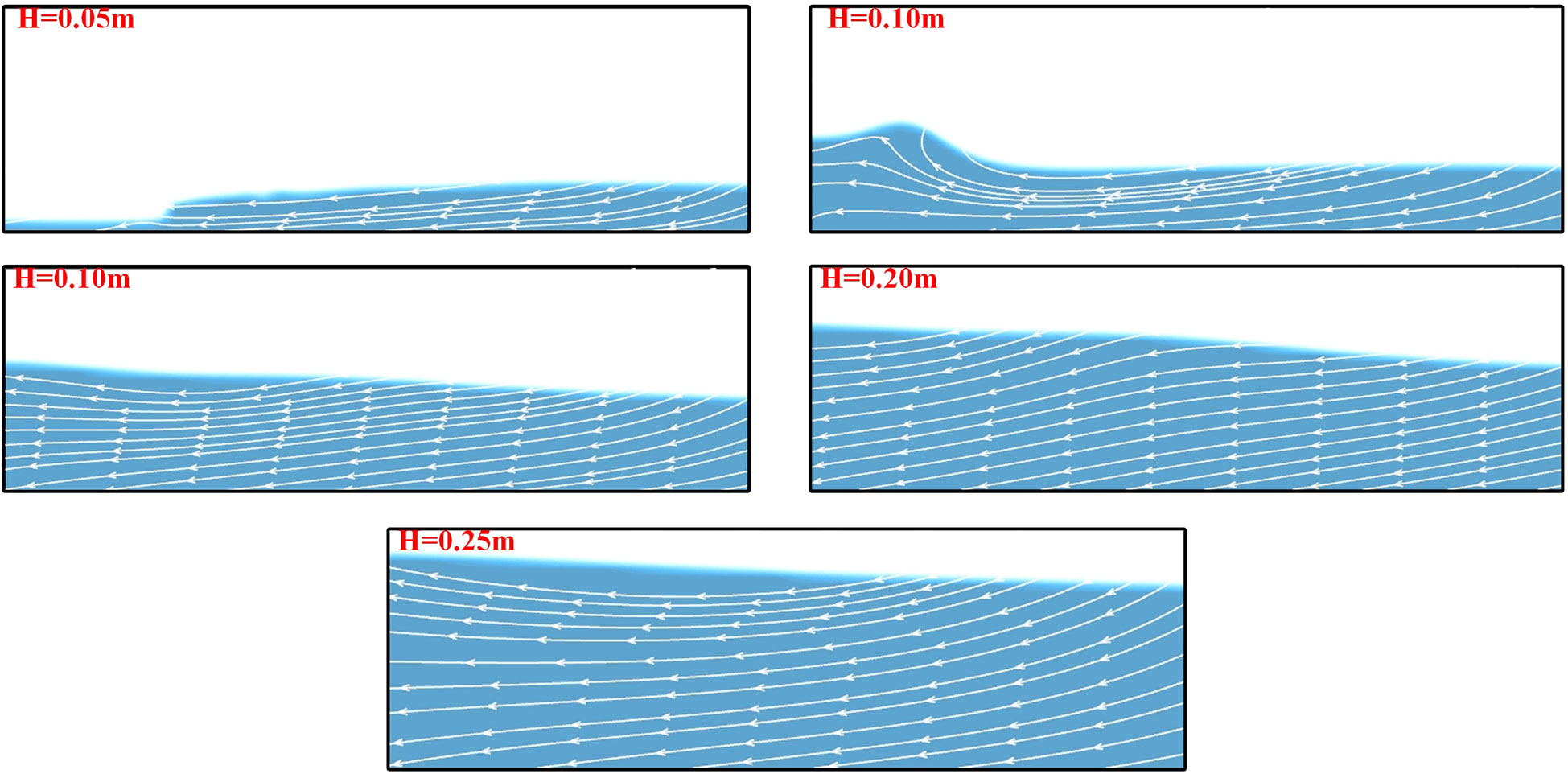
Figure 12 Streamline diagram of the square floating PBR with different culture depths at low-frequency excitation (ω=2.29 rad/s, t_{5 =} 5T). t₅ represents the moment at the fifth cycle, T represents sloshing period.

The DZFs of the floating PBRs with different culture fluid depths are shown in Figure 13. For the rectangular PBR, its DZFs were increased with the increase of culture depths, where the minimum DZF of 10.3% was achieved at the culture depth of 0.05 m. Compared with the rectangular PBR, the effects of culture depth on the DZFs of the square and cylindrical PBRs were more complicated, where their DZFs were both decreased with the increase of culture depths at first, and then were increased (Figure 12). The minimum DZFs of the square and cylindrical PBRs were 4.9% and 7.2%, respectively, which were achieved at the culture depths of 0.15 m and 0.10 m, respectively. This is because the external excitation frequencies of these two reactors above their corresponding culture depths (0.15 and 0.10 m), are both consistent with their corresponding natural frequencies, resulting in a resonance phenomenon, which intensifies the sloshing inside the reactors and reduces the DZFs. Notably, the effect of culture depths on DZF in open ponds is similar to that in square and cylindrical PBRs (Figure 13), while that for bubble column PBR and rectangular PBR is similar.

FIGURE 13

Figure 13 The dead zone volume fraction of algae cultivation systems with different culture depths.

As shown in this study, culture depth and PBRs’ structures have complex and interactive effects on the fluid dynamic of the floating PBRs. For instance, the floating PBRs pronounced upward flow at high culture depth (Figure 11), but they also were featured with high DZF simultaneously (Figure 13); the mixing of the rectangular PBR is sensitive to culture depth, and it can produce better mixing under low wave excitation; These results indicate that the optimal culture depth for the floating PBRs should be selected based on the interactive effect of structures and marine conditions. As guided by this study, in view of fluid dynamics, the following advices on the selection of optimal culture depth for the floating PBRs are proposed: for the rectangular PBR, we should choose low culture depth; the extremely low or high culture depth is inappropriate for square and cylindrical PBR, and the optimal culture depth is 0.1-0.15 m; the culture depth should be at about 0.15 m under high-frequency excitation for both of the floating PBRs, while 0.1 m under low-frequency excitation.

However, in addition to affecting the fluid dynamics, culture depth also affects the light transfer, where the thin culture depth has a high average light intensity (Gao et al., 2018), contributing to high biomass productivity and density. As reported, the highest biomass density of 2.24 g L^-1 and carbon utilization efficiency (CUE) of 83.3 ± 2.0% can be achieved in the cultivation of Spirulina at a culture depth of 0.05 m, which is about 1.6 and 1.5 fold higher than that of 0.1m cultures (Zhu et al., 2018). The high biomass density and CUE would help significantly reduce the harvesting cost and carbon source cost, which are considered two great parts of the total algae production costs (Zhu et al., 2021). On the other hand, the small culture volumes at the low culture depth will also increase the related operating costs and manpower costs, and require large land to produce the same biomass as that of high culture depth. To obtain an optimal culture depth for the best cost-effective microalgae production, the synergistic effect of the culture depth on microalgae production, including biomass density and productivity, as the costs of operation and harvesting, should be comprehensively evaluated with further study in the future.

4 Conclusions

This study studied the fluid dynamics inside the floating PBRs and their influencing mechanism by using the CFD technique. The numerical simulation results indicated that the liquid inside the floating PBRs followed a periodic sinusoidal and reciprocating flow, mainly horizontal. This liquid mixing was enhanced with the increasing external wave excitation frequencies, and it was also significantly affected by the configurations of the floating PBRs and their culture depths. The results demonstrated that the square PBR had more efficient liquid mixing at high wave excitation frequency, but the rectangular PBR produced more intense mixing at low wave excitation frequency. The PBRs with a high culture depth had high dead zone fractions although there was obvious upward flow at the high excitation frequency. Intensive studies are required to further enhance mixing of the floating PBRs in the future, including installing flow deflectors or baffles inside the floating PBRs for enhancement of their upward fluid flow, and using renewable energy such as wind energy and solar energy to supply supplementary mixing for the floating PBRs under poor waves.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author contributions

YZ: Conceptualization, Methodology, Software. GJ: Data curation, Writing- Original draft preparation. YC: Visualization, Investigation. HZ: Visualization, Investigation. ZC: Supervision, Ajay Kumar, Software, Validation. HS: Visualization, Investigation. CZ: Writing, Reviewing, and Editing. All authors contributed to the article and approved the submitted version.

Funding

This work was financially supported by the National Natural Science Foundation of China (42188102, 51822901, 31972843 and 31872610); LiaoNing Revitalization Talents Program (XLYC907139 and XLYC2007045); Dalian Technology Talents Program, Projects (2020RQ107 and 2020RJ02); Program from Key Laboratory of Environment Controlled Aquaculture, Ministry of Education, China (2021-MOEKLECA-KF-08).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

PBR, photobioreactor; CFD, computational fluid dynamics; unsteady Reynolds-averaged Navier-Stokes, URANS; UDF, user defined function; VOF, volume of fluid; PDEs, partial differential equations; FVM, finite volume method; CFL, courant friedrichs lewy.

References

Bitog J. P., Lee I.-B., Lee C.-G., Kim K.-S., Hwang H.-S., Hong S.-W., et al. (2011). Application of computational fluid dynamics for modeling and designing photobioreactors for microalgae production: A review. Comput. Electron. Agric. 76 (2), 131–147. doi: 10.1016/j.compag.2011.01.015

CrossRef Full Text | Google Scholar

Borowitzka M. A. (2013). High-value products from microalgae–their development and commercialisation. J. Appl. phycology 25 (3), 743–756. doi: 10.1007/s10811-013-9983-9

CrossRef Full Text | Google Scholar

Carvalho M., Montero D., Rosenlund G., Fontanillas R., Ginés R., Izquierdo M. (2020). Effective complete replacement of fish oil by combining poultry and microalgae oils in practical diets for gilthead sea bream (Sparus aurata) fingerlings. Aquaculture 529, 735696. doi: 10.1016/j.aquaculture.2020.735696

CrossRef Full Text | Google Scholar

Cheng J., Guo W., Cai C., Ye Q., Zhou J. (2018). Alternatively permutated conic baffles generate vortex flow field to improve microalgal productivity in a raceway pond. Bioresource Technol. 249, 212–218. doi: 10.1016/j.biortech.2017.10.031

CrossRef Full Text | Google Scholar

Chen Y., Xue M.-A. (2018). Numerical simulation of liquid sloshing with different filling levels using OpenFOAM and experimental validation. Water 10 (12), 1752. doi: 10.3390/w10121752

CrossRef Full Text | Google Scholar

Cho B. A., Pott R. W. M. (2019). The development of a thermosiphon photobioreactor and analysis using computational fluid dynamics (CFD). Chem. Eng. J. 363, 141–154. doi: 10.1016/j.cej.2019.01.104

CrossRef Full Text | Google Scholar

Delorme L., Colagrossi A., Souto-Iglesias A., Zamora-Rodríguez R., Botía-Vera E. (2009). A set of canonical problems in sloshing, part I: Pressure field in forced roll–comparison between experimental results and SPH. Ocean Eng. 36 (2), 168–178. doi: 10.1016/j.oceaneng.2008.09.014

CrossRef Full Text | Google Scholar

Dogaris I., Welch M., Meiser A., Walmsley L., Philippidis G. (2015). A novel horizontal photobioreactor for high-density cultivation of microalgae. Bioresource Technol. 198, 316–324. doi: 10.1016/j.biortech.2015.09.030

CrossRef Full Text | Google Scholar

Feng H., Sun C., Zhang C., Chang H., Zhong N., Wu W., et al. (2022). Bioconversion of mature landfill leachate into biohydrogen and volatile fatty acids via microalgal photosynthesis together with dark fermentation. Energy Conversion Manage. 252, 115035. doi: 10.1016/j.enconman.2021.115035

CrossRef Full Text | Google Scholar

Froehlich H. E., Koehn J. Z., Holsman K. K., Halpern B. S. (2022). Emerging trends in science and news of climate change threats to and adaptation of aquaculture. Aquaculture 549, 737812. doi: 10.1016/j.aquaculture.2021.737812

CrossRef Full Text | Google Scholar

Gao X., Kong B., Vigil R. D. (2015). CFD investigation of bubble effects on Taylor–couette flow patterns in the weakly turbulent vortex regime. Chem. Eng. J. 270, 508–518. doi: 10.1016/j.cej.2015.02.061

CrossRef Full Text | Google Scholar

Gao X., Kong B., Vigil R. D. (2018). Simulation of algal photobioreactors: Recent developments and challenges. Biotechnol. Lett. 40 (9), 1311–1327. doi: 10.1007/s10529-018-2595-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Guler B. A., Deniz I., Demirel Z., Oncel S. S., Imamoglu E. (2020). Computational fluid dynamics modelling of stirred tank photobioreactor for haematococcus pluvialis production: Hydrodynamics and mixing conditions. Algal Res. 47, 101854. doi: 10.1016/j.algal.2020.101854

CrossRef Full Text | Google Scholar

Hadiyanto H., Elmore S., Van Gerven T., Stankiewicz A. (2013). Hydrodynamic evaluations in high rate algae pond (HRAP) design. Chem. Eng. J. 217, 231–239. doi: 10.1016/j.cej.2012.12.015

CrossRef Full Text | Google Scholar

Hoffman J., Pate R. C., Drennen T., Quinn J. C. (2017). Techno-economic assessment of open microalgae production systems. Algal Research-Biomass Biofuels Bioproducts 23, 51–57. doi: 10.1016/j.algal.2017.01.005

CrossRef Full Text | Google Scholar

Huang J. J., Bunjamin G., Teo E. S., Ng D. B., Lee Y. K. (2016). An enclosed rotating floating photobioreactor (RFP) powered by flowing water for mass cultivation of photosynthetic microalgae. Biotechnol. Biofuels 9 (1), 218. doi: 10.1186/s13068-016-0633-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang S.-c., Teng B., Bai W., Gou Y. (2015). Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action. Ocean Eng. 108, 140–154. doi: 10.1016/j.oceaneng.2015.07.044

CrossRef Full Text | Google Scholar

Khor W.-H., Kang H.-S., Quen L. K., Jiang X., Ng C.-Y., Tan L.-K., et al. (2020). Hydrodynamic sloshing of microalgae in membrane type photobioreactor. IOP Conf. Series: Earth Environ. Sci. 463, 012162. doi: 10.1088/1755-1315/463/1/012162

CrossRef Full Text | Google Scholar

Kim Z. H., Park H., Hong S.-J., Lim S.-M., Lee C.-G. (2016). Development of a floating photobioreactor with internal partitions for efficient utilization of ocean wave into improved mass transfer and algal culture mixing. Bioprocess Biosyst. Eng. 39 (5), 713–723. doi: 10.1007/s00449-016-1552-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar V., Jain S. M. (2014). Plants and algae species: Promising renewable energy production source. Emirates J. Food Agric. 26 (8), 679–692. doi: 10.9755/ejfa.v26i8.18364

CrossRef Full Text | Google Scholar

Launder B. E., Spalding D. B. (1972). Lectures in mathematical models of turbulence.

Google Scholar

Lehr F., Posten C. (2009). Closed photo-bioreactors as tools for biofuel production. Curr. Opin. Biotechnol. 20 (3), 280–285. doi: 10.1016/j.copbio.2009.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Nzayisenga J. C., Farge X., Groll S. L., Sellstedt A. (2020). Effects of light intensity on growth and lipid production in microalgae grown in wastewater. Biotechnol. Biofuels 13 (1), 1–8. doi: 10.1186/s13068-019-1646-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Park H., Jung D., Lee J., Kim P., Cho Y., Jung I., et al. (2018). Improvement of biomass and fatty acid productivity in ocean cultivation of tetraselmis sp. using hypersaline medium. J. Appl. Phycology 30 (5), 2725–2735. doi: 10.1007/s10811-018-1388-3

CrossRef Full Text | Google Scholar

Viegas C., Gouveia L., Gonçalves M. (2021). Aquaculture wastewater treatment through microalgal. biomass potential applications on animal feed, agriculture, and energy. J. Environ. Manage. 286, 112187. doi: 10.1016/j.jenvman.2021.112187

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang C., Jiang C., Gao T., Peng X., Ma S., Sun Q., et al. (2022). Improvement of fish production and water quality in a recirculating aquaculture pond enhanced with bacteria-microalgae association. Aquaculture 547, 737420. doi: 10.1016/j.aquaculture.2021.737420

CrossRef Full Text | Google Scholar

Wang K., Khoo K. S., Leong H. Y., Nagarajan D., Chew K. W., Ting H. Y., et al. (2021). How does the Internet of things (IoT) help in microalgae biorefinery? Biotechnol. Adv. 54, 107819. doi: 10.1016/j.biotechadv.2021.107819

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang Z., Cheng J., Xu X., Zhou J., Cen K. (2016). Enhanced solution velocity between dark and light areas with horizontal tubes and triangular prism baffles to improve microalgal growth in a flat-panel photo-bioreactor. Bioresource Technol. 211, 519–526. doi: 10.1016/j.biortech.2016.03.145

CrossRef Full Text | Google Scholar

Yew G. Y., Chew K. W., Malek M. A., Ho Y.-C., Chen W.-H., Ling T. C., et al. (2019). Hybrid liquid biphasic system for cell disruption and simultaneous lipid extraction from microalgae chlorella sorokiniana CY-1 for biofuel production. Biotechnol. Biofuels 12 (1), 1–12. doi: 10.1186/s13068-019-1591-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang Q., Xue S., Yan C., Wu X., Wen S., Cong W. (2015). Installation of flow deflectors and wing baffles to reduce dead zone and enhance flashing light effect in an open raceway pond. Bioresource Technol. 198, 150–156. doi: 10.1016/j.biortech.2015.08.144

CrossRef Full Text | Google Scholar

Zhao Q., Huang H. (2021). Adaptive evolution improves algal strains for environmental remediation. Trends Biotechnol. 39 (2), 112–115. doi: 10.1016/j.tibtech.2020.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu C., Chen S., Ji Y., Schwaneberg U., Chi Z. (2021). Progress toward a bicarbonate-based microalgae production system. Trends Biotechnol. 40 (2), 180–193. doi: 10.1016/j.tibtech.2021.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu C., Chi Z., Bi C., Zhao Y., Cai H. (2019a). Hydrodynamic performance of floating photobioreactors driven by wave energy. Biotechnol. Biofuels 12 (1), 54. doi: 10.1186/s13068-019-1396-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu C., Han D., Li Y., Zhai X., Chi Z., Zhao Y., et al. (2019b). Cultivation of aquaculture feed isochrysis zhangjiangensis in low-cost wave driven floating photobioreactor without aeration device. Bioresource Technol. 293, 122018. doi: 10.1016/j.biortech.2019.122018

CrossRef Full Text | Google Scholar

Zhu C., Ji Y., Du X., Kong F., Chi Z., Zhao Y. (2022). A smart and precise mixing strategy for efficient and cost-effective microalgae production in open ponds. Sci. Total Environ. 852, 158515. doi: 10.1016/j.scitotenv.2022.158515

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu C., Zhai X., Wang J., Han D., Li Y., Xi Y., et al. (2018). Large-Scale cultivation of spirulina in a floating horizontal photobioreactor without aeration or an agitation device. Appl. Microbiol. Biotechnol. 102 (20), 8979–8987. doi: 10.1007/s00253-018-9258-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu C., Zhai X., Xi Y., Wang J., Kong F., Zhao Y., et al. (2019c). Progress on the development of floating photobioreactor for microalgae cultivation and its application potential. World J. Microbiol. Biotechnol. 35 (12), 190. doi: 10.1007/s11274-019-2767-x

PubMed Abstract | CrossRef Full Text | Google Scholar