ESPC-BCS-Net: A network-based CS method for underwater image compression and reconstruction

The Internet of Underwater Things (IoUT) is a typical energy-limited and bandwidth-limited system where the technical bottleneck is the asymmetry between the massive demand for information access and the limited communication bandwidth. Therefore, storing and transmitting high-quality underwater images is a challenging task. The data measured by cameras need to be effectively compressed before transmission to reduce storage and reconstruc-ted with minor errors, which is the best solution. Compressed sensing (CS) theory breaks through the Nyquist sampling theorem and has been widely used to reconstruct sparse signals accurately. For adaptive sampling underwater images and improving the reconstruction performance, we propose the ESPC-BCS-Net by combining the advantages of CS and Deep Learning. The ESPC-BCS-Net consists of three parts: Sampling-Net, ESPC-Net, and BCS-Net. The parameters (e.g. sampling matrix, sparse transforms, shrinkage thresholds, etc.) in ESPC-BCS-Net are learned end-to-end rather than hand-crafted. The Sampling-Net achieves adaptive sampling by replacing the sampling matrix with a convolutional layer. The ESPC-Net implements image upsampling, while the BCS-Net is used to image reconstruction. The efficient sub-pixel layer of ESPC-Net effectively avoids blocking artifacts. The visual and quantitative evaluation of the experimental results shows that the underwater image reconstruction still performs well when the CS ratio is 0.1 and the PSNR of the reconstructed underwater images is above 29.

1 Introduction

The internet of underwater things (IoUT) is an emerging communication ecosystem to facilitate an integrated, reliable, and coordinated communication network (Jahanbakht et al., 2021) that connects different underwater devices in water bodies (rivers, lakes, and oceans) and underwater environments. The underwater devices include underwater vehicles (sea-bots, remotely operated vehicles, underwater trackers) and underwater sensors (Bello and Zeadally, 2022). By connecting more and more devices to the IoUT, the ecosystem generates a huge amount of data, known as Big Data. However, due to the large size of the captured images and the low memory of low-power embedded devices, communication of underwater images becomes very difficult. Furthermore, the traditional big data processing methods (Cao et al., 2018) that rely on statistical properties lack generalization ability. JPEG and other traditional compression algorithms have limitations regarding reconstruction quality, data rate, and compression performance, making them unsuitable for resource-constrained IoUT (Monika et al., 2022b).

Compressed sensing (CS) theory has several names: compressive sampling, compressed sensing, and compressive sensing. CS theory breaks through Nyquist’s theorem, and it is a pre-processing technique that exploits the signal’s sparsity for sampling the data (Zhang et al., 2022). CS is more hardware-friendly, especially with simultaneous sampling and compression. Some CS-based methods have been proposed to solve underwater data processing. The SPIHT compression algorithm for underwater images was proposed based on embedded coding compression and CS (Cai et al., 2019). Zhang et al. (2021) used CS to overcome underwater image distortions. The CS multiscale entropy feature extraction method to process target radiation noise is efficient and accurate (Lei et al., 2022). Nevertheless, these traditional CS-based methods face the drawbacks of requiring manual parameter adjustment for the signal, time-consuming calculations, and poor generalization.

With the development of CS and Deep Learning, the network-based CS methods have been applied to magnetic resonance imaging (Kilinc et al., 2022), acoustic transmission (Atanackovic et al., 2020), and synthetic aperture radar imaging (Cheng et al., 2022). The network-based CS method allows the reconstruction of images quickly once the network has been trained. Yuan et al. (2020) proposed SARA-GAN based on Generative Adversarial Networks with the Self-Attention mechanism for CS-MRI reconstruction. In addition, a method called LightAMC based on CS and a convolutional neural network was proposed for a non-cooperative communication system (Wang Y et al., 2020). The parameters of these network-based CS methods are trained end-to-end rather than manually tuned, with the advantage of higher generalization and faster reconstruction.

To improve the CS performance of underwater image reconstruction, we propose ESPC-BCS-Net. The following are the particular contributions of the proposed ESPC-BCS-Net:

1. It is a novel network-based CS method where parameters (excluding hyperparameters) are trained end-to-end rather than through manual adjustment (including the sampling matrix and sparse matrix).

2. The ESPC-BCS-Net can be trained in unison, while the Sampling-Net can be used separately for underwater image sampling.

3. The Sampling-Net achieves adaptive sampling by replacing the fixed sampling matrix with a learnable convolutional layer.

4. The ESPC-Net avoids blocking artifacts and improves reconstruction quality.

2 Related works

This section will present related works and briefly introduce CS and CS-based reconstruction methods.

2.1 CS overview

Mathematically, CS reconstruction is to infer the objective signal x ∈ ℝ ^N from its randomized CS measurements:

$\begin{array}{ll}y= \Phi \Psi s=\Theta s=\Phi x & (1)\end{array}$

where Φ ∈ ℝ^M×N is the sampling matrix,  Θ is the sensing matrix,  Ψ is the sparse matrix, s is the sparse coefficient. CS ratio is defined as $\frac{M}{N}$, M ≪ N. In block compressed sensing (BCS), blocks of images are processed simultaneously rather than the entire image, which reduces the processing time. The image is divided into small blocks of size B×B. The vector y_i can be expressed as:

$\begin{array}{ll}{y}_i= {\Phi }_{Bi}{\mathit{x}}_i & (2)\end{array}$

where  x_i presents the vector form of the i^th image block and  Φ_bi is the i^th measurement matrix of size B×B. BCS solves the problem of high decoding computational complexity by independently measuring and recovering non-overlapping blocks, but the images can lead to blocking artifacts (Li et al., 2017).

2.2 CS reconstruction methods

We classify the existing CS into three categories: iteration-based method, optimization-based CS method, and network-based CS method. The general iteration-based method for CS reconstruction is:

$\begin{array}{ll}\underset{x}{\mathbf{m}\mathbf{i}\mathbf{n}} \frac{\mathbf{1}}{\mathbf{2}}\left|\right|\mathbf{\Phi }\mathbf{x}-\mathbf{y}|{|}_{2 }^2+\mathbf{\lambda }\mathbf{ℛ}(\mathbf{x}) & (3)\end{array}$

where the first term $\frac{1}{2}\Vert \Phi x-y{\Vert }_{2 }^2$ is the data fitting term, λ > 0 is the weighting parameter,  ℛ(·)  is the regularization term that requires reconstructed data satisfies the priori information. The optimization-based method for CS reconstruction is to solve the following optimization problem:

$\begin{array}{ll}\underset{x}{\mathbf{m}\mathbf{i}\mathbf{n}} \frac{\mathbf{1}}{\mathbf{2}}\left|\right|\mathbf{\Phi }\mathbf{x}-\mathbf{y}|{|}_2^2+\mathbf{\lambda }|\left|\mathbf{\Psi }x\right|{|}_1 & (4)\end{array}$

where the sparsity of the vector Ψx encouraged by the l₁ norm (Qin, 2020). In addition, the common idea of network-based CS method is to replace the operators in traditional CS methods with neural networks (Liu et al., 2021).

3 Proposed ESPC-BCS-Net

This section will briefly introduce the proposed method and then explain the novel ESPC-BCS-Net. As shown in Figure 1, the proposed ESPC-BCS-Net contains Sampling-Net, ESPC-Net, and BCS-Net. We will describe the design of these three networks in the following sub-sections.

FIGURE 1

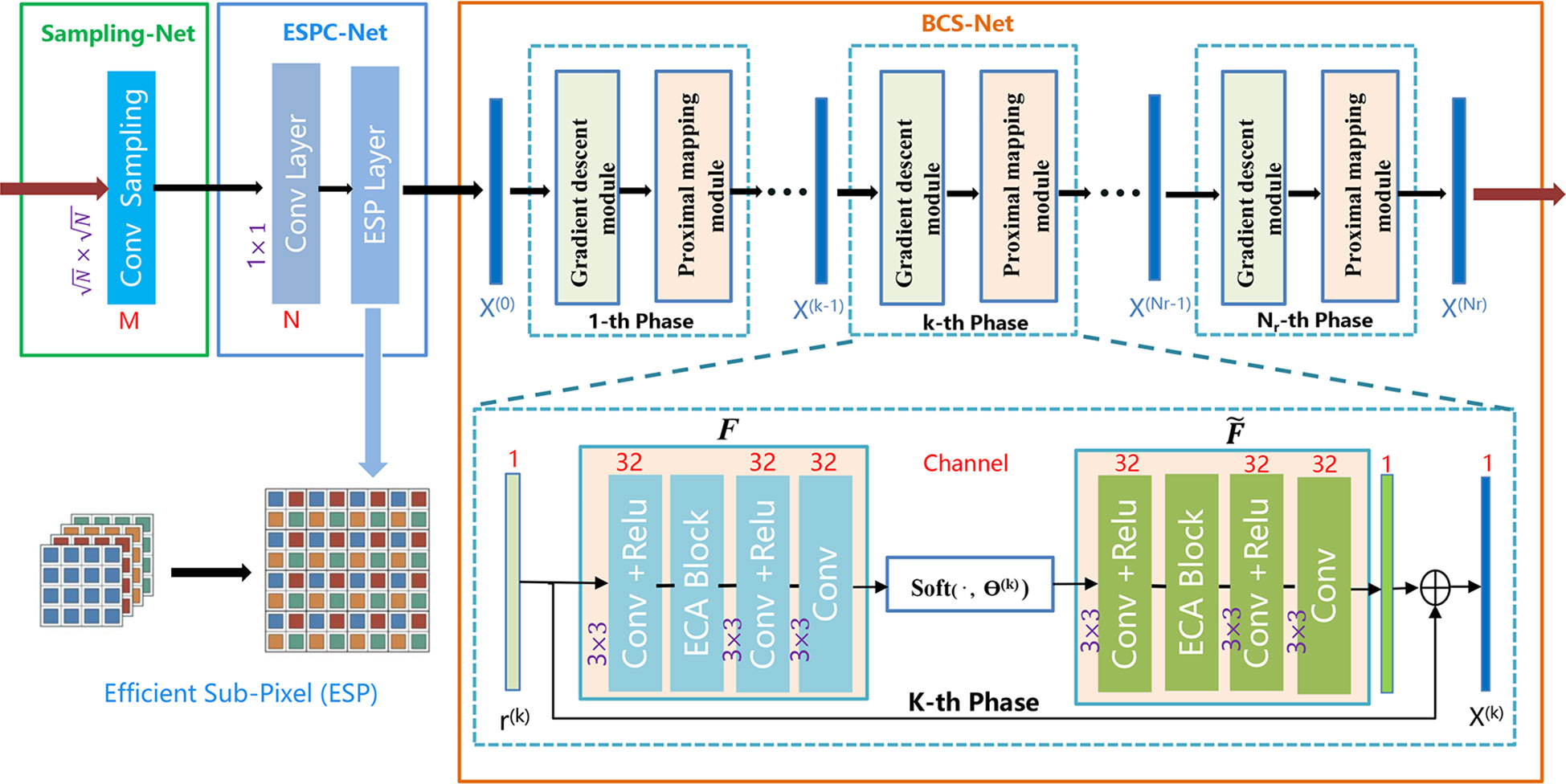
Figure 1 The schematic diagram of the proposed ESPC-BCS-Net consists of Sampling-Net, ESPC-Net, and BCS-Net.

3.1 Problem formulation

We divided CS reconstruction into two steps:

$\begin{array}{ll} {\mathbf{r}}^{(k)}={\mathbf{x}}_i{ }^{(k-1)}-\mathbf{\rho }*\mathbf{\nabla }\frac{\mathbf{1}}{\mathbf{2}}\left|\right|\mathbf{\Phi }{\mathbf{x}}_i^{(k-1)}-y|{|}_{2 }^2 & (5)\end{array}$

$\begin{array}{ll} x^{(k)}=arg \underset{x_i}{min} \frac{1}{2}\left|\right|\Phi x_i- r^{(k)}|{|}_{2 }^2+\lambda |\left|F_{(x_i)}\right|{|}_{1 } & (6)\end{array}$

Where  ρ is the step length of the gradient, ∇ express gradient operations, λ is the regularization parameter, F(·) is the transform function to sparse images, x_i is the image block. Inspired by a data-driven adaptively learned matrix (Hong and Zhu, 2018), we improve Equation (6) to learn sampling matrix Φ follow Equation (7):

$\begin{array}{ll} x^{(k)}=arg\underset{x_i,\Phi ,F}{min} \frac{1}{2}\left|\right|\Phi x_i-r^{(k)}|{|}_{2 }^2+\lambda ||F{(x_i)\left|\right|}_{1 } & (7)\end{array}$

3.2 Architecture of ESPC-BCS-Net

3.2.1 Sampling-Net

The traditional sampling matrix, such as the random Gaussian matrix, is computationally complex and takes up a lot of memory, so we design a learnable sampling matrix. Sampling-Net implements adaptive sampling, which is a learnable convolutional layer used to replace a fixed random matrix Φ ∈ ℝ^M×N. The convolutional layer uses M filters of size $\sqrt{\text{N}}\times \sqrt{\text{N}}$ to sample the image block x_i of size $\sqrt{\text{N}}\times \sqrt{\text{N}}$. After the sampling network, we get the result y_i=Φ_Bix_i with size 1 × 1 × M which easily compresses the underwater image. After the ESPC-BCS-Net network has been trained in unison, Sampling-Net can be used as a compression network. Compared to traditional compression algorithms, Sampling-Net is more suitable for low-power embedded devices as it compresses data through a simple convolution layer.

3.2.2 ESPC-Net

Inspired by the image super-resolution network (Shi et al., 2016), we designed the ESPC-Net (efficient sub-pixel convolutional neural network) for underwater image upsampling and reconstruction. The convolutional layer uses N filters of size 1 × 1 to replace the (Φ_Bi)^Ty_i=(Φ_Bi)^TΦ_Bix_i. After the convolutional layer, we get the result (Φ_Bi)^Ty_i with size 1 × 1 × N. Furthermore, the efficient sub-pixel operation is depicted in Figure 1. In the end, we obtained image blocks of the size $\sqrt{\text{N}}\times \sqrt{\text{N}}$ and used them as input to the BCS-Net.

3.2.3 BCS-Net

The BCS-Net (block compressed sensing network) is used for underwater image reconstruction and consists of N_r layers network, each containing a gradient module and a proximal module. In particular, the BCS-Net can be trained and used independently as a network for underwater image reconstruction.

Gradient module: corresponds to Equation (5), which is used to generate the r^(k). In Equation (8), we omit the calculation process for this $\nabla \frac{1}{2}\Vert \Phi x^{(k-1)}-y{\Vert }_{2 }^2={\Phi }^T(\Phi x^{(k-1)}-y)$. Φ^T is the transpose matrix of Φ.

$\begin{array}{ll} r^{(k)}=x^{(k-1)}-{\rho }^{(k)}*{\Phi }^T(\Phi x^{(k-1)}-y)& (8)\end{array}$

Proximal module: corresponds to Equation (7), which is used to generate the reconstruction result  x^(k). The soft thresholding function  Soft(·,θ^(k) ) is used to reduce image noise.

$\begin{array}{ll}{F}^{(k)}(x^{(k)})=Soft(F^{(k)}(r^{(k)}),{\theta }^{(k)})& (9)\end{array}$

We design the BCS-Net as a residual network structure and x^(k) is calculated by Equation (10).  F^(k) and ${\tilde{F}}^{(k)}$ have same structures, with an efficient channel attention (ECA) block (Wang Q et al., 2020) in each unit.

$\begin{array}{ll} x^{(k)}=r^{(k)}+ {\tilde{F}}^{(k)}(F^{(k)}(x^{(k)})) & (10)\end{array}$

3.3 Loss function

The loss function consists of three components, ℒ_constraint, ℒ_sparse, and ℒ_orth. The ℒ_constraint is for network accuracy and the ℒ_sparse is for signal sparsity. The ℒ_orth is an orthogonal constraint for the sampling matrix Φ. The end-to-end loss function for ESPC-BCS-Net as follows:

$\begin{array}{ll} {ℒ}_{\mathbf{t}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l}}= {ℒ}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{s}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}\mathbf{t}}+ {\mathbf{\lambda }}_1 {ℒ}_{\mathbf{s}\mathbf{p}\mathbf{a}\mathbf{r}\mathbf{s}\mathbf{e}}+ {\mathbf{\lambda }}_2 {ℒ}_{\mathbf{o}\mathbf{r}\mathbf{t}\mathbf{h}} & (11)\end{array}$

with:

$\begin{array}{ll} {ℒ}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{s}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}\mathbf{t}}=\frac{\mathbf{1}}{{\mathbf{N}}_b{\mathbf{N}}_x} {\displaystyle \sum _{\mathbf{i}=\mathbf{1}}^{{\mathbf{N}}_x}} {\displaystyle \sum _{k=1}^{N_r}} \left|\right|{\tilde{F}}^{(k)}( F^{(k)}(x_i))-x_i|{|}_{2 }^2 & (12)\end{array}$

$\begin{array}{ll}\underset{ }{ {\mathbf{ℒ}}_{\mathbf{s}\mathbf{p}\mathbf{a}\mathbf{r}\mathbf{s}\mathbf{e}} =} {\displaystyle \sum _{\mathbf{k}=\mathbf{1}}^{{\mathbf{N}}_{\mathbf{r}}}} \left|\right|{\mathbf{F}}^{(k)}{({\mathbf{r}}^{(k)})\left|\right|}_{1 } & (13)\end{array}$

$\begin{array}{ll}\underset{ }{ {ℒ}_{\mathbf{o}\mathbf{r}\mathbf{t}\mathbf{h}} =}\frac{\mathbf{1}}{{\mathbf{M}}^2}\left|\right|{\mathbf{\Phi }}^T\mathbf{\Phi }-{\text{I||}}_{2 }^2 & (14)\end{array}$

where the fixed hyperparameters λ₁ = 0.01, λ₂ = 0.01, the N_r is the total number of the BCS-Net phase, N_x is the total number of training blocks, N_b is the size of each block x_k, M is the size of Φ, I is the identity matrix.

4 Experiment results and discussion

4.1 Experiment setting

To fairly show the advantages of the ESPC-BCS-Net, we used the same training set (91 images) as ReconNet+ (Lohit et al., 2018) rather than thousands of images. All networks are trained on a workstation with Intel Core i9-10900KF CPU and NVIDIA RTX3060 GPU by PyTorch, taking about 22 hours for each CS ratio (0.5, 0.25, 0.1, 0.04, and 0.01). ESPC-BCS-Net parameters N_r = 10, N_x =88912, N_b =1089, and used Adam optimization with a learning rate of 0.0001. In training, the image block size $\sqrt{\text{N}}\times \sqrt{\text{N}}$ is 33×33. We used the ESPC-BCS-Net for our underwater image reconstruction experiments, and all the underwater images used were accessible through Monika et al. (2022a).

4.2 The results of underwater images

We select different underwater images to sample and reconstruct, including fish, turtles, corals, and underwater scenes. The visual quality comparison of the reconstructed underwater images at different CS ratios is shown in Figure 2. The original images contain three high-resolution images and three noisy images. PSNR (Peak Signal-to-Noise Ratio) and SSIM (structural similarity) evaluated the reconstruction quality. ESPC-BCS-Net has provided a relatively lower CS ratio with convincing visual reconstruction quality. When the CS ratio is 0.1, the PSNR is above 29. At a CS ratio below 0.1, underwater image reconstruction is challenging. As shown in Figure 2E, underwater images reconstructed by ESPC-BCS-Net are still distinguishable when the CS ratio is 0.04.

FIGURE 2

Figure 2 Reconstructed underwater images (size of 256×256) by ESPC-BCS-Net at different CS ratios. (A) The original underwater images. (B–F) Reconstructed underwater images.

4.3 Compared with BCS-Net

To demonstrate the usefulness of the Sampling-Net and the ESPC-Net, we conducted a comparative experiment using the BCS-Net and ESPC-BCS-Net. The Gaussian random matrix is used as the sampling matrix, and the same training set for ESPC-BCS-Net was then used to train BCS-Net. As shown in Figure 3, the original images contain a high-resolution image and a dark light image. As shown in Figures 3C, I, the image shows very obviously blocking artifacts with a PSNR below 23. Figures 3D–F, J–L show the results of the ESPC-BCS-Net reconstruction, all of which are better than BCS-Net. By comparison with the BCS-Net, the reconstructed underwater image PSNR and SSIM of the ESPC-BCS-Net are improved by approximately 3.5 and 0.14, respectively.

FIGURE 3

Figure 3 Visual comparison of BCS-Net and ESPC-BCS-Net. We evaluate the reconstructed underwater images by PSNR/SSIM. The size of (A-F) is 1024×678, and the size of (G-L) is 960×540.

4.4 Compared with other CS-based methods

To compare with other CS-based methods, we choose Set11 (Kulkarni et al., 2016) as the test set. We compare ESPC-BCS-Net with other CS-based methods, including GSR (Zhang et al., 2014), ReconNet+ (Lohit et al., 2018), BCS (Adler et al., 2017), CSNet (Shi et al., 2017), and FISTA-CSNET* (Xin et al., 2022). Note that the traditional CS-based methods enjoy the advantage of interpretability and do not require training but suffer from the disadvantage of manual adjustment of parameters and computational complexity. In addition, we use the average running time to evaluate these CS-based methods. The GSR is a traditional CS algorithm, which takes the longest time, about 4 minutes. Others CS-based methods are network-based CS methods, and all take less than 0.3 seconds. Table 1 shows each CS ratio’s average PSNR and SSIM for different methods. We highlight the best results in bold and underline the second-best results. Some methods were not trained and tested at a certain CS ratio. For example GSR was not evaluated at a CS ratio of 0.5. It is observed that the ESPC-BCS-Net outperforms the other CS-based methods across five different CS ratios. Even at the lowest CS ratio of 0.01, the PSNR of the reconstructed image is higher than 20. Compared with the BCS, ESPC-BCS-Net performance is superior. The proposed method still performs better reconstruction than the state-of-the-art FISTA-CSNet*. These results indicate that the proposed method produces better reconstruction results while maintaining fast runtime.

TABLE 1

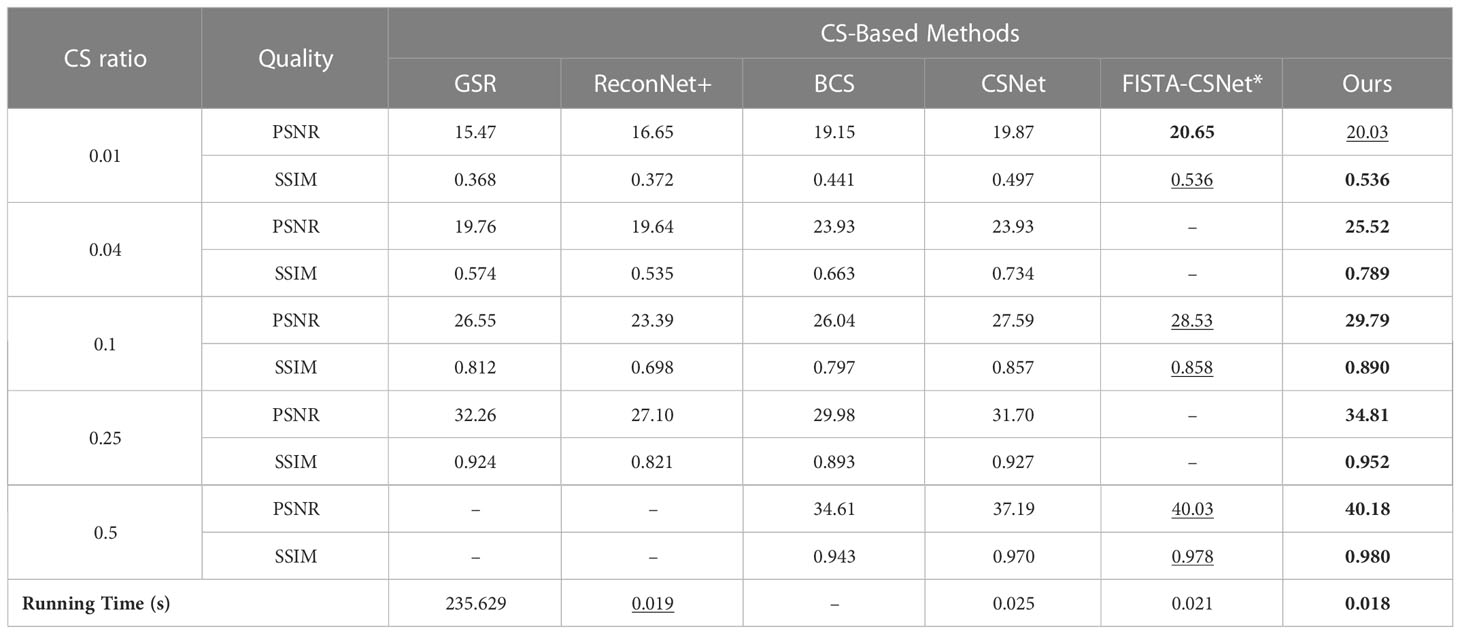
Table 1 Average PSNR and SSIM of different CS-based methods on Set11 and average running time (in sec) for reconstruction.

5 Conclusion

A novel network-based CS method named ESPC-BCS-Net for underwater image compression and reconstruction is proposed. All parameters (e.g. sampling matrix, sparse transforms, shrinkage thresholds, etc.) of the ESPC-BCS-Net are learned end-to-end, and its structure consists of Sampling-Net, ESPC-Net, and BCS-Net. The Sampling-Net achieves compressed sampling with only one convolutional layer, which reduces computational costs and is very suitable for resource-constrained IoUT. ESPC-Net and BCS-Net are used for underwater image reconstruction. Furthermore, the ESPC-Net effectively avoids blocking artifacts and improves the reconstruction performance. The results show that ESPC-BCS-Net achieves a PSNR of over 29 for underwater image reconstruction at a CS ratio of 0.1. It can be concluded that ESPC-BCS-Net has effectively improved underwater image compression and reconstruction quality while maintaining fast runtime. The ESPC-BCS-Net mainly focuses on the CS sampling and recovery of underwater images, which can be easily extended to medical images and other fields. The future scope is to implement the proposed method on the hardware platform.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

FY: conceptualization. ZL and FY: designed the experiments. GC and FY: funding acquisition. ZL: methodology. ZL: data processing. ZL: wrote the draft. GC: review and validation. All authors contributed to the article and approved the submitted version.

Funding

The following programs jointly supported this work: (1) the Laoshan Laboratory science and technology innovation projects under Grant No.LSKJ202204304; (2) the Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources under Grant No.2021-ZD-01.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adler A., Boublil D., Zibulevsky M. (2017). “Block-based compressed sensing of images via deep learning,” in 19th IEEE International Workshop on Multimedia Signal Processing (MMSP).

Google Scholar

Atanackovic L., Lampe L., Diaman R. (2020). “Deep-learning based ship-radiated noise suppression for underwater acoustic OFDM systems,” in Global OCEANS Singapore - U.S. Gulf Coast Conference. doi: 10.1109/IEEECONF38699.2020.9389436

CrossRef Full Text | Google Scholar

Bello O., Zeadally S. (2022). Internet Of underwater things communication: Architecture, technologies, research challenges and future opportunities. Ad Hoc Networks. 135. doi: 10.1016/j.adhoc.2022.102933

CrossRef Full Text | Google Scholar

Cai Y.-q., Zou H.-x., Yuan F. (2019). Adaptive compression method for underwater images based on perceived quality estimation. Front. Inf. Technol. Electronic Engineering. 20 (5), 716–730. doi: 10.1631/FITEE.1700737

CrossRef Full Text | Google Scholar

Cao X., Liu L., Cheng Y., Shen X. (2018). Towards energy-efficient wireless networking in the big data era: A survey. IEEE Commun. Surveys Tutorials. 20 (1), 303–332. doi: 10.1109/COMST.2017.2771534

CrossRef Full Text | Google Scholar

Cheng P., Chen W. Y., Cheng J. W., Xu X. M. , Zhao J. Q. (2022). A fast ISAR imaging method based on strategy weighted CAMP algorithm. IEEE Sensors J. 22 (17), 17022–17030. doi: 10.1109/JSEN.2022.3192534

CrossRef Full Text | Google Scholar

Hong T., Zhu Z. (2018). Online learning sensing matrix and sparsifying dictionary simultaneously for compressive sensing. Signal Processing. 153, 188–196. doi: 10.1016/j.sigpro.2018.05.021

CrossRef Full Text | Google Scholar

Jahanbakht M., Xiang W., Hanzo L., Azghadi M. R. (2021). Internet Of underwater things and big marine data analytics-a comprehensive survey. IEEE Commun. Surveys Tutorials. 23 (2), 904–956. doi: 10.1109/COMST.2021.3053118

CrossRef Full Text | Google Scholar

Kilinc O., Chu S., Baraboo J., Weiss E. K., Engel J., Maroun A., et al. (2022). Hemodynamic evaluation of type b aortic dissection using compressed sensing accelerated 4D flow MRI. J. Magnet Res. Imag. doi: 10.1002/jmri.28432

CrossRef Full Text | Google Scholar

Kulkarni K., Lohit S., Turaga P., Kerviche R., Ashok A., Ieee (2016). “ReconNet: Non-iterative reconstruction of images from compressively sensed measurements,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 449–458. doi: 10.1109/CVPR.2016.55

CrossRef Full Text | Google Scholar

Lei Z., Lei X., Zhou C., Qing L., Zhang Q. (2022). Compressed sensing multiscale sample entropy feature extraction method for underwater target radiation noise. IEEE Access. 10, 77688–77694. doi: 10.1109/ACCESS.2022.3193129

CrossRef Full Text | Google Scholar

Li R., Duan X., Guo X., He W., Lv Y. (2017). Adaptive compressive sensing of images using spatial entropy. Comput. Intell. Neurosci. doi: 10.1155/2017/9059204

CrossRef Full Text | Google Scholar

Liu J., Zhang R., Han G., Sun N., Kwong S. (2021). Video action recognition with visual privacy protection based on compressed sensing. J. Syst. Architecture. 113. doi: 10.1016/j.sysarc.2020.101882

CrossRef Full Text | Google Scholar

Lohit S., Kulkarni K., Kerviche R., Turaga P., Ashok A. (2018). Convolutional neural networks for noniterative reconstruction of compressively sensed images. IEEE Trans. Comput. Imag 4 (3), 326–340. doi: 10.1109/TCI.2018.2846413

CrossRef Full Text | Google Scholar

Monika R., Dhanalakshmi S., Kumar R., Narayanamoorthi R. (2022a). Coefficient permuted adaptive block compressed sensing for camera enabled underwater wireless sensor nodes. IEEE Sensors J. 22 (1), 776–784. doi: 10.1109/JSEN.2021.3130947

CrossRef Full Text | Google Scholar

Monika R., Dhanalakshmi S., Kumar R., Narayanamoorthi R., Lai K. W. (2022b). An efficient adaptive compressive sensing technique for underwater image compression in IoUT. Wireless Networks. doi: 10.1007/s11276-022-02921-1

CrossRef Full Text | Google Scholar

Qin S. (2020). Simple algorithm for L1-norm regularisation-based compressed sensing and image restoration. Iet Image Processing. 14 (14), 3405–3413. doi: 10.1049/iet-ipr.2020.0194

CrossRef Full Text | Google Scholar

Shi W., Caballero J., Huszar F., Totz J., Aitken A. P., Bishop R., et al. (2016). Real-time single image and video super-resolution using an efficient Sub-pixel convolutional neural network. IEEE Conf. Comput. Vision Pattern Recognit. pp, 1874–1883. doi: 10.1109/CVPR.2016.207

CrossRef Full Text | Google Scholar

Shi W., Jiang F., Zhang S., Zhao D., Ieee (2017). “DEEP NETWORKS FOR COMPRESSED IMAGE SENSING,” in IEEE International Conference on Multimedia and Expo (ICME), Hong Kong. 877–882. doi: 10.48550/arXiv.1707.07119

CrossRef Full Text | Google Scholar

Wang Q., Wu B., Zhu P., Li P., Zuo W., Hu. Q. (2020). “ECA-net: Efficient channel attention for deep convolutional neural networks,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR).

Google Scholar

Wang Y., Yang J., Liu M., Gui G. (2020). LightAMC: Lightweight automatic modulation classification via deep learning and compressive sensing. IEEE Trans. Vehicul. Technol0 69 (3), 3491–3495. doi: 10.1109/TVT.2020.2971001

CrossRef Full Text | Google Scholar

Xin L., Wang D., Shi W. (2022). FISTA-CSNet: a deep compressed sensing network by unrolling iterative optimization algorithm. Visual Comput. doi: 10.1007/s00371-022-02583-2

CrossRef Full Text | Google Scholar

Yuan Z., Jiang M., Wang Y., Wei B., Li Y., Wang P., et al. (2020). SARA-GAN: Self-attention and relative average discriminator based generative adversarial networks for fast compressed sensing MRI reconstruction. Front. Neuroinformat. 14. doi: 10.3389/fninf.2020.611666

CrossRef Full Text | Google Scholar

Zhang H., Ni J., Xiong S., Luo Y., Zhang Q. (2022). SR-ISTA-Net: Sparse representation-based deep learning approach for SAR imaging. IEEE Geosci. Remote Sens. Letters. 19. doi: 10.1109/LGRS.2022.3202557

CrossRef Full Text | Google Scholar

Zhang Z., Tang Y. G., Yang K. (2021). A two-stage restoration of distorted underwater images using compressive sensing and image registration. Adv. Manufact. 9 (2), 273–285. doi: 10.1007/s40436-020-00340-z

CrossRef Full Text | Google Scholar

Zhang J., Zhao D., Gao W. (2014). Group-based sparse representation for image restoration. IEEE Trans. Image Processing. 23 (8), 3336–3351. doi: 10.1109/TIP.2014.2323127

CrossRef Full Text | Google Scholar