Prediction of significant wave height based on EEMD and deep learning

Accurate and reliable wave significant wave height(SWH) prediction is an important task for marine and engineering applications. This study aims to develop a new deep learning algorithm to accurately predict the SWH of deep and distant ocean. In this study, we combine two methods, Ensemble Empirical Mode Decomposition (EEMD) and Long Short-Term Memory (LSTM), to construct an EEMD-LSTM model, and explore the optimal parameters of the model through experiments. A total of 5328 hours of SWH data from November 30, 2020, to July 9, 2021, are used to train and test the model to predict the SWH for the future 1h, 3h, 6h, 12h, and 18h. The results show that the EEMD-LSTM model has the best results compared with other comparative models for short-term and medium- and long-term predictions. The RMSEs are 0.0204, 0.0279, 0.0452, 0.0941, and 0.1949 for the SWH prediction in the future 1, 3, 6, 12, and 18 h. It can be used as a rapid SWH prediction system to ensure navigation safety to a certain extent, which has great practical significance and application value.

1. Introduction

Waves are an important area of study in physical oceanography. Sea waves are highly influenced by environmental changes and the Earth system, especially waves due to climate change (Lobeto et al., 2021). The wave period, wave direction, SWH, and other sea state characteristics are important safety factors that must be considered for activities such as marine engineering construction, maritime transportation, environmental protection, and military operations (Mahjoobi and Mosabbeb, 2009). Among them, the SWH of ocean is the most important. Accurate and reliable wave SWH prediction is an essential task for marine and engineering applications (Ali et al., 2021). Therefore, it is of great importance to combine the observation data to make accurate forecasts of the SWH.

As one of the two critical waters of the 21st Century Maritime Silk Road (Zhu and Wang, 2015), simulating and analyzing the SWH of the Indian Ocean will help explore and develop the wave energy of the sea and help the Chinese fleet navigate far away from the sea in the future. This is of positive significance to the development of both China and the coastal countries of the “Maritime Silk Road” and the building of the Maritime Silk Road and the Asian Community of Destiny (Zhao et al., 2021).

There are three main methods for predicting the SWH of ocean. The first one is based on empirical models. Wave prediction is performed by a priori model assumptions, such as the Auto-Regression and Moving Average Model (ARMA) (Ge and Kerrigan, 2016). Still, empirical models have limited predictive power and are not applicable to predicting non-linear and non-smooth wave heights. The second is a numerical model based on physical processes of wave generation and dissipation, such as SWAN (Booij et al., 1997), WAM (Group, 1988), and Wave Watch III (Tolman et al., 2009). Because the numerical model of waves has to be built on explicit physical processes, which require large computational resources and long computing time, its predictions lack real-time. The third one is the machine learning-based forecasting method. Because it is not limited by high-performance computing and large sample data set input and has a very high real-time performance, in recent years, machine learning methods such as Linear Regression (LR), Random Forests (RF), Long Short Term Memory (LSTM), and Gated Recurrent Unit (GRU) have been widely used for wave element prediction (Meng et al., 2021a; Meng et al., 2021b; Meng et al., 2021c; Meng et al., 2021d; Song et al., 2022), effectively compensating for the shortcomings of the other two wave prediction methods.

EMD is a signaling method for processing nonlinear nonstationary time series proposed by Huang et al. (1998). The EMD method can be theoretically applied to any type of signal decomposition and thus has a very obvious advantage in dealing with non-stationary and non-linear data. EEMD, which stands for Ensemble Empirical Mode Decomposition (Wu and Huang, 2009), is a noise-assisted data analysis method proposed to address the shortcomings of the EMD method, which effectively solves the mixing phenomenon of EMD. In recent years, EEMD has been widely used in wave factor prediction (Meng et al., 2022).

Currently, there are two widely used mesh discretization methods in ocean physical models: structured meshes and unstructured meshes. Unstructured meshes are meshes without regular topological relationships. An unstructured grid is one in which the interior points within the grid region do not have the same adjacent cells (Song et al., 2021).That is, there are different numbers of grids connected to different interior points within the grid section area. The unstructured grid has strong flexibility in modeling and can be good for shoreline boundary fitting. The data used in this study are the SWH data of the unstructured model.

The FVCOM model is an unstructured numerical model of the ocean (Chen et al., 2006). It uses a combination of alpha vertical coordinates and horizontal triangular unstructured mesh coordinates to simulate complex shore and seafloor topography better. The numerical model uses the finite volume method (FVM) and can be applied to a variety of oceanic problems, now has been widely used worldwide to study ocean processes (Chen et al., 2003).

To the best of our knowledge, there is no work to analyze and predict wave data based on unstructured ocean models using artificial intelligence methods. In this paper, according to the characteristics of non-smooth and non-linear wave SWH, the LSTM model, which is more suitable for time series prediction, is selected and combined with the EEMD method to train and predict the model using 5328 hours of deep-sea unstructured mode wave SWH data. The SWH for the next 1h, 3h, 6h, 12h, and 18h were predicted. Evaluation metrics such as RMSE, MSE, MAE, MAEP, and R2 were used to evaluate the model, and a number of different algorithms were also used to compare with the model to demonstrate the accuracy of the model predictions.

The main contribution of the work is as follows:

(1) To the best of our knowledge, this is the first work that presents the analysis and prediction of unstructured ocean model wave data using artificial intelligence methods. (2) An EEMD-LSTM model is proposed to predict the SWH of deep ocean for the next 1 to 18 hours.

(3) A comparative study with other machine learning and deep learning algorithms is conducted.

The remainder of the paper is organized as follows. Section 2 describes related work. Section 3 describes the methods used, the construction of the EEMD-LSTM model, the comparison model, and the model evaluation metrics. Section 4 describes the study area and the wave data used. In Section 5, the model is trained and predicted using 5328 h of SWH data for deep and distant ocean. The SWHs for the next 1h, 3h, 6h, 12h, and 18h are predicted and compared with the model using several different algorithms. Conclusions and limitations of this experiment are given in Section 6.

2. Related works

With the continuous progress of ocean observation technology, the volume and data dimension of ocean data has increased dramatically, and the use of traditional data analysis methods to analyze the huge amount of data has revealed many shortcomings (Lou et al., 2021). In recent years, data-driven approaches based on data are becoming well known and widely used. Data-driven methods can learn the dependencies between input and output data from historical data and build models, which can make predictions about future data. Machine learning methods are data-driven. Common machine learning methods such as LR and RF have been widely used in ocean forecasting. Ali M (Ali et al., 2020) designed a machine learning model based on multiple linear regression and covariance-weighted least square estimation for forecasting near real-time SWH values within half an hour. Pokhrel P (Pokhrel et al., 2020) proposed a random forest classifier-based algorithm to predict anomalous ocean surges, which achieved an overall accuracy of 89.57% - 91.81%. Memar S(Memar et al., 2021)applied two data-driven techniques, adaptive neuro-fuzzy inference system (ANFIS) and support vector regression (SVR), to predict the maximum seasonal wave height. Mahmoodi K (Mahmoodi and Nowruzi, 2021) proposed a new hybrid Natural Outlier Factor-Extreme Learning Machine(NOF-ELM) method for predicting extreme wave height occurrence based on meteorological data.

Being excellent in describing the long-term dependence of time series, the LSTM network has also been recently applied to wave height time series prediction (Fan et al., 2020; Guan, 2020; Raja et al., 2021). Abdullah (Abdullah et al., 2022) proposed a novel modeling approach based on LSTM neural network model. It is used to predict SWH in Indonesian waters. Hu H (Hu et al., 2021) applies a novel machine learning approach based on XGBoost and LSTM recurrent neural networks to predict the wave height and period of Lake Erie. GRU, a variant of LSTM, not only inherits the advantages of LSTM networks but also improves the training speed. Li X (Li et al., 2022) proposed a robust short- and long-term wave prediction method through a GRU network. Wei C C (Wei and Chang, 2021) combined GRU neural networks and convolutional neural networks (CNNs) to develop a typhoon-induced wind and wave height prediction model.

The EMD method can be used for adaptive time-frequency analysis of nonlinear and non-smooth data such as wave height. Moreover, pre-processing the data using the EMD method can effectively improve the performance of time series prediction models(Guo et al., 2020). Raj N (Raj and Brown, 2021) developed and applied a high-precision hybrid Boruta Random Forest (BRF)-EEMD-Bidirectional Long and Short Term Memory (BiLSTM) algorithm to predict the SWH. Zhou (Zhou et al., 2021) used a joint model of EMD and LSTM network to predict the giant wave height. Hao W (Hao et al., 2022) combined the 110 advantages of the LSTM model and EMD and found that the error of the EMD-LSTM method is lower than that of the LSTM model based on the prediction of SWH at three locations offshore China. Ali M (Ali and Prasad, 2019) combined an Extreme Learning Machine (ELM) model with an improved complete EEMD method with adaptive noise (ICEEMDAN) to predict the SWH along the eastern coast of Australia.

The data applied in this paper are from the FVCOM model, which is an unstructured ocean model that has also been widely used in recent years for ocean factor prediction. Soroush Sorourian et al. (Sorourian et al., 2020) used a fully coupled unstructured grid, three-dimensional, FVCOM-SWAVE model to study wave characteristics and wave-current interactions at six tidal inlets connecting the Barataria Basin to the northern Gulf of Mexico. Raharja I M D (Raharja et al., 2021) used a 3D oblique pressure hydrodynamic numerical simulation method of the FVCOM to simulate the tidal circulation.

Inspired by the above methods and models, we propose an EEMD-LSTM model for the analysis and prediction of unstructured ocean model SWH data. Section 3 describes in detail the principle of the method.

3. Methods

3.1. EEMD

EMD is a signaling method to deal with non-smooth time series (Wu and Huang, 2009), while the EEMD is based on the EMD by inserting a Gaussian white noise sequence, which effectively suppresses the edge effects and scale mixing phenomena appearing in the EMD method, so that the final decomposed eigenmode The IMF (Intrinsic Mode Function) component of the final decomposition is kept physically unique. Since the method does not require any predetermined basis functions, while the added white noise amplitude has a negligible impact on the final results, the method has good adaptability (Zheng et al., 2012).

IMFs are the signal components of each layer obtained after EMD decomposes the original signal. Any signal can be split into the sum of several IMFs. And the implicit mode components have two constraints.

(1) The number of extremal points and the number of trans-zero points must be equal or differ by at most one in the whole data segment.

(2) At any moment, the average value of the upper envelope formed by the local extreme value points and the lower envelope formed by the local minimal value points is zero, i.e., the upper and lower envelopes are locally symmetric with respect to the time axis.

After the EMD method decomposition (Lei et al., 2009), the original signal will decompose into a series of IMF and the remaining part of the linear superposition.

However, in the EMD method, the signal polarization point affects the IMF, and modal aliasing can occur if the distribution is not uniform.

The EEMD method introduces white noise into the signal to be analyzed. The spectrum of white noise is uniformly distributed, so the signal is automatically distributed to the appropriate reference scale. Due to the characteristics of zero-mean noise, the noise will cancel each other after several averaging calculations so that the calculation result of the integrated mean can be directly regarded as the final result.

The EEMD decomposition is mainly divided into 4 steps, as shown in Figure 1.

(1) Set the processing times of the original signal m

(2) add random white noise to each of the m original signals to form a new series of signals 148

(3) Perform EMD decomposition on the new signals to obtain a series of IMF components

(4) The EEMD decomposition results are obtained by averaging the IMF components of the corresponding modes.

FIGURE 1

Figure 1 Principle of EEMD.

EEMD can effectively suppress the modal mixing phenomenon of EMD, and the decomposition effect is better than that of EMD.

3.2. LSTM

A recurrent neural network (RNN) is a special kind of neural network structure that considers the input at the previous moment and gives the network a kind of ‘memory’ function for what came before.

RNN is called a recurrent neural network because the current output is also related to the previous output. This is because the network remembers the previous information and applies it to the current output, i.e., the nodes between the hidden layers are connected, and the input of the hidden layers includes not only the output of the input layer but also the output of the hidden layer at the previous moment.

RNN is very effective in dealing with time series problems, but there are still some problems: the tendency of gradient disappearance or gradient explosion.

LSTM is developed based on RNN. LSTM overcomes the problem of long-term dependence and gradient disappearance that RNN cannot handle using the input gate, forgetting gate, and output gate structure and can better handle time-series data. Figure 2 shows the structure of LSTM. There are three main phases within LSTM.

FIGURE 2

Figure 2 Structure of LSTM.

$\begin{array}{ll}{f}_t=\sigma (w_f·[h_{t-1},x_t]+b_f)& (1)\end{array}$

First is the forgetting phase. The calculated f_t is used as forgetting gating to control which of the last memory units C_t–1 need to be retained and which need to be forgotten. Equation (1) is the formula for f_t, where σ is the sigmoid activation function, W_f is the parameter estimated during modal training, h_t–1 is the state at the previous moment, x_t is the current input, and b_f denotes the bias.

$\begin{array}{ll}{\tilde{C}}_t=\tanh (W_C·[h_{t-1},x_t]+b_C)& (2)\end{array}$

$\begin{array}{ll}{i}_t=\sigma (W_i·[h_{t-1},x_t]+b_i)& (3)\end{array}$

The second is the selection memory phase. It is mainly a selection memory for input x_t. ${\tilde{C}}_t$ represents the cell state update value, which is obtained from the input data x_t and the state h_t–1 at the previous moment through a neural network layer. The activation function for the cell state update value usually uses the hyperbolic tangent activation function tanh. Equation (2) is the formula for ${\tilde{C}}_t$. i_t is called the input gate that controls which features of ${\tilde{C}}_t$ are used to update C_t. i_t, like f_t, is a vector with elements in the interval [0,1], and is also computed from x_t and h_t–1 via the sigmoid activation function. Equation (3) is the formula for i_t.

$\begin{array}{ll}{C}_t=f_t*C_{t-1}+i_t*{\tilde{C}}_t& (4)\end{array}$

The results obtained from the above two steps are summed to obtain the C_t transmitted to the next state, as shown in Equation (4).

$\begin{array}{ll}{o}_t=\sigma (W_0[h_{t-1},x_t]+b_o)& (5)\end{array}$

$\begin{array}{ll}{h}_t=o_t*\tanh (C_t)& (6)\end{array}$

The third is the output phase. This phase will decide what will be taken as the output of the current state. h_t represents the output of the hidden node. h_t is obtained from the output gate o_t and the cell state C_t. o_t is also calculated from x_t and h_t–1 via the sigmoid activation function, as shown in Equation (5). Equation (6) is the formula for h_t.

3.3. EEMD-LSTM prediction model

The SWH time series is a complex nonlinear, and non-smooth data signal and such characteristics make the prediction of LSTM models difficult. EEMD can smooth the SWH time series to obtain a series of smooth components with different frequencies and then use the LSTM model to predict these components and sum the prediction results to obtain the final SWH prediction. Because EEMD can fully extract the main features of SWH data, the EEMD-LSTM composite model can overcome the shortcomings of individual models by generating synergistic effects in the prediction (Meng et al., 2022), which is perhaps an effective method for predicting nonlinear and non-smooth SWHs. Therefore, in this study, an EEMD-LSTM prediction model is proposed for predicting the future multi-hourly SWH of deep-sea waves.

Figure 3 shows the flow chart of the EEMD-LSTM model implementation. The process of model implementation consists of three steps.

FIGURE 3

Figure 3 Flowchart of EEMD-LSTM model implementation.

Step 1: The wave SWH time series data are smoothed by EEMD to obtain a series of smooth components with different frequencies, i.e., IMFs and residuals.

Step 2: Normalize each IMF and build different LSTM prediction models to obtain the prediction results of each IMF separately and inverse normalize the results.

Step 3: Combine the prediction results of each IMF with equal weight superposition to get the final prediction results of SWH.

3.4. Comparative experimental methods and evaluation indicators

3.4.1. Linear regression (LR)

LR, the data are modeled using a linear predictive function, and the unknown model parameters are estimated from the data. These models are called linear models.

LR is a type of regression analysis that models the relationship between one or more independent and dependent variables using a least-square function called a LR equation.

The model is defined as shown in Equation (7) (Draper and Smith, 1998; Montgomery et al., 2021):

$\begin{array}{ll}f(x)=w_0+w_1{x}_1+w_2{x}_2+\cdots w_n{x}_n& (7)\end{array}$

Using the matrix to represent this is: f(x)=XW, where W is the set of parameters to be solved and X is the input data matrix.

3.4.2. Random forest (RF)

Integration learning has better generalization performance than a single learner by building multiple learners and integrating the results. Currently, there are two types of integrated learning methods: Boosting algorithms, which have strong dependencies between learners and learn serially, and Bagging algorithms, which have no dependencies between learners and can learn in parallel. RF is a typical Bagging integrated learning algorithm and is popular for its parallel training advantage in dealing with data problems today.

The process of constructing a RF is as follows.

(1) Random selection of samples (with put-back sampling). Suppose there are N samples, then N samples are selected randomly with put-back. Train a decision tree with these N samples as the samples at the root node of the decision tree.

(2) Random selection of features (the features are selected randomly during each node split). When each sample has M attributes, when each node of the decision tree needs to be split, m attributes are randomly selected from these M attributes to satisfy the condition m<<M. Then, some strategy is used to determine the divided attributes from these countries m attributes.

(3) Each node in the decision tree formation process is split according to step (2) until it can no longer be split. No pruning is done during the whole decision tree formation process.

(4) A large number of decision trees are built according to steps (1) to (3), which constitute a RF.

Different training sample sets are obtained by resampling the samples, training the learners separately on these new training sample sets, and finally merging the results of each learner as the final learning result, where the weights of each sample are the same.

3.4.3. GRU

GRU is a variant of the LSTM network (Cho et al., 2014). There are only two gates in the GRU model: the update gate and the reset gate. The specific structure is shown in Figure 4.

FIGURE 4

Figure 4 Structure of GRU.

$\begin{array}{ll}{r}_t=\sigma (w_r·[h_{t-1},x_t])& (8)\end{array}$

$\begin{array}{ll}{z}_t=\sigma \left(w_z\cdot \left[h_{t-1},x_t\right]\right)& (9)\end{array}$

$\begin{array}{ll}{\tilde{h}}_t=\tanh (W_{\tilde{h}}·[r_{t^{*}}{h}_{t-1},x_t])& (10)\end{array}$

$\begin{array}{ll}{h}_t=(1-z_t)*h_{t-1}+z_t*{\tilde{h}}_t& (11)\end{array}$

The rt and zt in the figure denote the reset gate and update gate, respectively. rt 230 is obtained from the 231 current input xt and the previous state h_t−1, as shown in Equation (8). The update gate controls how much information from the previous state is written to the current candidate set ${\tilde{h}}_t$. z_t is also obtained from xt and h_t−1, as shown in Eq. (9). Finally, ${\tilde{h}}_t$. z_t and ht are calculated from Eqs. (10) and (11).

3.4.4. Evaluation criterion

To quantitatively compare the prediction effects of the models, we use Root Mean Squared Error (RMSE), Mean Squared Error (MSE), Mean Absolute Error (MAE), Mean Absolute Error Percentage (MAEP), and Coefficient of Determination (R²), which calculates the deviation between the predicted and true values of the model (Gao et al., 2021, Bethel et al., 2022), are used to evaluate the model. m denotes the total number of predicted SWH, y_i is the true value, ${\widehat{y}}_i$ is the predicted value, and ${\stackrel{-}{y}}_i$ is the mean of the true values.

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{m}\sum _{i=1}^m{(y_i-{\widehat{y}}_i)}^2}& (12)\end{array}$

$\begin{array}{ll}MSE=\frac{1}{m}\sum _{i=1}^m{(y_i-{\widehat{y}}_i)}^2& (13)\end{array}$

$\begin{array}{ll}MAE=\frac{1}{m}\sum _{i=1}^m\left|(y_i-{\widehat{y}}_i)\right|& (14)\end{array}$

$\begin{array}{ll}MAEP=\frac{1}{m}\sum _{i=1}^m\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|& (15)\end{array}$

$\begin{array}{ll}{R}^2=1-\frac{{\sum }_{i=1}^m{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^m{(y_i-{\stackrel{-}{y}}_i)}^2}& (16)\end{array}$

4. Study area and data

4.1. Study area

Our study area is the sea area shown in Figure 5 in the Indian Ocean within the range of 15^∘S∼30^∘N , 30^∘E∼110^∘E . This sea area contains the main route of the 21st Century Maritime Silk Road: the Colombo - Kolkata - Nairobi route. The SWH prediction for the deep and distant sea of the Indian Ocean can guarantee the safety of ship travel to a great extent.

FIGURE 5

Figure 5 Study area.

4.2. Data

SWH is the actual wave height value counted according to certain rules. In any wave group consisting of n waves, the wave heights in the wave train are ranked from largest to smallest, and the first n/3 waves are determined to be the significant waves. The SWH and period are then equal to the average height and period of these n/3 waves.

As shown in Figure 6, there are 4434 unstructured grid nodes in our study area, and the study data are the SWH forecasts from the unstructured model FVCOM model for each grid node for a total of 222 days which is 5328 hours from November 30, 2020, to July 9, 2021. Because the FVCOM model can accurately forecast wave heights in several different environments and can also well simulate the characteristics and trends of wave height changes(Chen et al., 2006), the forecast data from the FVCOM model can be used as real wave height data to train the model. The SWH time series data are shown in Figure 7, which is the data with latitude and longitude 40.8965°E, 9.9087°S. The first 4262 hours of data are taken as the training set, which accounts for about 80% of the entire sequence length, and the rest of the data are used as the test set.

FIGURE 6

Figure 6 Unstructured grid in the study area.

FIGURE 7

Figure 7 SWH time-series data.

5. Experimental results and analysis

Our experiments are conducted on a PC with the following simulation environment.

(1) Hardware: I7-8750H processor, 32G RAM, 4 NVIDIA Tesla P100.

(2) System environment: Ubuntu 16.04 system, python 3.6.5, NumPy 1.18.5, Tensorflow 2.4.1, matplotlib 3.3.4.

5.1. Hyperparameter setting

To improve the prediction effect of the model, the hyperparameters of the model were tested in this study. The prediction effects of the EEMD-LSTM model were tested for different values of timestep and SWH data decomposed into different numbers of components in EEMD, respectively.

The meaning of the parameter Timestep is to predict the data in the next hour by how long the data in the past. For example, Timestep=8 means that the SWH data of the past 8 hours is used to predict the SWH of the future 1 hour. Firstly, the prediction effect of the EEMD-LSTM model for the SWH of the future one hour was tested under different values of the timestep. A total of seven sets of tests were conducted, setting the values of timestep from 6 to 12, respectively, and keeping other parameters consistent. The experimental results are shown in Table 1. It can be seen from Table 1 that when the value of timestep is 8, the EEMD-LSTM model has the best prediction effect on the SWH in the next 1 hour, in which the RMSE is only 0.0204 and the R² can reach 0.9965.

TABLE 1

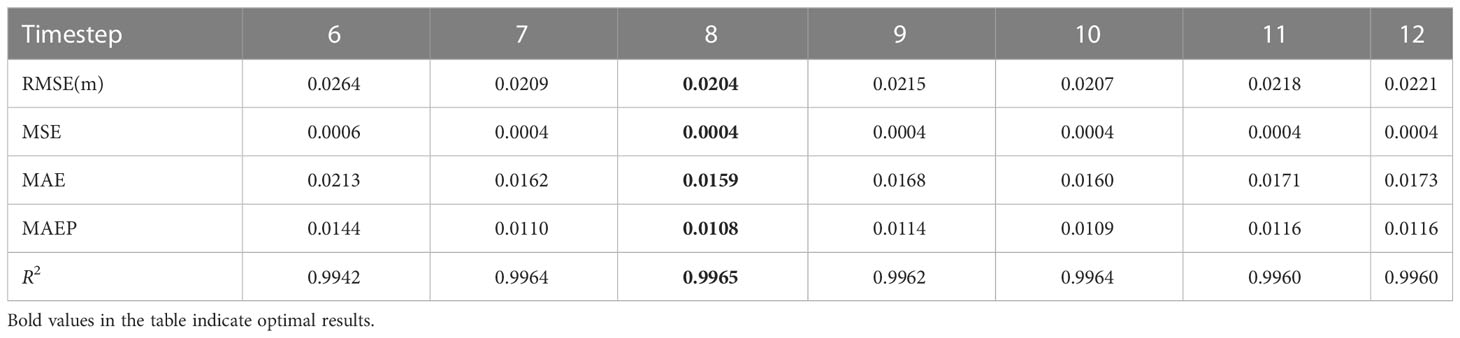
Table 1 Prediction results of EEMD-LSTM model for SWH in the next 1 hour for different values of timestep.

Then the prediction effectiveness of the proposed EEMD-LSTM model for the SWH in the next 1 hour is tested and compared when the SWH data are decomposed into different numbers of components using the EEMD algorithm, respectively. The specific procedure is as follows: The SWH data can be decomposed into up to 10 IMFs and a residual term. Firstly, the SWH data are decomposed into 1~10 components and a residual term by the EEMD algorithm. Then each IMF in these 10 decomposition states is predicted by the LSTM network, where the network parameters are kept consistent. The prediction results of each IMF are summed separately to obtain the final prediction results of each decomposition state and then compared with the true values to calculate the values of each evaluation index. When using EEMD, the increased noise amplitude is about 0.2 times the standard deviation of the sample data, according to the conclusions drawn by Wu and Huang (2009).

The experimental results are shown in Table 2, and the number of IMFs in the table does not include the number of residual terms. For example, when the number of IMFs is 3, the SWH time series data is decomposed into 3 IMFs and a remainder term.

TABLE 2

Table 2 Prediction effect of EEMD-LSTM model when the SWH data is decomposed into a different number of components by the EEMD algorithm.

From Table 2, it can be seen that the EEMD-LSTM model has the best prediction when the data is decomposed into 4 IMFs and a residual term.

Figure 8 shows the decomposition results of the SWH data into 4 IMFs and a residual term. IMF1 and IMF2 show high frequency fluctuations in the short term, while IMF3 to IMF5 have lower frequencies (IMF5 is the residual term), reflecting the characteristics of long wave height periods. Because we predetermine the number of components of the decomposition, i.e., we take the best prediction result of 4 IMFs and one residual term, so the residual term obtained from the decomposition in Figure 8 is not a monotonic residual term in the general sense of EEMD decomposition, but an intermediate quantity that can be further decomposed.

FIGURE 8

Figure 8 Decomposition results of SWH data into 4 IMFs and a residual term.

The prediction results of the proposed model for each component when decomposing the data into 4 IMFs and a residual term are shown in Figure 9. The thicker line in the figure is the true value and the thinner line is the predicted value. From Figure 9, we can see that except for IMF1, which has some deviation due to the high frequency, the prediction results of all the components can fit the observed values well, and has good results for predicting long-term characteristics. This proves that the method of decomposing by EEMD and then predicting separately can remove short-term disturbances and fluctuations that are not important for prediction.

FIGURE 9

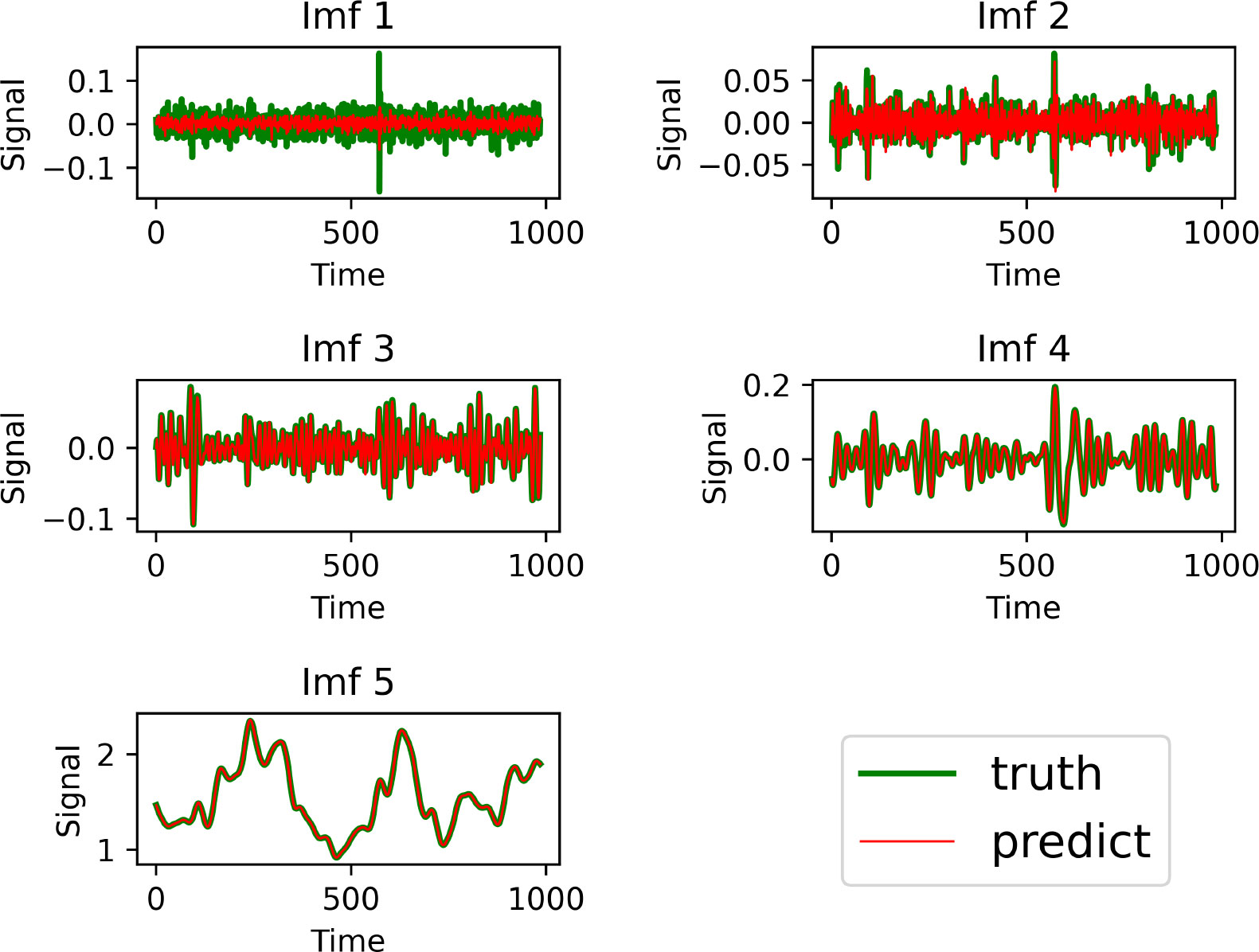
Figure 9 Prediction effect of the proposed model for each component decomposed by the EEMD algorithm.

In summary, we set the hyperparameters of the proposed model as follows: each SWH data is decomposed into 4 IMFs and a residual term by the EEMD algorithm. First LSTM layer (32 units), second LSTM layer (1 unit), timestep is 8, batchsize is 32, epoch is 200, using Adam optimization algorithm, the activation function is tanh.

5.2. Comparison of the prediction effect of the EEMD-LSTM model and other models

Four models, LR, RF, LSTM, and GRU, will be used to compare the prediction effect with the EEMD-LSTM model proposed in this paper. The parameter settings of each comparison model are shown in Table 3. s₀ represents the number of input layer units, num represents the number of trees, s₁ represents the number of hidden layer units, activation function represents the activation function used, s₂ is the number of output layer units, g represents the learning rate, and optimizer represents the type of optimizer used.

TABLE 3

Table 3 Parameter settings of each comparison model.

Table 4 compares the effectiveness of the EEMD-LSTM model with the four comparison models for the future 1-hour SWH prediction. From Table 4, it can be seen that the EEMD-LSTM model has the best performance among all the comparison models in terms of evaluation indexes such as RMSE, MSE, and R², and R² reaches 0.9965. It proves that our proposed EEMD-LSTM model has a smaller prediction error and higher accuracy for the future 1-hour SWH, and the prediction effect is better than other models.

TABLE 4

Table 4 Prediction effect of different models for future 1-hour SWH.

5.3. SWH prediction for many hours ahead

In this experiment, the SWH will be predicted for a long period.

As shown in Figure 10, the SWH at hour t+1 is first predicted using the data from the first 1~t hours, t = timestep, and then the SWH at hour t+2 is predicted using the data from hour 2~t+1, and so on for the next 1~18 hours.

FIGURE 10

Figure 10 Principles of SWH prediction for multiple hours ahead.

Figure 11 compares the predicted and true values of the EEMD-LSTM model and other comparative models predicting the SWH for the next 1 h, 3 h, 6 h, 12 h, and 18 h.

FIGURE 11

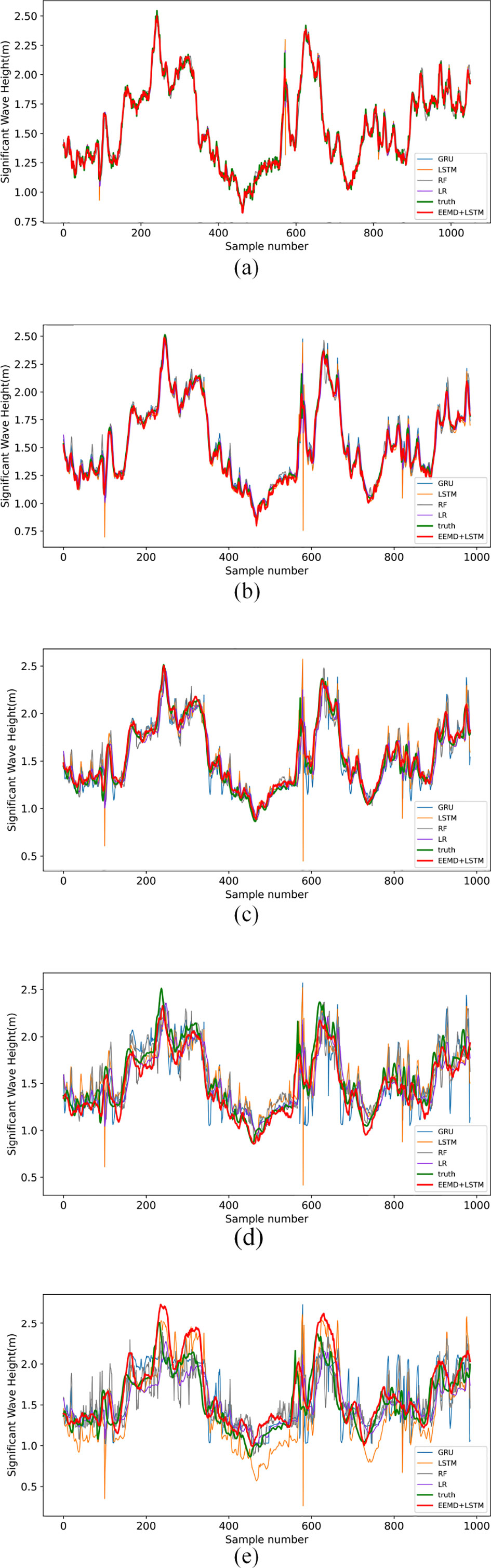
Figure 11 Comparison of predicted and true values of SWH predicted by each model for several future hours (A) 1 hour, (B) 3 hours, (C) 6 hours, (D) 12 hours, and (E) 18 hours.

As can be seen in Figures 11A, B, for the SWH predictions for the next 1 and 3 hours, the predicted values of our proposed EEMD-LSTM model are not much different from the true values. The predictions of the other models compared to it are also good, with only the LSTM model showing a few cases of large errors and the GRU model having slightly higher predicted values than the true values.

From Figure 11C, it can be seen that for the SWH prediction in the next 6 hours, the prediction results of the LSTM model, GRU model, and RF model all have some deviation from the true value, and LR has less error compared with other comparison models. The prediction results of our proposed EEMD-LSTM algorithm for the SWH in the next 6 hours are closest to the true values, and not only the trend of the SWH is well predicted, but also the predicted values are more accurate. This proves that the proposed method is the best for the prediction of SWH in the next 6 hours.

As shown in Figures 11D, E, for the SWH prediction in the next 12 and 18 hours, the prediction results of all four comparison models show substantial irregular deviations compared with the true values and can only predict the general wave height variation trend with large deviations in the predicted values. The LSTM, GRU, and RF models deviate the most, and the LR model deviates less, but the LR model predicted values have significant lags. The proposed EEMD-LSTM model also deviates from the true values, but the average difference is about 0.1 m for the prediction of the next 12 hours and 0.2 m for the prediction of the next 18 hours, which is the smallest deviation compared to the other comparison models. In particular, the EEMD-LSTM model can predict the trend of wave height variation well, which is very useful and meaningful in practical applications. In addition, although the predicted values of the EEMD-LSTM model also have some lags, the magnitude of the lags is smaller than that of the LR model.

In summary, the proposed EEMD-LSTM model has better predictions than the comparison model for both short-term and medium- to long-term SWH predictions. It can better predict the wave height variation trend and more accurately predict the value of wave height with smaller error. It indicates that decomposing the nonlinear non-stationary series into multiple smooth series and then predicting them separately can improve the prediction effect to a great extent.

Table 5 shows the values of each evaluation index for the prediction results of each model for the SWH of the next 3 to 18 hours. As can be seen from the table, for the RMSE, the RMSE of the EEMD-LSTM model is reduced by 52%~63% compared to the other comparison models for the prediction of the SWH for the next 3 hours; for the prediction of the next 6 hours, the RMSE is reduced by 62%~66%; for the prediction of the next 12 hours, the RMSE is reduced by 50%~55%; for the prediction of the next 18 hours forecasts, the RMSE is reduced by 14%~40%.

TABLE 5

Table 5 Comparison of the SWH prediction effects of each model for the next 3 to 18 hours.

For the SWH prediction in the next 3 hours, the R² of the EEMD-LSTM model reaches 0.9937; for the next 6 hours, the R² of the EEMD-LSTM model is 0.9836, which still remains very high. The R² of the other comparison models in contrast are all below 0.9. For the SWH prediction in the next 12 hours, the R² of the EEMD-LSTM model is 0.9295, which still remains above 0.9, while the R² of the other models is around 0.7. For the next 18 hours, the R² of the EEMD-LSTM model is close to 0.7 when the R² of the other comparison models is in the range of 0.13 to 0.58.

In summary, from all evaluation indexes, the EEMD-LSTM model has obvious advantages over other comparison models in terms of predicting SWH in both the short and long term.

Figure 12 depicts the error and R² of each model for the SWH prediction results for the future 1 to 18 hours, with the horizontal coordinates being the number of predicted future hours and the vertical coordinates being RMSE and R², respectively. From (a), it is obtained that the RMSE values of each model for SWH prediction increase gradually as the number of prediction hours increases. The RMSE values of the EEMD-LSTM model for the SWH prediction for the next 1 to 18 hours are smaller than those of the comparative models such as LR, LSTM, GRU, and RF, and the advantage is more obvious when predicting the next 6 and 12 hours. The accuracy of the proposed model predictions is fully demonstrated. From (b), R² of the prediction results of each model decreases gradually as the number of predicted hours increases. However, the R² of the EEMD-LSTM model is always larger than that of the other comparison models. It proves that the prediction results of the proposed model are more correlated with the true values and have better prediction results.

FIGURE 12

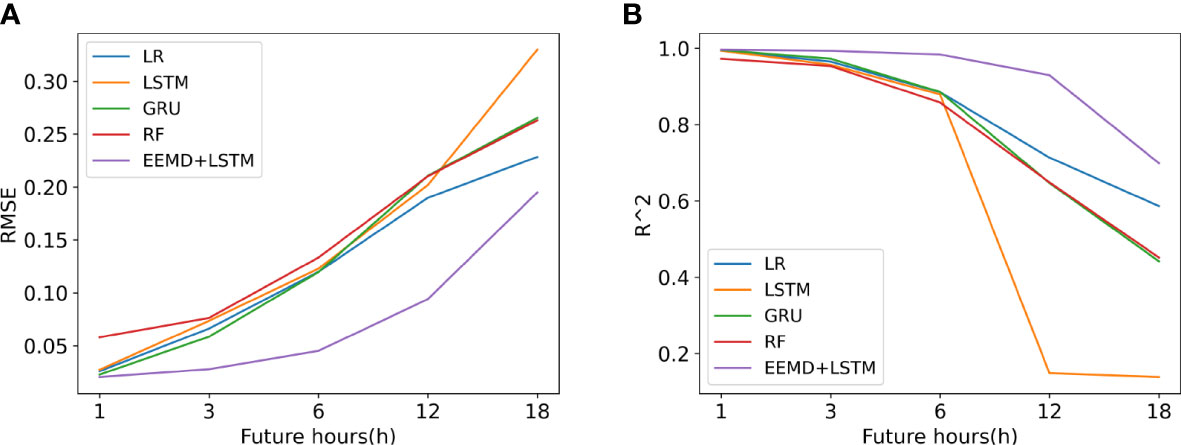
Figure 12 Rmse(M) And R2 Line Graphs Of The Swh Prediction Results Of Each Model For the next 1-18 hours (A) RMSE(m), (B) R2.

Figure 13 shows the scatter plots of the SWH prediction results of each model for the next 1-18 h. The horizontal coordinates are the true values, and the vertical coordinates are the predicted values. The scatter points of the EEMD-LSTM model are uniformly distributed on both sides of the line for the predicted SWH in the future 1h, 3h and 6h, and the dispersion is the least compared with other comparison models. The scatter points of the other comparison models are distributed in a wide range, and a few points have large deviations. For the SWH prediction in the next 12h and 18h, the scatter range of the EEMD-LSTM model is slightly expanded, but the dispersion of the EEMD-LSTM model is smaller and more concentrated on both sides of the straightline compared with other comparison models. For predicting the next 18 hours, the forecasts of large wave height have higher dispersion and larger forecast values. The reason may be that there are fewer data with large wave height in the dataset.

FIGURE 13

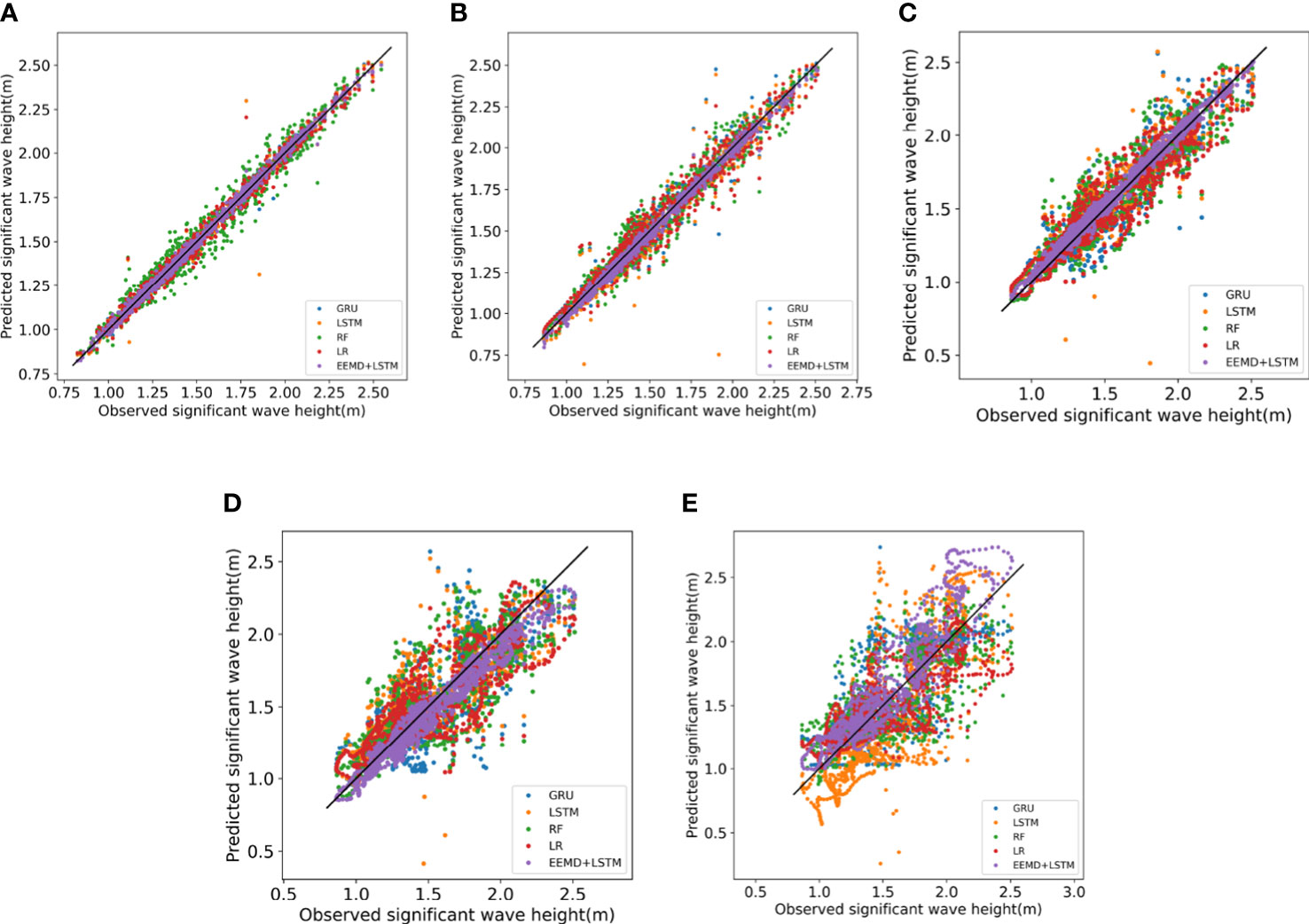
Figure 13 Scatter plots of the SWH prediction results for each model for the next 1 to 18 hours (A) 1 hour, (B) 3 hours, (C) 6 hours, (D) 12 hours, (E) 18 hours.

This proves that the proposed model has a smaller difference between the predicted and true values compared to other comparison models and has a better prediction effect.

5.4. Persistence forecast (PF)

Persistence Forecast (PF) (Rasp et al., 2020) is a simple forecasting method that treats the SWH of the previous hour as the forecast result of this hour, which is also the least computationally expensive forecasting method. If the prediction result obtained by the machine learning method is worse than the performance of persistent prediction, then it proves that the machine learning method is not very effective. PF can be used as a criterion to evaluate the feasibility of the machine learning method.

We compared the prediction effectiveness of Persistence Forecast and our proposed EEMD-LSTM model for the SWH from 1 to 18 hours in the future, and the results are shown in Table 6. From Table 6, we can see that the performance of each evaluation index of our proposed model is better than the Persistence Forecast, which proves the effectiveness and feasibility of the EEMD-LSTM model.

TABLE 6

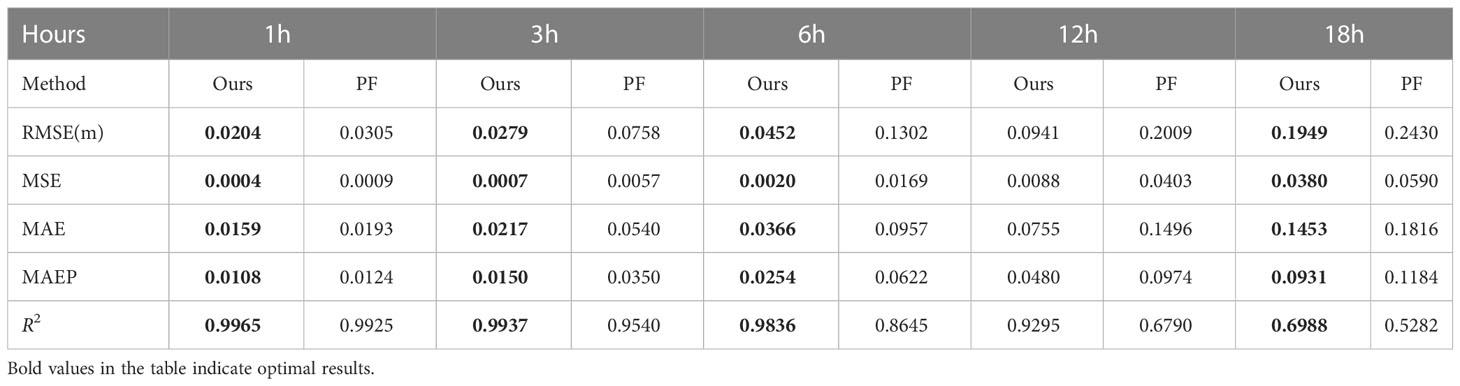
Table 6 Comparison of the prediction effect of PF and EEMD-LSTM models in predicting the SWH for the next 1 18 hours.

5.5. SWH prediction for the whole study area sea

Figure 14 shows the SWH prediction results of the EEMD-LSTM model for the future hours 1, 3, 6, 12, and 18. The leftmost column is the predicted value, the middle column is the true value, and the rightmost column is the difference between the predicted and true values. From Figure 14, it can be seen that the prediction results of the EEMD-LSTM model for 1 to 6 hours for the full study area of the sea are very close to the true values. The locations and ranges of the higher wave height areas are predicted very accurately, and the predicted values of the SWH are also very close to the true values. In the predictions for the next 12 and 18 hours, most of the predictions are accurate, and only a few regions with large wave heights are under-predicted, but the overall difference is not significant. It has been proved that the proposed method is very effective for SWH prediction and has great practical significance and application value.

FIGURE 14

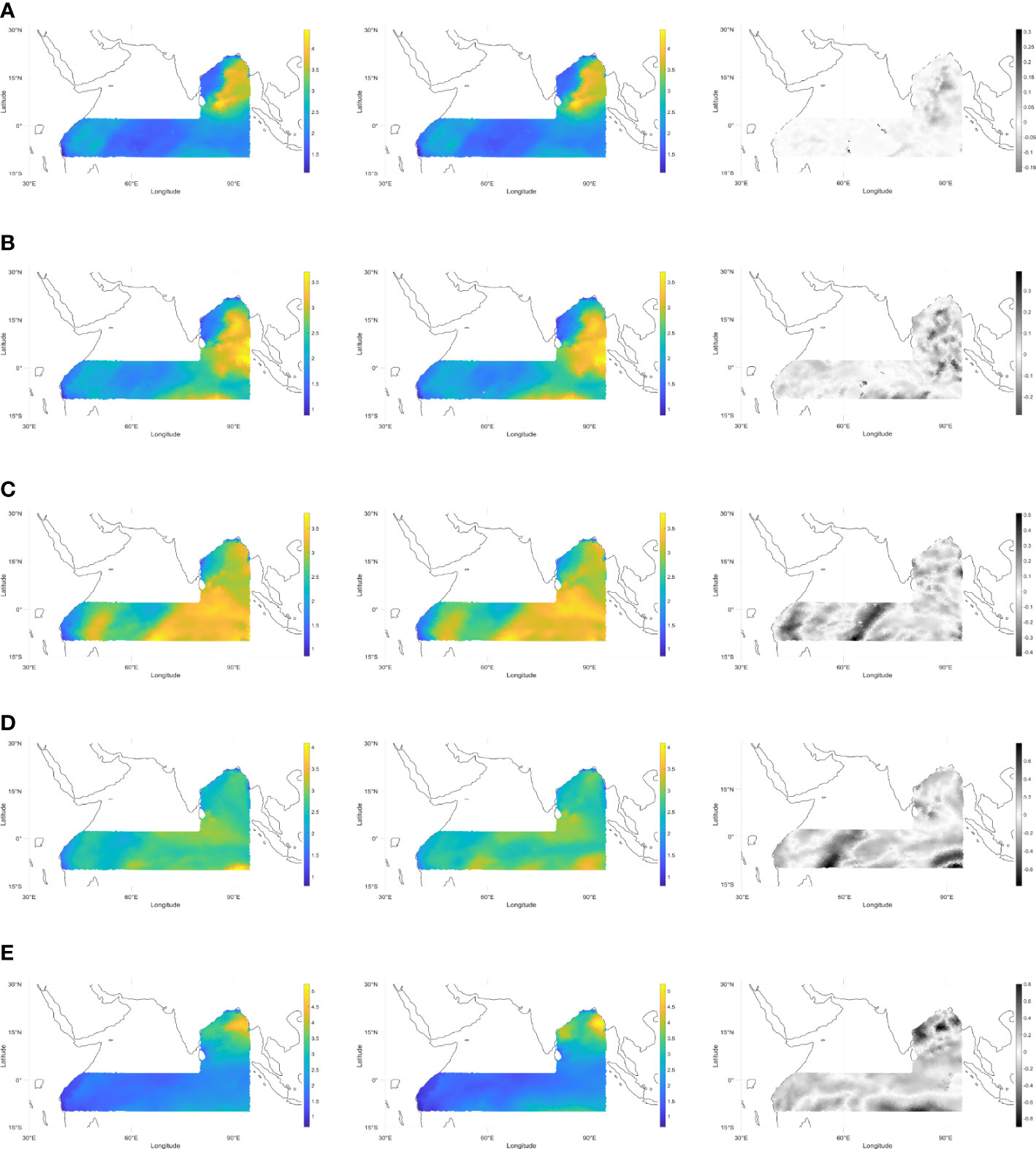
Figure 14 Prediction results of the EEMD-LSTM model for the future SWH from 1 to 18 hours for the whole study area (A) 1 hour, (B) 3 hours, (C) 6 hours, (D) 12 hours, (E) 18 hours. Coordinate axes are in meters.

6. Conclusions

In this paper, an EEMD-LSTM model for deep-sea wave SWH prediction is proposed, and the optimal parameters of the model are explored experimentally. A total of 5328 hours of SWH data from November 30, 2020 to July 9, 2021 are used to train and test the model to predict the SWH for the future 1h, 3h, 6h, 12h, and 18h. The prediction capability of the model is also evaluated using evaluation metrics such as RMSE, MSE, MAE, MAEP, and R². The results show that the EEMD-LSTM model has the best prediction compared with the comparative models such as LR, RF, LSTM, and GRU. Among them, for the SWH prediction of the next 1 h, the R² reaches 0.9965 and the RMSE is 0.0204; for the prediction of the next 3 h, 6 h and 12 h, the R² is greater than 0.92 and the RMSE is less than 0.1; for the prediction of the next 18 h, the EEMD-LSTM model also outperforms all the comparative models. In summary, our proposed EEMD-LSTM model for SWH prediction in deep and distant ocean has good results in both short-term and medium- and long-term predictions. It can be used as a fast SWH prediction system to ensure navigation safety to a certain extent, and has great practical significance and application value.

The limitation of this paper is that only one variable, the SWH, is used as the input condition for forecasting, and no more information on the variables is added. Moreover, the data we use is the forecast data of the unstructured model FVCOM model for SWH, which is not the real SWH data. Although it has been mentioned in the previous section that the FVCOM model is very accurate for wave height prediction and the predicted data can be used as real data for training the model, it is still one of the limitations of this study. In addition, as the model provides spatial result, so different spaces may have an effect on the model results. For future research, we can introduce more variables, such as sea surface wind speed, wind direction, sea surface pressure, etc., for the prediction of SWH. The results of SWH prediction can also be used to infer other relevant variables, such as the direction of ocean currents.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author contributions

Formal analysis, JW and FM; Funding acquisition, TS and DX; Investigation, WW; Methodology, JW; Software, RH and JH; Supervision, TS and DX; Visualization, JW; Writing—original draft, JW. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by National Natural Science Foundation of China U21A6001. Project Supported by Key Laboratory of Environmental Change and Natural Disaster of Ministry of Education, Beijing Normal University (Project No. 2022-KF-08). Project Supported by Key Laboratory of Marine Hazards Forecasting, Ministry of Natural Resources (No.LOMF2202). Innovation found project for graduate students of China University of Petroleum (East China) (No.CXJJ-2022-08).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdullah F., Ningsih N., Al-Khan T. (2022). Significant wave height forecasting using long short-term memory neural network in indonesian waters. J. Ocean Eng. Mar. Energy 8(2), 183–192. doi: 10.1007/s40722-022-00224-3

CrossRef Full Text | Google Scholar

Ali A., Fathalla A., Salah A., Bekhit M., Eldesouky E. (2021). Marine data prediction: An evaluation of machine learning, deep learning, and statistical predictive models. Comput. Intell. Neurosci. 2021. doi: 10.1155/2021/8551167

CrossRef Full Text | Google Scholar

Ali M., Prasad R. (2019). Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renewable Sustain. Energy Rev. 104, 281–295. doi: 10.1016/j.rser.2019.01.014

CrossRef Full Text | Google Scholar

Ali M., Prasad R., Xiang Y., Deo R. C. (2020). Near real-time significant wave height forecasting with hybridized multiple linear regression algorithms. Renewable Sustain. Energy Rev. 132, 110003. doi: 10.1016/j.rser.2020.110003

CrossRef Full Text | Google Scholar

Bethel B. J., Sun W., Dong C., Wang D. (2022). Forecasting hurricane-forced significant wave heights using a long short-term memory network in the caribbean sea. Ocean Sci. 18, 419–436. doi: 10.5194/os-18-419-2022

CrossRef Full Text | Google Scholar

Booij N., Holthuijsen L., Ris R. (1997). “The” swan” wave model for shallow water,” in Coastal engineering 1996, 668–676.

Google Scholar

Chen C., Beardsley R. C., Cowles G. (2006). Finite volume coastal ocean. Oceanography 19, 78. doi: 10.5670/oceanog.2006.92

CrossRef Full Text | Google Scholar

Chen C., Liu H., Beardsley R. C. (2003). An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries. J. atmospheric oceanic Technol. 20, 159–186. doi: 10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2

CrossRef Full Text | Google Scholar

Cho K., Van Merriënboer B., Gulcehre C., Bahdanau D., Bougares F., Schwenk H., et al. (2014). Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv preprint arXiv1406.1078. doi: 10.48550/arXiv.1406.1078

CrossRef Full Text | Google Scholar

Draper N. R., Smith H. (1998). Applied regression analysis Vol. vol. 326 (John Wiley & Sons).

Google Scholar

Fan S., Xiao N., Dong S. (2020). A novel model to predict significant wave height based on long short-term memory network. Ocean Eng. 205, 107298. doi: 10.1016/j.oceaneng.2020.107298

CrossRef Full Text | Google Scholar

Gao S., Huang J., Li Y., Liu G., Bi F., Bai Z. (2021). A forecasting model for wave heights based on a long short-term memory neural network. Acta Oceanologica Sin. 40, 62–69. doi: 10.1007/s13131-020-1680-3

CrossRef Full Text | Google Scholar

Ge M., Kerrigan E. C. (2016). “Short-term ocean wave forecasting using an autoregressive moving average model,” in 2016 UKACC 11th international conference on control (CONTROL) (IEEE), 1–6.

Google Scholar

Group T. W. (1988). The wam model–a third generation ocean wave prediction model. J. Phys. Oceanography 18, 1775–1810. doi: 10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2

CrossRef Full Text | Google Scholar

Guan X. (2020). “Wave height prediction based on cnn-lstm,” in 2020 2nd international conference on machine learning, big data and business intelligence (MLBDBI) (IEEE), 10–17.

Google Scholar

Guo Y., Cao X., Liu B., Peng K. (2020). El Niño index prediction using deep learning with ensemble empirical mode decomposition. Symmetry 12, 893. doi: 10.3390/sym12060893

CrossRef Full Text | Google Scholar

Hao W., Sun X., Wang C., Chen H., Huang L. (2022). A hybrid emd-lstm model for non-stationary wave prediction in offshore china. Ocean Eng. 246, 110566. doi: 10.1016/j.oceaneng.2022.110566

CrossRef Full Text | Google Scholar

Hu H., van der Westhuysen A. J., Chu P., Fujisaki-Manome A. (2021). Predicting lake erie wave heights and periods using xgboost and lstm. Ocean Model. 164, 101832. doi: 10.1016/j.ocemod.2021.101832

CrossRef Full Text | Google Scholar

Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q., et al. (1998). The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A: mathematical Phys. Eng. Sci. 454, 903–995. doi: 10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

Lei Y., He Z., Zi Y. (2009). Application of the eemd method to rotor fault diagnosis of rotating machinery. Mechanical Syst. Signal Process. 23, 1327–1338. doi: 10.1016/j.ymssp.2008.11.005

CrossRef Full Text | Google Scholar

Li X., Cao J., Guo J., Liu C., Wang W., Jia Z., et al. (2022). Multi-step forecasting of ocean wave height using gate recurrent unit networks with multivariate time series. Ocean Eng. 248, 110689. doi: 10.1016/j.oceaneng.2022.110689

CrossRef Full Text | Google Scholar

Lobeto H., Menendez M., Losada I. J. (2021). Future behavior of wind wave extremes due to climate change. Sci. Rep. 11, 1–12. doi: 10.1038/s41598-021-86524-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou R., Lv Z., Dang S., Su T., Li X. (2021). Application of machine learning in ocean data. Multimedia Syst., 1–10. doi: 10.1007/s00530-020-00733-x

CrossRef Full Text | Google Scholar

Mahjoobi J., Mosabbeb E. A. (2009). Prediction of significant wave height using regressive support vector machines. Ocean Eng. 36, 339–347. doi: 10.1016/j.oceaneng.2009.01.001

CrossRef Full Text | Google Scholar

Mahmoodi K., Nowruzi H. (2021). Extreme wave height detection based on the meteorological data, using hybrid nof-elm method. Ships Offshore Structures 17(11), 2520–2530. doi: 10.1080/17445302.2021.2005357

CrossRef Full Text | Google Scholar

Memar S., Mahdavi-Meymand A., Sulisz W. (2021). Prediction of seasonal maximum wave height for unevenly spaced time series by black widow optimization algorithm. Mar. Structures 78, 103005. doi: 10.1016/j.marstruc.2021.103005

CrossRef Full Text | Google Scholar

Meng F., Ma T., Xie P., Sun H., Xu D., Song T. (2021a). “Use ensemble learning to estimate the population and assets exposed to tropical cyclones,” in 2021 IEEE international geoscience and remote sensing symposium IGARSS (IEEE), 8476–8479.

Google Scholar

Meng F., Song T., Xu D., Xie P., Li Y. (2021b). Forecasting tropical cyclones wave height using bidirectional gated recurrent unit. Ocean Eng. 234, 108795. doi: 10.1016/j.oceaneng.2021.108795

CrossRef Full Text | Google Scholar

Meng F., Tian Q., Sun H., Xu D., Song T. (2021c). “Cyclone identify using two-branch convolutional neural network from global forecasting system analysis,” in 2021 IEEE international geoscience and remote sensing symposium IGARSS (IEEE), 8468–8471.

Google Scholar

Meng F., Xie P., Li Y., Sun H., Xu D., Song T. (2021d). “Tropical cyclone size estimation using deep convolutional neural network,” in 2021 IEEE international geoscience and remote sensing symposium IGARSS (IEEE), 8472–8475.

Google Scholar

Meng F., Xu D., Song T. (2022). Atdnns: An adaptive time–frequency decomposition neural network-based system for tropical cyclone wave height real-time forecasting. Future Generation Comput. Syst. 133, 297–306. doi: 10.1016/j.future.2022.03.029

CrossRef Full Text | Google Scholar

Montgomery D. C., Peck E. A., Vining G. G. (2021). Introduction to linear regression analysis (John Wiley & Sons).

Google Scholar

Pokhrel P., Ioup E., Hoque M. T., Simeonov J., Abdelguerfi M. (2020). Random forest classifier based prediction of rogue waves on deep oceans. arXiv preprint arXiv:2003.06431. doi: 10.48550/arXiv.2003.06431

CrossRef Full Text | Google Scholar

Raharja I., Radjawane I., Hendrawan I. (2021). “Characteristic of tidal currents in the lombok strait using 3d fvcom numerical model,” in IOP conference series: Earth and environmental science, vol. 925. (IOP Publishing), 012002.

Google Scholar

Raj N., Brown J. (2021). An eemd-bilstm algorithm integrated with boruta random forest optimiser for significant wave height forecasting along coastal areas of queensland, australia. Remote Sens. 13, 1456. doi: 10.3390/rs13081456

CrossRef Full Text | Google Scholar

Raja A. P. L., Ramadhan A. W., Adytia D., Adiwijaya A. (2021). “Long short-term memory approach for wave height prediction: Study case in jakarta bay, indonesia,” in 2021 international conference on software engineering & computer systems and 4th international conference on computational science and information management (ICSECS-ICOCSIM) (IEEE), 690–694.

Google Scholar

Rasp S., Dueben P. D., Scher S., Weyn J. A., Mouatadid S., Thuerey N. (2020). Weatherbench: a benchmark data set for data-driven weather forecasting. J. Adv. Modeling Earth Syst. 12, e2020MS002203. doi: 10.1029/2020MS002203

CrossRef Full Text | Google Scholar

Song T., Li Y., Meng F., Xie P., Xu D. (2022). A novel deep learning model by bigru with attention mechanism for tropical cyclone track prediction in the northwest pacific. J. Appl. Meteorology Climatology 61, 3–12. doi: 10.1175/JAMC-D-20-0291.1

CrossRef Full Text | Google Scholar

Song T., Wang J., Xu D., Wei W., Han R., Meng F., et al. (2021). Unsupervised machine learning for improved delaunay triangulation. J. Mar. Sci. Eng. 9, 1398. doi: 10.3390/jmse9121398

CrossRef Full Text | Google Scholar

Sorourian S., Huang H., Li C., Justic D., Payandeh A. R. (2020). Wave dynamics near Barataria Bay tidal inlets during spring–summer time Ocean Model. 147, 101553. doi: 10.1016/j.ocemod.2019.101553

CrossRef Full Text | Google Scholar

Tolman H. L., et al. (2009). “User manual and system documentation of wavewatch iii tm version 3.14,” in Technical note, MMAB contribution 276(220).

Google Scholar

Wei C.-C., Chang H.-C. (2021). Forecasting of typhoon-induced wind-wave by using convolutional deep learning on fused data of remote sensing and ground measurements. Sensors 21, 5234. doi: 10.3390/s21155234

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu Z., Huang N. E. (2009). Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. adaptive Data Anal. 1, 1–41. doi: 10.1142/S1793536909000047

CrossRef Full Text | Google Scholar

Zhao L., Hu R., Sun C. (2021). Analyzing the spatial-temporal characteristics of the marine economic efficiency of countries along the maritime silk road and the influencing factors. Ocean Coast. Manage. 204, 105517. doi: 10.1016/j.ocecoaman.2021.105517

CrossRef Full Text | Google Scholar

Zheng Y., Xiaofeng S., Jian C., Jun Y. (2012). Extracting pulse signals in measurement while drilling using optimum denoising methods based on the ensemble empirical mode decomposition. Petroleum Explor. Dev. 39, 798–801. doi: 10.1016/S1876-3804(12)60107-4

CrossRef Full Text | Google Scholar

Zhou S., Bethel B. J., Sun W., Zhao Y., Xie W., Dong C. (2021). Improving significant wave height forecasts using a joint empirical mode decomposition–long short-term memory network. J. Mar. Sci. Eng. 9, 744. doi: 10.3390/jmse9070744

CrossRef Full Text | Google Scholar

Zhu S., Wang Y. (2015). Fairway security of maritime silk road in 21st century. Transport Res. 1, 8–13.

Google Scholar